Simulation of Dynamic Evolution for Oil-in-Water Emulsion Demulsification Controlled by the Porous Media and Shear Action

1  Introduction

With ongoing industrialization, the demand for oil has steadily increased each year [1,2]. During oil field exploitation, large volumes of wastewater with high oil content are produced, which cannot be directly discharged or reinjected into the stratum. Hence, effective oil-removal treatment is crucial [3]. According to droplet size, oil in wastewater can be classified as floating oil, dispersed oil, emulsified oil, and dissolved oil. Among these, emulsified oil is the most difficult to remove. Emulsified oil droplets have diameters below 20 µm. Owing to electrostatic repulsion, neighboring oil droplets cannot coalesce and remain evenly dispersed in water, forming a stable oil-in-water (O/W) emulsion [4,5]. Currently, oil-bearing wastewater poses a significant environmental threat [6], making the development of efficient demulsification methods an urgent challenge.

Current techniques for emulsion demulsification can be broadly classified into three categories: chemical, microbiological, and physical [7]. Among these, chemical demulsification is the most widely used [8,9]. This approach involves the addition of demulsifiers such as polymeric surfactants [10], ionic liquids [11], and nanoparticles [12] to destabilize the emulsion. In a recent study on the stability of Pickering microemulsions, the authors [13] investigated the impact of polymer grafting density on the structure and thermodynamics of hairy droplets using Molecular Dynamics (MD) simulations. This computational study used pair potential models proposed by [14], which take into account repulsive and attractive interactions related to excluded volume forces between monomers and van der Waals forces between bare oil droplets. However, chemical demulsification can cause secondary environmental pollution in practical applications and does not enable the recovery of the contaminated oil products. Microbiological demulsification utilizes microorganisms to degrade petroleum hydrocarbons in wastewater into nutrients, thereby facilitating wastewater purification. However, the effectiveness of microbiological demulsification strongly depends on contaminant concentration, wastewater properties, and microbial activity. Hence, maintaining stable demulsification is challenging. The physical demulsification mainly includes thermal, electrical [15], ultrasonic [16], coalescence techniques and so on [17]. Thermal demulsification involves increasing the emulsion temperature to separate the oil and water phases [18]. Electrical demulsification employs a high-voltage electric field (direct or alternating current) to polarize, deform, and coalesce oil droplets, leading to emulsion demulsification. Ultrasonic demulsification utilizes ultrasound to induce droplet condensation and reduce oil viscosity. Among physical demulsification methods, coalescence technology provides distinct advantages such as low cost, high efficiency, and environmental friendliness. However, coalescence does not reduce the overall oil content in wastewater but alters the size distribution of oil droplets. Demulsification is achieved through the coalescence of small oil droplets into larger oil beads. Moreover, coalescence technology does not alter the properties of the original water, thereby preventing secondary pollution. Similarly, shear-induced demulsification is environmentally friendly and highly efficient. This demulsification process rapidly disrupts emulsion interfaces, resulting in effective oil–water separation. Therefore, shear-induced demulsification is particularly suitable for treating highly viscous and stable emulsion systems.

Current studies on demulsification in porous media and shear-induced demulsification have often focused on their individual effects. Research on demulsification in porous media has mainly relied on the passive interception effect of the porous media, leading to low overall demulsification efficiency [19,20]. Although shear forces can accelerate droplet coalescence [21], studies on shear-induced oil droplet aggregation have not fully captured the complexity of porous structures in real industrial scenarios. Building on previous research, this study simulated the morphological evolution of emulsion demulsification under porous media and shear forces. The effects of porous media distribution, flow conditions, and initial oil concentrations on emulsion demulsification were systematically examined through quantitative analyses. The dual-factor demulsification method enhances droplet coalescence via shear forces and porous media aggregation, thereby overcoming the low efficiency of each factor alone.

Experimental research and numerical simulations are commonly used to investigate emulsion demulsification. However, experimental approaches cannot precisely control all parameters or eliminate the impact of external factors. Additionally, monitoring the morphological changes of oil droplets at very small temporal and spatial scales is challenging. With advances in multiphase flow theory and computational technology, numerical simulations have been widely used. Numerous studies have used numerical simulations to investigate the mechanisms of oil–water demulsification under porous media or shear forces. Hou et al. [22] employed the Eulerian–Eulerian approach combined with the level set method to simulate the dynamic behavior of oil droplets in porous media. The analysis focused on separation efficiency and oil droplet trajectories under varying conditions, accounting for droplet deformation, kinetic viscosity, and inter-droplet interactions. Lu et al. [23] used the Eulerian–Lagrangian method to simulate collisions between oil droplets and fibers, and obtained the probability of collision under a certain particle size ratio and flow velocity range, and modified the probability of collision previously obtained through mathematical derivation. However, conventional Eulerian–Eulerian methods (e.g., fluid volume) face challenges such as excessive interface smearing and high computational costs in simulating the aggregation and rupture of dynamic droplets. Similarly, Eulerian–Lagrangian approaches (e.g., discrete particle method) are limited in simulating dense droplet systems owing to prohibitive particle-number constraints. Lattice Boltzmann method (LBM) inherently captures interactions among high-concentration droplet clusters through the density distribution function. LBM features intrinsic interface-capturing capability, high computational efficiency, and inherent parallelism [24,25]. The color-gradient lattice Boltzmann model has been widely applied to phase separation, droplet dynamics, and multiphase flows in porous media. For two-phase flow, the model captures interactions between particles of the same phase and accounts for collisions between particles of different phases at the interface. This study innovatively adopts a color-gradient lattice Boltzmann model to precisely capture emulsion phase separation under porous media and shear forces at the mesoscopic scale.

2  Mathematical Modeling

2.1 Lattice Boltzmann Method for Emulsion Evolution

LBM mainly describes the evolution of the distribution function fi(x,ξ,t), which represents the existence probability of particles with a certain velocity ξ at a specific time t and region x [26]. By discretizing the Boltzmann equation in time, space and velocity, the lattice Boltzmann equation for evolution of the O/W emulsion, namely the evolution equation of the distribution function fi(x,t), can be obtained:

fi(x+ciδt,t+δt)−fi(x,t)=−1τ(fi(x,t)−fi(eq)(x,t))(1)

where fi(x,t) denotes the distribution function at a fluid node in the emulsion, x represents the lattice point coordinates, t indicates the current time step, τ signifies the dimensionless relaxation time, and fi(eq)(x,t) denotes the equilibrium distribution function. For O/W emulsion flow in two-dimensional porous media, this study adopts the D2Q9 discrete velocity model. Here, 2 denotes the spatial dimension, 9 represents the number of discrete velocity directions, and ci indicates the discrete velocity vector. In the D2Q9 model, ci is expressed as follows:

ci={0,0i=0c(cos⁡(i−1)π2,sin⁡(i−1π2)i=1,2,3,42c(cos⁡(2i−1)π4,sin⁡(2i−1)π4)i=5,6,7,8(2)

here, c=δx/δt, where δx and δt indicate the grid and time steps, respectively. Typically, the grid steps in the x and y directions are equal. δx=δt=1 is commonly used.

A complete lattice Boltzmann model comprises the evolution equation of the distribution function, the discrete velocity model, and the equilibrium distribution function. The equilibrium distribution function can be expressed as follows:

fieq=ωiρ[1+ci⋅ucs2+(ci⋅u)22cs4−u22cs2](3)

where ωi denotes the weight coefficient and cs indicates the speed of sound. The parameters ωi and cs are defined as follows:

ωi={4/9i=11/9i=2,3,4,51/36i=6,7,8,9(4)

cs=c3(5)

The macroscopic density ρ and velocity u of the emulsion are determined as follows:

ρ=∑ifi(6)

u=1ρ∑ifici(7)

2.2 Color-Gradient Lattice Boltzmann Model for Emulsion Phase Separation

The color-gradient lattice Boltzmann model describes multiphase flow, with different colors assigned to each phase. Phase interactions are captured through the color-gradient mechanism. The detailed calculations are as follows:

Here, fki denotes the distribution function of different phases. In this study, “k” is equal to “b” or “r”, while “r” and “b” represent the red and blue phases, respectively. The red phase corresponds to the dispersed phase (oil), and the blue phase denotes the continuous phase (water). The evolution equation for the emulsion is given as follows:

fki(x+ci,t+1)=fki(x,t)+Ωki(fki(x,t))(8)

The collision factor Ωki(x,t) comprises three components:

Ωki(x,t)=Ωki3(x,t)(Ωki1(x,t)+Ωki2(x,t))(9)

where Ωki1(x,t) represents the collision operator, which simulates interactions among particles in the oil and water phases. Ωki2(x,t) denotes the interface perturbation operator, which accounts for the effects of surface tension. Ωki3(x,t) indicates the re-coloring operator, which drives particles toward regions of the same color. This mechanism prevents the oil-phase particles from penetrating the water phase, thereby maintaining phase separation.

The macroscopic densities of red and blue phases, the overall emulsion density, and the macroscopic velocity of the O/W emulsion are defined as follows:

ρk=∑ifkiρ=ρr+ρbu=1ρ∑i∑kfkici(10)

2.2.1 The Collision Operator

The collision force between particles in the emulsion is realized by the collision operator. The collision operator of single phase (red or bule phase) Ωki1 relaxes to the distribution function of the local equilibrium state, and the equation is shown as follows:

Ωki1(x,t)=fki(x,t)−τ(fki(x,t)−fki(eq)(x,t))(11)

where τ represents the relaxation factor and fki(eq) denotes the equilibrium distribution function.

fkieq=ρk(φik+ωi(3ciu+92(ciu)2−32u2))(12)

Here, ωi represents the weight coefficient of the particles in each velocity direction, and φik denotes a function of αk.

ωi={4/9i=11/9i=2,3,4,51/36i=6,7,8,9(13)

φik={αki=1(1−αk)/5i=2,3,4,5(1−αk)/20i=6,7,8,9(14)

2.2.2 The Interface Perturbation Operator

In this paper, the surface tension is simulated using the interface perturbation operator. The perturbation operator is expressed as:

Ωki2(x,t)=AK2|F|(Wi(F⋅ci)2|F|2)−Bi(15)

where the color gradient in the perturbation operator is defined as:

F(x)=∑ici(ρr(x+ci)−ρb(x+ci))(16)

Bi is defined as:

Bi={−4/27i=12/27i=2,3,4,55/108i=6,7,8,9(17)

where AK denotes a free parameter that couples the oil and water phases, but it does not guarantee that the two phases will not disturb each other at the interface. Therefore, the re-coloring operator Ωki3(x,t) is introduced.

2.2.3 The Re-Coloring Operator

The re-coloring operator mainly guides oil-phase particles at the interface toward the oil region and water-phase particles toward the water region. However, this re-coloring process involves complex calculations. To reduce computational cost, several researchers have proposed simplified methods. Leclaire et al. [27] developed an improved re-coloring operator based on previous research. The details are as follows:

Ωri3(fri)=ρrρfi+βρrρbρ2cos⁡(φi)∑kfkie(ρk,0,αk)(18)

Ωbi3(fbi)=ρrρfi−βρrρbρ2cos⁡(φi)∑kfkie(ρk,0,αk)(19)

The free parameter β must fall within 0<β<1 to ensure a positive distribution function. The value of this parameter directly affects the interface thickness [28]. Smaller values lead to a thicker interface, while larger values result in a thinner interface.

2.3 Boundary Conditions

Proper treatment of boundary conditions is crucial in physical simulations. Different models require specific approaches to accurately handle interactions at the boundaries. In this study, handling the boundary between porous media particles and the emulsion is crucial. As shown in Fig. 1, dashed and solid lines represent grid lines, intersections denote grid points, and the curved solid line represents the porous media boundary. Blue regions denote emulsions, while gray regions signify the porous media. The line connecting the fluid grid point xf and the solid grid points xb intersects the porous media boundary at the xw point. The vertical distance between grid points xf and xw is denoted as Δδx. The velocity of particles traveling from the fluid grid point xf to the solid grid point xb is represented by ci. The particle velocity from the solid grid point xb to the fluid grid point xf is designated as ci¯. Thus, ci=−ci¯, where uw=u(xw,t) denotes the velocity at point xw, and f~i represents the distribution function after collision. Notably, Δ satisfies the following relationship [29]:

Δ=‖xf−xw‖‖xf−xb‖(20)

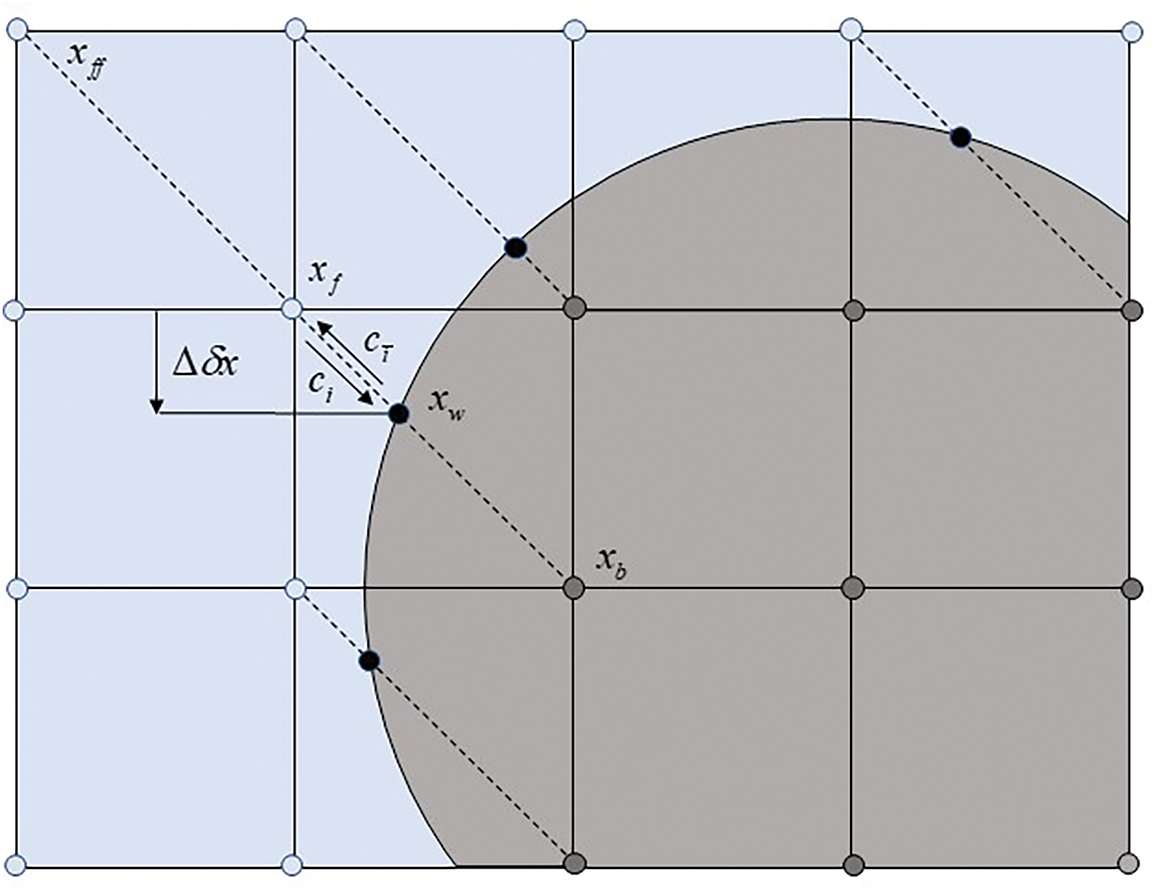
Figure 1: Rectangular grid and solid wall boundary

Vaseghnia et al. [30] used the processing idea of the rebound scheme to interpolate the distribution function. Researchers have further classified the interpolation into pre-collision and post-collision types based on specific Δ values. This method preserves the simplicity of the rebound scheme and achieves second-order numerical accuracy. Moreover, the interpolation method can be used to handle moving boundary conditions. Notably, at Δ=1/2, the scheme reduces to the standard rebound format. In this study, the rebound-scheme-based interpolation method is used to manage boundary conditions between porous media particles and emulsions. Considering the curve solid boundary shown in Fig. 1, interpolation is performed in two cases: At Δ<1/2, interpolation is applied before the migration and collision steps. At Δ≥1/2, interpolation is applied after the migration and collision steps. The interpolation formulas are as follows:

When Δ<12:

f~i¯(xb,t)=Δ(1+Δ)f~i(xf,t)+(1−4Δ2)f~i(xff,t)−Δ(1−2Δ)f~i(xff−ciδt,t)+3qi(ci⋅uw)(21)

When Δ≥12:

f~i¯(xb,t)=1Δ(1+Δ)f~i(xf,t)+2Δ−1Δfi¯(xff,t)−2Δ−12Δ+1fi¯(xff−ciδt,t)+3qiΔ(2Δ+1)(ci⋅uw)(22)

qi={2/299i=1,2,3,41/11818i=5,6,7,8(23)

In practice, the interpolation is calculated using the following formulas:

When Δ<12:

f~i¯(xb,t)=Δ(1+Δ)fi(xf+ciδt,t)+(1−4Δ2)fi(xf,t)−Δ(1−2Δ)fi(xf−ciδt,t)+3qi(ci⋅uw)(24)

When Δ≥12:

f~i¯(xb,t)=1Δ(1+Δ)fi(xf+ciδt,t)+2Δ−1Δfi¯(xf−ciδt,t)−2Δ−12Δ+1fi¯(xf−2ciδt,t)+3qiΔ(2Δ+1)(ci⋅uw)(25)

In this study, a two-dimensional grid of size 518×256 is used for the simulation. The upper and lower boundaries are configured as shear boundaries with equal magnitudes but opposite velocity directions. The left and right boundaries are periodic. As shown in Fig. 2, at the onset of simulation, the O/W emulsion with an initial oil concentration of 10% and porous medium with a porosity of 90% are arranged in the grid. Here, red regions represent oil droplets, gray regions denote the porous medium, and blue regions indicate water.

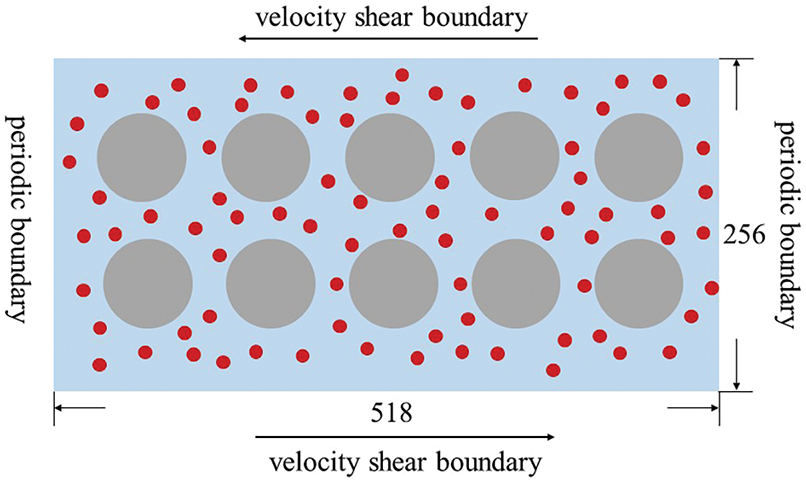
Figure 2: Rectangular grid and its surrounding boundary conditions

3  Simulation Results and Discussion

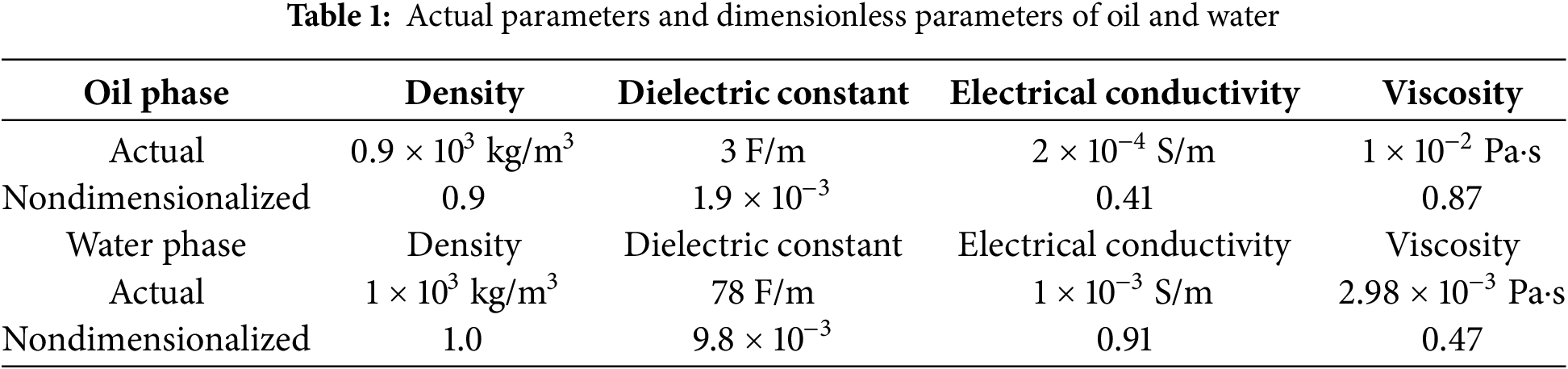
This study established a simulation model using crude oil–water parameters. Dimensionless transformations are applied to the actual parameters. This model provides a theoretical basis and new insights for treating actual oily wastewater. Here, sp,tp,σp represent the actual length, time, and interfacial tension coefficient, respectively. Moreover, s,t,σ denote the dimensionless length, time, and interfacial tension coefficient, respectively, with sp=s/10,tp=t/103,σ=σp/σu, σu as the reference interfacial tension coefficient. Similarly, εrp and εbp denote the actual dielectric constants of the oil droplets and water, respectively, while εr and εb represent the dimensionless dielectric constants. The relationship between the actual and dimensionless parameters is expressed as follows:

εr=εrpεrp+εbp,εb=εbpεrp+εbp(26)

Here, σrp and σbp represent the actual electrical conductivities of oil and water, respectively, while σr and σb denote the dimensionless electrical conductivities. The relationship between the actual and dimensionless values is expressed as follows:

σr=σrpσrp+σbp,σb=σbpσrp+σbp(27)

ρr and ρb represent the dimensionless densities of the oil droplets and water, respectively. ηrp and ηbp represent their actual viscosities. Moreover, ηr and ηb denote the dimensionless viscosities of the oil and water, respectively. The relationship between actual and dimensionless viscosities is expressed as follows:

ηr=ηrpηrp+ηbp,ηb=ηbpηrp+ηbp(28)

Overall, the dimensionless parameters in this paper were configured as follows: s=1,t=1,σ=1.8×10−2,εr=1.9×10−3,εb=9.8×10−3,σr=0.41,σb=0.91,ρr=0.9,ρb=1,ηr=0.87,ηb=0.47. Each porous medium has a radius of Rp=20, and the initial radius of the oil droplets is Rr=0.5. The specific parameters are shown in Table 1.

This section investigates the effects of porous media distribution, flow conditions, and initial oil concentration on O/W emulsion demulsification.

3.1 Effects of Porous Media Distribution on Emulsion Morphological Evolution

In emulsion evolution, porous media play a role similar to a filter bed. The complex pore structures of porous media promote inertia collisions among oil droplets. This section investigates the effects of the porosity and arrangement of porous media on emulsion morphology under a shear velocity of U=10−4 and an initial oil concentration of 10%.

3.1.1 Effects of Porosity on Emulsion Morphological Evolution

Porosity significantly influences emulsion demulsification. Fig. 3 illustrates the morphological evolution of emulsions at two porosities, 80% and 90%. The following conclusions can be obtained: (1) In the early stage of demulsification, oil droplets in the flow field are mainly classified into two groups owing to the porous media. The first group of oil droplets collides with the porous media, adhering on the surface of the porous media. Then other oil droplets further adhere on the surface of the porous media, or collide with oil droplets previously adhered on the surface of the porous media and form large oil beads; The second group of oil droplets bypasses the porous media and passes through deeper pores. These small oil droplets can be only slowly coalesced. (2) As time progresses, oil droplets continue to merge, forming increasingly larger oil films on the porous media surface until demulsification is complete. (3) In the later stage of demulsification, the 80% porosity flow field develops double-connected structures (Fig. 3Ic, IIc). In contrast, the 90% porosity flow field remains dominated by single-connected structures. As stated in literature [31], the higher the porosity, the more droplets that do not coalesce and pass through directly. This is consistent with what was discovered in literature [32]. In conclusion, the presence of porous media can enhance the ability of the flow field to coalesce oil droplets, while the increase of porosity prolongs the time required for demulsification and reduces the efficiency of demulsification.

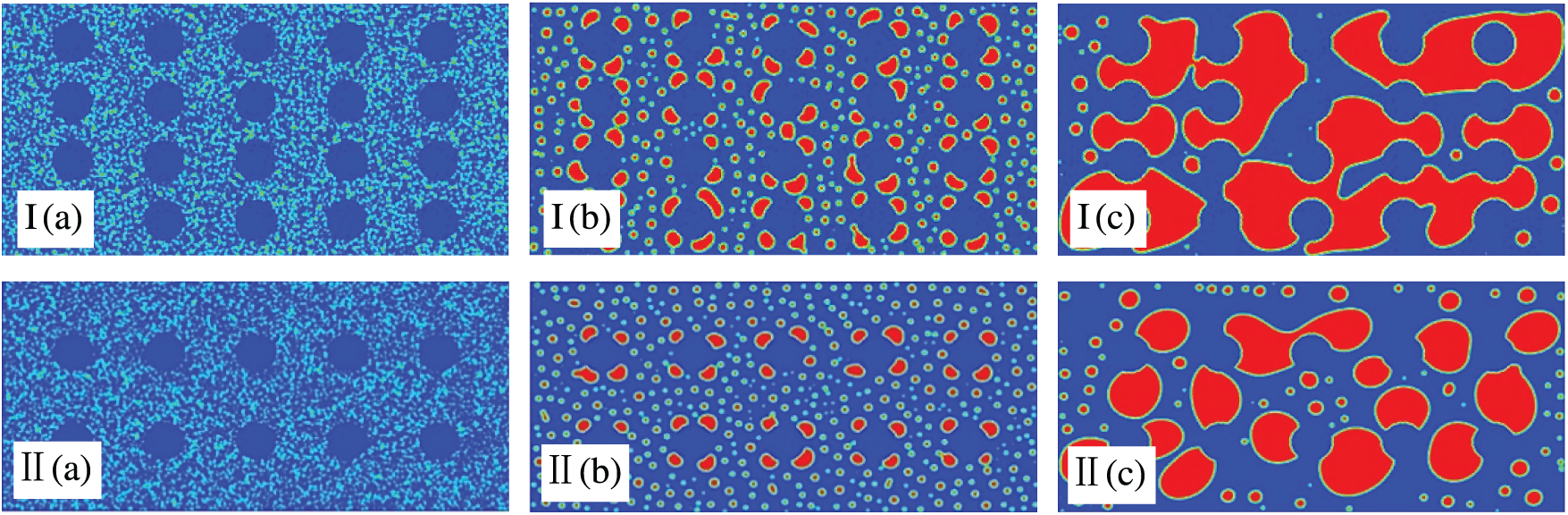
Figure 3: Impacts of the porosity on morphological evolution with U=10−4 and initial oil concentration of 10%, for (I) porosity of 80%, (I) porosity of 90%, at times (a)t=10T, (b)t=8×103T and (c)t=6×104T

3.1.2 Effects of Porous Media Arrangement on Emulsion Morphological Evolution

The ability of the flow field to capture and coalesce oil droplets is influenced by porosity and the arrangement of porous media. Fig. 4 shows the evolution of the emulsion under two porous media arrangements. By comparing Fig. 4I and II, it can be seen clearly: (1) In the initial stage of demulsification, small oil droplets in a flow field with regularly arranged porous media aggregate into large, dumbbell-shaped oil beads around the porous structures. However, it is difficult for the oil droplets to connect with each other in the irregularity of the pore structures. The oil droplets are forced to be stored in the shape of a circle or half-moon in the flow field. (2) In the later stage of demulsification, large oil films develop in the flow field with regular porous media, indicating near-complete demulsification. In contrast, only a few large oil beads form in the flow field with irregularly arranged porous media. Overall, the irregular arrangements of porous media hinder the coalescence of oil droplets, increase their susceptibility to breakage, and may lead to re-emulsification. Thus, a more regular arrangement of porous media improves demulsification performance.

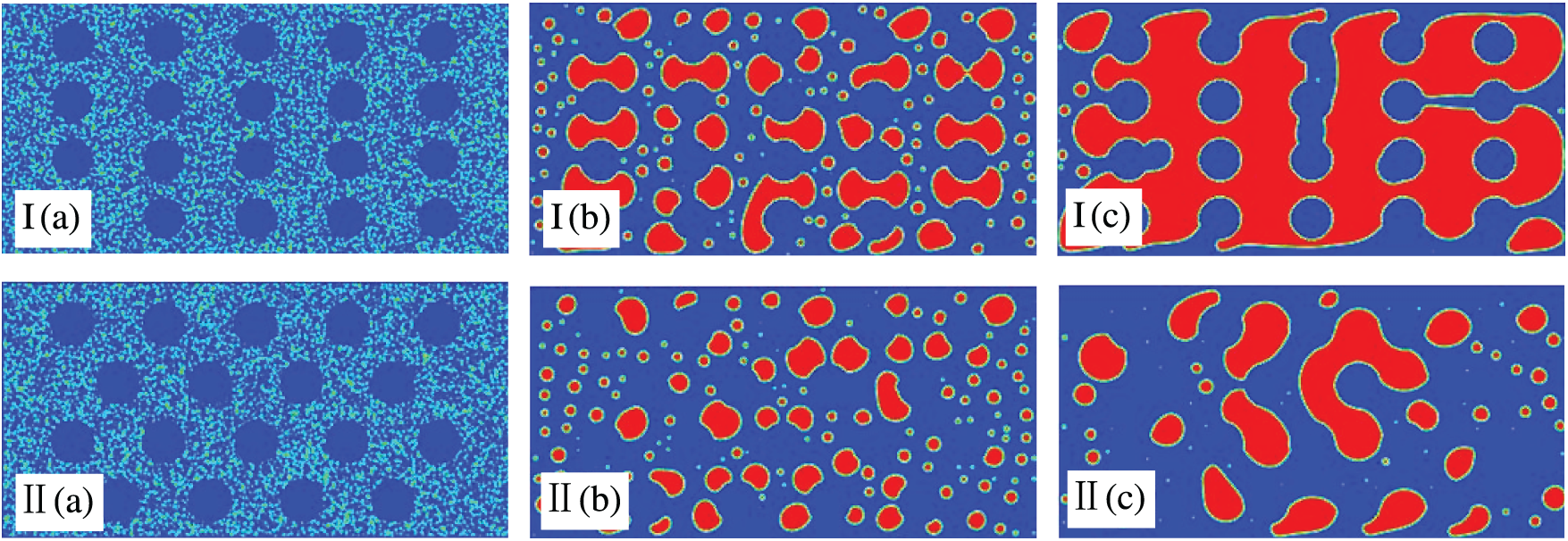
Figure 4: Impacts of the arrangement on morphological evolution with U=10−4, porosity of 80% and initial oil concentration of 10%, for (I) the regular arrangement of porous media, (II) the irregular arrangement of porous media, at times (a) t=10T, (b) t=2.4×104T and (c) t=105T

3.2 Effects of Flow Conditions on Emulsion Morphological Evolution

This section investigates the effects of different shear velocities and modes on emulsion morphological evolution in a flow field with regularly arranged porous media, 10% initial oil concentration, and 90% porosity.

3.2.1 Effects of Shear Velocity on Emulsion Morphological Evolution

Shear flow plays a critical role in emulsion demulsification. Fig. 5 shows the effects of shear velocity U on demulsification performance. A comparison of Fig. 5I and II reveals the following conclusions: (1) At a shear velocity of U=10−3, oil droplets near the upper and lower walls rapidly coalesce along the shear direction owing to strong shear forces, forming elongated, strip-shaped oil droplets. This behavior is consistent with the deformation patterns reported in the literature under steady shear [33]. However, at a shear velocity of U=10−5, the shear forces acting on the oil droplets are weaker. Consequently, the oil droplets mainly retain regular circular or half-moon shapes, with fewer strip-shaped structures. This is in line with what is stated in literature [34]. At very low shear rates, the dispersed phase mainly forms spherical droplets. As the shear rate increases, these spherical droplets gradually elongate, particularly near the upper and lower boundaries. (2) Additionally, increasing the shear velocity enhances the driving force for droplet coalescence. Therefore, the aggregated oil droplets in the flow field with U=10−3 are larger and denser than those in the flow field with U=10−5. In summary, higher shear velocities facilitate the formation of elongated, strip-shaped oil droplets near the upper and lower walls, which enhance oil–water separation.

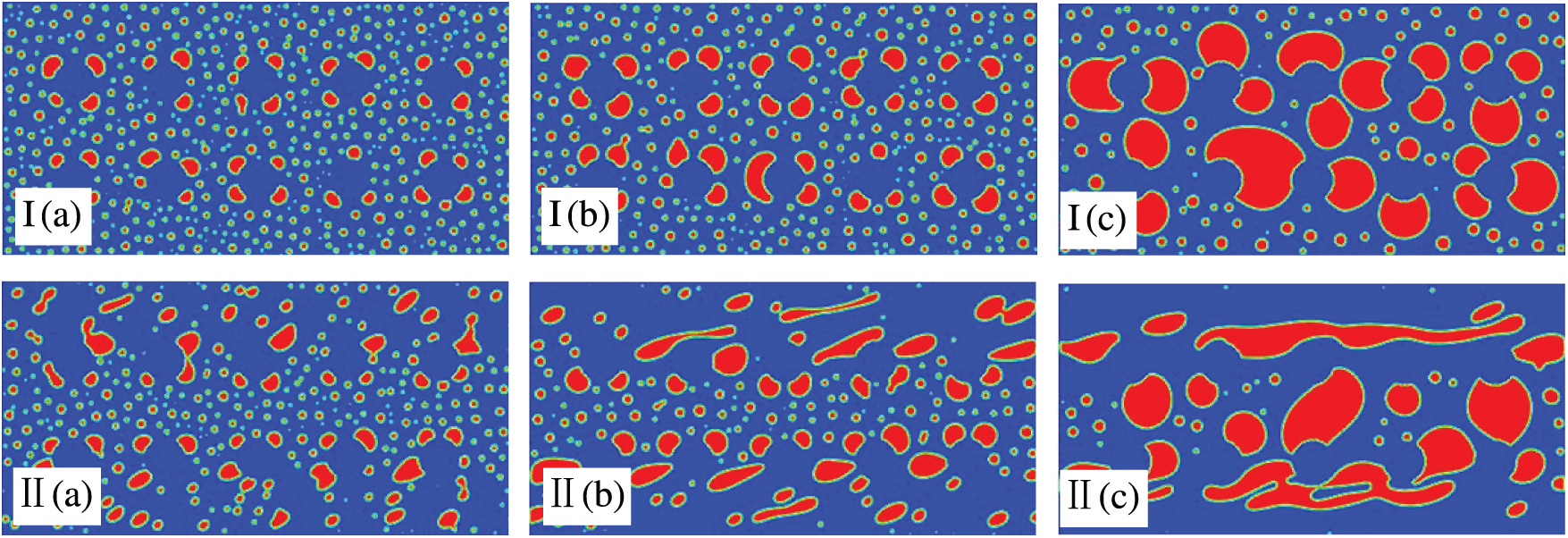
Figure 5: Impacts of the shear velocity on morphological evolution with porosity of 90% and initial oil concentration of 10%, for(I) U=10−5, (II) U=10−3, at times (a) t=8×103T, (b) t=1.8×104T and (c) t=6×104T

3.2.2 Effects of Shear Mode on Emulsion Morphological Evolution

In addition to steady shear, we investigated the morphological and structural evolution of emulsions under oscillatory shear. We set v=γcos⁡(2πft) as the oscillatory shear velocity of the upper wall. Here, γ denotes the shear velocity amplitude, and f represents the oscillation frequency. In this section, the oscillation frequency was set to f=10−4. The lower boundary oscillated in the opposite direction to the upper boundary.

By examining Fig. 6, we can draw the following conclusions: (1) Under steady shear flow, the shear force on the oil droplets is constant and uniform, resulting in stable droplet trajectories. However, under oscillatory shear flow, the oil droplets follow periodic trajectories owing to the alternating shear forces. Consequently, the oil droplets undergo continuous cycles of deformation and recovery. (2) A comparison of emulsion morphologies and structures under the two shear modes indicates that oil–water separation is more pronounced under steady shear flow than under oscillatory shear flow. Overall, oscillatory shear provides a less favorable condition for demulsification than steady shear.

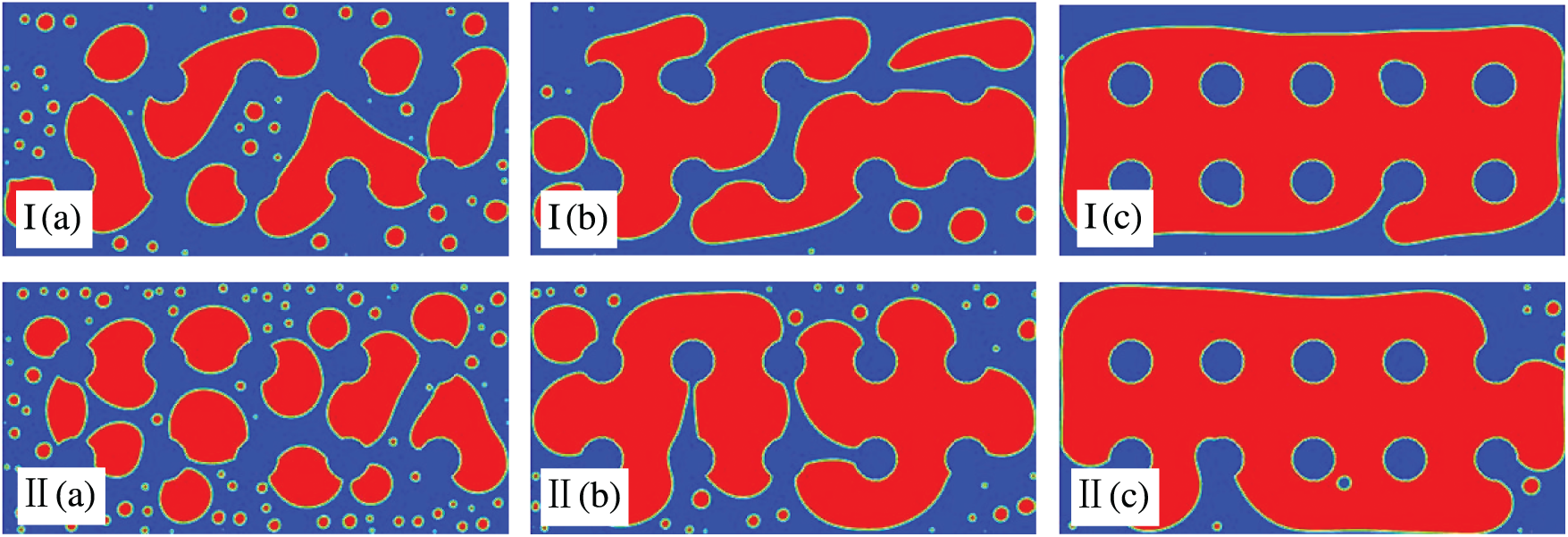
Figure 6: Impacts of the shear mode on morphological evolution with porosity of 90% and initial oil concentration of 10%, for(I) steady shear, (II) oscillatory shear, at times (a) t=8×104T, (b) t=1.6×105T and (c) t=4×105T

3.3 Combined Effects of Porosity and Shear Velocity on Emulsion Morphological Evolution

According to the analyses in Sections 3.1 and 3.2, the individual effects of porosity and shear velocity on emulsion morphological evolution can be summarized as follows: Increasing porosity reduces the degree of oil–water separation. However, higher shear velocity facilitates droplet coalescence and oil–water separation. In this section, we established a flow field with regular pore structures, an initial oil concentration of 10%, and a porosity of 80%. The results are then compared with those in Section 3.2.1 to examine the combined effects of porosity and shear velocity on the morphological evolution of emulsions.

A comparison of Figs. 5 and 7 yields the following conclusions: (1) If the porosity is constant, the oil droplets only become relatively dense due to the increase of shear velocity. However, if the shear velocity remains the same, a decrease in porosity will substantially augment the degree of oil-water separation. Namely, compared with shear velocity, porosity plays a dominant role on the process of demulsification. (2) By comparing Figs. 5II and 7II, it can be clearly seen that in a flow field with porosity of 90%, the oil droplets near the upper and lower walls only tend to flatten under the tensile action of shear. However, in a flow field with porosity of 80%, the oil droplets near the upper and lower walls are stretched into streamline-shaped with serious deformation. (3) A comparison of Figs. 5c and 7c indicates that regardless of shear velocity, double-connected structures form in the flow field with 80% porosity. In the 90% porosity field, most dispersed oil droplets remain as single-connected structures. In summary, at the same shear velocity, lower porosity leads to more severe deformation of oil droplets near the upper and lower walls. Additionally, porosity exerts a stronger impact on emulsion demulsification than shear velocity.

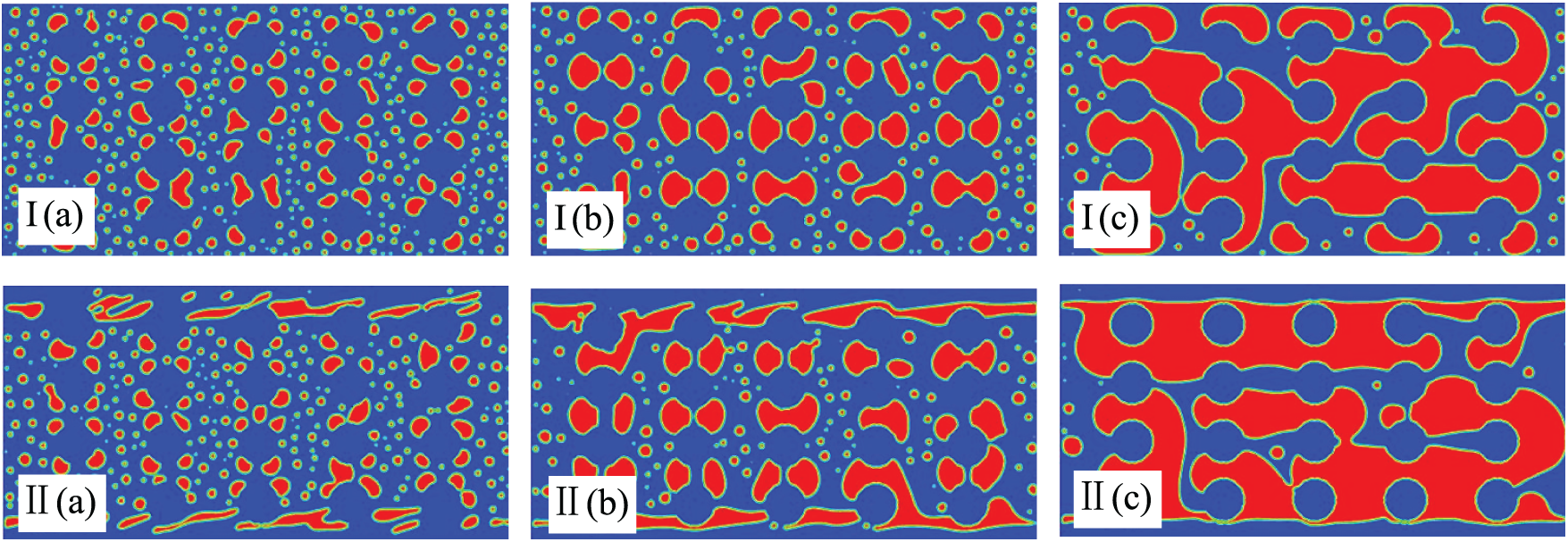
Figure 7: Impacts of the shear velocity on morphological evolution with porosity of 80% and initial oil concentration of 10%, for (I) U=10−5, (II) U=10−3, at times (a) t=8×103T, (b) t=1.8×104T and (c) t=6×104T

3.4 Effects of Initial Oil Concentration on Emulsion Morphological Evolution

As shown in Section 3.1.1, a flow field with lower porosity exhibits enhanced coalescence under the same conditions. This is due to the crucial role of collision in droplet coalescence, with the collision frequency directly affecting the probability of coalescence. The collision frequency between oil droplets is influenced by both porous media distribution and the initial oil concentration. Fig. 8 simulates the morphological evolution of emulsion when the shear rate is U=10−4, the porosity is 90%, and the porous media is arranged regularly. The following conclusions can be obtained by comparing Fig. 8I with 8II: (1) At an initial oil concentration of 10%, numerous oil droplets in the flow field increase collision frequency, thereby facilitating their aggregation into oil films. (2) At an initial oil concentration of 5%, very fine oil droplets are observed in the pore-throat structures of the flow field. The phenomenon exists for some reasons. When the emulsion flows through the throat of the pore, large oil droplets may be forced to deform or break because they cannot pass directly, while small oil droplets also may be further crushed by external forces such as the shear force and pressure gradient in the flow field. This phenomenon is more remarkable in the flow field with low initial oil concentration. Overall, higher initial oil concentrations significantly improve demulsification efficiency.

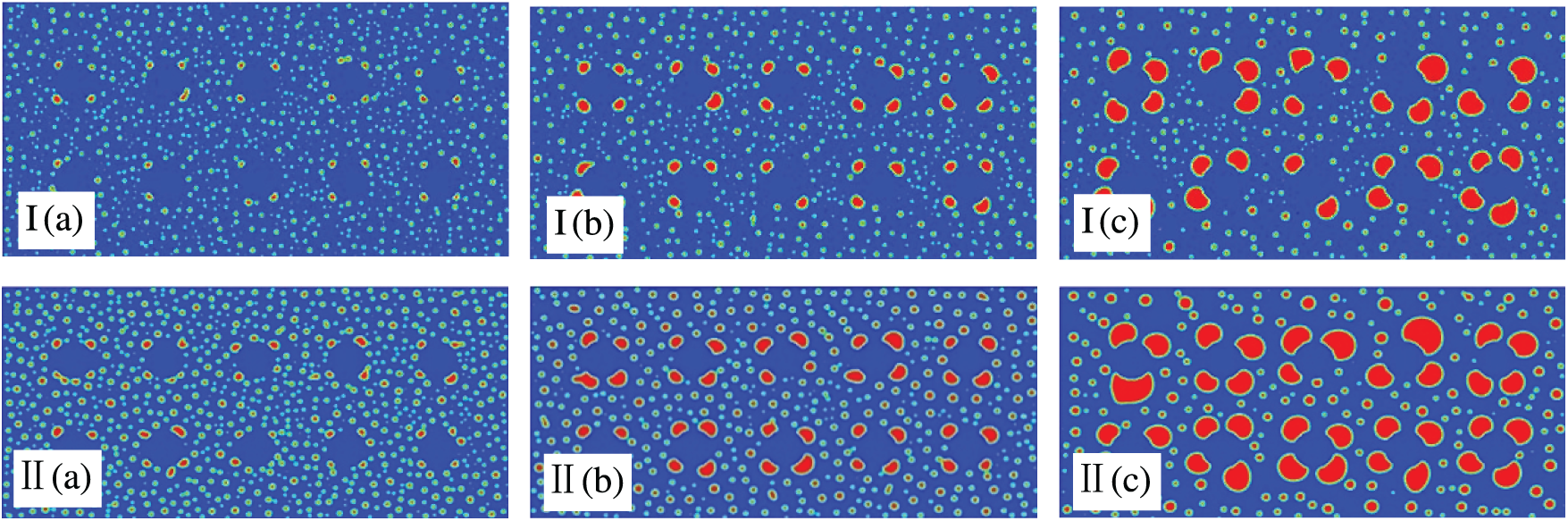
Figure 8: Impacts of initial oil concentration on morphological evolution with U=10−4 and porosity of 90%, for (I) initial oil concentration of 5%, (II) initial oil concentration of 10%, at times (a) t=2×103T, (b) t=8×103T and(c) t=2.8×104T

3.5 Growth Kinetics of Phase Separation

The oil droplets in the emulsion aggregate and connect under porous media and shear forces. To quantitatively assess demulsification performance, Dr (defined as Dr=Sr/Lr) was introduced to characterize the degree of droplet coalescence and deformation. Here, Sr denotes the total area of the oil droplets, and Lr represents their total circumference.

The key findings from Fig. 9 are as follows: (1) The degree of oil droplet coalescence increases linearly with time. Coalescence efficiency is higher in flow fields with lower porosity than in those with higher porosity. This is because the porosity is small, the effective coalescence area of porous media is large, the frequency and impulse of collision between oil droplets are increased, and the possibility of small oil droplets coalescing into large oil beads is increased. As the porosity increases, the oil droplets find it challenging to connect with each other due to the large permeability of the pores. Subsequently, they are susceptible to disintegration by shear forces, thereby resulting in the re-emulsification of the emulsion. (2) The slopes of the three lines differ significantly, as the ability of porous media to intercept oil droplets is highly sensitive to porosity. Even a slight increase in porosity can reduce coalescence efficiency. At 90% porosity, the slope stabilizes. With further increases in porosity, the effect of porous media on demulsification becomes negligible.

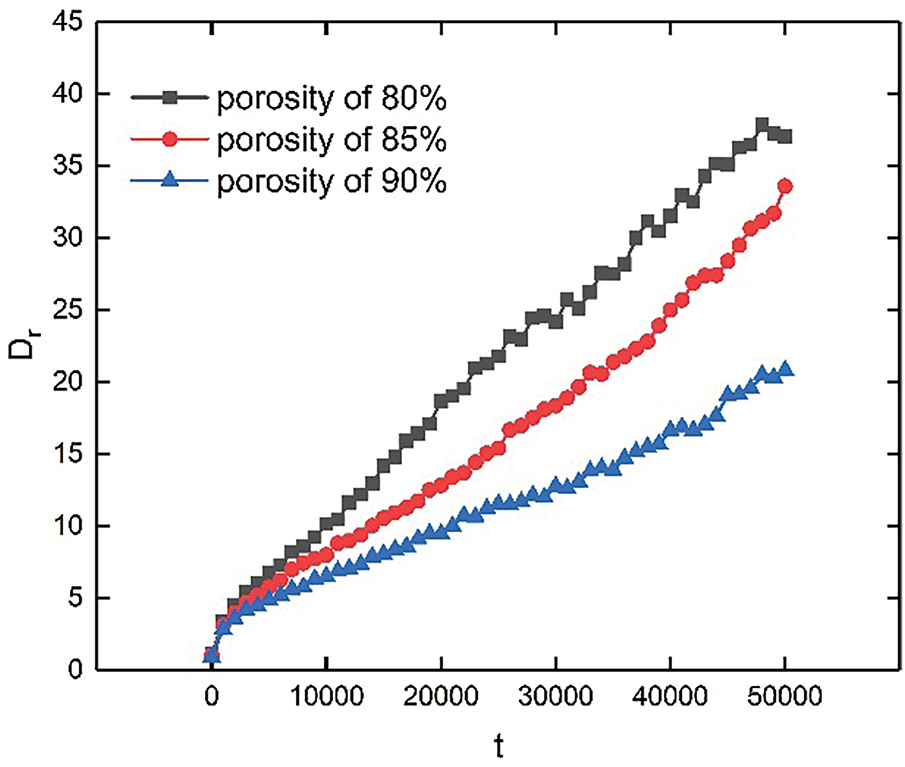
Figure 9: Typical time evolution characterization of Dr for different porosities

Oil droplets exhibit a higher degree of coalescence in flow fields with regularly arranged porous media (Fig. 10). This can be attributed to the following factors: (1) Regular pore structures increase the storage capacity of porous media for oil droplets and maintain the local continuity of dispersed oil droplets. Consequently, the droplets are less prone to breakage during motion. (2) When oil droplets pass through unevenly distributed porous media, the direction of motion must be constantly changed. Consequently, the shear force brought to the oil droplets by the flow field is consumed, increasing the velocity loss of the oil droplets. Oil droplets lack sufficient momentum to disrupt interfacial films, which hinders their aggregation and the formation of large oil beads on the porous media surface.

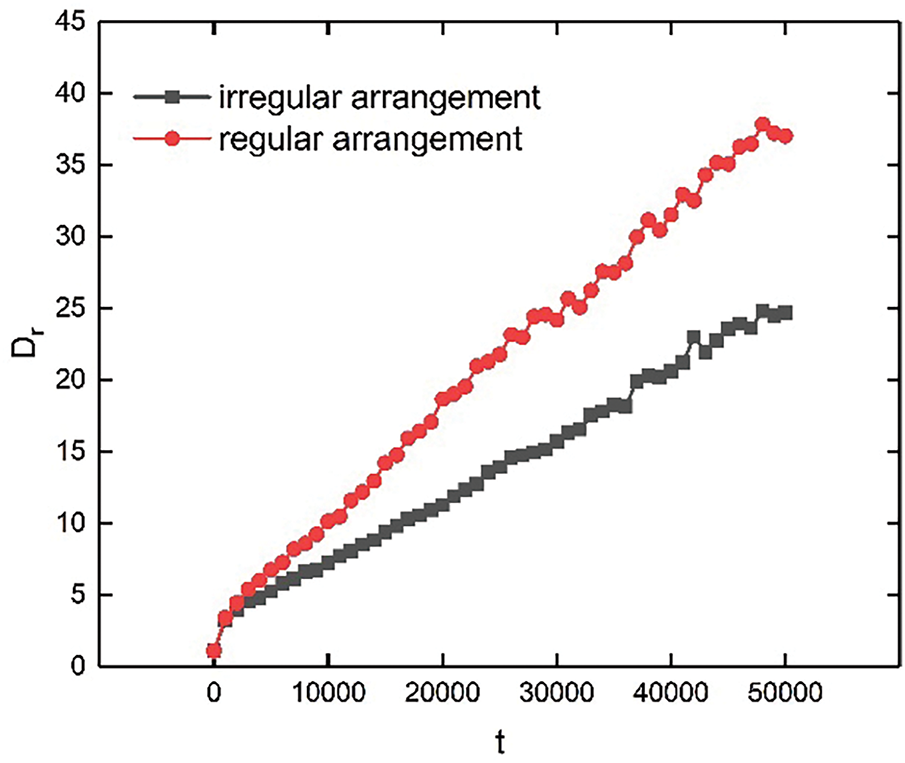
Figure 10: Typical time evolution characterization of Dr for different arrangements

The key findings from Fig. 11 are as follows: (1) The lines of U=10−4 and U=10−5 nearly overlap. At low shear velocities, the shear force on the oil droplets is minimal. Slight increases in shear velocity have minimal effect on droplet coalescence. (2) As the shear velocity increases to U=10−3, the coalescence of oil droplets significantly increases. This is due to the greater shear force on the oil droplets. Correspondingly, the combined forces driving droplet coalescence significantly exceed the interfacial tension. Additionally, oil droplets near the upper and lower walls are stretched into strip-like shapes owing to the strong shear, which facilitates their coalescence and enhances adaptation to the pores. (3) Compared with the lines of U=10−4 and U=10−5, the lines of U=10−3 exhibit slight oscillations during demulsification. This is because when the shear velocity is large, the shear force can both promote the coalescence of the oil droplets, and can also crush the oil droplets that have been coalesced, making emulsion emulsified again. Hence, there is the phenomenon of oscillation.

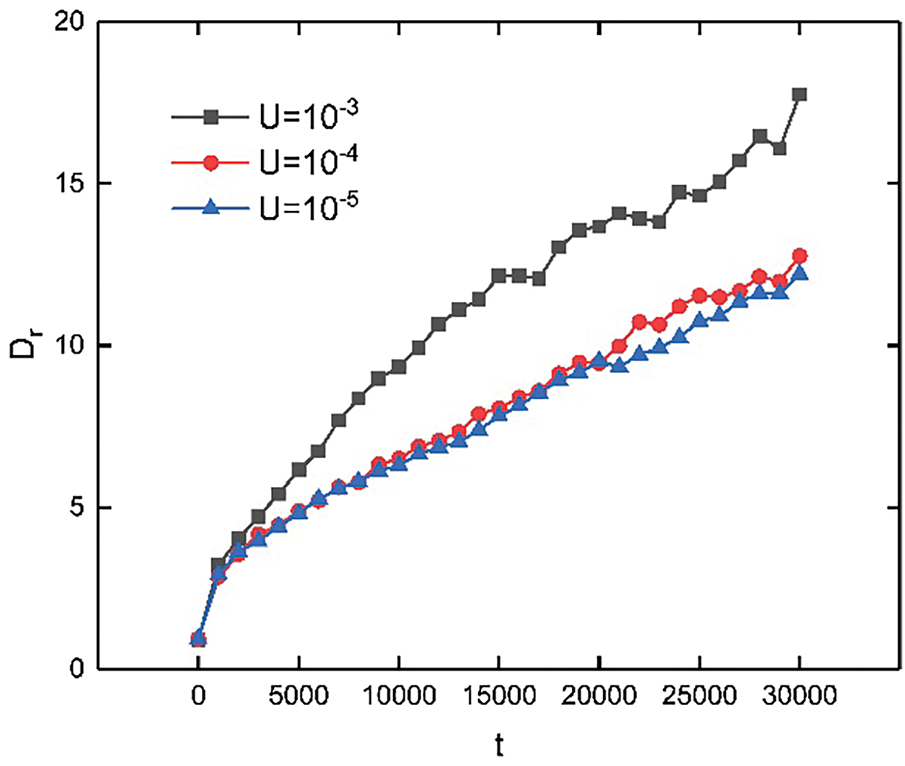
Figure 11: Typical time evolution characterization of Dr for different U

The following conclusions can be drawn from Fig. 12: As the time step increases from 0 to 200,000, the degree of oil droplet coalescence increases linearly. The enlarged image indicates that demulsification efficiency is higher under steady shear flow than under oscillatory shear flow. This is due to the constant magnitude and direction of the shear force in steady shear flow, which enables effective destabilization of the oil–water interfacial films. In contrast, although oscillatory shear can also cause instability and rupture of the interfacial films, the effect may not be as significant as that of steady shear due to its uneven distribution of shear force and the alterations of direction. (2) As the time step increases from 200,000 to 400,000, the effects of both oscillatory and steady shear on demulsification tend to stabilize. This is because in the late stage of demulsification, the stability of the emulsion has been greatly reduced, and the trend of coalescence and delamination between oil droplets has been significantly enhanced. At this point, most of the droplets have completed the initial process of coalescence, forming oil films wrapped on the surface of the porous media. (3) In the process of increasing the time step from 200,000 to 400,000, the lines for steady and oscillatory shear partially intertwine. This phenomenon is attributed to the factor as follows: In the later stage of demulsification, the shear force remains constant. However, the distribution and size of oil droplets and the strength of interfacial films undergo significant changes, causing uneven droplet responses to the shear force. For example, the coalescence of large oil beads may decelerate, while small oil droplets remain more susceptible to shear forces and further coalescence. Therefore, the overall degree of oil droplet coalescence under steady shear becomes similar to that under oscillatory shear.

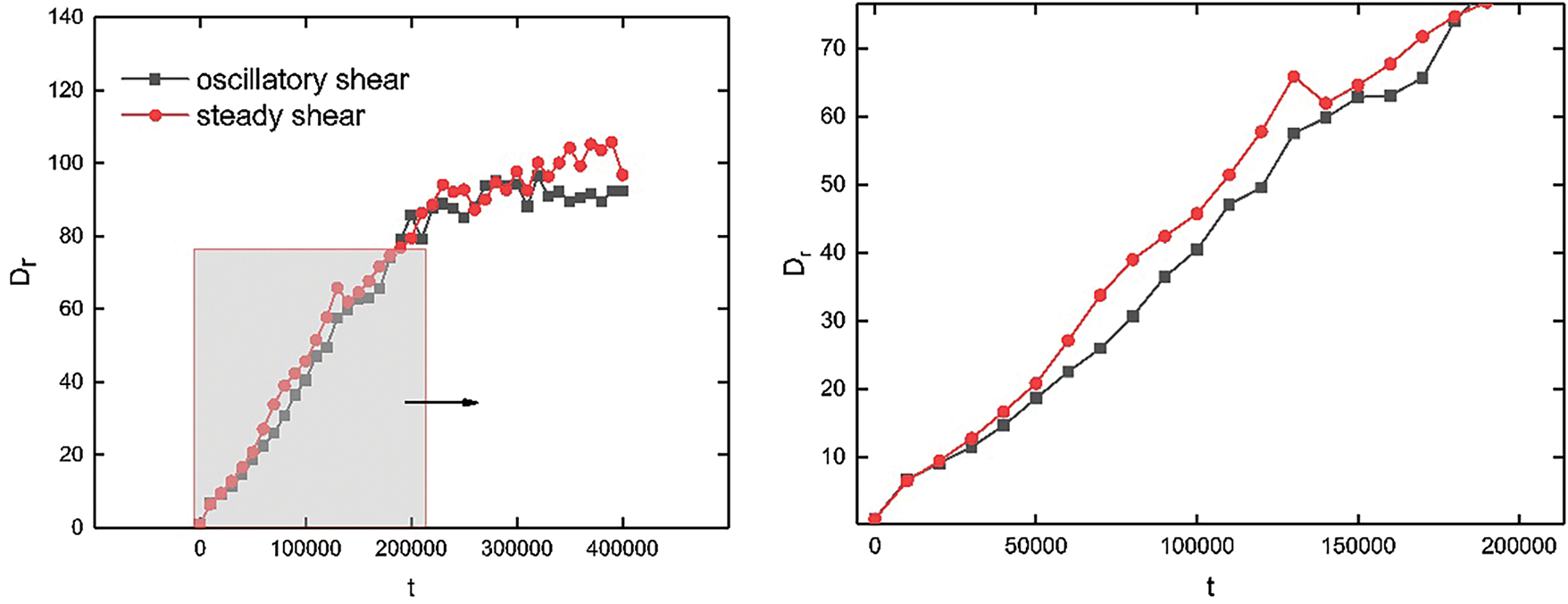
Figure 12: Typical time evolution characterization of Dr for different shear modes

Fig. 13 shows a quantitative analysis of the combined effects of shear velocity and porosity on emulsion evolution. The following points can be observed: (1) As previously mentioned, a decrease in porosity enhances coalescence efficiency. However, a decrease in the shear velocity reduces coalescence efficiency. (2) In a 90% porosity flow field, oil droplet coalescence is significantly higher than in an 80% porosity field, even if the shear velocity in the 90% porosity field increases to U=10−3. This indicates that porosity plays a dominant role in emulsion demulsification. Shear forces mainly affect the overall flow state of the emulsion, while porous media directly influence the coalescence of oil droplets. A slight decrease in porosity can cause oil droplets to accumulate more densely in local regions, thereby enhancing oil–water separation. In contrast, shear forces alone cannot effectively induce localized coalescence.

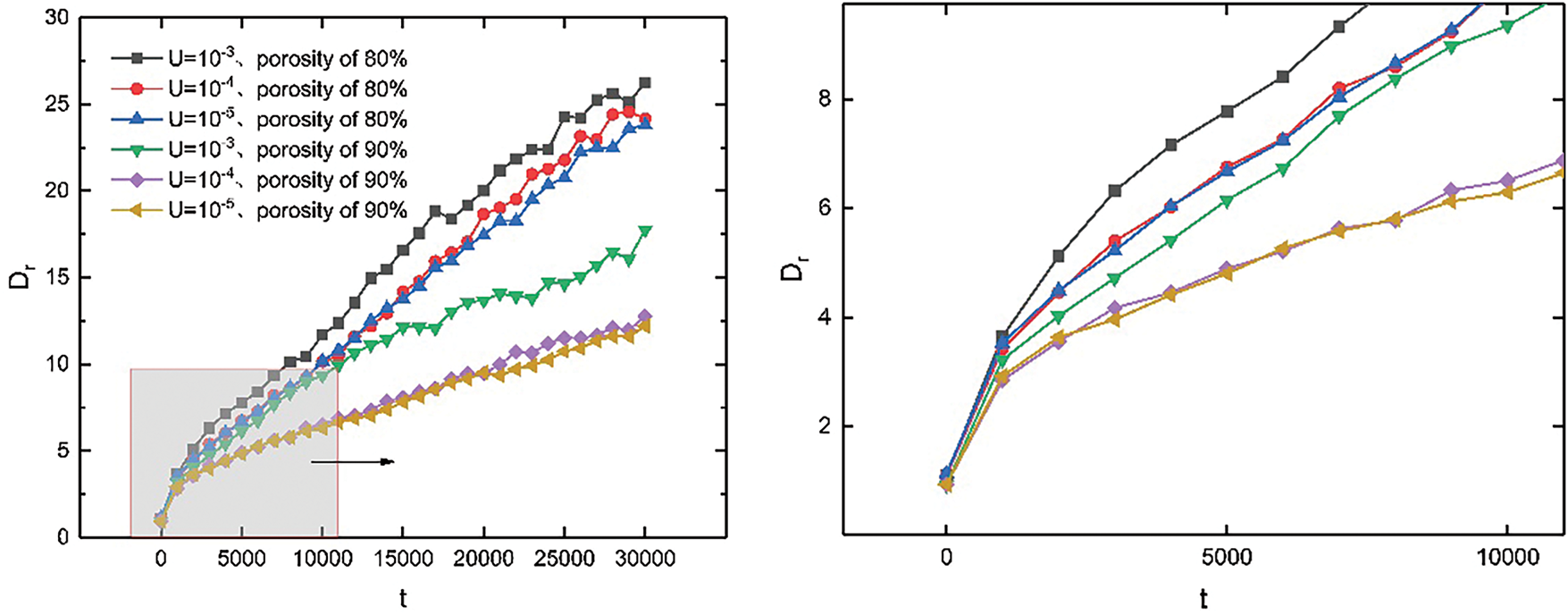
Figure 13: Typical time evolution characterization of Dr for different U and porosities

The flow field with a higher initial oil concentration exhibits greater coalescence efficiency (Fig. 14). At low initial oil concentrations, the frequency of collisions between oil droplets correspondingly decreases. In contrast, higher initial oil concentrations promote faster coalescence, leading to the earlier formation of oil films. However, nearly all oil droplets collide in very high-concentration emulsions. At this stage, collisions are not the main factor limiting oil droplet coalescence. Further increases in the oil concentration slightly improve demulsification efficiency.

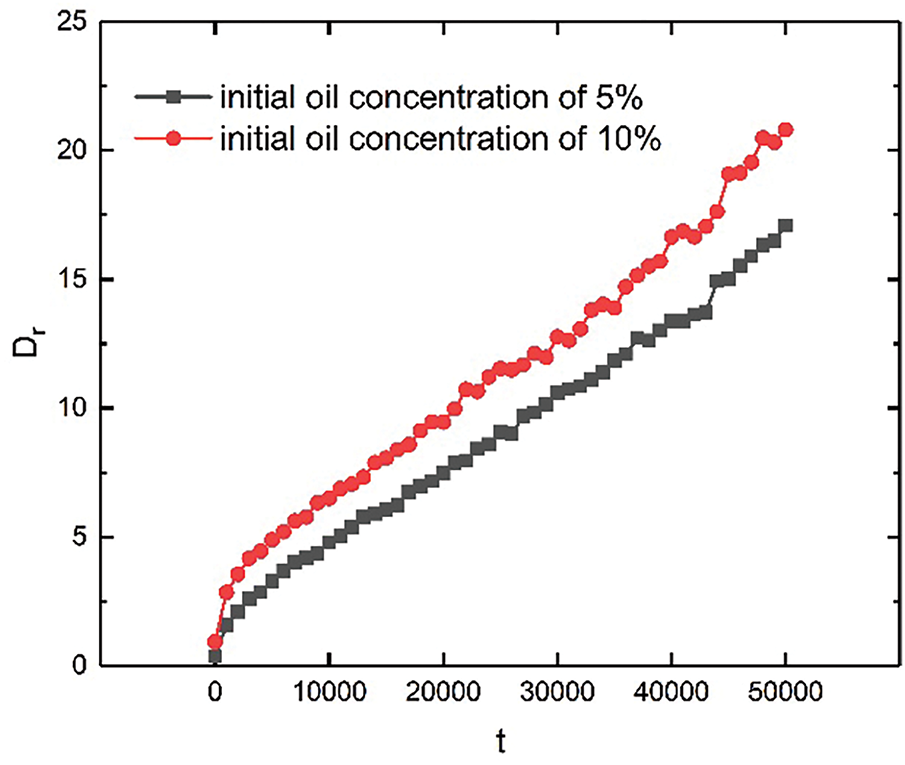
Figure 14: Typical time evolution characterization of Dr for different initial oil concentrations

4  Conclusion

In this study, a color-gradient-based lattice Boltzmann model was used to numerically simulate the morphologies and structures of O/W emulsion demulsification. The effects of porous media distribution (including porosity and arrangement), flow conditions (shear velocity and mode), and initial oil concentration on emulsion morphological evolution were investigated through controlled-variable experiments. The combined effects of porosity and shear velocity on emulsion demulsification were further analyzed through multiple sets of parallel experiments. Moreover, Dr was introduced to enable a quantitative analysis of oil–water separation. The main conclusions are as follows: (1) Porous media enhance the ability of the flow field to retain oil droplets. Lower porosity corresponds to higher demulsification efficiency. Additionally, an irregular arrangement of porous media prevents interconnection among oil droplets, further hindering demulsification. (2) Higher shear velocity causes oil droplets near the upper and lower walls to stretch more easily into strip-shaped structures, which facilitates connections between oil droplets. At the same shear velocity, switching from steady to oscillatory shear worsens the coalescence environment. Consequently, oil–water separation is less pronounced under oscillatory shear than under steady shear. (3) At the same shear velocity, oil droplets near the upper and lower walls undergo more pronounced deformation as porosity decreases. Overall, porosity has a greater impact on the morphological evolution and efficiency of emulsion demulsification than shear forces. (4) Higher initial oil concentrations increase the abundance of oil droplets in the flow field, leading to more frequent collisions and higher demulsification efficiency.

Although this study elucidates the demulsification mechanism of emulsions through numerical simulations, certain limitations remain and require further investigation. (1) To bridge the gap between theoretical simulations and practical applications, future research will extend beyond the circular porous structures adopted in this study. More complex geometries and pore-scale wettability variations will be incorporated for extensive demulsification studies. (2) Microfluidic experiments with controlled shear fields and porous structures will be designed to validate model reliability. High-speed imaging and interfacial tension measurement will be used to directly examine the emulsion demulsification process. Dimensionless parameters will be incorporated into the validated model to provide theoretical guidance for industrial wastewater treatment.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by the National Natural Science Foundation of China, grant number: 12161058. Heping Wang is the recipient of this funding. This research was funded by the National Natural Science Foundation of China, grant number: 12361096. Heping Wang is the recipient of this funding. This research was also funded by the Science and Technology Plan Project of Qinghai Province-Applied Basic Research Plan, grant number: 2023-ZJ-736. Yanggui Li is the recipient of this funding.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Heping Wang; methodology, Heping Wang, Yanggui Li; software, Heping Wang; validation, Ying Lu; investigation, Heping Wang; resources, Heping Wang; data curation, Ying Lu; writing—original draft preparation, Ying Lu; writing—review and editing, Heping Wang, Yanggui Li; visualization, Ying Lu; funding acquisition, Heping Wang, Yanggui Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Heping Wang, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li H, Chen X. Dynamic game analysis on China’s public and private oil stockpiles. Nat Hazards. 2016;84(1):715–23. doi:10.1007/s11069-016-2405-y. [Google Scholar] [CrossRef]

2. McPherson GR, Weltzin JF. Implications of peak oil for industrialized societies. Bull Sci Technol Soc. 2008;28(3):187–91. doi:10.1177/0270467608316098. [Google Scholar] [CrossRef]

3. Li S, Li B, Li Y, Liu H, Huang S, Yang Q, et al. Pilot study on a physical process for treating petrochemical wastewater. J Environ Manage. 2025;379:124891. doi:10.1016/j.jenvman.2025.124891. [Google Scholar] [PubMed] [CrossRef]

4. Raya SA, Mohd Saaid I, Abbas Ahmed A, Abubakar Umar A. A critical review of development and demulsification mechanisms of crude oil emulsion in the petroleum industry. J Petrol Explor Prod Technol. 2020;10(4):1711–28. doi:10.1007/s13202-020-00830-7. [Google Scholar] [CrossRef]

5. Saad MA, Kamil M, Abdurahman NH, Yunus RM, Awad OI. An overview of recent advances in state-of-the-art techniques in the demulsification of crude oil emulsions. Processes. 2019;7(7):470. doi:10.3390/pr7070470. [Google Scholar] [CrossRef]

6. Yao Y, Sun D, Xu JH, Wang B, Peng G, Sun B. Evaluation of enhanced oil recovery methods for mature continental heavy oil fields in China based on geology, technology and sustainability criteria. Energy. 2023;278:127962. doi:10.1016/j.energy.2023.127962. [Google Scholar] [CrossRef]

7. Wang D, Zhao Z, Qiao C, Yang W, Huang Y, McKay P, et al. Techniques for treating slop oil in oil and gas industry: a short review. Fuel. 2020;279:118482. doi:10.1016/j.fuel.2020.118482. [Google Scholar] [CrossRef]

8. Faisal W, Almomani F. A critical review of the development and demulsification processes applied for oil recovery from oil in water emulsions. Chemosphere. 2022;291(Pt 3):133099. doi:10.1016/j.chemosphere.2021.133099. [Google Scholar] [PubMed] [CrossRef]

9. Shen L, Ai G, Liu H, Zhu L, Lai L, Yan X, et al. Synthesis and demulsification performance of a novel low-temperature demulsifier based on trimethyl citrate. J Hazard Mater. 2024;472:134543. doi:10.1016/j.jhazmat.2024.134543. [Google Scholar] [PubMed] [CrossRef]

10. Zhai M, Wu M, Wang C, Li X. A novel silica-supported polyether polysiloxane quaternary ammonium demulsifier for highly efficient fine-sized oil droplet removal of oil-in-water emulsions. RSC Adv. 2020;10(32):18918–26. doi:10.1039/d0ra01679a. [Google Scholar] [PubMed] [CrossRef]

11. Adewunmi AA, Kamal MS. Demulsification of water-in-oil emulsions using ionic liquids: effects of counterion and water type. J Mol Liq. 2019;279:411–9. doi:10.1016/j.molliq.2019.02.008. [Google Scholar] [CrossRef]

12. Chen Y, Tian G, Liang H, Liang Y. Synthesis of magnetically responsive hyperbranched polyamidoamine based on the graphene oxide: application as demulsifier for oil-in-water emulsions. Int J Energy Res. 2019;43(9):4756–65. doi:10.1002/er.4614. [Google Scholar] [CrossRef]

13. Lazaar O, Hachem EK. Extensive study of droplet dynamics with end-grafted polymer chains in Pickering emulsions: molecular dynamics simulation and a generic model derived from the generalized Langevin equation. Comput Mater Sci. 2024;245:113305. doi:10.1016/j.commatsci.2024.113305. [Google Scholar] [CrossRef]

14. Benhamou M, Kaidi H, Hachem EK. Effective pair-potentials between droplets with end-grafted polymers within Pickering emulsions versus grafting-density, solvent quality and monomer concentration and phase diagrams architectures. J Mol Liq. 2020;318:114191. doi:10.1016/j.molliq.2020.114191. [Google Scholar] [CrossRef]

15. Yang S, Sun J, Wu K, Hu C. Enhanced oil droplet aggregation and demulsification by increasing electric field in electrocoagulation. Chemosphere. 2021;283:131123. doi:10.1016/j.chemosphere.2021.131123. [Google Scholar] [PubMed] [CrossRef]

16. Xu X, Cao D, Liu J, Gao J, Wang X. Research on ultrasound-assisted demulsification/dehydration for crude oil. Ultrason Sonochem. 2019;57:185–92. doi:10.1016/j.ultsonch.2019.05.024. [Google Scholar] [PubMed] [CrossRef]

17. Abdulredha MM, Siti Aslina H, Luqman CA. Overview on petroleum emulsions, formation, influence and demulsification treatment techniques. Arab J Chem. 2020;13(1):3403–28. doi:10.1016/j.arabjc.2018.11.014. [Google Scholar] [CrossRef]

18. Peng Y, Yu B, Zhang X, Li W, Gong H. Heat strengthening of double-field coupling demulsification of industrial waste oil emulsion. Appl Petrochem Res. 2019;9(1):13–22. doi:10.1007/s13203-018-0221-x. [Google Scholar] [CrossRef]

19. Lu H, Pan Z, Miao Z, Xu X, Wu S, Liu Y, et al. Combination of electric field and medium coalescence for enhanced demulsification of oil-in-water emulsion. Chem Eng J Adv. 2021;6:100103. doi:10.1016/j.ceja.2021.100103. [Google Scholar] [CrossRef]

20. Su X, Wang X, Jin P, Liao C. Droplet behaviors of W/O emulsions under the combination of electric field and medium coalescence. Sep Sci Technol. 2024;59(16):1659–70. doi:10.1080/01496395.2024.2397528. [Google Scholar] [CrossRef]

21. Nadeem H, Vigil RD, Samuel A, Sarkar A, Yeoh T, Olsen MG. Coalescence-induced phase separation of an oil in water emulsion under controlled shear and temperature conditions. Chem Eng Res Des. 2022;182:517–24. doi:10.1016/j.cherd.2022.04.024. [Google Scholar] [CrossRef]

22. Hou L, Liang CG, Ma FX, Hao B, Ma PC, Kuang D, et al. Numerical study of the dynamic aggregation behaviors of oil droplets in the porous filter media consisting of basalt particles. Powder Technol. 2025;452:120470. doi:10.1016/j.powtec.2024.120470. [Google Scholar] [CrossRef]

23. Lu H, Pan Z, Wang H, Liu Y, Dai P, Yang Q. Fiber coalescence treatment of oily wastewater: a new theory and application. J Hazard Mater. 2021;412:125188. doi:10.1016/j.jhazmat.2021.125188. [Google Scholar] [PubMed] [CrossRef]

24. Zhou JG. Macroscopic lattice Boltzmann method. Water. 2021;13(1):61. doi:10.3390/w13010061. [Google Scholar] [CrossRef]

25. Sudhakar T, Das AK. Evolution of multiphase lattice Boltzmann method: a review. J Inst Eng Ind Ser C. 2020;101(4):711–9. doi:10.1007/s40032-020-00600-8. [Google Scholar] [CrossRef]

26. Cheng Y, Wang S, Shao B, Yuan Z, Xie L. Lattice Boltzmann simulation of particle flow characteristics in porous media. Chin J Process Eng. 2023;2:188–98. (In Chinese). [Google Scholar]

27. Leclaire S, Reggio M, Trépanier JY. Numerical evaluation of two recoloring operators for an immiscible two-phase flow lattice Boltzmann model. Appl Math Model. 2012;36(5):2237–52. doi:10.1016/j.apm.2011.08.027. [Google Scholar] [CrossRef]

28. Haghani R, Erfani H, McClure JE, Flekkøy EG, Berg CF. Color-gradient-based phase-field equation for multiphase flow. Phys Rev E. 2024;109:035301. doi:10.1103/PhysRevE.109.035301. [Google Scholar] [PubMed] [CrossRef]

29. Li CS, Cai RR, Zhang LZ. An improved immersed moving boundary-based curved wetting condition method for the pseudopotential multiphase lattice Boltzmann model. Phys Fluids. 2024;36(11):112119. doi:10.1063/5.0238292. [Google Scholar] [CrossRef]

30. Vaseghnia H, Jettestuen E, Giljarhus KET, Aursjø O, Hiorth A. Evaluation of the non-Newtonian lattice Boltzmann model coupled with off-grid bounce-back scheme: wall shear stress distributions in Ostwald-de Waele fluids flow. Phys Rev E. 2024;110(1–2):015305. doi:10.1103/PhysRevE.110.015305. [Google Scholar] [PubMed] [CrossRef]

31. Mino Y, Hasegawa A, Shinto H, Matsuyama H. Lattice-Boltzmann flow simulation of an oil-in-water emulsion through a coalescing filter: effects of filter structure. Chem Eng Sci. 2018;177:210–7. doi:10.1016/j.ces.2017.11.027. [Google Scholar] [CrossRef]

32. Bansal S, Von Arnim V, Stegmaier T, Planck H. Effect of fibrous filter properties on the oil-in-water-emulsion separation and filtration performance. J Hazard Mater. 2011;190(1–3):45–50. doi:10.1016/j.jhazmat.2011.01.134. [Google Scholar] [PubMed] [CrossRef]

33. Wang H, Li X, Lin K, Geng X. Morphological simulation of phase separation coupled oscillation shear and varying temperature fields. J Low Temp Phys. 2018;191(3–4):153–73. doi:10.1007/s10909-018-1850-2. [Google Scholar] [CrossRef]

34. Fan J, Li W. Lattice Boltzmann simulation of the chemically reactive mixtures under simple and oscillatory shear flow. Acta Polym Sin. 2013;3:341–6. (In Chinese). doi:10.3724/sp.j.1105.2013.12223. [Google Scholar] [CrossRef]