 Open Access
Open Access
ARTICLE
Gradient Descent-Based Prediction of Heat-Transmission Rate of Engine Oil-Based Hybrid Nanofluid over Trapezoidal and Rectangular Fins for Sustainable Energy Systems
1 School of Mechanical Engineering, Hanyang University, 222 Wangsimni-ro, Seongdong-gu, Seoul, 04763, Republic of Korea
2 Faculty of Mathematics, Institute of Management, Kristu Jayanti Deemed to be University, K. Narayanapura, Kothanur, Bengaluru, 560077, India
3 Department of Mathematics and Statistics, College of Science, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, 11623, Saudi Arabia
4 Department of Mechanical Engineering, Sejong University, Seoul, 05006, Republic of Korea
* Corresponding Author: Se-Jin Yook. Email:
# These authors contributed equally to this work
(This article belongs to the Special Issue: Computational Intelligent Systems for Solving Complex Engineering Problems: Principles and Applications-III)
Computer Modeling in Engineering & Sciences 2026, 146(1), 20 https://doi.org/10.32604/cmes.2025.074680
Received 15 October 2025; Accepted 28 November 2025; Issue published 29 January 2026
Abstract
Fluid dynamic research on rectangular and trapezoidal fins is aimed at increasing heat transfer by means of large surfaces. The trapezoidal cavity form is compared with its thermal and flow performance, and it is revealed that trapezoidal fins tend to be more efficient, particularly when material optimization is critical. Motivated by the increasing need for sustainable energy management, this work analyses the thermal performance of inclined trapezoidal and rectangular porous fins utilising a unique hybrid nanofluid. The effectiveness of nanoparticles in a working fluid is primarily determined by their thermophysical properties; hence, optimising these properties can significantly improve overall performance. This study considers the dispersion of Graphene OxideKeywords
Fin is referred to as a thin, elongated, extended structure attached to a solid surface. Engineers realised in the early 20th century that heat dissipation through convection may be improved by expanding a solid surface’s surface area. Fins are widely employed in automotive, electronics, aerospace, steel, metallurgy and renewable energy industries to enhance heat transfer. The choice of fin type, size, shape, and spacing depends on the specific heat transfer requirements of the system and the constraints of the application. Fins with the best designs are in more demand. Aziz and Fang [1] examined temperature distribution in longitudinal fin focusing on trapezoidal, rectangular, and concave profiles. Han and Peng [2] investigated thermal management in a moving fin considering a radiative and convective environment. Pavithra et al. [3] analysed the temperature distribution in the dovetail longitudinal fin considering radiation and hybrid nanofluid. Riasat et al. [4] examined the Darcy model of internal heat generation in a radial fin. Luo et al. [5] used a deep generative model to analyse thermal performance in a fin. Abd-Elmonem et al. [6] analysed the heat transport via a fin in a vertical pipe using a machine learning technique. Rehman et al. [7] using ANN predicted improving buoyancy results in convective heat transfer in a T-shaped fin. Arshad [8] reported that the addition of a tree-shaped fin reduced heat sink temperature by 8%. Sowmya et al. [9] investigated thermal distribution in a rectangular fin incorporating magnetic and radiation. Basha et al. [10] investigated entropy generation and heat transport in nanofluid flow across a square enclosure fitted with a fin and estimated the optimal transport using machine learning technology. The development of extended surface technology has led to the replacement of conventional solid fin structures with porous ones. Conventional uses for heat transmission in porous media include solar collectors, heat exchangers, and reactor cooling. Kiwan and Al-Nimr [11] were the ones who first suggested using porous fins by presenting the Darcy model. They took up a comparative study between porous and conventional fins and noticed that the porous fin shows better performance in heat transfer. Ahmad et al. [12] applied an ANN model to analyse the optimal thermal dispersion considering a porous triangular moving fin by including radiation, surface temperature, and Peclet number parameters. Hu et al. [13] addressed thermal characteristics using structured porous fins. The study reported that structured porous fins (SPFs) significantly enhanced phase change material (PCM) heat transfer and achieved a 62% decrease in melting time. Alotaibi et al. [14] applied ANN and the ISPH method to analyse the optimal heat transfer performance. Their study reported that 15% of the temperature was reduced due to the addition of a triangular porous fin. Nandy and Balasubramanian [15] observed that a porous wavy fin in a microchannel improved thermos-hydraulic performance due to the use of design C at Re of 300.
The angle of inclination has a significant impact on fin performance. In particular, in natural convection, it influences the boundary layer growth, flow structure and the heat transfer coefficient. While in forced convection, it impacts the flow distribution and associated pressure drop. He et al. [16] asserted that by improving the inclination angle, the average heat transfer and heat flux of a solid-perforated spiral fin rose by 15.5%. Li et al. [17] demonstrated that micro-finned wall position and inclination angle play a crucial role in vapour-liquid distribution, heat transfer and flow dynamics. Dhaoui et al. [18] revealed that optimising fin angle remarkably enhances heat transfer and overall effectiveness of solar stills. Komathi et al. [19] carried out an analysis of heat transfer in an inclined wetted moving fin and reported that fin temperature declined with increasing wet porous, radiation, inclination angle and convective parameter. Zhong et al. [20] took up a detailed investigation on heat transfer considering four different fins, namely curved, vertical, serpentine and inclined fins. They noticed that heat transfer efficiency was more effective for the curved fin, and the serpentine fin exhibited outstanding heat transfer. Chen et al. [21] from 20 to 180 W, the bending heat type’s heat transfer is greatly improved by the observed small inclination angle. Choi and Eastman [22] first showed that the deferment of nanoparticles in a working fluid, like oil, ethylene glycol, and water, can greatly enhance their thermal properties and heat transfer performance. Owing to these advantages, nanofluids are increasingly used in heat transfer applications in commercial and engineering industries. In recent years, attention has shifted towards hybrid and ternary nanofluids. Bahiraei et al. [23] conducted an experimental study and described a hybrid nanofluid’s thermal characteristics, which involves the amalgamation of two distinct nanoparticles in a base fluid. Research confirms that hybrid nanofluid outperforms mono nanofluid with enhanced rheological characteristics. Ternary hybrid extends this concept by incorporating three distinct nanoparticles. Varatharaj et al. [24] analysed the impact of first-order slip, porous media, ternary hybrid nanofluid flow across a permeable stretching surface via joule heating and viscous dissipation. Mishra et al. [25] examined how slip affected a ternary hybrid nanofluid passing across a permeable plate. Gul et al. [26] elucidated that the incorporation of
A computational investigation of Cattaneo-Christov double diffusion and mixed convection effects in a non-Darcian Sutterby nanofluid was conducted by Rehman et al. [31] employing multi-objective optimization through Response Surface Methodology (RSM). Using a modified Buongiorno’s model, Wang et al. [32] examined the heat and mass transport of an Ag–H2O nano-thin film flowing over a porous medium. Rehman et al. [33] used response surface methods to study the impact of heat radiation and magnetohydrodynamics on shear-thinning Williamson nanofluids with stability analysis. Oscillatory convective gear-generalised differential quadrature analysis was studied by Xia et al. [34], Darcy-Forchheimer and Lorentz quadratic drag forces in second-grade fluids’ Taylor-Couette flows.
Novelty of the Present Study:
Despite extensive research on fin problems, inclined rectangular and triangular porous fins wetted with hybrid nanofluid remain largely unexplored with this combination. Therefore, because applications for sustainable energy systems are in high demand, this study aims to address the thermal performance of inclined porous rectangular and triangular porous fins wetted with a hybrid nanofluid (Engine Oil + Graphene Oxide (GO) + Molybdenum Disulfide (MOS2)) through machine learning gradient descent optimization technique forecasting the rate of heat transfer in rectangular and trapezoidal fins, the difference between expected and actual values is negligible, shows the precise thermal performance estimation for various fin geometries.
The interplay of conduction, convection, and radiation is used to analyse heat transmission in a fin. A differential control volume technique is used to move heat internally along the x-direction. The temperature gradient from the base temperature (Tb) causes the heat flux (qx) to change. Heat is lost through convection and radiation as it enters the surrounding environment after passing through the fin. The geometrical characteristics of the fin, including its thickness (tb), width (w), and length (L), are important in determining how heat is transferred and distributed. As internal conduction counteracts the heat loss at the surface, the temperature drops along the x-direction. Whereas radiative heat loss happens through thermal radiation to the surrounding environment at temperature (Ta), convective heat loss transfers energy to the surrounding fluid. The fin’s ensuing temperature gradient shows how internal heat conduction and outward heat dissipation are balanced. Comprehending these principles is essential for maximising thermal management in engineering systems, guaranteeing efficient heat dissipation for enhanced stability and performance.
The governing differential equation for this issue is provided by Khan et al. [35]
where, Hybrid nanofluid is denoted by the subscript hnf, C stands for specific heat capacity at constant pressure, ϕ for porosity, β for thermal expansion coefficient, k for thermal diffusivity, μ for effective kinematic viscosity, and ρ for effective mass density.
The following provides the corresponding boundary conditions:
The linearization of the T4 components as a function of temperature is possible with the Rosseland approximation, i.e.,
Now consider the dimensionless quantities:
Eq. (5) is obtained after solving by substituting Eq. (4) into Eq. (1)
Following the non-depersonalization process, the boundary conditions turn into
In the present study, normalization parameters are:
For ease of simplification,
Let
Now the equation becomes,
Fin’s heat transfer rate by using the study of Khan et al. [35]:
3 Methodology of the Present Study
3.1 Lobatto IIIa Collocation Method
• The given boundary conditions are then turned into a first-order system of differential equations, formulating the boundary value problem.
• The first mesh is created on the solution interval, and a good initial guess of the solution is provided.
• The ordinary differential equation (ODE) system is expressed as a function, and the boundary conditions are expressed as a separate boundary condition function.
• The Lobatto IIIa collocation approach is an internal approach used in the bvp5c solver of MATLAB to impose accuracy at collocation points.
• Tolerance error is 10−3, Step size is 0.01 and computational time is 5 s.
• The solver automatically optimises the mesh to meet error tolerances, and the solver is numerically stable.
3.2 Gradient Descent Machine Learning
• Input: Observe and preprocess the input information of important physical parameters.
• Influence of Features: Research the effect of parameters on physical quantities of the target.
• Model Training: Finding a minimum loss of a machine learning algorithm using gradient descent. The Cost function is
• Analysis: Producing the predictions of linear fits and determining their performance using such measures as mean squared error (MSE) and root mean squared error (RMSE).
An inclined longitudinal porous fin wetted with a hybrid nanofluid (Engine Oil Graphene Oxide Molybdenum Disulfide
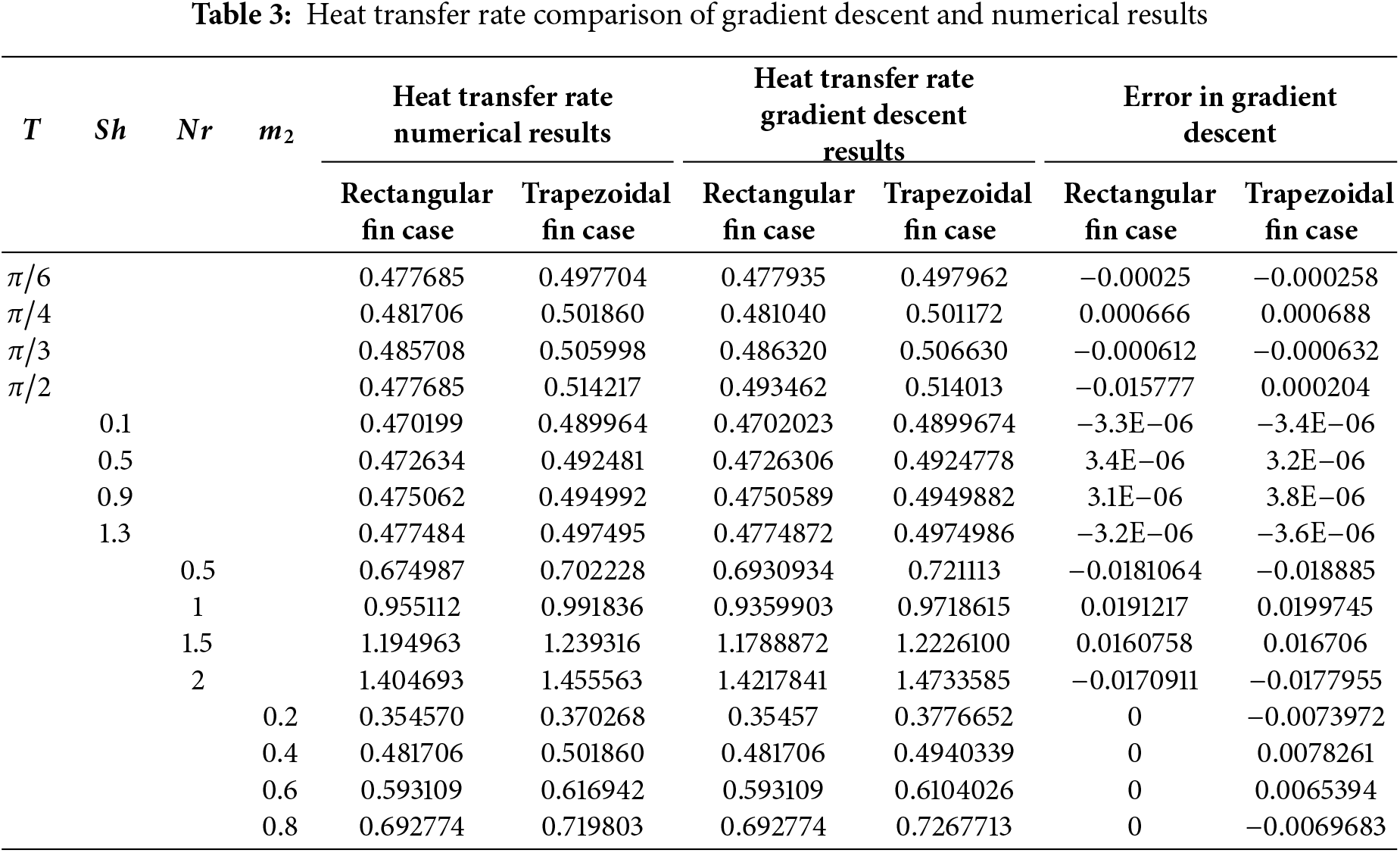
Figure 1: Applications of the current research
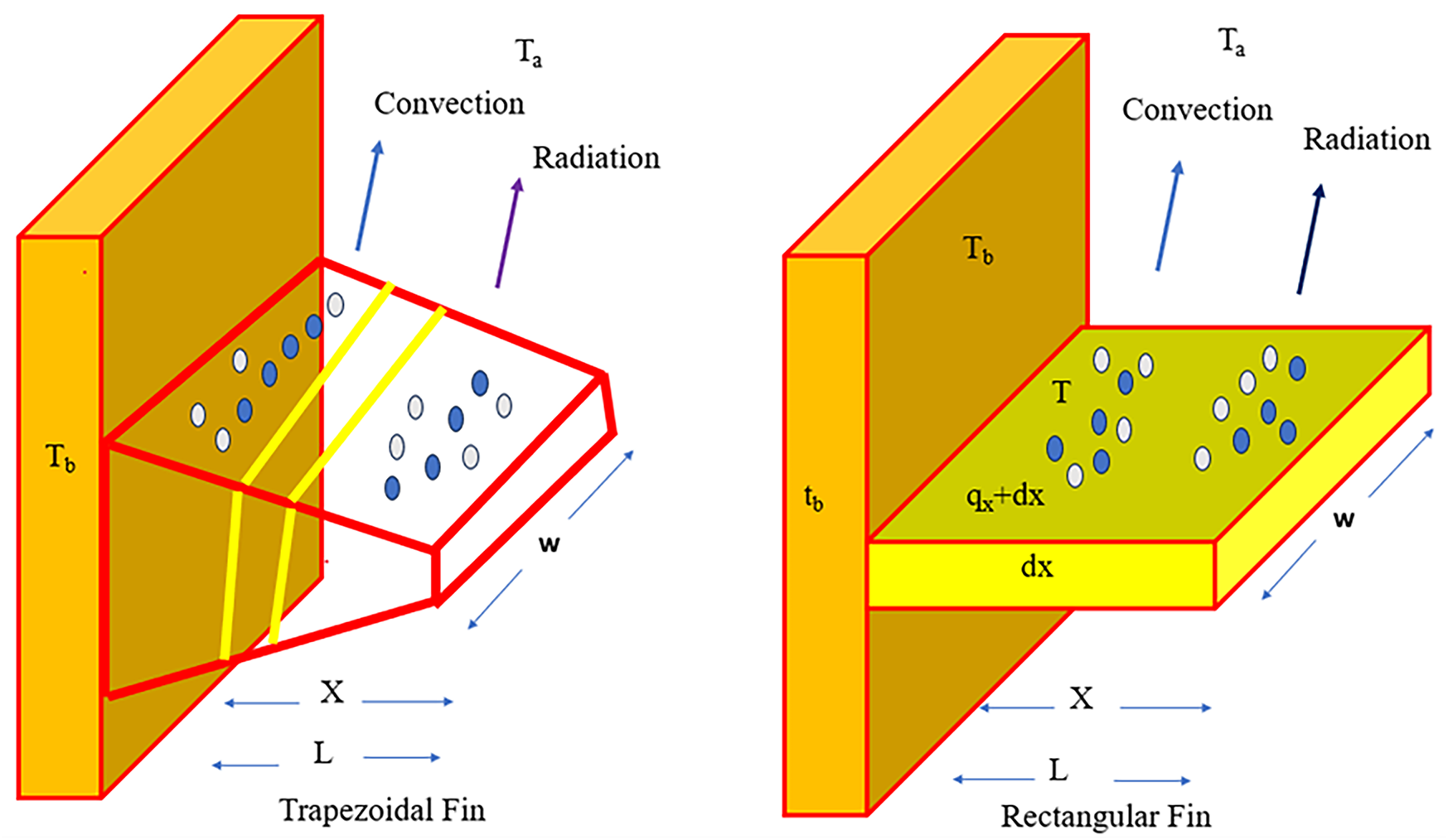
Figure 2: Schematic representation of the trapezoidal and rectangular fin
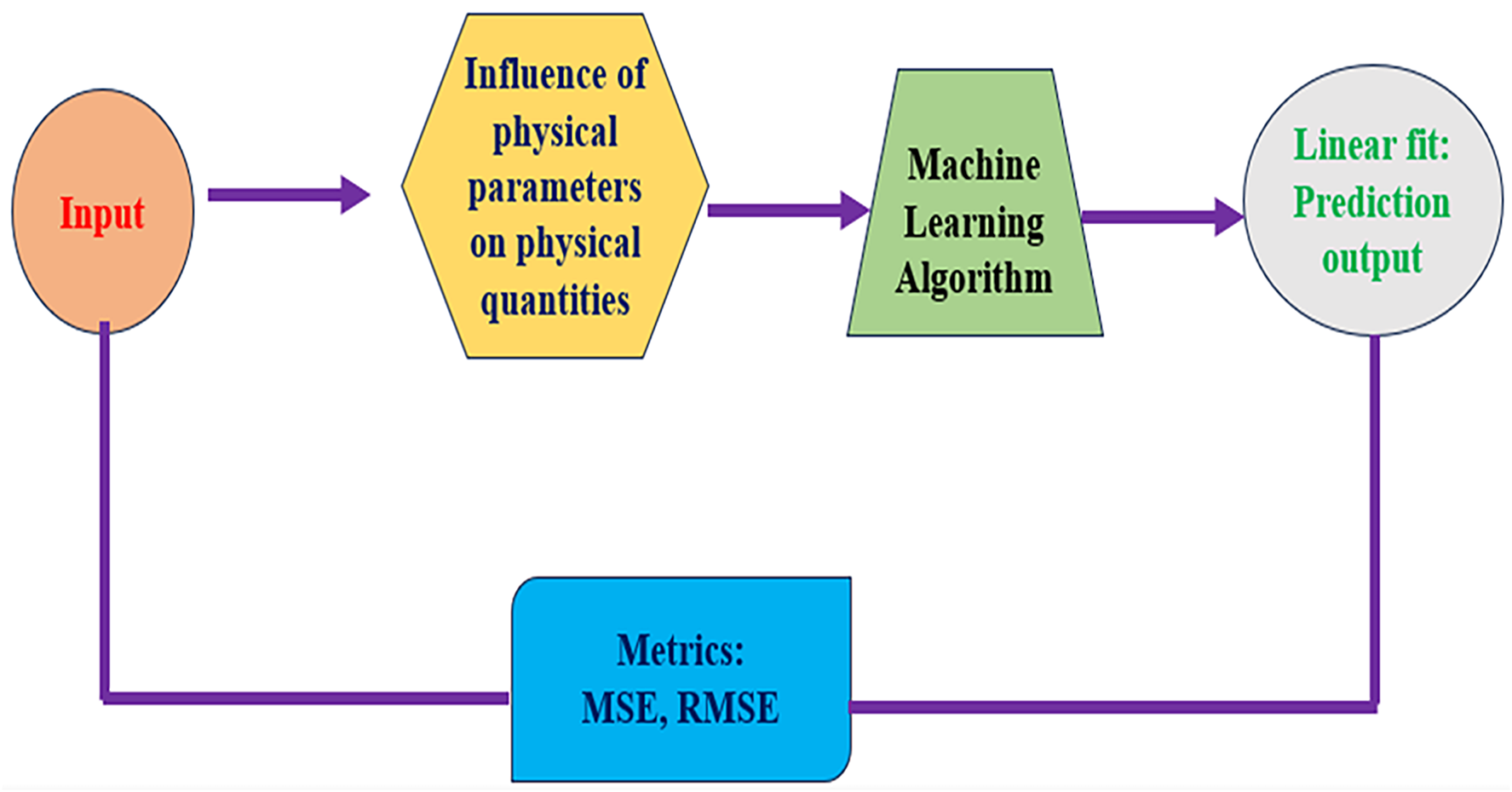
Figure 3: Gradient descent algorithm flow chart
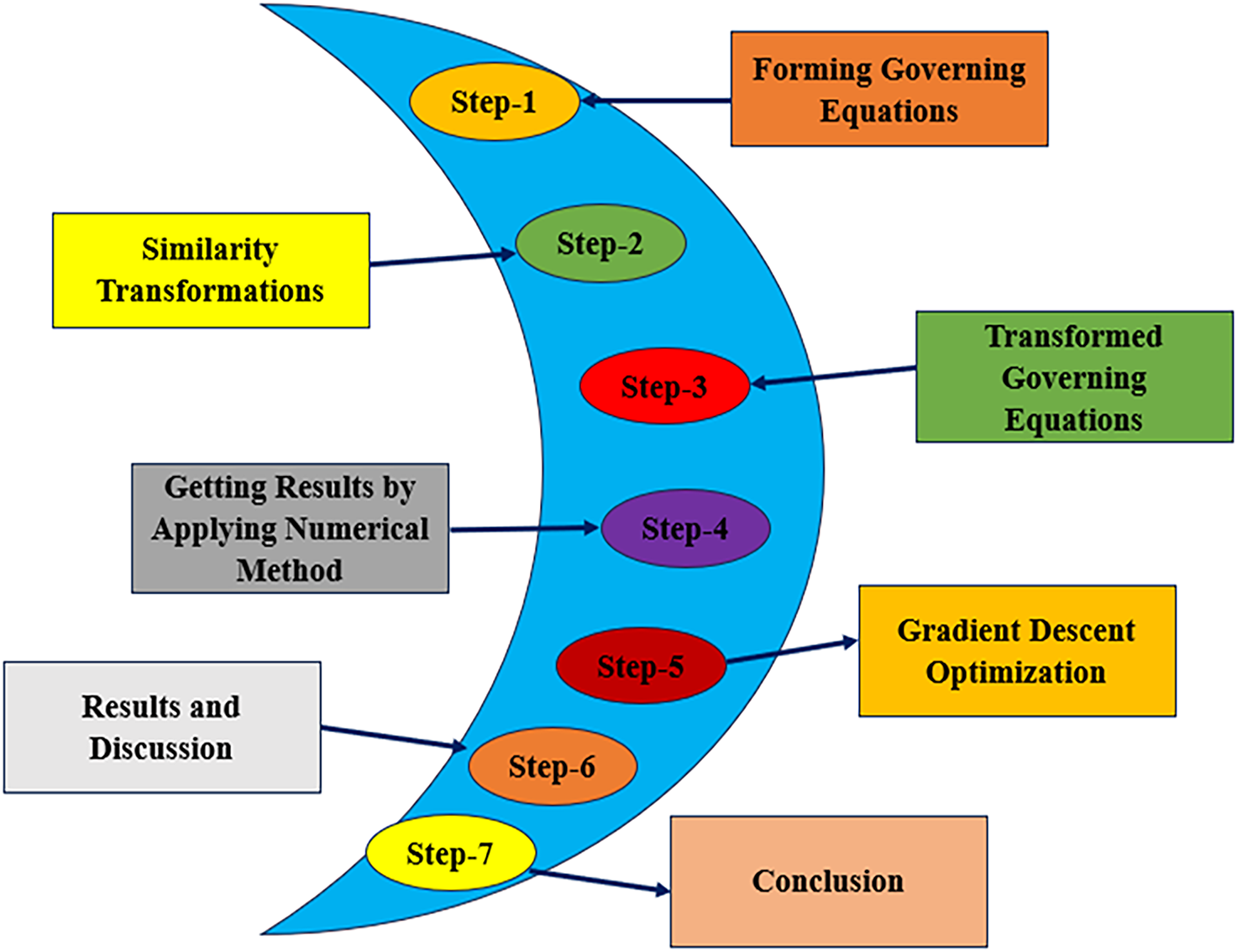
Figure 4: Methodology of the present study
4.1 Temperature Profiles for Various Parameters and Error Analysis
From Fig. 5 it is evident that as the wet porous parameter
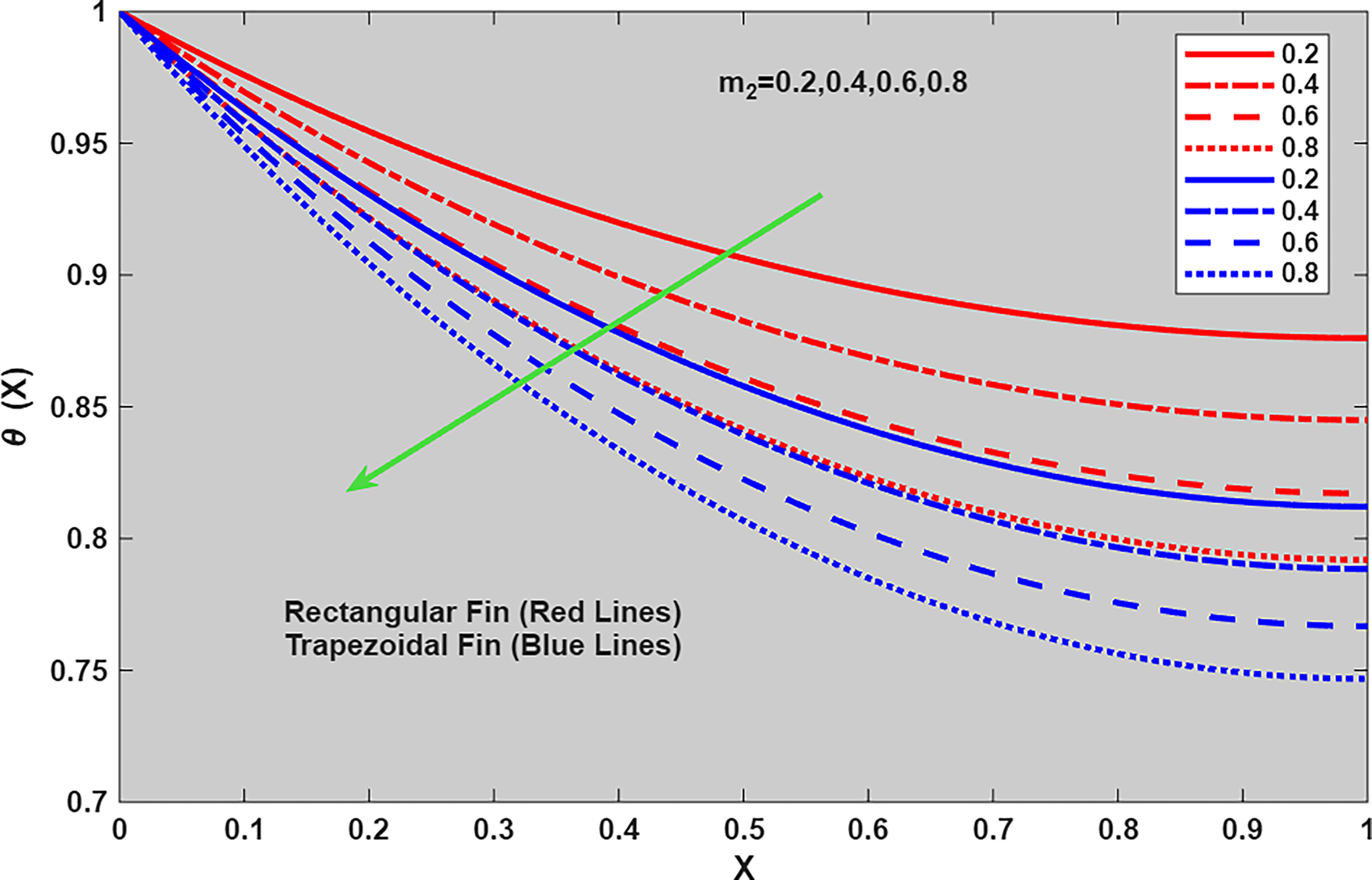
Figure 5: Plot of
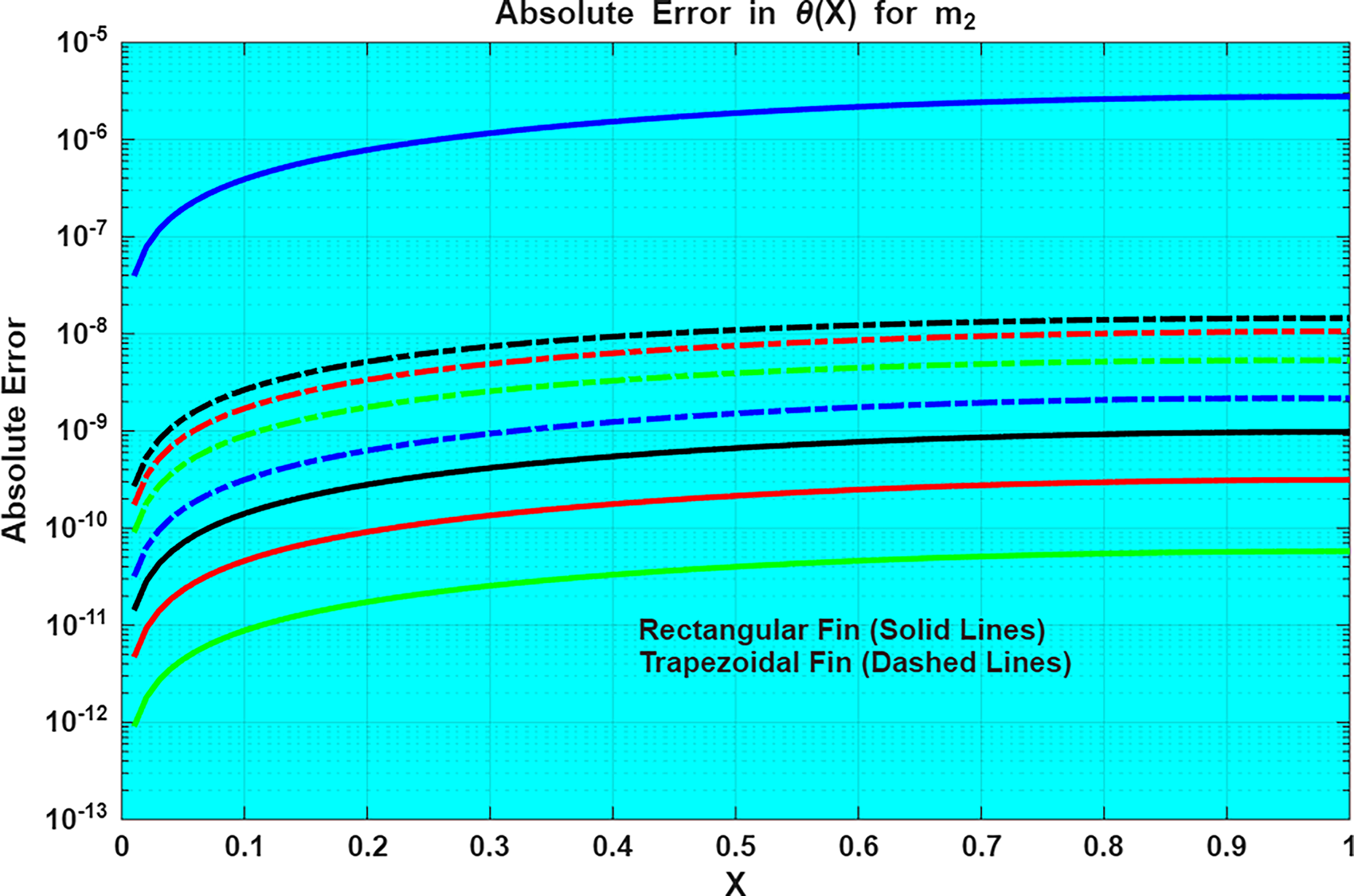
Figure 6: Absolute error of
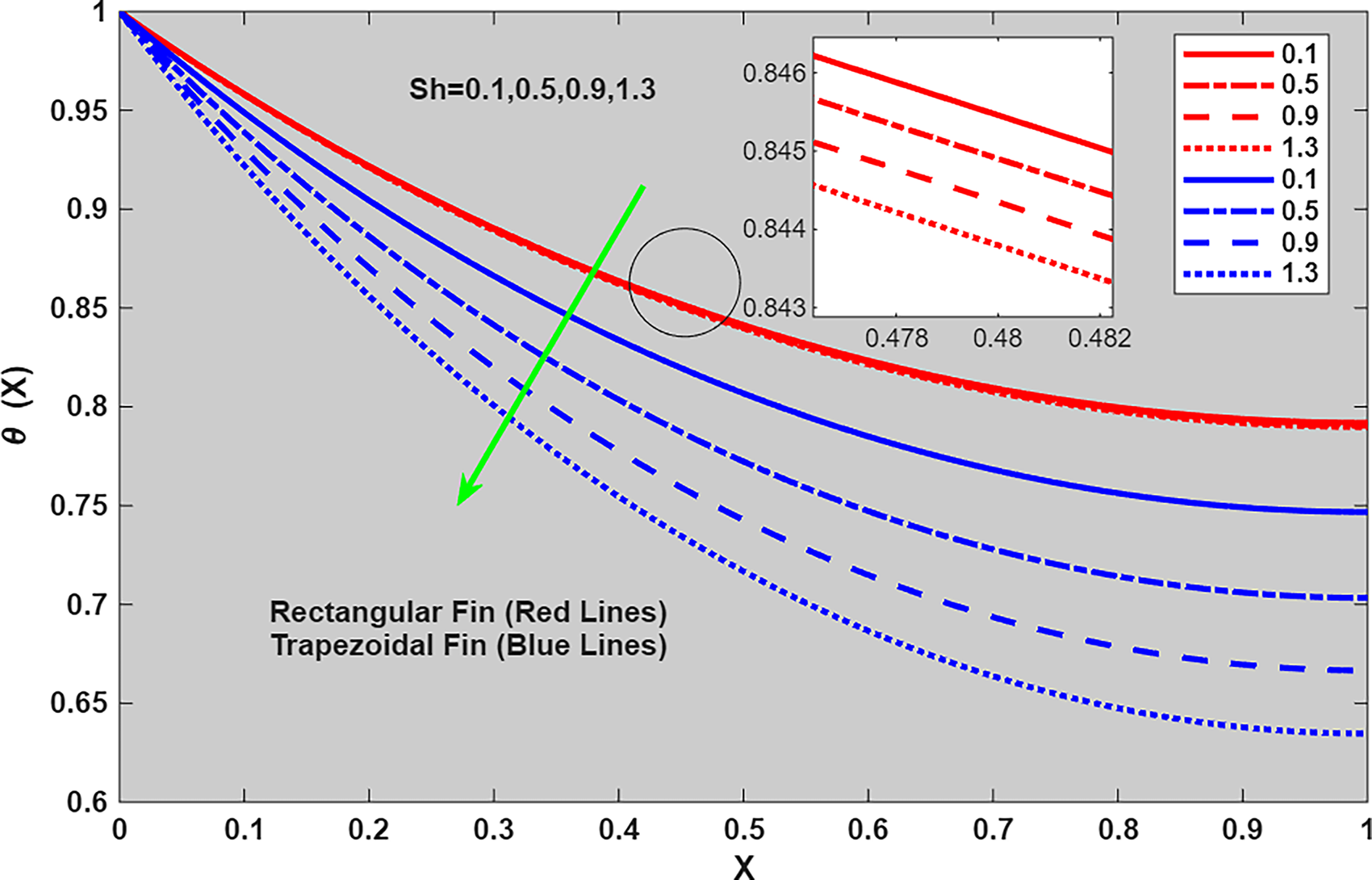
Figure 7: Plot of
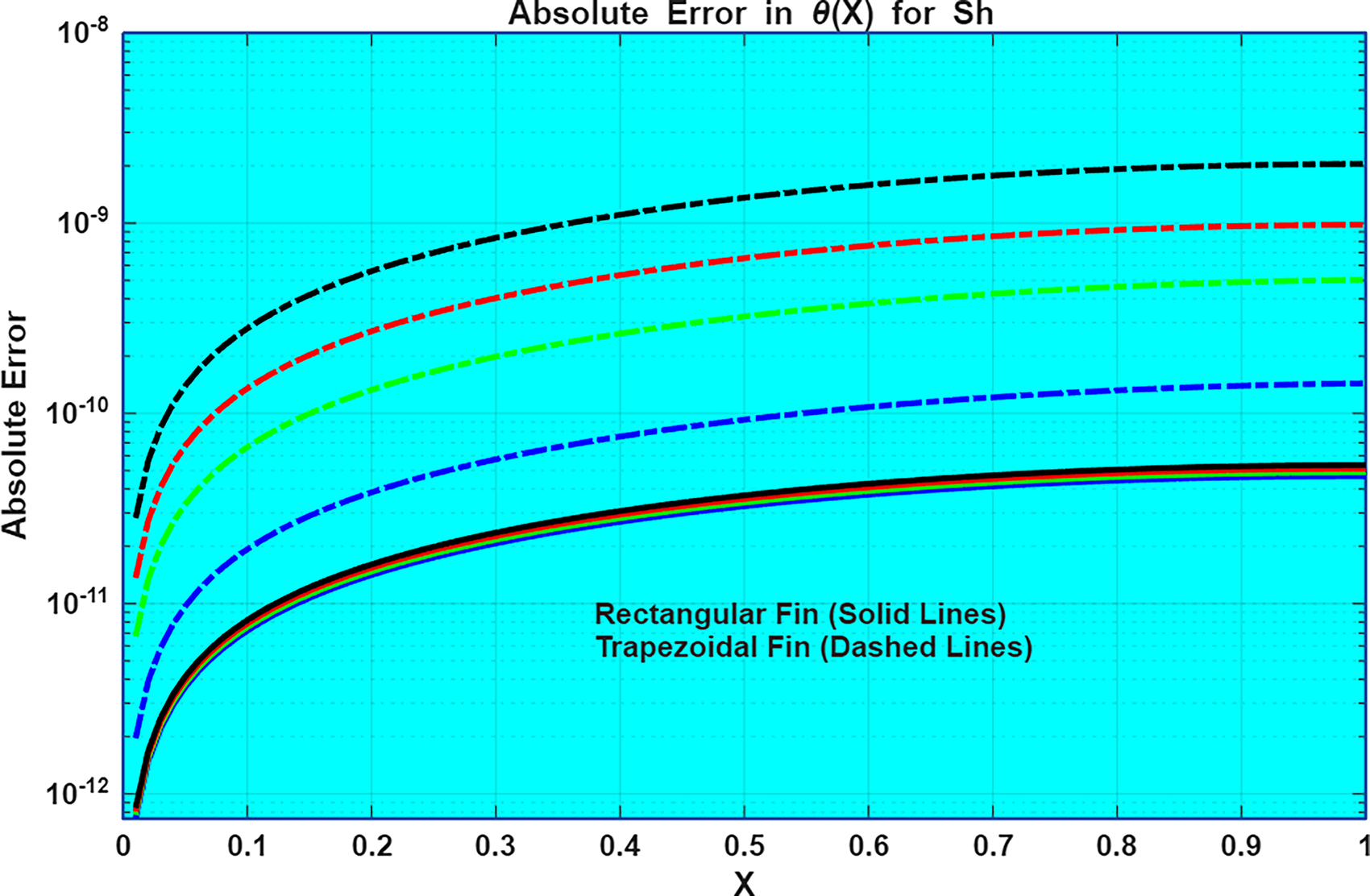
Figure 8: Absolute error of
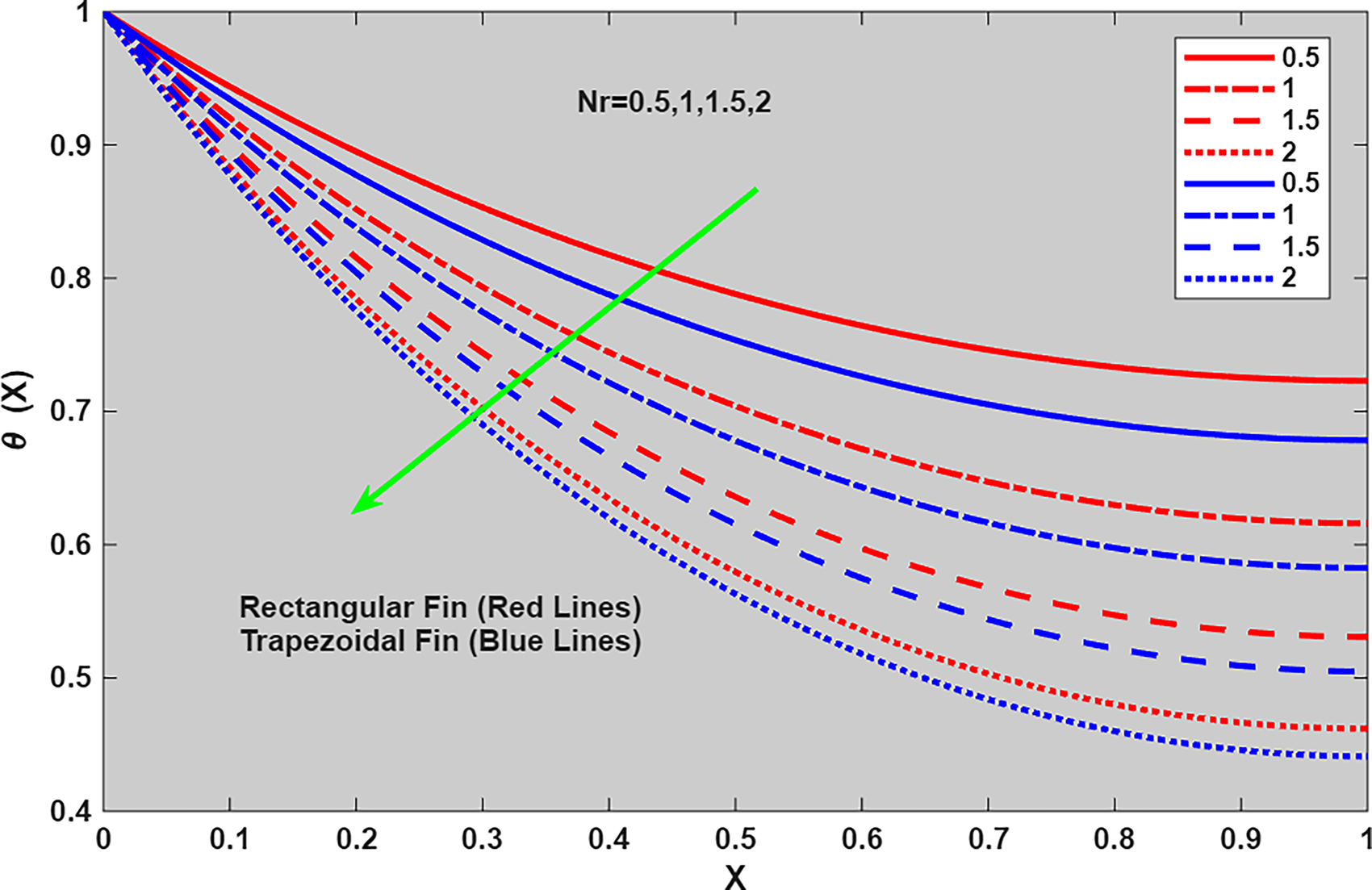
Figure 9: Plot of
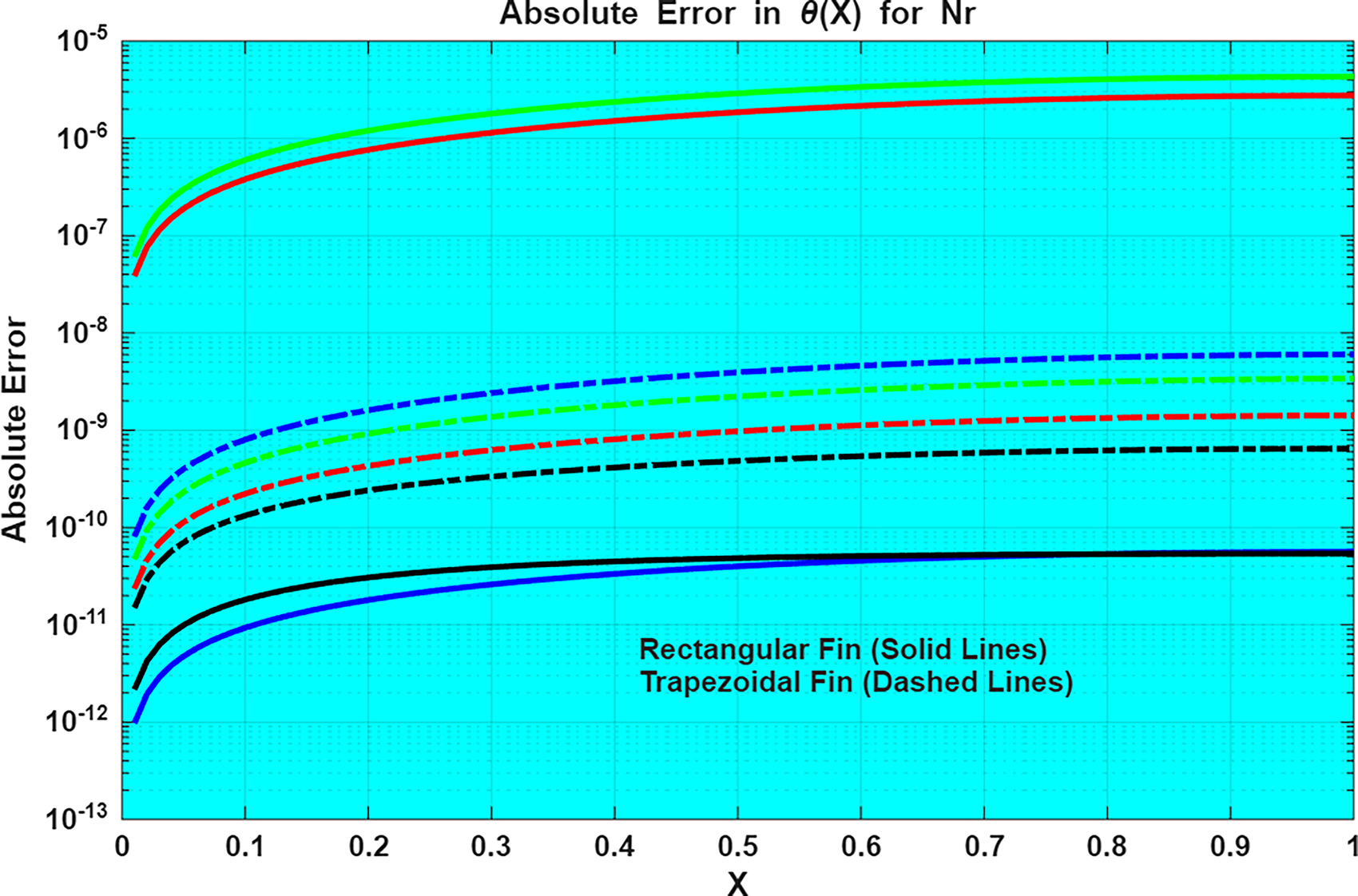
Figure 10: Absolute error of
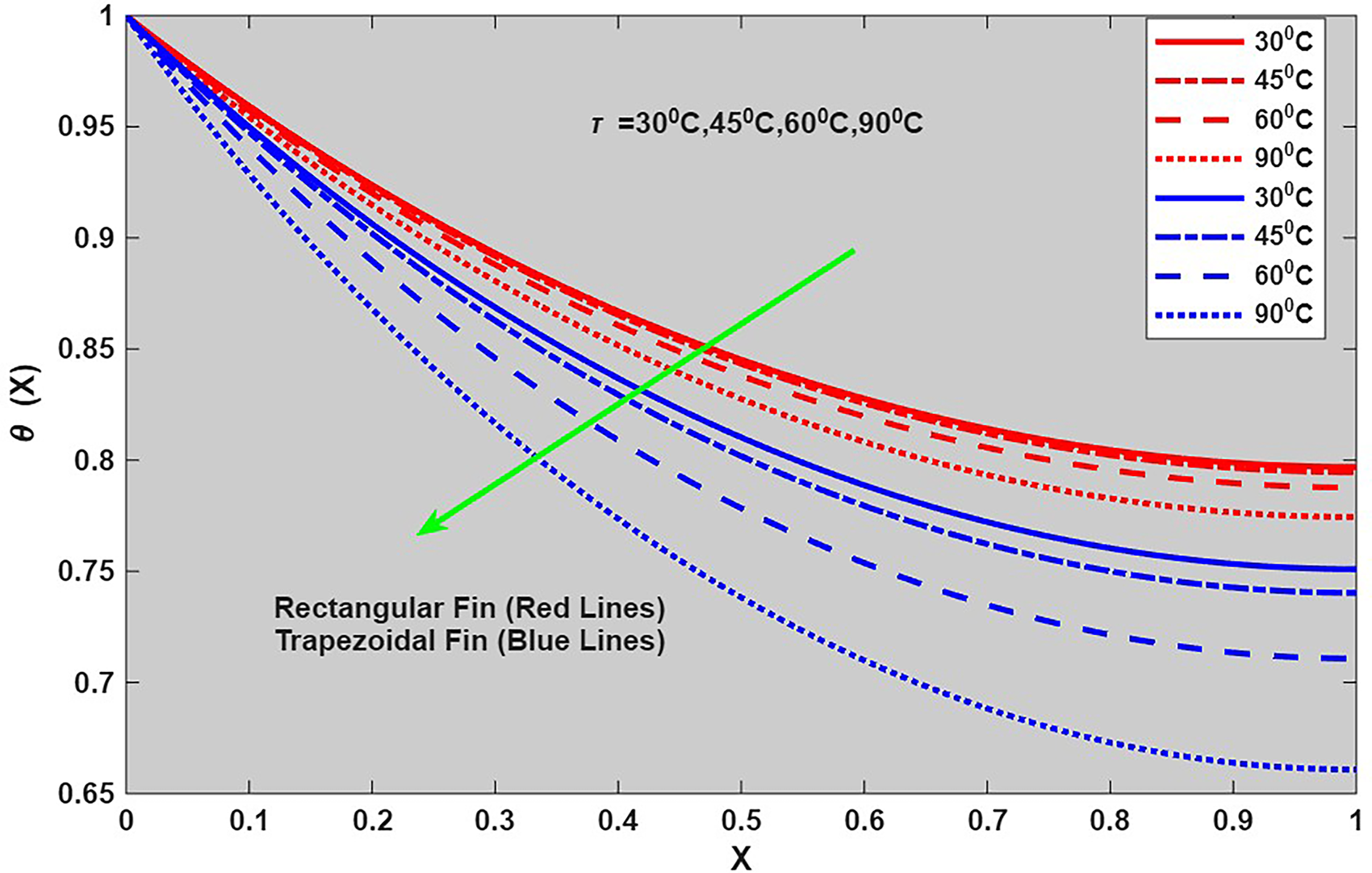
Figure 11: Plot of
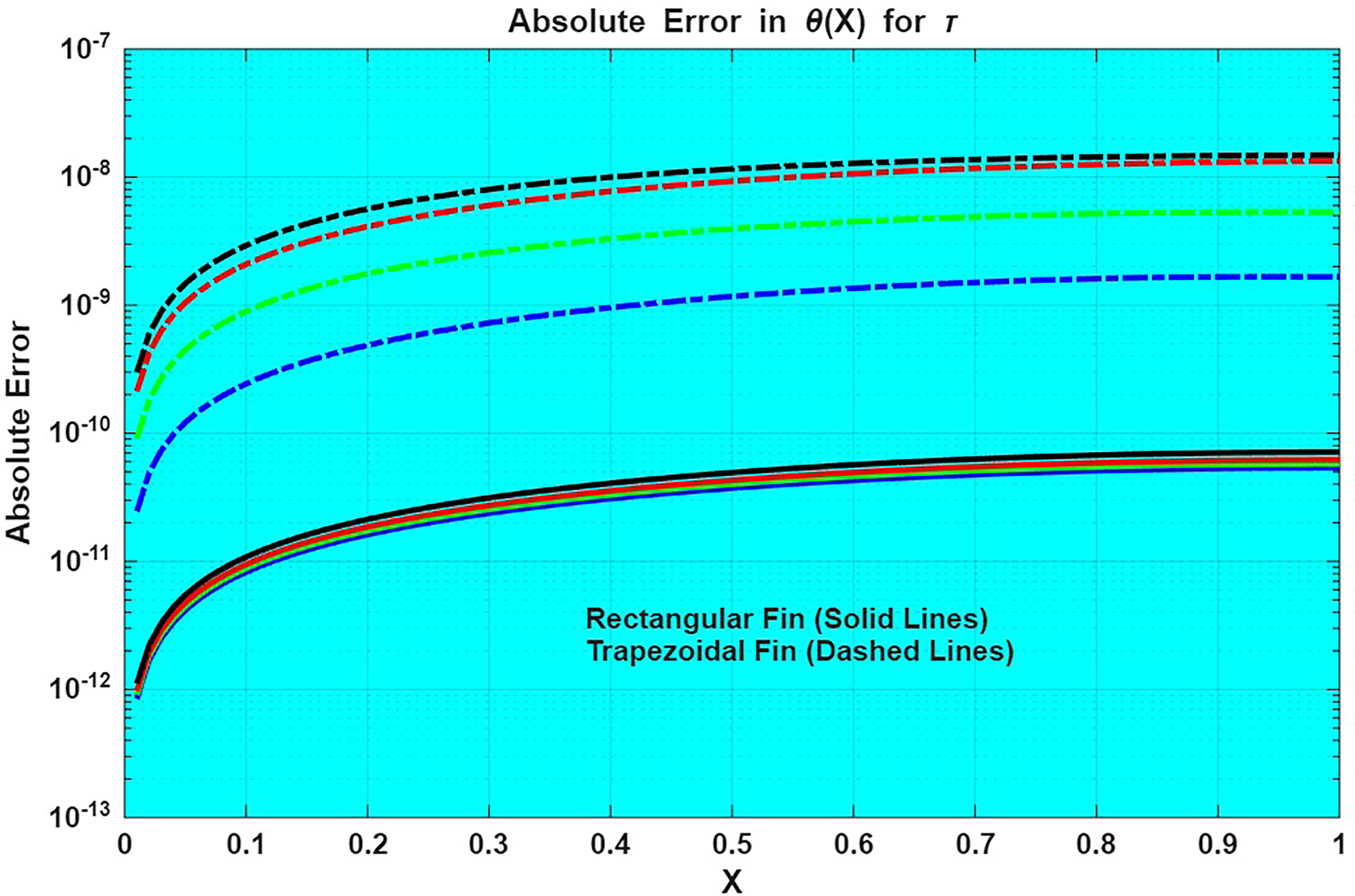
Figure 12: Absolute error of
The surface and contour plots in Figs. 13 and 14 explain the decline in temperature
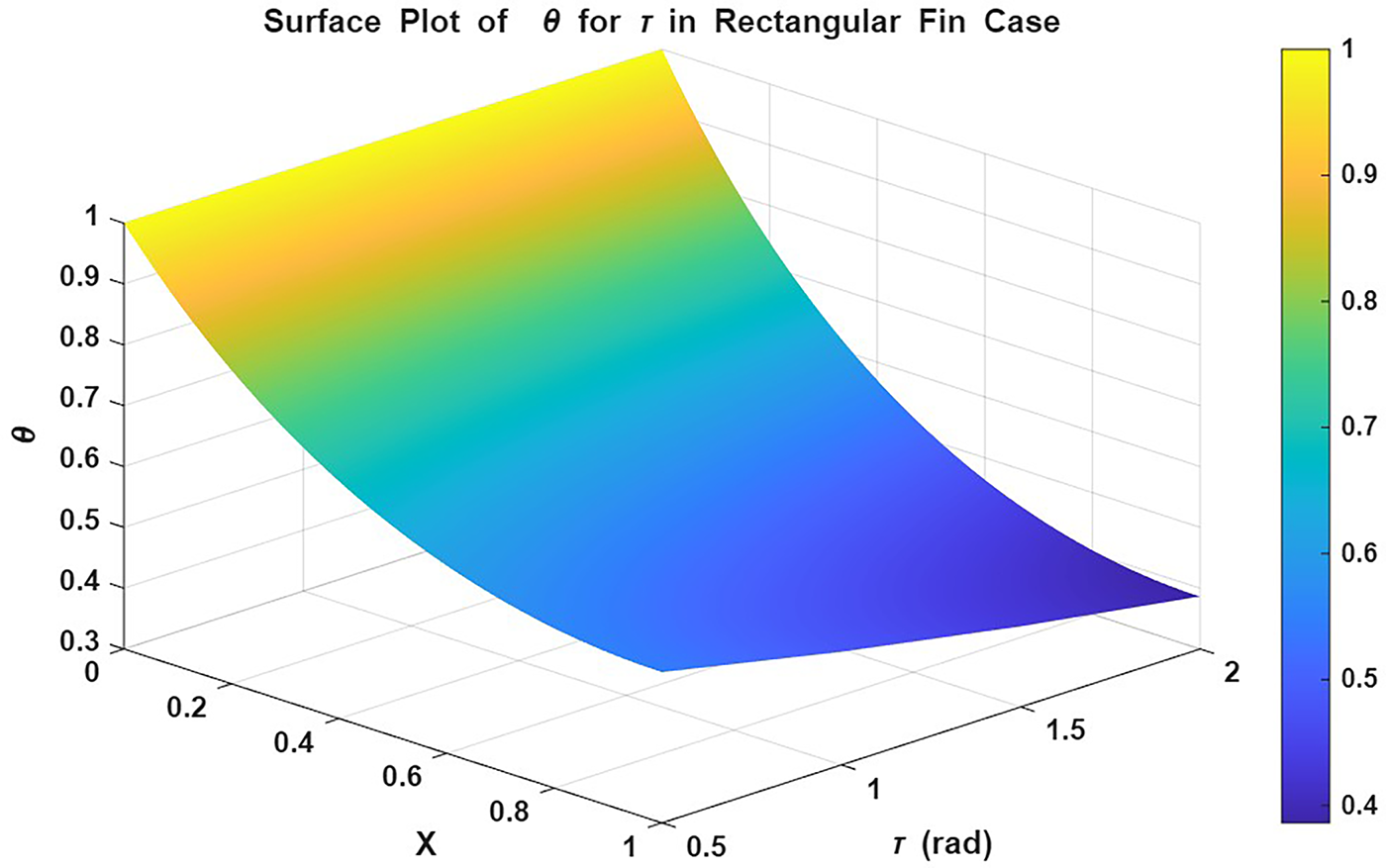
Figure 13: Surface plot of
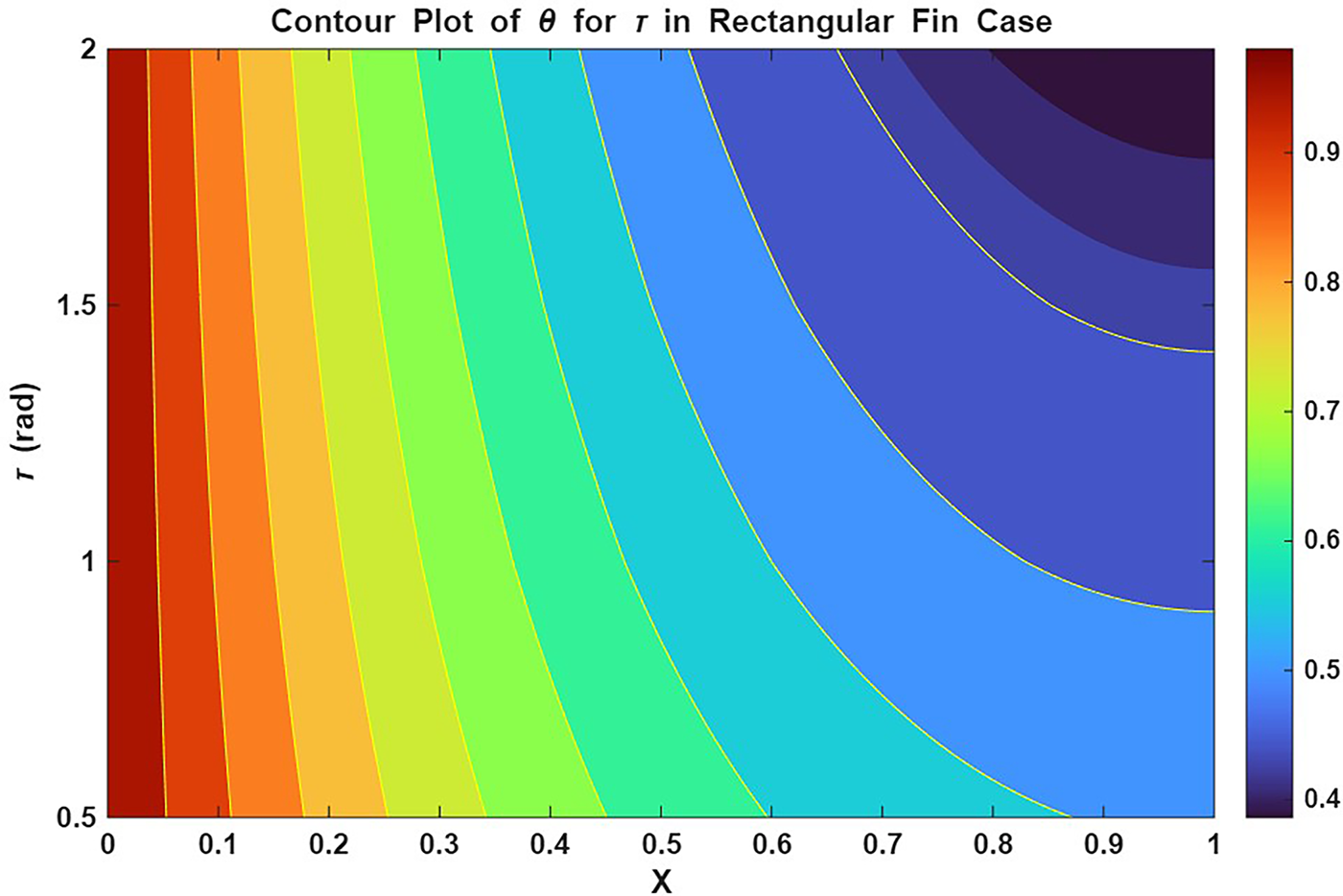
Figure 14: Contour plot of
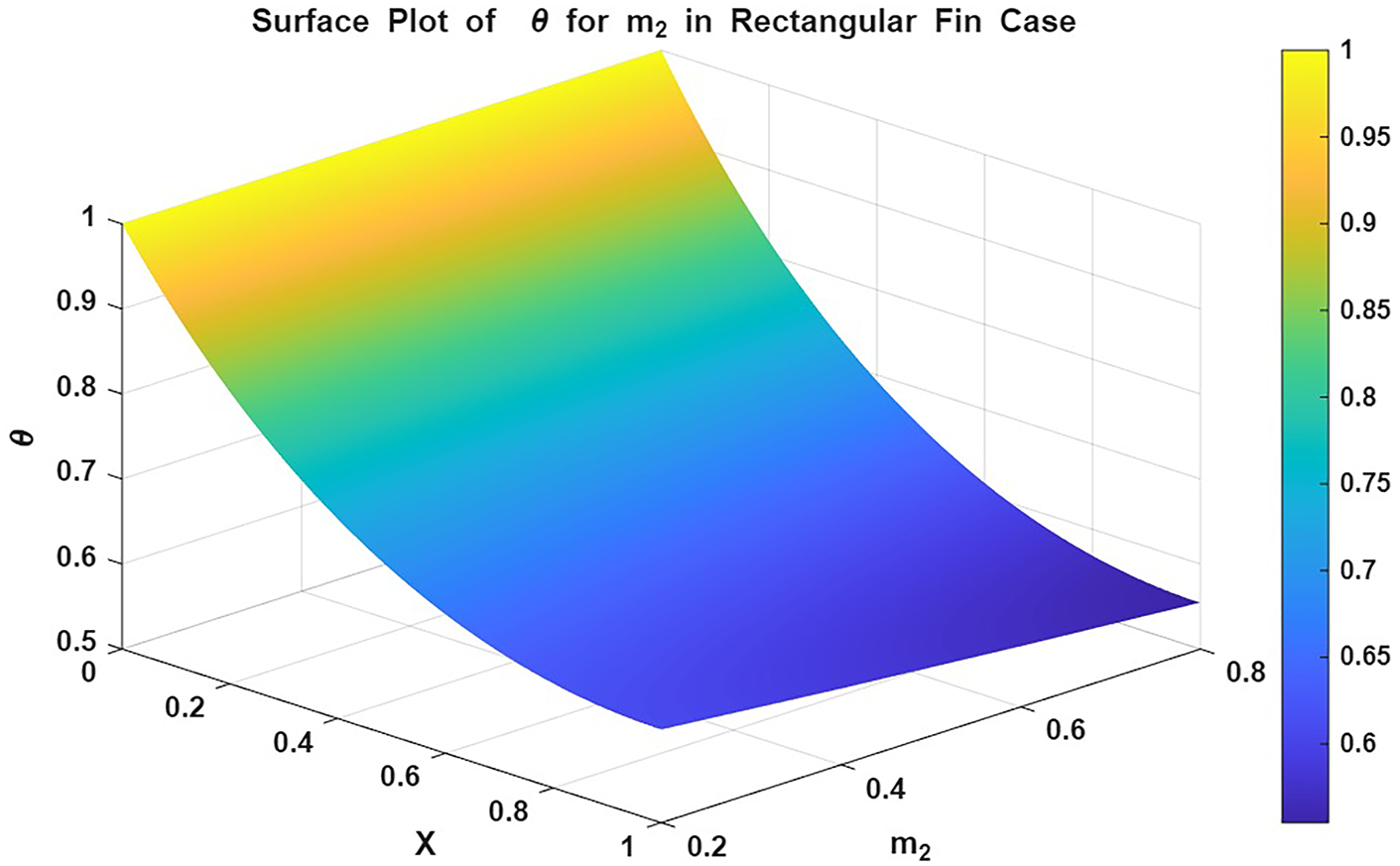
Figure 15: Surface plot of
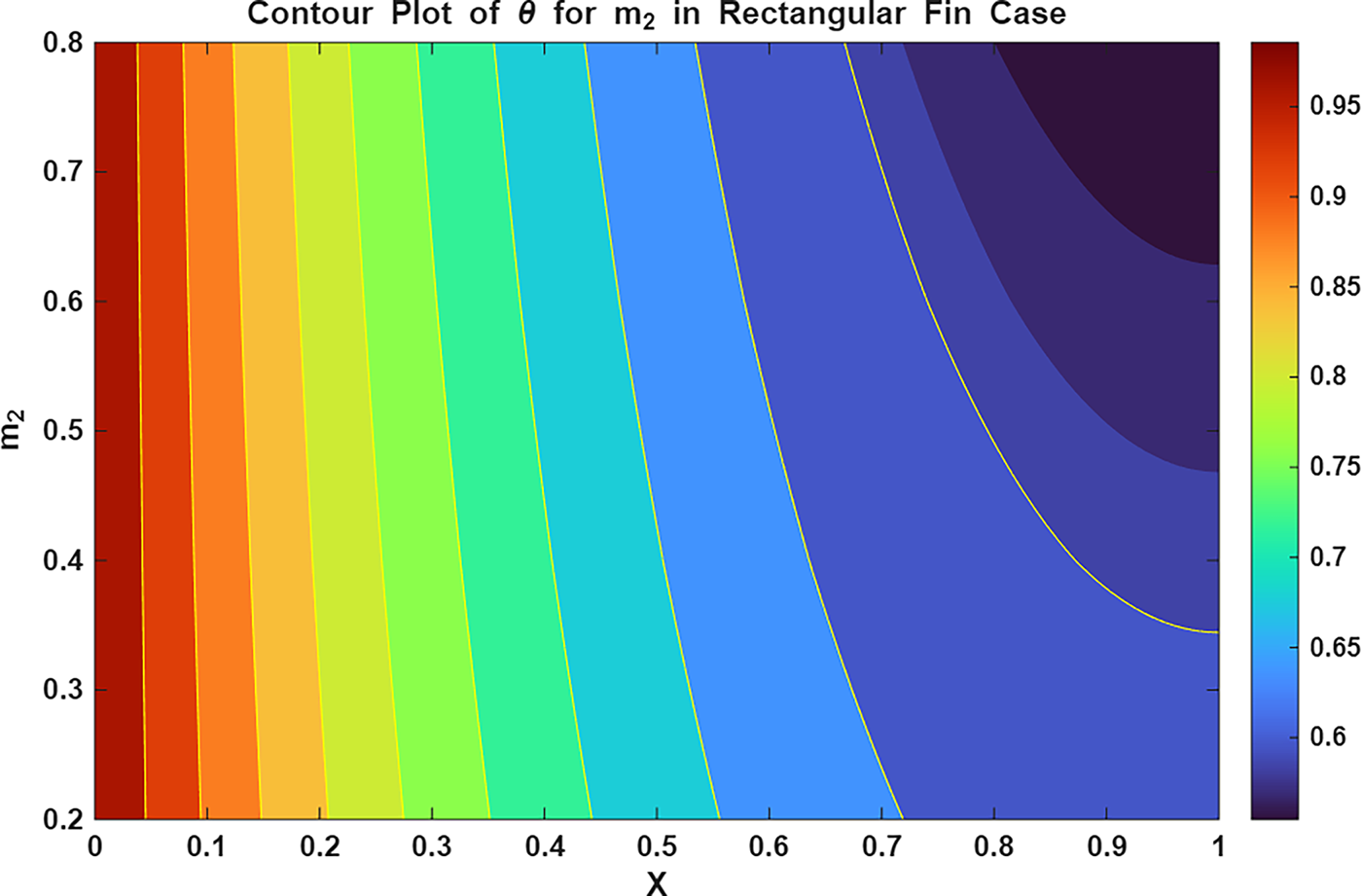
Figure 16: Contour plot of
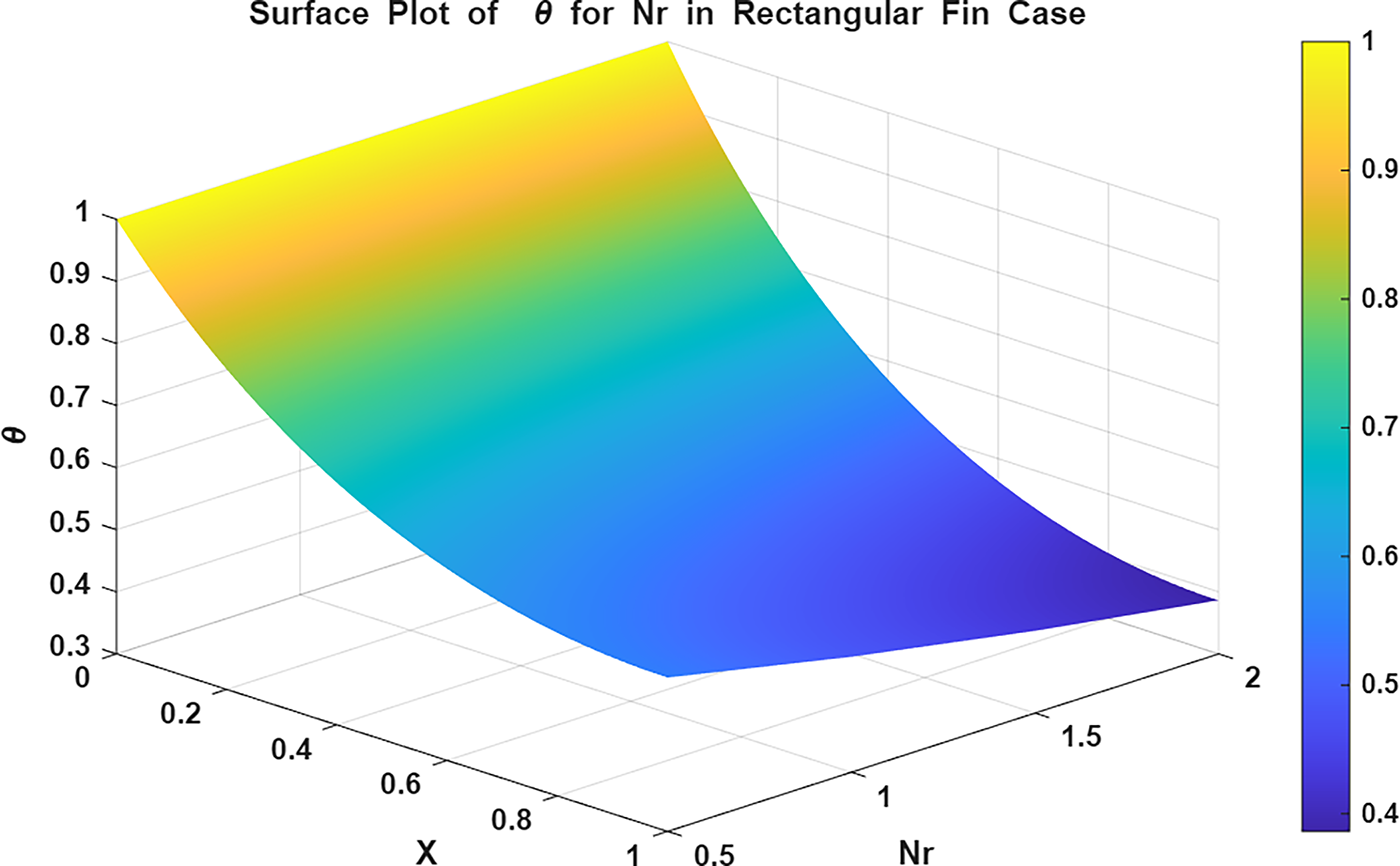
Figure 17: Surface plot of
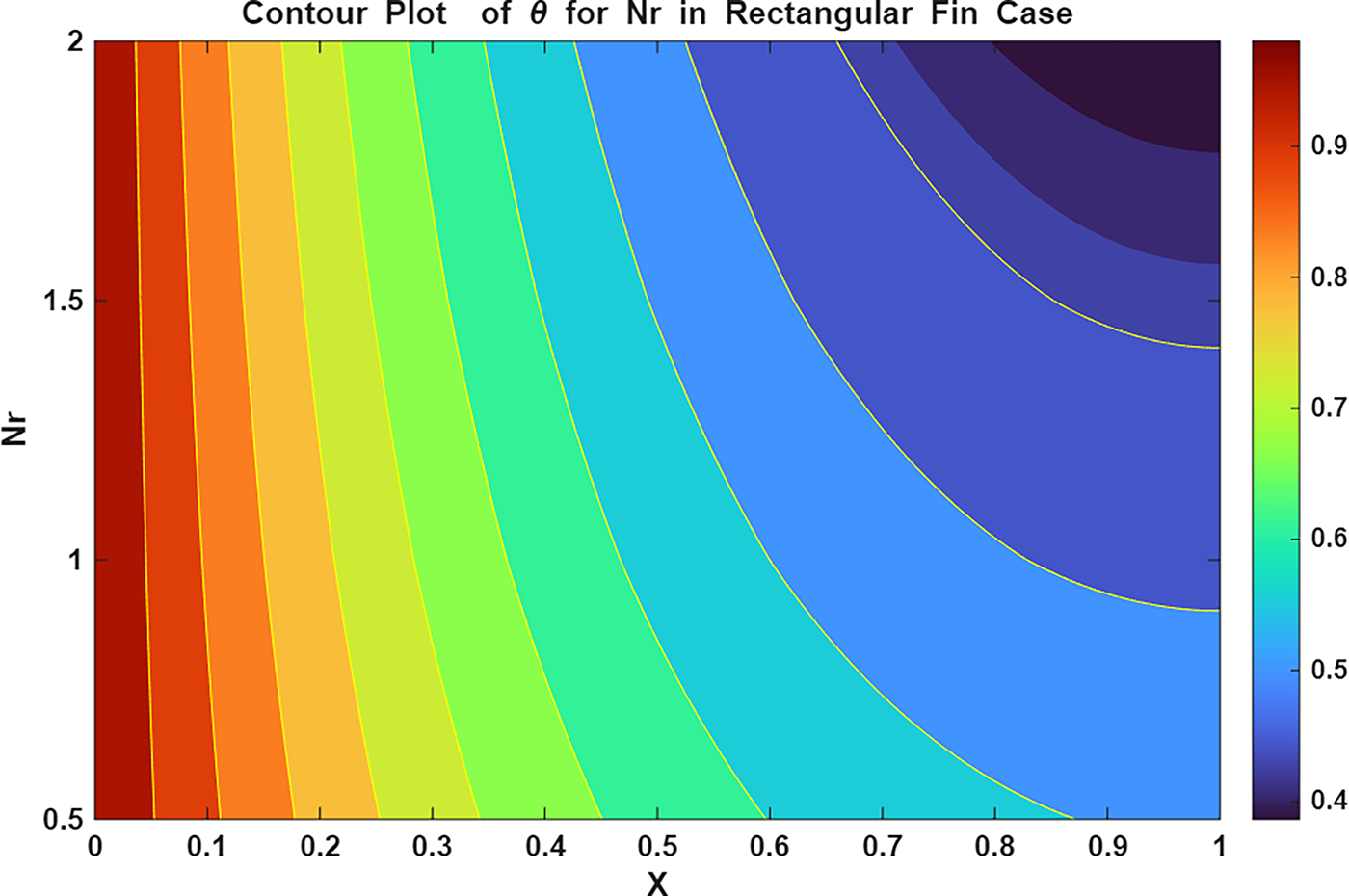
Figure 18: Contour plot of
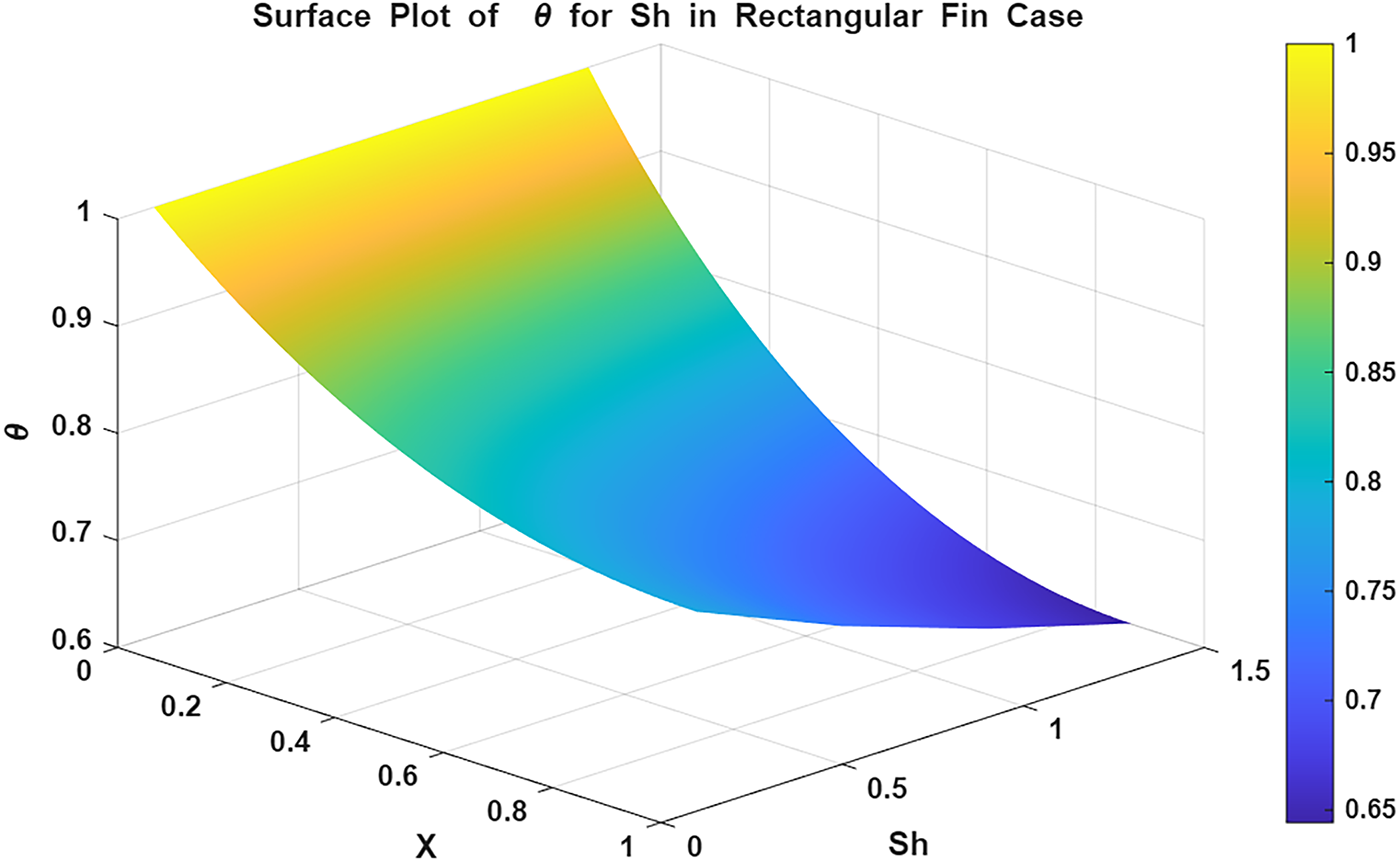
Figure 19: Surface plot of
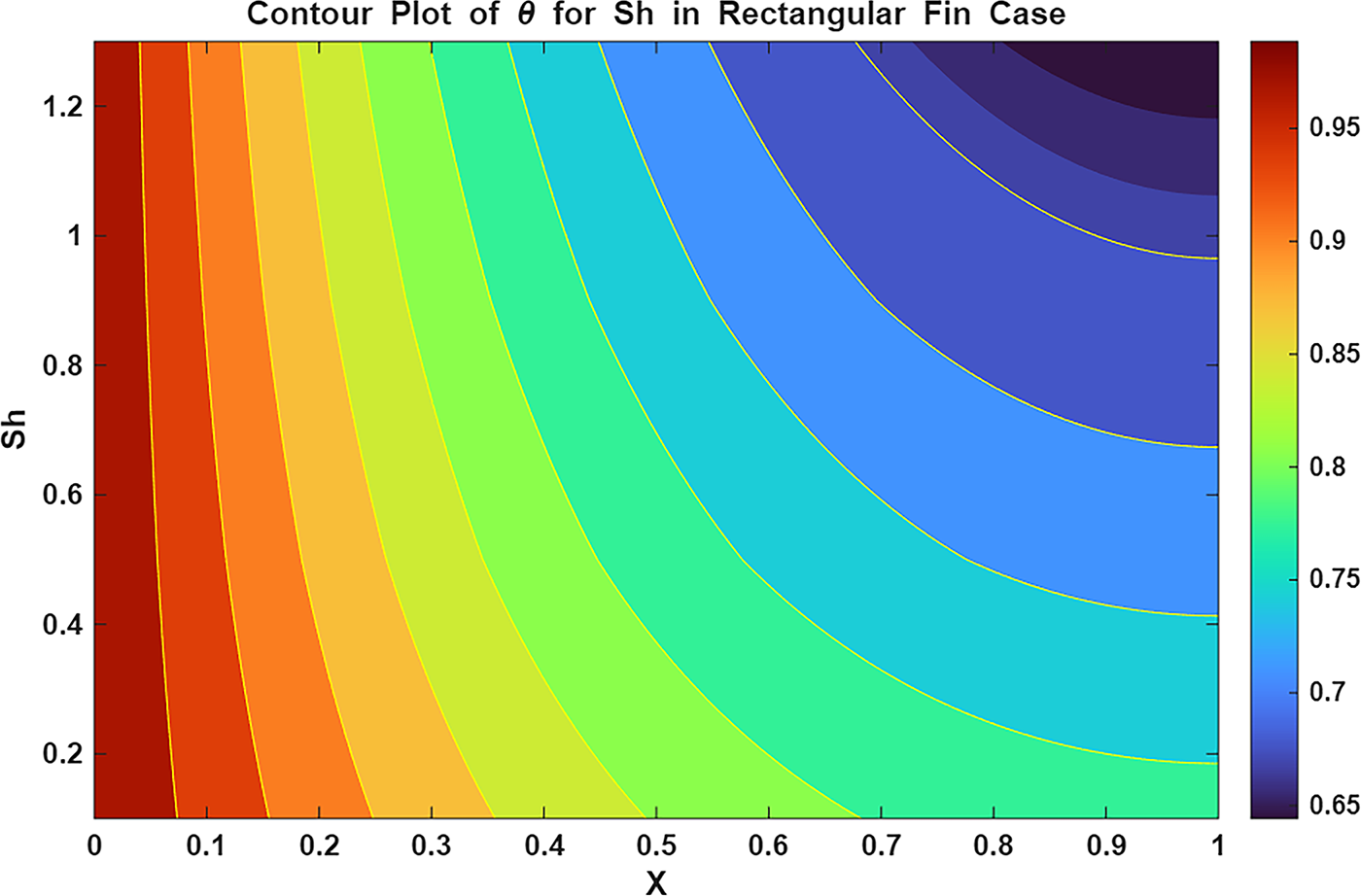
Figure 20: Contour plot of
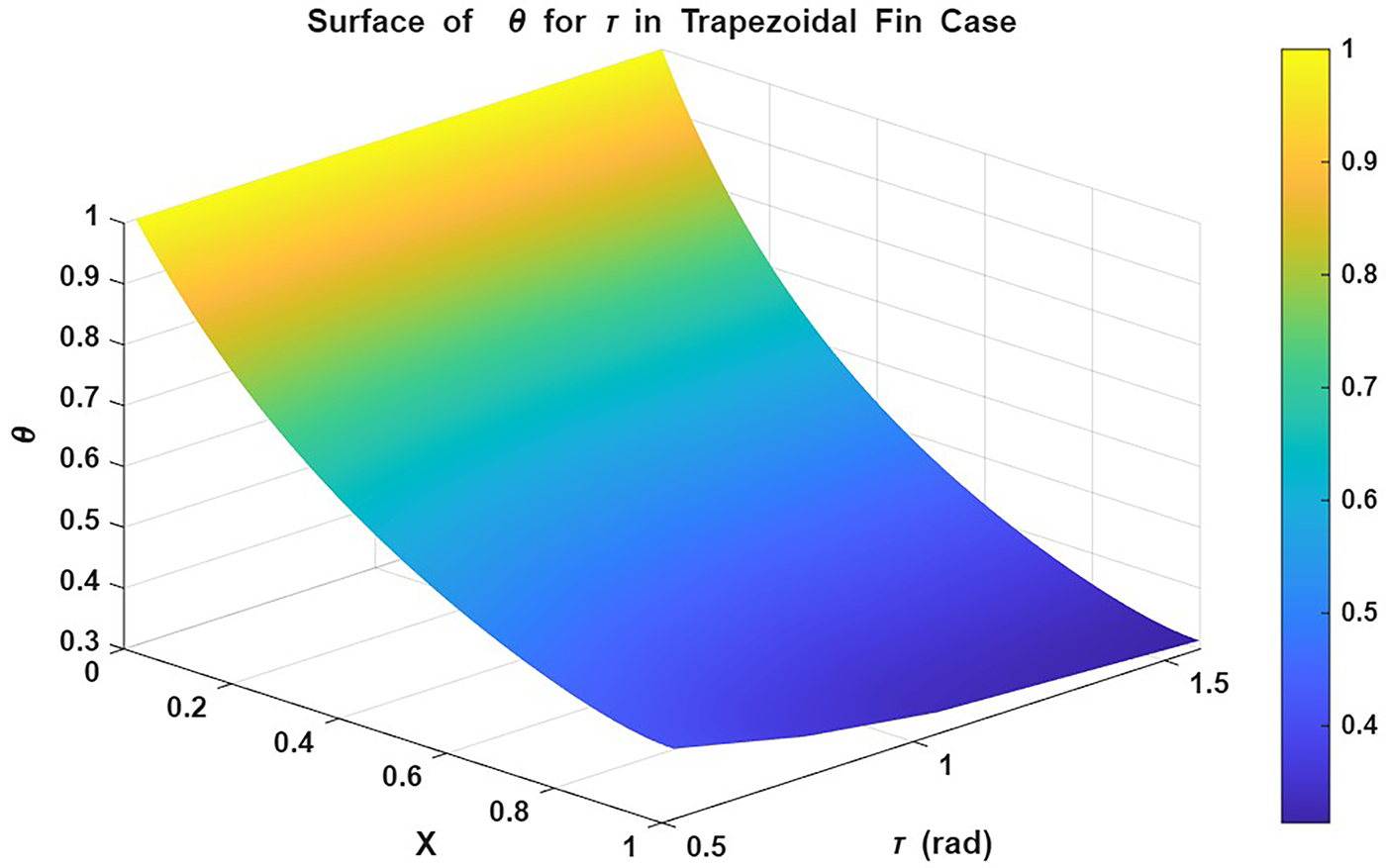
Figure 21: Surface plot of
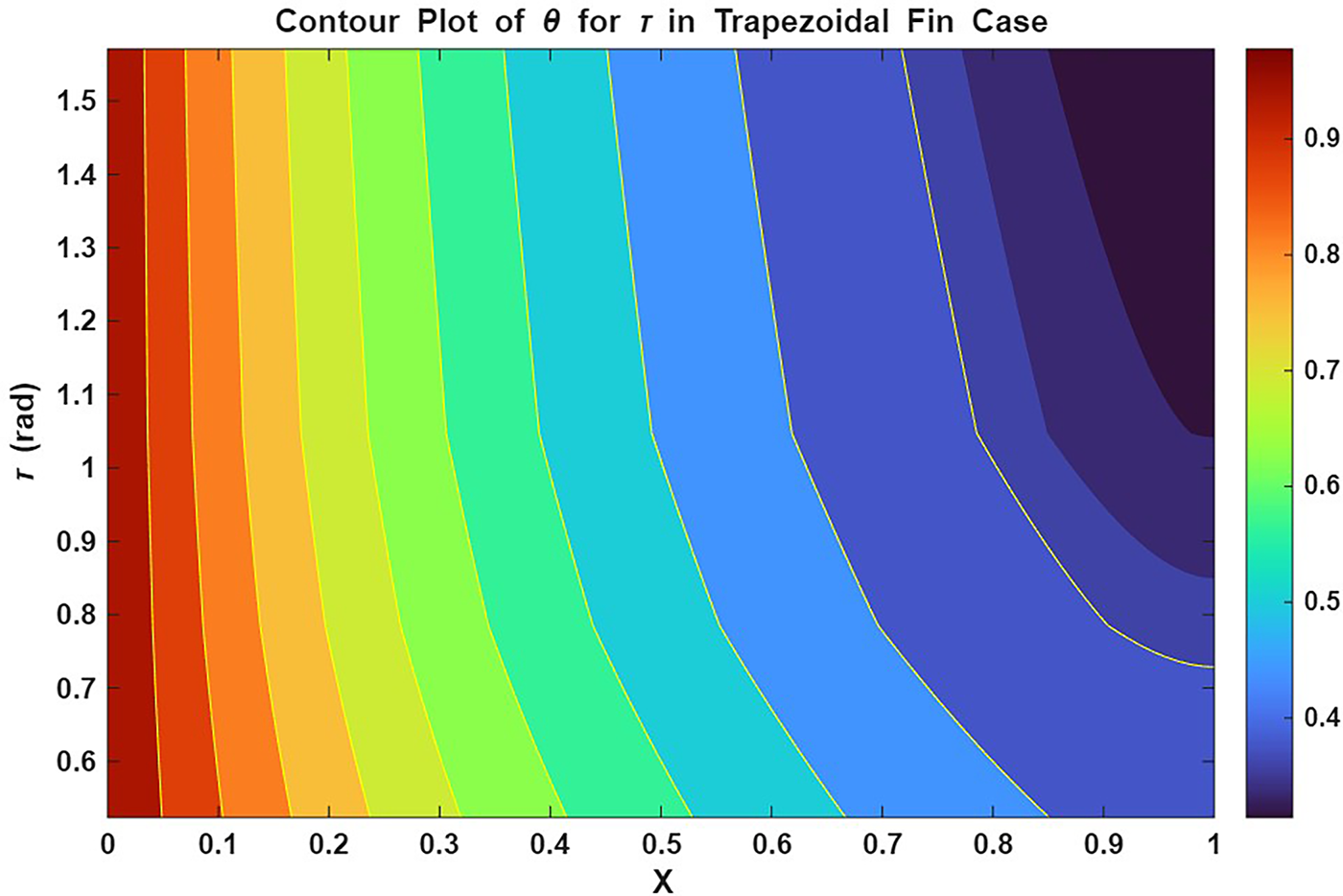
Figure 22: Contour plot of
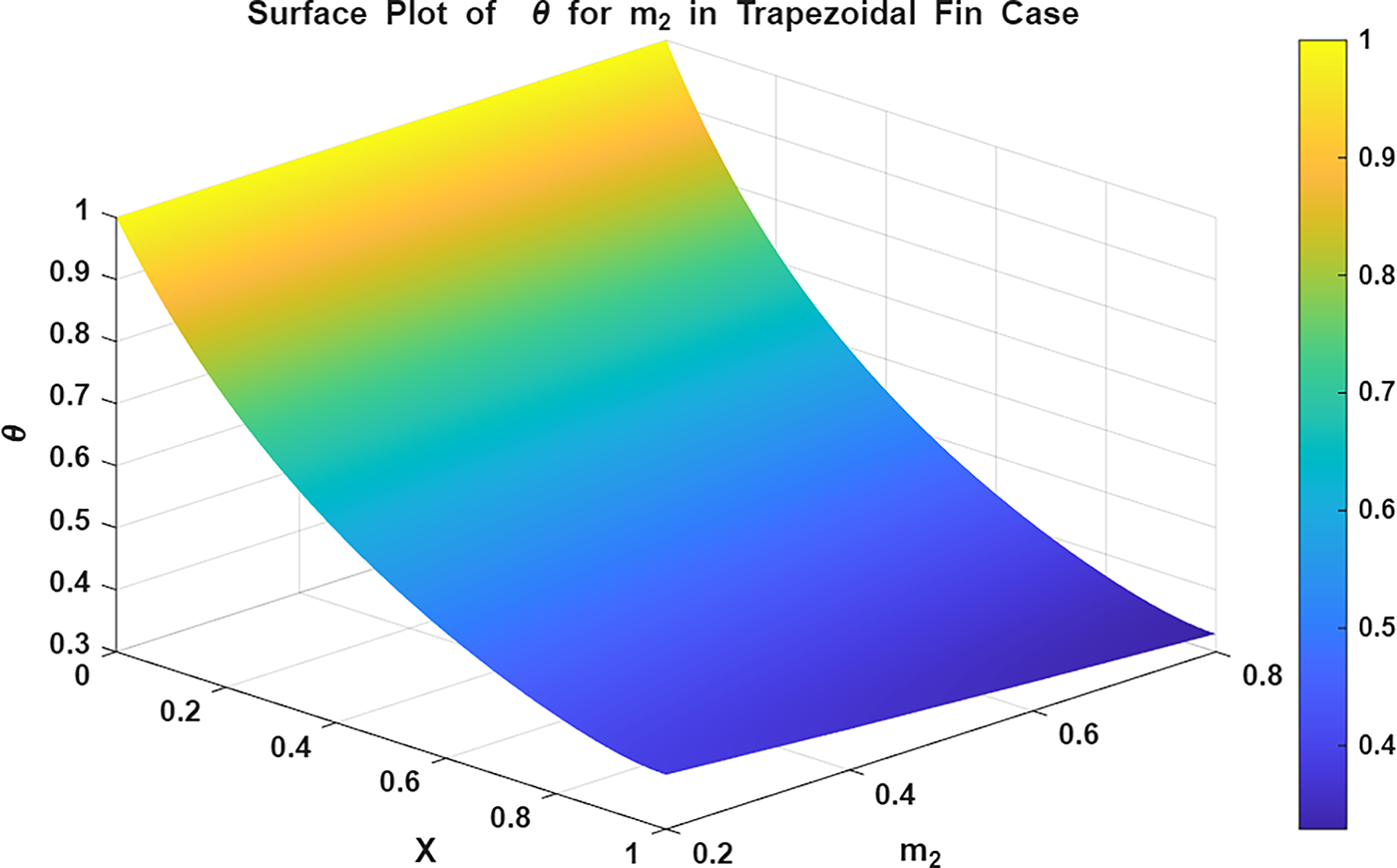
Figure 23: Surface plot of
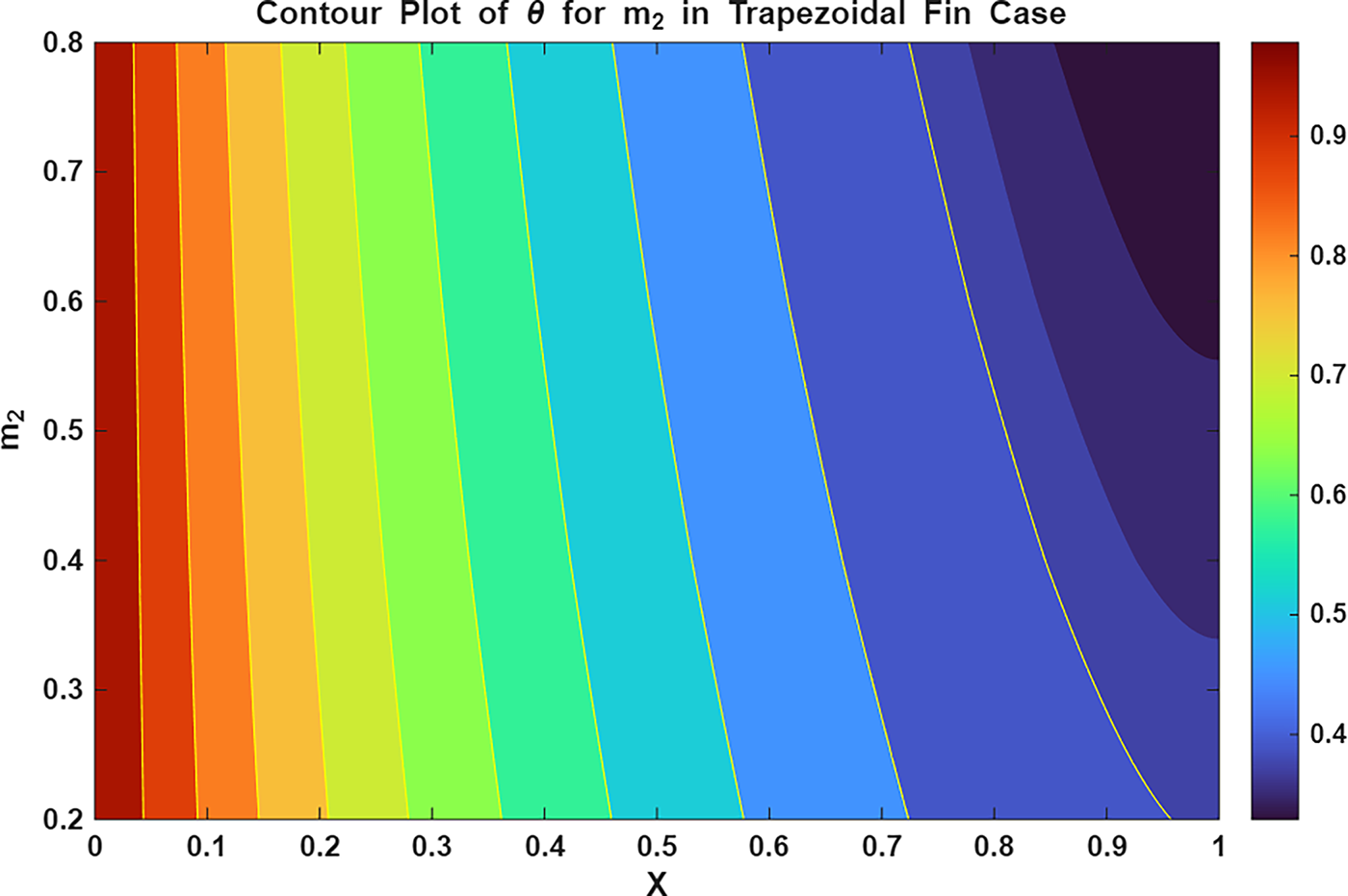
Figure 24: Contour plot of
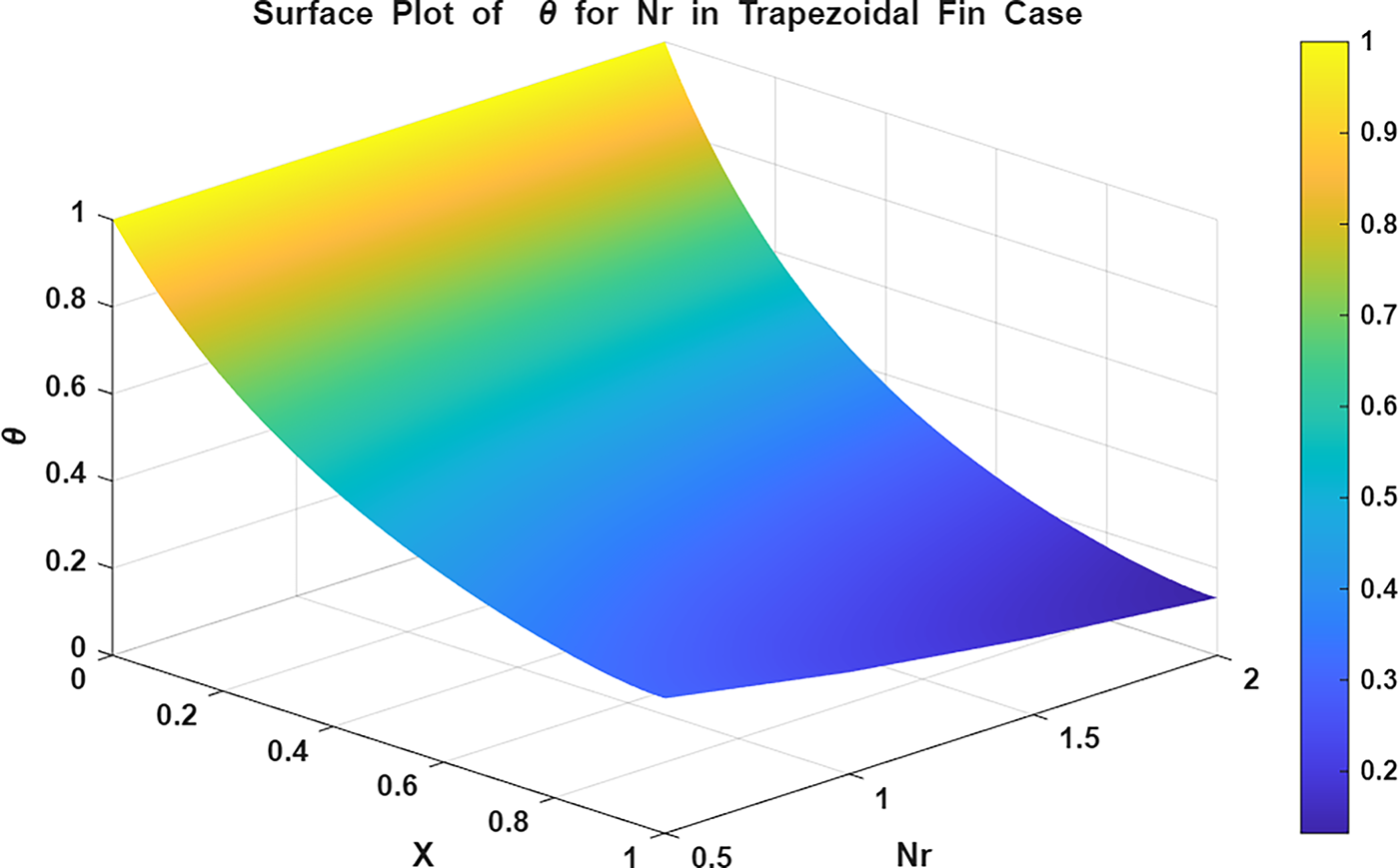
Figure 25: Surface plot of
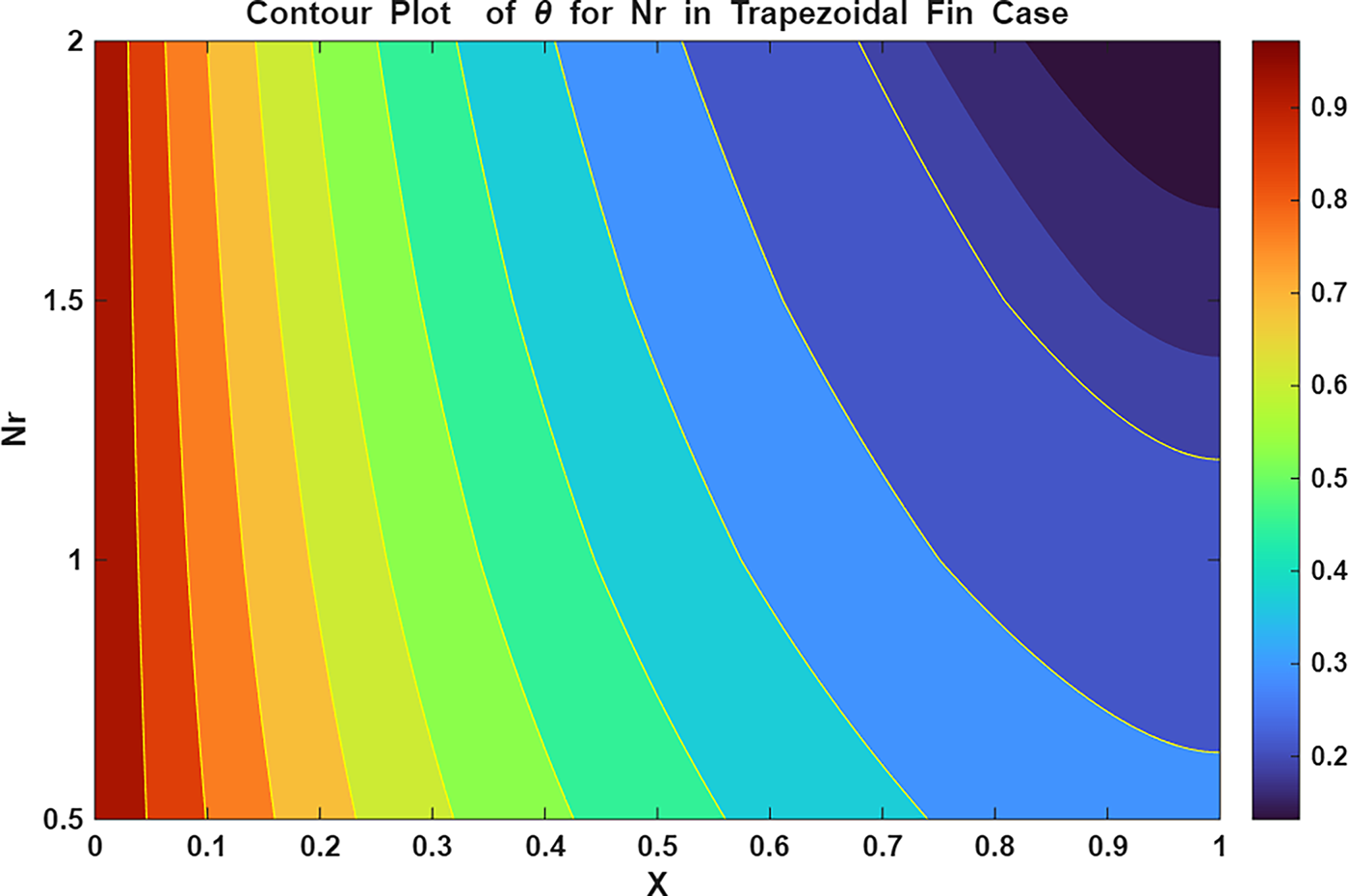
Figure 26: Contour plot of
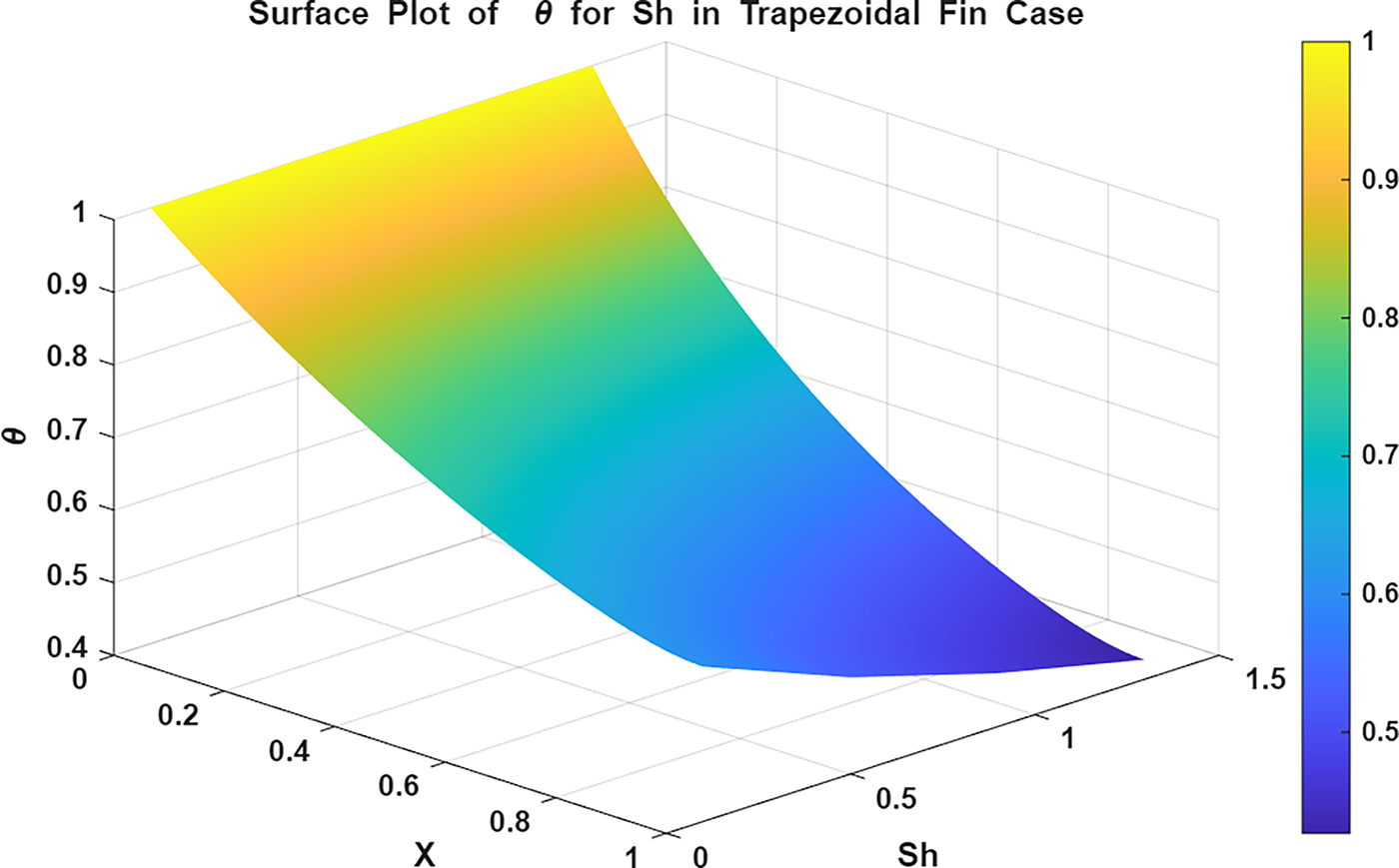
Figure 27: Surface plot of
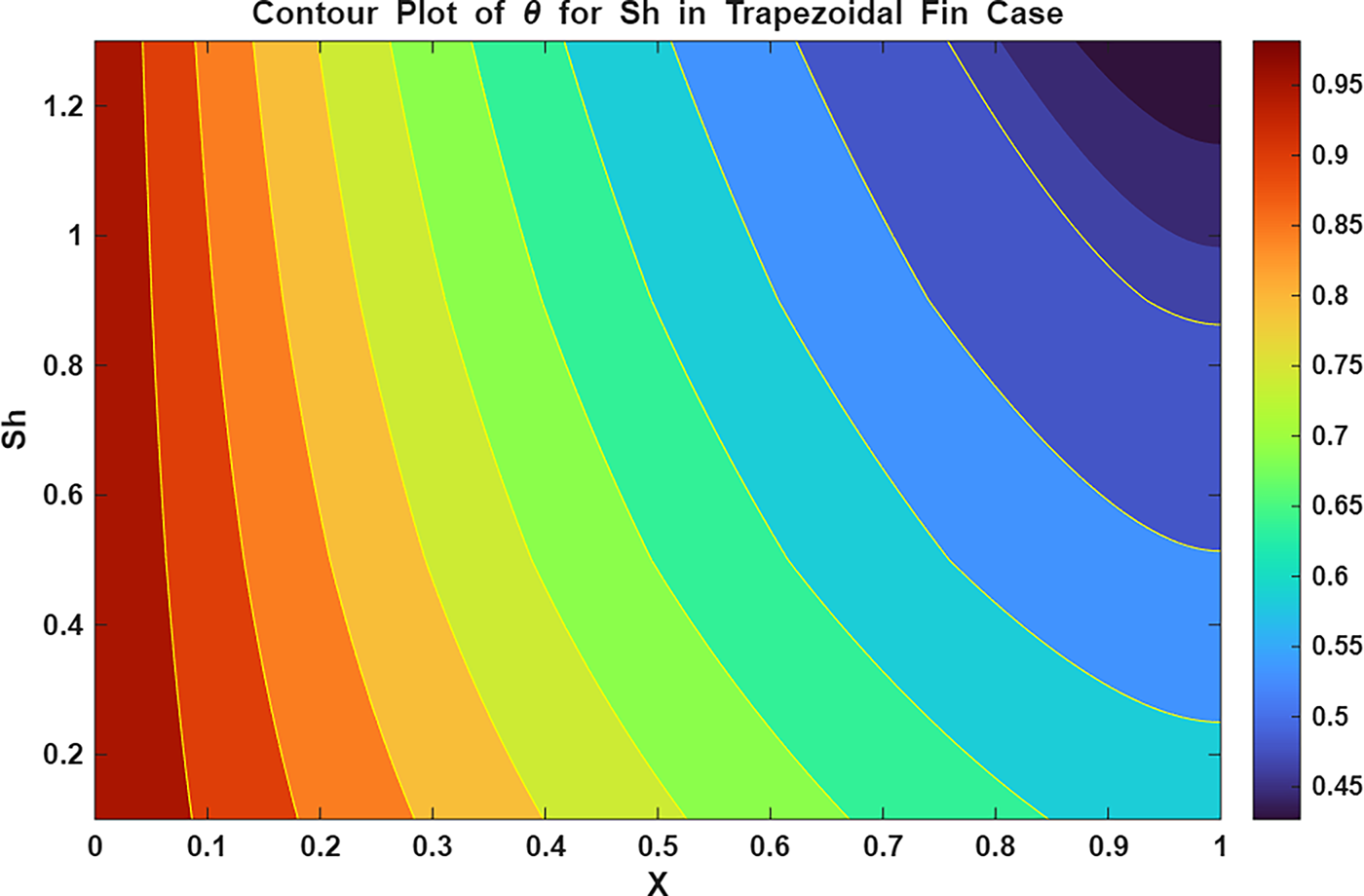
Figure 28: Contour plot of
4.3 Gradient Descent Optimization
The outcomes of the optimisation algorithm based on the Gradient Descent method.
Fig. 29 presents a linear fit plot of
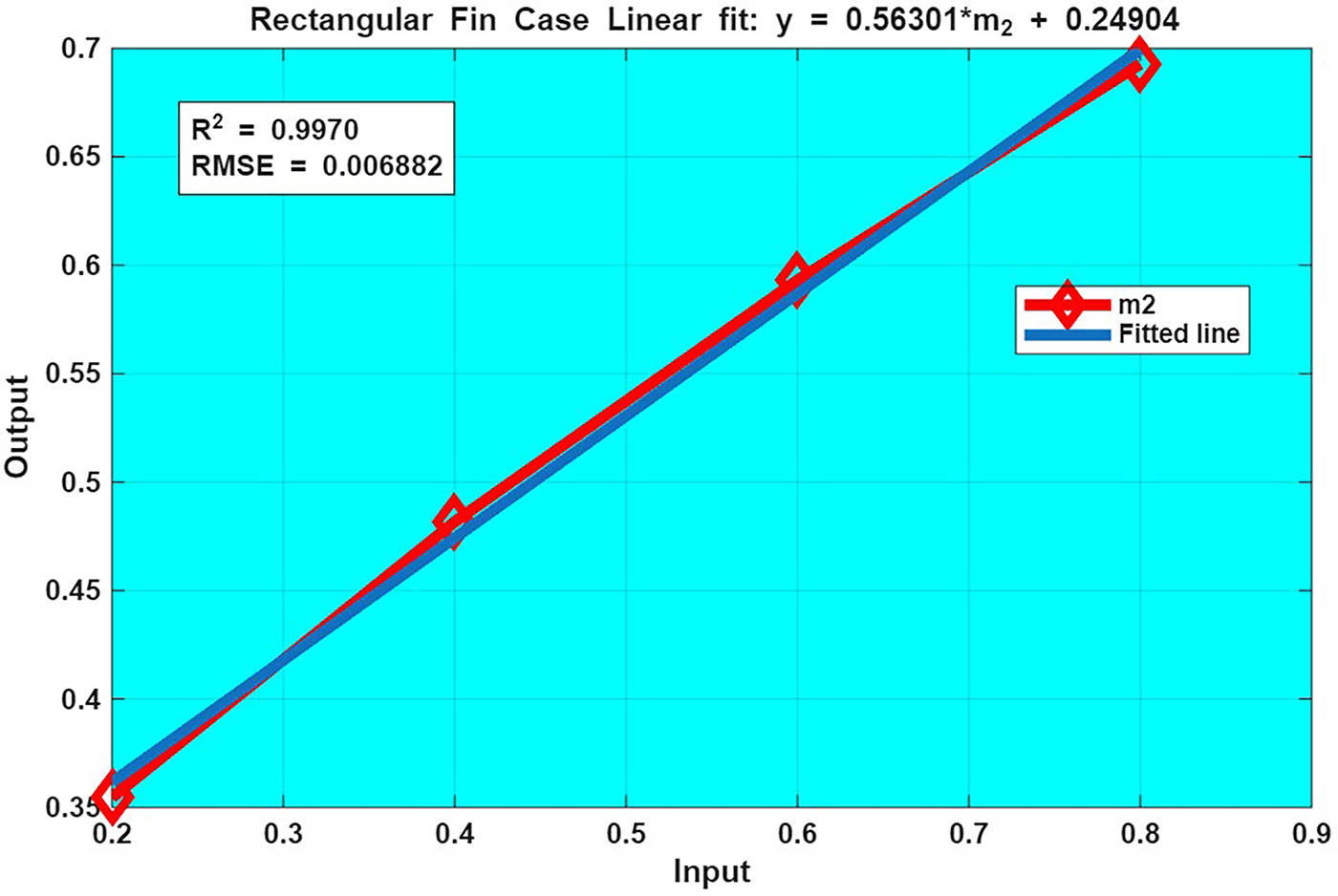
Figure 29: Fit Plot of
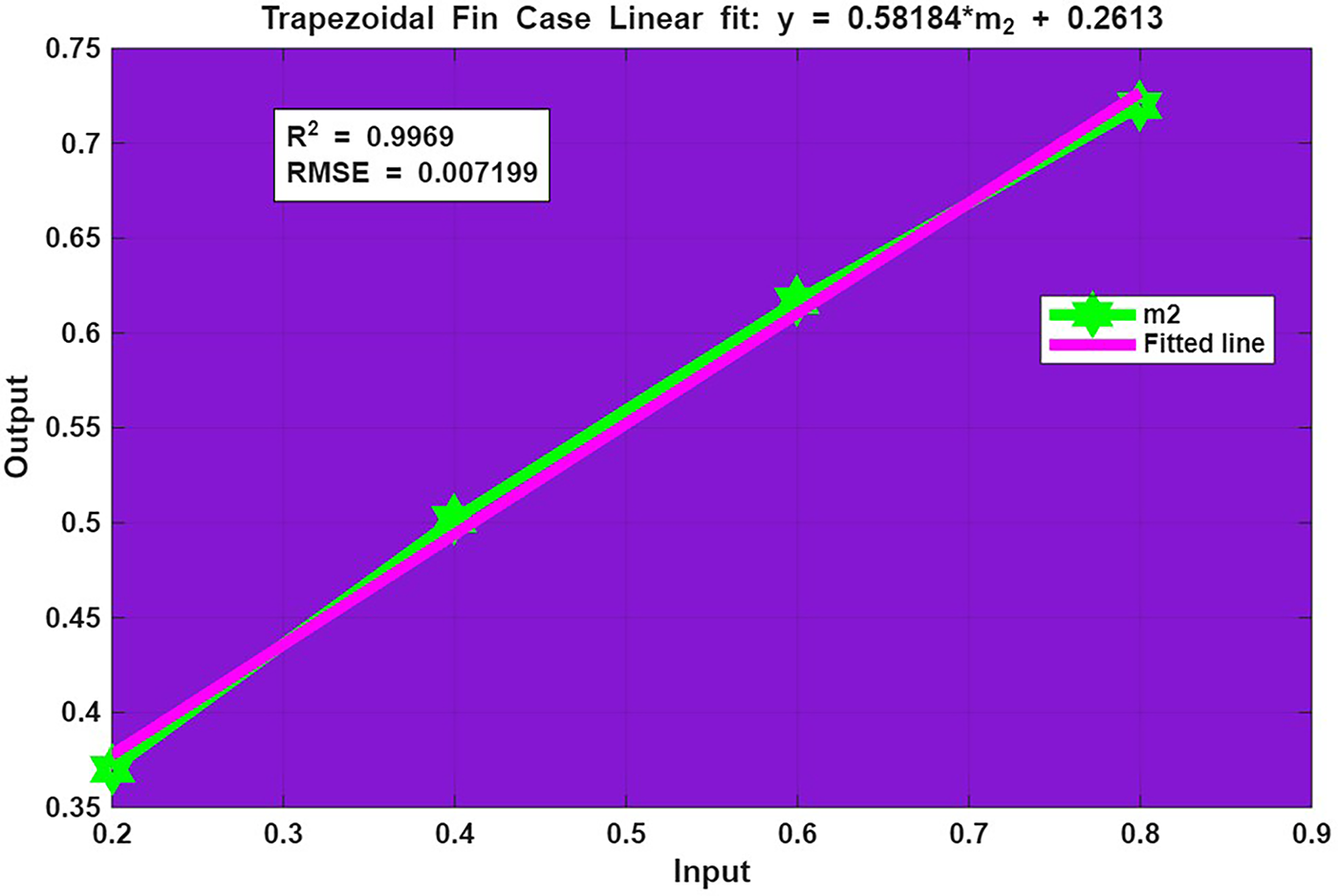
Figure 30: Fit Plot of
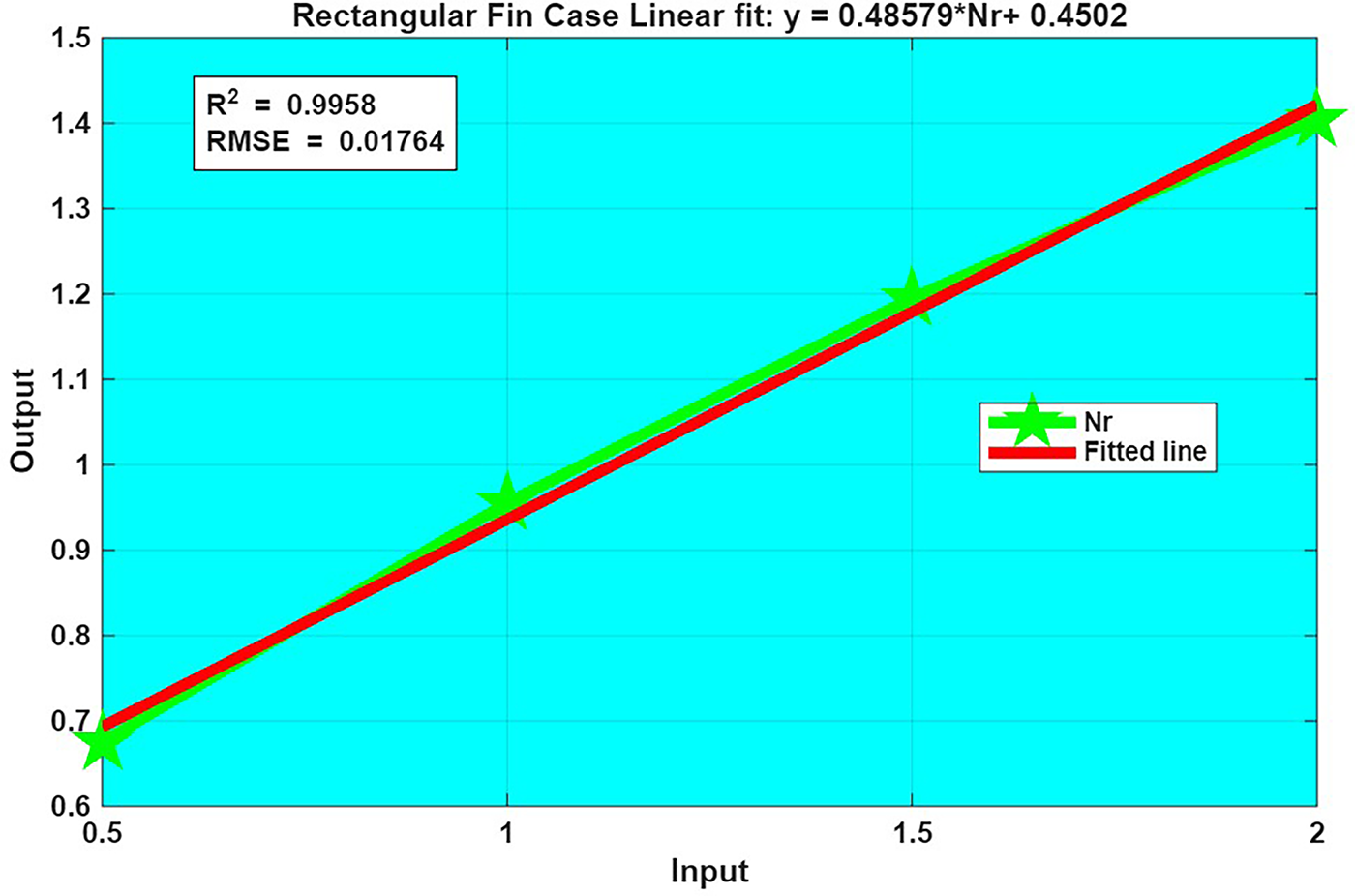
Figure 31: Fit Plot of
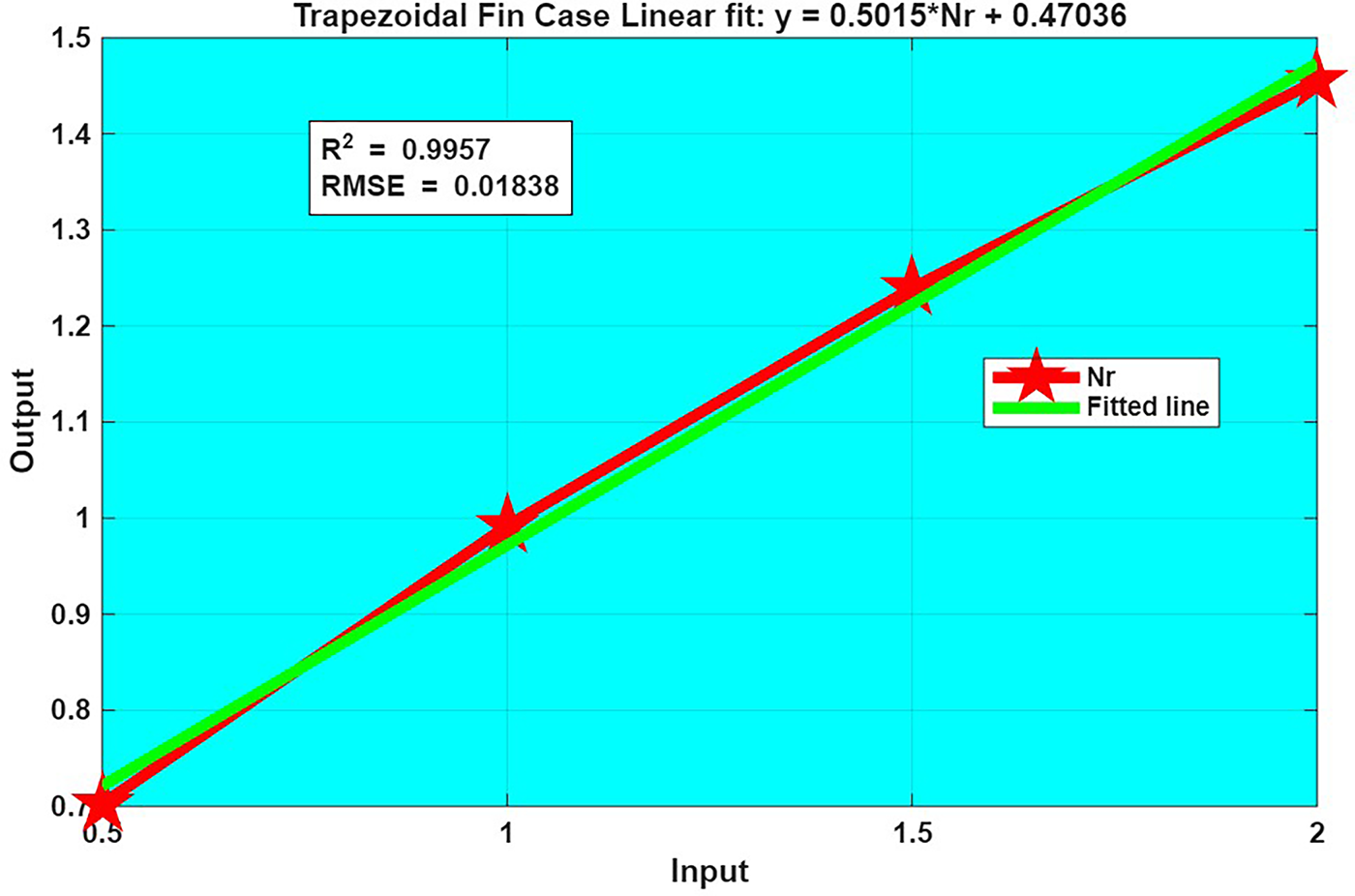
Figure 32: Fit Plot of
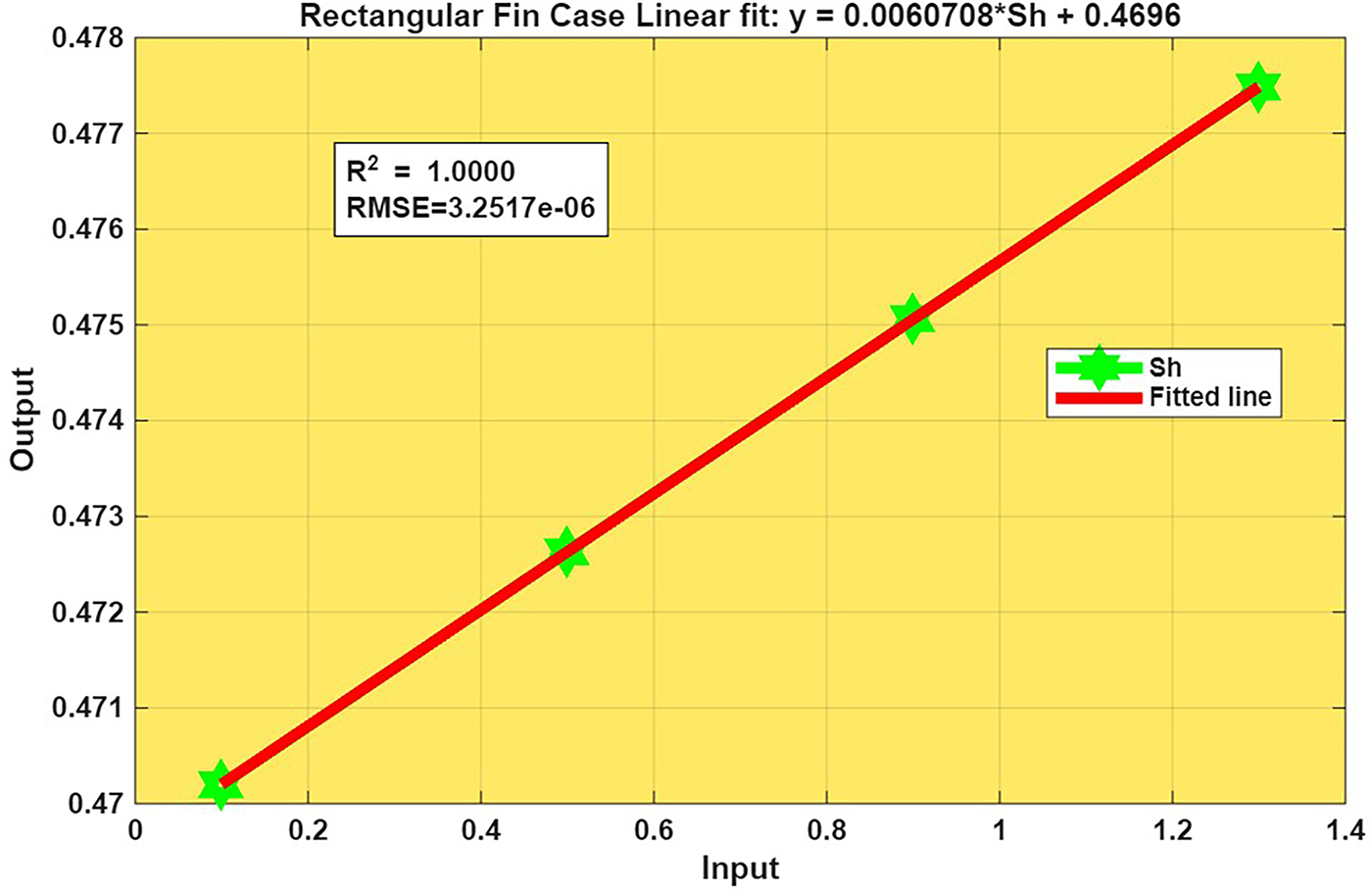
Figure 33: Fit Plot of
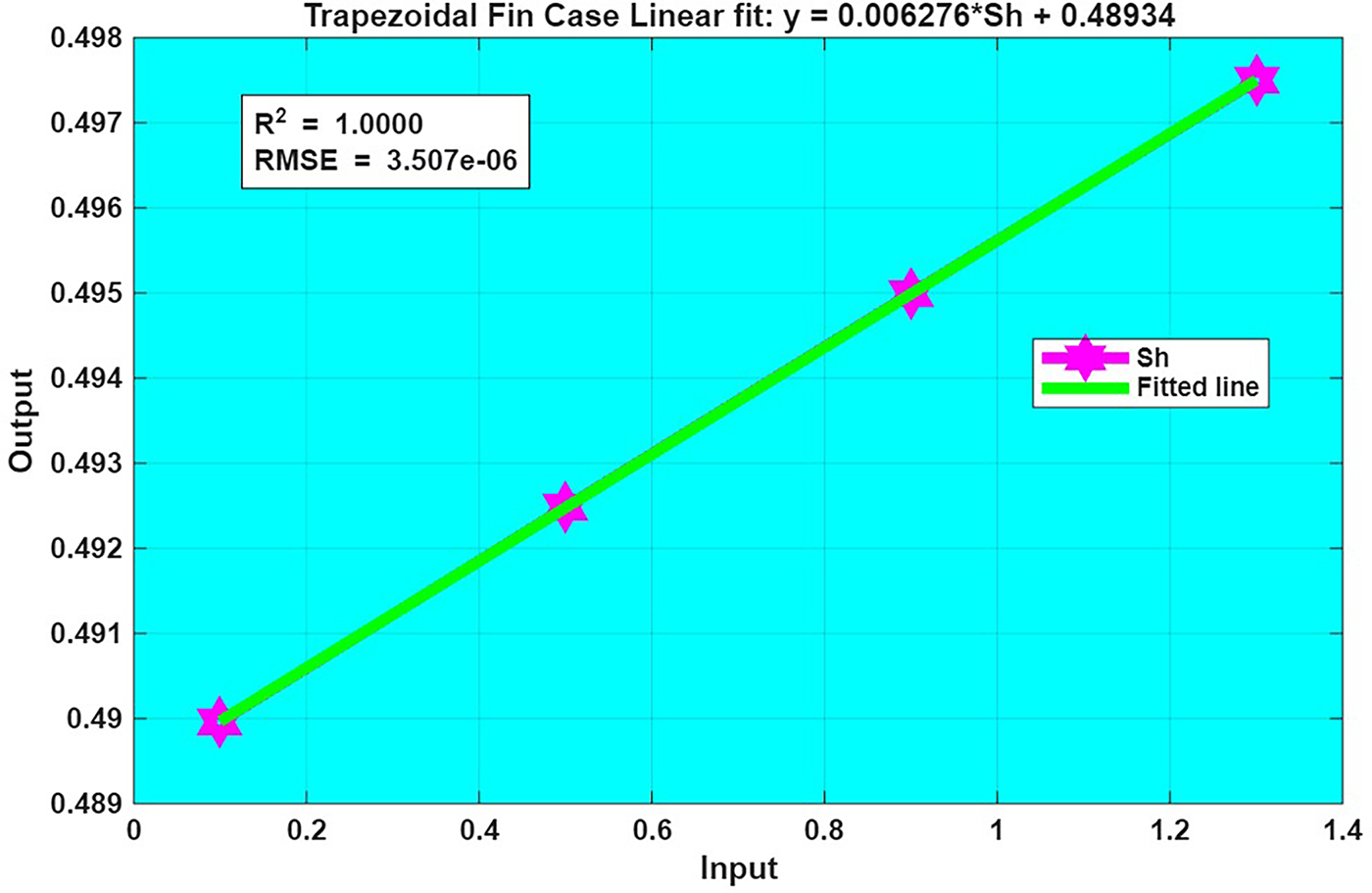
Figure 34: Fit Plot of
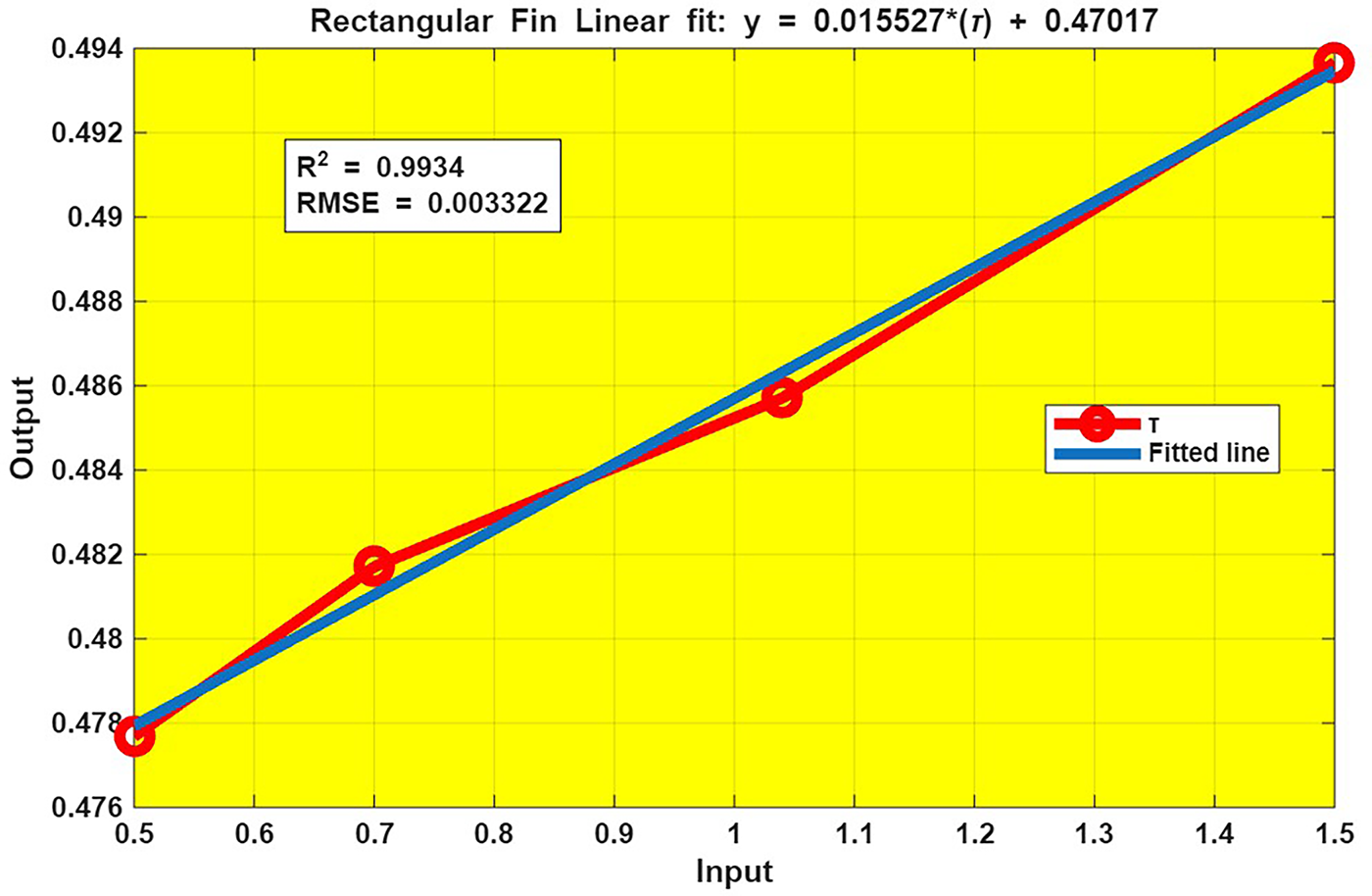
Figure 35: Fit Plot of
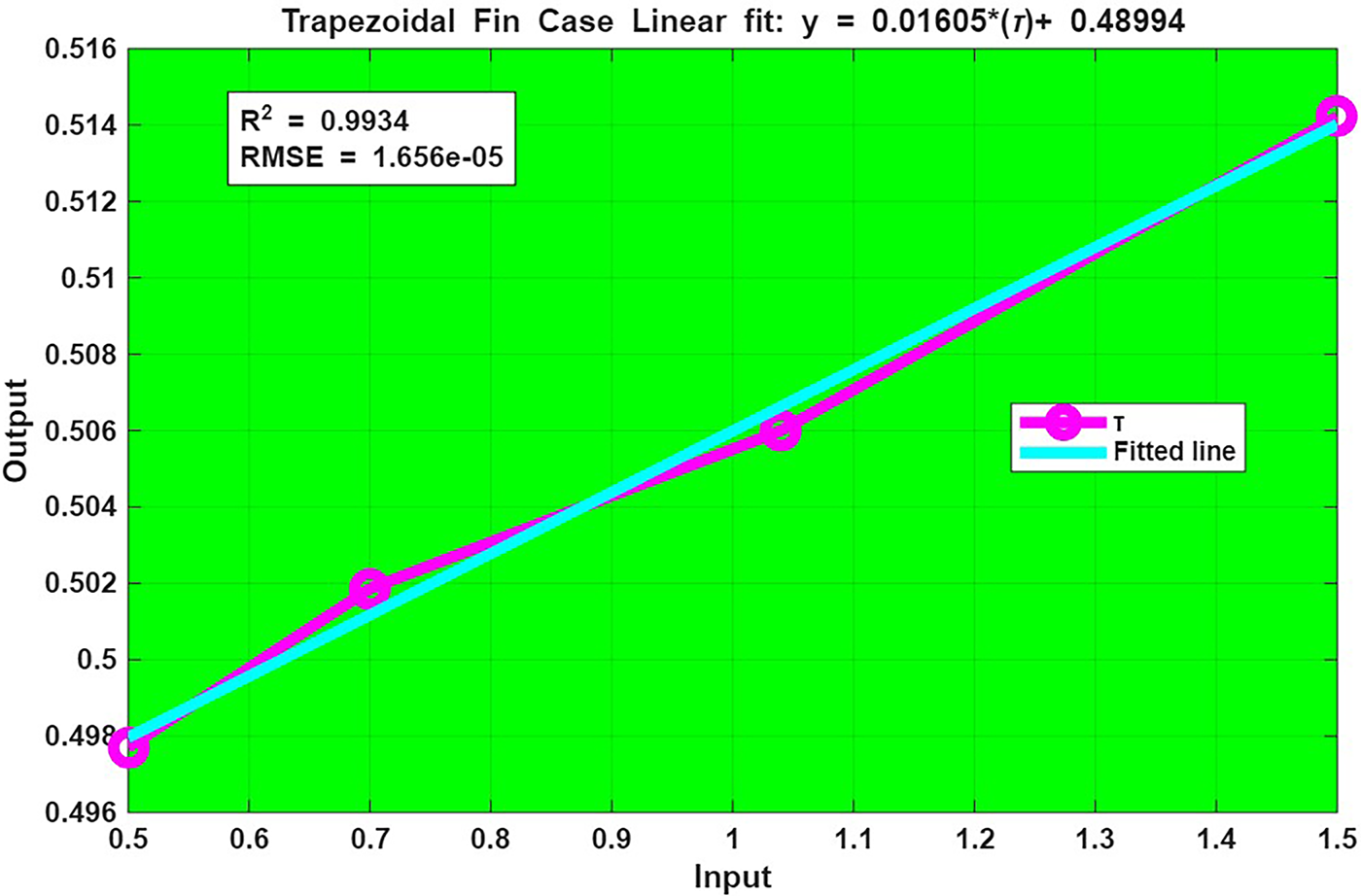
Figure 36: Fit Plot of
A variance-based technique for global sensitivity analysis, Sobol sensitivity analysis calculates the degree to which each input parameter
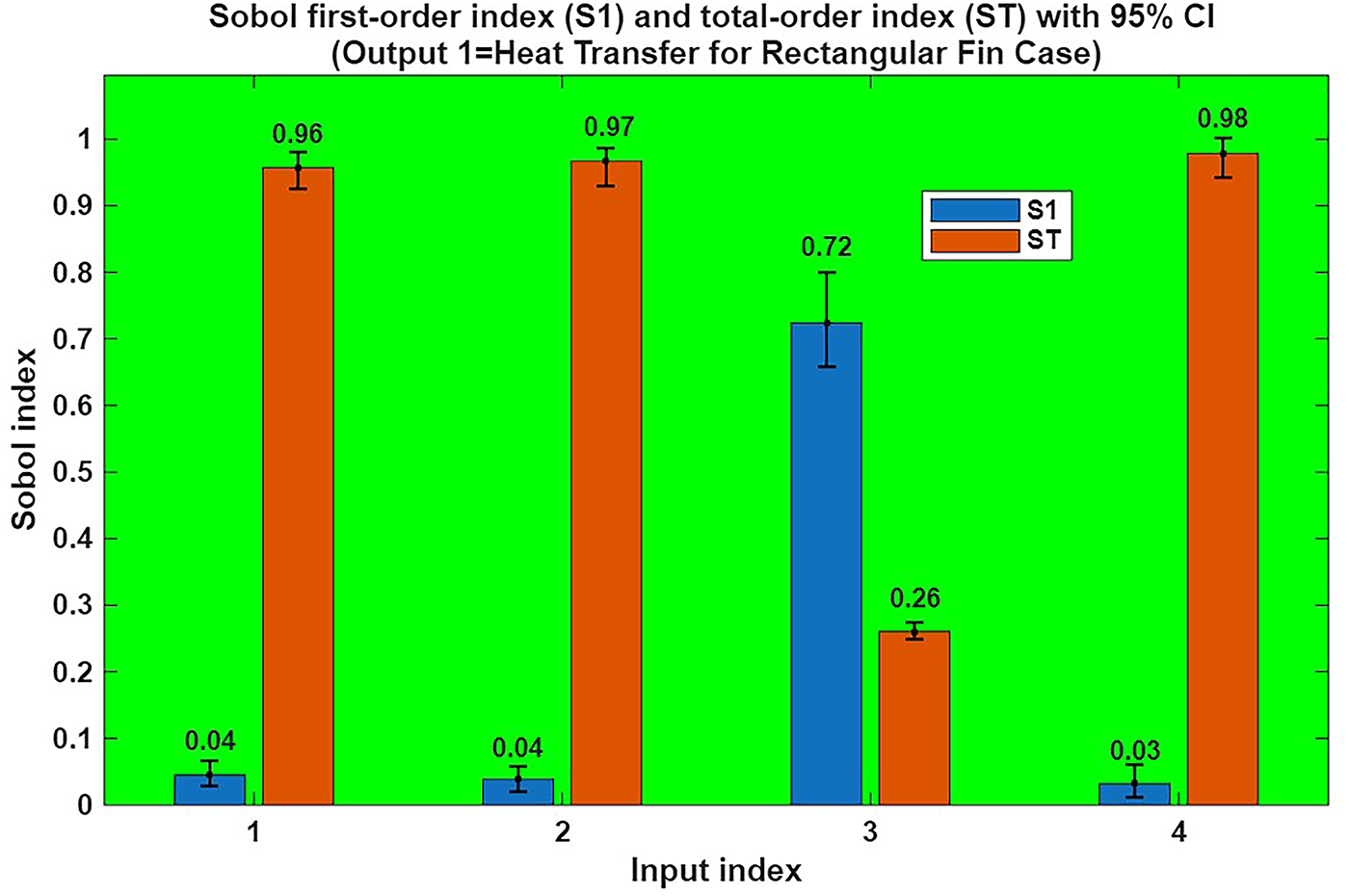
Figure 37: Sensitivity analysis plot for rectangular fin case
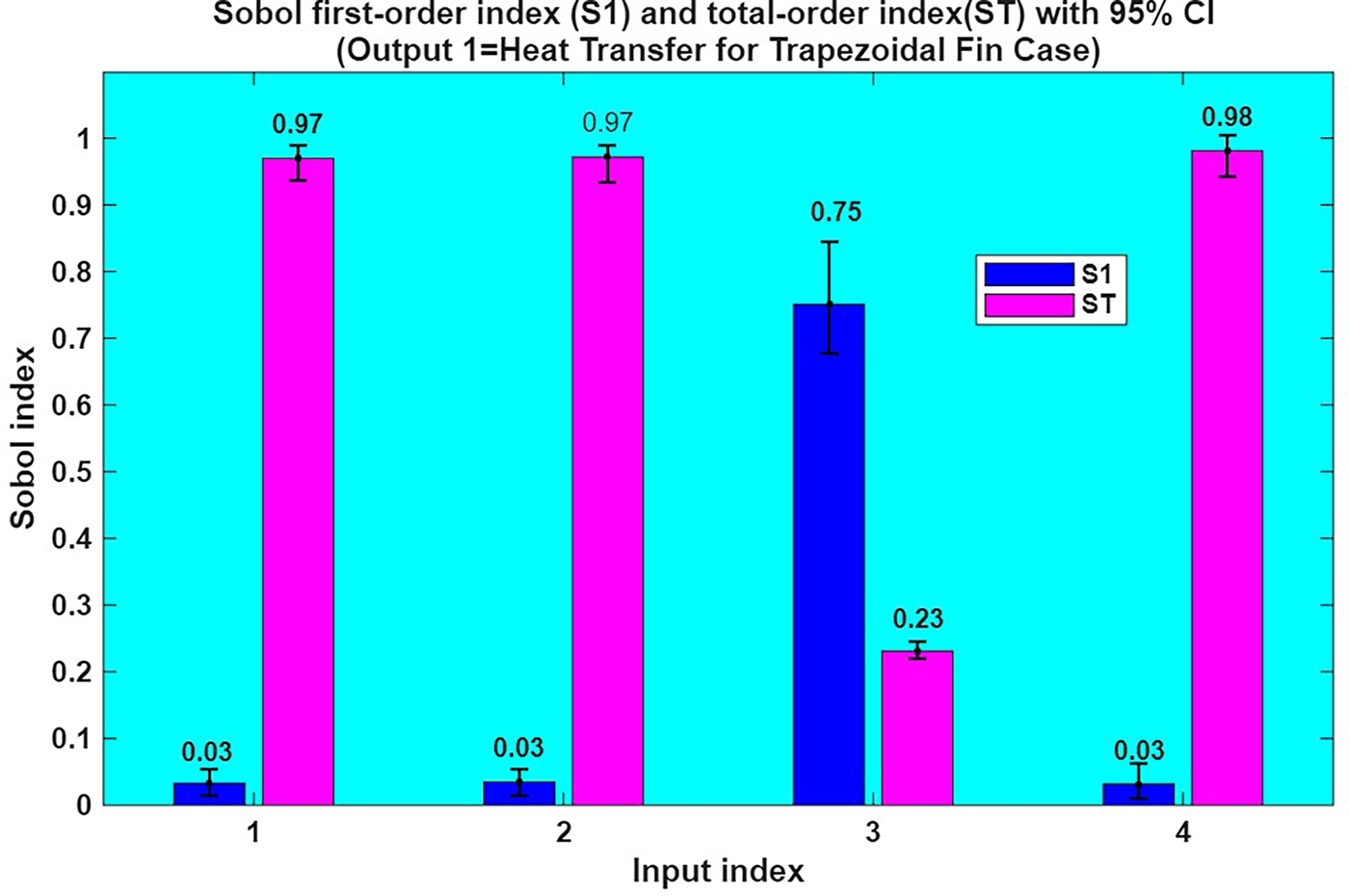
Figure 38: Sensitivity analysis plot for trapezoidal fin cas
4.5 Stability Analysis and Grid Independence Test
Fig. 39 shows that the results for both the medium and fine meshes agree in the rectangular and trapezoidal cases, indicating that the current study meets the criteria for grid independence testing. Fig. 40 depicts a linear rise in heat transfer with the parameter
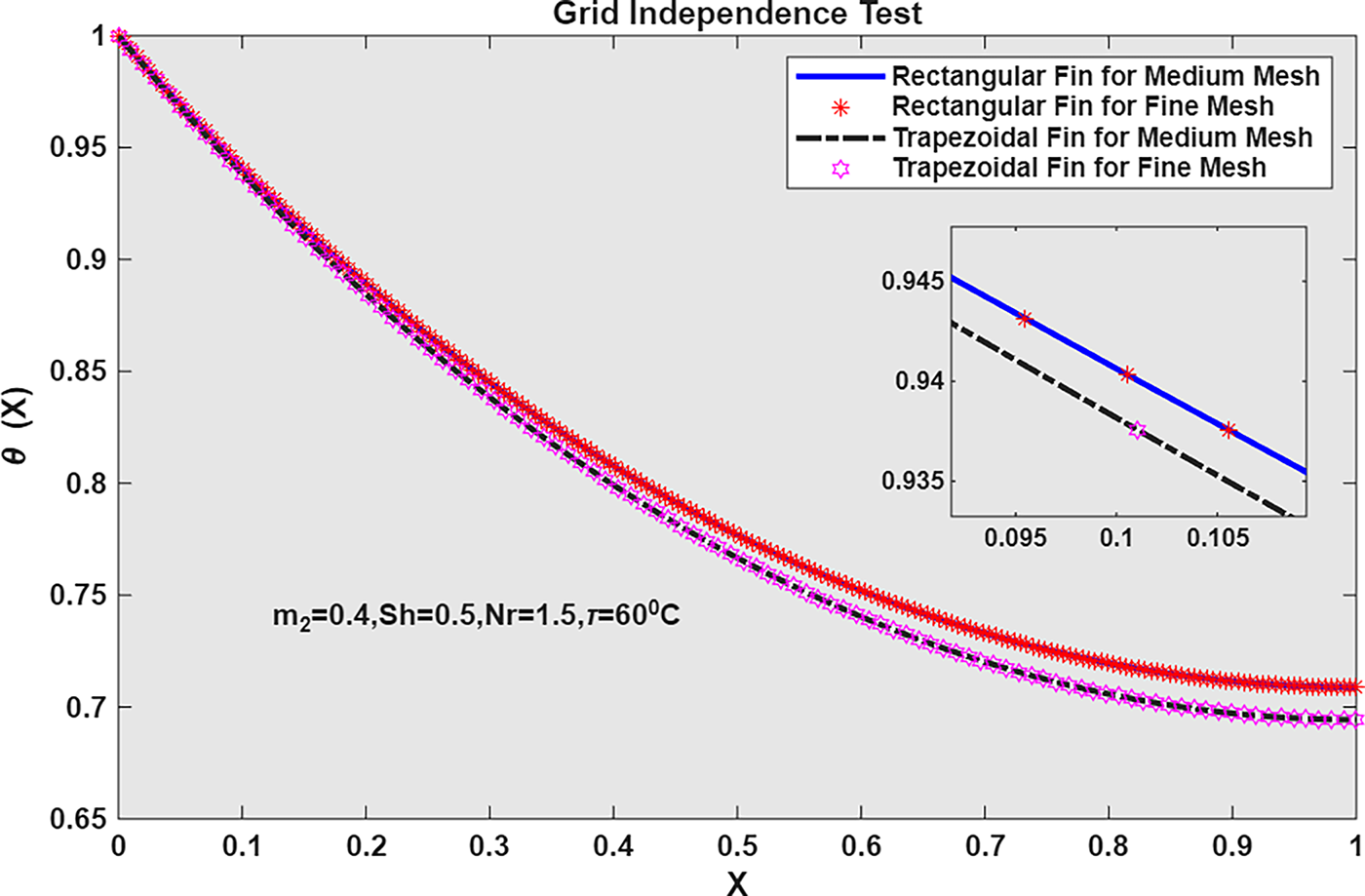
Figure 39: Grid independence test
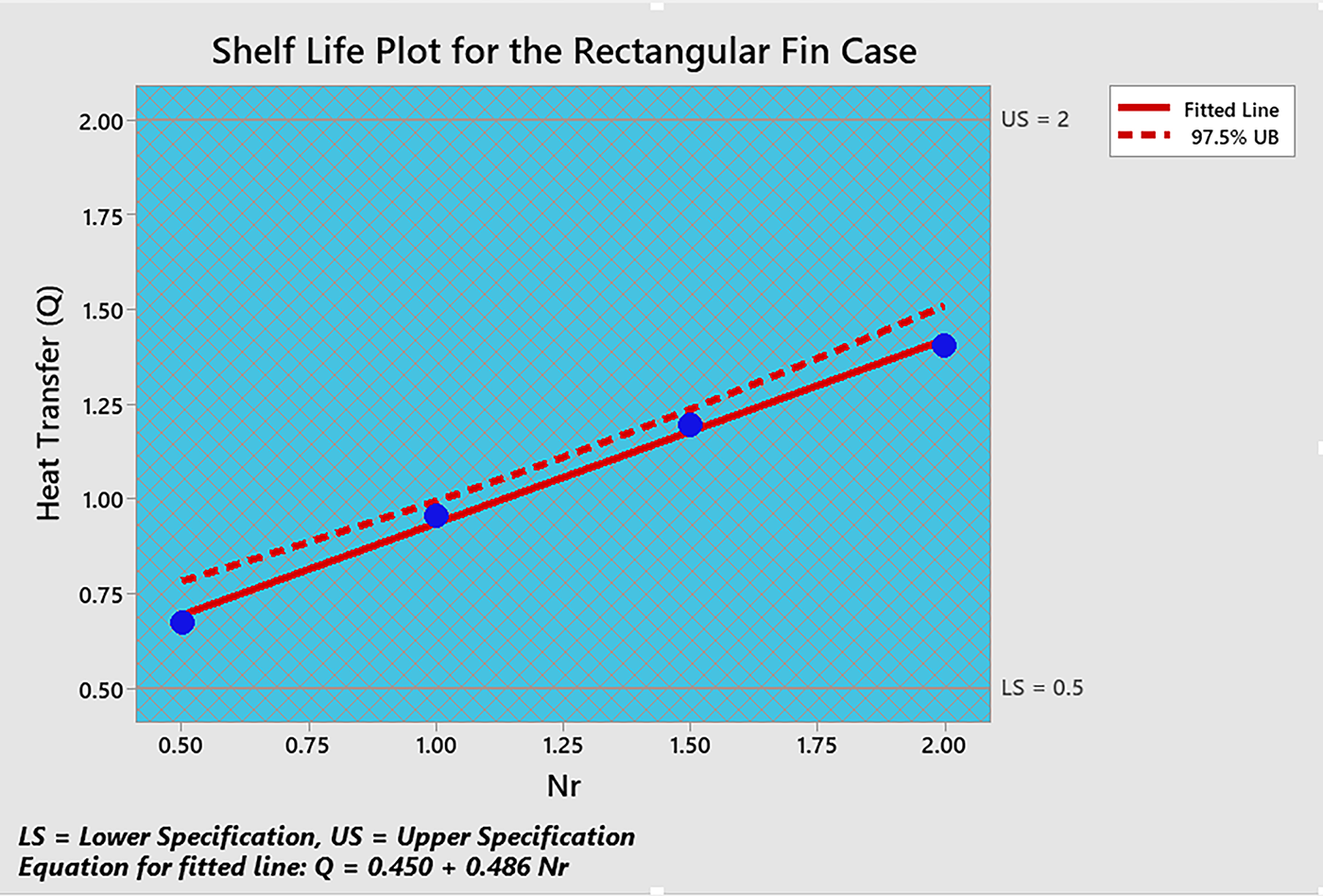
Figure 40: Numerical stability analysis for the rectangular fin
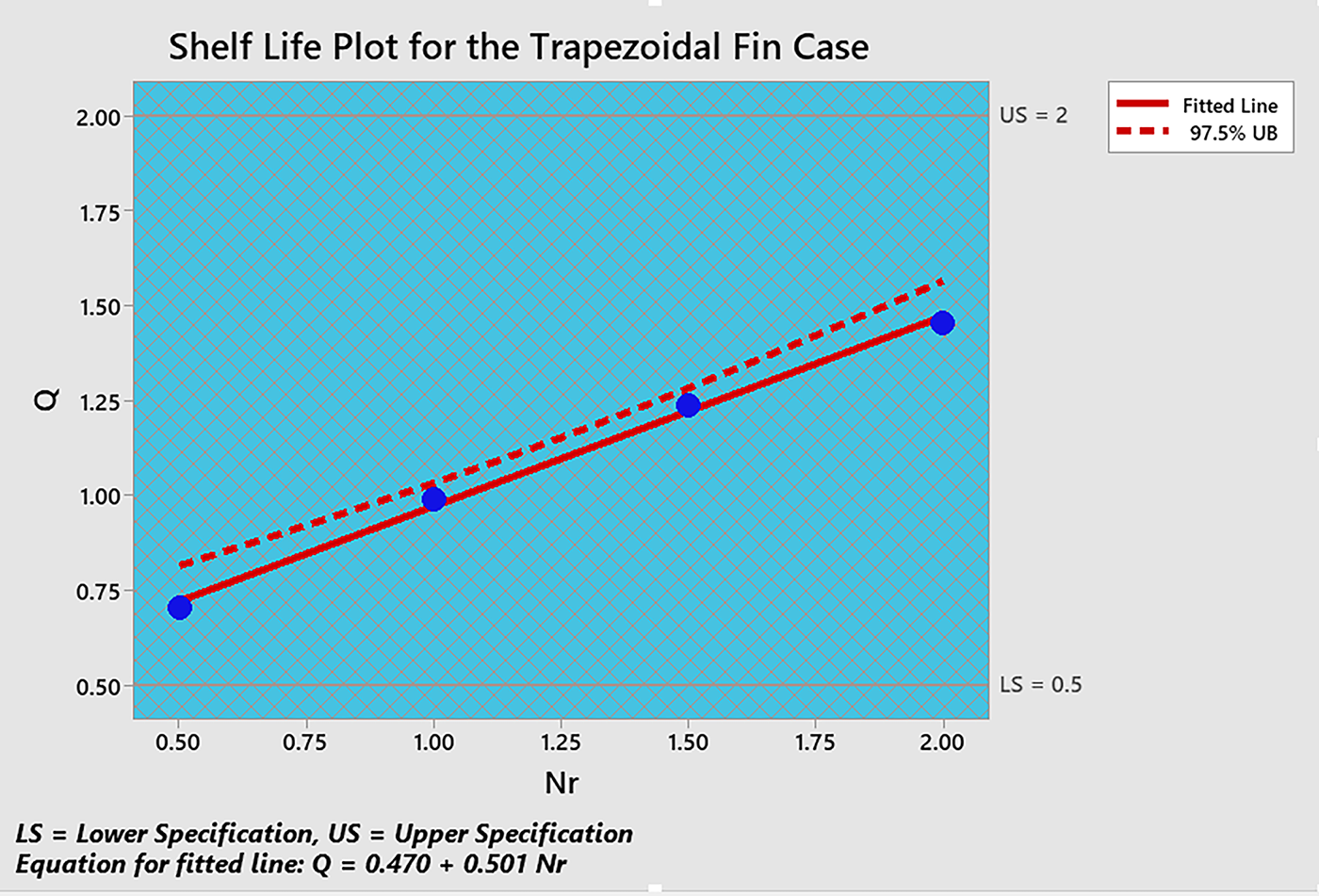
Figure 41: Numerical stability analysis for the trapezoidal fin
The thermal behaviour of a wetted hybrid nanofluid with inclined trapezoidal and rectangular porous fins was investigated in this work in MATLAB software with the Lobatto IIIa collocation method using the BVP5C solver to examine the impact of the inclination angle
Key Findings of the Present Study:
❖ The temperature decreases progressively with the rise in the inclination angle
❖ Trapezoidal fin consistently exhibits better heat transfer mechanism than rectangular fin due to its tapered geometry.
❖ Due to the increased permeability and solid-fluid interaction within the fin, the wet porous parameter and porosity significantly lower the temperature of the hybrid nanofluid.
❖ Integrating both radiative and convective heat transfer leads to effective thermal performance.
❖ The absolute error remains extremely small 10−12–10−6, validating that the adapted numerical method is highly accurate and stable.
❖ The linear regression results reveal excellent correlation between fitted and computed data, with R2 values are
Limitations of the Present Study:
❖ The present study examined a hybrid nanofluid only
❖ Comparison of results with experimental study
❖ In the present study, limited convective and radiative effects on heat transfer were considered.
❖ This study is limited to steady-state heat transfer
Future Scope:
To simplify the model, it was assumed that there was a perfect stationary state with homogeneous throughout flotation of the hybrid nanofluid. In the future, the aggregation, sedimentation and stability of nanoparticles will be taken into consideration with the aim of making the model have more practical considerations.
Acknowledgement: Not applicable.
Funding Statement: This research was supported by the “Regional Innovation System & Education (RISE)” through the Seoul RISE Center, funded by the Ministry of Education (MOE) and the Seoul Metropolitan Government (2025-RISE-01-027-04).
Author Contributions: Maddina Dinesh Kumar: Writing—original draft, Methodology, Resources, Software, Visualization, Validation. S. U. Mamatha: Writing—original draft, Methodology, Investigation, Formal analysis. Khalid Masood: Validation, Conceptualization, Methodology, Formal analysis. Nehad Ali Shah: Investigation, Supervision, Formal analysis, Methodology, Conceptualisation. Se-Jin Yook: Writing—review & editing, Software, Supervision, Project administration. Maddina Dinesh Kumar and Nehad Ali Shah contributed equally to this work and are co-first authors. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data will be available with the corresponding author on reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| Symbol | Description | SI units |
| Fin cross-sectional area | ||
| Specific heat at constant pressure | ||
| Variable temperature | ||
| Acceleration due to gravity | ||
| Heat transfer coefficient | ||
| Coefficient of heat transfer at temperature | ||
| Latent heat of water evaporation | ||
| Thermal conductivity | ||
| Permeability | ||
| Length of the fin | ||
| Constants | ||
| Wet porous parameter | ||
| Convection parameter | ||
| Radiative parameter | ||
| Porosity parameter | ||
| Base thickness of the fin | ||
| Fluid temperature | ||
| Ambient temperature | ||
| Base temperature | ||
| Semi fin thickness | ||
| Fin length | ||
| Non-dimensional axial co-ordinate | ||
| Greek Symbols | ||
| Non-dimensional temperature | ||
| Stefan-Boltzmann constant | ||
| Surface emissivity of fin | ||
| Density | ||
| Dynamic viscosity | ||
| Nanoparticle volume fraction parameter | ||
| Angle of inclination | ||
| Time constant | ||
| Subscript | ||
| Base fluid | ||
| Hybrid nanofluid | ||
References
1. Aziz A, Fang T. Alternative solutions for longitudinal fins of rectangular, trapezoidal, and concave parabolic profiles. Energy Convers Manag. 2010;51(11):2188–94. doi:10.1016/j.enconman.2010.03.012. [Google Scholar] [CrossRef]
2. Han Y, Peng X. Thermal performance of a moving fin with temperature-dependent thermal conductivity in convective and radiative environment. Heliyon. 2025;11(3):e42329. doi:10.1016/j.heliyon.2025.e42329. [Google Scholar] [PubMed] [CrossRef]
3. Pavithra CG, Gireesha BJ, Sushma S, Gowtham KJ. Analysis of convective-radiative heat transfer in dovetail longitudinal fins with shape-dependent hybrid nanofluids: a study using the Hermite wavelet method. Appl Math Mech Engl Ed. 2025;46(2):357–72. doi:10.1007/s10483-025-3218-9. [Google Scholar] [CrossRef]
4. Riasat S, Naz A, Ghachem K, Mir A, Alshammari BM, Kolsi L. Thermal stress analysis of radiated annular fin by considering platelet, hexahedron, and tetrahedron nanoparticles in the presence of magnetic field. J Radiat Res Appl Sci. 2025;18(2):101438. doi:10.1016/j.jrras.2025.101438. [Google Scholar] [CrossRef]
5. Luo JW, Yaji K, Chen L, Tao WQ. Data-driven multi-fidelity topology design of fin structures for latent heat thermal energy storage. Appl Energy. 2025;377:124596. doi:10.1016/j.apenergy.2024.124596. [Google Scholar] [CrossRef]
6. Abd-Elmonem A, Shams ZE, Imtiaz M, Ali K, Ahmad S, Jamshed W, et al. Flow dynamics in a vertical pipe with internal fins exposed to sunlight—a machine learning based evaluation of thermal signature. Energy Convers Manag X. 2025;25:100846. doi:10.1016/j.ecmx.2024.100846. [Google Scholar] [CrossRef]
7. Rehman KU, Shatanawi W, Yian LY. On nonlinear coupled differential system for heat transfer in magnetized enclosure with T-shaped baffle by using machine learning. Partial Differ Equ Appl Math. 2025;13:101078. doi:10.1016/j.padiff.2025.101078. [Google Scholar] [CrossRef]
8. Arshad A. A phase change material-based constructal design finned heat sink: an evolutionary design for thermal management. Int Commun Heat Mass Transf. 2025;161(1):108379. doi:10.1016/j.icheatmasstransfer.2024.108379. [Google Scholar] [CrossRef]
9. Sowmya G, Varun Kumar RS, Alsulami MD, Prasannakumara BC. Thermal stress and temperature distribution of an annular fin with variable temperature-dependent thermal properties and magnetic field using DTM-Pade approximant. Waves Random Complex Medium. 2025;35(1):2054–82. doi:10.1080/17455030.2022.2039421. [Google Scholar] [CrossRef]
10. Basha HT, Jang B. Heat transfer and entropy generation analysis in the buoyancy-driven flow of Fe3O4-MWCNT/water hybrid nanofluid within a square enclosure in the presence of fins using machine learning. J Therm Anal Calorim. 2025;150(4):2909–34. doi:10.1007/s10973-024-13647-x. [Google Scholar] [CrossRef]
11. Kiwan S, Al-Nimr MA. Using porous fins for heat transfer enhancement. J Heat Transf. 2001;123(4):790–5. doi:10.1115/1.1371922. [Google Scholar] [CrossRef]
12. Ahmad I, Zahid H, Zahoor Raja MA, Ilyas H, Mohayyuddin Z. Use of Levenberg-Marquardt networks for optimization of thermal dispersion in moving triangular porous fin. Int J Therm Sci. 2025;210(1):109613. doi:10.1016/j.ijthermalsci.2024.109613. [Google Scholar] [CrossRef]
13. Hu X, Chen P, Guo X, Zhang X. Numerical investigation on thermal behavior of PCM embedded in structured porous fins (SPFs) with various configurations and materials. Appl Therm Eng. 2025;274:126617. doi:10.1016/j.applthermaleng.2025.126617. [Google Scholar] [CrossRef]
14. Alotaibi MA, Alhejaili W, Aly AM, Almalki S. Magnetic field influence on heat transfer of NEPCM in a porous triangular cavity with a cold fin and partial heat sources: aI analysis combined with ISPH method. Alex Eng J. 2025;119:345–58. doi:10.1016/j.aej.2025.01.080. [Google Scholar] [CrossRef]
15. Nandy AK, Balasubramanian K. Solid/porous compound wavy fins bifurcation at crest and trough in the microchannel heat sink: thermo-hydraulic performance. Asia-Pacific J Chem Eng. 2025;20(4):e70032. doi:10.1002/apj.70032. [Google Scholar] [CrossRef]
16. He F, Hu C, Gao W, Li S, Meng X. Effect of inclination angles on heat transfer characteristics of solid and perforated spiral finned heat exchangers. Int Commun Heat Mass Transf. 2025;164:108920. doi:10.1016/j.icheatmasstransfer.2025.108920. [Google Scholar] [CrossRef]
17. Li B, Wang X, Tam L, Zeng M, Wang Q. Impact of inclination angle on flow boiling heat transfer of refrigerants in elliptical mini-channel with micro fins. Appl Therm Eng. 2025;269:126184. doi:10.1016/j.applthermaleng.2025.126184. [Google Scholar] [CrossRef]
18. Dhaoui S, Souaissa K, Bouabidi A, El Hadi Attia M, Chrigui M. Numerical and experimental analysis of the effect of fin inclination angle on the performance of a double-slope solar still. Appl Therm Eng. 2025;265:125659. doi:10.1016/j.applthermaleng.2025.125659. [Google Scholar] [CrossRef]
19. Komathi J, Magesh N, Venkadeshwaran K, Chandan K, Varun Kumar RS, Abdulrahman A. Heat transfer analysis of a fully wetted inclined moving fin with temperature-dependent internal heat generation using DTM-Pade approximant and machine learning algorithms. Pramana. 2025;99(1):23. doi:10.1007/s12043-024-02880-6. [Google Scholar] [CrossRef]
20. Zhong L, Su W, Shen Z. Effect of varying Reynolds numbers on the heat transfer and flow structure of vertical, curved, inclined, and serpentine pin fins. Int Commun Heat Mass Transf. 2025;161:108557. doi:10.1016/j.icheatmasstransfer.2024.108557. [Google Scholar] [CrossRef]
21. Chen H, Wang Z, Cheng WL. Effect of small inclination angle on heat transfer performance of Ω-grooved bending heat pipe. Appl Therm Eng. 2025;258:124662. doi:10.1016/j.applthermaleng.2024.124662. [Google Scholar] [CrossRef]
22. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. In: Proceedings of the ASME International Mechanical Engineering Congress & Exposition; 1995 Nov 12–17; San Francisco, CA, USA. [Google Scholar]
23. Bahiraei M, Hosseinalipour SM, Zabihi K. Experimental study of nanofluid convective heat transfer for implementation of dispersion model considering non-uniform particle distribution. Exp Heat Transf. 2014;27(5):452–71. doi:10.1080/08916152.2013.803174. [Google Scholar] [CrossRef]
24. Varatharaj K, Tamizharasi R, Vajravelu K. Ternary hybrid nanofluid flow and heat transfer at a permeable stretching sheet with slip boundary conditions. Eur Phys J Spec Top. 2025;234(8):2293–316. doi:10.1140/epjs/s11734-024-01295-z. [Google Scholar] [CrossRef]
25. Mishra A. Thompson and Troian slip effects on ternary hybrid nanofluid flow over a permeable plate with chemical reaction. Numer Heat Transf Part B Fundam. 2025;86(8):2640–68. doi:10.1080/10407790.2024.2346929. [Google Scholar] [CrossRef]
26. Gul M, Iqbal J, Abbasi FM. Impact of variable thermophysical properties on peristaltic propulsion of blood based casson ternary hybrid nanofluid for biomedical applications. BioNanoScience. 2025;15(3):346. doi:10.1007/s12668-025-01941-3. [Google Scholar] [CrossRef]
27. Anjum MW, Saqib SU, Shih YT, Hilali Jaghdam I, Becheikh N, Kolsi L. An intelligent soft computing model for predicting the thermal behavior of blood-based trihybrid nanofluids flow in biomedical drug delivery applications. Case Stud Therm Eng. 2025;74:106742. doi:10.1016/j.csite.2025.106742. [Google Scholar] [CrossRef]
28. Hussain S. Hydrodynamic and thermosolutal analysis of MHD ternary hybrid nanofluids in BFS configuration: high-order FEM for drag reduction and thermal enhancement. Int J Numer Meth Heat Fluid Flow. 2025;35(7):2577–607. doi:10.1108/hff-04-2025-0291. [Google Scholar] [CrossRef]
29. Jahan S, Nasrin R. Sensitivity study of thermal enhancement featuring ternary-hybrid nanofluid in a two-layered cross-flow microchannel heat exchanger. J Therm Anal Calorim. 2025;150(21):17591–616. doi:10.1007/s10973-025-14568-z. [Google Scholar] [CrossRef]
30. Hemmat Esfe M, Alidoust S, Toghraie D, Hatami H. Experimental study of thermal conductivity of SWCNT–TiO2–CuO (10:70:20)/water ternary hybrid nanofluid (THNF) and providing a new equation using response surface methodology. J Therm Anal Calorim. 2025;150(6):4177–89. doi:10.1007/s10973-025-14028-8. [Google Scholar] [CrossRef]
31. Israr Ur Rehman M, Chen H, Hamid A. Numerical investigation of Cattaneo-Christov double diffusion and mixed convection effects in non-Darcian Sutterby nanofluid using multi objective optimization through RSM. Int J Hydrog Energy. 2025;100:1219–30. doi:10.1016/j.ijhydene.2024.12.422. [Google Scholar] [CrossRef]
32. Wang F, Saeed AM, Puneeth V, Ali Shah N, Anwar MS, Geudri K, et al. Heat and mass transfer of Ag-H2O nano-thin film flowing over a porous medium: a modified Buongiorno’s model. Chin J Phys. 2023;84:330–42. doi:10.1016/j.cjph.2023.01.001. [Google Scholar] [CrossRef]
33. Israr Ur Rehman M, Hamid A, Wang X, Qi H. Magnetohydrodynamic and thermal radiation effects with stability analysis on shear-thinning Williamson nanofluid by using response surface methodology. J Therm Anal Calorim. 2025;150(20):16685–700. doi:10.1007/s10973-025-14635-5. [Google Scholar] [CrossRef]
34. Xia WF, Animasaun IL, Wakif A, Ali Shah N, Yook SJ. Gear-generalized differential quadrature analysis of oscillatory convective Taylor-Couette flows of second-grade fluids subject to Lorentz and Darcy-Forchheimer quadratic drag forces. Int Commun Heat Mass Transf. 2021;126:105395. doi:10.1016/j.icheatmasstransfer.2021.105395. [Google Scholar] [CrossRef]
35. Khan NA, Sulaiman M, Alshammari FS. Heat transfer analysis of an inclined longitudinal porous fin of trapezoidal, rectangular and dovetail profiles using cascade neural networks. Struct Multidiscip Optim. 2022;65(9):251. doi:10.1007/s00158-022-03350-6. [Google Scholar] [CrossRef]
36. Abbas Z, Mahmood I. Thermal property prediction in blood-based MHD Casson tri-hybrid nanofluids with TiO2 and carbon nanotubes using ANN and Tiwari-Das model. Eur Phys J Plus. 2025;140(6):519. doi:10.1140/epjp/s13360-025-06474-y. [Google Scholar] [CrossRef]
37. Gowtham KJ, Gireesha BJ. Exploring thermal efficiency of an inclined porous moving fins: comparative study of dovetail, trapezoidal, and rectangular profiles using fibonacci wavelet method and Physics-Informed neural networks. Appl Phys A. 2025;131(8):660. doi:10.1007/s00339-025-08734-1. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2026 The Author(s). Published by Tech Science Press.
Copyright © 2026 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools