Build Gaussian Distribution Under Deep Features for Anomaly Detection and Localization

1  Introduction

Anomaly detection (AD) is of utmost importance for numerous tasks in the field of computer vision, and it aims at precisely identifying abnormal images and often be seen as a binary classification task. AD has great significance and application value in the field of industrial inspection [1–3], medical image analysis [4], and surveillance [5,6]. However, defective samples are difficult to collect comprehensively, and labeled data is costly to obtain in many practical scenarios. Previous studies solved this challenge by following an unsupervised learning paradigm, such as one-class support vector machine (OC-SVM) [7,8]. However, these solutions are very sensitive to the feature space used. Hence, DeepSVDD [9] comes into existence and first introduces one-class classification to AD. Recently, there are some self-supervised learning methods [10,11] that design good pretext tasks to help the model extract more discriminative features.

Another feasible solution for AD is to use generative models, like AutoEncoder (AE) [12], and Generative Adversarial Network (GAN) [13,14]. These methods do not need pre-trained models and extra training data and detect anomalies by the reconstruction errors of the test images. However, these approaches treat each image as a whole, omitting the learning of local information, and the generalization characteristics of AE may reconstruct the abnormal inputs well, causing the anomaly detection task to fail. Hence, this kind of approach is not widely used.

Deep learning methods have been introduced for AD, and a property of neural network is that representations learned on vast datasets can be transferred to data-poor tasks, which is very convenient for industrial anomaly detection. Recent improvements thus leverage the pre-trained deep CNNs (e.g., ResNet18) to extract general features of normal images and build the distribution for anomaly detection.

We propose an unsupervised anomaly detection method that only uses anomaly-free images in training time, making our method very attractive for industrial anomaly detection. In addition, we extract deep features from a pre-trained network and model the distribution via MVG, then we use Mahalanobis distance [15] to detect defects. To alleviate the bias of the pre-trained network towards the task of natural image classification, we adopt mid-level feature representation. We also reduce redundancy in the extracted features to get critical features for AD and shortening running time. Finally, we evaluate the proposed method on the challenging MVTec anomaly detection dataset [3] and achieve an image-level anomaly detection AUROC score of 98.6%, a pixel-level anomaly detection AUROC score of 96.6%.

2  Related Work

In the current research literature, the existing methods of anomaly detection can be roughly divided into three categories: the reconstruction-based method, the classification-based method, and the distribution-based method.

2.1 Classification-based Methods

Classification-based anomaly detection methods aim to find a separating manifold between normal data and the rest of the input space. One paradigm is one-class Support Vector Machine (oc-SVM) [7], it trains a classifier to perform this separation. One of its most successful variants is support vector data description (SVDD) [16], it is a long-standing algorithm for AD tasks and it finds the minimal sphere which contains at least a given fraction of the data. DeepSVDD [9] trains a neural network by minimizing the volume of a hypersphere that encloses the network representations of the data. However, DeepSVDD requires the training of a neural network, the feature center needs to be designated by hand in the feature space, and model degradation occurs easily. PatchSVDD [10] extends SVDD to a patch-based method using self-supervised learning [17], it achieves more accurate anomaly localization performance, but the assumption that adjacent patch features are aggregated during training is not reasonable.

2.2 Reconstruction-based Methods

The most common anomaly detection methods are reconstruction-based, and this method is based on the assumption that each normal sample can be reconstructed accurately, and the reconstruction of the abnormal image will have a great reconstruction loss. A typical reconstruction-based method is based on AutoEncoders (AE) [18,19,20]. Reference [21] designs a deep yet efficient convolutional autoencoder and detect anomalous regions within images via feature reconstruction. Deep generative models based on generative adversarial network (GAN) [22] also can be used in this way. Furthermore, GAN-based methods have more appropriate anomaly score metrics, such as the output of the discriminator [23] and the latent space distance [24]. In order to improve the reconstruction quality of the image, [25] proposes to construct GAN ensemble for anomaly detection, as the GAN ensemble often outperforms a single GAN. However, these methods treat the image as a whole, it may be difficult for the generator to reconstruct images, leading to poor results in anomaly detection.

2.3 Distribution-based Methods

Distribution-based methods build a density estimation model for the distribution of normal data. Kernel density estimation [26], Gaussian, and nearest neighbors are all be seen as distributional. Recently, a pre-trained network is used to extract deep features, and the reuse of pre-trained features has also been widely used in anomaly detection [2,27]. These methods achieve great performance in detecting anomalous images but suffer from a critical drawback: real image data rarely follows simple parametric distributional assumptions. Student-teacher knowledge distillation [28] or normalizing flows [29] are used to learn bijective transformations between data distributions. Since flow-based methods have no dimensional reduction, the computation cost is significant.

3  Method

The proposed method is based on such assumptions that discriminative features do not necessarily vary enormously within the normal data in the anomaly detection task. The pipeline of the proposed method for unsupervised anomaly detection is depicted in Fig. 1.

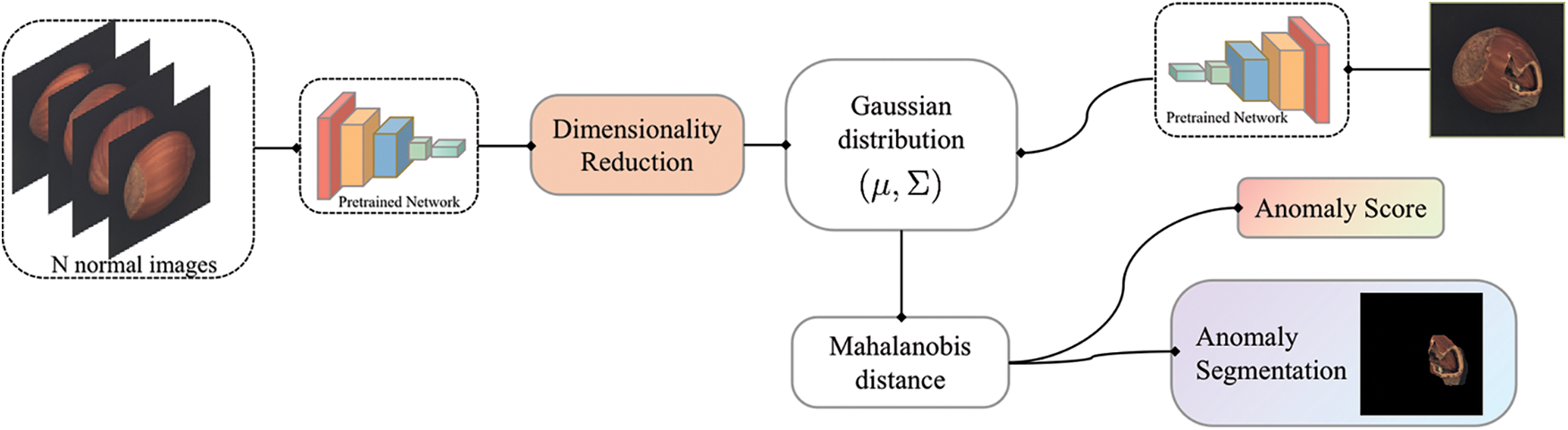
Figure 1: Overview of the proposed method

To coincide with the existing literature, we denote the pre-trained extractor by ϕ and define XN to denote the set of normal images at training time. Accordingly, XT denotes the set of test images, containing both normal and abnormal samples (∀xt∈XT:yxt∈{0,1}),y is the label of the test image.

3.1 Feature Extration

The network pre-trained on a large-scale dataset ensures the extraction of universal features. Hence, to avoid ponderous neural network optimization, we adopt the pre-trained EfficientNet [30] as the backbone and use 3∼7 (index from 0) layers to alleviate the bias to image classification. Specifically, we denote its final output of intermediate layer l with ϕl:Rcl−1×hl−1×wl−1→Rcl×hl×wl.

3.2 Dimensionality Reduction

A huge number of features have been extracted by ϕ, but the features may carry redundant information, hence, finding discriminative features between normal and anomalous images is critical for AD. For a good trade-off between efficiency and the cost of time, we propose applying the opposite operation in the principal component analysis (PCA) by retaining those principal components with the least variance (i.e., those with the smallest eigenvalues). For convenience, we use OPCA to indicate the opposite operation of PCA in the following. The PCA-based dimension reduction method discards dimensions that carry less information and retains the main features that are useful for anomaly detection.

3.3 Fit the Gaussian Distribution

The probability density function of multivariate Gaussian distribution (MVG) is given by:

φμ,Σ(x):=1(2π)n|detΣ|e−12(x−μ)TΣ−1(x−μ),(1)

with n being the number of dimensions. The MVG parameters comprise the mean vector, μ∈RD, and the symmetric covariance matrix, Σ∈RD×D, and Σ must be positive definite.

We learn the parameters of multivariate Gaussian distribution from the output of different layers of the backbone. Since the sample covariance matrix is only well-conditioned when the number of dimensions n is much lower than the number of samples m, we use the empirical mean μ and estimate Σ using shrinkage as proposed by Ledoit et al. [31]. We approximate both mean μ and covariance matrix Σ empirically from normal data x1, …, xm∈RD based on the sample covariance:

Σ^=1m−1∑i=1m(xi−x¯)(xi−x¯)T,(2)

where x¯ denotes the empirical mean of the observations and Σ^ denotes the empirical covariance matrix.

3.4 Anomaly Scoring

Under the distribution with mean μ and covariance Σ, Mahalanobis distance [15] is used to get a distance measure for a particular point x∈RD, which is defined as:

M(x)=(x−μ)TΣ−1(x−μ).(3)

To make the image-level anomaly score S more robust for test images, We measure the distance between the intermediate outputs of each layer of the network by Eq. (4) and then perform a simple summation to combine the anomaly scores of different layers. The scoring function for the test image xt is show in Eq. (4), where L is the total number of layers of ϕ.

S(xt):=∑l=1LMl.(4)

Anomaly localization is also an important criterion to estimate the validity of the method, and it hopes to detect anomalous pixels. Since intermediate features maintain spatial dimensions, we propose to apply Mahalanobis distance [15] to the features of the intermediate layer by Eq. (3), yielding a matrix Sl of size hl×wl, and upsample the spatial anomaly scores of each layer using bilinear interpolation and denote their unweighted mean as the final anomaly score per pixel.

4  Experiments

4.1 Experimental Setup

Dataset. We evaluate the proposed method on the MVTec AD dataset (MVTec). MVTec contains 15 categories of industrial products (10 for objects and 5 for textures) with a total of 5354 images. The MVTec follows the standard protocol where no anomalous images are used in the training stage. Each category has very few training images, which poses a unique challenge for learning deep representations.

Experimental Settings. The proposed method is implemented by PyTorch 1.2.0 and CUDA 11.3, and all experiments run with NVIDIA A100-PCIE-40GB GPU. All images in the MVTec are resized to a specific resolution (e.g., 380 × 380, 224 × 224) in the proposed method, and anomaly detection is performed on one category at a time. For training, we adopt the EfficientNet-b4 network with 3∼7 layers as the backbone and take the output of the intermediate layer as features. The default variance threshold of the OPCA approach is 0.05. We also use the ResNet-18 network as a supplementary experiment.

Evaluation Metrics. Image-level anomaly classification and pixel-level anomaly localization performance are measured via Area Under Receiver Operator Characteristics (AUROC). But, as mentioned in, AUROC is biased in favor of large anomalies. Hence, Per-Region-Overlap (PRO) was proposed to evaluate the performance of pixel-level anomaly localization. The higher the PRO score is, the better the localization performance of the anomaly is.

4.2 Comparison with State-of-the-Art

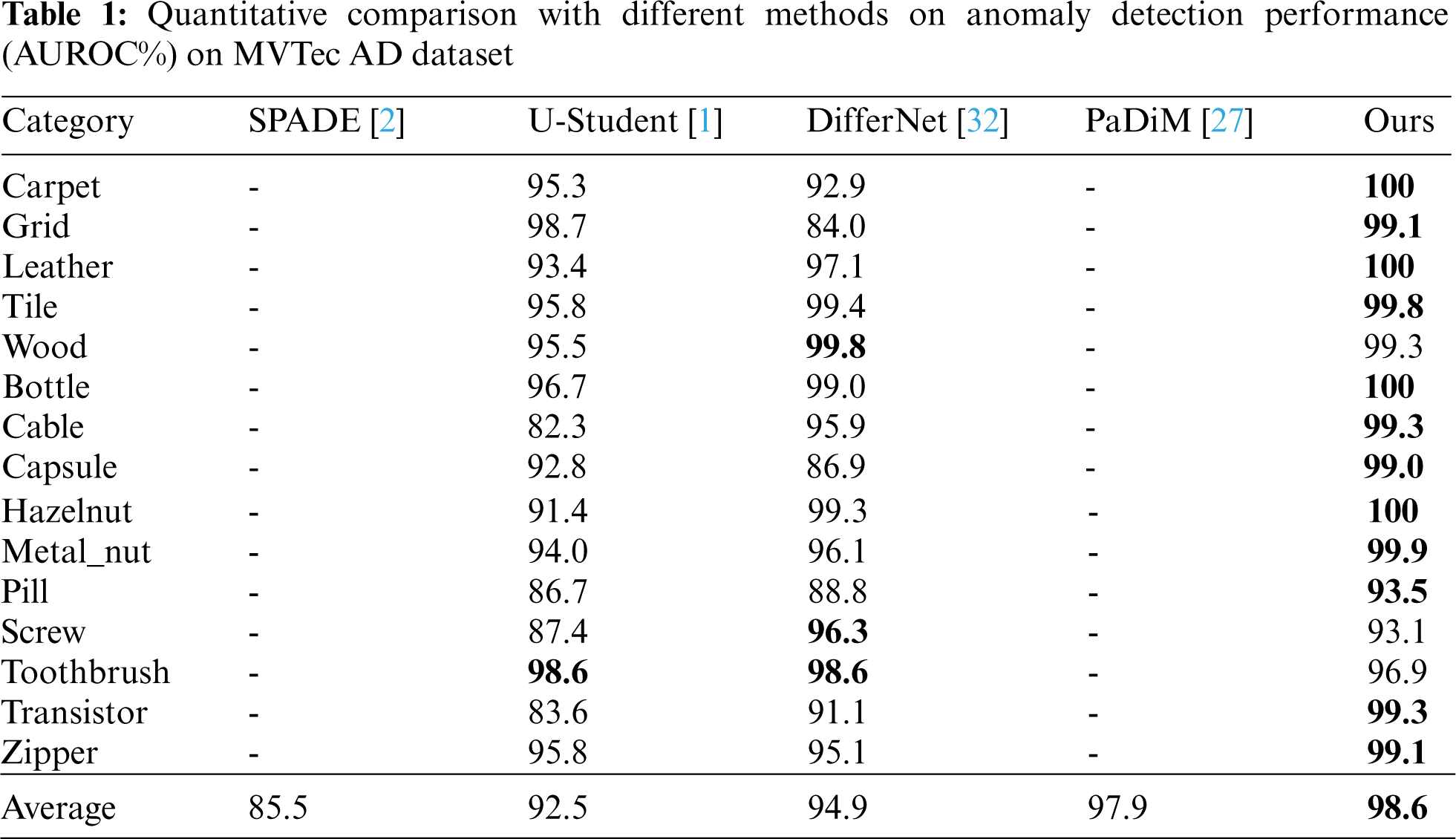
The quantitative results on image-level anomaly classification across the 15 classes are summarized in Table 1, and we further compare it to the current state-of-the-art performance reported in the existing literature. The best result of each category is highlighted in boldface. We do not reproduce those methods, taking the corresponding values directly from the linked sources. The proposed method significantly outperforms current state-of-the-art with 98.6% in anomaly classification. In all 15 categories, the proposed method achieves an AUROC of at minimum 93.1%, indicating that the proposed method can effectively deal with different kinds of defects. Furthermore, the results prove that not all the deep features are useful for the anomaly detection task. On the contrary, reducing the number of features can ensure detection efficiency and reduce memory requirements.

Anomaly localization requires a more fine-grained result that gives the label for each pixel. The performance of anomaly localization is an important criterion to verify the method’s validity. We compare the localization performance to current state-of-the-art results in Table 2, and the proposed method outperforms others by at least 0.6p.p in the AUROC.

The anomaly localization heatmaps of the proposed method on different classes are shown in Fig. 2. Remarkably, the proposed method can precisely locate defects in the images. It can be explained that the proposed method selects the features with the lowest variance which is effective in the anomaly detection task.

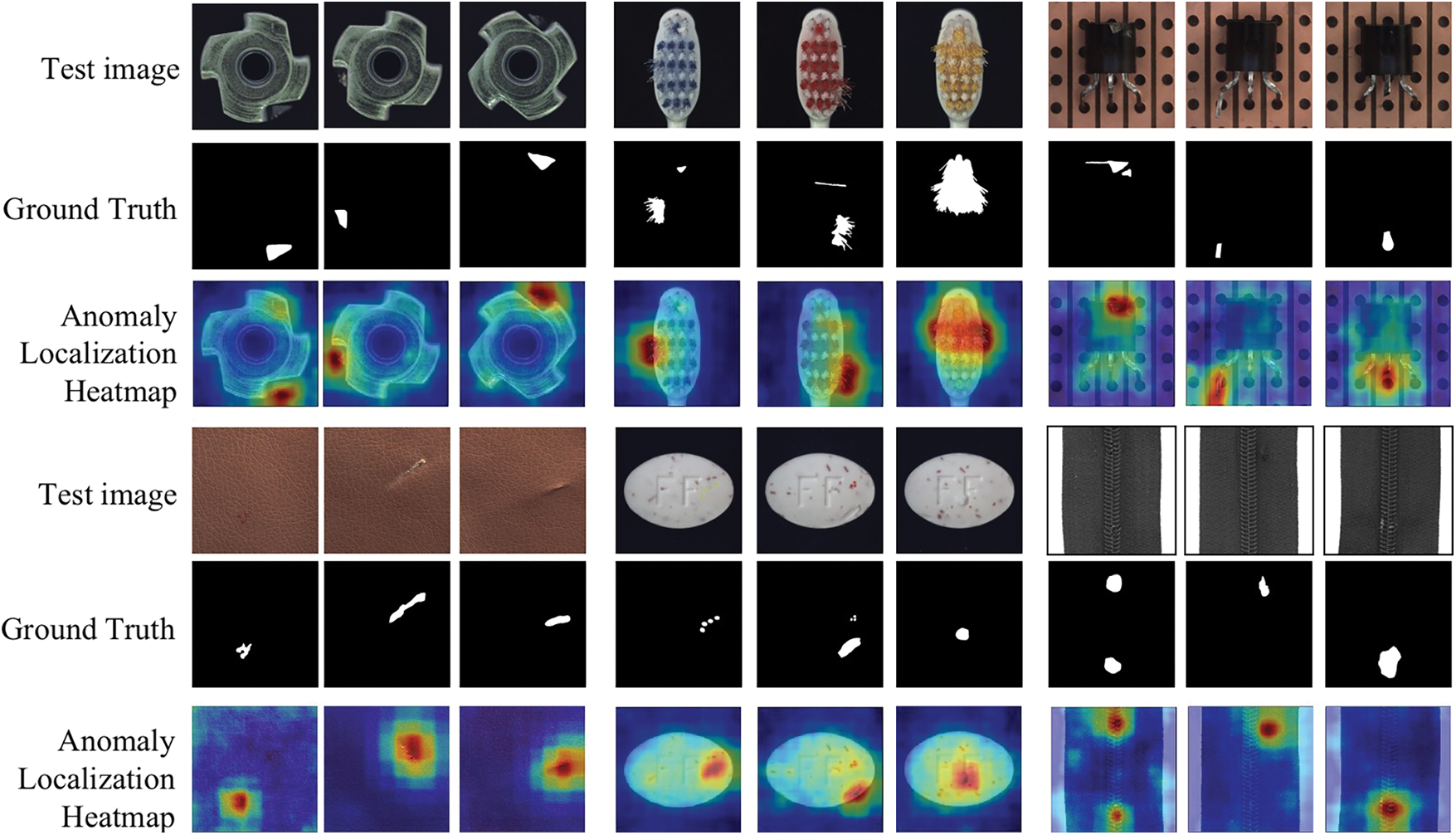
Figure 2: The visualization results on part categories of MVTec AD dataset

A visualization of the qualitative evaluation is presented in Fig. 3, we highlight the anomalies in red. To investigate the robustness of the method, we classified the defect types into two categories: large defects and subtle defects. Compared to the SPADE [2], which also uses the pre-trained network to extract anomaly-free features, the proposed method can locate anomalies precisely. Compared to the PaDiM [27], which is the runner-up in Table 1, our method is still competitive and accurately segments defects of different sizes and types.

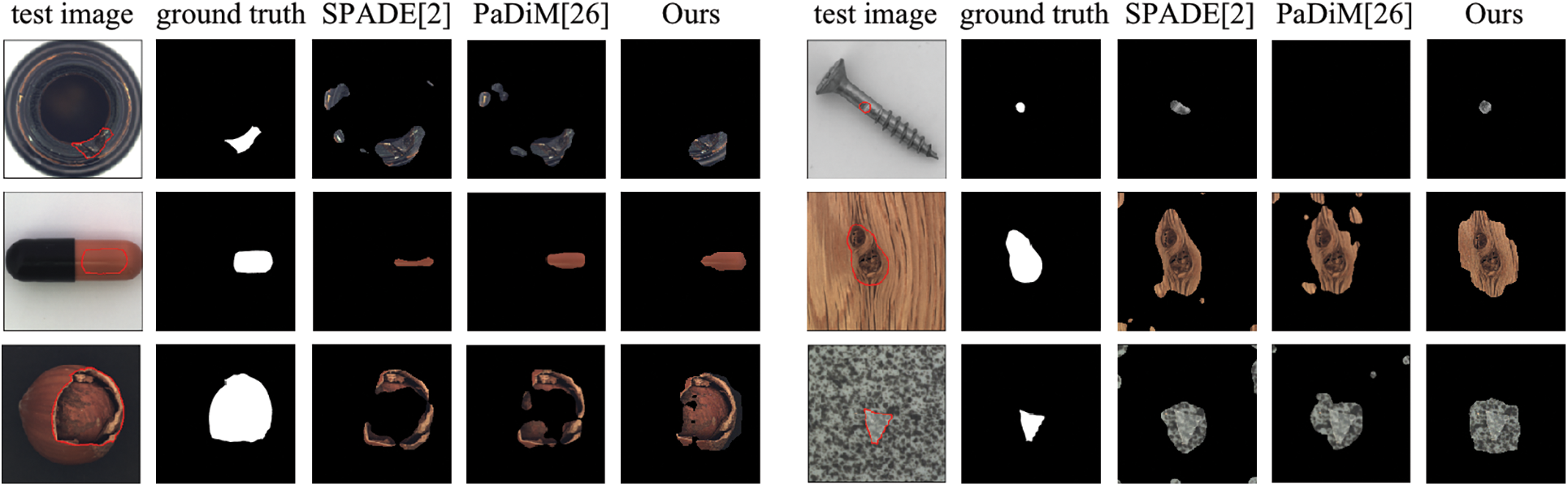
Figure 3: The visualization results on part categories of MVTec AD dataset

The proposed method generally surpasses previous methods by a wide margin, yielding 98.6% in image-level anomaly detection, 96.6% in pixel-level anomaly localization, and an 87.0% PRO score. The Dimensionality Reduction block can choose critical features to distinguish between anomaly-free images and anomalous images. While choosing discriminative features, we also throw away the noise in the features, and it allows our method not to localize non-anomalous regions.

4.3 Limitations

In addition, we show some failure detection cases in Fig. 4, the anomaly type from top to bottom are: defective toothbrush, hole on hazelnut and scratch on capsule. We provide normal samples as a reference. One limitation is pixel-wise anomaly localization, for instance, defects on the toothbrush and hazelnut. The proposed method can locate abnormal regions but lack accurate localization of anomalous pixels. Another limitation is that it may miss subtle anomalies, such as scratches on the capsule.

Figure 4: Bad case of false detection type

4.4 Running Time

Running time is the other dimension we are interested in. The main purpose of dimensionality reduction is to retain the most discriminative features for anomaly detection. We measure the running time of the proposed method using the NVIDIA A100-PCIE-40 GB GPU with serial implementation. We list the corresponding running times and the performance of detection for each category in the MVTec in Table 3. Please notice that each category has a different number of test images and we record the average running time of each category.

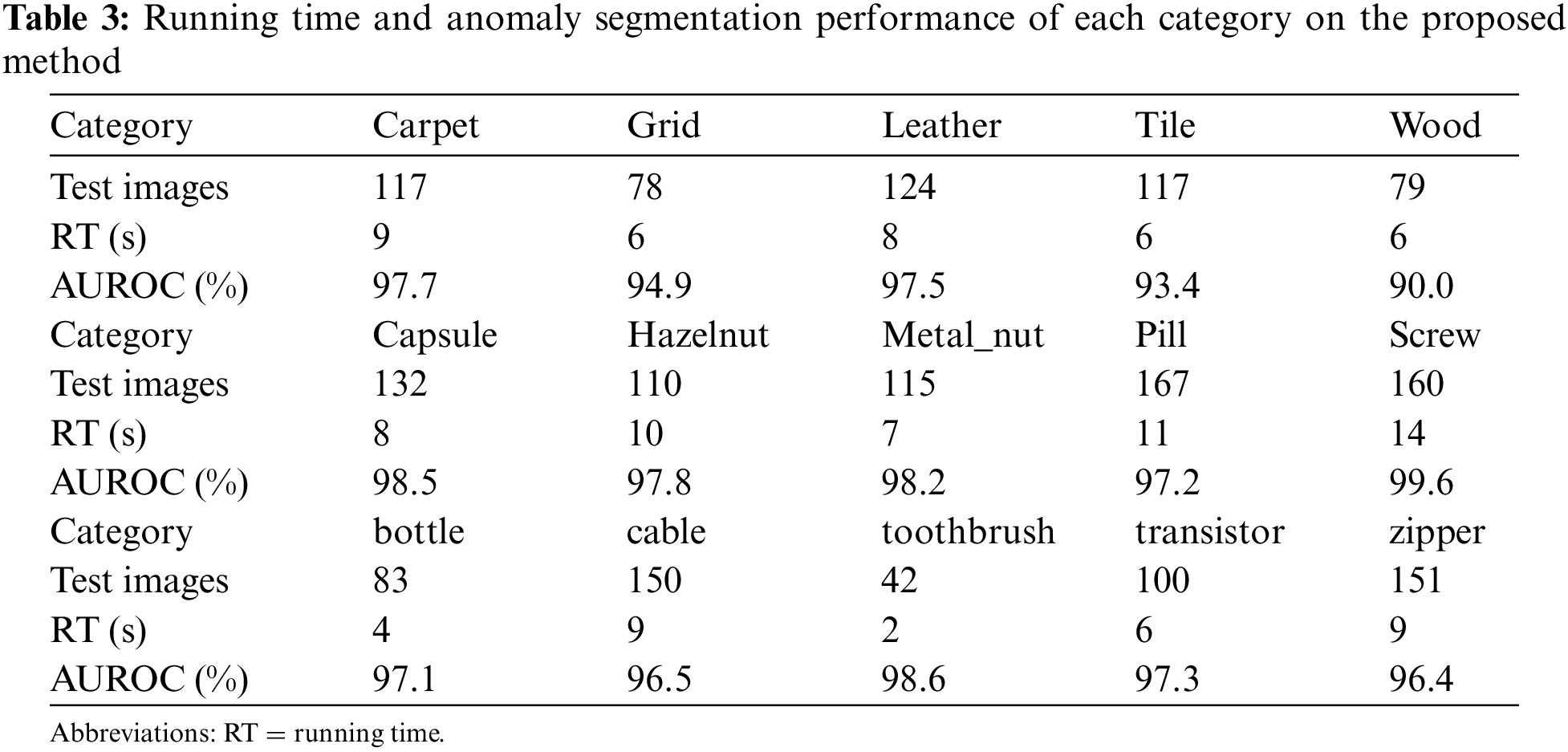
The proposed method uses EfficientNet-b4 pre-trained on ImageNet as a backbone, hence, we can focus more attention on the task of anomaly detection. The effectiveness of the proposed method suggests that it is better to use a pre-trained model than learn a model of normality from scratch using task-specific datasets.

4.5 Ablation Studies

We perform ablation studies on the MVTec AD dataset to answer the following questions: How much dimensionality reduction affects the performance of the proposed method, and which layer of the backbone provides the most information-rich features for anomaly detection?

4.5.1 Influence of Dimensionality Reduction

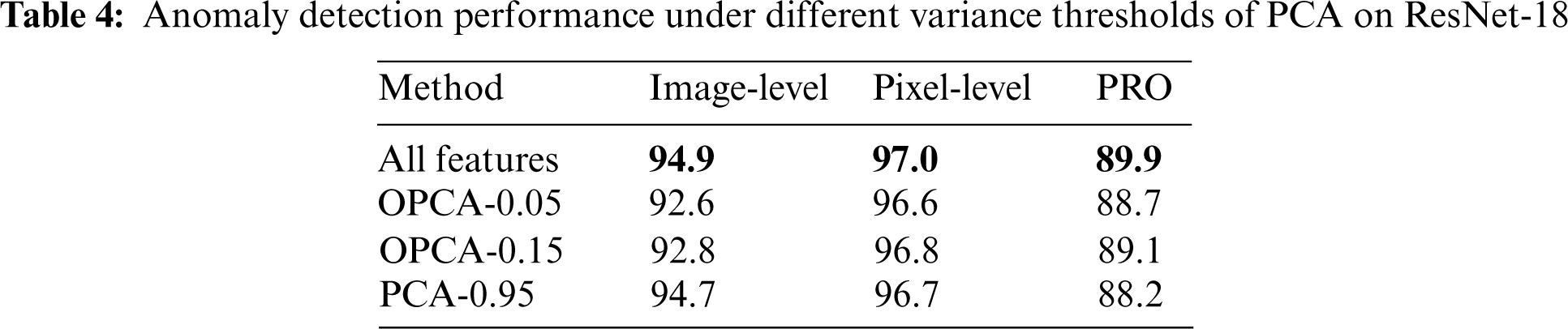
The goal of Dimensionality Reduction is to obtain appropriate features for the anomaly detection task and save computing time. First, we investigated the influence of anomaly detection on reducing partial features and using all features. The results on EfficientNet-b4 network are shown in Fig. 5. For instance, OPCA-0.05 means we retain principal components that account for 5% of the overall variance. Conversely, PCA-0.95 means we remove principal components that account for 5% of the total variance. Note that retaining an account of 5% of the variance can improve detection and localization performance.

Figure 5: Anomaly detection performance on EfficientNet-b4 network with different variance threshold

We experimented by using ResNet-18 to generate hierarchical convolution features for images to complete the experimental results. We use different layers of ResNet-18 to extract features using a default setting of 0∼3 layers (index from 0). The experimental results are shown in Table 4, and the best results are shown in boldface. Unlike the deep network, like the EfficientNet, shallow neural networks (non-deep networks) should use all features for the anomaly detection task. It can be explained that the shallow networks often extract simple features of the image, and filtrating partial features will easily lose the richer representation of the image and reduce the detection performance.

4.5.2 Network Hierarchy Selection

More global context can be achieved by higher the network hierarchy, but with the cost of reduced resolution and heavier ImageNet class bias. In Table 5, we show the performance of selecting a single layer of the EfficientNet-b4 network to extract features and using these features to detect and segment anomalies. We noticed that convolution features at different semantic levels could provide diverse and valuable information to detect anomalies. Features from layer five can achieve the best performance on detection, while features from layer four can give the best performance on localization.

5  Conclusion

In this study, we propose a novel framework for the challenging problem of unsupervised anomaly detection on the MVTec AD dataset. It comprehensively demonstrates that the principal components containing little variance in normal data are crucial for the anomaly detection task. Experimental results show that the proposed method can detect and locate anomalies quickly and effectively and have a great performance on the MVTec AD dataset. Furthermore, the proposed method uses the features extracted by the pre-trained CNN. We argue that using pre-trained CNN is a promising research direction in anomaly detection. Subsequent works can fine-tune the pre-trained network to obtain more discriminative and compact features and improve the performance of anomaly detection.

Acknowledgement: Thank my tutor for guiding my article and the help of my classmates.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declare that they have no conflicts of interest to report regarding the present study.

References

 1.  P. Bergmann, M. Fauser, D. Sattlegger and C. Steger, “Uninformed students: Student-teacher anomaly detection with discriminative latent embeddings,” in 2020 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 4182–4191, 2020. [Google Scholar]

 2.  N. Cohen and Y. Hoshen, “Sub-image anomaly detection with deep pyramid correspondences,” arXiv preprint arXiv:2005.02357, 2020. [Google Scholar]

 3.  P. Bergmann, M. Fauser, D. Sattlegger and C. Steger, “MVTec AD—A comprehensive real-world dataset for unsupervised anomaly detection,” in 2019 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 9584–9592, 2019. [Google Scholar]

 4.  C. Baur, B. Wiestler, S. Albarqouni and N. Navab, “Deep autoencoding models for unsupervised anomaly segmentation in brain MR images,” in Int. MICCAI Brainlesion Workshop, Granada, Spain, Springer, pp. 161–169, 2018. [Google Scholar]

 5.  W. Liu, W. Luo, D. Lian and S. Gao, “Future frame prediction for anomaly detection–A new baseline,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 6536–6545, 2018. [Google Scholar]

 6.  H. Park, J. Noh and B. Ham, “Learning memory-guided normality for anomaly detection,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 14372–14381, 2020. [Google Scholar]

 7.  B. Schölkopf, R. C. Williamson, A. Smola, J. Shawe-Taylor and J. Platt, “Support vector method for novelty detection,” Advances in Neural Information Processing Systems, vol. 12, pp. 582–588, 1999. [Google Scholar]

 8.  Y. Q. Chen, X. S. Zhou and T. S. Huang, “One-class SVM for learning in image retrieval,” in Proc. 2001 Int. Conf. on Image Processing, Thessaloniki, Greece, vol. 1, pp. 34–37, 2001. [Google Scholar]

 9.  L. Ruff, R. Vandermeulen, N. Goernitz, L. Deecke, S. A. Siddiqui et al., “Deep one-class classification,” in Int. Conf. on Machine Learning, Stockholm, Sweden, pp. 4393–4402, 2018. [Google Scholar]

10. J. Yi and S. Yoon, “Patch svdd: Patch-level svdd for anomaly detection and segmentation,” in Proc. of 15th Asian Conf. on Computer Vision, Kyoto, Japan, 2020. [Google Scholar]

11. C. L. Li, K. Sohn, J. Yoon and T. Pfister, “Cutpaste: Self supervised learning for anomaly detection and localization,” in 2021 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Nashville, TN, USA, pp. 9659–9669, 2021. [Google Scholar]

12. M. Sakurada and T. Yairi, “Anomaly detection using autoencoders with nonlinear dimensionality reduction,” in The MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis, New York, United States, pp. 4–11, 2014. [Google Scholar]

13. S. Akcay, A. Atapour-Abarghouei and T. P. Breckon, “GANomaly: Semi-supervised anomaly detection via adversarial training,” in 2018 14th Asian Conf. on Computer Vision, Perth, Australia, Springer, pp. 622–637, 2018. [Google Scholar]

14. S. Pidhorskyi, R. Almohsen and G. Doretto, “Generative probabilistic novelty detection with adversarial autoencoders,” in Advances in Neural Information Processing Systems, Cambridge, Massachusetts (USAvol. 31, 2018. [Google Scholar]

15. P. C. Mahalanobis, “On the generalised distance in statistics,” National Institute of Science of India, vol. 2, pp. 49–55, 1936. [Google Scholar]

16. D. M. Tax and R. P. Duin, “Support vector data description,” Machine Learning, vol. 54, no. 1, pp. 45–66, 2004. [Google Scholar]

17. J. Tack, S. Mo, J. Jeong and J. Shin, “CSI: Novelty detection via contrastive learning on distributionally shifted instances,” in Advances in Neural Information Processing Systems, Cambridge, Massachusetts (USAvol. 33, pp. 11839–11852, 2020. [Google Scholar]

18. D. P. Kingma and M. Welling, “Auto-encoding variational Bayes,” stat, vol. 1050, pp. 1, 2014. [Google Scholar]

19. D. Gong, L. Liu, V. Le, B. Saha, M. R. Mansour et al., “Memorizing normality to detect anomaly: Memory-augmented deep autoencoder for unsupervised anomaly detection,” in Proc. of the IEEE/CVF Int. Conf. on Computer Vision, Seoul, Korea (Southpp. 1705–1714, 2019. [Google Scholar]

20. T. W. Tang, W. H. Kuo, J. H. Lan, C. F. Ding, H. Hsu et al., “Anomaly detection neural network with dual auto-encoders GAN and its industrial inspection applications,” Sensors, vol. 20, no. 12, pp. 3336, 2020. [Google Scholar]

21. Y. Shi, J. Yang, and Z. Q. Qi, “Unsupervised anomaly segemntation via deep feature reconstruction,” Neurocomputing, vol. 424, pp. 9–22, 2021. [Google Scholar]

22. P. Perera, R. Nallapati and B. Xiang, “OCGAN: One-class novelty detection using GANs with constrained latent representations,” in 2019 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 2893–2901, 2019. [Google Scholar]

23. M. Sabokrou, M. Khalooei, M. Fathy and E. Adeli, “Adversarially learned one-class classifier for novelty detection,” in 2018 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 3379–3388, 2018. [Google Scholar]

24. D. Abati, A. Porrello, S. Calderara and R. Cucchiara, “Latent space autoregression for novelty detection,” in 2019 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 481–490, 2019. [Google Scholar]

25. X. Han, X. Chen and L. P. Liu, “GAN ensemble for anomaly detection,” arXiv preprint arXiv: 2012.07988, vol. 7, no. 8, 2020. [Google Scholar]

26. L. J. Latecki, A. Lazarevic and D. Pokra-jac, “Outlier detection with kernel density functions,” in Int. Workshop on Machine Learning and Data Mining in Pattern Recognition, Berlin, Heidelberg, Springer, pp. 61–75, 2007. [Google Scholar]

27. T. Defard, A. Setkov, A. Loesch and R. Audigier, “Padim: A patch distribution modeling framework for anomaly detection and segemntation,” in Int. Conf. on Pattern Recognition, Italy Milan, Springer, pp. 475–489, 2021. [Google Scholar]

28. M. Salehi, N. Sadjadi, S. Baselizadeh, M. H. Rohban and H. R. Rabiee, “Multiresolution knowledge distillation for anomaly detection,” in 2021 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Nashville, TN, USA, pp. 14897–14907, 2021. [Google Scholar]

29. D. P. Kingma and P. Dhariwal, “Glow: Generative flow with invertible 1 × 1 convolutions,” in Advances in Neural Information Processing Systems, Cambridge, Massachusetts (USAvol. 31, 2018. [Google Scholar]

30. M. Tan and Q. Le, “Efficientnet: Rethinking model scaling for convolutional neural networks,” in Int. Conference on Machine Learning. PMLR, pp. 6105–6114, 2019. [Google Scholar]

31. O. Ledoit and M. Wolf, “A well-conditioned estimator for large dimensional covariance matrices, ” Journal of Multivariate Analysis, vol. 88, no. 2, pp. 365–411, 2004. [Google Scholar]

32. M. Rudolph, B. Wandt and B. Rosenhahn, “Same same but DifferNet: Semi-supervised defect detection with normalizing flows,” in 2021 IEEE Winter Conf. on Applications of Computer Vision (WACV), Waikoloa, HI, USA, pp. 1906–1915, 2021. [Google Scholar]