 Open Access
Open Access
ARTICLE
La dilution urbaine au prisme de l’espace proxémique ; de la discontinuité au continuum des formes urbaines
Urban Dilution through the Prism of Proxemic Space; from Discontinuity to the Continuum of Urban Forms
Independent Researcher, Cergy, 95000, France
* Corresponding Author: Cyril Enault. Email:
Revue Internationale de Géomatique 2025, 34, 881-897. https://doi.org/10.32604/rig.2025.065740
Received 20 March 2025; Accepted 20 October 2025; Issue published 09 December 2025
RÉSUMÉ
Considérée souvent en France comme discontinue, la transition du bâti urbain-rural est largement envisagé comme continue au niveau international. Si la question de la forme urbaine n’est donc, aujourd’hui, plus en suspens du fait des très nombreuses études à l’échelle internationale, la limite urbain périurbain et rural isolé convient d’être néanmoins encore réinterrogée. La notion de proxémique développée dans les années 1970, pourrait permettre une résolution du problème. Utiliser cette notion pour revoir la métrique géographique pourrait permettre de réviser la limite urbain-campagne et raisonner alors sur un espace continu au-delà même des limites du périurbain.Abstract
Often considered discontinuous in France, the urban-rural transition is now widely considered continuous at the international level. While the question of urban form is no longer in abeyance, thanks to numerous international studies, the boundary between peri-urban and isolated rural areas needs to be re-examined. The notion of proxemics, developed in the 1970s, could provide a solution to this problem. Using this notion to revise geographical metrics could enable us to revise the urban-rural boundary and then reason about a continuous space beyond even peri-urban boundaries.MOTS CLÉS
Keywords
Le changement climatique est aujourd’hui au cœur de nos politiques d’aménagement comme le montre la loi dite « climat résilience » de 2021. Le « Zéro artificialisation nette », ou ZAN, est un de ces sujets traité par cette loi. Limiter l’étalement urbain est donc devenu pour les politiques une action structurante, comme le montre en Ile de France le Schéma Directeur de la région Ile de France (ou SDRIF) évoqué dans Delattre (2024) [1], Desjardins (2020) [2] et IPR (2020) [3]. Aussi, la question de l’étalement urbain s’impose donc comme un enjeu majeur de nos sociétés et en conséquence un sujet brûlant pour la géographie.
Comprendre ce phénomène, c’est d’abord étudier l’évolution des limites de la ville mais c’est aussi et surtout en définir la forme urbaine. Les géographes ne sont pas les seuls à avoir investis cette question. Depuis les années 1960, de nombreux auteurs économistes1 ou sociologues, ont utilisé la densité de population (Clark 1951 [4], Anas et al. 1998 [5]) Ensuite, les géographes ont mené des études sur ce phénomène par le bâti. L’analyse radiale par le bâti a longtemps été ignorée jusqu’au début des années 2000 (Guerois 2003 [6], Hirsh Weber 2000 [7]). C’est ainsi bien plus tard, avec le développement des bases de données satellite, que les études à grande échelle seront entreprises sur les grandes métropoles européennes (Guerois 2008 [8], Lemoy 2018 [9]), chinoises (Jiao 2015 [10], Lu et al. (2023) [11], Gao et al. (2025) [12]) pour finir par une étude à grande échelle internationale (Zheng et al. 2023 [13]). D’autres études ont appliqué cette même formule dite « urban land function » à un panel de 25 villes de l’Afrique (Xu et al. (2019) [14]).
Ce qui ressort de ces études est avant tout le profil relativement constant de l’ensemble des grandes agglomérations mais on pourra le retrouver également pour des villes de plus petite taille en France (Guerois 2003) [6].
Dans ces profils, la limite urbaine2, vue souvent comme une transition urbaine3, est jugée par certains auteurs comme discontinue (Guerois 2008 [8], Frankhauser 1994 [15], Hirsh et Weber 2000 [7]) alors que d’autres lui préfèrent la continuité (Enault 2003 [16], Jiao 2015 [10], Xu et al. 2019 [14] et Zheng and al 2023 [13]). Nous avons pu qualifier de dilution, cet espace flou entre ville centre et agglomération.
Par ailleurs, paraissant indépassable, la limite ville/campagne ou périurbain a longtemps eu du mal à être levée. Dans ces conditions, la discontinuité aurait pu être la seule voie pour analyser la forme urbaine.
Pourtant, Jiao (2015) propose une solution à ce problème en ajoutant un paramètre à la fonction de densité de bâti de base.
Aujourd’hui, nous apportons une nouvelle résolution à ce problème4 en introduisant une nouvelle notion ; la question de la proxémique, ce qui pourrait remplacer ce paramètre « c » ad hoc5 par un nouvel espace non euclidien6.
Le sujet est aujourd’hui bien connu par les psychologues et éthologues (1998 [17]) mais peu ou pas mobilisé par les géographes. Cette proxémique pourrait même être à l’origine d’un changement de paradigme en géographie. En ce sens, un espace proxémique7 pourrait-il donc ouvrir la voie à une nouvelle appréhension des formes urbaines ? Nous proposons de répondre à cette question en nous appuyant sur trois parties. Une première questionnera « l’urban land space » pour sa définition ; une seconde envisagera les problèmes de limite de l’urbain et enfin une troisième tentera d’introduire la proxémique pour redéfinir les formes urbaines.
2 Rappel sur la notion de dilution urbaine
2.1 Définition de la dilution urbaine
Dans ma thèse, j’introduis le concept de dilution et il recouvre deux phénomènes (Enault (2003) [16]).
Un premier ou le tissu urbain se fragmente spatialement, se morcèle dans le rural à mesure que l’on s’éloigne du centre de la ville.
Faire le choix de ce point comme reference, c’est envisage que l’ensemble de la ville, de son agglomeration et de son aire urbaine est plus ou moins dépendante de ce CBD (voir encadré 1).
Encadré 1: Pourquoi prendre le centre-ville des agglomérations comme point de référence ?
Dans la Nouvelle Économie Urbaine (NEU), la ville est concentrique de centre O et de rayon x. Elle est supposée comprendre l’ensemble des emplois en son centre le CBD (central Business District) (et cela que ce soit pour les villes américaines, asiatiques ou europénnes). Notons que dans ce modèle l’ensemble des habitants de la ville est censé vivre en périphérie et travailler dans ce centre.
Certes cette configuration de ville monocentrique est exagagérée, dans le monde, mais elle reste relativement vraie pour un grand nombre de villes françaises. Aussi, le CBD ou centre ville reste un lieu de pouvoir, de decision économique et polarise grandement l’ensemble de l’espace. Il est donc raisonnable de se reporter à ce point pour analyser l’ensemble de l’espace et plus particulièrement la forme urbaine donc la densité de bâti. Il est à noter que ce genre d’analyse est produite par les économistes pour la densité de population, et cela depuis les années 1960.
Un second, qui est un processus temporel par lequel la ville à la fois s’étale, mais en même temps se fragmente.
En cela, il n’existe pas véritablement de limite de la ville sous la forme d’une ligne mais, a priori, un ensemble de ruptures sous la forme d’une transition ville campagne, une sorte de zone tampon.
Notons que cette délimitation de l’espace peut être tout à fait complémentaire8 avec le zonage administratif de l’INSEE autrefois en ZAU (Zonage en aire urbaine) devenu aujourd’hui AAV (aires d’attraction des villes). La réalité qui sera exposé dans cet article recouvre donc partiellement le zonage de l’INSEE pour lequel on évalue la polarisation des villes sur les campagnes périurbaines9.
Dans sa partie purement statique, la dilution urbaine peut donc être appréhendée comme une probabilité d’existence d’espace urbain par rapport à la totalité de l’espace d’une couronne.
2.2 Expression de « l’urban-land density function » ou de la dilution
Pour modéliser cette probabilité10, le plus commun est d’employer la courbe logistique (largement ou ses variantes (Enault 2003)11. Le choix, pour la densité de bâti, a été celui de Zheng and al Formule (2) (2023) [13].
Avec Di(x) dilution ou densité de bâti, x la distance au centre de la ville, N le niveau de saturation indépassable (par défaut 100 si on raisonne en pourcentage et sinon 1), w le gradient de pente du modèle logistique et enfin p autre paramètre à ajuster. Remarquons que la fonction de Jiao (2015) [10] reprise par la suite dans une grande quantité d’articles était quasiment identique à l’exception du paramètre « c » qui permet l’ajustement sur le périurbain12.
Cette fonction est alors:
Avec Di(x), la densité de bâti, notée f(x) dans les articles de Jiao (2015 [10], 2023 [13]) «c» le seuil du périurbain, N = 1 et D et α, deux paramètres:
Ainsi, on passe d’un espace à 100% urbain à proximité du centre à un espace fondamentalement rural où la densité de surface bâtie tend vers 0 (dans le cas de dilution) ou vers un seuil « c » (dans le cas de urban-land function Jiao 2015).
Pour parvenir à la fonction de base (sans le périurbain: urbain pur), il suffit d’éliminer le « c » dans la fonction.
Comme D et α sont des paramètres, il est possible d’exprimer autrement cette Formule (2). On pose alors 2α/D = w et α = p et on obtient exactement la fonction (1).
On peut donc représenter graphiquement cette fonction (1) sous la forme suivante (voir Fig. 1).
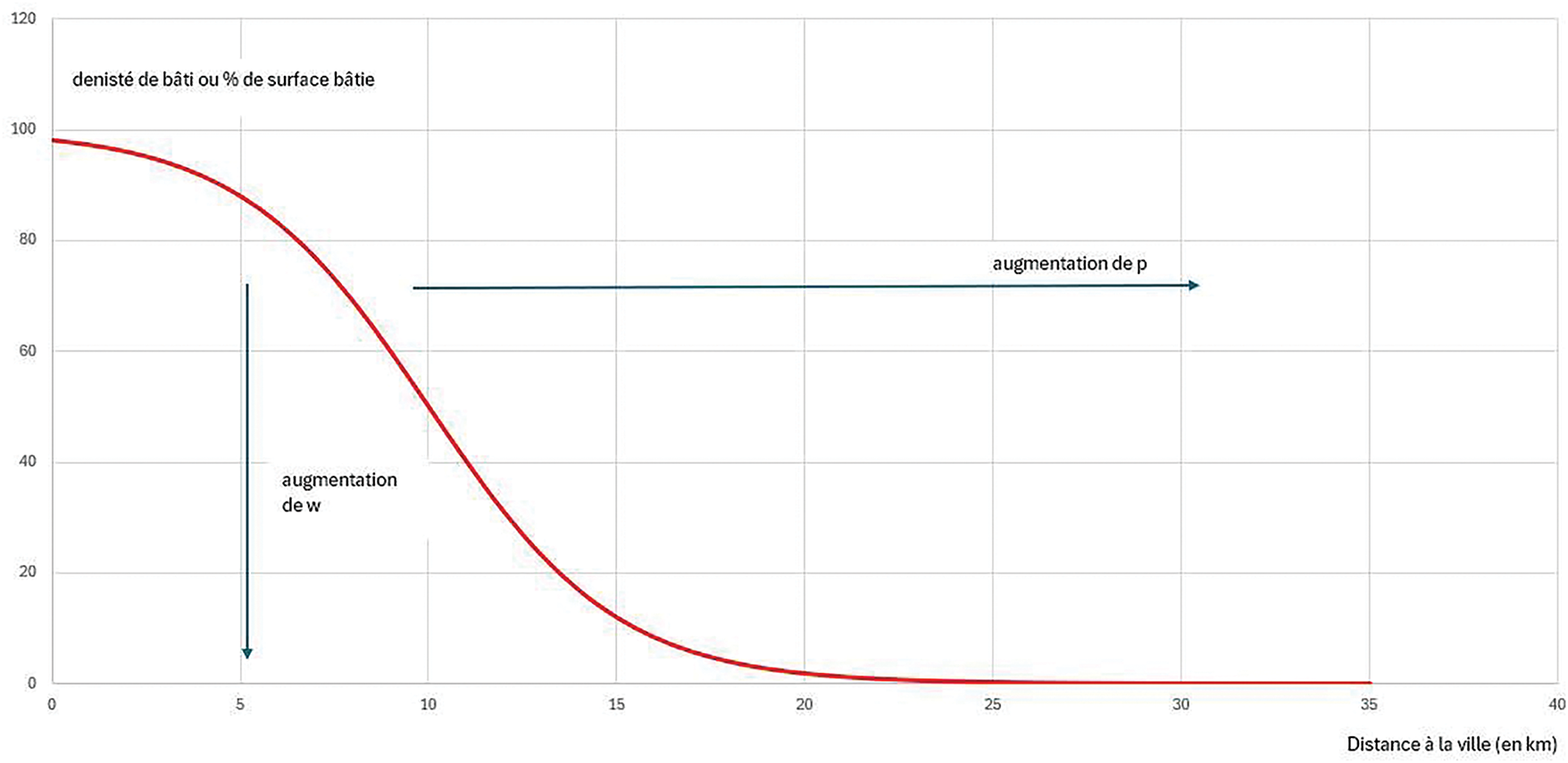
Figure 1: Courbe logistique
On obtient donc une courbe en S mais on lui préfère souvent sa transformation sous la forme d’un rapport dit LOGIT.
Ce rapport LOGIT est donc une droite. Tout l’intérêt de la suite sera d’analyser les ruptures de cette droite ou de proposer une solution sous forme de courbe.
Aussi, quand on analyse la dilution du bâti d’une ville on utilise ce rapport pour mettre en évidence les ruptures au niveau de l’espace. On dispose alors d’un nuage de points étiré selon plusieurs segments de droite.
C’est précisément ce que nous montrerons avec les données de bâti pour trois villes françaises.
3 La dilution entre ville et campagne: un problème de limite du phénomène urbain
3.1 Les données utilisées pour l’analyse de la densité de bâti
Guerois, en 2003 [6], les données les plus accessibles étaient celles de Corine Land Cover. Il s’agit de cartographie de l’Europe à des échelles médianes qui couvrent la plupart des grandes villes européennes.
On y trouve les modes d’occupation du sol rangés en 5 classes, 15 classes, 44 classes ou 50 classes.
Une simple sélection permet de retenir les espaces artificialisés.
L’auteur propose, alors, dans sa thèse, une analyse fouillée et comparative de plusieurs profils de capitales européennes pour leur surface bâtie.
Jiao, en 2015 utilise, quant à lui, les données des Landsat de 1990, 2000 et 2010 pour suivre l’évolution des agglomérations chinoises.
Dans notre thèse, nous nous intéressons à des données des années 2000 et historiques sur une agglomération et son aire urbaine Dijon. Ces données sont issues de BDTOPO IGN mais également d’autres sources plus anciennes comme des plans historiques remontant à 1050 pour le plus ancien.
3.2 Forme urbaine et description des limites
La question ici en suspens est celle des limites urbaines. La densité de bâti est-elle une voie pour cerner la ou les limites urbaines ? Nous nous proposons de répondre à cette question en nous appuyant sur trois exemples de trois villes de taille très différente: Paris, Bordeaux et Limoges. L’idée qui est alors derrière est de cerner les différences de limite (en termes d’éloignement à la ville) en fonction des tailles des agglomérations (10 millions, 1 million et 200 000)13.
Si dans les années 2000, le défi de cette analyse pouvait résulter de l’acquisition des données, ce n’est plus le cas actuellement. En effet, les progrès ont été importants pour Corine Land Cover qui donne aujourd’hui une résolution assez fine. Toutes les villes européennes sont donc accessibles. Nous aurions tout aussi bien pu prendre les données de BDTOPO (également en accès libre et tout aussi fiables) mais ces dernières sont limitées par les frontières régionales or nous souhaitions l’ensemble des données en auréoles concentriques autour des agglomérations sur de vastes superficies, principalement pour Paris (dépassant ainsi les limites de l’Ile de France). Pour ce motif, la continuité offerte par Corine Land Cover nous paraissait plus intéressante.
L’idée est donc de retenir des espaces urbains et périurbains autour des centres des agglomérations (100 km pour Paris, 50 km pour Limoges et 35 km pour Bordeaux).
Le choix de la distance est conditionné par l’absence d’autres agglomérations de grande taille à proximité pour perturber le modèle14.
Pour mettre en évidence ces limites à l’échelle de l’espace urbain, nous utilisons le rapport LOGIT (3).
Dès lors, les différentes limites font apparaitre 3 couronnes (dont découleront trois segments de droite dont le dernier (rural isolé) pourra ne pas être systématique présent). Cette analyse discontinue repose pour partie sur le profil de Pumain et Guerois (2008) auquel nous ajoutons le rural isolé (voir Fig. 2).
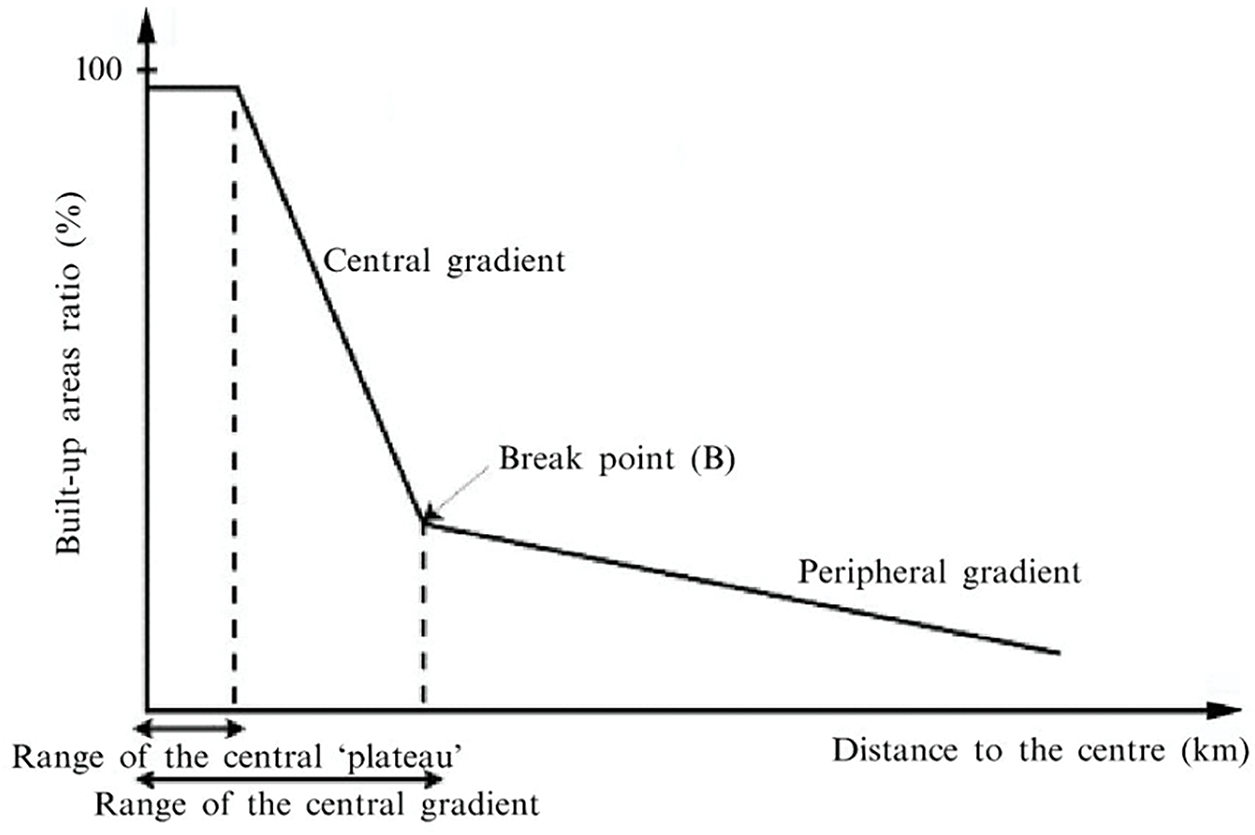
Figure 2: profil de la densité de bâti (avant transformation en LOGIT) du centre-ville au périurbain (Pumain Guerois 2008)
Pour obtenir le LOGIT de la densité de bâti, il convient de prendre le logarithme du rapport (densité de bâti/(100 — densité de bâti) si la densité de bâti est en pourcentage. On obtient alors un nuage de points s’étirant le long de segments de droites. On définira alors ces segments de droites selon les termes de ce graphique théorique15 (Fig. 3):

Figure 3: Profil du LOGIT de densité de bâti en fonction de la distance à la ville
A la lecture de ces graphiques se pose ensuite la question du centre. Comment le choisir ? La ville doit-elle être considérée comme monocentrique ?
Cette question a un réel sens dans la mesure où certaines agglomérations sont formées par plusieurs noyaux. Pour Zheng et al. (2023) ou Jiao (2015), une solution est trouvée par l’usage de multiples couronnes. Cette interrogation est toutefois moins pertinente pour les villes à un seul noyaux historique. Dans ces cas précis, le centre est avant tout le lieu de vie, le centre des activités (CBD) qui la plupart du temps dans les villes européennes se double avec le centre historique.
Pour les villes que nous étudierons c’est le cas, le centre sera aussi le cœur du noyau historique. C’est donc à partir de ce centre que nous analyserons les différentes couronnes concentriques. Aussi, à la lecture des trois graphiques suivants et de la figure théorique (Figs. 3–6)16, on constate que l’espace urbain est constitué de 3 couronnes concentriques17:
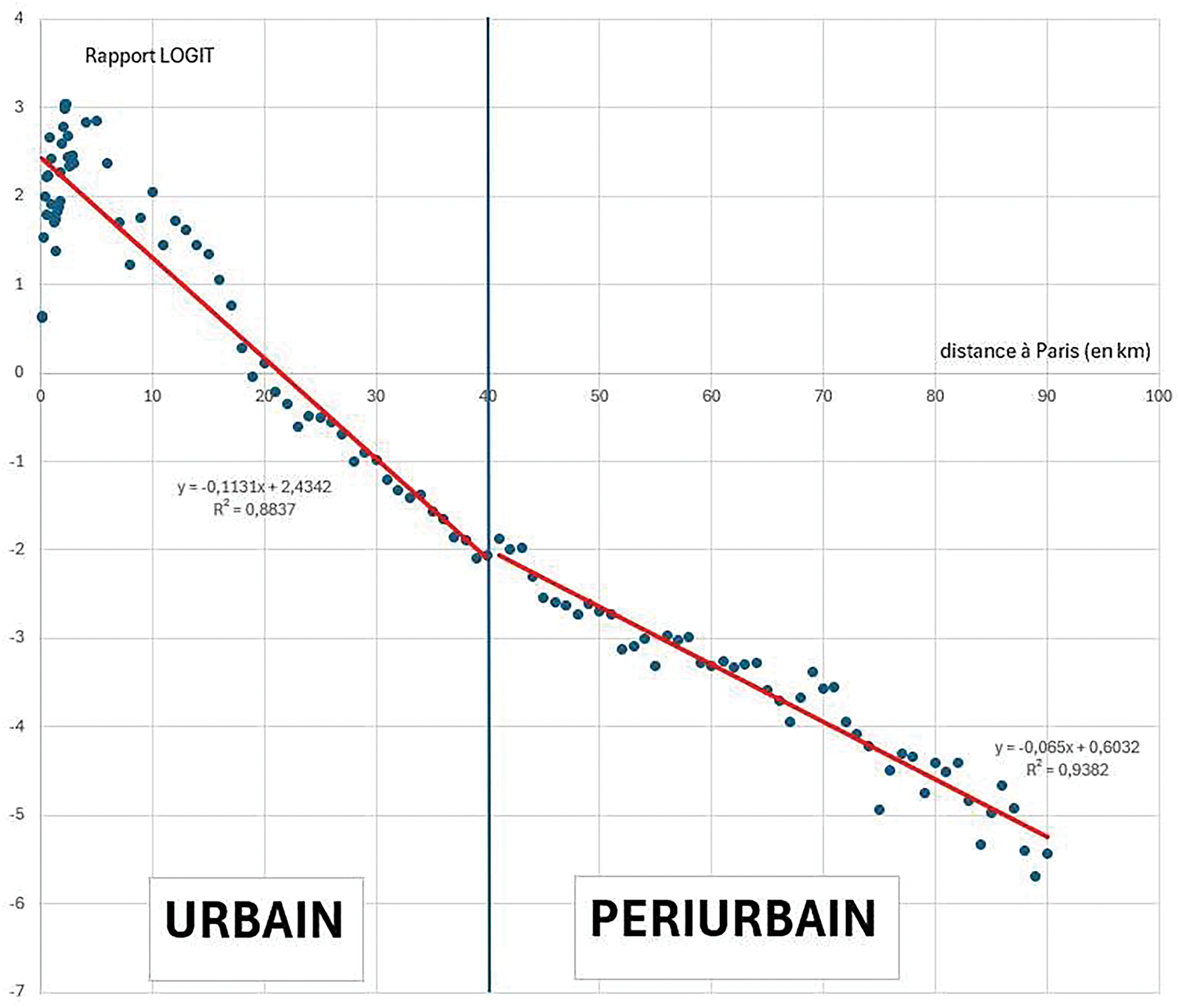
Figure 4: Discontinuité ville campagne pour les couronnes autour de Paris
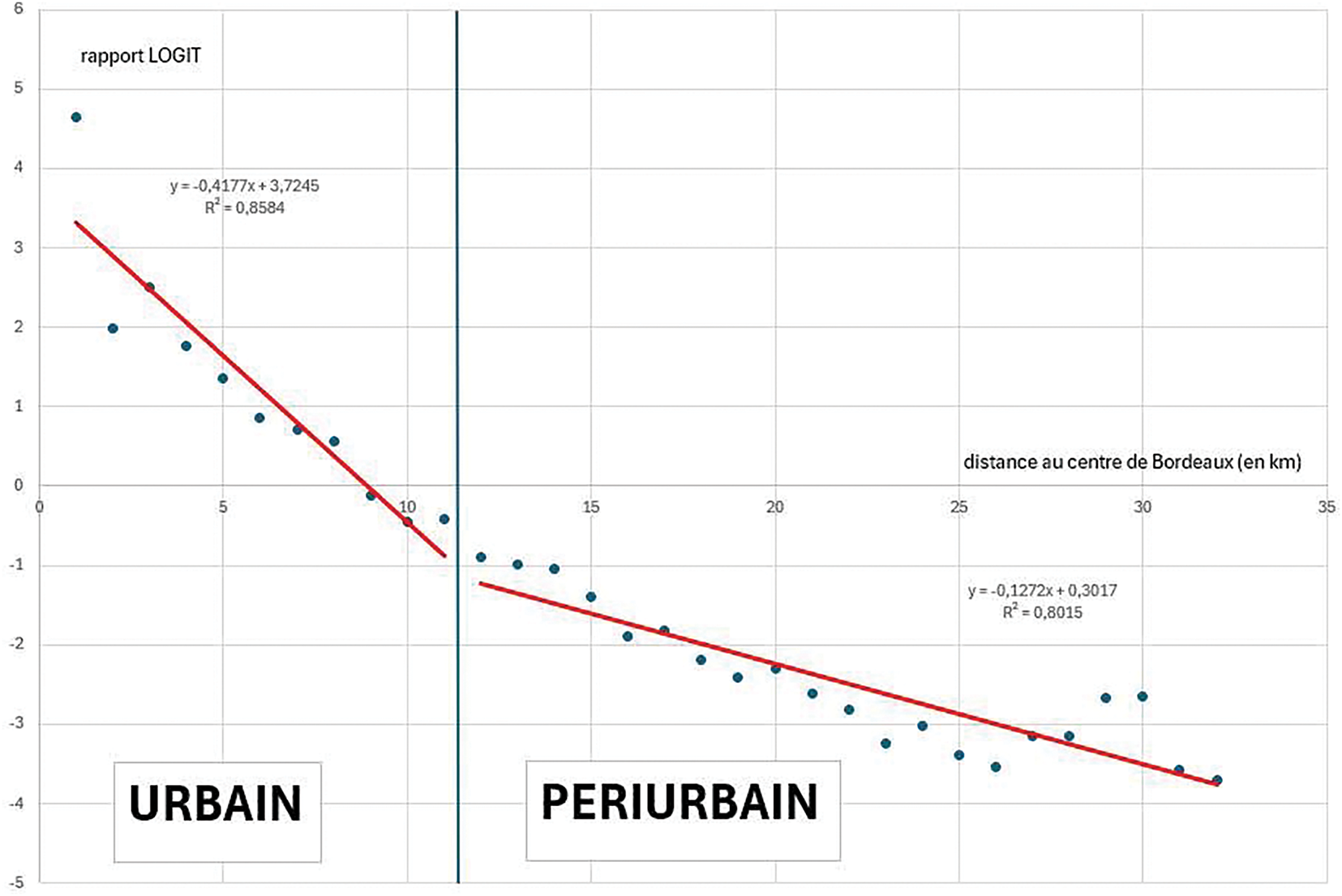
Figure 5: Discontinuité ville campagne pour les couronnes autour de Bordeaux
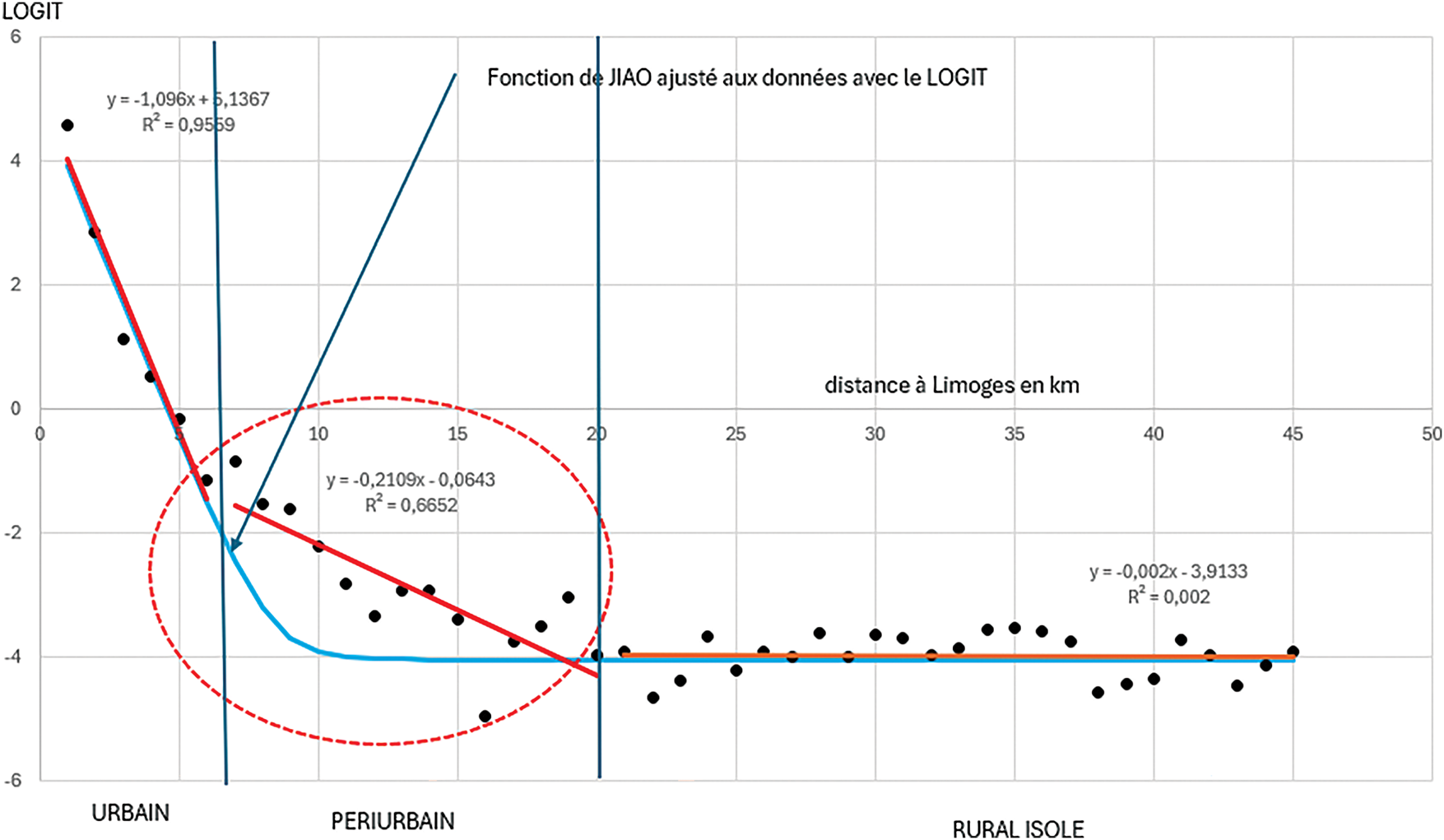
Figure 6: Discontinuités ville campagne pour les couronnes autour de Limoges
La première, et la plus proche du centre, est purement urbaine. Il s’agit du centre-ville et de son agglomération.
La seconde apparait après une première rupture de forme. Elle est caractérisée par un habitat plus diffus et fragmenté. Il s’agit essentiellement de villages ou de petites agglomérations. Cela forme la partie périurbaine.
Enfin, au-delà d’une seconde rupture, se trouve le rural isolé qui n’est alors plus polarisé par l’agglomération.
Ces trois couronnes varient en taille et en forme en fonction de la grandeur du pôle urbain. Plus la ville est importante, plus grandes seront les couronnes urbaines et périurbaines. Dans le cas de Paris, on a un rapport LOGIT qui diminue en pente forte avec une première limite urbain périurbain à 40 km18 (limite des villes nouvelles de l’Ile de France). Comme la pente du LOGIT sur le périurbain reste forte, cela signifie que cette couronne est très fortement polarisée. Sur la distance choisie, la dernière couronne (rural isolée) n’apparait pas car elle se situe plus loin de Paris.
Pour Bordeaux, la limite urbain-périurbain est à 12 km avec un espace périurbain polarisé au-delà de 35 km. Là encore, la couronne, rural isolé, n’est pas présente, car située au-delà de 35 km de Bordeaux.
Enfin, dans le cas de Limoges, cette limite urbain-périurbain est à 8 km avec un périurbain s’étendant jusqu’à 23 km et une nouvelle rupture apparait ensuite avant le rural isolé. Le rural isolé est bien visible car il n’y a quasiment plus de pente sur le rapport LOGIT ; l’espace n’est plus polarisé.
A la lumière de la Fig. 6 (qui présentait les 3 zones urbain, périurbain et rural isolé), on constate que la fonction de Jiao avec le paramètre « c » est parfaitement ajustée au domaine urbain et au rural isolé. En revanche, il convient beaucoup moins bien pour le périurbain. En somme, ce modèle se comporte comme si la transition douce était ignorée pour produire une rupture plus nette que dans la réalité.
Ainsi, que ce soit pour l’ajustement par droites sécantes ou par la fonction de Jiao, le résultat ne parait pas optimale. Pourquoi ne pas proposer d’autres solutions comme changer de métrique.
4 Vers une transition continue ville campagne: l’impact d’une révision de la métrique géographique
Le passage d’un espace euclidien à un espace non euclidien n’est pas nouveau pour le géographe. C’est dans les années 1970 que l’on initia ce mouvement avec les études portant sur les distances temps. D’autres auteurs ont pu, par la suite, poursuivre ce type de travaux (Lhostis 2014 [18]). Peguy (2000 [19]), quant à lui propose de substituer les distances physiques par des distances temps dans les modèles de densité de population afin de faire disparaitre les problèmes de limites urbain- périurbain notamment avec le modèle de Bussière (1975)19. C’est bien dans cet esprit, que nous proposons de raisonner sur les distances perçues pour le bâti.
Comment doit-on alors appréhender ce nouveau type d’espace ?
Pour définir l’espace égocentré, nous nous reporterons aux travaux d’A. Moles (1998) [17] dont sont issus ces deux schémas (Fig. 7).
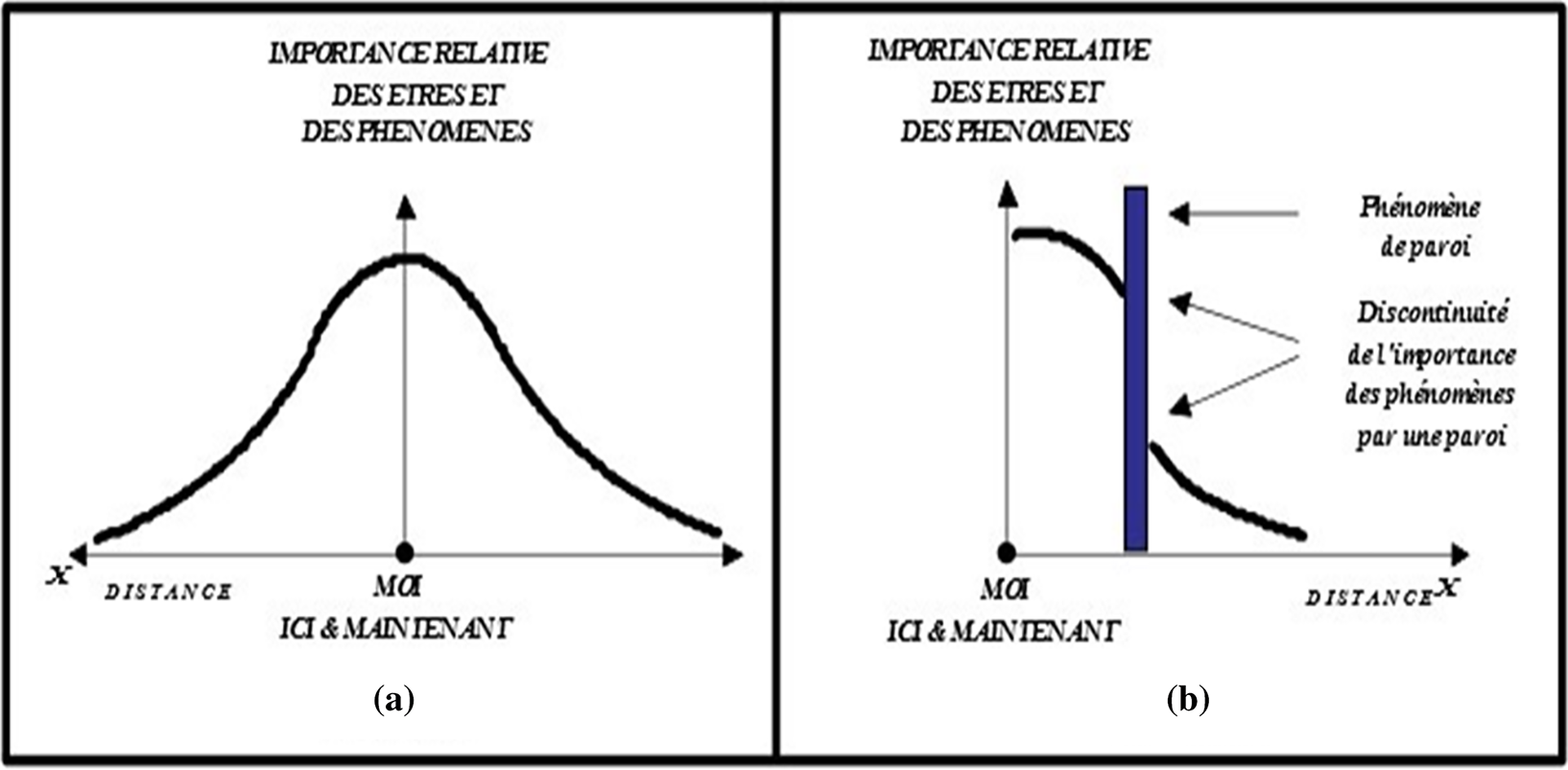
Figure 7: La Loi proxémique (a) et le phénomène de paroi (b) de Moles et Rohmer (1998)
A partir de cela, il devient possible d’extrapoler toute une construction mathématique.
4.1 Définition de l’espace perçu (égocentré)
En partant de ces principes théoriques de la proxémique, il est possible de définir toute une mathématique de la perception de l’espace à partir d’un ou plusieurs points donnés. Moles en 1998 esquisse une solution technique plus concrète au problème par ce graphique (Fig. 8):
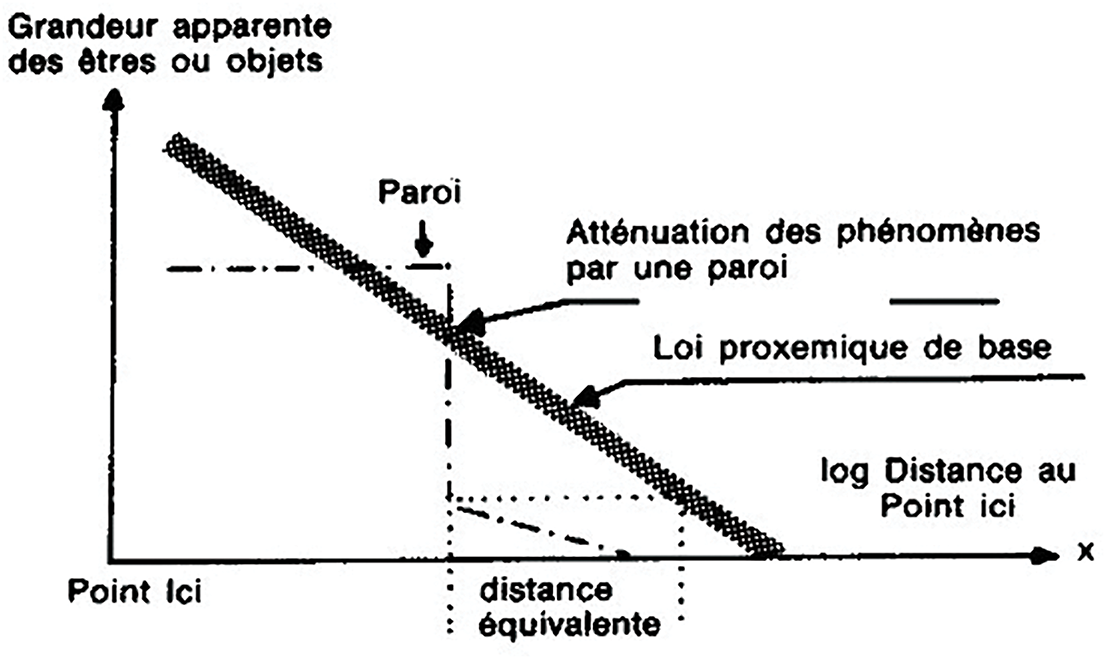
Figure 8: Valeur du mètre ou taille des espaces en fonction de la distance au point de de vue ici source Moles et Rhomer (1998)
Cette solution conduit donc à une expression de type20:
Avec L Valeur du mètre au point de vue Ici, r gradient de réduction du mètre et x distance au point de vue Ici.
Notons que dans cette expression on trouvera deux problèmes majeurs qui conduisent à faire un autre choix pour cette fonction.
La valeur du mètre L au point de de vue Ici tend vers l’infini, ce qui n’est pas possible.
La valeur du mètre coupe l’axe des abscisses à une distance x donnée alors que cette dernière devrait tendre vers 0.
C’est pour ces raisons que nous avons redéfini l’espace égocentré (2024a [20]) en vue de déformations cartographiques21.
Sur le principe, il repose donc sur deux éléments:
Un espace autocentré sur un lieu22 (un individu, un lieu où le centre d’une ville par exemple).
Un espace dont les métriques se réduisent à mesure que l’on s’éloigne de ce centre pour tendre vers 0 selon une loi dite d’airain de la proxémique:
Avec L(x) valeur du mètre perçu, L valeur du mètre au centre par défaut, r gradient de perception ou facteur de réduction du mètre23 et enfin x distance physique au centre. Notons que ce type d’espace existe déjà depuis le début du 20ième siècle en mathématique sous le nom de «disque de Poincaré» (Guys 2005 [21])24. L’espace est alors dit « hyperbolique ». Certains artistes ont cherché à représenter ce type d’espace dans le plan euclidien comme (Escher)25.
Appliquer cet espace à un unique individu est toujours possible mais il a été montré par Enault (2024a) également que la déformation est semblable pour un espace urbain avec comme centre du disque de déformation, le centre-ville (voir encadré 2).
Encadré 2: Passer de la proxémique individuelle à la proxémique à l’échelle d’une ville, le profil moyen.
L’idée de cet encadré est de montrer que si chaque individu a une vision proxémique spécifique, il est possible mathématiquement de démontrer que cette le profil moyen urbain repose sur une agrégation des profils individuelles.
Prenons d’abord comme hypothèse que la ville est de centre O et de rayon x. Alors, il devient possible de projeter la densité de population sur un segment radial pour retrouver une courbe indiquant la densité de population en fonction de la distance au centre x.
S’il existe de nombreuses lois pour mettre en relation la distance avec la densité dans les villes, la plus courante reste celle du modèle dit de Clark (1951) (Fig. 9).
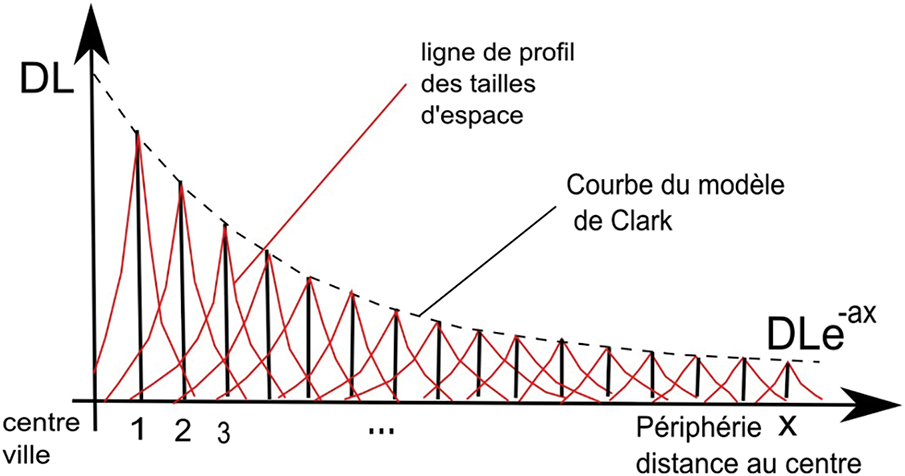
Figure 9: Tailles d’espace et modèle de Clark
Avec D(x) densité de population à une distance x du centre, D, densité extrapolée au centre et α, gradient de densité.
Les tailles d’espace représentent les métriques du collectif pour une distance donnée du centre-ville.
Pour chaque couronne de distance x, soit à chaque unité de distance, on somme le nombre d’individus.
Ainsi, le groupe d’individus à une distance x du centre est par nature:
Il est à noter que cette simplification est une des seules possibles pour pouvoir combiner le collectif avec la métrique individuelle, elle-même radiale. Par ailleurs, la solution du modèle de Clark est largement déployée dans la littérature économique pour analyser les formes urbaines. En cela, la ville est simplifiée mais représentative dans sa morphologie. D’autres options non formelles n’offriraient pas la possibilité d’aller vers une modélisation de la forme urbaine. Quant au choix du modèle de Clark au regard d’autres solutions plus complexes comme le modèle à cratère de densité nous le justifions par l’usage du modèle de Clark étendue (en version polynucléaire) pour les villes polycentriques qui forment aujourd’hui les types urbains les plus courants dans le monde.
Pour poursuivre notre démonstration, pour chaque couronne, il existe une métrique décroissante de la distance au centre qui décroit ensuite à la distance x − 1 et x + 1 selon Lr
En somme, si l’on désire obtenir la somme des métriques pour une distance x, il faut sommer toutes les métriques des autre distance x + ou − i.
Soit:
On obtient alors:
Ainsi S représente la métrique décroissante d’un groupe d’individus pour une distance x du centre de la ville.
Il est possible de trouver ensuite la distance dite égocentrée ou proxémique séparant le centre-ville à la distance physique x du centre.
Pour cela il faut sommer toutes les tailles d’espace du centre de la ville vers la périphérie. L’opération est plus complexe que précédemment.
On obtient avec sommes des termes d’une suite géométrique:
On retiendra alors, en simplifiant par A = D/(1 − r)
Cette fonction complexe en apparence donne en réalité une courbe simple qui ressemble à s’y méprendre à la courbe de la fonction (6).
Cette fonction tout à fait équivalente (6) sera donc reprise pour la suite de notre propos.
On utilise alors préférentiellement la fonction suivante pour définir cette fois ci la distance perçue entre le centre-ville et la distance physique x de la ville26.
Dans (6), X(x) est la distance perçue entre le centre-ville et la distance x physique du centre27.
Notons que cette métrique n’est pas uniquement le fait du centre et est donc naturellement adoptée par les habitants du centre de la ville mais également est reportée tout le long de la périphérie par des fractionnements de la distance physique. En somme tout l’espace urbain est affecté par cette métrique. Pour toute distance physique x correspond une distance perçue X(x).
4.2 Nouvelle formulation de la dilution avec la perception
La distance perçue (6) est ainsi une nouvelle métrique de l’espace. Si on prend comme principe que l’ensemble de ce qui est produit par l’homme résulte des métriques de son esprit, alors la production géographique pourrait reposer sur les métriques de l’esprit, à savoir celle de la perception.
Nous avions vu précédemment que la forme urbaine par le bâti pouvait être réduite à l’équation (3).
Remplaçons donc dans cette équation la distance physique x par une distance perçue X(x) soit (6).
On obtient alors:
Quand on calcule le rapport LOGIT avec (7), on n’obtient plus une ligne droite mais une courbe.
Cette dernière pourrait coïncider avec nos nuages de points pour le bâti pour nos trois villes.
4.3 La limite urbaine continue avec l’espace perçu
A partir de (7), il convient donc d’ajuster r, p et w pour faire coïncider le plus possible le nuage de points avec notre courbe.
Les Figs. 10–12 montrent un excellent ajustement pour le LOGIT et plus encore pour la densité de bâti.
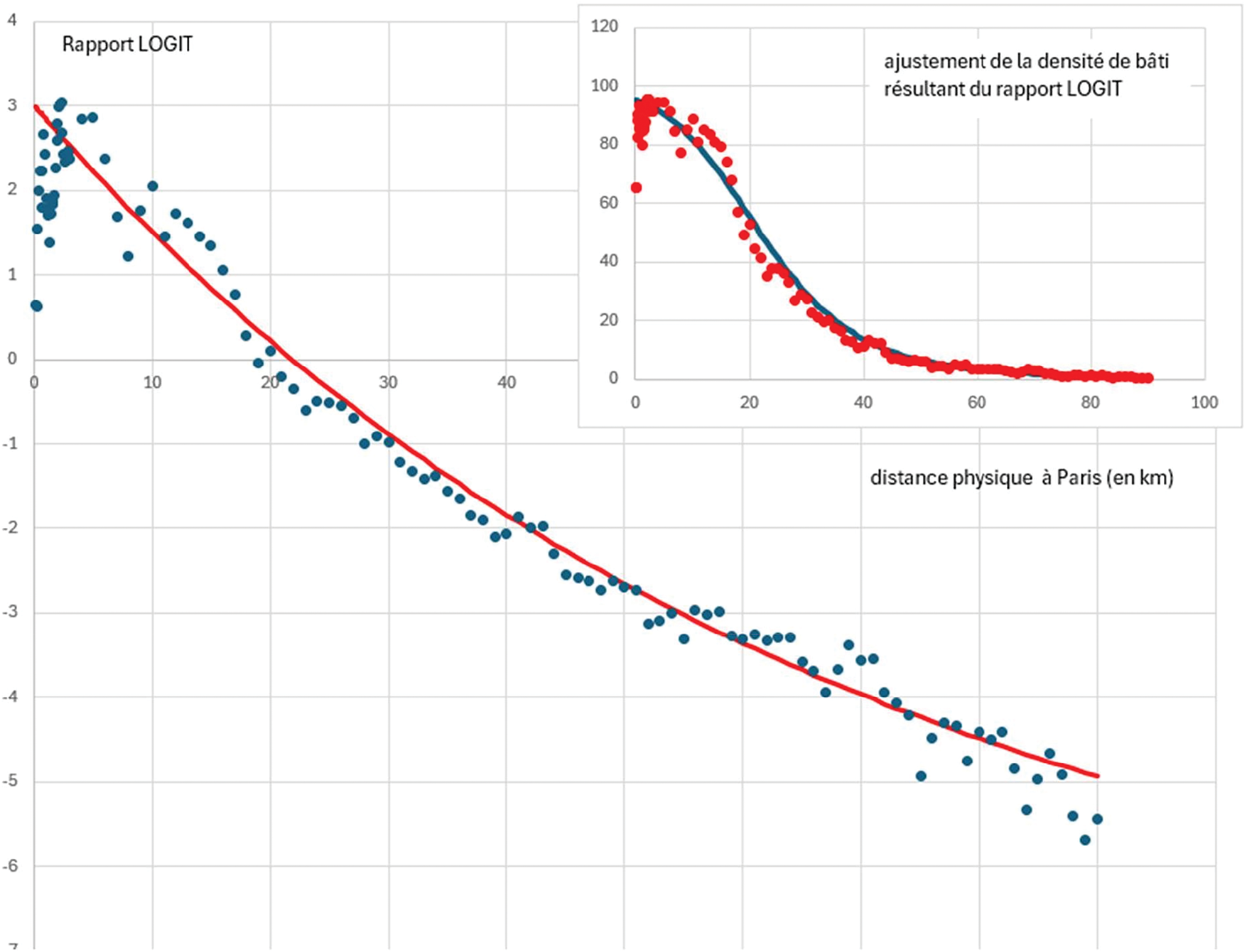
Figure 10: Ajustement du rapport LOGIT avec la distance physique à Paris selon la Formule (7)
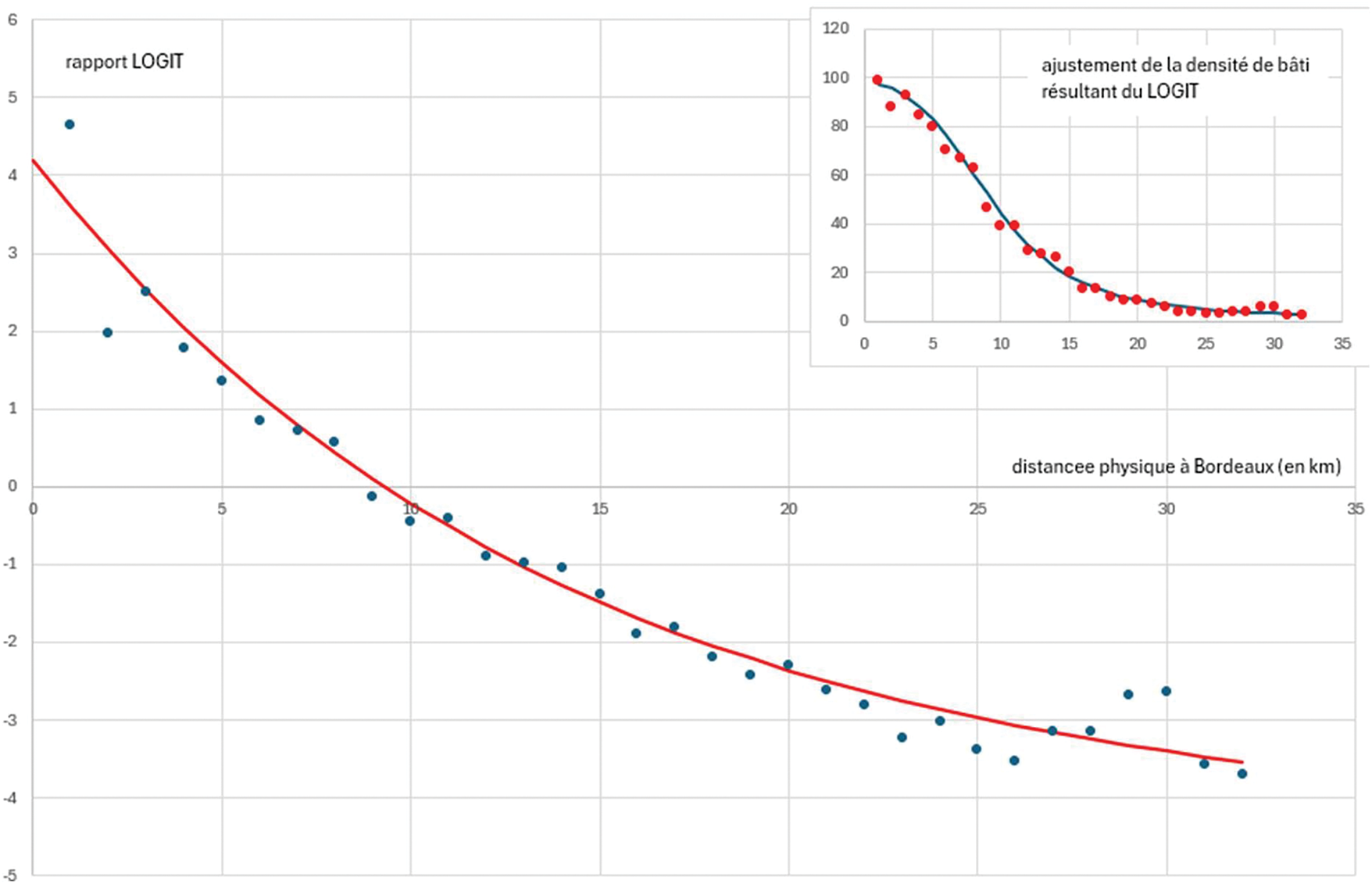
Figure 11: Ajustement du rapport LOGIT avec la distance physique à Bordeaux selon la Formule (7)
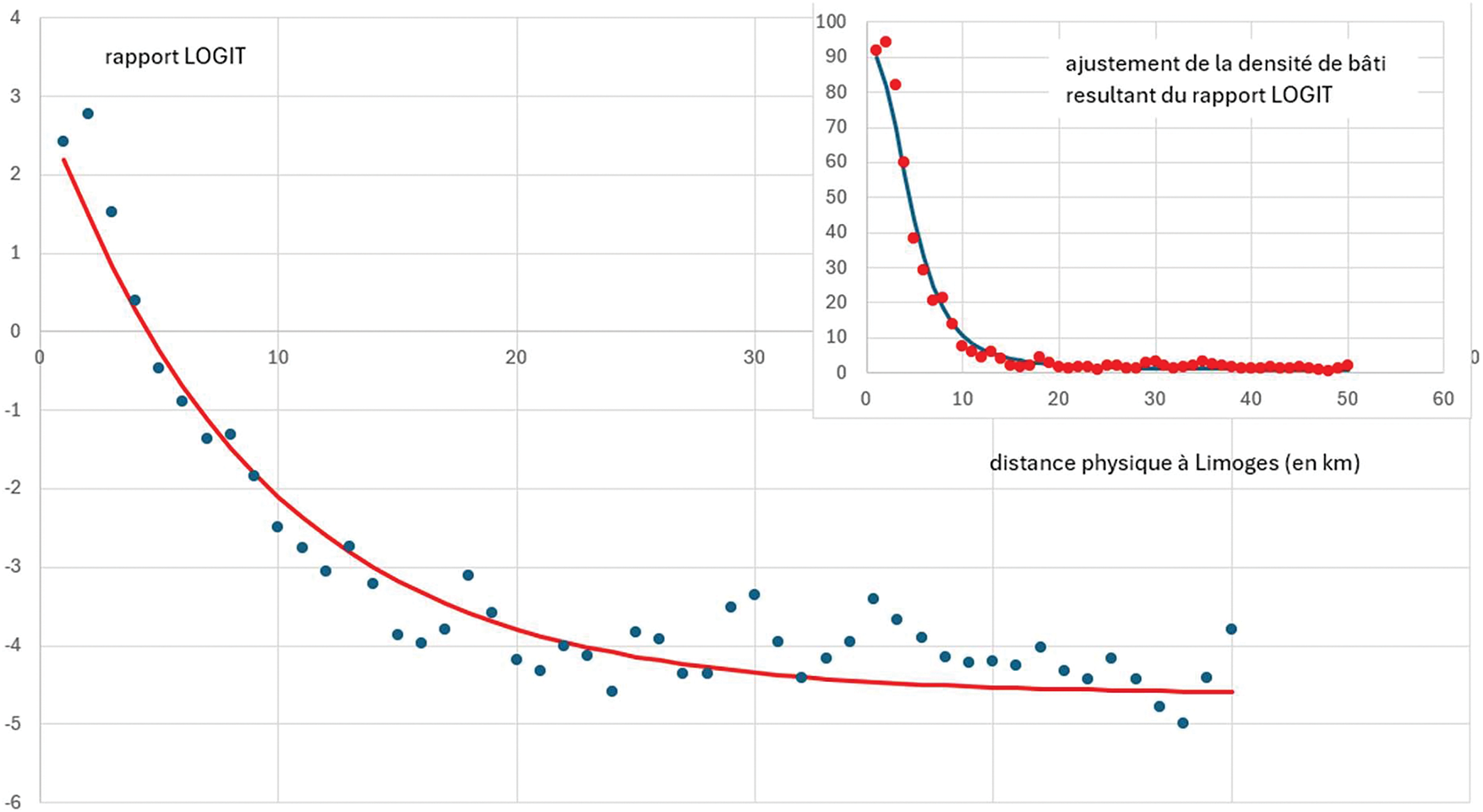
Figure 12: Ajustement du rapport LOGIT avec la distance physique à Limoges selon la Formule (7)
Sur le principe, l’ajustement de notre nouveau modèle (7) semble satisfaisant mais il est difficile de juger en l’absence d’indicateur.
Pour mieux comprendre l’intérêt de ce modèle, il convient de comparer l’ajustement par les droites sécantes du début, l’ajustement par la fonction de Jiao (2015) et enfin notre modèle.
Nous prenons ici le calcul du R2 (coefficient de détermination) dans sa formule générale:
Dans cette formule, yi désigne les valeurs y du nuage de points,

Nous concluons donc en montrant que la moyenne des R² des droites sécantes représente sans doute la méthode la moins intéressante avec surtout un R² de 0.1 pour Limoges pour la périphérie.
Autant la fonction s’ajuste correctement pour la partie urbaine et rural isolé, autant le décrochement est total dès lors que l’on rentre dans le périurbain ; la transition douce n’est pas prise en compte.
Ce n’est pas le cas pour notre modèle proxémique et c’est du reste le principal intérêt de ce modèle ; intégrer l’urbain et le rural dans son ensemble en modélisant l’ensemble de transition ville campagne. C’est le seul modèle étudié ici qui permet ce résultat.
Si l’analyse des formes urbaines par le bâti est connue depuis la fin des années 1990, l’analyse radiale par les densités de bâti est, quant à elle, bien plus récente. Les premières études remontent au début des années 2000 mais il faudra attendre 2015 pour que ce type de travaux soit généralisé dans le monde entier. Aujourd’hui, deux courants existent: — L’approche de la densité de bâti discontinue spécifiquement française — L’approche continue trouvant son origine en France et en Chine.
La question traitée par les différents types de méthodologie est alors celle de la limite ville campagne. Doit-on considérer cet espace comme fondamentalement discontinu ou au contraire doit on l’envisager comme une transition douce ?
Dans l’approche continue, la méthode est toujours celle de l’utilisation de la fonction logistique qu’elle soit simple ou bornée par le bas comme les études chinoises. Envisager l’usage d’un paramètre supplémentaire permet de s’affranchir d’une rupture entre l’urbain et le périurbain. Dans le cadre de l’application à trois espaces urbains français (Paris, Bordeaux et Limoges), nous avons pu montrer la diversité des situations (taille des espaces polarisés principalement avec une variation des différentes couronnes (urbain, périurbain et rural isolé) et en quoi l’usage de la simple fonction logistique était insuffisant pour modéliser la densité de bâti de l’ensemble de l’espace (autrement que par des droites sécantes).
Le modèle chinois logistique permet de pallier une partie du problème, à savoir modéliser la transition urbain périurbain.
Pour le reste, la solution est sans doute ailleurs. Aussi, nous avons introduit un espace non euclidien en substituant la distance physique par une distance perçue. Ce type de modélisation est très récent et a pu permettre d’ajuster, de manière satisfaisante, l’ensemble de la transition entre ville et campagne allant de l’urbain pur au rural isolé.
On montre alors que sur les trois types de modélisation proposés (sécante, logistique avec amendement et espace perçu), celle de l’espace perçu est la plus intéressante.
Les résultats sont sensibles, la forme urbaine par le bâti répond pleinement à la métrique de la perception, ce qui confirme les hypothèses phénoménologiques initiales, à savoir que les objets géographiques humains reposent sur des métriques de la perception.
Cette question de la perception est vaste et peut avoir de nombreuses applications, déjà pour les déformations cartographiques mais également dans le cadre d’approches modélisatrices plus complexes portant sur l’étalement urbain (Enault 2024b) [22].
Acknowledgement: Les auteurs tiennent à exprimer leur profonde gratitude envers tous ceux qui les ont soutenus et encouragés tout au long de ce travail de recherche.
Funding Statement: Les auteurs n’ont reçu aucun financement spécifique pour cette étude.
Availability of Data and Materials: Les principales données sont issues de data.gouv.fr.
Ethics Approval: Not applicable.
Conflicts of Interest: Les auteurs déclarent qu’ils n’ont pas de conflits d’intérêts à signaler en ce qui concerne la présente étude.
1En référence à la NEU (nouvelle économie urbaine) de Alonso 1964. Cette théorie classique de l’économie urbaine présuppose une ville circulaire, avec en son centre le CBD (central business district), et une decroissance des rentes en fonction de la distance au centre de la ville.
2Au sens de fin de la ville.
3Donc un espace et non une simple ligne.
4Ce qui pourrait lever un dernier problème sur la limite du périurbain et du rural isolé.
5Le parametre c apparait dans la forme fonctionnelle proposée par Jiao 2015 pour modéliser le forme urbaine au voisinage du périurbain.
6Une forme fonctionnelle de type exponentielle decroissante semble cohérente au regard des métriques qui ont été observées dans les formes urbaines (fractale) donnant naissance à des formes de plus en plus petites à mesure que l’on s’éloigne du centre.
7L’espace proxémique se définit comme un espace où l’importance des êtres et des choses, des événements diminuent avec la distance au sujet d’étude (par exemple un individu, un groupe d’individus, une ville).
8Ce zonage est purement morphologique car il ne repose que sur le bâti au sol.
9Le zonage en aires d’attraction des villes 2020 (AAV) est fondé sur l’identification de pôles de population et d’emploi, et sur la délimitation de leur aire d’attraction (couronnes) à partir des trajets domicile-travail. Il a pour objectif d’étudier les disparités territoriales selon la taille de l’aire d’attraction et la distinction entre les centres et leur périphérie.
L’aire d’attraction d’une ville correspond ainsi à un ensemble de communes, d’un seul tenant et sans enclave, constitué d’un pôle et d’une couronne, dont au moins 15 % des actifs travaillent dans le pôle. La commune la plus peuplée du pôle est appelée « commune-centre ». Dans certains cas, dont Paris, l’aire peut comprendre plusieurs pôles.
Plusieurs catégories d’aires d’attraction sont identifiées et classées suivant le nombre d’habitants:
• pôles et couronnes des aires de 700 000 habitants ou plus,
• pôles et couronnes des aires de 200 000 à 700 000 habitants,
• pôles et couronnes des aires de 50 000 à 200 000 habitants,
• pôles et couronnes des aires de moins de 50 000 habitants.
Les communes qui n’appartiennent pas à l’une de ces catégories sont dites « isolées », c’est-à-dire qu’elles sont situées en dehors de l’influence des pôles urbains. Le zonage en aires d’attraction des villes succède au zonage en aires urbaines de 2010.
Pour définir le pôle, on attribue des critères de seuil d’emploi de population et de densité. Pour la densité, un système de carroyage a été mis en place par l’INSEE pour évaluer la densité réellement vécue, à savoir la densité des zones peuplées et uniquement peuplées. On généralise alors cette densité « vraie » à l’ensemble de la commune.
10La forme (1) est la forme logistique la plus répandue en Economie ou en Géographie, la forme (2) en est une generalisation mais employée de manière plus restreinte pour des domaines particuliers.
11Les différentes variantes de la fonction logistique, fonction sigmoïde ou modèle de Verhulst sont décrites dans cette référence dans le cadre de la densité bâti mais également pour le calcul des vitesses de tronçons (le modèle est alors borné selon le même principe que la fonction urban land function). On le retrouve également pour modéliser les profils de vitesse moyenne en fonction de la distance au centre des villes (logistique croissant donc l’inverse de la fonction décrite dans cet article.
12Techniquement, il s’agit de soustraire un paramètre c au 100% de surface bâtie et de rajouter ensuite dans la fonction. Comme cela, on maintient le niveau de densité pour une distance donnée et au lieu de tendre vers 0, la fonction tend vers c dans le périurbain. Cela permet d’ajuster la fonction au périurbain.
13Le travail aurait pu être réalisé sur l’ensemble des villes françaises ou européennes mais nous n’en avons pas jugé l’utilité dans la mesure où ce type d’étude est aujourd’hui largement documenté à un niveau international. Le profil de densité de bâti est aujourd’hui bien connu statistiquement et modélisé.
14On notera toutefois que Zheng (2023) propose une vision polynucléaire de la fonction de densité de bâti (comme dans le cas de la conurbation de Lille Europe) et obtient des résultats semblables à une fonction mononucléaire.
15Toutes les villes et leurs périphéries répondent à priori à ce profil.
16On se réfèrera à Enault 2004 pour les opérations et requêtes dans le SIG pour obtenir ces graphiques.
17Pour l’identification des couronnes et donc des segments, nous avons agrégée empiriquement tous les points qui semblaient s’étirer selon une droite et dès qu’une rupture de pente a été observée nous avons commencé un nouveau segment linéaire.
18Les limites urbain/périurbain et rural isolé sont définies à la vue quand les pentes du nuage de points marquent une certaine rupture.
19Les modèles de densité évoqués sont monocentriques et définissent la densité de population ou la population cumulée (pour Bussière) en fonction de la distance à vol d’oiseau du centre de la ville. Initialement, avec cette distance physique, les modèles ne sont applicables que pour l’urbain. L’idée est alors de substituer cette distance par le temps de parcours au centre. Le modèle s’ajuste alors aux nouvelles données de temps y compris pour le périurbain.
20Dans l’expression (4), pourtant proposée par A.Moles, on ne distingue pas le principe de la paroi qui serait alors un raffinement supplémentaire. L’auteur montre alors que la valeur de l’espace décroît de manière logarithmique mais sans rupture donc que la decroissance est bien une fonction continue.
21Les déformations cartographiques n’auraient pas été possible avec la solution de Moles.
22Le point de vue ici de Moles 1998.
23Le paramètre r doit toujours être compris entre 0 et strictement inférieur à 1.
24Le disque de Poincaré représente un monde imaginaire dont les grandeurs se réduisent du centre du disque vers la périphérie pour tendre vers un infiniment petit au bord du disque. Cette construction purement mathématique a donné lieu à toute une géométrie dite hyperbolique. Nous verrons dans la suite de notre propos que cette construction qui peut paraitre éloignée de la Géographie ressemble à la géométrie de la proxémique.
25http://www.linternaute.com/science/art-et-science/escher/escher.shtml (accessed on 10 July 2025)
26Pour obtenir cette fonction, on part de L(x) = Lr
Pour chaque distance, on calcule la taille d’espace. On somme ensuite toutes les tailles d’espace L + Lr + Lr2 + Lr3 + … + Lrx
Cette somme est une somme remarquable. On obtient donc la fonction ci après.
27Pour le lien entre [4] et [5] voir Enault 2024 a.
References
1. Delattre R. Réguler l’étalement urbain: les services de l’Etat fran ? ais face aux projets d’urbanisme locaux. Paris: Espace et Société; 2024. (In French). [Google Scholar]
2. Desjardins X. Planification Urbaine, la ville en devenir. Paris: Armand Colin; 2020. 234 p. (In French). [Google Scholar]
3. IPR. Les espaces urbains au défi de la densification. Paris: Note rapide; 2020. (In French). [Google Scholar]
4. Clark C. Urban population densities. J R Stat Soc Ser A Gen. 1951;114(4):490. doi:10.2307/2981088. [Google Scholar] [CrossRef]
5. Anas A, Arnott R, Small KA. Urban spatial structure. J Econ Lit. 1998;36(3):1426–64. [Google Scholar]
6. Guerois M. Les formes des villes européennes vues du ciel. Une contribution de l’image Corine à la comparaison des grandes villes d’Europe occidentale, thèse de doctorat en géographie, université de Paris I Panthéon Sorbonne; 2003. (In French). [Google Scholar]
7. Weber C, Hirsch J. « Processus de croissance et limites urbaines », revue européenne de géographie, Cybergeo, n°158; 2000. (In French). [cited 2025 Jul 10]. Available from: https://journals.openedition.org/cybergeo/716. [Google Scholar]
8. Guérois M, Pumain D. Built-up encroachment and the urban field: a comparison of forty European cities. Environ Plan A. 2008;40(9):2186–203. doi:10.1068/a39382. [Google Scholar] [CrossRef]
9. Lemoy R, Caruso G. Evidence for the homothetic scaling of urban forms. Environ Plan B Urban Anal City Sci. 2020;47(5):870–88. doi:10.1177/2399808318810532. [Google Scholar] [CrossRef]
10. Jiao L. Urban land density function: a new method to characterize urban expansion. Landsc Urban Plan. 2015;139(4):26–39. doi:10.1016/j.landurbplan.2015.02.017. [Google Scholar] [CrossRef]
11. Lu H, Shang Z, Ruan Y, Jiang L. Study on urban expansion and population density changes based on the inverse S-shaped function. Sustainability. 2023;15(13):10464. doi:10.3390/su151310464. [Google Scholar] [CrossRef]
12. Gao H, Qiao X, Yang Y, Liu L, Zhang J, Zhou H, et al. Modeling urban land density with Gaussian and inverse S functions by analyzing urban expansion in Zhengzhou City. Sci Rep. 2025;15(1):18116. doi:10.1038/s41598-025-03009-4. [Google Scholar] [PubMed] [CrossRef]
13. Zheng M, Huang W, Xu G, Li X, Jiao L. Spatial gradients of urban land density and nighttime light intensity in 30 global megacities. Humanit Soc Sci Commun. 2023;10(1):404. doi:10.1057/s41599-023-01884-8. [Google Scholar] [CrossRef]
14. Xu G, Dong T, Cobbinah PB, Jiao L, Sumari NS, Chai B, et al. Urban expansion and form changes across African cities with a global outlook: spatiotemporal analysis of urban land densities. J Clean Prod. 2019;224(2–3):802–10. doi:10.1016/j.jclepro.2019.03.276. [Google Scholar] [CrossRef]
15. Frankhauser P. La Fractalité des structures urbaines. Paris: Anthropos, coll. « Villes »; 1994. (In French). [Google Scholar]
16. Enault C. Vitesse, accessibilité et étalement urbain, analyse et application à l’aire urbaine dijonnaise, thèse de doctorat en géographie sous la direction de Jean Jacques Bavoux, Université de Bourgogne, Dijon; 2003. (In French). [Google Scholar]
17. Moles A. Psychosociologie de l’espace, ed L’harmattan; 1998. Paris: L’harmattan. 158 p. (In French). [Google Scholar]
18. L’Hostis A. Le Détour, La Pause et l’optimalité, Essai Sur La Distance et Ses Apports Au Transport et à l’urbanisme, Habilitation à diriger des recherches. France: Université de Paris Marne la Vallée; 2014. (In French). [Google Scholar]
19. Peguy PY. Analyse économique des configurations urbaines et de leur étalement, thèse de doctorat en sciences économiques, université de Lyon II; 2000. (In French). [Google Scholar]
20. Enault C. Vers une transformation géométrique géocentrique des espaces urbains: la ville vue à partir du ou des centre(s). Revue Internationale de Géomatique. 2024;33(1):77–92. doi:10.32604/rig.2024.046591. [Google Scholar] [CrossRef]
21. Ghys E. “Poincaré et son disque”, article de l’ENS, Lyon; 2005. (In French). [Google Scholar]
22. Enault C. Proposition de modélisation de la dynamique du système Urbain: vitesse/densité/espace perçu Simulation de l’Ile de France. Revue Internationale de Géomatique. 2024;33(1):273–93. doi:10.32604/rig.2024.053490. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools