Enhanced sampling for lipid-protein interactions during membrane dynamics

Introduction

The biological membrane is an effective mechanism to selectively isolate the cell from its environment (Sackmann, 1995; Chernomordik and Kozlov, 2008; Alberts et al., 2015). Along evolution, a modular design progressively facilitated specialized transport mechanisms through the membranes (Honigmann and Pralle, 2016). With self-organization being a prevailing characteristic across cellular structures (Karsenti, 2008), protein homeostasis is guaranteed by complex cellular processes that determine the function, conformational states, abundance, and location of the approximately 25,000 proteins found in a human cell (Klaips et al., 2018). Remarkably, still far away from thermodynamic equilibrium (Mayorga et al., 2012), cellular homeostasis ultimately depends on an intricate network of mechanisms as yet waiting to be fully unveiled. As stated by Macklem in a 2008 viewpoint, survival requires adaptations, and during adaptation, homeostasis must preserve order (Macklem, 2008).

In the 70 s, the fluid mosaic model, originally proposed by Singer and Nicolson, was used to explain the gross organization and structure of proteins and lipids in biological membranes (Singer and Nicolson, 1972). In this simple model, the lipid bilayer is assumed as a two-dimensional permeability barrier that presents different faces to the cytoplasm and the extracellular environment. Within the model, amphipathic proteins appear dissolved in a fluid lipid bilayer solvent (Brown, 2017). This first approximation provided a useful framework for membrane analysis at the nanometer scale (Nicolson and Ferreira de Mattos, 2021) and served, for example, as a reference to Rothman and Lenard in 1977 to first discuss lipid asymmetries in biomembranes (Rothman and Lenard, 1977).

This review focuses on the current state of knowledge of enhanced molecular dynamics simulations applied to lipid-protein interactions in specific cellular problems, namely: membrane deformations, membrane fusion, and the fusion pore. Relevant recent computational approaches and advances are described herein. When appropriate, the experimental data that support these approaches are commented upon. The lipid bilayer is presented here as an extraordinarily heterogeneous many-body structure, emphasizing the dynamic interactions with proteins that may contain intrinsically disordered regions. Along the text, the reader is pointed to the most relevant literature on each specific topic.

Enhanced Sampling and Collective Variables

Computational methods are indisputably one of the common choices for studying biological problems at the molecular level. Among them, molecular dynamics is an excellent technique to describe protein and membrane dynamics within a wide range of scenarios. Moreover, in silico methods have been shown to produce useful biological information that, when combined with experimental data, benefit biomedical research. Remarkably, in terms of their historical trend, biomolecular simulations have already exceeded Moore’s law (Schlick and Portillo-Ledesma, 2021). In computer science, Moore’s law shows that the performance of integrated circuits has increased exponentially over the last half-century by doubling approximately every two years (Vendruscolo and Dobson, 2011), suggesting an interesting future of experimental and computational cooperation to address greater scientific challenges.

However, for most biological events, a detailed description at atomistic resolution is still unreachable by classic molecular dynamics. Although, since the first simulation of a protein in 1977 by McCammon et al. (1977) intelligent solutions have been found to speed up atomistic simulations (Ryckaert et al., 1977; Andersen, 1983; Hess et al., 1997; Miyamoto and Kollman, 1992; Feenstra et al., 1999; Olesen et al., 2018), the problem is inherent to the algorithm itself. Atomistic molecular dynamics require an integration step in the order of the femtoseconds (10−15 s) to correctly describe the fastest degrees of freedom, namely, the vibration of bonds and angles involving hydrogen atoms. With most biological processes (e.g., large conformational changes) happening in the order of the micro or even milliseconds (10−6 s–10−3 s), the overwhelming difference of 12 orders of magnitude makes the problem clear.

Therefore, from a numerical simulation point of view, most biological events of interest fall into the category of rare events, this is, events not easily observable within practical simulation times using classical molecular dynamics. From a thermodynamic point of view, large conformational changes in proteins or major lipid remodeling in biomembranes are events that require transitions along high-energy barriers that separate metastable states. From a statistical-mechanics point of view, relatively high-energy conformations have small probabilities of being visited during a molecular dynamics simulation (Laio and Parrinello, 2002; Fiorin et al., 2013; Masone and Grosdidier, 2014). Consequently, new approaches were needed to conveniently drive molecular dynamics to explore large-scale collective motions (Chen and Ferguson, 2018; Bernardi et al., 2015; Karplus and Petsko, 1990).

Enhanced sampling techniques have been shown to be a useful tool to overcome this problem. However, the reliability of these simulations depends critically on the choice of effective collective variables. The necessity to reduce the number of degrees of freedom in a numerical simulation into a few reaction coordinates led to the development of convenient collective variables that bias sampling and overcome high energy barriers (Laio and Parrinello, 2002; Fiorin et al., 2013; Hub and Awasthi, 2017; Masone et al., 2018). Collective variable-driven molecular dynamics then allow projecting the multidimensional space into one or two dimensions to intuitively plot a quantitative energy landscape (Fig. 1). Although higher dimensionality makes visual representations rather problematic (Lee and Verleysen, 2007); adequately enhanced samplings conveniently reduce the simulation time required to characterize a system. In spite of the curse of dimensionality (Fu and Pfaendtner, 2018; Bellman and Dreyfus, 2015), different approaches have been developed to take into account more variables that describe high-dimensional free energy surfaces (Hénin, 2021; Ming et al., 2015; Li et al., 2012).

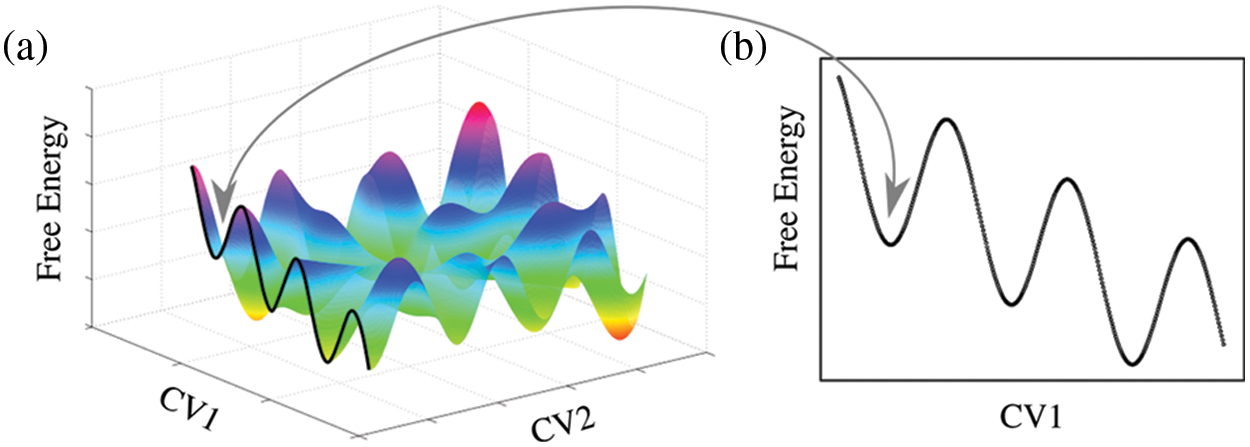
Figure 1: Alternative projections of a complex multidimensional free energy hypersurface. (a) Projection of the free energy over two collective variables (CV1 and CV2). (b) Projection over a single collective variable (CV1). The arrow indicates the same local minimum for both representations.

More than 40 years ago, Brito and Sousa (1981) eloquently discussed a classical analogy of the collective variable concept. They analyzed the extent to which it is possible to describe the behavior of a complex system (exhibiting a large number of degrees of freedom) by means of a reduced number of parameters that suppress unnecessary or redundant degrees of freedom. The concept of a collective variable assumes that the intrinsic and collective motions of a many-body system are sufficiently decoupled. Remarkably, such approximation allows for a significant reduction in the number of degrees of freedom to those necessary for the study of a particular behavior of a many-particle system.

However, the collective variable strategy has limitations. First, the computational cost to calculate a collective variable at each molecular dynamics step must be kept small, otherwise, the approach would generate the same problem seeking to be solved. Second, the definition of a collective variable is not an intuitive task. The problem of correctly projecting a free energy hypersurface (or manifold) into a few dimensions, with variables that correctly capture a biological event, is difficult (Hashemian et al., 2013). Badly defined collective variables can introduce wrong biases regarding how an event requiring large conformational changes should occur (Abrams and Vanden-Eijnden, 2010). Poor convergence or hysteresis are also problems associated with inadequate collective variables (Awasthi and Hub, 2016). With the aim to find better collective variables, several dimensionality reduction techniques that project data from biomolecular trajectories have been proposed (Tribello and Gasparotto, 2019; Wehmeyer and Noé, 2018; Hashemian et al., 2016). Particularly interesting are some innovative tools using machine learning (Doerr et al., 2021; Sidky et al., 2020) and neural network approaches (Hooft et al., 2021; Trapl et al., 2019).

Finally, during the study of the large majority of biological phenomena, long-lasting metastable states make classical sampling difficult, computationally too expensive, or even prohibitive (Zhang et al., 2019). Mainly by the umbrella sampling (Torrie and Valleau, 1977; Roux, 1995) and metadynamics (Laio and Gervasio, 2008) techniques, the development and improvement of collective variables have undoubtedly helped to overcome this problem (Pratyush and Berne, 2016). Still, new and better collective variables are objects of intense investigations (Zhang et al., 2019).

Membrane Deformations

Curvature-related processes play a key role during protein-membrane interactions. Lipids are now recognized to significantly determine the structure and function of membrane-associated proteins (Brown, 2017). Concurrently, the shape of the biomembrane is conditioned by the proteins that interact with its lipids (McMahon et al., 2010; François et al., 2014; Duncan et al., 2017; Masone and Bustos, 2019). Interesting studies have been conducted to reveal coupled properties between the membrane and proteins. Using Helfrich–Canham elastic theory (Helfrich, 1973), Sansom and collaborators (Fowler et al., 2016) showed that membrane stiffness highly depends on the concentration of membrane proteins such as aquaporin or an inwardly-rectifying potassium channel. Schulten and collaborators (Arkhipov et al., 2008; Yin et al., 2009) used computational means to extensively study how the adsorption of Bin/Amphiphysin/Rvs (BAR) domains containing an N-terminal amphipathic helix, induces bending. Consequently, the search for more accurate descriptions of the reciprocal interactions between membranes and proteins has been an initial step to unveiling the behaviors of real cell membranes.

From a lipocentric perspective, spontaneous curvature depends on the collective properties of the lipid bilayer. These properties are ultimately dictated by the membrane’s lipid packing (Israelachvili et al., 1977) and lipid shapes (Cooke and Deserno, 2006). In realistic models of biological membranes, lipid composition is highly heterogeneous, and lipid species are distributed asymmetrically between the hemilayers (Ingólfsson et al., 2014). Such organization has a high propensity to exhibit spontaneous local bending (Koldsø et al., 2014). Membrane curvature generally forms part of even larger lipid reorganization events for a wide range of cellular phenomena and processes, e.g., membrane fusion (di Bartolo and Masone, 2022) and fission (Lipowsky, 2022), endo and exocytosis (Tomes, 2015), cytokinesis (Schiel and Prekeris, 2013), and autophagy (Gómez-Sánchez et al., 2021). As pointed out by Torres-Sánchez et al. (2019), local density asymmetries result in small but noticeable changes in shape that can be observed in the curvature energy. Thermodynamically, bending appears to be a mechanism to maximize molecular contacts while minimizing the free energy of the system (Stroh and Risselada, 2021).

A common strategy in computer simulations is to replicate a biological event so that it can be later studied under different conditions of interest. Consequently, the development of new methods that enhance molecular dynamics simulations to induce curvature has significantly increased in recent years (Yang et al., 2019). Masone et al. (2018) proposed Ψ, a collective variable that induces membrane bending inspired by a previous concept by den Otter and collaborators (Tolpekina et al., 2004; Wohlert et al., 2006), originally used to form hydrophilic pores in lipid bilayers. Ψ takes advantage of the curvature as a collective response of the bilayers to increased local density (de Jesus et al., 2013), that produce out-of-plane forces. Remarkably, Ψ does not anticipate the curved shape of the bilayer, which spontaneously emerges as saddle-like (Alimohamadi and Rangamani, 2018). This essential characteristic has made Ψ a convenient tool to study protein mechanisms that induce or sense curvature, such as α-synuclein (Caparotta et al., 2020a) or the N-BAR domain (Masone et al., 2018).

Alternatively, Bubnis et al. (2016) used permutation symmetry to calculate lipid remodeling free energies via umbrella sampling. Also, Fiorin et al. (2020) proposed a method to quantify the mismatch between the shape of the bilayer and a reference, using this mismatch to induce different membrane shapes. Stroh and Risselada (2021) proposed a method to calculate bending free energies as a direct function of membrane curvature. Durrant and Amaro (2014) developed LipidWrapper, a multi-scale utility to create curved membrane models with geometries derived from experimental and theoretical sources. Finally, Yesylevskyy and Khandelia (2021) developed EnCurv (Enforced Curvature), a practical tool ported into PLUMED (Tribello et al., 2014) that induces bending in lipid bilayers in a controlled manner.

Simultaneously, convenient post-processing tools were also developed to analyze complex membrane surfaces from molecular dynamics trajectories. Lukat et al. (2013) used Voronoi diagrams to develop APL@Voro, a tool to analyze GROMACS (van der Spoel et al., 2005) trajectories of lipid bilayer simulations. Also, Buchoux developed the software Fast Analysis Toolbox for Simulations of Lipid Membranes (FATSLiM) (Buchoux, 2017) to extract physical properties from molecular dynamics simulations of membranes. Allen et al. (2009) developed GridMAT-MD to aid in the analysis of lipid bilayers from molecular dynamics trajectories. Sejdiu and Tieleman (2021) developed ProLint, a web-based framework to analyze and visualize lipid-protein interactions. Membrainy, developed by Carr and MacPhee (2015) is a user-friendly membrane analysis tool to calculate a variety of properties of different bilayers. Lastly, using Delaunay triangulations, Bhatia et al. (2019) developed MemSurfer to assess the undulations in the membrane.

Membrane Fusion

Membrane fusion is a fundamental process in many cellular events (both in the intra and the extracellular spaces), such as exocytosis, endocytosis, membrane genesis, viral infection, and fertilization (Arnold, 1995). To merge, initially independent membranes (Fig. 2a) follow different stages historically classified in an event-oriented manner. First, bilayers bend during recognition upon binding (Fig. 2b), and then, the fusion stalk forms (Fig. 2c). From the stalk, two possible paths exist: (i) a traversing water channel forms through it (Fig. 2d), connecting initially isolated spaces and initiating the formation of a nascent fusion pore, or a hemifusion diaphragm (Fig. 2e) emerges before the water channel forms (Fig. 2f). Finally, the fusion pore expands in its well-known toroidal shape (di Bartolo et al., 2022) (Fig. 2g).

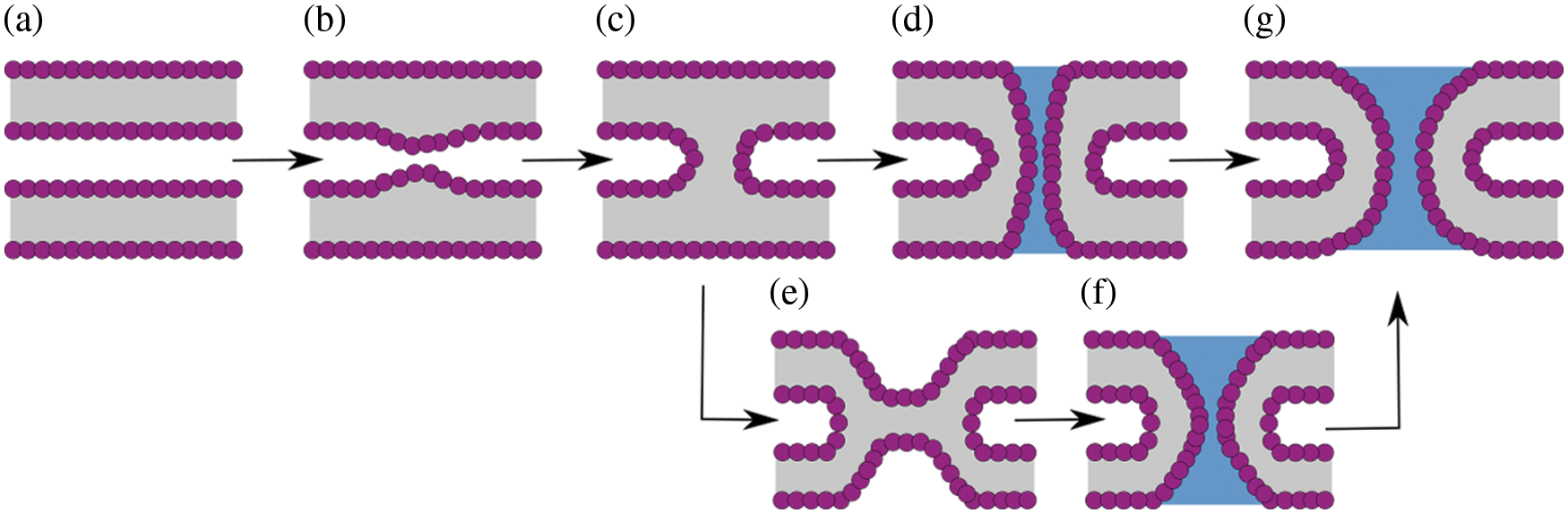
Figure 2: Possible pathways along membrane fusion and fusion pore formation. (a) Flat and parallel membranes. (b) Initial deformation and bending. (c) Fusion stalk. (d) Fusion pore nucleation from the stalk. (e) Hemifusion diaphragm. (f) Fusion pore nucleation from the diaphragm. (g) Fusion pore expansion (toroid-shaped).

As stated, the first stage in the membrane fusion process is the bending of the membrane (see Fig. 2b). However, to initiate effective membrane fusion, a substantial structural lipid reorganization is needed to either form the fusion stalk or the hemifusion diaphragm. In any case, lipid molecules forming the fusion stalk or surrounding the hemifusion diaphragm suffer from heavy tilting and splaying. Several studies have suggested that while membranes fuse, lipid acyl tails splay and protrude to the surface of the bilayers to initiate lipid mixing (Scheidt et al., 2020; Caparotta et al., 2020b; Pannuzzo et al., 2014; Smirnova et al., 2010; Smeijers et al., 2006).

Again, important efforts have been made to develop special-purpose computational methods to induce and study membrane fusion configurations. Kawamoto et al. (2014, 2015) used a continuum model to study the fusion stalk using coarse-grained molecular dynamics and to calculate its associated free energies of formation. Hub and collaborators (Hub and Awasthi, 2017; Poojari et al., 2021) proposed a novel collective variable to induce membrane fusion through the stalk mechanism. More than a decade ago, Chernomordik and Kozlov (2008) proposed that particular lipid geometries in proximal monolayers could facilitate or inhibit the formation of the hemifusion stalk. Nishizawa and Nishizawa (2013) studied pore propensity in hemifusion diaphragms using atomistic and coarse-grained molecular dynamics. Also, Risselada et al. (2012) used coarse-grained molecular dynamics to describe how the widening of the fusion stalk evolves into a single, bilayer H-shaped diaphragm. Gardner and Abrams (2017) studied the rate of expansion of large hemifusion diaphragms using solvent-free coarse-grained molecular dynamics.

The development of these tools allowed for further studies oriented to lipid-protein interactions. Caparotta et al. (2020b) studied membrane fusion and pore nucleation to describe synaptotagmin-1 C2B domain interactions with phosphatidylinositol 4, 5-bisphosphate lipids (PI (4,5) P2, or simply PIP2). di Bartolo and Masone (2022) described the effects on membrane fusion by a pair of synaptotagmin-1 C2B domains using a methodology by Hub and Awasthi for membrane fusion, 28 ported into PLUMED (Tribello et al., 2014) and freely available on GitHub: https://github.com/lautarodibartolo/MemFusion. Miyazaki et al. (2019) examined the free energy barrier for the creation of a pore in lipid membranes with and without multiple melittin peptides. Also, Hsiao et al. (2018) conducted a free energy study on cecropin B and its constituent domains to describe cooperative modes of action of antimicrobial peptides.

The Fusion Pores

The fusion stalk and the hemifusion diaphragm are intermediate metastable configurations that await the formation of a fusion pore. As widely accepted, the energetics along the membrane fusion paths towards the fusion pore (Fig. 2) highly depends on the lipid composition of the interacting bilayers (di Bartolo et al., 2022; Kawamoto and Shinoda, 2014; Fuertes et al., 2011; Aeffner et al., 2012; Cunill-Semanat and Salgado, 2019) as well as their hydration level for different inter-membrane distances (di Bartolo and Masone, 2022; Caparotta et al., 2020b; Poojari et al., 2021; Smirnova et al., 2015; Smirnova et al., 2019; Wu et al., 2021).

The exocytosis mechanism allows eukaryotic cells to release biological cargo and effectively transport molecules across the plasma membrane (Tomes, 2015; Rizo, 2022). The complexity of the fusion pore as a mechanism to connect intra-cellular organelles and release the contents of vesicles during exocytosis, has made it an interesting object of study both experimentally (Wu et al., 2021; Chang, Chiang and Jackson, 2017; Gucek et al., 2016; Bai et al., 2004) and computationally (Risselada and Grubmüller, 2021; Risselada and Mayer, 2020; Risselada et al., 2014). Fig. 3a shows a 3D time-averaged density of a fusion pore from an enhanced molecular dynamics trajectory. The fusion pore for this figure was induced with the collective variable ξe (di Bartolo et al., 2022; Hub, 2021) (freely available on GitHub: https://github.com/lautarodibartolo/FusionPore), and the trajectory density was generated using GROmaps (Briones et al., 2019). Fig. 3b is a representation of the possible free energy landscape along the different stages during the life of the fusion pore. Starting from membrane bending and ending with the expansion of the fusion pore, this schematic curve follows the path of pore nucleation through the fusion stalk. The shape of the estimated free energy profile is based on results by Caparotta et al. (2020b), di Bartolo and Masone (2022), di Bartolo et al. (2022) and is in good agreement with previous studies on the energetics of the fusion pore (Lipowsky, 2022; Kawamoto et al., 2015; Smirnova et al., 2015; Gorai et al., 2021; Dhara et al., 2020; François-Martin et al., 2017; Markvoort and Marrink, 2011).

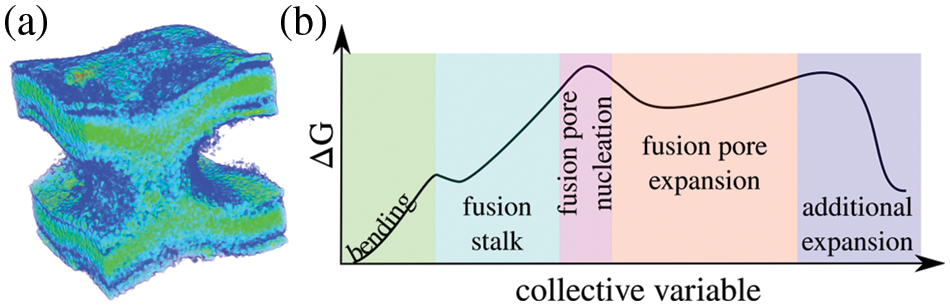
Figure 3: The fusion pore. (a) Time-averaged density of a fusion pore induced between two bilayers using enhanced molecular dynamics. For clarity, water molecules are not shown. (b) Schematics of the free energy landscape along membrane bending (green), the fusion stalk (light blue), fusion pore nucleation (pink), fusion pore expansion (orange), and possible further expansion (lilac).

The fusion pore is an excellent case of study to unveil complicated lipid-protein interactions. Recently, Caparotta et al. (2020b) showed that a single C2B domain of synaptotagmin-1 has negligible effects on the free energy during membrane fusion and fusion pore nucleation. Also, di Bartolo and Masone (2022) revealed a cooperative mechanism between a pair of C2B domains that significantly decrease the energy costs for the formation of the fusion stalk and the first traversing water channel. In another study, di Bartolo et al. (2022) demonstrated that C2B domains reduce the energy cost for fusion pore expansion and the probability of kiss-and-run events.

The Lipid-Protein Interplay

Lipid bilayers are composed of self-organizing molecules that form very stable structures. Hence, membrane fusion is thought to be mediated by protein fusogens that perturb their organization and dynamics (Pattnaik, Meher and Chakraborty, 2018; Joardar, Pattnaik and Chakraborty, 2022). Key proteins for evoked neurotransmitter release such as the synaptotagmin-1 C2B domains (Gruget et al., 2020) collaborate to overcome the energetic barriers for the fusion stalk (Di Bartolo and Masone, 2022) and fusion pore expansion (Di Bartolo et al., 2022; Nyenhuis et al., 2021; Das et al., 2020), possibly inducing PIP2 clusters (Caparotta et al., 2020b). Another significant example is myoblast fusion, where Myomaker and Myomerger promote the hemifusion diaphragm (Golani et al., 2021; Whitlock and Chernomordik, 2021). Also, local membrane deformations have been indicated to potentially affect the overall organization of signaling proteins and their biochemical functions (Orbach and Su, 2020).

The fusion pore is particularly interesting from a driving protein point of view. Undoubtedly, SNAREs are among the most studied proteins in inducing membrane fusion reactions inside eukaryotic cells, both experimentally (Tomes et al., 2002; Fang and Lindau, 2014; Bao et al., 2018; Amos et al., 2022) and computationally (Smirnova et al., 2019; Risselada and Mayer, 2020; Risselada et al., 2011; Risselada and Grubmüller, 2012; Sharma and Lindau, 2018; D’Agostino et al., 2018). The key role of SNAREs during fusion pore formation makes them an ideal object of study to develop and test new methods that describe lipid-protein interactions during membrane remodeling that can be later integrated with experiments. Other proteins involved in the membrane fusion process, such as the synaptotagmin family (Fernandez et al., 2001; Seven et al., 2013; Rizo, 2018), have also received significant attention within the biomedical sciences, both computationally (di Bartolo and Masone, 2022; di Bartolo et al., 2022; Caparotta et al., 2020b) and experimentally (Wu et al., 2021; Bendahmane et al., 2018; Ying et al., 2013; Lynch et al., 2008).

Shape transformations along the membrane due to specialized curvature-sensing and curvature-inducing proteins are also interesting lines of research (Brown, 2017; Alimohamadi and Rangamani, 2018). For example, the relation of α-synuclein to vesicle trafficking, membrane fusion, and fission has been extensively studied (Auluck et al., 2010; Nemani et al., 2010; Thayanidhi et al., 2010; Cooper et al., 2006; Kamp and Beyer, 2006), due to its implications in Parkison’s disease (Jao et al., 2008; Bodner et al., 2009) and other pathologies, broadly known as synucleinopathies. In particular, Middleton and Rhoades (Middleton and Rhoades, 2010) showed how α-synuclein preferably binds to highly curved lipid vesicles. Also, Braun et al. (2012) described how a truncated version (1–100) of α-synuclein is able to induce negative and positive curvature. Recent results in α-synuclein implications along the membrane fusion process have renewed the attention toward this protein (Huang et al., 2019; Khounlo et al., 2021; Liu et al., 2021). Experimentally, using a single vesicle-to-supported bilayer fusion assay, Khounlo et al. (2021) examined the role of α-synuclein in membrane fusion. Following an in vitro approach with v-SNARE–reconstituted nanodiscs and t-SNARE–reconstituted black lipid membrane (Das et al., 2020; Bao et al., 2018), Nellikka et al. (2021) studied α-synuclein modes of action in different time-scales. Both experimental procedures could be applied to synaptotagmin.

The detailed characterization of the full network of interactions between human proteins is a major scientific ambition (Cusick et al., 2009). Protein folding and protein-protein binding are interdependent processes (Sugase et al., 2007), ultimately determining protein functions. Moreover, membrane deformations due to lipid influences have been established for protein folding in membranes (Moon and Fleming, 2011; Honerkamp-Smith et al., 2009; Curnow et al., 2004). Consequently, strategies to approach the problem of lipid-protein interactions from a coupled point of view would improve the overall understanding of complex biological events, ultimately allowing better and more accurate predictions.

Intrinsic Disorder in Lipid-Protein Interactions

Many proteins have no stable 3D structures under physiological conditions, and their functions are determined dynamically by coexisting binding partners. These proteins have been historically classified as intrinsically unstructured (Wright and Dyson, 1999) or intrinsically disordered (Dunker et al., 2001). Such is the case of α-synuclein, which folds into two anti-parallel α-helices (Jao et al., 2008; Drescher et al., 2008; Chandra et al., 2003) upon binding to the membrane (see UniProt ID: P37840). Recently, Bondos et al. (2021) have compiled thirteen relevant papers that highlight the importance of intrinsic disorder in current biochemistry and cell biology.

The problem of intrinsically disordered regions in proteins that interact with lipid bilayers adds substantial complexity to the molecular description of the lipid-protein interplay. More two decades ago, Shoemaker et al. (2000) observed that a relatively unstructured protein could have a larger capture radius for a specific binding site with respect to the folded conformation. The fly-casting mechanism was then proposed (Shoemaker et al., 2000; Levy et al., 2007; Huang and Liu, 2009), where a disordered region of a protein binds weakly to its partner before folding. This hypothesis helped to highlight the importance of unstructured regions during protein binding and folding.

Accordingly, using enhanced molecular dynamics simulations, Caparotta et al. (2020a) showed that the intrinsically disordered region of α-synuclein is essential for the protein mechanism that induces bending in lipid bilayers. In agreement, Zeno et al. (2018) used Monte-Carlo simulations, in vitro, and live-cell measurements to show that proteins containing both structured and unstructured regions are significantly more sensitive to membrane curvature, with respect to fully-structured ones. Also, Busch et al. (2015) proposed that the large hydrodynamic radii of disordered domains generate a steric pressure that drives membrane bending.

Recently, new efforts have been made to improve computational modeling of intrinsically disordered proteins (Thomasen et al., 2022; Klein et al., 2021; Tran and Kitao, 2020). Several reviews have also been dedicated to the role of intrinsic disorder during lipid-protein interactions highlighting the effects on membrane curvature (Has, Sivadas and Das, 2022; Cornish et al., 2020; Fakhree, Blum and Claessens, 2019; Snead and Stachowiak, 2018). Intrinsic disorder presents itself as an additional complexity to the already difficult problem of lipid-protein interactions during biological events that require large configurational and conformational changes.

Lipid-protein interaction is a problem that could be addressed with an interdisciplinary approach, merging cell biology, chemistry, and physics. Such cross-disciplinary connections between different research fields, at experimental and computational levels, may help to find better descriptions with direct biomedical applications, e.g., to monitor disease development and to identify new targets for drug development.

Connecting Cell Biology and Physics

The idea of decomposing a biological problem into its fundamental building blocks in order to predict complex collective behaviors of the ensemble is an intelligent approach that for many years aimed to merge physics and cell biology (Alon, 2006; Hartwell et al., 1999; Gell-Mann, 1995). Among biological entities, each individual is characterized in part by its relations with other individuals (Nachtomy et al., 2002). Within the cell, the plasma membrane is a spatial boundary that actively isolates internal and external environments. A selective interchange of molecules takes place across the bilayers, and the properties of the bilayers are conditioned by their surrounding external and internal organizations.

In physics, the problem of reversibility is an elegant example that highlights collective behaviors. According to Fick’s first law, (Fick, 1995) a flux of particles evolves from regions of high concentrations to regions of low concentrations, with a magnitude proportional to the concentration gradient. From a microscopic point of view, each particle of the flux follows Newton’s laws, and its individual motion is fully reversible. However, when particles are taken together, they move collectively in a certain direction, following Fick’s first law (Dill et al., 2010). Reid and Latty (2016) recall that in a microbiological context, individual-level behaviors can lead to complex group-level patterns, which is well accepted. Richard Feynman observed that the behavior of a fluid depends very little on the nature of the individual particles in that fluid, for example, being the flow of sand very similar to the flow of water or a pile of ball bearings (Feynman et al., 2018). Communication seems to be the key between microbiological entities to transfer information and sense the environment to respond in ways that would be impossible for individuals to achieve on their own (Davies, 2004).

Almost twenty years ago, Davis (2004) commented on the problem of the minimum complexity needed by a system to exhibit emergent properties. As presented by Erwin Shcrödinger in 1944, life follows a spontaneous emergence of self-organized order (Schrödinger, 1944). Polanyi, already in 1968, commented on the irreducible structure of life, noting that although life obeys the laws of physics and chemistry, the design of living organisms is not ultimately determined by such laws (Polanyi, 1968). Although beyond the scope of this review, the philosophical discussion to distinguish between weak and strong emergent properties is of relevance and has been considered by others (O’Connor, 1994; Chalmers, 2006; Turkheimer et al., 2019).

From a thermodynamic point of view, order is more improbable than disorder, and also transitions from disordered configurations to ordered ones require energy (Macklem, 2008). Ikegami et al. (2017) clearly distinguished that these emergent phenomena are an extension of self-organization, being self-organization a one-way formation of macroscopic order from microdynamics. On the contrary, emergent phenomena require the two-way circulation of recurrent information between macro- and micro-scales. Such emergent phenomena in life might as well characterize many diseases (Macklem, 2008). Computational modeling is, therefore, an excellent tool for predicting the global emergent properties of a tissue starting from local cellular rules (Pebay-Peyroula et al., 2016).

Mathematical models have helped to understand the underlying mechanisms and emergent properties of the cell (Mayorga et al., 2018). Important advances have been made in fibration symmetries and the functionality of biological networks (Leifer et al., 2020; Monteiro et al., 2022). In particular, a convenient graph representation of the information flow has been proposed by Morone et al. (2020). In their work, the authors introduce the use of symmetries in biological networks by analyzing the well-known transcriptional regulatory network of Escherichia coli. These studies contribute to the identification of the building blocks in biological networks and are a step forward in understanding life as an emergent property of physics.

Conclusions

Today it is well accepted that membrane deformations and associated protein functions are coupled mechanisms (Haylock et al., 2020; Song et al., 2019), with complex emergent properties derived in part from the highly heterogeneous nature of the bilayers (Nicolson, 2014; Mohammad et al., 2019), or as suggested by Lamparter and Galic (2020), a versatile, adaptive composite material. Membrane proteins may dynamically modify their curvature preference upon external stimuli (Stroh and Risselada, 2021), also making the coupled mechanism dynamic. Additionally, lipid dynamics have been shown to play an active part in the protein-mediated fusion machinery, for example, by SNAREs or synaptotagmins (Amos et al., 2022).

Already in 1945, Novikoff highlighted the necessity of understanding lower level phenomena to understand higher level ones, even if the knowledge at lower levels does not completely describe, nor fully predicts, what will occur at higher ones (Novikoff Alex, 1945). Such observation is aligned with modern views of life as an emergent property. Therefore, a proper understanding of the lipid-protein interactions during key biological events, such as membrane curvature, membrane fusion, and fusion pore formation, would provide crucial information to face more complex biomedical problems.

The predictive capabilities of computational simulations have reached an interesting stage in the biomedical sciences. Improved simulation packages (Brooks et al., 2021; Suh et al., 2022), better force-fields (Klein et al., 2021; Souza et al., 2021; Cruz-León et al., 2021; Yungerman et al., 2022), unprecedented supercomputer power (Yamazaki et al., 2021; Kutzner et al., 2022) and creative sampling techniques (Gilabert et al., 2019; Bonati et al., 2021) have boosted the study of exceptionally complex biological problems (Mosalaganti et al., 2022; Lotz and Dickson, 2018). More studies combining theoretical approaches, computer simulations, and experiments are currently envisioning new possibilities (Sica and Smulski, 2021; Bernetti and Bussi, 2021; Miguel et al., 2021; Quevedo et al., 2019; Saen-oon et al., 2015). Although computational models containing conceptual simplifications may, of course, exhibit inherent limitations (Alessandri et al., 2019; Jarin et al., 2021; Masone et al., 2012), the recent overall progress in the biomolecular simulations field at varied lengths and timescales has been outstanding (Schlick and Portillo-Ledesma, 2021; Pezeshkian et al., 2020).

Acknowledgement: The author thanks Prof. Luis Mayorga for his useful suggestions.

Author Contribution: The author confirms sole responsibility for the manuscript preparation.

Ethics Approval: Not applicable.

Funding Statement: Grants from CONICET (PIP-0409CO) and ANPCyT (PICT2020-1897) are gratefully acknowledged.

Conflicts of Interest: The authors declares that they have no conflicts of interest regarding the present study.

References

Abrams CF, Vanden-Eijnden E (2010). Large-scale conformational sampling of proteins using temperature-accelerated molecular dynamics. Proceedings of the National Academy of Sciences 107: 4961–4966. DOI 10.1073/pnas.0914540107. [Google Scholar] [CrossRef]

Aeffner S, Reusch T, Weinhausen B, Salditt T (2012). Energetics of stalk intermediates in membrane fusion are controlled by lipid composition. Proceedings of the National Academy of Sciences 109: E1609. DOI 10.1073/pnas.1119442109. [Google Scholar] [CrossRef]

Alberts B, Bray D, Hopkin K, Johnson AD, Lewis J, Raff M, Roberts K, Walter P (2015). Essential Cell Biology. New York, NY, USA: Garland Science. [Google Scholar]

Alessandri R, Souza PCT, Thallmair S, Melo MN, de Vries AH, Mar-rink SJ (2019). Pitfalls of the martini model. Journal of Chemical Theory and Computation 15: 5448–5460. DOI 10.1021/acs.jctc.9b00473. [Google Scholar] [CrossRef]

Alimohamadi H, Rangamani P (2018). Modeling membrane curvature generation due to membrane-protein interactions. Biomolecules 8: 120. DOI 10.3390/biom8040120. [Google Scholar] [CrossRef]

Allen WJ, Lemkul JA, Bevan DR (2009). GridMAT-MD: A grid-based membrane analysis tool for use with molecular dynamics. Journal of Computational Chemistry 30: 1952–1958. DOI 10.1002/jcc.21172. [Google Scholar] [CrossRef]

Alon U (2006). An Introduction to Systems Biology: Design Principles of Biological Circuits. 1st edition. Boca Raton, Florida, USA: Chapman and Hall/CRC. [Google Scholar]

Amos C, Kiessling V, Schenk N, Mohan R, Doyle CA et al. (2022). Membrane order regulates SNARE mediated vesicle fusion in insulin-secreting cells. Biophysical Journal 121: 292a–293a. DOI 10.1016/j.bpj.2021.11.1281. [Google Scholar] [CrossRef]

Andersen HC (1983). Rattle: A “velocity” version of the shake algorithm for molecular dynamics calculations. Journal of Computational Physics 52: 24–34. DOI 10.1016/0021-9991(83)90014-1. [Google Scholar] [CrossRef]

Arkhipov A, Yin Y, Schulten K (2008). Four-scale description of membrane sculpting by BAR domains. Biophysical Journal 95: 2806–2821. DOI 10.1529/biophysj.108.132563. [Google Scholar] [CrossRef]

Arnold K (1995). In: Lipowsky R, Sackmann E (eds.Handbook of Biological Physics, vol. 1, pp. 903–957. North-Holland: Elsevier. [Google Scholar]

Auluck PK, Caraveo G, Lindquist S (2010). Alpha-Synuclein: Membrane interactions and toxicity in Parkinson’s disease. Annual Review of Cell and Developmental Biology 26: 211–233. DOI 10.1146/annurev.cellbio.042308.113313. [Google Scholar] [CrossRef]

Awasthi N, Hub JS (2016). Simulations of pore formation in lipid membranes: Reaction coordinates, convergence, hysteresis, and finite-size effects. Journal of Chemical Theory and Computation 12: 3261–3269. DOI 10.1021/acs.jctc.6b00369. [Google Scholar] [CrossRef]

Bai J, Wang CT, Richards DA, Jackson MB, Chapman ER (2004). Fusion pore dynamics are regulated by synaptotagmin.t-SNARE interactions. Neuron 41: 929–942. DOI 10.1016/S0896-6273(04)00117-5. [Google Scholar] [CrossRef]

Bao H, Das D, Courtney NA, Jiang Y, Briguglio JS, Lou X, Roston D, Cui Q, Chanda B, Chapman ER (2018). Dynamics and number of trans-SNARE com-plexes determine nascent fusion pore properties. Nature 554: 260–263. DOI 10.1038/nature25481. [Google Scholar] [CrossRef]

Baumgart T, Capraro BR, Zhu C, Das SL (2011). Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annual Review of Physical Chemistry 62: 483–506. DOI 10.1146/annurev.physchem.012809.103450. [Google Scholar] [CrossRef]

Bellman RE, Dreyfus SE (2015). Applied Dynamic Programming. Princeton, New Jersey, USA: Princeton University Press. [Google Scholar]

Bendahmane M, Bohannon KP, Bradberry MM, Rao TC, Schmidtke MW et al. (2018). The synaptotagmin C2B domain calcium-binding loops modulate the rate of fusion pore expansion. Molecular Biology of the Cell 29: 834–845. DOI 10.1091/mbc.E17-11-0623. [Google Scholar] [CrossRef]

Bernardi RC, Melo MCR, Schulten K (2015). Enhanced sampling techniques in molecular dynamics simulations of biological systems. Recent Developments of Molecular Dynamics 1850: 872–877. DOI 10.1016/j.bbagen.2014.10.019. [Google Scholar] [CrossRef]

Bernetti M, Bussi G (2021). Comparing state-of-the-art approaches to back-calculate SAXS spectra from atomistic molecular dynamics simulations. The European Physical Journal B 94: 180. DOI 10.1140/epjb/s10051-021-00186-9. [Google Scholar] [CrossRef]

Bhatia H, Ingólfsson HI, Carpenter TS, Lightstone FC, Bremer PT (2019). MemSurfer: A tool for robust computation and characterization of curved membranes. Journal of Chemical Theory and Computation 15: 6411–6421. DOI 10.1021/acs.jctc.9b00453. [Google Scholar] [CrossRef]

Bodner CR, Dobson CM, Bax A (2009). Multiple tight phospholipid-binding modes of alpha-synuclein revealed by solution NMR spectroscopy. Journal of Molecular Biology 390: 775–790. DOI 10.1016/j.jmb.2009.05.066. [Google Scholar] [CrossRef]

Bonati L, Piccini G, Parrinello M (2021). Deep learning the slow modes for rare events sampling. Proceedings of the National Academy of Sciences 118: e2113533118. DOI 10.1073/pnas.2113533118. [Google Scholar] [CrossRef]

Bondos SE, Dunker AK, Uversky VN (2021). On the roles of intrinsically disordered proteins and regions in cell communication and signaling. Cell Communication and Signaling 19: 88. DOI 10.1186/s12964-021-00774-3. [Google Scholar] [CrossRef]

Braun AR, Sevcsik E, Chin P, Rhoades E, Tristram-Nagle S, Sachs JN (2012). Alpha-synuclein induces both positive mean curvature and negative gaussian curvature in membranes. Journal of the American Chemical Society 134: 2613–2620. DOI 10.1021/ja208316h. [Google Scholar] [CrossRef]

Briones R, Blau C, Kutzner C, de Groot BL, Aponte-Santamaría C (2019). GROmaps: A GROMACS-Based toolset to analyze density maps derived from molecular dy-namics simulations. Biophysical Journal 116: 4–11. DOI 10.1016/j.bpj.2018.11.3126. [Google Scholar] [CrossRef]

Brito LP, Sousa CA (1981). Classical analogy of the concept of collective variables. Journal of Physics A: Mathematical and General 14: 2239–2249. DOI 10.1088/0305-4470/14/9/019. [Google Scholar] [CrossRef]

Brooks CL, Case DA, Plimpton S, Roux B, van der Spoel D, Tajkhorshid E (2021). Classical molecular dynamics. The Journal of Chemical Physics 154: 100401. DOI 10.1063/5.0045455. [Google Scholar] [CrossRef]

Brown MF (2017). Soft matter in lipid-protein interactions. Annual Review of Biophysics 46: 379–410. DOI 10.1146/annurev-biophys-070816-033843. [Google Scholar] [CrossRef]

Bubnis G, Risselada HJ, Grubmüller H (2016). Exploiting lipid permutation symmetry to compute membrane remodeling free energies. Physical Review Letters 117: 188102. DOI 10.1103/PhysRevLett.117.188102. [Google Scholar] [CrossRef]

Buchoux S (2017). FATSLiM: A fast and robust software to analyze MD simulations of membranes. Bioinformatics 33: 133–134. DOI 10.1093/bioinformatics/btw563. [Google Scholar] [CrossRef]

Busch DJ, Houser JR, Hayden CC, Sherman MB, Lafer EM, Stachowiak JC (2015). Intrinsically disordered proteins drive membrane curvature. Nature Communications 6: 7875. DOI 10.1038/ncomms8875. [Google Scholar] [CrossRef]

Caparotta M, Bustos DM, Masone D (2020a). Order-disorder skewness in alpha-synuclein: A key mechanism to recognize membrane curvature. Physical Chemistry Chemical Physics 22: 5255–5263. DOI 10.1039/C9CP04951G. [Google Scholar] [CrossRef]

Caparotta M, Tomes CN, Mayorga LS, Masone D (2020b). The synaptotagmin-1 C2B domain is a key regulator in the stabilization of the fusion pore. Journal of Chemical Theory and Computation 16: 7840–7851. DOI 10.1021/acs.jctc.0c00734. [Google Scholar] [CrossRef]

Carr M, MacPhee CE (2015). Membrainy: A ‘smart’, unified membrane analysis tool. Source Code for Biology and Medicine 10: 3. DOI 10.1186/s13029-015-0033-7. [Google Scholar] [CrossRef]

Chalmers DJ (2006). Strong and weak emergence. In: Davies P, Clayton P (eds.The Re-Emergence of Emergence: The Emergentist Hypothesis from Science to Religion. Oxford, England: Oxford University Press. [Google Scholar]

Chandra S, Chen X, Rizo J, Jahn R, Südhof TC (2003). A broken α-helix in folded α-synuclein. Journal of Biological Chemistry 278: 15313–15318. DOI 10.1074/jbc.M213128200. [Google Scholar] [CrossRef]

Chang CW, Chiang CW, Jackson MB (2017). Fusion pores and their control of neurotransmitter and hormone release. The Journal of General Physiology 149: 301–322. DOI 10.1085/jgp.201611724. [Google Scholar] [CrossRef]

Chen W, Ferguson AL (2018). Molecular enhanced sampling with autoencoders: On-the-fly collective variable discovery and accelerated free energy landscape exploration. Journal of Computational Chemistry 39: 2079–2102. DOI 10.1002/jcc.25520. [Google Scholar] [CrossRef]

Chernomordik LV, Kozlov MM (2008). Mechanics of membrane fusion. Nature Structural & Molecular Biology 15: 675–683. [Google Scholar]

Cooke IR, Deserno M (2006). Coupling between lipid shape and membrane curvature. Biophysical Journal 91: 487–495. DOI 10.1529/biophysj.105.078683. [Google Scholar] [CrossRef]

Cooper AA, Gitler AD, Cashikar A, Haynes CM, Hill KJ et al. (2006). Alpha-synuclein blocks ER-Golgi traffic and Rab1 rescues neuron loss in Parkinson’s models. Science 313: 324–328. DOI 10.1126/science.1129462. [Google Scholar] [CrossRef]

Cornish J, Chamberlain SG, Owen D, Mott HR (2020). Intrinsically disordered proteins and membranes: A marriage of convenience for cell signalling? Biochemical Society Transactions 48: 2669–2689. DOI 10.1042/BST20200467. [Google Scholar] [CrossRef]

Cruz-León S, Grotz KK, Schwierz N (2021). Extended magnesium and calcium force field parameters for accurate ion-nucleic acid interactions in biomolecular simulations. The Journal of Chemical Physics 154: 171102. DOI 10.1063/5.0048113. [Google Scholar] [CrossRef]

Cunill-Semanat E, Salgado J (2019). Spontaneous and stress-induced pore formation in membranes: Theory, experiments and simulations. The Journal of Membrane Biology 252: 241–260. DOI 10.1007/s00232-019-00083-4. [Google Scholar] [CrossRef]

Curnow P, Lorch M, Charalambous K, Booth PJ (2004). The reconstitution and activity of the small multidrug transporter EmrE is modulated by non-bilayer lipid composition. Journal of Molecular Biology 343: 213–222. DOI 10.1016/j.jmb.2004.08.032. [Google Scholar] [CrossRef]

Cusick ME, Yu H, Smolyar A, Venkatesan K, Carvunis AR et al. (2009). Literature-curated protein interaction datasets. Nature Methods 6: 39–46. DOI 10.1038/nmeth.1284. [Google Scholar] [CrossRef]

Das D, Bao H, Courtney KC, Wu L, Chapman ER (2020). Resolving kinetic intermediates during the regulated assembly and disassembly of fusion pores. Nature Communications 11: 231. DOI 10.1038/s41467-019-14072-7. [Google Scholar] [CrossRef]

Davies PCW (2004). Emergent biological principles and the computational properties of the universe. arXiv preprint astroph/0408014. [Google Scholar]

de Jesus AJ, Kastelowitz N, Yin H (2013). Changes in lipid density induce membrane curvature. RSC Advances 3: 13622–13625. DOI 10.1039/c3ra42332h. [Google Scholar] [CrossRef]

Dhara M, Mantero Martinez M, Makke M, Schwarz Y, Mohrmann R, Bruns D (2020). Synergistic actions of v-SNARE transmembrane domains and membrane-curvature modifying lipids in neurotransmitter release. eLife 9: e55152. DOI 10.7554/eLife.55152. [Google Scholar] [CrossRef]

di Bartolo AL, Masone D (2022). Synaptotagmin-1 C2B domains cooperatively stabilize the fusion stalk via a master-servant mechanism. Chemical Science 13: 3437–3446. DOI 10.1039/D1SC06711G. [Google Scholar] [CrossRef]

di Bartolo AL, Tomes CN, Mayorga LS, Masone D (2022). Enhanced expansion and reduced kiss-and-run events in fusion pores steered by synaptotagmin-1 C2B domains. Journal of Chemical Theory and Computation 18: 4544–4554. DOI 10.1021/acs.jctc.2c00424. [Google Scholar] [CrossRef]

Dill KA, Bromberg S, Stigter D (2010). Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience. New York, NY, USA: Garland Science. [Google Scholar]

Doerr S, Majewski M, Pérez A, Krämer A, Clementi C, Noe F, Giorgino T, De Fabritiis G (2021). TorchMD: A deep learning framework for molecular simulations. Journal of Chemical Theory and Computation 17: 2355–2363. DOI 10.1021/acs.jctc.0c01343. [Google Scholar] [CrossRef]

Drescher M, Veldhuis G, van Rooijen BD, Milikisyants S, Subramaniam V, Huber M (2008). Antiparallel arrangement of the helices of vesicle-bound alpha-synuclein. Journal of the American Chemical Society 130: 7796–7797. DOI 10.1021/ja801594s. [Google Scholar] [CrossRef]

Duncan AL, Reddy T, Koldsø H, Hélie J, Fowler PW, Chavent M, Sansom MSP (2017). Protein crowding and lipid complexity influence the nanoscale dynamic organization of ion channels in cell membranes. Scientific Reports 7: 16647. DOI 10.1038/s41598-017-16865-6. [Google Scholar] [CrossRef]

Dunker AK, Lawson JD, Brown CJ, Romero P, Oh JS et al. (2001). Intrinsically disordered protein. Journal of Molecular Graphics and Modelling 19: 26–59. DOI 10.1016/S1093-3263(00)00138-8. [Google Scholar] [CrossRef]

Durrant JD, Amaro RE (2014). LipidWrapper: An algorithm for generating large-scale membrane models of arbitrary geometry. PLoS Computational Biology 10: e1003720. DOI 10.1371/journal.pcbi.1003720. [Google Scholar] [CrossRef]

D’Agostino M, Risselada HJ, Endter LJ, Comte-Miserez V, Mayer A (2018). SNARE-mediated membrane fusion arrests at pore expansion to regulate the volume of an organelle. The EMBO Journal 37: e99193. DOI 10.15252/embj.201899193. [Google Scholar] [CrossRef]

Fakhree MAA, Blum C, Claessens MMAE (2019). Shaping membranes with disordered proteins. Archives of Biochemistry and Biophysics 677: 108163. DOI 10.1016/j.abb.2019.108163. [Google Scholar] [CrossRef]

Fang Q, Lindau M (2014). How could SNARE proteins open a fusion pore? Physiology 29: 278–285. DOI 10.1152/physiol.00026.2013. [Google Scholar] [CrossRef]

Feenstra KA, Hess B, Berendsen HJC (1999). Improving efficiency of large time-scale molecular dynamics simulations of hydrogen-rich systems. Journal of Computational Chemistry 20: 786–798. DOI 10.1002/(ISSN)1096-987X. [Google Scholar] [CrossRef]

Fernandez I, Arac D, Ubach J, Gerber SH, Shin OH, Gao Y, Anderson RGW, Südhof TC, Rizo J (2001). Three-dimensional structure of the synaptotagmin 1 C2B-Domain: Synaptotagmin 1 as a phospholipid binding machine. Neuron 32: 1057–1069. DOI 10.1016/S0896-6273(01)00548-7. [Google Scholar] [CrossRef]

Feynman RP, Hey T, Allen RW (2018). Feynman Lectures on Computation. Boca Raton, Florida, USA: CRC Press. [Google Scholar]

Fick A (1995). On liquid diffusion. Journal of Membrane Science 100: 33–38. DOI 10.1016/0376-7388(94)00230-V. [Google Scholar] [CrossRef]

Fiorin G, Klein ML, Hénin J (2013). Using collective variables to drive molecular dynamics simulations. Molecular Physics 111: 3345–3362. DOI 10.1080/00268976.2013.813594. [Google Scholar] [CrossRef]

Fiorin G, Marinelli F, Faraldo-Gómez JD (2020). Direct derivation of free energies of membrane deformation and other solvent density variations from enhanced sampling molecular dynamics. Journal of Computational Chemistry 41: 449–459. DOI 10.1002/jcc.26075. [Google Scholar] [CrossRef]

Fowler PW, Hélie J, Duncan A, Chavent M, Koldsø H, Sansom MS (2016). Membrane stiffness is modified by integral membrane proteins. Soft Matter 12: 7792–7803. DOI 10.1039/C6SM01186A. [Google Scholar] [CrossRef]

François Q, Sigurdsson Jon K, Marianne R, Atzberger Paul J, Patricia B, David L (2014). Shape matters in protein mobility within membranes. Proceedings of the National Academy of Sciences 111: 5083–5087. DOI 10.1073/pnas.1321054111. [Google Scholar] [CrossRef]

François-Martin C, Rothman JE, Pincet F (2017). Low energy cost for optimal speed and control of membrane fusion. Proceedings of the National Academy of Sciences 114: 1238–1241. DOI 10.1073/pnas.1621309114. [Google Scholar] [CrossRef]

Fu C, Pfaendtner J (2018). Lifting the curse of dimensionality on enhanced sampling of reaction networks with parallel bias metadynamics. Journal of Chemical Theory and Computation 14: 2516–2525. DOI 10.1021/acs.jctc.7b01289. [Google Scholar] [CrossRef]

Fuertes G, Giménez D, Esteban-Martín S, Sánchez-Muñoz OL, Salgado J (2011). A lipocentric view of peptide-induced pores. European Biophysics Journal 40: 399–415. DOI 10.1007/s00249-011-0693-4. [Google Scholar] [CrossRef]

Gardner JM, Abrams CF (2017). Rate of hemifusion diaphragm dissipation and ability to form three-junction bound HD determined by lipid composition. The Journal of Chemical Physics 147: 134903. DOI 10.1063/1.4994320. [Google Scholar] [CrossRef]

Gell-Mann M (1995). The Quark and the Jaguar: Adventures in the Simple and the Complex. St. Martin's Press. New York, NY, USA: Macmillan. [Google Scholar]

Gilabert JF, Grebner C, Soler D, Lecina D, Municoy M et al. (2019). PELE-MSM: A monte carlo based protocol for the estimation of absolute binding free energies. Journal of Chemical Theory and Computation 15: 6243–6253. DOI 10.1021/acs.jctc.9b00753. [Google Scholar] [CrossRef]

Golani G, Leikina E, Melikov K, Whitlock JM, Gamage DG, Luoma-Overstreet G, Millay DP, Kozlov MM, Chernomordik LV (2021). Myomerger promotes fusion pore by elastic coupling between proximal membrane leaflets and hemifusion diaphragm. Nature Communications 12: 1–18. DOI 10.1038/s41467-020-20804-x. [Google Scholar] [CrossRef]

Gorai B, Sahoo AK, Srivastava A, Dixit NM, Maiti PK (2021). Concerted interactions between multiple gp41 trimers and the target cell lipidome may be required for HIV-1 entry. Journal of Chemical Information and Modeling 61: 444–454. DOI 10.1021/acs.jcim.0c01291. [Google Scholar] [CrossRef]

Gruget C, Bello O, Coleman J, Krishnakumar SS, Perez E, Rothman JE, Pincet F, Donaldson SH (2020). Synaptotagmin-1 membrane binding is driven by the C2B domain and assisted cooperatively by the C2A domain. Scientific Reports 10: 18011. DOI 10.1038/s41598-020-74923-y. [Google Scholar] [CrossRef]

Gucek A, Jorgacevski J, Singh P, Geisler C, Lisjak M, Vardjan N, Kreft M, Egner A, Zorec R (2016). Dominant negative SNARE peptides stabilize the fusion pore in a narrow, release-unproductive state. Cellular and Molecular Life Sciences 73: 3719–3731. DOI 10.1007/s00018-016-2213-2. [Google Scholar] [CrossRef]

Gómez-Sánchez R, Tooze SA, Reggiori F (2021). Membrane supply and remodeling during autophagosome biogenesis. Current Opinion in Cell Biology 71: 112–119. DOI 10.1016/j.ceb.2021.02.001. [Google Scholar] [CrossRef]

Hartwell LH, Hopfield JJ, Leibler S, Murray AW (1999). From molecular to modular cell biology. Nature 402: C47–C52. DOI 10.1038/35011540. [Google Scholar] [CrossRef]

Has C, Sivadas P, Das SL (2022). Insights into membrane curvature sensing and membrane remodeling by intrinsically disordered proteins and protein regions. The Journal of Membrane Biology 255: 237–259. DOI 10.1007/s00232-022-00237-x. [Google Scholar] [CrossRef]

Hashemian B, Millán D, Arroyo M (2013). Modeling and enhanced sampling of molecular systems with smooth and nonlinear data-driven collective variables. The Journal of Chemical Physics 139: 214101. DOI 10.1063/1.4830403. [Google Scholar] [CrossRef]

Hashemian B, Millán D, Arroyo M (2016). Charting molecular free-energy landscapes with an atlas of collective variables. The Journal of Chemical Physics 145: 174109. DOI 10.1063/1.4966262. [Google Scholar] [CrossRef]

Haylock S, Friddin MS, Hindley JW, Rodriguez E, Charalambous K, Booth PJ, Barter LMC, Ces O (2020). Membrane protein mediated bilayer communi-cation in networks of droplet interface bilayers. Communications Chemistry 3: 77. DOI 10.1038/s42004-020-0322-1. [Google Scholar] [CrossRef]

Helfrich W (1973). Elastic properties of lipid bilayers: Theory and possible experiments. Zeitschrift für Naturforschung C 28: 693–703. DOI 10.1515/znc-1973-11-1209. [Google Scholar] [CrossRef]

Hess B, Bekker H, Berendsen HJC, Fraaije JGEM (1997). LINCS: A linear constraint solver for molecular simulations. Journal of Computational Chemistry 18: 1463–1472. DOI 10.1002/(ISSN)1096-987X. [Google Scholar] [CrossRef]

Honerkamp-Smith AR, Veatch SL, Keller SL (2009). An introduction to critical points for biophysicists; observations of compositional heterogeneity in lipid membranes. Biochimica et Biophysica Acta (BBA)–Biomembranes 1788: 53–63. DOI 10.1016/j.bbamem.2008.09.010. [Google Scholar] [CrossRef]

Honigmann A, Pralle A (2016). Compartmentalization of the cell membrane. Journal of Molecular Biology 428: 4739–4748. DOI 10.1016/j.jmb.2016.09.022. [Google Scholar] [CrossRef]

Hooft F, Pérez de Alba Ortíz A, Ensing B (2021). Discovering collective variables of molecular transitions via genetic algorithms and neural networks. Journal of Chemical Theory and Computation 17: 2294–2306. DOI 10.1021/acs.jctc.0c00981. [Google Scholar] [CrossRef]

Hsiao YW, Hedström M, Losasso V, Metz S, Crain J, Winn M (2018). Cooperative modes of action of antimicrobial peptides characterized with atomistic simulations: A study on cecropin B. The Journal of Physical Chemistry B 122: 5908–5921. DOI 10.1021/acs.jpcb.8b01957. [Google Scholar] [CrossRef]

Huang Y, Liu Z (2009). Kinetic advantage of intrinsically disordered proteins in coupled folding-binding process: A critical assessment of the “Fly-Casting” mechanism. Journal of Molecular Biology 393: 1143–1159. DOI 10.1016/j.jmb.2009.09.010. [Google Scholar] [CrossRef]

Huang M, Wang B, Li X, Fu C, Wang C, Kang X (2019). Alpha-Synuclein: A mul-tifunctional player in exocytosis, endocytosis, and vesicle recycling. Frontiers in Neuroscience 13: 28. DOI 10.3389/fnins.2019.00028. [Google Scholar] [CrossRef]

Hub JS (2021). Joint reaction coordinate for computing the free-energy landscape of pore nucleation and pore expansion in lipid membranes. Journal of Chemical Theory and Computation 17: 1229–1239. DOI 10.1021/acs.jctc.0c01134. [Google Scholar] [CrossRef]

Hub JS, Awasthi N (2017). Probing a continuous polar defect: A reaction coordinate for pore formation in lipid membranes. Journal of Chemical Theory and Computation 13: 2352–2366. DOI 10.1021/acs.jctc.7b00106. [Google Scholar] [CrossRef]

Hénin J (2021). Fast and accurate multidimensional free energy integration. Journal of Chemical Theory and Computation 17: 6789–6798. DOI 10.1021/acs.jctc.1c00593. [Google Scholar] [CrossRef]

Ikegami T, Mototake YI, Kobori S, Oka M, Hashimoto Y (2017). Life as an emergent phenomenon: studies from a large-scale boid simulation and web data. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 375: 20160351. DOI 10.1098/rsta.2016.0351. [Google Scholar] [CrossRef]

Ingólfsson HI, Melo MN, van Eerden FJ, Arnarez C, Lopez CA, Wasse-naar TA, Periole X, de Vries AH, Tieleman DP, Marrink SJ (2014). Lipid organization of the plasma membrane. Journal of the American Chemical Society 136: 14554–14559. DOI 10.1021/ja507832e. [Google Scholar] [CrossRef]

Israelachvili JN, Mitchell D, Ninham BW (1977). Theory of self-assembly of lipid bilayers and vesicles. Biochimica et Biophysica Acta (BBA)–Biomembranes 470: 185–201. DOI 10.1016/0005-2736(77)90099-2. [Google Scholar] [CrossRef]

Jao CC, Hegde BG, Chen J, Haworth IS, Langen R (2008). Structure of membrane-bound alpha-synuclein from site-directed spin labeling and computational refinement. Proceedings of the National Academy of Sciences 105: 19666–19671. DOI 10.1073/pnas.0807826105. [Google Scholar] [CrossRef]

Jarin Z, Newhouse J, Voth GA (2021). Coarse-grained force fields from the perspective of statistical mechanics: Better understanding of the origins of a MARTINI hangover. Journal of Chemical Theory and Computation 17: 1170–1180. DOI 10.1021/acs.jctc.0c00638. [Google Scholar] [CrossRef]

Joardar A, Pattnaik GP, Chakraborty H (2022). Mechanism of membrane fusion: Interplay of lipid and peptide. The Journal of Membrane Biology 255: 211–224. DOI 10.1007/s00232-022-00233-1. [Google Scholar] [CrossRef]

Kamp F, Beyer K (2006). Binding of alpha-synuclein affects the lipid packing in bilayers of small vesicles. Journal of Biological Chemistry 281: 9251–9259. DOI 10.1074/jbc.M512292200. [Google Scholar] [CrossRef]

Karplus M, Petsko GA (1990). Molecular dynamics simulations in biology. Nature 347: 631–639. DOI 10.1038/347631a0. [Google Scholar] [CrossRef]

Karsenti E (2008). Self-organization in cell biology: A brief history. Nature Reviews Molecular Cell Biology 9: 255–262. DOI 10.1038/nrm2357. [Google Scholar] [CrossRef]

Kawamoto S, Klein ML, Shinoda W (2015). Coarse-grained molecular dynamics study of membrane fusion: Curvature effects on free energy barriers along the stalk mechanism. The Journal of Chemical Physics 143: 243112. DOI 10.1063/1.4933087. [Google Scholar] [CrossRef]

Kawamoto S, Shinoda W (2014). Free energy analysis along the stalk mechanism of mem-brane fusion. Soft Matter 10: 3048–3054. [Google Scholar]

Khounlo R, Hawk BJD, Khu TM, Yoo G, Lee NK, Pierson J, Shin YK (2021). Membrane binding of α-synuclein stimulates expansion of SNARE-dependent fusion pore. Frontiers in Cell and Developmental Biology 9: 663431. DOI 10.3389/fcell.2021.663431. [Google Scholar] [CrossRef]

Klaips CL, Jayaraj GG, Hartl FU (2018). Pathways of cellular proteostasis in aging and disease. The Journal of Cell Biology 217: 51–63. DOI 10.1083/jcb.201709072. [Google Scholar] [CrossRef]

Klein F, Barrera EE, Pantano S (2021). Assessing SIRAH’s capability to simulate intrinsically disordered proteins and peptides. Journal of Chemical Theory and Computation 17: 599–604. DOI 10.1021/acs.jctc.0c00948. [Google Scholar] [CrossRef]

Koldsø H, Shorthouse D, Helie J, Sansom MSP (2014). Lipid clustering correlates with membrane curvature as revealed by molecular simulations of complex lipid bilayers. PLoS Computational Biology 10: 1–11. DOI 10.1371/journal.pcbi.1003911. [Google Scholar] [CrossRef]

Kutzner C, Kniep C, Cherian A, Nordstrom L, Grubmüller H, de Groot BL, Gapsys V (2022). GROMACS in the cloud: A global supercomputer to speed up alchemical drug design. Journal of Chemical Information and Modeling 62: 1691–1711. DOI 10.1021/acs.jcim.2c00044. [Google Scholar] [CrossRef]

Laio A, Gervasio FL (2008). Metadynamics: A method to simulate rare events and re-construct the free energy in biophysics, chemistry and material science. Reports on Progress in Physics 71: 126601. DOI 10.1088/0034-4885/71/12/126601. [Google Scholar] [CrossRef]

Laio A, Parrinello M (2002). Escaping free-energy minima. Proceedings of the National Academy of Sciences 99: 12562–12566. DOI 10.1073/pnas.202427399. [Google Scholar] [CrossRef]

Lamparter L, Galic M (2020). Cellular membranes, a versatile adaptive composite mate-rial. Frontiers in Cell and Developmental Biology 8: 684. DOI 10.3389/fcell.2020.00684. [Google Scholar] [CrossRef]

Lee JA, Verleysen M (2007). Nonlinear Dimensionality Reduction. 1st edition, Berlin/Heidelberg, Germany: Springer. [Google Scholar]

Leifer I, Morone F, Reis SDS, Andrade J, Sigman M, Makse HA (2020). Circuits with broken fibration symmetries perform core logic computations in biological networks. PLoS Computational Biology 16: e1007776. DOI 10.1371/journal.pcbi.1007776. [Google Scholar] [CrossRef]

Levy Y, Onuchic JN, Wolynes PG (2007). Fly-casting in protein-DNA binding: Frustration between protein folding and electrostatics facilitates target recognition. Journal of the American Chemical Society 129: 738–739. DOI 10.1021/ja065531n. [Google Scholar] [CrossRef]

Li W, Rudack T, Gerwert K, Gräter F, Schlitter J (2012). Exploring the multidimensional free energy surface of phosphoester hydrolysis with constrained QM/MM dynamics. Journal of Chemical Theory and Computation 8: 3596–3604. DOI 10.1021/ct300022m. [Google Scholar] [CrossRef]

Lipowsky R (2022). Remodeling of membrane shape and topology by curvature elasticity and membrane tension. Advanced Biology 6: 2101020. DOI 10.1002/adbi.202101020. [Google Scholar] [CrossRef]

Liu C, Zhao Y, Xi H, Jiang J, Yu Y, Dong W (2021). The membrane interaction of alpha-synuclein. Frontiers in Cellular Neuroscience 15: 1–7. DOI 10.3389/fncel.2021.633727. [Google Scholar] [CrossRef]

Lotz SD, Dickson A (2018). Unbiased molecular dynamics of 11 min timescale drug unbinding reveals transition state stabilizing interactions. Journal of the American Chemical Society 140: 618–628. DOI 10.1021/jacs.7b08572. [Google Scholar] [CrossRef]

Lukat G, Krüger J, Sommer B (2013). APL@Voro: A voronoi-based membrane analysis tool for GROMACS trajectories. Journal of Chemical Information and Modeling 53: 2908–2925. DOI 10.1021/ci400172g. [Google Scholar] [CrossRef]

Lynch KL, Gerona RRL, Kielar DM, Martens S, McMahon HT, Mar-tin TFJ (2008). Synaptotagmin-1 utilizes membrane bending and SNARE binding to drive fusion pore expansion. Molecular Biology of the Cell 19: 5093–5103. DOI 10.1091/mbc.e08-03-0235. [Google Scholar] [CrossRef]

Macklem PT (2008). Emergent phenomena and the secrets of life. Journal of Applied Physiology 104: 1844–1846. DOI 10.1152/japplphysiol.00942.2007. [Google Scholar] [CrossRef]

Markvoort AJ, Marrink SJ (2011). Current Topics in Membranes, vol. 68, pp. 259–294. Amsterdam, Netherlands, Elsevier: Academic Press. [Google Scholar]

Masone D, Bustos DM (2019). Transmembrane domain dimerization induces cholesterol rafts in curved lipid bilayers. Physical Chemistry Chemical Physics 21: 268–274. DOI 10.1039/C8CP06783J. [Google Scholar] [CrossRef]

Masone D, Cabeza de Vaca I, Pons C, Recio JF, Guallar V (2012). H-bond network optimization in protein-protein complexes: Are all-atom force field scores enough? PROTEINS: Structure, Function, and Bioinformatics 80: 818–824. DOI 10.1002/prot.23239. [Google Scholar] [CrossRef]

Masone D, Grosdidier S (2014). Collective variable driven molecular dynamics to improve protein-protein docking scoring. Computational Biology and Chemistry 49: 1–6. DOI 10.1016/j.compbiolchem.2013.12.003. [Google Scholar] [CrossRef]

Masone D, Uhart M, Bustos DM (2018). Bending lipid bilayers: A closed-form collective variable for effective free-energy landscapes in quantitative biology. Journal of Chemical Theory and Computation 14: 2240–2245. DOI 10.1021/acs.jctc.8b00012. [Google Scholar] [CrossRef]

Mayorga LS, Cebrian I, Verma M, Hoops S, Bassaganya-Riera J (2018). Reconstruction of endosomal organization and function by a combination of ODE and agent-based modeling strategies. Biology Direct 3: 25. DOI 10.1186/s13062-018-0227-4. [Google Scholar] [CrossRef]

Mayorga LS, López MJ, Becker WM (2012). Molecular thermodynamics for cell biology as taught with boxes. CBE Life Sciences Education 11: 31–38. DOI 10.1187/cbe.11-07-0053. [Google Scholar] [CrossRef]

McCammon JA, Gelin BR, Karplus M (1977). Dynamics of folded proteins. Nature 267: 585–590. DOI 10.1038/267585a0. [Google Scholar] [CrossRef]

McMahon HT, Kozlov MM, Martens S (2010). Membrane curvature in synaptic vesicle fusion and beyond. Cell 140: 601–605. DOI 10.1016/j.cell.2010.02.017. [Google Scholar] [CrossRef]

Middleton ER, Rhoades E (2010). Effects of curvature and composition on alpha-synuclein binding to lipid vesicles. Biophysical Journal 99: 2279–2288. DOI 10.1016/j.bpj.2010.07.056. [Google Scholar] [CrossRef]

Miguel V, Sánchez-Borzone ME, Mariani ME, García DA (2021). Modulation of membrane physical properties by natural insecticidal ketones. Biophysical Chemistry 269: 106526. DOI 10.1016/j.bpc.2020.106526. [Google Scholar] [CrossRef]

Ming C, Tang-Qing Y, Tuckerman Mark E (2015). Locating landmarks on high-dimensional free energy surfaces. Proceedings of the National Academy of Sciences 112: 3235–3240. DOI 10.1073/pnas.1418241112. [Google Scholar] [CrossRef]

Miyamoto S, Kollman PA (1992). Settle: An analytical version of the SHAKE and RAT-TLE algorithm for rigid water models. Journal of Computational Chemistry 13: 952–962. DOI 10.1002/(ISSN)1096-987X. [Google Scholar] [CrossRef]

Miyazaki Y, Okazaki S, Shinoda W (2019). Free energy analysis of membrane pore formation process in the presence of multiple melittin peptides. Biochimica et Biophysica Acta (BBA)–Biomembranes 1861: 1409–1419. DOI 10.1016/j.bbamem.2019.03.002. [Google Scholar] [CrossRef]

Mohammad IL, Mateos B, Pons M (2019). The disordered boundary of the cell: Emerging properties of membrane-bound intrinsically disordered proteins. Biomolecular Concepts 10: 25–36. DOI 10.1515/bmc-2019-0003. [Google Scholar] [CrossRef]

Monteiro HS, Leifer I, Reis SDS, Andrade JS, Makse HA (2022). Fast algorithm to identify minimal patterns of synchrony through fibration symmetries in large directed networks. Chaos 32: 033120. DOI 10.1063/5.0066741. [Google Scholar] [CrossRef]

Moon CP, Fleming KG (2011). Side-chain hydrophobicity scale derived from trans-membrane protein folding into lipid bilayers. Proceedings of the National Academy of Sciences 108: 10174–10177. DOI 10.1073/pnas.1103979108. [Google Scholar] [CrossRef]

Morone F, Leifer I, Makse HA (2020). Fibration symmetries uncover the building blocks of biological networks. Proceedings of the National Academy of Sciences 117: 8306–8314. DOI 10.1073/pnas.1914628117. [Google Scholar] [CrossRef]

Mosalaganti S, Obarska-Kosinska A, Siggel M, Taniguchi R, Turoňová B et al. (2022). AI-based structure prediction empowers integrative structural analysis of human nuclear pores. Science 376: 1158–1159. [Google Scholar]

Nachtomy O, Shavit A, Smith J (2002). Leibnizian organisms, nested individuals, and units of selection. Theory in Biosciences 121: 205–230. DOI 10.1007/s12064-002-0020-9. [Google Scholar] [CrossRef]

Nellikka RK, Bhaskar BR, Sanghrajka K, Patil SS, Das D (2021). α-Synuclein kinetically regulates the nascent fusion pore dynamics. Proceedings of the National Academy of Sciences 118: e2021742118. DOI 10.1073/pnas.2021742118. [Google Scholar] [CrossRef]

Nemani VM, Lu W, Berge V, Nakamura K, Onoa B, Lee MK, Chaudhry FA, Nicoll RA, Edwards RH (2010). Increased expression of alpha-synuclein reduces neurotransmitter release by inhibiting synaptic vesicle reclustering after endocytosis. Neuron 65: 66–79. DOI 10.1016/j.neuron.2009.12.023. [Google Scholar] [CrossRef]

Nicolson GL (2014). The fluid—mosaic model of membrane structure: Still relevant to understanding the structure, function and dynamics of biological membranes after more than 40 years. Biochimica et Biophysica Acta (BBA)–Biomembranes 1838: 1451–1466. DOI 10.1016/j.bbamem.2013.10.019. [Google Scholar] [CrossRef]

Nicolson GL, Ferreira de Mattos G (2021). A brief introduction to some aspects of the fluid-mosaic model of cell membrane structure and its importance in membrane lipid replacement. Membranes 11: 947. DOI 10.3390/membranes11120947. [Google Scholar] [CrossRef]

Nishizawa M, Nishizawa K (2013). Molecular dynamics simulation analysis of membrane defects and pore propensity of hemifusion diaphragms. Biophysical Journal 104: 1038–1048. DOI 10.1016/j.bpj.2013.01.022. [Google Scholar] [CrossRef]

Novikoff Alex B (1945). The concept of integrative levels and biology. Science 101: 209–215. DOI 10.1126/science.101.2618.209. [Google Scholar] [CrossRef]

Nyenhuis SB, Karandikar N, Kiessling V, Kreutzberger AJB, Thapa A, Liang B, Tamm LK, Cafiso DS (2021). Conserved arginine residues in synaptotagmin 1 regulate fusion pore expansion through membrane contact. Nature Communications 12: 761. DOI 10.1038/s41467-021-21090-x. [Google Scholar] [CrossRef]

Olesen K, Awasthi N, Bruhn DS, Pezeshkian W, Khandelia H (2018). Faster simulations with a 5 fs time step for lipids in the CHARMM force field. Journal of Chemical Theory and Computation 14: 3342–3350. DOI 10.1021/acs.jctc.8b00267. [Google Scholar] [CrossRef]

Orbach R, Su X (2020). Surfing on membrane waves: Microvilli, curved membranes, and immune signaling. Frontiers in Immunology 2187: 1–11. DOI 10.3389/fimmu.2020.02187. [Google Scholar] [CrossRef]

O’Connor T (1994). Emergent properties. American Philosophical Quarterly 31: 91–104. [Google Scholar]

Pannuzzo M, de Jong DH, Raudino A, Marrink SJ (2014). Simulation of polyethy-lene glycol and calcium-mediated membrane fusion. The Journal of Chemical Physics 140: 124905. DOI 10.1063/1.4869176. [Google Scholar] [CrossRef]

Pattnaik GP, Meher G, Chakraborty H (2018). Biochemical and Biophysical Roles of Cell Surface Molecules, pp. 69–78. Singapore: Springer. [Google Scholar]

Pebay-Peyroula E, Ziegler C, Nury H, Parcy F, Ruigrok RWH, Cugliandolo LF (2016). From molecules to living organisms: An interplay between biology and physics. In: Lecture Notes of the Les Houches School of Physics, vol. 102. Oxford University Press, Oxford, England: Oxford University Press. [Google Scholar]

Pezeshkian W, König M, Wassenaar TA, Marrink SJ (2020). Backmapping triangulated surfaces to coarse-grained membrane models. Nature Communications 11: 2296. DOI 10.1038/s41467-020-16094-y. [Google Scholar] [CrossRef]

Polanyi M (1968). Life’s irreducible structure. Science 160: 1308–1312. DOI 10.1126/science.160.3834.1308. [Google Scholar] [CrossRef]

Poojari CS, Scherer KC, Hub JS (2021). Free energies of membrane stalk formation from a lipidomics perspective. Nature Communications 12: 6594. DOI 10.1038/s41467-021-26924-2. [Google Scholar] [CrossRef]

Pratyush T, Berne BJ (2016). Spectral gap optimization of order parameters for sampling complex molecular systems. Proceedings of the National Academy of Sciences 113: 2839–2844. DOI 10.1073/pnas.1600917113. [Google Scholar] [CrossRef]

Quevedo MF, Bustos MA, Masone D, Roggero CM, Bustos DM, Tomes CN (2019). Grab recruitment by Rab27A-Rabphilin3a triggers Rab3A activation in human sperm exocytosis. Biochimica et Biophysica Acta (BBA)-Molecular Cell Research 1866: 612–622. DOI 10.1016/j.bbamcr.2018.12.005. [Google Scholar] [CrossRef]

Reid CR, Latty T (2016). Collective behaviour and swarm intelligence in slime moulds. FEMS Microbiology Reviews 40: 798–806. DOI 10.1093/femsre/fuw033. [Google Scholar] [CrossRef]

Risselada HJ, Bubnis G, Grubmüller H (2014). Expansion of the fusion stalk and its implication for biological membrane fusion. Proceedings of the National Academy of Sciences 111: 11043–11048. DOI 10.1073/pnas.1323221111. [Google Scholar] [CrossRef]

Risselada HJ, Grubmüller H (2012). How SNARE molecules mediate membrane fusion: Recent insights from molecular simulations. Current Opinion in Structural Biology 22: 187–196. DOI 10.1016/j.sbi.2012.01.007. [Google Scholar] [CrossRef]

Risselada HJ, Grubmüller H (2021). How proteins open fusion pores: insights from molecular simulations. European Biophysics Journal 50: 279–293. DOI 10.1007/s00249-020-01484-3. [Google Scholar] [CrossRef]

Risselada HJ, Kutzner C, Grubmüller H (2011). Caught in the act: Visualization of SNARE-mediated fusion events in molecular detail. ChemBioChem 12: 1049–1055. DOI 10.1002/cbic.201100020. [Google Scholar] [CrossRef]

Risselada HJ, Marelli G, Fuhrmans M, Smirnova YG, Grubmüller H, Mar-rink SJ, Muller M (2012). Line-Tension controlled mechanism for influenza fusion. PLoS One 7: 1–14. DOI 10.1371/journal.pone.0038302. [Google Scholar] [CrossRef]

Risselada HJ, Mayer A (2020). SNAREs, tethers and SM proteins: How to overcome the final barriers to membrane fusion? Biochemical Journal 477: 243–258. DOI 10.1042/BCJ20190050. [Google Scholar] [CrossRef]

Risselada H, Smirnova Y, Grubmüller H (2014). Free energy landscape of rim-pore expansion in membrane fusion. Biophysical Journal 107: 2287–2295. DOI 10.1016/j.bpj.2014.08.022. [Google Scholar] [CrossRef]

Rizo J (2018). Mechanism of neurotransmitter release coming into focus. Protein Science 27: 1364–1391. DOI 10.1002/pro.3445. [Google Scholar] [CrossRef]

Rizo J (2022). Molecular mechanisms underlying neurotransmitter release. Annual Review of Biophysics 51: 377–408. DOI 10.1146/annurev-biophys-111821-104732. [Google Scholar] [CrossRef]

Rothman JE, Lenard J (1977). Membrane asymmetry. Science 195: 743–753. DOI 10.1126/science.402030. [Google Scholar] [CrossRef]

Roux B (1995). The calculation of the potential of mean force using computer simulations. Computer Physics Communications 91: 275–282. DOI 10.1016/0010-4655(95)00053-I. [Google Scholar] [CrossRef]

Ryckaert JP, Ciccotti G, Berendsen HJC (1977). Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. Journal of Computational Physics 23: 327–341. DOI 10.1016/0021-9991(77)90098-5. [Google Scholar] [CrossRef]

Sackmann E (1995). Biological membranes architecture and function. Structure and Dynamics of Membranes 1: 1–63. [Google Scholar]

Saen-oon S, Cabeza de Vaca I, Masone D, Medina M, Guallar V (2015). A theoretical multiscale treatment of protein-protein electron transfer: The ferredoxin/ferredoxin-NADP+ reductase andflavodoxin/ferredoxin-NADP+ reductase systems. Biochimica et Biophysica Acta (BBA)–Bioenergetics 1847: 1530–1538. DOI 10.1016/j.bbabio.2015.09.002. [Google Scholar] [CrossRef]

Scheidt HA, Kolocaj K, Konrad DB, Frank JA, Trauner D, Langosch D, Huster D (2020). Light-induced lipid mixing implies a causal role of lipid splay in membrane fusion. Biochimica et Biophysica Acta (BBA)–Biomembranes 1862: 183438. DOI 10.1016/j.bbamem.2020.183438. [Google Scholar] [CrossRef]

Schiel JA, Prekeris R (2013). Membrane dynamics during cytokinesis. Current Opinion in Cell Biology 25: 92–98. DOI 10.1016/j.ceb.2012.10.012. [Google Scholar] [CrossRef]

Schlick T, Portillo-Ledesma S (2021). Biomolecular modeling thrives in the age of technology. Nature Computational Science 1: 321–331. DOI 10.1038/s43588-021-00060-9. [Google Scholar] [CrossRef]

Schrödinger E (1944). What is Life? The Physical Aspect of the Living Cell. Cambridge, England: Cambridge University Press. [Google Scholar]

Sejdiu BI, Tieleman DP (2021). ProLint: A web-based framework for the automated data analysis and visualization of lipid-protein interactions. Nucleic Acids Research 49: W544–W550. DOI 10.1093/nar/gkab409. [Google Scholar] [CrossRef]

Seven AB, Brewer KD, Shi L, Jiang QX, Rizo J (2013). Prevalent mechanism of membrane bridging by synaptotagmin-1. Proceedings of the National Academy of Sciences 110: E3243–E3252. DOI 10.1073/pnas.1310327110 [Google Scholar] [CrossRef]

Sharma S, Lindau M (2018). Molecular mechanism of fusion pore formation driven by the neuronal SNARE complex. Proceedings of the National Academy of Sciences 115: 12751–12756. DOI 10.1073/pnas.1816495115. [Google Scholar] [CrossRef]

Shoemaker BA, Portman JJ, Wolynes PG (2000). Speeding molecular recognition by using the folding funnel: The fly-casting mechanism. Proceedings of the National Academy of Sciences 97: 8868–8873. DOI 10.1073/pnas.160259697. [Google Scholar] [CrossRef]

Sica MP, Smulski CR (2021). Coarse grained molecular dynamic simulations for the study of TNF receptor family members’ transmembrane organization. Frontiers in Cell and Developmental Biology 8: 1–11. DOI 10.3389/fcell.2020.577278 [Google Scholar] [CrossRef]

Sidky H, Chen W, Ferguson AL (2020). Machine learning for collective variable discovery and enhanced sampling in biomolecular simulation. Molecular Physics 118: 5. DOI 10.1080/00268976.2020.1737742. [Google Scholar] [CrossRef]

Singer SJ, Nicolson GL (1972). The fluid mosaic model of the structure of cell membranes. Science 175: 720–731. DOI 10.1126/science.175.4023.720. [Google Scholar] [CrossRef]

Smeijers AF, Markvoort AJ, Pieterse K, Hilbers PAJ (2006). A detailed look at vesicle fusion. The Journal of Physical Chemistry B 110: 13212–13219. DOI 10.1021/jp060824o. [Google Scholar] [CrossRef]

Smirnova YG, Fuhrmans M, Vidal IAB, Müller M (2015). Free-energy calculation methods for collective phenomena in membranes. Journal of Physics D 48: 343001. DOI 10.1088/0022-3727/48/34/343001. [Google Scholar] [CrossRef]

Smirnova YG, Marrink SJ, Lipowsky R, Knecht V (2010). Solvent-exposed tails as prestalk transition states for membrane fusion at low hydration. Journal of the American Chemical Society 132: 6710–6718. DOI 10.1021/ja910050x. [Google Scholar] [CrossRef]

Smirnova YG, Risselada HJ, Müller M (2019). Thermodynamically reversible paths of the first fusion intermediate reveal an important role for membrane anchors of fusion proteins. Proceedings of the National Academy of Sciences 116: 2571–2576. DOI 10.1073/pnas.1818200116. [Google Scholar] [CrossRef]

Snead WT, Stachowiak JC (2018). Structure vs. stochasticity-the role of molecular crowding and intrinsic disorder in membrane fission. Journal of Molecular Biology 430: 2293–2308. DOI 10.1016/j.jmb.2018.03.024. [Google Scholar] [CrossRef]

Song W, Yen HY, Robinson CV, Sansom MSP (2019). State-dependent lipid inter-actions with the A2a receptor revealed by MD simulations using in vivo-mimetic membranes. Structure 27: 392–403.e3. DOI 10.1016/j.str.2018.10.024. [Google Scholar] [CrossRef]

Souza PCT, Alessandri R, Barnoud J, Thallmair S, Faustino I et al. (2021). Martini 3: A general purpose forcefield for coarse-grained molecular dynamics. Nature Methods 18: 382–388. DOI 10.1038/s41592-021-01098-3. [Google Scholar] [CrossRef]

Stroh KS, Risselada HJ (2021). Quantifying membrane curvature sensing of peripheral proteins by simulated buckling and umbrella sampling. Journal of Chemical Theory and Computation 17: 5276–5286. DOI 10.1021/acs.jctc.1c00021. [Google Scholar] [CrossRef]

Sugase K, Dyson HJ, Wright PE (2007). Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 447: 1021–1025. DOI 10.1038/nature05858. [Google Scholar] [CrossRef]

Suh D, Feng S, Kim S, Lee H, Park S-J, Zhang H, Choi S, Wang K, Lee J, Im W (2022). CHARMM-GUI Enhanced Sampler for molecular dynamics simulations with collective variables and various enhanced sampling methods. Biophysical Journal 121: 274a. DOI 10.1016/j.bpj.2021.11.1376. [Google Scholar] [CrossRef]

Thayanidhi N, Helm JR, Nycz DC, Bentley M, Liang Y, Hay JC (2010). Alpha-synuclein delays endoplasmic reticulum (ER)-to-Golgi transport in mammalian cells by antagonizing ER/Golgi SNAREs. Molecular Biology of the Cell 21: 1850–1863. DOI 10.1091/mbc.e09-09-0801. [Google Scholar] [CrossRef]

Thomasen FE, Pesce F, Roesgaard MA, Tesei G, Lindorff-Larsen K (2022). Improving martini 3 for disordered and multidomain proteins. Journal of Chemical Theory and Computation 18: 2033–2041. DOI 10.1021/acs.jctc.1c01042. [Google Scholar] [CrossRef]

Tolpekina TV, den Otter WK, Briels WJ (2004). Nucleation free energy of pore formation in an amphiphilic bilayer studied by molecular dynamics simulations. The Journal of Chemical Physics 121: 12060–12066. DOI 10.1063/1.1815296. [Google Scholar] [CrossRef]

Tomes C (2015). The proteins of exocytosis: Lessons from the sperm model. Biochemical Journal 465: 359–370. DOI 10.1042/BJ20141169. [Google Scholar] [CrossRef]

Tomes CN, Michaut M, Blas GD, Visconti P, Matti U, Mayorga LS (2002). SNARE complex assembly is required for human sperm acrosome reaction. Developmental Biology 243: 326–338. DOI 10.1006/dbio.2002.0567. [Google Scholar] [CrossRef]

Torres-Sánchez A, Millán D, Arroyo M (2019). Modelling fluid deformable surfaces with an emphasis on biological interfaces. Journal of Fluid Mechanics 872: 218–271. DOI 10.1017/jfm.2019.341. [Google Scholar] [CrossRef]

Torrie G, Valleau J (1977). Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. Journal of Computational Physics 23: 187–199. DOI 10.1016/0021-9991(77)90121-8. [Google Scholar] [CrossRef]

Tran DP, Kitao A (2020). Kinetic selection and relaxation of the intrinsically disordered region of a protein upon binding. Journal of Chemical Theory and Computation 16: 2835–2845. DOI 10.1021/acs.jctc.9b01203. [Google Scholar] [CrossRef]

Trapl D, Horvacanin I, Mareska V, Ozcelik F, Unal G, Spiwok V (2019). Anncolvar: Approximation of complex collective variables by artificial neural networks for analysis and biasing of molecular simulations. Frontiers in Molecular Biosciences 6: 1–9. DOI 10.3389/fmolb.2019.00025. [Google Scholar] [CrossRef]

Tribello G, Bonomi M, Branduardi D, Camilloni C, Bussi G (2014). PLUMED 2: New feathers for an old bird. Computer Physics Communications 185: 604–613. DOI 10.1016/j.cpc.2013.09.018. [Google Scholar] [CrossRef]

Tribello GA, Gasparotto P (2019). Using dimensionality reduction to analyze protein trajectories. Frontiers in Molecular Biosciences 6: 46. DOI 10.3389/fmolb.2019.00046. [Google Scholar] [CrossRef]

Turkheimer FE, Hellyer P, Kehagia AA, Expert P, Lord LD, Vohryzek J, de Faria Dafflon J, Brammer M, Leech R (2019). Conflicting emergences. Weak vs. strong emergence for the modelling of brain function. Neuroscience and Biobehavioral Reviews 99: 3–10. DOI 10.1016/j.neubiorev.2019.01.023. [Google Scholar] [CrossRef]

van der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE, Berendsen HJC (2005). GROMACS: Fast, flexible, and free. Journal of Computational Chemistry 26: 1701–1718. DOI 10.1002/(ISSN)1096-987X. [Google Scholar] [CrossRef]

Vendruscolo M, Dobson CM (2011). Protein dynamics: Moore’s law in molecular biology. Current Biology 21: R68–R70. DOI 10.1016/j.cub.2010.11.062. [Google Scholar] [CrossRef]

Wehmeyer C, Noé F (2018). Time-lagged autoencoders: Deep learning of slow collective variables for molecular kinetics. The Journal of Chemical Physics 148: 241703. DOI 10.1063/1.5011399. [Google Scholar] [CrossRef]

Whitlock JM, Chernomordik LV (2021). Flagging fusion: Phosphatidylserine signaling in cell-cell fusion. Journal of Biological Chemistry 296: 100411. DOI 10.1016/j.jbc.2021.100411. [Google Scholar] [CrossRef]

Wohlert J, den Otter WK, Edholm O, Briels WJ (2006). Free energy of a trans-membrane pore calculated from atomistic molecular dynamics simulations. The Journal of Chemical Physics 124: 154905. DOI 10.1063/1.2171965. [Google Scholar] [CrossRef]

Wright PE, Dyson HJ (1999). Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. Journal of Molecular Biology 293: 321–331. DOI 10.1006/jmbi.1999.3110. [Google Scholar] [CrossRef]

Wu Z, Dharan N, McDargh ZA, Thiyagarajan S, O’Shaughnessy B, Karatekin E (2021). The neuronal calcium sensor Synaptotagmin-1 and SNARE proteins cooperate to dilate fusion pores. eLife 10: e68215. DOI 10.7554/eLife.68215. [Google Scholar] [CrossRef]

Yamazaki T, Igarashi J, Yamaura H (2021). Human-scale brain simulation via super-computer: A case study on the cerebellum. Neuroscience 462: 235–246. DOI 10.1016/j.neuroscience.2021.01.014. [Google Scholar] [CrossRef]

Yang YI, Shao Q, Zhang J, Yang L, Gao YQ (2019). Enhanced sampling in molecular dynamics. The Journal of Chemical Physics 151: 070902. DOI 10.1063/1.5109531. [Google Scholar] [CrossRef]

Yesylevskyy S, Khandelia H (2021). EnCurv: Simple technique of maintaining global membrane curvature in molecular dynamics simulations. Journal of Chemical Theory and Computation 17: 1181–1193. DOI 10.1021/acs.jctc.0c00800. [Google Scholar] [CrossRef]

Yin Y, Arkhipov A, Schulten K (2009). Simulations of membrane tubulation by lattices of amphiphysin N-BAR domains. Structure 17: 882–892. DOI 10.1016/j.str.2009.03.016. [Google Scholar] [CrossRef]

Ying L, Jiajie D, Yanxin L, Yuji I, Zengliu S, Klaus S, Taekjip H, Yeon-Kyun S. (2013). Fusion pore formation and expansion induced by Ca2+ and synaptotagmin 1. Proceedings of the National Academy of Sciences 110: 1333–1338. [Google Scholar]

Yungerman I, Starodumov I, Fulati A, Uto K, Ebara M, Moskovitz Y (2022). Full-atomistic optimized potentials for liquid simulations and polymer consistent force field models for biocompatible shape-memory poly(epsilon-caprolactone). The Journal of Physical Chemistry B 126: 3961–3972. DOI 10.1021/acs.jpcb.2c01973. [Google Scholar] [CrossRef]

Zeno WF, Baul U, Snead WT, DeGroot ACM, Wang L, Lafer EM, Thirumalai D, Stachowiak JC (2018). Synergy between intrinsically disordered domains and structured proteins amplifies membrane curvature sensing. Nature Communications 9: 4152. DOI 10.1038/s41467-018-06532-3. [Google Scholar] [CrossRef]

Zhang YY, Niu H, Piccini G, Mendels D, Parrinello M (2019). Improving collective variables: The case of crystallization. The Journal of Chemical Physics 150: 094509. DOI 10.1063/1.5081040. [Google Scholar] [CrossRef]