A developed ant colony algorithm for cancer molecular subtype classification to reveal the predictive biomarker in the renal cell carcinoma

Introduction

As cancer lesions are reflected in abnormal expression of cellular genes in the body (Zakiryanova et al., 2019), the study of gene expression data can be useful both for making early judgments about a patient’s cancer status and for the precise treatment of drugs (Vamathevan et al., 2019). The important process in the early detection and treatment of cancer is to identify the subtypes of the high-dimensional cancer gene expression data (Sayed et al., 2019). Therefore, a large number of methods have been proposed to classify those datasets.

Feature selection methods have been utilized since the 1990s (Yu and Liu, 2003; Li and Yin, 2013; Bolón-Canedo et al., 2014). For instance, a new feature selection method based on iBPSO was proposed for cancer diagnosis and classification, the classification performance of which was superior to the other compared algorithms (Jain et al., 2018). To select desired feature subset, two feature selection methods including relevant estimation and redundant estimation are combined (Kavitha et al., 2020), which used different criteria for attribute selection. Moreover, as one of the various feature selection methods, the Relief-F technique is widely used for selecting the most relevant features (Robnik-Šikonja and Kononenko, 2003). Hakim et al. (2021) applied ReliefF-support Vector Machine (SVM) in seven biomedical datasets for classification and concluded that ReliefF outperformed compared with correlation-based feature selection (CFS). To remove redundancy in microarray data, we used the k-means method as the clustering approach for feature selection, which could classify similar features (Aydadenta and Adiwijaya, 2018). Kang et al. (2019) combined relaxed Lasso and generalized SVM to solve tumor classification and verified that the proposed method had better performance in reduction and accuracy of classification. However, due to the dimension curse and high data noise of those cancer gene expression datasets, classification is a challenging task to perform the classification. Therefore, it is urgent to propose an effective method to enhance the classification accuracy and choose the optimal feature subset on those cancer gene expression datasets.

Recently, swarm intelligence methods have aroused universal interest due to their strong robustness, simplicity, self-organization and extensibility (Li et al., 2011, 2015; Islam et al., 2018; Wang et al., 2020a; Mitra et al., 2022). Consequently, more and more classification methods are developed based on swarm intelligence. For instance, Li et al. (2017) combined the genetic algorithm and the grey wolf optimization algorithm were combined to address the classification task. This hybrid approach yielded the best subset of features by changing the initial position and changing the group position in real-time. An improved artificial bee colony algorithm combined with the SVM classifier was proposed by Zhang (2016), which obtained a subset of features with better classification performance. The optimal subset of features was chosen by the combination of the genetic algorithm and the SVM classifier by Huerta et al. (2006). The authors proposed a novel hybrid swarm intelligence method based on the chaos-based firefly algorithm and the other heuristic method to reduce computing costs (Dash et al., 2019). To select the optimal feature set, an Altruistic Whale Optimization Algorithm (AWOA) was proposed which could get the global optima (Kundu et al., 2022). Dash et al. (2019) used an ASVM method that combined the Shuffled Frog Leaping Algorithm and proposed an SVM that proposed and performed better than SVM based on Grid Search and Random Search.

As one of the swarm intelligence methods, the ant colony optimization (ACO) algorithm is a heuristic evolutionary algorithm inspired by foraging ants (Dash et al., 2019). Ant colony optimization has the characteristics of parallel, robust and positive feedback (Peake et al., 2018; Dhanasekaran et al., 2020). Now, the ant colony algorithm has extensive use in combinatorial optimization problems such as the traveling salesman problem (Gülcü et al., 2018), vehicle routing problems (Yan, 2018), and mobile robot path planning (Ajeil et al., 2020). The ACO algorithm is widely applied to solve the problem of high-dimensional feature selection (Ma et al., 2021). For instance, a fuzzy adaptive ACO was proposed by Wang et al. (2015). Could achieve better classification results under specific conditions. Based on ACO, a classification system for microarray data was designed (Bir-Jmel et al., 2019) and the study proved that the F-score could increase by 0.86 when combined with ACO. In (Aldryan et al., 2018), the authors proposed a new method (ACO-FLANN) that combined ACO and functional link artificial neural network. However, the shortcomings in traditional ACO are obvious: local optimal solution and slow convergence speed (Mallick et al., 2021), affecting negatively the efficiency of algorithm optimization.

Therefore, to address those problems in the traditional ACO algorithm, we propose the development of an ACO algorithm (DACO) to conduct the classification task. First, the initial pheromone concentration based on the weight ranking vector is proposed to accelerate the convergence speed; second, a dynamic pheromone volatility factor is designed to prevent the convergence premature; last, the pheromone update rule in the Ant Colony System is employed to update the pheromone globally and locally. In the experiment, eight high-dimensional cancer gene expression datasets and a renal cell carcinoma dataset are employed to demonstrate the excellent performance of the proposed algorithm. Then, we compare the proposed algorithm with effective methods from different perspectives. Experimental results show that DACO outperforms the other comparative methods in terms of the accuracy and the optimal number of feature subsets.

Methodology

Feature selection methods for cancer gene expression data always suffer from the curse of dimensionality. Indeed, the redundant and irrelevant features can adversely affect the classification accuracy, since noise information is added more than useful information. In this paper, we propose a novel algorithm (DACO) based on the ACO algorithm to enhance the quality of classification and minimize the number of irrelevant features. In DACO, two states are split in each feature, with corresponding ants passing through or not passing through the node. To obtain the optimal subset of features, the search process is iterated multiple times in the proposed algorithm.

Ant colony algorithm

Inspired by the social intelligence of ants, the ant colony algorithm mimics the foraging behaviors of ants. Studies have shown that it is difficult for one ant to find the food; instead, in colony of ants, the path information can be shared, so that food and the shortest path can be found with ease. To be more specific, during the process of foraging, subsequent ants are led rationally to choose suitable paths through the pheromone released on the paths. The paths with more pheromones are more likely to be chosen by ants. Eventually, after continuous positive feedback, the shortest route accumulates the most pheromones. Generally speaking, and with multiple iterations, ongoing pheromone updates are essential to finding the best solution for the optimization problem. Furthermore, the ant colony algorithm follows the following rules in the search process:

1.    Each ant searches the path independently and the communication between ants is based only on the pheromones.

2.    Each ant does not repeatedly pass through the nodes that it has already passed through during each iteration.

(1) In each iteration of the ant k, the possibility pijk is utilized to make ant k select the next node j at the current node i , which is calculated using the following equation:

pijk={τijα(t)∗ηijβ(t)∑k∈allowedk⁡τijα(t)∗ηijβ(t)k∈allowedk0others (1)

where allowedk indicates the set of nodes to be selected by the ant k in the next step, which is updated at once when the ant k passes through a path. It is worth noting that the empty allowedk denotes the end of the current iterative process of the ant k . For pijk , τij is the pheromone concentration on path (i,j) at the current moment t ; η is the heuristic factor, which is the reciprocal of dij ; dij is the distance between node i and node j ; α and β are the information heuristic factor and expectation heuristic factor, respectively.

(2) In each iteration of the ACO algorithm, the initial pheromone concentration on each path is the same. After that, update rules are used to update the following pheromone concentrations, which are denoted as follows:

τij(t+1)=(1−ρ)∗τij(t)+Δτij(t) (2)

Here, ρ is the pheromone volatility factor (0 < ρ < 1); Δτij(t) denotes the pheromone concentration on path (i,j) at the iteration t , which is updated in the following equation:

Δτij(t)=∑k=1N⁡Δτijk(t) (3)

Here, Δτijk(t) is the pheromone concentration released by the ant k on path (i,j) at the iteration t . The equation that can update Δτijk(t) is defined as follows:

Δτijk(t)={QLk(t)ifantkpassesthroughpathij0others (4)

Here, Lk(t) is the length of the route that the ant k takes to find food throughout the whole iteration. Q is a constant.

Development of an ant colony optimization algorithm

Considering the shortcomings of the traditional ACO algorithm, a developed ACO algorithm (DACO) is proposed in this paper.

First, the traditional ACO algorithm is prone to slow convergence speed during early iterations. This is partly due to the fact that the initial pheromone concentration is the same between features, leading to the ants selecting the features randomly initially. In the initial search, the randomness makes the ants blind and increases the time cost of the initial search. In addition, this drawback can be aggravated due to the high dimensionality of the research object. To address this problem, the initial pheromone concentration is positively correlated with the weights of features. The definition is as follows:

τ(0)=τ0exp((1+rnf)2) (5)

Here, τ0 is a hyperparameter for pheromone concentration; nf stands for the number of genetic features participating in the ACO; and r is the weight ranking vector of the features filtered by the Relief-F algorithm.

Then, to prevent the algorithm from getting stuck in the local optimal solution, we designed a dynamic pheromone volatility factor to resize itself adaptively. Early in each iteration, pheromones are released on features that pass through what is likely to be locally optimal solutions, thus attracting more ants to pass through these solutions. As time accumulates, the positive feedback can widen the difference between the local optimal solution and other solutions, restricting the ACO algorithm get stuck in the local optimal solution. The adaptive calculation formula is as follows:

ρ(t)={ρ0t≤100.9∗ρ(t−1)0.9∗ρ(t−1)>0.2,gap(t)<10−40.20.9∗ρ(t−1)≤0.2ρ(t−1)others (6)

And

gap(t)={fit(t)−fit(t−10)ift>101others (7)

Here, ρ0 is the initial value of the pheromone volatility factor; ρ has a minimum value of 0.2; gap (t) represents the gap between the global optimal solution at the iteration t and the iteration (t−10) . Alternatively, if the gap is less than 0.0001, or the algorithm may enter the stagnation period, ρ is updated to 0.9 times in terms of the pheromone volatility factor of the previous iteration. The fit(t) is the evaluation value of the optimal solution for the iteration t . It is worth noting that the optimal solution gets better when the evaluation value reduces. Lastly, we utilized the pheromone update rule in the ant colony system as follows to address the problem that was stuck in the local optimal solutions:

(1) For each path of the best routine in each iteration, the pheromone is updated globally after the completion of the current iteration with the following equation:

τij=(1−ξ)∗τij+ξ∗Δτij (8)

Here, ξ is a hyperparameter on the pheromone update (0 < ξ < 1), τij is the pheromone concentration of the path (i,j) where the ant with the optimal solution in the current iteration passes; Δτij is equal to the reciprocal of fG ; and fG is the optimal solution in the current iteration.

(2) The pheromone concentration is updated locally for each passed path. The local updating rule of pheromone is expressed as follows:

τij=(1−ρ)∗τij+ρ∗τ0 (9)

In each iteration, the search efficiency is enhanced by the difference between the pheromone concentration of the best solution and other solutions. Meanwhile, the probability of searching for unused paths for the ants can be increased by the local update rule of pheromone, effectively avoiding the stagnation of the algorithm. In specific, the pseudocode of the proposed DACO algorithm is described in Algorithm 1:

:

Results

Data collection

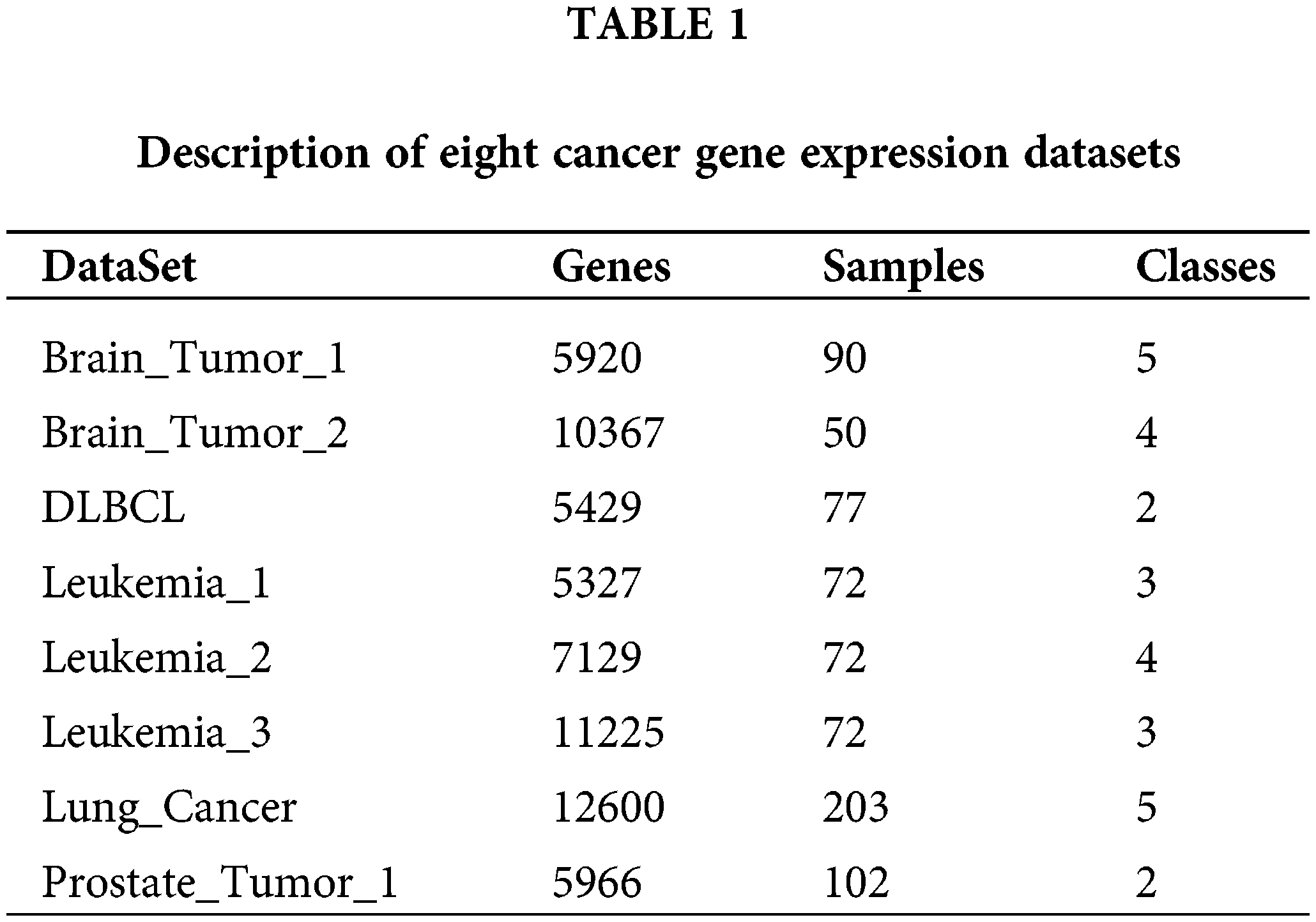
The proposed algorithm and other comparative algorithms were evaluated on eight cancer gene expression datasets, including Brain_Tumor_1, Brain_Tumor_2, DLBCL, Leukemia_1, Leukemia_2, Leukemia_3, Lung Cancer, and Prostate_Tumor_1. Table 1 shows the description of these datasets specifically, consisting of the number of features, samples and classes. As can be seen from Table 1, most of the datasets have multiple categories, the number of features varied from 5429 to 12600, and the number of samples from 72 to 203. In the data pre-processing phase, the number of features in these datasets was greatly reduced by the Relief-F algorithm (Robnik-Šikonja and Kononenko, 2003), which removes the irrelevant features among all the features using the weights. Meanwhile, the 200 most important features were retained for each cancer gene expression dataset.

Parameter setting

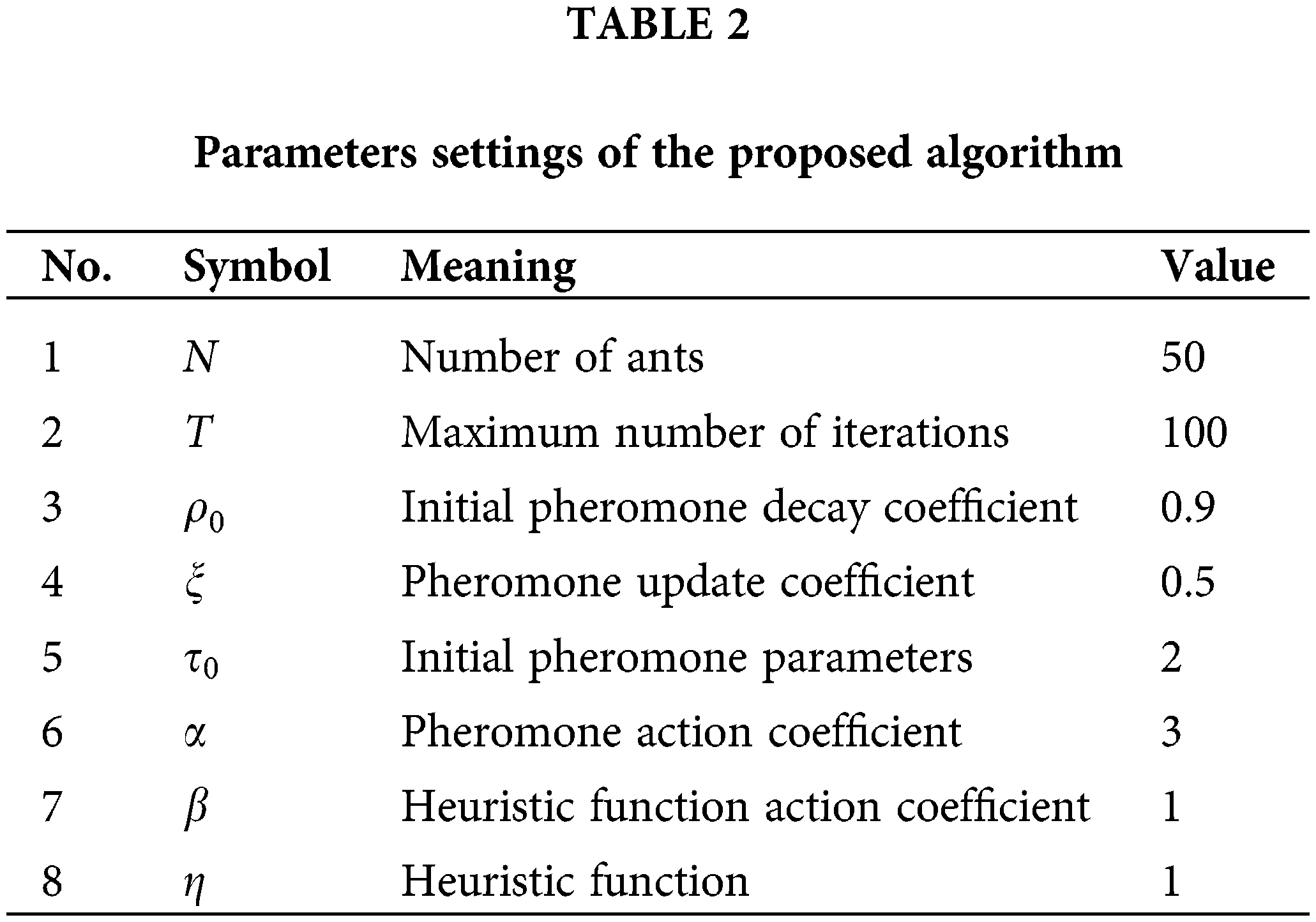
For the proposed algorithm, the number of ants, the maximum number of iterations, the initial pheromone decay coefficient, the pheromone update coefficient, the initial pheromone parameters, and the pheromone action coefficient are essential parameters. All the parameter settings are detailed in Table 2. For a fair comparison, the ratio of the training and test sets is set to 8 to 2 (Tang et al., 2017; Wang et al., 2020b), the K-Nearest Neighbor (KNN) algorithm was used as an evaluation function for all the comparison algorithms. The hyperparameter K in the KNN algorithm was set to 10. All other classifiers used the 10-fold cross-validation method. Moreover, each algorithm runs 20 times independently on each dataset.

Other related methods from literature

To verify the performance of the developed ant colony algorithm, several swarm intelligence algorithms were compared with the proposed algorithm, including particle swarm optimization (PSO) (Kennedy and Eberhart, 1995), genetic algorithm (GA) (Ghareb et al., 2016), differential evolution algorithm (DE) (Fleetwood, 2004), and ACO algorithm (Dorigo et al., 2006). Each algorithm represents a specific algorithm paradigm. PSO originated from the study of the predatory behavior of birds, obtaining the optimal solution by leveraging the information sharing of individuals in a group. GA searches for the best solution by simulating the natural evolutionary process. DE is a global optimization algorithm, which could be applied in terms of accuracy, speed, and stability of solutions. ACO is the basic algorithm of the proposed algorithm.

Comparison with the related methods

Classification results under different classifiers

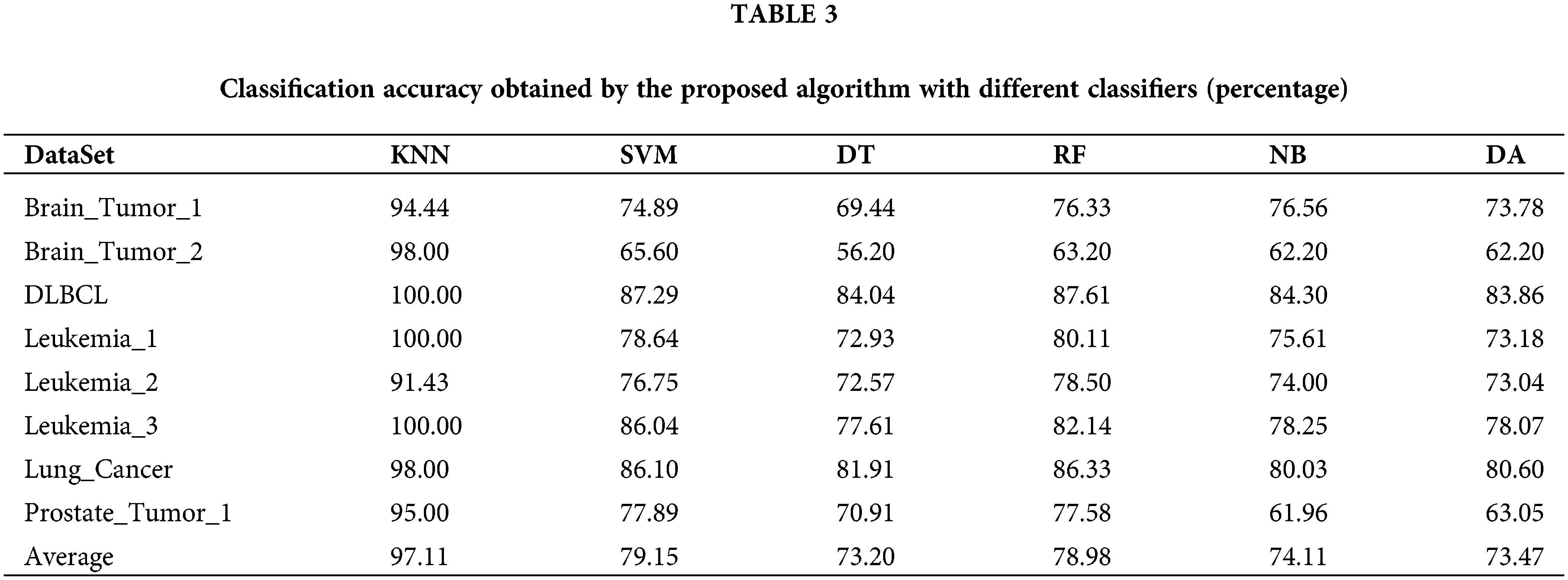
In this section, our proposed algorithm with five other different classifiers including SVM, Decision Tree (DT), Random Forest (RF), Naïve Bayesian (NB), and Discriminant Analysis (DA), is used to compare with our algorithm. The experiment is repeated 20 times on each cancer gene expression dataset independently. The comparison results are summarized in Table 3. As shown in Table 3, for each row in the table, the classification accuracy obtained by our proposed algorithm with different classifiers varied greatly. The classification accuracy of our proposed algorithm is much better than that of the other five classifiers. Meanwhile, the accuracy of the proposed algorithm with the other five classifiers also differed greatly from each other. For instance, the algorithm with RF outperformed that with DT by 7% on Leukemia_1 and the proposed algorithm with SVM outperforms that with DA by 14% on Prostate_Tumor_1. We conclude that KNN is appropriate for our proposed algorithm to conduct the cancer molecular subtype classification task.

Comparison between two ant colony algorithms

To investigate whether the developed ant colony algorithm can overcome the problems of slow convergence in the initial iterations and fall into local optimum, the traditional ACO algorithm was used to compare with our proposed algorithm DACO. In particular, two classifiers were employed in those two algorithms respectively. The algorithms were repeated 20 times independently on each cancer gene expression dataset and the average classification accuracy is summarized in Table 4. Moreover, the convergence curves of those two algorithms under the KNN classifier are shown in Fig. 1. We choose the error rate as the fitness value, which is equal to 1-accuracy.

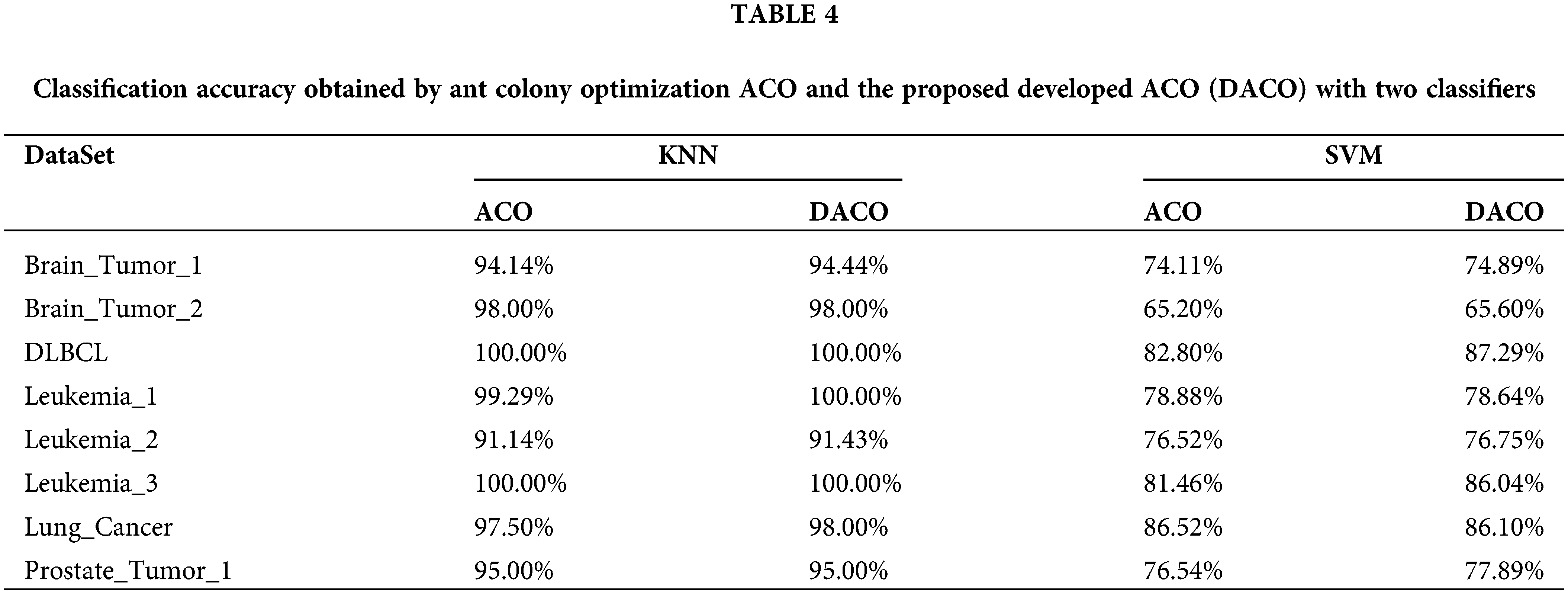
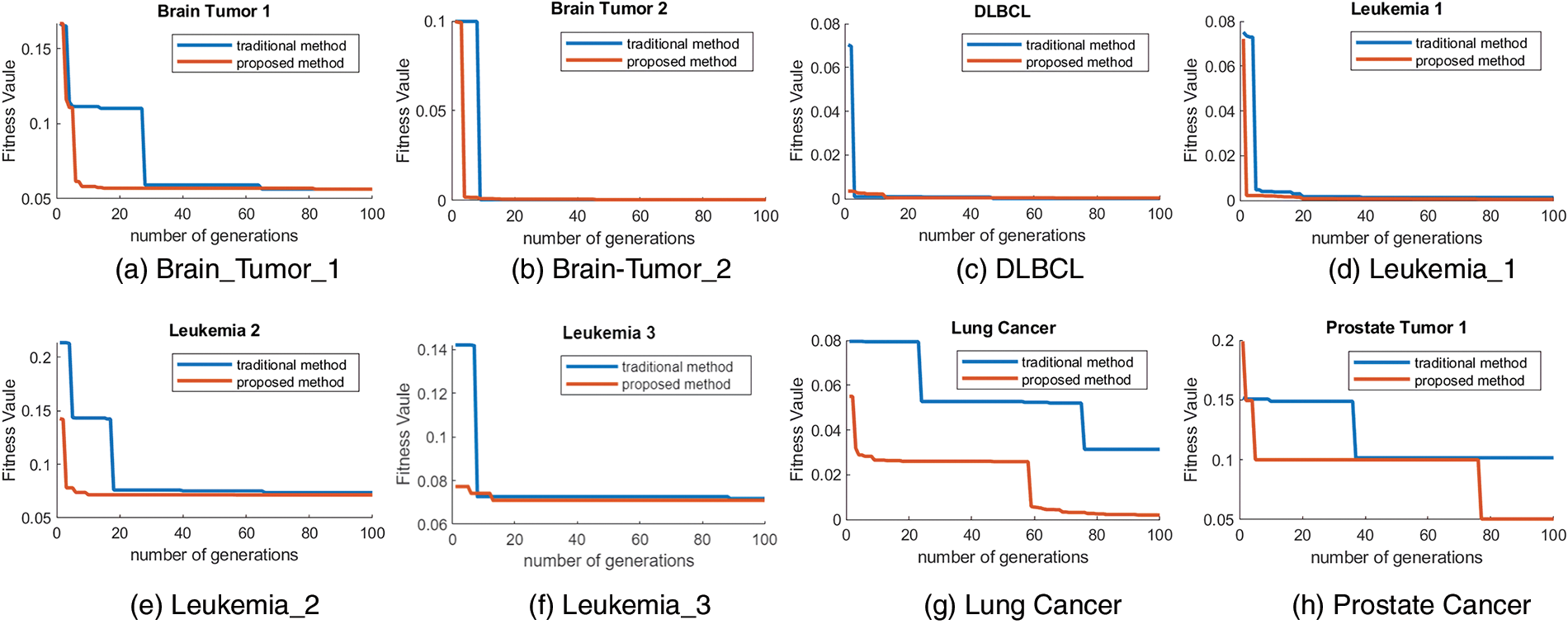
Figure 1: The convergence curves of the traditional method of ant colony optimization ACO and the proposed developed ACO (DACO) method.

From Table 4, the average classification accuracy obtained by our proposed algorithm DACO was generally higher under both KNN and SVM classifiers. In particular, the classification accuracy of the eight feature subsets obtained by DACO was above 90% under the KNN classifier and mostly above 75% under the SVM classifier.

As shown in Fig. 1, the fitness value decreased as the number of iterations increased. The convergence curves of DACO were always at the lower left of the convergence curve of ACO, demonstrating the convergence performance and classification accuracy of the proposed algorithm are better than the other algorithm. More specifically, the proposed algorithm converged faster in the early iterations compared to the conventional algorithm. From the perspective of the convergence curve, DACO has the potential to find the global optimal solution, since it can jump out of the local optimal solution several times.

Effect of different feature subset sizes on classification accuracy

Different sizes of feature subsets were set to explore the classification accuracy under different sizes of feature subsets obtained by the proposed method. Specifically, the feature subset size ranged from 10 to 150. The average accuracy obtained by our proposed algorithm with different numbers of features on those eight cancer gene expression datasets is summarized in Fig. 2.

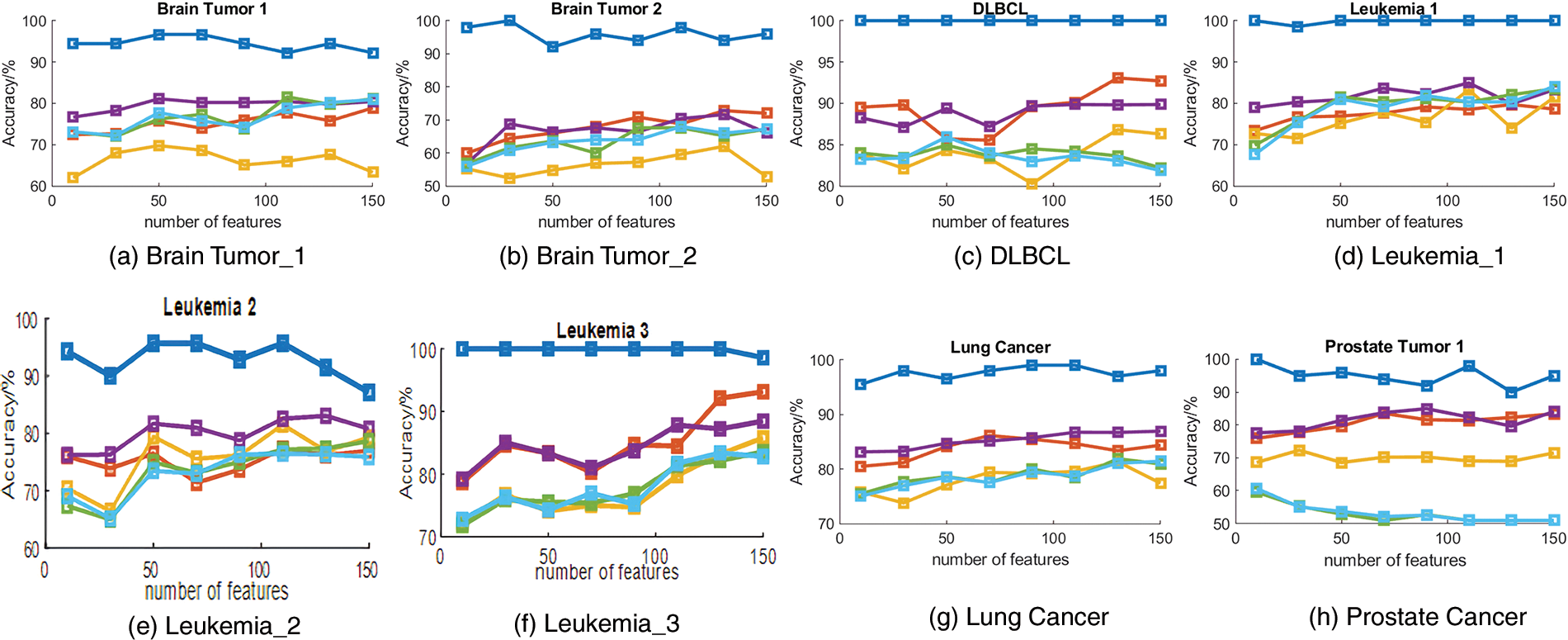
Figure 2: The accuracy obtained by developed ant colony optimization (DACO) using different feature subset sizes on eight cancer gene expression datasets.

As can be seen from Fig. 2, the curves of the classification accuracy did not increase monotonically. In addition, as the number of features increases, the classification accuracy shows a smooth trend of Brain_Tumor_1, DLBCL and Prostate_Tumor_1; a small increase in Brain_Tumor_2, Leukemia_1, Leukemia_2 and Lung_Cancer; and a large increase in Leukemia_3. In conclusion, as more and more features are gradually involved in the classification task, more meaningless features can negatively interfere with the classification accuracy.

Comparison with different swarm intelligence optimization algorithms

To evaluate the performance of the proposed algorithm, we compared DACO with multiple swarm intelligence optimization algorithms including PSO, DE, GA, and ACO. The sizes of the feature subsets obtained by different comparative algorithms are summarized in Table 5, and the classification accuracy of different swarm intelligence methods is shown in Fig. 3.

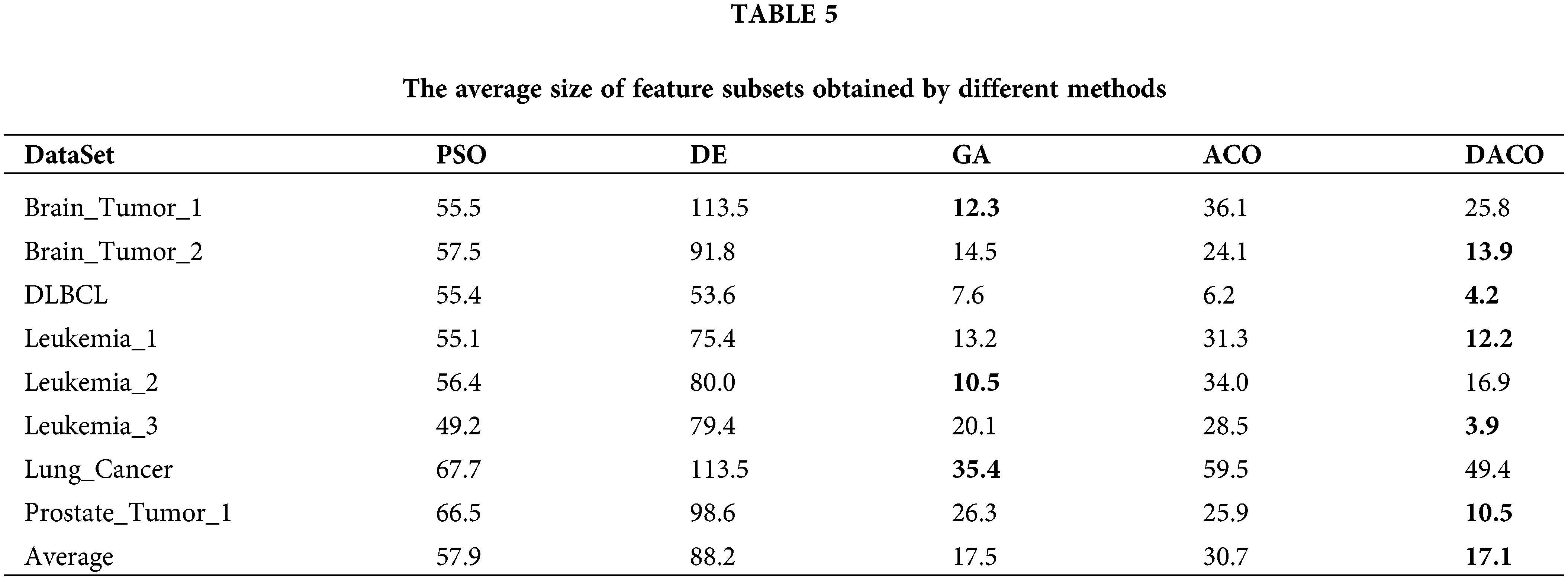
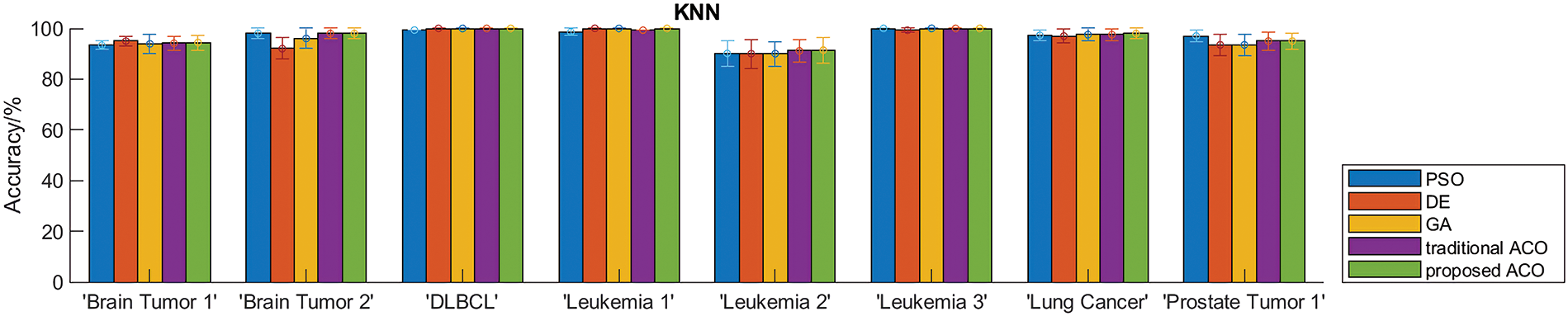
Figure 3: Classification accuracy obtained by different algorithms.

Table 5 indicates that the proposed ant colony algorithm DACO could greatly reduce the size of the feature subset, that is, redundant features can be removed to a large extent. For instance, the average number of feature subsets obtained by the developed ant colony algorithm is 3.9 for the Leukemia_3 dataset. Fig. 3 shows the classification accuracy of different comparison algorithms based on KNN and SVM respectively. Clearly, the proposed algorithm performed better than other swarm intelligence algorithms on most cancer gene expression datasets, which could also verify the good performance of the proposed method in cancer subtype classification.

Case study and biological analysis

To further demonstrate the biological performance of the proposed algorithm, we applied it to analyze the renal cell carcinoma dataset GSE40435 from the Gene Expression Omnibus database. Renal cell carcinoma (RCC) is one of the most lethal urological tumors and takes about 3% of all diagnosed cancers in humans (Padala et al., 2020). It is characterized by different subtypes such as the clear cell RCC (ccRCC) which accounts for ~75% of cases (Patergnani et al., 2020). Although ccRCC patients have improved survival rates through surgical techniques and specific targeted therapy, the predictability of outcome is still poor (Ma et al., 2013). Therefore, the pathogenesis of ccRCC needs to be further studied.

From our algorithm DACO, we selected a number of genes using the Relief-F algorithm on GSE40435, then 13 genes including CAPS, CD27, CP, DMBX1, EEPD1, EXOSC2, GSTM4, MRPL43, MRPL55, NAP1L1, PPM1F, TIMM9 and TTTY2 are selected.

First, we employed the Gene Expression Profiling Interactive Analysis (GEPIA) (Tang et al., 2017) and the University of Alabama at Birmingham CANcer (UALCAN) (Chandrashekar et al., 2017) websites to analyze the difference between tumor tissues and normal tissues. GEPIA is used to profile cancer and normal gene expression and analyze the interactive, available at http://gepia.cancer-pku.cn/; UALCAN is used for tumor gene expression and survival analyses, which can be found in http://ualcan.path.uab.edu/. The RNA sequencing expression data based on thousands of samples in those tissues were from the Cancer Genome Atlas (TCGA) and Genotype Tissue-Expression (GTEx) databases (Tang et al., 2017). The differential expression of those 13 genes using the GEPIA and UALCAN websites are summarized in Fig. 4. Fig. 4 shows that CAPS, CD27, and CP have different expression levels between tumor tissues and normal tissues in TCGA and GTEx databases. Therefore, CAPS, CD27, and CP can be used as biomarkers in ccRCC.

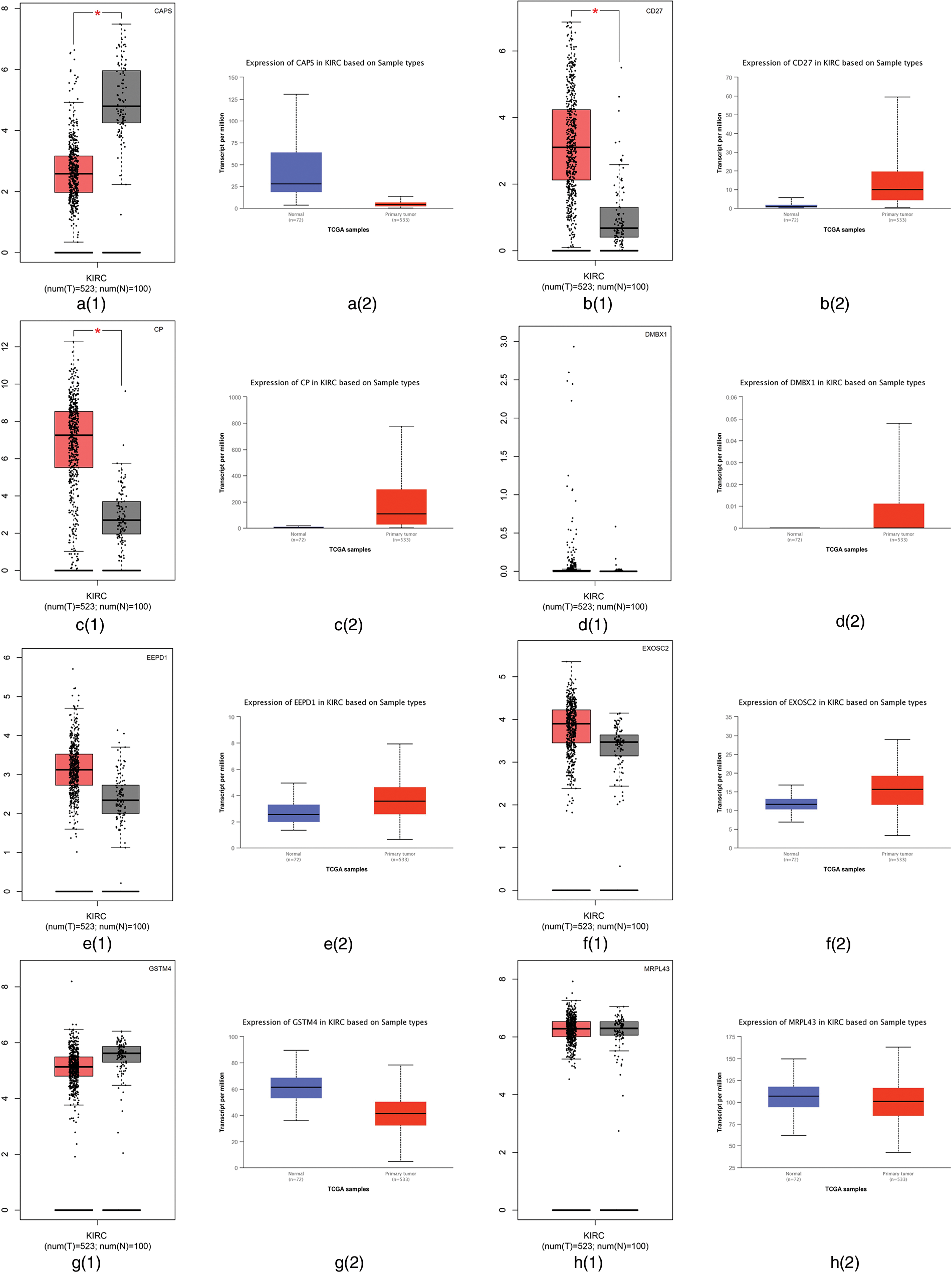
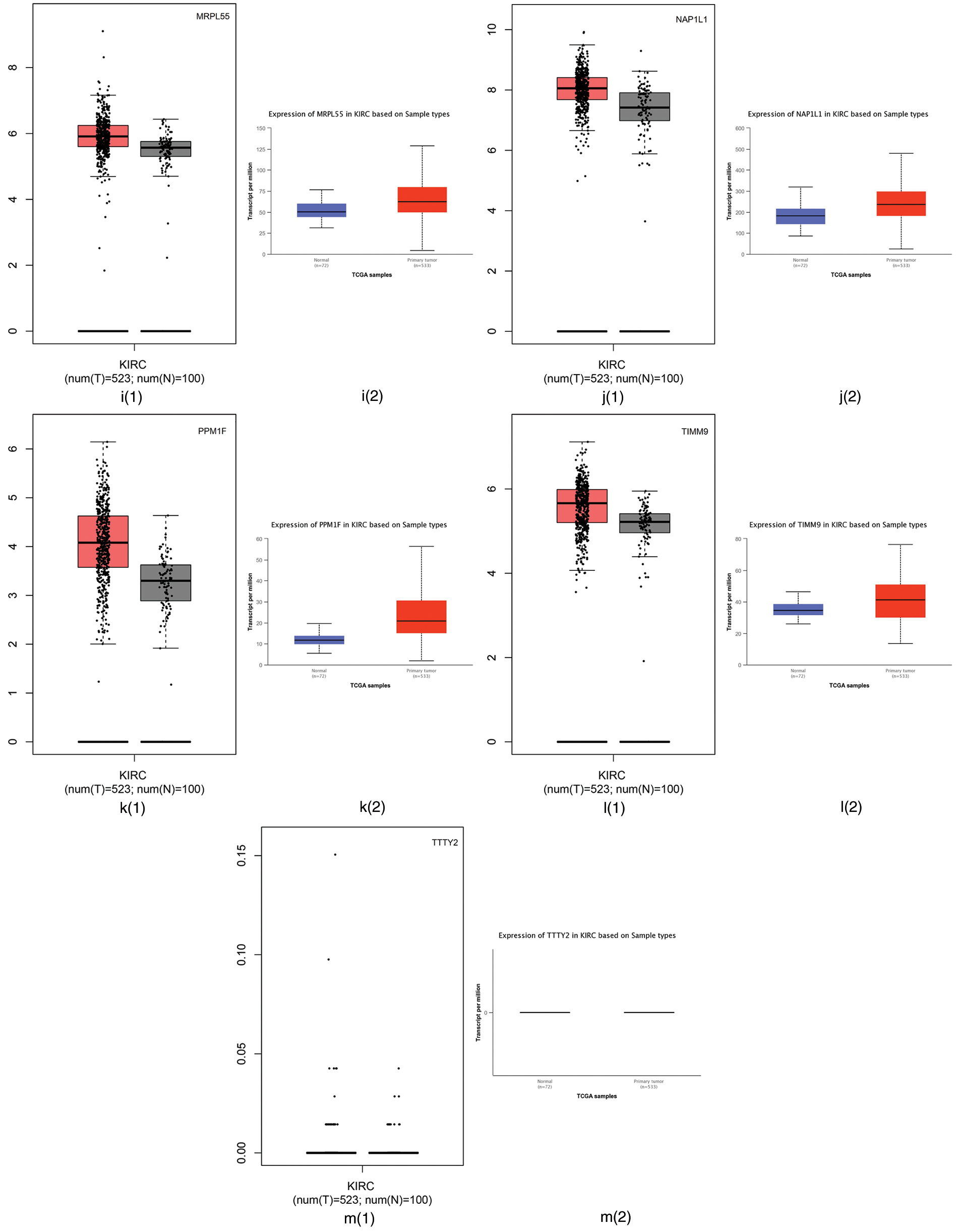
Figure 4: The differential expression of those 13 genes selected by our proposed algorithm using Gene Expression Profiling Interactive Analysis (GEPIA) and the University of Alabama at Birmingham CANcer data analysis Portal (UALCAN) websites.

Then, to demonstrate whether the gene expression of those three genes can affect the clinical outcome of RCC, we applied the GEPIA website and Kaplan-Meier plotter to analyze the survival rate of the three genes (Fig. 5). The results indicate that the expression of CAPS is prognostic of poor clinical outcomes for RCC.

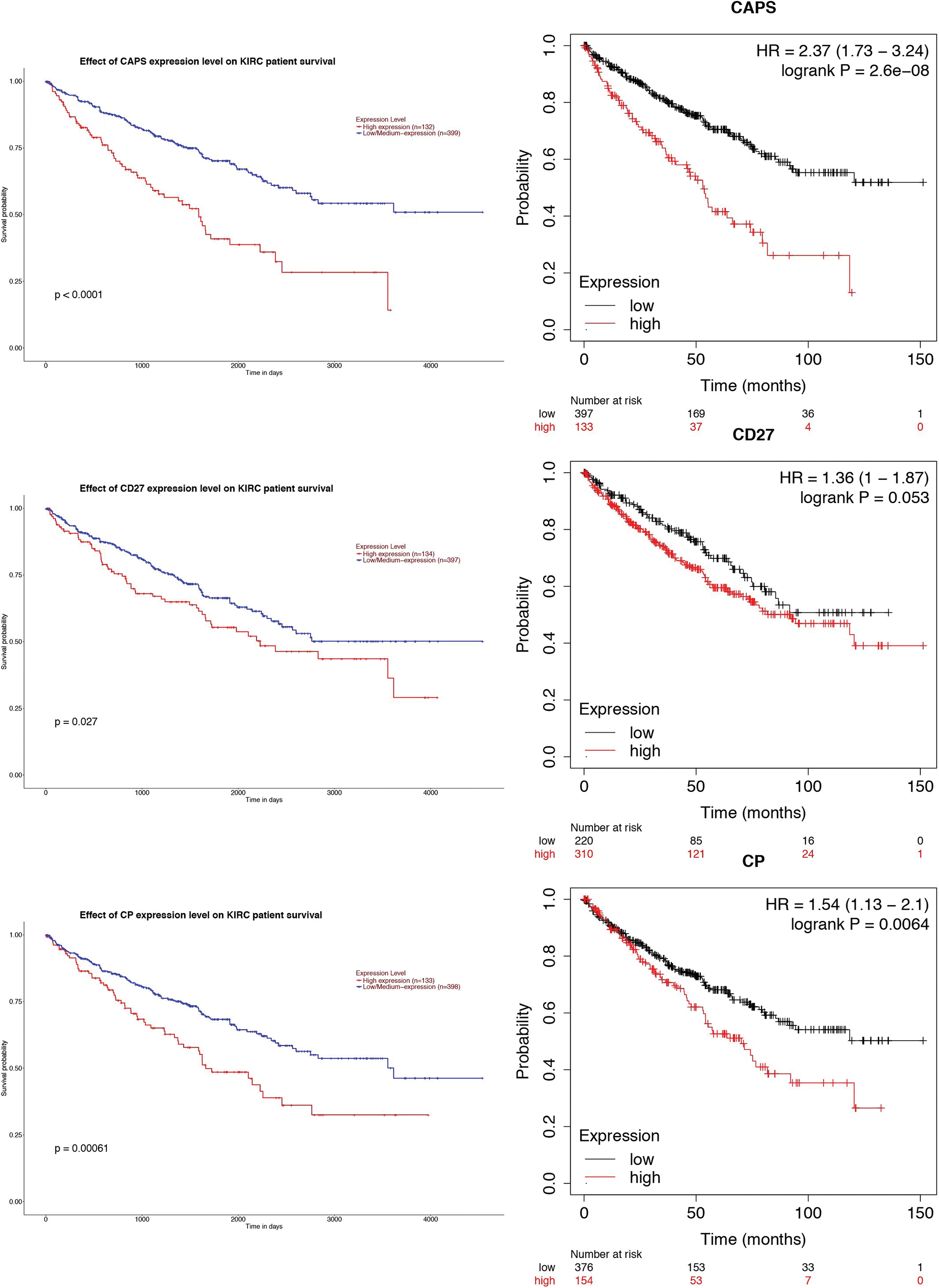
Figure 5: The survival rate of CAPS, CD27, and CP by Gene Expression Profiling Interactive Analysis (GEPIA) website and Kaplan-Meier plotter, respectively.

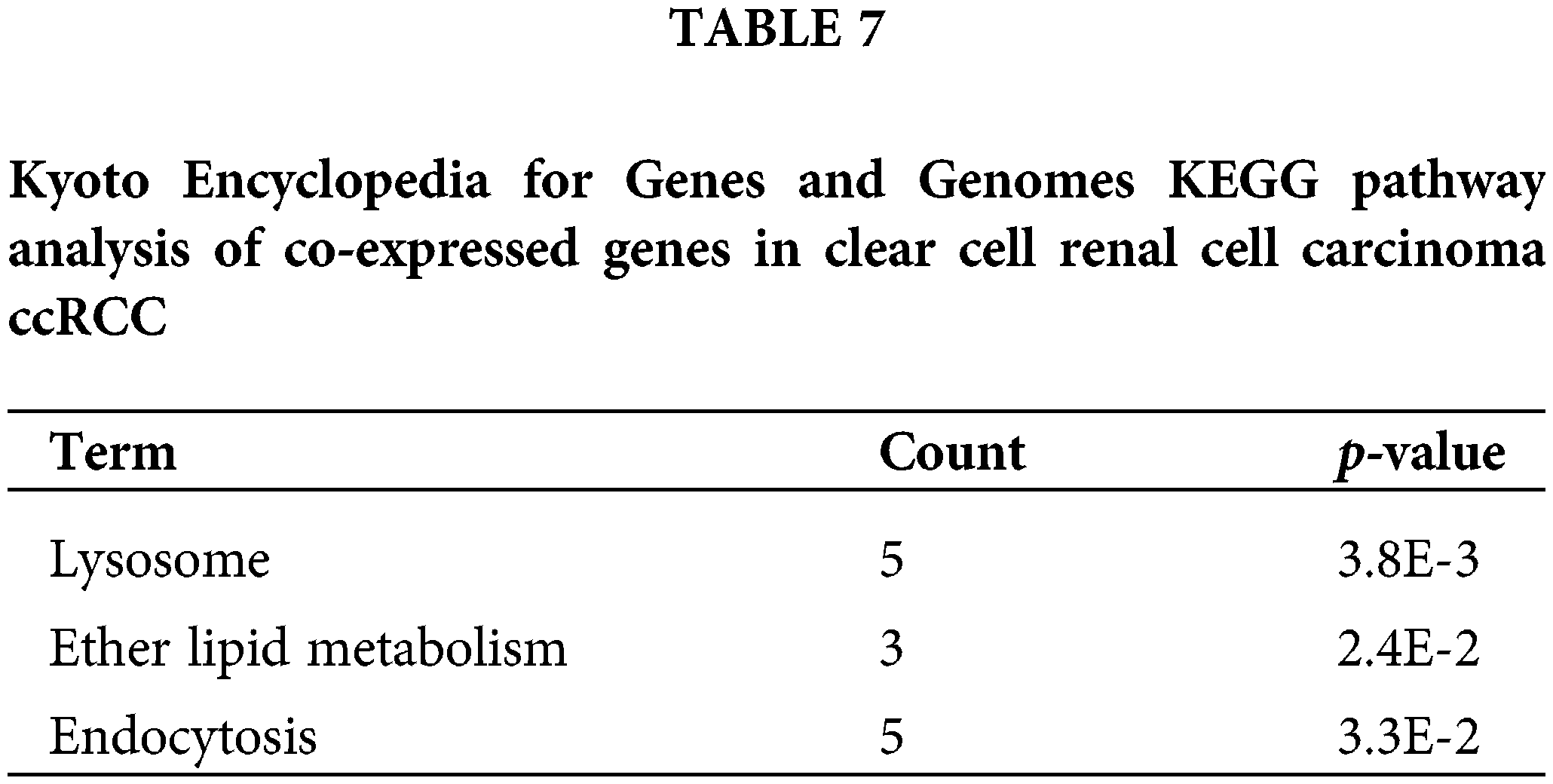
Finally, to identify the potential function of the expression of CAPS, we searched for genes co-expressed with CAPS in RCC from the cBioportal database (Gao et al., 2013) and discovered 20041 genes. Then we select 150 genes with the highest Spearman’s correlation coefficient. All the 150 genes were analyzed by the Database for Annotation, Visualization, and Integrated Discovery (DAVID) (Huang et al., 2009) software and the results of GO analysis tabulated in Table 6 indicate that the co-expressed genes are particularly enriched in cell cycle and methylation. We also conducted the Kyoto Encyclopedia for Genes and Genomes (KEGG) analysis, the results of which are summarized in Table 7. According to Table 7 we demonstrate that co-expressed genes are enriched in the lysosome, ether lipid metabolism and Endocytosis. Based on the above analysis, we infer that CAPS can be used as a biomarker and an important potential target drug in the treatment of ccRCC. That provides evidence that our algorithm can bring us new insights to identify important genes in the cancer gene expression data.

Discussion

In this paper, we propose a DACO to classify cancer gene expression data. First, the initial pheromone concentration based on the weight ranking vector was proposed to accelerate the convergence speed; then, to prevent the algorithm from getting stuck in the local optimal solution, we proposed a dynamic pheromone volatility factor to resize itself adaptively; finally, the pheromone update rule in the Ant Colony System was utilized to update the pheromone globally and locally. To demonstrate the performance of the proposed algorithm, eight cancer gene expression datasets and a renal cell carcinoma dataset were employed. The experiment results showed that the proposed algorithm not only provides excellent performance in terms of classification accuracy but also in the small size of the feature subset. The proposed algorithm outperformed other existing methods. By our proposed algorithm, CAPS of the renal cell carcinoma dataset was screened and may play a crucial role in the occurrence and development of renal clear cell carcinoma from multiple bioinformatics analyses. These results can provide a novel idea for the future treatment of renal clear cells. In the future, we plan to apply our proposed algorithm to other real cancer gene expression datasets. We would also like to test the expression of CAPS between the cancer issue and the normal issue with IHC.

Availability of Data and Materials: The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Author Contribution: The authors confirm contribution to the paper as follows: study conception and design: Zekun Xin, Yudan Ma; data collection: Weqiang Song; analysis, and interpretation of the results: Hao Gao, Lijun Dong; drafted manuscript preparation: Zhilong Ren; revised the manuscript: Bao Zhang; All authors reviewed the results and approved the final version of the manuscript.

Ethics Approval: Not applicable.

Funding Statement: This study was supported by the Langfang Science and Technology Plan Project (No. 2018013151) from Hebei Petro China Central Hospital.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

Ajeil FH, Ibraheem IK, Azar AT, Humaidi AJ (2020). Grid-based mobile robot path planning using aging-based ant colony optimization algorithm in static and dynamic environments. Sensors 20: 1880. DOI 10.3390/s20071880. [Google Scholar] [CrossRef]

Aldryan DP, Adiwijaya, Annisa A (2018). Cancer detection based on microarray data classification with ant colony optimization and modified backpropagation conjugate gradient Polak-Ribiére. 2018 International Conference on Computer, Control, Informatics and its Applications (IC3INA), pp. 13–16. Tangerang: IEEE. [Google Scholar]

Aydadenta H, Adiwijaya A (2018). A clustering approach for feature selection in microarray data classification using random forest. Journal of Information Processing Systems 14: 1167–1175. DOI 10.3745/JIPS.04.0087. [Google Scholar] [CrossRef]

Bir-Jmel A, Douiri SM, Elbernoussi S (2019). Gene selection via a new hybrid ant colony optimization algorithm for cancer classification in high-dimensional data. Computational and Mathematical Methods in Medicine 2019: 1–20. DOI 10.1155/2019/7828590. [Google Scholar] [CrossRef]

Bolón-Canedo V, Sánchez-Marono N, Alonso-Betanzos A, Benítez JM, Herrera F (2014). A review of microarray datasets and applied feature selection methods. Information Sciences 282: 111–135. DOI 10.1016/j.ins.2014.05.042. [Google Scholar] [CrossRef]

Chandrashekar DS, Bashel B, Balasubramanya SAH, Creighton CJ, Ponce-Rodriguez I et al. (2017). UALCAN: A portal for facilitating tumor subgroup gene expression and survival analyses. Neoplasi 19: 649–658. DOI 10.1016/j.neo.2017.05.002. [Google Scholar] [CrossRef]

Dash R, Dash R, Rautray R (2019). An evolutionary framework based microarray gene selection and classification approach using binary shuffled frog leaping algorithm. Journal of King Saud University-Computer and Information Sciences 34: 880–891. DOI 10.1016/j.jksuci.2019.04.002.2019040101. [Google Scholar] [CrossRef]

Dash S, Thulasiram R, Thulasiraman P (2019). Modified firefly algorithm with chaos theory for feature selection: A predictive model for medical data. International Journal of Swarm Intelligence Research 10: 1–20. DOI 10.4018/IJSIR. [Google Scholar] [CrossRef]

Dhanasekaran B, Siddhan S, Kaliannan J (2020). Ant colony optimization technique tuned controller for frequency regulation of single area nuclear power generating system. Microprocessors and Microsystems 73: 102953. DOI 10.1016/j.micpro.2019.102953. [Google Scholar] [CrossRef]

Dorigo M, Birattari M, Stutzle T (2006). Ant colony optimization. IEEE Computational Intelligence Magazine 1: 28–39. DOI 10.1109/MCI.2006.329691. [Google Scholar] [CrossRef]

Fleetwood K (2004). An introduction to differential evolution. Proceedings of Mathematics and Statistics of Complex Systems (MASCOS) One Day Symposium, pp. 785–791. Brisbane. [Google Scholar]

Gao J, Aksoy BA, Dogrusoz U, Dresdner G, Gross B et al. (2013). Integrative analysis of complex cancer genomics and clinical profiles using the cBioPortal. Science Signaling 6: pl1. DOI 10.1126/scisignal.2004088. [Google Scholar] [CrossRef]

Ghareb AS, Bakar AA, Hamdan AR (2016). Hybrid feature selection based on enhanced genetic algorithm for text categorization. Expert Systems with Applications 49: 31–47. DOI 10.1016/j.eswa.2015.12.004. [Google Scholar] [CrossRef]

Gülcü Ş., Mahi M, Baykan ÖK, Kodaz H (2018). A parallel cooperative hybrid method based on ant colony optimization and 3-Opt algorithm for solving traveling salesman problem. Soft Computing 22: 1669–1685. DOI 10.1007/s00500-016-2432-3. [Google Scholar] [CrossRef]

Hakim MAN, Adiwijaya A, Astuti W (2021). Comparative analysis of ReliefF-SVM and CFS-SVM for microarray data classification. International Journal of Electrical and Computer Engineering 11: 3393. DOI 10.11591/ijece.v11i4.pp3393-3402. [Google Scholar] [CrossRef]

Huang DW, Sherman BT, Lempicki RA (2009). Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nature Protocols 4: 44–57. DOI 10.1038/nprot.2008.211. [Google Scholar] [CrossRef]

Huerta EB, Duval B, Hao JK (2006). A hybrid GA/SVM approach for gene selection and classification of microarray data. In: EvoWorkshops 2006: Applications of Evolutionary Computing, pp. 34–44. [Google Scholar]

Islam T, Islam ME, Ruhin MR (2018). An analysis of foraging and echolocation behavior of swarm intelligence algorithms in optimization: ACO, BCO and BA. International Journal of Intelligence Science 8: 1–27. DOI 10.4236/ijis.2018.81001. [Google Scholar] [CrossRef]

Jain I, Jain VK, Jain R (2018). Correlation feature selection based improved-binary particle swarm optimization for gene selection and cancer classification. Applied Soft Computing 62: 203–215. DOI 10.1016/j.asoc.2017.09.038. [Google Scholar] [CrossRef]

Kang C, Huo Y, Xin L, Tian B, Yu B (2019). Feature selection and tumor classification for microarray data using relaxed Lasso and generalized multi-class support vector machine. Journal of Theoretical Biology 463: 77–91. DOI 10.1016/j.jtbi.2018.12.010. [Google Scholar] [CrossRef]

Kavitha KR, Prakasan A, Dhrishya PJ (2020). Score-based feature selection of gene expression data for cancer classification. 2020 Fourth International Conference on Computing Methodologies and Communication, pp. 261–266. Erode. [Google Scholar]

Kennedy J, Eberhart RC (1995). Particle swarm optimization. IEEE International Conference on Neural Networks, pp. 1942–1948. Perth. [Google Scholar]

Kundu R, Chattopadhyay S, Cuevas E, Sarkar R (2022). AltWOA: Altruistic Whale Optimization Algorithm for feature selection on microarray datasets. Computers in Biology and Medicine 144: 105349. DOI 10.1016/j.compbiomed.2022.105349. [Google Scholar] [CrossRef]

Li Q, Chen H, Huang H, Zhao X, Cai Z et al. (2017). An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis. Computational and Mathematical Methods in Medicine 2017: 1–15. DOI 10.1155/2017/9512741. [Google Scholar] [CrossRef]

Li X, Wang J, Zhou J, Yin M (2011). A perturb biogeography based optimization with mutation for global numerical optimization. Applied Mathematics and Computation 218: 598–609. DOI 10.1016/j.amc.2011.05.110. [Google Scholar] [CrossRef]

Li X, Yin M (2013). Multiobjective binary biogeography based optimization for feature selection using gene expression data. IEEE Transactions on NanoBioscience 12: 343–353. DOI 10.1109/TNB.2013.2294716. [Google Scholar] [CrossRef]

Li X, Zhang X, Yin M, Wang J (2015). A genetic algorithm for the distributed assembly permutation flowshop scheduling problem. 2015 IEEE Congress on Evolutionary Computation 9: 3096–3101. DOI 10.1109/CEC.2015.7257275. [Google Scholar] [CrossRef]

Ma J, Siegel R, Jemal A (2013). Pancreatic cancer death rates by race among US men and women, 1970–2009. Journal of the National Cancer Institute 105: 1694–1700. DOI 10.1093/jnci/djt292. [Google Scholar] [CrossRef]

Ma W, Zhou X, Zhu H, Li L, Jiao L (2021). A two-stage hybrid ant colony optimization for high-dimensional feature selection. Pattern Recognition 116: 107933. DOI 10.1016/j.patcog.2021.107933. [Google Scholar] [CrossRef]

Mallick PK, Satapathy SK, Mishra S, Panda AR, Mishra D (2021). Feature selection and classification for microarray data using ACO-FLANN framework. Intelligent and Cloud Computing 1: 491–501. DOI 10.1007/978-981-15-5971-6. [Google Scholar] [CrossRef]

Mitra A, Basu D, Ghosh A (2022). Swarm intelligence-based smart city applications: A review for transformative technology with artificial intelligence. Data Science and Security 462: 81–92. DOI 10.1007/978-981-19-2211-4. [Google Scholar] [CrossRef]

Padala SA, Barsouk A, Thandra KC, Saginala K, Mohammed A et al. (2020). Epidemiology of renal cell carcinoma. World Journal of Oncology 11: 79–87. DOI 10.14740/wjon1279. [Google Scholar] [CrossRef]

Patergnani S, Guzzo S, Mangolini A, dell’Atti L, Pinton P et al. (2020). The induction of AMPK-dependent autophagy leads to P53 degradation and affects cell growth and migration in kidney cancer cells. Experimental Cell Research 395: 112190. DOI 10.1016/j.yexcr.2020.112190. [Google Scholar] [CrossRef]

Peake J, Amos M, Yiapanis P, Lloyd H (2018). Vectorized candidate set selection for parallel ant colony optimization. In: Proceedings of the Genetic and Evolutionary Computation Conference Companion, pp. 1300–1306. Kyoto. [Google Scholar]

Robnik-Šikonja M, Kononenko I (2003). Theoretical and empirical analysis of ReliefF and RReliefF. Machine Learning 53: 23–69. DOI 10.1023/A:1025667309714. [Google Scholar] [CrossRef]

Sayed S, Nassef M, Badr A, Farag I (2019). A nested genetic algorithm for feature selection in high-dimensional cancer microarray datasets. Expert Systems with Applications 121: 233–243. DOI 10.1016/j.eswa.2018.12.022. [Google Scholar] [CrossRef]

Tang C, Wang D, Tan AH, Miao C (2017). EEG-based emotion recognition via fast and robust feature smoothing. International Conference on Brain Informatics, vol. 2017, 83–92. Cham: Springer. [Google Scholar]

Tang Z, Li C, Kang B, Gao G, Li C et al. (2017). GEPIA: A web server for cancer and normal gene expression profiling and interactive analyses. Nucleic Acids Research 45: W98–W102. DOI 10.1093/nar/gkx247. [Google Scholar] [CrossRef]

Vamathevan J, Clark D, Czodrowski P, Dunham I, Ferran E et al. (2019). Applications of machine learning in drug discovery and development. Nature Reviews Drug discovery 18: 463–477. DOI 10.1038/s41573-019-0024-5. [Google Scholar] [CrossRef]

Wang G, Chu HCE, Zhang Y, Chen H, Hu W et al. (2015). Multiple parameter control for ant colony optimization applied to feature selection problem. Neural Computing and Applications 26: 1693–1708. DOI 10.1007/s00521-015-1829-8. [Google Scholar] [CrossRef]

Wang Y, Ma Z, Wong KC, Li X (2020a). Nature-inspired multiobjective patient stratification from cancer gene expression data. Information Sciences 526: 245–262. DOI 10.1016/j.ins.2020.03.095. [Google Scholar] [CrossRef]

Wang Y, Ma Z, Wong KC, Li X (2020b). Evolving multiobjective cancer subtype diagnosis from cancer gene expression data. IEEE/ACM Transactions on Computational Biology and Bioinformatics 18: 2431–2444. DOI 10.1109/TCBB.2020.2974953. [Google Scholar] [CrossRef]

Yan F (2018). Autonomous vehicle routing problem solution based on artificial potential field with parallel ant colony optimization (ACO) algorithm. Pattern Recognition Letters 116: 195–199. DOI 10.1016/j.patrec.2018.10.015. [Google Scholar] [CrossRef]

Yu L, Liu H (2003). Feature selection for high-dimensional data: A fast correlation-based filter solution. Proceedings of the 20th International Conference on Machine Learning, pp. 856–863. Washington DC. [Google Scholar]

Zakiryanova GK, Kustova E, Urazalieva NT, Baimuchametov ET, Nakisbekov NN et al. (2019). Abnormal expression of c-Myc oncogene in NK cells in patients with cancer. International Journal of Molecular Sciences 20: 756. DOI 10.3390/ijms20030756. [Google Scholar] [CrossRef]

Zhang Y (2016). A modified artificial bee colony algorithm-based feature selection for the classification of high-dimensional data. Journal of Computational and Theoretical Nanoscience 13: 4088–4095. DOI 10.1166/jctn.2016.5255. [Google Scholar] [CrossRef]