Optimized Evaluation of Mobile Base Station by Modern Topological Invariants

1  Introduction

Currently, there has been an enormous expansion in rush hour traffic demand for communication services in cellular mobile networks. The frequency spectrum dispensed to the frameworks is restricted; thus, how to utilize frequency diverts most efficiently whether the frameworks depend on the Frequency division multiple access (FDMA) or the Time division multiple access (TDMA) [1]. FDMA is the correspondence procedure utilized in communicating, land-versatile two-way radio, and so forth. It starts with a band of frequencies, which is distributed by the Federal communications commission (FCC). This band of frequency is additionally partitioned into a few thin groups of frequencies, where every frequency, otherwise called a channel, is utilized for full-duplex correspondence. The correspondence connection is kept up within the two headings, either in the frequency space or in the time area. This is represented by two fundamental modes of tasks known as the Frequency division duplex (FDD) and Time division duplex (TDD). These subjects, alongside FDMA range the executives and its credits, are introduced in this section [2]. In new mobile radio frameworks, TDMA is utilized. Every versatile hub doles out frequencies for the utilization of the period on a repeating premise. Generally, a telecaster doesn’t have full admittance to the game’s data transmission for a specific timeframe. The frequency of the framework, then again, is partitioned into sub-groups, each involving TDMA for shared confirmation [3]. The network structure used in a cellular network system is a hexagonal structure with two variants [4]. The study technique is used to evaluate and optimize the physical layout of the mobile base station to fulfill the optimal traffic demand in rush hours. It can be done by solving the topology of cellular networks by modern invariants and predicting the physical characteristics of the honeycomb network used in the mobile base station network.

A mobile telephone base station is a transmission and gathering station in a decent area, comprising of at least one get/send receiving wire, microwave dish and electronic hardware used to deal with cell traffic. It fills in as an extension between all mobile clients on a phone and interfaces mobile calls to the mobile exchanging focus. It is fundamentally the main issue that all clients interface within a center and talked style network [5].

In material sciences, honeycomb networks play a fundamental part in various fields, particularly in wireless base stations, image processing and graphics. Honeycomb networks are formed by the iterative utilization of hexagonal tiles in a particular plan. We mean the n-layered honeycomb network with hexagons among focal and boundary hexagons by HCn. HCn are built by adding a layer of hexagon around HCn−1. Its evaluation is also useful in other fields of computer science like microprocessors, memory interconnection and processor interconnection. As another arising science is developed with the help of computer sciences, mathematics, and chemistry called cheminformatics, whose significant segments incorporate Quantitative structure-activity relationship (QSAR) and Quantitative structure-property relationships (QSPR) and the segments can add to the examination of the physicochemical characteristics of synthetic mixtures. QSAR is a modeling tool used to solve the topology of networks or structure of compounds and model the efficient and best performer networks or structures. QSPR is also a modeling tool that correlates the properties of network structures with the help of mathematical equations or expressions. It also provides the quantitative relationship between properties of networks or chemical structures. Angles of topology in the form of numeric values can be portrayed with the help of a graph because of invariance. It is done due to the automorphism property of the graph. A k-banhatti sombor index is a topological index which is a number associated with a network graph that captures the symmetry of the network structure and provides a scientific language for predicting the characteristics of the network. In the fields of computer sciences and chemistry, there are a lot of applications of graph theory [6].

On the other hand, V. R. Kulli in 2022, define another vertex degree-based invariant graph named Quadratic-contraharmonic indices (QCI) are used to get the sharp lower and upper limits of the related networks and the characteristics of the network showing up at the boundaries. There are two varieties of quadratic-contraharmonic indices, the first is a QCI and the second one is a CQI [7]. A QCI is a topological invariant which is a number related to a network graph that gets the evenness of the network design and gives a coherent language to expecting the characteristics of the network.

The research work concentrates on the topological properties and solutions of mobile base station networks. The topological properties include lower bounds, upper bounds and prediction qualities of deduced mathematical results to resolve the issues related to connectivity, scalability, routing, node density, mobility among the nodes, link formation between the nodes modeling the network and simulation. Though mobile base station networks are modeled through these solved results. So, engineers and manufacturers foresee concerning networks before manufactured or developing them. After that Topological invariants (TIs) allow us to accumulate information about algebraic structures and mathematically predict hidden properties of various networks like hexagons and honeycomb etc.

This paper first introduces the problem statement with Honeycomb and regular hexagonal networks and KBSO and QCIs, secondly review the literature, thirdly discusses objectives, significance, research gap, and method in the research methodology section, in the fourth section analyze data and in the last section write results and conclude the research. The study has implications in the fields of computer science, physics, chemistry, mathematics, and bioinformatics for modeling purposes of networks, cellular networks, and chemical compounds. KBSO topological invariants and QCIs allow us to accumulate information about algebraic structures and mathematically predict hidden properties of various structures such as Honeycomb and regular hexagonal networks used in mobile base station networks.

2  Background

In a cellular mobile communication framework, to treat the traffic demand at the necessary grade of administration, some number of frequency channels ought to be allocated to every cell of the framework under the electromagnetic limitations, for example, co-channel imperative, contiguous channel requirement and co-site imperative. The quantity of frequency channels apportioned to a cellular framework is limited on account of the restricted frequency spectrum [8]. In any case, lately, interest in frequency channels has been expanded definitely. Consequently, how to appoint the expected number of frequency channels to every cell under the above requirements turns into a significant issue. This issue is called FAP. It has been broadly utilized as a choice measure of FAP to limit the most extreme range of the frequency channels utilized in a cellular framework [9]. This paper study enhances the efficiency of mobile cellular networks by evaluating the cellular base station networks’ topology mathematically by newly prepared topological indices. So issues are started to resolve from the gross root level [10]. This study solved and optimized the MBSNs in context with the topology of the network.

3  Literature Review

The calculation of the irregularity indices of honeycomb networks, hexagonal networks, oxide networks, and silicate networks is done. The results are very helpful in understanding the behavior of different computer networks and chemical networks. After understanding these formulas different researchers can construct their own best networks in chemistry and computer also [11]. Further, the study elaborates that graph theory is a field through which they calculate topological indices for finding the properties of different chemicals without performing any types of experiments on them. It may be understanding only mathematical formulas or equations which are deduced for them. It also calculates topological indices form-polynomial block shift networks which are a part of different chemical compounds with the help of the division of edge [12].

The readings explain that another arising science is cheminformatics which is a combination of chemistry, mathematics, and computer science. It is the main concern and constituent part is QSAR and QSPR which mainly explore physicochemical properties of chemicals and their structures. This paper tended to the OTIS traded networks and bi-swapped networks and investigated their topological indices. They decided the overall randi ć, general aggregate availability, first and second zagreb, first and second multiple zagreb, hyper zagreb molecule bond, and mathematical indices for both the group of networks by considering the premise network as way Pn and k-customary graph Rk. They likewise gave express formulae for ABC4 and GA5 indices of these networks with the premise Rk network [13].

In the view of the study, the headway of large-scale integrated circuit innovation has empathy for the development of complex interconnected networks. Graph theory gives a key apparatus to designing and evaluating such networks. Connected networks and graph theory give a detailed comprehension of these connected themes. Chemical graph theory is a part of numerical science wherein they apply devices of graph theory to demonstrate the chemical wonder numerically. In-network vertex addresses network hub like PC, switch, switch some other gadget and an edge addresses a network path through which transmission completed. These topological indices or invariants are also numeric values related to computer networks, their interconnections, their properties, etc. It calculates the different topological indices of eccentricity-based for a binary tree up to k-level. The results of a paper can be used for computer networks and chemical networks in topological characterization [14].

Chemical graph theory manages the essential properties of a molecular graph. In graph theory, we relate molecular descriptors to the properties of molecular structures. Here, we calculate some Banhatti molecular descriptors for water-dissolvable dendritic uni-molecular polyether micelle. Our outcomes end up being extremely important to comprehend the way of behaving of water-dissolvable dendritic unimolecular polyether micelle as a drug-delivery agent [15].

Multiprocessor interconnection networks are habitually expected to join numerous indistinguishable processor-memory matches that are rehashed everyone is alluded to as a handling hub [16]. Message passing instead of divided memory is much of the time utilized for synchronization of correspondence among the handling hubs for the execution of the program. Multiprocessor interconnection networks are most drawn in networks because of the accessibility of strong and cheap microchips and memory chips. By rehashing normal polygons, intermittent plane decorations can be handily constructed [17]. For direct interconnection organizations, this plan is vital as it offers high worldwide execution. A few equal organizations that start from well-known networks are hexagonal and honeycomb [18].

With the assistance of the topological index (TI), we can figure out various properties of molecular structures. TI empowers us to connect a number with a molecular construction. Various mixtures can be changed into various shapes like trees, cycles, and so on. This paper is about the reverse Zagreb indices, hyper turn around Zagreb invariants, and their polynomials for metal-natural structures [19].

In the field of chemical graph theory, topological indices are vital. The topological index is a mathematical amount reliant upon various invariants or molecular graph qualities. In the current article, the topological indices of para desert plants chain graph are determined, for example, iota bond availability, mathematical number juggling, first k-banhatti, second k-banhatti, first k-hyper banhatti, second k-hyper banhatti, adjusted first k-banhatti, altered second k-banhatti and consonant k-banhatti utilizing their M-polynomials by the equations given in. Graphical examination of the discoveries is additionally shown the capacity to recuperate the topological indices [20].

To increase the effectiveness of observing and conservation endeavors, it is of key importance to foster sound quantitative techniques that can indicate which key areas and site components play a noticeable and critical job in the working of territory mosaics. In this article, a new emerging study will compute different indices of bridge networks. The results will play a vital role in determining the properties of these networks and their uses in the computer industry, electronics, chemistry, pharmacy, etc. It will also perform index analysis on certain networks which may be beneficial for people who are working in the field of computer science, mathematics and chemistry also. In the end, formulate a mathematical formula to construct a computer network or processor design or chemical compound, check the properties of concerning before and also check the feasibility of anyone which discuss earlier [21].

Chemical graph theory is a subfield of numerical chemistry that is exceptionally valuable in the advancement of the computational examination of chemical mixtures. A chemical graph is the result of the molecular design by applying some graph The exhibit of chemical mixtures with the M-polynomials is a creating thought and the M-polynomial of various molecular structures upholds us to ascertain numerous topological indices. In this paper we ascertain M-polynomial and topological indices for the starphene graph, then, at that point, we recuperate various topological indices utilizing the M-polynomials [22].

The momentum disclosure of various kinds of nanostructures has propelled scientists to concentrate on the uses of these structures in various fields. In this review, the study dissected the boron three-sided nanotube through topological indices. M-polynomial of a boron three-sided nanotube can recuperate the topological indices which are reliant upon the level of the vertex. We have introduced the outcomes in a graphical structure [23].

These topological indices can contribute to getting the natural, chemical and actual qualities of a molecule. Along these lines, the topological index plays a vital part in addressing the chemical design of a particle in a genuine number and is utilized to communicate the atom which is tried. These outcomes are useful in understanding and determining the physicochemical properties of these chemical structures [24].

Another study told that topological indices and network polynomials are invariants of molecular graphs. Expected properties of structures of molecules can be studied with the help of invariants. In benzene networks, honeycomb networks are significantly used. In the current article, new topological portrayals of honeycomb networks are given as degree-based descriptors. They, for the first time, used some consistency indices and a few co-indices identified with this network without a line graph and complement also. These indices of honeycomb networks are very much effective to understand the physicochemical properties of chemicals. These realities might be valuable for individuals working in software engineering and science who experience honeycomb networks. An ideal level of a specific index can be acquired by putting a limitation on n [25].

Another study conveyed that since computers are a tool used in the world as a source of information, they increase in numbers numerously. To such an extent, today, it is hard to track down any space, logical or other, which is not dependent on their application. Indeed, even general sets of laws have been affected by novel processing and data strategies. A considerable lot of these QSAR procedures depend on the utilization of structural boundaries, which are mathematical arrangements that classify helpful structural data and empathy relationships among structure and natural properties [26].

KBSO index and its reduced version have a good potential for prediction in the field of computer science, mathematics, chemistry, pharmacy, informatics, and biology in context with physical and chemical structures and networks. On the other hand, the CQI and its reverse form are also having the same prediction quality as mentioned earlier.

4  Research Methodology

The methodology is based on quantitative inquiry. The purpose of this research is to explore and develop an understanding of critical concerns error-free, failure-free, efficient utilization and having advanced capabilities in cellular networks, interconnection networks of processors and chemical compound structures.

4.1 Objectives

The main objective of this study is to investigate the topological invariants of mobile cellular networks like honeycomb and regular hexagonal networks. The study finds out the intensity of seriousness of topological indices in certain networks like mobile cellular networks, interconnection networks of processors, parallel processors, chemical structures, etc. This paper study explains the k-banhatti sombor indices, their reduced form, CQIs, and its other variant. It also discusses the benefits of each. This article explains and is aware recent use of KBSO inavariants and QCI and CQI. Its prime objective is to develop formulas so that it can check the topology and performance of mobile base station networks without performing experiments and also before manufacturing them. The work deduced some results which are used in the modeling of mobile-cellular networks.

4.2 Significance

The study is very significant these days because it creates awareness about Topological invariants of certain networks like cellular networks, interconnection networks of processors and chemical structures for efficient utilization. It is also discovering new and significant solutions or formulas for modeling mobile networks [27].

4.3 Hypothesis

The study considers the following hypothesis for the development of mobile cellular networks because vendors and manufacturers need error-free, failure-free and best performer mobile-cellular networks [28].

4.4 Contribution

The expected contribution of this research is to analyze how existing mobile base station networks can be improved by optimizing their adaptability. During the said research honeycomb and regular hexagonal were solved and modeled through deduced results by topological invariants. These results will be developed over the solution of networks graphically by freshly prepared topological indices. Existing MBSNs have been studied for topological perspectives and QSPR and QSAR models are developed and analyzed. The relation between lower bounds and upper bounds of the network or graph has been discovered. The outcomes of the research will provide designing guidelines for advanced MBSNs and chemical compound interconnection networks [29].

4.5 Method

This systematic study will take an existing Honeycomb and regular hexagonal networks, associate it with a graph and solve the topology of the graph with the help of k-banhatti Sombor indices, its reduced form, QCI and the CQI. The concerning results in the form of formulas will compare with existing results and used for modeling purposes of cellular networks [30]. This model is particularly disrupting as it handled the geography of a mobile base station network including regular hexagonal network and honeycomb network in numeric and graphical construction and gives careful results. After examination, an entertainment device maple is used for the affirmation and endorsement of results.

5  Experimental Results

A honeycomb graph is a graph obtained from several graphs of HCn−1 associated with each in a layer. KBSO indices have two variants, k-banhatti sombor index and its reduced version.

KBSO(G)=∑ue⁡du2+dϱ2(1)

The graph theory introduced many graph invariants and studied also but Eq. (1) shows the KBSO index which will be used for the solution of honeycomb and regular hexagonal networks mentioned in Figs. 1 and 4. This invariant has a capability to calculate and found sharp upper bounds at the boundaries.

KBSOrϱd_(G)=∑ue⁡(du−1)2+(dϱ−1)2(2)

The graph theory introduced many graph invariants and studied also but Eq. (2) shows the KBSO reduced index which will be used for the solution of honeycomb and regular hexagonal networks in Figs. 1 and 4. This invariant has a capability to calculate and found sharp lower bounds at the boundaries.

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)(3)

The graph theory introduced many graph invariants and studied also but Eq. (3) shows the CQI which will be used for the solution of honeycomb and regular hexagonal networks in Figs. 1 and 4. This invariant has a capability to calculate and found sharp upper bounds at the boundaries.

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)(4)

The graph theory introduced many graph invariants and studied also but Eq. (4) shows the QCI which will be used for the solution of honeycomb and regular hexagonal networks in Figs. 1 and 4. This invariant has a capability to calculate and found sharp lower bounds at the boundaries.

de = du + dv–2

Tab. 1 describes the edge partitions with their frequencies of honeycomb network given in Fig. 1. The study found vertices of G are either 5, 7 or 9 shown in Tab. 1 and Fig. 1 also. After the calculation the number of edges formed are 6, 12(n − 1), 6(n − 1) and 9n2 – 21n + 12 shown in above table.

5.1 Main Results of Honeycomb Network

Fig. 1 shows honeycomb networks in which n-number of layers of hexagonal networks are exist and used in mobile base stations network. Every cell has 6 vertices and 6 edges. Every cell is surrounded by 6 other hexagonal cells which make it the structure of honeycomb network for mobile base station.

Figure 1: Honeycomb network with n number of cells (HCn)

5.1.1 Honeycomb Graph

Let G = HCn the n-layered honeycomb network with n hexagons among middle and boundary hexagons by HCn. HCn is developed by adding a layer of hexagon around HCn−1 (see Fig. 4). The order and size of HCn are 6n2 and 9n2–3n, separately. Tab. 1, explains in detail the edges partition.

5.1.2 Theorem 1

Let G be a graph of honeycomb, then, KBSO and KBSOred indices are

KBSO(G)=689+55(12n−12)+75(6n−6)+337(9n2−21n+12)(5)

KBSOred(G)=665+97(12n−12)+205(6n−6)+153n2−357n+204(6)

Eqs. (5) and (6) represent the proven results of the graph of honeycomb mentioned in Fig. 1.

5.1.3 Investigation of Honeycomb Graphs by KBSO Indices

Proof

KBSO(G)=∑uedu2+dϱ2

KBSO(G)=52+82(6)+52+102(12(n−1))+72+142(6(n−1))−92+162(9n2−21n+12)

KBSO(G)=689+55(12n−12)+75(6n−6)+337(9n2−21n+12)

KBSOrϱd_(G)=∑ue(du−1)2+(dϱ−1)2

KBSOred(G)=(5−1)2+(8−1)2(6)+5(5−1)2+(10−1)2(12(n−1))

                      +4(7−1)2+(14−1)2(6(n−1))+(9−1)2+(16−1)2(9n2−21n+12)

KBSOred(G)=665+97(12n−12)+205(6n−6)+153n2−357n+204

Fig. 2 results show little sharp lower and upper bounds (Eqs. (5) & (6)) of KBSO indices and their reduced form in red and blue lines respectively.

Figure 2: KBSO and KBSOred for honeycomb network (HCn)

5.1.4 Theorem 2

Let G be a graph of honeycomb, then, CQI and QCI indices are

CQI(G)=33+1411(12n−12)+116179(6n−6)−123(9n2−21n+12)(7)

QCI(G)=43+41111(12n−12)+16179179(6n−6)+233(9n2−21n+12)(8)

Eqs. (7) and (8) represent the proven results of the graph of the honeycomb network mentioned in Fig. 1 with the help of CQI and QCI.

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)

CQI(G)=2((5)2+(5)2)5+5(6)+2((5)2+(7)2)5+7(12(n−1))+2((7)2+(9)2)7+9(6(n−1))+2((9)2+(9)2)9+9(9n2−21n+12)

CQI(G)=33+1411(12n−12)+116179(6n−6)−123(9n2−21n+12)

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)

QCI(G)=5+52((5)2+(5)2)(6)+5+72((5)2+(7)2)(12(n−1))+7+92((7)2+(9)2)(6(n−1))+9+92((9)2+(9)2)(9n2−21n+12)

QCI(G)=43+41111(12n−12)+16179179(6n−6)+233(9n2−21n+12)

Fig. 3 results represesnt sharp upper and lower bounds (Eqs. (7) & (8)) of KBSO indices and their reduced form in red and blue lines respectively.

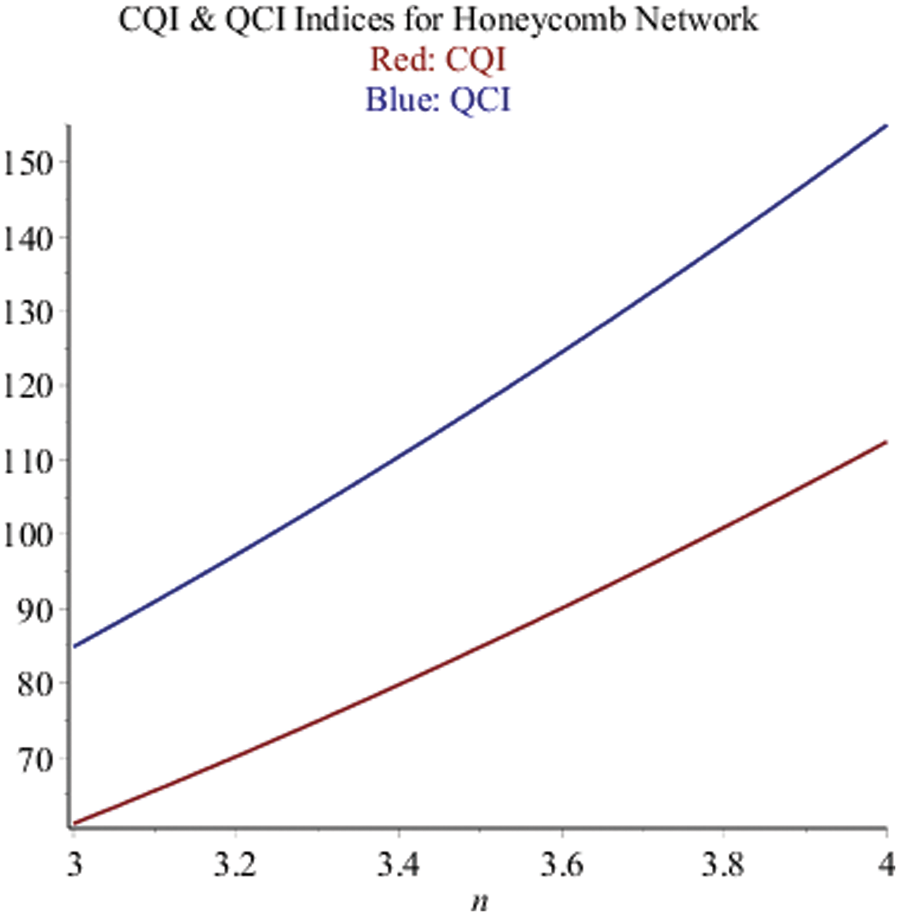
Figure 3: CQI and QCI for honeycomb network (HCn)

5.2 Main Results of Regular Hexagonal Cell Network

Fig. 4 shows regular hexagonal networks used in mobile base stations network with six sides consecutively attached.

Figure 4: Regular hexagonal cells network

5.2.1 Regular Hexagonal Cells Network

Let G = RHm, n. The vertices of G are both of degree 2 or 3, as referenced in Fig. 2. By estimation, we get that G has 4mn + 4m + m − 2 vertices and 6mn + 5m + n − 4 edges. In G, there are three kinds of edges in light of the level of end vertices of each edge Tab. 2 provides a detailed description of the edge set.

Tab. 2 describes the edge partitions with frequencies regarding them in the graph of the regular hexagonal cells network given in Fig. 4 with frequencies. The study found vertices of G are either 2 or 3 shown in Tab. 1 and Fig. 1 also. After the calculation the number of edges formed are 2n + 4, 4m + 4n + 4 and 6mn + m − 5n − 4 shown in above table.

5.2.2 Theorem 3

Let G be a graph of regular hexagonal network Then KBSO and KBSOred are

KBSO(G)=22(2n+4)+13(4m+4n−4)+30mn+5m−25n−20(9)

KBSOred(G)=2(2n+4)+5(4m+4n−4)+13(6mn+m−5n−4)(10)

Eqs. (9) and Eqs. (10) represent the proven results of the graph of regular hexagonal mentioned in Fig. 4. with the help of the KBSO Index and its reduced form.

5.2.3 Investigation of Regular Hexagonal by K-Banhatti Sombor Indices

Proof

KBSO(G)=∑uedu2+dϱ2

KBSO(G)=22+22(2n+4)+22+32(4m+4n−4)+32+42(6mn+m−5n−4)

KBSO(G)=22(2n+4)+13(4m+4n−4)+30mn+5m−25n−20

KBSOrϱd_(G)=∑ue⁡(du−1)2+(dϱ−1)2

KBSOred(G)=(2−1)2+(2−1)2(2n+4)+(2−1)2+(3−1)2(4m+4n−4)

                       +(3−1)2+(4−1)2(6mn+m−5n−4)

KBSOred(G)=2(2n+4)+5(4m+4n−4)+13(6mn+m−5n−4)

Fig. 5 shows the results (Eqs. (9) & (10)) of CQI and QCI in red and blue colors respectively in the 3D version which shows sharp upper and lower bounds of a network.

Figure 5: KBSO and KBSOred for regular hexagonal network

5.2.4 Theorem 4

Let G be a graph of Regular Hexagonal Network Then CQI and QCI are

CQI(G)=12(2n+4)3+15(4m+4n−4)17+123(6mn+m−5n−4)(11)

QCI(G)=23(2n+4)3+517(4m+4n−4)17+233(6mn+m−5n−4)(12)

Eqs. (11) and (12) represent the proven results of the graph of regular hexagonal mentioned in Fig. 4.

5.2.5 Investigation of Regular Hexagonal Network by CQIs

Proof

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)

CQI(G)=2((2)2+(2)2)2+2(rs−2r)+2((2)2+(3)2)2+3(4)+2((2)2+(4)2)2+4(2r−4)+2((3)2+(4)2)(2)+2((4)2+(4)2)4+4(r−3)3+4

CQI(G)=12(2n+4)3+15(4m+4n−4)17+123(6mn+m−5n−4)

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)

CQI(G)=2+22((2)2+(2)2)(rs−2r)+2+32((2)2+(3)2)(4)+2+42((2)2+(4)2)(2r−4)+3+42((3)2+(4)2)(2)+4+42((4)2+(4)2)(r−3)

QCI(G)=23(2n+4)3+517(4m+4n−4)17+233(6mn+m−5n−4)

Fig. 6 shows the results with clear upper and lower bounds (Eqs. (11) & (12)) of CQI and QCI in red and blue colors respectively in the 3D version.

Figure 6: CQI and QCI for regular hexagonal network

6  Conclusion

TIs have lots of uses and implementations in many fields of computer science, chemistry, biology, informatics, arithmetic, material sciences, and many more. But the utmost significant application is in the non-exact QSPR and QSAR. TIs are associated with the structure of mobile networks which are hexagonal layered structures called honeycombs. The study discusses the KBSO invariants and CQIs which are freshly presented and have numerous prediction qualities for different variants of hexagonal graphs or networks, i.e., honeycomb and regular hexagonal. Figs. 2 and 5 give the graphical representation with sharp upper and lower bound of KBSO indices for handling high traffic load and minimal load by improving the physical layout according to deduced results. On the other hand, Figs. 3 and 6 give the graphical representation of CQIs for mobile base station networks. These deduced results will be used for the node density, mobility among the nodes, link formation between the nodes, modeling and simulation of Cellular base station networks, and chemical interconnection networks.

Acknowledgement: The authors, therefore, gratefully acknowledge DSR technical and financial support.

Funding Statement: This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under Grant No. (RG−11–611–43).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  P. Kainan, A. Sinchai, P. Tuwanut and P. Wardkein, “New pulse oximetry detection based on the light absorbance ratio as determined from amplitude modulation indexes in the time and frequency domains,” Biomedical Signal Processing and Control, vol. 75, no. 1, pp. 103627, 2022. [Google Scholar]

 2.  S. Faruque, “Frequency division multiple access (FDMA),” in Radio Frequency Multiple Access Techniques Made Easy, Grand Forks, GF, USA: Springer, pp. 21–33, 2019. [Google Scholar]

 3.  L. Hota, B. P. Nayak, A. Kumar, G. G. M. N. Ali and P. H. J. Chong, “An analysis on contemporary MAC layer protocols in vehicular networks: State-of-the-art and future directions,” Future Internet, vol. 13, no. 11, pp. 11, 2021. [Google Scholar]

 4.  Y. Lou and N. Ahmed, Link Performance Enhancement Techniques in Underwater Communications and Networks, Cham, CM, Switzerland: Springer, pp. 243–267, 2022. [Google Scholar]

 5.  M. C. Meyer, Y. Wang and T. Watanabe, “Real-time cost minimization of fog computing in mobile-base-station networked disaster areas,” IEEE Open Journal of the Computer Society, vol. 2, no. 1, pp. 53–61, 2021. [Google Scholar]

 6.  M. W. Sarwar, A. Riaz, S. M. R. Dilshad, A. Al-Qahtani, M. S. Nawaz-Ul-Rehman et al., “Structure activity relationship (SAR) and quantitative structure activity relationship (QSAR) studies showed plant flavonoids as potential inhibitors of dengue NS2B-NS3 protease,” BMC Structural. Biology, vol. 18, no. 1, pp. 6, 2018. [Google Scholar]

 7.  V. Kulli, “Contraharmonic quadratic index of certain nanostar dendrimers,” International Journal of Mathematical Archive, vol. 13, no. 1, pp. 1–7, 2022. [Google Scholar]

 8.  J. Jung and R. Katz, “Spectrum flexibility and mobile telecommunications development,” Utilities Policy, vol. 75, no. 1, pp. 101351, 2022. [Google Scholar]

 9.  X. Li, L. Lu, W. Ni, A. Jamalipour, D. Zhang et al., “Federated multi-agent deep reinforcement learning for resource allocation of vehicle-to-vehicle communications,” IEEE Transactions on Vehicular Technology, vol. 1, no. 1, pp. 1–10, 2022. [Google Scholar]

10. R. D. Gaudenzi, M. Luise and L. Sanguinetti, “The open challenge of integrating satellites into (beyond-) 5G cellular networks,” IEEE Network, vol. 36, no. 2, pp. 168–174, 2022. [Google Scholar]

11. J. Liu, L. Cai, A. R. Virk, W. Akhtar, S. A. Maitla et al., “Computation of irregularity indices of certain computer networks,” Mathematical Problems in Engineering, vol. 2020, no. 1, pp. 2797286, 2020. [Google Scholar]

12. M. Cancan, I. Ahmad and S. Ahmad, “Study of topology of block shift networks via topological indices,” Proyecciones (Antofagasta), vol. 39, no. 4, pp. 887–902, 2020. [Google Scholar]

13. A. Aslam, S. Ahmad, M. A. Binyamin and W. Gao, “Calculating topological indices of certain OTIS interconnection networks,” Open Chemistry, vol. 17, no. 1, pp. 220–228, 2019. [Google Scholar]

14. M. Imran, M. A. Iqbal, Y. Liu, A. Q. Baig, W. Khalid et al., “Computing eccentricity-based topological indices of 2-power interconnection networks,” Journal of Chemistry, vol. 2020, no. 1, pp. 1–12, 2020. [Google Scholar]

15. J. H. Tang, “On computation of edge degree-based banhatti indices of a certain molecular network,” Journal of Mathematics, vol. 2021, no. 1, pp. e5185270, 2021. [Google Scholar]

16. Y. Yao, Y. Song, H. Ge, Y. Huang and D. Zhang, “A Communication-aware and predictive list scheduling algorithm for network-on-chip based heterogeneous muti-processor system-on-chip,” Microelectron. Journal, vol. 121, no. 1, pp. 105367, 2022. [Google Scholar]

17. B. B. Yusuf, T. Maqsood, F. Rehman and S. A. Madani, “Energy aware parallel scheduling techniques for network-on-chip based systems,” IEEE Access, vol. 9, no. 1, pp. 38778–38791, 2021. [Google Scholar]

18. E. C. Onyibo and B. Safaei, “Application of finite element analysis to honeycomb sandwich structures: A review,” Reports in Mechanical Engineering, vol. 3, no. 1, pp. 1–21, 2022. [Google Scholar]

19. R. S. Haoer and A. U. R. Virk, “Some reverse topological invariants for metal-organic networks,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 24, no. 2, pp. 499–510, 2021. [Google Scholar]

20. F. Afzal, H. Hussain, D. Afzal, M. R. Farahani, M. Cancan et al., “On computation of latest topological descriptors of some cactus chains graphs via m-polynomial,” Journal of Information and Optimization Sciences, vol. 42, no. 7, pp. 1437–1446, 2021. [Google Scholar]

21. S. Hayat and M. Imran, “Computation of topological indices of certain networks,” Applied Mathematics and Computation, vol. 240, no. 1, pp. 213–228, 2014. [Google Scholar]

22. F. Chaudhry, M. Ehsan, D. Afzal, M. R. Farahani, M. Cancan et al., “On computation of m-polynomial and topological indices of starphene graph,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 24, no. 2, pp. 401–414, 2021. [Google Scholar]

23. S. Hussain, F. Afzal, D. Afzal, M. Cancan, S. Ediz et al., “Analyzing the boron triangular nanotube through topological indices via m-polynomial,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 24, no. 2, pp. 415–426, 2021. [Google Scholar]

24. F. Chaudhry, M. Farahani, M. Cancan, İ. Çiftçi and F. Afzal, “Degree based topological indices of tadpole graph via m-polynomial [665],” Eurasian Chemical Communications, vol. 3, no. 1, pp. 146–153, 2021. [Google Scholar]

25. M. Riaz, W. Gao and A. Q. Baig, “M-Polynomials and degree-based topological indices of some families of convex polytopes,” Open Journal of Mathematical Sciences, vol. 2, no. 1, pp. 18–28, 2018. [Google Scholar]

26. S. Bordoloi and B. Kalita, “Designing graph database models from existing relational databases,” International Journal of Computer Applications, vol. 74, no. 1, pp. 25–31, 2013. [Google Scholar]

27. H. Khalid, M. W. Iqbal, A. U. R. Virk, M. U. Ashraf, A. M. Alghamdi et al., “K-banhatti sombor invariants of certain computer networks,” Computer,” Materials and Continua, vol. 73, no. 1, pp. 15–31, 2022. [Google Scholar]

28. A. Virk, S. Bilal and K. Hamid, “Irregularity invariants for chemical structures used in the treatment of COVID-19,” Scientific Inquiry and Review, vol. 4, no. 3, pp. 38–60, 2020. [Google Scholar]

29. K. Hamid, M. W. Iqbal, H. A. B. Muhammad, Z. Fuzail, Z. T. Ghafoor et al., “Usability evaluation of mobile banking applications in digital business as emerging economy,” International Journal of Computer Science and Network Security, vol. 22, no. 2, pp. 250–271, 2022. [Google Scholar]

30. G. Yasin, S. F. Abbas and M. W. Iqbal, “Carbon emission-aware routing protocol in vehicular ad-hoc networks,” in 9th Int. Conf. on Application of Information and Communication Technologies (AICT), Rostov-on-Don, Russia, pp. 461–466, 2015. [Google Scholar]