Solar Energy Harvesting Using a Timer-Based Relay Selection

1  Introduction

In solar energy harvesting, the harvested power is proportional to the radiation intensity I(t) [1–3]. The radiation intensity is the sum of a deterministic radiation intensity I1(t) and a random radiation intensity I2(t) [4–7]. I1(t) is a deterministic radiation intensity that depends on time t in hour, month and season. I1(t) is maximum at t = 12 h and zero at t = 6 and t = 18 [8–10]. I2(t) is a random attenuation due to weather effects as well as clouds occlusion [11–15]. I2(t) has a zero mean Gaussian distribution with variance a2 [1]. Therefore, the harvested power has a Gaussian density. In this article, we study cooperative communications with energy harvesting from sun. The source and relays harvest energy using a photo voltaic system. The source use the harvested power to transmit data to relays. Relay nodes harvest energy from sun and set a timer to a value proportional to the inverse of its Signal to Noise Ratio (SNR). The timer of relay with largest SNR will expire first. This relay amplifies the source signal and its signal will be detected by the other relays that will remain idle to avoid collisions. We use Opportunistic Amplify and Forward (OAF), Partial and Reactive Relay Selection (PRS and RRS). The main contributions of the paper are

A simple timer based relay selection is used. The throughput, the collision and the delay of timer based relay selection will be derived. The throughput is maximized by optimizing harvesting duration.

The motivation of this work is to evaluate the throughput and delays with solar energy harvesting. Another motivation is to evaluate the performance of the suggested timer based relay selection. The main contribution of the paper is to derive the statistics of SNR with solar energy harvesting. The throughput, waiting time and total delay are evaluated with solar energy harvesting. A simple relay selection process using a timer is suggested. No signalization is required and the selection process is very simple since each relays uses a timer initialized to a value proportional to the inverse of its SNR. The relay with largest SNR transmits and the other relays remain idle when they detect its signal to avoid collisions. The throughput and delay analysis with energy harvesting from sun were not yet derived.

Section 2 studies the statistics of the harvested power from sun. The collision probability of timer based relay selection is evaluated in Section 3. Section 4 evaluates the throughput, packets’ waiting time and total delay. Section 5 comments on the obtained results. Section 6 concludes the paper.

2  Solar Energy Harvesting

Fig. 1 shows the system model where the source S and relays Ri harvest energy from sun using a Photo Voltaic (PV) system. Then, S sends data to relays Ri. A selected relay amplifies the signal to the destination D. The harvested solar power using a PV system at noon is approximately 1000 W/m2. The harvested power P at the source S and relays Ri using a PV system is proportional to the radiation intensity.

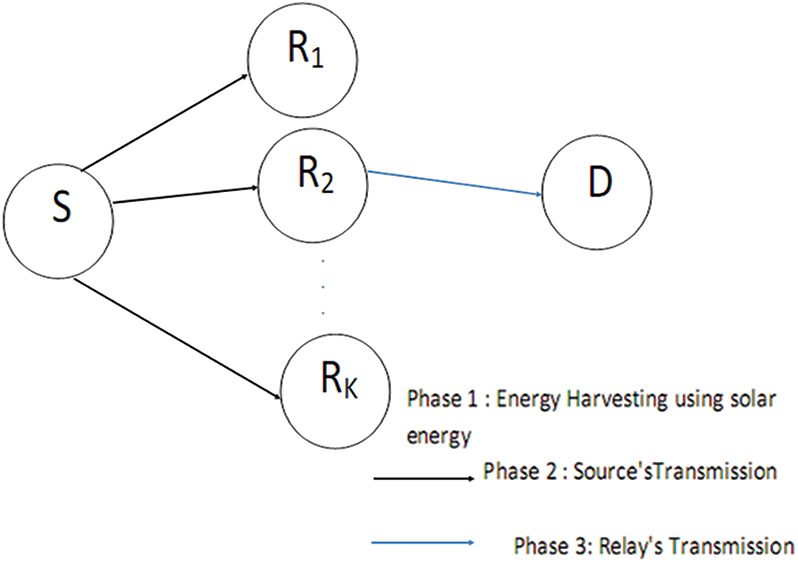
Figure 1: Network model

P=ηI(t),(1)

I(t)=I1(t)+I2(t)(2)

I1(t)=Imax(−3+t23−t236)(3)

The harvested solar power using a PV system at noon t = 12 is approximately 1000 W/m2. For a PV system of 2 m2, the maximum solar radiation intensity is Imax = 2000 W. I2(t) is a random attenuation due to weather effects as well as clouds occlusion. I2(t) has a zero mean Gaussian distribution with variance a2 [1]. Therefore, the Probability Density Function (PDF) of I(t) is expressed as [1]

fI(x)=12πa2exp⁡(−(x−I1(t))22a2)(4)

where x > 0 is the variable of PDF function and a2 is the variance of random attenuation I2(t).

Energy harvesting from the PV system is performed continuously. The harvested energy during αT seconds is used to transmit data by S and a selected relay during (1−α)T/2 s where 0 < α < 1 and T is frame length. The harvested energy by the source and relays during αT seconds is expressed as [1]

E=αTP(5)

The symbol energy Es is the ratio of the harvested energy E given in (5) and the number of transmitted symbols (1−α)T/Ts [1]

Es=2TsE(1−α)T=2αηTsI(t)1−α(6)

where Ts is the symbol duration.

Since I(t) has a Gaussian distribution, Es follows also a Gaussian distribution with PDF

fEs(x)=12πσ2exp⁡(−(x−m(t))22σ2)(7)

where m(t) and σ2 are the mean and the variance of Es written as

m(t)=η2αTsI1(t)1−α(8)

β2=[aη2αTsI1(t)1−α]2(9)

The SNR at relay Rk is written as

γSRk=Es|hSRk|2N0(10)

where hXY is channel gain of the X-Y link and N0 is noise variance.

Let E(|hSRk|2) = λk = PL d0PLE/dSRkPLE where PL is the path loss at distance d0, dXY is the distance from X to Y. Let Zk = |hSRk|2/N0. For Rayleigh channels, Xk follows an exponential distribution with Cumulative Distribution Function (CDF) equal to

FZk(x)=1−exp⁡(−xN0k),(11)

Therefore, the SNR is the product a Gaussian random variable (r.v.) Es and an exponential r.v. Xk. The Cumulative Distribution Function (CDF) of the SNR can be computed as follows [19]:

FγSRk(x)=∫0+∞fEs(y)FZk(xy)dy(12)

The CDF of SNR of Rk-D link is written similarly.

3  Collision Probability

The relay selection process uses a timer. Each relay sets a timer proportional to the inverse of its SNR. Therefore, the timer of the relay with best SNR expires the first and amplifies the signal to the destination. When the relay transmits the other relays detects its signals and remain idle to avoid collisions. Let Xk be the timer of relay Rk

Xk=βγSRk(13)

when Partial Relay Selection (PRS) is employed. β>0 is a constant used to set the timer.

Xk=βγRkD(14)

when Reactive Relay Selection (RRS) is employed.

Xk=βγSRkD(15)

when opportunistic relay selection is employed and γSRkD = min(γSRk, γRkD).

Let X(1) be the timer of best relay and X(k) be the timer of k-th best relay: X(1) < X(2) < … < X(K).

There is a collision if the gap between the timer of second best relay X(2) and that of the best relay X(1) is lower than the propagation between d between relay nodes:

X(2)<X(1)+d(16)

The joint PDF of X(1) and X(2) is expressed as [20]

fX(1),X(2)(x1,x2)=∑i=1K∑j≠i,j=1KfXj(x2)fXi(x1)∏k=1,k≠i,k≠jK[1−FXk(x2)],(17)

The collision probability is equal to

cp=∫x2=d+∞∫x1=x2−d+∞fX(1),X(2)(x1,x2)dx1dx2(18)

fXk(x) is computed by a simple derivative of FXk(x).

4  Throughput and Delay Analysis

The throughput at D using OAF and a timer based relay selection is computed as:

ThrOAF=0.5(1−a)[1−cp]log⁡2(M)[1−PEPOAF],(19)

where M is the constellation size, cp is the collision probability and PEPOAF is the Packet Error Probability (PEP) of OAF.

The throughput of PRS with timer based relay selection is computed as:

ThrPRS=0.5(1−a)[1−cp]log⁡2(M)[1−PEPPRS],(20)

PEPPRS is the PEP of PRS.

The throughput of RRS with timer based relay selection is computed as:

ThrRRS=0.5(1−a)[1−cp]log⁡2(M)[1−PEPRRS],(21)

where PEPRRS is the PEP of RRS relaying.

The PEP of different relaying techniques are computed as [19]

PEPOAF<FγOAF(TH)(22)

PEPPRS<FγPRS(TH)(23)

PEPOAF<FγOAF(TH)(24)

TH=∫0+∞1−[1−SEP(w)]Ldw,(25)

L is packet length and [21]

SEP(w)=2(1−1M)erfc(3wM−1),(26)

The average waiting time W of packets is given by the Pollaczek Khinchin formula [22]:

W=λE(TR2)T22(1−λE(TR))+0.5T,(27)

λ is packet arrival rate, TR is the number of transmission attempts [21]

E(TR)=11−PEP,(28)

E(TR2)=3PEP2(1−PEP)2+31−PEP−2,(29)

The total delay D is equal to the average waiting time plus the service time, E(TR)T, expressed as

D=W+E(TR)T,(30)

5  Theoretical and Simulation Results

Figs. 2–4 depict the throughput of timer based relay selection using OAF, PRS and RRS for cp = 0.2, 0.1, 0.05. The curves were plotted vs. the average Signal to Noise Ratio (SNR) per it Eb/N0. Eb is the average transmitted energy per bit and N0 is noise variance. The distance between source and relays is 5 and the distance between relays and destination is 4. The path loss exponent was set to three. The size of the PV system was 0.5 m2 . The used parameters are η=0.5, α = 0.5, the variance of radiation intensity is a2 = 1 and t = 12. The number of relays is K = 2. We observe that the performance improves as cp decreases and becomes close to best relay selection due to less collisions. In fact as cp decreases as there are less collisions and a larger throughput is achieved. Fig. 5 shows that OAF offers the best performance as it uses the SNR of two hops. PRS is better than RRS since the relays are closer to the destination. In fact, PRS selects the best relay of first hop and offers good performance when relays are close to the destination. RRS selected the best relay of second hop and offers good performance when relays are close to the source. Fig. 6 shows that the throughput of OAF is better at t = 12 since the solar energy is larger than t = 8. Fig. 7 shows that we can increase the throughput of OAF by optimizing the value of harvesting duration α. When α is very small, the harvested power is small and the performance is bad. When α is very large, the harvested power is large but the remaining time for communication is small leading to a small throughput. Fig. 8 shows that the throughput can be easily maximized as it is a concave function with respect to α and there is a single maximum. Fig. 9 shows the total delay for T = 1 ms and arrival rate λ = 0.001. We observe that the timer based relay selection offers similar delays to best relay selection for cp = 0.05 since there are only few collisions.

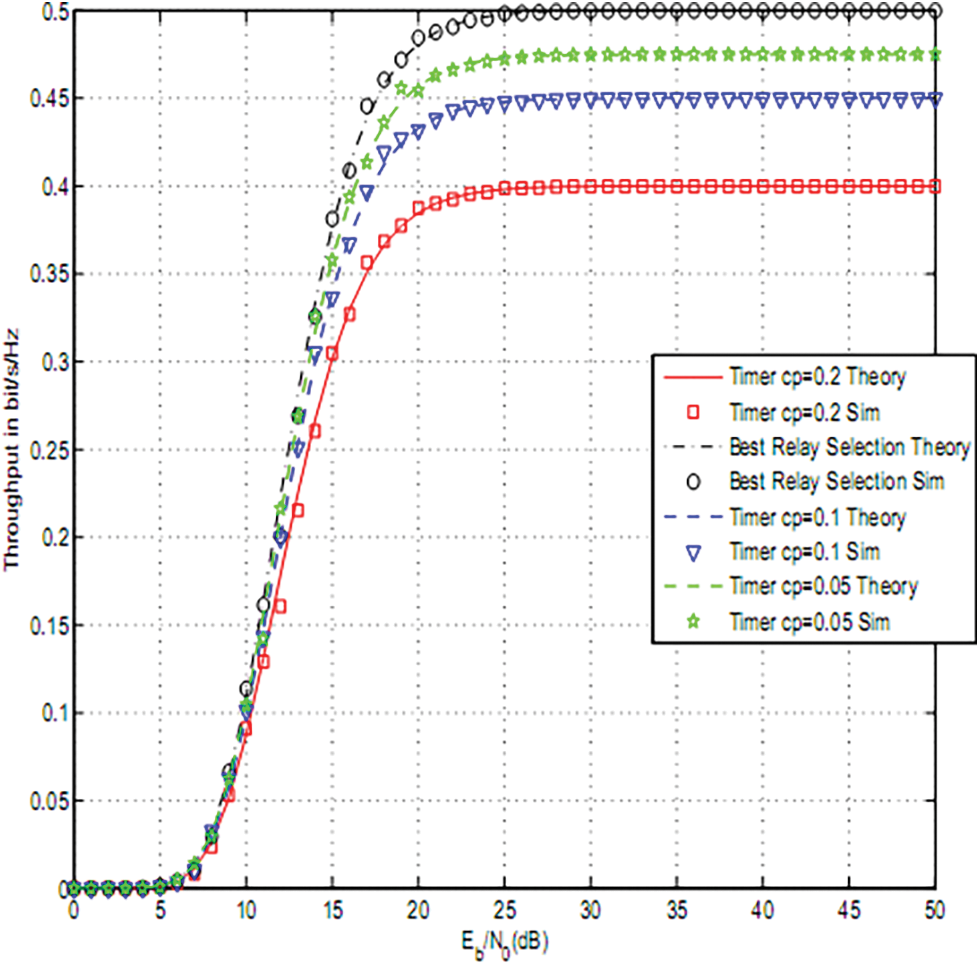
Figure 2: OAF using a timer based relay selection

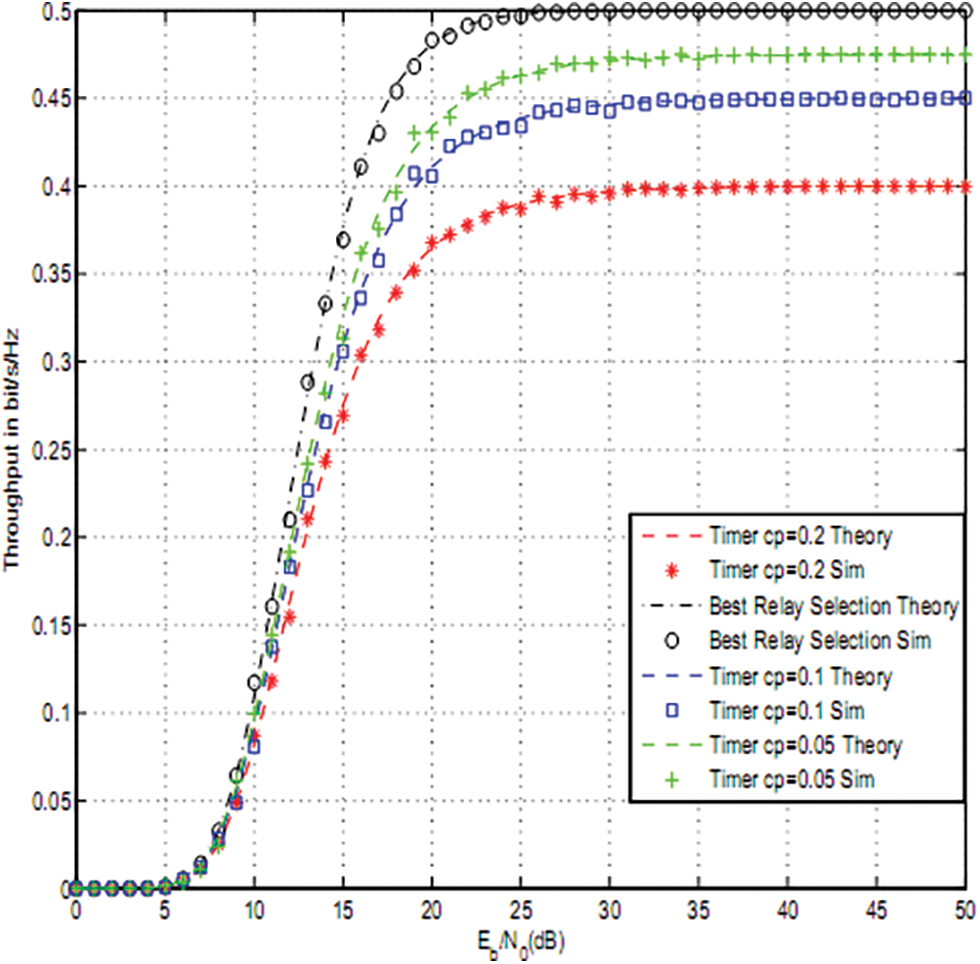
Figure 3: PRS using a timer-based relay selection

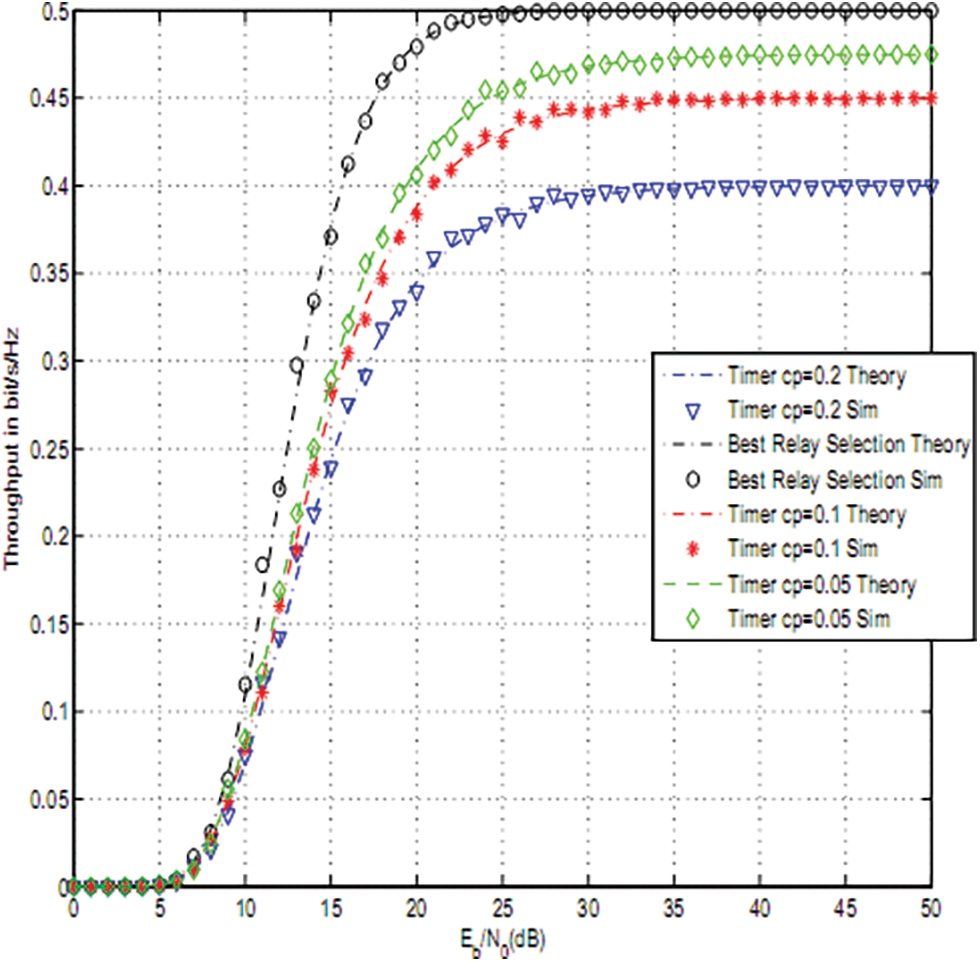
Figure 4: RRS using a timer based relay selection

Figure 5: OAF, PRS and RRS for cp = 0.05

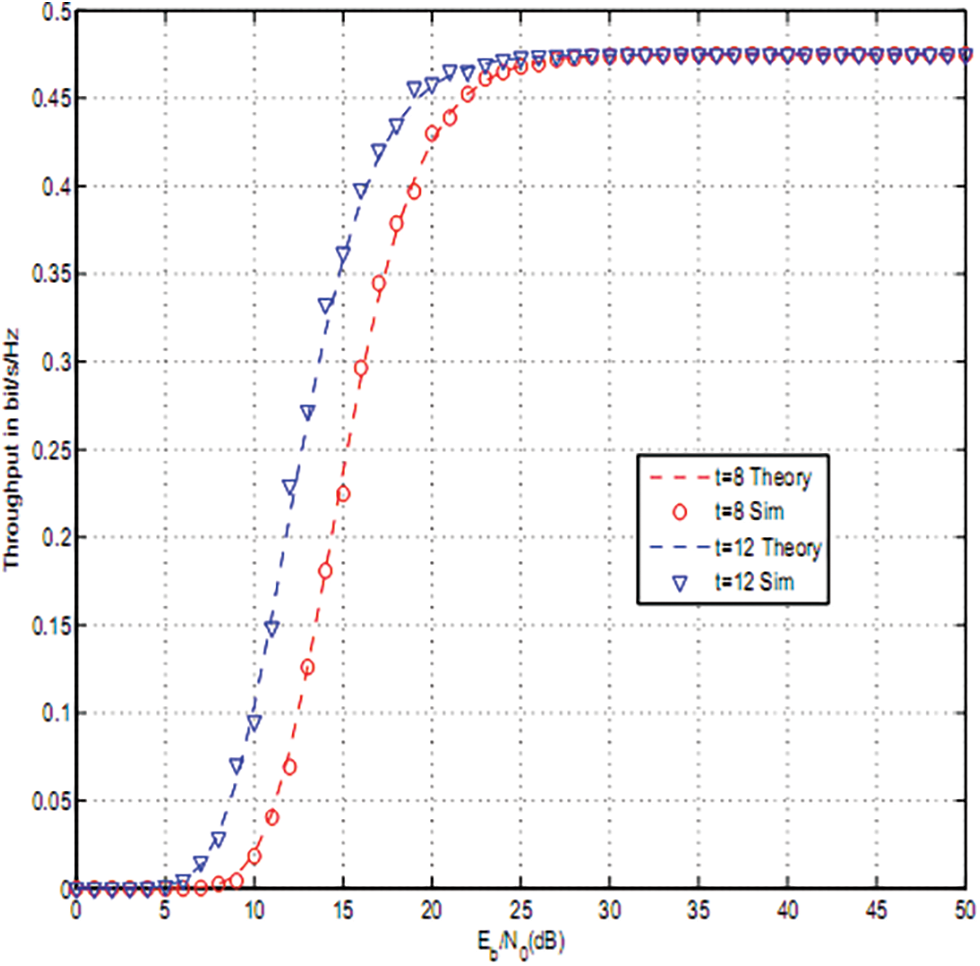
Figure 6: Throughput of OAF for cp = 0.05, K = 2 and t = 8, 12

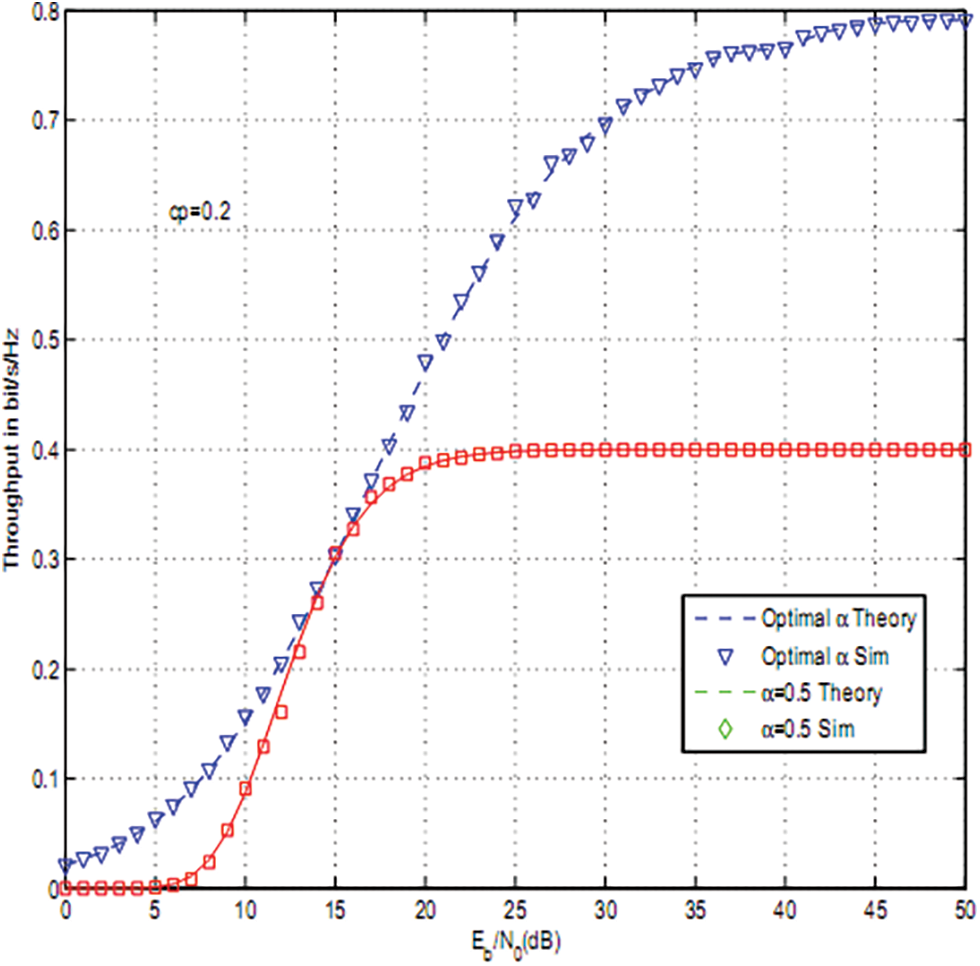
Figure 7: Throughput optimization of OAF for cp = 0.2

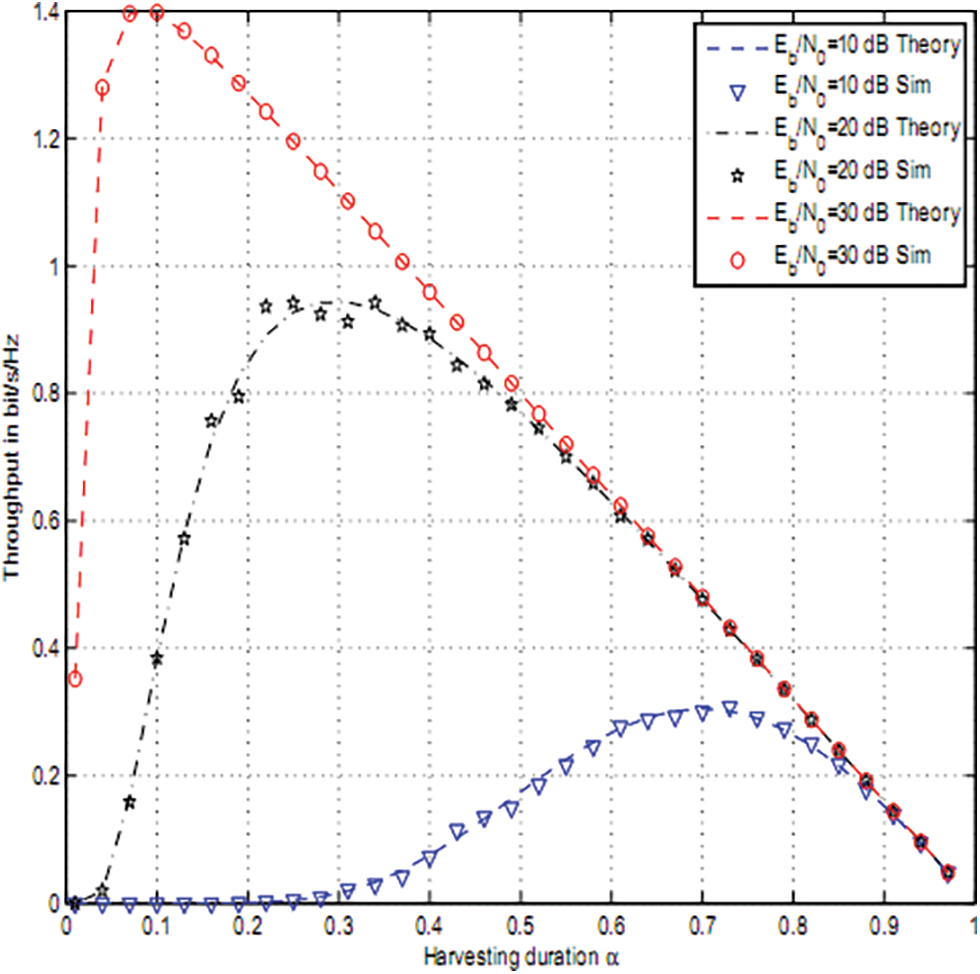
Figure 8: Throughput of OAF vs. α for cp = 0.2

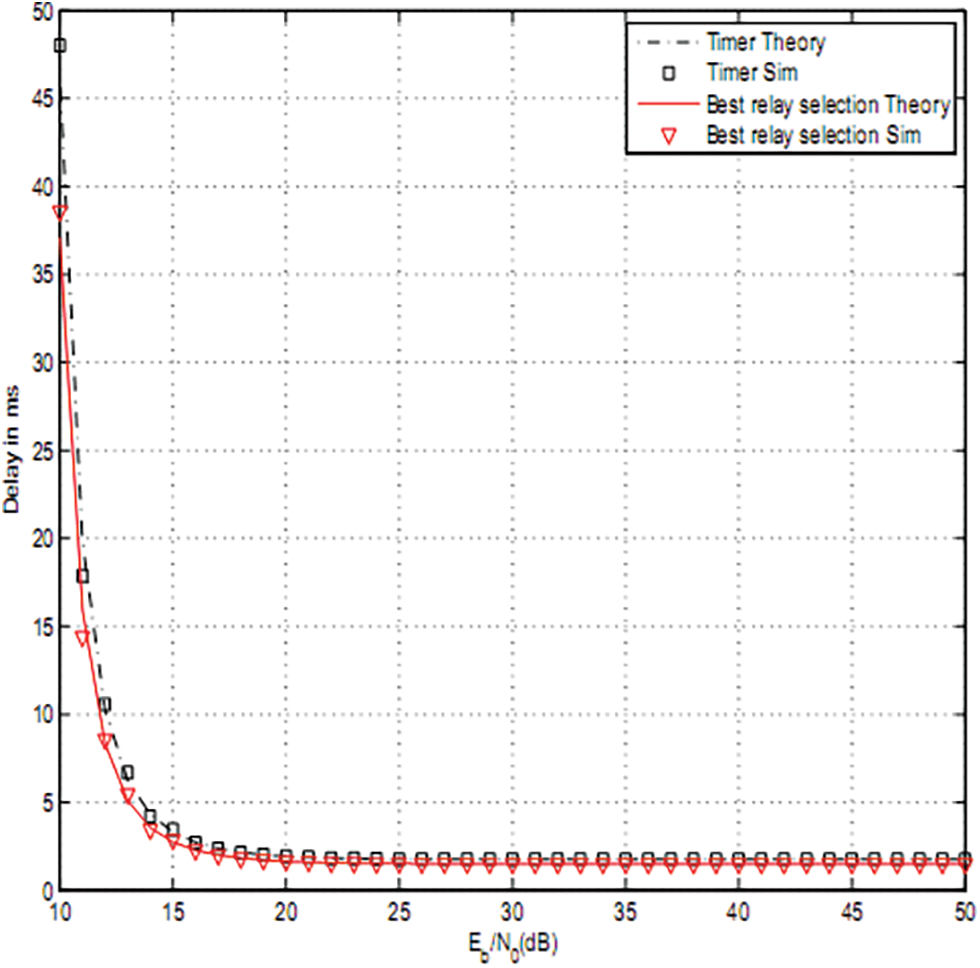
Figure 9: Total delay of OAF for cp = 0.05

6  Conclusions

In this article, the throughput, packets’ waiting time and total delay of cooperative communication with solar energy harvesting are derived. The relay selection process uses a timer. Each relay sets a timer proportional to the inverse of its SNR. Therefore, the timer of the relay with best SNR expires the first and amplifies the signal to the destination. When the relay transmits the other relays detects its signals and remain idle to avoid collisions. The throughput was also maximized by optimizing harvesting duration.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at Saudi Electronic University for funding this research work through the project number 8092.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. Xu, Y. Zhao, L. Tao and Z. Xu, “Resource allocation strategy for dual UAVs-assisted MEC system with hybrid solar and RF energy harvesting,” in 3rd Int. Conf. on Computer Communication and the Internet (ICCCI), Rhodes, Greece, 29 September-1 October 2021. [Google Scholar]

 2.  R. B. Roy, M. Rokonuzzaman, N. Amin, M. Mishu, S. Alahakoon et al., “A comparative performance analysis of ANN algorithms for MPPT energy harvesting in solar PV system,” IEEE Access, vol. 9, pp. 102137–102152, 2021. [Google Scholar]

 3.  P. Soonsawad, K. Jeon and J. She, “Improved energy harvesting with one-time adjusted solar panel for BLE beacon,” in IEEE 93rd Vehicular Technology Conf. (VTC2021-Spring), 27 September-28 October, Virtual conference, 2021. [Google Scholar]

 4.  H. D. Tuan, A. A. Nasir, A. V. Savkin, H. V. Poor and E. Dutkiewicz, “MPC-based UAV navigation for simultaneous solar-energy harvesting and two-way communications,” IEEE Journal on Selected Areas in Communications, vol. 39, no no. 11, pp. 3459–3474, 2021. [Google Scholar]

 5.  S. C. Chadrarathna and J. Lee, “A self-resonant boost converter for solar energy harvesting with 97% tracking efficiency, 80 mV self-startup and ultra-wide range source tracking,” in IEEE Custom Integrated Circuits Conf. (CICC), pp. 25–30, April, Virtual conference, 2021. [Google Scholar]

 6.  Y. Chen, X. Cheng, Y. Yao and B. Wan, “Short interval solar power prediction for energy harvesting with low computation cost on edge computation network,” in IEEE 11th Annual Computing and Communication Workshop and Conf. (CCWC), Virtual conference, pp. 27–30, January 2021. [Google Scholar]

 7.  M. L. Ku and T. Lin, “Neural network-based power control prediction for solar-powered energy harvesting communications,” IEEE Internet of Things Journal, vol. 8, no. 16, pp. 12983–12998, 2021. [Google Scholar]

 8.  M. Hamza, M. Rehman, A. Riaz, Z. Maqsood and W. T. Khan, “Hybrid dual band radio frequency and solar energy harvesting system for making battery-less sensing nodes,” in IEEE Radio and Wireless Symposium (RWS), San Diego, USA, pp. 17–20, January 2021. [Google Scholar]

 9.  W. An, L. Hong, Y. Luo, K. Ma, J. Ma et al., “A wideband dual-function solar cell dipole antenna for both energy harvesting and wireless communications,” IEEE Transactions on Antennas and Propagation, vol. 69, no. 1, pp. 544–549, 2021. [Google Scholar]

10. J. Park, M. Jeong, J. Kang and C. Yoo, “Solar energy-harvesting buck–boost converter with battery-charging and battery-assisted modes,” IEEE Transactions on Industrial Electronics, vol. 68, no. 3, pp. 263–2172, 2021. [Google Scholar]

11. D. Yadav, “Solar energy harvesting by carbon nanotube optical rectenna: A review,” in 2020 IEEE Int. Symp. on Sustainable Energy, Signal Processing and Cyber Security (iSSSC), Gunupur, Odisha, India, pp. 16–17, December 2020. [Google Scholar]

12. F. M. Abdel, K. R. Mahmoud, M. Hussein and S. S. A. Obayya, “Design and analysis of hexagonal dipole nano-rectenna based on MIIM diode for solar energy harvesting,” in 8th Int. Japan-Africa Conf. on Electronics, Communications, and Computations (JAC-ECC), Virtual Conference, New York, McGraw-Hill, pp. 14–15, December 2020. [Google Scholar]

13. W. Liu, W. Yin, J. Xie, R. Luo and S. Hu, “Do we really need complicated solar energy harvesting circuits for low cost sensor nodes?,” in IEEE 2nd Int. Conf. on Circuits and Systems (ICCS), Amsterdam, Netherlands, pp. 3–5, June 2020. [Google Scholar]

14. A. Aliakbari and V. Vahidinasab, “Optimal charging scheduling of solar plugin hybrid electric vehicles considering on-the-road solar energy harvesting,” in 10th Smart Grid Conf. (SGC), Kashan, Iran, pp. 16–17, December 2020. [Google Scholar]

15. P. Poulose and D. P. Sreejaya, “Energy harvesting technology using dye sensitized solar cell for low power devices,” in 2020 Int. Conf. on Power Electronics and Renewable Energy Applications (PEREA), Kannur, Kerala, India, pp. 27–28, November 2020. [Google Scholar]

16. M. Ali, S. Ali, H. Abbas, A. Murtaza, M. Khurram et al., “Development of experimental model for water desalination by harvesting solar energy,” in 2020 IEEE 23rd Int. Multitopic Conf. (INMIC), Bahawalpur, Pakistan, pp. 5–7, November 2020. [Google Scholar]

17. H. Shatnawi and A. Aldossary, “Outdoor investigation of high concentrator photovoltaic under uniform and non-uniform illumination,” Journal of Daylighting, vol. 7, no. 1, pp. 1–12, 2020. [Google Scholar]

18. A. Dragulinescu and A. Dragulinescu, “Solar cell types and technologies with applications in energy harvesting,” in 2020 IEEE 26th Int. Symp. for Design and Technology in Electronic Packaging (SIITME), Online conference, pp. 21–24, October 2020. [Google Scholar]

19. Y. Xi, A. Burr, J. Wei and D. Grace, “A general upper bound to evaluate packet error rate over quasi-static fading channels,” IEEE Trans. Wireless Communications, vol. 10, no. 5, pp. 1373–1377, May 2011. [Google Scholar]

20. R. J. Vaughan and W. N. Venables, “Permanent expressions for order statistics densities,” Journal of Royal Statistical Society Series B, vol. 34, pp. 308–310, 1972. [Google Scholar]

21. J. Proakis, “Digital communications,” in Mac Graw-Hill, 5th ed., 2007. [Google Scholar]

22. W. C. Chan, T. C. Lu and R. J. Chen, “Pollaczek–Khinchin formula for the M/G/1 queue in discrete time with vacations,” IET Computer and Digital. Techniques, vol. 144, no. 4, pp. 222–226, Jul. 1997. [Google Scholar]