Fusion Strategy for Improving Medical Image Segmentation

1  Introduction

Medical images are increasingly used in healthcare for diagnosis, medication preparation, treatment directing, and disease progression tracking. Medical imaging primarily processes data that is unclear, incomplete, ambiguous, complementary, conflicting, overlapping, contradictory, skewed, and has a clear structural character. One of the general ways to understand an image is to match the previously stored models with the features and features that were extracted from the image. In order to obtain a high-level model, full knowledge of the objects to be modeled and their relationship to each other, how to use the information obtained in the model, and the best time to use it. Magnetic resonance imaging (MRI) offers detailed three-dimensional (3D) details on the anatomy of human soft tissues [1]. It is noninvasive and does not use ionising radiation like X-rays to expose fine details of anatomy.

In recent years, applications that use the morphologic contents of MRI have often required segmentation of the image volume into tissue types due to the wealth of anatomy knowledge provided by MRI [2]. For example, determining white matter (WM) and grey matter volume in brain magnetic resonance images (MRI) has become an important measurement tool for multiple sclerosis (MS) patient monitoring and research [3–5]. A number of different approaches for brain tissue segmentation have been identified in the literature, including histogram-based techniques, edge detection, region-based segmentation [6,7], fuzzy clustering [8–12], graph cuts [13,14], genetic algorithms [15–17], threshold approaches [18–21], and hybrid techniques [22,23].

To deal with the complexity of MRI structure, hybrid techniques that combine more than one method are required [24]. One of the most popular image segmentation techniques is multi-level thresholding. The techniques used to select the threshold value determine the segmented image quality [25], for example an extensive survey was conducted, using meta-inference optimization algorithms, the performance of image segmentation methods was compared.

The aim of image segmentation is to divide pixels into two or more classes based on their intensity levels and a threshold value. The procedure used to pick the threshold determines the accuracy of the segmentation. To determine the best multilevel threshold of image segmentation, various optimization techniques have been developed. the behaviour of birds flocking in search of food is a machine-learning technique [26]. It is made up of a group of particles that collectively travel through the search space (e.g., image pixels) in search of the global optimum (e.g., maximising the between-class variance of the distribution of intensity levels in the given image). However, a common issue with the PSO and other optimization algorithms is that they may get stuck in a local optimum, causing them to function in some cases but not in others [27]. The image segmentation problem is also solved using an improved Cuckoo Search optimization algorithm based on the levy function (IM.CS), which mimics the behaviour of a cuckoo in nature. It is a modification of the regular Cuckoo Search (CS) algorithm called CS McCulloch algorithm with Otsu’s (CSMC otsu). To analyses CS algorithm results, McCulloch’s method for Lévy flight generation is combined with Otsu’s objective functions. One of the most common techniques for finding the best solution from a collection of solutions provided to a particular problem is the genetic algorithm. In their operations, chromosomes are used separately to find the right solutions. At the start of the optimization process, chromosomes are chosen at random, then other generations are created, and the target function is determined in each generation.

In this paper, we introduce a technique based on combining these four different meta-heuristic algorithms with decision fusion to produce the greatest improvement in classification accuracy. This technique starts by partitioning the given source MRI image into several segments using multi-level threshold technique. Then we combine the result of 4 algorithms with decision fusion rule like Max, Min, Mean, Median and Product rules. As a result, image segmentation and fusion output estimation remain an open problem that needs further attention from the scientific community. Furthermore, results from experiments show that our algorithm can generate better image segments than some popular approaches.

The rest of the paper organized as follows. A brief review of the algorithms and fusion methods are presented in Section 2. The presented technique described in Section 3. In Section 4, the experimental results are presented. Our conclusion is presented in Section 5.

2  Image Segmentation Algorithms

The most commonly used radiographic techniques are known as computed tomography (CT), magnetic resonance Imaging (MRI) and Positron Emission Tomography (PET). PET scan images display the internal formation of tumours and cancer cells by using the metabolism of the body parts, while other imaging methods such as CT and MRI only show the physiology of the body parts. Labeling pixels in 2D and 3D images is called segmentation. Typically, what is meant by regions is to divide the image into parts. It is essential to map 3D visualization and specific structures in medical imaging. There are different techniques for image segmentation, one of the most attractive methods that are called intelligent methods. In this section we will focused on Particle Swarm Optimization (PSO), Cuckoo search, modification of Cuckoo Search (CS McCulloch) and Genetic algorithms because it is more stable and efficiency.

2.1 Partical Swarm Optimization (PSO)

The PSO primarily edges from the principle of swarm intelligence, which could be a property of a system that enables undeveloped agents to communicate locally with their environment and create coherent global career patterns [28]. Consider a flock of birds, each of which cries loudly in proportion to the quantity of food available in its current location. At the same time, every bird can discover the presence of alternative birds close and verify that of them is creating a bang. There is a better chance that the flock can realize an area with the foremost food if every bird follows a path that combines three rules: (i) the swarm flies within the same direction; (ii) return to the positioning wherever it found the most important quantity of insects thus far; and (iii) go to the next bird crying the loudest [29]. Particles are the expected solutions in traditional PSO. These particles travel around the search space, communicating and sharing information with other particles to find the perfect solution, that is the best individual solution (best locally) and therefore the best neighborhood account. Additionally, the best global solution obtained in the entire swarm is modified at every stage of the algorithm. Particles apprehend the positions of the search space where progress was achieved using all of this knowledge [30,31].

A fitness function is employed to check particle success at every step of the algorithm. To model the swarm, every particle n moves during a multidimensional space according to position xtn and velocity vtn values which are highly dependent on local best (x˘tn), neighborhood best (n˘tn) and global best (g˘tn) information:

vt+1n=wvtn+ρ1r1((g˘tn−xtn)+ρ2r2(x˘tn−xtn)+ρ3r3(g˘tn−xtn)(1)

xt+1n=xtn+vt+1n(2)

The coefficients w, ρ1, ρ2 and ρ3 determine the weights that affect inertia, the local best, the global best and the neighborhood best when determining the new velocity, respectively. Typically, the inertial influence is set to a value slightly less than 1. ρ1, ρ2 and ρ3 are constant integer values, which represent ‘‘cognitive’’ and ‘‘social’’ components. However, different results can be obtained by distribution different influences for every component. For example, some techniques do not consider the neighborhood best and ρ3 is set to zero. Reliance on the application and the characteristics of the problem, adjusting parameters leads to good results. The parameters r1, r2 and r3 are random vectors with every component generally a uniform random number between 0 and 1. Rather than multiplying the same random component with every particle’s velocity dimension, the aim is to multiply a new random component per velocity dimension.

The particles within the PSO are evaluated for the fitness function, that is defined as the between-class variance σB2 of the image intensity distributions.

∅C=maxσBC2(tjC).(3)

1<t1C<…<tn−1C<L

C={R,G,B}

First, we set the particle velocities to zero, the choice of sites depends on the search area, and this area depends on the density levels, Particles are spread between 0 and 255 if the frames are 8-bit images, as shown in Fig. 1.

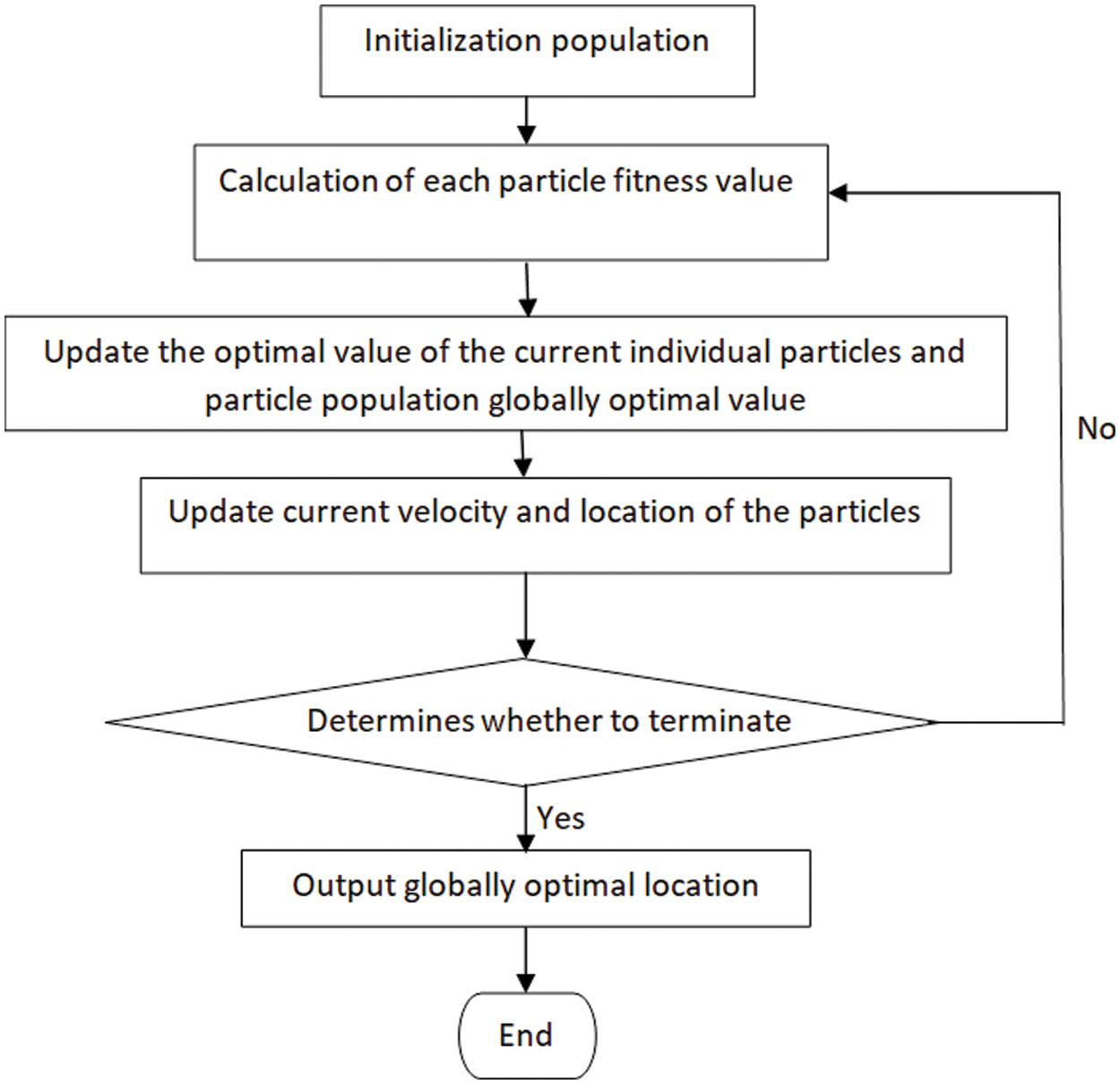
Figure 1: Particle swarm optimization flowchart

Given the nature of the problem, the local neighborhood and global bests are initialized with the worst possible values. Population size and stopping conditions are the other factors that need to be tweaked. To get an overall successful solution in a reasonable amount of time, Population size should be improved. The implicit connection between particles is explained by PSO (similar to broadcasting) through updating neighborhood and global knowledge, which affects the velocity and consequent location of particles. Stopping criteria may be a predefined number of iterations without having better results or other criteria, depending on the issue. Due to the implementation of random multipliers, there is also a stochastic exploration effect (r1, r2 and r3). Many applications of the PSO have been successful, including robotics [32–34], electric systems [28,35], and sports engineering [36].

2.2 Cuckoo Search (CS) Algorithm

Cuckoo Search (CS) is a recent heuristic algorithm taken from the parasitic behavior of some cuckoo species’ obligatory brooding when laying their eggs in host bird nests. Some cuckoos will imitate the colours and patterns of eggs from a limited number of host species. Egg abandonment is less likely as a result of this. If the host bird notices unusual eggs. They either abandon the eggs or discard them. The parasitic cuckoo selects a nest where the host bird’s eggs will be laid. Cuckoo eggs hatch before their hosts’ eggs, and when they do, the host’s eggs are pushed out of the nests. As a result, cuckoo chicks get a lot of food and occasionally imitate the host chicks’ voice to get more food [37]. Cuckoos usually hunt for food using a simple random walk, which is a Markov chain whose next location is determined by the current position and the transfer probability of the next position. Singing instead of simple random walks, Lévy flights boost search capabilities. Lévy flight is a heavy-tailed probability distribution-based random walk in step-lengths [38,39]. In CS, there are three fundamental idealised laws. According to the first law, each cuckoo lays one egg and deposits it in a random nest. The second rule states that the nest with the highest fitness will be passed on to future generations, while the third rule states that the number of available host nests is set, and the cuckoo egg is found by the host bird with a probability of p [0, 1]. The host bird either throws the egg away or abandons the nest, depending on p. Just a fraction p of nests are thought to be replaced by new nests. The cuckoo quest has been applied based on the three laws. To generate a new solution xit+1 for ith cuckoo, Lévy flight is performed. This step is called global random walk and is given by

xit+1=xit+α⊗Le´vy(λ)(xbest−xit(4)

The local random walk is given by:

xit+1=xit+α⊗H(p−ϵ)⊗(xjt−xkt)(5)

where xit is the preceding solution, α > 0 is the step size regarding to issue scales and ⊗ is entry wise multiplication. Here xjt and xkt are randomly chosen solutions and xbest is the immediate best solution. The random step length via Lévy flight is considered due to more efficiency of Lévy flights in exploring the search space and is drawn from a Lévy distribution having infinite variance and mean.

Le´vy∼ {λΓ(λ) sin (πλ/2)π1s1+λ (s≫s0>0)(6)

Since Lévy flights produce a portion of new solutions, the local quest accelerates. Any of the solutions should be produced using far field randomization to avoid the system being stuck in a local optimum., Γ (λ) is the gamma function, p is the switch probability, ε is a random number and (1 < λ ≤ 3). Due to large scale randomization, the step length in cuckoo search is heavy-tailed, and any large step is probable.

The following algorithm [40] gives the pseudo-code for CS.

2.3 CS McCullocha Algorithm with Otsu (CSMC_Otsu)

By merging McCulloch’s method, this is a modification of the standard Cuckoo Search (CS) algorithm [41], which proposed a computationally efficient image segmentation algorithm. By merging the computationally efficient McCulloch’s technique for steady random number generation, the CS-McCulloch algorithm adjusting the Lévy flight generation strategy in the CS algorithm. When compared to other bio-inspired algorithms such as PSO, Darwinian PSO, ABC algorithm, CS-Lévy flight, and CS-Mantegna algorithm using Otsu’s process, Kapur’s entropy, and Tsalli’s entropy as objective functions, the proposed CS-McCulloch algorithm emerged as the most promising and computationally efficient for segmenting satellite images [25]. To boost the cuckoo search method’s convergence rate and efficiency in time-constrained scenarios, a new technique for modelling levy flight in the cuckoo search method is proposed. Chambers, Mallows, and Stuck proposed this algorithm to model levy flight by presenting stable random variable generation in a less costly way. For the generation of stable random numbers, a larger number of methods have been proposed, much of it depends on the inverse distribution (in the interval 0 to 1) pseudo-random numbers [42].

J.H McCulloch [43] encoded the approach proposed for many workable applications. As a result, this procedure is known as the McCulloch algorithm. The McCulloch algorithm produces a n m matrix of random numbers. The scaling parameter y, the position defining parameter λ, the skewness measure, and the characteristic exponent value β are all necessary parameters [41,44]. On the foundation of exponent value β, many cases can be explained for this method. Due to humble possibility of overflow, the minimum value characteristic exponent is 0.1.

The skewness α = 0 for uniform case and β ≠ 1, step size (xz) can be computed as:

xz=y[cos(1−β)φω]1β−1[sin(βφ)cos(φ)]1β+λ(7)

To avert overflow, β should be maintained within the range 0 ≤ β ≤ 2.

Special cases:

1.    Gaussian case, β = 2

xz=y2wsin⁡(φ)+λ(8)

2.   Cauchy case, β = 1

xz=ytan⁡(φ)+α(9)

ω=log10(randn(n,m))andφ=(rand(n,m)−12)π(10)

2.4 Genetic Algorithm

Genetic algorithms use natural choice, as discovered by Charles Darwin [45]. They use natural selection of the fittest as the best solution to problems. The standard exchange of genetic material between the parents is used to achieve the enhancement. The parent gives birth to children. The health of the offspring is measured [46–48]. Only the most physically fit people are allowed to reproduce. Within the machine world, genetic material is replaced by strings of bits, and natural selection is replaced by a fitness function. Parental mat is replicated by hybridization and mutation processes [49]. A simple GA (Fig. 2) is made up of five steps [47], which are summarised in the algorithm below.

Figure 2: Flow chart for genetic algorithm

2.5 Fusion Methods

After you’ve built your segmentation, you’ll need to figure out how to combine their outputs effectively. Fusion is usually used wherever several methods are needed to perform at the data or decision level [50].

In this research, we focus on fusion method using equivalent architectures. The problem can be explained as follows. The target to evaluate each image point y to one class label βi out of D class labels α = {w1, w2,…, wD}. To complete this job, a set of R segmentation approach may be consulted. The output of each approach can be one of two kinds:

a)   Hard label, which Wi € α. b) Soft label, D element vector Wi = [wi,1, wi,2,…, wi,D]T which represent the supports to the D classes. Some segmentation approaches produce hard outputs so we need to convert from hard label to soft label. This establish by using Gaussian membership function. The Gaussian membership function is a popular technique that defines how each point in the input space is mapped to a membership value. The mathematical tractability given by the following equation:

P(wi/y)=p(y/wi)P(wi)P(y),(11)

p(y/wi)=12πσe−(y−μ)2/2σ2,μ=1wi∑y∈wi⁡y,σ2=1|wi|−1∑yϵwi⁡(y−μ)2

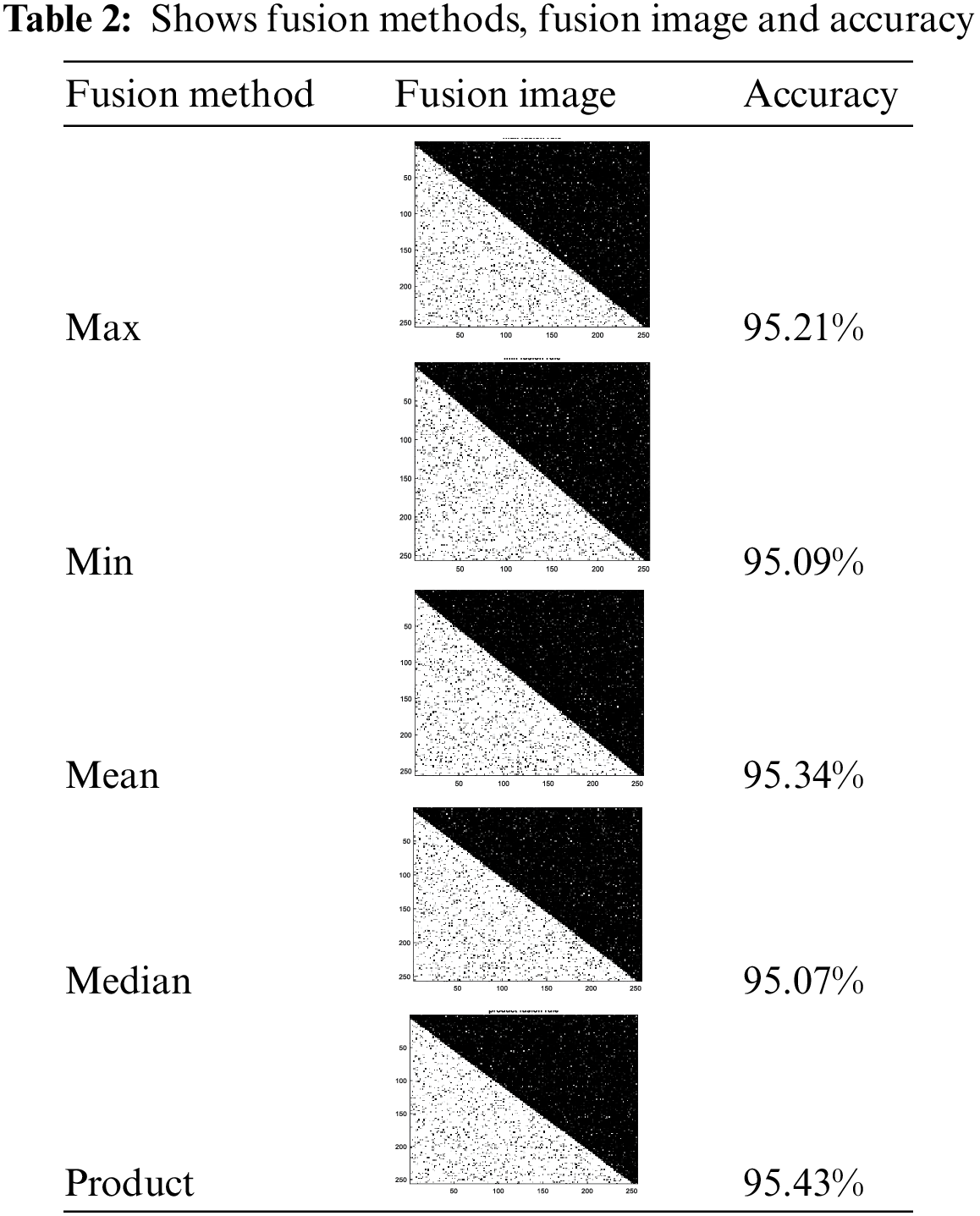
We have a tendency to use the fusion techniques to combine the results of the 4 meta-heuristic algorithms that we used in MRI segmentation in order to improve the segmentation accuracy. There are many decision fusion approaches for each kind of outputs. In this paper, we will use many of them, namely the median, maximum, minimum, mean and output rules for soft outputs. The simple fusion rules (Max, Min, Sum, Product, and Median) acquire the system output by operating every column of DP(X) [51].

•   Max rule is

dj(X)=max1≤i≤l⁡ci,j(X),j=1,2,…,m.(12)

The Max rule takes the maximum of each DP(X) column as the fused output C(X).

•   Min rule is

dj=min1≤i≤l⁡ci,j(X),j=1,2,…,m(13)

The Min rule takes the minimum of each DP(X) column as the fused output C(X)

•   Sum rule is

dj=∑i=1I⁡ci,j(X), j=1,2,…,m(14)

The Sum rule computes the sum of each DP(X) column as the fused output C(X). It is conjointly known as the mean rule once it computes the mean; these are simply two forms of the same rule.

•   Product rule is

dj(X)=∏i=1l⁡ci,j(X), j=1,2,…,m(15)

The output rule calculate the outputs of each DP(X) column as the fused output C(X).

•   Median rule is

dj(X)=median ci,j(X),i=1lj=1,2,…,m.(16)

The average rule computes the median of each DP(X) column as the fused output C(X). If l is an even number, then the mean of two medians is taken as the result of a column.

3  The Proposed Method

We propose an approach based on integrating the fusion concepts into the segmentation process. The architecture of multiple classifier systems is used to categories them. The serial suite and the parallel suite are the two basic groups in this regard [52]. Combination methods may also be categorised based on the type of data produced by the individual segmentation methods: Crisp segmentation output (class mark or hard), ranked list of data classes, and measurement level (soft) outputs [24]. Since no information about possible alternatives is available, the crisp labels provide the bare minimum of input information for fusion methods. Segmentation methods that generate outputs in the form of class rankings may provide some additional useful information. Fusion methods based on segmentation methods with soft/fuzzy outputs, on the other hand, are expected to increase classification accuracy the most.

The target of this paper is to introduce a new strategy for improving segmentation accuracy that is focused on decision fusion. Instead of focusing on a single approach, this new paradigm considers a variety of them. It consists of a series of segmentation methods that are used in parallel in its most common form. After that, a fusion module blends the decisions of the different methods. In this case, the individual strategies are capable of working independently and concurrently. A comparative analysis is also presented to show whether one fusion process outperforms the others in terms of segmentation. Several advances are discussed here, including how to improve the accuracy of multiple segmentation methods using fusion methods, as well as how to test these methods when applied to different data sets (medical and non-medical data).

The introduced algorithm begins with dividing the source image into several segments using 4 different meta-heuristic algorithms, Particle Swarm Optimization (PSO)algorithm, Cuckoo search algorithm, CS McCulloch algorithm and Genetic algorithm. The result of the segmentation methods are the input of decision fusion techniques to improvement the MRI segmentation accuracy. The purpose of the fusion step is to combine each result of segmentation method to produce a segmentation accuracy better than the accuracy of each method taken separately (as shown in Fig. 3. The fused image should be more useful for human visual inspection or machine perception. maximum, Minimum, mean, median, and output rules for soft outputs are used.

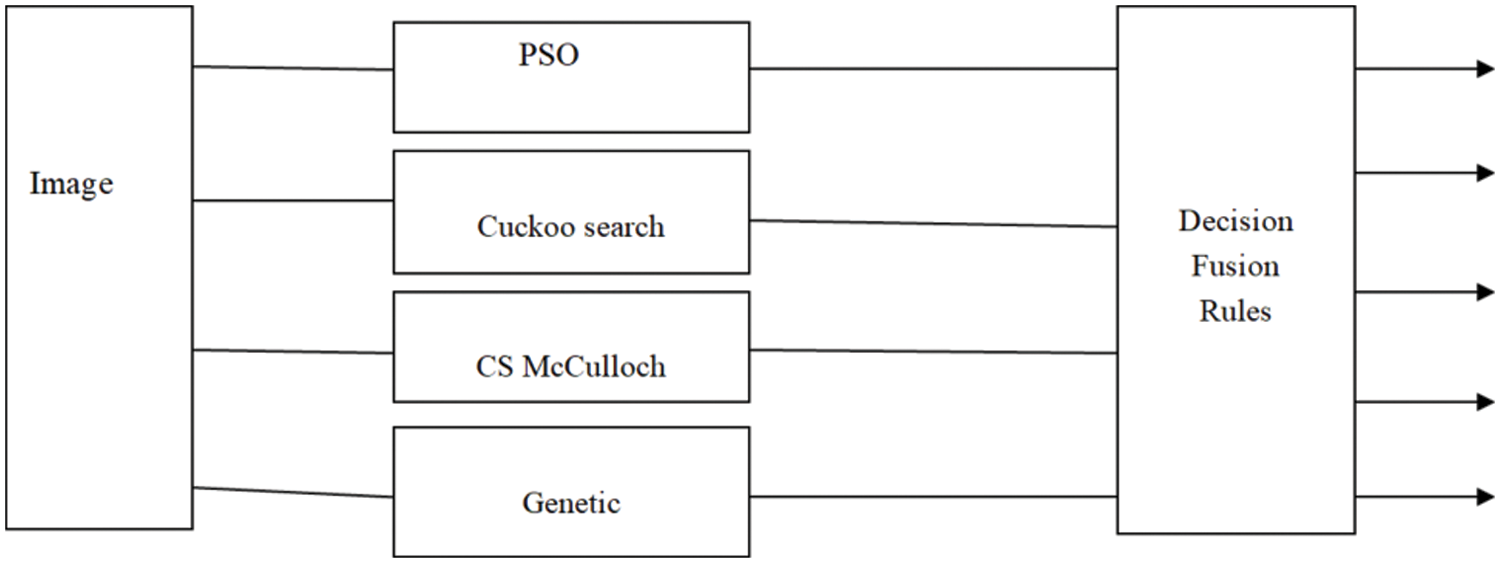
Figure 3: The architecture of the proposed method

Image fusion is a method for combining a multispectral image with high spectral resolution but low spatial resolution with a panchromatic image with high spatial resolution but low spectral resolution. The merged image should have more information than the multispectral and panchromatic images combined. Image fusion is more practical and cost-effective than developing an advanced sensor that meets all resolution requirements. Image fusion can be done at three different stages, depending on the stage of the fusion process: pixel, function, and decision [53]. At the feature level, algorithms must be capable of identifying artifacts in a variety of data sources, for example, based on statistical characteristics of dimension, form, and edge. In this case, segmentation procedures may be useful. The study’s aim is to segment a multispectral image into individual regions and assess the quality of different image fusion techniques.

4  Result Analysis

Several data sets are used for experiments, where the first experiment consists of simple synthetic images with image size 256 × 256 pixels and corrupted by 9% salt and pepper noise. The another group T1-weighted MR data with sliver density of 1 mm, no intensity inhomogeneities and 3% noise, with 258 × 258 image size, we got it from McGill University’s classic brain simulation.

We present an approach based on combining 4 different meta-heuristic algorithms with decision fusion to produce the greatest improvement in classification accuracy. This method starts with partitioning the given source MRI image into many segments. Then we combine the result of four algorithms with decision fusion rule like Max, Min, Mean, Median and Product rules.

The segmentation method relies heavily on the consistency of the segmentation algorithm. Every algorithm’s comparison score S is proposed in [54], which defined as:

S=|A∩ArefA∪Aref|,(17)

where A denotes the set of pixels belonging to a class as determined by a specific procedure and Aref denotes the reference segmented image’s set of pixels belonging to the same class (ground truth).

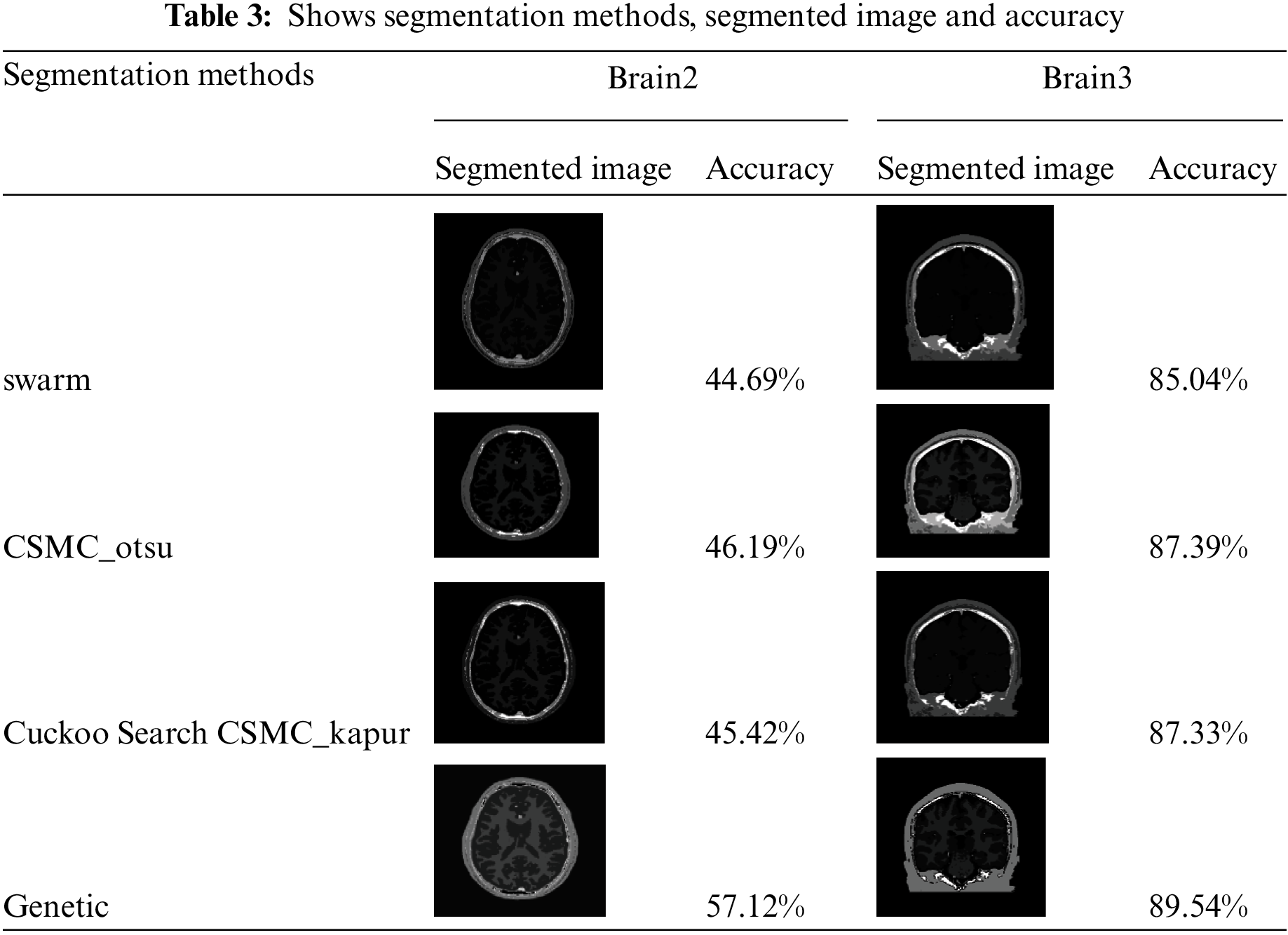
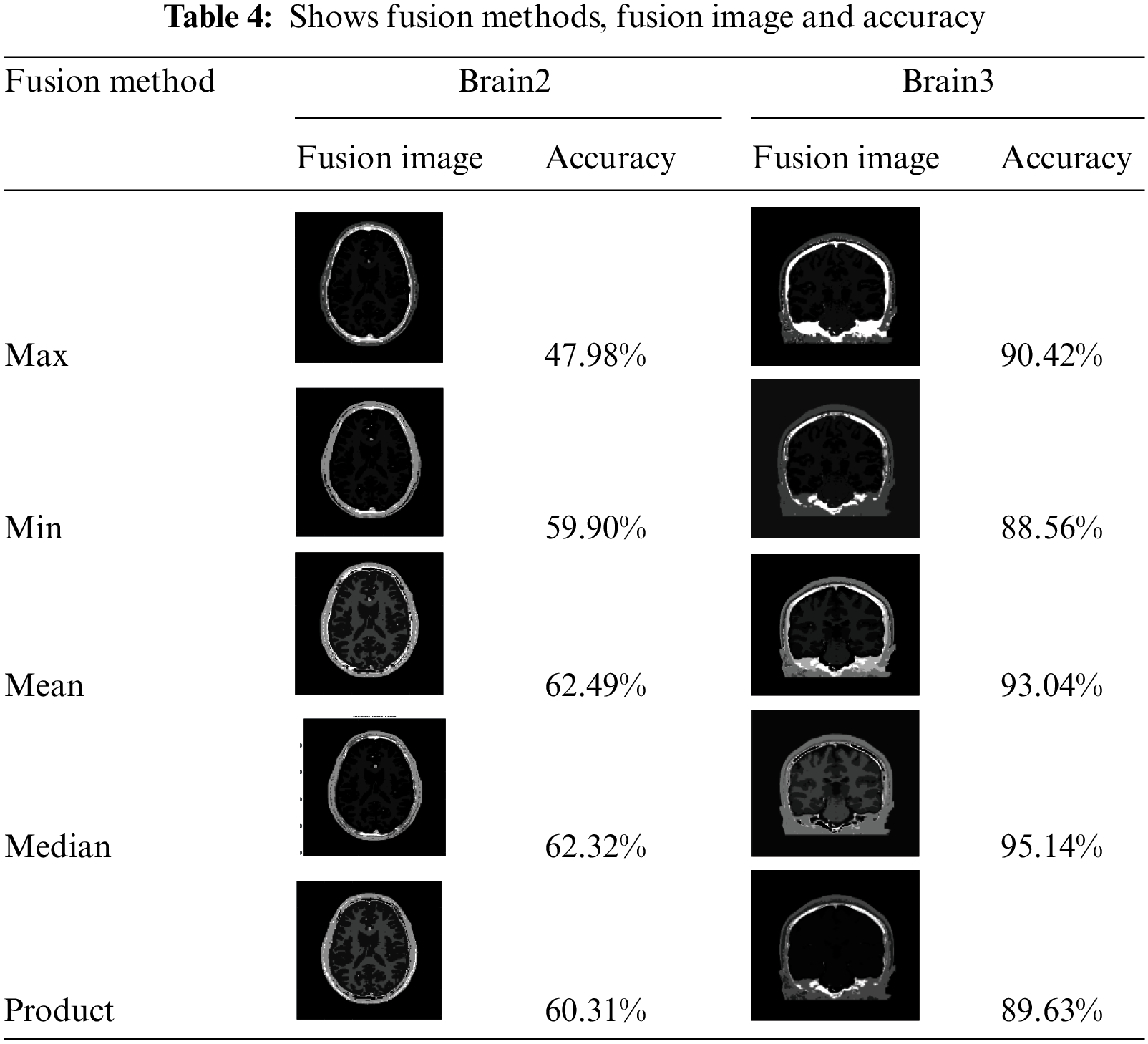
We use 4 different meta-heuristic algorithms, Particle Swarm Optimization (PSO) algorithm, Cuckoo search algorithm, CS McCulloch algorithm and Genetic algorithm. Every method from these segmentation methods applied in practice to different images with different sizes; every method was applied on original black/white images and MRI images, as in Tabs. 1 and 3. Our approach applied on original black/white images and MRI images, as in Tabs. 2 and 4

As shown in Tab. 1 every segmentation method was applied on original black/white image. It shows the values of accuracy for the 4 segmentation methods and it is clear that in the Swarm algorithm, we obtained the highest accuracy followed by CSMC_otsu algorithm then Cuckoo Search CSMC_kapur algorithm and the lowest accuracy obtained when applying the genetic algorithm.

As shown in Tab. 2, where our approach was applied on original black/white image and it is shown that the values of accuracy for the decision fusion rules and it is clear that in the Product rule, we obtained the highest accuracy followed by Mean rule, followed by Max rule, then Min rule and the lowest accuracy obtained with the Median rule. Through this table, we obtained the highest accuracy in segmentation, using the product integration rule. It gives an improvement about 1.86% over the accuracy of the best method in Tab. 1.

As shown in Tab. 3, every segmentation method was applied on MR image and it shows the values of accuracy for the 4 segmentation methods and it is clear that in the genetic algorithm, we obtained the highest accuracy followed by CSMC_otsu algorithm then Cuckoo Search CSMC_kapur algorithm and the lowest accuracy obtained when applying the Swarm algorithm.

As shown in Tab. 4 our approach was applied on MRI images and it shows the values of accuracy for the decision fusion rules and it is clear that we obtained the highest accuracy with the Mean rule, followed by Median rule, followed by Product rule, then Min rule and the lowest accuracy obtained with the Max rule. The Mean fusion rule yields the highest partition accuracy, as shown in Tab. 3. It improves on the accuracy of the best method in Tab. 3 by 5.34%.

Figs. 4 and 5 show that, we obtained segmentation accuracy from the proposed method better than the segmentation accuracy that we obtained from the 4 segmentation methods, Particle Swarm Optimization (PSO) algorithm, Cuckoo search, CS McCulloch and Genetic algorithm. When compared to max, min and product image fusion techniques, it has been proven that median and mean fusion procedures preserves more spectral information. Our strategy increases the performance of traditional methods by selective feature fusion, as demonstrated by experimental results. From Fig. 6 four segments are obtained after applying Swarm, CSMC_otsu, Cuckoo Search CSMC_kapur, Genetic and presented hybrid method to brain 2 image. Even with misleading of true tissue of validity indexes, the presented technique is more stable and achieves significantly better performance than others in all classes. Computing the accuracy of the present methods and the proposed technique are shown in Tabs. 3 and 4. Obviously, the presented approach gains the best segmentation execution. It is very interesting to mention other possibility for applying the results on different directions [55–57]. Also, an important application and different treatments of the present proposal can be used to understand the impact of COVID-19 [58,59]. In Fact, the demand of medical images analysis based on magnetic resonance images, computed tomography images and chest images is increasing to detect new viral infections such as Covid-19 and other, where the segmentation of medical images and knowledge of what its contain has become an important topic [60–67].

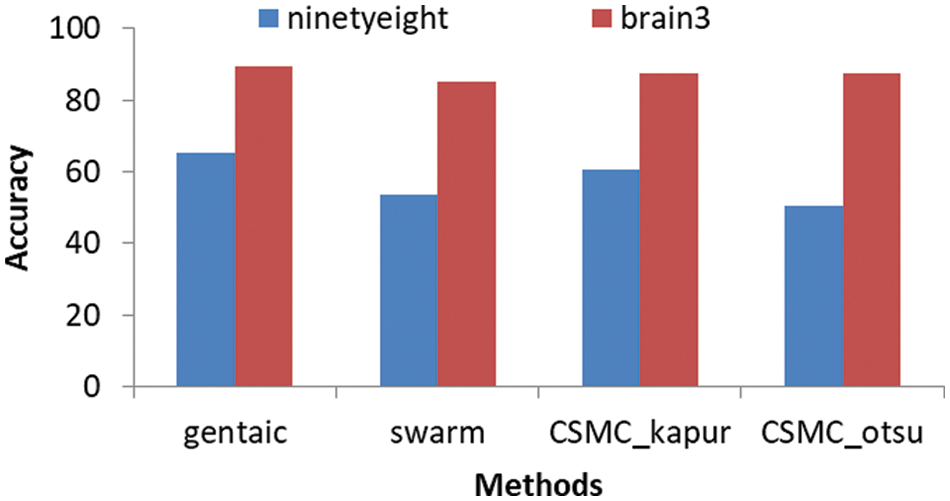
Figure 4: The segmentation accuracy of the 4 segmentation methods

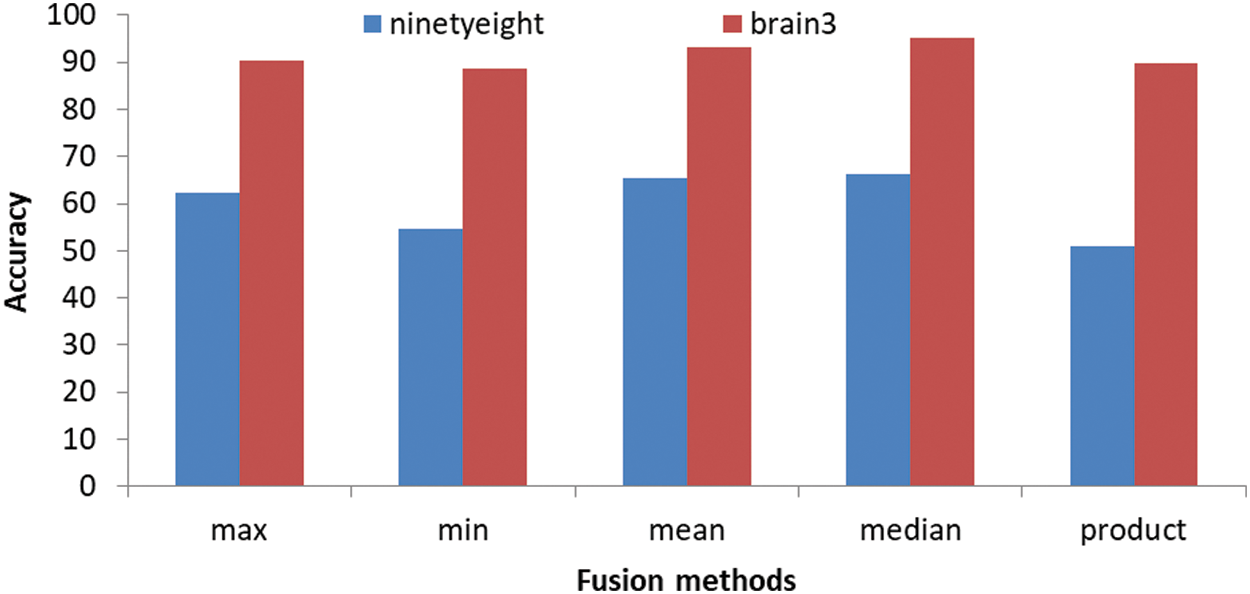
Figure 5: The segmentation accuracy of the proposed method

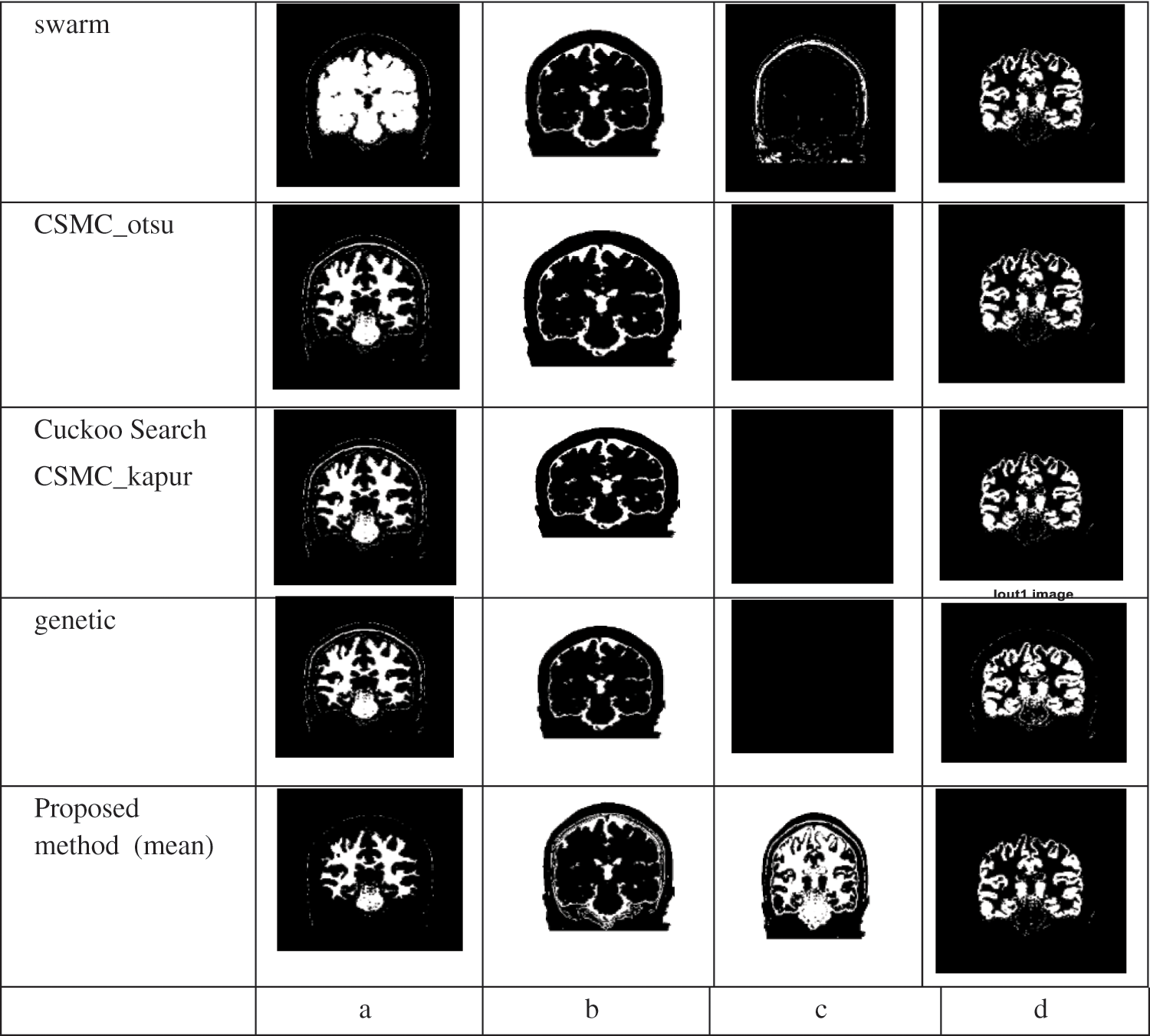
Figure 6: Segmentation results using the various methods

5  Conclusion

In this research, we present a strategy that combines four segmentation algorithms using fusion modules to improve when compared to utilize each method independently. The Particle Swarm Optimization (PSO) algorithm, Cuckoo search algorithm, CS McCulloch algorithm and Genetic algorithm are used to partition the provided image into various segments. The proposed approach was tested with MRIs data then implemented in Matlab. The proposed median, maximum, minimum, mean, and product have demonstrated to be higher robustness to segment many different types of brain images data. The segmentation accuracy proved that median and mean fusion techniques preserves more spectral information as compared with max, min and product Image fusion techniques. It is easier to determine the contributions of these components in the fused image and select the best fusion method that meets the user’s needs using the fusion methods used in this analysis. As seen in Tab. 4, the Mean fusion rule provides the best segmentation accuracy. It improves segmentation accuracy by 5.34% over the genetic method, which is the best way in Tab. 3, and the highest segmentation accuracy is attained using the Product fusion rule table, as shown in Tab. 2. It improves accuracy by 1.86% over the Swarm technique, which yields the best result in Tab. 1. Future research could concentrate on enhancing the accuracy of region categorization procedures and band wise quality assessment of fusion techniques. Experiments also indicate that our system can generate better image segments than some popular approaches.

Acknowledgement: The authors would like to thanks Taif University Researchers for Supporting Project number (TURSP-2020/214), Taif University, Taif Saudi Arabia.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors have no conflicts of interest to report regarding the present study.

References

 1.  J. W. Peterson, L. Bo and S. Mork, “Transected neuritis, apoptotic neurons, and reduced inflammation in cortical multiple sclerosis lesions,” Annals of Neurology, vol. 50, no. 3, pp. 389–400, 2001. [Google Scholar]

 2.  B. A. Abrahim, Z. A. Mustafa, I. A. Yassine, N. Zayed and Y. M. Kadah, “Hybrid total variation and wavelet thresholding speckle reduction for medical ultrasound imaging,” Journal of Medical Imaging and Health Informatics, vol. 2, no. 2, pp. 1–11, 2012. [Google Scholar]

 3.  H. S. Abdel-Aziz, E. A. Zanaty, M. Khalifa Saad and H. A. Ali, “Generating bézier curves for medical image reconstruction,” Results in Physics Journal, vol. 23, no. 4, pp. 1–8, 2021. [Google Scholar]

 4.  S. K. Elagan, M. H. Alkinani, E. A. Zanaty, H. Alotaibi and S. F. Abdelwahab, “Remote detection coronavirus disease (COVID-19) system based on intelligent healthcare and internet of things,” Results in Physics, vol. 22, pp. 1–8, 2021. [Google Scholar]

 5.  E. A. Zanaty, M. H. Alkinani and S. Hashad, “A novel algorithm for medical image compression based on combining wavelets with particle swarm optimization,” Computers, Materials & Continua, 2021. [Google Scholar]

 6.  M. Del-Fresno, M. Vénere and A. Clausse, “A combined region growing and deformable model method for extraction of closed surfaces in 3D CT and MRI scans,” Computerized Medical Imaging and Graphics, vol. 33, no. 5, pp. 369–376, 2009. [Google Scholar]

 7.  L. Wang, L. Chunming, S. Quansen, X. Deshen and K. Chiu-Yen, “Brain MR image segmentation using local and global intensity fitting active contours/surfaces,” Medical Image Computing and Computer-Assisted Intervention (MICCAI 2008), Part 1, LNCS 5241, vol. 11, pp. 384–392, 2008. [Google Scholar]

 8.  A. Liew, W. Chung and H. Yan, “An adaptive spatial fuzzy clustering algorithm for MR image segmentation,” IEEE Transactions Medical Image, vol. 22, no. 9, pp. 1063–1075, 2003. [Google Scholar]

 9.  E. A. Zanaty and S. Aljahdali, “Fuzzy algorithms for automatic magnetic resonance image segmentation,” International Arab Journal of Information Technology (IAJIT), vol. 7, no. 3, pp. 271–279, 2010. [Google Scholar]

10. E. A. Zanaty, S. Aljahdali and N. Debnath, “Improving fuzzy algorithms for automatic magnetic resonance image segmentation,” in Proc. of Seventeenth Int. Conf. of Software Engineering and Data Engineering, Los Angeles, California, USA, pp. 60–66, 2008. [Google Scholar]

11. E. A. Zanaty, S. Aljahdali and N. Debnath, “Akernelized fuzzy C-means algorithm for automatic magnetic resonance image segmentation,” Journal of Computational Methods in Science and Engineering (JCMSE), vol. 9, no. 1, pp. 123–136, 2009. [Google Scholar]

12. L. Zhang, J. Wang and Z. An, “FCM fuzzy clustering image segmentation algorithm based on fractional particle swarm optimization,” Journal of Intelligent & Fuzzy Systems, vol. 38, no. 4, pp. 3575–3584, 2020. [Google Scholar]

13. B. Peng and O. Veksler, “Parameter selection for graph cut based image segmentation,” in British Machine Vision Conf., BMVC, vol. 32, pp. 42–44, 2008. [Google Scholar]

14. B. Peng, L. Zhang, D. Zhang and J. Yang, “Image segmentation by iterated region merging with localized graph cuts,” Pattern Recognition, vol. 44, no. 10, pp. 2527–2538, 2011. [Google Scholar]

15. C. C. Laia and C. Y. Chang, “A hierarchical evolutionary algorithm for automatic medical image segmentation,” Expert Systems with Applications, vol. 36, no. 1, pp. 248–259, 2009. [Google Scholar]

16. K. E. Melkemi, M. Batouche and S. Foufou, “A multiagent system approach for image segmentation using genetic algorithms and extremal optimization heuristics,” Pattern Recognition Letters, vol. 27, no. 11, pp. 1230–1238, 2006. [Google Scholar]

17. U. Maulik, “Medical image segmentation using genetic algorithms,” IEEE Transactions on Information Technology in Biomedicine, vol. 13, no. 2, pp. 166–173, 2009. [Google Scholar]

18. E. A. Zanaty, “A modified watershed transformation for distorted brain tissue segmentation,” Journal of Medical Imaging and Health Informatics, vol. 2, no. 4, pp. 393–399, 2012. [Google Scholar]

19. S. De and F. Haque, “Multilevel image segmentation using modified particle swarm optimization,” Intelligent Analysis of Multimedia Information, IGL global, pp. 106–142, 2017. [Google Scholar]

20. L. Duan, S. Yang and D. Zhang, “Multilevel thresholding using an improved cuckoo search algorithm for image segmentation,” The Journal of Supercomputing, vol. 77, pp. 6734–6753, 2021. [Google Scholar]

21. R. Kalyani, P. D. Sathya and V. P. Sakthivel, “Image segmentation with kapur, otsu and minimum cross entropy based multilevel thresholding aided with cuckoo search algorithm,” in IOP Conf. Series: Materials Science and Engineering, vol. 1119, no. 1, pp. 012019, 2021. [Google Scholar]

22. T. Logeswari and M. Karnan, “Hybrid self-organizing map for improved implementation of brain MRI segmentation,” in Signal Acquisition and Processing, IEEE, pp. 248–252, 2010. [Google Scholar]

23. C. C. Kang and W. J. Wang, “Fuzzy based seeded region growing for image segmentation,” Annual Meeting of the North American Fuzzy Information Processing Society NAFIPS 2009, IEEE, pp. 1–5, 2009. [Google Scholar]

24. E. A. Zanaty, “An approach based on fusion concepts for improving brain magnetic resonance images (MRIs) segmentation,” Journal of Medical Imagining and Health Informatics, vol. 3, no. 1, pp. 30–37, 2013. [Google Scholar]

25. S. Pare, A. Kumar, G. K. Singh and V. Bajaj, “Image segmentation using multilevel thresholding: A research review,” Iranian Journal of Science and Technology, Transaction of Electrical Engineering, vol. 44, pp. 1–29, 2020. [Google Scholar]

26. R. Eberhart and J. Kennedy, “A new optimizer using particle swarm theory,” in MHS'95 Proc. of the IEEE Sixth Int. Symp. on Micro Machine and Human Science, pp. 39–43, 1995. [Google Scholar]

27. M. S. Couceiro, N. M. Ferreira, M. Machado and J. A. Tenreriro Machado, “In fractional order darwinian particle swarm optimization,” in Symp. on Fractional Signals and Systems, pp. 127–136, 2011. [Google Scholar]

28. D. Wang, D. Tan and L. Liu “Particle swarm optimization algorithm: An overview,” Soft Computing, vol. 22, no. 2, pp. 387–408, 2018. [Google Scholar]

29. R. V. Kulkarni and G. K. Venayagamoorthy, “Bio-inspired algorithms for autonomous deployment and localization of sensor,” IEEE Transactions on Systems, vol. 40, no. 6, pp. 663–675, 2010. [Google Scholar]

30. P. Ghamisi, S. M. Couceiro, J. A. Benediktsson and M. F. Ferreira, “An efficient method for segmentation of images based on fractional calculus and natural selection,” Expert Systems with Applications, vol. 39, no. 16, pp. 12407–12417, 2012. [Google Scholar]

31. P. Xia, Y. Lin and Z. Li-Hua, “An improved PSO-FCM algorithm for image segmentation,” IOP Conf. Series: Earth and Environmental Science, vol. 267, no. 4, pp. 042081, 2019. [Google Scholar]

32. M. S. Couceiro, J. M. A. Luz, C. M. Figueiredo and N. M. F. Ferreira, “Modeling and control of biologically inspired flying robots,” Robotica, vol. 30, no. 1, pp. 107–121, 2012. [Google Scholar]

33. E. J. S., Pires, P. B. M., Oliveira, J. A. Tenreriro Machado and J. B. Cunha, “Particle swarm optimization versus genetic algorithm in manipulator trajectory planning,” in 7th Portuguese Conf. on Automatic Control, pp. 1–7, 2006. [Google Scholar]

34. J. Tang, J. Zhu and Z. Sun, “A novel path panning approach based on appart and particle swarm optimization,” in Proc. of the 2nd Int. Symp. on Neural Networks, LNCS, vol. 3498, pp. 253–258, 2005. [Google Scholar]

35. M. R. Alrashidi and M. E. El-Hawary, “A survey of particle swarm optimization applications in power system operations,” Electric Power Component Systems, vol. 34, no. 12, pp. 1349–1357, 2006. [Google Scholar]

36. M. S. Couceiro, J. M. A. Luz, C. M. Figueiredo, N. M. F. Ferreira and G. Dias, “Parameter estimation for a mathematical model of the golf putting,” in WACI’10–Proc. of Workshop Applications of Computational Intelligence ISEC-IPC, December 2, Coimbra, Portugal, pp. 1–8, 2010. [Google Scholar]

37. J. Rahaman and M. Sing, “An efficient multi level thresholding based satellite image segmentation,” Expert System with Application, vol. 174, pp. 114633, 2021. [Google Scholar]

38. X. S. Yang and S. Deb, “Cockoo search via lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing, pp. 210–214, 2009. [Google Scholar]

39. W. Jiao, W. Chen and J. Zhang, “An improved cuckoo search algorithm for multithreshold image segmentation,” Security and Communication Networks, vol. 20, pp. 1–10, 2021. [Google Scholar]

40. R. Salgotra, U. Singh and S. Saha, “New cuckoo search algorithms with enhanced exploration and exploitation properties,” Expert Systems with Applications, vol. 95, pp. 384–420, 2018. [Google Scholar]

41. S. Suresh and S. Lal, “An efficient cuckoo search algorithm based multilevel thresholding for segmentation of satellite images using different objective functions,” Expert Syst. Appl., vol. 58, pp. 184–209, 2016. [Google Scholar]

42. A. K. Santhos, A. Kumar, V. Bajaj and G. K. Singh, “Mcculloch’s algorithm inspired cuckoo search optimizer based mammographic image segmentation,” Multimedia Tools and Application, vol. 79, no. 7, pp. 30453–30488, 2020. [Google Scholar]

43. J. M. Chambers, C. L. Mallows and B. Stuck, “A method for simulating stable random variables,” Journal of the American Statistical Association, vol. 71, no. 354, pp. 340–344, 1976. [Google Scholar]

44. M. Leccardi, “Comparison of three algorithms for levy noise generation,” in Proc. of Fifth Euromech Nonlinear Dynamics Conf., pp. 1–14, 2005. [Google Scholar]

45. N. V. Benjamin, R. D. Boutin, A. J. Chaudhari and K. L. Ma, “Genetic algorithm based L4 Identification and Psoas segmentation,” in BIOIMAGING, pp. 120–127, 2021. [Google Scholar]

46. S. Cagnoni, A. B. Dobrzeniecki, R. Poli and J. C. Yanch, “Genetic algorithm-based interactive segmentation of 3D medical images,” Image and Vision Computing, vol. 17, no. 12, pp. 881–895, 1999. [Google Scholar]

47. C. R. Reeves “Genetic algorithms and grouping problems,” IEEE Transactions on Evolutionary Computation, vol. 5, no. 3, pp. 297–298, 2001. [Google Scholar]

48. C. Tan, Y. Sun, G. Li, B. Tao, S. Xu et al., “Image segmentation technology based on genetic algorithm,” in ICDSP 2019: Proc. of the 2019 3rd Int. Conf. on Digital Signal Processing, pp. 27–31, 2019. [Google Scholar]

49. D. Kaushik, U. Singh and P. Singhal., “Medical image segmentation using genetic algorithm,” International Journal of Computer Applications, vol. 81, no. 18, pp. 10–15, 2013. [Google Scholar]

50. L. Lam and C. Y. Suen, “Application of majority voting to pattern recognition: An analysis of its behavior and performance,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 27, no. 5, pp. 553–568, 1997. [Google Scholar]

51. A. Mi, L. Wang and J. Qi, “A multiple classifier fusion algorithm using weighted decision templates,” Hindawi Publishing Corporation, Scientific Programming, 2016. [Google Scholar]

52. R. Ranawana, and V. Palade, “Multi-classifier systems-review and a roadmap for developers,” International Journal of Hybrid Intelligent Systems, vol. 3, no. 1, pp. 35–61, April 2006. [Google Scholar]

53. C. Pohl and J. L. Van Genderen, “Review article multi sensor image fusion in remote sensing: Concepts, methods and applications,” International Journal of Remote Sensing, vol. 19, no. 5, pp. 823–854, 1998. [Google Scholar]

54. A. P. Zijdenbos, “MRI segmentation and the quantification of white matterlesion,” Ph.D. Thesis, Vanderbilt University, Electrical Engineering Department, Nashville, Tennessee, 1994. [Google Scholar]

55. M. Zidan, A. -H. Abdel-Aty, A. El-Sadek, E. A. Zanaty and M. Abdel-Aty, “Low-cost autonomous perceptron neural network inspired by quantum computation,” in AIP Conf. Proc., vol. 1905, no. 1, p. 020005, AIP Publishing LLC, 2020. [Google Scholar]

56. G. M. Ismail, H. R. Abdl-Rahim, H. R. Abdel-Aty, R. Kharabsheh, W. Alharbi, “An analytical solution for fractional oscillator in a resisting medium,” Chaos, Solitons and Fractals, vol. 130, p. 109395, 2020. [Google Scholar]

57. A. -H. Abdel-Aty, M. M. A. Khater, R. A. M. Attia, M. Abdel-Aty and H. Eleuch, “On the new explicit solutions of the fractional nonlinear space-time nuclear model,” Fractals, 2020. [Google Scholar]

58. A. A. M. Teamah, W. A. Afifi, J. Gani Dar, A. Al-Aziz Hosni El-Bagoury and S. Naji Al-Aziz, “Optimal discrete search for a randomly moving COVID19,” J. Stat. Appl. Prob, vol. 9, no. 3, pp. 473–481, 2020. [Google Scholar]

59. A. A. H. Ahmadini, N. K. Adichwal, M. Zico Meetei, Y. Singh Raghav, M. A. H. Ahmadini et al., “Knowledge, awareness and practices (KAP) about COVID-19 in Jazan,” J. Stat. Appl. Prob., vol. 10, no. 2, pp. 487–497, Jul. 2021. [Google Scholar]

60. H. El Maroufy, A. Lahrouz and P. G. L. Leach, “Qualitative behaviour of a model of an SIRS epidemic: Stability and permanence,” Applied Mathematics & Information Sciences, vol. 5, no. 2, pp. 220–238, 2011. [Google Scholar]

61. H. A. A. El-Saka, “The fractional-order SIR and SIRS epidemic models with variable population size,” Mathematical Science Letters, vol. 2, no. 3, pp. 195–200, 2013. [Google Scholar]

62. A. M. Yousef, S. Z. Rida, Y. G. Gouda and A. S. Zaki, “On dynamics of a fractional-order SIRS epidemic model with standard incidence rate and its discretization,” Progress Fractional Differentiation and Applications, vol. 5, no. 4, pp. 297–306, 2019. [Google Scholar]

63. W. M. Abd-Elhafiez and H. H. Amin, “The digital transformation effects in distance education in light of the epidemics (COVID-19) in Egypt,” Information Science Letters, vol. 10, no. 1, pp. 141–152, 2021. [Google Scholar]

64. P. Veeresha, W. Gao, D. G. Prakasha, N. S. Malagi, E. Ilhan et al., “New dynamical behaviour of the coronavirus (2019-NCOV) infection system with non-local operator from reservoirs to people,” Information Science Letters, vol. 10, no. 2, pp. 205–212, May 2021. [Google Scholar]

65. W. Mustafa Shrink, “An efficient construction algorithm for minimum vertex cover problem,” Information Science Letters, vol. 10, no. 2, pp. 255–261, 2021. [Google Scholar]

66. O. Y. M. Al-Rawi, W. S. Al-Dayyeni and I. Reda, “COVID-19 impact on education and work in the kingdom of Bahrain: Survey study,” Information Science Letters, vol. 10, no. 3, pp. 427–433, Sep. 2021. [Google Scholar]

67. I. Atia, M. L. Salem, A. Elkholy, W. Elmashad and G. A. M. Ali, “In-silico analysis of protein receptors contributing to SARS-COV-2 high infectivity,” Information Science Letters, vol. 10, no. 3, pp. 561–570, Sep. 2021. [Google Scholar]