Numerical Procedure for Fractional HBV Infection with Impact of Antibody Immune

1  Introduction

The hepatitis B virus (HBV) is known as a threatening disease, which directly attacks the healthy liver. Around 257 million individuals get infected per year, among them the top disease is HBV [1]. To investigate this serious viral HBV infection, a number of mathematical systems have been introduced. Bangham and Nowak were known as the pioneer to introduce the mathematical form of the with three categories, the free virus, uninfected and infected [2–6]. It is observed that the virus adopts a certain procedure using these measures, i.e., an uninfected cell with the major points is replicated, encapsulation and decapitation [7,8]. This significant viral procedure represents a new compartment in the traditional dynamical viral system [9]. The process of humoral insusceptibility is used to decrease the intensity of the viral disease [10]. This insusceptibility frequently represents the antibodies, which are produced from B cells to attack and defuse the diseases [11]. Based on the HBV dynamics and its antibodies, several mathematical systems have been proposed using the ordinary differential equations [12].

The fractional order (FO) derivative is a significant operator to design a real apparatus. A number of the FO derivatives have been used in the nonlinear models [13–15]. The nonlocal operator makes the FO derivative different to the integer order. To calculate the FO derivative at t = t1, the starting to desired time (t = t0 to t = t1) is reported in the literature. Therefore, the phenomena to calculate more real results of the mathematical FO derivatives has been motivated by many researchers [16]. It is also signified that the biological based FO derivatives have been analyzed to produce the rheological cell’s characteristics [17]. The FO derivatives have also been used in the electrical cell’s conductance based on the biological organism [18]. In the mechanical field, FO derivatives have been used to indicate the effectiveness of the complex behavior of various physical models [19,20]. Few investigations have been presented based on the FO derivatives, few of them are a local wave fractional model based on the fractal string presented by Bhatter et al. [21]. FO differential system were also used to model the Drinfeld Sokolov Wilson model, KdV and Kawahara equations [22,23]. A number of discussions that have been presented to discuss the behavior of the viral infections using the FO differential models [24,25]. The optimal control systems, immune models and tumor cells have been discussed using the FO derivatives [26,27]. FO tuberculosis and diabetes systems of optimal control have been discussed by Baleanu et al. [28]. The model based on the blood and liver using the FO derivative is presented by Jajarmi et al. [29]. Moreover, FO derivatives have been used in the spread of the dengue fever [30] and many other of utmost significance [31–38].

A fractional order HBV differential infection system (FO-HBV-DIS) with the response of antibody immune is classified into five modules, healthy hepatocytes (H), infected hepatocytes (I), capsids (D), free virus (V) and antibodies (W). It is examined that time-fractional derivative has numerous applications to designate the different forms of dynamical model. The derivative shows the remembrance, while the memory function represents the FO derivative. The time-fractional derivative shows the characteristics of real-world models [39,40]. The general form of the nonlinear FO-HBV-DIS with the response of antibody immune is provided along with its initial conditions (ICs) as [41]:

{DαH(τ)=S−kH(τ)V(τ)−μH(τ),H0=i1,DαI(τ)=kH(τ)V(τ)−δI(τ),I0=i2,DαD(τ)=aI(τ)−βD(τ)−δD(τ),D0=i3,DαV(τ)=βD(τ)−uV(τ)−qV(τ)W(τ),V0=i4,DαW(τ)=gV(τ)W(τ)−hW(τ),W0=i5.(1)

It is observed that the hepatocytes (H) increase, decay with the rates S and μH, while it infected through virus at the kHV rate. The infected based hepatocytes (I) reduce at δI rate. The category of the capsids (D) is produced using the infected cells with aI rate that are unconfined in blood, got viruses with βD rate and naturally die with δD rate. The dynamics of free virus (V) reduces at uV and counteracted by antibodies with qVW. The last dynamics in the nonlinear FO-HBV-DIS is antibodies (W), which develops in the response of free virus with rate and reduces with hW rate. The ICs are represented by i1, i2, i3, i4 and i5, respectively.

The novelty of this work is to perform the numerical simulations of the nonlinear FO-HBV-DIS with the response of antibody immune using the optimization based stochastic schemes of the Levenberg-Marquardt backpropagation (LMB) neural networks (NNs), i.e., LMBNNs. The stochastic LMBNNs measures have never applied before to solve the nonlinear FO-HBV-DIS with the response of antibody immune. The data magnitudes are implemented 75% for training, 10% for certification and 15% for testing to solve the FO-HBV-DIS with the response of antibody immune. The stochastic numerical procedures have the competence and ability to solve the linear models as well as various stiff complex nonlinear systems [42–50]. These numerical performances of the integer order motivated the authors to present the numerical simulations of FO derivatives of nonlinear equations. Therefore, a well-known mathematical FO-HBV-DIS model with antibody immune response is presented to check the reliability of the proposed stochastic LMBNNs. Few novel characteristics of the present study for solving the nonlinear FO-HBV-DIS with the response of the antibody immune are presented as:

•   A fractional order nonlinear mathematical system of differential equations is numerically handled successfully using the stochastic techniques.

•   The design of the artificial NNs along with the LMB method is provided first time to solve the FO-HBV-DIS with the response of the antibody immune model.

•   Three different FO variations have been presented for solving the biological nonlinear FO-HBV-DIS with the response of antibody immune.

•   The correctness of the stochastic scheme is observed using the comparison of the obtained and numerical Adams-Bashforth-Moulton approach.

•   The calculated absolute error (AE) validates the accuracy of the designed scheme for the biological nonlinear FO-HBV-DIS with the response of antibody immune.

•   The performances based on the regression, error histograms (EHs), mean square error (MSE), state transitions (STs) and correlation authorize the reliability of the designed LMBNNs procedure for the biological FO-HBV-DIS with the response of the antibody immune system.

The remaining sections are organized as: The LMBNNs procedure is described in Section 2. The numerical simulations of the FO-HBV-DIS using the LMBNNs are presented in Section 3. Concluding notes are presented in the last Section.

2  Methodology

The designed procedures for the biological nonlinear FO-HBV-DIS with the response of the antibody immune system are presented in this section. The classification of the LMBNNs procedure is provided in two steps. First, the essential executions based on the LMBNNs are provided, while the implementation process is provided in second phase. An optimization method is drawn in Fig. 1 using the multi-layer process, while Fig. 2 presents a structure of single neurons. The stochastic computing processes through ‘nftool’ built-in command is presented in MATLAB. The statistics proportions are pragmatic 75% for training, 10% for certification and 15% for testing to solve the FO-HBV-DIS with the response of antibody immune.

Figure 1: Workflow diagram of the designed LMBNNs procedure for the biological FO-HBV-DIS with the response of antibody immune

Figure 2: Design of proposed single neuron

3  Numerical Presentations of the Nonlinear FO-HBV-DIS

In this section, the numerical presentations of the nonlinear FO-HBV-DIS are provided by using the LMBNNs. The literature values to solve the nonlinear FO-HBV-DIS are S=2.5, k=1.67×10−13, μ=0.01, δ=0.053, a=150, β=0.87, q=0.5, g=1×10−11, u=3.8, h=0.1, i1=0.1, i2=0.2, i3=0.3, i4=0.1 and i5=0.5. Three variants of the nonlinear FO-HBV-DIS based on the FO values, 0.5, 0.7 and 0.9 have been discussed. The results comparison is performed for each class of FO-HBV-DIS, which is found in [0,1] interval with minimum step size (0.01). Twelve numbers of neurons have been used in this study and the data proportions are applied 75% for training, 10% for certification and 15% for testing to solve the FO-HBV-DIS with the response of antibody immune. The obtained results using the 12 neurons based on the LMBNNs for solving the FO-HBV-DIS are given in Fig. 3.

Figure 3: LMBNNs structure for the FO-HBV-DIS

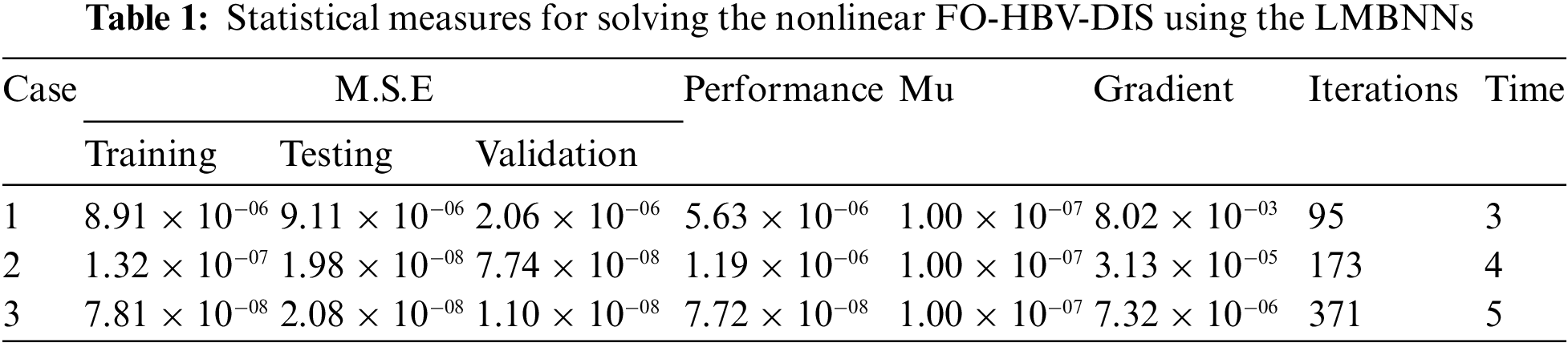
The graphical plots have been derived using the LMBNNs for solving the FO-HBV-DIS in Figs. 4 to 8. The MSE and STs performances have been provided for solving the FO-HBV-DIS in Fig. 4. The MSE measures for best curves, testing, training and verification are demonstrated in Figs. 4a to 4c, whereas the STs best values for solving the FO-HBV-DIS are exemplified in Figs. 4d to 4f at iterations 95, 173 and 371. The achieved presentations have been calculated at 2.1604 × 10−06, 7.7456 × 10−07 and 1.102 × 10−08, respectively. The gradient measures based on the proposed LMBNNs to solve the nonlinear FO-HBV-DIS are calculated 8.0165 × 10−03, 3.1268 × 10−05 and 7.3161 × 10−06, respectively. The achieved values in these figures represent the precision, convergence and accuracy of the proposed LMBNNs for the FO-HBV-DIS. The values of the fitting curve have been drawn in Figs. 5a to 5c for solving the FO-HBV-DIS using the proposed LMBNNs. These values have been drawn using the comparison presentations of the results. Figs. 5d to 5f is drawn using the EHs, which are found 2.173 × 10−03, 6.68 × 10−04 and 1.21 × 10−04 for 1st, 2nd and 3rd variation. The performances based on the regression are derived in Fig. 6. These values of the regression authenticate the performances, which lie around 1 to designate the perfect model. The performances of the verification, testing and training have been illustrated to represent the accuracy and precision of LMBNNs to solve FO-HBV-DIS. Additionally, the convergence through the MSE measure with these representations of the complexity, epochs, training, confirmation, backpropagation and testing is tabulated in Tab. 1 for the nonlinear FO-HBV-DIS.

Figure 4: MSE (a to c) and STs (d to f) for the FO-HBV-DIS using the LMBNNs

Figure 5: Valuations of the outcomes (a–c) and EHs (d–f) for the FO-HBV-DIS using the LMBNNs

Figure 6: Regression measures for the nonlinear FO-HBV-DIS using the LMBNNs

Figure 7: Result for solving the nonlinear FO-HBV-DIS using the LMBNNs

Figure 8: AE for solving the nonlinear FO-HBV-DIS using the LMBNNs

The AE plots AE have been derived using the comparisons based on the nonlinear FO-HBV-DIS in Figs. 7 to 8. The numerical values are provided for each class of the nonlinear FO-HBV-DIS with the response of antibody immune using the proposed LMBNNs. The numerical results are provided in Figs. 7a–7c, that shows the matching of proposed and reference results. These overlapping represent the accuracy and correctness of the proposed LMBNNs for nonlinear FO-HBV-DIS with the response of antibody immune.

The AE measures for each category of the nonlinear FO-HBV-DIS with the response of antibody immune are demonstrated in Figs. 8a to 8c. The AE values for the healthy hepatocytes H(τ) lie 10−03 to 10−04 for variation 1, 10−03 to 10−06 for variation 2 and 10−04 to 10−06 for variation 3 for solving the nonlinear FO-HBV-DIS. The AE values for the infected hepatocytes I(τ) lie 10−03 to 10−05 for variation 1, 10−04 to 10−05 for variation 2 and 10−04 to 10−06 for variation 3 for solving the nonlinear FO-HBV-DIS.

The AE values for the capsids D(τ) lie around 10−02 to 10−04, 10−03 to 10−04 and 10−03 to 10−05 for case 1 to 3 for solving the nonlinear FO-HBV-DIS. The AE values for the free virus V(τ) lie 10−03 to 10−05 for case 1 and 2, while for case 3 the AE is found around 10−04 to 10−06 for solving the nonlinear FO-HBV-DIS. The AE values for the antibodies class W(τ) lie 10−03 to 10−07, 10−04 to 10−06 and 10−04 to 10−07 cases 1 to 3 of the nonlinear FO-HBV-DIS. The AE plots enhance the correctness and exactness of the stochastic scheme for the nonlinear biological model.

4  Conclusions

The aim of this study is to present the numerical simulations of the fractional order HBV differential infection system with the response of antibody immune using the stochastic procedures of the LMBNNs. The fractional order HBV differential infection system is implemented to solve three different deviations using different values of the fractional order. The data magnitudes are implemented 75% for training, 10% for certification and 15% for testing to solve the FO-HBV-DIS with the response of antibody immune. Twelve numbers of neurons have been implemented to solve the biological differential system. The solutions of the FO-HBV-DIS with the response of antibody immune have been presented by using the LMBNNs, however the comparative performances have been accessible through the reference results. The numerical performances of FO biological system have been simulated using the LMBNNs to lessen the MSE. To authenticate the reliability, aptitude and capability of the LMBNNs, the numerical outcomes have been plotted using the STs, regression, Ehs, MSE and correlation. The matching performances indicate the precision of the designed stochastic method. The AE in good assortments shows the correctness of the nonlinear biological fractional order system. The other performance plots signify the consistency and dependability of the proposed method.

In future work, the stochastic LMBNNs procedures have been used to achieve the numerical measures/treatments of the many potential nonlinear fractional/integer order systems [51–55]. Additionally, one may use alternative stochastic solver based on neural networks optimized with evolutionary and swarming techniques for the presented bioinformatics study for better performance in terms of accuracy and convergence.

Funding Statement: This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (grant number B05F640092).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  World Health Organization, “Progress towards access to hepatitis B treatment worldwide,” 2018. [Online]. Available: http://www.who.int/hepatitis/newsevents/cdc-hepatitis-b-article/en/. [Google Scholar]

 2.  M. A. Nowak, S. Bonhoeffer, A. M. Hill, R. Boehme, H. C. Thomas et al., “Viral dynamics in hepatitis B virus infection,” Proceedings of the National Academy of Sciences of The United States of America, vol. 93, no. 9, pp. 4398–4402, 1996. [Google Scholar]

 3.  Y. Zheng, L. Min, Y. Ji, Y. Su and Y. Kuang, “Global stability of endemic equilibrium point of basic virus infection model with application to HBV infection,” Journal of Systems Science and Complexity, vol. 23, no. 6, pp. 1221–1230, 2010. [Google Scholar]

 4.  K. Wang and W. Wang, “Propagation of HBV with spatial dependence,” Mathematical Biosciences, vol. 210, no. 1, pp. 78–95, 2007. [Google Scholar]

 5.  M. A. Nowak and C. R. Bangham, “Population dynamics of immune responses to persistent viruses,” Science, vol. 272, no. 5258, pp. 74–79, 1996. [Google Scholar]

 6.  J. Li, K. Wang and Y. Yang, “Dynamical behaviors of an HBV infection model with logistic hepatocyte growth,” Mathematical and Computer Modelling, vol. 54, no. 1–2, pp. 704–711, 2011. [Google Scholar]

 7.  D. Ganem and A. M. Prince, “Hepatitis B virus infection—Natural history and clinical consequences,” New England Journal of Medicine, vol. 350, no. 11, pp. 1118–1129, 2004. [Google Scholar]

 8.  V. Bruss, “Envelopment of the hepatitis B virus nucleocapsid,” Virus Research, vol. 106, no. 2, pp. 199–209, 2004. [Google Scholar]

 9.  K. Manna and S. P. Chakrabarty, “Chronic hepatitis B infection and HBV DNA-containing capsids: Modeling and analysis,” Communications in Nonlinear Science and Numerical Simulation, vol. 22, no. 1–3, pp. 383–395, 2015. [Google Scholar]

10. S. Wang and D. Zou, “Global stability of in-host viral models with humoral immunity and intracellular delays,” Applied Mathematical Modelling, vol. 36, no. 3, pp. 1313–1322, 2012. [Google Scholar]

11. G. Ada, “Vaccines and vaccination,” New England Journal of Medicine, vol. 345, no. 14, pp. 1042–1053, 2001. [Google Scholar]

12. A. M. Elaiw and N. H. Alshamrani, “Global analysis for a delay-distributed viral infection model with antibodies and general nonlinear incidence rate,” Journal of the Korean Society for Industrial and Applied Mathematics, vol. 18, no. 4, pp. 317–335, 2014. [Google Scholar]

13. Z. Masood, M. A. Z. Raja, N. I. Chaudhary, K. M. Cheema and A. H. Milyani, “Fractional dynamics of stuxnet virus propagation in industrial control systems,” Mathematics, vol. 9, no. 17, pp. 1–27, 2021. [Google Scholar]

14. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A novel design of fractional Meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2641–2659, 2021. [Google Scholar]

15. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Meyer wavelet neural networks to solve a novel design of fractional order pantograph Lane-Emden differential model,” Chaos Solitons & Fractals, vol. 152, no. 2, pp. 1–14, 2021. [Google Scholar]

16. Y. A. Rossikhin and M. V. Shitikova, “Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids,” Applied Mechanics Reviews, vol. 50, no. 1, pp. 15–67, 1997. [Google Scholar]

17. R. J. I. I. Marks and M. Hall, “Differintegral interpolation from a bandlimited signal’s samples,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 29, no. 4, pp. 872–877, 1981. [Google Scholar]

18. K. S. Cole, “Electric conductance of biological systems,” in Cold Spring Harbor Symposia on Quantitative Biology, 1st ed., vol. 1. New York, USA: Cold Spring Harbor Laboratory Press, pp. 107–116, 1933. [Google Scholar]

19. Z. Sabir, T. Botmart, M. A. Z. Raja, R. Sadat, M. R. Ali et al., “Artificial neural network scheme to solve the nonlinear influenza disease model,” Biomedical Signal Processing and Control, vol. 75, no. 103594, pp. 1–13, 2022. [Google Scholar]

20. J. Singh, D. Kumar, D. Baleanu and S. Rathore, “On the local fractional wave equation in fractal strings,” Mathematical Methods in the Applied Sciences, vol. 42, no. 5, pp. 1588–1595, 2019. [Google Scholar]

21. S. Bhatter, A. Mathur, D. Kumar and J. Singh, “A new analysis of fractional Drinfeld-Sokolov–Wilson model with exponential memory,” Physica A: Statistical Mechanics and its Applications, vol. 537, no. 2, pp. 1–13, 2020. [Google Scholar]

22. S. Bhatter, A. Mathur, D. Kumar, K. S. Nisar and J. Singh, “Fractional modified Kawahara equation with Mittag-Leffler law,” Chaos Solitons & Fractals, vol. 131, no. 1, pp. 1–6, 2020. [Google Scholar]

23. A. Boukhouima, K. Hattaf and N. Yousfi, “Dynamics of a fractional order HIV infection model with specific functional response and cure rate,” International Journal of Differential Equations, vol. 2017, pp. 1–8, 2017. [Google Scholar]

24. A. Sunarto, P. Agarwal, J. Sulaiman and J. V. L. Chew, “Computational approach via half-sweep and preconditioned AOR for fractional diffusion,” Intelligent Automation and Soft Computing, vol. 31, no. 2, pp. 1173–1184, 2022. [Google Scholar]

25. T. A. Yildiz, A. Jajarmi, B. Yildiz and D. Baleanu, “New aspects of time fractional optimal control problems within operators with nonsingular kernel,” Discrete and Continuous Dynamical Systems-Series S, vol. 13, no. 3, pp. 407–428, 2020. [Google Scholar]

26. D. Baleanu, A. Jajarmi, S. S. Sajjadi and D. Mozyrska, “A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 29, no. 8, pp. 1–15, 2019. [Google Scholar]

27. A. Jajarmi, B. Ghanbari and D. Baleanu, “A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 29, no. 9, pp. 1–15, 2019. [Google Scholar]

28. D. Baleanu, A. Jajarmi, H. Mohammadi and S. Rezapour, “A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative,” Chaos, Solitons & Fractals, vol. 134, no. 4, pp. 1–7, 2020. [Google Scholar]

29. A. Jajarmi, S. Arshad and D. Baleanu, “A new fractional modelling and control strategy for the outbreak of dengue fever,” Physica A: Statistical Mechanics and its Applications, vol. 535, no. 7, pp. 122524, 2019. [Google Scholar]

30. A. Khan, T. Abdeljawad, J. F. Gómez-Aguilar and H. Khan, “Dynamical study of fractional order mutualism parasitism food web module,” Chaos, Solitons & Fractals, vol. 134, no. 1, pp. 1–15, 2020. [Google Scholar]

31. A. Khan, J. F. Gomez-Aguilar, T. Abdeljawad and H. Khan, “Stability and numerical simulation of a fractional order plantnectar-pollinator model,” Alexandria Engineering Journal, vol. 59, no. 1, pp. 49–59, 2020. [Google Scholar]

32. A. Khan, H. M. Alshehri, T. Abdeljawad, Q. M. Al-Mdallal and H. Khan, “Stability analysis of fractional nabla difference COVID-19 model,” Results in Physics, vol. 22, no. 1, pp. 1–8, 2021. [Google Scholar]

33. J. F. Gomez-Aguilar, T. Cordova-Fraga, T. Abdeljawad, A. Khan and H. Khan, “Analysis of fractal-fractional malaria transmission model,” Fractals, vol. 28, no. 8, pp. 1–25, 2020. [Google Scholar]

34. K. Khan, R. Zarin, A. Khan, A. Yusuf, M. Al-Shomrani et al., “Stability analysis of five-grade Leishmania epidemic model with harmonic mean-type incidence rate,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–27, 2021. [Google Scholar]

35. A. Khan, J. F. Gómez-Aguilar, T. S. Khan and H. Khan, “Stability analysis and numerical solutions of fractional order HIV/AIDS model,” Chaos, Solitons & Fractals, vol. 122, no. 21, pp. 119–128, 2019. [Google Scholar]

36. P. Bedi, A. Kumar, T. Abdeljawad and A. Khan, “Existence of mild solutions for impulsive neutral Hilfer fractional evolution equations,” Advances in Difference Equations, vol. 2020, no. 1, pp. 1–16, 2020. [Google Scholar]

37. P. Bedi, A. Kumar, T. Abdeljawad and A. Khan, “Study of Hilfer fractional evolution equations by the properties of controllability and stability,” Alexandria Engineering Journal, vol. 60, no. 4, pp. 3741–3749, 2021. [Google Scholar]

38. B. Ghanbari and S. Djilali, “Mathematical analysis of a fractional-order predator-prey model with prey social behavior and infection developed in predator population,” Chaos, Solitons & Fractals, vol. 138, pp. 1–13, 2020. [Google Scholar]

39. B. Ghanbari and S. Djilali, “Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative,” Mathematical Methods in the Applied sciences, vol. 43, no. 4, pp. 1736–1752, 2020. [Google Scholar]

40. J. Danane, K. Allali and Z. Hammouch, “Mathematical analysis of a fractional differential model of HBV infection with antibody immune response,” Chaos, Solitons & Fractals, vol. 136, no. 1–3, pp. 1–9, 2020. [Google Scholar]

41. K. Nisar, Z. Sabir, M. A. Z. Raja, A. A. A. Ibrahim, F. Erdogan et al., “Design of morlet wavelet neural network for solving a class of singular pantograph nonlinear differential models,” IEEE Access, vol. 9, pp. 77845–77862, 2021. [Google Scholar]

42. K. Nisar, Z. Sabir, M. A. Z. Raja, A. Ibrahim, A. Asri et al., “Evolutionary integrated heuristic with Gudermannian neural networks for second kind of Lane-Emden nonlinear singular models,” Applied Sciences, vol. 11, no. 11, pp. 1–16, 2021. [Google Scholar]

43. N. H. Aljahdaly, R. P. Agarwal, R. Shah and T. Botmart, “Analysis of the time fractional-order coupled burgers equations with non-singular kernel operators,” Mathematics, vol. 9, no. 2326, pp. 1–24, 2021. [Google Scholar]

44. E. Ilhan and İ.O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]

45. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Solution of novel multi-fractional multi-singular Lane-Emden model using the designed FMNEICS,” Neural Computing and Applications, vol. 33, no. 24, pp. 17287–17302, 2021. [Google Scholar]

46. H. M. Baskonus, H. Bulut and T. A. Sulaiman, “New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 141–150, 2019. [Google Scholar]

47. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]

48. P. Yang, G. Liu, X. Li, L. Qin and X. Liu, “An intelligent tumors coding method based on drools,” Journal of New Media, vol. 2, no. 3, pp. 111–119, 2020. [Google Scholar]

49. Z. Sabir, K. Nisar, M. A. Z. Raja, A. A. B. A. Ibrahim, J. J. Rodrigues et al., “Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations,” Alexandria Engineering Journal, vol. 60, no. 6, pp. 5935–5947, 2021. [Google Scholar]

50. Z. Sabir, M. Munawar, M. A. Abdelkawy, M. A. Z. Raja, C. Ünlü et al., “Numerical investigations of the fractional-order mathematical model underlying immune-chemotherapeutic treatment for breast cancer using the neural networks,” Fractal and Fractional, vol. 6, no. 4, pp. 1–16, 2022. [Google Scholar]

51. A. ul Rehman, R. Singh and P. Agarwal, “Modeling, analysis and prediction of new variants of COVID-19 and dengue co-infection on complex network,” Chaos, Solitons & Fractals, vol. 150, no. 1, pp. 1–39, 2021. [Google Scholar]

52. S. M. E. K. Chowdhury, M. Forkan, S. F. Ahmed, P. Agarwal, A. S. Ali et al., “Modeling the SARS-CoV-2 parallel transmission dynamics: Asymptomatic and symptomatic pathways,” Computers in Biology and Medicine, vol. 143, pp. 1–11, 2022. [Google Scholar]

53. P. Agarwal, J. J. Nieto, M. Ruzhansky and D. F. Torres, Analysis of infectious disease problems (COVID-19) and their global impact, 1st ed., Singapore: Springer, 2021. [Google Scholar]

54. T. Xie, R. Liu and Z. Wei, “Improvement of the fast clustering algorithm improved by-means in the big data,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 1–10, 2020. [Google Scholar]

55. B. Kouider and A. Polat, “Optimal position of piezoelectric actuators for active vibration reduction of beams,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 385–392, 2020. [Google Scholar]