Novel Scheme for Robust Confusion Component Selection Based on Pythagorean Fuzzy Set

1  Introduction

In this age of the 21st century where technology reaches its new heights, secure communication is a big challenge for researchers. Different communication channels are increasingly being utilized for online data transfer from one location to another which requires security and confidentiality that can be achieved by the use of cryptography. Cryptography is used to obscure the meaning of the data which results in the protection of information from unauthorized access. In cryptography, efficient algorithms are used for encryption purposes, which are characterized by private key and public key cryptographic algorithms. A modern block cipher is a part of private key cryptographic algorithms, which uses the similar key both for encoding and decoding purposes. S-box is an essential nonlinear part in many modern block cipher techniques, responsible for creating confusion during encryption. S-box with strong confusion ability is more sustainable in distorting the input information. Numerous techniques have been presented in writing for the structure of a reliable S-box [1–3].

Decision-making (DM) entails, choosing the best option from the set of feasible options. It is an essential part of human life. As humans make decisions almost every day to perform their daily tasks. The human-based decision involves uncertainty and vagueness in their preferences. L. A. Zadeh [4] suggested the fuzzy set (FS) concept in 1965 as an addition to classical set theory for dealing with uncertain and unclear information. In classical set theory, every component has designated a value called the membership degree from {0, 1}; however, in fuzzy set theory, each element is provided a membership degree from the unit interval [0, 1] by utilizing the membership function. The degree of membership is not provided by FS. To address this, Attanassov (1986) [5] suggested an intuitionistic fuzzy set (IFS) where both the membership and non-membership values (preference values) are given with the property that their sum is less than or equal to 1. In actual decision-making applications, there are circumstances where the above condition may not be satisfied. To deal with such situations Yagar [6,7] proposed the Pythagorean fuzzy set (PFS) as an expansion of IFS with the property that the sum of the square of its preference values does not exceed 1. An example of its support would be that a value of 0.9 is assigned to an object as a membership value and 0.2 is added as a non-membership value (0.9)2 + (0.2)2 < 1. PFS is a more efficient approach for modeling uncertainty in real-world applications than IFS.

Multicriteria decision-making (MCDM) is a set of systems used in various decision-making applications. The goal of MCDM is to choose the most excellent option from a group of alternatives characterized by multiple, usually conflicting criteria. Researchers have introduced various MCDM methods in the past few decades to successfully tackle decision-making problems [8–11]. TOPSIS [12] is a well-known MCDM technique that is utilized to locate the optimal result which is nearer to a positive ideal solution (PIS) and a long way from a negative ideal solution (NIS). Many scholars have successfully employed the TOPSIS approach to tackle MCDM issues in different fuzzy environments [13–16]. TOPSIS approach based on PFS was extended by Zhang et al. [17]. The authors in [18] discussed the financial problem of different companies using seven MCDM methods and compared using two verification methods. Abughazalah et al. [19] proposed optimum criteria for the selection of nonlinear components using MCDM. Kannan et al. [20] presented an industrial-based application of fuzzy MCDM. The authors in [21] implemented a Fuzzy MCDM standard for the choice of natural fiber for organic uses in the aerospace cabin interior. Taghipour et al. [22] suggested a fuzzy MCDM integrated technique for the choice of suppliers of voice identification devices in IT projects. Moreover, we have selected some S-boxes with good cryptographic properties to choose the best of all by using the proposed TOPSIS method [23–30]. Some algebraic properties of these S-boxes have been described by many researchers [31–37].

In this research, an MCDM approach was employed to select the desired S-box used in encryption applications. In this regard, we first investigate the results of cryptographic properties of some standard S-boxes [23–30]. The suitability of S-boxes in encryption applications cannot be identified by the above outcomes concerning the given criteria. As a result, the aforesaid results are further analyzed by using the technique of extended TOPSIS method with a Pythagorean fuzzy set [17].

In this article, a decision-making algorithm is utilized to select the suitable S-box. Our contributions are summarized as follows:

•   We first investigate into the results by investigating the cryptographic properties of some standard S-boxes.

•   Secondly, the TOPSIS procedure depending on the interval-valued Pythagorean fuzzy (IVPF) set is applied to analyze the above outcoming results to reach the final decision.

The remainder of the research is categorized as follows: segment 2 is devoted to the background; cryptographic analysis is presented in segment 3; IVPF-based TOPSIS structure is employed to choose the desired S-box in segment 4; last, the conclusion is discussed in segment 5.

2  Backgrounds

2.1 Fuzzy Set [1]

A fuzzy set F in G is defined as.

F={(g,αF(g))|g∈G,αF:G→[0,1]},(1)

where G is a universe of discourse and αF(g) denotes the membership degree of a component g ∈G to the set F.

2.2 Intuitionistic Fuzzy Set [2]

An intuitionistic fuzzy set I in G is characterized as

I={<g,αI(g),βI(g)>|g∈G},(2)

where G is a universe of discourse and αI:G→[0,1] and βI:G→[0,1] denotes the preference values of an element g∈G to the set I correspondingly, with the property that 0≤αI(g), βI(g) ≤1. The hesitancy degree is given by πI(g)=1−(αI(g) + βI(g)). For simplicity Yager and Xu called the pair (αI(g), βI(g)) an IF number and is denoted by I = (αI, βI).

Let G be a ground set. An intuitionistic fuzzy set (IFS) I in G is described as.

I={(g,αI(g),βI(g))|g∈G},(3)

where αI:G→[0,1] and βI:G→[0,1] indicates the membership value and non-membership value of every element g∈G to I correspondingly, with the condition 0≤αI(g) + βI(g) ≤1. The indeterminacy value is given by ρI(g)=1−αI(g) −βI(g). For simplicity, Yager and Xu called the pair (αI(g), βI(g)) an IF number and is represented by I = (αI, βI).

2.3 Pythagorean Fuzzy Set [9]

A Pythagorean fuzzy set (PFS) P in G is defined as:

P={<g,(αp(g),βp(g))>|g∈G},(4)

where G is a universe of discourse and αp:G→[0,1] and βp:G→[0,1] denotes the preference values of an element g ∈G to the set I correspondingly, with the property that 0≤ (αp(g))2, (βp(g))2≤1. The hesitancy degree is defined as:

πp(g)=(1−(αp(g))2+(βp(g))2)(5)

For simplicity, Zhang and Xu called the pair (αp(g), βp(g)) as PF number denoted by P = (αP, βP).

Let G be a ground set. A Pythagorean fuzzy set (PFS) P in G is defined as.

P={(g,(αP(g),βP(g)))|g∈G},(6)

where αP:G→[0,1] indicates the membership value and βP:G→[0,1] signifies the non-membership value of a component g∈G to the set P correspondingly, with condition 0≤ (αP(g))2 + (βP(g))2≤1. The indeterminacy value is given by

ρP(g)=(1−((αP(g))2+(βP(g))2))0.5.(7)

2.4 Natural Quasi-Ordering [7]

Let P1 = (αP1, βP1) and P2= (αP2, βP2), be two PF numbers, a natural quasi-ordering is defined as: P1> P2 iff αP1> αP2 and βP1< βP2.

2.5 Score Function [17]

For any PF number P = (αP, βP), a score function is given by

s(p)=(αp)2−(βp)2(8)

2.5.1 Proposition [17]

Let P = (αP, βP) be a PF number then score function −1≤ s (p) ≤ 1.

2.5.2 Example [17]

Let p = (0.8, 0.3) then s(p) = 0.64 – 0.09 = 0.55 ∈[−1,1].

2.5.3 Proposition [17]

For any two PFNs P1 = (αP1, βP1) and P2 = (αP2, βP2), the score function has properties.

1.    P1 < P2 if s(P1) < s(P2).

2.    P1> P2 if s(P1)> s(P2).

3.    P1 ∼ P2 if s(P1) = s(P2).

2.5.4 Example

Let P1 = (0.8, 0.3), P2= (0.9, 0.3) then s(P1) = 0.55, s(P2) = 0.72

Clearly s (P1) < s(P2) hence P1 < P2

But if we consider P1 = (0.3, 0.3), P2= (0.5, 0.5) then s(P1) = 0, s(P2) = 0 then by definition 2.2 P1 ∼ P2 but in fact, it is absurd, hence to counter this problem Peng and Yang introduce an accuracy function [23].

2.6 Distance Between Two Pythagorean Fuzzy Numbers [17]

For any two (PF) numbers P1 = (αP1, βP1) and P2 = (αP2, βP2) the distance between them is defined as.

D(P1,P2)=(0.5)(|(αP1)2−(αP2)2|+|(βP1)2−(βP2)2|+|(πP1)2−(πP2)2|)(9)

3  Cryptographic Assets of S-Boxes

In this segment, we examine some cryptographic features of S-boxes used in this work. We also show the findings obtained using the extended TOPSIS structure recommended by Zhang et al. [17].

3.1 Nonlinearity

The least distance of any Boolean function f to the set of all affine functions An is the nonlinearity (NL) measure, which is determined using the following expression:

Nf=minaϵAnd(f,a)

Nonlinearity determines the robustness of an S-box. The high value of NL is desired since it enhances resistance to cryptanalytic attack [31].

3.2 Strict Avalanche Criterion (SAC)

Strict Avalanche Criteria (SAC) is an examination test of an S-box in which each resultant bit is changed with the probability of 1/2. SAC has an optimum value of 0.5 [25].

3.3 Bit Independent Criterion

Bit independent criteria (BIC) are applied to the input bits that remain unchanged. The correlation coefficient is employed to compute the BIC value. It is observed that if nonlinearity and SAC are satisfied then BIC is also satisfied [33].

3.4 Absolute Indicator and Sum of Square

The highest absolute value of δf(w) ∀ w ∈{1,…,2n−1} is indicated as  ACf, which is the absolute indicator of a Boolean function f. The autocorrelation of the n-variable Boolean function f is symbolized by the δ(w), and the sum of the square indicators of f is provided by the ∑w(δ(w))2.

3.5 Algebraic Degree

The algebraic degree is the highest quantity of confusion elements in the truth table. A high-value of algebraic degree is required to resist any cryptanalytic attack [32].

3.6 Algebraic Immunity

Algebraic immunity (AI) provides a challenge to an S-box against any cryptanalytic attack. A high value of AI is required to overcome the algebraic attacks in breaking an encryption system [33].

3.7 Transparency Order

A low value of transparency order is required to resist any differential power analysis (DPA) attack [34].

3.8 Robustness to Differential Cryptanalysis

Suppose F = (f1, f2,……,fs) be an n × s S-box, where fj (j = 1,…,s) is a function on GF (2n). If L is the highest value of differential characteristic Table on F and k is the number of non-zero values in the first column of the table where the value of 2n is not calculated in either case [35]. Then F is ε – robustness against the differential cryptanalysis, where ε is specified by:

ε=(1−K2n)(1−L2n)(10)

3.9 Signal to Noise Ratio (SNR)

The robustness of DPA counter to differential and linear cryptanalysis correlates positively with the signal-to-noise ratio (SNR) of the algorithm. Good quality cryptographic S-boxes are assessed because of high SNR. A high SNR value refers to strong signal strength concerning noise level [36].

3.10 Confusion Coefficient Variance

The confusion coefficient variance is the resistance of an S-boxes against any cryptanalytic attack. A high value of confusion coefficient variance is required [37].

4  Pythagorean Fuzzy Set Based TOPSIS Method

The TOPSIS technique [12] is a powerful MCDM approach that is used to find the best feasible solution in various decision-making applications. Different researchers have introduced different extensions to the TOPSIS system for explaining decision problems in various fuzzy contexts in the last few years, such as in [14] Yue extended for the intuitionistic fuzzy environment, Joshi in [15] extended for the interval-valued fuzzy environment, but all of the above extensions were unable to solve decision problems using Pythagorean fuzzy information. In (2014), Zhang et al. [17] suggested the PF TOPSIS design for resolving real-life decision problems using the PF set. In this section, we utilized the technique described in [17] to select the best S-box. For this purpose, let Sjb = {S1b, S2b, S3b, S4b, S5b, S6b} be six standard S-boxes which are to be evaluated. These S-boxes are evaluated with the aid of the following criterion:

(i)   Nonlinearity

(ii)   BIC Nonlinearity

(iii)    SAC

(iv)   BIC SAC

(v)   Sum of square indicator

(vi)   Transparency order

(vii)   Composite algebraic immunity

(viii)   Absolute Indicator

(ix)   Robustness to differential cryptanalysis

(x)   Algebraic degree

(xi)   Signal to noise ratio (SNR) (DPA)

(xii)   Algebraic immunity

(xiii)   Confusion coefficient variance,

and is represented by the set C:

C={C1,C2,…,C13}t.(11)

Let us consider equal weights for criteria that are W = {0.07692,0.07692,0.07692,0.07692,0.07692,0.07692,0.07692,0.07692,0.07692,0.07692,0.07692,0.07692,0.07692}t such that ∑w = 1. The S-boxes will be analyzed by using PF data required by the decision-maker based on the criteria listed above. Suppose that P = (Ci(sjb))13×6=(αij,βij)13×6 be a Pythagorean fuzzy decision matrix defined in Table 1, where αij represents how much an S-box Sjb (j = 1,2,…,6) satisfies the criterion Ci and βij represents how much an S-box Sjb (j = 1,2,…,6) dissatisfies the criteria Ci (i = 1,2,3,…,m) with the property that (αij)2 + (βij)2 ≤1. The process for the PF TOPSIS approach is explained below.

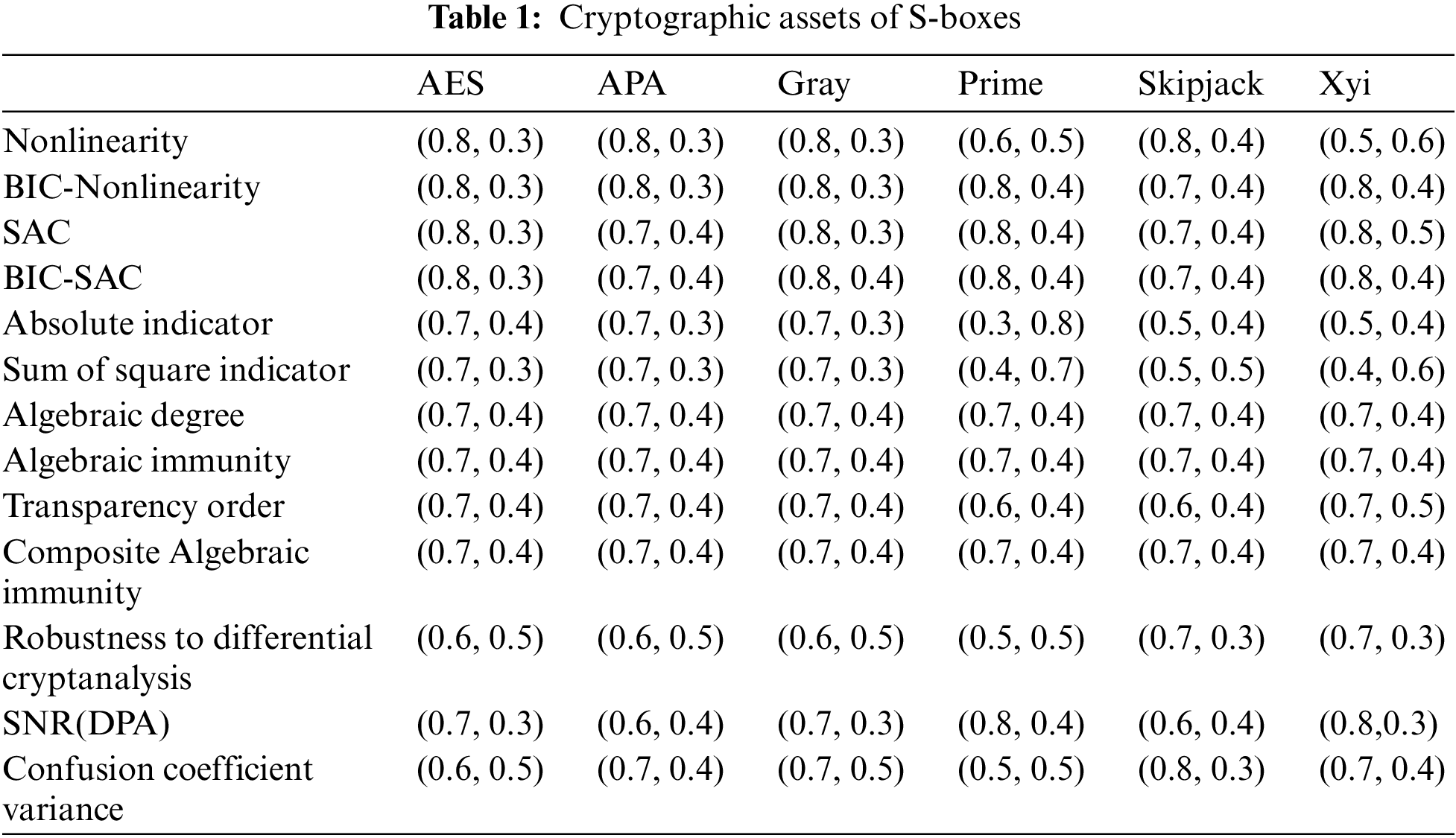
In Table 1, the element C1(s1b) = (0.8, 0.3) corresponding to AES and nonlinearity is expressed as, the degree to which an S-box (AES) satisfies the nonlinearity is 0.8, and the degree to which an S-box (AES) dissatisfies the nonlinearity is 0.3, the remaining elements in Table 1 represents the same meaning.

Step 1: To begin, we use formulas (3) and (4) to compute the Pythagorean fuzzy positive ideal solution (PFPIS) and Pythagorean fuzzy negative ideal solution (PFNIS) concerning the score function defined in (1).

pi+={p1+,p2+,p3+,p4+,p5+,p6+,p7+,p8+,p9+,p10+,p11+,p12+,p13+}t,pi+={<Ci,maxj(uij,vij)|i=(1,2,…,13)},(12)

pi−={p1−,p2−,p3−,p4−,p5−,p6−,p7−,p8−,p9−,p10−,p11−,p12−,p13−}t,pi−={<Ci,maxj(uij,vij)|i=(1,2,…,13)},(13)

Table 2 summarizes the findings.

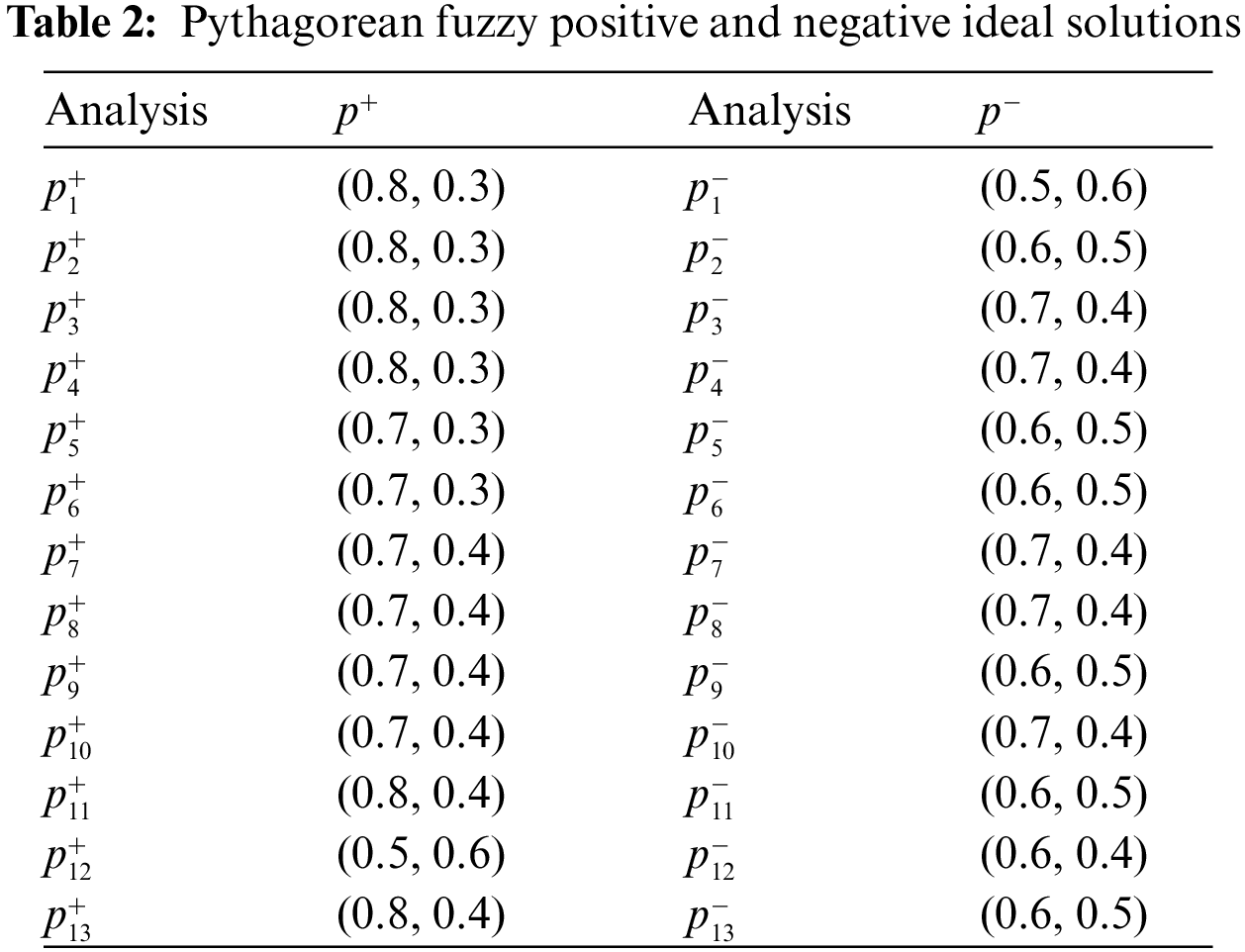
In Table 2 the element (0.8, 0.3) is the maximum element of Table 1 corresponding to criteria non-linearity. Similarly, other elements in Table 2 represent a similar meaning corresponding to other criteria. Moreover, in Table 2 the element (0.5, 0.6) is the minimum element of Table 1 corresponding to criteria non-linearity. Similarly, other elements in Table 2 represent a similar meaning corresponding to other criteria. The separation measure of each S-box from PFPIS and PFNIS is provided in Table 3.

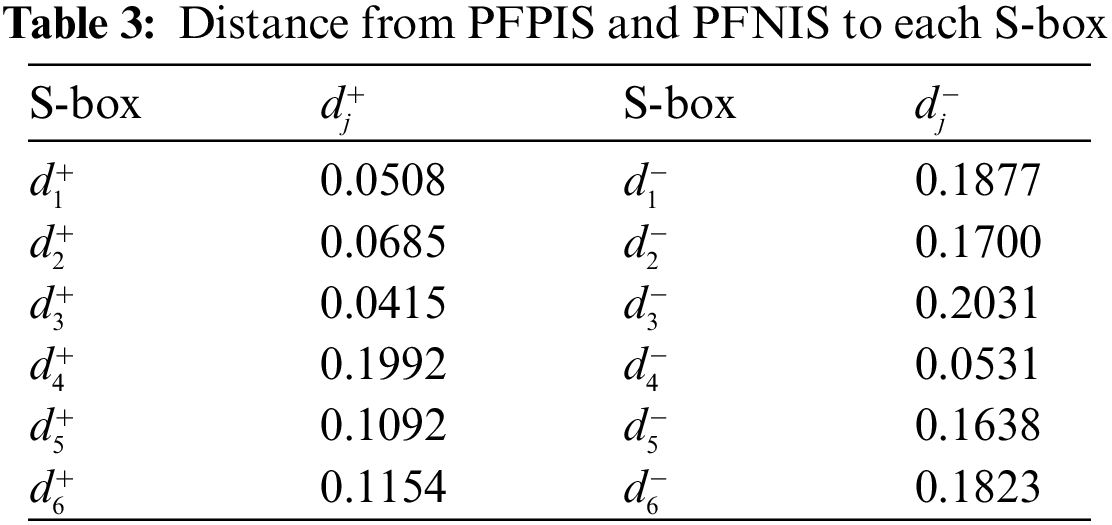
Step 2: Next, we use Eq. (5) to calculate the distance of each S-box from the PFPIS and Eq. (6) to compute the distance of each S-box from PFNIS concerning the distance formula stated in (2).

dj+={d1+,d2+,d3+,d4+,d5+,d6+}dj+=∑i=1mwi∗D(Ci(sjb),pi+),j=1,2…,6(14)

dj−={d1−,d2−,d3−,d4−,d5−,d6−}dj−=∑i=1m⁡wi∗D(Ci(sjb),pi−),j=1,2…,6(15)

Table 3 shows the outcomes of the calculations. For better visualization, the results are presented geometrically, as displayed in Fig. 1. It is seen that the distance between Gray S-box and PFPIS is minimum whereas the distance between Gray S-box and PFNIS is maximum.

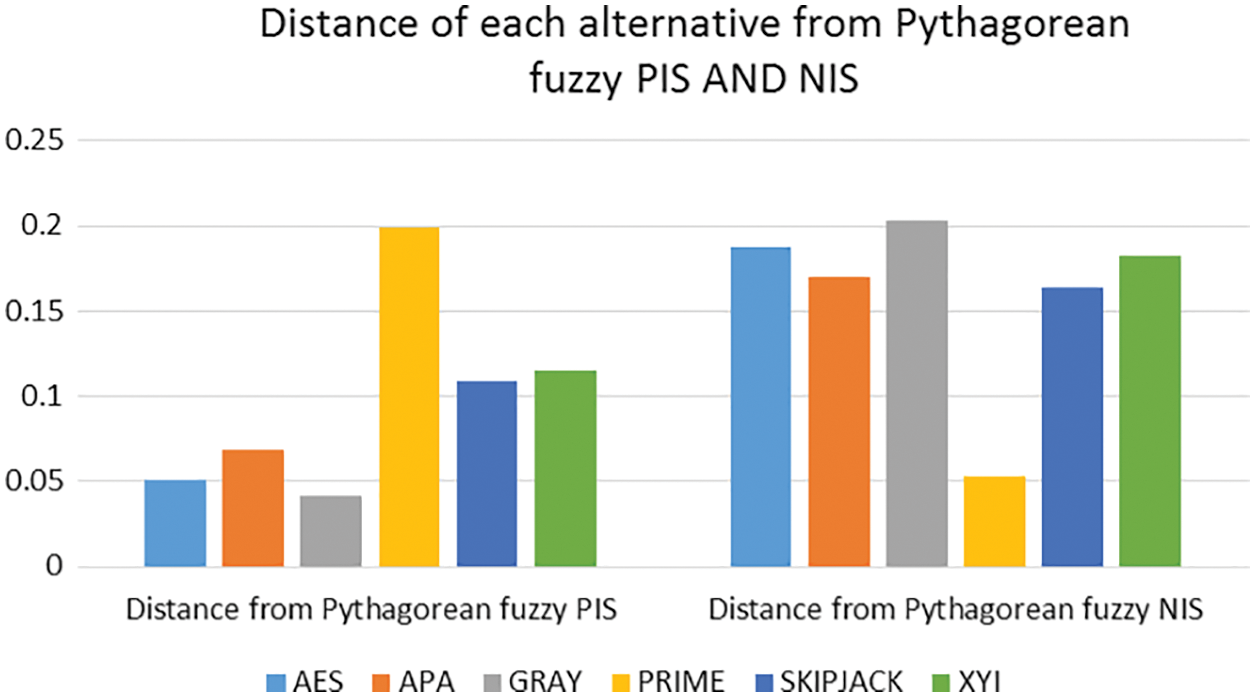
Figure 1: Distance from PFPIS and PFNIS to each S-box

The distance between Gray S-box and PFPIS is minimum in Fig. 1, whereas the distance between Gray S-box and PFNIS is maximum.

Step 3:

Now to determine the performance score of all S-boxes, we have to calculate the relative closeness. Closeness rCi of all S-boxes from PFPIS which is given by Eq. (7) and results are seen in Table 4.

rCi=di−maxdi−−di+mindi+(16)

Step 4:

The S-box with the highest rank is considered the best S-box, and Table 4 shows that the S-box in third place, Gray S-box, has the highest rank. Hence Gray S-box is the best S-box based on previously defined criteria. It can be visualized geometrically as displayed in Fig. 2.

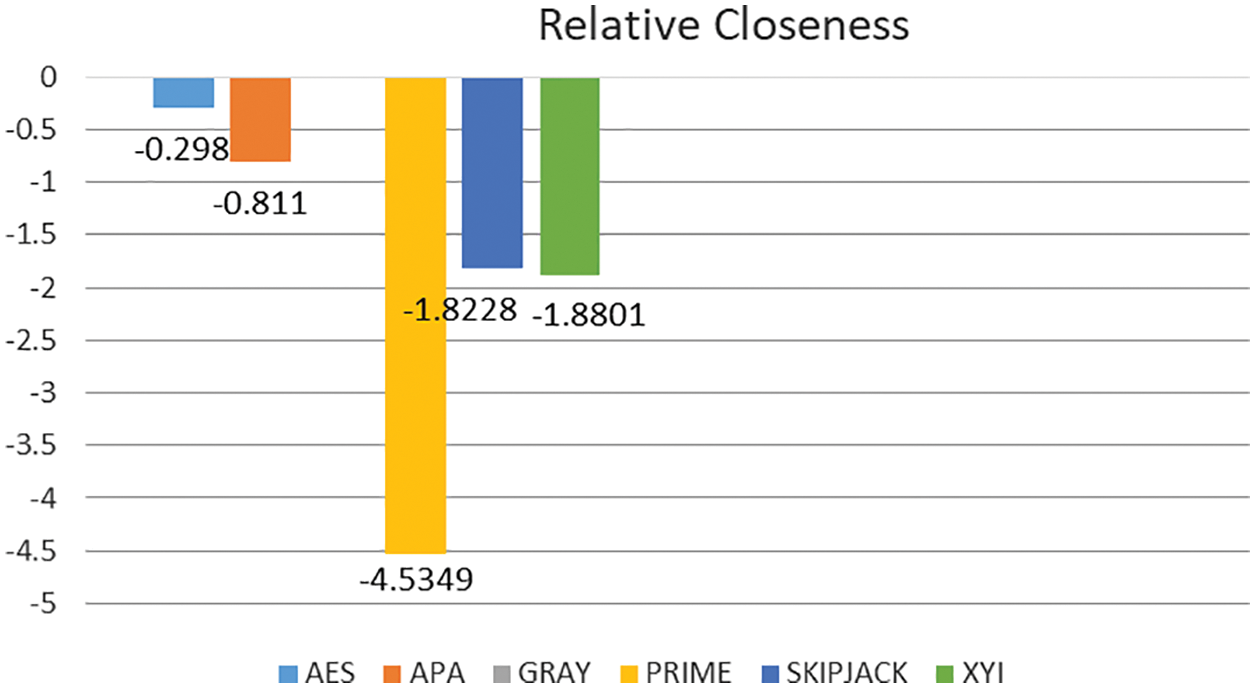
Figure 2: Relative closeness of each alternative 4 TOPSIS process depending on IVPFS

5  Conclusion

The primary intention of this study is to figure out which S-box is better for encryption applications. To do this, a decision-making algorithm namely the extended TOPSIS technique based on PFS is applied to a matrix containing data in the form of a PF number as displayed in Table 1. The findings clearly show that the Gray S-box is the best S-box, as given in Table 4. In the future, additional analyses can be added to further strengthen the proposed criteria.

Acknowledgement: This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R87), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R87), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Khan and T. Shah, “An efficient construction of substitution box with fractional chaotic system,” Signal Image and Video Processing, vol. 9, no. 6, pp. 1335–1338, 2015. [Google Scholar]

 2.  M. Khan, T. Shah and S. I. Batool, “A new approach for image encryption and watermarking based on substitution box over the classes of chain rings,” Multimedia Tools and Applications, vol. 76, no. 22, pp. 24027–24062, 2017. [Google Scholar]

 3.  N. Munir and M. Khan, “A generalization of algebraic expression for nonlinear component of symmetric key algorithms of any characteristic p,” in Int. Conf. on Applied and Engineering Mathematics (ICAEM), Taxila, Pakistan, IEEE, pp. 48–52, 2018. [Google Scholar]

 4.  R. E. Bellman and L. A. Zadeh, “Decision-making in a fuzzy environment,” Management Science, vol. 17, no. 4, pp. 141–163, 1970. [Google Scholar]

 5.  K. Atanassov, “Intuitionistic fuzzy sets,” International Journal Bio Automation, vol. 20, pp. 1, 2016. [Google Scholar]

 6.  R. R. Yager, “Pythagorean fuzzy subsets,” in Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, IEEE, pp. 57–61, 2013. [Google Scholar]

 7.  R. R. Yager, “Pythagorean membership grades in multicriteria decision making,” IEEE Transactions on Fuzzy Systems, vol. 22, no. 4, pp. 958–965, 2013. [Google Scholar]

 8.  N. Abughazalah, M. Khan, N. Munir and A. Zafar, “Optimum criterion for lightweight nonlinear confusion component with multi-criteria decision making,” Journal of Intelligent & Fuzzy Systems, vol. 40, no. 6, pp. 12399–12410, 2021. [Google Scholar]

 9.  G. Villacreses, J. M. Gómez, D. Jijón and M. Cordovez, “Geolocation of photovoltaic farms using eeographic information systems (GIS) with multiple-criteria decision-making (MCDM) methods: Case of the ecuadorian energy regulation,” Energy Reports, vol. 8, no. 3, pp. 3526–3548, 2022. [Google Scholar]

10. A. Gohari, A. B. Ahmad, A. T. Balasbaneh, A. Gohari, R. Hasan et al., “Significance of intermodal freight modal choice criteria: MCDM-based decision support models and SP-based modal shift policies,” Transport Policy, vol. 121, no. 6, pp. 46–60, 2022. [Google Scholar]

11. H. Çalışkan, B. Kurşuncu, C. Kurbanoğlu and S. Y. Güven, “Material selection for the tool holder working under hard milling conditions using different multi criteria decision making methods,” Materials & Design, vol. 45, pp. 473–479, 2013. [Google Scholar]

12. Ž. Stević, S. Miškić, D. Vojinović, E. Huskanović, M. Stanković et al., “Development of a model for evaluating the efficiency of transport companies: PCA-DEA–MCDM model,” Axioms, vol. 11, no. 3, pp. 140, 2022. [Google Scholar]

13. Z. Yue, “TOPSIS-based group decision-making methodology in intuitionistic fuzzy setting,” Information Sciences, vol. 277, pp. 141–153, 2014. [Google Scholar]

14. G. Torlak, M. Sevkli, M. Sanal and S. Zaim, “Analyzing business competition by using fuzzy TOPSIS method: An example of Turkish domestic airline industry,” Expert Systems with Applications, vol. 38, no. 4, pp. 3396–3406, 2011. [Google Scholar]

15. D. Joshi and S. Kumar, “Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making,” European Journal of Operational Research, vol. 248, no. 1, pp. 183–191, 2016. [Google Scholar]

16. Z. Xu and H. Hu, “Projection models for intuitionistic fuzzy multiple attribute decision making,” International Journal of Information Technology & Decision Making, vol. 9, no. 2, pp. 267–280, 2010. [Google Scholar]

17. X. Zhang and Z. Xu, “Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets,” International Journal of Intelligent Systems, vol. 29, no. 12, pp. 1061–1078, 2014. [Google Scholar]

18. M. Baydaş and D. Pamučar, “Determining objective characteristics of MCDM methods under uncertainty: An exploration study with financial data,” Mathematics, vol. 10, no. 7, pp. 1115, 2022. [Google Scholar]

19. N. Abughazalah, M. Khan, N. Munir and A. Zafar, “Optimum criterion for lightweight nonlinear confusion component with multi-criteria decision making,” Journal of Intelligent & Fuzzy Systems, vol. 40, no. 6, pp. 12399–12410, 2021. [Google Scholar]

20. N. S. Kannan, R. Parameshwaran, P. T. Saravanakumar, P. M. Kumar and M. L. Rinawa, “Performance and quality improvement in a foundry industry using Fuzzy MCDM and lean methods,” Arabian Journal for Science and Engineering, 2022. http://dx.doi.org/10.1007/s13369-022-06627-6. [Google Scholar]

21. D. Bhadra and N. R. Dhar, “Selection of the natural fiber for sustainable applications in aerospace cabin interior using fuzzy MCDM model,” Materialia, vol. 21, no. 3, pp. 101270, 2022. [Google Scholar]

22. A. Taghipour, B. D. Rouyendegh, A. Ünal and S. Piya, “Selection of suppliers for speech recognition products in IT projects by combining techniques with an integrated fuzzy MCDM,” Sustainability, vol. 14, no. 3, pp. 1777, 2022. [Google Scholar]

23. X. Peng and Y. Yang, “Some results for Pythagorean fuzzy sets,” International Journal of Intelligent Systems, vol. 30, no. 11, pp. 1133–1160, 2015. [Google Scholar]

24. S. Heron, “Advanced encryption standard (AES),” Network Security, vol. 2009, no. 12, pp. 8–12, 2009. [Google Scholar]

25. L. Cui and Y. Cao, “A new S-box structure named affine-power-affine,” International Journal of Innovative Computing, Information and Control, vol. 3, no. 3, pp. 751–759, 2007. [Google Scholar]

26. M. T. Tran, D. K. Bui and A. D. Duong, “Gray S-box for advanced encryption standard,” in Int. Conf. on Computational Intelligence and Security, Suzhou, China, IEEE, vol. 1, pp. 253–258, 2008. [Google Scholar]

27. E. S. Abuelyman, A. A. S. Alsehibani and S. Arabia, “An optimized implementation of the S-Box using residue of prime numbers,” International Journal of Computer Science and Network Security, vol. 8, no. 4, pp. 304–309, 2008. [Google Scholar]

28. R. Housley, P. Yee and W. Nace, Encryption Using KEA and SKIPJACK. USA, RFC Editor, 2000. [Online]. Available: https://dl.acm.org/doi/10.17487/RFC2773. [Google Scholar]

29. X. Yi, S. Xin, C. Xiao, H. You and K. Lam, “A method for obtaining cryptographically strong 8x8 S-boxes,” in IEEE Global Telecommunications Conf., Phoenix, AZ, vol. 2, pp. 689–693, 1997. [Google Scholar]

30. A. Alghafis, “Quantum half ad full spinning operator-based nonlinear confusion component,” IEEE Access, vol. 9, pp. 31256–31267, 2021. [Google Scholar]

31. I. Hussain and T. Shah, “Literature survey on nonlinear components and chaotic nonlinear components of block ciphers,” Nonlinear Dynamics, vol. 74, no. 4, pp. 869–904, 2013. [Google Scholar]

32. Y. Zheng and X. M. Zhang, “Improved upper bound on the nonlinearity of high order correlation immune functions,” in Int. Workshop on Selected Areas in Cryptography, Berlin, Heidelberg, Springer, pp. 262–274, 2000. [Google Scholar]

33. Y. Nawaz, K. C. Gupta and G. Gong, “Algebraic immunity of S-boxes based on power mappings analysis and construction,” IEEE Transactions on Information Theory, vol. 55, no. 9, pp. 4263–4273, 2009. [Google Scholar]

34. B. Mazumdar, D. Mukhopadhyay and I. Sengupta, “Constrained search for a class of good bijective $ S $-Boxes with improved DPA resistivity,” IEEE Transactions on Information Forensics and Security, vol. 8, no. 12, pp. 2154–2163, 2013. [Google Scholar]

35. B. Mazumdar, D. Mukhopadhyay and I. Sengupta, “Design for security of block cipher S-Boxes to resist differential power attacks,” in 25th Int. Conf. on VLSI Design, Hyderabad, India, IEEE, pp. 113–118, 2012. [Google Scholar]

36. S. Guilley, P. Hoogvorst and R. Pacalet, “Differential power analysis model and some results,” in Smart Card Research and Advanced Applications Vi, Boston, MA: Springer, pp. 127–142, 2004. [Google Scholar]

37. Y. Fei, A. A. Ding, J. Lao and L. Zhang, “A statistics-based fundamental model for side-channel attack analysis,” IACR Cryptol. ePrint Arch, vol. 2014, pp. 152, 2014. [Google Scholar]