Metaheuristic Optimization of Time Series Models for Predicting Networks Traffic

1  Introduction

In the context of network traffic analysis and prediction, network traffic management is defined. Use of Internet traffic management is used to control network traffic, minimize congestion, improve information security and make the most of network resources. Internet traffic is growing at an exponential rate due to the widespread use of smartphones and data subscriptions. Accurate network traffic prediction is necessary for network capacity planning in order to handle this tremendous expansion. Network operators will be at danger if they do not have access to a model that accurately and quickly predicts network traffic. Effective network traffic management necessitates proper network management and modeling [1].

The traditional system administration structure cannot keep up with the rapid advancements in Internet technology and the growing ubiquity of high-tech mobile phones. If we can estimate network traffic patterns using past data, we will be able to allocate and schedule resources more effectively, and improved planning of the network is more likely to take place. For optimal resource allocation through simple bandwidth provisioning and maintaining maximum network utilization, models and forecasts of network traffic are critical. As a result, a robust forecasting model is essential for planning and constructing the network’s capacity. The requirement for a method to dynamically allot bandwidth and minimize congestion is influenced by the dynamic nature of network traffic. We can only accurately measure network traffic if we have a model. With greater Quality of Service (QoS) and better future traffic engineering, reliable network traffic modeling and prediction are necessary. Furthermore, several developers and academics have used linear and non-linear time series models to model network traffic.

Network traffic prediction models can help network engineers choose traffic engineering solutions that can even handle unpredicted future scenarios. In network planning and bandwidth provisioning, network traffic prediction algorithms can play an important role. The planning of network traffic has grown in importance in the scientific community. It’s becoming increasingly difficult for network administrators to keep track of all the people who are using the network at the same time. For this reason, it is critical to keep an eye on the network between the two points and to model the incoming traffic and make predictions about what it will be. To keep tabs on network activity, network traffic analysis is becoming increasingly critical. In order to determine what is happening in the network, network analysts collect and analyze network traffic. There are various different names for network analysis, including “network analysis,” “protocol analysis,” and “packet analysis”. There are several techniques that may be used to analyze network traffic on a packet or level-by-packet basis. It is also possible to do network traffic analysis on a variety of other types of data, including the identity and location of the organizations interacting as well as the length and complexity of their communication streams. As a result, network traffic modeling has become an integral aspect of network design and bandwidth management. The Poisson model is the initial model used in the telephone network to model and forecast arrivals. In spite of this, as contemporary telecommunications have evolved, network traffic has grown enormously and is now more complicated and erratic than speech traffic was previously. To effectively control network traffic, network management and suitable modeling are required.

In order to model and predict network traffic, a lot of academics and developers have worked on these problems. The genetic algorithm [2,3], the Artificial Neural Network [4], fuzzy logic [5], and so on are examples of these intelligence algorithms. In order to improve the ability to forecast network traffic, they integrate a neural network with a robust model based on fuzzy logic. When compared to the individual, the combination has produced the best results. The Recurrent Convolution Neural Network has been suggested as a possible alternative to this approach. The deep neural networks (DNN) may also be used to forecast traffic flow. A reduction in prediction errors was shown to be a benefit of deep learning. Because of the importance of this issue and our desire to make a meaningful contribution to the effort to intelligently estimate network traffic, we undertook this study. A higher QoS and the best future network traffic engineering both depend on accurate network traffic modeling and predictions.

2  Literature Review

After a review of the current research models, it can be seen that there are still significant gaps in the field, which will be addressed in the proposed study. To improve network resource efficiency, it is necessary to understand network traffic in order to forecast future demand owing to the complicated in-network data from a variety of network applications [3]. Network traffic and traffic prediction have been addressed by a slew of time series models, including statistical models [4,5], machine-learning models [6–9], and hybrid schemes [10]. All network traffic prediction systems are examined, and deep learning algorithms are applied to improve network traffic forecasting. Predictive network demand is based on convolution and recurrent neural networks [11,12]. An approach like convolution and recurrent neural networks is used to improve performance prediction [13]. The long short-term memory (LSTM) is used to estimate network traffic in [14]. Researchers have used a variety of relevant models to improve network performance in traffic forecasting. Using the auto-regressive integrated moving average (ARIMA) model and the ON-OFF model, authors in [15] presented the fusion based ARIMA (FARIMA) model, authors in [16] considered the mobility model, authors in [17,18] explored the network traffic model, and authors in [19] used the stable model, and authors in [20–24] presented models to explore the network traffic features, such as performance, planning and trend and seasonal traffic further. Modern signal processing methods, such as those in [25,26], are used to forecast the properties of network traffic. Kalman filtering and compressive sensing methods were used to record traffic evolutions in [25–30]. Network traffic modeling is critical in large-scale networks since it aids in planning and improves network performance. There is a model for predicting network traffic in [31–33]. The ARIMA model is presented in [34,35] for network traffic analysis and forecasting. Network traffic may be predicted using non-linear models such as deep learning and neural networks, which are discussed in [36,37]. There are a number of important time series prediction models in the literature. Stochastic time series models, such as the Single Moving Average, Holt-Winters, Exponential Smoothing [38], and ARMA models, are the most often used and most widely accepted. As time goes on, we learn more and more about the stochastic nature of the data. Some of these additional models are branches of the auto-regressive model, such as auto regressive and seasonal auto-regressive moving averages (SARIMA) [39]. To predict seasonal time series such as SARIMA, the Box and Jenkins technique has been presented [40].

The Fusion Deep Learning (FDL) model for forecasting traffic speed was described in [7]. For accuracy and stability, the suggested model was shown to be superior to the other models tested. In order to forecast outgoing passenger volume, researchers in [41] developed a neural network. Improved passenger flow control was achieved by applying the suggested model, which identified the potential stations that had the greatest influence on the outgoing volumes at the target stations. A deep feature leaning model was used to estimate short-term traffic by authors in [42]. Using the suggested model, traffic may be predicted for the following day. An approach for optimizing the parameters of a deep learning model using particle swarm optimization was also provided. Traffic flow features may be predicted using the DNN model presented in [43]. According to authors in [44], traffic flow may be predicted using a Bayesian combination model with deep learning. It is possible to improve the suggested model by using three sub-predictors: radial basis function neural network (RBFNN), autoregressive integrated moving average, and a neural network. An evaluation of the deep learning model against the most recent available models shows that it performs better. This research helps improve network design, network security, and network administration by anticipating network traffic. It is hoped that the new proposed model would strengthen the existing models. This model can aid in the prediction of network packet loading and burst arrivals.

3  Methodology

The proposed methodology is based on optimizing the hyperparameters of long short-term memory (LSTM) to boost the prediction accuracy of wireless network traffic volume. Therefore, this section starts by presenting the structure of LSTM and showing the parameters that are optimized, and then the proposed optimization algorithm is presented and discussed.

3.1 Long Short-Term Memory

Because of its ability to simulate complicated time series with time delays of undetermined size, the Long Short-Term Memory (LSTM) model has recently gained favor as a recurrent neural network [27]. It is the usage of self-loops where the gradient may flow for lengthy periods of time without disappearing or bursting that is the main idea of LSTM. A forget-gate, in conjunction with this, allows the LSTM to build up information that may be “forgotten” later, depending on the input data. For the first time, LSTM models have been utilized to model short-term network flow sizes of fine granularity. The following recursive equations characterize LSTMs:

ct=it⊙c~t+ft⊙ct−1

ot=σ(WoXt+Uoht−1+bo)

ft=σ(WfXt+Ufht−1+bf)(1)

it=σ(WiXt+Uiht−1+bi)

c~t=tanh(WcXt+Ucht−1+bc)

ht=ot⊙tanh⁡(ct)

where bf, Xt, ht, ot, ct, c~t, it, ft are the bias value, input data, hidden state, output gate, current state, candidate state, input gate, and forget gate, respectively. The values of Wo, Wc, Wi, and Wf represent the weights for output gate, candidate state gate, input gate, and forget gate, respectively. The values of Uo, Uc, Ui, and Uf are the recurrent weights for the output gate, current state, input gate, and forget gate, respectively. The Hadamard product, ⊙, refers to the sigmoid function. The bias terms for output gate, candidate state, input gate, and forget gate is denoted by, bo, bc, bi, and bf, respectively. Fig. 1 shows the architecture of an LSTM network from where we can see the internal structure of the LSTM unit at time t, as well as how it connects to past and future states to form a recurrent neural network.

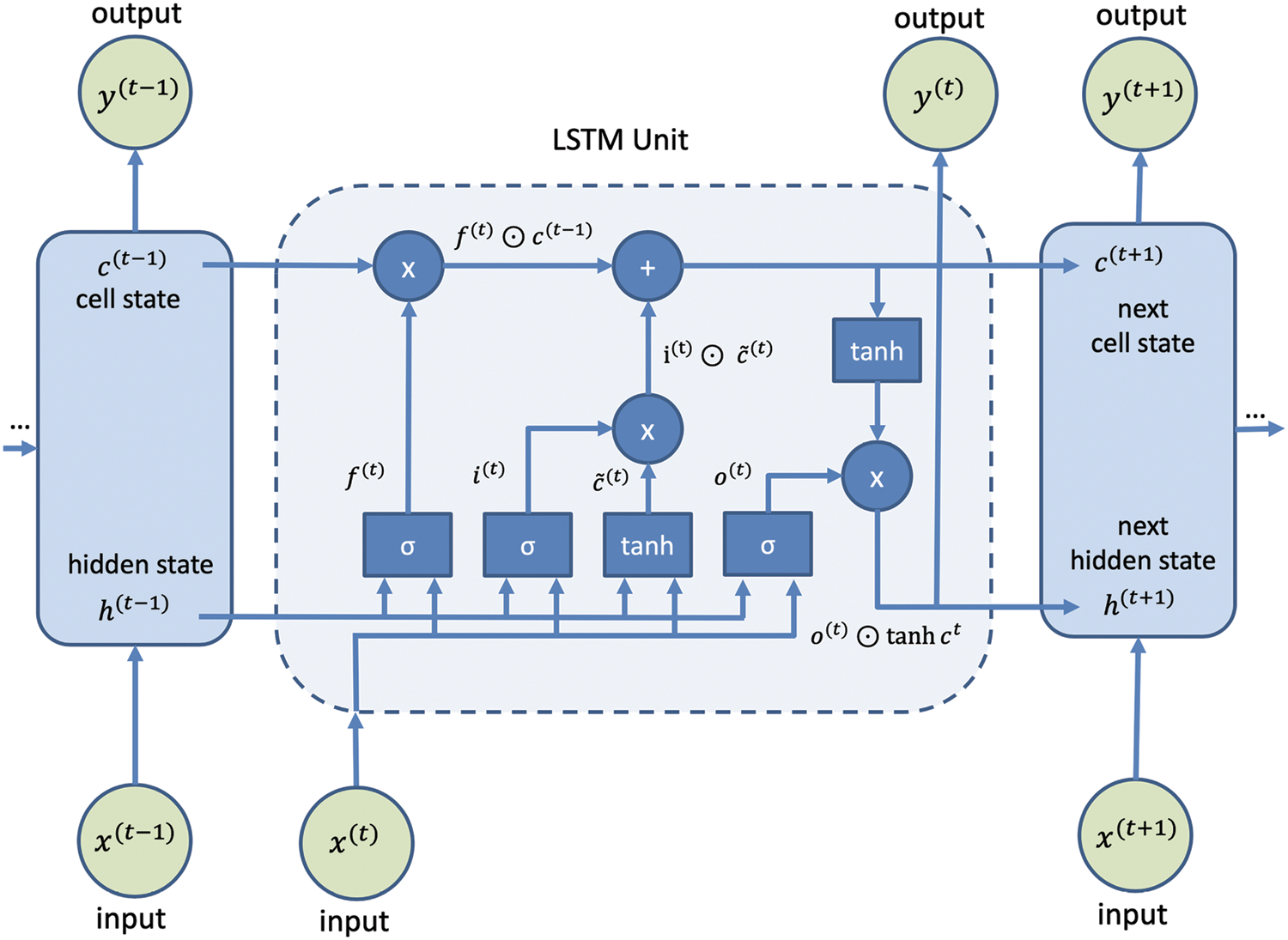
Figure 1: Standard structure of the LSTM network

3.2 Grey Wolf Optimizer (GWO)

An initial random population is generated by the grey wolf optimizer; the next iterations modify this population. Exports and exploitation are kept under check by GWO. In order to find potential places in the search space, exportation is used. Exploitation is a search strategy that makes use of promising points in the search space to identify the best possible advantageous points. To the problem-solver, each and every one of us is a potential solution. The fitness function is then determined for each solution. In this way, the three major gamma frequencies may be distinguished [45]. To keep track of where each wolf is at any one time, we utilize the equations below.

D→=|D→.X→p(t)−X→(t)|(2)

X→(t+1)=|X→p+1(t)−A→.D→|(3)

where A→ and C→ are two coefficient vectors, X→, X→p and t are the grey wolf position and prepositions, and the iteration number is denoted by t. The following equations present the calculation of these vectors:

A→=2a→.r→1−a→(4)

C→=2r→2(5)

Over the course of iterations, the value of a→ decreases linearly from 2 to 0, whereas r→1 and r→2 are random numbers between [0; 1]. The following equation of alpha, beta, and delta calculations are used to recalculate the pack’s position, and then an attack is launched.

X→1=X→α−A→1∗D→α

X→2=X→β−A→2∗D→β

X→3=X→δ−A→3∗D→δ

D→α=|C→1∗X→α−X→|(6)

D→β=|C→2∗X→β−X→|

D→δ=|C→3∗X→δ−X→|

The average of the three solutions, D→1,D→2,D→3 is used to calculate the population’s updated positions denoted by D→(t+1) as follows:

D→(t+1)=D→1+D→2+D→33(7)

3.3 Dipper Throated Optimization (DTO)

The Cinclidsae family of birds includes the Dipper Throated bird, which is renowned for its bobbing or dipping motions while perched. Unlike other passerines, birds are able to dive, swim, and hunt underwater. Flying straight and swiftly with no stops or glides is made possible by the small and flexible wings. The Dipper Throated bird has a unique hunting strategy due to its fast bending motions and white breast. To catch its prey, it plunges headfirst into any turbulent or fast-flowing water. The sinking of the ocean floor has a negative impact on aquatic invertebrates, including aquatic insects, fish, and tiny crustaceans. The dipper uses its hands to move on the ocean floor. It’s possible to catch prey by lowering your head and walking down the bottom of the water with your body bent at an angle. When diving into the water and purposefully submerging, it may use its wings to propel itself through the water and stay below for lengthy periods of time while using its wings to propel itself through the water. The Dipper-Throated Optimization (DTO) technique argues that a flock of birds is swimming and flying in search of food supplies. This matrix may be used to depict the position and speed of a flock of birds (BL, BS). In order to choose features, the binary DTO is used. An alternative approach employs a continuous DTO for fine-tuning neural network parameters during classification [46].

V=[S1,1S1,2S1,3…S1,dS2,1S2,2S2,3…S2,dS3,1S3,2S3,3…S3,d……………Sm,1Sm,2Sm,3…Sm,d](8)

L=[L1,1L1,2L1,3…L1,dL2,1L2,2L2,3…L2,dL3,1L3,2L3,3…L3,d……………Lm,1Lm,2Lm,3…Lm,d](9)

where Li,j refers to the ith bird in the jth dimension for i∈1,2,3,…,m and j∈1,2,3,…,d. A bird’s speed in the jth dimension for i∈1,2,3,…,m and j∈1,2,3,…,d is indicated by Si,j. There is a uniform distribution of the initial positions of Li,j.

3.4 DTO+FGW Algorithm

Based on the formulation of DTO and GWO discussed in the previous sections, we proposed a new optimization algorithm that exploits the advantages of both algorithms to improve the efficiency of the LSTM network and thus boost the prediction accuracy. The steps of the proposed algorithm are listed in Algorithm 1.

3.5 Traffic Model

It’s possible to simulate any stationary time series system using the formula: [y(t-1), y(t-2),…, y(t-m)]. A single function termed f(.) cannot accurately predict the full-time series for a non-stationary time series, which necessitates a collection of functions, each of which has its own set of independent components. Because of this, non-stationary time series can be modeled as:

y(t)=∑i=1kpitfi(t)(10)

∑i=1kpit=1(11)

where fi(t) can be modeled as a collection of random processes to account for the nonstationary nature of the time series. A non-stationary time series can be established by the number of users and their arrival patterns, the number and size of individual user sessions, and the number of sessions between arrivals of the same user.

Tr(t)=∑i=1kpitfi(t)(12)

where f1(t) is a discrete value continuous-time process where the number of users and the pattern of their arrival are both random processes, the pattern of user arrival is a time-varying Poisson process [18], and the distribution of users is either uniform or lognormal. User session is a Lognormal or time-varying Poisson process, while session inter-arrival is a BiPareto, Weibull or Markov Modulated Poisson process (MMPP). The discrete value and continuous-time random process of f2(t) is the random process of the number of sessions and the inter-arrival pattern. In discrete-value continuous-time processes, f3(t) represents the size of each session and can be either Bipareto or Lognormal random [47].

3.6 ARIMA Model

The ARMA process is a well-established statistical model and forecasting method for stationary time series. Moving Average (MA) value aims to reduce the influence of unknown series beginning value by increasing the order of Auto Regression (AR) value captures the seasonal pattern of time series and leads to an improved approximation of stationary time series. It is possible to eliminate series dependence on unknown beginning values by combining the AR and MA processes, resulting in very accurate predictions of stationary time series. Time series decomposition into transitory (stationary) and permanent (non-stationary) components can help improve forecasting and approximation for non-stationary data, but it is not possible to use a simple ARMA process in this case because time series only represents one realization of a set of stochastic processes.

y(t)=yp(t)+yk(t)(13)

Permanent components are represented by yp(t), whereas transitory components are represented by yk(t). The LRD and SRD parameters of the time series may be determined individually using this decomposition technique. Differentiating a non-stationary process y(t) by d times transforms it into an LRD process with a specific parameter d.

(1−L)dy(t)=δ+x(t)(14)

In this case, y(t) = [y(t-1)] where L is the backward shift operator. where x(t) is an ARMA process whose SRD qualities are determined by the ARMA process parameters p and q. Non-stationary processes are called ARIMA in this context (p, d, q). The estimate of the differencing term d is critical to the accuracy of non-stationary time series prediction. This process is known as the FARIMA(p, d, q) process when the degree of differencing d is permitted to assume a non-integral value. A non-stationary time series may be predicted using the FARIMA(p, d, q) process if it is described by the FARIMA process.

y^(n)=∑j=1∞⁡πjnyn−j(15)

πjn=πj+n−1−∑i=1n−1⁡πiπjn+1(16)

πj=(−1)jΓ(1+d)Γ(1+j)Γ(1+d−j)(17)

where πj1=πj and y^(.) is the projected time series from the calculated FARIMA process, whereas Γ(.) is the gamma function.

4  Experimental Results

The parameters of LSTM that are optimized using the proposed algorithm are listed in Table 1. In this table, the parameters are defined with initial values. These values are then updated during the optimization process to find the optimal value that can boost the prediction accuracy of the network traffic volume.

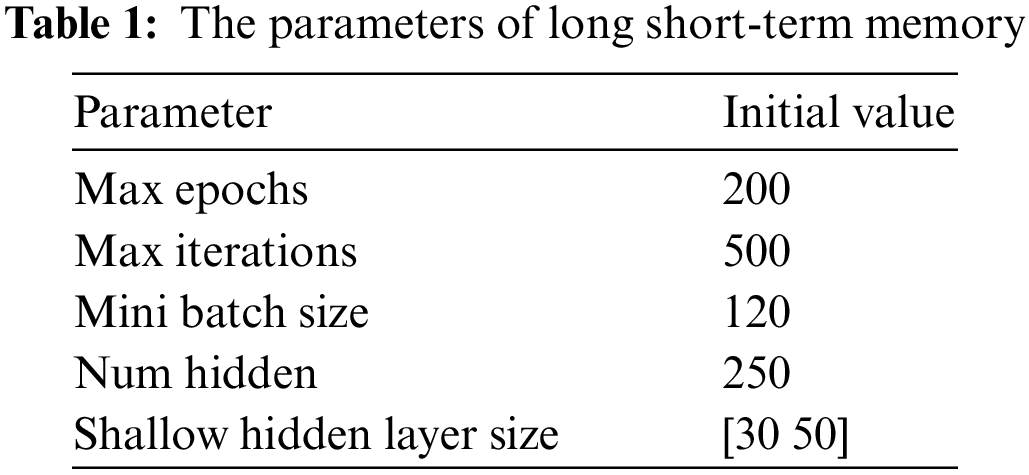
Using the optimized LSTM, wireless data traffic is predicted using time series derived from data extraction. Time series data extraction from wireless traffic is made possible by the CRAWDAD repository’s wireless trace [48]. For one second, ten seconds, and one minute, the original dataset comprises the traffic trace of 476 wireless APs over an 11-week period. Here, the traffic prediction is restricted to one AP. To extract the detailed traffic from a tcpdump file, this SNMP trace is used to filter the original trace file and only acquire the traffic of a specific AP. In order to determine the quantity of traffic in terms of bytes per unit time, the filtered traffic trace is further analyzed. Traffic between an AP and a group of wireless clients is included in the filtered trace for one day. One millisecond is coupled with a second to produce one minute, and so on and so forth in order to form the other time scales. It is possible to predict traffic for a variety of time steps using the time series obtained from network trace. Prior to doing n-step ahead prediction, the filtered traffic must be normalized [49–53]. The LSTM predictor is trained and tested using the time series derived from the trace. A random sample of 1000 is used to choose the individuals for training and testing.

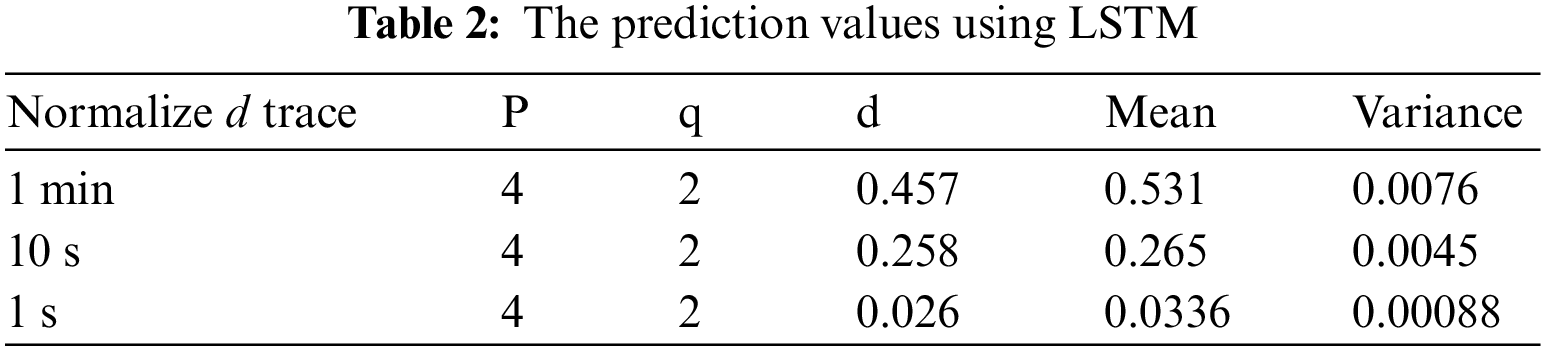
Once the wireless trace has been described, the FARIMA model may be used to predict network traffic on a variety of time scales based on this model. Four phases are involved in the construction of the FARIMA model. In the first step, the traffic data is normalized, and the zero mean time series is obtained. When the Hurst Parameter (H) is calculated using the Variancetime plot of a normalized trace’s Variancetime, the Hurst Parameter (d) is approximated using the Hurst Parameter (H). Fractionally differing y(t) to get x(t) of Eq. (13) (ARMA model of the original time series) yields the precise value of d, which can then be used to get the exact value of d. After that, the ARMA process parameters p and q, which should begin with the fewest possible values, are identified and checked during the model identification and diagnostic checking phase. Table 2 lists the model parameters for different temporal granularities. The projected future steps of the time series are derived from the estimated FARIMA process and the current and previous values of the time series. One and ten percent are the expected step sizes. These results are achieved by the traditional LSTM model without optimization.

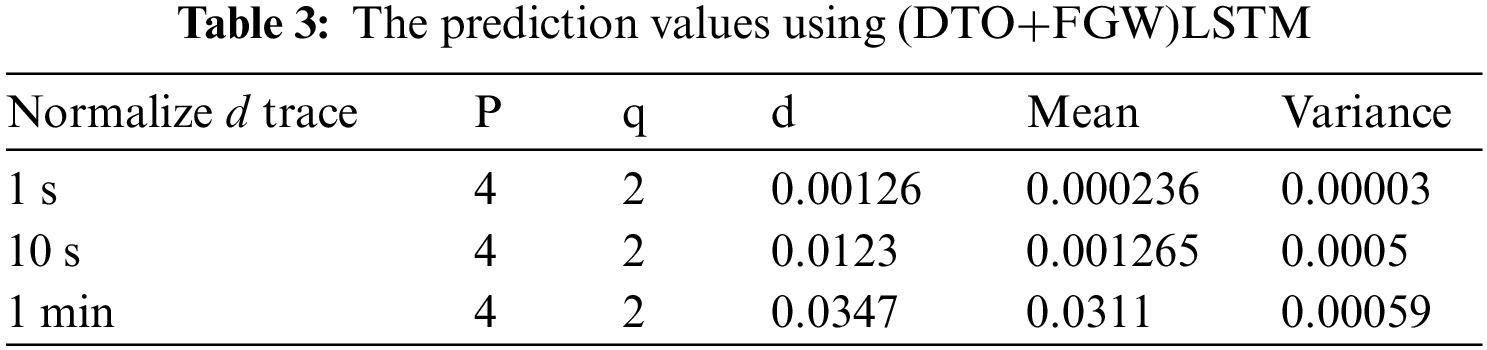
On the other hand, the prediction results using the optimized LSTM based on the proposed optimization approach are presented in Table 3. In this table, the mean and variance are much better than those achieved by the traditional LSTM. These results prove the effectiveness of the proposed approach.

To confirm the effectiveness of the proposed approach, the plots in Fig. 2 depict the performance of the proposed approach. In this figure, the homoscedasticity plot and residual plots are used to show the accuracy of the prediction results. As shown in these plots, the errors in prediction are tiny, and this emphasizes the robustness of the proposed approach. In addition, the QQ plot and ROC curve also show promising performance.

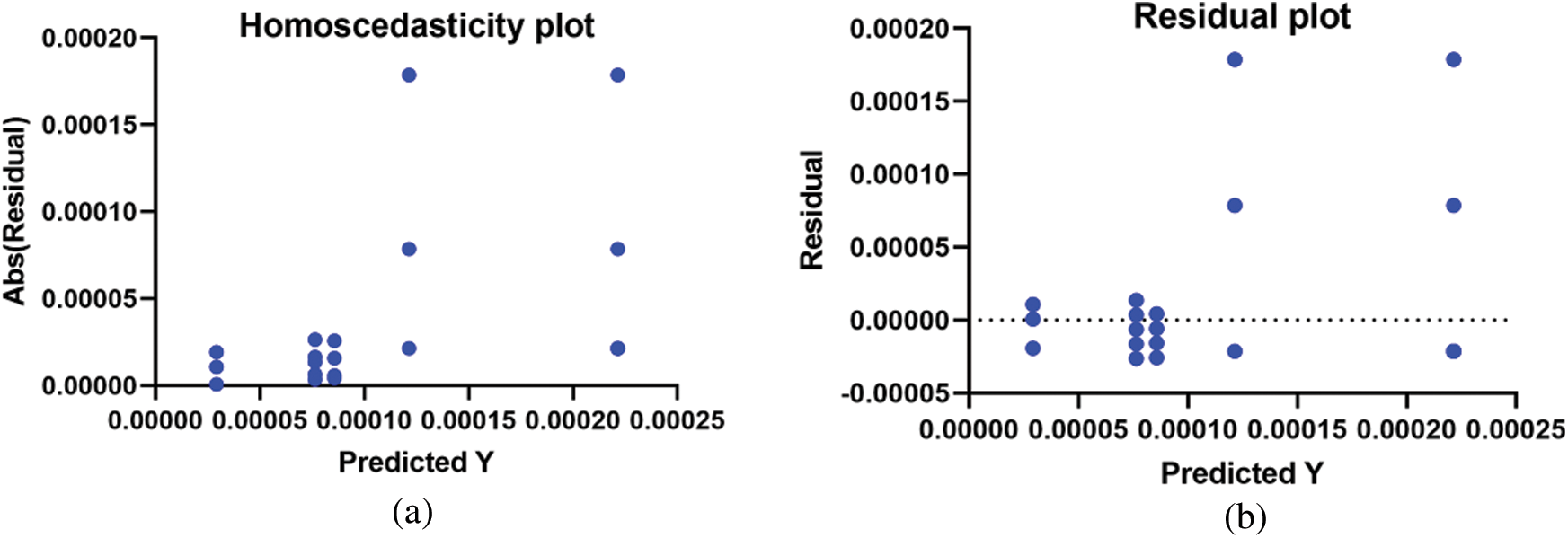
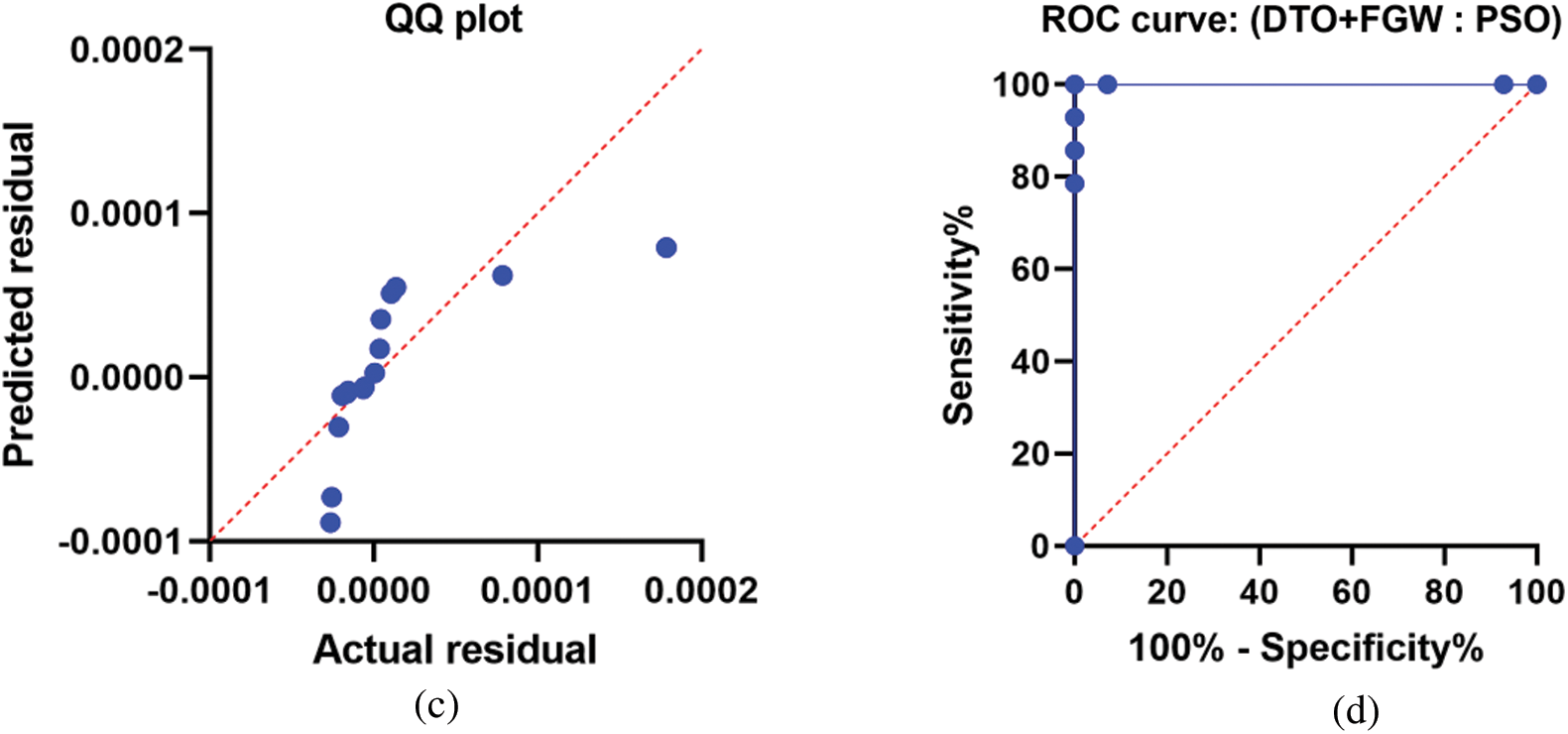
Figure 2: Analysis plots of the achieved results using the proposed optimization algorithm

Fig. 3 shows the histogram of the residuals of the recorded results. As shown in this figure, the results recorded using the proposed DTO+FGW are (0.00001) with a large number of values. However, the histogram of the residual values using the other approaches is greater than that of the proposed approach. This indicates that the proposed approach outperforms the other methods.

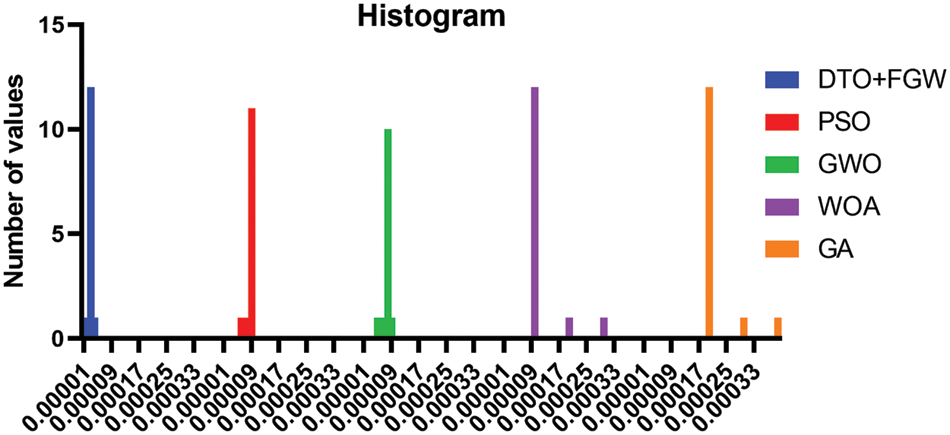
Figure 3: One way analysis of variance test

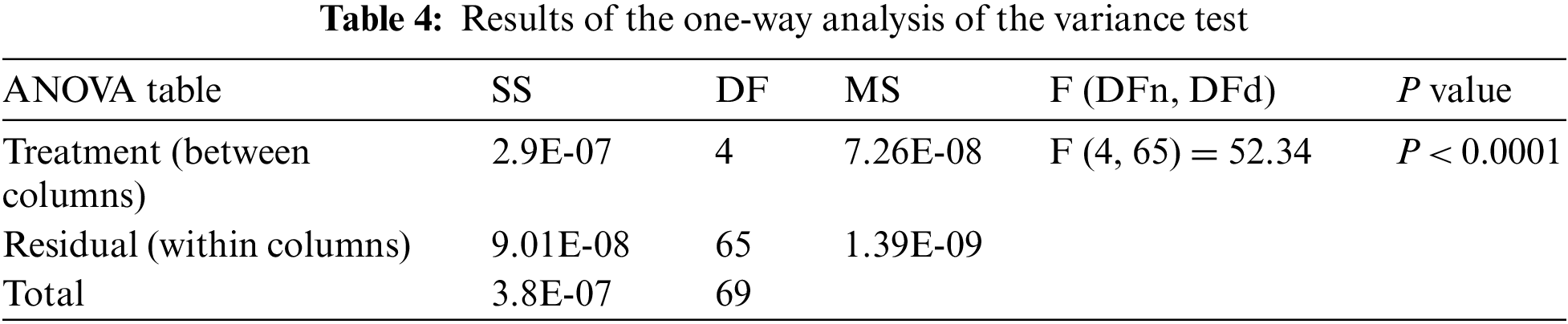
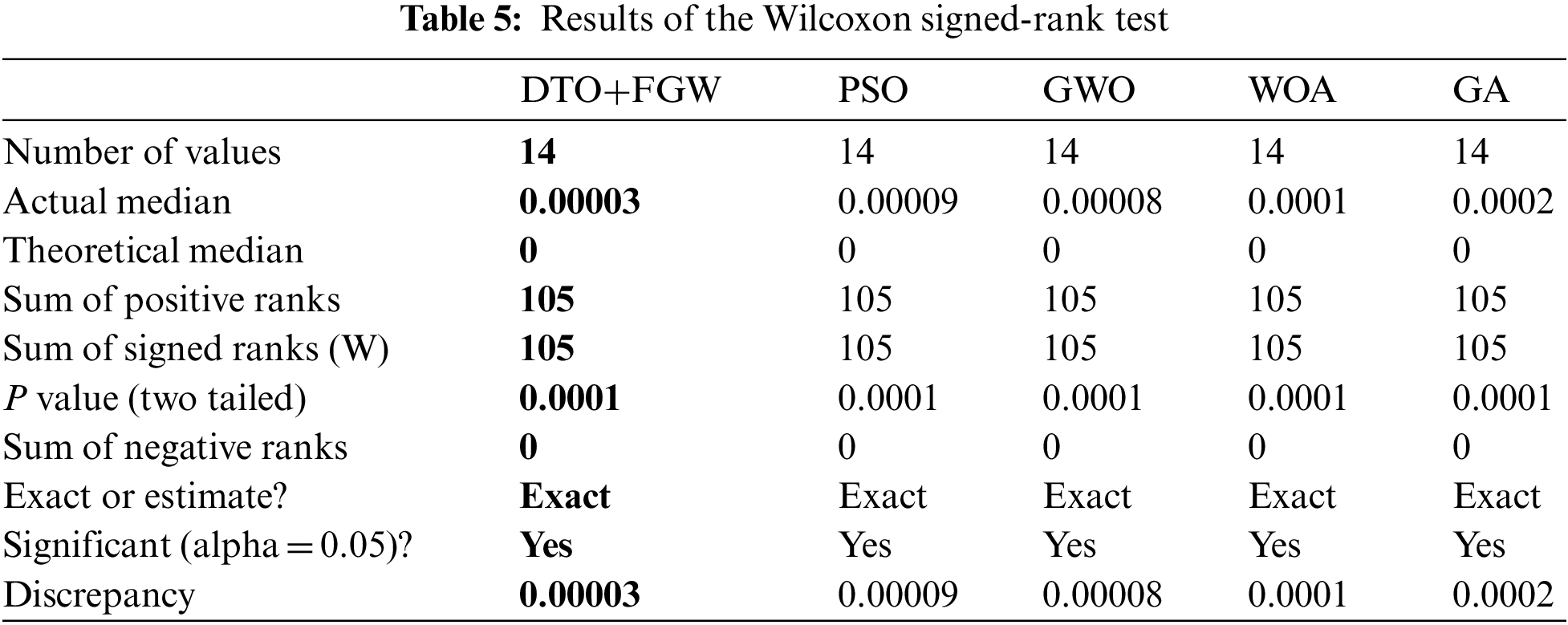
Moreover, the plot shown in Fig. 4 depicts the variance values using the proposed approach compared to the other methods. In this plot, the value of the objective function using the proposed method achieves the minimum values when compared to the other methods. This confirms the previous findings of the superiority of the proposed approach. To study the stability and significance of the propose approach, two tests were performed. The first test is the one-way analysis of variance (ANOVA) test, presented in Table 4, whereas the second test is the Wilcoxon test, presented in Table 5. The presented results in these tables reflect the statistical significance of the proposed approach when compared to the other competing approaches.

Figure 4: Variance of the predicted values of wireless traffic volumes

5  Conclusions

Network management relies heavily on Quality of Service (QoS) since it may assist in determining the volume of traffic on a particular network. Traffic predictions have grown increasingly crucial as networks become increasingly complicated and diversified. It is possible to alleviate network congestion by predicting traffic volumes more accurately. Time series prediction methods are used to predict future traffic numbers. By creating a link between the present and expected traffic quantities, it may be possible to boost the network’s performance this way. In order to increase network quality of service, it has been recommended that time series models should be improved. In this paper, we improved the prediction accuracy by optimizing the parameters of LSTM network using the proposed optimization algorithm based on a hybrid of grey wolf and dipper throated optimization methods. We increase the performance of LSTM time series model by employing metaheuristic optimization techniques. Real-world data from a distinct network was used to test and evaluate the proposed approach. Tests conducted with current time series models demonstrate that using the proposed approach greatly decreased the prediction results. On the other hand, the proposed approach is compared to other methods and proved to achieve better performance. In addition, a statistical analysis is performed to study the significance and stability of the proposed approach. Overall, the network traffic volume prediction is improved significantly using the proposed approach.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R323), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R323), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. E. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]

    2. T. H. H. Aldhyani and M. R. Joshi, “Intelligent time series model to predict bandwidth utilization,” International Journal of Computer Science Applications, vol. 14, no. 2, pp. 130–141, 2017. [Google Scholar]

    3. A. Azari, M. Ozger and C. Cavdar, “Risk-aware resource allocation for URLLC: Challenges and strategies with machine learning,” IEEE Communication Magazine, vol. 57, no. 3, pp. 42–48, 2019. [Google Scholar]

    4. C. Qiu, Y. Zhang, Z. Feng, P. Zhang and S. Cui, “Spatio-temporal wireless traffic prediction with recurrent neural network,” IEEE Wireless Communication Letter, vol. 7, no. 4, pp. 554–557, 2018. [Google Scholar]

    5. S. S. M. Ghoneim, T. A. Farrag, A. A. Rashed, E. -S. M. El-Kenawy and A. Ibrahim, “Adaptive dynamic meta-heuristics for feature selection and classification in diagnostic accuracy of transformer faults,” IEEE Access, vol. 9, pp. 78324–78340, 2021. [Google Scholar]

    6. H. D. Trinh, L. Giupponi and P. Dini, “Mobile traffic prediction from raw data using LSTM networks,” in 2018 IEEE 29th Annual Int. Symp. on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, pp. 1827–1832, 2018. [Google Scholar]

    7. Y. Wu, H. Tan, L. Qin, B. Ran and Z. Jiang, “A hybrid deep learning based traffic flow prediction method and its understanding,” Transportation Research Part C: Emerging Technologies, vol. 90, pp. 166–180, 2018. [Google Scholar]

    8. M. A. Shoorehdeli, M. Teshnehlab and A. K. Sedigh, “Training ANFIS as an identifier with intelligent hybrid stable learning algorithm based on particle swarm optimization and extended kalman filter,” Fuzzy Sets and Systems, vol. 160, no. 7, pp. 922–948, 2009. [Google Scholar]

    9. J. Wang, J. Tang, Z. Xu, Y. Wang, G. Xue et al., “Spatiotemporal modeling and prediction in cellular networks: A big data enabled deep learning approach,” in IEEE INFOCOM 2017-IEEE Conf. on Computer Communications, Atlanta, GA, USA, pp. 1–9, 2017. [Google Scholar]

  10. A. Abdelhamid and S. R. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]

  11. C. -W. Huang, C. -T. Chiang and Q. Li, “A study of deep learning networks on mobile traffic forecasting,” in 2017 IEEE 28th Annual Int. Symp. on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, pp. 1–6, 2017. [Google Scholar]

  12. R. Li, Z. Zhao, X. Zhou, J. Palicot and H. Zhang, “The prediction analysis of cellular radio access network traffic: From entropy theory to networking practice,” IEEE Communications Magazine, vol. 52, no. 6, pp. 234–240, 2014. [Google Scholar]

  13. G. Lai,W. -C. Chang, Y. Yang and H. Liu, “Modeling long-and short-term temporal patterns with deep neural networks,” in Proc. of the 41st Int. ACM SIGIR Conf. on Research & Development in Information Retrieval, Ann Arbor, MI, USA, pp. 95–104, 2018. [Google Scholar]

  14. A. Azzouni and G. Pujolle, “NeuTM: A neural network-based framework for traffic matrix prediction in SDN,” in Proc. of 2018 IEEE/IFIP Network Operations and Management Symp., Taipei, Taiwan, pp. 1–5, 2018. [Google Scholar]

  15. A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]

  16. S. Skaperas, L. Mamatas and A. Chorti, “Real-time algorithms for the detection of changes in the variance of video content popularity,” IEEE Access, vol. 8, pp. 30445–30457, 2020. [Google Scholar]

  17. O. Cappe, E. Moulines, J. -C. Pesquet, A. P. Petropulu and X. Yang, “Long-range dependence and heavy-tail modeling for teletraffic data,” IEEE Signal Processing Magazine, vol. 19, no. 3, pp. 14–27, 2002. [Google Scholar]

  18. F. Ashtiani, J. A. Salehi and M. R. Aref, “Mobility modeling and analytical solution for spatial traffic distribution in wireless multimedia networks,” IEEE Journal on Selected Areas in Communications, vol. 21, no. 10, pp. 1699–1709, 2003. [Google Scholar]

  19. K. Tutschku and P. Tran-Gia, “Spatial traffic estimation and characterization for mobile communication network design,” IEEE Journal on Selected Areas in Communications, vol. 16, no. 5, pp. 804–811, 1998. [Google Scholar]

  20. L. Xiang, X. -H. Ge, C. Liu, L. Shu and C. -X. Wang, “A new hybrid network traffic prediction method,” in Proc. of IEEE Global Telecommunications Conf. GLOBECOM, Miami, FL, USA, pp. 1–5, 2010. [Google Scholar]

  21. G. Xiaohu, S. Yu, W. -S. Yoon and Y. -D. Kim, “A new prediction method of alpha-stable processes for self-similar traffic,” in Proc. of IEEE Global Telecommunications Conf. GLOBECOM, Dallas, TX, USA, pp. 675–679, 2004. [Google Scholar]

  22. M. Z. Shafiq, L. Ji, A. X. Liu, J. Pang and J. Wang, “Geospatial and temporal dynamics of application usage in cellular data networks,” IEEE Transactions on Mobile Computing, vol. 14, no. 7, pp. 1369–1381, 2015. [Google Scholar]

  23. M. E. Crovella and A. Bestavros, “Self-similarity in world wide Web traffic: Evidence and possible causes,” IEEE/ACM Transactions on Networking, vol. 5, no. 6, pp. 835–846, 1997. [Google Scholar]

  24. W. E. Leland, M. S. Taqqu, W. Willinger and D. V. Wilson, “On the self-similar nature of ethernet traffic,” IEEE/ACM Transactions on Networking, vol. 2, no. 1, pp. 1–15, 1994. [Google Scholar]

  25. M. Roughan, Y. Zhang, W. Willinger and L. Qiu, “Spatio-temporal compressive sensing and internet traffic matrices,” IEEE/ACM Transactions on Networking, vol. 20, no. 3, pp. 662–676, 2012. [Google Scholar]

  26. A. Soule, A. Lakhina, N. Taft, K. Papagiannaki, K. Salamatian et al., “Traffic matrices: Balancing measurements, inference and modeling,” ACM SIGMETRICS Performance Evaluation Review, vol. 33, no. 1, pp. 362–373, 2005. [Google Scholar]

  27. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. E. Takieldeen, T. M. Hassan et al., “Meta-heuristics for feature selection and classification in diagnostic breast cancer,” Computers, Materials & Continua, vol. 73, no. 1, pp. 749–765, 2022. [Google Scholar]

  28. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. Ibrahim, S. H. Abd Elkhalik et al., “Improved prediction of metamaterial antenna bandwidth using adaptive optimization of LSTM,” Computers, Materials & Continua, vol. 73, no. 1, pp. 865–881, 2022. [Google Scholar]

  29. E. -S. M. El-Kenawy, H. F. Abutarboush, A. W. Mohamed and A. Ibrahim, “Advance artificial intelligence technique for designing double T-shaped monopole antenna,” Computers Materials & Continua, vol. 69, no. 3, pp. 2983–2995, 2021. [Google Scholar]

  30. R. Li, Z. Zhao, Y. Wei, X. Zhou and H. Zhang, “GM-PAB: A grid-based energy saving scheme with predicted traffic load guidance for cellular networks,” in Proc. of IEEE Int. Conf. on Communications (ICC), Ottawa, ON, Canada, pp. 1160–1164, 2012. [Google Scholar]

  31. N. K. Hoong, P. K. Hoong, I. K. T. Tan, N. Muthuvelu and L. C. Seng, “Impact of utilizing forecasted network traffic for data transfers,” in Proc. of the 13th Int. Conf. on Advanced Communication Technology (ICACT2011), Gangwon, Korea (Southpp. 1199–1204, 2011. [Google Scholar]

  32. P. K. Hoong, I. K. T. Tan and C. Y. Keong, “BitTorrent network traffic forecasting with ARMA,” International Journal of Computer Networks and Communications, vol. 4, no. 4, pp. 143–156, 2012. [Google Scholar]

  33. N. Sadek and A. Khotanzad, “Multi-scale high-speed network traffic prediction using k-factor gegenbauer ARMA model,” in Proc. of the IEEE Int. Conf. on Communications, Paris, France, pp. 2148–2152, 2004. [Google Scholar]

  34. Y. Yu, J. Wang, M. Song and J. Song, “Network traffic prediction and result analysis based on seasonal ARIMA and correlation coefficient,” in Proc. of the Network Traffic Prediction and Result Analysis Based on Seasonal ARIMA and Correlation Coefficient, Changsha, China, pp. 980–983, 2010. [Google Scholar]

  35. Y. Shu, M. Yu, J. Liu and O. W. W. Yang, “Wireless traffic modeling and prediction using seasonal ARIMA models,” in Proc. of the IEEE Int. Conf. on Communications, Anchorage, AK, USA, pp. 1675–1679, 2003. [Google Scholar]

  36. E. S. Yu and C. Y. R. Chen, “Traffic prediction using neural networks,” in Proc. of GLOBECOM ‘93. IEEE Global Telecommunications Conf., Houston, TX, USA, pp. 991–995, 1993. [Google Scholar]

  37. S. Chabaa, A. Zeroual and J. Antari, “ANFIS method for forecasting internet traffic time series,” in Proc. of the Mediterrannean Microwave Symp. (MMS), Tangiers, Morocco, pp. 1–4, 2009. [Google Scholar]

  38. A. Abdelhamid, E. M. El-Kenawy, B. Alotaibi, G. Amer, M. Abdelkader et al., “Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm,” IEEE Access, vol. 10, pp. 49265–49284, 2022. [Google Scholar]

  39. G. P. Zhang, “Time series forecasting using a hybrid ARIMA and neural network model,” Neurocomputing, vol. 50, pp. 159–175, 2003. [Google Scholar]

  40. J. Wang, Q. Gu, J. Wu, G. Liu and Z. Xiong, “Traffic speed prediction and congestion source exploration: A deep learning method,” in Proc. of the IEEE 16th Int. Conf. on Data Mining (ICDM), Barcelona, Spain, pp. 499–508, 2016. [Google Scholar]

  41. L. Li, L. Qin, X. Qu, J. Zhang, Y. Wang et al., “Day-ahead traffic flow forecasting based on a deep belief network optimized by the multi-objective particle swarm algorithm,” Knowledge-Based Systems, vol. 172, pp. 1–14, 2019. [Google Scholar]

  42. Y. Gu, W. Lu, L. Qin, M. Li and Z. Shao, “Short-term prediction of lane-level traffic speeds: A fusion deep learning model,” Transportation Research Part C: Emerging Technologies, vol. 106, pp. 1–16, 2019. [Google Scholar]

  43. Y. Gu, W. Lu, X. Xu, L. Qin, Z. Shao et al., “An improved Bayesian combination model for short-term traffic prediction with deep learning,” IEEE Transactions on Intelligent Transportation Systems, vol. 21, no. 3, pp. 1332–1342, 2020. [Google Scholar]

  44. H. Li, Y. Wang, X. Xu, L. Qin and H. Zhang, “Short-term passenger flow prediction under passenger flow control using a dynamic radial basis function network,” Applied Soft Computing, vol. 83, pp. 1– 13, 2019. [Google Scholar]

  45. E. S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

  46. A. Takieldeen, E.-S. M., El-kenawy, E. Hadwan and M. Zaki, “Dipper throated optimization algorithm for unconstrained function and feature selection,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1465–1481, 2022. [Google Scholar]

  47. S. Gowrishankar and P. Satyanarayana, “A time series modeling and prediction of wireless network traffic,” International Journal of Interactive Mobile Technologies (iJIM), vol. 3, no. 1, pp. 53–62, 2008. [Google Scholar]

  48. H. Rajabi, CRAWDAD Dataset, Dartmouth College, USA, 2022, [Online]. Available: https://doi.org/10.15783/08kw-7n74. [Google Scholar]

  49. E. -S. M. El-kenawy, A. Ibrahim, N. Bailek, B. Kada, M. Hassan et al., “Sunshine duration measurements and predictions in Saharan Algeria region: An improved ensemble learning approach,” Theoretical and Applied Climatology, vol. 147, pp. 1015–1031, 2022. [Google Scholar]

  50. A. Salamai, A. Ageeli and E. -S. M. El-kenawy, “Forecasting E-commerce adoption based on bidirectional recurrent neural networks,” CMC-Computers, Materials and Continua, vol. 70, no. 1, pp. 10.32604, 2021. [Google Scholar]

  51. M. Eid, E. -S. M. El-kenawy and A. Ibrahim, “A new hybrid video encryption technique based on chaos cryptography,” Journal of Computer Science and Information Systems, vol. 2, no. 2, pp. 1–8, 2021. [Google Scholar]

  52. E. -S. M. El-kenawy, M. Saber and R. Arnous, “An integrated framework to ensure information security over the internet,” International Journal of Computer Applications, vol. 178, no. 1, pp. 13–15, 2019. [Google Scholar]

  53. E. -S. M. El-kenawy, A. Ibrahim, S. Mirjalili, Y. Zhang, S. Elnazer et al., “Optimized ensemble algorithm for predicting metamaterial antenna parameters,” Computers, Materials & Continua, vol. 71, no. 1, pp. 4989–5003, 2022. [Google Scholar]