Efficient Resource Allocation Algorithm in Uplink OFDM-Based Cognitive Radio Networks

1  Introduction

This section describes research background, research gap, research objectives and the related works.

1.1 Background

According to the Federal Communications Commission (FCC), approximately 70% of the spectrum band is vacant in the USA [1,2]. Consequently, to meet the high demand for wireless spectrum bands, open spectrum access and CRs have been considered as a resourceful system to resolve the under utilization issue in the spectrum band. Hence, cognitive radio (CR) will be one of the best candidates for fifth-generation wireless networks (5G) to provide better spectrum utilization with respectable quality of service.

In CRNs, the problematic of resource allocation (RA) is important and has managed in many researches [3–7]. Moreover, the orthogonal frequency-division multiplexing (OFDM) multicarrier technique is considered a promising method for cognitive radio networks (CRNs) due to its consistency and flexibility in managing resources to CR users [8–10]. In the OFDM network, both CR and PU exist close to each other, which results in common interference, which is a preventive factor affecting the performance of both CRNs and PUNs [11].

The analogy between CRNs and the real market gives a strong motivation to adopt game and pricing scheme as a key to the problem of resource allocations in CRNs. Furthermore, Pricing-based game theory can be adopted to achieve good network performance in terms of rate maximization without harming the PUs. Moreover, adding pricing scheme to the resource allocation model resulted in simple mathematical optimization problem from which the optimal solution could be easily obtained [12]. However, the main challenge in adopting game and pricing scheme is to prove the point of equilibrium, i.e., Nash equilibrium (NE). In addition, how fast convergence to the NE is another challenge to consider to solve the problem of RA in a given scenarios, such as ad-hoc CRNs [13].

1.2 Related Works

Game and pricing theories are considered essential tools to resolve the problem of RA resourcefully with a lesser amount of complexity. Hence, game theory and pricing techniques are adopted to resolve the problem of RA in CR in a number of research papers, for example [14–25]. Optimal resource allocation problem-based noncooperative game theory in the uplink scenario was proposed in [14]. Noncooperative game model is adopted to enhance the performance of the uplink transmission in 5G network by maximizing the sum rate for an uplink scenario. However, the existence and uniqueness of the Nash equilibrium (NE) have been ignored in this research. Moreover, the convergence of the NE has been ignored. In [15], the authors proposed RA and power control in the device-to-device (D2D) uplink network using a coalitional game. Similar to [14], the authors ignored the analysis of the mathematical model regarding the Nash bargaining solution.

Joint channel allocation and pricing in CR multihoming networks using Stackelberg game was adopted in [16]. In this work, PU is considered to be the leader and takes the responsibility of setting the price of the channel, whereas the cognitive users are followers who are allocating the channel according to the price announced by the primary network. The interference analysis between cognitive radio and the primary network has been ignored in this work. Moreover, the pricing scheme is announced without any interference consideration, which makes the proposed network quite similar to the classical network where no secondary users exist.

A power control problem using pricing scheme in a CRN is proposed in [17]. Furthermore, super modular game is assumed to solve problem of power allocation, where price rate is announced individually by each user. Moreover, the pricing scheme is used as a metric to control and manage the generated interference. The convergence of the Nash equilibrium has been proved by simulation. However, the convergence to the NE is somewhat slow, and this is because of adopting a genetic algorithm rather than providing a close-form solution to the proposed problem. A resource allocation-based interference pricing scheme in a multiuser CRN was presented in [18]. In this setup, the PU controls transmission of cognitive radio and the related interference by a pricing scheme using a Stackelberg game. The key point of this work is to make the most of the revenue for the PU and maintain quality of service for CRs. Even though the work presented in this paper is solid, the solution of the NE was ignored.

Resource allocation algorithm using pricing scheme in vehicle-to-everything (V2X) communications in an uplink cellular network was developed in [19]. In the proposed algorithm, both vehicle users and cellular users share the same spectrum using Stackelberg-based pricing game theory. Although the proposed algorithm adopted pricing techniques, it was not used adequately to manage interference between different users. Thus, it is not certain how the proposed algorithm will perform in a real scenario. In [20], a novel algorithm was proposed to manage spectrum fragility in 5G networks where both certified and unlicensed bands are available to access. Furthermore, pricing has been adopted to manage the power of users in CR band with aim of controlling spectrum fragility. The solution of the presented algorithm to the NE was not obtained directly and was obtained via S-modular game theory, which might further increase the complexity of the proposed algorithm. Furthermore, the authors in [21] proposed an algorithm for power control using the Stackelberg game and pricing theory in a shared-spectrum cognitive radio network. However, a pricing function has been proposed to manage the profit of the primary users (PUs). Hence, it is not clear how the presented solution can be used to manage and control CR users to provide a better engagement environment.

The algorithm in [22] proposed a power control using a pricing scheme to reduce the interference in a D2D scenario. The power control algorithm in D2D is modeled using noncooperative game theory with a pricing scheme that offers efficient connectivity with slight power consumption. Although authors claim that the proposed pricing scheme helps reduce interference, there was no evidence in the results to prove that the proposed algorithm can be adopted to reduce interference between different wireless devices.

The authors in [23] adopted Stackelberg game theory based on pricing technique to provide a multi-mode channel sharing in 5G ad hoc network. Pricing technology has been adopted to facilitate the sharing and management of users’ access to spectrum. However, there is no evidence of convergence with the Nash equilibrium. Moreover, the pricing technique was formed to manage users’ access to the available spectra and not to reduce the complexity of the presented algorithm.

Software-defined network based on pricing Stackelberg game theory for 5G ad-hoc network has been proposed in [24]. Although the problem is appropriately formulated, the proposed pricing schemes do not reflect the real solution to the optimization problem in the V2V 5G network. Hence, the presented model is not appropriate for a real-world 5G application. Finally, power allocation in underlay CR non-orthogonal multiple access (NOMA) scheme using game and pricing scheme is proposed in [25]. The mathematical model is properly formulated to attain effective power control and reduce interfering PUs. However, the computational complexity has been ignored and no evidence shown of how efficient of the presented algorithm in real scenarios and practical implementation.

The motivational question that arises at this point is how to adopt a pricing scheme to provide flexibility in resource allocation in an uplink cognitive radio scenario and make the scenario more suitable for practical applications. This gap has not been answered in previous work and is carefully addressed in this paper to allocate resources efficiently. The main objective is to offer quality of service to cognitive radios while maintain the interference limit to the primary user. Furthermore, the main contribution of this work is the adoption of pricing scheme to attain two objectives: (i) reducing the difficulty of the presented optimization model and (ii) offering flexibility in managing interference produced to primary user. Moreover, for simulation verification, the results have been compared with [26,27], and [28].

The rest of this work is organized like so. Section 2 describes setup of CR network that has been developed, including network setting and interference calculation. An optimization problem is formulated in Section 3. In Section 4, the uplink-pricing model is modeled, including managing of subcarrier algorithm, price-power control, and solution of the NE. A comparison study and simulations of the presented algorithm are described in Section 5. Finally, the conclusion of this paper presented in Section 6.

2  System Model

This section defines the system model, which includes description of uplink CR scheme setting and description of the interference mathematical models.

2.1 Setting of the OFDM-CRN Uplink

In this work, the OFDM-based CR network was assumed to exist with a PUN in uplink spectrum-sharing scenario, as given in Fig. 1a. Moreover, side-by-side frequency allocation is considered among cognitive radio users, CRs, and PUs, where the bandwidth is divided into N-subcarriers, as displayed in Fig. 1b.

Figure 1: System setup: (a) CR and PU deployment scenario and (b) active and inactive bands

Furthermore, B1PU,B2PU,…,BρPU is the frequency band occupied by ρ primary user in which M-CR users can occupy it such that the interference does not exceed the interference threshold, (Intth). Additionally, gm−ρ,ic is defined as the channel gain between the mth CR and ρth PU on the ith subcarrier, and the gain of link among the ρth PU and the mth CR is symbolized by χρ−m,i. Note that the superscripts (c) indicate cognitive radio users. Furthermore, the solid line in Fig. 1a is the intended communication link and the dashed line in the interference link from CRs to the PUs.

2.2 Model of Interference

2.2.1 Interference on the PUs

To achieve fair sharing among CR users and the users of the primary network, the interference should be well defined to prevent any deficiency in the quality of the primary network. Let ϑi(f) be the power spectral density (PSD) of the ith subcarrier, which was formulated along the lines of [29,30].

ϑi(f)=pi,mT(sin⁡πfTπfT)(1)

where pi,m is the overall power generated by the mth CRs on the ith subcarrier. The interference produced by cognitive users to the primary user can be described as follows:

Definition 1: The interference produced to the ρth PU from the mth CR on a particular subcarrier, ith, symbolized by Im,iPUρ(diρ,pi,m), can be defined as the integration of the ϑi(f) through the ρth primary user, which is formulated according to [29].

Im,iPUρ(diρ,pi,m)=Pi,mΩi,mρ;Ωi,mρ=∫di−Bρ/2di+Bρ/2|gm−ρ,ic|2∗ϑi(f)df(2)

where diρ & Ωi,mρ are the spacing and interference factors among the ith subcarrier and the ρth PU’s band.

2.2.2 Interference with the CRs

The generated interference from primary user to cognitive radio can be defined accordingly:

Definition 2: The interference produced by the  ρth  PU to the mth cognitive user, indicated by Iρ,iCRm, can be modeled as the integration of the ϑi(f) of the ρth primary user, which is given in (3) [29].

Iρ,iCRm(diρ,Pρ)=∫diρ−Δf2diρ+Δf2|χρ−m,i|2∗ϑi(f)df(3)

3  Problem Formulation

This work attempts to manage the problem of RA in OFDM-CRN in an uplink scenario involving power and subcarrier allocation. Furthermore, a mathematical model is defined in this section, and pricing techniques are adopted to model the problem of protecting the primary users by addressing the interference presented by CRs. Hence, interference and power model can be expressed according to definitions 3 and 4.

3.1 Interference and Power Consideration

Assume that Intth is the interference threshold for the PUs and P~m is the maximum transmission power for the mth CR, which is assumed constant across CR users. Hence, the constraint of interference and power can be defined according to definitions 3 and 4.

Definition 3: total interference on the ρth PU can be formulated according to (4). That means that each primary user in the given scenario can receive a certain level of interference from neighbor subcarrier that been occupied by cognitive radio, which is less than the threshold limit, Intth. That is,

∑m=1M∑i=1Nsi,mpi,mΩi,mρ≤Intth,∀ρ∈{1,2,…,ρ}(4)

Definition 4: Assume that the local power limit for each CR is P~m. Therefore, the total power constraint for the CRs is formulated as follows:

∑i=0NSi,mpi,m≤Pm~(5)

where si,m=1 if CR occupied the ith subcarrier and si,m=0 otherwise.

3.2 Mathematical Model

Assume that pi,m is the power of the mth CR on the ith carrier. Hence, the signal-to-interference ratio, abbreviated as SINR, is modelled as follows:

γim=pi,m|hi,m|2δAWGN+∑ρ=1ρIρ,iCRm=pi,m|hi,m|2ITot(6)

where δAWGN is the mean variance of the Gaussian noise and ITot represent the total interference that can be formulated according to (7).

ITot=δAWGN+∑ρ=1ρIρ,iCRm(7)

Furthermore, the interference factor from the primary user to cognitive users, (Il,iCRm), is considered the superposition of a large number of independent random variables, ∑ρ=1ρIρ,iCRm. Thus, with the help of the central limit theorem, (Iρ,iCRm) is presented as additive white Gaussian noise (AWGN). Consequently, transmission rate of the mth cognitive user on the ith subcarrier is defined according to (8).

Rim=Δflog2⁡(1+γim).(8)

Maximizing the transmission rate of the network is the primary objective of the optimization problem, and this can be done by considering the interference generated to the PU and the per-CR power constraint as defined in Eqs. (4) and (5), respectively. Hence, the optimization problem in the uplink scenario is modeled according to (P1).

P.1:maxpi,m(Rim),

s.t.

{C1:si,m∈{0,1},∀i,m,C2:∑m=1Msi,m≤1,∀i,C3:∑m=1M∑i=1Nsi,mpi,mΩi,mρ≤Intth∀ρ∈{1,2,…,ρ},C4:∑i=1Nsi,mpi,m≤P~m,∀mC5:pi,m≥P¯m,(P.1)

The inequality subcarrier constraint, C2 in (P.1), means that the subcarrier should be occupied by only one CR. Moreover, the last constraint, C5, refers to the minimum power constraint. Furthermore, (P.1) is mixed-integer optimization mathematical model, which is a nondeterministic polynomial (NP)-hard problem. Therefore, in the following section, an appropriate solution will be provided by adopting a pricing model.

4  Uplink Price Model

As an alternative approach to the optimal algorithm, the RA problem is resolved according to the following stages:

1.    Cost function formulation: In this stage, the cost function is the rate maximization subtracted from the pricing scheme.

2.    Subcarrier allocations (SAs): In this stage, the suboptimal algorithm will be adopted to allocate subcarriers to CRs.

3.    Uplink-Price power allocation (UPPA): In this stage, a power-based pricing algorithm will be evaluated.

Therefore, the RA problem is achieved by decomposing the mathematical model, (P.1), into two sub-problems: the SA problem and the UPPA problem, as presented in the following subsections.

4.1 Subcarrier Allocation Algorithm

In a downlink OFDM scenario, the optimal subcarrier allocation is attained by assigning subcarrier to users holding maximum SINR as shown in [31]. However, this method is not effective in CR-uplink scenario due to per-user power constraints. In addition, subcarrier allocation method adopted in the classical uplink-based multicarrier network is not efficient for the CRN scenario because the interference generated from CRs to the users of the primary network does not exist in the classical uplink scenario. Consequently, to obtain an effective SA in an uplink scenario, the adopted algorithm should assign subcarriers by considering each user’s power, channel quality, and interference. Hence, the algorithm presented in [26] is implemented in this paper. However, a simple modification has been made to the adopted algorithm to make it compatible with the UPPA algorithm. The subcarrier algorithm is described in Table 1. However, the proposed SA in this work is obtained with no concern for minimum rate constraints. Thus, the U set is expected to always be an empty set, and there is no constraint in assigning the subcarriers to any user.

4.2 Uplink Price Power Allocation (UPPA)

UPPA can be decomposed into two subproblems: the subcarrier is allocated to cognitive users in the first stage, and price-based power assignment is developed in the second subproblem. More specifically, UPPA can be defined as follows:

Definition 5: The uplink-price power allocation problem denoted as UPPA is made up of three components as follows:

UPPA⟨M, {aiction},{Sc(⋅)}⟩

where M={1,2,…,M} is the set of cognitive radios in CRN or decision-makers, {aiction} is the action space, and Sc(⋅) is the cost function. Assume that the power strategy for cognitive users is a compact convex bounded set with maximum and minimum power stated by P^i,m=[P¯m,P~m]. Note that the minimum power for all CRs is assumed to be zero, that is, P¯m=0.

The pricing scheme in this paper, compared to the others, has been inserted into the mathematical model to provide flexibility in managing the interference generated from CRs to the users of the primary network. Moreover, this flexibility provides a better implementation of CRs in a more practical scenario where many CRs can share the available spectrum with PUs without exceeding the interference threshold.

4.3 Design of the Cost Function

The transmission rate is one of the common utility functions adopted in market theory. Moreover, the cost function can be stated according to definition 7.

Definition 7: The cost function in UPPA is the action chosen by decision-maker m and the actions chosen by all decision-makers in the network except those of decision-maker m. Mathematically speaking, the cost function is modeled as shown below:

Si,mc(pi,m,p−i,m)=∑i=1Nlog2⁡(1+γimIiTot)−pim∑l=1LαlΩi,ml(13)

where αl is the pricing factor that manages and address the interference level. Consequently, the pricing factor is adopted to facilitate solving (P.1) by ignoring the interference constraint, C3, and letting αl in (13) manage and address the interference to PUs. Hence, by adopting the cost function, (P.1) can be remodeled as shown below.

P.2:maxp^i,m(Si,mc),

s.t.

{C1:∑i∈Nmp^i,m≤P~m,∀mC2:p^i,m≥P¯m,∀i(P.2)

where m in p^i,m indicates a cognitive user with assigned subcarrier i, i.e., si,m=1, and Nmindicates the subcarriers that are given to the mth CR. Moreover, the optimal solution for (P.2) can be easily designed because the resulting optimization problem, P.2, is a convex optimization problem. Furthermore, the solution of (P.2) can be defined by Theorem 1.

Theorem 1: The Nash equilibrium (NE) exists in the optimization problem if the below conditions are satisfied:

1)   P^i,m, is closed and bounded convex set.

2)   Si,mc(⋅), the cost function, is a concave function.

Proof: The first conditions can be easily established because P^i,m in (13) is modelled by the maximum and minimum power.

Then, the second condition in Theorem 1 can be secured by following Lemma 1.

Lemma 1: The cost function defined in (13) is a concave function.

Proof: following set of equations must be solved: ∂2Si,mc∂2pim<0. This gives

∂2Si,mc∂2pim=−|hi,m|2(ITot+pi,m|hi,m|2)2<0.

This result proves the presence of the NE in the proposed UPPA since both conditions in Theorem 1 were proven.

4.4 Power Allocation Algorithm

The proposition below is used to derive the UPPA.

Proposition 1: If the mathematical problem in (P.2) is adopted to allocate power to subcarriers, then the power algorithm is modeled according to (14).

p^i,m=[1∑m=1Mβuser+∑ρ=1ραlΩi,mρ−Itotal|hi,m|2]+(14)

Proof: The optimal solution for (P.2) is derived by adopting the Lagrange method. Therefore, the Lagrange function is solved, as shown below:

Γ(p^i,m)=∑i=1Nlog2⁡(1+p^i,m|hi,m|2ITot)−p^i,m∑l=1ραlΩi,mρ−∑m=1Mβm(∑i=1Np^i,m−P~)+∑i=1Np^i,mλi(15)

Moreover, the Karush–Kuhn–Tucker (KTT) conditions can be formed according to (16).

p^i,m≥P¯,∀i∈{1,2,…,N},βm≥0,∀m∈{1,2,…,M},λi≥0∑m=1Mβm(p^i,m−P~)=0,βip^i,m=0,∀i∈{1,2,…,N}(16)

where β and λ are Lagrange multipliers.

By applying the partial derivative to (15) with respect to p^i,m, the result is equal to zero. The optimal solution can be simplified as follows:

∂Γ∂p^i,m=(ITot(ITot+p^i,m|hi,m|2)∗ITot|hi|2(ITot)2−∑ρ=1ραlΩi,mρ+∑m=1Mβm=0(17)

Rearranging (17), the optimal solution can be defined according to (18).

p^i,m=[1∑m=1Mβm+∑ρ=1ραlΩi,mρ−ITot|hi,m|2]+(18)

where [⋅]+=max(0,⋅). Note that there is one Lagrange multiplier, (βm), in (18) compared to two Lagrange multipliers in some related works in the literature. Hence, the complexity of the optimal solution is reduced, which is one of the benefits of adoption of the pricing scheme in this work. The Lagrange multiplier in (18) is derived for each CR user. This is due to the per-user power constraint available in uplink scenario. Hence, βm can be modeled by substituting (18) into constraint C1 in (P.2), i.e., C1:∑i=1Np^i,m≤P~m. Hence,

∑i=1N[1∑m=1Mβm+∑ρ=1ραlΩi,mρ−ITot|hi,m|2]=P~m(19)

To facilitate the calculation of (19), the interference component Ωi,mρ has been replaced by the average interference component (Ωavg). Therefore, (19) can be reformulated according to (20).

|N|∑m=1Mβm+∑ρ=1ραlΩavg−∑i=1N(ITot|hi,m|2)=P~m(20)

For the sake of description clarity, if ∑m=1Mβm=mβuser and substituting it into (20), we have

|N|mβuser+∑ρ=1ραlΩavg−∑i=1N(ITot|hi,m|2)=P~m(21)

By rearranging (21), the Lagrange multiplier (βuser) can be formulated according to (22).

βuser=m|N|ψρ(P~m+∑i=1NITot|hi,m|2)−∑l=1LαlΩavgm(22)

where ψρ is a controlling component that compensates for replacing the interference factor with the average interference factor and is modeled as follows: ψρ=∑i=1N(Ωi,mρITot|hi,m|2)+Intth. Hence, the UPPA algorithm is reformulated by including the summation of the Lagrange multiplier for all CRs, that is,

p^i,m=[1∑m=1Mβuser+∑l=1LαlΩi,mρ−ITot|hi,m|2]+(23)

Furthermore, the UPPA procedure is shown in Table 2, and the details of the UPPA are described according to the following stages:

a)   Definition stage: Parameters related to UPPA are defined, which include N,M,P~m,P¯m,αl,Ωi,ml,ITot.

b)   Power-allocation stage: The available powers must be distributed to the subcarriers by adopting the pricing technique. The optimal solution to UPPA is obtained by resolving (P.2), that is,

P.2:maxp^i(Si,mc),

s.t.{C1:∑i=1Np^i,m≤P~m,∀m∈{1,2,…,M}C2:p^i,m≥P¯m∀i∈{1,2,…,N}

c)   Respecting Interference Constraint: The interference constraint related to the PUs is respected and managed by adopting the pricing factor. This results in flexible management of the interference to the primary user. In this step, the interference constraint should be respected, that is, ∑i=1Np^i,mΩi,mρ≤Intth.

Furthermore, the flowchart of the proposed UPPA algorithm is shown in Fig. 2.

Figure 2: Subcarriers and power allocation in an uplink scenario

5  Performance Analysis

The simulation setting and results are defined and presented in this section. Moreover, the results have been compared with the PI algorithm, Wang algorithm, and GC-NPGP algorithm.

5.1 Simulation Setting

The CRN consists of five CRs, i.e., M = 5, with N = 32 as a total number of subcarriers. Subcarrier bandwidth is represented by Δf and δAWGN is the mean variance of the AWGN. Moreover, the simulation settings are provided in Table 3.

Intth1 and Intth2 are interference thresholds for the PUs. Furthermore, the fading gain, g and y, is considered to be the outcome of (i.i.d) Rayleigh distributed random variables with a mean equal to one. Further, simulation results have been averaged over one thousand (1000) iterations.

5.2 Performance Analysis & Comparison

The simulation setup is defined according to the network scenario presented in Fig. 2. Moreover, two active bands, PU, and two interference thresholds are assumed, that is, L = 2; B1PU=B2PU are the bandwidth of the PUs and  Intth1=Intth2 in an underlay spectrum sharing, as shown in Fig. 3. Therefore, the CR users are allowed to occupy both active and inactive licensed bands while observing respect to the specified interference limit (Intth1 and Intth2).

Figure 3: Spectrum-band distribution

Moreover, the proposed UPPA algorithm is compared with the following related uplink algorithms:

1)   Wang Algorithm [27]: In the Wang algorithm, the subcarriers are assigned to the users with the best channel quality. The preliminary assignment is adjusted when the subcarriers are assigned to different CR users using an improved water-filling algorithm that adopts the interference temperature constraints.

2)   PI Algorithm [26]: Power interference algorithm. In the PI algorithm, the subcarriers are assigned using Algorithm 1. Additionally, the power is assigned to subcarriers using three steps as follows: (i) an interference-based water-filling algorithm, (ii) CAP-limited water-filling [32], and (iii) a power level readjustment step.

3)   GC-NPGP Algorithm [28]: the proposed algorithm in this work assigns power using noncooperative game model with pricing scheme. The cost function contains exponential pricing factor and a linear pricing factor with a fixed pricing component to assign power to the users of CRN. Linear pricing with a fixed pricing component is adopted from [28] to ensure a fair evaluation with the proposed UPPA.

Note that the main idea behind the Wang algorithm compared to the PI algorithm and the proposed UPPA is that the Wang algorithm adopted the interference temperature instead of the defined interference threshold as a metric to quantify the generated interference to PUs. Moreover, the pricing scheme is included in the UPPA algorithm to simplify the optimization model, (P.1), which is a unique contribution to the proposed algorithm. Fig. 4 shows the achieved capacity for the CR network vs. the interference threshold, Intth1=Intth2. The overall rate increases as the interference limit increases. This is because each user has flexibility to assign more power to their subchannels. Moreover, the performance of the UPPA algorithm outperforms that of the Wang algorithm and the PI algorithm.

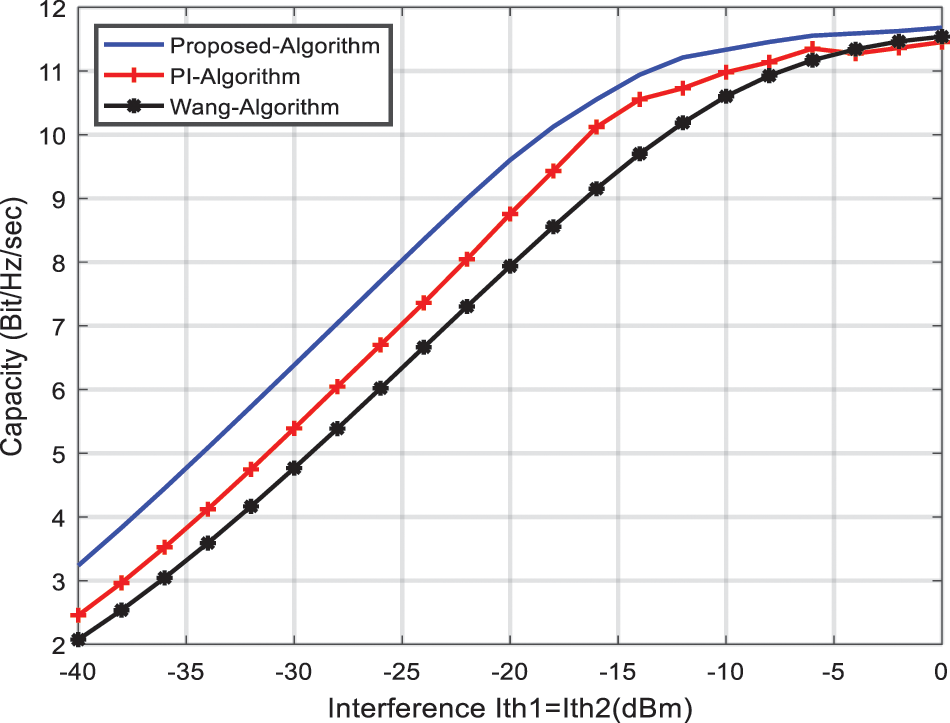
Figure 4: Achieved capacity with interference limit

The overall interference produced to the primary user by considering the UPPA, Wang algorithm, PI algorithm, and GC-NPGP algorithm with Intth1=Intth2  is illustrated in Figs. 5 and 6.

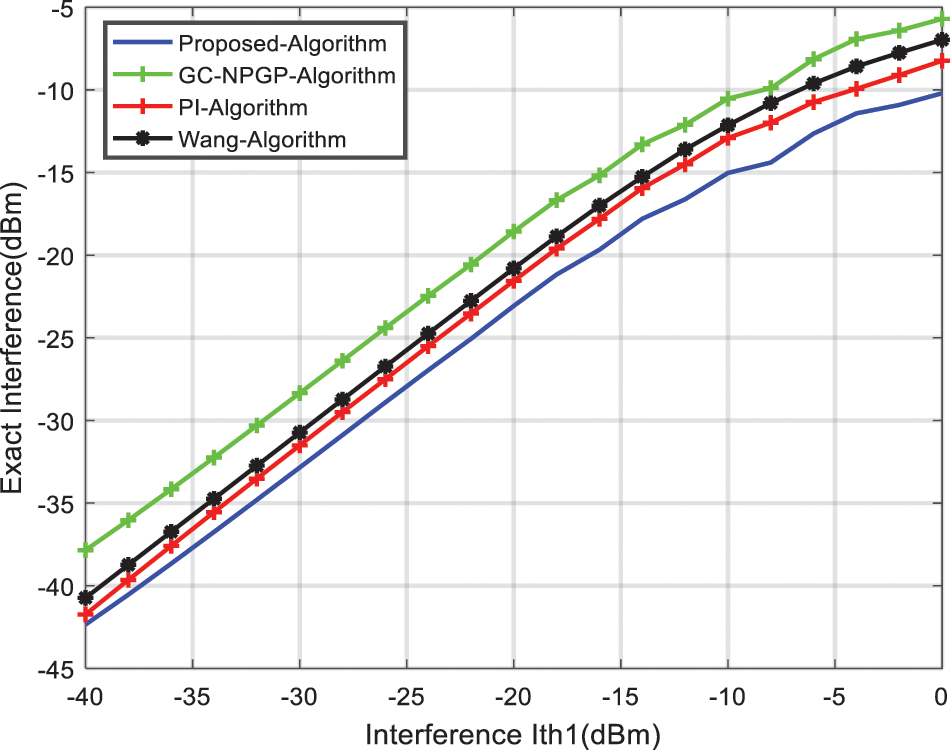
Figure 5: Interference produced to PU (Intth1)

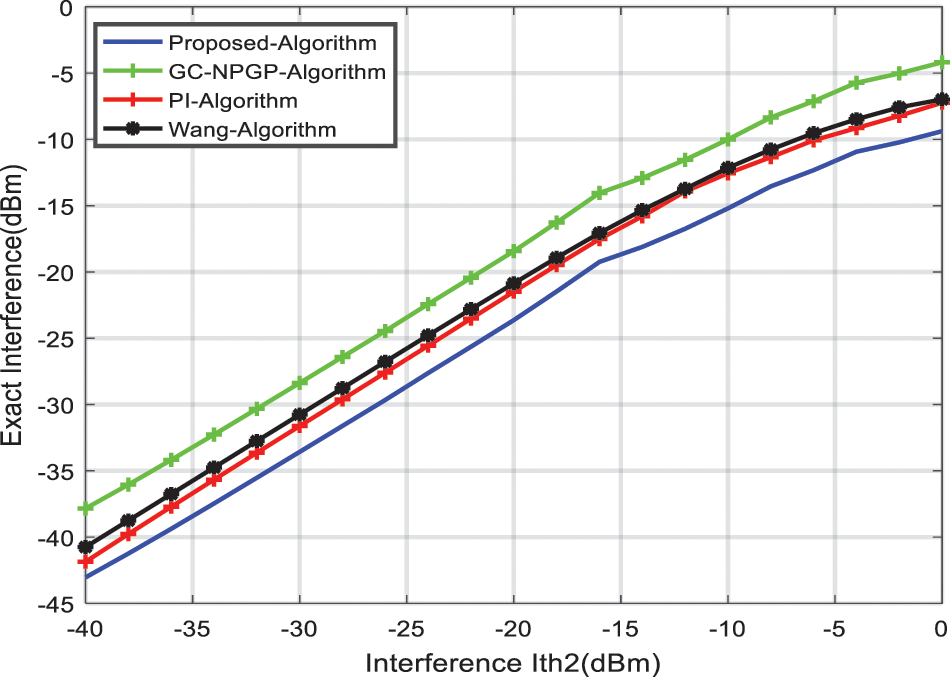
Figure 6: Interference produced to PU (Intth2)

The net interference using the proposed UPPA meets the predetermined interference limits in bands B1PU and B2PU. Furthermore, adopting a pricing scheme in the UPPA algorithm offers more freedom with regard to interference management than that in the PI algorithm, Wang algorithm, and GC-NPGP algorithm. The flexibility in interference management is demonstrated by changing the pricing factor and examining the interference to the primary users in both active bands.

It can be noted that by raising the pricing cost, the interference to the PUs decreases, and by reducing the pricing factor, the interference to the primary users increases, as presented in Figs. 7 to 10. In the PI algorithm and Wang algorithm, in contrast, the parameters are predefined in the power algorithm, which results in unchanging interference components regardless of the value of the interference threshold. For this reason, the UPPA algorithm can be implemented in various scenarios that have various interference thresholds, and this makes the UPPA algorithm more appropriate in terms of respecting different interference thresholds for several primary network providers.

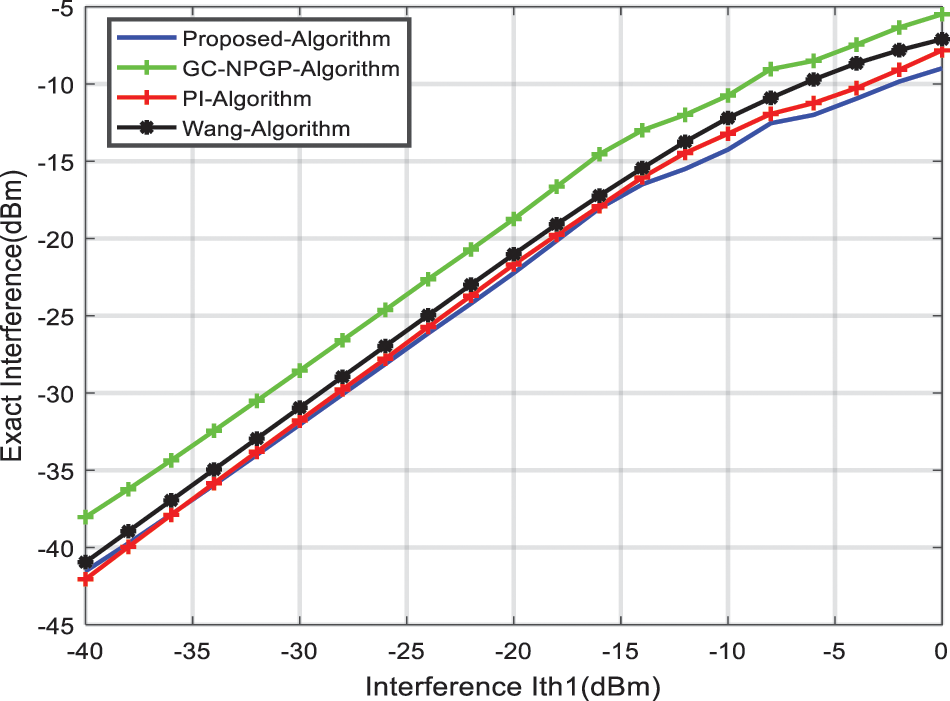
Figure 7: Interference to the PU (Intth1) by decreasing the pricing factor

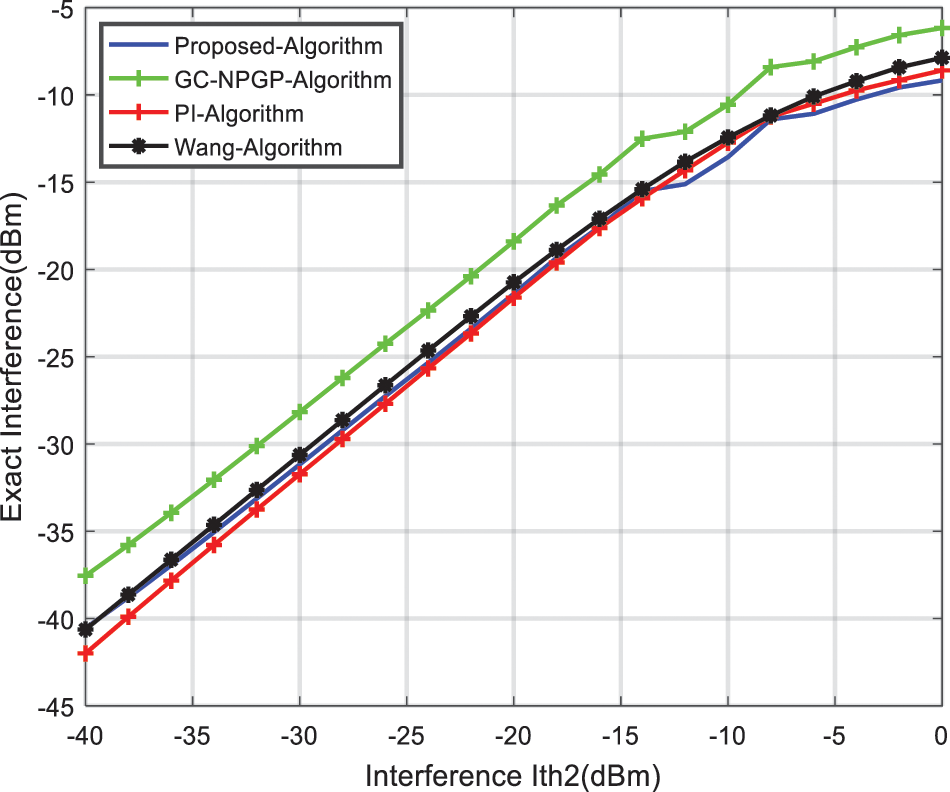
Figure 8: Interference threshold of the PU (Intth2) by decreasing the pricing factor

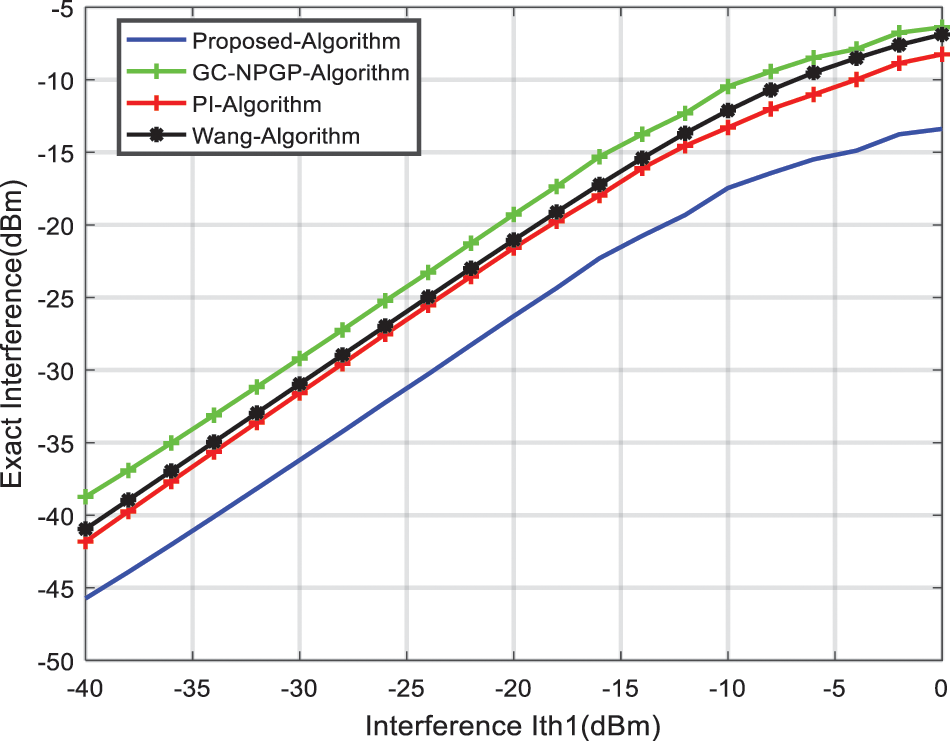
Figure 9: Interference threshold of the PU (Intth1) by increasing the pricing factor

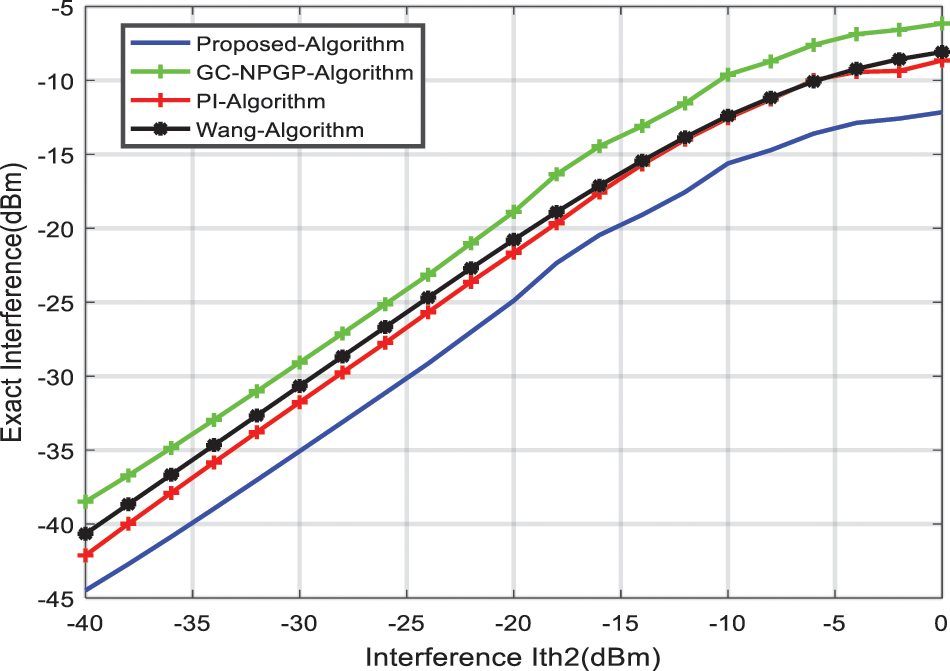
Figure 10: Interference threshold of the PU (Intth2) by increasing the pricing factor

Furthermore, in Figs. 11 and 12, the number of CRs is increased from M = 5 CRs to M = 10 CRs, and the interference constraints are tested accordingly.

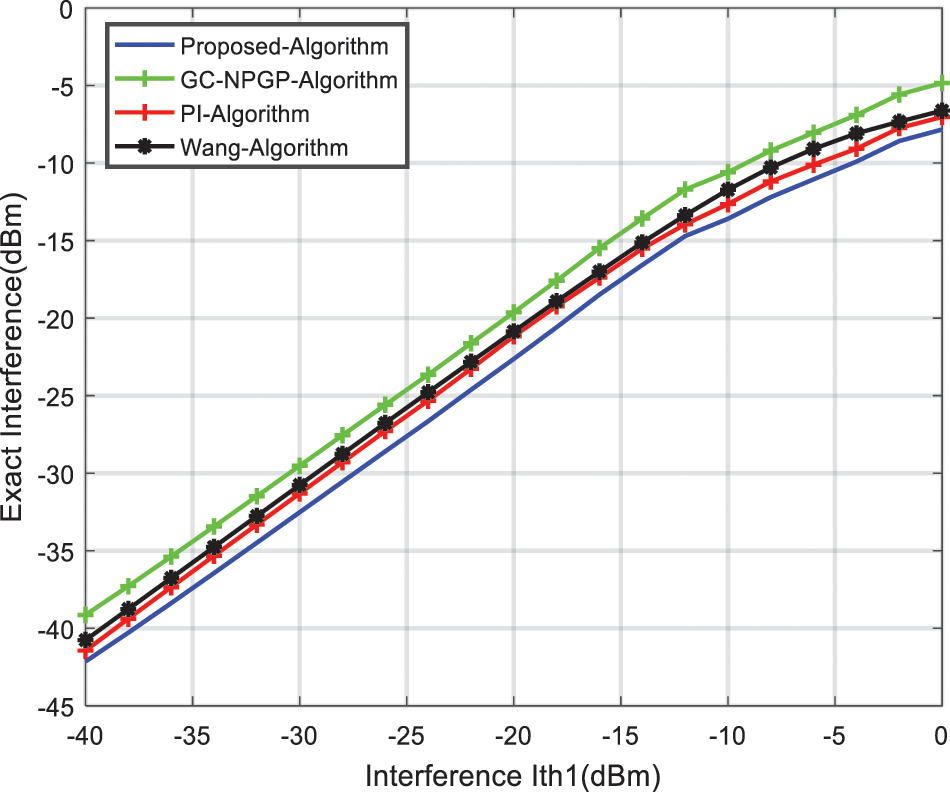
Figure 11: Interference to PU (Intth1) for M = 10

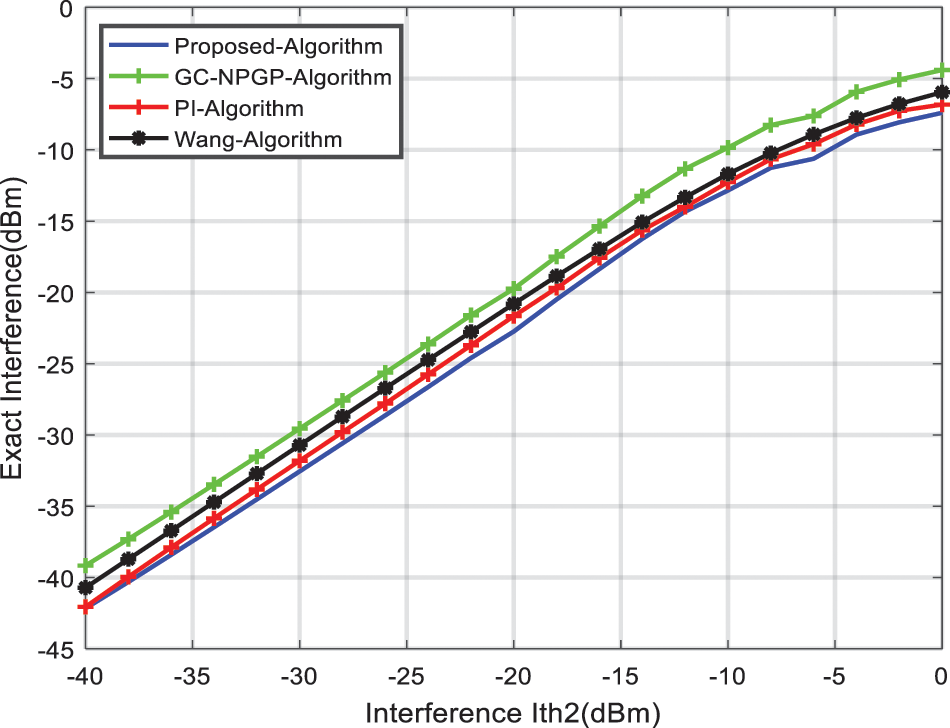
Figure 12: Interference to PU (Intth2) for M = 10

Both interference constraints, Intth1=Intth2, for both bands have been respected as well, and there is no violation for the whole range of the given interference. Hence, the UPPA algorithm can be implemented in more practical scenarios where more secondary users try to access the licensed band for the purpose of spectrum utilization improvement.

6  Computational Complexity

Recall that the optimization problem has been solved in two stages: subcarriers to CR allocation conducted in the first stage and the power allocation in the second stage. Hence, the complexity of the first stage can be found by considering the overall number of cognitive radios, M, and subcarriers, N. Note that each subcarrier requires a maximum of M rounds to be allocated to one user. Hence, the computational complexity is O(NM). Moreover, the proposed UPPA needs one operation of the water-filling power algorithm because the interference constraint was ignored by considering the pricing scheme. Hence, the complexity for the second stage, UPPA, is similar to that in conventional water-filling, which is O(Nlog(N)).

Therefore, the overall computational complexity, comptot, can be formulated according to (24).

Comptot=comp. of (stage_1 (SA)+stage_2(UPPA))(24)

By following Eq. (24), the overall complexity is O(NM) + O(Nlog(N)). Furthermore, Table 4 shows a summary of the computational complexity of the presented algorithms in this work.

The proposed pricing scheme provides flexibility in managing and controlling overlaps of PUs in central CRNs. However, the main limitation of the proposed mathematical model using a pricing scheme is its inefficiency in a distributed manner whereby cognitive users take an independent action to allocate resources. Hence, a combination of game theory and evolutionary algorithms is required to allocate resources that will further complicate the algorithm.

7  Conclusion

In this work, a price-based power allocation in an uplink CRN termed UPPA has been proposed. The pricing scheme has been adopted to manage the produced interference from the CRs to the PUs, on the one hand, and to simplify the optimization problem by relaxing some constraints, on the other hand. Moreover, the mathematical problem is an NP-hard problem, and the problem has been solved using two steps: the subcarrier is assigned in the first step, and the power is allocated in the second step. Furthermore, the computational complexity of the proposed algorithm was O(NM) + O(Nlog(N)). Compared to the complexity of the optimal algorithm, i.e., O(N3MN), the proposed UPPA algorithm provides lesser computational complexity.

Acknowledgement: Authors would like to thank The American University of Kurdistan and King Khalid University for their kind support.

Funding Statement: Authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Groups Project under Grant Number RGP.2/111/43. Furthermore, Musbah Shaat work was supported in part by the Agencia Estatal de Investigación, Ministerio de Ciencia e Innovación (MCIN/AEI/10.13039/501100011033) through the R + D + i Project under Grant PID2020-115323RB-C31; and in part by the Grant from the Spanish Ministry of Economic Affairs and Digital Transformation and the European Union-NextGenerationEU under Grant UNICO-5G I + D/AROMA3D-Hybrid TSI-063000-2021-71.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. F. Zhou, Z. Chu, H. Sun, R. Q. Hu and L. Hanzo, “Artificial noise aided secure cognitive beamforming for cooperative miso-noma using swipt,” IEEE Journal on Selected Areas in Communications, vol. 36, no. 36, pp. 918–931, 2018. [Google Scholar]

2. Z. Chu, F. Zhou, Z. Zhu, R. Q. Hu and P. Xiao, “Wireless powered sensor networks for internet of things: Maximum throughput and optimal power allocation,” IEEE Internet of Things Journal, vol. 5, no. 1, pp. 310–321, 2018. [Google Scholar]

3. Z. Yang, W. Jiang and G. Li, “Resource allocation for green cognitive radios: Energy efficiency maximization,” Wireless Communications and Mobile Computing, vol. 2018, no. 5, pp. 1–16, 2018. [Google Scholar]

4. W. Shaowei, G. Mengyao and Z. Wentao, “Energy-efficient resource allocation for ofdm-based cognitive radio networks,” IEEE Transactions on Communications, vol. 61, no. 8, pp. 3181–3191, 2013. [Google Scholar]

5. X. Gong, A. Ispas, G. Dartmann and G. Ascheid, “Outageconstrained power allocation in spectrum sharing systems with partial csi,” IEEE Transactions on Communications, vol. 62, no. 2, pp. 452–466, 2014. [Google Scholar]

6. H. Xu, H. Gao, C. Zhou, R. Duan and X. Zhou, “Resource allocation in cognitive radio wireless sensor networks with energy harvesting,” Sensors, vol. 19, no. 23, pp. 5115, 2019. [Google Scholar] [PubMed]

7. C. Sun, B. Zhang, W. Zheng and J. Shu, “Price learning in joint resource allocation and power control game in heterogeneous cellular networks,” in IEEE Int. Conf. on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking, Exeter, United Kingdom, pp. 1354–1358, 2020. [Google Scholar]

8. I. Budiarjo, H. Nikookar and L. P. Ligthart, “Cognitive radio modulation techniques,” IEEE Signal Processing Magazine, vol. 25, no. 6, pp. 24–34, 2008. [Google Scholar]

9. B. Farhang-Boroujeny and R. Kempter, “Multicarrier communication techniques for spectrum sensing and communication in cognitive radios,” IEEE Communications Magazine, vol. 46, no. 4, pp. 80–85, 2008. [Google Scholar]

10. A. Salman, I. M. Qureshi, S. Saleem and S. Saeed, “Optimization of resource allocation for heterogeneous services in ofdm based cognitive radio networks using artificial bee colony,” in Int. Symp. on Recent Advances in Electrical Engineering (RAEE), Islamabad, Pakistan, pp. 1–5, 2019. [Google Scholar]

11. M. Shaat and F. Bader, “Computationally efficient power allocation algorithm in multicarrier-based cognitive radio networks: Ofdm and fbmc systems,” EURASIP Journal on Advances in Signal Processing, vol. 2010, pp. 1–13, 2010. [Google Scholar]

12. O. Abdulghafoor, M. Ismail, R. Nordin and M. M. R. Shaat, “Resource allocation in multiuser multi-carrier cognitive radio network via game and supermarket game theory: Survey, tutorial, and open research directions,” KSII Transactions on Internet and Information Systems Journal, vol. 8, pp. 3674–3710. 2014. [Google Scholar]

13. O. Abdulghafoor, M. Ismail, R. Nordin and M. M. R. Shaat, “Fast and distributed power control algorithm in underlay cognitive radio networks,” Journal of Communicaitons, vol. 9, pp. 634–643, 2014. [Google Scholar]

14. A. Mudassir, S. A. Hassan, H. Pervaiz, S. Akhtar and H. Kamel, “Game theoretic efficient radio resource allocation in 5G resilient networks: A data driven approach,” Transactions on Emerging Telecommunications Technologies, vol. 30, no. 8, pp. e3582, 2019. [Google Scholar]

15. Y. Sun, F. Wang and Z. Liu, “Coalition formation game for resource allocation in D2D uplink underlaying cellular networks,” IEEE Communications Letters, vol. 23, no. 5, pp. 888–891, 2019. [Google Scholar]

16. L. Xu, “Joint spectrum allocation and pricing for cognitive multi-homing networks,” IEEE Transactions on Cognitive Communication and Network, vol. 4, no. 3, pp. 597–606, 2018. [Google Scholar]

17. A. Abdelaziz Salem and M. Shokair, “Game theoretic utility optimization based power control on cognitive sensor network,” in 34th National Radio Science Conf. (NRSC 2017), Port Said, Egypt, pp. 294–300, 2017. [Google Scholar]

18. B. Ning, G. Sun, J. Li, A. Zhang, W. Hao et al., “Resource allocation in multi-user cognitive radio network with stackelberg game,” IEEE Access, vol. 2020, no. 8, pp. 58260–58270, 2020. [Google Scholar]

19. Y. Cheng and Y. Zhao, “Price-based resource allocation scheme for v2x communications underlying uplink cellular network,” in 7th Annual Int. Conf. on Network and Information Systems for Computers (ICNISC), Guiyang, China, pp. 801–806, 2021. [Google Scholar]

20. P. Vamvakas, E. E. Tsiropoulou and S. Papavassiliou, “On controlling spectrum fragility via resource pricing in 5G wireless networks,” IEEE Networking Letters, vol. 1, no. 3, pp. 111–115, 2019. [Google Scholar]

21. X. Bai, C. Zhao, L. Guan and W. Dao, “Cognitive radio optimal price power control algorithm based on stackelberg game,” in Int. Conf. on Wireless Communications and Smart Grid (ICWCSG), Hangzhou, China, pp. 367–372, 2021. [Google Scholar]

22. A. Saif, K. Noordin, K. Dimyati, N. Shahida, Y. Ali et al., “An efficient game theory-based power control algorithm for D2D communication in 5G networks,” KSII Transactions on Internet and Information Systems, vol. 15, no. 7, pp. 2631–2649, 2021. [Google Scholar]

23. B. Qian, H. Zhou, T. Ma, Y. Xu, K. Yu et al., “Leveraging dynamic stackelberg pricing game for multi-mode spectrum sharing in 5G-VANET,” IEEE Transactions on Vehicular Technology, vol. 69, pp. 6374–6387, 2020. [Google Scholar]

24. A. Alioua, S. Simoud, S. Bourema, M. Khelifi, S. M. Senouci et al., “A stackelberg game approach for incentive V2V caching in software-defined 5G-enabled VANET,” in IEEE Symp. on Computers and Communications (ISCC), Rennes, France, 2020. [Google Scholar]

25. S. Abidrabbu and H. Arslan, “Efficient power allocation for cognitive radio NOMA using game-theoretic based pricing strategy,” in IEEE 93rd Vehicular Technology Conf. (VTC2021-Spring), Helsinki, Finland, 2021. [Google Scholar]

26. M. Shaat and F. Bader, “Efficient resource allocation algorithm for uplink in multicarrier-based cognitive radio networks with fairness consideration,” IET Communications, vol. 16, no. 5, pp. 2328–2338, 2011. [Google Scholar]

27. W. Wang, W. Wang, Q. Lu and T. Peng, “An uplink resource allocation scheme for ofdma-based cognitive radio networks,” International Journal of Communication Systems, vol. 22, no. 5, pp. 603–623, 2009. [Google Scholar]

28. F. Mukhlif, N. Ithnin, O. B. Abdulghafoor, F. Alotaibi and N. Saad Alotaibi, “Game theory-based IoT efficient power control in cognitive uav,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1561–1578, 2022. [Google Scholar]

29. G. Bansal, J. Hossain and V. K. Bhargava, “Optimal and suboptimal power allocation schemes for ofdm-based cognitive radio systems,” IEEE Transactions on Wireless Communications, vol. 11, no. 7, pp. 4710–4718, 2008. [Google Scholar]

30. W. Shaowei, H. Fangjiang and Z. Zhi-Hua, “Fast power allocation algorithm for cognitive radio networks,” IEEE Communications Letters, vol. 15, no. 8, pp. 845–847, 2011. [Google Scholar]

31. O. Abdulghafoor, M. Shaat, I. Shayea, F. Mahmood, R. Nordin et al., “Efficient power allocation algorithm in downlink cognitive radio networks,” ETRI Journal, vol. 44, pp. 400–412, 2022. [Google Scholar]

32. N. Papandreou and T. Antonakopoulos, “Bit and power allocation in constrained multicarrier systems: The single-user case,” EURASIP Journal on Advances in Signal Processing, vol. 2008, pp. 1–14, 2008. [Google Scholar]