Efficient Group Blind Signature for Medical Data Anonymous Authentication in Blockchain-Enabled IoMT

1  Introduction

Internet of medical things (IoMT) is the direction for traditional healthcare service systems with the increasing number of wearable and mobile medical devices [1]. IoMT establishes a medical network that aggregates dispersive medical data created by many smart medical devices. Although these massive amounts of medical data can contribute much to patient treatment, drug discovery, and medical equipment manufacturing, they also face many security issues as they contain sensitive information about the patient and medical institution. Therefore, the security of medical data and user privacy is more important for data sharing through IoMT [2].

Blockchain technology brings new vitality to traditional IoMT and helps to establish the distributed medical data management platform called blockchain-based Internet of medical things (BIoMT) [3]. The public blockchain ledger guarantees that data and operation records are not tampered with, which can well solve the centralized management problem in traditional IoMT [4]. Through this distributed platform, the patient can freely choose the needed medical institution and get more precise treatment with historical medical data, the doctor can improve the efficiency of diagnosis with more comprehensive medical data, and the researcher can develop the level of drug discovery and medical equipment manufacturing with massive amounts of medical data. By focusing on these goals, more and more BIoMT frameworks and proposes are emerging in recent years, such as Healthchain, Fortified-chain, and so on [5–15]. Meanwhile, some AI-powered methods also appear to improve data-handling capacity and analysis efficiency, such as machine learning and federated learning [16,17]. However, these works mainly focus on medical data management and utilization but rarely care about the security of medical data and user privacy using the cryptographic algorithm [18].

Privacy-preserving is the main challenge for BIoMT [19]. As identity privacy is generally inserted in medical data, it can be divulged easily with centralized management forms, insecure data transmission, or man-made sabotage. Meanwhile, medical data are indicators of patients’ physical condition, which are also personal privacies, especially for important persons. Blockchain transactions contain the operator’s signature, essential in verifying transaction legitimacy, confirming the operator’s identity, and data traceability for medical disputes [20]. For the privacy security of medical data in BIoMT, the signer’s anonymity is a more critical issue. A group signature allows one member to represent the group for signing, and the verifier can verify the signature’s legitimacy but not confirm which one is the real signer [21–26]. Meanwhile, a blind signature utilizes a blind factor to blind the message to be signed [27–30]. Some protocols with these two properties have been proposed, which can guarantee anonymous of the user identity and data information [31–33]. Therefore, this paper plans to combine these two signatures to design a GBS scheme and establish an anonymous authentication model for privacy-preserving in BIoMT.

This paper mainly focuses on the problems of authentication difficulty and privacy leakage in the medical data-sharing process. It contributes to the privacy-preserving method for medical data and users in the BIoMT system. A four-ledger architecture for the BIoMT system has been introduced first, and an anonymous authentication model has been designed to strengthen the security of the data-sharing process in the network ledger. Then, a GBS scheme has been proposed to achieve anonymous authentication. The detailed contributions of this work are as follows:

•   A four-ledger architecture for the BIoMT system has been introduced, which contains four layers of the perceptual, network, platform, and application. From data collection to application, this distributed peer-to-peer platform can guarantee the transparency and integrity of medical data. Meanwhile, an anonymous authentication model has been designed, which can strengthen the security of the data-sharing process in the network ledger.

•   A GBS scheme has been proposed to achieve anonymous authentication. It provides anonymity for the signer as the group can be represented by one member for signing. The blind property can protect the message to be signed as it is anonymous to the signer, but the signer cannot deny a valid signature signed by himself. Meanwhile, this scheme is based on lattice assumption, which can also guarantee the security of anti-quantum attacks.

•   The correctness analysis and security proof have been given, which show that the GBS scheme can capture properties of blindness, traceability, and non-flammability. The comparison analysis and performance evaluation of key size show that the GBS scheme is efficient.

In the following, Section 2 presents the reviews of related work, Section 3 gives an anonymous model for BIoMT, Section 4 proposes a new GBS scheme, Section 5 shows the security proof and analysis, section 6 presents the efficiency comparison and performance, and Section 7 concludes.

2  Related Work

2.1 Blockchain-Enabled Internet of Medical Things

The distributed BIoMT platform and application are constructed by blockchain, Hyperledger, management model, cryptographic algorithm, etc. Xu et al. proposed a double chain Healthchain system for large-scale medical data management, which contains the userchain and doctorchain [5]. Using blockchain and Hyperledger Fabric, Chenthara et al. constructed a Healthchain system to protect patient privacy and medical data [6]. Li et al. established a novel peer-to-peer platform for medical data management and proposed a Stackelberg pricing algorithm to promote medical data sharing between different medical institutions [7]. Moreover, Hylock et al. presented a Healthchain system around the patient, which can help patients participate in medical data curation and dissemination [8]. Rahoof et al. established a Healthchain system using private and consortium blockchain technology for intra-regional and inter-regional communication [9]. Egala et al. proposed a Fortified-chain for security and privacy-assured IoMT based on blockchain, which mainly focuses on the access control mechanism for medical data [10]. These distributed peer-to-peer platforms give new directions to realize secure medical sharing among different medical users and institutions.

Some new frameworks are also based on blockchain and artificial intelligence (AI) technologies. Singh et al. designed a privacy-preserving model for IoT healthcare data based on federated learning and blockchain [11]. Qahtan et al. focused on security in IoT healthcare industry 4.0 systems and presented a multi-security and privacy benchmarking framework with blockchain [12]. AI-Sumaidaee et al. utilized the Hyperledger fabric to perform the distributed healthcare platform with private blockchain [13]. Zhao et al. established a Brooks-Iyengar quantum Byzantine agreement-centered blockchain networking for smart healthcare [14]. Baucas et al. gave a federated learning and blockchain-enabled fog-IoT platform for wearables in predictive healthcare [15]. Although these platforms based on blockchain and AI has certain security capabilities for medical data, they cannot resist attacks from malicious adversaries with high computing power. There is also a need the cryptographic protocols, such as encryption schemes, signature schemes, and key agreement schemes, to strengthen the system security of BIoMT.

2.2 Anonymous Authentication Protocols

Many anonymous authentication methods exist to blind the signer’s identity or message. The group signature and blind signature are standard protocols that can achieve this function. In the group signature (GS) scheme, one group member can serve as the representative to perform the signing operation. The signature can be verified valid without knowing who signs it [21]. Perera et al. gave a GS scheme with lattice assumption, which can achieve verifier-local revocation with time-bound keys [22]. Xie et al. presented a GS scheme to strengthen the security of anonymous authentication for IoT users [23]. Şahin et al. proposed dynamic GS scheme based on lattice assumptions, and applied the quantum random oracle model to show that the proposed scheme could achieve of anonymity, traceability, and non-fremability [24]. Zhang et al. gave a GS scheme with the verifier-local revocation mechanism based on lattice assumption [25]. Tang et al. designed a GS scheme with multiple managers, which can achieve privacy-preserving for BIoMT [26]. Then, the blind signature (BS) scheme utilizes the blind factor to blind the message to be signed by the signer, which can provide anonymity for this message. Vora et al. proposed a BS scheme that depends on the hardness of big integer decomposition to protect medical data in an e-health system [27]. Li et al. constructed a BS scheme and a proxy BS scheme with lattice assumption, which can strengthen the anti-quantum property for blockchain-based systems [28,29]. Xu et al. introduced a certificateless signcryption scheme with blockchain technology to improve privacy security in an edge computing environment [30]. GS or BS only provides individual security properties for information systems, so it cannot satisfy the demands for group anonymity and message blinding.

Moreover, there also exist some group blind signature schemes, which aggregate the merits of the former two kinds of signature schemes. Kong et al. introduced a practical GBS scheme for privacy-preserving in smart grids [31]. Fan et al. applied the fast GBS scheme to construct a refreshing algorithm of dynamic nodes [32]. Kastner et al. proposed a pairing-free blind signature scheme based on the Algebraic group model. They proved it could reduce to the weakest possible assumption compared with known reduction techniques [33]. These schemes can provide both group anonymity and message blinding and improve the privacy security for users and data in information systems. However, considering the difficult authentication problems and privacy leakage in the medical data-sharing process, these protocols are unsuitable for anonymous authentication for privacy-preserving in the BIoMT system.

3  Anonymous Model for BIoMT System

This section first descripts the architecture of BIoMT. Then, the anonymous authentication model is presented for BIoMT system.

3.1 Architecture of BIoMT

Fig. 1 shows the architecture of BIoMT, which mainly contains four layers for medical data management. Here, the layers are divided according the four life cycle phases of data collection, storage, share and analyze. Therefore, from the medical data generation to expiration, it generally needs to pass four layers of the perceptual, network, platform, and application. Detail function introductions of every layer are as follows:

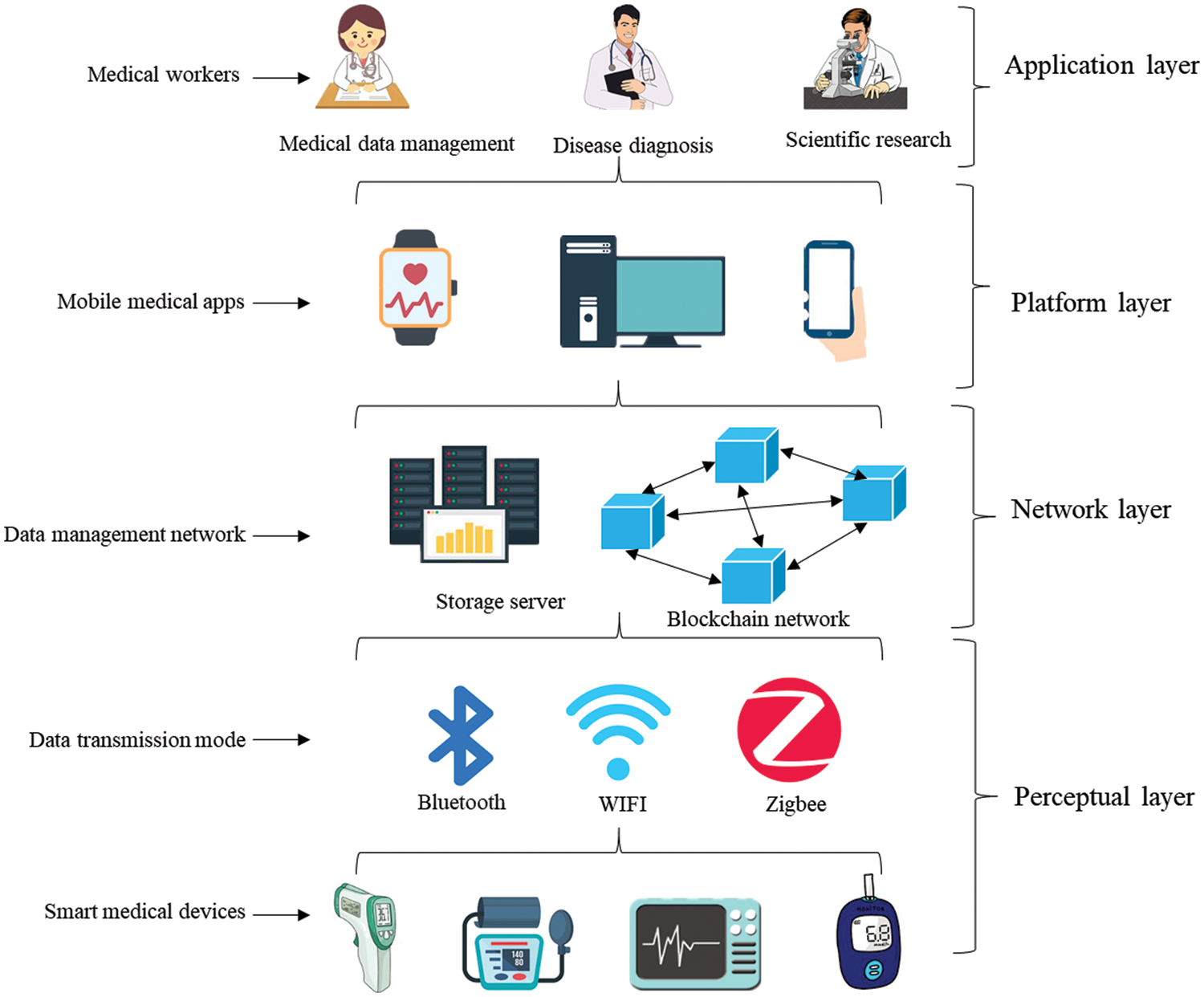
Figure 1: The architecture of BIoMT

•   Perceptual layer: This layer contains the smart medical device, such as the clinical thermometer, digital blood pressure monitor, cardio kickboxing, and glucose meter. The patient’s physical condition data will be collected by these devices and uploaded to the BIoMT network. This layer is the edge data collection network, which also preprocesses the data to improve their interoperability for cross-institutional data sharing. Then, First, the data transmission mode generally contains Bluetooth, WIFI, and Zigbee, and these modes upload the medical data to the data management network in the network layer.

•   Network layer: This is a distributed IoMT network based on blockchain technology, and it can solve the centralized problem compared with the traditional IoMT system. An anonymous authentication model has been introduced to protect the patient’s privacy. After the collection process, the medical data will be signed with the signer's private key. This model also adds the function of GBS signature to strengthen the anonymity of medical data. Here, real medical data will be stored in a native storage server, and storage address and operation behavior will be recorded onto the blockchain ledger. Here, the user must first visit the public blockchain ledger, and then he can get the storage address and obtain real medical data. This mechanism will prevent the problems of data loss and privacy leakage by direct access to data. Meanwhile, the lightweight storage of address and operation behavior will provide data traceability and audit links and decrease the redundancy of the public blockchain ledger. This layer guarantees the security of storage and sharing processes by utilizing the distributed peer-to-peer network and untampered blockchain ledger.

•   Platform layer: medical workers can access and operate the medical data from BIoMT servers through these platforms. The watch, desktop, telephone, and other mobile medical devices and apps can all link to the BIoMT network. Note that the current smartwatch can serve as a medical data management platform and a perceptual device to collect medical data. This layer connects the medical in-network layer and the application layer. A valid user can access medical data from these platforms. Meanwhile, this layer takes responsibility for presetting access control privileges, which can protect users' and medical data privacy more refined.

•   Application layer: This layer contains different kinds of medical workers, such as doctors, nurses, researchers, insurance salespeople, and supervisors. These medical data can be used for disease diagnosis, scientific research, and drug development. They also provide evidence for market regulation and medical dispute tracing. Medical workers take responsibility for data management and can utilize these data for disease diagnosis and scientific research. For a piece of medical data, the signature embedded in it can help check its validity. The GBS scheme allows one group member to perform a signing operation on behalf of the group. This signature can be verified as legitimate without knowing who the signer is. Meanwhile, the blind function makes the signature anonymous to the signer.

This BIoMT performs data acquisition, storage, and management roles to support data sharing between medical institutions. The medical data are collected by the smart medical device, stored in the native storage server, shared by the distributed blockchain ledger, managed by different medical platforms, and used by different medical workers. Blockchain technology guarantees transparency and integrity, but user authentication and privacy security are still the weak aspects of BIoMT. There always exist some problems of authentication difficulties and privacy leakage in the medical data sharing process. Especially in the face of quantum computation attacks, current mathematic hard problems-based cryptographic protocols are vulnerable. An anonymous authentication model is introduced for BIoMT in the following subsection, focusing on privacy security in the network layer.

3.2 The Anonymous Authentication Model for BIoMT

The framework of the model is shown in Fig. 2. This model mainly contains an anonymous authentication scheme and an IoMT blockchain ledger. Here, the anonymous authentication scheme is established with a GBS scheme which can ensure the anonymous verifiability of the signer and the authenticity of medical data. The IoMT blockchain ledger takes responsibility for recording the data store address and operation records to guarantee storage security and traceability.

Figure 2: Anonymous authentication model for BIoMT

•   Anonymous authentication scheme: This scheme establishes an anonymous authentication mechanism for cross-institutional medical data sharing. This scheme is a GBS scheme based on lattice assumption. When smart medical devices collect medical data, they will be signed by the corresponding medical workers. Then, the signed medical data will be uploaded and packaged into the blockchain transaction. Here, as the patient’s condition needs to synthesize various detection results for comprehensive judgment, it generally needs various detection equipment to cooperate. There is also a need for some medical workers to consult together when the patient’s condition is very complex. The GBS improves the security of medical data and allows one group member to sign messages. The message to be signed is also blind to the signer, which can improve medical data security. Moreover, the medical store address and operations are recorded as transactions and uploaded into the ledger. This scheme establishes an anonymous authentication mechanism for cross-institutional medical data sharing.

•   IoMT blockchain ledger: This is a unified ledger for the whole network of BIoMT, which establishes a secure cross-institutional medical data-sharing platform. This ledger only contains lightweight messages as the storage addresses and operations records, which can improve the data sharing efficiency by a more lightweight ledger. When medical workers want to view some medical data, they can derive the original data from the storage address by obtaining access control permission. Meanwhile, they will form a hinged record ledger with time stamps and establish permanent, immutable records. This ledger can provide evidence and traceability for verifying medical data when a medical dispute arises. Every valid user can check the validity of medical data without losing any private information.

4  The Proposed Anonymous Authentication Protocol

To protect the sensitive information security, a GBS scheme based on lattice cryptography has been designed for anonymity authentication. This GBS scheme is based on lattice assumption ℜ−SISq,n,m,βκ, where κ is a uniform distribution. Meanwhile, the algorithms for ℜ=Z is performed by the same work way in rings ℜ=Z[x]/(xn+1). Although the work way becomes simple, the hardness of this lattice assumption Z−SISq,n,m,βκ has not decreased. Here, the GM represents the group manager, the GG represents group guest (Signer), the GU represents group user (Message owner), the SV represents signature verifier, and the SO represents signature opener. To generate a valid group signature, these four parties perform the following six algorithms, such as KeyGen., Join, Blind Sign, Verify, Open, and Revoke. This GBS scheme can also realize that the group members free join and revoke.

Moreover, the bimodal Gaussian distribution has been applied into the GBS scheme, which can improve the efficiency of reject sampling [34] and make the GBS scheme more efficient. Following are the detailed step descriptions of the GBS scheme.

Key Gen.: According to the rules in Ref. [35], parameters n,m,q,κ,σ are defined, where κ is security parameter, and m=O(nlog⁡q). Then, the system parameters are generated by the following steps:

•   Choose a short matrix SA∈Z2qm∗n, as ‖S~‖≤O(nlog⁡q);

•   Generate matrix A∈Z2qn∗m such that ASA=A(−SA)=qIn(mod2q);

•   Choose a short matrix SB∈Z2qm∗n;

•   Generate the matrix B∈Z2qn∗m which satisfies BSB=B(−SB)=qIn(mod2q);

•   Derive (Ui,SUi) according the former principle;

•   Output gpk=(A,B) as group public key, gmsk=SA as group master secret key, tmsk=SB as tracing manager’s (opener’s) secret key, (upki=Ui,uski=SUi) as guest i’s key pair.

Join algorithm: This algorithm contains two parts: one is that GG sends a registration message to GM, the other is that GM generates a member certificate to GG. GG also sets a leaving date and time for registration to prevent pretending by some malicious adversaries.

(1) GG performs:

•   Selects vectors xi1,xi2←Dσ1m, as Dσ1m is the bimodal Gaussian distribution;

•   Computes yi1=SUixi1 and yi2=Bxi2;

•   Computes zi=xi1+xi2;

•   Sets a leaving date and time tri;

•   Sends (yi1,yi2,zi,tri) to group manager.

(2) GM performs:

•   Samples ri←SampleD(SA,A,qzi,σ2);

•   Sets the revocation token Tokeni=A⋅ri;

•   Computes ci1←H(Ayi1mod2q,Tokeni) with the received yi1;

•   Selects a∈{0,1}n randomly;

•   Computes wi1←yi1+(−1)aSAci1;

•   Derives (wi1,ci1) with probability min(Dσ1Tokeni(wi1)M1Dci1,σ1Tokeni(wi1),1); otherwise, restart;

•   Records GG i’s registration reg[i]←(i,yi1,tri,ri,1), here “1” represents this GG i is active;

•   Outputs the member certificate mci=(wi1,ci1,Tokeni) for GG i.

Blind sign algorithm: This algorithm contains four parts: GG verifies the date and sends the commitment to GU, GU blind the message to be signed and sends it to GG, GG signs the blind message and returns it back to GU, and GU recover the signature for original message. GG i first verifies the validation of his member certificate mci=(wi1,ci1,tri). Here, ‖wi1‖>T1 with the conditions of T1=ηmσ1, and η can be verified with probability 1−2−κ for the security parameter κ (in practice η∈[1.1,1.4]). Next is the detailed steps of this blind sign algorithm.

1) GG performs:

•   Verifies the validity of member certificate mci;

•   If ‖wi1‖>T1 or ‖wi1‖∞>q/4, terminates and restarts Join algorithm;

•   Continues iff ci1←H(Awi1+qci1mod2q,A⋅ri);

•   Sends (yi1,yi2) to the user.

2) GU performs:

•   Selects a blind vector yi3←Dσ2m;

•   Computes ci2←H(Ayi1+yi2+Ayi3mod2q,M) with the former computed (yi1,yi2);

•   Selects b∈{0,1}nrandomly;

•   Computes μ←(−1)bci2;

•   Drives μ with probability min(Dσ2M(μ)M2Dci2,σ2M(μ),1), and sends it to GG; otherwise, restart.

3) GG performs:

•   Confirms the signature expiration date ts<tri, Otherwise restart;

•   GG computes wi2←wi1+xi2+μSA with wi1 and the former selected vector xi2;

•   Derives the blind signature (wi2,ci1,ts) of μ with probability min(Dσ1m(wi2)M1DμSA,σ1m(wi2),1), and sends it to GU; otherwise, restart;

4) GU performs:

•   GU computes ei←yi3+wi2 with the former selected blind vector yi3.

•   Recovers signature (ei,ci1,ci2,tri,ts) with probability min(Dσ2m(ei)M2Dyi3,σ2m(ei),1); Otherwise, restart;

Verify algorithm: SV performs verification process and gives Accept or Reject.

•   SV checks the date and time tv<ts and ts<tri, otherwise restart;

•   If ‖ei‖>T1 or ‖ei‖∞>q/4, Reject

•   Iff ci2←H(Aei+qci1+qci2mod2q,M), Accept.

Open algorithm: Though this algorithm, it can confirm who is the real signer in the group.

•   Samples ri′←SampleD(SA,A,Uiyi1+SByi2,σ2);

•   If r′i=ri, returns GG’s index i; Otherwise, restart.

Revoke algorithm: GM executes the following steps to change group member and records the revocation information to a list RL.

•   Queries on reg[i] to get Tokeni=A⋅ri;

•   Updates state (1) to inactive (0), and records (A⋅ri) into RL;

5  Security Analysis

5.1 Correctness

(1) Member certificate correctness: The member certificate mci is valid when it satisfies three conditions. First is‖wi1‖<T1, as T1 is defined in the Sign algorithm. Second is ‖wi1‖∞<q/4, as this condition is restricted system security reason. Third is ci1←H(Awi1+qci1mod2q,A⋅ri), as that it is based on the following Eq. (1) holds.

Awi1+qci1=A(yi1+(−1)aSAci1)+qci1   =Ayi1+(−1)aASAci1+qci1   =Ayi1+(−1)aqci1+qci1   =Ayi1mod2q(1)

(2) Signature correctness: The signature ei is valid for message M which also needs those three conditions holds. As in the Verify algorithm, the former two conditions are ‖ei‖<T1 and ‖ei‖∞<q/4, and the third is ci2←H(Aei+qci1+qci2mod2q,μ) as the following Eq. (2) holds.

Aei+qci1+qci2=A(yi3+wi2)+qci1+qci2=Ayi3+A(wi1+xi2+μSA)+qci1+qci2=Ayi3+A(yi1+(−1)aSAci1)+Axi2+(−1)bqci2+qci1+qci2=Ayi3+Ayi1+Axi2+(−1)aqci1+qci1+(−1)bqci2+qci2=Ayi1+yi2+Ayi3mod2q(2)

Meanwhile, the signature is correct, which also needs the following conditions to hold. Firstly, a user with a fake expiration date cannot pass verification as the new guest has set a leaving date and time tri for the member certificate. Secondly, the signature generation time ts is verified at step 1 of Sign algorithm, only the no expired group member can perform the following signing steps. Thirdly, the verification time tv is compared with signature generation time ts. If the user does not have a correct signature expiration date, he will be rejected. Moreover, the signature cannot be accepted, created by the revoked group member whose revocation token is in list RL.

(3) Opening correctness: On inputting tmsk=SB, the signature is generated by guest i if ri′=ri, where ri′←SampleD(SA,A,Uiyi1+SByi2,σ2). The correctness of that open algorithm is based on the following Eq. (3).

Uiyi1+SByi2=UiSUixi1+BSBxi2=qxi1+qxi2=q(xi1+xi2)=qzimod2q(3)

5.2 Security Proof

This section provides the security proof of the proposed GBS scheme to show it can achieve dynamical-almost-full anonymity, blindness, traceability and non-frameability.

(1) Dynamical-almost-full anonymity: With the free joining and revoking mechanism, one signature cannot be confirmed which group member is the signer, and two different signatures cannot be distinguished who is the real signer between two different signers without the information of group muster’s secret key.

Theorem 1: In random oracle model, this GBS scheme can capture dynamical-almost-full anonymity with the hardness of ℜ−SISq,n,m,βκ.

Proof: A query-respond game has been established between the adversary A and challenger C, and challenger can utilize the forged signature created by adversary to solve ℜ−SISq,n,m,βκ instance with non-negligible probability. Detailed proving processes are shown as follows.

Game 0: Suppose adversary A can get some information of usk. Based on the hardness of ℜ−SISq,n,m,βκ, A cannot distinguish that one signature’s real signer is user i0 or user i1 by the query-respond game with C. Meanwhile, A can add new user into the group, and perform queries on the opened signatures and member’s revocation token. If A asks to add a new user, C first confirms whether this user’s identity is registered or not. C performs registration process to generate the registration information when this identity does not exist and returns it back. C also establish an empty registration list ListRU to store the registration information. Here, the returned registration information does not contain the revocation token and key-expiration time. When A asks to reveal the revocation token for user i, C checks ListRU and finds out user i’s registration information. He returns member certificate mci back, and updates ListRU. Then, C gives two challenge indices (i0,i1) with relate to M, and derives signature (ei∗,ci1∗,ci2∗,tri∗,ts∗) with a random τ←{0,1} when he confirms that (i0,i1) are newly recorded in ListRU. After that, A gives his guess τ′←{0,1}. It will derive 1 when τ′=τ, and 0 when τ′≠τ. Moreover, A needs to give two different expiration dates for indices i0 and i1. A cannot pass validation process if he does not provide a right key-expiration date which should satisfy tri>ts≥tv. Even worse, A provides two correct expiration dates, C will derive challenging signature for verification. A will attack the anonymity of signer in this GBS scheme with time-bound keys.

Game 1: C executes KeyGen. and derives key pair (Ui∗,SUi∗) for the challenging signature. If A performs query on an opened signature (ei,M), C will quit and select a random bit as response. Note that it cannot distinguish this game with Game 0. Next, C performs the following games.

Game 2: C executes Join algorithm to answer for the query on random oracle H. If A performs query on an opened signature (ei,M), C calculates ci2←H(Ayi1+yi2+Ayi3mod2q,M). Meanwhile, C executes Join algorithm and calculates H(Ayi1mod2q,A⋅ri) to get ci1. Next, C derives signature (ei,ci1,ci2,tri,ts) as response. Here, A cannot get anything from this collision-resistant random oracle as he has nothing about the newly registered user. Note that it cannot distinguish this game with the former two games.

Game 3: As ei←yi3+wi2 is related with yi3 and wi2. C randomly chooses a blind vector for yi3, and executes the Blind sign algorithm to generate wi2. Meanwhile, C can compute wi1 from the following Game 4, and derives (ei,ci1,ci2) with probability min(Dσ2m(ei)M2Dyi3,σ2m(ei),1). Note that it cannot distinguish this game with the former games.

Game 4: C randomly selects a vector ri∗ and calculates Tokeni=Ari∗. Then, C calculates wi1←yi1+(−1)aSAci1 with yi1 and ci1, here ci1 is derived with Tokeni∗ from Game 2. The generation probability of (wi1,ci1) is min(Dσ1Tokeni(wi1)M1Dci1,σ1Tokeni(wi1),1).

Game 5: As C generates Tokeni with challenging bit τ, ei is derived uniformly. C chooses a random vector η∈Zqn and sets ei=η. Here, (ei,ci1,ci2) is a proper ℜ−SISq,n,m,βκ instance. If A can find a solution for this hard problem, he can make a correct distinction between ei and η. Note that it cannot distinguish this game with the former games.

Game 6: ei∗ is generated independently with τ. Note that it cannot distinguish this game with the former games. Therefore, it is impossible for A to forge a valid signature as ℜ−SISq,n,m,βκ is hard.

Now, it can say that this GBS scheme can capture dynamical-almost-full anonymity.

(2) Blindness

Blindness: The signer cannot deny his signature inserted in one message which he does not know what it is, here this signature can be verified to be true.

Theorem 2: In random oracle model, this GBS scheme can capture statistically blind with the hardness of ℜ−SISq,n,m,βκ.

Proof: Suppose adversary AdvBSblind(S∗) can interact with two different users u0 and u1, it can prove that signatures e0 and e1 generated by two users cannot be distinguished. The blind message μ0 and μ1are generated with probability probability min(Dσ1m(wi2)M1DμSA,σ1m(wi2),1). As μ←(−1)bci2, it tailors μ0 and μ1 to be distributed according to the same distribution Dσ2m by rejection sampling lemma [34]. Therefore, it can derive Δ(μ0,μ1)=0, and these two blind messages are distributed independently from the original message. Then, from the blind sign and revoke steps, the blind signature (wi2,ci1,ts) is generated by wi2←wi1+xi2+μSA with probability min(Dσ1m(wi2)M1DμSA,σ1m(wi2),1), and the signature (ei,ci1,ci2,tri,ts) generated by ei←yi3+wi2 with probability min(Dσ2m(ei)M2Dyi3,σ2m(ei),1). It can derive two signatures e0 and e1 which also satisfy Δ(e0,e1)=0. Meanwhile, they are independent from the original message to be signed. Now, it can say that this GBS scheme can capture statistically blind to the attacks from adversary S∗.

(3) Traceability

Traceability: The signer with relate to one valid signature can be confirmed by the open algorithm, and he cannot deny this signature.

Theorem 3: In random oracle model, this GBS scheme is traceable with the hardness of ℜ−SISq,n,m,βκ.

Proof: Suppose adversary A can forge a valid signature, and he has ability to add new group user by replacing user’s upk. Meanwhile, the revocation token can also be queried by A. Next, challenger C1utilizes a pseudo polynomial time (PPT) algorithm to perform a query-answer game with A to solve ℜ−SISq,n,m,βκ instance. A can execute queries on the KeyGen., Join, and Blind sign algorithms with enough times, and C1 responds them one by one. Then, A can forge a signature (ei′, ci1′, ci2′, tri′, ts′) for M′ with enough queried information. With the former hypothesis, this signature (ei′, M′) derived by A is valid. Now, C1 can create a new valid signature (ei′∗,M) with (ei′∗,ci1′∗,ci2′∗,tri′∗,ts′∗) by Forking Lemma [36]. Hence, C1 obtains two equations Uiyi1′+SByi2′=qzi′mod2q and Uiyi1′∗+SByi2′∗=qi′∗mod2q, and then generates two vectors zi and zi′∗ (zi≠zi′∗) respectively. There also has A(ri′−ri′∗)=q(zi′−zi′∗)mod2q. Here, it has ri′−ri′∗≠0mod2qas zi′≠zi′∗, and v=ri′−ri′∗ is a solution for ℜ−SISq,n,m,βκ instance as Av=0mod2q. However, this is impossible with current computation. So the hypothesis for adversary A fails, and the GBS scheme is traceable.

(4) Non-frameability

Non-frameability: It cannot generate a legitimate signature by impersonating other people, no matter the group manager and other members.

Theorem 4: In random oracle model, this GBS scheme can capture non-frameability with the hardness of ℜ−SISq,n,m,βκ.

Proof: Suppose adversary A can forge a valid signature. This signature also opens to user i, but this user has never generated the signature. Then, there exists a challenge PPT algorithm C2 which can solve SIS problem from the query-answer game with A. A signs up a new user i by working as the corrupted group member, and makes some queries to the main algorithms in the GBS scheme. C2 answers the queries with the system keys gpk, gmsk and tmsk. When A asks for a signature with relate to message M, C2 generates and sends back the corresponding signature (ei′, ci1′, ci2′, tri′, ts′). A makes these queries for many times, and obtains enough information for the system keys. Next, A forges a signature (ei″,ci1″,ci2″,tri″,ts″) for the target message C2 which opens to user i∗. Based on the former assumption for A, (ei″,M″) is a legitimate signature with overwhelming probability. As C2 also can generate a legitimate signature (ei″,M″), it can derive H(Aei″+qci1″+qci2″mod2q,M″)=H(Aei″∗+qci1″∗+qci2″∗mod2q,M″). Then, there will exist Aei″+qci1″+qci2″=Aei″∗+qci1″∗+qci2″∗ because it does exist hash collision. Meanwhile, it also can derive A(ei″−ei″∗)=0mod2q as ci1″=ci1″∗ and ci2″=ci2″∗. Until now, C2 finds out a solution for the ℜ−SISq,n,m,βκ instance.

6  Efficiency Comparison

This section provides the efficiency comparison between the proposed GBS with the other three similar schemes. Key size is an essential index to reflect the scheme performance as that more small key size leads to more efficient scheme performance. Here, the parameters n,m,q,σ in [22,23], and the proposed GBS are unified and the parameter k and l in [24] are converted with the principle of k=0.96n and l=m. Then, the key comparison results with some other similar schemes are shown in Table 1. As for the gpk and gmsk, the proposed GBS is a little bigger than those in the other two schemes. But the keys’ distribution with bimodal Gaussian by modeling 2q can make the scheme more secure. As for the tmsk, its size in the proposed GBS is nearly half of that in Ref. [23]. As for the signature size, the proposed GBS has a great advantage in the signature verification efficiency with more small size.

Then, to clearly view the difference between the proposed GBS scheme with similar three schemes. The performance environment is a Windows 10 desktop with Intel(R) Core (TM) i7 CPU 3.2 GHz and 16G RAM. The key size is performed on Matlab R2016a with two security levels of 80-bit and 192-bit, where the parameters n and q are setting as n=512,q=223 and n=1024,q=227 respectively. The parameter m=3545 for 80-bit and m=8323 for 192-bit as it satisfies m≥n⌈log⁡q⌉, the message length is preset to l=80, and σ=230 is set according the principle in [29]. From the performance results in Fig. 3, gpk is almost the same, and tmsk in GBS scheme is smaller than [23]. Furthermore, the signature size comparison is shown independently in Fig. 4, and the signature size in the GBS scheme has more advantages than the other two similar schemes. As the gpk, gmsk, and tmsk can be pre-generated to save algorithm time, the signature size makes essential effects on the signature generation and verification. Therefore, the small signature size in the GBS scheme can improve the efficiency.

Figure 3: Key size comparison with two different security level

Figure 4: The signature size comparison

7  Conclusion

This paper solves the problems of authentication difficulty and privacy leakage in the BIoMT system. A four-ledger architecture for the BIoMT system is introduced first, which contains the perceptual, network, platform, and application. Meanwhile, an anonymous authentication model has been designed to strengthen the security of the data-sharing process in the network ledger. This model integrates the anonymous authentication scheme and untampered blockchain ledger, which can guarantee the traceability of the signature and the anonymity of the signer’s identity privacy at the same time. Then, a GBS scheme has been proposed to achieve anonymous authentication. It keeps the signer’s anonymity through the group representative signing mechanism and protects data privacy with the message binding mechanism. Moreover, the security proof and analysis show that this GBS scheme can capture the needed security properties of dynamical-almost-full anonymity, blindness, traceability, and non-frameability. The efficiency comparison and performance evaluation of key size show that the proposed anonymous authentication model and signature scheme are efficient and practical.

With the number of smart medical devices increasing, the security problems of privacy leakage, data loss, and unauthorized access have become more and more serious. To maximize the value of medical data, privacy security, identity authentication, and access control are the main security issues that should be put into continuous efforts. Therefore, there still exist some exciting research directions in BIoMT, such as the data fine-grained access control, anonymous authentication, and lightweight storage in the cross-institutional sharing process.

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant 61962009, the Doctor Scientific Research Fund of Zhengzhou University of Light Industry under Grant 2021BSJJ033, the Key Scientific Research Project of Colleges and Universities in Henan Province (CN) under Grant No.22A413010, the Foundation and Cutting-Edge Technologies Research Program of Henan Province (CN) under Grant No. 222102210161, the Natural Science Foundation of Henan Province (CN) under Grant No. 222300420582.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. G. J. Joyia, R. M. Liaqat, A. Farooq and S. Rehman, “Internet of medical things (IoMTApplications, benefits and future challenges in healthcare domain,” Journal of Communications, vol. 12, no. 4, pp. 240–247, 2017. [Google Scholar]

2. G. Yang, Z. Pang, M. J. Deen, M. Dong, Y. T. Zhang et al., “Homecare robotic systems for healthcare 4.0: Visions and enabling technologies,” IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 9, pp. 2535–2549, 2020. [Google Scholar] [PubMed]

3. M. Mettler, “Blockchain technology in healthcare: The revolution starts here,” in 2016 IEEE 18th Int. Conf. on E-Health Networking, Applications and Services (Healthcom), Munich, Germany, IEEE, pp. 1–3, 2016. [Google Scholar]

4. M. Papaioannou, M. Karageorgou, G. Mantas, V. Sucasas, I. Essop et al., “A survey on security threats and countermeasures in internet of medical things (IoMT),” Transactions on Emerging Telecommunications Technologies, vol. 33, no. 6, pp. e4049, 2022. [Google Scholar]

5. J. Xu, K. Xue, S. Li, H. Tian, J. Hong et al., “Healthchain: A blockchain-based privacy preserving scheme for large-scale health data,” IEEE Internet of Things Journal, vol. 6, no. 5, pp. 8770–8781, 2019. [Google Scholar]

6. S. Chenthara, K. Ahmed, H. Wang, F. Whittaker and Z. Chen, “Healthchain: A novel framework on privacy preservation of electronic health records using blockchain technology,” PLoS One, vol. 15, no. 12, pp. e0243043, 2020. [Google Scholar] [PubMed]

7. C. Li, M. Dong, J. Li, G. Xu, X. Chen et al., “Healthchain: Secure EMRs management and trading in distributed healthcare service system,” IEEE Internet of Things Journal, vol. 8, no. 9, pp. 7192–7202, 2021. [Google Scholar]

8. R. H. Hylock and X. Zeng, “A blockchain framework for patient-centered health records and exchange (HealthChainEvaluation and proof-of-concept study,” Journal of Medical Internet Research, vol. 21, no. 8, pp. e13592, 2019. [Google Scholar] [PubMed]

9. T. P. A. Rahoof and V. R. Deepthi, “HealthChain: A secure scalable health care data management system using blockchain,” in Int. Conf. on Distributed Computing and Internet Technology, Cham, Bhubaneswar, India, Springer, pp. 380–391, 2020. [Google Scholar]

10. B. S. Egala, A. K. Pradhan, V. Badarla and S. P. Mohanty, “Fortified-chain: A blockchain based framework for security and privacy assured internet of medical things with effective access control,” IEEE Internet of Things Journal, vol. 8, no. 14, pp. 11717–11731, 2021. [Google Scholar]

11. S. Singh, S. Rathore, O. Alfarraj, A. Tolba and B. Yoon, “A framework for privacy-preservation of IoT healthcare data using federated learning and blockchain technology,” Future Generation Computer Systems, vol. 129, no. 2, pp. 380–388, 2022. [Google Scholar]

12. S. Qahtan, K. Y. Sharif, A. A. Zaidan, H. A. Alsattar, O. S. Albahri et al., “Novel multi security and privacy benchmarking framework for blockchain-based IoT healthcare industry 4.0 systems,” IEEE Transactions on Industrial Informatics, vol. 18, no. 9, pp. 6415–6423, 2022. [Google Scholar]

13. G. Al-Sumaidaee, R. Alkhudary, Z. Zilic and A. Swidan, “Performance analysis of a private blockchain network built on Hyperledger Fabric for healthcare,” Information Processing & Management, vol. 60, no. 2, pp. 103160, 2023. [Google Scholar]

14. Z. Zhao, X. Li, B. Luan, W. Jiang, W. Gao et al., “Secure Internet of things (IoT) using a novel Brooks-Iyengar quantum Byzantine agreement-centered blockchain networking (BIQBA-BCN) model in smart healthcare,” Information Sciences, vol. 629, pp. 440–455, 2023. [Google Scholar]

15. M. J. Baucas, P. Spachos and K. N. Plataniotis, “Federated learning and blockchain-enabled fog-IoT platform for wearables in predictive healthcare,” IEEE Transactions on Computational Social Systems, pp. 1–10, 2023. [Online]. Available: https://ieeexplore.ieee.org/abstract/document/1001889 [Google Scholar]

16. H. N. Dai, Y. Wu, H. Wang, M. Imran and N. Haider, “Blockchain-empowered edge intelligence for internet of medical things against COVID-19,” IEEE Internet of Things Magazine, vol. 4, no. 2, pp. 34–39, 2021. [Google Scholar]

17. Y. Chen, J. Sun, Y. Yang, T. Li, X. Niu et al., “PSSPR: A source location privacy protection scheme based on sector phantom routing in WSNs,” International Journal of Intelligent Systems, vol. 37, no. 2, pp. 1204–1221, 2021. [Google Scholar]

18. C. Li, M. Dong, J. Li, G. Xu, X. B. Chen et al., “Efficient medical big data management with keyword-searchable encryption in Healthchain,” IEEE Systems Journal, vol. 16, no. 4, pp. 5521–5532, 2022. [Google Scholar]

19. R. Kumar and R. Tripathi, “Towards design and implementation of security and privacy framework for Internet of medical things (iomt) by leveraging blockchain and ipfs technology,” The Journal of Supercomputing, vol. 77, no. 8, pp. 7916–7955, 2021. [Google Scholar]

20. C. Li, Y. Guo, M. Dong, G. Xu, X. B. Chen et al., “Efficient certificateless authenticated key agreement for blockchain-enabled internet of medical things,” CMC-Computers, Materials & Continua, vol. 75, no. 1, pp. 2043–2059, 2023. [Google Scholar]

21. L. Chen and T. P. Pedersen, “New group signature schemes,” Lecture Notes in Computer Science, vol. 950, pp. 171–181, 1995. [Google Scholar]

22. M. N. S. Perera and T. Koshiba, “A guests managing system with lattice-based verifier-local revocation group signature scheme with time-bound keys,” in Proc. of the Fifth Int. Conf. on Mathematics and Computing, Singapore, Springer, pp. 81–96, 2021. [Google Scholar]

23. R. Xie, C. He, C. Xu and C. Gao, “Lattice-based dynamic group signature for anonymous authentication in IoT,” Annals of Telecommunications, vol. 74, no. 7, pp. 531–542, 2019. [Google Scholar]

24. M. S. Şahin and S. Akleylek, “A constant-size lattice-based partially-dynamic group signature scheme in quantum random oracle model,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 10, pp. 9852–9866, 2022. [Google Scholar]

25. Y. Zhang, X. Liu, Y. Hu, H. Jia and Q. Zhang, “An improved group signature scheme with VLR over lattices,” Security and Communication Networks, vol. 2021, no. 16, pp. 1–10, 2021. [Google Scholar]

26. F. Tang, Z. Feng, Q. Gong, Y. Huang and D. Huang, “Privacy-preserving scheme in the blockchain based on group signature with multiple managers,” Security and Communication Networks, vol. 2021, no. 1, pp. 1–8, 2021. [Google Scholar]

27. J. Vora, P. DevMurari, S. Tanwar, S. Tyagi, N. Kumar et al., “Blind signatures based secured e-healthcare system,” in 2018 Int. Conf. on Computer, Information and Telecommunication Systems (CITS), IEEE, Alsace, Colmar, France, pp. 1–5, 2018. [Google Scholar]

28. C. Li, G. Xu, Y. Chen, H. Ahmad and J. Li, “A new anti-quantum proxy blind signature for blockchain-enabled internet of things,” CMC-Computers, Materials & Continua, vol. 61, no. 2, pp. 711–726, 2019. [Google Scholar]

29. C. Li, Y. Tian, X. B. Chen and J. Li, “An efficient anti-quantum lattice-based blind signature for blockchain-enabled systems,” Information Sciences, vol. 546, no. 2, pp. 253–264, 2021. [Google Scholar]

30. G. Xu, J. Dong, C. Ma, J. Liu and U. G. O. Cliff, “A certificateless signcryption mechanism based on blockchain for edge computing,” IEEE Internet of Things Journal, pp. 1, 2022. [Online]. Available: https://ieeexplore.ieee.org/abstract/document/9714261 [Google Scholar]

31. W. Kong, J. Shen, P. Vijayakumar, Y. Cho and V. Chang, “A practical group blind signature scheme for privacy protection in smart grid,” Journal of Parallel and Distributed Computing, vol. 136, no. 1, pp. 29–39, 2020. [Google Scholar]

32. H. Fan and J. Rao, “A security refreshing algorithm of dynamic node based on fast group-blind signature,” Journal of Physics: Conference Series. IOP Publishing, vol. 1575, no. 1, pp. 012014, 2020. [Google Scholar]

33. J. Kastner, J. Loss and J. Xu, “On pairing-free blind signature schemes in the algebraic group model,” in Public-Key Cryptography-PKC 2022: 25th IACR Int. Conf. on Practice and Theory of Public-Key Cryptography, Virtual Event, pp. 468–497, 2022. [Google Scholar]

34. L. Ducas, A. Durmus, T. Lepoint and V. Lyubashevsky, “Lattice signatures and bimodal Gaussians,” in Advances in Cryptology-CRYPTO 2013: 33rd Annual Cryptology Conf., Santa Barbara, CA, USA, pp. 40–56, 2013. [Google Scholar]

35. C. Y. Li, X. B. Chen, Y. L. Chen, Y. Y. Hou and J. Li, “A new lattice-based signature scheme in post-quantum blockchain network,” IEEE Access, vol. 7, pp. 2026–2033, 2018. [Google Scholar]

36. E. Brickell, D. Pointcheval, S. Vaudenay and M. Yung, “Design validations for discrete logarithm based signature schemes, Public Key Cryptography,” in Public Key Cryptography: Third Int. Workshop on Practice and Theory in Public Key Cryptosystems, PKC 2000, Melbourne, Victoria, Australia, pp. 276–292, 2000. [Google Scholar]