Time Highlighted Multi-Interest Network for Sequential Recommendation

1  Introduction

Recommender systems explore users’ potential interests based on historical interactions and then analyze the correlation between interests and items to provide personalized recommendations. Collaborative filtering [1] is a classic algorithm of recommender systems, and it works based on the fact that similar users may share similar preferences and similar items may be liked by users. Many traditional methods [2–4] are designed based on it to alleviate the problem of data sparsity. With the advent of deep learning, neural network-based approaches [5] are proposed for their capacity for representation. For example, Guo et al. [6] combined deep learning and factorization machines to learn both high-order and low-order feature interactions. Wang et al. [7] captured richer embedding representations based on high-order connectivity in the user-item graph. However, the above methods learn fixed user embeddings, which cannot capture dynamic demands as user preferences always change over time.

Sequential recommendation treats historical interactions as a chronological sequence that contains the evolution of user preferences to guarantee more accurate, customized, and dynamic recommendations. The early research on the sequential recommendation predominantly relied on Markov Chains (MC) [8], which made the assumption that the dependency of each interaction lies in its preceding sequence. Recent methods [9,10] have achieved satisfactory performance by converting information into low-dimensional embeddings and using neural networks to learn user representations. For more effective and interpretable recommendations, some methods [11–13] utilized auxiliary relations in knowledge graph to capture more connections between items to enrich item embedding, rather than being limited to a sequence. In addition, the idea of self-supervised [14] which adaptively adjusts parameters by the difference between the current optimal solution and the global optimal solution has been introduced into recommendation systems, several models [15,16] extracted user embeddings from multiple perspectives and make the distance between them closer to obtain more accurate representation of users and improve model performance.

To better match the real-world recommendation scenarios, multi-interest-based models [17,18] have been proposed to extract multiple interests that represent different aspects of user preferences. Following the idea, Tan et al. [19] constructed intent prototypes and assign different weights to obtain various interests. Chen et al. [20] explored the periodicity and interactivity of user behavior sequences to enrich item embedding and utilized an attention network to extract multiple interests. Nevertheless, these methods have the following two problems: (1) they only answer the question “What are the interests of users” without distinguishing the importance of different interests in predicted time; (2) the transition trends of items in sequences that can simulate the potential interest of users over time are not fully mined. This work argues that temporal information is a key factor in extracting user interests, and transition trends can reflect possible points of interest. As shown in Fig. 1, the user interacted with three categories of products in the last week: laptops, clothes, and desks. Previous models tend to treat each interest equally, resulting in content that users are not interested in still being recommended. By contrast, this work considers timestamps when extracting interests, pays more attention to recent interests, and recommends items that the user may be like based on the trends. Besides, Fig. 2a shows the distribution of time intervals between two adjacent items on Amazon Books, it can be seen that the timespan in the historical sequences might be large. Traditional approaches treat user interests (items marked with black, blue, and green series) equally, but the time gap between the interactions related to the black series and the last interaction exceeds 100 days, the user (whose most recent interests are blue and green series) is unlikely to be interested in it, suggesting the possibility of utilizing temporal information. Fig. 2b plots the behavior analysis of a user’s last thirty interactions, revealing that interactions tend to be grouped within a short period of time, while the items that are interacted within a short period of time often have correlations. So, the transformation of items in the sequence can reflect the dynamic changes of points of interest to a certain extent.

Figure 1: An example of sequential recommendation using temporal information. Two more recent interests “clothes & desks” and possible trends of them are mainly considered when predicting the top four items

Figure 2: Analysis of temporal information about user interactions on Amazon Books. (a) Is the distribution of time intervals between two consecutive interactions (the long tail of the distribution is not included). (b) Is the behavior analysis of a user’s last thirty interactions. The X-axis denotes the time since the first interaction, while the Y-axis denotes the interaction count. Items with different categories are represented by circles of different colors

Aiming at the problems that the existing multi-interest methods cannot capture the temporal dynamics of user preferences, and do not make full use of interaction history to simulate the changing trends of user interests. This paper proposes a novel method called time highlighted multi- interest network for sequential recommendation (TimiRec), which assigns different weights to multiple interests based on the prediction moment, and aggregates the updated neighbor item representations as the transition trends of the current item. The main contributions of this work are summarized as follows:

•   Based on the prediction moment, a linear time interval function is designed to generate time interval information as the key factor to extract multiple interests from the user’s behavior sequence.

•   A time-attentive aggregation layer is introduced to aggregate neighbor items, in which an attention network is used to update the representations of neighbor items by considering the time intervals between the item and its neighbors, thereby capturing the changing trends of points of interest. And a gated unit is deployed to adaptively fuse the initial items embeddings and the captured trends.

•   The effectiveness of the proposed algorithm is evaluated by comparing it with various baseline methods on three real-world datasets, and the results convincingly establish the superior performance of the proposed model over state-of-the-art baselines.

2  Related Work

2.1 Sequential Recommendation

Sequential recommender systems treat users’ historical behaviors in chronological order and model the dependencies between items to provide more accurate recommendations. The model based on Markov Chains [8,21] is one of the most classical models. Nevertheless, a significant shortcoming of MC-based methods is their limited consideration of long-term dependencies, since they only rely on the most recent interactions. The field of sequential recommendation has embraced the advancements in deep learning, incorporating Recurrent Neural Network (RNN) and its variants, such as Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU). Zhou et al. [22] used GRU to increase the accuracy of prediction by supervising the hidden state. However, RNN-based methods that utilize the current state and previous state as input still have several problems, such as difficulty in parallelization and learning long-term dependencies. To tackle these problems, inspired by Transformer [23], Kang et al. [10] stacked self-attention layers to capture item relevance. Moreover, recent studies focused on incorporating interaction timestamps into the sequential modeling process. For instance, Li et al. [24] added relative time interval and position information into item embeddings. Following a normal distribution, Wang et al. [11] introduced two distinct temporal kernel functions to explicitly model the evolution of user preferences over time in terms of “complement” and “substitute” relations. Jiang et al. [25] designed a time weighting function to enhance the influence of the time effect of evaluation.

2.2 Attention Mechanism

Attention mechanism is a technique that considers the importance of each item in the input sequence to the output, recognizing that not all items in the sequence are equally important. Chen et al. [26] introduced attention mechanism into recommender systems as an additional component earlier. Xiao et al. [27] combined attention networks and Factorization Machine (FM) to improve the performance and interpretability of the model. Wang et al. [28] learned an attentive transactional context embedding which paid more attention to relevant items. And Cai et al. [29] measured the importance of different friends in social networks based on attention mechanism. More Recently, Vaswani et al. [23] proposed a sequence-to-sequence method named Transformer with a pure attention mechanism, which surpasses Convolutional Neural Network (CNN)/RNN-based approaches and achieves state-of-the-art performance. Unlike sequentially propagating sequence information, Transformer introduces the concept of query, key, and value to capture the relationship between items in the sequence, and then updates each item based on the similarity. This enables the model to simultaneously focus on all relevant parts of the sequence, which allows for better long-term dependencies modeling and improving the overall performance of the model.

3  Methodology

In this section, we begin by formulating the task of sequential recommendation and subsequently present the approach to map time intervals to corresponding vectors and construct the neighbor-aware graph, as well as the details of the proposed framework.

3.1 Problem Formulation

Let U and V denote the set of users and items respectively. Xu=[x1u,x2u,…,x|Xu|u] is the interaction sequence of user u∈U, and Tu=[t1u,t2u,…,t|Tu|u] is the corresponding timestamp sequence, where |Xu| (or |Tu|) is the length of the sequence. Given user u, historical interaction sequence Xu, and corresponding timestamp sequence Tu, the sequential recommendation task is to generate predictions of the next items that u is likely to interact with from V at a given time tr.

3.2 Linear Time Interval

To capture temporal dynamics, a simple way is to use a time decay function [11,30], but its disadvantages are that the fitting capacity is limited and the importance weights are not normalized. Another way [24,31] is to map timestamps to vectors, although it can improve model performance, its calculation of relative time intervals is overly dependent on the minimum value.

Besides, note that in Fig. 2b, interactions tend to be grouped in a short time, indicating the importance of ensuring the small range of time intervals are treated equally. Taking advantage of the above two approaches, this paper designs a linear time interval function to model the effect of temporal information. Specifically, for a given anonymous time sequence T=[t1,t2,…,t|T|], the linear time interval between interaction at time t and recommendation moment is defined as follows:

it=⌈α∗(tr−tt)⌉(1)

where tr represents the timestamp of the target item, and α is the coefficient of the linear function. By adjusting the value of α, ensure that the time interval is the same within the range of α. And then the linear time interval sequence is transformed into I=[i1,i2,…,i|T|] with a clip operation to avoid sparse relation encoding:

it=clip(it)=min(it,m)(2)

where m is the threshold.

3.3 Neighbor-Aware Graph Construction

Generally, adjacent interactions in sequence are often related to similar interests. To capture the changing trends of items and enrich the representation of item xi, we attentively aggregate the embedding of its neighbors Nδ(xi) (i.e., δ-neighbor set) in graph G, which is generated based on the pairwise item transitions in interaction records of all users. Since the time interval between paired items can indicate their correlation, utilizing it to distinguish the importance of different neighbors is necessary. Note that the same pairwise item transition may occur at multiple different time intervals, so choose the largest one to cover all possible situations and ensure the comprehensiveness of the model.

Specifically, for any item xiu in a user’s interaction sequence Xu, the δ-neighbor set of xiu contains items with a distance no more than δ in the sequence, which is defined as Nδ(xiu)={xju|xiu∈Xu,j∈(i,i+δ)}. The definition of graph G formed by neighbor items is G=(V,ℰ), where V={vi∪vj|vi∈V,vj∈Nδ(vi)} denotes the node set, and ℰ=max{i~ij|(vi,vj)|vi∈V,vj∈Nδ(vi)} represents the set of edges, the process of i~ij is consistent with Section 3.2. To keep efficiency and save resources, top-H neighbor items with the highest frequency are selected for any item vi.

3.4 TimiRec Framework

Fig. 3 provides an overview of our proposed framework, TimiRec. Each part of the model will be described in detail next.

Figure 3: The architecture of TimiRec. The linear function is applied to time interval information. A neighbor-aware construct and a time-attentive aggregation layer are deployed to sample top-H collaborative neighbors and model the trends of items over time, respectively. Finally, the multi-interest extraction layer is introduced to generate diverse preferences from the output of the gated fusion unit

3.4.1 Embedding Layer

The interaction sequence [x1,x2,…,x|X|] is converted into a fixed-length sequence X=[x1,x2,…,xL], where L represents the maximum length. If the sequence is longer than L, only the most recent L items are kept, and zero pad the sequence with zero on the left of the sequence if it is shorter than L. The time interval sequence [i1,i2,…,i|T|] is also transformed into I=[i1,i2,…,iL] to maintain the corresponding time interval of each interaction.

EX∈R|V|∗d is the learnable embedding matrix for all items, where d represents the latent dimension. Then, the embedding of the behavior sequence X∈RL∗d is obtained by a lookup operation. Similar to the behavior sequence, another embedding matrix EI∈Rm∗d is created for linear time interval sequence I, where m represents the maximum number of time intervals. After retrieval, the time interval sequence embedding I∈RL∗d is obtained.

3.4.2 Time-Attentive Neighbor Relation Aggregation

As shown in Fig. 4, based on the graph obtained by item transitions from all sequences, the time interval I~∈RH∗d between an item and its top-H collaborative neighbors are generated following the idea mentioned in the previous section. The only difference is the threshold of I~ is n. Then, for each item, mean pooling is used to gather information about neighbors.

Figure 4: Illustration of the time-attentive aggregation layer, which aggregates the representation of neighbor items by considering time interval information

eNvi=1|Nδ(vi)|∑vj∈Nδ(vi)evj∗(3)

where evj∗∈Rd denotes the embedding of item vj obtained by the time-attentive aggregation layer, and d is the dimension. To differentiate the significance of various neighbors to vi, neighbor embeddings are extended by time interval vectors I~, and the normalized score π(vi,vj) is then generated with an attention network as follows:

π(vi,vj)=exp(eviT(evj+i~ij))∑vk∈Nδ(vi)exp(eviT(evk+i~ik))(4)

evj∗=π(vi,vj)evj(5)

where i~ij∈Rd is the time interval between item vi and one of its top-H neighbor vj, evi,evj∈Rd are the embedding of item vi and vj, respectively.

Inspired by GRU which uses gating signals to update states, a gated unit is designed to dynamically balance the contributions of the item itself and its neighbors. For item vi, the representation evi and the aggregation representation eNvi of its neighbors are combined as follows:

gi=σ(W1evi+W2eNvi)(6)

ci=gi∗evi+(1−gi)∗eNvi(7)

where W1,W2∈Rd∗d are learnable transformation parameters, and σ is the sigmoid function. The gating signal gi∈Rd is employed to regulate the impact of the initial item and the aggregated neighbors. Finally, the fused result Cu=[c1u,c2u,…,cLu] is obtained.

3.4.3 Multi-Interest Extraction Layer

Considering the impact of temporal dynamics, the temporal embedding I∈RL∗d is used as the query of attention mechanism to selectively aggregate behavior sequences:

S=ATC(8)

A=softmax(tanh(IW3)W4)(9)

where W3∈Rd∗4d and W4∈R4d∗K are learnable parameters. A∈RL∗K estimates the contribution of each item in the sequence to the multiple interests, S∈RK∗d indicates multiple interests and K is the number of interests.

3.4.4 Model Training

After obtaining the interest embeddings from the multi-interest extraction layer, for the target item v, the argmax operator is used to select the corresponding interest vector from K candidate interest representations as user embedding:

s=S[:,argmax(Sev)](10)

When provided with a training sample (u,v) containing the user embedding s and item embedding ev, the probability of user u will interact with item v is calculated as follows:

Pθ(v|u)=exp(sTev)∑k∈Vexp(sTek)(11)

Since the sum operator in Eq. (11) is computationally time-consuming, a sampled softmax method is introduced to minimize the following objective function:

loss=∑u∈U∑v∈Xu−logPθ(v|u)(12)

3.4.5 Model Testing

Different from the training phase, different interests representing different aspects of user preferences can independently provide top-N items in the testing phase. To get the final top-N prediction results from K∗N candidate items, a straightforward approach is to select those items with the greatest similarity as the final prediction based on the inner product of candidate items and user interests, and it’s defined as:

f(u,v)=max1≤k≤K(evTsk)(13)

where ev is the embedding of a candidate item, and sk indicates the k-th interest.

4  Experiments

In this section, to validate the effectiveness of the proposed framework, extensive experiments with other state-of-the-art baseline methods are carried out on three real-world datasets.

4.1 Experimental Settings

4.1.1 Datasets

TimiRec is evaluated on three public datasets of diverse domains and sizes, Table 1 presents the statistics information of these datasets.

•   Amazon1: A commonly used review dataset that comprises various sub-datasets, and the following two specific sub-datasets are used: Books and Beauty.

•   MMTD2: Million Musical Tweets Dataset (MMTD) [32] is a dataset of listening events collected from Twitter.

To ensure data quality, interactions involving users and items with less than 5 occurrences are filtered out, and all users are split into training/validation/test sets in a ratio of 8:1:1. For model training, the complete sequences of interactions from the training users are utilized. More specifically, for a user sequence Xu=[x1u,x2u,…,x|Xu|u], each training sample ([x1u,x2u,…,xtu],xt+1u) uses the first t behaviors to predict the (t+1)−th interaction, where t=4,5,…,|Xu|−1. The number of neighbors H is 20, and the distance δ between the item and neighbors is set to 2. Each training sample is truncated to 20. For model testing, the first 80% of interactions of the user sequence from validation and test users are used as input of the trained model to infer user embeddings, and metrics are calculated by predicting the remaining 20% of interactions.

4.1.2 Evaluation Metrics

To evaluate the performance of the proposed TimiRec, three widely adopted evaluation criteria for top-N recommendation are used in our experiments, i.e., Recall, Normalized Discounted Cumulative Gain (NDCG), and Hit Ratio (HR). Among them, Recall@N represents the proportion of ground truth items included in the recommended N candidates, NDCG@N is a position-aware metric that assigns higher scores to ground truth items appearing at higher positions in the recommendation list, and HR@N focuses on determining whether the ground-truth item is present among the recommended items. N is set to 20 and 50 in our experiments.

4.1.3 Baselines

Comparative evaluations are conducted with TimiRec and the following methods:

•   YouTube DNN [33]: it is a deep learning model designed for an industrial recommendation that applies deep neural networks to YouTube video recommendation (YouTube DNN).

•   GRU4Rec [9]: it first applies GRU for the sequential recommendation.

•   MIND [17]: it is a multi-interest model that incorporates a capsule network to extract multiple user interests.

•   ComiRec-DR [18]: it follows MIND that extracts multiple interests using dynamic routing, and considers both diversity and accuracy of recommendation with a controllable factor.

•   ComiRec-SA [18]: another variant of ComiRec that utilizes self-attention to extract diverse interests.

•   PIMI [20]: a state-of-the-art model based on ComiRec-SA, periodicity and interactivity of user behavior sequence are explored to collect features before extracting multiple interests.

4.1.4 Details

TimiRec is implemented with TensorFlow. The embedding dimension is set to 64. For Books, MMTD, and Beauty, the reciprocal of the coefficient 1/α are set to 1 day, 1 min, and 1 day, the number of time interval thresholds m/n are set to 32/8, 128/16, and 64/16, respectively, and the number of interest embedding is 4. The number of samples for sampled softmax loss is set to 10. The maximum number of training iterations is set to 1 million. A widely used optimizer Adam [34] is adopted for optimization with a learning rate lr = 0.001.

4.2 Overall Performance

Table 2 shows a comprehensive summary of the performance of various methods across different datasets. Compared with GRU4Rec and YouTube DNN, which represent users as a single vector, multi-interest methods MIND, ComiRec, and PIMI achieve significant improvement, which implies that extracting multiple interests is more consistent with real-world scenarios. By incorporating the concepts of periodicity and interactivity in user behavior sequence, PIMI obtains notable enhancements compared to ComiRec. Our proposed method, TimiRec, consistently outperforms other baseline methods by effectively capturing the temporal dynamics of user interests.

4.3 Ablation Study

Table 3 presents the comparison results under the evaluation metrics of Recall@20, NDCG@20, and HR@20, where TimiRec-time and TimiRec-neigh denote TimiRec without temporal information and neighbor aggregate unit respectively. It can be found that removing any part harms results, suggesting that both of them are important to capture sequential information. Besides, lacking temporal information will lead to bigger performance loss. This is because the time interval information directly affects the weight of the current item when extracting interests, while neighbors are aggregated into items to enrich the item representation.

4.4 Time Interval Function

To verify the effectiveness of the designed linear time interval function, we removed the neighbor-aggregation layer (i.e., TimiRec-neigh in Section 4.3), and modify the Eq. (1) as:

it=⌈β∗log((tr−tt))+1⌉(14)

it=⌈(tr−tt)/min(iu)⌉(15)

Eq. (14) represents the logarithmic function, β is a coefficient, which assumes the effect of time on user interests gradually slows down as the time interval increases. Eq. (15) is the processing method in the paper proposed by Li et al. [24], min(iu) means the minimum time interval of user u. Because each training sample relies on the first t behaviors to predict the (t+1)-th interaction, leading to the value of min(iu) may change, so the relation between items will also change. Table 4 illustrates the performance when the time function changes. Experimental results demonstrate the great improvement brought by the proposed method.

4.5 Study on Hyper-Parameters

In order to gain a deeper understanding of how different hyper-parameters impact the performance of the model, the effect of time interval threshold m and n, the coefficient of time interval function α, and the number of interests K are studied.

As shown in Tables 5 and 6, the values of time interval thresholds m and n are varied to investigate the effect of modeling temporal dynamics. The parameter m controls the maximum time scope that directly affects user interests, and n ensures the quality of aggregated neighbor items. The values of m and n are selected from {16, 32, 64, 128} and {2, 4, 8, 16}, respectively. Experimental results on Amazon Books show that model achieves the best performance when m/n is set to 32/8. An excessively large time interval threshold may result in sparse encoding, conversely, setting a time interval threshold that is too small may lead to insufficient learning.

Fig. 5 illustrates the comparison of model performance on Amazon Books across different values of the coefficients α. The X-axis indicates 1/α, which is chosen from {0.25 day, 0.5 days, 1 day, 1.5 days, 2 days}. As is observed, TimiRec has the best performance when 1/α is 1 day. Combined with the best setting of 32 for m, it can be further inferred that a person reads a book in about one month.

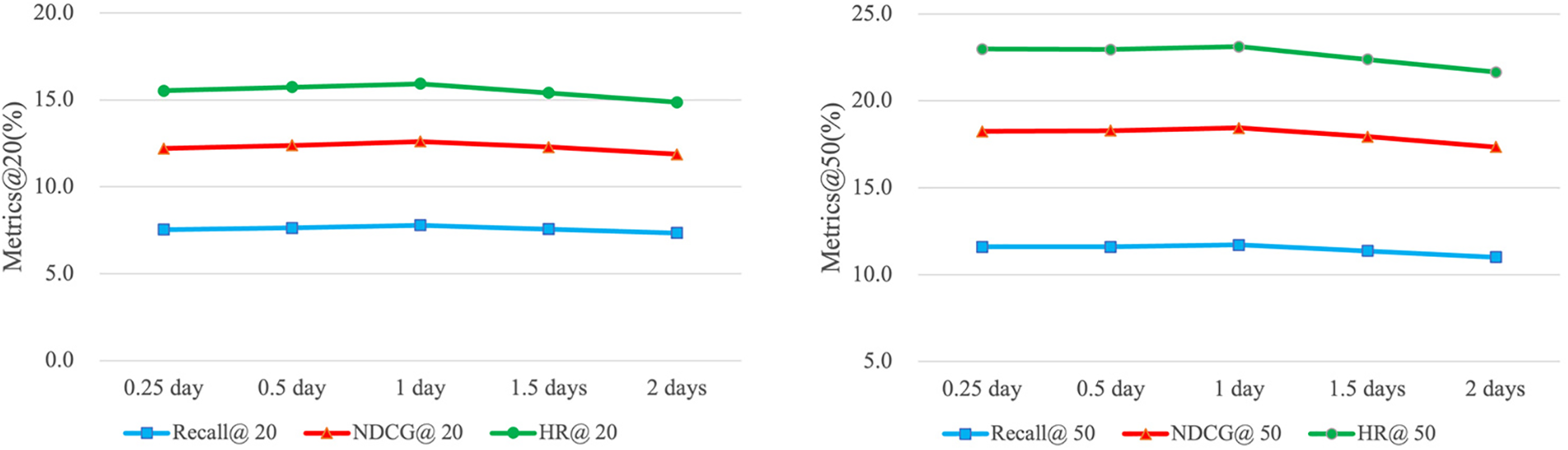
Figure 5: Performance comparison for the number of coefficients α on Amazon Books

Fig. 6 presents the Metrics@20 and Metrics@50 results, demonstrating the effect of the interest number K on Amazon Books. TimiRec obtains the best performance when K is 4. Increasing the number of interests does not always improve the model effect, which is in line with real-world recommendation scenarios, where users usually do not have too many or too few interests.

Figure 6: Effect of the number of interest K on Amazon Books

4.6 Training Efficiency

As shown in Fig. 7, the metrics of Recall@20 are tested on Amazon Books during the training process for the proposed model and two other state-of-the-art methods to show training efficiency compared to the proposed model. It can be observed that the evaluation metric of Recall@20 has roughly the same trend with iteration on three models. In terms of the average time per iteration, TimiRec takes an average of 0.050 s, which is 1.79 times larger than ComiRec-SA, which attributes to the aggregation of neighbor information and the preprocessing of time interval information. But compared with PIMI with an average iteration time of 0.100 s, the training efficiency of our model has been greatly improved, this is because the computation of the stacked three-layer self-attention network in the interactivity module is very time-consuming.

Figure 7: Training efficiency on Amazon Books

4.7 Case Study

The attention weights among multiple interests and items in the input sequence are visualized, which demonstrates the advantage of the proposed method by comparison with ComiRec-SA. Fig. 8 illustrates the heatmap of the attention weights (corresponding to the value of A in Eq. (9)) associated with a user randomly selected from Amazon Books. Compared with ComiRec-SA which is not aware of time, it can be seen that for items under the same interest, TimiRec will assign higher weights to the more recently interacted items. And for items of the same category with smaller timespans, TimiRec will assign similar weights (Interest 2).

Figure 8: Heatmap of attention weights among multiple interests and input items. I represents the linear time interval sequence corresponding to the input sequence of a user from Amazon Books

5  Conclusion

This work proposes a novel framework named TimiRec, which utilizes temporal information to extract multiple user interests. Specifically, multiple interests of users are generated by highlighting the time intervals in the multi-interest extraction layer, and combined with the neighbor-aware aggregation unit to capture possible trends of points of interest. The effectiveness and efficiency of the proposed model have been empirically verified through experiments conducted on three real-world datasets. In future work, we will combine temporal information and knowledge graph to build bridges between items and further explore their relationships to capture the possible trend of interests more comprehensively.

Acknowledgement: The resources and computing environment are provided by Chongqing University, Chongqing, China. We are thankful for their support.

Funding Statement: This work is supported in part by the National Natural Science Foundation of China under Grant 61702060.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design, analysis and interpretation of result: Jiayi Ma; draft manuscript preparation: Jiayi Ma, Tianhao Sun; data collection: Jiayi Ma, Xiaodong Zhang; All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors have shared the link to the data in the paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1http://jmcauley.ucsd.edu/data/amazon/.

2http://www.cp.jku.at/datasets/MMTD/.

References

1. D. Goldberg, D. Nichols, B. M. Oki and D. Terry, “Using collaborative filtering to weave an information tapestry,” Communications of the ACM, vol. 35, no. 12, pp. 61–70, 1992. [Google Scholar]

2. Y. Hu, Y. Koren and C. Volinsky, “Collaborative filtering for implicit feedback datasets,” in Eighth IEEE Int. Conf. on Data Mining, Pisa, Italy, pp. 263–272, 2009. [Google Scholar]

3. S. Rendle, “Factorization machines,” in IEEE Int. Conf. on Data Mining, Sydney, NSW, Australia, pp. 995–1000, 2010. [Google Scholar]

4. B. Sarwar, G. Karypis, J. Konstan and J. Riedl, “Item-based collaborative filtering recommendation algorithms,” in Proc. of WWW, New York, NY, USA, pp. 285–295, 2001. [Google Scholar]

5. J. Tang and K. Wang, “Personalized top-n sequential recommendation via convolutional sequence embedding,” in Proc. of WSDM, New York, NY, USA, pp. 565–573, 2018. [Google Scholar]

6. H. Guo, R. Tang, Y. Ye, Z. Li and X. He, “DeepFM: A factorization-machine based neural network for CTR prediction,” in Proc. of IJCAI, Melbourne, Australia, pp. 1725–1731, 2017. [Google Scholar]

7. X. Wang, X. He, M. Wang, F. Feng and T. S. Chua, “Neural graph collaborative filtering,” in Proc. of SIGIR, New York, NY, USA, pp. 165–174, 2019. [Google Scholar]

8. S. Rendle, C. Freudenthaler and L. Schmidt-Thieme, “Factorizing personalized Markov chains for next-basket recommendation,” in Proc. of WWW, New York, NY, USA, pp. 811–820, 2010. [Google Scholar]

9. B. Hidasi, A. Karatzoglou, L. Baltrunas and D. Tikk, “Session-based recommendations with recurrent neural networks,” arXiv:1511.06939, 2016. [Google Scholar]

10. W. C. Kang and J. McAuley, “Self-attentive sequential recommendation,” in IEEE Int. Conf. on Data Mining, Singapore, pp. 197–206, 2018. [Google Scholar]

11. C. Wang, M. Zhang, W. Ma, Y. Liu and S. Ma, “Make it a chorus: Knowledge- and time-aware item modeling for sequential recommendation,” in Proc. of SIGIR, New York, NY, USA, pp. 109–118, 2020. [Google Scholar]

12. P. Wang, Y. Fan, L. Xia, W. X. Zhao, S. Niu et al., “KERL: A knowledge-guided reinforcement learning model for sequential recommendation,” in Proc. of SIGIR, New York, NY, USA, pp. 209–218, 2020. [Google Scholar]

13. J. Yao, K. Cheng, M. Ge, X. Li and Y. Wang, “KGSR-GG: A noval scheme for dynamic recommendation,” Computers, Materials & Continua, vol. 73, no. 3, pp. 5509–5524, 2022. [Google Scholar]

14. A. Bhatt, P. Dimri and A. Aggarwal, “Self-adaptive brainstorming for jobshop scheduling in multicloud environment,” Software: Practice and Experience, vol. 50, no. 8, pp. 1381–1398, 2020. [Google Scholar]

15. Z. Lin, C. Tian, Y. Hou and W. X. Zhao, “Improving graph collaborative filtering with neighborhood-enriched contrastive learning,” in Proc. of WWW, New York, NY, USA, pp. 2320–2329, 2022. [Google Scholar]

16. Z. Wang, H. Liu, W. Wei, Y. Hu, X. L. He et al., “Multi-level contrastive learning framework for sequential recommendation,” in Proc. of CIKM, New York, NY, USA, pp. 2098–2107, 2022. [Google Scholar]

17. C. Li, Z. Liu, M. Wu, Y. Xu, H. Zhao et al., “Multi-interest network with dynamic routing for recommendation at tmall,” in Proc. of CIKM, New York, NY, USA, pp. 2615–2623, 2019. [Google Scholar]

18. Y. Cen, J. Zhang, X. Zou, C. Zhou, H. Yang et al., “Controllable multi-interest framework for recommendation,” in Proc. of KDD, New York, NY, USA, pp. 2942–2951, 2020. [Google Scholar]

19. Q. Tan, J. Zhang, J. Yao, N. Liu, J. Zhou et al., “Sparse-interest network for sequential recommendation,” in Proc. of WSDM, New York, NY, USA, pp. 598–606, 2021. [Google Scholar]

20. G. Chen, X. Zhang, Y. Zhao, C. Xue and J. Xiang, “Exploring periodicity and interactivity in multi-interest framework for sequential recommendation,” in Proc. of IJCAI, Montreal, Canada, pp. 1426–1433, 2021. [Google Scholar]

21. R. He and J. McAuley, “Fusing similarity models with Markov chains for sparse sequential recommendation,” in IEEE 16th Int. Conf. on Data Mining, Barcelona, Spain, pp. 191–200, 2016. [Google Scholar]

22. G. Zhou, N. Mou, Y. Fan, Q. Pi, W. Bian et al., “Deep interest evolution network for click-through rate prediction,” in The Thirty-Third AAAI Conf. on Artificial Intelligence, Honolulu, Hawaii, USA, pp. 5941–5948, 2019. [Google Scholar]

23. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones et al., “Attention is all you need,” in Proc. of NIPS, Red Hook, NY, USA, pp. 6000–6010, 2017. [Google Scholar]

24. J. Li, Y. Wang and J. McAuley, “Time interval aware self-attention for sequential recommendation,” in Proc. of WSDM, New York, NY, USA, pp. 322–330, 2020. [Google Scholar]

25. W. Jiang, J. Chen, Y. Jiang, Y. Xu, Y. Wang et al., “A new time-aware collaborative filtering intelligent recommendation system,” Computers, Materials & Continua, vol. 61, no. 2, pp. 849–859, 2019. [Google Scholar]

26. J. Chen, H. Zhang, X. He, L. Nie, W. Liu et al., “Attentive collaborative filtering: Multimedia recommendation with item- and component-level attention,” in Proc. of SIGIR, New York, NY, USA, pp. 335–344, 2017. [Google Scholar]

27. J. Xiao, H. Ye, X. He, H. Zhang, F. Wu et al., “Attentional factorization machines: Learning the weight of feature interactions via attention networks,” in Proc. of IJCAI, Melbourne, Australia, pp. 3119–3125, 2017. [Google Scholar]

28. S. Wang, L. Cao and L. Hu, “Attention-based transactional context embedding for next-item recommendation,” in Proc. of AAAI, New Orleans, Louisiana, USA, pp. 2532–2539, 2018. [Google Scholar]

29. C. Cai, H. Xu, J. Wan, B. Zhou and X. Xie, “An attention-based friend recommendation model in social network,” Computers, Materials & Continua, vol. 65, no. 3, pp. 2475–2488, 2020. [Google Scholar]

30. J. Wu, R. Cai and H. Wang, “Déjà vu: A contextualized temporal attention mechanism for sequential recommendation,” in Proc. of WWW, New York, NY, USA, pp. 2199–2209, 2020. [Google Scholar]

31. W. Ye, S. Wang, X. Chen, X. Wang, Z. Qin et al., “Time matters: Sequential recommendation with complex temporal information,” in Proc. of SIGIR, New York, NY, USA, pp. 1459–1468, 2020. [Google Scholar]

32. D. Hauger, M. Schedl, A. Kosir and M. Tkalvcivc, “The million musical tweet dataset: What we can learn from microblogs,” in Proc. of ISMIR, Curitiba, Brazil, pp. 189–194, 2013. [Google Scholar]

33. P. Covington, J. Adams and E. Sargin, “Deep neural networks for youtube recommendations,” in Proc. of RecSys, New York, NY, USA, pp. 191–198, 2016. [Google Scholar]

34. D. Kingma and J. Ba, “ADAM: A method for stochastic optimization,” arXiv:1412.6980, 2014. [Google Scholar]