Hybrid Hierarchical Particle Swarm Optimization with Evolutionary Artificial Bee Colony Algorithm for Task Scheduling in Cloud Computing

1  Introduction

Cloud computing resource scheduling refers to the process of efficiently allocating and managing computing resources, such as virtual machines, storage, and networking, within a cloud infrastructure. The primary objective of resource scheduling in cloud computing is to optimize resource utilization, ensure high availability, and meet the performance requirements of applications and services hosted in the cloud environment. This involves making dynamic decisions on how to allocate resources to various tasks, workloads, or users in a way that maximizes efficiency and minimizes costs while maintaining a balanced and responsive system [1,2]. Furthermore, resource scheduling in cloud computing is a critical component for ensuring the allocating of cloud resources effectively and real-time adaptation of requirements. It involves load balancing, provisioning, and de-provisioning resources, as well as considering factors like workload priorities, resource constraints, and cost management. A seamless and efficient computing experience would help cloud users easily and effectively operate the underlying infrastructure. Effective resource scheduling is important in the scalability, flexibility, and cost-effectiveness of cloud computing services.

Additionally, the cloud computing resources can be divided into homogeneous and heterogeneous. As for the homogeneous one, there is a set of resources with the same or similar nature components. When they are processed by virtual machines, there are few fluctuations in processing speed. The time cost is low, and the load is less. On the contrary, the heterogeneous resources are composed of different resources with different natures. Cloud computing usually needs to deal with various resources, such as the requirement of storage space, varied computational speed, accuracy of data processing, and so on. So far, the investigations on the resource-scheduling techniques in heterogeneous multi-cloud environments are mainly focused on resource scheduling, provisioning, and clustering, which are usually limited to a single cloud platform. Resource scheduling with better adaptability used in higher-level, large-scale, and heterogeneous multi-cloud scenarios is still a challenge. Moreover, although most metaheuristic algorithms on heterogeneous resources improve the comprehensive performance, the complexity is also increased. Additionally, they usually tend to fall into local ones during the iterative convergence phase of the algorithm to find the optimal solution. The scheduling time is prolonged, reducing efficiency.

Currently, there are many optimization algorithms, like the cuckoo-improved particle swarm optimization (PSO). In literature [3], Levy flight in Rhododendron was introduced into PSO to solve the problem of particle swarm being trapped in local optimization. Gray wolf optimization was used in the literature [4], in which the wolf pack fitness function was optimized to process multiple targets with a single fitness. It overcomes the serious sensitivity to the initial population settings. Additionally, the random value used in the algorithm to update the position of the Wolf was limited to the search range. In literature [5–7], the researchers carried out the cat swarm algorithm to improve the search efficiency. In which, the algorithm divides cats into two categories and optimizes them at the same time. For the elite algorithm and the idea of the Pareto optimal frontier, the introduced cat colony improvement effectively accelerated the convergence of the optimal solution [5]. Although the disadvantages of the cat swarm algorithm like the requirement of more iterations to achieve effective optimization still exist, these studies also guide future research. In addition, particle swarm algorithm [8–10], seagull optimization algorithm [11], and other emerging intelligent algorithms [12–15], have been proposed to optimize the cloud-computing resource scheduling. Among these algorithms, PSO may be more mature and have more application, while it is easy to fall into local optimum. Therefore, by modifying the varied and crossover operators of the backtracking search algorithm (BSA) via neighborhood, the PSO-BSA algorithm has been proposed to accelerate the convergence speed [8]. Such as the ant colony optimization was carried out to improve the convergence accuracy and avoid local optima [12–15]. This algorithm has strong parallelism, and it is suitable for large-scale problems. Nevertheless, its insufficient convergence speed in the early stage notably increases the early computing time cost in resource scheduling. To reduce time cost, pseudo-random state transfer rules were used for path selection, and the state transfer probability was calculated based on the current optimal solution and the number of iterations as well as optimal and worst solutions were used to improve the global pheromone update [13]. In recent years, numerous emerging algorithms have shown novel and infinite potential, although they were proposed later than the aforementioned algorithms. For example, the dwarf mongoose optimization algorithm [16] can achieve a balance between exploration and exploitation by incorporating principles which makes it an effective metaheuristic approach for solving complex optimization problems. Its convergence speed is low, however, there will be more heuristic algorithms to enhance algorithm robustness on this base in the future. The gazelle optimization algorithm that mimics the process of a gazelle chasing its prey in the natural world to search for the optimal solution [17] displays fast convergence speed, high precision, ease of implementation, and significant applicability in solving complex optimization problems. While it would converge prematurely in some cases.

In addition, the artificial bee colony (ABC) algorithm, as an intelligent algorithm, is also a popular swarm intelligence algorithm [18]. It has been widely used in cloud computing resource scheduling due to its advantages of fast convergence, strong global optimization capability, and easy implementation [19,20]. These studies mainly focus on improving the performance of the algorithm, exploring its application in different scenarios, and/or combining it with other optimization algorithms. Moreover, some researchers have also proposed modified ABC algorithms, such as hybrid ABC algorithms [20] used to adapt to the complex and dynamic environment of cloud computing better. Achieving a multi-objective optimal solution in a complex environment by combining with another algorithm. Overall, the research on the ABC algorithm in cloud computing resource scheduling is still ongoing, and there is still room for further exploration and improvement.

In this work, an evolutionary artificial bee colony algorithm (EABC) has been proposed to make the solution more diverse to avoid falling into local optimum by adding random perturbation to ABC. The probability of onlooker bees choosing honey sources was introduced to improve the inertia weight decline of the particle swarm algorithm. The average of fitness was taken into the original equation to determine whether it was far from the optimal solution and to increase the accuracy of the selection of the solution. Considering that the improved algorithm cannot effectively improve the processing speed of heterogeneous resources, we proposed an improved hierarchical particle swarm optimization (HPSO) algorithm and incorporated it into the EABC to obtain a hybrid hierarchical particle swarm and evolutionary artificial bee colony algorithm (Hierarchical particle swarm optimization-evolutionary artificial bee colony, HPSO-EABC), which is more robust in improving load balancing, processing different resources faster, and reducing the cost in resource scheduling. However, this paper also has some defects, such as the performance of the improved algorithm (EABC, HPSO-EABC) highly depends on the algorithm and parameter settings. Choosing the appropriate parameter values is critical to the performance, but parameter selection is often a challenging task and may require trial and error and adjustment to obtain the best results. Introducing more mechanisms and additional steps also leads to an increase in the complexity of the algorithm.

The remaining sections of this paper are organized as follows: Section 2 presents the research content and the proposed algorithms of this work, namely EABC, HPSO, and HPSO-EABC. This section provides a detailed description of the ideas and steps involved in these proposed algorithms. In Section 3, we focus on the experiments conducted in both homogeneous and heterogeneous resource scenarios. The performance of our proposed algorithms is also compared with other algorithms in terms of convergence speed, task execution time, load balancing, and operational cost. Finally, Section 4 concludes this investigation and outlines future work.

2  Methods

2.1 Cloud Computing Resource Scheduling Algorithm

The principle of cloud computing task scheduling involves dividing the problem to be executed into two parts Map and Reduce. The submitted task of the user is split into several smaller tasks by the Map program. Through cloud virtualization technology, these sub-tasks are assigned to virtual machine computing resources with a certain scheduling method. The Reduce step integrates the computation results and puts out the ultimate ones. Throughout this process, the virtual machines are independent of each other, and each sub-task only can run on one virtual machine resource. On the other hand, heterogeneous resources are composed of different components with diverse properties. Cloud computing encompasses a variety of resources. Some tasks require large storage space with minimal computing speed requirements, while others have the opposite characteristics [21]. Current challenges in heterogeneous resource scheduling include resource orchestration, provisioning, and clustering. These challenges often restrict the resource scheduling techniques to within a single cloud platform, which lacks higher-level and multi-cloud scheduling capabilities, and exhibits limited adaptability to large-scale and heterogeneous scenarios.

In comparison to homogeneous resources, most heuristic algorithms designed for handling heterogeneous resources tend to increase overall performance at the expense of complexity. During the iterative convergence process of these algorithms, it is easy to get trapped in local solutions, resulting in longer scheduling time and lower efficiency. The EABC algorithm proposed here combines the advantages of global search, robustness, and high efficiency, which belongs to bee colony optimization. Compared to the ABC algorithm, the EABC algorithm effectively improves task completion time and algorithm convergence within different environments. Additionally, the HPSO-EABC algorithm integrates the rapid convergence and the strong global search capability from the HPSO algorithm on the base of the EABC algorithm. It addresses the deficiency of EABC in terms of heterogeneous resource scheduling speed and ensures a more balanced workload allocation for virtual machines during resource scheduling. The framework of the cloud computing resource scheduling used here is shown in Fig. 1.

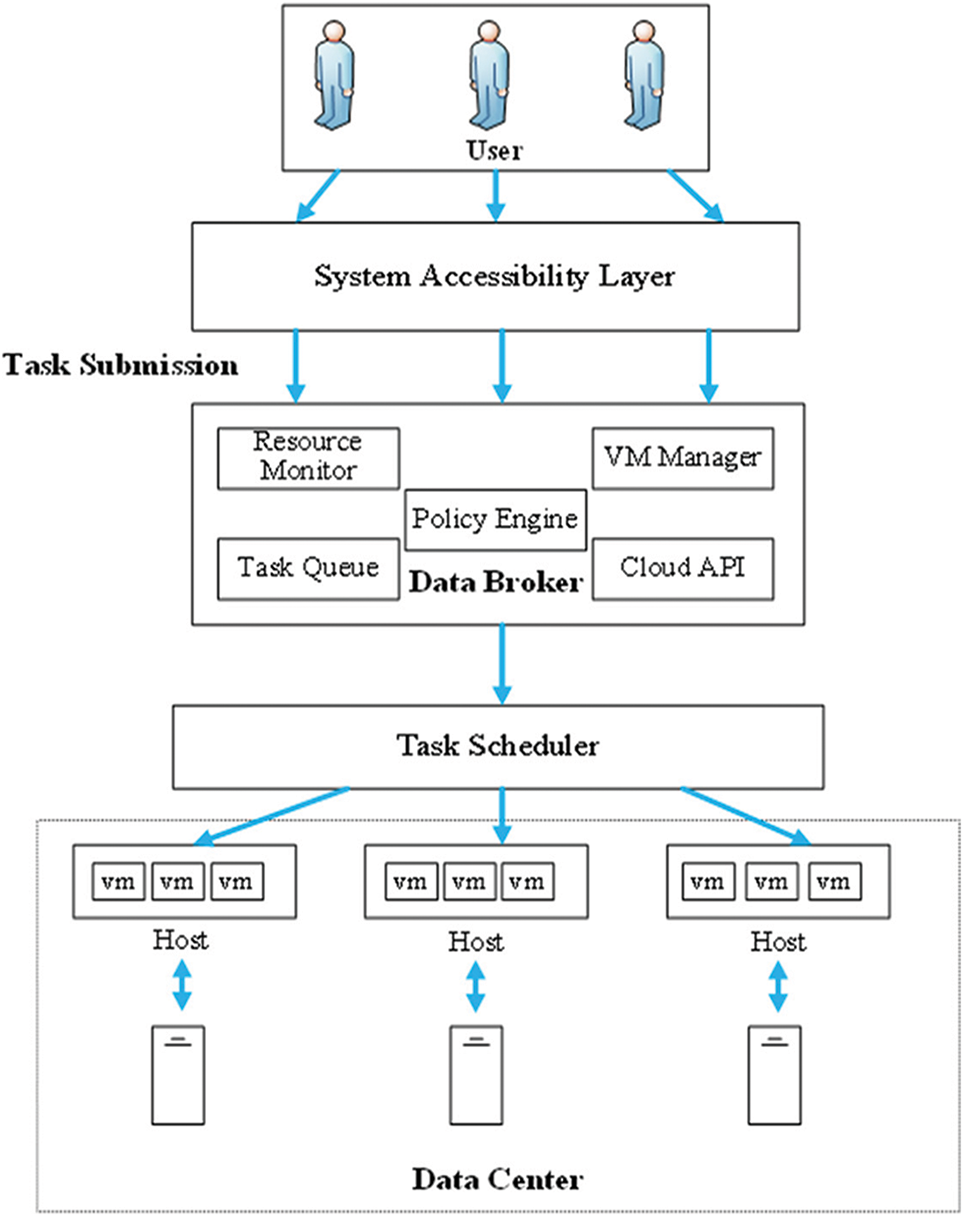
Figure 1: The cloud resource management framework

In detail, the scheduling process is abstracted as m subtasks executing on n VM nodes. T={t1,t2,t3,…,tm} is the set of m subtasks, where (i=1,2,3,…,m) is the i-th subtask. VM={vm1,vm2,vm3,…,vmn}, which is the set of n virtual machines, where vmj (j=1,2,3,…,n) is the j-th VM compute node. As a result, the allocation relationship between them can be described as m×n matrix TVM as Eq. (1).

TVM=[tvm11…tvm1n…tvmij…tvmm1…tvmmj](1)

where tvmij takes two separate values of 0 and 1. When tvmij is 0, it means the subtask ti is not assigned to the vmj virtual machine. On the contrary, if tvmij is 1, the subtask is assigned to the vmj virtual machine. Each subtask can only be assigned to one virtual machine, denoted as ∑j=1ntvmij=1. The execution time of a subtask on a virtual machine is represented by the matrix ETC as Eq. (2).

ETC=[etc11…etc1n…etcij…etcm1…etcmn](2)

where etcij denotes the running time of the subtask ti on the virtual machine vmj. It can be calculated with Eq. (3).

etcij=lengthimipsj(3)

where lengthi denotes the length of subtask i, while mipsj denotes the processing speed of virtual machine j. The final goal of the whole scheduling is the minimum time for task completion. It can be expressed by Makespan [22], and calculated with Eq. (4).

Makespan=maxj=1n∑i=1sum(j)etcij(4)

where sum(j) denotes the total number of tasks assigned to the virtual machine vmj.

2.2 Cloud Computing Resource Scheduling Based on Evolutionary Artificial Bee Colony Algorithm

The artificial bee colony algorithm is an optimization method proposed by imitating the behavior of bees. It does not need to know the special information about the problem, but comparing the advantages and disadvantages of the problem is required. Based on the local optimization-seeking behavior of each bee, the global optimum value will be deduced, which has a fast convergence speed. Furthermore, the process of gathering honey is regarded as a task assignment. The bee species are roughly divided into employed and non-employed bees. The non-employed bees are further divided into onlooker and scouter bees. The employed bees can pass their honey-harvesting information to the onlooker ones through the “waggle dance”. The onlooker bees will select the nectar source based on the information passed from the employed ones and continue to exploit. When a nectar source reaches the threshold value and does not update its position, one of the employed bees will turn into a scouter to re-exploit a new nectar source. After the iteration, the optimal solution will be decided according to the predefined criteria [19].

2.2.1 Honey Source Initialization

At the initial stage of this algorithm, there is no prior experience for the bee. All the bees are scouters. The population number was set as N. That is, there are N initial solutions. The location of the i-th nectar source can be expressed as Xi=(xi1,xi2,…,xiD), where D denotes the dimension, that is the number of tasks. Each component of the nectar source was mapped into the ID number of the VM according to the corresponding mapping rules. Thus, the location of a nectar source corresponds to a virtual machine. The feasible equation for each initial solution of a virtual machine assignment scheme is described as Eq. (5).

xij=xminj+rand(0,1)(xmaxj−xminj)(5)

where xij is the nectar source location, j is any number from the set of 1 to D, xmaxj and xminj respectively denotes the maximum and minimum value in each dimension, i.e., the upper and lower bounds of the task number, and rand (0,1) represents a random number from 0 to 1.

2.2.2 Improved Location Update and Search Strategy

This section discusses the improvements in the search strategy of onlooker bees, in the standard ABC algorithm, the employed bees conduct a neighborhood search first, then the onlooker bees collect nectar through the information transmitted by the “waggle dance” of the employed bees. If a nectar source has a higher fitness value, the probability of being selected by the onlooker bees is also higher, there will be more onlooker bees in the neighborhood to exploit it. When onlooker bees are in the neighborhood search phase, the location of the new nectar source can be generally calculated using the following Eq. (6) [19].

vij=xij+r(xij−xkj)(6)

where i and k are not equal, r is a random number in the range 0 to 1, k∈{1,2,3,…,N}, j∈{1,2,3,…,D}, xij is the current nectar source location, and vij is the new nectar source obtained within the neighborhood search [19]. It is worth mentioning that the neighborhood search method of the employed bees is also referred to in Eq. (6). Moreover, this section does not improve the location update strategy of employed bees, while it is the other way for the onlooker bees.

On the other hand, it is hard to derive the optimal solution quickly with the steps mentioned above. To overcome this lack, the learning factor in the particle swarm algorithm was introduced. As a result, the swarm can locate the better nectar source more precisely through the guidance of the current optimal solution during the neighborhood search. Eq. (6) is further modified as Eq. (7).

vij=xij+α(xbestj−xkj)(7)

where xbestj is the current best nectar source location, and α represents a random number from 0 to 1. Although Eq. (7) crosses the optimal solution and the current position, the neighborhood search may lead to a depressed exploitation capability. It is easy to fall into local solutions, reducing the exploration of other nectar sources [23]. Therefore, a random perturbation is added to optimize Eq. (7) and to increase its search capability. The final equation after improvement is presented as Eq. (8).

vij=xij+α(xbestj−xkj)+β(xr1j−xr2j)(8)

where r1 and r2 are the two random numbers with different values, and β is a random number, which will be set to a random number in the range of −0.5 to 1.5 after several rounds of testing. In this way, the onlooker bees will unconsciously favor some random nectar sources in the neighborhood search on the original guidance, providing the opportunity for nectar with optimal solutions to be exploited.

2.2.3 Improved Selection Strategy

For the traditional ABC algorithms, the selection probability is achieved by the roulette wheel. It will lead the poorer nectar sources to abandon, reducing the diversity of the population, and finally making the algorithm premature. Here, an improved selection strategy in the initial algorithm is carried out, which is described as Eq. (9).

Pi=(1−γ)∗(fi/fmax)+γ(9)

where Pi is the selection probability of the ith onlooker bee, fi and fmax are the ith nectar source fitness value and the current maximum fitness value, respectively. γ is a coefficient of 0.1, when the selection strategy is optimal after several rounds of test. Nevertheless, due to ignoring the degree of converging to the optimal solution of the algorithm, the accuracy of the derived result with Eq. (9) is not enough. To improve it, the sensitivity was introduced in the free search algorithm [24,25]. The improved probability is described as Eq. (10).

S1(i)={|(fi−favg)/(fmax−favg)|fmax≠favg0the others(10)

where S1(i) is the probability of the ith nectar source being selected, and generating another number that S2(i) indicates the probability of each onlooker bee selecting that source, S2(i)∼U(0,1). When S2(i)<S1(i), the search is performed, or vice versa, and the original nectar source location is kept unchanged.

2.2.4 Steps of the EABC Algorithm

The flow chart of our EABC algorithm is shown in Fig. 2. The detailed steps of our EABC algorithm are as follows:

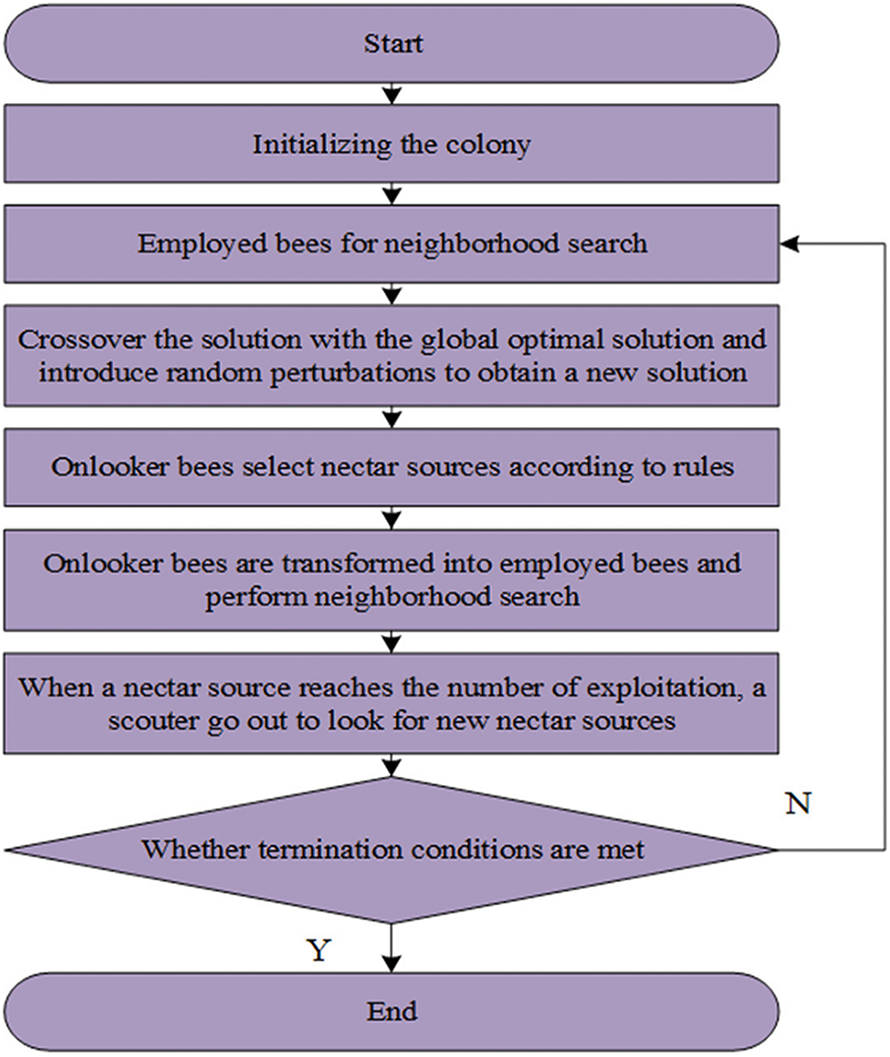
Figure 2: The flow chart of our proposed EABC algorithm

For ease of reading, in the following steps, the employed bees had been defined as “Bee A,” the onlooker bees were labeled as “Bee B,” and the scouters were described as “Bee C”.

Step 1: Initialize the relevant parameters, set the maximum number of iterations of the population, the number of nectar sources and the maximum number of exploitation, the number of bee populations, etc., where Bee A and Bee B account each for half.

Step 2: Initialize the population by generating random initial solutions according to Eq. (5) and assign cloud tasks to corresponding virtual machines.

Step 3: Bee A performs neighborhood searches on honey sources, generating new honey source search solutions. These new solutions are compared with the original solutions mapped into virtual machine allocation schemes to select the solution with a shorter resource scheduling time.

Step 4: Bee B, guided by the “waggle dance” of Bee A, chooses nectar sources based on probability.

Step 5: Bee B continues to exploit the selected nectar sources. They repeat Step 3, crossing the solutions from the neighborhood search with the global optimum solution and introducing perturbation. The better solution is selected based on a greedy principle.

Step 6: If the maximum number of nectar sources has been mined, only one Bee A will transform into Bee C to produce new nectar sources and reinitialize.

Step 7: If the termination condition has been reached, find the optimal solution and the optimal resource allocation solution found by all the current bees.

Step 8: Incorporate the obtained allocation plans into both heterogeneous and homogeneous resource allocation, output the results, and analyze them.

The maximum number of iterations is set as T, and the current number of iterations is t. Based on the above theory, the EABC algorithm is implemented below.

2.3 Cloud Computing Resource Scheduling Algorithm Based on Hierarchical Particle Swarm Optimization-Evolutionary Artificial Bee Colony Algorithm

In fact, for our proposed EABC algorithm, there are still some shortcomings that need to be improved, including

(a) Difficult to model heterogeneous resources. As for the heterogeneous resources, there are many different performance metrics and usage constraints, like CPU, memory, bandwidth, etc. It is hard for our EABC to model these different resource attributes effectively, which leads to trouble in fully utilizing the resource characteristics.

(b) Excessive search space. In some resource scheduling, the search space is usually very large and high complexity. It makes the EABC face inefficient searches, and failure to find the optimal solution in a limited time.

(c) Difficult adjustment of algorithm parameters. The EABC depends largely on the setting parameters of population size, number of iterations, local search, and so on. Furthermore, these parameters are difficult to adjust effectively for the heterogeneous resource scheduling, which will cause lower efficiency and valid performance of the algorithm.

Fortunately, PSO has a global search capability. It can find the global optimal solution in the multi-dimensional search space. Besides handling complex resource scheduling, it also can search for the optimal solution quickly, improving scheduling efficiency.

Therefore, to overcome the shortcomings of EABC, PSO is used to improve the velocity update formula of particles and to stratify the particles. That is HPSO, and it is also fused with the EABC algorithm, giving rise to the HPSO-EABC algorithm.

2.3.1 Description of the HPSO Algorithm

To improve our algorithm, we have done more in-depth research on PSO [26–28]. In [26], to solve the many-objective optimization problem, the author proposed a binary particle swarm optimization with a two-level particle cooperation strategy. A many-objective reset operation is also done to enable the algorithm to jump out of the local optimum. In [27], an improved localized FS approach based on multi-objective binary PSO was proposed, it addressed fault diagnosis from a novel perspective that takes advantage of the local distribution of data without balancing strategies. In [28], a cooperative coevolutionary algorithm based on the genetic algorithm (GA) and PSO was proposed to search for the feature subsets with and without entropy-based cut points simultaneously. Enlightened by these works, the HPSO is proposed here based on the standard PSO.

For PSO, the velocity and position update equations are exhibited in Eqs. (11) and (12).

vidk1+1=vidk1+c1r3(pidk1−xidk1)+c2r4(pgdk1−xidk1)(11)

and

xidk1+1=xidk1+vidk1+1(12)

where vidk1 and xidk1 respectively represent the d-dimensional component of the velocity and position vector of particle i in the k1th iteration, pidk1 indicates the optimal value of the d-dimensional component of the position vector of particle i since the k1th iteration, i.e., the local optimal value, pgdk1 indicates the optimal value of the d-dimensional component of the position vector of all particles since the k1th iteration, i.e., the global optimal value, c1 represents the cognitive term factor, c2 represents the social term factor that regulates the maximum step size of learning, and r3 and r4 represent two random numbers. Eq. (11) consists of three components the inertial term, the cognitive term, and the social term. Then the velocity update formula was improved as

vidk1+1=vidk1+c1r3(μpidk1+(1−μ)pgdk1−xidk1)+c2r4(pgdk1−xidk1)(13)

where μ represents the ratio of the current optimal value to the global optimal value and is defined as

μ=pidk1/pgdk1(14)

As a result, the guidance of the global optimal solution can be obtained, when the particles perform cognitive term learning. The increase in value μ may indicate the pidk1 is close to pgdk1, and the guidance of pgdk1 to the particles is weakened. The particles are more inclined to the local optimal position pidk1, and vice versa to the global optimal position pgdk1. The ability to jump out of the local optimal solution for the particles is improved, which also enhances the diversity and global search capability of the population.

Besides, the particles will be stratified according to the number of iterations, and are further labeled as the pre-particle, mid-particle, and post-particle, respectively. The particles in different layers will be given different Inertia weighting factors ω as their separate inertia terms. The improved velocity update formula can be described as

vidk1+1=ωvidk1+c1r3(μpidk1+(1−μ)pgdk1−xidk1)+c2r4(pgdk1−xidk1)(15)

where ω is dynamically decreasing and discontinuous. It satisfies the Eq. (16).

ω={λ−λ1k1/nλ2+n/(λ3k1)λ4k1/n<1/31/3≤k1/n≤2/3k1/n>2/3(16)

where λ, λ1, λ2, λ3, λ4 are the different coefficients, k1 is the current number of iterations, and n represents the maximum number of iterations. When the number of iterations of the population reaches n/3, the corresponding particle is regarded as the pre-particle. Currently, to make the particle expand the search range and increase the development of the algorithm, the value of ω is set to linear decrease largely. After testing, the value of λ may be set as 0.9, and that of λ1 can be set to 1.5 for the best effect. With the increase in the number of iterations, the ratio of the current number to n is over 1/3, while less than 2/3, the population enters the middle one, and the particle becomes the middle one. After the pre-search, to reduce the particle search range fluctuation and increase the stability of the algorithm, the ω will decrease slowly and tend to smooth with the iteration number, which follows an inverse proportional function. Additionally, when the particle just enters the middle stage, ω should be no much difference in value from the end of the previous period. Otherwise, it may lead to a large change in the trajectory of the particles. As a test result, the optimized value of λ2 is set to 0.1. The value of λ3 determines the smoothness of the curves. It is set to 10 after many tests, which is the most favorable. Meanwhile, the ω has already reached a much lower value after the initial two downward evolutions. If ω continues to decrease, it will lead to a decrease in the quality of the optimal solution due to the lack of particle search range. Thus, when the particle enters the later stage, the λ4 is set as a constant. As mentioned above, since the inertia factor for the two stages should not vary so much, λ4 is set as 0.2. To show it more intuitively, the trend of ω with n in the range of 0 to 10000 is plotted, and shown in Fig. 3.

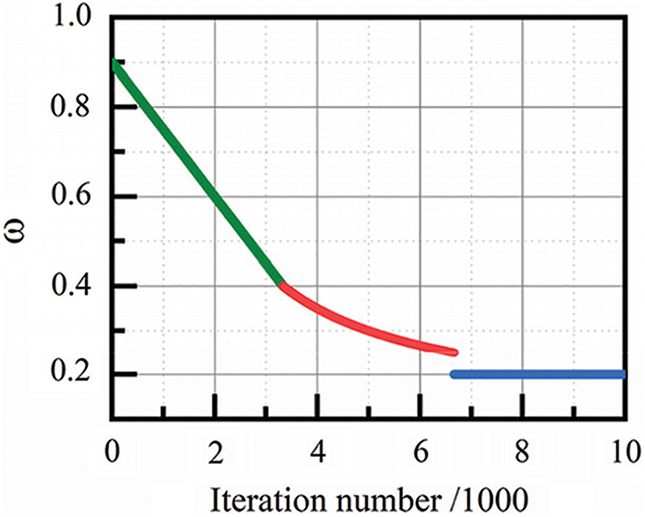
Figure 3: Trend of ω

2.3.2 Description of the HPSO-EABC Algorithm

The Particle Swarm Optimization algorithm with Inertia Weight Optimization demonstrates increased adaptability following inertia weight optimization. Combining it with EABC allows for the synergistic utilization of their respective advantages, further enhancing the robustness and ensuring the stability of resource scheduling solutions. It also increases scalability to meet resource scheduling requirements in various environments.

In this integrated algorithm, the HPSO is responsible for generating initial solutions after the initialization by the EABC. During the EABC initialization, the particle population transformed into a new type of bee species named “initial bees.” These initial bees inherit the learning attributes of particles in the EABC algorithm. As per Eqs. (12) and (13), each initial bee undergoes position and velocity updates, while the inertia weight is updated according to Eq. (15). The final positions obtained by the initial bees after a full iteration cycle serve as the initial nectar source position in the artificial bee colony algorithm. In essence, the HPSO algorithm is executed first, and its solutions are integrated into the EABC one.

In contrast to Eq. (5), the solutions obtained from the initial bees inherit the high stability characteristic of the PSO algorithm. It enables the bee colony to have both a clear sense of direction and randomness at the beginning of iterations. This fused algorithm effectively addresses the neighborhood-search limitation of the bee colony algorithm and avoids falling into local optima.

2.3.3 Steps of the HPSO-EABC Algorithm

The HPSO-EABC is a two-stage optimization approach. First, the HPSO algorithm is initialized with specific parameters. Initial velocities and positions are assigned to each particle, and then the individual and global best solutions are updated. The particle velocities are updated iteratively, and such process continues until a specified number of iterations is reached. The best solution is recorded and named the “initial bee”. Next, the “initial bee” which represents the result from the previous HPSO, serves as the initial source position for the EABC algorithm and further is initialized with its parameters. After that, the population is divided into employed bees and onlooker bees. The employed bees perform neighborhood searches based on the “initial bee” position, and the results obtained are communicated to the onlooker bees. The onlooker bees then continue to explore When a honey source reaches its maximum exploitation limit, a randomly employed bee will be transformed into a scouter to reset the nectar source.

These processes mentioned above are repeated until the best solution is found. The HPSO-EABC algorithm initially leverages the HPSO optimization to benefit from its strong exploitation capabilities, improving efficiency and robustness. Then it combines the concurrency of the EABC algorithm to ensure stability in later-stage solutions. As a result, the merged algorithm exhibits higher scalability and can adapt to resource scheduling in different environments. The specific flowchart of the HPSO-EABC algorithm is shown in Fig. 4.

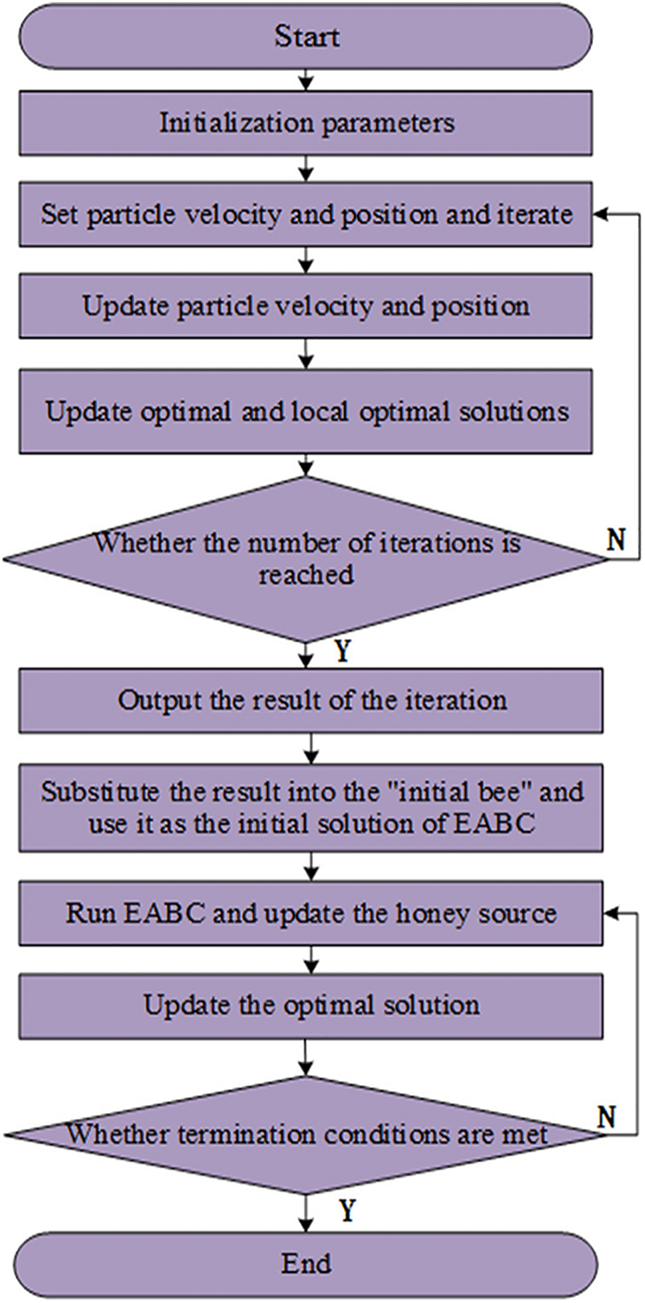
Figure 4: The flow chart of the HPSO-EABC

Since the subsequent HPSO algorithm is similar to that of the EABC algorithm, it will not be repeated here. Even so, early on the HPSO algorithm is implemented below in detail.

3  Simulation Results and Analysis

The CloudSim platform [29] with an Intel i5 processor, a 16 GB RAM, and the Windows 10 operating system were used for simulation. ABC [22], PSO [22], and our proposed EABC, HPSO, and HPSO-EABC are compared and analyzed within the convergence speed, the task completion time, and the load balancing degree. For simulated homogeneous resource processing, a uniform mips value for processing was used. Setting the mips value to fluctuate within a certain range was done for the heterogeneous resource processing. More specifically, in all the following comparison graphs, the mips value will be set to 3000 for homogeneous resource processing scenarios, and it fluctuates in the range of 1000-10000 for heterogeneous ones for ease of display.

Other parameter settings and values used in the simulation are listed in Tables 1 and 2. Since the parameters used in the hybrid HPSO-EABC algorithm are not changed, Table 2 only shows the parameters done for the ABC, EABC, PSO, and HPSO algorithms.

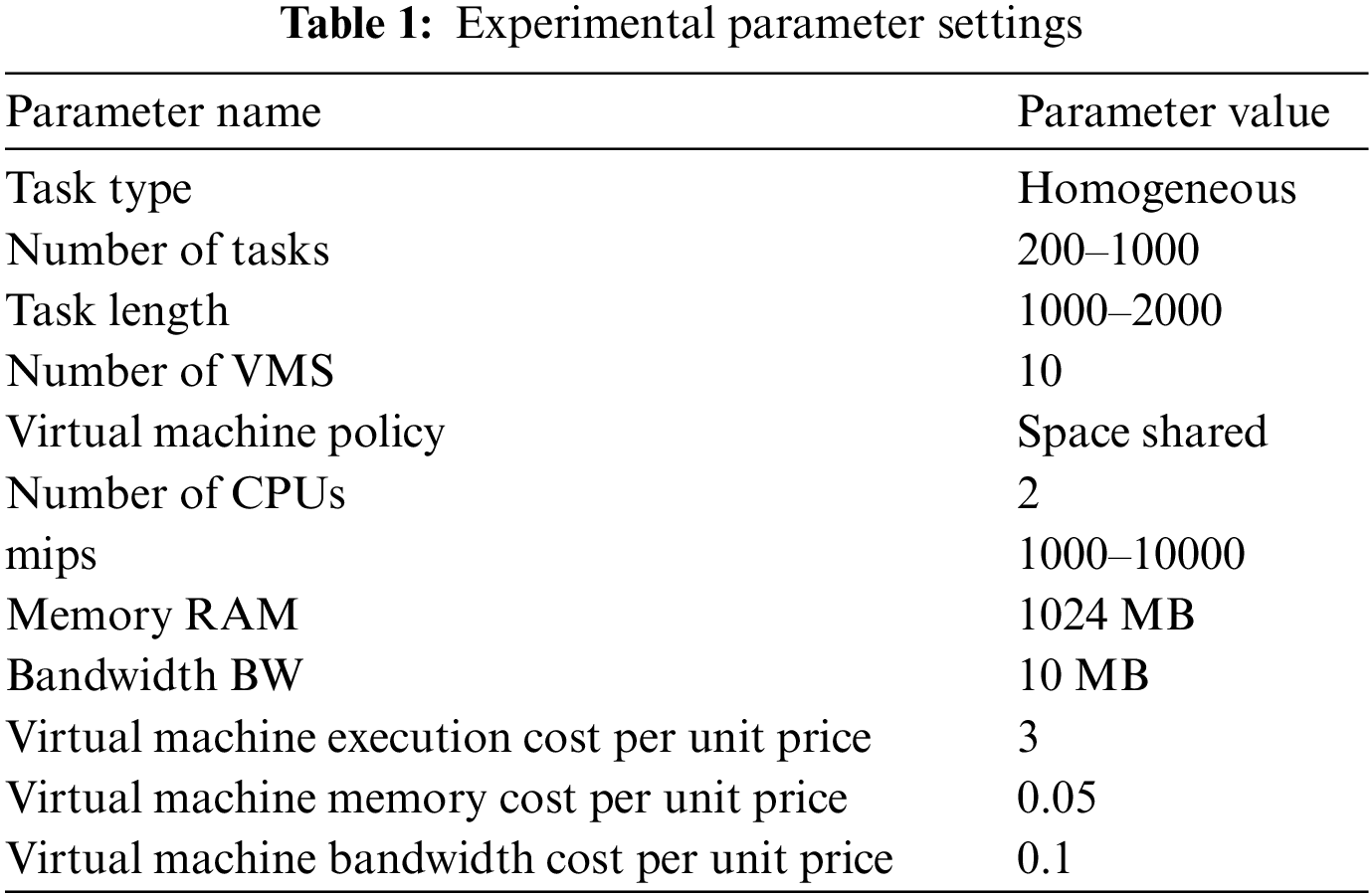
Firstly, the convergence of each algorithm is tested. The initial number of scheduling tasks is set to 1000. There are 10 computing resources, and the number of iterations varies from 1000 to 10000. The completion time is calculated with Eq. (4), which is the value of the makespan. As a result, the iteration number-dependent computing time cost with the ABC, PSO, EABC, HPSO, and HPSO-EABC algorithms for both homogeneous and heterogeneous resources are displayed respectively in Figs. 5a and 5b. For a fixed number of tasks, as the number of iterations increases, the convergence of the algorithm has been improved, resulting in better optimal solutions and corresponding allocation schemes. Consequently, the overall resource scheduling completion time is reduced.

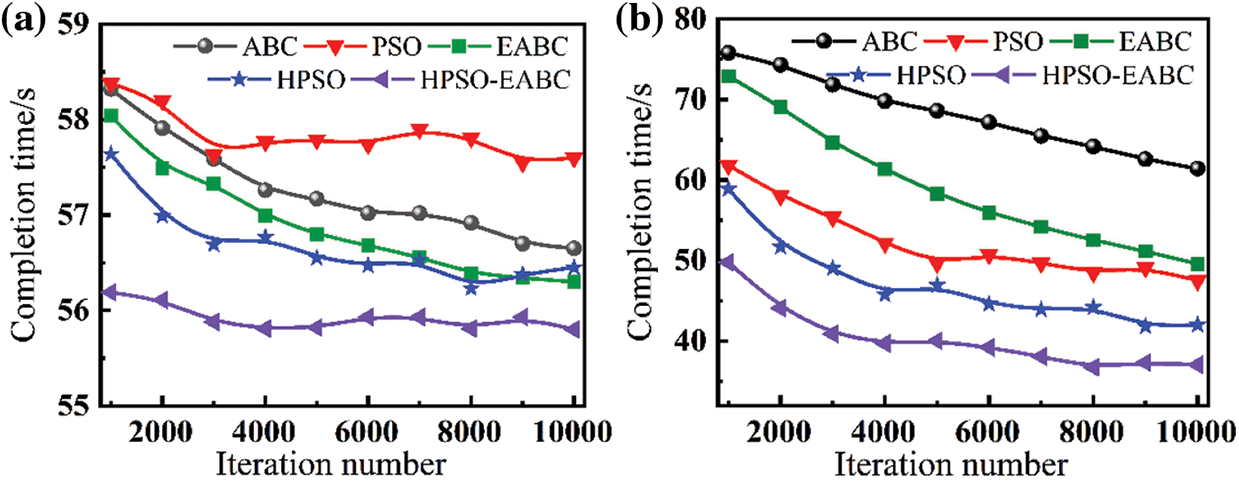
Figure 5: Iteration number-dependent convergence comparison for (a) homogeneous and (b) heterogeneous task scheduling

As shown in Fig. 5, the HPSO-EABC consistently has a faster convergence speed and shorter completion time compared to other algorithms no matter for the homogeneous and heterogeneous environment. The EABC, when compared to the ABC, also improves in terms of convergence speed with lower completion time. For the homogeneous ask scheduling, the EABC slightly outperforms the ABC and the PSO. However, as displayed in Fig. 5a, when the progressing iteration number increases from 3000 to 4000, the decline of the PSO notably diminishes, while that of ABC continues to decrease steadily. This indicates that the PSO tends to get trapped in local optima, and the quality of the solutions is without significant improvement. However, the overall runtime has improved considerably. Introducing a global optimum to the cognitive component and setting appropriate weightings has effectively addressed the inadequate search scope of the PSO. The tiered inertia weight reduces runtime in the early stages and helps HPSO maintain stability in the middle and later stages. For the EABC, though the downward trend is obvious, its task completion time cost in the early iterations is lower than that of the HPSO. At 1000, 2000, and 3000 iterations, the EABC needs more corresponding completion time of 0.4, 0.5, and 0.64 s than the HPSO algorithm, respectively. After the 9000th iteration, the time cost of the EABC is the same as that of the HPSO. Notably, it keeps decreasing and is slightly less than that of the HPSO after the 10000th iteration, although it is still a divergence. Considering experimental deviation and randomness of the task lengths, the HPSO tends to have a stable completion time between 5000-6000 iterations. Thus, both the EABC and the HPSO have their advantages and disadvantages for the homogeneous environment. The EABC, with its parallel processing capability, can steadily approach the optimal solution. However, with a lesser number of iterations, the solution quality needs to be optimized, and the convergence speed is slower. Although the HPSO can obtain better solutions earlier, its solution quality in the later stages is slightly lower than that of the EABC. Therefore, by combining the fast obtaining the optimal solution with the HPSO and optimizing it with the EABC, the advantages can be effectively taken, resulting in less runtime and enhancing convergence.

However, for the heterogeneous resource scheduling, as shown in Fig. 5b, following the MIPS value changing continuously, both the ABC and the EABC perform worse than PSO and HPSO. This suggests that swarm algorithms like ABC and EABC are not as effective as particle swarm algorithms. On the contrary, the PSO can deal with such resources with significant variability. That is, there is lesser scalability of the ABC and EABC algorithms. For the HPSO, it consistently reduces runtime while maintaining stability and convergence. Hence, the hybrid HPSO-EABC inherits the advantages of both the EABC and the HPSO. At the initial iteration, the HPSO-EABC has respective lower runtime of 26.03, 12.09, 23.13, and 9.1 s than that of the ABC, PSO, EABC, and HPSO, which translates to percentage improvements of 34.34%, 19.54%, 31.73%, and 15.46%. Around the 8000th iteration, the HPSO-EABC starts to converge. At the 10000th iteration, its runtime is 24.37, 10.47, 12.55, and 4.97 s less than that of the ABC, PSO, EABC, and HPSO, respectively, which is a percentage improvement of 39.68%, 22.03%, 25.3%, and 11.83%. Moreover, following the iteration increases from 1000 to 10000, the reduced runtime for the ABC, PSO, EABC, HPSO, and HPSO-EABC is respective 1.67, 0.78, 1.74, 1.19, and 0.39 s for the homogeneous scenario. Those for the heterogeneous one are 14.38, 14.34, 23.3, 16.85, and 12.72 s, respectively. The lowest runtime reduction of the HPSO-EABC algorithm after 10000 iterations among all algorithms indicates its best stability and convergence.

Different task loads, typical 200, 400, 600, 800, and 1000 tasks are selected with a fixed number of iterations of 10000 and were used to demonstrate the performance time of each algorithm. The completion time of the ABC, PSO, EABC, HPSO, and HPSO-EABC is calculated with Eq. (4), and the results are shown in Figs. 6a and 6b respectively for the homogeneous and heterogeneous sources. For homogeneous resource scheduling, as shown in Fig. 6a, our proposed EABC and HPSO algorithms display slightly less virtual machine runtime for each number of tasks. The reduced completion time for the EABC algorithm may be caused by the improvements in the position updating and selection strategies. The reduced runtime for the HPSO algorithm is a result of achieving a better optimal solution from a larger search range and avoiding local optima with the hierarchical approach of particle search. Moreover, as shown in Fig. 6a, the less time of the EABC algorithm than that of the HPSO, suggests that the bee colony algorithm is more advantageous than particle swarm algorithms in processing homogeneous resources. Notably, the HPSO-EABC algorithm reduced the virtual machine runtime by 0.85, 1.8, 0.5, and 0.65 s for the 1000 tasks, separately compared to the ABC, PSO, EABC, and HPSO algorithms. This is attributed to the further reduction in the virtual machine runtime with particle swarm guidance on the base of the EABC algorithm. In the case of heterogeneous resource scheduling, as shown in Fig. 6b, five algorithms have close runtime for the lowest 200 tasks. Nevertheless, with the task loads increasing, the runtime with our proposed EABC and HPSO algorithms are significantly reduced, respectively compared to the traditional ABC and PSO algorithms. In detail, the EABC algorithm reduces the completion time by 11.82 s compared with the ABC algorithm, and the HPSO algorithm reduces the completion time by 4.25 s compared with the PSO algorithm with a task number of 1000. As the dimension of the solution space increases with the number of tasks, the random perturbation introduced in the EABC algorithm increases the possibility of finding the optimal solution, which significantly improves the effectiveness, and leads to its low runtime. As for the HPSO algorithm, the introduction of the inertial weight effectively avoids premature convergence and enlarges the search space and dimension of the solution.

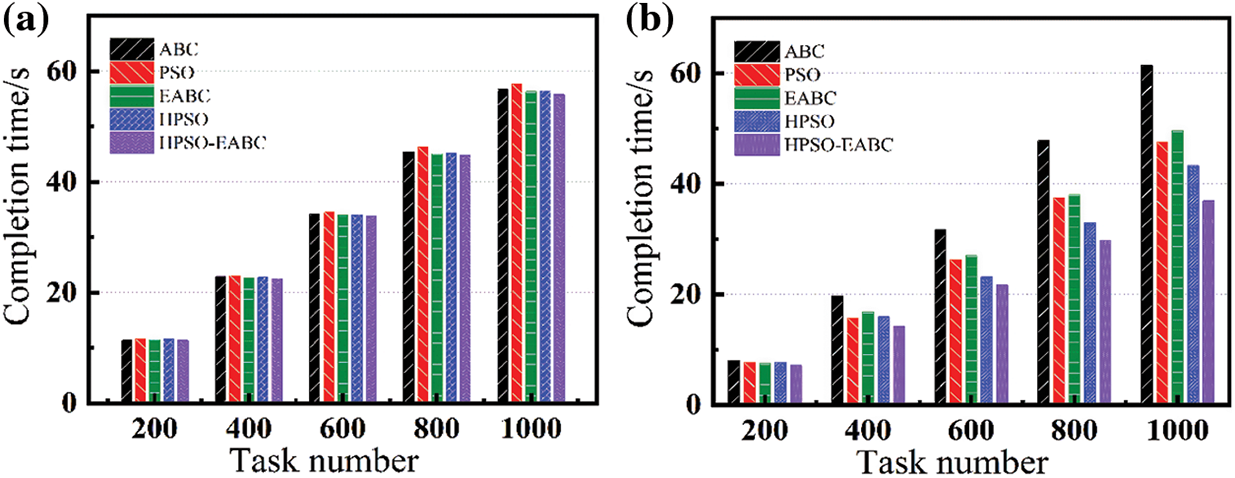
Figure 6: Comparison of (a) homogeneous and (b) heterogeneous task completion time

Furthermore, as shown in Fig. 6b, the HPSO-EABC algorithm can reduce the completion time by 24.49, 10.59, 12.67, and 6.34 s compared to ABC, PSO, EABC, and HPSO algorithms, respectively. Therefore, such a hybrid algorithm HPSO-EABC not only overcomes the shortcomings mentioned above but also reduces the completion time. Following the optimal solution obtained by the particle swarm algorithm, the blindness and randomness of the initial solution obtained by the bee colony algorithm are improved. As a result, the completion time has been dramatically reduced with the HPSO-EABC algorithm. To give the load balance of our algorithms, the degree of imbalance (DI) was defined and used to calculate the imbalance degree among the virtual machines, which is expressed as Eq. (17).

DI=∑j=1n(Timej−AL)2n(17)

where AL is the average load of virtual machines is the average completion time of virtual machines, Timej is the task completion time on the jth virtual machine, and n is the number of virtual machines. The smaller the value of DI is, the more balanced the VMs are, and the higher the degree of load balancing is, the more reasonable the scheduling policy is under this algorithm.

The DI value for each ABC, PSO, EABC, HPSO, and HPSO-EABC algorithm for typical tasks of 200, 400, 600, 800, and 1000 is calculated and plotted in Figs. 7a and 7b for the homogeneous and heterogeneous sources, respectively. For a homogeneous environment and as shown in Fig. 7a, the PSO has the most uneven workload. Its DI is significantly higher than the other algorithms, which even exceeds 1 at the task of 1000. The EABC has lower DI values than that of the ABC. The new honey source update strategy introduced in the EABC makes the algorithm more stable when searching for the optimal solution. In the task range of 200–600, the EABC algorithm performs the best with a relatively low and steady increased DI value. Additionally, the HPSO also demonstrates a lower DI value than that of the PSO, which is a result of the introduced inertia weight and the increased stability as the task dimension increases. However, when the number of tasks is over 800, the HPSO-EABC algorithm has the lowest DI value and even shows a decreasing trend. This suggests that the hybrid HPSO-EABC algorithm holds the best balance degree, as a result of inheriting the high concurrency exploratory and load stability of the EABC algorithm as well as making full use of particle assignment through gradually following the current global optimal solution.

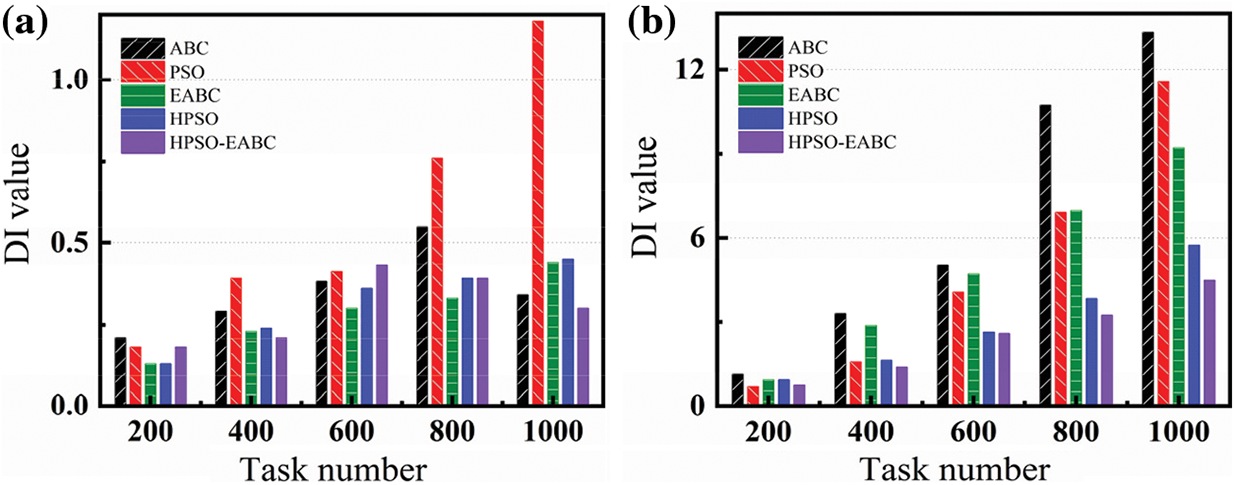
Figure 7: Comparison of (a) homogeneous and (b) heterogeneous tasks load balancing

For the heterogeneous environment, as shown in Fig. 7b, the DI value for each algorithm is larger than that of homogeneous sources, which is due to the fluctuation of the mips value. However, the DI value of the EABC and HPSO is still lower than that of the traditional ABC and PSO. For the HPSO-EABC algorithm, its global search ability is improved, which makes it more adaptable and robust to various types of problems. As a result, the HPSO-EABC exhibited the lowest DI among all algorithms, as shown in Fig. 7b. Hence, when dealing with fluctuating mips resources, the HPSO-EABC algorithm achieves the most evenly distributed node loads for virtual machines, with a DI value that remains stable at less than 5, although the number of tasks reaches 1000. That is, our proposed hybrid HPSO-EABC algorithm can achieve the most evenly distributed node loads on dealing with mips resources.

A statistical test on the runtime and the load balance is carried out further to exhibit the difference between our proposed algorithms and other ones. The task-dependent statistical analysis results of runtime and standard deviation for each algorithm within homogeneous and heterogeneous scheduling scenarios are shown in Tables S1 and S2, respectively. The completion time displayed in Fig. 6 is taken from their average values, while the DI values shown in Fig. 7 correspond to the standard deviation. As listed in Tables S1 and S2, the EABC surpasses the ABC algorithm, and the HPSO excels over the PSO one. The enhanced algorithms have reduced the average runtime, as previously discussed. Moreover, the runtime in the best and worst cases has also improved, with a noticeable reduction in the difference between the longest and shortest runtime. Consequently, the corresponding standard deviation has decreased, leading to a more balanced workload. Therefore, the hybrid HPSO-EABC algorithm, which combines the strengths of both the HPSO and the EABC algorithms, exhibits the best performance. Although the standard deviation of runtime for the HPSO-EABC algorithm is not the smallest in initial low tasks as listed in Table S2, suggests that there may still be room for improvement in such fused algorithms.

Since the EABC algorithm proposed here mainly combines two kinds of improvements: the location update strategy of neighborhood search of the onlooker bee and the honey source selection strategy, the ablation experiments were carried out on the EABC algorithm to further verify its rigor. All the experimental contents and data analysis of this part are provided in the part of Supplementary Materials of the paper. In detail, all the results are shown in Tables S3-S8. In detail, the experiment was divided into three groups. For the first one, we only retain the improvement of the location update strategy in the EABC algorithm, which is recorded as the EABC-A algorithm and compared with the ABC algorithm. Detailed data are recorded in Tables S3 and S4. For the second group, we only retain the improvement of the selection strategy in the EABC algorithm, which is recorded as the EABC-B algorithm and compared with the ABC algorithm. Detailed data are recorded in Tables S5 and S6. For the last group, we compare the EABC-A and the EABC-B algorithms, which contain only one improved strategy, with the EABC algorithm in this paper. Detailed data are recorded in Tables S7 and S8. The comparison of the first two groups, as listed in lower values shown in Tables S3–S6, proves that the two improved methods used in the EABC algorithm proposed here are effective. The comparison results of the third group prove once again that the effect of our EABC algorithm is better than that of both the EABC-A and EABC-B algorithms, which contain only one improved strategy.

Furthermore, the operating cost of resource scheduling C with a unit of US dollars for each algorithm was calculated with Eq. (18).

C=c1makespan+c2RAM+c3BW(18)

where the variable c1 represents the unit cost of time running, c2 represents the unit cost of memory, and c3 represents the unit cost of bandwidth. According to Table 1, the values of c1, c2, and c3 are respectively 3, 0.05, and 0.1. The calculated C for all five algorithms with different task loads within the homogeneous and heterogeneous resource scheduling are respectively displayed in Figs. 8a and 8b. On one side, for the homogeneous resource scheduling shown in Fig. 8a, all algorithms show a close value of C regardless of the task number, although HPSO-EABC holds a slightly lower value. Nonetheless, the HPSO-EABC exhibited much less cost. Furthermore, the cost reductions can separately reach $73.47, $31.77, $38.0, and $19.02 compared to the ABC, PSO, EABC, and HPSO algorithms. It indicates that HPSO-EABC is more cost-efficient for many tasks.

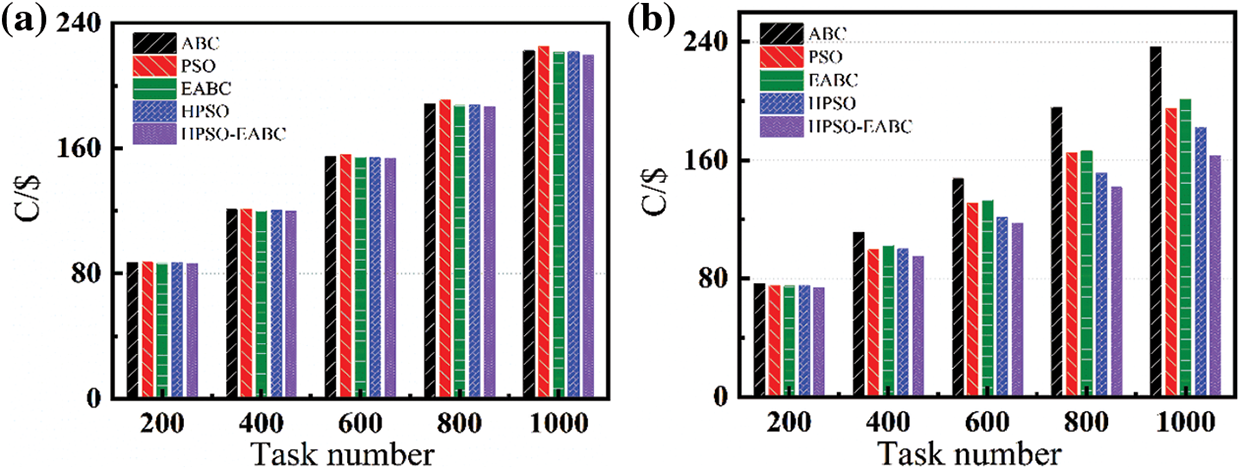
Figure 8: Comparison of resource scheduling costs for (a) homogeneous and (b) heterogeneous resources

4  Conclusion and Future Work

In summary, the HPSO-EABC algorithm, as a hybrid HPSO with the EABC algorithm, has been proposed and used for multi-objective task scheduling optimization in a cloud computing environment.

•   The EABC based on the ABC algorithm has been proposed to make the solution more diverse to avoid falling into local optimum. As a result of the sensitivity in the free search, the EABC algorithm has enhanced algorithm parallelism.

•   The HPSO has been proposed to accelerate the processing speed of heterogeneous resources on the base of the traditional PSO algorithm.

•   The HPSO-EABC that hybrid EABC and HPSO has been proposed to further improve the stability and convergence of the algorithm, which is not only robust and easy to develop, but also can effectively reduce resource scheduling completion time and make the virtual machine operating load more balanced with low virtual machine operating costs for both homogeneous and heterogeneous scenarios.

Considering the integration of other algorithms or modifying the optimization strategies of the EABC algorithm and the inertia weight strategies of the HPSO algorithm could be explored in future work. The algorithm proposed here may be expanded to and applied in other fields like path planning, cluster control, and so on.

Acknowledgement: The authors thank the anonymous referees for their careful readings and provisions of helpful suggestions to improve the presentation.

Funding Statement: This work was jointly supported by the Jiangsu Postgraduate Research and Practice Innovation Project under Grant KYCX22_1030, SJCX22_0283 and SJCX23_0293, the NUPTSF under Grant NY220201.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: S. Zhao, H. Yan; data collection: H. Yan, Q. Lin, X. Feng, H. Chen; analysis and interpretation of results: S. Zhao, H. Yan, D. Zhang; draft manuscript preparation: S. Zhao, H. Yan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

Supplementary Materials: The supplementary material is available online at https://doi.org/10.32604/cmc.2023.045660.

References

1. S. B. Mehdi, E. S. Mohammad, R. M. G. Mohammad and H. S. J. Hamid, “Multi-objective tasks scheduling using bee colony algorithm in cloud computing,” International Journal of Electrical and Computer Engineering, vol. 12, no. 5, pp. 5657–5666, 2022. [Google Scholar]

2. Y. H. Ahmed and H. A. Monagi, “Task scheduling optimization in cloud computing based on genetic algorithms,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3289–3301, 2021. [Google Scholar]

3. A. Bouyer and A. Hatamlou, “An efficient hybrid clustering method based on improved cuckoo optimization and modified particle swarm optimization algorithms,” Applied Soft Computing, vol. 67, no. 6, pp. 172–182, 2018. [Google Scholar]

4. G. Natesan and A. Chokkalingam, “An improved grey wolf optimization algorithm based task scheduling in cloud computing environment,” The International Arab Journal of Information Technology, vol. 17, no. 1, pp. 73–81, 2020. [Google Scholar]

5. M. Orouskhani, M. Teshnehlab and M. A. Nekoui, “EMCSO: An elitist multi-objective cat swarm optimization,” Journal of Optimization in Industrial Engineering, vol. 11, no. 2, pp. 107–117, 2018. [Google Scholar]

6. H. Siqueira, C. Santana, M. Macedo, E. Figueiredo, A. Gokhale et al., “Simplified binary cat swarm optimization,” Integrated Computer-Aided Engineering, vol. 28, no. 1, pp. 35–50, 2021. [Google Scholar]

7. K. M. Ajitha and I. N. Chenthalir, “Principal component regression based adaptive multiple extrema seeking cat swarm resource optimized task scheduling in cloud computing,” International Journal of Next-Generation Computing, vol. 13, no. 2, pp. 189–206, 2022. [Google Scholar]

8. H. R. R. Zaman and F. S. Gharehchopogh, “An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems,” Engineering with Computers, vol. 38, no. 10, pp. 2797–2831, 2022. [Google Scholar]

9. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN’95–Int. Conf. on Neural Networks, Perth, WA, Australia, vol. 4, pp. 1942–1948, 1995. [Google Scholar]

10. S. Saeedi, R. Khorsand, S. G. Bidgoli and M. Ramezanpour, “Improved many-objective particle swarm optimization algorithm for scientific workflow scheduling in cloud computing,” Computers and Industrial Engineering, vol. 147, no. 9, pp. 1–23, 2020. [Google Scholar]

11. P. Krishnadoss, V. K. Poornachary, P. Krishnamoorthy and L. Shanmugam, “Improvised seagull optimization algorithm for scheduling tasks in heterogeneous cloud environment,” Computers, Materials & Continua, vol. 74, no. 2, pp. 2461–2478, 2023. [Google Scholar]

12. Q. N. Menga and X. Xu, “Price forecasting using an ACO-based support vector regression ensemble in cloud manufacturing,” Computers and Industrial Engineering, vol. 125, no. 11, pp. 171–177, 2018. [Google Scholar]

13. Q. Luo, H. Wang, Y. Zheng and J. He, “Research on path planning of mobile robot based on improved ant colony algorithm,” Neural Computing and Applications, vol. 32, no. 6, pp. 1555–1566, 2020. [Google Scholar]

14. C. Chandrashekar, P. Krishnadoss, V. K. Poornachary, B. Ananthakrishnan and K. Rangasamy, “HWACOA Scheduler: Hybrid weighted ant colony optimization algorithm for task scheduling in cloud computing,” Applied Sciences, vol. 13, no. 6, pp. 3433, 2023. [Google Scholar]

15. S. Tao, Y. Xia, L. Ye, C. Yan and R. Gao, “DB-ACO: A deadline-budget constrained ant colony optimization for workflow scheduling in clouds,” IEEE Transactions on Automation Science and Engineering, pp. 1–16, 2023. [Google Scholar]

16. O. J. Agushaka, A. E. Ezugwu and L. Abualigah, “Dwarf mongoose optimization algorithm,” Computer Methods in Applied Mechanics and Engineering, vol. 391, pp. 114570, 2022. [Google Scholar]

17. O. J. Agushaka, A. E. Ezugwu and L. Abualigah, “Gazelle optimization algorithm: A novel nature-inspired metaheuristic optimizer,” Neural Computing and Applications, vol. 35, no. 5, pp. 4099–4131, 2023. [Google Scholar]

18. H. Wang, W. Wang, S. Xiao, Z. Cui, M. Xu et al., “Improving artificial bee colony algorithm using a new neighborhood selection mechanism,” Information Sciences, vol. 527, pp. 227–240, 2020. [Google Scholar]

19. M. R. Thanka, P. Uma Maheswari and E. B. Edwin, “An improved efficient: Artificial bee colony algorithm for security and QoS aware scheduling in cloud computing environment,” Cluster Computing, vol. 22, pp. 10905–10913, 2019. [Google Scholar]

20. J. Li and Y. Han, “A hybrid multi-objective artificial bee colony algorithm for flexible task scheduling problems in cloud computing system,” Cluster Computing, vol. 23, no. 4, pp. 2483–2499, 2020. [Google Scholar]

21. M. Karaja, A. Chaabani, A. Azzouz and L. Said, “Efficient bi-level multi objective approach for budget-constrained dynamic Bag-of-Tasks scheduling problem in heterogeneous multi-cloud environment,” Applied Intelligence, vol. 53, no. 8, pp. 9009–9037, 2023. [Google Scholar]

22. O. Gkalp, “Performance evaluation of heuristic and metaheuristic algorithms for independent and static task scheduling in cloud computing,” in 29th Signal Processing and Communications Applications Conf. (SIU), Istanbul, Turkey, pp. 1–4, 2021. [Google Scholar]

23. K. Li, L. Jia and X. Shi, “IPSOMC: An improved particle swarm optimization and membrane computing based algorithm for cloud computing,” International Journal of Performability Engineering, vol. 17, no. 8, pp. 135, 2021. [Google Scholar]

24. L. Li, Z. Zhang and X. Wang, “Analysis of convergence for free search algorithm in solving complex function optimization problems,” in Proc. of the CICA, Hangzhou, China, pp. 1201–1207, 2012. [Google Scholar]

25. W. Xu, R. Wang and J. Yang, “An improved league championship algorithm with free search and its application on production scheduling,” Journal of Intelligent Manufacturing, vol. 29, no. 1, pp. 165–174, 2018. [Google Scholar]

26. Y. Zhou, J. Kang and H. Guo, “Many-objective optimization of feature selection based on two-level particle cooperation,” Information Sciences, vol. 532, pp. 91–109, 2020. [Google Scholar]

27. Y. Zhou, L. Gao, D. Wang, W. Wu, Z. Zhou et al., “Imbalanced multifault diagnosis via improved localized feature selection,” IEEE Transactions on Instrumentation and Measurement, vol. 72, pp. 1–11, 2023. [Google Scholar]

28. Y. Zhou, J. Kang and X. Zhang, “A cooperative coevolutionary approach to discretization-based feature selection for high-dimensional data,” Entropy, vol. 22, no. 6, pp. 613, 2020. [Google Scholar] [PubMed]

29. J. D. Sawarka and M. E. Patil, “To study optimization method in scheduling for cloud computing,” Scandinavian Journal of Information Systems, vol. 35, no. 1, pp. 433–439, 2023. [Google Scholar]