 Open Access
Open Access
ARTICLE
A New Encrypted Traffic Identification Model Based on VAE-LSTM-DRN
1 College of Computer and Control Engineering, Qiqihar University, Qiqihar, 161006, China
2 Heilongjiang Key Laboratory of Big Data Network Security Detection and Analysis, Qiqihar University, Qiqihar, China
* Corresponding Authors: Haizhen Wang. Email: ; Jinying Yan. Email:
Computers, Materials & Continua 2024, 78(1), 569-588. https://doi.org/10.32604/cmc.2023.046055
Received 16 September 2023; Accepted 17 November 2023; Issue published 30 January 2024
Abstract
Encrypted traffic identification pertains to the precise acquisition and categorization of data from traffic datasets containing imbalanced and obscured content. The extraction of encrypted traffic attributes and their subsequent identification presents a formidable challenge. The existing models have predominantly relied on direct extraction of encrypted traffic data from imbalanced datasets, with the dataset’s imbalance significantly affecting the model’s performance. In the present study, a new model, referred to as UD-VLD (Unbalanced Dataset-VAE-LSTM-DRN), was proposed to address above problem. The proposed model is an encrypted traffic identification model for handling unbalanced datasets. The encoder of the variational autoencoder (VAE) is combined with the decoder and Long-short term Memory (LSTM) in UD-VLD model to realize the data enhancement processing of the original unbalanced datasets. The enhanced data is processed by transforming the deep residual network (DRN) to address neural network gradient-related issues. Subsequently, the data is classified and recognized. The UD-VLD model integrates the related techniques of deep learning into the encrypted traffic recognition technique, thereby solving the processing problem for unbalanced datasets. The UD-VLD model was tested using the publicly available Tor dataset and VPN dataset. The UD-VLD model is evaluated against other comparative models in terms of accuracy, loss rate, precision, recall, F1-score, total time, and ROC curve. The results reveal that the UD-VLD model exhibits better performance in both binary and multi classification, being higher than other encrypted traffic recognition models that exist for unbalanced datasets. Furthermore, the evaluation performance indicates that the UD-VLD model effectively mitigates the impact of unbalanced data on traffic classification. and can serve as a novel solution for encrypted traffic identification.Keywords
In recent years, as the Internet has continued to advance, there has been a growing awareness of network security among individuals. Encryption technology has seen widespread adoption [1,2], and encrypted traffic now constitutes the predominant form of network traffic [3]. Encrypted traffic serves the dual purpose of safeguarding data integrity and concealing the underlying network infrastructure from potential hacker attacks. However, the inherent difficulty in collecting and annotating encrypted traffic data has led to a significant imbalance in the class distribution of datasets [4]. Such imbalance poses a substantial challenge for encrypted traffic classification [5], consequently elevating security risks. As such, the identification and classification of encrypted traffic have emerged as crucial challenges within the contemporary field of cybersecurity. As mentioned above, collecting encrypted traffic data is difficult. Therefore, different from [6], which collects real-time traffic data from various sources, our work focuses on the encrypted traffic classification with imbalanced data distribution based on public datasets.
Traditional machine learning methods based on Random Forests [7], Bayesian Networks [8], and Decision Trees [9] have also been employed for encrypted traffic network classification. However, such methods are highly dependent on feature selection [10], and their model performance hinges on features designed by humans, thereby restricting their generality and overall generalization capabilities. On the other hand, deep learning methods possess the capacity to autonomously optimize feature engineering [11,12], a capability that markedly enhances model performance and renders them better suited for traffic classification tasks in comparison to traditional machine learning approaches. In most deep learning methods, the unbalance of encrypted traffic dataset categories is not considered. Convolution with other deep learning methods is incorporated to effectively capture local data features, which helps minimize the impact of overall class distribution unbalance on the model’s data processing. Thus, even though certain class samples have considerably fewer numbers, convolution can still extract useful features therefrom. Nevertheless, convolution comes with high computational complexity, and the direction considered in the present study was to avoid the drawback of long computation time associated with convolution.
Balancing the initially imbalanced dataset serves to enhance the model’s robustness, elevate its generalization capacity, and mitigate the issue of extreme imbalances between positive and negative samples. At present, for unbalanced dataset processing, the following three methods are commonly used. The first method involves the use of the SMOTE algorithm, which analyzes minority class samples and artificially generates new samples based on them to augment the dataset. However, a drawback of this approach is its susceptibility to sample overlap issues and the generation of samples that lack meaningful information [13]. The second method involves the use of generative adversarial networks (GAN). The third method involves the use of Variational Autoencoders (VAE), which is a format-independent and generalized data enhancement method. In summary, both GAN and VAE can generate new sample data with different attributes or noise, which can effectively expand the dataset for model training and enhance the model’s generalization and robustness. However, GAN often face issues like prolonged training times and a high number of parameters, which can make them less cost-effective in practical applications. On the other hand, VAE transforms the original sample data into an ideal data distribution using an encoder network and then reconstructs data from this distribution using a decoder network to maintain the quality of the generated data. In addition, VAE tends to converge more easily compared to GAN.
To address the aforementioned problem, a new encrypted traffic identification model, UD-VLD, was proposed in the present study. The proposed model is based on the data enhancement scheme of VAE and integrates a Long-short Term Memory (LSTM) network and DRN. The contributions of the present study are as follows:
(1) A new deep learning cryptography traffic recognition model UD-VLD was proposed, which can enhance high-dimensional unbalanced data and identify traffic types;
(2) To enhance the data, LSTM was incorporated into the encoding and decoding of VAE, and the purpose of temporal data enhancement was achieved by processing the features of temporal data through LSTM;
(3) To overcome the gradient descent issue during model training, the residual block structure in DRN was modified based on the temporal features of the data. The original convolutional layers were replaced with Dense layers, and the flattened layer was removed from the original DRN before being replaced with a Dropout layer. This adjustment reduces the model’s computation time and helps prevent model overfitting;
(4) The proposed model supports classification training on publicly available encrypted traffic datasets. Results show that UD-VLD achieved high accuracy and F1-score on both publicly available Tor and VPN datasets, demonstrating strong generalization capabilities.
The rest of the paper is organized as follows. Section 2 briefly describes the related work in this field. In Section 3, the design of the UD-VLD model is elaborated. Section 4 provides the experimental analysis. Section 5 is the results and discussion. Finally, the conclusion of the paper is discussed in Section 6.
Shapira et al. [14] used packet size distributions at different times to create images, which were referred to as FlowPics. Subsequently, these FlowPics were fed into a conventional CNN model for classification, and notable results were obtained in the final experiments. Despite such endeavors, the FlowPic method has limitations, including feature conflicts caused by the size distribution of individual packets that can affect the accuracy of VPN flow classification. Lan et al. [15] introduced a cascade model known as DarknetSec, which combines a one-dimensional convolutional neural network (CNN) with a bi-directional long and short-term memory network (LSTM). The model was designed to capture local spatio-temporal features within packet payloads. Further, they incorporated a self-attention mechanism into the feature extraction network to uncover inherent relationships and concealed connections among the previously extracted content features. Lin et al. [16] proposed an encrypted traffic categorization method known as ET-BERT, which utilizes a bi-directional encoder representation called a Transformer. The model is capable of pre-training deep contextualized datagram-level representations using extensive unlabeled data. Subsequently, the pre-trained model can be fine-tuned with a limited amount of task-specific labeled data, achieving state-of-the-art performance in five distinct encrypted traffic classification tasks. Ma et al. [17] proposed a high-precision encrypted network traffic classification method-based traffic reconstruction, which extracts the first 500 bytes of the payload as key data, and inserts the length threshold identifier in the payload header. Then, a one-dimensional convolutional neural network is used to classify the reconstructed traffic.
Guo et al. [18] proposed an unbalanced traffic classification framework ITCGAN, in which the author uses GAN to oversample a small number of traffic flows to rebalance the unbalanced traffic data. The addition of a Classifier to the traditional GAN makes the fusion of oversampling and training possible, which helps the classification results reach the global optimum. Li et al. [19] proposed Dynamic Chaotic Cross-Optimized Bidirectional Residual Gated Recurrent Units (DCCSO-Res-BIGRU) and Adaptive Wasserstein Generative Adversarial Networks with Generative Feature Domains (GFDA-WGAN), in which feature extraction is realized using DCCSO-Res-BIGRU. GFDA-WGAN can then be used to detect unbalanced attack traffic. Liu et al. [20] used a VAE-based data enhancement scheme combined with deep learning-based IDS to improve the F1-score of the model.
The UD-VLD model framework is shown in Fig. 1. The framework mainly includes three parts: data preprocessing, model training, and model testing. The VAE model improved by LSTM is used to enhance the data for unbalanced data, and then DRN classifies the generated balanced data samples with encrypted traffic.

Figure 1: Flowchart of the UD-VLD model
Data preprocessing includes the division of the training and test sets, and the normalization and numerical processing of the data (Section 4.2 for the processing). The preprocessed data are reshaped using the reshape function to perform shape reconstruction of the array without changing the data. The reshaped data are used as the input layer data for the LSTM improved VAE model, and the augmented data samples are generated by the model. Finally, both the generated samples and the original samples are input into the DRN. After passing through eight residual blocks within the DRN, the issue of gradient vanishing is effectively addressed. Subsequently, the data is classified using a softmax classifier. The loss function employed in the study was Mean Squared Error (MSE), with a learning rate set at 0.00001.
3.2 Variational Autoencoder (VAE)
VAE is an unsupervised learning method similar to the traditional autoencoder algorithm [21], and its structure is shown in Fig. 2.

Figure 2: Original variational autoencoder architecture
VAE consists of an encoder and a decoder, where the encoder encodes the input raw data into a Gaussian distribution, and the decoder randomly samples one sample from this distribution and uses it as an input to the decoder, obtaining an output that approximates the input of the encoder. VAE enhances the model’s robustness and mitigates the rigidity error by assuming a probabilistic distribution for the latent variable
The encoder computes the mean
The decoder uses vectors in the latent space to generate vectors in the real-time space, and the role of the decoder is to complete the reconstruction from the latent variable
In the training process of VAE, to make
The core concept of the VAE training process is to maximize the likelihood of generating
LSTM stands for Long-short Term Memory, which is a specialized type of recurrent neural network (RNN). LSTM is used for analyzing data with temporal sequences, and its unit structure is illustrated in Fig. 3.

Figure 3: Structure of LSTM cell
The first step involves data filtration using a forget gate, which determines which information should be discarded. The forget gate reads the previous state passed down
The second step involves determining the update values for the unit through a sigmoid activation function. A new candidate vector is created by a tanh layer and added to the unit state. The specific formula is shown in Eq. (5).
Finally, the output unit state is determined in part through a sigmoid activation function. The unit’s output is then obtained by multiplying the output of the previous sigmoid layer with the output of the tanh layer (which maps values to the range between −1 and 1). The specific formulae are shown in Eqs. (6) and (7).
In UD-VLD, LSTM replaced conventional neural networks in VAE to better analyze temporal data features, using default activation functions.
In UD-VLD, the neural networks in the encoder and decoder of VAE were replaced with LSTM, aiming to achieve better feature encoding and decoding of raw time-series data, thus obtaining augmented sample data. The improved VAE network structure is illustrated in Fig. 4. Inputting raw data samples into VAE, the LSTM encoder automatically extracts the input time-series data, which is then encoded to obtain the mean

Figure 4: Improved VAE network structure based on LSTM
LSTM operates by taking in 23-dimensional time series features from the input dataset, which includes details like connection start time, connection end time, and timestamp information (28 dimensions in the Tor dataset). It employs its neurons and gating mechanisms for feature extraction while regulating information flow through gate states. This enables LSTM to capture long-term dependencies and store this information in cell states, facilitating propagation along the sequence and preserving the temporal aspects of the input sequence. Ultimately, the output data is generated through a tanh operation.
Finally, the original samples are integrated with the generated new samples to obtain the dataset that represents the augmented samples. In the improved VAE, the LSTM layer has 32 neurons, and the ‘return_sequences’ parameter is set to True. The hidden layer with 64 neurons is used for computing the latent variable
In neural networks, during the backpropagation process, gradients need to be propagated continuously. As the network’s depth increases, there is a tendency for gradients to diminish during the propagation process. This can result in the problem of gradient saturation or even degradation in network accuracy. Deep Residual Networks (DRN) were developed to address the described issue. The core idea of DRN is to facilitate gradient propagation by inserting shortcut connections between convolutional layers. These shortcut connections directly add their output to the output of the convolutional layer they bypass. In the process of backpropagation, half of the gradients are routed through the shortcut connections to deeper convolutional layers, while the remaining half passes through the convolutional layers that were bypassed. This architectural arrangement is referred to as a residual network block. By stacking and replicating these blocks, a deep residual network is constructed.
Based on experiments and the temporal characteristics of the dataset, two improvements were proposed for the design of residual networks based on Xu [24]. One involves transforming the convolutional layer in the deep residual network into a dense layer for faster deep extraction of temporal features. The second involves changing the Flatten layer between the residual block and the fully connected layer to a Dropout layer, to prevent overfitting and improve the model’s generalization ability, As shown in Fig. 5, the residual blocks in the deep residual network consist of three sequential operations.

Figure 5: Residual block structure based on dense layers
(1) Dense: Extracts features from time-series data with high-dimensional multiclass features.
(2) Batch-normalization: Scales weights to unit norms to reduce internal covariate shift during training and fine-tune learning rates for accelerated network training.
(3) ReLU: Provides stable performance and simplicity without adding computational complexity.
The complete deep residual network structure used in the present study is shown in Fig. 6. Unlike the original residual network structure, there is no need for global pooling operation after the residual block structure. The rest of the structure remains the same as the original residual network.

Figure 6: Deep residual network structure
Based on the experimental results, the choice was made to construct deep residual network blocks with a total of 8 blocks. Each layer within a residual block comprised 80 neurons. Regarding the selection of the number of residual blocks, a series of comparative experiments was conducted using 5, 6, 8, and 9 residual blocks. As depicted in Table 1, the model performed optimally with 8 residual blocks. There was a relatively small difference in performance between eight and nine residual blocks. However, employing nine blocks led to longer processing times and a slight reduction in accuracy and F1-score.

The datasets used in the present study were ISCX-VPN-nonVPN [25] and ISCXTor2016 [26], both of which were released by the ISCX Research Center at the University of New Brunswick (UNB), Canada.
The ISCX-VPN-nonVPN dataset originally had a size of 28 GB. In this dataset, Scenario A aimed to identify encrypted traffic using VPN labels. The dataset consists of a total of 14 different traffic categories, including 7 regular types of traffic and 7 VPN types of traffic, such as Web, Email, Chat, Streaming, File Transfer, IP Voice, and P2P. The various traffic categories in the dataset are shown in Table 2. In the experiment, traffic types within ISCX were categorized into VPN and Non-VPN traffic first, and then encrypted data was further divided for traffic identification. A total of 7 traffic categories for identification and classification were selected, resulting in a dataset comprising 9,793 records.
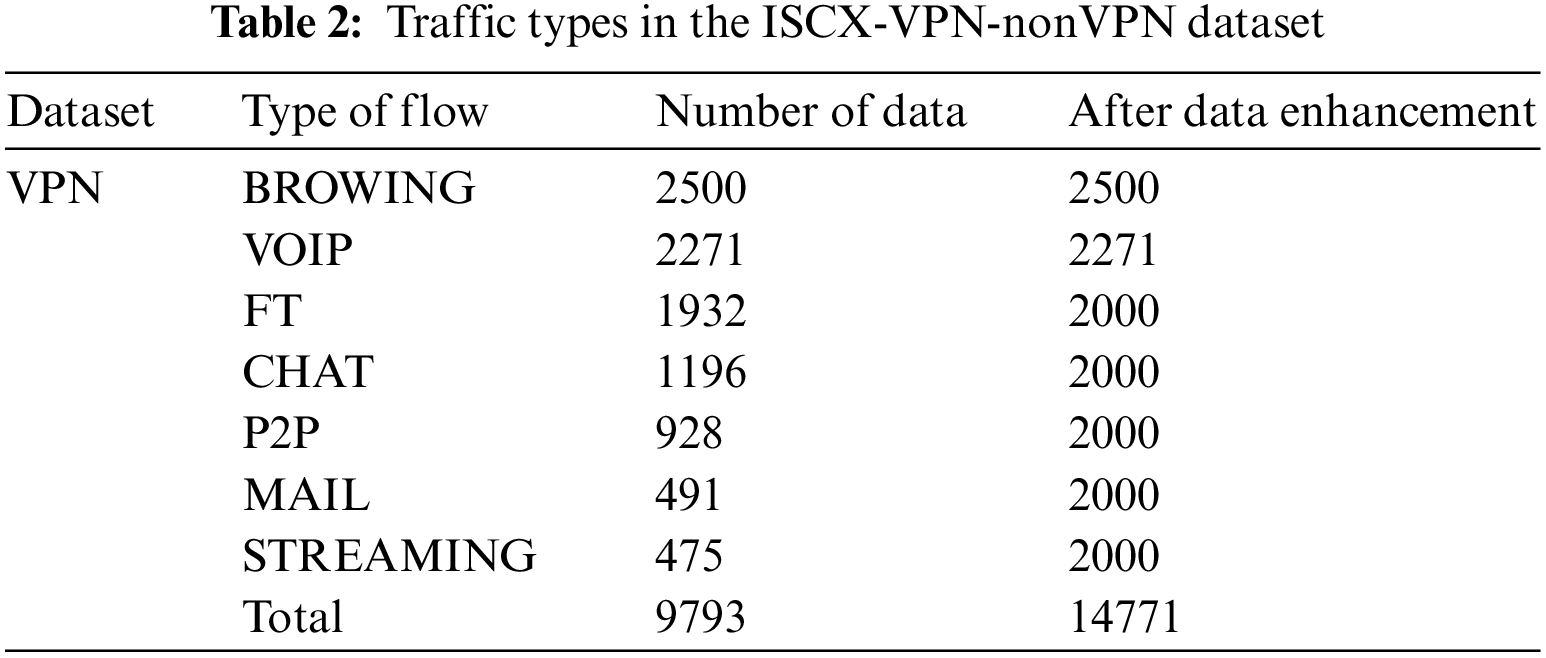
The ISCXTor2016 dataset initially had a size of 22 GB. Tor is a circuit-based protocol where all traffic from the gateway to the entry node is encrypted and sent over the same connection. The dataset defines 8 categories, namely Browsing, Email, Chat, Audio-streaming, Video-streaming, File Transfer, VoIP, and P2P. The various traffic categories in the dataset are shown in Table 3. A total of 8 traffic categories were selected for identification and classification, resulting in a dataset comprising 8,044 records.
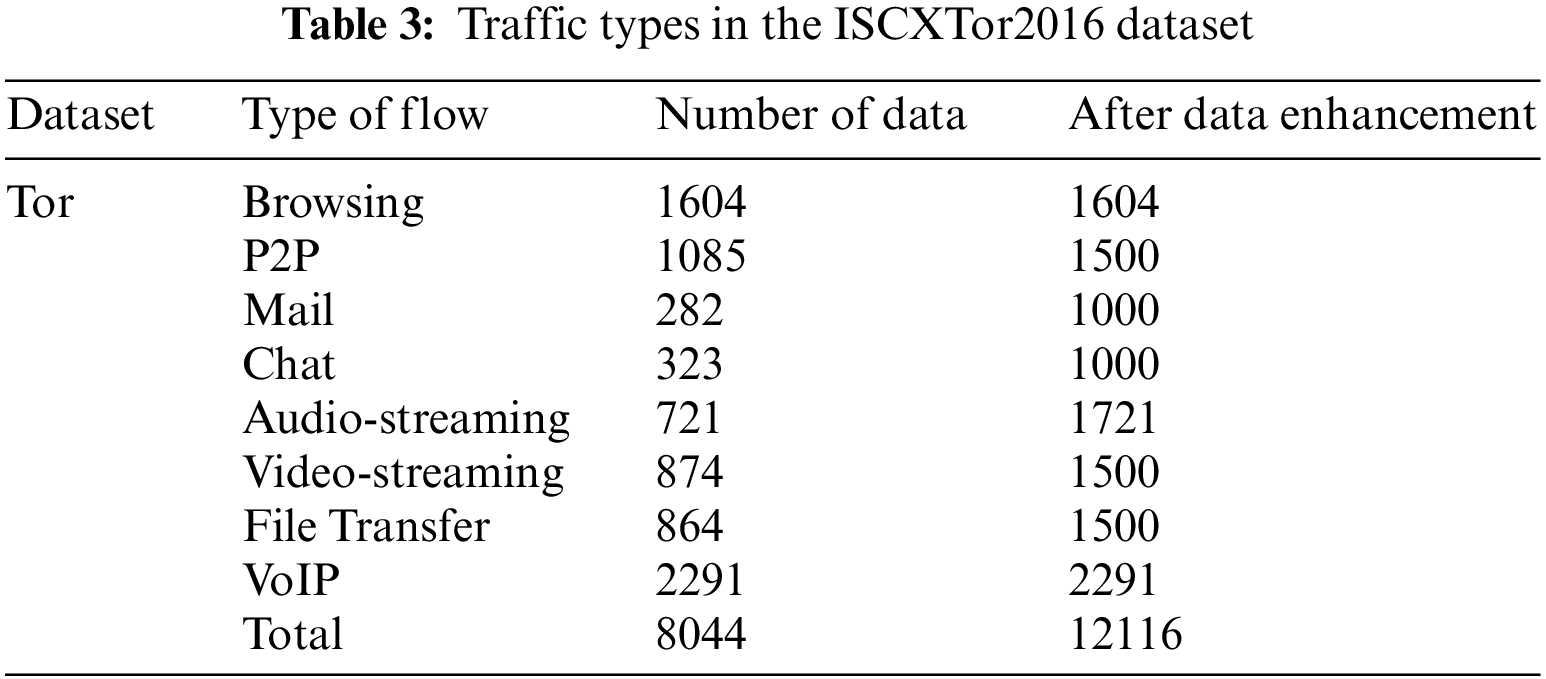
In the present study, the ISCX-VPN-nonVPN dataset and the ISCXTor dataset were used. For the VPN dataset, data format conversion was performed using Wireshark and Weka, converting pcap files and arff files into csv format. The data were divided into training and testing sets. For the Tor dataset, the csv files provided in the dataset were directly used. The LabelEncoder function from the sklearn. Preprocessing package was utilized to convert non-numeric data in both datasets into numeric label types. The StandardScaler function from the sklearn.preprocessing package was used to standardize the overall feature data of the dataset, setting the mean to 0 and the variance to 1. The ratio of the training set to the testing set was 8:2.
4.3 Experimental Evaluation Metrics
In the evaluation of encrypted traffic recognition within the UD-VLD framework, critical performance metrics were employed, namely accuracy, recall, precision, and F1-score. Accuracy gauged the model’s overall performance by quantifying the ratio of correctly identified samples to the total dataset. Meanwhile, recall measured the model’s specific detection rate, focusing on the ratio of correctly identified positive samples among all actual positives. Precision evaluated the model’s classification ability for each category by calculating the ratio of true positive samples to all samples identified as positive. Lastly, the F1-score, a comprehensive metric, took into account both the model’s classification accuracy and its ability to detect positive cases, expressed as the harmonic mean of precision and recall. These metrics, as described by Eqs. (8)–(10), relied on variables such as true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN) to provide a thorough assessment of the encrypted traffic recognition model’s performance.
5.1 Training Results of the Model
During the model training process, UD-VLD was subjected to experiments with different numbers of iterations on the ISCXVPN2016 dataset: 50, 100, 150, 200, and 250 iterations, as shown in Fig. 7. For the ISXTor2016 dataset, experiments were conducted with 10, 50, 100, and 150 iterations, as illustrated in Fig. 8. From the experimental data and analysis, a conclusion can be drawn that when the number of iterations was set to 200, the model achieved the best training performance on the VPN dataset, with an accuracy of 0.961 and a loss rate of 0.007, as depicted in Fig. 9. Meanwhile, with 100 iterations, the model achieved the best training performance on the Tor dataset, with an accuracy of 0.990 and a loss rate of 0.003, as shown in Fig. 10.

Figure 7: The experimental results on the ISCX-VPN-nonVPN dataset with different numbers of epochs

Figure 8: The experimental results on the ISCXTor2016 dataset with different numbers of epochs

Figure 9: Accuracy and loss rate of UD-VLD on the ISCX-VPN-nonVPN dataset

Figure 10: Accuracy and loss rate of UD-VLD on the ISCXTor2016 dataset
5.2 Ablation Experiments and Result Analysis
To assess the effectiveness of UD-VLD in managing unbalanced datasets for traffic recognition, both ablation and comparative experiments were conducted on the datasets. UD-VLD primarily comprises VAE, LSTM, and DRN components, each of which can be partially ablated to evaluate their contributions. The ablation experiments encompassed VAE, VAE-LSTM, DRN, and VAE-DRN configurations, and the results are presented in Tables 4 and 5. As previously mentioned in the evaluation metrics, given the proposed model’s focus on multi-class recognition within unbalanced datasets, precision, recall, and F1-score in the overall experimental results are Macro Averaged. In the VAE-LSTM ablation experiment, the key difference from the proposed model was the absence of DRN for neural network layer processing. Results were obtained directly using a softmax classifier, potentially leading to the problem of gradient vanishing. In the case of DRN ablation, VAE-LSTM was not employed for handling unbalanced data, which can impact subsequent model training. In the VAE-DRN ablation scenario, LSTM was omitted for handling time-based features and extraction, while other neural network parameters remained consistent with UD-VLD.
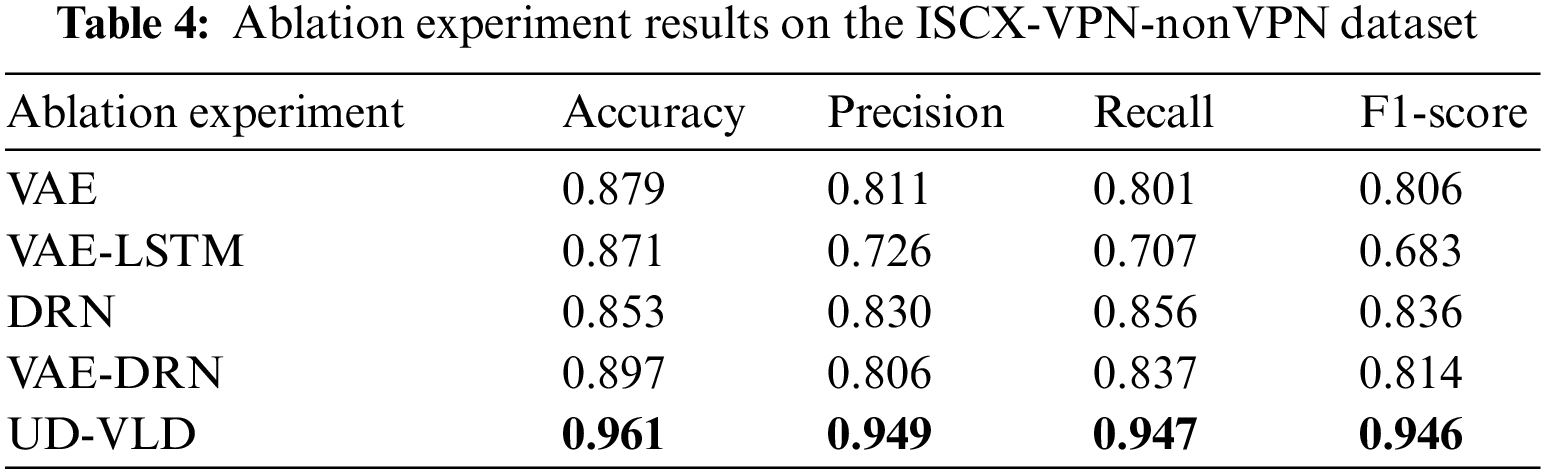
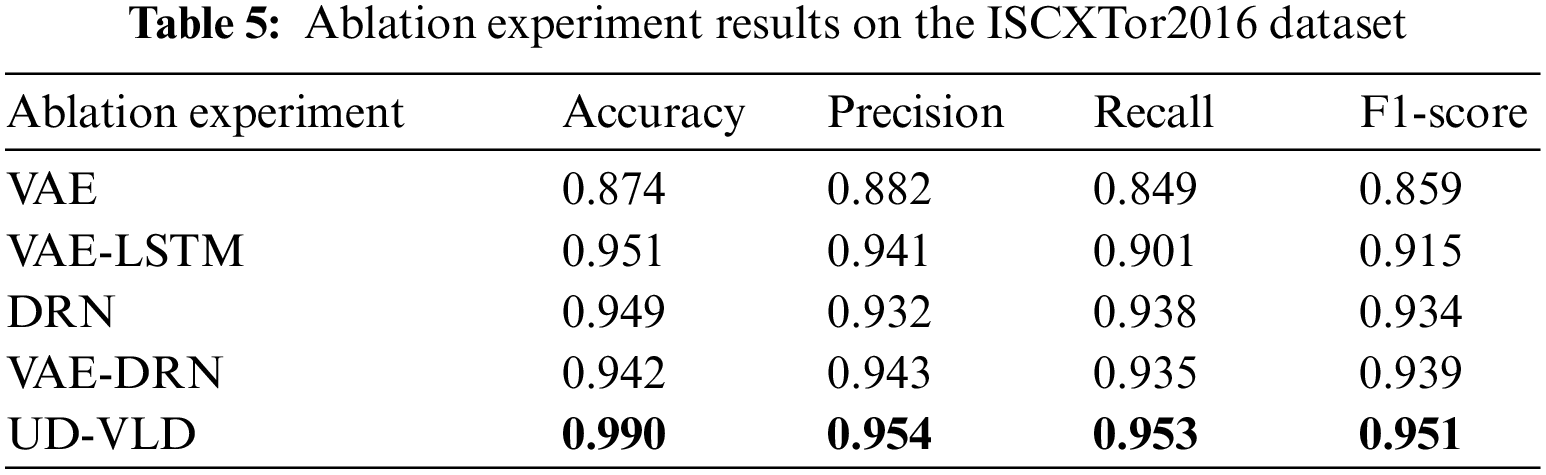
In the proposed model, a batch_size of 32 was used, and the optimal number of iterations was 200 for the VPN dataset and 100 for the Tor dataset. The optimizer employed in the model was the Adam optimization algorithm. Based on the analysis from the tables, an observation can be made that within the same module, the model using the improved VAE for unbalanced data augmentation showed a relatively higher F1-score, precision, recall, and macro average, indicating that data augmentation played a certain role.
5.3 Analysis of Comparative Experiment Results
In the present study, UD-VLD was compared with five other deep learning models that deal with unbalanced datasets. The experimental results on the VPN dataset and Tor dataset are shown in Tables 6 and 7. The parameters of the five compared models, CMTSNN, CSCNN, CostSAE, GAN-DRN, and Tree-RNN, were all reproduced based on the original descriptions and tuned to their optimal settings. Nevertheless, the model’s performance in the study did not achieve the optimal values reported in the original papers. This discrepancy can be attributed to variations in the dataset categories and differences in feature dimensions, which can impact the model’s performance. As depicted in the figures, the proposed UD-VLD model exhibited higher overall performance in terms of accuracy, recall, precision, and F1-score when compared to the other five deep learning models. As shown in the tables, while CostSAE required less time for training on the VPN dataset, its accuracy was 8.1% lower compared to UD-VLD, and its precision, recall, and F1-score did not exceed 0.85.
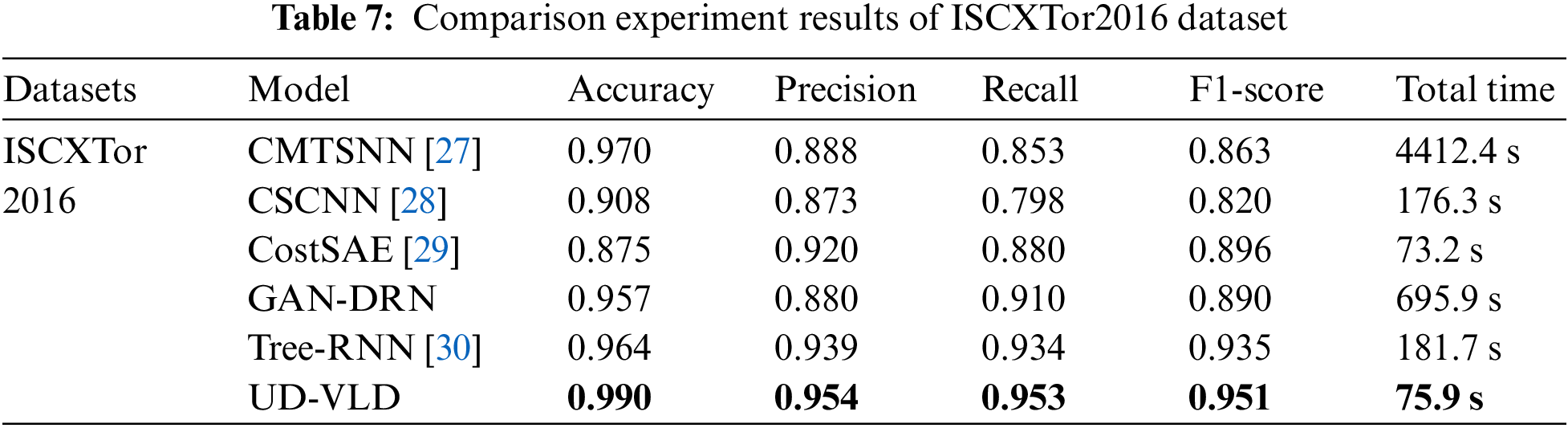
Tree-RNN, a deep-learning traffic recognition model that does not employ an enhanced data augmentation process, was also included. This model was evaluated alongside other deep-learning traffic recognition models using the augmented dataset. Additionally, GAN-DRN, a method that leverages GAN for data augmentation, was considered. However, GAN-DRN exhibited longer processing times and comparatively lower F1-score and accuracy when compared to UD-VLD. Consequently, it can be concluded that the proposed model maintains an advantage in recognizing unbalanced data for traffic classification.
For further comparison with the five deep learning models, the F1-score for each category of the two datasets after handling unbalanced data was obtained, as shown in Tables 8 and 9. Analyzing Table 8 reveals that in multi-class recognition, CMTSNN had an F1-score for the “Browsing” category that was 0.02 higher than that of UD-VLD. Therefore, the performance of the two models needed to be evaluated from multiple perspectives. As indicated by the comparative tables in the previous sections, the training time for the CMTSNN model was significantly longer than UD-VLD, and both its accuracy and macro average values were lower than UD-VLD. Trading an extensive amount of time for an improvement in the recognition rate of a single category may not be a favorable decision. In the remaining six categories, CMTSNN’s F1-scores were not prominent and even fell below 0.8 for one category. According to the analysis, a conclusion could be drawn that the proposed model UD-VLD demonstrated stronger and more stable performance.

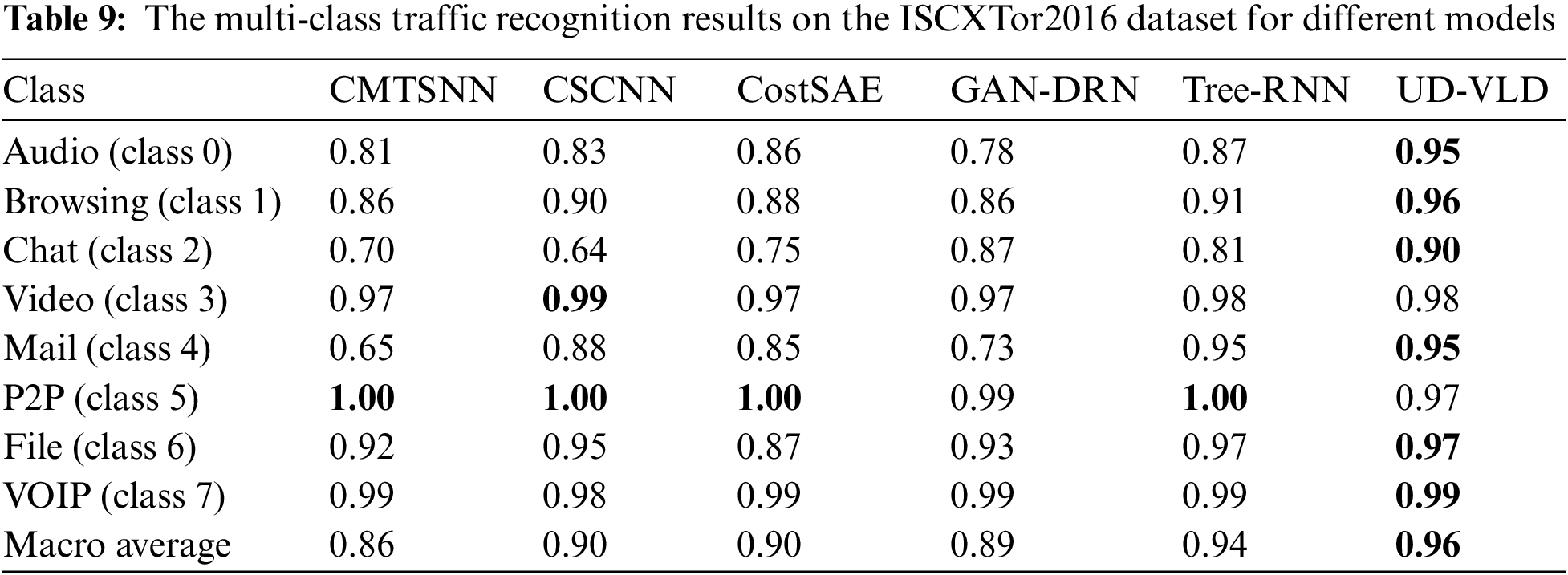
Based on the observations from Table 9, several noteworthy insights emerge. In the P2P category, four deep learning models achieved an impressive F1-score of 1, whereas the F1-score for the proposed model stood at 0.97. In the Video category, the CSCNN model achieved a slightly higher F1-score than UD-VLD by 0.01. Notably, all three comparative experiments in the present study, namely CMTSNN, CSCNN, and CostSAE, incorporated a cost-sensitive matrix. When comparing CSCNN with UD-VLD by considering time, macro average, recall, and precision, CSCNN exhibited a significantly longer processing time, requiring an additional 100.4 s, while its accuracy and F1-score were lower by 0.082 and 0.131, respectively. Examining the macro average and Table 9, it becomes evident that CSCNN, despite using a cost-sensitive matrix to address data imbalance, encountered difficulties in identifying certain sample categories, resulting in low F1-scores. Specifically, in identifying the “Chat” category, F1-scores for CMTSNN, CSCNN, CostSAE, and Tree-RNN all dropped below 0.8, while UD-VLD consistently achieved F1-scores above 0.90 for various traffic types. Through this analysis, it is evident that UD-VLD excels in stable and high-accuracy multi-class sample recognition. This finding further validates that the proposed model effectively mitigates the impact of unbalanced data on traffic classification.
In addition to assessing model applicability and effectiveness based on loss rate and accuracy, the models were also compared using F1-score and ROC curves. F1-score combines precision and recall, providing a more comprehensive analysis of each model’s performance in traffic identification. A larger area under the ROC curve (represented by the area value in the graph) indicates better model performance, approaching 1. Figs. 11 and 12 depict ROC curves for the ISCX-VPN-nonVPN and ISCXTor2016 datasets, respectively.
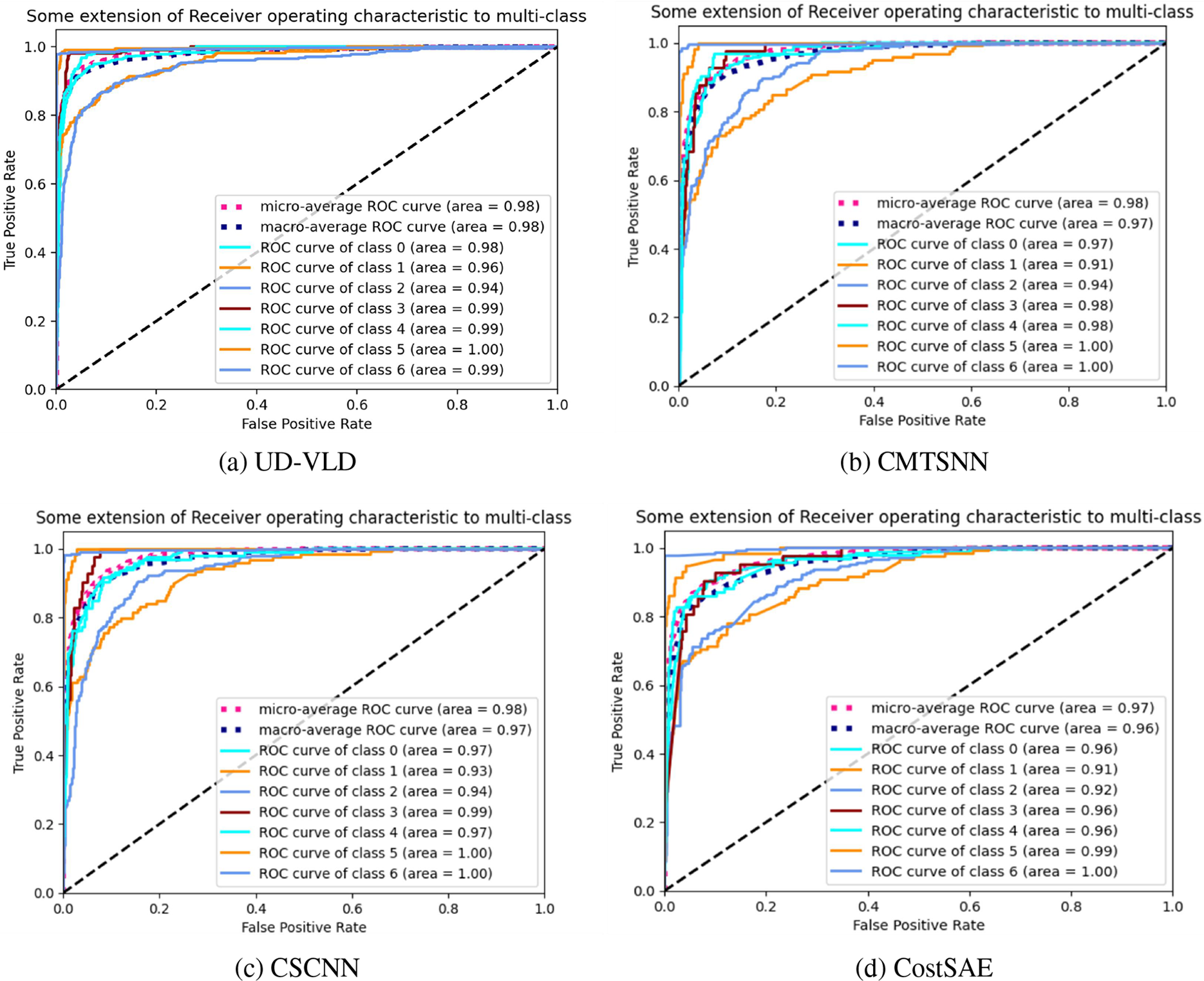
Figure 11: ROC curve graphs for four experiments in the VPN dataset


Figure 12: ROC curve graphs for four experiments in the ISCXTor2016 dataset
Through the ROC curve graphs generated after training each model and their characteristics, a conclusion could be drawn that UD-VLD had the largest area under the ROC curve (closest to 1) on both datasets. As such, UD-VLD exhibited the best performance in all comparative experiments.
In the present study, an encrypted traffic recognition model known as UD-VLD was proposed. The model is based on deep learning techniques, combining VAE, LSTM, and DRN. The proposed LSTM-based VAE generates enhanced samples through latent variables and internal probabilistic distribution transformations and combines these new samples with the original samples to achieve traffic identification through deep residual networks. This approach effectively achieves data augmentation and feature extraction, thus mitigating the adverse effects of unbalanced data on model efficiency. It simultaneously enhances feature extraction efficiency, resolves gradient vanishing issues, and reduces the loss rate.
The experimental results demonstrate that UD-VLD achieved higher F1-scores and the maximum AUC values on ROC curves for encrypted traffic recognition compared to other methods. Further, UD-VLD addresses the challenges of processing encrypted traffic data using traditional ML and DL methods, proposing a novel approach for encrypted traffic identification. In future endeavors, UD-VLD holds the potential for adaptation to recognize traffic from multiple channels and real-time traffic, thereby enabling the tackling of more complex tasks in this domain.
Acknowledgement: None.
Funding Statement: This work was supported by the Fundamental Research Funds for Higher Education Institutions of Heilongjiang Province (145209126), and the Heilongjiang Province Higher Education Teaching Reform Project under Grant No. SJGY20200770.
Author Contributions: Study conception and design: H. Wang, J. Yan; data collection: J. Yan, N. Jia; analysis and interpretation of results: H. Wang, J. Yan, N. Jia; draft manuscript preparation: H. Wang, J. Yan. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used in the study are all available on the UNB official website (https://www.unb.ca/cic/datasets/index.html).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. J. Cheng, Y. Wu and E. Y., “MATEC: A lightweight neural network for online encrypted traffic classification,” Computer Networks, vol. 199, pp. 108472, 2021. [Google Scholar]
2. F. Thabit, S. Alhomdy and S. Jagtap, “A new data security algorithm for the cloud computing based on genetics techniques and logical-mathematical functions,” International Journal of Intelligent Networks, vol. 2, pp. 18–33, 2021. [Google Scholar]
3. Z. Wang, K. W. Fok and V. L. L. Thing, “Machine learning for encrypted malicious traffic detection: Approaches, datasets, and comparative study,” Computers & Security, vol. 113, pp. 102542, 2022. [Google Scholar]
4. Z. Tang, J. Wang and B. Yuan, “Markov-GAN: Markov image enhancement method for malicious encrypted traffic classification,” IET Information Security, vol. 16, no. 6, pp. 442–458, 2022. [Google Scholar]
5. S. Rezaei and X. Liu, “Deep learning for encrypted traffic classification: An overview,” IEEE Communications Magazine, vol. 57, no. 5, pp. 76–81, 2019. [Google Scholar]
6. R. Jain, S. Dhingra, K. Joshi, A. K. Rana and N. Goyal, “Enhance traffic flow prediction with real-time vehicle data integration,” Journal of Autonomous Intelligence, vol. 6, no. 2, pp. 574, 2023. [Google Scholar]
7. M. Elnawawy, A. Sagahyroon and T. Shanableh, “FPGA-based network traffic classification using machine learning,” IEEE Access, vol. 8, pp. 175637–175650, 2020. [Google Scholar]
8. K. L. Dias, M. A. Pongelupe and W. M. Caminhas, “An innovative approach for real-time network traffic classification,” Computer networks, vol. 158, pp. 143–157, 2019. [Google Scholar]
9. S. B. Kotsiantis, “Decision trees: A recent overview,” Artificial Intelligence Review, vol. 39, pp. 261–283, 2013. [Google Scholar]
10. S. Mantach, A. Ashraf, H. Janani and B. Kordi, “A convolutional neural network-based model for multi-source and single-source partial discharge pattern classification using only single-source training set,” Energies, vol. 14, no. 5, pp. 1355, 2021. [Google Scholar]
11. D. E. Kislov, K. A. Korznikov, J. Altman, A. S. Vozmishcheva and P. V. Krestov, “Extending deep learning approaches for forest disturbance segmentation on very high-resolution satellite images,” Remote Sensing in Ecology and Conservation, vol. 7, no. 3, pp. 355–368, 2021. [Google Scholar]
12. M. Al-Sarem, A. Alsaeedi, F. Saeed, W. Boulila and O. AmeerBakhsh, “A novel hybrid deep learning model for detecting COVID-19-related rumors on social media based on LSTM and concatenated parallel CNNs,” Applied Sciences, vol. 11, no. 17, pp. 7940, 2021. [Google Scholar]
13. X. Tan, S. Su and Z. Huang, “Wireless sensor networks intrusion detection based on SMOTE and the random forest algorithm,” Sensors, vol. 19, no. 1, pp. 203, 2019. [Google Scholar] [PubMed]
14. T. Shapira and Y. Shavitt, “FlowPic: A generic representation for encrypted traffic classification and applications identification,” IEEE Transactions on Network and Service Management, vol. 18, no. 2, pp. 1218–1232, 2021. [Google Scholar]
15. J. Lan, X. Liu, B. Li, Y. Li and T. Geng, “DarknetSec: A novel self-attentive deep learning method for darknet traffic classification and application identification,” Computers & Security, vol. 116, pp. 102663, 2022. [Google Scholar]
16. X. Lin, G. Xiong, G. Gou, Z. Li, J. Shi et al., “ET-BERT: A contextualized datagram representation with pre-training transformers for encrypted traffic classification,” in Proc. of Association for Computing Machinery, New York, NY, USA, pp. 633–642, 2022. [Google Scholar]
17. Q. Ma, W. Huang, Y. Jin and J. Mao, “Encrypted traffic classification based on traffic reconstruction,” in Proc. of Int. Conf. on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, pp. 572–576, 2021. [Google Scholar]
18. Y. Guo, G. Xiong, Z. Li, J. Shi, M. Cui et al., “Combating imbalance in network traffic classification using GAN based oversampling,” in Proc. of IFIP Networking Conf. (IFIP Networking), Espoo and Helsinki, Finland, pp. 1–9, 2021. [Google Scholar]
19. K. Li, W. Ma, H. Duan, H. Xie, J. Zhu et al., “Unbalanced network attack traffic detection based on feature extraction and GFDA-WGAN,” Computer Networks, vol. 216, pp. 109283, 2022. [Google Scholar]
20. C. Liu, R. Antypenko, I. Sushko and O. Zakharchenko, “Intrusion detection system after data augmentation schemes based on the VAE and CVAE,” IEEE Transactions on Reliability, vol. 71, no. 2, pp. 1000–1010, 2022. [Google Scholar]
21. D. P. Kingma and M. Welling, “An introduction to variational autoencoders,” Foundations and Trends in Machine Learning, vol. 12, no. 4, pp. 307–392, 2019. [Google Scholar]
22. J. Chang, L. Xie, J. Zhao and Y. Yang, “An anomaly detection algorithm for ship trajectory data based on VAE-LSTM model,” Journal of Transport Information and Safety, vol. 38, no. 6, pp. 1–8, 2020. [Google Scholar]
23. J. Zhang and Y. Zhao, “Research on intrusion detection method based on generative adversarial network,” in Proc. of Int. Conf. on Big Data Analysis and Computer Science (BDACS), Kunming, China, pp. 264–268, 2021. [Google Scholar]
24. Z. Xu, “Research on deep learning model and algorithm for network intrusion detection,” M. S. thesis, Jiangxi University of Science and Technology, China, 2022 (In Chinese). [Google Scholar]
25. G. Drapper-Gil, A. H. Lashkari, M. S. I. Mamun and A. A. Ghorbani, “Characterization of encrypted and vpn traffic using time-related features,” in Proc. of Int. Conf. on Information Systems Security and Privacy (ICISSP), Rome, Italy, pp. 407–414, 2016. [Google Scholar]
26. A. H. Lashkari, G. Draper-Gil, M. S. I. Mamun and A. A. Ghorbani, “Characterization of tor traffic using time based features,” in Proc. of Int. Conf. on Information Systems Security and Privacy (ICISSP), Porto, Portugal, pp. 253–262, 2017. [Google Scholar]
27. S. Zhu, X. Xu, H. Gao and F. Xiao, “CMTSNN: A deep learning model for multiclassification of abnormal and encrypted traffic of Internet of Things,” IEEE Internet of Things Journal, vol. 10, no. 13, pp. 11773–11791, 2023. [Google Scholar]
28. S. Soleymanpour, H. Sadr and M. N. Soleimandarabi, “CSCNN: Cost-sensitive convolutional neural network for encrypted traffic classification,” Neural Process Letters, vol. 53, no. 5, pp. 3497–3523, 2021. [Google Scholar]
29. A. Telikani, A. H. Gandomi, K. K. R. Choo and J. Shen, “A cost-sensitive deep learning-based approach for network traffic classification,” IEEE Transactions on Network and Service Management, vol. 19, no. 1, pp. 661–670, 2022. [Google Scholar]
30. X. Ren, H. Gu and W. Wei, “Tree-RNN: Tree structural recurrent neural network for network traffic classification,” Expert Systems with Applications, vol. 167, pp. 114363, 2021. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools