A Lightweight, Searchable, and Controllable EMR Sharing Scheme

1  Introduction

In today’s information age, data is considered an important asset [1]. However, in the healthcare sector, the secure and efficient sharing of electronic medical records has always been a challenge. Since 2020, the cost of healthcare data breaches has increased by 53.3%, and for the 13th consecutive year, the healthcare industry has reported the most costly data breaches with an average loss of $10.93 million [2]. Healthcare data contains a large amount of private information such as patients’ identity and medical history, which can pose serious security risks to patients if compromised [3]. However, electronic healthcare data sharing has become a key trend in healthcare. Most patients are willing to share their personal medical data under the premise of ensuring patient privacy and data security [4]. The Healthcare Medical Data Compliance Circulation Standard provides a regulatory framework for healthcare data circulation [5], which is a major advancement in healthcare data circulation.

Medical data includes sensitive data such as medical history and personal health information. Once illegally accessed, it not only violates personal privacy, but also may lead to serious consequences such as identity theft. At the same time, the rights and interests of data owners cannot be safeguarded due to the lack of sufficient trust between data owners and data visitors. Therefore, it is very important to ensure the rights and interests of the data owner and privacy, while at the same time achieve efficient access to e-medical data by data visitors. On the basis of CP-ABE, Zheng et al. [6] proposed the ciphertext policy-based keyword searchable attribute-based encryption (CP-ABKS) scheme, which allows to retrieve the encrypted documents through keyword search while maintaining fine-grained access control, but the use of a tree structure is less efficient and cannot achieve the resistance to the keyword guessing attack, and also the data owner’s controllability over the data, thus effectively guaranteeing the data owner’s rights and privacy while ensuring the data visitor’s efficient access to the electronic medical data. Zhang et al. [7] proposed a partial policy hiding scheme against attribute value guessing attack using interactive online privacy protection test, which can resist offline dictionary guessing attack, but with low efficiency and no controllability of data by data owner. Li et al. [8] realized data sharing based on proxy re-encryption, and at the same time, realized a certain controllability of data by data owner. The data sharing is based on proxy re-encryption technique, while the data owner has some control over the data, and the blockchain is used to verify the user privileges and record the request content to achieve a certain degree of regulatory control, but the scheme is not able to resist the offline dictionary guessing attack, and the sharing efficiency also needs to be improved. In order to promote efficient and secure sharing of healthcare data, new technologies and strategies must be used to address these issues.

To address the above problems, this paper proposes a lightweight, searchable, and controllable EMR sharing scheme, which utilizes a large attribute domain and a linear secret sharing structure to improve the flexibility and efficiency of medical data sharing, reduces the encryption and decryption overhead of the medical data during the sharing process, and decrypts the ciphertext with a constant level of computation. Using Intel SGX technology, a secure container Enclave is opened in the system to re-encrypt the data and change the structure of the data, thus realizing the resistance to offline dictionary guessing attacks and avoiding the interaction of data visitors in the server during the search process. Adopting dynamic accumulator technology, the data owner can flexibly manage authorized users, including the update and revocation of privileges, etc., which enhances the owner’s controllable degree of its own data. The summary and Hash of the access rows of the data visitors are uploaded to the blockchain, and by using the characteristics of blockchain such as tampering, the regulation can trace the request process of the data, and carry out credible judgments and pursuing responsibilities when there is anomalous behavior. The main contributions of this paper are summarized as follows.

The solution adopts the LSSS structure and supports large attribute domains, which further improves the flexibility and efficiency of the existing solution and can be adapted to devices with limited computing resources.

The application of Intel SGX further guarantees the security of the data sharing process.

The combination of dynamic accumulator technology and blockchain technology further increases the rights and interests of data owners in the sharing process.

The paper is organized as follows. The second part presents the related research work. The third part provides the basics of the theoretical model. The fourth part first introduces the design of the scheme and details the key processes such as algorithms in the scheme. The fifth part is the security analysis of the scheme. The sixth part is the experimental verification and analysis. Finally, the seventh part summarizes and discusses.

2  Related Work

In recent years, the emergence of emerging technologies such as Deep Learning [9], Edge Computing [10] and Knowledge Graphs [11] has contributed significantly to the research on efficient sharing of data. In sensitive domains such as electronic medical record sharing, fine-grained data access control mechanisms are required. However, some traditional searchable encryption (SE) schemes do not support fine-grained access control [12]. In this context, Attribute-Based Encryption (ABE) [13] has been proposed as an effective solution to achieve finer-grained access control. Sun et al. [14] extended this concept and implemented a verifiable CP-ABKS scheme in a multiuser environment, which supports user revocation and is resistant to keyword guessing Attacks. Access policies may reveal sensitive information about the data owner, which makes it crucial to hide the access policies, but none of the above schemes support policy hiding. Nishide et al. [15] proposed a wildcard-based scheme for policy hiding, but it only supports the “and gate” structure, which makes it more demanding and less flexible in terms of computing resources. However, only the “and gate” structure is supported, which makes it more demanding on computational resources and less flexible. In order to overcome these limitations, Lai et al. [16] proposed a more flexible partial policy hiding scheme based on ensemble groups using Linear Secret Sharing Scheme (LSSS), but this scheme also does not support keyword search.

Qiu et al. [17] proposed a new CP-ABKS scheme that supports policy hiding with resistance to keyword guessing attacks and effectively restricts the possibility of unauthorized users to perform searches, but there is a lack of research on data encryption. Based on this, Wang et al. [18] proposed a data owner attribute-based encryption scheme with policy hiding that can be searched and revoked to enable data sharing by multiple owners. Miao et al. [19] proposed a keyword search scheme with privacy preservation and support for multi-owner cooperation that supports policy hiding and user tracking. However, schemes [17–19] are based on the partial policy hiding implemented in Nishide et al.’s [15] scheme, with low flexibility and scalability of access control, and none of them can resist offline dictionary guessing attacks. Ma et al. [20] proposed an innovative EMR access control model and fine-grained data sharing mechanism for resource-constrained mobile devices, and addressed challenges of data privacy protection and challenges such as computational efficiency optimization, but fails to achieve controllability of data by the data owner. The DNACDS scheme proposed by Singh et al. [21] and the LBP-RDH technique proposed by Sahu et al. [22] also provide some new ideas for healthcare data security and sharing.

While improving the efficiency of healthcare data access control, the controllability of the data flow of the data owner’s data during the sharing process is equally important. Since the emergence of Bitcoin in 2009, its underlying blockchain technology has gradually received attention from the research field of healthcare data sharing controllability due to its characteristics. Xia et al. [23] proposed MeDShare, a healthcare data management system in a trustless environment, where data manipulation behaviors are logged and user permissions are managed, but there is a high overhead in verifying user permissions. Gao et al. [24] designed a blockchain-based medical data sharing scheme using searchable encryption and secret sharing techniques. The scheme takes into account the problem that cloud storage servers are not fully trusted and uses secret sharing techniques to support sharing by multiple users, but the interaction process of the scheme is relatively complex and the system coupling is relatively high. Sun et al. [25] proposed a blockchain- and smart contract technology based distributed electronic searchable scheme for medical data, which achieves decentralization of data storage and fine-grained control of data access, and at the same time adopts an attribute-based encryption scheme to ensure data privacy, but the system efficiency needs to be further improved. Wu et al. [26] proposed a blockchain-based smart healthcare system, which has fine-grained privacy protection, and can reliably exchange and share data among different users but cannot resist offline dictionary guessing attacks.

Zhou et al. [27] designed a sharing scheme for healthcare data by combining attribute-based encryption and blockchain technology from access control in the time dimension. Although a regulatory center is set up to manage the user’s identity, there is little flexibility to restrict data sharing from the time dimension. Chelladurai et al. [28] used blockchain smart contracts to provide a secure, efficient and seamless solution to support healthcare information exchange and peer-to-peer contracts with cryptographic hash functions to ensure high security and integrity, but the user cannot achieve effective data control. Lin et al. [29] proposed the UDVSP scheme and the EMRChain system to achieve efficient and secure blockchain-based EMR sharing with bilinear unpaired and anti-malicious propagation, which was demonstrated through a comprehensive performance evaluation shows that these schemes are feasible, but cannot resist offline dictionary guessing attacks. Gao et al. [30] proposed a blockchain-based searchable encryption scheme that implements fine-grained access control and EHR sharing on the cloud, ensuring data integrity and fairness of transactions, while resisting adaptive keyword selection attacks, but with poor data controllability for the data owner.

Based on the above statement, the current scheme does not simultaneously weigh the relationship between efficient encryption and decryption of medical data and sharing and the effective controllability of data owners’ data, therefore, in this paper, we propose a lightweight searchable and controllable electronic medical record sharing scheme, which adopts the large attribute domain, the LSSS structure, and the Intel SGX technology to realize the function of keyword search, policy hiding, and offline dictionary guessing attack. The keyword search, strategy hiding and offline dictionary guessing attack functions, which improve the sharing efficiency and ensure the security of the data at the same time; through the combination of dynamic accumulator technology and blockchain technology, it is to realize the controllability of the data by the data owner and the credible judgment and accountability of the regulator, which fully protects the rights and interests of the data owner.

3  Preliminaries

3.1 Composite Order Bilinear Group

Apply a bilinear group of composite order Q=p1p2p3, where p1, p2 and p3 are three different prime numbers. G and GT are two multiplicative cyclic groups of order Q=p1p2p3. Gpi is a subgroup of G with order pi, and Gpipj(i≠j) is a subgroup of G with order pipj. The bilinear mapping e: G×G→GT satisfies the following properties:

1)   Bilinearity: for any u,v∈G and a,b∈Zp, has e(ua,vb)=e(u,v)ab.

2)   Non-degeneracy: there exists g∈G such that the order of e(g,g) in GT is Q.

3)   Computability: for any u,v∈G, there exists an efficient algorithm to compute e(u,v).

4)   Orthogonality of subgroups: for ∀gi∈Gpi and ∀gj∈Gpj(i≠j), has e(gi,gj)=1.

3.2 Access Structure

In order to achieve effective control of the data owner over the data visitor, it is necessary to customize the access authorization set, which is satisfied to continue access, otherwise access is denied. Let {P1,P2,⋯,Pn} be a set of entities comprising n participants. For set A⊆2{p1,p2,⋯,pn}, if ∀B,C where B∈A and B⊆C, has C∈A, then A is said to be monotone. If A is a non-empty subset of {P1,P2,⋯,Pn}, that is, A⊆2{p1,p2,⋯,pn}∖{∅}, then A is considered an access structure. All sets included in A are termed as authorized sets, and those not included in A are termed as non-authorized sets.

3.3 Intel SGX

Intel SGX is an extension of the existing Intel architecture, comprising a new set of instruction sets and memory access mechanisms [31] that allow applications to create an isolated execution environment known as an Enclave. An Enclave serves as a trusted and secure entity for storing data and executing code. It possesses three key security features: Isolation, sealing, and attestation [32]. The feature of isolation restricts access to a protected area of memory hardware to only specific Enclaves. The encryption is performed using a sealing key that is private to a specific Enclave, and no process other than an exact replica of the Enclave is able to decrypt or modify it. Attestation allows verifiers to authenticate that the code is running securely within an Enclave and has not been tampered with. SGX offers two types of attestation: Local and remote [33]. Local attestation is used for authentication between two Enclaves on the same platform, where they can derive a shared key using a root sealing key shared between them. Remote attestation enables an Enclave to generate reports that can be verified by any remote entity.

4  Scheme Design

4.1 Scheme Overview

The lightweight searchable and controllable electronic medical record sharing scheme (EMR_LSCSS) designed in this paper is shown in Fig. 1. The system mainly includes six participating entities: Cloud Server (CS), Regulatory and Authorization Center (RAC), Data Owner (DO), Data Visitor (DV), Blockchain (BC), and Enclave.

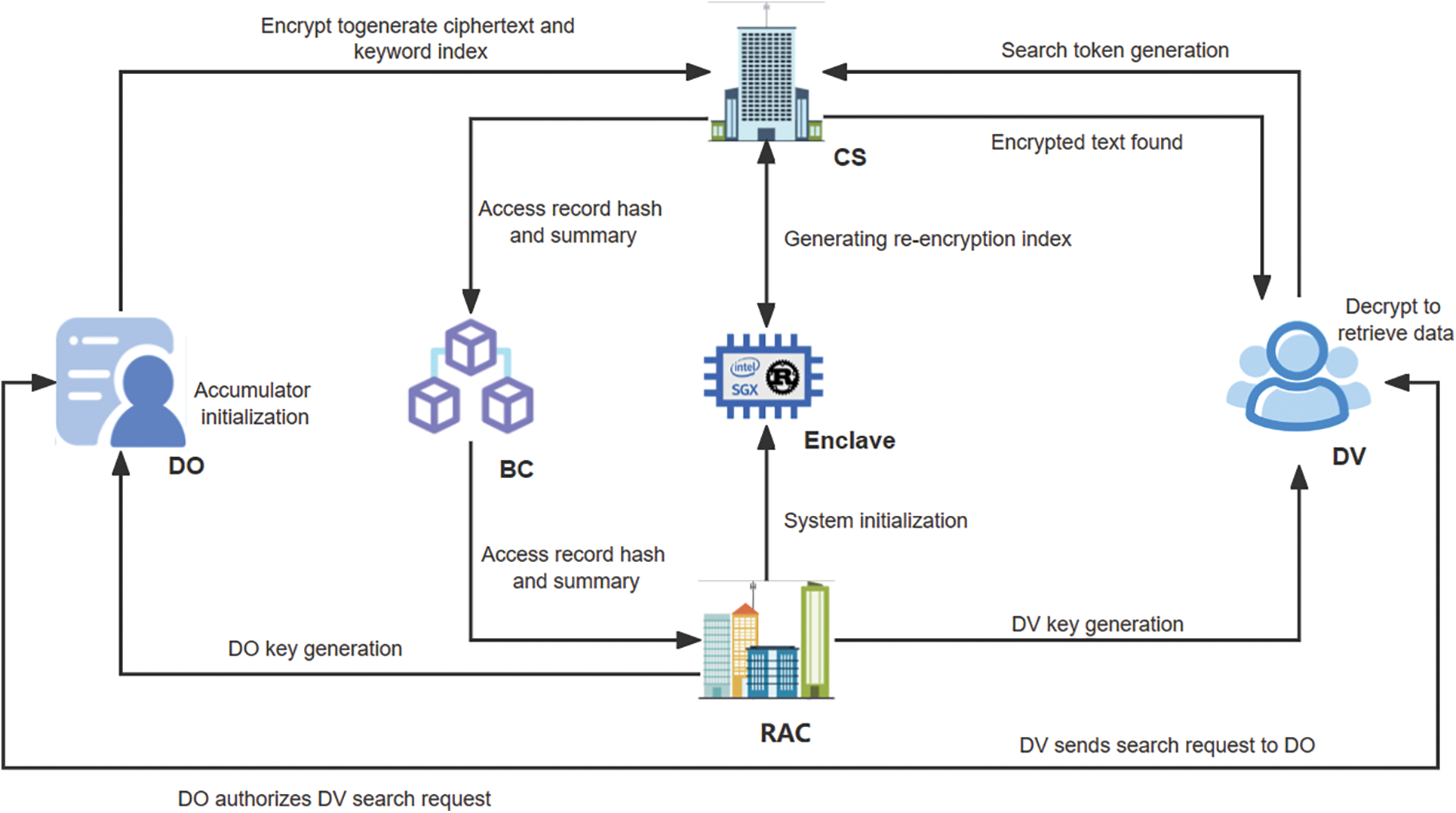
Figure 1: EMR_LSCSS framework diagram

4.2 Specific Algorithm Processes

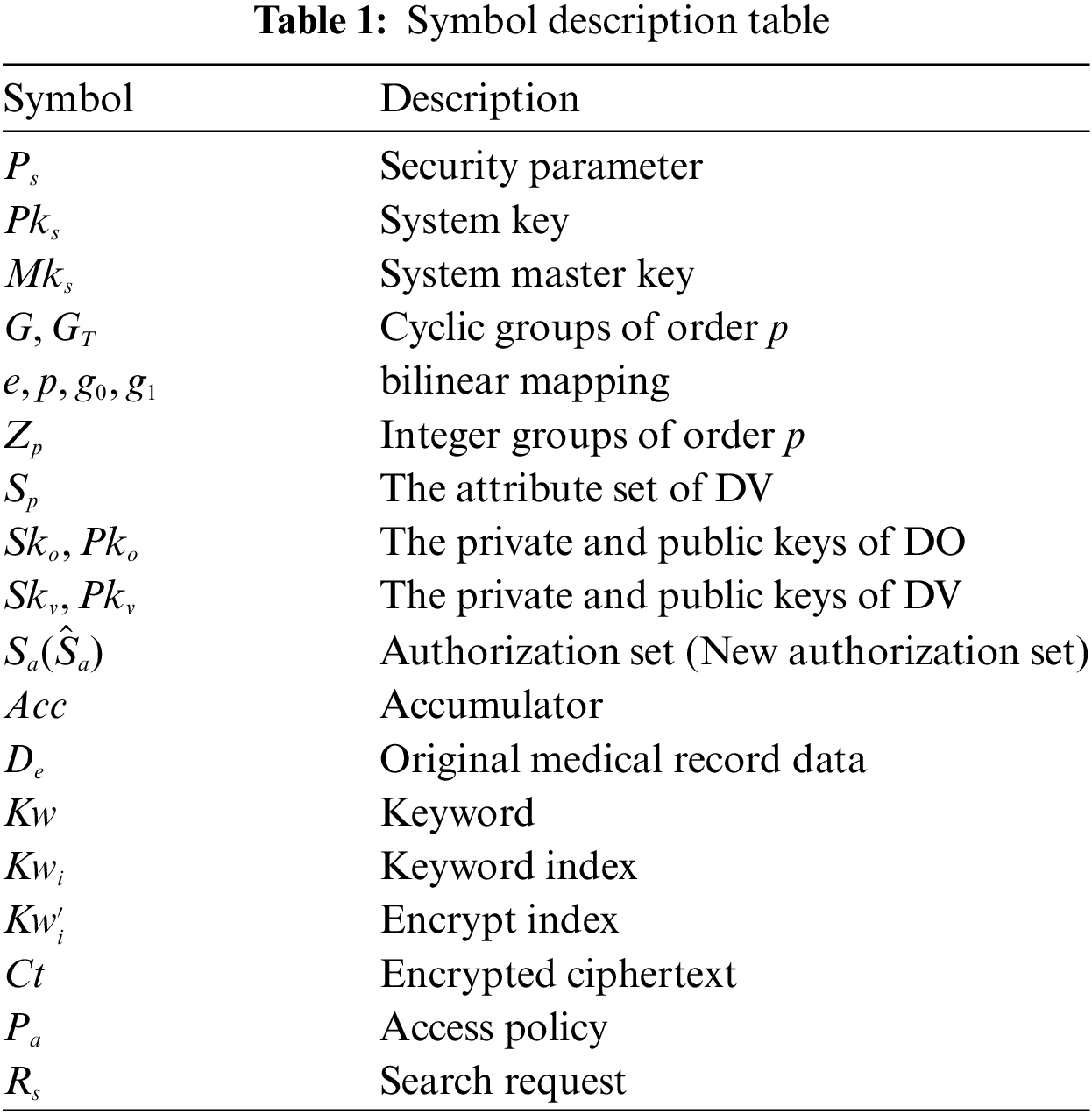
The scheme presented in this article primarily comprises algorithms for System initialization, Key generation, Accumulator initialization, Encryption, Re-encryption, Search request, Authorization search, Search token generation, Search and Decryption. The symbol description is shown in Table 1 and specific algorithmic processes are as follows.

1. Key generation algorithm. This algorithm is executed by RAC.

2. Accumulator initialization algorithm. This algorithm is executed by DO.

3. Encryption algorithm. This algorithm is executed by DO.

4. Re-Encryption algorithm. This algorithm is executed by Enclave.

5. Search request algorithm. This algorithm is executed by DV.

6. Authorization search algorithm. This algorithm is executed by DO.

7. Search token generation algorithm. This algorithm is executed by DV.

8. Search algorithm. This algorithm is executed by CS.

9. Decryption algorithm. This algorithm is executed by DV.

5  Security Analysis of the Scheme

The scheme has the ability to resist offline dictionary guessing attacks and is controllable by the data owner. This section proves its security.

5.1 Proof of Security against Offline Dictionary Guessing Attacks

Offline Dictionary Guessing Attacks generally target keywords or attribute values. In this paper’s solution, the keywords and attribute values are included in the keyword index and the search tokens. Therefore, the following will provide a security analysis for resistance to Offline Dictionary Guessing Attacks from the perspectives of the keyword index and search tokens. In this context, the CS acts as the attacker, with the attributes {ci,vi} and keywords Kwi all being elements from the offline dictionary.

Assumption 1: CDH (Computational Diffie-Hellman problem) Assumption

Let us presume a multiplicative cyclic group G with its order being a prime number p, and g being a generator of the cyclic group G. Calculation parameters a,b∈Zp are selected randomly. The CDH assumption can be understood as: It is quite difficult to solve gab through ga and gb.

Theorem 1: If the CDH assumption holds, then the scheme proposed in this paper can resist offline dictionary guessing attacks based on keywords and indices.

Proof: During the system encryption phase, CS receives an index Index=(I1,{Ii,1,Ii,2}i=1l), where I1=ges, Ii,1=gdri, and Ii,2=gaλiH(πi)−riH1(Kw). Under the CDH assumption, it is challenging for an attacker, who knows g, gd, and ga, to calculate gad. Consequently, the attacker cannot guess the attribute values and keywords included in the index by verifying whether the discriminant e(I1,gad)=∏i=1l(e(Ii,2,gd)e(Ii,1,H(vi)1H1(Kw ′)))Kwi holds. The proof is thus completed.

Theorem 2: The scheme proposed in this paper can resist offline dictionary attacks directed at search tokens.

Proof: During the system search phase, the attacker receives a search token Ts=(Ts1,Ts2,{Tsi}i=1h), where Ts1=gkdtθ, Ts2=gakdtθe, and Tsi=H(vi)ktzθH1(Kw ′). The z element included in Tsi is one of the system master keys, which CS cannot obtain. Therefore, CS cannot guess the attributes and keywords in the search token by verifying whether the discriminant e(gd,Tsi)=e(Ts1,H(vi)1H(Kw ′)) holds. The proof is thus completed.

According to the above proof it can be seen that the attacker finds a polynomial in polynomial time and puts the keywords and attribute values from the offline dictionary into the discriminant in order to check whether the discriminant is valid or not, and it turns out that the discriminant is invalid, so this paper’s scheme is resistant to offline dictionary guessing attack security.

5.2 Proof of Security for Data Owner’s Control over Their Data

Assumption 2: Given the fulfillment of the following conditions, the data owner has controllability over their own data, that is, the scheme proposed in this paper offers data controllability security.

Pr [Initialization(Ps)→(Pks,Mks),

KeyGeneration(Pks,Mks,Sp)→(Sko,Pko,Skv,Pkv,Skr,Pkr),

AccInitialization(Pkv)→(Acc,Sa),

SearchRequest(Pks,Kw ′,Kv,Pko)→

reqSearch:AuthorizationSearch(Pks,Pko ′,Rs,Acc,Sa)→0

]≥1−f(μ)

In the aforementioned equation, f(μ) is a negligible function, implying that the probability of DV not receiving authorization from DO is approaching 1.

Theorem 3: During the process in which the data visitor requests the data owner for data sharing, only those data visitors authorized by the data owner can obtain the corresponding data. That is, the data owner has controllability over personal data.

Proof: When the DV, labeled as cj, requests authorization from DO, DO updates the accumulator as Accnew=AcccjmodN, updates the authorization set Sa to S^a, and generates evidence ω=u∏i=1ci≠cjncimodN, where ci=S^a The CS verification process is ωcj=(u∏i=1ci≠cjnci)cjmodN=u∏i=1ncimodN, where ci∈S^a. The latest accumulator is Accnew=u∏i=1ncimodN, where ci∈S^a. That is, Accnew=ωcj, a necessary condition for CS to return data. When ω is not the correct authorization evidence, according to the strong RSA assumption, Accnew is not equal to ωcj, leading to CS validation failure and data not being returned. Therefore, the scheme proposed in this paper provides controllability of data from DO. Proof completed.

Based on the above proof, it can be seen that DO can control the flow of its own data, i.e., it can flexibly authorize data access to other DVs or revoke the authorization to a certain DV to ensure the controllability of its own data.

6  Performance Analysis of the Scheme

6.1 Experimental Environment

In order to gain a more intuitive understanding of the performance of the proposed scheme, this simulation experiment uses Java language and calls a third-party Java pairing based encryption (JPBC) library to simulate some of the algorithms in this scheme. The experimental environment configuration is shown in Table 2.

In this paper, an extension of the Type A elliptic curve characterized by the equation y2=x3+x is employed for simulative experiments. The encrypted Electronic Medical Record dataset utilized is the COVID-19 Dataset [34], which is provided by the Mexican government and comprises a vast amount of anonymized patient-related information, including preexisting conditions. The original dataset consists of 21 unique features and 1,048,576 unique patients. During simulation experiments, the range of attribute numbers n and the number of rows in the matrix I were both set within the interval [0,50], with the number of candidate values per attribute ni set as 5.

6.2 Function Analysis

This section compares the seven functions of keyword search and large attribute domains, resistance to offline dictionary guessing attacks, constant decryption overhead, access structure, controllability, and trusted accountability with the schemes of Miao et al. [19], Zhang et al. [7], and Gao et al. [30]. The comparison results are shown in Table 3.

The comparative results presented in the table above allow for the following conclusions. Firstly, the scheme by Miao solely supports keyword search functionality, with an access structure that employs an AND-gate paradigm. Notably, the decryption overhead in their scheme is closely linked to the count of data owners and collaborating parties, which makes it impossible to achieve a constant decryption cost. Secondly, Zhang, despite supporting a vast attribute space and the incorporation of a LSSS structure, and endowing the capability to withstand offline dictionary guessing attacks, exhibit a decryption overhead similar to that of Miao. This cost is not constant either but varies with the number of user attributes. Lastly, Gao have accomplished fine-grained access control and sharing of EMR in the cloud, albeit lacking in mechanisms to counteract offline dictionary attacks and in providing data owners with the power of control.

This study takes into consideration the advantages of the aforementioned schemes and incorporates technologies such as dynamic accumulators and blockchain. By utilizing these technologies, ensure controllability by data owners over data access and accountable trustworthiness, all the while fulfilling the requirement for low computational resource overhead. Compared to the previous schemes, the proposal in this paper exhibits significant merits.

6.3 Computational Overhead

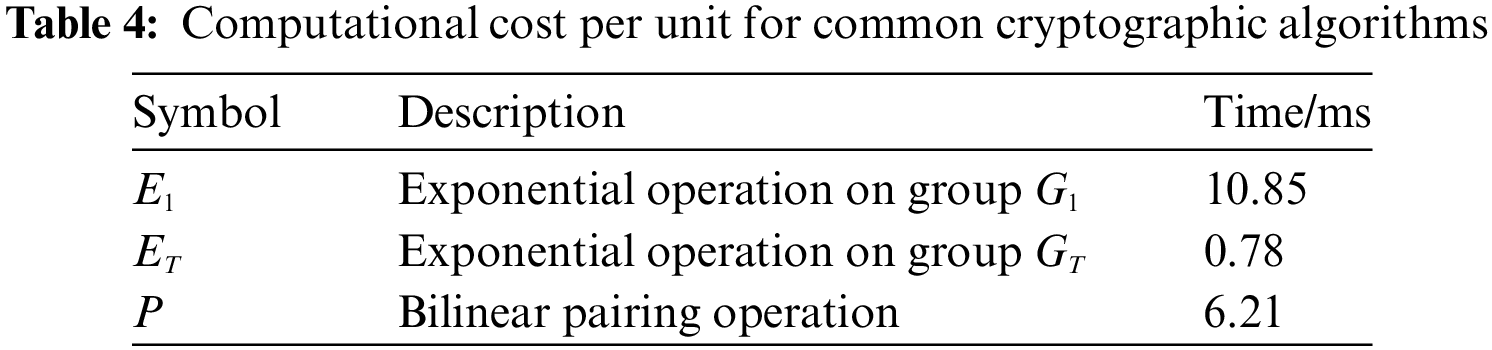
Drawing on the comparative experiments of Miao and Zhang, this section will evaluate the computational cost of some algorithm processes in this paper through theoretical and simulation experiments. By conducting 500 tests and taking the average, the specific unit time results are shown in Table 4.

1) The computational overheads of the proposed scheme in comparison to other schemes during system initialization, key generation, encryption, and shared decryption phases are delineated in Table 5 below. Within this context, ni denotes the number of candidates per attribute, n represents the number of attributes, I corresponds to the number of rows in the access matrix, and d signifies the number of collaborators of the data owner. During the system initialization phase, the computational overhead for Miao is related to both the number of system attributes n and the number of candidate values per attribute ni. In contrast, the proposed scheme in this paper, akin to that of Zhang, is predicated upon a large attribute space, hence the computation overhead remains a constant at a constant-time complexity, which is significantly less than that of Miao.

Moreover, the computational overhead of the scheme presented in this paper is also marginally lower than that of Zhang. In the key generation phase, the computational overhead of our scheme is reduced by at least nE1 compared to other benchmark schemes. The encryption phase of the scheme under consideration includes both data and index encryption. The computational overhead of Miao is contingent upon the number of collaborators d of the data owner, which diverges from the focus of our scheme. Relative to Zhang, the encryption cost of our scheme is approximately 2IE1 lower. During the search token generation stage, the computational overhead of our approach is comparable to that of other schemes.

Owing to the adoption of LSSS structure within the scheme proposed in this article, the reconstruction of the secret values entails exponential operations, thus rendering the computational overhead during the search phase of our scheme relatively higher compared to that of Zhang. Nevertheless, the computational overhead of ET is marginal; therefore, the additional overhead introduced in the search phase is deemed acceptable. Ultimately, in the decryption phase, the computational cost of the scheme by Zhang. is contingent upon the number of user attributes n, whereas the overhead of the scheme elucidated in this work is fixed at a constant-time complexity, which confers a considerable advantage.

The scheme from Miao involves the number of data owner’s collaborators d during the encryption, key generation, and decryption phases. However, this variable is not included in the scheme presented in this paper and that of Zhang For ease of comparison between the schemes, d=1, and then a comparison is performed.

The temporal overhead associated with system initialization is depicted in Fig. 2. During the system initialization phase, the time overhead of the scheme proposed by Miao exhibits a linear growth trend with respect to the number of attributes m. In contrast, the time overhead for the scheme presented in this paper as well as that by Zhang remains constant, with notably lower expenses.

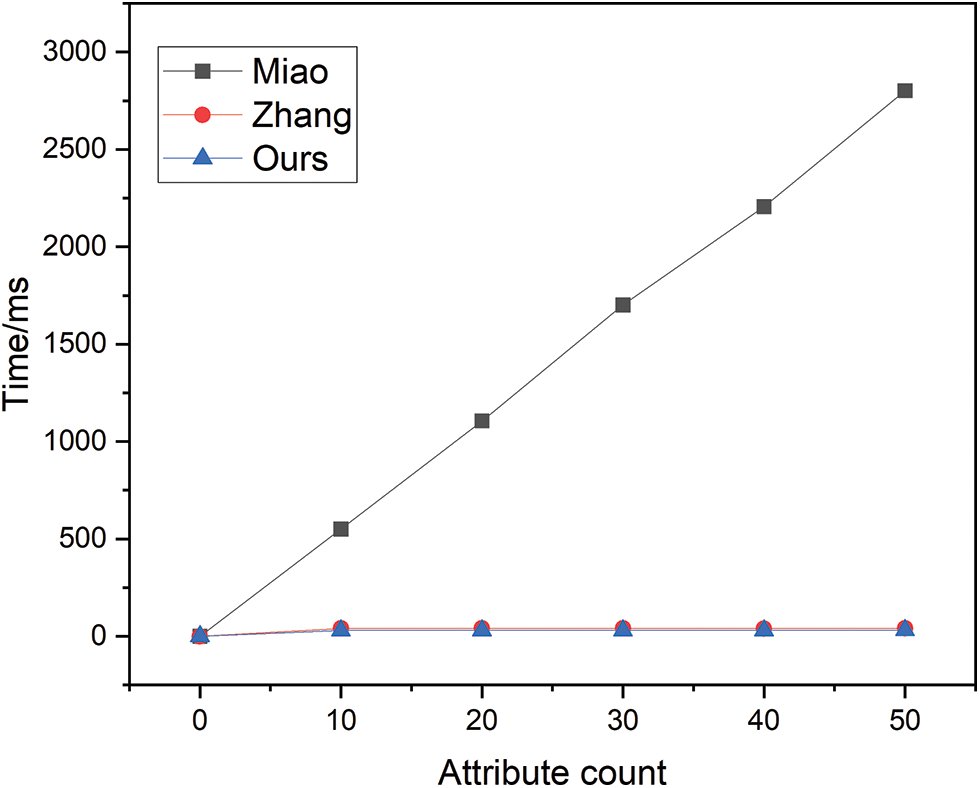
Figure 2: System initialization time overhead

The encryption time overhead is illustrated in Fig. 3. During the encryption phase, the time overhead for the schemes proposed by Miao and Zhang both display an exponential growth as a function of the increase in the number of rows I in the sharing matrix. Although the time overhead for the scheme presented in this paper also rises with an increase in the number of rows I, under the stipulated assumptions, the rate of increase for this paper’s scheme is substantially slower than that of Zhang, and is only slightly higher than that of Miao. Furthermore, considering that the cooperating number of data owners d is a relatively large value, and not merely d=1, in practical scenarios, the growth rate of Miao would be much faster than that of the scheme proposed in this paper.

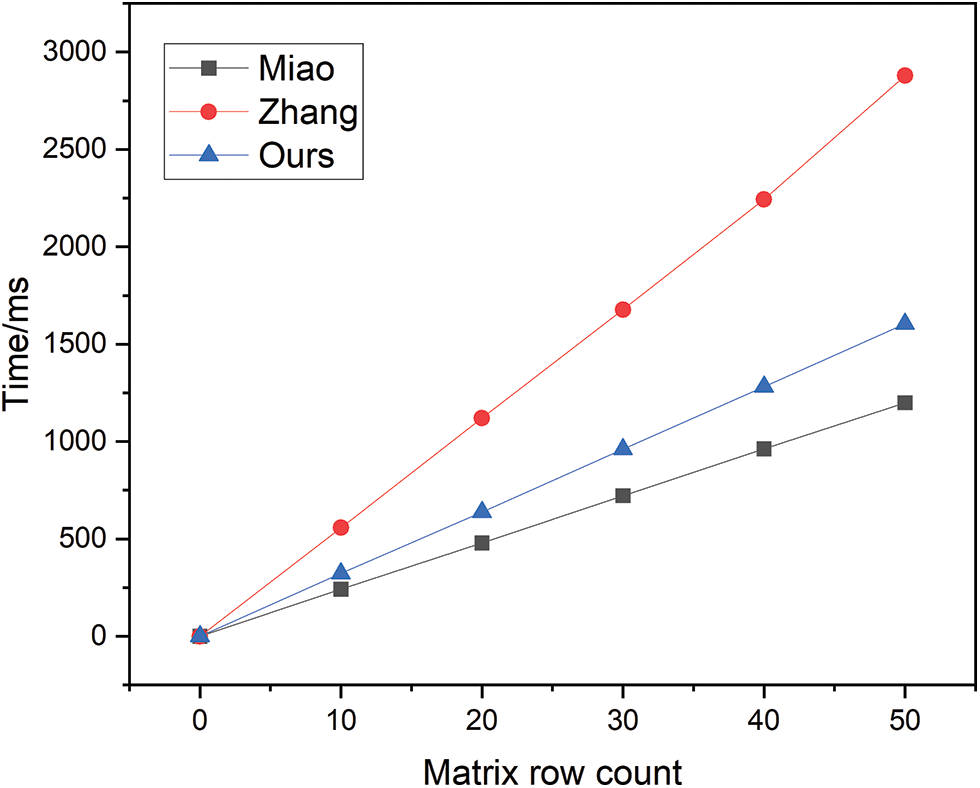
Figure 3: Encryption time overhead

The temporal overhead of the key generation phase is depicted in Fig. 4. Although the scheme in this paper grows linearly with the schemes of Miao and Zhang, the growth rate is significantly lower than that of Miao and Zhang.

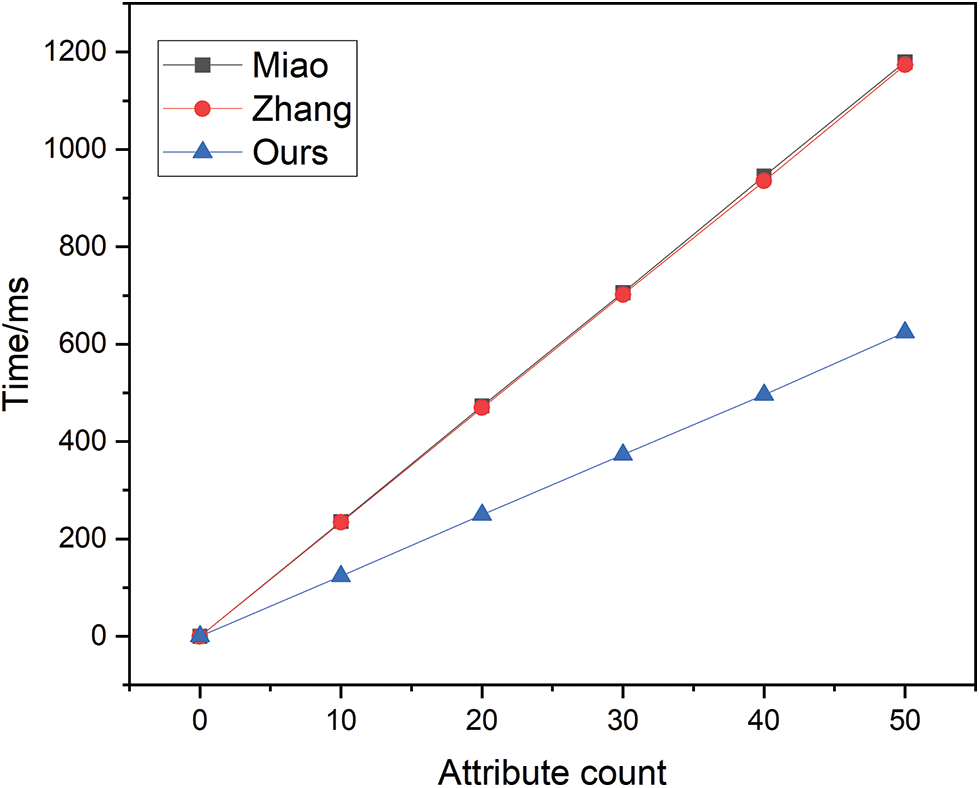
Figure 4: Key generation time overhead

The decryption time overhead is illustrated in Fig. 5. The program of Miao has a significantly higher growth rate than the program in this paper. Although the time overhead for Zhang is a relatively small constant when the variable d is presumed to be a constant value of one, in practical scenarios, d is often significantly greater than this value. In contrast, the decryption time overhead of the scheme presented within this paper remains constant and invariant. Consequently, in comparison, the computation during this phase is more efficient in the approach proposed by this study.

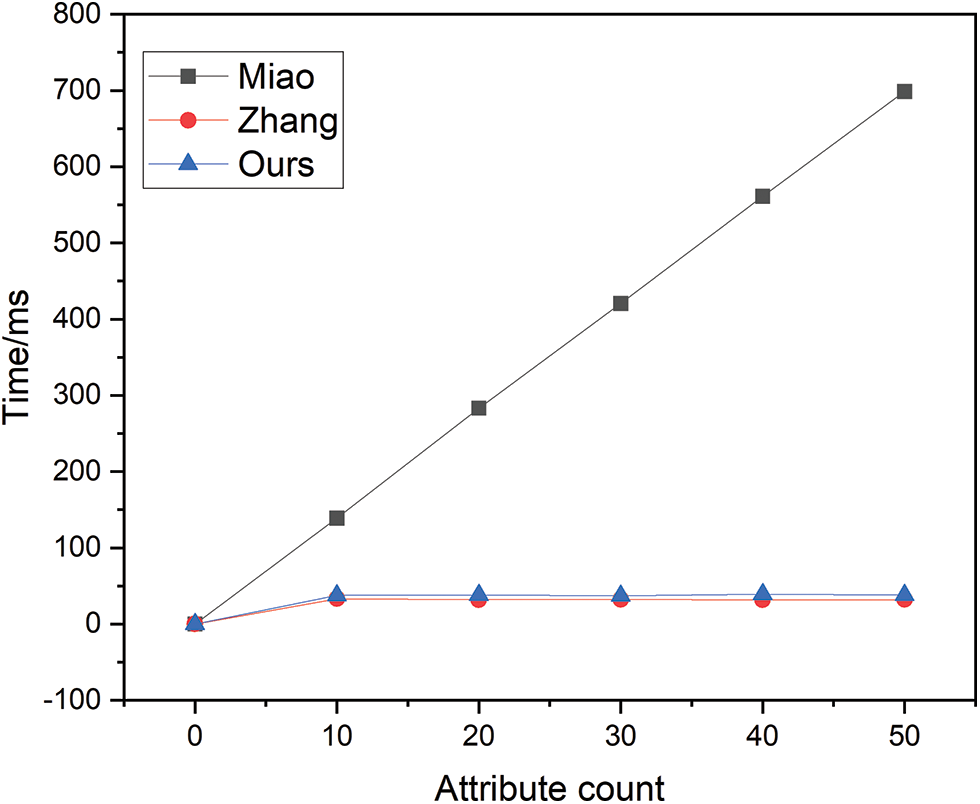
Figure 5: Decryption time overhead

As discerned from Table 6. During the system initialization phase, when n = 50, the time overhead for the scheme by Miao amounts to 2801.6 ms, for Zhang, it is 40.7 ms, whereas for the scheme proposed in this paper it accounts for 30.9 ms. Consequently, the scheme proposed in this paper demonstrates a significant advantage during the system initialization stage. In the key generation phase, the scheme proposed by Miao incurs a time expense of 1179.5 ms, while that of Zhang amounts to 1173.5 ms, with both exhibiting comparable temporal overheads. In contrast, the scheme presented in this paper demonstrates a significantly reduced time consumption of 624.1 ms, markedly outperforming the approaches of Miao and Zhang. In the encryption stage, when I = 50, the time overhead for the scheme proposed in this paper is 1605.2 ms, for Miao it is 1198.7 ms, and for the scheme of Zhang it is 2878.9 ms. In actual scenarios, the scheme presented in this paper holds a distinct advantage in terms of time overhead. In the decryption stage, the time overhead associated with Zhang exhibits a noticeable increase with the addition of attributes. Under the assumption of specific conditions, the time overhead for the scheme by Miao is 32.1 ms, while that for Zhang and colleagues’ scheme is 698.7 ms, and the approach introduced in this article incurs a time expense of 38.1 ms, has a clear advantage.

In terms of the search token generation and search time overhead, a comparison is drawn between the scheme presented in this paper and that of Miao, as the scheme by Zhang does not incorporate these two stages. The temporal overhead during the search phase is comparable between the two approaches; however, in the phase of search token generation, the scheme of Miao almost doubles the time expense of the scheme proposed in this article. Therefore, the approach delineated herein proves to be more efficient in both of these stages.

In the stages of re-encryption, accumulator initialization, search requests, and authorization requests, the scheme proposed in this paper adds several functionalities compared to the schemes by Miao and Zhang. Through logical analysis and simulation experiments, these additional functionalities are deemed to be within a reasonable range.

6.4 Storage Overhead

This section will analyze the partial overhead associated with the proposed scheme in the context of non-blockchain storage. Herein, |G1| denotes the size of elements in the group G1, and similarly, |G2|,|GT| and |Zp| represent the sizes of elements in the groups G2,GT and Zp, respectively. Under the elliptic curve defined by the equation y2=x3+x, it holds that |G1|=|G2|=|GT|. Due to functional discrepancies between the scheme introduced in this paper and those by Miao and Zhang, a comparative assessment of storage overhead is limited to five key aspects: System public keys, system master keys, private keys, search tokens, and encrypted indexes—specifically, ciphertexts associated with indexes. The outcomes are tabulated in Table 7.

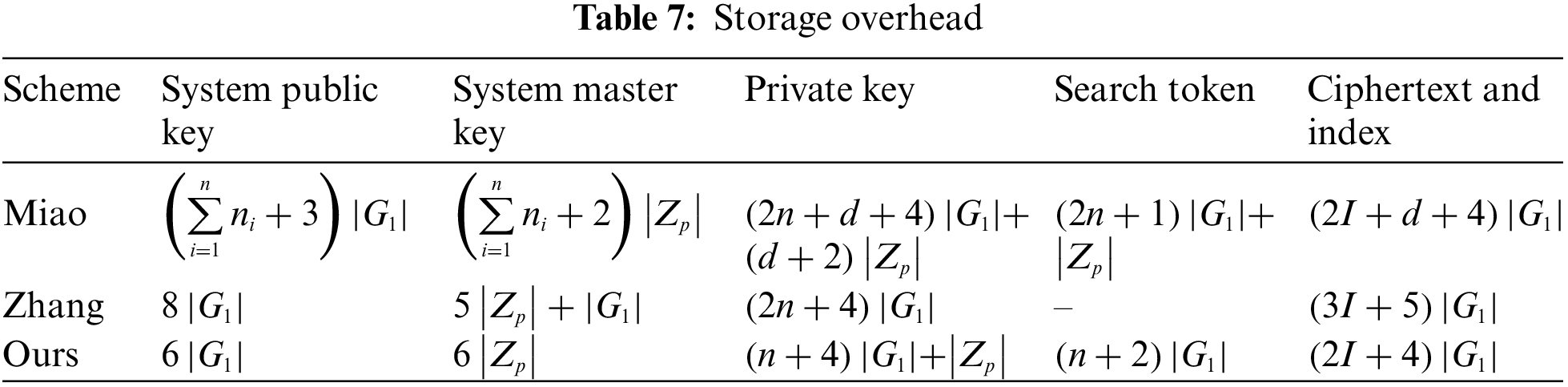
As observed from Table 7, in terms of the storage overhead for system public keys, the scheme presented in this paper incurs a constant overhead of 6|G1|, which is significantly less than the (∑i=1nni+3)|G1| required by Miao, and slightly less than the 8|G1| required by Zhang. Regarding the system master key storage overhead, the overhead for the proposed scheme is a constant 6|Zp|, which is markedly less than the (∑i=1nni+2)|Zp| needed by Miao and is comparable to Zhang is 5|Zp|+|G1|. In the aspect of private key storage overhead, the proposed scheme requires (n+4)|G1|+|Zp|, while the private key storage overhead for the schemes by Miao and Zhang is nearly double that of the proposed scheme. With regards to the search token storage overhead, the scheme introduced here necessitates an overhead of (n+2)|G1|, which is almost half of that incurred by the search tokens of Miao. Since Zhang’s scheme does not address search token storage overhead, a comparison cannot be made.

Lastly, for the storage of ciphertexts and indexes, the proposed scheme’s overhead is (2I+4)|G1|, whereas the overhead for both the other schemes surpasses that of the scheme detailed in this document. A theoretical analysis and simulation experiments were conducted on the other functional modules of the proposed scheme for their storage overhead, and the results indicate that the overhead is also within a reasonable range.

7  Summary

The current work introduces a lightweight, searchable, and controllable EMR sharing scheme. The proposed framework integrates keyword search with policy hiding, employing large attribute domains and a linear key-sharing structure to enhance the scalability and flexibility of access control. Within this scheme, Intel SGX technology is utilized to re-encrypt data, effectively thwarting offline dictionary guessing attacks and reducing decryption computational overhead to a constant level, catering to users with limited computing resources. To precisely manage data access, the scheme implements dynamic accumulator technology, enabling data owners to grant or revoke access permissions to data requesters flexibly. Additionally, the generation of data requester access logs and the uploading of corresponding hash values to the blockchain efficiently prevent denial and tampering of data. Furthermore, the inclusion of regulatory bodies to evaluate and hold accountable data access requests further elevates the system’s trustworthiness and security.

Through simulation experiments, the feasibility and superiority of the proposed strategy have been confirmed. Relative to existing solutions, the presented scheme exhibits significant advantages. However, the implementation of the current study has been confined to theoretical simulation due to resource constraints. Consequently, future research endeavors should focus on deploying the proposed strategy within real-world healthcare settings to further validate its effectiveness and practicality.

Acknowledgement: This study was supported by the Natural Science Foundation of Hebei Province, China, under Project F2021201052. I would like to express my heartfelt gratitude to Professor Xiaohui Yang for his valuable guidance and support throughout this research. I also want to thank all the classmates who provided valuable suggestions for the experiments. Lastly, I am grateful to this esteemed journal for providing an opportunity for further learning.

Funding Statement: Yang’s work was supported by the Natural Science Foundation of Hebei Province under Grant Number F2021201052.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Xiaohui Yang, Peiyin Zhao; data collection: Peiyin Zhao; analysis and interpretation of results: Xiaohui Yang, Peiyin Zhao; draft manuscript preparation: Peiyin Zhao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. M. Nolin, “Data as oil, infrastructure or asset? Three metaphors of data as economic value,” J. Inf. Commun. Ethics Soc., vol. 18, no. 1, pp. 28–43, 2020. doi: 10.1108/JICES-04-2019-0044. [Google Scholar] [CrossRef]

2. IBM, “Cost of a Data Breach Report 2023,” Accessed: Apr. 30, 2023. [Online]. Available: https://www.ibm.com/reports/data-breach [Google Scholar]

3. H. J. Wang, J. T. Ning, X. Y. Huang, G. Y. Wei, G. S. Poh and X. M. Liu, “Secure fine-grained encrypted keyword search for E-healthcare cloud,” IEEE Trans. Dependable Secure Comput., vol. 18, no. 3, pp. 1307–1319, 2021. [Google Scholar]

4. L. J. Kish and E. J. Topol, “Unpatients—why patients should own their medical data,” Nat. Biotechnol., vol. 33, no. 9, pp. 921–924, 2015. doi: 10.1038/nbt.3340. [Google Scholar] [PubMed] [CrossRef]

5. Skyflow, “Healthcare Medical Data Compliance Circulation Standards,” Accessed: Mar. 22, 2023. [Online]. Available: http://www.cinsa.org.cn/2023/0901/c33219a517345/page.htm [Google Scholar]

6. Q. J. Zheng, S. H. Xu, and G. Ateniese, “VABKS: Verifiable attribute-based keyword search over outsourced encrypted data,” in Proc. IEEE Conf. Comput. Commun.,Toronto, Toronto, ON, Canada, Piscataway, IEEE Press, 2014, pp. 522–530. [Google Scholar]

7. Z. S. Zhang, W. Zhang, and Z. G. Qin, “A partially hidden policy CP-ABE scheme against attribute values guessing attacks with online privacy-protective decryption testing in IoT assisted cloud computing,” Future Gener. Comp. Syst., vol. 123, no. 4, pp. 181–195, 2021. doi: 10.1016/j.future.2021.04.022. [Google Scholar] [CrossRef]

8. L. Li, Q. X. Zeng, Y. H. Wen, and S. C. Wang, “Data sharing scheme based on the blockchain and the proxy re-encryption,” Netinfo Secur., vol. 20, no. 8, pp. 16–24, 2020. [Google Scholar]

9. M. Hooshmand and D. Hosahalli, “Network anomaly detection using deep learning techniques,” CAAI Trans. Intel. Tech., vol. 7, no. 2, pp. 228–243, 2022. doi: 10.1049/cit2.12078. [Google Scholar] [CrossRef]

10. M. Wang, H. Yi, F. Jiang, L. Lin, and M. Gao, “Review on offloading of vehicle edge computing,” J. Artif. Intell. and Technol., vol. 2, no. 4, pp. 132–143, 2022. doi: 10.37965/jait.2022.0120. [Google Scholar] [CrossRef]

11. Y. Deng, Z. Zeng, K. Jha, and D. Huang, “Problem-based cybersecurity lab with knowledge graph as guidance,” J. Artif. Intell. and Technol., vol. 2, no. 2, pp. 55–61, 2022. doi: 10.37965/jait.2022.0066. [Google Scholar] [CrossRef]

12. S. Kamara, C. Papamanthou, and T. Roeder, “Dynamic searchable symmetric encryption,” in Proc. 2012 ACM Conf. Comput. Commun. Secur., New York, NY, USA, ACM Press, 2012, pp. 965–976. [Google Scholar]

13. P. Jiang, Y. Mu, F. C. Guo, and Q. Y. Wen, “Secure-channel free keyword search with authorization in manager-centric databases,” Comput. Secur., vol. 69, no. 2, pp. 50–64, 2017. doi: 10.1016/j.cose.2016.11.015. [Google Scholar] [CrossRef]

14. W. H. Sun, S. C. Yu, W. J. Lou, Y. T. Hou, and H. Li, “Protecting your right: Verifiable attribute-based keyword search with fine-grained owner-enforced search authorization in the cloud,” IEEE Trans. Parallel Distrib. Syst., vol. 27, no. 4, pp. 1187–1198, 2016. doi: 10.1109/TPDS.2014.2355202. [Google Scholar] [CrossRef]

15. T. Nishide, K. Yoneyama, and K. Ohta, “Attribute-based encryption with partially hidden encryptor-specified access structures,” in Int. Conf. Appl. Crypto. Netw. Secur, Berlin, Germany, Springer, 2008, pp. 111–129. [Google Scholar]

16. J. Z. Lai, R. H. Deng, and Y. J. Li, “Expressive CP-ABE with partially hidden access structures,” in Proc. 7th ACM Symp. Inform., Comput. Commun. Secur., New York, USA, ACM Press, 2012, pp. 18–19. [Google Scholar]

17. S. Qiu, J. Q. Liu, Y. F. Shi, and R. Zhang, “Hidden policy ciphertext-policy attribute-based encryption with keyword search against keyword guessing attack,” Sci. China Inf. Sci., vol. 60, no. 5, pp. 1–12, 2016. [Google Scholar]

18. S. P. Wang, T. T. Gao, and Y. L. Zhang, “Searchable and revocable multi-data owner attribute-based encryption scheme with hidden policy in cloud storage,” PLoS One, vol. 13, no. 11, pp. e0206126, 2018. doi: 10.1371/journal.pone.0206126. [Google Scholar] [PubMed] [CrossRef]

19. Y. Miao, X. Liu, K. K. R. Choo, and R. H. Deng, “Privacy-preserving attribute-based keyword search in shared multi-owner setting,” IEEE Trans. Dependable and Secure Comput., vol. 18, no. 3, pp. 1080–1094, 2019. doi: 10.1109/TDSC.2019.2897675. [Google Scholar] [CrossRef]

20. H. Ma, R. Zhang, G. Yang, Z. Song, K. He and Y. Xiao, “Efficient fine-grained data sharing mechanism for electronic medical record systems with mobile devices,” IEEE Trans. Depend. and Secure Comput., vol. 17, no. 5, pp. 1026–1038, 2018. doi: 10.1109/TDSC.2018.2844814. [Google Scholar] [CrossRef]

21. A. Singh, A. Kumar, and S. Namasudra, “DNACDS: Cloud IoE big data security and accessing scheme based on DNA cryptography,” Front. Comput. Sci., vol. 18, pp. 181801, 2024. doi: 10.1007/s11704-022-2193-3. [Google Scholar] [CrossRef]

22. M. Sahu, N. Padhy, S. S. Gantayat, and A. K. Sahu, “Local binary pattern-based reversible data hiding,” CAAI T Intell. Techno., vol. 7, no. 4, pp. 695–709, 2022. [Google Scholar]

23. Q. Xia, E. B. Sifah, K. O. Asamoah, J. B. Gao, X. J. Du and M. Guizani, “MeDShare: Trustless medical data sharing among cloud service providers via blockchain,” IEEE Access, vol. 5, pp. 14757–14767, 2017. [Google Scholar]

24. M. J. Gao and H. Q. Wang, “Blockchain-based searchable medical data sharing scheme,” (in ChineseJ. Nanjing Univ. Posts Telecommun: Natural Sci. Ed., vol. 39, no. 6, pp. 94–103, 2019. [Google Scholar]

25. J. Sun, L. Ren, S. Wang, and X. Yao, “A blockchain-based framework for electronic medical records sharing with fine-grained access control,” PLoS One, vol. 15, no. 10, pp. e0239946, 2020. doi: 10.1371/journal.pone.0239946. [Google Scholar] [PubMed] [CrossRef]

26. G. Wu, S. Wang, Z. Ning, and B. Zhu, “Privacy-preserved electronic medical record exchanging and sharing: A blockchain-based smart healthcare system,” IEEE J. Biomed. Health Inform., vol. 26, no. 5, pp. 1917–1927, 2021. [Google Scholar]

27. Z. Q. Zhou, Y. L. Chen, T. Li, X. J. Ren, and X. Y. Qing, “Medical data security sharing scheme based on consortium blockchain,” J. Appl. Sci., vol. 39, no. 1, pp. 123–134, 2021. [Google Scholar]

28. U. Chelladurai and S. Pandian, “A novel blockchain based electronic health record automation system for healthcare,” J. Ambient Intell. Human Comput., vol. 13, no. 1, pp. 693–703,2021, 2022. doi: 10.1007/s12652-021-03163-3. [Google Scholar] [CrossRef]

29. C. Lin, X. Huang, and D. He, “Efficient blockchain-based electronic medical record sharing with anti-malicious propagation,” IEEE Trans. Serv. Comput., vol. 16, no. 5, pp. 3294–3304, 2023. doi: 10.1109/TSC.2023.3289319. [Google Scholar] [CrossRef]

30. H. Gao, H. Huang, L. Xue, F. Xiao, and Q. Li, “Blockchain-enabled fine-grained searchable encryption with cloud-edge computing for electronic health records sharing,” IEEE Internet Things J., vol. 10, no. 20, pp. 18414–18425, 2023. doi: 10.1109/JIOT.2023.3279893. [Google Scholar] [CrossRef]

31. S. Shinde, Z. L. Chua, V. Narayanan, V. Narayanan, and P. Saxena, “Preventing page faults from telling your secrets,” in Proc. 11th ACM on Asia Conf. Comput. Commun. Secur., New York, ACM Press, 2016, pp. 317–328. [Google Scholar]

32. J. T. Ning, X. Y. Huang, W. Susilo, K. T. Liang, X. M. Liu and Y. H. Zhang, “Dual access control for cloud-based data storage and sharing,” IEEE Trans. Depend. Secure Comput., vol. 19, no. 2, pp. 1036–1048, 2022. [Google Scholar]

33. B. Fisch, D. Vinayagamurthy, D. Boneh, and S. Gorbunov, “IRON: Functional encryption using intel SGX,” in Proc. 2017 ACM SIGSAC Conf. Comput. Communi. Secur., New York, USA, ACM Press, 2017, pp. 765–782. [Google Scholar]

34. Datos Abiertos, “Información Referente a Casos COVID-19 en México,” 2020. Accessed: May 15, 2023. [Online]. Available: https://datos.gob.mx/busca/dataset/informacion-referente-a-casos-covid-19-en-mexico [Google Scholar]