 Open Access
Open Access
ARTICLE
Upper and Lower Bounds of the α-Universal Triple I Method for Unified Interval Implications
1 School of Computer and Information, Hefei University of Technology, Hefei, 230601, China
2 Department of Electrical and Computer Engineering, University of Alberta, Edmonton, AB T6R 2V4, Canada
* Corresponding Author: Jianwei Gao. Email:
(This article belongs to the Special Issue: Emerging Trends in Fuzzy Logic)
Computers, Materials & Continua 2024, 79(1), 1063-1088. https://doi.org/10.32604/cmc.2024.049341
Received 03 January 2024; Accepted 07 March 2024; Issue published 25 April 2024
Abstract
The α-universal triple I (α-UTI) method is a recognized scheme in the field of fuzzy reasoning, which was proposed by our research group previously. The robustness of fuzzy reasoning determines the quality of reasoning algorithms to a large extent, which is quantified by calculating the disparity between the output of fuzzy reasoning with interference and the output without interference. Therefore, in this study, the interval robustness (embodied as the interval stability) of the α-UTI method is explored in the interval-valued fuzzy environment. To begin with, the stability of the α-UTI method is explored for the case of an individual rule, and the upper and lower bounds of its results are estimated, using four kinds of unified interval implications (including the R-interval implication, the S-interval implication, the QL-interval implication and the interval t-norm implication). Through analysis, it is found that the α-UTI method exhibits good interval stability for an individual rule. Moreover, the stability of the α-UTI method is revealed in the case of multiple rules, and the upper and lower bounds of its outcomes are estimated. The results show that the α-UTI method is stable for multiple rules when four kinds of unified interval implications are used, respectively. Lastly, the α-UTI reasoning chain method is presented, which contains a chain structure with multiple layers. The corresponding solutions and their interval perturbations are investigated. It is found that the α-UTI reasoning chain method is stable in the case of chain reasoning. Two application examples in affective computing are given to verify the stability of the α-UTI method. In summary, through theoretical proof and example verification, it is found that the α-UTI method has good interval robustness with four kinds of unified interval implications aiming at the situations of an individual rule, multi-rule and reasoning chain.Keywords
As the core of fuzzy logic [1–3], fuzzy reasoning plays an important role in intelligent control, affective computing, machine vision, large models and other fields [4–7]. Fuzzy reasoning itself has two key problems. The first problem is fuzzy modus ponens (FMP):
The other one is fuzzy modus tollens (FMT):
Since Zadeh came up with the compositional rule of inference (CRI) [8,9] method in 1973, it has been widely adopted in various fields such as industrial control and artificial intelligence. So far, many scholars have presented various fuzzy reasoning methods. Among them, Wang’s triple I (TI) method [10] is one of the most influential methods.
Due to the strong logical completeness of the TI method, many scholars have carried out more in-depth research in this direction. Many methods are proposed to enhance the TI method, such as the α-triple I constraint degree method [11], the α-universal triple I (α-UTI) method (proposed by us in [12]), the quintuple implicational method [13,14], symmetric implicational methods [15] and similarity-base inference methods [16]. These methods all enhance the performance of the TI method to a certain extent. It is necessary to test the different properties of these methods in order to analyze their performance.
Among them, robustness is a crucial property, which refers to the resistance of the method to perturbations. It can be quantified by calculating the gap between the output of the fuzzy reasoning method with interference and the output without interference. The smaller the gap, the smaller the impact of interference. Distance [17–19] (or dissimilarity) is a common tool, including the Chebyshev distance [20], the Minkowski distance [21] and the Hamming distance [22]. The concepts of maximum ε-disturbance, α-similarity, fuzzy set approximate equality derived from Chebyshev distance are explored in detail in [23–26]. Therefore, the Chebyshev distance is also used in this study to measure the gap between the original output and the disturbed output to evaluate the robustness.
Fuzzy implication plays a key role in fuzzy reasoning strategy. Different implications will also have different effects on the robustness of the method. Reference [26] studied the robustness of the CRI method when adopting R-implications, S-implications and QL-implications, and demonstrates that CRI had strong stability. In [17], the robustness of the BKS (Bandler-Kohout subproduct) method with S-implications and QL-implications was discussed in the context of interval perturbation. Wang et al. [27] discovered the robustness of the TI method.
The main formula of the α-UTI method for FMP is as below [12] (
The α-UTI method has been widely recognized in the field of fuzzy reasoning as a generalization of the CRI method and the TI method. The α-UTI method is also a generalization of the universal triple I (UTI) method proposed in [12]. In detail, when α = 1, the α-UTI method degenerates into the UTI method.
The current research gaps in this field include the following two aspects:
• On the one hand, how to give the solution of chain reasoning, a special form of reasoning, is a tough problem in fuzzy reasoning. In this regard, we can consider starting from the α-UTI method to construct a scheme oriented towards chain reasoning.
• On the other hand, it is not clear how the interval stability of the α-UTI method is. In particular, can the upper and lower bounds of its reasoning be estimated? This aspect has not yet been discussed. This has aroused our great interest, and also constitutes the research goal of this paper.
In this study, we explore the interval robustness of the α-UTI method, which is embodied by interval stability.
Fig. 1 shows the detailed schematic diagram of the proposed study.
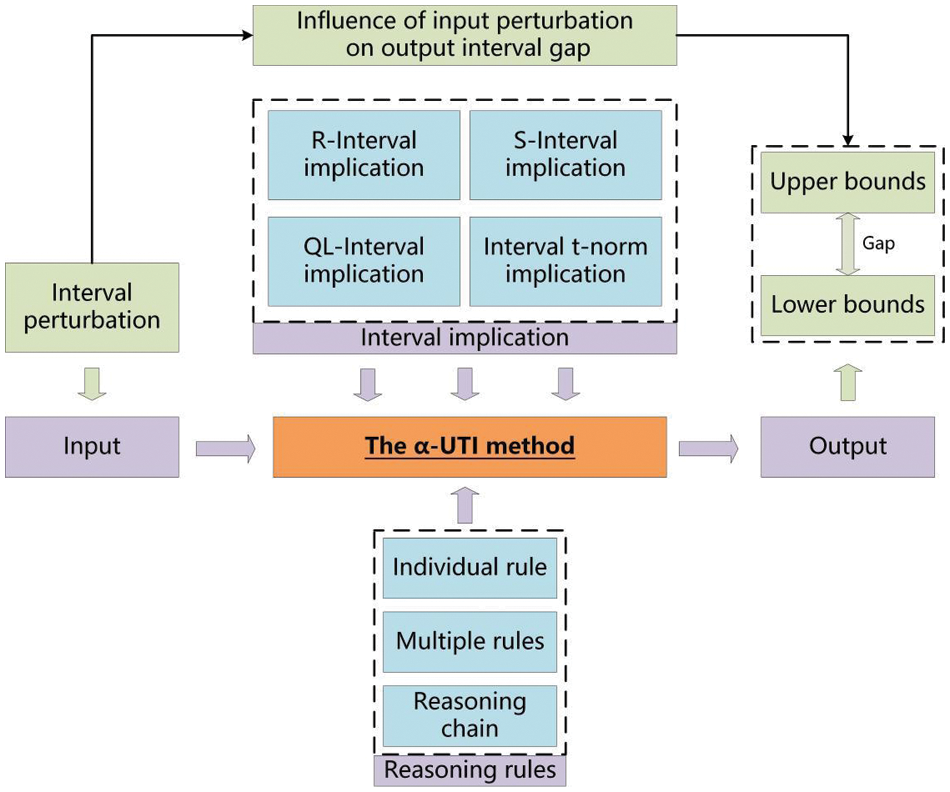
Figure 1: The detailed schematic diagram of the proposed study
The proposed study includes the following aspects:
• To begin with, we discuss the robustness of the α-UTI method in the case of an individual rule, and give an estimate of the upper and lower bounds. Therein, four kinds of unified interval implications mentioned above are employed in turn. It is important to note that each kind of implication actually contains a lot of specific implications, so this study can incorporate many implications into its framework. The process and flow chart of the corresponding algorithm are given. The results show that the α-UTI method is stable in the individual rule case under the interval perturbation.
• Moreover, we provide the estimation for upper and lower bounds for the multiple rules case of the α-UTI method. Here, four kinds of unified interval implications are respectively examined in the α-UTI method. The results show that, in the context of the interval perturbation, the α-UTI method is stable for the situation of multiple rules.
• In addition, for the problem of chain reasoning, we put forward a strategy based upon the α-UTI method, which is called the α-UTI reasoning chain method. We provide an intelligent algorithm to estimate its upper and lower bounds, and draw the corresponding flow chart. In this case, the four types of interval implications are adopted in turn. It is found the α-UTI reasoning chain method is stable for the problem of chain reasoning.
• Lastly, the α-UTI method is analyzed through two application examples in affective computing. Here we propose the scheme of emotional deduction based on the α-UTI method. These examples verify the stability of the α-UTI method.
To sum up, the results show that in three cases of individual rule, multiple rules and reasoning chain, the α-UTI method has good interval stability when it respectively adopts four kinds of unified interval implications mentioned above.
The structure of this paper is as follows. Section 2 gives the fundamental knowledge and related work. Sections 3 and 4 prove the robustness of the α-UTI method from the perspectives of individual rule and multiple rules, respectively. Section 5 probes into the robustness of the α-UTI reasoning chain method and its robustness. Section 6 gives two examples. Section 7 summarizes all the work and provides the prospect.
This section mainly introduces the basic knowledge of fuzzy reasoning, and provides some interval implications and interval connectives.
Definition 2.1 [26–28]. Let
There are two functions
For any
Definition 2.2 [28–30]. For any
a)
b)
c)
d)
In order to facilitate the subsequent operation, we give two tokens, namely
Definition 2.3 [30,31]. The operation
For the definition of interval fuzzy implication, there are other definitions, such as the need for incrementality with regard to the second variable. But here conditions (5) and (6) are often basic conditions, and generally need to be met. In summary, Definition 2.3 here is a classical and fundamental definition of interval fuzzy implication.
Two important operations are further defined here, in which these two concepts are mutually symmetric.
Definition 2.4 [32,33]. An operation
Definition 2.5 [28,34]. An operation
The interval t-norm and the interval t-conorm are symmetric concepts. As the opposite structure of conventional operations, interval fuzzy negation is defined as below.
Definition 2.6 [28,30,34,35]. An operation
a)
b)
c)
On the basis of interval fuzzy negation, if it still has:
d)
then this is a strong interval fuzzy negation.
Subsequently, three important classes of interval fuzzy implication are defined as below.
Definition 2.7 [30]. An interval fuzzy implication is called an R-interval implication denoted by
Definition 2.8 [30]. An interval fuzzy implication is under the title of an S-interval implication denoted by
Definition 2.9 [30]. An interval fuzzy implication is called a QL-interval implication represented by
The interval t-norm can also be regarded as an interval fuzzy implication, called the interval t-norm implication.
Definition 2.10 [26]. Suppose
then
In what follows, the idea of interval disturbance is provided.
Definition 2.11 [26]. Suppose
holds, then
Definition 2.12 [26]. Suppose
In this work,
Lemma 2.1 [26]. Let
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Lemma 2.2 [17] Let
a)
b)
c)
d)
Example 2.1 Let
a)
b)
c)
d)
e)
f)
g)
Example 2.2 Here are three representative interval t-norms, which are the Gödel norm
a)
b)
c)
3 Interval Perturbation of the α-UTI Method for an Individual Rule
For an individual rule, assume that
Theorem 3.1 Let
Proof: The R-interval implication is decreasing with respect to the first parameter and increasing with respect to the second parameter. From Lemma 2.1 and Lemma 2.2, it can be obtained as follows:
Moreover, one has
In summary, we have proved that (16) holds.
Theorem 3.1 gives a estimation of the corresponding α-UTI solutions for the case of the interval perturbation with an individual rule. In other words, it respectively provides an upper bound and a lower bound of the α-UTI solutions for R-interval implications.
Theorem 3.2, Theorem 3.3 and Theorem 3.4 can be achieved in a similar mode, in which the interval t-norm implication, the S-interval implication, the QL-interval implication are employed, respectively.
Theorem 3.2 Let
Theorem 3.3 Let
Theorem 3.4 Let
In light of Theorem 3.1 to Theorem 3.4, in the case of an individual rule, if related operators including the interval t-norm, the interval t-conorm and so on, then the α-UTI method is stable with regard to S-, QL- and interval t-norm implication. The α-UTI method is stable with respect to R-interval implication if the R-interval implication and the interval t-norm are continuous. All in all, the α-UTI method is robust for the individual rule.
Suppose that for the α-UTI method, there exists a perturbation array of input
Besides, the consequent properties are satisfied:
In detail, we have from (23) that
Others can be analogously expanded.
Considering that
When the continuity condition is satisfied, then
holds. In other words, if the above-mentioned continuity condition is effective, the outcome of the α-UTI method stably converges to a value. As a consequence, in light of the stable definition given in Definition 2.12, the α-UTI method is stable in the individual rule case.
For Theorem 3.1, we give an intelligent algorithm (see the following Algorithm 1) to deal with such operations. For the other theorems, we can get corresponding algorithms.

Fig. 2 shows the flow chart of Algorithm 1.
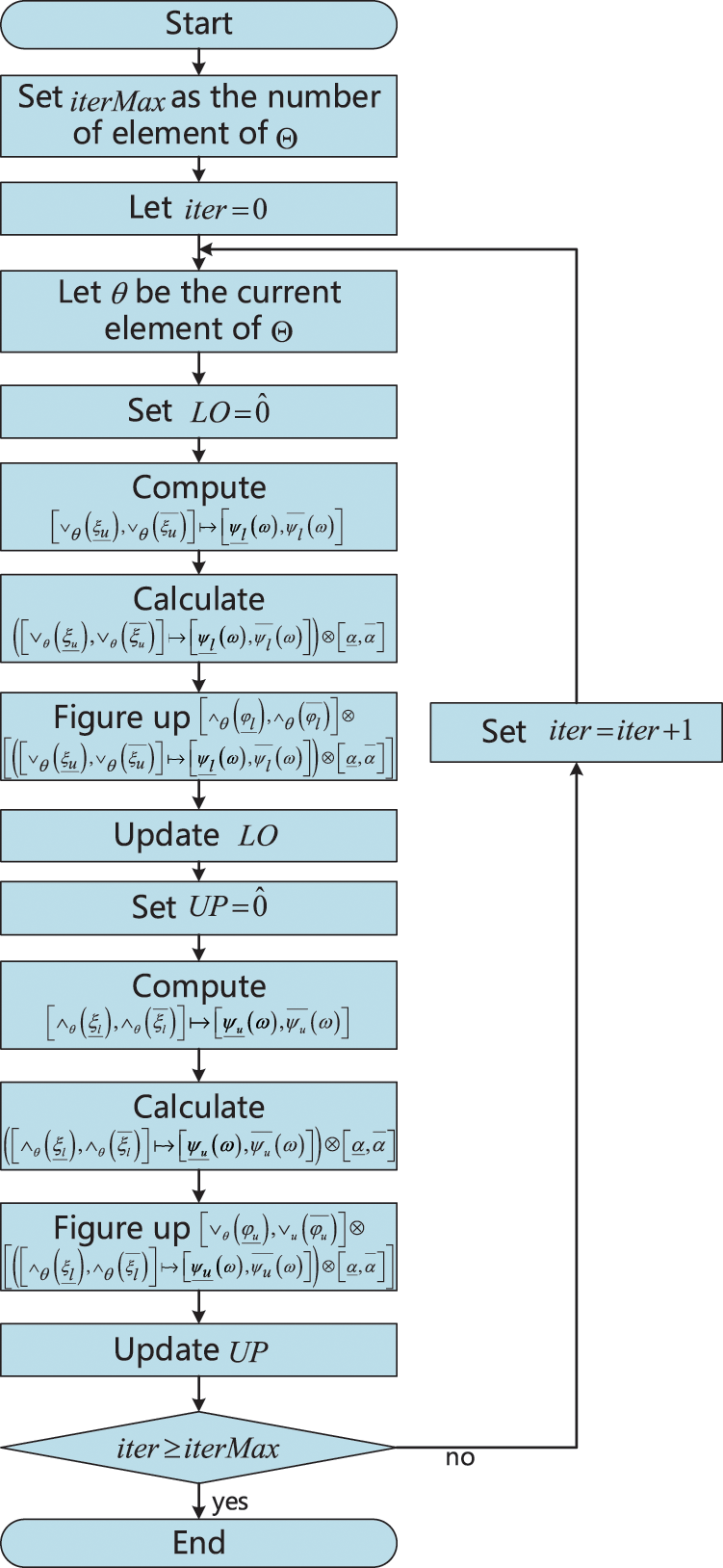
Figure 2: The flow chart of Algorithm 1
4 Interval Perturbation of the α-UTI Method for Multiple Rules
For multiple rules, the notation for representing fuzzy intervals is similar for the individual rule. It is denoted that
Theorem 4.1 Assume that
Proof: When
hold for two fuzzy sets
It follows from Lemma 2.1 and Lemma 2.2 that one has
In a similar structure, we can also find
To sum up, we can find that (28) is valid. The proof is accomplished.
Theorem 4.2, Theorem 4.3 and Theorem 4.4 can be proved in an analogous mode, in which four kinds of unified interval implications are employed in turn.
Theorem 4.2 Assume that
Theorem 4.3 Assume that
Theorem 4.4 Assume that
By virtue of Theorem 4.1 to Theorem 4.4, in the case of multiple rules, if operations in Definitions 2.4–2.6 are continuous, the α-UTI method is stable for multiple rules with respect to S-interval implication, QL-interval implication and interval t-norm implication. In addition, the α-UTI method is stable with respect to R-interval implication if the interval t-norm and the R-interval implication are continuous. All in all, the α-UTI fuzzy reasoning method is stable for multiple rules. In short, the α-UTI method is robust aiming at the multiple rules.
Suppose that for the α-UTI method, there exists a perturbation array of input
Besides, the consequent properties are satisfied
In detail, we have from (36) that
Others can be analogously analyzed.
Noting that
When the continuity condition is satisfied, then
is effective. That is, if the above-mentioned continuity condition is effective, the outcome of the α-UTI method stably converges to a value. Thereout, in light of the stable definition, the α-UTI method is stable for the situation of the multiple rules.
Similar to Theorem 3.1 and Algorithm 1, we can obtain corresponding algorithms for Theorems 4.1, 4.2, 4.3 and 4.4.
5 The α-UTI Reasoning Chain Method and Its Interval Perturbation
Here we propose the α-UTI reasoning chain method. Let
To begin with, we employ the α-UTI method to get
Because of multiple reasoning, chain reasoning may lead to errors that may expand, so it is naturally more difficult to maintain stability. So the stability study of the α-UTI reasoning chain method is more important.
Now we discuss the problem of upper and lower bounds of inference results of the α-UTI reasoning chain method. First of all, we analyze the case of the S-interval implication.
Theorem 5.1 Let
Therein two notions are as follows
Proof: It follows from the conclusion of Theorem 3.3 that one has
Let us denote
Thus, it can be obtained
Furthermore, it can be derived
in which,
With similar treatment, we can end up with the following formula:
To sum up, (41) holds. The proof is accomplished.
Moreover, we further discover the case of the R-interval implication, where the proof process is similar to that obtained.
Theorem 5.2 Let
Therein two notions are as follows
Along similar lines, we can prove the following two theorems with regard to the interval t-norm implication and the QL-interval implication.
Theorem 5.3 Let
Therein two notions are as follows
Theorem 5.4 Let
Therein two notions are as follows
For Theorem 5.1, we provide an intelligent algorithm (see the following Algorithm 2). For the other theorems, we can similarly obtain corresponding algorithms.
Fig. 3 shows the flow chart of Algorithm 2.
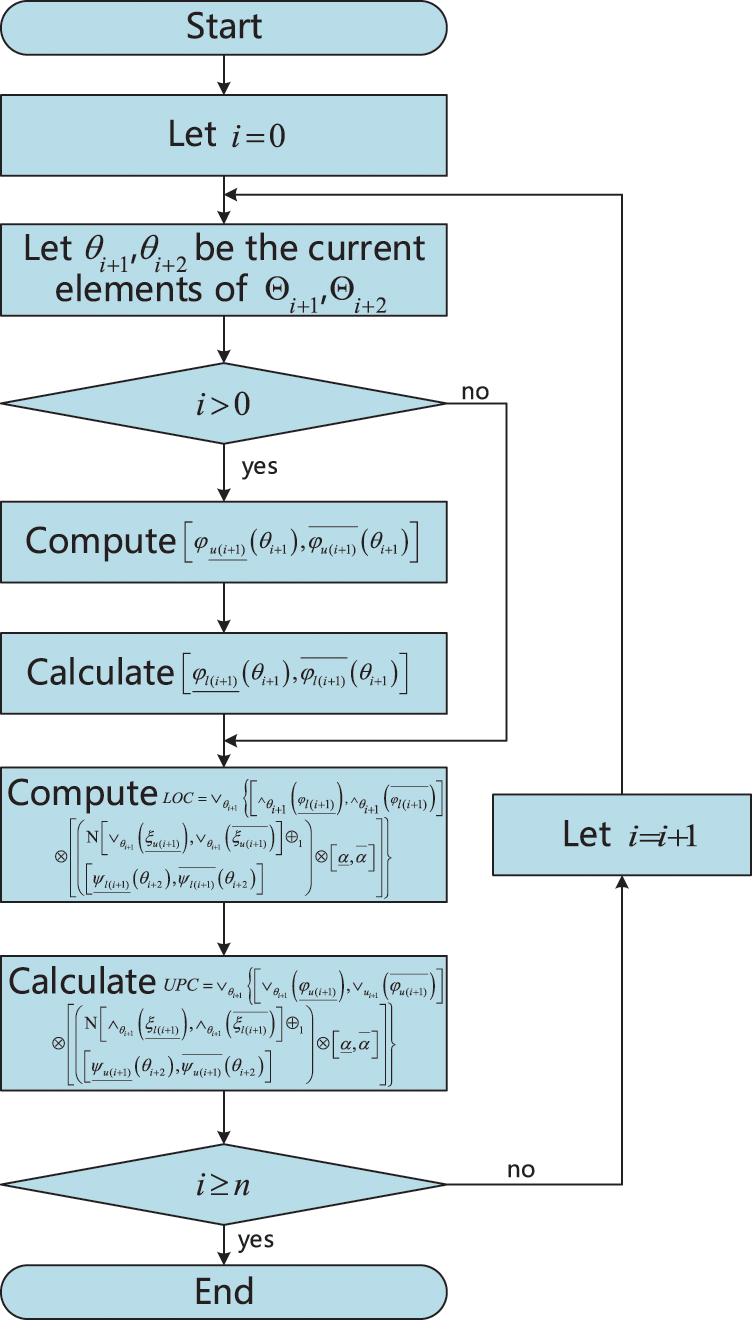
Figure 3: The flow chart of Algorithm 2
By virtue of Theorem 5.1 to Theorem 5.4, if the underlying operations in Definitions 2.4–2.6 are continuous, then the α-UTI reasoning chain method about
Assume that for the α-UTI reasoning chain method, there is a perturbed queue with input

Besides, the consequent properties are satisfied:
In detail, we have from (62) that
Others can be similarly expanded.
From Theorem 5.1 to Theorem 5.4,
When the continuity condition is satisfied, one has
is effective. In other words, the outcome of the α-UTI reasoning chain method gradually converges to a value when the continuity condition holds. As a consequence, in light of the stable definition provided in Definition 2.12, the α-UTI reasoning chain method is stable for the issue of chain reasoning.
6 Applications in Affective Computing
In summary, the α-UTI method is stable in the case of an individual rule, multiple rules and reasoning chain under the interval perturbation. In this section, we employ two examples to verify the interval stability of the α-UTI method.
Example 6.1. The first example is when the following rule is adopted:
The input is
For testing, we use a structure with interval perturbation in the input. We use Theorem 3.1 with the R-interval implication
For one situation, we take
For another situation, we let
The interval of the second input is obviously smaller than that of the first input. It can be seen that the α-UTI method will eventually converge under the interval disturbance as the interval disturbance decreases under the reasonable input and rule.
For the background of Example 6.1, the input corresponds to the values of sorrow, anger, and hate, and the output corresponds to the value of joy (noting that these four are all basic emotions in affective computing). This reflects the relationship between several basic emotions. Comparing the two situations in Example 6.1, it can be seen that when the three input emotions are subjected to smaller interval perturbations, the change of output emotions tends to be stable.
Affective computing is receiving extensive attention. Emotion deduction (exploring how to reason about the membership of other emotions from some basic emotions) is significant in many ways (e.g., emotional state transitions when building a large emotional corpus, etc.) and is an essential task in affective computing. Here we give an example of the application of the method in emotion deduction to demonstrate the robustness of the α-UTI method.
Example 6.2. We compute the emotion aspect by the α-UTI method, which
The input is
Here, the input
For one situation, we take
For another situation, we let
Fig. 4 shows the emotion deduction process of Example 6.2.
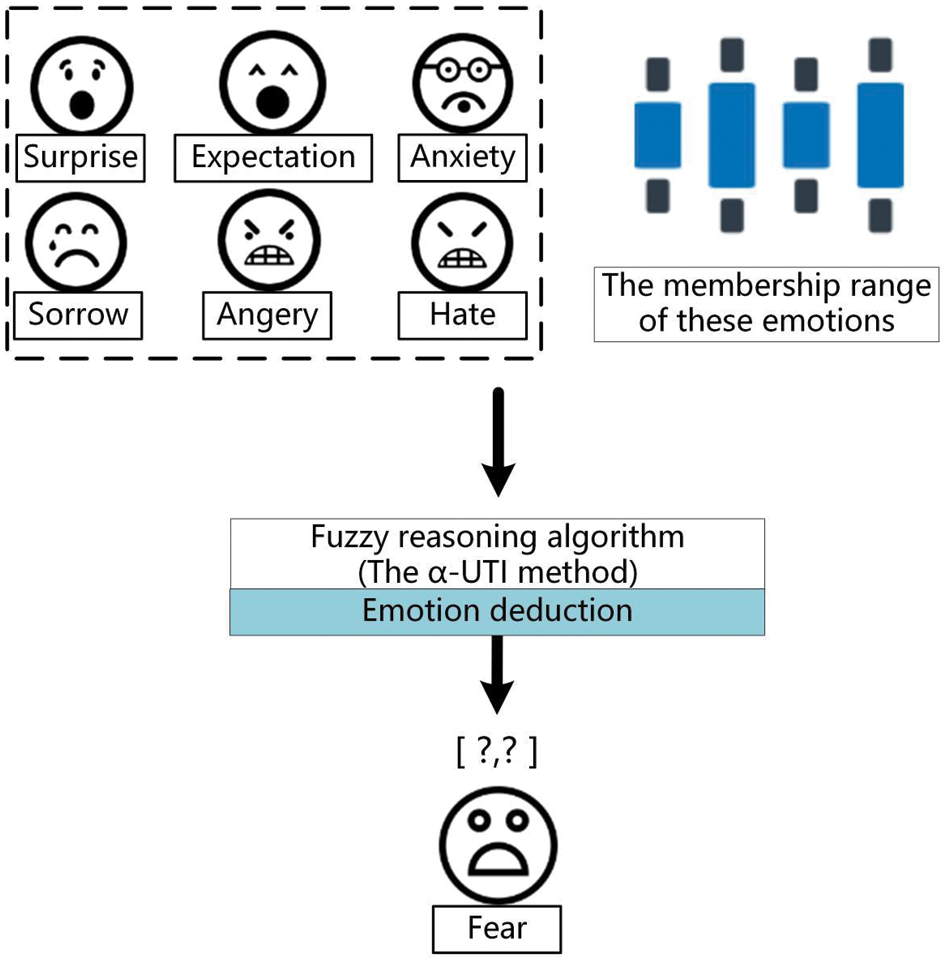
Figure 4: The emotion deduction process of Example 6.2
The context of Example 6.2 is emotional deduction. Emotion corpus is one of the key issues in affective computing. We have done a lot of work in constructing an emotion corpus, but the emotion corpus is often based on basic emotions, such as the eight basic emotions mentioned above. However, in the real world, there are many kinds of emotions, far more than these basic emotions. Obtaining values for other emotions, then, has become a recognized puzzle in the field of affective computing. That is why emotional deduction comes in.
Here we put forward the scheme of emotional deduction based on the α-UTI method, and naturally hope that such emotional deduction scheme is stable. Through the comparison of the two situations in Example 6.2, we can see that when the input interval disturbance is smaller, the obtained result also belongs to a smaller range, so the emotional deduction result is stable for multiple rules. This validates that our proposed emotional deduction scheme based on the α-UTI method is effective and practicable.
In this study, we investigate the interval robustness (embodied by the interval stability) of the α-UTI method of fuzzy reasoning. The main contributions of this paper are reflected in the following aspects:
First of all, the stability of the α-UTI method is examined for an individual rule, and the upper and lower bounds are estimated for the α-UTI solutions. Here the analysis is conducted on the basis of four kinds of unified interval implications. The analysis shows that the α-UTI method exhibits good interval stability for an individual rule.
In addition, the stability of the α-UTI method is found in the context of multi-rule conditions, while the upper and lower bounds of its outcomes are estimated. Therein, four kinds of unified interval implications are adopted. It is observed that the α-UTI method is stable in the case of multiple rules.
Furthermore, the α-UTI reasoning chain method is put forward, containing a chain structure with multiple layers. The corresponding solutions are given and the interval perturbations are analyzed. The upper and lower bounds of the outcomes are estimated, involving four kinds of unified interval implications. The results show that the α-UTI reasoning chain method is stable from the viewpoint of interval perturbation.
Finally, the α-UTI method is studied through two application examples, incorporating an application of the α-UTI method in emotion deduction of affective computing. These examples show that the α-UTI solution converges stably to a value if the continuity condition is effective, which verifies the stability of the α-UTI method.
The novelty of this paper is manifested in the following aspects. To begin with, the estimation of the upper and lower bounds of interval perturbations is a novel problem to be explored for the α-UTI method. Moreover, we propose the α-UTI reasoning chain method as a new multi-layer inference mechanism. Lastly, we investigate the interval robustness of fuzzy reasoning under the interval-valued fuzzy environment.
The merits of this study are as follows. Firstly, we propose the α-UTI reasoning chain method, which consists of a chain structure with multiple layers. This method presents a new scheme to solve the problem of chain reasoning. Secondly, four kinds of important unified interval implications are considered in this work, which have certain universality. Finally, the upper and lower bounds are estimated for the α-UTI method in the interval-valued fuzzy environment. The results indicate that the α-UTI method has good interval robustness in situations involving an individual rule, multi-rule and reasoning chain.
The demerits of this study are outlined as follows. On the one hand, we do not consider the use of specific interval implications in the α-UTI method, especially those that do not belong to these four kinds of interval implications. The interval robustness of this kind of the α-UTI method is not considered. On the other hand, we have explored the interval robustness of the α-UTI method in the interval-valued fuzzy environment. However, other environments, such as the intuitionistic fuzzy environment, have not been discussed. These can be the guidelines for the upcoming work.
In future studies, we will consider incorporating the latest clustering algorithms [36,37] into the α-UTI method to build cluster-driven algorithms and explore their interval robustness. In addition, we will further explore other application areas of α-UTI fuzzy reasoning, such as inventory modeling [38,39].
Acknowledgement: A preliminary version of this work was presented at the 3rd International Conference on Artificial Intelligence Logic and Applications (AILA 2023), and its title is “On interval perturbation of the α-universal triple I algorithm for unified interval implications”.
Funding Statement: This work was supported by the National Natural Science Foundation of China under Grants 62176083, 62176084, 61877016, and 61976078, the Key Research and Development Program of Anhui Province under Grant 202004d07020004, the Natural Science Foundation of Anhui Province under Grant 2108085MF203.
Author Contributions: Conceptualization, Y.T. and Y.H.; methodology, Y.T. and J.G.; software, Y.T. and J.G.; validation, Y.T., Y.H., and J.G.; formal analysis, J.G.; investigation, Y.T. and J.G.; resources, J.G.; data curation, J.G.; writing—original draft preparation, Y.T. and Y.H.; writing—review and editing, Y.T. and J.G.; visualization, J.G.; supervision, Y.T.; project administration, J.G.; funding acquisition, Y.T. All authors have read and agreed to the published version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. P. A. Ejegwa, S. Wen, W. Feng, and N. Tang, “Novel Pythagorean fuzzy correlation measures via Pythagorean fuzzy deviation, variance and covariance with applications to pattern recognition and career placement,” IEEE Trans. Fuzzy Syst., vol. 30, no. 6, pp. 1660–1668, Jun. 2022. doi: 10.1109/TFUZZ.2021.3063794. [Google Scholar] [CrossRef]
2. P. Liu and S. M. Chen, “Group decision making based on Heronian aggregation operators of intuitionistic fuzzy numbers,” IEEE Trans. Cybern., vol. 47, no. 9, pp. 2514–2530, Sep. 2017. doi: 10.1109/TCYB.2016.2634599. [Google Scholar] [PubMed] [CrossRef]
3. J. Q. Yang, C. H. Chen, J. Y. Li, D. Liu, T. Li and Z. H. Zhan, “Compressed-encoding particle swarm optimization with fuzzy learning for large-scale feature selection,” Symmetry, vol. 14, no. 6, pp. 1142, Jun. 2022. doi: 10.3390/sym14061142. [Google Scholar] [CrossRef]
4. D. Yan, K. Wu, P. A. Ejegwa, X. Xie, and Y. Feng, “Pythagorean fuzzy partial correlation measure and its application,” Symmetry, vol. 15, no. 1, pp. 216, Jan. 2023. doi: 10.3390/sym15010216. [Google Scholar] [CrossRef]
5. Y. M. Tang, Z. F. Pan, W. Pedrycz, F. J. Ren, and X. C. Song, “Viewpoint-based kernel fuzzy clustering with weight information granules,” IEEE Trans. Emerg. Topics Comput. Intell., vol. 7, no. 2, pp. 342–356, Apr. 2023. doi: 10.1109/TETCI.2022.3201620. [Google Scholar] [CrossRef]
6. W. Pedrycz, “Information granularity, information granules, and granular computing,” in Granular Computing: Analysis and Design of Intelligent Systems, 1st ed. Boca Raton, FL, USA: CRC Press, 2013, vol. 1, pp. 1–18. [Google Scholar]
7. L. X. Wang, “The mathematics of fuzzy systems and control,” in A Course in Fuzzy Systems and Control, 1st ed. NJ, USA: Prentice-Hall, 1996, vol. 1, pp. 19–88. [Google Scholar]
8. L. Zadeh, “Outline of a new approach to the analysis of complex systems and decision processes,” IEEE Trans. Syst. Man Cybern, vol. 3, no. 1, pp. 28–44, Jan. 1973. doi: 10.1109/TSMC.1973.5408575. [Google Scholar] [CrossRef]
9. K. K. Ang, C. Quek, and M. Pasquier, “POPFNN-CRI(SPseudo outer product based fuzzy neural network using the compositional rule of inference and singleton fuzzifier,” IEEE Trans. Syst. Man Cybern. B, Cybern, vol. 33, no. 6, pp. 838–849, Dec. 2003. doi: 10.1109/TSMCB.2003.812850. [Google Scholar] [PubMed] [CrossRef]
10. G. Wang, “On the logic foundation of fuzzy reasoning,” Inf. Sci., vol. 117, no. 1, pp. 47–88, Jul. 1999. doi: 10.1016/S0020-0255(98)10103-2. [Google Scholar] [CrossRef]
11. S. Song, C. Feng, and E. S. Lee, “Triple I method of fuzzy reasoning,” Comput. Math. Appl., vol. 44, no. 12, pp. 1567–1579, Dec. 2002. doi: 10.1016/S0898-1221(02)00279-1. [Google Scholar] [CrossRef]
12. Y. M. Tang and X. P. Liu, “Differently implicational universal triple I method of (1, 2, 2) type,” Comput. Math. Appl., vol. 59, no. 6, pp. 1965–1984, Mar. 2010. doi: 10.1016/j.camwa.2009.11.016. [Google Scholar] [CrossRef]
13. B. Zhou, G. Xu, and S. Li, “The quintuple implication principle of fuzzy reasoning,” Inf. Sci., vol. 297, no. 1, pp. 202–215, Mar. 2015. doi: 10.1016/j.ins.2014.11.024. [Google Scholar] [CrossRef]
14. M. Luo and K. Zhou, “Logical foundation of the quintuple implication inference methods,” Int. J. Approx. Reason., vol. 101, no. 1, pp. 1–9, Oct. 2018. doi: 10.1016/j.ijar.2018.06.001. [Google Scholar] [CrossRef]
15. Y. M. Tang, W. Pedrycz, and F. J. Ren, “Granular symmetric implicational method,” IEEE Trans. Emerg. Topics Comput. Intell., vol. 6, no. 3, pp. 710–723, Jun. 2022. doi: 10.1109/TETCI.2021.3100597. [Google Scholar] [CrossRef]
16. I. Turksen and Z. Zhong, “An approximate analogical reasoning approach based on similarity measures,” IEEE Trans. Syst. Man Cybern., vol. 18, no. 6, pp. 1049–1056, Nov.–Dec. 1988. doi: 10.1109/21.23107. [Google Scholar] [CrossRef]
17. Y. M. Tang and W. Pedrycz, “Oscillation-bound estimation of perturbations under Bandler-Kohout subproduct,” IEEE Trans. Cybern., vol. 52, no. 7, pp. 6269–6282, Jul. 2022. doi: 10.1109/TCYB.2020.3025793. [Google Scholar] [PubMed] [CrossRef]
18. Z. Deng and J. Wang, “New distance measure for Fermatean fuzzy sets and its application,” Int. J. Intell. Syst., vol. 37, no. 1, pp. 1903–1930, Dec. 2022. doi: 10.1002/int.22760. [Google Scholar] [CrossRef]
19. B. Gohain, R. Chutia, and P. Dutta, “Distance measure on intuitionistic fuzzy sets and its application in decision-making, pattern recognition, and clustering problems,” Int. J. Intell. Syst., vol. 37, no. 1, pp. 2458–2501, Dec. 2022. doi: 10.1002/int.22780. [Google Scholar] [CrossRef]
20. J. Rathee, P. Kaur, and A. Singh, “Evaluating the performance of fuzzy clustering using different distance metrics for image segmentation,” in Proc. ICONAT, Goa, India, Jan. 2022, pp. 1–5. [Google Scholar]
21. F. Feng, Y. Zheng, B. Sun, and M. Akram, “Novel score functions of generalized orthopair fuzzy membership grades with application to multiple attribute decision making,” Granul. Comput., vol. 7, no. 1, pp. 95–111, Feb. 2022. doi: 10.1007/s41066-021-00253-7. [Google Scholar] [CrossRef]
22. D. Wu, Z. Zhu, K. Ullah, L. Liu, X. Wu and X. Zhang, “Analysis of Hamming and Hausdorff 3D distance measures for complex Pythagorean fuzzy sets and their applications in pattern recognition and medical diagnosis,” Complex Intell. Syst., vol. 9, no. 1, pp. 4147–4158, Dec. 2022. doi: 10.1007/s40747-022-00939-8. [Google Scholar] [CrossRef]
23. C. Pappis, “Value approximation of fuzzy systems variables,” Fuzzy Sets Syst., vol. 39, no. 1, pp. 111–115, Jan. 1991. doi: 10.1016/0165-0114(91)90070-7. [Google Scholar] [CrossRef]
24. S. Dai, D. Pei, and S. Wang, “Perturbation of fuzzy sets and fuzzy reasoning based on normalized Minkowski distances,” Fuzzy Sets Syst., vol. 189, no. 1, pp. 63–73, Feb. 2012. doi: 10.1016/j.fss.2011.07.012. [Google Scholar] [CrossRef]
25. D. Hong and S. Hwang, “A note on the value similarity of fuzzy systems variables,” Fuzzy Sets Syst., vol. 66, no. 3, pp. 383–386, Sep. 1994. doi: 10.1016/0165-0114(94)90107-4. [Google Scholar] [CrossRef]
26. G. Cheng and Y. Fu, “Error estimation of perturbations under CRI,” IEEE Trans. Fuzzy Syst., vol. 14, no. 6, pp. 709–715, Dec. 2006. doi: 10.1109/TFUZZ.2006.877333. [Google Scholar] [CrossRef]
27. G. Wang and J. Duan, “On robustness of the full implication triple I inference method with respect to finer measurements,” Int. J. Approx. Reason., vol. 55, no. 3, pp. 787–796, Mar. 2014. doi: 10.1016/j.ijar.2013.09.023. [Google Scholar] [CrossRef]
28. B. C. Bedregal and A. Takahashi, “Interval valued versions of t-conorms, fuzzy negations and fuzzy implications,” in Proc. FUZZ-IEEE, Vancouver, BC, Canada, 2006, pp. 1981–1987. [Google Scholar]
29. R. Bedregal and B. Bedregal, “Intervals as a domain constructor,” Trends Comput. Appl. Math., vol. 2, no. 1, pp. 43–52, Oct. 2001. [Google Scholar]
30. B. C. Bedregal, R. H. N. Santiago, R. H. S. Reiser, and G. P. Dimuro, “Analyzing properties of fuzzy implications obtained via the interval constructor,” in Proc. SCAN 2006, Duisburg, 2006, pp. 1–8. [Google Scholar]
31. R. Reiser and B. Bedregal, “Interval-valued intuitionistic fuzzy implications-construction, properties and representability,” Inf. Sci., vol. 248, no. 1, pp. 68–88, Nov. 2013. doi: 10.1016/j.ins.2013.06.020. [Google Scholar] [CrossRef]
32. B. R. C. Bedregal and A. Takahashi, “Interval t-norms as interval representations of t-norms,” in Proc. FUZZ '05, Reno, NV, USA, 2005, pp. 909–914. [Google Scholar]
33. B. Bedregal and A. Takahashi, “The best interval representations of t-norms and automorphisms,” Fuzzy Sets Syst., vol. 157, no. 24, pp. 3220–3230, Dec. 2006. doi: 10.1016/j.fss.2006.06.013. [Google Scholar] [CrossRef]
34. E. P. Klement, R. Mesiar, and E. Pap, “Construction of t-norms,” in Triangular Norms, 1st ed. Dordrecht, NL: Kluwer Academic Publishers, 2000, vol. 1, pp. 53–100. [Google Scholar]
35. H. Bustince, P. Burillo, and F. Soria, “Automorphisms, negations and implication operators,” Fuzzy Sets Syst., vol. 134, no. 2, pp. 209–229, Mar. 2003. doi: 10.1016/S0165-0114(02)00214-2. [Google Scholar] [CrossRef]
36. Y. M. Tang, J. J. Huang, W. Pedrycz, B. Li, and F. J. Ren, “A fuzzy clustering validity index induced by triple center relation,” IEEE Trans. Cybern., vol. 53, no. 8, pp. 5024–5036, Aug. 2023. doi: 10.1109/TCYB.2023.3263215. [Google Scholar] [PubMed] [CrossRef]
37. Y. M. Tang, Z. F. Pan, X. H. Hu, W. Pedrycz, and R. H. Chen, “Knowledge-induced multiple kernel fuzzy clustering,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 45, no. 12, pp. 14838–14855, Dec. 2023. doi: 10.1109/TPAMI.2023.3298629. [Google Scholar] [PubMed] [CrossRef]
38. S. K. De, “Solving an EOQ model under fuzzy reasoning,” Appl. Soft Comput., vol. 99, no. 1, pp. 106892, Feb. 2021. doi: 10.1016/j.asoc.2020.106892. [Google Scholar] [CrossRef]
39. S. K. De, K. Bhattacharya, and B. Roy, “Solution of a pollution sensitive supply chain model under fuzzy approximate reasoning,” Int. J. Intell. Syst., vol. 36, no. 10, pp. 5530–5572, Jun. 2021. doi: 10.1002/int.22522. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools