 Open Access
Open Access
ARTICLE
Research on Maneuver Decision-Making of Multi-Agent Adversarial Game in a Random Interference Environment
1 Equipment Management and UAV Engineering College, Air Force Engineering University, Xi’an, 710051, China
2 National Key Laboratory of Unmanned Aerial Vehicle Technology, Xi’an, 710051, China
3 College of Information Technology, Nanjing Police University, Nanjing, 210023, China
* Corresponding Author: Le Ru. Email:
Computers, Materials & Continua 2024, 81(1), 1879-1903. https://doi.org/10.32604/cmc.2024.056110
Received 15 July 2024; Accepted 29 August 2024; Issue published 15 October 2024
Abstract
The strategy evolution process of game players is highly uncertain due to random emergent situations and other external disturbances. This paper investigates the issue of strategy interaction and behavioral decision-making among game players in simulated confrontation scenarios within a random interference environment. It considers the possible risks that random disturbances may pose to the autonomous decision-making of game players, as well as the impact of participants’ manipulative behaviors on the state changes of the players. A nonlinear mathematical model is established to describe the strategy decision-making process of the participants in this scenario. Subsequently, the strategy selection interaction relationship, strategy evolution stability, and dynamic decision-making process of the game players are investigated and verified by simulation experiments. The results show that maneuver-related parameters and random environmental interference factors have different effects on the selection and evolutionary speed of the agent’s strategies. Especially in a highly uncertain environment, even small information asymmetry or miscalculation may have a significant impact on decision-making. This also confirms the feasibility and effectiveness of the method proposed in the paper, which can better explain the behavioral decision-making process of the agent in the interaction process. This study provides feasibility analysis ideas and theoretical references for improving multi-agent interactive decision-making and the interpretability of the game system model.Keywords
Multi-agent systems play a crucial role in modern complex systems, such as autonomous driving of unmanned vehicles, energy management in smart grids, financial market trading strategies, and coordinated confrontation of drone swarms. In these domains, multiple agents need to coordinate and make decisions to achieve optimal overall benefits. The coordinated confrontation of drone swarms in the aerial domain, as a typical application, involves not only various maneuvers and tactical strategies of the agents but also the interactive behaviors of both sides in a constantly changing dynamic environment. Each agent must make real-time decisions in a complex and dynamic environment to ensure maximum overall effectiveness. Ensuring that agents make optimal decisions in dynamic environments has gradually become a hot topic in current academic research.
In the aerial confrontation scenario, the strategy interaction and behavior decision-making of agents are highly complex and rapidly dynamic macro-process [1]. Influenced by the dynamic changes of the situational environment, the asymmetry of the game player’s perceived information, the random and sudden situation, other external interference, and many other factors, the game evolution process of agents is highly uncertain [2–4]. These uncertain emergencies are difficult to predict effectively, which will directly affect the strategy formulation and action execution of game players and have a significant impact on the final results of the game. The level of decision-making and the formulation of operational strategies can largely determine the outcome of the game and even affect the development of the macro confrontation scenario [5]. Therefore, conducting in-depth research on the behavioral strategy evolution mechanisms of aerial game agents in environments with random disturbances, exploring the behavioral learning processes of intelligent agents, and identifying and predicting potential adversarial mechanisms and behavior patterns can lead to a better understanding and prediction of various random emergent situations in real-world aerial confrontation scenarios. This research can reveal how tactics and strategies of intelligent agents undergo natural selection and evolution under different environments and conditions. Consequently, it can aid in the development of more efficient and intelligent decision support systems, enabling strategies to adapt to continuously changing situational environments. This, in turn, enhances the adaptability and flexibility of autonomous decision-making systems, providing more accurate decision recommendations and theoretical foundations for command-control personnel to formulate more effective counter-strategies. Such advancements hold significant theoretical value and practical significance for the improvement and development of multi-agent decision-making systems in the real world.
Until now, numerous scholars have conducted research and achieved corresponding results in solving decision-making problems in aerial simulation confrontation scenarios. Specific solutions include differential games, matrix games, deep reinforcement learning, heuristic algorithms [6,7], and others. In terms of differential games, relevant literature describes the strategies and behavioral state changes of both adversarial parties in continuous time by establishing differential models of dynamic systems. In the 1960s, Isaacs [8] firstly studied the pursuit-evasion maneuvering decision problem based on differential games from a mathematical perspective and proposed an analytical method for optimal strategies. Although the research results were not entirely satisfactory due to model simplifications and the limitations of mathematical methods, it provided inspiration for future studies. Garcia et al. [9] investigated the active defense cooperative differential game problem involving three game participants, focusing on the target differential game problem of active control. Park et al. [10] proposed a method based on differential game theory to study within-visual-range air combat for Unmanned Combat Aerial Vehicles (UCAVs). This algorithm employs a hierarchical decision-making structure and uses differential game theory to compute the scoring function matrix, thereby solving for the optimal maneuvering strategies to address dynamic and challenging combat situations. These studies primarily analyze the aerial combat process in continuous time and space, enabling precise simulation of dynamic changes during air battles. However, the modeling process is complex, the models are highly dependent, the solution difficulty is high, real-time performance is low, and it is challenging to address multi-dimensional and multi-variable problems.
In terms of matrix games, related research employs a discretization approach to describe the strategy space and payoffs of the opposing sides. Austin et al. [11] was the first to utilize matrix game methods to study one-on-one low-altitude air combat maneuvering decisions in a hilly battlefield environment. Li et al. [4] proposed a constrained-strategy matrix game approach for generating intelligent decisions for multiple UCAVs in complex air combat environments using air combat situational information and time-sensitive information. Li et al. [12] proposed a dimensionality reduction-based matrix game solving algorithm for solving large-scale matrix games in a timely manner. The modeling process of matrix games is relatively straightforward, allowing for an intuitive demonstration of the strategy choices and payoff situations of both players. However, it heavily relies on prior knowledge, lacks flexibility in application, and struggles to effectively handle continuous state and action spaces. Additionally, it is unable to respond in real-time to complex dynamic adversarial environments, making it challenging to solve large-scale scenario problems.
In terms of deep reinforcement learning, relevant research primarily utilizes deep neural networks and reinforcement learning algorithms, which are capable of addressing adversarial problems in high-dimensional and complex environments. Cao et al. [13] addressed the problem that UCAVs are difficult to quickly and accurately perceive situational information and autonomously make maneuvering decisions in modern air wars that are susceptible to the influence of complex factors, and proposes an UCAVs maneuvering decision-making algorithm combining deep reinforcement learning and game theory. Liles et al. [14] developed a Markov Decision Process model of the stochastic dynamic allocation problem for the efficient and intelligent multi-program allocation decision-making problem faced by air force combat managers and uses approximate dynamic programming techniques to learn to find a high-quality solution for the Air Battle Management Problem (ABMP). Léchevin et al. [15] proposed a hierarchical decision-making and information system designed to provide coordinated aircraft path planning and deception warfare missions in real time. Zhang et al. [16] constructed beyond-visual-range air combat training environment and proposed a heuristic Q-network method that incorporates expert experience. This method aims to improve the efficiency of reinforcement learning algorithms in exploring strategy spaces, achieving self-learning of air combat maneuver strategies. Li et al. [17] proposed a UCAV autonomous maneuvering decision-making method based on game theory that considers the partially observable state of the adversary. Poropudas et al. [18] presented a new game-theoretic approach for validating discrete-event air combat simulation models and simulation-based optimization. Sun et al. [19] proposed a novel Multi-Agent Hierarchical Policy Gradient (MAHPG) Algorithm that learns various strategies and outperforms expert cognition through adversarial self-game learning. Deep reinforcement learning exhibits strong adaptability, allowing for continuous improvement of strategies during the training process. It is capable of handling problems with continuous time and continuous state spaces. However, the training process requires substantial amounts of data and computational resources. The results of model training are highly dependent on the quality and diversity of the training data, which may lead to overfitting or underfitting issues. Furthermore, the “black box” nature of the model limits its credibility and interpretability, making it challenging to explain and understand the specific formation process of the strategies.
Additionally, there are other relevant literature analyses that discuss the dynamic evolution process of aerial adversarial games. Hu et al. [20] studied the evolutionary mechanism of Unmanned Aerial Vehicle (UAV) swarm cooperative behavioral strategies in communication-constrained environments. Gao et al. [21] proposed an evolutionary game theory-based target assignment method for multi-UAV networks in 3D scenarios. Sheng et al. [22] proposed a posture evolution game model for the UAV cluster dynamic attack-defense problem. However, these studies did not take into account the interference of random environmental factors during confrontation.
To a certain extent, these methods provide effective solutions for multi-agent game decision-making, but there are also some limitations. In particular, the existing research results are mainly based on the premise of complete rationality of the players, focusing on solving the optimal strategy in a particular moment or situation, i.e., Nash equilibrium, failing to give full consideration to the dynamic changes in the process of confrontation, and neglecting the stochastic complexity of the environment and the uncertainty of information interference, lacking the analysis of the specific influencing factors of the dynamic game process and unable to analyze and study the whole process of the player’s coping strategy selection from a global perspective. In contrast, stochastic evolutionary game theory takes into account the bounded rationality and dynamic learning processes of agents, as well as the impact of random disturbances. This allows for the simulation of participants’ strategy selection processes over time, reflecting the dynamic changes in the maneuvering behaviors of agents in aerial confrontation. Therefore, this paper investigates the strategy interactions and decision-making behaviors of bounded rationality game agents in simulated adversarial scenarios under the influence of random disturbances, based on stochastic evolutionary game theory. Specifically, the main research content and contributions of this paper are as follows:
(1) Considering the risks that random disturbances in complex situational environments may pose to the autonomous decision-making of game players, as well as the impact of participants’ maneuvering behaviors on the state changes of game players in simulated adversarial scenarios, a nonlinear mathematical model is established to describe the strategy decision-making process of participants in this context.
(2) Through simulation experiments, the interactive relationships of strategy selection among game players, the stability of strategy evolution, and the dynamic decision-making processes were studied and validated. The study delves into the mechanisms by which certain factors influence agent behavior choices in specific environments. The results indicate that environmental disturbance factors and parameters related to agents’ maneuvering actions have varying impacts on the selection and evolution speed of agents’ strategies.
(3) This research explores the decision-making behaviors of multiple agents in aerial combat games, providing a new perspective for the study of agent strategy selection mechanisms. It offers a reliable quantitative analysis foundation for the observed results and fills a research gap in this field. The findings not only help decision-makers understand the dynamic changes in strategies under different factors and environmental conditions but also provide feasible analytical approaches and theoretical references to enhance the interpretability of multi-agent interactive decision-making and game system models.
In the multi-agent simulation confrontation scenario, the behavioral decision-making of the agent is a highly complex game process involving the interaction of multiple variables and factors, and the state and behavior of the agent evolve with the escalation of the conflict between both game players and the change of the situation. Among them, the maneuvers executed by the agent are crucial to the implementation of their maneuvering strategies, and the quality of the execution of these maneuvers not only directly affects the effectiveness of the strategies but also has a significant impact on the game state of the entire simulation confrontation.
Maneuvers of the agent refer to the flight techniques and maneuvering strategies adopted by the agent in conflict to gain an advantage, avoid risk, or achieve a specific purpose. Currently, there are two common ways of dividing maneuvers: basic maneuvers based on the operational mode [23], and typical maneuvers based on tactical maneuver theory. The National Advisory Committee for Aeronautics scholars has classified the most commonly used maneuvers into seven basic maneuvers based on the operational mode [24,25] including straight line uniform flight, maximum acceleration flight, maximum deceleration flight, maximum overload left turn, maximum overload right turn, maximum overload climb, and maximum overload dive. Complex maneuvers can be generated by combining and arranging the basic maneuvers in this group. From the point of view of tactical theory and demonstration effect, the typical maneuvers include [26,27]: High-G Turn, Roll, Barrel Roll, Split-S, Scissors, Immelman Turn, Pougatcheff Cobra maneuver, Falling Leaves, Loop, High Yo-Yo, Low Yo-Yo, and others.
However, these two types of maneuvers are still essentially two-dimensional or even multi-dimensional combinations of typical basic maneuvers such as straight flight, turn, pitch, etc., and there are some limitations in the way they are divided. In the division based on the operational mode, this mode mainly focuses on the physical operation level of the agent, oversimplifies the complexity of actual confrontation, ignores the application and effect of these maneuvers in specific situations, and does not fully consider the impact of the differences in the performance of the game players on the use of complex maneuvers. In the division based on the tactical maneuver theory, the approach is highly dependent on the specific environment, equipment performance, and the posture of both sides. It is difficult to comprehensively cover all the possible changes and the opponent’s reaction, and there are discrepancies and lags between daily training and practical application, which cannot reflect the latest tactical dynamics promptly. In general, the two divisions have their focuses, but they have some common problems. In the rapidly developing and highly technological modern confrontation, neither of them can fully cover all possible maneuvers, and the maneuvers are often interrelated and affect each other, so it is difficult for a single division to reflect the interaction and synergistic effect between different maneuvers. To overcome these problems, a more integrated division is needed that takes into account both the practicality and flexibility of the operation and the theoretical and practical applicability of the maneuvers while being constantly updated to accommodate technological developments and the accumulation of practical experience.
Therefore, based on these two classifications, this paper, regarding the maneuver design of the literature [28,29], combines the strategic intent during the interactive confrontation and divides the typical strategy maneuvers commonly used by players in actual confrontation based on the characteristics and expected goals of different maneuvers, which can be classified into three specific categories: offensive maneuvers, defensive maneuvers, and offensive-defensive maneuvers. Offensive maneuvers have the primary goal of maximizing strike effectiveness, focusing on using the performance advantages and firepower systems of the game players to execute precision strikes against incoming targets, mainly including direct flight turns, target tracking, and fire attacks. Defensive maneuvers have the priority goal of ensuring the game players’ safety and survival, focusing on evading the opponent’s attack and protecting the game players from damage. The strategy involves a high degree of maneuverability and the ability to quickly adapt to the environment and mainly includes straight flight turns, danger warnings, and circling evasions. Offensive-defensive maneuvers can be used both as offensive strategies to enhance the effectiveness of the game players in attack, and as defensive strategies to provide effective defense flight maneuvers when necessary. The strategy has a balanced performance in terms of speed, maneuverability, concealment, and reaction speed, the maneuver is mainly loop maneuvers. The specific divisions are shown in Fig. 1.
Figure 1: Maneuvers division
3 Deterministic Evolutionary Game Model
In the multi-agent simulation confrontation scenario, both game players must be based on the ever-changing environment and a flexible choice of offensive or defensive strategies to ensure that the benefits of attacking the target and their own safety and survival are maximized. This confrontation is a dynamic decision-making process, both game players will have mutual conversion and attack-defense transposition on the situation. The game players, in the choice of strategy, must weigh the potential payoffs and possible costs in the assumption of a certain risk at the same time and strive to obtain the maximum return to ensure that every maneuver and decision-making can lay the foundation for the ultimate victory. Evolutionary game theory provides a framework for explaining strategy interactions and behavioral decisions in multi-agent systems, and it helps us understand how individuals or groups form and adjust their strategies during long-term interactions by modeling natural selection and learning processes [30].
Assuming that both game players are limited rational groups with autonomous intelligent decision-making abilities, both sides are in the range of each other’s effective firepower in the confrontation process, and their strategy choices have a certain dynamic evolutionary law. Specifically, in the decision-making process, agents are capable of real-time perception of environmental changes and opponent behaviors, independently making judgments and autonomously adjusting strategies. However, constrained by incomplete information acquisition, limited computational capabilities, and finite response times, agents cannot achieve a level of fully rational decision-making. Consequently, collective decision-making often results in locally optimal or near-optimal outcomes under specific conditions. The Multi-agent Interactive Confrontation Game Evolution Model (MAICGEM) can be expressed as a quaternion array, i.e.,
(1)
(2)
(3)
(4)
The benefits available to both players under different tactical maneuvering strategies differ, mainly: basic flight gains for straight flight turning maneuvers
where:
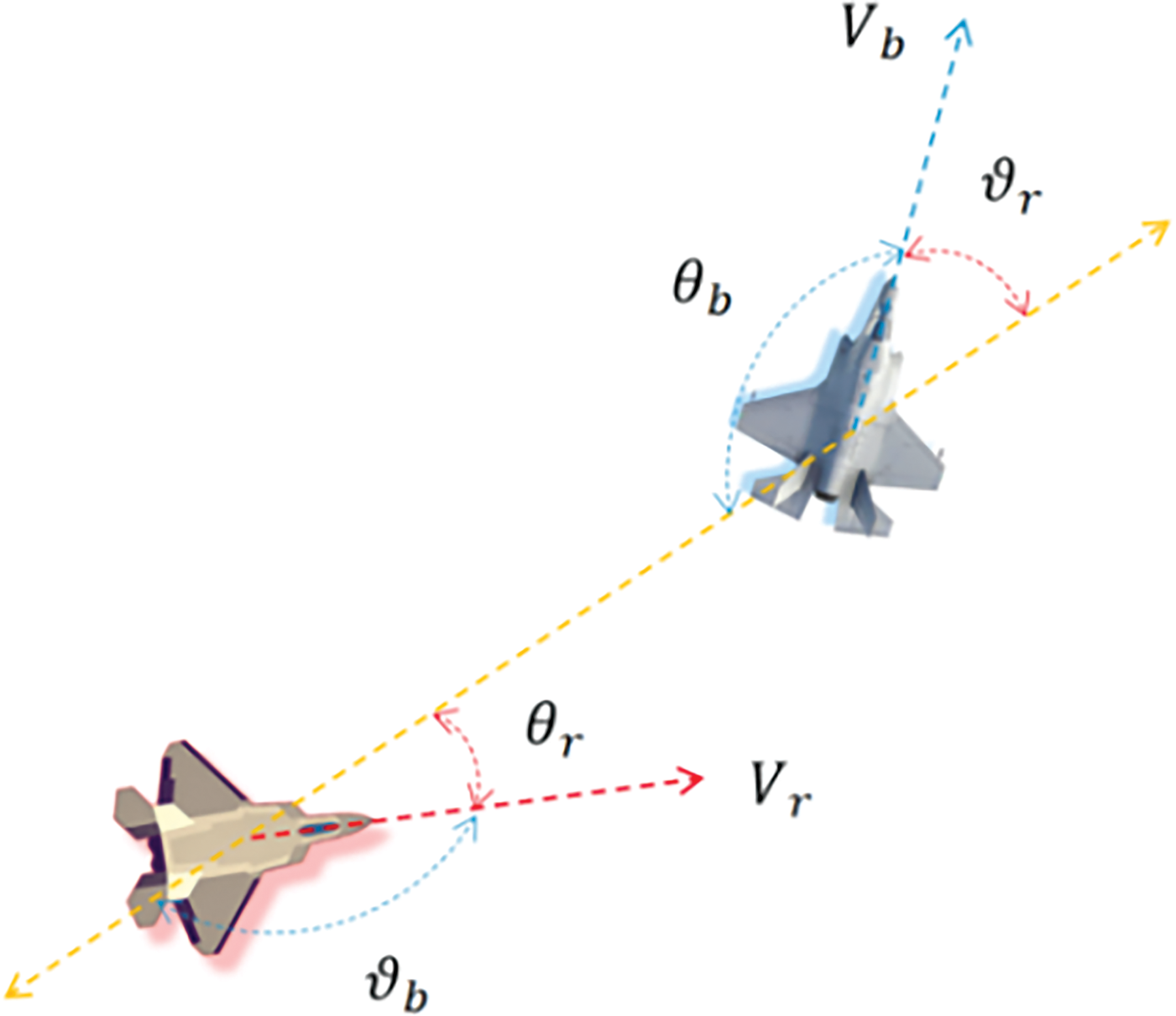
Figure 2: Schematic diagram of the simulation confrontation
In an evolutionary game, both game players no longer take Nash Equilibrium as the final strategy choice, but in the continuous competition, learning, and imitation, the participants with low returns will learn from the high-return players to optimize and improve their own strategies and gradually seek for Evolutionary Stable Strategy (ESS). The attack-defense game tree is shown in Fig. 3.
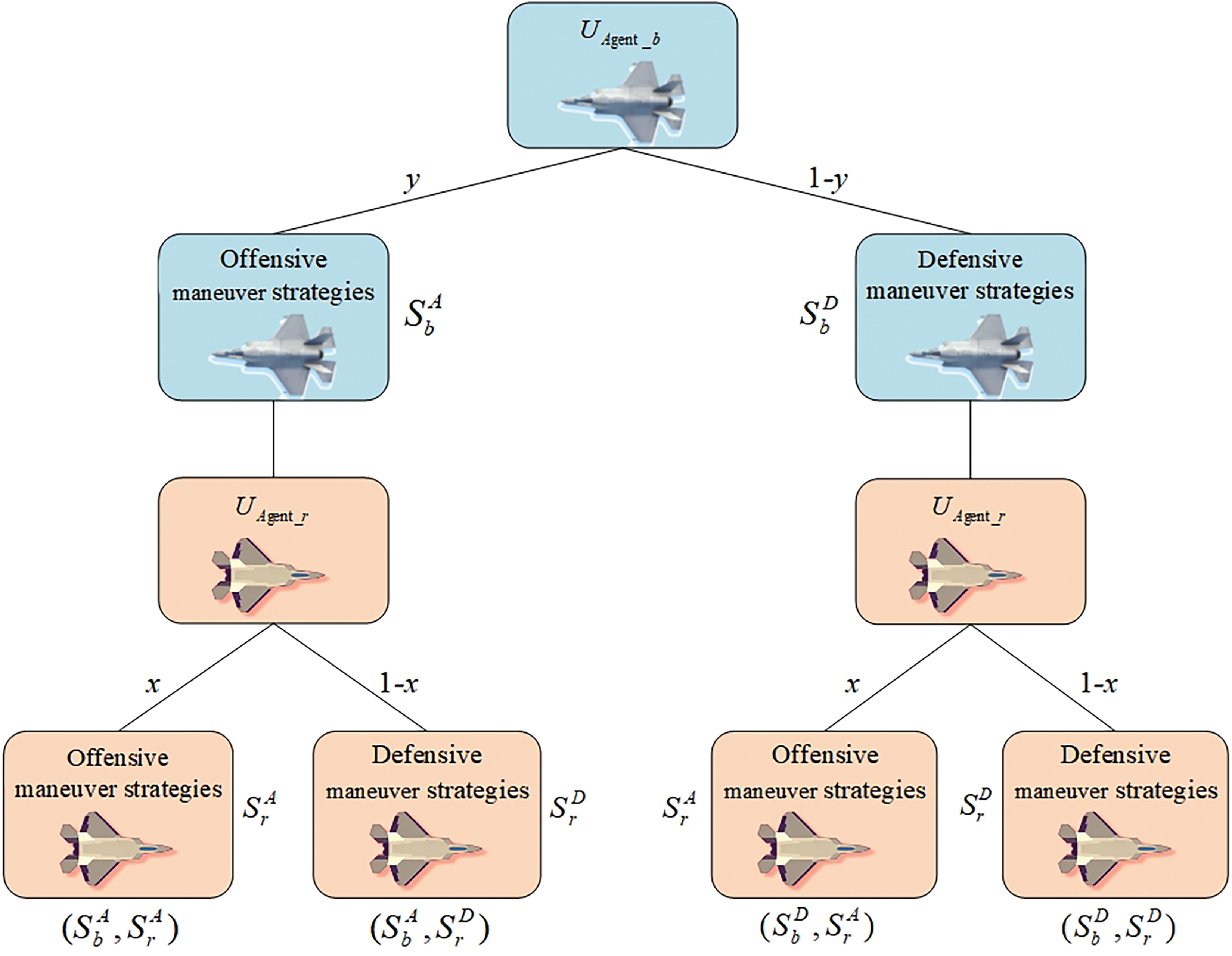
Figure 3: Confrontation game tree
From the game tree, there are four scenarios for the strategy combinations of the antagonists:

From Table 1, the expected gains of the
Further the dynamic replication equation for the
Similarly, the expected gains of the
Further the dynamic replication equation for
4 Stochastic Evolutionary Game Model
4.1 Stochastic Evolutionary Game
Although the evolutionary game theory overcomes the shortcoming of the classical game theory which the decision-maker is completely rational, it discusses the strategic behavior in a deterministic system [31], and the multi-agent simulation confrontation is a macro-complex system with uncertainty and randomness in its evolving dynamical mechanism. In actual confrontation, the change of environment and the interference of other external factors have a certain degree of randomness, so the game decision-making is also affected by the dynamic change of the complex environment, and the traditional evolutionary game theory lacks the research on the strategy dynamic evolution of the game players in a random dynamic interference environment, which cannot describe the uncertainty and random dynamics of the complex environment. Gaussian white noise is a nonlinear random noise whose amplitude obeys the Gaussian distribution and power spectral density obeys the uniform distribution, which can better describe the random external environment [32,33]. Therefore, this paper introduces the Gaussian white noise, which is combined with the stochastic differential equations [34] for describing the various types of random interference factors in complex adversarial environments [35]. Considering
where
Accordingly, it can be seen that Formulas (7), (8) are both one-dimensional
where
Since
where,
Taylor expansion is the basis for the numerical solution of stochastic differential equations. In practice, we generally use discrete stochastic processes to approximate the continuous solutions of stochastic differential equations. There are two main solution methods, Euler method and Milstein method. Euler method is more direct in the solution process, and Milstein method uses
Referring to the Formulas (11), (7) and (8) are expanded and solved to obtain as follows:
Aiming at the possible equilibrium solutions in the confrontation game system, the stability analysis of both game players is carried out according to the stability discrimination theorem of stochastic differential equations [40]. Let there exist a continuously differentiable smooth function
(1) If there exists a positive constant
(2) If there exists a positive constant
Among them,
For Formulas (7) and (8), let
If the Zero-solution P-order moment index of Formulas (15) and (16) are stable, the following requirements need to be satisfied:
If the Zero-solution P-order moment index of Formulas (15) and (16) are unstable, the following requirements need to be satisfied:
Simplifying Formulas (17) and (18), respectively, then we can obtain the conditions under which the Formulas (15) and (16) satisfy the stability of the Zero-solution P-order moment index:
(a) When
(b) When
(c) When
(d) When
In summary, the stochastic evolutionary game system consisting of the two parties involved in the game satisfies the condition of exponential stability of the zero-solution expectation moments as
5 Numerical Simulation Analysis
In order to confirm the correctness of the previous theoretical derivation and verify the validity of the model, the decision-making evolution process of the two players of the game is simulated and analyzed here. Before performing the numerical simulation, it is necessary to initialize the numerical simulation by assigning values according to the system stability constraints, so the following values are taken according to the constraints in the previous section. The initial selection probability of both players of the game is set to 0.5, the intensity coefficients of random environmental disturbances are taken as
5.1 Interference Intensity Factors
Fig. 4 shows the dynamic evolution process of the game players’ strategy in different random environmental interference intensities. From the figure, it can be seen that the magnitude of the interference intensity has a huge impact on the evolutionary results of the system. When the interference intensity is small, the system evolution results show different degrees of volatility, but they can still maintain a certain stability and consistency in general. This stability enables the system to evolve around one or some dominantly advantageous strategies. Although there are fluctuations in the process, these fluctuations usually do not change the overall evolution direction of the system, and the evolution results show a progressive stability state. With the continuous increase of interference intensity, the internal stability of the system is destroyed, and the system may enter a more dynamic and unstable state. In this case, the strategy selection of the game players becomes more difficult to predict and control. The strategy evolution shows persistent fluctuations, decision wandering and even reversals. This phenomenon reveals the important influence of the uncertainty in random environment on strategy selection and the challenge of maintaining or adjusting strategies in complex and dynamic environments.
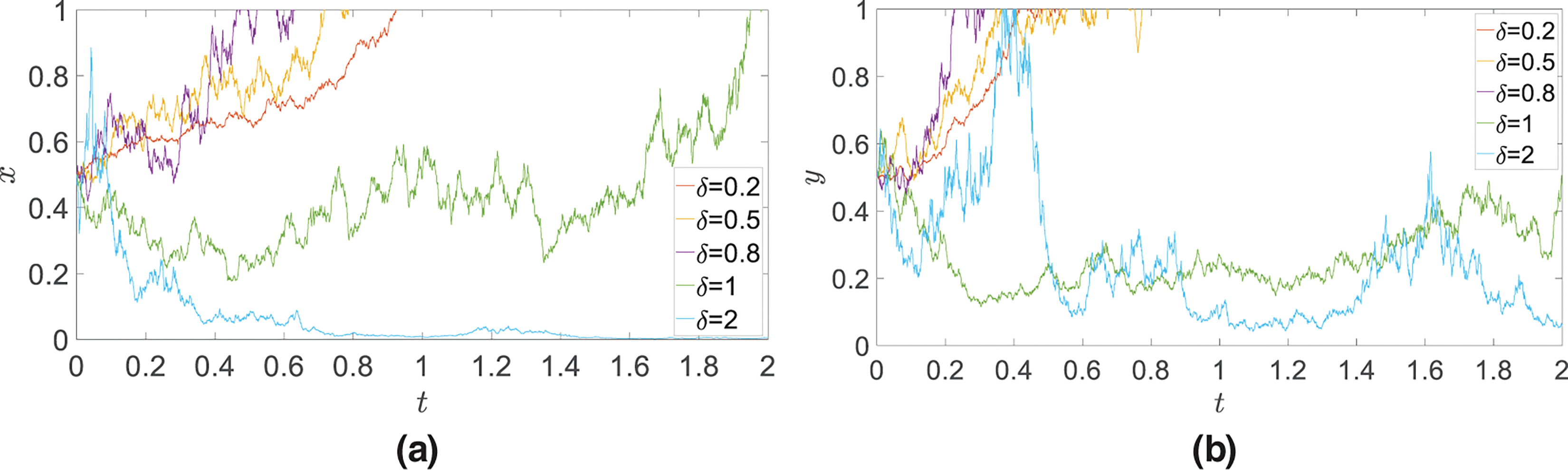
Figure 4: Dynamic evolution process of game player’s strategy under uncertainty conditions (a)
Moreover, the evolutionary trends and rates exhibited by the curves at different time points and under varying interference intensities differ, with some time segments even displaying reversal phenomena. These reversals are manifestations of the impact of random environmental interference on agents’ decision-making process. The degree of curve fluctuation varies, with greater random interference leading to larger fluctuations and a higher probability of reversals. Furthermore, the occurrence of random environmental interference at any given moment is stochastic, with random variables at two different time points being not only uncorrelated but also statistically independent. This induces uncertainty and randomness in the system’s evolutionary process both temporally and spatially, thereby increasing the overall unpredictability of the system’s evolution. Consequently, strategy evolution curves exhibit diverse fluctuations or reversals at different time points. Over extended time periods, despite the influence of random environmental interference, these fluctuations typically do not alter the overall evolutionary direction of the system. The agents’ strategy evolution ultimately converges to a certain strategic equilibrium state. Furthermore, the system’s evolutionary process exhibits a “threshold effect” characteristic of nonlinear dynamics, with a nonlinear relationship between interference intensity and system response. As a result, the system’s response characteristics differ under various interference levels. Smaller interference may induce minor fluctuations in the system, particularly near certain thresholds where significant changes in system behavior may occur, such as accelerated response speeds, increased amplitudes, or state transitions. Conversely, larger interference may exceed the system’s threshold range, triggering more complex nonlinear behaviors and leading to system state transformations.
5.2 System Sensitivity Analysis
The strategy selection of the game players will be affected by the comprehensive influence of many factors. According to the previous analysis of the strategy stability of both game players, the key parameters are selected and assigned different values to further explore the impact of the value of the key factors on the strategy of the game players caused by the trajectory of the stochastic evolution of the trajectory. The selection of parameters is based on the initial assignment, and the stochastic environmental interference intensity coefficient is uniformly valued as
(1) Target azimuth
In the case of ensuring that the initial values of other parameters remain unchanged, only the value of
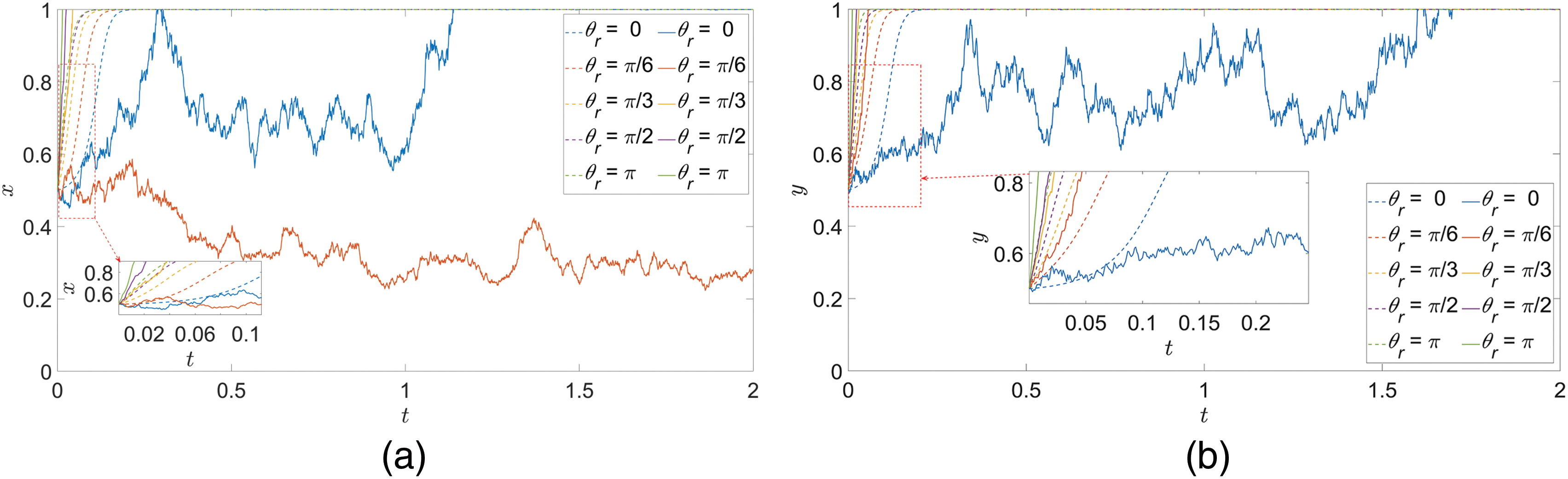
Figure 5:
Considering the reason for this phenomenon, it is due to the fact that the target azimuth angle directly affects the relative positions of the two players, the possible engagement distance, and the acquisition and processing of information, and the change of the azimuth angle directly affects the perceptual judgment of the two sides of the game on the battlefield environment, which in turn affects the initial choice of the game player to the strategy and adjustment. In the small azimuth, it means that the two players are more directly face-to-face conflict, the two players of the game in this scenario are in the optimal working interval of the airborne electronic sensing system and air-to-air missiles, at this time there is more time and space to respond to changes in the target’s strategy. In addition, due to the frequent and large amounts of information updates and rapid and dynamic strategy adjustments, decision-making requires more time to assess the effects of different strategies and possible consequences, resulting in their relatively low rate of strategy evolution. Moreover, the players under this layout is more sensitive to the perception of environmental uncertainty and random interference, which increases the complexity and unpredictability of strategy implementation, leading to greater fluctuations in its strategy selection, and its strategy adjustment becomes more conservative or hesitant, which may result in wavering and even cause strategy results opposite to those expected, further reducing the rate of strategy evolution. Under the large azimuth angle, the initial layout of the two players is more lateral or back-to-back. Although the urgency of direct conflict is reduced, the two players need to adjust their strategies more quickly to adapt to the other player’s possible flanking or backward actions and to maintain their own positional advantage, which leads to a faster rate of strategy evolution. Especially the environmental uncertainty can affect the perception and judgment of the two players more significantly under the layout, which further speeds up the strategy evolution rate of the game players.
(2) Target entry angle
In the case of ensuring that the initial values of other parameters remain unchanged, only the value of
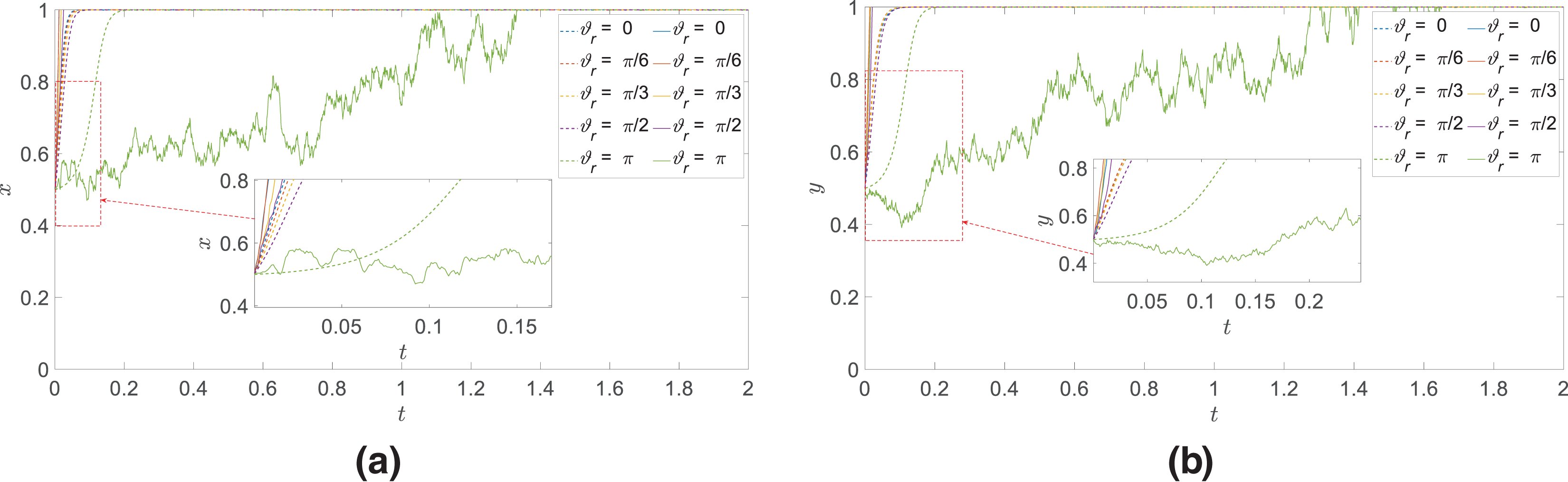
Figure 6:
Consider that the phenomenon is due to the fact that different target entry angles affect the perception and judgment of both players, which in turn affects the timeliness of perception, decision-making and action. Small target entry angle means that both game players are in a tailgate situation, and the smaller the entry angle, the easier the target is to escape maneuvers. when the game players need to make quick decisions to achieve the target’s strikes to intercept, especially by the random factors of the environment, the environmental disturbances may exacerbate the uncertainty of the two players of the strategy when the small entry angle, resulting in the urgency of the decision-making and the frequency of the decision-making is increased, and the need for faster information processing capabilities, which in turn cause the game players must adjust their strategies faster to adapt to the rapid response of the opponent’s maneuvers and tactics as well as the constant changes of the battlefield environment. For large target entry angles, it means that both players of the game are in a head-on posture, when the missile attack area has a larger range and a better angular posture, so there is more time and space to respond to changes in the environment and target strategy.
(3) Inherent value of the game player
In the case of ensuring that the initial values of other parameters remain unchanged, only the value of
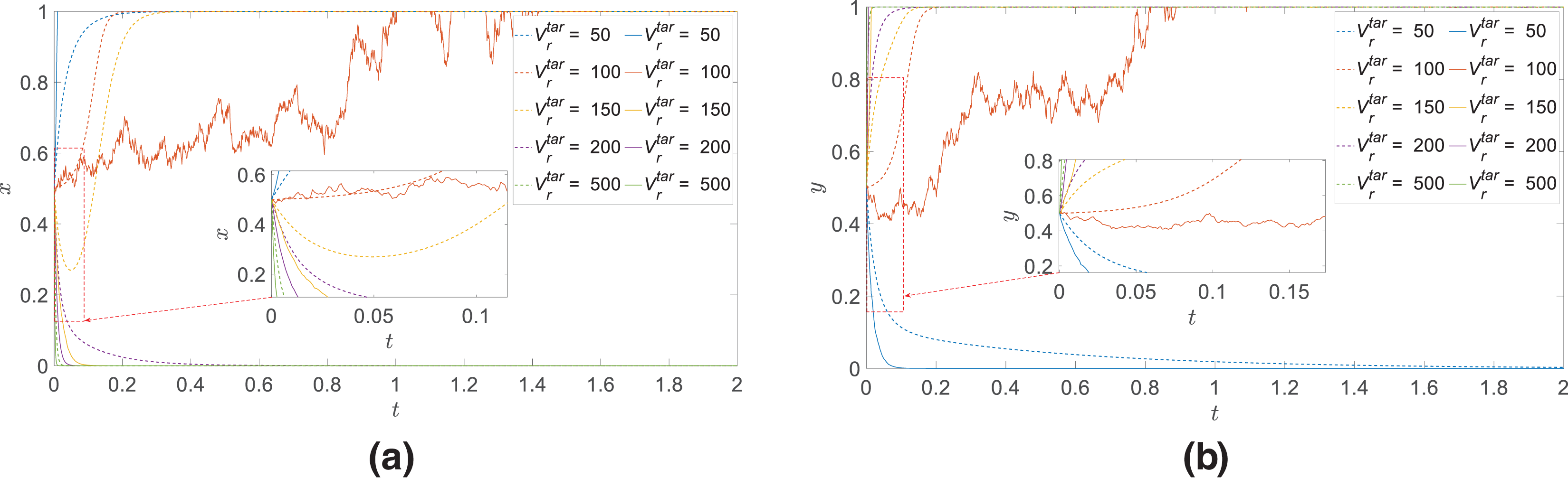
Figure 7:
Considering the reason for this phenomenon, it is because when the inherent value of the agent player is small, even if the agent is shot down and destroyed by the other side, its own loss is relatively small, so it is more aggressive and adventurous in the choice of strategy in order to seek to maximize the benefits or quickly change the battlefield situation. With the increase in the value of the agent player, the cost of the loss is also increased accordingly, so it is more conservative and hesitant in the tactics and pays attention to the cost-benefit calculation trade-offs and risk management to reduce and avoid potential losses. In addition, high-value agent players are more risky in uncertain environments, and benefit analysis becomes more complex and the consideration of risk more delicate, so they are more prudent in decision-making, leading to an increase in the volatility of tactical choices. This is one of the key reasons why countries around the world are now more willing to adopt high-volume, low-cost unmanned aerial vehicle to replace manned aerial vehicle.
(4) Basic probability of fire-strike process
In the case of ensuring that the initial values of other parameters remain unchanged, only the value of
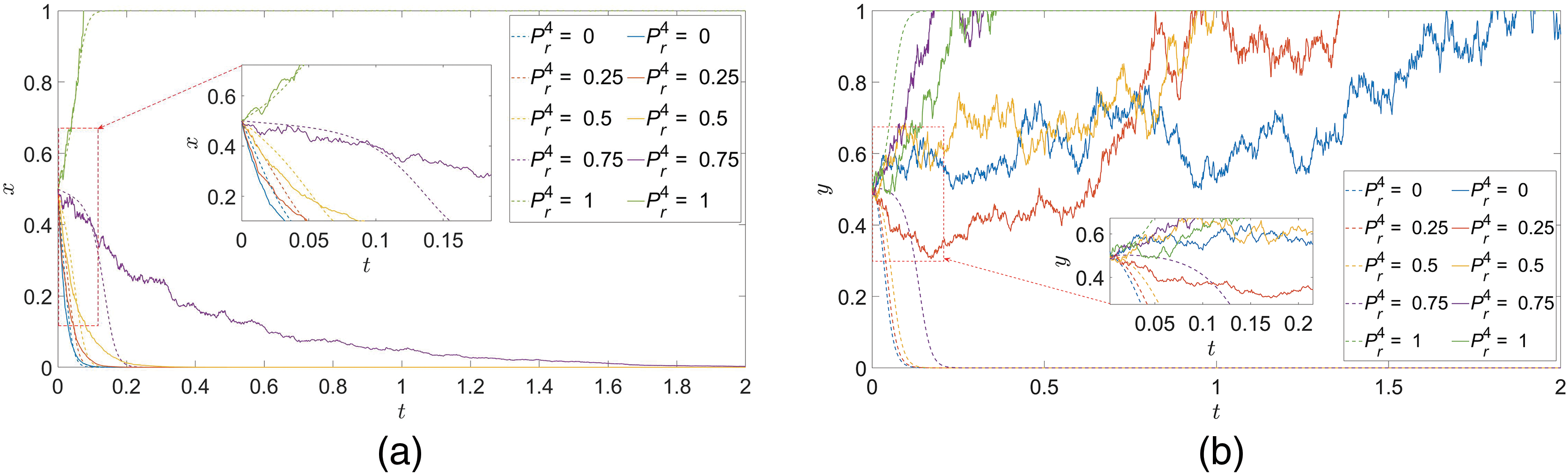
Figure 8:
Consider that the reason for this phenomenon is that because the lower weapon damage probability means that the
(5) Remaining time to evade missiles
In the case of ensuring that the initial values of other parameters remain unchanged, only the value of
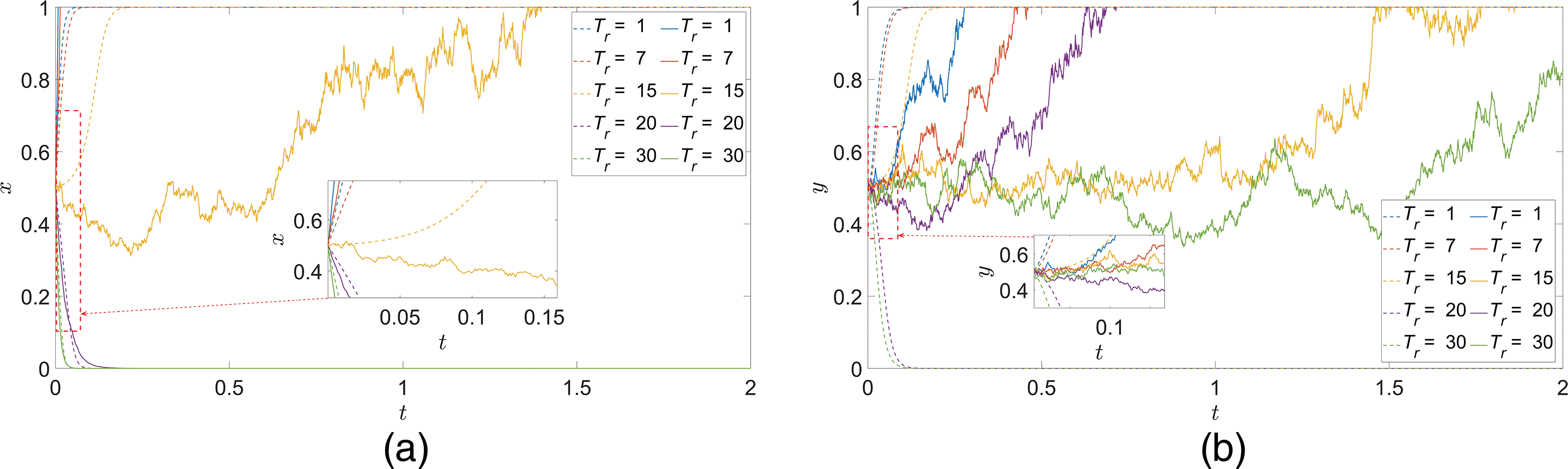
Figure 9:
Consider that the reason for this phenomenon is due to the fact that when the remaining time to evade the interceptor missiles is shorter, it means that the
(6) Missile consumption costs
In the case of ensuring that the initial values of other parameters remain unchanged, only the value of
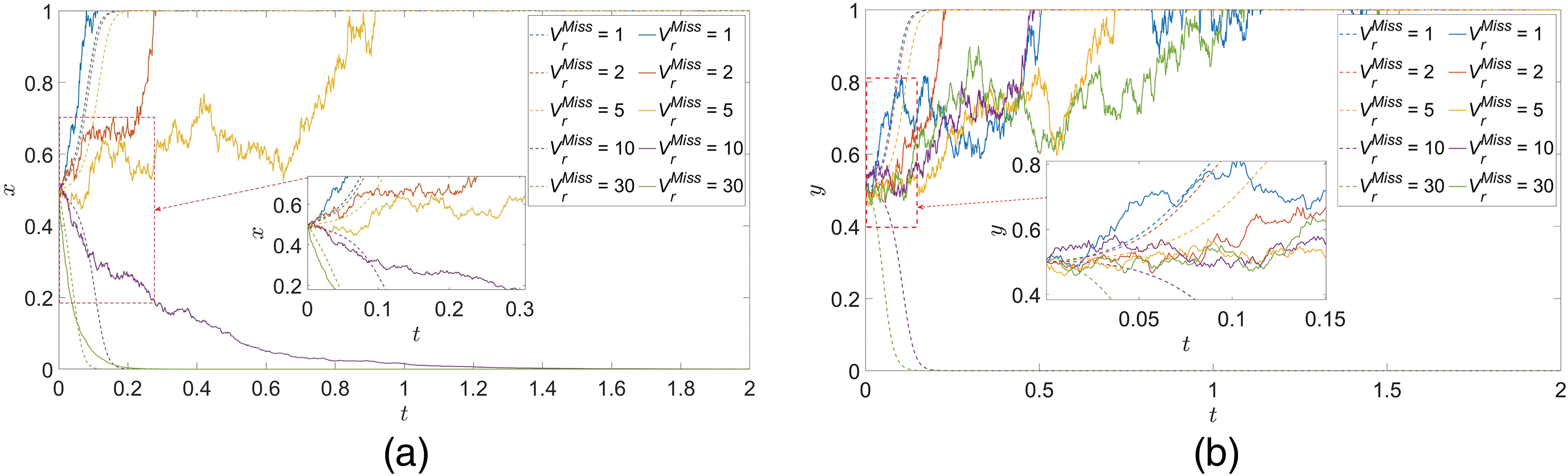
Figure 10:
Consider that the reason for this phenomenon is due to the fact that when the remaining time to evade the interceptor missiles is shorter, it means that the
It is clear from the previous analysis that the evolution of the system will be subject to the interference of random factors in the external environment, and the greater the intensity of random environmental interference, the greater the fluctuation of the decision-making of the game players in the process of strategy evolution, and the more difficult it is for both game players to predict the changes in the environment accurately. The introduction of random disturbances increases the uncertainty of the system so that the decision-making process of the game players is no longer entirely based on rational analysis and expected returns but is affected by more uncontrollable factors. This randomness leads to the diversity and unpredictability of the system’s evolutionary path.
In addition, factors such as target azimuth, target entry angle, the inherent value of the game players, the basic probability of fire-strike process, the remaining time to evade missiles, and the missile consumption costs all have different impacts on the rate of evolution and the results of the game. Specifically, factors such as target azimuth, target entry angle, and the inherent value of the game players themselves have a relatively minor impact on the strategic evolution outcomes of both parties involved in the game, but they significantly influence the rate of evolution. Conversely, factors such as the basic probability of fire-strike process, the remaining time to evade missile, and the missile consumption cost have a relatively minor impact on the strategy evolution outcomes of the parameter owner itself, but they significantly affect the other party involved in the game. Therefore, in the actual operational process, decision-makers need to combine the specific environment, strategic objectives, tactical considerations, the psychology and behavior of the two game players and other factors to conduct a comprehensive analysis. They must understand the effect of various parameters in regulating different aspects of the decision-making process of the game players, and take into account the changes caused by a multitude of factors on the evolution of decision-making on both game players. Especially in a highly uncertain environment, even a small information asymmetry or miscalculation may have a significant impact on decision-making.
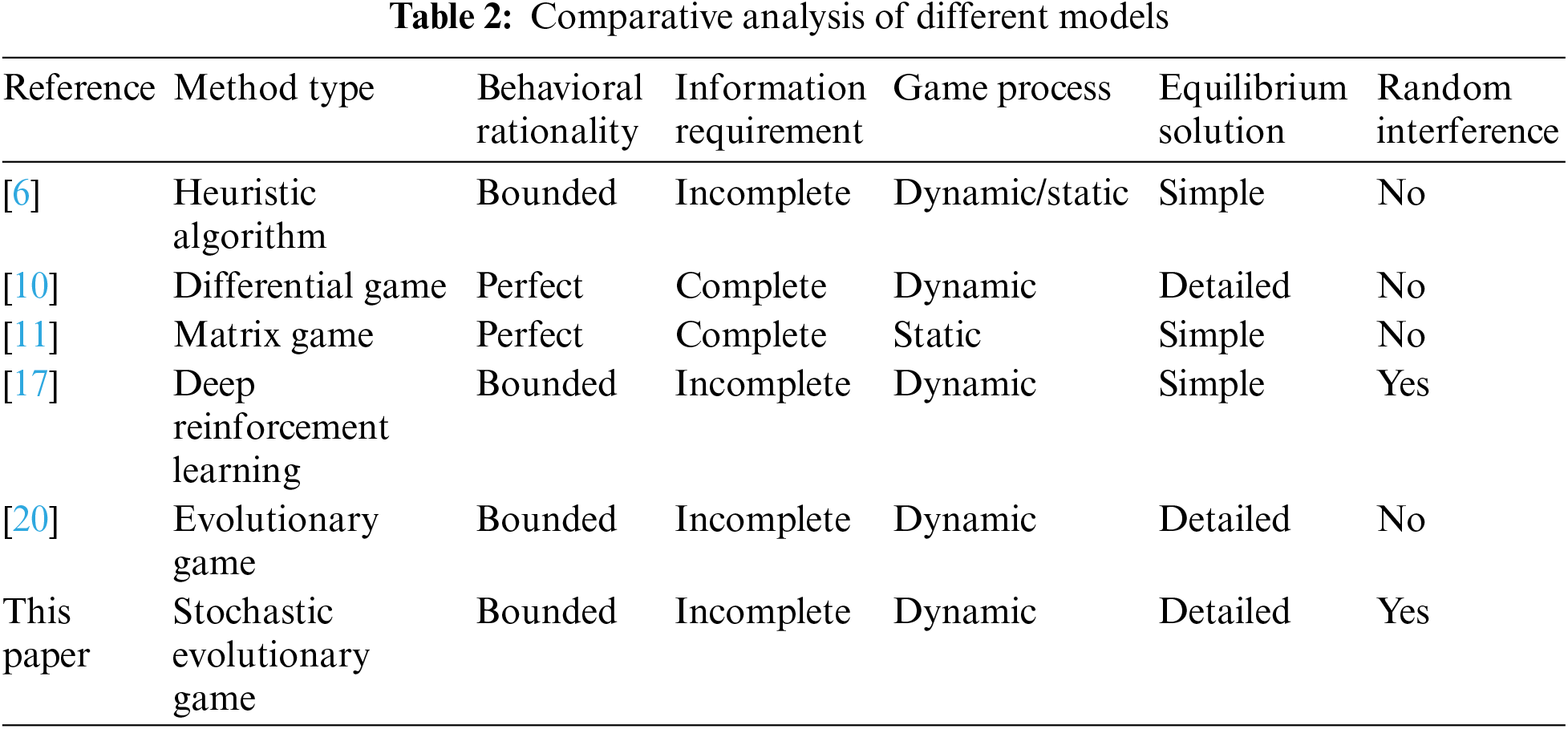
The method proposed in this paper is compared with other literatures, and the results are shown in Table 2. In the table, the method type refers to the theoretical approach adopted in the corresponding literature. Behavioral rationality indicates whether the literature considers the agents involved in adversarial decision-making as fully rational or boundedly rational, which affects the model’s alignment with real-world problems and, consequently, the algorithm’s practicality and generalizability. Information requirement denotes whether the adversarial decision-making process considers if agents can obtain complete environmental situational information. If agents can access all information in the adversarial environment, it is considered a complete information condition, otherwise, it is an incomplete information condition. The game process refers to the phased and state-based characteristics exhibited in the air attack-defense confrontation process, indicating whether the game process is dynamic or static, with dynamic processes featuring rapid state changes and more complex solution processes. Equilibrium solution indicates whether the algorithm’s equilibrium solving process is detailed and specific, as incomplete information dynamic adversarial games are more challenging to solve for equilibrium compared to complete information adversarial games and static adversarial games. Therefore, the level of detail in equilibrium solving directly affects the practicality and interpretability of the algorithm. Random environmental interference refers to whether the model considers the impact of random environmental factors on agent decision-making, which determines if the model can more accurately describe interference factors present in real-life scenarios.
Aiming at the maneuvering decision-making problem of agents in the interaction process of multi-agents in a random interference environment, the paper considers the specific impact of maneuvering actions on the game state, analyzes the possible risks caused by random interference in the complex environment on the maneuver decision-making of the game players, establishes a stochastic evolutionary mathematical model of multi-agent game behavior strategy, and researches the strategy selection interaction relationship, evolutionary stability, and dynamic decision-making process of each game player in a random interference environment. The results show that the parameters related to the maneuvering actions of the agent have different effects on the selection and evolution speed of the agent’s strategy, and the influence of environmental interference on the different parameters of the maneuver is also different. This also confirms the feasibility and effectiveness of the proposed method, which can better explain the behavior decision-making process of the agent in the interaction process.
This study quantifies the decision-making processes of agents through mathematical methods, providing a foundational model and analytical framework for subsequent research. It not only aids decision-makers in understanding the dynamics of strategies under various factors and environmental conditions but also offers feasible analytical approaches and theoretical references for improving decision-making in multi-agent interactions and enhancing the interpretability of game system models. Compared to other methods such as differential games, matrix games, deep reinforcement learning, and genetic algorithms, the proposed method in this paper takes into account the agents’ bounded rationality, dynamic learning processes, and the impact of random disturbances, making it more aligned with real-world scenarios. It can simulate the strategy selection process of participants over time, reflect the dynamic changes in agents’ maneuvering behaviors during aerial combat, and describe the various tactics in air warfare. This is beneficial for predicting the evolution of tactics and identifying optimal strategy combinations, thereby assisting decision-makers in better understanding the potential behaviors and responses of both friendly and adversary forces, ultimately enhancing the scientific rigor of air combat training and strategy development.
However, the paper primarily analyzes the impact of maneuver actions in environments with stochastic disturbances on the behavioral strategies of agents. It offers a solution that is interpretable for specific problems, but its universality is somewhat limited. We are committed to expanding our research scope in future studies. In subsequent research, we will conduct more refined experimental designs and employ more complex mathematical models to further analyze the specific impacts of different factors in various contexts. Additionally, we aim to provide more detailed mechanistic explanations to uncover the specific mechanisms and principles underlying these complex relationships, thereby enhancing the specificity and operability of the research findings. We also consider combining the self-learning capability of deep reinforcement learning and the strategy analysis capability of game theory to provide a more comprehensive solution to the air combat problem.
Acknowledgement: We would like to thank everyone who provided comments on this work.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Study conception and design: Shiguang Hu, Le Ru, Bo Lu, Zhenhua Wang; data collection: Shiguang Hu, Xiaolin Zhao, Wenfei Wang, Hailong Xi; analysis and interpretation of results: Shiguang Hu, Le Ru, Xiaolin Zhao, Bo Lu; draft manuscript preparation: Shiguang Hu, Le Ru. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article or its supplementary materials.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. F. Jiang, M. Xu, Y. Li, H. Cui, and R. Wang, “Short-range air combat maneuver decision of UAV swarm based on multi-agent Transformer introducing virtual objects,” Eng. Appl. Artif. Intell., vol. 123, 2023, Art. no. 106358. doi: 10.1016/j.engappai.2023.106358. [Google Scholar] [CrossRef]
2. Z. Ren, D. Zhang, S. Tang, W. Xiong, and S. Yang, “Cooperative maneuver decision making for multi-UAV air combat based on incomplete information dynamic game,” Def. Technol., vol. 27, no. 3, pp. 308–317, 2023. doi: 10.1016/j.dt.2022.10.008. [Google Scholar] [CrossRef]
3. J. Xu, Z. Deng, and Q. Song, “Multi-UAV counter-game model based on uncertain information,” Appl. Math. Comput., vol. 366, no. 3, 2020, Art. no. 124684. doi: 10.1016/j.amc.2019.124684. [Google Scholar] [CrossRef]
4. S. Li, M. Chen, Y. Wang, and Q. Wu, “Air combat decision-making of multiple UCAVs based on constraint strategy games,” Def. Technol., vol. 18, no. 3, pp. 368–383, 2022. doi: 10.1016/j.dt.2021.01.005. [Google Scholar] [CrossRef]
5. Z. Chen et al., “Tripartite evolutionary game in the process of network attack and defense,” Telecommun. Syst., vol. 86, no. 2, pp. 351–361, May 2024. doi: 10.1007/s11235-024-01130-9. [Google Scholar] [CrossRef]
6. Y. Huang, A. Luo, T. Chen, M. Zhang, B. Ren and Y. Song, “When architecture meets RL plus EA: A hybrid intelligent optimization approach for selecting combat system-of-systems architecture,” Adv. Eng. Inform., vol. 58, Oct. 2023, Art. no. 102209. doi: 10.1016/j.aei.2023.102209. [Google Scholar] [CrossRef]
7. Y. Wang, X. Zhang, R. Zhou, S. Tang, H. Zhou and W. Ding, “Research on UCAV maneuvering decision method based on heuristic reinforcement learning,” Comput. Intell. Neurosci., vol. 2022, pp. 1–13, Mar. 2022. doi: 10.1155/2022/1477078. [Google Scholar] [PubMed] [CrossRef]
8. R. Isaacs, “A mathematical theory with applications to warfare and pursuit, control and optimization,” in Differential Games. New York, NY, USA: Wiley, 1965. [Google Scholar]
9. E. Garcia, D. Casbeer, and M. Pachter, “Active target defence differential game: Fast defender case,” IET Control Theory Appl., vol. 11, no. 17, pp. 2985–2993, Sep. 2017. doi: 10.1049/iet-cta.2017.0302. [Google Scholar] [CrossRef]
10. H. Park, B. Lee, and D. Yoo, “Differential game based air combat maneuver generation using scoring function matrix,” Int. J. Aeronaut. Space, vol. 17, no. 2, pp. 204–213, Jun. 2016. doi: 10.5139/IJASS.2016.17.2.204. [Google Scholar] [CrossRef]
11. F. Austin, G. Carbone, H. Hinz, M. Lewis, and M. Falco, “Game theory for automated maneuvering during air-to-air combat,” J. Guid. Control Dyn., vol. 13, no. 6, pp. 1143–1149, Dec. 1990. doi: 10.2514/3.20590. [Google Scholar] [CrossRef]
12. S. Li, M. Chen, and Q. Wu, “A fast algorithm to solve large-scale matrix games based on dimensionality reduction and its application in multiple unmanned combat air vehicles attack-defense decision-making,” Inform. Sci., vol. 594, no. 4, pp. 305–321, 2022. doi: 10.1016/j.ins.2022.02.025. [Google Scholar] [CrossRef]
13. Y. Cao, Y. Kou, and A. Xu, “Autonomous maneuver decision of UCAV air combat based on double deep Q network algorithm and stochastic game theory,” Int. J. Aerosp. Eng., vol. 2023, pp. 1–20, Jan. 2023. doi: 10.1155/2023/3657814. [Google Scholar] [CrossRef]
14. J. Liles, M. Robbins, and B. Lunday, “Improving defensive air battle management by solving a stochastic dynamic assignment problem via approximate dynamic programming,” Eur J. Oper. Res., vol. 305, no. 3, pp. 1435–1449, 2023. doi: 10.1016/j.ejor.2022.06.031. [Google Scholar] [CrossRef]
15. N. Léchevin and C. Rabbath, “A hierarchical decision and information system for multi-aircraft combat missions,” Proc. Inst. Mech. Eng. Part G J. Aerosp., vol. 224, no. 2, pp. 133–148, Feb. 2010. doi: 10.1243/09544100JAERO563. [Google Scholar] [CrossRef]
16. X. Zhang, G. Liu, C. Yang, and J. Wu, “Research on air confrontation maneuver decision-making method based on reinforcement learning,” Electron., vol. 7, no. 11, Nov. 2018, Art. no. 279. doi: 10.3390/electronics7110279. [Google Scholar] [CrossRef]
17. S. Li, Q. Wu, and M. Chen, “Autonomous maneuver decision-making of UCAV with incomplete information in human-computer gaming,” Drones, vol. 7, no. 3, Feb. 2023, Art. no. 157. doi: 10.3390/drones7030157. [Google Scholar] [CrossRef]
18. J. Poropudas and K. Virtanen, “Game-theoretic validation and analysis of air combat simulation models,” IEEE Trans. Syst. Man Cyber.-Part A: Syst. Hum., vol. 40, no. 5, pp. 1057–1070, Sep. 2010. doi: 10.1109/TSMCA.2010.2044997. [Google Scholar] [CrossRef]
19. Z. Sun et al., “Multi-agent hierarchical policy gradient for Air Combat Tactics emergence via self-play,” Eng. Appl. Artif. Intell., vol. 98, 2021, Art. no. 104112. doi: 10.1016/j.engappai.2020.104112. [Google Scholar] [CrossRef]
20. S. Hu, L. Ru, and W. Wang, “Evolutionary game analysis of behaviour strategy for UAV swarm in communication-constrained environments,” IET Control Theory Appl., vol. 18, no. 3, pp. 350–363, Nov. 2023. doi: 10.1049/cth2.12602. [Google Scholar] [CrossRef]
21. Y. Gao, L. Zhang, and Q. Wang, “An evolutionary game-theoretic approach to unmanned aerial vehicle network target assignment in three-dimensional scenarios,” Mathematics, vol. 11, no. 19, Oct. 2023, Art. no. 4196. doi: 10.3390/math11194196. [Google Scholar] [CrossRef]
22. L. Sheng, M. Shi, and Y. Qi, “Dynamic offense and defense of uav swarm based on situation evolution game,” (in Chinese), Syst. Eng. Electron., vol. 8, pp. 2332–2342, Jun. 2023. doi: 10.12305/j.issn.1001-506X.2023.08.06. [Google Scholar] [CrossRef]
23. C. Liu, S. Sun, and B. Xu, “Optimizing evasive maneuvering of planes using a flight quality driven model,” Sci. China Inform. Sci., vol. 67, no. 3, Feb. 2024. doi: 10.1007/s11432-023-3848-6. [Google Scholar] [CrossRef]
24. H. Huang, H. Cui, H. Zhou, and J. Li, “Research on autonomous maneuvering decision of UAV in close air combat,” in Proc. 3rd 2023 Int. Conf. Autonom. Unmanned Syst., Singapore, Springer, 2023, vol. 1171. doi: 10.1007/978-981-97-1083-6_14. [Google Scholar] [CrossRef]
25. Z. Li, J. Zhu, M. Kuang, J. Zhang, and J. Ren, “Hierarchical decision algorithm for air combat with hybrid action based on reinforcement learning,” (in Chinese), Acta Aeronaut. et Astronaut. Sinica, Apr. 2024. doi: 10.7527/S1000-6893.2024.30053. [Google Scholar] [CrossRef]
26. D. Lee, C. Kim, and S. Lee, “Implementation of tactical maneuvers with maneuver libraries,” Chin. J. Aeronaut., vol. 33, no. 1, pp. 255–270, 2020. doi: 10.1016/j.cja.2019.07.007. [Google Scholar] [CrossRef]
27. H. Duan, Y. Lei, J. Xia, Y. Deng, and Y. Shi, “Autonomous maneuver decision for unmanned aerial vehicle via improved pigeon-inspired optimization,” IEEE Trans. Aerosp. Electron. Syst., vol. 59, no. 3, pp. 3156–3170, Jun. 2023. doi: 10.1109/TAES.2022.3221691. [Google Scholar] [CrossRef]
28. J. Zhu, M. Kuang, and X. Han, “Mastering air combat game with deep reinforcement learning,” Def. Technol., vol. 34, no. 4, pp. 295–312, 2024. doi: 10.1016/j.dt.2023.08.019. [Google Scholar] [CrossRef]
29. W. Kong, D. Zhou, and Y. Zhao, “Hierarchical reinforcement learning from competitive self-play for dual-aircraft formation air combat,” J. Comput. Des. Eng., vol. 10, no. 2, pp. 830–859, Mar. 2023. doi: 10.1093/jcde/qwad020. [Google Scholar] [CrossRef]
30. S. Deng and Y. Yuan, “A data intrusion tolerance model based on an improved evolutionary game theory for the energy internet,” Comput. Mater. Contin., vol. 79, no. 3, pp. 3679–3697, Jan. 2024. doi: 10.32604/cmc.2024.052008. [Google Scholar] [CrossRef]
31. X. Richter and J. Lehtonen, “Half a century of evolutionary games: A synthesis of theory, application and future directions,” Phil. Trans. R. Soc. B, vol. 378, no. 1876, May 2023, Art. no. 489. doi: 10.1098/rstb.2021.0492. [Google Scholar] [PubMed] [CrossRef]
32. E. L. N. Ekassi, O. Foupouapouognigni, and M. S. Siewe, “Nonlinear dynamics and Gaussian white noise excitation effects in a model of flow-induced oscillations of circular cylinder,” Chaos Solitons Fract., vol. 178, 2024, Art. no. 114374. doi: 10.1016/j.chaos.2023.114374. [Google Scholar] [CrossRef]
33. A. V. Balakrishnan and R. R. Mazumdar, “On powers of Gaussian white noise,” IEEE Trans. Inf. Theory, vol. 57, no. 11, pp. 7629–7634, 2011. doi: 10.1109/TIT.2011.2158062. [Google Scholar] [CrossRef]
34. D. Cheng, F. He, H. Qi, and T. Xu, “Modeling, analysis and control of networked evolutionary games,” IEEE Trans. Automat. Control, vol. 60, no. 9, pp. 2402–2415, Sep. 2015. doi: 10.1109/TAC.2015.2404471. [Google Scholar] [CrossRef]
35. G. Jumarie, “Approximate solution for some stochastic differential equations involving both Gaussian and Poissonian white noises,” Appl. Math. Lett., vol. 16, no. 8, pp. 1171–1177, 2003. doi: 10.1016/S0893-9659(03)90113-3. [Google Scholar] [CrossRef]
36. H. Zhang, Y. Mi, X. Liu, Y. Zhang, J. Wang and J. Tan, “A differential game approach for real-time security defense decision in scale-free networks,” Comput. Netw., vol. 224, 2023, Art. no. 109635. doi: 10.1016/j.comnet.2023.109635. [Google Scholar] [CrossRef]
37. J. Armstrong and A. Ionescu, “Itô stochastic differentials,” Stoch. Proc. Appl., vol. 171, Apr. 2024, Art. no. 104317. doi: 10.1016/j.spa.2024.104317. [Google Scholar] [CrossRef]
38. B. Moghaddam, A. Lopes, J. Machado, and Z. Mostaghim, “Computational scheme for solving nonlinear fractional stochastic differential equations with delay,” Stoch. Anal. Appl., vol. 37, no. 6, pp. 893–908, Nov. 2019. doi: 10.1080/07362994.2019.1621182. [Google Scholar] [CrossRef]
39. K. Kang, L. Bai, and J. Zhang, “A tripartite stochastic evolutionary game model of complex technological products in a transnational supply chain,” Comput. Ind. Eng., vol. 186, Dec. 2023, Art. no. 109690. doi: 10.1016/j.cie.2023.109690. [Google Scholar] [CrossRef]
40. J. Yang, X. Liu, and X. Liu, “Stability of stochastic functional differential systems with semi-Markovian switching and Levy noise by functional Itô’s formula and its applications,” J. Franklin Inst., vol. 357, no. 7, pp. 4458–4485, May 2020. doi: 10.1016/j.jfranklin.2020.03.012. [Google Scholar] [CrossRef]
41. Y. Xu, B. Hu, and R. Qian, “Analysis on stability of strategic alliances based on stochastic evolutionary game including simulations,” (in Chinese), Syst. Eng. Theory Pract., vol. 31, pp. 920–926, May 15, 2011. doi: 10.12011/1000-6788(2011)5-920. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools