Login
Register
Submit a Paper
Propose a Special lssue
Open Access
ARTICLE
An Efficient Anti-Quantum Blind Signature with Forward Security for Blockchain-Enabled Internet of Medical Things
1 School of Information Science and Technology, North China University of Technology, Beijing, 100144, China
2 State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing, 100876, China
3 School of Mathematical Science, Heilongjiang University, Harbin, 150080, China
4 School of Digtial and Intelligence Industry, Inner Mongolia University of Science and Technology, Baotou, 014010, China
5 Institute for Network Sciences and Cyberspace, Tsinghua University, Beijing, 100084, China
6 Yunnan Key Laboratory of Blockchain Application Technology, Kunming, 650233, China
7 Yunnan Innovation Institute of Beihang University, Kunming, 650233, China
* Corresponding Author: Kejia Zhang. Email:
Computers, Materials & Continua 2025, 82(2), 2293-2309. https://doi.org/10.32604/cmc.2024.057882
Received 29 August 2024; Accepted 08 November 2024; Issue published 17 February 2025
View Full Text
Download PDFAbstract
Blockchain-enabled Internet of Medical Things (BIoMT) has attracted significant attention from academia and healthcare organizations. However, the large amount of medical data involved in BIoMT has also raised concerns about data security and personal privacy protection. To alleviate these concerns, blind signature technology has emerged as an effective method to solve blindness and unforgeability. Unfortunately, most existing blind signature schemes suffer from the security risk of key leakage. In addition, traditional blind signature schemes are also vulnerable to quantum computing attacks. Therefore, it remains a crucial and ongoing challenge to explore the construction of key-secure, quantum-resistant blind signatures. In this paper, we introduce lattice-based forward-secure blind signature (LFSBS), a lattice-based forward-secure blind signature scheme for medical privacy preservation in BIoMT. LFSBS achieves forward security by constructing a key evolution mechanism using a binary tree structure. This mechanism ensures that even if future encryption keys are leaked, past data can still remain secure. Meanwhile, LFSBS realizes post-quantum security based on the hardness assumption of small integer solution (SIS), making it resistant to potential quantum computing attacks. In addition, we formally define and prove the security of LFSBS in a random oracle model, including blindness and forward-secure unforgeability. Comprehensive performance evaluation shows that LFSBS performs well in terms of computational overhead, with a reduction of 22%–73% compared to previous schemes.Keywords
The Internet of Medical Things (IoMT) has significantly transformed the traditional healthcare industry in recent years [1]. It comprises a range of smart medical devices that can sense medical data, along with transmitters that enable the secure transmission of sensitive information [2]. By interconnecting these devices and transmitters, IoMT facilitates real-time monitoring of the health status of patients. At the same time, the vast amount of sensitive medical data, such as electronic health records (EHRs), presents significant challenges for data security and privacy protection [3]. Therefore, IoMT incorporating blockchain technology has been proposed (e.g., [4–7]). The decentralized nature of blockchain and data immutability enhances the security of medical data.
However, traditional blockchain-enabled IoMT schemes [8–12] rely on public transaction records and digital signatures to ensure data integrity. Although medical information such as electronic medical records are uploaded to the blockchain after signing, they are still at risk of leakage as the data is transparent to the signer.
To overcome these obstacles, many scholars have applied blind signature technology to BIoMT [13–16], which allows users to sign without knowing the content of EHRs. Blind signatures protect the security of medical data and verify its integrity.
Unfortunately, these solutions are either ineffective against the risks associated with quantum computing attacks or face the potential for key compromise. Specifically, the key required for the user to sign in several schemes is constant after generation [13–17]. It means that if the key is compromised due to an external attack or improper storage, adversaries could potentially compromise the content of data previously signed by the signer. For instance, in the scheme [13], a trusted organization generates a pair of large numbers as public and private keys for each user. The user applies a blind signature to the data using their individual private key. However, the private key is retained by the user and remains unchanged throughout the duration of the scheme, which exposes it to the risk of key leakage [18]. On the other hand, as quantum computers advance, blind signature schemes reliant on the discrete-logarithm problem or number-theoretic hard problems, including Elliptic Curve Cryptography (ECC) [19] and Rivest-Shamir-Adleman (RSA) [12], will cease to be secure. The computational prowess offered by quantum computers can convert these hard problems into polynomial time-solvable ones through the application of Shor’s algorithm [20].
We introduce lattice based forward-secure blind signature (LFSBS), an efficient lattice-based blind signature scheme with forward security for blockchain-enabled IoMT, aimed at enhancing the protection of sensitive medical data. The scheme is not only resistant to quantum attacks, but also supports forward security. LFSBS addresses two key challenges in blockchain-enabled IoMT, as outlined below.
The first challenge is to achieve quantum resistance for blind signatures. The security of lattice-based cryptosystems relies on the intractability of problems on the lattice, such as the least integer solution (SIS). These problems also have no significant computational advantage on quantum computers. Therefore, lattice-based cryptographic regimes are considered to be resistant to attacks on quantum computation. LFSBS constructs an anti-quantum blind signature protocol based on the lattice theory. In addition, computational complexity and communication efficiency are taken into account in the protocol design to ensure that the anti-quantum nature is satisfied while still maintaining efficient execution performance.
The second challenge is how to design a forward-secure key evolution mechanism, which provides strong forward security to ensure that past keys are not compromised by leakage of existing keys. LFSBS assigns time periods to the leaf nodes of a binary tree. When the time period changes, the corresponding leaf nodes change accordingly. The ExtBasis algorithm [21] is then applied to update the keys associated with these leaf nodes.
In summary, the contributions of this work are shown below:
• We introduce a quantum-resistant forward-secure blind signature scheme, LFSBS, which realizes an attack on quantum computing based on the SIS assumption. In addition, we further design a forward secure key evolution mechanism for LFSBS to prevent key leakage.
• We formally define and prove the blindness and forward unforgeability of LFSBS in the Random Oracle Model (ROM). We show through comprehensive experimental results that LFSBS has significant efficiency advantages over previous techniques in signature generation and verification. For instance, when n=25, Sign and Verify in LFSBS are about 1.2×–3.4× and 3.5×–16× faster than other schemes, respectively. The total time reduction is 22%–73%.
As blockchain technology rapidly advances and is widely adopted in the IoMT, privacy protection has increasingly become a significant concern. Blockchain offers a new approach for securely transmitting and storing medical data through its decentralized and tamper-proof characteristics [22]. However, IoMT devices face serious privacy challenges when collecting and transmitting sensitive health data. How to effectively protect user privacy while securing data has become an urgent challenge. Garg et al. [6] introduced a novel blockchain-based scheme for authentication and key management called BAKMP-IoMT, which ensures the reliability of medical data during transmission by establishing a secret pairing key between an individual, a medical device, and a server, but it involves a large number of key management issues. In [11], Rachakonda et al. introduced the SaYoPillow system, which designs secure data transmission, storage, and communication protocols for uploading and retrieval in order to reduce malicious attacks on medical data during interaction with the blockchain, but it suffers from deficiencies in data validity validation, which may affect its security and reliability in practical applications. Nie et al. [23] proposed a novel blockchain-assisted data transfer scheme in which Bloom filters with hash functions were designed to ensure data authenticity. Meanwhile, Bhattacharjya et al. [24] used elliptic curve digital signature for signing medical information to verify the reliability of data. However, in these designs, the signer has high visibility to the specific content of the data, which may affect the effectiveness of privacy protection. To further protect the data privacy of distributed ledgers in blockchain-enabled IoMT and improve the reliability of transactions, a privacy-preserving scheme utilizing ElGamal blind signatures was proposed by Le et al. [12]. Meanwhile, Li et al. [14] introduced the concept of ‘swarm’ on the basis of blind signatures, and implemented the mechanism of co-signing by multiple entities in the blockchain, which improves the security of the signing process.
However, none of the above schemes considered security under quantum attacks, Li et al. [25] then developed a blind signature scheme using lattice assumptions to counter quantum attacks. Qu et al. [26] designed a novel quantum blockchain-based system for medical data processing (QB-IMD). The system features a quantum blockchain framework that leverages quantum signatures and authentication to guarantee data integrity and protection against tampering. The above blind signature techniques, nevertheless, are still unable to cope with the risk of key leakage, leading to the fact that even with anti-quantum blind signatures to enhance data protection, the security of historical data may still be threatened in case of key leakage. Therefore, introducing forward security in blind signatures can effectively solve this problem by periodically updating the key or using a new key in each session to ensure that past data remains secure even if the key is cracked in the future. Currently, most solutions [27–30] are based on number-theoretic assumptions or only support ordinary signatures, and thus lack security against quantum attacks.
We present the preparatory knowledge involved in the program in this section.
Definition 1. Let the matrix B=(b1,…,bn)∈Zm×n, where the vectors are linearly independent of each other. The lattice with matrix B as the basis is Λ(B):={∑i=ni=1bixi|xi∈Z}⊆Zm. (When vectors are linearly independent, it is the discrete points generated by them that cover the entire discrete space and uniquely represent any vector in the space).
Definition 2. Given a matrix A∈Zm×nq, a vector u∈Znq, the q-order integer lattice is defined as follows:
Λ⊥q(A)={x∈Zm|Ax≡0modq}(1)
Λuq(A)={x∈Zm|Ax≡umodq}(2)
Definition 3 [31]. For any parameter σ>0, x∈Rm, there is a Gaussian distribution function centred on c as ρσ,c(x)=exp(−π∥x−c∥2/σ2). Let Λ⊆Zm be a lattice, the discrete Gaussian distribution on Λ is is given by DΛ,σ,c(x)=ρs,c(x)ρσ,c(Λ).
Lemma 1(Rejection Sampling) [16, Lemma 4.5]. Given a subset V={v∈Zm:∥v∥≤T} and a real number s=ω(Tlog√m), Define a probability distribution h:V→R on V. There is a universal constant M=O(1) such that the statistical distance Δ(𝒜,ℬ):=2−ω(logm)/M between the outputs of the two algorithms is negligible.
(𝒜) With probability 1/M, output (z,v) where v←h,z←𝒟mσ.
(ℬ) With probability min (𝒟mσ(z,)M𝒟mv,σ(z),1), output (z,v) where v←h,z←𝒟mv,σ.
Moreover, the probability that 𝒜 outputs something is at least (1−2−ω(logm))/M. For any α>0 and s=αT, the constant M=e12/α+1/(2α2), Δ(𝒜,ℬ) is 2−100/M.
Lemma 2 [16]. For any v∈Zm, if s=α⋅∥v∥, where α>0, there exists a probability Pr[𝒟ms(x)/𝒟ms,v(x)≤e12/α+1/(2α2):x←𝒟ms]≥1−2−100.
TrapGen(n,m,q) [32]: Let n, q=poly(n), and m≥5nlogq be integers. There exists a polynomial-time algorithm TrapGen that outputs a pair of matrices (A∈Zn×mq,T∈Zm×m), where A is uniformly distributed over Zn×mq, and T is a basis for Λ⊥q(A) with the property that ∥T∥≤O(√nlogq).
ExtBasis(A,TA2)[21]: Let a matrix A=[A1,A2,A3]. If there exists TA2 which is a basis for Λ⊥q(A2), then there exists a deterministic polynomial-time algorithm ExtBasis that outputs a basis TA for Λ⊥q(A) such that ∥~TA∥=∥~TA2∥.
SampleKey(A,T,r,K) [33]: Given the output (A,T) of the algorithm TrapGen, a real number r>∥˜T∥, and a matrix K∈Zn×kq, there exists a polynomial-time algorithm SampleKey that outputs a random matrix S∈Zm×k such that each column S[j]∈D:{s∈Zm:∥s∥≤r√m] for all j∈[k], and A⋅S=K(modq) with overwhelming probability.
commit(M,b3)[12]: Given a message M∈{0,1}∗ and a stream of characters b3∈{0,1}n, there exists an algorithm commit with statistical hiding and computational constraints that outputs a commitment string.
3.3 Difficult Assumptions in Lattice
Definition 4 (↕2−SISq,n,m,β problem) [16]. For a random matrix A$←Zn×mq, find a vector z∈Zm{0} with Az=0(modq) and ∥z∥≤β.
Lemma 3 [34]. For any A∈Zn×mq, where m>64+n⋅logq/log(2d+1), and any random vector s$←{−d,…,0,…,d}m, the probability that there exists another vector s′∈{−d,…,0,…,d}m such that As=As′ is 1−2−100.
This section provides a formal description of the target problem addressed in this paper. We first briefly describe the system model for LFSBS. Following that, we present the LFSBS definition and security model. Details of the notations used can be found in Table 1.
An LFSBS scheme consists of the following four entities, as depicted in Fig. 1. They are the smart medical devices in the perception layer, the accounting nodes and the blockchain-enabled IoMT in the network layer and the medical personnel in the application layer.
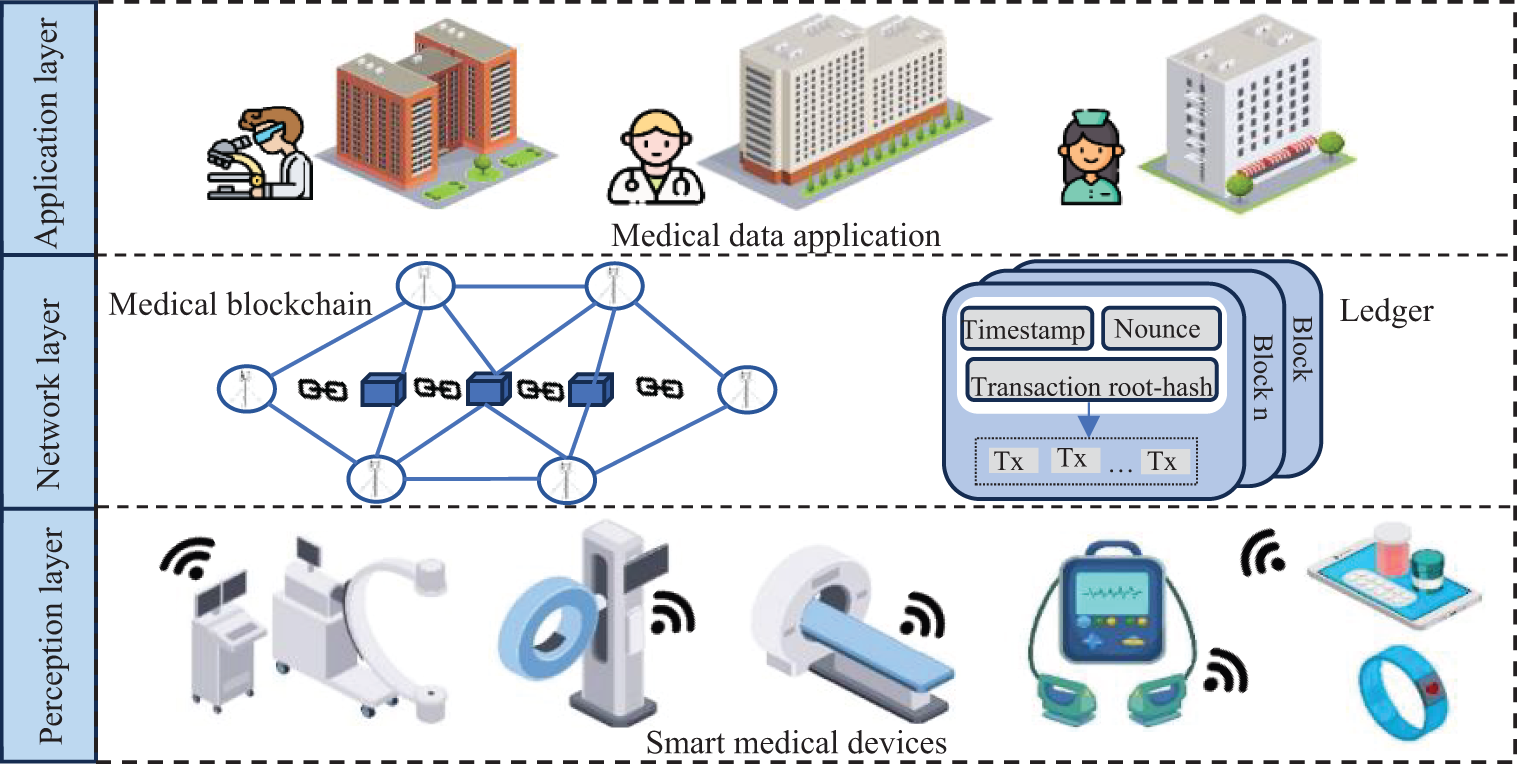
Figure 1: system model
• Smart Medical Devices: Smart medical devices monitor and record the patient’s physiological parameters, such as blood glucose and blood pressure. in real time through inbuilt sensors within the perceptual layer of the system. The raw medical data collected by these devices is initially processed to generate an electronic medical record and transmitted to the accounting node via a secure communication protocol.
• Accounting Nodes: The accounting node is responsible for ensuring the authenticity and privacy protection of the data. Upon receiving the electronic medical records, the accounting node will sign the data blindly to maintain privacy. It also ensures the non-repudiation of the signature due to the non-forgeability of the blind signature, which enhances the trustworthiness of the entire system. The master accounting node that obtains the right to establish the block broadcasts the signature data to other accounting nodes in the chain, which use the public key to verify the data with the signature. When all nodes have completed the verification, they return the results to the master accounting node, which eventually embeds the data in the transaction record and incorporates it into the blockchain network.
• Medical Blockchain Network: The medical blockchain network is responsible for storing and verifying the data. All signed data verified by the accounting node is recorded in the distributed ledger. The decentralised nature of the blockchain ensures that each piece of data cannot be tampered with after it is written and the integrity of the data is confirmed through a consensus mechanism.
• Medical Personnel: The data on the blockchain can be accessed by medical personnel through a permission management system for necessary analyses and decision making.
A set of probabilistic polynomial time (PPT) algorithms ∏LFSBS = (Setup, KeyGen, Sign, Verify) are the foundation of an LFSBS scheme, and they are defined as follows:
• (pp,pk,sk0)←Setup(1λ,1dp): is an algorithm executed by the authorised agency. It takes a security parameter λ and a binary tree depth dp as input. It outputs a public parameter pp, a public key pk, and an initial private key sk0.
• skt+1←KeyGen(pp,skt,t): is an algorithm executed by the Key Generation Centre (KGC). It takes the public parameter pp, the binary tree depth dp, and a time period t as input. It outputs a private key skt+1 for time period t+1.
• (v,S)←Sign(pp,pk,skt,t,M): is an algorithm executed by the signer. It takes the public parameter pp, the public key pk, the private key skt, the time period t, and a message M as input. It outputs a signature pair (v,S).
• value←verify(pp,pk,t,S,M): is an algorithm executed by the verifier. It takes the public parameter pp, the public key pk, the time period t, the signature S, and the message M as input. It outputs a return value value.
We introduce two security concepts for the LFSBS scheme: one is called blindness in order to ensure privacy during the signature process; the other is called forward unforgeability for the reliability of the signature.
The unforgeability of LFSBS is determined by the interaction between 𝒞 and 𝒜, where 𝒞 denotes the challenger and 𝒜 denotes the attacker.
Setup(1λ): The challenger 𝒞 provides the attacker 𝒜 with a public parameter pp, a public key pk, and a private key sk0 using the initialization algorithm.
Challenge: The attacker 𝒜 chooses two distinct messages M1 and M1 and submits them to the challenger 𝒞. Subsequently, 𝒞 randomly selects a bit b and engages with 𝒜 as a signer, resulting in the generation of two pairs of signatures (vb,Sb) and (v1−b,S1−b).
Output: 𝒜 outputs a bit b′∈{0,1}.
𝒜 will win the game described above if b=b′.
We define the advantage of the attacker in the blindness game as AdvBlindness𝒜=Pr[𝒜wins]−1/2.
Definition 1: If the AdvBlindness𝒜 can be ignored by any PPT attacker 𝒜, then the LFSBS scheme is considered perfectly blind.
4.3.2 Forward-Secure Unforgeability
The unforgeability of LFSBS is determined by the interaction between 𝒞 and 𝒜, where 𝒞 denotes the challenger and 𝒜 denotes the attacker.
Setup(1λ): The challenger 𝒞 provides the attacker 𝒜 with a public parameter pp and a public key pk using the initialisation algorithm.
Query: At a time period t, the attacker 𝒜 can adaptively perform the following polynomial-time random queries.
1) Key oracle 𝒦𝒪(t) query: The attacker 𝒜 interacts with the random oracle 𝒦𝒪 to obtain the corresponding private key skt+1 if t<ρ−1; Otherwise, it returns an empty string.
2) Hash oracle ℋ𝒪(t,M) query. The attacker 𝒜 interacts with the random oracle ℋ𝒪 to obtain the corresponding hash value.
3) Signing oracle 𝒮𝒪(t,M). query: The attacker 𝒜 interacts with the random oracle 𝒮𝒪 to obtain corresponding signature.
4) Intrusion oracle ℐ𝒪(˜t) query: The attacker 𝒜 interacts with the random oracle ℐ𝒪 to obtain corresponding private key sk˜t and transfer the gaming process to the output phase.
Output: 𝒜 outputs a signature (v∗,S∗) with a message M∗ at time period t∗.
𝒜 will win the game described above if t∗<˜t and verify(M∗,pk,S∗)=1.
We define Advunforgeability𝒜=Pr[𝒜wins].
Definition 2: If the Advunforgeability𝒜 can be ignored for any PPT attacker 𝒜, then the LFSBS scheme is considered forward-secure unforgeable.
We describe in detail the individual algorithms involved in the LFSBS scheme in this section.
The system is initialized by the authorized agency through the execution of the algorithm Setup. Initially, the agency chooses prime numbers q=ploy(n), m=O(nlogq), k1, k2, ρ=2dp−1, σ ,…,σ3, and randomly selects matrices A1←Znq, (A01,A11,…,A0dp,A1dp)←Zn×mq. To ensure system security within random oracles, the agency picks a hash function: H:{0,1}∗→{e2∈{−1,0,1}(dp+1)m,||e2||≤k2}, where H is a one-way hash function that maps strings to a vector e2. Additionally, the agency defines the commit function commit:{0,1}∗×{0,1}n→{0,1}∗ and executes the algorithm TrapGen(n,m,q), to acquire a pair of matrices (A,TA), where A∈Zn×mq and TA∈Zm×mq is the basis for Λ⊥q(A) satisfying ||~TA||≤O(√nlogq). The public key pk is the set of matrices (A,A01,A11,…,A0dp,A1dp,A1), and the private key skroot is TA. The system’s public parameters pp is generated as pp=(q,m,n,k1,k2,ρ,σ,…,σ3,H,commit).
The KGC obtains the keys of all internal nodes that can generate previous keys by executing the algorithm Keygen, which utilizes the key evolution mechanism.
Each time period ρ corresponds in order from left to right to a leaf node l in a binary tree of depth dp. For any leaf node l, there is a minimal subset of nodes, denoted as Note(l), that includes at least one ancestor node common to all leaves from l to the last leaf ρ−1, while excluding any ancestor node of any leaf from 0 to l−1. Such as using binary codes for node names as illustrated in Fig. 2. Note(l=0)={root}, Note(l=1)={01,1}, Note(l=2)={1}, Note(l=3)={11}. The private key skt, corresponding to time period t, consists of the private keys of all nodes in the minimal subset Note(l=t). As shown in Fig. 2, skroot=sk0={TA}, sk1={T01,T1}, sk2={T1}, sk3={T11}, where T01, T1, and T11 are trapdoors associated with [A||A01||A12], [A||A11] and [A||A11||A12], respectively.
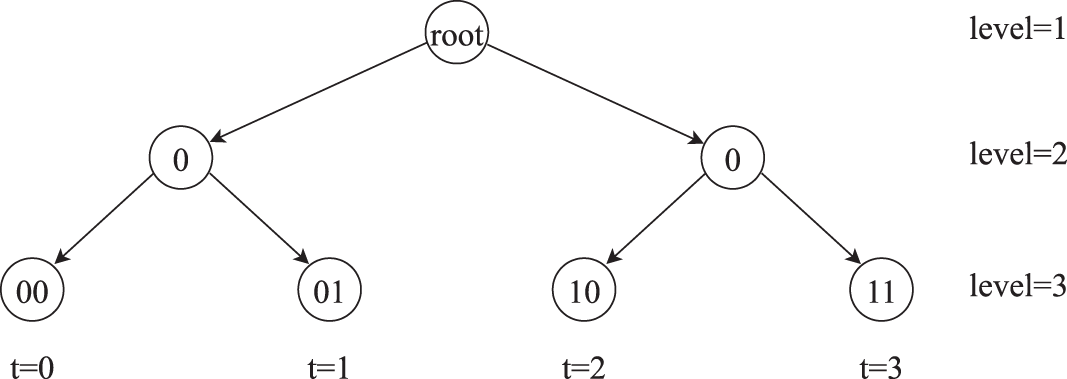
Figure 2: Binary tree with depth dp=2 and time period ρ=4
The update from the private key skt to skt+1 using the trapdoor delegation mechanism with the algorithm ExtBasis, consider a leaf node l(i) with binary representation {0,1}i. The matrix corresponding to the private key skl(i) is Tl(i), which is computed from the initial private key TA via ExtBasis(Al(i),TA), where Al(i)=[A||Al(i)1||⋯||Al(i)i]. Therefore, if the private key Tt(j) of any ancestor node from time period t(i) is known, along with the associated matrix At(j), it is possible to derive the private key of Tt(i), provided that t(j)<t(i).
The accounting node acts as a signer generates the signature by interacting with the user executing the algorithm Sign. The interactive process is as follows:
Step 1: The signer first constructs a matrix At(i) = [A||At(i)1||⋯||At(i)dp]∈Zn×(dp+1)mq for time period t(i). The signer then uses the algorithm SampleKey to obtain a temporary private key SKt, which satisfies At(i)⋅SKt=A1. Next, the signer calculates x∈Znq=At(i)r after sampling the vector r∈Z(i+1)×m←D(i+1)×mσ2, and sends x to the user.
Step 2: The user obtains the vector x and samples random vectors as follows: b1←D(dp+1)mσ3,b2←D(dp+1)mσ1, and b3←{0,1}n. The user then computes the hash value h=H(d,c), where vector d=At(i)b1+x(modq) and c=commit(M,b3). Rejection sampling is subsequently employed to obtain the blinded challenge e=h+b2, which is then returned to the signer with probability min{1,Dmσ1(e)N1⋅Dmσ1,h(e)}.
Step 3: The signer computes the blind signature s=SKt+e+r, employing rejection sampling to confirm that the distribution of s is consistent with that of r. The signature s is then sent back to the user with probability min{1,D(dp+1)mσ2(s)N2⋅D(dp+1)mσ2,SKte(s)}.
Step 4: The user receives a blind signature s and employs rejection sampling to compute the corresponding unblinded signature us=s+b1 with probability min{1,D(dp+1)mσ3(us)N3⋅D(dp+1)mσ3,s(us)}, ensuring us and s remain independent of each other. If ∥us∥<σ3√(dp+1)m) holds true, the user returns the final signature S=(b2,b3,h,us) to the signer, with result=′′valid′′. Otherwise, it outputs result=(b1,b2,h,c).
Step 5: If the result=′′valid′′, output (v=(r,e,s),S). Otherwise, the signer performs the following checks and re-executes the signature algorithm. First, calculates d=At(i)b1+A1b2+x(modq) and d′=At(i)b1−A1h+At(i)s(modq). Then, verifies whether e−b2=h=H(d′,c) and ∥s+b1∥≥σ3√(dp+1)m). If these conditions are satisfied, revert to Step 1.
The validity of the signature S is checked by the verifier by executing the algorithm Verify. Initially, the verifier constructs the matrix At(i) = [A||At(i)1||⋯||At(i)dp] associated with t(i) and computes h′=H(At(i)(us−b2−h)−A1(modq),commit(M,b3)). The verifier returns 1 if both h=h′ and ∥us∥≤σ3√(1+dp)m are satisfied; otherwise, it returns 0.
In this section, we provide a comprehensive assessment of the security of the LFSBS scheme with respect to the following three aspects: correctness, blindness, and forward-secure unforgeability.
According to Lemma 2, the probability of Dms(x)/Dms,v(x)≤e12/12+1/(2⋅122) is guaranteed to be at least 1−1/2100. Lemma 1 shows that rejection sampling necessitates Dms(x)/(N⋅Dms,c(x))≤1, which means that this condition holds only if N≥e1+1/288. Therefore, the signature algorithm generates a valid signature at most e3 times repeatedly. Given a valid signature S=(b3,h,us), we have:
At(i)(us−b2−h)−A1(modq)=At(i)s+At(i)b1−At(i)b2−At(i)h−A1(modq)=At(i)(SKt+e+r)+At(i)b1−At(i)b2−At(i)(e−b2)−A1(modq)=A1+At(i)e+At(i)r+At(i)b1−At(i)b2−At(i)e+At(i)b2−A1(modq)=x+At(i)b1(modq)=d(3)
Assuming that an adversary 𝒜 is unable to discriminate between blind signatures created by different messages, the proposed technique fulfills blindness. H is a hash function resistant to collisions, while commit is a statistically hidden commitment function.
Proof. In the following, we employ users u0 and u1 as challengers 𝒞 to interact with adversary 𝒜 played by the signer.
Initialization. The adversary 𝒜 selects the security parameter λ, the binary tree depth dp and executes the function Setup to obtain a public parameter pp along with the public and initial private keys.
Challenge: Adversary 𝒜 initially selects time periods t0 and t1, where t0 and t1 are not necessarily distinct. The adversary then obtains private keys skt0 and skt1, which correspond to the outputs of the algorithm KeyGen, along with distinct messages M0 and M1. 𝒜 relays these messages to challenger 𝒞, who then randomly picks a bit b∈{0,1} and uses the algorithm Sign to interactively sign the messages with adversary 𝒜, resulting in the signatures (Sb=(b2b,b3b,hb,usb),vb=(rb,eb,sb)) and ((S1−b=(b21−b,b31−b,h1−b,us1−b),v1−b=(r1−b,e1−b,s1−b)).
Analysis: The adversary 𝒜 constructs the blind signatures (rb,r1−b) and (sb,s1−b) using the signature algorithm. Since these signatures are self-generated, they are disregarded in the analysis. Additionally, the rejection sampling ensures that (eb,e1−b) and (usb,us1−b) follow the same distributions D(dp+1)mσ1, and D(dp+1)mσ3 respectively. The random sampling of the blind factors, coupled with the hash function H possessing the one-way collision-resistant property, implies that the adversary 𝒜 cannot extract valid information from (b2b,b21−b), (b3b,b31−b) and (hb,h1−b). Even if the adversary 𝒜 receives the result=(b1,b2,h,c) and restarts the signature process at Step 5, this does not increase the adversary’s chances of winning the game. This can be attributed to the fact that the blind factors b1 and b2 are generated through fresh random sampling by the user, while c is obtained by statistically concealing the commitment function commit. In summary, adversary 𝒜 is unable to establish a correlation between the signature and the message.
6.3 Forward-Secure Unforgeability
Assuming an adversary 𝒜 can break the forward-secure unforgeability of the proposed scheme with non-negligible probability using randomized oracle queries, then a polynomial-time algorithm B will exist that can solve the l2−SISq,n,(1+2dp)m problem with probability: β=max{(σ2+2σ3)√(1+dp)m,2(σ3+σ1+1)√(1+dp)m}.
Proof. Consider an instance of the l2_SISq,n,(1+2dp)m problem is given by the equation A⋅z=0modq with ∥z∥≤β, where A=[A0||U01||U11||⋯||U0dp||U1dp]∈Zn×(1+2dp)mq and z∈Z(1+2dp)mq. Algorithm B will succeed in solving this instance if it can find a non-zero integer vector z.
Initialization. Algorithm B sets a public parameter pp according to the initialization algorithm Setup, and defines the public key as follows. For each i≤dp, At∗ii=Ut∗ii, B obtains (Abi,TAbi) by executing algorithm TrapGen for each bit b where b≠t∗i. Then B sets A1=At(i)⋅SKt, where SKt∗←D(1+dp)mσ, At(i) = [A||At(i)1||⋯||At(i)dp]∈Zn×(dp+1)mq. Subsequently, B sends the public parameter pp and the public key pk to the adversary 𝒜 while keeping SKt∗ secret. Finally, B maintains an initially empty table T for storing random predictor queries (d,c) and their corresponding hash value h, and prepares a set of values {h1,…,hiH}←SH in response to the hash queries.
Queries:
Algorithm B acts as a signer and interacts with adversary 𝒜 to form a signature. Adversary 𝒜 is allowed to perform these specific oracle queries to B.
Key oracle 𝒦𝒪(t(i)). If t(i)∗≥t(i), the query is aborted, where t(j)=(t1,…,tdp). Otherwise, B identifies k1 as the minimum index with k1≤i and tk1≠t∗k1. Subsequently, B obtains the matrix Ttk1←ExtBasis(At(k1),TAtk1k1) associated with the private key sktk1, where At(k1)=[A||At11||⋯||Atk1k1].
Hash oracle ℋ𝒪(d,c). Upon receiving a hash query request from adversary 𝒜, algorithm B first checks if the hash value corresponding to (d,c) is already present in the table T. If it is, B sends corresponding hash value to 𝒜. If not, B selects the first unused hash value hi from the set {h1,…,hiH}, sends hi to 𝒜, and updates table T at the same time.
Signing oracle 𝒮𝒪(t(i),M). If t(i)∗≠t(i), algorithm B computes TAt(i)←ExtBasis(At(i),TAtk1k1) and SKt(i)←SampleKey(At(i),TAt(i),σ,A1), where At(i)=[A||At11||⋯||Atdpdp]. Otherwise, B sets SKt(i)∗=SKt(i)∗.
Intrusion queries (TQ(t(i)))). If t(i)<t(i)∗, B aborts the query. Otherwise, B sets the intrusion time ˜t(i)←t(i), calculates the corresponding private key sk˜t(i), and provides it to 𝒜.
Output: 𝒜 Output of falsified data: (t1(i)∗,M∗1,S∗1=(b∗31,b∗21,h∗1,us∗1)), where h∗1=H(At(i)∗(us∗1−b∗21−h∗1)−A1(modq),commit(M∗1,b∗31)). B accepts the signature if t1(i)∗=t(i)∗.
Analysis: Let i denote the target fork index with i≤iH and hi=h∗1. B employs a backtracking strategy to retain the set {h1,…,hi−1} and selects a fresh set {h′i,…,h′iH}. Together, they form the returned set {h1,…,hi−1,h′i,…,h′iH} for the hash query. Similarly, 𝒜 outputs a new signature (t2(i)∗,M∗2,S∗2=(b∗32,b∗22,h∗2,us∗2)) via the above oracle, where h∗2=h′i. If t2(i)∗≠t(i)∗ or h∗2=h∗1, then B aborts. If h∗2≠h∗1, B returns the data pair (At(i)∗(us∗1−b∗21−h∗1)−A1(modq),commit(M∗1,b∗31), At(i)∗(us∗2−b∗22−h∗2)−A1(modq),commit(M∗2,b∗32)). Additionally, we have At(i)∗˜v=0(modq), where ˜v=(us∗1−us∗2+b∗22−b∗21+h∗2−h∗1), since the data pair originates from the consent hash query and the commitment function is binding. According to Lemma 3, there exists at least one key SK′ such that At(i)∗SK∗=At(i)∗SK′ with SK′≠SK∗. Therefore, at least one ˜v≠0 exists with At(i)∗˜v=0(modq). Note that ∥b2∗{1,2}∥≤σ1√(1+dp)m, ∥us∗{1,2}∥≤σ3√(dp+1)m, ||h∗{1,2}||≤√(dp+1)m. Therefore, ∥˜v∥≤2(σ3+σ1+1)√(1+dp)m.
In the following we consider the case where adversary 𝒜 forges a signature by restarting the signature interaction. Specifically, when A returns result=(b1,b2,h,c) to B, B can only restart the interaction with 𝒜 if h=(At(i)∗(us−b2−h)−A1(modq),c). Suppose adversary 𝒜 successfully produces a valid signature ˆS=(^b2^,b3,ˆh,^us) after passing ^result=(^b1,^b2,ˆh,ˆc) to B. This implies that the following equation must hold: e−^b2=ˆh=H(At(i)∗b1+x(modq),c)=H(At(i)∗(^us−^b2−ˆh)−A1(modq),commit(M∗,^b3)), where ∥^us∥≤σ3√(1+dp)m. If ˆh≠h, then B aborts. Otherwise, we have At(i)∗^us(modq)=At(i)∗b1+At(i)∗s(modq), leading to At(i)∗ˆv(modq)=0, where ˆv=b1+s−^us≠0. If ˆv=0, then ∥b1+s∥=∥^us∥≤λσ3√m, which contradicts ∥s+b1∥≥σ3√(dp+1)m) from Step 5. Therefore, ∥ˆv∥≤∥b1∥+∥s∥+∥^us∥≤(2σ3+σ2)√(1+dp)m. Finally, we obtain the matrix A by inserting the correlation matrix U1−t∗ii into the matrix At(i)∗. Similarly, the vector v is derived by inserting the element 0 into the corresponding position of the vector ˆv. Thus we obtain an instantiation of the SIS problem l2_SISq,n,(1+2i)m. The probability of solving it successfully is given by β=max{(σ2+2σ3)√(1+dp)m,2(σ3+σ1+1)√(1+dp)m}.
7 Performance Evaluation and Comparison
We conducted a thorough experimental evaluation of the LFSBS and compared its performance with other schemes. All experiments were carried out on a Windows 11 operating system using an 11th Gen Intel(R) Core(TM) i5-8250U @ 1.60 GHz processor and 12 GB of RAM. The LFSBS scheme was fully implemented in the Python. Finally, the relevant parameter settings involved in the experiment are presented in Table 2.
We assessed the effectiveness of our LFSBS scheme in this section, particularly focusing on the signature generation and verification algorithms, as these are the most time-consuming operations in LFSBS.
We assessed the computational overhead associated with the Sign and Verify algorithms within LFSBS. Additionally, we evaluate the computational efficiencies of LFSBS with those of other schemes during the signing and verification processes, including cutting-edge lattice-based blind signature schemes [9,35,36]. As shown in Table 3.
7.1.2 Storage and Communication Overhead
In our LFSBS scheme, both public and private keys are composed of matrices. We evaluated the storage and communication costs of the Sign and Verify algorithms by determining the dimensions of the public key, private key and signature, as detailed in Table 4.
We compare four schemes in terms of blindness, quantum resistance and unforgeability, respectively in the Table 5. It’s evident that our scheme offers functional advantages and improved feasibility.
We provide an analytical comparison of the performance with the current lattice-based blind signatures schemes [9,35,36] in this section.
The running times of the verification and signature algorithms for our LFSBS scheme and those suggested in [9,35,36] are shown in Fig. 3. As shown, our LFSBS scheme outperforms the others significantly. For example, when n = 25, the signature and verification times for our scheme are 2.15 and 0.04 s, respectively. In comparison, the signature and verification algorithms of the schemes proposed in [9,35,36] take the following times: [35] takes 7.45 s for signature and 0.67 s for verification, [36] takes 3.02 s for signature and 0.14 s for verification, and [9] takes 2.67 s for signature and 0.15 s for verification. Therefore, we conclude that our LFSBS scheme is approximately 1.2× to 3.4× faster for signature algorithms and 3.5× to 16× faster for verification algorithms compared to those in [9,35,36]. As shown by the total computation time in Fig. 3. our LFSBS scheme is more efficient in generating signatures and verifying them than other schemes. In addition, we introduce a forward-secure key evolution mechanism to further enhance the key security.
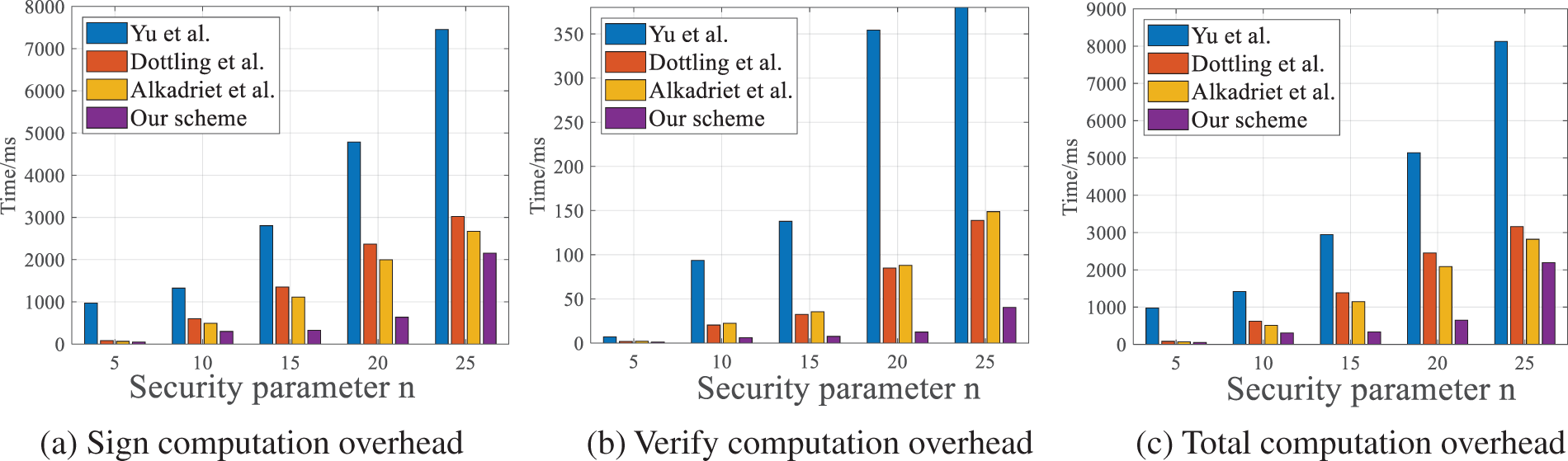
Figure 3: Comparison of the computation overhead associated with the attributes between our LFSBS and current lattice-based blind signature schemes [9,35,36]
In summary, our LFSBS scheme exhibits higher efficiency in signature generation and verification compared to existing lattice-based blind signature schemes. In addition, the scheme is not only resistant to attacks from quantum computers, but also possesses forward security, which better ensures the long-term security of the system and the integrity of the data.
The LFSBS designed in this paper is an anti-quantum blind signature scheme with forward security for BIoMT, which provides blind signatures for auditing users in BIoMT to protect medical information. Meanwhile, we introduce forward security to prevent key leakage and rely on lattice cryptography to defend against potential attacks from quantum computing. Experimental results show that the overhead of the algorithms in this scheme is effective for medical data sharing scenarios. In the future, we would like to further experiment this scheme in real BIoMT environments to ensure its performance and stability in real applications.
Acknowledgement: The authors extend their gratitude to the members of the research group for their invaluable support.
Funding Statement: This work was funded by the Yunnan Key Laboratory of Blockchain Application Technology (202105AG070005, 202305AG340008) & YNB202301, NSFC (Grant Nos. 72293583, 72293580, 62476007, 62176273, 62271234), and the Open Foundation of State Key Laboratory of Networking and Switching Technology (Beijing University of Posts and Telecommunications) (SKLNST-2024-1-06), the Project of Science and Technology Major Project of Yunnan Province (202302AF080006), Open Foundation of State Key Laboratory of Public Big Data (Guizhou University) under Grant No. PBD2022-16, Double First-Class Project for Collaborative Innovation Achievements in Disciplines Construction in Heilongjiang Province under Grant No. GXCG2022-054.
Author Contributions: The authors confirm their contributions to the paper as follows: study conception, design, simulation, analysis, interpretation of results and draft manuscript preparation: Gang Xu, Xinyu Fan, Xin Liu; interpretation of results and draft manuscript preparation: Xiu-Bo Chen, Zongpeng Li, Yanhui Mao, Kejia Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data is unavailable due to the nature of this research; participants did not provide consent for their data to be publicly shared. Therefore, supporting data is not accessible.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. X. Chen, S. Xu, Y. He, Y. Cui, J. He and S. Gao, “LFS-AS: Lightweight forward secure aggregate signature for e-health scenarios,” in IEEE Int. Conf. Commun., Seoul, Republic of Korea, 2022, pp. 1239–1244. [Google Scholar]
2. C. Li et al., “Efficient privacy-preserving in IoMT with blockchain and lightweight secret sharing,” IEEE Internet Things J., vol. 10, no. 24, pp. 22051–22064, 2023. doi: 10.1109/JIOT.2023.3296595. [Google Scholar] [CrossRef]
3. X. Chen, S. Xu, T. Qin, Y. Cui, S. Gao and W. Kong, “AQ-ABS: Anti-quantum attribute-based signature for EMRs sharing with blockchain,” in IEEE Wireless Commun. Netw. Conf. (WCNC), Austin, TX, USA, 2022, pp. 1176–1181. [Google Scholar]
4. G. Xu et al., “PPSEB: A postquantum public-key searchable encryption scheme on blockchain for E-healthcare scenarios,” Secur. Commun. Netw., vol. 2022, no. 1, 2022, Art. no. 3368819. doi: 10.1155/2022/3368819. [Google Scholar] [CrossRef]
5. J. Miao, Z. Wang, Z. Wu, X. Ning, and P. Tiwari, “A blockchain-enabled privacy-preserving authentication management protocol for Internet of Medical Things,” Expert. Syst. Appl., vol. 237, 2024, Art. no. 121329. doi: 10.1016/j.eswa.2023.121329. [Google Scholar] [CrossRef]
6. N. Garg, M. Wazid, A. K. Das, D. P. Singh, J. J. Rodrigues and Y. Park, “BAKMP-IoMT: Design of blockchain enabled authenticated key management protocol for internet of medical things deployment,” IEEE Access, vol. 8, pp. 95956–95977, 2020. doi: 10.1109/ACCESS.2020.2995917. [Google Scholar] [CrossRef]
7. S. Xu, X. Chen, Y. Guo, S. Yiu, S. Gao and B. Xiao, “Efficient and secure post-quantum certificateless signcryption for internet of medical things,” Crypt. ePrint Arch., vol. 2024, 2024, Art. no. 965. [Google Scholar]
8. S. F. Ahmed, M. S. B. Alam, S. Afrin, S. J. Rafa, N. Rafa and A. H. Gandomi, “Insights into Internet of Medical Things (IoMTData fusion, security issues and potential solutions,” Inf. Fusion, vol. 102, 2024, Art. no. 102060. doi: 10.1016/j.inffus.2023.102060. [Google Scholar] [CrossRef]
9. N. A. Alkadri, Nabil, R. E. Bansarkhani, and J. Buchmann, “BLAZE: Practical lattice-based blind signatures for privacy-preserving applications,” in Int. Conf. Financial Cryptog. Data Secur., Kota Kinabalu, Malaysia, 2020, pp. 484–502. [Google Scholar]
10. G. Xu, F. Yun, S. Xu, Y. Yu, X. Chen and M. Dong, “A blockchain-based log storage model with efficient query,” Soft Comput., vol. 27, no. 19, pp. 13779–13787, 2023. doi: 10.1007/s00500-023-08975-3. [Google Scholar] [CrossRef]
11. L. Rachakonda, A. K. Bapatla, S. P. Mohanty, and E. Kougianos, “SaYoPillow: A blockchain-enabled, privacy-assured framework for stress detection, prediction and control considering sleeping habits,” 2020, arXiv:2007.07377. [Google Scholar]
12. H. Le, D. H. Duong, and W. Susilo, “A blind ring signature based on the short integer solution problem,” in Inform. Secur. Appl: 20th Int. Conf., WISA 2019, Jeju Island, Republic of Korea, Aug. 21–24, 2019, pp. 92–111. [Google Scholar]
13. Y. Sun, J. Liu, K. Yu, M. Alazab, and K. Lin, “PMRSS: Privacy-preserving medical record searching scheme for intelligent diagnosis in IoT healthcare,” IEEE Trans. Ind. Inform., vol. 18, no. 3, pp. 1981–1990, 2021. doi: 10.1109/TII.2021.3070544. [Google Scholar] [CrossRef]
14. C. Li, B. Jiang, Y. Guo, and X. Xin, “Efficient group blind signature for medical data anonymous authentication in blockchain-enabled IoMT,” Comput. Mater. Contin., vol. 76, no. 1, pp. 591–606, 2023. doi: 10.32604/cmc.2023.038129. [Google Scholar] [CrossRef]
15. M. Bhavin, S. Tanwar, N. Sharma, S. Tyagi, and N. Kumar, “Blockchain and quantum blind signature-based hybrid scheme for Healthcare 5.0 applications,” J. Inf. Secur. Appl., vol. 56, 2021, Art. no. 102673. doi: 10.1016/j.jisa.2020.102673. [Google Scholar] [CrossRef]
16. V. Lyubashevsky, “Lattice signatures without trapdoors,” in Annual Int. Conf. Theory Appl. Cryptograph. Tech., Cambridge, UK, Apr. 15–19, 2012, pp. 738–755. [Google Scholar]
17. G. Xu et al., “A model value transfer incentive mechanism for federated learning with smart contracts in AIoT,” IEEE Internet Things J., 2024. doi: 10.1109/JIOT.2024.3468443. [Google Scholar] [CrossRef]
18. S. Xu, Y. Cao, X. Chen, Y. Zhao, and S. Yiu, “Post-quantum public-key authenticated searchable encryption with forward security: General construction, and applications,” in Int. Conf. Inform. Secur. Crypt., Hangzhou, China, Dec. 9–10, 2023, pp. 274–298. [Google Scholar]
19. S. H. Islam, R. Amin, G. P. Biswas, M. S. Obaidat, and M. K. Khan, “Provably secure pairing-free identity-based partially blind signature scheme and its application in online e-cash system,” Arab. J. Sci. Eng., vol. 41, no. 8, pp. 3163–3176, 2016. doi: 10.1007/s13369-016-2115-5. [Google Scholar] [CrossRef]
20. J. Howe, T. Pöppelmann, M. O’neill, E. O’sullivan, and T. Güneysu, “Practical lattice-based digital signature schemes,” ACM Trans. Embed. Comput. Syst., vol. 14, no. 3, pp. 1–24, 2015. doi: 10.1145/2724713. [Google Scholar] [CrossRef]
21. S. Agrawal, D. Boneh, and X. Boyen, “Efficient lattice (H)IBE in the standard model,” in Adv. Crypt.–EUROCRYPT 2010: 29th Annual Int. Conf. Theory Appl. Cryptog. Tech., Riviera, French, May 30–Jun. 3, 2010, pp. 553–572. [Google Scholar]
22. X. Chen, S. Xu, Y. Cao, Y. He, and K. Xiao, “AQRS: Anti-quantum ring signature scheme for secure epidemic control with blockchain,” Comput. Netw., vol. 224, 2023, Art. no.109595. doi: 10.1016/j.comnet.2023.109595. [Google Scholar] [PubMed] [CrossRef]
23. X. Nie, A. Zhang, J. Chen, Y. Qu, and S. Yu, “Blockchain-empowered secure and privacy-preserving health data sharing in edge-based IoMT,” Secur. Commun. Netw., vol. 2022, no. 1, 2022, Art. no. 8293716. doi: 10.1155/2022/8293716. [Google Scholar] [CrossRef]
24. A. Bhattacharjya, K. Kozdrój, G. Bazydło, and R. Wisniewski, “Trusted and secure blockchain-based architecture for Internet-of-Medical-Things,” Electronics, vol. 11, no. 16, 2022, Art. no. 2560. doi: 10.3390/electronics11162560. [Google Scholar] [CrossRef]
25. C. Li, Y. Tian, X. Chen, and J. Li, “An efficient anti-quantum lattice-based blind signature for blockchain-enabled systems,” Inf. Sci., vol. 546, no. 6, pp. 253–264, 2021. doi: 10.1016/j.ins.2020.08.032. [Google Scholar] [CrossRef]
26. Z. Qu, Y. Meng, B. Liu, G. Muhammad, and P. Tiwari, “QB-IMD: A secure medical data processing system with privacy protection based on quantum blockchain for IoMT,” IEEE Internet Things J., vol. 11, no. 1, pp. 40–49, 2021. doi: 10.1109/JIOT.2023.3285388. [Google Scholar] [CrossRef]
27. M. Drijvers and G. Neven, “Forward-secure multi-signatures,” Crypt. ePrint Arch., vol. 2019, 2019, Art. no. 261. [Google Scholar]
28. M. Abdalla, F. Benhamouda, and D. Pointcheval, “On the tightness of forward-secure signature reductions,” J. Cryptol., vol. 32, no. 1, pp. 84–150, 2019. doi: 10.1007/s00145-018-9283-2. [Google Scholar] [CrossRef]
29. Q. Xue, Z. Lu, and T. Zhang, “Attribute-based proxy signature scheme with dynamic strong forward security,” Int. J. Sens. Netw., vol. 44, no. 4, pp. 214–225, 2024. doi: 10.1504/IJSNET.2024.138518. [Google Scholar] [CrossRef]
30. J. Lee, J. E. Kim, and H. K. Oh, “Forward-secure multi-user aggregate signatures based on zk-SNARKs,” IEEE Access, vol. 9, pp. 97705–97717, 2021. doi: 10.1109/ACCESS.2021.3093925. [Google Scholar] [CrossRef]
31. S. Xu et al., “Lattice-based public key encryption with authorized keyword search: Construction, implementation, and applications,” Crypt. ePrint Arch., vol. 2023, 2023, Art. no. 1715. [Google Scholar]
32. C. Ma, H. Gao, and B. Hu, “Ciphertext policy attribute-based encryption scheme supporting Boolean circuits over ideal lattices,” J. Inf. Secur. Appl., vol. 84, 2024, Art. no. 103822. doi: 10.1016/j.jisa.2024.103822. [Google Scholar] [CrossRef]
33. S. Xu, X. Chen, C. Wang, Y. He, K. Xiao and Y. Cao, “A lattice-based ring signature scheme to secure automated valet parking,” in Int. Conf. Wireless Algor., Syst. Appl., Nanjing, China, Jun. 25–27, 2021, pp. 70–83. [Google Scholar]
34. H. Q. Le et al., “Lattice blind signatures with forward security,” in Inform. Secur. Priv.: 25th Australasian Conf., ACISP 2020, Perth, Australia, Nov. 30–Dec. 2, 2020, pp. 3–22. [Google Scholar]
35. H. Yu and L. Baim, “Post-quantum blind signcryption scheme from lattice,” Front. Inform. Techn. Elect. Eng., vol. 22, no. 6, pp. 891–901, 2021. doi: 10.1631/FITEE.2000099. [Google Scholar] [CrossRef]
36. N. A. Alkadri, N. Dottling, and S. Pu, “Practical lattice-based distributed signatures for a small number of signers,” in Int. Conf. App. Crypt. Netw. Secur., Abu Dhabi, United Arab Emirates, Mar. 01, 2024, pp. 367–402. [Google Scholar]
37. E. Crites, C. Komlo, M. Maller, S. Tessaro, and C. Zhu, “Snowblind: A threshold blind signature in pairing-free groups,” in Annual Int. Crypt. Conf., Santa Barbara, CA, USA, Aug. 09, 2023, pp. 710–742. [Google Scholar]
38. G. Xu et al., “A novel post-quantum blind signature for log system in blockchain,” Comput. Syst. Sci. Eng., vol. 41, no. 3, pp. 945–958, 2022. doi: 10.32604/csse.2022.022100. [Google Scholar] [CrossRef]
Cite This Article
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Downloads
Citation Tools
