 Open Access
Open Access
ARTICLE
A Trusted Distributed Oracle Scheme Based on Share Recovery Threshold Signature
1 He’nan Province Key Laboratory of Information Security, Zhengzhou, 450000, China
2 School of Cyberspace Security, Zhengzhou University, Zhengzhou, 450000, China
* Corresponding Author: Xuehui Du. Email:
Computers, Materials & Continua 2025, 82(2), 3355-3379. https://doi.org/10.32604/cmc.2024.059722
Received 15 October 2024; Accepted 05 December 2024; Issue published 17 February 2025
Abstract
With the increasing popularity of blockchain applications, the security of data sources on the blockchain is gradually receiving attention. Providing reliable data for the blockchain safely and efficiently has become a research hotspot, and the security of the oracle responsible for providing reliable data has attracted much attention. The most widely used centralized oracles in blockchain, such as Provable and Town Crier, all rely on a single oracle to obtain data, which suffers from a single point of failure and limits the large-scale development of blockchain. To this end, the distributed oracle scheme is put forward, but the existing distributed oracle schemes such as Chainlink and Augur generally have low execution efficiency and high communication overhead, which leads to their poor applicability. To solve the above problems, this paper proposes a trusted distributed oracle scheme based on a share recovery threshold signature. First, a data verification method of distributed oracles is designed based on threshold signature. By aggregating the signatures of oracles, data from different data sources can be mutually verified, leading to a more efficient data verification and aggregation process. Then, a credibility-based cluster head election algorithm is designed, which reduces the communication overhead by clarifying the function distribution and building a hierarchical structure. Considering the good performance of the BLS threshold signature in large-scale applications, this paper combines it with distributed oracle technology and proposes a BLS threshold signature algorithm that supports share recovery in distributed oracles. The share recovery mechanism enables the proposed scheme to solve the key loss issue, and the setting of the threshold value enables the proposed scheme to complete signature aggregation with only a threshold number of oracles, making the scheme more robust. Finally, experimental results indicate that, by using the threshold signature technology and the cluster head election algorithm, our scheme effectively improves the execution efficiency of oracles and solves the problem of a single point of failure, leading to higher scalability and robustness.Keywords
Nomenclature
| The credibility of oraclei | |
| The initial value of ci | |
| SK | The general private key of the oracle set |
| The private key of oraclei | |
| The key share fragment from oraclei to oraclej | |
| H(m) | The hash result of message m |
| The aggregate signature for H(m) of the oracle set | |
| The signature for H(m) of oraclei | |
| The professional experience of oraclei | |
| The performance score of oraclei | |
| The data acquisition capability of oraclei | |
| PK | The general public key of the oracle set |
| The public key of oraclei |
Currently, the decentralization and the immutability of the blockchain have gradually attracted attention, and blockchain has been widely used in various fields, such as data tamper prevention [1,2], data reliable transmission protection [3], and data traceability management. Although the smart contract of blockchain can verify and execute the terms of the agreement automatically in the blockchain environment [4], but the usability of smart contracts is primarily limited to on-chain data without access to the external systems (i.e., off-chain) where real-world data and events reside. This connectability to off-chain data for smart contracts and blockchain is an open practical problem referred to as the “oracle problem” and is defined as how real-world data can be transferred into/from the blockchain. Hence, blockchain oracle mechanism is introduced and implemented in the form of application programming interfaces connecting the real world to the blockchain for mitigating such a limitation [5].
Oracle can obtain data from the real world and transmit it to the blockchain smart contract. As a middleware connecting the two parties, its responsibility is to respond to data requests of smart contracts and then access data sources to obtain data in the real world and transmit reliable data to the blockchain. After the smart contract obtains the data transmitted by the oracle, it can perform operations on these data. Therefore, the reliability of the data provided by the oracle directly affects the credibility of the implementation of the smart contract.
Centralized oracle [6,7] has been widely used in the first wave of blockchain applications because of its high execution efficiency and low cost. However, with the extensive application of blockchain, the problems of centralized oracles also appear. First, the centralized oracle needs the support of a centralized platform, which violates the decentralization of blockchain. Second, the centralized oracle may suffer from a single point of failure [8], and it is difficult to guarantee the quality of the data. The distributed oracle can solve the above problems, so it has attracted much attention from researchers.
The distributed oracle employs the multi-point deployment mechanism, which combines multiple oracle agencies into one oracle set and makes them undertake the data acquisition task together. When a smart contract issues a data request, the oracle agencies in the whole oracle set obtain data from their own data sources and respond to the data request after data verification and data aggregation. Attributed to the multi-point deployment, the distributed oracle scheme avoids the dependence on a single oracle and eliminates the risk of a single point of failure. Meanwhile, compared with the centralized oracle, data from multiple oracles has stronger reliability and accuracy after verification and aggregation, so smart contracts can be supported by more reliable data.
At present, many achievements have been made in the study of distributed oracles [9–11]. However, there are many problems in existing distributed oracle schemes. First, the existing distributed oracle schemes do not validate the obtained data off-chain, but instead transfer the data directly to the blockchain, which cause a large burden of data validation for the blockchain, resulting in low execution efficiency. Second, these schemes blindly feed data to the blockchain without effective data screening mechanisms, which makes many redundant or invalid data transferred from the oracle to the blockchain, resulting in high communication costs. Third, these schemes lack effective key recovery mechanism, which is difficult to deal with the case of key loss, resulting in poor robustness.
To solve the problems with distributed oracles, this paper proposes a trusted distributed oracle scheme based on threshold signature with share recovery mechanism. The main contributions of this paper are as follows:
1. A data verification method of distributed oracle is designed based on threshold signature, and the data verification of the oracle is integrated into the signature aggregation stage of the threshold signature. The verification results of the data are determined by the signature aggregation results, which avoids the frequent and complicated interaction between multiple nodes during data verification, improving the efficiency of data verification. Meanwhile, the threshold signature technology needs just threshold number of oracles to complete the signature aggregation. This reduces the time cost and avoids efficiency reduction caused by waiting, making the proposed oracle scheme more robust and expandable.
2. A credibility-based cluster head election algorithm is designed. The algorithm defines the responsibilities of each oracle and assigns the functions of data acquisition, data verification, data aggregation, and data transmission to different oracles, leading to reliable and efficient data summaries. Also, the algorithm introduces the evaluation and stimulation mechanism to evaluate the whole process of the distributed oracle, and it implements rewards and punishments according to the evaluation results, thereby providing support for constructing a dynamic and reasonable hierarchical technical architecture of distributed oracles.
3. Based on the Boneh-Lynn-Shacham (BLS) signature, a BLS share recovery threshold signature algorithm is designed. All oracles in the algorithm execute as signers and finish the key share generation, message signing, and signature verification in a distributed way. When the algorithm generates the key share by using a secret sharing method, a share recovery mechanism is integrated. The oracle can follow the mechanism to send the share recovery request and recover the key share by receiving the response from other oracles.
The rest of the paper is organized as follows: Section 2 summarizes the related works on the oracle and mainly introduces distributed oracle schemes. Section 3 presents the background knowledge and mathematical principles used in this paper. In Section 4, the framework, design details, and function of the proposed scheme are introduced in detail. In Section 5, the BLS share recovery threshold signature algorithm is described in detail. Then, experimental results are analyzed in Section 6, and the safety of the proposed scheme is proved in Section 7. Finally, Section 8 summarizes this paper.
Blockchain oracle can be divided into centralized oracle and distributed oracle according to the deployment mode. The former relies on a single oracle to obtain data from the data source and complete the data verification task, while the latter adopts multi-point deployment of oracles and relies on multiple oracles to complete the data acquisition and data verification tasks.
As a verification data feed oracle system based on Trusted Execution Environment (TEE), Town Crier uses a hardware-based security enclave to verify data integrity. It employs the Software Guard Extensions (SGX) of Intel to generate a digital signature, and by verifying this digital signature, it can prove that the Town Crier instance is securely running in the SGX security zone, thereby guaranteeing that the instance has not been tampered with and the data sent by Town Crier is reliable.
Provable [12], another representative centralized oracle scheme, provides centralized data transfer services for platforms such as Ethereum, EOS, and Hyperledger Fabric, and it is responsible for ensuring the security of the data transport layer of smart contracts. Provable takes external data from an API or a data source specified by the smart contract and proves that the data is correct and was obtained from the specified API or data source at a specific time, thus ensuring the verifiability and availability of the data.
Although centralized oracle has been widely used, it also has problems such as single point of failure. To solve these problems, the research of distributed oracles has been paid great attention to.
Chainlink [13] is the first distributed oracle project based on the Ethereum platform. It uses reputation mechanisms and on-chain aggregation models to achieve secure data transmission. However, on-chain aggregation has a high cost, and frequent data submission brings much communication overhead.
SCOs-Bos [14] aims to solve the problem of single-point failure in the construction industry. In this study, a construction supply chain management system is studied to manage the data in the construction process. However, the management system shows low execution efficiency in actual work.
BLOR [15] is a distributed oracle architecture with reinforcement learning mechanism. By using the Bayesian cost-dependent reputation model and knowledge gradient algorithm, a new model is constructed to identify untrustworthy and low-cost oracles and find the most rewarding ones. However, it lacks effective key recovery mechanism to deal with the problem of single point of failure.
Literature [16] proposes a secure and trustworthy oracle scheme to obtain off-chain data. A novel node selection algorithm is designed to select high-quality nodes, and a sliding window-based data filtering algorithm is proposed to improve data consistency and data acquisition efficiency. However, this scheme cannot guarantee the data accuracy in low acquisition time.
P2RP [17] proposes a novel protocol to maintain security and user privacy while ensuring the trustworthiness of blockchain oracles by using decentralized identity-based reputation systems. However, this article lacks discussion of fault tolerance, which makes it difficult to deal with unexpected situations.
Literature [18] proposes a novel approach utilizing Long Short-Term Memory (LSTM) neural networks to forecast interest rate swaps. This article mainly focuses on the analysis of financial markets, and neglects to study the robustness and scalability of oracles.
The analysis and comparison of the oracle schemes proposed in recent years are presented in Table 1.
The Threshold Signature Scheme (TSS) is an encrypted digital signature protocol. Within a set of signers, a subset of signers, instead of the entire set, can sign a message. If the threshold is set to (t, n), it implies that in a set of n signers, any t signers can sign the message on behalf of the whole set. When using threshold signature in a distributed oracle scheme, each oracle in the oracle set is a signer to obtain data and sign it separately. Then, the oracles in the set aggregate the data signatures. If the number of signatures for the same data exceeds t, an aggregate signature can be formed for the data, indicating that the data can be submitted to the blockchain.
The BLS signature scheme was originally proposed by Boneh et al. from Stanford University in 2001 [26]. In 2018, Boneh et al. from IBM Research Institute updated this signature scheme [27]. The BLS signature scheme adopts the elliptic curve matching technology based on bilinear mapping for signature verification and aggregation. The threshold signature algorithm designed by the BLS signature scheme is characterized by high aggregation efficiency and strong scalability.
Other commonly used signature schemes in blockchain include the ECDSA algorithm [28] and the Schnorr algorithm [29]. Since the threshold scheme of the ECDSA algorithm is complicated and has poor practicability, it is not suitable for distributed oracle schemes. The Schnorr threshold signature algorithm has limited function and scalability. Given the three algorithms, this paper realizes the threshold signature algorithm based on the BLS signature scheme, which is responsible for signing and aggregating the data obtained by oracles.
In distributed system schemes, attacks against oracles are frequent [19,30]. Through the attack, the attacker can make the oracle lose the current state and key share, leading to the loss of the signature capability of the oracle and reducing the execution efficiency of the whole oracle set. To solve this problem, improve the ability to handle emergencies, such as reboot attack, and ensure the accuracy of data verification, this paper designs a share recovery mechanism. In this scheme, the key share consisting of key share fragments is generated in a distributed way. The key share fragments are calculated by multiple oracles respectively and sent to the corresponding oracles, and then oracles generate their own key share after summary. In this approach, when the key share is lost, the oracle can send share recovery requests with identity to other oracles and recover the key share by collecting share fragments.
Bilinear mapping is described as follows:
Let G1 and G2 be two multiplicative cyclic groups of order q, where q is a large prime number. Then, e is a bilinear pair if the mapping e: G1 × G2→GT (where GT is a multiplicative cyclic group of order q) has the following properties:
• Bilinear: Given
• Non-degenerate: If
• Computable: For all
The BLS threshold signature algorithm supporting share recovery is designed in this paper based on bilinear mapping e: G1 × G2→GT, and it has the above three properties. These properties will be used in subsequent algorithm descriptions and security proofs.
3.4 Security Properties and Hard Problem
Definition 1. (EUF-IBS-CMA) [31]: An identity-based signature scheme
It should be noted that the requirements id* and (id*, m*) cannot be equal to any query for the oracles OE(·) and OS(·,·), respectively, and OE(·) cannot be queried twice for the same id. Based on this property, an existential unfalsifiable (EU-CMA) model can be constructed.
Definition 2. Computational Diffie-Hellman Problem (CDH): Given g, ga, gb∈G,
4.1.1 The Design of the Framework
In the existing distributed oracle schemes, data is usually processed in off-chain verification and on-chain aggregation, i.e., the data obtained by the oracle will be verified off the chain, then submitted to the blockchain, and aggregated on the chain finally. However, the original verification method involves many oracle interactions and data submissions, resulting in much time and communication cost, and the data aggregation process on the chain will consume lots of computing resources of the blockchain. To solve these problems, this paper designs a trusted distributed oracle scheme based on a share recovery threshold signature, as illustrated in Fig. 1.
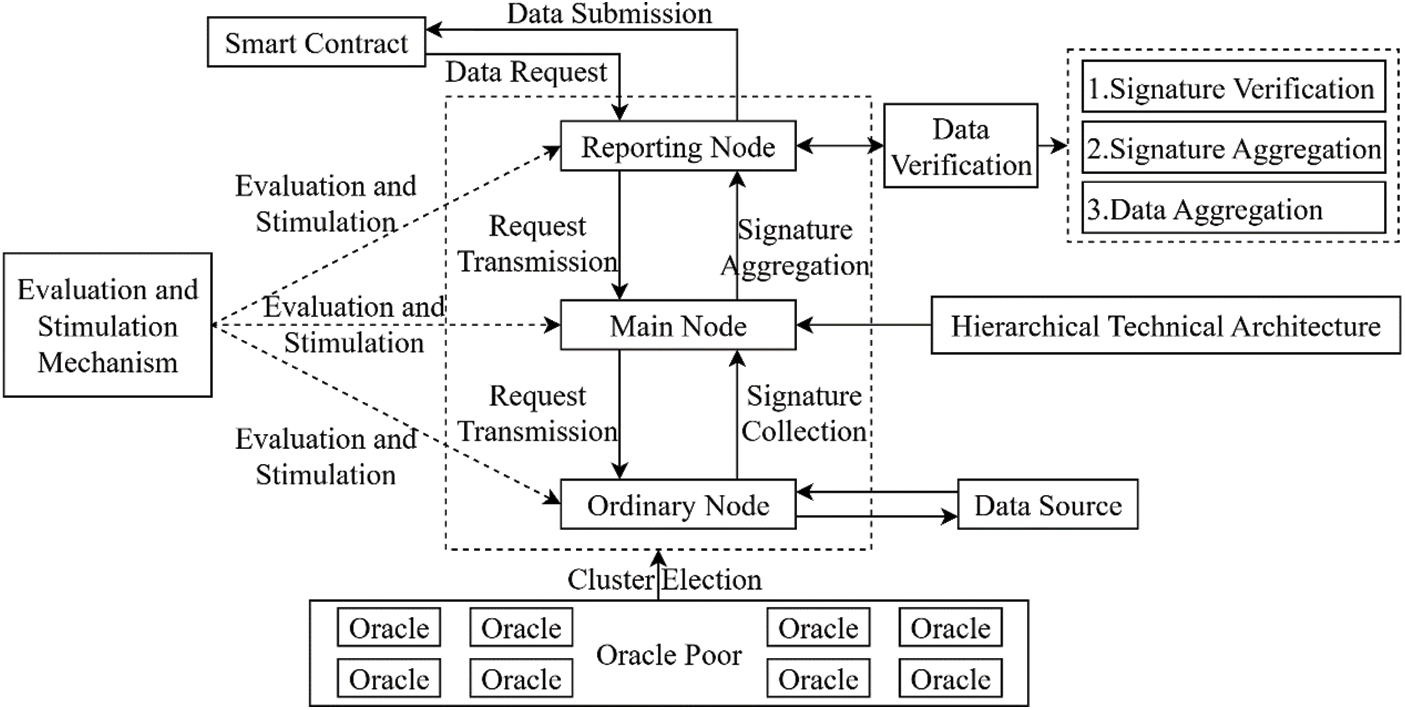
Figure 1: The schematic diagram of the oracle scheme in this paper
To solve the problem that on-chain data aggregation consumes a large amount of blockchain computing resources, a data verification method of distributed oracle is designed based on threshold signature. Each oracle uses its key share to sign data to form a signature, and the correctness of the signature can be verified by the public key of the oracle. In the signature aggregation stage, the signature shares that reach the threshold are aggregated, and the process of forming an aggregated signature also verifies the reliability of the data. This method simplifies the verification process of data and improves the execution efficiency of the system. Also, the process of data aggregation is implemented off-chain, which effectively reduces the computing overhead of the blockchain.
Then, to address the issue of the limited capacity of centralized oracles, a credibility-based cluster head election algorithm is designed when implementing the architecture of the distributed oracle. By assigning functions to different oracles, each oracle can specialize in its own work, which reduces the communication complexity of the whole set of oracles. Meanwhile, through constructing a hierarchical technical architecture, the process of data transmission and data submission is clearly planned, which reduces network communication overhead.
Meanwhile, this paper designs a BLS share recovery threshold signature algorithm, which allows a threshold number of oracles to complete data aggregation. The share recovery mechanism allows the oracle to actively recover its lost key share, thereby guaranteeing the execution of the system in case of an emergency, ensuring the accuracy of data verification and the fairness of the oracle evaluation, and improving the robustness of the scheme.
In this paper, a trusted distributed oracle scheme is proposed based on a share recovery threshold signature, which is a scheme with low delay and high robustness. The execution process of the scheme is shown in Fig. 2.
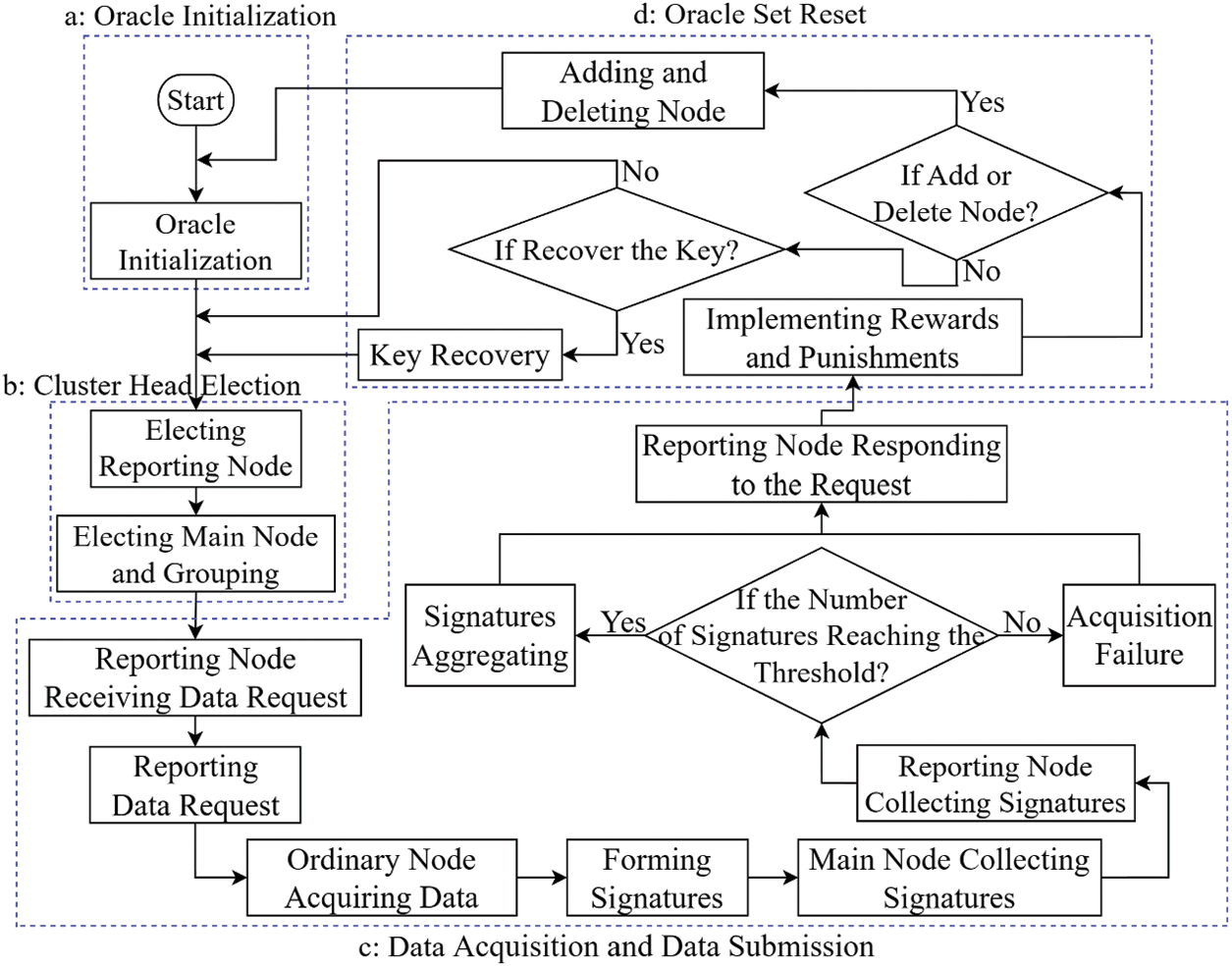
Figure 2: The execution process of the oracle scheme proposed in this paper
Our proposed scheme mainly consists of the following four stages:
(1) Oracle initialization
Oracle initialization is performed before the scheme is executed. This process mainly involves two parts: the authentication part and the key generation part. The former is responsible for verifying the identity of oracles, ensuring that they have the working ability and credible qualifications, and collecting their working performance, such as work proficiency, equipment performance, and data acquisition ability; the latter is responsible for organizing the oracles to complete distributed key generation so that they can respond to data requests. During key generation, each oracle generates a random t − 1-order polynomial and values the polynomial one by one according to the serial number.
Additionally, it is necessary to determine an appropriate threshold t according to the number of oracles to ensure that the scheme does not lose robustness due to an excessively high threshold, nor does it compromise the accuracy of the data due to an excessively low threshold. Specifically, the setting of threshold during the initialization phase is dynamically adjusted according to the current state of network communication. In good network conditions, the threshold will be adjusted higher to pursue higher security and data accuracy. In poor network conditions, the threshold will be adjusted lower, trying to ensure the data supply to the blockchain and the efficiency of the scheme. The dynamic adjustment of the threshold further improves the robustness of our scheme.
Oracle initialization only needs to be performed once, unless there are oracles to join or leave.
(2) Cluster head election
In this paper, a credibility-based cluster head election algorithm is designed to perform cluster-head election and hierarchy division for all the oracles in the set. First, the reporting node is selected to be responsible for data aggregation and data submission. Then, the main node is selected from the remaining nodes. Next, the remaining ordinary nodes are randomly grouped, and each main node is responsible for messaging and data collection within a group. In this approach, a hierarchical technical architecture of distributed oracles is formed, which transforms the original complex communication mode between oracles to the centralized interaction mode of main nodes, significantly decreasing the communication volume of signature aggregation of oracles and effectively reducing the network burden. In this stage, the number of main nodes needs to be determined according to the number of oracles to fully leverage the role of the main nodes.
(3) Data aggregation and data submission
The process of responding to data requests from the blockchain consists of three parts: data acquisition, data aggregation, and data submission. First, the reporting node receives the data request and transmits it, and then ordinary nodes are connected to the data sources to obtain the corresponding data. The ordinary nodes sign the obtained data and send it to the main node of their own group. Then, the main node collects the signed data of its group and sends it to the reporting node. The reporting node aggregates all signatures received and judges whether the request can be completed according to the aggregation results. If the data aggregation can be completed, the aggregation results are submitted to the blockchain as a reply, and the feedback of each oracle is submitted together; otherwise, the failure of the data request is reported to the blockchain, and the feedback of each node is attached. Then, the signed message returned from the blockchain is passed down. Based on the performance of each oracle in this process, the oracle stimulation mechanism evaluates each oracle and implements rewards and punishments to promote oracles to provide more accurate data.
(4) Oracle set reset
To process applications of new oracles in a timely manner and remove negative oracles that affect execution efficiency, the set of oracles is checked after each data request. First, it is checked whether to add or delete oracles: if the number of authenticated oracle applications to join reaches a certain number, or the set needs to eliminate the negative oracles with poor credit, then the oracle set is reset to make all the oracles perform initialization and cluster head election, and then the newly formed oracle set is responsible for responding to data requests. If no add or delete operation is required, the share recovery request is processed, and the next data request is responded to until the requests processed by the current oracle set reach a certain threshold.
4.2 Credibility-Based Cluster Head Election Algorithm
A credibility-based cluster head election algorithm is designed in this paper to construct a hierarchical technical architecture of trusted distributed oracles and decrease the communication complexity of the oracle set. The design idea of the algorithm is: the value of m which is the number of groups is determined first according to the number of oracles in the oracle set and the quality of network communication. After that, the reporting node is elected from all oracles, and then m main nodes are elected from the remaining ordinary oracles. Next, the remaining ordinary nodes are randomly divided into m groups, and each group is randomly assigned to a main node. The reporting node and the main nodes are selected according to their credibility and professional ability.
The credibility of an oracle is denoted as ci, which plays an important role in the probabilistic selection of cluster head election, and its value reflects the trustworthiness of the oracle. In the algorithm, the initial value of ci of the oracle is set to c0, and then it is increased or decreased according to the data accuracy of the oracle to each data request. Each time the oracle set completes the data request, the performance of each oracle will be evaluated according to the data submitted by this oracle. For the oracle that provides correct data, its value of ci will be increased to increase the probability of the oracle being selected as the reporting node and main node; for an oracle that provides incorrect data or no data, its value of ci will be decreased. By measuring the performance of the oracles in the whole process of implementing rewards and punishments, the scheme can stimulate oracles to process data requests effectively.
Professional ability measures the performance conditions and data acquisition ability of an oracle, which mainly includes the following factors: The first one is professional experience, which is determined by the number of data request completed by the oracle; the second one is to obtain the performance score according to the performance of each oracle to guarantee that it can work normally; the third one is data acquisition capability. The main task of oracles is to provide rich and accurate trusted data for the blockchain, and the ability to obtain data is critical. The algorithm measures this ability on the number of authoritative databases connected to each oracle, and the above three factors are denoted was workn, scoren, and on, respectively.
The cluster head election algorithm probabilistically selects the reporting node based on the numerical value of various factors. It ensures that the better the performance in credibility and professional ability, the higher the probability of the oracle being selected.
The probability of oraclei being selected is:
where, ci denotes the credibility of oraclei, c0 is the initial value of ci, and n is the number of oracles in oracle set. The three weighted values a, b, and c need to be determined by the oracle set according to the number and performance of oracles.
In the process of cluster head election, each oracle in the set has a determined function. Specifically, the ordinary node is responsible for responding to data requests and providing replies by querying the database; the main node is responsible for transmitting data requests to its group and collecting the replies to the reporting node; the reporting node is responsible for receiving and passing data requests published by the blockchain, and aggregating and submitting the replies submitted by the main node to the blockchain. The principle of the credibility-based cluster head election algorithm designed in this paper is presented in Fig. 3.
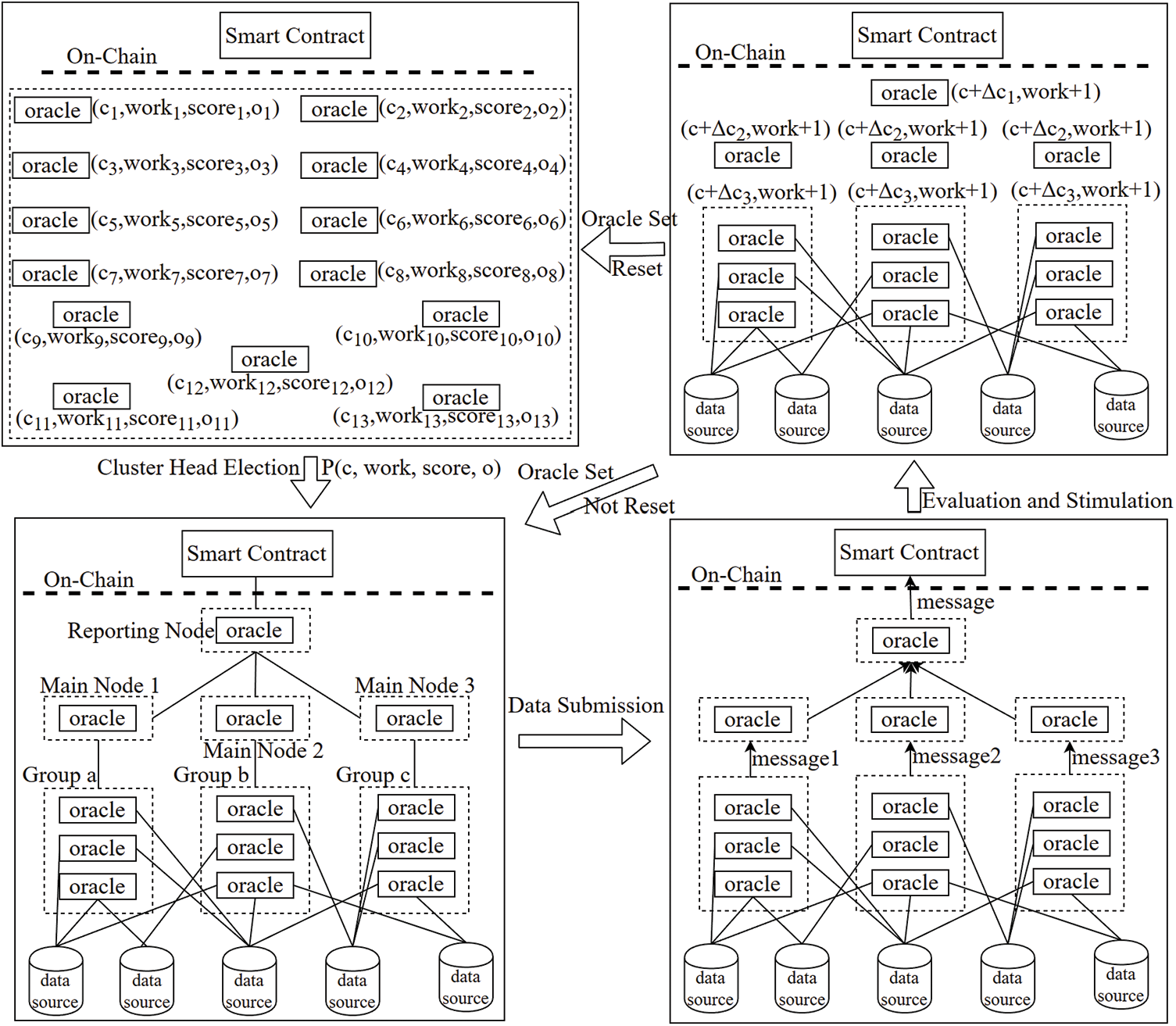
Figure 3: The implementation of the oracle scheme proposed in this paper
To stimulate oracles to respond to data requests positively and ensure the execution efficiency of the scheme, an evaluation and stimulation mechanism is designed in the cluster head election algorithm, and it includes four modules. In addition to the already mentioned credibility ci, there are also security deposits, reward and punishment measures, and a reporting mechanism. The credibility ci plays an important role in cluster head election. Security deposit is a guarantee to maintain the initiative of the oracle, and it can prevent the oracle from negatively responding to data requests and thus ensure the efficiency of data aggregation. The reporting mechanism is a supervisory measure to ensure fairness. To prevent the main node and reporting node from using their power for personal gain and maliciously concealing the reply of ordinary nodes to maintain their leading position, the scheme sets a complete message reply mechanism. Specifically, ordinary nodes determine whether their feedback is submitted to the blockchain by comparing the response of superior nodes with the final submission results and then report the malicious concealment nodes found.
After grouping, each oracle has a clear function and forms a hierarchical structure. Then, according to the hierarchy, the data is transmitted and uniformly submitted by the reporting node. This reduces unnecessary data transmission and data submission, avoiding a lot of communication costs and waiting time. Meanwhile, after the functions are clarified, the tasks of data verification and data aggregation are assigned to the main node and reporting node, respectively, which effectively improves the algorithm’s execution efficiency.
The design of the credibility-based cluster head election algorithm is shown in Algorithm 1.
During the cluster head election process, the operations of elections and hierarchy divisions are performed by smart contract. Oracles first transmit their own information to the smart contract, who will select the reporting node and the main nodes from them. Smart contract then divides the remaining oracles into m groups and broadcasts the grouping results to all the oracles. After data submission, the smart contract records the oracles’ performances based on the data accuracy, and there is no additional communication overhead. The communication complexity of the cluster head election algorithm is

According to the message reply mechanism, the diagram of message flow for each stage of the oracle is illustrated in Fig. 4.
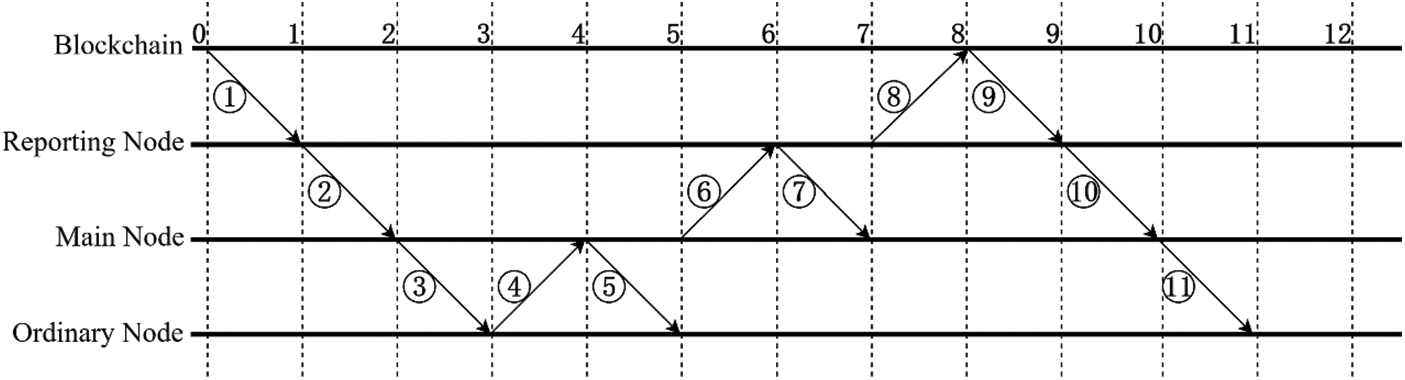
Figure 4: The implementation of the oracle scheme proposed in this paper
①~③: Data requests are passed from the blockchain to the reporting node, main node, and ordinary nodes;
④: The ordinary node signs data with its key and sends it to the main node;
⑤: The main node replies to the ordinary nodes to confirm receipt of the message from the nodes in the group;
⑥: The main node sends all replies received in the group to the reporting node;
⑦: The reporting node replies to the main node to confirm receipt of the message;
⑧: The reporting node aggregates the replies received to obtain the result of the data request, and then it sends the result and the reply of each node to the blockchain after signing with its key;
⑨~⑪: After receiving the result, the blockchain signs the message and passes the signature to the reporting node, main nodes, and ordinary nodes in turn. The main nodes and ordinary nodes confirm this signature to judge whether their data replies have been concealed or underreported.
5 BLS Share Recovery Threshold Signature Algorithm
To enhance the execution efficiency of the scheme and reduce the time cost of waiting for messages, this paper designs the BLS share recovery threshold signature algorithm based on the distributed oracle. By combining the oracle and threshold signature, the number of threshold oracles that can complete the data aggregation is decreased, thereby reducing the time cost of waiting for all the oracles. Also, data verification is integrated into the signature aggregation process to improve the efficiency of data verification. Meanwhile, the share recovery mechanism is introduced to design a secure share recovery method, which not only guarantees that the owner can recover its key share by collecting share fragments from other oracles but also ensures that non-key owner cannot recover the key share it does not own. The algorithm adopts bilinear mapping G1 × G2→GT. The algorithm is initialized as follows:
Given bilinear mapping e: G1 × G2→GT, where G1 and G2 are multiplicative cyclic groups of order p, and their generators are g1 and g2, respectively, and GT represents the multiplicative cyclic groups of order q. The safe hash function is H: {0, 1}*→G1. The public parameters of the algorithm are (G1, G2, GT, e, g1, g2, p, H).
5.2 Distributed Key Generation
To avoid the threat to the key security of oracles by introducing centralized elements in key generation, this paper designs a distributed key generation algorithm. When the key is generated, each oracle generates its own polynomial and values the polynomial according to the sequence number, and then the key share fragment is calculated. Subsequently, these key share fragments are sent to the oracle with the corresponding sequence number so that each oracle can use the share fragments generated by itself and those generated by other oracles to generate its own key share and then calculate the corresponding public key based on the key share. In this process, each oracle participates in the generation of the key share, which guarantees that the key generation process is not controlled by a single oracle. Meanwhile, since the generation of the key share requires the shared fragment from each oracle, including the one generated by the share owner for itself, if the share owner protects this share fragment well, it can prevent other oracles from collecting fragments to obtain the owner’s key share.
Distributed key generation mainly includes the following processes:
(1) Key Share Generation
Let the key share of oraclej be skj, the number of oracles be n, and the threshold be t. In the process of distributed key generation, oraclei generates a t − 1 polynomial
Polynomial fi(x) is:
The key share skj of oraclej is:
The key share fragment of skj is:
The key share of oraclej is calculated:
(2) Polynomial Merging
Each oracle has its own polynomial. The polynomials of all oracles can be combined to obtain the merged polynomial f(x) representing the entire oracle set, and the value at x = 0 is the general private key SK of the whole set. At this time, the polynomial fi(x) of oraclei is a part of the combined polynomial f(x), and its key share ski is the result of the combined polynomial f(i) at x = i. Therefore, in theory, the general private key SK can be recovered by Lagrange interpolation using the key shares held by multiple oracles. The recovery process is as follows:
The combined polynomial f(x) is:
The general private key SK is:
The key share skj of oraclej is:
According to Lagrange interpolation, there is:
When x = 0, there is:
The value of the combined polynomial f(x) can be calculated through Lagrange interpolation:
When x = 0, the general private key SK is:
xi and xj are the sequence numbers of oracles. From the above process, when the number of collected oracle private keys reaches t, the general private key can be aggregated and recovered by the aggregability of private keys. However, in the algorithm execution, for the sake of security, the general private key SK cannot be recovered, and each oracle does not allow its own polynomial and key share to be exposed. Therefore, the combined polynomial is not actually generated, and the recovery of the general private key is only theoretically feasible.
The public keys and the signatures of the oracles generated by the private keys are also aggregable. As a result, when the general public key is generated, the threshold number of public keys of oracles can be collected, and the general public key can be formed by public key aggregation. This property can also be exploited to aggregate the threshold number of signatures to generate aggregate signatures.
(3) Public Key Generation
After the process of distributed key share generation, each oracle uses its own key share to calculate its public key pki, and then the general public key PK is calculated from multiple public keys.
The generation of the public key relies on group G2 in the BLS threshold signature algorithm. For the bilinear pair mapping e: G1 × G2→GT, the generator of group G2 is g2, and the public key generated by oraclei is:
The general public key PK is calculated by using multiple public keys:
The generation of the keys for each oracle and the general public key for the oracle set is now completed. The distribution mechanism of the algorithm’s key share fragments is demonstrated in Fig. 5.

Figure 5: The BLS share recovery threshold signature algorithm
The design of the distributed key generation algorithm is presented in Algorithm 2.

When the share needs to be recovered, the oracle sends a share recovery request to other oracles to obtain the key share fragments to restore its key share:
On receiving the share recovery request, other oracles generate share fragments and send them to this oracle. After collecting the share fragments, this oracle aggregates them with its calculated share fragment to recover its own key share. Since the share fragment fj(j) is not exposed, the key of this oracle cannot be recovered by other oracles during the share recovery process because they cannot obtain the share fragment fj(j). The design of the share recovery algorithm is presented in Algorithm 3.

Particularly, in our scheme, the scale of share fragments is small and only a very low communication bandwidth is required to transmit, which brings negligible communication overhead. Even in the case of poor network conditions, as long as there is normal network communication, it has no significant impact on the transmission of share fragments. If faced with extremely harsh network conditions, oracle can report the loss of keys to the blockchain. In this case, due to the strong robustness of our scheme, data aggregation and data verification can still be completed through the threshold number of signature messages, so the failure of a small number of oracles will not affect the efficiency of the scheme.
Message m is first hashed to convert it to a point H(m) in G1.
The message signed by oraclei is:
The aggregate signature representing the entire set of oracles should be:
When an aggregate signature is generated, the sigi(H(m)) that reaches the threshold is collected and aggregated to generate an aggregate signature sig(H(m)) for message m. In this approach, the aggregate signature of message m representing the entire oracle set is obtained.
Based on the key aggregation theory of the BLS threshold signature algorithm, the signature aggregation method of the algorithm is introduced as follows:
The signature sigi(H(m)) of oraclei is:
The aggregated signature sig(H(m)) is:
Under the threshold (t, n), if more than t correct signatures can be collected, an aggregate signature can be generated using these signatures.
In our algorithm, through using the threshold signatures aggregation, we also implement the aggregation and validation of data from different oracles instead of performing these two operations specifically. And the aggregation result can reflect the data correctness. For an aggregated signature, using less signatures represents that the data correctness is higher. If the aggregation fails, it represents the data from different oracles are various and cannot reach consensus, resulting in the failure of the data validation. This design greatly improves the efficiency of our algorithm.
Signature verification involves single signature verification and aggregate signature verification, and they require the personal public key of the oracle and the general public key of the oracle set respectively. The former corresponds to the private key share of a single oracle and can verify its signature, while the latter corresponds to the general private key for the entire oracle set and can verify the aggregated signature.
When verifying a single signature using a personal public key, the bilinear map e: G1 × G2→GT has the property:
Then there is:
Here, g2 is the generator of G2. From the above deduction, the signature sigi(H(m)) can be verified using public key pki.
When using the general public key to verify the aggregate signature, there is:
From the above deduction, the aggregate signature sig(H(m)) can be verified using general public key PK.
In this paper, the BLS share recovery threshold signature algorithm is designed for data signature, aggregation, and verification in the oracle scheme, and its execution efficiency will directly affect the execution efficiency of the oracle scheme. In the field of blockchain, the ECDSA algorithm, Schnorr algorithm, and BLS algorithm are the three commonly used signature algorithms. Since the ECDSA algorithm is difficult to implement threshold signatures and the corresponding threshold scheme is very complex, it is not suitable for the scheme proposed in this paper. Therefore, the Schnorr threshold signature algorithm was selected to conduct a comparison experiment with the proposed algorithm.
The scheme was simulated and tested in a virtual machine on the VMware Workstation Pro platform. The virtual machine runs the Ubuntu 20.04 operating system, with 4 processor cores and 8 GB memory. The host computer was equipped with a 12th Gen Intel(R) Core(TM) i9-12900H process (2.50 GHz). The algorithm proposed in this paper and the Schnorr threshold signature algorithm were implemented using the Go language, and then the smart contract was deployed and tested on the Fabric chain.
6.2 Experimental Analysis of Scalability
During the experiment, the proposed algorithm and the Schnorr threshold signature algorithm were used to test the scheme respectively, and the execution time of the scheme with different numbers of nodes was calculated to measure the scalability of the scheme. The experimental results are shown in Figs. 6 and 7.
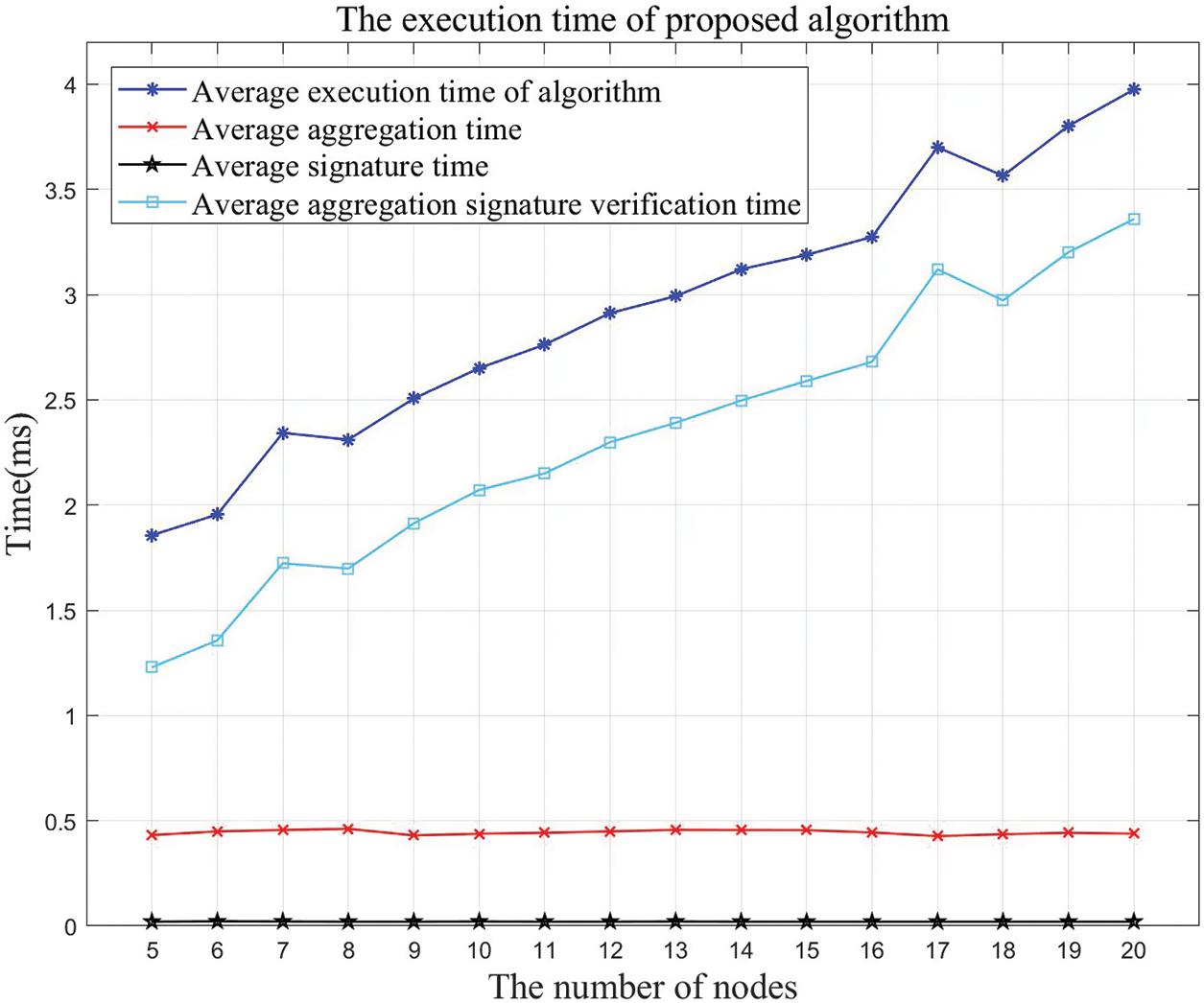
Figure 6: The execution time of the proposed algorithm with different number of nodes
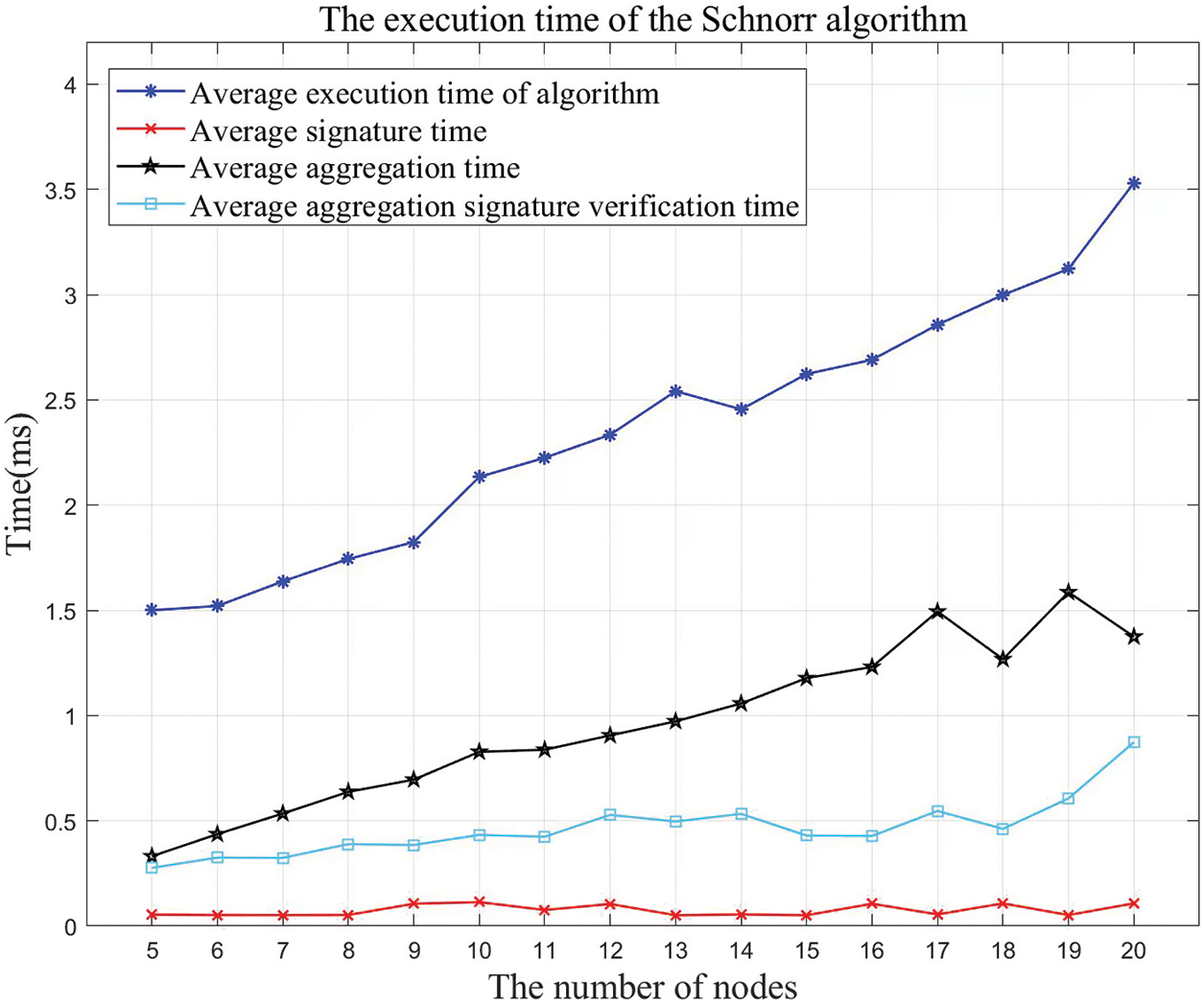
Figure 7: The execution time of the Schnorr algorithm with different number of nodes
Compared Figs. 6 with 7, as the number of oracle nodes in the scheme increases, the signature aggregation time of the algorithm proposed in this paper is almost unchanged, while the verification time of aggregate signature increases accordingly. This is because this algorithm is designed based on the BLS threshold signature algorithm, which has no advantage in signature verification.
The Schnorr threshold signature algorithm can maintain a high signature generation rate, but as the number of nodes increases, the time for signature aggregation and aggregate signature verification gradually increases. Meanwhile, the curve shows that the execution time of the Schnorr algorithm increases significantly faster than that of the proposed algorithm. This is because when the Schnorr signature algorithm is adopted to implement threshold signature, a Merkle tree of the public key needs to be constructed. When the number of nodes is small, the design of the Merkle tree makes the algorithm have higher execution efficiency, but when there are numerous nodes, the constructed Merkle tree has a large size, resulting in a significant decrease in execution efficiency. In contrast, although the algorithm designed in this paper based on the BLS threshold signature algorithm has low pairing efficiency and long signature verification time, its design is friendly to key aggregation, so it can perform better in the signature aggregation and maintain stable performance when the number of nodes increases.
6.3 Experimental Analysis of Execution Efficiency
In the experiment, the proposed algorithm and the Schnorr threshold signature algorithm are used to simulate the scheme, and the execution time of the scheme in different execution rounds is counted to obtain the average execution efficiency of the two algorithms. The obtained experimental results are shown in Figs. 8 and 9.
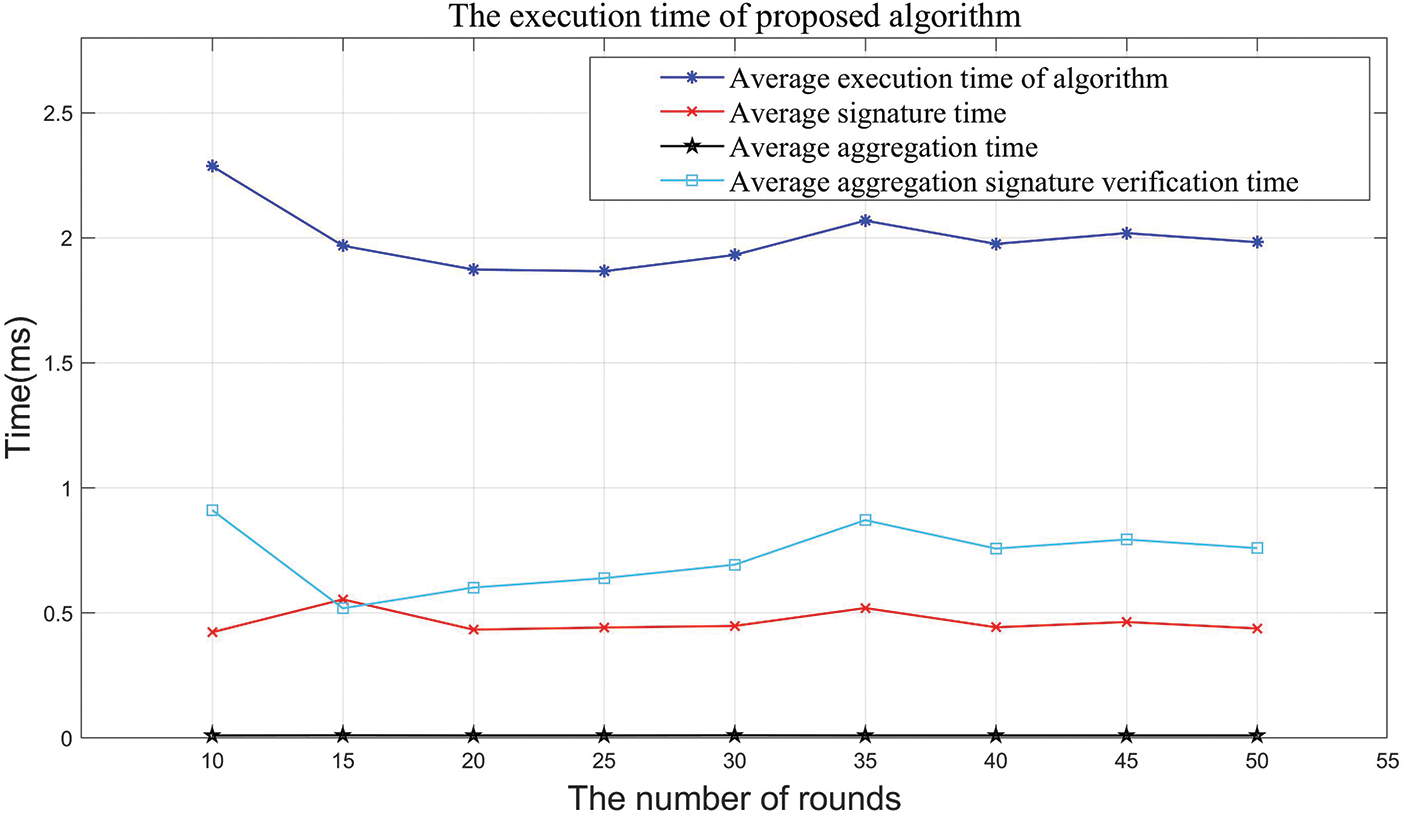
Figure 8: The execution time of the proposed algorithm in different execution rounds
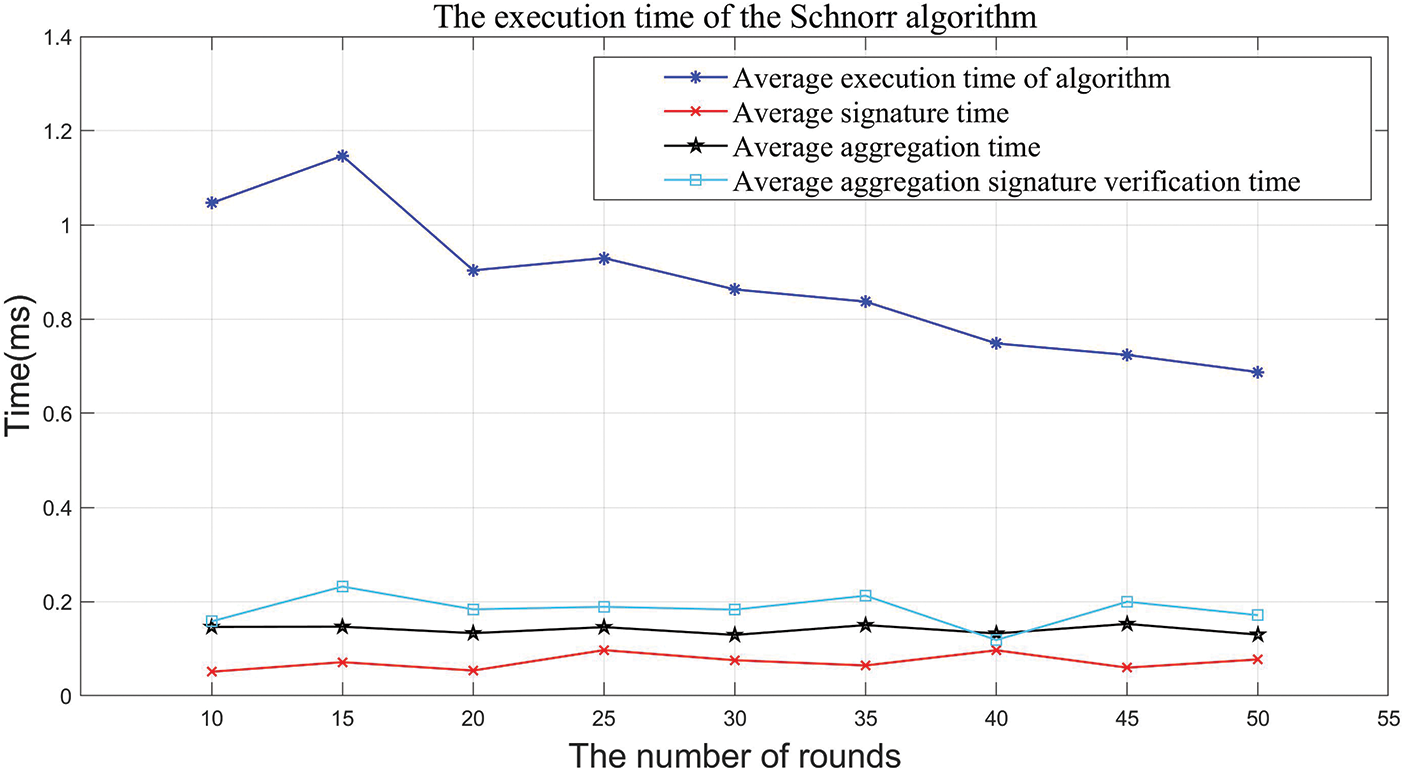
Figure 9: The execution time of the Schnorr algorithm in different execution rounds
Compared Figs. 8 with 9, it can be found that with the increase in the number of execution rounds, the average execution time of the schemes using the two algorithms fluctuates. Compared with the Schnorr algorithm, although the proposed algorithm has lower efficiency in message signing and a longer time in aggregate signature verification, it performs significantly better than the latter in signature aggregation. This is because the BLS threshold signature algorithm is friendly to key aggregation, and this advantage will be more prominent when the algorithm is applied on a large scale.
It can be seen from Fig. 10 that with the continuous expansion of the node scale, the proposed algorithm using the BLS signatures has more and more obvious advantages in execution time compared with the Schnorr algorithm. Specifically, our algorithm has designed cluster head election algorithm and share recovery threshold signature algorithm to perform the operations of key generation, signature aggregation, data verification and data submission, which uses off-chain aggregation and off-chain verification to make our algorithm of great execution efficiency. Meanwhile, the communication costs to transmit the data is also reduced significantly. These two advantages make our algorithm more capable of dealing with large-scale nodes working simultaneously.
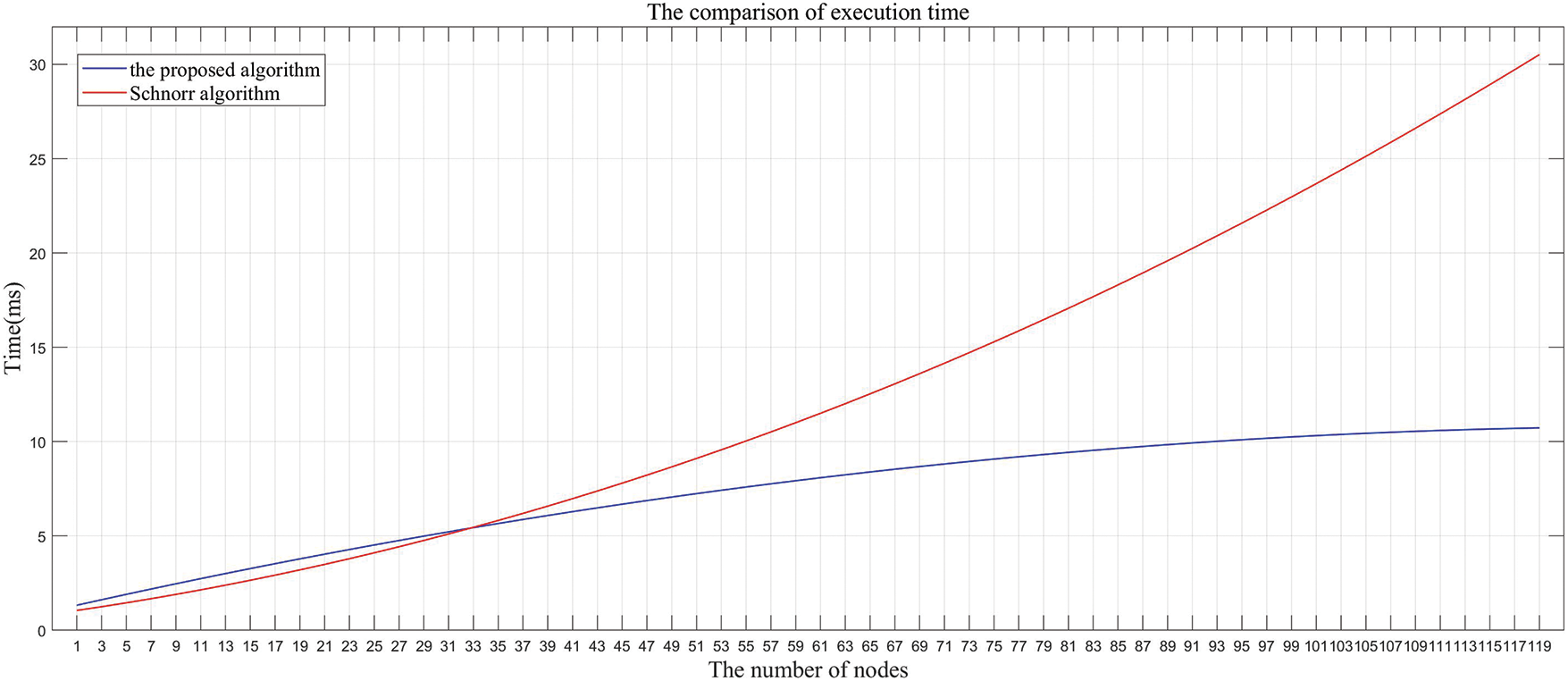
Figure 10: The execution time of the two algorithms in large-scale applications
From Figs. 6–10, we can find that the threshold signature algorithm in this paper has advantages in scalability and signature aggregation. Meanwhile, it uses one point instead of two points on the elliptic curve when signing, and the length of the signature formed by the same data is only half of the Schnorr algorithm or ECDSA algorithm, which is more convenient for the transmission of a large amount of data. More importantly, the threshold signature algorithm in this paper introduces the share recovery mechanism, which gives the scheme better emergency handling ability and stronger fault tolerance.
6.4 Experimental Analysis of Fault Tolerance
In the experiment, we also compare our scheme with BLOR scheme in the performance of fault tolerance. Based on the different election strategy for oracles, the fault tolerance of the scheme in the execution stage will also change, which will be experimented in this section. Note that the share recovery is temporarily not considered in the experiment process because of the complexity of the fault’s types.
In Fig. 11, there is comparison of fault tolerance. We compare our scheme with BLOR scheme and oracles selected randomly in the ability of fault tolerance. It can be found that our scheme and BLOR scheme both have more advantages than oracles selected randomly. BLOR uses machine learning algorithm to select oracles with high quality to maintain the data accuracy and our scheme use cluster head election algorithm to achieve the result. Meanwhile, after adding the share recovery mechanism, our scheme will have an additional increase in fault tolerance.
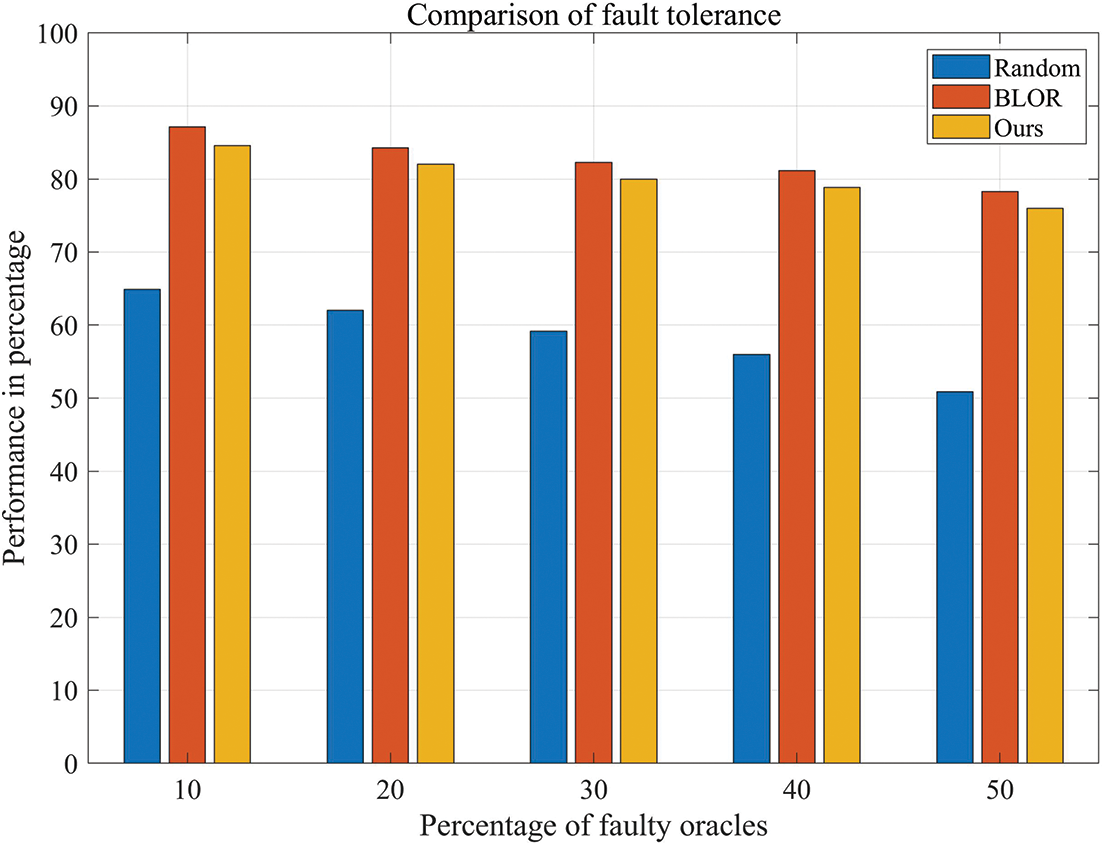
Figure 11: The comparison of fault tolerance
The BLS share recovery threshold signature algorithm designed in this paper is a digital signature scheme based on bilinear mapping, and the security of the scheme is guaranteed by the CDH problem. The following is the proof of the security of this scheme under the random oracle model.
Theorem. Under the random oracle model, suppose the hash function H is a random oracle. If the CDH problem is difficult, the proposed scheme is provably secure in the EU-CMA security model with a reduction loss L = qH, where qH is the number of hash queries to the random oracle.
The proof is given below:
Assuming that in the EU−CMA security model, there is an adversary A that can break the algorithm in polynomial time, then a simulator B can be constructed to call adversary A to solve the CDH problem.
CDH problem instances can be obtained according to Definition 2. Given g, ga, gb∈G,
Setup. Let H be a random oracle controlled by the simulator. B can call adversary A to query. B sets the public key h = ga, where the secret key is a. The public key is available for the problem instance. Though the simulator does not know the private key, it can construct a signature that can be simulated without using the private key and design a signature that can be reduced for adversary A.
H-Query. The adversary A makes hash queries mi to simulator B in this phase. B queries the random oracle to obtain the hash result H(mi) and returns it to the adversary. Before receiving queries from adversary A, simulator B selects a random number i∗∈[1, qH], where qH denotes the number of hash queries to the random. Then, B prepares an empty hash list to record all queries and responds as follows.
Let the i-th hash query be mi. If mi is already in the hash list, B responds to this query following the hash list; otherwise, B randomly chooses wi from
Simulator B responds to this query with H(mi) and adds (i, mi, wi, H(mi)) to the hash list.
Query. Adversary A makes signature queries in this phase. For a signature query on mi, if mi is the i∗-th queried message in the hash list, abort, and otherwise, H(mi) = gwi.
B computes
According to the signature definition and simulation, we have
Therefore,
Forgery. The adversary returns a forged signature
Then, based on this signature, simulator B can calculate
In this way, the solution gab to the CDH problem instance is obtained.
It can be found that if there is an adversary that can break the algorithm in polynomial time with probability
The existing oracle schemes all have some problems: Centralized oracles have a single data source and are easy to produce a single point of failure, while distributed oracles have low execution efficiency and high communication cost. To solve these problems, this paper proposes a trusted distributed oracle scheme based on a share recovery threshold signature, which provides an efficient, secure, and stable scheme for the trusted use and large-scale development of distributed oracles. First, a data verification method of distributed oracles is designed based on threshold signature, which aggregates data signatures through threshold signature and verifies data reliability in the aggregation, enabling the proposed scheme to eliminate the previous interactive data verification mode. Second, a credibility-based cluster head election algorithm is proposed, which assigns the functions of data acquisition, signature aggregation and data submission to different oracles to enhance the execution efficiency of the proposed scheme. Also, the network communication overhead is reduced by constructing a hierarchical technical architecture. Finally, a BLS share recovery threshold signature algorithm is designed to improve the robustness and scalability of the proposed scheme through share recovery and threshold signature. In the future, we will further improve the proposed threshold signature algorithm to make it have higher execution efficiency and a stronger ability to resist attacks.
Acknowledgement: We are grateful to our families and friends for their unwavering understanding and encouragement.
Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant No. 62102449) and the Central Plains Talent Program under Grant No. 224200510003.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shihao Wang; data collection: Shihao Wang, Wenjuan Wang, Yu Cao, Aodi Liu; analysis and interpretation of results: Shihao Wang, Xuehui Du, Xiangyu Wu; draft manuscript preparation: Shihao Wang, Xuehui Du, Qiantao Yang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Xuehui Du, upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. G. S. Aujla and A. Jindal, “A decoupled blockchain approach for edge-envisioned IoT-based healthcare monitoring,” IEEE J. Sel. Areas Commun., vol. 39, no. 2, pp. 491–499, 2020. doi: 10.1109/JSAC.2020.3020655. [Google Scholar] [CrossRef]
2. S. Gupta, H. K. Sharma, and M. Kapoor, Blockchain for Secure Healthcare Using Internet of Medical Things (IoMT). Berlin, Germany: Springer, 2023. [Google Scholar]
3. X. Wu, X. Du, Q. Yang, N. Wang, and W. Wang, “Redactable consortium blockchain based on verifiable distributed chameleon hash functions,” J. Parallel Distr. Comput., vol. 183, 2024, Art. no. 104777. doi: 10.1016/j.jpdc.2023.104777. [Google Scholar] [CrossRef]
4. Z. Zheng et al., “An overview on smart contracts: Challenges, advances and platforms,” Future Gener. Comput. Syst., vol. 105, no. 2020, pp. 475–491, 2020. doi: 10.1016/j.future.2019.12.019. [Google Scholar] [CrossRef]
5. A. Pasdar, Y. C. Lee, and Z. Dong, “Connect API with blockchain: A survey on blockchain oracle implementation,” ACM Comput. Surv., vol. 55, no. 10, pp. 1–39, 2023. doi: 10.1145/3567582. [Google Scholar] [CrossRef]
6. F. Zhang, E. Cecchetti, K. Croman, A. Juels, and E. Shi, “Town crier: An authenticated data feed for smart contracts,” in Proc. 2016 ACM SIGSAC Conf. Comput. Commun. Secur., Vienna, Austria, Oct. 2016, pp. 270–282. doi: 10.1145/2976749.2978326. [Google Scholar] [CrossRef]
7. A. Beniiche, “A study of Blockchain Oracles,” 2020, arXiv:2004.07140. [Google Scholar]
8. A. Egberts, “The oracle problem—An analysis of how blockchain oracles undermine the advantages of decentralized ledger systems,” SSRN J., vol. 5, 2017, Art. no. 655. doi: 10.2139/ssrn.3382343. [Google Scholar] [CrossRef]
9. J. Peterson and J. Krug, “Augur: A decentralized, open-source platform for prediction markets,” 2015, arXiv:1501.01042. [Google Scholar]
10. Dos Network, “Dos network: A decentralized oracle service boosting blockchain usability with off-chain data & verifiable computing power,” Oct. 25, 2021. Accessed: Aug. 10, 2024. [Online]. Available: https://s3.ama-zonaws.com/whitepaper.dos/DOS+Network+Technical+Whitepaper.pdf [Google Scholar]
11. H. Ritzdorf, K. Wüst, A. Gervais, G. Felley, and S. Capkun, “TLS-N: Non-repudiation over TLS enabling ubiquitous content signing,” 2018. doi: 10.14722/ndss.2018.23272. [Google Scholar] [CrossRef]
12. Provable, “Provable,” 2020. Accessed: Aug. 10, 2024. [Online]. Available: https://provable.xyz/papers/randomdatasource-rev1.pdf [Google Scholar]
13. L. Breidenbach et al., Chainlink 2.0: Next Steps in the Evolution of Decentralized Oracle Networks. Chainlink Labs, 2021, vol. 1, pp. 1–136. [Google Scholar]
14. W. Lu, X. Li, F. Xue, R. Zhao, L. Wu and A. Yeh, “Exploring smart construction objects as blockchain oracles in construction supply chain management,” Autom. Constr., vol. 129, 2021, Art. no. 103816. doi: 10.1016/j.autcon.2021.103816. [Google Scholar] [CrossRef]
15. M. Taghavi, J. Bentahar, H. Otrok, and K. Bakhtiyari, “A reinforcement learning model for the reliability of blockchain oracles,” Expert. Syst. Appl., vol. 214, 2023, Art. no. 119160. doi: 10.1016/j.eswa.2022.119160. [Google Scholar] [CrossRef]
16. P. Liu, Y. Xian, C. Yao, P. Wang, L. -E. Wang and X. Li, “A trustworthy and consistent Blockchain oracle scheme for industrial Internet of Things,” IEEE Trans. Netw. Serv. Manage., vol. 21, no. 5, pp. 5135–5148, Oct. 2024. doi: 10.1109/TNSM.2024.3399837. [Google Scholar] [CrossRef]
17. S. You, K. Radivojevic, J. Nabrzyski, and P. Brenner, “Persona preserving reputation protocol (P2RP) for enhanced security, privacy, and trust in blockchain oracles,” Cluster Comput., vol. 27, pp. 3945–3956, 2024. doi: 10.1007/s10586-023-04222-4. [Google Scholar] [CrossRef]
18. G. Vijayakumar, K. Singh, and S. K. Karthika, “Privacy preserving decentralized swap derivative with deep learning based oracles leveraging blockchain technology and cryptographic primitives,” Comput. Electr. Eng., vol. 119, 2024, Art. no. 109510. doi: 10.1016/j.compeleceng.2024.109510. [Google Scholar] [CrossRef]
19. L. Luu, J. Teutsch, R. Kulkarni, and P. Saxena, “Demystifying incentives in the consensus computer,” in Proc. 22nd ACM SIGSAC Conf. Comput. Commun. Secur., 2015, pp. 706–719. [Google Scholar]
20. J. Adler, R. Berryhill, A. Veneris, Z. Poulos, N. Veira and A. Kastania, “Astraea: A decentralized blockchain oracle,” in 2018 IEEE Int. Conf. Internet of Things (IThings) and IEEE Green Comput. Commun. (GreenCom) and IEEE Cyber, Phys. Soc. Comput. (CPSCom) and IEEE Smart Data (SmartData), IEEE, 2018, pp. 1145–1152. [Google Scholar]
21. Tellor, “Tellor,” 2021. Accessed: Aug. 10, 2024. [Online]. Available: https://docs:tellor:io/tellor/whitepaper/ [Google Scholar]
22. H. Huilgolka, “Razor network: A decentralized oracle platform,” 2019. Accessed: Aug. 10, 2024. [Online]. Available: https://razor:network/whitepaper:pdf [Google Scholar]
23. Bandchain, “Band protocol,” 2020. Accessed: Aug. 10, 2024. [Online]. Available: https://docs.bandchain.org/whitepaper [Google Scholar]
24. D. Network, “Decentralized information asset (DIA),” 2021. Accessed: Aug. 10, 2024. [Online]. Available: https://docs:diadata:org/documentation [Google Scholar]
25. Kylin, “Kylin network,” 2021. Accessed: Aug. 10, 2024. [Online]. Available: https://kylin:network/ [Google Scholar]
26. D. Boneh, B. Lynn, and H. Shacham, “Short signatures from the Weil pairing,” in Int. Conf. Theory Appl Cryptol Inform Secur. Berlin, Heidelberg, Berlin Heidelberg: Springer, 2001, pp. 514–532. [Google Scholar]
27. D. Boneh, M. Drijvers, and G. Neven, “Compact multi-signatures for smaller blockchains,” in Adv. Cryptol.–ASIACRYPT 2018: 24th Int. Conf. Theory Appl. Cryptol. Inform. Secur., Brisbane, QLD, Australia, 2018, pp. 435–464. [Google Scholar]
28. G. Castagnos, D. Catalano, F. Laguillaumie, F. Savasta, and I. Tucker, “Two-party ECDSA from hash proof systems and efficient instantiations,” in Adv. Cryptol.–CRYPTO 2019: 39th Annu. Int. Cryptol. Conf., Santa Barbara, CA, USA, 2019, pp. 191–221. [Google Scholar]
29. D. R. Stinson and R. Strobl, “Provably secure distributed Schnorr signatures and a (t, n) threshold scheme for implicit certificates,” in Australasian Conf. Inform. Secur. Priv., Berlin, Germany, 2001, pp. 417–434. [Google Scholar]
30. Y. Zhu et al., “Distributed random beacon for blockchain based on share recovery threshold signature,” Sensors, vol. 22, no. 16, 2022, Art. no. 6004. doi: 10.3390/s22166004. [Google Scholar] [PubMed] [CrossRef]
31. D. Galindo and F. D. Garcia, “A Schnorr-like lightweight identity-based signature scheme,” in Progress Cryptol.-AFRICACRYPT 2009: Second Int. Conf. Cryptol. Africa, Gammarth, Tunisia, Jun. 21–25, 2009, pp. 135–148. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF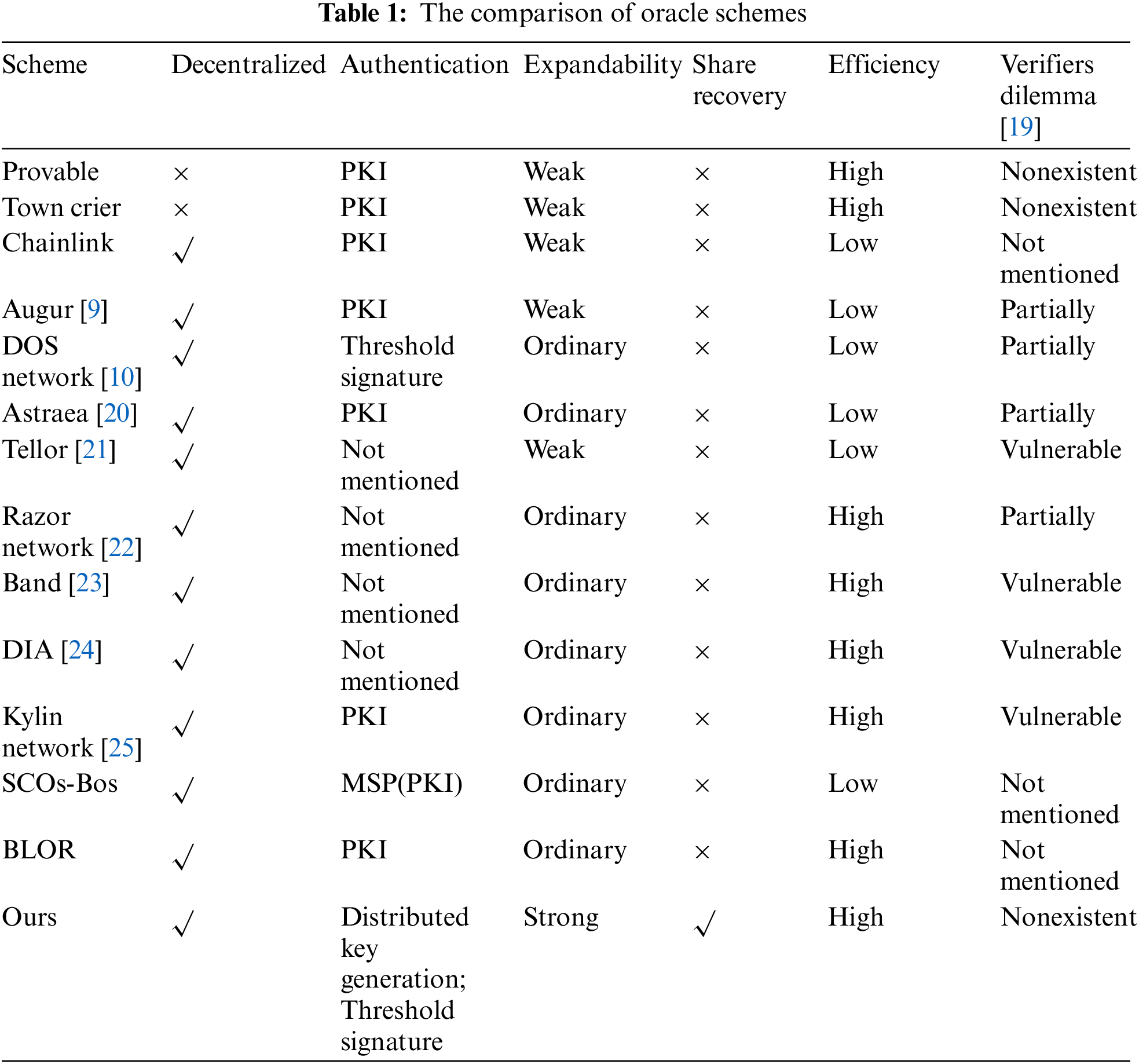
 Downloads
Downloads
 Citation Tools
Citation Tools