Machine Learning-Based Methods for Materials Inverse Design: A Review

1  Introduction

Over the past few decades, significant advancements have been made in materials science and engineering, driving the development of many new materials and advanced technologies [1,2]. From electronic devices to aerospace, and from medical devices to energy technologies, the development and application of novel materials are crucial. Historically, material discovery has largely relied on traditional methods, such as experience, trial and error, or serendipitous findings, to identify materials with desired properties. This involves progressively adjusting the chemical composition and structural parameters of materials to achieve the required performance [3]. However, due to the vastness of the materials design space, traditional methods require substantial time and resources, and their efficiency and reliability struggle to meet the growing demands for materials design [4]. Therefore, there is an urgent need for more efficient and intelligent methods to accelerate material discovery and optimization [5,6].

In recent years, materials inverse design methods have emerged prominently in the field of materials science and have been widely applied to the discovery and development of new materials [7]. Materials are fundamental elements of the material world and can be defined by ACS, which stands for Atoms (the basic units of all matter, composed of protons, neutrons, and electrons), Composition (the chemical makeup, including the types of elements and their relative amounts in a material), and Structure (the arrangement of atoms or molecules and their spatial relationships, such as crystal structure). Since the target properties of materials vary across different fields, inverse design methods that start from specific performance requirements to find materials with target properties have become a major research direction in future materials science and engineering [8,9]. The forward design of materials is a process that starts from the composition and structure of materials, using experiments and simulations to predict and optimize material properties. It can be represented as ACS->P(ACS). On the other hand, inverse design starts from the desired material properties and works backward to determine the composition and structure, thereby discovering materials with the target properties. This can be represented as P(ACS)->ACS, where P denotes the material properties. The processes of forward and inverse design are illustrated in Fig. 1.

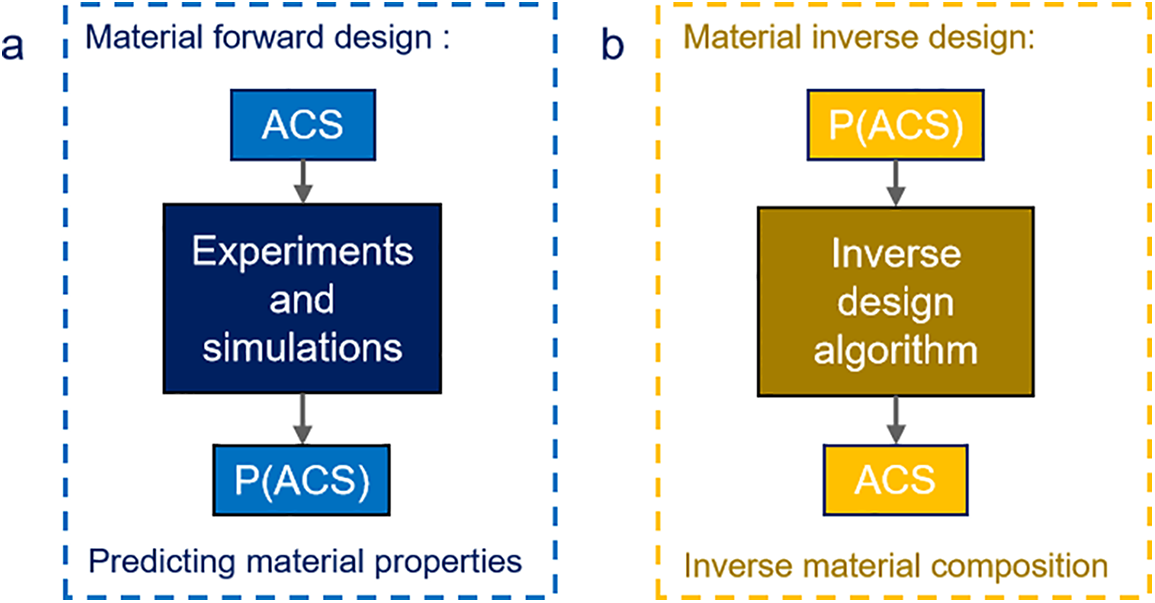
Figure 1: The specific processes of forward design and inverse design. (a) Forward design process: Based on the material’s ACS, the material’s P(ACS) is predicted through experiments and simulations. (b) Inverse design process: Based on a given material’s P(ACS), the material’s ACS is deduced using inverse design algorithms

Material databases are crucial resources for supporting materials inverse design, providing the essential data foundation for the development and training of machine learning models. Machine learning is a technique that learns from data and improves automatically to perform specific tasks [8–10]. Using machine learning algorithms can accelerate the process of discovering and designing materials. In materials science, machine learning can handle large volumes of complex data [11], by learning and training from existing data, it can extract the mapping relationship between ACS and P(ACS) from extensive experimental data. Based on the given performance, it can predict the ACS of new materials, thus enabling materials inverse design [12]. Section 2 of this paper provides an overview of the basic concepts and roles of material databases.

However, machine learning-based materials inverse design methods also face numerous challenges. For instance, the cost of data acquisition and labeling is high, and the scale of existing datasets is limited [13]. Machine learning models have weak generalization abilities and poor interpretability, making it difficult to provide materials scientists with deep insights and understanding. In addition, low optimization efficiency, slow convergence speed, and incomplete search of the solution space during the design process are issues that need to be addressed in current research [14]. To address the aforementioned challenges, this paper proposes three solutions for inverse design based on exploration, modeling, and optimization. Additionally, it discusses strategies for selecting machine learning methods and highlights the importance of model performance evaluation and benchmarking standards for assessing and comparing results, which will be detailed in Section 3. Furthermore, inverse design has made significant research progress in fields such as alloys, optics, and acoustics. This paper will provide a detailed overview of the advancements in these areas in Section 4.

In this paper, we provide a comprehensive review of machine learning-based materials inverse design methods. This field has witnessed rapid development in recent years, with steadily increasing research interest. As shown in Fig. 2, the number of publications related to the application of machine learning in materials design and materials inverse design has exhibited a year-on-year growth trend in the Web of Science database, with particularly remarkable growth over the past five years. This trend indicates that, with the continuous optimization of machine learning algorithms and the growing demands of material science, researchers are paying increasing attention to this interdisciplinary field. In 2024, the number of publications related to machine learning-based materials inverse design reached 361, representing a significant increase compared to previous years. This data highlights the potential of this field and its critical role in advancing innovation in material science, making it deserving of greater attention and deeper investigation.

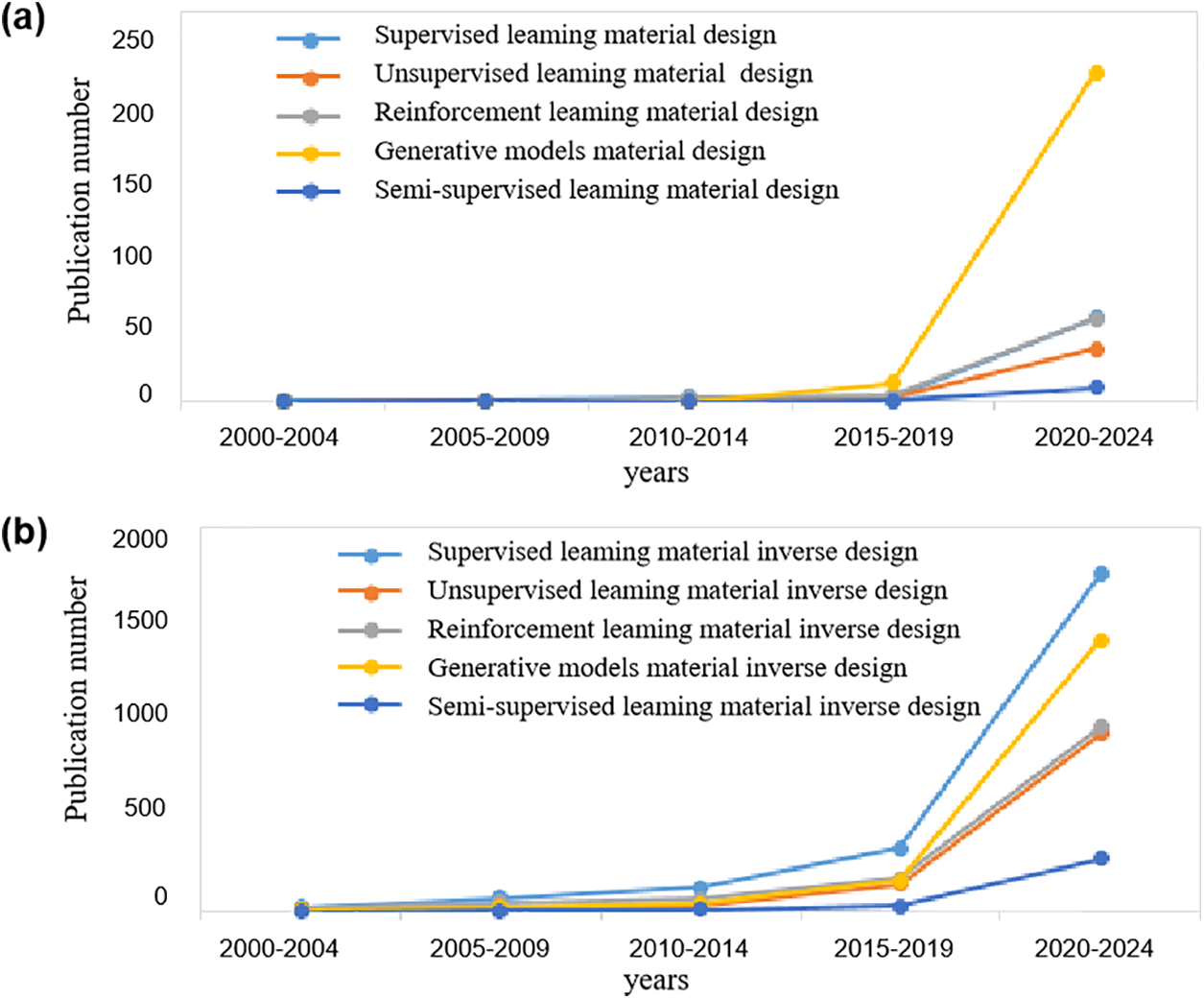
Figure 2: Trend chart of related publications in recent years. (a) Annual number of publications on various machine learning methods and materials design extracted from the Web of Science database. (b) Annual number of publications on various machine learning methods and materials inverse design extracted from the Web of Science database

We begin with an overview of material databases, analyzing their critical role in supporting materials inverse design. Additionally, we systematically classify and evaluate materials using inverse design methods, describing them based on different scenarios and delving into the performance evaluation of models and benchmarking standards. Furthermore, we summarize the current progress in inverse design research within the field of materials science. Through this paper, we aim to provide scholars interested in materials inverse design with a comprehensive perspective, helping them quickly understand various methods and their practical applications. In the future, with improvements in database quality and advancements in machine learning algorithms, materials inverse design is expected to play an increasingly significant role in the discovery of new materials, performance optimization, and engineering design.

2  Materials Database

In June 2011, the American White House announced the launch of the “Materials Genome Initiative for Global Competitiveness” (MGI) [15]. This initiative aims to accelerate material research and development processes and reduce development costs through advanced technologies such as high-throughput computation, big data analysis, and multiscale simulation [16]. Among these efforts, the construction and sharing of databases became a critical component of the Materials Genome Initiative. These databases not only store vast amounts of material data (e.g., composition, structure, properties), providing essential support for material discovery and simulation but also facilitate high-efficiency data accumulation and automated processing. This supports in-depth data analysis based on machine learning, offering intelligent guidance for new material development. Material data serves as the core driver of machine learning algorithm applications. In recent years, attention has shifted from being model-centric to data-centric. Improvements in model performance depend not only on architectural innovation and algorithm optimization but are also closely tied to data quality [17]. This shift emphasizes the importance of data—every step, from data collection and annotation to cleaning and augmentation, can profoundly impact the final effectiveness of machine learning.

Jia et al. adopted a rigorous data preprocessing strategy to optimize the dataset by removing low-quality and mixed data [18]. Additionally, when constructing the machine learning model, they introduced a composition-based cross-validation method to prevent data with the same composition but different temperatures from being allocated to both the training and test sets. This approach effectively avoided the model capturing only temperature-dependent trends, ensuring its ability to generalize to unknown materials. This segmentation method, based on data characteristics, demonstrated that data-splitting strategies play a critical role in model performance. Furthermore, the model was validated using newly published experimental data from 2023, which further confirmed its robustness and predictive capabilities, emphasizing the importance of continually updating data. These findings highlight that in the application of machine learning in materials science, data quality, and processing methods are increasingly becoming key factors influencing model performance.

The foundation of machine learning lies in the availability of existing data, which is typically sourced from literature, online repositories, or directly generated from experimental results. Some commonly used material databases are listed in Table 1 [19]. Data serves as the fundamental building block for training machine learning models, with experimental data being particularly critical because it accurately reflects real-world conditions. However, even if potentially promising materials are identified through computational screening, it may still take years to successfully synthesize them in the laboratory. Consequently, the performance of models is often constrained by the limited availability of data [20]. Although computational material databases like Materials Project, Open Quantum Materials Database (OQMD), and Starrydata2 have provided abundant resources for high-throughput screening and performance prediction in recent years, issues such as data scarcity and quality inconsistency persist. These challenges are especially pronounced in emerging material fields or complex material systems, where data acquisition and organization remain significant obstacles. Therefore, efficiently utilizing existing data while mining and generating high-quality new data is a core challenge for applying machine learning in materials science. To address this, valuable information can be extracted from vast amounts of literature to construct and refine material databases, thereby enriching research data sources. By integrating experimental validation with machine learning model predictions, new data can be generated and supplemented, filling gaps in existing databases. These approaches not only address data scarcity and quality issues but also further expand research data sources, providing a solid foundation for material science research and driving progress in materials design and optimization.

As the data quality of material databases directly impacts the effectiveness of data analysis and mining, and ultimately their practical applications, building high-quality databases has become a critical issue in the field of materials science [21]. Constructing such databases requires not only integrating scattered experimental and computational data but also implementing rigorous data cleaning and validation strategies to ensure reliability, consistency, and completeness. Additionally, the diversity and coverage of the database are essential to support the analysis and prediction of various material properties. High-quality material databases provide a solid foundation for machine learning algorithms, enabling the discovery of scientific principles hidden within the data, accelerating materials design and optimization, and facilitating practical applications. However, challenges arise during construction, as errors may exist in the original literature or during the data extraction process. Moreover, databases used for building machine learning models should maintain uniformity—comprising either entirely experimental or computational data. Experimental data, in particular, more accurately reflect the actual performance of materials, making the identification and removal of low-quality data a crucial step in improving accuracy. With advances in experimental technologies, the latest data typically offer higher quality. To ensure the timeliness and relevance of databases, outdated data from older publications should be excluded, and additional data can be extracted from recent literature to validate the credibility and robustness of the models. This ensures that models remain relevant and accurate when utilizing up-to-date material data. By adopting these strategies, material databases can more effectively support the development of machine learning algorithms, providing robust backing for the discovery, performance prediction, and optimization of new materials. This will significantly accelerate research and progress in the field of materials science.

3  Inverse Design

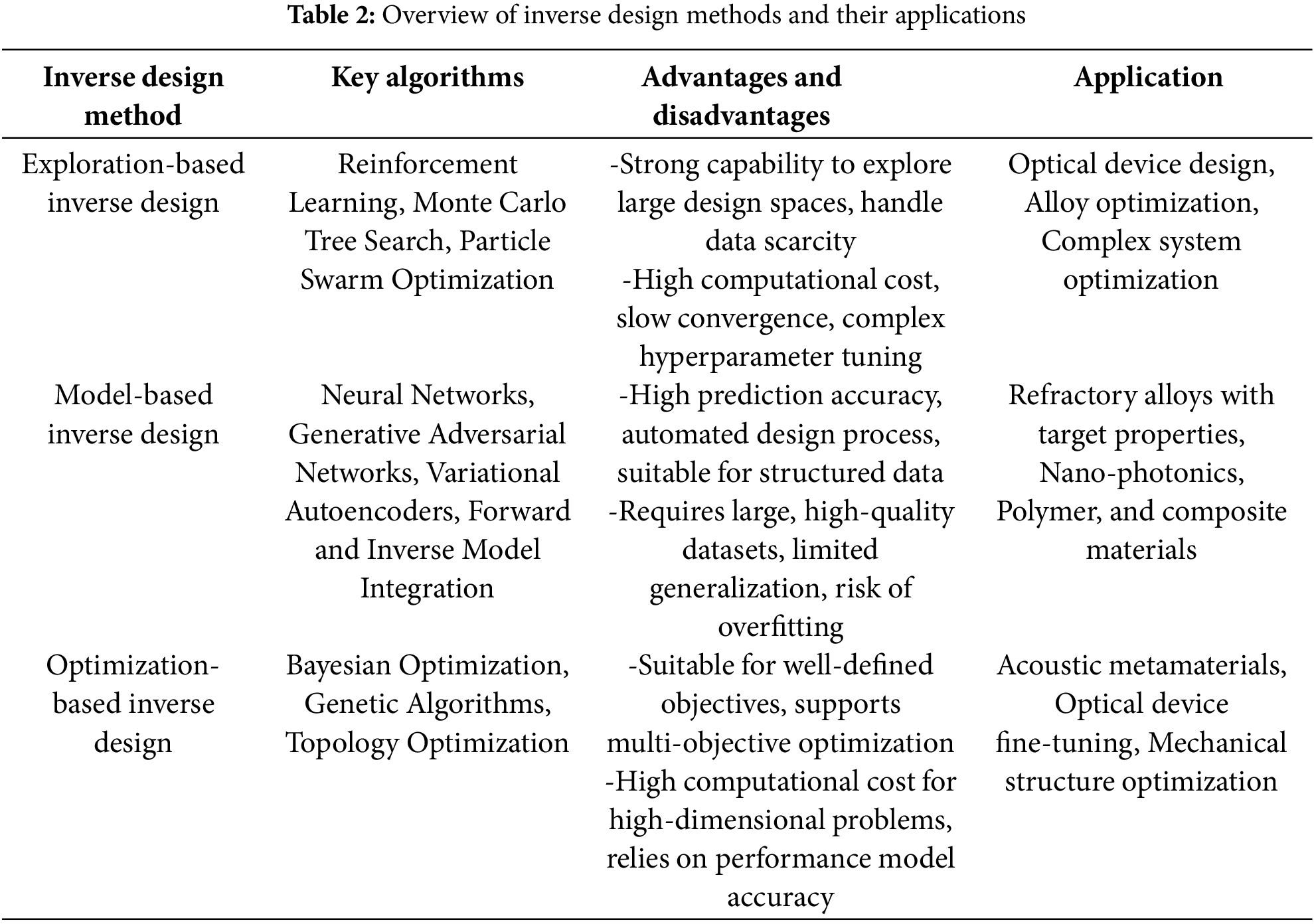
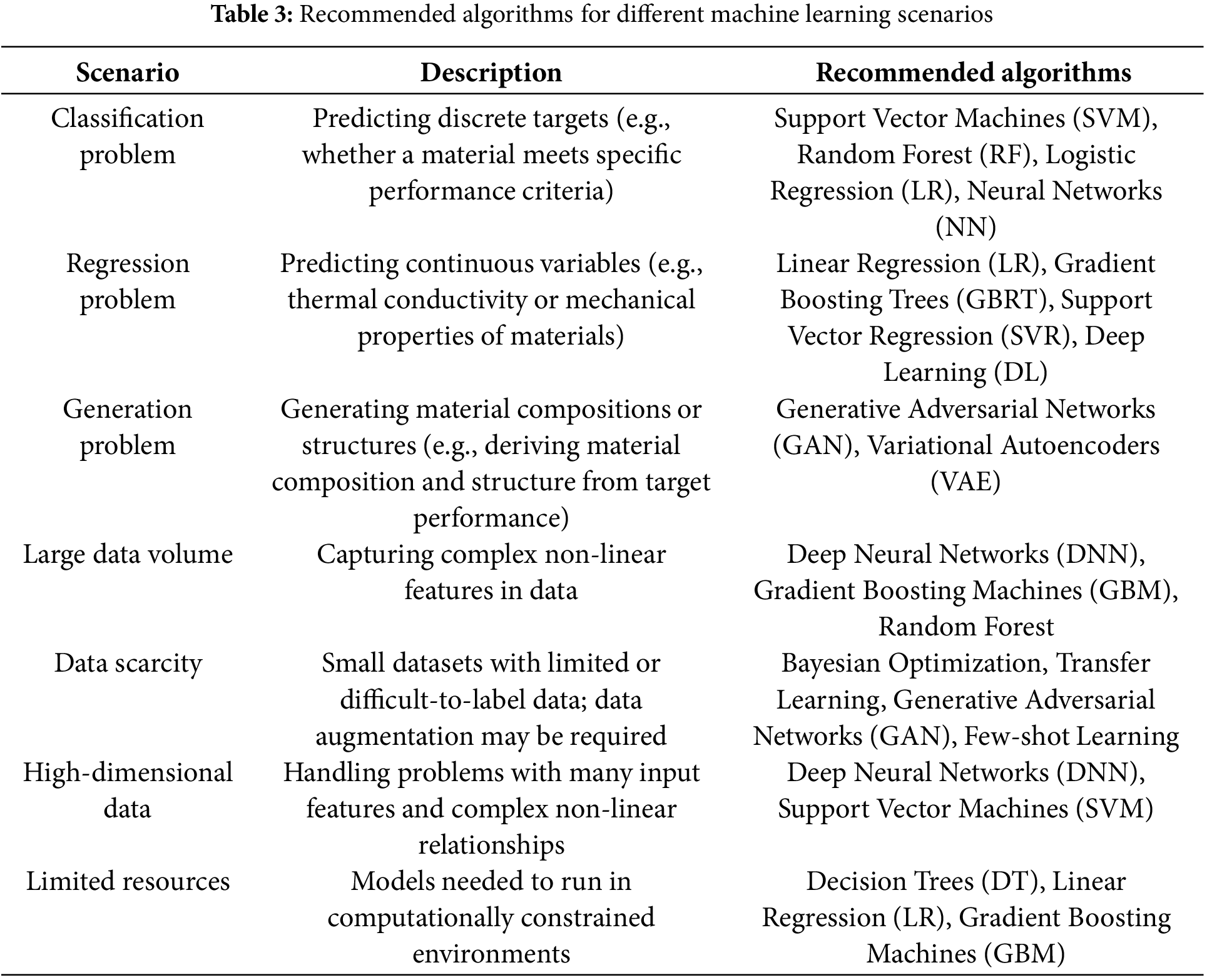
Inverse design is a method that starts with the desired performance and works backward by adjusting design variables to meet these performance requirements. Compared to traditional forward design, inverse design is more challenging because it requires finding design solutions that satisfy specific requirements within a vast design space. At the same time, machine learning-based materials inverse design methods face several difficulties, such as the high cost of data acquisition and labeling, poor generalization capability of machine learning models, and low optimization efficiency during the design process. These challenges can be addressed through exploratory analysis, model design, and optimization strategies. Table 2 describes three inverse design methods, along with their key algorithms, advantages and disadvantages, and application scenarios.

3.1 Exploration-Based Inverse Design

Exploration-based inverse design is a method focused on exploring unknown or entirely new design targets, particularly suitable for situations with scarce data. The conceptual design diagram is shown in Fig. 3. This method emphasizes gradually approaching the optimal solution through local rules and random exploration, allowing it to handle complex multidimensional design problems and efficiently discover potential optimal design solutions in a vast design space. Reinforcement learning and heuristic search are typical exploration strategies that can better discover optimized designs. The following sections will specifically describe the applications of exploration-based inverse design in materials.

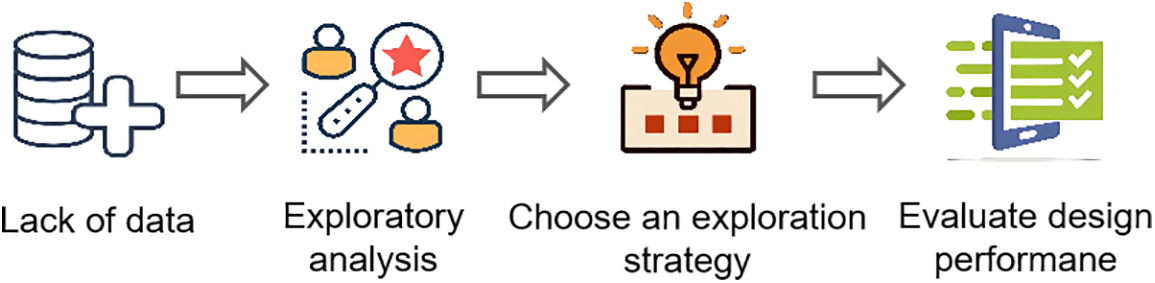
Figure 3: Exploratory-based inverse design concept diagram

Reinforcement learning methods differ from traditional supervised learning in that they do not rely on large amounts of labeled data. Instead, they accumulate experience through the interaction between the agent and the environment during the learning pro cess [22,23]. In situations with scarce data, reinforcement learning can still effectively explore vast and complex unknown design spaces. Hwang et al. proposed an inverse design framework based on deep reinforcement learning, which includes the Inverse Design Agent (IDEA) and the Critical-Value-Based Tree (CVBT) algorithm [24]. Initially, based on the Advantage Actor-Critic (A2C) method, the agent learns the relationship between the geometric parameters of optical devices and their performance through trial and error without any prior knowledge. The agent continuously adjusts the geometric parameters and receives rewards from the environment to optimize the design parameters. Finally, CVBT proposes multiple candidate designs to enhance the diversity and robustness of the solutions, gradually achieving the design goals that meet the target performance.

Monte Carlo Tree Search (MCTS) is a tree search algorithm based on random simulations [25,26], with high heuristic search capabilities. MCTS does not strictly belong to the traditional definition of machine learning but is often combined with Reinforcement Learning (RL) in inverse design as a strategy optimization method [27–29]. Without complete data, MCTS can discover potential optimal paths and solutions through random simulations and probability estimates. Banik et al. proposed a Continuous Action Space Tree search framework (CAST) based on reinforcement learning, where MCTS serves as a heuristic search method, exploring the search space through random sampling and tree search strategies [30]. RL balances exploration and exploitation, optimizing the search path. The heuristic search of MCTS and the strategy optimization of RL complement each other, enabling the agent to conduct effective exploration and optimization even in data-scarce situations. This achieves structural and topological optimization in complex and high-dimensional search environments, significantly enhancing the efficiency and accuracy of crystal structure prediction and multidimensional system optimization. Patra et al. combined MCTS with Molecular Dynamics (MD) simulations to achieve efficient exploration and optimization of polymer molecular sequences [31]. MD simulations may face issues of insufficient or expensive experimental data, but MCTS, with its efficient heuristic search capabilities, can quickly identify and optimize target sequences in a large design space under data-limited conditions. Through continuous optimization and expansion, the MCTS algorithm is expected to play a greater role in more materials science and engineering design problems.

Particle Swarm Optimization (PSO) optimizes objectives by moving a swarm of particles, utilizing heuristic and intelligent exploration strategies for global search in complex and uncertain design spaces. This method can efficiently find optimal input parameters in multidimensional spaces through collaboration and information sharing among particles with minimal data or information, thus improving design efficiency [32–34]. Mi et al. used the PSO algorithm to optimize the input parameters of neural networks, achieving inverse design through input optimization [35]. Khadikar et al. combined Self-Consistent Field Theory (SCFT) with PSO to optimize the structure and composition of Block Copolymer (BCP) films. PSO simulates the self-assembly behavior of biological systems, conducting global exploration in multidimensional design spaces to find the optimal formulation parameters for the target morphology [36]. By combining PSO with SCFT to handle high-density metastable states of free energy, heuristic search finds stable target morphologies.

In summary, exploration-based inverse design demonstrates significant advantages in handling unknown targets and data scarcity issues, making it an effective tool for discovering new materials and optimizing complex systems. However, this method also faces challenges such as high computational resource requirements and slow convergence speeds. Future research and technological innovations are needed in areas such as computational acceleration, adaptive tuning, hybrid optimization, intelligent algorithms, and uncertainty handling. By continuously improving algorithm efficiency, the robustness and adaptability of models can be enhanced. Overall, exploration-based inverse design is expected to play a greater role in materials science, engineering design, and other complex fields, driving innovation and technological progress.

3.2 Model-Based Inverse Design

Model-Based Inverse Design is a method that uses data-driven or physics-driven inference models for materials design [37]. This approach builds predictive models that establish the relationship between performance and composition or structure based on material databases, enabling the inference of corresponding material components or structures starting from target performance. The conceptual design diagram is shown in Fig. 4. Currently, various strategies such as combining forward and inverse models, generative models, and surrogate models are widely used in materials inverse design. The following will introduce several model-based inverse design strategies [38].

Figure 4: Conceptual diagram of model-based inverse design

Inverse design often involves mapping multiple outputs from two or fewer inputs, making it prone to overfitting when using only inverse models. Combining forward and inverse models enables bidirectional exploration between performance and composition, effectively addressing the overfitting issue. Wang et al. proposed a machine learning design system (MLDS) for the inverse design of copper alloys in 2019 [39]. Jiang et al. also applied MLDS to the inverse design of aluminum alloys [40]. MLDS consists of two artificial neural networks built based on a database. One of the models predicts the properties of alloys from their compositions (i.e., composition→performance, C2P), and the other model predicts the compositions of alloys according to the targeted properties (i.e., performance→composition, P2C). The P2C model is first used to generate multiple candidate material combinations, which are then input into the more reliable C2P model to obtain more accurate predictions. The predicted values are compared with the target values, and the error is calculated. Based on the error, a combination design solution is selected or the model is retrained. If the error exceeds the preset threshold, the P2C model is retrained until reasonable alloy composition design solutions are selected. The MLDS design process is shown in Fig. 5. In addition to the alloy field, Liu et al. also applied forward and inverse models to the field of nano-photonics [41]. We find that combining inverse “pre-design” with traditional “post-analysis” can comprehensively cover the design space, improving design efficiency and accuracy, and accelerating the discovery of target materials.

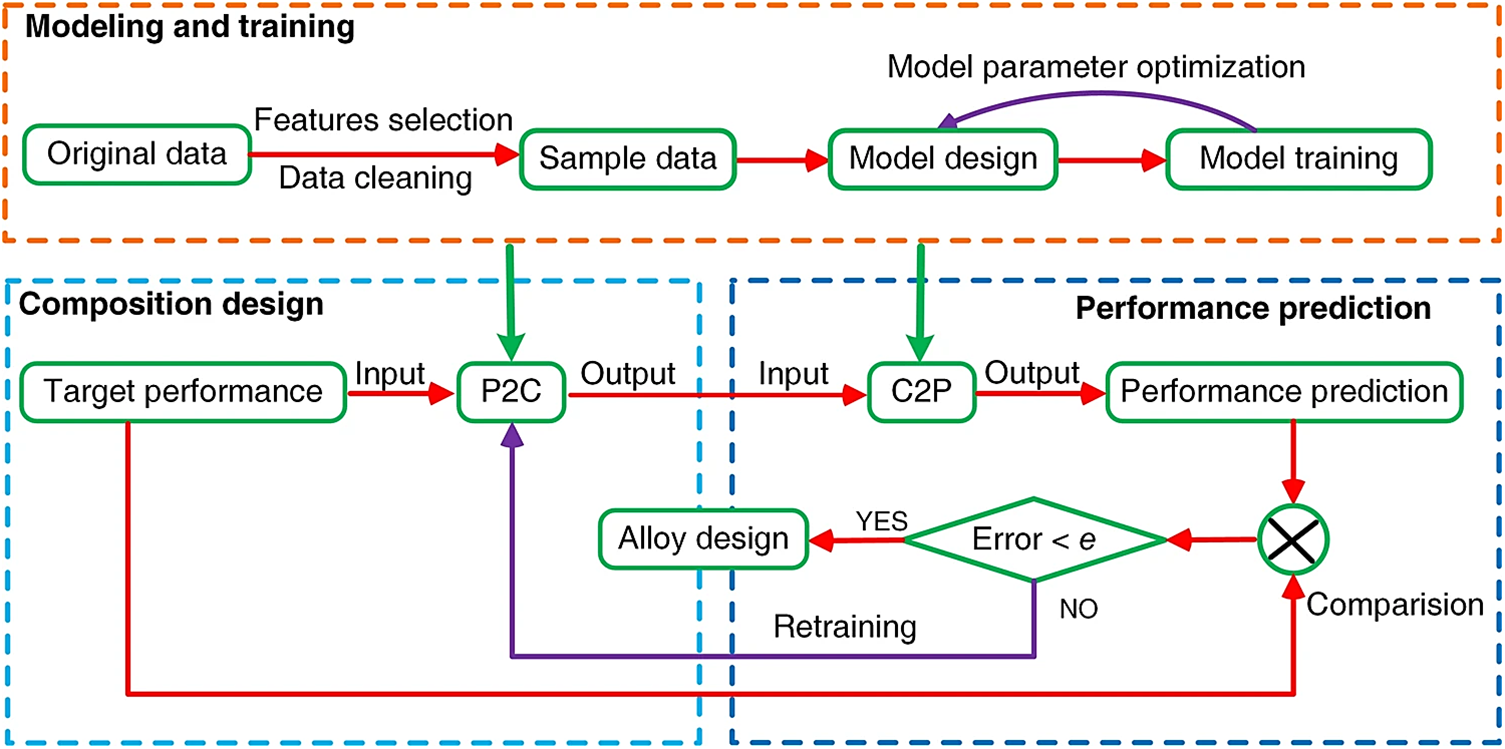
Figure 5: MLDS design flowchart [39]

Generative models are deep learning models capable of generating new data points. They can directly generate material compositions or structures based on target performance in a data-driven manner. This strategy typically employs advanced machine learning techniques such as Generative Adversarial Networks (GAN) [42] and Variational Autoencoders (VAE) [43]. Debnath et al. utilized Conditional Generative Adversarial Networks (cGAN) to achieve the inverse design of refractory high-entropy alloys [44], as shown in Fig. 6. The cGAN provides an additional conditional vector in the generator compared to ordinary GANs. This conditional vector, which usually includes the target performance that the material needs to have, directly influences the generated material data. The generator creates material data according to this conditional vector. The discriminator also receives this conditional vector and compares it with the generator’s output to determine the authenticity of the generated material data. In this way, the generator can create material combinations under imposed conditions based on the input conditional vector, exploring diverse combinations within the target performance range to compensate for the limitations brought by a single target value. Pei et al. proposed an Inverse Design Network (IDN) [45]. First, a regression model is trained to predict the relationship between material performance and element concentration. Then, a VAE model is used to represent material structure in the latent space, capable of inverse-generating element concentrations from this space. The IDN uses the trained network weights and biases to transform the latent space representation into actual element concentrations, completing the mapping from target performance to material composition, thereby achieving the inverse design of alloys with highly similar microstructure images.

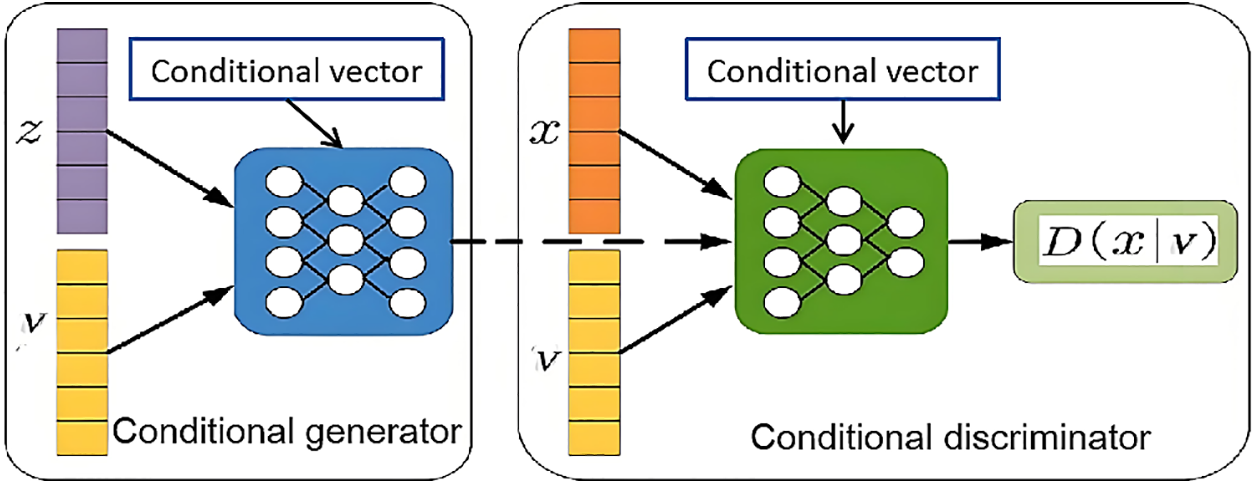
Figure 6: cGAN inverse design process

A surrogate model is a simplified representation of a complex function that approximates the mapping relationship between design parameters and performance. It enables efficient design optimization and experimental validation by utilizing optimization algorithms to adjust input parameters, thereby maximizing or minimizing target performance. Liow et al. proposed an inverse design surrogate model that combines statistical interpolation techniques, machine learning, and optimization design for efficient cathode materials design and experimental validation [46]. The surrogate model was constructed using a random forest algorithm to train the model, learning the relationship between cathode materials design parameters and discharge capacity, and predicting design variables that meet the target discharge capacity, demonstrating strong predictive and optimization capabilities. Dong et al. integrated a transfer learning-based artificial intelligence surrogate model with traditional optimization algorithms to successfully predict optical materials based on given target spectra [47]. First, the dataset was divided into a small dataset B, and the remaining dataset A. The parameters of model A (trained using dataset A) were then transferred to model B (fine-tuned using dataset B). Finally, the results obtained from model B were used for inverse design through spectral fitting with traditional optimization algorithms. The framework diagram of the transfer learning-based artificial intelligence surrogate model is shown in Fig. 7.

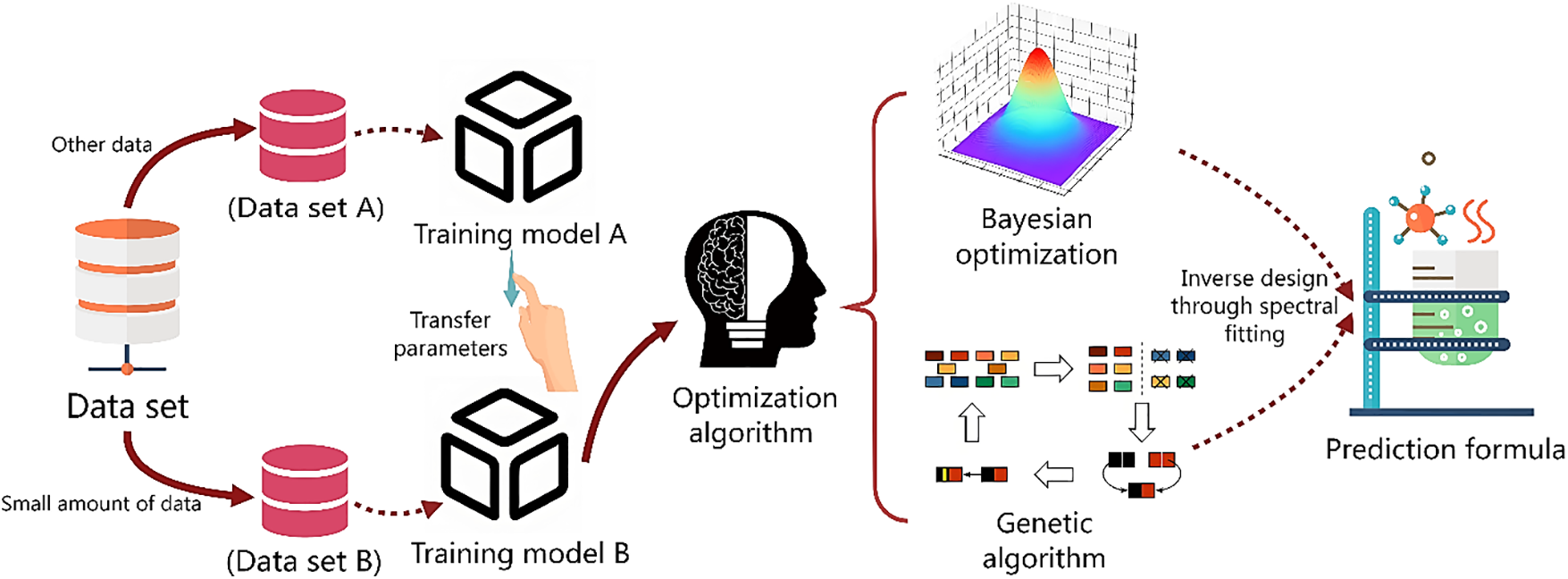
Figure 7: Framework diagram of transfer learning-based AI surrogate model

Model-based inverse design focuses on utilizing design models, enabling efficient mapping from performance to parameters through data-driven methods. This approach is suitable for design problems with existing data or models. By appropriately selecting and combining these models, it is possible to accurately predict or generate new design schemes. These models not only enhance the automation and accuracy of the design process but also expand the diversity and possibilities of design. However, model-based inverse design faces challenges such as model stability and high demand for training data. Future research needs to address these technical challenges, explore more model integration with practical applications, and promote the rapid discovery and performance optimization of new materials.

3.3 Optimization-Based Inverse Design

Optimization-based inverse design views inverse design as an optimization problem, specifying target performance and using optimization algorithms to adjust material composition or structure to achieve specific target performance. The concept diagram is shown in Fig. 8. In this type of design, the target performance is usually defined as one or more optimization objectives. To achieve these objectives, the design process relies on various optimization algorithms. Choosing the appropriate optimization algorithm can greatly enhance model optimization efficiency.

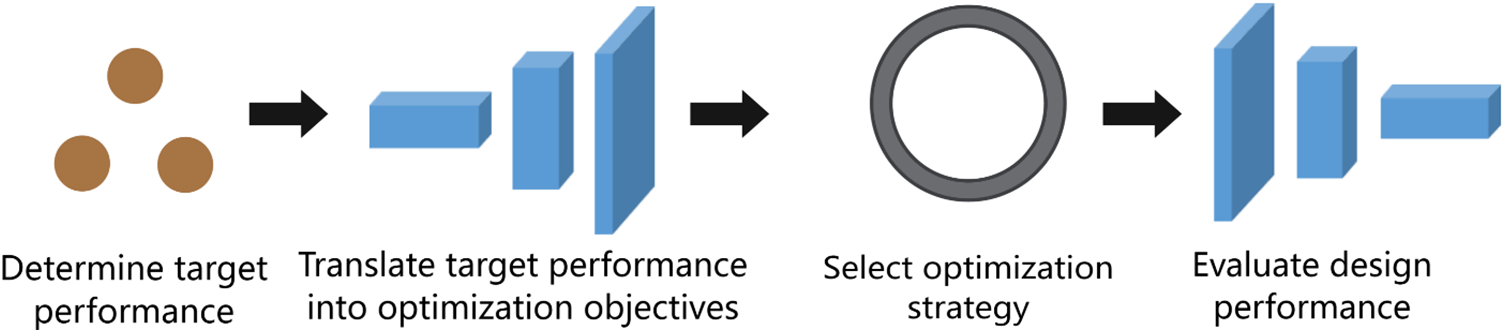
Figure 8: Optimization-based inverse design concept diagram

Bayesian optimization combines Bayesian inference and Gaussian processes to dynamically adjust design parameters, improving optimization efficiency and accuracy [48–50]. Zheng et al. describe an inverse design method based on Gaussian Bayesian models (GB) [51]. First, a Gaussian process is used to establish an initial model relating acoustic performance to design parameters. Then, based on current optimization results, an adaptive acquisition function is employed to select new observation points, thus enhancing optimization efficiency. This is followed by iterative calculations and parameter updates to gradually optimize structural parameters and approach an optimal design. Finally, numerical simulations and experimental validations are conducted to ensure that the optimized design meets the expected performance. Tagade et al. combined Bayesian theorem and unsupervised learning for inverse design [52]. They used unsupervised learning to quantify prior probabilities, ensuring that the search space remained within a valid range. Then, they applied the Bayesian theorem to update the prior probability distribution and optimized the molecular structure with new evidence. A large number of valid molecular structures were generated by sampling from the posterior distribution, and their effectiveness was validated through numerical simulations and experiments.

Genetic algorithms (GA) are optimization algorithms that search for optimal configurations by simulating the process of natural selection [53]. By incorporating constraints and multi-stage optimization, GAs can achieve efficient optimization for complex molecular designs. In inverse design, the adaptive nature of genetic algorithms ensures that generated solutions meet both structural similarity and target performance optimization requirements. Bhat et al. proposed a design method using category-based optimization to predict the optimal Al alloy compositions. This approach outperformed traditional class-agnostic optimization techniques in predicting alloys with enhanced tensile strength and elongation, identifying key alloying elements for targeted optimization. The method was further improved by introducing data-driven classification techniques to train class-specific regression models. These models were then individually combined with genetic algorithms to search for alloys with high strength and high ductility [54].

Topology optimization (TopOpt) is an optimization method that provides powerful tools and techniques for inverse design by adjusting material distribution to optimize structural performance [55]. Christiansen et al. described a density-based topology optimization strategy, which adjusts material distribution to optimize structural performance and uses adjoint analysis for efficient gradient computation to optimize design variables [56]. This method has been widely applied to achieve high-performance structural designs. Chen et al. used topology optimization to maximize near-field enhancement effects in nanoparticle dimers [57]. They first adjusted design variables through material interpolation methods, then used adjoint methods to compute the gradient information of the design objectives concerning design variables. Finally, based on the gradient information, iterative methods were used to update design variables, gradually approaching the optimal solution. TopOpt demonstrates strong optimization capabilities and flexibility in handling large-scale and high-dimensional design problems, significantly enhancing design efficiency and flexibility in mechanics, photonics, and plasma science. Future developments can further optimize computational efficiency, improve considerations for manufacturing constraints, and promote the application and innovation of topology optimization in more fields.

Optimization-based inverse design methods are particularly well-suited for materials design problems with clear design objectives and optimization requirements. This method can accommodate various types of objective functions and constraints, making it broadly applicable. However, for high-dimensional design problems, the computational cost of optimization algorithms can be significant. Additionally, the optimization results depend on the accuracy of performance prediction models; inaccurate models may lead to suboptimal or incorrect designs. In the future, optimization-based inverse design will play a larger role in addressing complex, high-dimensional materials design problems. As optimization algorithms and performance prediction models continue to improve, this method will further enhance the efficiency and accuracy of materials design, providing powerful tools for the discovery and development of high-performance materials.

3.4 Machine Learning Method Selection

The selection of machine learning models is a crucial aspect of materials inverse design. Different task types, data characteristics, and practical application scenarios present varying requirements for model selection. The right machine learning model can not only improve the accuracy and efficiency of predictions but also significantly optimize the design process and accelerate material development. However, the complexity and diversity of material science problems mean that model selection is not fixed but needs to be considered comprehensively, taking into account factors such as the specific problem type, data scale and quality, computational resources, and model interpretability. To assist researchers in selecting the most appropriate machine learning method, Table 3 summarizes model selection strategies based on task type, data characteristics, computational costs, and other factors. These strategies provide systematic guidance for choosing machine learning models in materials inverse design, helping to improve design efficiency and the reliability of results.

3.5 Model Performance Evaluation and Benchmarking Standards

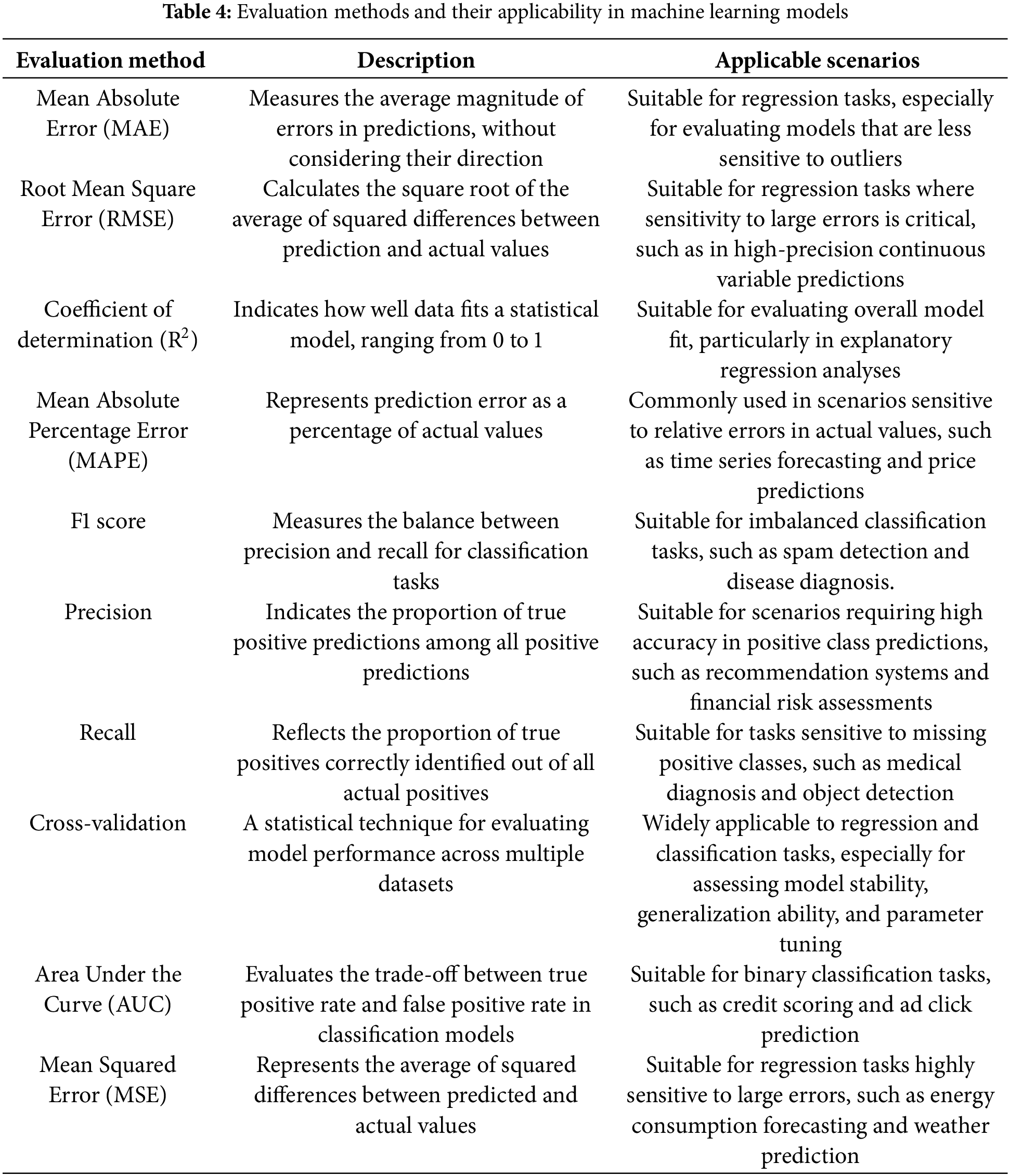
In materials inverse design, model performance evaluation and benchmarking standards are key components for assessing the effectiveness and applicability of machine learning methods. Performance evaluation, as one of the key factors to consider when designing, developing, configuring, and tuning computer systems, should span all stages of the system lifecycle to ensure its effectiveness and reliability in various application scenarios [58]. As shown in Table 4, different evaluation methods provide researchers with multi-dimensional performance measurement tools. Through scientifically sound performance evaluation, one can gain a comprehensive understanding of the model’s prediction accuracy, generalization ability, and adaptability to complex materials design tasks in various application scenarios.

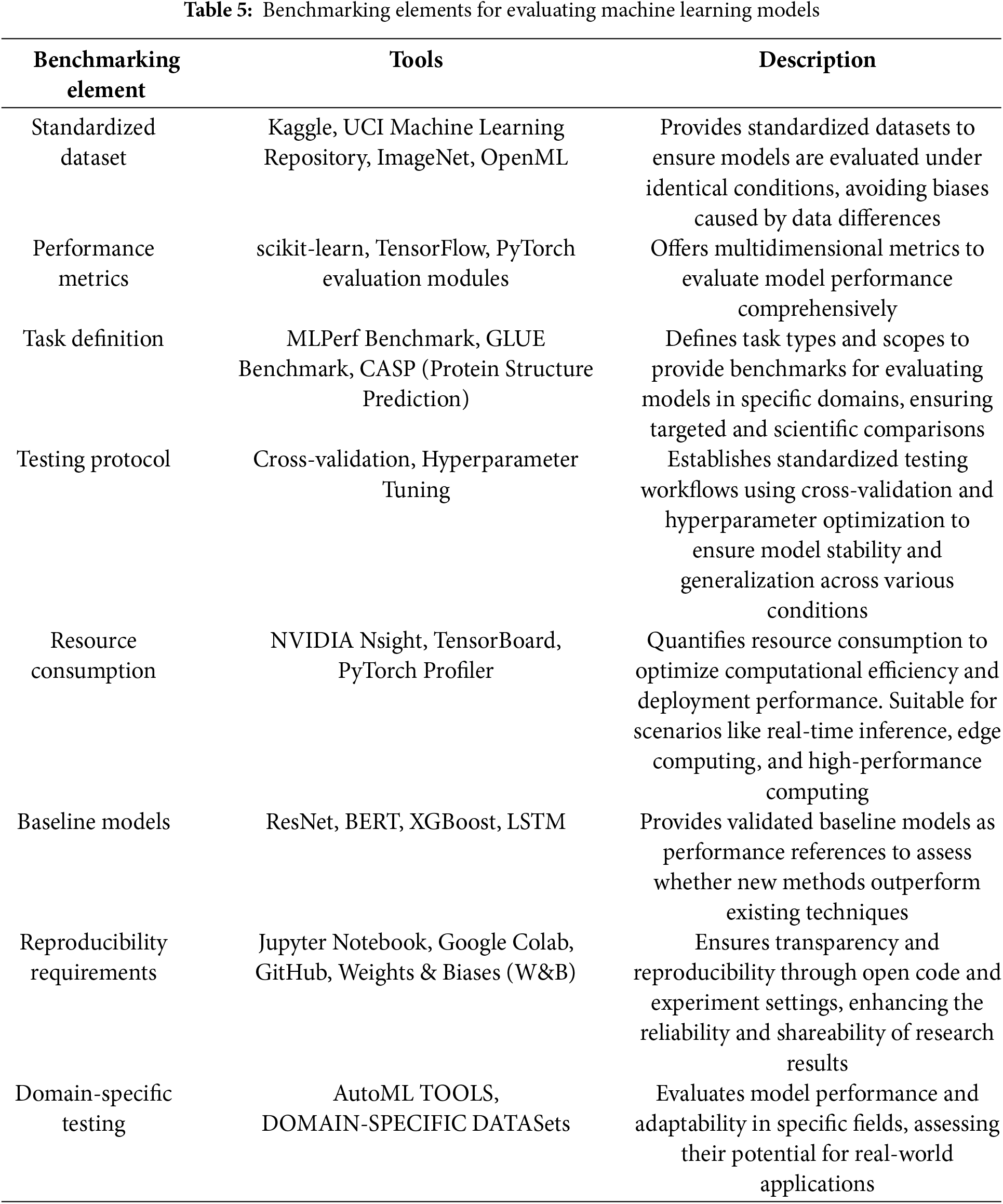
The establishment of benchmarking standards provides a unified comparison framework for different methods and models, allowing researchers to evaluate the performance and applicability of technologies on the same basis [59]. This not only helps identify the strengths and weaknesses of models but also promotes cross-validation of different research works and the reproducibility of results. Table 5 summarizes the key elements of benchmarking standards, commonly used methods or tools, and the applicable model types, offering an important reference for establishing a benchmarking framework.

4  Applications of Inverse Design

Inverse design, as an innovative approach in modern engineering design, has been widely applied across various fields of materials science and engineering technology. Through inverse design, researchers and engineers can use advanced computing technology and experimental data to improve and optimize existing materials and devices or develop entirely new high-performance materials. This method not only enhances design efficiency but also significantly reduces R&D costs. The following will provide a detailed introduction to the specific applications of inverse design in several key types of materials, including alloy materials, optical materials and photonic devices, acoustic materials, and other materials.

4.1 Alloy Materials

Alloy materials are widely used in aerospace, automotive, electronics, and military fields due to their excellent properties [60–63]. With the advancement of industrial technology and the increasing demands for material performance, combining the inherent properties of alloys with structural design to achieve specific performance indicators has become a significant research direction in materials design. The composition, microstructure, and manufacturing process of alloys have a significant impact on their properties. By adjusting these factors, the performance of alloys can be precisely controlled to meet the needs of various applications [64]. In alloy design, mechanical properties are fundamental [65]. Tensile strength and ductility are commonly used and easily tested in engineering, and are often selected as target performances [66]. Inverse design, by constructing a relationship model between composition and performance and using optimization algorithms to iteratively adjust design variables, can efficiently find alloy combinations that meet specific performance requirements.

Building relationship models between the composition, thermal processing conditions, microstructure, and performance of alloy materials are crucial in alloy inverse design [67]. Machine learning algorithms can efficiently analyze and mine large amounts of experimental data to establish accurate relationship models, guiding optimization algorithms to quickly find optimal alloy combinations that meet target performance [68,69]. Hu et al. systematically reviewed the research progress of machine learning in alloy design, detailing the three major obstacles faced in alloy inverse design [70]. The basic process of alloy materials inverse design is shown in Fig. 9.

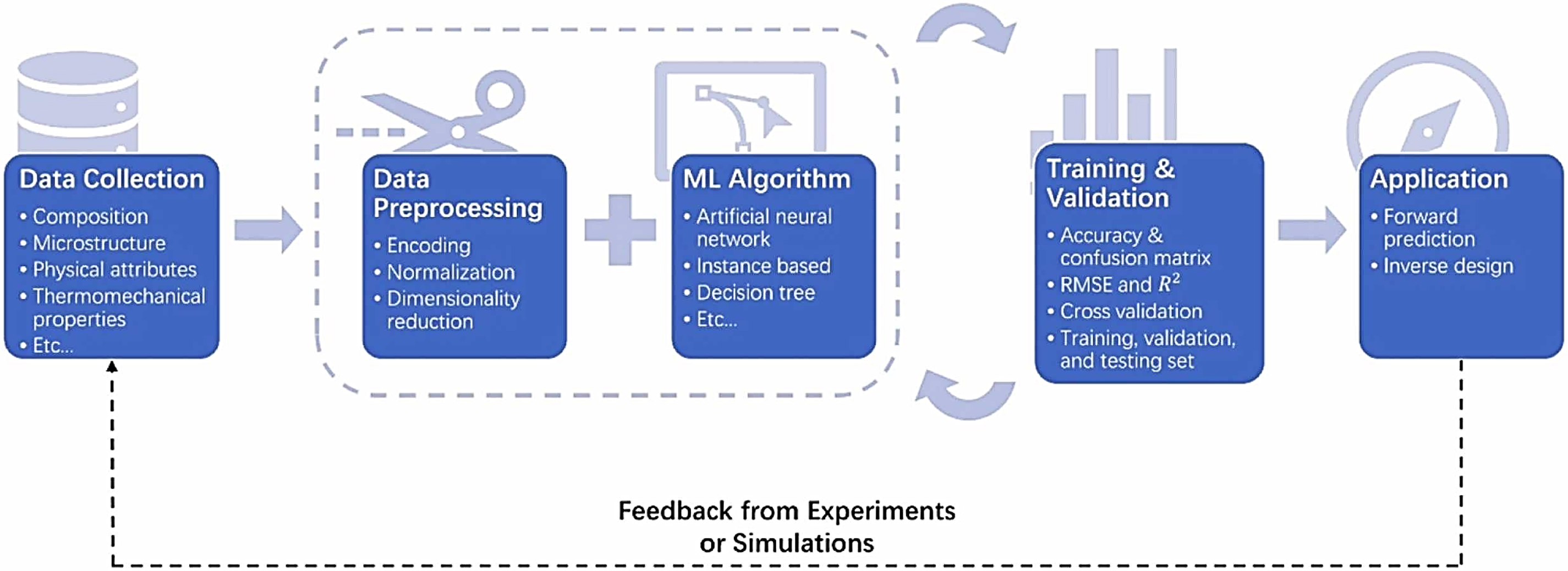
Figure 9: Basic process flowchart for alloy materials inverse design [70]

As the composition of alloys becomes increasingly complex and elements continue to increase, the design space expands, making it more challenging to discover alloys with target performance [71]. Optimization algorithms can simplify this search process and accelerate the discovery of new materials. Dudiy et al. used Genetic Algorithms (GA) as search and optimization algorithms to help find alloy materials with specific light absorption capabilities [72]. This target performance depends on structural configurations, with each structural configuration element discovered in the Gap shown in Fig. 10a. The process first optimizes the atomic structure through evolution to find the optimal configuration. Then, a fitness function is used to define the difference between the calculated values and the target values, thus driving the GA optimization process. This method efficiently explores vast design spaces, progressively optimizing alloy composition and structure to quickly find alloys that meet target performance requirements. Although this optimization algorithm can effectively accelerate the search speed, it often generates multiple material combinations, leading to issues of non-uniqueness and uncertainty. To address the non-uniqueness issue, Jiang et al. proposed an adaptive strategy, interactively using forward models and inverse models [40]. Candidate solutions proposed by the inverse model are validated through the forward model, and uncertainty is assessed. After each optimization iteration, new validated data is fed back into the forward model to continuously update the model and improve prediction accuracy. This adaptive updating method evolves the model, progressively converging to the optimal solution, as shown in the model flowchart in Fig. 10b. However, single-objective optimization can no longer meet the diverse needs of alloy materials; therefore, it is necessary to find alloys that simultaneously meet multiple performance requirements. Padhy et al. collected alloys’ magnetic, electrical, and mechanical properties and designed a database [73]. For this database, they developed a multi-objective performance machine learning model and combined it with Bayesian algorithms to optimize in the multi-objective performance space. This method can optimize alloy composition while considering multiple performance indicators and finding alloy combinations that meet various performance requirements. Additionally, Bhat et al. trained a multi-objective random forest regression model to predict three mechanical properties (yield strength, tensile strength, and elongation) [74]. They used the multi-objective random forest regression model to predict alloy composition and employed a random forest classifier to predict processing conditions. Through this multi-objective optimization strategy, they successfully met multiple performance requirements in alloy inverse design, improving the efficiency and accuracy of alloy design, as shown in Fig. 10c.

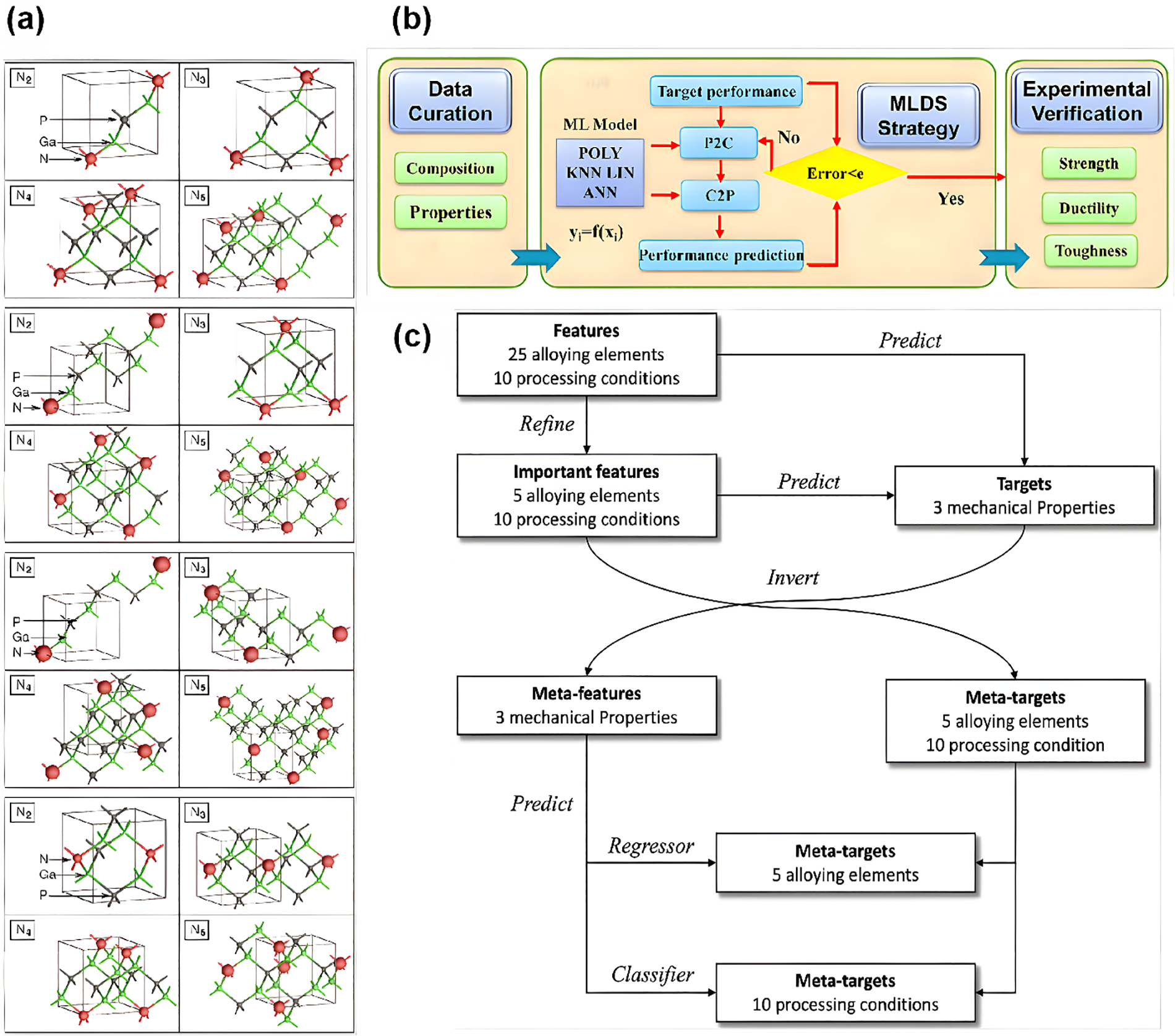
Figure 10: (a) Identification of Np cluster configurations with the deepest defect layer, shallowest defect layer, highest oscillation intensity, and lowest strain capacity in the Gap [72]; (b) Rational design method for new ultra-strong and high-toughness aluminum alloys [40]; (c) Summary of the engineering process for aluminum alloy inverse design [74]

Currently, alloy inverse design methods based on machine learning have made significant progress. Researchers have successfully predicted the composition and process parameters of new alloys by constructing large-scale alloy databases and utilizing advanced machine learning technologies, and these predictions have been validated through experiments. However, alloy materials inverse design still faces many challenges, including data quality, model interpretability, and algorithm accuracy. In summary, alloys with target performance can reduce the time and cost of discovering new materials. With ongoing research and innovation, machine learning-based alloy inverse design methods will bring greater advancements and development to the design and application of alloy materials.

4.2 Optical Materials and Photonic Devices

Optical materials and photonic devices are widely used in fields such as optical communications, laser technology, and optical sensing due to their specific optical properties (e.g., refractive index and absorption rate) [75,76]. One of the core challenges in contemporary optics is how to optimally combine the inherent properties of materials with photonic structures to achieve the desired performance. The composition, structure, and manufacturing processes of materials significantly impact their optical performance. By adjusting these factors, precise control over the optical properties can be achieved to meet various optical application needs [77,78]. Traditional optical materials design methods typically start from fixed structural parameters and predict their optical performance, which is a unidirectional process lacking feedback adjustment. This approach can limit optimization and speed, especially in the design of complex or large-scale photonic devices. In contrast, inverse design begins with the desired optical response and uses inverse engineering to determine the necessary materials and structures, allowing for the rapid discovery of new materials. This method has become an active research direction in the field of photonics engineering [79–83].

Molesky et al. systematically introduced the major developments of inverse design in the field of nanophotonics [84]. In the early stages, adjoint methods and evolutionary algorithms were already applied to photonic inverse design [85]. However, adjoint methods can get trapped in local optima when facing multi-modal problems, making it difficult to find the global optimum. Evolutionary algorithms can be computationally expensive and slow to converge when dealing with complex or non-smooth objective functions, which may make these optimization methods less suitable. To overcome these shortcomings, several emerging inverse design methods have been developed in recent years.

Using machine learning to learn patterns and rules in datasets enables the prediction of the performance and behavior of photonic structures, providing rapid prediction and optimization capabilities. Peurifoy et al. trained a neural network to simulate the interaction of light with nanoscale materials, mapping the relationship between the thickness of each shell of the nanoparticle and the scattering cross-sections at different wavelengths in the scattering spectrum [86]. The inverse problem was solved using backpropagation, and the trained model can approximate complex physical simulations. The framework of this neural network model is shown in Fig. 11a. Compared to traditional methods, neural networks are more capable of searching for global optima and offer faster computational speeds. Although machine learning can accelerate the inverse design process in some cases, there are still challenges. A common issue is the occurrence of non-uniqueness in data, where the same input can result in different outputs [87], such as in inverse scattering problems [41], the “one-to-many” nature of target spectra [88], and multiple solutions that satisfy transparency conditions [24]. Cleaning training data, adjusting network structures, or introducing forward models can help address this issue. For example, Liu et al. overcame the non-uniqueness problem by cascading forward and inverse models [41], as shown in Fig. 11b. However, machine learning methods heavily rely on large amounts of high-quality data, and the lack of data resources and poor model interpretability remain major bottlenecks in optical materials inverse design. In optical systems, building datasets requires collecting spectral data [89], imaging data, etc., which demands substantial time and resources, making it challenging to gather sufficient training data.

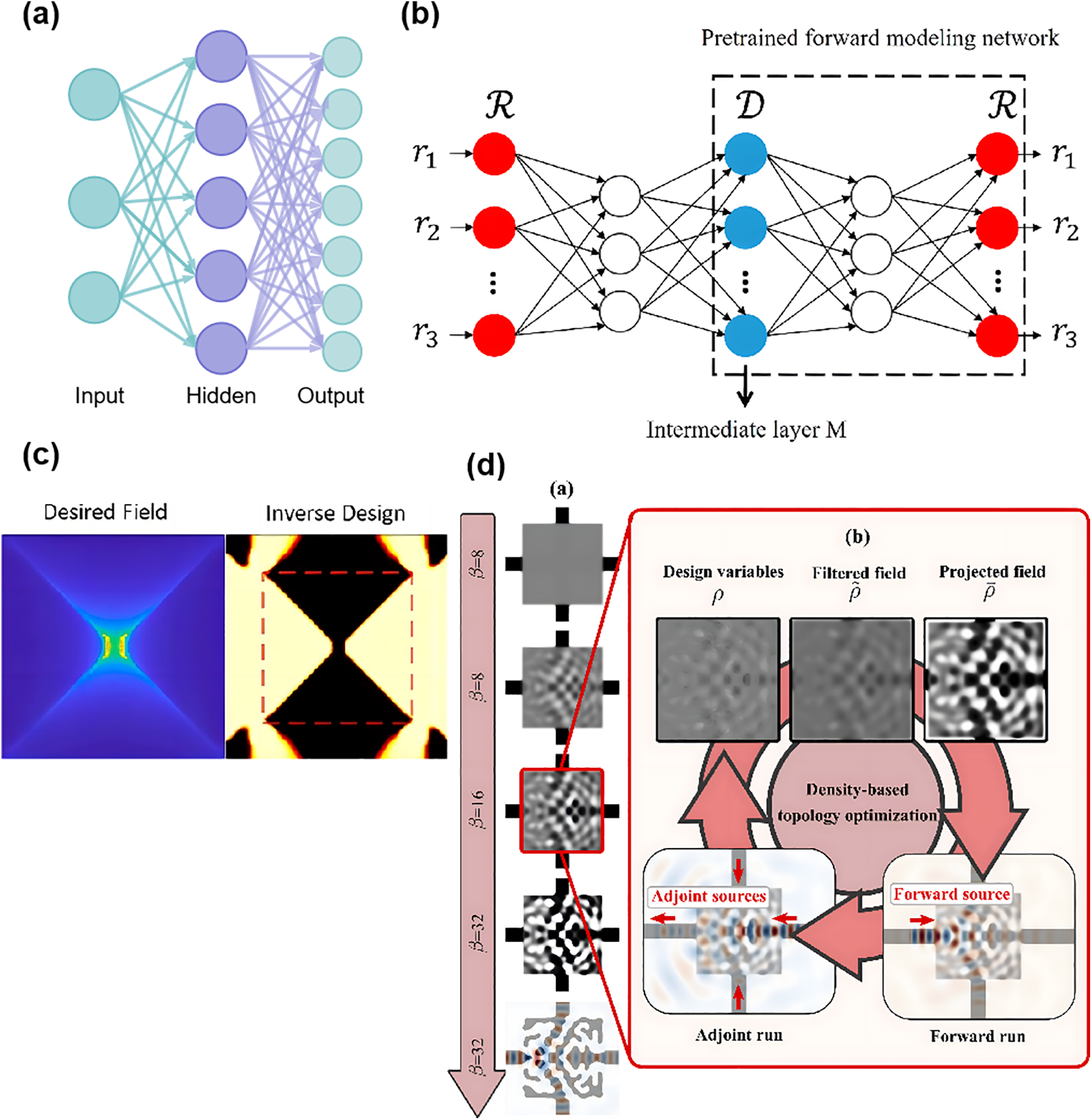
Figure 11: (a) Neural network architecture iagram; (b) Series network connecting the forward network and the inverse network [41]; (c) Schematic diagram of inverse design for plasmonic structures [91]; (d) Density-based photonic topology optimization: First, the design variables are filtered and projected, then a forward run is performed to evaluate the objective function, and finally, the adjoint sources, determined by the results of the forward run, are applied for optimization [92]

Given the limitations of traditional methods (adjoint methods and evolutionary algorithms) and emerging methods (machine learning), there is a need for an approach that combines multiple advantages. In the optical field, topology optimization, which combines the physical accuracy and numerical efficiency of traditional methods with low data dependency, has become a powerful tool for solving optical inverse design problems [90]. Zeng et al. proposed a density-based topology optimization framework for the inverse design of plasmonic structures [91], as illustrated in Fig. 11c. They converted time-domain finite difference results to the frequency domain for optimization analysis and integrated it with a frequency-domain discrete adjoint method within the density-based topology optimization framework. Through topology optimization, innovative structures and design solutions that are difficult to find with traditional design methods can be discovered. Similarly, Hammond et al. introduced a density-based topology optimization framework that combines time/frequency domain adjoint variable methods and automatic differentiation techniques to efficiently compute gradients for any number of optimization objectives (FOM) or multiple frequency gradients within the design domain [92]. They also incorporated automatic differentiation techniques for user-defined photonic optimization objectives, achieving efficient inverse design of complex nanophotonic structures, as shown in Fig. 11d. In summary, topology optimization in optics is a powerful design tool that enhances the performance and functionality of optical devices by optimizing material distribution and structure. With advances in computational power and optimization algorithms, the application of topology optimization in optical design will become more widespread, providing crucial support for the design and innovation of next-generation optical devices.

The significance and application potential of inverse design has been fully demonstrated in photonics research, providing an effective approach to designing novel optical materials. At the same time, with ongoing technological advancements and increasing computational resources, inverse design is expected to play a greater role in the development of optical devices in the future, driving innovation and breakthroughs in the field of optics.

4.3 Acoustic Materials

In recent years, the field of acoustics has gained significant attention due to the increasing demand for designing phononic crystals, acoustic metamaterials, and other acoustic structures. These materials have widespread applications in vibration reduction, noise control, filtering, acoustic lenses, and acoustic imaging, which are crucial for industries such as information technology, communication, and healthcare [93]. The target performance in acoustics typically includes specific functions or characteristics of acoustic structures, such as sound wave scattering [94,95], absorption performance [96], group velocity profiles [97], and bandgap distribution. By adjusting geometric parameters, absorption spectra, and elastic wave propagation behaviors of acoustic materials, their acoustic performance can be altered, thus affecting the functionality of acoustic devices. Traditional design methods rely on analytical and numerical approaches to predict the performance of acoustic structures. As the complexity of the structures increases, these methods require evaluating numerous structural parameters, leading to extended design times and resource consumption issues. To overcome these limitations, the field of acoustics has begun to shift towards inverse design, where the desired acoustic characteristics are used to infer the corresponding structures [98].

Jin et al. have provided an excellent review of the development of machine learning in the field of phononic metamaterials, including machine learning-driven on-demand design [99]. The review covers the use of supervised learning, unsupervised learning, reinforcement learning, and other methods to achieve acoustic inverse design. Early acoustic design was primarily based on optimization, including methods such as topology optimization [100], genetic algorithms, level set methods, and particle swarm optimization, which have long been applied to various phononic crystal materials. However, as the structures of acoustic materials become increasingly complex, these optimization methods can be time-consuming and require precise control of certain factors (such as sound waves). Therefore, relying solely on optimization algorithms makes it difficult to discover new materials, and machine learning needs to be introduced to assist in the design process.

With advancements in machine learning technology, its application in acoustics has become a key focus of research. Through machine learning algorithms, researchers can mine nonlinear physical patterns in high-dimensional spaces from large datasets of candidate structures, enabling efficient and accurate design of acoustic materials. Cheng et al. developed a deep neural network model for two-dimensional input performance parameters and four-dimensional output geometric parameters [101]. Based on this deep neural network model, a deep autoencoder network (DAE) was also proposed to enhance model accuracy, ensuring the reliability and stability of the model in acoustic inverse design. The framework of this deep autoencoder network is shown in Fig. 12a. This model can rapidly search and optimize the design space, accelerating the process of finding acoustic structures that meet specific requirements. Li et al. trained a deep learning model to extract topological features from a large number of sample images, revealing the complex relationship between the topological structure and band gaps of phononic crystals [102]. The model demonstrates excellent fitting capability even in very complex situations, thus achieving on-demand design of acoustic materials. The design process is shown in Fig. 12b. As data continues to be updated, the deep learning model can also self-evolve, avoiding real-time computations. Moreover, this deep learning model can be applied to the design of other structural mechanical materials. Sun et al. used deep neural networks to identify the intrinsic relationship between isoelectric effects and acoustic properties [103]. The trained model can automatically generate isoelectric effect parameters for structures and calculate corresponding geometric parameters through linear predictive analysis, achieving the expected sound insulation and noise reduction effects for multi-order Helmholtz resonators and acoustic filters. This design process is shown in Fig. 12c. This method makes the design and optimization of acoustic structures faster and more efficient compared to traditional methods, while also improving the accuracy of achieving specific acoustic performance.

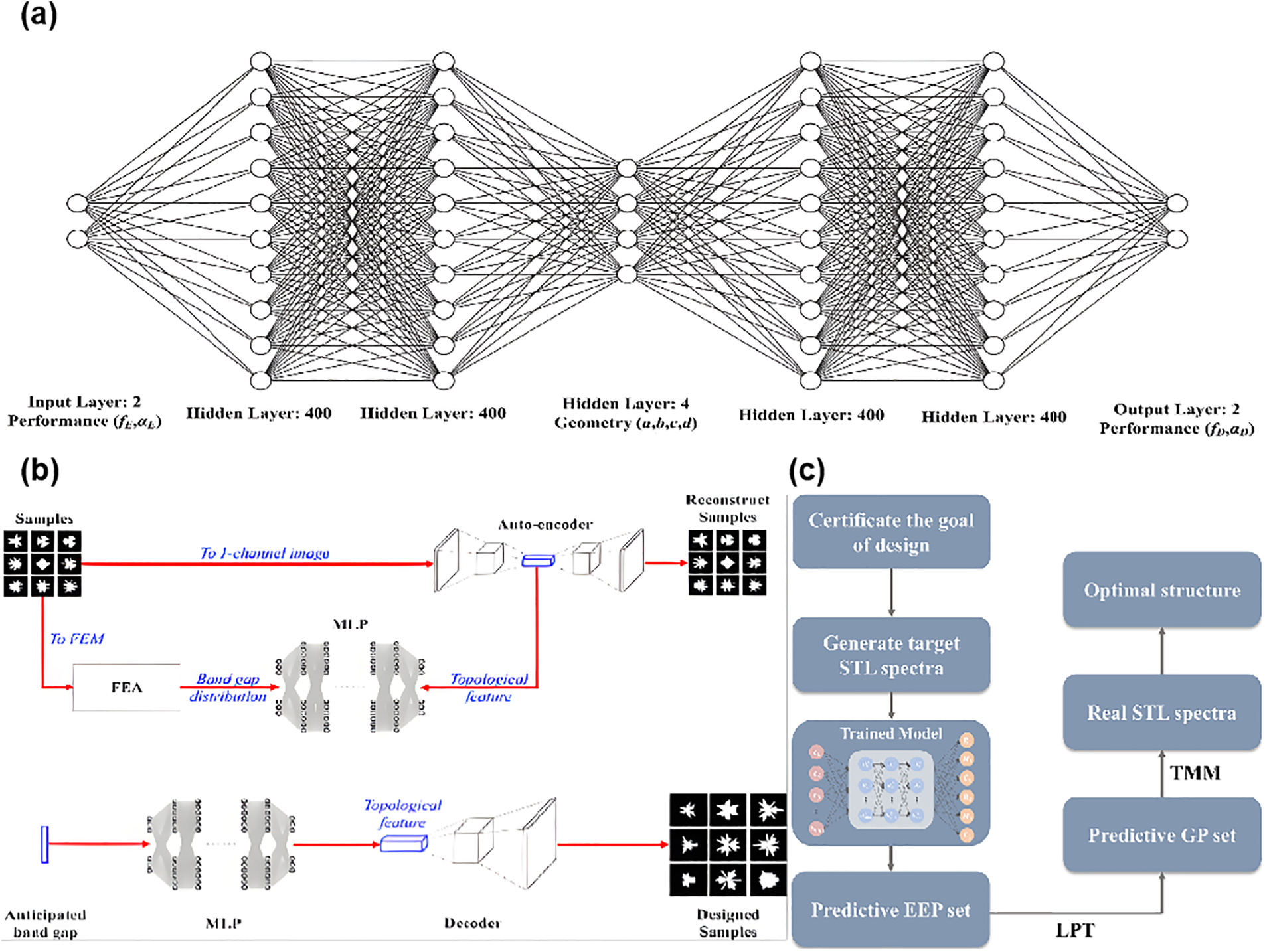
Figure 12: (a) The architecture of the DAE model [101]; (b) Design workflow for photonic crystals with the desired bandgap [102]; (c) Conceptual diagram of using neural networks to address acoustic inverse design [103]

However, due to limitations in equipment and technology, the data obtained often suffer from inconsistencies and limited quantity, which complicates the acquisition and processing of acoustic data and affects the modeling and predictive performance of machine learning models. Therefore, in inverse design, data collection and processing for acoustic materials become crucial for achieving on-demand design and performance prediction. The construction of a dataset typically involves extensive acoustic performance evaluations, which can be completed through numerical simulations, experimental measurements, or theoretical derivations. After data collection, the data processing steps include cleaning, transforming, and feature extraction to prepare the data for training and prediction in machine learning models. Data collection can be achieved through numerical simulations. For example, finite element methods or other numerical techniques can be used to calculate acoustic performance such as absorption spectra, transmission spectra, or reflection spectra of acoustic materials. These data can cover variations in frequency ranges, material parameters, and structural geometries to ensure the diversity and representativeness of the dataset.

In summary, inverse design in the field of acoustics requires efficient, versatile, and automated design methods, as well as a deep understanding of the complex relationships between acoustic characteristics and structures. The introduction of machine learning technologies offers new ideas and methods to address these challenges, providing more flexible and efficient pathways for the design and optimization of acoustic devices. In the future, data-driven approaches will become the mainstream for optimizing acoustic structures [104]. By improving the quality and availability of acoustic data and generating and processing large datasets, it will be possible to predict acoustic materials with target performance more accurately [105].

4.4 Other Materials

The inverse design of materials using machine learning algorithms also extends to other fields. Polymers, known for their light weight, good plasticity, and high chemical stability, are widely used in various domains [106,107]. Mechanical properties, thermal stability, and chemical resistance can be influenced by factors such as molecular structure, side chain structure, and molecular weight [108]. Designing and optimizing the structure and composition of polymers is crucial for achieving the desired performance. Sattari et al. have provided a comprehensive review of optimization algorithms in the inverse design of polymers [109]. Kumar et al. used particle swarm optimization combined with neural networks for inverse design, successfully predicting and synthesizing polymers with specific cloud points [110]. Patra et al. employed MCTS to search for specific polymer sequences and combined it with molecular dynamics (MD) simulations in inverse design strategies to identify particular copolymers [31]. In the study of inorganic solid materials, inverse design is gradually becoming an efficient and promising approach. Zunger have reviewed the inverse design of inorganic solid materials extensively [111]. Other materials related to inverse design research are listed in Table 6.

5  Conclusions

In modern materials science and engineering applications, the limitations of traditional forward design methods have gradually become apparent with the continuous advancement of technology. Facing complex multidimensional design spaces and diverse performance requirements, finding optimal design solutions has become increasingly challenging. To overcome these challenges, materials inverse design has emerged. By starting from the desired performance and utilizing advanced algorithms and models, inverse design not only addresses the limitations of traditional design but also provides an effective approach for discovering and optimizing new materials. With the development of materials science, inverse design has become a key tool in driving the discovery and optimization of new materials.

In this paper, we focus on three machine learning-based materials inverse design methods: exploration-based inverse design, model-based inverse design, and optimization-based inverse design. Exploration-based inverse design uses techniques such as reinforcement learning, Monte Carlo Tree Search, and Particle Swarm Optimization to efficiently search for and approximate optimal design solutions in scenarios with limited data. Model-based inverse design improves the accuracy of predictions by enhancing existing models. Optimization-based inverse design seeks optimal solutions in complex multidimensional design spaces using optimization algorithms such as genetic algorithms and Bayesian optimization.

These inverse design methods have been widely applied in fields such as alloys, optics, and acoustics. For example, in the optical field, inverse design can optimize the geometric structure of optical devices to enhance optical performance. In the acoustics field, inverse design is used to develop new acoustic materials for efficient control of sound waves. In the alloy field, inverse design helps scientists discover and optimize new alloy materials with outstanding performance.

Nevertheless, the widespread application of materials inverse design still faces several challenges:

•   Data Scarcity and Quality Issue—The lack of high-quality data required for training machine learning models limits the effectiveness of inverse design methods.

•   Prohibitively large search space—Materials design involves a wide range of possible elements and processing methods, and the design process requires considering numerous potential combinations.

•   Multi-objective tasks—Finding materials that can simultaneously meet different performance requirements is very challenging, as optimizing one property may negatively impact others.

•   Integration of Interdisciplinary Knowledge-Materials design is inherently interdisciplinary, requiring knowledge from fields such as chemistry, physics, engineering, and computational science.

These challenges can be effectively addressed through a series of solutions. Data scarcity and quality issues can be improved by combining experimental data with high-throughput computational data, and by employing techniques such as data augmentation and transfer learning. In the case of the prohibitively large search space, efficient optimization methods such as Bayesian optimization and reinforcement learning can help reduce computational burdens and focus on the most promising design areas. Performance conflicts in multi-objective tasks can be balanced using multi-objective optimization algorithms, and the evaluation process can be accelerated by utilizing surrogate models. Finally, the interdisciplinary nature of materials design requires close collaboration among experts from various fields. By integrating knowledge from chemistry, physics, engineering, and computational science, interdisciplinary teams can offer more comprehensive solutions. Furthermore, combining computational models from different disciplines can provide more accurate predictions and optimizations for materials design. The implementation of these measures will significantly enhance the efficiency and effectiveness of materials inverse design, driving innovation and progress in the field of materials science.

With the continuous advancement of computing resources and innovations in machine learning algorithms, the methods and applications of materials inverse design will become more extensive and in-depth. By integrating multidisciplinary knowledge and developing more intelligent and efficient algorithms, we are expected to achieve more breakthroughs in materials design. Additionally, with the increase in data sharing and collaborative research, the inverse design will be able to utilize larger-scale and higher-quality data, further enhancing its accuracy and practicality. In the future, we look forward to seeing widespread applications of materials inverse design in cutting-edge fields such as new energy materials, biomaterials, and nanomaterials, advancing scientific and technological progress and contributing more to solving global challenges.

Acknowledgement: The authors would like to express their gratitude to the editors and reviewers for their detailed review and insightful advice.

Funding Statement: This research was funded by the National Natural Science Foundation of China (52061020), Major Science and Technology Projects in Yunnan Province (202302AG050009), and Yunnan Fundamental Research Projects (202301AV070003).

Author Contributions: Resources: Yingli Liu, Sheng Lei; Conceptualization: Yingli Liu, Tao Shen; Investigation: Yingli Liu, Haihe Zhou; Writing—original draft: Yingli Liu; Writing—review&editing: Yuting Cui; Methodology: Yuting Cui, Haihe Zhou, Sheng Lei, Tao Shen, Jiancheng Yin; Formal analysis: Haibin Yuan; Supervision: Haibin Yuan, Jiancheng Yin. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Bai J, Xue Y, Bjorck J, Bras RL, Rappazzo B, Bernstein R, et al. Phase mapper: accelerating materials discovery with AI. AI Mag. 2018;39(1):15–26. [Google Scholar]

2. De Pablo JJ, Jackson NE, Webb MA, Chen LQ, Moore JE, Morgan D, et al. New frontiers for the materials genome initiative. npj Comput. Mater. 2019;5(1):41. doi:10.1038/s41524-019-0173-4. [Google Scholar] [CrossRef]

3. Zheng X, Zhang X, Chen TT, Watanabe I. Deep learning in mechanical metamaterials: from prediction and generation to inverse design. Adv Mater. 2023;35(45):2302530. doi:10.1002/adma.202302530. [Google Scholar] [PubMed] [CrossRef]

4. Schön CF, Van Bergerem S, Mattes C, Yadav A, Grohe M, Kobbelt L, et al. Classification of properties and their relation to chemical bonding: essential steps toward the inverse design of functional materials. Sci Adv. 2022;8(47):eade0828. doi:10.1126/sciadv.ade0828. [Google Scholar] [PubMed] [CrossRef]

5. Cheetham AK, Seshadri R. Artificial intelligence driving materials discovery? Perspective on the article: scaling deep learning for materials discovery. Chem Mater. 2024;36(8):3490–5. doi:10.1021/acs.chemmater.4c00643. [Google Scholar] [PubMed] [CrossRef]

6. Li C, Zheng K. Methods, progresses, and opportunities of materials informatics. InfoMat. 2023;5(8):e12425. doi:10.1002/inf2.12425. [Google Scholar] [CrossRef]

7. Wei J, Chu X, Sun XY, Xu K, Deng HX, Chen J, et al. Machine learning in materials science. InfoMat. 2019;1(3):338–58. doi:10.1002/inf2.12028. [Google Scholar] [CrossRef]

8. Gomes CP, Selman B, Gregoire JM. Artificial intelligence for materials discovery. MRS Bull. 2019;44(7):538–44. doi:10.1557/mrs.2019.158. [Google Scholar] [CrossRef]

9. Chan CH, Sun M, Huang B. Application of machine learning for advanced material prediction and design. EcoMat. 2022;4(4):e12194. doi:10.1002/eom2.12194. [Google Scholar] [CrossRef]

10. Juan Y, Dai Y, Yang Y, Zhang J. Accelerating materials discovery using machine learning. J Mater Sci Technol. 2021;79:178–90. doi:10.1016/j.jmst.2020.12.010. [Google Scholar] [CrossRef]

11. Li J, Sun Y, Zhang Z. Perspective on machine learning in energy material discovery. SmartMat. 2023;4(4):e1171. doi:10.1002/smm2.1171. [Google Scholar] [CrossRef]

12. Cai J, Chu X, Xu K, Li H, Wei J. Machine learning-driven new material discovery. Nanoscale Adv. 2020;2(8):3115–30. doi:10.1039/D0NA00388C. [Google Scholar] [PubMed] [CrossRef]

13. Jordan MI, Mitchell TM. Machine learning: trends, perspectives, and prospects. Science. 2015;349(6245):255–60. doi:10.1126/science.aaa8415. [Google Scholar] [PubMed] [CrossRef]

14. Liao TW, Li G. Metaheuristic-based inverse design of materials—a survey. J. Materiomics. 2020;6(2):414–30. doi:10.1016/j.jmat.2020.02.011. [Google Scholar] [CrossRef]

15. Nosengo N. Can artificial intelligence create the next wonder material? Nature. 2016;533(7601):22–5. doi:10.1038/533022a. [Google Scholar] [PubMed] [CrossRef]

16. Kalidindi SR, Brough DB, Li S, Cecen A, Blekh AL, Congo FYP, et al. Role of materials data science and informatics in accelerated materials innovation. MRS Bull. 2016;41(8):596–602. [Google Scholar]

17. Zhu L, Zhou J, Sun Z. Materials data toward machine learning: advances and challenges. J Phys Chem Lett. 2022;13(18):3965–77. doi:10.1021/acs.jpclett.2c00576. [Google Scholar] [PubMed] [CrossRef]

18. Jia X, Aziz A, Hashimoto Y, Li H. Dealing with the big data challenges in AI for thermoelectric materials. Sci China Mater. 2024;67(4):1173–82. doi:10.1007/s40843-023-2777-2. [Google Scholar] [CrossRef]

19. Butler KT, Davies DW, Cartwright H, Isayev O, Walsh A. Machine learning for molecular and materials science. Nature. 2018;559(7715):547–55. doi:10.1038/s41586-018-0337-2. [Google Scholar] [PubMed] [CrossRef]

20. Draxl C, Scheffler M. The NOMAD laboratory: from data sharing to artificial intelligence. J Phys Mater. 2019;2(3):036001. [Google Scholar]

21. Fu Z, Liu W, Huang C, Mei T. A review of performance prediction based on machine learning in materials science. Nanomater. 2022;12(17):2957. [Google Scholar]

22. Milani S, Topin N, Veloso M, Fang F. Explainable reinforcement learning: a survey and comparative review. ACM Comput Surv. 2024;56(7):1–36. doi:10.1145/3616864. [Google Scholar] [CrossRef]

23. Kim H, Choi H, Kang D, Lee WB, Na J. Materials discovery with extreme properties via reinforcement learning-guided combinatorial chemistry. Chem Sci. 2024;15(21):7908–25. doi:10.1039/D3SC05281H. [Google Scholar] [PubMed] [CrossRef]

24. Hwang HS, Lee M, Seok J. Deep reinforcement learning with a critic-value-based branch tree for the inverse design of two-dimensional optical devices. Appl Soft Comput. 2022;127:109386. doi:10.1016/j.asoc.2022.109386. [Google Scholar] [CrossRef]

25. Iwata H, Nakai T, Koyama T, Matsumoto S, Kojima R, Okuno Y. VGAE-MCTS: a new molecular generative model combining the variational graph auto-encoder and monte carlo tree search. J Chem Inf Model. 2023;63(23):7392–400. doi:10.1021/acs.jcim.3c01220. [Google Scholar] [PubMed] [CrossRef]

26. Browne CB, Powley E, Whitehouse D, Lucas SM, Cowling PI, Rohlfshagen P, et al. A survey of monte carlo tree search methods. IEEE Trans Comput Intell AI Games. 2012;4(1):1–43. doi:10.1109/TCIAIG.2012.2186810. [Google Scholar] [CrossRef]

27. Sridharan B, Mehta S, Pathak Y, Priyakumar UD. Deep reinforcement learning for molecular inverse problem of nuclear magnetic resonance spectra to molecular structure. J Phys Chem Lett. 2022;13(22):4924–33. doi:10.1021/acs.jpclett.2c00624. [Google Scholar] [PubMed] [CrossRef]

28. Vodopivec T, Samothrakis S, Ster B. On monte carlo tree search and reinforcement learning. J Artif Intell Res. 2017;60:881–936. doi:10.1613/jair.5507. [Google Scholar] [CrossRef]

29. Song Z, Zhou Q, Lu S, Dieb S, Ling C, Wang J. Adaptive design of alloys for CO2 activation and methanation via reinforcement learning monte carlo tree search algorithm. J Phys Chem Lett. 2023;14(14):3594–601. doi:10.1021/acs.jpclett.3c00242. [Google Scholar] [PubMed] [CrossRef]

30. Banik S, Loefller T, Manna S, Chan H, Srinivasan S, Darancet P, et al. A continuous action space tree search for INverse desiGn (CASTING) framework for materials discovery. NPJ Comput Mater. 2023;9(1):177. doi:10.1038/s41524-023-01128-y. [Google Scholar] [CrossRef]

31. Patra TK, Loeffler TD, Sankaranarayanan SKRS. Accelerating copolymer inverse design using monte carlo tree search. Nanoscale. 2020;12(46):23653–62. doi:10.1039/D0NR06091G. [Google Scholar] [PubMed] [CrossRef]

32. Wang D, Tan D, Liu L. Particle swarm optimization algorithm: an overview. Soft Comput. 2018;22(2):387–408. doi:10.1007/s00500-016-2474-6. [Google Scholar] [CrossRef]

33. Zhou YP, Tang LJ, Jiao J, Song DD, Jiang JH, Yu RQ. Modified particle swarm optimization algorithm for adaptively configuring globally optimal classification and regression trees. J Chem Inf Model. 2009;49(5):1144–53. doi:10.1021/ci800374h. [Google Scholar] [PubMed] [CrossRef]

34. Namasivayam V, Bajorath J. Searching for coordinated activity cliffs using particle swarm optimization. J Chem Inf Model. 2012;52(4):927–34. doi:10.1021/ci3000503. [Google Scholar] [PubMed] [CrossRef]

35. Mi X, Tian L, Tang A, Kang J, Peng P, She J, et al. A reverse design model for high-performance and low-cost magnesium alloys by machine learning. Comput Mater Sci. 2022;201:110881. doi:10.1016/j.commatsci.2021.110881. [Google Scholar] [CrossRef]

36. Khadilkar MR, Paradiso S, Delaney KT, Fredrickson GH. Inverse design of bulk morphologies in multiblock polymers using particle swarm optimization. Macromolecules. 2017;50(17):6702–9. doi:10.1021/acs.macromol.7b01204. [Google Scholar] [CrossRef]

37. Raccuglia P, Elbert KC, Adler PDF, Falk C, Wenny MB, Mollo A, et al. Machine-learning-assisted materials discovery using failed experiments. Nature. 2016;533(7601):73–6. doi:10.1038/nature17439. [Google Scholar] [PubMed] [CrossRef]

38. Wang T, Shao M, Guo R, Tao F, Zhang G, Snoussi H, et al. Surrogate model via artificial intelligence method for accelerating screening materials and performance prediction. Adv Funct Mater. 2021;31(8):2006245. doi:10.1002/adfm.202006245. [Google Scholar] [CrossRef]

39. Wang C, Fu H, Jiang L, Xue D, Xie J. A property-oriented design strategy for high performance copper alloys via machine learning. npj Comput Mater. 2019;5(1):87. doi:10.1038/s41524-019-0227-7. [Google Scholar] [CrossRef]

40. Jiang L, Wang C, Fu H, Shen J, Zhang Z, Xie J. Discovery of aluminum alloys with ultra-strength and high-toughness via a property-oriented design strategy. J Mater Sci Technol. 2022;98:33–43. doi:10.1016/j.jmst.2021.05.011. [Google Scholar] [CrossRef]

41. Liu D, Tan Y, Khoram E, Yu Z. Training deep neural networks for the inverse design of nanophotonic structures. ACS Photonics. 2018;5(4):1365–9. doi:10.1021/acsphotonics.7b01377. [Google Scholar] [CrossRef]

42. Brzin T, Brojan M. Using a generative adversarial network for the inverse design of soft morphing composite beams. Eng Appl Artif Intell. 2024;133:108527. doi:10.1016/j.engappai.2024.108527. [Google Scholar] [CrossRef]

43. Kim Y, Park HK, Jung J, Asghari-Rad P, Lee S, Kim JY, et al. Exploration of optimal microstructure and mechanical properties in continuous microstructure space using a variational autoencoder. Mater Des. 2021;202:109544. doi:10.1016/j.matdes.2021.109544. [Google Scholar] [CrossRef]

44. Debnath A, Krajewski AM, Sun H, Lin S, Ahn M, Li W, et al. Generative deep learning as a tool for inverse design of high-entropy refractory alloys. J Mater Inform. 2021;1:3. doi:10.20517/jmi.2021.05. [Google Scholar] [CrossRef]

45. Pei Z, Rozman KA, Doğan ÖN, Wen Y, Gao N, Holm EA, et al. Machine-learning microstructure for inverse material design. Adv Sci. 2021;8(23):2101207. doi:10.1002/advs.202101207. [Google Scholar] [PubMed] [CrossRef]

46. Liow CH, Kang H, Kim S, Na M, Lee Y, Baucour A, et al. Machine learning assisted synthesis of lithium-ion batteries cathode materials. Nano Energy. 2022;93:107214. doi:10.1016/j.nanoen.2022.107214. [Google Scholar] [CrossRef]

47. Dong R, Dan Y, Li X, Hu J. Inverse design of composite metal oxide optical materials based on deep transfer learning. Comput Mater Sci. 2021;188:110166. doi:10.1016/j.commatsci.2020.110166. [Google Scholar] [CrossRef]

48. Mi X, Dai L, Jing X, She J, Holmedal B, Tang A, et al. Accelerated design of high-performance Mg-Mn-based magnesium alloys based on novel bayesian optimization. J Magnes Alloys. 2024;12(2):750–66. doi:10.1016/j.jma.2024.01.005. [Google Scholar] [CrossRef]

49. Raßloff A, Seibert P, Kalina KA, Kästner M. Inverse design of spinodoid structures using Bayesian optimization. arXiv:2402.13054. 2024. [Google Scholar]

50. Zuo Y, Qin M, Chen C, Ye W, Li X, Luo J, et al. Accelerating materials discovery with Bayesian optimization and graph deep learning. Mater Today. 2021;51:126–35. doi:10.1016/j.mattod.2021.08.012. [Google Scholar] [CrossRef]

51. Zheng B, Yang J, Liang B, Cheng JC. Inverse design of acoustic metamaterials based on machine learning using a Gauss-Bayesian model. J Appl Phys. 2020;128(13):134902. doi:10.1063/5.0012392. [Google Scholar] [CrossRef]

52. Tagade PM, Adiga SP, Pandian S, Park MS, Hariharan KS, Kolake SM. Attribute driven inverse materials design using deep learning Bayesian framework. npj Comput Mater. 2019;5(1):127. doi:10.1038/s41524-019-0263-3. [Google Scholar] [CrossRef]

53. Ren Y, Zhang L, Wang W, Wang X, Lei Y, Xue Y, et al. Genetic-algorithm-based deep neural networks for highly efficient photonic device design. Photonics Res. 2021;9(6):B247. doi:10.1364/PRJ.416294. [Google Scholar] [CrossRef]

54. Lee Y, Choi G, Yoon M, Kim C. Genetic algorithm for constrained molecular inverse design. arXiv:2112.03518. 2021. [Google Scholar]

55. Jensen JS, Sigmund O. Topology optimization for nano-photonics. Laser Photonics Rev. 2011;5(2):308–21. doi:10.1002/lpor.201000014. [Google Scholar] [CrossRef]

56. Christiansen RE, Sigmund O. Inverse design in photonics by topology optimization: tutorial. J Opt Soc Am B. 2021;38(2):496. doi:10.1364/JOSAB.406048. [Google Scholar] [CrossRef]

57. Chen Y, Hu Y, Zhao J, Deng Y, Wang Z, Cheng X, et al. Topology optimization-based inverse design of plasmonic nanodimer with maximum near-field enhancement. Adv Funct Mater. 2020;30(23):2000642. doi:10.1002/adfm.202000642. [Google Scholar] [CrossRef]

58. Heidelberger P, Lavenberg SS. Computer performance evaluation methodology. IEEE Trans Comput. 1984;33(12):1195–220. doi:10.1109/TC.1984.1676394. [Google Scholar] [CrossRef]

59. Wang AYT, Murdock RJ, Kauwe SK, Oliynyk AO, Gurlo A, Brgoch J, et al. Machine learning for materials scientists: an introductory guide toward best practices. Chem Mater. 2020;32(12):4954–65. [Google Scholar]

60. Liu Y, Ren H, Hu WC, Li DJ, Zeng XQ, Wang KG, et al. First-principles calculations of strengthening compounds in magnesium alloy: a general review. J Mater Sci Technol. 2016;32(12):1222–31. doi:10.1016/j.jmst.2016.04.003. [Google Scholar] [CrossRef]

61. Feng X, Wang Z, Jiang L, Zhao F, Zhang Z. Simultaneous enhancement in mechanical and corrosion properties of Al-Mg-Si alloys using machine learning. J Mater Sci Technol. 2023;167:1–13. doi:10.1016/j.jmst.2023.04.072. [Google Scholar] [CrossRef]

62. Lee CY, Jui CY, Yeh AC, Chang YJ, Lee WJ. Inverse design of high entropy alloys using a deep interpretable scheme for materials attribution analysis. J Alloys Compd. 2024;976:173144. doi:10.1016/j.jallcom.2023.173144. [Google Scholar] [CrossRef]

63. Lee JW, Park C, Do Lee B, Park J, Goo NH, Sohn KS. A machine-learning-based alloy design platform that enables both forward and inverse predictions for thermo-mechanically controlled processed (TMCP) steel alloys. Sci Rep. 2021;11(1):11012. doi:10.1038/s41598-021-90237-z. [Google Scholar] [PubMed] [CrossRef]

64. Wang ZL, Adachi Y. Property prediction and properties-to-microstructure inverse analysis of steels by a machine-learning approach. Mater Sci Eng A. 2019;744:661–70. doi:10.1016/j.msea.2018.12.049. [Google Scholar] [CrossRef]

65. Wang H, Luo XC, Zhang DT, Qiu C, Chen DL. High-strength extruded magnesium alloys: a critical review. J Mater Sci Technol. 2024;199:27–52. doi:10.1016/j.jmst.2024.01.089. [Google Scholar] [CrossRef]

66. Wang H, Gao SL, Wang BT, Ma YT, Guo ZJ, Zhang K, et al. Recent advances in machine learning-assisted fatigue life prediction of additive manufactured metallic materials: a review. J Mater Sci Technol. 2024;198:111–36. doi:10.1016/j.jmst.2024.01.086. [Google Scholar] [CrossRef]

67. Li C, Bao L, Ji Y, Tian Z, Cui M, Shi Y, et al. Combining machine learning and metal-organic frameworks research: novel modeling, performance prediction, and materials discovery. Coord Chem Rev. 2024;514:215888. doi:10.1016/j.ccr.2024.215888. [Google Scholar] [CrossRef]

68. Fu H, Zhang H, Wang C, Yong W, Xie J. Recent progress in the machine learning-assisted rational design of alloys. Int J Miner Metall Mater. 2022;29(4):635–44. doi:10.1007/s12613-022-2458-8. [Google Scholar] [CrossRef]

69. Lu Z, Zhang Y, Li W, Wang J, Liu X, Wu Y, et al. Materials genome strategy for metallic glasses. J Mater Sci Technol. 2023;166:173–99. doi:10.1016/j.jmst.2023.04.074. [Google Scholar] [CrossRef]

70. Hu M, Tan Q, Knibbe R, Xu M, Jiang B, Wang S, et al. Recent applications of machine learning in alloy design: a review. Mater Sci Eng R Rep. 2023;155:100746. doi:10.1016/j.mser.2023.100746. [Google Scholar] [CrossRef]

71. Cann JL, De Luca A, Dunand DC, Dye D, Miracle DB, Oh HS, et al. Sustainability through alloy design: challenges and opportunities. Prog Mater Sci. 2021;117:100722. doi:10.1016/j.pmatsci.2020.100722. [Google Scholar] [CrossRef]

72. Dudiy SV, Zunger A. Searching for alloy configurations with target physical properties: impurity design via a genetic algorithm inverse band structure approach. Phys Rev Lett. 2006;97(4):046401. doi:10.1103/PhysRevLett.97.046401. [Google Scholar] [PubMed] [CrossRef]

73. Padhy SP, Chaudhary V, Lim YF, Zhu R, Thway M, Hippalgaonkar K, et al. Experimentally validated inverse design of multi-property Fe-Co-Ni alloys. iScience. 2024;27(5):109723. doi:10.1016/j.isci.2024.109723. [Google Scholar] [PubMed] [CrossRef]

74. Bhat N, Barnard AS, Birbilis N. Inverse design of aluminium alloys using multi-targeted regression. J Mater Sci. 2024;59(4):1448–63. doi:10.1007/s10853-023-09317-2. [Google Scholar] [CrossRef]

75. Sebbag Y, Talker E, Naiman A, Barash Y, Levy U. Demonstration of an integrated nanophotonic chip-scale alkali vapor magnetometer using inverse design. Light Sci Appl. 2021;10(1):54. doi:10.1038/s41377-021-00499-5. [Google Scholar] [PubMed] [CrossRef]

76. Liu Z, Zhu D, Raju L, Cai W. Tackling photonic inverse design with machine learning. Adv Sci. 2021;8(5):2002923. doi:10.1002/advs.202002923. [Google Scholar] [PubMed] [CrossRef]

77. Pilozzi L, Farrelly FA, Marcucci G, Conti C. Machine learning inverse problem for topological photonics. Commun Phys. 2018;1(1):57. doi:10.1038/s42005-018-0058-8. [Google Scholar] [CrossRef]

78. MacLellan B, Roztocki P, Belleville J, Romero Cortés L, Ruscitti K, Fischer B, et al. Inverse design of photonic systems. Laser Photonics Rev. 2024;18(5):2300500. doi:10.1002/lpor.202300500. [Google Scholar] [CrossRef]

79. So S, Mun J, Rho J. Simultaneous inverse design of materials and structures via deep learning: demonstration of dipole resonance engineering using core-shell nanoparticles. ACS Appl Mater Interfaces. 2019;11(27):24264–8. doi:10.1021/acsami.9b05857. [Google Scholar] [PubMed] [CrossRef]

80. Yeung C, Tsai R, Pham B, King B, Kawagoe Y, Ho D, et al. Global inverse design across multiple photonic structure classes using generative deep learning. Adv Opt Mater. 2021;9(20):2100548. [Google Scholar]

81. Yang J, Guidry MA, Lukin DM, Yang K, Vučković J. Inverse-designed silicon carbide quantum and nonlinear photonics. Light Sci Appl. 2023;12(1):201. doi:10.1038/s41377-023-01253-9. [Google Scholar] [PubMed] [CrossRef]

82. Deng R, Liu W, Shi L. Inverse design in photonic crystals. Nanophotonics. 2024;13(8):1219–37. doi:10.1515/nanoph-2023-0750. [Google Scholar] [PubMed] [CrossRef]

83. Yu L, Kokenyesi RS, Keszler DA, Zunger A. Inverse design of high absorption thin-film photovoltaic materials. Adv Energy Mater. 2013;3(1):43–8. doi:10.1002/aenm.201200538. [Google Scholar] [CrossRef]

84. Molesky S, Lin Z, Piggott AY, Jin W, Vuckovic J, Rodriguez AW. Outlook for inverse design in nanophotonics. Nat Photonics. 2018;12(11):659–70. doi:10.1038/s41566-018-0246-9. [Google Scholar] [CrossRef]

85. Yeung C, Ho D, Pham B, Fountaine KT, Zhang Z, Levy K, et al. Enhancing adjoint optimization-based photonic inverse design with explainable machine learning. ACS Photonics. 2022;9(5):1577–85. doi:10.1021/acsphotonics.1c01636. [Google Scholar] [CrossRef]

86. Peurifoy J, Shen Y, Jing L, Yang Y, Cano-Renteria F, DeLacy BG, et al. Nanophotonic particle simulation and inverse design using artificial neural networks. Sci Adv. 2018;4(6):4206. doi:10.1126/sciadv.aar4206. [Google Scholar] [PubMed] [CrossRef]

87. Ma W, Cheng F, Xu Y, Wen Q, Liu Y. Probabilistic representation and inverse design of metamaterials based on a deep generative model with semi-supervised learning strategy. Adv Mater. 2019 Aug 28;31(35):792. doi:10.1002/adma.201901111. [Google Scholar] [PubMed] [CrossRef]

88. Li Z, Pestourie R, Park JS, Huang YW, Johnson SG, Capasso F. Inverse design enables large-scale high-performance meta-optics reshaping virtual reality. Nat Commun. 2022 May 3;13(1):2409. doi:10.1038/s41467-022-29973-3. [Google Scholar] [PubMed] [CrossRef]

89. Yu L, Zunger A. Identification of potential photovoltaic absorbers based on first-principles spectroscopic screening of materials. Phys Rev Lett. 2012;108(6):068701. doi:10.1103/PhysRevLett.108.068701. [Google Scholar] [PubMed] [CrossRef]

90. Nanda A, Kues M, Calà Lesina A. Exploring the fundamental limits of integrated beam splitters with arbitrary phase via topology optimization. Opt Lett. 2024;49(5):1125. doi:10.1364/OL.512100. [Google Scholar] [PubMed] [CrossRef]

91. Zeng Z, Venuthurumilli PK, Xu X. Inverse design of plasmonic structures with FDTD. ACS Photonics. 2021;8(5):1489–96. doi:10.1021/acsphotonics.1c00260. [Google Scholar] [CrossRef]

92. Hammond AM, Oskooi A, Chen M, Lin Z, Johnson SG, Ralph SE. High-performance hybrid time/frequency-domain topology optimization for large-scale photonics inverse design. Opt Express. 2022;30(3):4467. doi:10.1364/OE.442074. [Google Scholar] [PubMed] [CrossRef]

93. Tao Y, Ren M, Zhang H, Peijs T. Recent progress in acoustic materials and noise control strategies—a review. Appl Mater Today. 2021;24:101141. doi:10.1016/j.apmt.2021.101141. [Google Scholar] [CrossRef]

94. Liu CX, Yu GL. Predicting the dispersion relations of one-dimensional phononic crystals by neural networks. Sci Rep. 2019;9(1):15322. doi:10.1038/s41598-019-51662-3. [Google Scholar] [PubMed] [CrossRef]

95. Morales N, Manocha D. Efficient wave-based acoustic material design optimization. Comput-Aided Des. 2016;78:83–92. doi:10.1016/j.cad.2016.05.011. [Google Scholar] [CrossRef]

96. Gao N, Wang M, Cheng B, Hou H. Inverse design and experimental verification of an acoustic sink based on machine learning. Appl Acoust. 2021;180:108153. doi:10.1016/j.apacoust.2021.108153. [Google Scholar] [CrossRef]

97. Goh H, Kallivokas LF. Inverse band gap design of elastic metamaterials for P and SV wave control. Comput Methods Appl Mech Eng. 2020;370:113263. doi:10.1016/j.cma.2020.113263. [Google Scholar] [CrossRef]

98. Wu RT, Jokar M, Jahanshahi MR, Semperlotti F. A physics-constrained deep learning based approach for acoustic inverse scattering problems. Mech Syst Signal Process. 2022;164:108190. doi:10.1016/j.ymssp.2021.108190. [Google Scholar] [CrossRef]

99. Jin Y, He L, Wen Z, Mortazavi B, Guo H, Torrent D, et al. Intelligent on-demand design of phononic metamaterials. Nanophotonics. 2022;11(3):439–60. doi:10.1515/nanoph-2021-0639. [Google Scholar] [PubMed] [CrossRef]

100. Dühring MB, Jensen JS, Sigmund O. Acoustic design by topology optimization. J Sound Vib. 2008;317(3–5):557–75. doi:10.1016/j.jsv.2008.03.042. [Google Scholar] [CrossRef]

101. Cheng B, Wang M, Gao N, Hou H. Machine learning inversion design and application verification of a broadband acoustic filtering structure. Appl Acoust. 2022;187:108522. doi:10.1016/j.apacoust.2021.108522. [Google Scholar] [CrossRef]

102. Li X, Ning S, Liu Z, Yan Z, Luo C, Zhuang Z. Designing phononic crystal with anticipated band gap through a deep learning based data-driven method. Comput Methods Appl Mech Eng. 2020;361:112737. doi:10.1016/j.cma.2019.112737. [Google Scholar] [CrossRef]

103. Sun X, Jia H, Yang Y, Zhao H, Bi Y, Sun Z, et al. Acoustic structure inverse design and optimization using deep learning. 2021 [cited 2024 May 20]. Available from: https://www.researchsquare.com/article/rs-255615/v1. [Google Scholar]

104. Pollice R, dos Passos Gomes G, Aldeghi M, Hickman RJ, Krenn M, Lavigne C, et al. Data-driven strategies for accelerated materials design. Acc Chem Res. 2021;54(4):849–60. doi:10.1021/acs.accounts.0c00785. [Google Scholar] [PubMed] [CrossRef]

105. Huang K, Li Y, Lai Y, Liu X. Neural network-based inverse design of nonlinear phononic crystals. IEEE Open J Ultrason Ferroelectr Freq Control. 2023;3:166–75. doi:10.1109/OJUFFC.2023.3314396. [Google Scholar] [CrossRef]

106. McDonald SM, Augustine EK, Lanners Q, Rudin C, Catherine Brinson L, Becker ML. Applied machine learning as a driver for polymeric biomaterials design. Nat Commun. 2023;14(1):4838. doi:10.1038/s41467-023-40459-8. [Google Scholar] [PubMed] [CrossRef]

107. Yan C, Li G. The rise of machine learning in polymer discovery. Adv Intell Syst. 2023;5(4):2200243. doi:10.1002/aisy.202200243. [Google Scholar] [CrossRef]

108. Celina MC. Review of polymer oxidation and its relationship with materials performance and lifetime prediction. Polym Degrad Stab. 2013;98(12):2419–29. doi:10.1016/j.polymdegradstab.2013.06.024. [Google Scholar] [CrossRef]

109. Sattari K, Xie Y, Lin J. Data-driven algorithms for inverse design of polymers. Soft Matter. 2021;17(33):7607–22. doi:10.1039/D1SM00725D. [Google Scholar] [PubMed] [CrossRef]

110. Kumar JN, Li Q, Tang KYT, Buonassisi T, Gonzalez-Oyarce AL, Ye J. Machine learning enables polymer cloud-point engineering via inverse design. npj Comput Mater. 2019;5(1):73. doi:10.1038/s41524-019-0209-9. [Google Scholar] [CrossRef]

111. Zunger A. Inverse design in search of materials with target functionalities. Nat Rev Chem. 2018;2(4):0121. doi:10.1038/s41570-018-0121. [Google Scholar] [CrossRef]

112. Kim K, Kang S, Yoo J, Kwon Y, Nam Y, Lee D, et al. Deep-learning-based inverse design model for intelligent discovery of organic molecules. npj Comput Mater. 2018;4(1):67. doi:10.1038/s41524-018-0128-1. [Google Scholar] [CrossRef]

113. Geng Y, van Anders G, Glotzer SC. Predicting colloidal crystals from shapes via inverse design and machine learning. arXiv:1801.06219. 2018. [Google Scholar]

114. Xie Y, Feng S, Deng L, Cai A, Gan L, Jiang Z, et al. Inverse design of chiral functional films by a robotic AI-guided system. Nat Commun. 2023;14(1):6177. doi:10.1038/s41467-023-41951-x. [Google Scholar] [PubMed] [CrossRef]

115. Wang Q, Zhang L. Inverse design of glass structure with deep graph neural networks. Nat Commun. 2021;12(1):5359. doi:10.1038/s41467-021-25490-x. [Google Scholar] [PubMed] [CrossRef]

116. Wang Q, Chumak AV, Pirro P. Inverse-design magnonic devices. Nat Commun. 2021;12(1):2636. doi:10.1038/s41467-021-22897-4. [Google Scholar] [PubMed] [CrossRef]

117. Zheng X, Jia G. Active learning based reverse design of hydrogen production from biomass fuel. Fuel. 2024;357:129948. doi:10.1016/j.fuel.2023.129948. [Google Scholar] [CrossRef]