kProtoClust: Towards Adaptive k-Prototype Clustering without Known k

1  Introduction

Clustering is to discover natural data groups with maximal intra-cluster similarity yet minimal inter-cluster similarity. As one of the most well known algorithms, k-means adopts an iterative strategy with conditional termination, in which labeling each data sample to the nearest cluster centroid and recalculating the centroids are alternately conducted. Due to insufficient prior knowledge, discovering data groups is an exploration procedure toward the target data. First, a predefined K is frequently impractical before we judge the exact distribution pattern, e.g., customer segmentation, and anomaly detection [1,2]. Second, k-means ultimately does input space partition insensitive to the data distribution boundary. Therefore, a data set can be partitioned differently, and the random selection of initial cluster centroids can aggravate ineradicable instability. Third, under the K constraint, partitioning input space in terms of circle-like patterns requires further exploration to deal with arbitrary cluster shapes.

Considering the challenges above, many insightful works can be found in the literature. Without the prior knowledge of K, two representative methods are distance-based and vote-based analysis after running k-means for a range of K values (e.g., 5–20). For the former, elbow curve and silhouette coefficient analysis [3] are two typical methods. For each K, elbow curve analysis calculates average distances to the centroid across all data samples and finds the point where the average distance from the centroid falls suddenly. Unlike elbow curve analysis, silhouette coefficient analysis measures how similar a data sample is within a cluster (cohesion) compared to other clusters (separation). An average score on each K will be obtained before making a judgment. Besides, authors in [4] introduce enhanced gap statistic (EGS) to measure the standardized difference between the log-transformed within-cluster sums of squares from a reference dataset of exponential distribution. A better K should reduce the variation. For the latter, Fred et al. [5] suggest evidence accumulation (EAC) to combine multiple results under a vote strategy. It works well in identifying arbitrarily shaped cluster, particularly on low-dimensional data with clear boundaries. Since the initialization phase strongly influences the obtained accuracy and computational load, a common sense of coping strategy is to restart k-means several times under one of seeding strategies and keep the final result with the lowest error. Besides the random seeding strategy employed by the classic k-means, the other popular strategies include Forgy’s approach [6], probabilistic-based strategy [7,8], and the most recent split-merge approach [9]. For k-means and its variants, the circle-like pattern hypothesis is preserved. Therefore, split-merge [5,9], multiprototype [10], and multiple kernels-based strategy [11] are mainly adopted for imbalanced clusters. In addition, the outlier removal matching k-means is getting more attention for accuracy. Despite the above representative methods making improvements on accuracy, efficiency or adaptability for k-means, the requirement of K approximating the ground truth is almost kept. Furthermore, even if K is given, the intrinsic input space division strategy and the circle-like pattern hypothesis also can not match irregular cluster shapes [9], since they should be considered along with the exploration of unknown K clusters.

Despite challenges, k-means inspires us for its simplicity, intuition, and efficiency. In this paper, an adaptive k-prototype clustering namely kProtoClust is designed to cast off the K dependence, optimize seeds extraction, and reduce the influence from circle-like pattern description. The discovered clusters can change in number and shape and become apparent along with the global and local position relationship analysis. The main contributions of this work lie in:

(1) Inspired by the concept of support vector data description (SVDD), convex hulls of variable sizes described by boundary patterns [12] are employed as prototypes. Discarding the circle-like pattern assumption, kProtoClust is never an input space division method but a boundary discovery-based clustering method with a convex decomposition strategy that prefers one-cluster-multiple-prototypes. Thus, arbitrary-shaped clusters can be well discovered and described.

(2) K is no longer an objective for input space division but a starting point for cluster exploration. Based on a union analysis of the global and local position relationship for data samples, we find solid evidence for split and mergence. Begin with an initial K for a sketchy division of input space, kProtoClust discovers optimal clusters in accord with data distribution. The prior knowledge K is bypassed due to giving no constraint on the final cluster number Kf.

(3) To reduce redundant computations, we propose a careful seeding strategy with position analysis (S2PA) in which a lightweight data grouping algorithm and logical inner analysis are carefully introduced. It gets two critical yet intuitive features: K seeds selection must evade outliers and boundaries and should not be limited to existing samples in the target data. As an assistant of kProtoClust in an early collection of cluster centers, k-means++ with S2PA contributes to accurate prototype analysis in stability and efficiency.

(4) By integrating the aforementioned designs, kProtoClust is proposed to achieve a better understanding of clusters from the basic component of convex hull. For efficiency, complete cluster exploration is conducted in input space. Furthermore, to reduce the impact of sparse data space on separability, a near maximin and random sampling (NMMRS) [13] is recommended for large and high dimensional dataset. More exploration spirits with the descriptive ability can be found in kProtoClust that motivates it to discover the accurate data distribution, not to divide the input data space under an inflexible rule. Compared with k-means-like algorithms [14], the cost of a slight efficiency drop is acceptable in practical data analysis.

The remainder of this paper proceeds as follows. Section 2 gives preliminaries of k-means++, SVDD, shrinkable edge pattern selection, and NMMRS. Section 3 describes the proposed kProtoClust with its critical components, e.g., S2PA, evidence of split and mergence, and convex decomposition based prototypes extraction. Section 4 evaluates the performance of kProtoClust. In Section 5, we discuss related work. In Section 6, we conclude this work.

2  Preliminaries

2.1 k-means++

Consider a data set 𝒳 with N samples {x1,x2,⋯,xN}, C={c1,c2,⋯,cK} is the set of expected K cluster centers where xi,cv∈Rd with i=1,⋯,N;v=1,⋯,K and the integer d is the dimension. Let Z=[ziv]N×K, where ziv∈{0,1} indicates whether xi belongs to the v-th cluster. Then, we formulate the objective function of k-means by

minZ,C∑i=1N∑v=1Kziv||xi−cv||2.(1)

Generally, k-means++ selects the first center c1 at random from 𝒳, and repeatedly collects the next center ci=x′∈𝒳 with probability D(x′)2∑x∈𝒳D(x)2 until a total of K centers are initialized. Here, D(x) is the shortest distance from x to the closest center we have already chosen. Then, the solver of k-means++ iteratively updates the cluster centers and memberships formulated by the following equations:

cv=∑i=1Nzivxij∑i=1Nzivziv={1if ||xi−cv||2=min1≤v≤K||xi−cv||20otherwise.(2)

Here, ||xi−cv|| is the Euclidean distance between xi and the cluster center cv. Apparently, to conduct the iterative procedure, the initial K centers are pivotal and the root of instability. Meanwhile, K is also the prior knowledge because the iteration will end with K clusters.

2.2 Support Vector Data Description

Giving a nonlinear function Φ(⋅), SVDD maps data samples into the feature space and obtains the minimum sphere which contains most of the data samples. Let α and R denote its center and radius, respectively, the objective function is

minR,α,ξiR2+C∑iξis.t.||Φ(xi)−α||2≤R2+ξi,(3)

where ξi is a slack variable, and C makes the trade-off between simplicity and error [15]. Its dual problem can be formulated by

minβj∑i,jβiβjK(xi,xj)s.t.∑jβj=1,0≤βj≤C,j=1,…,N(4)

with α=∑jβjΦ(xj) if the Gaussian kernel K(xi,xj)=e−q||xi−xj||2 with kernel width q is adopted. α is a linear combination of data samples in feature space with weight factors βj. Similar to k-means, only a part of data samples with βj>0 contribute to the center. Those with 0<βi<C located on the sphere’s boundary are support vectors (SVs), which are essential for describing the sphere, clusters’ shapes, and connectivity.

2.3 Shrinkable Edge Pattern Selection

As depicted by Fig. 1, in geometrical, a cluster’s boundary consists of an edge and a border [16]. An edge belongs to one cluster, while a border appears in an overlapping region and is shared by two adjacent clusters which are generally considered as two components with the same cluster label. However, in unsupervised learning, it is difficult to find the border. Therefore, similar to SVDD, the edge contains the most informative samples that accurately describe the distribution structure. From this perspective, it can be considered a superset of SVs. In line with [12], the critical steps of shrinkable edge pattern selection (SEPS) for a given xi with its ke nearest neighbors xj(j=1,2,…,ke) are described as follows:

•   Setting two thresholds γl and γu (0<γl<γu≤1) to respectively control the curvature and the shrinkage degree of the aforementioned surface.

•   Generating the normal vector ni=∑j=1keuij, where uij=xj−xi.

•   Calculating li=1ke∑j=1keg(niT⋅uij), where (⋅) means inner product and the function g(x) returns 1 if x≥0, otherwise it returns 0.

•   Cluster boundary identification. If li∈[γl,γu], then xi is considered as one of the boundary patterns.

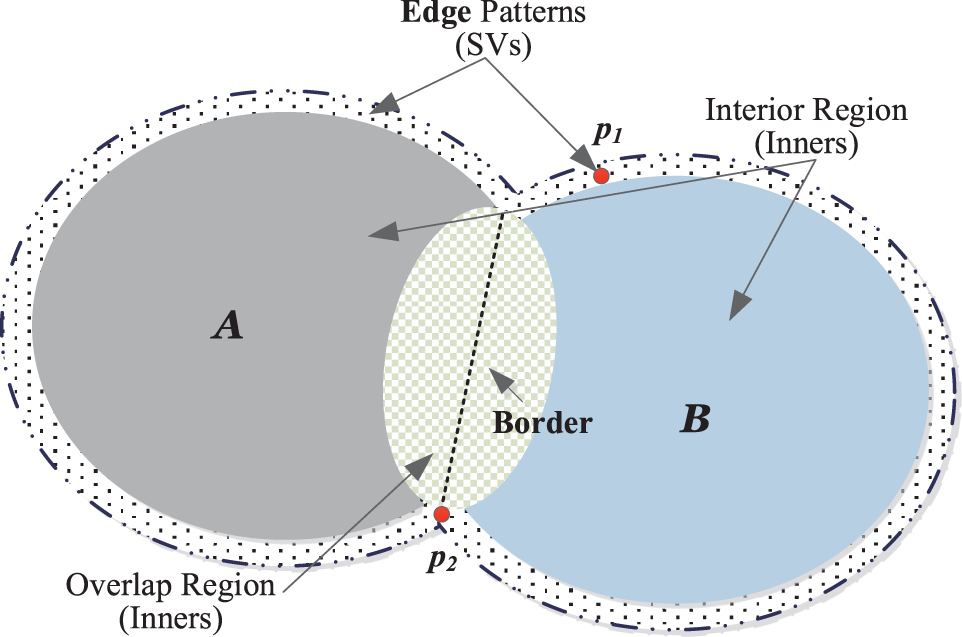
Figure 1: Edge patterns and border

2.4 Near Maximin & Random Sampling

Desired from the maximin sampling rule, NMMRS focuses on accurately portraying the distribution of 𝒳 in the q-dimensional downspace by maximin and random sampling (MMRS) where q≤d. Let 𝒳ds⊂Rq be a downspace data of 𝒳⊂Rd which is obtained by employing a random projection (RP). Following [13], NMMRS conducts three steps as follows:

•   Step 1: Collect k′ maximin samples. NMMRS finds the k′ maximin samples in 𝒳ds, which are furthest from each other. Begin with a random data sample, it chooses the second maximin sample which is furthest from the initial one with respect to a chosen distance measure. The third one should have the maximum distance from the first two. This process continues until k′ maximin samples are collected.

•   Step 2: Group each data sample with its nearest maximin sample. By grouping each data sample in 𝒳ds with its nearest maximin sample, we get k′ groups of data {Gi}i=1k′ associating to k′ maximin samples, respectively.

•   Step 3: Randomly select data near each maximin sample to obtain n samples. The final data 𝒳s of size Ns(Ns≪N) is built by selecting random samples from each group Gi(i=1,…,k′). The number ni of samples collected from Gi is proportional to the number of data samples in Gi, i.e., ni=⌈Ns×|Gi|/N⌉.

3  The Proposed kProtoClust

Towards discovering clusters without the ground truth, kProtoClust adopts edge-based cluster analysis since edges describe clusters and contribute to the connectivity analysis. Therefore, split analysis with S2PA given random seed K is designed to collect all the edge patterns forming convex hulls in local view. Mergence analysis tries to find the connectivity evidence of two neighboring convex hulls from a global view. In this section, we successively present the designs of edge collection, split and mergence analysis strategy, and finally give the algorithm description of kProtoClust.

3.1 Edges in Global and Local View

In kProtoClust, convex hulls with variable sizes are employed as the prototypes to support one-cluster-multiple-prototypes. From the perspective of SVDD following [12,17,18], the boundary is critical for convex hull extraction since the latter can be decomposed from the former. Even though a border is shared by two neighboring and connected convex hulls in the local view, it should be removed to accurately describe a cluster comprised of these two convex hulls in the global view. Therefore, although commonality exists, different perspectives frequently lead to very distinguished results. Without considering the border, the edge becomes the primary focus for kProtoClust.

Towards accurately and visually describing the difference between edges discovered in the global and local view, we consider one cluster with two prototypes (convex hulls) denoted by A and B in Fig. 2. A and B are centers of the respective convex hulls. Generally, the global view is important to recognize edge patterns and make correct cluster judgments. As shown in Fig. 2a, we theoretically expect edge patterns in the global view to be a minimum set of data samples traveling along the cluster boundary. Due to the existence of non-convex turning points p1 and p2, we have to accept the fact that there are two convex hulls. In the following context, we call these turning points split points since they are edge patterns in a cluster yet do not satisfy convexity [17] as the others. Apparently, p3 and p4 are inners, and SEPS can not extract them due to the balanced normal vectors radiating all around in their ke nearest neighboring (KNN) regions.

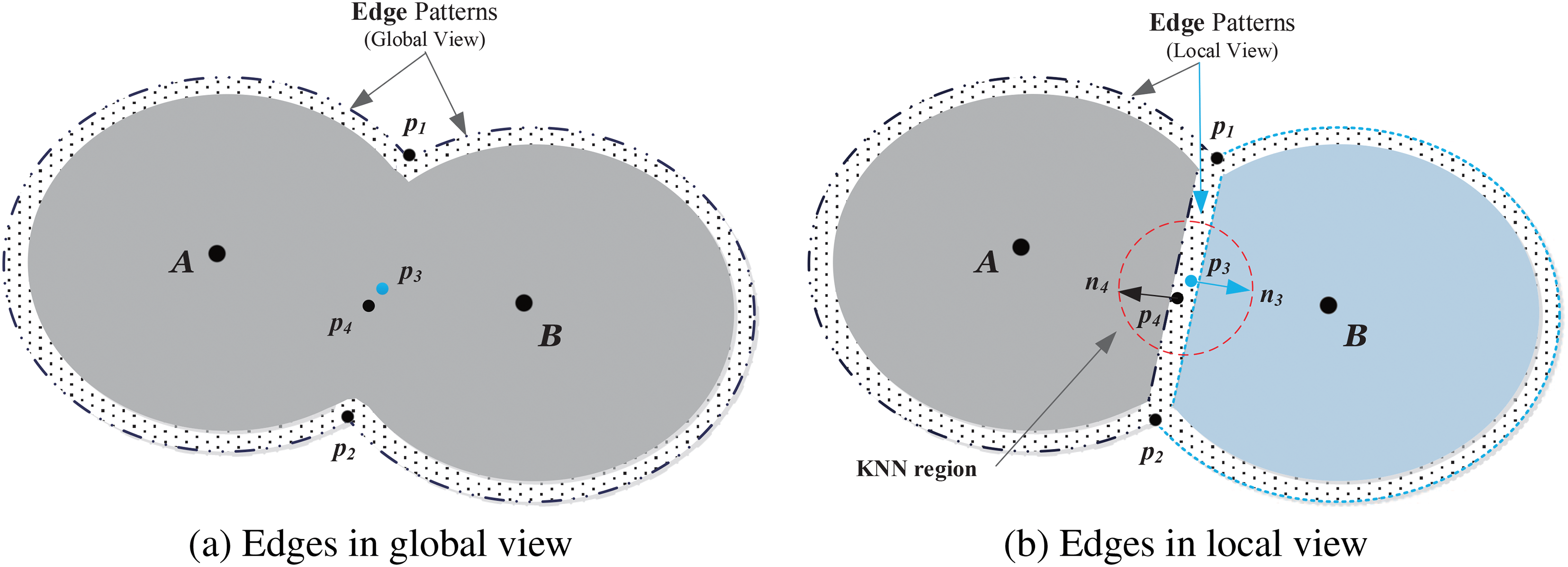
Figure 2: Edge analysis of two connected components in global and local view. In b), the two components are assigned with different labels after k-means++

Due to inaccurate data grouping or input space division, in the process of cluster exploration, inners like p3 and p4 may be chosen as edge patterns when A and B are split from a cluster. As depicted in Fig. 2b, in a local view, edge patterns p3 and p4 may have distinct convergence directions n3 and n4 such that they belong to different clusters A and B. This phenomenon is the same as what has been discussed in [18]. Even so, we can fortunately expect that those edge patterns collected in the global view (Fig. 2a) are still here and will not be missed (at least most of them) by SEPS in the local view with the same ke. This is the commonality of edge pattern collection from global and local perspectives. Naturally, the only difference is the occurrence of extra edges, which are the borders, if we finally get the evidence that A and B belong to the same cluster. Undoubtedly, sampled from the extra edges, p3 and p4 keep their correct roles of inners when we switch the edge analysis from their KNN regions back to the global view from the local view. That means, for the edge selection rule of ℓ∈[γl,γu], p3 and p4 are violating samples that exist in local analysis yet disappear from the perspective of global analysis.

Taking two irregularly shaped clusters Chameleon [19] as an example, edge patterns collected in a local view after k-means++ with K=5 and in the global view (K=1 equivalently) are shown in Fig. 3a,c, respectively. Obvious violating samples exist between adjacent clusters or convex hulls with connection relationships, e.g., cluster pairs {3, 5}, {5, 1}, and {1, 4}. A similar result with respect to the difference between Fig. 3c,d when we change K to 3 further confirms that the existence of violating samples is related to the connectivity determination of any two neighboring clusters or convex hulls.

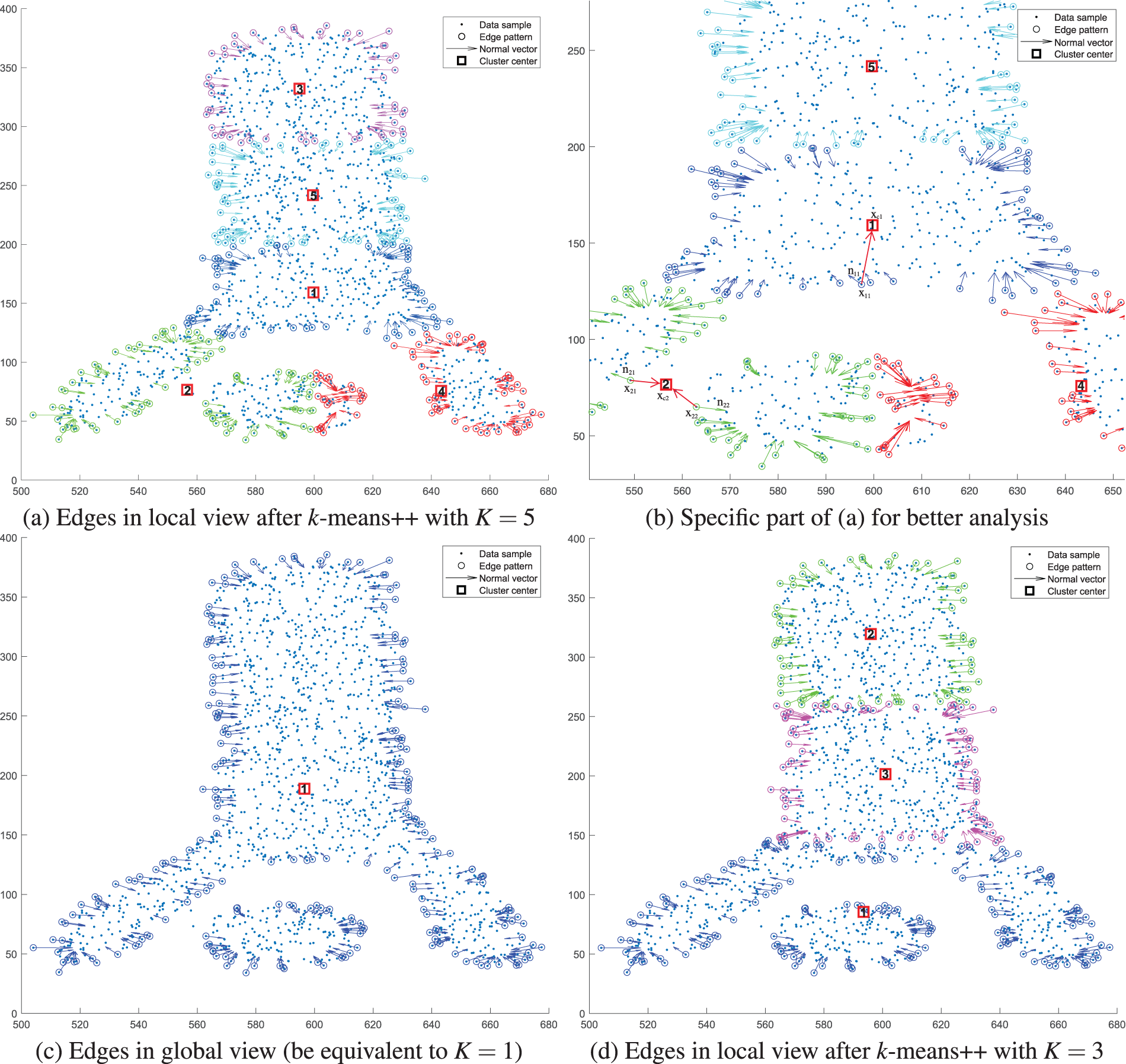
Figure 3: Edge analysis on two classes of Chameleon in global and local view with Ke=30,γl=0.85,γu=1. Each cluster is marked with the cluster index on its center

3.2 Split Analysis with S2PA

The input space division strategy of k-means+ + allows us to efficiently observe data distribution patterns in a local view. Besides the separation of components of one cluster, components from different clusters can also be mistakenly grouped due to the circle-like hypothesis. As shown in Fig. 3a, cluster 2 covers two components that should be assigned with different labels. A similar result occurs in cluster 4. Before discovering the disconnection evidence, we first retrospect the convex hull definition following [17,20].

Definition 1 (convex hull). In Euclidean space, the convex hull of a data set 𝒳h with Nh data samples {x1,x2,⋯,xNh} and xi∈Rd(i∈[1,Nh]) is defined to contains all the line segments connecting each pair of 𝒳h. Let CH(𝒳h) be the convex hull, it can be formulated by

CH(𝒳h)={x|x=∑i=1Nhλixi,∑i=1Nhλi=1,0≤λi≤1}.(5)

In CH(𝒳h), a vertex x is the data sample which does not satisfy x=λxi+(1−λ)xj with any two distinct samples xi,xj∈𝒳h and i,j=1,…,Nh if λ≠{0,1}. Following the circle-like hypothesis, ideally, each cluster obtained by k-means++ should be a convex hull. Therefore, based on the Definition 1, the center of each circle-like cluster formulated by Eq. (2) must be located in the corresponding convex hull. That means each center is an inner from the perspective of SVDD. However, the center of cluster 2 in Fig. 3a goes against this rule that motivates us to reconsider the cluster’s reasonability. In other words, the current center of cluster 2 even should not be a good seed for data regrouping.

Proposition 1. For a convex hull CH(𝒳h) with vertices 𝒳v, the included angle between the normal vector nv of any vertex xv(∈𝒳v) and its direction pointing to the cluster center xc is less than 90∘.

Proof. Based on Definition 1, there are Nh data samples in the convex hull CH(𝒳h) with center xc. As an inner of the convex hull, xc can be formulated by xc=∑i=1Nhλixi with 0<λi<1. The vector between xc and xv is ∑i=1Nhλixi−xv. Following Section 2.3, the normal vector nv of any vertex xv is ∑i=1Nh(xi−xv). We can formulate the cosine value of the included angle between the normal vector of xv and its direction pointing to the cluster center xc as

cos⁡∠xcxvnv=xvxc→⋅nv||xvxc→||×||nv||.(6)

The numerator of Eq. (6) is

xvxc→⋅nv=(∑i=1Nhλixi−xv)⋅(∑i=1Nh(xi−xv))====∑λi=1(∑i=1Nhλixi−∑i=1Nhλixv)⋅(∑i=1Nh(xi−xv))=(∑i=1Nhλi(xi−xv))⋅(∑i=1Nh(xi−xv))=====x¯i=xi−xv(∑i=1Nhλix¯i)⋅(∑i=1Nhx¯i)<(∑i=1Nh1⋅x¯i)⋅(∑i=1Nhx¯i)=||∑i=1Nhx¯i||2.

Meanwhile, due to ∃λi>0 for i=1,…,Nh, we have xvxc→⋅nv>(∑i=1Nh0⋅x¯i)⋅(∑i=1Nhx¯i)=0. Thus, we get cos⁡∠xcxvnv∈(0,1) and the included angle has arccos⁡∠xcxvnv∈(0,90∘). ◻

Based on the properties of convex hull and convex hull based decomposition [17], experimental result on Chameleon shown in Fig. 3b confirms the aforementioned two features.

•   First, the center xc2 of cluster 2 violates the convex hull’s property. The center should be an inner of a convex hull. A similar situation can be found in cluster 4. They are not appropriate centers or suitable for acting as seeds for k-means++. To reduce redundant computations, the proposed S2PA strategy is quite simple and intuitive: to avoid non-inner samples becoming seeds for k-means++ based on the position analysis of SEPS.

•   Second, xc2 is also a violating sample of the Proposition 1. x21 and x22 are two randomly selected data samples in cluster 2 judged by k-means++ with normal vectors n21 and n22, respectively. Obviously, both ∠n21x21xc2 and ∠n22x22xc2 are greater than 90∘. It means that cluster 2 either contains at least two convex hulls from different clusters or has two prototypes of convex hulls due to irregular cluster shapes. Therefore, a cluster is suggested to be split if it violates the rule of the Proposition 1. On the contrary, xc1 follows the Proposition 1 well with a randomly chosen ∠n11x11xc1<90∘.

Based on the aforementioned S2PA strategy and violating sample analysis, an essential cluster split for mistake correction can be briefly illustrated in Algorithm 1. Given a set of edge pattern groups Xe={Xe1,Xe2,⋯,XeK} with the corresponding normal vector set Ne={Ne1,Ne2,⋯,NeK}, and the set of centroids C={c1,c2,⋯,cK}, the algorithm SplitAnalysis checks each cluster’s reasonability, conducts iterative split analysis with irrefutable evidence, and outputs an updated set of edge pattern groups Xe={Xe1,Xe2,⋯,XeKp} with centroids C={c1,c2,⋯,cKp} where Kp≥K. Notice that the working set Xw⊆Xei selection in line 2 is employed for efficiency while avoiding missing sufficient evidence of cluster split. To avert excessive split, we suggest an accumulated analysis by

pd=1|Xw|∑j=1|Xw|sign(−cos⁡∠cixjnj),(7)

where |Xw| is the size of Xw, xj∈Xw, and nj∈Nei. The function sign(x) returns 1 if x>0, otherwise it returns 0. The other function isInner (ci,ke) is to check whether the data x is an inner (true) or not (false) by employing SEPS. Following Proposition 1, isInner (ci,ke) can also be simplified by checking the included angle ∠cixini where xi is the nearest neighbor of ci in the same cluster. The replacement and update works in lines 6–8 are simple, e.g., line 6 does Xe←{Xe∖{Xei}}⋃{Xei1,Xei2}. Apparently, through the recursive call of SplitAnalysis in line 9, we transfer the flaw of the circle-like pattern hypothesis into its advantage of forming convex hulls with different sizes. These convex hulls are the cornerstone of multiple prototype support in cluster analysis. Meanwhile, following the previous discussion and [12,17] we can check the included angle declared in Proposition 1 for the evidence of cluster split or mergence in stead of direct constructing convex hulls for simplicity.

3.3 Mergence Analysis

According to the analysis in Section 3.1, violating samples exist in the overlapping region of two adjacent clusters or convex hulls. Therefore, as shown in Algorithm 2, the mergence analysis of convex hulls extracted by SplitAnalysis is quite intuitive: find out violating samples and merge the associated convex hulls to add prototypes for the corresponding cluster.

Algorithm 2 of MergenceAnalysis invokes EdgeSel(⋅) firstly, which implements SEPS to collect edge patterns Xge in the global view. Then, DiffSet(⋅) gets the difference set ΔXe between Xge and Xe. Here, Xe are edge patterns collected in local view, and ΔNe in line 3 is the set of normal vectors corresponding to ΔXe. Based on ΔXe and ΔNe, lines 4–27 try to check the connectivities among k-prototype obtained by SplitAnalysis. Each prototype is represented by its center ci∈C for simplicity.

If the current convex hull has no violating samples, lines 5–9 find two nearest edge patterns xi and xj separately from it and the remaining unconnected convex hulls. As a specific case extended from the KNN region, the normal vectors ni and nj keep similar directions, although they are mistakenly divided into different groups. Thus, lines 7–9 set the adjacent matrix with Aij=1 and Aij=1 to declare the connection while cos⁡∠ninj>τm. Here, τm is the threshold for this judgment.

Line 10 starts a series of distinguished works with violating samples in the current convex hull. Each KNN Region around the violating point will be carefully checked to obtain an accumulated imbalance for each adjacent prototype pair. When KNNRegion(⋅) checks the nearest ke neighbors of xv from ΔXe, we have introduced a specific constraint that every considered neighbor xj should have different convergence direction with xv unless it has the same label with xv. That means the included angle ∠nvxvnj must be greater or equal to 90∘ if Lj≠i; otherwise we skip this neighbor and let ke←ke−1 in this round. The constraint is to avoid excessive sampling beyond the overlapping area. Thus, KNNRegion(⋅) returns the number of neighbors nv in the convex hull of xv, the number of neighbors nj from the largest class with label Lj and Lj≠i. The complete procedure is presented by Algorithm 3. To assist the connectivity analysis, we accumulate all the imbalance degrees of KNN Regions by considering all the data samples in the overlapping region between each adjacent prototypes-pair. Following [21], the imbalance degree of the KNN Region around xv is formulated by

b=nv+nj2×min{nv,nj},(8)

where only two different labels {i,Lj} are considered. The greater the gap between nv and nj is, the larger the imbalance is in the KNN Region. The imbalance degree is 1 for a balanced region when we have nv=nj. Consequently, as shown in lines 18–22 of Algorithm 2, an accumulated imbalance lower than or equal to τim suggests that the two adjacent prototypes are connected. Finally, we find all the standalone and connected prototypes based on A. The former means a cluster with one prototype, whereas the latter suggests multiple prototypes in a cluster. The finally discovered cluster number Kf is the number of subsets in P.

3.4 Implementation of kProtoClust

Based on the split and mergence analysis, the proposed kProtoClust is detailed by Algorithm 4.

On the basis of keeping data distribution patterns, data sampling and dimension reduction are effective ways for efficiency. As data preparation works, however, they are frequently optional since only some of the data sets to be analyzed are large-scale with high dimensions. Therefore, Algorithm 4 prefers NMMRS [13] in lines 1–2 to make the following analysis done in the downspace if the target data is large-scale with high dimensions. Then, a standard k-means++ is employed to partition data into K clusters for further edge pattern selection in the local view. Since the difference of edge patterns collected in terms of local and global views mainly lies in the border patterns, which are also inners in the perspective of SVDD. K is not a decisive prior knowledge. How to init the K value in the first round of line 3 only depends on the efficiency requirement from EdgeSel(⋅) (using SEPS) in line 4. By introducing the global analysis, SplitAnalysis(⋅) in line 5 will try to find all the divisible ones from K clusters and decompose them into different numbers of convex hulls. In general, the number of decomposed convex hulls Kp is greater than or equal to K. As prototypes, all the convex hulls’ connection relationships are determined by MergeAnalysis(⋅) in line 6, which groups all the convex hulls with the same label together. By now, each group of connected convex hulls Pi∈P forms a cluster. So, the final cluster number discovered is not limited to K or Kp. The last phase is to assign all the data samples with appropriate labels based on their distance to prototypes. In this step, kProtoClust prefers each prototype to be represented by its center, i.e., the mean of the convex hull’s vertices. For ease of reading, we summarize all the notations in Algorithm 4 in Table 1.

3.5 Time Complexity

As shown in Algorithm 4, kProtoClust comprises six critical tasks. NMMRS consists of the first two lines yet optional data preparation works, as discussed in [13], which are suggested to be invoked if 𝒳⊂Rd is a large-scale and high dimensional dataset. RP is a simple computation work that consumes O(dqN) where q is the final dimension reduced from d following the Johnson-Lindenstrauss Lemma [22]. With an appropriate ρ to keep data distribution pattern, MMRS requires O(qk′N) to divide data into k′ groups and extract a subset 𝒳s(⊂𝒳ds) which has Ns(≪N) samples for the following analysis and prototypes extraction.

Leaving NMMRS, k-means++ [7] costs O(qKNs) to divide 𝒳s into K clusters. Then, EdgeSel(⋅) takes O(Ns2) to collect edge patterns in local view. The following two phases are critical for K rectification because kProtoClust does not consider K a prior knowledge for k-means++. First, SplitAnalysis(⋅) is a recursive algorithm. For each round, the worst situation is that k-means++(𝒳ei, 2) with O(2qNei) cannot be avoided, whereas the best situation is no further division required. Consider a K centers’ traversal on average, invoking k-means++ K times means that all the edge patterns take part in the division, i.e., Ne=∑i=1KNei. So the cost for each round can be approximated to O(2qNe). Assume that there are ℓ rounds of recursion, SplitAnalysis(⋅) may be finished in O(2qℓNe). Second, MergeAnalysis(⋅) is conducted based on the Kp convex hulls discovered by SplitAnalysis(⋅). Due to |ΔXe|=∑i=1Kp|ΔXei|, lines 4–27 consume O(|ΔXe|2) if we have to invoke KNNRegion(⋅). It is the same as the requirement of line 28. However, we find that EdgeSel(⋅) in line 2 is the most time-consumption work for edge patterns extracted from 𝒳s in global view since |ΔXe|≪Ns. Therefore, MergeAnalysis(⋅) costs O(Ns2). Hereto, all the k-prototype unevenly distributed in different clusters are collected. So the last task LabelAssignment(⋅) can be finished in O(KpN).

The overall computational complexity of kProtoClust is O(dqN+qk′N+qKNs+2Ns2+2qℓNe+KpN). Simply stated, it ranges from O(Ns2) to O(N2) corresponding to employing the sampling strategy or not.

4  Experimental Results

4.1 Datasets and Experimental Settings

Inspired by a union analysis in the local and global view, kProtoClust provides adaptive multiple prototypes support while guaranteeing the fundamental principle of k-means. We conduct the following four series of experiments on various datasets to achieve a complete performance analysis.

•   Do parameter sensitivity analysis on clustering accuracy and the discovered cluster number with respect to parameters K, τd, τm and τim, even though the last three are suggested to be derived from the human’s basic cognition of cluster discrimination. That means τd, τm and τim can be either fixed values for universality or may vary with each individual because different peoples can have distinct connectivity assertions of weak connection. The remaining parameters {γl,γu} and ke were respectively discussed by [12] and [16].

•   Perform descriptive ability analysis for kProtoClust, in terms of accuracy, on classic datasets (type I in Table 2) with known cluster numbers. Since the foremost design of kProtoClust is to collect and well utilize the difference captured by local and global analysis, for fairness, we consider a compact version of kProtoClust including only lines 3–7 of Algorithm 4. Eight state-of-the-art algorithms are baselines: k−means, k−means++, Ball k−means [2], deep k−means with pretraining [23], coordinate descent based k-means (CDKM) [24], t-k-means, t-k-means++ [25], and a hybrid method of k-means with split-merge strategy (SMKM) [9]. Besides, k-median [26], k-medoid [27], a clustering method from the t-mixture model (TMM) [25], and EAC [5] are also introduced.

•   Check the cluster discovery ability of the compact kProtoClust on datasets of type I in Table 2 without the prior knowledge of cluster number Kc. The selected baselines are those methods with relatively better performance in the second experiment.

•   Explore some applicable suggestions by verifying the effectiveness of kProtoClust with NMMRS (lines 1–2 of Algorithm 4) denoted by kProtoClust (RS) on datasets of type II in Table 2 which have either large number of samples or high dimensionality.

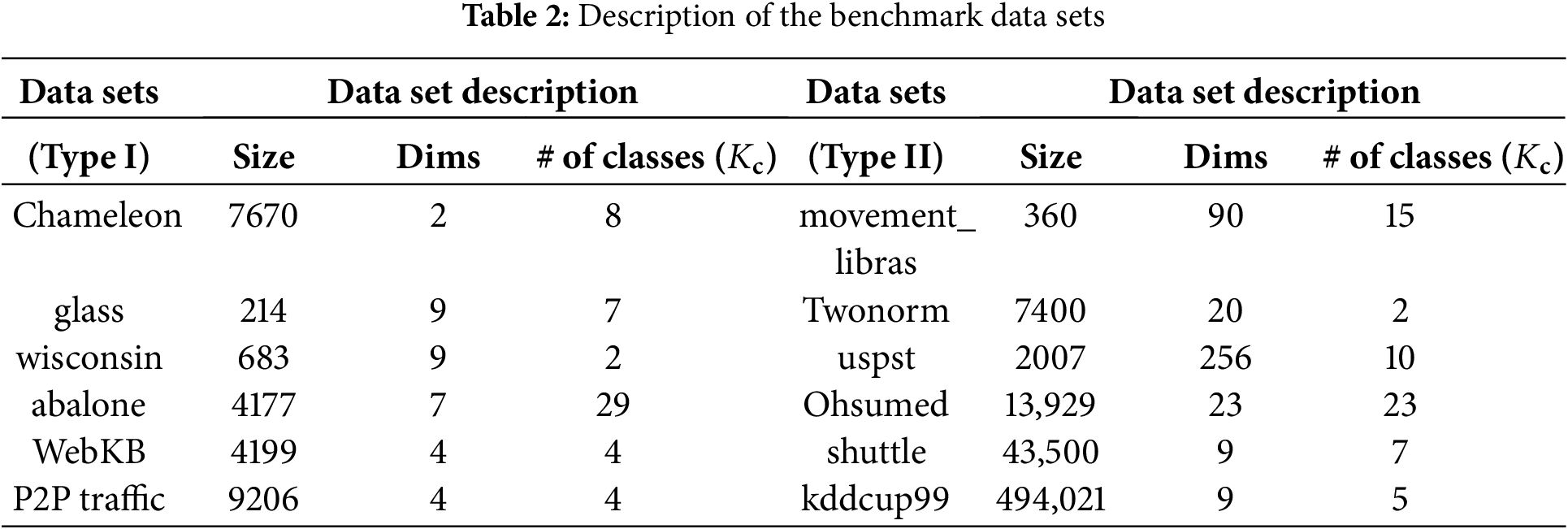
Table 2 lists the twelve employed datasets’ statistical information. Type I denotes small data with very irregular cluster shapes, while type II means more samples or higher dimensionality. They will be considered separately in different experiments to achieve a clear analysis. glass, wisconsin, abalone, movement_libras, Twonorm, uspst, and shuttle are from UCI repository [28]. WebKB [29] and Ohsumed [30] are pre-processed versions from [12]. Chameleon is provided by [19], and P2P traffic has 9206 flows’ features extracted by [31]. kddcup99 is a 9-dimensional data set extracted from KDD Cup 1999 Data [32] which is typical for intrusion detection. All the datasets are listed in the sequence of complexity NdKc from lowest to highest, where Kc corresponds to “# of classes” in Table 2.

To evaluate the accuracy, adjusted rand index (ARI) [33], normalized mutual information (NMI) [34], and F-measure [35] are preferred. All the compared algorithms are implemented by MATLAB 2021b on a mobile workstation with Intel I9-9880H and 128 GB DRAM running Windows 10-X64. Since the main objectives are to verify the descriptive and cluster discovery abilities of the proposed kProtoClust, we do not pursue the maximal efficiency and the run-time is for limited reference.

4.2 Parameter Sensitivity Analysis

4.2.1 Initial Cluster Number K

Generally, unsupervised learning faces the critical challenge of lacking sufficient prior knowledge, such as the cluster number Kc. For instance, along with various variants of intrusion behavior appearing, we can not simply consider Kc being equivalent to the number of categories. Different perspectives of the bounds for data grouping frequently lead to distinct clustering results. By fixing τd=0.3,τm=0.1 and τim=1.2, Chameleon [36] with eight irregular clusters is adopted to make an intuitive analysis of the influence from the initial cluster number K on accuracy and the final cluster number Kf. Fig. 4a depicts the results in which ARI’s mean and standard variance and the discovered Kf are separately collected for each K. As K increases, kProtoClust gets stable accuracies whose mean values fluctuate in a range [−5.10%,8.86%] around 0.4994. In contrast, accuracies achieved by k-means++ have a relatively large fluctuation from 0 to 0.4982. Particularly, the best accuracies obtained by k-means++ are 0, 0.1229, and 0.4025 when K is set to 1, 2, and 4, respectively. In theory, kProtoClust may fail when K is set to 1 since edge patterns collected in terms of local view and global view are the same. However, lines 5–10 of Algorithm 2 bring a chance to reconsider the connectivity of prototype-pairs split by Algorithm 1 under a human basic cognition parameter τm. Even so, K=1 should be avoided to get the utmost out of union analysis. The mean value of the discovered Kf ranges from 6.0 to 13.2. Even though it is a relatively large fluctuation around the ground truth 8, the majority falls within [6.8,9.8], and the dramatic change begins with K≥16. This phenomenon gives us a notice about the choice of cluster number, i.e., the voting strategy also works even though we begin with different K. Therefore, kProtoClust can benefit from further data analysis for reducing the constraint from the prior knowledge of cluster number.

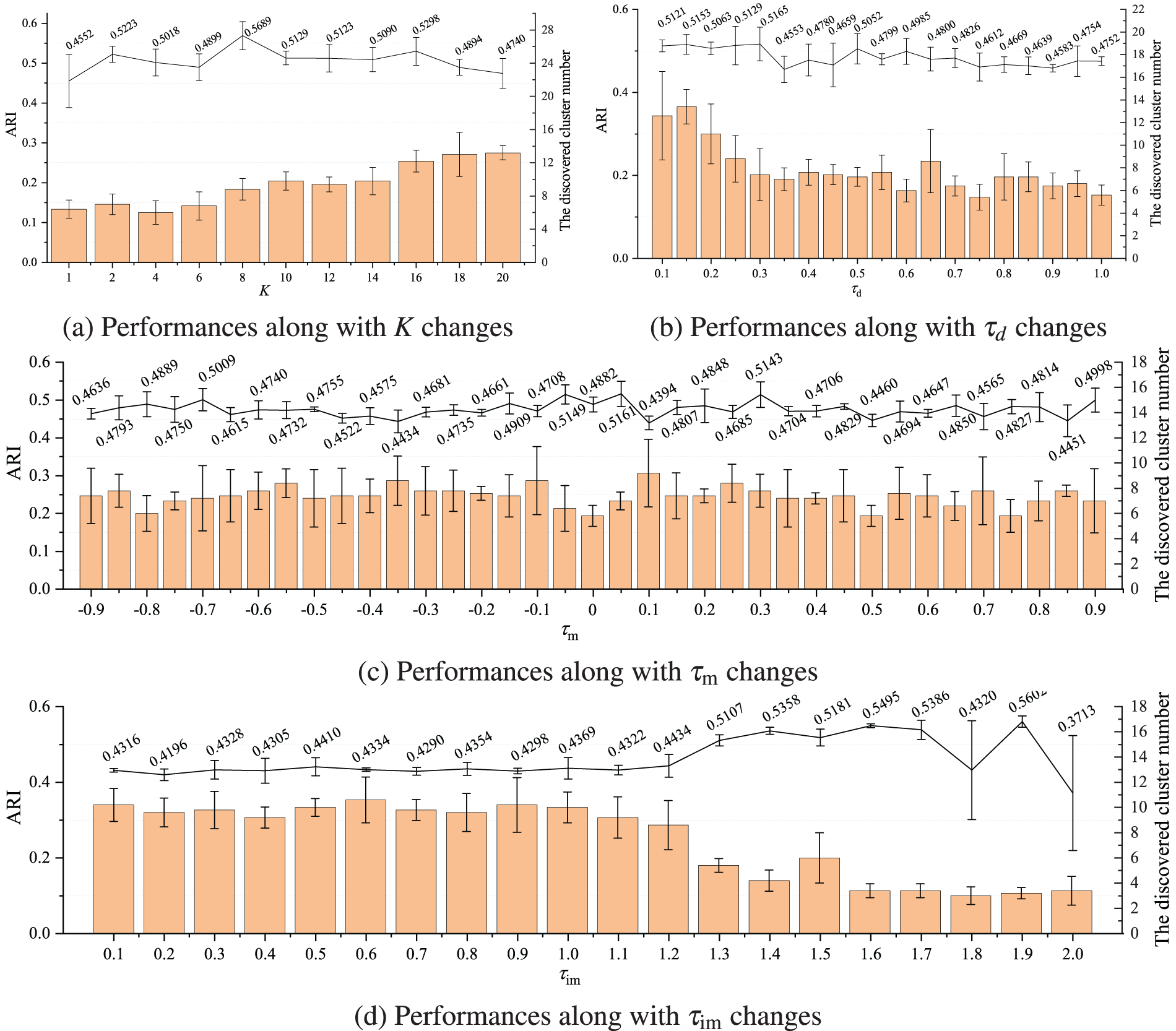
Figure 4: Sensitive analysis by means and standard variations of accuracy (ARI) and the cluster number (Kf) discovered by the compact version of kProtoClust on Chameleon along with the change of K,τd,τm and τim while γl=0.85,γu=1 and ke=30. These four parameters are fixed to K=8 (the same as Kc), τd=0.3,τm=0.1 and τim=1.2 when we do sensitivity analysis for each of them

4.2.2 Hyperparameters τd, τm and τim

τd is defined in Algorithm 1. It is an upper bound for the allowed proportion of edge patterns in a cluster yet has a distinct convergence direction rather than pointing to the cluster center. The smaller the chosen value of τd is, the more confidence kProtoClust emphasizes cluster splitting. As shown in Fig. 4b, given K=8, the discovered Kf with τd<0.3 is obviously greater than that of found with τd≥0.3. Due to imbalanced data distribution, we also reach greater ARIs with more clusters decomposed from the given data space in these cases. As τd increases, only a few changes in the discovered Kf are naturally determined by the data distribution structure. Therefore, in this study, we accept τd=0.3 as the reference line for checking whether a cluster is worthy of being split. Notice that one can fix τd to any other value to meet his personal decision although kProtoClust has relatively stable performances with τd>0.3.

Due to imbalanced distribution, non-accurate parameter settings in SEPS may miss some border patterns even though the nearest neighboring convex hulls are split from one cluster. To deal with this case, τm is introduced in lines 5–10 of Algorithm 2. It should be considered a relatively extreme condition but not always exists. Results shown in Fig. 4c confirm that both of the accuracy and discovered Kf have relatively high stability as τm increases. Because, Chameleon without noise has a relatively clear boundary in which an edge pattern can hardly have its nearest neighbor from another cluster. Therefore, without loss of generality, based on Proposition 1, we prefer τm=−0.3 (i.e., 107.5∘) not τm=0.0 (i.e., 90.0∘) or τm=−0.2 (i.e., 101.5∘) to tolerate uncertainty of convergence direction although the latter two has smaller variance values. In another way, based on the observation, τm can be set flexibly if the target data has a clear boundary.

In KNN region, the more balanced the edge patterns from different clusters are, the cumulative imbalance degree is close to 1. Theoretically, the bound τim in line 22 of Algorithm 2 should be greater than or equal to 1. We add a range of [0.1,1) to τim to make the analysis more comprehensive. Apparently, the trends of the accuracies and the discovered Kf in Fig. 4d show sufficient evidence. Along with the increase of τim, many more extremely weak-connected convex hulls are considered connected, leading to continuous reduction of Kf. In this study, we take τim=1.2 as the bound for connection.

4.3 Performance Contrast with the Prior Knowledge K_c

The prior knowledge of cluster number is critical for k-means and its variants. Although kProtoClust is also derived from k-means, the design strategy of multiple prototypes support is to break through this constraint by emphasizing the descriptive ability. To verify the effectiveness, we compare it with twelve state-of-the-art methods on datasets of type I in terms of three accuracy metrics after thirty times of evaluations. The achieved mean and mean-square deviation (std) for each metric is illustrated in Table 3. Since descriptive ability is a common concern for all the methods considered from different perspectives, such as initialization strategy, data distribution description, or voting analysis, we omit efficiency comparisons for insignificant differences in low-complexity data despite having irregular clusters.

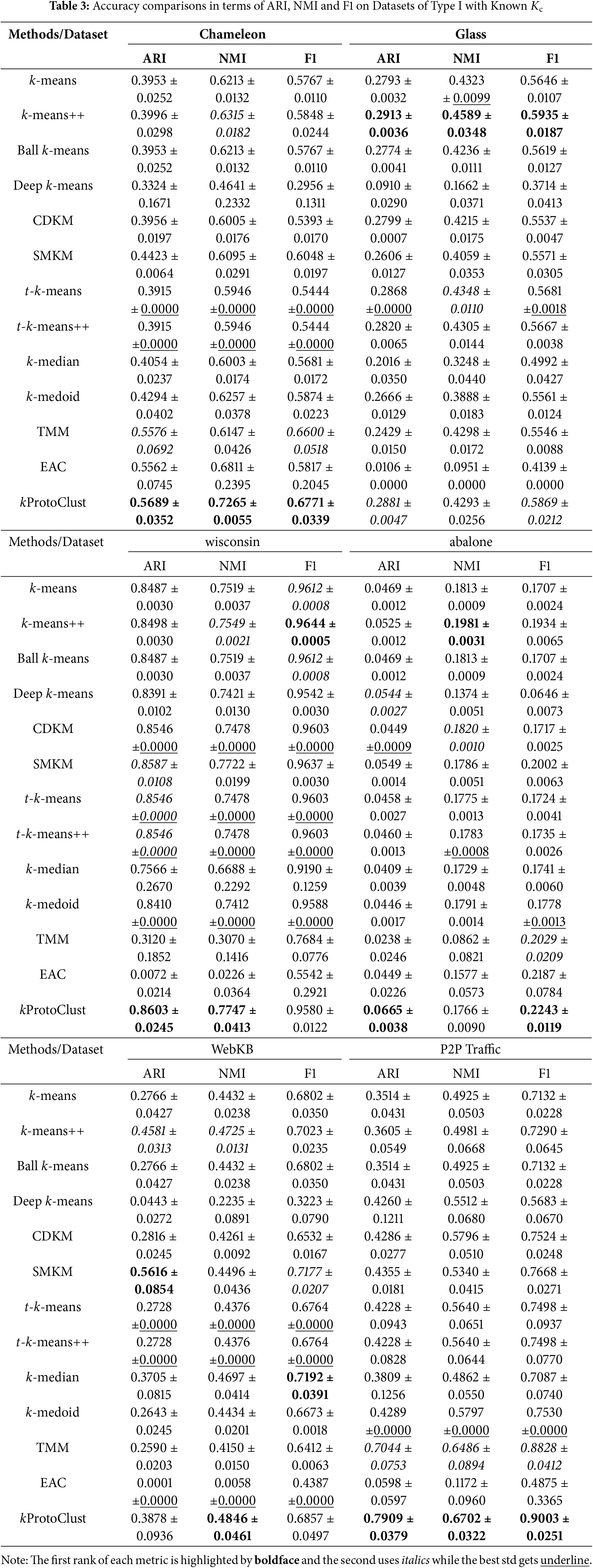
Consider data description in Table 2, we can get the following observations:

•   Performances related to ARI, NMI, and F1 have similar trends for most cases. In terms of ARI, kProtoClust reaches the first rank on Chameleon, wisconsin, abalone, and P2P Traffic while performing the second on glass and the third on WebKB. Similarly, kProtoClust also reaches the best performance on four datasets in terms of NMI and on three data sets in terms of F1. Even though kProtoClust is not ranked first, it frequently gets into the first three ranks or obtains comparable accuracies. Relatively, kProtoClust has a significant advantage on datasets with small dimensions but more samples, e.g., Chameleon and P2P Traffic. Generally, in these cases, the more irregular the cluster shape is, the greater advantage it achieves.

•   Besides kProtoClust, SMKM and k-means++ perform better than the others. They separately have the best ARI on glass and WebKB. Compared with k-means, coincidentally, they both achieve improvement by introducing the initialization strategy of centroid selection. k-means++ selects K centroids far away from each other, whereas SMKM introduces a cheap split-merge step to re-start k-means after reaching a fixed point. Compared with k-means++, SMKM has advantages on all the other five datasets. What follows is CDKM, which achieves comparable accuracies with SMKM and k-means++ yet performs more stable with much lower mean-square deviations.

•   Unfortunately, there are no obvious advantages for Deep k-means, t-k-means, t-k-means++, and TMM, even though they tend to build distribution models for these datasets with extremely irregular cluster shapes. Similar performance can be found in k-means, Ball k-means, k-median, and k-medoid. Like CDKM, t-k-means and t-k-means++ have significant stability advantages due to pursuing the global optimization of Eq. (1). However, limited by the circle-like pattern hypothesis, global optimization usually does not mean the best cluster description for irregular shapes and imbalance distribution. Among these methods, EAC outperforms most of the others on low-dimensional datasets with clear shapes, e.g., Chameleon. However, noises and higher dimensions frequently make it fail, e.g., glass, wisconsin, WebKB, and P2P Traffic.

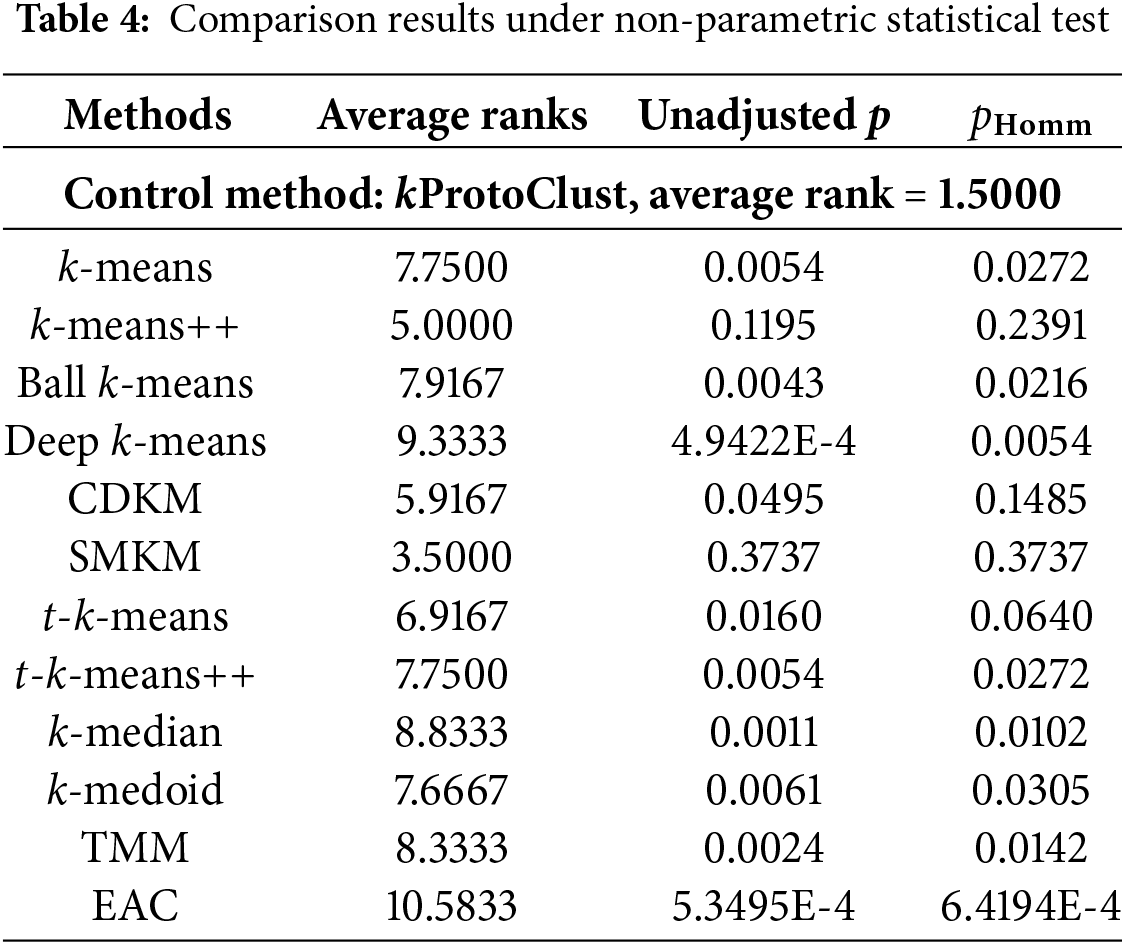
To further confirm the effectiveness of kProtoClust, we give results of pair comparisons in Table 4 following [37]. Taking kProtoClust as the control method, a typical nonparametric statistical test of Friedman test is adopted to get the average ranks and unadjusted p values. By introducing the Bergmann-Hommel procedure [38], the adjusted p-value denoted by pHomm corresponding to each comparison is obtained. Obviously, kProtoClust reaches the best performance. Since the Bergmann-Hommel procedure rejects those hypotheses with p-values ≤0.0167, together with the values of pHomm, kProtoClust performs better than SMKM, k-means++ and CDKM, and outperforms the others. The weakness is that several rounds of invoking k-means++ (i.e., lines 3 and 5 of Algorithm 4) may cause accumulative instability. Thus, kProtoClust frequently has greater mean-square deviations than that achieved by k-means++ and CDKM.

4.4 Exploration Contrast without the Prior Knowledge Kc

For many real-world problems, e.g., intrusion behavior analysis, data owners can not have the prior knowledge Kc. Due to polymorphism, the expected class number Kc (column 5 in Table 2) is sometimes not the same as the real cluster number, which generally corresponds to the actual distribution pattern. Therefore, we conduct experiments to check the cluster discovery ability of kProtoClust on datasets of Type I without the prior knowledge Kc. Based on results in Tables 3 and 4, we take k-means, SMKM, k-means++, t-k-means++, CDKM, and k-median as baselines. On datasets of type I, the reserved methods either reach close accuracies with kProtoClust or have significant stability advantages. Fig. 5 shows the accuracies achieved by all the compared methods and the obtained cluster numbers Kf with respect to different initialized K by kProtoClust.

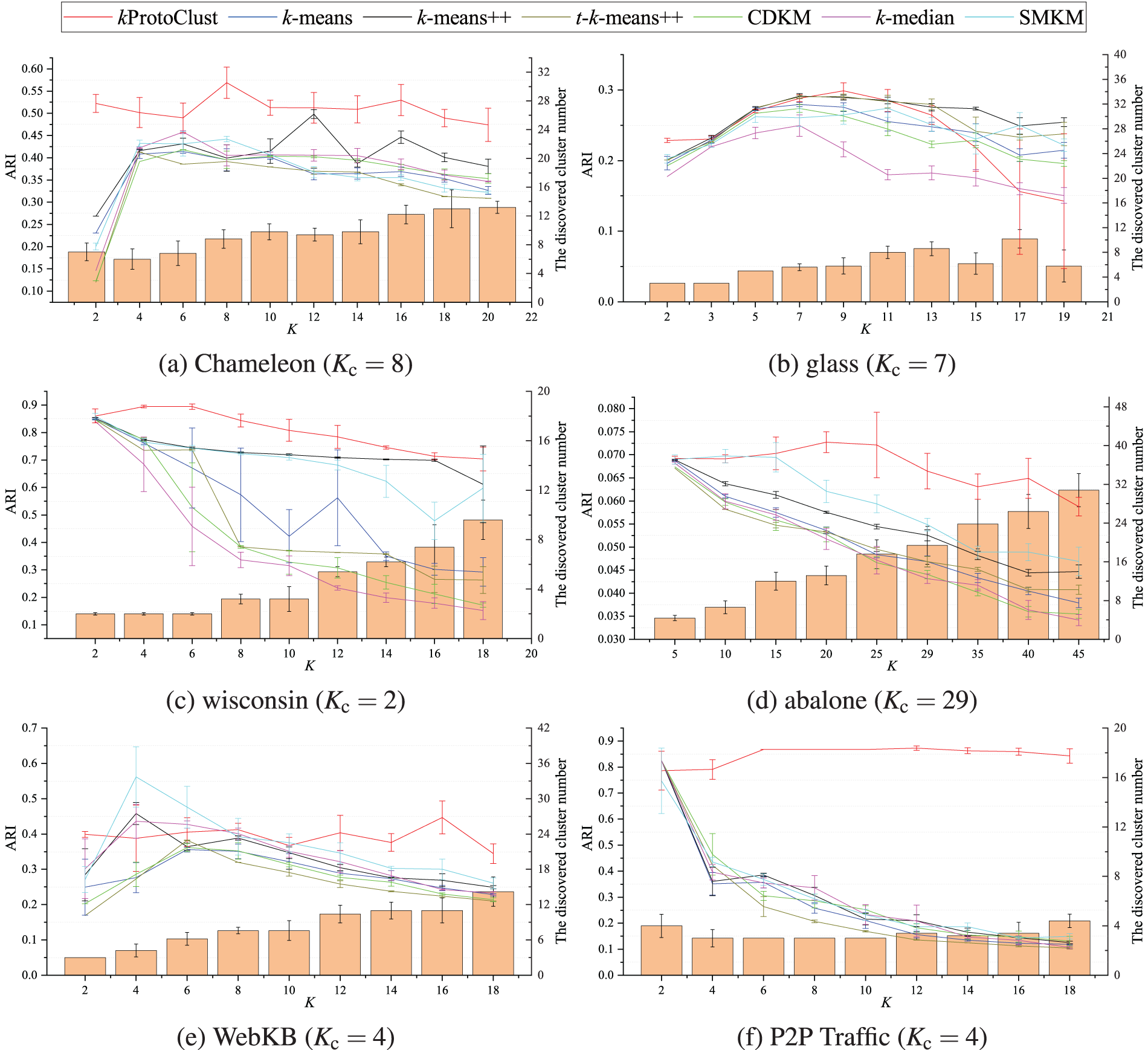
Figure 5: Accuracy (ARI) for all the compared methods and the cluster number found by kProtoClust without Kc

Intuitively, without enough attention to the actual distribution, k-means, k-means++, and k-median try to do data division under different initialization strategies or distance measures. Although CDKM researches instability reduction by perusing the global optimization, t-k-means++ pays more attention to data distribution by introducing t-mixture distribution model, and SMKM adopts split-merge strategy to adjust clusters, they have to ensure the input space is divided into K clusters. Therefore, they can not avoid a severe deviation from the truth cluster number if we get an incorrect assumption of K. In contrast, the objective of split and merge analysis in kProtoClust is to dynamically generate an unfixed number of convex hulls of different sizes. Considering these convex hulls as prototypes, kProtoClust can better profile clusters with arbitrary shapes. Even though the discovered cluster number may not be equal to Kc, it is located around the expected value in a relatively small error range on Chameleon, glass, and P2P Traffic. In general, data separability reduces for high dimensional data with inadequate samples. Therefore, the discovered cluster numbers on wisconsin and abalone show increasing trends when K becomes much greater than the actual number. Even so, these deviations are still much smaller than those discovered by the other variants.

Regarding ARI, the obtained accuracies show evidence of imbalanced distribution and irregular cluster shapes. For instance, accuracies obtained on Chameleon by the baseline methods are not falling off a cliff along with the increase of K, and the best accuracy on P2P Traffic is achieved when K=2, not K=Kc (i.e., 4). Besides k-means++ reaches the best accuracy with K=12 on Chameleon while Kc=8, the baselines share a common characteristic of a downtrend as K increases, especially when K is far from the ground truth. Fortunately, we can find that kProtoClust has remarkable performances in stability which outperform the others for most cases, e.g., Chameleon, wisconsin, abalone, WebKB, and P2P Traffic. k-means++ and SMKM have comparable performances which rank only second to kProtoClust, whereas CDKM and t-k-means++ have similar performance. Although k-means does cluster analysis well, it frequently gets greater std than k-median. Therefore, we believe that kProtoClust outperforms the others when we can not have the actual cluster number as the prior knowledge.

Additionally, several other cues may be found from Fig. 5. First, for most cases, performances of baselines have specific decreases in accuracy when K is far from Kc. Similar trends happened to kProtoClust on glass and wisconsin. It means that a small cluster number assumed by k-means++ (line 3 of Algorithm 4) is unsuitable for convex decomposition towards prototype finding. Although the discovered cluster number by kProtoClust is frequently close to the ground truth. One can try several times and then avoid making K fall into a range where the discovered cluster numbers have large fluctuations. However, an appropriate assessment method for accurate cluster numbers may benefit from finding an optimal K for all the methods. Second, although the cluster discovery ability of kProtoClust on datasets of type I has been confirmed, too few samples in a dataset is also a challenge for kProtoClust, e.g., the 9-dimensional dataset glass with only 214 samples in 7 clusters. For a dataset like this particular case, CDKM, k-means, and k-means++ are recommended for simplicity if we get a K value close to the ground truth.

4.5 Necessity Analysis of NMMRS for kProtoClust

Based on the analysis in Sections 3.5 and 4.4, when we fix the data size N, a greater dimensionality d not only increases its complexity but also reduces the separability. However, if d is fixed, the increase of N increases the complexity but will not permanently change (either increase or reduce) the separability. Therefore, we introduce NMMRS (lines 1–2 of Algorithm 4) into kProtoClust and denote it by kProtoClust(SR) in the following necessity analysis.

As discussed in Section 3.5, EdgeSel consumes O(N2) which may be the most time-consumption phase in kProtoClust. By employing the “Run and Time” analysis provided by MATLAB, we separately list all the time-consumptions required by each phase of kProtoClust and kProtoClust(SR) on Chameleon in Table 5. Obviously, the first two significant time-consuming phases are MergeAnalysis and EdgeSel which occupy 54.95% and 30.27% of kProtoClust, respectively. Furthermore, EdgeSel is one of the main phases invoked by MergeAnalysis in line 2 of Algorithm 2. In kProtoClust(SR), their time-consumptions are separately reduced to 43.52% and 9.32%, and the total occupation is reduced to 52.84% from 85.22%. Relatively, LabelAssignment has been increased to 26.75% from 5.81%. Unlike experiments in Section 4.3, we restrict the max iteration of k-means++ to 10 for all the invocations (i.e., lines 3 and 5), and do not consider any parallel strategy for each phase.

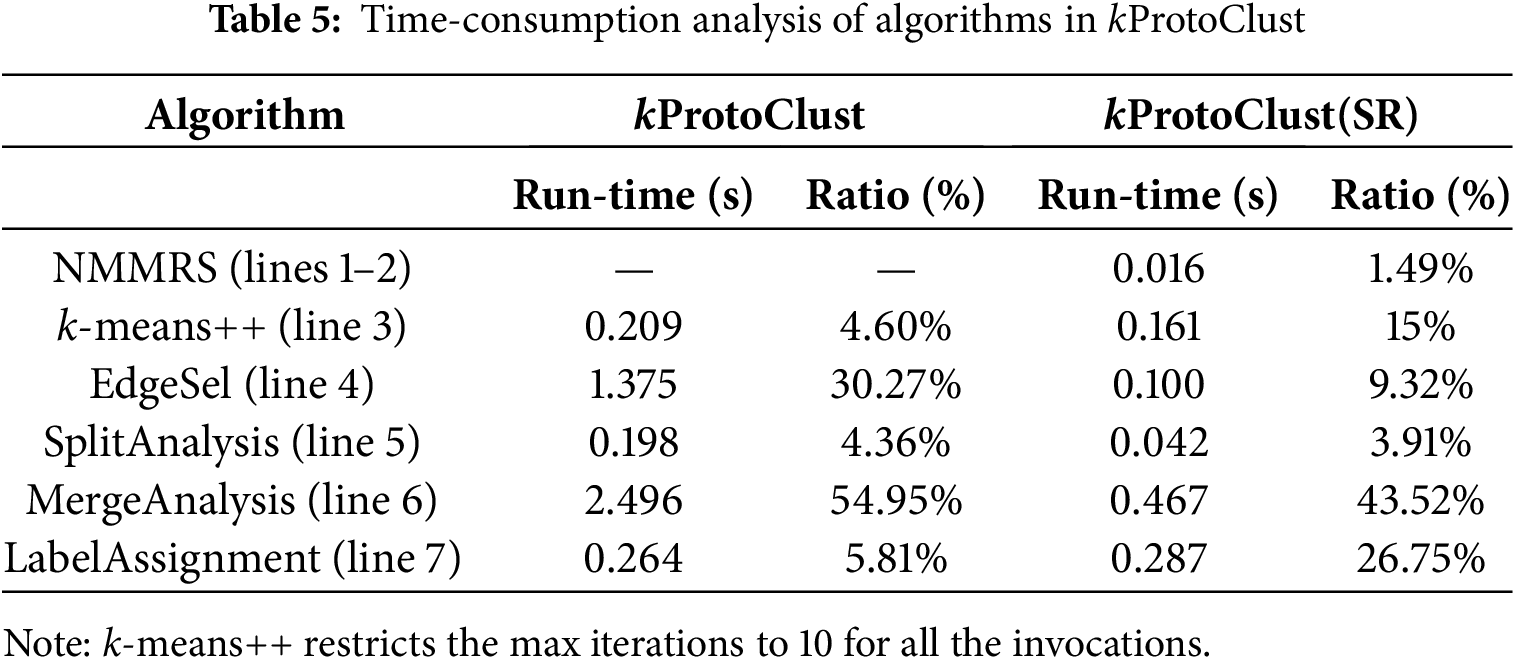
kProtoClust(SR) is a variant of k-means++ with split and mergence strategy. Meanwhile, SMKM also prefers a split-merge strategy and performs closely to kProtoClust(SR) in terms of accuracy on datasets of type I. In this section, we take k-means++ and SMKM as the baselines for further comparative analysis with kProtoClust and kProtoClust(SR). Results of accuracies in terms of ARI are depicted in Fig. 6 in which run-time costs required by kProtoClust and kProtoClust(SR) are also given. Due to dKc>N, NMMRS is employed by kProtoClust(SR) to make dimensionality reduction for movement_libras and uspst, while data reduction is preferred for the other four datasets since dKc≪N. As shown in Fig. 6, kProtoClust(SR) and kProtoClust consistently achieve the first two ranks of accuracy except for uspst. Obviously, the advantage usually rises along with N increases, e.g., results corresponding to kddcup99. On uspst, kProtoClust and k-means++ have comparable results while kProtoClust(SR) and SMKM perform similarly. Furthermore, a greater d frequently influences the std of accuracy for kProtoClust(SR) and SMKM, particularly for SMKM. It means that dimensionality reduction may not be the best choice if the dimensionality d of a dataset is high and dKc>N. Because the ability of structure kept of NMMRS reduces significantly if we want to do distance-based analysis among data samples more than the nearest neighbors.

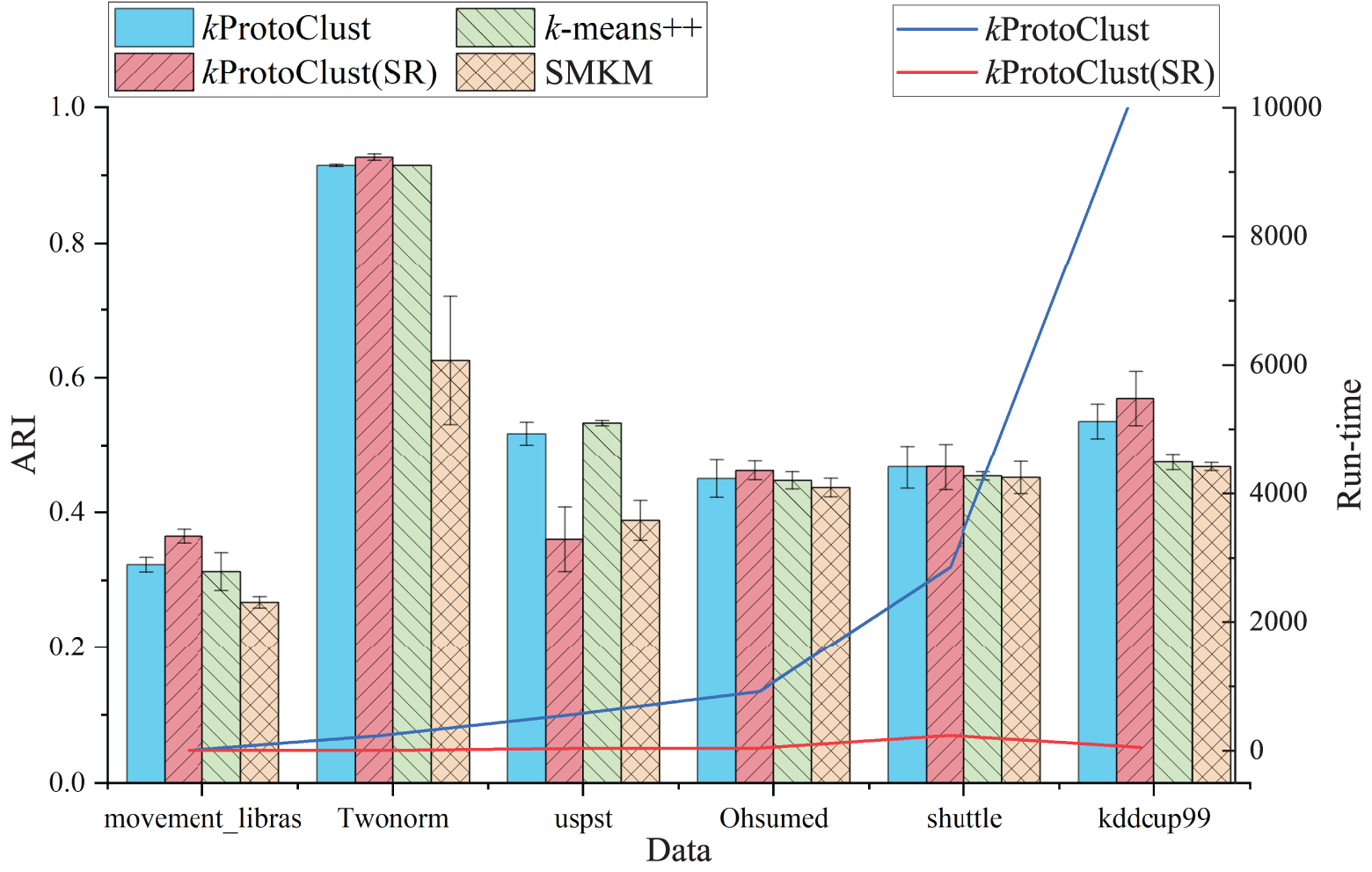
Figure 6: Performance analysis for kProtoClust with or without sampling and dimensionality reduction by taking k-means++ and SMKM as baselines. Ns=N and q=10≪d are set for movement_libras and uspst while Ns=5000≪N and q=d are preferred for the other datasets

In terms of efficiency, kProtoClust(SR) has a significant advantage over kProtoClust due to the introduction of NMMRS. On Twonorm, Ohsumed, shuttle and kddcup99, kProtoClust(SR) finish cluster analysis in 2.5, 40.7, 233.5 and 49.7 s, respectively. The run-time required by shuttle is greater than kddcup99 because the iterative analysis is more complex in SplitAnalysis (line 5 of Algorithm 4) due to extremely imbalanced distribution. Furthermore, results corresponding to all the datasets of type II confirm the contributions from NMMRS and suggest that the reduced dataset should have N>dKc or keep Ns>qKc to avoid affecting data separability.

5  Related Works

k-means is the inspiration source of kProtoClust. Due to some intrinsic flaws inherited from the partition-based clustering strategy, the literature mainly focuses on further efficiency improvements, initialization strategy, stability optimization, and specific data types and patterns support.

The classical k-means selects K samples at random as the initial centroids and iteratively conducts the assignment and refinement until all the centroids do not change. For efficiency, besides hardware parallelization, fast convergence [7], result approximation [39], and distance computation reduction [14] are mainly focused. The last one receives the most attention for its generalization ability of computation optimization. Those representative works include avoiding unnecessary membership analysis by storing the different number of bounds for either centroids or data samples [40], and introducing group pruning and centroids regrouping strategy in the iteration [41]. For efficiency, Ryšavý et al. [42] makes a tighter centroid drift bound by employing the distance between the origin sample and the corresponding centroid, Bottesch et al. [43] adopts the Hölder’s inequality and norms, while Broder et al. [44] introduce a pre-assignment search around each centroid which greatly reduces distance computations. Recently, to optimize cluster assignment, Ball k-means [2] utilizes centroid distance. Besides, k-median [26] and k-medoid [27] can also be considered variants of k-means since the former introduces the Manhattan distance while the latter chooses existing data samples as centroids.

Many valuable solutions [45] corresponding to the initialization strategy, the main works are to estimate an appropriate K for centroids initialization. For the former, the mainstream way is parameter tweaking or evaluating models with different K settings [46] before finding out the usable K. Meanwhile, combining multiple clustering results with some voting strategies like EAC [5] or introducing some extensions of criterion such as Elbow index [47] are also considered. For the latter, besides pre-analysis of a set of potential centroids, Peña et al. [48] suggest that dividing a data set into K clusters and iteratively collecting K representative instances are practical. Furthermore, k-means++ [7] is a representative adopting the latter strategy since it chooses K centroids far away from each other.

Stability optimization is strongly related to the initialization strategy because the random initialization increases the instability. Recently, Capó et al. [9] present a split-merge strategy to restart k-means after reaching a fixed point. Therefore, their variant of k-means, namely SMKM, improves stability. However, multiple rounds of invocations to k-means and the split-merge strategy make it more suitable for dealing with clusters with irregular shapes. Another typical work in the most recently is CDKM [24], which designs a coordinate descent method for k-means to reach the global optimization of Eq. (1).

Different data types frequently relate to different application domains and distinct data patterns. In the literature, most works prefer doing special designs of k-means for a specific application. For instance, privacy-preserving k-means is presented for encrypted data analysis [49], global k-means based neural network performs well on sound source localization [50], while k-means with bagging neural network is suitable for short-term wind power forecasting [51]. Consider those mixed data types, the major attentions prefer fuzzy method [52], distance calculation mechanism [45], and hybrid framework [14]. Towards challenges from arbitrary cluster shapes, Li et al. [25] present t-k-means and t-k-means++ by assuming data sampled from the t-mixture distribution. Besides, Khan et al. [53] consider an exponential distribution to standardize data and propose EGS to estimate the optimal number of clusters. Fard et al. [23] present a joint solution namely deep k-means by integrating k-means and deep learning, while Peng et al. [54] adopt deep learning to re-describe k-means. Given the cluster number K, another exciting work [55] introduces k-means into SVDD such that it supports K groups of submodel of SVDD to describe different clusters in a data set. Lacking the prior knowledge of cluster number, EAC [5] clusters data with k-means based evidence accumulation. It conducts result combination with a specific vote strategy that well support low-dimensional data with clear and simple shape.

Despite many insightful works, they treat clusters fairly in size due to the limitation of the distance-based data partition. Few works change the initialized K in the clustering procedure. However, arbitrarily shaped clusters are very common in practice which motivates us to break the restriction of inaccurate prior-knowledge K and partition data into clusters with different sizes and connection relationships. Even though an optimal K is estimated by [53], utilizing K fixed clusters and K data samples as prototypes for label assignments can not match the human’s cognition of discovering clusters from their shapes, sizes, and connection relationships well. Therefore, kProtoClust takes convex hulls of varying sizes as prototypes following [17] and allows the change of K to support multiple prototypes in one cluster to improve cluster description ability.

6  Conclusion

With a specific distance measure, k-means find K data samples as prototypes to partition data space into clusters. However, not only the cluster number is unknown, but many practical datasets do not have a balanced and regular distribution as what k-means expected. To discover clusters following a general human cognition (corresponding to {γl,γu,τd,τm,τim}), we propose kProtoClust to replace prototypes with convex hulls of varying sizes. Given K selected at random, k-means++ divides the input space into K clusters. Regarding the local geometry view, edge patterns of each cluster are collected and split into subgroups if they can not construct a single convex hull. In terms of the global geometry view, all the violating samples existing in the overlapping region of two adjacent convex hulls are located. Since violating samples are not the actual edge patterns, removing violating samples means the mergence of the associated convex hulls increases the number of prototypes for the corresponding cluster. Finally, one-cluster-multiple-prototypes are supported by kProtoClust in which the adaptive prototype size contributes to the ability of arbitrary cluster shape’s description. As the composite indicators for a specific human cognition, the five additional thresholds are relatively insensitive to the clustering result. They can be preset fixedly following either the recommendations in Section 4.2 or user preferences.

Although kProtoClust achieves accuracy improvement with fair efficiency on datasets of imbalanced distribution and irregular cluster shapes, some shortcomings still exist, e.g., a certain instability inherited from k-means++. Meanwhile, the ways of handling high dimensional data with low separability and making the cluster number assessment more accurate are worthy of further investigation, as well as further improving the generalizability and adaptability across different scenarios, including semi-supervised clustering and clustering data streams.

Acknowledgment: We thank all the authors for their research contributions.

Funding Statement: This work is supported by the National Natural Science Foundation of China under Grant No. 62162009, the Key Technologies R&D Program of He’nan Province under Grant No. 242102211065, the Scientific Research Innovation Team of Xuchang University under Grant No. 2022CXTD003, and Postgraduate Education Reform and Quality Improvement Project of Henan Province under Grant No. YJS2024JD38.

Author Contributions: Conceptualization, methodology, and draft manuscript preparation: Yuan Ping; Huina Li; data collection, visualization, and analysis: Yuan Ping; Chun Guo; Bin Hao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kansal T, Bahuguna S, Singh V, Choudhury T. Customer segmentation using k-means clustering. In: 2018 International Conference on Computational Techniques, Electronics and Mechanical Systems (CTEMS); 2018; Belgaum, India. p. 135–9. [Google Scholar]

2. Xia S, Peng D, Meng D, Zhang C, Wang G, Giem E, et al. Ball k-means: fast adaptive clustering with no bounds. IEEE Trans Pattern Anal Mach Intell. 2022;44(1):87–99. doi:10.1109/TPAMI.2020.3008694. [Google Scholar] [PubMed] [CrossRef]

3. Banerji A. k-mean: getting the optimal number of clusters; 2022 [cited 2024 Oct 20]. Available from: https://www.analyticsvidhya.com/blog/2021/05/k-mean-getting-the-optimal-number-of-clusters/. [Google Scholar]

4. Khan IK, Daud HB, Zainuddin NB, Sokkalingam R, Abdussamad, Museeb A, et al. Addressing limitations of the k-means clustering algorithm: outliers, non-spherical data, and optimal cluster selection. AIMS Math. 2024;9(9):25070–97. doi:10.3934/math.20241222. [Google Scholar] [CrossRef]

5. Fred ALN, Jain AK. Data clustering using evidence accumulation. In: Proceedings of the 16th International Conference on Pattern Recognition (ICPR’02); 2002; Quebec City, QC, Canada. p. 276–80. [Google Scholar]

6. Celebi ME, Kingravi HA, Vela PA. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert Syst Appl. 2013;40(1):200–10. doi:10.1016/j.eswa.2012.07.021. [Google Scholar] [CrossRef]

7. Arthur D, Vassilvitskii S. k-means++: The advantages of careful seeding. In: Proceedings of The Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA ’07); 2007; New Orleans, LA, USA. p. 1027–35. [Google Scholar]

8. Fränti P, Sieranoja S. How much can k-means be improved by using better initialization and repeats? Pattern Recognit. 2019;93(9):95–112. doi:10.1016/j.patcog.2019.04.014. [Google Scholar] [CrossRef]

9. Capó M, Pérez A, Lozano JA. An efficient split-merge re-start for the k-means algorithm. IEEE Trans Knowl Data Eng. 2022;34(4):1618–27. doi:10.1109/TKDE.2020.3002926. [Google Scholar] [CrossRef]

10. Lu Y, Cheung Y-M, Tang YY. Self-adaptive multiprototype-based competitive learning approach: a k-means-type algorithm for imbalanced data clustering. IEEE Trans Cybern. 2021;51(3):1598–612. doi:10.1109/TCYB.2019.2916196. [Google Scholar] [PubMed] [CrossRef]

11. Yao Y, Li Y, Jiang B, Chen H. Multiple kernel k-means clustering by selecting representative kernels. IEEE Trans Neural Netw Learn Syst. 2021;32(11):4983–96. doi:10.48550/arXiv.1811.00264. [Google Scholar] [CrossRef]

12. Ping Y, Hao B, Li H, Lai Y, Guo C, Ma H, et al. Efficient training support vector clustering with appropriate boundary information. IEEE Access. 2019;7(10):146964–78. doi:10.1109/ACCESS.2019.2945926. [Google Scholar] [CrossRef]

13. Rathore P, Kumar D, Bezdek JC, Rajasegarar S, Palaniswami M. A rapid hybrid clustering algorithm for large volumes of high dimensional data. IEEE Trans Knowl Data Eng. 2019;31(4):641–54. doi:10.1109/TKDE.2018.2842191. [Google Scholar] [CrossRef]

14. Wang S, Sun Y, Bao Z. On the efficiency of k-means clustering: evaluation, optimization, and algorithm selection. Proceedings VLDB Endowment. 2020;14(2):163–75. doi:10.48550/arXiv.2010.06654. [Google Scholar] [CrossRef]

15. Tax DMJ, Duin RPW. Support vector domain description. Pattern Recognit Lett. 1999;20:1191–9. doi:10.1023/B:MACH.0000008084.60811.49. [Google Scholar] [CrossRef]

16. Li YH, Maguire L. Selecting critical patterns based on local geometrical and statistical information. IEEE Trans Pattern Anal Mach Intell. 2011;33(6):1189–201. doi:10.1109/TPAMI.2010.188. [Google Scholar] [PubMed] [CrossRef]

17. Ping Y, Tian Y, Zhou Y, Yang Y. Convex decomposition based cluster labeling method for support vector clustering. J Comput Sci Technol. 2012;27(2):428–42. doi:10.1007/s11390-012-1232-1. [Google Scholar] [CrossRef]

18. Li H, Ping Y, Hao B, Guo C, Liu Y. Improved boundary support vector clustering with self-adaption support. Electronics. 2022;11(12):1854. doi:10.3390/electronics11121854. [Google Scholar] [CrossRef]

19. Karypis G, Han E-H, Kumar V. CHAMELEON: a hierarchical clustering algorithm using dynamic modeling. Computer. 1999;32(8):68–75. doi:10.1109/2.781637. [Google Scholar] [CrossRef]

20. Liparulo L, Proietti A, Panella M. Fuzzy clustering using the convex hull as geometrical model. Adv Fuzzy Syst. 2015;2015(1):265135. doi:10.1155/2015/265135. [Google Scholar] [CrossRef]

21. Pan C, Rana JSSPV, Milenkovic O. Machine unlearning of federated clusters. arXiv:2210.16424. 2022. [Google Scholar]

22. Johnson WB, Lindenstrauss J. Extensions of lipschitz mappings into a hilbert space. Contemp Math. 1984;26(1):189–206. doi:10.1090/conm/026/737400. [Google Scholar] [CrossRef]

23. Fard MM, Thonet T, Gaussier E. Deep k-means: jointly clustering with k-means and learning representations. Pattern Recognit Lett. 2020;138(10):185–92. doi:10.1016/j.patrec.2020.07.028. [Google Scholar] [CrossRef]

24. Nie D, Xue J, Wu D, Wang R, Li H, Li X. Coordinate descent method for k-means. IEEE Trans Pattern Anal Mach Intell. 2022;44(5):2371–85. doi:10.1109/TPAMI.2021.3085739. [Google Scholar] [PubMed] [CrossRef]

25. Li Y, Zhang Y, Tang Q, Huang W, Jiang Y, Xia S-T. t-k-means: a robust and stable k-means variant. In: ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2021; Toronto, ON, Canada. p. 3120–4. [Google Scholar]

26. Arora S, Raghavan P, Rao S. Approximation schemes for euclidean k-medians and related problems. In: Proceedings of the 30th Annual ACM Symposium on Theory of Computing (STOC’ 98); 1998; Dallas, TX, USA. p. 106–13. [Google Scholar]

27. Kaufman L, Rousseeuw P. Clustering by means of meoids. North-Holland: Faculty of Mathematics and Informatics; 1987. [Google Scholar]

28. Frank A, Asuncion A. UCI machine learning repository. Irvine: University of California, School of Information and Computer Sciences; 2010 [cited 2024 Oct 20]. Available from: http://archive.ics.uci.edu/ml. [Google Scholar]

29. Graven M, DiPasquo D, Freitag D, McCallum A, Mitchell T, Nigam K, et al. Learning to extract symbolic knowledge form the world wide web. In: Proceedings of 15th Nat’l Conference for Artificial Intelligence (AAAI’98); 1998; Madison, WI, USA. p. 509–16. [Google Scholar]

30. Hersh WR, Buckley C, Leone TJ, Hickam DH. Ohsumed: an interactive retrieval evaluation and new large test collection for research. In: Proceedings of 17th Annual ACM SIGIR Conference; 1994; Dublin, Ireland. p. 192–201. [Google Scholar]

31. Peng J, Zhou Y, Wang C, Yang Y, Ping Y. Early tcp traffic classification. J Appl Sci. 2011;29(1):73–7. doi:10.1016/j.dcan.2022.09.009. [Google Scholar] [CrossRef]

32. Department of Information and Computer Science, University of California. KDD cup 99 intrusion detection dataset. Irvine: Department of Information and Computer Science, University of California; 1999 [cited 2024 Oct 20]. Available from: http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html. [Google Scholar]

33. Xu R, Wunsch DC. Clustering. Hoboken, New Jersey: A John Wiley&Sons; 2008. [Google Scholar]

34. Strehl A, Ghosh J. Cluster ensembles—a knowledge reuse framework for combining multiple partitions. J Mach Learn Res. 2002;3(12):583–617. doi:10.1162/153244303321897735. [Google Scholar] [CrossRef]

35. Sasaki Y. The truth of the f-measure; 2007 [cited 2024 Oct 20]. Available from: https://www.toyota-ti.ac.jp/Lab/Denshi/COIN/people/yutaka.sasaki/F-measure-YS-26Oct07.pdf. [Google Scholar]

36. Ping Y, Zhou Y, Yang Y. A novel scheme for accelerating support vector clustering. Comput Inform. 2012;31(3):1001–26. [Google Scholar]

37. Garcia S, Herrera F. An extension on “statistical comparisons of classifiers over multiple data sets” for all pairwise comparisons. J Mach Learn Res. 2008;9(Dec):2677–94. [Google Scholar]

38. Bergmann G, Hommel G. Improvements of general multiple test procedures for redundant systems of hypotheses. Mult Hypotheses Test. 1988;70:100–15. [Google Scholar]

39. Newling J, Fleuret F. Nested mini-batch k-means. In: Proceedings of the 13th Annual Conference on Neural Information ProcessingSystems (NIPS’16); 2016; Barcelona, Spain. p. 1352–60. [Google Scholar]

40. Newling J, Fleuret F. Fast k-means with accurate bounds. In: Proceedings of the 33rd International Conference on Machine Learning (ICML ’16); 2016; New York City, NY, USA. p. 936–44. [Google Scholar]

41. Kwedlo W. Two modifications of yinyang k-means algorithm. In: Proceedings of 16th International Conference on Artificial Intelligence and Soft Computing (ICAISC ’17); 2017; Zakopane, Poland. p. 94–103. [Google Scholar]

42. Ryšavý P, Hamerly G. Geometric methods to accelerate k-means algorithms. In: Proceedings of the 2016 SIAM International Conference on Data Mining (SDM ’16); 2016; Miami, FL, USA. p. 324–32. [Google Scholar]

43. Bottesch T, Bühler T, Kächele M. Speeding up k-means by approximating euclidean distances via block vectors. In: Proceedings of the 33rd International Conference on Machine Learning (ICML ’16); 2016. p. 2578–86. [Google Scholar]

44. Broder A, Garcia-Pueyo L, Josifovski V, Vassilvitskii S, Venkatesan S. Scalable k-means by ranked retrieval. In: Proceedings of the 7th ACM International Conference on Web Search and Data Mining (WSDM ’14); 2014; New York City, NewYork, USA. p. 233–42. [Google Scholar]

45. Ahmed M, Seraj R, Islam SMS. The k-means algorithm: a comprehensive survey and performance evaluation. Electronics. 2020;9(8):1295:1–12. doi:10.3390/electronics9081295. [Google Scholar] [CrossRef]

46. Ikotun AM, Ezugwu AE, Abualigah L, Abuhaija B, Heming J. K-means clustering algorithms: a comprehensive review, variants analysis, and advances in the era of big data. Inf Sci. 2023;622:178–210. doi:10.1016/j.ins.2022.11.139. [Google Scholar] [CrossRef]

47. Rykov A, De Amorim RC, Makarenkov V, Mirkin B. Inertia-based indices to determine the number of clusters in k-means: an experimental evaluation. IEEE Access. 2024;12:11761–73. doi:10.1109/ACCESS.2024.3350791. [Google Scholar] [CrossRef]

48. Peña JM, Lozano JA, Larrañaga PL. An empirical comparison of four initialization methods for the k-means algorithm. Pattern Recognit Lett. 1999;20(10):1027–40. doi:10.1016/S0167-8655(99)00069-0. [Google Scholar] [CrossRef]

49. Yuan J, Tian Y. Practical privacy-preserving mapreduce based k-means clustering over large-scale dataset. IEEE Trans Cloud Comput. 2019;7(2):568–79. doi:10.1109/TCC.2017.2656895. [Google Scholar] [CrossRef]

50. Yang X, Li Y, Sun Y, Long T, Sarkar TK. Fast and robust RBF neural network based on global k-means clustering with adaptive selection radius for sound source angle estimation. IEEE Trans Antennas Propag. 2018;66(6):3097–107. doi:10.1109/TAP.2018.2823713. [Google Scholar] [CrossRef]

51. Wu W, Peng M. A data mining approach combining k-means clustering with bagging neural network for short-term wind power forecasting. IEEE Internet Things J. 2017;4(4):979–86. doi:10.1109/JIOT.2017.2677578. [Google Scholar] [CrossRef]

52. Nie F, Zhao X, Wang R, Li X, Li Z. Fuzzy k-means clustering with discriminative embedding. IEEE Trans Knowl Data Eng. 2022;34(3):1221–30. doi:10.1109/TKDE.2020.2995748. [Google Scholar] [CrossRef]

53. Khan IK, Daud HB, Zainuddin NB, Sokkalingam R, Farooq M, Baig ME, et al. Determining the optimal number of clusters by enhanced gap statistic in k-mean algorithm. Egypt Inform J. 2024;27(1):100504. doi:10.1016/j.eij.2024.100504. [Google Scholar] [CrossRef]

54. Peng X, Li Y, Tsang IW, Zhu H, Lv J, Zhou JT. Xai beyond classification: interpretable neural clustering. J Mach Learn Res. 2022;23(6):1–28. doi:10.48550/arXiv.1808.07292. [Google Scholar] [CrossRef]

55. Gornitz N, Lima LA, Muller K-R, Kloft M, Nakajima S. Supprt vector data descriptions and k-means clustering: one class? IEEE Trans Neural Netw Learn Syst. 2018;29(9):3994–4006. doi:10.1109/TNNLS.2017.2737941. [Google Scholar] [PubMed] [CrossRef]