MMH-FE: A Multi-Precision and Multi-Sourced Heterogeneous Privacy-Preserving Neural Network Training Based on Functional Encryption

1  Introduction

Machine learning technology has been widely used in many fields, including computer vision, natural language processing, and audio and speech processing, becoming a core component of the development of modern technology. Many companies, such as Google and IBM, provide Infrastructure as a Service (IaaS) in the current business environment. These services are designed to help users who lack computing resources use cloud computing resources to train and deploy machine learning models. However, when using these services, data privacy and security issues are particularly important, especially when dealing with sensitive data such as medical or financial data. Therefore, meeting such privacy concerns of users as well as legal and regulatory requirements poses a huge challenge to the implementation of machine learning solutions.

Suppose a bank wants to assess the credit risk of its users and decides to outsource this task to a company that provides IaaS. In this scenario, the bank provides the user’s financial transaction history as input, and the IaaS company uses this data to predict whether the user is likely to default. This data is extremely sensitive and cannot be directly disclosed to the service provider due to the personal financial information involved. In this privacy-preserving environment, the credit risk assessment must be conducted without directly revealing the transaction history to the company.

With the development of various intelligent devices [1]. To cope with the privacy issues that may arise during this process, a privacy-preserving machine learning (PPML) framework needs to be implemented. In the field of PPML, various technical approaches have been proposed to protect data privacy [2]. We summarize some of the representative PPML methods in Table 1. As shown in the literature [3], non-cryptographic solutions like differential privacy and federated learning require strong security parameters for privacy. For example, differential privacy needs a strict privacy budget, reducing the usability of neural network models. In contrast, cryptographic schemes, such as secure multi-party computation [4], provide robust security. However, they have very high computational costs and require significant communication overhead. This results in poor computational performance, making them less suitable for large-scale applications. Homomorphic encryption schemes, such as those proposed in the literature [5,6], require the execution of complex arithmetic operations and often utilize approximations to replace the activation function, which limits both time efficiency and accuracy. Except for some existing functional encryption methods (e.g., CryptoNN [7], NN-EMD [8]), most cryptographic methods address the privacy problem in the prediction phase without focusing on the privacy problem in the training phase.

The remainder of this paper is organized as follows: It summarizes related work in Section 2. In Section 3, we introduce background knowledge and preliminaries. In Section 4, we propose the MMH-FE framework and describe the technical details. In Section 5, we conduct experimental analyses and evaluate. Finally, conclusions are drawn in Section 6.

2  Related Work

2.1 Functional Encryption

Functional encryption (FE) scheme was first proposed by Sahai et al. in [10], and an exhaustive formal definition was provided by Boneh et al. in the literature [11]. Functional encryption has become an innovative technique in public key cryptography as more and more scholars have invested in this area of research [12–14]. This technique constructs a theoretical framework that abstracts a variety of existing encryption mechanisms, including fine-grained access control [15], dynamic decentralized functional encryption [16], and a new paradigm of quadratic public-key functional encryption [17]. Unlike traditional encryption schemes, which reveal either all plaintext or all ciphertext, functional encryption strategies have a unique feature. Their decryption keys reveal only limited information about the plaintext. Specifically, they disclose the result of a computation performed on the plaintext using a particular function. In addition, functional encryption contrasts with homomorphic encryption techniques, which are widely used today, and which usually consume a certain amount of resources to additionally decrypt the final result. In contrast, this unique property of functional encryption brings new research and application prospects in the field of data privacy and information security.

In the existing literature, a variety of functional encryption constructs have been proposed to handle different types of functions, such as inner products [18], sequential comparisons [11], and access control [19]. In addition, researchers have also explored the use of secure multi-party computation [20] and multilinear mapping [21,22] to construct functional encryption schemes, or the use of functional encryption techniques to implement other cryptographic applications. However, most of these schemes are still in the theoretical research stage and have not been sufficiently translated into practical applications. Compared with existing work, our method is not only theoretically innovative but also practically feasible. The work presented in the literature [23,24] is part of our cryptosystem underlying this paper.

2.2 Secure Neural Networks

In recent years, with the rapid development of neural network technology [25], the issue of data security has received widespread attention. The homomorphic encryption [26–28] technique, as an advanced encryption method, has attracted much attention from researchers for its application in privacy-preserving ML. ML confidential [29] describes a binary classification mechanism that combines polynomial approximation and homomorphic encryption. Faster CryptoNets [30] accelerates prediction performance in deep learning models by utilizing sparse representations in the underlying cryptosystem through techniques of pruning and quantization. Secure Multi-Party Computing [4] discusses a privacy-preserving protocol that uses SGD (Stochastic Gradient Descent) optimization algorithm to train a neural network model. Homomorphic encryption and secure multi-party computation can both be applied to neural networks to protect data privacy. However, homomorphic encryption incurs a high computational cost, as the process of encrypting and decrypting data consumes substantial computational resources. In contrast, secure multi-party computation requires a large number of messages to be exchanged between participants. As the number of participants increases, the complexity and difficulty of implementing secure multi-party computation also rise. Therefore, implementing secure neural networks on servers with limited computational resources is not feasible.

This article focuses on the use of functional encryption as a way to build a secure neural network training process. In an earlier study, Ligier et al. [31] developed an inner-product functional encryption scheme for classifying encrypted data. They utilized Extreme Random Tree (ERT) classifiers trained on the MNIST dataset, focusing primarily on private machine learning prediction using inner product functional encryption. Following this, Dufour-Sans et al. [32] proposed a new quadratic encryption scheme, Ryffel et al. [33] and Nguyen et al. [34] applied it to quadratic networks to classify encrypted data. In addition, CryptoNN [7] investigated the possibility of applying functional encryption to train neural networks on the MNIST dataset, which is comparable to the traditional MNIST model in terms of accuracy. NN-EMD [8] used a multilayer perceptron (MLP) for neural network training on the same dataset, with the difference that it uses a lookup table method to compute discrete logarithms during decryption. Its classification accuracy also rivals the traditional MNIST model.

In this paper, we use Euclidean Division to reconstruct the data representation and achieve moderation of the accuracy of the data in this framework. At the same time, the space cost of the lookup table is significantly reduced during the function decoding process. To reduce the space cost in function encryption computation, we implement this method in Single-Input Function Encryption and Multi-Input Function Encryption. To improve the training accuracy of the model, we apply it in the neural network training process.

3  Preliminaries

3.1 Single-Input Functional Encryption

The single-input functional encryption scheme(SIFE) for the inner-product function is defined as the following four PPT algorithms: .

The algorithm is implemented as follows:

•   : , and on the security parameters and , and then set mpk = and msk = . Return the pair (mpk, msk).

•   : Return the function derived key by master secret key msk and vector .

•   : Choose a random number and compute . Compute for each . Return the ciphertext .

•   : Compute . The recovered result is .

3.2 Multi-Input Functional Encryption

The multi-input functional encryption scheme(MIFE) for the inner-product is defined as the following five PPT algorithms: .

The algorithm is implemented as follows:

•   : , and then generate several samples as , , . Generate the master public key mpk = and master private key msk = .

•   : Return partial private key by .

•   : Partition into , where is equal to . Return the function derived key

•   : Choose a random number . Return the ciphertext .

•   : Compute . The recovered result is .

3.3 Multi-Precision Fixed-Point Arithmetic

Multi-precision fixed-point arithmetic is a common method for large-number multiplication. It is based on the Karatsuba algorithm, which breaks large numbers into smaller ones for multiplication. Here we review the double-precision fixed-point arithmetic technique.

Let m be integers. Decompose m into a pair of integers corresponding to the quotient and the remainder of division , where is a positive integer.

(1)

with . The multiplication of two decomposed integers and satisfies:

(2)

4  The Proposed MMH-FE Framework

4.1 Overview

This paper proposes a multi-precision and multi-sourced heterogeneity privacy-preserving neural network (MMH-FE) framework. Three main entities are involved: the client, the server, and the key generation authority(KGA).

•   Client: The client has two ways to provide data: The first is by supplying horizontal data, where each data owner holds a complete sample that includes all feature information. The second is by supplying longitudinal data, where each data owner holds a sample that contains only a subset of the features. When combined, these partial datasets form the full dataset.

•   Server: After the server integrates the encrypted data sets uploaded by the client, it uses this data to construct a knowledge system for the model. This process ultimately generates a prediction model with high accuracy and strong privacy protection.

•   KGA: The KGA is mainly responsible for initializing the underlying cryptosystem, setting up key credentials, and distributing the relevant public keys to the client and the server. In the training phase, KGA will interact with the server to obtain the functional private key and get the functional encryption result. However, from start to finish, KGA cannot obtain or access the encrypted training data, thus effectively guaranteeing the confidentiality of the data.

Fig. 1 depicts the details of our proposed MMH-FE framework. The whole architecture is built by three entities including the client, the KGA, and the server. The client provides multi-sourced data for model training. For multi-sourced data, if each data source contains complete information, the data will be decomposed with multi-precision using the protocol in Fig. 2, and each data source will be encrypted and protected using the underlying SIFE; If each data source is a subset of the complete message, the data is encrypted and protected by multi-precision decomposition using the protocol in Fig. 3, which utilizes the underlying MIFE. Also, the labels are stored in clear text information, which does not reveal any private information as described in the literature [8]. The server uses appropriate metrics (e.g., learning rate, momentum, etc.) to train the model on the received multi-precision multi-sourced data and optimize the parameters to get a good model result.

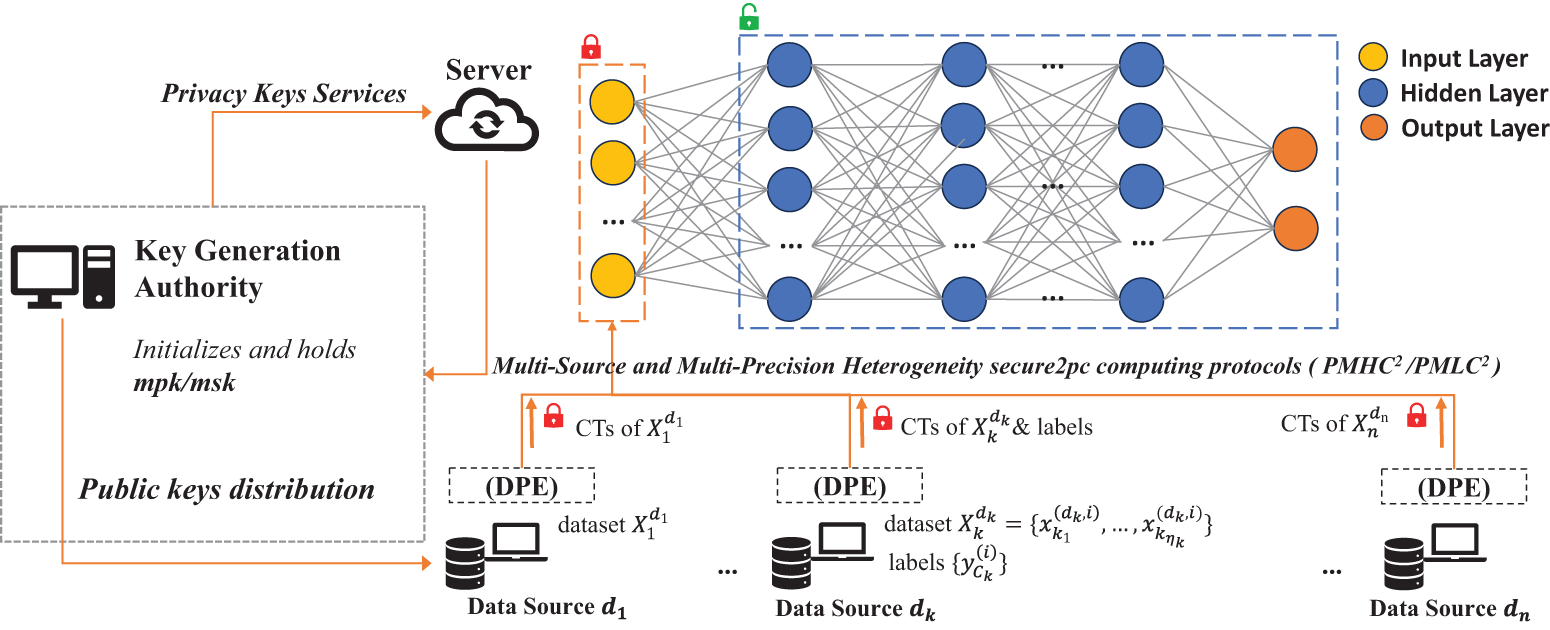
Figure 1: An overview of the framework of our proposed effective methods for training neural networks with multi-precision and multi-sourced hybridization

Figure 2: Describes in detail the execution of the protocol

Figure 3: Describes in detail the execution of the protocol

As shown in Fig. 4. We use to denote the dataset owned by Client , the Client needs to perform data processing and data encryption as follows:

•   Data Processing: The Client performs precision decomposition using Euclidean division for each data in dataset . The decomposition results in datasets .

•   Data Encryption: The Client requests an encryption key from the KGA, and uses this key to encrypt each decomposed dataset to obtain the ciphertext set CTs of the dataset .

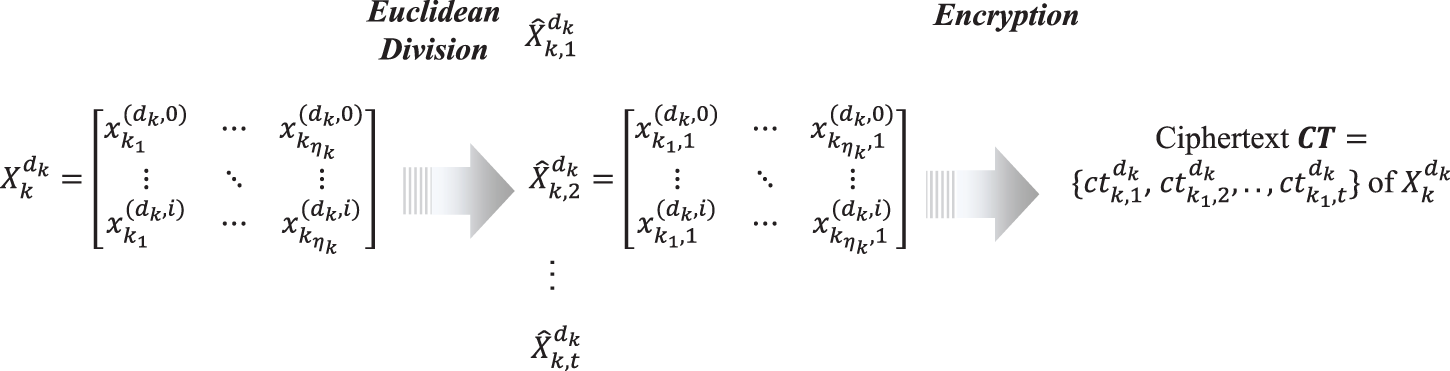
Figure 4: Data processing and data encryption

4.2 FE with Double Precision

Definition 1 (Vector-oriented Euclidean division). Let be a vector. By Euclidean division, can be expressed as:

(3)

where and denote the Element-wise addition and subtraction, respectively.

According to Definition 1, the decomposition of a vector is

(4)

Conversely, the recombination of is

(5)

Further, it can be extended to high-precision decomposition for a vector , such as:

(6)

and high-precision decomposition recombination for a vector set , such as:

(7)

Definition 2 (2-tuple Ciphertext base on Euclidean Division). Let be a 2-tuple ciphertext. The remainder of by base is defined as:

(8)

where and denotes the ciphertext of a vector encrypted by Algorithm of Sections 3.1 and 3.2.

Lemma 1 (Double-precision inner-product function). Let be a 2-tuple ciphertext of a vector . Let be a functional derived key. Then:

(9)

where , and , the is of or of and .

Proof. According to algorithms of Sections 3.1 and 3.2, it is clear that , and . Then, we have

(10)

For (2), we can get , the proof is complete. □

4.3 FE with Multi-Precision

We define the operations corresponding to Double Ciphertext Euclidean Division for t-tuple representations of ciphertexts.

Definition 3 (T-tuple Ciphertext Euclidean Division). Let be a t-tuple ciphertext. The remainder of by base is defined as:

(11)

where .

Lemma 2 (Multi-precision inner product function). Let be a ciphertext. Let be a functional derived key. Then:

(12)

where and the is or .

Proof. According to algorithms of Sections 3.1 and 3.2, it is clear that . Then, we have

(13)

According to Eq. (2), it can be deduced by analogy that , the proof is complete. □

4.4 Joint Computational Methods with Multi-Precision

To be able to train normal PPML in complex scenarios, we construct computational methods to cope with two kinds of complex scenarios based on FE with multi-precision. Two privacy-preserving computational methods are proposed for horizontal and longitudinal data from multiple sources. We propose a Privacy Multi-Precision Horizontal Cooperative Computing Protocol (, as described in Fig. 2) for horizontal data and a Privacy Multi-Precision Longitudinal Cooperative Computing Protocol (, as described in Fig. 3) for longitudinal data. The communication of both protocols is non-interactive and both require only one-way communication from the client to the server. Both protocols privacy-preserving computing protocols use Functional encryption methods with multi-precision to ensure the underlying security of the data. The key difference is that in , each client provides the server with the full dataset for model construction. In contrast, in , each client only provides a subset of the full dataset for model building.

: The specific implementation of is depicted in Fig. 2. This protocol is based on SIFE with multi-precision. For , the training dataset is composed of multiple clients, each of which will provide all of its local data (data containing all features). This is common in real-world scenarios. is different from the traditional methods, such as the traditional method in literature [7], which only analyzes the possibility of multi-client scenarios, and [8] is just normal inner product functional encryption. Our protocols are based on multi-precision with better performance and provide higher computational depth.

: Fig. 3 depicts the execution of the protocol. This protocol is built on top of MIFE with multi-precision. It is worth noting that the multiple clients in this paper must ensure that some of the features of the input data are of the same length and do not include overlapping parts between the features. The server will go through the training dataset generated by the combination of clients to complete the model construction.

4.5 MMH-FE Framework

In this paper, we propose an MMH-FE framework. The framework consists of a client, server, and KGA to ensure that data privacy and security are guaranteed when data processing and computation are performed with multiple parties involved.

As described in Algorithm 1. First, initialize the model parameters . These parameters are obtained by random initialization. Next, initialize the and protocols. These two protocols handle equally distributed and differently distributed data sources, respectively, ensuring privacy protection of data during transmission and computation.

The client dataset is iterated over to obtain each data source . Assuming that contains the dataset , it is then determined whether the data type is horizontally distributed (as described in line 5 of Algorithm 1). If the data distribution is consistent, the protocol is applied to the input data to obtain the first layer of the neural network results in plaintext. Normal forward propagation is performed for the obtained results. For backward propagation, since all layers except the first layer of the neural network propagate information in plaintext, so special treatment of the first layer is sufficient. For the first layer, we use SIFE to get the first layer back propagation results to update the gradient. For longitudinal data, we perform a similar operation. The difference is that the underlying longitudinal data uses MIFE instead of SIFE. In this paper, we do not expand on the specifics of the prediction phase of the MMH-FE model because the prediction process only involves forward propagation based on the trained model and does not contain additional complex operations. Nevertheless, the model can effectively guarantee data privacy during the prediction phase without exposing sensitive information. This feature ensures that, in practice, the data is protected during the prediction process with the same level of security as in the training phase.

5  Experimental Results

5.1 Setup

To comprehensively evaluate the performance of the MMH-FE framework. We select three publicly available datasets for our experiments. The details of these datasets are described below:

•   MNIST: The MNIST dataset [35] is a standard benchmark dataset widely used for image classification tasks, mainly for handwritten digit recognition. The dataset contains 10 categories (digits 0 to 9) with a total of 70,000 grey-scale images of dimension 28 28 pixels, including 60,000 training images and 10,000 test images.

•   Fashion-MNIST: The Fashion-MNIST dataset [36] is a clothing image dataset provided by Zalando for more challenging image classification tasks. The dataset contains 10 categories of fashion merchandise images, such as t-shirts, skirts, shoes, bags, etc., each of which is a grey-scale image of dimension 28 28 pixels. The dataset contains 60,000 training images and 10,000 test images.

•   CIFAR-10: The CIFAR-10 dataset [37] is a standard dataset for image classification of natural scenes, containing 60,000 color images(RGB) of dimension 32 32 pixels in 10 categories covering a wide range of objects such as cars, planes, cats, dogs, birds, etc. The dataset is divided into 50,000 training images and 10,000 test images.

We implement our proposed MMH-FE based on the object-oriented high-level programming language Python and the numpy, gmpy2 library. We use standardization and normalization to pre-process the datasets Mnist, Fashion-Mnist, and CiFar10. Functional encryption requires solving the difficult problem of computing discrete logarithms during decryption. This step is crucial to the overall execution of the encryption process. To speed up the computation, we use a bounded lookup table approach. Specifically, we design a data representation for x as (S, , ). This means . The variable represents the number of tuples, as defined in Definition 3. In the discrete logarithm , we compute the discrete log by setting up a hash table H. The hash table stores the pair , where . To the best of our knowledge, the size of the hash table to solve functional encryption of discrete log problems relies on the precision of the preserved decimal places in encoding for floating-point numbers, since our method underlies the use of the FE with multi-precision. The resource space consumed for discrete logarithm table storage will be greatly reduced. The complexity consumed by our discrete log table lookup operation is , which is better than the traditional time complexity of big-step small-step algorithm.

The security parameters are set to 256 bits, and the running time of the program relies on Python’s built-in time package for measurement. Increasing the security will correspondingly increase the size of the ciphertext, requiring an increase in the size of the lookup table, resulting in an increase in the space cost of the framework. Larger security parameters lead to an increased computational burden during encryption and decryption, which in turn affects the model training time and memory consumption. 256-bit security parameters are currently a popular choice, and in this paper, we use 256-bit for the related performance analysis. All experiments are conducted on a 3.8 GHz 8-Core AMD Ryzen 7 platform with 32 GB of RAM. Throughout the process, the model training relies only on the CPU.

5.2 Evaluation of Ciphertext Computational Efficiency

Since the MMH-FE proposed in this paper supports multi-precision inner-product functional encryption, we first explore the advantages and disadvantages of the multi-precision inner-product functional ciphertext computation scheme compared to other schemes. Table 2 explores the comparison between our FE with multi-precision and the existing conventional methods under different computational precision (Note that our FE with multi-precision method in this paper uses balanced decomposition for both ciphertext decomposition and combination). From the data, it can be seen that for the traditional method, the consumption of computational space increases significantly after the increase of the computational precision . In our method, the computational space is still kept in a relatively small range after the precision is increased. For the case that the and , it shows that the computational space consumes only 696 KB, which is about times better than that of the traditional method.

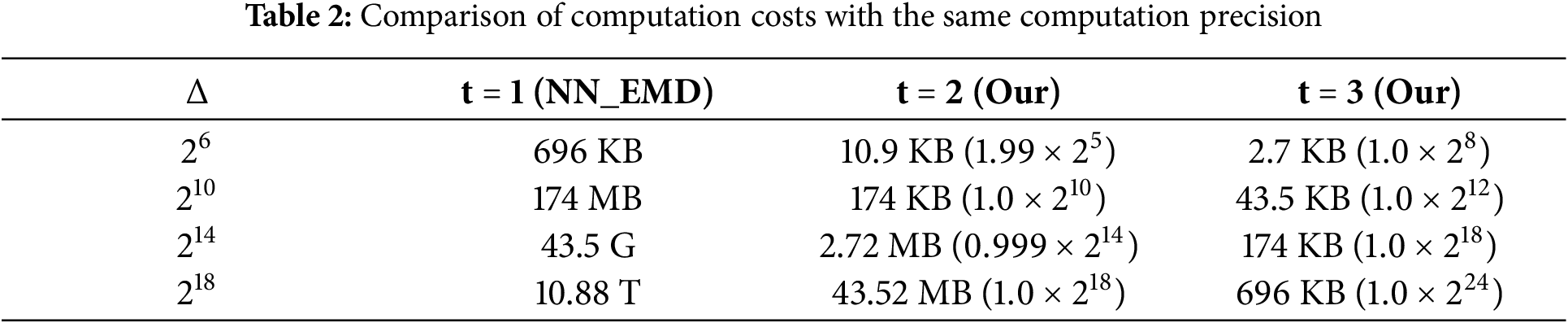
Based on Table 2, we further analyze the computational precision that can be calculated under different space costs. As shown in Table 3, traditional methods often have limited precision in smaller computational spaces. They cannot meet the demands of realistic scenarios. To address this, more computational space is often required. Our method can achieve high computational precision even when the computational space is limited. For example, in the case of 1 MB computing space, the traditional method can only reach , while our method can reach , which is more than times higher. For the case of higher , the calculation precision will continue to improve. This greatly solves the problem of not being able to train a good neural network due to the lack of computational precision when training neural networks in ciphertext.

We set the from to and test the time consumed for encryption and decryption as shown in Table 4. In both CryptoNN and NN-EMD methods, the encryption time is stabilized at 40s compared to our method, which is 4 to 6 times faster. For decryption, the NN-EMD and our methods do not change much with increasing precision, but the CryptoNN decryption time increases significantly with increasing precision. This is caused by the use of the BSGS method on each discrete logarithmic computation, and the time required will increase significantly as the precision of the computation increases. In general, to train a better model, the precision must be kept high. Therefore, we can conclude that our proposed method has significant advantages and is more suitable for PPML.

The space cost of the scheme varies under different precision decomposition parameters. Assuming that the data precision is S, the CryptoNN [7] directly stores a lookup table of length to satisfy the lookup demand during the decryption process. In contrast, a lookup table of length is all that is required when the data is precision decomposed using the method of this paper, which significantly reduces the size of the lookup table needed for each decryption, and thus reduces the cost of the space drop. The same principle is used in Table 4, where we fix the space to analyze the limiting data precision achievable by the scheme.

5.3 Model Training Performance Evaluation

5.3.1 Baseline Model

In this experiment, we use two separate base models for in-depth analyses of different experimental objectives. For the temporal performance exploration, we use the same multilayer perceptron as the NN-EMD model on the handwriting dataset mnist. This model has a simpler structure consisting of multiple layers of fully connected neurons with low computational complexity and is therefore well suited for evaluating the time overhead required for the model to be trained. The choice of the MLP model can help us to better understand the performance of the time efficiency in different experimental setups, especially in large-scale data processing tasks. For accuracy exploration, based on the complexity of the dataset, we chose to build a custom neural network model identical to the ResNet18 framework. This network framework incorporates a residual module to better capture features in complex data, thus ensuring high accuracy performance in classification tasks.

5.3.2 Computational Time Efficiency Evaluation

As shown in Fig. 5, we perform time performance tests for different frameworks. The results show that the training time increases linearly as the epoch grows. CryptoNN takes the most time to train 30 epochs, for our PMH approach takes 5.1 times longer than NN-EMD (HPT) in 1 thread, and our PML approach takes 4.7 times longer than NN-EMD (VPT) in 1 thread. But both of the methods can be about 20 faster than NN-EMD in 6 threads.

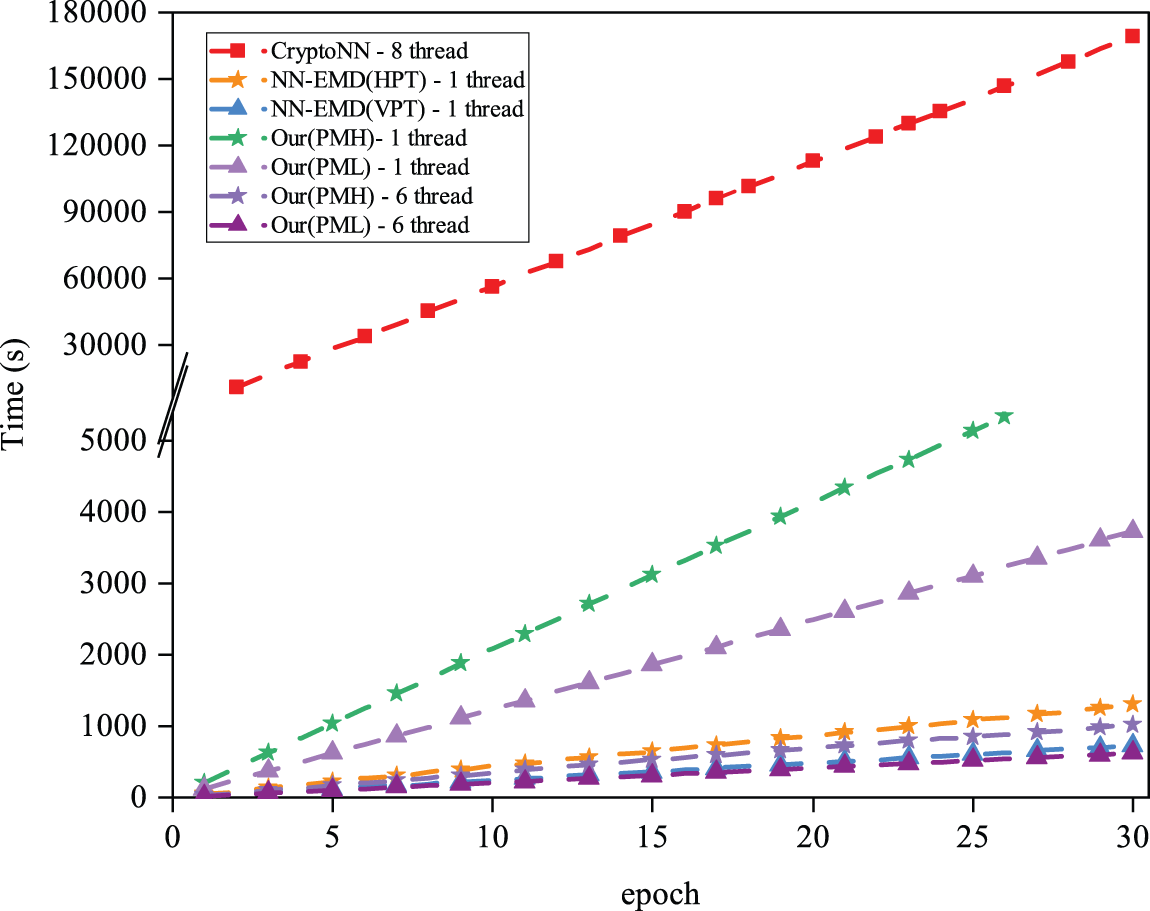
Figure 5: Training time of different schemes as epoch increases

We analyze the reason for this result, which is mainly because our method is probing the result of time consumption on the client side t = 2 and the server side t = 3. Since the time overhead is mainly spent on the decryption operation, our method will get 6 combinations based on Definition 3 for the final decryption result. As a result, we conduct 6-threaded experiments, where each thread computes one of each combination, and our multi-threaded approach takes relatively minimal time in solving discrete logarithms, as the discrete logarithm table queried by our method has a very small time consumption. The final training consumes less time than NN-EMD as we expected.

5.3.3 Model Accuracy Evaluation

As shown in Fig. 6, we conduct experimental analyses of accuracy for three different datasets on 1 MB discrete logarithmic storage space, and the training process was carried out for a total of 50 epochs. From the experimental results, the traditional way in the accuracy method can only reach the level of . In our proposed MMH-FE method, however, the accuracy is significantly improved to when the parameter t = 2, and the accuracy is further improved to when t = 3. Note that our MMH-FE is a cryptosystem that computes based on integers rather than floating-point numbers, and thus as expected, both of our methods obtain high accuracy concerning conventional methods. It can be observed from Fig. 6a that on the simple MNIST dataset, the accuracy increases from 97.03% to 98.04%, a rise of about 1% when increases from to . In Fig. 6b, for the relatively complex Fashion-MNIST dataset, the accuracy increases from 84.85% to 89.75%, a rise of about 6% when increases from to . However, in Fig. 6c, when the model is trained on the more complex CIFAR-10 dataset, the accuracy improves from 55.57% to 75.81%, an increase of about 30% when increases from to . As the value of increases, the amount of retained raw information also increases. For simple datasets, less information is sufficient to capture the relationships between the data, so a smaller value can still yield a relatively complete model. However, for complex datasets, retaining more raw information helps to capture the finer details and complex relationships between the data, thereby improving the performance of the trained model. Therefore, when dealing with complex datasets, larger value of a helps to enhance the model’s learning capability and generalization ability. Therefore, it can be concluded that our method demonstrates significant effectiveness when applied to handling complex datasets.

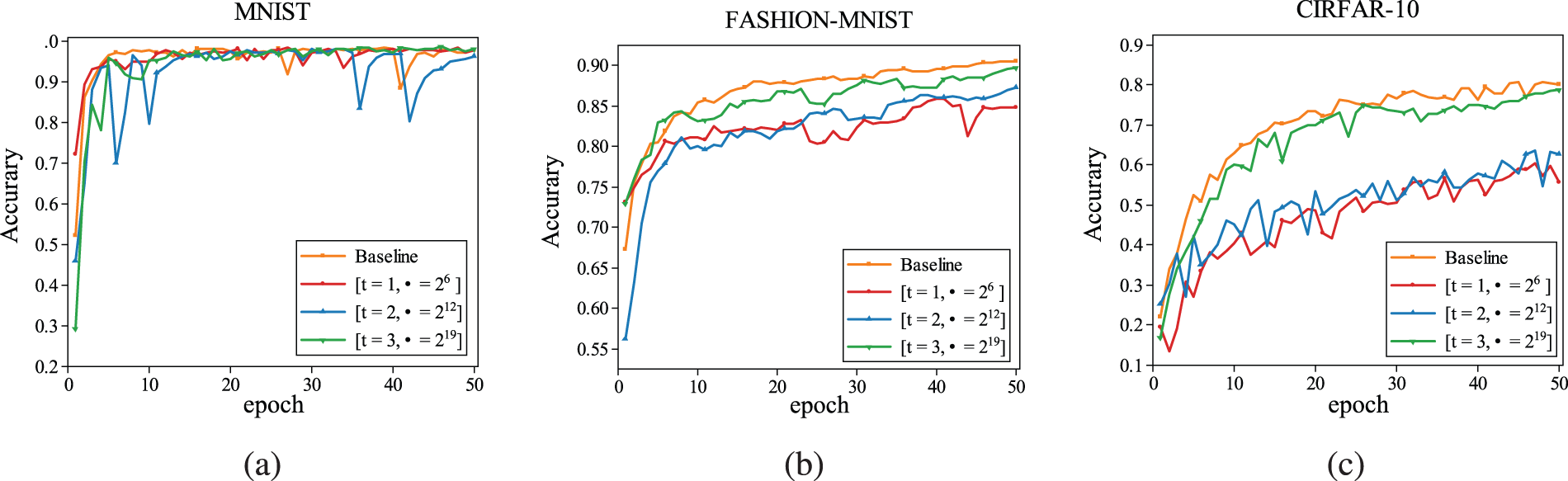
Figure 6: Comparison of model accuracy with the base species model on three datasets. (a) MNIST. (b) FASHION-MNIST. (c) CIRFAR-10

6  Conclusion

With the development of cloud computing and machine learning, users can upload data to the cloud for training machine learning models. However, untrustworthy clouds may leak or speculate user data, leading to user privacy leakage. In this paper, we propose an MMH-FE framework with functional encryption as the underlying security algorithm for supporting neural network training using encrypted data. Experiments show that MMH-FE can indeed ensure the accuracy of the model while guaranteeing privacy. However, when dealing with more complex network architectures, such as Long Short-Term Memory (LSTM) networks and Generative Adversarial Networks (GAN), the performance of the framework remains to be verified. These models typically have higher computational complexity and data processing demands, which could lead to performance bottlenecks due to the encryption computation. As the model becomes more complex, challenges related to real-time training and computational efficiency arise. To optimize model performance, improvements can be made to the encryption algorithms, hardware acceleration can be adopted, and optimizations can be applied to reduce the number of encryption operations. Additionally, we plan to combine differential privacy with homomorphic encryption and other privacy protection techniques to enhance the model’s privacy protection capabilities and adaptability, better addressing the diverse application scenarios and more complex network architectures.

Acknowledgment: We express our gratitude to the members of our research group, i.e., the Intelligent System Security Lab (ISSLab) of Guizhou University, for their invaluable support and assistance in this investigation. We also extend our thanks to our university for providing essential facilities and environment.

Funding Statement: This work was supported by Natural Science Foundation of China (Nos. 62303126, 62362008, author Z. Z, https://www.nsfc.gov.cn/, accessed on 20 December 2024), Major Scientific and Technological Special Project of Guizhou Province ([2024]014), Guizhou Provincial Science and Technology Projects (No. ZK[2022]General149), author Z. Z, https://kjt.guizhou.gov.cn/, accessed on 20 December 2024), The Open Project of the Key Laboratory of Computing Power Network and Information Security, Ministry of Education under Grant 2023ZD037, author Z. Z, https://www.gzu.edu.cn/, accessed on 20 December 2024), Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China (No. ICT2024B25), author Z. Z, https://www.gzu.edu.cn/, accessed on 20 December 2024).

Author Contributions: The authors confirm contribution to the paper as follows: research conception and design: Hao Li; Data collection: Zhenyong Zhang, Xin Wang, Mufeng Wang; Analysis and interpretation of results: Hao Li, Kuan Shao; draft manuscript preparation: Hao Li, Kuan Shao, Zhenyong Zhang; Funding support: Zhenyong Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Liu M, Teng F, Zhang Z, Ge P, Sun M, Deng R, et al. Enhancing cyber-resiliency of DER-based smart grid: a survey. IEEE Trans Smart Grid. 2024 Sep;15(5):4998–5030. doi:10.1109/TSG.2024.3373008. [Google Scholar] [CrossRef]

2. Xiao T, Zhang Z, Shao K, Li H. SeP2CNN: a simple and efficient privacy-preserving CNN for AIoT applications. In: 2024 International Conference on Artificial Intelligence of Things and Systems (AIoTSys); 2024; Hangzhou, China. p. 1–7. doi:10.1109/AIoTSys63104.2024.10780672. [Google Scholar] [CrossRef]

3. Xu R, Baracaldo N, Zhou Y, Anwar A, Joshi J, Ludwig H. FedV: privacy-preserving federated learning over vertically partitioned data. In: Proceedings of the 14th ACM Workshop on Artificial Intelligence and Security; 2021; New York, USA. p. 181–92. doi:10.1145/3474369.3486872. [Google Scholar] [CrossRef]

4. Mohassel P, Zhang Y. SecureML: a system for scalable privacy-preserving machine learning. In: 2017 IEEE Symposium on Security and Privacy; 2017; San Jose, CA, USA. p. 19–38. doi:10.1109/SP.2017.12. [Google Scholar] [CrossRef]

5. Gilad-Bachrach R, Dowlin N, Laine K, Lauter K, Naehrig M, Wernsing J. Cryptonets: applying neural networks to encrypted data with high throughput and accuracy. In: Proceedings of the International Conference on Machine Learning; 2016; New York, USA. p. 201–10. [Google Scholar]

6. Hesamifard E, Takabi H, Ghasemi M. CryptoDL: deep neural networks over encrypted data. 2017. doi:10.48550/arXiv.1711.05189. [Google Scholar] [CrossRef]

7. Xu R, Joshi JBD, Li C. CryptoNN: training neural networks over encrypted data. In: 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS); 2019; Dallas, TX, USA. p. 1199–209. doi:10.1109/ICDCS.2019.00121. [Google Scholar] [CrossRef]

8. Xu R, Joshi J, Li C. NN-EMD: efficiently training neural networks using encrypted multi-sourced datasets. IEEE Trans Dependable Secure Comput. 2022 Jul–Aug 1;19(4):2807–20. doi:10.1109/TDSC.2021.3074439. [Google Scholar] [CrossRef]

9. Phan TC, Tran HC. Consideration of data security and privacy using machine learning techniques. Int J Data Inform Intell Comput. 2023;2(4):20–32. doi:10.59461/ijdiic.v2i4.90. [Google Scholar] [CrossRef]

10. Sahai A, Waters B. Fuzzy identity-based encryption. In: Proceedings of the 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2005; Aarhus, Denmark. p. 457–73. doi:10.1007/11426639_27. [Google Scholar] [CrossRef]

11. Boneh D, Sahai A, Waters B. Functional encryption: definitions and challenges. In: Proceedings of the 8th Theory of Cryptography Conference; 2011; Providence, RI, USA. p. 253–73. doi:10.1007/978-3-642-19571-6_16. [Google Scholar] [CrossRef]

12. Francati D, Friolo D, Maitra M, Malavolta G, Rahimi A, Venturi D. Registered (inner-product) functional encryption. In: Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security; 2023; Guangzhou, China. p. 98–133. doi:10.1007/978-981-99-8733-7_4. [Google Scholar] [CrossRef]

13. Chang Y, Zhang K, Gong J, Qian H. Privacy-preserving federated learning via functional encryption, revisited. IEEE Trans Inf Forensics Secur. 2023;18:1855–69. doi:10.1109/TIFS.2023.3255171. [Google Scholar] [CrossRef]

14. Agrawal S, Goyal R, Tomida J. Multi-input quadratic functional encryption from pairings. In: Proceedings of the 41st Annual International Cryptology Conference; 2021; Springer. p. 208–38. doi:10.1007/978-3-030-84259-8_8. [Google Scholar] [CrossRef]

15. Abdalla M, Catalano D, Gay R, Ursu B. Inner-product functional encryption with fine-grained access control. In: Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security; 2020; Daejeon, Republic of Korea: Springer. p. 467–97. doi:10.1007/978-3-030-64840-4_16. [Google Scholar] [CrossRef]

16. Chotard J, Dufour-Sans E, Gay R, Phan DH, Pointcheval D. Dynamic decentralized functional encryption. In: Proceedings of the Annual International Cryptology Conference; 2020; Santa Barbara, CA, USA: Springer. p. 747–75. doi:10.1007/978-3-030-56784-2_25. [Google Scholar] [CrossRef]

17. Gay R. A new paradigm for public-key functional encryption for degree-2 polynomials. In: Proceedings of the IACR International Conference on Public-Key Cryptography; 2020; Edinburgh, UK: Springer. p. 95–120. doi:10.1007/978-3-030-45374-9_4. [Google Scholar] [CrossRef]

18. Kim S, Lewi K, Mandal A, Montgomery H, Roy A, Wu DJ. Function-hiding inner product encryption is practical. In: Proceedings of the International Conference on Security and Cryptography for Networks; 2018; Amalfi, Italy: Springer. p. 544–62. doi:10.1007/978-3-319-98113-0_29. [Google Scholar] [CrossRef]

19. Lewko A, Okamoto T, Sahai A, Takashima K, Waters B. Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Proceedingsof the 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2010; Berlin, Heidelberg:Springer. p. 62–91. doi:10.1007/978-3-642-13190-5_4. [Google Scholar] [CrossRef]

20. Gorbunov S, Vaikuntanathan V, Wee H. Functional encryption with bounded collusions via multi-party computation. In: Proceedings of the 32nd Annual Cryptology Conference; 2012; Santa Barbara, CA, USA: Springer. p. 162–79. doi:10.1007/978-3-642-32009-5_11. [Google Scholar] [CrossRef]

21. Carmer B, Malozemoff AJ, Raykova M. 5Gen-C: multi-input functional encryption and program obfuscation for arithmetic circuits. In: Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security; 2017; Dallas, TX, USA: ACM. p. 747–64. doi:10.1145/3133956.3133983. [Google Scholar] [CrossRef]

22. Lewi K, Malozemoff AJ, Apon D, Carmer B, Foltzer A, Wagner D, et al. 5Gen: a framework for prototyping applications using multilinear maps and matrix branching programs. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security; 2016; Vienna, Austria: ACM. p. 981–92. doi:10.1145/2976749.2978314. [Google Scholar] [CrossRef]

23. Abdalla M, Bourse F, Caro ADe, Pointcheval D. Simple functional encryption schemes for inner products. In: Proceedings of the IACR International Workshop on Public Key Cryptography; 2015; Gaithersburg, MD, USA: Springer. p. 733–51. doi:10.1007/978-3-662-46447-2_33. [Google Scholar] [CrossRef]

24. Abdalla M, Catalano D, Fiore D, Gay R, Ursu B. Multi-input functional encryption for inner products: function-hiding realizations and constructions without pairings. In: Proceedings in Cryptology-CRYPTO 2018: 38th Annual International Cryptology Conference; 2018; Santa Barbara, CA, USA: Springer. p. 597–627. doi:10.1007/978-3-319-96884-1_20 [Google Scholar] [CrossRef]

25. Zhang Z, Liu M, Sun M, Deng R, Cheng P, Niyato D, et al. Vulnerability of machine learning approaches applied in IoT-based smart grid: a review. IEEE Internet Things J. 2024 Jun 1;11(11):18951–75. doi:10.1109/JIOT.2024.3349381. [Google Scholar] [CrossRef]

26. Bourse F, Minelli M, Minihold M, Paillier P. Fast homomorphic evaluation of deep discretized neural networks. In: Proceedings in Cryptology-CRYPTO 2018: 38th Annual International Cryptology Conference; 2018; Santa Barbara, CA, USA: Springer. p. 483–512. doi:10.1007/978-3-319-96878-0_17. [Google Scholar] [CrossRef]

27. Chillotti I, Gama N, Georgieva M, Izabachene M. Faster fully homomorphic encryption: bootstrapping in less than 0.1 seconds. In: Proceedings in Cryptology-ASIACRYPT 2016: 22nd International Conference on the Theory and Application of Cryptology and Information Security; 2016; Hanoi, Vietnam: Springer. p. 3–33. doi:10.1007/978-3-662-53887-6_1. [Google Scholar] [CrossRef]

28. Zhang Z, Cheng P, Wu J, Chen J. Secure state estimation using hybrid homomorphic encryption scheme. IEEE Trans Control Syst Technol. 2021 Jul;29(4):1704–20. doi:10.1109/TCST.2020.3019501. [Google Scholar] [CrossRef]

29. Graepel T, Lauter K, Naehrig M. ML confidential: machine learning on encrypted data. In: Proceedings of the International Conference on Information Security and Cryptology; 2012; Seoul, Republic of Korea: Springer. p. 1–21. doi:10.1007/978-3-642-37682-5_1. [Google Scholar] [CrossRef]

30. Chou E, Beal J, Levy D, Yeung S, Haque A, Fei-Fei L. Faster cryptonets: leveraging sparsity for real-world encrypted inference. 2018. doi:10.48550/arXiv.1811.09953. [Google Scholar] [CrossRef]

31. Ligier D, Carpov S, Fontaine C, Sirdey R. Privacy preserving data classification using inner-product functional encryption. In: Proceedings of the International Conference on Information Systems Security and Privacy; 2017. p. 423–30. doi:10.5220/0006206704230430. [Google Scholar] [CrossRef]

32. Dufour-Sans E, Gay R, Pointcheval D. Reading in the dark: classifying encrypted digits with functional encryption. Cryptology EPrint Archive. 2018 [cited 10 December 2024]. Available from: https://eprint.iacr.org/2018/206. [Google Scholar]

33. Ryffel T, Dufour-Sans E, Gay R, Bach F, Pointcheval D. Partially encrypted machine learning using functional encryption. 2019. doi:10.48550/arXiv.1905.10214. [Google Scholar] [CrossRef]

34. Nguyen T, Karunanayake N, Wang S, Seneviratne S, Hu P. Privacy-preserving spam filtering using homomorphic and functional encryption. Comput Commun. 2023;197:230–41. doi:10.1016/j.comcom.2022.11.002. [Google Scholar] [CrossRef]

35. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86(11):2278–324. doi:10.1109/5.726791. [Google Scholar] [CrossRef]

36. Xiao H, Rasul K, Vollgraf R. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. 2017. doi:10.48550/arXiv.1708.07747. [Google Scholar] [CrossRef]

37. Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images [Ph.D. dissertation]. Canada: University of Toronto; 2009. [Google Scholar]