Unknown DDoS Attack Detection with Sliced Iterative Normalizing Flows Technique

1  Introduction

Threat actors execute malicious cyber attacks, and organizations worldwide face a significant risk from attacks that cause widespread disruption by overwhelming services and denying access to users (DDoS). Such attacks possess the potential to cripple entire network systems, making them unreachable for legitimate users and leading to significant interruptions in both service dependability and availability. Cybersecurity defense teams employ intrusion detection systems (IDS) to minimize the harm inflicted by such attacks [1].

Identifying and counteracting DDoS threats is now crucial to safeguarding the robustness and protection of essential infrastructure systems. As DDoS attacks grow more frequent and intricate in today’s cybersecurity realm, establishing robust IDS mechanisms is critical for preserving the stability and continued accessibility of network frameworks [2]. Anomaly detection (AD) is a key technology in IDS design, identifying and flagging patterns or behaviors that deviate from normal operations in computer networks, systems, or applications [3]. Traditional IDS approaches, which rely on predefined signatures and rules, often fail to detect novel and sophisticated DDoS attacks. This limitation underscores the necessity for more advanced detection techniques capable of adapting to evolving attack patterns.

Models based on deep learning have surfaced as a potential solution for identifying and counteracting these attacks through the autonomous discovery of intricate patterns within network traffic information. DL outperforms traditional machine learning methods in handling large and complex datasets. A range of deep learning models is currently being developed to improve the ability to detect DDoS incidents. Despite its advantages, deep learning models frequently fall short in handling uncertainty, resulting in overly assertive yet incorrect predictions, which poses a serious challenge in vital fields like cybersecurity [4,5]. The integration of DL in IDS allows for the automatic extraction of features from raw data, eliminating the need for manual feature engineering and enabling the detection of subtle anomalies that may escape human analysts.

The ever-changing behavior of attacks and the continual evolution of network vulnerabilities make it exceedingly difficult to keep models up to date. Another significant challenge is the lack of necessary data for practical training, resulting in insufficient large, high-quality datasets for training DL models [6]. Uncertainty in this context is divided into aleatoric (random) and epistemic (knowledge-based). Aleatoric uncertainty arises from data and can be mitigated by having more training data, whereas epistemic uncertainty stems from model parameters and can be reduced by improving the model [7]. The continuous evolution of DDoS attack strategies necessitates frequent model updates to ensure that IDS remains effective against new threats.

Although anomaly-based IDS can detect unknown attacks, current designs still require specific attack data to train the models. Existing IDS models demand substantial quantities of precisely labeled data for every attack type and cannot identify novel threats. Unsupervised IDS models can detect new attacks without training data but suffer from lowered precision and challenges when distinguishing between different forms of attacks. Current IDS models are not well-adapted to the evolution of modern attacks, which can generate various variants. Recent research indicates that current models, whether machine learning or deep learning, are ineffective in handling attacks that have not been previously trained on [8]. This highlights the need for IDS to adaptively learn from new and unseen data without compromising detection accuracy.

Open-Set Recognition (OSR) helps identify and classify objects or instances not encountered during training. OSR has achieved significant milestones recently [9]. Traditional closed-set recognition systems are limited to predefined categories and fail to recognize unknown instances, making OSR a crucial advancement for IDS in handling unknown DDoS attacks. This paper introduces an OSR technique called Sliced Iterative Normalizing Flows (SINF), a deep learning algorithm that uses the Sliced Wasserstein distance to transform probability distributions. SINF can generate high-quality samples and perform efficient density estimation, particularly well with small datasets. Compared to traditional flow-based or autoencoder-based methods, SINF incrementally adapts its latent space slicing across iterations. This iterative slicing approach allows the model to preserve essential properties of the data distribution, thereby robustly estimating tail distributions necessary for unknown DDoS detection in high-dimensional data with limited samples. This algorithm is stable, less dependent on hyperparameters, and does not use mini-batching or gradient descent [10]. By incorporating SINF, IDS can maintain high detection performance even when encountering novel attack patterns.

The ever-growing threat of DDoS attacks necessitates the development of advanced IDS that can detect and mitigate both known and unknown attacks. Leveraging deep learning and OSR techniques, notably the SINF algorithm, presents a promising direction for enhancing the robustness and reliability of IDS in dynamic and evolving cyber threat environments. This paper aims to explore the application of SINF in IDS, providing insights into its effectiveness in detecting unknown DDoS attacks and addressing the challenges of model uncertainty and data scarcity.

The key contributions of this study lie in integrating Autoencoder and SINF for detecting Unknown DDoS Attacks. The autoencoder, a widely used method for data representation, reduces dimensionality by eliminating redundant information while preserving essential features. SINF, a state-of-the-art Normalizing Flow technique, enables the transformation of a simple base distribution into complex ones that effectively model intricate data patterns. Unlike traditional approaches, our method applies SINF not to raw data but to the encoded representations generated by the autoencoder. This design enhances the system’s ability to capture high-dimensional data structures with greater precision and robustness. By optimizing the modeling process, this framework significantly improves the estimation of sample distributions, ensuring higher adaptability and sensitivity to previously unseen attack patterns. Comparative analysis with established techniques in unknown DDoS attack detection, including Gaussian Mixture Models (GMM) [11], DBSCAN-SVM [12], CNN-Geometrical Metrics [13], and AlexNet-Fuzzy C-Means Clustering (FCM) [14] demonstrates the superior performance of our approach, particularly under conditions of data scarcity and high-dimensional complexity. This synergy between the autoencoder and SINF modules represents a substantial advancement in detecting Unknown DDoS Attacks, effectively bridging critical gaps in existing IDS.

The remainder of this paper is organized as follows: Section 2 reviews related work; Section 3 details our methodology; Section 4 presents the experiments, results, and discussion; and Section 5 provides the conclusion.

2  Related Work

2.1 Traditional and Machine Learning Approaches in Intrusion Detection Systems

IDS has been a vital element in ensuring network security for a considerable period. Traditional IDS approaches can be broadly categorized into signature-based and anomaly-based systems. Signature-based intrusion detection systems depend on established patterns and preset rules to recognize existing threats. While highly efficient in recognizing familiar attack methods, they struggle when confronting novel or emerging dangers. Conversely, anomaly-based detection systems identify irregularities that deviate from typical behavioral norms. While more adaptable to unknown attacks, these systems frequently encounter high false alarm rates, stemming from challenges in precisely characterizing what constitutes’ normal activity, as noted by [15,16].

Machine learning (ML) approaches have seen growing applications in intrusion detection systems to overcome the shortcomings of conventional techniques. These methodologies are typically divided into supervised, unsupervised, and semi-supervised learning approaches. Supervised learning strategies, including decision trees, support vector machines, and neural networks, rely on labeled data for training and excel at differentiating between harmless and harmful actions. However, the effectiveness of these models is significantly influenced by the availability and quality of labeled datasets, as highlighted by [17].

Unsupervised learning techniques, such as clustering methods like k-means and anomaly detection models like random forests, operate without labeled data and can recognize novel attack patterns. These methods are beneficial for detecting unknown threats but often struggle with accuracy and interpretability, as discussed by [18]. Semi-supervised learning methods attempt to leverage labeled and unlabeled data to improve detection performance, making them a promising area of research for IDS, as indicated by [19].

DL models represent a significant advancement in IDS, offering superior performance in processing and analyzing large and complex datasets. CNN and Recurrent Neural Networks (RNNs) are among the most widely used DL architectures for IDS. CNNs are effective at extracting spatial features from network traffic data. At the same time, RNNs are well-suited for capturing temporal dependencies in sequential data. Gueriani et al. [20] developed a robust attack detection model based on the combination of CNN and RNN. Additionally, Iliyasu et al. [21] have pointed out that CNN and Generative Adversarial Networks (GANs) are also employed to enhance anomaly detection capabilities, providing robust mechanisms for identifying deviations from normal network behavior. Chalapathy et al. [22] discussed the application of these techniques in their comprehensive survey on deep learning for anomaly detection. Recent advancements address these challenges through innovative frameworks and hybrid approaches. For instance, the BDIP framework integrates tensor-based representation with tensor-train decomposition to efficiently manage high-dimensional, multi-modal network data. Combining preprocessing, denoising, and classification achieves 99.19% accuracy in DDoS detection while maintaining computational efficiency and scalability, even in big data environments [23]. Similarly, hybrid techniques such as ML-Entropy for SDN environments combine entropy-based statistical techniques with ML algorithms to enhance detection accuracy and reduce computational overhead. This approach has demonstrated superior speed in model convergence, achieving over 99% accuracy with significantly faster training than standalone ML models [24].

Recent advancements in intrusion detection have explored various methodologies to improve accuracy and adaptability in dynamic environments. Wang et al. proposed a tensor-based network attack detection framework for SDN security, leveraging principal component analysis to enhance the detection of sophisticated threats through high-dimensional data representation [25]. Similarly, Rabie et al. introduced a hybrid model combining Decisive Red Fox optimization and Radial Basis Function classification, demonstrating its efficacy in detecting IoT-based intrusions while optimizing computational efficiency [26]. The research of Srivastava et al. and Shitharth et al. on intelligent edge computing further highlights the integration of advanced machine learning techniques with security paradigms to address emerging threats across diverse IoT and edge systems [27,28].

Despite the advantages of DL models, they cannot often represent uncertainty, leading to overly confident and sometimes inaccurate predictions. This limitation is particularly problematic in critical applications like cybersecurity, where false positives and false negatives can have severe consequences [29]. Hariharan et al. [30] utilized XAI (Explainable AI) techniques alongside black-box deep learning models in developing an intrusion detection system. This approach not only enhances the transparency and reliability of the model but also improves its performance by optimizing features based on the provided explanations.

Table 1 provides a comparative summary of recent studies, highlighting their methodologies, strengths, and weaknesses while underscoring the advantages of our approach in achieving superior detection accuracy and adaptability.

2.2 Open-Set Recognition in Cybersecurity

OSR has emerged as a critical advancement in cybersecurity, addressing the limitations of traditional closed-set recognition systems that can only identify predefined categories of attacks. The fundamental concept of OSR enables systems to identify and classify objects or instances not encountered during training, thereby enhancing the ability to detect novel and evolving threats. Wang et al. emphasize the importance of OSR in scenarios where the diversity of potential threats is vast and constantly changing [41].

In network security, OSR techniques have shown significant promise in improving the detection of unknown or zero-day attacks. These techniques differ from traditional anomaly detection methods by flagging anomalies and providing mechanisms to recognize new attack classes. This capability is particularly crucial given the rapid evolution of cyber threats. Recent studies have demonstrated the application of various OSR techniques in network intrusion detection, demonstrating their effectiveness in maintaining high detection rates while reducing false positives [42].

Significant differences emerge when comparing OSR-based IDS with traditional closed-set systems, particularly in their ability to handle unknown DDoS attacks. Traditional IDS rely heavily on static signatures and predefined datasets, which limit their capacity to detect novel or evolving threats. In contrast, OSR-based systems adopt more adaptive techniques capable of modeling complex data distributions and identifying anomalies that deviate from expected patterns. These systems offer greater flexibility and robustness in dynamic network environments, enabling them to effectively address the limitations of static detection models. For example, clustering techniques such as FCM have been applied to group network traffic patterns, allowing the identification of anomalous behaviors that may indicate unknown attacks [14]. Similarly, probabilistic methods like Gaussian Mixture Models have demonstrated their effectiveness in modeling network traffic distributions, capturing subtle deviations that might signal intrusion attempts [40]. One-Class Support Vector Machines (OC-SVM) have also been employed to create decision boundaries around standard traffic data, effectively flagging outliers as potential threats [13].

Additionally, AE has been utilized for reconstructing normal network behavior, where significant reconstruction errors can signal the presence of anomalous traffic [37]. These approaches excel in dynamic environments where attack patterns constantly evolve and labeled datasets are often incomplete. By integrating such techniques, OSR-based IDS achieve higher adaptability and accuracy in detecting previously unseen DDoS attack patterns, outperforming traditional static detection models.

Incorporating probabilistic approaches in OSR, such as the Probabilistic Autoencoder (PAE), allows for a more flexible representation of latent spaces by learning the distribution of latent weights, which can help address outliers and anomalies in network traffic. As demonstrated by [43], the PAE leverages a Normalizing Flow (NF) to produce high-quality latent space representations and detect outliers efficiently. The latent space density learned from NF offers a robust outlier detection metric, making it highly applicable to the challenges posed by OSR in Cybersecurity.

Implementing OSR in IDS involves several challenges, including robust models that can accurately distinguish between known and unknown instances and the requirement for efficient algorithms that can operate in real-time. Advanced machine learning and deep learning techniques, such as Sliced Iterative Normalizing Flows (SINF), have been explored to address these challenges. Reference [10] discusses how SINF leverages the Sliced Wasserstein distance to transform probability distributions, enabling the generation of high-quality samples and efficient density estimation. By effectively handling the uncertainty and variability of modern cyber threats, OSR-equipped IDS can provide more robust protection against known and unknown attacks, ensuring critical network services’ continuous availability and integrity [44].

2.3 Sliced Iterative Normalizing Flows

Sliced Iterative Normalizing Flows (SINF) represent a cutting-edge approach in deep learning, particularly effective for applications requiring efficient density estimation and sample generation from complex distributions. Introduced by [10], SINF employs the Sliced Wasserstein distance to transform probability distributions iteratively. This method has demonstrated significant potential in addressing the challenges associated with data scarcity and high-dimensional spaces.

The primary advantage of SINF is its ability to generate high-quality samples and perform robust density estimation, even with limited data. Unlike many deep learning algorithms that necessitate extensive training data and complex optimization processes, SINF operates without requiring mini-batching or gradient descent. This simplification not only enhances the training process but also improves the stability and scalability of the model, making it highly suitable for real-time applications in cybersecurity. In the context of Intrusion Detection Systems, SINF provides substantial improvements over conventional methods. Traditional IDS models often struggle to adapt to new and unseen attack patterns because they rely on predefined signatures or exhaustive labeled datasets. SINF addresses these limitations by leveraging the flexibility of iterative normalizing flows, which can dynamically adapt to evolving threat landscapes without frequent retraining or extensive hyperparameter tuning.

SINF’s application in anomaly detection and OSR is particularly noteworthy. By transforming the underlying data distribution iteratively, SINF can accurately model known and unknown data points, thereby enhancing IDS’s ability to detect novel attacks. This capability is crucial for maintaining the security and integrity of network infrastructures where new threats are constantly emerging. Integrating SINF into OSR frameworks offers a robust solution to the challenges posed by unknown attacks. OSR techniques are designed to identify and classify instances that were not encountered during training, a critical requirement for effective cybersecurity. SINF’s ability to perform efficient density estimation and generate high-quality samples makes it an ideal candidate for OSR, enabling the IDS to maintain high detection rates while reducing false positives.

3  Methodology

The training phase of our model follows a structured process, as depicted in Fig. 1. Initially, the training set undergoes data preprocessing to clean and prepare the data for subsequent stages. This preprocessing step ensures that the input data is suitable for the model training process.

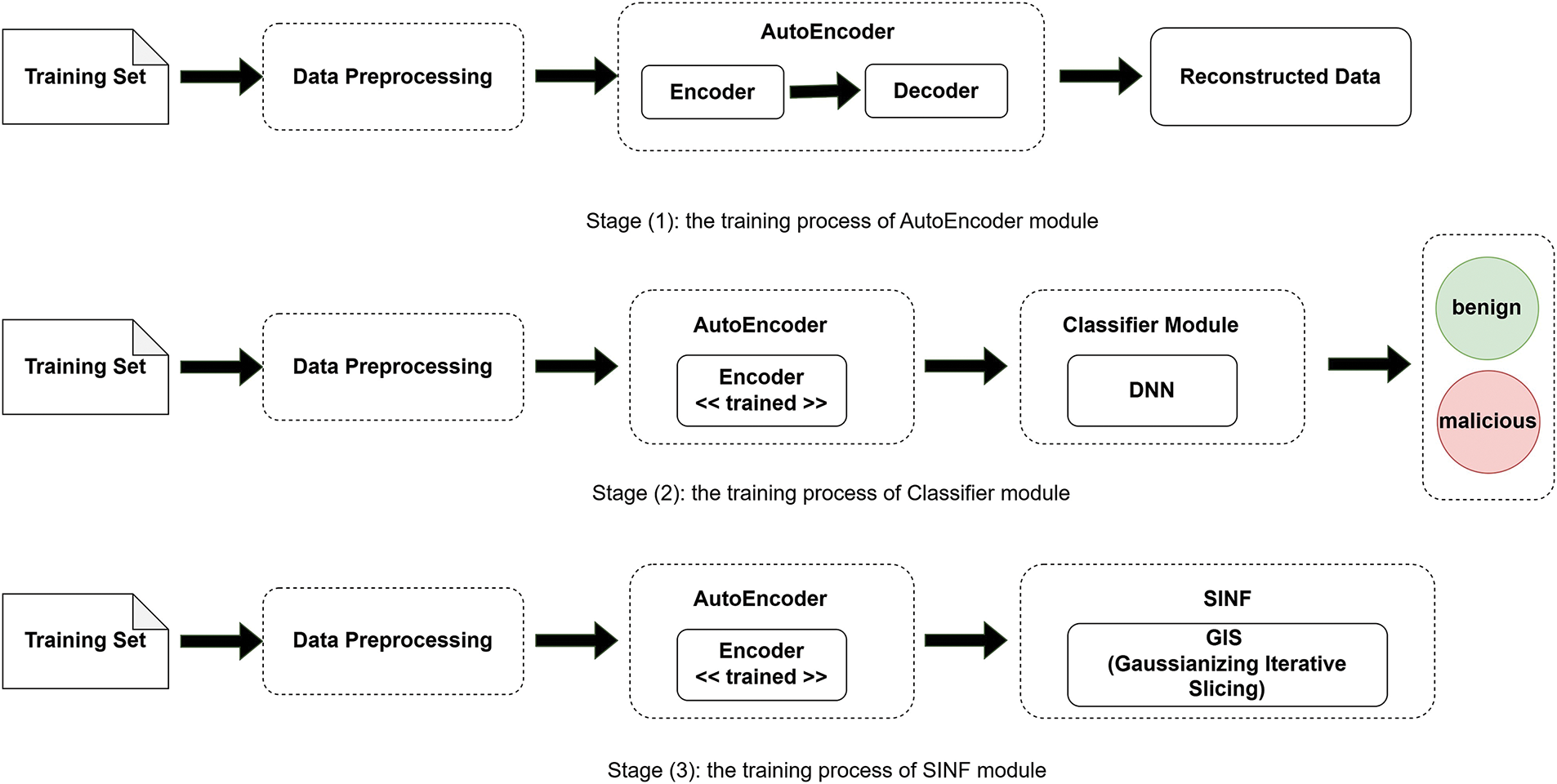
Figure 1: The training phase of the proposed system

In the first stage, the preprocessed data is fed into an autoencoder consisting of an encoder and a decoder. The encoder compresses the input data into a lower-dimensional representation, while the decoder attempts to reconstruct the original data from this compressed form. The goal is to minimize the reconstruction error, ensuring that the model learns a compact and efficient representation of the input data. The output of this stage is the reconstructed data.

In the second stage, the training set, after data preprocessing, is again fed into the trained autoencoder to generate encoded representations. These representations are then passed to a classifier module, which utilizes a Deep Neural Network (DNN) to classify the encoded data into benign or malicious categories. The classifier is trained to distinguish between normal and anomalous patterns based on the features extracted by the autoencoder.

The preprocessed training data is encoded in the third stage using the trained autoencoder. The encoded data is then input into the SINF module, specifically the Gaussianizing Iterative Slicing (GIS) component. This component tries to learn and approximate the complex distribution of the encoded dataset, aiding in identifying novel and evolving threats. Combining autoencoder-based feature extraction and SINF-based sample generation enhances the system’s ability to detect known and unknown attacks effectively. Our model integrates OSR concepts into the third stage, where SINF scores are used to measure how’ familiar’ a sample is. If the score is below a certain threshold, the system treats it as an unseen type of attack. This approach helps isolate unknown attacks by design rather than forcing them into known class categories.

The evaluation phase of our system in Fig. 2 begins with the evaluating set undergoing data processing to clean and prepare it for analysis. The preprocessed data is then passed through a trained autoencoder, which compresses the data into lower-dimensional representations using its encoder and reconstructs it with the decoder. These encoded representations are subsequently fed into a classifier module comprising a Deep Neural Network (DNN), which categorizes the data as benign or malicious based on the features extracted by the autoencoder. Along with that, for encoded data, the process continues with the Unknown Detecting Module, utilizing the GIS (Gaussianizing Iterative Slicing) component of the SINF module. This module performs density estimation from the training set and checks if the incoming data fits within the learned distributions, flagging data points that deviate as suspicious. Finally, a threshold is applied to determine the classification, with data points exceeding this threshold marked for further investigation. This comprehensive evaluation ensures that the IDS effectively detects known and potential unknown threats, enhancing overall network security.

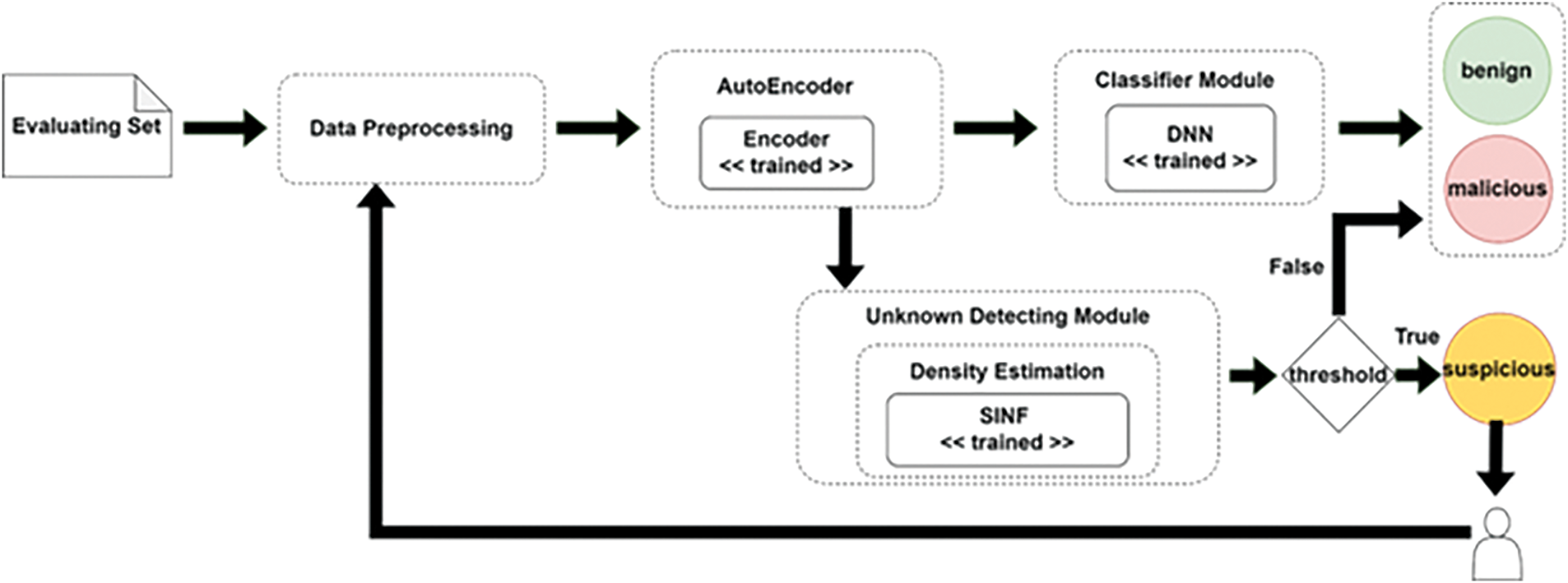
Figure 2: The evaluation phase of the proposed system

3.1 Mathematical Notations

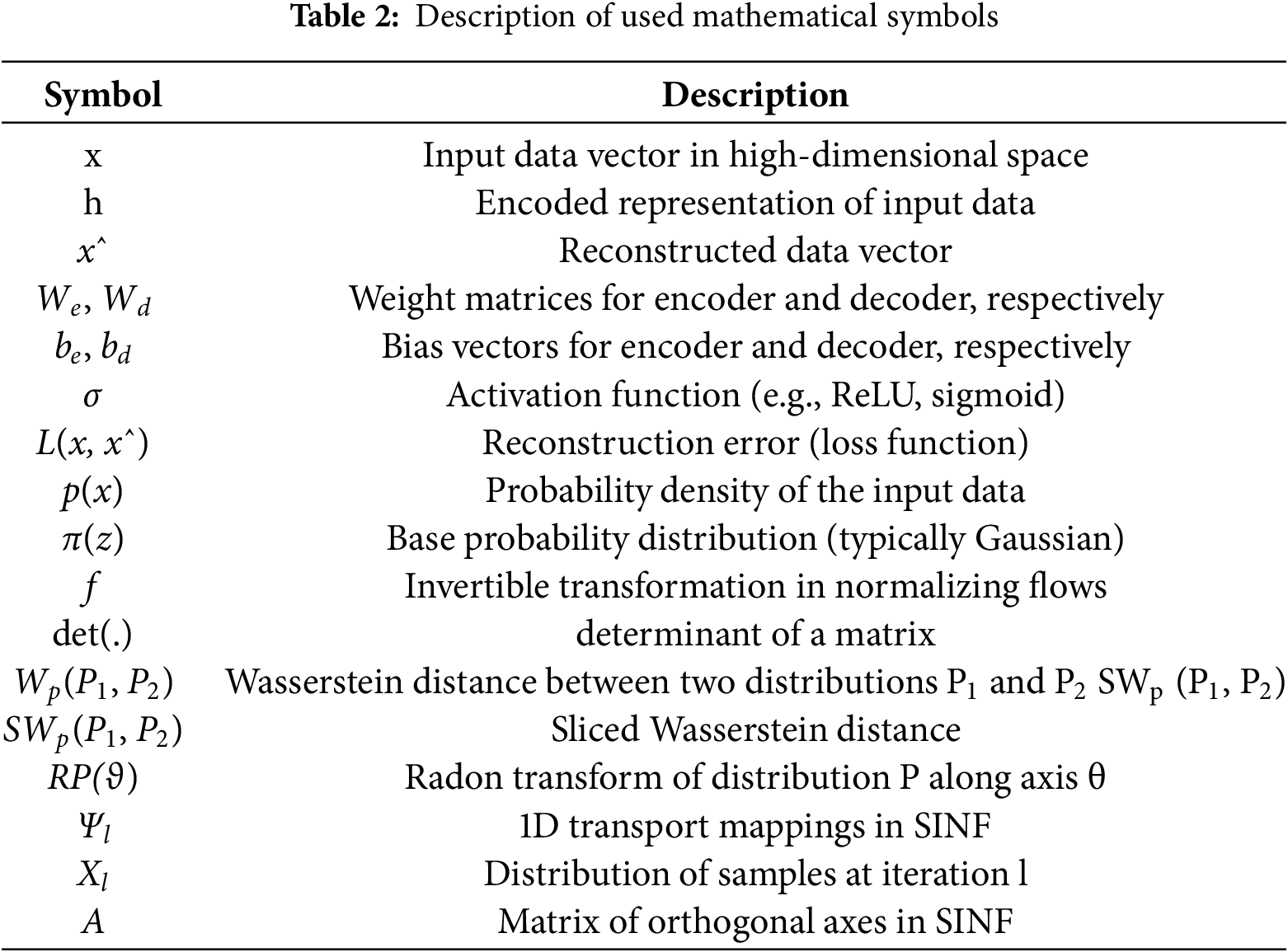
To improve clarity and ensure the readability of the mathematical notations used throughout this manuscript, we provide symbol descriptions in Table 2. This table summarizes the key symbols and their meanings, enabling readers to follow the equations and understand the underlying principles more effectively. The descriptions also highlight the relationships between the variables, which are critical for interpreting the proposed methodology.

3.2 Auto Encoder

Autoencoders are a type of neural network used to learn efficient representations of input data unsupervised, making them particularly effective for anomaly detection tasks, such as identifying unusual patterns in network traffic that may indicate security threats like DDoS attacks. An autoencoder consists of an encoder and a decoder, as depicted in Fig. 3.

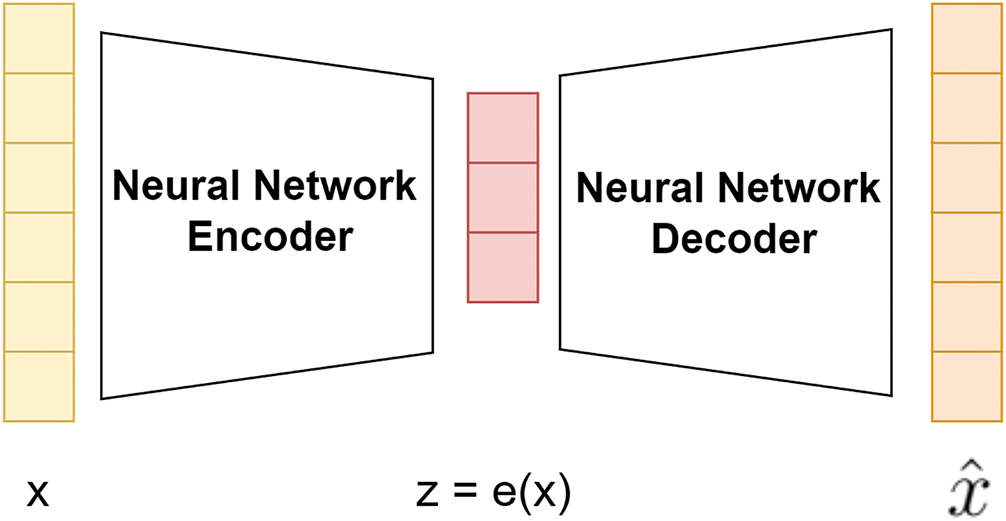
Figure 3: Autoencoder architecture

The encoder compresses the input data x∈Rn into a lower-dimensional representation h∈Rm using the function fθ. As shown in Formula (1), the encoder performs this compression efficiently by applying weights and biases to the input data.

h=fθ(x)=σ(Wex+be)(1)

where We∈Rm×n is the weight matrix.

The decoder maps h back to the reconstructed input x^∈Rn using the function gθ. As described in Formula (2), the decoder reconstructs the input data using the latent representation h.

x^=gθ(h)=σ(Wdh+bd)(2)

where Wd∈Rn×m is the weight matrix, bd∈Rn is the bias vector, and σ is an activation function.

The objective of training an autoencoder is to minimize the reconstruction error between x and x^, often, using the mean squared error (MSE). As expressed in Formula (3), the reconstruction error is measured as the mean squared error between x and x^:

L(x,x,^)=1n∑i=1n(xi−xi^)2(3)

Thus, the goal is to find the parameters θ and θ′ that minimize the average reconstruction error across all training examples. As defined in Formula (4), the objective is to reduce the reconstruction error across all training:

minθ,θ′=1N∑inL(x(i),x^(i))(4)

In cybersecurity, autoencoders are trained on normal network traffic data to learn a compact representation of typical behavior. Once trained, the autoencoder can reconstruct new network traffic data, and if the reconstruction error for a given data point is significantly higher than average, it may indicate an anomaly, such as a potential intrusion. By monitoring the reconstruction error, an IDS equipped with autoencoders can effectively detect unusual patterns in network traffic, enabling timely identification and mitigation of security threats. This method leverages the autoencoder’s ability to capture the underlying structure of normal data, making it a powerful tool for anomaly-based intrusion detection.

3.3 Principle of SNIF

Sliced Iterative Normalizing Flows (SINF) represent an advanced deep learning algorithm that iteratively transforms an arbitrary probability distribution function (PDF) into a target PDF. This transformation is achieved by performing iterative optimal transport on a series of one-dimensional (1D) slices, leveraging the Sliced Wasserstein distance to align the marginal distributions along each slice. By selecting orthogonal slices to maximize the PDF difference, the algorithm efficiently scales to high-dimensional spaces.

Flows use a sequence of differentiable and invertible transformations to map data from a simple base distribution to a complex target distribution. The target distribution represents the underlying data distribution we aim to learn and approximate. Formally, a high-dimensional data point x is transformed into a latent variable z through a series of invertible mappings, such that f=fn∘fn−1∘fn−2∘⋅⋅⋅∘f2∘f1z=f(x). Here, fi denotes the differentiable transformations applied sequentially. The invertibility of these mappings ensures that the probability density of the target distribution can be computed effectively using the change of variables formula. Fig. 4 illustrates this process, where data is iteratively transformed through a series of flows until it matches the target distribution.

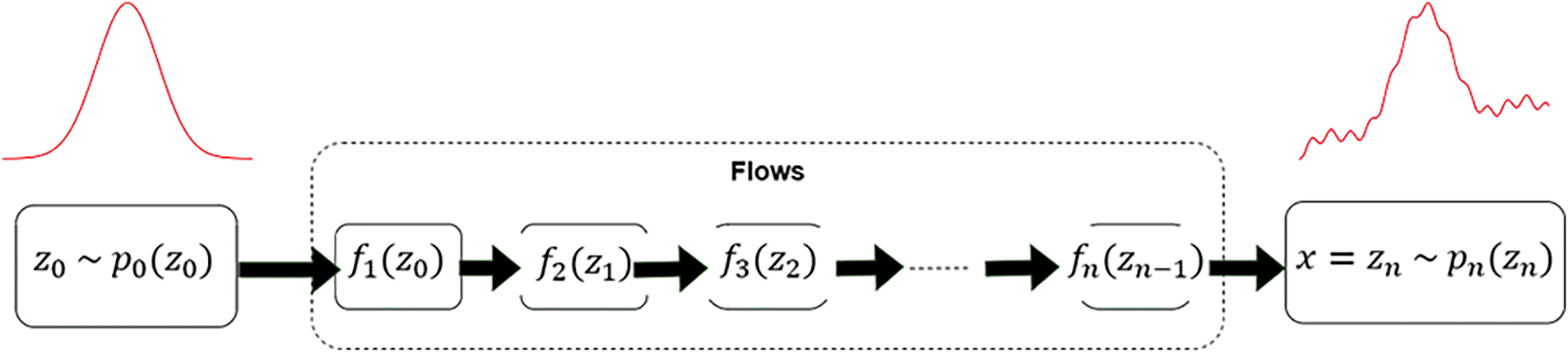
Figure 4: Architecture of the normalizing flows method

The density of x can be computed using the change of variables as presented in Formula (5):

p(x)=π(f(x))|det(∂f(x)∂x)|(5)

where π(z) is typically chosen to be a standard normal distribution and det(∂f(x)∂x) is the Jacobian determinant of the transformation.

This determinant must be easy to compute for density evaluation, and the transformation f should be easy to invert for efficient sampling. The SINF algorithm iteratively solves for the orthogonal axes where the marginals of two distributions are most different, defined by the maximum K-sliced Wasserstein Distance (max K-SWD). The distance between two probability distributions, P1 and P2, is defined in Formula (6):

Wp(P1,P2)=infγ∈Π(P1,P2)(E(x,y)∼γ[‖x−y‖p])1p(6)

where Π(P1,P2) is the set of all possible joint distributions with marginals P1 and P2.

The core principle of SINF lies in its ability to iteratively transform a base probability distribution into a more complex target distribution. Unlike traditional Wasserstein metrics, SINF leverages the Sliced Wasserstein Distance (SWD), which projects high-dimensional distributions onto one-dimensional slices using the Radon transform, simplifying the computation while retaining essential information about the distribution. SWD is defined in Formula (7):

SWp(P1,P2)=(∫Sd−1Wpp(RP1(⋅,θ),RP2(⋅,θ))dθ)1p(7)

where RP(⋅,θ) denotes the projection of the distribution P onto the slice determined by the axis θ. By averaging the Wasserstein distances over all possible slices, SWD provides a robust measure of similarity between two distributions. To enhance efficiency in high-dimensional settings, SINF employs max K-Sliced Wasserstein Distance (max K-SWD), which optimizes over a set of Korthonormal axes θ1,…,θK, focusing on directions where the distributions differ most significantly, which is detailed in Formula (8):

max−K−SWDp(P1,P2)=max{θ1,…,θK} orthonormal(1K∑k=1KWpp((RP1)(⋅,θk),(RP2)(⋅,θk)))1p(8)

where Rp denotes the Radon transform of P projecting the distribution onto 1D slices. This targeted optimization allows SINF to concentrate on informative dimensions, significantly improving performance in high-dimensional spaces.

The SINF algorithm iteratively optimizes the orthonormal axes θk and matches the 1D marginals along these axes, as follows:

a.   Initialization: Randomly initialize the matrix 𝒜∈VK(Rd), where VK(Rd) is the Stiefel manifold of orthonormal K-frames in Rd.

b.   Iterative Optimization: For each iteration, update the orthogonal axes to maximize the max K-SWD and compute the optimal transport mapping for each axis.

c.   Marginal Matching: Apply the 1D transport maps along the optimized axes to transform the distribution.

The transformation at the iteration l of samples Xl can be written as Formula (9):

Xl+1=𝒜Ψl(𝒜TXl)+Xl(9)

where Xl⊥ = Xl−𝒜l𝒜lTXl contains the components orthogonal to the axes θk and Ψl=[Ψl1,…,ΨlK]T represents the 1D marginal mappings, which are monotonic and differentiable. This transformation can be inverted easily by following Formula (10):

Xl=𝒜lΨl−1(𝒜lTXl+1)+Xl⊥(10)

The Jacobian determinant of this transformation is as Formula (11):

det(∂Xl+1∂Xl)=∏k=1KdΨlk(x)dx(11)

The algorithm iteratively minimizes the max K-SWD between the transformed and target distributions, leveraging the inverse Radon transform and Cramer-Wold theorem to match the high-dimensional distributions by aligning their 1D slices. This approach ensures that the SINF algorithm can effectively handle high-dimensional data and generate high-quality samples, making it a powerful tool for density estimation and sample generation in complex applications such as cybersecurity. Fig. 5 illustrates the functioning of the SNIF algorithm.

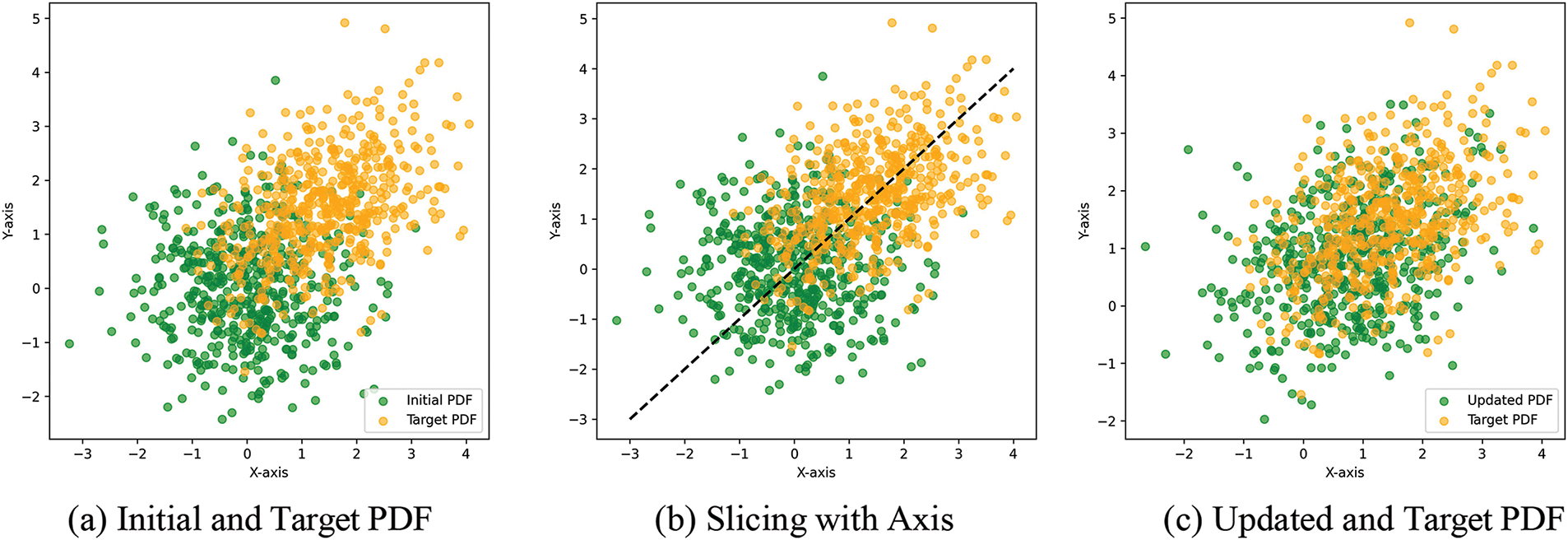
Figure 5: Illustration of the SNIF algorithm

Fig. 5a shows the initial alignment significant deviation between the initial and target distributions. Fig. 5b shows the slicing of the axis with the most difference between the two PDFs. Fig. 5c illustrates the reduced discrepancy between the updated and target distribution after applying the SINF algorithm.

3.4 Computational Complexity Analysis

The time complexity of the proposed algorithm primarily arises from two key stages: the Autoencoder module and the SINF module. In the Autoencoder module, the complexity per training epoch can be expressed as shown in Formula (12).

O(L⋅n⋅m)(12)

where L represents the number of layers in the autoencoder, n is the dimensionality of the input data, and m is the dimensionality of the encoded representation.

In the SINF module, the iterative density estimation and transformation contribute to the overall time complexity, represented in Formula (13).

O(K⋅D)(13)

where K denotes the number of slicing directions per iteration, and D represents the dataset dimensionality.

The combination of these two stages results in an overall time complexity approximately expressed in Formula (14).

O(L⋅n⋅m+N⋅K⋅D)(14)

This indicates that the computational time scales linearly with the size of the dataset and the number of iterations in the SINF module.

The space complexity is primarily dictated by the need to store model parameters and intermediate representations from both the Autoencoder and SINF stages. The autoencoder requires space proportional to Formula (15).

O(n⋅m+m)(15)

where n⋅m represents the weight matrices and m accounts for bias terms.

For the SINF module, additional memory is required to store density estimation parameters and intermediate slice mappings, as shown in Formula (16).

O(K⋅D)(16)

Combining both stages can approximate the overall space complexity using Formula (17).

O(n⋅m+m+K⋅D)(17)

This space requirement grows linearly with the number of optimized slicing directions and the dimensionality of the dataset.

The system was tested on our computational platform. The Autoencoder module completed training in approximately 2.5 h per epoch on the CICIDS2017 dataset during our experiments. The SINF module, performing iterative density estimation, required an average of 3.2 h per iteration for a dataset of similar scale.

These empirical observations demonstrate that while the computational requirements are non-trivial, they remain feasible within standard hardware configurations. Moreover, incremental learning significantly reduces the retraining burden, ensuring scalability for real-world deployment scenarios.

3.5 Unknown Detection Module

We propose a novel method for the unknown detection module by combining SINF with an autoencoder. The SINF method is a prominent and advanced recent Normalizing Flow technique that transforms a base distribution into a more complex one. It allows for learning and approximating the complex distribution of the dataset. The autoencoder excels in compressing data, retaining essential features, and eliminating redundancies.

Here, SINF is not applied directly to the raw data but rather to the data encoded by the autoencoder. In other words, SINF approximates the data distribution represented in a different space where critical information has been condensed. Using the autoencoder before applying SINF helps reduce the complexity of the data and eliminate unnecessary noise, thereby making the learning process of SINF more effective. Through this combination, the distribution of the dataset can be learned and estimated efficiently, enabling more accurate identification of unknown samples compared to traditional methods.

After performing the density estimation for the training dataset, we obtain a set of density values corresponding to each sample. To define the threshold for our system, we calculate the percentile of these density values. The threshold is selected based on this percentile to effectively distinguish between normal and anomalous samples. This threshold will later serve as a key parameter in the detection phase, determining whether new data points are classified as anomalies. The following Algorithm 1 outlines the detailed steps of the threshold selection mechanism.

Here, we set the threshold to the 1st percentile of the output. We can adjust the threshold based on our experience on the dataset and our domain to perform well. Fig. 6 illustrates the process of detecting unknown attacks. Fig. 7 illustrates the process of selecting the threshold.

Figure 6: Unknown detection mechanism

Figure 7: Threshold selection mechanism

3.6 Incremental Learning

After passing through the Unknown DDoS Detection module, suspicious traffic samples will be stored by the system and manually verified by network experts. The network experts will analyze the new unknown samples flagged by the system and label them as normal or attack. Subsequently, the system will perform incremental learning on the newly labeled data. Incremental learning, also known as continuous learning, enhances this adaptability by enabling the system to update dynamically with newly labeled data without retraining from scratch. This approach is particularly valuable in dynamic environments like network security, where new data types and attacks frequently emerge. Incremental learning ensures sustained performance in real-world scenarios with constantly evolving threats by complementing static detection strategies.

Let 𝒟t={(xi,yi)}i=1Nt represent the dataset at time t, where xi is the input data and yi is the corresponding label. In incremental learning, the model parameters θt are updated iteratively as new data 𝒟t arrives, rather than retraining the model from scratch using the entire dataset.

The goal is to minimize the loss function L(θt;𝒟t), which measures the discrepancy between the predicted and actual outputs. The update rule for the parameters θt at time t can be expressed as Formula (18).

θt+1=θt−η∇θtL(θt;𝒟t)(18)

where η is the learning rate, and ∇θtL(θt;𝒟t) is the gradient of the loss function with respect to the model parameters θt.

4  Methodology

4.1 Datasets

In this research, we evaluated our Intrusion Detection System (IDS) utilizing two datasets, namely CICIDS2017 and CICDDoS2019. These datasets, widely respected in the cybersecurity community, were created by the Canadian Institute for Cyber Security (CIC). Their purpose is to simulate a variety of cyber threats and typical network behaviors in realistic scenarios, providing a comprehensive setup that includes actual traffic data and network configurations. This setup enables detailed analyses of IDS effectiveness, algorithm refinement, and feature extraction.

The CICIDS2017 dataset contains network activity from Wednesday and Friday, showcasing a mix of benign traffic and various attack types. On Wednesday, the dataset records 319,186 benign packets (64.26%) and 159,049 packets from DoS Hulk attacks (32.021%), alongside smaller attack instances like DoS GoldenEye (7647 packets), DoS Slowloris (5071 packets), and DoS Slowhttptest (5109 packets). Additionally, 11 packets were associated with the HeartBleed vulnerability.

The proposed model uses all 80 features from the CICIDS2017 dataset, comprehensively representing flow-level, packet-level, temporal, and protocol-specific network traffic characteristics. No additional features were engineered as the dataset’s existing features already cover the critical indicators for detecting DDoS attacks. Basic flow metrics such as Flow Duration, Total Fwd Packets, and Total Backward Packets capture traffic volume and direction, which is essential for identifying unusual activity. Packet size statistics, including Fwd Packet Length Mean, Bwd Packet Length Max, and Packet Length Variance, provide insights into data distribution, which is often disrupted during DDoS attacks. Temporal features, such as Flow IAT Mean, Idle Mean, and Active Std, highlight abnormalities in inter-arrival times and connection activity, which are strong indicators of attack behavior.

Additionally, flag-based features (e.g., SYN Flag Count, RST Flag Count, and ACK Flag Count) help detect patterns associated with TCP-based flooding attacks. Rate-based metrics like Flow Bytes/s and Fwd Packets/s further support anomaly detection by capturing traffic bursts typical in DDoS attacks. To justify the inclusion of these features, each category contributes uniquely to attack prediction by capturing deviations in network behavior caused by malicious traffic. For instance, temporal and flag-based features are particularly effective in identifying attack traffic that mimics legitimate flows but exhibits subtle anomalies.

On Friday, the CICIDS2017 dataset logs 128,027 benign packets (56.713%) and 97,718 DDoS attack packets (43.287%). The CICDDoS2019 dataset, meanwhile, focuses on DDoS attacks and other network threats. For example, the LDAP attack dominates with 2,179,928 packets (99.927%), while only 1602 benign packets (0.073%) were recorded. Other significant attacks include MSSQL (4,522,489 packets), DNS (5,071,002 packets), NetBIOS (4,093,273 packets), and UDP (3,134,643 packets), with NTP and SYN attacks also recorded in substantial numbers.

These datasets serve as a pivotal foundation for tasks like training, validating, and benchmarking IDS models and assessing the comparative performance of different detection algorithms. Furthermore, they enable researchers to refine feature selection methodologies and test IDS robustness under various conditions.

4.2 Preprocessing Steps

Data preprocessing is a crucial step to ensure the accuracy and reliability of experimental results. In our research, we applied several data-cleaning techniques to address errors and inconsistencies in the dataset. Preprocessing also helps remove noise, handle missing values, and normalize features, improving the model’s performance and ability to generalize to unseen data. Precisely, we followed these procedures:

–   For data samples where any feature value is missing, we eliminated those samples.

–   For data samples where any feature value is NaN, we eliminated those samples.

–   Any features possessing INF values were substituted by 1010.

–   In the case of negative values, these were swapped out for 0.

For feature transformation, we used the following Formula (19):

X←log10⁡(X+1)10(19)

After transformation, all feature values were scaled to fall within the range of [0, 1].

For label encoding, we used the One-hot Encoding method. In this study, we focus on binary classification. Therefore, we are only concerned with whether the traffic is normal traffic or an attack. Table 3 describes the labels grouped as attacks from CICIDS2017 and CICDDoS2019.

After processing the data according to the outlined steps, we directly utilize them for training and evaluation. In this study, we prioritize evaluating the model performance on the original dataset. Consequently, techniques like outlier removal or data augmentation are not applied.

4.3 Evaluation Metrics

In machine learning, performance metrics are indispensable for evaluating how well a model operates and its overall efficiency. Such metrics offer a mechanism to gauge and contrast how models perform when faced with specific challenges or tasks. In this study, the following key metrics were applied for performance evaluation:

–   Accuracy (Acc): Measures the proportion of predictions that were accurate out of the total predictions made by the model.

–   Precision (Prec): Measures the proportion of true positive outcomes in relation to the overall predicted positive cases.

–   Recall: Determines the fraction of true positives compared to the total number of actual positive instances.

–   F1 score (F1): Delivers a harmonized metric that incorporates both precision and recall to give a balanced evaluation.

–   Fowlkes-Mallows Index (FM) [45]: Represents the geometric average of precision and recall, providing a well-rounded measure particularly effective for reducing both false positives and false negatives.

The choice of metrics accuracy, precision, recall, F1 score, and Fowlkes-Mallows Index (FM) was driven by the multifaceted nature of intrusion detection tasks. Accuracy provides a general overview of the model’s correctness but may be misleading in imbalanced datasets where the majority class dominates. precision is critical in minimizing false positives, especially in cybersecurity contexts where misclassifying benign traffic as malicious can lead to resource wastage. On the other hand, recall emphasizes the ability to identify actual attacks, minimizing false negatives that might leave threats undetected. F1 score harmonizes precision and recall, offering a balanced metric for overall performance assessment. Finally, the Fowlkes-Mallows Index complements these by providing a geometric mean of precision and recall, ensuring robustness in scenarios with skewed distributions. In our study, precision and recall hold particular significance, as they directly influence the system’s reliability in detecting and responding to threats. Precision ensures that detected threats are genuine, while recall ensures comprehensive coverage of all potential attacks. This balance is essential for an IDS to operate efficiently and effectively in dynamic and high-risk environments.

The calculations for these performance indicators are outlined in Formulas (20)–(24):

Accuracy=TP+TNTP+FP+TN+FN(20)

Precision=TPTP+FP(21)

Recall=TPTP+FN(22)

F1 score=2×Precision×RecallPrecision+Recall(23)

FM=Precision×Recall(24)

where

–   the TP is the number of true positive predictions.

–   the TN is the number of true negative predictions.

–   the FP is the number of false positive predictions.

–   the FN is the number of false negative predictions.

4.4 Framework

For this research, a system running Ubuntu 20.04 was utilized. The machine is equipped with powerful hardware, including an AMD Ryzen 5700X processor with eight cores and 16 threads, 96 GB of DDR4 RAM, and two GPUs—the Nvidia RTX2060 and RTX3070—serving as computational accelerators. As for the framework employed in model development, we used PyTorch 2.0.1 + cu118, Sklearn 1.3.0 and Python 3.11.5, for programming and testing purposes.

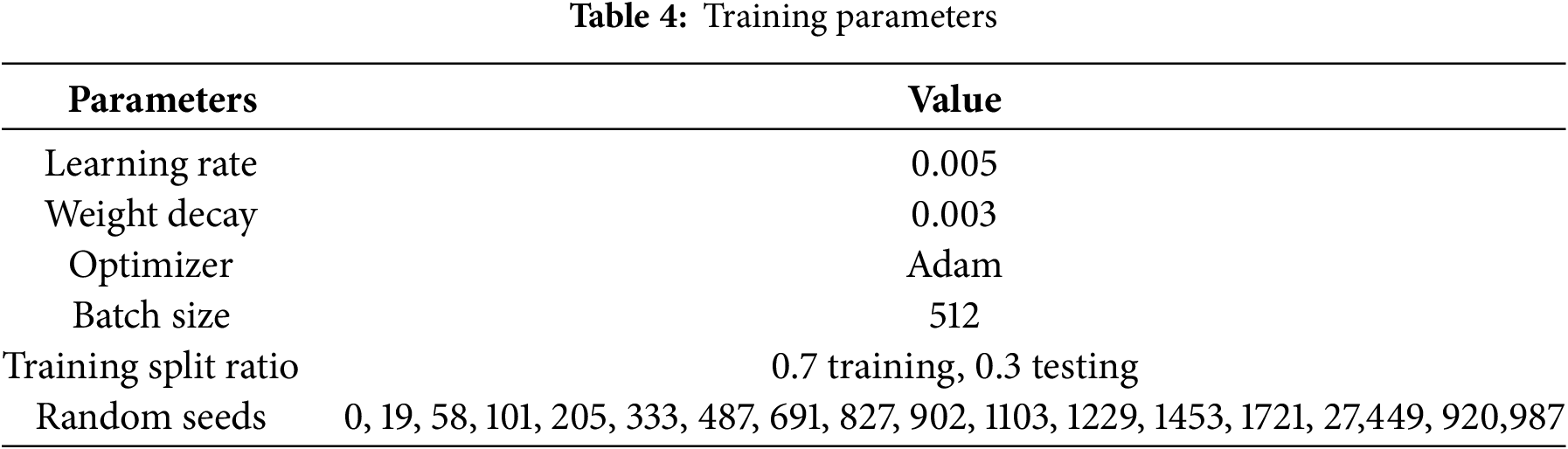
In this experiment, the PyTorch framework was leveraged to construct the model, while Sklearn was used to compute the performance metrics. To evaluate how well the model performed, we performed ten distinct training iterations, each using a different random seed to vary the training process. Adam was selected as the optimizer to enhance the model’s learning efficiency. The detailed configuration of the parameters is presented in Table 4.

We employed 16 distinct random seeds to train the suggested model twenty times. Subsequently, we calculated the average results to validate the model’s performance in closed sets. The data presented in Table 5 and Fig. 8 demonstrates the high efficacy of the model when applied to the closed dataset.

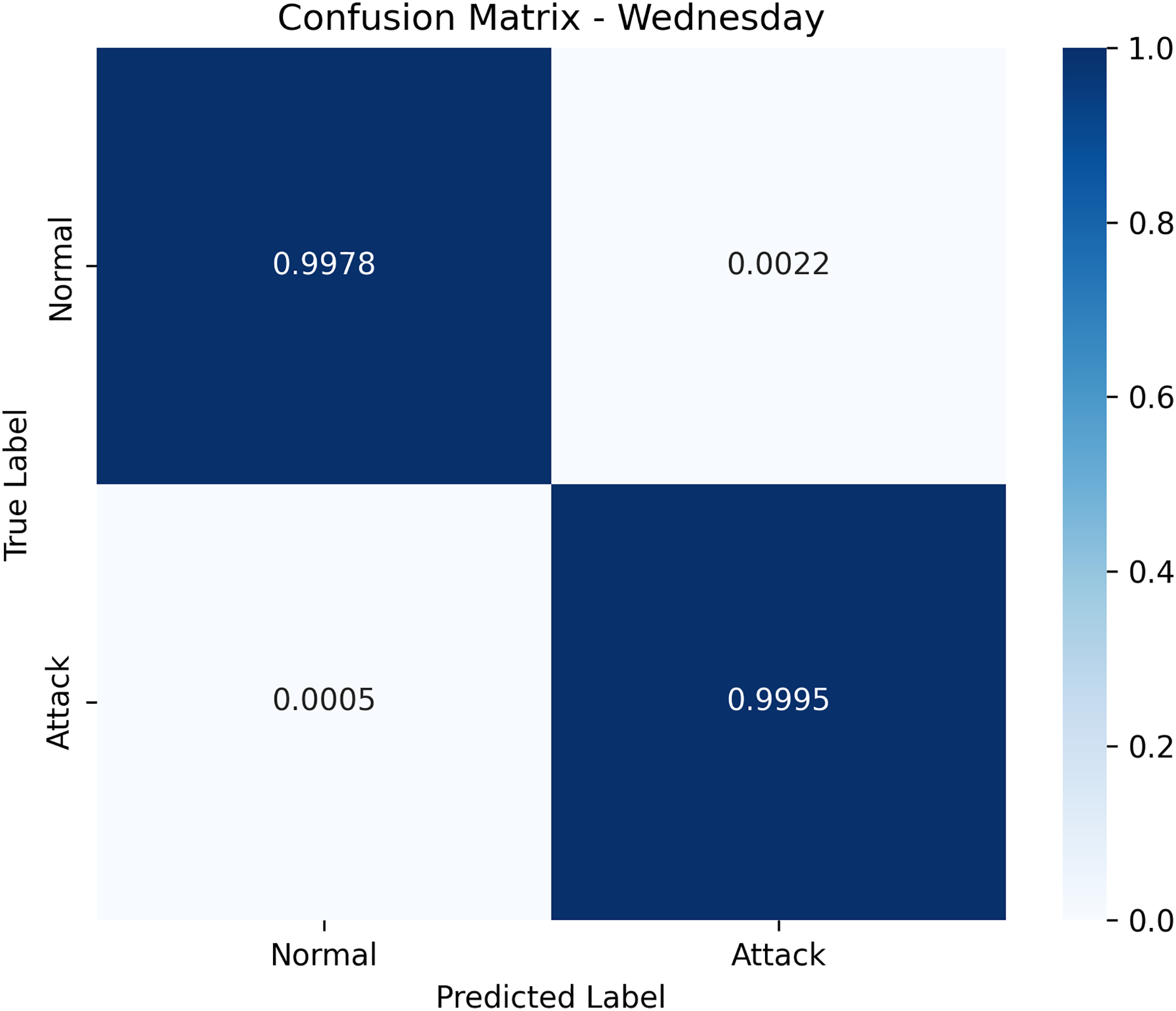
Figure 8: Known attack confusion matrix for CICIDS2017-Wednesday

4.5 Results and Analysis

4.5.1 Density Estimation

In the density estimation method, selecting the threshold based on the training sample’s log(Density) values plays a crucial role, as it directly affects the system’s ability to classify samples. Data samples evaluated with log(Density) values lower than the threshold are considered unknown samples. When a low threshold is used, the system applies a stricter check, identifying fewer unknown samples. This helps reduce the number of samples that require labeling by network experts and lowers the cost of system updates through incremental learning. However, if the threshold is too low, the system risks missing important unknown samples, decreasing detection efficiency.

In contrast, when a higher threshold is used, the system becomes less strict, resulting in more unknown samples being identified. This includes some previously known samples, increasing the workload of network experts for labeling and raising the cost of updates. Therefore, the threshold should be chosen carefully to be small enough to detect unknown samples effectively but not so low that it misses important ones. A well-considered threshold will optimize system performance and minimize operational costs.

In this study, we will estimate the Density of the CICIDS2017-Wednesday dataset in the training phase. As mentioned earlier, the threshold here is set as the 1st percentile of the results, with a value of −23.30. Fig. 9 shows the density estimation for CICIDS2017-Wednesday.

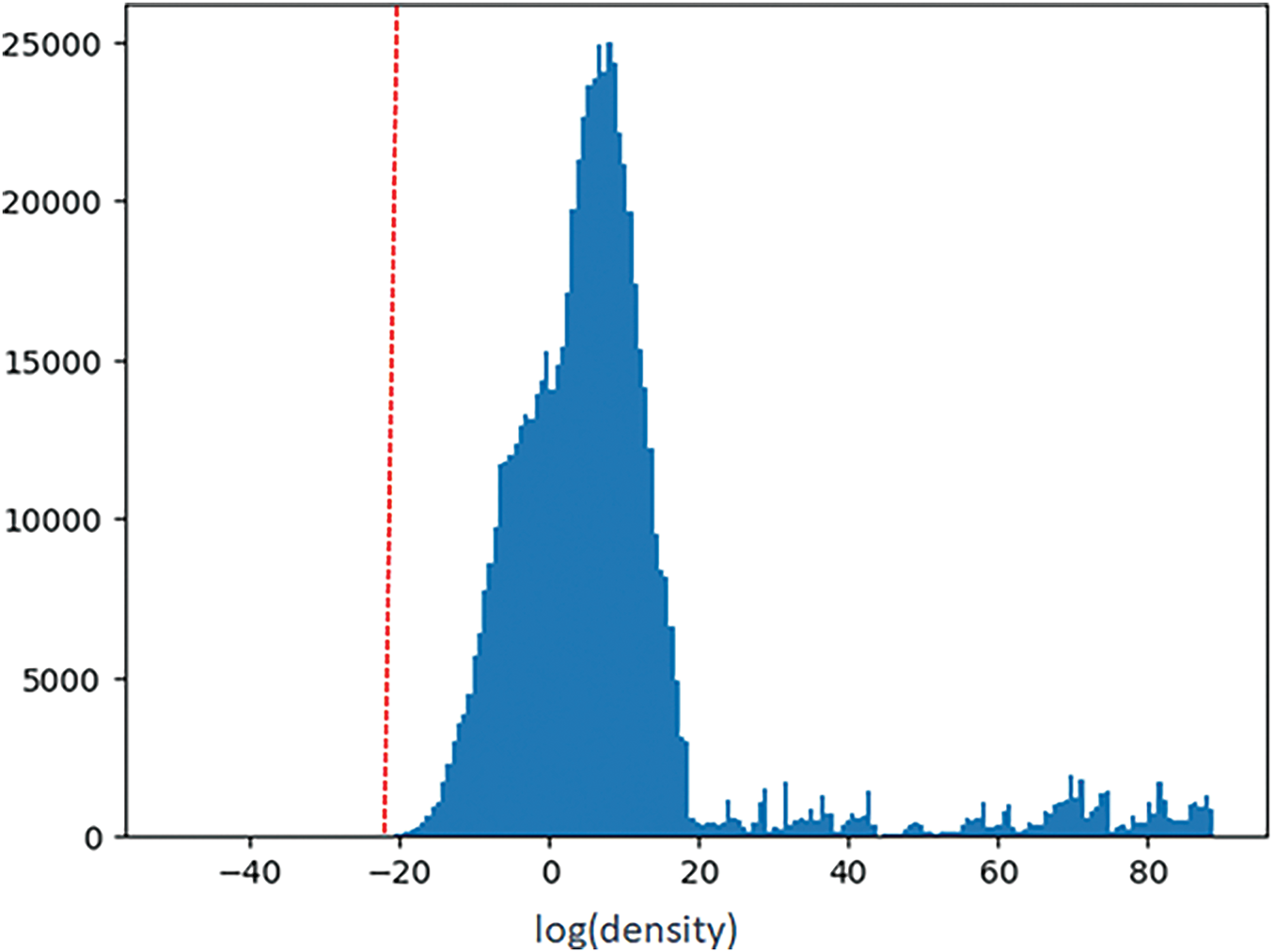
Figure 9: The Density histogram chart of CICIDS2017-Wednesday

In the evaluating phase, we will estimate the Density of other datasets to detect unknown attacks. If the density value is smaller than the threshold, −23.30, the traffic will be marked as an unknown attack. Fig. 10 shows the density estimation for CICIDS2017-Friday.

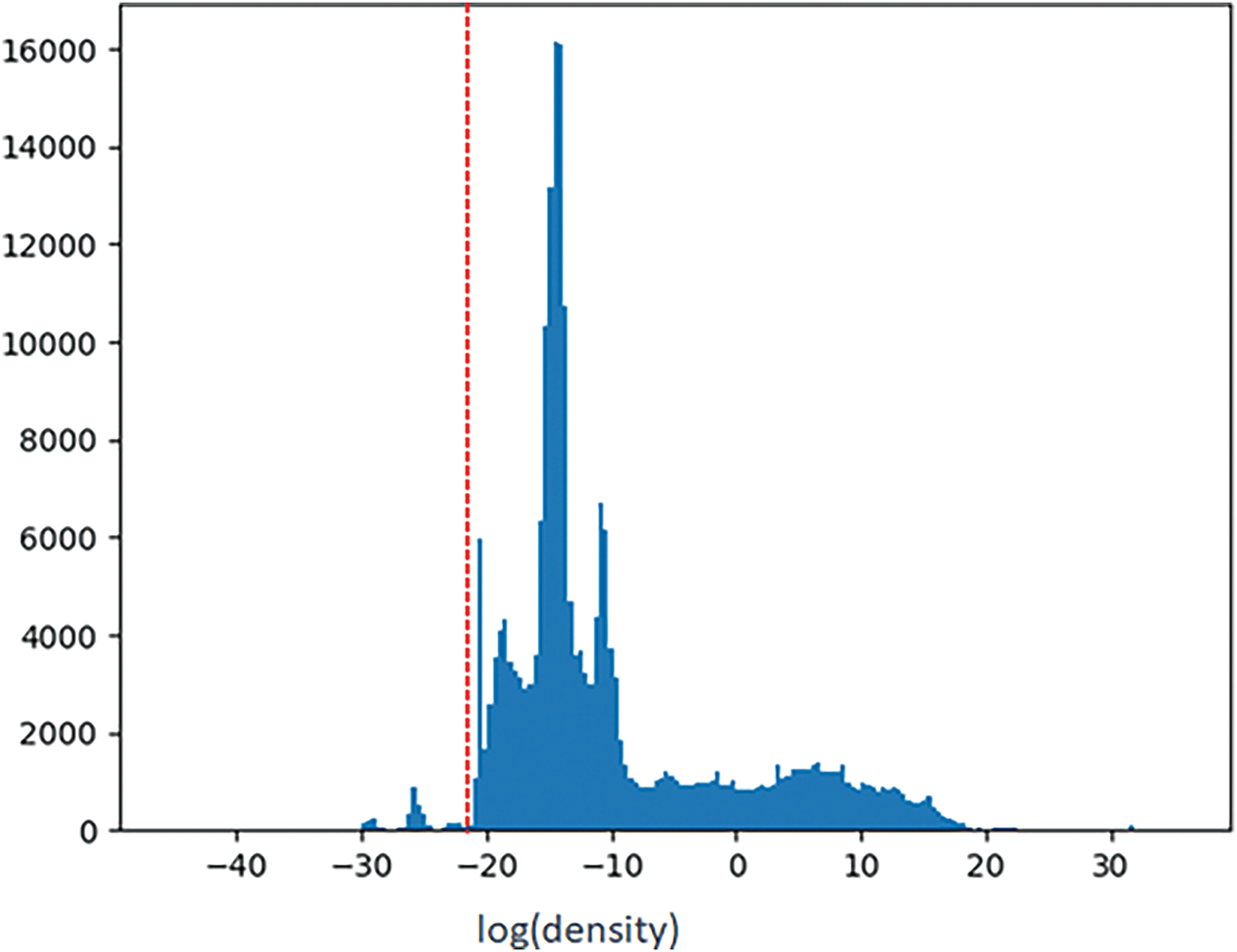
Figure 10: The Density histogram chart of CICIDS2017-Friday

4.5.2 Density Estimation

The proposed methodology has demonstrated strong efficacy in countering known attacks. Afterward, we initiated an evaluation to determine how well we could defend against unidentified DDoS threats. At the start, the CICIDS2017-Friday dataset was used to measure the effectiveness of our model. Table 6 displays the outcomes and the comparisons.

When analyzing the CICIDS2017-Friday dataset, the model achieved an accuracy score of 0.7809, with other performance metrics showing favorable results. Since the CICIDS2017-Friday and -Wednesday datasets were collected under similar conditions, they share specific characteristics, especially within the benign traffic. However, the findings reveal that the standalone model struggles to detect newly emerging attacks. Following this, we applied CICDDoS2019 to conduct additional assessments of the framework’s performance. Table 7 highlights the detection outcomes and association analysis for the CICDDoS2019 dataset.

The model’s performance is significantly inadequate when assessing it using the CICDDoS2019 dataset. Despite being collected by the same organization, the CICDDoS2019 and CICIDS2017 datasets exhibit notable differences. The simulation environments and gathered features vary, and the model is unfamiliar with the attack behaviors in the CICDDoS2019 dataset. As a result, the trained model erroneously classified new attacks as normal network activity. In order to resolve this problem, incorporating an Unknown DDoS Detection module into the model is crucial to enhance the system’s overall functionality.

4.5.3 Outlier Detection

In this study, the Outlier Detection Rate (ODR) was computed to evaluate how well the module performs in detecting unknown DDoS attacks.

ODR=NNOutlier(25)

where NOutlier indicates the quantity of unidentified samples flagged by our system for further examination by network specialists, and N is the total number of samples processed.

Table 8 demonstrates that our Unknown DDoS Detection module performs exceptionally well in identifying outlier samples.

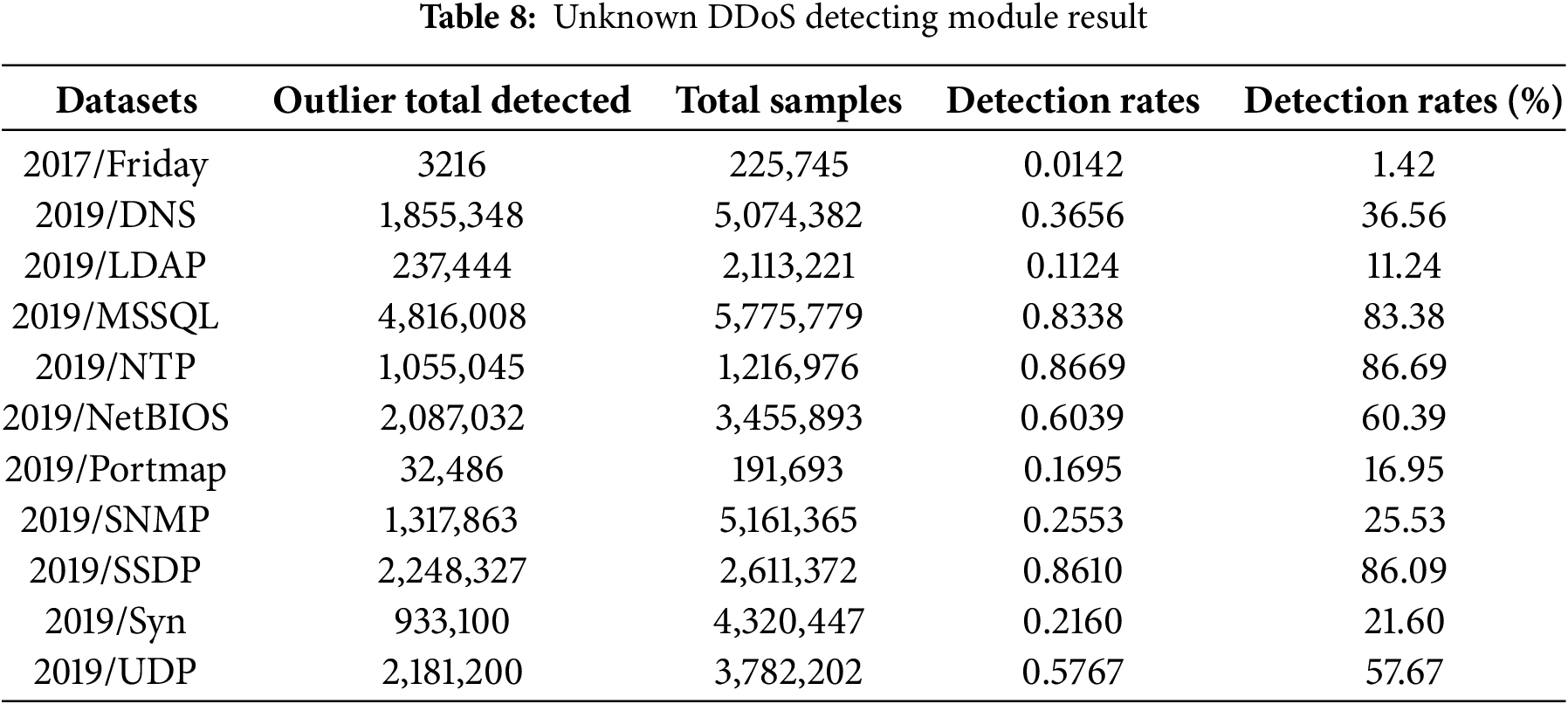
CICIDS2017-Friday and -Wednesday datasets, having been gathered under identical conditions, show high similarity. Consequently, the ODR for CICIDS2017-Friday is as low as 0.0142. On the other hand, the ODRs for the CICDDoS2019 datasets show notable variation, spanning from 0.11 to 0.86.

4.5.4 Incremental Learning Results

Network specialists will examine and label suspicious samples after processing them using the Unknown DDoS Detection module. The newly labeled data will then be utilized for incremental learning. This method improves the machine learning model without necessitating total retraining. Our incremental learning approach was comprehensively evaluated across multiple data splits from CICIDS2017 and CICDDoS2019, where we gradually introduced new DDoS attack variants to update the model’s knowledge while retaining performance on previously learned attacks. Throughout these successive training rounds, we carefully tracked accuracy, F1 score, and open-set detection rates before and after each incremental step to confirm that the system maintained robust recognition of older threats. This design closely mimics real-world scenarios where novel DDoS vectors emerge over time, and our results show stable performance, indicating minimal forgetting of existing knowledge and effective assimilation of unfamiliar traffic patterns. We also examined precision/recall on old classes, accuracy and F1 scores on newly added attacks, and open-set detection metrics for genuinely unknown behaviors to provide a balanced evaluation. The consistency across multiple incremental phases, combined with consideration of practical constraints such as limited appearances of newly emerging attacks, demonstrates the sufficiency of our current experiment design.

To ensure the robustness and generalization of our proposed model, we adopted multiple strategies to mitigate potential overfitting issues. Cross-validation was employed using multiple random seeds to evaluate the model’s performance across different data splits, reducing bias from a specific data partition. The model was trained and validated for each iteration across varying subsets of the CICIDS2017 and CICDDoS2019 datasets. The average metrics over these folds confirm the consistency of the model’s performance, demonstrating minimal variance.

Additionally, we incorporated Dropout regularization within the autoencoder layers to prevent the model from over-relying on specific neurons during training. Dropout randomly deactivates a subset of neurons, enhancing the model’s generalization ability to unseen data. This technique proved effective in stabilizing performance and avoiding overfitting on known attacks. Experimental results validate that the model maintains high accuracy and F1 scores, even after incremental learning on unseen datasets. The model’s output after incremental learning is shown in Table 9.

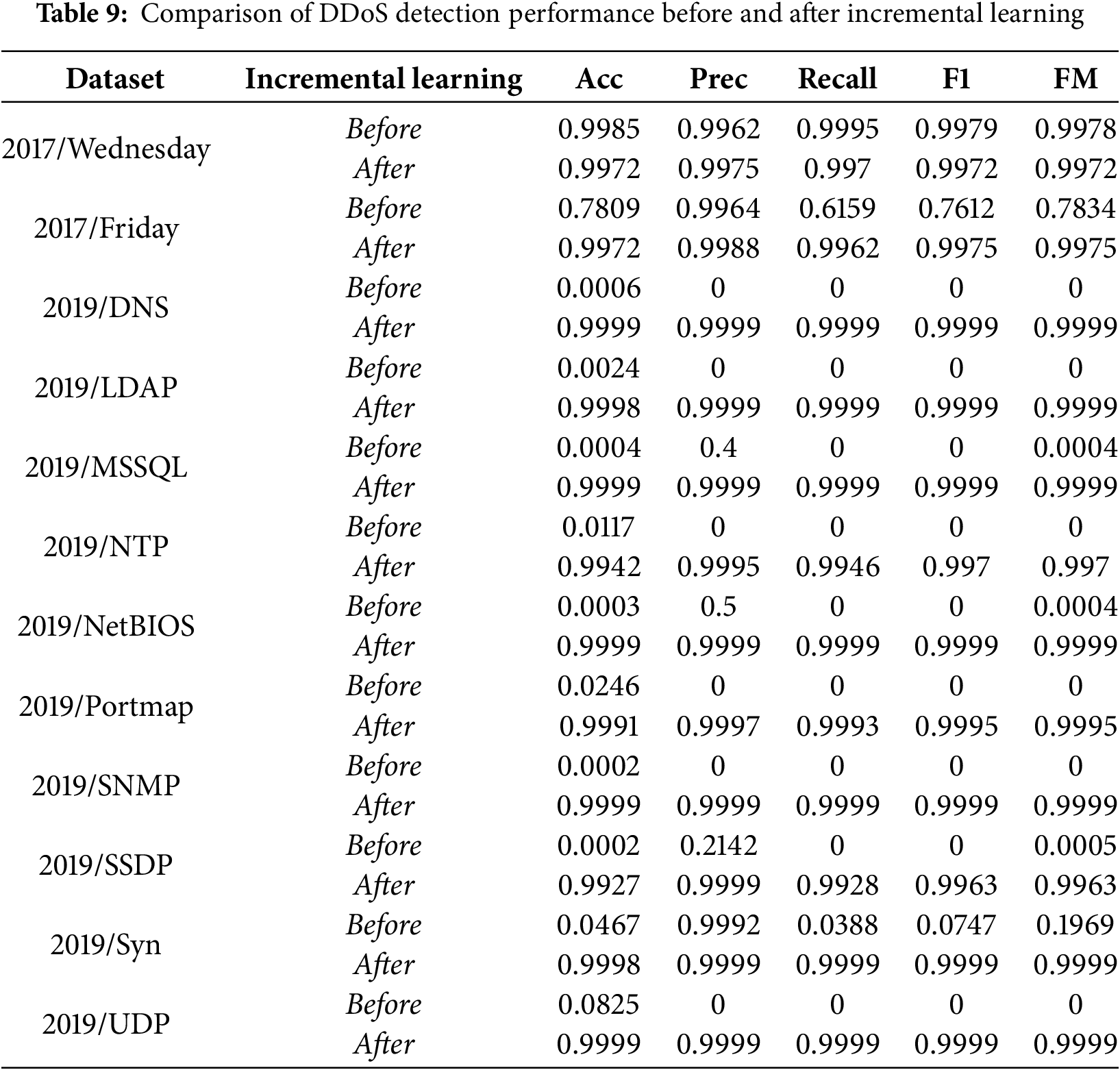
The model has significantly improved in performance after incremental learning. An accuracy gain of roughly 0.2 has been achieved for the CICIDS2017-Friday dataset with an ODR rate of 0.0142. All of the measured parameters for the CICDDoS2019 dataset surpassed 0.99, which was the expected value. Remarkably, for certain datasets of CICDDoS2019, such as LDAP, Portmap, SNMP, and Syn, the Outlier Detection Rate (ODR) is not very high, remaining below 26% (Table 5). However, the results are still outstanding, similar to those of other datasets. This illustrates how well the suggested model separates known from unknown traffic. The majority of samples that are marked as unknown are not acquainted with the system and improve performance. The incremental learning process does not only enhance the autoencoder and classifier modules. It also helps improve the SINF system, which is the core of the unknown detection module. Through this process, density estimation for new samples is performed. Since new samples used for incremental learning have scores lower than the threshold, the threshold will be adjusted to a value smaller than the previous one. This ensures the system’s sensitivity to new patterns. As a result, the system’s maximum degree of assurance on its capacity to identify unknown assaults is provided.

This result also demonstrates the effective generalization capability of the model, as it was trained on the CICIDS2017 dataset and can detect and update unknown samples on the unknown CICDDoS2019 dataset. Both datasets were collected by the Canadian Institute for Cybersecurity and utilized a similar feature extraction method (NetFlow), exhibiting a certain compatibility level. However, for other datasets, we will need to conduct separate studies while exploring feature mapping or transformation methods due to differences in data collection and feature extraction methods. This ensures an objective and accurate evaluation of the model’s performance on these datasets.

4.5.5 Comparison

For the comparison, we drew extensively on current research on DDoS attack detection. Chosen algorithms include Stacked Auto-Encoders (SAE) [37], Random Forest and Decision Tree (RF & DTC) [38], CNN-LSTM Hybrid [39], Multilayer Perceptron [46], Deep Neural Network with Genetic Algorithms [47], and AlexNet with Fuzzy C-Means clustering [14]. Each algorithm underwent evaluation using the CICIDS2017 dataset to detect previously known DDoS attacks. Table 10 compares our approach and other modern machine learning algorithms following incremental learning.

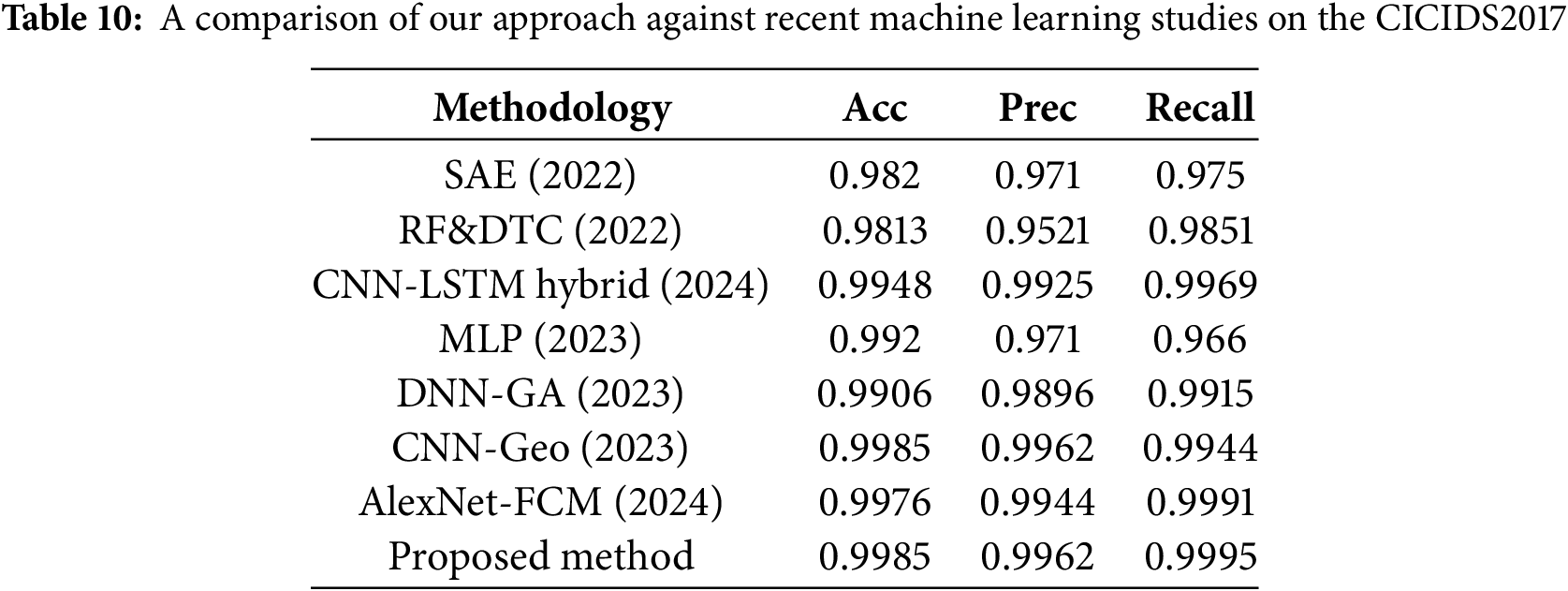
Our method’s performance metrics surpass those obtained by SAE, RF&DTC, CNN-LSTM Hybrid, DNN-GA, MLP, CNN-Geo, and AlexNet-FCM. The performance indicators, such as accuracy, precision, and recall, are on par with or exceed the results of competing algorithms. Compared to SAE, our approach provides better adaptability to dynamic datasets through incremental learning, while SAE requires retraining from scratch when encountering new attack patterns. Similarly, RF & DTC exhibit strong anomaly detection capabilities but struggle with scalability in real-time environments, an area where our approach excels due to its computational efficiency during incremental updates.

We then compared our approach to other algorithms to identify previously unknown attacks. The selection of algorithms for comparison included GMM [11], DBSCAN combined with SVM (DBSCAN-SVM) [12], DBSCAN paired with Random Forest (DBSCAN-RF) [12], a Convolutional Neural Network utilizing geometrical Metrics [13], 1D-DHRNet-OCSVM [48], and AlexNet integrated with Fuzzy C-Means clustering [14]. Each algorithm was trained using the CICIDS2017 dataset and tested across other datasets CICDDoS2019. The overall system’s performance metrics can be found in Table 11.

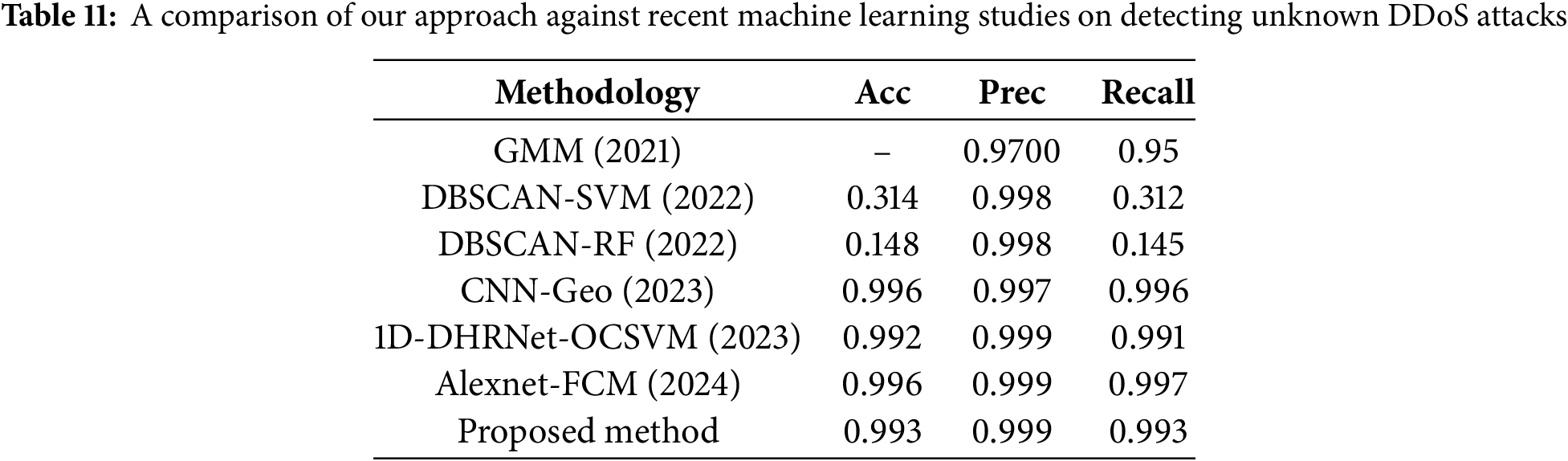
Our approach shows marginally higher performance metrics than GMM (2021) and 1D-DHRNet-OCSVM (2022). Our performance metrics have slight and negligible differences compared with CNN-Geo (2023) and ALexnet-FCM (2024). When considering known and unknown attack detection scenarios, our results are on par with or exceed the effectiveness of alternative methods. The CNN-LSTM Hybrid method demonstrates excellent accuracy; however, its high training complexity limits scalability on large datasets. In contrast, our method maintains comparable accuracy while optimizing computational efficiency through incremental updates. Similarly, DNN-GA performs effectively in structured datasets but struggles with irregular patterns often seen in unknown DDoS attacks. Our Autoencoder-SINF integration addresses this limitation by providing stable and adaptive density estimation mechanisms. CNN-Geo, 1D-DHRNet- OCSVM, and AlexNet-FCM all demonstrate high detection accuracy and precision, particularly in structured datasets. However, they share a significant limitation: computational intensity, especially when applied to large-scale datasets, poses challenges for real-time scalability and deployment in resource-constrained environments. In contrast, our approach balances precision and scalability by leveraging efficient density estimation via SINF and incremental learning mechanisms, enabling our system to adapt dynamically to evolving threats without excessive computational overhead.

4.6 Discussion

4.6.1 Incremental Learning Performance Across Datasets

The analysis of the experimental results is visualized in Fig. 11, comparing the performance metrics before and after the incremental learning process on multiple datasets. These radar charts provide a comprehensive view of key evaluation metrics, including precision, recall, accuracy, and F1 score. Fig. 11a,b represents the outcomes for the CICIDS2017-Wednesday and -Friday datasets, respectively, while Fig. 11c,d highlights the results for the CICDDoS2019 LDAP and the CICDDoS2019 SYN datasets.

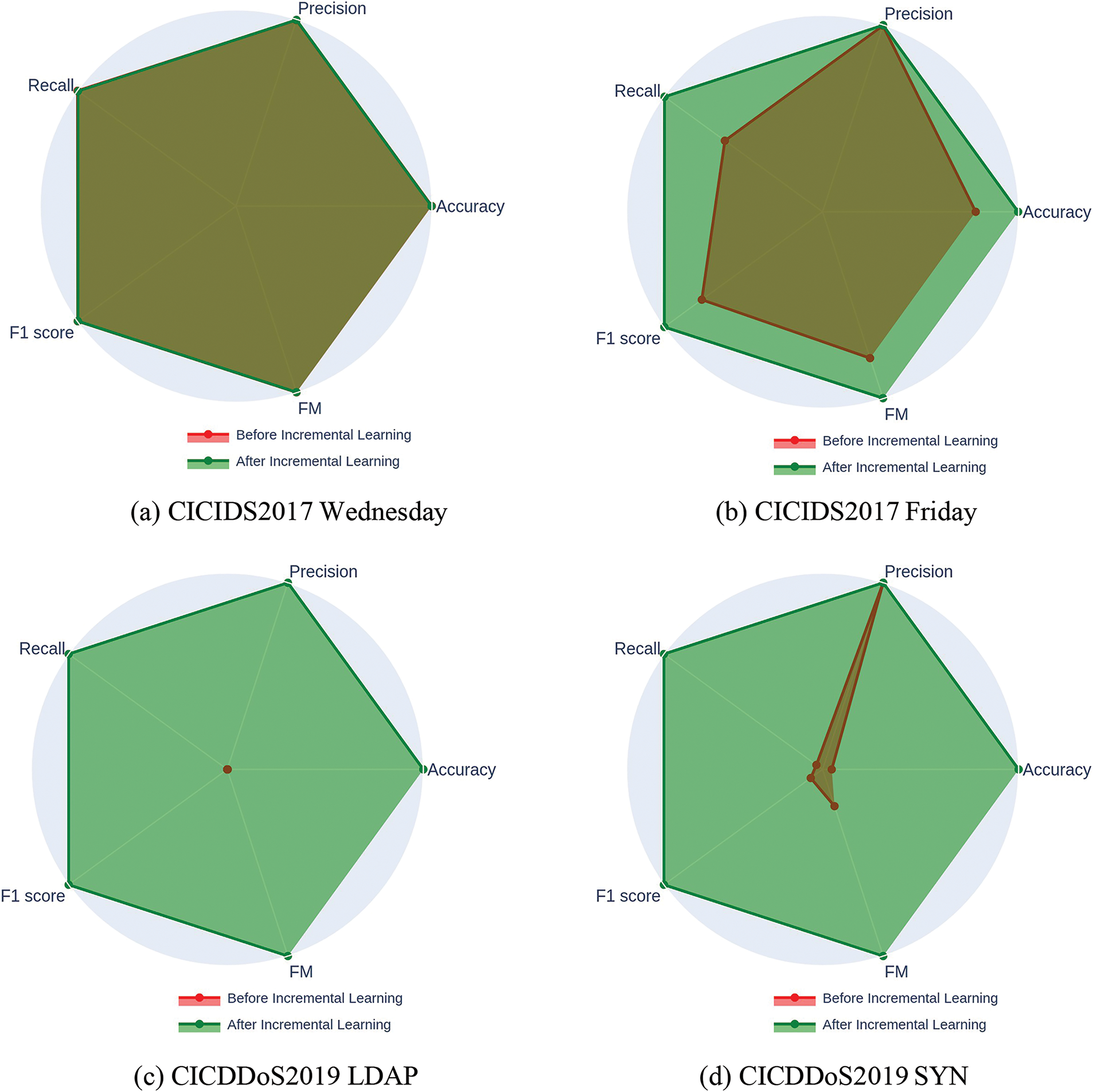
Figure 11: Compared outcomes before and after incremental learning on multiple datasets

The results on the CICIDS2017-Wednesday dataset (Fig. 11a) show that incremental learning did not significantly change the detection performance on the training dataset. Key metrics like accuracy, precision, recall, and F1 score remain stable before and after the learning update. This indicates that adding new data does not cause the system to “forget” what it learned from older datasets. The system performs well on the previous dataset, showing that it can adapt to new information without losing its effectiveness on known attacks.

The evaluation results on the CICIDS2017-Friday dataset (Fig. 11b) show a different pattern than Wednesday’s. Before incremental learning, the detection metrics were already fairly decent, largely because this dataset was collected in the same environment as the Wednesday training set. The similarity between these datasets means the system could detect known patterns effectively, even before updating the model. However, after applying incremental learning, there is a noticeable improvement across all key metrics, confirming that the updated model better captures common and subtle variations in attack behavior without compromising its original detection capabilities. This emphasizes that although the initial performance was good, incremental learning further enhances the system’s adaptability and precision.

The results on the CICDDoS2019 LDAP dataset (Fig. 11c) show a noticeable difference compared to CICIDS2017. The initial detection performance was poor since CICDDoS2019 was collected in a different environment with different attack scenarios. The model struggled to identify these new attacks because it was initially trained on CICIDS2017 data, which has various features and behaviors. However, after applying incremental learning, the performance metrics improved significantly. This shows that incremental learning allows the model to adapt to new attack patterns from different environments, making it more effective at detecting a wider range of threats.

Following the improvements seen with the CICDDoS2019 LDAP dataset, the results for the CICD- DoS2019 SYN dataset present an interesting anomaly in Fig. 12. Before incremental learning, precision was unusually high despite other metrics like recall and F1 scores being much lower.

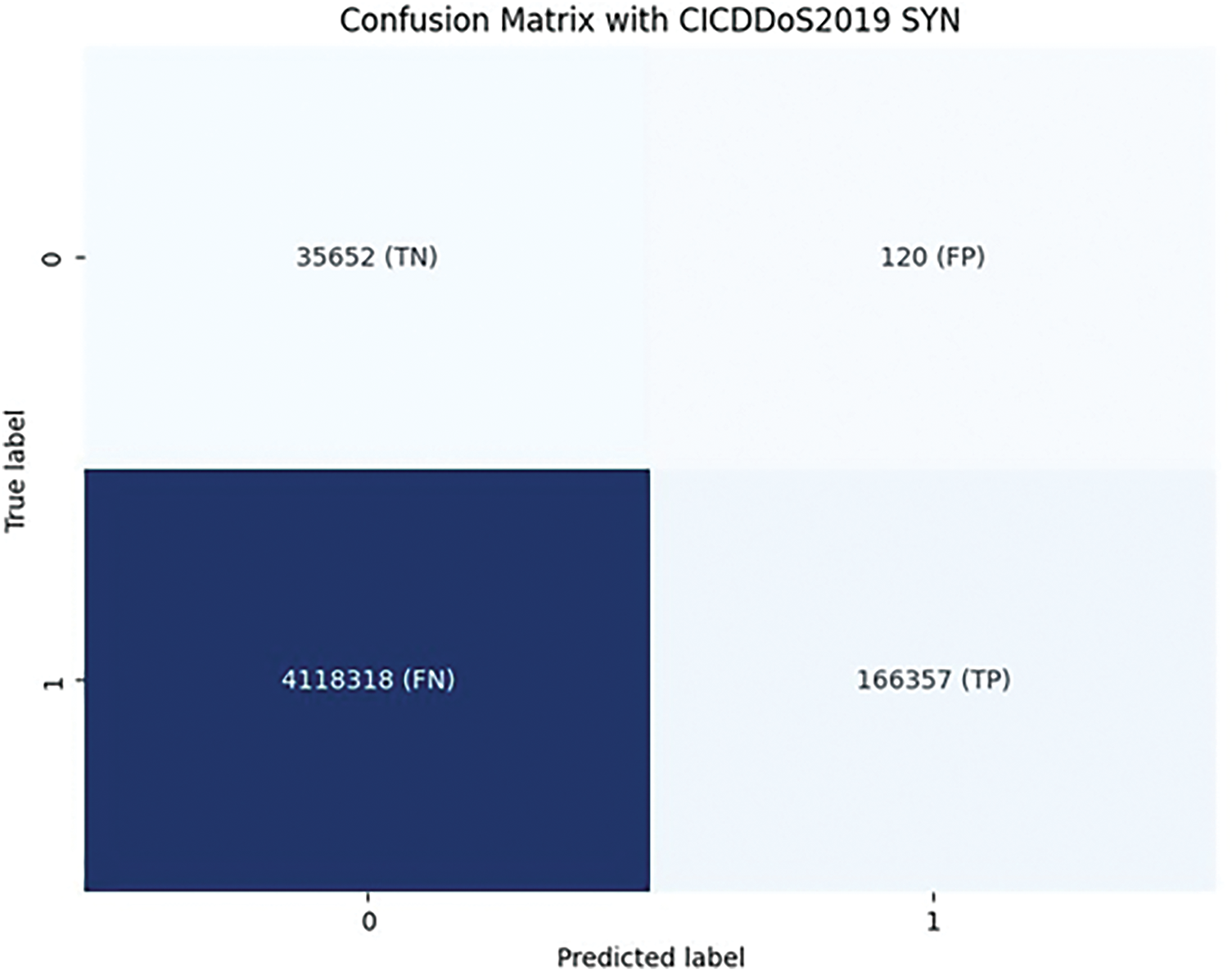
Figure 12: Unknown detection mechanism

4.6.2 Impact of Threshold Adjustment on Outlier Detection and Model Performance

One key aspect influencing anomaly detection systems’ performance is the threshold selection for identifying outliers. In our approach, the initial threshold was set at the 1st percentile of the anomaly scores, resulting in a value of −23.30. However, during incremental learning with newly detected unknown samples, it became evident that this threshold might not fully optimize the balance between sensitivity and specificity when dealing with evolving datasets. To address this, we recalculated the threshold using a subset of data, specifically the CICIDS2017-Wednesday dataset combined with unknown samples from the CICIDS2017-Friday dataset, resulting in a refined threshold value of −24.07.

The new threshold was then applied across three representative datasets, LDAP, MSSQL, and NTP, to evaluate its impact on outlier detection and overall system performance. The results revealed a reduction in detected outliers across all three datasets compared to the initial threshold, as shown in Table 12.

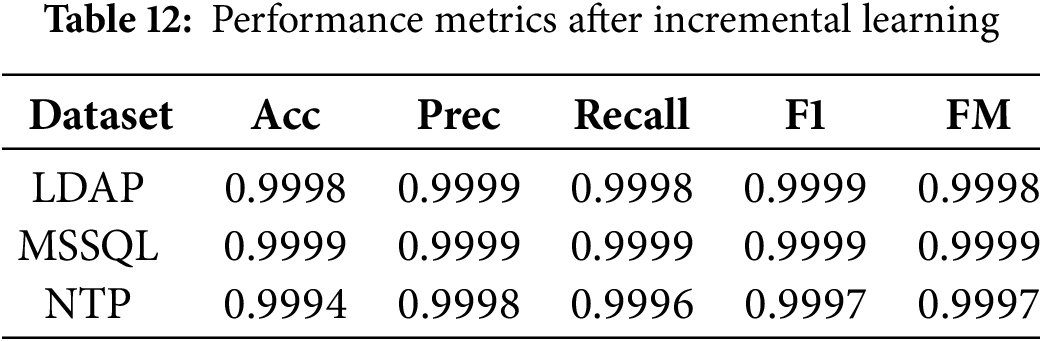
The results indicate that the overall performance metrics remain consistently high despite the reduction in detected outliers. This suggests that the outliers identified using the refined threshold are highly representative and contribute meaningfully to the incremental learning process.

Adjusting the threshold based on dataset characteristics has significant implications for system optimization. While a strict percentile-based threshold (1st percentile) ensures sensitivity, it may introduce unnecessary computational overhead and include borderline anomalies with limited representational value. In contrast, fine-tuning the threshold based on dataset-specific characteristics enables better trade-offs between detection sensitivity and computational efficiency. The refined threshold effectively reduced computational overhead by filtering less representative anomalies while maintaining high performance across key metrics. This adjustment highlights the importance of dynamic threshold tuning in balancing detection sensitivity and efficiency, especially in evolving datasets. This presents a promising direction for our future research, where we aim to develop adaptive thresholding mechanisms to enable real-time self-optimization, enhancing the system’s scalability and reliability in dynamic cybersecurity environments.

4.6.3 Research Challenges and Future Improvements

The proposed SINF-based framework addresses key challenges in IDS, particularly false positive reduction, deployment complexities, and broader applicability to diverse cybersecurity problems. Reducing false positives is critical, as misclassifying benign traffic as malicious can result in unnecessary alerts and resource overhead. Using a density-based threshold optimized with the 1st percentile of log density values effectively distinguishes benign traffic from anomalies, as demonstrated in Figs. 9 and 10. Incremental learning further enhances the model by incorporating newly labeled data, improving precision from 0.9964 to 0.9988 on the CICIDS2017-Friday dataset (Table 9), while maintaining high recall. This refinement significantly reduces false positives, as highlighted by confusion matrices in Fig. 12. Future work will further explore adaptive thresholding and adversarial training to minimize false alarms in dynamic environments.

Deploying the system in real-world scenarios introduces challenges, including system integration and resource requirements. Integration with existing infrastructures may face compatibility issues, particularly in legacy systems. A modular design with standardized APIs can streamline deployment without disrupting operations. The computational demands of SINF, especially in real-time scenarios, can be mitigated through GPU acceleration, parallel computing, and adaptive slicing strategies. For resource-constrained environments such as IoT networks, lightweight models optimized via feature prioritization, quantization, and pruning ensure efficiency while preserving accuracy. These strategies collectively enhance the system’s scalability and adaptability across diverse operational contexts.

In addition to its high detection accuracy, the proposed system provides interpretability through the SINF density estimation mechanism. By analyzing the probability distributions learned through SINF, the model can highlight specific feature distributions associated with suspicious flows. For flagged alerts, SINF identifies deviations in density values, which can serve as interpretable insights for security analysts. These insights help understand which aspects of the network traffic caused the system to classify a flow as anomalous or unknown. This interpretability is particularly valuable in practical settings, as it enables analysts to investigate alerts efficiently and validate the model’s decisions, thereby improving trust and utility in real-world deployment.

Furthermore, the iterative slicing approach used in SINF retains the underlying structure of high-dimensional traffic data, which aids in identifying key features that contribute most to the detection of novel attacks. This interpretable information bridges the gap between automated decision-making and human analysis, allowing for actionable insights that enhance incident response and mitigation. These efforts aim to refine the system into a more scalable, adaptable, and resilient solution for modern cybersecurity challenges.

5  Conclusion

By adding Sliced Iterative Normalizing Flows to intrusion detection systems (IDS), this paper describes a new way to improve the detection of unknown DDoS attacks. Traditional IDS models struggle with detecting novel attacks due to their reliance on predefined signatures and extensive labeled datasets. Our suggested method uses SINF’s ability to change probability distributions repeatedly using the sliced Wasserstein distance. This gives us a reliable way to estimate Density and make good samples even when we only have a small amount of data. Using OSR techniques, the system can find and classify attack patterns that have not been seen before. This solves important problems related to uncertainty and changing cyber threats.

Evaluations of the CICIDS2017 and CICDDoS2019 datasets show that the combined method keeps detection rates high and lowers the number of false positives. This makes it a scalable and valuable way to protect real-time networks. The research highlights the potential of combining deep learning algorithms like SINF with OSR frameworks to enhance the resilience of IDS against both known and unknown threats. Applying such techniques could be extended to other domains of cybersecurity, paving the way for more adaptive and intelligent defense mechanisms in the ever-evolving landscape of cyber threats.

Acknowledgement: We would like to thank the National Science and Technology Council, Taiwan, for funding this research.

Funding Statement: This research was partly supported by the National Science and Technology Council, Taiwan with grant numbers NSTC 112-2221-E-992-045, 112-2221-E-992-057-MY3, and 112-2622-8-992- 009-TD1.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Thanh-Tuan Nguyen, Chin-Shiuh Shieh; data collection: Thanh-Lam Nguyen; analysis and interpretation of results: Thanh-Lam Nguyen, Mong-Fong Horng, Thanh-Tuan Nguyen; draft manuscript preparation: Thanh-Tuan Nguyen, Thanh-Lam Nguyen; supervision: Chin-Shiuh Shieh, Mong-Fong Horng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data supporting the reported results are available upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Alfatemi A, Rahouti M, Amin M, ALJamal S, Xiong K, Xin Y. Advancing DDoS attack detection: a synergistic approach using deep residual neural networks and synthetic oversampling. arXiv:2401.03116. 2024. [Google Scholar]

2. Mittal M, Kumar K, Behal S. Deep learning approaches for detecting DDoS attacks: a systematic review. Soft Comput. 2023;27(18):13039–75. doi:10.1007/s00500-021-06608-1. [Google Scholar] [PubMed] [CrossRef]

3. Malliga S, Nandhini PS, Kogilavani SV. A comprehensive review of deep learning techniques for the detection of (distributed) denial of service attacks. Inf Technol Contr. 2022;51(1):180–215. doi:10.5755/j01.itc.51.1.29595. [Google Scholar] [CrossRef]

4. Hnamte V, Ahmad Najar A, Nhung-Nguyen H, Hussain J, Sugali MN. DDoS attack detection and mitigation using deep neural network in SDN environment. Comput Secur. 2024;138(21):103661. doi:10.1016/j.cose.2023.103661. [Google Scholar] [CrossRef]

5. Najafimehr M, Zarifzadeh S, Mostafavi S. DDoS attacks and machine-learning-based detection methods: a survey and taxonomy. Eng Rep. 2023;5(12):e12697. doi:10.1002/eng2.12697. [Google Scholar] [CrossRef]

6. Agostinello D, Genovese A, Piuri V. Anomaly-based intrusion detection system for DDoS attack with deep learning techniques. In: Proceedings of the 20th International Conference on Security and Cryptography; 2023 Jul 10–12; Rome, Italy: SCITEPRESS-Science and Technology Publications. p. 267–75. doi:10.5220/0012146100003555 [Google Scholar] [CrossRef]

7. Kumar D, Pateriya RK, Gupta RK, Dehalwar V, Sharma A. DDoS detection using deep learning. Procedia Comput Sci. 2023;218(1):2420–9. doi:10.1016/j.procs.2023.01.217. [Google Scholar] [CrossRef]

8. Elubeyd H, Yiltas-Kaplan D. Hybrid deep learning approach for automatic DoS/DDoS attacks detection in software-defined networks. Appl Sci. 2023;13(6):3828. doi:10.3390/app13063828. [Google Scholar] [CrossRef]

9. Shieh CS, Ho FA, Horng MF, Nguyen TT, Chakrabarti P. Open-set recognition in unknown DDoS attacks detection with reciprocal points learning. IEEE Access. 2024;12(4):56461–76. doi:10.1109/ACCESS.2024.3388149. [Google Scholar] [CrossRef]

10. Dai B, Seljak U. Sliced iterative normalizing flows. arXiv:2007.00674. 2021. [Google Scholar]

11. Chapaneri R, Shah S. Multi-level Gaussian mixture modeling for detection of malicious network traffic. J Supercomput. 2021;77(5):4618–38. doi:10.1007/s11227-020-03447-z. [Google Scholar] [CrossRef]

12. Najafimehr M, Zarifzadeh S, Mostafavi S. A hybrid machine learning approach for detecting unprecedented DDoS attacks. J Supercomput. 2022;78(6):8106–36. doi:10.1007/s11227-021-04253-x. [Google Scholar] [PubMed] [CrossRef]

13. Shieh CS, Nguyen TT, Horng MF. Detection of unknown DDoS attack using convolutional neural networks featuring geometrical metric. Mathematics. 2023;11(9):2145. doi:10.3390/math11092145. [Google Scholar] [CrossRef]

14. Nguyen TL, Kao H, Nguyen TT, Horng MF, Shieh CS. Unknown DDoS attack detection with fuzzy C-means clustering and spatial location constraint prototype loss. Comput Mater Contin. 2024;78(2):2181–205. doi:10.32604/cmc.2024.047387. [Google Scholar] [CrossRef]

15. Maseer ZK, Kadhim QK, Al-Bander B, Yusof R, Saif A. Meta-analysis and systematic review for anomaly network intrusion detection systems: detection methods, dataset, validation methodology, and challenges. IET Netw. 2024;13(5–6):339–76. doi:10.1049/ntw2.12128. [Google Scholar] [CrossRef]

16. Udurume M, Shakhov V, Koo I. Comparative analysis of deep convolutional neural network—bidirectional long short-term memory and machine learning methods in intrusion detection systems. Appl Sci. 2024;14(16):6967. doi:10.3390/app14166967. [Google Scholar] [CrossRef]

17. Lansky J, Ali S, Mohammadi M, Majeed MK, Karim SHT, Rashidi S, et al. Deep learning-based intrusion detection systems: a systematic review. IEEE Access. 2021;9:101574–99. doi:10.1109/ACCESS.2021.3097247. [Google Scholar] [CrossRef]

18. Laskar M, Huang J, Smetana V, Stewart C, Pouw K, An A, et al. Extending isolation forest for anomaly detection in big data via k-means. ACM Transact Cyber-Phys Syst. 2021;5(4):41. doi:10.1145/3460976. [Google Scholar] [CrossRef]

19. Zheng X, Yang S, Wang X. SF-IDS: an imbalanced semi-supervised learning framework for fine-grained intrusion detection. In: ICC 2023-IEEE International Conference on Communications; 2023 May 28–Jun 1. Rome, Italy: IEEE; 2023. p. 2988–93. doi:10.1109/ICC45041.2023.10279032 [Google Scholar] [CrossRef]

20. Gueriani A, Kheddar H, Mazari AC. Enhancing IoT security with CNN and LSTM-based intrusion detection systems. In: 2024 6th International Conference on Pattern Analysis and Intelligent Systems (PAIS); 2024 Apr 24–25. EL OUED, Algeria: IEEE; 2024. p. 1–7. doi:10.1109/PAIS62114.2024.10541178 [Google Scholar] [CrossRef]

21. Iliyasu AS, Deng H. N-GAN: a novel anomaly-based network intrusion detection with generative adversarial networks. Int J Inf Technol. 2022;14(7):3365–75. doi:10.1007/s41870-022-00910-3. [Google Scholar] [CrossRef]

22. Chalapathy R, Chawla S. Deep learning for anomaly detection: a survey. arXiv:1901.03407. 2019. [Google Scholar]

23. Fan Q, Li X, Wang P, Jin X, Yao S, Miao S, et al. BDIP: an efficient big data-driven information processing framework and its application in DDoS attack detection. IEEE Trans Netw Serv Manag. 2024. doi:10.1109/TNSM.2024.3464729. [Google Scholar] [CrossRef]

24. Santos-Neto MJ, Bordim JL, Alchieri EAP, Ishikawa E. DDoS attack detection in SDN: enhancing entropy-based detection with machine learning. Concurr Comput. 2024;36(11):e8021. doi:10.1002/cpe.8021. [Google Scholar] [CrossRef]

25. Wang P, Yang LT, Nie X, Ren Z, Li J, Kuang L. Data-driven software defined network attack detection: state-of-the-art and perspectives. Inf Sci. 2020;513(4):65–83. doi:10.1016/j.ins.2019.08.047. [Google Scholar] [CrossRef]

26. Rabie OBJ, Selvarajan S, Hasanin T, Alshareef AM, Yogesh CK, Uddin M. A novel IoT intrusion detection framework using Decisive Red Fox optimization and descriptive back propagated radial basis function models. Sci Rep. 2024;14(1):386. doi:10.1038/s41598-024-51154-z. [Google Scholar] [PubMed] [CrossRef]

27. Srivastava G, Reddy KD, Supriya Y, Yenduri G, Hegde P, Gadekallu TR, et al. Federated learning enabled edge computing security for Internet of Medical Things: concepts, challenges and open issues. In: Srivastava G, Ghosh U, Lin JC-W, editors. Security and risk analysis for intelligent edge computing. Cham, Switzerland: Springer; 2023. p. 67–89. [Google Scholar]

28. Shitharth S, Mohammed GB, Ramasamy J, Srivel R. Intelligent intrusion detection algorithm based on multi-attack for edge-assisted internet of things. In: Security and risk analysis for intelligent edge computing. 1st ed. Cham, Switzerland: Springer; 2023. Vol. 103, p. 119–35. [Google Scholar]

29. Gawlikowski J, Tassi C, Ali M, Lee J, Humt M, Feng J, et al. A survey of uncertainty in deep neural networks. Artif Intell Rev. 2023;56(S1):1513–89. doi:10.1007/s10462-023-10562-9. [Google Scholar] [CrossRef]

30. Hariharan S, Rejimol Robinson RR, Prasad RR, Thomas C, Balakrishnan N. XAI for intrusion detection system: comparing explanations based on global and local scope. J Comput Virol Hacking Tech. 2023;19(2):217–39. doi:10.1007/s11416-022-00441-2. [Google Scholar] [CrossRef]

31. Lin H, Wu C, Masdari M. A comprehensive survey of network traffic anomalies and DDoS attacks detection schemes using fuzzy techniques. Comput Electr Eng. 2022;104:108466. doi:10.1016/j.compeleceng.2022.108466. [Google Scholar] [CrossRef]

32. Alduailij M, Khan QW, Tahir M, Sardaraz M, Alduailij M, Malik F. Machine-learning-based DDoS attack detection using mutual information and random forest feature importance method. Symmetry. 2022;14(6):1095. doi:10.3390/sym14061095. [Google Scholar] [CrossRef]

33. Mihoub A, Ben Fredj O, Cheikhrouhou O, Derhab A, Krichen M. Denial of service attack detection and mitigation for Internet of Things using looking-back-enabled machine learning techniques. Comput Electr Eng. 2022;98(3):107716. doi:10.1016/j.compeleceng.2022.107716. [Google Scholar] [CrossRef]

34. Saghezchi FB, Mantas G, Violas MA, de Oliveira Duarte AM, Rodriguez J. Machine learning for DDoS attack detection in Industry 4.0 CPPSs. Electronics. 2022;11(4):602. doi:10.3390/electronics11040602. [Google Scholar] [CrossRef]

35. Balasubramaniam S, Vijesh Joe C, Sivakumar TA, Prasanth A, Satheesh Kumar K, Kavitha V, et al. Optimization enabled deep learning-based DDoS attack detection in cloud computing. Int J Intell Syst. 2023;2023(1):2039217. doi:10.1155/2023/2039217. [Google Scholar] [CrossRef]

36. Aktar S, Yasin Nur A. Towards DDoS attack detection using deep learning approach. Comput Secur. 2023;129(9):103251. doi:10.1016/j.cose.2023.103251. [Google Scholar] [CrossRef]

37. Choobdar P, Naderan M, Naderan M. Detection and multi-class classification of intrusion in software defined networks using stacked auto-encoders and CICIDS2017 dataset. Wirel Pers Commun. 2022;123(1):437–71. doi:10.1007/s11277-021-09139-y. [Google Scholar] [CrossRef]

38. Phulre AK, Verma M, Mathur JPS, Jain S. Approach on machine learning techniques for anomaly-based web intrusion detection systems: using CICIDS2017 dataset. In: Verma OP, Wang L, Kumar R, Yadav A, editors. Machine intelligence for research and innovations. Singapore: Springer Nature Singapore; 2024. p. 59–72. [Google Scholar]

39. Halbouni A, Gunawan TS, Habaebi MH, Halbouni M, Kartiwi M, Ahmad R. CNN-LSTM: hybrid deep neural network for network intrusion detection system. IEEE Access. 2022;10(11):99837–49. doi:10.1109/ACCESS.2022.3206425. [Google Scholar] [CrossRef]

40. Shieh CS, Lin WW, Nguyen TT, Chen CH, Horng MF, Miu D. Detection of unknown DDoS attacks with deep learning and Gaussian mixture model. Appl Sci. 2021;11(11):5213. doi:10.3390/app11115213. [Google Scholar] [CrossRef]

41. Wang Y, Mu J, Zhu P, Hu Q. Exploring diverse representations for open set recognition. Proc AAAI Conf Artif Intell. 2024;38(6):5731–9. doi:10.1609/aaai.v38i6.28385. [Google Scholar] [CrossRef]

42. Korba AA, Boualouache A, Ghamri-Doudane Y. Zero-X: a blockchain-enabled open-set federated learning framework for zero-day attack detection in IoV. IEEE Trans Veh Technol. 2024;73(9):12399–414. doi:10.1109/TVT.2024.3385916. [Google Scholar] [CrossRef]

43. Bahm V, Seljak U. Probabilistic autoencoder. arXiv:2006.05479. 2022. [Google Scholar]

44. Sivagaminathan V, Sharma M, Henge SK. Intrusion detection systems for wireless sensor networks using computational intelligence techniques. Cybersecurity. 2023;6(1):27. doi:10.1186/s42400-023-00161-0. [Google Scholar] [CrossRef]

45. Fowlkes EB, Mallows CL. A method for comparing two hierarchical clusterings. J Am Stat Assoc. 1983;78(383):553–69. doi:10.1080/01621459.1983.10478008. [Google Scholar] [CrossRef]

46. Mohammed Sharif D, Beitollahi H, Fazeli M. Detection of application-layer DDoS attacks produced by various freely accessible toolkits using machine learning. IEEE Access. 2023;11:51810–9. doi:10.1109/ACCESS.2023.3280122. [Google Scholar] [CrossRef]

47. Zhao J, Xu M, Chen Y, Xu G. A DNN architecture generation method for DDoS detection via genetic alogrithm. Future Internet. 2023;15(4):122. doi:10.3390/fi15040122. [Google Scholar] [CrossRef]

48. Shieh CS, Nguyen TT, Chen CY, Horng MF. Detection of unknown DDoS attack using reconstruct error and one-class SVM featuring stochastic gradient descent. Mathematics. 2023;11(1):108. doi:10.3390/math11010108. [Google Scholar] [CrossRef]