A Comparative Study of Optimized-LSTM Models Using Tree-Structured Parzen Estimator for Traffic Flow Forecasting in Intelligent Transportation

1  Introduction

Short-term traffic prediction is one of the crucial factors for urban transportation management that provide significant benefits for efficient traffic control and optimization [1]. By accurately forecasting traffic patterns, authorities can proactively implement dynamic traffic signal adjustments, refine traffic management strategies, and optimize resource allocation, to mention a few. These measures help mitigate congestion, reduce travel time, and enhance the overall efficiency of the road networks [2,3]. Furthermore, precise traffic predictions contribute to sustainability by minimizing fuel consumption through optimal route selection and reducing emissions via adaptive traffic management systems [4].

Effective traffic management depends on accurate traffic flow prediction, among other critical factors. The Long Short-term Memory (LSTM) network has emerged as a widely utilized deep learning algorithm for capturing temporal dependencies in traffic data, enabling the forecasting of traffic conditions over both short and long time intervals [5]. Additionally, the LSTM networks effectively model the sequential nature of time-dependent traffic dynamics, making them well-suited for traffic prediction tasks [6–8].

Several researchers have developed LSTM-based models for short-term traffic prediction, achieving varying degrees of accuracy. In [9], a method is proposed that integrates Random Forest-Recursive Feature Elimination (RF-RFE) for feature selection with the LSTM network optimized through Bayesian optimization. This approach effectively addresses imbalanced traffic data using the Synthetic Minority Over-Sampling Technique (SMOTE). A dynamically optimized LSTM model for short-term traffic flow prediction is introduced in [10]. The preprocessing phase employs Asym-Gentle Adaboost with a Cost-Sensitive support vector machine (AGACS) to eliminate outliers. Additionally, the model’s hidden layer structure is optimized using Chaotic Particle Swarm Optimization (CPSO), enhancing both efficiency and generalization. The study in [11] presents a model that leverages Variational Mode Decomposition (VMD) with Improved Dung Beetle Optimization to refine the LSTM-based approach (IDBO-LSTM), thereby improving predictive accuracy. Furthermore, reference [12] proposes an Improved Particle Swarm Optimization (IPSO) with radial basis function combined with LSTM model. This method incorporates the Support Vector Machine (SVM) for feature fusion, further strengthening its predictive capabilities.

To address the aforementioned challenges, this research proposes a Tree-structured Parzen Estimator-optimized LSTM (TPE-LSTM) model for short-term traffic prediction. The input data undergoes preprocessing, including data smoothing and normalization, before being fed into the TPE-LSTM model. The core of the model is the LSTM network, which directly processes the input data streams. The Tree-structured Parzen Estimator (TPE) iteratively optimizes the hyperparameters of the LSTM by evaluating performance at the hidden layer. It employs two probability density functions—one representing well-performing hyperparameters (classified as “good” when their probability is below a predefined threshold) and the other capturing suboptimal configurations (classified as “bad” when their probability meets or exceeds the threshold). This optimization process enhances the model’s predictive accuracy and efficiency in traffic forecasting. Such combinations enable selecting the best setups for improved and accurate output predictions. The contributions of this work are:

•   The Tree-structured Parzen Estimator (TPE) is utilized with the LSTM to tune its hyperparameters that are involved in the hidden layers and affect traffic prediction at the output. This optimization dynamically adjusts the hyperparameters of the LSTM unless the accuracy of the prediction reaches the desired limit.

•   A comparison of optimizers: Adaptive Moment Estimation (Adam), Root Mean Square Propagation (RMSProp), and Stochastic Gradient Descend with Momentum (SGDM) is performed to choose the most accurate optimization for the LSTM to perform the traffic prediction.

•   Comparison of the proposed model with the latest deep learning hybrid algorithms involving LSTM is performed to validate its accuracy.

The remaining part of this paper is organized as follows: Section 2 explains related work, while Section 3 introduces the methodology description of the proposed model and describes the performance evaluation indicators. Section 4 presents the simulation results and discussion, while Section 5 concludes the paper and highlights future investigations.

2  Literature Review

This section studies the latest deep learning algorithms used for traffic prediction involving LSTM. The scheme in [13] optimizes toll lane schedules with a Particle Swarm Optimization-Long Short-term Memory (PSO-LSTM) model, but oversimplifies traffic dynamics and convergence to local minima issues. The model in [14] performs short-term traffic prediction by integrating attention mechanism and convolutional networks with LSTM. The Tent mapping-enhanced Dung Beetle Optimization (TDBO) is utilized for feature selection and parameters optimization in [15]. However, these methods are complex in terms of processing and convergence. The Whale Optimization Algorithm (WOA) and LSTM with self-attention, as explained in [16], optimize traffic flow forecasting by incorporating spatial, temporal, and weather-related features. But the focuses majorly remain on long-term data trends. The method in [17] employs the LSTM merged with the Dijkstra algorithm for optimizing real-time route guidance to avoid congestion and pollution. However, the algorithm convergence is time-consuming. The authors in [18] utilize three algorithms: the Empirical Mode Decomposition (EMD), which decomposes traffic data into components, the LSTM network to predict telecom base station traffic and a Whale optimization with the LSTM for improved accuracy. Also, the Empirical Mode Decomposition (EMD) decomposes non-smooth telecom base station traffic data into intrinsic mode functions, which is often devoid of distinct physical or practical meanings. However, it has a high computational time. The scheme in [19] proposes an Autonomous Underwater Vehicle (AUV) trajectory prediction model called the Nonlinear Kepler Optimization-BiLSTM Variable Attention for capturing temporal and variable dependencies alongside with the Nonlinear Kepler Optimization (NKO) for hyperparameters tuning. However, it requires prior knowledge of the underwater route. The authors propose an LSTM-based prediction model optimized by the Improved Genetic Algorithm (IGA) to enhance road traffic flow forecasting accuracy in [20]. It prioritizes enhancing the LSTM parameters through the Improved Genetic Algorithm (IGA), which leads to complexity of computation. In [21] and [22], the authors propose Cosine Adaptive Particle Swarm Optimization with LSTM (CAPSO-LSTM) for urban green area prediction and Particle Swarm Optimization with LSTM (PSO-LSTM) for short-term urban rail passengers flow forecasting. However, the algorithms tend to convergence to local extrema. The study in [23] evaluates YOLOv8 for vehicle detection in Intelligent Transportation System (ITS), demonstrating an 18% precision improvement and faster inference times compared to YOLOv5, using aerial drone data. However, factors such as a vehicle shape, lighting conditions, and relative sizes affect the performance. The scheme in [24] explores vehicle detection in ITS using YOLOv8, focusing on aerial images captured via modified unmanned aerial vehicles (UAVs) to enhance algorithm adaptability across varied scenarios. YOLOv8x outperformed YOLOv8n with higher precision, recall, and F1 scores, highlighting its superior detection capabilities. However, the study’s limitations include the lack of exploration of computational efficiency and real-world deployment challenges for unmanned aerial vehicles-based ITS applications.

The reviewed literature explores various LSTM-based optimization techniques applied to traffic and route prediction. However, these methods often suffer from high computational complexity, convergence to local optima during hyperparameter tuning, limited generalizability of input data, and restricted prediction accuracy. To address these challenges, this paper proposes the TPE-LSTM model, which enhances road traffic forecasting while reducing computational overhead. The model leverages the Tree-structured Parzen Estimator (TPE) to optimize the LSTM hyperparameters through a probabilistic approach with adaptive search, distinguishing between favorable and unfavorable objective function values. This optimization strategy ensures faster and more accurate convergence. Subsequently, the optimized LSTM model performs accurate traffic prediction. Furthermore, the study compares three optimizers: Adam SGDM and RmsProp, for the LSTM to determine the most effective optimizer for the model.

3  Methodology Description of the Proposed Model

In this section, the proposed model is described that consists of a description of the data preprocessing TPE and LSTM.

3.1 Data Smoothing

Gaussian smoothing, also known as Gaussian blur, is applied to the traffic dataset to reduce noise and discrepancies in data. This technique is particularly effective for datasets contaminated with random noise. The foundation of Gaussian smoothing lies in the convolution of the dataset with a Gaussian function [25], which is a bell-shaped curve defined by the following probability density function:

G(x)=12πσ2e−x22σ2(1)

where G(x) is the Gaussian function, x is the variable, and σ is the standard deviation of the distribution.

The parameter σ controls the width of the Gaussian curve; a large σ results in high smoothing, while a small σ preserves the detail in the proportional manner. For the noisy traffic dataset, we apply Gaussian smoothing by convolving the dataset with the Gaussian function. Mathematically, the convolution of a dataset f(x) with a Gaussian function (x) is formulated as follows:

(f∗G)(x)=∫−∞∞f(t)G(x−t)dt(2)

This convolution integral effectively weights the nearby values of the dataset according to the Gaussian function, thereby averaging out noise. In discrete form, for a dataset represented as a sequence of values fi, the convolution can be expressed as:

(f∗G)i=∑j=−kkfi−jGj(3)

here, k is the number of points over which the Gaussian function is defined (usually determined by the standard deviation σ), and Gj is the discrete value of the Gaussian function.

In this convolution, we obtain an entirely new dataset, all points being averages of their neighboring points within a weighted context that can be computed using the Gaussian function. This process smooths out abrupt changes, reduces the effect of random noise, and produces a clean and easily interpretable dataset.

3.2 Data Normalization

After smoothing the original traffic data to reduce discrepancies in the dataset, it is streamlined and normalized to ensure that it falls within a standard range, making it easy to compare and process [25].

Data normalization is a method used to scale data to a specific range, typically [0, 1] or [−1, 1].

Given a smoothed dataset fi′, Min-Max normalization can be performed using the formula below:

fi′′=fi′−min(f′)max(f′)−min(f′)(4)

>here, fi′ represents the smoothed data points, while min(f′) and max(f′) are the minimum and maximum values of the smoothed dataset, respectively. The parameter fi″ denotes the normalized data point. This conversion rescales the data such that the minimum value becomes 0 and the maximum value becomes 1, and all other value are proportionally adjusted between these limits. If a different range is desired, such as [−1, 1], the corresponding mathematical formula is:

fi′′=2(fi˙′−min(f′)max(f′)−min(f′))−1(5)

3.3 Long Short-Term Memory (LSTM)

The LSTM network is used to overcome the vanishing gradient problem in Recurrent Neural Networks (RNNs). It is designed to predict both long and short-term time-series data [26]. The network consists of memory cells with self-connected recurrent units that can store information over time and are controlled by three gates: the input gate, the output gate, and the forget gate, as shown in Fig. 1 [27]. These gates control the flow of information into, out of, and within each cells to select, recall, or forget information depending on the context of the input sequence. The formulated expressions of the internal process of the LSTM framework are [28,29]:

ft=σ[(Wfh∗ht−1)+(Wfx∗xt)+bf](6)

Ctf=Ct−1∗ft(7)

it=σ[(Wih∗ht−1)+(Wix∗Xt)+bi](8)

gt=tanh⁡[(Wgh∗ht−1)+(Wgx∗Xt)+bg](9)

Cti=it∗gt(10)

Ct=Cti+Ctf(11)

Ot=σ[(Woh∗ht−1)+(Wox∗Xt)+b0](12)

ht=tanh⁡(Ct)∗Ot(13)

where ft, it, gt and Ot represent the forget gate, input gate, input node and output gate, respectively, with corresponding weights Wf, Wi, Wg and Wo. In t time step, cell memory Cti represents the updated state. The final state of the cell memory at the time step t is Ct, which is utilized in subsequent time step memory operations, and ℎt denotes the ultimate output memory unit. The parameters Wfℎ, Wiℎ, Wgℎ and Woℎ are the weights from the previous hidden state, while bf, bi, bg and bo are used as biases in the LSTM cell memory. The symbol * shows element-wise multiplication. The sigmoid function (x) and the tanh function tanℎ(x) are given by:

σ(x)=11+e−x(14)

tanh⁡(x)=1−e−x1+e−x(15)

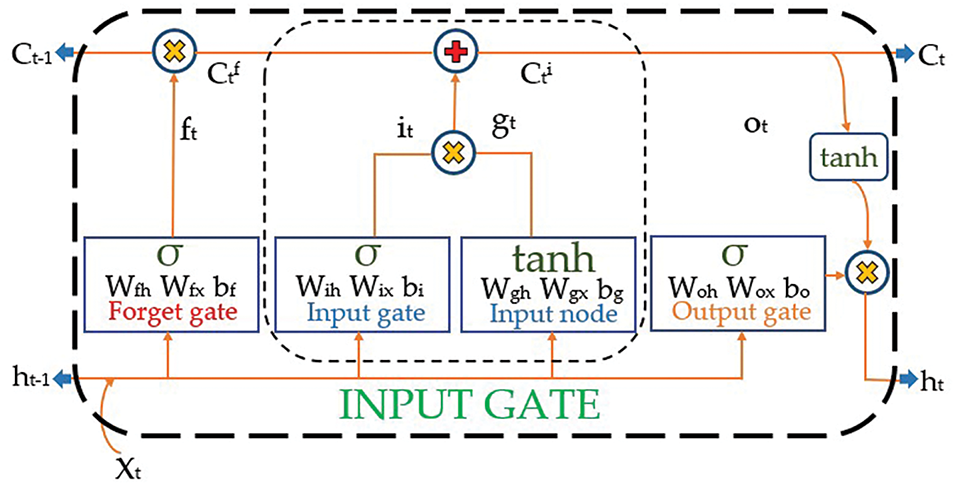
Figure 1: Framework structure of the LSTM network, demonstrating full process of input data through gates (forget gate, input gate and output gate) and activation functions (sigmoid and tanh)

3.4 Tree-Structured Parzen Estimator

The TPE is an advanced and modified Bayesian optimization method. Traditional Bayesian optimization method relies on Gaussian Processes (GPs) to model the surrogate function, which is used to predict the performance of hyperparameters [30]. However, the TPE uses a different approach by modeling the Probability Density Function (PDF) of good and bad hyperparameters separately using Kernel Density Estimation (KDE) [31].

The TPE structure, depicted in Fig. 2, involves defining hyperparameters within a search space, sampling points, and refining them based on model performance. Initially, hyperparameters to be optimize are identified. Gaussian Mixture Models (GMMs) generate random samples, and the acquisition function determines the next sampling points for performance evaluation.

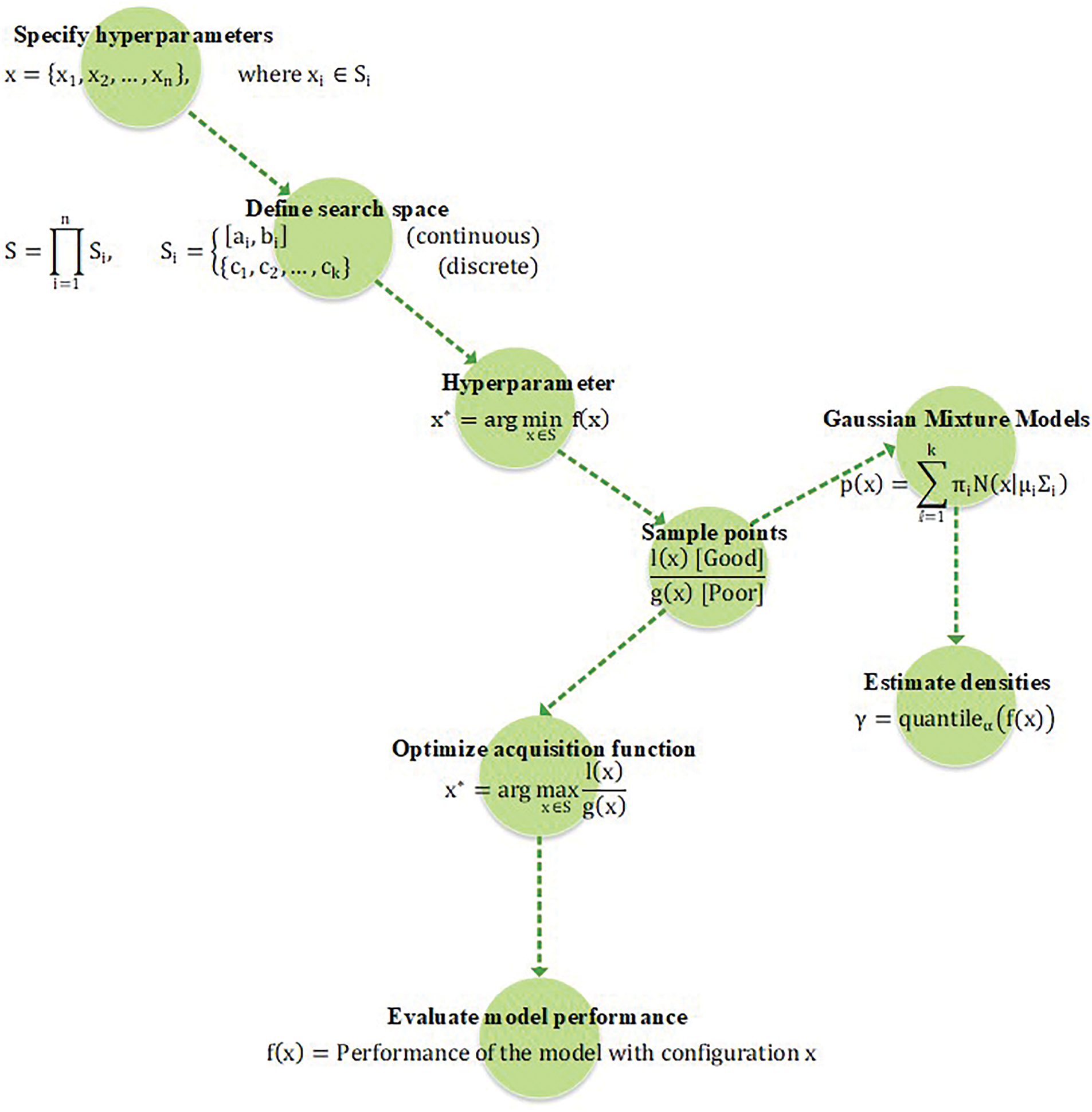
Figure 2: The Tree-structured Parzen Estimator (TPE) structural scenario. This structure illustrates the steps involved in the TPE for optimizing the GMMs to enhance the accuracy of predicted outcome

Fig. 3 outlines the mathematical workflow of TPE, from initialization to optimization [32]. The process begins with an initial hyperparameter set D = {(x1, y1), (x2, y2), …, (xn, yn)}, evaluated against the objective function. A thresholdlpartitions the data into good points Dl (objective values below l) and bad points Dg (above l). The KDE estimates PDFs l(x) and g(x). The acquisition function is optimized to find the next configuration x* by implementing (17), which is evaluated iteratively until optimal configurations are achieved.

α(x)=l(x)g(x)(16)

x∗=arg maxx⁡α(x)(17)

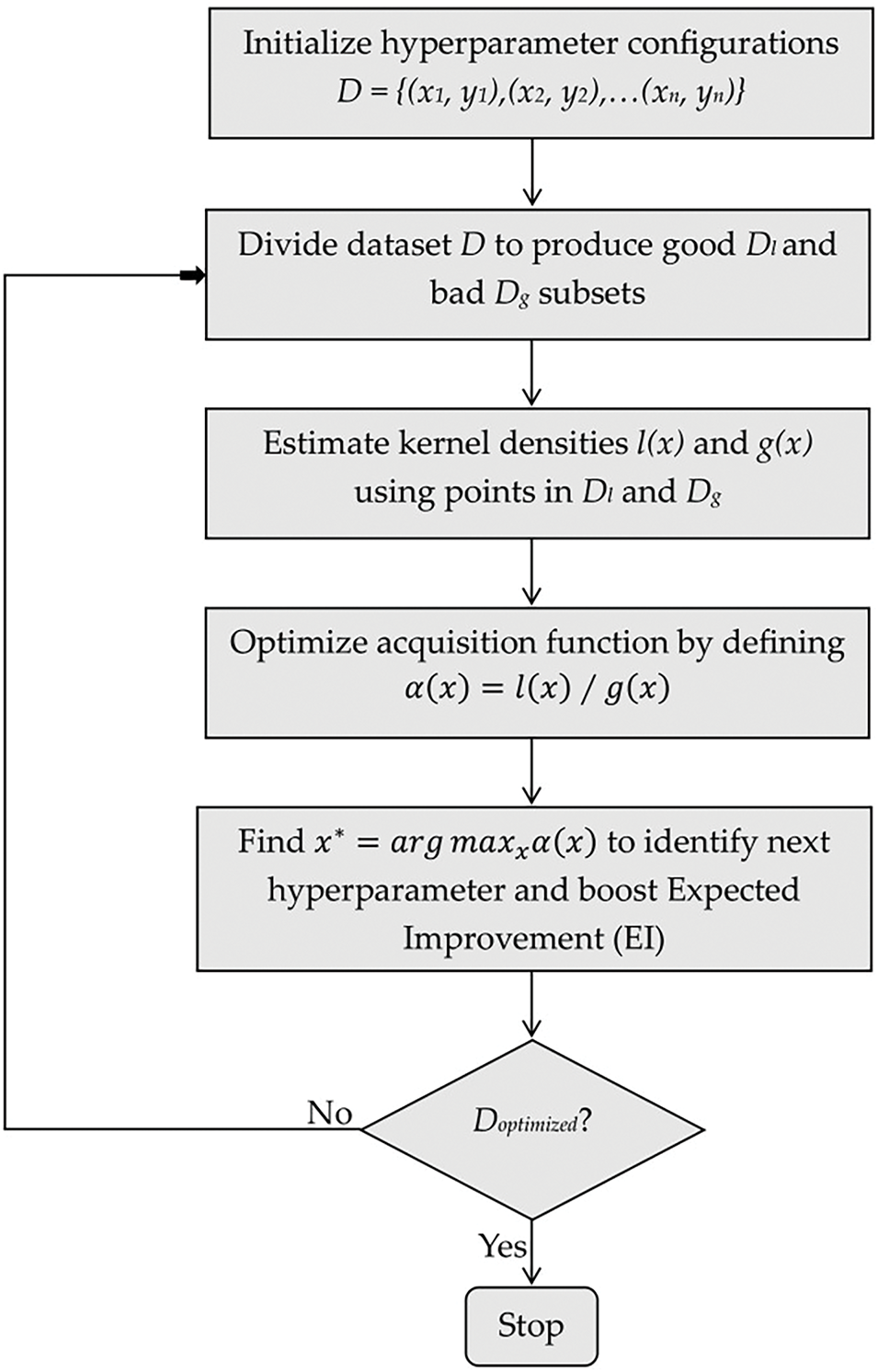
Figure 3: Algorithmic flowchart of the Tree-structured Parzen Estimator TPE for optimizing hyperparameters

Mathematically, TPE reformulates the optimization problem by expressing it in terms of two densities in Eqs. (18) and (19): l(x) for the hyperparameters that result in losses less than a certain threshold l, and g(x) for the hyperparameters that result in losses greater than or equal to l.

l(x)=p(x|y < l)(18)

g(x)=p(x|y ≥ l)(19)

where x represents the hyperparameters, and y represents the loss or performance metric of the model. The threshold l is often set to a quantile of the observed losses, ensuring a balance between exploration and exploitation.

The Expected Improvement (EI) criterion is used to select the next hyperparameters to evaluate, which are formulated as follows:

EI(x)=∫−∞l(l−y)p(y|x)dy(20)

Using Bayes’ theorem, the EI can be expressed in terms of l(x) and g(x) as:

EI(x)αl(x)g(x)[l−E[y|x,y<l]](21)

Eq. (21) allows the TPE to efficiently balance between exploring new hyperparameters and exploiting known good regions.

3.5 TPE-LSTM (Proposed Model)

The TPE and LSTM models are integrated to construct the TPE-LSTM model to predict short-term traffic flow as shown in Fig. 4. First, in data preprocessing, data smoothing is applied, specifically the Gaussian smoothing technique, to reduce noise and severe fluctuations in the data. This produces a more stable and continuous dataset. The smoothed data is then fed into the Min–Max normalization method, which transforms the data to a common scale without distorting differences in the ranges of values. Before feeding it into LSTM network further, pre-processed output captures how time series data changes over time while TPE uses an efficient way of exploring hyperparameters by modeling objective function distributions and focusing on regions that look promising.

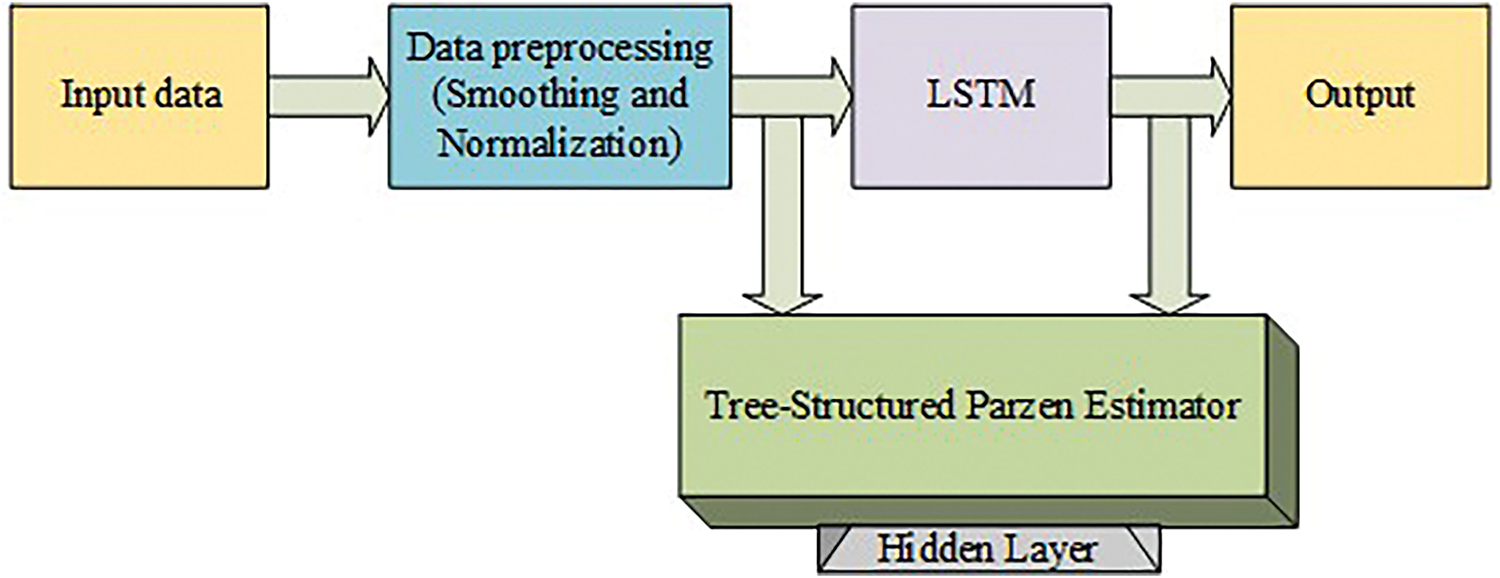
Figure 4: Block architecture of the proposed framework, showing the implementation process from input to output

The combination of the TPE with LSTM helps to optimize hyperparameters and improve time series prediction. We fine-tune parameters like number of hidden layers, total epochs count, LSTM optimizer and learning rate, all aimed at improving accuracy in traffic flow measurements.

3.6 Error Evaluation Indicators

Three evaluation indices are used to verify the performance of the suggested hybrid prediction model for short-term traffic flow. These evaluation metrics include Mean Square Error (MSE), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE), defined as follows:

MSE=1N∑i=1N(yi−y^i)2(22)

RMSE=∑i=1N(y^i−yi)2N(23)

MAE=1N∑i=1N|yi−y^i|(24)

here, N denotes the traffic volume (number of vehicles flowing per day), yi represents the real traffic flow, y^i is the predicted traffic flow, y¯ is the mean of the observed traffic data.

4  Simulation Results and Discussion

4.1 Dataset Description

The original traffic datasets from the Great Britain Traffic Database contain daily vehicles flow data spanning from 2000 to 2023. However, for this study, only the most recent traffic data from the past four years (2020–2023) is utilized for traffic flow prediction. The yearly traffic flow data was collected from various roads across England, UK, and is freely accessible [33].

The datasets contain traffic volume data from UK roads for the years 2020–2023, as shown in Table 1. In Dataset 1, the recorded traffic volumes were 27,000 (2020), 32,811 (2021), 26,196 (2022), and 23,364 (2023). Dataset 2 shows consistent traffic levels of around 22,373, 22,297, 22,240, and 22,257 for the respective years, while Dataset 3 recorded the respective values of 42,674, 42,562, 42,455, and 42,508.

Table 2 includes a Ryzen 5 5600X processor, AMD Radeon RX 5600 XT GPU, 16 GB RAM (3200 MHz), and a 256 GB SSD. An adequate air cooling system, and a 650-watt power supply supports the components. The system runs on Windows 11 (x64 bit) and uses MATLAB R2021a with the DL and ML Toolboxes.

4.2 Simulation Plots with Explanation

In the proposed research study, first data is preprocessed using Gaussian smoothing and data normalization methods. Fig. 5 demonstrates that the original traffic data exhibits high variability with sharp spikes, reflecting sudden traffic volume changes due to factors like peak hours, events, or accidents. In contrast, the smoothed data, obtained through Gaussian smoothing, shows a more uniform pattern with reduced fluctuations. This technique minimizes noise from random variations, sensor inaccuracies, and transient events, making it easier to identify underlying traffic trends.

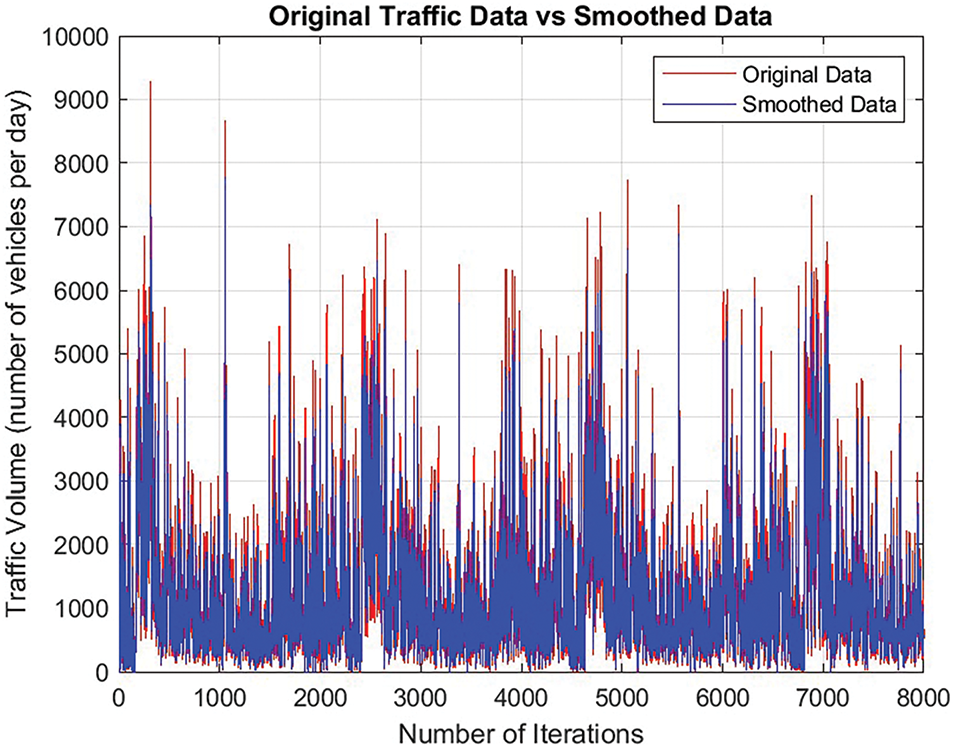
Figure 5: Gaussian smoothing technique is applied to the actual traffic volume

Fig. 6 shows normalized transport data on a scale from 0 to 1, facilitating input into an LSTM network for easier training. The peaks in the chart represent periods of high transportation activity, typically during rush hours, special events, weather-related disruptions, or accidents. These peaks reflect increased traffic due to factors like morning and evening commutes, large events, or adverse weather conditions, leading to higher traffic volumes or congestion. The variability in the data highlights the dynamic nature of transportation patterns.

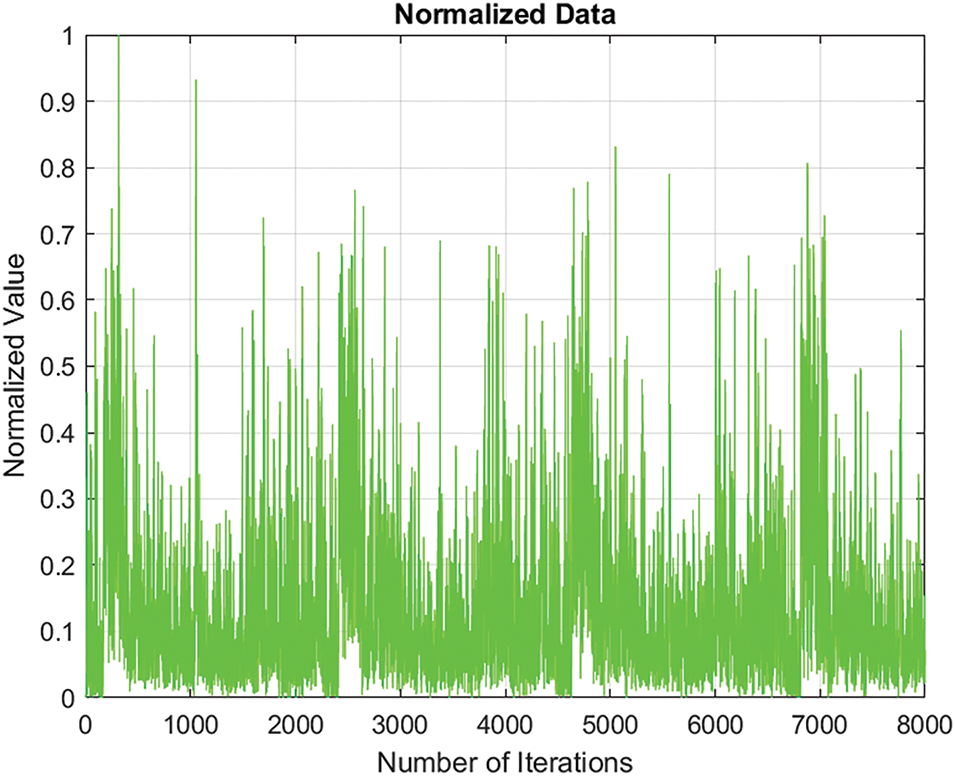
Figure 6: Data normalization method is implemented to measure and place the traffic data into a common range

After preprocessing steps were applied on actual traffic from 2020 until 2023, the data is smoothed and normalized for better readability and scalability prior to implementing the main model. Then the TPE is applied to measure the minimum observed objective and estimate the minimum objective in a probabilistic manner to guide the search for optimal hyperparameters. During optimization by TPE, the minimum observed objective reflects the actual minimum values of the objective function. It starts from a high value and then decreases. Initially, both the observed and estimated objectives drop rapidly, demonstrating significant early progress. As the process progresses, stress fluctuations suggest potential minima in different solution regions, causing some misalignment. As the process continues, both estimated and observed values converge to similar values that shows the stability of the algorithm to convergence. Table 3 highlights convergence values for the Adam, SGDM and RMSProp, with Adam showing the fastest performance.

Table 4 summarizes the key parameters used at each data processing stage, comparing the proposed model with counterpart schemes. It highlights optimization frameworks for training LSTM models, including TPE-LSTM, BO-LSTM, GA-LSTM, Att-LSTM, and TF-LSTM. All models utilize 40 hidden-layer neurons, a learning rate of 0.001, 20 epochs (8000 iterations), 125 dense layers, and mini-batches of 400.

The impact of a 0.7 dropout rate on the performance of the TPE-LSTM model is illustrated through error loss during training and testing with three optimizers: Adam, SGDM, and RMSProp. A 0.7 dropout rate deactivates 70% of the network’s neurons during training to prevent overfitting. Adam demonstrates rapid error loss reduction and quick convergence, effectively mitigating overfitting. SGDM occasionally shows slow and noisy error reduction, but benefits from dropout in controlling overfitting. RMSProp achieves stable gradient updates with low training and testing errors, indicating effective regularization.

The consistent use of a 0.7 dropout rate across Adam, SGDM, and RMSProp effectively reduces overfitting by encouraging the network to learn redundant representations, enhancing robustness and generalization. Among these, Adam achieved the best results on all traffic datasets, as shown in Table 5.

The TPE-LSTM model optimized with the Adam optimizer outperforms SGDM and RMSProp in predicting vehicle counts, as shown in Table 6. Adam’s adaptive learning rates and momentum enable superior generalization, allowing it to accurately capture traffic trends with minimal deviation during testing. In contrast, SGDM struggles due to fixed learning rates and slow convergence, while RMSProp underperforms because of its limited adaptability and lack of momentum.

Adam achieves the lowest training and testing losses for dataset 1 (0.0346 and 0.0337, respectively), compared to SGDM (0.0348 and 0.0340) and RMSProp (0.0347 and 0.0338). Error losses for datasets 2 and 3 are displayed in Table 6. Therefore, Adam is selected to enhance the accuracy of the TPE-LSTM model in traffic flow prediction.

The proposed TPE-LSTM model utilizes the TPE for optimization. To evaluate its performance in traffic prediction, the TPE is replaced by alternative optimizers in the counterpart schemes. These optimizers include Bayesian Optimization (BO), Genetic Algorithm-based Optimization (GA), Attention Optimization (Att), and Transformer-based (TF) prediction models. The Transformer-LSTM and Attention-LSTM approaches are implemented in [31,32], respectively, for predictive purposes.

Fig. 7 presents the actual and predicted traffic data from 2020 to 2023 for the proposed framework and other schemes. A refined search space for hyperparameters is built using the Tree-structured Parzen Estimator (TPE), which outperforms other methods by effectively identifying optimal regions for hyperparameters. This improves the LSTM network’s ability to capture complex temporal relationships. In BO-LSTM, the balance between exploration and exploitation is crucial; improper tuning may lead to local minima or inefficient exploration. In GA-LSTM, random mutations or premature convergence can slow down the search. While Att-LSTM’s attention mechanism helps focus on key features, they tend to cause overfitting or inefficiency with long sequences. Similarly, TF-LSTM’s self-attention mechanism may fail to capture high-frequency traffic variations, especially during peak times.

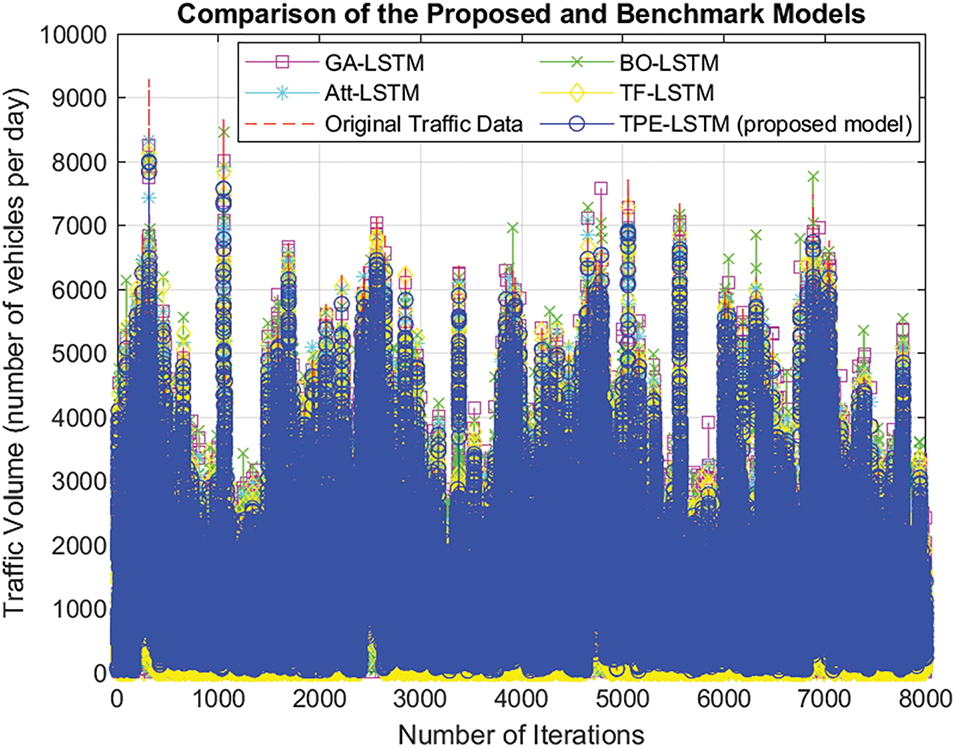
Figure 7: Traffic volume prediction (number of vehicles/day) comparison between the proposed model and counterpart of last four years (2020–23)

The prediction performance of traffic flow is evaluated using three metrics. MSE (Fig. 8a,b) calculates the average squared differences between predicted and actual values. RMSE (Fig. 9a,b) gives more weight to large errors due to squaring. MAE (Fig. 10a,b) measures the average magnitude of errors without considering their direction.

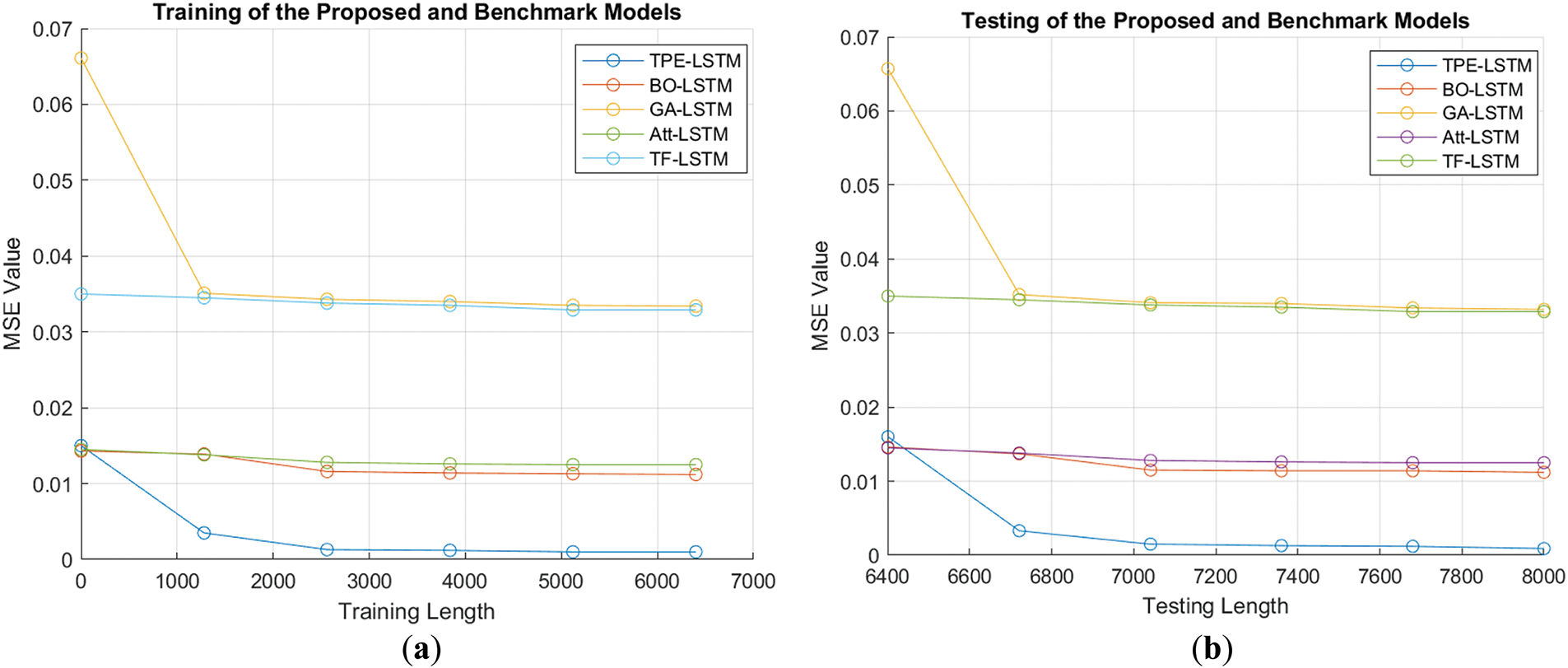
Figure 8: (a, b): Comparison of the MSE across training and testing lengths for the TPE-LSTM and counterpart

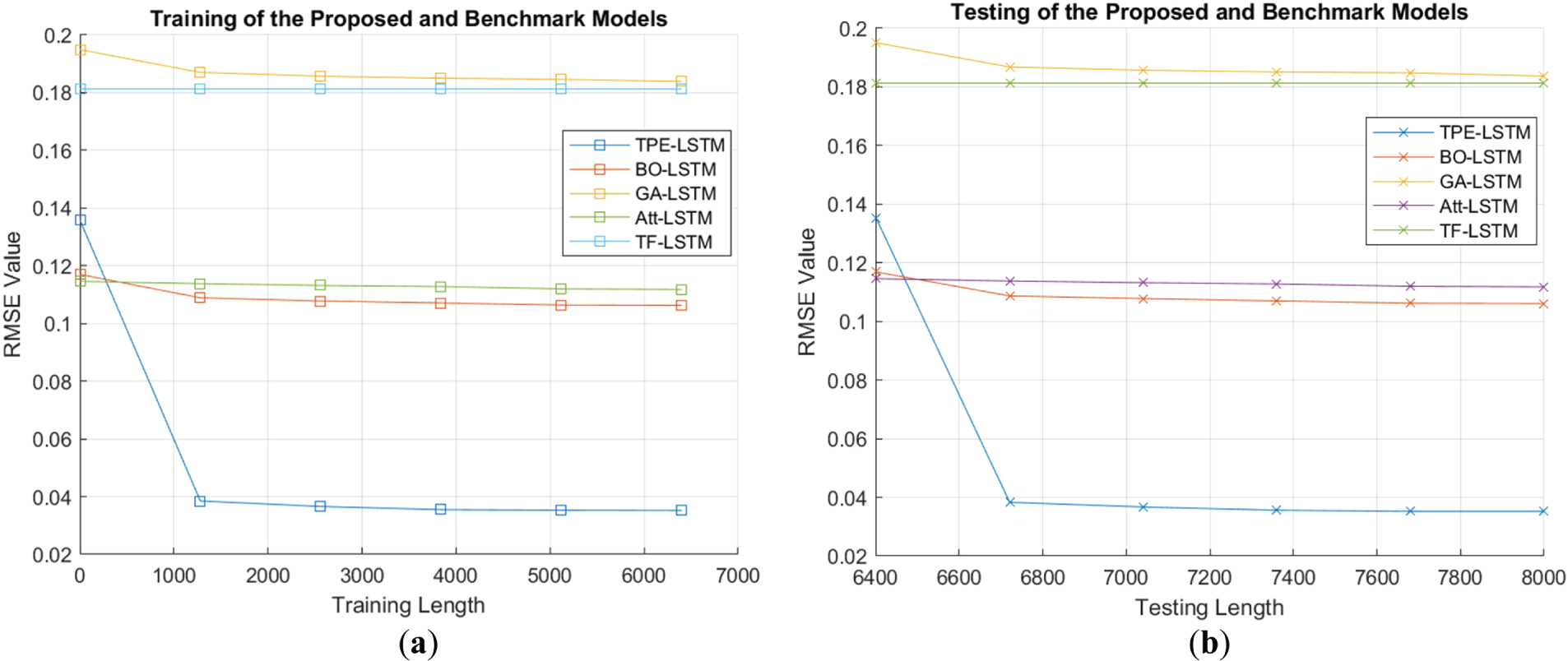
Figure 9: (a, b): Comparison of the RMSE across training and testing lengths for the TPE-LSTM and counterpart schemes

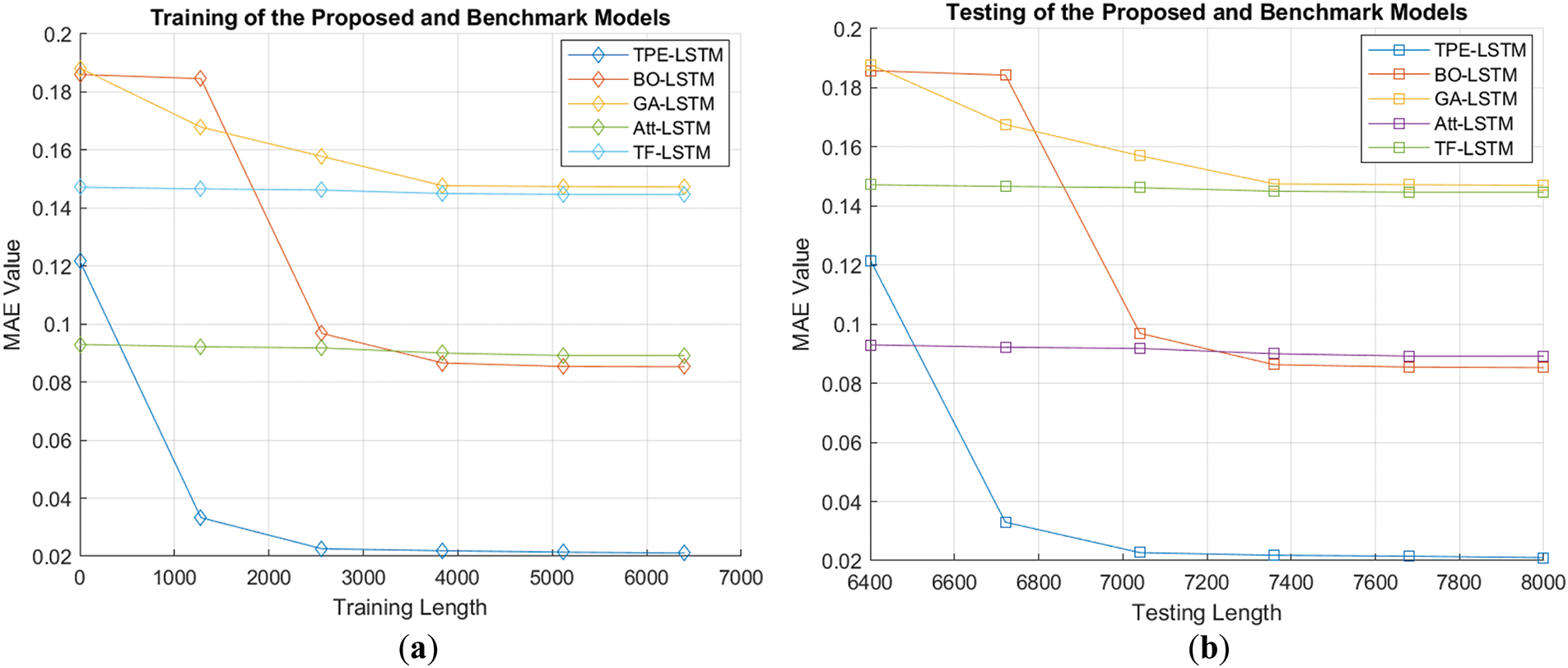
Figure 10: (a, b): Comparative analysis of MAE for the proposed and benchmark architectures over training and testing lengths

The MSE values for TPE-LSTM, BO-LSTM, Att-LSTM, TF-LSTM, and GA-LSTM on dataset 1 are 0.0012, 0.0114, 0.0125, 0.0329, and 0.0341, respectively, while the results for datasets 2 and 3 are detailed in Table 7.

The TPE-LSTM model outperforms the counterpart schemes in MSE due to its probabilistic search, effectively locating optimal hyperparameters by modeling their likelihood in good or bad regions. The BO-LSTM, using Bayesian Optimization with a surrogate model, struggles with high-dimensional, noisy datasets like traffic data, resulting in suboptimal configurations and high MSE. GA-LSTM, which optimizes hyperparameters through selection, crossover, and mutation, faces premature convergence in complex datasets, reducing population diversity and increasing MSE. While Att-LSTM improves accuracy by prioritizing relevant inputs, its attention mechanism is prone to overfitting in noisy datasets. Similarly, TF-LSTM, despite its ability to model complex dependencies through self-attention and sequential patterns with LSTM, struggles with computational inefficiencies and overparameterization in high-dimensional traffic data.

Fig. 9a,b compares the RMSE during training and testing for the proposed and counterpart models on dataset 1, with values of 0.0354, 0.1068, 0.1118, 0.1813, and 0.1846 for TPE-LSTM, BO-LSTM, Att-LSTM, TF-LSTM, and GA-LSTM, respectively. RMSE values for datasets 2 and 3 are provided in Table 7. The RMSE and MSE values are lower for TPE-LSTM indicating better accuracy than the counterpart methods. This is done through the usage of TPE which efficiently explores hyperparameter space. Fig. 10a,b demonstrates the MAE comparison of all the models with the same training and testing lengths, respectively.

The results of all error indicators proved that the TPE-LSTM on all traffic datasets achieved better results in testing phase, indicating improved accuracy for traffic prediction, as shown in Table 7. This suggests that the model effectively avoids overfitting.

To handle traffic data, the proposed model incorporates an adaptive mechanism within the TPE framework, which dynamically optimizes hyperparameters to maintain efficiency even if data volumes increase. This ensures the model’s ability to process and analyze large-scale traffic data streams without significant latency, a critical requirement for smart city systems.

To address noisy or incomplete traffic data, robust preprocessing techniques are used such as Gaussian smoothing and data normalization. Gaussian smoothing helps mitigate the impact of outliers and abrupt fluctuations by applying a weighted average to the data points. Data normalization further ensures that all input features are scaled to a uniform range. By combining these techniques with the sequential learning capability of the LSTM architecture, the TPE-LSTM model can effectively reconstruct reliable patterns and maintain prediction accuracy even when faced with noisy or incomplete data. The TPE-LSTM has diverse applications in ITS, including traffic flow prediction and dynamic route optimization to reduce congestion and improve travel time reliability, to mention a few.

The developed TPE-LSTM model demonstrates significant potential for improving short-term traffic flow predictions in ITS. However, like any machine learning approach, it has certain limitations that must be acknowledged and critically examined. One key challenge lies in the model’s black-box nature, as LSTM networks, combined with the TPE optimization process, do not inherently provide insights into how predictions are made. This lack of interpretability can hinder trust and adoption in critical ITS applications where transparency is essential. Additionally, the model might struggle to adapt to rapid changes in traffic behavior caused by long-term infrastructural developments or policy changes, such as new traffic regulations or the introduction of autonomous vehicles. These scenarios may require continuous retraining and validation, which could be resource-intensive and time-consuming. Furthermore, the reliance on historical data may limit the model’s ability to predict unprecedented traffic scenarios or disruptions. Finally, while TPE helps in optimizing hyperparameters efficiently, it might overlook unconventional or highly specific hyperparameter settings that could yield better performance for niche ITS scenarios. Addressing these issues may involve incorporating explainable techniques, developing adaptive learning mechanisms, and combining data-driven approaches with rule-based systems to improve robustness and flexibility.

To evaluate the contributions of different preprocessing techniques, optimization methods, and model architectures, comprehensive ablation studies are conducted. Table 8 summarizes the performance of various configurations, highlighting the incremental improvements achieved through specific modifications. These experiments were conducted on three traffic datasets to ensure robustness and generalizability.

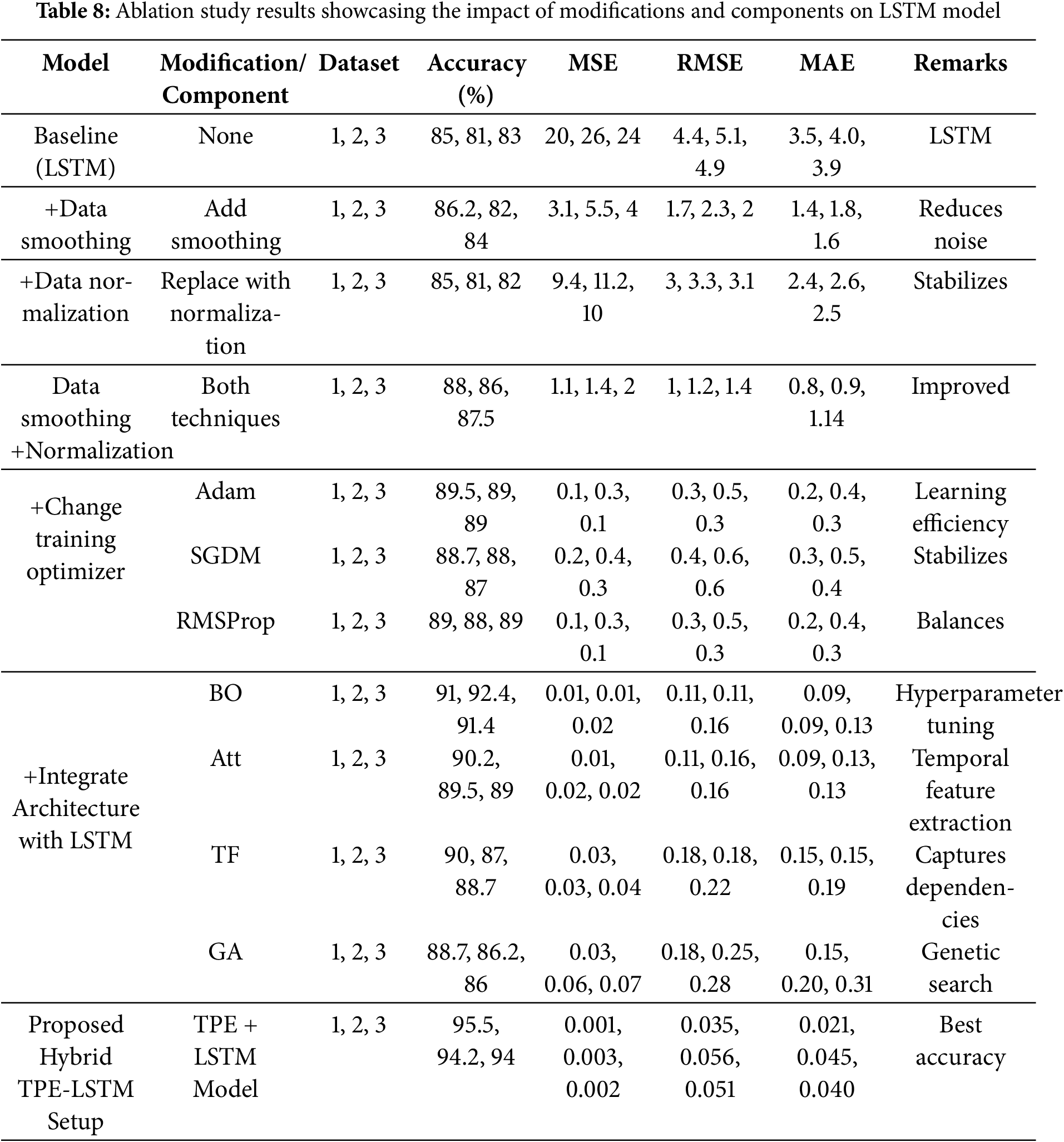
The results demonstrate that each modification positively impacts the model’s performance, with the proposed Hybrid TPE-LSTM setup achieving the highest accuracy and the lowest error metrics across all datasets. This indicates the effectiveness of combining TPE-based optimization with LSTM architecture, showcasing its potential as one of the state-of-the-art solutions for traffic flow prediction.

5  Conclusions and Future Work

The short-term traffic prediction in intelligent transportation is performed by optimizing the hyperparameters of the LSTM using Tree-Structured Parzen Estimator (TPE) making TPE-LSTM as the proposed model. The TPE reduced the error accuracy by an adaptive probabilistic research and divided the objective function into good and bad values. This also reduced the computational efficiency by avoiding convergence to local optima and performing random search, which is generally time-intensive with reduced error accuracy. The comparison of the proposed model verified its accuracy over benchmark schemes, achieving an accuracy of 95.5%, with MSE (0.0012), RMSE (0.0354), and MAE (0.0214) for traffic dataset 1. For dataset 2, the model achieved an accuracy of 94.2%, with corresponding values of 0.0032 (MSE), 0.0566 (RMSE), and 0.0452 (MAE). Dataset 3 reported an accuracy of 94%, with 0.0026 (MSE), 0.0510 (RMSE), and 0.0407 (MAE). The model is capable to predict traffic for transportation networks and can be effectively used within an acceptable threshold of accuracy for short-term traffic prediction. To make the model further effective, it could be utilized in future investigation for real-time traffic flow prediction by using the convolutional networks for features extraction directly from the real-time traffic data.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Hamza Murad Khan implemented the idea of the proposed work under the supervision of Anwar Khan. Santos Gracia Villar and Luis Alonso Dzul Lopez provided resources, performed revision and evaluated the technical content of the manuscript. Abdulaziz Almaleh and Abdullah M. Al-Qahtani contributed to data curation, analysis and streamlined the overall flow of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data openly available in a public repository. “The data that support the findings of this study are openly available in [UK Traffic Dataset site] at [https://roadtraffic.dft.gov.uk (accessed on 2 November 2024)]”.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhu F, Lv Y, Chen Y, Wang X, Xiong G, Wang FY. Parallel transportation systems: toward IoT-enabled smart urban traffic control and management. IEEE Trans Intell Transp Syst. 2020;21(10):4063–71. doi:10.1109/TITS.2019.2934991. [Google Scholar] [CrossRef]

2. Qiao J. Smart city and intelligent upgrading of urban transportation system: based on sustainable investment strategy. In: 2022 Second International Conference on Advanced Technologies in Intelligent Control, Environment, Computing & Communication Engineering (ICATIECE); 2022 Dec 16–17; Bangalore, India. p. 1–6. doi:10.1109/ICATIECE56365.2022.10047675. [Google Scholar] [CrossRef]

3. Ma Y, Zhang Z, Ihler A. Multi-lane short-term traffic forecasting with convolutional LSTM network. IEEE Access. 2020;8:34629–43. doi:10.1109/ACCESS.2020.2974575. [Google Scholar] [CrossRef]

4. Zhao D, Chen F. A hybrid ensemble model for urban lane-level traffic flow prediction. IEEE J Radio Freq Identif. 2022;6:820–4. doi:10.1109/JRFID.2022.3217031. [Google Scholar] [CrossRef]

5. Cheng Z, Lu J, Zhou H, Zhang Y, Zhang L. Short-term traffic flow prediction: an integrated method of econometrics and hybrid deep learning. IEEE Trans Intell Transp Syst. 2021;23(6):5231–44. doi:10.1109/TITS.2021.3052796. [Google Scholar] [CrossRef]

6. Zhang Y, Xin D. A diverse ensemble deep learning method for short-term traffic flow prediction based on spatiotemporal correlations. IEEE Trans Intell Transp Syst. 2022;23(9):16715–27. doi:10.1109/TITS.2021.3131248. [Google Scholar] [CrossRef]

7. Haputhanthri D, Wijayasiri A. Short-term traffic forecasting using LSTM-based deep learning models. In: 2021 Moratuwa Engineering Research Conference (MERCon); 2021 Jul 27–29; Moratuwa, Sri Lanka. p. 602–7. doi:10.1109/mercon52712.2021.9525670. [Google Scholar] [CrossRef]

8. Li J, Zhang Z, Meng F, Zhu W. Short-term traffic flow prediction via improved mode decomposition and self-attention mechanism based deep learning approach. IEEE Sens J. 2022;22(14):14356–65. doi:10.1109/JSEN.2022.3181451. [Google Scholar] [CrossRef]

9. Shang Q, Feng L, Gao S. A hybrid method for traffic incident detection using random forest-recursive feature elimination and long short-term memory network with Bayesian optimization algorithm. IEEE Access. 2020;9:1219–32. doi:10.1109/ACCESS.2020.3047340. [Google Scholar] [CrossRef]

10. Zhang Y, Xin D. Dynamic optimization long short-term memory model based on data preprocessing for short-term traffic flow prediction. IEEE Access. 2020;8:91510–20. doi:10.1109/ACCESS.2020.2994655. [Google Scholar] [CrossRef]

11. Zhao K, Guo D, Sun M, Zhao C, Shuai H. Short-term traffic flow prediction based on VMD and IDBO-LSTM. IEEE Access. 2023;11:97072–88. doi:10.1109/ACCESS.2023.3312711. [Google Scholar] [CrossRef]

12. Zhang T, Xu J, Cong S, Qu C, Zhao W. A hybrid method of traffic congestion prediction and control. IEEE Access. 2023;11:36471–91. doi:10.1109/ACCESS.2023.3266291. [Google Scholar] [CrossRef]

13. Wang P, Zhao J, Gao Y, Sotelo MA, Li Z. Lane work-schedule of toll station based on queuing theory and PSO-LSTM model. IEEE Access. 2020;8:84434–43. doi:10.1109/ACCESS.2020.2992070. [Google Scholar] [CrossRef]

14. Zhang W, Shen W, Lin X. A short-term traffic flow prediction method of improved PSO-LSTM. In: 2023 3rd International Conference on Intelligent Communications and Computing (ICC); 2023 Nov 24–26; Nanchang, China. p. 394–9. doi:10.1109/ICC59986.2023.10421500. [Google Scholar] [CrossRef]

15. Li Y, Zhang J, Yan Y, Lei Y, Yin C. Enhancing network intrusion detection through the application of the dung beetle optimized fusion model. IEEE Access. 2024;12:9483–96. doi:10.1109/ACCESS.2024.3353488. [Google Scholar] [CrossRef]

16. Cao K, Liu Y, Duan L, Xu S, Jung H. Research on regional traffic flow prediction based on MGCN-WOALSTM. IEEE Access. 2023;11(5):126436–46. doi:10.1109/ACCESS.2023.3330909. [Google Scholar] [CrossRef]

17. Zhang Z, Fang C, Zhang J, Qian J, Su Q. Traffic guidance based on LSTM neural network and dual tracking dijkstra algorithm. In: 2020 IEEE 3rd International Conference on Information Systems and Computer Aided Education (ICISCAE); 2020 Sep 27–29; Dalian, China. 497503 p. doi:10.1109/iciscae51034.2020.9236823. [Google Scholar] [CrossRef]

18. Cheng J, Zhang H, Xu J. Traffic prediction model for telecommunication base stations based on improved WOA optimized LSTM and EMD. In: 2023 IEEE 5th International Conference on Power, Intelligent Computing and Systems (ICPICS); 2023 Jul 14–16; Shenyang, China. p. 1075–84. doi:10.1109/ICPICS58376.2023.10235735. [Google Scholar] [CrossRef]

19. Yao J, Yang J, Zhang C, Zhang J, Zhang T. Autonomous underwater vehicle trajectory prediction with the nonlinear Kepler optimization algorithm-bidirectional long short-term memory-time-variable attention model. J Mar Sci Eng. 2024;12(7):1115. doi:10.3390/jmse12071115. [Google Scholar] [CrossRef]

20. Zhang J, Qu S, Zhang Z, Cheng S. Improved genetic algorithm optimized LSTM model and its application in short-term traffic flow prediction. PeerJ Comput Sci. 2022;8:e1048. doi:10.7717/peerj-cs.1048. [Google Scholar] [PubMed] [CrossRef]

21. Tian H, Yuan H, Yan K, Guo J. A cosine adaptive particle swarm optimization based long-short term memory method for urban green area prediction. PeerJ Comput Sci. 2024;10(1):e2048. doi:10.7717/peerj-cs.2048. [Google Scholar] [PubMed] [CrossRef]

22. Liu S, Mariano VY. Short term passenger flow forecast of urban rail transit based on PSO-LSTM. In: 2023 International Conference on Advances in Electrical Engineering and Computer Applications (AEECA); 2023 Aug 18–19; Dalian, China. p. 758–62. doi:10.1109/AEECA59734.2023.00139. [Google Scholar] [CrossRef]

23. Bakirci M. Utilizing YOLOv8 for enhanced traffic monitoring in intelligent transportation systems (ITS) applications. Digit Signal Process. 2024;152(2):104594. doi:10.1016/j.dsp.2024.104594. [Google Scholar] [CrossRef]

24. Bakirci M. Enhancing vehicle detection in intelligent transportation systems via autonomous UAV platform and YOLOv8 integration. Appl Soft Comput. 2024;164(5):112015. doi:10.1016/j.asoc.2024.112015. [Google Scholar] [CrossRef]

25. Saleh MA, Ameen ZS, Altrjman C, Al-Turjman F. Computer-vision-based statue detection with Gaussian smoothing filter and EfficientDet. Sustainability. 2022;14(18):11413. doi:10.3390/su141811413. [Google Scholar] [CrossRef]

26. Chen Y, Guo J, Xu H, Huang J, Su L. Improved long short-term memory-based periodic traffic volume prediction method. IEEE Access. 2023;11:103502–10. doi:10.1109/ACCESS.2023.3305398. [Google Scholar] [CrossRef]

27. Khan A, Fouda MM, Do DT, Almaleh A, Rahman AU. Short-term traffic prediction using deep learning long short-term memory: taxonomy, applications, challenges, and future trends. IEEE Access. 2023;11:94371–91. doi:10.1109/ACCESS.2023.3309601. [Google Scholar] [CrossRef]

28. Tang J, Xu L, Wu X, Chen K. A short-term forecasting method for ionospheric TEC combining local attention mechanism and LSTM model. IEEE Geosci Remote Sens Lett. 2024;21:1001305. doi:10.1109/LGRS.2024.3373457. [Google Scholar] [CrossRef]

29. Xia L, Wang R, Ye H, Jiang B, Li G, Ma C, et al. Hybrid LSTM-transformer model for the prediction of epileptic seizure using scalp EEG. IEEE Sens J. 2024;24(13):21123–31. doi:10.1109/JSEN.2024.3401771. [Google Scholar] [CrossRef]

30. Kraemer R, Düzgöl O, Li S, Calabretta N. Data-driven SOA parameter discovery and optimization using Bayesian machine learning with a parzen estimator surrogate. J Light Technol. 2024;42(2):721–31. doi:10.1109/JLT.2023.3316353. [Google Scholar] [CrossRef]

31. Liu JX, Leu JS. Enhancing short-term load forecasting with technical indicators and tree-structured parzen estimator. In: 2023 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm); 2023 Oct 31–Nov 3; Glasgow, UK. p. 1–6. doi:10.1109/SmartGridComm57358.2023.10333876. [Google Scholar] [CrossRef]

32. Massaoudi M, Abu-Rub H, Refaat SS, Trabelsi M, Chihi I, Oueslati FS. Enhanced deep belief network based on ensemble learning and tree-structured of parzen estimators: an optimal photovoltaic power forecasting method. IEEE Access. 2021;9:150330–44. doi:10.1109/ACCESS.2021.3125895. [Google Scholar] [CrossRef]

33. UK traffic data site. [cited 2025 Jan 1]. Available from: https://roadtraffic.dft.gov.uk. [Google Scholar]