Numerical Homogenization Approach for the Analysis of Honeycomb Sandwich Shell Structures

1  Introduction

In the realm of engineering, there has been a notable shift towards the use of fewer resources and the enhancement of the design of lightweight structures, particularly within transportation systems, in response to ecological trends [1]. This evolution has led to the widespread adoption of Additive Manufacturing (AM) technologies, serving as a direct response to these trends. AM processes offer a wide parameter space that significantly influences the mechanical properties, while simultaneously reducing the manufacturing costs through a decreased material usage [2,3].

Recent advancements in AM have emphasized the integration of sustainable practices and energy-efficient production methods. Binder jetting and directed energy deposition techniques have revealed to be optimal to achieve a high material utilization while minimizing waste, making them suitable for large-scale industrial applications [4,5]. Moreover, the development of hybrid AM systems has facilitated the production of multi-material components with enhanced mechanical and thermal properties [6,7].

The rapid expansion of AM technologies can be attributed to their flexible processes, ability to incorporate multi-materials, and capability to modify function, structure, and material properties, while reducing the production costs up to 50% [8]. The Artificial Intelligence (AI) and machine learning tools have increasingly been integrated into AM workflows to optimize the process parameters, to detect defects, and to predict material properties, leading to an improved efficiency and product quality [9,10]. These tools are particularly valuable for automating the design of complex lattice structures [11].

This complexity in AM production processes enables the creation of periodic structures, which boast advantageous mechanical properties relative to weight or volume ratios [3]. Among these highly periodic structures, lattice cells and porous cellular structures, presenting different applications and potentials due to their tailored properties [12–14]. A recent work has also explored the use of AM in creating bio-inspired designs for energy absorption and impact resistance, with potential applications in aerospace and automotive engineering.

To fully harness the potential of AM, engineers must identify and integrate the most affecting process parameters for design and modeling phases, requiring the development and selection of appropriate design tools [8], such as the Representative Volume Element (RVE). The RVE serves as the smallest statistically representative volume or cellular element of the entire domain, ensuring a constitutive response error below 5% [15]. It must strike a balance between being smaller than the overall structural domain, yet large enough to encompass defects for a realistic mechanical response [16,17].

Recent advancements in computational modeling, such as phase-field approaches, have improved the simulation of RVE properties under complex loading conditions, enabling a more accurate prediction of the material behavior [18,19]. These methods, together with traditional finite element strategies, are particularly useful for anisotropic and heterogeneous materials.

Various studies have proposed methods to determine the optimal size of the RVE to maintain the computational efficiency [20,21]. Notable contributions in literature, including works by Masters et al. [22], Christensen [23], and Wang et al. [24,25], have provided solutions for deriving the equivalent mechanical properties from RVE definitions, predominantly relying on the description of cellular components through Euler-Bernoulli beams. Alternative approaches, such as energy equivalence methods, offer solutions for more complex cellular topologies [26,27].

Numerous studies have explored the wave propagation in lattice structures and their corresponding frequency response [28–30]. The recent research has introduced novel approaches for bandgap engineering in lattice structures, enabling their use in vibration isolation and noise reduction applications [31,32].

Homogenization techniques allow for the investigation of an equivalent continuum representation of periodic solid cellular structures. Asymptotic expansion approaches have facilitated the development of multiscale methods [33,34]. In such a context, the Finite Element Method (FEM) remains the predominant tool for analyzing continuum micromechanics problems, with periodic homogenization methods leveraging single repeating volume elements [35,36].

Innovative hybrid homogenization approaches combine experimental data and numerical simulations, thus enhancing the accuracy of material property predictions for AM components [37,38]. These techniques are particularly beneficial for high-performance applications in aerospace and biomedical engineering.

Recent advancements, such as the mechanics of structural genome, offer innovative approaches to periodic homogenization, allowing for the analysis and division of structures into basic repeating elements for macro-to-micro scale transitions [39]. Noteworthy studies about the homogenization procedure of periodic cellular structures, including those by Seiler et al. [40], Alaimo et al. [41], Mantegna et al. [42], and Tumino et al. [43], have introduced novel concepts, such as waviness and simplified homogenization approaches.

Advanced studies, such as the investigation of thermo-elastic buckling in honeycomb micro plates integrated with FG-GNPs reinforced Epoxy skins [44], provide valuable insights that complement our methodology. In the last years, the advancement in the field of auxetic honeycomb structures has further emphasized their potential in engineering applications. For instance, Kiani et al. [45] conducted a detailed thermo-mechanical bending analysis of sandwich cylindrical panels with auxetic honeycomb cores, highlighting their enhanced mechanical behavior under combined loading conditions. Similarly, Amirabadi et al. [46] explored the free vibrational behavior of conical sandwich shells with functionally graded auxetic honeycomb cores, focusing on the dynamic advantages of such structures. These studies underscore the growing interest and utility of auxetic honeycomb designs, aligning with the focus of this work on innovative lattice-based materials.

From an analytical point of view in the existing literature, a comprehensive investigation into the structural behavior of doubly-curved shells reinforced with honeycomb cores has been conducted by Tornabene et al. [47]. Their study encompasses the modal analysis of a large variety of shell geometries across various practical applications of such shells. Utilizing a theoretical framework grounded in the equivalent single layer and principles of differential geometry, as extensively discussed in another study [48], numerical computations were carried out employing the generalized differential quadrature method [49].

In conclusion, this study significantly contributes to advancing the understanding of honeycomb sandwich panels and lattice structures, validated through the work of Tornabene et al. [47] and based on the research by Valvano [50] for the application of the RVE method. The integration of advanced computational tools, sustainable practices, and bio-inspired designs demonstrates the potential of AM to revolutionize engineering applications. By leveraging recent innovations in AI, multi-material systems, and hybrid modeling, this study provides a valid reference for a further development in the field of lightweight and high-performance structures.

2  Homogenization Theory

The central idea behind the sandwich core, as employed here, relies on lattice structures. In particular, rectangular, hexagonal, and reentrant cell geometries are considered, as they represent the most commonly used cell configurations in practical applications and they are extensively documented in literature. In the present study, these cellular geometries are examined in two distinct scenarios: in the first one, the model is validated through cell geometries existing in the literature, in particular the cell geometries investigated by Tornabene et al. [47]. In the second scenario, the equivalent volume among the three geometries remains constant. In this context, the homogenization of these cells plays a pivotal role in understanding and analizing the structural properties of sandwich panels. The homogenization approach, the same used by Valvano in his work [50], allows for the simplification of the complexity of cell structures by treating the composite material of the panel as a continuous medium with uniform properties. Specifically, considering rectangular, hexagonal, and reentrant cell geometries, the homogenization procedure is applied to characterize the effective mechanical behavior of the sandwich panel. Based on this homogenization technique, the intricate variations within the cell geometries are effectively considered, facilitating accurate predictions of the overall structural response of the sandwich sructure. Importantly, the utilisation of homogenization techniques not only ensures a computational efficiency but also guarantees a comprehensive analysis of the plate behavior, thus enhancing the reliability and robustness of the engineering design process.

In the numerical code used herein, each cell has been drawn as a three dimentional (3D) solid, as shown in Fig. 1. The discretization process of the cells involves the use of C3D20R elements, i.e., a 20-node quadratic brick, with reduced integration. The reduced integration is a numerical method used to solve the numerical “locking” problem, usually linked to thin-walled structures [51–53]. The mesh convergence study is not reported here for the sake of brevity.

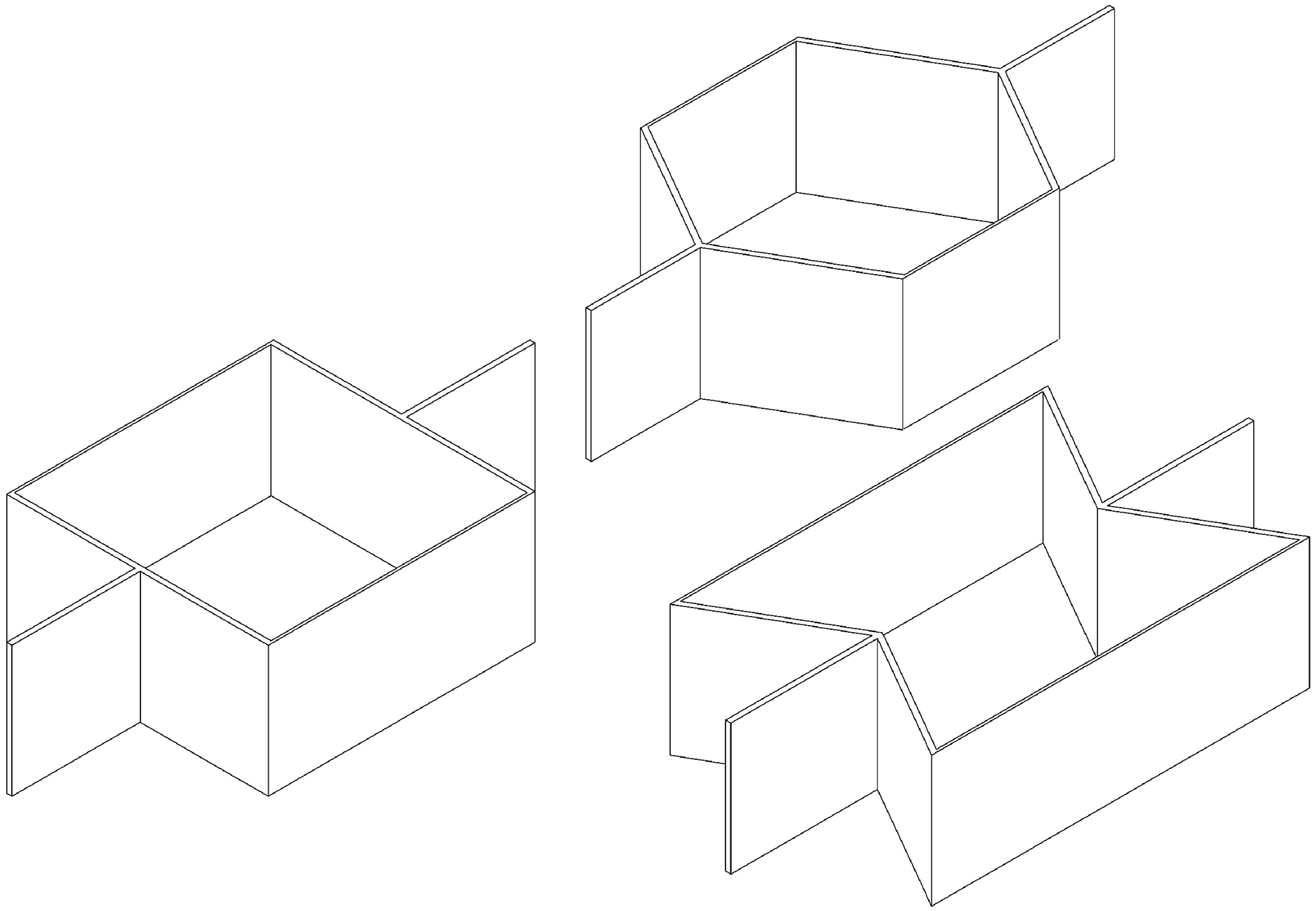
Figure 1: Representation of the honeycomb cells: rectangular, hexagonal and reentrant geometry

In materials science, RVEs (Fig. 2) serve as crucial tools for characterizing the mechanical properties of complex structures, particularly in the case of honeycomb sandwich panels. RVEs represent the minimum repeating unit within these structures (cells), encapsulating the essential statistical variations in material properties. By defining the RVE, researchers can extract the key mechanical core properties such as Young’s modulus (E), Poisson’s ratio (ν), and shear modulus (G). For honeycomb lattice panels, whose cells exhibit an isotropic behavior under traction or shear loading, these properties suffice. For cells with an anisotropic behavior, additional properties are considered (i.e., Ei, νij and Gij, with i,j=x,y,z). Also, the kinematic components referred to the x,y and z directions are indicated as u,v and w, respectively. This approach facilitates the development of accurate computational models and enhances the knowledge of the material behavior, crucial for the advancement in engineering and design.

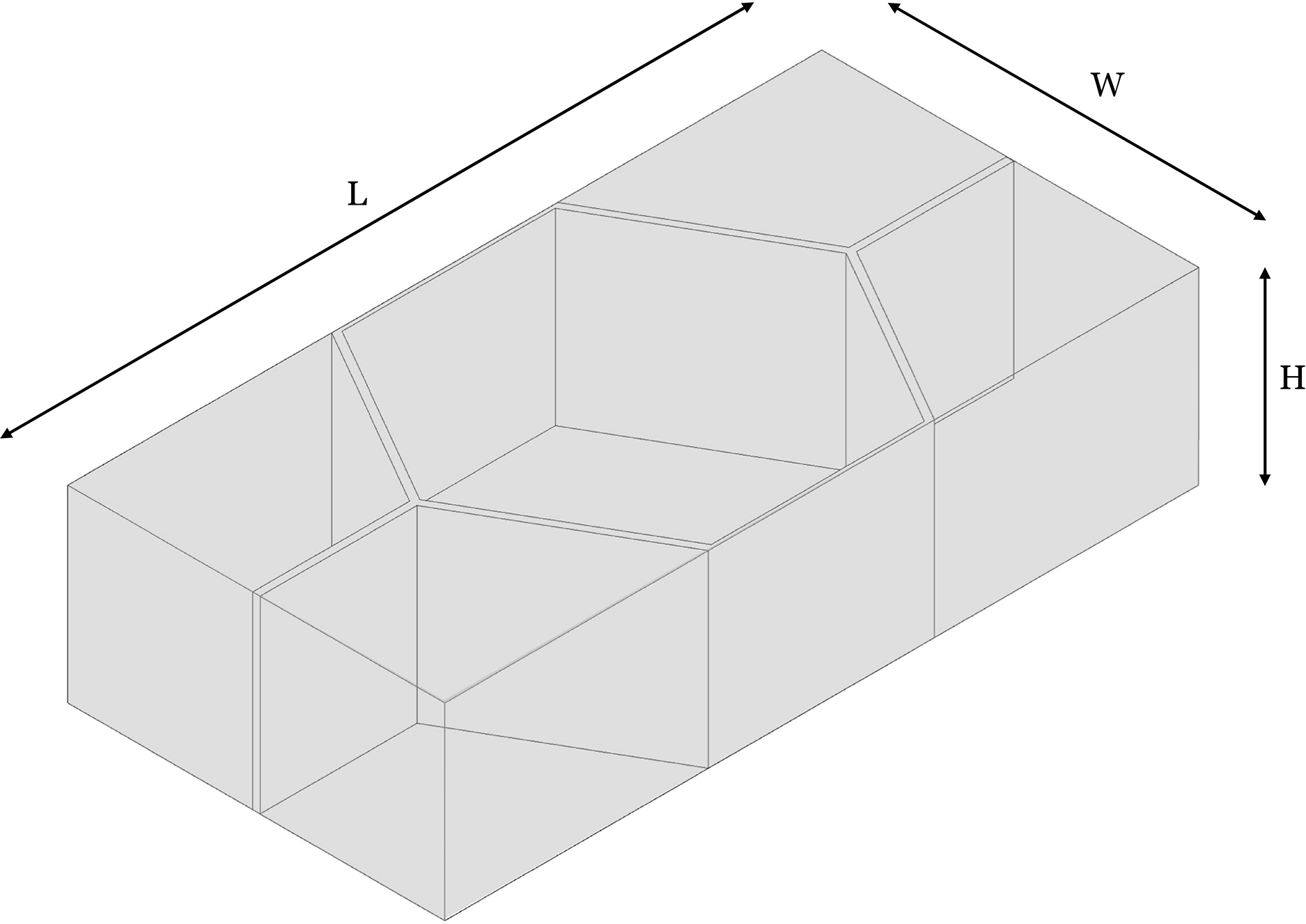
Figure 2: RVE for an arbitrary hexagonal cell

For consistency reasons, in the current homogenization campaign is essential to ensure the displacement compatibility along the faces of the RVE by applying double periodic boundary conditions to surfaces with normals differing from the loaded face. Fig. 3 illustrates an example of hexagonal cell, with three positive surfaces in each direction named x+, y+ and z+. For readability purposes, the negative surfaces are not depicted in the figure. According to Valvano [50], the notion of periodicity entails that the RVE undergoes uniform deformations, without separation or overlap among neighboring volume elements [35,54]. This condition of periodicity can be formulated as follows:

ui=ϵ¯ikxk+ui∗(1)

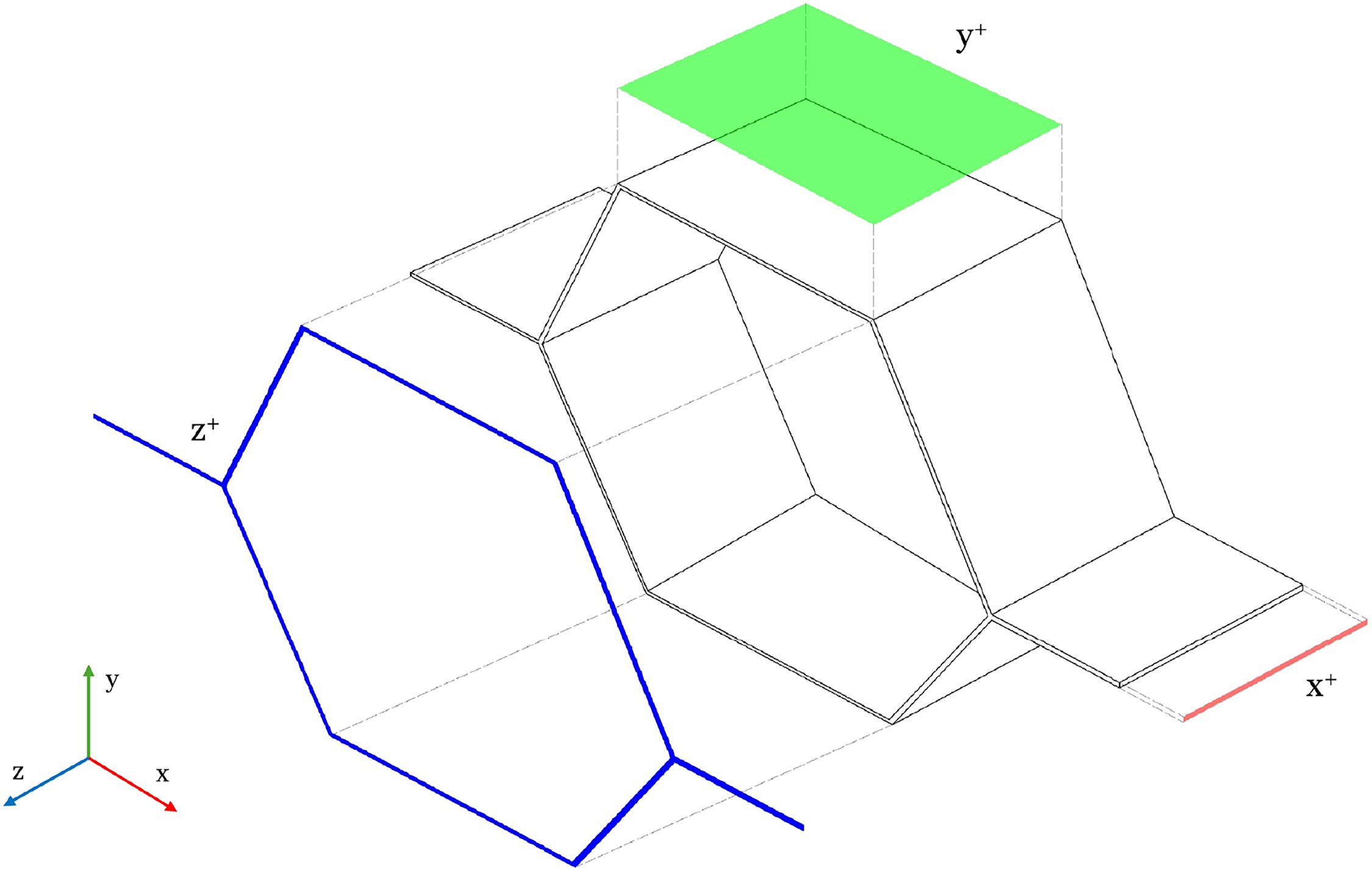
Figure 3: Constrained faces and reference system of an arbitrary hexagonal cell

ui are the mechanical displacements for a generic i-th direction (i.e., i=1,2,3 refers to the displacement components along x,y and z directions, in compact notation). Thus, the displacements on a pair of opposite boundary surfaces writes:

uij+=ϵ¯ikxkj++ui∗uij−=ϵ¯ikxkj−+ui∗(2)

Here, ϵ¯ik represents the average strains, and ui∗ denotes the unknown periodic component of the displacement components on the boundary surfaces. In this context, index j denotes the normal direction for both the upper (+) and lower (–) boundary surfaces. The displacement variation between the upper and lower boundary surfaces can be characterized as:

uij+−uij−=ϵ¯ik(xkj+−xkj−)=ϵ¯ikΔxkj(3)

For a RVE in cubic shape, and in more general parallelepiped volume elements, the constant nature of Δxkj holds. As a result, a generalized formulation of periodic boundary conditions can be defined in the following manner:

uij+(x,y,z)−uij−(x,y,z)=cij(4)

In this equation, the constants cij refer to the stretching or contracting factors of the RVE. It is possible to define the average stresses σ¯ij and strains ϵ¯ij of the RVE as follows [50]:

ϵ¯ik=1V∫VϵijdV;σ¯ik=1V∫VσijdV(5)

The integrands ϵij and σij in Eq. (5) represent the local strains and stresses of the constituent volume elements.

To implement the double periodicity within the numerical code used, a novel routine has been here implemented in the Abaqus environment, which verifies the position of corresponding nodes placed on the opposite boundary surfaces (i.e., at x+ and x−). For each pair of nodes located on the external surfaces, a series of constraint equations is generated, as outlined below [42], i.e.,

ui+−ui−=Δuvi+−vi−=Δvwi+−wi−=Δw(6)

with

Δu=uref+−uref−Δv=vref+−vref−Δw=wref+−wref−(7)

In Eq. (6), the fundamental constraint equations are presented for a single direction. The mechanical displacements for each pair of i-th nodes can be correlated by introducing a Δ term, representing the stretch or dilation properties of the cellular structure. This parameter is determined based on a selected reference (ref) pair of nodes. Upon implementing the double periodicity condition, nodes within the mesh may intersect two distinct boundary surfaces with different normals. These intersecting nodes must remain unconstrained. For a fixed variation of loading and boundary conditions necessary to assess parameters such as Young’s modulus E, Poisson’s ratio ν, or shear modulus G, a comprehensive summary of boundaries, here adopted to define the orthotropic homogenized properties for the cell (i.e., Ex,Ey,Ez,νxy,νxz,νyz,Gxy,Gxz,Gyz), is provided in Table 1. In order to determine the Young modulus Ei in each direction i, traction has been enforced on the positive surfaces x+, y+ and z+ (Fig. 3), alternatively, through a prescribed displacement along the selected direction. Furthermore, the reaction force could be obtained from the lower boundary surfaces x−, y− and z−, where the prescribed displacement is set to zero only for the component in the load direction (i.e., x, y and z), as shown in Fig. 4 for the y-direction traction. To apply the boundary conditions, the definition of the outer boundary surfaces with respect to the direction of its normal is a crucial aspect. The boundary conditions are defined by enforcing a prescribed displacement on the FEM nodes lying on the boundary surfaces.

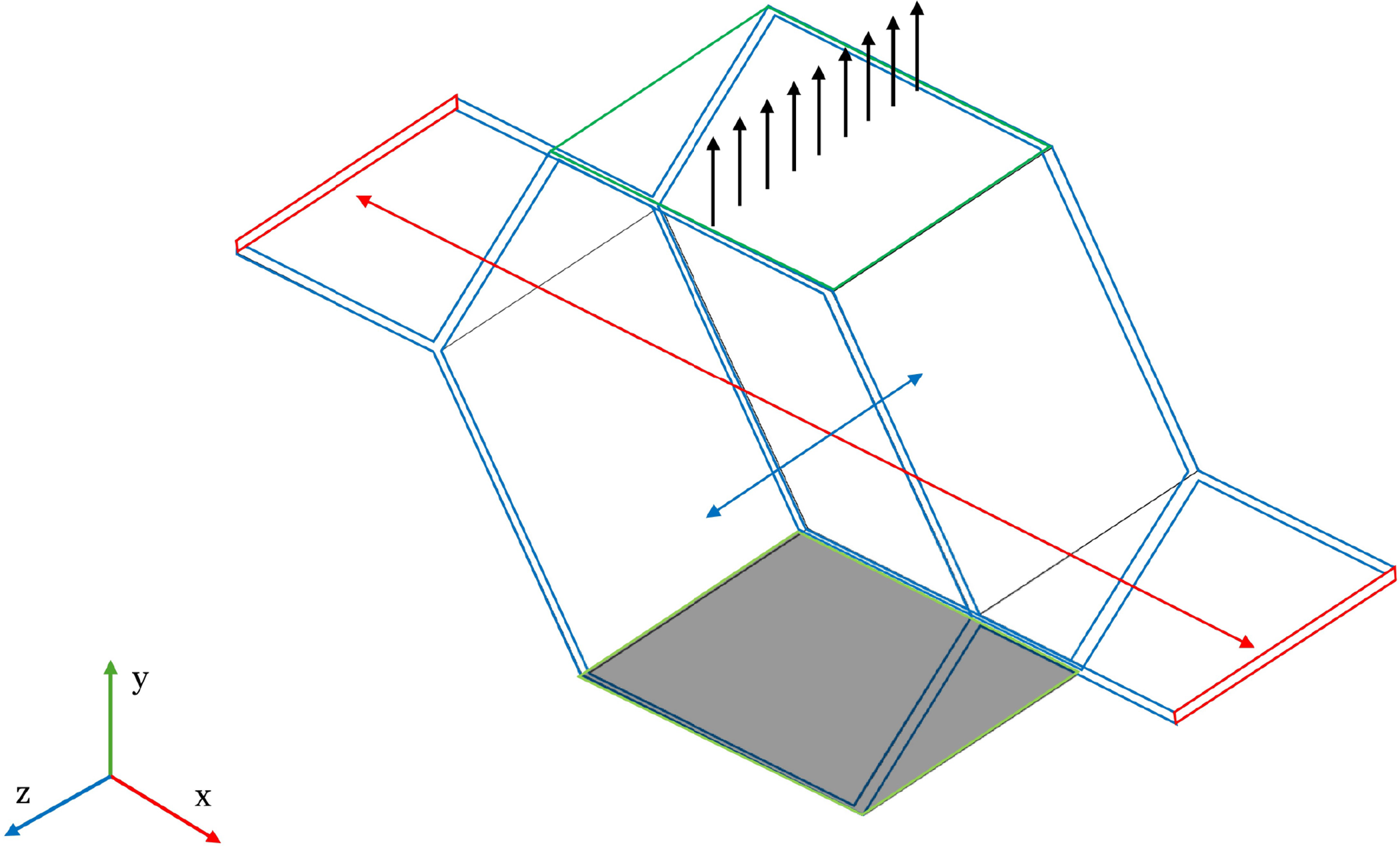
Figure 4: Traction test in y-direction. The load is applied on the y+ surface, while the y− surface (grey) is constrained in the y-direction

A series of pure traction tests are conducted to assess the Young’s modulus E and Poisson’s coefficient ν. Various geometries of the cell are examined, i.e., rectangular, hexagonal, and reentrant shapes. According to the Hooke’s law σ=Eϵ, the Young’s modulus E can be deduced from stress and strain data. Strain values are readily available since traction is applied as prescribed displacement on a boundary surface. The corresponding stress state can be computed using the reaction forces obtained from the opposite boundary surface, where the prescribed displacement is restricted solely to the component of the loading direction. Additionally, the equivalent stresses are determined as follows:

σeq=∑FreacAeq(8)

Here, Aeq is the area of the box cell where the load is applied (it is H∗W for a load applied in the x-direction, L∗W for a load applied in the z-direction, L∗H for a load applied in the y-direction). Freac represents the sum of reactions on the constrained face in the loading direction. At the same time, the Poisson’s coefficint ν writes:

νeq=−ϵtransvϵload(9)

As previously stated, ϵload is determined from the prescribed loading displacement. Conversely, ϵtransv needs to be computed along the two transversal directions using the following simple expressions, here shown for the specimen loaded in the z-direction: ϵxx=(ux+−ux−)/L or ϵyy=(vy+−vy−)/H. The same procedure must be applied for each loading direction. It is possible to obtain the shear modulus G, by knowing the stress and the strain and by using the Hooke law: τ=Gϵ.

In Figs. 5 and 6, the shear loading is represented. In particular, to define the shear modulus Gxy, the faces with normal y and z are constrained with double periodic boundary conditions (arrows), while the x-normal-positive face is loaded in the y-direction. Its opposite face (grey face) is constrained in the x and y directions. Gyx is calculated considering the faces with normal x and z constrained with double periodic boundary conditions (arrows), while the y-normal-positive face is loaded in the x-direction. Its opposite face (grey face) is constrained in the x and y directions. In any case, the shear modulus is calculated based on the reaction force in the load direction and generated on the parallel and opposite face of the loaded one, namely the restrained one.

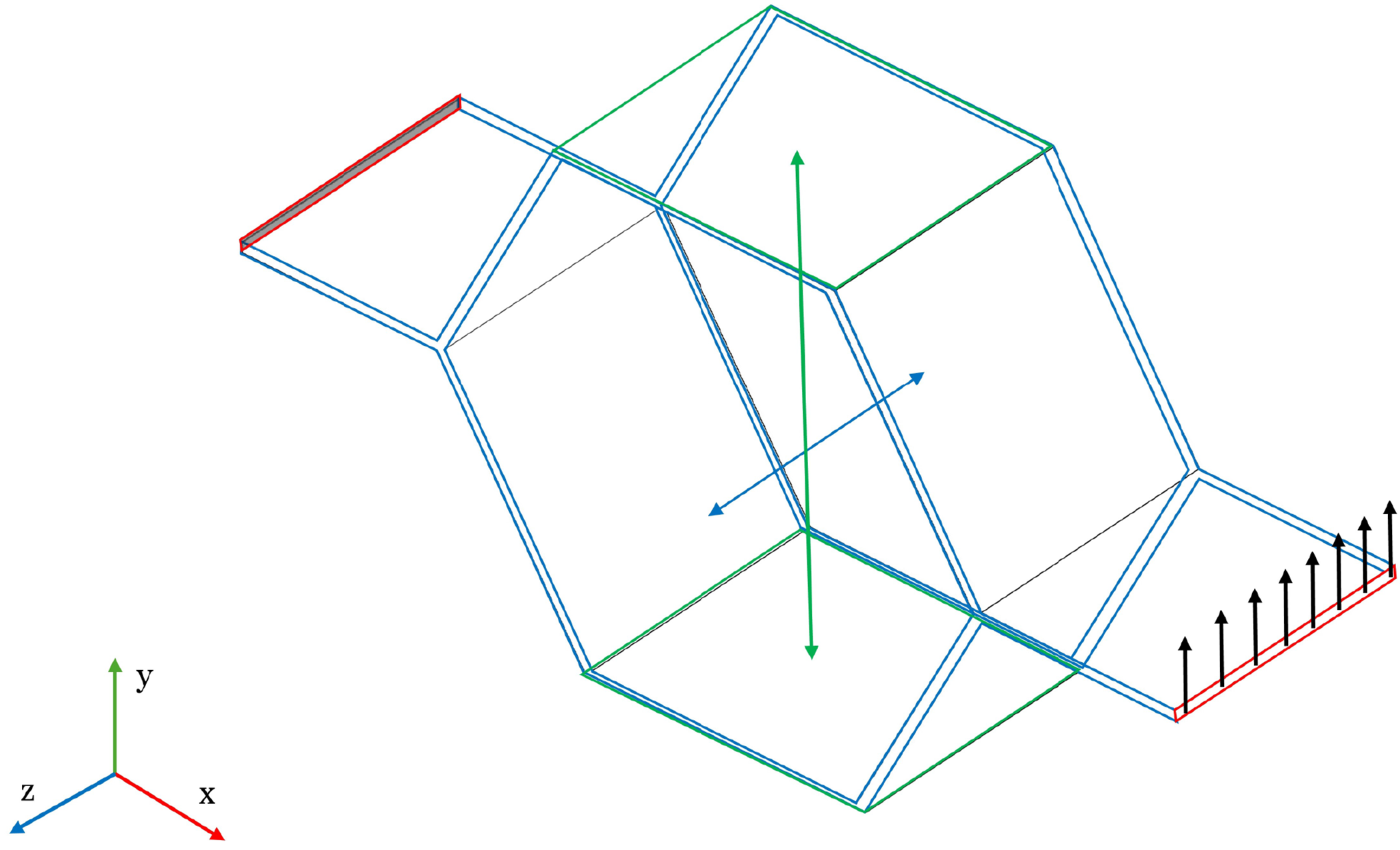
Figure 5: Loaded cell for the definition of the shear modulus Gxy

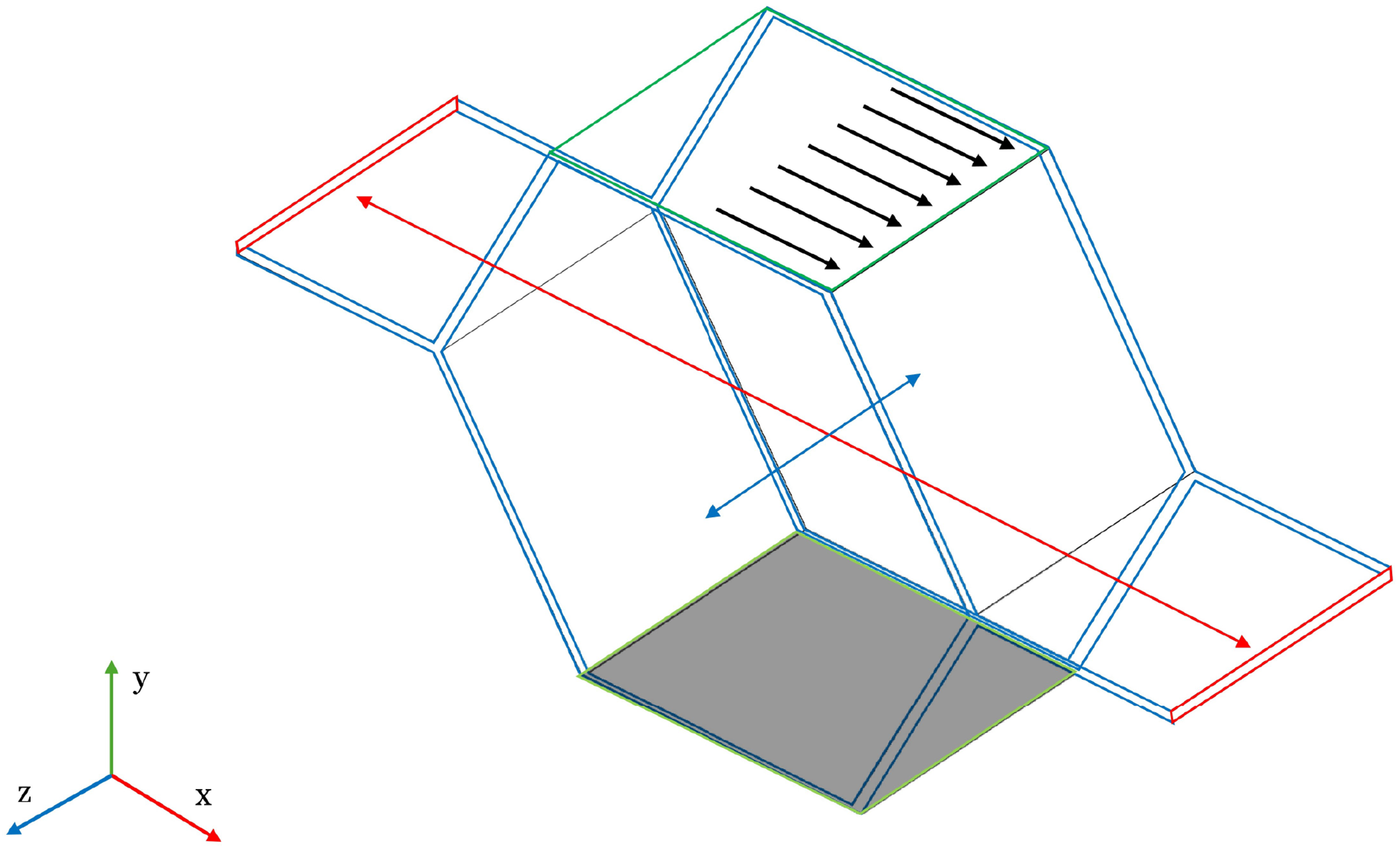
Figure 6: Loaded cell for the definition of the shear modulus Gyx

Given the asymmetrical behavior of the cells under consideration, all shear moduli will be different each other. This will result in the definition of a homogenized material with non-isotropic properties. In particular, it is considered the equilibrium equation τij=τji resulting from the equilibrium assumption that avoids the specimen torsion, such that:

τij=τji⇒Gij∂uj∂i=Gji∂ui∂j(10)

being i the direction of the load, and j the transverse direction. Since the response of the cell to shear stresses is not symmetrical (as shown in Figs. 5 and 6), it is clear that Gij≠Gji and Eq. (10) becomes:

∂uj∂i=GjiGij∂uj∂i(11)

In this way, knowing one of the two tangential stresses (e.g., τji) and both shear moduli Gji and Gij, it is possible to define the tangential stress in the other direction. Once the strain and shear stresses in both directions are known, it is possible to define the homogenized shear modulus as follows:

G¯ij=τij+τjiϵij+ϵji(12)

Finally, to fully characterize the homogenized properties of the generic aluminium cell, the equivalent density has been determined as: ρ=ρall(Vcell/Vcube cell), where Vcell represents the volume of the considered cell structure, and Vcube cell denotes the volume of the equivalent full parallelepiped cell.

3  Results

3.1 Honeycomb Panels with Different Lattice Cells

Among different geometries of the cells, the inclination θ of the sides of length a is varied from 0∘ (for rectangular cells) to ±30∘ (for hexagonal and reentrant cells). The same isotropic material is applied for all cell geometries, i.e., Aluminium with ρ=2700kg/m^3, E=70GPa, ν=0.33. The external bounding box defining the cell dimensions (Fig. 2), is a parallelepiped with edges of length L=20mm, H=10mm and W=5mm representing the cell length, height and depth respectively. In all analyzed cells, the wall thickness, s, measures 0.1 mm uniformly. However, it reduces by half, i.e., to 0.05mm, along walls oriented normally to the y-axis.

The geometrical dimensions of the cells, depicted in Fig. 7 measure l=4.97E−3 m,l2=10.0E−3 m,θ=0deg for the rectangular cell, l=5.77E−3 m,l2=7.11E−3 m,θ=30deg for the hexagonal cell and l=5.98E−3 m,l2=13.39E−3 m,θ=−30deg for the reentrant cell.

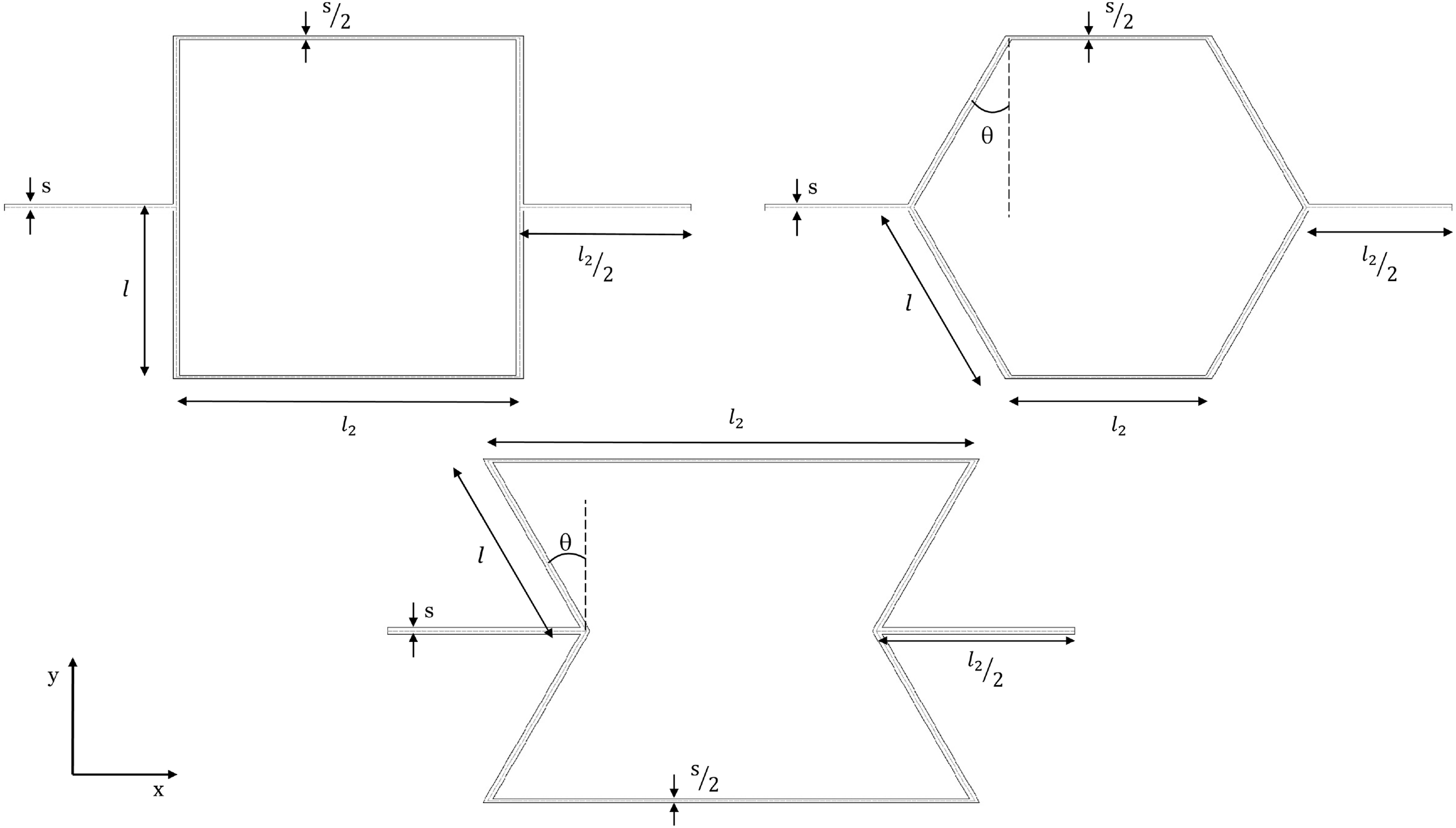
Figure 7: Geometry of the rectangular, hexagonal and reentrant cells

The homogenized orthotropic properties of the cell for various geometries are presented in Table 2.

In the same manner, the homogenized properties of cells modeled with dimensions equal to those used by Tornabene et al. [47] have been defined. The resulting properties are listed in Table 3.

This subsection validates the current approach for 3D homogenizations of equivalent orthotropic materials by examining an infinite sandwich panel under double-periodic boundary conditions. To this end, two sandwich structures are modeled, for a fixed geometry. The first panel consists of two external aluminium skins with thickness of 1 mm and a central core of thickness 5 mm with cells aligned in a single row. The other panel, on the other hand, has a central core with homogenized properties, as previously defined, while the skins are made of aluminum. As mentioned before, the panel has double boundary conditions at each lateral face. The first ten natural frequencies are computed for each cell geometry, as reported in Tables 4 and 5 for cells with equal volume and those modeled according to Ref. [47], respectively. Fig. 8 shows the first four frequencies of a 3D plate made of rectangular cells with a costant volume.

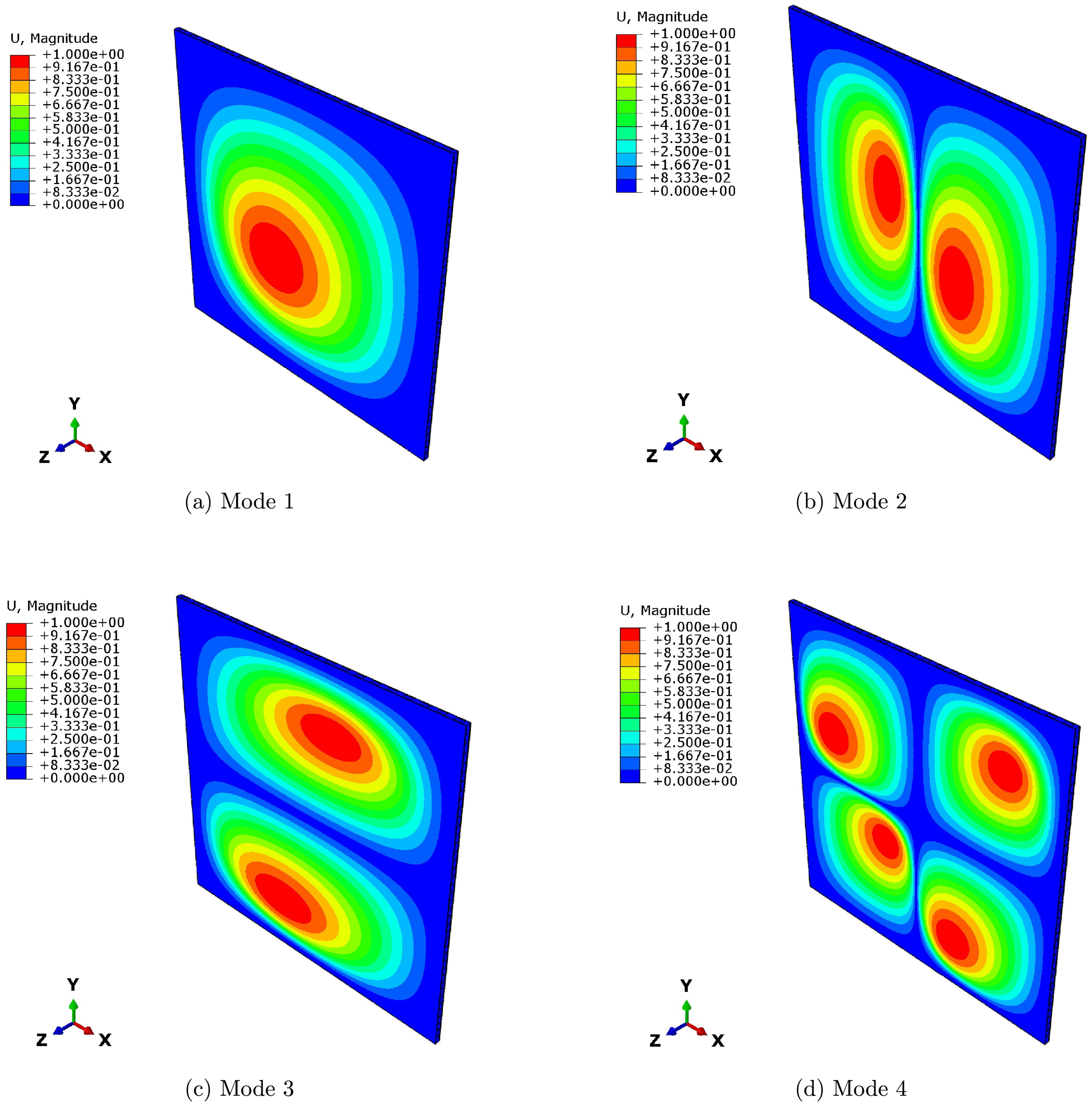
Figure 8: First four frequencies (Hz) of the rectangular plate modeled with a 3D lattice core

It is evident from the results in Tables 4 and 5 that the homogenization method proposed in this study effectively approximates the 3D behavior, with a significantly lower computational cost and an overall error mostly below 5%.

Furthermore, a comparison among results in Table 5 with predictions by Tornabene et al. [47] shows the good accuracy of the proposed approach, despite the reduced number of degrees of freedom (DOFs) by an order of magnitude.

Table 5 reports the results obtained by considering shear components for out-of-plane bending only, instead of considering the full shear components calculated by Eq. (12) for a general orthotropic material. This decision is based on the issue described earlier, specifically the difference between shear components, where Gij≠Gji, which are typically related by the equilibrium equation τij=τji.

To mitigate this inconsistency in the future, one could consider adopting a different starting point for the formulation of the constitutive equations, using τij≠τji. This approach would result in independent values for Gij and Gji.

3.2 Honeycomb Panels with Various Material Cells

The investigation of lattice structures with varying cell materials stands at the forefront of materials science and engineering, particularly in the context of homogenized property studies. Within this realm, the exploration of lattice structures with diverse cell geometries offers invaluable insights into the mechanical properties, but also in general thermal or functional characteristics of materials.

This study examines the homogenized properties of lattice structures with varying cell geometries, transitioning from aluminum to two distinct materials: steel and isotropic metal matrix composite AlSiC (Aluminum Silicon Carbide) with short fibers [55]. The sequential analysis highlights the influence of the material composition on the overall behavior of lattice structures, favoring tailored material design and optimization across a spectrum of applications. A systematic analysis explores the relation between cell geometry and material properties, advancing the understanding of lattice structures and their potential for practical implementation in diverse engineering domains.

The mechanical properties applied in the model for the two materials just introduced, i.e., steel and AlSiC, are reported in Table 6. AlSiC is widely used in advanced engineering applications due to its exceptional combination of high thermal conductivity, low density, and excellent mechanical properties. These characteristics make it a preferred choice for applications requiring lightweight yet robust materials, especially in thermal management and structural integrity. This section focuses on the analysis of AlSiC to highlight its suitability for the investigated scenarios. The volume fraction Vf of the AlSiC material is here considered equal to 0.70%.

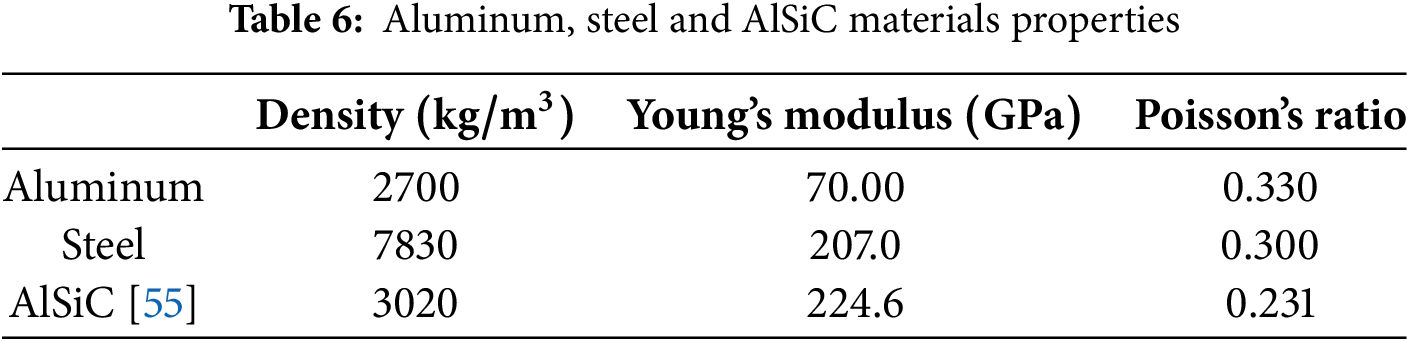
To define the equivalent properties of cells composed of the steel and AlSiC materials, the techniques described in the previous section are employed, and the results are presented in Table 7, for cells whose volume remains constant as the angle θ varies.

Homogenization of cells within lattice structures involves different materials in these cells, often leading to a complex nature of the mechanical properties. Understanding these relationships is pivotal, as it can significantly reduce the computational time by circumventing the need for recalculating finite element analyzes. By discerning the homogenized properties of one material, it becomes feasible to define those of another through established relationships, as summarized in Table 8, referring to a rectangular cell. This approach streamlines the design process, enabling engineers to leverage existing data and models to predict the mechanical behavior of novel materials without the burden of extensive recalculations.

The parameters listed in Table 8 are derived from the ratio between the equivalent property for a fixed geometry and the actual property of the material. This ratio is calculated for each of the 9 mechanical properties. Knowing the mechanical properties of materials and their homogenized properties for one of them, it is possible to define the homogenized properties of other materials. To do this, one multiplies the normalised value, i.e., those in Table 8, by the corresponding material property. For instance, if one wants to determine the Young’s modulus Ex of steel using the homogenized properties of aluminum, these quantities should multiply the Young’s modulus of steel Esteel by Exrel of aluminum.

This approach enables engineers to efficiently extrapolate the mechanical behavior of various materials within lattice structures, significantly reducing the computational burden and accelerating the design process. By leveraging these established relationships, designers can make informed decisions regarding the material selection and structural optimization, ultimately enhancing the performance and reliability of lattice-based systems. Therefore, the first 10 frequencies (Table 9) of the panel with the core composed by homogenized properties of steel and AlSiC materials were computed for each cell geometry. In Table 2 the equivalent properties for aluminium material are reported. It is easy to notice that the frequencies decrease as the material stiffness increases, as also observed in the plate composed of steel cells.

3.3 Honeycomb Curved Lattice Shells

Introducing curved lattice structures, we delve into a realm where traditional engineering meets innovative design, offering a myriad of possibilities across various applications. These structures, characterized by their curvature and interconnected lattice patterns, exhibit unique mechanical properties and aesthetic appeal. From architectural marvels to aerospace components, curved lattice structures have garnered a significant attention for their lightweight nature, structural integrity, and adaptability to complex geometries.

In this context, the present study focuses on the modeling of cylindrical and spherical panels with cores composed of materials exhibiting homogenized properties. By integrating lattice structures into curved panels, the work aims to explore the synergies between curvature and lattice geometry, leveraging the enhanced mechanical characteristics of homogenized materials. The objective of this study is to analyze the variation in natural frequencies of such panels as their curvature and dimensions change. By systematically investigating how the curvature and size of curved lattice panels influence their natural vibration modes, the work aims to provide insights into the dynamic behavior of these structures. This analysis will not only deepen the understanding of the relationship between curvature and natural frequencies, but also it will improve the design and optimization of curved lattice structures for specific engineering applications.

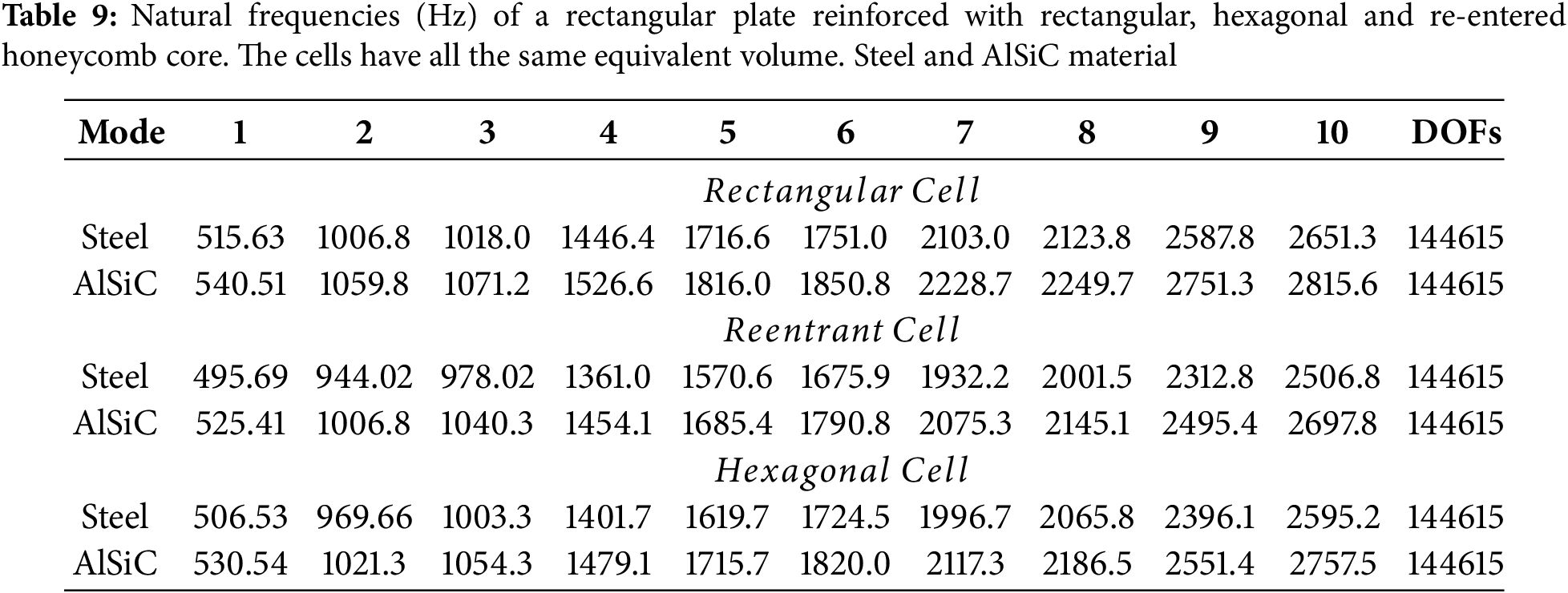
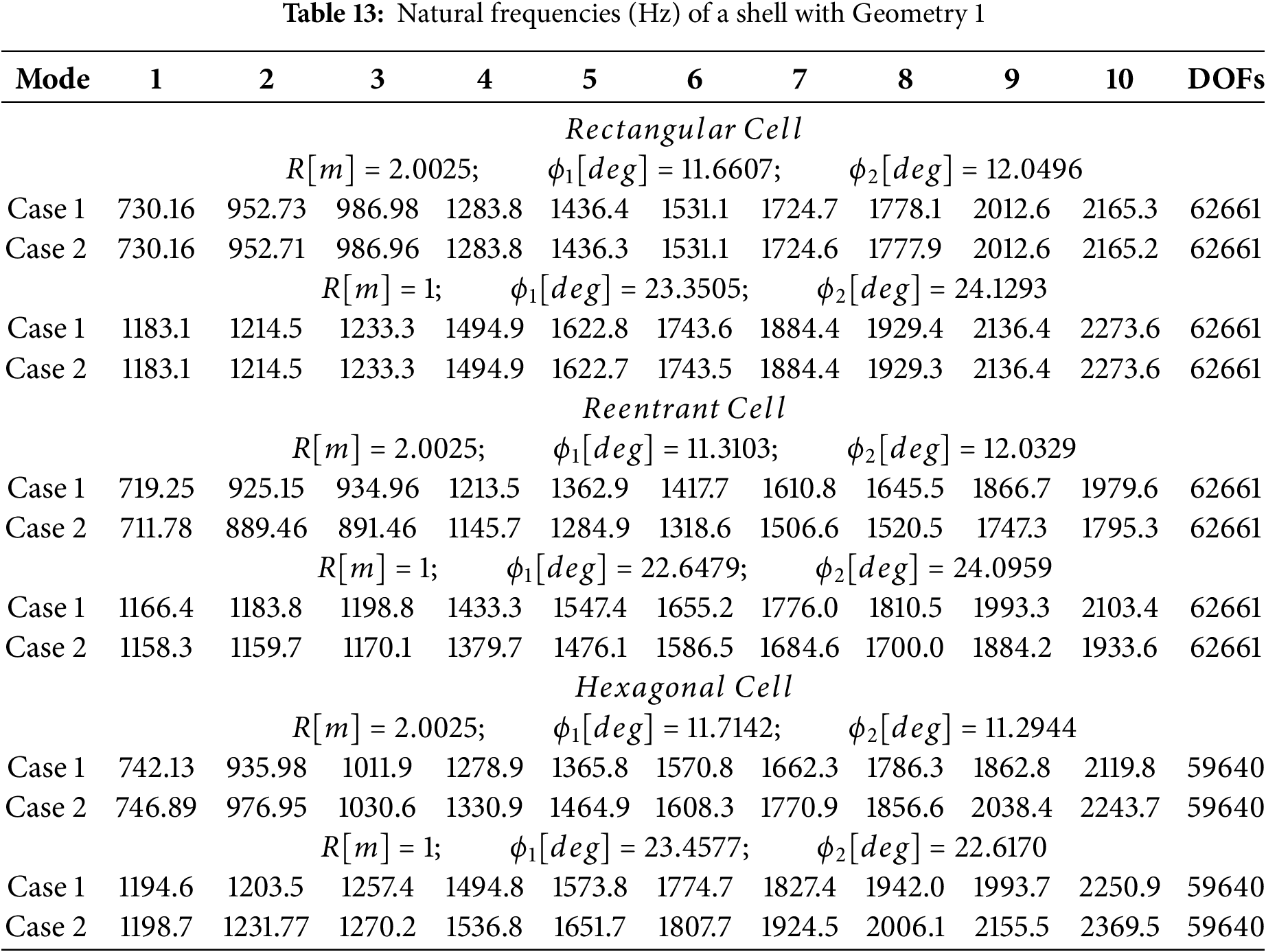
Tables 10–15 summarize the natural frequencies for cylindrical and spherical panels with radii of 2.0025 and 1 m, considering various plate dimensions and homogenized properties derived from rectangular, hexagonal, and indented cells. Three dimensions are considered, named Geometry 1, 2 and 3. The value of the varying parameters is indicated in each table. The three geometries are applied to both a cylindrical panel (Tables 10–12) and a spherical one (Tables 13–15). The homogenized properties applied to the sandwich core are derived from the cells analyzed in the current study at a constant equivalent volume (Case 1), as well as those from the same work by Tornabene et al. [47] (Case 2).

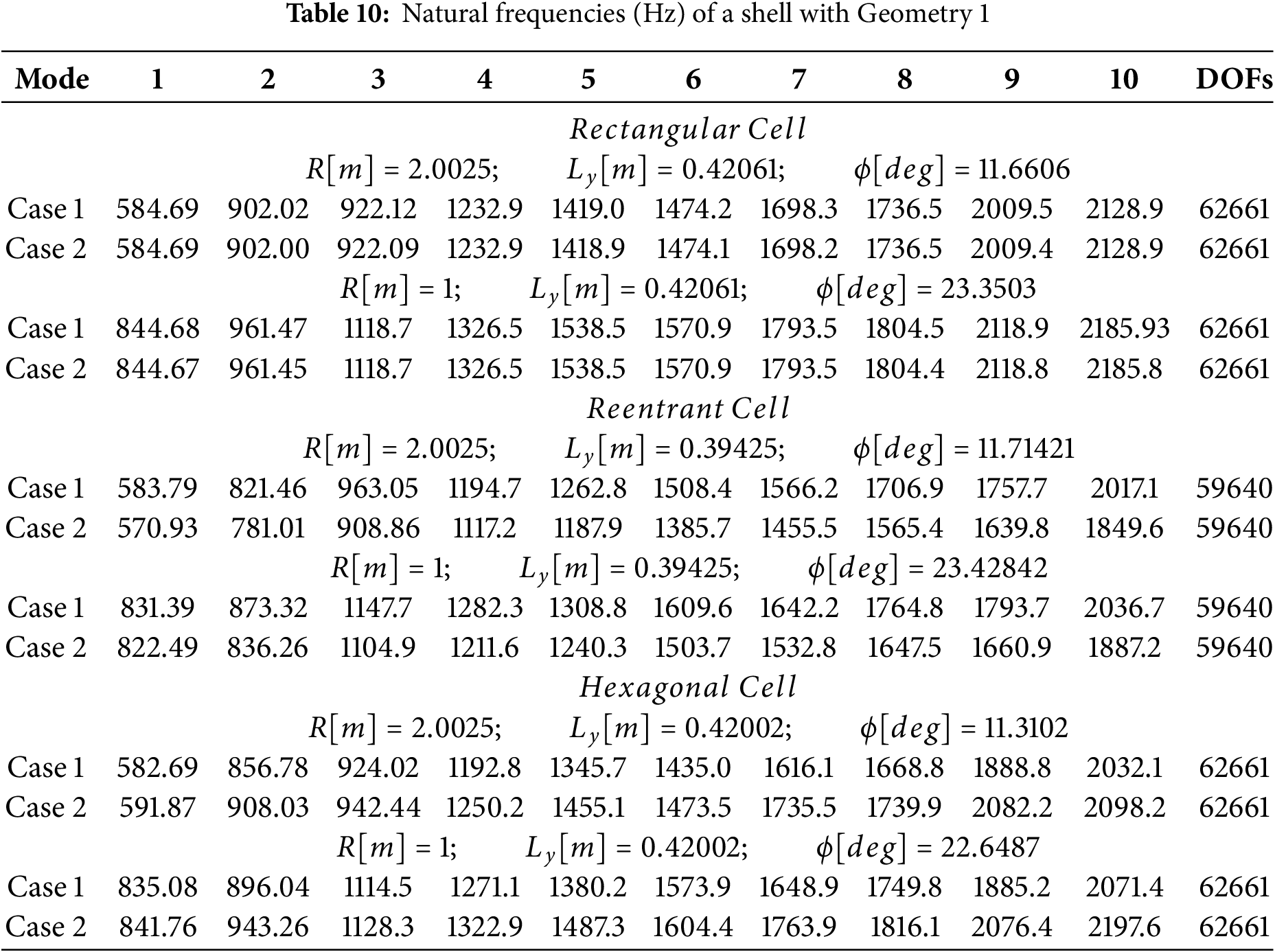
Based on results in Table 10, it can be noticed that frequencies increase as curvature increases. This correlation suggests a direct relationship between curvature and frequency, indicating that higher degrees of curvature lead to higher frequencies in the observed phenomena. Moreover, an interesting observation emerges regarding the impact of plate dimensions on results. Despite the variations in dimensions of the plates used in this study, the differences in size seem to have a minimal effect on the outcomes. This suggests that the variations in plate dimensions do not significantly alter the relationship between curvature and frequency. Such robustness in the findings underscores the reliability and generalizability of the observed trend across different plate sizes.

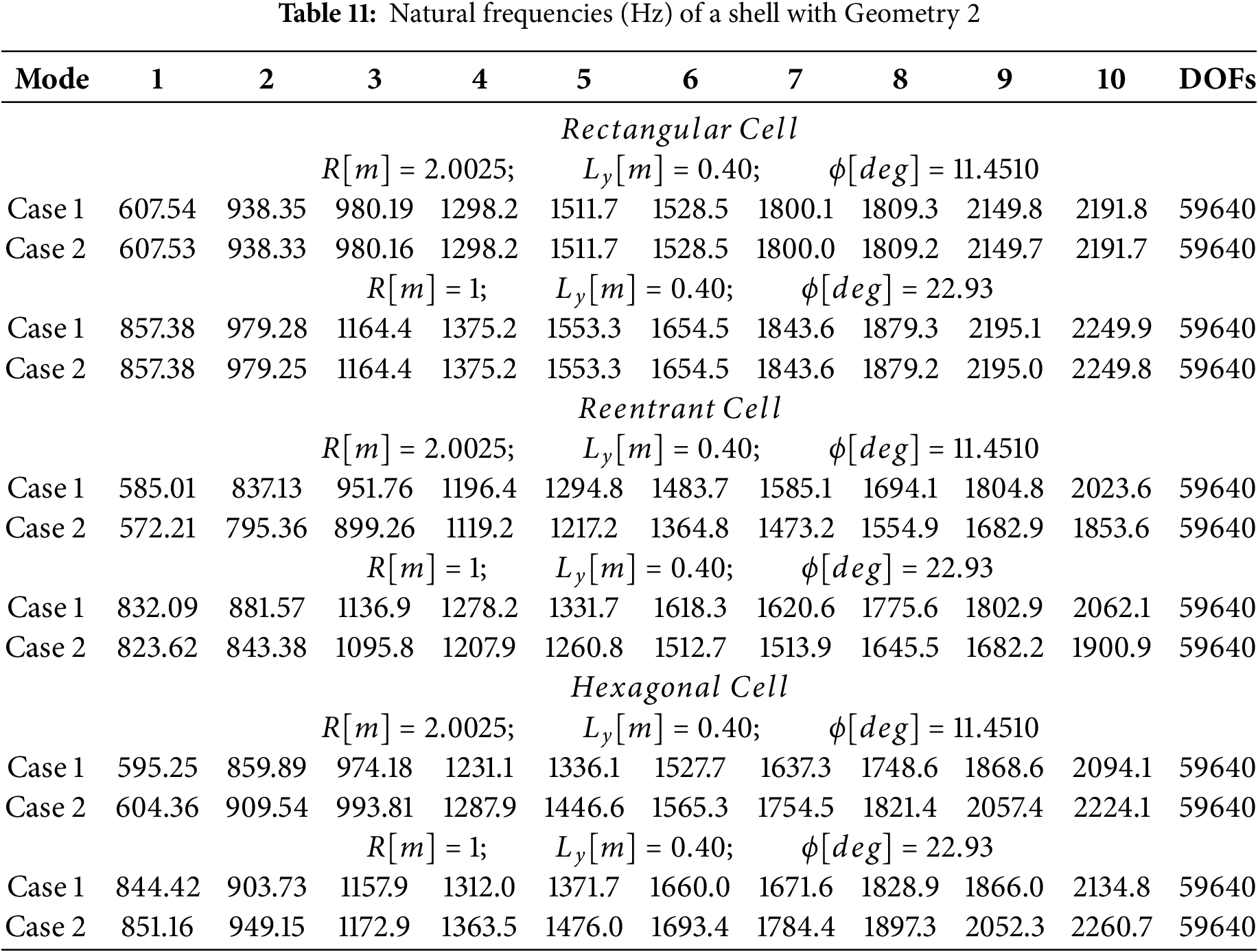
In Table 11, the influence of cell shape within the core of the sandwich structure is explored, while keeping constant the plate dimensions. Despite the uniformity in plate dimensions, the core material comprises cells with equal volumes but varying shapes. This manipulation allows for a nuanced investigation into how the geometric characteristics of the core cells impact the overall behavior of the sandwich structure. The observed results underscore the significance of cell shape in governing the global response of the sandwich panel. By keeping the plate dimensions consistent, any variations in the structural response can be attributed primarily to differences in cell shape. This finding highlights the intearaction between material microstructure and macroscopic behavior, revealing how minor differences in cell characteristics can result in significant alterations in the overall performance of composite structures.

The findings from Table 12 align with those of Table 10, reinforcing the observed trend regarding the impact of shell curvature on the overall behavior of the plate studied with only Case 2. Once again, the data suggest a direct correlation between increasing curvature and changes in the global response of the plate. This consistency across different modeling setups underscores the robustness of the observed phenomenon and highlights its significance in understanding the structural behavior of these composite systems.

The results reported in the tables of the current section reveal an increase in the natural frequency values, as the curvature radius decreases. This trend is particularly pronounced in spherical panels, where curvature exists in both directions of the panel, contributing to increase the overall structural stiffness.

Additionally, there is a notable alignment between the results obtained for rectangular cells compared to hexagonal or re-entered cells. This alignment stems from the regular geometry of rectangular cells, allowing for a more precise approximation of mechanical properties through various analytical or numerical formulations.

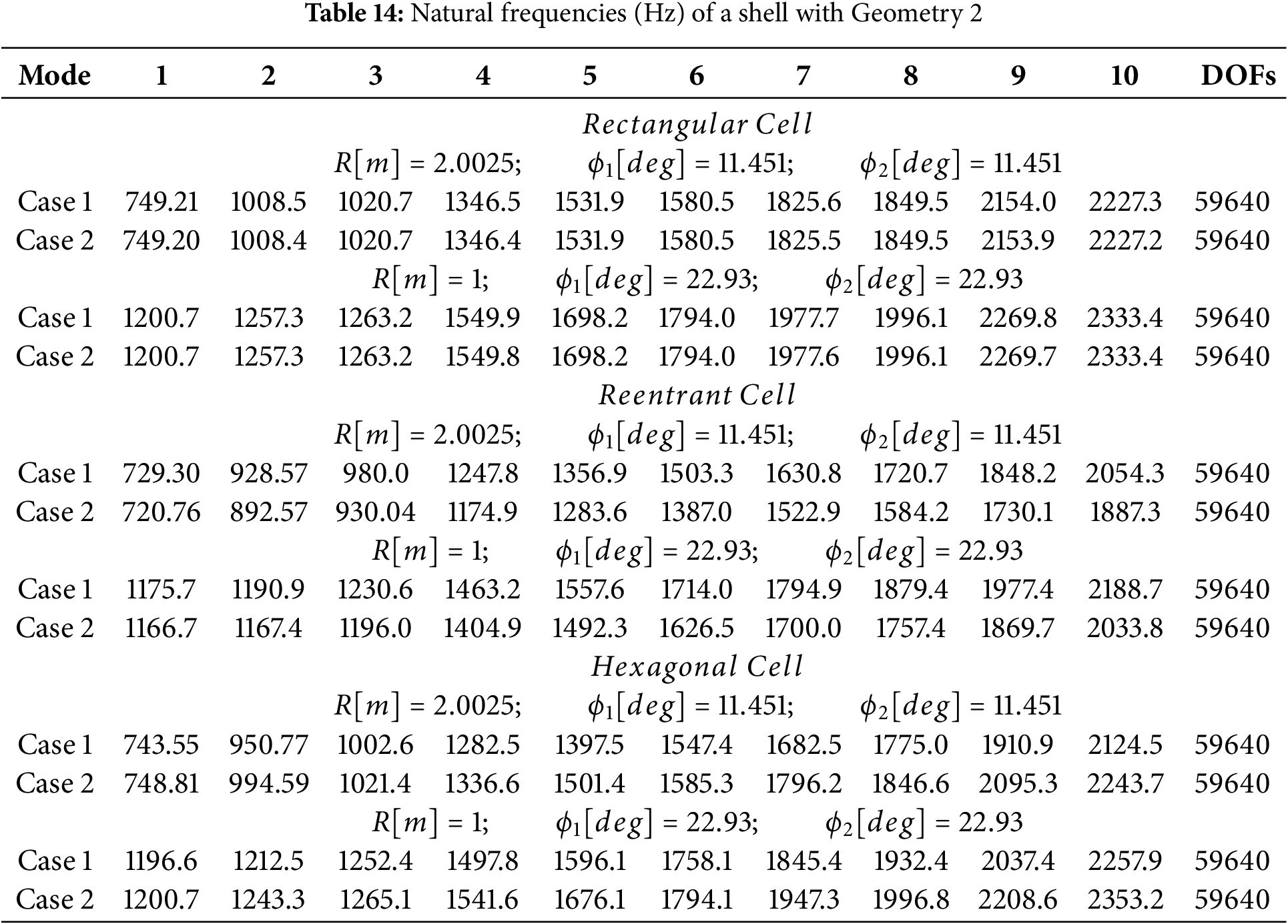
This consistency across different cell types suggests that, despite differences in shape and structure, the resulting homogenized properties are coherent and reliable, providing a solid foundation for the design and optimization of curved lattice panels. The first four freqencies are also shown in Figs. 9 and 10, referred to a sandwich shell with an honeycomb core modeled with homogenized properties deriving from rectangular cells.

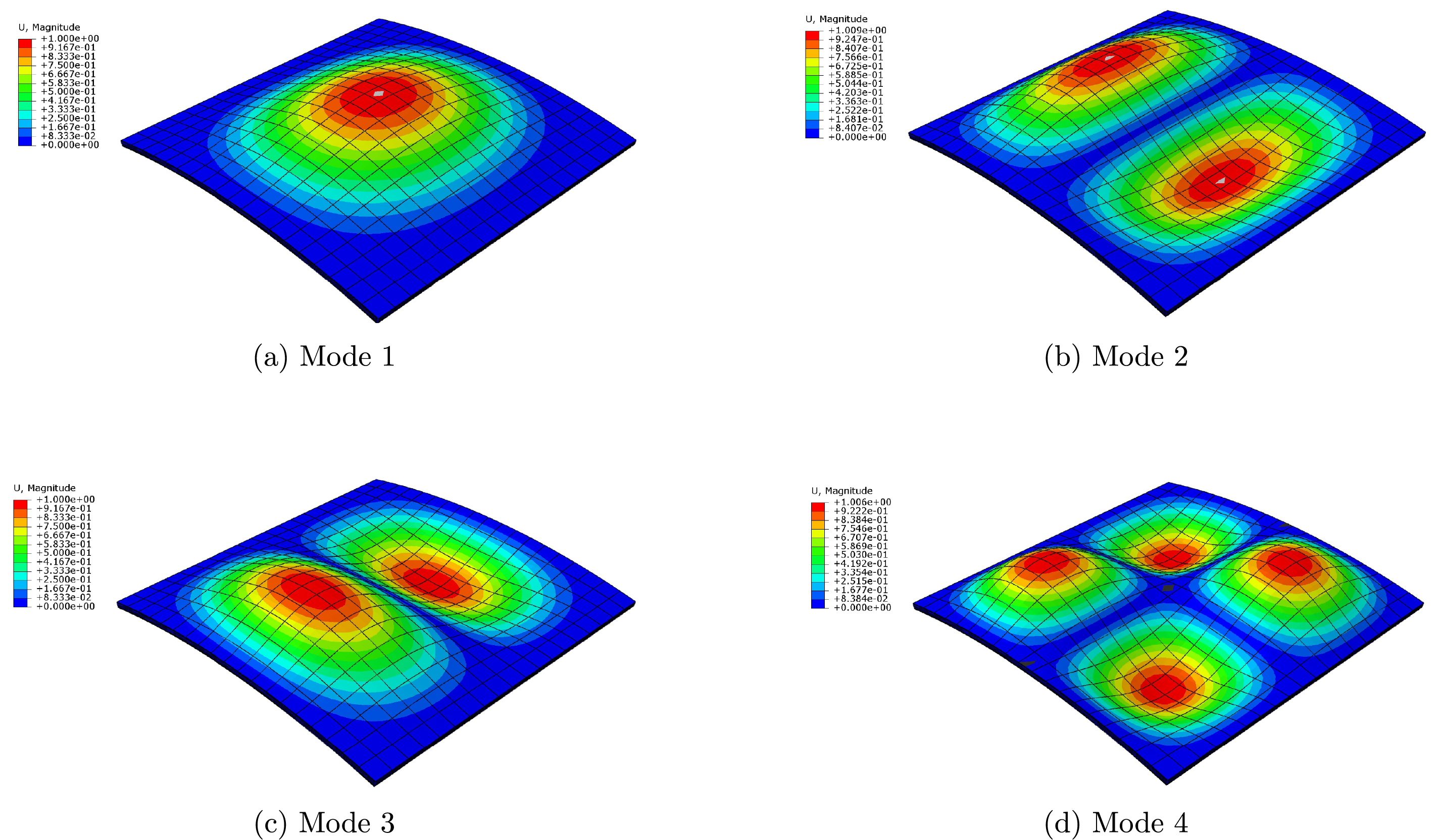
Figure 9: First four frequencies (Hz) of a cylindrical panel with radius R=1.00 m. The core has homogenized properties deriving from rectangular cells

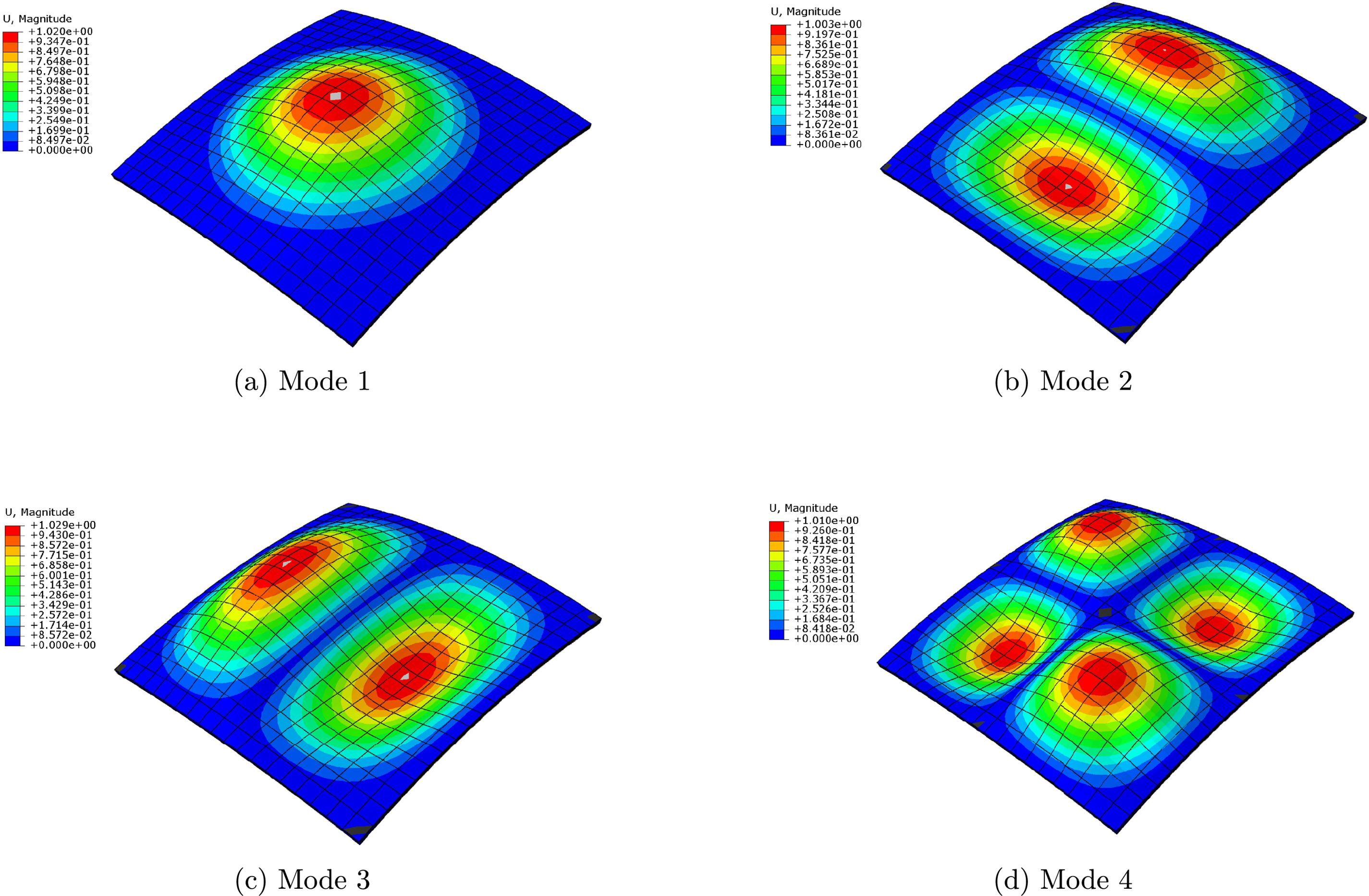
Figure 10: First four frequencies (Hz) of a spherical plate with radius R=1.00 m. The core has homogenized properties deriving from rectangular cells

Based on the results obtained, it was found that the frequencies increase with the increase in curvature. This suggests a direct relationship between curvature and frequency, where an increased curvature leads to an increased in frequencies. Moreover, despite variations in size of the plates used in the study, the size differences seem to have a minimal effect on the results. The relationship between curvature and frequency appears to be robust and independent of plate size, reinforcing the reliability and generalizability of the observed trend across different plate formats. This behavior suggests that plate dimensions do not significantly alter the overall behavior of the structure. In a subsequent analysis, the influence of the cell shape within the core of the sandwich structure was investigated, keeping the plate dimensions constant. Despite the uniform plate dimensions, the core material consists of cells with equal volumes but varying shapes. This targeted manipulation allowed for investigating how the geometric characteristics of the cells influence the overall behavior of the sandwich structure. Based on the main results of this analysis, it has been observed that the variations in cell shape affect significantly the structural behavior while keeping the volume constant. In addition, differences in structural responses can be attributed mainly to the variation in cell shape, confirming the importance of the material microstructure in the overall behavior of the composite structure. This highlights the interaction between cell geometry and macroscopic behavior of the structure, suggesting that even small differences in microstructure can lead to significant changes in the global performance of the structure.

A final analysis was conducted on the influence of core material and geometry, with particular attention to the cell shape. The results of this analysis showed slight variations between the different core materials and geometries. In particular, frequency variations were relatively subtle compared to the previous cases but still significant. Differences in structural behavior were more evident in the geometric configurations, suggesting a certain sensitivity of the system to geometric modifications. This aspect is crucial during the design optimization phase, as small changes in geometric configuration can affect the structural performance, necessitating careful balancing between form and material to optimize the design according to performance criteria.

4  Conclusions

This study provides a comprehensive analysis of honeycomb sandwich panels, employing advanced numerical homogenization techniques to model their core lattice structures. Several key findings emerged, offering significant insights for engineering applications:

•   Enhanced Predictive Modeling: The developed homogenization approach demonstrated its capability to accurately predict the mechanical behavior of honeycomb cores, aligning well with existing literature, particularly for geometries like rectangular cells. This highlights its potential for reliable applications in structural design optimization.

•   Material and Geometry Influence: A systematic relationship was identified between material stiffness and natural frequencies of the panels. The study established that stiffer materials reduce the natural frequencies, while less stiff materials have the opposite effect. This insight is critical for tailoring material properties to achieve desired vibrational characteristics.

•   Efficiency in Material Substitution: The study introduced a material normalization strategy, enabling efficient derivation of equivalent properties for diverse materials without repetitive simulations. This approach significantly reduces computational costs and time, fostering faster prototyping and material testing.

•   Impact of Curvature on Structural Performance: The analysis revealed that higher panel curvature (smaller radii) leads to increased natural frequencies, with doubly curved panels exhibiting superior stiffness and vibrational properties compared to singly curved ones. These findings underscore the importance of curvature in optimizing structural performance for specific applications.

•   Practical Applications: The insights gained from this study are directly applicable to designing lightweight, high-performance structures in aerospace, automotive, and civil engineering domains. By understanding the interaction of material properties, geometry, and structural behavior, engineers can make informed decisions to enhance performance and reliability.

The proposed RVE methodology offers several significant advantages, primarily its ability to provide a comprehensive description of material heterogeneities at multiple scales while maintaining the computational efficiency. This approach enhances the accuracy of the predictions for mechanical properties and facilitates the design of advanced materials with tailored properties.

Furthermore, the method is designed to yield the equivalent constants of the core efficiently, with a minimal computational effort. This is achieved through systematic modeling and normalization strategies that eliminate the need for repetitive simulations for different configurations. Consequently, the methodology is both practical and versatile, suitable for a wide range of engineering applications where accuracy and efficiency are paramount.

The study paves the way for further exploration into more complex geometries, material combinations, and experimental validation to enhance the reliability of predictive models. Additionally, extending the framework to dynamic loading scenarios could broaden its applicability.

Acknowledgement: The authors thank all collaborators who contributed to the development of this work.

Funding Statement: This research received no specific funding.

Author Contributions: Martina Rinaldi: Writing—original draft, Investigation, Formal analysis, Resources, Software, Data curation. Stefano Valvano, and Francesco Tornabene: Writing—review and editing, Supervision, Methodology, Data curation, Conceptualization. Rossana Dimitri: Writing—review and editing, Supervision, Data curation, Conceptualization. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data presented in this work are fully included within the manuscript and are not available elsewhere.

Ethics Approval: This study did not involve human participants or animals.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Blakey-Milner B, Gradl P, Snedden G, Brooks M, Pitot J, Lopez E, et al. Metal additive manufacturing in aerospace: a review. Mater Des. 2021;209(12):110008. doi:10.1016/j.matdes.2021.110008. [Google Scholar] [CrossRef]

2. Jihong Z, Han Z, Chuang W, Lu Z, Shangqin Y, Zhang W. A review of topology optimization for additive manufacturing: status and challenges. Chin J Aeronaut. 2021;34(1):91–110. doi:10.1016/j.cja.2020.09.020. [Google Scholar] [CrossRef]

3. Plocher J, Panesar A. Review on design and structural optimisation in additive manufacturing: towards next-generation lightweight structures. Mater Des. 2019;183(4):108164. doi:10.1016/j.matdes.2019.108164. [Google Scholar] [CrossRef]

4. Cooper D, Stanford M, Ferrari G. Binder jetting additive manufacturing: a review of process, materials, and methods. Addit Manuf. 2020;32:101009. doi:10.1016/j.addma.2020.101009. [Google Scholar] [CrossRef]

5. Zhai W, Zhang C, Du L. Scaling up binder jetting for industrial applications. J Mater Sci. 2023;58:1023–39. doi:10.1007/s10853-023-07244-6. [Google Scholar] [CrossRef]

6. Zhu H, Zhang W. Multi-material additive manufacturing: opportunities and challenges. Addit Manuf. 2023;64:102350. doi:10.1016/j.addma.2023.102350. [Google Scholar] [CrossRef]

7. Li W, Wang Y. Advanced applications of multi-material am in thermal management systems. Mater Des. 2022;224(6417):111212. doi:10.1016/j.matdes.2022.111212. [Google Scholar] [CrossRef]

8. Aboulkhair NT, Everitt NM, Ashcroft I, Tuck C. Reducing porosity in alsi10mg parts processed by selective laser melting. Addit Manuf. 2014;1:77–86. doi:10.1016/j.addma.2014.08.001. [Google Scholar] [CrossRef]

9. Nguyen V, Tran M. Ai-driven optimization in additive manufacturing: process parameters and defect reduction. J Manuf Process. 2023;92(7):223–39. doi:10.1016/j.jmapro.2023.05.010. [Google Scholar] [CrossRef]

10. Kumar R, Das A. Machine learning for additive manufacturing: recent trends and future directions. Addit Manufact Lett. 2023;1:100013. doi:10.1016/j.addlet.2023.100013. [Google Scholar] [CrossRef]

11. Wang J, Zhang W. Automated topology optimization for am lattice structures using AI-driven methods. Addit Manuf. 2022;59:102458. doi:10.1016/j.addma.2022.102458. [Google Scholar] [CrossRef]

12. Chen L-Y, Liang S-X, Liu Y, Zhang L-C. Additive manufacturing of metallic lattice structures: unconstrained design, accurate fabrication, fascinated performances, and challenges. Mat Sci Eng: R: Rep. 2021;146(8):100648. doi:10.1016/j.mser.2021.100648. [Google Scholar] [CrossRef]

13. Plessis AD, Broeckhoven C, Yadroitsava I, Yadroitsev I, Hands CH, Kunju R, et al. Beautiful and functional: a review of biomimetic design in additive manufacturing. Addit Manuf. 2019;27(Suppl. 1):408–27. doi:10.1016/j.addma.2019.03.033. [Google Scholar] [CrossRef]

14. Sohrabian M, Vaseghi M, Khaleghi H, Dehrooyeh S, Kohan MSA. Structural investigation of delicate-geometry fused deposition modeling additive manufacturing scaffolds: experiment and analytics. J Mater Eng Perform. 2021;30(9):6529–41. doi:10.1007/s11665-021-05894-y. [Google Scholar] [CrossRef]

15. Drugan WJ, Willis JR. A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites. J Mech Phys Solids. 1996;44(4):497–524. doi:10.1016/0022-5096(96)00007-5. [Google Scholar] [CrossRef]

16. Hashin Z. Analysis of composite materials—a survey. J Appl Mech. 1983 Sep;50(3):481–505. [Google Scholar]

17. Gitman IM, Askes H, Sluys LJ. Representative volume: existence and size determination. Eng Fract Mech. 2007;74(16):2518–34. doi:10.1016/j.engfracmech.2006.12.021. [Google Scholar] [CrossRef]

18. Liu H, Zhang J. Phase-field modeling for additive manufacturing: applications in defect analysis. Acta Mater. 2023;250:111241. doi:10.1016/j.actamat.2023.111241. [Google Scholar] [CrossRef]

19. Xie M, Chen H. Damage modeling in am materials using phase-field approaches. Mech Mater. 2022;174:104591. doi:10.1016/j.mechmat.2022.104591. [Google Scholar] [CrossRef]

20. Kanit T, Forest S, Galliet I, Mounoury V, Jeulin D. Determination of the size of the representative volume element for random composites: statistical and numerical approach. Int J Solids Struct. 2003;40(13–14):3647–79. doi:10.1016/S0020-7683(03)00143-4. [Google Scholar] [CrossRef]

21. Borbely A, Biermann H, Hartmann O. Fe investigation of the effect of particle distribution on the uniaxial stress-strain behaviour of particulate reinforced metal-matrix composites. Mat Sci Eng: A. 2001;313(1–2):34–45. doi:10.1016/S0921-5093(01)01144-3. [Google Scholar] [CrossRef]

22. Masters IG, Evans KE. Models for the elastic deformation of honeycombs. Compos Struct. 1996;35(4):403–22. doi:10.1016/S0263-8223(96)00054-2. [Google Scholar] [CrossRef]

23. Christensen RM. Mechanics of cellular and other low-density materials. Int J Solids Struct. 2000;37(1–2):93–104. doi:10.1016/S0020-7683(99)00080-3. [Google Scholar] [CrossRef]

24. Wang A-J, McDowell DL. In-plane stiffness and yield strength of periodic metal honeycombs. J Eng Mater Technol. 2004;126(2):137–56. doi:10.1115/1.1646165. [Google Scholar] [CrossRef]

25. Wang A-J, McDowell DL. Yield surfaces of various periodic metal honeycombs at intermediate relative density. Int J Plast. 2005;21(2):285–320. doi:10.1016/j.ijplas.2003.12.002. [Google Scholar] [CrossRef]

26. Kumar RS, McDowell DL. Generalized continuum modeling of 2-D periodic cellular solids. Int J Solids Struct. 2004;41(26):7399–422. doi:10.1016/j.ijsolstr.2004.06.038. [Google Scholar] [CrossRef]

27. Burgardt B, Cartraud P. Continuum modelling of beamlike lattice trusses. UK: Civil-Comp Press; 1996. p. 51–59. [Google Scholar]

28. Phani AS, Woodhouse J, Fleck NA. Wave propagation in two-dimensional periodic lattices. J Acoust Soc Am. 2006;119(4):1995–2005. doi:10.1121/1.2179748. [Google Scholar] [PubMed] [CrossRef]

29. Martinsson PG, Movchan AB. Vibrations of lattice structures and phononic band gaps. Quart J Mech Appl Mathem. 2003;56(1):45–64. doi:10.1093/qjmam/56.1.45. [Google Scholar] [CrossRef]

30. Hussein MI, Hulbert GM, Scott RA. Band-gap engineering of elastic waveguides using periodic materials. In: ASME 2003 International Mechanical Engineering Congress and Exposition; 2003; Washington, DC, USA. p. 799–807. doi:10.1115/IMECE2003-41886. [Google Scholar] [CrossRef]

31. Li H, Zhang J. Vibration isolation in aerospace applications using am lattice structures. Aerosp Sci Technol. 2023;139:108036. doi:10.1016/j.ast.2023.108036. [Google Scholar] [CrossRef]

32. Maraghi AK, Arefi M, Afshari H. Dynamics of a rotating ring-stiffened sandwich conical shell with an auxetic honeycomb core. Appl Math Mech. 2024;45(3):312–24. doi:10.1007/s10483-024-3124-7. [Google Scholar] [CrossRef]

33. Fish J, Chen W. Higher-order homogenization of initial/boundary-value problem. J Eng Mech. 2001;127(12):1223–30. doi:10.1061/(ASCE)0733-9399(2001)127:12(1223). [Google Scholar] [CrossRef]

34. Fish J, Chen W, Nagai G. Non-local dispersive model for wave propagation in heterogeneous media: multi-dimensional case. Int J Numer Methods Eng. 2002;54(3):347–63. doi:10.1002/nme.424. [Google Scholar] [CrossRef]

35. Suquet P. Elements of homogenization for inelastic solid mechanics. Homogeniz Techniq Compos Media. 1987;272:193–278. doi:10.1007/3-540-17616-0. [Google Scholar] [CrossRef]

36. Michel JC, Moulinec H, Suquet P. Effective properties of composite materials with periodic microstructure: a computational approach. Comput Methods Appl Mech Eng. 1999;172(1–4):109–43. doi:10.1016/S0045-7825(98)00227-8. [Google Scholar] [CrossRef]

37. Kumar SP, Elangovan S, Mohanraj R, Ramakrishna JR. A review on properties of inconel 625 and inconel 718 fabricated using direct energy deposition. Mater Today: Proc. 2021;46(5):7892–906. doi:10.1016/j.matpr.2021.02.566. [Google Scholar] [CrossRef]

38. Liu J, Yu H. Concurrent deposition path planning and structural topology optimization for additive manufacturing. Rapid Prototyp J. 2017;23(5):930–42. doi:10.1108/RPJ-05-2016-0087. [Google Scholar] [CrossRef]

39. Yu W, Tang T. Variational asymptotic method for unit cell homogenization of periodically heterogeneous materials. Int J Solids Struct. 2007;44(11–12):3738–55. doi:10.1016/j.ijsolstr.2006.10.020. [Google Scholar] [CrossRef]

40. Seiler PE, Li K, Deshpande VS, Fleck NA. The influence of strut waviness on the tensile response of lattice materials. J Appl Mech. 2021;88(3):031011. doi:10.1115/1.4049140. [Google Scholar] [CrossRef]

41. Alaimo A, Marino F, Valvano S. Bcc lattice cell structural characterization. Rep Mechal Eng. 2021;2(1):77–85. doi:10.31181/rme200102077v. [Google Scholar] [CrossRef]

42. Mantegna G, Vindigni CR, Valvano S, Esposito A, Tumino D, Alaimo A, et al. Representative volume element homogenisation approach to characterise additively manufactured porous metals. Mech Adv Mater Struct. 2023;30(5):1073–82. doi:10.1080/15376494.2022.2124002. [Google Scholar] [CrossRef]

43. Tumino D, Alaimo A, Mantegna G, Orlando C, Valvano S. Mechanical properties of bcc lattice cells with waved struts. Int J Interact Des Manuf. 2023;18(8):1–14. doi:10.1007/s12008-023-01359-9. [Google Scholar] [CrossRef]

44. Khorasani M, Soleimani-Javid Z, Arshid E, Lampani L, Civalek Ö. Thermo-elastic buckling of honeycomb micro plates integrated with FG-GNPs reinforced epoxy skins with stretching effect. Compos Struct. 2021;258(3):113430. doi:10.1016/j.compstruct.2020.113430. [Google Scholar] [CrossRef]

45. Kiani M, Arefi M, Afshari H. Thermo-mechanical bending analysis of a sandwich cylindrical panel with an auxetic honeycomb core and gnp-reinforced face sheets. Arch Civil Mech Eng. 2024;25(1):1–15. doi:10.1007/s43452-024-01043-z. [Google Scholar] [CrossRef]

46. Amirabadi H, Mottaghi A, Sarafraz M, Afshari H. Free vibrational behavior of a conical sandwich shell with a functionally graded auxetic honeycomb core. J Vib Control. 2024. online first. doi:10.1177/10775463241240215. [Google Scholar] [CrossRef]

47. Tornabene F, Viscoti M, Dimitri R, Aiello MA. Higher order formulations for doubly-curved shell structures with a honeycomb core. Thin-Walled Struct. 2021;164(9):107789. doi:10.1016/j.tws.2021.107789. [Google Scholar] [CrossRef]

48. Tornabene F, Bacciocchi M. Anisotropic doubly-curved shells: higher-order strong and weak formulations for arbitrarily shaped shell structures. Bologna, Italy: Società Editrice Esculapio; 2019. [Google Scholar]

49. Shu C, Chen W, Xue H, Du H. Numerical study of grid distribution effect on accuracy of DQ analysis of beams and plates by error estimation of derivative approximation. Int J Numer Methods Eng. 2001;51(2):159–79. doi:10.1002/nme.150. [Google Scholar] [CrossRef]

50. Valvano S. Homogenised properties of lattice metal composite cell. Facta Univ Ser: Mech Eng. 2024. doi:10.22190/FUME240125015V. [Google Scholar] [CrossRef]

51. Valvano S, Carrera E. Multilayered plate elements with node-dependent kinematics for the analysis of composite and sandwich structures. Facta Univ Ser: Mech Eng. 2017;15(1):1–30. doi:10.22190/FUME170315001V. [Google Scholar] [CrossRef]

52. Pagani A, Valvano S, Carrera E. Analysis of laminated composites and sandwich structures by variable-kinematic mitc9 plate elements. J Sandwich Struct Mat. 2018;20(1):4–41. doi:10.1177/1099636216650988. [Google Scholar] [CrossRef]

53. Carrera E, Pagani A, Valvano S. Shell elements with through-the-thickness variable kinematics for the analysis of laminated composite and sandwich structures. Compos Part B: Eng. 2017;111(3):294–314. doi:10.1016/j.compositesb.2016.12.001. [Google Scholar] [CrossRef]

54. Xia Z, Zhang Y, Ellyin F. A unified periodical boundary conditions for representative volume elements of composites and applications. Int J Solids Struct. 2003;40(8):1907–21. doi:10.1016/S0020-7683(03)00024-6. [Google Scholar] [CrossRef]

55. Kumar SS, Bai VS, Rajkumar KV, Sharma GK, Jayakumar T, Rajasekharan T. Elastic modulus of al-si/sic metal matrix composites as a function of volume fraction. J Phy D: Appl Phy. 2009;42(17):175504. doi:10.1088/0022-3727/42/17/175504. [Google Scholar] [CrossRef]