Entropy-Bottleneck-Based Privacy Protection Mechanism for Semantic Communication

1  Introduction

The rapid development of artificial intelligence (AI) and the widespread popularity of Internet of Things (IoT) devices have led to a explosive growth in the amount of global data [1]. Applications ranging from smart city infrastructure to autonomous vehicles rely on efficient and robust communication systems to support the real-time transmission of vast amounts of data. However, as the volume of data produced by IoT devices and sensors continues to grow, conventional communication technologies are increasingly struggling to meet these demands [2,3]. Traditional communication methods primarily focus on transmitting data at the bit level without considering its semantic significance. This approach not only results in excessive communication overhead but also leads to inefficient bandwidth utilization and increased energy consumption [4]. Moreover, the expansion of transmitted data heightens the risk of data breaches, making privacy protection a critical concern [5]. Therefore, there is an urgent need for a new communication paradigm that can efficiently transmit data based on its semantic relevance, optimize communication efficiency, and enhance privacy protection.

To address these limitations, semantic communication has emerged as an innovative method. It converts raw data into semantic information for transmission, focusing on the actual meaning of information rather than simply pursuing the integrity of data [6–8]. Initially inspired by Shannon’s communication theory, semantic communication extends its foundations by introducing a semantic layer, which focuses on conveying essential and high-value information while minimizing redundancy and enhancing transmission efficiency [9,10]. By selectively transmitting only the most relevant information, semantic communication significantly reduces bandwidth consumption and improves overall system performance. However, as device-to-device interactions become more frequent, this transmission paradigm also introduces new privacy challenges. The extracted semantic information may contain sensitive personal data, making it susceptible to privacy breaches and adversarial attacks during transmission. Thus, ensuring secure and privacy-preserving semantic communication remains a critical research challenge.

In the context of image transmission, semantic communication plays a crucial role in optimizing data efficiency. Images usually contain a lot of redundant information, and not all data is equally important in different application scenarios. By extracting and transmitting only the most relevant semantic features, semantic communication significantly reduces data volume while maintaining the necessary information quality for specific applications [11]. In [12], a vehicle shares visual data to aid remote driving decisions. Since operators focus on moving objects like pedestrians and traffic signals, the proposed system uses semantic segmentation to distinguish regions of interest (ROI) from non-interest (RONI). By leveraging semantic communication networks with different bandwidths, it ensures high-quality ROI transmission with minimal overhead. By distinguishing between ROI and RONI, semantic communication systems can intelligently allocate network resources, minimizing unnecessary data transmission while prioritizing bandwidth for processing essential information.

Although there have been some works in semantic communication that have attempted to classify ROI and RONI in images through semantic segmentation, these methods have failed to fully utilize the data compression capabilities of semantic communication, resulting in high data redundancy and unnecessary communication overhead, and there is still a risk of privacy leakage during the compression process [11,12]. Therefore, the challenge is not only to accurately identify and segment ROI and RONI, but also to design a compression strategy that can fully compress ROI and RONI under the condition of protecting privacy.

By adopting this approach, the proposed system effectively reduces the volume of transmitted data, enabling high-quality semantic communication while preserving privacy. The method first performs semantic segmentation on the image to identify ROI and RONI, and then efficiently converts the latent features into a compact bitstream through probabilistic modeling. By communicating in this way, the proposed system can significantly reduce the amount of transmitted data and achieve high-quality semantic communication while protecting privacy. The main contributions of this paper are summarized as follows:

•   We introduce a semantic communication framework that combines semantic segmentation with entropy bottleneck technology. By distinguishing between ROI and RONI and applying differentiated compression strategies, we not only optimize the communication efficiency but also significantly enhance the privacy protection capability.

•   A probabilistic modeling and compression method based on entropy bottleneck is proposed, which can effectively encode the latent features and convert them into a compact bit stream, thereby reducing the overall overhead of data transmission and reducing the correlation between the original data and the transmitted content.

•   The experiments have shown that the mechanism proposed in this paper is superior to traditional methods in terms of transmission efficiency and reconstruction quality while protecting privacy.

The rest of this paper is organized as follows: Section 2 reviews the related research work on semantic communication. Section 3 explains the basic definition of semantic communication. Section 4 introduces the framework and implementation of the proposed system in detail. Section 5 shows the experimental results along with a comprehensive analysis and discussion of their implications. Section 6 presents the conclusion of this study and discusses potential directions for future research.

2  Related Work

In recent years, with explosive growth in data and increasing demand for transmission efficiency, semantic communication is expected to become a new paradigm for 6G communications and has rapidly developed into a cutting-edge research direction in the field of communications. In response to different application scenarios and needs, researchers have proposed a variety of semantic communication models and methods, and have deeply explored their potential applications in multiple fields, showing broad prospects and innovative value.

Xie et al. first proposed a system framework consisting of a semantic encoder and decoder [13], laying the foundation for semantic communication. Gündüz et al. further proposed the concept of goal oriented semantic communication [14]. This method no longer focuses on higher-level information, but selectively transmits information with a goal oriented approach to ensure that only the content required to achieve the goal is transmitted. Xie et al. designed an innovative hierarchical Transformer that facilitates the fusion of multimodal data by adding connections between each encoder and decoder layer [15]. Numerical results indicate that the proposed model outperforms traditional communication methods in terms of channel robustness, computational complexity, transmission delay, and various task-specific performance metrics. Zhou et al. proposed a novel semantic communication system based on the Universal Transformer [16]. Compared to traditional Transformers, the Universal Transformer incorporates an adaptive recurrence mechanism which can achieve better end-to-end performance under diverse channel conditions.

Zhang et al. proposed a part-of-speech-based encoding strategy and a context-based decoding strategy, in which various deep learning models were introduced to learn semantic and contextual features as background knowledge. With this background knowledge, our strategy can be applied to some non-jointly designed communication scenarios with uncertainties [17]. Zhang et al. proposed a communication system for image transmission, where the sender is unaware of the task, and the data environment is dynamic [18]. Semantic communication faces challenges in balancing the preservation of semantic information and the retention of complex details. To address these limitations, Tang proposed a contrastive learning-based semantic communication system [19]. Dai et al. developed novel adaptive rate transmission and hyperprior-assisted codec enhancement mechanisms to upgrade deep joint source-channel coding [20]. Beyond coding and transmission, efficient semantic representation and retrieval also play a crucial role in semantic communication. Yan et al. [21] proposed a task-adaptive attention mechanism for image captioning, which dynamically selects relevant features based on task requirements, aligning with the goal of extracting task-relevant semantic information in semantic communication. Additionally, Yan et al. [22] developed a deep multi-view enhancement hashing method for efficient image retrieval, demonstrating how compact and discriminative feature representations can facilitate effective information processing. These works collectively highlight the importance of learning-based feature extraction, adaptive compression, and efficient retrieval in advancing semantic communication systems.

While semantic communication is developing rapidly, it is also facing a variety of security issues [23]. Introducing corrupted data into the training set will cause the performance of the semantic codec to degrade and become unable to complete the task [7]. Adversarial samples can guide the semantic codec to generate wrong information [24]. At the same time, semantic noise is also misleading, thus affecting the performance of semantic communication.

The concept of the entropy bottleneck, as introduced in [25], offers an efficient approach to encoding latent features using entropy principles. Experimental results have shown the significant effect of entropy bottleneck in optimizing image compression performance. Subsequently, this innovative entropy encoding method was extended to the field of video compression [26], demonstrating the outstanding performance of entropy compression in improving video data compression efficiency. The effectiveness of entropy bottleneck in deep learning compression has been fully demonstrated in computer vision tasks. At the same time, by entropy encoding the information before transmission, the efficiency and security of communication can be improved, making it very suitable for semantic communication.

3  Problem Formulation

This section begins by defining the concept of semantic communication, outlining its fundamental structure and key components. It then examines the current state of semantic communication transmission, highlighting its advantagesand challenges. Following this, the concept of the entropy bottleneck is introduced, explaining its role in modeling the probability distribution of intermediate features to enhance compression efficiency. By leveraging this approach, the system achieves efficient transmission while simultaneously preserving privacy, addressing critical limitations in existing semantic communication frameworks.

3.1 Semantic Communication Definition

As shown in Fig. 1, semantic communication system consists of several core components, including semantic encoder, communication channel with noise, semantic decoder and knowledge base. These components work together to efficiently transmit the meaning of information.

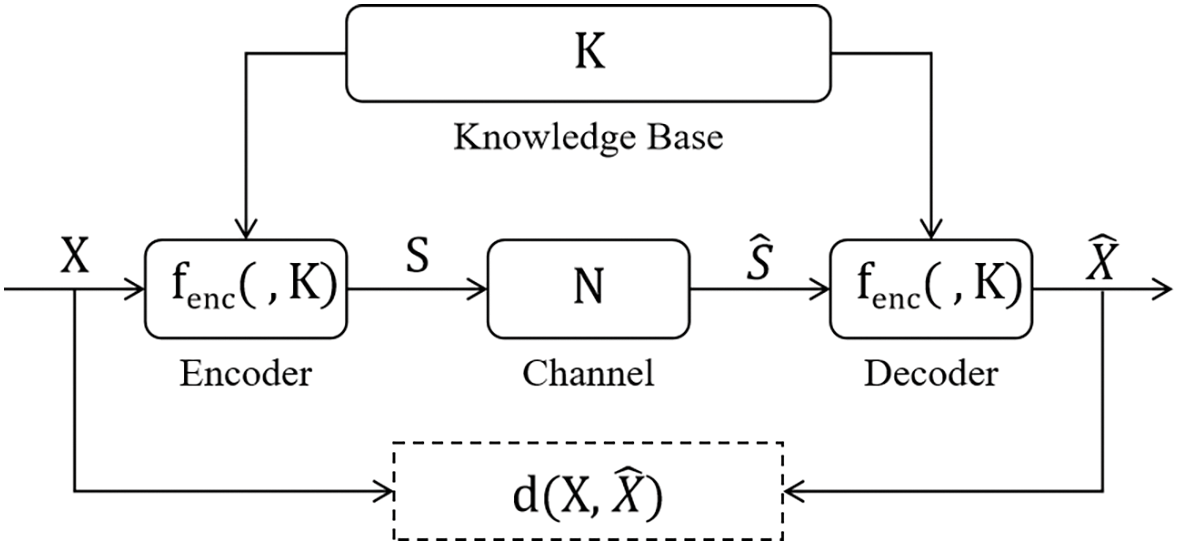
Figure 1: Formulation of semantic communication system

The original input data is represented as X, which typically contains not only essential content but also a substantial amount of redundant information. Unlike traditional communication systems, which transmit X directly at the bit level, semantic communication systems focus on capturing and encoding only the core semantic content of X. This is accomplished by a semantic encoding function fenc(⋅), which transforms X into a compact semantic representation S:

S=fenc(X,K)(1)

where K represents the shared knowledge base. The knowledge base K provides contextual information that aids the encoder in identifying the essential semantic content, resulting in a reduced representation S that is more efficient to transmit.

Once the semantic representation S is generated, it is transmitted through a noisy communication channel. Due to various physical limitations, the channel introduces noise into the transmission, represented by N. Thus, the signal received by the decoder, S^, can be expressed as:

S^=S+N(2)

where N is often modeled as additive Gaussian noise, following a normal distribution N∼𝒩(0,σ2). Unlike traditional communication systems that focus on bit-level accuracy, semantic communication systems are designed to tolerate a certain level of noise as long as the semantic content remains interpretable.

After receiving the noisy signal S^, the system proceeds to semantic decoding. The semantic decoder applies a decoding function fdec(⋅) that leverages the shared knowledge base K to reconstruct the semantic meaning of the original input X. The decoding process can be described as follows:

X^=fdec(S^,K)(3)

where X^ represents the reconstructed output. By utilizing the knowledge base K, the decoder can effectively restore the essential meaning of X, even if noise has introduced some errors in the transmission.

The knowledge base K contains shared domain-specific knowledge that both the encoder and decoder use to interpret semantic content. This shared knowledge ensures consistent understanding of the transmitted meaning, enhancing the system’s ability to accurately encode and decode semantic information. Mathematically, the knowledge base contributes to increasing the mutual information I(X;Y|K) between the input X and the output Y, defined as:

I(X;Y|K)=H(X|K)−H(X|Y,K)(4)

where H(⋅) denotes entropy. By incorporating K, we reduce the conditional entropy H(X|Y,K), facilitating efficient and accurate transmission of semantic information.

3.2 Objective and Challenges

Traditional communication usually adopts a fixed format of simply transmitting bit streams or data packets for communication without considering the actual meaning of the data. Semantic communication compresses the original data into feature vectors through neural networks, and transmits them according to the type of data and the requirements of specific tasks, ensuring that the receiver can effectively complete the task based on the received information. Semantic communication greatly reduces data redundancy and retains the key information required for the task by encapsulating semantic information in feature vectors. Feature vectors effectively compress the main features of information, allowing the receiver to accurately decode, reconstruct or directly understand its core meaning. For ease of storage and transmission, feature vectors usually exist in the form of matrices.

Since semantic communication relies on deep learning frameworks, its feature vectors are usually represented in the form of multi-dimensional floating-point arrays. Although this representation can accurately describe the semantic features of information, it also brings about the problem of data redundancy. Since high-precision floating-point numbers require a lot of memory, especially when using high-dimensional feature vectors, the communication cost will rise sharply. As the dimension of the feature vector increases, the communication overhead will increase linearly. This high bandwidth requirement may become a bottleneck for efficient transmission in resource-constrained environments.

On the other hand, feature vectors essentially perform semantic extraction of raw data, which makes it contain key semantic information. If the feature vector is not encrypted during transmission, it may be stolen by malicious attacks, resulting in privacy leakage. Therefore, in the design of semantic communication, we need to pay attention not only to the compactness and transmission efficiency of the feature vector, but also to introduce a privacy protection mechanism to ensure the security of data during transmission and storage.

In order to deal with these problems, entropy coding technology can be combined to perform probabilistic modeling and compression on the feature vector, which can reduce the communication overhead while improving the privacy protection capability by reducing the correlation between the feature vector and the original data.

3.3 Entropy Bottleneck Definition

Entropy bottleneck differs from traditional compression methods in that it does not directly compress the raw data. Instead, it enhances the efficiency of the encoding process by accurately modeling the probability distribution of feature data. By assigning lower probabilities to less likely feature values and higher probabilities to more likely values, it ensures efficient entropy coding of the feature map. This approach enables the model to identify and leverage statistical patterns within the data, producing a more compact bit stream. Such compactness not only significantly reduces the bandwidth required for data transmission but also ensures the integrity and fidelity of the reconstructed information.

During training, the entropy bottleneck is optimized to balance two objectives: minimizing the reconstruction loss and minimizing the bit rate, which corresponds to the entropy of the encoded feature map. The loss function for the entropy bottleneck L is defined as:

L=λ⋅D+R(5)

where D represents the reconstruction loss, R represents the bit rate loss, and λ is a hyperparameter balancing the two terms. The reconstruction loss D quantifies the dissimilarity between the original input X and the reconstructed output X^. It is typically measured using metrics such as mean squared error (MSE) or structural similarity index (SSIM). The bit rate loss R is defined as the entropy of the semantic representation S. The hyperparameter λ determines the trade-off between reconstruction quality and compression efficiency.

By minimizing L, the model balances maintaining high-quality reconstructions and producing a compact low-entropy representation of the input data.

3.4 Entropy Bottleneck in Privacy Protection

Entropy bottleneck enhances privacy protection by reducing the leakage of sensitive information Y through the compressed data X′. This is primarily achieved by minimizing the mutual information between X′ and Y, which quantifies how much sensitive information is revealed by the compressed data.

Mutual information I(X′;Y) is defined as the difference between the entropy of the compressed data H(X′) and the conditional entropy H(X′|Y), which represents the uncertainty of X′ given the sensitive information Y. The entropy bottleneck mechanism works by removing redundant parts of the data that are highly predictable or less informative, thereby reducing H(X′) and increasing H(X′|Y). This adjustment leads to a decrease in mutual information I(X′;Y), meaning less sensitive information is revealed during compression.

Moreover, the entropy bottleneck increases the conditional entropy H(X|Y), which represents the uncertainty of the original data X when Y is known. The entropy of the compressed data X′ under the condition of Y becomes larger. This increase in conditional entropy means that the data X′ becomes less predictable when Y is known, which in turn reduces the leakage of sensitive information. In essence, the entropy bottleneck reduces the reliance of X on Y by eliminating redundant or less informative parts of the data.

In the case of tensor data X, the entropy bottleneck further optimizes the data’s distribution structure. Tensor data often contains high-dimensional arrays with varying degrees of sparsity and frequency across different dimensions. The entropy bottleneck mechanism prioritizes high-frequency information, which carries more relevant or distinctive features, while reducing the influence of sparse or less relevant features. This leads to a more compact representation of the data, which minimizes the statistical correlation between different tensor dimensions and sensitive information Y. By reducing these correlations, the entropy bottleneck reduces the risk of sensitive information leakage.

In [27], Smith proposes an entropy-based quantification method to evaluate how the original information is leaked to an eavesdropper through the signal in a communication system. The paper first establishes a communication model with privacy protection mechanisms, where the original information is encoded into the signal, which is then transmitted through the channel. By calculating the relative entropy between the transmitted information and the signal received by the eavesdropper, the degree of information leakage can be quantified. A smaller relative entropy indicates that the information obtained by the eavesdropper from the signal is significantly different from the original information, thus indicating better privacy protection.

Based on this approach, we design a scheme to evaluate the impact of entropy encoding on privacy protection in semantic communication. We construct a semantic communication model with privacy protection mechanisms, where the original information X is first transformed into the encoded signal S by the semantic encoder, then S is further transformed into S′ via entropy encoding, and finally, S′ is transmitted through the channel.

Compared to S, S′ effectively reduces the entropy of the data, thereby reducing the likelihood of information leakage. The entropy encoding process introduces noise and randomness, making the encoded signal S′ more complex and uncertain than the original signal S. Since S′ has a lower information entropy, the difficulty for the eavesdropper to recover the original information X from the signal is greatly increased. Moreover, the noise introduced during the entropy encoding process further increases the difficulty of data recovery, as the noise makes the signal lack a directly decodable structure, further obscuring the characteristics of the original information. Therefore, entropy encoding not only limits the amount of information the eavesdropper can obtain by lowering the entropy of the signal, but also effectively enhances the difficulty of data recovery through the interference of noise, thus improving privacy protection.

4  Architecture of the Proposed System

The system takes semantic communication as its core framework, and the entropy bottleneck undertakes the dual tasks of privacy protection and compression optimization. The input data is first extracted through semantic segmentation to extract ROI and RONI, and the semantic coding module is used to compress ROI and RONI. The entropy bottleneck generates an efficient bit stream through dynamic probability modeling and quantization, while blurring the correlation between features and original data, thereby enhancing the privacy of communication. The communication channel is responsible for transmitting the entropy-coded bit stream, and the decoding module decodes and reconstructs according to the same entropy model.

The framework of the proposed system is shown in Fig. 2. The proposed system aims to optimize communication efficiency by prioritizing essential information according to specific task requirements and reduce bandwidth consumption by applying selective compression strategies to ROI and RONI of the images. The system is built around five main components: semantic segmentation, semantic encoder, entropy bottleneck, semantic decoder, and image combination. The structures of the semantic encoder and decoder are based on [28], each consisting of three convolutional neural networks (CNNs).

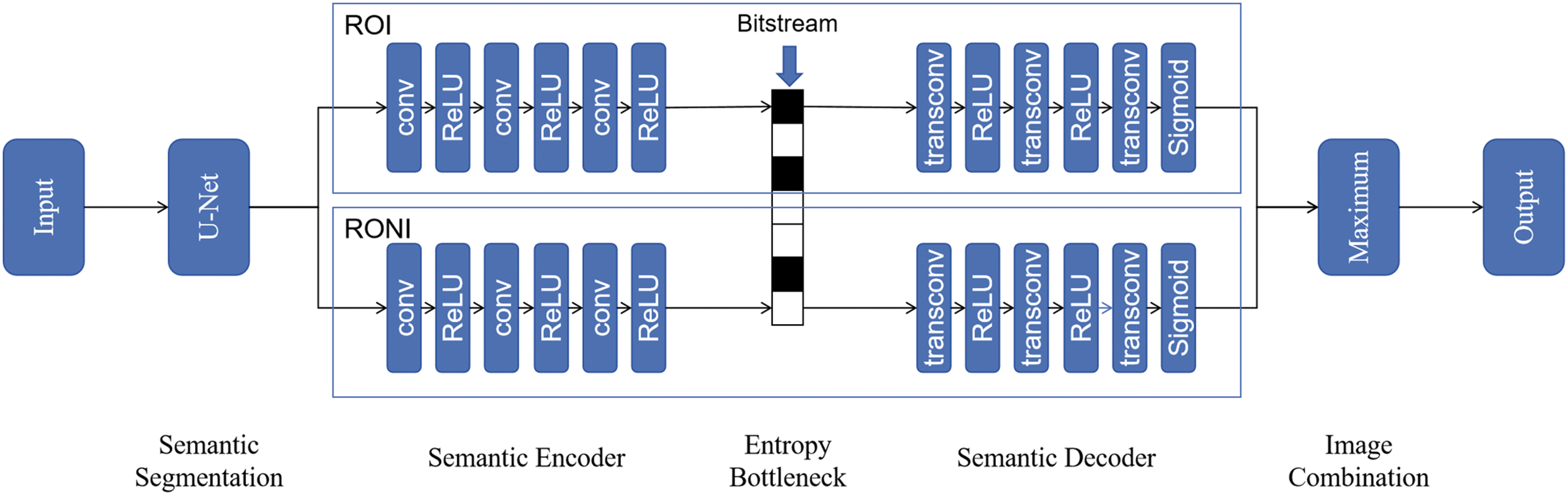
Figure 2: Framework of the proposed system

4.1 Semantic Segmentation

The semantic segmentation is to analyze and partition an input image into distinct regions based on their semantic content and relevance to the specific application. By classifying each pixel in the image, the module distinguishes between ROI, which contain high-priority information crucial for the task, and RONI, which hold lower-priority background information.

To achieve semantic segmentation, the system employs a deep learning-based U-Net model. U-Net is a widely used model for image segmentation, featuring a U-shaped structure with a symmetrical encoder-decoder architecture. The encoder part progressively extracts image features, transforming them into abstract, high-level representations through layers of convolution and pooling operations. The decoder then restores the spatial resolution step-by-step through upsampling and feature fusion, mapping these features back to the original image size. By combining feature information during the encoding and decoding stages, the U-Net model retains fine spatial details in the output, making it well-suited for tasks requiring precise pixel-level segmentation.

The input image is represented as X∈RH×W×C, where H, W, and C denote the height, width, and number of channels, respectively. The semantic segmentation module is employed to determine the category to which each pixel belongs:

M=fseg(X)(6)

where fseg denotes the semantic segmentation process, and M is the resulting category map. Each pixel value in category map M indicates whether it belongs to the ROI (Mi,j=1) or the RONI (Mi,j=0).

By using this mask, the ROI and RONI are extracted as:

XROI=X⊙M,XRONI=X⊙(1−M)(7)

where ⊙ represents element-wise multiplication. XROI contains the task-critical regions, while XRONI retains the less important background information.

The separation of ROI and RONI through semantic segmentation brings significant advantages for subsequent semantic encoding. The segmentation mask enables differentiated processing of ROI and RONI, allowing higher fidelity encoding for ROI to preserve critical semantic details, while applying more aggressive compression to RONI to save bandwidth.By isolating irrelevant background information in RONI, the system minimizes data redundancy, improving the overall transmission efficiency.

4.2 Semantic Encoder

The semantic encoder is responsible for transforming the segmented image regions, including ROI and RONI, into compact latent feature representations that capture their essential semantic information. By focusing on transmitting meaningful, high-level features instead of raw pixel data, the encoder significantly enhances transmission efficiency and reduces data size.

After the semantic segmentation step separates the input image into ROI and RONI, the semantic encoder processes each region independently. The segmented regions be denoted as XROI and XRONI, respectively. The encoder maps these regions into latent representations:

SROI=fenc(XROI),SRONI=fenc(XRONI)(8)

where SROI and SRONI refer to the latent representations of the ROI and RONI, respectively. fenc(⋅) represents the encoding function, which is implemented using convolutional neural networks due to their ability to efficiently extract and compress semantic features with low computational cost.

The encoding process is designed to prioritize the preservation of meaningful features within the ROI, ensuring that high-priority regions are encoded with greater fidelity for accurate reconstruction. In contrast, RONI undergoes more aggressive compression, resulting in smaller data sizes while retaining sufficient contextual information. This selective approach aligns with the demand-oriented paradigm, enabling the system to optimize bandwidth utilization and focus resources on task-critical information.

4.3 Entropy Bottleneck

The feature vectors generated by the semantic encoding module are further compressed in the entropy bottleneck, and the amount of data is reduced by entropy coding technology, thereby minimizing communication overhead while ensuring that semantic information is not lost, and enhancing privacy protection capabilities. By applying entropy coding, the entropy bottleneck achieves effective encoding of feature vectors, resulting in a compact bitstream that is very suitable for bandwidth-constrained transmission scenarios. At the same time, the correlation between the original data and the features is weakened by the compression process, effectively reducing the risk of privacy leakage.

After the semantic encoder processes the input data and generates feature representations for the ROI and the RONI, the entropy bottleneck quantizes the probability distribution of these feature vectors, quantizing the latent features S into discrete values S^. Direct quantization is non-differentiable, which hinders gradient-based optimization. To address this, an additive uniform noise ϵ∼𝒰(−0.5,0.5) is introduced during training to simulate quantization while maintaining feature continuity. This ensures the entire model can be optimized through gradient descent.

The quantized features S^ are passed to an entropy model, which predicts their probability distribution P(S^). Assuming a Gaussian distribution, the entropy model estimates the mean μ and variance σ2 for each feature. The probability of S^i is computed as:

P(S^i)=12πσi2exp⁡(−(S^i−μi)22σi2)(9)

where i means the ith data. Learnable parameters for μ and σ2 enable the entropy bottleneck to adapt to diverse data distributions, improving compression flexibility and efficiency.

The rate R(S^), representing the encoding length required for the quantized feature, is calculated as the negative log-likelihood of S^ under its estimated probability distribution:

R(S^)=−∑ilog2⁡P(S^i)(10)

The R(S^) indicates the compression efficiency of entropy coding, with higher probability features requiring fewer bits for encoding.

The entropy bottleneck incorporates a demand-oriented selective compression strategy. For ROI, the compression retains as much detail as possible to ensure high reconstruction quality. In contrast, RONI undergoes more aggressive compression to minimize data size while preserving sufficient contextual information. By modeling the probability distribution and applying entropy coding, the entropy bottleneck reduces the correlation between the original data and the compressed features. This process blurs the semantic details of the original data, making it challenging for adversaries to reconstruct sensitive information. Additionally, the inherent randomness introduced during quantization further obfuscates the feature representations, enhancing data privacy.

4.4 Semantic Decoder

The semantic decoder is responsible for reconstructing the ROI and the RONI from the compressed bitstreams received after transmission. Semantic decoder applies the inverse processes of encoding and compression, ensuring that the high-priority information in the ROI is accurately restored, while maintaining sufficient detail in the RONI. The goal of this module is to deliver a high-quality reconstructed image, even under low-bandwidth conditions, by prioritizing the semantic integrity of critical regions.

The decoder reconstructs the quantized features S^ by sampling from the Gaussian distribution characterized by μ and σ2. For each feature S^i, the reconstruction is given by:

S^i=μi+σi⋅ϵi,(11)

where ϵi∼𝒩(0,1) represents variable sampled from the standard normal distribution. The reconstructed feature vector S^ is then represented as S^=[S^1,S^2,…,S^n].

After entropy decoding, the reconstructed latent feature representations for the ROI and RONI are passed to the semantic decoder for image reconstruction. The semantic decoder applies the inverse transformation of the encoding step. Let the input features be z^ROI and z^RONI, then the reconstructed ROI and RONI regions are given by:

XROI=fdec(S^ROI),XRONI=fdec(S^RONI)(12)

where fdec(⋅) represents the decoding function implemented by a neural network.

For ROI regions, the semantic decoding process prioritizes high fidelity, reconstructing the details necessary to meet the specific demands of the task. RONI regions, in contrast, are reconstructed with lower fidelity, balancing quality with efficiency by focusing on general structure rather than detailed accuracy. This differential reconstruction aligns with the system’s demand-oriented approach, ensuring that critical regions receive the attention they need while conserving resources on less important areas.

4.5 Image Combination

In the semantic communication system, the image combination module is essential for merging data from different segments to reconstruct a complete image. After transmission, ROI and RONI previously separated by semantic segmentation, are integrated to create the output image. Rather than simply layering the regions, the system utilizes a pixel-wise maximum selection method to fuse the two segments. This approach prioritizes important details at the boundaries between ROI and RONI, reduces the impact of less significant areas, and enhances the quality of the reconstructed image.

The process starts with the semantic decoder, which decodes the compressed data to produce the respective outputs for the ROI and RONI. A maximum combination algorithm then merges these decoded sections according to the formula:

Xoutput=max(Xroi,Xroni)(13)

where Xroi and Xroni denote the reconstructed images for the ROI and RONI, respectively. The resulting Xoutput serves as the final output image. This method effectively minimizes the influence of less essential information from lower-priority regions, ensuring high-quality reconstruction while enhancing transmission efficiency.

5  Performance Evaluations

The section provides a detailed overview of the experimental setup and evaluation criteria. It outlines the specific datasets, metrics, and methods applied, ensuring a rigorous evaluation of system performance. This is followed by an in-depth analysis and discussion of the experimental results.

5.1 Experiment Setup

In this experiment, we use the Cityscapes dataset to evaluate the performance of the proposed system [29]. The Cityscapes dataset is widely used for autonomous driving and urban environment perception tasks. It contains high-resolution images collected from urban street scenes in various European cities, representing diverse urban environments. The Cityscapes dataset not only provides abundant image data but also includes fine pixel-level annotations, covering key objects such as roads, buildings, pedestrians, and vehicles, making it suitable for tasks such as semantic segmentation and object detection.

In this study, the image data undergoes several preprocessing steps. First, to reduce computational load, each input image is resized to 512×256. Then, the pixel values are normalized to the range [0, 1], and standardized using the training set’s mean (0.485, 0.456, 0.406) and standard deviation (0.229, 0.224, 0.225) to ensure zero mean and unit variance for each channel.

The experiment is implemented using the PyTorch deep learning platform. To optimize training, we use the Adam optimizer, which combines momentum and adaptive learning rates to adjust according to the historical gradient of each parameter, accelerating convergence and reducing gradient fluctuations for stability. A batch size of 128 is chosen to maximize GPU utilization, enhance computing efficiency, and stabilize gradient updates. The initial learning rate is set to 0.0005 to ensure faster convergence while avoiding instability or overshooting the optimal solution. Additionally, a learning rate decay strategy is applied, gradually reducing the learning rate during training to fine-tune the model, improving accuracy and generalization.

In the comparative experiment, the three image transmission schemes, JPEG, Joint Source-Channel Coding (JSCC), and Semantic Segmentation-based Semantic Communication (SSSC), are evaluated in terms of computational complexity, reconstruction quality, and noise resilience to assess their performance under different conditions. JPEG is a traditional image compression standard that utilizes Discrete Cosine Transform (DCT) to compress image data. JSCC is a deep learning-based joint source-channel coding method that maps image data directly to channel symbols through end-to-end training. SSSC is a method based on semantic segmentation, specifically optimized for image transmission tasks. It preprocesses images through semantic segmentation to prioritize essential semantic information, thereby enhancing the effectiveness of transmission.

5.2 Evaluation Criteria

In this experiment, two main metrics are used to evaluate the effectiveness of the proposed semantic communication system: compression ratio (CR) and image quality. The image quality includes Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) as well as an extended metric called θPSNR, which can better evaluate the reconstruction quality of ROI and RONI. We define transmission efficiency as the ability of a communication system to transmit image data effectively at a specific CR, while ensuring that the quality of the reconstructed image at the receiver remains high. In other words, transmission efficiency captures how well the system balances the trade-off between data compression and the preservation of image quality during the transmission process.

Compression Ratio (CR)In semantic communication systems, the CR is a crucial metric for assessing communication efficiency. It measures the degree of data reduction achieved by comparing the size of the compressed data to the original data. Effective data compression significantly reduces communication overhead, improving bandwidth utilization and system efficiency. The CR can be expressed as:

CR=Total BitsC×W×H×Bpp(14)

where Total Bits represents the total number of bits after compression, C is the number of channels in the image, such as 3 for an RGB image, W and H are the width and height of the image, respectively, Bpp denotes the bit depth per channel.

Peak Signal-to-Noise Ratio (PSNR)PSNR is a widely used metric for measuring image quality, primarily to quantify the difference between a compressed image and its original version [30]. A higher PSNR indicates a closer resemblance to the original image, reflecting better image quality, while a lower PSNR value suggests greater distortion due to compression.

The PSNR is computed as follows:

PSNR=10log10⁡(MAX2MSE)(15)

where MAX represents the maximum possible pixel value in the image. For normalized images, MAX is typically set to 1. The Mean Squared Error (MSE) quantifies the pixel-wise differences between the original and compressed images.

Structural Similarity Index Measure (SSIM)The SSIM is a metric used to assess the similarity between two images, commonly applied in image quality evaluation. Unlike traditional metrics like Mean Squared Error (MSE), which only consider pixel-wise differences, SSIM evaluates the perceived quality of an image by comparing structural information. It takes into account luminance, contrast, and texture, aligning more closely with human visual perception. SSIM values range from −1 to 1, with a value of 1 indicating perfect similarity between the two images. This metric is widely used in image processing tasks, as it better correlates with subjective human judgment of image quality.

The SSIM between two images x and y is defined as:

SSIM(x,y)=(2μxμy+C1)(2σxy+C2)(μx2+μy2+C1)(σx2+σy2+C2)(16)

where μx and μy are the average intensities of the images x and y, σx2 and σy2 are the variances of x and y, σxy is the covariance between x and y, C1 and C2 are small constants to avoid division by zero.

Weighted Peak Signal-to-Noise Ratio (θPSNR)To better capture the quality differences in ROI and RONI during reconstruction, an improved evaluation metric called θPSNR is introduced. This metric assigns different weights to the MSE values for the ROI and RONI, allowing for a more nuanced quality assessment that prioritizes critical areas. The θPSNR is calculated as follows:

θPSNR=10log10⁡(MAX2θ⋅MSEROI+(1−θ)⋅MSERONI)(17)

where MSEROI and MSERONI represent the Mean Squared Errors for the ROI and RONI, respectively. The weight coefficient θ adjusts the emphasis on the MSE of the ROI relative to the RONI, where 0≤θ≤1. This weighted approach provides a comprehensive quality assessment, focusing on crucial regions while still considering overall image quality.

5.3 Experimental Results

We start by investigating how the dimensionality of the bottleneck layer affects the overall performance of the model. The dimensionality of the bottleneck layer could potentially influence the model’s ability to capture and process essential features. However, it is important to highlight that the dimensionality of the bottleneck does not impact the communication load in this system. This is because the communication load is governed by the information entropy of the transmitted data rather than by the size of the bottleneck itself. Thus, while the bottleneck dimension play a significant role in determining model accuracy or efficiency, it does not directly influence the volume of information that needs to be transmitted across the communication channel.

Fig. 3 shows the PSNR values for various bottleneck dimensions, highlighting how dimension size impacts image reconstruction quality. The results demonstrate that increasing the bottleneck dimension consistently improves PSNR across different CR. Specifically, a dimension of 128 yields the highest PSNR, while a dimension of 4 results in the lowest. This indicates that larger bottleneck dimensions allow the model to retain more feature information, enhancing reconstruction quality. With respect to CR, the PSNR increases with higher CR, as more information is retained, leading to better quality. However, the performance stabilizes at higher CR values, especially at a dimension of 128, suggesting diminishing returns with further increases in dimension and CR. From a practical standpoint, increasing the bottleneck dimension increases computational overhead. A dimension of 64 offers a good balance between performance and computational cost, making it optimal for most CR conditions.

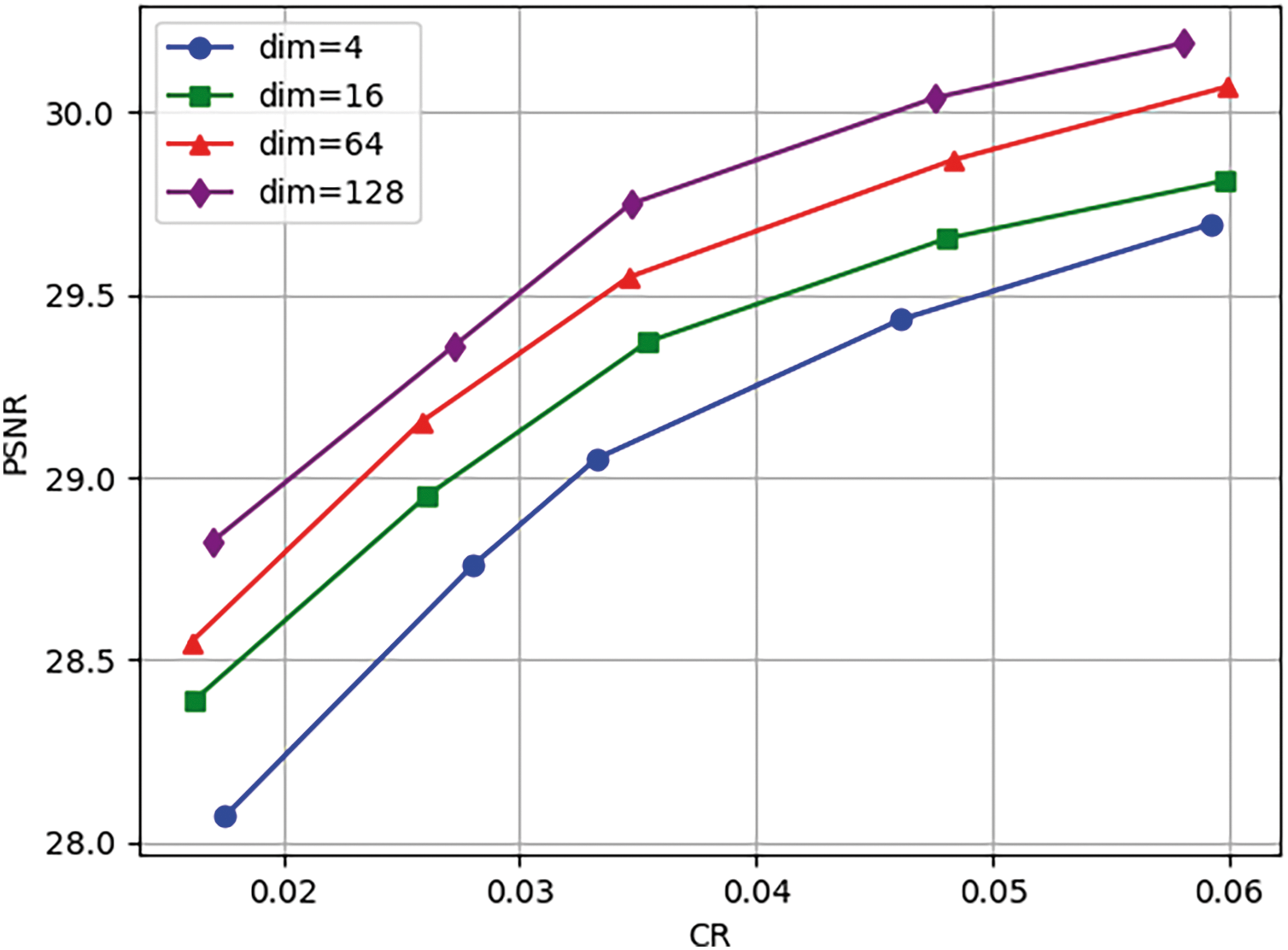
Figure 3: The PSNR values under different bottleneck dimensions

Table 1 demonstrates the ablation experiments showing the impact of semantic segmentation and the entropy bottleneck on system performance. The baseline system, without these modules, achieves reasonable reconstruction quality. Semantic segmentation improves performance by using two separate semantic encoders and decoders for encoding and decoding ROI and RONI independently. This approach avoids interference between ROI and RONI, allowing the system to allocate resources more effectively to critical areas. Essentially, semantic segmentation optimizes performance by trading additional computational resources for better results. The entropy bottleneck itself can also improve performance by compressing feature representation and preserving essential information, thereby improving image fidelity. When the two modules are combined together, the system achieves the best performance. This shows that semantic segmentation and entropy bottleneck together ensure higher reconstruction quality and higher representation and transmission efficiency.

Fig. 4 shows the PSNR values at different CR, highlighting the impact of compression on the quality of reconstructed regions of interest under varying signal-to-noise ratio (SNR) conditions. At SNR = 20 dB, the proposed scheme consistently achieves the highest PSNR, demonstrating its effectiveness in preserving image quality. The SSSC scheme outperforms the JSCC scheme, with both showing improved PSNR as CR increases, indicating that SSSC is better at reconstruction under high SNR. In contrast, the JPEG scheme exhibits the lowest PSNR and minimal improvement with increasing CR, revealing its limitations in retaining image details compared to deep learning-based methods. At SNR = 10 dB, PSNR values decrease across all schemes, but the proposed method still performs the best, proving its robustness in low SNR environments. SSSC outperforms JSCC in most cases, suggesting it better preserves image features in noisy conditions. The PSNR of JPEG remains low, below 20, with little improvement as CR increases, confirming its poor performance in noisy environments.

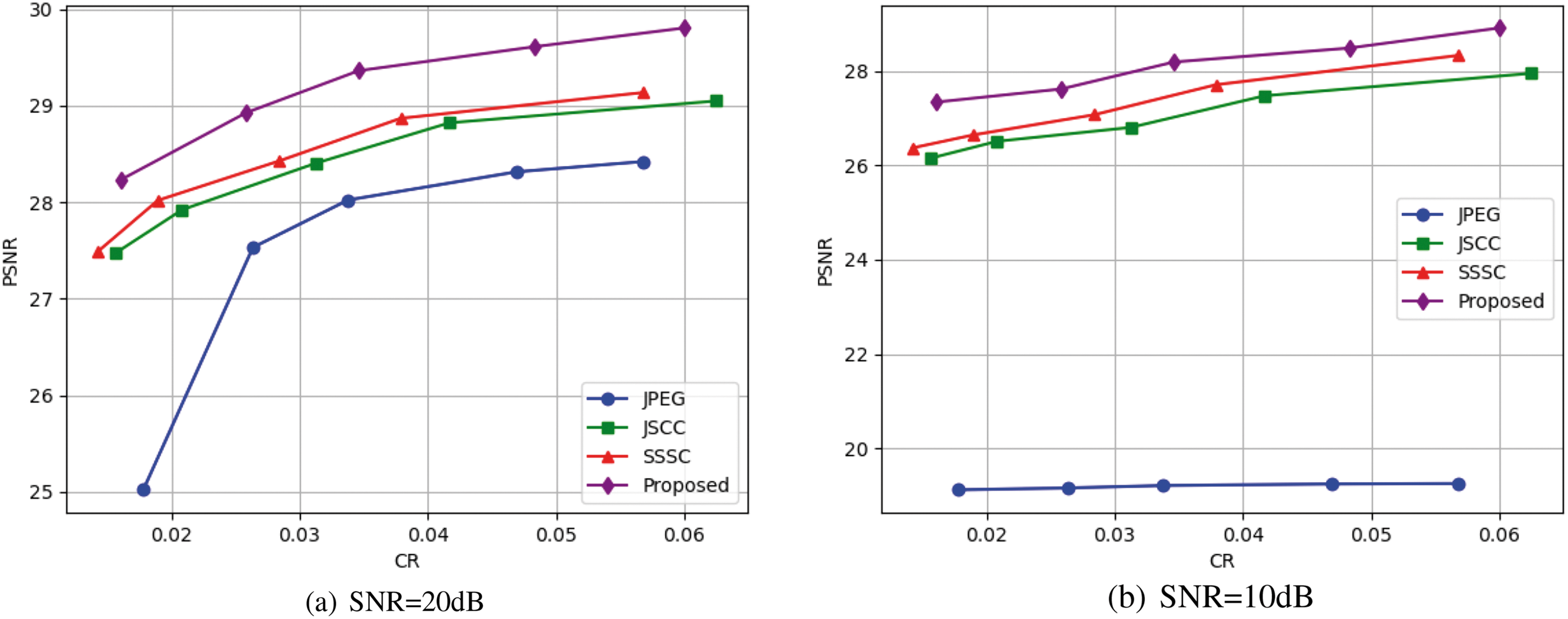
Figure 4: The θPSNR values at different CR

Fig. 5 demonstrates the robustness of the proposed system across various SNR conditions and for different values of the parameter θ (specifically, θ=0.6 and θ=0.8). As θ increases, the focus on ROI becomes stronger. For θ=0.6, the proposed scheme consistently achieves the highest θPSNR across all SNR conditions, showing excellent image reconstruction quality and robustness to SNR fluctuations. The θPSNR improves only slightly as SNR increases. The SSSC scheme follows closely, with stable θPSNR slightly lower than the proposed scheme. The JSCC scheme performs a bit worse than SSSC but still shows steady θPSNR improvement as SNR increases. In contrast, the JPEG scheme exhibits significantly lower θPSNR at lower SNRs, with a noticeable rise at higher SNRs, though it still lags behind deep learning-based schemes, indicating poor noise resilience. For θ=0.8, the relative performance remains similar to that at θ=0.6. The proposed scheme again leads with the highest θPSNR, demonstrating optimal reconstruction and robustness against noise, even with the stronger ROI focus. SSSC continues to outperform JSCC, with both schemes showing slight θPSNR improvements as SNR increases. The θPSNR of JPEG remains low at lower SNRs and increases linearly with higher SNR, but it never reaches the performance of the deep learning-based methods.

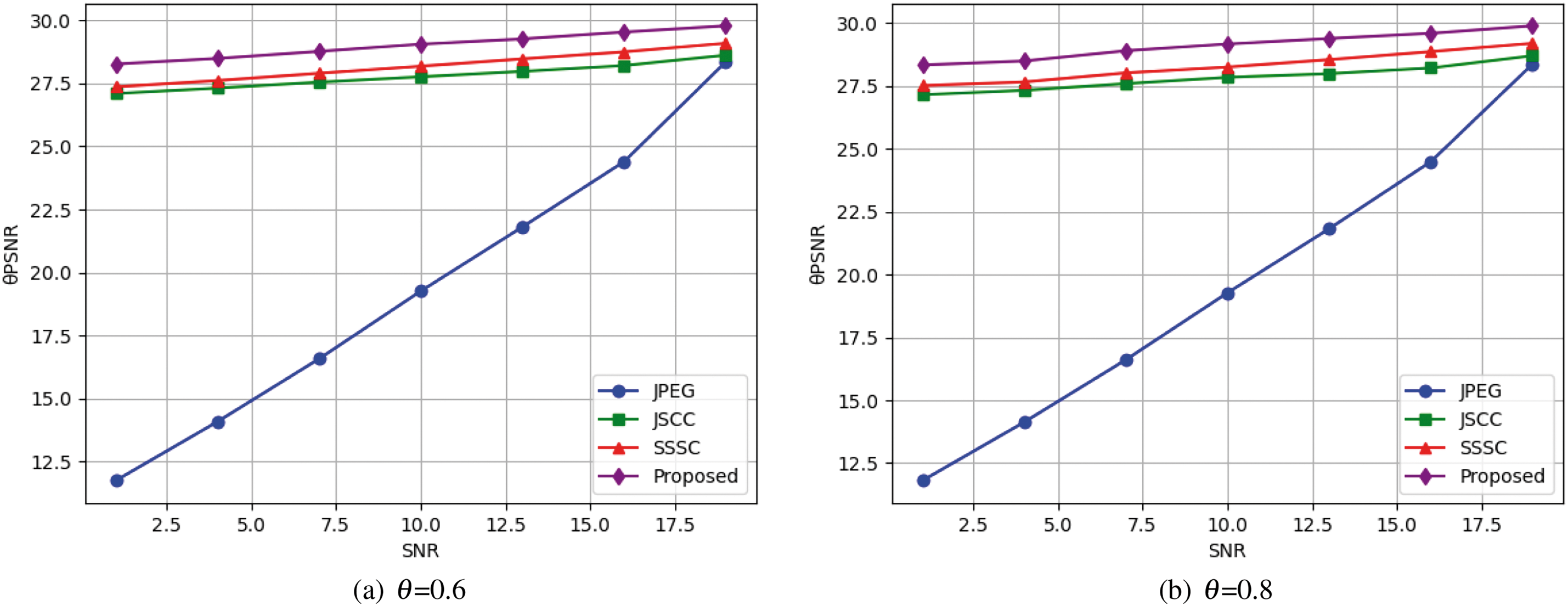
Figure 5: The θPSNR values at different SNR

5.4 Computational Complexity

The computational complexity of various image transmission schemes, including JPEG, JSCC, SSSC, and the proposed system, varies significantly.

JPEG has a complexity of O(nlog⁡n), making it efficient for resource-limited scenarios. However, it performs poorly in low SNR conditions and doesn’t optimize semantic information, limiting its robustness in noisy environments. JSCC, which uses deep learning for joint source and channel encoding, has a higher complexity of O(n2) or more, especially during training. While it performs well in noisy environments, its high computational cost makes it suitable for resource-rich applications. SSSC also has a complexity of around O(n2) due to a simple deep networks like U-Net. Despite the added cost, it improves reconstruction quality in low SNR conditions by focusing on semantic information. The proposed method introduces additional computational load for entropy calculation but reduces communication overhead by efficiently compressing data. This balance makes it suitable for high-quality reconstructions with manageable computational costs.

6  Conclusion

In this paper, we propose an entropy-bottleneck-based privacy protection mechanism for semantic communication, integrating semantic segmentation with entropy-based compression techniques to enhance both transmission efficiency and privacy protection in bandwidth-constrained environments. The proposed method distinguishes between ROI and RONI, applying differentiated compression strategiesto optimize data transmission. This approach not only significantly reduces communication overhead but also ensures the preservation of critical information, enabling high-quality reconstruction. Furthermore, the probabilistic modeling and feature quantization process within the entropy bottleneck effectively reduces the correlation between the original data and its compressed representation, thereby enhancing privacy protection and mitigating the risk of sensitive information leakage during transmission.

Acknowledgement: None.

Funding Statement: This research was supported in part by the Innovation and Entrepreneurship Training Program for Chinese College Students (No. 202410128019), in part by JST ASPIRE Grant Number JPMJAP2325, and in part by Support Center for Advanced Telecommunications Technology Research (SCAT).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Kaiyang Han; data collection: Yalong Li; analysis and interpretation of results: Kaiyang Han, Xiaoqiang Jia, Jiale Wu; draft manuscript preparation: Kaiyang Han, Yangfei Lin, Tsutomu Yoshinaga. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in the Cityscapes dataset repository at https://www.cityscapes-dataset.com/ (accessed on 31 January 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Nguyen DC, Ding M, Pathirana PN, Seneviratne A, Li J, Niyato D, et al. 6G internet of things: a comprehensive survey. IEEE Internet Things J. 2021;9(1):359–83. doi:10.1109/JIOT.2021.3103320. [Google Scholar] [CrossRef]

2. Kumari A, Gupta R, Tanwar S. Amalgamation of blockchain and IoT for smart cities underlying 6G communication: a comprehensive review. Comput Commun. 2021;172(1):102–18. doi:10.1016/j.comcom.2021.03.005. [Google Scholar] [CrossRef]

3. Alahi MEE, Sukkuea A, Tina FW, Nag A, Kurdthongmee W, Suwannarat K, et al. Integration of IoT-enabled technologies and artificial intelligence (AI) for smart city scenario: recent advancements and future trends. Sensors. 2023;23(11):5206. doi:10.3390/s23115206. [Google Scholar] [PubMed] [CrossRef]

4. Alsabah M, Naser MA, Mahmmod BM, Abdulhussain SH, Eissa MR, Al-Baidhani A, et al. 6G wireless communications networks: a comprehensive survey. IEEE Access. 2021;9:148191–243. doi:10.1109/ACCESS.2021.3124812. [Google Scholar] [CrossRef]

5. Sandeepa C, Siniarski B, Kourtellis N, Wang S, Liyanage M. A survey on privacy for B5G/6G: new privacy challenges, and research directions. J Ind Inf Integr. 2022;30:100405. [Google Scholar]

6. Luo X, Chen HH, Guo Q. Semantic communications: overview, open issues, and future research directions. IEEE Wirel Commun. 2022;29(1):210–9. doi:10.1109/MWC.101.2100269. [Google Scholar] [CrossRef]

7. Yang W, Du H, Liew ZQ, Lim WYB, Xiong Z, Niyato D, et al. Semantic communications for future internet: fundamentals, applications, and challenges. IEEE Commun Surv Tutor. 2022;25(1):213–50. doi:10.1109/COMST.2022.3223224. [Google Scholar] [CrossRef]

8. Qin Z, Tao X, Lu J, Tong W, Li GY. Semantic communications: principles and challenges. arXiv:2201.01389. 2021. [Google Scholar]

9. Lan Q, Wen D, Zhang Z, Zeng Q, Chen X, Popovski P, et al. What is semantic communication? A view on conveying meaning in the era of machine intelligence. J Commun Inf Netw. 2021;6(4):336–71. doi:10.23919/JCIN.2021.9663101. [Google Scholar] [CrossRef]

10. Shi G, Xiao Y, Li Y, Xie X. From semantic communication to semantic-aware networking: model, architecture, and open problems. IEEE Commun Mag. 2021;59(8):44–50. doi:10.1109/MCOM.001.2001239. [Google Scholar] [CrossRef]

11. Wu J, Wu C, Lin Y, Yoshinaga T, Zhong L, Chen X, et al. Semantic segmentation-based semantic communication system for image transmission. Digit Commun Netw. 2024;10(3):519–27. doi:10.1016/j.dcan.2023.02.006. [Google Scholar] [CrossRef]

12. Lin Y, Wu C, Wu J, Zhong L, Chen X, Ji Y. Meta-networking: beyond the shannon limit with multi-faceted information. IEEE Netw. 2023;37(4):256–64. doi:10.1109/MNET.013.2300115. [Google Scholar] [CrossRef]

13. Xie H, Qin Z, Li GY, Juang BH. Deep learning enabled semantic communication systems. IEEE Trans Signal Process. 2021;69:2663–75. doi:10.1109/TSP.2021.3071210. [Google Scholar] [CrossRef]

14. Gündüz D, Qin Z, Aguerri IE, Dhillon HS, Yang Z, Yener A, et al. Beyond transmitting bits: context, semantics, and task-oriented communications. IEEE J Sel Areas Commun. 2022;41(1):5–41. [Google Scholar]

15. Xie H, Qin Z, Tao X, Letaief KB. Task-oriented multi-user semantic communications. IEEE J Sel Areas Commun. 2022;40(9):2584–97. doi:10.1109/JSAC.2022.3191326. [Google Scholar] [CrossRef]

16. Zhou Q, Li R, Zhao Z, Peng C, Zhang H. Semantic communication with adaptive universal transformer. IEEE Wirel Commun Lett. 2021;11(3):453–7. doi:10.1109/LWC.2021.3132067. [Google Scholar] [CrossRef]

17. Zhang Y, Zhao H, Wei J, Zhang J, Flanagan MF, Xiong J. Context-based semantic communication via dynamic programming. IEEE Trans Cogn Commun Netw. 2022;8(3):1453–67. doi:10.1109/TCCN.2022.3173056. [Google Scholar] [CrossRef]

18. Zhang H, Shao S, Tao M, Bi X, Letaief KB. Deep learning-enabled semantic communication systems with task-unaware transmitter and dynamic data. IEEE J Sel Areas Commun. 2022;41(1):170–85. doi:10.1109/JSAC.2022.3221991. [Google Scholar] [CrossRef]

19. Tang S, Yang Q, Fan L, Lei X, Nallanathan A, Karagiannidis GK. Contrastive learning based semantic communications. IEEE Trans Commun. 2024;72(10):6328–43. [Google Scholar]

20. Dai J, Wang S, Tan K, Si Z, Qin X, Niu K, et al. Nonlinear transform source-channel coding for semantic communications. IEEE J Sel Areas Commun. 2022;40(8):2300–16. doi:10.1109/JSAC.2022.3180802. [Google Scholar] [CrossRef]

21. Yan C, Hao Y, Li L, Yin J, Liu A, Mao Z, et al. Task-adaptive attention for image captioning. IEEE Trans Circuits Syst Video Technol. 2021;32(1):43–51. doi:10.1109/TCSVT.2021.3067449. [Google Scholar] [CrossRef]

22. Yan C, Gong B, Wei Y, Gao Y. Deep multi-view enhancement hashing for image retrieval. IEEE Trans Pattern Anal Mach Intell. 2020;43(4):1445–51. doi:10.1109/TPAMI.2020.2975798. [Google Scholar] [PubMed] [CrossRef]

23. Guo S, Wang Y, Zhang N, Su Z, Luan TH, Tian Z, et al. A survey on semantic communication networks: architecture, security, and privacy. arXiv:2405.01221. 2024. [Google Scholar]

24. Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. arXiv:1412.6572. 2014. [Google Scholar]

25. Ballé J, Minnen D, Singh S, Hwang SJ, Johnston N. Variational image compression with a scale hyperprior. arXiv:180201436. 2018. [Google Scholar]

26. Li J, Li B, Lu Y. Deep contextual video compression. Adv Neural Inf Process Syst. 2021;34:18114–25. [Google Scholar]

27. Smith G. On the foundations of quantitative information flow. In: International Conference on Foundations of Software Science and Computational Structures; 2009; Berlin/Heidelberg: Springer. p. 288–302. [Google Scholar]

28. Bourtsoulatze E, Kurka DB, Gündüz D. Deep joint source-channel coding for wireless image transmission. IEEE Trans Cogn Commun Netw. 2019;5(3):567–79. doi:10.1109/TCCN.2019.2919300. [Google Scholar] [CrossRef]

29. Cordts M, Omran M, Ramos S, Rehfeld T, Enzweiler M, Benenson R, et al. The cityscapes dataset for semantic urban scene understanding. In: Proceedings of the IEEE Conference on Computer Vision And Pattern Recognition; 2016; Las Vegas, NV, USA: IEEE. p. 3213–23. [Google Scholar]

30. Korhonen J, You J. Peak signal-to-noise ratio revisited: is simple beautiful? In: 2012 Fourth International Workshop on Quality of Multimedia Experience; 2012; New York, NY, USA: IEEE. p. 37–8. [Google Scholar]