 Open Access
Open Access
ARTICLE
Single Qubit Quantum Logistic-Sine XYZ-Rotation Maps: An Ultra-Wide Range Dynamics for Image Encryption
1 Research Center for Quantum Computing and Materials Informatics, Faculty of Computer Science, Dian Nuswantoro University, Semarang, 50131, Indonesia
2 Department of Cyber Forensics and Information Security, Behala Government Polytechnic, 756, Upendra Nath Banerjee Road, Parnasree, Behala, Kolkata, 700060, India
3 Thai Nguyen University of Technology, Thai Nguyen University, Thai Nguyen, 240000, Vietnam
4 Department of Computer Science, Federal University of Petroleum Resources, Effurun, 330102, Nigeria
* Corresponding Author: De Rosal Ignatius Moses Setiadi. Email:
Computers, Materials & Continua 2025, 83(2), 2161-2188. https://doi.org/10.32604/cmc.2025.063729
Received 22 January 2025; Accepted 10 March 2025; Issue published 16 April 2025
Abstract
Data security has become a growing priority due to the increasing frequency of cyber-attacks, necessitating the development of more advanced encryption algorithms. This paper introduces Single Qubit Quantum Logistic-Sine XYZ-Rotation Maps (SQQLSR), a quantum-based chaos map designed to generate one-dimensional chaotic sequences with an ultra-wide parameter range. The proposed model leverages quantum superposition using Hadamard gates and quantum rotations along the X, Y, and Z axes to enhance randomness. Extensive numerical experiments validate the effectiveness of SQQLSR. The proposed method achieves a maximum Lyapunov exponent (LE) of ≈55.265, surpassing traditional chaotic maps in unpredictability. The bifurcation analysis confirms a uniform chaotic distribution, eliminating periodic windows and ensuring higher randomness. The system also generates an expanded key space exceeding 1040, enhancing security against brute-force attacks. Additionally, SQQLSR is applied to image encryption using a simple three-layer encryption scheme combining permutation and substitution techniques. This approach is intentionally designed to highlight the impact of SQQLSR-generated chaotic sequences rather than relying on a complex encryption algorithm. The encryption method achieves an average entropy of 7.9994, NPCR above 99.6%, and UACI within 32.8%–33.8%, confirming its strong randomness and sensitivity to minor modifications. The robustness tests against noise, cropping, and JPEG compression demonstrate its resistance to statistical and differential attacks. Additionally, the decryption process ensures perfect image reconstruction with an infinite PSNR value, proving the algorithm’s reliability. These results highlight SQQLSR’s potential as a lightweight yet highly secure encryption mechanism suitable for quantum cryptography and secure communications.Keywords
In today’s modern world, the acceleration of data transmission has increased the demand for data protection techniques. In addition, due to the rapid increase in both the volume and complexity of cyberattacks [1,2], conventional encryption methods began to face more and more difficulties [3]. A new paradigm of increasing attention is chaos-based cryptography, which possesses the properties of being sensitive to initial conditions, ergodicity, and unpredictability [4–6]. In general, chaos maps are categorized into one-dimensional (1D), two-dimensional (2D), and high-dimensional (HD) maps [7–10]. HD chaotic maps, such as hyperchaotic maps, have complex dynamics and more control parameters, thus providing a high level of security in encryption applications [11]. However, implementing these maps often requires longer computation time and more resources. To overcome this, compression and encryption can be combined to reduce computational complexity while increasing encryption efficiency [12]. However, designing and improving chaotic models can directly improve encryption performance.
The 1D chaotic maps have a simple structure, are easy to implement, and require minimal computational resources, making them an attractive choice for many practical applications, including image encryption [13]. However, traditional 1D chaotic maps, such as Logistic Map and sine maps, have inherent limitations, like uneven bifurcation distribution, periodic windows, and limited Lyapunov exponent (LE) range. These limitations reduce the effectiveness of 1D maps for high-security scenarios and advanced applications such as image encryption. Research [14] has created a cryptanalysis method to break the encryption of hill and chaotic variants such as logistic, sine, and Chebyshev. Hence, the development of chaos methods becomes urgent.
Several studies have developed 1D chaotic maps, such as Han’s [15] study, which proposed the Modified Logistic Map to improve the sensitivity to initial conditions and expand the chaotic range of the Logistic Map. Other 1D methods have also been proposed, such as Fractional 1D chaotic map [13] for high-speed image encryption and 1D Sine Powered (1DSP) [16], which integrates two control parameters to produce a wider range of chaos and higher complexity. The 1D Sine-Map-Coupling-Logistic-Map (1D-SMCLM) coupling system was also developed by Hu et al. [17], which overcomes the shortcomings of small parameters in the Sine Map and Logistic Map. In addition, an Improved Logistic Map (1D-ILM) and an Improved Quadratic Map (1D-IQM) were also proposed by Khairullah et al. [18]. These developments reflect significant efforts to improve the efficiency and security of 1D-based chaotic systems.
The advancement of quantum computing technology, such as Quantum Key Distribution (QKD), has been widely developed in data communication. QKD can be distributed very securely, making it difficult for attackers to steal. QKD has also been applied to protect key distribution in image encryption [19–21], but quantum development for image encryption has not been widely developed. The way quantum computing works by converting bits into qubits makes the randomness patterns produced by chaotic systems stronger [22,23]. The superposition principle allows qubits to be in a linear combination of two or more states simultaneously, providing the ability to increase randomness significantly [24,25]. Moreover, entanglement between qubits strengthens the correlation between elements in a chaotic system even though they are physically separated. Quantum rotation, mediated by rotation gates such as Hadamard and CNOT, provides additional complexity in manipulating the system’s randomness.
Several studies have utilized quantum approaches to chaotic maps [26–28]. Rehman [29] integrated quantum principles with sine-based chaos maps. Wang [30] proposed fast adaptive synchronization on discrete logistic quantum chaos maps. Rajan et al. [31] also introduced an image encryption model that combines quantum rotation and chaos maps. While Abd el-Latif et al. [32] used a quantum-inspired method to integrate the properties of quantum walks and logistic-sine maps. The development of quantum chaos is crucial because it can expand the control parameters that directly increase the key space, increase the complexity of system dynamics, and overcome the periodicity weaknesses in traditional chaotic systems, especially 1D ones.
This research objective is to introduce Single Qubit Quantum Logistic-Sine XYZ-Rotation Maps (SQQLSR), a powerful and simple 1D quantum chaos map. SQQLSR utilizes quantum principles to produce more random and unpredictable 1D chaotic behavior. Quantum superposition is implemented through the Hadamard gate, which allows qubits to be in a linear combination of multiple states simultaneously, expanding the space of possible system dynamics. In addition, three types of quantum rotations are used—X, Y, and Z Rotations—each providing an additional dimension to manipulating randomness. Combining these elements makes SQQLSR produce superior performance in terms of randomness and security. The SQQLSR map is also tested and applied in a new image encryption framework, where the resulting chaotic sequence is used for substitution and permutation processes. RGB images expand one chaotic sequence into three sequences for red, green, and blue channels. A high floating point normalization technique is applied to adjust the initial distribution range of the chaotic sequence, making it compatible with the number of image layers without compromising the randomness quality of the system.
2.1 Traditional Chaotic Maps and Background
In traditional chaos maps such as Logistic Map and Sine Map, bifurcations are often concentrated in certain regions, especially when the value of the control parameter (

Figure 1: Bifurcation diagram of traditional chaotic map (a) Logistic map; (b) Sine map; (c) Tent map; (d) Piecewise-linear chaotic map
The Tent Map bifurcation graph in Fig. 1c shows chaotic behavior starting from the control parameter value
The Lyapunov exponent (LE) is an essential metric for assessing the sensitivity of a system to small changes in initial conditions. Positive LE values indicate a better chaotic pattern. Conversely, low values mean that the chaotic pattern is more predictable, thus reducing the strength of the encryption key. In traditional chaotic maps such as Logistic and Sine Map, LE values tend to be low in the

Figure 2: LE of traditional chaotic map (a) Logistic map; (b) Sine map; (c) Tent map; (d) Piecewise-linear chaotic map
The LE of the Tent Map (see Fig. 2c) shows a pattern different from that of the Logistic and Sine Map. In the
Another important factor in chaotic systems is the range of control parameters. A more extensive range of control parameters directly expands the available key space, which is one of the critical elements in cryptographic security [33,34]. In traditional chaotic maps such as Logistic Map, the range of control parameters is generally limited to the interval [0, 4]. Ullah et al. [34] proposed 1D Cosine Chaotic Equation (1D-CCE) with a range of control parameters [0, 10], showing improved flexibility and randomness compared to the Logistic Map. Another study [33] developed a hybrid chaotic map using three dynamic parameters, where one parameter has a range of [0, 4], and the other two parameters have a range of [0, 2]. Although there is an improvement over traditional maps, the limited range of parameters is still a constraint in expanding the key space. Therefore, expanding the control parameters in 1D chaotic maps remains a significant need to improve security, especially in the key space and complexity of chaotic systems.
Traditional chaotic maps have been modified to improve deficiencies such as narrow bifurcation range, low LE, and instability in specific parameter ranges. Modified Logistic Map [15] is designed to increase sensitivity to initial conditions, expand the range of control parameters to [0, 10], and obtain complete mapping
Another development of 1D chaotic map is called sine powered chaotic map (1DSP) [16] such as research using two control parameters, namely
Another map, the Fractional 1D chaotic map [13], also uses two control parameters, namely
Furthermore, a recent study [34] proposed 1-Dimensional Cosine Chaotic Equation (1D-CCE). CCE has a wider range of control parameters, namely
The development of the 1D chaotic map models above has indeed succeeded in expanding the range of chaos and increasing sensitivity to initial conditions. However, quantum chaotic maps have been developed with a relatively limited parameter range and relatively unstable chaotic behavior. Study [35] is one of the early studies that utilized quantum chaotic maps as pseudo-random number generators (PRNG). It is said that a high level of non-periodicity was obtained based on the evaluation of the Scale Index Technique. In addition, there are also dissipative quantum corrections, which provide additional dynamics.
Furthermore, Rehman [29] implemented quantum coding and 1-D Sine-based Chaotic Maps for image encryption. Furthermore, Rajan et al. [31] combined classical chaotic maps, such as logistic-sine hybrid chaotic maps, with quantum chaotic maps to increase randomness and sensitivity to initial conditions. The unique characteristics of qubits, such as entanglement and superposition, are exploited to expand the key space and strengthen encryption security against classical and quantum threats. Unfortunately, this study does not discuss the bifurcation diagram, Lyapunov exponent, and trajectory. However, there is a discussion of the phase diagram, which shows very complex and unexpected dynamics, in addition to the claim of a significant increase in the key space.
Recent research introduces a distributed quantum logistic model in three dimensions (3D) [30], utilizing the coupling parameter (
2.3 Motivation and Research Contribution
Traditional chaos maps face limitations such as uneven bifurcation distribution, low Lyapunov exponent (LE), and narrow key space. The development of chaos maps has been carried out and has obtained positive results, but considering the increasingly developing technology, the sophistication of chaos maps still needs to be developed. Quantum technology is a leap of innovation and has the potential to develop chaos map performance. The previously carried out quantum approach offers more complex dynamics, although it can be more complex and still has limited chaos space. SQQLSR is designed to overcome this problem by utilizing the principles of superposition and quantum rotation, resulting in a more even bifurcation distribution, stable LE, and a more expansive dynamic key space. More detailed contributions of this research are:
1. Designing SQQLSR by simply using single qubits to reduce computational complexity.
2. The principles of superposition (Hadamard) and quantum rotation (X, Y, Z) are used to expand chaos dynamics and increase sensitivity.
3. SQQLSR offers higher and stable LE and dynamic bifurcation distribution over an ultra-wide parameter range.
4. Implementing and testing SQQLSR for image encryption.
3.1 Design Single Qubit Quantum Logistic-Sine XYZ-Rotation Maps
Single Qubit Quantum Logistic-Sine XYZ-Rotation Maps (SQQLSR) is a quantum-based chaos map design that utilizes the properties of quantum superposition and rotation to produce more complex and unpredictable chaotic dynamics. Compared with classical chaos maps, SQQLSR provides significant advantages regarding a more expansive key space, higher randomness, and better sensitivity to initial conditions. It should be noted that the number of qubits in a quantum computing system significantly impacts computational complexity. Each additional qubit increases the information storage capacity exponentially and enlarges the state space that must be managed, thereby increasing operational complexity and resource requirements [36,37]. Based on this theory, this research considers designing the system using a single qubit, making it simpler than multi-qubit based models but still sophisticated. This single-qubit design reduces the computational complexity while maintaining strong chaotic properties. Efficiently exploiting quantum superposition and rotation in a simpler framework makes near-term quantum hardware more feasible. The unitary operator of SQQLSR can be written in Eq. (1).
where
where

Figure 3: Quantum circuit design of SQQLSR
Based on the circuit plot in Fig. 3, the more detailed workings of the proposed quantum circuit are as follows:
1. Initial Hadamard gate: prepares the qubit in the initial superposition state, allowing the qubit to be in a linear combination of its basis states
2. The first rotation about the Z-axis (
3. The second rotation about the Y-axis (
4. The third rotation about the X-axis (
5. The End Hadamard Gate is used to bring the qubit back to the superposition basis to maximize quantum interference that reflects the overall dynamics of the system.
6. Pauli-Z measurement
3.2 Proposed Image Encryption Method Using SQQLSR
The SQQLSR is used as a chaotic sequence generator as the primary key (
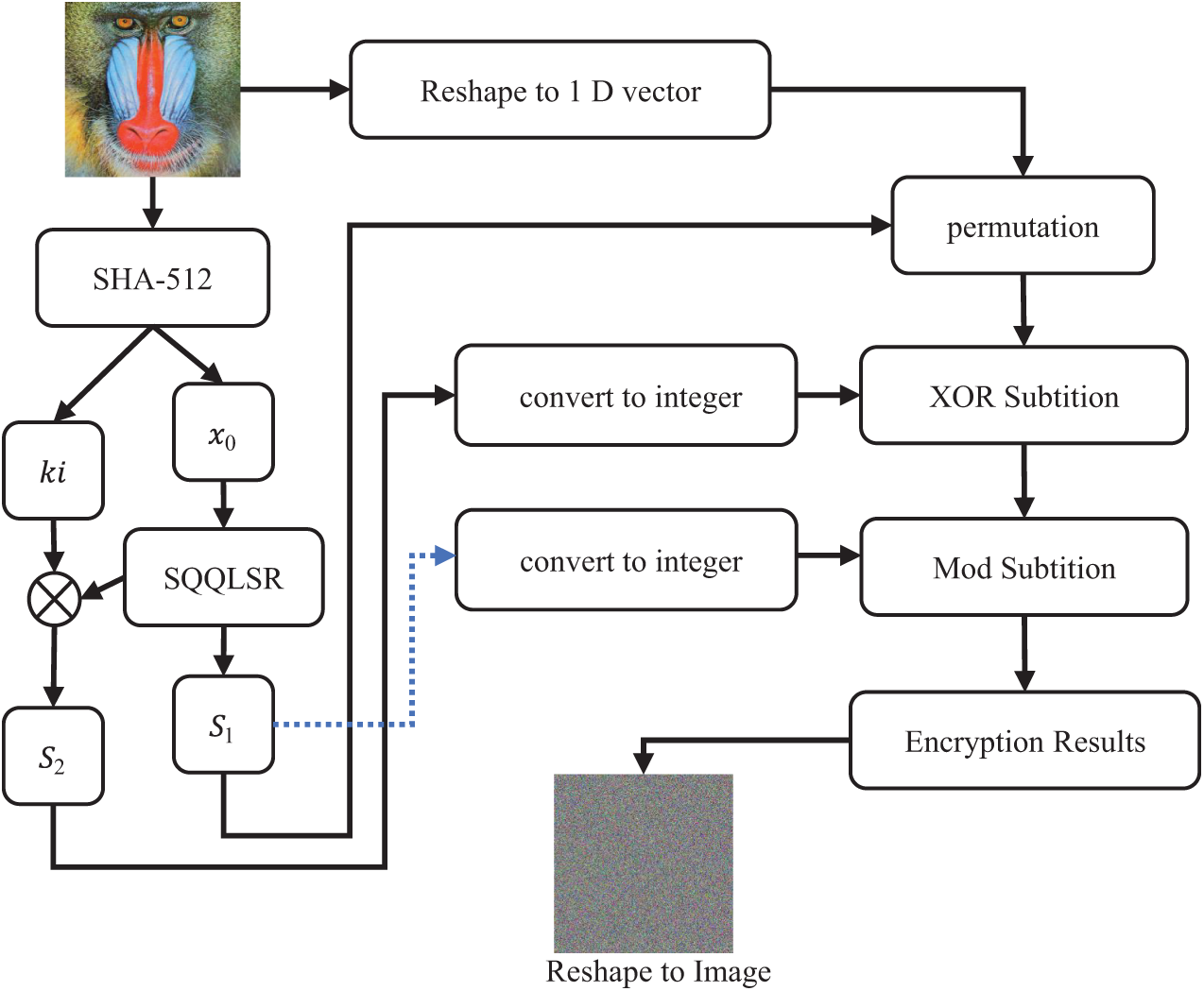
Figure 4: Proposed encryption scheme
3.2.1 Initialization and Key Generation
1. A plain image
2. The chaotic sequence
where
3. After obtaining two chaotic sequences
1. Stage 1: In this stage involves a sort permutation operation to shuffle the positions of image pixels. This step introduces a high level of randomness to the spatial distribution of pixel intensities, effectively obscuring the original image structure. The chaotic sequence
here,
2. Stage 2: XOR Substitution is performed by XOR operation between the first stage encrypted image
3. Stage 3: The final stage is modulus substitution, where the chaotic sequence
4. The
1. Read the final encrypted image
2. Stage 1: Perform modulus Substitution Inversion on
3. Stage 2: Perform XOR substitution inversion on
4. Stage 3: Restore the pixel position of
5. After three stages decryption, reconstructed
This section presents the results and analysis of the SQQLSR model, evaluated through comprehensive simulations. The experiments were conducted in a Python environment using Google Colab, utilizing the PennyLane quantum simulator to implement and test the chaotic properties of SQQLSR. The implementation leveraged PennyLane for quantum circuit simulations, NumPy for numerical computations, Matplotlib for visualization, and Pandas for data handling. OpenCV and PIL libraries were also employed for image preprocessing, encryption, and visualization. The proposed quantum chaotic system was examined using bifurcation diagrams, Lyapunov exponent analysis, trajectory plots, and phase-space representations to validate its capability to generate highly complex and unpredictable dynamics.
Section 4.1 provides an in-depth analysis of SQQLSR, including its parameter sensitivity, chaotic range, and key performance metrics, demonstrating its advantages over traditional chaotic maps. Meanwhile, Section 4.2 implements SQQLSR for image encryption, applying a simple three-layer scheme combining permutation and substitution techniques. This approach is intentionally designed to isolate and highlight the impact of SQQLSR on encryption performance rather than relying on a complex encryption algorithm. By focusing on the chaotic sequence generated by SQQLSR, the evaluation emphasizes its effectiveness in enhancing diffusion and confusion, ensuring robust security against statistical and differential attacks.
4.1 Single Qubit Quantum Logistic-Sine XYZ-Rotation Maps (SQQLSR)
In this section, the results of the SQQLSR test are measured and analyzed using bifurcation diagrams, LE, and chaos trajectories. In addition, this section also aims to validate the hypothesis that the selection of parameters such as scaling factor, iteration variation, and rotation offset can expand the range of control parameters, increase sensitivity to initial conditions, and strengthen chaotic dynamics. In SQQLSR, apart from the parameter
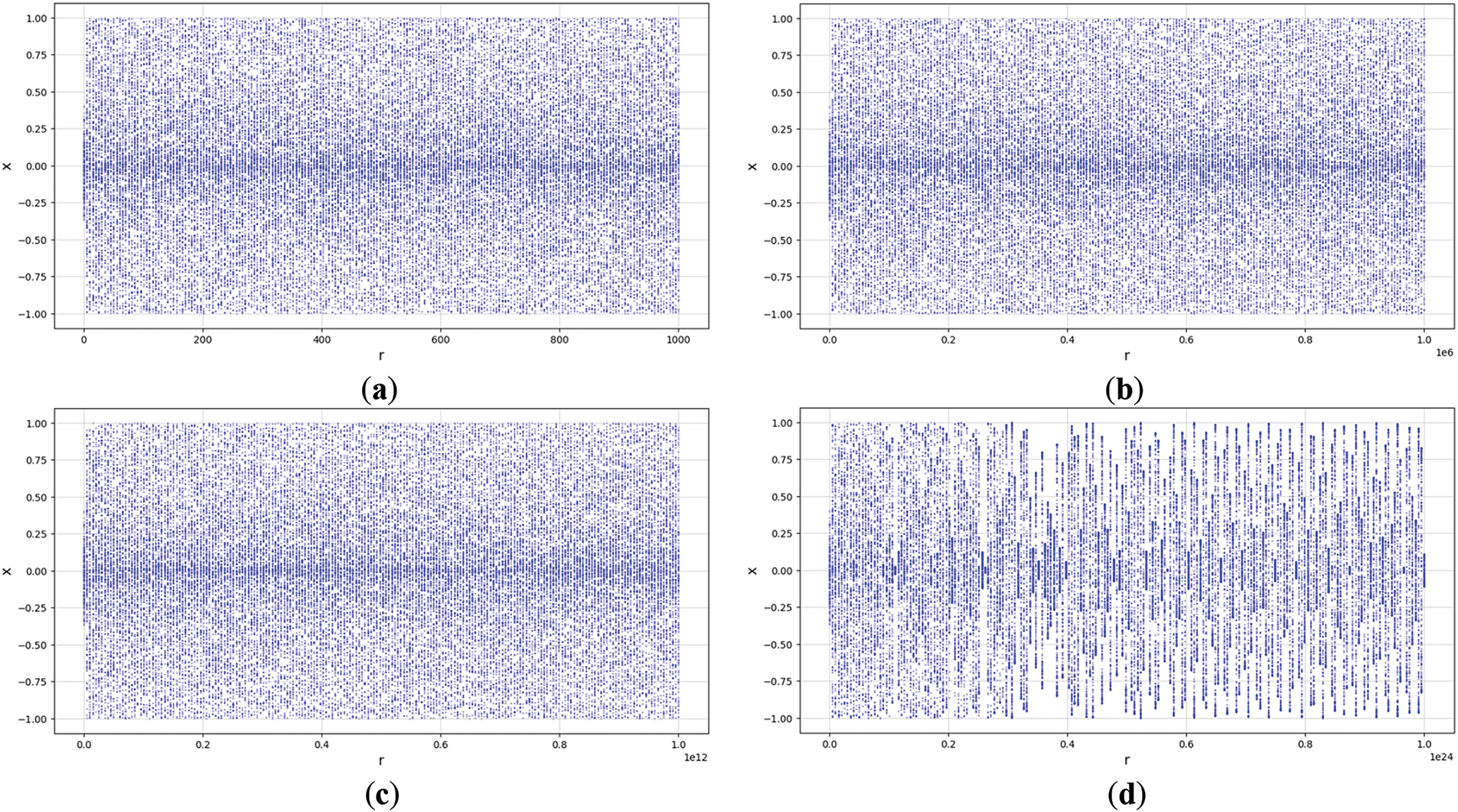
Figure 5: Bifurcation diagram of SQQLSR (a)
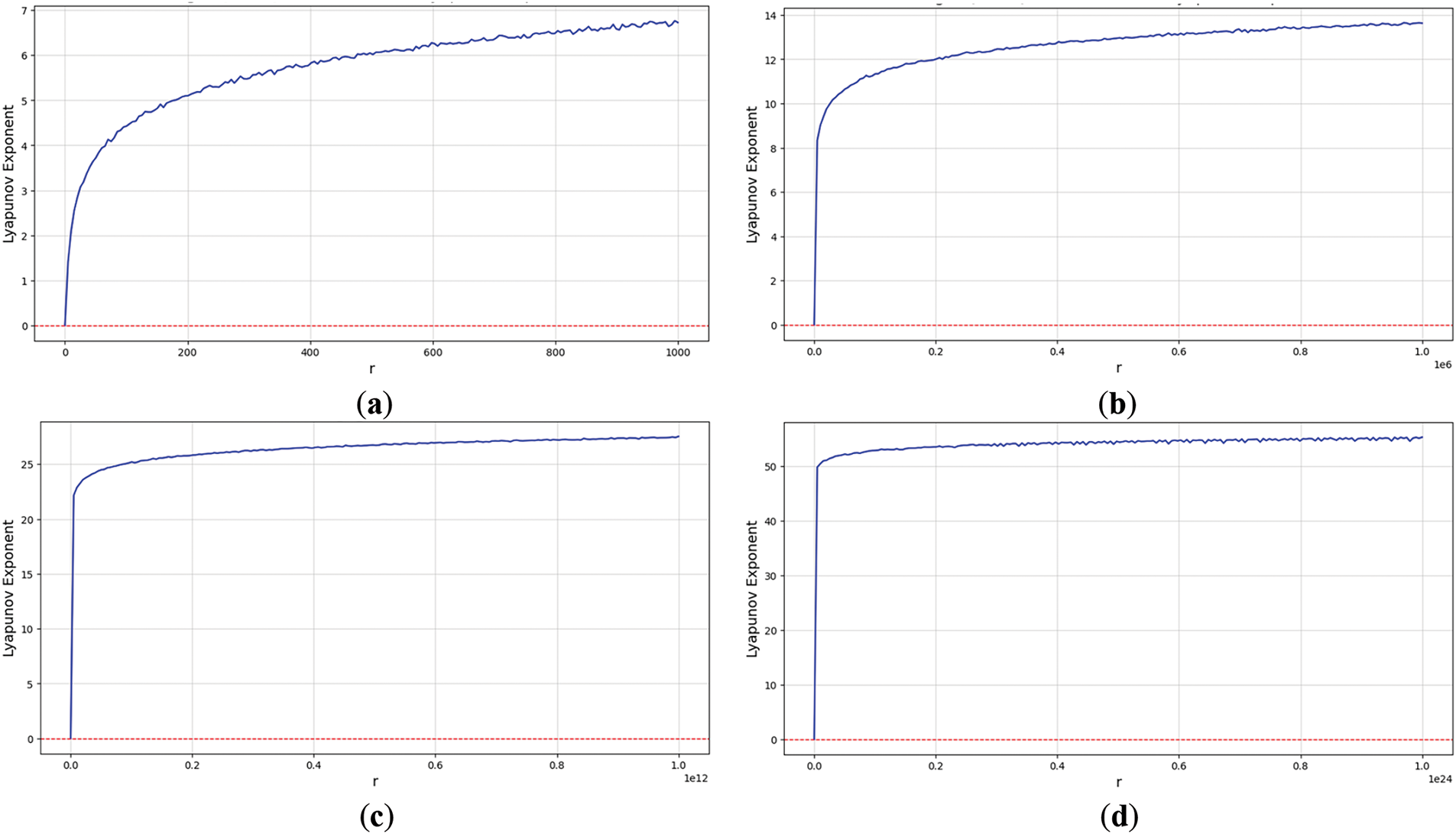
Figure 6: Lyapunov exponent of SQQLSR (a)
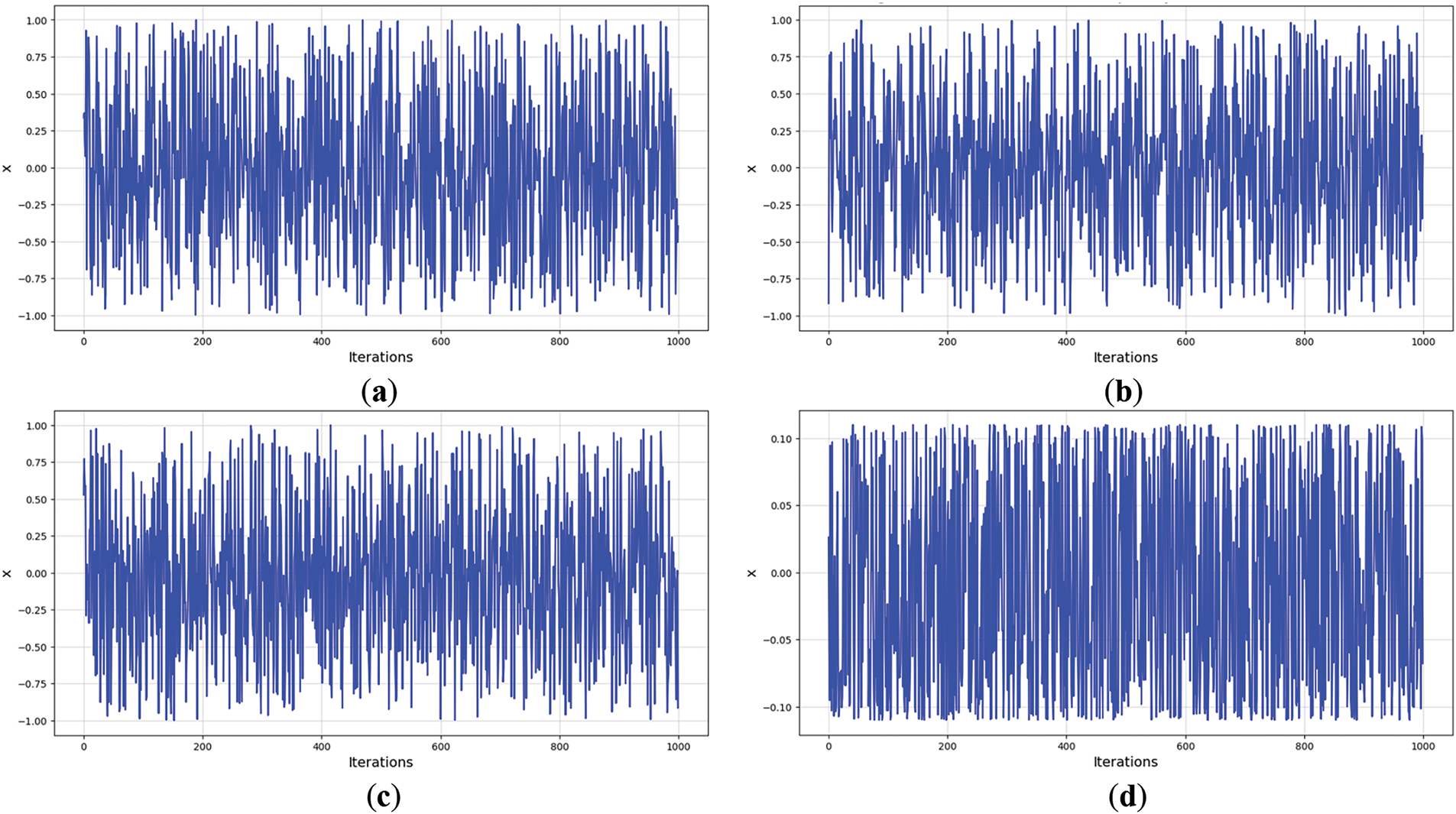
Figure 7: Trajectory diagram of SQQLSR (a)
The simulation results of SQQLSR show excellent capability in generating complex and unpredictable chaotic dynamics. The bifurcation diagram (Fig. 5) shows a uniform distribution of variable x in the range [−1, 1] without “blank windows” for Fig. 5a–c, indicating that SQQLSR successfully overcomes the weakness of the stability of traditional chaos maps. However, “blank windows” begin to appear in Fig. 5d, so our test is limited to
Based on the observation in Fig. 6, the LE value shows a relatively stable increase along with a significant increase compared to the traditional chaos map at
The chaotic attractor diagram in Fig. 8 also confirms the superior chaotic dynamics of SQQLSR. The diagram presents a dense, non-repeating point distribution highlighting the system’s ability to explore a wide range of state spaces. In Fig. 8a–c, the attractor maintains its density and complexity while avoiding periodic regions, thus ensuring robust and unpredictable dynamics. At
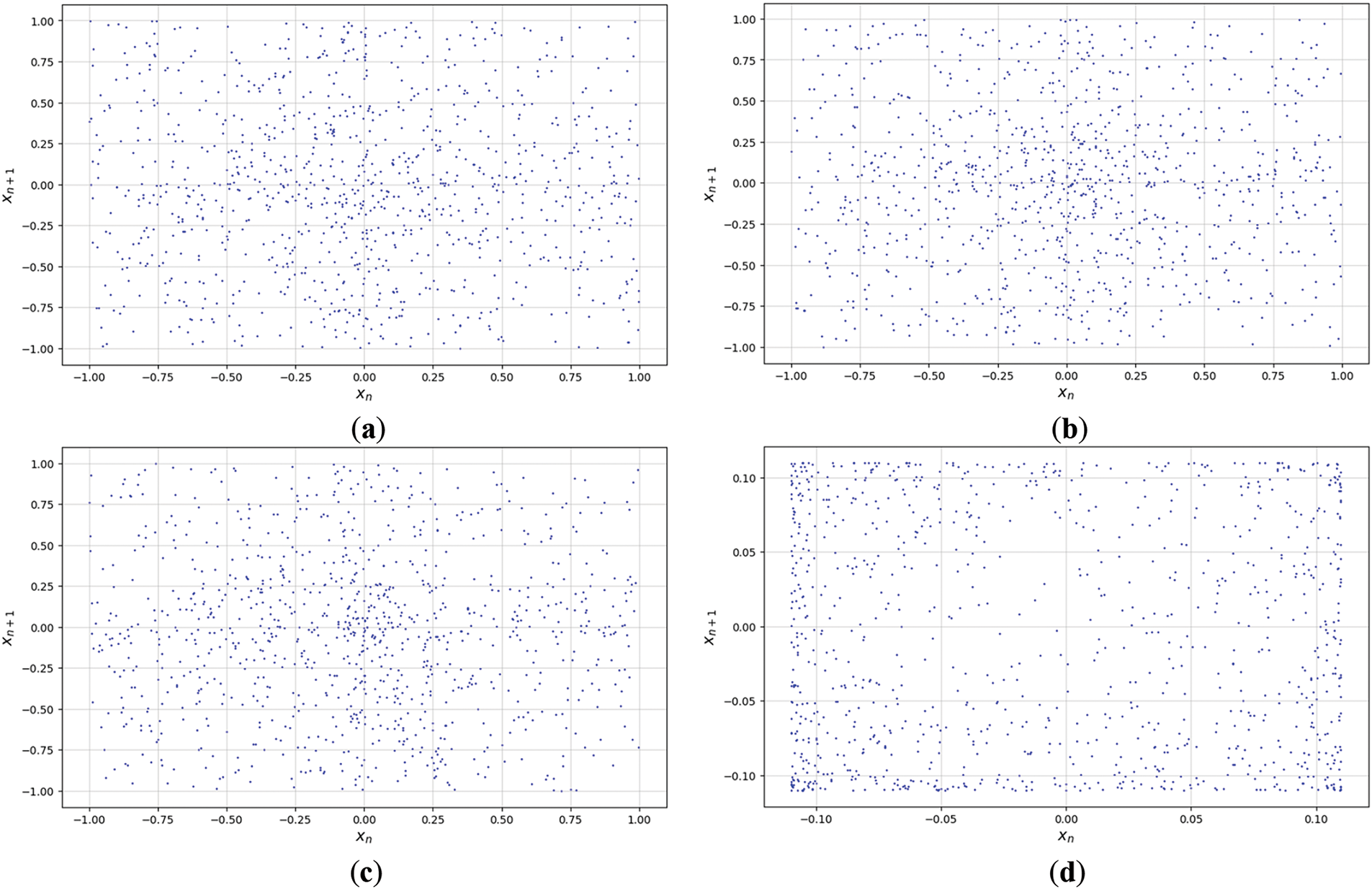
Figure 8: Chaotic attractor of SQQLSR (a)
The phase space diagrams of SQQLSR presented in Fig. 9 demonstrate strong chaotic behavior across an ultra-wide range of the control parameter
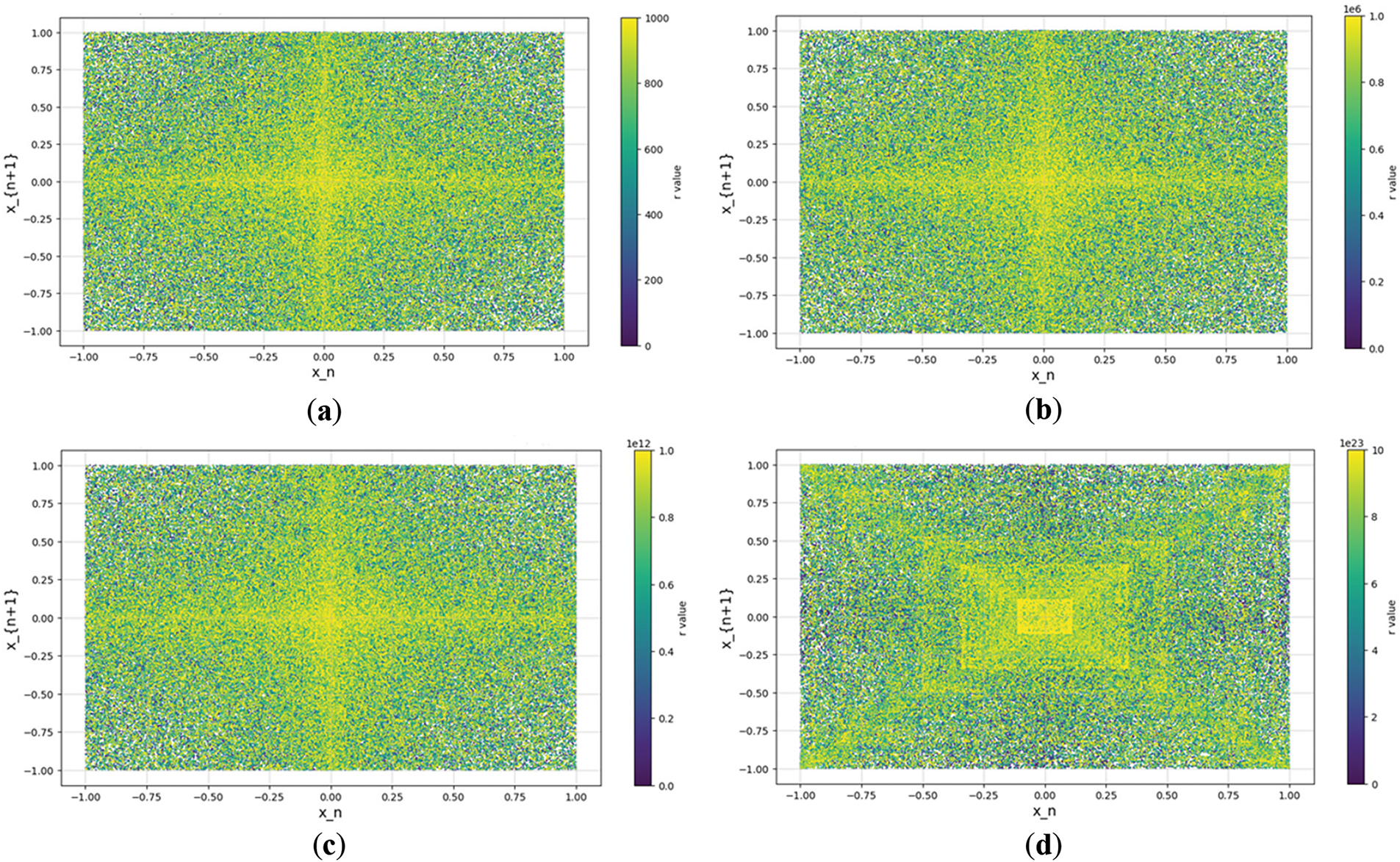
Figure 9: Phase space diagram of SQQLSR (a)
The carefully designed parameter selection also supports this success. To determine optimal values, we conducted multiple experimental trials to evaluate the sensitivity of each parameter to chaotic behavior. In the graphs above, we used 1000 iterations (
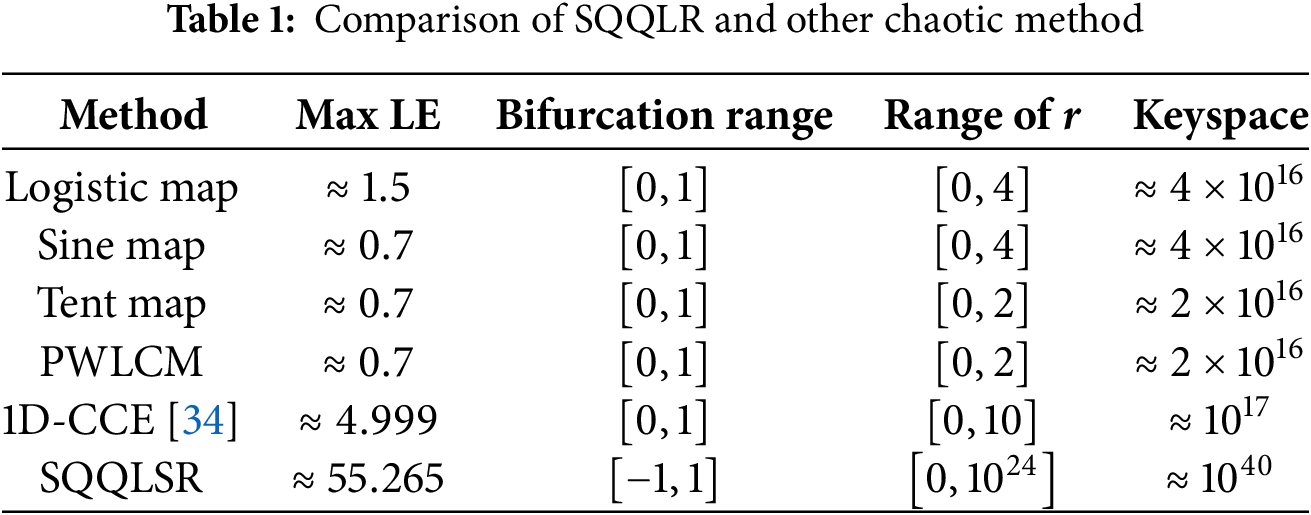
Table 1 highlights the superiority of SQQLSR over traditional chaotic maps in key aspects such as Lyapunov exponent (LE), bifurcation range, and key space size. SQQLSR exhibits a significantly higher LE (≈55.265), indicating extreme sensitivity to initial conditions compared to classical methods, which typically have LE ≤ 1.5. Its bifurcation range [−1, 1] is broader than conventional maps, suggesting enhanced chaotic behavior. Moreover, its key space (≈1040) is orders of magnitude larger than classical methods, reinforcing its robustness against brute-force attacks. Overall, SQQLSR offers significant advantages regarding large key space, unpredictable randomness, and high sensitivity to initial conditions, making it a strong candidate for developing quantum-based security technologies.
4.2 Implementation SQQLSR for Image Encryption
In this section, we test SQQLSR with
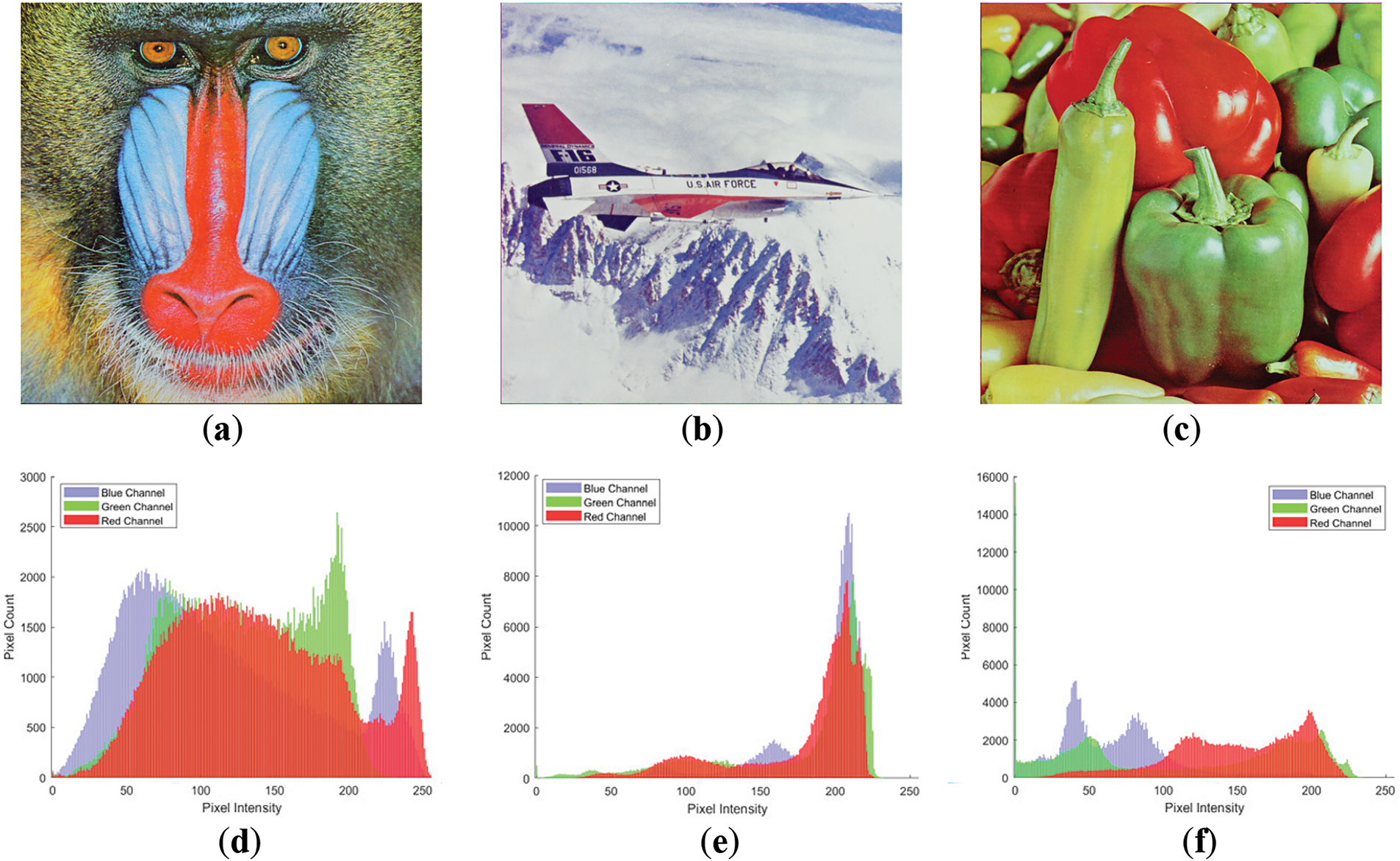
Figure 10: Standard image used (a) 4.2.03 Baboon; (b) 4.2.05; (c) 4.2.07 Peppers; (d–f) Corresponde Histogram

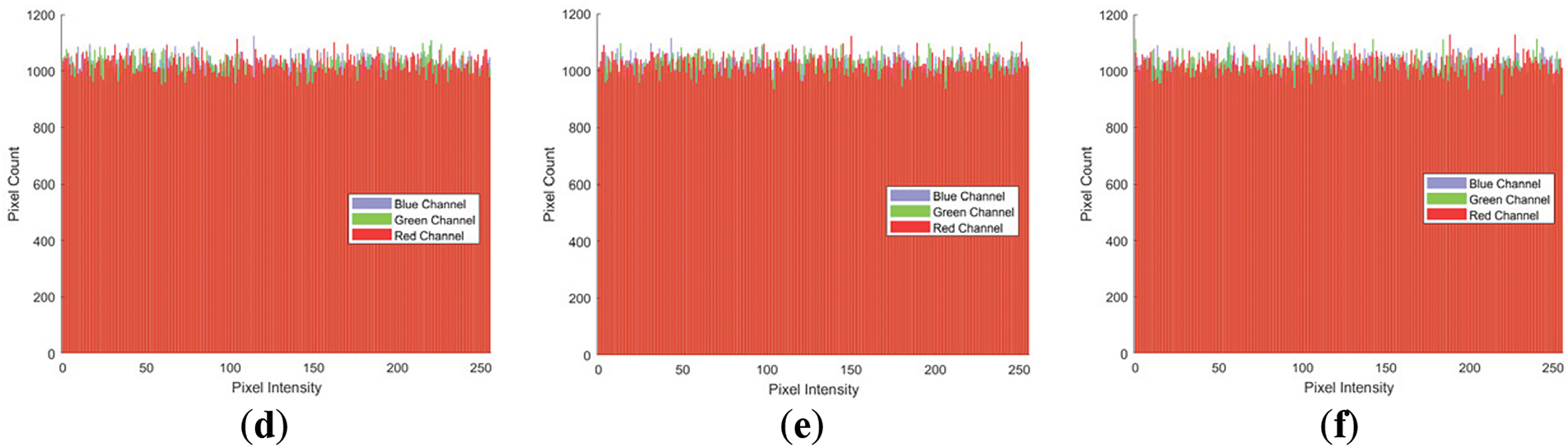
Figure 11: Encryption results (a) 4.2.03 Baboon; (b) 4.2.05; (c) 4.2.07 Peppers; (d–f) Corresponde Histogram
In the context of chi-square analysis on images with a dimension of 512 × 512 pixels, it is important to understand that the ideal chi-square value results from a uniform distribution of pixel intensities after encryption. For grayscale images, the ideal distribution is that each intensity level has the same frequency. With a total of 512 × 512 = 262,144 pixels evenly distributed among 256 intensity levels, the ideal frequency (
where
To evaluate whether the results are ideal, it is necessary to compare the calculated chi-square value with the critical value at a certain significance level. If the degrees of freedom are 255 and the significance level is 0.05, then the critical chi-square value is around 293.25. If the calculated chi-square value is smaller than this critical value, then the intensity distribution can be considered statistically uniform.
The chi-square calculation results in Table 2 show that all are below the critical value. This indicates that the pixel intensity has been distributed evenly, approaching the characteristics of a uniform distribution. In other words, the encryption algorithm has successfully hidden the original pattern of the image, ensuring security against statistical analysis.
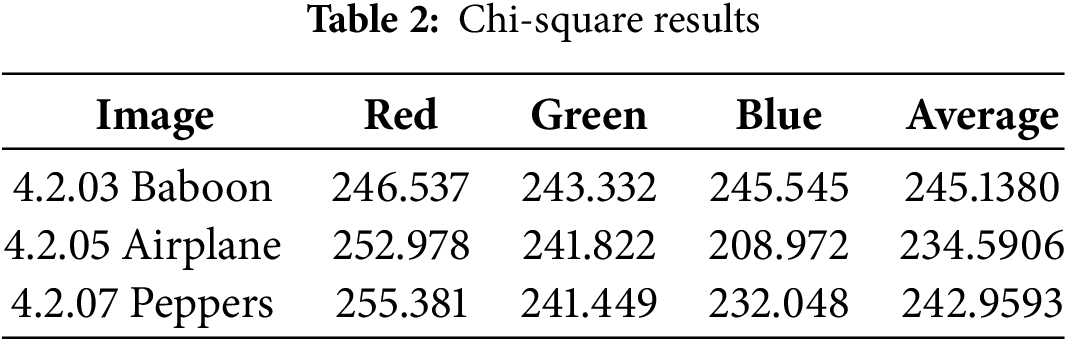
Entropy is an important metric to measure the randomness of the pixel intensity distribution in an encrypted image. The maximum entropy for an 8-bit digital image is calculated using Shannon information theory and is expressed in Eq. (17).
where
The entropy values for global entropy calculations are presented in Table 3. The average entropy values across all color channels show high consistency, ranging from 7.9993 to 7.9994, which signifies a nearly ideal randomness level.
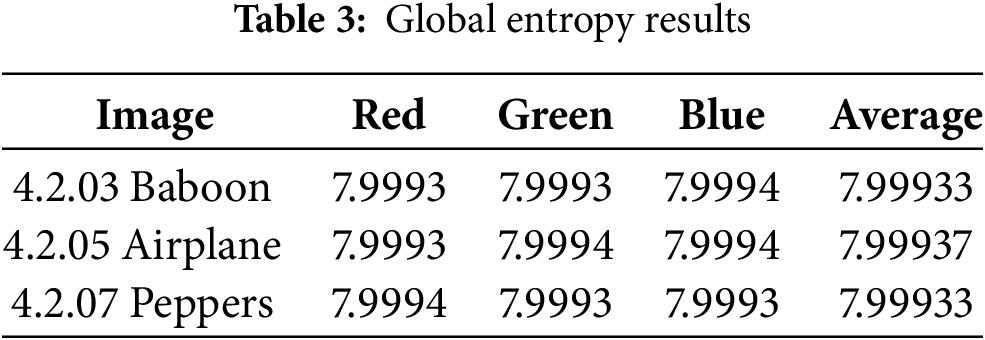
The results in Table 3 indicate that the global entropy values approach the theoretical maximum, meaning that the pixel intensity distribution is highly randomized, making it challenging to extract any meaningful patterns.
To further assess the randomness across different image regions, a local Shannon entropy test was conducted using 120 randomly selected blocks, each containing 1936 pixels. This configuration was carefully adjusted based on the methodology outlined in [39]. The local entropy was computed for each block, and the min, max, and mean local entropy values were reported to evaluate localized randomness within the encrypted images comprehensively.
The local entropy values presented in Table 4 confirm a high level of randomness across different regions of the encrypted images. The mean entropy values for the red, green, and blue channels consistently range between 7.9014 and 7.9038, indicating a nearly uniform pixel intensity distribution across different color channels. The minimum entropy values exhibit slight variations, with the lowest recorded entropy being 7.8771 (Red-Airplane), while the maximum entropy values remain within a narrow range, peaking at 7.9295 (Blue-Airplane). These variations demonstrate localized differences in randomness, which are inherent in encryption processes but remain within an acceptable range. The consistency of minimum and maximum entropy values across different channels reinforces the robustness of the encryption scheme, ensuring that no discernible pattern exists within the encrypted images. This study provides a more detailed randomness assessment by complementing global entropy analysis with local entropy evaluation, further validating the encryption method’s resilience against statistical attacks.
4.2.3 Correlation of Adjacent Pixel Analysis
Adjacent pixel correlation analysis is one of the important methods to evaluate the efficiency of encryption algorithms in eliminating the relationship between neighboring pixels. In the original image, adjacent pixels, either horizontally, vertically, or diagonally, tend to correlate highly due to consistent visual patterns. However, the correlation should be close to zero in an ideal encrypted image, indicating that the relationship between pixels has been wholly randomized [40]. The calculation of the correlation coefficient is done by randomly selecting 100,000 pairs of adjacent pixels from the image in three directions: horizontal (H), vertical (V), and diagonal (D). The correlation coefficient is calculated using Eq. (18).
where
In the encrypted image, the correlation values in all three directions (H, V, and D) for each color channel are very close to zero, as shown in Table 5. The pixel correlation in the original image, shown in Fig. 12, appears to have a high value because it has a diagonal pattern of pixel intensity distribution. In contrast, the results in Fig. 13 for the encrypted image show an almost random intensity distribution without any clear pattern because all points are evenly distributed. These results highlight the algorithm’s efficiency in creating a random intensity distribution, where the original visual relationships are entirely randomized, making them unrecognizable.
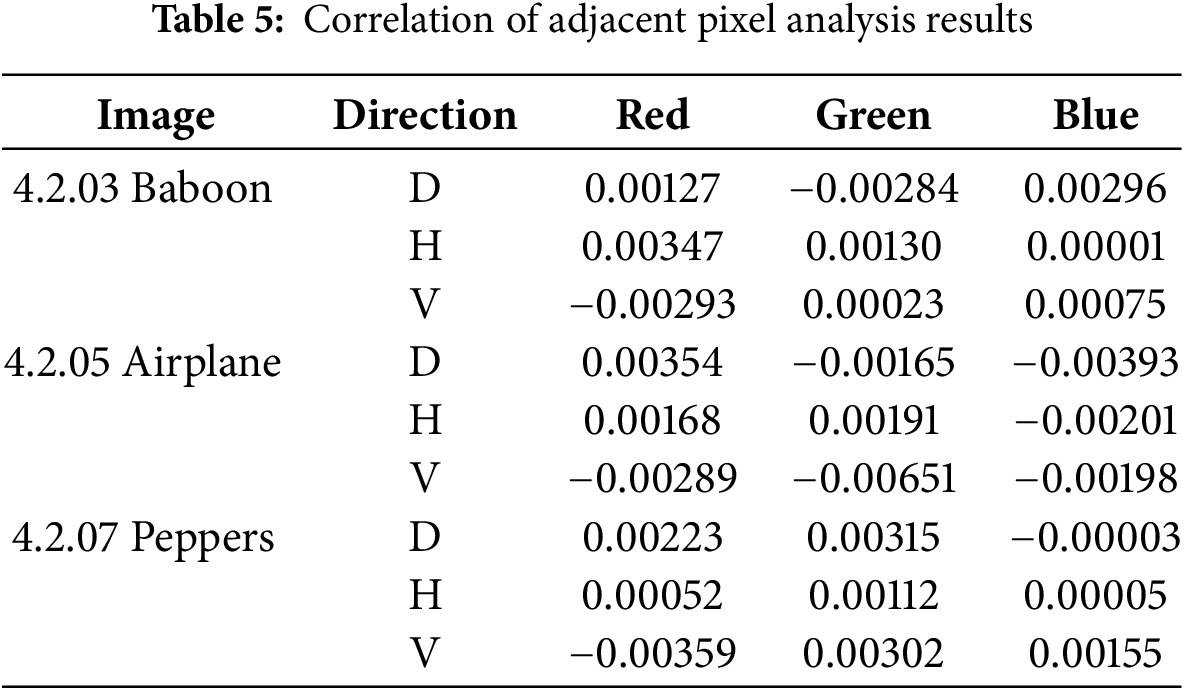

Figure 12: Plot of correlation analysis of original baboon image (column 1) red channel; (column 2) green channel; (column 3) blue channel

Figure 13: Plot of correlation analysis of encrypted baboon image (column 1) red channel; (column 2) green channel; (column 3) blue channel
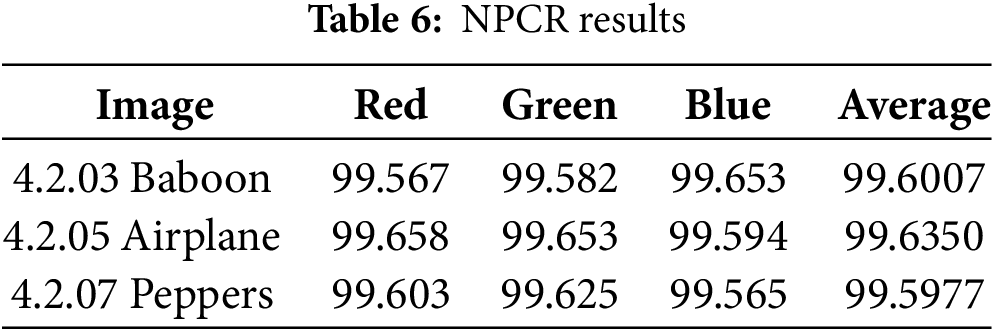
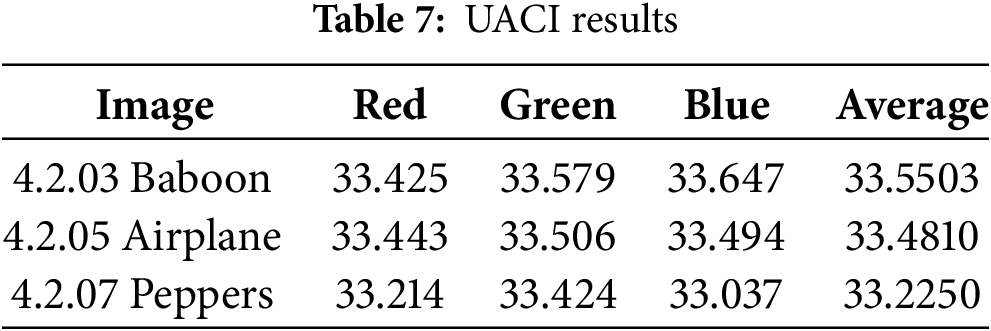
Differential analysis, including the measurement of the Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI), is used to assess the sensitivity of the encryption algorithm to small changes in the original image, such as modifying a single pixel. NPCR on a grayscale image can be calculated by Eq. (19), while UACI is calculated by Eq. (20).
where
The ideal value for NPCR comes from the assumption of a uniform random distribution, calculated from the probability that a pixel value changes after a slight change in the original image, which is
The differential analysis results in Table 6 show that the NPCR values for all test images are within the ideal range. This confirms that the algorithm is susceptible to small changes in the original image, such as one-pixel modification, so the original pattern is difficult to recognize after encryption. Table 7 also shows the UACI results for all test images, with average values ranging from 33.2250% to 33.5503%. This value is within the ideal range of 32.8%–33.8%, indicating that the change in pixel intensity between two encrypted images due to slight modifications to the original image is close to a perfectly random distribution.
A key space assessment is an important factor in determining the security provision of an encryption algorithm when subjected to brute force attacks. The larger key space guarantees that the algorithm will have a high level of resistance to exhaustive key-guessing attacks. In the proposed encryption algorithm, SQQLSR is used to produce chaotic sequences that assist in the key generation together with some key parameters that considerably broaden the key space as follows:
1. The initial seed is obtained from hashing the original image using the SHA-512 method. The hashing process produces a numerical vector of 512 bits (
2. The adjustment parameter is calculated using Eq. (6), which introduces an additional layer of randomness based on the value of <1. Since the original image directly influences <1,
3. The control parameter
4. The chaotic sequence SQQLSR generated by SQQLSR is normalized to produce
In conclusion, the estimated key space of the proposed algorithm incorporates contributions from several factors. First, the SHA-512 function provides a key space of
The robustness test is important in estimating the strength of cryptographic schemes against the totality of data attacks such as cropping/loss, noise addition, and compression. These tests imitate practical situations where the encrypted data is incomplete or is of lower quality than the intended one due to the loss sustained during transmission or storage. In this case, some areas of the encrypted image have been cut or masked to zero, emulating data loss. Following this, the strength of the decryption technique has been examined by inspecting the image built from the decryption process. As depicted in Fig. 14, two trimming forms were evaluated, namely, 200 × 200 and 400 × 400 cropping losses. The resilience being displayed connotes an extensive retention mechanism, and the algorithm can disperse the key information across the whole area of the image so that losing some data locally will not be detrimental to the utilization of the image. Noticeable degradation occurred with larger cropping sizes, demonstrating the limitations of extreme data loss. However, the object’s shape in the image can still be recognized visually.

Figure 14: Robustness test under crop/loss attack (a) Encrypted image with loss 200 × 200 pixels; (b) Decrypted image after loss 200 × 200 pixels; (c) Encrypted image with loss 400 × 400 pixels; (d) Decrypted image after loss 400 × 400 pixels
In this case, the second robustness measure introduced salt and pepper noises of intensity equal to 0.05 and 0.1 to the already encrypted image. This form of noise model roughly simulates pixel errors that might happen to a pixel during its transmission or storage. The results, shown in Fig. 15, prove that the algorithm under consideration can properly process noisy data. The encryption algorithm has good noise immunity and can handle severe random damage. This strength also comes from the algorithm’s parametrization, which is highly sensitive, and the use of non-linear chaotic mapping, which guarantees that the encryption does not depend on neighborhood pixel values.

Figure 15: Robustness test under noise additional attack (a) Encrypted image under salt & pepper 0.05; (b) Decrypted image after salt & pepper 0.05; (c) Encrypted image under salt & pepper 0.1; (d) Decrypted image after loss salt & pepper 0.1
Lastly, JPEG compression with quality settings of Q = 75 and Q = 50 were used in assessing the algorithm’s performance concerning lossy compression. These values are intended to imitate actual situations in which images must be compressed to minimize the use of space in storage or bandwidth. As shown in Fig. 16, the algorithm performs well with lossy compression such as JPEG. The uninformation diffusion seems to be aided by the chaotic mapping within the image, which enables successful decryption even after a considerable amount of quality has been sacrificed.

Figure 16: Robustness test under JPEG compression attack (a) Compressed using Q = 75; (b) Decrypted image after JPEG compression Q = 75; (c) Compressed using Q = 50; (d) Decrypted image after JPEG compression Q = 50
4.2.7 Decryption and Key Sensitivity Analysis
The ability of an encryption algorithm to perfectly decrypt an image is a key indicator of the reliability of the method used. Key sensitivity analysis is also important to evaluate the algorithm’s security against small changes in the key or initial parameters. Fig. 17 shows that decryption with the correct key (Fig. 17b) results in a fully recovered image, while a tiny change in the initial seed (−0.00000001) results in an unrecognizable image (Fig. 17a). This confirms the high sensitivity of the algorithm to the key, thus preventing brute-force attacks or correlation-based key guessing. The decryption process with the correct key shows the peak signal-to-noise ratio (PSNR) value reaching infinity, proving that data integrity is maintained without any information loss. Thus, the SQQLSR algorithm offers high security through key sensitivity and guarantees perfect decryption when the correct key is used, making it highly reliable for image encryption applications.

Figure 17: Decryption result (a) using a slight modification of initial seed (−0.00000001); (b) using the correct key
4.2.8 Comparison with Related Work
Performance comparisons are performed using the same dataset as published papers. This allows for a fair and direct comparison of the effectiveness of the proposed encryption methods. In this study, the encryption method is designed with a simple approach so that the performance of SQQLSR can be seen more dominantly. This approach is deliberately carried out to focus on evaluating the randomness and complexity produced by SQQLSR so that in the future, this method is still open to further development that is more integrated with complex encryption systems. In Table 8, the comparison results using Peppers images show that the NPCR value for the proposed method is very competitive with existing methods, even higher for some color channels, such as the green channel (99.625%). The UACI value of this method is slightly lower than some references but is still within the ideal range (32.8%–33.8%), indicating adequate sensitivity to small changes in the original image. Meanwhile, the proposed method appears relatively superior based on entropy and pixel correlation analysis.
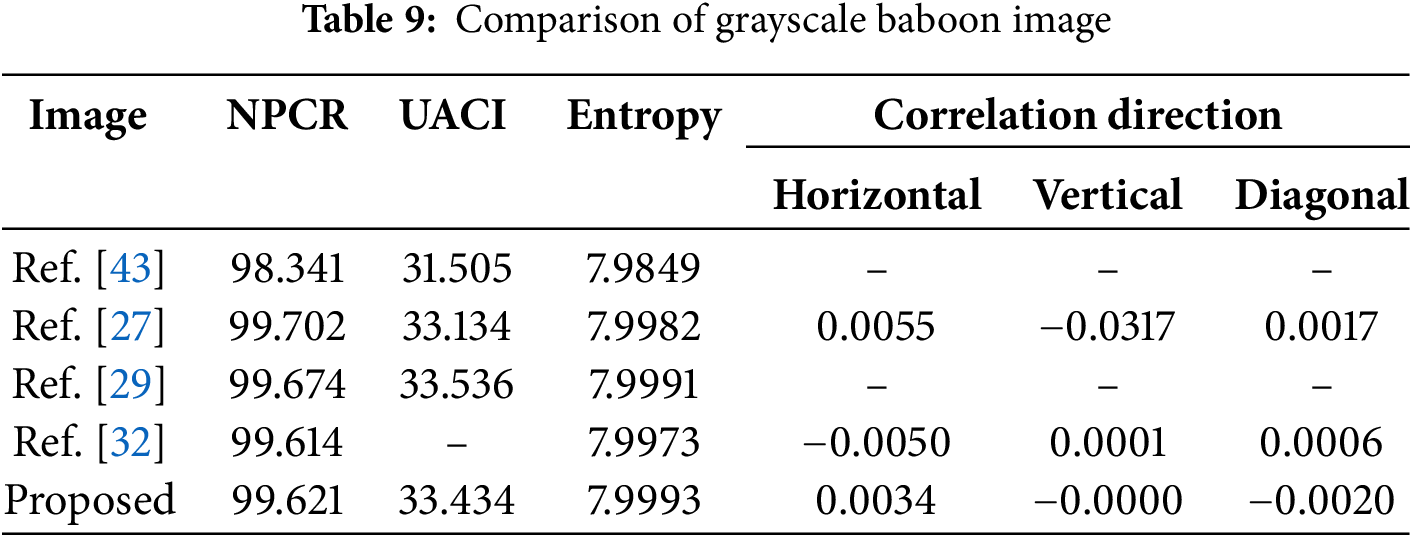
In Table 9, we re-encrypt the baboon image and convert it to a grayscale image. The proposed method shows the highest NPCR result (99.621%), surpassing most other methods. The UACI value is also very competitive (33.434%), indicating that this method successfully produces significant intensity changes between pixels in the encrypted image. The entropy of the encrypted image also shows the most superior value. While the adjacent correlation also has outstanding results, competing with Ref. [32].
Although the encryption method is relatively simple, the results are very competitive compared to previous methods. The proposed method performs better in some aspects, such as NPCR and entropy. This shows that SQQLSR has great potential for further development, not only as a randomness generator but also as a core part of more complex encryption methods in the future.
The proposed SQQLSR significantly advances 1D chaotic systems by integrating quantum principles such as superposition using Hadamard and quantum rotations. This study highlights how SQQLSR achieves ultra-wide chaotic dynamics, characterized by a broad bifurcation range without periodic windows, exceptional Lyapunov Exponent values reaching up to ≈55.265, and a significantly expanded keyspace. The ultra-wide range of the r control parameter alone provides a key space of up to
While the study includes image encryption as a proof-of-concept, the encryption method was deliberately kept simple to focus on showcasing SQQLSR’s core capabilities. The evaluations, including metrics like NPCR, UACI, entropy, and robustness, demonstrate that even with this simplified approach, the system delivers competitive and, in some cases, superior performance compared to existing methods. These results affirm SQQLSR’s potential as a foundational component for advanced cryptographic and security applications.
Although this study primarily focuses on image encryption, SQQLSR holds strong potential for broader cryptographic applications, particularly in lightweight encryption for IoT devices, secure communication protocols, and real-time key generation for quantum-based security frameworks. The ability of SQQLSR to operate on a single qubit while maintaining strong chaotic properties makes it an attractive choice for resource-constrained environments where computational efficiency is a critical factor. Additionally, the inherent unpredictability of SQQLSR’s chaotic dynamics can be leveraged for key expansion techniques, secure authentication mechanisms, and random number generation, making it a viable candidate for next-generation security frameworks.
Given that our study uses Pennylane quantum simulators, we acknowledge that practical implementation on real quantum hardware presents additional challenges, such as gate fidelity, decoherence, and execution time constraints. Addressing these challenges will be a key focus of future research, where we plan to evaluate SQQLSR’s performance on actual quantum processors and explore optimizations for hardware-specific noise resilience and efficient gate decompositions. Moreover, in-depth cryptanalysis is necessary to assess SQQLSR’s resistance to quantum attacks and side-channel vulnerabilities, ensuring its robustness in real-world cryptographic implementations.
In conclusion, SQQLSR lays the groundwork for future research into integrating quantum chaotic systems with more sophisticated cryptographic frameworks. Its adaptability and strong performance make it a promising tool for enhancing security in various domains, paving the way for further innovations in quantum and chaos-based technologies.
Acknowledgement: This research was supported by the Ministry of Higher Education, Science, and Technology (Kemdiktisaintek), Indonesia. The authors also express gratitude to those who provided administrative and technical assistance.
Funding Statement: This research was funded by Kementerian Pendidikan Tinggi, Sains, dan Teknologi (Kemdiktisaintek), Indonesia, grant numbers 108/E5/PG.02.00.PL/2024; 027/LL6/PB/AL.04/2024; and 061/A.38-04/UDN-09/VI/2024.
Author Contributions: Conceptualization: De Rosal Ignatius Moses Setiadi; Data curation: T. Sutojo; Formal analysis: Supriadi Rustad, Sudipta Kr Ghosal, and Minh T. Nguyen; Investigation: De Rosal Ignatius Moses Setiadi, Minh T. Nguyen, and Arnold Adimabua Ojugo; Methodology: De Rosal Ignatius Moses Setiadi; Project administration: Supriadi Rustad; Resources: Muhamad Akrom and T. Sutojo; Software: T. Sutojo and Muhamad Akrom; Supervision: De Rosal Ignatius Moses Setiadi; Validation: De Rosal Ignatius Moses Setiadi, Supriadi Rustad, and Muhamad Akrom; Visualization: T. Sutojo; Writing—original draft: De Rosal Ignatius Moses Setiadi; Writing—review & editing: De Rosal Ignatius Moses Setiadi, Supriadi Rustad, Minh T. Nguyen, and Arnold Adimabua Ojugo. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Malik SK. Secure framework for cyber data. In: 2023 International Conference on Artificial Intelligence and Smart Communication (AISC); 2023 Jan 27–29; Greater Noida, India. p. 124–7. [Google Scholar]
2. Çetin A, Öztürk S. Comprehensive exploration of ensemble machine learning techniques for IoT cybersecurity across multi-class and binary classification tasks. J Future Artif Intell Technol. 2025;1(4):371–84. doi:10.62411/faith.3048-3719-51. [Google Scholar] [CrossRef]
3. Kallapu B, Dodmane R, Krishnaraj Rao NS, Thota S, Sahu AK. Enhancing cloud communication security: a blockchain-powered framework with attribute-aware encryption. Electronics. 2023;12(18):3890. doi:10.3390/electronics12183890. [Google Scholar] [CrossRef]
4. Alawida M, Sen TJ, Samsudin A, Alshoura WH. An image encryption scheme based on hybridizing digital chaos and finite state machine. Signal Process. 2019;164(1):249–66. doi:10.1016/j.sigpro.2019.06.013. [Google Scholar] [CrossRef]
5. Liu Y, Qin Z, Liao X, Wu J. A chaotic image encryption scheme based on Hénon-Chebyshev modulation map and genetic operations. Int J Bifurc Chaos. 2020;30(6):2050090. doi:10.1142/S021812742050090X. [Google Scholar] [CrossRef]
6. Teng L, Wang X, Xian Y. Image encryption algorithm based on a 2D-CLSS hyperchaotic map using simultaneous permutation and diffusion. Inf Sci. 2022;605(6):71–85. doi:10.1016/j.ins.2022.05.032. [Google Scholar] [CrossRef]
7. Winarno E, Nugroho K, Adi PW, Setiadi DRIM. Combined interleaved pattern to improve confusion-diffusion image encryption based on hyperchaotic system. IEEE Access. 2023;11:69005–21. doi:10.1109/ACCESS.2023.3285481. [Google Scholar] [CrossRef]
8. Setiadi DRIM, Rijati N. An image encryption scheme combining 2D cascaded logistic map and permutation-substitution operations. Computation. 2023;11(9):178. doi:10.3390/computation11090178. [Google Scholar] [CrossRef]
9. Setiadi DRIM, Robet R, Pribadi O, Widiono S, Sarker MK. Image encryption using half-inverted cascading chaos cipheration. J Comput Theor Appl. 2023;1(2):61–77. doi:10.33633/jcta.v1i2.9388. [Google Scholar] [CrossRef]
10. Raghunandan KR, Dodmane R, Bhavya K, Rao NSK, Sahu AK. Chaotic-map based encryption for 3D point and 3D mesh fog data in edge computing. IEEE Access. 2023;11(10):3545–54. doi:10.1109/ACCESS.2022.3232461. [Google Scholar] [CrossRef]
11. Tong XJ, Wang Z, Zhang M, Liu Y, Xu H, Ma J. An image encryption algorithm based on the perturbed high-dimensional chaotic map. Nonlinear Dyn. 2015;80(3):1493–508. doi:10.1007/s11071-015-1957-9. [Google Scholar] [CrossRef]
12. Lin Y, Xie Z, Chen T, Cheng X, Wen H. Image privacy protection scheme based on high-quality reconstruction DCT compression and nonlinear dynamics. Expert Syst Appl. 2024;257(5):124891. doi:10.1016/j.eswa.2024.124891. [Google Scholar] [CrossRef]
13. Talhaoui MZ, Wang X. A new fractional one dimensional chaotic map and its application in high-speed image encryption. Inf Sci. 2021;550(2):13–26. doi:10.1016/j.ins.2020.10.048. [Google Scholar] [CrossRef]
14. Wen H, Lin Y, Yang L, Chen R. Cryptanalysis of an image encryption scheme using variant Hill cipher and chaos. Expert Syst Appl. 2024;250(1):123748. doi:10.1016/j.eswa.2024.123748. [Google Scholar] [CrossRef]
15. Han C. An image encryption algorithm based on modified logistic chaotic map. Optik. 2019;181(4):779–85. doi:10.1016/j.ijleo.2018.12.178. [Google Scholar] [CrossRef]
16. Mansouri A, Wang X. A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme. Inf Sci. 2020;520:46–62. doi:10.1016/j.ins.2020.02.008. [Google Scholar] [CrossRef]
17. Hu Y, Wang X, Zhang L. 1D sine-map-coupling-logistic-map for 3D model encryption. Front Phys. 2022;10:1–15. doi:10.3389/fphy.2022.1006324. [Google Scholar] [CrossRef]
18. Khairullah MK, Alkahtani AA, Bin Baharuddin MZ, Al-Jubari AM. Designing 1D chaotic maps for fast chaotic image encryption. Electronics. 2021;10(17):2116. doi:10.3390/electronics10172116. [Google Scholar] [CrossRef]
19. Setiadi DRIM, Rijati N, Muslikh AR, Indriyono BV, Sambas A. Secure image communication using galois field, hyper 3D logistic map, and B92 quantum protocol. Comput Mater Contin. 2024;81(3):4435–63. doi:10.32604/cmc.2024.058478. [Google Scholar] [CrossRef]
20. Morissa VSG, Setiadi DRIMS. Implementation of a mixed triple logistic map and the BB84 quantum key distribution for secure image communication. In: 2024 International Seminar on Application for Technology of Information and Communication; 2024 Sep 21–22; Semarang, Indonesia. [Google Scholar]
21. Kamran MI, Khan MA, Alsuhibany SA, Ghadi YY, Arshad A, Arif J, et al. A highly secured image encryption scheme using quantum walk and chaos. Comput Mater Contin. 2022;73(1):657–72. doi:10.32604/cmc.2022.028876. [Google Scholar] [CrossRef]
22. Ho WW, Choi S. Exact emergent quantum state designs from quantum chaotic dynamics. Phys Rev Lett. 2022;128(6):060601. doi:10.1103/PhysRevLett.128.060601. [Google Scholar] [PubMed] [CrossRef]
23. Choi J, Shaw AL, Madjarov IS, Xie X, Finkelstein R, Covey JP, et al. Preparing random states and benchmarking with many-body quantum chaos. Nature. 2023;613(7944):468–73. doi:10.1038/s41586-022-05442-1. [Google Scholar] [PubMed] [CrossRef]
24. Yuan X, Zhou H, Cao Z, Ma X. Intrinsic randomness as a measure of quantum coherence. Phys Rev A. 2015;92(2):022124. doi:10.1103/PhysRevA.92.022124. [Google Scholar] [CrossRef]
25. Mendoza BD, Lara DA, López-Aparicio J, Armendáriz G, López-Hernández L, Velázquez V, et al. Quantum chaos in time series of single photons as a superposition of wave and particle states. Photonics. 2021;8(8):326. doi:10.3390/photonics8080326. [Google Scholar] [CrossRef]
26. Zhang J, Huo D. Image encryption algorithm based on quantum chaotic map and DNA coding. Multimed Tools Appl. 2019;78(11):15605–21. doi:10.1007/s11042-018-6973-6. [Google Scholar] [CrossRef]
27. Wang Y, Chen L, Yu K, Gao Y, Ma Y. An image encryption scheme based on logistic quantum chaos. Entropy. 2022;24(2):1–22. doi:10.3390/e24020251. [Google Scholar] [PubMed] [CrossRef]
28. Anitha R, Vijayalakshmi B. Image encryption using multi-scroll attractor and chaotic logistic map. Comput Mater Contin. 2022;72(2):3447–63. doi:10.32604/cmc.2022.021519. [Google Scholar] [CrossRef]
29. Rehman MU. Quantum-enhanced chaotic image encryption: strengthening digital data security with 1-D sine-based chaotic maps and quantum coding. J King Saud Univ-Comput Inf Sci. 2024;36(3):101980. doi:10.1016/j.jksuci.2024.101980. [Google Scholar] [CrossRef]
30. Wang S. Fast adaptive synchronization of discrete quantum chaotic maps. Results Phys. 2023;52(7):106833. doi:10.1016/j.rinp.2023.106833. [Google Scholar] [CrossRef]
31. Rajan AA, Vetrian V. QMedShield: a novel quantum chaos-based image encryption scheme for secure medical image storage in the cloud. J Mod Opt. 2024;71(13–15):524–42. doi:10.1080/09500340.2024.2436521. [Google Scholar] [CrossRef]
32. Abd El-Latif AA, Abd-El-Atty B, Amin M, Iliyasu AM. Quantum-inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications. Sci Rep. 2020;10(1):1930. doi:10.1038/s41598-020-58636-w. [Google Scholar] [PubMed] [CrossRef]
33. Alnajim AM, Abou-Bakr E, Alruwisan SS, Khan S, Elmanfaloty RA. Hybrid chaotic-based PRNG for secure cryptography applications. Appl Sci. 2023;13(13):7768. doi:10.3390/app13137768. [Google Scholar] [CrossRef]
34. Ullah F, Faheem M, Hashmi MA, Bashir R, Khan AR. A Novel 1-dimensional cosine chaotic equation and digital image encryption technique. IEEE Access. 2024;12(4):118857–74. doi:10.1109/ACCESS.2024.3447889. [Google Scholar] [CrossRef]
35. Akhshani A, Akhavan A, Mobaraki A, Lim SC, Hassan Z. Pseudo random number generator based on quantum chaotic map. Commun Nonlinear Sci Numer Simul. 2014;19(1):101–11. doi:10.1016/j.cnsns.2013.06.017. [Google Scholar] [CrossRef]
36. Auzzi R, Baiguera S, De Luca GB, Legramandi A, Nardelli G, Zenoni N. Geometry of quantum complexity. Phys Rev D. 2021;103(10):106021. doi:10.1103/PhysRevD.103.106021. [Google Scholar] [CrossRef]
37. Dalzell AM, Harrow AW, Koh DE, La Placa RL. How many qubits are needed for quantum computational supremacy? Quantum. 2020;4:264. doi:10.22331/q-2020-05-11-264. [Google Scholar] [CrossRef]
38. USC Viterbi School of Engineering. SIPI Image Database [Internet]. [cited 2019 Mar 27]. Available from: http://sipi.usc.edu/database/. [Google Scholar]
39. Wu Y, Zhou Y, Saveriades G, Agaian S, Noonan JP, Natarajan P. Local Shannon entropy measure with statistical tests for image randomness. Inf Sci. 2013;222:323–42. doi:10.1016/j.ins.2012.07.049. [Google Scholar] [CrossRef]
40. Andono PN, Setiadi DRIM. Improved pixel and bit confusion-diffusion based on mixed chaos and hash operation for image encryption. IEEE Access. 2022;10:115143–56. doi:10.1109/ACCESS.2022.3218886. [Google Scholar] [CrossRef]
41. Wen H, Zhang C, Chen P, Chen R, Xu J, Liao Y, et al. A quantum chaotic image cryptosystem and its application in IoT secure communication. IEEE Access. 2021;9:20481–92. doi:10.1109/ACCESS.2021.3054952. [Google Scholar] [CrossRef]
42. AbdElHaleem SH, Abd-El-Hafiz SK, Radwan AG. A generalized framework for elliptic curves based PRNG and its utilization in image encryption. Sci Rep. 2022;12(1):1–16. doi:10.1038/s41598-022-17045-x. [Google Scholar] [PubMed] [CrossRef]
43. Cheng G, Wang C, Xu C. A novel hyper-chaotic image encryption scheme based on quantum genetic algorithm and compressive sensing. Multimed Tools Appl. 2020;79(39–40):29243–63. doi:10.1007/s11042-020-09542-w. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF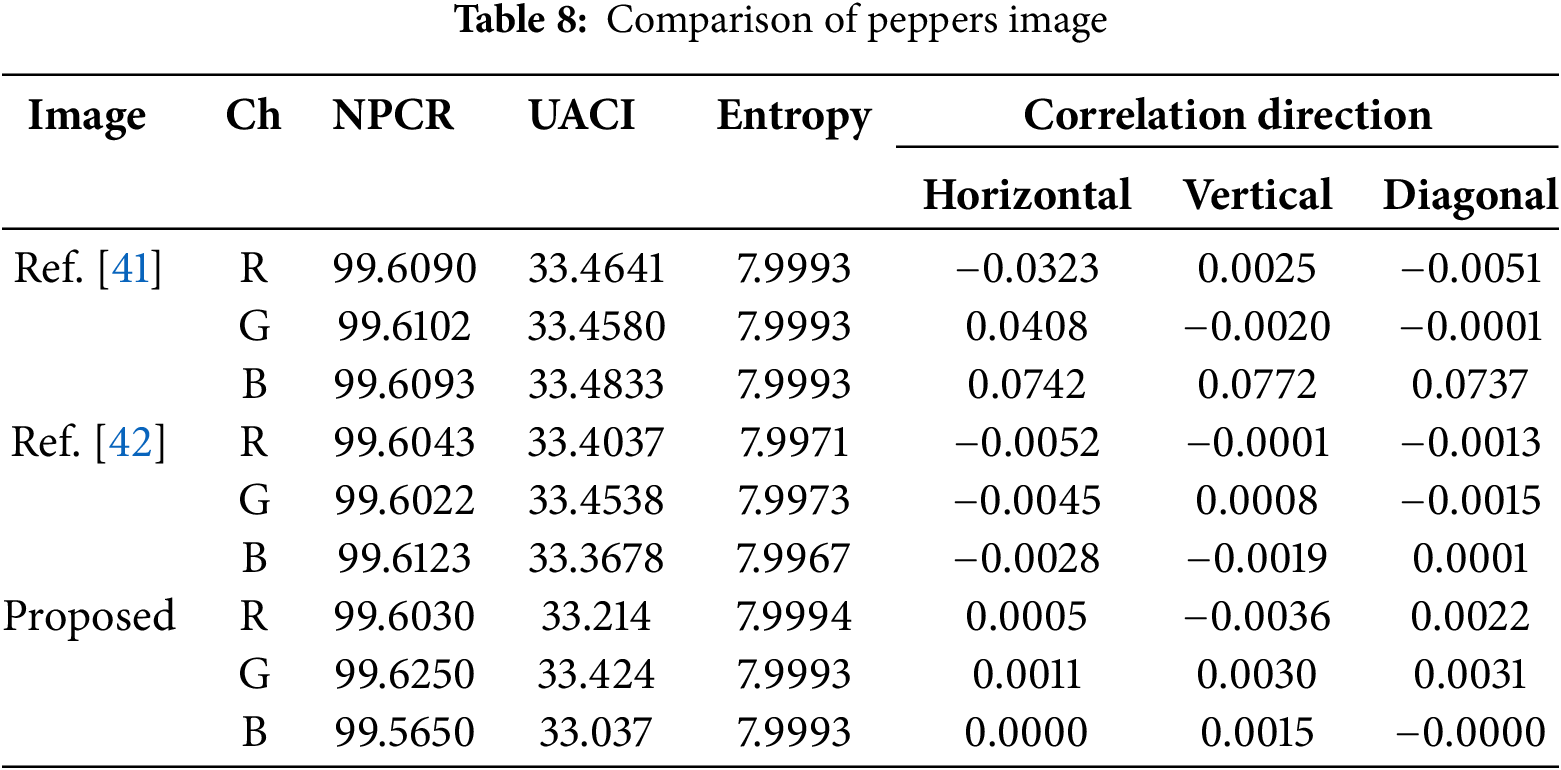
 Downloads
Downloads
 Citation Tools
Citation Tools