UAV 3D Path Planning Based on Improved Chimp Optimization Algorithm

1  Introduction

1.1 Research Background

UAVs play a pivotal role in various fields due to their cost-effectiveness and operational flexibility. Among the many aspects of Unmanned Aerial Systems (UAS), UAV path planning is a critical task, with its core objective being the determination of an optimal path from the starting point to the target point. Over the past few decades, UAV technology has advanced rapidly. Through autonomous flight or remote control, UAVs can perform a wide range of tasks and are widely applied across numerous sectors, including military, agriculture, logistics, environmental monitoring, and disaster rescue. In the military sector [1], UAVs conduct military rescue operations in complex terrain and hostile environments; in agriculture, UAVs assist in farmland mapping and precision pesticide spraying, thereby enhancing crop yield and quality; in aerial photography, UAVs capture images from unique perspectives, providing valuable materials for film, television, and geographic exploration; in environmental monitoring, UAVs collect real-time data on atmospheric conditions, water quality, and more, enabling timely identification of environmental issues; in logistics, UAVs facilitate efficient distribution; and in disaster rescue, UAVs enable the deployment of rescue materials across multiple locations.

Therefore, designing an efficient and rational UAV path planning scheme is crucial. This design must not only ensure that the UAV effectively avoids various threatening areas, such as adverse weather conditions, no-fly zones, and obstacles, but also guarantee smooth navigation to the destination, ultimately improving the efficiency and safety of mission execution.

1.2 Research Status

To identify the optimal flight path, researchers have employed both traditional algorithms and intelligent optimization algorithms. Traditional methods, such as the artificial potential field method [2,3], Dijkstra’s algorithm [4,5], and intelligent optimization algorithms, such as the ant colony algorithm [6] and the grey wolf algorithm [7], have contributed to the development of UAV path planning to varying extents. However, these algorithms exhibit several limitations, such as slow convergence speed, a tendency to fall into local optima, or poor accuracy and efficiency in path planning within complex environments. In response, many scholars have actively worked on improving these algorithms, aiming to overcome existing bottlenecks and enhance the performance and quality of UAV path planning.

For instance, Na et al. [8] proposed an IA-RRT* algorithm (Improved A* algorithm integrating RRT* Thought) for solving path planning problems. The algorithm modifies the cost evaluation function of the A* algorithm and combines the concept of randomness of the RRT* algorithm with the inflection penalty term to find a path with fewer inflection points. Wang et al. [9] proposed a parallel particle swarm optimization and augmented sparrow search algorithm for UAV path planning, which enhances random jumps in the producer’s position to ensure global search capability, each forager continuously learns from the producer’s experience, and also incorporates an elite reverse search strategy to improve diversity. Sonny et al. [10] proposed a UAV path planning framework based on an improved particle swarm optimization algorithm, which first determines the optimal communication position with the user and then searches for energy-efficient obstacle-avoidance paths, achieving favorable results in terms of energy consumption, time, and user rate. Hao et al. [11] improved the traditional artificial potential field method by introducing a collision risk assessment mechanism and virtual subgoals, solving the local minima and target unreachability problems, and optimizing the flight path. Nguyen et al. [12] proposed a multi-UAV cooperative path planning algorithm based on game theory and particle swarm optimization, using game theory to find equilibrium solutions and hierarchical particle swarm optimization to find the global optimum, thereby achieving efficient formation path planning. Diao et al. [13] introduced the Artificial Potential Field-Improved Rapidly-exploring Random Trees (APF-IRRT*) algorithm by combining the artificial potential field and the improved Rapidly-exploring Random Tree (RRT*) algorithm, addressing slow convergence and unsmooth paths, with excellent performance in both static and dynamic environments. Zhang et al. [14] proposed a heuristic crossing search and rescue optimization algorithm (HC-SAR), which combines the heuristic crossing strategy with the underlying SAR to improve the convergence speed and maintain the population diversity during the optimization process. In addition, a real-time path adjustment strategy is proposed to straighten the UAV flight path. He et al. [15] proposed an improved chaotic sparrow search algorithm, in which a piecewise chaotic mapping strategy, a nonlinear dynamic weighting factor strategy, and an enhanced sine-cosine algorithm strategy are used for optimization and improvement in order to overcome the problems of slow convergence and falling into local optimums in the path planning of UAVs in three-dimensional complex environments. Ouyang et al. [16] proposed a dual-strategy improved sparrow search algorithm (DSSA), which employs circle mapping and specular reflection learning strategies to solve the UAV path planning problem. Oliva et al. [17] used a chaotic algorithm to improve the probability of whale position updates to increase the performance of the optimization algorithm in global search. Shankar et al. [18] proposed a hybrid approach for mobile robot path planning combining Particle Swarm Optimization (PSO) technique and Artificial Potential Field (APF) method for locating feasible routes in environments with many static obstacles. Tang et al. [19] proposed a nonlinear time-varying hybrid particle swarm algorithm and a differential evolution algorithm based on ranked adaptive strategies, and fused the two to enhance the effectiveness of path planning.

1.3 Research Motivation, Innovation and Methodology

Despite the advancements in existing algorithms, their convergence speed and optimization search accuracy remain limited. In complex environments, traditional path planning algorithms often struggle to find the shortest paths, leading to inefficient and less stable task execution. To address these limitations, this study proposes an improved Chimp Optimization Algorithm (IChOA) [20]. The main innovations are as follows:

(1)   Sine Chaos Mapping Initialization: Unlike the random initialization in the original Chimp Optimization Algorithm (ChOA), the Sine chaos mapping method is employed to generate the initial chimp population. This approach enhances population diversity, enabling broader exploration of the solution space and reducing the likelihood of getting trapped in local optima. The chaotic sequences’ rich diversity and unpredictability offer a better starting point for the algorithm, improving the chances of finding the global optimal solution.

(2)   Improved Linear Convergence Factor: The original ChOA’s linearly decreasing convergence factor is replaced with a nonlinear convergence factor. This new factor adaptively adjusts the search behavior of the population throughout the algorithm’s execution. In the early stages, it promotes extensive global exploration to avoid overlooking potential high-quality solutions. In the middle stages, it accelerates convergence towards promising areas, and in the late stages, it maintains a level of local exploitation to refine the solution. This enhances both the overall convergence speed and solution accuracy.

(3)   Dynamic Adjustment of Search Strategies: In the IChOA, the number of chimpanzee advance echelons is dynamically adjusted based on the magnitude of the coefficient vector. During the global exploration phase, a larger number of high-quality solutions are retained as pioneers to thoroughly explore the search space. In the local exploitation phase, the number is reduced to focus on fine-tuning the search around potential optimal solutions, achieving a better balance between global and local search and optimizing the algorithm’s performance.

In conclusion, by proposing a multi-strategy improvement to the IChOA algorithm, this paper overcomes the limitations of existing algorithms and makes a significant contribution to the field of UAV path planning. Through extensive simulations and comparisons with other algorithms, the effectiveness and superiority of IChOA in UAV 3D path planning are demonstrated, providing a more reliable and efficient solution for practical applications.

2  System Modeling and Problem Description

2.1 Problem Description

The core objective of path planning is to find an optimal flight path in a complex three-dimensional space that meets the UAV’s performance requirements while effectively avoiding obstacles such as mountain peaks and sources of threat. First, an accurate 3D mission environment model must be established. Based on this model, the constraints associated with UAVs performing missions in 3D space are comprehensively considered. An objective function model is then constructed according to these mission requirements, leading to the design of a path planning algorithm with superior performance.

2.2 Environmental Threat Constraints

(1) Topographical constraints

The terrain barrier h is a 3D spatial model that combines a ground model h1 and a peak model h2 to simulate a near-real environment. The original digital terrain model is defined by h1(x,y) and the peak equivalent model is constructed by h2(x,y).

h=max(h1,h2)

h1(x,y)=sin(y+a)+b×sin(x)+c×cos(d∗x2+y2)+e×cos(y)+f×sin(g×x2+y2)

h2(x,y)=∑i=1NHiexp[−(x−Aoiasi)2−(y−Aoibsi)2](1)

where Hi denotes the height of peak i, (Aoi,Aoi) represents the position of the center of peak i, and (asi,bsi) denotes the attenuation coefficient of peak i, which reflects the steepness of the peak.

(2) Hazardous area restraints

The ground threat was modelled as a hemispherical kill zone proportional to the threat level. Additionally the area that must not be accessed during UAV flight is defined as a no-fly zone, which is simplified to a height-adjustable cylinder for ease of analysis. The threat modeling function is shown in Eq. (2).

Wi(x,y,z)=∑i=1N(x−xo)2+(y−yo)2+(h−ho)2=r2(h≥0)(2)

where r denotes the radius of the sphere, (x,y,z) are the coordinates of any point on the sphere, and (x0,y0,z0) are the coordinates of the center of the sphere.

2.3 Path Cost

(1) Path Length Cost

The path length cost plays a crucial role in path planning. When calculating this cost, both the UAV’s flight trajectory and the distance between each path point must be considered comprehensively to derive a surrogate value that accurately reflects the UAV’s flight cost. The path length cost is shown in Eq. (3).

Path Cost=∑i=1ndist(pi−1,pi)(3)

where n denotes the number of nodes on the path, and (Pi−1,Pi) denotes the distance between node Pi−1 and node Pi.

(2) Altitude Difference Cost

Excessive altitude variation during UAV flight increases energy consumption and threatens flight stability and safety. Therefore, the altitude difference cost is quantified using Eq. (4), which evaluates the altitude change along the flight path by summing the altitude differences between neighboring path points.

High Cos t=∑i=1n|zi−zi−1|(4)

where n represents the number of nodes on the path, z represents the height value of each node on the path, and Zi represents the height of the ith node on the path, ∣Zi−Zi−1∣ represents the absolute value of the height difference between node Pi−1 and node Pi

(3) Turning Angle cost

During the planning process, a formula based on the change in direction between neighboring path points is used to quantify the turning angle cost. By optimizing this metric, the goal is to select paths with small turning angles and low frequencies, thereby reducing energy consumption and improving flight efficiency while ensuring the UAV’s safety and stability during flight. The expression for this evaluation function is shown in Eq. (5).

Corner Cos t=∑i=1n(cosθ−C(i))(5)

where θ=π2 and C(i) denotes the cosine of the steering angle between two consecutive points, point (i) and point (i + 1).

In this paper, multiple cost indicators are normalized and combined into a comprehensive cost function model, as shown in Eq. (6).

Cos t=ω1×Path Cos t+ω2×High Cos t+ω3×Corner Cos t(6)

where ω1, ω2 and ω3 are the relative weight coefficients corresponding to the three cost indicators, and ω1+ω2+ω3=1. In this paper, 0.4 is taken ω1, 0.4 is taken ω2, and 0.2 is taken ω3.

3  Improved Chimp Optimization Algorithm

The Chimp Optimization Algorithm (ChOA) suffers from limitations such as weak global search capability and unbalanced local exploitation, making it prone to falling into local optima. To enhance the performance of ChOA, this paper proposes three strategies: introducing the Sine chaotic mapping strategy, improving the linear convergence factor, and dynamically adjusting the search strategy.

3.1 Sine Chaotic Mapping Initialization

The initialization approach used in the original Chimp Optimization Algorithm (ChOA) [21] has several limitations. First, the randomness of the initialization process can lead to insufficient population diversity, causing the algorithm to become trapped in local optima and increasing the difficulty of finding a globally optimal solution. Second, random initialization can result in slow convergence and unnecessary computational overhead. Additionally, randomly generated individuals may lack search experience, which limits the optimization process and negatively impacts the final optimization accuracy.

To overcome these issues, this paper introduces the Sine chaotic mapping method for initializing the chimp population. Yang et al. [22] demonstrated that the Sine chaos model exhibits more complex nonlinear properties than the Logistic chaos model, with an infinite folding number. Therefore, the Sine chaos model is adopted for the population initialization of the chimp population. This method generates chaotic sequences through a one-dimensional self-mapping expression (Eq. (7)), and its distribution properties are illustrated in Fig. 1.

{xi+1=k4×sin(π⋅xi)k∈(0,4](7)

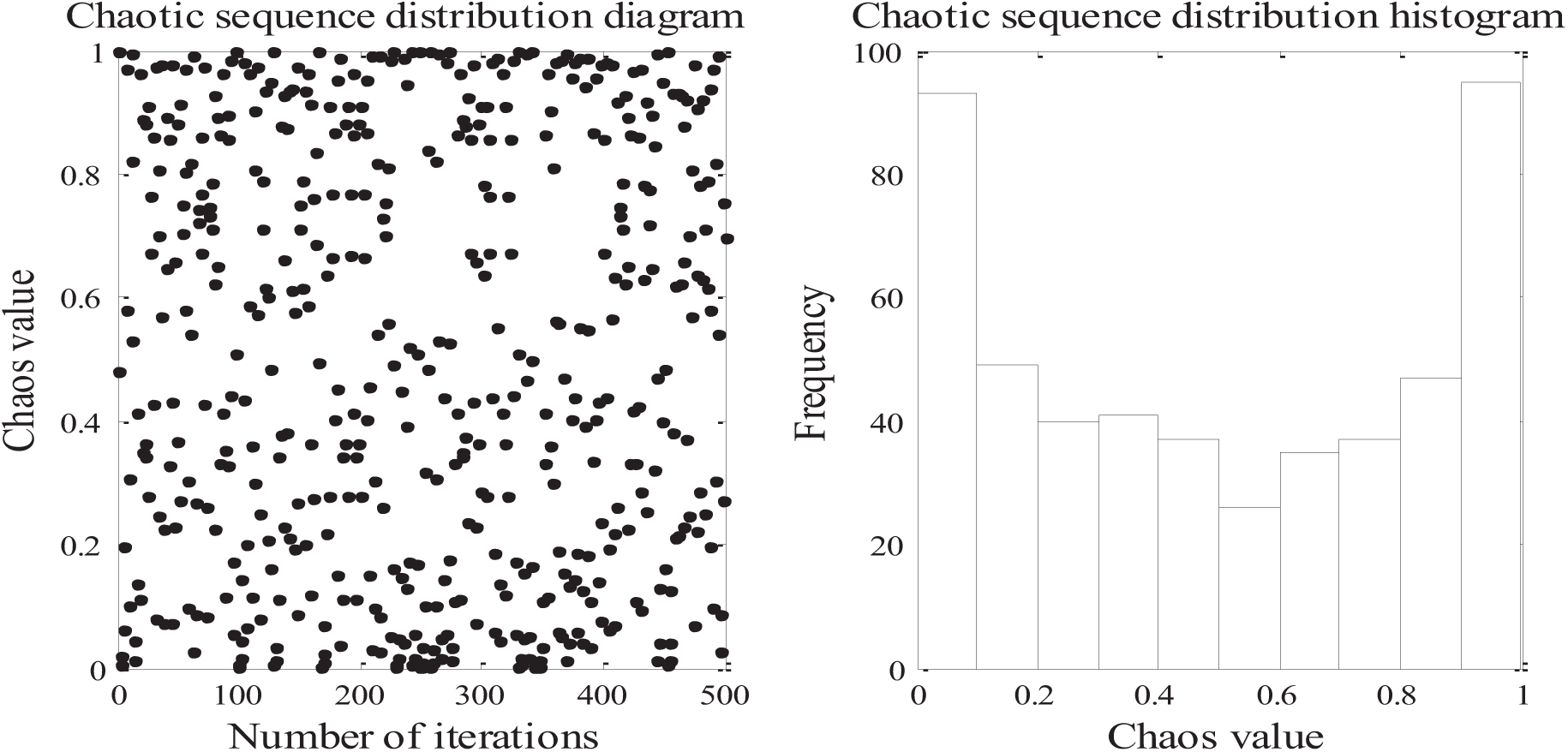
Figure 1: Sine chaotic sequence distributions

where xi represents each value in the iterative sequence, i is a non-negative integer indicating the number of iterations, x0 belongs to the interval (0, 1), and k is a system parameter with values in the range (0, 4]. In the experiments of this paper, setting k=4 generates Sine chaotic sequences with specific properties.

Sine chaotic mapping, as a nonlinear dynamical system, is capable of generating chaotic sequences with high diversity. This property enables the ChOA to achieve a broader distribution of the initial population within the search space during the initialization phase, thereby covering more potential solution areas. This improves the likelihood of the algorithm identifying the globally optimal solution. Additionally, the randomness and unpredictability of chaotic mapping allow the algorithm to escape local optima, thereby enhancing its global exploration capability. Furthermore, this chaotic mapping improves the algorithm’s convergence speed, enabling faster convergence to the vicinity of the optimal solution and reducing computational costs.

3.2 Improved Linear Convergence Factor

In the Chimp Optimization Algorithm (ChOA), the coefficient vector a plays a central role, as its magnitude directly influences the population’s search strategy. When (|a| > 1), the population disperses, enhancing global exploration capability. Conversely, when (|a| < 1), the population focuses its search, improving local exploitation capability. However, the linearly decreasing convergence factor f in the original algorithm has notable shortcomings. During the initial phase, the linear decrease in f may lead to under-exploration, potentially missing high-quality solutions. Later in the process, the premature reduction of f can cause the algorithm to fall into local optima, hindering a fine-grained search.

To overcome these limitations, this paper introduces an improved nonlinear convergence factor f′, whose mathematical expression is provided in Eq. (8). A comparison of the degradation rates between the original and improved factors is shown in Fig. 2.

f′=f0−(f02)×(1−cos(IMax_iterπ))(8)

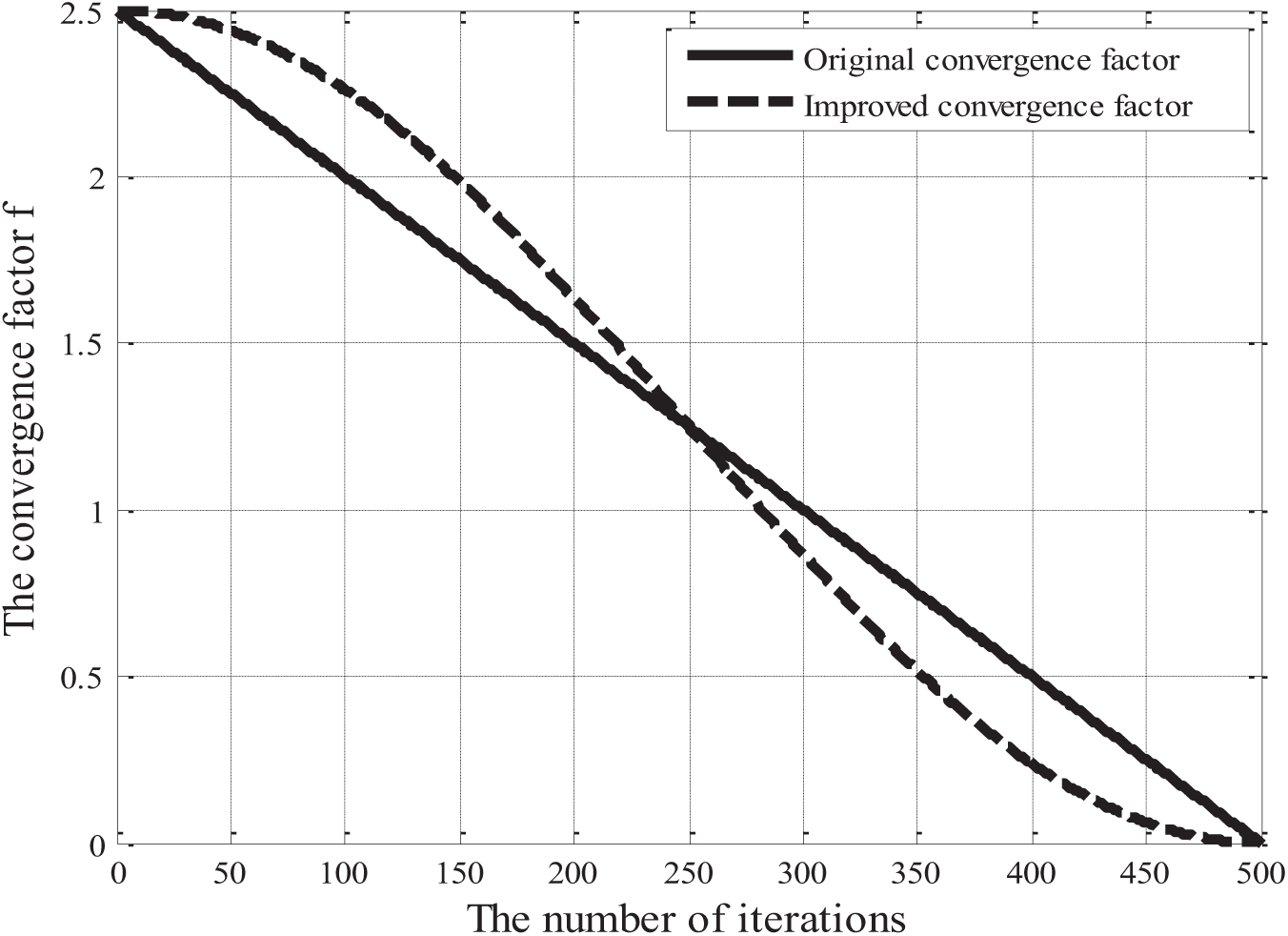
Figure 2: Convergence factor improvement before and after

The proposed nonlinear convergence factor initially declines slowly, then decreases rapidly in the middle stage, and slows down again in the later stages of the algorithm. This pattern promotes broad exploration of the search space early on, preventing premature convergence and enhancing global search. In the middle stage, it accelerates convergence toward high-quality solutions, improving efficiency. In the later stages, it refines the search process, reducing the risk of local optima and enhancing local exploitation. By incorporating the nonlinear convergence factor, the Chimp Optimization Algorithm adaptively adjusts the search step size, balancing global exploration and local exploitation, ultimately improving both convergence speed and solution accuracy.

3.3 Dynamic Adjustment of Search Strategies

In the original Chimp Optimization Algorithm (ChOA), the four best solutions form the vanguard echelon, which guides the other chimpanzee individuals in exploring the solution space and updates their positions using Eqs. (9)–(11).

{dAttacker=|c1×xAttacker−m1×x|dBarrier=|c2×xBarrier−m2×x|dChaser=|c3×xChaser−m3×x|dDriver=|c4×xDriver−m4×x|(9)

{x1=xAttacker−a1×dAttackerx2=xBarrier−a2×dBarrierx3=xChaser−a3×dChaserx4=xDriver−a4×dDriver(10)

x(t+1)=(x1+x2+x3+x4)4(11)

To improve the algorithm’s efficiency and performance, this paper proposes a dynamic adjustment strategy for the number of precedence echelons. By considering the magnitude of the coefficient vector a, the algorithm flexibly adjusts the size of the first echelon. During the global exploration phase (|a| > 0.5), the algorithm retains the maximum number of first echelons, utilizing position update Formula (11) to preserve a sufficient number of high-quality solutions as pioneers. This facilitates extensive search space exploration, preventing premature convergence to local optima. Conversely, in the local exploitation phase (|a| < 0.5), the number of leading echelons is reduced, retaining only a few optimal solutions as pioneers and applying position update Eq. (12) to enhance search efficiency and accelerate convergence toward potential optimal solutions.

x(t+1)=(x1+x2)2(12)

This dynamic adjustment strategy not only retains the leading echelon guidance of the original Chimp Optimization Algorithm but also enhances its efficiency and adaptability. By balancing global exploration and local exploitation, it significantly improves the algorithm’s overall search performance.

3.4 Pseudo-Code for the IChOA Algorithm

IChOA algorithm pseudo-code as shown in Algorithm 1.

4  Algorithm Simulation and Result Analysis

4.1 Experimental Setup

This study was implemented in MATLAB R2019b and executed on an Intel(R) Core(TM) i7-8750H CPU. To comprehensively evaluate the proposed algorithm’s performance, eight existing algorithms were selected for comparison: the Chimp Optimization Algorithm (ChOA) [21], Particle Swarm Optimization (PSO) [23], and its improved versions TACPSO [24] and MPSO [25]. Additionally, the Escape Algorithm (ESC) [26], Pied Kingfisher Optimizer (PKO) [27], Sine Cosine Algorithm (SCA) [28], and Beetle Antennae Search Algorithm (BAS) [29] were included.

The simulation experiment involves ten benchmark functions as shown in Table 1. Functions F1–F7 are unimodal and primarily assess optimization performance in simple scenarios, testing global search ability, convergence rate, and solution accuracy. In contrast, F8–F10 are multimodal functions, containing multiple local optima that increase in complexity with higher dimensionality. These functions evaluate the algorithms’ exploration capability, particularly their effectiveness in navigating complex search spaces and avoiding local optima.

To ensure stability and reproducibility, all experiments were conducted under identical computational conditions with uniform parameter settings. Multiple adjustments were made to parameter selection across different experimental conditions to ensure both fairness and accuracy. The study found that a small population size or dimensionality often led to premature convergence, while excessively large values increased computational costs and slowed convergence. Additionally, convergence trend analysis indicated that setting the maximum number of iterations to 500 achieved an optimal balance between accuracy and computational efficiency. Thus, the parameters were set as follows: N = 50, Max_iter = 500, and Dim = 30, ensuring both enhanced global search capability and efficient computation.

4.2 Comparison Test

Each algorithm was independently tested 30 times on ten benchmark functions. After each test, detailed records were maintained, and the mean, standard deviation, and optimal value of the 30 trials were calculated. Table 2 summarizes the results, providing a performance comparison of the nine optimization algorithms across the benchmark functions.

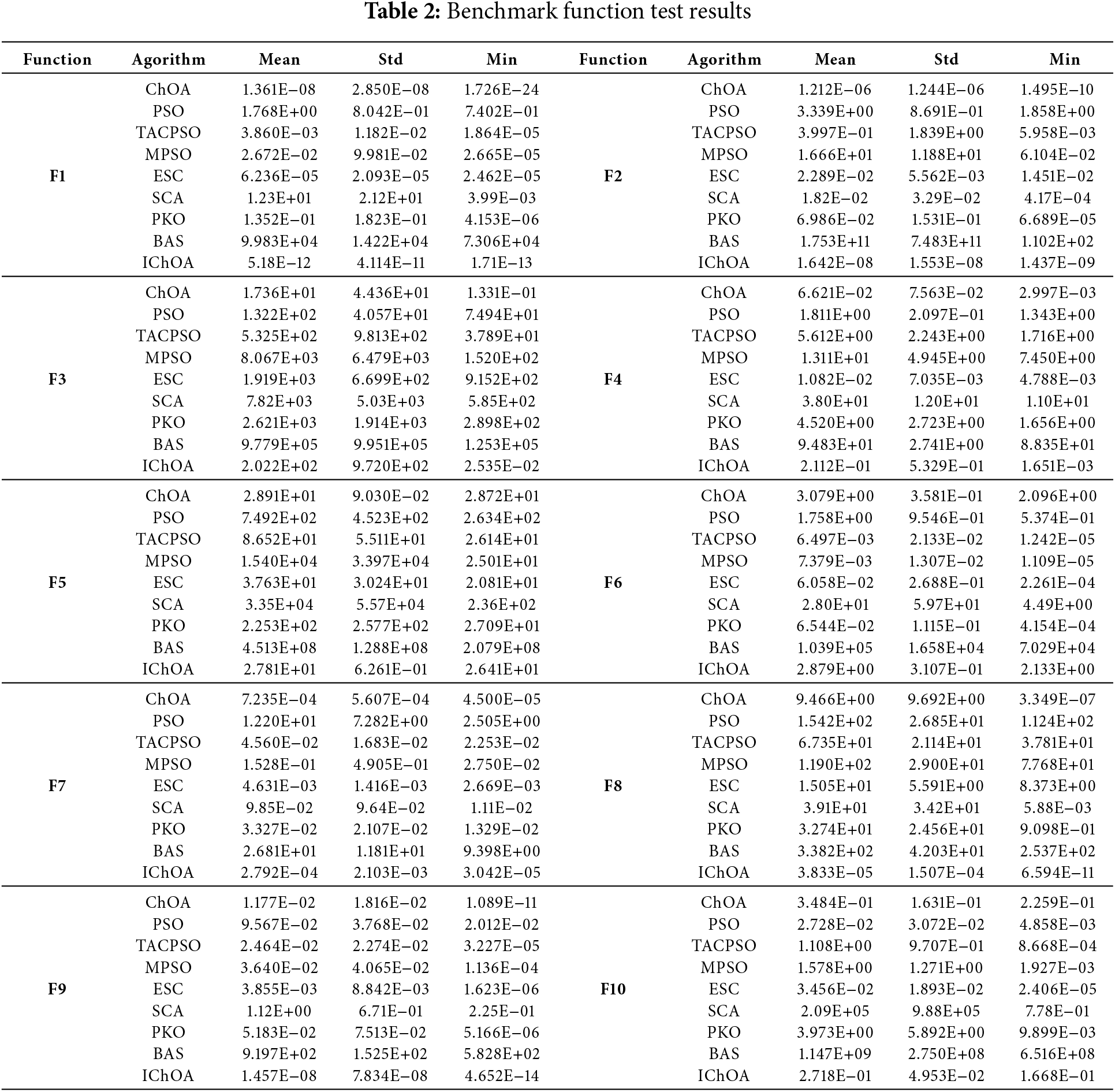
The IChOA algorithm demonstrated strong optimality-seeking performance in tests involving unimodal benchmark functions. In terms of mean values, IChOA consistently achieved low results across most test functions, indicating its reliable ability to approach the global optimal solution. The algorithm’s small standard deviation in several test functions further verifies its stability in handling unimodal problems. Additionally, IChOA achieved competitive minimum values in multiple test functions, demonstrating its frequent ability to locate positions close to the global optimum. Compared to other algorithms, IChOA exhibits superior performance in terms of optimality-seeking capability, stability, and robustness.

For multimodal benchmark functions, the test results indicate that IChOA outperforms the other eight optimization algorithms. In F8, F9, and F10, IChOA demonstrates strong global search ability and stability. Notably, in F8 and F9, the optimal value of IChOA shows significant improvement over other algorithms, confirming its accuracy in locating the global optimal solution. In F10, although IChOA does not achieve the lowest optimal value, its mean and standard deviation outperform those of other algorithms, reflecting its robust overall performance. Overall, IChOA exhibits clear advantages in multimodal optimization problems, excelling in both solution accuracy and algorithmic stability. These characteristics make it a promising choice for solving such problems.

4.3 Algorithm Convergence Curve Analysis

The convergence curve of the IChOA algorithm is a crucial tool for analyzing its convergence trend. It provides an intuitive comparison of convergence speed, accuracy, and the ability to escape local optima across different algorithms. To effectively evaluate IChOA’s optimization accuracy and convergence speed, six test functions were selected to compare nine optimization algorithms, and their corresponding convergence curves were plotted. Fig. 3 presents the average convergence curves from 30 independent optimization tests. Fig. 3a–d corresponds to unimodal functions F1–F4, while Fig. 3e,f represents multimodal functions F8 and F9, respectively. The vertical axis denotes the objective function value, and the horizontal axis represents the number of iterations.

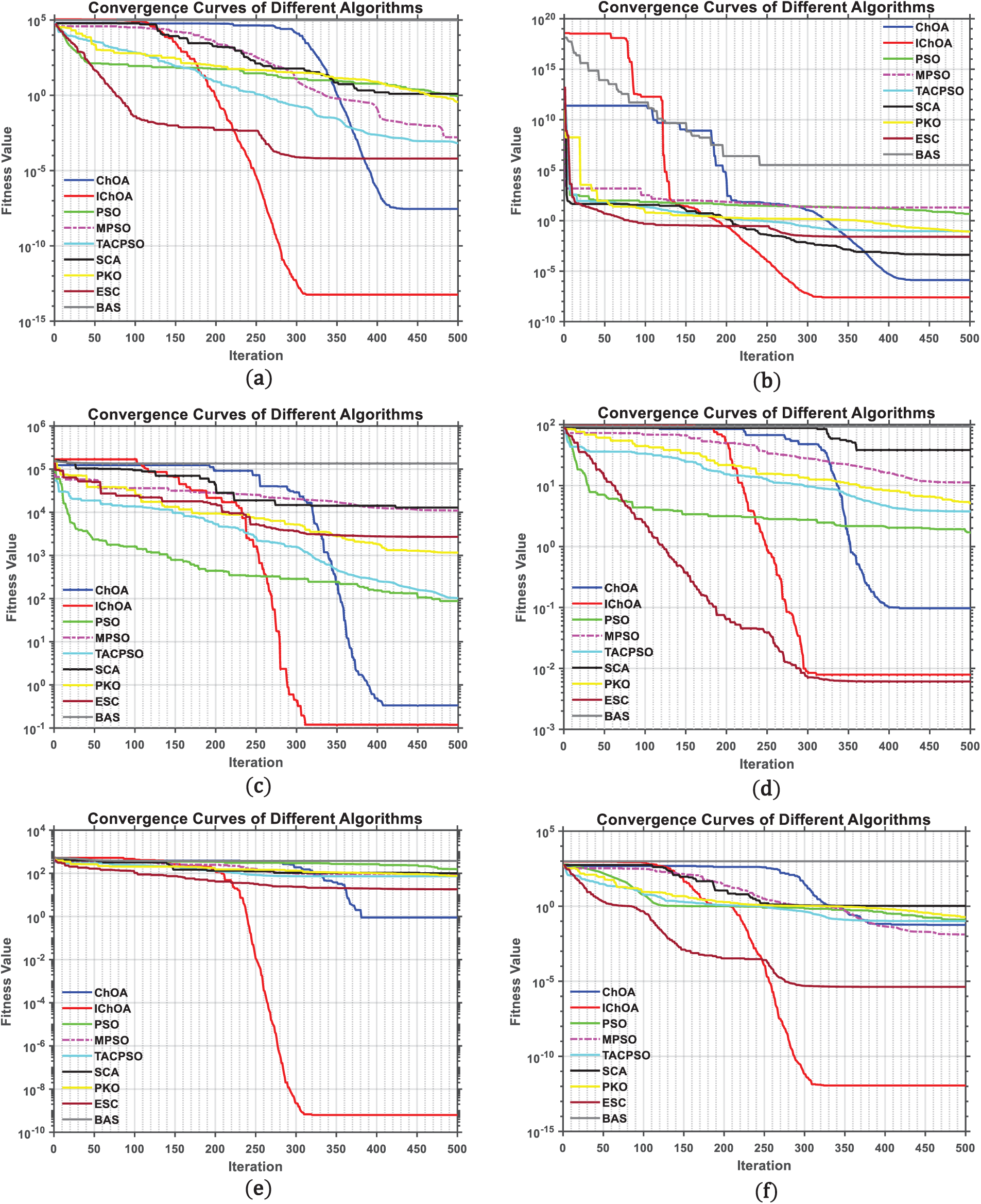
Figure 3: Convergence curve comparison plot

When comparing the convergence curves of IChOA with those of other algorithms, it is observed that IChOA employs Sine chaos mapping to initialize the population, enabling a more comprehensive search of the solution space. Consequently, its convergence curves may not initially lie entirely below those of other algorithms. However, this does not indicate inferior performance; rather, it reflects IChOA’s initial emphasis on global exploration over rapid convergence. As iterations progress, particularly in the middle and later stages, IChOA exhibits a superior convergence trend, with increased speed and higher optimization accuracy. This improvement is attributed to key optimization mechanisms in IChOA, such as the enhanced nonlinear convergence factor and the dynamic adjustment strategy for the number of chimpanzees in the first echelon.

The IChOA algorithm demonstrates strong performance on both unimodal and multimodal functions. In single-objective optimization, it achieves higher objective function values within the same number of iterations, delivering the fastest optimization speed and highest convergence accuracy. For multi-objective optimization, IChOA effectively escapes local optima, converging faster and requiring fewer iterations. Comparative analysis reveals that IChOA not only surpasses other algorithms in final convergence accuracy but also outperforms them in convergence speed. Overall, IChOA exhibits enhanced global search capability and convergence performance, making it a highly competitive optimization algorithm.

4.4 Wilcoxon Rank Sum Test

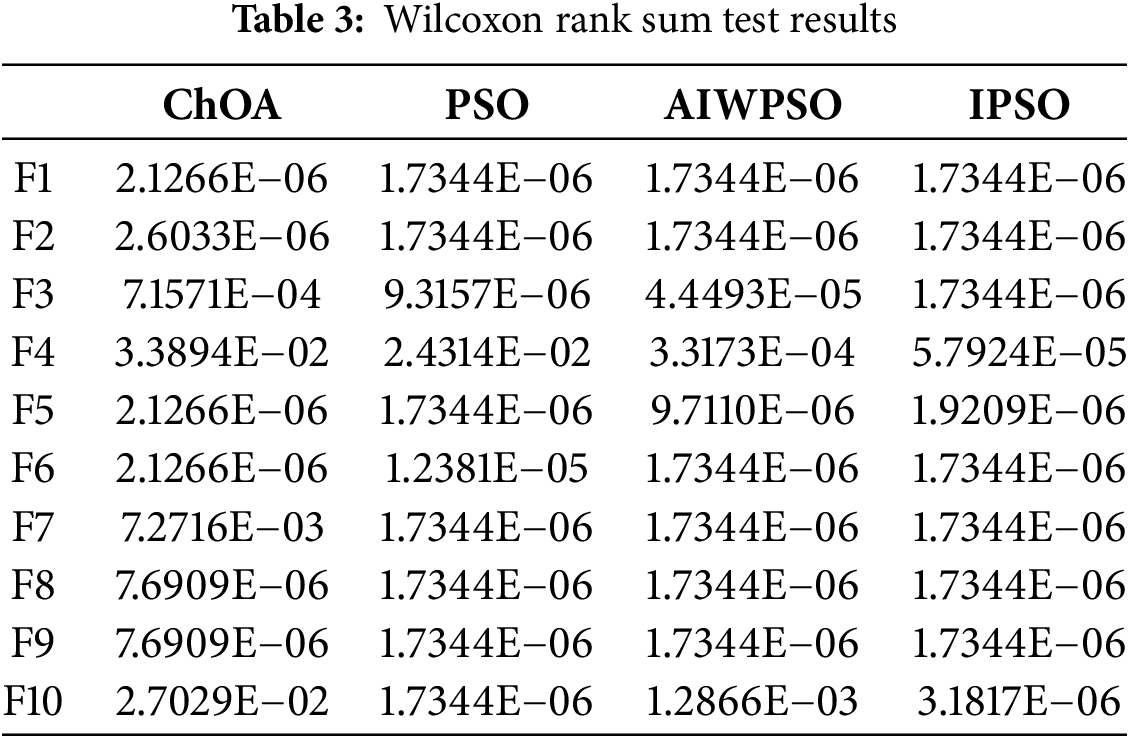
To further compare IChOA with other algorithms, this study employs the Wilcoxon rank-sum test, a nonparametric statistical method, to analyze performance differences based on results from multiple simulation runs. Traditional data analysis methods often rely solely on the mean and standard deviation, which are insufficient for effectively comparing algorithmic performance across multiple runs, making such approaches less rigorous. To comprehensively evaluate IChOA’s performance, ten test functions were selected, and the results of IChOA were compared with those of four other algorithms using the Wilcoxon rank-sum test [30]. The p-value was calculated, where (p < 0.05) indicates a significant difference between the two algorithms, while (p > 0.05) suggests their performances are comparable with no statistically significant difference.

As shown in Table 3, the p-values for IChOA are less than 0.05 in most cases, indicating that IChOA statistically outperforms the other algorithms in solving basic function optimization problems. These findings further demonstrate the robustness and stability of IChOA.

4.5 Time Complexity Analysis

Time complexity is a crucial metric for assessing an algorithm’s operational efficiency. In the ChOA algorithm, let the population size be N, the dimensionality of the search space be n, the time for parameter initialization be t1, and the time for generating random numbers be t2. The time complexity of the population initialization phase can thus be expressed as:

O(t1+N(nt2))=O(n+f(n))(13)

During the iterative phase, the following time-related settings are considered: the time to calculate the fitness values for each individual in the population is denoted as f(n); the time to compare fitness values and select the four optimal individuals is t3; the time to update the convergence factor is t4; and the time for the remaining individuals to update their positions based on the four optimal individuals is t5. Consequently, the time complexity of this phase is:

O(N(f(n)+t3+t4+t5))=O(n+f(n))(14)

Thus, the overall time complexity of the ChOA algorithm for the optimization problem is:

T(n)=O(n+f(n))+O(n+f(n))=O(n+f(n))(15)

For the IChOA algorithm, the time required for population parameter initialization remains the same as in the ChOA algorithm, with the additional time for each one-dimensional sine chaotic mapping represented as t6. The time complexity for the population initialization phase in IChOA is therefore:

O(t1+N(nt6))=O(n+f(n))(16)

In the iterative phase, the following assumptions are made: f(n) represents the time to compute the fitness values for each individual; t7 represents the time to update the improved nonlinear convergence factor; and t8 represents the time for implementing the dynamic priority rank strategy. Accordingly, the time complexity of this phase is:

O(Nf(n)+t7+t8)=O(n+f(n))(17)

The overall time complexity of the improved IChOA algorithm is:

T(n)=O(n+f(n))+O(n+f(n))=O(n+f(n))(18)

In conclusion, the time complexity of the IChOA algorithm remains of the same order of magnitude as the standard ChOA algorithm, ensuring that the improvements do not increase the computational cost.

5  UAV 3D Path Planning Based on IChOA Algorithm

5.1 Simulated Experimental Environment

The experimental environment is configured using MATLAB R2019b and an Intel(R) Core(TM) i7-8750H processor to ensure the experiment is conducted efficiently and accurately.

5.2 Experimental Setup

To evaluate the feasibility and effectiveness of IChOA, this section presents a comprehensive assessment of the improved algorithm using several simulation examples. The continuous space is discretized by constructing a rectangular grid to cover the UAV’s mission range. Using the spatial slicing method, N planes are divided to generate N path points. The specific parameters of the 3D path planning environment model used in the experiments are listed in Tables 4–6.

In this subsection, MATLAB is utilized for constructing the 3D environment. Based on the data provided, the simulation environment for UAV path planning is established. Fig. 4 illustrates the simulation environment for the no-threat scenario, while Fig. 5 depicts the simulation environment for the threat scenario.

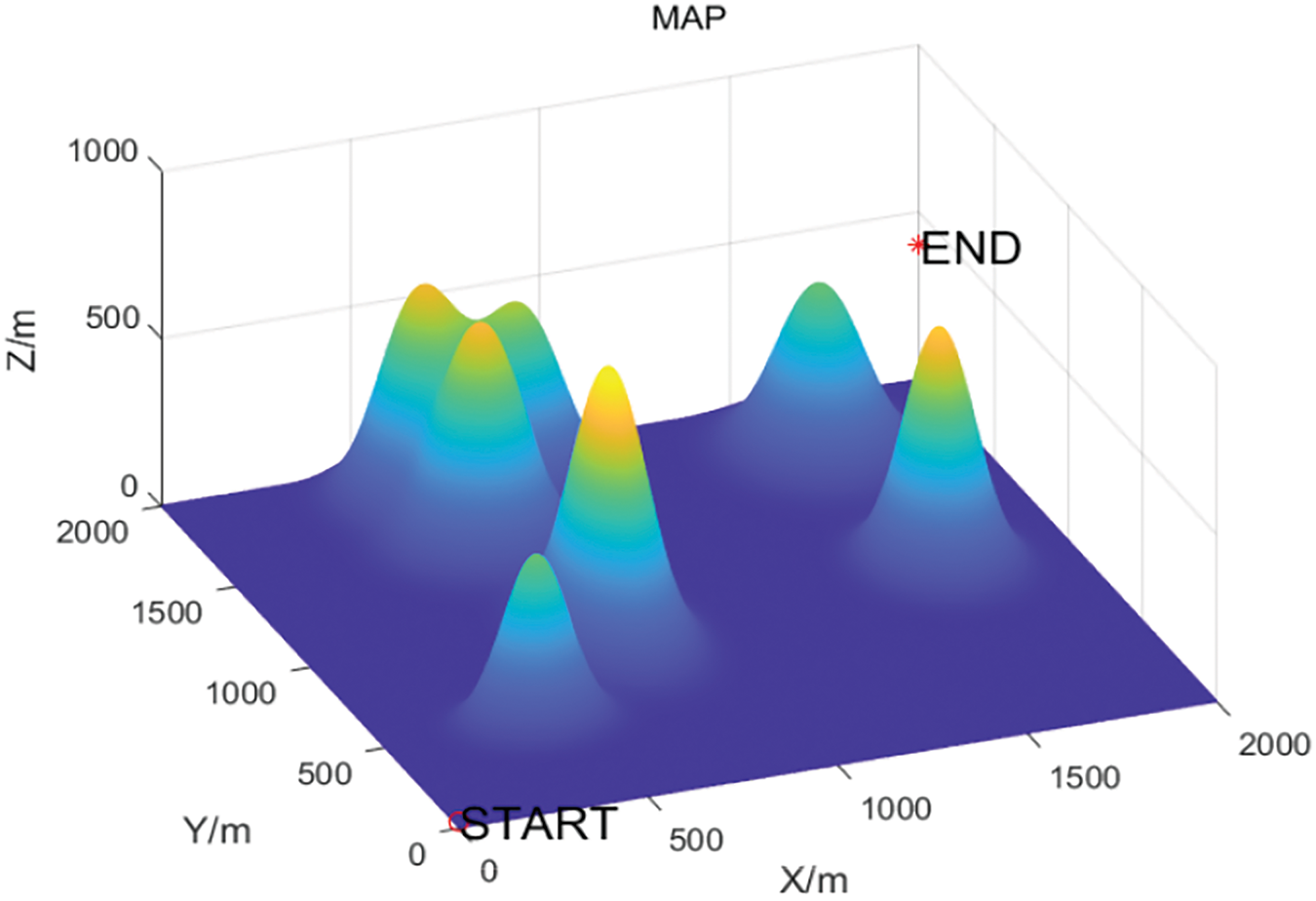
Figure 4: Threat-free simulation environment

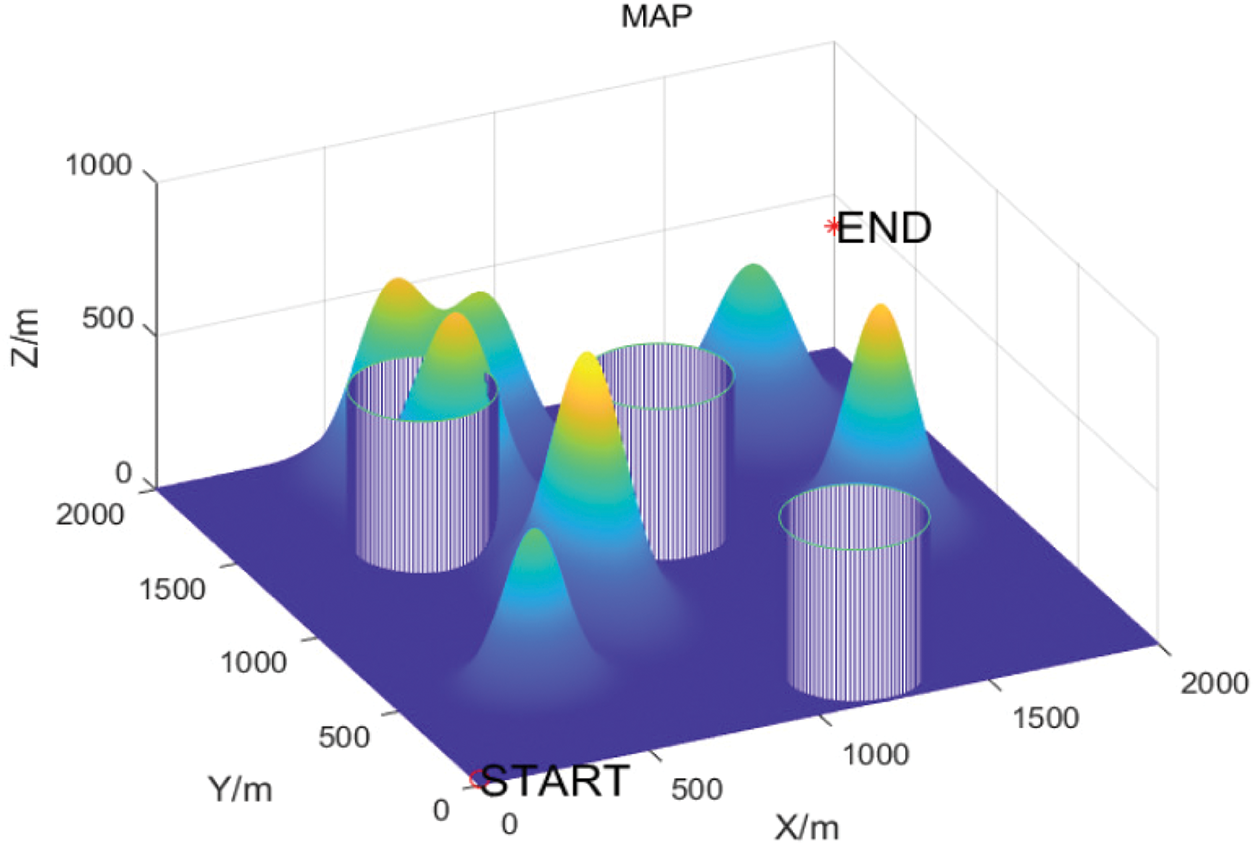
Figure 5: Threat modelling environment

5.3 Experimental Results and Analysis

(1) UAV 3D path planning based on IChOA algorithm

In this section, the Improved Chimp Optimization Algorithm is used to plan the flight path of the UAV in the non-threatening and threatening simulation environments, respectively. The number of chimpanzee population is set to 70, the maximum number of iterations is set to 100, and the number of path nodes between the start and end points is set to 4. The path search results after the simulation are shown as the red lines in Figs. 6 and 7, and the changes of the iteration curves of the cost function are shown in the following figure under the consideration of the path cost only.

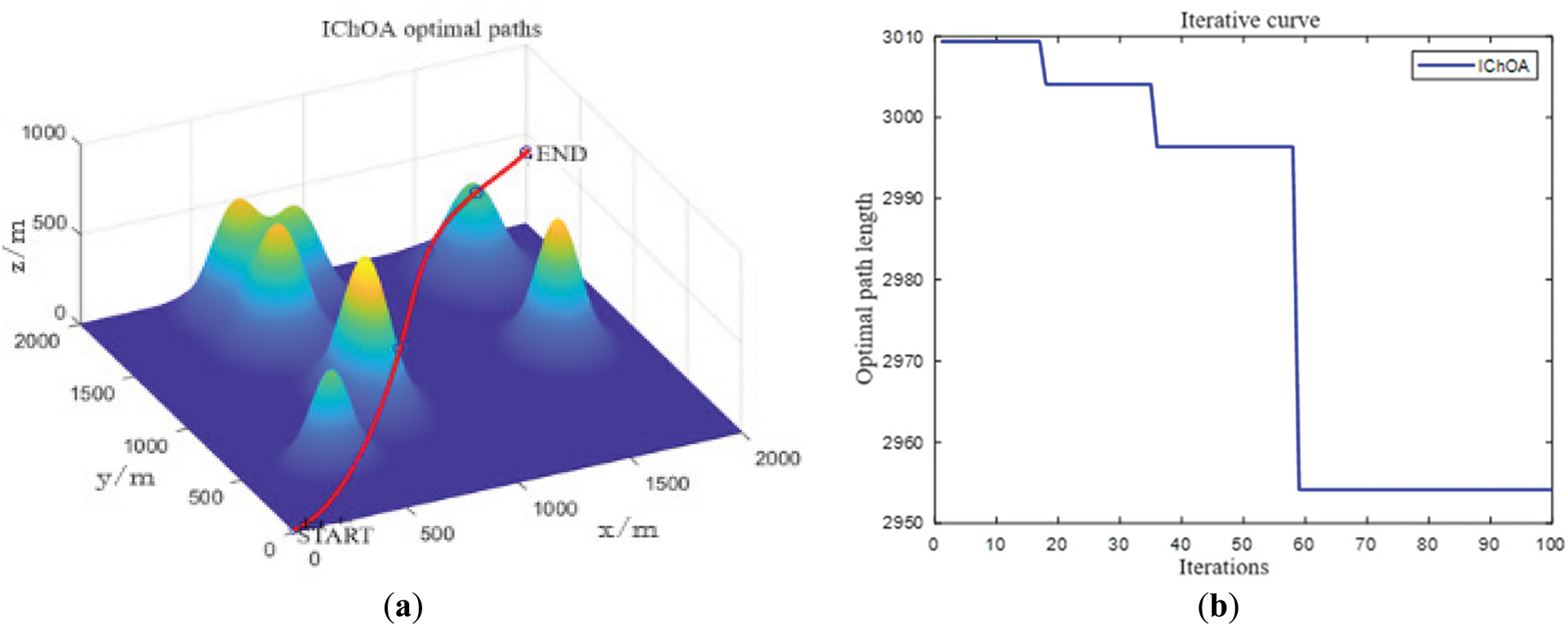
Figure 6: Threat-free simulation environment. (a) 3D path planning simulation; (b) Path cost function iteration curve

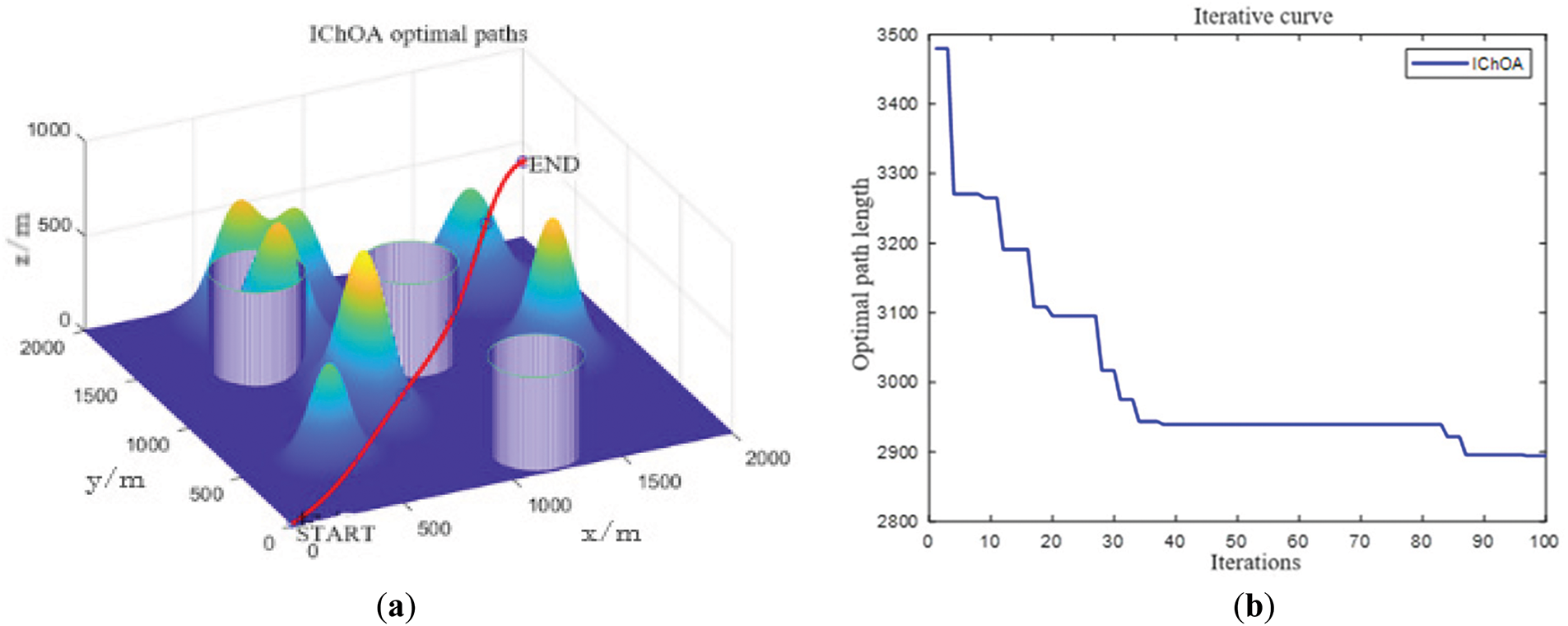
Figure 7: Threat modelling environment. (a) 3D path planning simulation; (b) Path cost function iteration curve

(2) Simulation Comparison of 3D Path Planning Algorithms

In this section, the performance of IChOA and several swarm intelligence algorithms in 3D path planning is compared through an experiment. In a simulated environment containing a hazardous area, uniform simulation conditions are applied across all algorithms: the population size is set to 70, the number of iterations to 100, and the UAVs are ensured to start flying at an altitude of 20 m above the ground. A cost function is designed to evaluate the performance of each algorithm by considering key factors such as path length, altitude variation, and turning angle.

The experimental results are detailed in Fig. 8. Specifically, Fig. 8a presents the three-dimensional path trajectories planned by five optimization algorithms, comparing the paths generated by IChOA, ChOA, SSA (Sparrow Search Algorithm), PSO, and IPSO (Improved Particle Swarm Optimization). Fig. 8b illustrates the convergence curves based on the cost function, providing an intuitive representation of the optimization performance of each algorithm.

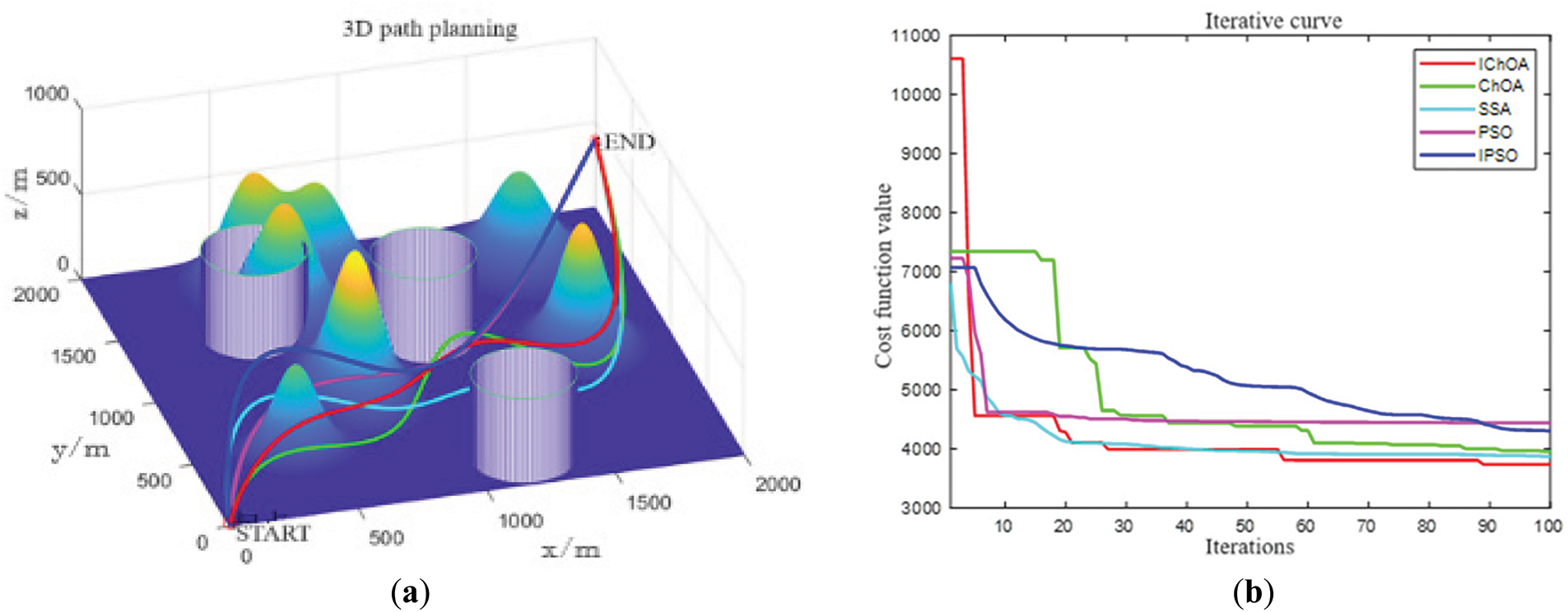
Figure 8: Comparison of five algorithms for 3D simulation. (a) 3D path planning simulation; (b) Path cost function iteration curve

In this section, to evaluate the algorithms’ optimality in search performance, a 3D path simulation environment with three no-fly zones and a search space of (2000 × 2000) is constructed. The optimal, worst, mean, and standard deviation of the cost functions obtained after running each algorithm 20 times are summarized in Table 7.

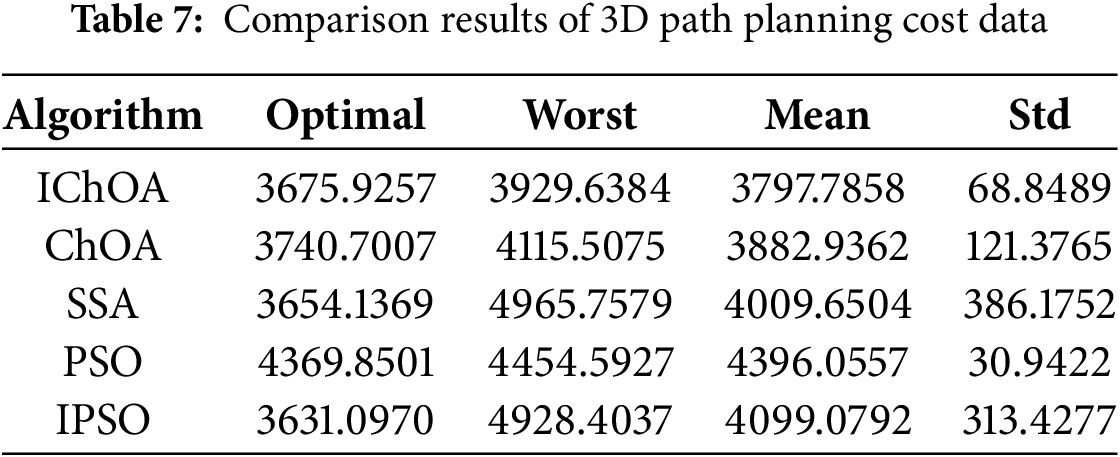
As shown in Table 6, the IChOA algorithm demonstrates significant advantages in the simulation study of 3D task maps. Specifically, its performance in finding the optimal path is close to the theoretical optimal solution, and the worst value of its cost function is the lowest among the five algorithms compared. After 20 repetitions of simulation experiments, the IChOA algorithm not only achieves a lower average surrogate value than the other four algorithms but also exhibits a standard deviation that reflects a high degree of stability. This indicates that the IChOA algorithm can consistently find shorter paths under varying simulation conditions.

The effectiveness of the IChOA algorithm is further validated by analyzing the changes in path trajectories and convergence curves in the 3D environment. These statistical results not only highlight the efficiency of the IChOA algorithm in finding the shortest path but also confirm the high stability of its execution process.

6  Conclusion

This paper proposes a multi-strategy improved chimpanzee optimization algorithm (IChOA) for UAV 3D path planning. First, a sinusoidal chaotic mapping strategy is introduced to initialize the population, enhancing coverage of the solution space and increasing population diversity. Next, a nonlinear convergence factor is employed to adaptively adjust the search process, improving both convergence speed and solution accuracy. Finally, a dynamically tuned search strategy is utilized to balance global and local search by varying the number of chimpanzee advance teams.

To validate the effectiveness of the IChOA algorithm, an experimental comparison was conducted with eight other algorithms. In benchmark function tests, IChOA demonstrated strong stability and optimization capability, achieving low mean values, small standard deviations, and superior optimal values on both unimodal and multimodal functions. In the convergence curve analysis, although IChOA does not dominate in the initial stages, it surpasses other algorithms in convergence speed and accuracy during subsequent iterations. Its superiority is statistically verified using the Wilcoxon rank-sum test. Notably, IChOA maintains a time complexity comparable to the original algorithm.

Subsequently, 3D path planning experiments for UAVs were conducted using the IChOA algorithm. The algorithm successfully planned feasible flight paths in various simulated environments. Compared to other intelligent algorithms, IChOA consistently finds shorter paths, as evidenced by the lower standard deviation of the cost function.

In conclusion, the IChOA algorithm effectively addresses the limitations of the original algorithm and demonstrates excellent performance and practical value in UAV 3D path planning, providing a reliable solution and contributing to advancements in the field.

Acknowledgement: Not applicable.

Funding Statement: This work was supported by the Shaanxi Province Natural Science Basic Research Program Project (2024JC-YBMS-572), partially funded by Yan’an University Graduate Education Innovation Program Project (YCX2023032, YCX2023033, YCX2024094, YCX2024097) and the “14th Five Year Plan Medium and Long Term Major Scientific Research Project” (2021ZCQ015) of Yan’an University.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Wenli Lei and Xinghao Wu; methodology, Wenli Lei, Xinghao Wu, Kun Jia and Jinping Han; software, Wenli Lei and Xinghao Wu; validation, Wenli Lei and Xinghao Wu; formal analysis, Xinghao Wu; investigation, Wenli Lei and Xinghao Wu; resources, Wenli Lei; data curation, Wenli Lei and Xinghao Wu; writing—original draft preparation, Xinghao Wu; writing—review and editing, Xinghao Wu; visualization, Xinghao Wu; supervision, Wenli Lei; project administration, Wenli Lei; funding acquisition, Wenli Lei. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the Corresponding Author, Wenli Lei, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Wan Y, Zhong Y, Ma A, Zhang L. An accurate UAV 3-D path planning method for disaster emergency response based on an improved multiobjective swarm intelligence algorithm. IEEE Trans Cybern. 2023;53(4):2658–71. doi:10.1109/TCYB.2022.3170580. [Google Scholar] [PubMed] [CrossRef]

2. Gao X, Zhang L, Hu G, Yang Z, Gao B. UAV trajectory planning algorithm based on plane-constrained artificial potential field. Aviation Sci Technol. 2023;34(8):68–76. (In Chinese). [Google Scholar]

3. Chen Y, Yu Q, Han D, Jiang H. UAV path planning: integration of grey wolf algorithm and artificial potential field. Concurr Comput Pract Exp. 2024;36(15):e8120. doi:10.1002/cpe.8120. [Google Scholar] [CrossRef]

4. Yin Y, Li Y, Li P. Research on improved Dijkstra-based navigation path planning algorithm for unmanned scrapers. J Kunming Metall Coll. 2023;39(6):55–61, 106. (In Chinese). [Google Scholar]

5. Wang J, Li Y, Li R, Chen H, Chu K. Trajectory planning for UAV navigation in dynamic environments with matrix alignment Dijkstra. Soft Comput. 2022;26(22):12599–610. doi:10.1007/s00500-022-07224-3. [Google Scholar] [CrossRef]

6. Dorigo M, Birattari M, Stutzle T. Ant colony optimization. IEEE Comput Intell Mag. 2006;1(4):28–39. doi:10.1109/MCI.2006.329691. [Google Scholar] [CrossRef]

7. Dewangan RK, Shukla A, Wilfred GW. Three dimensional path planning using Grey wolf optimizer for UAVs. Appl Intell. 2019;49(6):2201–17. doi:10.1007/s10489-018-1384-y. [Google Scholar] [CrossRef]

8. Liu N, Hu ZH, Wei M, Guo PF, Zhang SH, Zhang AD. Improved A* algorithm incorporating RRT* thought: a path planning algorithm for AGV in digitalised workshops. Comput Oper Res. 2025;177(4):106993. doi:10.1016/j.cor.2025.106993. [Google Scholar] [CrossRef]

9. Wang ZW, Sun GK, Zhou KP, Zhu LQ. A parallel particle swarm optimization and enhanced sparrow search algorithm for unmanned aerial vehicle path planning. Heliyon. 2023;9(4):e14784. doi:10.1016/j.heliyon.2023.e14784. [Google Scholar] [CrossRef]

10. Sonny A, Yeduri SR, Cenkeramaddi LR. Autonomous UAV path planning using modified PSO for UAV-assisted wireless networks. IEEE Access. 2023;11:70353–67. doi:10.1109/ACCESS.2023.3293203. [Google Scholar] [CrossRef]

11. Hao G, Lv Q, Huang Z, Zhao H, Chen W. UAV path planning based on improved artificial potential field method. Aerospace. 2023;10(562):1–20. doi:10.3390/aerospace10060562. [Google Scholar] [CrossRef]

12. Nguyen L, Phung MD, Ha QP. Game theory-based optimal cooperative path planning for multiple UAVs. IEEE Access. 2022;10:108034–45. doi:10.1109/ACCESS.2022.3213035. [Google Scholar] [CrossRef]

13. Diao Q, Zhang J, Liu M, Yang J. A disaster relief UAV path planning based on APF-IRRT* fusion algorithm. Drones. 2023;7(5):323. doi:10.3390/drones7050323. [Google Scholar] [CrossRef]

14. Zhang C, Zhou WJ, Qin WD, Tang WD. A novel UAV path planning approach: heuristic crossing search and rescue optimization algorithm. Expert Syst Appl. 2023;215(13):119243. doi:10.1016/j.eswa.2022.119243. [Google Scholar] [CrossRef]

15. He Y, Wang M. An improved chaos sparrow search algorithm for UAV path planning. Sci Rep. 2024;14(1):366. doi:10.1038/s41598-023-50484-8. [Google Scholar] [PubMed] [CrossRef]

16. Ouyang L, Zhu M, Li M, Li, W, Zhu Y, Zou G. UAV path planning method based on dual-strategy improved sparrow search algorithm. In: 5th International Conference on Computer Engineering and Application (ICCEA); 2024 Apr 12–14; Hangzhou, China; 2024. p. 1345–8. doi:10.1109/ICCEA62105.2024.10603975. [Google Scholar] [CrossRef]

17. Oliva D, Abd El Aziz M, Hassanien AE. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl Energy. 2017;200:141–54. doi:10.1016/j.apenergy.2017.05.029. [Google Scholar] [CrossRef]

18. Shankar M, Sushnigdha G. A hybrid path planning approach combining artificial potential field and particle swarm optimization for mobile robot. IFAC-PapersOnLine. 2022;55(22):242–7. doi:10.1016/j.ifacol.2023.03.041. [Google Scholar] [CrossRef]

19. Tang B, Zhu Z, Luo J. Hybridizing particle swarm optimization and differential evolution for the mobile robot global path planning. Int J Adv Robot Syst. 2016;13(3):86. doi:10.5772/63812. [Google Scholar] [CrossRef]

20. Lei W, Jia K, Zhang X, Lei Y. Research on chaotic chimp optimization algorithm based on adaptive tuning and its optimization for engineering application. J Sens. 2023;2023(1):5567629. doi:10.1155/2023/5567629. [Google Scholar] [CrossRef]

21. Khishe M, Mosavi MR. Chimp optimization algorithm. Expert Syst Appl. 2020;149(1):113338. doi:10.1016/j.eswa.2020.113338. [Google Scholar] [CrossRef]

22. Yang HD, E JQ. An adaptive chaos immune optimization algorithm with mutative scale and its application. Control Theory Appl. 2009;26(10):1069–74. (In Chinese). doi:10.7641/j.issn.1000-8152.2009.10.ccta080581. [Google Scholar] [CrossRef]

23. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks; 1995 Nov 27–Dec 1; Perth, WA, Australia. doi:10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]

24. Tang Z, Zhang D. A modified particle swarm optimization with an adaptive acceleration coefficients. In: 2009 Asia-Pacific Conference on Information Processing; 2009 Jul 18–19; Shenzhen, China. p. 330–2. doi:10.1109/APCIP.2009.217. [Google Scholar] [CrossRef]

25. Liu H, Zhang X, Tu L. A modified particle swarm optimization using adaptive strategy. Expert Syst Appl. 2020;152(3):113353. doi:10.1016/j.eswa.2020.113353. [Google Scholar] [CrossRef]

26. Ouyang KC, Fu SW, Chen Y, Cai QF, Heidari AA, Chen HL. Escape: an optimization method based on crowd evacuation behaviors. Artif Intell Rev. 2024;58(1):19. doi:10.1007/s10462-024-11008-6. [Google Scholar] [CrossRef]

27. Bouaouda A, Hashim FA, Sayouti Y, Hussien AG. Pied kingfisher optimizer: a new bio-inspired algorithm for solving numerical optimization and industrial engineering problems. Neural Comput Appl. 2024;36(25):15455–513. doi:10.1007/s00521-024-09879-5. [Google Scholar] [CrossRef]

28. Mirjalili S. SCA: a Sine Cosine Algorithm for solving optimization problems. Knowl-Based Syst. 2016;96(63):120–33. doi:10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

29. Jiang X, Li S. BAS: beetle antennae search algorithm for optimization problems. Neural Evol Comput.2017. doi:10.48550/arXiv.1710.10724. [Google Scholar] [CrossRef]

30. Yao X, Liu Y, Lin G. Evolutionary programming made faster. IEEE Trans Evol Comput. 1999;3(2):82–102. doi:10.1109/4235.771163. [Google Scholar] [CrossRef]