Enhancing Medical Data Sharing: A Cooperative Game Incentive Approach Based on Blockchain

1  Introduction

With the continuous improvement of digitalization levels and the large-scale production of medical data, the medical industry is facing an important transition. A wealth of medical data resources can be transformed into valuable knowledge that can help in scientific decision-making. As the advantages of cloud storage become more evident, an increasing number of organizations are opting to store their data in the cloud. Nevertheless, once organizations and individuals outsource their data to the cloud, they lose full control over it. Especially when data is stored in plaintext, semi-trusted cloud servers can pose a threat to data privacy. Consequently, the process of data sharing brings problems such as data sharing risk, data sharing cost, and data ownership, which makes many data owners reluctant to share data [1,2]. This poses a great challenge to facilitate medical data sharing.

Traditional data-sharing solutions face issues such as slow response times, data vulnerability to tampering, and insecure transmission. Existing cloud data-sharing schemes face the challenge of trusted but curious cloud servers, and data requesters worry about their private data being leaked or tampered with [3,4]. Traditional data-sharing schemes are no longer suitable for scenarios involving smart healthcare and the explosive growth of data in the cloud. With the continuous advancement of cloud storage technology, storing data in the cloud has become an emerging trend, and the security of transactions has become increasingly important. This necessitates guaranteeing that data users receive accurate and complete data after payment, while data owners receive appropriate returns when providing data. In data-driven multi-party collaboration models, ensuring the high integrity and reliability of data transactions has become a key factor for successful cooperation. Traditional solutions often rely on the involvement of authoritative third-party institutions, which not only impose additional costs on users but also usually regard these third parties as semi-trusted [5].

Blockchain technology’s emergence presents novel strategies for resolving the issues that data sharing confronts, and it has been effectively applied to data management [6,7]. The essence of blockchain is a distributed ledger. Firstly, the distributed feature of blockchain ensures the tamper-proofness of data sharing and circulation. Secondly, the automatic execution of smart contracts in blockchain could standardize the process to realize the transparency of rewards and punishments. Through the blockchain, all data transaction information can be traced one by one, which can not only ensure the integrity and ownership of data but also efficiently solve transaction conflicts. Consequently, integrating blockchain with data sharing can standardize the data management process and realize the right confirmation of shared data, to establish an open data-sharing ecosystem [8,9].

In data sharing, because the process of gathering information can be carried out independently by various organizations [10], there should be incentive measures to improve the service level and revenue. The Shapley value in cooperative game theory is commonly used to evaluate fair revenue distribution among participating entities based on individual contributions. An et al. [11] applied the Shapley value method for profit distribution in a three-stage system, promoting resource sharing and significantly optimizing the system’s overall performance.

Based on the existing work, we aim to design a data-sharing framework combining blockchain and Shapley value, which can realize collaborative sharing and data security [12]. Then, a dynamic incentive mechanism suitable for multi-party data sharing is designed using Shapley values, aiming to achieve a fair distribution of participants’ rewards. The mechanism adjusts incentives based on each data owner’s contribution at different stages, ensuring that all participants receive rewards corresponding to their contributions. The dynamic incentive mechanism not only motivates data owners to share more data but also enhances the quality of the data shared.

Overall, the main contributions of this paper are listed as follows:

•   Based on the blockchain platform, we use attribute-based Searchable encryption (ABSE) technology to achieve fine-grained access control of on-chain encrypted data. Participants are authorized by the consortium blockchain to ensure data privacy and security. Given the potential threat to data security and privacy posed by cloud servers, our solution ensures that they only store encrypted data.

•   We propose a dynamic and fair multi-party data-sharing incentive mechanism based on Shapley value. Unlike traditional schemes, it’s automatically executed by blockchain smart contracts, ensuring system reliability and consistency. In medical data sharing, the Shapley value method accurately measures each party’s contribution and distributes revenues reasonably, promoting more efficient and fair medical data sharing.

The rest of the paper is organized as follows. We present the related work in Section 2 and Section 3 introduces the preliminaries. Section 4 describes the system model of ours. Incentive mechanisms using cooperative game theory are proposed in Section 5. Performance analysis is presented in Section 6. At last, we summarize the paper in Section 7.

2  Related Work

2.1 Data Sharing

Data sharing has attracted much attention due to its convenience and economy. Numerous medical data-sharing schemes exist. Yang et al. [13] proposed a medical data-sharing service platform from the perspectives of medical data collection, sharing, and management, and then realized a medical data sharing system BDMISS based on cloud storage. Sahai et al. [14] introduced the concept of Attribute-Based Encryption (ABE) in 2005, enabling fine-grained access control over ciphertexts. In the context of smart healthcare and data outsourcing, Mamta et al. [15] combined ABE with searchable encryption, called ABSE, to achieve fine-grained access control and keyword search capabilities. Abdelfattah et al. [16] proposed a scheme based on the medical cloud, which uses cloud servers to achieve fairness in data trading. Zhang et al. [17] studied a verifiable ABSE scheme, which introduces a third-party and shared multi-owner mechanism to achieve the verifiability of search results. However, the two schemes proposed in [16,17] rely on semi-trusted cloud servers, and storing data on the cloud may lead to privacy leakage for users [3]. Moreover, malicious cloud servers could exploit outsourced data, such as intentionally tampering with data or providing false information.

Blockchain has gained widespread attention in data sharing due to its advantages such as decentralization and immutability [18,19]. Das et al. [20] proposed a blockchain-based incentive minimization scheme. In Delay Tolerant Networks (DTNs), this scheme optimizes incentive distribution by combining resource and efficient caching routing protocols to prevent malicious node behaviors. Azaria et al. [9] proposed MedRec, a decentralized record supervision system for electronic medical records based on blockchain technology, which provides secure access to diagnostic data and comprehensive, immutable logs. Shrestha et al. [21] proposed a blockchain-based platform that enables users to benefit from the data-sharing process while ensuring the integrity of transaction data.

However, although these schemes use blockchain to ensure transaction reliability, they suffer from issues of low system efficiency and heavy computational burdens on the user side. There is an urgent need for more efficient and secure solutions for medical data sharing. Mamta et al. [22] proposed a blockchain-based cloud-assisted computing scheme, which uses the consortium chain for system initialization and partial search token generation. Although shifting a large amount of computation to consensus nodes alleviates the computational burden on users, these nodes also need to perform additional calculations. In another scheme, Su et al. [23] used two smart contracts to verify the correctness of the search results and used the computing power of the cloud server to improve the efficiency. However, the existing blockchain consensus algorithms incur relatively high computational overheads and are not suitable for high-frequency data-sharing scenarios. Therefore, it is necessary to adopt improved consensus algorithms to enhance the system’s efficiency.

2.2 Incentive Mechanism

In practice, data owners may be reluctant to share data due to privacy concerns or other factors. Therefore, to incentivize data owners, it is essential to design a fair and reasonable incentive mechanism to ensure that data owners receive the corresponding revenues they deserve. The theories used to design incentive mechanisms in data sharing mainly include auction theory, contract theory, and evolutionary game theory.

Zhao et al. [24] put forward an incentive mechanism, which is designed to facilitate the online selection of workers in real-time scenarios. Nevertheless, due to the diversity of tasks and multiple other factors during the auction process, the reverse auction fails to adapt to complex requirements. In the Internet of Vehicles, due to the trust issues in the traditional crowdsourcing incentive mechanism, Chen et al. [25] proposed a quality-driven auction incentive mechanism, which uses a consortium blockchain to ensure the integrity and traceability of the data. Kazmi et al. [26] proposed an incentive mechanism based on contract theory to encourage vehicles to participate in resource sharing, thereby reducing the resource burden of the vehicular network and maximizing social welfare. Liu et al. [27] constructed an incentive model for enterprise data-sharing, and utilized evolutionary game theory to explore the evolutionary strategies in various conditions.

However, contract theory assumes that both parties have complete knowledge of all key information in the contract, and in data sharing, the data owner may not be able to fully understand the intention of the data consumer. Evolutionary game theory usually considers the evolutionary process with a long time scale, which makes it difficult to adapt to the rapidly changing data-sharing environment. The assumption based on individual rationality may ignore other influencing factors. Therefore, in multi-participant data-sharing, it is necessary to find a suitable mechanism that can encourage data owners to participate in sharing and ensure fair distribution of benefits.

Cooperative game theory is an effective tool for designing the desired incentive mechanisms. The Shapley value is commonly used in models of contribution-based revenue distribution. Ying et al. [28] proposed CHASER, an incentive mechanism specifically developed for blockchain-based Edge-assisted Mobile Crowd-sensing (BEMCS) systems. CHASER can meet incentive requirements such as budget balance, bilateral individual rationality, and high social welfare, attracting more participants. Under the federated learning framework, Yang et al. [29] proposed Weighted Truncation (WT) to improve the state-of-the-art Shapley Value algorithm for the scenario of industrial safety inspection data joint modeling. This is aimed at eliminating unnecessary computations. Our work is to provide a contribution-based revenue distribution method for multi-participant data-sharing collaboration and encourage them to share data.

3  Preliminaries

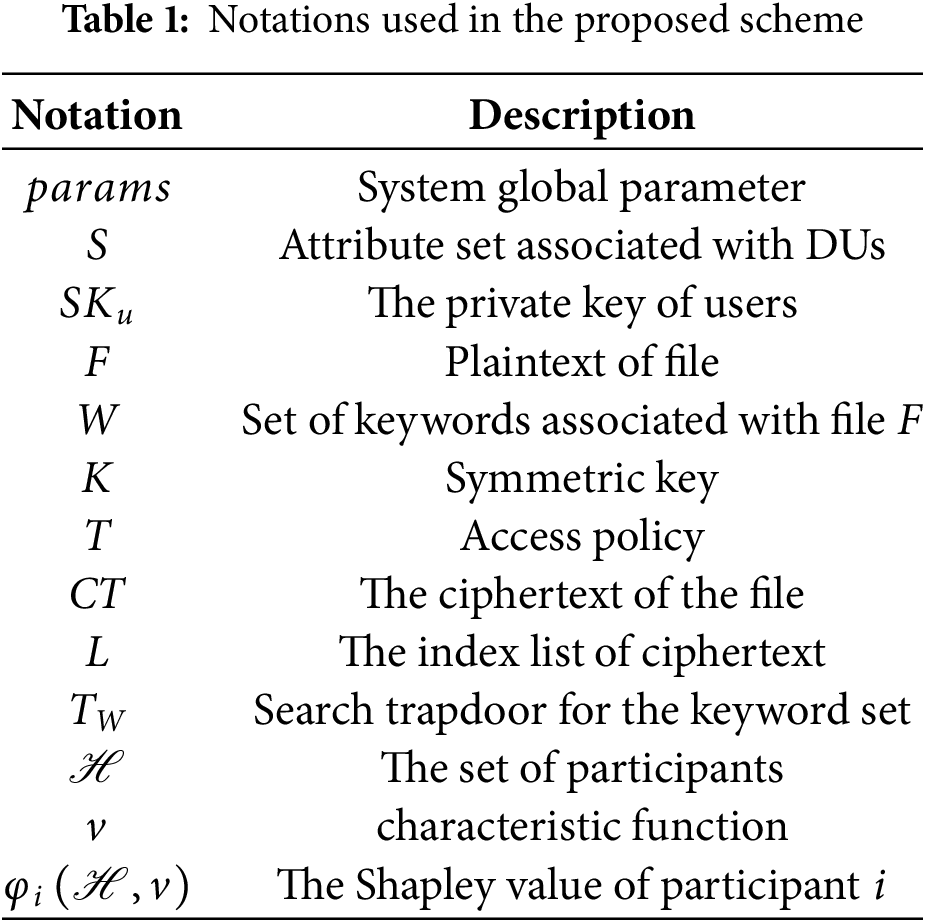
For better understanding, this section first presents some notations applied in the presented scheme in Table 1. Then, the background knowledge and relevant technologies that will be used are introduced.

3.1 Shapley Value

In multi-party data sharing, measuring each participant’s contribution is key to ensuring fair revenue distribution. The Shapley value from cooperative game theory effectively addresses this issue by focusing on evaluating each participant’s marginal contribution in multi-party collaboration. This method embodies the principles of cooperation and effectively encourages the positive participation of all members [30].

Suppose the set of participants is denoted as ℋ. We define any non-empty subset S of ℋ (where S⊆ℋ and S≠∅) as a coalition of participants. Considering a set of participants denoted as ℋ where |ℋ| denotes the number of participants. We call any nonempty subset S∈ℋ a coalition of the participants. A coalition can generate revenue by internally collaborating to share medical data. For every coalition S, we use v(S) as the value function. Specifically, v(ℋ) is defined as the total revenue generated by all the participants within the set ℋ, Let SPi(S) indicate the revenue of participant i within coalition S:

v(ℋ)=Σi∈SSPi(S).(1)

Therefore, the contribution of the participant to the coalition is represented by the value function v as follows.

Definition 1. We define the marginal contribution of participant i to a coalition S (with the condition that S⊆ℋ∖{i}) as Δi(v,S). Specifically, it is expressed by the equation:

Δi(v,S)=v(S∪{i})−v(S).(2)

In cooperation, as participants gradually join the coalition, the marginal contribution of each participant within the coalition will also change. According to the variation of the value function v in Definition 2, the Shapley value is calculated as follows.

Definition 2. The Shapley value is defined by

φi(ℋ,v)=Σs∈Siw(|s|)Δi(v,s),∀i∈𝒩.(3)

where w(|s|)=(|ℋ|−|s|−1)!|s|!|ℋ|! is defined as the weighting factor and Si represents a collection of all subsets of ℋ excluding the player i. The effectiveness of Eq. (3) is as follows:

Σi∈𝒩φi(ℋ,v)=v(ℋ).(4)

Shapley value quantifies the contribution of each participant in a cooperative scenario by accumulating their marginal contributions. Our main work is to design an incentive mechanism suitable for multi-party data-sharing scenarios using Shapley value theory.

3.2 Blockchain and Smart Contract

The essence of blockchain is a decentralized distributed ledger, jointly maintained and managed by multiple decentralized nodes within the network. Through consensus algorithms, the nodes achieve synchronization and sharing of the ledger. Currently, blockchain technology is being widely studied and applied in fields such as Internet finance, e-healthcare, the Internet of Things, and cloud computing. Consortium blockchain based on the Practical Byzantine Fault Tolerance (PBFT) algorithm has advantages such as fault tolerance, strong consistency, privacy protection, and low latency, which can provide participants with a secure, reliable, and efficient data-sharing platform [31].

The smart contract, proposed by computer scientist Nick Szabo in 1994, is an automatically executable program code that is transparent and immutable on the blockchain and has been applied in various fields. Smart contracts ensure the security, transparency, and reliability of contracts through the decentralized feature of blockchain [32,33].

Therefore, we utilize blockchain technology as the infrastructure for data-sharing. This facilitates the verification of historical transactions and ensures security and privacy during the data-sharing process. By combining incentive mechanisms and smart contract technology, fair distribution of interests among participants can be achieved without assuming the honesty of a third party. Smart contractsensure the reliability, consistency, and verifiability of the incentive mechanism.

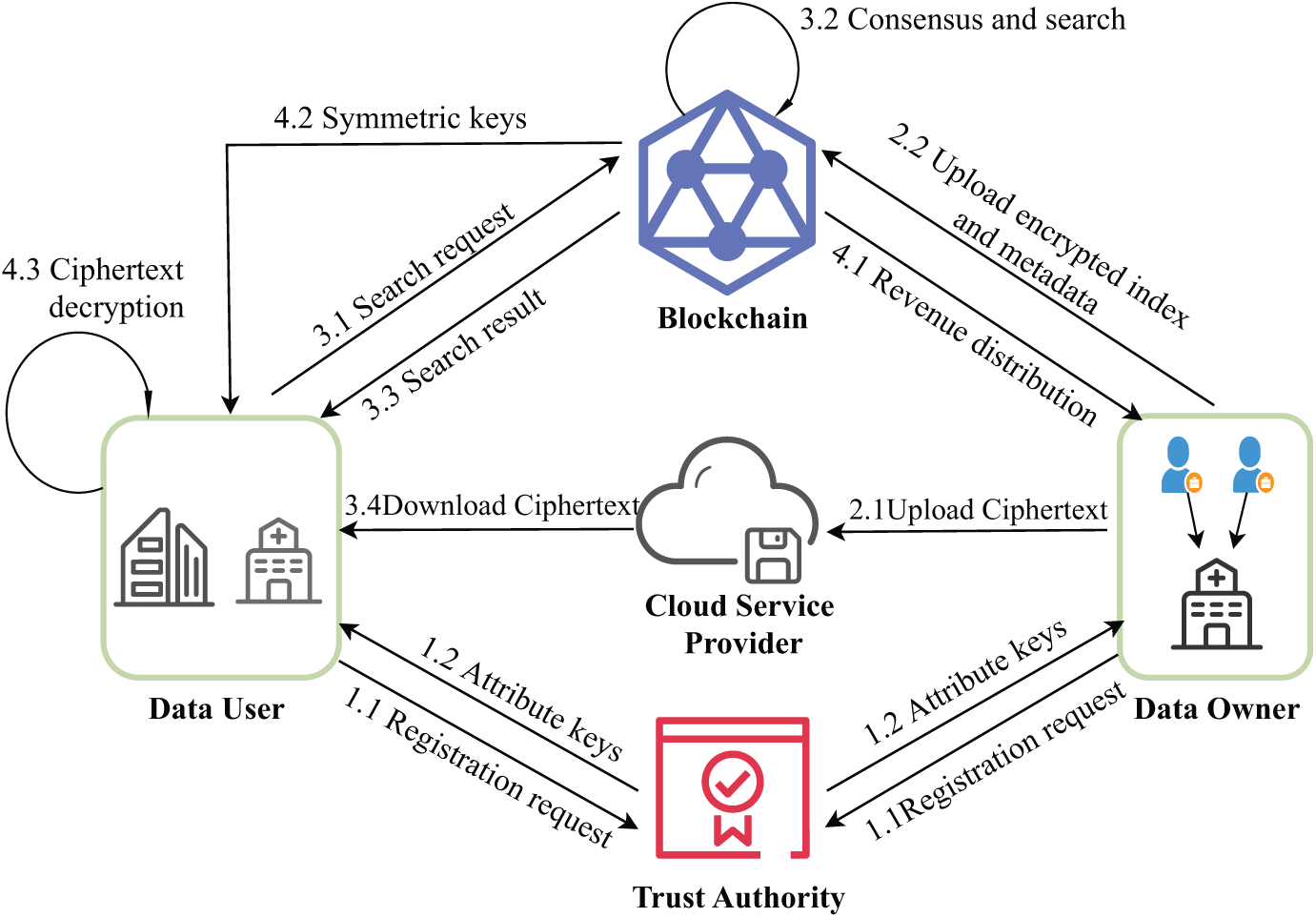
Figure 1: System model of medical data sharing

4  Framework of Data Sharing

As shown in Fig. 1, the framework is composed of five entities. It provides a platform for all participants to achieve data sharing and revenue distribution.

4.1 System Model

1)   Trust Authority (TA): TA is regarded as completely trustworthy by the rest of the participants. It generates public parameters params, master key msk within the system, and the secret keysSK corresponding to the attributes assigned to DO and DU.

2)   Data Owner (DO): DOs are those who own electronic health records (EHRs) and are willing to take part in the data-sharing process. DO encrypts EHRs and keywords using the Encrypt algorithm. The encrypted EHR is then sent to the Cloud Service Provider, while the encrypted index and other information are sent to the blockchain to enable the Data Users to execute the Search algorithm.

3)   Data User (DU): DUs encompass entities like data users, such as doctors, hospitals, and research institutions. To retrieve EHRs with specific keywords, the DU sends a request to the blockchain network. This request contains the set of attributes of DU as well as the target keyword of the search operation. At the same time, the symmetric key of the relevant ciphertext can be obtained only after the transaction is completed. Then, DU decrypts the intermediate ciphertext obtained from the Cloud Service Provider.

4)   Cloud Service Provider (CSP): CSP possesses powerful storage and computing capabilities. It can efficiently address the storage challenges faced by the blockchain. It can be utilized to store encrypted data and perform pre-decryption tasks. In this way, it can not only significantly enhance the execution efficiency of the solution but also effectively reduce the processing burden on the user side.

5)   Blockchain (BC): BC employed is a consortium blockchain. This type of blockchain serves as a repository for keyword ciphertext, and its access is restricted solely to consortium members. Inside the BC network, the consensus nodes are made up of various hospitals and research institutions. Once a user submits a request, these consensus nodes execute the algorithm to reach consensus. Subsequently, they conduct a search for the relevant index according to the provided attribute set and keywords.

4.2 Basic Definition

1)   {params,msk}←Setup(1λ): TA executes this task. By inputting the security parameter λ, TA outputs the system parameters params and the master key msk.

2)   SKu←KeyGen(params,uid∈UID,S): The generation algorithm is carried out by TA. Inputting the system parameters params, the user identifier uid, and the attribute set S from the user, generates the attribute key SKu.

3)   {IW,CT}←Encrypt(params,SK,W,T,F,K): is run by DO through taking system parameters params, DO’s SKu, keyword set W, access policy T, original file F, and symmetric key K as input. It outputs encrypted keyword index IW and encrypted file CT.

4)   TW←TrapDoor(Params,SKU,W): This algorithm is run by the DU. After inputting the system parameters params, DU’s private key SKu, and keyword set W for which a search is to be conducted, the DU obtains the search trapdoor TW.

5)   0/1←Consensus(H2(TW)): when DU sends H(TW) to the blockchain network, the consensus nodes will process this hash value, execute the corresponding algorithm to achieve the consensus operation, and the final output will be either 1 or 0.

6)   CTor⊥←Search(params,IW,TW): is executed by the smart contract SearchSC. The operation takes in the system parameters params, search trapdoor TW, and encrypted keyword index IW. Then, it carries out the task of matching the trapdoor against the indexes. Finally, CSP returns search results CT to DU, otherwise returns ⊥.

7)   F←DecEhr(params,CT,K): DU executes the algorithm. By inputting the symmetric key K, system parameters params, and the ciphertext CT, DU can obtain the original file F as the output.

8)   RegisterSC: The smart contract, deployed by the TA, is responsible for handling user registration requests. When the user initiates a registration request, the contract verifies the user’s identity, calls KeyGen to generate and return the attribute key, and broadcasts the related registration information to the blockchain.

9)   SearchSC: DO deploys this smart contract. Once the smart contract detects that the consensus nodes have attained a consensus-in other words, when the output of the Consensus algorithm is 1, it invokes the Search function and sends the retrieved file index back to DU.

10)   IncentivizeSC: TA deploys this smart contract. Once the user initiates a transaction, the contract is triggered. This contract automatically distributes benefits derived from transactional data to participants according to their contributions to the data-sharing collaboration. The exact allocation method and mechanism details are covered in Section 5.

4.3 System Workflow

The workflow is shown in Fig. 2 and mainly consists of four stages. The details are as follows.

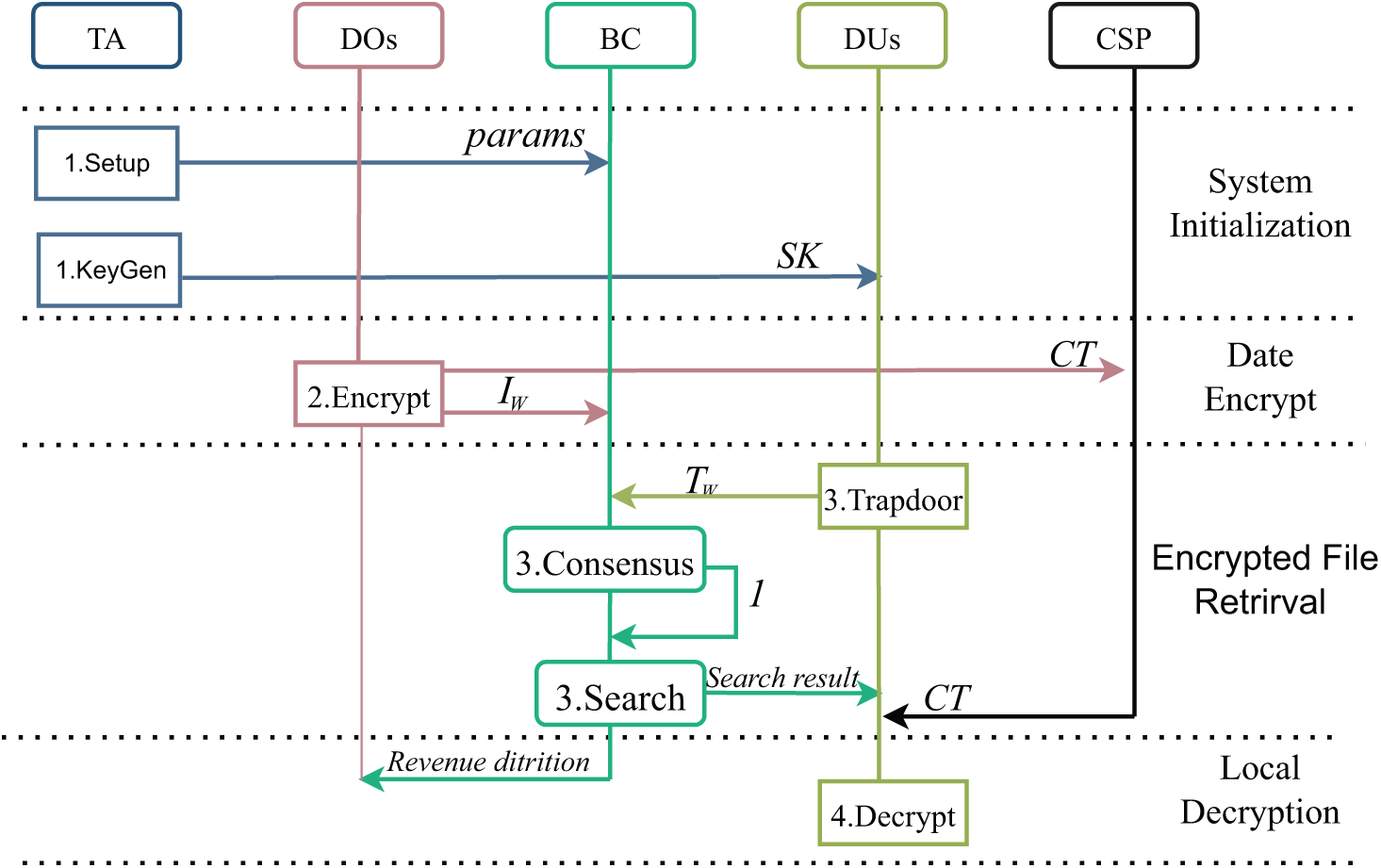
Figure 2: The workflow of system model

Step 1: This stage mainly includes system initialization and registration.

Setup: TA executes the algorithm and chooses the security parameter λ for the system initialization.

1)   Given a bilinear mapping e:G1×G1→GT, where G1 and GT are the multiplicative cycle groups of prime order p and g is one generator of the group G1. Three secure hash functions are selected by the TA. Specifically, H:{0,1}∗→Zq∗, H1:{0,1}∗→G1, H2:{0,1}∗→{0,1}l.

2)   Define Δi,S(x)=Πj∈S,j≠ix−ji−j as the Lagrange coefficient, S represents the set of attributes, i,j∈Zq∗.

3)   After that, it selects α,β∈Zq∗ at random, and calculates the values of gα,gβ,e(g,g)α. Finally, the system master key msk={e(g,g)α,gβ} is obtained, and the global system parameters params={G1,GT,e,g,H,H1,H2} are published.

Keygen: TA accepts DO (or DU) requests and verifies the user’s identity. Upon successful verification, TA generates a key relevant to the user’s attribute set S.

1)   TA randomly selects r∈Zq∗, and computes SKu1=gβ,SKu2=g,SKu3=gr.

2)   Then, it randomly selects a number r within Zq∗ and computes according to the steps below: SKua=SKu3×H1(att)ra, SKua′=gra. The algorithm generates the user’s secret key SKu, as follows: SKu={SKu1,SKu2,SKu3,{SKua,SKua′}att∈S}.

3)   Finally, the secret key SKu is sent by the TA to DU (or DO) via a secure channel.

Remark: Based on real identity authentication, it ensures the uniqueness and legitimacy of each identity, which makes our scheme resistant to Sybil attacks.

Step 2: This stage mainly includes data plaintext encryption and keyword encryption:

Plaintext encryption: DO selects the EHRs’ plaintext file set F={f1,f2,…,fn}.

1)   DO randomly choose Kj∈Zq∗ as the symmetric key, where j∈[1,n].

2)   For f∈F compute the corresponding hash value h(f) and encrypted file CT=ε.EncKf. Here, ε.Enc is used to represent the well-recognized symmetric encryption algorithm.

Keyword encryption: DO executes the algorithm, and for f∈F, extracts the set of keywords W={w1,w2,…,wm}, then sets the access tree T.

1)   DO selects a secret value s∈Zq∗ and computes as follows: Cwi=e(gH(wi)s,g)e(g,g)as, i∈[1,m], and Cw′=gβs.

2)   First, DU executes the secret sharing algorithm and selects a polynomial qx for each node x in the access tree T.

X is defined as the set of leaf nodes within the access tree T. Starting from the root node t, define qt(0)=s. Regarding any other node x, define qx(0)=qparent(x)(idx(x)).

(b)   Compute Cx=gqx(0),Cx′=H1(attr(x))qx(0) for x∈X.

Finally, the encrypted index is generated as IW={CWi,CW′,{Cx,Cx′}x∈X}. DO send CT to the CSP, IW, and metadata to the blockchain.

Step 3: The main components of this stage are the generation of the trapdoor and keyword search:

Trapdoor generation: The algorithm is executed by DU when the search keyword set W′={w1′,w2′,…,wm′} is given.

1)   DU randomly choose r1∈Zq∗, and computes T1,i=SKu1×SKu2Σni−1H(wi′)×SKu2r1=g,i∈[1,m].

2)   For each attribute, ∀att∈S, DU computes as follow: Ta′=SKua′, Ta=SKua×gr1=gr+r1×H(att)ra.

Finally, the search trapdoor TW={T1,i,{Ta,Ta′}att∈S} is obtained and sent to the blockchain network.

Consensus: DU initiates a data request to the blockchain network, and consensus nodes execute the following algorithm to return the consensus result.

1)   Then, for n consensus nodes, DU uses the (k,n) Shamir’s secret sharing scheme to compute the shares of H2(TW), H2(TW)i∣i=1n.

2)   The calculation of e(g,g)H2(TW)i is carried out by k′ honest consensus nodes, and then this result is broadcasted to the blockchain network.

If k′≥k, k consensus nodes integrate their H2(TW)i∣i=1n, and obtain: H2(TW)′=∏i=1ke(g,g)H2(TW)i. SearchSC checks the following equation: H2(TW)′=?H2(TW). Return 1 if the equation holds; otherwise, return 0.

(b)   If k′<k, return 0.

Keyword search: Given an index IW and a search trapdoor TW, the smart contract SearchSC executes the algorithm when Consensus’s is 1. x represents a node within the access tree T.

1)   When node x is a leaf node, set att=attr(x), where att represents the attributes related to leaf node x.

If att∈S, then the following calculation is performed:

Fx=e(Ta,Cx)e(Ta′,Ca′)=e(gr+r1,gqx(0))e(H1(att)ra,gqx(0))e(gra,H1(attr(x))qx(0))=e(g,g)(r+r1)qx(0)

(b)   If att∉S, then Fx=⊥.

When x is a non-leaf node, for every child node z of node x, the outcome of the algorithm is represented as Fz. Set Ux retains all values where Fz≠⊥, and kx is the threshold value for node x.

(a)   If |Ux|<kx, it indicates that the node threshold is not satisfied, terminate and return ⊥.

(b)   If |Ux|≥kx, it indicates that the node threshold is satisfied. Choose kx values at random from set Ux, then calculateF in conjunction with Lagrange coefficients:

Fx=∏z∈UxFzΔi,Sx(0)=∏z∈Ux(e(g,g)(r+r1)qparent(z)(idx(z)))Δi,Sx(0)=e(g,g)(r+r1)qx(0),

where i=idx(z), Sx={∀z∈Ux:idx(z)}, Δi,S(x) refers to the Lagrange coefficients.

When the user’s set of attributes meets the requirements of the access tree, recursively calculate to obtain the final execution result as Ft=e(g,g)(r+r1)qt(0)=e(g,g)(r+r1)s, and return the search result to the DU.

Step 4: Data decryption and verification:

After the SearchSC is executed, IncentiveSC is triggered to calculate the contribution of each participant based on the Shaplay value, and the rewards are distributed accordingly. DU then obtains the corresponding encrypted file from CSP and executes the decryption algorithm DecEhr to obtain the plaintext data f=ε.DecKC.

Blockchain records relevant transactions through a distributed ledger. Due to its tamper-proof feature, the traceability of transaction data is achieved. This traceability not only ensures the integrity of the data but also safeguards the data ownership, effectively resolving transaction conflicts.

5  Incentive Mechanism for Data Sharing Based on Cooperative Game

In this section, we initially introduce the proposed cooperation model and explore how to measure each participant’s contribution to the data-sharing process. Subsequently, we offer a detailed explanation of achieving fair revenue distribution through contribution-based incentive mechanisms.

5.1 Cooperation Model

The decentralized data-sharing framework and its revenue distribution process have been systematically elaborated above. With the development of digitalization, data users have become more stringent in their requirements for the reliability and verifiability of shared data. Encouraging users to share more high-quality data has become a pressing issue. Therefore, it is necessary to design an incentive mechanism suitable for multi-party data-sharing scenarios, ensuring fair revenue distribution, motivating data owners to collaborate actively, and improving the quality of shared data.

We categorize participants into three types: data owners, blockchain networks, and data users. The set of participants is 𝒩=ℛ∪ℬ∪ℋ, where ℛ={R1,R2,...,R|ℛ|} denotes a set of data users, ℬ denotes a blockchain network, and ℋ={H1,H2,…,H|ℋ|} denotes a set of data owners. We denote Di={d1,d2,…,d|Di|} as the set of sharing data provide by Hi. Fig. 3 shows a cooperation model where |ℛ| = 1, |ℋ| = 3, and ℬ as a medium for interaction between DO and DU, ensuring reliable and fair execution of the incentive mechanism.

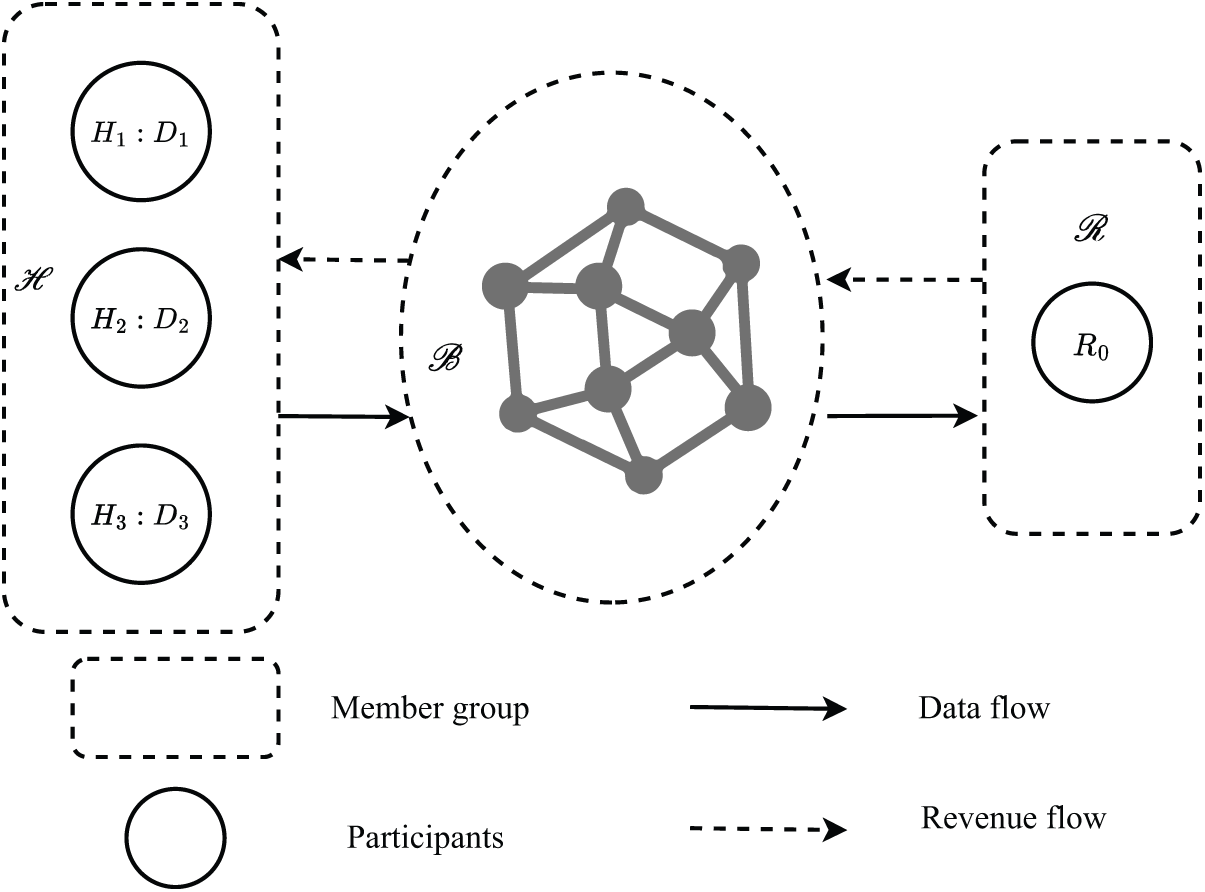
Figure 3: The cooperation model based on Blockchain

In our proposed scheme, points are used as incentive tokens. These points can be accumulated and later exchanged for services or benefits within the consortium, fostering a positive feedback loop for data sharing. When a data user (DU) requests data from the blockchain, the network performs a search after reaching a consensus. Rewards are then distributed based on the contributions of the participants, thereby encouraging active participation in data sharing.

5.2 Methods for Measuring the Value of Medical Data

This subsection aims to evaluate the contributions of each participant in the process of data sharing. It is assumed that the contribution of the data provided by each participant is reflected in the incremental improvement of the overall data quality. Therefore, we choose a generic metric to measure the dataset as a signifier of the value function in Eq. (2). In this research, information entropy (IE) is used to relate the value of medical data to the volume of data. This method can measure data’s value in the process of data-sharing, and further calculate the contribution of participants in data sharing. In the data-sharing model, we use IE as a measure of value, which is based on both the quantity and quality of shared data.

In this process, information entropy is an indicator to measure the degree of uncertainty or confusion of data. We abstract it as a method for comprehensively evaluating data volume and data quality. Applying information entropy to the volume and quality of shared data enables us to better understand each participant’s contribution to the overall data-sharing process. Specifically, the higher the amount of shared data and data quality of participants, the greater their contribution to revenue. This indicates that data quality is as crucial as data volume, and low-quality data will undermine the overall contribution, regardless of its quantity. Thus, by leveraging information entropy to measure the contribution of participants, a new way is provided to assess the value of shared medical data and infer the contribution of participants to revenue accordingly.

The information entropy of player Hi is calculated as follows:

IE(Hi)=−∑k=1|Di|P(dk)log⁡(P(dk)), (i=1,2,…,|ℋ|)(5)

where 𝒟i represents the data set shared by participant Hi this time, P(dk) represents the probability of occurrence of medical data dk, which is calculated by using the index of transaction times, and IE(Hi) represents the information entropy of participant Hi.

During multi-party data sharing, the initial coalition is seen as the state having the most significant effect on the system’s overall performance. To better reflect the relative contributions of different participants, we introduce a weighted Shapley model. Specifically, by adjusting the weights, we consider the unique contributions made by members of the initial coalition in aspects such as coalition establishment, coordination, and attraction of other members. We aim to explore the incentive effects of the model on different types of participants by adjusting the weights of the initial coalition participants’ information entropy, that is when s=ℋ, Δi(IE,ℋ)=λ(IE(ℋ∪{Hi})−IE(ℋ)).

The weighted model was dynamically adjusted to explore its impact on the distribution of participants’ revenue, improving the fairness of revenue distribution and participants’ enthusiasm. However, to ensure the rationality and fairness of the proposed method, we must continuously adjust and optimize it while taking into account the interests of all parties.

5.3 Revenue Distribution of Cooperation Model

We have designed an incentive mechanism based on Shapley values, utilizing the method described in Section 5.2 to calculate participants’ marginal contributions in cooperation, aiming to effectively incentivize participants and fairly distribute profits.

Let’s presume that data owner Hi∈ℋ participates in data sharing, and the total revenue in this model is v(ℋ), which belongs to all data owners participating in sharing. Since all participants have a positive influence on the coalition, every participant should be involved in the revenue distribution. In any subset of ℋ, we focus on the information entropy obtained from the dataset provided by the participants.

We measure the contribution to the IE of each participant through Δi(IE,s)=IE(s∪{Hi})−IE(s), where IE(s) represents the entropy value of the dataset of the coalition s. The marginal contribution Δi(v,S) defined in Eq. (2) is similar to it. That is, the information gain ΔHi(IE,s) is measured as the marginal contribution of Hi in coalition s.

Given any model system (𝒩,v), we put forward the Shapley value relying on the IE as:

φi(ℋ,v)=Σs∈Siw(|s|)Δi(IE,s)IE(ℋ)v(ℋ),∀i∈ℋ(6)

where Si={s|s⊆ℋ/{i}} represents the set of all subsets of ℋ with participant i excluded. In Eq. (6), we divide by IE(ℋ) as a form of normalization. This makes Eq. (4) hold, that is, Σi∈ℋφi(ℋ,v)=v(ℋ).

We denote φHi as the Shapley value-based revenue that is assigned to Hi. The subsequent theorem, based on Eq. (2), elaborates on the revenue distribution of data owners in the scenario of multi-party data-sharing cooperation.

Theorem 1 (Shapley value allocated to participants)

Assume a set of data owners ℋ participates in data sharing. We establish Sℋi as the set that consists of all subsets of ℋ with the exclusion of the data owner Hi, formally defined as Sℋi={ℋ′⊆ℋ/{Hi}}. Regarding the marginal contribution to the IE, the revenue of the Shapley value for each participant is expressed as follows:

φi(ℋ,v)=φHi(ℋ)v(ℋ),∀Hi∈ℋ,(7)

where the normalized Shapley values {φH1,φH2,…,φH|ℋ|} are:

φHi(ℋ)=∑ℋ′∈Sℋiw(|ℋ′|),∀Hi∈ℋ.(8)

The revenue v(ℋ) allocated to data owner Hi is determined by the normalized Shapley value φHi, which represents the percentage of the total coalition revenue attributed to Hi. Essentially, this value reflects the weighted sum of the participant’s marginal contributions ΔHi(IE,ℋ′) across all possible subcoalitions.

Theorem 2 (Consistency of Shapley value allocation)

In the cooperative game framework, the total revenue distribution of the coalition must satisfy the collective rationality axiom, meaning that the sum of the Shapley values of all participants is exactly equal to the total revenue of the coalition, denoted as ϕℋ=∑Hi∈ℋφ(Hi). The revenue v(ℋ) should be distributed to the relevant data owners in specific proportions. Specifically, the revenue v(ℋ) should not be shared by participants who have not contributed. We use normalized Shapley values to assess each participant’s contribution to the revenue in the system, thus ensuring that the revenue is fairly distributed among the participants.

For participants Hi and Hj, if for any coalition s that does not include Hi or Hj, the condition IE(s∪{Hi})=IE(s∪{Hj}) holds true, then φHi=φHj. This demonstrates that the order or labeling of stakeholders does not affect the distribution of benefits.

6  Performance Evaluation

6.1 Experimental Setup

To validate the rationality and performance of the proposed solution, we conducted numerical evaluations using the following hardware specifications: Intel Core i5-8500HQ CPU, the processor speed is 3.0 GHz, and the RAM is 8 GB. The Java Pairing-Based Cryptography Library (JPBC) [34] was employed to assess the fundamental cryptographic operations. We conducted multiple runs of various algorithms under different attribute counts to assess the computational overhead at each stage. Subsequently, theoretical analysis and simulation experiments validated the effectiveness and rationality of the incentive mechanism.

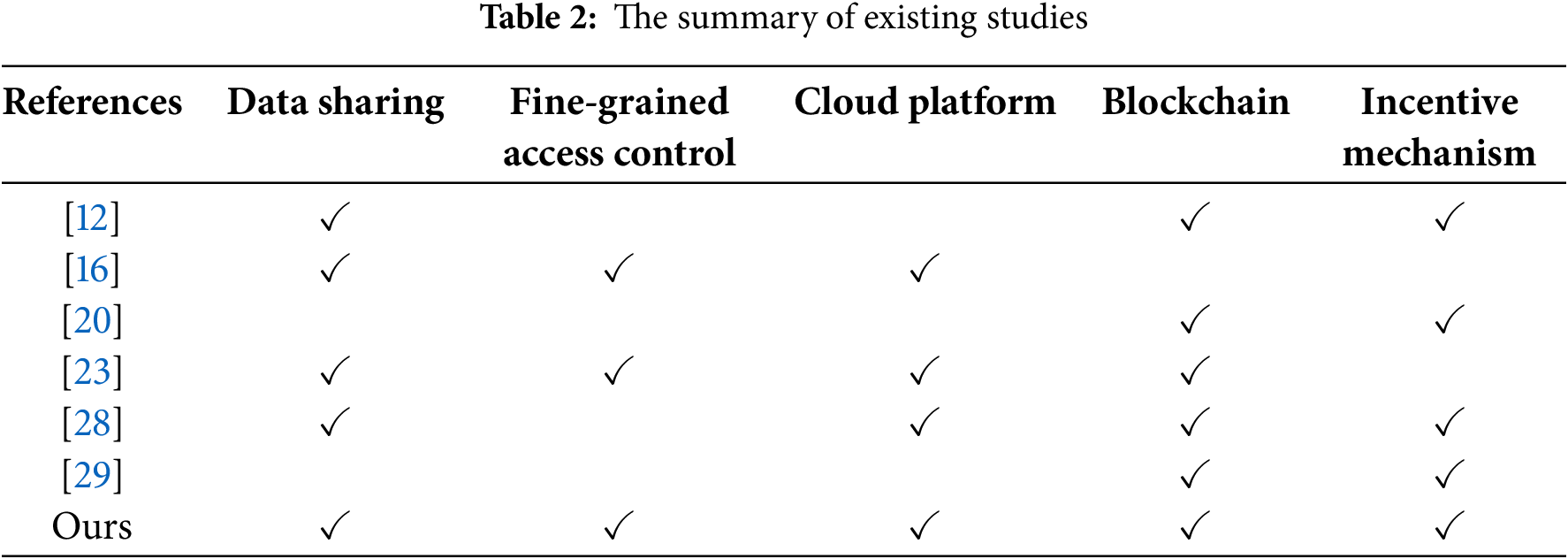
We conducted a functional comparison of the proposed scheme and existing studies, summarizing their key features in Table 2.

6.2 Algorithm Efficiency and Smart Contract Cost

In Figs. 4 and 5, we show the overhead of the algorithms and smart contracts in different stages respectively. In the experimental analysis, we evaluated the computational overhead associated with three critical attribute-related operations in the data-sharing scheme: key generation, encryption, and search. In Section 4.3, we detail the construction of each algorithm and experimentally confirm the linear growth between attribute count and execution time. As shown in Fig. 4, the execution time of each algorithm shows a linear growth trend under different scales of attributes. It is worth noting that even when the scale of attributes reaches 25, the execution time of each operation remains within 0.5 seconds, which is acceptable in most application scenarios. In Fig. 5, we use gas as a metric to measure the overhead of smart contracts and the graph shows the gas overhead of RegisterSC, SearchSC, and IncentiveSC. The deployment cost is one-time and the highest, while the transaction cost consists of the execution cost and the basic transaction cost.

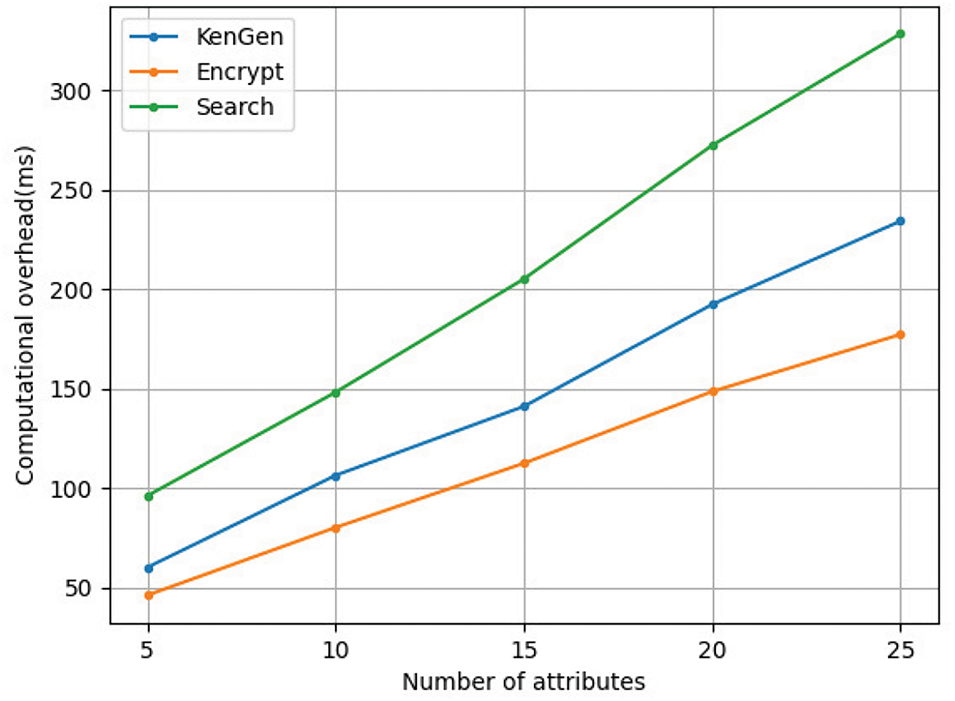
Figure 4: Computation overhead of algorithms

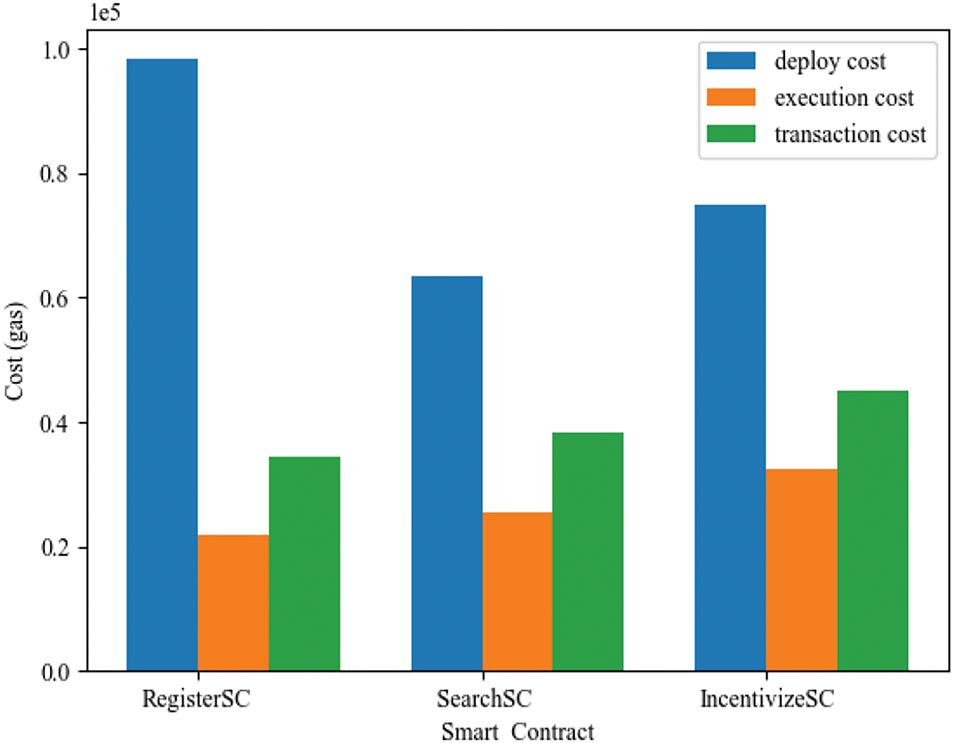
Figure 5: Consumption of smart contracts

Since the consensus mechanism of the consortium blockchain primarily employs Practical Byzantine Fault Tolerance (PBFT), as discussed in references [22] and [23], it is worth noting that PBFT is a consensus algorithm with a complexity of O(n2). Therefore, we have made improvements to the consensus algorithm. In the experiments, a multi-threaded program written in Java is used to simulate the consensus process between nodes. PBFT algorithm requires that the node scale satisfies the constraint N≥3n+1, where n is the number of fault-tolerant nodes. Based on this requirement, the number of nodes starts at 4 with a step size of 3.

To evaluate the performance of the consensus algorithm, we tested the time required to reach consensus under different node scales, as shown in Fig. 6. Within the PBFT framework, we reconstructed the consensus mechanisms from references [22] and [23] to ensure consistency in experimental conditions. It is noteworthy that scheme [23] requires consensus nodes to act as proxies for executing user-side computations, which results in a time overhead similar to that of [22], but with higher resource consumption. Experimental results show that when the number of nodes exceeds 10, the overhead of traditional schemes [22] and [23] increases exponentially. In contrast, the consensus mechanism designed in this work, based on Shamir’s secret sharing, exhibits a linear increase in time overhead as the node scale grows, significantly improving consensus efficiency, and making it more suitable for the demands of healthcare IoT scenarios.

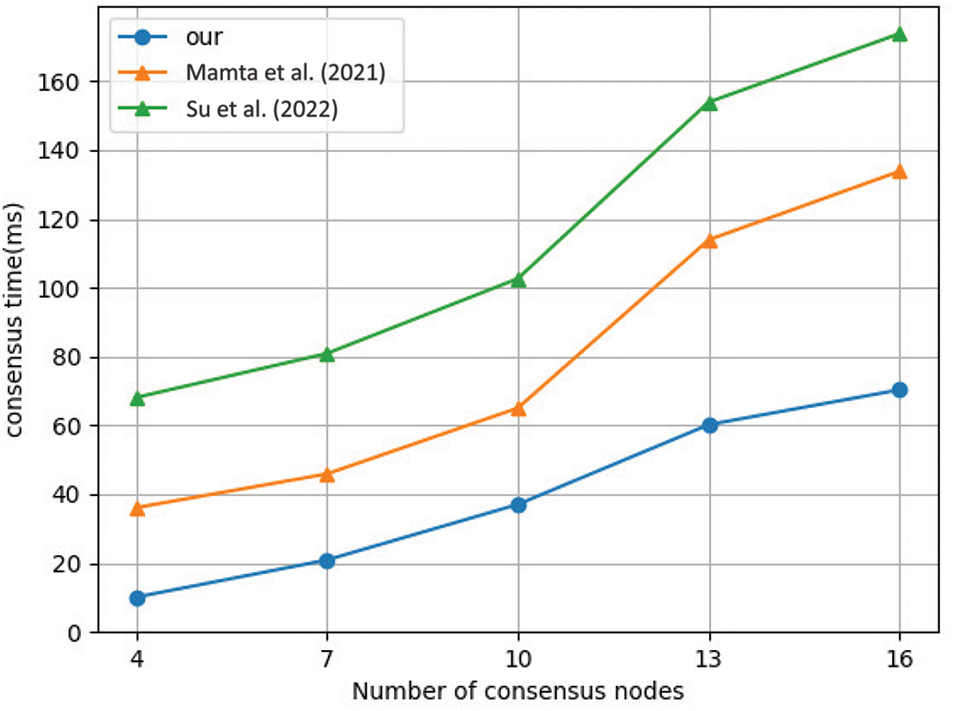
Figure 6: Computation overhead of consensus [22,23]

6.3 Performances of the Proposed Incentive Mechanism

6.3.1 Influence of Data Contribution and Rationality

We initially performed a theoretical analysis of the proposed method. By adjusting the weights of key parameters in the coalition based on the cooperative model in Section 5.1, where |ℋ| = 4 and |ℛ| = 1, we validated the effectiveness and theoretical rationality of the approach.

Fig. 7 shows the information entropy, Shapley value, and corresponding revenue percentage for four players sharing the dataset when the coalition size |ℋ| = 4. We can observe that players with higher initial information entropy (IE) also have higher Shapley values and higher payoff percentages. In addition, participants with low initial information entropy will have their Shapley value and corresponding payoff percentage increased relative to the initial value because the Shapley value considers all possible feature subsets and the contribution of participants is a weighted average, which is beneficial to encourage new participants to participate in data sharing. Concurrently, our method of measuring the value of data also ensures that high-quality participants will get higher payoffs relative to low-quality participants, thus providing the equity of high-quality participants.

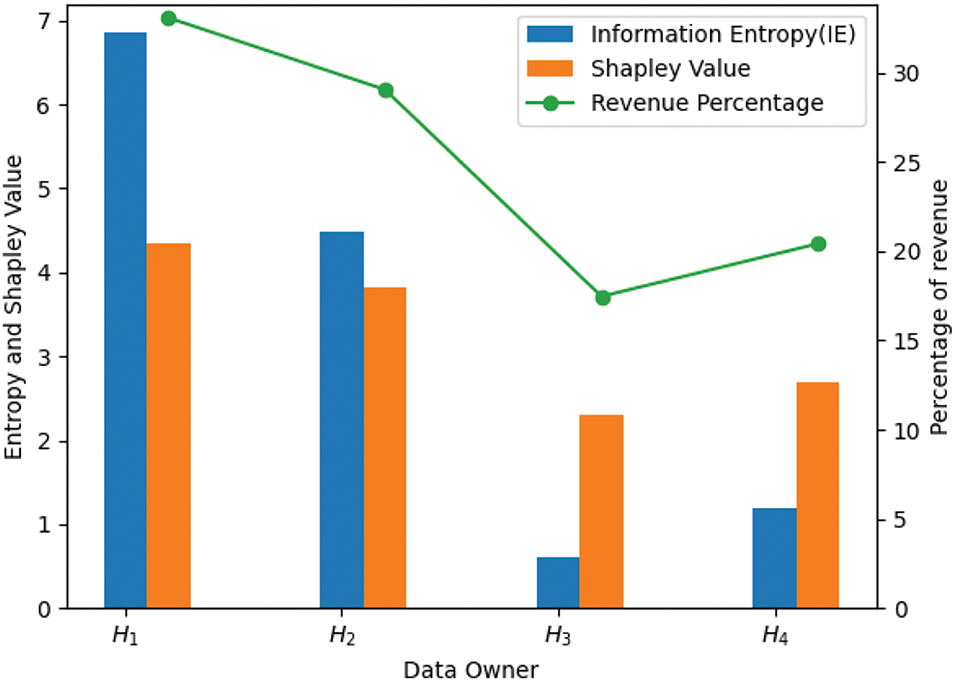
Figure 7: The Shapley value revenue under the unit model with different IE

In Fig. 8, we consider when the initial coalition is regarded as the state with the greatest impact on the overall system performance, denoted as state s=ℋ. Consequently, we increase the weight of information entropy at state s=ℋ to investigate the effect of different values of λ on the participants’ revenue. The figure illustrates the variation in revenue distribution of data owners as λ changes. We can observe that the percentage gain of H1 and H2 increases with the increase of λ, while the percentage gain of H3 and H4 decreases with the increase of λ. It encourages the improvement of data quality by bias increasing the reward for participants with high-quality data contribution, and promotes the circulation and sharing of high-quality data in the whole network. By adjusting the parameters, we can achieve the desired incentive effect, thus selecting the appropriate model according to different goals and scenario requirements.

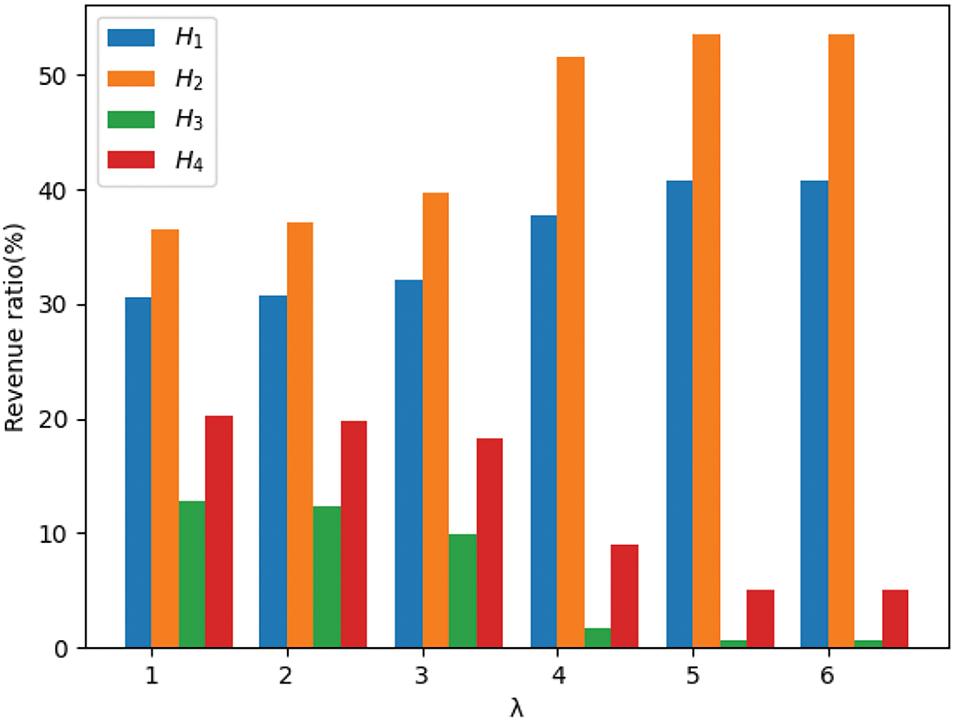
Figure 8: The relationship between revenue and λ

6.3.2 Incentive Mechanism Simulation Experiment Analysis

To evaluate the proposed incentive mechanism, this study simulated scenarios of data sharing and conducted simulation experiments. Taking an example of a platform with 50 medical institutions and 1500 artificially simulated medical data records, as the experiments progressed, each medical institution decided whether to increase the quantity of shared data based on the profits obtained.

In the experimental simulations, we compared two different incentive mechanisms: the first one is the incentive mechanism based on fixed value, where participants can only receive predetermined rewards. This mechanism is simple to implement but may lack the ability to motivate participants to improve data quality or quantity. The second one is the incentive mechanism proposed in this paper based on cooperative game theory, which allocates revenue according to the actual contributions of participants. This can better reflect the value of each participant’s contribution.

As shown in Fig. 9, the changes in the amount of shared data in the system over time under different incentive mechanisms are displayed. We can observe a significant growth trend in medical data in the system as time progresses. Under the incentive mechanism based on cooperative game theory, where profits are fairly distributed based on participants’ contributions, this differentiated reward mechanism motivates participants. Compared to fixed-value incentive mechanisms, incentive mechanisms based on cooperative game theory can achieve more efficient and flexible revenue distribution, which helps promote data sharing and enhance cooperation efficiency.

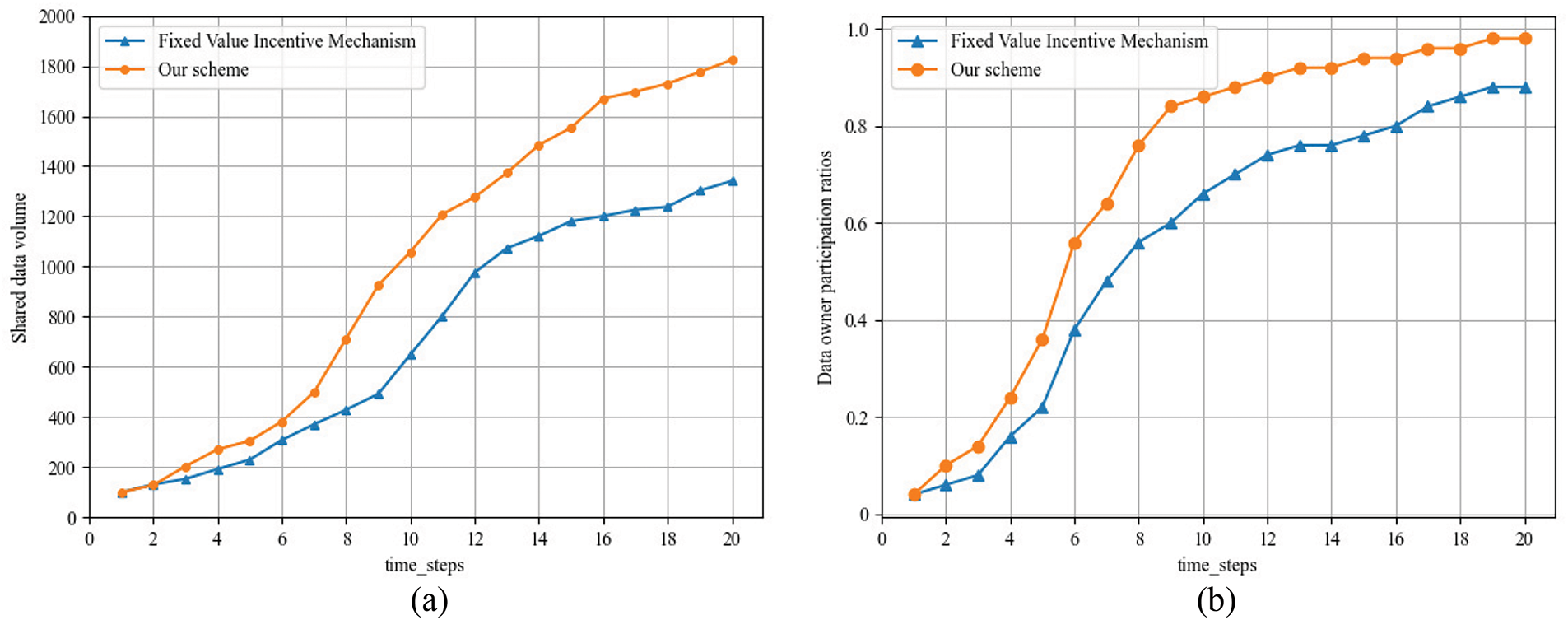
Figure 9: The comparison (a) between proposed incentive mechanisms and fixed value (b) incentive mechanisms. (a) Shared data volume; (b) data owner participation ratios

7  Conclusion

In this research, we design a data-sharing scheme based on attribute-based searchable encryption and the Shapley value method to meet the practical data-sharing requirements. The scheme supports fine-grained access control over encrypted data. Moreover, it achieves dynamic and fair distribution of revenues to data-sharing participants and guarantees fairness and traceability of transactions with the help of blockchain technology. Compared with other schemes, our scheme is more suitable for the multi-party medical data-sharing scenario. Through performance analysis and simulation experiments, this method can encourage more data owners to participate in data-sharing and enhance the security and fairness of the sharing process. We believe that this work has positive implications for multi-party data-sharing. In future work, we will investigate other factors influencing contribution distribution and user motivation, to make the incentive mechanism more reasonable and fair.

Acknowledgement: I would like to express my heartfelt gratitude to Professor Xiaohui Yang for his guidance and support throughout the research process. I also thank the other classmates for their valuable suggestions in the study. Lastly, we appreciate the valuable comments from the editor and anonymous reviewers, which helped improve the paper.

Funding Statement: This work was supported by the Natural Science Foundation of Hebei Province of China (F2021201052).

Author Contributions: Shuo Huang: Conceptualization, Methodology, Validation, Writing—original draft, Formal analysis. Xiaohui Yang: Conceptualization, Methodology, Validation, Writing—original draft. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No datasets were utilized or analyzed in the course of this research.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhang H, Fan W, Wang J. Bidirectional utilization of blockchain and privacy computing: issues, progress, and challenges. J Netw Comput Appl. 2024;222(9):103795. doi:10.1016/j.jnca.2023.103795. [Google Scholar] [CrossRef]

2. Zhang H, Liu W. Research on the application of blockchain in the safe and trusted sharing of Government data. In: 2023 2nd International Conference on Artificial Intelligence and Blockchain Technology (AIBT); 2023; Zibo, China. p. 52–5. [Google Scholar]

3. Hei Y, Liu Y, Li D, Liu J, Wu Q. Themis: an accountable blockchain-based P2P cloud storage scheme. Peer Peer Netw Appl. 2020;14(1):225–39. doi:10.1007/s12083-020-00967-6. [Google Scholar] [CrossRef]

4. Singh A, Chatterjee K. Securing smart healthcare system with edge computing. Comput Secur. 2021;108(1):102353. doi:10.1016/j.cose.2021.102353. [Google Scholar] [CrossRef]

5. Wang H. Identity-based distributed provable data possession in multicloud storage. IEEE Transact Serv Comput. 2015;8(2):328–40. doi:10.1109/TSC.2014.1. [Google Scholar] [CrossRef]

6. Fan K, Wang S, Ren Y, Li H, Yang Y. MedBlock: efficient and secure medical data sharing via blockchain. J Med Syst. 2018 Aug;42(8):1–11. doi:10.1007/s10916-018-0993-7. [Google Scholar] [PubMed] [CrossRef]

7. Nakamoto S. Bitcoin: a peer-to-peer electronic cash system; 2008. [Online]. [cited 2024 Mar 7]. Available from: https://bitcoin.org/bitcoin.pdf [Google Scholar]

8. Chi J, Li Y, Huang J, Liu J, Jin Y, Chen C, et al. A secure and efficient data sharing scheme based on blockchain in industrial Internet of Things. J Netw Comput Appl. 2020;167(3):102710. doi:10.1016/j.jnca.2020.102710. [Google Scholar] [CrossRef]

9. Azaria A, Ekblaw A, Vieira T, Lippman A. MedRec: using blockchain for medical data access and permission management. In: 2016 2nd International Conference on Open and Big Data (OBD); 2016; Vienna, Austria. p. 5–30. [Google Scholar]

10. Huang Q, Huang S, Gao C. A differentiated service based incentive mechanism in P2P file-sharing systems. In: 2007 IFIP International Conference on Network and Parallel Computing Workshops (NPC 2007); 2007; Dalian, China. p. 419–24. [Google Scholar]

11. An Q, Wen Y, Ding T, Li Y. Resource sharing and payoff allocation in a three-stage system: integrating network DEA with the Shapley value method. Omega. 2019;85(1):16–25. doi:10.1016/j.omega.2018.05.008. [Google Scholar] [CrossRef]

12. Zhu L, Dong H, Shen M, Gai K. An incentive mechanism using shapley value for blockchain-based medical data sharing. In: 2019 IEEE 5th International Conference on Big Data Security on Cloud (BigDataSecurityIEEE International Conference on High Performance and Smart Computing, (HPSC) and IEEE International Conference on Intelligent Data and Security (IDS); 2019; Washington, DC, USA . p. 113–8. [Google Scholar]

13. Yang Y, Chen T. Analysis and visualization implementation of medical big data resource sharing mechanism based on deep learning. IEEE Access. 2019;7:156077–88. doi:10.1109/ACCESS.2019.2949879. [Google Scholar] [CrossRef]

14. Sahai A, Waters B. Fuzzy identity-based encryption. In: Cramer R, editor. Advances in cryptology–EUROCRYPT 2005. Berlin/Heidelberg: Springer; 2005. p. 457–73. [Google Scholar]

15. Mamta, Gupta BB, Lytras MD. Fog-enabled secure and efficient fine-grained searchable data sharing and management scheme for IoT-based healthcare systems. IEEE Trans Eng Manag. 2022;71:1–13. [Google Scholar]

16. Abdelfattah S, Baza M, Mahmoud MMEA, Fouda MM, Abualsaud KA, Guizani M. Multidata-owner searchable encryption scheme over medical cloud data with efficient access control. IEEE Syst J. 2022;16(3):5067–78. doi:10.1109/JSYST.2021.3123956. [Google Scholar] [CrossRef]

17. Zhang Y, Zhu T, Guo R, Xu S, Cui H, Cao J. Multi-keyword searchable and verifiable attribute-based encryption over cloud data. IEEE Transact Cloud Comput. 2023;11(1):971–83. doi:10.1109/TCC.2021.3119407. [Google Scholar] [CrossRef]

18. Shen W, Hu T, Zhang C, Ma S. Secure sharing of big digital twin data for smart manufacturing based on blockchain. J Manufact Syst. 2021;61(7775):338–50. doi:10.1016/j.jmsy.2021.09.014. [Google Scholar] [CrossRef]

19. Zou R, Lv X, Zhao J. SPChain: blockchain-based medical data sharing and privacy-preserving eHealth system. Inform Process Manag. 2021;58(4):102604. doi:10.1016/j.ipm.2021.102604. [Google Scholar] [CrossRef]

20. Das N, Basu S, Bit SD. Incentive minimization using energy and buffer efficient routing protocol over Blockchain enabled DTN. Peer-to-Peer Network Applicat. 2024;17(5):3239–54. doi:10.1007/s12083-024-01737-4. [Google Scholar] [CrossRef]

21. Shrestha AK, Vassileva J. Blockchain-based research data sharing framework for incentivizing the data owners. In: Chen S, Wang H, Zhang LJ, editors. Blockchain–ICBC 2018. Cham: Springer; 2018. p. 259–66. [Google Scholar]

22. Mamta, Gupta BB, Li KC, Leung VCM, Psannis KE, Yamaguchi S. Blockchain-assisted secure fine-grained searchable encryption for a cloud-based healthcare cyber-physical system. IEEE/CAA J Automat Sinica. 2021;8(12):1877–90. doi:10.1109/JAS.2021.1004003. [Google Scholar] [CrossRef]

23. Su J, Zhang L, Mu Y. BA-RMKABSE: blockchain-aided ranked multi-keyword attribute-based searchable encryption with hiding policy for smart health system. Future Generat Comput Syst. 2022;132(10):299–309. doi:10.1016/j.future.2022.01.021. [Google Scholar] [CrossRef]

24. Zhao D, Li XY, Ma H. Budget-feasible online incentive mechanisms for crowdsourcing tasks truthfully. IEEE/ACM Transact Network. 2016;24(2):647–61. doi:10.1109/TNET.2014.2379281. [Google Scholar] [CrossRef]

25. Chen W, Chen Y, Chen X, Zheng Z. Toward secure data sharing for the IoV: a quality-driven incentive mechanism with on-chain and off-chain guarantees. IEEE Int Things J. 2020;7(3):1625–40. doi:10.1109/JIOT.2019.2946611. [Google Scholar] [CrossRef]

26. Kazmi SMA, Dang TN, Yaqoob I, Manzoor A, Hussain R, Khan A, et al. A novel contract theory-based incentive mechanism for cooperative task-offloading in electrical vehicular networks. IEEE Transact Intell Transport Syst. 2022;23(7):8380–95. doi:10.1109/TITS.2021.3078913. [Google Scholar] [CrossRef]

27. Liu R, Huang M, Yu Y. Incentive mechanism and simulation of data sharing in blockchain based on evolutionary game. In: 2022 International Conference on Information Technology, Communication Ecosystem and Management (ITCEM); 2022; Bangkok, Thailand. p. 146–52. [Google Scholar]

28. Ying C, Jin H, Li J, Si X, Luo Y. Incentive mechanism design via smart contract in blockchain-based edge-assisted crowdsensing. Frontiers Comput Sci. 2025;19(3):193802. doi:10.1007/s11704-024-3542-1. [Google Scholar] [CrossRef]

29. Yang C, Liu J, Sun H, Li T, Li Z. WTDP-shapley: efficient and effective incentive mechanism in federated learning for intelligent safety inspection. IEEE Transact Big Data. 2024;10(6):1028–37. doi:10.1109/TBDATA.2022.3198733. [Google Scholar] [CrossRef]

30. Jiang X, Wang L, Cao B, Fan X. Benefit distribution and stability analysis of enterprises’ technological innovation cooperation alliance. Comput Indust Eng. 2021;161(5):107637. doi:10.1016/j.cie.2021.107637. [Google Scholar] [CrossRef]

31. Xu Y, Zhang C, Wang G, Qin Z, Zeng Q. A blockchain-enabled deduplicatable data auditing mechanism for network storage servicesy. IEEE Transact Emerg Top Comput. 2021;9(3):1421–32. doi:10.1109/TETC.2020.3005610. [Google Scholar] [CrossRef]

32. Lone AH, Naaz R. Applicability of Blockchain smart contracts in securing Internet and IoT: a systematic literature review. Comput Sci Rev. 2021;39(1):100360. doi:10.1016/j.cosrev.2020.100360. [Google Scholar] [CrossRef]

33. Xuan S, Zheng L, Chung I, Wang W, Man D, Du X, et al. An incentive mechanism for data sharing based on blockchain with smart contracts. Comput Elect Eng. 2020;83(1):106587. doi:10.1016/j.compeleceng.2020.106587. [Google Scholar] [CrossRef]

34. De Caro A, Iovino V. jPBC: Java pairing based cryptography. In: 2011 IEEE Symposium on Computers and Communications (ISCC); 2011; Kerkyra, Greece . p. 850–5. [Google Scholar]