Non-Singular Fast Terminal Sliding Mode Control of PMSM Based on Disturbance Observer

1  Introduction

Due to its advantages of high efficiency and compact structure, permanent magnet synchronous motor (PMSM) is widely used in many fields with high-performance requirements such as exoskeleton robots and aerospace [1]. However, in actual operation, PMSM systems often suffer from performance degradation and jitter due to parameter changes and external interference. To enhance the system’s robustness and improve the dynamic response-ability, it is essential to conduct in-depth research on the control strategy [2]. At present, common control strategies include PI control [3], robust control [4], predictive control [5], adaptive control [6], and sliding mode control [7]. For example, literature [8] designed a fractional order PID controller based on sigmoid function for the design of a voltage regulation system, and literature [9] based on the use of adaptive Neuro-Fuzzy control for intelligent path planning of vehicles in dynamic environments, these control methods have certain advantages in solving specific problems with characteristics. However, when it is applied to PMSM control, it will face complex controller design, and it is difficult to achieve the ideal effect due to the specific rules of the algorithm. As a nonlinear control method, sliding mode control is widely used in PMSM control because of its simple design and significant advantages in the face of uncertainty and strong disturbance [10].

A hybrid adaptive iterative learning sliding mode control (AILS) method is proposed in [11]. The iterative learning sliding mode control (ILSMC) strategy is used to reduce the effect of periodic interference in the system but AILS is designed as a hybrid superposition of two controllers with relatively many parameters, and the proportion of nonlinear interference factors in the seeker coordination system is large, so the parameter design is more complicated and cumbersome. To solve the problems of slow convergence time and unknown disturbance in sliding mode control, a new non-singular fast terminal sliding mode control (NFTSMC) based on super torsional sliding mode observer (STA-STO) was designed in literature [12], but the system buffeting suppression was not significant enough.

To reduce the torque pulsation and improve dynamic response, literature [13] proposes an improved approach law combined with a disturbance sliding mode observer to estimate disturbances online and improve the robustness of the system. However, unknown disturbances are not sufficiently considered. In literature [14], sensorless control driven by PMSM is realized through the generalized proportional integral observer and Kalman filter, but the design of the observer is complicated, which will have a certain impact on the system response. Literature [15] proposes a sensorless control method based on fractal-order terminal sliding mode observer to suppress high-frequency harmonics, but the real-time performance of the method has not been thoroughly analyzed and optimized, especially under high speed and high dynamic changes, to verify the response speed and control accuracy of the method. In reference [16], an interference observer is designed for feedback compensation for PMSM with matching and mismatch interference, but the designed sliding mode controller is not obvious enough to suppress the chattering phenomenon of the system, and the principle analysis of higher-order sliding mode differentiator is not deep enough. This study will also design the interference observer based on the principle of high-order sliding mode differentiator and further analyze the principle of differentiator combined with PMSM to further simplify the design and improve the observation effect.

Because whether the parameters of the controller match directly affects the performance of the system, to avoid repeated trial-and-error of parameters and shorten the development cycle, common intelligent algorithms include particle swarm algorithm [17], genetic algorithm [18], gray Wolf algorithm [19] and Zebra algorithm [20]. In addition, some other intelligent algorithms are also common. For example, literature [21] is used to adjust the neuroendocrine-PID controller based on the improved Marine predator algorithm, but the algorithm design is complicated, and the scalability is poor. To optimize the key parameters of the controller, an improved particle swarm optimization algorithm (IPSO) was designed based on chaos theory in literature [22]. However, in the optimization process, there was a risk of continuous loss of population diversity, which reduced the accuracy of parameter adjustment. Particle swarm optimization (PSO) and gray wolf optimization (GWO) algorithms are used to optimize the sliding mode control (SMC) gain of the double-fed induction generator (DFIG) system in the literature [23]. It is used to enhance reference tracking, but the overall computational complexity is increased, and the PSO is prone to premature convergence to the local optimal solution, resulting in parametric dependence. Compared with the above algorithms, the zebra optimization algorithm (ZOA) has the characteristics of simple structure, fewer control parameters, fast convergence speed, ease of implementation, etc., has been applied to many intelligent control fields, and is still suitable for the motor field.

The ZOA is a relatively new meta-heuristic algorithm, proposed in literature [24] in 2022. Its core idea is to imitate zebra’s foraging behavior and defense behavior against predators. In literature [25], a controller combining fuzzy proportional-integral (PI) and fractional proportional-fractional filtering derivatives is proposed, and the ZOA is used to optimize the controller parameters. Literature [26] proposes to adjust the parameters of the PID controller based on the ZOA to improve the transient response of the system. In literature [27], the ZOA is combined with the variable step size perturbation method to reduce the probability of falling into the local optimal value, reduce the energy loss in the oscillation process, and improve the convergence speed.

In summary, to solve the jitter problem of the PMSM system, this study proposes an improved non-singular fast terminal sliding mode controller (INFTSMC) and designs a disturbance observer based on the principle of higher-order sliding mode differentiator to observe the disturbance in real time and compensate the sliding mode controller. Due to the defects of premature convergence and local optimization in traditional ZOA, an improved zebra optimization algorithm (IZOA) is proposed to be applied to PMSM for parameter tuning. The improved method includes using chaotic mapping to initialize the population, introducing random disturbance, and adjusting the disturbance frequency adaptively, to improve the global search ability of the algorithm.

The organizational structure of this paper is as follows: Section 2 establishes the mathematical model of PMSM, Section 3 describes the design of the interference observer, Section 4 describes the design of the controller, Section 5 carries out the design of IZOA algorithm, Section 6 analyzes the simulation results, Section 7 verifies the experiment, and Section 8 gives the conclusion.

2  PMSM Mathematical Model

To simplify the analysis, core saturation, hysteresis, and eddy current losses are not taken into account, and the effects due to friction of the rotor shaft and stator slot irregularities are neglected, and the mathematical model in the axial coordinate system is [28]:

{ud=Rsid+Ldi˙d−ωeLqiquq=Rsiq+Lqi˙q−ωe(Ldid+ψf)θ˙m=ωmJω˙m=Te−TL−Bωm(1)

where ud and id, uq and iq denote the voltage and current in the d−q axis coordinate system, respectively; Ld and Lq denote the inductance in the axial coordinate system, respectively; Rs is the stator resistance; ψd and ψq denote the d−q axis magnetic chain, respectively; ψf is the magnetic chain of the permanent magnet; Pn is the number of motor pole pairs; ωe is the electrical angular velocity; ωm is the mechanical angular velocity; θm is the mechanical angle of the motor; J is the rotational moment of inertia; TL is the torque of the load; B is the friction coefficient. Since the d−q axis inductance of the surface-mounted PMSM is equal, the electromagnetic torque equation is Te=1.5Pniqψf.

3  Disturbance Observer Design

The state variables for designing the PMSM system are shown below:

{x1=e=ωref−ωmx2=e˙=x˙1=ω˙ref−ω˙m(2)

where ωm is the mechanical angular speed, ωref is the set mechanical angular speed of the motor, e is the speed error, x1 and x2 are the system state variables.

Due to the existence of parameter errors in the actual system, the nominal value parameters of the PMSM: rotational inertia Jn, magnetic chain ψf, friction coefficient Bn, and load torque TLn may change, and these nominal value parameters are expressed as follows: J=Jn+ΔJ, B=Bn+ΔB, TL=TLn+ΔTL and ψ=ψf+Δψ, where ΔJ,ΔB,ΔTL,Δψ are the system perturbation, to obtain the equation of motion of the permanent magnet synchronous motor for the non-ideal case as:

ω˙m=32(Jn+ΔJ)pn(ψf+Δψ)iq−TLJn+ΔJ−Bn+ΔBJn+ΔJω(3)

The equation of state x˙1 of its system is organized into the form of an ideal model with a perturbation term as follows:

x˙1=ω˙ref−ω˙m=ω˙ref−3(ψfn+Δψf)2(Jn+ΔJ)pniq+TL(Jn+ΔJ)+(Bn+ΔB)(Jn+ΔJ)ωm=ω˙ref−3Pniqψfn2Jn+TLJn+BnωmJn–3pniq(ΔψfJn−ψfnΔJ)+2TLΔJ−2ΔJωm(ΔB−Bn)2(Jn+ΔJ)Jn=x2−3pniq(ΔψfJn−ψfnΔJ)+2TLΔJ−2ΔJω(ΔB−Bn)2(Jn+ΔJ)Jn=x2+F1(4)

where F1 is the perturbation term. Similarly, the state of the system x˙2 is represented as an ideal model with a perturbation term of the form.

x˙2=ω¨ref−ω¨m=ω¨ref−3pni˙q(ψfn+Δψf)2(Jn+ΔJ)+T˙L(Jn+ΔJ)+(Bn+ΔB)(Jn+ΔJ)ω˙m=ω¨ref+(Bn+ΔB)(Jn+ΔJ)(ωref−x2)−3pni˙qψfn2Jn−3pni˙q(ΔψfJn−ψfnΔJn)2(Jn+ΔJ)Jn+T˙LJn+ΔJ+(Bn+ΔB)(Jn+ΔJ)ωref=−BnJnx2−3pnψfn2Jni˙q+ω¨ref+(Bn+ΔB)(Jn+ΔJ)ωref−3pni˙q(ΔψfJn−ψfnΔJn)2(Jn+ΔJ)Jn+T˙LJn+ΔJ+(Bn+ΔB)(Jn+ΔJ)ωref=−Dnx2−Eni˙q+F2(5)

where Dn=BnJn,En=3pnψfn2Jn,F2 is the corresponding perturbation term, and in summary, the state equation of the PMSM is given by:

{x˙1=x2+F1x˙2=−Dnx2−Eni˙q+F2(6)

Based on the system model in Eq. (6), the disturbance observer based on the principle of higher order sliding mode differentiator is designed as follows:

{x^˙1=x2+y1y1=−r1|x^1−x1|3/4⋅sgn(x^1−x1)+F^1F^˙1=−r2|F^1−y1|1/3⋅sgn(F^1−y1)x^˙2=−Dnx2−Eni˙q+y2y2=−r3|x^2−x2|3/4⋅sgn(x^2−x2)+F^2F^˙2=−r4|F^2−y2|1/3⋅sgn(F^2−y2)(7)

where x^˙1 is the estimate of the systematic velocity error, x^˙2 is the estimate of the derivative of the systematic velocity error, sgn(x) is the sign function, y1 and y2 are the intermediate variables, F^1 and F^2 are the disturbance estimates, and r1∼4 are the strictly positive gain parameters of the disturbance observer.

As shown in Fig. 1, the control principle block diagram of the simplified interference observer shows, that when calculating the intermediate variables y1 and y2, the disturbance estimates F^1 and F^2 participate in the calculation, respectively. This connection mode makes the intermediate variables y1 and y2 contain disturbance information, which provides a basis for the subsequent state estimation and disturbance update. In a real system, when the system is disturbed to cause changes in x1 and x2, F^1 and F^2 can adjust the values of y1 and y2 in time, thus affecting the state estimation and control signals.

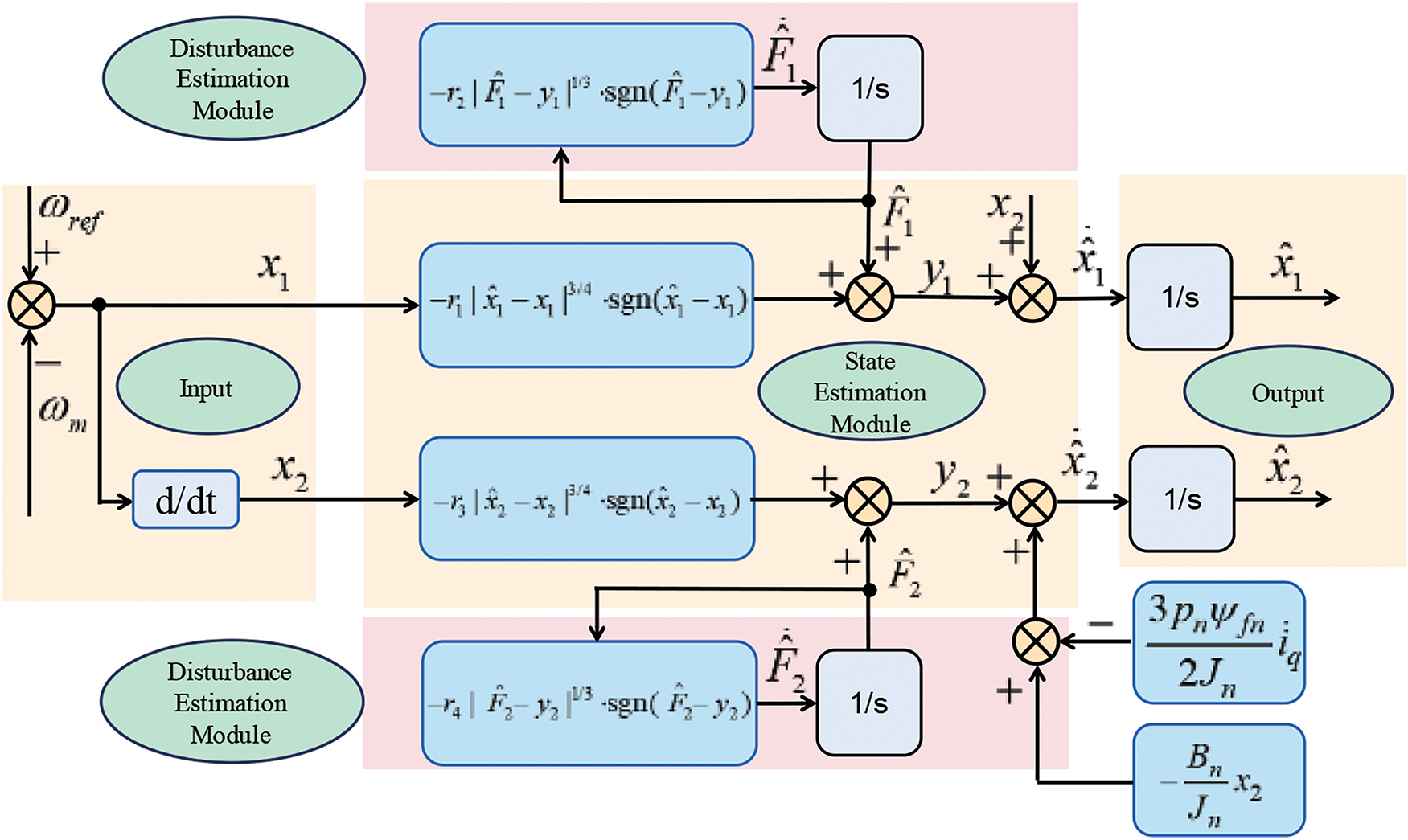
Figure 1: Disturbance observer control block diagram

In the state estimation module, calculating x^˙1 requires the value of y1, while y1 contains the information of F^1; calculation x^˙2 depends on y2, and y2 contains F^2. Therefore, the perturbation estimate indirectly affects the system state estimate by affecting the intermediate variable. When the motor is disturbed by the load, changes in F^1 and F^2 cause x^˙1 and x^˙2 to adjust, resulting in a more accurate estimate of the system state.

In addition, the disturbance estimation module has its own feedback adjustment mechanism. In the case of F^1, calculating F^˙1 relies on the difference between F^1 and y1, which, after a series of operations, is used to update F^1. The F^2 update is a similar principle. With this feedback adjustment, F^1 and F^2 can be continuously optimized to provide more accurate disturbance information for system control.

4  Controller Design

4.1 INFTSMC Design

To improve the convergence speed and robustness of the system, the following non-singular fast terminal sliding mode surface is selected:

s=x2+β1x1+β2x1p/q(8)

where p,q are odd and p > q > 0, β1 and β2 are positive integral gains.

The convergence speed of the sliding mode controller is directly affected by the convergence law, the traditional convergence law control is not effective, to improve the convergence speed and reduce the jitter, a new type of convergence law is proposed as follows:

s˙=−k1tanh⁡(s)α+(1+1/δ|x1|−α)σ−m|s|−k2s(9)

where tanh⁡(s) is the hyperbolic tangent function; the system state variable x1 satisfies: limt→t0x1=0; k1, k2, α, δ, σ and m is the parameter to be designed, and satisfies k1>0, k2>0, m>0, 0<α<1, 0<δ<1 and σ>1.

Derivation of the sliding mode surface Eq. (8) and combining Eqs. (6) and (7) yields:

s˙=−Dnx2−Eni˙q+F^2+β1(x2+F^1)+β2pqx1pq−1(x2+F^1)(10)

Combined with Eq. (9), the system control law can be obtained as:

i˙q=1En[−Dnx2+F^2+(β1+β2pqxpq−1)(x2+F^1)+k1tanh⁡(s)α+(1+1δ|x1|−α)σ−m|s|+k2s)(11)

4.2 Convergence Law Comparison and System Stability Analysis

The new convergence law proposed in this paper is compared and analyzed with the classical isotropic convergence law s˙=−εsign(s), exponential convergence law s˙=εsign(s)−qs, and idempotent convergence law s˙=−q|s|αsign(s). The phase trajectory diagrams and convergence times are shown in Fig. 2.

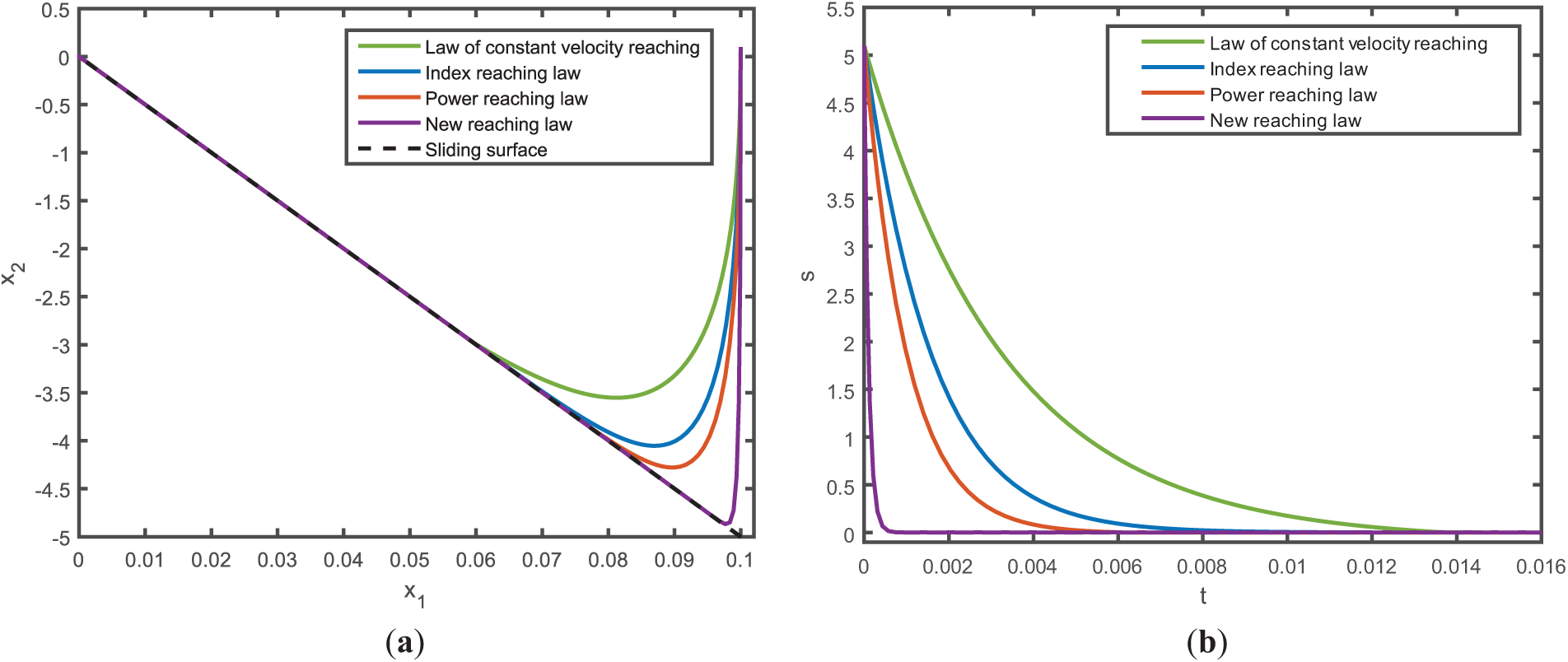
Figure 2: (a) Comparison of phase trajectories of the reaching law. (b) Comparison of convergence times for reaching law

As shown in Fig. 2a, from the phase trajectory diagram of the sliding mold movement, it can be intuitively seen that the new convergence law has a faster convergence process, and takes the lead in arriving at the sliding mold surface. From the time required for the convergence process in Fig. 2b, it can be seen that the convergence time of the new convergence law is 8×10−4 s, which is faster than that of the isotropic convergence law by 1.22×10−2 s, and the convergence time is shortened by 93.85%; it is faster than that of the idempotent convergence law by 7.2×10−3 s, and the time is shortened by 90%; and it is faster than that of the exponential convergence law by 4.2×10−3 s, and the time is shortened by 84%.

In order to verify the stability of the new reaching law proposed in this paper, the Lyapunov function is chosen: V=0.5s2. From the Lyapunov principle, the system is stable when V˙ is semi-negative timing, which leads to:

V˙=ss˙=−sk1tanh⁡(s)α+(1+1/δ|x1|−α)σ−m|s|−k2s2(12)

According to the design parameters k1, k2 and m are greater than 0, so k2s2 > 0. α and δ are greater than 0 and less than 1, σ is greater than 1, and the hyperbolic tangent function and s have the same positive and negative can be known: σ−m|s| > 0 1+1/δ|x1|−α > 0, so the first numerator expression meets sk1tanh⁡(s) > 0, denominator expression meets α+(1+1/δ|x1|−α)σ−m|s| > 0. In summary V˙ ≤ 0, the control system is asymptotically stable.

5  ZOA Design

It is well known that the traditional manual parameter tuning method is not only a tedious and inefficient process, but also difficult to achieve the optimal configuration. To address this problem, this paper improves the ZOA for complex parameter tuning by improving it and verifying it by test functions.

5.1 Traditional ZOA

In the foraging strategy, the best-performing individual is regarded as the lead zebra, guiding the other group members toward their position in the exploration space. The positional update during the foraging phase can be represented as:

Xi,jnew,P1=Xi,j+r(PZj−IXi,j)(13)

Xi={Xinew,P1,Finew,P1 < FiXi,else(14)

where Xi,jnew,P1 denotes the new position of the individual zebra in the foraging phase, r is a random number between [0, 1], PZj denotes the optimal pioneer zebra, I is a random value of the set {1, 2}, and Fi denotes the value of the objective function for the i-th zebra.

In response to a predator threat, the zebra chooses either a defense or an attack strategy. When attacked, the zebra will avoid the attack near its location, and this strategy can be represented by S1 in Eq. (15). When a zebra chooses an attack strategy, the other zebras in the herd will approach the attacked zebra and try to intimidate or confuse the predator by establishing a defense structure, which can be represented by S2 in Eq. (15). The value of Ps is used in the procedure to select either S1 or S2 computational strategy.

Xi,jnew,P2={S1:Xi,j+R(2r−1)(1−t/Tmax)Xi,j,Ps≤0.5S2:Xi,j+r(AZj−IXi,j),else(15)

Xi={Xinew,P2,Finew,P2<FiXi,else(16)

where Xi,jnew,P2 denotes the new position of the zebra individual in the attack or defense phase, R=0.01, Ps∈[0,1] denote the probability of choosing attack or defense when a threat is received, Tmax denotes the maximum number of iterations, and AZj denotes the state of the zebra when threatened.

5.2 IZOA Design

5.2.1 Iterative Chaotic Map

The traditional initialization method often generates the initial solution randomly, which may cause the distribution of the initial solution of the algorithm to be uneven, and affect the convergence speed and solution quality of the algorithm. Using the Iterative chaotic map with ergo and randomness to initiate the Iterative chaotic map can make the initial solutions more evenly distributed in the search space, increase the search diversity, and help the algorithm avoid falling into the local optimal solution. Using iterative chaotic mapping to initialize the population can be obtained:

Zi,j=lbj+(ubj−lbj)sin⁡(π2Xi,j)(17)

where Zi,j is the initialized population individual, lbj is the lower bound of the optimal value and ubj is the upper bound of the optimal value.

5.2.2 Stochastic Perturbation Mechanism

The IZOA algorithm introduces a random disturbance mechanism. In the foraging behavior stage and defense strategy stage, the current solution is randomly disturbed according to the comparison of random number and disturbance frequency. This mechanism increases the search diversity of the algorithm and helps the algorithm to jump out of the local optimal solution. The position update in the foraging phase can be expressed as:

Xi={Xinew,P1+r(1−t/Tmax),Xinew,P1,r<Fperelse(18)

where t denotes the number of iterations, Tmax is the maximum number of iterations, and Fper is the adaptive perturbation frequency threshold, which is expressed as:

Fper=h(1−t/Tmax)(19)

where h is a constant indicating the adaptive initial value, which is 0.3. In the early stages of the algorithm, the frequency threshold is high to encourage individuals to explore, and the threshold is gradually lowered in the later stages to promote convergence.

Similarly, in the defense strategy phase, the value of Ps is used in the procedure to select a computational strategy of S1 or S2, and the values of r and Fper are used to determine whether to add a perturbation strategy. The positional updates of S1 and S2 can be represented as, respectively:

Xi,jnew,P2={S1:Xi,j+R(2r−1)(1−t/Tmax)Xi,j+ r(1−t/Tmax),S1:Xi,j+R(2r−1)(1−t/Tmax)Xi,j,r<Fperelse(20)

Xi,jnew,P2={S2:Xi,j+r(AZj−IXi,j+1−t/Tmax)r<FperS2:Xi,j+r(AZj−IXi,j)else(21)

5.2.3 IZOA Pseudo-Code

The implementation steps of the algorithm are as follows (Algorithm 1):

5.2.4 IZOA Performance Comparison

To confirm the performance of IZOA, this study compares it with the standard ZOA, Whale Optimization Algorithm (WOA), Grey Wolf Optimization algorithm (GWO) and Sparrow Search Algorithm (SSA). They were tested using national standard benchmark functions, including single-peak and multi-peak functions as shown in Table 1. Each algorithm was set to run independently 30 times with a population size of 50 and 500 iterations. The default values of the original algorithms were used for the remaining parameters, and the results are shown in Fig. 3.

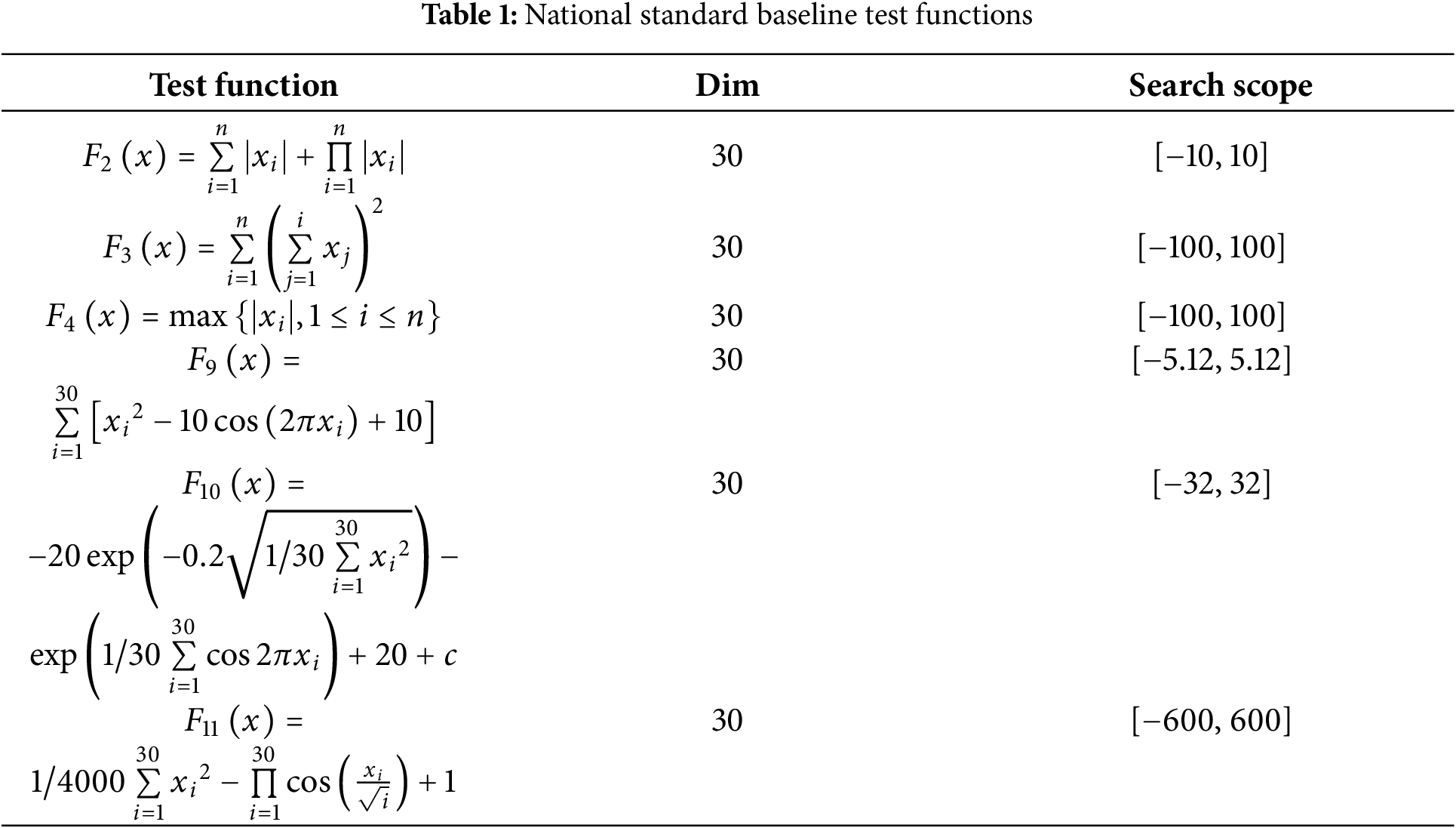
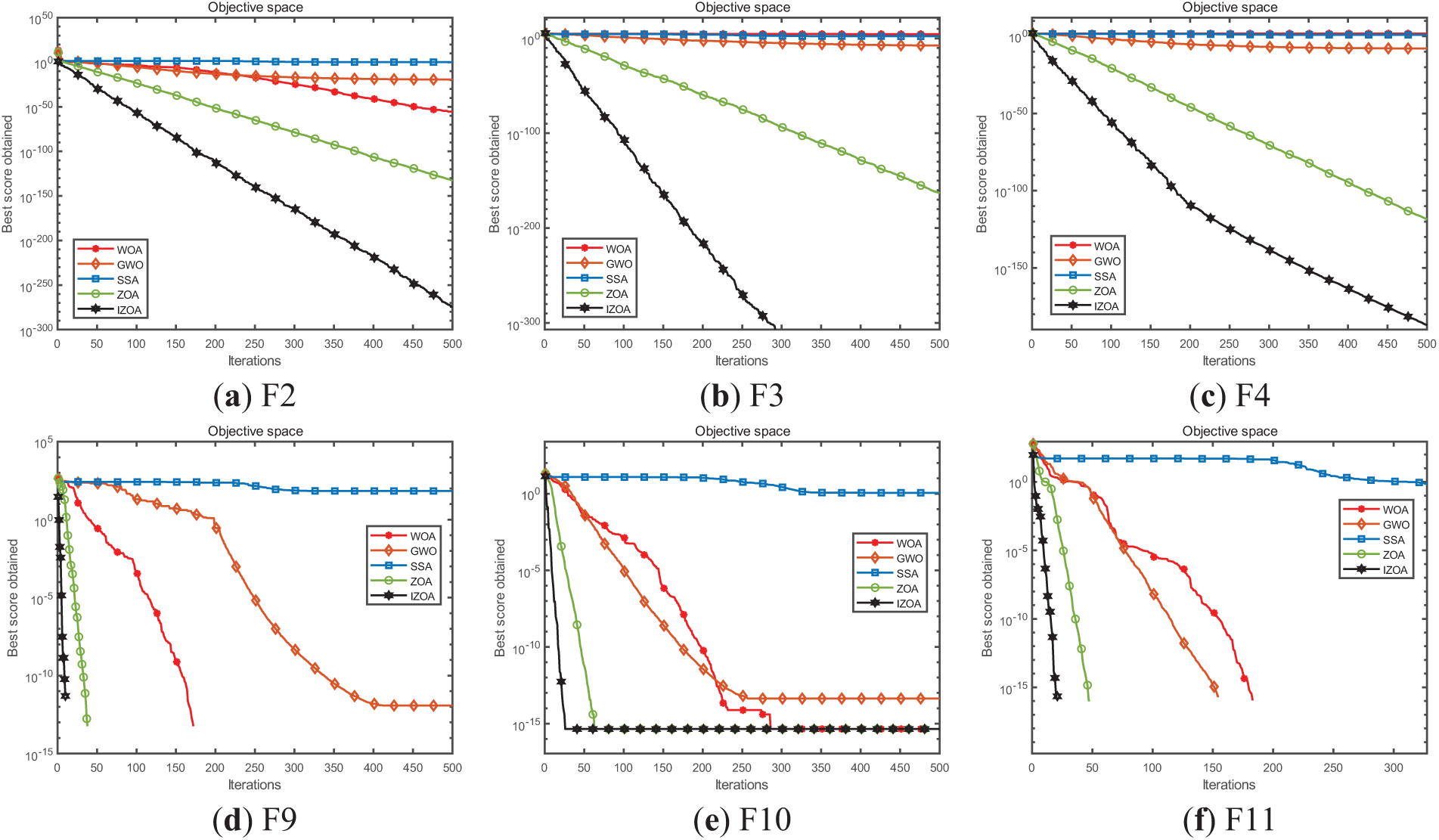
Figure 3: Comparison of algorithms

From Fig. 3, it can be seen that IZOA has a clear advantage in solving single-peak and multi-peak problems with faster convergence and lower fitness values.

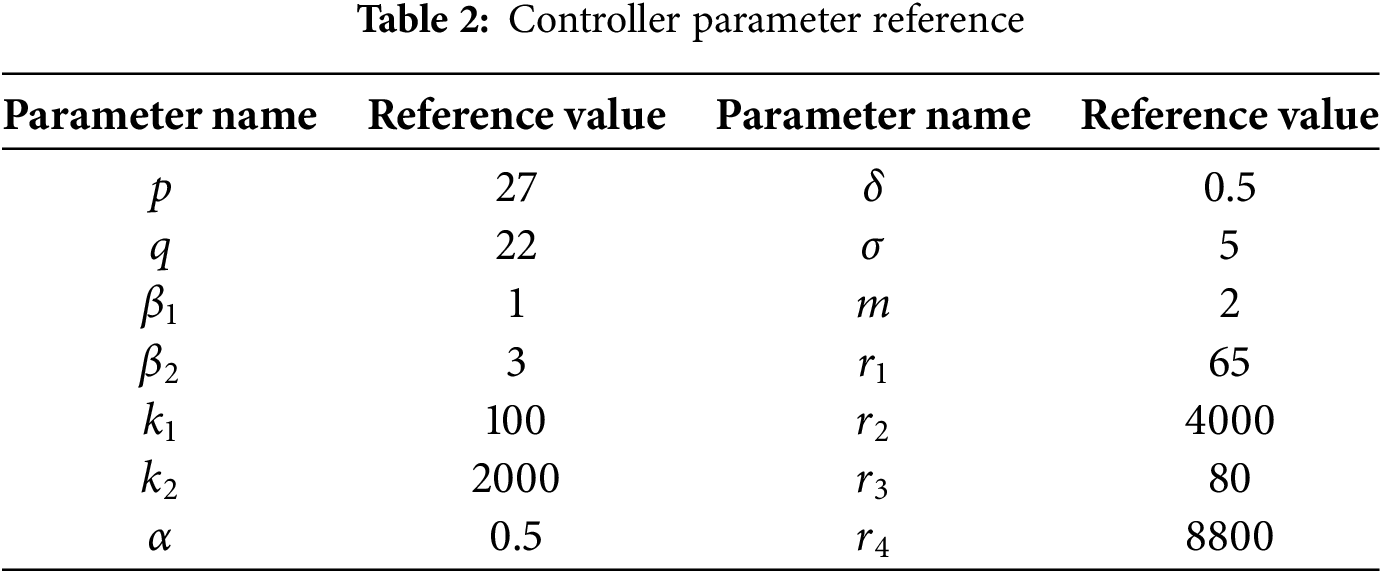
Finally, the controller parameters are preliminarily adjusted by IZOA, as shown in Table 2. It is worth noting that if the parameters need to be fine-tuned, the following suggestions are given: The choice of exponential parameter p/q has an important impact on the convergence speed and stability of the system, and the recommended range is 1 < p/q < 2. In addition, a larger value of r1,r2,r3,r4 can significantly improve the performance of the observer, but too large a value will cause system chattering. Therefore, it is recommended to consider these two factors at the same time and appropriately select the value of the gain parameter according to the actual situation. The remaining parameters should also meet the basic conditions required by the formula above. In addition, the current loop adopts PI control, with Ki=6,Kp=1916.

6  Analysis of Simulation Results

6.1 Model Construction

To test the effectiveness of the improved non-singular fast terminal sliding mode controller with disturbance observer (DO-INFTSMC) and the practical applicability of IZOA, a vector control system for a tabletop permanent magnet synchronous motor is constructed in MATLAB/Simulink. The overall control structure of the control system is shown in Fig. 4.

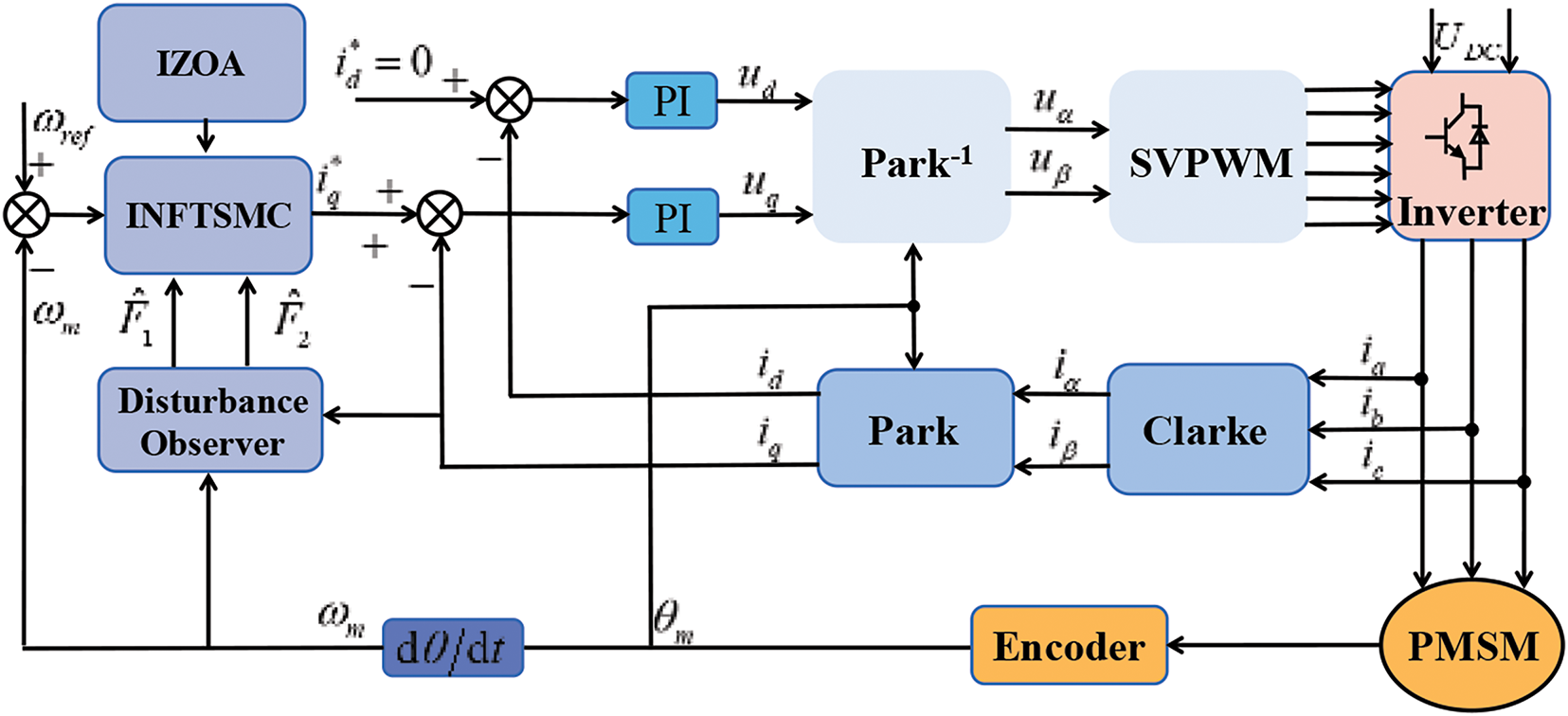
Figure 4: Block diagram of the vector control structure of PMSM

The parameters of the PMSM model used in the simulation are shown in Table 3 below.

6.2 IZOA Verification

In order to verify the practical application ability of IZOA, it is made to regulate the controller parameters with ZOA, WOA, GWO, and SSA, respectively. To compare the simulation results, the current loop parameters are kept unchanged, and the optimization of the controller parameters is carried out using the above-mentioned intelligent algorithms, respectively, the parameters include: p, q, β1, β2, k1, k2, α, δ, σ,m, r1,r2,r3,r4.

6.2.1 Step Response Simulation Experiment

The position is set to 1 rad, and a 5 N · m load is added at 1.5 s to perform the step simulation. The simulation results are shown in Fig. 5. From Fig. 5b, it can be seen that the parameters adjusted by these five methods can make the PMSM follow the step signal quickly, but the parameters adjusted by GWO converge slower, and the adjustment time (Settling Time) is 0.875 s; the adjustment times of WOA, SSA, and ZOA are 0.75, 0.63, and 0.60 s, respectively; while the parameters adjusted by IZOA have faster adjustment speed when approaching the target position, and their adjustment times are 0.75, 0.63, and 0.60 s. The parameter has a faster adjustment speed when approaching the target position, and its adjustment time is 0.17 s. The adjustment time of IZOA is 71.67%, 73.02%, 77.33%, and 80.60% shorter than that of ZOA, SSA, WOA, and GWO, respectively.

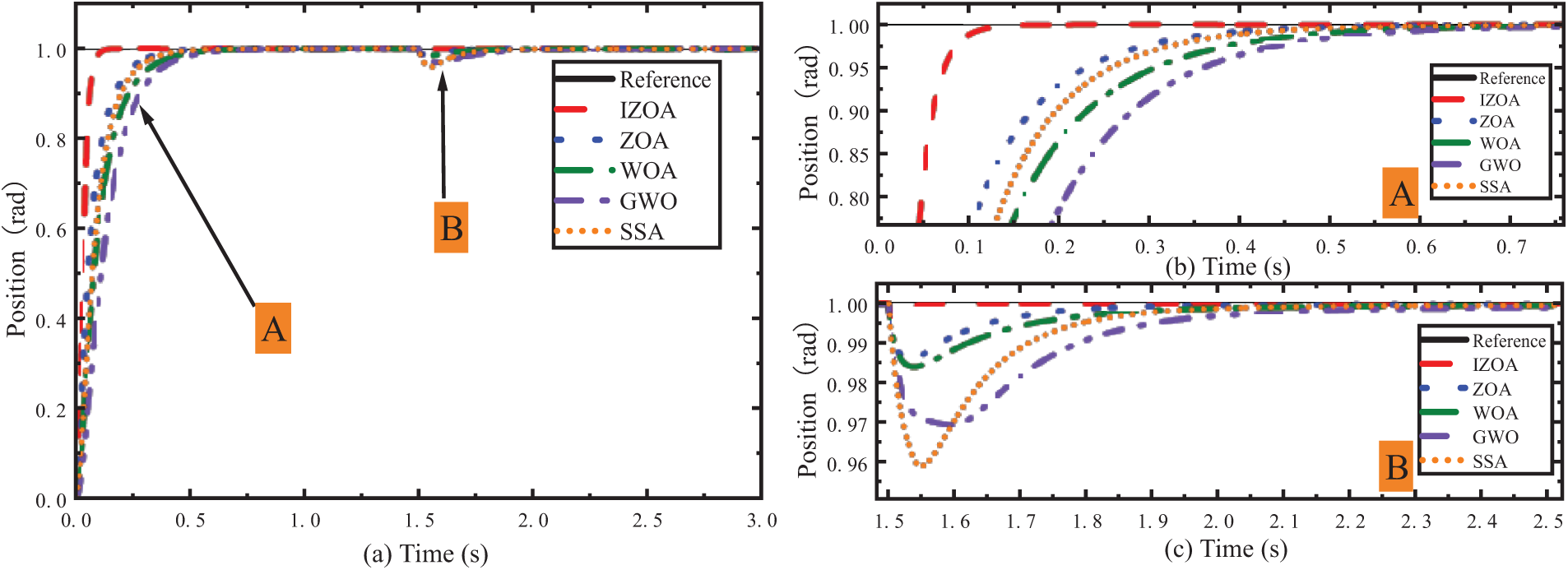
Figure 5: Step response experiment

When the load disturbance is increased, it can be seen from Fig. 5c that the parameters regulated by SSA have limited adaptability to the load, and the position fluctuation is 0.041 rad; the position fluctuations of GWO, WOA, and ZOA are 0.031 rad, 0.016 rad, and 0.014 rad, respectively; whereas, the parameters regulated by IZOA have a stronger anti-disturbance ability, and the position fluctuation is only 0.004 rad, and the recovery time is shorter.

6.2.2 Sinusoidal Signal Following Experiment

In the actual working conditions, the PMSM needs to rotate at different angles according to the instructions. To verify the controller’s robustness to external interference, y1=π/3sin⁡(4πt) is selected as the position tracking reference curve, y2=π/4sin⁡(4πt) is selected as the load change curve, and the motor is started with the load. The controller parameters are also adjusted using the above five methods, and the position following the curve is shown in Fig. 6.

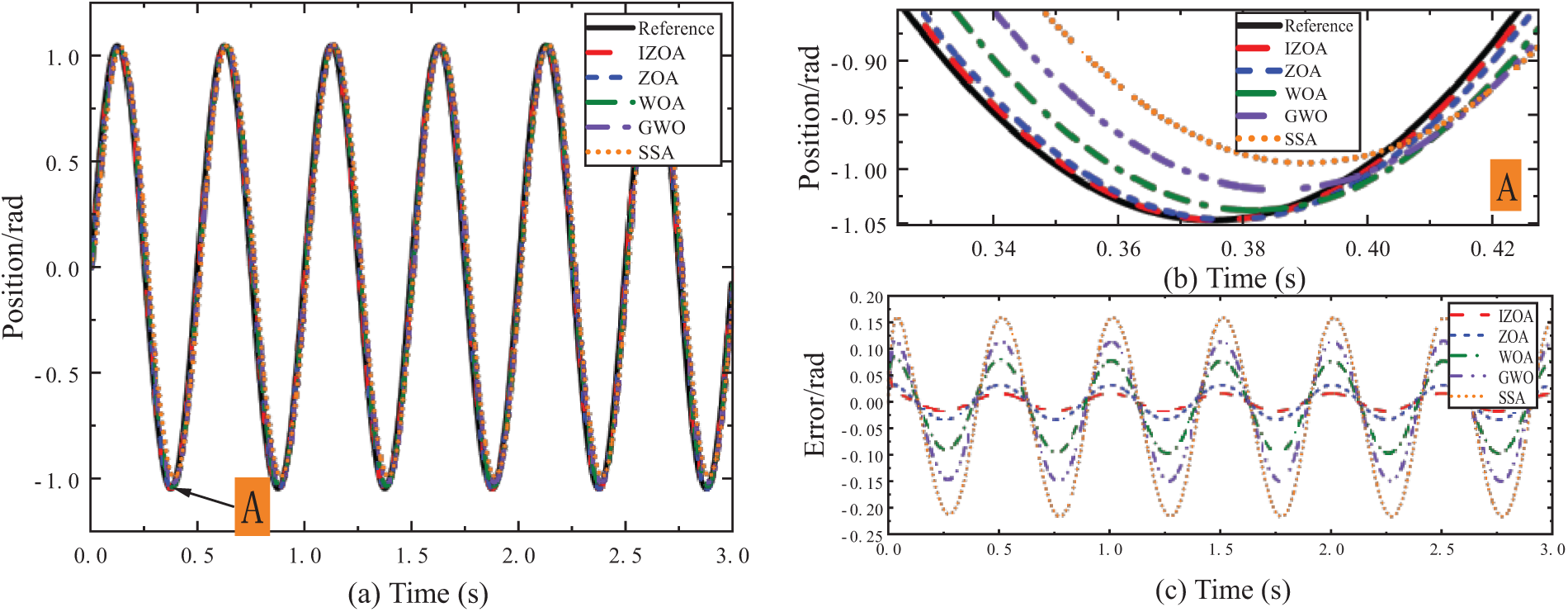
Figure 6: Sinusoidal signal following experiment

From Fig. 6a, it can be seen that the various methods can make the motor follow the reference curve effectively, but the SSA-based method has obvious errors with lagging, caused by the SSA method appearing to converge prematurely and easily falling into the local optimum. Fig. 6b demonstrates a local zoomed-in view of the following effect, it can be concluded that the parameters regulated by IZOA have a better following effect, thanks to the perturbation strategy that makes the algorithm jump out of the local optimum solution. Fig. 6c shows the following error curves, the SSA-adjusted parameter produces a large following error of 0.160 rad for the PMSM; the maximum following errors of 0.115 rad, 0.079 rad, and 0.033 rad for the GWO, WOA, and ZOA, respectively, and the maximum following error of 0.016 rad for the IZOA, which is 90% lower than that of 0.016 rad for the SSA, GWO, WOA, and ZOA, respectively, and ZOA are reduced by 90%, 86.09%, 79.75%, and 51.52%, respectively.

6.3 DO-INFTSMC Verification

To verify the anti-disturbance capability of the DO-INFTSMC designed in this paper, a time-varying load is used to verify the robustness of the control system, which is compared with the traditional NFTSMC, the improved INFTSMC, and the disturbance observer-based DO-INFTSMC, respectively. Firstly, a load of 10 N.m is applied abruptly to the PMSM system at 0.2 s, and the load is released at 0.4 s to set the rotational speed. The response curves of the PMSM system are shown in Fig. 7a,b. Fig. 7c shows the observation error of the disturbance observer on the disturbed parts F1 and F2.

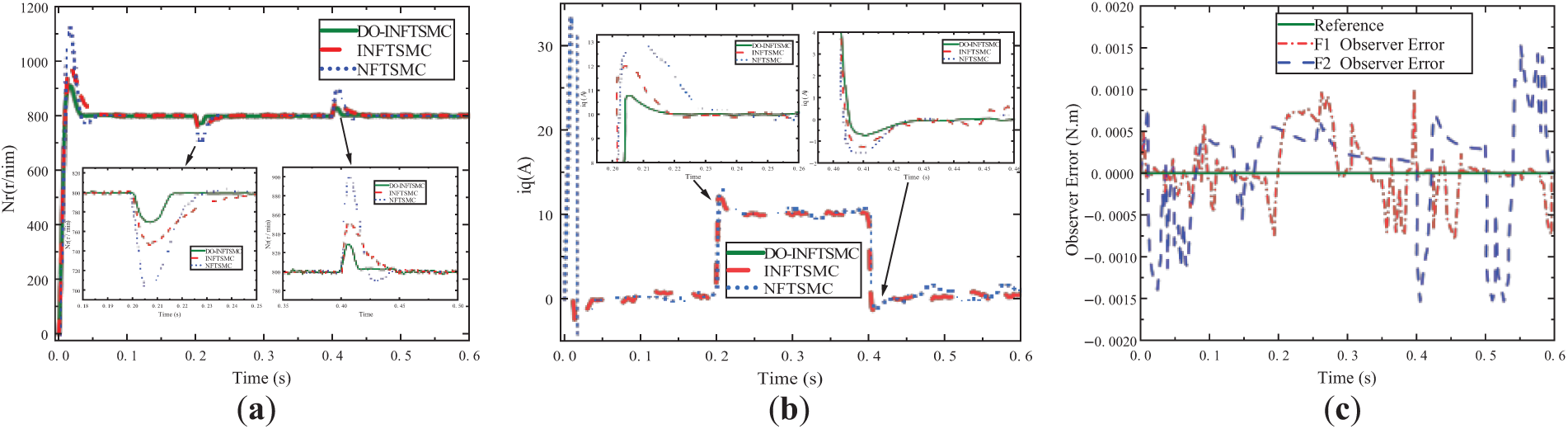
Figure 7: (a) Interference suppression capability verification curve. (b) q-axis current response curve. (c) Observation error of interference observer

From Fig. 7a, it can be seen that the proposed INFTSMC has a faster response speed and a smaller instantaneous landing of the rotational speed compared with the traditional NFTSMC when a load of 10 N.m is applied abruptly at 0.2 s. The proposed DO-INFTSMC has a significant effect on the system jitter. The proposed DO-INFTSMC not only has a faster response speed and a smaller instantaneous speed drop compared with the previous two control strategies but also has an obvious effect on the vibration of the system. Similarly, after releasing the load at 0.4 s, the response of the proposed INFTSMC is better than that of the NFTSMC, while the proposed DO-INFTSMC can recover the rotational speed to 800 r/min the fastest, and the system vibration suppression ability is significant.

From Fig. 7b, it can be seen that at the initial moment, the q-axis current response of INFTSMC is better than that of NFTSMC, while the proposed DO-INFTSMC is able to respond the fastest, and at the same time, the overshoot is the smallest when the load is applied suddenly at 0.2 s, and the current is able to respond faster to the recovery after releasing the load at 0.4 s, and since the q-axis current is proportional to the torque, it indicates that the system is more resistant to the interference.

It can be seen from Fig. 7c that the observation error of the disturbance F1 is within the range of 1×10−3 N⋅m and the observation error of the disturbance F2 is within the range of 1.5×10−3 N⋅m, indicating that the designed interference observer can perform a good error estimation and further verify the anti-interference capability of the designed DO-INFTSMC.

7  Experimental Validation and Analysis

In order to further verify the actual performance of the DO-INFTSMC proposed in this paper, the experimental platform shown in Fig. 8 is set up, and the TMS320F28379 is selected as the main control unit for the experiments, and three control strategies, namely, NFTSMC, INFTSMC, and DO-INFTSMC, are adopted, respectively. In the experimental setup, the motor parameters include: rated speed ω=3000 r/min, frequency 50 HZ, rated voltage UDC=36 V, number of pole pairs Pn=4, stator resistance Rs=0.523 Ω, and winding interphase inductance Ls=0.554 mH. This experiment is to verify the dynamic response performance of the PMSM under sudden speed change and load change conditions, so as to confirm the effectiveness and practicality of the proposed scheme.

Figure 8: Experimental platforms

7.1 Sudden Change of Rotational Speed under No Load

In order to verify the no-load stability and response characteristics of the designed DO-INFTSMC, the rotational speed is abruptly changed from 800 to 1600 r/min under no-load condition of the PMSM, and the experimental results are shown in Figs. 9–11.

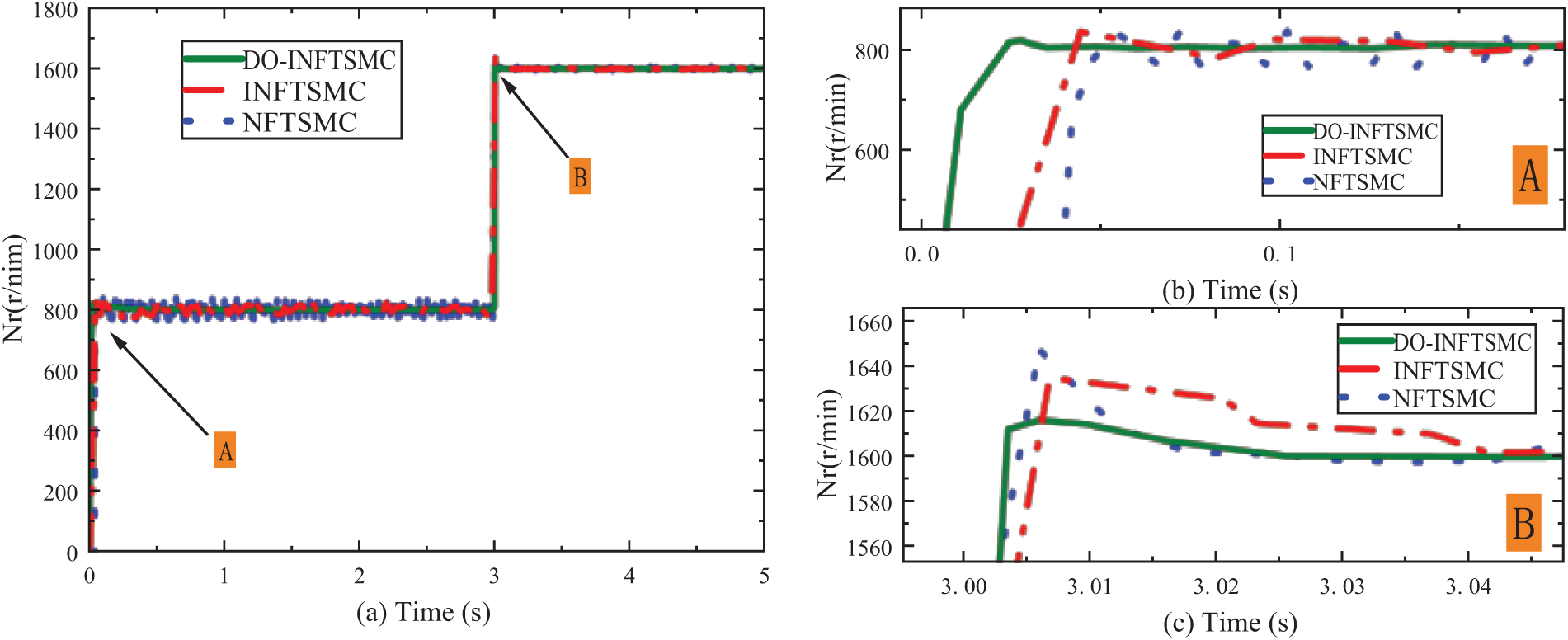
Figure 9: Nr response to sudden changes in rotational speed

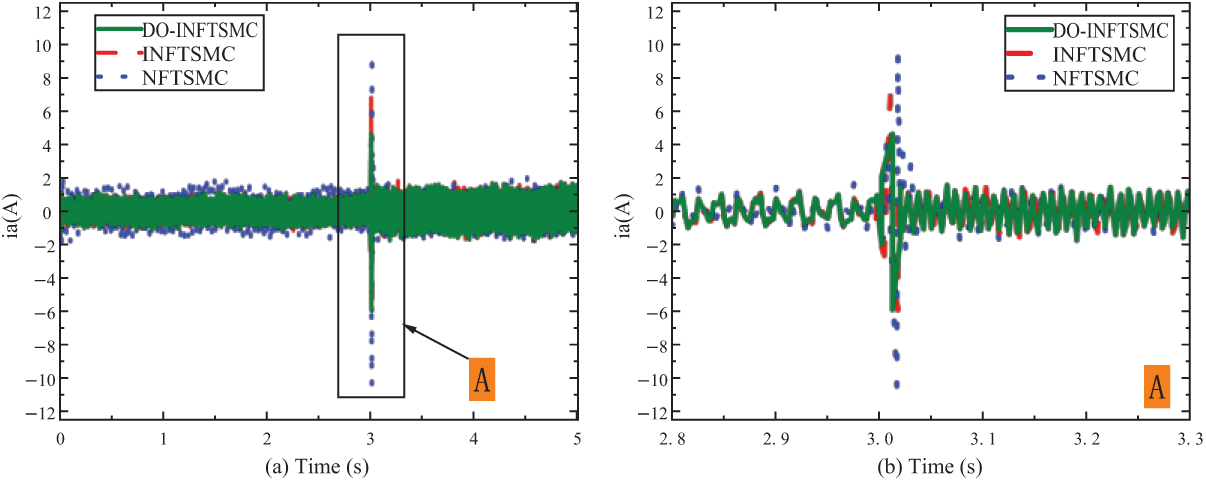
Figure 10: ia response to sudden changes in rotational speed

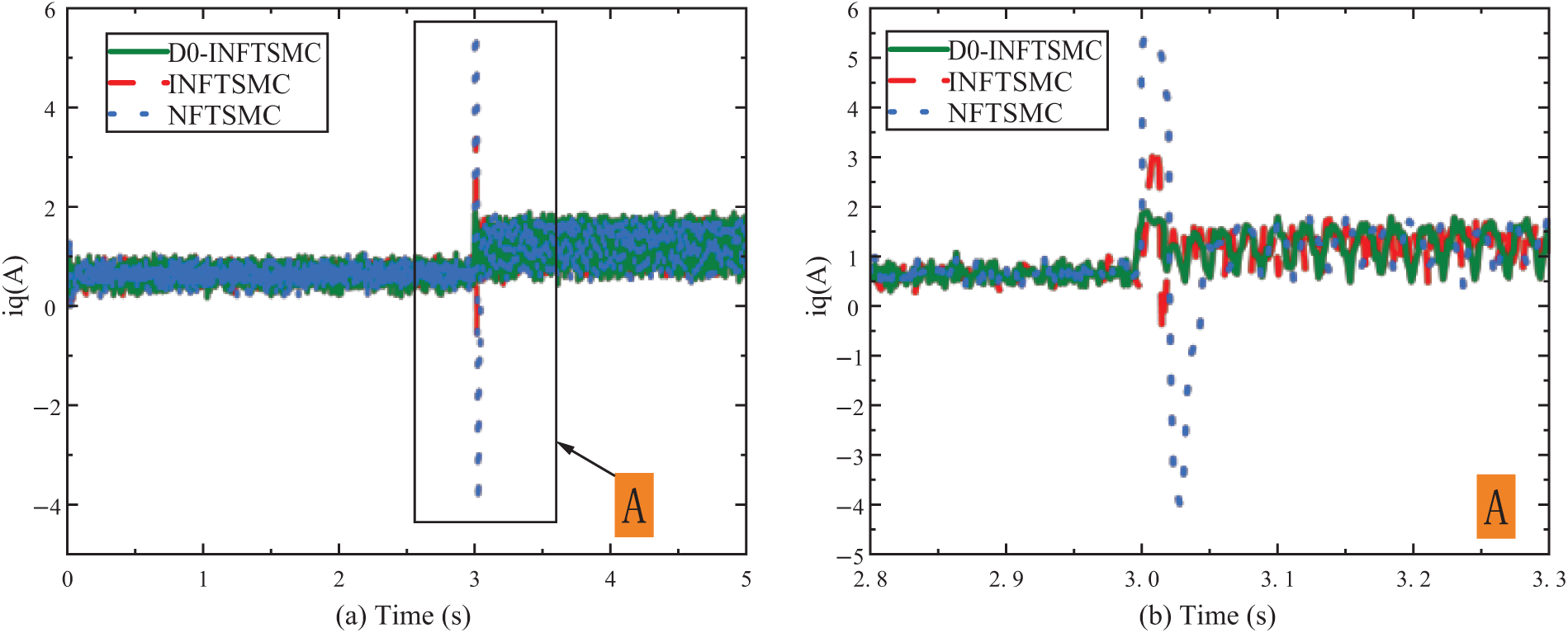
Figure 11: iq response to sudden changes in rotational speed

As can be seen from Fig. 9, when three control strategies are respectively adopted, DO-INFTSMC control strategy not only has faster speed response characteristics, but also has better speed stability. In addition, at the 3 s speed change, the NFTSMC control strategy has an overshoot of 2.5%, INFTSMC has an overshoot of 1.88%, and DO-INFTSMC only has an overshoot of 0.63%, which improves the performance by about 74.8% compared with NFTSMC.

From Fig. 10, when the speed changes rapidly, the maximum value of ia reaches 10 A when NFTSMC is used, and the maximum value of ia when INFTSMC is used reaches 7 A. When DO-INFTSMC is used, the maximum value of ia is about 6 A, and ia has better response characteristics than NFTSMC. With DO-INFTSMC, ia is less volatile and improves performance by about 40% compared to NFTSMC.

From Fig. 11, when the speed changes rapidly, the maximum value of iq reaches 5.5 A when NFTSMC is used, and the maximum value of iq when INFTSMC is used reaches 3 A. When DO-INFTSMC is used, the maximum value of iq is about 2 A, and compared with NFTSMC, iq has better response characteristics. Similarly, DO-INFTSMC showed less volatility, with a performance improvement of approximately 63.64% compared to NFTSMC.

7.2 Sudden Load and Load Release Test

To verify the robustness and anti-interference capability of the designed DO-INFTSMC with load, a load of 5 N · m is added abruptly at 2 s at a given speed of 800 r/min, and the load is reduced to no-load operation after 3 s, and the experimental results are shown in Figs. 12–14.

Figure 12: Nr response to sudden load changes

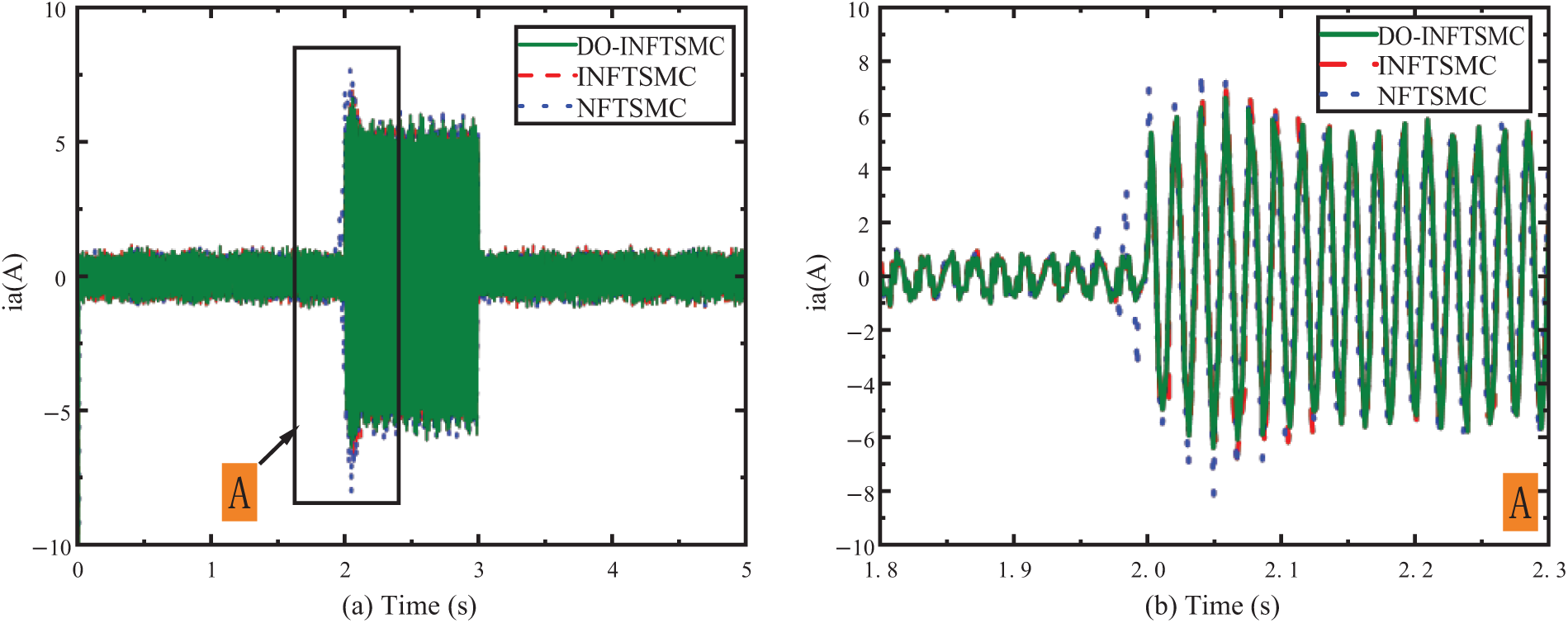
Figure 13: ia response to sudden load changes

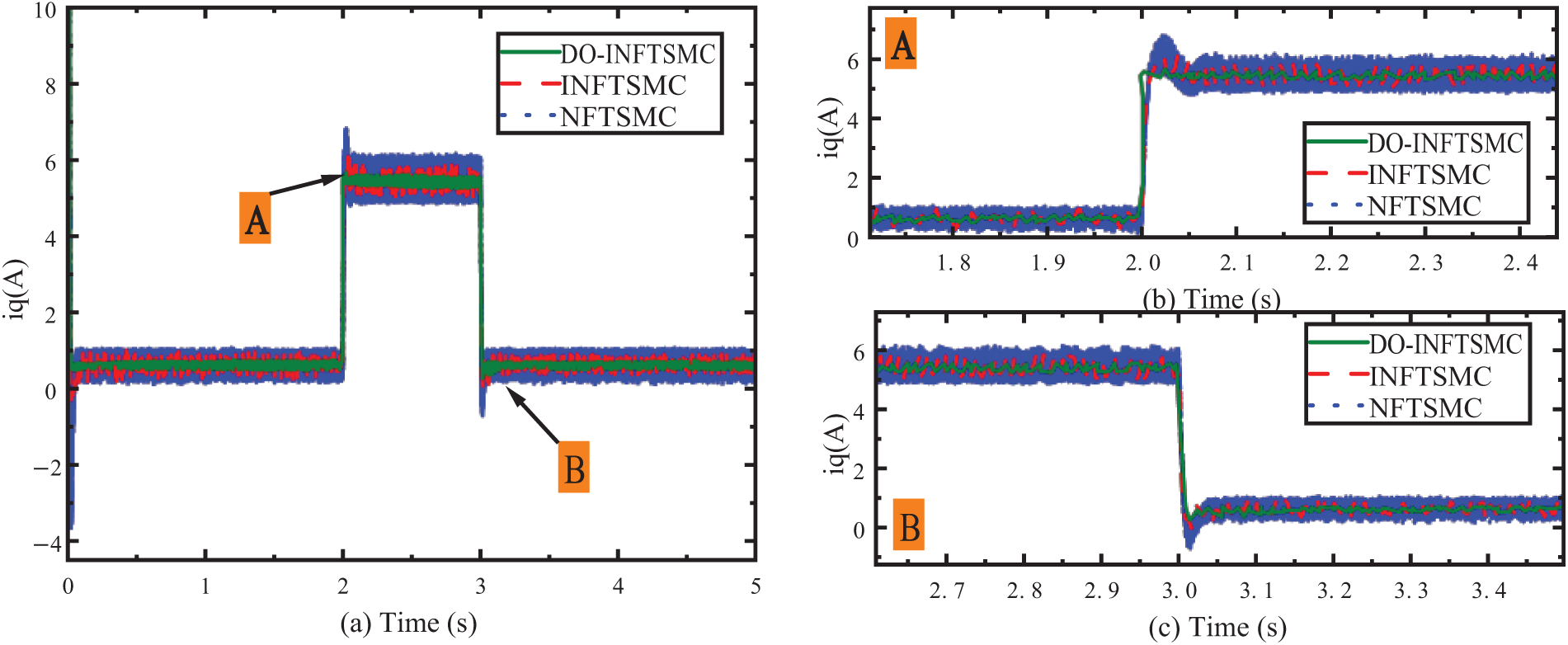
Figure 14: iq response to sudden load changes

From Fig. 12, when the load is suddenly applied for 2 s, the speed decrease percentage is about 15.63% when NFTSMC is used, about 12.5% when INFTSMC is used, and about 6.25% when DO INFTSMC is used, indicating a significant speed response effect. After the 3 s load release, the overshoot percentage was 31.25% under NFTSMC control, 9.38% under INFTSMC control, and only 3.13% under DO-INFTSMC control. It can be seen that DO-INFTSMC has obvious advantages in overshoot control after load release, which can effectively reduce the overshoot and improve the stability and dynamic performance of the system.

From Fig. 13 that when the load changes, the maximum value of ia is about 8 A when NFTSMC is used, and the maximum value of ia when INFTSMC is used is about 7 A. When DO-INFTSMC is used, the maximum value of ia is about 6 A. Compared with NFTSMC, ia has better response characteristics, and the fluctuation of ia is less when DO-INFTSMC is used, and the performance is improved by about 25% compared with NFTSMC.

From Fig. 14, when the load is suddenly applied, the overshoot of iq under NFTSMC control is the largest, about 7.2 A; overshoot under NFTSMC control is about 6.5 A; overshoot is about 6 A when DO-INFTSMC is used, and the performance is improved by about 16.67%. When the load is released at the 3 s, the NFTSMC current drop is about 1 A and INFTSMC current drop is about 0.2 A, which is A great improvement, while the current drop is about 0.05 A when using DO-INFTSMC control, which is also less volatile, and the performance is improved by about 95% compared with NFTSMC.

8  Conclusion

To improve the PMSM control performance, this study has designed an improved non-singular fast terminal sliding mode controller with a disturbance observer. Firstly, a novel reaching law and disturbance observer are introduced to reduce the system jitter and improve the disturbance immunity effectively. Secondly, IZOA is proposed for parameter tuning, and the practicality of IZOA is demonstrated by the test function, and a step response simulation test is set up to verify that the tuning time of IZOA is shortened by 71.67%, 73.02%, 77.33%, and 80.60% compared with that of ZOA, SSA, WOA, and GWO, respectively. Setting up the sinusoidal signal following the test verifies that the maximum following error of IZOA is reduced by 90%, 86.09%, 79.75%, and 51.52% compared to SSA, GWO, WOA, and ZOA, respectively. Finally, the effectiveness of the designed DO-INFTSMC control strategy is further verified in the experimental part using the speed-abrupt and load-abrupt conditions, respectively. In addition, despite the advantages of the controller designed in this paper, there is still a certain amount of overshooting of the rotational speed in real working conditions, and the controller can be further optimized in future work.

Acknowledgement: The authors would like to express their sincere gratitude to the Lower Limb Rehabilitation Exoskeleton Joint Motion Research Team of Guizhou University for the technical support of this study and financial support from PowerChina Guiyang Engineering Co. Ltd.

Funding Statement: This work was supported by the Key Technology of Flexible Regulation of Energy in Green High-Efficiency/Carbon-Efficient Buildings under the Smart Park System of PowerChina Guiyang Co., Ltd. (YJ2022-12) and the Science and Technology Support Plan of Guizhou Province “Research and Application Development of Key Technologies for Flexible Regulation of Energy in High-Efficiency/Carbon-Efficient Buildings (Guizhou Science and Technology Cooperation Support [2023] General 409).

Author Contributions: The authors acknowledge their contributions to the study as follows: study concept and design: Lang Qin, Zhengrui Jiang; data collection: Xueshu Xing, Xiao Wang; analysis and interpretation of results: Yaohua Yin, Yuhui Zhou and Zhiqin He. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors declare that all data supporting the findings of this study are available within the article. No additional data are required to understand, replicate, or build upon the findings. All relevant details are included in the main text, tables, and figures provided.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhou S, Wang D, Du M, Li Y, Cao S. Double update intelligent strategy for permanent magnet synchronous motor parameter identification. Comput Mater Contin. 2023;74(2):3391–404. doi:10.32604/cmc.2023.033397. [Google Scholar] [CrossRef]

2. Brescia E, Tipaldi M, Torelli F, Massenio PR, Savastio LP, Cascella GL, et al. A continuous sliding mode current control based on the sensitivity theory for PMSM drives. IEEE Open J Ind Applicat. 2025;6:48–58. doi:10.1109/OJIA.2025.3526628. [Google Scholar] [CrossRef]

3. Li Y, Yin Z, Zhang Y, Yuan D, Gao Y, Liu J. Overvoltage suppression strategy for electrolytic capacitorless drives using sliding mode controller based on improved variable rate reaching law. IEEE Trans Ind Electron. 2025;3519595. doi:10.1109/TIE.2024.3519595. [Google Scholar] [CrossRef]

4. Wang H, Gan C, Zhang C, Ren H, Qu R. Parameter robust predictive current control for PMSM drives based on self-tuning incremental model and voltage constraint compensation. IEEE Trans Power Electron. 2025;3539434. doi:10.1109/TPEL.2025.3539434. [Google Scholar] [CrossRef]

5. Cao H, Deng Y, Liu J, Zuo Y, Liu X, Wang H, et al. Improved deadbeat predictive current control of PMSM drives with repetitive control-based disturbance correction observer. IEEE Trans Power Electron. 2025;40(1):801–12. doi:10.1109/TPEL.2024.3482315. [Google Scholar] [CrossRef]

6. Riaz S, Qi R, Tutsoy O, Iqbal J. A novel adaptive PD-type iterative learning control of the PMSM servo system with the friction uncertainty in low speeds. PLoS One. 2023;18(1):e0279253. doi:10.1371/journal.pone.0279253. [Google Scholar] [PubMed] [CrossRef]

7. Liu J, Li M, Xie E. Noncascade structure equivalent SMC for PMSM driving based on improved ESO. IEEE Trans Power Electron. 2025;40(1):611–24. doi:10.1109/TPEL.2024.3471866. [Google Scholar] [CrossRef]

8. Sahin AK, Cavdar B, Ayas MS. An adaptive fractional controller design for automatic voltage regulator system: sigmoid-based fractional-order PID controller. Neural Comput Appl. 2024;36(23):14409–31. doi:10.1007/s00521-024-09816-6. [Google Scholar] [CrossRef]

9. Ambuj, Machavaram R. Intelligent path planning for autonomous ground vehicles in dynamic environments utilizing adaptive Neuro-Fuzzy control. Eng Appl Artif Intell. 2025;144:110119. doi:10.1016/j.engappai.2025.110119. [Google Scholar] [CrossRef]

10. Li K, Ding J, Sun X, Tian X. Overview of sliding mode control technology for permanent magnet synchronous motor system. IEEE Access. 2024;12(12):71685–704. doi:10.1109/ACCESS.2024.3402983. [Google Scholar] [CrossRef]

11. Zhang C, Qi R, Li B, Riaz S. Experimental validation and analysis of hybrid adaptive iterative learning sliding mode control for PMSM seeker coordinator. Eng Sci Technol Int J. 2024;58(7):101826. doi:10.1016/j.jestch.2024.101826. [Google Scholar] [CrossRef]

12. Li G, Zhang X, Jiang C, Li H. Non-singular fast terminal sliding mode control of permanent magnet synchronous linear motor based on superhelix algorithm. In: 2024 3rd International Conference on Smart Grids and Energy Systems (SGES); 2024 Oct 25–27; Zhengzhou, China. p. 183–6. doi:10.1109/SGES63808.2024.10824163. [Google Scholar] [CrossRef]

13. Yang Z, Sun J, Sun X, Wang B, Feng L. Direct instantaneous torque control for six-phase SRM with nonsingular fast terminal sliding mode controller. IEEE J Emerg Sel Top Power Electron. 2023;12(1):505–15. doi:10.1109/JESTPE.2023.3333802. [Google Scholar] [CrossRef]

14. Yu K, Li S, Zhu W, Wang Z. Sensorless control scheme for PMSM drive via generalized proportional integral observers and Kalman filter. IEEE Trans Power Electron. 2025;40(3):4020–33. doi:10.1109/TPEL.2024.3502396. [Google Scholar] [CrossRef]

15. Cheng Z, Li L, Liu X, Bai X, Liu J. Sensorless control based on discrete fractional-order terminal sliding mode observer for high-speed PMSM with LCL filter. IEEE Trans Power Electron. 2025;40(1):1654–68. doi:10.1109/TPEL.2024.3443401. [Google Scholar] [CrossRef]

16. Li D, Feng S, Dou L. Disturbance observer-based improved non-singular fast terminal sliding mode control for the PMSM with matched and mismatched disturbances. In: 2024 36th Chinese Control and Decision Conference (CCDC); 2024 May 25–27; Xi’an, China. p. 4158–63. doi:10.1109/CCDC62350.2024.10588341. [Google Scholar] [CrossRef]

17. Zhang Y, Li S, Yi W, Yang Y, Cao K, Luo B. A robust model predictive current closed-loop control with parameter estimation strategy based on immune chaotic antipredator PSO for PMSM. IEEE Trans Power Electron. 2025;40(1):1836–48. doi:10.1109/TPEL.2024.3476118. [Google Scholar] [CrossRef]

18. Bendjedia B, Chouireb S, Houichiti A, Zakhrouf A, Chaoui H. Optimization of PMSM sensorless control based on EKF for electric vehicle applications. In: 2024 IEEE Vehicle Power and Propulsion Conference (VPPC); 2024 Oct 7–10; Washington, DC, USA. p. 1–8. doi:10.1109/VPPC63154.2024.10755275. [Google Scholar] [CrossRef]

19. Bae SB, Choi DS, Min SG. Artificial hunting optimization: a novel method for design optimization of permanent magnet machines. IEEE Trans Transp Electrif. 2024;10(2):3305–19. doi:10.1109/TTE.2023.3293909. [Google Scholar] [CrossRef]

20. Wang X, Yu X, Liu Y. DV-Hop localization Based on parameter correction and Improved Zebra optimization algorithm. In: 2024 IEEE 12th International Conference on Information, Communication and Networks (ICICN); 2024 Aug 21–24; Guilin, China. p. 413–8. doi:10.1109/ICICN62625.2024.10761302. [Google Scholar] [CrossRef]

21. Mohd Tumari MZ, Ahmad MA, Suid MH, Ghazali MR, Tokhi MO. An improved marine predators algorithm tuned data-driven multiple-node hormone regulation neuroendocrine-PID controller for multi-input-multi-output gantry crane system. J Low Freq Noise Vib Act Contr. 2023;42(4):1666–98. doi:10.1177/14613484231183938. [Google Scholar] [CrossRef]

22. Yue P, Xu B, Zhang M. An improve nonlinear robust control approach for robotic manipulators with PSO-based global optimization strategy. Sci Rep. 2024;14(1):21447. doi:10.1038/s41598-024-72156-x. [Google Scholar] [PubMed] [CrossRef]

23. Ibrahim B, Abdelkader H, Hartani MA, Kayisli K. Optimization of sliding mode control for doubly fed induction generator systems using particle swarm and grey wolf algorithms. Electr Power Compon Syst. 2024;52(10):1782–95. [Google Scholar]

24. Trojovská E, Dehghani M, Trojovský P. Zebra optimization algorithm: a new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access. 2022;10:49445–73. doi:10.1109/ACCESS.2022.3172789. [Google Scholar] [CrossRef]

25. Ghadi YY, Neamah NM, Hossam-Eldin AA, Alqarni M, AboRas KM. State-of-the-art frequency control strategy based on an optimal fuzzy PI-FOPDFλ for SMES and UPFC integrated smart grids using Zebra optimization algorithm. IEEE Access. 2023;11:122893–910. doi:10.1109/ACCESS.2023.3328961. [Google Scholar] [CrossRef]

26. Pazhanimuthu C, Saravanan G, Suresh KP, Kumar RS. Performance analysis of voltage profile improvement in AVR system using zebra optimization algorithms based on PID controller. e-Prime–Adv Electr Eng Electron Energy. 2023;6(1):100380. doi:10.1016/j.prime.2023.100380. [Google Scholar] [CrossRef]

27. Wei XY, Zhang T, Liu RZ. MPPT control strategy of photovoltaic based on improved zebra optimization algorithm. J Phys Conf Ser. 2024;2831(1):012029. [Google Scholar]

28. Ghosh S. Method for fault diagnosis and speed control of PMSM. Comput Syst Sci Eng. 2023;45(3):2391–404. doi:10.32604/csse.2023.028931. [Google Scholar] [CrossRef]