Toward Intrusion Detection of Industrial Cyber-Physical System: A Hybrid Approach Based on System State and Network Traffic Abnormality Monitoring

1  Introduction

The rapid integration of advanced information technologies—such as the Industrial Internet of Things (IIoT), cloud computing, big data, and artificial intelligence—is driving an unprecedented transformation in manufacturing industries. Intelligent manufacturing has emerged as a central theme in global competition, with the Industrial Cyber-physical System (ICPS) playing a central role [1]. The advent of ICPS has driven Industrial Control Systems from traditional electromechanical architectures to interconnected, intelligent systems. While this evolution enhances automation and intelligence, it also expands the attack surface, exposing ICPS to sophisticated cybersecurity threats. The deep integration of information and physical components in ICPS means that cyberattacks on any component can propagate across the entire industrial network. Several high-profile cyberattacks have underscored these vulnerabilities. In 2013, hackers infiltrated Haifa’s highway control systems, causing substantial financial losses. In December 2015, a cyberattack on Ukraine’s power grid disrupted electricity for 22,500 residents. In 2017, a Chernobyl nuclear power plant in Ukraine subway and other national facilities were infected by the NotPetya extortion virus. More recently, on 07 May 2021, a ransomware attack forced the Colonial Pipeline—the largest fuel pipeline in the United States—to shut down operations, causing widespread disruptions. These incidents highlight the urgent need for robust, adaptive, and intelligence-driven security mechanisms to protect ICPS from evolving cyber threats [2].

Traditional communication network security has been studied extensively, focusing on network anomaly-based and signature-based detection techniques [3,4]. While these methods have demonstrated effectiveness in protecting IT infrastructures, ICPS security poses unique challenges due to its distinct operational and structural characteristics [5,6].

(1)   System Integrity vs. Data Confidentiality: Traditional communication network security primarily safeguards the confidentiality of critical data. In contrast, ICPS security prioritizes system integrity, including the physical sensory system, the information system, and the overall control system to ensure reliable operation.

(2)   Resource Constraints: Unlike IT communication network systems with relatively ample computational resources, ICPS often operate under strict energy and processing limitations. Consequently, cybersecurity measures must enable real-time monitoring while minimizing computational overhead.

(3)   Complexity and Heterogeneity: ICPS comprise hybrid wired-wireless networks with diverse communication protocols. The heterogeneity of controllers, sensors, and data acquisition systems across industries complicates cybersecurity. However, once deployed, ICPS configurations remain largely static.

(4)   Non-interruptible Maintenance: Unlike IT communication network systems that can undergo periodic updates and patches, ICPS operates continuously, limiting downtime for updates. The intrusion detection of ICPSs must provide real-time threat detection and alarm, particularly identifying unknown and covert attacks.

To sum up, ICPS exhibit relatively stable traffic state with trackable system states, enabling intrusion detection through system anomaly monitoring [7]. Existing ICPS intrusion detection methods can be broadly classified into traffic anomaly-based and state anomaly-based intrusion detection technologies [8].

Traffic anomaly-based detection analyzes time-dependent node-level and network-level characteristics to identify network intrusions and classify attack types. A critical step is effective feature representation, where clustering techniques, such as K-means clustering, are commonly used. However, traditional K-means clustering suffers from initialization sensitivity, poor global search capability, and susceptibility to local optima. Evolutionary K-means (EKM) integrates genetic algorithms to optimize initialization, but its reliance on the silhouette index (SI) for clustering evaluation weakens its robustness against noise [9].

On the other hand, cyberattacks on sensors, controllers, actuators, or network transmissions can disrupt ICPS stability by altering system input-output signals. Researchers have explored fault diagnosis-inspired methodologies, such as outlier detection, for intrusion detection. Linear and nonlinear system models have been used to detect attacks, like replay attacks and denial-of-service (DoS) attacks [10]. Shinohara et al. [11] presented the optimal security investment problem as a discrete-time linear time-invariant system. These studies demonstrate that as long as not all sensors fail simultaneously, state anomaly-based intrusion detection can effectively identify small, rare, and unknown faults.

Concerning the system modeling, the commonly used method characterizes the ICPS as a linear time-varying system, with the Kalman filtering frequently employed. For instance, Pasqualetti et al. [12] and Lee et al. [13] model the ICPS attacks using a linear time-invariant system with unknown inputs and time-varying process and measurement noise. Zhang et al. [14] advanced distributed state estimation in binary sensor networks by integrating variation Bayesian methods to handle noisy, uncertain environments. However, these methods assume known or invariant noise, making them overly reliant on prior noise statistics, which limits their applicability in dynamic ICPS environments.

To overcome the above issues, adaptive Kalman filtering models, such as Bayesian inference, maximum likelihood estimation, correction and covariance matching methods, have been explored. Among them, the Bayesian method is the most widely used [15]. For instance, Liu et al. [16] introduced an adaptive Kalman filtering method with time-varying process noise and measurement noise covariance matrix. However, these methods still assume linear time-invariant system constraints, neglecting the inherent nonlinearity of ICPS dynamics, which is critical for analyzing stability, faults, and attacks in complex industrial processes.

To capture time-varying and nonlinearity in ICPS, nonlinear ICPS modeling that adapts to process and measurement noise is essential. Many exploratory studies have been carried out. For instance, Yuan et al. [17] proposed a model-driven ICPS, leveraging an extended Kalman filter (EKF) to calibrate the empirical model with online measured data for online diagnosis and monitoring. However, this approach fails to detect covert attacks (e.g., replay attacks), which do not significantly alter measurement values.

To address the above challenges, an improved variation Bayesian-based noise covariance-adaptive nonlinear Kalman filtering (IVB-NCA-NKF) is proposed for the nonlinear system modeling of complex ICPSs. IVB-NCA-NKF can model the adaptive nonlinear time-varying system with the unknown process and measurement noise covariance matrices. It is mainly used for sensor system-related attack detection in ICPSs. To realize the overall security monitoring of networked industrial control systems, a hybrid intrusion detection framework for securing ICPSs that combines state anomaly detection of the sensor systems and the network traffic anomaly detection is proposed. The main contributions can be summarized as follows:

(1)   A hybrid intrusion detection framework is proposed by combining sensor state anomaly and network traffic anomaly detection, ensuring multi-layered ICPS security from sensors to network communication systems.

(2)   An IVB-NCA-NKF is proposed for modeling nonlinear time-varying ICPSs, leveraging a cluster-based sensor system model and state estimation to enable cybersecurity monitoring of large-scale distributed ICPS.

(3)   An online adaptive network traffic pattern learning approach for network communication system intrusion detection is proposed, incorporating a cache-based pattern library to enhance the detection of sparse and unknown attack modes in ICPS.

The rest of this article is organized as follows. Section 2 briefly reviews the theoretical foundations of the EKF and K-means algorithm. Section 3 details the proposed hybrid intrusion detection approach. Section 4 makes extensive confirmatory and comparative experiments. Section 5 summarizes the whole article with possible extensions of this work.

2  Preliminaries

This section briefly reviews the principles of EKF and the K-Mean Algorithm.

2.1 Exended Kalman Filter (EKF)

The Kalman filter is a powerful and standard approach for state estimation. However, the standard Kalman filter is limited to linear systems, whereas most real-world systems exhibit nonlinearity, necessitating its extension to handle nonlinear dynamics. The EKF [18] is undoubtedly the most widely used nonlinear form of the standard Kalman filter. The EKF state transfer equations and observation equations can be expressed as,

xk=f(xk−1,uk−1)+sk(1)

yk=h(xk,uk)+vk(2)

where xk∈Rn represents the system state vector, uk∈RD denotes the operation vector, yk∈Rm stands for the observation or measurement vector; f and h are nonlinear differentiable functions representing the transfer and measurement function, respectively; sk and vk represent the system and measurement noises, and satisfies sk∼𝒩(sk|0,Qk), vk∼𝒩(vk|0,Rk), where 𝒩(x|µ,Σ) stands for a multivariate normal distribution with the mean vector of µ and variance matrix of Σ.

Based on the Taylor’s expansion, xk in Eq. (1) can be expressed as,

xk=f(x^k−1,uk−1)+Fk−1(xk−1−x^k−1)+sk(3)

where x^k−1 is the estimation vector of the time t − 1. Based on the Taylor expansion at the state prediction value x^k|k−1 of this round, we have,

yk=h(x^k|k−1,uk)+Hk(xk−x^k|k−1)+vk(4)

where Fk−1 and Hk, respectively, represent the function and the Jacobian matrix at x^k−1 and x^k|k−1.

Based on the Gaussian assumption, according to Eq. (4), under a known system state xk, there is,

p(yk|xk,uk)=𝒩(yk|h(x^k|k−1,uk)+Hk(xk−x^k|k−1),Rk)(5)

When xk−1 is known, according to Eq. (3), there is,

p(xk|xk−1)=𝒩(xk|f(x^k−1,uk−1)+Fk−1(xk−1−x^k−1),Qk)(6)

Kalman filter is designed to estimate xk based on historical observations, y1:k. That is, to iteratively calculate the model parameters x^k,Σk in p(xk|y1:k,u1:k)=𝒩(xk|x^k,Σk). The main iterative steps are as follows:

(1) Estimate the state of the system at the current moment using the historical observations y1:k−1, i.e.,

p(xk|y1:k−1,u1:k−1)=∫p(xk−1|y1:k−1,u1:k−1)p(xk|xk−1)dxk−1=𝒩(xk|x^k|k−1,Σk|k−1)(7)

where x^k|k−1=f(µk−1,uk−1) and Σk|k−1=Fk−1Σk−1Fk−1T+Qk.

(2) Update p(xk|y1:k,u1:k) based on the currently obtained observation vector xk,

p(xk|y1:k,u1:k)∝p(xk|y1:k−1,u1:k−1)p(yk|xk,uk)=𝒩(xk|x^k,Σk)(8)

where Σk=(I−KkHk)Σk|k−1, x^k=x^k|k−1+Kk(yk−h(x^k|k−1,uk)), and,

Kk=Δ⁡Σk|k−1HkT(HkΣk|k−1HkT+Rk)−1(9)

By iterating steps (1) and (2), EKF can realize the Gaussian nonlinear dynamic system modeling.

2.2 K-Means Clustering-Based Pattern Learning

K-means clustering [19] is known as a simple and scalable pattern learning (pattern mining) method. Given a data set X={x1,x2,⋯,xN}, where xi∈RD, K-means is used to categorize X into K clusters. The pattern learning results are usually expressed by the mean vectors of the K clusters, {µk|k=1,⋯, K}. To achieve the clustering results, a cluster-assigning notation of points, rnk∈{0,1}, referring to that data point xn is assigned to the cluster k if rnk=1, and rnj=0 for j≠k. Thus, the K-means clustering is to minimize the following optimization objective, i.e.,

J=∑n=1N∑k=1Krnk‖xn−µk‖2(10)

The commonly used expectation maximization (EM) algorithm can be used to address the above optimization problem. The iteration steps are as follows:

(1) E step. It tries to assign the optimal rnk for each point based on the clustering results, {µk|k=1,⋯, K}, of the last step, i.e.,

rnk={1 if k=arg minj‖xn−µj‖20 otherwise(11)

Namely, each point will be assigned to its nearest cluster.

(2) M step. Based on the assigned rnk of each point in the E step, the clustering centers, {µk|k=1,⋯, K}, can be optimized by setting the partial derivative of the optimization objective J over each clustering center be zero, i.e., ∂J∂µk=2∑n=1Nrnk(xn−µk)=0, which can be easily solved to achieve,

µk=∑n=1Nrnkxn∑n=1Nrnk(12)

Iterating the Steps E step M until a convergent result is reached. K-mean clustering is straightforward to implement with high computational efficiency. However, the clustering results are affected greatly by the presupposed cluster number (K) and the initialized clustering centers.

Numerous studies have addressed the initialization problem in the K-means algorithm, focusing either on determining the optimal number of clusters or selecting appropriate initial cluster centers for a given cluster count. A common approach is to perform multiple clustering operations with varying cluster numbers or initial centers and then select the best results based on predefined cluster validity indices (CVIs) [20]. Arbelaitz et al. [21] conducted a comprehensive comparative study of approximately 30 CVIs, including the Dunn index, Silhouette index, and Cluster Separation (CS) measure, to evaluate clustering performance and optimize algorithm parameters. Some researchers have integrated both cluster number selection and center initialization using evolutionary algorithms. For instance, the genetic algorithm (GA) was combined with the K-mean algorithm to achieve an evolutionary K-mean (EKM) algorithm [22].

3  Proposed ICPS-Oriented Intrusion Detection Scheme

The proposed hybrid intrusion detection framework addresses cybersecurity in ICPS from two key aspects: system state anomaly detection and network traffic anomaly detection, aiming for comprehensive protection, as illustrated in Fig. 1.

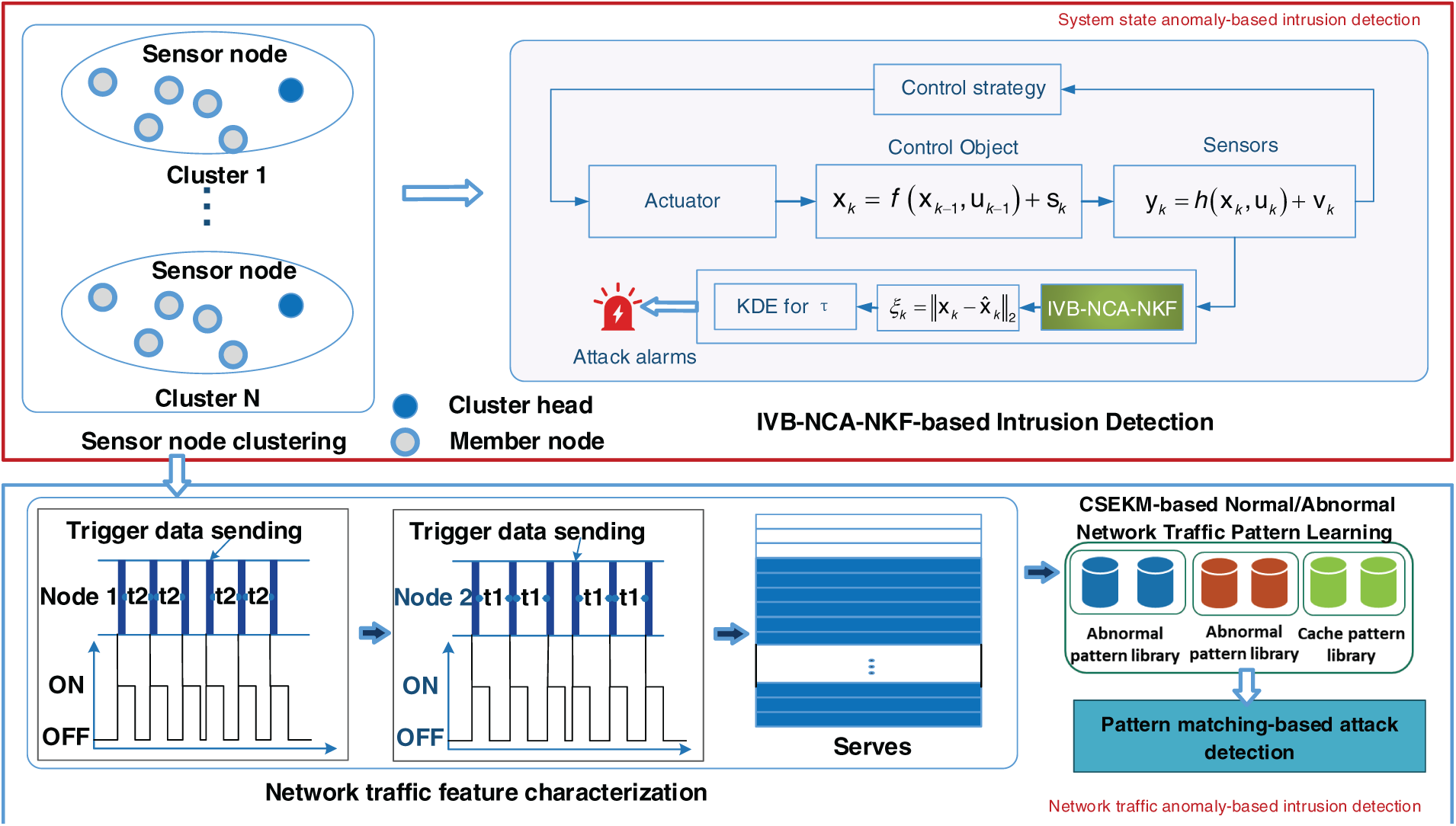
Figure 1: Intrusion detection framework

As shown in Fig. 1, the sensor system state anomaly detection model leverages data from ICPS sensor nodes for real-time anomaly monitoring. A significant system state estimation residual may indicate potential anomalies, such as sensor system attacks. To mitigate computational and communication constraints, a sensor grading strategy is adopted, clustering sensor nodes and assigning each cluster a state estimation detector for anomaly detection, thereby reducing system complexity and cost. Simultaneously, a network traffic pattern matching-based anomaly detection mechanism is introduced for network security monitoring. An improved N-Burst model is proposed to represent ICPS network traffic patterns, while an enhanced clustering stability-based evolutionary K-Means (CSEKM) algorithm is employed for network traffic pattern learning. By analyzing both node-level and system-level traffic patterns, an intrusion detector is implemented using the pattern-matching scheme.

The main detection steps can be summarized as follows:

(1)   Sensor node clustering and cluster node head setting;

(2)   For each sensor cluster:

(2.1)   Perform IVB-NCA-NKF to estimate the state vector xk, measuring noise covariance matrix Rk, and system noise covariance matrix Σk|k−1;

(2.2)   Compute the system state prediction residual;

(2.3)   Determine whether an intrusion occurs based on the system residual threshold.

(3)   Perform the network traffic anomaly-based intrusion detection:

(3.1)   Perform N-burst model-based node-level and communication network-level traffic feature representation;

(3.2)   Perform CSEKM-based Normal/Abnormal network traffic pattern learning;

(3.3)   Perform pattern matching-based network intrusion detection.

3.1 Sensory System State Anomaly-Based Intrusion Detector

Sensor system anomaly-based intrusion detection are detected by analyzing the state estimation residual—the difference between the actual detected state and the estimated state—based on the proposed IVB-NCA-NKF model. To minimize transmission delays and enable distributed intrusion detection, sensor nodes are clustered [23], with each cluster assigned a detector.

3.1.1 Sensor Node Clusters

Following Sarehati’s sensor clustering approach [23], controllers and their associated sensor nodes (including sensors and actuators) are grouped into clusters. Each cluster is managed by a controller as the cluster head, while the associated sensor nodes act as members. To enhance distributed attack detection, active collaboration among member nodes is employed. Sensor nodes periodically transmit local and shared information—including suspicious activity from neighboring nodes and confirmed attack warnings—to their linked nodes. The cluster head then aggregates and forwards this data to the next hop or data transfer node. A schematic representation of sensor node collaboration is shown in Fig. 2.

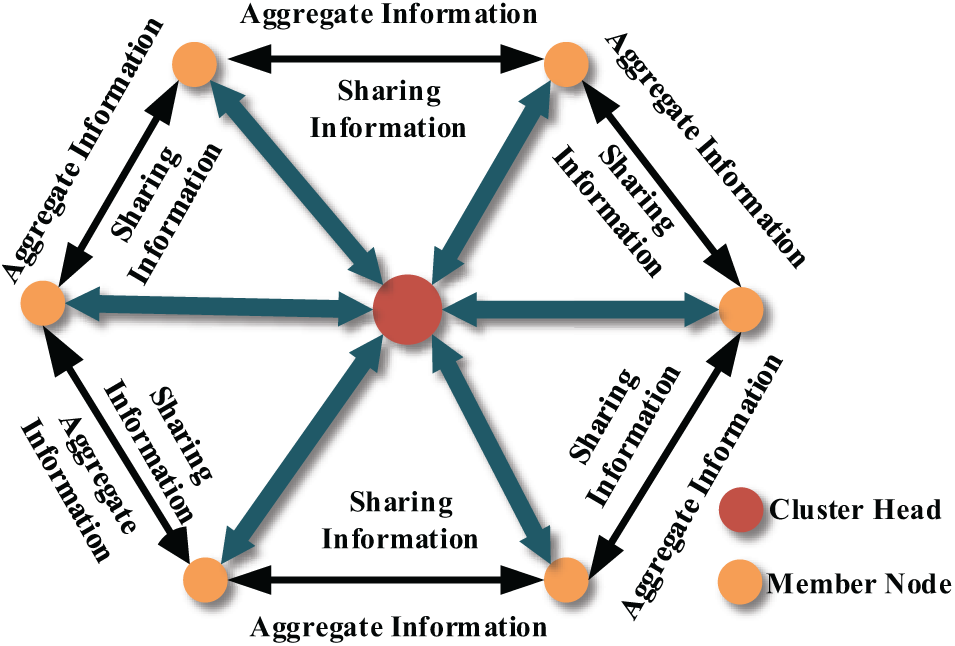
Figure 2: Collaborative work diagram of sensor node

3.1.2 IVB-NCA-NKF-Based Intrusion Detection

The proposed IVB-NCA-NKF is an optimal EKF based on the variation inference for the system modeling of unknown process and measurement noise covariance matrixes.

First of all, assuming that a nonlinear sensor system is expressed by Eqs. (1) and (2), under the Gaussian assumption, the random vector of the state, xk, and observation, yk, are also Gaussian, i.e.,

xk|xk−1∼𝒩(f(xk−1,uk−1),Σk|k−1)(13)

yk|xk∼𝒩(h(xk,uk),Rk)(14)

Although we can model the dynamic system by iterating Eqs. (7) and (8), the system noise information, Σk|k−1 in (13) and the measurement noise, Rk, in (14) are actually unknown (system noise and measurement noise are time-varying). Therefore, the classic EKF model may cause an accumulation of system estimation errors due to the inaccuracy of process and measurement noise estimation in the system modeling, results in an inaccurate system model that is far from the real system.

Chang et al. [24] have pointed out that a good solution for modeling the noise-unknown systems is to use the variation Bayesian method to measure the system state and measurement noise covariance matrices jointly. Huang et al. [25] have also extended the Kalman filter model with unknown measurement noises. The results show that the proposed method is more robust to the uncertainty factors in the process and measurement of linear dynamic systems. However, the abovementioned methods are linear system models, which are not suitable for nonlinear systems.

In this work, the linear system modeling method is extended to the nonlinear dynamic system modeling. The proposed IVB-NCA-NLKF is aimed at estimating the sensory system state, observation and process noise covariance matrixes jointly by the variation inference based on the sensor observations, i.e., to achieve a posterior probability, p(xk,Σk|k−1,Rk|y1:k).

Since the analytic solution of the posterior, p(xk,Σk|k−1,Rk|y1:k), is intractable, the variation Bayesian inference method is introduced to optimally approximate it, where p(xk,Σk|k−1,Rk|y1:k) is assumed to be factorable approximately, i.e.,

p(xk,Σk|k−1,Rk|y1:k)≈q(xk)q(Σk|k−1)q(Rk)(15)

where q(xk),q(Σk|k−1),q(Rk) should be achieved by,

{q^(xk),q^(Σk|k−1),q^(Rk)}=arg min{KLD(p(xk,Σk|k−1,Rk|y1:k)||q(xk)q(Σk|k−1)q(Rk))}(16)

where KLD stands for the Kullback–Leibler Divergenc, and KLD(p(x)||q(x))=∫p(x)log⁡p(x)/q(x)dx.

Based on the variation inference, the optimal solution of Eq. (16) can be expressed as,

log⁡q^i(θi)=Ej≠i[log⁡p(θ,y1:k)],where θ=(θ1,θ2,θ3)=(xk,Σk|k−1,Rk)(17)

To achieve q^i(θi) in Eq. (17), the total probability formula, p(θ,y1:k), should be achieved in advance. According to the Bayesian rule, p(θ,y1:k)=p(xk,Σk|k−1,Rk,y1:k) can be expressed as,

p(xk,Σk|k−1,Rk,y1:k)=p(y1:k−1)p(Rk|y1:k−1).p(Σk|k−1|y1:k−1)p(xk|y1:k−1,Σk|k−1).p(yk|xk,Rk)(18)

In Eq. (18), p(xk|y1:k−1,Σk|k−1) and p(yk|xk,Rk) are Gaussian density. Rk and Σk|k−1 are the covariance matrixes of Gaussian models, whose prior distribution is known to be the Inverse-Wishart (IW) distribution [24]. By the introduction of the IW distribution, it can ensure that their posterior distribution has the same distribution form as the prior distribution, which is conducive to the probability calculation. Detailed information of IW distribution can be found in Appendix A. Briefly, these prior distributions are selected as,

p(xk|y1:k−1,Σk|k−1)=𝒩(xk|x^k|k−1,Σk|k−1)p(yk|xk,Rk)=𝒩(yk|y^k|k−1,Rk)p(Rk|y1:k−1)=IW(Rk|d^k|k−1,Dk|k−1)p(Σk|k−1|y1:k−1)=IW(Σk|k−1|t^k|k−1,Tk|k−1)(19)

where x^k|k−1=f(x^k−1|k−1,uk−1), y^k|k−1=h(x^k|k−1,uk)+Hk(xk−x^k|k−1).

By these prior distributions, we can achieve the posterior of the dynamic system state based on Formula (17). A detailed estimation procedure of q(xk),q(Σk|k−1),q(Rk) is shown in Appendix B.

The state estimation residual can be computed by,

ξk=‖xk−x^k‖2(20)

where ‖⋅‖2 stands for the 2-norm. If the industrial control system is affected by malicious attacks, it may yield state mutation, leading to a deviation from the stable state. Thus, when ξk is beyond a preset threshold, τ, the system is considered to have an abnormal state or attack. The threshold value τ is generally determined by chi-square detection or by kernel density estimation of ξk based on a predefined confidence level.

Here below is an illustrative example to validate the performance of the proposed IVB-NCA-NKF model. Given a stochastic discrete-time nonlinear dynamic system (DC motor system) has the following state and measurement expression,

(ωkck)=(ωk−1+(uk−1−ck−1ωk−1)Ts/Jck−1)+qkyk=(ωk(uk−ckωk)/J)+rk(21)

where uk represents the control value, J = 10, Ts = 0.01, and qk∼𝒩(0,Qk), rk∼𝒩(0,Rk) are the noise vectors of the system state equation and the measurement equation, respectively, where the covariance matrixes, Qk, Rk, are time-varying.

Fig. 3 presents a comparative analysis of the prediction results for the nonlinear system described in Eq. (21) using the IVB-NCA-NLKF model and traditional EKF methods. As can be seen from Fig. 3, the proposed model demonstrates higher accuracy, particularly for the step state variable. Overall, the predicted system state closely aligns with the actual state, highlighting the effectiveness of the IVB-NCA-NLKF model for nonlinear system modeling under unknown process and measurement noise conditions.

Figure 3: Example of IVB-NCA-NLKF-based nonlinear system modeling

3.2 Network Traffic Anomaly-Based Intrusion Detector

Network traffic anomaly-based intrusion detection consists of offline learning of normal and abnormal traffic patterns, followed by online anomaly detection with continuous pattern library updates. A schematic representation of this process is shown in Fig. 4.

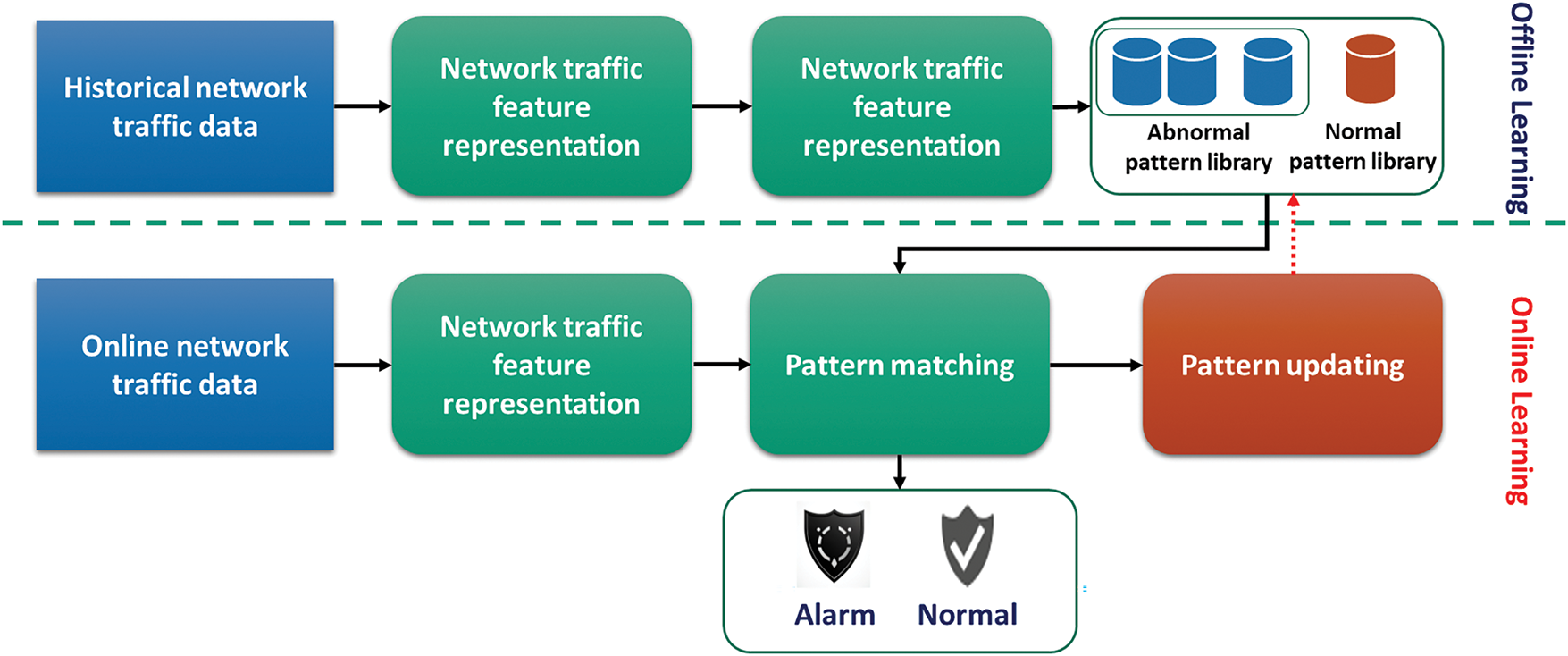
Figure 4: Network traffic anomaly detector

3.2.1 Network Traffic Feature Extraction and Representation

Inspired by Huang et al.’s study [26], a N-Burst model is adopted for the network traffic representation. As described in Huang et al.’s work [26], the N-Burst model expresses an arrival process of superposition of traffic streams from N-independent and statically identical ON/OFF sources. As described in Fig. 5, each ON/OFF source consists of an ON period, i.e., 1 burst, and an OFF period. A more detailed description of the N-Burst model can be found in the literature [26].

Figure 5: ON/OFF source model

In the ICPS, the ON/OFF source involves actuators and sensors. The ON stage refers to the stage in which the node transmits data, with a randomly varying duration. The OFF stage refers to the idle stage of the node, and the duration is also random. The end of each ON phase follows the previous OFF phase. When the system is running, the sensor data is collected according to the predetermined sequence and period. After a specific event triggers data transmission, the pre-set sequence and cycle are restored, and the sensor data is collected. Due to the coupling relationship between nodes, different nodes enter the ON period according to a certain time interval. The ON/OFF model-based data feature for the network traffic representation is shown in Table 1.

3.2.2 CSEKM-Based Normal/Abnormal Network Traffic Pattern Learning

The Silhouette Index (SI) is widely regarded as one of the most effective clustering validity indices (CVIs) for evaluating cluster compactness and separability [27]. However, SI is sensitive to noise, as outliers can significantly alter its values, affecting clustering results. To overcome the initialization problem of K-Means and improve the robustness, He et al. [27] introduced the clustering stability index as an alternative to SI for performance evaluation. Inspired by He’s study, the CSEKM algorithm was introduced for normal/abnormal network traffic pattern learning. Using the learned pattern libraries, traffic anomalies can then be detected via pattern matching.

The main procedure of the clustering stability-based K-means model selection is to learn a set of K-means models using a set of perturbed versions of training samples and choose the minimum instability of each K-means clustering model as the final model. The clustering instability is often computed as the average distance between clusters on different perturbed training samples. However, as stated in the literature [27,28], this criterion may be misleading in the case of EKM. Besides the average distance between clusters, the other commonly used method for evaluating cluster stability is the Consensus Matrix (CM)–based approach. As suggested in Yu et al.’s study [29], the Aggregation Consensus Matrix (ACM), a modified rand index calculated based on discrete CM to evaluate clustering stability to determine K, was applicable. In this work, the ACM-based clustering stability analysis is adopted. By combining the EKM and clustering stability analysis, a CSEKM-based is adopted for the normal traffic pattern and abnormal traffic pattern learning. Detailed CSEKM algorithm steps can be found in the literature [27].

3.2.3 Pattern Matching-Based Anomaly Detection and Online Pattern Updating

Once normal and abnormal network traffic pattern libraries are established, anomaly detection via pattern matching becomes straightforward. However, the dynamic nature of ICPS networks and evolving intrusion tactics cause attack patterns to deviate from their original features, leading to new intrusion variants. Traditional intrusion detection models, which rely on predefined intrusion characteristics, struggle to detect emerging attacks in such dynamic environments.

To enhance adaptability in dynamic ICPS network environments, an online pattern updating mechanism is incorporated into the intrusion detection model, building on our previous work [30]. The process, illustrated in Fig. 6, integrates a cache pattern library (CPL) alongside the pre-learned normal pattern library (NPL) and the abnormal pattern library (APL) to handle unforeseen or evolving network behaviors.

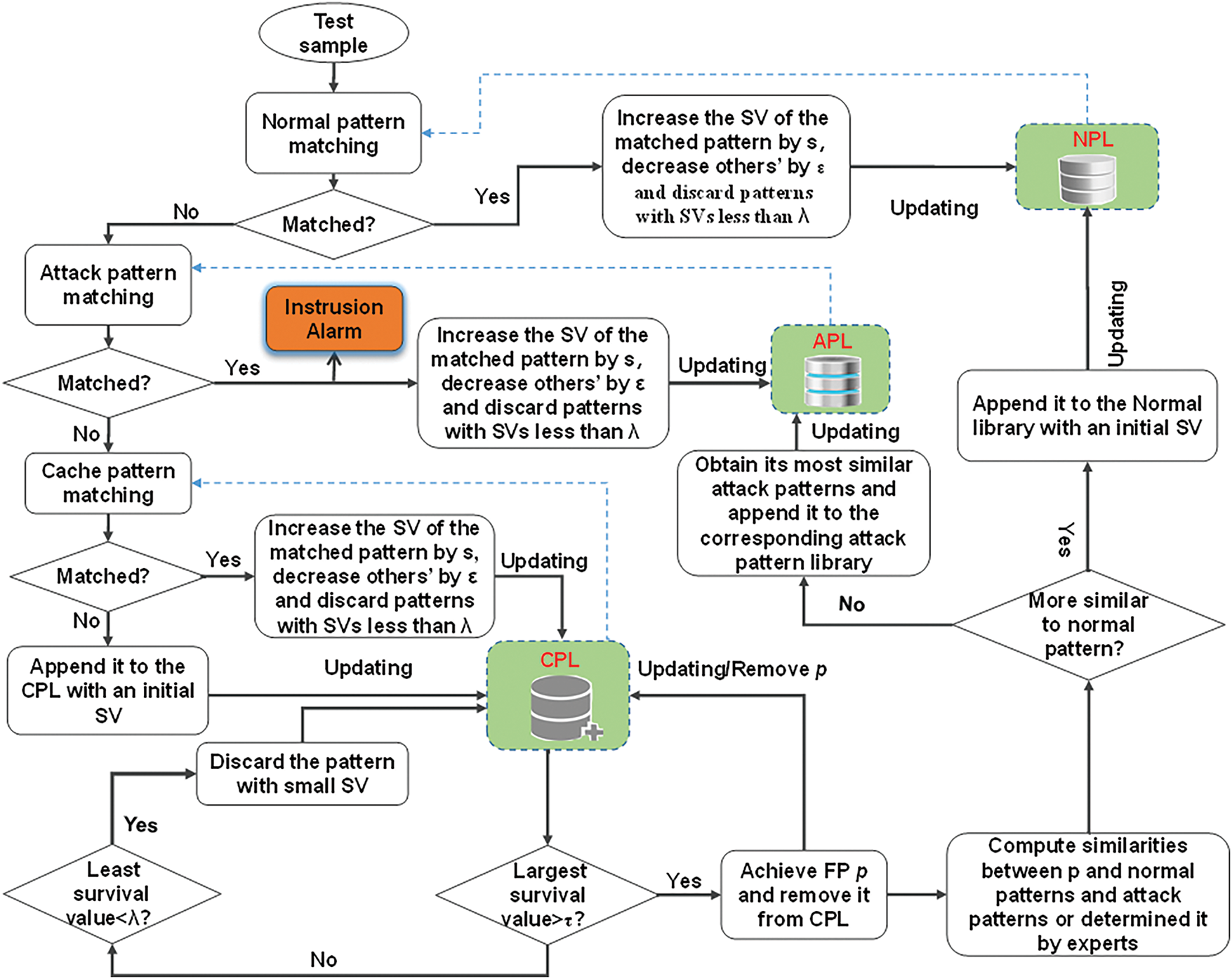
Figure 6: Pattern matching-based intrusion detection and online pattern updating

Each learned pattern in the libraries is assigned a survival value (SV) to track its activity. Patterns with SVs below a predefined threshold are discarded to maintain an updated library. Upon receiving a new network traffic instance, pattern matching is performed sequentially.

•   Normal Pattern Matching: If a match is found in the NPL, the SV of the matched pattern increases by s (e.g., by 1 in experiments), while others in the NPL decrease by ε(≪1). Patterns with SVs below the threshold (λ) are removed.

•   Attack Pattern Matching: If no match is found in the NPL, the instance is checked against the APL. A successful match triggers an intrusion alarm and updates the APL similarly to the NPL.

•   Cache Pattern Matching: If no match is found in either NPL or APL, the instance is compared with patterns in the CPL. A match leads to CPL updates following the same principle. If unmatched, the instance is added to the CPL with an initial confidence value (CV).

For any pattern in CPL, if its CV is larger than a high threshold (τ), this pattern can be referred as to a frequent pattern (FP). And it will perform pattern matching of the FP with NPL and APL, if it is more like to a normal pattern, the NPL will be updated accordingly. Oppositely, if the FP is more like to an abnormal pattern, the APL will be updated accordingly.

Many vector distance measurement approaches can be used for pattern matching, such as Pearson correlation coefficient, Euclidean distance, Cosine similarity, Manhattan distance, Lance Williams distance, and so on [31]. In this work, the simple cosine similarity is adopted to measure the dissimilarity of two network records, given by,

d(x,y)=xTy‖x‖‖y‖(22)

where x,y stands for two patterns. The smaller the value of d(x,y), the smaller the angle between x and y, and the greater the similarity between x and y.

4  Experimental Validation and Result Analysis

This section details the confirmatory and comparative experiments with result discussions.

4.1 State Anomaly-Based Intrusion Detection

4.1.1 Attacking Models

Four typical and common attacks in the ICPS are considered in this work, namely, the denial of service (DoS), spoof attack, noise and scaling attacks as described in Liu et al.’s study [32]. In the following attacking model, n represents the number of sensors in the ICPS, yi(t) represents acquired value of the ith sensor at the t time, ui(t) stands for the received control signal of the sensor i at the time of t and the attacking duration is [ts,te].

(1) DoS

Attackers introduce attacking signals to yi(t) or control signals ui(t) to prevent the collection of correct control commands or actual sensory data by offsetting the normal signals, i.e.,

y^i(t)={yi(t)t∉[ts,te]yi(t)+ay,ay=−yi(t)t∈[ts,te],u^i(t)={ui(t)t∉[ts,te]ui(t)+au,au=−ui(t)t∈[ts,te](23)

(2) Spoof attack

The spoof attack occurs when an attacker steals historical data and replaces the current system data with the historical data in the sensory system. This is a covert intrusion that cannot be easily detected,

y^i(t)={yi(t)t∉[ts,te]ay,ayis historical data t∈[ts,te],u^i(t)={ui(t)t∉[ts,te]au,au is historical data t∈[ts,te](24)

(3) Noise attack

Attackers target acquisition signals yi(t) or control signals ui(t) by constructing specific noises. It can affect or even change the state of the system, leading to system fluctuation and even process faults,

y^i(t)={yi(t)t∉[ts,te]yi(t)+ay,ay=ω′(t)t∈[ts,te],u^i(t)={ui(t)t∉[ts,te]ui(t)+au,au=υ′(t)t∈[ts,te](25)

(4) Scaling attack

Attackers collect the sensor signal, yi(t), or control signal, ui(t), and then scale up or down them with a certain range to change the actual system state, i.e.,

y^i(t)={yi(t)t∉[ts,te]ayyi(t)t∈[ts,te],ayyi(t)∈[yimin,yimax]yimint∈[ts,te],ayyi(t)<yiminyimaxt∈[ts,te],ayyi(t)>yimax,u^i(t)={ui(t)t∉[ts,te]auui(t)t∈[ts,te],auui(t)∈[uimin,uimax]uimint∈[ts,te],auui(t)<uiminuimaxt∈[ts,te],auui(t)>uimax(26)

4.1.2 Experimental Result Analysis

This section verifies the effectiveness of the proposed IVB-NCA-NLKF-based sensor system intrusion detection method by a numerical simulation system.

(1) Numerical system description and data preparation

Suppose the nonlinear system is expressed as follows,

y1(t1,t2)=u(t1)+sin⁡(u(t1))+ε(t2)u(t1)=t1+sint1,t1,t2≥0y2(t1,t2)=u(t1)2+cos⁡(u(t1))+ε(t2)u(t1)=t1+cost1,t1,t2≥0y3(t1,t2)=4u(t1)+3u(t1)2+ε(t2)u(t1)=t1+t12,t1,t2≥0y4(t1,t2)=2cos⁡(u(t1))+3u(t1)+ε(t2)u(t1)=t1+2cost1,t1,t2≥0y5(t1,t2)=exp⁡(u(t1))+2u(t1)2+ε(t2)u(t1)=t1+expt1,t1,t2≥0(27)

where y1,y2,y3,y4,y5 represent the five observational variables; ε is a Gaussian noise.

In the experiment, four groups of normal sample data are generated based on the system model in (27), forming four sensory clusters in the ICPS perceptual execution layer. Correspondingly, four attack modes are introduced as attack samples. These normal and attack samples constitute the initial training set, with each cluster containing 500 data samples.

Three different working modes (model 1, model 2 and model 3) are given. Each of the three modes produces 200 sets of samples as the initial training set,

model1={t1:Uniform(2,1.5)t2:Normal(0,0.1)(28)

model2={t1:Uniform(0,2)t2:Normal(0,0.1)(29)

model3={t1:Uniform(2,1)t2:Normal(0,0.1)(30)

Based on the normal working condition data, under three modes, the variables y1,y2,y3,y4,y5 of different attack signals are introduced from the 151st sampling data to the 350th sampling data. The DoS attacks and spoof attacks are added, respectively, that is, from the 151st to 350th group, and they are considered as samples with attack. From the 251st to the 401 sampling data, they have added the noise attack and the scaling attack, respectively.

As expressed in Eq. (20), the residual threshold τ is an important factor to the intrusion detection performance. In this work, τ is determined by crossing validation experiments. Multiple parameter values were tested. As can be seen from Fig. 7, to achieve a relatively high intrusion detection accuracy with low false alarm rate (FAR), the residual threshold τ=0.8 is a trade-off setting value. Therefore, the residual threshold was fixed as 0.8 in the following experiments.

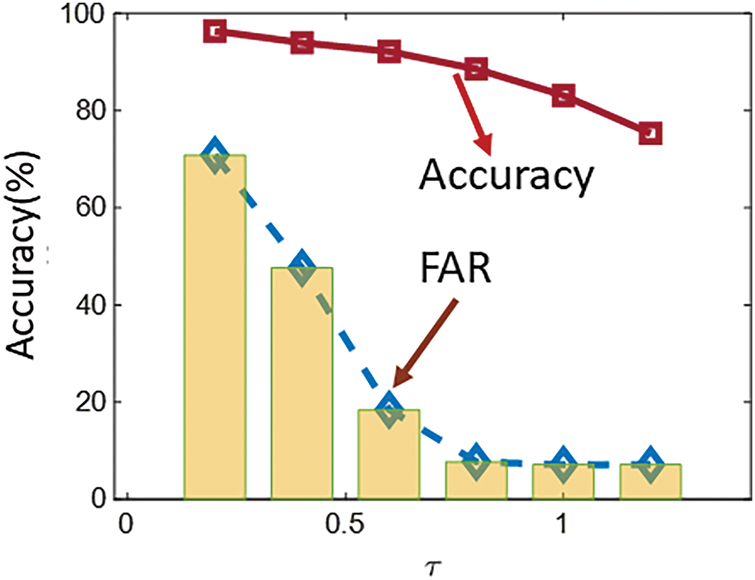
Figure 7: Effect of residual threshold τ

(2) Experimental results and discussions

Intrusion detection results of the simulated three models as described in (28) to (30) are displayed in Fig. 8. It can be seen from Fig. 8 that when attacks are introduced into the sensory system models (different clusters under each model), the system state fluctuations will occur. Though the system state fluctuations of the same attack vary under different models, they exhibit great differences between the system prediction results and the actual system state, resulting in a significant difference in the state estimation residual. By comparing the residual threshold of the system state prediction, attacks can be detected accurately.

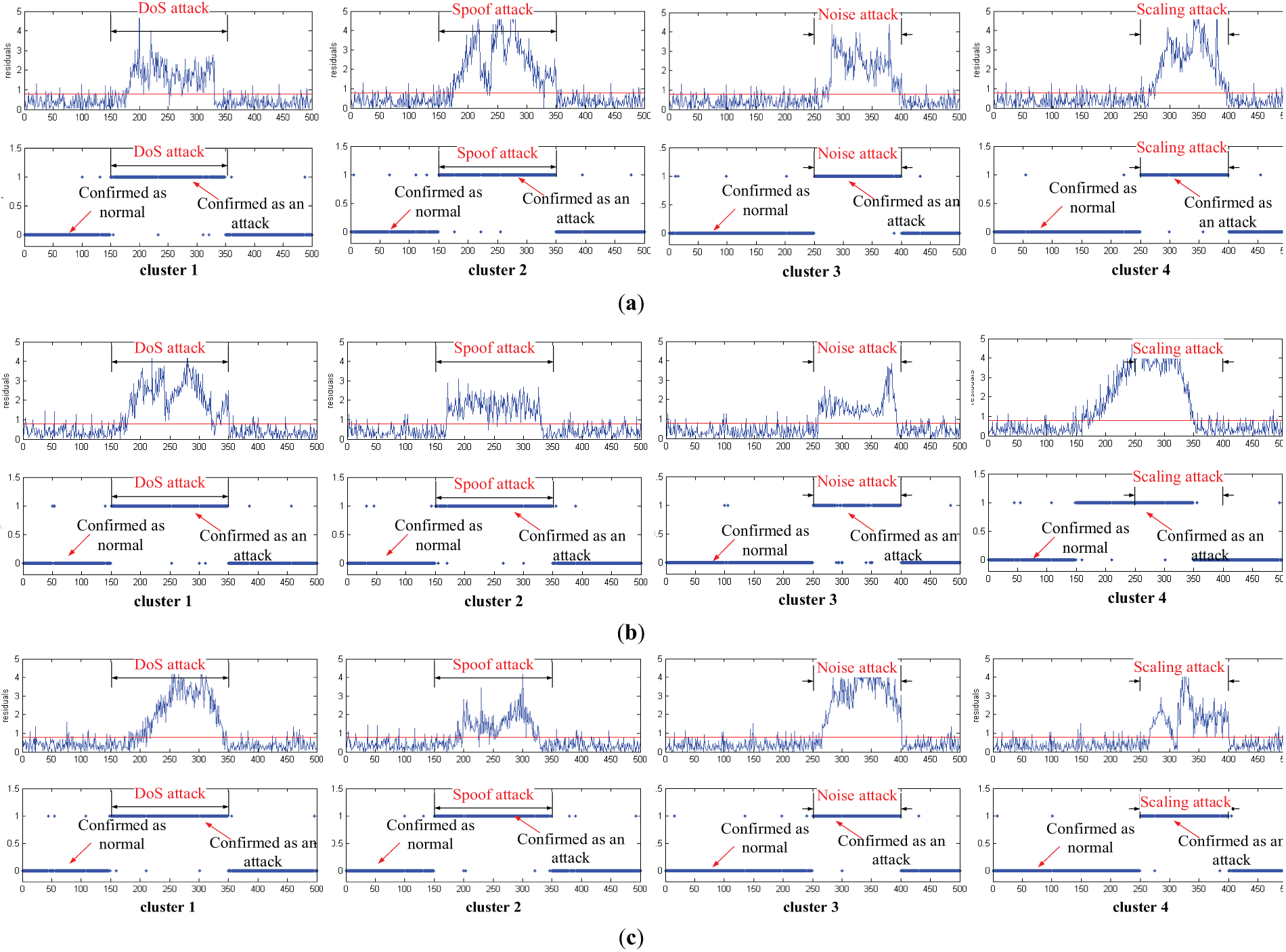
Figure 8: Experimental results of different models. (a) model 1; (b) model 2; (c) model 3

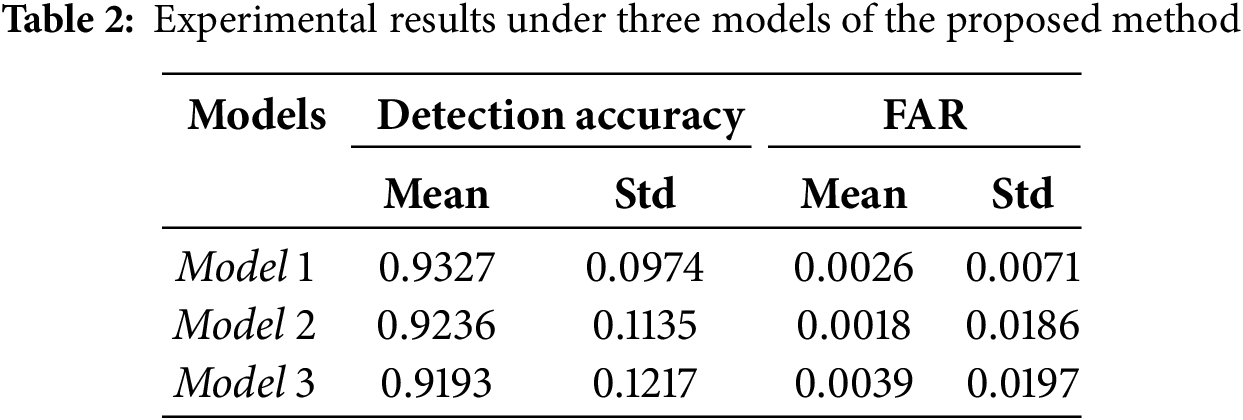
To further analyze the effectiveness of the proposed method, the intrusion detection accuracies and FARs of different clusters under each model are listed in Fig. 9. It can be seen from Fig. 9 that although the detection accuracy and FAR of different clusters fluctuate in different models, the accuracy rates are generally over 90%, and the proposed method can achieve lower FARs for different attacks with different models. In addition, statistics of the detection performance, mean and standard deviation of the detection accuracies and FARs under different models are counted and listed in Table 2. It can be seen from Table 2 that no matter the system model, a high detection rate and lower FAR can be achieved.

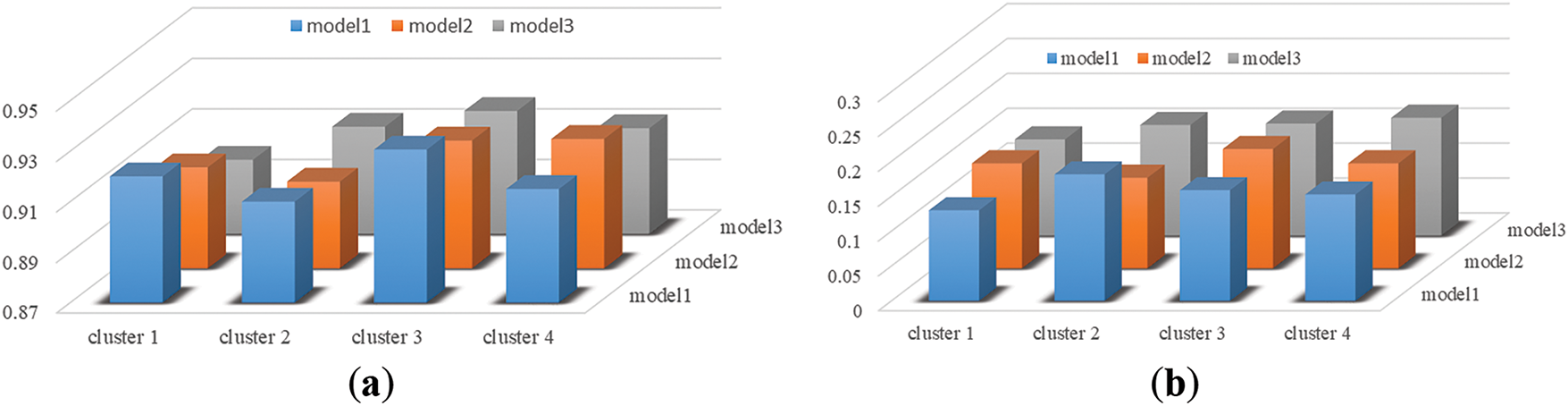
Figure 9: Detection accuracies and FAR. (a) Accuracies; (b) FAR

Moreover, to further verify the effectiveness of IVB-NCA-NLKF, three representative and analogous methods, namely, H∞-EKF [33], novel switching unscented Kalman filter (NS-UKF) [34], EKF and recursive last-square estimator (EKF-RLSE) [35], were used for the comparative experiment. The comparative results are listed in Table 3. As shown in Table 3, IVB-NCA-NLKF can achieve the highest detection accuracies with the lowest FAR. In addition, the proposed method can achieve relatively low standard deviation values of the detection accuracies and FAR, which means that the proposed method can achieve more stable detection results. In other words, the overall performance of the proposed method outperforms that of these comparative methods, which can realize effective intrusion detection of the sensory system.

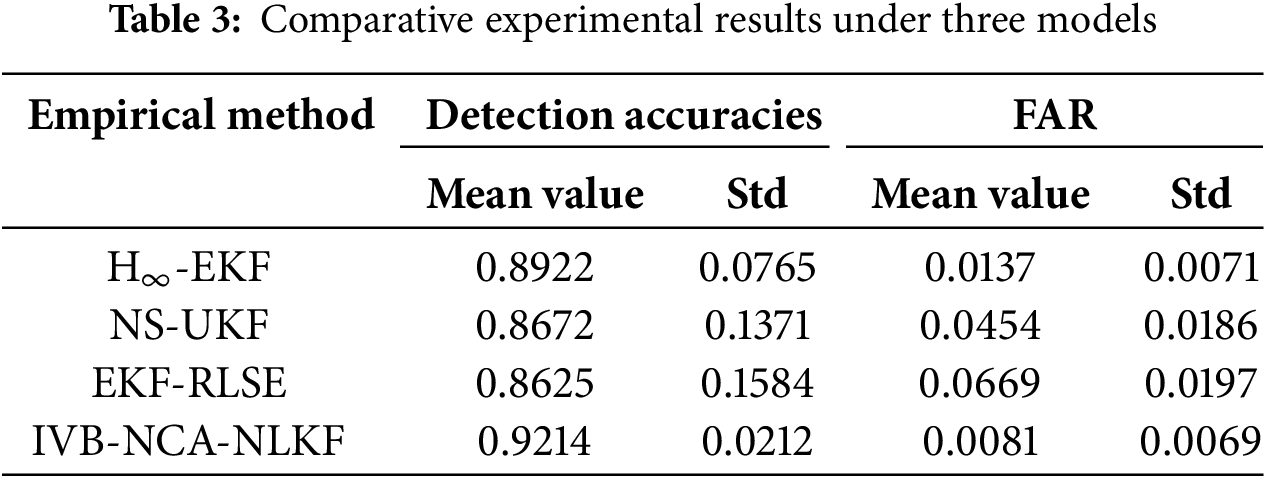
The IVB-NCA-NLKF method outperforms other methods due to several key advantages. First, the IVB-NCA-NLKF jointly estimates the system state, process noise, and measurement noise covariance matrices using variation inference based on sensor observations. This results in a more accurate and robust estimation of the system’s state, even in the presence of uncertainties or noise in both the process and the measurements. The adoption of Bayesian inference techniques in IVB-NCA-NLKF allows for adaptive noise covariance estimation, which improves the model’s ability to handle dynamic and uncertain environments. This flexibility is particularly beneficial in ICPSs, where both system dynamics and measurement noises can be highly nonlinear and unpredictable. Furthermore, the IVB-NCA-NLKF’s ability to extend traditional linear system models to nonlinear systems makes it more suitable for the intricate behaviors of ICPSs. Unlike previous linear models that may struggle with nonlinearities, the proposed method can effectively estimate the system state in more complex and realistic settings.

4.2 Network Traffic-Based Intrusion Detection

The TrueTime toolbox (https://www.control.lth.se/research/tools-and-software/truetime/, accessed on 2 April 2025) was used to build the simulated network control system for simulating an ICPS. Detailed parameters of the simulation environment are as follows: Version-TrueTime 2.0; Operating system-Windows 10; Processor−1.99 GHz; Running memory−8 GB; Network protocol-CSMA/CD (Ethernet).

The simulated ICPS involves interference nodes, sensors, controllers and actuators, whose network structure is illustrated in Fig. 10. The simulated process system model structure is shown in Fig. 11. Some important factors of network transmission, such as data transmission delay, packet loss, and so on, will affect the system performance of the process system. By setting the interference node and acting on the whole system, various attacks are simulated. In the ICPS network system, the greater the impact on network traffic, the greater the packet loss rate, the greater the impact on system performance. When the packet loss rate reaches a certain degree, the system will no longer be stable.

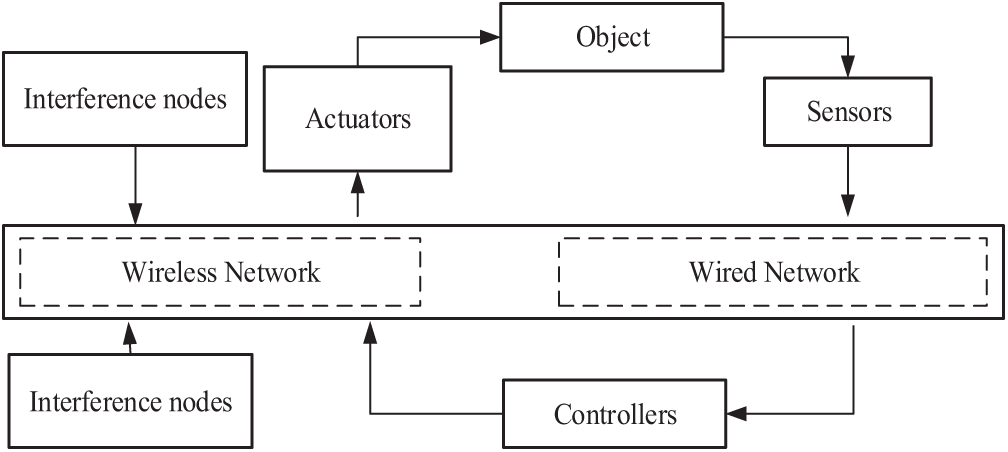
Figure 10: ICPS System block diagram

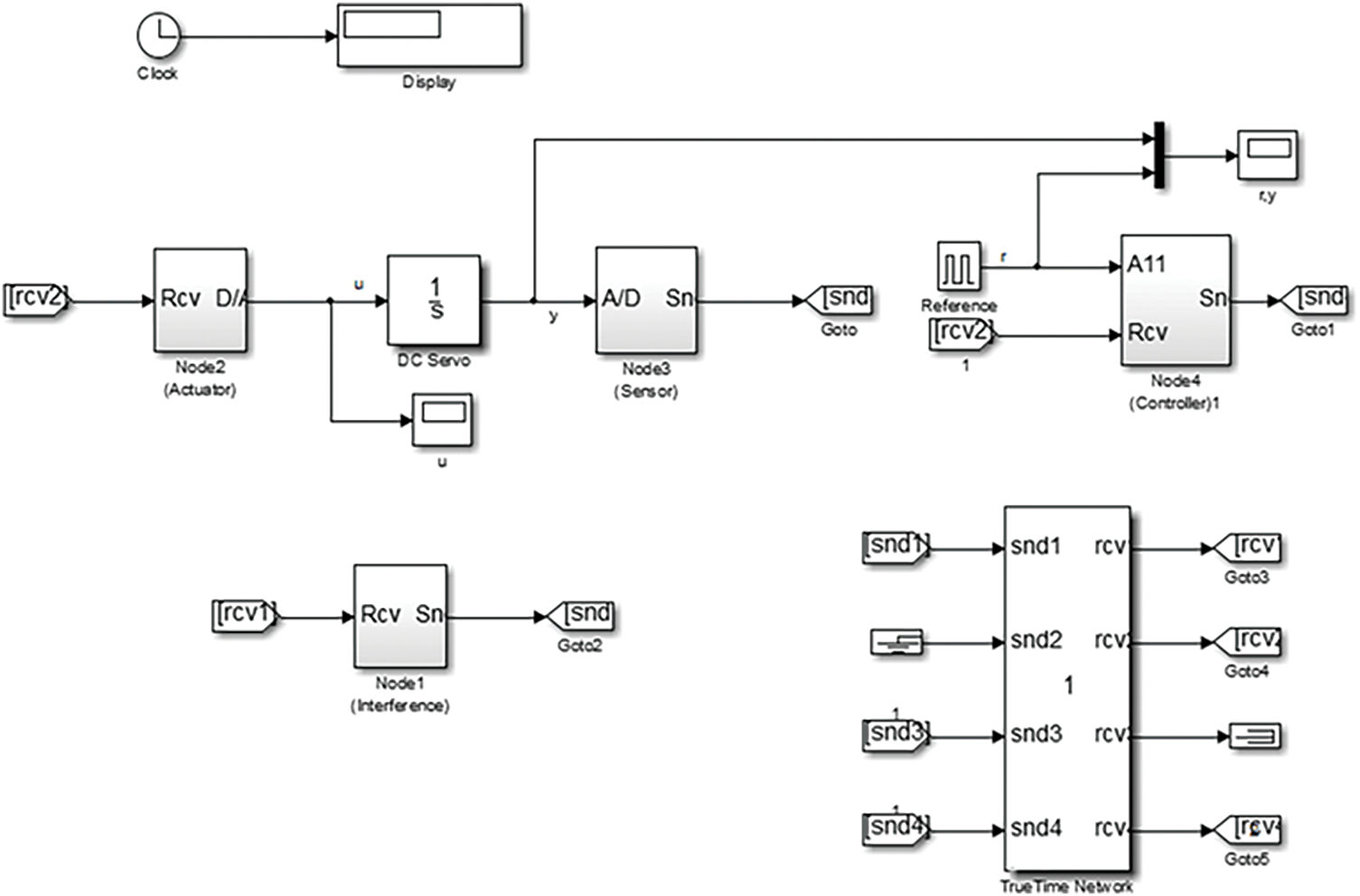
Figure 11: System simulation model

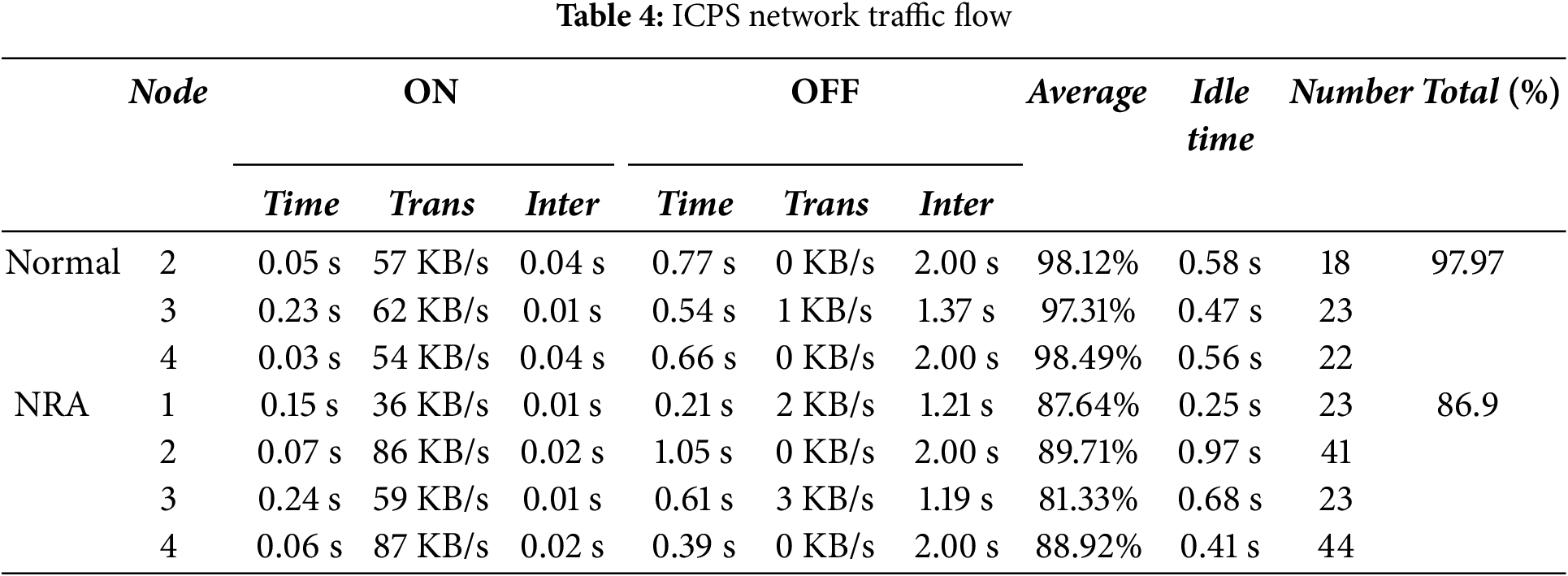
Table 4 presents the normal system state and real-time data obtained from the simulation after introducing a node replication attack (NRA) at the interference node (node 1). The results show that, compared to the normal state, the average flow through the actuator (node 2) and controller (node 4) increases after the NRA attack, prolonging the ON phase and shortening the OFF phase. Moreover, the NRA attack reduces the average transmission rate of packets in the sensor node (node 3) due to bandwidth occupation. This leads to decreased transmission efficiency and an increased sensor transmission rate during the OFF phase. Although no data is sent to the controller in the OFF phase, the presence of interference nodes adds to the communication burden, further straining the system.

To summarize, five common attacks, namely Man-In-The-Middle (MITM), Node Replication Attack (NRA), and Node Compromise Attack (NCA), DoS attack, and Node blocking attack, were tested to evaluate the effects of different attacks on network traffic. Experimental results are shown in Fig. 12. Fig. 12a shows the flow mode under normal conditions (no attack). Fig. 12b–d shows the network traffic flow mode after adding the corresponding attacks, respectively. It can be seen from Fig. 12 that the three attacks caused the packet loss rate of 0.1, 0.12, and 0.19, respectively, with different effects on the flow rate.

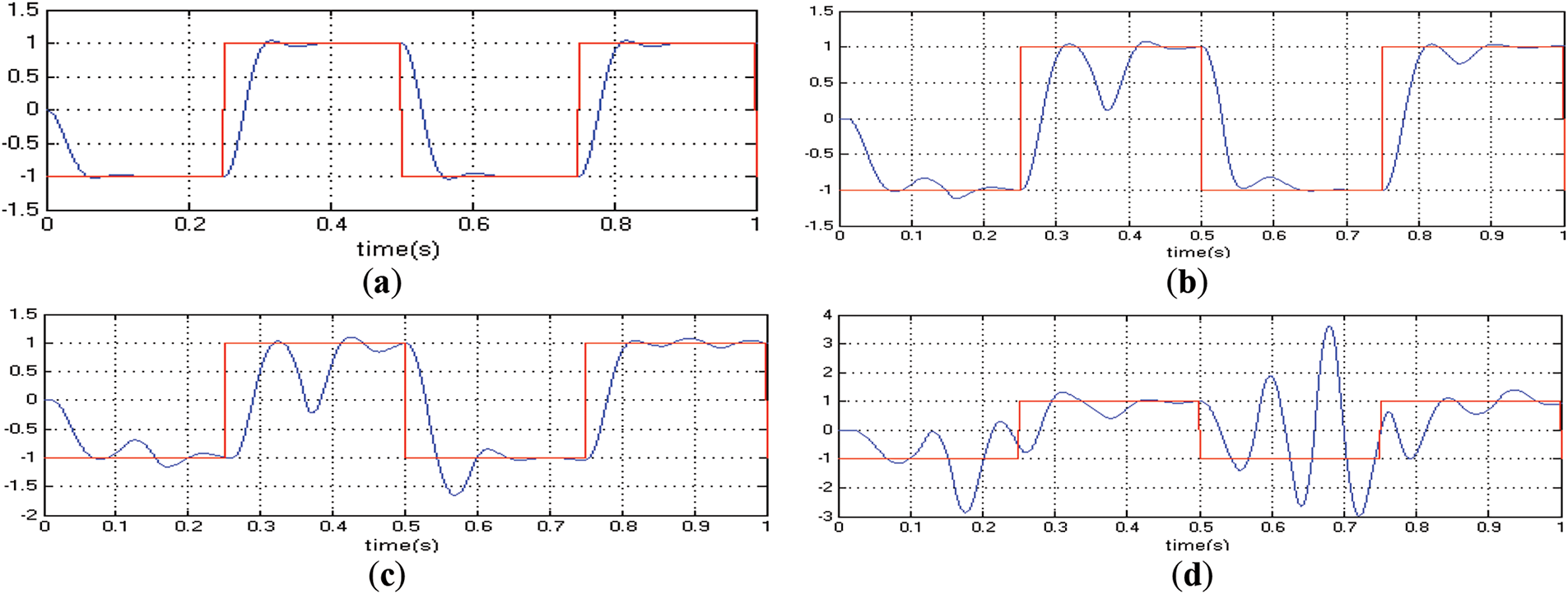
Figure 12: Impact of attacks on traffic. (a) Normal (no packet loss); (b) MITM (packet loss rate 0.1); (c) NRA (packet loss rate 0.12); (d) NCA (packet loss rate 0.19)

This experiment evaluates the detection rate and false alarm rate (FAR) of the proposed intrusion detection method, with results presented in Fig. 13. As shown, the detection rate improves as the number of training samples increases, stabilizing when the training data reaches 2000. Notably, even with fewer training samples, the model achieves a high detection rate. Additionally, the FAR decreases as training data increases, with lower FAR observed in cases of limited training data. These results demonstrate that the proposed method ensures high detection accuracy and low error rates, performing effectively even with small sample sizes.

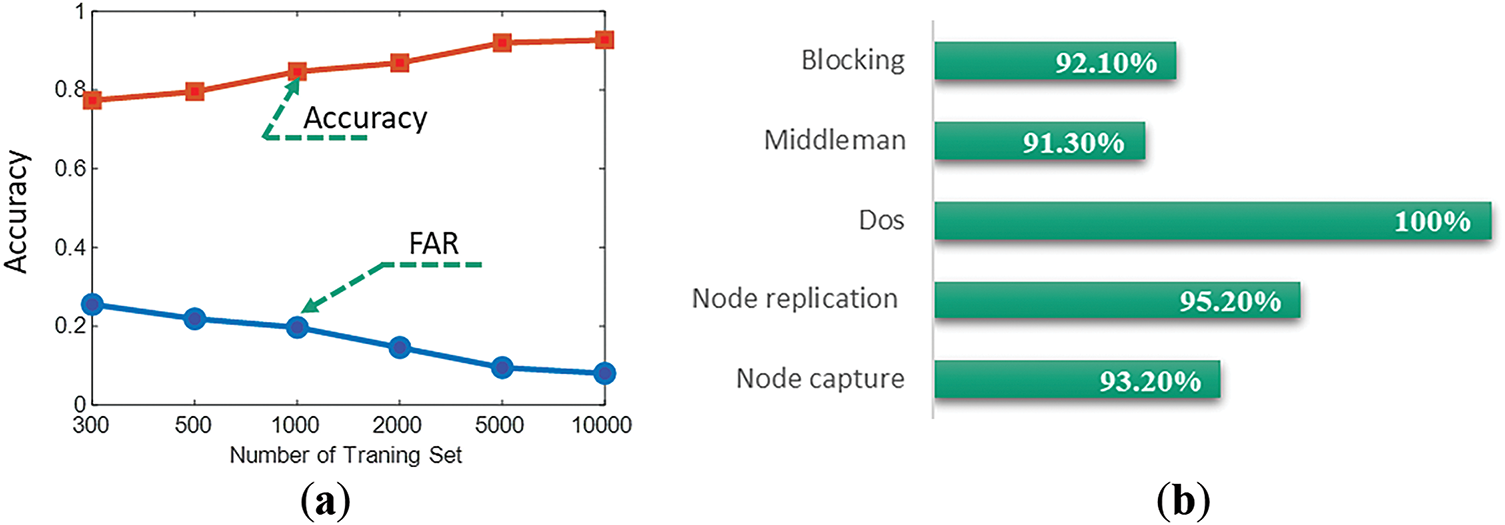
Figure 13: Relationship between detection effect and number of training sets. (a) Detection accuracy and FAR with different number of training samples; (b) Detection accuracies of different attacks

The detection results of the proposed method for different attacks are shown in Fig. 13b. As shown, the detection rates of other attacks are generally high, except in channel blocking attacks and middleman attacks because the traffic changes caused by these attacks are obvious and easy to detect. Channel-blocking attacks and middleman attacks have no great effect on traffic.

To further validate the effectiveness of the proposed intrusion detection method, some representative methods, including the CUSUM Model with Regression Strategy (CUSUM-RS) [36], Dictionary-based Compression Theory (DBCT) [37], and Hidden Semi-Markov Model (HSMM) [38], were also conducted for intrusion detection performance comparison. The detection rate (DR), FAR, and detection time (DT) are recorded as the comparison indexes. The comparative experimental results are shown in Table 5.

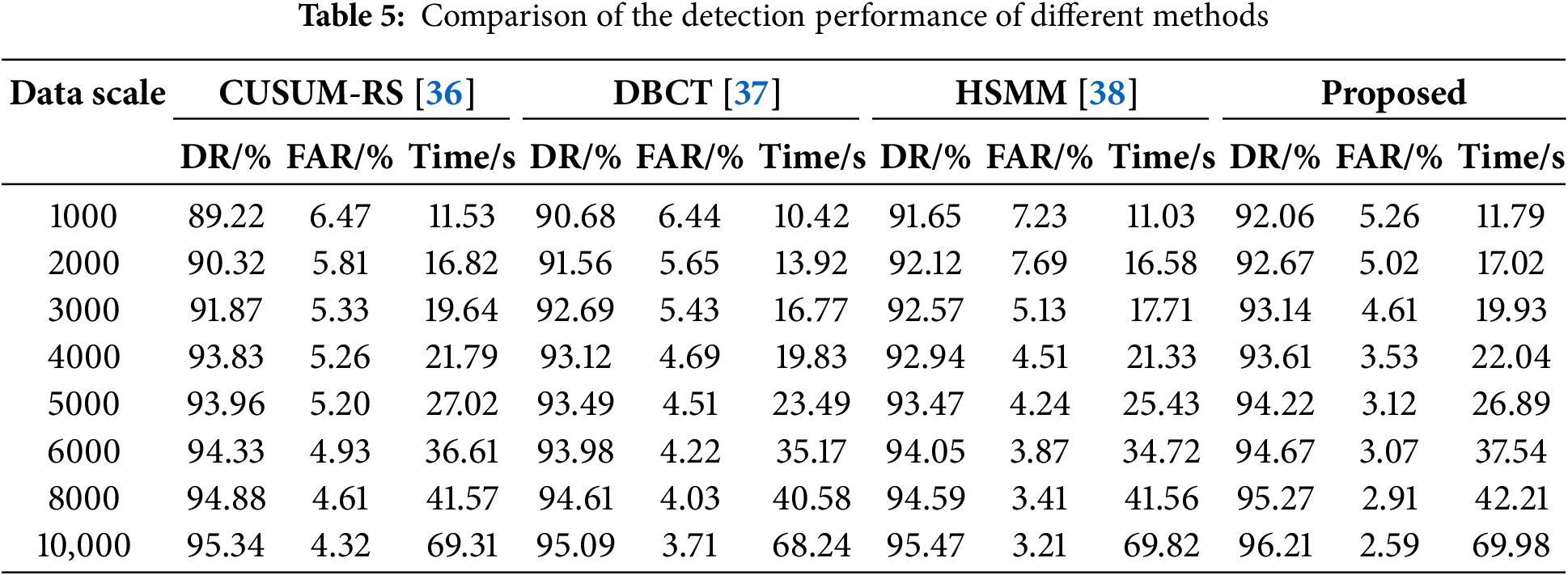
Table 5 shows that the FAR of HSMM is higher than that of the proposed method. Although HSMM outperforms simple average-based schemes, it struggles to effectively differentiate between attacks and normal traffic. Its reliance on detecting spatiotemporal patterns in wake-up packet generation leads to a higher FAR. In contrast, the proposed intrusion detection method achieves higher accuracy than CUSUM-RS and DBCT. By analyzing captured data, it simultaneously extracts node-level and network-level traffic, providing a more comprehensive understanding of data characteristics and enhancing detection performance.

Beyond detection accuracy, detection efficiency is also crucial, as it directly impacts real-time performance. To ensure the real-time performance of the detection method, the detection efficiency should also be maintained at a high level. As shown in Table 5, when the sample size reaches 10,000, the detection time is only 69.98 s, demonstrating the proposed method’s ability to detect attacks rapidly. While the detection time is slightly higher than that of other methods, this is due to the inclusion of CPL for dynamic network pattern learning and updating, which primarily adds time when a pattern does not match normal or abnormal cases. The system determines whether a pattern is frequent before updating the pattern library. However, given the high detection accuracy and low false alarm rate (FAR), this slight increase in detection time is negligible. Overall, the experimental results confirm that the proposed method achieves a high detection rate with relatively short detection time, proving its effectiveness for cybersecurity monitoring in ICPS networks.

5  Conclusions

To adapt to the dynamic changes of the industrial control network system environment and improve the detection effect, a hybrid ICPS-oriented intrusion detection approach is proposed. In order to detect ICPS attacks more comprehensively, intrusion detection is carried out from two aspects, i.e., the system state anomaly monitoring and network traffic flow anomaly monitoring. Namely, an IVB-NCA-NLKF-based sensor system state anomaly detector and an online network pattern learning-based network traffic anomaly detector, are incorporated, to achieve a comprehensive cybersecurity monitoring of large-scale ICPSs. At the same time, an online pattern updating mechanism is also introduced to adjust the model automatically during the intrusion detection process to realize real-time cybersecurity monitoring. Extensive confirmatory and comparative experiments carried out by the numerical simulation system and TrueTime-based simulated network control system have demonstrated the effectiveness and superiority of the proposed method. However, the proposed ICPS security protection method in this work is based on the situation that the system is deterministic. In the current large-scale ICPS, sensors, actuators, and controllers are all likely to be dynamically added. Therefore, further work will focus on how to extend the method of this work to the system resources-dynamically changing ICPS and the real ICPSs.

Acknowledgement: Not applicable.

Funding Statement: This work is supported by the National Natural Science Foundation of China (NSFC) under grant No. 62371187 and the Hunan Provincial Natural Science Foundation of China under Grant Nos. 2024JJ8309 and 2023JJ50495.

Author Contributions: Conceptualization, Jinping Liu and Wuxia Zhang; methodology, Junbin He, Guangyi Yang and Jinping Liu; software, Wuxia Zhang and Guangyi Yang; formal analysis, Wuxia Zhang; investigation, Junbin He, Wuxia Zhang and Jinping Liu; resources, Wuxia Zhang, Guangyi Yang and Xianyi Liu; data curation, Xianyi Liu; writing—original draft preparation, Jinping Liu, Wuxia Zhang and Xianyi Liu; writing—review and editing, Jinping Liu and Wuxia Zhang; funding acquisition, Jinping Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A IW Distribution

Inverse Wishart (IW) distribution, also termed inverted Wishart distribution, is a probability distribution model defined over real-valued, symmetric, positive-definite matrices. In the Bayesian estimation, it is mainly used to describe the conjugate prior distribution of the covariance matrix of multivariate normal distribution samples. The probability density of IW distribution can be expressed as [14],

IW(R|λ,D)=|R|−(λ+d+1)/2ZIWexp⁡{−12tr(DR−1)}(A1)

where R are d×d symmetric positive definite matrices; D∈Rd×d is a symmetric positive definite matrix, also known as an inverse scale matrix; tr(⋅) means the trace of a matrix; λ stands for the degrees of freedom, and ZIW=2λd/2Γd(λ/2)|D|−λ/2, Γd is a d-D Gamma function.

When λ>d+1, the IW distribution has the following properties,

E[R]=Dλ−d−1(A2)

The variance of each element of R is,

var[Rij]=(λ−d+1)Dij2+(λ−d+1)DiiDjj(λ−d)(λ−d−1)2(λ−d−3)(A3)

Given n i.i.d d-D Gaussian variables, X=[X1,⋯,Xn], drawn from the distribution of 𝒩(X|0,R), the conditional distribution of p(R|X) has an IW distribution of IW(R|λ+n,A+D), where A=XXT. Due to its conjugacy to the multivariate Gaussian, it can integrate out the covariance parameter in Gaussian by,

p(X|λ,D)=∫p(X|R)p(R|λ,D)dR=|R|λ/2Γλ(n+λ2)πnd2|R+A|n+λ2Γλ(λ2)(A4)

Appendix B Detailed q(xk),q(Σk|k−1),q(Rk) Estimation Procedure

Firstly, by the expansion of the Formula (18), we can achieve,

log⁡p(xk,Σk|k−1,Rk,y1:k)=−12(d^k|k−1+m+2)log⁡|Rk|−12tr(Dk|k−1Rk−1)−12(t^k|k−1+n+2)log⁡|Σk|k−1|−12tr(Tk|k−1Σk|k−1−1)−12(xk−x^k|k−1)TΣk|k−1−1(xk−x^k|k−1)−12(yk−y^k|k−1)TRk−1(yk−y^k|k−1)+Cθ(A5)

where Cθ represents terms that do not related to parameters, θ={xk,Σk|k−1,Rk}.

(1) q(Σk|k−1) Estimation

Denote θ=Σk|k−1, according to the Formula (17), we can achieve,

log⁡q(i+1)(θ)=−12(d^k|k−1+m+2)E(i)[log⁡|Rk|]−12E(i)[tr(Dk|k−1Rk−1)]−12(t^k|k−1+n+2)log⁡|Σk|k−1|−12tr{(Ak(i)+Tk|k−1)Σk|k−1−1}−12E(i)[(yk−y^k|k−1)TRk−1(yk−y^k|k−1)]+Cθ=CΣk|k−1+12(t^k|k−1+n+2)log⁡|Σk|k−1|−12tr{(Ak(i)+Tk|k−1)Σk|k−1−1}(A6)

where q(i+1)(θ) represents the i+1 iteration of q(θ) estimation, and,

Ak(i)=E(i)[(xk−x^k|k−1)(xk−x^k|k−1)T]=E(i)[(xk−x^k(i)+x^k(i)−x^k|k−1)(xk−x^k(i)+x^k(i)−x^k|k−1)T]=E(i)[(xk−x^k(i))(xk−x^k(i))T]+(x^k(i)−x^k|k−1)(x^k(i)−x^k|k−1)T=Σk|k(i)+(x^k(i)−x^k|k−1)(x^k(i)−x^k|k−1)T(A7)

According to the Formulae (A6) and (A1), we can see that q(i+1)(Σk|k−1) also obey an IW distribution, i.e.,

q(i+1)(Σk|k−1)=IW(Σk|k−1|t^k(i+1),Tk(i+1))(A8)

where t^k(i+1)=Δ t^k|k−1 + 1, Tk(i+1) =Δ Ak|k−1(i) + Tk|k−1.

(2) q(Rk) Estimation

log⁡q(i+1)(Rk)=−12(d^k|k−1+m+2)log⁡|Rk|−12tr((Dk|k+Bk(i))Rk−1)−12(t^k|k−1+n+2)E(i)[log⁡|Σk|k−1|]−12E(i)[tr(Tk|k−1Σk|k−1−1)]−12E(i)[(xk−x^k|k−1)TΣk|k−1−1(xk−x^k|k−1)]+Cθ=CRk+12(d^k|k−1+m+2)log⁡|Rk|−12tr((Dk|k−1+Bk(i))Rk−1)(A9)

where,

Bk(i)=E[(yk−y^k|k−1)(yk−y^k|k−1)T]=E{E(yk−h(x^k|k−1)−Hkxk+Hkx^k|k−1)⋅(yk−h(x^k|k−1)−Hkxk+Hkx^k|k−1)T}=E{E(yk−Hkxk|k(i)+Hkxk|k(i)−Hkxk+Hkx^k|k−1−h(x^k|k−1))⋅(yk−Hkxk|k(i)+Hkxk|k(i)−Hkxk+Hkx^k|k−1−h(x^k|k−1))T}=(yk−h(x^k|k−1))(yk−h(x^k|k−1))T+HkΣk|k(i)HkT(A10)