ONTDAS: An Optimized Noise-Based Traffic Data Augmentation System for Generalizability Improvement of Traffic Classifiers

1  Introduction

Network traffic is an important carrier of Internet data which contains a lot of valuable information. Traffic classification can classify network traffic into specific categories and enable effective analysis and handling. Therefore, traffic classification plays an important role in many fields, such as joint cloud computing monitoring, Internet of Vehicles, and cyberspace security. Especially in cyberspace security, it is necessary to identify malicious traffic for network anomaly detection [1,2].

In recent years, many traffic classification methods have been developed for different application scenarios. The existing methods fall mainly into four types: port-based, payload-based, machine learning-based, and deep learning-based [3–5]. Classic port-based methods achieve good performance in applications that use specific port numbers, but now they are rarely reliable due to dynamic port allocation [6]. Payload-based methods rely on payload or data packet inspection (DPI), and focus on patterns or keywords in these data. Since encrypted traffic contains less constant features and discriminative patterns, these methods are only suitable for unencrypted traffic [7,8]. Machine learning-based methods are developed to overcome this problem. Researchers select features that reflect the characteristics of traffic and train classical machine learning algorithms for classification [9]. However, the quality of features largely limits the performance of these methods. Compared to machine learning-based methods, deep learning-based methods can automatically perform feature extraction from large amounts of traffic data and select the optimal feature combination. They also have high learning capacity for the non-linear relationship between the original input traffic and the corresponding output categories [10].

As more attackers utilize encryption technology to hide traffic content, learning-based methods are increasingly appealing for traffic classification [11]. However, traffic in real-world network environments often differs from that in datasets. Models are required not only to correctly classify known traffic, but also to have sufficient generalizability to deal with unknown malicious traffic. As a result, learning-based methods need large amounts of labeled data for model training, while collecting and correctly labeling traffic is time-consuming and requires massive manual work [12]. Moreover, it is much more difficult to collect malicious samples than benign samples. The resulting imbalanced category distribution has posed serious challenges. Traffic classifiers trained by imbalanced datasets lead to anomalously high recognition for specific categories [13]. In addition, the rapid evolution of attack techniques makes current datasets obsolete, even combining different datasets does not yield sufficient diversification.

These issues make data augmentation an ideal solution. Data augmentation aims to improve the size and diversity of datasets by generating new data points or entirely new samples [14]. Data augmentation has been widely used in computer vision and natural language processing. However, classical methods in these fields cannot be directly applied to traffic data augmentation. Unlike image and natural language, traffic features are highly heterogeneous. Unlike pixels and words, traffic data have different physical meanings [15]. In order to apply data augmentation to traffic data, this paper proposes a novel optimized noise-based traffic data augmentation system, ONTDAS. This system uses optimized noise for traffic data augmentation. Its advantages include:

1.    The system uses optimized noise for data augmentation. Optimized noise can enrich datasets, prevent traffic classifiers from overfitting, and improve their generalizability when dealing with unknown malicious traffic.

2.    A noise conversion module generates classical noise from special distributions and transforms it into converted noise. Subsequently, an noise optimization module optimizes the converted noise in terms of shape and scale. These two modules enable the noise to adapt to different traffic features and ensure that the noised samples follow the distribution of original samples.

3.    By synthesizing noised samples, the system expands the size of datasets. These noised samples are labeled as malicious and combined with original samples for training. This approach helps traffic classifiers fully learn the category boundary.

4.    An improved bagging algorithm calculates the weights of trained base traffic classifiers according to their precision and integrates all classification results. This balances the performance between benign and malicious samples, and further improves the generalizability.

The remainder of this paper is organized as follows. Section 2 reviews important and recent learning-based methods of traffic classification, as well as data augmentation, bagging algorithms, and noise injection. Section 3 offers a thorough introduction to ONTDAS. Section 4 presents the experimental results. Section 5 proposes possible future directions for work based on ONTDAS. Section 6 concludes the paper.

2  Related Work

2.1 Machine Learning-Based Traffic Classification Methods

Machine learning-based methods do not require complex analysis on traffic data. They can be well applied to both encrypted and unencrypted traffic classification. Ma et al. [16] propose an improved K-Nearest Neighbors (KNN) to weight the features, and further establish a three-layer framework for encrypted traffic classification. Zhang et al. [17] propose an encrypted traffic classification scheme employing Random Forest (RF) for imbalanced learning, which balances the number of majority class and minority class by traffic features selection. Draper-Gil et al. [18,19] publish the ISCX VPN-nonVPN and ISCX Tor-nonTor datasets and use machine learning models such as C4.5 decision tree and KNN to perform encrypted traffic classification. Shafiq et al. [20] make a systematic review on machine learning-based methods step by step and apply four machine learning models, Bayes Net, C4.5 decision tree, Naive Bayes and SVM for comparative analysis.

2.2 Deep Learning-Based Traffic Classification Methods

Compared to machine learning-based methods, deep learning-based methods can automatically perform feature selection through training. Adaptive Clustering based Intrusion Detection (ACID) [11] uses a novel adaptive clustering algorithm to learn low-dimensional representations of traffic features. This model resolves the challenge of traffic classifiers’ sensitivity to slight changes in traffic features. Huang et al. [21] propose an encrypted malicious traffic classification method, which captures global semantic features through the Bidirectional Encoder Representations from Transformers (BERT) model and extracts local spatiotemporal features through the Bidirectional Gated Recurrent Unit (BiGRU) model and the Text Convolutional Neural Network (TextCNN) model. The fusion of these features serves as the final representation of malicious traffic. Hong et al. [22] construct attribute KNN graphs based on encrypted traffic and employ the Graph SAmple and aggreGatE (GraphSAGE) to detect malicious traffic. Pan et al. [23] employ graph convolution network and Long-Short Term Memory (LSTM) to extract spatial and temporal features from network flow data, and further propose a traffic classification model based on these features.

2.3 Data Augmentation

Data augmentation can increase the size and diversity of datasets by adding synthetic samples and has been widely used in traffic classification. Li et al. [24] propose an abnormal traffic detection method based on a novel Denoise AutoEncoder-Generative Adversarial Network (DAE-GAN) model. This method employs multiple DAEs to perform efficient data augmentation. Hajaj et al. [14] propose an innovative data augmentation system which relies on the LSTM model to create data points. This system can significantly enrich the dataset and improve classification efficiency. Rapier [25] fully utilizes different distributions of normal and malicious traffic in the sample space to correct label noise and address the problem of low-quality dataset. Liu et al. [10] propose a data augmentation scheme based on the Variational AutoEncoder (VAE) to address the dataset imbalance, the model learns the probability distribution of real traffic and generates reconstructed traffic to enhance the number of minority samples. Qing et al. [26] propose a attention-based Synthetic Minority Over-sampling Technique (SMOTE) to improve the generalizability in DDoS detection tasks.

2.4 Bagging Algorithms

The main idea behind bagging algorithms is using a combination of multiple models instead of a single model to improve the performance. They are very efficient and powerful in improving the stability and generalizability of traffic classifiers. Chowdhury et al. [27] propose a novel network intrusion detection system, which uses the decision tree-based bagging ensemble algorithm and Moth Flame Optimization (MFO) algorithm to detect malicious traffic. Wang et al. [28] propose a highly accurate and robust traffic classification model based on an ensemble learning framework, in which three Convolutional Recurrent Neural Networks (CRNN) are integrated into the bagging to train traffic classifiers using only small-scale datasets. Xu et al. [29] use bagging algorithm to combine three types of base neural network and form a strong traffic classifier. These networks are trained separately, and the final prediction result is determined by weight voting.

2.5 Noise Injection

Noise injection, as a classical data augmentation method, is able to inhibit overfitting in models and provide more generalization. Liu et al. [30] introduce a noise-based data augmentation method to improve model’s generalizability towards unknown malicious inputs in black-box test settings. The noise used for augmentation is composed of Gaussian noise and Salt-and-Pepper noise. Bilali et al. [31] employ adaptive boosting models and noise-based data augmentation to overcome the limitation of predicting the faecal coliform using small datasets. The data augmentation module significantly improve the generalizability. Khadidja et al. [32] use Synthetic Minority Over-sampling Technique (SMOTE) and the additive noise to improve model’s performance in malware identification. The noise is composed of Gaussian noise, Laplacian noise and Poisson noise. Xiao et al. [33] calculate the pathwise stochastic gradient estimate regarding the standard deviation of Gaussian noise added to each neuron of the network, in order to optimize the noise distribution and obtain the optimal model parameters during training to improve robustness and maintain original performance. Duan et al. [34] optimize the level of injected noise by gradient descent to obtain a wide range of useful activation functions and improve the generalizability of neural networks. Wang et al. [15] employ two searching algorithms to generate optimized smoothing noise and propose a general robustness certification framework for deep learning-based traffic analysis systems.

In summary, most existing data augmentation systems address the hot issues in traffic classification, such as correcting label noise and alleviating dataset imbalance. Generalizability is merely an additional benefit brought by these systems. There are also some studies that inject fixed noise into samples. However, the magnitudes of noise are not manually controlled, but set in an arbitrary manner, which requires a lot of work to strike a balance between original task performance and generalizability. In addition, researchers are also committed to adding optimized noise to the model. This approach is limited by the structure of traffic classifiers and completely ignores the potential role of samples. The system we proposed focuses on generalizability improvement and innovatively optimizes noise based on training samples. The optimized noise is injected into samples rather than models for data augmentation. As a result, it can effectively solve the above problems.

3  Methodology

3.1 System Architecture

In this paper, we introduce the ONTDAS for data augmentation of network traffic. ONTDAS mainly includes three modules: noise conversion, noise optimization, and ensemble learning. Fig. 1 illustrates the framework of ONTDAS.

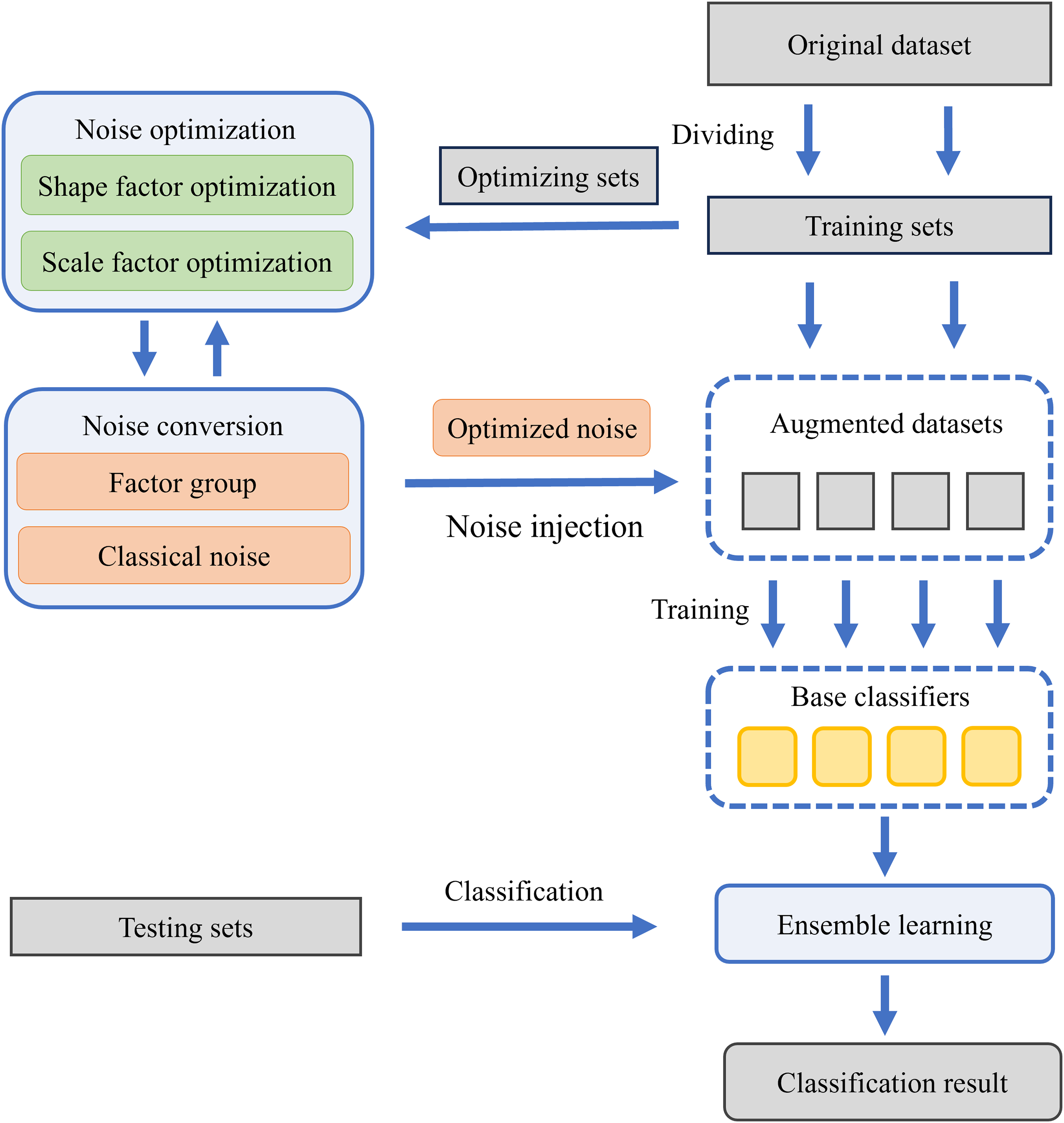
Figure 1: Framework of ONTDAS

In the noise conversion module, isotropic classical noise is generated from three symmetrical distributions. Subsequently, the noise is transformed into anisotropic noise through a conversion formula. The formula uses the shape factor to represent the relative noise distributions between different dimensions and the scale factor to represent the overall scale of noise distributions in all dimensions. Significantly, these factors serve as weights to superimpose the classical noise from different distributions in the form of a weighted linear sum.

The converted noise is optimized separately in terms of shape and scale. The shape factors are determined by a gradient-based searching algorithm. The scale factors are determined by the improved Bayesian optimizer Heteroscedastic Evolutionary Bayesian Optimization (HEBO) [35]. The combination of shape factors and scale factors, called a factor group, is collected after optimization. Significantly, there are some differences between the optimization of scale factors for benign samples (benign scale factors) and malicious samples (malicious scale factors). For benign scale factors, the original dataset is divided into multiple sub datasets before optimization, and each sub dataset is used for independent optimization. For malicious scale factors, multiple superior factors are collected after optimization instead of the single optimal factor. These strategies allow for the acquisition of multiple factor groups from a single dataset. These factor groups are then applied to the conversion formula to obtain optimized noise. The optimized noise is injected into original samples for data augmentation.

The ensemble learning module treats noised samples as pseudo-malicious samples and combines them with original samples. Subsequently, multiple base traffic classifiers are trained on these samples. An improved bagging algorithm calculates these traffic classifiers’ weights based on their precision, and integrates them into a strong traffic classifier. The details of ONTDAS will be explained in the following sections.

3.2 Noise Conversion

Traditional noise-based data augmentation simply adds the same noise to all features, regardless of their diversity, which is not flexible enough to handle high-dimensional traffic data. The noise conversion module generates classical isotropic noise from three symmetrical distributions, and converts it into anisotropic noise by dimension. Each dimension of noise is added separately to the corresponding feature. This strategy enables the converted noise to adapt to the diverse distributions of features, improves its representation capability for different physical meanings, and ensures that the noised samples can be more realistic. The framework of noise conversion module is shown in Fig. 2.

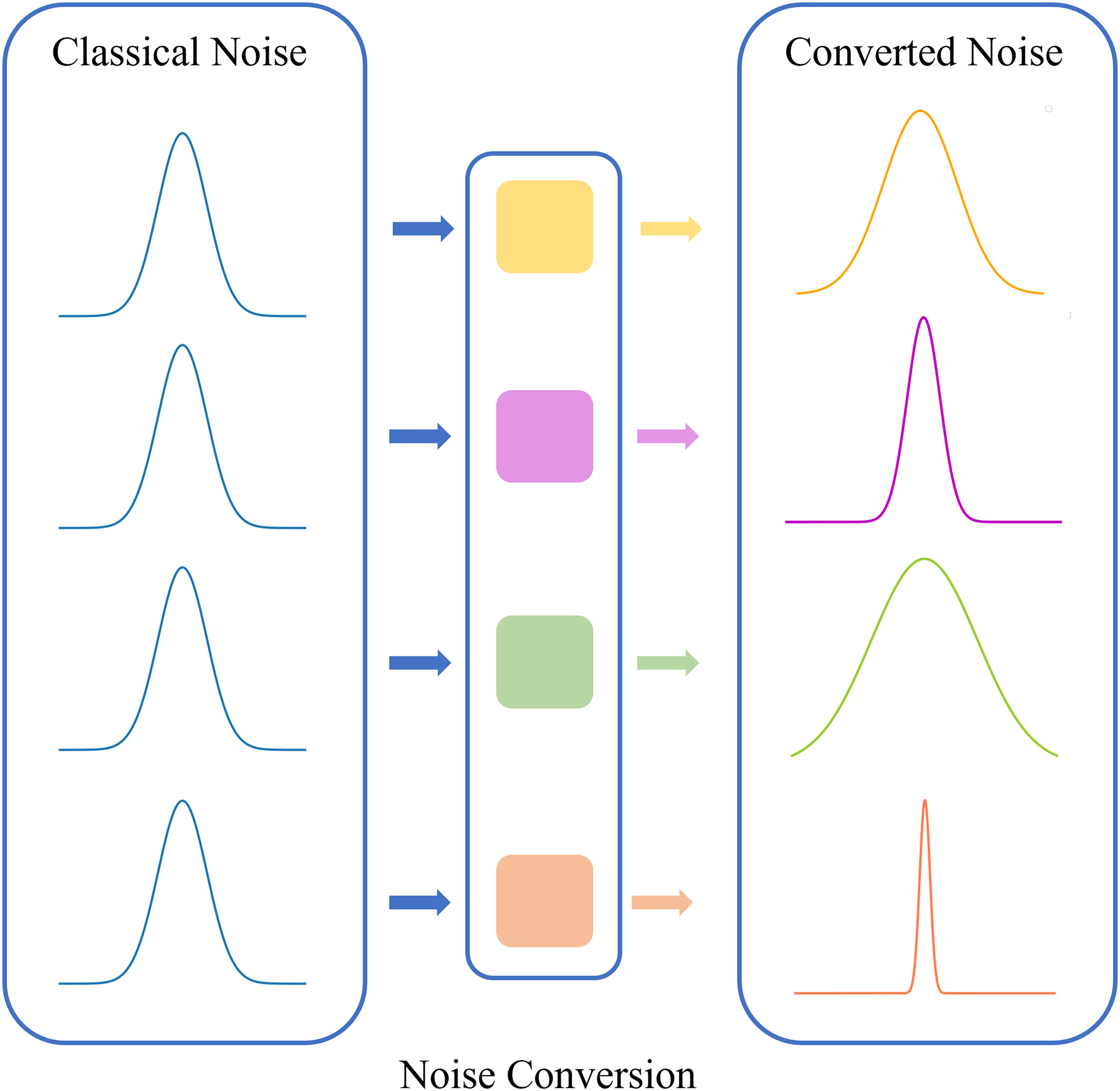
Figure 2: Framework of noise conversion

Given the original sample x and the additive noise ε, the noised sample xn can be defined as:

(1)xn=x+ε(1)

Consider that classical isotropic noise follows the distribution Dc, and converted anisotropic noise follows the distribution Do, the noise conversion formula can be defined as a map from classical noise to converted noise. Thus, the overall conversion formula is:

(2)εo=Ψ(εc)(2)

where εc is the classical noise, εo is the converted noise, Ψ is the overall conversion.

Suppose that the number of features is Nf and the number of special distributions is Nd, the detailed conversion formula for the i-th dimension of noise is as follows:

(3)Ψ(εci)=t⋅∑d=1Nd(wsd+wii,d)(Fsd)−1(Fc(εci)), i=1,2…,Nf(3)

where εci is the i-th dimension of classical noise added to the i-th feature, t is the weight parameters shared by all special distributions in all dimensions, wsd is the weight parameters shared by the d-th special distribution in all dimensions, wii,d is the weight parameters only used by the d-th special distribution in the i-th dimension independently, Fsd is the cumulative distribution function of the d-th special distribution, Fc is the cumulative distribution function of the standard normal distribution.

Among the above parameters, wsd and wii,d compose the trainable shape factors, and t represents the trainable scale factor. These factors will be optimized in the following module.

3.3 Noise Optimization

Noise optimization module uses a searching algorithm to optimize the shape factor and an improved Bayesian optimizer to optimize the scale factor. The optimized noise ensures that the noised samples can simulate real samples, enables traffic classifiers to learn a more general boundary between benign and malicious samples. The framework of noise optimization module is shown in Fig. 3.

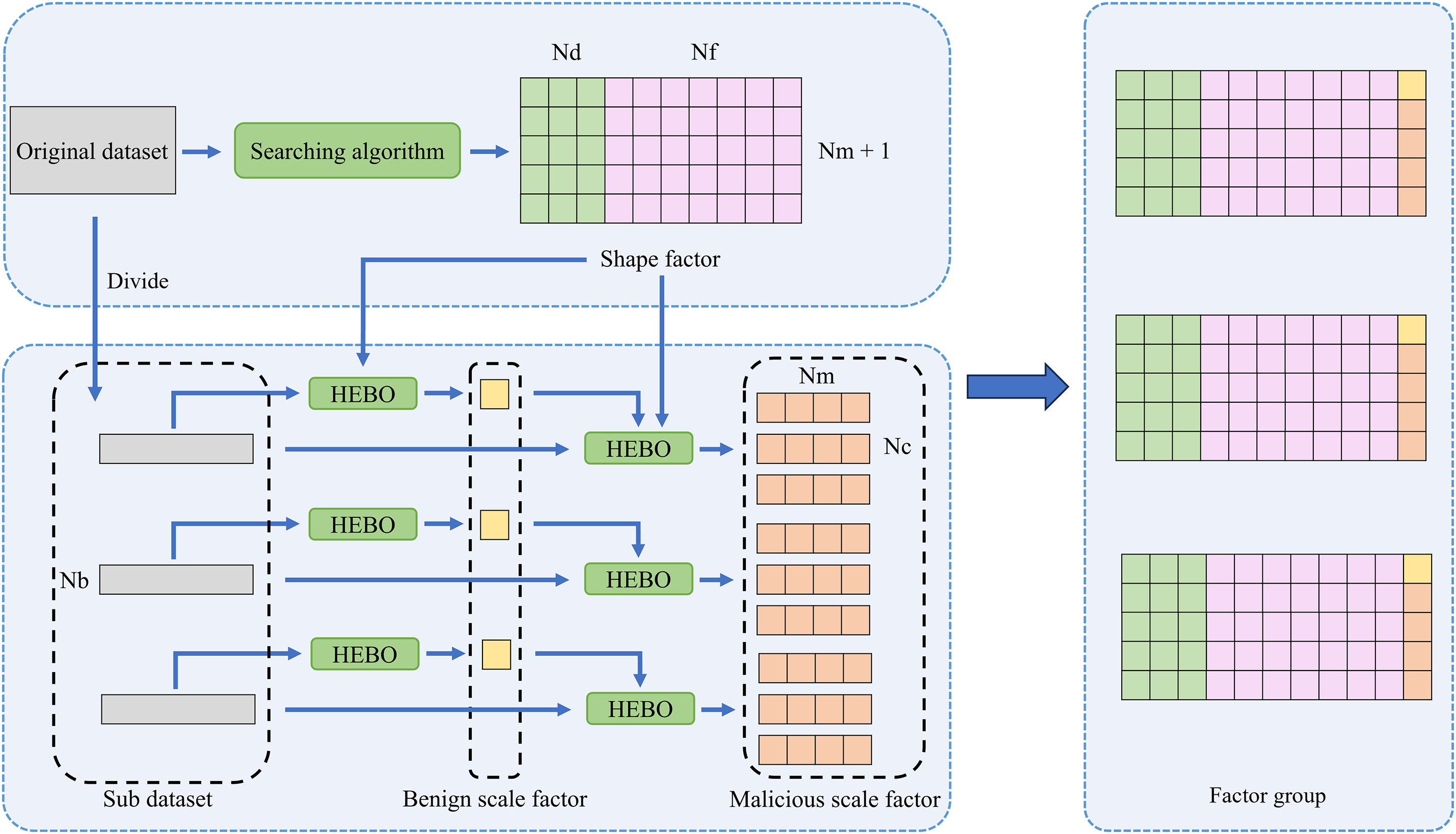
Figure 3: Framework of noise optimization

3.3.1 Shape Factor Optimization

Noise shape represents the relative noise distributions between different dimensions. It should be as close to the classification boundary as possible to adapt to heterogeneous traffic features.

When optimizing shape factors, inspired by the Generative Adversarial Network (GAN), the noise conversion module serves as a generator. It generates converted noise based on Eq. (3), and injects it into original samples to obtain noised samples. The traffic classifier, trained by original samples, serves as a discriminator. It uses the noised samples as the testing set and perform classification. The loss function in Eqs. (5)–(7) is calculated according to the traffic classifier’s performance. In each round of optimization, the shape factors (parameters ws and wi in Eq. (3) are updated based on gradients back-propagated from the loss function. After a certain number of rounds, the optimized shape factors are obtained.

Given a traffic classifier f, the classification for a traffic sample can be defined as:

(4)f(x)=arg⁡maxc∈CSP(m(x)=c)(4)

where m is the model of the traffic classifier, x is the traffic sample, Cs is the class set, c is a class in Cs, P is the probability that the output of the model is equal to c. The classification obtains the class to which x is most likely to belong.

Considering the number of original samples used for training is Ns and the set of shape factors to be optimized, ws and wi, is θ, the loss function is:

L=1Ns∑i=1Ns(Lw(xi,εo)+Lc(xi,εo))+λ∑w∈θlog⁡(1+e−w)(5)

where L is the overall loss function which consists of three parts including the loss function for wrongly-classified noised samples Lw, the loss function for correctly-classified noised samples Lc and a regularizer with a hyper-parameter λ controlling the regularization strength.

The loss function for wrongly-classified noised samples Lw is defined as:

Lw(xi,εo)=I{f(xi+εo)≠f(xi)}⋅1|Cs|∑c∈Cslog⁡(1+e(I{c≠f(xi+εo)}−I{c=f(xi+εo)})⋅Sf⁡(c))(6)

where I is the indicator function, f is the trained traffic classifier, Sf is the softmax probability of f, xi is an original sample, εo is the converted noise, Cs is the class set, c is a class in Cs. When the noised sample xi + εo is wrongly-classified, Lw calculates a value based on the softmax probability and adds it to the overall loss function L.

The loss function for correctly-classified noised samples Lc is defined as:

Lc(xi,εo)=I{f(xi+εo)=f(xi)}⋅1|Cs|∑c∈Cslog⁡(1+e(I{c=f(xi+εo)}−I{c≠f(xi+εo)})⋅Sf⁡(c))(7)

where I is the indicator function, f is the trained traffic classifier, Sf is the softmax probability of f, xi is an original sample, εo is the converted noise, Cs is the class set, c is a class in Cs. When the noised sample xi + εo is correctly-classified, Lc calculates a value based on the softmax probability and adds it to the overall loss function L.

3.3.2 Scale Factor Optimization

Noise scale represents the overall scale of the noise distributions in all dimensions. It determines the location of noised sample in sample space. The categories of traffic in the training set are limited, resulting in the existence of empty regions in sample space. These regions are likely to contain unknown malicious samples. Noise scale factors should make noised samples move to the empty regions as possible.

Similarly to shape factor optimization, scale optimization also treats the noise conversion module as a generator. The module generates converted noise based on Eq. (3), and injects it into original samples to obtain noised samples. A traffic classifier serves as a discriminator. It performs classification according to Eqs. (8)–(11). The loss functions are calculated based on its performance.

HEBO is a novel parameter optimizer. It uses the Gaussian process model to fit the black-box function, and obtain the optimal parameter by an improved acquisition function. When optimizing scale factors, HEBO treats the above process as a black-box function. The input of the function is the noised samples, and the output is the scale factor (parameter t in Eq. (3). In each round of optimization, the scale factor is updated based on the loss function. After a certain number of rounds, the optimized scale factor is obtained.

There are some differences between the optimization of benign scale factors and malicious scale factors. Noised benign samples are treated as pseudo-malicious samples. The benign scale factor should enable the traffic classifier to learn the boundary between these samples and the real benign samples as much as possible. Therefore, the discriminator is trained on the dataset composed of noised benign samples (labeled as malicious) and real benign samples. After training, it performs classification on real malicious samples. Additionally, to obtain multiple optimized benign scale factors from a single dataset, the original dataset is divided into several sub datasets before optimization. Each sub dataset is further divided into a training set Tr, a testing set Te, and an optimizing set To. The size of To is the same as that of Te, but only To is used in the current optimization, while Te is reserved for subsequent ensemble learning module. Based on these datasets, the loss function of benign scale factors can be defined as:

Lb=AccBi⁡(Trb,To)(8)

Trb=Xb∪(Xb+εo)(9)

where Lb is the loss function. The discriminator is trained by the dataset Trb. Trb consists of two parts: all benign samples Xb within Tr, and noised benign samples Xb+εo, where εo is the converted noise. The trained discriminator performs binary classification on To, its accuracy is represented as AccBi. Considering the number of sub datasets is Nb, hence, the number of benign scale factors is also Nb.

Noised malicious samples are treated as pseudo-malicious samples. The malicious scale factor should enable the traffic classifier to correctly classify malicious samples of all categories as accurately as possible based on the noised samples of a single category. Therefore, the discriminator is trained on the dataset composed of noised malicious samples (labeled as malicious) and real malicious samples, both of which belong to the same single category. After training, it performs classification on real malicious samples of all categories. Additionally, to obtain multiple optimized malicious scale factors from a single optimization, several superior factors are collected instead of the single optimal factor. The loss function of scale factors for malicious samples of class c can be defined as:

Lmc=AccBi⁡(Trm,To)(10)

Trm=Xb∪Xnb∪Xc∪(Xc+εo)(11)

where Lmc is the loss function of class c. The discriminator is trained by the dataset Trm. Trm consists of four parts: all benign samples Xb within Tr, noised benign samples Xnb, all malicious samples Xc of class c within Tr, and noised malicious samples Xc + εo, where εo is the converted noise. The trained discriminator performs binary classification on To, its accuracy is represented as AccBi. Given that the number of factors collected each time is Nc, and the number of malicious classes is Nm, the total number of malicious scale factors is Nb × Nc × Nm.

3.3.3 Noise Injection

The distributions of benign and malicious samples are different [25]. The benign samples are relatively representative and tend to have a denser distribution. The malicious samples are relatively manifold and their distribution tends to be more sparse. In sample space, samples with high densities are benign while those with low densities are malicious. Unknown malicious samples that are hard to detect are mainly located in two specific regions. First, they may move closer to benign samples over time and be located in the boundary region. The region is outside the benign samples and yet very close to it, since sophisticated attackers are likely to imitate normal behaviors to avoid detection. Second, considering that unknown malicious samples use more novel attack techniques compared to known malicious samples, they may be different from both benign and known malicious samples, and located in the empty regions outside all known samples.

In noise injection, each factor group is used to generate a corresponding batch of optimized noise, both benign and malicious samples are augmented by these noise. The noised benign samples simulate unknown malicious samples that are close to benign samples, while the noised malicious samples simulate unknown malicious samples located in empty regions. The sample spaces before and after noise injection are shown in Fig. 4.

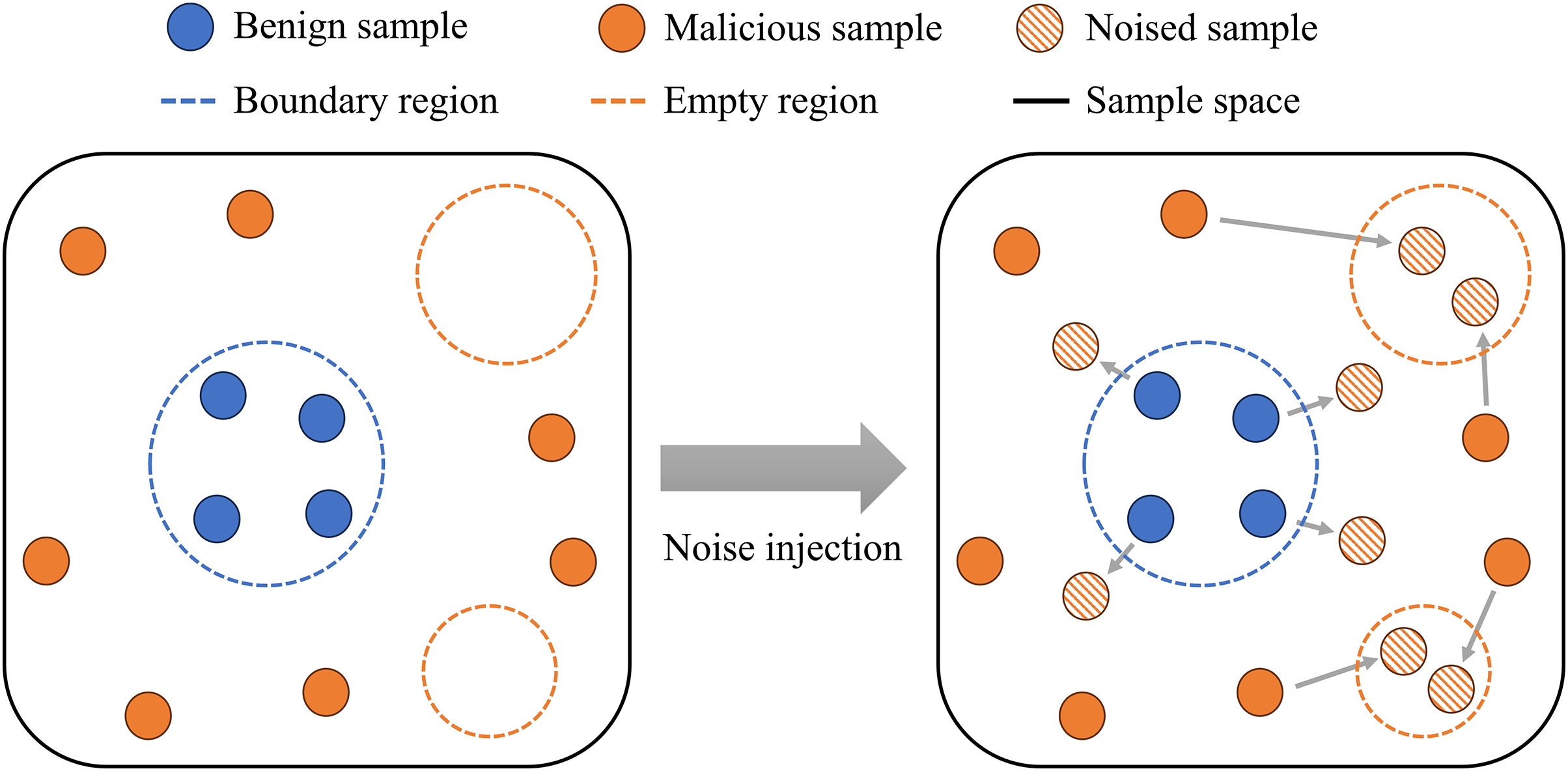
Figure 4: Sample spaces before and after noise injection

The scale factor optimization is carried out on every category. Shape factors are combined with scale factors of all categories to form a factor group. Given that the number of sub dataset is Nb, the number of malicious scale factors collected each time is Nc, the number of factor groups is Nb × Nc. Each factor group can independently and effectively perform noise injection. As a result, there are Nb × Nc groups of noised samples.

3.4 Ensemble Learning

The noise optimization module generates Nb × Nc groups of noised datasets. Each dataset is used to train a base traffic classifier separately. The ensemble learning module uses an improved bagging algorithm to aggregate the results of all base traffic classifiers. Compared to traditional bagging algorithms, the applied algorithm obtains training subsets by noised sample generation instead of extraction from the original samples.

When noised benign samples are treated as pseudo-malicious samples, base traffic classifiers can learn the category boundary more thoroughly. However, this approach also makes base traffic classifiers biased towards the malicious category during classification, and slightly reduces their precision on benign samples. As a result, the applied algorithm sets the precision as the standard for weight calculation. This strategy balances the performance on both unknown malicious and benign samples. These weights are used to weight the results of all base traffic classifiers. The improved bagging algorithm is shown as Algorithm 1.

The input of the algorithm consists of three parts: N (Nb × Nc) noised training sets Tn1, ⋯,TnN, an optimizing set Tob, and a testing set Teu. Tn are the noised datasets generated after noise optimization. These datasets are used to train base traffic classifiers. Tob and Teu are derived from the optimizing set To and the testing set Te when optimizing benign scale factors. Tob contains only the benign samples within To and is used to measure the precision. Teu includes all the samples within Te and additional unknown malicious samples. It is used to calculate the final generalizability. The algorithm uses Tn to train all base traffic classifiers and performs classification on Teu. Then, it calculates the error rate e and the weight update factor β according to the precision. These two parameters are used to update base traffic classifiers’ weights. Finally, the algorithm outputs the weighted classification result F.

4  Experiments

4.1 Dataset

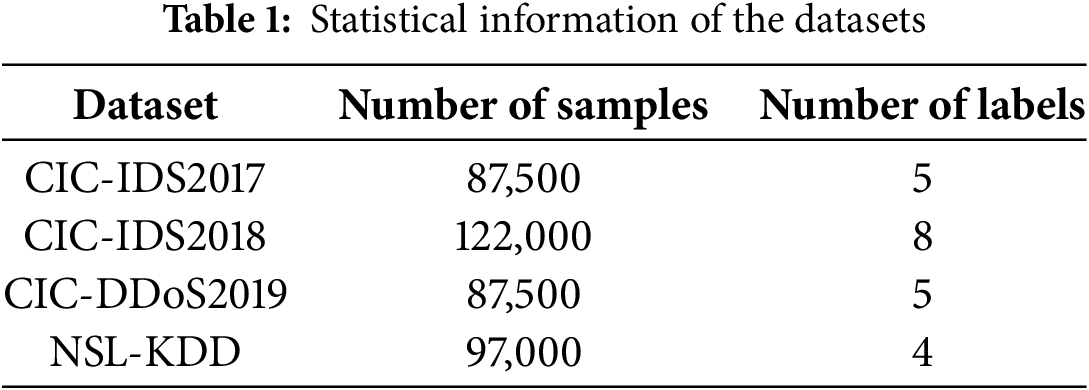
For the classification task in this paper, we use the CIC-IDS2017, CIC-IDS2018, CIC-DDoS2019 and NSL-KDD datasets [36–38]. These datasets contain benign and the latest common malicious samples, which resemble the real-world data. In preprocessing, we clean these datasets by filtering out samples that contain missing and infinite values. We then remove traffic features related to IP address, port number and timestamp, which are difficult to be augmented. Finally, we normalize the remaining features. Table 1 shows the statistical information of the datasets.

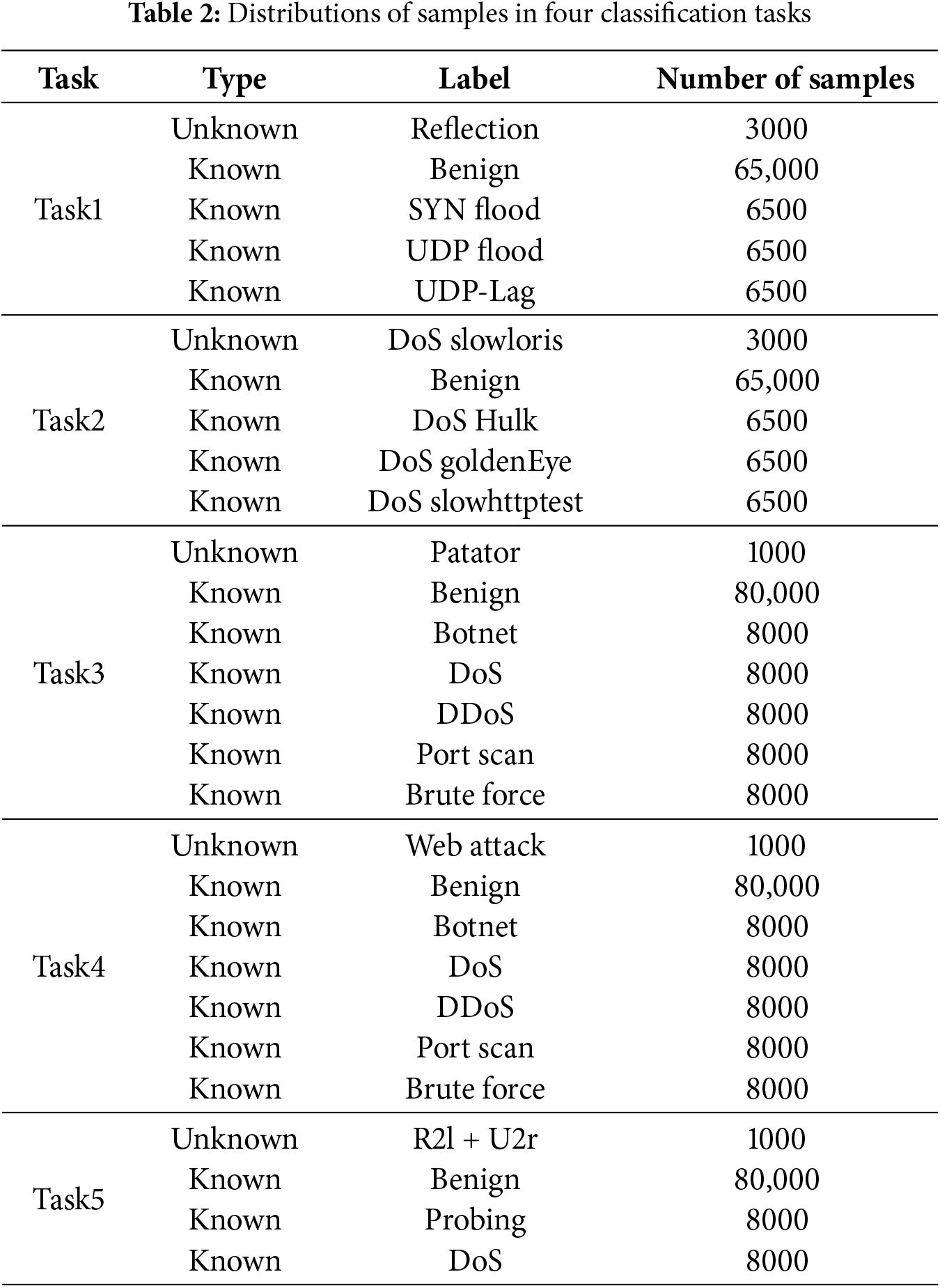
To comprehensively evaluate the effectiveness of ONTDAS, we perform a detailed analysis and quantification of the preprocessed datasets, and construct five classification tasks that utilize ONTDAS for data augmentation. We categorize samples into two types according to their availability for training. Samples with a sufficient quantity are marked as “known”, while samples with a smaller quantity are marked as “unknown”. Known samples are included in both training sets and testing sets for data augmentation and model training. Unknown samples are exclusively reserved for testing sets to calculate the generalizability. The distributions of samples in five classification tasks are shown in Table 2.

4.2 Experimental Environment and Setup

The experiments are performed using Python version 3.8, with the Windows10 operating system. The processor is an Intel(R) Core(TM) i7-12700KF @ 3.60 GHz, and the graphics processing unit is a single NVIDIA GeForce RTX 4060, with a 8 GB graphics processing unit memory. All experiments are based on PyTorch.

The model parameters are set as follows: In the noise conversion module, the number of features Nf is set to 76 in Task1–Task4 and 33 in Task5, the number of special distributions Nd is set to 3. In the noise optimization module, we set the hyper-parameter λ to 0.01, the number of sub datasets Nb to 3 and the number of scale factors collected each time Nc to 3.

Moreover, the base traffic classifier is set as CNN, KNN, RF, C4.5 decision tree, AutoEncoder and ACID [11]. The special distributions are set to ISRU, Gaussian, and Arctan. In Task1 and Task2, we divide the dataset into a training set, a testing set, and an optimizing set in a ratio of 9:2:2. In Task3, Task4 and Task5, the ratio is 6:1:1.

4.3 Evaluation Metrics

In this study, we use the following metrics: Accuracy, Precision, Recall, and F1-score. When evaluating the base traffic classifier, TP (True Positive) represents the cases where the benign samples are correctly classified, TN (True Negative) represents the cases where the malicious samples are correctly classified, FP (False Positive) represents the cases where the malicious samples are incorrectly classified, and FN (False Negative) represents the cases where the benign samples are incorrectly classified. The calculation formulas of these metrics are as follows:

Accuracy=TP+TNTP+TN+FP+FN(12)

Precision=TPTP+FP(13)

Recall=TPTP+FN(14)

F1-score=2⋅Precision⁡ ⋅ RecallPrecision+Recall(15)

4.4 Results of Overall Performance

In each classification task, we first train a base traffic classifier with a known training set and employ it to perform binary classification on a known testing set. Then, we add unknown samples to the known testing set and employ the trained traffic classifier to perform binary classification on the mixed testing set. Finally, we train a new base traffic classifier with an noised dataset and employ it to perform binary classification on the mixed testing set. The first classification result is the original performance of the base traffic classifier, representing its learning ability for known samples. The second classification obtains the performance for unknown malicious samples before augmentation, where the base traffic classifier can only rely on the category boundary learned from known samples. The last classification result is the performance for unknown malicious samples after augmentation. To measure the overall performance, we calculate the accuracy, precision, recall and F1-score based on Eqs. (12)–(15).

Table 3 shows the results of CNN. Compared to the original performance, after adding unknown samples, the average accuracy decreases by 4.79%, the average F1-score decreases by 3.40%, and the average recall decreases by 6.58%. After data augmentation, the average accuracy increases by 2.17%, the average F1-score increases by 1.49%, the average recall increases by 3.20%, the average precision decreases by 0.42%.

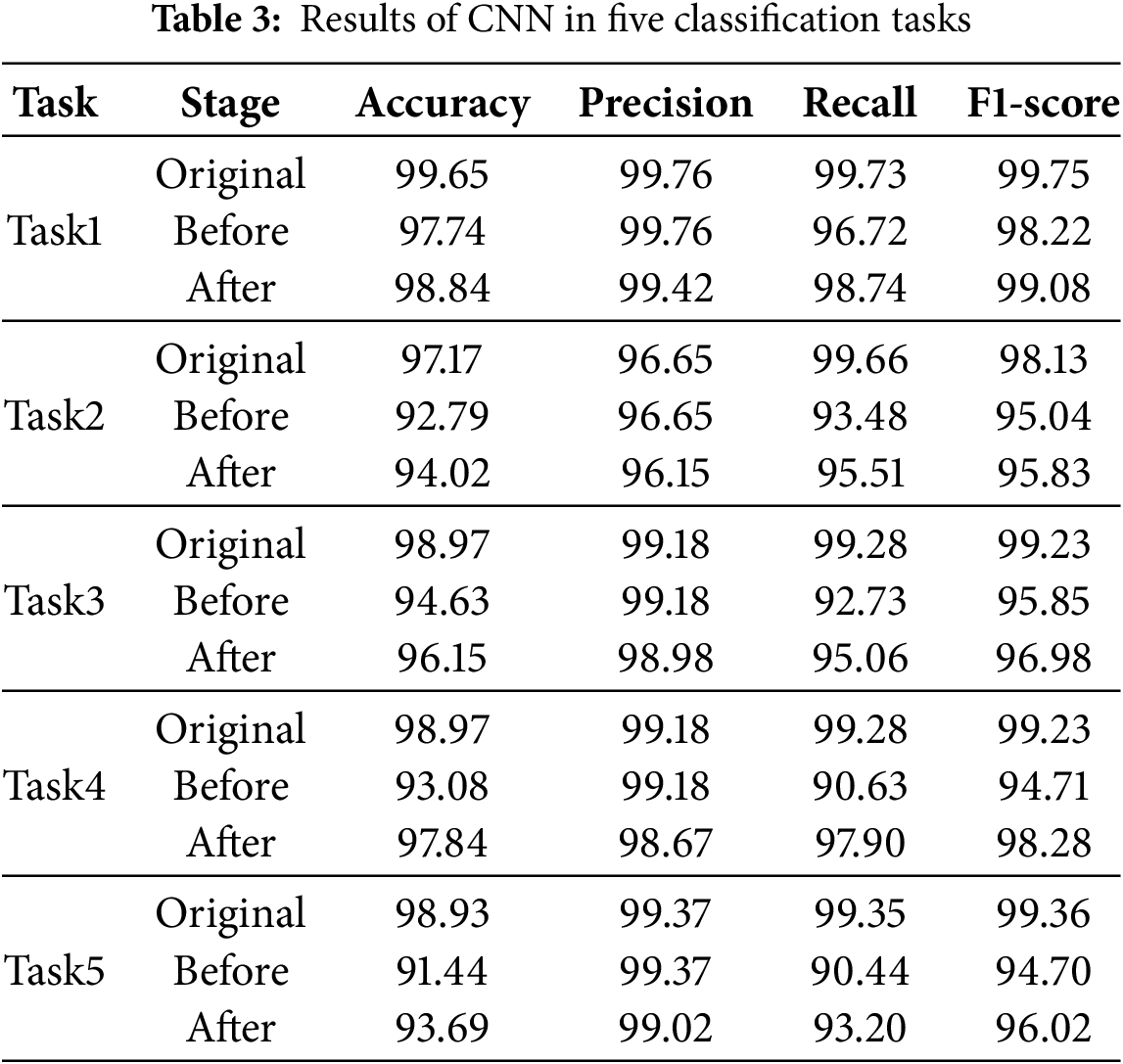
Table 4 shows the results of KNN. Compared to the original performance, after adding unknown samples, the average accuracy decreases by 4.36%, the average F1-score decreases by 3.13%, and the average recall decreases by 6.04%. After data augmentation, the average accuracy increases by 2.09%, the average F1-score increases by 1.42%, the average recall increases by 3.15%, the average precision decreases by 0.41%.

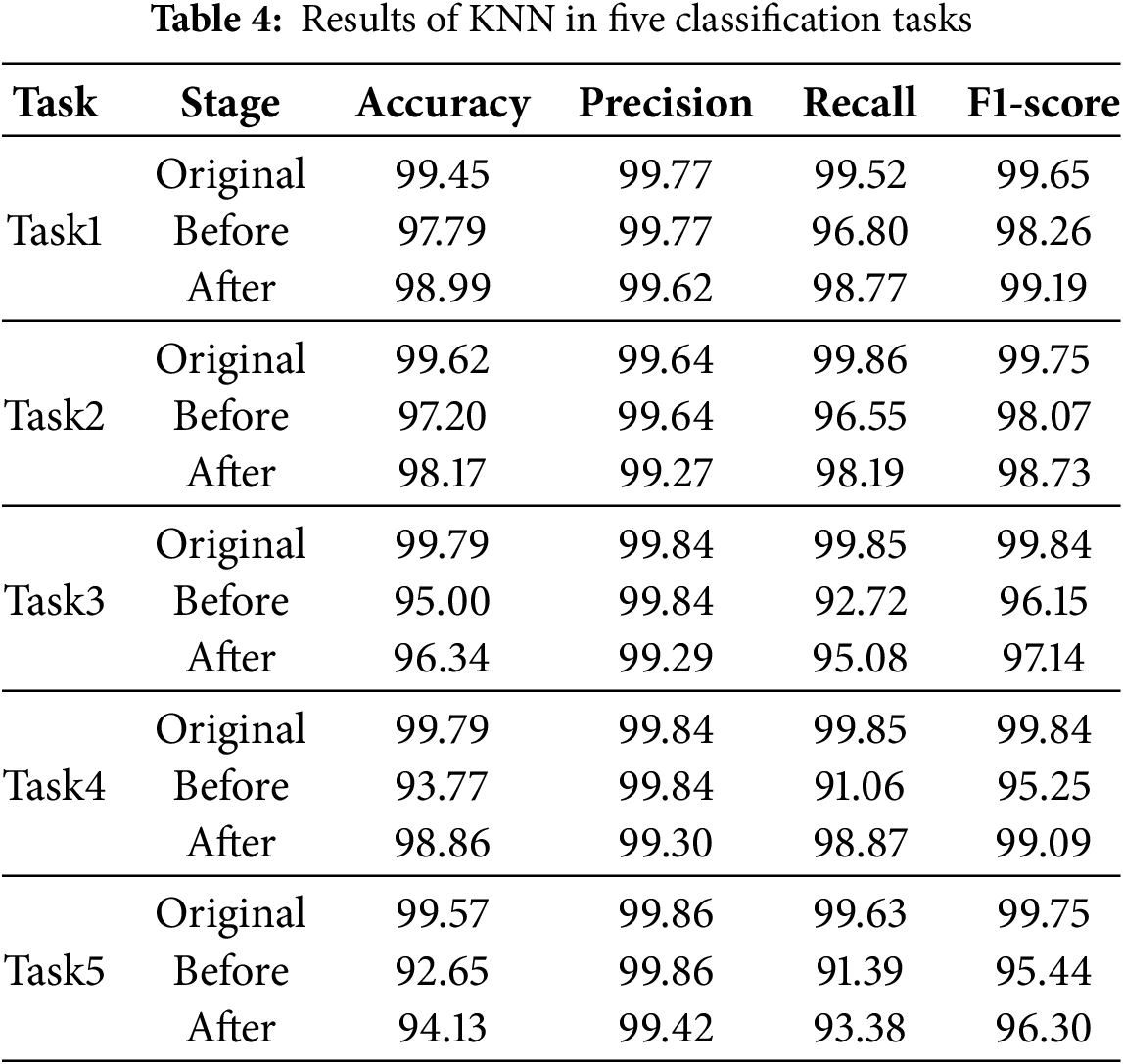
Table 5 shows the results of RF. Compared to the original performance, after adding unknown samples, the average accuracy decreases by 4.77%, the average F1-score decreases by 3.31%, and the average recall decreases by 6.35%. After data augmentation, the average accuracy increases by 1.86%, the average F1-score increases by 1.27%, the average recall increases by 2.85%, the average precision decreases by 0.45%.

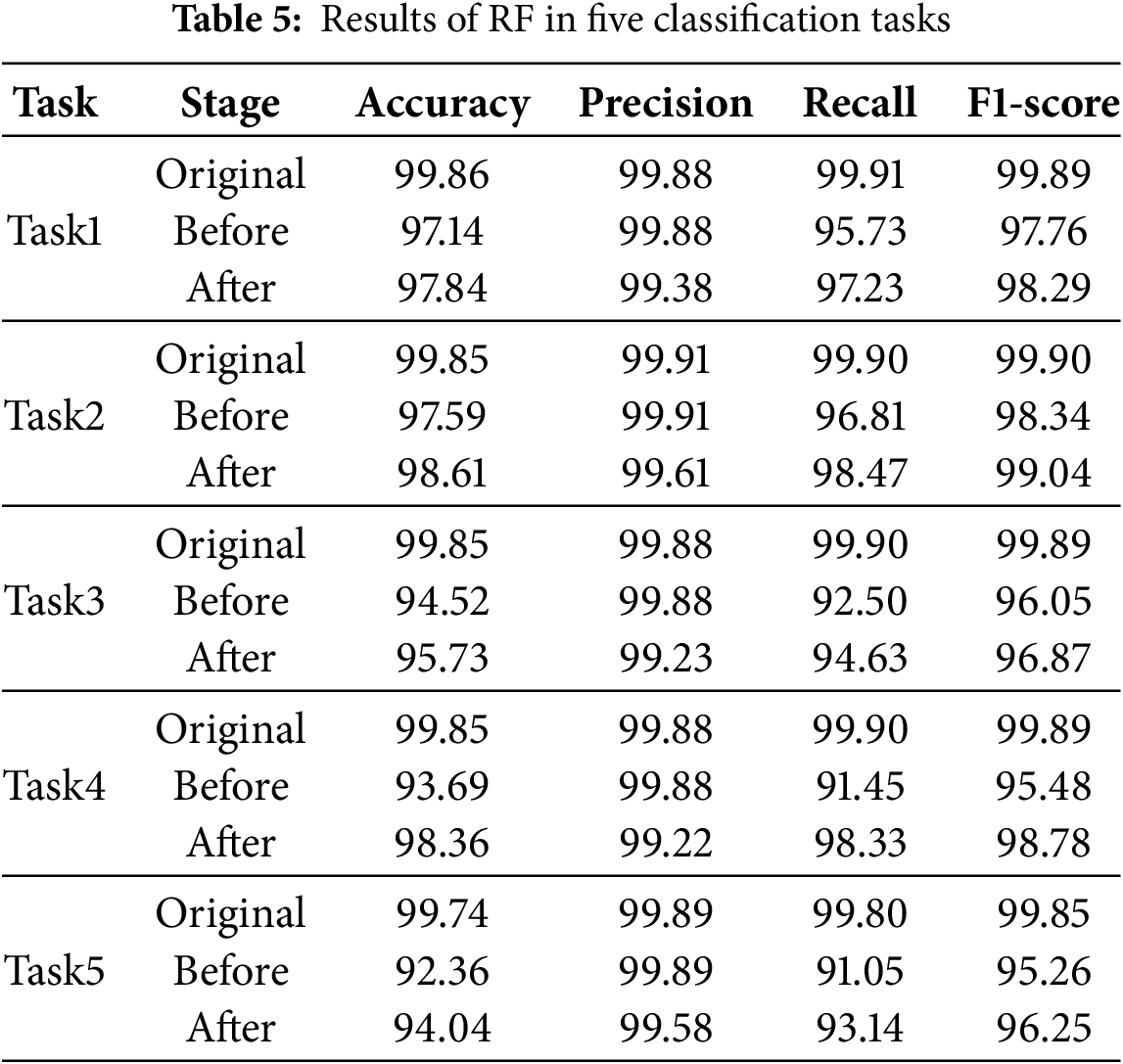
Table 6 shows the results of C4.5 decision tree. Compared to the original performance, after adding unknown samples, the average accuracy decreases by 4.46%, the average F1-score decreases by 3.16%, and the average recall decreases by 6.23%. After data augmentation, the average accuracy increases by 1.47%, the average F1-score increases by 0.96%, the average recall increases by 2.19%, the average precision decreases by 0.31%.

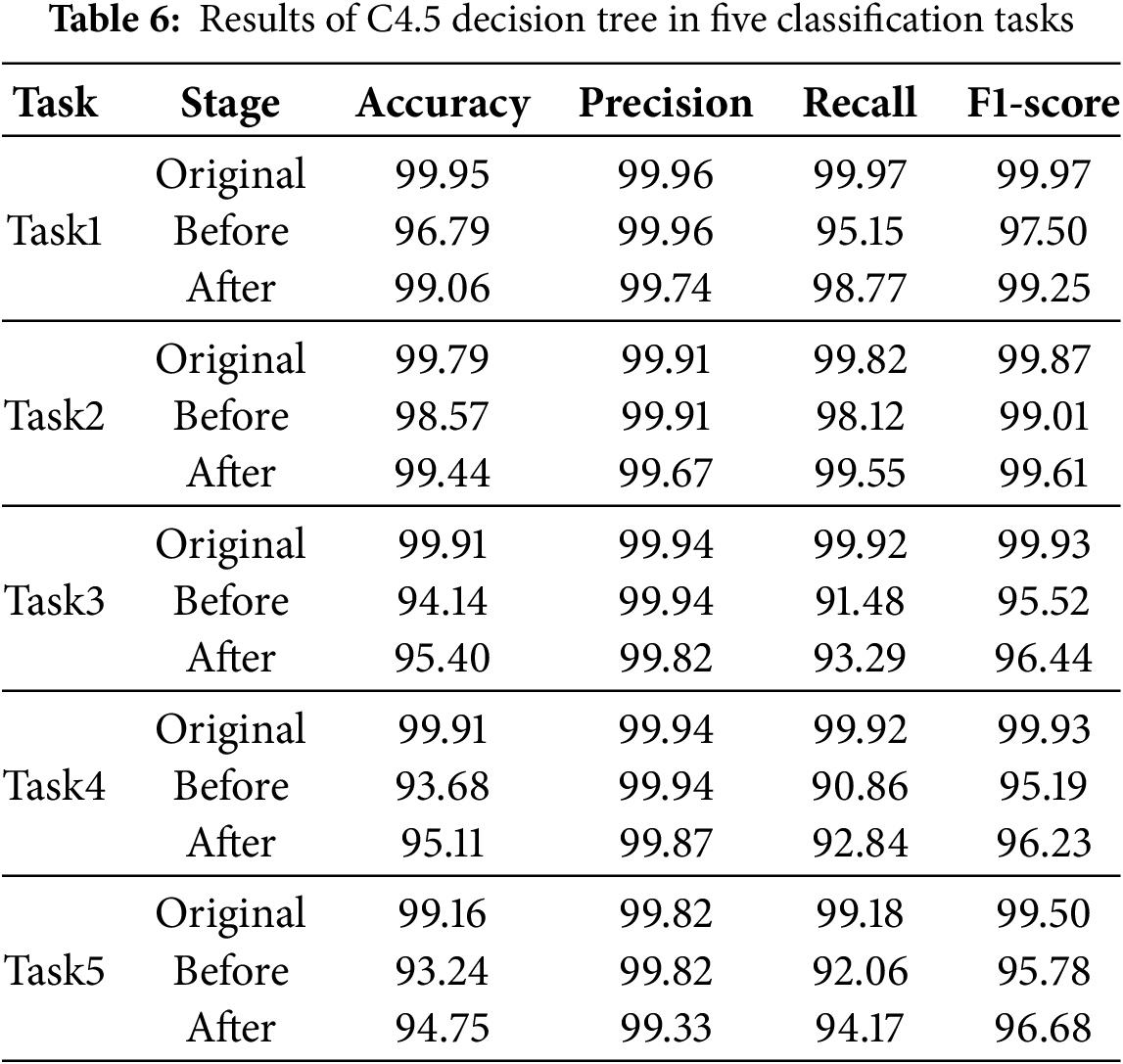
Table 7 shows the results of AutoEncoder. Compared to the original performance, after adding unknown samples, the average accuracy decreases by 4.52%, the average F1-score decreases by 3.20%, and the average recall decreases by 6.24%. After data augmentation, the average accuracy increases by 2.02%, the average F1-score increases by 1.39%, the average recall increases by 3.20%, the average precision decreases by 0.49%.

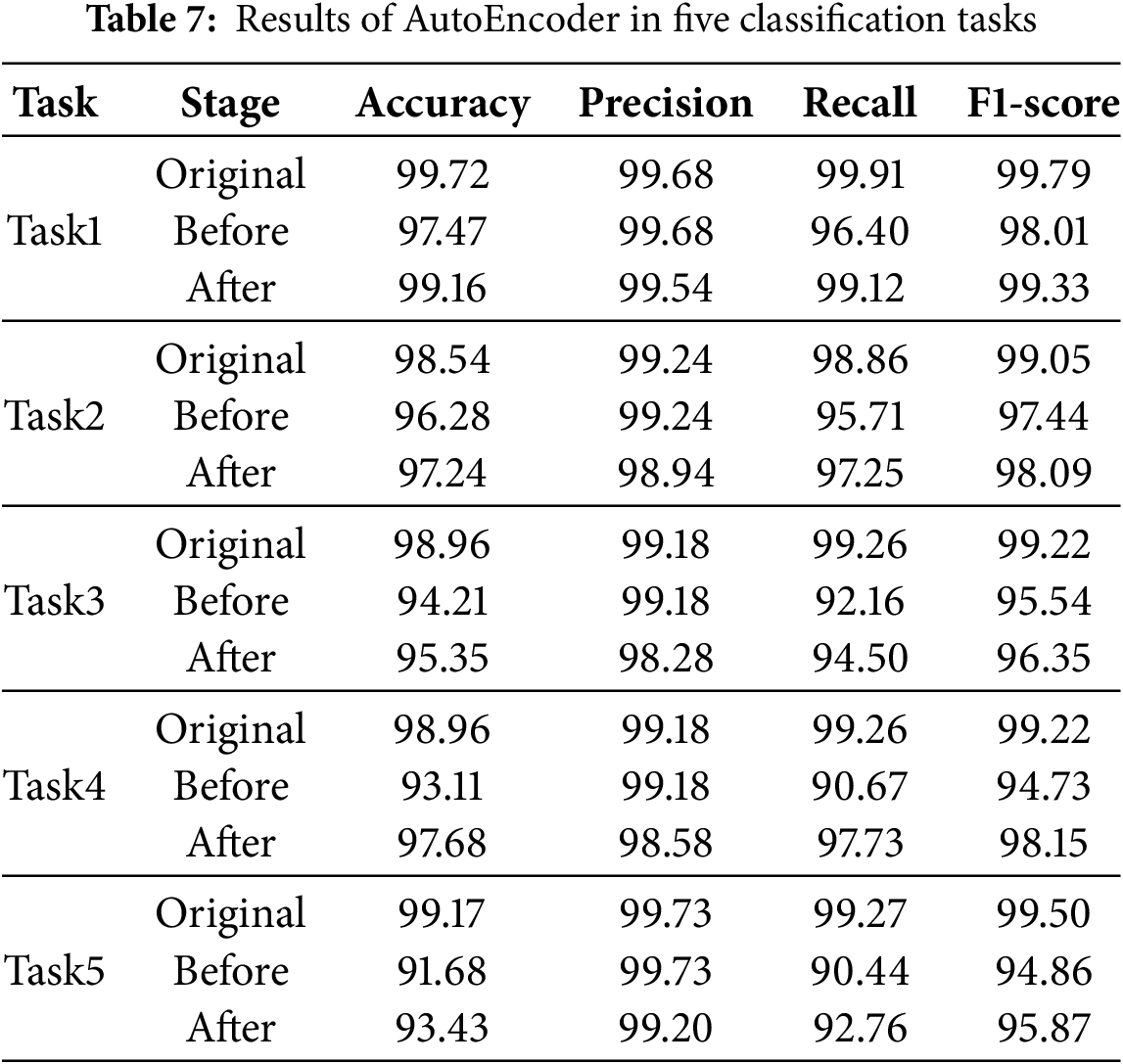
Table 8 shows the results of ACID. Compared to the original performance, after adding unknown samples, the average accuracy decreases by 5.04%, the average F1-score decreases by 3.63%, and the average recall decreases by 7.02%. After data augmentation, the average accuracy increases by 2.69%, the average F1-score increases by 1.90%, the average recall increases by 4.31%, the average precision decreases by 0.64%.

The experimental results show that the addition of unknown malicious samples leads to a decrease in performance. The base traffic classifier incorrectly identifies these samples as benign samples, resulting in the decrease in accuracy, F1-score, and recall. However, the precision focuses only on benign samples and does not decrease. The experimental results also show that ONTDAS improves the overall performance. ONTDAS enables the base traffic classifier to correctly classify unknown malicious samples, resulting in the increase in accuracy, F1-score, and recall. Because all noised benign samples are treated as pseudo-malicious samples, the precision slightly decreases, but this is acceptable compared to the significant improvement in other metrics.

4.5 Results of Recall on Unknown Malicious Samples

We use the recall on unknown malicious samples to measure the generalizability of base traffic classifier. Table 9 and Fig. 5 show the recall before and after data augmentation.

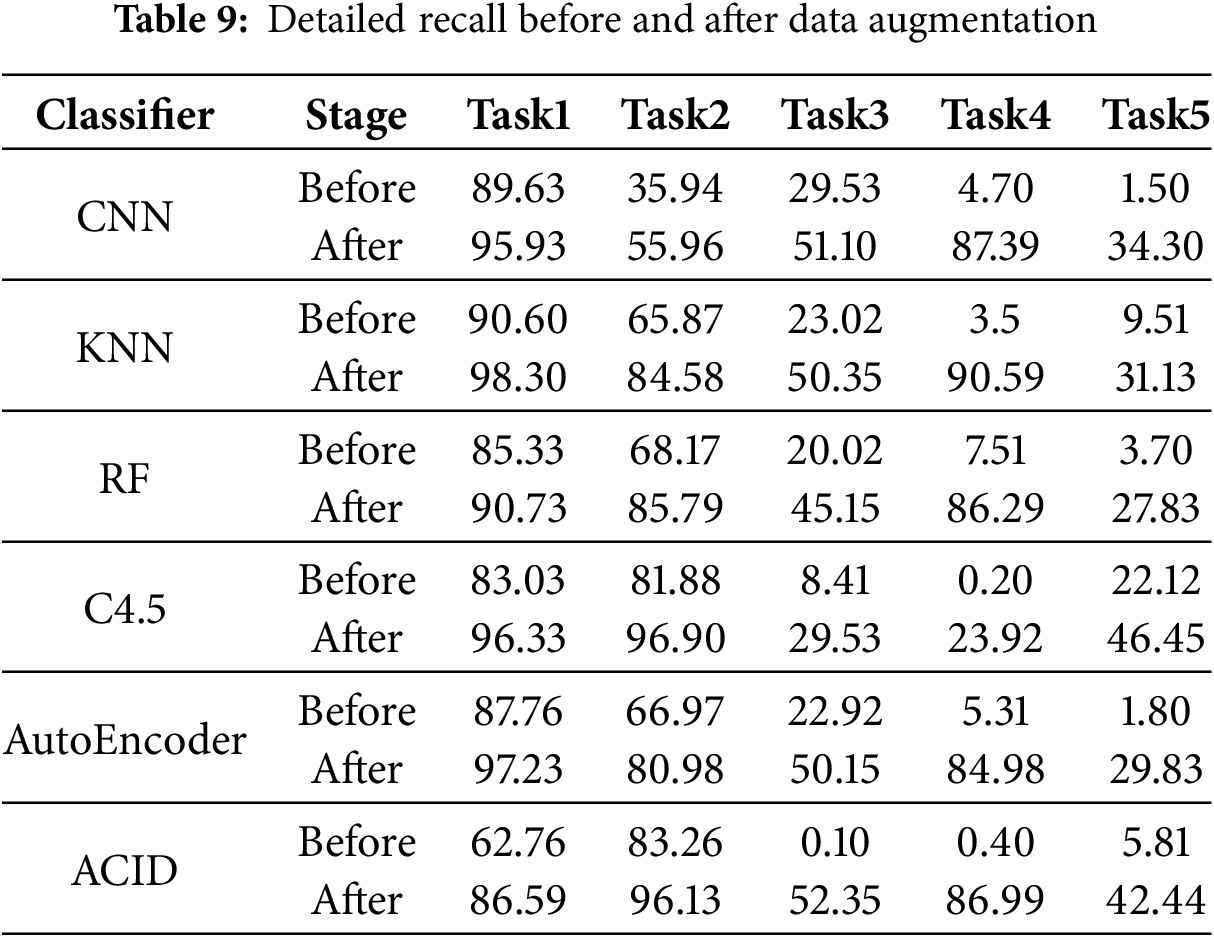
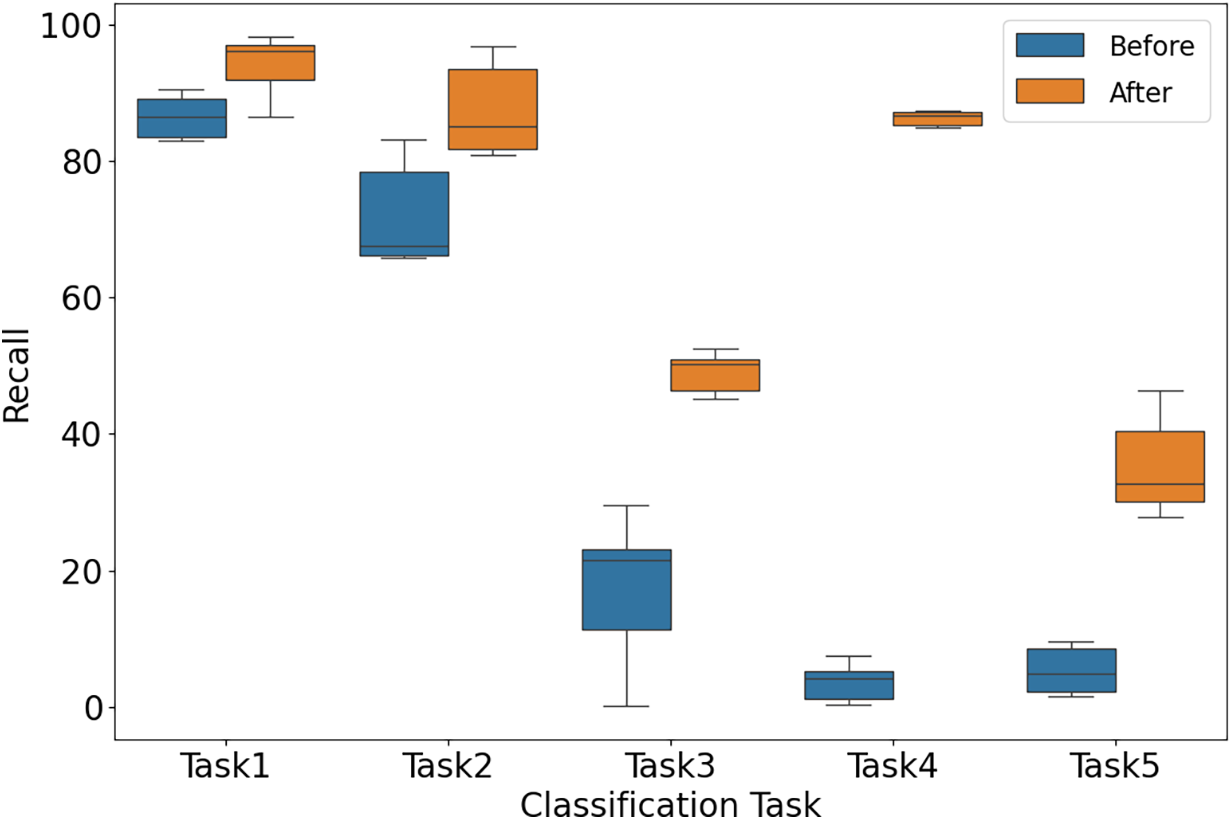
Figure 5: Overall recall before and after data augmentation

Unknown malicious samples in Task1 and Task2 simulate samples located in the empty regions, and the trained base traffic classifier can roughly classify them before augmentation. Unknown malicious samples in Task3, Task4 and Task5 simulate samples located in the boundary region outside the benign samples, and the trained base traffic classifier misclassifies them as benign samples before augmentation. These results demonstrate that ONTDAS can significantly increase the recall and improve the generalizability of base traffic classifier.

4.6 Comparison with Baselines

To validate the effectiveness of ONTDAS, we select eight methods (Rapier [25], BARS [15], SMOTE [39], Pyraug [40], Random Over Sampling (ROS), Attention-based SMOTE (Optimized SMOTE) [26], SMOTE-noise [32] and learnable noise [34]) as baselines. The experiments are carried out on ACID and Task4. For ROS, we only replicate malicious samples to increase their number. For learnable noise, we add learnable Gaussian noise to the activation function of ACID. For other baselines, we perform data augmentation on malicious samples and treat generated samples as pseudo-malicious samples. Table 10 shows the classification results of all baselines. Fig. 6 shows the recall on unknown malicious samples of all baselines. The experimental results indicate that although the precision is slightly lower, our system achieves the best performance in accuray, F1-score, and recall, and improves generalizability the most.

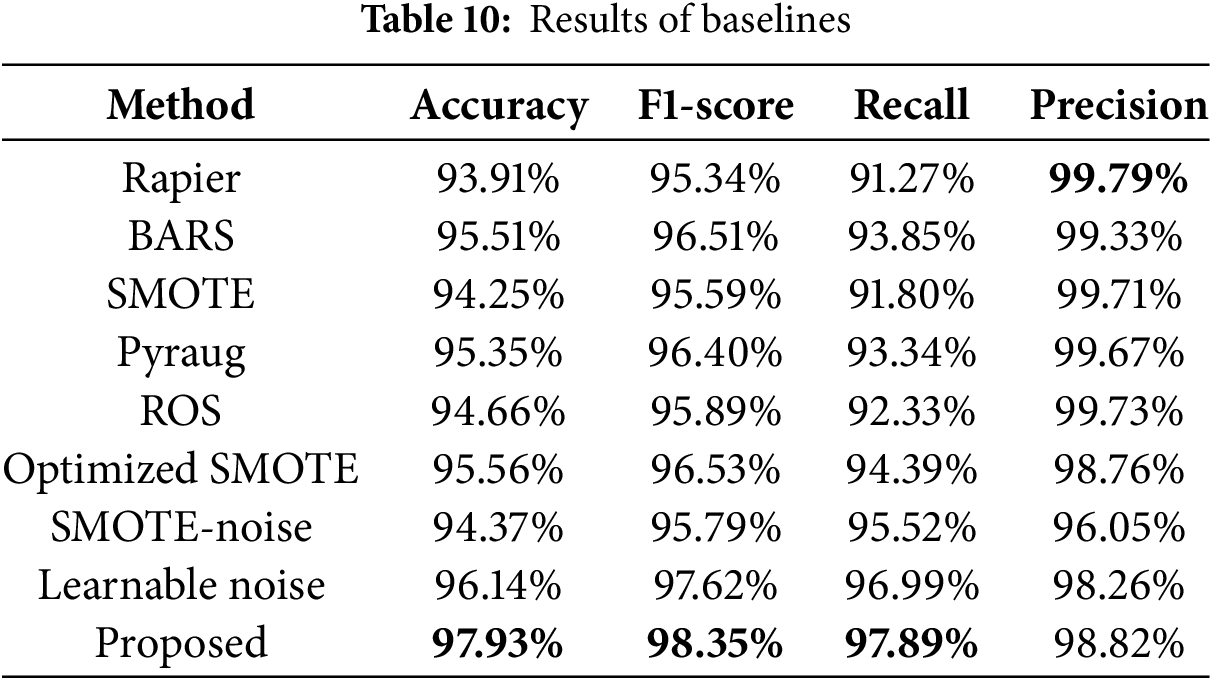
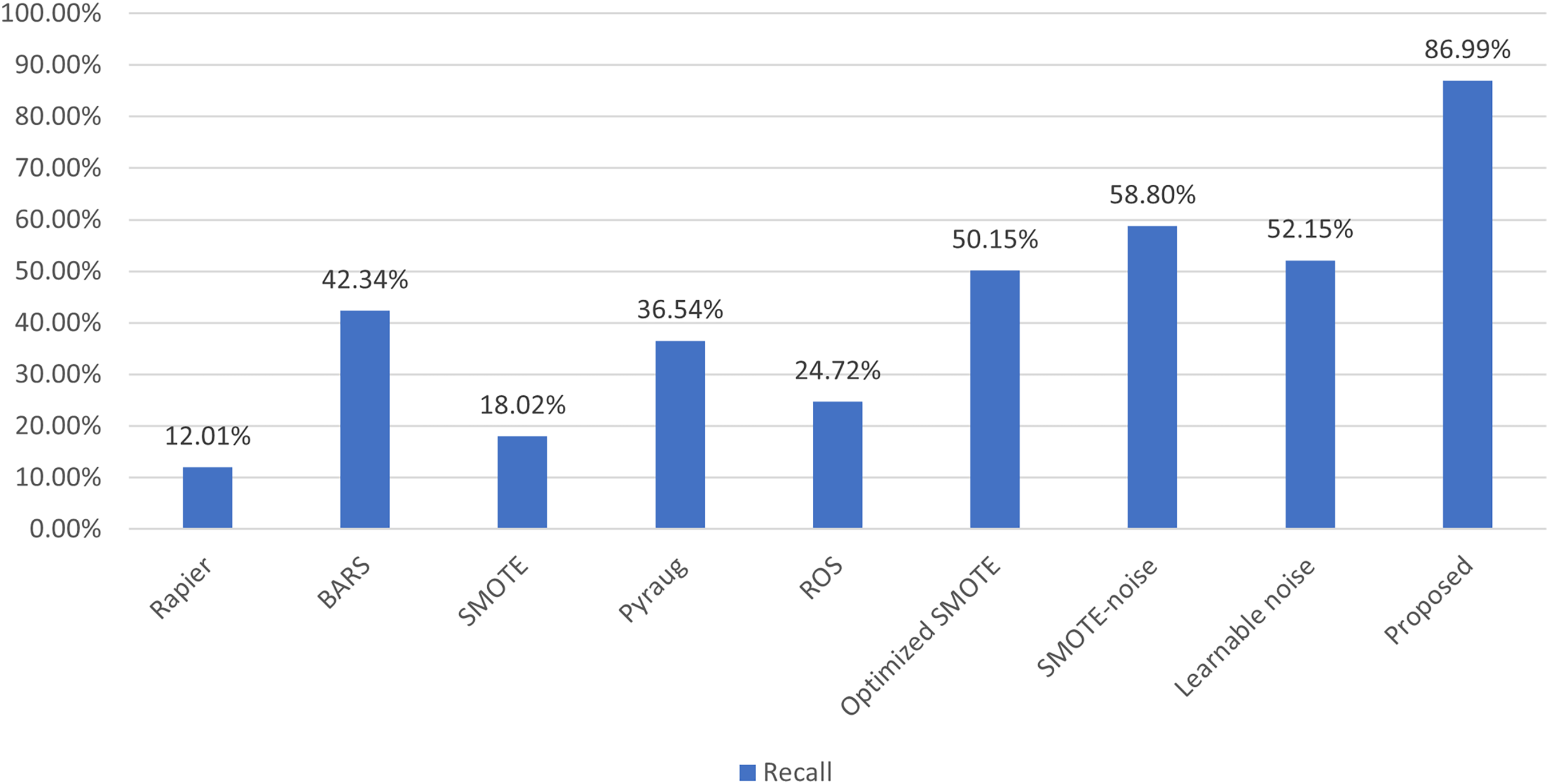
Figure 6: Recall on unknown malicious samples of baselines

Upon thorough analysis, the proposed system outperforms all baseline methods, and the reasons can be summarized as follows. Baseline methods like Rapier and BARS do not focus on generalizability. Instead, they focus on removing label noise and improving robustness, generalizability is merely an additional benefit. This makes it difficult for them to effectively deal with unknown malicious samples. SMOTE and its derivative methods, such as Attention-based SMOTE and SMOTE-noise, overly rely on the original data distribution when generating new samples. Consequently, the pseudo-malicious samples lack diversity and are unable to fully expand the sample space of the training set. This greatly limits the generalizability of the base traffic classifier. Although Pyraug uses a VAE to generate samples, in experimental scenarios involving high-dimensional traffic, the quality of its generated samples still lags behind that of the proposed system. ROS simply replicates malicious samples, which not only fails to increase sample diversity but is also likely to cause overfitting. The strategy of adding learnable Gaussian noise to the activation function is limited by the model structure. It cannot comprehensively improve generalizability.

4.7 System Parameter Analysis

When optimizing scale factors, HEBO searches for the best parameters within a given range. A search range that is too large will prevent HEBO from obtaining the best parameters in a short period of time, while a search range that is too small will cause HEBO to skip the best parameters directly. Therefore, an appropriate search range is crucial. Considering that the lower bound of the search range is 0, we conduct experiments on the upper bound based on ACID and Task4. We set the scale factors to 0.01, 0.025, 0.05, 0.1, 0.25, and 0.5, respectively. The results are shown in Fig. 7.

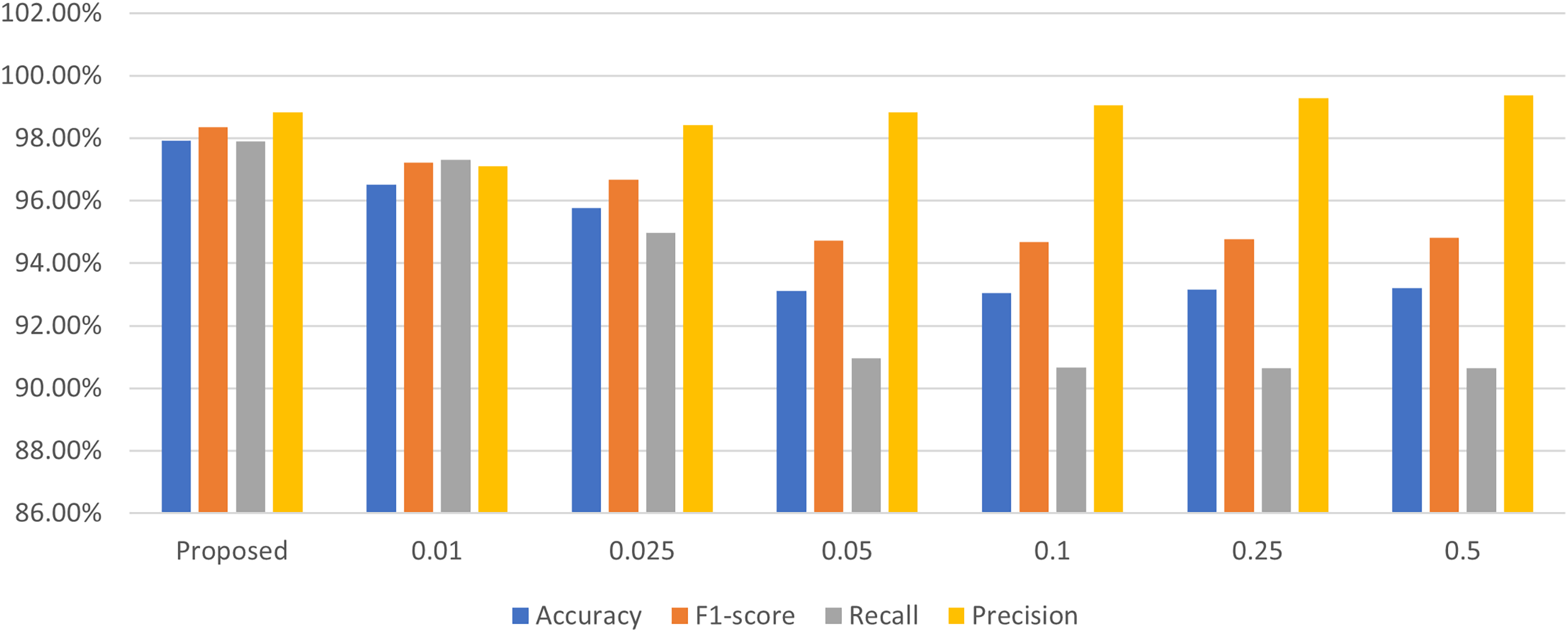
Figure 7: Results of different scale factors

The experimental results show that as the upper bound increases, the improvement in generalizability weakens. The excessively large factor causes the noised features to deviate from the original distribution, and makes noised samples no longer similar to original samples. Therefore, we set the search range to [0, 0.01], and the scale factors optimized within this range achieve the best performance.

To verify the indispensability of each module, we design three ablation experiments based on ACID and Task4. The first experiment removes the noise optimization module and injects raw noise for data augmentation. The second experiment removes the HEBO and directly uses the noise optimized by the shape factors for data augmentation. The third experiment removes the ensemble learning module and averages the results of all base traffic classifiers. The results are shown in Fig. 8.

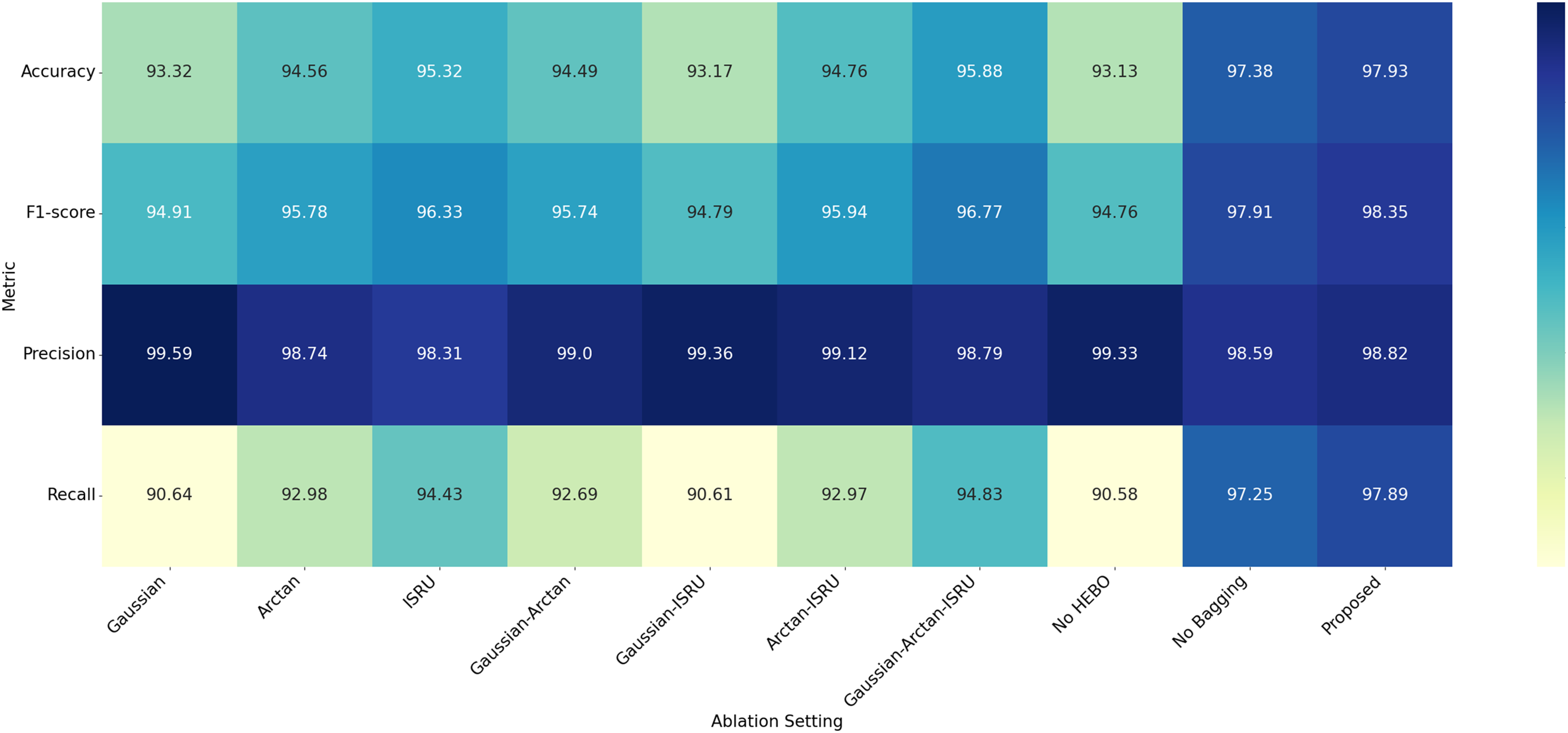
Figure 8: Results of different ablation settings

The experimental results indicate that the proposed system outperforms others. The first experiment simply injects noise from the combination of different distributions, the second experiment does not optimize the overall scale of the noise distributions, and the third experiment focuses too much on unknown malicious samples, without balancing the performance of all samples.

We also conduct experiments on hyperparameters Nb and Nc based on ACID and Task4. Nb controls the number of sub dataset when optimizing scale factors, Nc controls the number of malicious scale factors collected each time. Nb and Nc ensure the diversity of noise, enabling the ensemble learning module to achieve more improvement in generalizability. The results are shown in Figs. 9 and 10.

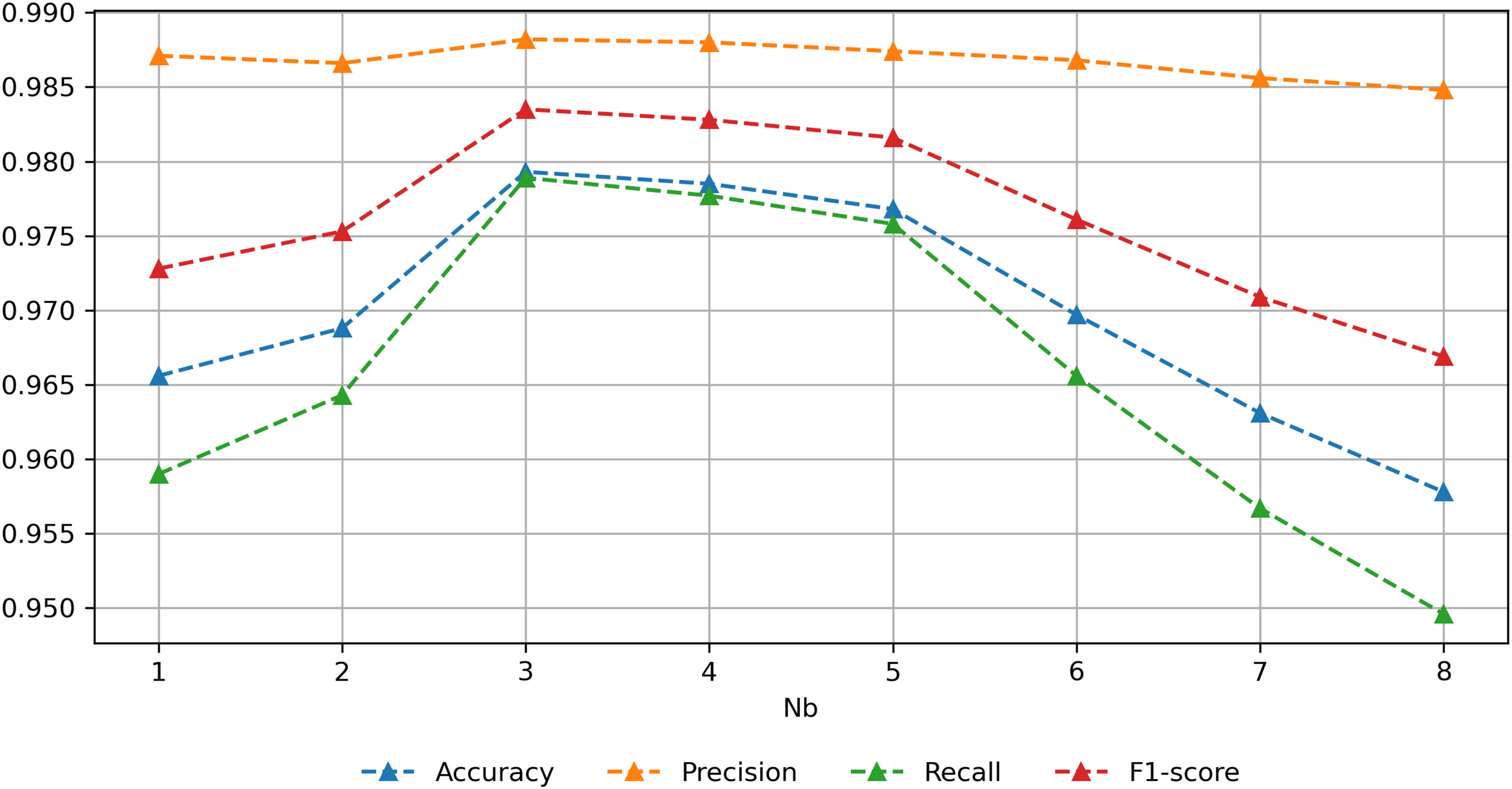
Figure 9: Results of different Nb

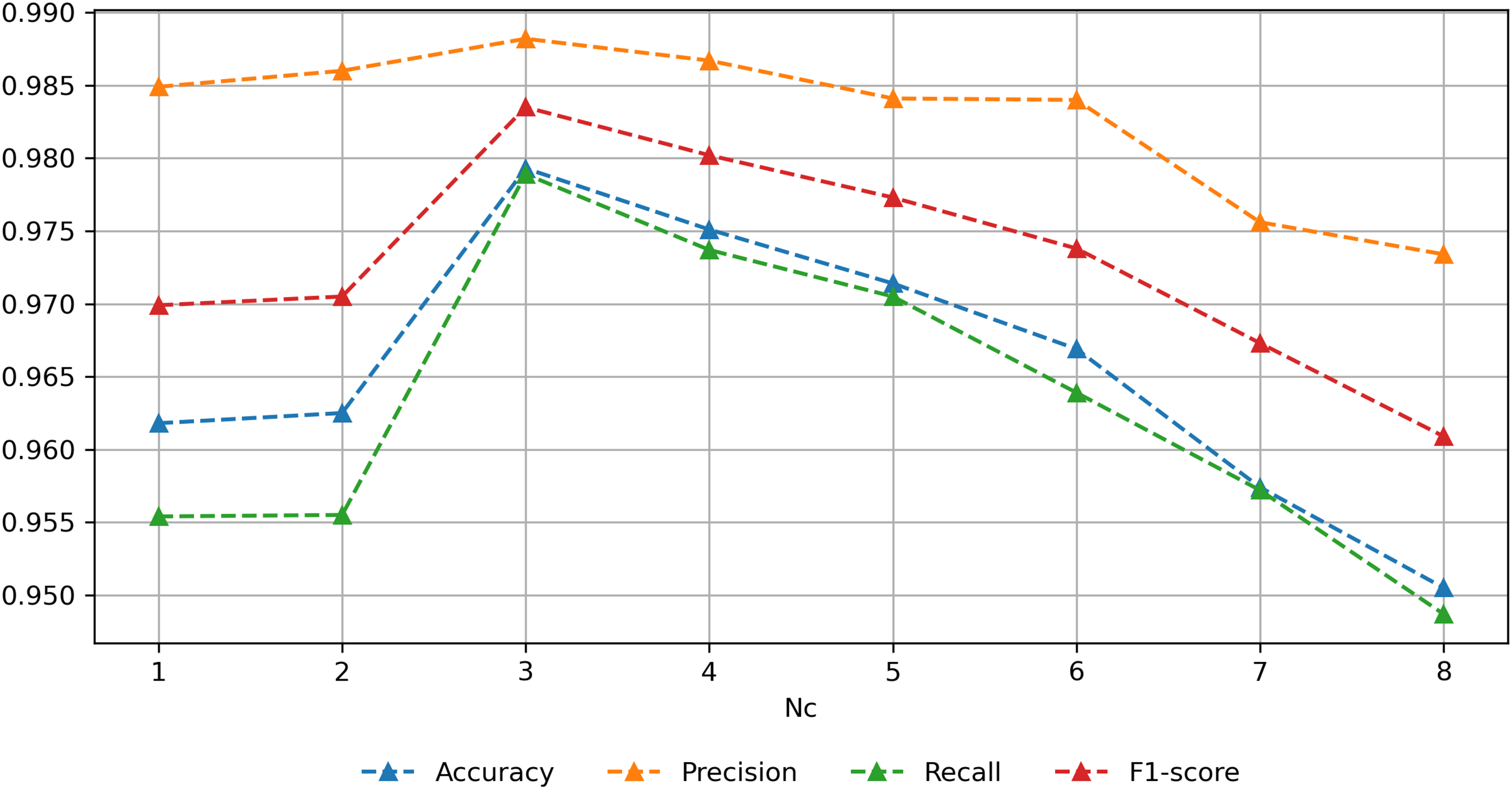
Figure 10: Results of different Nc

When Nc is set to 3, the performance first increases and then decreases as Nb increases, reaching its peak value when Nb is 3. An excessively small Nb fails to bring sufficient diversity to the noised samples, while an excessively large Nb makes sub datasets too small, reducing the representation capability of optimized noise. When Nb is set to 3, the performance first increases and then decreases as Nc increases, reaching its peak value when Nc is 3. Similar to Nb, an excessively small Nc does not bring sufficient diversity to the noised samples, while an excessively large Nc leads to the scale factors with poor effects being collected, thus reducing the quality of the noised samples. Moreover, excessively large Nb and Nc increase the time consumption for optimization and training. Therefore, both of them are finally set to 3.

4.8 Results of Dataset Imbalance

In addition to above experiments, we also conduct an experiment which uses ONTDAS to solve dataset imbalance. We reduce the number of malicious samples in the training set of Task4 to its one tenth, while keeping the number of benign samples unchanged. At this point, the ratio of the number of majority and minority categories becomes 100:1. When alleviating dataset imbalance, our main focus is on minority samples, namely malicious samples. As the amount of malicious samples is no longer sufficient for optimization, we uniformly set malicious scale factors to 0.1. For the majority samples, namely benign samples, we neither collect factors nor perform data augmentation. Before augmentation, we use the imbalanced dataset to train a base traffic classifier and perform multi classification. Then, we train a new base traffic classifier with the noised dataset and perform multi classification again.

Table 11 shows the results of two classifications. Figs. 11 and 12 show the confusion matrices before and after augmentation. Confusion matrices are usually used to analyze the classification results and provide a better understanding of performance. The rows in the confusion matrix represent the true labels of the samples, and the columns in the confusion matrix represent the predicted labels inferred by the traffic classifiers. Compared to the performance before augmentation, the accuracy, F1-score, recall and precision after augmentation increase by 5.89%, 10.11%, 1.27% and 15.03%, respectively. The results show that ONTDAS can also be used effectively to solve dataset imbalance.

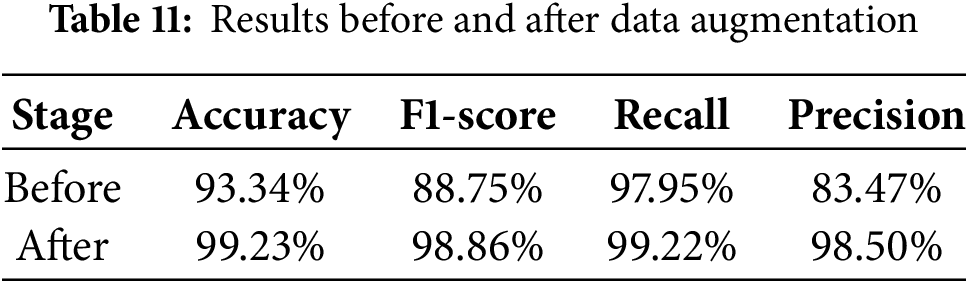
Figure 11: Confusion matrix before augmentation

Figure 12: Confusion matrix after augmentation

5  Future Work

The ever-updating attack techniques lead to the emergence of unknown malicious traffic, which poses challenges to traffic classifiers trained on limited samples. Improving the generalizability of traffic classifiers through data augmentation requires continuous in-depth research and innovation. Our proposed system has only been validated on a few publicly available datasets. For real unknown malicious traffic in the complex network environment, the system needs to evolve accordingly. Potential future work includes, but is not limited to, the following points:

Optimize noise conversion module. In the proposed system, we use three special distributions to convert classical noise to anisotropic noise. In the future, we will explore more distributions to improve the performance of ONTDAS.

Explore more data augmentation applications. ONTDAS processes multi-dimensional traffic data. It can be applied to other learning-based heterogeneous tabular data analysis systems, such as spam URL detection and KPI anomaly detection. In addition to tabular data, we will also extend ONTDAS to augment sequence data and image data.

Better balance of the performance of benign samples and unknown malicious samples. The experimental results show that, when the generalizability is significantly improved, the precision decreases slightly. This can be solved in the future by more scientific bagging algorithms or selecting algorithms of noised benign samples.

Use feature selection techniques. ONTDAS adds noise to all features, which significantly increases the time consumption of noise optimization. In the future, we will select the features that are sensitive to generalizability, and perform noise injection only on these features.

6  Conclusion

In order to address the issues of low generalizability of traffic classifiers, this paper proposes an optimized noise-based traffic data augmentation system, ONTDAS. The system first uses the noise conversion module and the noise optimization module to obtain optimized noise, and injects it into the original samples for augmentation. Then, the base traffic classifiers are trained by noised samples and integrated by the ensemble learning module. The experimental results show that ONTDAS, compared to other methods, achieves the optimal performance and significantly improves the generalizability on unknown malicious samples. In addition, ONTDAS can effectively alleviate dataset imbalance. At the same time, the ablation experiment proves the indispensability of each module. ONTDAS provides a solution for the next generation of intelligent systems in traffic data augmentation.

Acknowledgement: The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.

Funding Statement: This work was supported in part by the National Key Research and Development Program of China (No. 2022YFB4500800) and the National Science Foundation of China (No. 42071431).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Rongwei Yu, Jie Yin; data collection: Jingyi Xiang, Qiyun Shao; analysis and interpretation of results: Jie Yin, Jingyi Xiang; draft manuscript preparation: Rongwei Yu, Jie Yin, Lina Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Publicly available datasets used in this paper are obtained from the CIC Dataset. Available online via the following link: https://www.unb.ca/cic/datasets/ (accessed on 17 January 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Aceto G, Ciuonzo D, Montieri A, Pescapé A. Mobile encrypted traffic classification using deep learning: experimental evaluation, lessons learned, and challenges. IEEE Trans Netw Serv Manag. 2019 Feb 12;16(2):445–58. doi:10.1109/TNSM.2019.2899085. [Google Scholar] [CrossRef]

2. Lin X, Xiong G, Gou G, Li Z, Shi J, Yu J. Et-bert: a contextualized datagram representation with pre-training transformers for encrypted traffic classification. In: Proceedings of the ACM Web Conference 2022; 2022 Apr 25; New York, NY, USA. p. 633–42. [Google Scholar]

3. Lin K, Xu X, Gao H. TSCRNN: a novel classification scheme of encrypted traffic based on flow spatiotemporal features for efficient management of IIoT. Comput Netw. 2021 May 8;190:107974. doi:10.1016/j.comnet.2021.107974; [Google Scholar] [CrossRef]

4. Shen M, Zhang J, Zhu L, Xu K, Du X. Accurate decentralized application identification via encrypted traffic analysis using graph neural networks. IEEE Trans Inf Forensics Secur. 2021 Jan 11;16:2367–80. doi:10.1109/TIFS.2021.3050608. [Google Scholar] [CrossRef]

5. Sauber-Cole R, Khoshgoftaar TM. The use of generative adversarial networks to alleviate class imbalance in tabular data: a survey. J Big Data. 2022 Aug 22;9(1):98. doi:10.1186/s40537-022-00648-6. [Google Scholar] [CrossRef]

6. Aceto G, Ciuonzo D, Montieri A, Pescapé A. DISTILLER: encrypted traffic classification via multimodal multitask deep learning. J Netw Comput Appl. 2021 Jun 1;183:102985. doi:10.1016/j.jnca.2021.102985. [Google Scholar] [CrossRef]

7. Rezaei S, Liu X. Deep learning for encrypted traffic classification: an overview. IEEE Commun Mag. 2019 May 13;57(5):76–81. doi:10.1109/MCOM.2019.1800819. [Google Scholar] [CrossRef]

8. Chai Y, Zhu Y, Lin W, Li D. Combo Packet: an encryption traffic classification method based on contextual information. Comput Mater Contin. 2024 Apr 1;79(1):1223–43. doi:10.32604/cmc.2024.049904. [Google Scholar] [CrossRef]

9. Shi Z, Luktarhan N, Song Y, Yin H. TSFN: a novel malicious traffic classification method using BERT and LSTM. Entropy. 2023;25(5):821. doi:10.3390/e25050821. [Google Scholar] [PubMed] [CrossRef]

10. Liu C, Antypenko R, Sushko I, Zakharchenko O. Intrusion detection system after data augmentation schemes based on the VAE and CVAE. IEEE Trans Reliab. 2022 Apr 22;71(2):1000–10. doi:10.1109/TR.2022.3164877. [Google Scholar] [CrossRef]

11. Diallo AF, Patras P. Adaptive clustering-based malicious traffic classification at the network edge. In: IEEE INFOCOM 2021—IEEE Conference on Computer Communications; 2021 May 10; Piscataway, NJ, USA: IEEE. p. 1–10. [Google Scholar]

12. Sun B, Yang W, Yan M, Wu D, Zhu Y, Bai Z. An encrypted traffic classification method combining graph convolutional network and autoencoder. In: 2020 IEEE 39th International Performance Computing and Communications Conference (IPCCC); 2020 Nov 6; Piscataway, NJ, USA: IEEE. p. 1–8. [Google Scholar]

13. Wang P, Li S, Ye F, Wang Z, Zhang M. PacketCGAN: exploratory study of class imbalance for encrypted traffic classification using CGAN. In: ICC 2020—2020 IEEE International Conference on Communications (ICC); 2020 Jun 7; Piscataway, NJ, USA: IEEE. p. 1–7. [Google Scholar]

14. Hajaj C, Aharon P, Dubin R, Dvir A. The art of time-bending: data augmentation and early prediction for efficient traffic classification. Expert Syst Appl. 2024 Oct 15;252:124166. doi:10.1016/j.eswa.2024.124166. [Google Scholar] [CrossRef]

15. Wang K, Wang Z, Han D, Chen W, Yang J, Shi X, et al. BARS: local robustness certification for deep learning based traffic analysis systems. In: NDSS; 2023 Feb 27–Mar 3; San Diego, CA, USA. doi:10.14722/ndss.2023.24508. [Google Scholar] [CrossRef]

16. Ma C, Du X, Cao L. Improved KNN algorithm for fine-grained classification of encrypted network flow. Electronics. 2020 Feb 13;9(2):324. doi:10.3390/electronics9020324. [Google Scholar] [CrossRef]

17. Zhang F, Shang T, Liu J. Imbalanced encrypted traffic classification scheme using random forest. In: 2020 International Conferences on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics); 2020 Nov 2; Piscataway, NJ, USA: IEEE. p. 837–42. [Google Scholar]

18. Draper-Gil G, Lashkari AH, Mamun MS, Ghorbani AA. Characterization of encrypted and vpn traffic using time-related features. In: Proceedings of the 2nd International Conference on Information Systems Security and Privacy (ICISSP); 2016 Feb 19; Setúbal, Portugal. p. 407–14. [Google Scholar]

19. Lashkari AH, Gil GD, Mamun MS, Ghorbani AA. Characterization of tor traffic using time based features. In: International Conference on Information Systems Security and Privacy; 2017 Feb 19; Setúbal, Portugal: SciTePress. p. 253–62. [Google Scholar]

20. Shafiq M, Yu X, Laghari AA, Yao L, Karn NK, Abdessamia F. Network traffic classification techniques and comparative analysis using machine learning algorithms. In: 2016 2nd IEEE International Conference on Computer and Communications (ICCC); 2016 Oct 14; Piscataway, NJ, USA: IEEE. p. 2451–5. [Google Scholar]

21. Huang H, Zhang X, Lu Y, Li Z, Zhou S. An encrypted malicious traffic classification method integrating global semantic and spatiotemporal features. Comput Mater Contin. 2024 Mar 1;78(3):3929–51. doi:10.32604/cmc.2024.047918. [Google Scholar] [CrossRef]

22. Hong Y, Li Q, Yang Y, Shen M. Graph based encrypted malicious traffic detection with hybrid analysis of multi-view features. Inf Sci. 2023 Oct 1;644:119229. doi:10.1016/j.ins.2023.119229. [Google Scholar] [CrossRef]

23. Pan Y, Zhang X, Jiang H, Li C. A network traffic classification method based on graph convolution and lstm. IEEE Access. 2021 Nov 15;9:158261–72. doi:10.1109/ACCESS.2021.3128181. [Google Scholar] [CrossRef]

24. Li Z, Chen S, Dai H, Xu D, Chu CK, Xiao B. Abnormal traffic detection: traffic feature extraction and DAE-GAN with efficient data augmentation. IEEE Trans Reliab. 2022 Sep 14;72(2):498–510. doi:10.1109/TR.2022.3204349. [Google Scholar] [CrossRef]

25. Qing Y, Yin Q, Deng X, Chen Y, Liu Z, Sun K, et al. Low-quality training data only? A robust framework for detecting encrypted malicious network traffic. arXiv:2309.04798. 2023 Sep 9. [Google Scholar]

26. Qing Y, Liu X, Du Y. Mitigating data imbalance to improve the generalizability in IoT DDoS detection tasks. J Supercomput. 2024 May;80(7):9935–60. doi:10.1007/s11227-023-05829-5. [Google Scholar] [CrossRef]

27. Chowdhury R, Sen S, Roy A, Saha B. An optimal feature based network intrusion detection system using bagging ensemble method for real-time traffic analysis. Multimed Tools Appl. 2022 Nov;81(28):41225–47. doi:10.1007/s11042-022-12330-3. [Google Scholar] [CrossRef]

28. Wang X, Wei W, Liu C, Zhang X, Lu W, Zhong Y. Network traffic classification with small-scale datasets using ensemble learning. In: ICC 2024-IEEE International Conference on Communications; 2024 Jun 9; Piscataway, NJ, USA: IEEE. p. 1–6. [Google Scholar]

29. Xu L, Zhou X, Ren Y, Qin Y. A traffic classification method based on packet transport layer payload by ensemble learning. In: 2019 IEEE Symposium on Computers and Communications (ISCC); 2019 Jun 29; Piscataway, NJ, USA: IEEE. p. 1–6. [Google Scholar]

30. Liu X, Wang H, Zhang Y, Wu F, Hu S. Towards efficient data-centric robust machine learning with noise-based augmentation. arXiv:2203.03810. 2022 Mar 8. [Google Scholar]

31. Bilali AE, Taleb A, Bahlaoui MA, Brouziyne Y. An integrated approach based on Gaussian noises-based data augmentation method and AdaBoost model to predict faecal coliforms in rivers with small dataset. J Hydrol. 2021 Aug 1;599:126510. doi:10.1016/j.jhydrol.2021.126510. [Google Scholar] [CrossRef]

32. Khadidja B, Mohamed A, Imene A, Okba Z. Enhancing malware detection using deep learning with SMOTE and noise-based augmentation. In: International Conference on Advanced Aspects of Software Engineering (ICAASE); 2024 Nov 9; Piscataway, NJ, USA: IEEE. p. 1–8. [Google Scholar]

33. Xiao L, Zhang Z, Huang K, Jiang J, Peng Y. Noise optimization in artificial neural networks. IEEE Trans Autom Sci Eng. 2024 Apr 8;22:2780–93. doi:10.1109/TASE.2024.3384409. [Google Scholar] [CrossRef]

34. Duan F, Chapeau-Blondeau F, Abbott D. Optimized injection of noise in activation functions to improve generalization of neural networks. Chaos Solit Fractals. 2024 Jan 1;178:114363. doi:10.1016/j.chaos.2023.114363. [Google Scholar] [CrossRef]

35. Cowen-Rivers AI, Lyu W, Tutunov R, Wang Z, Grosnit A, Griffiths RR, et al. Hebo: pushing the limits of sample-efficient hyper-parameter optimisation. J Artif Intell Res. 2022 Jul 11;74:1269–349. doi:10.1613/jair.1.13643. [Google Scholar] [CrossRef]

36. Sharafaldin I, Lashkari AH, Ghorbani AA. Toward generating a new intrusion detection dataset and intrusion traffic characterization. Vol. 1. In: Proceedings of the 4th International Conference on Information Systems Security and Privacy ICISSP; 2018; Funchal, Madeira, Portugal. p.108–16. [Google Scholar]

37. Sharafaldin I, Lashkari AH, Hakak S, Ghorbani AA. Developing realistic distributed denial of service (DDoS) attack dataset and taxonomy. In: 2019 International Carnahan Conference on Security Technology (ICCST); 2019 Oct 1; Piscataway, NJ, USA: IEEE. p. 1–8. [Google Scholar]

38. Tavallaee M, Bagheri E, Lu W, Ghorbani AA. A detailed analysis of the KDD CUP 99 data set. In: 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications; 2009 Jul 8; Piscataway, NJ, USA: IEEE. p. 1–6. [Google Scholar]

39. Chawla NV, Bowyer KW, Hall LO, Kegelmeyer WP. SMOTE: synthetic minority over-sampling technique. J Artif Intell Res. 2002 Jun 1;16:321–57. doi:10.1613/jair.953. [Google Scholar] [CrossRef]

40. Zou Y, Zhu Z, Xu Z, Zhou X, Mao S. PyrAug: gaussian pyramid-based multi-scale data augmentation for panoptic plant segmentation with ambiguous boundary. In: 2022 IEEE International Conference on Robotics and Biomimetics (ROBIO); 2022 Dec 5; Piscataway, NJ, USA: IEEE. p. 1140–5. [Google Scholar]