Optimizing Feature Selection by Enhancing Particle Swarm Optimization with Orthogonal Initialization and Crossover Operator

1  Introduction

Particle Swarm Optimization (PSO) is a powerful stochastic optimization technique inspired by swarm intelligence, first introduced by James Kennedy and Russell Eberhart in 1995 [1]. PSO simulates the social behaviors of animals such as bird flocking and fish schooling. Its flexibility, simplicity, and ease of implementation have made it one of the most widely adopted metaheuristic optimization methods. Over the years, PSO has been successfully applied to a range of problems, including feature selection [2,3], feature extraction [4,5], hyperparameter optimization [6,7], clustering [8,9], neural network training [10,11], forecasting [12,13], and multi-objective optimization [14,15].

Despite its widespread use, PSO suffers from limitations such as premature convergence, slow convergence, and stagnation [16]. To address these challenges, various improvements have been proposed, including enhanced velocity handling techniques [17], new position update mechanisms [18], control parameter adaptation strategies [14], swarm adaptation methods [19,20], modifications to neighborhood topologies [21], and fitness landscape analysis tools [22].

However, PSO continues to face difficulties—particularly premature convergence—when applied to complex datasets [16,23]. To overcome these issues, this study introduces advanced strategies to enhance PSO’s performance, especially in the context of high-dimensional and complex medical datasets. Specifically, we incorporate orthogonal initialization and a crossover operator to improve population diversity and mitigate premature convergence. Detailed descriptions of these enhancements will be provided in the following sections.

The motivation behind this research stems from the critical role of feature selection in improving the efficiency and interpretability of machine learning models. By identifying the most relevant subsets of features from large datasets, feature selection helps to address the challenges associated with the exponential growth of data—often referred to as the “curse of dimensionality” [24]. Our proposed method addresses this issue by selecting informative features, thereby improving predictive performance through the elimination of noisy, irrelevant, and redundant data. Below is a summary of the key contributions of this research:

1.    Enhancement of PSO’s efficiency and convergence stability using orthogonal initialization and crossover techniques.

2.    Integration of the optimized PSO framework with machine learning to improve feature selection and model interpretability.

3.    Evaluation and comparison of feature selection techniques on complex medical datasets.

The rest of the paper is organized as follows: Section 2 provides a literature review, covering recent advancements in PSO and its applications in feature selection. Section 3 outlines the proposed method and implementation process. Section 4 discusses the datasets and evaluates the proposed approach on various medical datasets. Finally, Section 5 concludes the study and presents future research directions.

2  Literature Review

Building on the introduction of PSO and its limitations mentioned in Section 1, this literature review examines various methods that have been proposed to address issues such as premature convergence, slow convergence, and stagnation [19]. Modifications to the PSO algorithm can be categorized into several approaches [16]. We review six of these categories below, before discussing the broader machine learning problem of feature selection and existing applications of PSO in this domain.

2.1 Methods of Velocity Handling

In the context of velocity handling, several key techniques have emerged in the literature to enhance the efficiency of PSO. These techniques primarily involve modifications to velocity initialization methods, velocity updating strategies, and velocity clamping approaches. Proper adjustment of these components is crucial for achieving a balance between exploration and convergence efficiency.

Typically, the initial velocity of particles is set to zero. While this approach stabilizes initial convergence, it restricts exploration capabilities. Random initialization, on the other hand, promotes greater swarm diversity [25]. Similarly, Gaussian Disturbance PSO [26] employs the Gaussian distribution to boost the likelihood of escaping from local optimum points. Techniques such as Velocity-free Boolean PSO [27] employ random velocity initialization to enhance performance. The Self-Balanced PSO [28] focuses on refining the velocity updating process by utilizing the current global best to enhance the cognitive component. This approach not only improves swarm diversity but also helps control exploitation abilities, thereby enhancing overall convergence. Additionally, Modified Particle Velocity-based PSO (MPV-PSO) [29] introduces an adaptive velocity updating equation, which increases insensitivity to local optima.

2.2 Position Update Mechanisms

To address limitations in traditional PSO—particularly its difficulty in handling constrained optimization—several position update strategies have been proposed. Zhao and Li [30] introduced a Two-Stage Multi-Swarm PSO, which employs multiple swarms for global exploration in the first stage, followed by local exploitation using elite solutions in the second. This approach enhances both search diversity and convergence stability. Another variant, Constrained Multi-Swarm PSO Without Velocity [31], eliminates the component entirely and updates particle positions through a linear combination of the personal best and global best. Both methods reflect ongoing efforts to improve position updates in PSO, particularly for constrained and complex search spaces.

2.3 Control Parameter Adaptation

In the initial PSO algorithm, particle velocity was not controlled, resulting in a tendency for particles to explore large regions of the search space. Several approaches have modified the calculation process of inertia weight, including PSO with Self-Regulating Inertia Weight [32], Selective Multiple Inertia Weights [33], and Exponential Dynamic Inertia Weight PSO [34]. Additionally, the well-known Constriction Factor PSO and Ramp Rate Constriction Factor PSO [35] have been developed by incorporating advanced techniques to control cognitive and social coefficients.

PSO is heavily dependent on initial settings, which can lead to premature convergence. By adapting the control parameters based on the current situation, the likelihood of the algorithm reaching the global optima can be enhanced. One variant using this technique is Unique Adaptive PSO [36], where particles are encouraged to learn solely from their feasible solutions. Furthermore, optimally selecting control parameters is crucial for enhancing exploration capabilities, reducing premature convergence, and minimizing the number of parameters involved.

2.4 Swarm Adaptation

Swarm initialization methods and swarm size significantly impact PSO’s effectiveness and should be tailored to specific optimization problems. Researchers typically use uniform or Gaussian distributions for initializing particle coordinates in PSO, but these can limit search space coverage. Studies indicate that using different distributions, such as logarithmic or normal, can significantly improve convergence speeds. One innovative approach is Generalized Opposition-based PSO, which involves Generalized Opposition-based Learning to help trapped particles escape from local optima [37]. Additionally, Chaotic PSO (CPSO) has shown promising results by integrating chaos into initialization and PSO mechanics, improving performance across various scenarios [38].

With the introduction of the algorithm in 1995, the authors suggested setting the population size between 20 and 50 particles. However, Piotrowski et al. recommended larger swarm sizes (70–500 particles), noting these generally yield improved performance across various PSO variants, particularly for more complex problems. Conversely, they suggested smaller swarm sizes when addressing unimodal problems for most PSO variants [20].

2.5 Neighborhood Topologies

After the introduction of PSO, researchers investigated what might be the best social structure for particles and showed that the performance of PSO is significantly affected by neighborhood topology, with the effects varying depending on the function being optimized. A subsequent study examined neighborhood topology across PSO, Bare-bones PSO (BBPSO), and an extension of BBPSO, using six different topologies: ring, fully connected, mesh, star, toroidal, and tree. Their findings indicated that PSO performs best with toroidal, mesh, and ring topologies, while BBPSO excels with fully connected, star, or tree structures [39,40]. This demonstrates that the choice of topology should be made thoughtfully, depending on the specific algorithm employed.

2.6 Fitness Landscape Analysis

In understanding and improving the behavior of metaheuristic algorithms, fitness landscape analysis is helpful. Fitness landscape modification can effectively eliminate many local optima that could lead the search away from the global optimum [41]. In this approach, the fitness values of some particles are estimated, while those of others are obtained from objective functions.

2.7 Feature Selection (FS)

Having reviewed various PSO modification techniques, we now turn to the application domain of our study: feature selection. The exponential growth of data has led to significant challenges associated with high dimensionality, commonly referred to as the “curse of dimensionality” [24]. One effective approach to addressing this issue is feature selection, which involves identifying and selecting the most important features from a dataset to enhance the performance of specific machine learning algorithms. Applying feature selection improves predictive accuracy by eliminating noisy, irrelevant, and redundant data.

There are two categories of FS methods based on the method of evaluation of features: feature ranking method and subset selection method [42]. In feature ranking methods, based on predefined criteria, each feature gets a score and using a threshold, the low score features are eliminated. In subset selection methods, the optimum subset is chosen from all the possible subsets, which makes it an NP-hard problem. When the problem becomes more complicated, metaheuristic algorithms such as Tabu search [43], Ant Colony Algorithm (ACO) [44], Genetic algorithm [45], Gravitational Search Algorithm [46], and many more have been utilized in feature selection.

2.8 Utilization of PSO in Feature Selection

An extensive evaluation was conducted on the use of metaheuristic algorithms—particularly swarm-based methods—for feature selection. The analysis compared the effectiveness and limitations of various algorithms, including Particle Swarm Optimization (PSO), Firefly Algorithm (FA), Differential Evolution (DE), Ant Colony Optimization (ACO), Artificial Bee Colony Optimization (ABC), Gravitational Search Algorithm (GSA), Bat Algorithm (BA), Cuckoo Optimization Algorithm (COA), Whale Optimization Algorithm (WOA), Gray Wolf Optimization (GWO), and Salp Swarm Algorithm (SSA), across six diverse medical datasets with varying feature dimensions. The results demonstrated that PSO consistently outperformed the other methods in terms of average classification accuracy, performance stability, feature selection efficiency, and execution time [42,47].

The literature has seen significant advancements in utilizing PSO as a feature selection method. Researchers have integrated PSO with Support Vector Machines (SVM) to optimize feature selection and reduce computational demands. Other notable developments include enhancing particle updating methods for feature selection tasks and employing binary PSO alongside Hamming distance in classification tasks [12,45]. Yong et al. proposed a multi-objective PSO algorithm aimed at classifying unreliable data, introducing new search operators to enhance performance [48]. Zhang et al. introduced a multi-objective PSO method for cost-effective feature selection [49]. Jain et al. applied a modified binary PSO for gene selection and cancer classification [50]. Recent advancements have also included hybrid methods for selecting relevant features from DNA microarray data.

Building on these findings and addressing the limitations identified in the literature, we introduce an advanced PSO method for improved feature selection in this study. The next section describes our proposed method in detail.

3  Methods

In this section, we provide a detailed discussion of Particle Swarm Optimization (PSO) and introduce our proposed algorithm, Orthogonal Particle Swarm Optimization with Crossover (OrPSOC). We begin by explaining the fundamental concepts and mathematical formulation of the standard PSO algorithm, followed by a comprehensive description of our enhancements designed to overcome its limitations when applied to complex feature selection problems.

3.1 Particle Swarm Optimization

The main points of Particle Swarm Optimization (PSO) are collaboration, exploration, and exploitation. Imagine a Cartesian coordinate system where each point represents a bird in a swarm [1]. Initially, each bird (or particle) is assigned a random position. Each particle has a velocity that determines its movement through the solution space, which evolves over time based on both individual experiences and the collective experience of the swarm. Each particle keeps track of its personal best position and the global best position found by the swarm. At each iteration, particles update their velocity by considering their personal best and the swarm’s global best. The algorithm updates the position and velocity of each particle iteratively to find the optimal solution [51]. The velocity update equation is a crucial part of PSO, combining the particle’s personal experience and the collective knowledge of the swarm. The equation is given by:

Vid(t+1)=w×Vid(t)+c1×r1×(pbestid−Pid(t))+c2×r2×(gbest−Pid(t))(1)

here, Vid(t) represents the velocity of particle i in dimension d at time t, w is weight, c1 and c2 are cognitive and social components, respectively, guiding the particle towards its personal best position pbestid and the global best position gbest. The random variable r1 and r2, drawn from the uniform distribution, add stochasticity to the search process.

The position of each particle is then updated using the new velocity:

Pid(t+1)=Pid(t)+Vid(t+1)(2)

This equation shifts the particle from its current position Pid(t) in the direction determined by its velocity. The continuous adjustment of positions and velocities allows the swarm to explore the solution space, converging towards the optimal solution.

3.2 The Proposed Method

In this section, we discuss enhancements to the PSO mechanism by introducing orthogonal initialization, which improves the algorithm’s exploratory behavior. Additionally, we integrate crossover techniques to enhance diversity and prevent premature convergence.

3.2.1 Orthogonal Initialization

Orthogonal initialization is a method used to generate a diverse and well-distributed initial population of particles in optimization algorithms [52]. This technique leverages orthogonal vectors to ensure that the initial particles effectively cover the search space, thereby enhancing the exploration capabilities of the algorithm.

We constructed the orthogonal matrix [H]n×d where n represents the number of particles and d is dimensions or features. Each element Hij of the matrix H is calculated using the formula:

Hij=(2i+1)(2j+1)2(n×d)  where  i=0,1,2,…,n−1;j=0,1,2,…,d−1(3)

This formula ensures that the elements of the matrix are arranged in a specific pattern that promotes orthogonality. To achieve orthogonal initialization in PSO, we employ Singular Value Decomposition (SVD) to obtain orthogonal vectors [47]. This process helps to decompose H into three matrices such as:

H=UΣVT(4)

where U is n×n orthogonal matrix, Σ is n×d diagonal matrix, and V is d×d orthogonal matrix. The orthogonal matrix U contains vectors that are linearly independent and orthogonal to each other.

After creating the orthogonal matrix, we utilize the orthogonal components from the matrix U. Specifically, we take the first d columns of matrix U and consider their absolute values to ensure non-negativity, defined as:

P=|U[:,0:d]|(5)

In matrix P, each row represents a starting position for a particle, and these positions spread out in the search space. Finally, the initialized particles in matrix P are scaled to conform to the boundaries of the search space such as:

P=P×(upperbound−lowerbound)+lowerbound(6)

This scaling ensures that all particles are positioned within the feasible region of the search space, ready for the optimization process to begin.

For clearer understanding, suppose we initialize a swarm with n=3 particles in a d=2 dimensional space. First, we compute each element Hij of the matrix H∈R3×2 as: H=[0.0830.250.250.750.4171.25]. Next, we apply Singular Value Decomposition (SVD) to decompose the matrix H into: H=UΣVT. Where U∈R3×3 is the left orthogonal matrix, Σ∈R3×2 is the diagonal matrix of singular values, and V∈R2×2 is the right orthogonal matrix.

We then extract the first d=2 columns of U, take their absolute values to ensure non-negativity and define: P=|U[:,0:2]|∈R3×2. This gives us a matrix P∈R3×2 representing the orthogonally initialized positions of the 3 particles in the search space. Then finally we scale P according to the problem bounds using Eq. (6).

3.2.2 Crossover Operator

Once the initialization is completed, particles update their velocity and position based on personal best and global best positions. At each iteration, the crossover mechanism is applied to selected particles to introduce genetic diversity and create new potential solutions [45].

During each iteration, particles are randomly selected for the crossover operation based on a predetermined crossover probability. This probability determines whether a particle will undergo crossover with another particle. A random binary mask m=[m1,m2,…,md], of the same length d is generated, where each element mi is determined as follows:

mi={1withprobabilitycrossoverrate0otherwise}(7)

This mask determines which dimensions of the particle will be inherited from each parent. For each dimension, an offspring o=[o1,o2,…,od], is created by combining elements from two parent particles, p1 and p2 based on the mask m:

oi=mi.pi,i+(1−mi).p2,i(8)

If mi=1, the offspring inherits the gene from the first parent (pi,i) and if mi=0, the offspring inherits the gene from the second parent (p2,i). This process combines characteristics from both parents. If the offspring has a better fitness score than either parent, it replaces the parents in the population until the best solution is obtained. This introduction of genetic diversity helps prevent the algorithm from converging prematurely to a suboptimal solution, thereby avoiding local optima [25]. The detailed pseudocode of the proposed algorithm (OrPSOC) is provided in Algorithm 1.

Hence by strategically combining orthogonal initialization and the crossover mechanism, the proposed OrPSOC algorithm not only enhances initial diversity but also continuously introduces new genetic material into the population. This dual approach ensures that the algorithm maintains a balance between exploring new areas of the search space and exploiting known good solutions, thereby optimizing performance more effectively than traditional PSO methods. The complete experimental layout, model details, and other relevant aspects of the experiment are illustrated in Fig. 1.

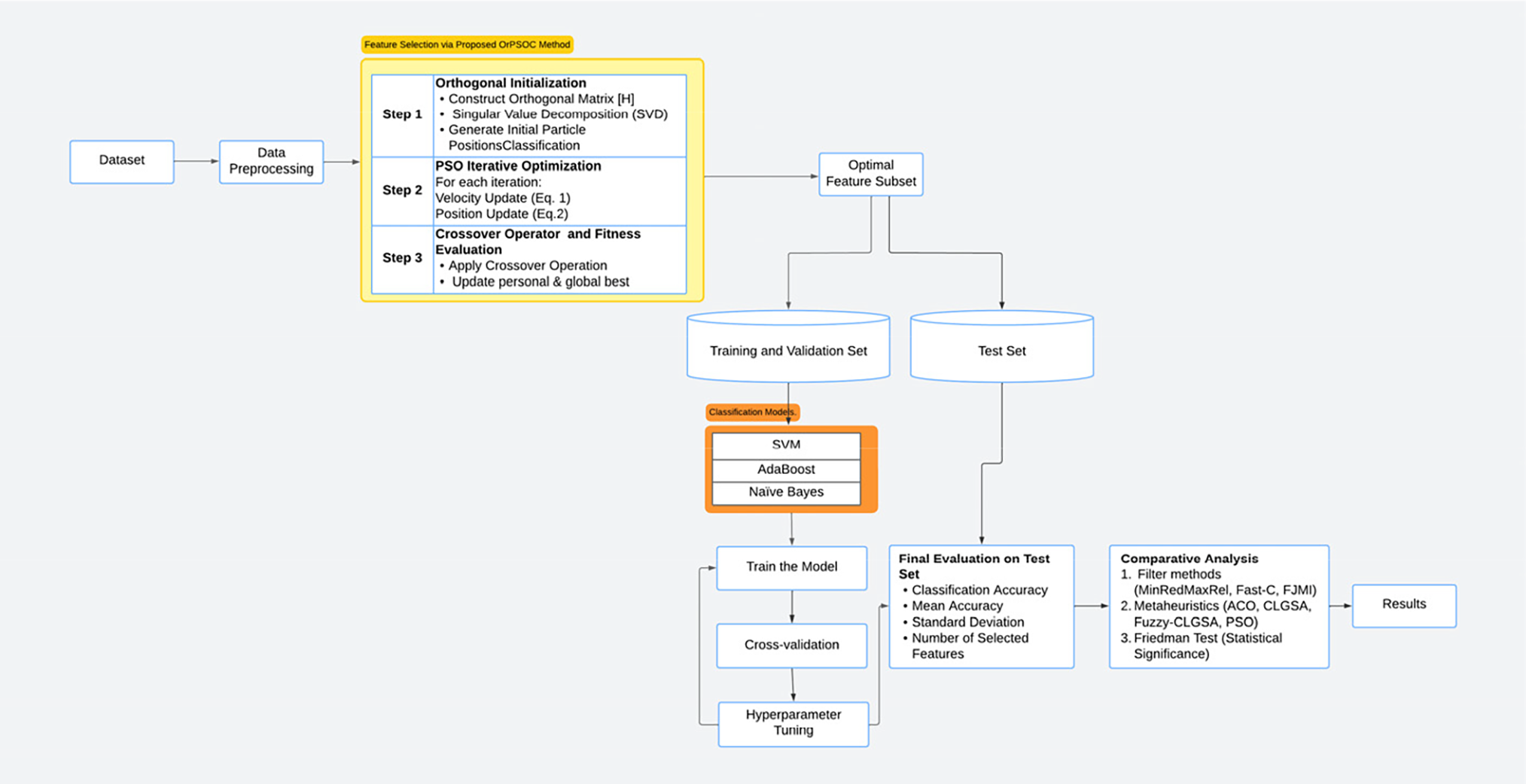
Figure 1: Overview of the experimental framework used in this study

4  Experimental Setting and Results Discussion

This section assesses the effectiveness of our newly developed feature selection strategy. We measure performance based on the number of features selected and the classification accuracy [53], computed using the formula:

CA=TP+TNTP+TN+FP+FN(9)

here, TN, TP, FN, and FP denote the counts of true negatives, true positives, false negatives, and false positives respectively. We conduct ten iterations of each feature selection method, averaging the outcomes to gauge methodological efficacy. For each iteration, we standardize the dataset and split it into a training set (70%) and a testing set (30%), using the training set for feature selection and the testing set for method validation. This consistent approach across all tested methods ensures comparability.

To evaluate the effectiveness of the proposed Orthogonal PSO with Crossover (OrPSOC) method, we compared it against a carefully selected set of baseline algorithms, including both traditional filter-based techniques and nature-inspired metaheuristic approaches. The choice of these benchmarks was based on their wide acceptance in the feature selection literature, their demonstrated effectiveness in high-dimensional settings, and their complementary strengths [49–51].

The filter-based methods—Fast clustering-based Feature Selection (Fast-C) [54], Minimum Redundancy Maximum Relevance (MinRedMaxRel) [55], and Five-way Joint Mutual Information (FJMI) [56]—were chosen for their simplicity, computational efficiency, and strong performance in ranking relevant features across various domains. These techniques serve as robust, non-iterative baselines commonly used in feature selection studies, enabling a clear performance contrast against iterative optimization-based methods.

In addition, we included four nature-inspired metaheuristic algorithms: the original Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO) [44], Comprehensive Learning Gravitational Search Algorithm (CLGSA) [57], and its fuzzy-based variant (FCLGSA) [58]. These were selected for several reasons. First, PSO serves as the foundational baseline to demonstrate the improvements introduced by the OrPSOC enhancements. ACO was selected as a classical swarm intelligence technique often benchmarked in feature selection tasks. CLGSA and FCLGSA, more recent and advanced algorithms, represent hybrid and enhanced metaheuristic strategies that have shown competitive performance in prior studies involving high-dimensional and imbalanced data. This diverse set of metaheuristics allows for a fair and comprehensive comparison, evaluating the effectiveness of OrPSOC not only against its predecessor but also against broader state-of-the-art optimization strategies.

Together, these methods cover a spectrum from traditional statistical approaches to cutting-edge heuristic techniques, offering a balanced and rigorous evaluation framework. All methods were implemented in Python using consistent experimental protocols and libraries such as Scikit-learn, PySwarms, DEAP, and pymrmr, ensuring reproducibility and comparability across results.

4.1 Datasets

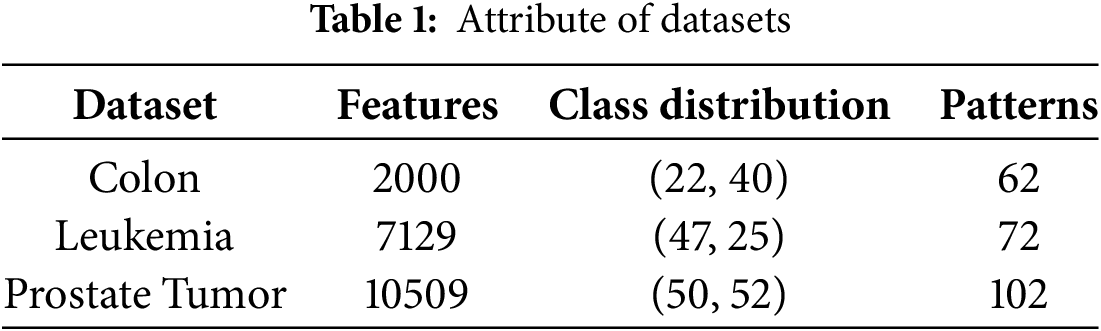
This study utilizes three specialized medical datasets to assess the performance of the proposed method. These datasets are chosen for their unique properties and relevance to specific medical conditions: Colon, Leukemia, and Prostate Tumor. The Colon and Leukemia datasets are available from the Bioinformatics Research Group at Universidad Pablo de Olavide [59], and the Prostate Tumor dataset is sourced from the Gene Expression Model Selector at Vanderbilt University [60].

Table 1 elaborates on the specifics of the three chosen medical datasets, each selected for their distinct attributes, such as the number of features they contain. The Prostate Tumor dataset is particularly notable for its high-dimensional feature space coupled with a relatively small sample size. These datasets—Colon, Leukemia, and Prostate Tumor—are used for binary classification tasks aimed at cancer detection. In some cases, these datasets include attributes with a broad range of values, where larger values can overshadow smaller ones. To address this, max-min normalization is applied. Additionally, there are instances of missing values within some datasets. To rectify this, missing values are replaced by calculating the average of the available data for the corresponding attributes.

4.2 Parameters and the Utilised Classifies

The implementation of the proposed OrPSOC method requires careful setting of various parameters. Initial values for these parameters are determined through trial and error based on preliminary runs, though these values are not necessarily optimal. In PSO, the parameters w, c1, and c2 are crucial as they represent the inertia weight, cognitive learning rate, and social learning rate, respectively. To effectively balance deep exploration (diversification) and focused exploitation (intensification), these parameters are initially set to 0.6, 0.2, and 0.2. Additionally, as outlined in the methods section, the crossover rate is configured at 0.6, with the number of particles and the number of iterations both set at 100.

To assess the efficiency of the proposed OrPSOC method across various scenarios, this study employs three distinct classifiers: Support Vector Machine (SVM) [61], and AdaBoost (AdaB) [62], Naïve Bayes (NaBa) [63]. SVM is a well-established supervised learning algorithm designed to optimize the separation margin between data points, and it has demonstrated robust performance in both classification and regression tasks. Naïve Bayes (NaBa) consists of a set of probabilistic processes that apply Bayes’ theorem, assuming independence among features. Lastly, AdaBoost (AdaB) enhances its efficacy by adjusting the weights of misclassified instances in successive iterations, increasingly focusing on the more challenging cases.

4.3 Results

This part of the discussion analyzes the performance of the OrPSOC approach by comparing it with traditional filter-based and subsequent nature-inspired metaheuristic techniques. The comparisons focus on two primary criteria: classification accuracy and the quantity of features selected. The parameter settings for each approach were adopted from the relevant literature or determined through preliminary trials when optimal values were not specified.

Initially, we assess the performance of the OrPSOC approach against well-known filter-based feature selection strategies using different classifiers. Table 2 summarizes the mean classification accuracy percentages from ten separate runs for each method, including MinRedMaxRel, Fast-C, FJMI, and OrPSOC, across three different datasets. The entries in Table 2 include both the mean accuracy and the standard deviation (in parentheses) for these runs, providing a comprehensive overview of each method’s performance stability and effectiveness.

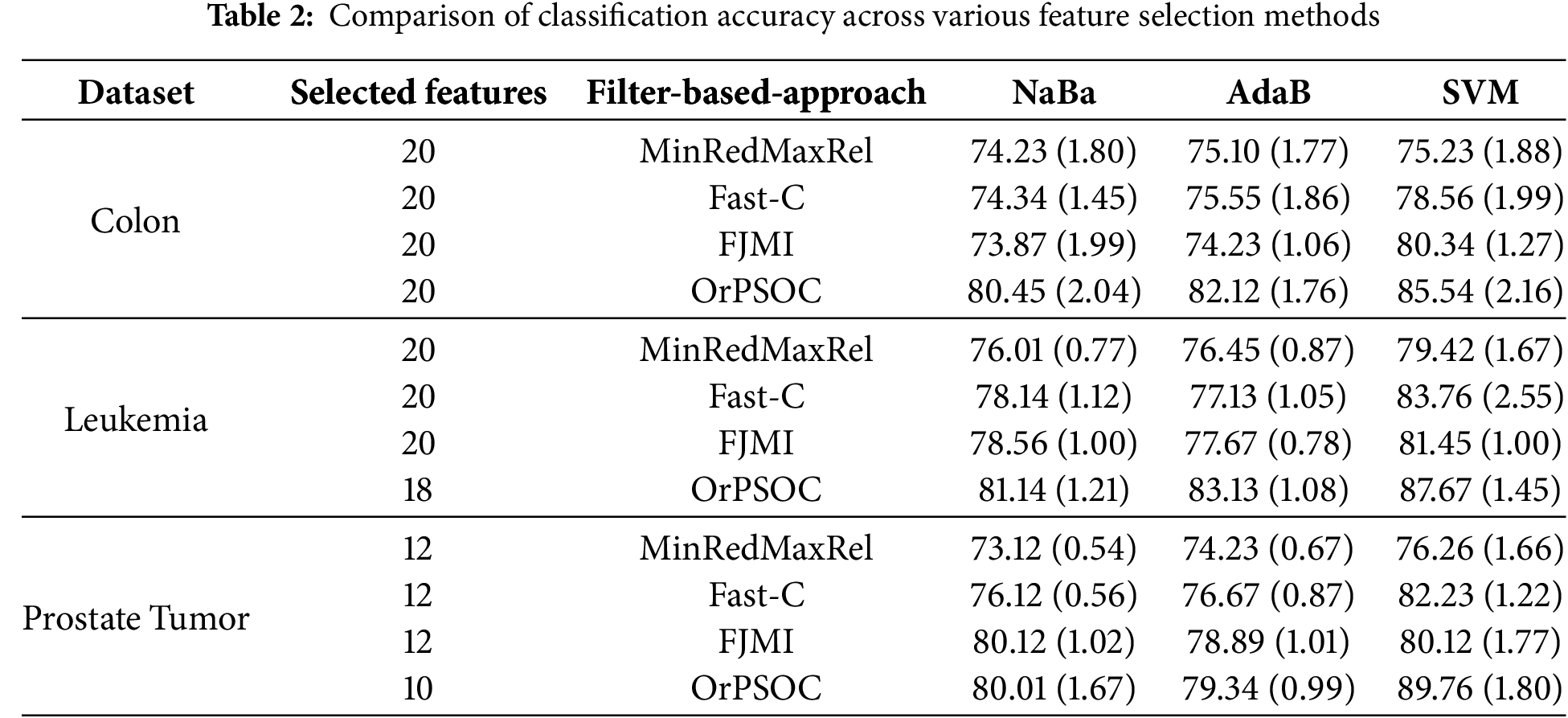
According to Table 2, the OrPSOC method consistently outperforms the other feature selection methods across all datasets and classifiers, underscoring its effectiveness in enhancing classification accuracy. This method shows particularly strong synergy with the SVM classifier, leading to the most significant performance gains. Among the traditional filter methods, FJMI often exhibits superior or competitive performance, especially with the SVM classifier, indicating its effectiveness in extracting valuable features that positively impact classification outcomes. The performance variation across different datasets is noteworthy, with the Prostate Tumor dataset showing significant improvements when using OrPSOC, even with a reduced number of features. This suggests that OrPSOC is not only effective in feature selection but also efficient in utilizing fewer, more impactful features. Additionally, the reported performance metrics, including mean accuracy and standard deviation, confirm the statistical stability of the results—an essential factor in validating the reliability of feature selection methods for practical applications.

This consistency is particularly noteworthy given that the three selected datasets vary significantly in both feature dimensionality and sample size, which offers a valuable testbed to evaluate the robustness of OrPSOC. For instance, the Prostate Tumor dataset contains over 10,000 features but only 102 samples, presenting an extreme case of high dimensionality with limited observations. Leukemia is similarly high-dimensional with a small sample size, while Colon has a moderate number of features and samples. Despite these challenges, OrPSOC consistently achieved strong performance across all datasets. This demonstrates the algorithm’s adaptability to both feature redundancy and sparsity. The crossover operator appears particularly effective in managing noise in high-dimensional settings, while orthogonal initialization ensures a diverse search from the outset, helping to mitigate overfitting in small-sample scenarios.

In Table 3, which showcases classification accuracies and computational times (in seconds) for various nature-inspired metaheuristic algorithms, the first column corresponds to the SVM technique without any metaheuristic enhancement. The results show that several metaheuristics outperform the baseline SVM model. OrPSOC consistently achieves the highest accuracy across all datasets—85.64% for Colon, 88.02% for Leukemia, and 89.74% for Prostate Tumor—highlighting its strong capability in identifying relevant features for medical diagnostics. Among the competing methods, PSO emerges as the closest in performance, trailing OrPSOC by approximately 5–6% across the datasets. ACO, on the other hand, exhibits the lowest accuracy, particularly underperforming on the Prostate Tumor dataset with only 76.12%. This may reflect its limited effectiveness in navigating high-dimensional medical data. Regarding computational efficiency, all algorithms require similar time, with OrPSOC occasionally taking slightly longer. For example, on the Colon dataset, OrPSOC takes 56 s compared to PSO’s 54 s. However, this modest increase in time is justified by the notable improvement in classification accuracy.

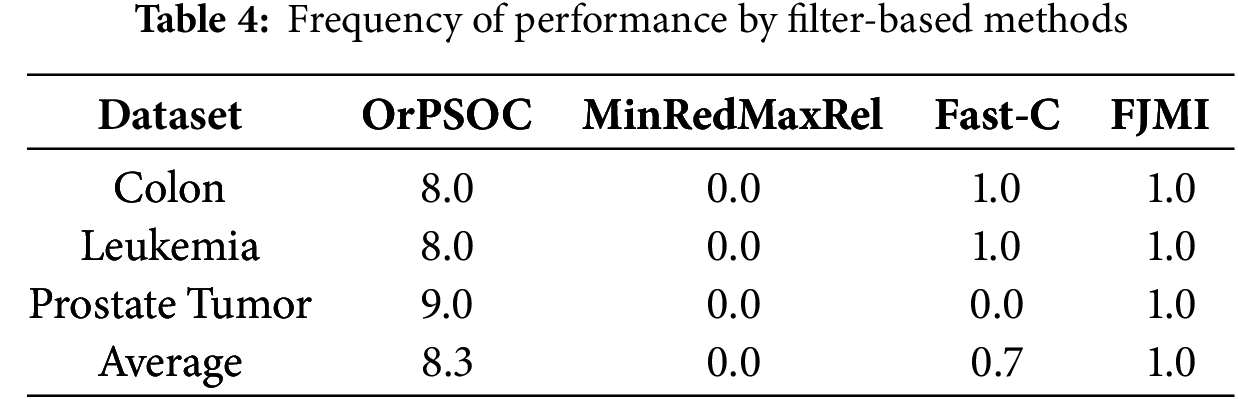
Tables 4 and 5 detail the frequency with which different feature selection methods achieved the highest performance across these datasets on filter-based and metaheuristic-based, respectively. These tables collectively underscore OrPSOC’s dominant efficacy in both filter-based and metaheuristic-based feature selection categories across various medical datasets, indicating its robustness and reliability as a feature selection method in diverse diagnostic scenarios.

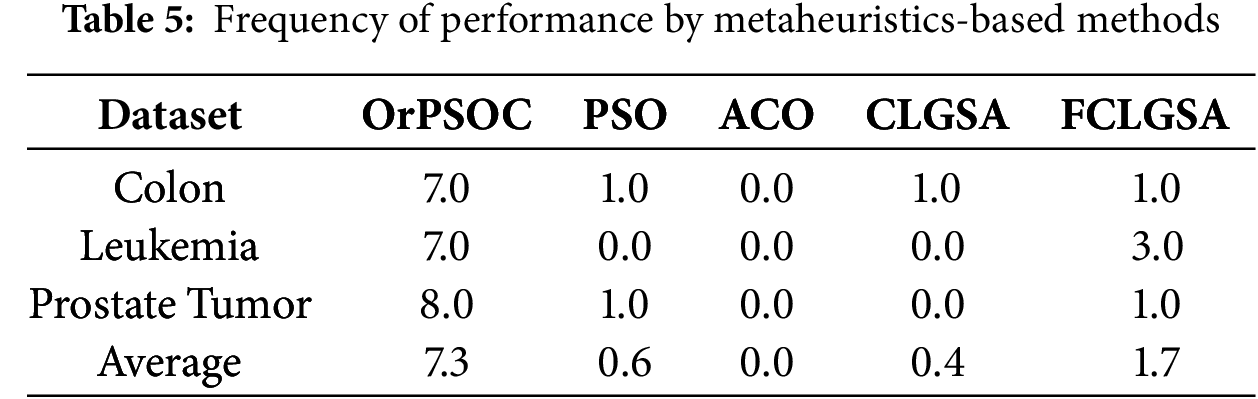
The performance variation of OrPSOC across different datasets and classifiers can be explained by the interplay between dataset characteristics and classifier behavior. High-dimensional and low-sample-size datasets such as Prostate Tumor benefit significantly from OrPSOC’s orthogonal initialization, which enhances diversity in the swarm and prevents premature convergence. This mechanism ensures that the search space is explored more effectively from the outset. Additionally, the crossover operator in OrPSOC maintains population diversity during the convergence phase, which is particularly valuable in complex, nonlinear datasets like Leukemia. From a classifier standpoint, SVM perform notably well due to their sensitivity to feature relevance and decision boundaries, which complements OrPSOC’s ability to prune irrelevant features. In contrast, Naïve Bayes, with its assumption of feature independence, is less able to capitalize on the refined feature subsets, leading to more modest performance gains.

Overall, OrPSOC demonstrates its strength in handling high-dimensional, sparse, and noisy data—scenarios where maintaining diversity and controlled convergence are critical. Its superiority over standard PSO is evidenced by consistent improvements in classification accuracy: 6.3% (Colon), 5.9% (Leukemia), and 6.3% (Prostate Tumor), despite both algorithms sharing identical control parameters and search operators. These improvements are directly attributable to the integration of orthogonal initialization and crossover. Together, these enhancements boost the algorithm’s robustness and effectiveness in challenging feature selection tasks.

4.4 Sensitivity Analysis of Crossover Parameter

To understand the impact of the crossover rate on classification accuracy, we conducted a detailed sensitivity analysis, as depicted in Fig. 2. This analysis explores the effects of varying crossover rates on three medical datasets: Colon, Leukemia, and Prostate Tumor, using SVM, NaBa, and AdaB classifiers.

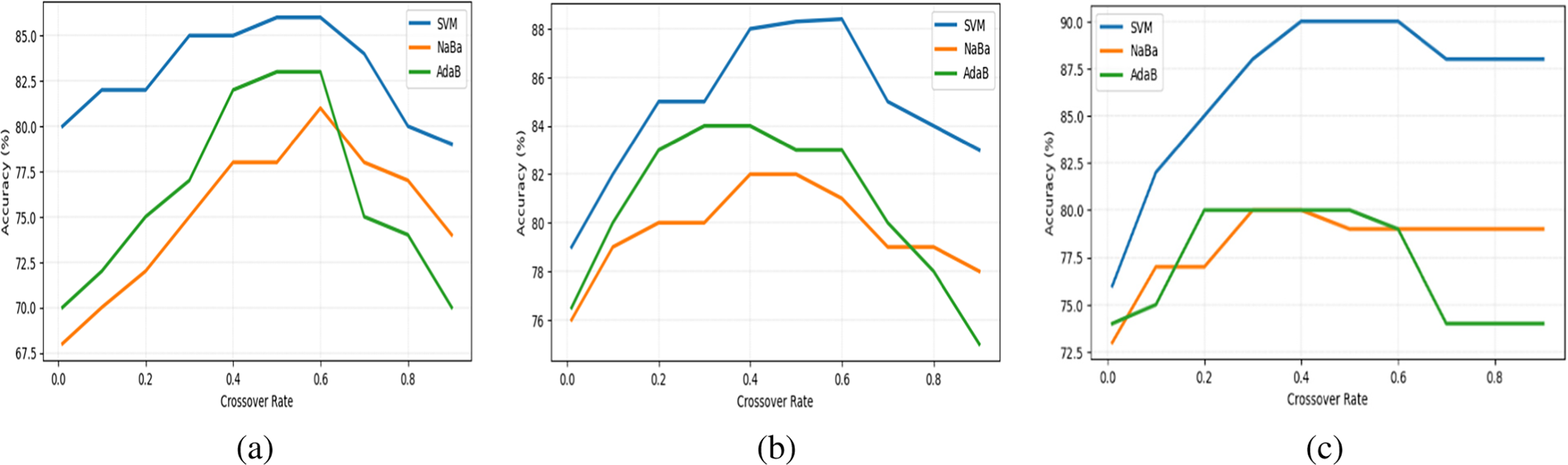
Figure 2: Average classification accuracy across 10 independent runs at varying crossover rates for (a) Colon dataset; (b) Leukemia dataset; and (c) Prostate Tumor dataset

The analysis reveals that for the SVM classifier, there is a noticeable improvement in performance as the crossover rate increases, peaking at around a rate of 0.4 to 0.5. Beyond this point, the performance plateaus before eventually experiencing a slight decline, suggesting an optimal range where crossover effectively enhances feature recombination for SVM. The AdaB classifier also shows improvement with increasing crossover rates, particularly up to 0.4–0.5, before gradually declining. In contrast, NaBa demonstrates a steady performance gain until mid-range crossover rates, but drops sharply beyond 0.6, suggesting overfitting or loss of useful feature combinations at higher crossover levels.

Notably, the findings indicate that adjusting the crossover parameter to 0.6 enhances the classification accuracy of the OrPSOC approach across various datasets. These observations underscore the importance of tailoring crossover rates to each classifier and dataset combination. Optimally adjusting crossover rates can significantly enhance classifier accuracy by introducing beneficial diversity. However, excessively high rates might disrupt learning processes by breaking down beneficial feature combinations, thus hindering performance.

4.5 Statistical Analysis

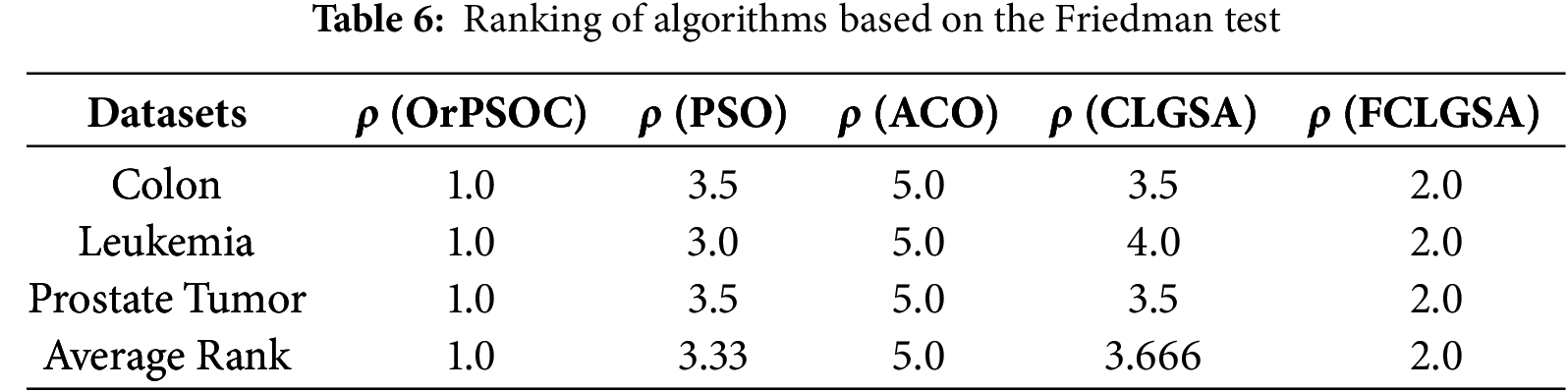
This section presents a statistical evaluation of the outcomes utilizing the Friedman test [64]. The Friedman test, a nonparametric method, assesses the efficacy of various approaches across multiple datasets. Due to the stochastic characteristics of the metaheuristic algorithms used in this study, the Friedman test is well-suited for assessing the comparative performance of these methods when applied with the SVM classifier. Each entry in our dataset denotes the accuracy achieved by each algorithm for each dataset, creating a perfect framework for the Friedman test, as all algorithms were evaluated consistently across the same three datasets.

Continuing the analysis, the Friedman test was administered with the assumption that all algorithms would perform equivalently across the datasets (null hypothesis) vs. the possibility that one or more algorithms would exhibit distinct performance (alternative hypothesis). The test generated a Friedman statistic of 11.862 with a p-value of 0.0184, which is significant at a 5% threshold (α=0.05). Consequently, the null hypothesis was rejected, confirming meaningful variations in how the algorithms performed across the datasets.

To further analyse which algorithms differed significantly, rankings based on performance within each dataset were assigned. These rankings (ρ) were averaged across all datasets to determine the overall performance of each algorithm, as presented in Table 6. This ranking methodology helps identify not only the existence of performance differences but also how each algorithm stands in relation to others in terms of performance. According to Table 6, the proposed algorithm OrPSOC achieved rank 1 across all datasets, highlighting its superiority. While ACO did not perform well, PSO and CLGSA proved to be strong competitors. This section validates the effectiveness of metaheuristic algorithms in improving feature selection outcomes.

5  Conclusion and Future Scope

This study presented OrPSOC, a novel enhancement of the Particle Swarm Optimization (PSO) algorithm, incorporating orthogonal initialization and a crossover operator. The orthogonal initialization strategy generates a diverse and well-distributed initial population, significantly improving the algorithm’s exploratory capabilities. The integration of a crossover operator promotes genetic diversity throughout the search process, effectively mitigating premature convergence and improving robustness in high-dimensional feature spaces.

We evaluated OrPSOC on three benchmark medical datasets, demonstrating its superior performance in feature selection tasks compared to traditional filter methods and state-of-the-art metaheuristic algorithms. The algorithm consistently achieved the highest classification accuracy while selecting fewer, yet more informative, features. A sensitivity analysis of the crossover rate provided further insight into parameter tuning, and statistical validation using the Friedman test confirmed OrPSOC’s significant advantage in performance.

These results highlight OrPSOC’s effectiveness and reliability in handling complex, high-dimensional data, particularly in medical diagnostics. Its strong performance underscores its potential as a powerful and interpretable tool for feature selection. However, since the method was tested primarily on classification tasks with labeled data, its generalization to unsupervised learning scenarios or large-scale real-time applications requires further validation.

Looking forward, OrPSOC can be extended to a broader range of applications, including unsupervised learning tasks such as clustering. We are currently planning extended research to explore its performance in clustering-based applications and across other domains such as finance, cybersecurity, and bioinformatics—further validating its adaptability and practical impact in diverse data-driven fields.

Acknowledgement: The authors would like to thank the University of Adelaide for providing computational support and access to resources required for this research.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Indu Bala; methodology, Indu Bala; formal analysis, Indu Bala; implementation, Indu Bala and Wathsala Karunarathne; validation, Wathsala Karunarathne; writing—original draft preparation, Indu Bala; writing—review and editing, Indu Bala, Wathsala Karunarathne and Lewis Mitchell; supervision, Lewis Mitchell; critical review, Lewis Mitchell. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used in this study are publicly available through the Bioinformatics Research Group at Universidad Pablo de Olavide and the Gene Expression Model Selector at Vanderbilt University. These sources are also cited in the references for easy access. The code for the proposed algorithm can be made available upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of ICNN’95—International Conference on Neural Networks; 1995 Nov 27–Dec 1; Perth, WA, Australia. doi:10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]

2. Amoozegar M, Minaei-Bidgoli B. Optimizing multi-objective PSO based feature selection method using a feature elitism mechanism. Expert Syst Appl. 2018;113(1):499–514. doi:10.1016/j.eswa.2018.06.027. [Google Scholar] [CrossRef]

3. Kunhare N, Tiwari R, Dhar J. Particle swarm optimization and feature selection for intrusion detection system. Sadhana. 2020;45(1):109. doi:10.1007/s12046-020-1308-5. [Google Scholar] [CrossRef]

4. Ogundokun RO, Awotunde JB, Sadiku P, Adeniyi EA, Abiodun M, Dauda OI. An enhanced intrusion detection system using particle swarm optimization feature extraction technique. Procedia Comput Sci. 2021;193(1):504–12. doi:10.1016/j.procs.2021.10.052. [Google Scholar] [CrossRef]

5. Al-Andoli MN, Tan SC, Sim KS, Lim CP, Goh PY. Parallel deep learning with a hybrid BP-PSO framework for feature extraction and malware classification. Appl Soft Comput. 2022;131(1):109756. doi:10.1016/j.asoc.2022.109756. [Google Scholar] [CrossRef]

6. Guo Y, Li JY, Zhan ZH. Efficient hyperparameter optimization for convolution neural networks in deep learning: a distributed particle swarm optimization approach. Cybern Syst. 2021;52(1):36–57. doi:10.1080/01969722.2020.1734932. [Google Scholar] [CrossRef]

7. Tani L, Veelken C. Comparison of Bayesian and particle swarm algorithms for hyperparameter optimisation in machine learning applications in high energy physics. Comput Phys Commun. 2024;294(2):108955. doi:10.1016/j.cpc.2023.108955. [Google Scholar] [CrossRef]

8. Rengasamy S, Murugesan P. PSO based data clustering with a different perception. Swarm Evol Comput. 2021;64(1):100895. doi:10.1016/j.swevo.2021.100895. [Google Scholar] [CrossRef]

9. Loganathan S, Arumugam J. Energy efficient clustering algorithm based on particle swarm optimization technique for wireless sensor networks. Wirel Pers Commun. 2021;119(1):815–43. doi:10.1007/s11277-021-08292-0. [Google Scholar] [CrossRef]

10. Chatterjee S, Dey S, Paul S, Dey S. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Comput Appl. 2017;28(1):2005–16. doi:10.1007/s00521-016-2223-3. [Google Scholar] [CrossRef]

11. Rauf HT, Lali MIU, Lali MIU, Raza M, Khan MA, Rehman A. Training of artificial neural network using PSO with novel initialization technique. In: Proceedings of the 2018 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT); 2018 Nov 18–20; Sakhier, Bahrain. doi:10.1109/3ICT.2018.8855771. [Google Scholar] [CrossRef]

12. Chouikhi N, Ammar A, Alimi AM. PSO-based analysis of Echo State Network parameters for time series forecasting. Appl Soft Comput. 2017;55(4):211–25. doi:10.1016/j.asoc.2017.01.039. [Google Scholar] [CrossRef]

13. ShafieiChafi Z, Afrakhte H. Short-term load forecasting using neural network and particle swarm optimization (PSO) algorithm. Math Probl Eng. 2021;2021(2):5598267. doi:10.1155/2021/5598267. [Google Scholar] [CrossRef]

14. Zhang W, Gong D, Sun X, Guo Y. A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization. Swarm Evol Comput. 2019;50(2):100569. doi:10.1016/j.swevo.2019.100569. [Google Scholar] [CrossRef]

15. Zhang X, Liu H, Tu L. A modified particle swarm optimization for multimodal multi-objective optimization. Eng Appl Artif Intell. 2020;95:103905. doi:10.1016/j.engappai.2020.103905. [Google Scholar] [CrossRef]

16. Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-Qaness MAA, Gandomi AH. Particle swarm optimization algorithm: review and applications. Metaheuristic Optim Algorithms. 2024;2024(6):1–14. doi:10.1016/B978-0-443-13925-3.00019-4. [Google Scholar] [CrossRef]

17. Bala I, Yadav A. Optimal reactive power dispatch using gravitational search algorithm to solve IEEE-14 bus system. In: Proceedings of the International Conference on Communication and Intelligent Systems; 2019 Nov 9–10; Jaipur, India. doi:10.1007/978-981-15-3325-9_36. [Google Scholar] [CrossRef]

18. Ang KM, Lim WH, Mat Isa NA, Tiang SS, Wong CH. A constrained multi-swarm particle swarm optimization without velocity for constrained optimization problems. Expert Syst Appl. 2020;140:112882. doi:10.1016/j.eswa.2019.112882. [Google Scholar] [CrossRef]

19. Bala I, Yadav A. Gravitational search algorithm: a state-of-the-art review. In: Yadav N, Yadav A, Bansal J, Deep K, Kim J, editors. Harmony search and nature inspired optimization algorithms. Singapore: Springer; 2018. doi: 10.1007/978-981-13-0761-1_3. [Google Scholar] [CrossRef]

20. Piotrowski AP, Napiorkowski JJ, Piotrowska AE. Population size in particle swarm optimization. Swarm Evol Comput. 2020;58(3):100718. doi:10.1016/j.swevo.2020.100718. [Google Scholar] [CrossRef]

21. Liu L, Wu J, Meng S. Analysis and improvement of neighborhood topology of particle swarm optimization. J Comput Methods Sci Eng. 2019;19(4):955–68. doi:10.3233/JCM-193929. [Google Scholar] [CrossRef]

22. Jain M, Saihjpal V, Singh N, Singh SB. An overview of variants and advancements of PSO algorithm. Appl Sci. 2022;12(17):8392. doi:10.3390/app12178392. [Google Scholar] [CrossRef]

23. Tang Y, Gong D, Sun X, Guo Y. Multi-subswarm cooperative particle swarm optimization algorithm and its application. Inf Sci. 2024;677(1):120887. doi:10.1016/j.ins.2024.120887. [Google Scholar] [CrossRef]

24. Fernandez-Martinez JL, Fernandez-Muniz Z. The curse of dimensionality in inverse problems. J Comput Appl Math. 2020;369(3):112571. doi:10.1016/j.cam.2019.112571. [Google Scholar] [CrossRef]

25. Karunarathne W, Bala I, Chauhan D, Roughan M, Mitchell L. Modified CMA-ES algorithm for multi-modal optimization: incorporating niching strategies and dynamic adaptation mechanism. arXiv:2407.00939. 2024. [Google Scholar]

26. Sun H, Li C, Zhang H, Wang Y. Particle swarm optimisation by adding Gaussian disturbance item guided by hybrid narrow centre. Int J Comput Sci Math. 2020;11(4):327–37. doi:10.1504/IJCSM.2020.109939. [Google Scholar] [CrossRef]

27. Quan W, Gorse D. A novel multi-objective velocity-free Boolean particle swarm optimization. In: Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC); 2022 Oct 9–12; Prague, Czech Republic. doi:10.1109/SMC53654.2022.9945131. [Google Scholar] [CrossRef]

28. Mumtaz F, Yahaya NZ. A self-balancing PSO-tuned PI controller for integrating parallel converters with variable renewable sources. J Hunan Univ Nat Sci. 2023;50(2):1–10. doi:10.55463/issn.1674-2974.50.2.8. [Google Scholar] [CrossRef]

29. Sen T, Pragallapati N, Agarwal V, Kumar R. Global maximum power point tracking of PV arrays under partial shading conditions using a modified particle velocity-based PSO technique. IET Renew Power Gener. 2018;12(5):555–64. doi:10.1049/iet-rpg.2017.0324. [Google Scholar] [CrossRef]

30. Zhao Q, Li C. Two-stage multi-swarm particle swarm optimizer for unconstrained and constrained global optimization. IEEE Access. 2020;8:124905–27. doi:10.1109/ACCESS.2020.3007255. [Google Scholar] [CrossRef]

31. Liu R, Tang K, Yao X. A coevolutionary technique based on multi-swarm particle swarm optimization for dynamic multi-objective optimization. Eur J Oper Res. 2017;261(3):1028–51. doi:10.1016/j.ejor.2017.03.018. [Google Scholar] [CrossRef]

32. Chen Y, Wang S, Yang Z, Wang Y, Zuo Z. Self-regulating and self-perception particle swarm optimization with mutation mechanism. J Intell Robot Syst. 2022;105(2):30. doi:10.1007/s10846-021-01509-7. [Google Scholar] [CrossRef]

33. Gupta IK, Choubey A, Choubey S. Particle swarm optimization with selective multiple inertia weights. In: Proceedings of the 2017 8th International Conference on Computing, Communication and Networking Technologies (ICCCNT); 2017 Jul 3–5; Delhi, India. doi:10.1109/ICCCNT.2017.8203999. [Google Scholar] [CrossRef]

34. Kiani AT, Rehman A, Nazir A, Alqahtani A, Rauf HT. Optimal PV parameter estimation via double exponential function-based dynamic inertia weight particle swarm optimization. Energies. 2020;13(15):4037. doi:10.3390/en13154037. [Google Scholar] [CrossRef]

35. Maharana HS, Dash SK. Ramp rate and constriction factor based dual objective economic load dispatch using particle swarm optimization. Int J Energy Power Eng. 2017;11(6):636–40. [Google Scholar]

36. Isiet M, Gadala M. Self-adapting control parameters in particle swarm optimization. Appl Soft Comput. 2019;83(1):105653. doi:10.1016/j.asoc.2019.105653. [Google Scholar] [CrossRef]

37. Zhang B, Guo S, Wang Z, Wang H, Chen X. State of health prediction of lithium-ion batteries using particle swarm optimization with Levy flight and generalized opposition-based learning. J Energy Storage. 2024;84(4):110816. doi:10.1016/j.est.2024.110816. [Google Scholar] [CrossRef]

38. Tian D, Zhao X, Shi Z. Chaotic particle swarm optimization with sigmoid-based acceleration coefficients for numerical function optimization. Swarm Evol Comput. 2019;51(1):100573. doi:10.1016/j.swevo.2019.100573. [Google Scholar] [CrossRef]

39. Qiu C, Zuo X. Barebones particle swarm optimization with a neighborhood search strategy for feature selection. In: Proceedings of the Bio-Inspired Computing: Theories and Applications: 13th International Conference, BIC-TA 2018; 2018 Nov 2–4; Beijing, China. doi:10.1007/978-981-13-1810-5_2. [Google Scholar] [CrossRef]

40. Zhang L, Lim CP, Liu C. Enhanced bare-bones particle swarm optimization based evolving deep neural networks. Expert Syst Appl. 2023;230(1):120642. doi:10.1016/j.eswa.2023.120642. [Google Scholar] [CrossRef]

41. Engelbrecht AP, Bosman P, Malan KM. The influence of fitness landscape characteristics on particle swarm optimisers. Nat Comput. 2022;21(1):179–95. doi:10.1007/s11047-022-09902-5. [Google Scholar] [CrossRef]

42. Rostami M, Berahmand K, Nasiri E, Forouzandeh S. Review of swarm intelligence-based feature selection methods. Eng Appl Artif Intell. 2021;100(1):104210. doi:10.1016/j.engappai.2021.104210. [Google Scholar] [CrossRef]

43. Prajapati VK, Jain M, Chouhan L. Tabu search algorithm (TSAa comprehensive survey. In: Proceedings of the 2020 3rd International Conference on Emerging Technologies in Computer Engineering (ICETCE); 2020 Feb 7–8; Jaipur, India. doi:10.1109/ICETCE48112.2020.9091772. [Google Scholar] [CrossRef]

44. Ma W, Li X, Xu J, Liu Y, Wang X. A two-stage hybrid ant colony optimization for high-dimensional feature selection. Pattern Recognit. 2021;116(1):107933. doi:10.1016/j.patcog.2021.107933. [Google Scholar] [CrossRef]

45. Guha R, Biswas A, Ganguly A, Saha S, Das S. Deluge based genetic algorithm for feature selection. Evol Intell. 2021;14:357–67. doi:10.1007/s12065-020-00397-4. [Google Scholar] [CrossRef]

46. Sarhani M, El Afia A, Faizi R. Facing the feature selection problem with a binary PSO-GSA approach. Recent Dev Metaheuristics. 2018;447–62. doi:10.1007/978-3-319-67669-2_17. [Google Scholar] [CrossRef]

47. Almomani O. A feature selection model for network intrusion detection system based on PSO, GWO, FFA and GA algorithms. Symmetry. 2020;12(6):1046. doi:10.3390/sym12061046. [Google Scholar] [CrossRef]

48. Zhang Y, Gong DW, Zhang WQ. Feature selection of unreliable data using an improved multi-objective PSO algorithm. Neurocomputing. 2016;171:1281–90. doi:10.1016/j.neucom.2015.07.057. [Google Scholar] [CrossRef]

49. Zhang Y, Gong D, Sun X, Guo Y. A PSO-based multi-objective multi-label feature selection method in classification. Sci Rep. 2017;7(1):376. doi:10.1038/s41598-017-00382-y. [Google Scholar] [CrossRef]

50. Jain I, Jain VK, Jain R. Correlation feature selection based improved-binary particle swarm optimization for gene selection and cancer classification. Appl Soft Comput. 2018;62(1):203–15. doi:10.1016/j.asoc.2017.10.040. [Google Scholar] [CrossRef]

51. Ileberi E, Sun Y, Wang Z. A machine learning based credit card fraud detection using the GA algorithm for feature selection. J Big Data. 2022;9(1):24. doi:10.1186/s40537-022-00536-6. [Google Scholar] [CrossRef]

52. Bala I, Chauhan D, Mitchell L. Orthogonally initiated particle swarm optimization with advanced mutation for real-parameter optimization. arXiv:2405.12542. 2024. [Google Scholar]

53. Bala I, Kelly TL, Lim R, Gillam MH, Mitchell L. An effective approach for multiclass classification of adverse events using machine learning. J Comput Cogn Eng. 2022;1(1):1–10. doi:10.47852/bonviewjcce32021924. [Google Scholar] [CrossRef]

54. Elankavi R, Kalaiprasath R, Udayakumar R. A fast clustering algorithm for high-dimensional data. Int J Civ Eng Technol. 2017;8(5):1220–7. [Google Scholar]

55. Zhao Z, Anand R, Wang M. Maximum relevance and minimum redundancy feature selection methods for a marketing machine learning platform. In: Proceedings of the 2019 IEEE International Conference on Data Science and Advanced Analytics (DSAA); 2019 Oct 5–8; Washington, DC, USA. doi:10.1109/DSAA.2019.00022. [Google Scholar] [CrossRef]

56. Tang X, Dai Y, Xiang Y. Feature selection based on feature interactions with application to text categorization. Expert Syst Appl. 2019;120(15):207–16. doi:10.1016/j.eswa.2018.11.023. [Google Scholar] [CrossRef]

57. Bala I, Yadav A. Comprehensive learning gravitational search algorithm for global optimization of multimodal functions. Neural Comput Appl. 2020;32:7347–82. doi:10.1007/s00521-019-04244-2. [Google Scholar] [CrossRef]

58. Bala I, Malhotra A. Fuzzy classification with comprehensive learning gravitational search algorithm in breast tumor detection. Int J Recent Technol Eng. 2019;8(2):2688–94. doi:10.35940/ijrte.b2801.078219. [Google Scholar] [CrossRef]

59. Dataset Repository. UPOBioinfo Group. Sevilla, Spain. [cited 2021 Sep 1]. Available from: http://www.bioinfocabd.upo.es/. [Google Scholar]

60. Statnikov A, Tsamardinos I, Dosbayev Y, Aliferis CF. GEMS: a system for automated cancer diagnosis and biomarker discovery from microarray gene expression data. Int J Med Inform. 2005;74(7–8):491–503. doi:10.1016/j.ijmedinf.2005.05.002. [Google Scholar] [PubMed] [CrossRef]

61. Abdullah DM, Abdulazeez AM. Machine learning applications based on SVM classification: a review. Qubahan Acad J. 2021;1(2):81–90. doi:10.48161/qaj.v1n2a50. [Google Scholar] [CrossRef]

62. Favaro P, Vedaldi A. AdaBoost. In: Ikeuchi K, editor. Computer vision: a reference guide. Cham, Switzerland: Springer; 2021. doi: 10.1007/978-3-030-03243-2_208-1. [Google Scholar] [CrossRef]

63. Chen S, He L, Wang H, Liu Y. A novel selective naïve Bayes algorithm. Knowl Based Syst. 2020;192(1):105361. doi:10.1016/j.knosys.2019.105361. [Google Scholar] [CrossRef]

64. Fadeyi OB. Robustness and comparative statistical power of the repeated measures ANOVA and Friedman test with real data [dissertation]. Detroit, MI, USA: Wayne State University; 2021. [Google Scholar]