NGP-ERGAS: Revisit Instant Neural Graphics Primitives with the Relative Dimensionless Global Error in Synthesis

1  Introduction

Three-dimensional (3D) reconstruction of a scene from a group of images is a primary task in computer vision [1–4]. It plays a vital role in many applications, such as self-driving, augmented reality, and medical diagnosis. This task has advanced significantly due to recent developments in learning-based neural rendering approaches. By training a fully connected neural network, i.e., a multilayer perceptron (MLP), learning-based neural rendering approaches [1] can implicitly reconstruct a given 3D scene via photorealistic novel view synthesis only with some posed images.

The first among these neural rendering approaches is the Neural Radiance Fields (NeRF) [1], which achieves novel view synthesis of a given scene by implicitly encoding volumetric density and color through an MLP. The success of NeRF has sparked a wave of using implicit expressions for 3D reconstruction and significantly changed the field of computer vision and computer graphics. However, the rendering quality of NeRF needs further improvements, and the NeRF training is still expensive, even on a graphic processing unit (GPU). Then, various methods are proposed to improve NeRF further. Some of them focused on improving the rendering quality. For example, Xie et al. [4] designed a nonlocal multiplex training paradigm for NeRF by proposing the stochastic structural similarity (S3IM) loss term and incorporating it into the loss function. Different from most of the existing works, the Instant Neural Graphics Primitives (Instant-NGP) [5] method focuses on improving the efficiency of training and rendering of neural graphics primitives while maintaining accuracy by exploiting the multi-resolution hash coding and linear interpolation. Similar to NeRF, Instant-NGP also optimizes a point-wise loss and makes point-wise predictions. It obtained state-of-the-art performance. Most importantly, it makes applying neural rendering to real applications possible. However, the qualitative results of Instant-NGP, especially some fine details shown in the red bounding box in Fig. 1, still need improvements. Such the fine details loss of the Instant-NGP is fatal to applications such as augmented reality, self-driving, and medical diagnosis, which hinders its application in practice. Improving the rendering quality of Instant-NGP further while remaining efficient is still a challenge.

Figure 1: Qualitative results on DL3DV dataset. The 1st and 4th rows show the ground truth, the 2nd and 5th rows show the results of Instant-NGP, and the 3rd and 6th rows show the results of our NGP-ERGAS. Notice details marked by red rectangles

To further enhance the rendering quality of delicate details while maintaining efficiency, an improved Instant-NGP method with the relative dimensionless global error in synthesis (Erreur Relative Globale Adimensionnelle de Synthese, ERGAS [6]), i.e., NGP-ERGAS, is proposed in this paper. Inspired by S3IM [4], the collective supervision of a group of pixels with rich structural information instead of the point-wise supervision of the original Instant-NGP is used. First, a thread-based strategy in which multiple threads are set as a custom thread block to process image pixels collectively is proposed to extend the pixel-based strategy of Instant-NGP [5]. It can overcome the deficiency that the strategy of S3IM [4] cannot be applied to Instant-NGP due to the parallel programming’s independence and the tiles-based rendering’s inapplicability of Instant-NGP. Then, ERGAS is applied to efficiently collect the overall information of custom thread blocks and incorporated into the loss function to supervise the neural network training. Extensive experiments on open datasets validate the proposed NGP-ERGAS. It can dramatically improve the qualitative results of Instant-NGP with fewer iteration steps. Amazing reconstruction effects can be obtained, especially for delicate structures and details such as lines and continuous structures. The main contributions of this paper can be summarized as follows:

(1)   A new NeRF method, NGP-ERGAS, is proposed to collect the nonlocal structure information to supervise the neural network training, which can dramatically improve the qualitative results of novel view synthesis with fewer iteration steps.

(2)   ERGAS is applied to a custom thread block to collect the nonlocal structural information of threads instead of an image patch, which can overcome the deficiency of Instant-NGP that the independence of parallel programming and the inapplicability of tiles-based rendering.

(3)   Extensive experiments on open datasets are performed to validate the proposed NGP-ERGAS.

The rest of this paper is organized as follows: Section 2 presents the background and related work. Section 3 elaborates on the proposed method. Section 4 reports experimental results. Finally, Section 5 concludes this paper.

2  Background and Related Work

2.1 Novel View Synthesis

Given images of a scene or object from certain views, novel view synthesis aims to generate images of novel viewpoints different from those of any given image. According to the scene representation model, the novel view synthesis methods can roughly be classified as mesh-based, volume-based, and neural rendering fields-based.

The mesh-based methods exploit the mesh-based representations [7,8], which can generate new view images using gradient-based mesh optimization based on image reprojection. However, the optimization is generally challenging due to poor conditioning and local minima of the loss function. Moreover, this class of methods needs a good initialized template mesh with fixed topology, which is generally unavailable for real applications.

The volume-based methods use volumetric representation to realize novel view image synthesis. Early work [9] directly rendered the voxel grid using the observed images. Recent methods [10,11] first utilized deep learning techniques to predict 3D scenes in volumetric representations, then rendered the desired new views. These volume-based methods have achieved impressive results in novel view synthesis. Especially, they have fewer visual artifacts in comparison with mesh-based methods. However, the volume-based methods are hard to scale to high-resolution and large-scale scenes due to their explicit representation’s poor time and space complexity.

Unlike existing methods, the newly emerging neural radiance fields-based methods [1,2,4,5] use the implicit expression to fulfill novel view synthesis. The neural radiance fields-based novel view synthesis methods implicitly encode a volume of the scene within the parameters of a fully connected neural network, i.e., an MLP. These methods can dramatically reduce the storage cost and boost the quality of novel view synthesis, which opens a new era of novel view synthesis. However, although some neural radiance fields-based methods, such as Instant-NGP [5] and so on, have significantly boosted the quantitative results and speed, the qualitative results (i.e., the visual effects), especially some fine details, still need improvements.

2.2 Neural Radiance Fields

NeRF [1] maps a scene represented by a 5D function (x,y,z,θ,ϕ) to the view-dependent RGB color c=(r,g,b) and corresponding volume density σ with an MLP network: fΘ:(x,d)→(c,σ), where x=(x,y,z) is a 3D location, (θ,ϕ) is a 2D viewing direction whose 3D Cartesian unit vector is d, and Θ is the MLP’s weights [1]. NeRF estimates Θ via minimizing the mean square error (MSE) between the rendered image pixel color value C^(r) for camera ray r and the ground truth pixel color value C(r) for all camera rays {r}, i.e., the loss function,

L(Θ)=1|R|Σr∈R‖C^(r)−C(r)‖2(1)

where r(t)=o+td represents the ray/pixel of a target view with pose which is with origin o, ray unit direction d and transmittance distance along the ray t, R={r}, and |R| is the cardinality of the set R, and the rendered pixel color value C^(r) of camera ray r(t) with near and far bounds tn and tf [12] is

C^(r)=∫tntfT(t)σ(t)c(t)dt(2)

where T(t)=exp(−∫tntσ(s)ds) denotes the accumulated transmittance along the ray from tn to t. NeRF significantly advances the novel view synthesis.

Then, various variants and improvements [13–15] have been developed for different application scenarios. One class of them focuses on improving the rendering quality. For example, Mip-NeRF [13] improved the ability to render details using tapered rays. Xie et al. [4] found that NeRF only considers the differences between single pixels and cannot reflect the rich structural information in the image; then, they proposed a nonlocal multiplex training paradigm, S3IM, to improve the rendering quality. D-NeRF [14] extends NeRF to the dynamic domain.

The others aim to improve training and rendering efficiency, such as Instant-NGP [5], Plenoxels [16], DVGO [17], and TensoRF [18]. The Plenoxels [16] method completely eliminates the dependence on MLPS and directly uses sparse voxel grids to represent scenes, thus achieving efficient reconstruction. DVGO [17] follows a similar route and accelerates the scene reconstruction process by introducing a sparse voxel grid and combining a shallow MLP to further extract features. These two methods make full use of the high efficiency of voxel structure in representing the geometric information of the scene. However, both face the dilemma of high accuracy and computational complexity caused by fine voxel partitioning. Then, TensoRF [18] adopts tensor decomposition technology to decompose the high-dimensional voxel grid into low-rank factors, which realizes the dimensionality reduction and compression of high-dimensional data and significantly reduces space occupation. TensoRF dramatically reduces the memory consumption caused by additional voxel modeling. However, it is only suited to limited scenes and cannot handle unbounded scenes with both foreground and background content. Unlike previous methods that directly store high-dimensional voxel data, Instant-NGP [5] uses multi-resolution hash coding combined with shallow neural networks to significantly accelerate the training and rendering of NeRF. It achieves fast training and real-time rendering while maintaining high-quality image rendering. It is the state-of-art and the most popular NeRF.

Due to its state-of-the-art performance, Instant-NGP [5] has been taken as the basis of many works on the editability of NeRF. For example, LAENeRF [19] learned a mapping from the desired light termination to the final output color, enabling style modification. Shum et al. [20] realized the addition or removal of objects in 3D models. Most of the latest published work takes Instant-NGP as the 3D model generation tool. However, the visual effect of Instant-NGP still needs further improvements. The proposed NGP-ERGAS improves the visual effect of Instant-NGP, which can achieve high performance even with low iteration steps of network training.

2.3 Instant-NGP

NeRF [1] takes the frequency encoding [21] for each element of position x=(x,y,z), which encodes a scalar position p∈R as a multi-resolution (L∈N) sequence of sine and cosine functions as follows:

Enc(p)=(sin⁡(20πp),sin⁡(21πp),⋯,sin⁡(2L−1πp),cos⁡(20πp),cos⁡(21πp),⋯,cos⁡(2L−1πp))(3)

Frequency encoding in NeRF must traverse every point on a ray, resulting in high computational cost.

Instant-NGP [5] achieves fast training speed by introducing multi-resolution hash coding and linear interpolation. It divides the space into voxels of different resolutions and determines the voxel position based on the points on the ray. The values of points are calculated by voxel vertex interpolation, and the position in each resolution is concatenated to generate feature vectors, which are input into the MLP for training. It significantly improves rendering speed with a smaller MLP network. However, its visual effects, especially some fine details shown in Fig. 1, still need improvements.

Some latest works [19,20] take the Instant-NGP as the basis to extend the editability of NeRF. The others further improve the Instant-NGP. NGP-RT [22] deals with the hash conflicts by sorting color and density as hash features and using the attention mechanism. It also applies the precomputed occupancy distance grid to reduce computation cost. Korhonen et al. [23] proposed an efficient NeRF with an online hard sample mining strategy. It significantly improves the efficiency of Instant-NGP. Different from these works, the proposed NGP-ERGAS improves the visual effect by incorporating the nonlocal structure information of pixels into the trained network.

2.4 S3IM

Considering that NeRF [1] only considered the differences between single pixels when computing the loss function, which omitted the rich structural information in the image, Xie et al. [4] proposed the stochastic structural similarity (S3IM) to improve the rendering quality of novel views.

S3IM [4] introduces the Structural Similarity (SSIM) [24], which is a commonly used quality metric for image quality assessment, into the loss function of NeRF. Since directly adding the SSIM of multiple pixels within an area centered at the rendering pixel could not improve the rendering quality, S3IM takes a stochastic strategy to form a rendered patch via randomly sampling pixels to compute its SSIM. Then, repeat the random patch forming and SSIM computing M times. Finally, take the average of the M computed SSIM as the S3IM to supervise the learning of neural fields. Due to the collective and nonlocal structural information contained in a group of data points being considered, the S3IM significantly improves the rendering quality of novel views.

However, for each rendering pixel, performing S3IM involves M times random patch forming and SSIM computing. That is, its computational cost is heavy. So, the S3IM could not be applied to the instant NeRF methods, such as Instant-NGP, due to their independence of parallel programming and inapplicability of tiles-based rendering. Different from S3IM, the proposed NGP-ERGAS takes a thread-based strategy and the ERGAS-based loss function to incorporate the nonlocal structural information. It significantly improves the visual effect of Instant-NGP with fewer iterations.

2.5 ERGAS

ERGAS (Erreur Relative Globale Adimensionnelle de Synthese) [6] is a metric first proposed to assess the quality of remote sensing images. It is commonly used to evaluate the performance of image processing or compression algorithms.

In image fusion, the ERGAS metric is applied to two images with different spatial resolutions: the reference image (ground truth) and the fused new image [25]. The formula for ERGAS is as follows:

ERGAS=100hl1NΣKk=1(RMSE(Bk)μ(k))2(4)

where h and l are the spatial resolutions of the fused and reference images, K is the number of spectral bands, k is the index of each band, RMSE(Bk) is the root mean square error of the fused and reference image k-bands, and μ(k) is the mean value of the reference image k-bands. The ERGAS formula is convenient and concise, which can reduce the requirements for hardware computing capability.

3  Method

Similar to Instant-NGP shown in Fig. 2, the proposed NGP-ERGAS also serves to train the NeRF’s neural network. NeRF takes a group of images with known positions and orientations as input and outputs the rendered novel view’s image. In fact, NeRF fulfills this task in the pixel-wise way that each independent thread realizes efficient spatial sampling through a parallel ray casting mechanism [26]. Similarly, NGP-ERGAS also trains NeRF in a pixel-wise way.

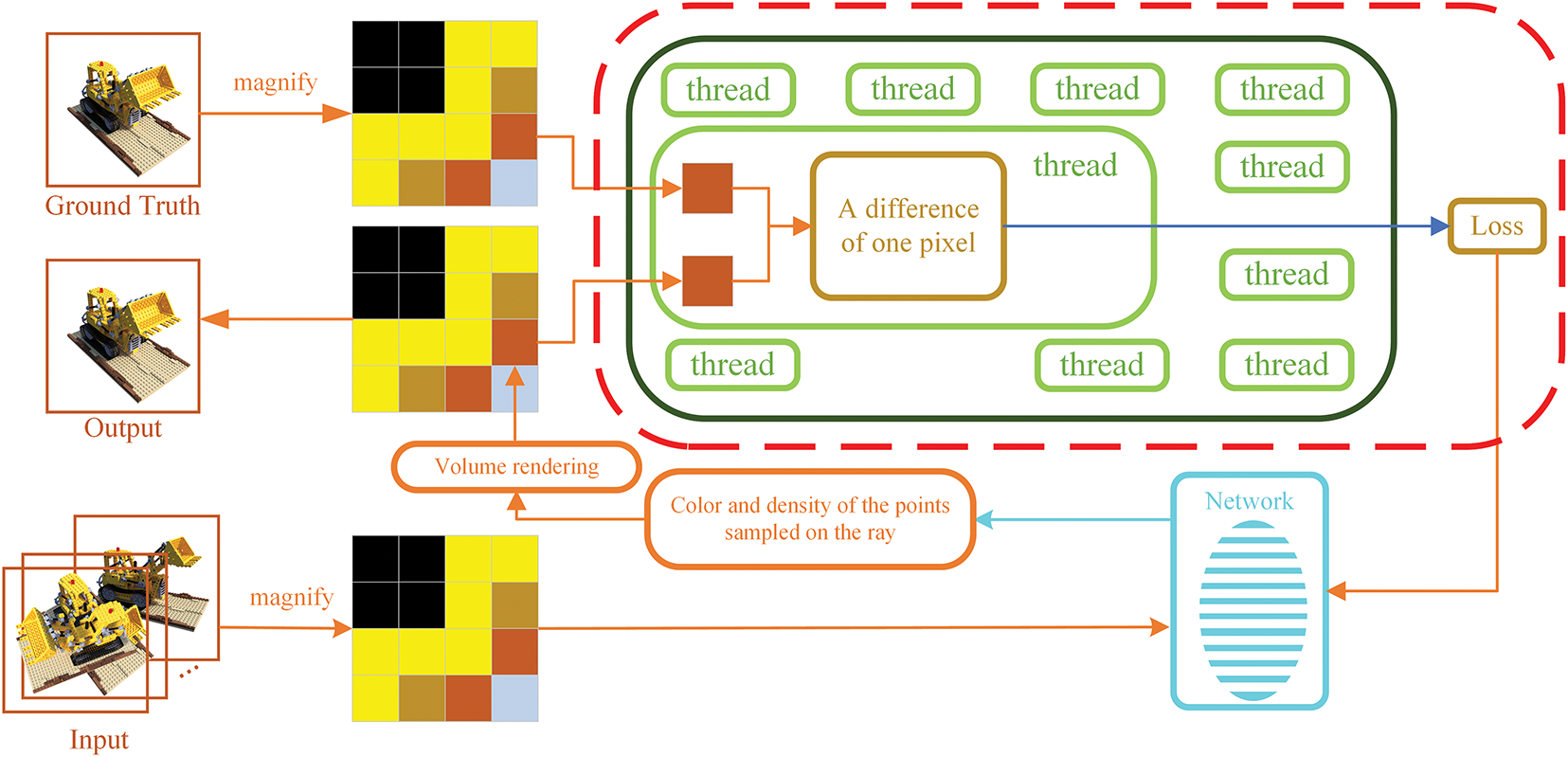
Figure 2: Flow scheme of Instant-NGP. Instant-NGP calculates the difference between the rendered pixel and the ground truth, and directly takes it as the loss value for network training, where one pixel difference is calculated by one thread. The core of Instant-NGP is marked by red bounding box

During the training stage of NeRF, NGP-ERGAS takes the output rendered novel view image and the corresponding ground truth image as the input and outputs the optimized network parameters of NeRF. Firstly, the NeRF network with initial parameters predicts the pixel-wise RGB color of the rendered novel view image. Next, NGP-ERGAS takes the predicted pixels and the corresponding ground truth as the input to construct the custom thread block to collect nonlocal structure information. Then, the ERGAS value and SSIM value of the thread block are calculated and added to the loss function to supervise the training of the NeRF network. After that, the NeRF network outputs the newly rendered output image with supervised learned network parameters, which are input into NGP-ERGAS. Iterate this process until the loss function converges or meets the stop criterion. Finally, the optimized NeRF network parameters are obtained.

In this section, we apply the strategy of efficiently collecting the overall information of custom thread blocks via the ERGAS loss and incorporating it into the Instant-NGP to improve the novel view synthesis performance.

3.1 Custom Thread Block

As shown in Fig. 2, when Instant-NGP computes the loss function, calculating the difference between each pixel pair is assigned to a graphic processing unit (GPU) thread, one thread for each pixel pair. Therefore, threads in the original Instant-NGP can be regarded as independent pixels, and the idea of randomly generating image blocks from pixels in S3IM can be introduced into Instant-NGP by setting custom thread blocks instead of image blocks.

Since each GPU thread determines its specific task with its one-dimensional thread index in the original Instant-NGP, we can set the thread block according to the index. Set the adjustable custom thread block containing M1 threads and the thread with index m^ as its dominant thread. The index range of the custom thread block is defined as [mmin,mmax], where mmin=⌈m^−M12⌉, mmax=⌊m^+M12⌋.

Except for the dominant thread, the remaining threads in the custom thread block are auxiliary threads. Moreover, each thread has a chance to act as the dominant thread. If the index of an auxiliary thread is 0 or out of range, this thread will be skipped.

Before calculating the loss function, we must save the pixel information according to the custom thread block we set. With the help of the thread index, the pixel information of each thread in the custom thread block is collected. The set of truth colors corresponding to all threads in a thread block is denoted as follows:

C(m)={C(m)|m^−M12≤m≤m^+M12,m∈N}(5)

The set of rendered colors contained in all threads in a thread block is denoted as

C^(m)={C^(m)|m^−M12≤m≤m^+M12,m∈N}(6)

3.2 ERGAS for Custom Thread Blocks

In S3IM [4], stochastically selected image pixels are considered as a virtual patch and treated as a whole when training the neural network. However, for each rendering pixel, S3IM involves M times random patch forming and SSIM computing, which has a computational cost that the Instant-NGP could not afford. In addition, the strategy of S3IM could not directly apply to Instant-NGP due to the parallel programming technique adopted in Instant-NGP, where each thread is responsible for the computation task of one pixel. So, the proposed method transforms the pixel-based strategy into a thread-based strategy, and multiple threads are set as a custom thread block to process image pixels collectively. To reduce the computational cost, ERGAS, instead of SSIM, is applied.

The scheme chart of the proposed method is illustrated in Fig. 3. We introduce the adjustable custom thread block to compute pixel differences in the GPU thread. To improve the computation of pixel differences, a thread centered on the custom thread block is considered the dominant thread.

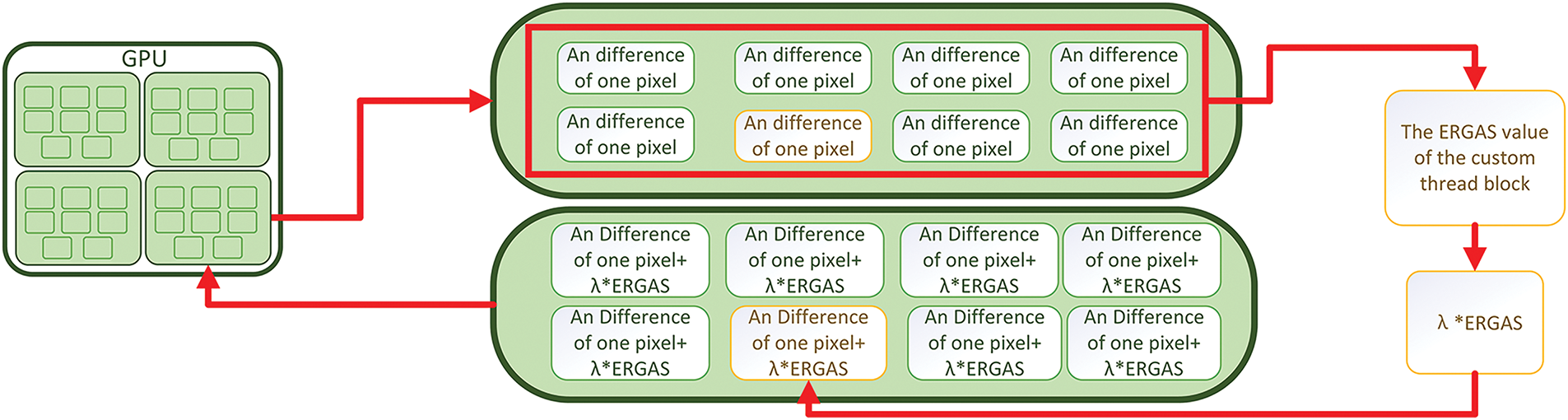
Figure 3: Pipeline of the proposed NGP-ERGAS’s core algorithm. It substitutes for the part marked by the red bounding box in Fig. 2. NGP-ERGAS introduces the nonlocal consideration of S3IM into Instant-NGP, which considers threads nonlocally. ERGAS values of custom thread blocks are calculated and incorporated into the loss function

For RGB images, there are only three bands (i.e., color channels), so K in ERGAS is set to 3, M1 is the number of threads in a thread block, Ckm represents the ground truth color value of the kth band of the pixel corresponding to the mth thread in the thread block, C^km represents the rendered color value of the kth band of the pixel corresponding to the mth thread. In the same thread block, the numbers of threads are the same, so the coefficient h/l equals 1. Ultimately, we have the following ERGAS:

ERGAS=10013Σ3k=1(1M1ΣM1m=1(Ckm−C^km)21M1ΣM1m=1Ckm)2(7)

The error of these pixels is globally considered when calculating the ERGAS in a custom thread block, and the E(m^) term of the dominant thread is obtained.

E(m^,M1)=1M1ΣM1m^=1ERGAS(𝒞^(m^)−𝒞(m^))(8)

where M1 is the number of threads in the thread block, 𝒞^(m^) and 𝒞(m^) denote the set of rendered colors and the set of truth colors corresponding to the thread in the thread block, respectively.

Since ERGAS itself cannot directly calculate the gradient, we average it and merge it with the original color loss of the dominant thread, i.e., Eq. (1), to complete the transformation of the loss function of the dominant thread. The new loss function is

LERGAS(Θ)=1|R|Σm^∈R‖C(m^)−C^(m^)+λ1E(m^,M1)‖2(9)

where λ1 is the weight parameter of E(m^,M1), and R and |R| are same with those shown in Eq. (1).

To further enforce the constraint of local structural information, the SSIM loss term

LSSIM=1−SSIM(10)

is also added to the loss function, whose computation formula can be found in [4]. Then, the final loss function has the form:

Lall=LERGAS+λ2LSSIM(11)

where λ2 is the weight coefficient of the SSIM loss term.

Regarding the selection of hyperparameters, we first perform multiple experiments by adding a single LERGAS loss term to obtain the best value of λ1. Fixing λ1, and then performing experiments after adding the LSSIM loss term, the best value was determined to be λ2.

The proposed method can be summarized as Algorithm 1. Since more pixels/threads are considered in the loss function to train the network, the loss function is enriched. So, more pixel information and the thread block’s global information are considered when training the network, and the proposed NGP-ERGAS can quickly reconstruct and render the structural integrity of the scene with significant quality improvement and low iteration steps. At the same time, because of the addition of the idea of centralized consideration of the custom thread block, the mutual influence between the pixels in the thread block is introduced, which leads to the rendering and reconstruction efficiency being slightly lower than the original Instant-NGP.

4  Experiments

4.1 Performance Evaluation

Firstly, the public datasets NeRF_synthetic provided by NeRF [1] are used to validate the proposed NGP-ERGAS. NeRF_synthetic is a synthetic dataset consisting of the training set with 100 images and the test set with 200 images. To ensure a fair comparison with the standard Instant-NGP [5] (Standard), all MLP networks are trained on the same RTX4060 with the same setting. Networks are trained in 4000 steps in each scenario.

Quantitative results are shown in Table 1. It can be seen that the performance of our NGP-ERGAS is improved in terms of the four indicators of Peak Signal-to-Noise Ratio (PSNR) [27], Structural SImilarity Metric (SSIM) [24], Learned Perceptual Image Patch Similarity (LPIPS) [28] and Universal Quality Index (UQI) [29], while the running times are slightly inferior to the original algorithm. Qualitative results are shown in Fig. 4. It can be seen that the visual effect of rendered images obtains significant improvements. In Fig. 4, for the reflective area of the smooth surface on the top of the Drums image, i.e., the area marked by the pink rectangle in the first row, our NGP-ERGAS renders the spot successfully, while the standard Instant-NGP fails. As shown in the second row, for the area marked by the green square in the Drums image, the reflective area rendered by our NGP-ERGAS matches the size of the true image well, while the standard Instant-NGP fails. In the last row, our NGP-ERGAS successfully renders the lights in the Ship image marked by the yellow rectangle, while the standard Instant-NGP fails. Therefore, our method exhibits higher quality in reconstructing fine details, such as metallic luster and lighting.

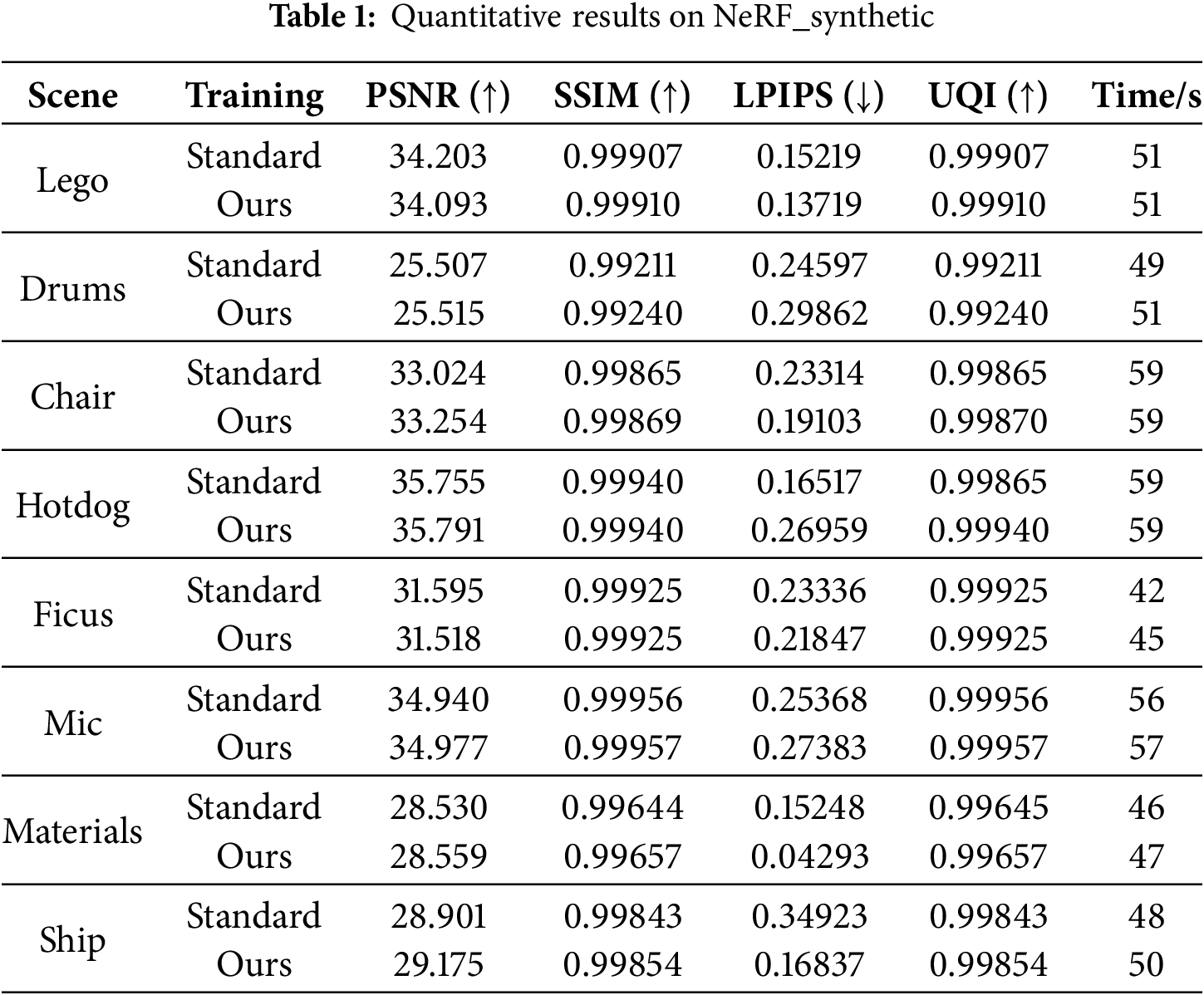
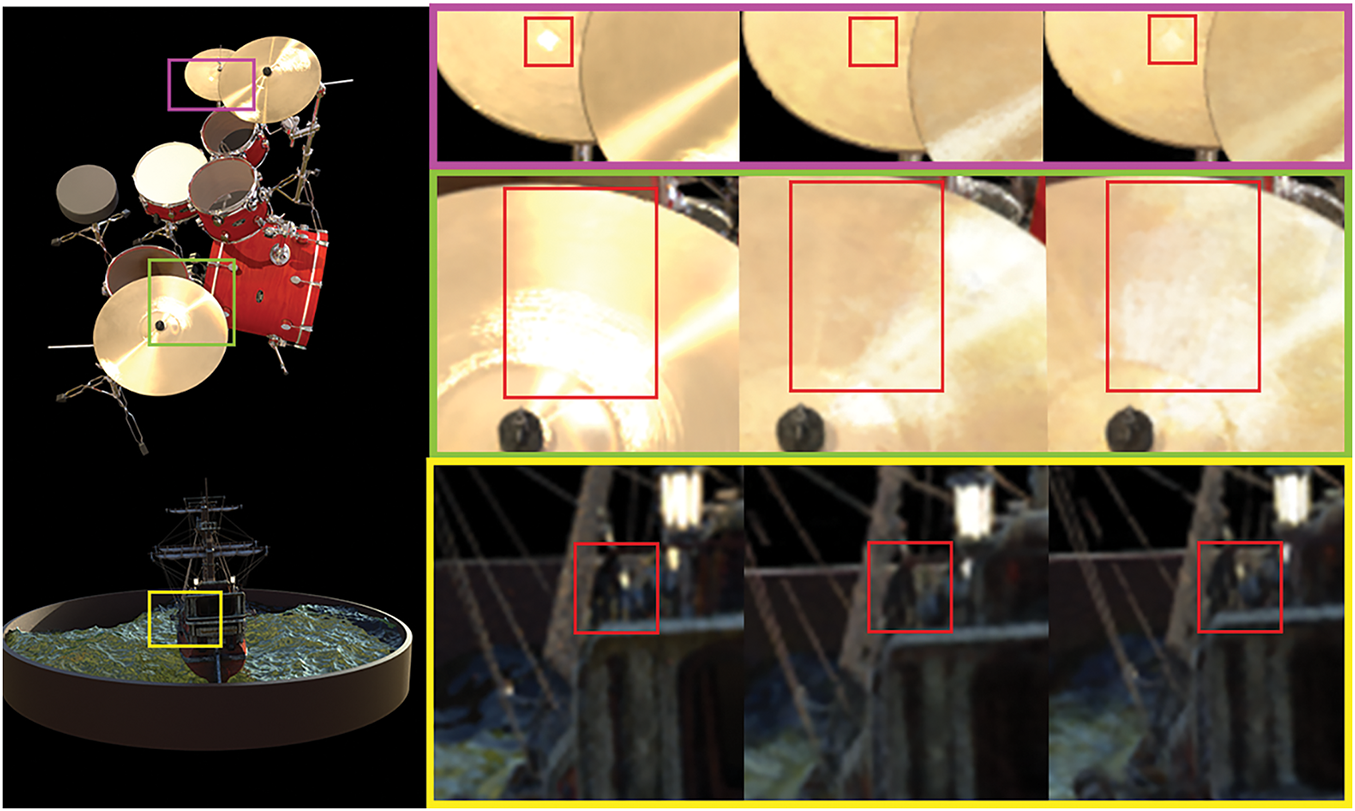
Figure 4: Qualitative results on NeRF_synthetic dataset. The 1st column shows ground truth images of Drums and Ship. The 2nd to 4th column shows enlarged details of the ground truth, result of Instant-NGP (Standard) and result of NGP-ERGAS (Ours), respectively

Then, the Tanks & Temple Dataset [30] is used to perform further evaluation. To make a comparison, the results of the DVGO-S3IM [17] and Instant-NGP are also reported. The number of iteration steps is 4000. The experiment uses two sub-datasets. One consists of the first three scenes shown in Table 2, which is used in DVGO-S3IM, and the other consists of scenes from the Tanks & Template dataset. The former’s training and test sets are the same as those in DVGO-S3IM. For the latter, the test set consists of images with numbers divisible by 10, and the remaining images form the training set. Due to UQI being unavailable for DVGO-S3IM, only PSNR, SSIM, and LPIPS are reported.

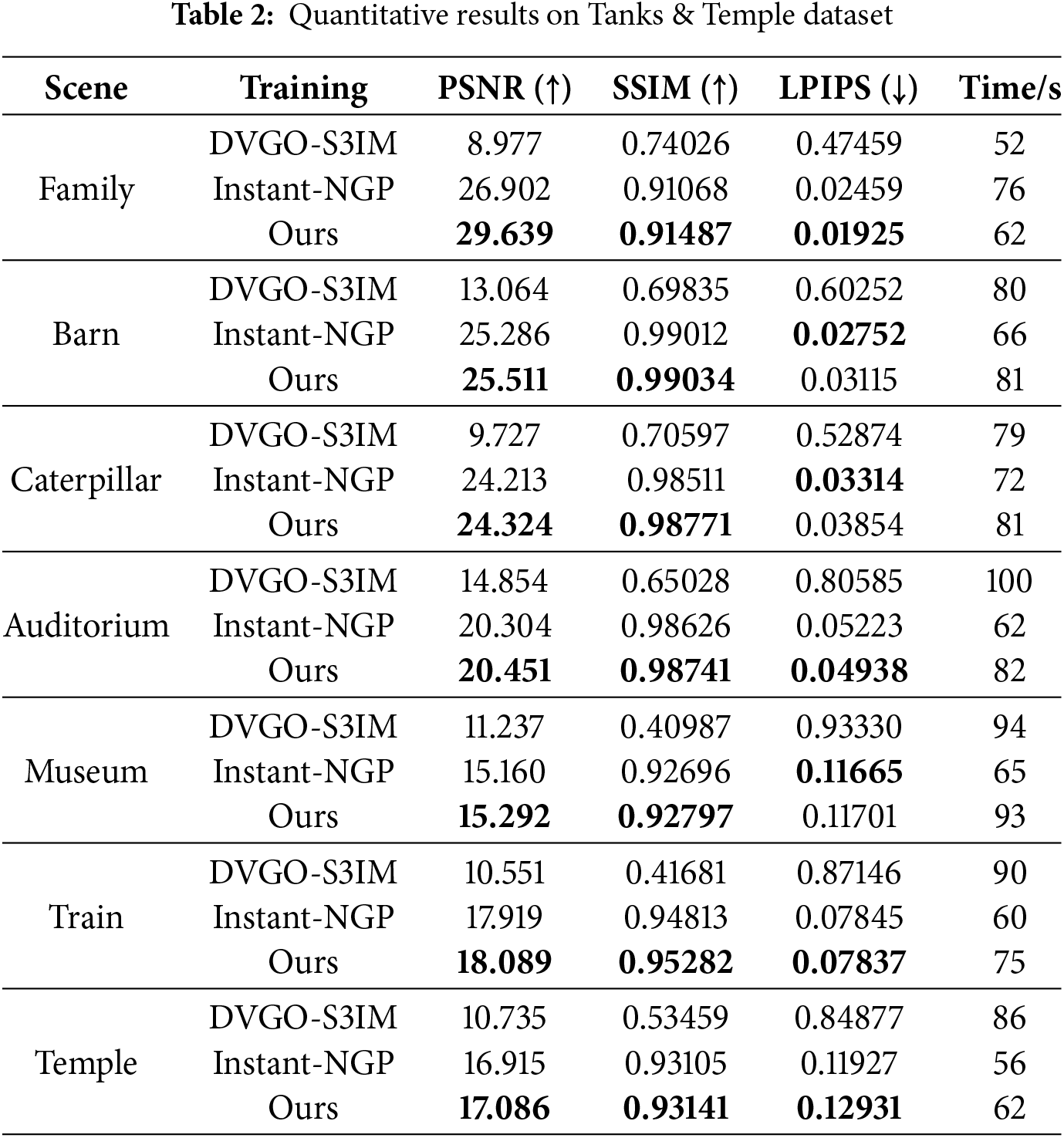
Quantitative results are shown in Table 2. It can be seen that our NGP-ERGAS has a significant improvement in PSNR and SSIM, and the values of LPIPS are comparable to those of Instant-NGP. The qualitative results are shown in Fig. 5, where our method shows significant advantages in visual effects. In the first row, our model renders a much sharper face compared to Instant-NGP. The bulbs and triangles in the second and third rows have sharper contours compared to Instant-NGP. For the railing part of the fourth and fifth rows, our method is able to effectively retain the railing details, while there is an omission in Instant-NGP. Overall, NGP-ERGAS achieves significant improvements in visual quality. The rendering results are amazing, especially for details such as line contours. The improved algorithm can better restore the line contour in the true image in fewer iteration steps. In addition, the number of network parameters is also reported in Fig. 5. The network parameter numbers of the proposed NGP-ERGAS and the standard Instant-NPG are about 10K, while those of DVGO-S3IM are about 22K.

Figure 5: Qualitative results on the Tanks & Template dataset. From left to right, each column corresponds to the ground truth, DVGO-S3IM results, Instant-NGP results, and our NGP-ERGAS results, respectively. Network parameters of three methods are 22K, 10K and 10K in turn. Notice details bounded by red rectangles

It should be pointed out that DVGO-S3IM has a costly GPU consumption, which is trained and tested on an L40 GPU with 48 GB memory. In contrast, NGP-ERGAS and Instant-NGP do not require such high GPU costs, which are only trained and tested on an RTX4060 GPU. So, the Time shown in Table 2 is only a reference.

We conducted experiments with Gaussian noise added to the ship scene in the NeRF_synthetic dataset to test the robustness of our work. As shown in Table 3, our work still performs well with Gaussian noise as without noise. Moreover, it surpasses the Instant-NGP more on the evaluation index.

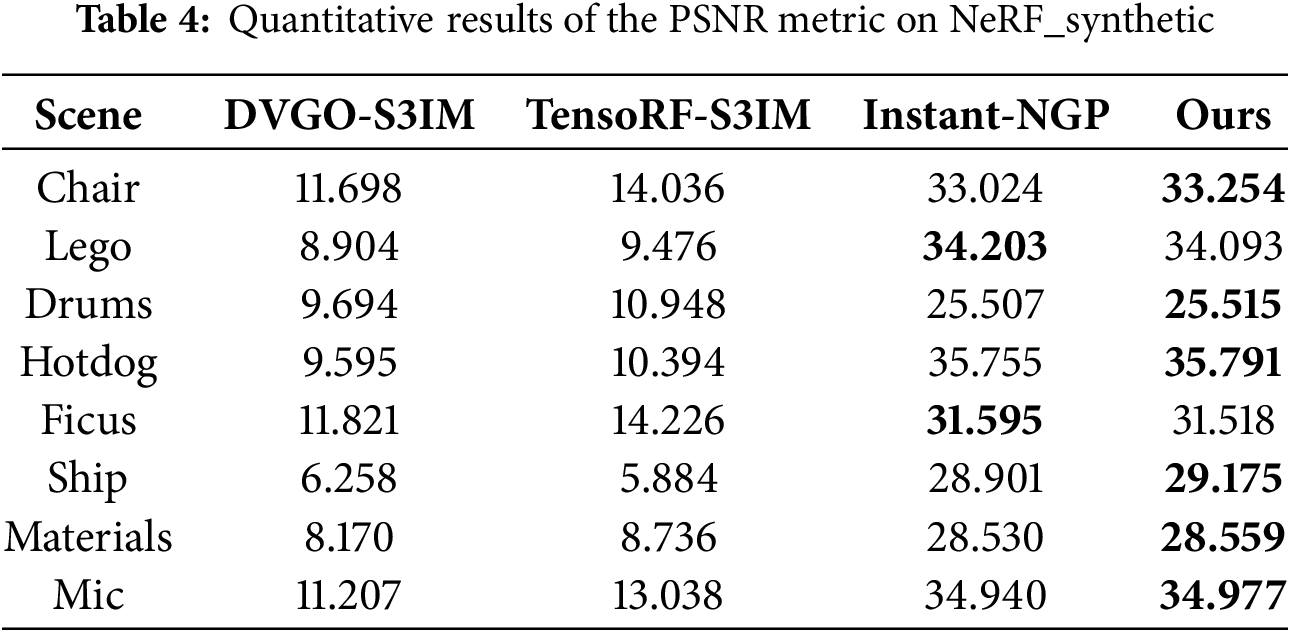
In Table 4, we compare the PSNR metrics of NGP-ERGAS with DVGO-S3IM [17] and TensoRF-S3IM [18] on the NeRF_synthetic dataset. We can see that only Instant-NGP and our work based on NGP have high quality reconstruction at low iteration steps.

4.2 Ablation Study

An ablation study on the scene Drums of the NeRF_synthetic dataset [1] is conducted to validate the proposed NGP-ERGAS. Firstly, the ERGAS loss shown in Eq. (8) is first added to the original MSE loss function shown in Eq. (1). After that, the SSIM loss shown in Eq. (10) is added to the original MSE loss function. Finally, the loss function contains both the ERGAS loss term and SSIM loss term, in addition to the original MSE loss term, as shown in Eq. (11). Experimental results are shown in Table 5.

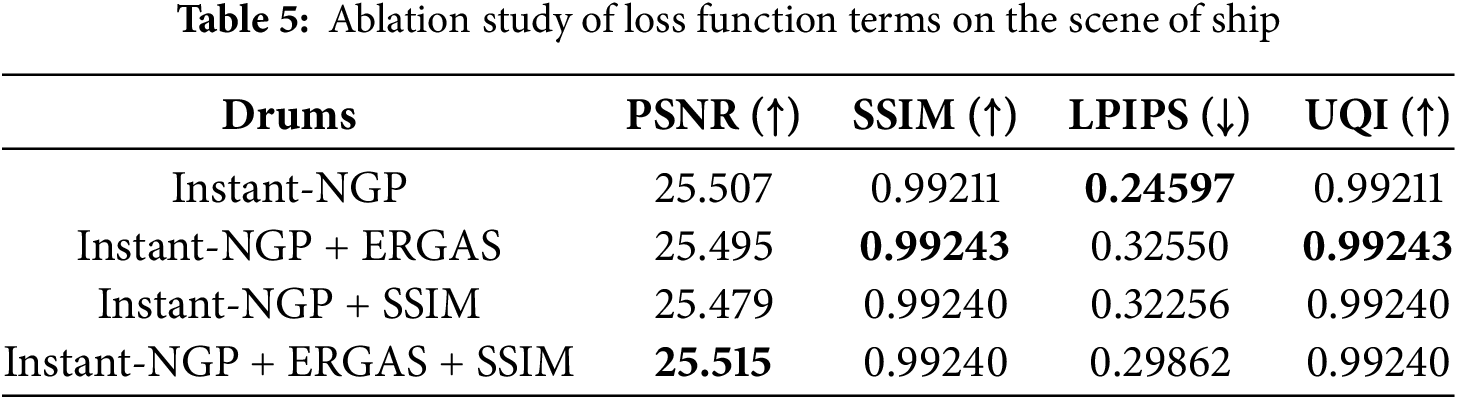
It can be seen that the loss function with ERGAS term has the better SSIM metric, and the loss function with ERGAS plus SSIM terms is better in terms of PSNR metrics. Among them, there is little difference between SSIM index and UQI index. Experiments on other scenes also show a similar performance. It is the reason why the loss function of the proposed NGP-ERGAS shown in Eq. (11) consists of the MSE, ERGAS, and SSIM loss terms.

4.3 Generalization Ability

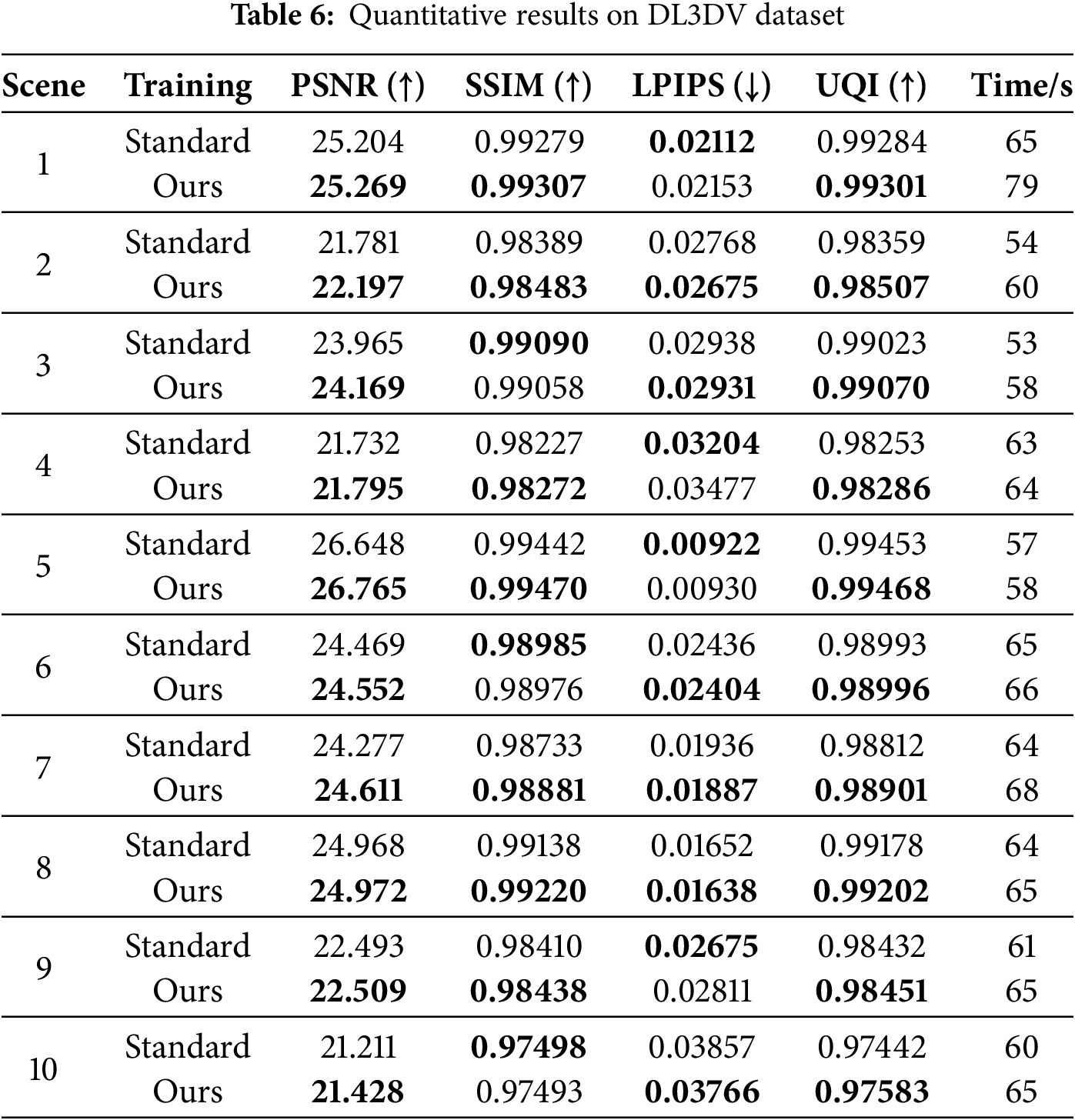
Experiments are performed on the DL3DV [31] dataset to evaluate the generalization ability. The DL3DV [31] is a large-scale dataset published in CVPR 2024, which consists of posed images and can be used to evaluate NeRF algorithms in various aspects. The experiment configuration is the same as that of the second sub-dataset of the Tanks & Template dataset reported in Section 4.1.

Quantitative results are shown in Table 6. It can be seen that the proposed NGP-ERGAS (Ours) performs better than Instant-NGP in terms of PSNR, SSIM, and UQI, and has similar LPIPS. That is, the proposed method has comparable or even better performance in comparison with the original Instant-NGP methods on quantitative results. In addition, there is only a slight delay in the training time for NGP-ERGAS compared to Instant-NGP.

Qualitative results are shown in Fig. 1. It can be seen that the proposed NGP-ERGAS dramatically improves the visual effects. NGP-ERGAS significantly outperforms Instant-NGP for detail rendering, especially for continuous structures such as railings. The Instant-NGP generally ignores distant objects, while NGP-ERGAS can better render these objects and provide higher structure integrity. NGP-ERGAS also performs better in rendering details such as contours and lines. It is because, under the same training conditions, NGP-ERGAS considers more threads/pixels simultaneously, significantly improving rendering quality while the training time only increases slightly.

The enhanced structural completeness achieved by NGP-ERGAS shows particular promise for real applications demanding rigorous environmental reconstruction accuracy. Our method’s improved railing reconstruction (as shown in Fig. 1) could help prevent critical obstacle omission errors for a self-driving car requiring precise collision prediction. Similarly, for virtual reality applications and immersive gaming environments, the ability to guarantee high integrity of architectural structures during rapid scene generation addresses the fundamental requirements of spatial presence and interactive authenticity. While these initial results demonstrate the framework’s potential for time-sensitive 3D reconstruction tasks, further engineering optimizations remain necessary for industrial-scale implementation.

5  Conclusion

This paper presents a novel NeRF method, NGP-ERGAS, to improve the performance of novel view synthesis. To overcome the deficiency that S3IM cannot be applied to Instant-NGP due to the independence of parallel programming and not rendering tiles of Instant-NGP, the proposed method transforms the pixel-based strategy to a thread-based strategy and sets multiple threads as a custom thread block to process image pixels collectively. Then, ERGAS is applied to collect the nonlocal information of custom thread blocks efficiently and incorporates it into the loss function to supervise the neural network training. Finally, extensive experiments on open datasets are performed to validate the proposed NGP-ERGAS. Experimental results show that the proposed NGP-ERGAS can dramatically improve the quality of novel view synthesis with fewer iteration steps, especially visual effects for fine structures and details.

Limitations and future work: While NGP-ERGAS demonstrates significant performance improvements, our current implementation introduces moderate computational overhead due to the parallel processing architecture’s increased per-thread workload. Future research will prioritize optimizing thread-task distribution through load-balancing strategies and dynamic task allocation mechanisms to accelerate training convergence. From an application perspective, we recognize the critical need for both model efficiency and inference speed in practical deployment scenarios. Subsequent investigations will explore neural network quantization techniques and parameter pruning approaches to achieve more compact model representations without compromising reconstruction quality.

Acknowledgement: We would like to thank the editor and reviewers for their useful feedback that improved this paper.

Funding Statement: This work was supported in part by National Natural Science Foundation of China under Grant No. 62473013, and Key Project of Science and Technology Innovation and Entrepreneurship of TDTEC (No. 2022-TD-ZD004).

Author Contributions: Study conception and design: Dongheng Ye, Heping Li, Ning An, Jian Cheng, Liang Wang; data collection: Dongheng Ye, Liang Wang; analysis and interpretation of results: Dongheng Ye, Heping Li, Ning An, Jian Cheng, Liang Wang; draft manuscript preparation: Dongheng Ye, Heping Li, Liang Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The NeRF_synthetic, Tanks & Temple and DL3DV Dataset used in this article are available at https://www.matthewtancik.com/nerf (accessed on 22 May 2025), https://www.tanksandtemples.org/ (accessed on 22 May 2025) and https://huggingface.co/DL3DV, respectively (accessed on 22 May 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Mildenhall B, Srinivasan PP, Tancik M, Barron JT, Ramamoorthi R, Ng R. NeRF: representing scenes as neural radiance fields for view synthesis. Commun ACM. 2021;65(1):99–106. doi:10.1007/978-3-030-58452-8_24. [Google Scholar] [CrossRef]

2. Zhang Z, Zhang L, Wang L, Wu H. Scene 3-D reconstruction system in scattering medium. Comput Mater Contin. 2024;80(2):3405–20. doi:10.32604/cmc.2024.052144. [Google Scholar] [CrossRef]

3. Wang L, Sun L, Duan F. CT-MVSNet: curvature-guided multi-view stereo with transformers. Multimed Tools Appl. 2024;83(42):90465–86. doi:10.1007/s11042-024-19227-3. [Google Scholar] [CrossRef]

4. Xie Z, Yang X, Yang Y, Sun Q, Jiang Y, Wang H, et al. S3IM: stochastic structural similarity and its unreasonable effectiveness for neural fields. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2023 Oct 2–3; Paris, France. p. 18024–34. doi:10.1109/ICCV51070.2023.01652. [Google Scholar] [CrossRef]

5. Müller T, Evans A, Schied C, Keller A. Instant neural graphics primitives with a multiresolution hash encoding. ACM T Graphic. 2022;41(4):1–15. doi:10.1145/3528223.3530127. [Google Scholar] [CrossRef]

6. Wald L. Quality of high resolution synthesised images: is there a simple criterion? In: Proceedings of the Third Conference Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images; 2000 Jan; Sophia Antipolis, France. p. 99–103. [Google Scholar]

7. Waechter M, Moehrle N, Goesele M. Let there be color! Large-scale texturing of 3D reconstructions. In: Proceedings of the Computer Vision–ECCV 2014: 13th European Conference; 2014 Sep 6–12; Zurich, Switzerland. p. 836–50. doi:10.1007/978-3-319-10602-1_54. [Google Scholar] [CrossRef]

8. Wu L, Zhao S, Yan LQ, Ramamoorthi R. Accurate appearance preserving prefiltering for rendering displacement-mapped surfaces. ACM T Graphic. 2019;38(4):1–14. doi:10.1145/3306346.3322936. [Google Scholar] [CrossRef]

9. Huang YH, He Y, Yuan YJ, Lai YK, Gao L. StylizedNeRF: consistent 3D scene stylization as stylized NeRF via 2D-3D mutual learning. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022 Jun 18–24; New Orleans, LA, USA. p. 18342–52. doi:10.1109/cvpr52688.2022.01780. [Google Scholar] [CrossRef]

10. Srinivasan PP, Tucker R, Barron JT, Ramamoorthi R, Ng R, Snavely N. Pushing the boundaries of view extrapolation with multiplane images. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019 Jun 15–20; Long Beach, CA, USA. p. 175–84. doi:10.1109/CVPR.2019.00026. [Google Scholar] [CrossRef]

11. Zhou T, Tucker R, Flynn J, Fyffe G, Snavely N. Stereo magnification: learning view synthesis using multiplane images. ACM T Graphic. 2018;37(4):1–12. doi:10.1145/3197517.3201323. [Google Scholar] [CrossRef]

12. Siddiqui Y, Porzi L, Buló SR, Müller N, Nießner M, Dai A, et al. Panoptic lifting for 3D scene understanding with neural fields. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023 Jun 17–24; Vancouver, BC, Canada. p. 9043–52. doi:10.1109/cvpr52729.2023.00873. [Google Scholar] [CrossRef]

13. Barron JT, Mildenhall B, Tancik M, Hedman P, Martin-Brualla R, Srinivasan PP. Mip-NeRF: a multiscale representation for anti-aliasing neural radiance fields. In: Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021 Oct 11–17; Montreal, BC, Canada. p. 5855–64. doi:10.1109/ICCV48922.2021.00580. [Google Scholar] [CrossRef]

14. Pumarola A, Corona E, Pons-Moll G, Moreno-Noguer F. D-NeRF: neural radiance fields for dynamic scenes. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021 Jun 20–25; Nashville, TN, USA. p. 10313–22. doi:10.1109/CVPR46437.2021.01018. [Google Scholar] [CrossRef]

15. Xu Y, Liu B, Tang H, Deng B, He S. Learning with unreliability: fast few-shot voxel radiance fields with relative geometric consistency. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2024 Jun 16–22; Seattle, WA, USA. p. 20342–51. doi:10.1109/CVPR52733.2024.01923. [Google Scholar] [CrossRef]

16. Fridovich-Keil S, Yu A, Tancik M, Chen Q, Recht B, Kanazawa A. Plenoxels: radiance fields without neural networks. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022 Jun 18–24; New Orleans, LA, USA. p. 5501–10. doi:10.1109/CVPR52688.2022.00542. [Google Scholar] [CrossRef]

17. Sun C, Sun M, Chen HT. Direct voxel grid optimization: super-fast convergence for radiance fields reconstruction. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022 Jun 18–24; New Orleans, LA, USA. p. 5449–59. doi:10.1109/CVPR52688.2022.00538. [Google Scholar] [CrossRef]

18. Chen A, Xu Z, Geiger A, Yu J, Su H. TensoRF: tensorial radiance fields. In: Proceedings of the European Conference on Computer Vision; 2022 Oct 23–27; Tel Aviv, Israel. Cham, Switzerland: Springer Nature; 2022. p. 333–50. doi:10.1007/978-3-031-19824-3_20. [Google Scholar] [CrossRef]

19. Radl L, Steiner M, Kurz A, Steinberger M. LAENeRF: local appearance editing for neural radiance fields. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2024 Jun 16–22; Seattle, WA, USA. p. 4969–78. doi:10.1109/CVPR52733.2024.00475. [Google Scholar] [CrossRef]

20. Shum KC, Kim J, Hua BS, Nguyen DT, Yeung SK. Language-driven object fusion into neural radiance fields with pose-conditioned dataset updates. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2024 Jun 16–22; Seattle, WA, USA. p. 5176–87. doi:10.1109/CVPR52733.2024.00495. [Google Scholar] [CrossRef]

21. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. In: Proceedings of the 31st International Conference on Neural Information Processing Systems; 2017 Dec 4–9; Long Beach, CA, USA. p. 6000–10. doi:10.5555/3295222.3295349. [Google Scholar] [CrossRef]

22. Hu Y, Guo X, Xiao Y. NGP-RT: fusing multi-level hash features with lightweight attention for real-time novel view synthesis. In: Proceedings of the European Conference on Computer Vision; 2024 Sep 29–Oct 4; Milan, Italy. Cham, Switzerland: Springer Nature; 2024. p. 148–65. doi:10.1007/978-3-031-72670-5_9. [Google Scholar] [CrossRef]

23. Korhonen J, Rangu G, Tavakoli HR, Kannala J. Efficient NeRF optimization-not all samples remain equally hard. In: Proceedings of the European Conference on Computer Vision; 2024 Sep 29–Oct 4; Milan, Italy. Cham, Switzerland: Springer Nature; 2024. p. 198–213. doi:10.1007/978-3-031-72764-1_12. [Google Scholar] [CrossRef]

24. Xing Z, Feng Q, Chen H, Dai Q, Hu H, Xu H, et al. A survey on video diffusion models. ACM Comput Surv. 2024;57(2):1–42. doi:10.1145/3696415. [Google Scholar] [CrossRef]

25. Renza D, Martinez E, Arquero A. A new approach to change detection in multispectral images by means of ergas index. IEEE Geosci Remote S. 2012;10(1):76–80. doi:10.1109/LGRS.2012.2193372. [Google Scholar] [CrossRef]

26. Xie Y, Takikawa T, Saito S, Litany O, Yan S, Khan N, et al. Neural fields in visual computing and beyond. Comput Graph Forum. 2022;41(2):641–76. doi:10.1111/cgf.14505. [Google Scholar] [CrossRef]

27. Tian C, Chunwei L. Deep learning on image denoising: an overview. Neural Netw. 2020;131(11):251–75. doi:10.1016/j.neunet.2020.07.025. [Google Scholar] [PubMed] [CrossRef]

28. Zhang R, Isola P, Efros AA, Shechtman E, Wang O. The unreasonable effectiveness of deep features as a perceptual metric. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. p. 586–95. doi:10.1109/CVPR.2018.00068. [Google Scholar] [CrossRef]

29. Azam MA, Khan KB, Salahuddin S, Rehman E, Khan SA, Khan MA, et al. A review on multimodal medical image fusion: compendious analysis of medical modalities, multimodal databases, fusion techniques and quality metrics. Comput Biol Med. 2022;144(3):105253. doi:10.1016/j.compbiomed.2022.105253. [Google Scholar] [PubMed] [CrossRef]

30. Knapitsch A, Park J, Zhou QY, Koltun V. Tanks and temples: benchmarking large-scale scene reconstruction. ACM Trans Graph. 2017;36(4):1–13. doi:10.1145/3072959.3073599. [Google Scholar] [CrossRef]

31. Ling L, Sheng Y, Tu Z, Zhao W, Xin C, Wan K, et al. DL3DV-10K: a large-scale scene dataset for deep learning-based 3D vision. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Pattern Recognition; 2024 Jun 23–28; Columbus, OH, USA. p. 22160–9. doi:10.1109/CVPR52733.2024.02092. [Google Scholar] [CrossRef]