 Open Access
Open Access
ARTICLE
Neural Architecture Search via Hierarchical Evaluation of Surrogate Models
School of Computer Science and Engineering, Northeastern University, Wenhua Road, Heping District, Shenyang, 110819, China
* Corresponding Author: Xiaofeng Liu. Email:
(This article belongs to the Special Issue: Neural Architecture Search: Optimization, Efficiency and Application)
Computers, Materials & Continua 2025, 84(2), 3503-3517. https://doi.org/10.32604/cmc.2025.064544
Received 18 February 2025; Accepted 22 May 2025; Issue published 03 July 2025
Abstract
The rapid development of evolutionary deep learning has led to the emergence of various Neural Architecture Search (NAS) algorithms designed to optimize neural network structures. However, these algorithms often face significant computational costs due to the time-consuming process of training neural networks and evaluating their performance. Traditional NAS approaches, which rely on exhaustive evaluations and large training datasets, are inefficient for solving complex image classification tasks within limited time frames. To address these challenges, this paper proposes a novel NAS algorithm that integrates a hierarchical evaluation strategy based on Surrogate models, specifically using supernet to pre-train weights and random forests as performance predictors. This hierarchical framework combines rapid Surrogate model evaluations with traditional, precise evaluations to balance the trade-off between performance accuracy and computational efficiency. The algorithm significantly reduces the time required for model evaluation by predicting the fitness of candidate architectures using a random forest Surrogate model, thus alleviating the need for full training cycles for each architecture. The proposed method also incorporates evolutionary operations such as mutation and crossover to refine the search process and improve the accuracy of the resulting architectures. Experimental evaluations on the CIFAR-10 and CIFAR-100 datasets demonstrate that the proposed hierarchical evaluation strategy reduces the search time and costs compared to traditional methods, while achieving comparable or even superior model performance. The results suggest that this approach can efficiently handle resource-constrained tasks, providing a promising solution for accelerating the NAS process without compromising the quality of the generated architectures.Keywords
With the continuous development of evolutionary deep learning [1], various neural architecture search algorithms [2–5] based on evolutionary algorithms have emerged [6]. GraTO [7] a neural architecture search-based framework [8,9] that addresses the over-smoothing problem in Graph Neural Networks by balancing model performance and representation smoothness, achieving competitive accuracy and robustness with increasing layers. BSO [10] is an orthogonal learning framework for brain storm optimization that improves exploration and exploitation by using two orthogonal design engines, achieving superior performance in complex function optimization and association rule mining. Evolutionary deep learning is often widely used to solve multiple complex optimization problems [11–13]. In the traditional method, individuals in the population are converted into CNNs with corresponding structures through gene structure mapping [14], etc. Then, the weights [15,16] of the network structure are initialized, the network parameters are trained based on the stochastic gradient descent method, and the process needs to go through dozens or even hundreds of periods. The dataset must be traversed iteratively based on the preset batch sizes and other iterations to perform training in each period. This above training before fitness evaluation often takes hours or even days [17,18]. Improvements Achieved Through Multi-Objective Lightweight Deep Neural Network Architecture Search [19,20]. Such a time-consuming and enormous evaluation cost, coupled with the demand for models with complex tasks and many parameters, makes it impossible for ordinary researchers to design task-specific network structures through evolutionary deep learning under limited time and conditions.
One of the common approaches in existing work to accelerate the evaluation of search adaptation of neural architectures is the use of Surrogate model performance predictors. For example, Ref. [21] proposes an efficient fuzzy neural architecture search (NAS) framework for defect recognition, which effectively handles uncertain data and achieves high accuracy with fewer parameters. SDGP [3] introduces a Single-Domain Generalized Predictor that leverages meta-learning and multi-head attention to improve architecture search efficiency, achieving superior generalization and performance with minimal GPU usage. P-NAS [22] uses a multilayer perceptron (MLP) as a performance predictor to evaluate the performance of candidate neural network architectures, avoiding the expensive model training and evaluation process to achieve the acceleration effect. Still, much data is required to ensure the predictor’s performance stability. Sun et al. [23] proposed a performance predictor based on random forests, which can predict the performance of neural networks more quickly. The random forest model has good generalization ability and flexibility without the need for many training datasets and can adaptively learn different types of neural network architectures in the face of various neural network architecture search scenarios. Inspired by this work [24], to reduce the time cost associated with training neural networks, the performance predictor of random forests that does not require a large training dataset has certain advantages, but its drawback is that offline performance predictors are unable to capture the complexity of the neural network structure, which leads to inaccurate performance prediction. These papers [25,26] introduce self-adaptive weight algorithms with dual-attention for differentiable neural architecture search, which effectively mitigates performance collapse and improves network architecture performance, achieving competitive results on CIFAR-10, CIFAR-100, and ImageNet. Therefore, in this work, to improve the efficiency of neural architecture search, supernet is utilized to accelerate the training process of network architecture due to its weight-sharing mechanism,random forests are used as network structure-assisted performance predictors, and to ensure the predictor performance and search performance, a Neural Architecture Search via Hierarchical Evaluation of Surrogate Models (HESM-NAS) to improve the neural architecture search for image classification.
This work proposes a neural architecture search model based on the hierarchical evaluation of Surrogate models. The model’s main framework is shown in Fig. 1, which includes the search space design, evolutionary process, and Surrogate model prediction or accurate evaluation process. It organically combines the decision tree random forest prediction and the network architecture fully trained evaluation. It constructs the Surrogate model hierarchical evaluation strategy to solve the time-consuming problem of traditional neural network evaluation and effectively improve the inaccuracy of the Surrogate model predictor. The following sections provide a detailed description of each part of the model.
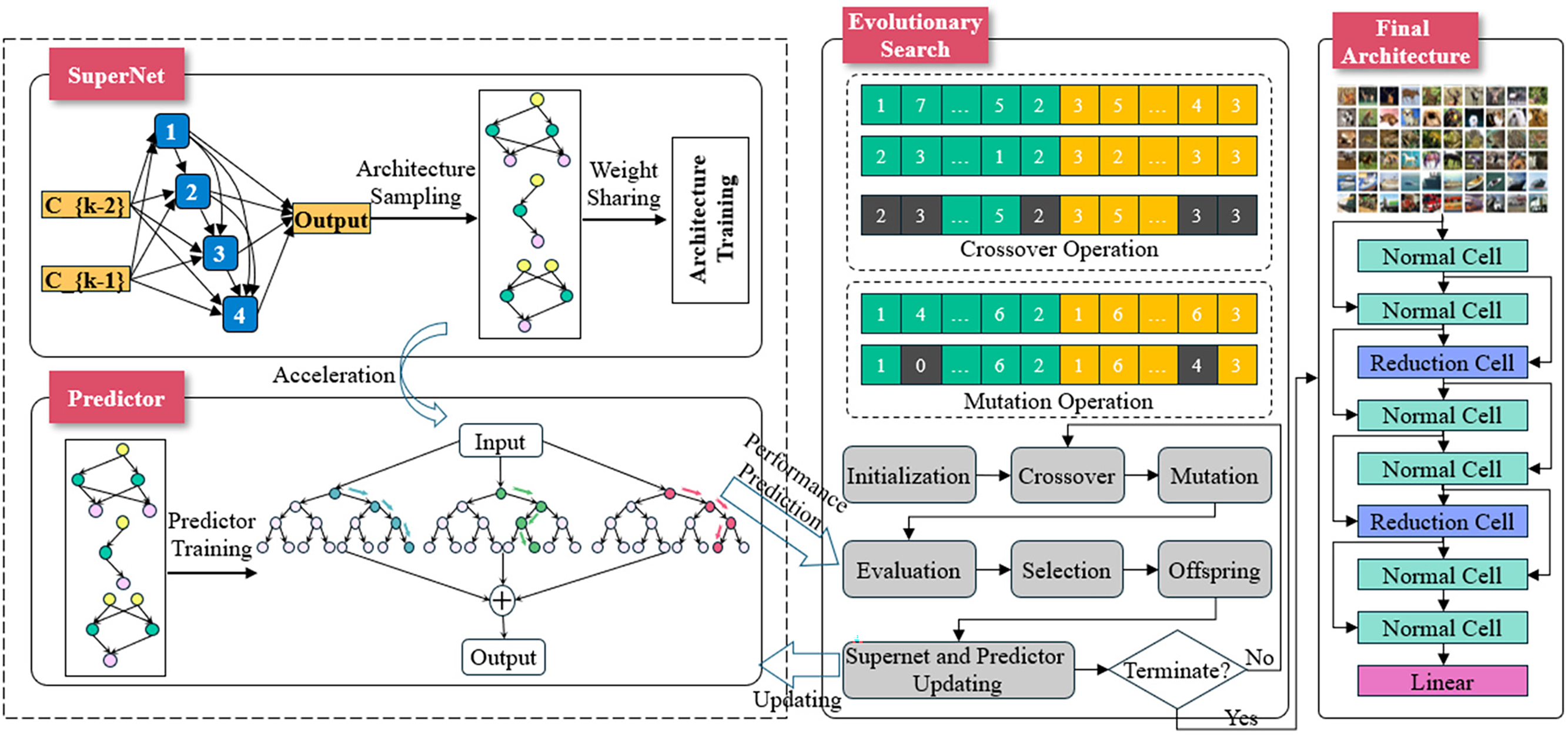
Figure 1: Framework for neural architecture search based on evolutionary hierarchical evaluation
This algorithm is based on the classical Evolutionary Neural Architecture Search (ENAS) [16,27] process combined with the hierarchical evaluation of the Surrogate model for improvement; the specific process is as follows: first of all, train a supernet, initialize the number of population individuals, encode the neural network individuals to be searched, and then according to coding, sample the corresponding subnet from the supernet and fine-tune. Then, all the network individuals are reviewed by traditional precise evaluation [28,29], and then the fitness values of the population individuals are obtained. Then, the evaluated population of individuals is used to construct and update the decision tree random forest. Then, the fitness values are sorted, and the first M individuals with higher fitness values are selected and put into the elite archive Arc-T. A parent individual is selected from the parent population and the elite archive by roulette. The crossover or mutation operator generates an offspring individual through the evolution operation, and then the operation is cycled until the size of the candidate populations reaches N. Random forest is used to predict the performance of N individual architectures, and the architectures with the highest predicted values are fully trained and used to update random forest and supernet. Then, enter the next round of the population cycle until the preset conditions are reached. The process is expressed as follows (Algorithm 1):

2.3 Surrogate Modeling for Efficient Evaluation
2.3.1 Architecture Encoding for Surrogate Modeling
This section’s training data for the random forest is composed of data pairs, each of which includes the network architecture CNNs and their fitness values. Since natural language descriptions cannot be directly used as inputs to the random forest, this section devises an efficient encoding [27,28] method. This method extracts the features of the CNN neural network as numerical values and further serves as input sample data to the random forest.
The CNNs architecture search space of this algorithm consists of a Normal cell and a Reduction cell, and each cell maps two inputs to one output; the cell contains 7 nodes, the first two nodes are the outputs of the previous cell, the last node is the output node of the cell, the middle 4 nodes can be chosen to be connected to any of the previous nodes, so there are 14 connection possibilities. Therefore, there are 14 connection possibilities; the specific structure schematic can be seen in Fig. 2. The candidate operations in each cell include none, max_pool_3 × 3, avg_pool_3 × 3, skip_connect, sep_conv_3 × 3, sep_conv_5 × 5, dil_conv_3 × 3, dil_conv_5 × 5. 5 × 5 for a total of eight. Represent this search space as a matrix with a matrix size of 2 × 14 × 8.
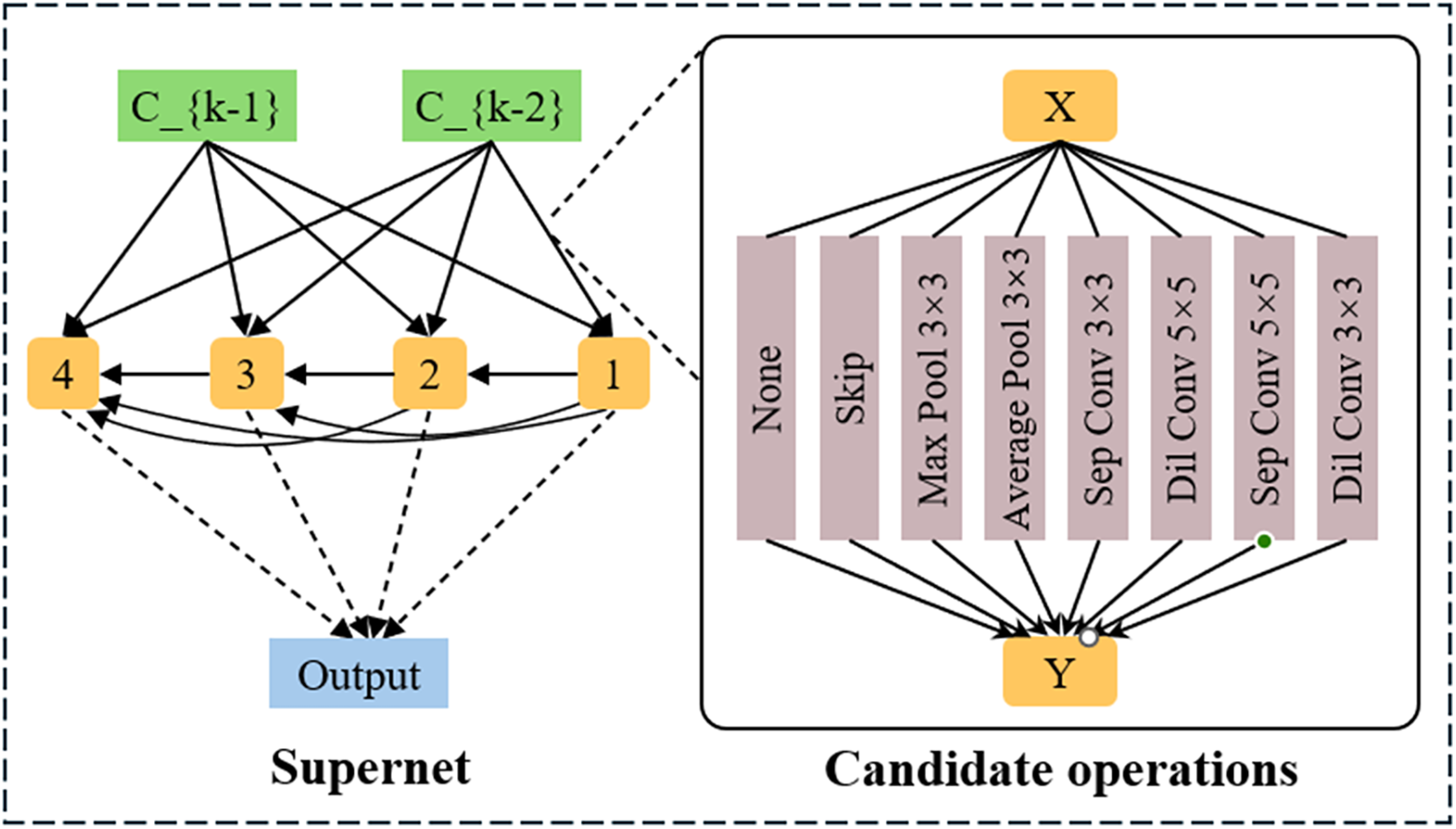
Figure 2: Search space unit internal structure
To encode the neural network architecture into a format that random forest can handle, it needs to be transformed into a feature vector, where each operational edge in each basic unit is considered a feature, and each feature takes the value of a One-Hot [2] vector. All of its feature vectors are concatenated for each basic unit to form a feature vector for one basic unit. Then, the feature vectors of two basic units are concatenated again to form a neural network architecture feature vector.
Specifically, for each operation in a Normal cell, a One-Hot vector of length 8 represents the operation used by that node. The detailed coding is shown in Table 1:
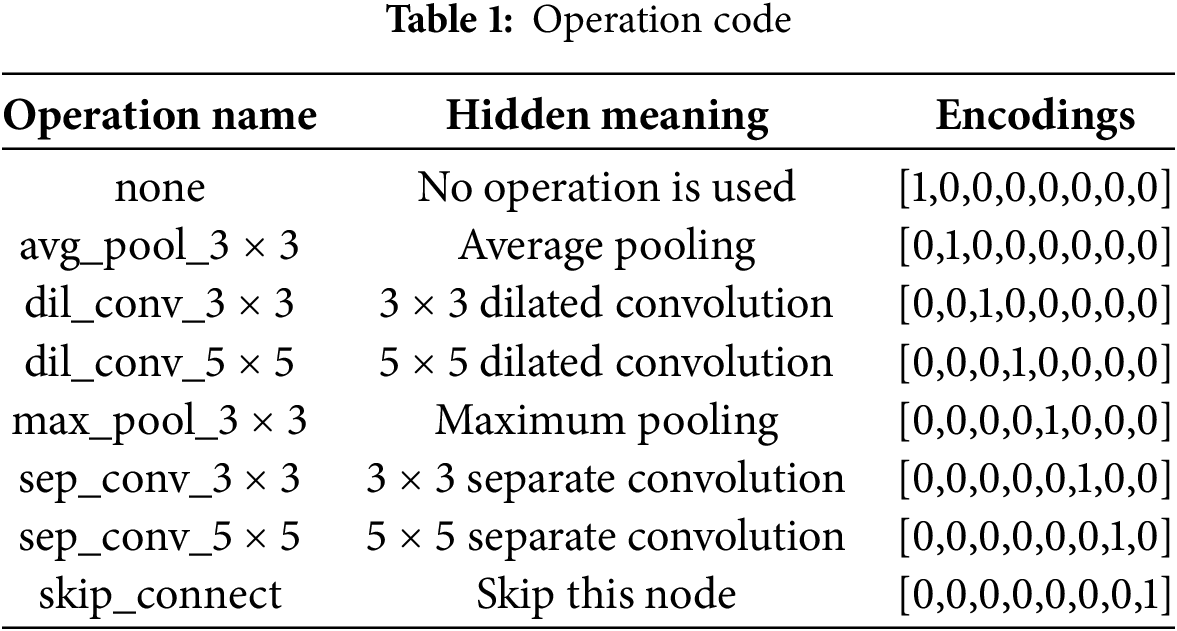
The Reduction cell is represented by a vector of length 14 × 8. The coding of the nodes and edges of the Normal and Reduction units is spliced into two long vectors, which are then spliced together to form a longer vector. Ultimately, this long vector is used as the input to the random forest, and the corresponding labels are the accuracies of the neural networks trained by this structure.
2.3.2 Supernet-Based Candidate Generation
Supernet is an efficient technology widely adopted in Neural Architecture Search (NAS), whose core function is to reduce computational costs significantly through a weight-sharing mechanism. Traditional NAS methods require the independent training and evaluation of each candidate architecture, resulting in enormous computational overhead, whereas the supernet integrates all possible subnet into a unified framework, allowing them to share the same set of weights [22]. Specifically, during the training process, different subnetworks (such as different layers, channels, or connection methods) inherit weights from the Supernet rather than training from scratch. This mechanism not only avoids redundant calculations but also enables the approximate evaluation of the performance of a large number of candidate architectures through a single training, thereby enhancing search efficiency by several orders of magnitude. The training process of the supernet is shown in Fig. 3 below.
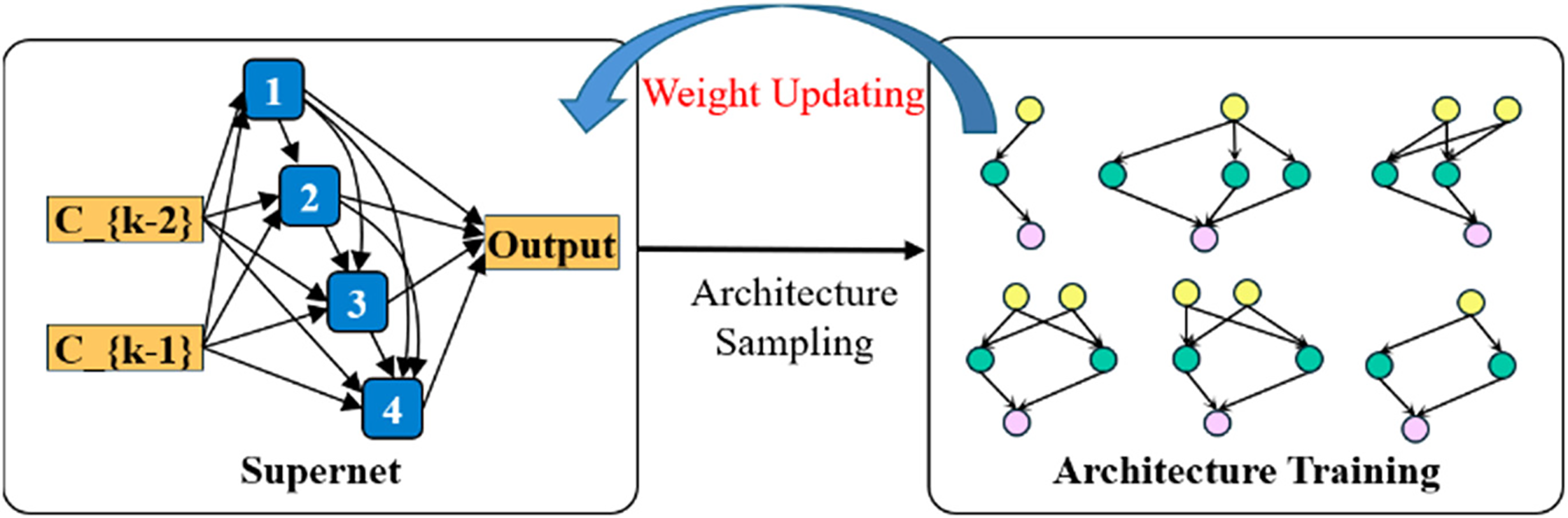
Figure 3: Schematic diagram of supernet training
Firstly, design a discrete search space based on the task requirements, covering all possible architectural options (such as convolution types, layer numbers, and channel numbers, etc.). Then, integrate these options into a differentiable super network, encompassing all possible sub-architectures by superimposing all possible operations. During the training phase, the super network alternates between sampling sub-architectures and optimizing architectural parameters and network weights.
2.3.3 Construction of a Random Forest-Based Surrogate Model
Random forest is a very efficient algorithm that can directly take discrete data as input without extensive labeling, making it the first choice of algorithm for this word. During the training process, each decision maker randomly selects a part of the feature set and learns the mapping from features to target. In contrast, during the testing process, each decision maker selects the same features as in the training phase and outputs the corresponding prediction results [22]. The construction process is shown in Fig. 4 below:
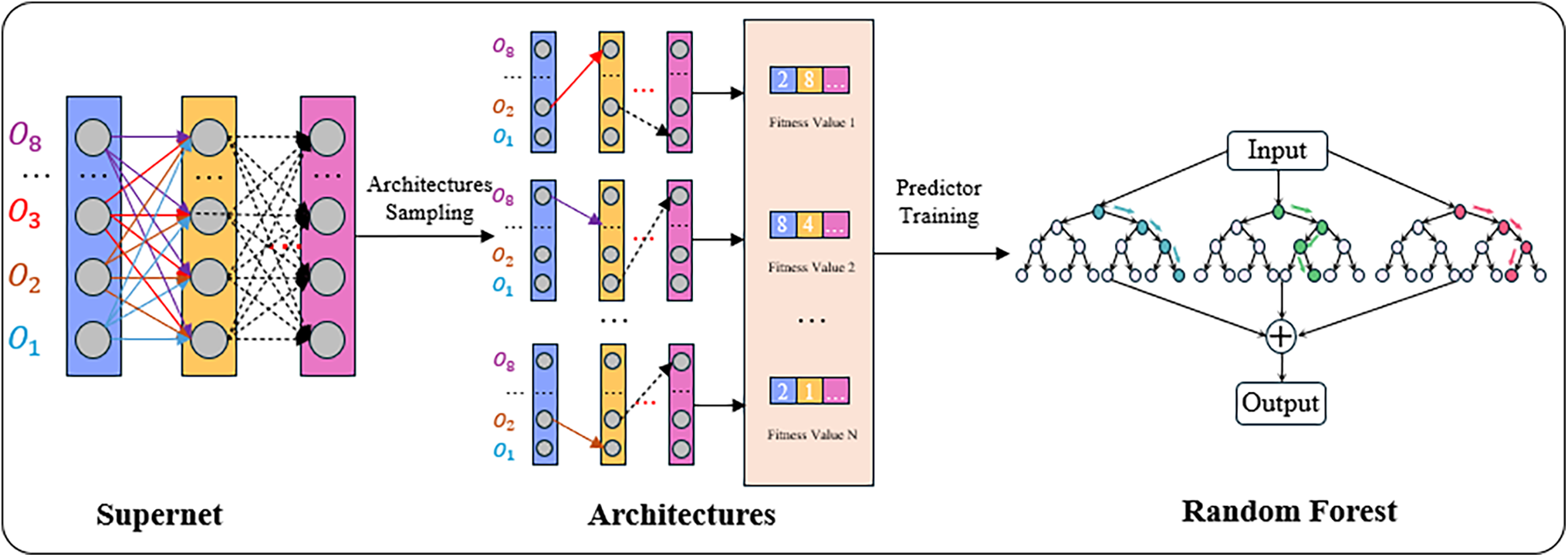
Figure 4: Schematic diagram of random forest surrogate model construction
To start, the CNN architecture will be fully trained on the training set until it achieves convergence. Its performance will then be thoroughly assessed using the validation set. Following this, the network architecture will be encoded as discrete data along with the corresponding performance values to create training samples for the random forest. In each generation of the neural architecture search, accurately evaluated individuals will serve as the training data for the random forest. During the prediction and evaluation process, the new population of individuals not participating in the training will be encoded as inputs to the random forest, and their fitness values will be predicted.
The random forest of the algorithm in this work uses the CART [30] decision tree as the base learner, and the specific process is as follows:
Individual samples from a CNN network coding set are selected using bootstrap sampling to form a training set. One sample is selected at a time until nnn samples are extracted to construct the dataset. A CART decision tree is then generated using these nnn samples as the root nodes. During the decision tree construction, each sample has D attributes. When splitting each decision tree node, a subset of d features is randomly selected. The feature space is divided by minimizing the squared error criterion. For each decision node, the best feature is chosen based on criteria such as information gain, which helps determine the dividing attribute of the node. The final decision tree partitions the feature space into different regions based on these splits. Eq. (1) is the squared error formula: each division divides the feature space into two parts.
Firstly, in the feature space, the traversal selects the feature axis m to divide and selects a cut point n at m to obtain the
After selecting
Cycling through the above steps, each node is split during the decision tree construction process according to the previous steps, if the next node selects the same attribute as the one selected by its parent node for classification, then the node is considered as a leaf node and stops to continue the splitting process, which is carried out until it can not be split any more. A decision tree is generated as shown in Eq. (5), and the decision tree divides the input sample space into M regions, each corresponding to a node on the decision tree. The non-leaf nodes of the decision tree hold the best cut feature and cut point of the current node, while the leaf nodes hold the average of the labels of all the samples within that node. After that, the above steps are repeated k times to generate k decision trees to obtain the random forest Surrogate model.
In order to reduce the risk of overfitting in the random forest model, two issues in particular should be paid attention to in the construction process: random sampling and complete splitting. Firstly, for row sampling, N samples are selected from N samples for training the decision tree using a method with put-back, which makes the training data of each tree not all samples with a certain degree of randomness due to the repeatable sampling nature of the samples, which can reduce the overfitting of the model; followed by column sampling, which randomly selects d attributes (d << D) for splitting the nodes. Secondly, when constructing the decision tree, the strategy of complete splitting is used, i.e., each leaf node is either undividable or contains samples that all belong to the same classification. By sampling at the initial stage of the decision tree, this algorithm ensures randomness and thus avoids the risk of overfitting; therefore, no additional pruning is required to reduce the effect of overfitting.
A random forest of trained K-CART decision trees is used to predict the test samples, and the final prediction results are evaluated using the voting method approach.
2.4 Hierarchical Evaluation Strategy Combining Surrogate and Precise Models
The hierarchical evaluation strategy in this work integrates both fast Surrogate model evaluation and traditional precise evaluation to enhance search efficiency while maintaining evaluation accuracy. The random forest model, constructed in Section 2.3.3, plays a critical role in the Surrogate model evaluation, which significantly reduces the time and computational costs associated with full evaluations.
In this strategy, candidate architectures are first evaluated using the random forest model. The RF, which was trained on previously evaluated networks, predicts the performance of new candidate architectures based on their encoded features. This Surrogate evaluation allows us to quickly estimate the fitness of candidate networks without requiring full training.
However, as the Surrogate model is not always perfectly accurate, we combine it with a traditional precise evaluation. In this evaluation, the candidate networks undergo full training on the dataset, and their performance is evaluated on a validation set to obtain the exact fitness values. This process ensures that while the Surrogate model accelerates the search, the final selection of architectures is based on precise evaluation, guaranteeing the accuracy of the model selection.
In the hierarchical evaluation strategy of the algorithm in this work, the application of the random forest Surrogate model reduces the overhead of complete evaluation and improves the search efficiency for the whole algorithm, and the use of precise evaluation ensures the accuracy of the model evaluation, as shown in Fig. 5, where the two parts interact with each other to form a complete evaluation system.

Figure 5: Schematic diagram of hierarchical assessment
The time overhead saved for the whole search process by the evaluation system used in this work compared to the full evaluation method can be expressed as Eq. (6).
where T is the maximum number of iterations,
3 Empirical Validation and Performance Benchmarking
3.1 Benchmark Datasets and Experimental Protocol
The experiment uses two well-known image classification datasets: CIFAR-10 [28] and CIFAR-100 [31]. These datasets were initially released in 2009 by researchers Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton from the University of Toronto to advance the field of computer vision, particularly image classification techniques. CIFAR-10 contains 60,000 32 × 32 pixel color images, with pixel values ranging from 0 to 255. The categories in CIFAR-10 include relatively simple objects, making it suitable for testing basic image classification algorithms. In contrast, CIFAR-100 is an extended version of CIFAR-10, featuring more categories and images. Like CIFAR-10, CIFAR-100 consists of 60,000 32 × 32 pixel color images, but the images are divided into 100 distinct categories, each containing 600 images—500 for training and 100 for testing. More complex than CIFAR-10, the 100 categories in CIFAR-100 are further grouped into 20 superclasses.
CIFAR-10 offers a relatively simple task, making it suitable for validating basic image classification models. CIFAR-100 requires models to capture more complex image features and finer classification criteria. It is often used to test more sophisticated deep learning models, particularly convolutional neural networks (CNNs). The more significant number of categories and more granular labels in CIFAR-100 make it a classic dataset in image classification, and it serves as a benchmark for evaluating algorithm performance.
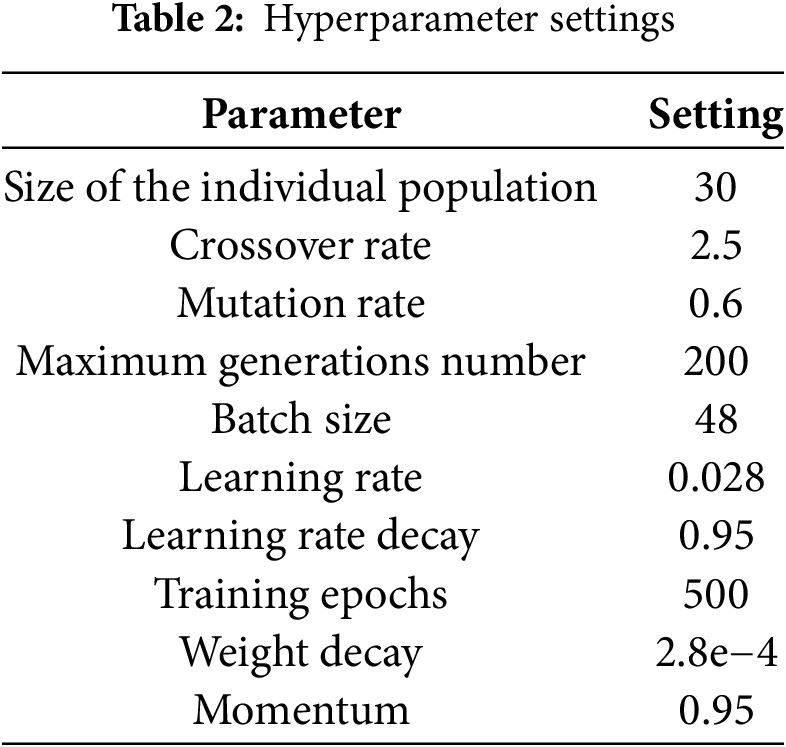
The neural architecture search algorithm code applied to image classification in this work runs on an Intel(R) Xeon(R) W2250 CPU@3.70 GHz CPU, an NVIDIA A4000 GPU with 16 GB of video memory, an operating system of Ubuntu 22.04, and an experimental framework of PyTorch. Due to the large memory requirements of the supernet search space for the memory requirements, the algorithm in this work sets the number of model cell stacks to 8 and the initial channel size to 16, and other parameters are set as shown in Table 2:
3.2 Performance Evaluation Criteria
In this work we use three key metrics to evaluate the search performance: classification accuracy (Accuracy), search time (Search Time), and model size (Model Size). Classification accuracy reflects the neural network’s performance on a specific dataset, typically quantified using methods like cross-validation. In this work, the exact calculation method for accuracy is shown in the Eq. (7).
here, Tp (True Positive) denotes true cases and refers to the number of samples that are actually positive and predicted to be positive, FP (False Positive) is false positive and refers to the number of samples that are actually negative but predicted to be positive, Fn (False Negative) is false negative and refers to the number of samples that are actually positive but predicted to be negative, and Tn (True Negative) is the true counterexample, which refers to the number of samples that are actually negative and are predicted to be negative. The size of the model refers to the size of the storage space occupied by the model, which is calculated and expressed in this method using the number of model parameters as an indicator. Search time refers to the time required to find the best neural network structure, which is expressed in this work in terms of the number of days consumed by the GPUs required for the search.
3.3 Comparative Results and Discussion
The architecture search process follows the settings in Table 1, and after the search is complete, the searched optimal architecture needs to be completely retrained on the dataset to evaluate its performance. For this, the re-training process follows the DARTS network, where the units obtained from the search are constructed into a larger network, with the number of unit stacks set to 20, the initial number of channels to 36, the total number of training generations to 600, and the rest of the settings are the same as in Table 1.
After several experiments on CIFAR-10 and CIFAR-100, Fig. 6 lists the training performance graphs of the algorithm searching the architecture on CIFAR-10, and Table 3 lists the comparison between this algorithm and the manual design as well as other NAS algorithms, which contains information on the accuracy of the searched models, model size (number of parameters), and search duration.
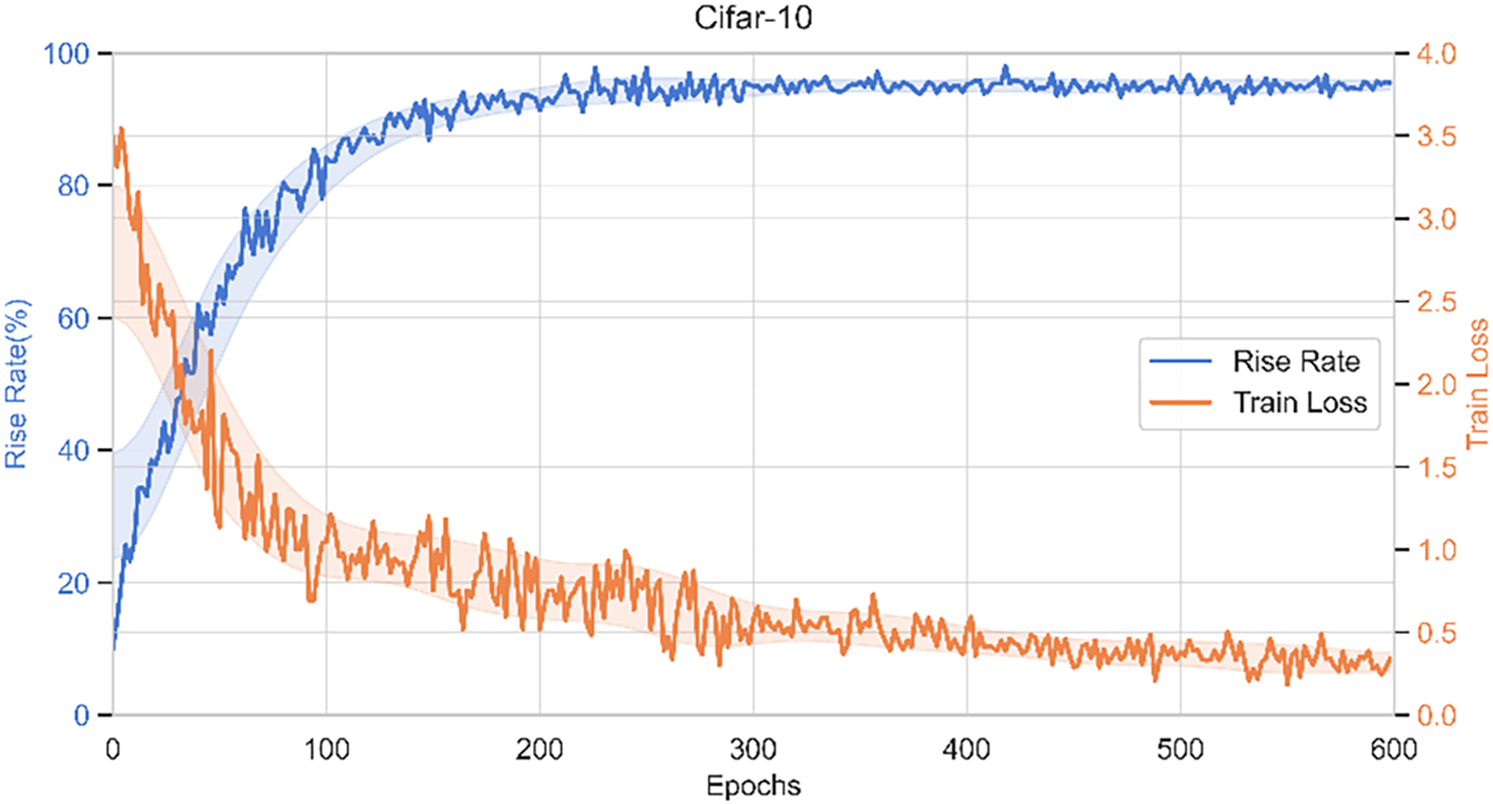
Figure 6: Network architecture training accuracy-loss
The results show that HESM-NAS searches on CIFAR-10 to obtain better network architectures than some of the more classical manually designed, gradient-based, RL-based or EA-based algorithms. When compared in terms of GPU days, i.e., the cost of search time, it can be found that the present algorithm can perform the architecture search process in a shorter time and obtain better search results compared to other EA algorithms.
The cellular structures obtained from the architectural search of this algorithm on CIFAR-10 and CIFAR-100 are presented in the following figures, where Fig. 7 shows the optimal architecture on CIFAR-10 and Fig. 8 shows the optimal architecture obtained on CIFAR-100.
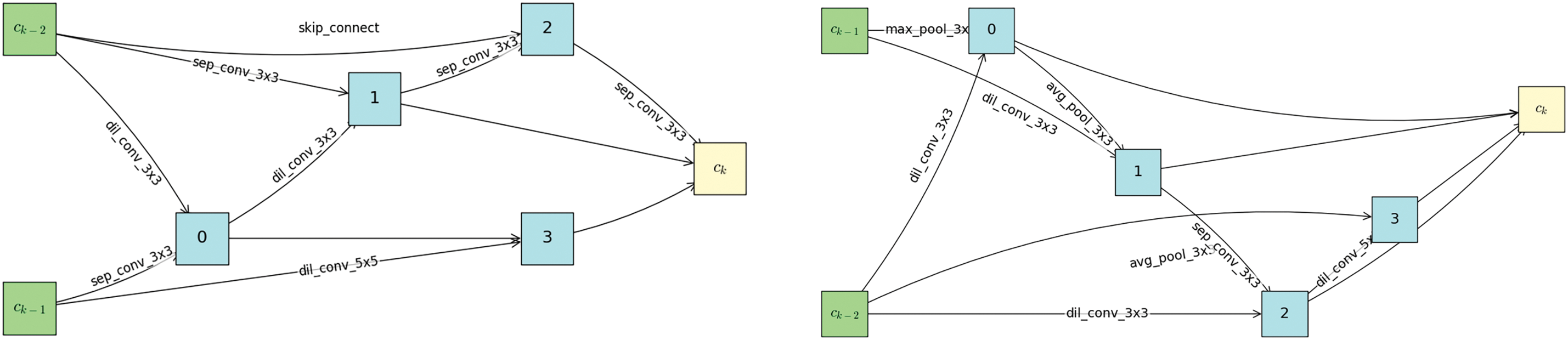
Figure 7: Optimal architecture on CIFAR-10

Figure 8: Optimal architecture on CIFAR-100
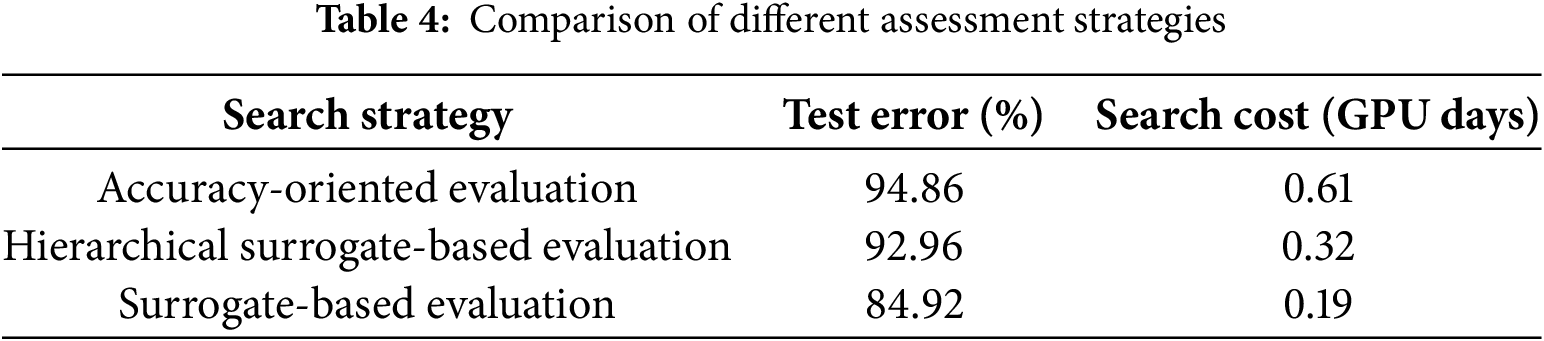
Based on different search strategies, three experimental scenarios were designed using the control variable method to verify the proposed method’s effectiveness, including assessment using traditional Accuracy-Oriented evaluation, evaluation based solely on a random forest Surrogate model and evaluation using the proposed Hierarchical Surrogate-Based Evaluation strategy. The effect of search accuracy is shown in Fig. 9, and the result data obtained from the search is shown in Table 4. From the graphical data, it can be seen that the accuracy obtained from the traditional. Accuracy-Oriented evaluation is higher, but its search time is the maximum value, the search time can be greatly shortened by using only the Surrogate-Based evaluation, but its accuracy is reduced a lot compared with that of the precise evaluation, and the efficiency of the search using the Hierarchical Surrogate-Based Evaluation is much improved compared with that of the traditional precise evaluation, and the search accuracy is not as good as the precise evaluation, but it is much better than that using only the Surrogate model evaluation. The search accuracy is not as high as that of accurate evaluation, but it is much higher than that of Surrogate-only model evaluation. From this analysis, it can be seen that the proposed method may strike a balance between accuracy and search time, and greatly improve the search efficiency and reduce the search cost under the premise of guaranteeing a certain performance effect.
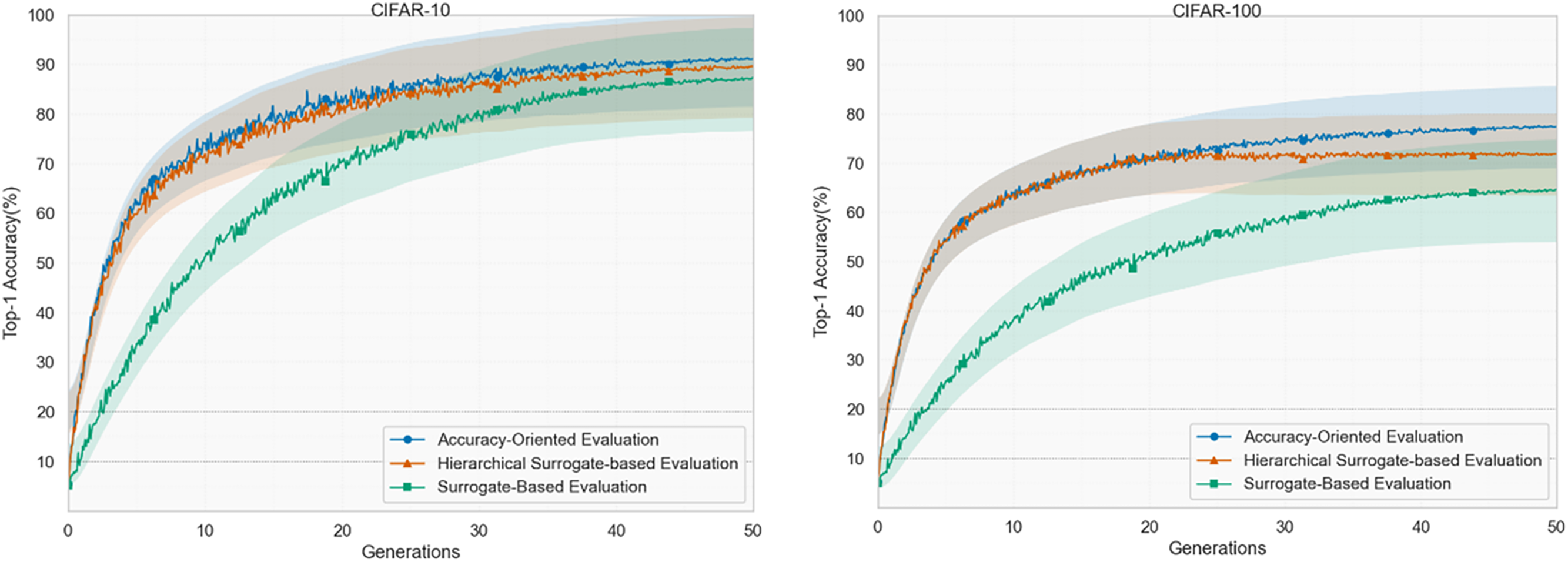
Figure 9: Variation of accuracy for different evaluation strategies
To dive into the challenges of neural architecture search (NAS) in resource-limited image classification scenarios, this work introduces a novel strategy that leverages a hierarchical evaluation mechanism guided by Surrogate models. Central to the approach is a combination of a supernet and a random forest-based Surrogate model, which jointly helps minimize the amount of expensive neural network training. By integrating fast Surrogate evaluations with selective full evaluations, the method strikes a balance between efficiency and performance. The proposed NAS framework is detailed from both architectural and algorithmic perspectives, followed by the design and role of the hierarchical evaluation system. Experimental studies utilize clearly defined benchmarks and metrics, with findings indicating that the proposed method markedly improves search efficiency while maintaining evaluation accuracy. In contrast to conventional strategies that lack a hierarchical framework, this approach yields more consistent performance in constrained environments. Future research will aim to enhance the generalization performance of the Surrogate model, refine the evaluation strategy, and investigate the applicability of this approach to additional vision tasks.
Acknowledgement: Not applicable.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Xiaofeng Liu and Yubin Bao; methodology, Xiaofeng Liu; software, Xiaofeng Liu; validation, Yubin Bao; formal analysis, Xiaofeng Liu and Yubin Bao; investigation, Xiaofeng Liu; resources, Xiaofeng Liu; data curation, Fangling Leng; writing—original draft preparation, Xiaofeng Liu; writing—review and editing, Yubin Bao; visualization, Fangling Leng; supervision, Xiaofeng Liu; project administration, Xiaofeng Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Hu YF, Belkhir N, Angulo J, Yao AEL, Franchi G. Learning deep morphological networks with neural architecture search. Pattern Recogn. 2022;131(4):108893. doi:10.1016/j.patcog.2022.108893. [Google Scholar] [CrossRef]
2. Ding ZX, Chen YR, Li NN, Zhao DB, Chen CL. Stacked BNAS: rethinking broad convolutional neural network for neural architecture search. IEEE Trans Syst Man Cybern. 2023;53(9):5679–90. doi:10.1109/tsmc.2023.3275128. [Google Scholar] [CrossRef]
3. Ma LB, Kang HD, Yu G, Li Q, He Q. Single-domain generalized predictor for neural architecture search system. IEEE Trans Comput. 2024;73(5):1400–13. doi:10.1109/tc.2024.3365949. [Google Scholar] [CrossRef]
4. Chen ZH, Qiu GH, Li P, Zhu L, Yang XK, Sheng B. MNGNAS: distilling adaptive combination of multiple searched networks for one-shot neural architecture search. IEEE Trans Pattern Anal Mach Intell. 2023;45(11):13489–508. doi:10.1109/tpami.2023.3293885. [Google Scholar] [PubMed] [CrossRef]
5. Li N, Xue B, Ma L, Zhang M. Automatic fuzzy architecture design for defect detection via classifier-assisted multiobjective optimization approach. IEEE Trans Evol Comput. 2025;28(1):1. doi:10.1109/tevc.2025.3530416. [Google Scholar] [CrossRef]
6. Salmani Pour Avval S, Eskue ND, Groves RM, Yaghoubi V. Systematic review on neural architecture search. Artif Intell Rev. 2025;58(3):73. doi:10.1007/s10462-024-11058-w. [Google Scholar] [CrossRef]
7. Feng XS, Wan HR, Feng SB, Wang HR, Zheng QH, Zhou J, et al. GraTO: graph neural network framework tackling over-smoothing with neural architecture search. In: Proceedings of the 31st ACM International Conference on Information and Knowledge Management; 2022 Oct 17–21; Atlanta, GA, USA. [Google Scholar]
8. Shi CK, Hao YX, Li GY, Xu SY. EBNAS: efficient binary network design for image classification via neural architecture search. Eng Appl Artif Intel. 2023;120(8):105845. doi:10.1016/j.engappai.2023.105845. [Google Scholar] [CrossRef]
9. Ding ZX, Chen YR, Li NN, Zhao DB, Sun ZQ, Chen CLP. BNAS: efficient neural architecture search using broad scalable architecture. IEEE Trans Neural Netw Learn Syst. 2022;33(9):5004–18. doi:10.1109/tnnls.2021.3067028. [Google Scholar] [PubMed] [CrossRef]
10. Ma LB, Cheng S, Shi YH. Enhancing learning efficiency of brain storm optimization via orthogonal learning design. IEEE Trans Syst Man Cybern. 2021;51(11):6723–42. doi:10.1109/tsmc.2020.2963943. [Google Scholar] [CrossRef]
11. Cereda E, Crupi L, Risso M, Burrello A, Benini L, Giusti A, et al. Deep neural network architecture search for accurate visual pose estimation aboard nano-UAVs. IEEE Int Conf Robot. 2023;2019:6065–71. doi:10.1109/icra48891.2023.10160369. [Google Scholar] [CrossRef]
12. Dabbu M, Karuppusamy L, Pulugu D, Vootla SR, Reddyvari VR. Water atom search algorithm-based deep recurrent neural network for the big data classification based on spark architecture. Int J Mach Learn Cyb. 2022;13(8):2297–312. doi:10.1007/s13042-022-01524-8. [Google Scholar] [CrossRef]
13. Hou WX, Liu LJ, Zhang HA, Sun HB, Zheng NN. DFSNet: dividing-fuse deep neural networks with searching strategy for distributed DNN architecture. Neurocomputing. 2022;483(3):488–500. doi:10.1016/j.neucom.2021.08.144. [Google Scholar] [CrossRef]
14. Sun YN, Xue B, Zhang MJ, Yen GG. Completely automated CNN architecture design based on blocks. IEEE Trans Neural Netw Learn Syst. 2020;31(4):1242–54. doi:10.1109/tnnls.2019.2919608. [Google Scholar] [PubMed] [CrossRef]
15. Risso M, Burrello A, Conti F, Lamberti L, Chen Y, Benini L, et al. Lightweight neural architecture search for temporal convolutional networks at the edge. IEEE Trans Comput. 2023;72(3):744–58. doi:10.1109/tc.2022.3177955. [Google Scholar] [CrossRef]
16. Zhang HY, Jin YC, Hao KR. Evolutionary search for complete neural network architectures with partial weight sharing. IEEE Trans Evol Comput. 2022;26(5):1072–86. doi:10.1109/tevc.2022.3140855. [Google Scholar] [CrossRef]
17. Li LT, Jiang HK, Wang RX, Yang Q. A reinforcement neural architecture search convolutional neural network for rolling bearing fault diagnosis. Meas Sci Technol. 2023;34(11):115122. doi:10.1088/1361-6501/acec06. [Google Scholar] [CrossRef]
18. Li JL, Cao X, Chen RX, Zhang X, Huang XZ, Qu YZ. Graph neural network architecture search for rotating machinery fault diagnosis based on reinforcement learning. Mech Syst Signal Process. 2023;202(2):110701. doi:10.1016/j.ymssp.2023.110701. [Google Scholar] [CrossRef]
19. Jiang P, Xue Y, Neri F. Score predictor-assisted evolutionary neural architecture search. EEE Trans Emerg Top Comput Intell. 2025;2025:1–15. doi:10.1109/tetci.2025.3526179. [Google Scholar] [CrossRef]
20. Xue Y, Zha J, Pelusi D, Chen P, Luo T, Zhen L, et al. Neural architecture search with progressive evaluation and sub-population preservation. IEEE Trans Evol Comput. 2024. doi:10.1109/tevc.2024.3393304. [Google Scholar] [CrossRef]
21. Ma LB, Li N, Zhu PC, Tang KK, Khan A, Wang F, et al. A novel fuzzy neural network architecture search framework for defect recognition with uncertainties. IEEE Trans Fuzzy Syst. 2024;32(5):3274–85. doi:10.1109/tfuzz.2024.3373792. [Google Scholar] [CrossRef]
22. Liu CX, Zoph B, Neumann M, Shlens J, Hua W, Li LJ, et al. Progressive neural architecture search. Comput Vis. 2018;11205(1):19–35. doi:10.1007/978-3-030-01246-5_2. [Google Scholar] [CrossRef]
23. Sun N, Zhang S, Peng T, Zhang N, Zhou J, Zhang H. Multi-variables-driven model based on random forest and Gaussian process regression for monthly streamflow forecasting. Water. 2022;14(11):1828. doi:10.3390/w14111828. [Google Scholar] [CrossRef]
24. Huang G, Liu Z, Van Der Maaten L, Weinberger KQ. Densely connected convolutional networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2017 Jul 21–26; Honolulu, HI, USA. [Google Scholar]
25. Xue Y, Han X, Wang Z. Self-adaptive weight based on dual-attention for differentiable neural architecture search. IEEE Trans Ind Inform. 2024;20(4):6394–403. doi:10.1109/tii.2023.3348843. [Google Scholar] [CrossRef]
26. Xue Y, Han X, Neri F, Qin J, Pelusi D. A gradient-guided evolutionary neural architecture search. IEEE Trans Neural Netw Learn Syst. 2024;36(3):4345–57. doi:10.1109/tnnls.2024.3371432. [Google Scholar] [PubMed] [CrossRef]
27. Chen HJ, Huang H, Zuo XQ, Zhao XC. Robustness enhancement of neural networks via architecture search with multi-objective evolutionary optimization. Mathematics. 2022;10(15):2724. doi:10.3390/math10152724. [Google Scholar] [CrossRef]
28. Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images [dissertation]. Toronto, ON, Canada: University of Toronto; 2009. [Google Scholar]
29. Real E, Moore S, Selle A, Saxena S, Suematsu YL, Tan J, et al. Large-scale evolution of image classifiers. In: Proceedings of the International Conference on Machine Learning; 2017 Aug 6–11; Sydney, Australia. [Google Scholar]
30. Loh WY. Classification and regression trees. Wiley Data Min Knowl Discov. 2011;1(1):14–23. [Google Scholar]
31. Zheng Y, Huang H, Chen J. Comparative analysis of various models for image classification on Cifar-100 dataset. In: Proceedings of the 2023 International Conference on Machine Learning and Automation; 2023 Oct 18; Adana, Turkey. [Google Scholar]
32. Zhang X, Zhou XY, Lin MX, Sun R. ShuffleNet: an extremely efficient convolutional neural network for mobile devices. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2018 Jun 18–23; Salt Lake City, UT, USA. [Google Scholar]
33. Bungert L, Roith T, Tenbrinck D, Burger M. A Bregman learning framework for sparse neural networks. J Mach Learn Res. 2022;23. [Google Scholar]
34. Srinivasan S, Rajakumar K. Ant colony optimized AmoebaNet-A algorithm for hyperspectral image classification. In: Proceedings of the 2022 6th International Conference on Electronics, Communication and Aerospace Technology; 2022 Jan 1–3; Coimbatore, India. [Google Scholar]
35. Godara S, Kumar R, Singh D, Parsad R, Marwaha S. CNN-GA: deep learning-based response surface modelling integrated with genetic algorithm for extracting optimal solutions in highly nonlinear response surfaces. Curr Sci. 2024;127(10):1194–201. [Google Scholar]
36. Cai H, Wang TZ, Wu ZH, Wang K, Lin J, Han S. On-device image classification with proxyless neural architecture search and quantization-aware fine-tuning. In: Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops; 2019 Oct 27–Nov 2; Seoul, Republic of Korea. [Google Scholar]
37. Pham H, Guan MY, Zoph B, Le Q, Dean J. Efficient neural architecture search via parameter sharing. In: Proceedings of the International Conference on Machine Learning; 2018 Jul 10–15; Stockholm, Sweden. [Google Scholar]
38. Zhang R, Gao MR, Zhang PY, Zhang YM, Fu LH, Chai YF. Research on an ultrasonic detection method for weld defects based on neural network architecture search. Measurement. 2023;221(2):113483. doi:10.1016/j.measurement.2023.113483. [Google Scholar] [CrossRef]
39. Cai L, Fu YL, Huo WL, Xiang YJ, Zhu T, Zhang Y, et al. Multiscale attentive image de-raining networks via neural architecture search. IEEE Trans Circuits Syst Video Technol. 2023;33(2):618–33. doi:10.1109/tcsvt.2022.3207516. [Google Scholar] [CrossRef]
40. Zoph B, Vasudevan V, Shlens J, Le QV. Learning transferable architectures for scalable image recognition. In: Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2018 Jun 18–23; Salt Lake City, UT, USA. [Google Scholar]
41. Lu ZC, Whalen I, Dhebar Y, Deb K, Goodman E, Banzhaf W, et al. NSGA-Net: neural architecture search using multi-objective genetic algorithm. In: Proceedings of the Genetic and Evolutionary Computation Conference; 2019 Jul 13–17; Prague, Czech Republic. [Google Scholar]
42. Lu ZC, Whalen I, Dhebar Y, Deb K, Goodman ED, Banzhaf W, et al. Multiobjective evolutionary design of deep convolutional neural networks for image classification. IEEE Trans Evol Comput. 2021;25(2):277–91. doi:10.1109/tevc.2020.3024708. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF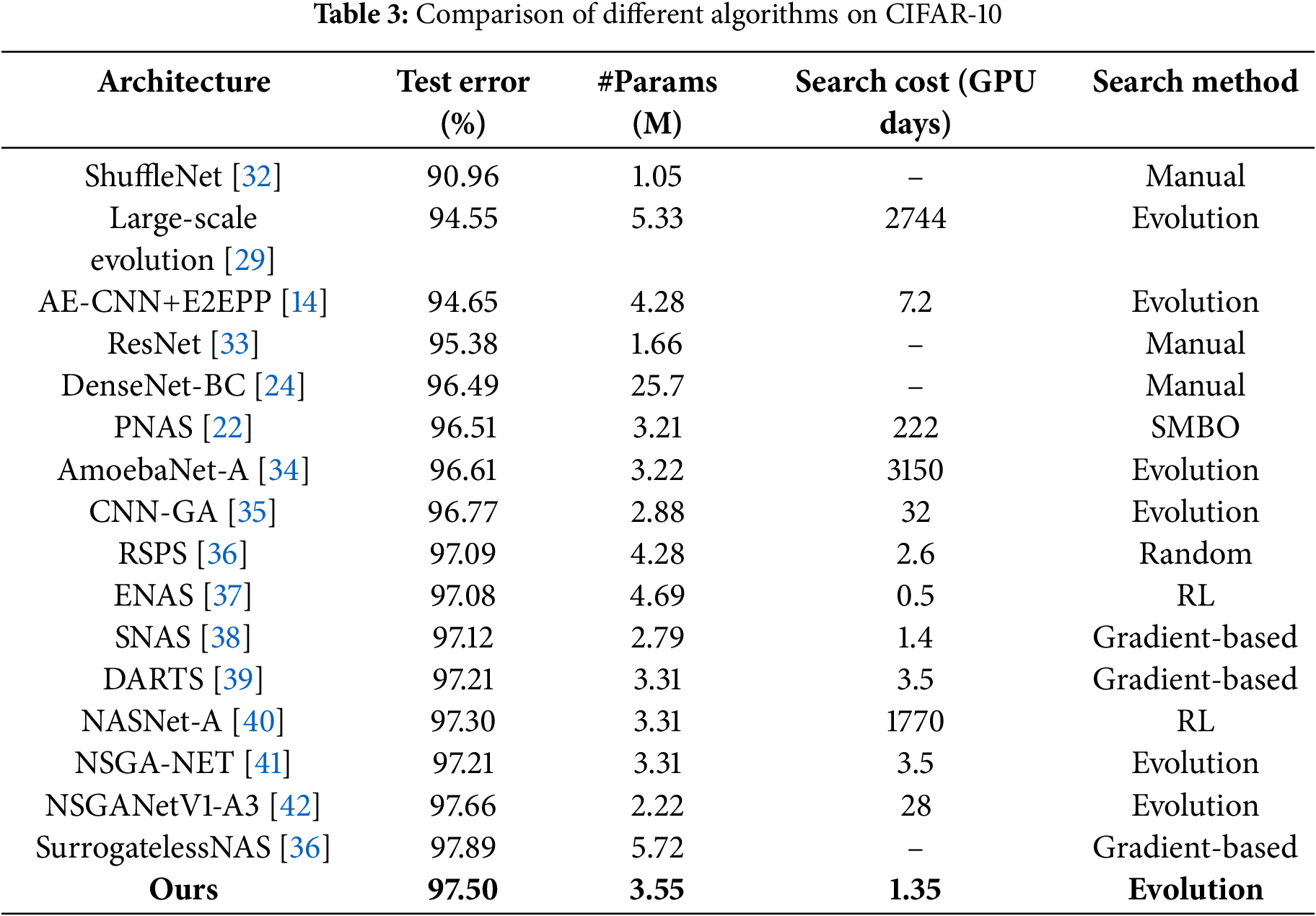
 Downloads
Downloads
 Citation Tools
Citation Tools