Research on Adaptive Reward Optimization Method for Robot Navigation in Complex Dynamic Environment

1  Introduction

The proliferation of service robots in public spaces—from hospital logistics to commercial guidance systems—has created unprecedented demands for safe and efficient navigation in human-dominated environments [1,2]. While traditional navigation algorithms achieve satisfactory performance in structured industrial settings [3], their effectiveness diminishes significantly in dynamic crowd scenarios characterized by rapidly evolving pedestrian movements, heterogeneous motion patterns, and time-varying social constraints [4]. This limitation becomes particularly critical in safety-sensitive domains like medical delivery, where collision risks could lead to catastrophic consequences, and mall environments requiring socially compliant navigation to ensure user acceptance [5].

Deep reinforcement learning (DRL) approaches have demonstrated remarkable progress in handling environmental uncertainties through end-to-end policy learning [6–9]. Still, their reliance on fixed reward mechanisms creates fundamental limitations in real-world crowd navigation. A primary constraint lies in the static safety-efficiency trade-offs of conventional multi-objective reward functions, which assign fixed weights to collision avoidance and navigation efficiency [4,6,10] while ignoring the context-dependent nature of human-robot interaction. This rigidity becomes particularly problematic when considering scenario variations: safety constraints should dominate in high-density environments like hospital corridors during peak hours to prevent collisions. In contrast, efficiency should take priority in sparse settings such as late-night commercial spaces to optimize energy consumption and task completion time. Additionally, existing Gaussian-based reward formulations [11] exhibit inadequate risk quantification by failing to capture emergent risks from collective crowd dynamics, including pedestrian group movements and velocity-dependent collision probabilities. This deficiency intensifies when handling risk superposition effects in dense crowds [3]. Another critical limitation stems from computational inefficiency, where the quadratic computational complexity of pairwise distance evaluations in dense environments severely degrades real-time performance. This bottleneck often forces robots to adopt overly conservative navigation strategies that compromise operational fluency [12], highlighting the need for adaptive algorithmic frameworks in practical deployments.

These limitations stem from a critical gap in current research: the absence of dynamic reward mechanisms that explicitly couple environmental complexity with navigation objectives. While recent works attempt to enhance adaptability through different approaches, they exhibit distinct limitations. For instance, GST + HH Attn [9] introduces attention-based interaction modeling and multi-step trajectory prediction to improve intention awareness. Yet its reward function relies on fixed penalties for predicted collisions without dynamically reweighting safety-efficiency tradeoffs based on real-time crowd density. In contrast, TGRF [11] proposes a flexible Gaussian-shaped reward structure to reduce hyperparameter tuning, but its adaptability primarily targets static object characteristics rather than explicitly addressing dynamic crowd motion patterns. Both methods lack mechanisms to dynamically reweight safety-efficiency objectives based on real-time crowd density and motion characteristics.

To address these challenges, this work makes three primary contributions: (1) A Gaussian kernel-based spatiotemporal risk field that quantifies environmental complexity by integrating crowd density, relative distance, and pedestrian velocity into a unified risk metric, enabling real-time assessment of emergent crowd behaviors. (2) An exponential decay reward mechanism that nonlinearly adjusts safety constraints based on instantaneous risk levels, automatically prioritizing collision avoidance in dense regions while permitting efficient navigation in sparse areas. (3) A parametric optimization framework establishes explicit mappings between risk parameters and navigation performance, providing interpretable guidelines for deploying service robots across diverse operational scenarios.

Our experimental validation demonstrates that this approach fundamentally transforms the safety-efficiency trade-off paradigm. In high-density environments (0.21 persons/m2), the proposed method achieves a 9.0% higher success rate than state-of-the-art baselines while reducing human space intrusion time by 10.7%. These advancements hold significant implications for deploying service robots in real-world applications where adaptive behavior is paramount, from hospital logistics to crowded urban service platforms.

The remainder of this paper is organized as follows: Section 2 reviews related works in navigation algorithms and reward shaping. Section 3 details our risk field modeling and adaptive reward framework. Sections 4 and 5 present experimental results and discussions, respectively. Finally, Section 6 concludes with future research directions.

2  Related Works

2.1 Research on Robot Navigation Methods

There has been a notable transition in research methodologies in robot navigation, shifting from conventional deterministic algorithms to learning-based approaches. Early navigation algorithms primarily relied on search-based methods, such as the A* algorithm [13]. These methods guarantee completeness and optimality in discrete spaces; however, their computational complexity grows exponentially with increasing dimensions, leading to the “curse of dimensionality” [14]. Subsequently, methods based on artificial potential fields have garnered significant attention. Algorithms like the Dynamic Window Approach (DWA) and the Timed Elastic Band (TEB) employ virtual potential fields to avoid obstacles. Still, they often become trapped in local optima in complex dynamic environments. As research advanced, the Optimal Reciprocal Collision Avoidance (ORCA) [15] identifies the optimal path in the velocity space through linear programming to mitigate potential deadlocks or oscillations in dense environments, thereby resolving local optima issues and achieving robust navigation in complex dynamic scenarios.

Recent advancements in deep reinforcement learning (DRL) and graph neural networks (GNNs) have enabled novel solutions for robot navigation in socially complex environments. Recent advancements in deep reinforcement learning (DRL) and graph neural networks (GNNs) have enabled novel solutions for robot navigation in socially complex environments. DRL trains agents through trial-and-error interactions to maximize cumulative rewards, allowing robots to adapt to human behaviors and environmental uncertainties dynamically. GNNs, meanwhile, excel at modeling relational dynamics in scenarios with multiple interacting agents, such as human-robot coexistence. For example, Chen et al. [12] designed an attention-based DRL framework to improve navigation by explicitly encoding human-robot and human-human interactions. At the same time, Liu et al. [6] proposed a Decentralized Structured Recurrent Neural Network (DS-RNN) capable of operating in dense crowds and partially observable settings. Furthermore, GNNs are increasingly being incorporated into navigation frameworks: Chen et al. [16] leveraged Graph Convolutional Networks (GCNs) to optimize navigation by learning human attention weights, and Zhou and Garcke [17] developed a spatiotemporal graph architecture with attention mechanisms to capture human intentions and social norms, thereby enhancing navigation performance. Nevertheless, challenges persist in ensuring decision stability and real-time responsiveness in highly dynamic, densely populated environments.

Despite these advancements, existing methods still face critical limitations in highly dynamic crowd environments. Traditional search-based algorithms (e.g., A*) suffer from the curse of dimensionality and lack adaptability to dynamic obstacles. While ORCA improves obstacle avoidance through motion prediction, it struggles in high-density scenarios due to limited predictive accuracy for collective crowd behaviors. Although DRL and GNN-based approaches enable end-to-end learning and social interaction modeling, their reliance on fixed reward weights often leads to suboptimal trade-offs between safety and efficiency across varying crowd densities. These limitations highlight the need for adaptive mechanisms that dynamically adjust risk assessment and reward allocation based on real-time environmental complexity.

2.2 Design of Reward Functions

The design of the reward functions represents the primary challenge in reinforcement learning-based robot navigation [18], as their mathematical formulation directly influences strategy convergence and operational safety [19].

Existing research [6,20–22] primarily utilizes multi-objective weighted fusion to optimize navigation, incorporating reward components for target approach, collision avoidance, social distance maintenance, and path efficiency. Social distance and path efficiency rewards typically utilize distance-based penalty functions such as L2 norms [9] or Gaussian distributions [11], which quantify discomfort through human-robot distance metrics while integrating prior knowledge of socially acceptable spacing [23–25]. For efficiency quantification, researchers commonly adopt L2-based metrics. Though their weighting coefficients remain fixed, these reward values undergo dynamic adjustment through time-varying distance calculations between the robot and the target.

However, suboptimal reward design may cause policy learning to diverge from intended objectives, while the inherent conflict between sparse safety rewards and dense efficiency rewards can induce robot behavior freezing [26]. Furthermore, the hyperparameter combinatorial explosion in multi-objective systems significantly increases policy search dimensionality [27].

To address these challenges, Kim et al. [11] introduced the Transformable Gaussian Reward Function (TGRF), which leverages a Gaussian distribution with three tunable hyperparameters—weight, mean, and standard deviation—to adjust penalties based on proximity to humans dynamically. The TGRF incorporates normalization to stabilize reward magnitudes across varying standard deviations, enabling adaptable risk-sensitive navigation while reducing hyperparameter redundancy. Despite these advancements, relying on Gaussian-derived exponential operations for distance-based penalties introduces computational overhead, particularly when evaluating dense crowds in real-time scenarios.

3  Methodology

In the context of autonomous navigation tasks, the navigation problem is typically modeled as a Markov decision process (MDP). This modeling approach enables the utilization of reinforcement learning techniques for path planning and obstacle avoidance. An MDP is typically defined as a quintuple ⟨S,A,P,R,γ⟩, where S denotes the state space, which encompasses information such as the robot’s position, speed, and the presence of surrounding pedestrians, and A represents the action space, specifying the navigation decisions (e.g., speed and direction adjustments) that the robot can execute at each time step. The state transition probability P(st+1|st,at) signifies the likelihood of the robot transitioning from state st to st+1 following the execution of an action at. Developing a reward function, denoted by R(st,at), is essential to ensure safety and efficiency in path planning. This function guides the robot’s behavior, providing incentives for approaching the goal, penalizing collisions with obstacles and pedestrians, and ensuring smooth navigation through a comfort reward. Within the framework of this MDP, the objective of robot navigation is to identify a strategy, denoted by π(at|st), that maximizes the robot’s cumulative discounted reward throughout the task. This strategy is the probability distribution of selecting an action at in a state st. The cumulative discounted reward can be expressed as Eq. (1).

Gt=Eπ[∑k=0∞γkR(st+k,at+k)],(1)

the discount factor γ∈[0,1] indicates that future rewards are discounted, the γk indicates the discount weight at k-step, and R(st+k,at+k) indicates the immediate reward received after performing action at+k in state st+k.

The present paper utilizes a risk field to quantify the scene complexity in the environment and adjust the reward function. The structure of the paper, which follows the MDP paradigm, is shown in Fig. 1. First, the density of people and the speed of pedestrians within the robot’s current visual range in the scene are evaluated to obtain a risk score for the scene complexity. The robot’s collision reward is scaled according to the score. In the subsequent phase, for robots entering dense areas, the reward is attenuated according to the action taken by applying an exponential decay function to the reward. This can assign exponentially increasing negative rewards to the robot’s actions of approaching pedestrians, to guide the robot to reduce the intrusion time ratio.

Figure 1: Follow the structural diagram of the MDP paradigm. The gray individuals symbolize pedestrians outside the robot’s field of view, and the yellow individuals represent pedestrians within the field of view. They are employed to calculate the scene’s complexity, and the red individuals represent pedestrians too close to the robot. The blue dashed circle with the robot at its center represents the robot’s field of view

3.1 Scenario Complexity Modeling Based on Risk Fields

In a dynamic crowd environment, the risk impact of pedestrians at a specific location on a robot is not discrete; rather, it gradually decreases with increasing distance and decreasing speed. Inspired by this, this paper proposes a modeling method based on the risk field, comprehensively considering the three key factors of spatial distance, pedestrian speed, and crowd density. First, the spatial scope of risk propagation can be flexibly adjusted by introducing the parameter σ to control the attenuation rate in the exponential term. Concurrently, the speed component vi of each pedestrian can be used as a weighting factor to integrate dynamic characteristics into the risk assessment effectively. Pedestrians with higher speeds will generate higher risk values, consistent with the risk distribution characteristics in real scenarios. The risk field modeling method based on the Gaussian kernel has good mathematical continuity and differentiability, which facilitates subsequent path planning optimization and intuitively reflects the risk distribution law in human-computer interaction scenarios.

The present study utilizes a risk field function to model the potential risk of each pedestrian within the robot’s field of view. This function incorporates spatial distance and motion characteristics (speed)into the evaluation model (Eq. (2)). The combination of the distance from the pedestrian to the robot di and the pedestrian’s speed vi enables the dynamic evaluation of the relative risk between the robot and the pedestrian. Furthermore, the range of the risk impact can be controlled by adjusting only one parameter, to suit the complexity requirements of different scenarios.

C(σ)=∑i=1nviexp(di22σ2),(2)

where di represents the distance from the robot to the third person, vi represents the speed of the third person, and σ is the range factor of the risk field, which controls the decay rate of the risk field intensity with distance. When σ is small, the risk field exhibits a rapid spatial attenuation characteristic. This parameter configuration is suitable for accurately assessing close-range risks in open spaces. When σ is large, the risk field has stronger spatial extensibility and can effectively assess potential risks at medium and long distances. This characteristic is fundamental in crowded scenes. As shown in Fig. 2, different σ correspond to differentiated risk assessment models.

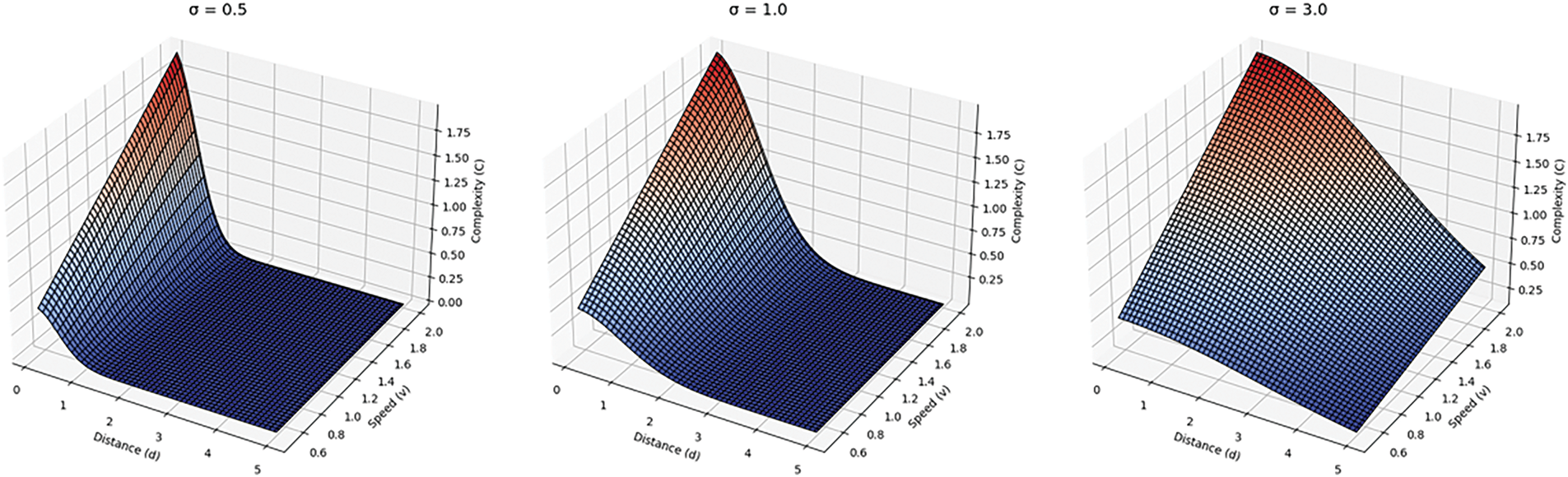
Figure 2: The influence of different σ values on complexity calculation. The figure on the far left represents the distribution of scene complexity with pedestrian speed and distance between the pedestrian and the robot when σ = 0.5. The figure in the middle represents the distribution of scene complexity with pedestrian speed and distance between the pedestrian and the robot when σ = 1.0. The figure on the far right represents the distribution of scene complexity with pedestrian speed and distance between the pedestrian and the robot when σ = 3.0

The three-dimensional surface in Fig. 2 reveals the regulatory mechanism of the parameter σ on the complexity of the risk field. In this example, when σ = 0.5, the effective action radius of the risk field shrinks to within 1 m, and its intensity gradient shows a steep attenuation characteristic. This parameter setting is particularly suitable for modeling the close-range risks in high-density scenarios such as subway stations and commercial centers. When σ = 1.0, the risk gradient curve exhibits a smooth transition characteristic, maintaining significant risk perception ability at a moderate distance of 1 to 3 m. This balanced characteristic suits medium-density scenarios such as shopping malls and office areas. When σ = 3.0, the range of action of the risk field extends to more than 3 m, and its slow decay characteristic can accurately capture the potential long-distance interaction risks in low-density scenarios such as open squares and stadiums.

Fig. 3 shows the risk field distribution under different crowd densities: in low-density scenarios, the risk field presents discrete and independent peaks, and the risk value is generally low (base speed0.5 m/s), providing the robot with flexible navigation space; while in high-density crowd behaviors (such as walking side by side), the risk superposition caused by the crowd effect leads to the formation of significant high-risk areas in local areas, forcing the robot to adopt conservative strategies such as deceleration and increasing the avoidance distance. This dynamic risk field drives the robot’s navigation strategy from proactive to conservative.

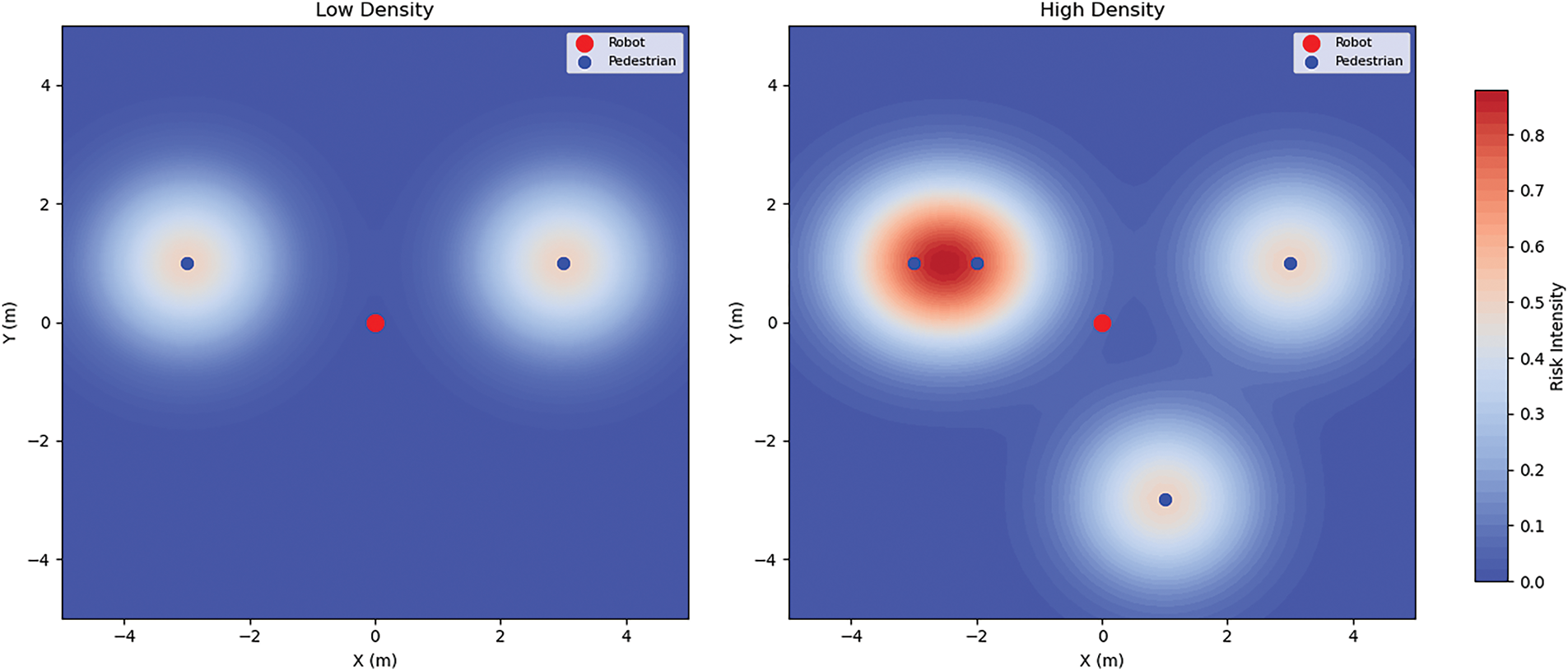
Figure 3: A schematic diagram of the risk field under different population densities. The left side of the diagram shows a sparse pedestrian scene, and the right side shows a dense pedestrian scene. The red dots are robots, and the blue dots are pedestrians. The darker the red around the pedestrians, the higher the risk

3.2 Design of Reward Functions

Unlike previous research [11], this paper explicitly designs a scenario complexity score to adjust the collision penalty in different pedestrian density scenarios, prompting the robot to take more cautious actions to maintain appropriate social distance in high-density scenarios. When the robot acts according to the learned strategy, the reward or penalty obtained will be adjusted according to the complexity value C(σ), that is, the penalty rcol for the robot colliding in a crowded scene will be increased, as in Eq. (3).

rcol=−10⋅C(σ).(3)

In addition, this paper also designs an exponential decay reward mechanism to modulate the reward for dangerous areas, as shown in Eq. (4). When the robot enters a dangerous area (dmin within rcol) determined by the nearest human distance (denoted as dmin), it will be punished by rcol. To make the reward function adaptive and able to reflect environmental changes dynamically, this section combines the scene complexity in Section 3.1 to design a reward for dangerous areas that measures the risk of pedestrian distribution in the current scene.

rdisc=C(σ)2⋅exp⁡(1−dmin⋅λ),(4)

where rdisc is designed to prevent the robot from colliding with humans in dense scenes, it follows the exponential decay law. At this time, the sensitivity to distance is greater than that to scene complexity, so C(σ) is weighted and reduced here.

The exponential decay mechanism in this paper only uses one hyperparameter to adjust the reward effect. The researchers can control the sensitivity of the reward decay to the distance by adjusting the value of the decay rate λ. In addition, this paper follows the definitions of the punishment for future trajectory conflicts between robots and pedestrians and the potential field reward from previous work [9].

rpredi(st)=mink=1,…,K(1it+krcol2k),rpred(st)=mini=1,…,nrpredi(st).(5)

When using the trajectory prediction model, rpred(st) is calculated as a penalty term, as in Eq. (5). rpred(st) represents the potential risk of a collision between the robot and the pedestrian’s future trajectory. The 1it+k calculates whether the robot will enter the predicted position of the i pedestrian at time t+k. The value of rpred(st) takes the minimum penalty value of all potential conflicts and represents the lowest collision risk faced by the robot.

The potential field reward rpot is used to guide the robot to the reward obtained when approaching the target, as in Eq. (6). Where dgoalt is the L2 distance between the robot position and the target position at a given time t.

rpot=dgoalt+1−dgoalt(6)

Finally, the reward function defined in this paper is as in Eq. (7).

r(st,at)={10,if st∈Sgoalrcol,if st∈Scollisionrpred(st)+rdisc(st),if st∈Sconfined zone.rpred(st)+rpot(st),otherwise(7)

4  Experiments and Results

This section describes this paper’s simulation environment, experimental setup, and results. We tested models that did not use the method in this paper and compared them with the latest research and the method in this paper. We also compared navigation performance at different population densities and compared two hyperparameters in the method in this paper to explore their impact on the navigation strategy.

4.1 Experimental Environment

As in the previous work [6,9,11,27], we used the CrowdSim framework for all simulation experiments. CrowdSim is an open-source 2D robot navigation crowd navigation simulator based on OpenAI Gym, obtained from the GitHub code warehouse disclosed in Liu et al.’s work [9]. This environment comprises a 12 m × 12 m planar workspace, where the robot and pedestrians are modeled as circular agents with collision radii. The robot perceives its surroundings through a 360° field of view (FOV) and a lidar sensor with a detection range of 5 m. Pedestrians follow the ORCA (Optimal Reciprocal Collision Avoidance) algorithm for collision avoidance, while the robot is invisible to pedestrians to simulate unidirectional interaction.

The robots’ and pedestrians’ starting and target positions are randomly generated in the 2D plane. Upon reaching their destinations, pedestrians are dynamically reassigned to new random targets, ensuring continuous movement patterns. A medium-density scenario with 20 pedestrians (density ρ = 0.15 persons/m2) is adopted for model training.

px[t+1]=px[t]+vx[t]Δt,py[t+1]=py[t]+vy[t]Δt.(8)

Regarding the kinematic model, this paper uses the overall kinematic equation (Eq. (8)) to update the robot’s and pedestrians’ positions. At each time step: t, the movement of each agent is represented by the desired velocity at=[vx,vy] in the x-axis and y-axis, and both the robot and the human can reach the desired velocity immediately within the time frame of △t. The robot employs a continuous action space with a maximum speed of 1 m/s, consistent with real-world service robots. A collision radius of 0.3 m constrains the robot’s motion, while pedestrians have radii ranging from 0.3 to 0.5 m and speeds between 0.5 and 1.5 m/s.

During training, the robot’s and pedestrians’ initial positions are regenerated at the start of each new episode by invoking the environment’s reset method. This ensures diverse training scenarios through randomized configurations, where each episode begins with a unique layout determined by a fixed random seed and predefined parameters. The visibility between agents is determined solely by the two-dimensional field of view (FOV) and distance thresholds. Specifically, a pedestrian or robot is considered visible if it lies within another agent’s FOV cone and a maximum detection range (5 m), regardless of potential occlusions by other agents along the line of sight. This simplified perception model resembles a third-person perspective rather than simulating physical volume-based occlusions in three-dimensional space.

The Proximal Policy Optimization (PPO) algorithm was implemented with γ = 0.99 discount factor, 4e−5 learning rate, and 0.2 clip parameter across 16 parallel environments, while risk field parameters used σ = 8 spatial decay and λ = 0.1 exponential reward decay. The experiment was conducted on a workstation with a GeForce GTX TITAN GPU and an AMD Ryzen 3990X CPU. A total of 20,820 training iterations were performed, with the model achieving the highest average reward selected for testing.

4.2 Relevant Evaluation Indicators

In terms of evaluation methodology, this study assesses all approaches using 500 randomized test cases and evaluates their performance through navigation and social awareness metrics, consistent with prior research [9]. Navigation metrics quantify pathfinding quality through three key indicators: success rate (SR), average navigation time (NT, in seconds), and mean path length (PL, in meters) across successful cases. Social metrics analyze robotic social compliance through two primary measures: the intrusion-to-time ratio (ITR) and mean social distance (SD, in meters) at intrusion instances. ITR represents the temporal proportion during which the robot violates pedestrian spaces across all test scenarios. During intrusion events, SD is computed as the average minimum distance between the robot and surrounding pedestrians. All intrusion determinations utilize ground-truth pedestrian trajectory data from subsequent timesteps to maintain comparative validity.

4.3 Results

Experiments were conducted with a fixed random seed for environment initialization and policy training to mitigate training stochasticity. The reported results are averaged across 500 test cases to ensure statistical reliability.

4.3.1 Experimental Results of Reward Mechanism Comparison

To comprehensively evaluate the performance advantages of the proposed method, we conducted systematic comparative experiments with five robot navigation strategies. The baseline methods include DS-RNN [6], three attention-based variants (Const vel + HH Attn, Truth + HH Attn, GST + HH Attn [9]), and TGRF [11]. DS-RNN is a model that uses RNN but does not include pedestrian trajectory prediction and a self-attention mechanism. The baseline models that include pedestrian trajectory prediction and self-attention mechanisms include Const vel + HH Attn (which assumes that pedestrians move at a constant speed for trajectory prediction), Truth + HH Attn (which assumes that the robot can obtain the true future trajectory of the pedestrian), GST + HH Attn (which uses the GST model for nonlinear trajectory prediction), and TGRF (which performs reward adjustment based on the transformable Gaussian reward function). In contrast, our method introduces dynamic risk field modeling and adaptive exponential decay rewards. This design enables real-time prioritization of safety in dense crowds (via risk score amplification) and efficiency in sparse regions (via exponential decay suppression), addressing the rigidity of fixed-weight approaches.

Table 1 compares various models’ performance when implementing our proposed risk field modeling and exponential decay reward method under ORCA-governed pedestrian dynamics. The hyperparameters were configured with σ=8.0 (risk diffusion coefficient) and λ=0.1 (decay factor). Both quantitative analysis from Table 1 and qualitative visualization in Fig. 4 reveal three significant improvements attributable to our risk field model implementation.

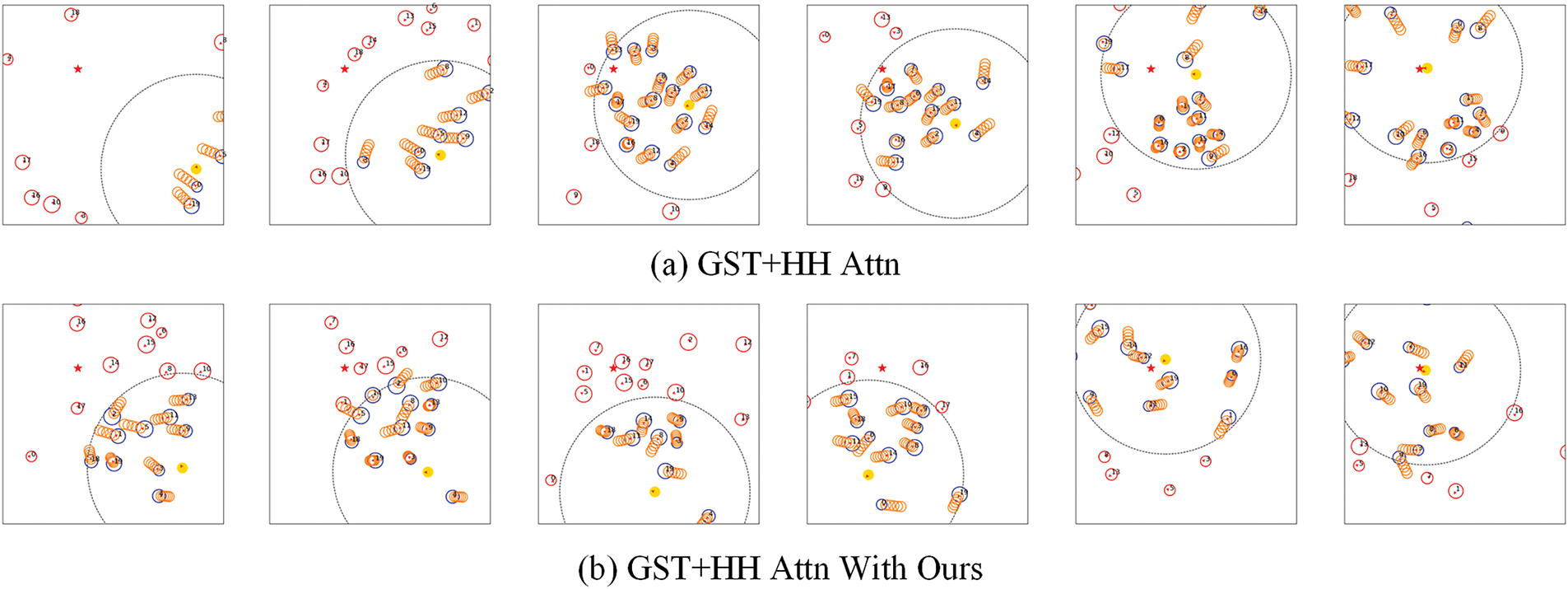
Figure 4: Comparison of robot strategies in a simulated environment. The yellow circles represent the robot, the blue circles represent humans within the sensor range, the red circles represent humans outside the sensor range, and the orange circles in front of the blue circles indicate the predicted trajectory of the GST + HH Attn model

Firstly, the proposed methodology demonstrates substantial improvements in navigation safety metrics. Regarding success rate (SR), the GST With Ours method attains a success rate of 97.0%, 4% higher than the benchmark GST + HH Attn method (93%) and 2% higher than the TGRF method’s 95.0%. This finding signifies that the GST With Ours method demonstrates enhanced reliability in accomplishing navigation tasks. Concurrently, the intrusion-to-time ratio (ITR) has undergone a substantial reduction. The ITR of the GST + HH Attn With Ours method is 2.94%, considerably lower than the 4.36% of the TGRF method, and the time of intruding into the crowd has been reduced by 32.56%. This superiority stems from the adaptive reward mechanism: the exponential decay function amplifies collision penalties in dense crowds while suppressing inefficiency penalties in sparse regions. Unlike fixed-weight methods, which rigidly balance safety and efficiency, our approach adapts weights to real-time risk levels. For instance, in high-density scenarios (Fig. 4b), the exponential decay mechanism imposes exponentially increasing penalties as the robot approaches pedestrians, forcing proactive detours. Conversely, in low-density scenarios, reduced penalties allow faster navigation without compromising safety.

Secondly, while prioritizing safety, the method maintains competitive navigation efficiency despite inherent trade-offs. Given the need to navigate congested areas cautiously, this approach has significantly increased navigation time (NT) and path length (PL). However, this increase remains within the acceptable range. A comparison with the baseline GST + HH Attn method reveals that navigation time (NT) increased from 16.33 to 18.44 s (an increase of 12.9%), and path length (PL) increased from 22.31 to 24.38 m (an increase of 9.3%). Notably, both indicators exhibit a marked superiority over conventional methodologies, such as the DS-RNN approach, which recorded times of 20.76 s and 22.71 m, respectively.

Finally, the approach delineated in this paper enhances the robot’s comprehension of crowd density, thereby reducing the incidence of collisions. As illustrated in Fig. 4a, robots that do not employ this method frequently exhibit aggressive navigation, characterized by sudden movements into crowds and subsequent collisions with pedestrians. This behavior signifies an inability to comprehend pedestrian intentions and to balance reward functions. In contrast, Fig. 4b demonstrates the robot’s enhanced performance when utilizing the proposed method, which anticipates pedestrian congregation and proactively avoids dense areas. This enhanced navigation facilitates safer and more socially acceptable movement while ensuring efficient progress toward the destination.

4.3.2 Results of the Crowd Density Adaptation Experiment

This paper proposes a crowd density gradient test to compare models’ generalization ability. The basic model, which is trained with N = 20 pedestrians (corresponding to a density of ρ = 0.15 people/m2), is used as the test object. Two extreme scenarios of low density (N = 10/15, ρ = 0.07/0.11 person/m2) and high density (N = 25/30, ρ = 0.21/0.25 person/m2), respectively. These scenarios are then compared with the GST + HH Attn and TGRF models in Table 1.

Risk fields and exponential decay methods in high-density scenarios show significant advantages in environmental adaptation. As shown in Table 2, in the extreme scenario of ρ = 0.21, our method improves the success rate (SR) by 7.0% compared to the GST model (82.0% vs. 75.0%) and 9.0% compared to the TGRF model (82.0% vs. 73.0%). In comparison, the intrusion-to-time ratio (ITR) decreased by 7.2% (6.74% vs. 7.26%) compared to the GST + HH Attn model and by 10.7% (6.74% vs. 7.55%) compared to the TGRF model. This shows that in complex high-density environments, the model proposed in this paper can more effectively identify and avoid potential collision risks, thereby improving the safety and reliability of navigation. In contrast, TGRF employs a transformable Gaussian reward function but relies on fixed weights, which fail to prioritize safety in dense scenarios (ITR = 7.55% at ρ = 0.21).

The superiority of our method stems from its adaptive reward mechanism. Unlike fixed-weight approaches, the exponential decay function imposes nonlinearly increasing penalties as the robot approaches pedestrians (Fig. 4b). This forces proactive detours in high-density scenarios while allowing efficient navigation in sparse regions. Mathematically, the penalty term rcol scales with real-time risk scores C(σ), dynamically amplifying safety constraints when crowd density increases. This contrasts with TGRF’s static Gaussian formulation, which cannot adjust penalty intensity based on spatiotemporal risk levels.

The method shows a more substantial performance advantage as the density of the environment decreases. In the low-density scenario of ρ = 0.07, the navigation success rate increases to 100%, and both the benchmark methods GST + HH Attn (98%) and TGRF model (98%) achieve completely reliable navigation performance. At the same time, the intrusion-to-time ratio (ITR) decreased to 1.11%, a 52.6% reduction compared to the benchmark method GST + HH Attn (2.13%) and a 39.7% reduction compared to the TGRF model (1.84%).

This result shows that the method in this paper performs well in low-density environments and has better generalization ability than the GST + HH Attn and TGRF models in higher-density environments. It can efficiently complete navigation tasks and maintain a low intrusion rate when interacting with pedestrians.

4.3.3 Model Hyperparameter Analysis

The selection of hyperparameters has a certain impact on the training and final performance of the model. To deeply analyze the impact of hyperparameters on the model, we quantitatively evaluate the synergistic effect of the risk field range coefficient (σ) and the exponential decay rate (λ) on navigation performance through a cross-over experiment. The results are shown in Table 3. The experimental design covers 16 parameter combinations of σ ∈ {2, 6, 8, 10} and λ ∈ {0.005, 0.05, 0.1, 0.2}. It analyzes the mechanism of hyperparameter action from three dimensions: success rate, navigation efficiency (navigation time and path length), and safety (intrusion time ratio and social distance).

Fig. 5 illustrates the impact of λ (0.005, 0.05, 0.1, 0.2) on loss and reward curves with σ = 8. λ = 0.005 accelerates early optimization through fine-grained perception, leading to rapid loss reduction (Fig. 5a) and stable reward convergence (Fig. 5b), effectively suppressing policy oscillations. However, λ = 0.05 shows a non-monotonic reward decline, suggesting a suboptimal attractor. λ = 0.2 excessively smooths rewards, slowing early convergence and delaying reward growth until 15,000 iterations. λ = 0.1 achieves the best balance, ensuring smooth loss convergence and a stable reward near 20, moderating the exploration-exploitation trade-off.

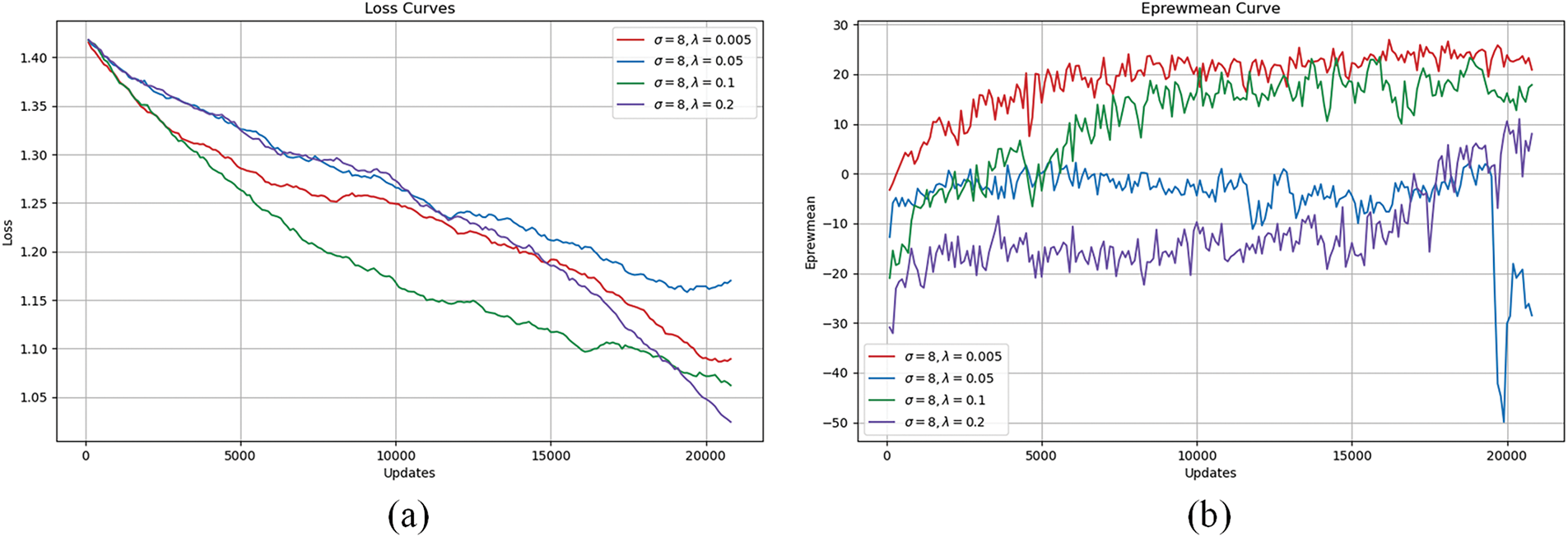
Figure 5: Training loss curve and average reward curve corresponding to different values of λ when σ=8

Fig. 6 illustrates the effect of σ (2, 6, 8, 10) on loss and reward curves with λ = 0.1. A narrow perception range (σ = 2) quickly attenuates nearby risks, leading to rapid loss reduction (Fig. 6a), but makes the reward highly sensitive to disturbances, causing a sharp drop from 25 to −45 after 8000 iterations (Fig. 6b). Increasing σ to 6 balances local and global risks, ensuring gradual loss convergence and stable rewards around 20. At σ = 8, the model maintains stability while optimizing path length and invasion time. However, σ = 10 causes state space explosion, blurring risk boundaries, and stagnating rewards at −8 (Fig. 6b). Table 3 confirms that σ = 6 and λ = 0.1 achieve optimal success (94%), while σ = 10 leads to decision confusion and a drop in success rate to 14%.

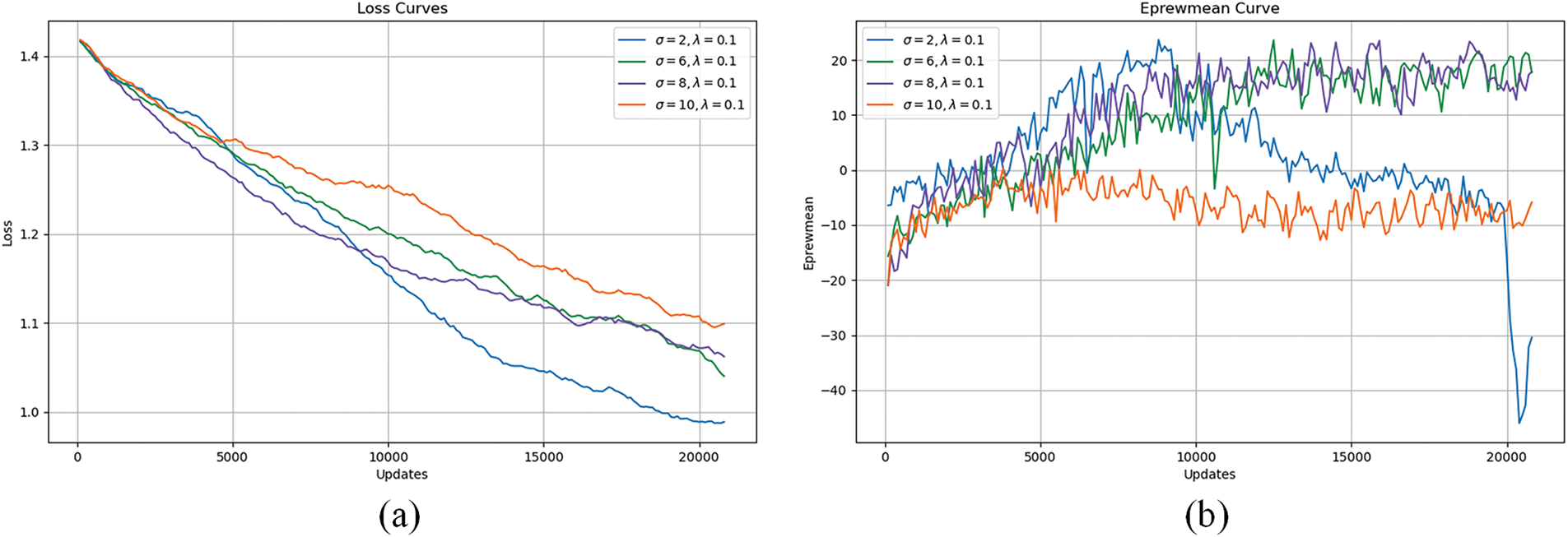
Figure 6: Training loss curve and average reward curve corresponding to different σ values when λ = 0.1

Hyperparameter tuning must align with environmental dynamics. As shown in Table 3, σ = 6 and λ = 0.1 achieve optimal balance (SR = 94%, ITR = 5.25%) in medium-to-high densities (ρ ≥ 0.15). Here, σ = 6 ensures moderate risk coverage, while λ = 0.1 stabilizes reward convergence (Fig. 5). In contrast, extreme parameters (e.g., σ = 10, λ = 0.2) cause decision confusion (SR = 7%), as excessive risk field ranges blur critical boundaries.

The training curves in Figs. 5 and 6 further illustrate behavioral implications. For λ = 0.1, smooth loss reduction (Fig. 5a) correlates with gradual learning of socially compliant paths (Fig. 4b), whereas λ = 0.005’s rapid convergence may lead to overly conservative strategies. Similarly, σ = 8’s stable reward curve (Fig. 6b) reflects the balanced perception of local and global risks, enabling proactive detours in crowded zones.

In light of the results above, the hyperparameter tuning process is advised to adhere to the following principles: In scenarios characterized by low density (ρ<0.10 people/m2), it is recommended to employ σ=2 and λ=0.05 to enhance efficiency through the utilization of local perception, thereby achieving a success rate of 91% and a path length of 22.56 m. This approach enables the management of a higher intrusion time ratio (ITR = 5.82%), attributable to the sparse pedestrian population. In scenarios of medium-to-high density (ρ ≥ 0.15 people/m2), it is recommended to select σ=6 (or σ=8) and λ=0.1 to achieve a balanced risk coverage and reward decay rate, thereby facilitating a trade-off between safety and efficiency (success rate 94%–97%, ITR ≤ 5.25%). Avoiding extreme parameter combinations or preventing policy instability or convergence failure is imperative.

5  Discussion

The experimental results demonstrate that the proposed adaptive reward optimization method effectively addresses the safety-efficiency trade-off in complex dynamic environments through spatiotemporal risk field modeling and exponential decay mechanisms. Compared to conventional fixed-weight approaches [6,9,11,12], our method achieves superior generalization across varying crowd densities by dynamically amplifying collision penalties in high-risk scenarios while relaxing constraints in sparse regions. This adaptability stems from the Gaussian kernel-based risk field, which quantifies scene complexity through integrated analysis of pedestrian speed, density, and distance—an advancement over static Gaussian formulations that lack spatiotemporal awareness [9,11]. The exponential decay reward further enhances responsiveness by assigning nonlinearly increasing penalties as the robot approaches pedestrians, forcing proactive detours without sacrificing navigation efficiency. These innovations explain the 9.0% improvement in success rates and 10.7% reduction in intrusion time observed in high-density scenarios, outperforming state-of-the-art methods like TGRF [11] and GST + HH Attn [9].

The proposed method aligns with recent advancements in adaptive perception and decision-making systems for robotic navigation. For instance, Yi and Guan [28] emphasize the integration of hybrid deliberative-reactive architectures in reinforcement learning to balance strategic planning and real-time responses, a principle echoed in our adaptive reward mechanism. Their work highlights the scalability of DRL across diverse robotic platforms. At the same time, our method extends this by introducing interpretable hyperparameter tuning mechanisms (e.g., σ and λ) to address dynamic crowd dynamics. Similarly, Zhou and Garcke [17] leverage spatiotemporal graphs with attention mechanisms to model crowd interactions, demonstrating the critical role of temporal reasoning in proactive navigation. While their approach focuses on graph-based intention prediction, our work complements this by dynamically adjusting reward weights based on real-time risk assessments, bridging the gap between crowd behavior understanding and adaptive decision-making.

A critical distinction lies in the interpretability of our method. While deep reinforcement learning (DRL) methods often operate as “black boxes” [6,7], our risk field explicitly links environmental dynamics to reward adjustments, enabling systematic hyperparameter tuning. For example, the correlation between σ values and risk coverage (Fig. 2) provides actionable insights for adapting to specific scenarios—a feature absent in end-to-end DRL approaches [28]. This interpretability complements vision-based semantic navigation systems that rely on transparent object detection metrics (e.g., mAP (mean Average Precision) and ODR (Object detection rate) [29]), collectively advancing trustworthy robotic decision-making. Furthermore, our exponential decay mechanism addresses computational inefficiencies in dense crowds, resonating with Zhou and Garcke [17] emphasis on efficient spatiotemporal aggregation but extending it through reward shaping rather than trajectory prediction.

However, limitations persist. The 2D simulation environment simplifies occlusion modeling and sensor noise, potentially overestimating performance in real-world settings. Future integration with multimodal perception systems, such as the YOLO v8-based semantic navigation frameworks [29], could enhance environmental understanding by combining risk field dynamics with real-time object detection. Additionally, while our method reduces hyperparameter sensitivity compared to fixed-weight approaches, optimal σ and λ selection remain scenario-dependent. Automated parameter adaptation, inspired by the self-tuning mechanisms in graph-based navigation [17] and hybrid DRL architectures [28], could improve robustness across diverse environments. These extensions would bridge the gap between reward optimization and perception, fostering holistic navigation systems operating in structured and unstructured dynamic spaces.

6  Conclusions

This paper proposes a navigation method based on spatiotemporal risk field modeling and adaptive reward optimization to address the safety-efficiency trade-off in robotic navigation through complex dynamic environments. By constructing a risk field model that integrates crowd density distribution and pedestrian motion patterns, our approach enables real-time quantification of environmental complexity. Coupled with an exponential decay reward mechanism, this methodology addresses the adaptability limitations of conventional fixed-weight reward functions in varying crowd density scenarios. Experimental results demonstrate that, in comparison with the baseline method, the proposed method enhances the navigation success rate by 9% in high-density scenes and reduces intrusion time by 10.7%. This outcome substantiates the efficacy of balancing safety and efficiency through nonlinear safety constraint enhancement and dynamic adjustment of efficiency weight. Future work will construct a real-world environment testbed containing multimodal sensor data to verify the transferability of our methods from simulation to reality.

Acknowledgement: We sincerely acknowledge the financial support from the Sichuan Science and Technology Program. We also thank our laboratory members for their invaluable collaboration in experimental execution and data validation.

Funding Statement: This work was supported by the Sichuan Science and Technology Program (2025ZNSFSC0005).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Jie He; methodology, Jie He; data collection and experimental design, Dongmei Zhao and Qingfeng Zou; formal analysis and writing—original draft preparation, Jie He and Jian’an Xie; supervision and project administration, Tao Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used in this paper can be requested from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Fragapane G, De Koster R, Sgarbossa F, Strandhagen JO. Planning and control of autonomous mobile robots for intralogistics: literature review and research agenda. Eur J Oper Res. 2021;294(2):405–26. doi:10.1016/j.ejor.2021.01.019. [Google Scholar] [CrossRef]

2. Kim SS, Kim J, Badu-Baiden F, Giroux M, Choi Y. Preference for robot service or human service in hotels? impacts of the COVID-19 pandemic. Int J Hosp Manag. 2021;93(2):102795. doi:10.1016/j.ijhm.2020.102795. [Google Scholar] [PubMed] [CrossRef]

3. Le H, Saeedvand S, Hsu CC. A comprehensive review of mobile robot navigation using deep reinforcement learning algorithms in crowded environments. J Intell Robot Syst. 2024;110(4):1–22. doi:10.1007/s10846-024-02198-w. [Google Scholar] [CrossRef]

4. Bai Y, Shao S, Zhang J, Zhao X, Fang C, Wang T, et al. A review of brain-inspired cognition and navigation technology for mobile robots. Cyborg Bionic Syst. 2024;5(1):0128. doi:10.34133/cbsystems.0128. [Google Scholar] [PubMed] [CrossRef]

5. Feng Z, Xue B, Wang C, Zhou F. Safe and socially compliant robot navigation in crowds with fast-moving pedestrians via deep reinforcement learning. Robotica. 2024;42(4):1212–30. doi:10.1017/S0263574724000183. [Google Scholar] [CrossRef]

6. Liu S, Chang P, Liang W, Chakraborty N, Driggs-Campbell K. Decentralized structural-RNN for robot crowd navigation with deep reinforcement learning. In: Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA); 2021 May 30–Jun 5; Xi’an, China. doi:10.1109/ICRA48506.2021.9561595. [Google Scholar] [CrossRef]

7. Zhou Z, Zhu P, Zeng Z, Xiao J, Lu H, Zhou Z. Robot navigation in a crowd by integrating deep reinforcement learning and online planning. Appl Intell. 2022;52(13):15600–16. doi:10.1007/s10489-022-03191-2. [Google Scholar] [CrossRef]

8. Sun X, Zhang Q, Wei Y, Liu M. Risk-aware deep reinforcement learning for robot crowd navigation. Electronics. 2023;12(23):4744. doi:10.3390/electronics12234744. [Google Scholar] [CrossRef]

9. Liu S, Chang P, Huang Z, Chakraborty N, Hong K, Liang W, et al. Intention aware robot crowd navigation with attention-based interaction graph. In: Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA); 2023 May 29–Jun 2; London, UK. doi:10.1109/ICRA48891.2023.10160660. [Google Scholar] [CrossRef]

10. Kim J, Kwak D, Rim H, Kim D. Belief aided navigation using Bayesian reinforcement learning for avoiding humans in blind spots. In: Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); 2024 Oct 14–18; Abu Dhabi, United Arab Emirates. doi:10.1109/IROS58592.2024.10802765. [Google Scholar] [CrossRef]

11. Kim J, Kang S, Yang S, Kim B, Yura J, Kim D. Transformable gaussian reward function for socially aware navigation using deep reinforcement learning. Sensors. 2024;24(14):4540. doi:10.3390/s24144540. [Google Scholar] [PubMed] [CrossRef]

12. Chen C, Liu Y, Kreiss S, Alahi A. Crowd-robot interaction: crowd-aware robot navigation with attention-based deep reinforcement learning. In: Proceedings of the 2019 International Conference on Robotics and Automation (ICRA); 2019 May 20–24; Montreal, QC, Canada. doi:10.1109/ICRA.2019.8794134. [Google Scholar] [CrossRef]

13. Hart PE, Nilsson NJ, Raphael B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans Syst Sci Cybern. 1968;4(2):100–7. doi:10.1109/TSSC.1968.300136. [Google Scholar] [CrossRef]

14. Sotirchos G, Ajanovic Z. Search-based versus sampling-based robot motion planning: a comparative study. arXiv:240609623. 2024. [Google Scholar]

15. Van Den Berg J, Guy SJ, Lin M, Manocha D. Reciprocal n-body collision avoidance. In: Proceedings of the 14th International Symposium ISRR; 2009 Aug 31–Sep 3; Lucerne, Switzerland. [Google Scholar]

16. Chen Y, Liu C, Shi BE, Liu M. Robot navigation in crowds by graph convolutional networks with attention learned from human gaze. IEEE Robot Autom Lett. 2020;5(2):2754–61. doi:10.1109/LRA.2020.2972868. [Google Scholar] [CrossRef]

17. Zhou Y, Garcke J. Learning crowd behaviors in navigation with attention-based spatial-temporal graphs. In: Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA); 2024 May 13–17; Yokohama, Japan. doi:10.1109/ICRA57147.2024.10610279. [Google Scholar] [CrossRef]

18. Zhu K, Zhang T. Deep reinforcement learning based mobile robot navigation: a review. Tsinghua Sci Technol. 2021;26(5):674–91. doi:10.26599/TST.2021.9010012. [Google Scholar] [CrossRef]

19. Ibrahim S, Mostafa M, Jnadi A, Salloum H, Osinenko P. Comprehensive overview of reward engineering and shaping in advancing reinforcement learning applications. IEEE Access. 2024;12:175473–500. doi:10.1109/ACCESS.2024.3504735. [Google Scholar] [CrossRef]

20. Montero EE, Mutahira H, Pico N, Muhammad MS. Dynamic warning zone and a short-distance goal for autonomous robot navigation using deep reinforcement learning. Complex Intell Syst. 2024;10(1):1149–66. doi:10.1007/s40747-023-01216-y. [Google Scholar] [CrossRef]

21. Patel U, Kumar NKS, Sathyamoorthy AJ, Manocha D. DWA-RL: dynamically feasible deep reinforcement learning policy for robot navigation among mobile obstacles. In: Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA); 2021 May 30–Jun 5; Xi’an, China. doi:10.1109/ICRA48506.2021.9561462. [Google Scholar] [CrossRef]

22. Oh J, Heo J, Lee J, Lee G, Kang M, Park J, et al. Scan: socially-aware navigation using Monte Carlo tree search. In: Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA); 2023 May 29–Jun 2; London, UK. doi:10.1109/ICRA48891.2023.10160270. [Google Scholar] [CrossRef]

23. Jeong H, Hassani H, Morari M, Lee DD, Pappas GJ. Deep reinforcement learning for active target tracking. In: Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA); 2021 May 30–Jun 5; Xi’an, China. doi:10.1109/ICRA48506.2021.9561258. [Google Scholar] [CrossRef]

24. Samsani SS, Mutahira H, Muhammad MS. Memory-based crowd-aware robot navigation using deep reinforcement learning. Complex Intell Syst. 2023;9(2):2147–58. doi:10.1007/s40747-022-00906-3. [Google Scholar] [CrossRef]

25. Rios-Martinez J, Spalanzani A, Laugier C. From proxemics theory to socially-aware navigation: a survey. Int J Soc Robot. 2015;7(2):137–53. doi:10.1007/s12369-014-0251-1. [Google Scholar] [CrossRef]

26. Goyal P, Niekum S, Mooney RJ. Using natural language for reward shaping in reinforcement learning. arXiv:190302020. 2019. [Google Scholar]

27. Xu J, Zhang W, Cai J, Liu H. SafeCrowdNav: safety evaluation of robot crowd navigation in complex scenes. Front Neurorobot. 2023;17:1276519. doi:10.3389/fnbot.2023.1276519. [Google Scholar] [PubMed] [CrossRef]

28. Yi Y, Guan Y. Research on autonomous navigation and control algorithm of intelligent robot based on reinforcement learning. Scalable Comput Pract Exp. 2025;26(1):423–31. doi:10.12694/scpe.v26i1.3841. [Google Scholar] [CrossRef]

29. Alotaibi A, Alatawi H, Binnouh A, Duwayriat L, Alhmiedat T, Alia OM. Deep learning-based vision systems for robot semantic navigation: an experimental study. Technologies. 2024;12(9):157. doi:10.3390/technologies12090157. [Google Scholar] [CrossRef]