Semantic Secure Communication Based on the Joint Source-Channel Coding

1  Introduction

Semantic secure communication is an emerging field that combines the principles of source-channel coding with the need for secure data transmission [1]. Traditional communication systems focus on accurately transmitting bits over noisy channels, while emantic secure communication aims to identify and transmit the most valuable information efficiently, considering human perceptual loss and machine task accuracy as the distortion metrics [2]. This paradigm shift is driven by the fusion of information and communication technology (ICT) advances and artificial intelligence (AI) innovations [3]. Semantic secure communication can resist some common attacks including cryptanalysis [4,5], eavesdropping [6], image verification code bypassing [7,8], and man-in-the-middle attacks [9,10]. There is also evidence on using semantic secure communications to protect privacy [11]. How to retain the advantages of both has become a scientific problem that continues to be solved. Thus, it is necessary to do some research on semantic secure communication.

Semantic secure communication refers to a framework that ensures both the efficient transmission of task-critical information (semantic level) and robust protection against eavesdropping or adversarial tampering. Unlike traditional semantic communication, which focuses on compressing contextual meaning, our approach integrates cryptographic guarantees (e.g., indistinguishability under chosen plaintext attacks) to safeguard semantic features during transmission. One approach to achieving semantic secure communication is through joint source-channel coding (JSCC), which integrates the design of source and channel processing [12]. JSCC has been extensively studied in the field of information theory and coding theory, but conventional JSCC schemes have limitations in handling complex sources and optimizing for human perception or machine tasks directly. However, recent advancements in deep learning models have shown promise in optimizing JSCC for specific end-to-end transmission objectives [13]. For example, deep JSCC approaches have been successful in wireless image transmission, surpassing traditional separation-based source compression combined with channel coding methods [14]. These deep JSCC models optimize the trade-off between reconstruction quality and channel bandwidth cost, which is crucial for high-resolution media transmission, especially in air traffic communication [15] and high-speed trains [16]. Nonlinear transform source-channel coding (NTSCC) has been proposed to achieve content-aware variable-length JSCC by introducing an entropy model on semantic latent representations [17].

While existing end-to-end transmission approaches have shown success in optimizing the trade-off over source datasets and wireless channel responses, they might not be optimal for every test instance for security concerns. In AI, this could be due to limited model capacity and imperfect optimization, especially when the testing data distribution or channel response is different from the training stage. To address this challenge, a new online learning approach [18] has been explored, optimizing network parameters or semantic representations during the model inference stage based on the current target source data and wireless channel domain [19]. In data compression and encryption, handling these two processes in tandem might result in inefficiencies. To solve this problem in digital signal processing, compression-combined digital image encryption [20] has been presented. In data sharing, sending all data has been changed to sending necessary data only [21], which greatly increases the security.

Inspired by insights from traditional source compression codes and the improvement ideas mentioned above, this paper aims to solve the following problems.

•   To design an automated JSCC algorithm with adaptive modulation (BPSK/QPSK/16QAM) based on packet length.

•   To propose a semantically secure encryption scheme (RIAC) resistant to ciphertext attacks.

•   To validate the framework’s efficiency (transmission time) and security (attack resistance) under real-world channel conditions.

In this paper, we proposes a domain adaptive joint source-channel coding architecture for semantic secure communication [22]. The proposed method incorporates online learning to overfit the instant source data sample and channel state information, enhancing the end-to-end communication system’s performance. The system introduces an additional model stream to update the JSCC decoder and synthesis transform parameters at the receiver, considering the costs of sending model updates [23]. The overall system design is formulated as an optimization problem, aiming to minimize the tripartite trade-off among data stream bandwidth cost, model stream bandwidth cost, and end-to-end distortion [24]. For a better description, several contributions of this paper are listed below.

•   We design an automated joint source-channel coding algorithm.

•   We designed an encryption and decryption algorithm based on semantic security.

•   We designed a secure communication solution based on the designed joint source-channel coding algorithm.

The remaining sections of this paper are organized as follows. Section 2 is the related work, which proposes some recent research related to semantic secure communication based on joint source-channel coding. Section 3 is the proposed method. In this section, the secure communication solution based on the designed joint source-channel coding algorithm will be stated in detail. Section 4 is the syntax and security models, in which we analyze the security of our proposed method theoretically. Section 5 is the experiment, which states how our proposed methods are superior to state-of-the-art methods in performance. Section 6 is the conclusion, which gives an overall review of this paper and provides the conclusion. The future work is also proposed in this section.

2  Related Work

This section introduces concepts about channel transmission and points out the security issues in communication and the limitations of existing methods. This section introduces concepts about channel transmission and points out the security issues in communication and the limitations of existing methods. Both the joint methodology and the importance of applying semantic secure communication in the joint coding are stressed.

The general process of channel transmission is “original text → encryption → compression → encoding → channel → decoding → decompression → decryption → original text”, and the order cannot be changed under normal circumstances [25]. Encryption is the process of converting original text into ciphertext to protect the confidentiality of data and prevent it from being read or tampered with without authorization [26]. The encryption operation is based on the original text, not the compressed data, so compression before encryption will cause the encryption algorithm to be unable to correctly process the compressed data. Compression is the process of reducing the storage space or transmission bandwidth of data through a certain algorithm, to improve data transmission efficiency and storage efficiency. Encoding is the process of converting data into a specific format or rules so that it can be decoded and processed correctly during transmission or storage. The encoding operation serves transmission, so the last step before transmission should be the encoding operation. To sum up, before the sender enters the channel to perform transmission, the order of encryption, compression, and encoding must be “encryption → compression → encoding”. After the receiver obtains the data transmitted by the channel, it performs the “decoding → decompression → decryption” operation accordingly to ensure that the original data that the sender wants to send can be obtained.

In the encoding operation, traditional communication systems usually encode the source first and then the channel [27]. This separate encoding method can effectively reduce the error rate during data transmission, but there are certain limitations in data transmission efficiency. Fig. 1 shows the complete procedures of sending and receiving in communication, which uses the traditional source-channel coding. In source-channel joint coding, source coding and channel coding operations are performed simultaneously. Joint coding can reduce the amount of data transmitted and the bandwidth required for transmission as much as possible while ensuring transmission reliability when improving the transmission efficiency and reliability of the communication system. Source channel joint coding usually uses some efficient coding algorithms, such as Turbo codes [28], LDPC codes [29] and FEC codes [30], which are widely used in wireless communications [31–33], satellite communications [34,35], digital television [36,37], and other fields. Fig. 2 shows the complete procedures of sending and receiving in communication using the joint source-channel coding that improves from the traditional one, using joint source-channel coding and joint source-channel decoding.

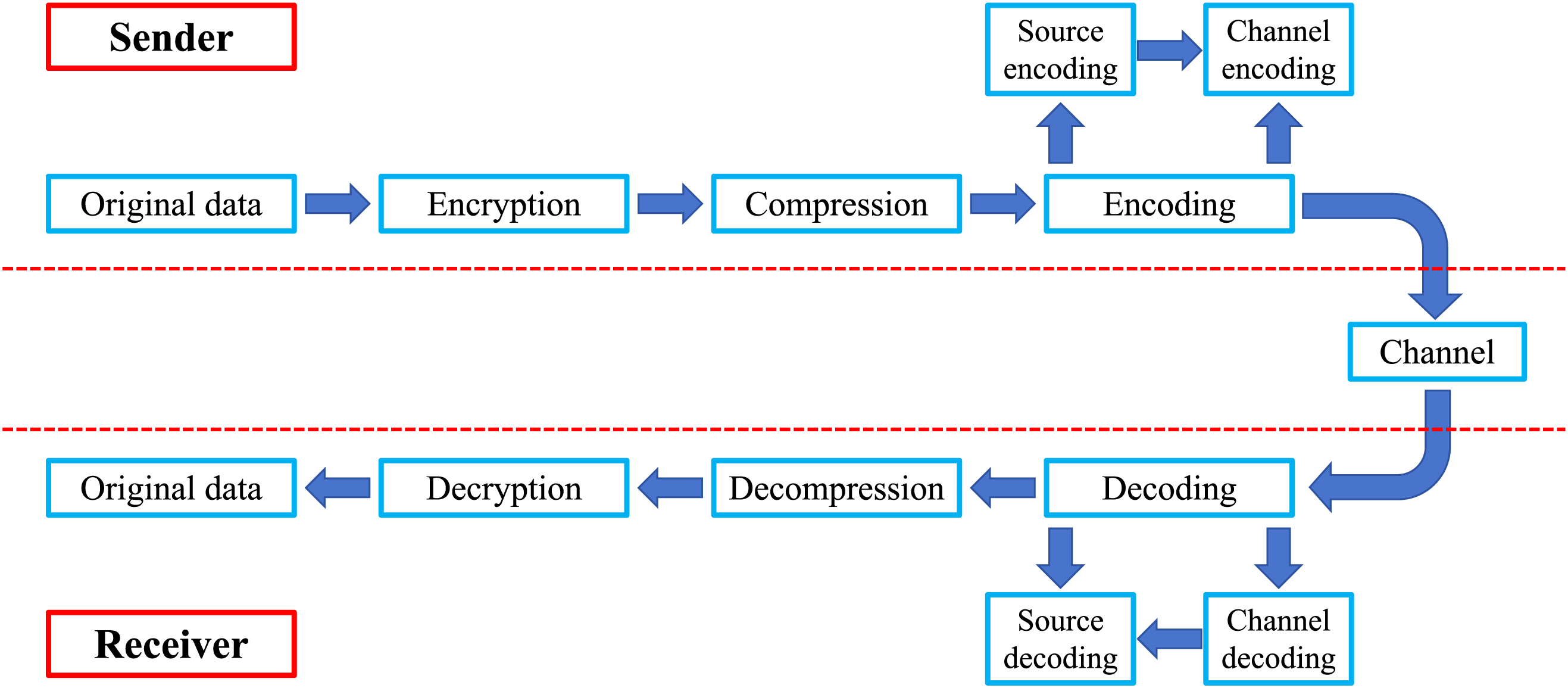
Figure 1: The complete procedures of sending and receiving in communication using the traditional channel-source coding. Channel type: AWGN with SNR 0–20 dB. Adaptive modulations: BPSK/QPSK/16QAM

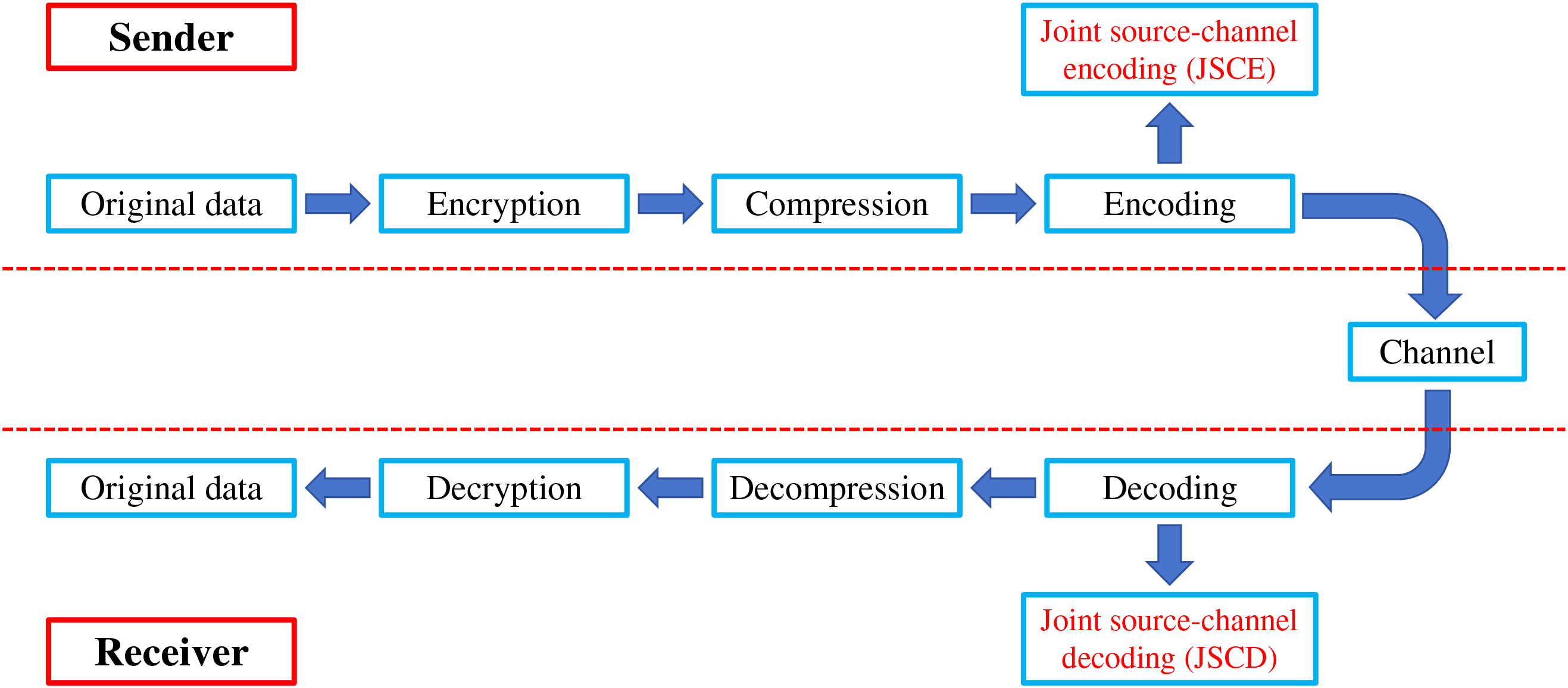
Figure 2: The complete procedures of sending and receiving in communication using the joint channel-source coding that improves from the traditional one. Channel type: AWGN with SNR 0–20 dB. Adaptive modulations: BPSK/QPSK/16QAM

Traditional channel transmission algorithms can often only guarantee data confidentiality, but cannot guarantee data integrity and availability. Semantic secure communication based on joint source-channel coding can solve this problem well, and it can provide a higher level of security, including data confidentiality, integrity, and availability. Although artificial intelligence-assisted communication has been proposed, the uncertainty and unexplainability of AI are still difficult to handle with rigorous mathematical proofs [38] in secure communication processes since AI algorithms are seldom exact algorithms.

3  Proposed Method

This section introduces the automated joint source-channel coding algorithm we proposed. Then, a novel encryption and decryption algorithm based on semantic security is described. Finally, the secure communication solution based on the designed joint source-channel coding algorithm is stated in detail.

3.1 Automated Joint Source-Channel Coding Algorithm

If the source information entropy is not greater than the channel capacity, separate channel coding and source coding can be found to complete error-free transmission of information [39]. Although this theory can achieve the best results for both channel coding and source coding, when each is optimal, the information transmission performance of the entire communication system is not necessarily optimal.

The purpose of source encoding is to remove redundant information within the source and improve effectiveness. Channel coding requires adding check bits to the original bit sequence to implement error detection and correction functions, thereby improving the authenticity of the bit sequence transmitted on a noisy channel.

From a design perspective, source compression and channel coding are opposites. If designed separately, it would be difficult to compromise. The joint design of source compression and channel coding can enable the communication system to achieve end-to-end optimal performance. Jointly optimizing compression and encryption can also avoid cascaded inefficiencies.

We use Huffman coding to encode the source. Huffman coding is a variable-length prefix encoding technique that assigns shorter codes to more frequently occurring symbols and longer codes to less frequently occurring symbols. This technology effectively eliminates redundancy in the source and improves transmission efficiency.

The automatic joint source-channel coding algorithm is automatically reflected in automatically selecting a matching channel coding algorithm for encoding according to the packet length. For channel coding, our proposed automatic joint source-channel coding algorithm will automatically select one of the three channel coding algorithms: Binary Phase Shift Keying (BPSK) [40], Quadrature Phase Shift Keying (QPSK) [41], or Quadrature Amplitude Modulation (16QAM) [42] for the channel encoding. BPSK modulates a digital signal into two different phase states, each phase state representing a binary bit. QPSK (Quadrature Phase Shift Keying) modulates digital signals into four different phase states, each phase state represents two binary bits. 16QAM (Quadrature Amplitude Modulation) modulates digital signals into 16 different states, each state represents four binary bits.

When choosing a modulation method, the packet length needs to be considered. Packet length refers to the number of bits represented by each symbol. For longer packet lengths, such as data transmission of multiple bits, 16QAM can provide higher data transmission rates and spectral efficiency because it can represent more bits of information. For shorter packet lengths, such as single-bit data transmission, BPSK, and QPSK are more suitable because they have lower complexity and lower bit error rates. Since QPSK and 16QAM have restrictions on the length of the packet when the packet length does not meet QPSK and 16QAM, the automatic joint source channel coding uses BPSK for channel coding by default. Otherwise, the channel coding algorithm corresponding to the packet length is used for channel coding.

The automatic joint source-channel coding algorithm selects different modulation methods according to different packet lengths, which makes the algorithm perform better than the original joint source channel. On the one hand, the data transmission rate and spectral efficiency can be improved by choosing an appropriate modulation method. Using 16QAM to transmit multiple bits of data can transmit more information under the same bandwidth and improve the data throughput of the system. On the other hand, selecting the modulation method according to the packet length simplifies the system design and reduces the complexity. For short packet lengths, using BPSK or QPSK can simplify the demodulation and detection process and reduce the calculation and processing volume of the system. The bit error rate is also an important indicator to measure the modulation method. Automatically selecting the appropriate modulation method according to different packet lengths can reduce the bit error rate. Different modulation methods have different anti-noise properties. By selecting an appropriate modulation method, the system’s tolerance to noise and interference can be improved, and the reliability of data transmission can be improved.

3.2 Encryption and Decryption Algorithm Based on Semantic Security

The Randomized Iterative Affine Cipher (RIAC) [43] is built on the classical affine cipher, where a linear transformation and a mode operation are used to encrypt and decrypt the plaintext [44]. Affine cipher is a simple and ancient encryption technique that has been used for centuries. In an affine cipher, each letter of the plaintext is replaced by a letter from the alphabet using a mathematical function.

The encryption process involves two key components: a multiplicative key (k1) and an additive key (k2). The letter p in the plaintext is encrypted to become the letter c in the ciphertext using Eq. (1), where mod “n” ensures that the result is within the range of cipher text space. Additionally, n is the size (e.g., n=256 for 8-bit data) and n is co-prime with k1. The key k=(k1,k2)∈K should satisfy k1×k1−1=1(mod n). By operating on the ciphertext C according to Eq. (2), the plaintext P information can be obtained.

c≡Ek(p)≡k1×p+k2(mod n)(1)

p≡Dk(c)≡k1−1(c−k2)(mod n)(2)

Different from the traditional affine cipher algorithm, the RIAC incorporates additional layers of security and randomness. Building upon the principles of the affine cipher, RIAC introduces multiple rounds of iteration and randomization to enhance encryption. It utilizes a set of randomly generated keys and applies affine transformations iteratively, increasing the complexity and security of the encryption process. By introducing randomness and multiple iterations, RIAC provides a higher level of resistance against frequency analysis attacks and other cryptographic attacks. It offers a stronger level of security compared to the traditional affine cipher, making it suitable for applications that require higher encryption strength.

Algorithm 1 describes the key generation algorithm of the random iterative affine cipher (RIAC), where e represents the accuracy of the encoding, s represents the length of the key and r represents the number of iteration rounds. In accordance with the tradittional affine ciper algorithm, A and W are similar to k1 and k2 respectively, where gcd(wi,ai)=1 are satisfy for all i∈[0,s]. The generator g and the scalar x are selected randomly. The detailed process of how to generate a key is shown in Algorithm 1.

The encryption steps are as follows. Encode the plaintext through ⌊(e×(M+τ))⌋ to obtain the encoded plaintext M. Randomly select a number y and calculate c1←(y×g)%w0,c2←(M+y×h)%w0. The encrypted ciphertext is repeatedly encrypted for multiple rounds, using different coprime numbers a and modulus w in each round. In each round of encryption, the second ciphertext part is updated through (ai×c2)%wi. Where i is the number of iteration rounds, ai is the i-th element in A, and wi is the i-th element in W. Eventually, the ciphertext C=(c1,c2) should be the output.

Algorithm 2 describes the encryption algorithm of the random iterative affine cipher (RIAC), where K represents the key, M stands for the plaintext, and τ is the transaction. The key of the encryption algorithm of RIAC is how to encrypt the plaintext by using the randomly generated key matrix K=(A,W,g,x). During the cycle of encryption, c1 remains whilst c2 is iteratively produced.

Algorithm 3 describes the decryption algorithm of random iteration affine cipher (RIAC), where C stands for the ciphertext, K represents the key, q represents the multiple, and b is the multiple times.

Both RIAC encryption and RIAC decryption algorithms have a time complexity of O(r), where r is the iteration rounds (default=5). For 1 KB data, encryption takes 2.1 µs on a CPU (vs. 4.8 µs for AES-256), making it suitable for low-latency applications.

3.3 A Novel Secure Communication Solution

Based on the proposed Automated joint source-channel coding algorithm and encryption and decryption algorithm based on semantic security, this paper proposes a novel secure communication solution. Fig. 3 shows the procedures of the novel secure communication solution we proposed, applying the automated joint source-channel coding algorithm and the cryptography algorithms based on semantic security.

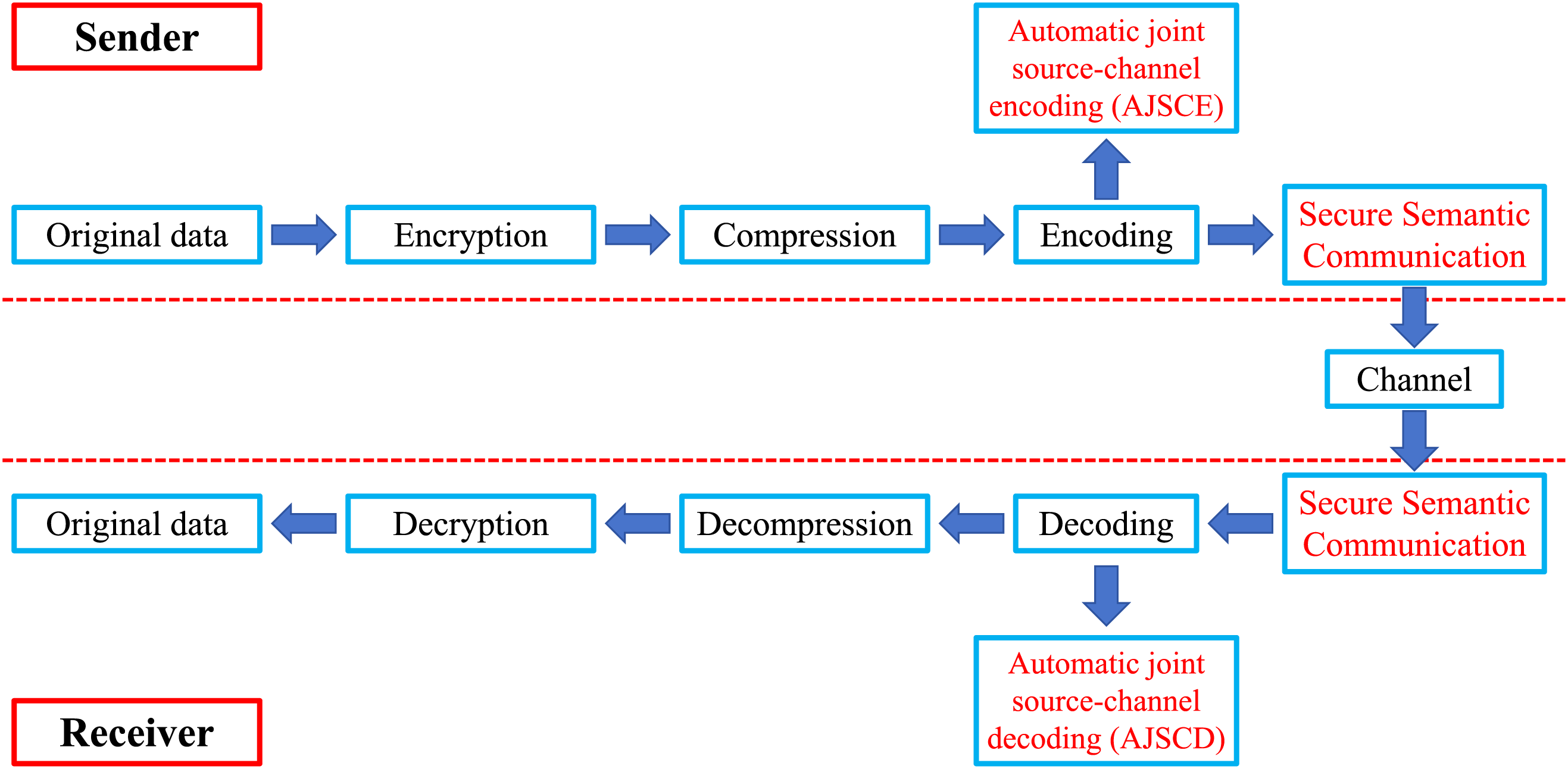
Figure 3: The complete procedures of sending and receiving in communication with secure semantic communication supported using the solution we proposed

During the channel transmission process, the original text M is first converted into ciphertext C through encryption, and the ciphertext C is then compressed to obtain C′. Then C′ is input into the Automated joint source-channel coding algorithm for encoding to obtain the encoded data D. Then we use the RIAC algorithm to encrypt the obtained data D to obtain D′. D′ is the data transmitted in the channel. After the receiving end receives the data D′, it first uses the RIAC algorithm to decrypt D′ to obtain the data D, and then D Input it into the Automated joint source-channel coding algorithm for decoding, and get the decoded data C′. Then it is decompressed and decrypted to obtain the original data M. At this point, the process of transmitting information on the channel is over. This is the novel secure communication solution proposed in this article. The secure communication solution is encoded with a novel randomized iterative affine cipher for homomorphic encryption that preserves semantic security, which enables our communication solution to provide a higher level of security, including data confidentiality, integrity, and availability.

4  Security Models

This section focuses on using mathematics to prove the security of our proposed method. Different models are presented for in-depth analysis.

4.1 Two Mathematical Problems

The security of the RIAC algorithm is based on two mathematical problems, the modular inversion problem and the discrete logarithm problem.

Modular Inversion Problem. Given a modulus n and an integer a, find the multiplicative inverse of a modulo n. The difficulty of this problem is that calculating the inverse element modulo n requires finding the integer a′ that satisfies the multiplicative inverse condition, that is, the integer ainv that satisfies (a×a′)≡1 mod n.

In this algorithm, the selected parameters w and a satisfy the mutual prime relationship, that is, the greatest common divisor of the two numbers is 1. This is done to ensure that in each round of encryption and decryption, the inverse element modulo w (i.e., the multiplicative inverse element modulo w) exists.

Discrete Logarithm Problem. Given a large prime number p and a finite field Zp, a is a primitive element on Zp, for Integer b, find the unique integer c such that ac=b mod p.

In this algorithm, the parameters g and x are chosen to generate the public and private keys. where g is a generator and x is a scalar. The difficulty of this problem is that calculating the discrete logarithm requires finding an integer x that satisfies the exponential operation conditions.

These two mathematical problems are widely considered to be difficult, i.e., no efficient algorithm can solve them in polynomial time given current computing power.

4.2 Proof of the Difficulty of the Modular Inversion Problem

Suppose there is a polynomial-time algorithm (i.e., one that can be solved in polynomial time) to solve the modular inversion problem. We will show that this leads to the existence of polynomial-time algorithms for the integer factorization problem, which is considered a difficult problem.

Suppose we have a number N and we want to factor it into the product of two prime numbers p and q, i.e., N=p×q. We can think of N as the modulus m in the modular inversion problem, and we are trying to find a number a such that a×b≡1 mod m. If we can find such a, then we can find p and q by calculating the greatest common divisor of a2−N.

Now let’s assume that we have a polynomial time algorithm to solve the modular inversion problem. We can use this algorithm to find a number a such that a×b≡1 mod N. Then we calculate the greatest common divisor of a2−N. If the result is a non-trivial factor, then we have found a factor of N. Otherwise, we can continue to try other numbers a.

In this way we can find the factors of N in polynomial time, thus solving the integer factorization problem. Therefore, if the modular inversion problem is easy to solve, then the integer factorization problem will also be easy to solve, which contradicts the difficulty of the integer factorization problem.

Therefore, we can conclude that the modular inversion problem is difficult.

4.3 Security Models of IND-CCA2

If the DLP problem on group G is hard, then the RIAC scheme is IND-CCA2 secure.

Setup: The challenger 𝒞 executes Setup algorithm to generate (A, W, g, x).

Phase 1: Adversary 𝒜 can perform a series of decryption queries. When the adversary submits a ciphertext C for query, challenger 𝒞 returns the result of Dec(K,C) to the adversary 𝒜.

Challenge: 𝒜 generates and sends two equal length plain text m0 and m1 on which it wishes to be challenged. 𝒞 selects a random bit δ∈{0,1}. Then 𝒞 calculates C∗=Enc(pk,mδ) and sends C∗ to 𝒜.

Phase 2: Adversary 𝒜 can continue to perform decryption queries, here it is required that the adversary cannot query the challenge ciphertext C∗.

Guess: Ultimately, 𝒜 outputs a guess bit δ′∈{0,1} and she win the game if δ=δ′. The advantage for 𝒜 attacking this scheme is defined as a function related to the security parameter λ shown in Eq. (3).

Adv𝒜(λ):=|Pr[δ=δ′]−12|(3)

If for any of the above polynomial time adversary 𝒜, its advantages over the encryption scheme are negligible, then the encryption scheme is said to be IND-CCA2 secure.

4.4 Proof of IND-CCA2 Secure

Proof: Suppose there is an adversary 𝒜 that can break the IND-CCA2 security of the RIAC algorithm, then there is a polynomial time algorithm ℬ that can solve the discrete logarithm problem.

Setup: The algorithm ℬ executes KeyGen algorithm to generate key K=(pk,sk). Algorithm ℬ selects the key size s, the key round r, and the encoding precision e. The key generation algorithm acts as follows. First, a series of bit arrays A, W corresponding to the key round numbers are generated. For each key round number, an integer w with a specific number of bits s is randomly selected. A random number ar between [0,1] is randomly generated. a is a random integer of ⌊s×ar⌋ bits, and a and w are prime numbers to each other. Randomly generate a generator g and a scalar x. Calculate h with the equation h≡(g×x) mod w0. Then give the public key pk=(A,W,g,h,e to 𝒜).

Phase 1: Adversary 𝒜 can perform a series of decryption queries. When the adversary 𝒜 submits a ciphertext C for query, algorithm ℬ first determines whether the ciphertext is an integer 0 and does not meet specific multiple and modulus requirements. If so, it outputs “the ciphertext is invalid”. If not, it outputs M=Dec(sk,C).

Challenge: When the adversary 𝒜 decides to end Phase 1, it generates and sends two equal-length plain text m0 and m1 on which it wishes to be challenged. ℬ selects a random bit γ∈0,1. Then 𝒞 calculates C∗=Enc(pk,mγ) and sends C∗ to 𝒜.

Phase 2: Adversary 𝒜 can continue to perform decryption queries, here it is required that the adversary cannot query the challenge ciphertext C∗. Algorithm ℬ uses a strategy similar to Phase 1 to respond to adversary 𝒜 queries.

Guess: Ultimately, 𝒜 outputs a guess bit γ′∈{0,1}. If γ=γ′, then the algorithm outputs β′=1 as a guess for the DLP problem. Otherwise, it outputs β′=0.

If there is an adversary that can crack the RIAC algorithm 𝒜, then the ability of 𝒜 can be used to solve the discrete logarithm problem. This shows that the security of the RIAC algorithm is related to the intractability of the discrete logarithm problem.

5  Experiments and Results

This section first presents the experimental environments for better reimplementation. Subsequently, the experiments presenting the detailed test instances and performance metrics will be described. Eventually, this section provides the experimental results and discusses the related phenomena. We set up two baselines. The first baseline is the traditional coding method, which performs two encoding procedures in series. The second baseline is the state-of-the-art joint source-channel coding, which is mainly used to show that our proposed method increases security while almost losing no efficiency. Since we optimized the second baseline model using Huffman coding and object-oriented programming, we also compared the two baseline models.

5.1 Experimental Enviroments

The experiment is accomplished on 11th Gen Intel(R) Core(TM) i7-11800H CPU 2.30 GHz 8 cores, NVIDIA GeForce RTX 3060 Laptop GPU, 24 GB RAM, 512 GB SSD, and 1024 GB HDD under Windows 10 Pro 22H2 x64. The operating system is on the SSD. The codes and the datasets are on the HDD. All the codes are in Python programming language and run by Python 3.6.8. Please note that since the running time of the program will vary depending on the state of the machine each time it is measured and the resources owned by the program are different on different machines, the time-consuming values of each run will basically be different but the trends and the speed ratios in each run should be consistent with those in this paper.

5.2 Test Instances

All test instances are randomly generated, which are non-single strings with a length of no less than 2. For testing the security, a is set to 5.33, c is set to −3.55, the general scale is set to −3.1, and the scale of c is set to 2.5. The number of rounds in each group of experiments is set to 1000.

5.3 Evaluation Metrics

In order to evaluate the new method we proposed fairly, we quantify it through two evaluation metrics, time consumption and symbol error rate.

In order to test the time consumption of the three algorithms, for each group of data to be transferred, 1000 rounds of independent experiments are tested. Subsequently, the average time of the corresponding 1000 rounds of independent experiments will be collected and computed, representing the time consumption for each group. This can avoid the time consumption being 0 since the time consumption is extremely small but not exactly 0 in each round. Since the time consumption of each round is usually within 1µs, the unit of the time consumption for each group is set to µs. After running 10 groups of independent experiments, we compute the average time consumption of the 10 groups of independent experiments to present a more exact time consumption of each algorithm.

The error rate and the bit error rate refer to the same concept, which is the rate of errors occurring during data transmission. The error rate represents the proportion of incorrect bits in the transmitted data, while the bit error rate represents the average number of incorrect bits in the transmitted data. Let’s represent the variables as follows.

•   Error rate: ER

•   Bit error rate: BER

•   Number of incorrectly decoded bits: Nerror

•   Total number of transmitted bits: Ntotal

The mathematical formula to represent the relationship between error rate and bit error rate can be shown as ER=BER=NerrorNtotal. Here, we mainly compare our proposed method with the second baseline, the joint source-channel coding.

5.4 Results and Discussion

Fig. 4 shows the overall comparison of time consumption between the two baselines and our proposed method. Table 1 presents the time consumption of the traditional source-channel coding and the joint source-channel coding. The average time consumption for the traditional source-channel coding is 180.349507µs, while for the joint source-channel coding, it is 68.962002µs. It can be observed that the joint source-channel coding has a significantly lower time consumption compared to the traditional source-channel coding, with an improvement of 61.830591%. This indicates that the joint source-channel coding has better performance in terms of time consumption.

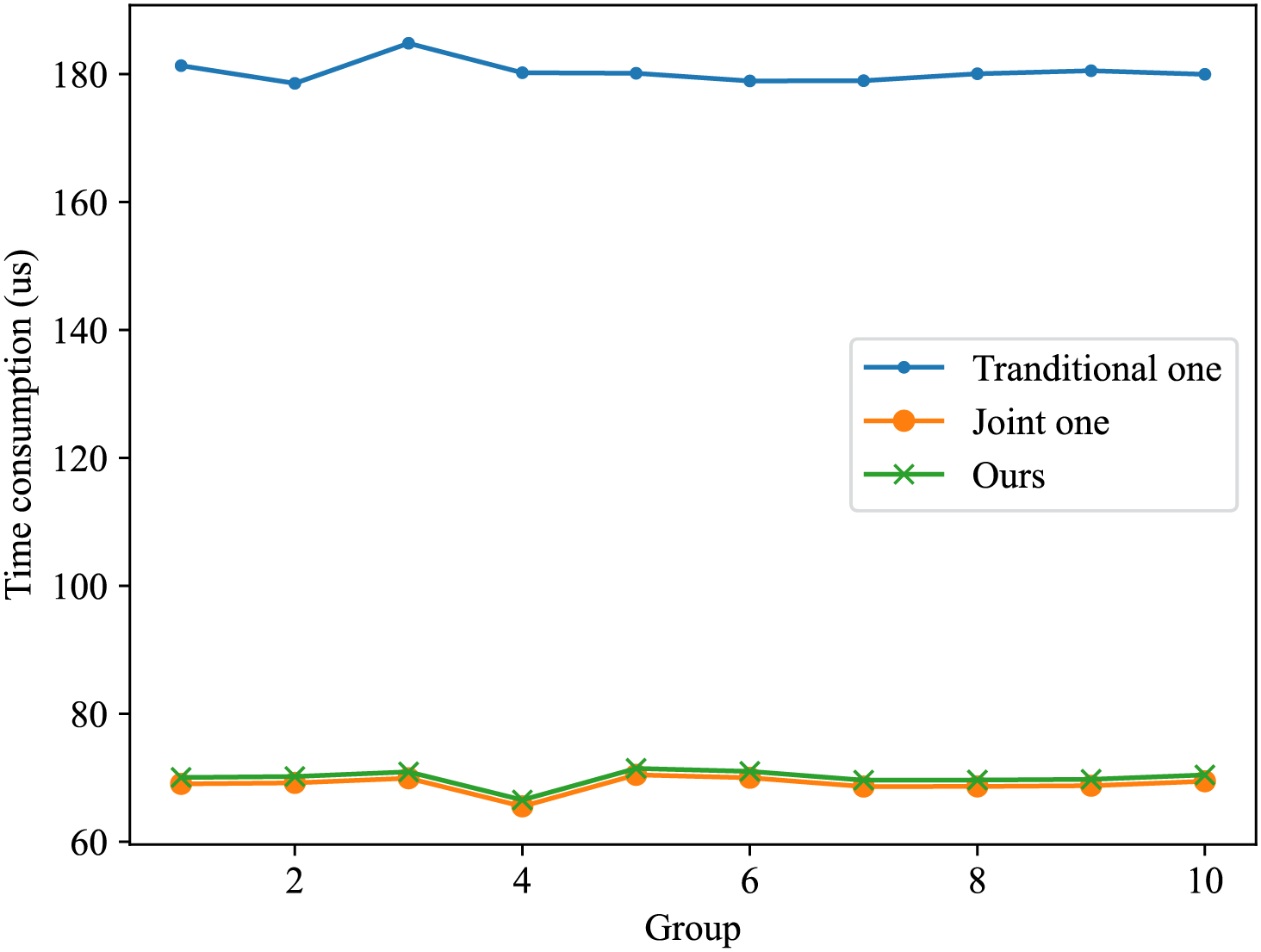
Figure 4: The time consumption of the three methods

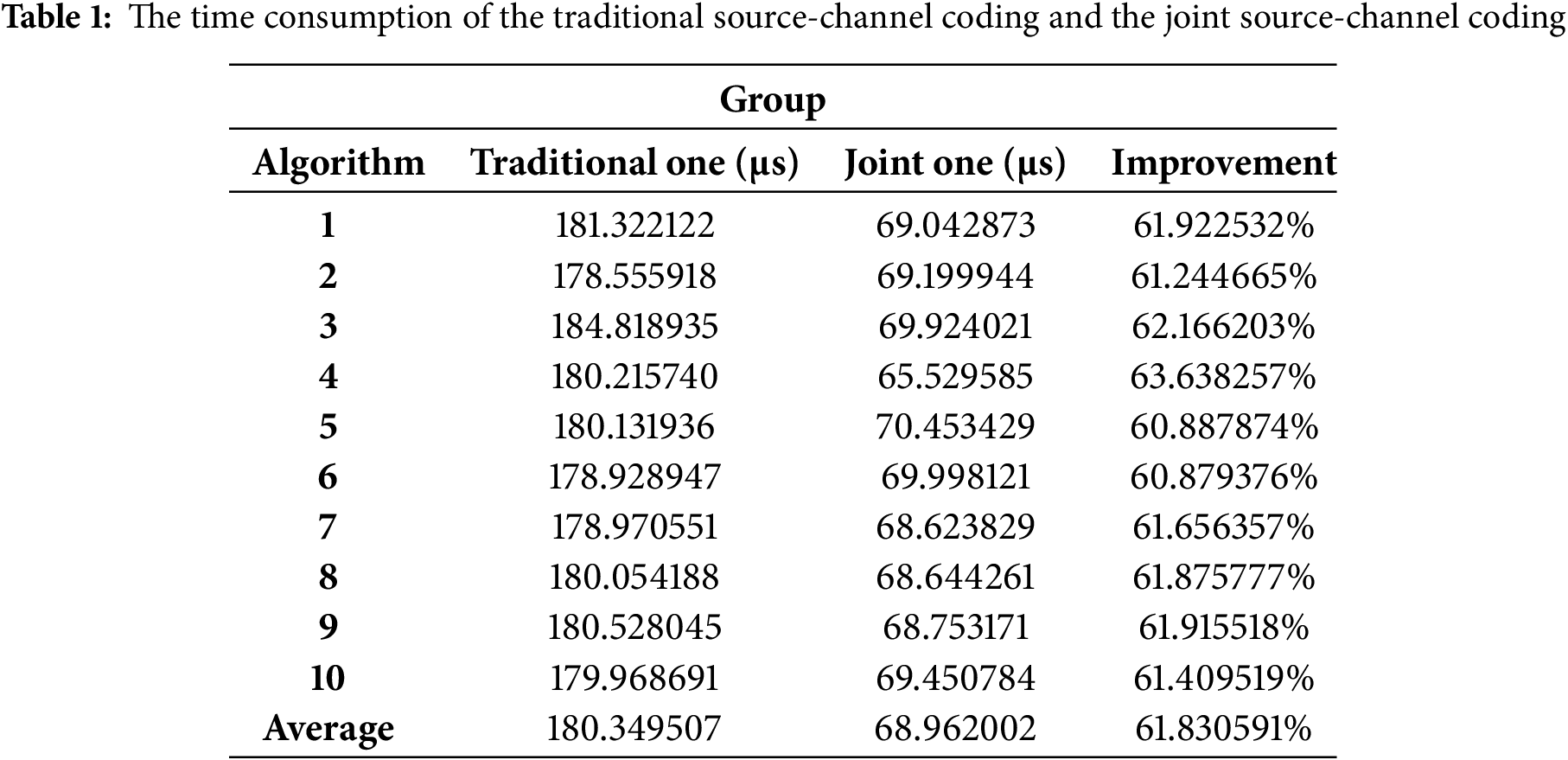
Table 2 shows the time consumption of the traditional source-channel coding and our proposed algorithm. The average time consumption for the traditional source-channel coding is 180.349507µs, while for our proposed algorithm it is 69.958305µs. The improvement for our proposed algorithm is approximately 61.209595%, indicating a sharp decrease in time consumption compared to the baseline method. Therefore, our proposed method is of high efficiency in coding compared with the first baseline, the traditional source-channel coding. In practice, it will be better if the error rate can be further optimized.

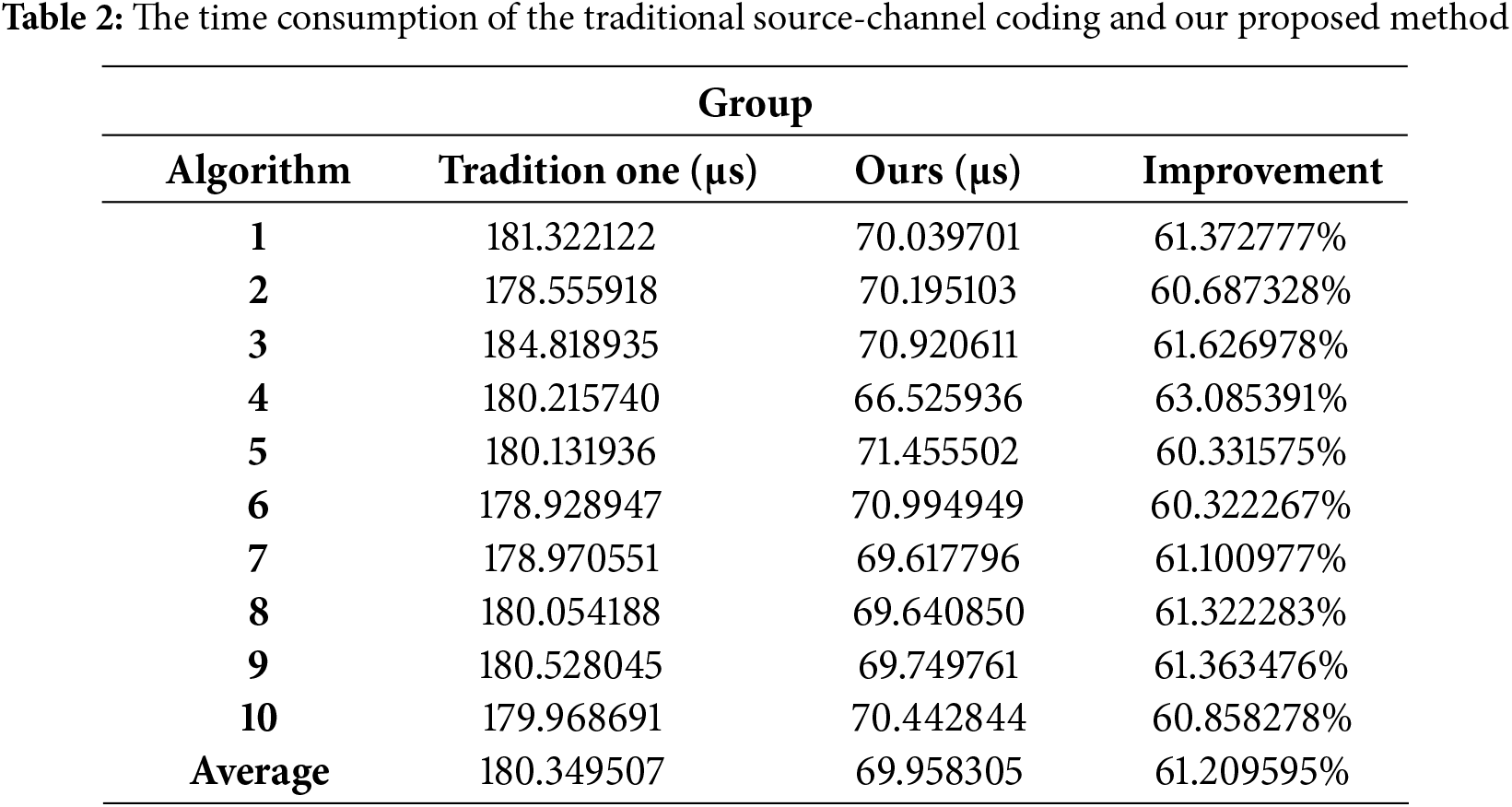
Table 3 shows the time consumption of the joint source-channel coding and our proposed algorithm. The average time consumption for the joint source-channel coding is 68.962002µs, while for our proposed algorithm it is 69.958305µs. The improvement for our proposed algorithm is approximately −1.428436%, indicating a slight increase in time consumption compared to the second baseline, the joint source-channel coding. However, this increase is negligible. Therefore, with the addition of mathematically proven secure semantic communication, our proposed approach barely impacts the time consumption of the joint source-channel coding.

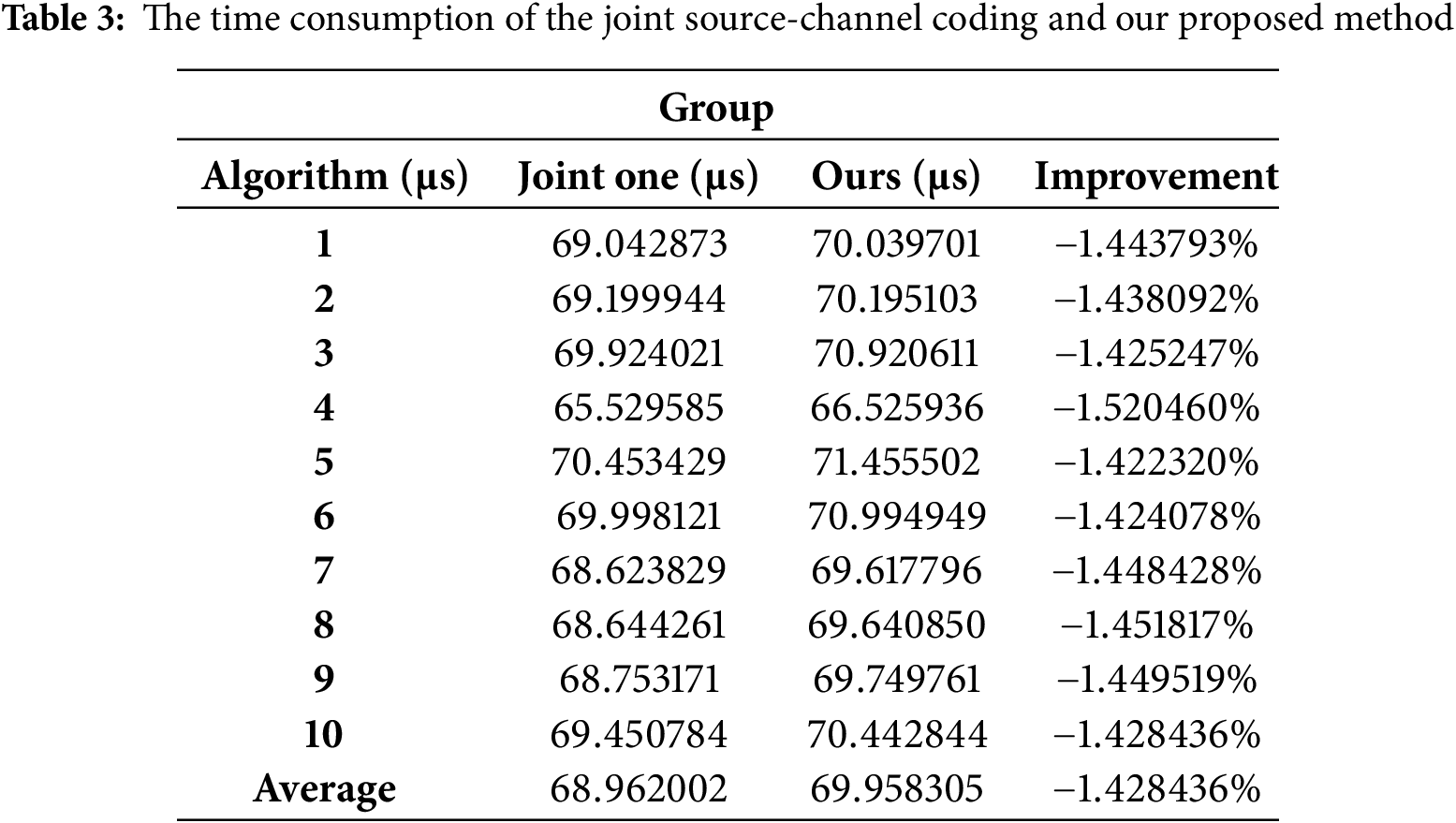
As a matter of fact, efficiency and security are usually conflicts. While security requires more checks and filters, efficiency just requires codes to be run as fast as possible. For example, in Python programming language, programmers usually use the “isinstance” function to check whether the input parameters are of correct types in functions, which will slow down the running efficiency but make the codes more secure. In the C/C++ programming language, programmers usually use “if (nullptr != pointer)” to examine whether a pointer is valid, which will slow down the running efficiency but avoid potential vulnerabilities. In this work, we integrate semantically secure communication into a state-of-the-art joint source-channel coding (JSCC) framework, resulting in an automated JSCC system with semantic security guarantees. Therefore, our primary objective should be to first ensure semantic security, followed by rigorous performance optimization. When we just slightly lower the efficiency to implement a semantic secure communication, it should be a success. This is like adjusting the architecture of a large language model (LLM) and then it achieves a challenging task with training time extending one minute from the original several days.

Based on the similar computation method and the evaluation metric of the error rate, the average value of the error rate of the 10 groups is gathered for each algorithm. The error rate of the joint source-channel coding is 5.93%, while that of our proposed method is 5.83%. This indicates that our proposed method has a slightly lower error rate compared to the joint source-channel coding. After combining the mathematically proven secure semantic communication, our proposed approach barely impacts the error rate of joint source-channel coding.

In conclusion, compared to the traditional source-channel coding, our proposed method is much more efficient in terms of time consumption. Our proposed method has a slightly higher time consumption and lower error rate compared to the joint source-channel coding. With the secure semantic communication supported, our proposed approach barely impacts the performance of joint source-channel coding. Consequently, on the one hand, our proposed method is better than the traditional source-channel coding. On the other hand, our proposed method can support secure semantic communication with little impact on the performance of the state-of-the-art joint source-channel coding.

6  Conclusion

This paper proposes a secure communication solution based on a designed joint source-channel coding algorithm and an automated joint source-channel coding algorithm. The automated joint source-channel coding distinguishes itself by selecting different modulation methods according to different packet lengths, which makes the algorithm perform better than the original joint source-channel coding. The time consumption of traditional source-channel coding, joint source-channel coding, and our proposed algorithm is tested respectively, showing that our proposed method is 61.21% faster than the first baseline method, the traditional source-channel coding. While implementing the secure semantic communication techniques, our proposed method is only 1.42% slower than the second baseline, the state-of-the-art joint source-channel coding, exhibiting nearly no increases in time consumption compared to it. Moreover, with secure semantic communication supported, there is no obvious impact on the error rate in our proposed method. Compared with the two baselines, our proposed algorithm outperforms the two algorithms in security by resisting 2 more types of attacks. In conclusion, our proposed method demonstrates superior performance compared to traditional source-channel coding approaches. Furthermore, it effectively supports secure semantic communication while maintaining minimal impact on the performance of state-of-the-art joint source-channel coding systems. These findings underscore the robustness and versatility of our approach in advancing secure and efficient communication frameworks. This framework is deployable in IoT networks for secure medical data transmission and military communications where semantic security is critical.

Our work also has some limitations. The automated joint source-channel coding algorithm can be further expanded. Providing more source coding methods and channel coding methods to choose from and improving coding efficiency can be two major future research directions. How to design the best automated joint coding algorithm by combining multiple procedures including encryption and compression deserves in-depth research. In the future, we will try to solve these issues. In addition, the proposed framework relies on accurate channel state information (CSI). For large payloads (>10 MB), the computational load is higher than AES.

Acknowledgement: Thanks to Donghong Cai, from College of Cyber Security, Jinan University, for providing fundamental knowledge of secure computer communication. Thanks to the editors for the warm invitation. Thanks to the anonymous reviewers for their insightful comments, which improved the quality of this paper.

Funding Statement: This work was supported in part by the National Key R&D Program of China under Grant 2022YFB3103500, in part by the National Natural Science Foundation of China under Grant 62302195.

Author Contributions: Yifeng Lin designed this study, investigated the state-of-the-art joint source-channel coding schemes, and wrote the first version of the manuscript. Yuer Yang conducted the experimental schemes, implemented the experiments, and gathered the experimental results. Jianxiang Xie edited the LaTeX, polished English expressions, and formatted the manuscript. Tong Ji arranged the figures, tables, and algorithms in this manuscript. Peiya Li supervised this study, revised the first version of the manuscript, and provided funding. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: For the codes and datasets used in the experiments in this manuscript, please visit https://github.com/yiyistudy/SSC-JSCC (accessed on 08 April 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Tung TY, Gündüz D. Deep joint source-channel and encryption coding: secure semantic communications. In: ICC 2023—IEEE International Conference on Communications; 2023 May 28–Jun 1; Rome, Italy; 2023. p. 5620–5. [Google Scholar]

2. Dai J, Zhang P, Niu K, Wang S, Si Z, Qin X. Communication beyond transmitting bits: semantics-guided source and channel coding. IEEE Wirel Commun. 2022;30(4):170–7. doi:10.1109/mwc.017.2100705. [Google Scholar] [CrossRef]

3. Shao Z, Wu Q, Fan P, Cheng N, Chen W, Wang J, et al. Semantic-aware spectrum sharing in internet of vehicles based on deep reinforcement learning. IEEE Internet Things J. 2024;11(23):38521–36. doi:10.1109/jiot.2024.3448538. [Google Scholar] [CrossRef]

4. Benkouider K, Sambas A, Sulaiman IM, Mamat M, Kottakkaran S. Secure communication scheme based on a new hyperchaotic system. Comput Mater Contin. 2022;73:1019–35. doi:10.32604/cmc.2022.025836. [Google Scholar] [CrossRef]

5. Guo S, Wang Y, Zhang N, Su Z, Luan TH, Tian Z, et al. A survey on semantic communication networks: architecture, security, and privacy. IEEE Commun Surv Tutor. 2024; early access. [Google Scholar]

6. Won D, Woraphonbenjakul G, Wondmagegn AB, Tran AT, Lee D, Lakew DS, et al. Resource management, security, and privacy issues in semantic communications: a survey. IEEE Commun Surv Tutor. 2024; early access. [Google Scholar]

7. Ding W, Luo Y, Lin Y, Yang Y, Lian S. VeriBypasser: an automatic image verification code recognition system based on CNN. Comput Commun. 2024;217(24):246–58. doi:10.1016/j.comcom.2023.12.022. [Google Scholar] [CrossRef]

8. Ji T, Luo Y, Lin Y, Yang Y, Zheng Q, Lian S, et al. ImageVeriBypasser: an image verification code recognition approach based on Convolutional Neural Network. Expert Syst. 2024;41(10):e13658. doi:10.1111/exsy.13658. [Google Scholar] [CrossRef]

9. Ba L, Guan J, Jiang J. Semantic-based defense mechanism for AI model networks using rich semantic identifier mapping. Comput Electr Eng. 2025;122(8):109977. doi:10.1016/j.compeleceng.2024.109977. [Google Scholar] [CrossRef]

10. Mohamed N, Ahmed AA. AI in combatting man-in-the-middle attacks: a comprehensive review. In: 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT); 2024; Kamand, India. p. 1–6. [Google Scholar]

11. Han K, Jia X, Lin Y, Yoshinaga T, Li Y, Wu J. Entropy-bottleneck-based privacy protection mechanism for semantic communication. Comput Mater Contin. 2025;83(2):2971–88. doi:10.32604/cmc.2025.061563. [Google Scholar] [CrossRef]

12. Dommel J, Utkovski Z, Simeone O, Stańczak S. Joint source-channel coding for semantics-aware grant-free radio access in IoT fog networks. IEEE Signal Proces Lett. 2021;28:728–32. doi:10.1109/lsp.2021.3072278. [Google Scholar] [CrossRef]

13. Erdemir E, Tung TY, Dragotti PL, Gündüz D. Generative joint source-channel coding for semantic image transmission. IEEE J Sel Areas Commun. 2023;41(8):2645–57. doi:10.1109/jsac.2023.3288243. [Google Scholar] [CrossRef]

14. Jiang P, Wen CK, Jin S, Li GY. Deep source-channel coding for sentence semantic transmission with HARQ. IEEE Transact Communicat. 2022;70(8):5225–40. doi:10.1109/tcomm.2022.3180997. [Google Scholar] [CrossRef]

15. Ge S, Ren J, Shi Y, Zhang Y, Yang S, Yang J. Audio-text multimodal speech recognition via dual-tower architecture for mandarin air traffic control communications. Comput Mater Contin. 2024;78(3):3215–45. doi:10.32604/cmc.2023.046746. [Google Scholar] [CrossRef]

16. Han D, Qi H, Wang S, Hou D, Wang C. Adaptive stepsize forward-backward pursuit and acoustic emission-based health state assessment of high-speed train bearings. Struct Health Monit. 2024;24(12):1. doi:10.1177/14759217241271036. [Google Scholar] [CrossRef]

17. Dai J, Wang S, Tan K, Si Z, Qin X, Niu K, et al. Nonlinear transform source-channel coding for semantic communications. IEEE J Select Areas Communicat. 2022;40(8):2300–16. doi:10.1109/jsac.2022.3180802. [Google Scholar] [CrossRef]

18. Fang Z, Hu S, Wang J, Deng Y, Chen X, Fang Y. Prioritized information bottleneck theoretic framework with distributed online learning for edge video analytics. IEEE Trans Netw. 2025. doi:10.1109/globecom52923.2024.10900993. [Google Scholar] [CrossRef]

19. Dai J, Wang S, Yang K, Tan K, Qin X, Si Z, et al. Toward adaptive semantic communications: efficient data transmission via online learned nonlinear transform source-channel coding. IEEE J Sel Areas Commun. 2023;41(8):2609–27. doi:10.1109/jsac.2023.3288246. [Google Scholar] [CrossRef]

20. Lin Y, Yang Y, Li P. Development and future of compression-combined digital image encryption: a literature review. Digit Signal Process. 2024;158(2):104908. doi:10.1016/j.dsp.2024.104908. [Google Scholar] [CrossRef]

21. Wang X, Lin Y, Yang Y, Xu H, Luo Z. A secure physical health test data sharing scheme based on token distribution and programmable blockchains. Comput Commun. 2023;209(2):444–54. doi:10.1016/j.comcom.2023.06.019. [Google Scholar] [CrossRef]

22. Zhong X, Sham C-W, Ma SL, Chou H-F, Mostaani A, Vu TX, et al. Joint source-channel coding system for 6G communication: design, prototype and future directions. arXiv:2310.01024. 2023. [Google Scholar]

23. Liu S, Gao Z, Chen G, Su Y, Peng L. Transformer-based joint source channel coding for textual semantic communication. In: 2023 IEEE/CIC International Conference on Communications in China (ICCC); 2023 Aug 10–12; Dalian, China. p. 1–6. [Google Scholar]

24. Lu K, Zhou Q, Li R, Zhao Z, Chen X, Wu J, et al. Rethinking modern communication from semantic coding to semantic communication. IEEE Wirel Commun. 2022;30(1):158–64. doi:10.1109/mwc.013.2100642. [Google Scholar] [CrossRef]

25. Zheng Z, Peng T. A scheme of steganography and transmission based on AMR-WB fixed codebook. In: 2022 IEEE 8th International Conference on Computer and Communications (ICCC); 2022 Dec 9–12; Chengdu, China. p. 972–6. [Google Scholar]

26. Jyothi VE, Prasad B, Mojjada RK. Analysis of cryptography encryption for network security. In: IOP conference series: materials science and engineering. Vol. 981. Bristol, UK: IOP Publishing; 2020. [Google Scholar]

27. Gastpar M, Vetterli M. Source-channel communication in sensor networks. In: Information processing in sensor networks. Cham, Switzerland: Springer; 2003. p. 162–77 doi:10.1007/3-540-36978-3_11. [Google Scholar] [CrossRef]

28. Divsalar D, Pollara F. On the design of turbo codes. In: The telecommunications and data acquisition progress report 42-123. Washington, DC, USA: NASA; 1995. [Google Scholar]

29. Liva G, Song S, Lan L, Zhang Y, Lin S, Ryan WE. Design of LDPC codes: a survey and new results. J Commun Soft Syst. 2006;2(3):191–211. doi:10.24138/jcomss.v2i3.283. [Google Scholar] [CrossRef]

30. Tzimpragos G, Kachris C, Djordjevic IB, Cvijetic M, Soudris D, Tomkos I. A survey on FEC codes for 100 G and beyond optical networks. IEEE Communicat Surv Tutor. 2014;18(1):209–21. doi:10.1109/COMST.2014.2361754. [Google Scholar] [CrossRef]

31. Pfletschinger S, Mourad A, Lopez E, Declercq D, Bacci G. Performance evaluation of non-binary LDPC codes on wireless channels. In: Proceedings of ICT Mobile Summit; 2009 Jun 10–12; Santander, Spain. p. 1–8. [Google Scholar]

32. Arora K, Singh J, Randhawa YS. A survey on channel coding techniques for 5G wireless networks. Telecommun Syst. 2020;73(4):637–63. doi:10.1007/s11235-019-00630-3. [Google Scholar] [CrossRef]

33. Fei Z, Yuan J, Huang Q. Error control codes for next-generation communication systems: opportunities and challenges. Wirel Commun Mob Comput. 2018;2018(1):2643205. doi:10.1155/2018/2643205. [Google Scholar] [CrossRef]

34. Barbulescu SA. Turbo codes on satellite communications. In: Turbo code applications: a journey from a paper to realization. Cham, Switzerland: Springer; 2005. p. 257–99. [Google Scholar]

35. Wang P, Yin L, Lu J. Design of check-hybrid LDPC codes for data communications over helicopter-satellite channels. In: 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall); 2017 Sep 24–27; Toronto, ON, Canada. p. 1–5. [Google Scholar]

36. Valenti MC, Cheng S, Seshadri RI. Turbo and LDPC codes for digital video broadcasting. In: Turbo code applications. Dordrecht, The Netherland: Springer; 2005. p. 301–19. doi: 10.1007/1-4020-3685-x_12. [Google Scholar] [CrossRef]

37. Michael L, Kan M, Muhammad N, Asjadi H, Fay L. Latest trends in worldwide digital terrestrial broadcasting and application to the next generation broadcast television physical layer. In: ATSC Symposium on Next Generation Broadcast Television; 2010; Rancho Mirage, CA, USA. [Google Scholar]

38. Wang Z, Tabassum M. A holistic secure communication mechanism using a multilayered cryptographic protocol to enhanced security. Comput Mater Contin. 2024;78(3):4417–52. doi:10.32604/cmc.2024.046797. [Google Scholar] [CrossRef]

39. Cover TM, Thomas JA. Channel capacity. In: Elements of information theory. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 1991. p. 191–205. [Google Scholar]

40. Sacher WD, Green WM, Gill DM, Assefa S, Barwicz T, Khater M, et al. Binary phase-shift keying by coupling modulation of microrings. Optics Express. 2014;22(17):20252–9. doi:10.1364/oe.22.020252. [Google Scholar] [PubMed] [CrossRef]

41. Saha D, Birdsall TG. Quadrature-quadrature phase-shift keying. IEEE Transact Commun. 1989;37(5):437–48. doi:10.1109/26.24595. [Google Scholar] [CrossRef]

42. El-Nahal F. Coherent 16 quadrature amplitude modulation (16 QAM) optical communication systems. Photonics Lett Poland. 2018;10(2):57–9. doi:10.4302/plp.v10i2.809. [Google Scholar] [CrossRef]

43. Yao H, Wang J, Dai P, Bo L, Chen Y. An efficient and robust system for vertically federated random forest. arXiv:2201.10761. 2022. [Google Scholar]

44. Kazemi M, Naraghi H, Golshan HM. On the affine ciphers in cryptography. In: Informatics Engineering and Information Science: International Conference, ICIEIS 2011; 2011 Nov 12–14; Kuala Lumpur, Malaysia. p. 185–99. [Google Scholar]