A Multi-Objective Joint Task Offloading Scheme for Vehicular Edge Computing

1  Introduction

The development of Intelligent Transportation Systems (ITS) and CAVs has brought significant improvements to modern transportation [1]. As a result, numerous compute-intensive and delay-sensitive vehicular applications have emerged in Internet of Vehicles (IoV) scenarios, including navigation, communication services, entertainment, and autonomous driving, etc. [2,3].

Vehicular edge computing (VEC) can coordinate with roadside base stations, edge devices, and cloud servers to distribute the content and functions of centralized networks to the edge, shortening the transmission path between vehicles and servers, thereby enhancing task computing efficiency [4]. In recent years, UAVs have been increasingly used in various fields, taking advantage of their flexibility and ability to operate without geographical limitations. And UAVs can provide edge computing capabilities to ground users [5]. By integrating them into vehicular edge computing, they can effectively reduce the computational load on vehicles, thereby enhancing the overall performance and efficiency of the vehicular network system. Therefore, the UAV-MEC framework has become a research hotspot [6].

In real traffic conditions, vehicles experience high dynamics, coexistence of various services, and uneven distribution of traffic flow in both temporal and spatial domains [7]. IoV applications impose stringent latency requirements and frequently depend on the stability of IoV communications [8].

Recent vehicular edge computing advancements strategically reconcile latency-energy tradeoffs through intelligent task offloading, dynamic resource orchestration, and game-theoretic coordination [9,10]. For task offloading schemes, recent advances employ a hierarchical deep reinforcement learning framework named Sequential Quadratic Programming-based Dueling Double Deep Q Networks reduces system costs and task loss rates [11], Proximal Policy Optimization (PPO)-based method decreases total delay and dropped task ratios [12], a Hybrid Average Reward Proximal Policy Optimization algorithm (hybrid-ARPPO) that combines optimized offloading decisions, transmission rates, and edge server allocation without the discount factor [13], Double Q-learning improving user service quality [14], Digital Twin-assisted Predictive Adaptive Intelligent Offloading scheme to reduce computation latency [15], Exploration and Exploitation Assisted Contract Theory (EEACT) scheme optimal offloading strategies by minimizing task processing costs [16] and a Mobile-Aware Computation Efficiency Task Offloading and Resource Allocation scheme to optimize transmission efficiency [17]. Resource-saving strategies focus on balancing Quality of Service (QoS) and energy consumption through cooperative models [18], PPO-based to balance the long-term cost between minimizing task delay and energy consumption [19], semi-distributed algorithm to solve the task offloading and service caching problem [20], based on Non-Orthogonal Multiple Access (NOMA) to minimize the total system cost [21], and convex programming-driven power allocation via iterative offloading ratio derivation [22]. Game theory applications further enhance system equilibrium through Nash equilibrium solutions [23], a Minority Game (MG)-based scheme and found the optimal solution by probabilistically adjusting decisions, achieving near-optimal performance and stability [24] and a decentralized offloading game algorithm to solve task offloading problems in edge computing [25].

Despite significant advancements in Intelligent Transportation Systems and Connected and Automated Vehicles, current research has not fully addressed the challenges introduced by highly dynamic vehicular environments, diverse service requirements, and heterogeneous resource distributions. A thorough analysis of these issues reveals the necessity for a robust system model and an optimization framework that can effectively balance the conflicting objectives of delay minimization and energy efficiency under stringent constraints. Therefore, designing an effective strategy for task offloading and resource allocation that also minimizes costs presents a significant challenge [26].

In this paper, we propose a three-stage hybrid multi-objective task offloading strategy for UAV-assisted MEC systems to minimize the total system delay and overall energy consumption while ensuring performance under resource constraints. The control decisions include Offload task allocation, UAV selection, and UAV computation resource allocation. The primary contributions of this study are listed below:

1.    This paper comprehensively considers the computing offloading problem in sustainable UAVs-MEC systems and formulates it as a multi-objective optimization problem, consisting of two optimization objectives, i.e., delay and energy consumption with several constraints.

2.    This paper proposes a three-stage hybrid multi-objective optimization scheme, called DVCG-MWOA, to address the above-formulated problem. A mobile-aware dynamic clustering algorithm (MDCA) is proposed to dynamically link vehicles and UAVs in the first stage. Then, a cooperative game model with delay constraints is established for each cluster, allocating UAV resources for coordinated utilization. The Pareto front solution is derived using an improved multi-objective whale optimization algorithm.

3.    We conducted multiple experiments across application scenarios of different scales to thoroughly assess the effectiveness and adaptability of the proposed scheme. Additional parameter analysis reveals that the scheme can flexibly regulate energy consumption, computation delay, and system performance in response to varying resource constraints and task demands, ultimately enhancing the overall efficiency of task offloading.

2  System Model and Problem Formulation

In this section, we detail the UAV-assisted edge computing offloading scheme model, aiming to minimize delay and energy consumption, and formulate the computation offloading problem as a multi-objective optimization problem. Table 1 summarizes the main notations in this model.

2.1 System Model

The UAV-assisted vehicular ad-hoc network system is shown in Fig. 1. The tasks generated by the vehicles for offloading can be computed by the vehicles themselves, roadside base stations, and deployed UAVs. Vehicles in the area are represented by V={v1,v2,…,vn}, UAVs is U={u1,u2,…,uc}, and an edge server is deployed. Assuming the vehicles have the same configuration, each vehicle only communicates with one UAV, and the UAVs are at the same height h above the vehicles, described using cartesian coordinates. The set of tasks generated by vehicles is W={w1,w2,…,wn}, the i-th task wi is represented by a triplet {Di,Ci,τi}.

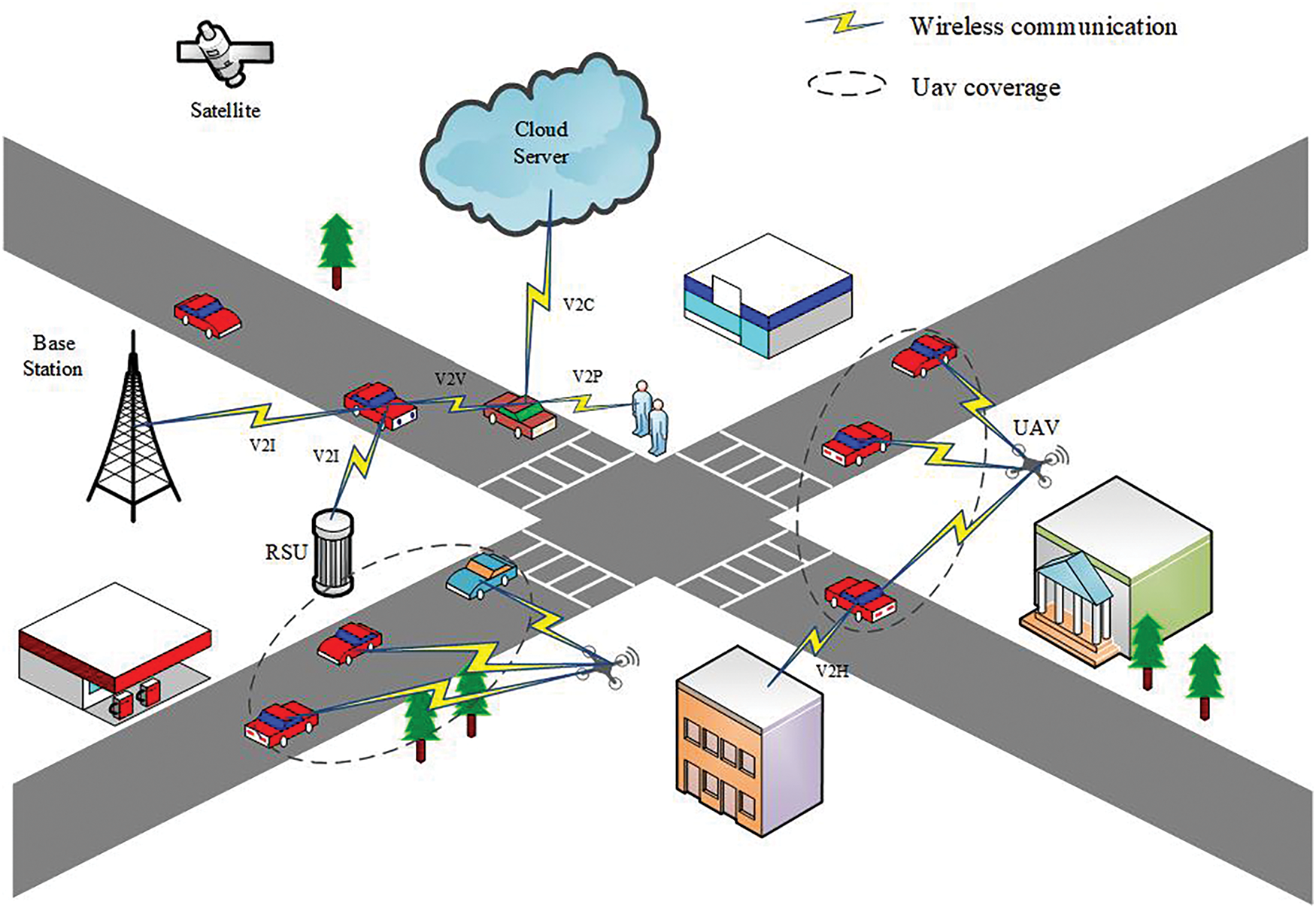
Figure 1: Model of UAV-assisted Vehicular Ad-Hoc Network (VANET) system

Assuming the tasks are divisible, ailocal, aiedge and aiuav, respectively represent the proportions of tasks computed locally, offloaded to the roadside base station, and offloaded to the UAV, with their sum equal to 1.

The transmission rate between vehicles and the edge base station or UAV can be calculated using Shannon’s theorem [27]:

vtra=Blog2⁡(1+pitrahiBN0)(1)

2.2 Local Vehicle Computing Model

In the local computing process, the amount of data allocated to the vehicle itself can be represented by ailocal×Di, the power consumed in the computing process can be represented by kv×(fv)3, the local computing delay and energy consumption are represented by:

ti_local=Ci×ailocal×Difv,(2)

Ei_local=kv×Ci×ailocal×Di×(fv)2.(3)

2.3 Roadside Base Station Computing Model

In the roadside base station computing process, the amount of data allocated to the roadside base station can be represented by aiedge×Di, the delay and energy consumption generated by transmitting tasks from the vehicle to the roadside base station represented by:

ti_edgetra=Ci×aiedge×Divedgetra,(4)

Ei_edgetra=pi_edgetra×ti_edgetra.(5)

The computing power used by the roadside base station to process the task is represented by kedge×(fedge_i)3. The computing power used by the roadside base station to process the task is represented by:

ti_edgemid=Ci×aiedge×Difedge_i,(6)

Ei_edgemid=kedge×Ci×aiedge×Di×(fedge_i)2.(7)

After the task is processed, the result is returned to the vehicle i.

In the roadside base station computing process, the total task processing delay is represented by the sum of the transmission delay and the computing delay, and the total energy consumption is represented similarly.

2.4 UAV Computing Model

In the UAV computing process, the amount of data allocated to the UAV can be represented by aiuav×Di the delay and energy consumption generated by transmitting tasks from the vehicle to the UAV are represented by:

ti_uavtra=Ci×aiuav×Divtra,(8)

Ei_uavtra=pi_uavtra×ti_uavup.(9)

The computing power used by the UAV to process the task is represented by ku×(fuav_i)3, the computing delay, and energy consumption is represented by:

ti_uav=Ci×aiuav×Difuav_i,(10)

Ei_uav=ku×Ci×aiuav×Di×(fuav)2.(11)

After the task is processed, the result is returned to the vehicle i.

In the UAV computing process, the total task processing delay is represented by the sum of the transmission delay and the computing delay, and the total energy consumption is represented similarly.

2.5 Formulation of Problem

The total delay and total energy consumption of the task processing process for vehicle i are represented as follows:

Ti_sum=ti_local+ti_edge+ti_uav,(12)

Ei_sum=Ei_local+Ei_edge+Ei_uav.(13)

The problem of local offloading, roadside base station, and UAV edge computing for multiple mobile vehicles in the area is modeled as a multi-objective optimization constraint problem Z, and the mathematical model is constructed as follows:

Z=min{∑i=1NTi_sum,∑i=1NEi_sum},(14)

s.t.

ailocal+aiedge+aiuav=1,∀i∈[1,2,3,…,n],(14a)

ti_sum≤τi,∀i∈[1,2,3,…,n],(14b)

∑i=1nfedge_i≤fedge,(14c)

where Eq. (14a) indicates the sum of the ratios at which tasks are allocated to different offloading terminals. Eq. (14b) indicates the total processing delay of the task should be lower than the maximum tolerable delay. Eq. (14c) indicates the sum of the computing resources allocated by the edge server to each vehicle should be less than its own computing resources.

3  Proposed Optimization Solution

In this section, which first performs dynamic clustering of vehicles, determines the optimal resource allocation scheme for each cluster head-unmanned aerial vehicle (CH-UAV) through cooperative game theory. To further improve performance, this study develops an enhanced multi-objective whale optimization algorithm to efficiently explore the global optimal solution of the objective function.

3.1 MDCA Clustering Algorithm

The high-speed mobility of vehicular nodes introduces critical IoV challenges including dynamic topology fluctuations, scalability constraints, and routing efficiency demands. Clustering approaches that leverage mobility metrics tend to outperform traditional methods in enhancing cluster stability. Metrics such as vehicle density, relative velocity, relative distance, and moving direction are particularly well-suited for the dynamic environment of VANET system.

In this part, a new clustering algorithm named MDCA that is based on mobility values and vehicle dynamic characteristics is proposed. Considering the mobility and communication quality of each vehicle, dynamically allocate vehicles into clusters with UAVs as cluster heads. Utilize vehicle clustering to enhance UAV offloading efficiency. Continuously adjust UAV positions based on vehicle dynamics at each moment to ensure data processing quality, better addressing the dynamic mobility environment of VANET system.

The following discusses the details of various components and their communication. Vehicles and UAVs serve as the mobile nodes and key elements of our network architecture, and they are equipped with GPS devices. On-board units (OBUs) provide mutual wireless communication via vehicle-to-vehicle (V2V) and vehicle-to-UAV (V2U). A vehicle is assigned to a single cluster at any time slot. Each cluster, headed by a UAV, is responsible for the overall management of the cluster and overseeing the efficient allocation of resources.

We propose a task offloading metric that integrates mobility measurement, task offloading volume, and communication quality as follows:

WSi=wmvMVi∑q∈ClMVq+wwlWLi∑q∈ClWLq×Qi∑q∈ClQq,(15)

Qi is the communication quality between vehicle i and the UAV, represented by the reciprocal of the Euclidean distance:

Qi=1Dis(i,UAV)2.(16)

Mobility measurement [28] MVi is defined as follows:

MVi=LSi(t)Vnsi+(ln⁡(1−ArνiVmax))2+ADimaxDi.(17)

The algorithm process is detailed in Algorithm 1. The main objective is to divide n vehicles into c distinct CH-UAV clusters during each time slot. The location and speed of vehicles can be acquired either through integrated GPS modules or by employing appropriate localization techniques.

Initialize the CH-UAV positions and store them in matrix R, and the vehicle positions are stored in matrix Q. Initialize a link matrix AM of size x×n, AMcd is the link relationship between UAV c and vehicle d. Vehicle d is clustered to UAV c, AMcd is 1, otherwise, AMcd is 0. Initially, link each vehicle to the nearest UAV based on Euclidean distance.

The process of dynamic task offloading and communication binding begins by calculating the dynamic task offloading metric WS for each vehicle in a cluster using Eq. (15) and determining the cluster’s average WS¯. The UAV position is then updated to be directly above the vehicle with the smallest absolute WS value. Next, the communication range is assessed: if all vehicles are within the UAV’s range, those farther away may select a UAV with a closer Euclidean distance, and the link relationship matrix AM is updated accordingly. If some vehicles are outside the range, their positions are checked for coverage by other UAVs. If covered, links are established with those UAVs, and AM is updated; otherwise, V2V communication is established with the nearest vehicle to form a multi-hop routing connection to the UAV, and the matrix is modified. This process completes the communication binding for the current time slot. Finally, UAV positions are continuously adjusted in real-time based on road conditions to enhance data transmission quality and ensure network stability, with the updated link relationship matrix AM outputted at the end.

3.2 Intra-Cluster Cooperative Game

The algorithm clusters vehicles with offloading tasks based on movement similarity, using UAVs as cluster heads. A coalition formation game coordinates resource allocation within each cluster. To handle unpredictable task demands, the approach employs conditional value-at-risk (CVaR) for risk assessment and introduces a negotiation mechanism to optimize allocation while ensuring task completion within tolerable latency. By integrating consensus auctions, the approach maintains UAV autonomy and stability in the coalition structure. The UAV resource allocation problem as a cooperative game model among the vehicles:

𝒢={𝒩,𝒮𝒜,𝒫(𝒮)},(18)

where 𝒩 is the set of all vehicles of each cluster, 𝒮𝒜 is the set of all sub-resource allocation strategies, and 𝒫(𝒮) represents the multi-objective utility function of strategy 𝒮, which is the sum of the delay and energy consumption generated by q vehicles in the cluster.

𝒫(𝒮)={∑i=1qTi,∑i=1qEi}.(19)

Definition 1 (Coalition structure): The coalition structure ∏={𝒮0,𝒮1,…,𝒮q}, is a disjoint partition of the vehicleresource allocation set. Each coalition ∏∈𝒮𝒜 is specific to the subresourceallocationset. Each element 𝒮k represents the proportion of UAV resources allocated to vehicle k.

Definition 2 (Negotiation mechanism): For vehicle k∈𝒩, if vehicle k changes its strategy, it needs to satisfy the conditions:

Tk(fuav−k′)≤Tkτ∪Ei(fuav−k′)≤Ek(fuav−k),∀k∈𝒩,(20)

𝒫(𝒮′)<𝒫(𝒮),(21)

where 𝒮′ represents the changed strategy. fuav−k′ represents the UAV computing capacity allocated to vehicle k after the strategy change. Tkτ represents the maximum tolerable delay for the UAV processing the task portion, expressed as the product of the proportion of the task processed by the UAV and the maximum tolerable delay of the task, i.e., akuav×τk.

The UAV resource allocation game algorithm process is shown in Algorithm 2. In the initial stage, input the link matrix AM of vehicles and UAVs from the clustering stage, and the task information to be allocated for each vehicle.

In the initial iteration, the UAV’s computing power is evenly distributed among the vehicles in the cluster. Determine whether each task meets the delay tolerance requirement. For tasks that meet the delay requirement, use the gradient descent method to reduce computing power allocation; for tasks that do not meet the delay requirement, use the gradient ascent method to increase computing power allocation. Continuously iterate under the constraints of the negotiation mechanism to seek the optimal strategy set 𝒮∗.

In this cooperative game model, delay is used as a constraint for the optimization goal. Gradient calculations are performed based on energy consumption to derive the optimal utility strategy. The complexity of each vehicle’s task, data size, task period, and switching capacitance values are set as constants ok, Ek denoted as:

Ek=ok×(𝒮k×fuav)2,(22)

where ok is ku×Ck×akuav×Dk.

Computing the partial derivatives 𝒮k to calculate the gradient.

Update the strategy of each vehicle in the direction opposite to the gradient using the stochastic gradient algorithm, ensuring it continuously meets the conditions of (20) and (21). The update rule is as follows:

𝒮k(I+1)=𝒮k(I)±η×∇E(𝒮k).(23)

Define 𝒮k(I+1) as the strategy for the next iteration, continue iterating until the optimal strategy for the cooperative game model is obtained. Output the proportion of UAV resources allocated.

3.3 Proposed MWOA Offloading Optimization Strategy

In multi-objective optimization (MOO), the inherent conflict between objectives creates a Pareto optimal set where improving one metric necessitates compromising others. While the Whale Optimization Algorithm (WOA) has emerged as an effective MOO solver due to its exploration-exploitation balance and computational efficiency, existing multi-objective WOA variants still face limitations in handling complex vehicular scenarios. To address this, we propose an enhanced MOWOA integrating swarm-based whale search with evolutionary mechanisms. Each whale solution encodes vehicle/UAV capabilities and task offloading ratios across three layers (vehicles, RSUs, UAVs), with dual optimization objectives of latency and energy consumption. As detailed in Algorithm 3, two critical improvements are implemented over baseline MOWOA to achieve parallel optimization.

The process is as follows:

Step 1: Good point set initialization population: GD is a unit cube in the D dimensional Euclidean space, D represents the dimension of the target solution, points γ in the Euclidean space can be represented by D dimensional vectors, i.e., γ=(γ1,γ2,…,γD),γ∈GD, where 0≤γj≤1, be represented as:

γj=2cos(2jπσ),1≤j≤D,(24)

where j is a dimension in D, σ is the smallest prime number that satisfies (σ−3)2≥D, generating the good point set PM(m):

PM(m)={(γ1×m),…,(γD×m)},1≤m≤M,(25)

where M is the number of whale individuals in the population, m=1,2,…,M, with m representing an individual whale in the population, γj×m represents a good point, PM(m) is the good point set matrix of size D×M, which is mapped to the search space as:

PM(m)=Lbj+(Ubj−Lbj)×mod({PM(m)},1),1≤j≤D,(26)

where Lbj is the lower bound of the jth dimensional decision variable Ubj is the upper bound of the jth dimensional decision variable. PM(m) mapped is the initial position of the whale population.

Step 2: Establish Pareto front storage mechanism: An external archive stores Pareto non-dominated solutions, replacing lower-fitness ones when capacity is exceeded to ensure dynamic updates.

Step 3: Non-dominated sorting: Individuals are ranked based on dominance, selecting non-dominated ones as the first level and iterating until all are classified.

Step 4: Crowding distance sorting mechanism: to maintain diversity and explore the solution space, crowding distance guides the algorithm toward the Pareto front by measuring distribution density. Solutions with greater distances are prioritized to ensure uniform coverage and enhance optimization.

Step 5: Elite retention mechanism: whale individuals from parent and offspring generations are sorted by crowding distance within each Pareto level. Those with the largest distances are stored in the archive until full, while the rest are discarded.

Step 6: Leader selection strategy: a whale individual with the smallest Pareto rank is randomly selected from the archive to guide the group’s movement in each iteration.

Step 7: Enhancement of individual location update strategy: the fixed 0.5 selection probability in the original whale optimization algorithm causes an imbalance between global exploration and local exploitation, slowing convergence. We propose a dynamic feedback threshold mechanism to adjust these probabilities, improving both convergence speed and optimization performance. The selection probability pth is updated dynamically as follows:

pth(t+1)={pth(t)+(ra/M),ra>01−pth(t),ra=0,(27)

where M is the total number of whale individuals in the population, and ra represents the number of populations whose fitness values have improved compared to the previous iteration. At the first iteration, pth is set to 0.5, and in subsequent iterations, pth(t+1) is updated based on the value of pth from the previous iteration.

The rest of the process is updated according to the WOA.

3.4 Method Overview

This paper considers the task offloading and resource allocation problem as a multi-objective optimization problem, aiming to minimize latency and energy consumption. Firstly, dynamic clustering is formed through the current positions and mobility characteristics of vehicles and UAVs, enabling cooperation in each time slot. Subsequently, a cooperative game model constrained by latency is used for intra-cluster resource allocation. To find the optimal task assignment strategy and resource utilization, an improved parallel MOWOA algorithm is employed for multi-objective optimization. This scheme is potentially very effective in balancing the trade-off between latency and energy consumption, providing efficient solutions in complex environments. The proposed scheme process is shown in Fig. 2.

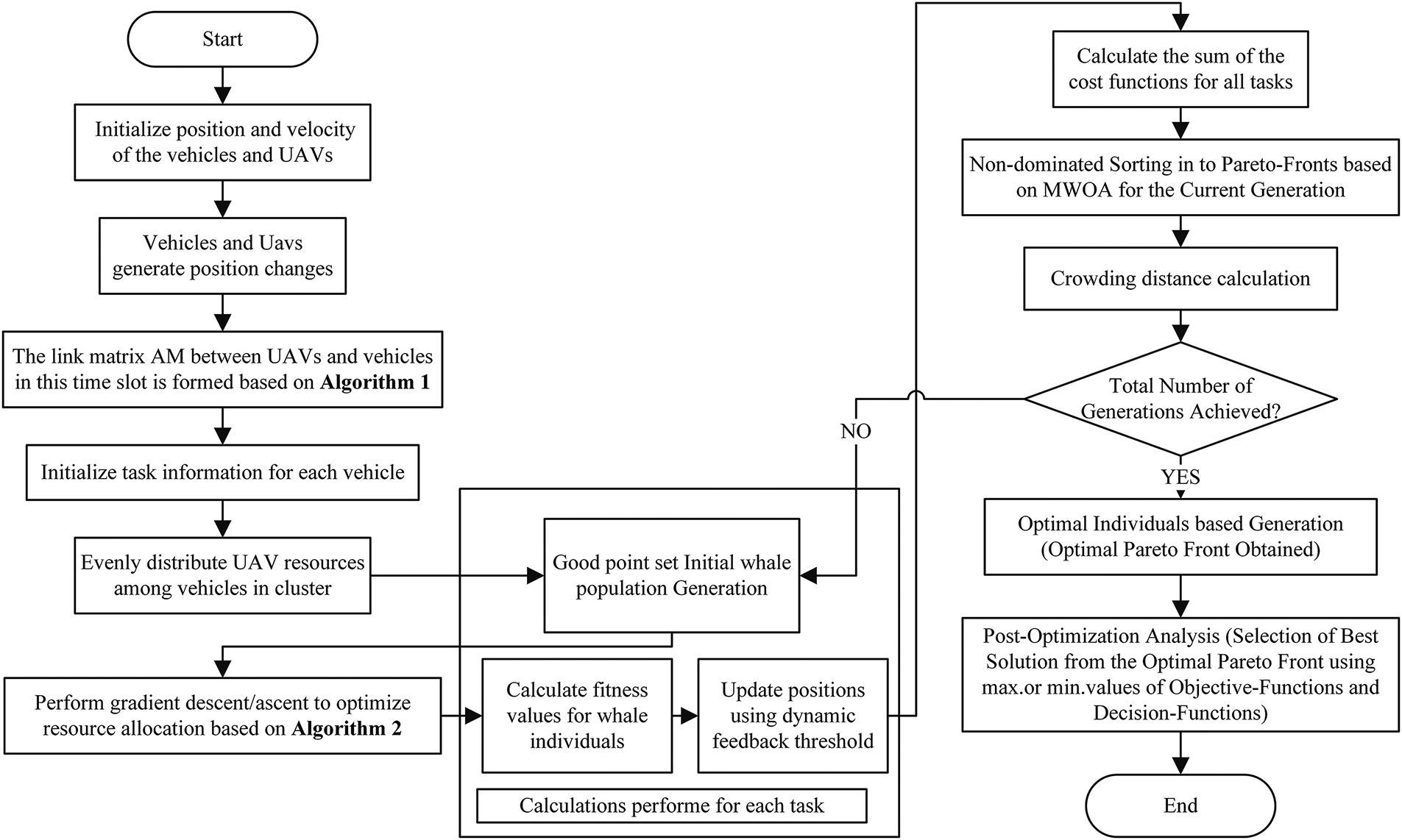
Figure 2: The flow chart of DVCG-MWOA

4  Experimental Evaluation

In this section, a simulation is performed to evaluate the effectiveness of the proposed joint strategy. The experiment is conducted in MATLAB R2022b, and run on a personal computer with Intel (R) Core (TM) i9-13900 CPU and 32.0 GB RAM. The results are based on the average of 30 Monte Carlo simulations.

4.1 Experimental Environment

In our experiment, we simulate an intersection composed of two perpendicular roads, each 500 m in length. A roadside base station is set on one side of the road, and drones are randomly distributed in the area. Five experimental vehicle scales are set up, with vehicles randomly generated according to a Poisson distribution. The clustering cycle between drones and vehicles is 3 s (ignoring the time required for drone movement), and task offloading is performed every 6 s. The experiment runs for 6 min, and the results are averaged over 10 task offloads. The experimental parameters set in this paper are shown in Table 2. The communication standard employed in our experiments is the IEEE 802.11p standard. Specifically, simulation map is based on [29], the vehicle speed configuration references [30], the task complexity and chip switching capacitance as suggested in [31].

4.2 Task Offloading Strategies

4.2.1 Benchmark Offloading Location Schemes

In the simulation experiments, we mainly study the vehicles, edge servers, and UAVs to collaborate for computation task offloading called Local, Edge and Air Computation Offloading (LEACO), This scheme was compared with the following three benchmark offloading location schemes.

1.    LCO (Local Computation Only) scheme, where tasks are only offloaded locally.

2.    ECO (Edge Computation Only) scheme, where tasks are only offloaded to edge servers.

3.    LECO (Local and Edge Computation Offloading) scheme, where tasks are offloaded both locally and to edge servers.

4.2.2 Performance Metrics

In our experiments, to facilitate comparison with single-objective experiments, we not only considered delay and energy consumption separately but also considered the weighted sum of these two normalized optimization objectives to represent the total system cost. The definitions are as follows.

Q=α×Delay_w+(1−α)×Energy_w,(28)

where Delay_w and Energy_w represent the normalized delay and normalized energy consumption, respectively, and α represents the weight factor. Particularly, two normalized objective values Delay_w and Energy_w are calculated as follows.

Delay_w=2×DelayallDelayallL+DelayallE,(29)

Energy_w=2×EnergyallEnergyallL+EnergyallE,(30)

where DelayallL and DelayallE represent the total delay when all tasks are executed in LCO scheme and all tasks are executed in ECO scheme, respectively. EnergyallL and EnergyallE represent the total energy consumption when all tasks are executed in LCO scheme and all tasks are executed in ECO scheme, respectively. These two objective values can be in the same order of magnitude, so the weighted sum can simultaneously reflect the algorithm’s comprehensive performance in terms of delay and energy consumption.

4.3 Comparative Optimization Approaches

We compare the proposed joint scheme with the following methods, which combine offloading methods and optimization algorithms.

4.3.1 Offloading Methods

1.    Random Sequential Scheme (RS): Vehicles are randomly bound to a UAV, which then offloads tasks sequentially.

2.    Distance-First Averaging Scheme (DA): Vehicles bind only with the nearest UAV, and the UAV’s computational resources are evenly distributed.

3.    Cyclic Balanced Scheme (CB): Sort all vehicle offloading tasks by size, then sequentially assign these sorted tasks to the available UAVs with the most idle computing resources for computation.

4.3.2 Optimization Algorithms

We also compare these offloading strategies using several intelligent optimization algorithms to evaluate their effectiveness in minimizing system costs:

1.    Single-objective Comparison: Particle Swarm Optimization (PSO), Genetic Algorithm (GA) and Improved Whale Optimization Algorithm (IWOA).

2.    Multi-objective Comparison: Non-dominated Sorting Genetic Algorithm III (NSGA-III), Multi-objective Pareto Envelope-based Selection Algorithm II (PESA-II) and Multi-objective Whale Optimization Algorithm (MOWOA).

By integrating these intelligent optimization algorithms with the offloading methods, we aim to compare their performance with our proposed joint scheme, focusing on finding the optimal system cost.

4.4 Simulation Results

Fig. 3 shows we conducted a set of experiments to explore the optimal alpha value and number of UAVs in the LEACO scenario, laying the foundation for subsequent research. In terms of methodology, we adopted a difference-based optimization strategy, selecting the alpha value and UAV quantity that minimized the total system cost difference, thereby effectively reducing subjective bias in the experimental process.

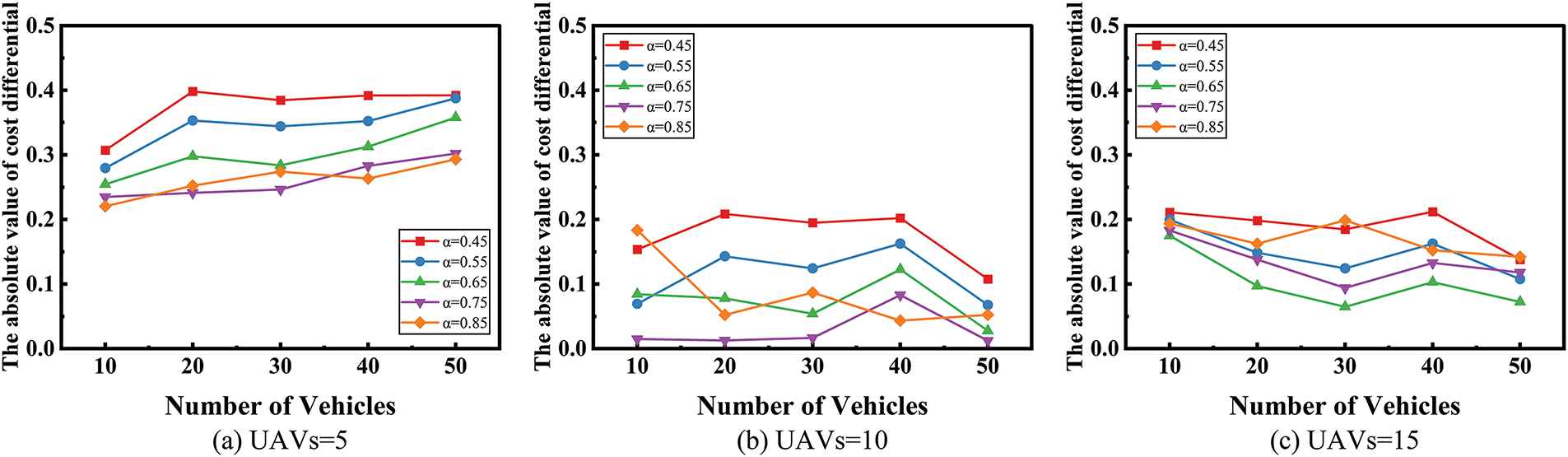
Figure 3: The variation in the absolute difference in costs between the LECO and LEACO offloading modes under different numbers of UAVs, as the value of alpha changes for different vehicle quantities

This approach not only validated the effectiveness of the LEACO scenario but also ensured the reliability and scientific rigor of the experimental results. Specifically, we conducted experiments in both LEACO and LECO scenarios under different alpha values (0.45, 0.55, 0.65, 0.75) and varying numbers of UAVs (5, 10, 15). For each configuration, we calculated the difference in total system cost for different vehicle quantities (10, 20, 30, 40, 50). As shown in the figure, when the alpha value is 0.75 and the number of UAVs is 10, the system cost difference reaches its minimum, and thus we follow this indicator for subsequent experiments. Optimizing the system cost difference under complex and variable conditions ensures that the chosen alpha value and number of UAVs demonstrate significant feasibility and robustness in practical applications. Consequently, this provides a solid theoretical foundation and a reliable experimental basis for subsequent studies.

Fig. 4 shows the experimental results of DVCG-MWOA compared to single-objective hybrid comparison schemes in terms of delay and energy consumption weight, we calculated the average value of the component in the Pareto solution set. As shown in the figure, across five different experimental environments with varying vehicle quantities, the proposed hybrid strategy reduced the time delay weights by an average of 27.63%, 18.02%, and 8.71% compared to the single-objective hybrid strategies (RS-PSO, DA-GA, CB-IWOA), and reduced the energy weights by an average of 22.12%, 33.69%, and 10.51% compared to the single-objective hybrid strategies, respectively. DVCG-MWOA shows clear advantages compared to these single-objective comparison algorithms.

Figure 4: The delay weight comparison results and energy weight comparison results with the single target experiment under different experimental sizes

Fig. 5 compares the Pareto frontiers of the proposed DVCG-MWOA with six baseline combinations of offloading methods and optimization algorithms under varying vehicular densities (10/30/50 vehicles). The hybrid baselines exhibit distinct limitations: RS-NSGA-III induces latency spikes and energy fluctuations due to uncoordinated task allocation and stochastic vehicle-UAV binding, while DA-PESA-II suffers from progressive performance decay as its static proximity-based binding exacerbates congestion at nearest UAVs. Although CB-MOWOA mitigates load imbalance through sorted task scheduling, its rigid cyclic allocation incurs computational overheads under high-density scenarios (50 vehicles), leading to suboptimal resource utilization. In contrast, DVCG-MWOA integrates mobility-aware game-theoretic coordination with latency-constrained optimization, dynamically adjusting UAV-vehicle binding based on real-time trajectories. This dual adaptation mechanism reduces total system costs by 22%–35% in Pareto dominance metrics, while maintaining stable energy-delay trade-offs even under extreme densities. Furthermore, it outperforms single/multi-objective baselines in convergence precision (12.7%–29.4% improvement) and solution diversity, demonstrating superior adaptability to dynamic vehicular environments.

Figure 5: The comparison results with multi-objective algorithm experiments under different numbers of vehicles

Fig. 6 illustrates the task offloading success rates of different strategies under varying maximum tolerable delays, with vehicle counts set to 20 and 40, respectively. The results indicate a positive correlation between the probability of successful task offloading and the tolerable delay. The RS-NSGA-III shows a gradual increase in offloading rates as the delay increases, but overall, its performance remains conservative, particularly with a higher number of vehicles. In comparison, the DA-PESA-II achieves slightly higher offloading rates across all delay conditions, although its growth trend is relatively moderate. The CB-MOWOA exhibits a stable growth trend, performing particularly well under high delay conditions; it achieves a high offloading rate at 750 ms, with smaller increases thereafter. Among the schemes, the DVCG-MWOA consistently outperforms the others under all delay conditions, nearing saturation in high delay scenarios and showing superior performance across both vehicle scales.

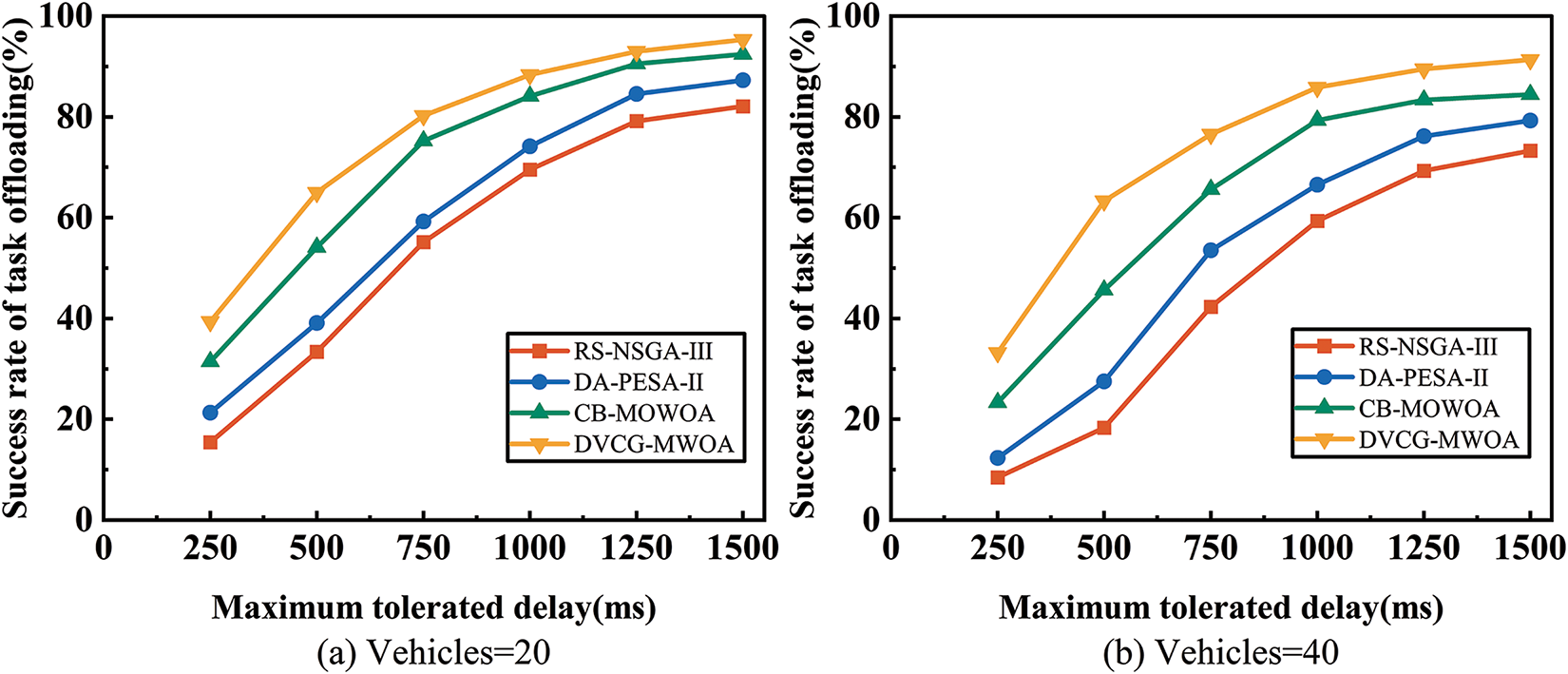
Figure 6: The comparison results in maximum tolerable delay and task offloading success rate when the number of vehicles is 20 and 40, respectively

5  Conclusion

In this paper, we comprehensively study sustainable edge computing in the Internet of Vehicles, considering the complex and variable vehicle conditions, reasonable resource allocation optimization, and UAV-assisted edge computing issues in practical scenarios of the Internet of Vehicles. We formulate the computation offloading problem as a multi-objective optimization problem with the goal of minimizing latency and energy consumption. Further, we design a three-stage hybrid offloading strategy to effectively solve the above problems. The first step is to cluster the vehicles, followed by resource allocation within the clusters, and then solve using an improved parallel multi-objective whale optimization algorithm. In this way, we achieve the goal of reducing latency and energy consumption.

Acknowledgement: The authors sincerely appreciate the editor and reviewers for their valuable feedback.

Funding Statement: This research was funded by Shandong University of Technology Doctoral Program in Science and Technology, grant number 4041422007.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, methodology and writing, Yiwei Zhang; supervision and project administration, Xin Cui; formal analysis, Qinghui Zhao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Xin Cui, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Matin A, Dia H. Impacts of connected and automated vehicles on road safety and efficiency: a systematic literature review. IEEE Trans Intell Transp Syst. 2023;24(3):2705–36. doi:10.1109/TITS.2022.3227176. [Google Scholar] [CrossRef]

2. Shi J, Du J, Shen Y, Wang J, Yuan J, Han Z. DRL-based V2V computation offloading for blockchain-enabled vehicular networks. IEEE Trans Mob Comput. 2023;22(7):3882–97. doi:10.1109/TMC.2022.3153346. [Google Scholar] [CrossRef]

3. Wang J, Zhu K, Hossain E. Green Internet of vehicles (IoV) in the 6G era: toward sustainable vehicular communications and networking. IEEE Trans Green Commun Netw. 2022;6(1):391–423. doi:10.1109/TGCN.2021.3127923. [Google Scholar] [CrossRef]

4. Liu L, Chen C, Pei Q, Maharjan S, Zhang Y. Vehicular edge computing and networking: a survey. Mob Netw Appl. 2021;26(3):1145–68. doi:10.1007/s11036-020-01624-1. [Google Scholar] [CrossRef]

5. Mozaffari M, Saad W, Bennis M, Nam YH, Debbah M. A tutorial on UAVs for wireless networks: applications, challenges, and open problems. IEEE Commun Surv Tutor. 2019;21(3):2334–60. doi:10.1109/COMST.2019.2902862. [Google Scholar] [CrossRef]

6. Dai X, Xiao Z, Jiang H, Lui JCS. UAV-assisted task offloading in vehicular edge computing networks. IEEE Trans Mob Comput. 2024;23(4):2520–34. doi:10.1109/TMC.2023.3259394. [Google Scholar] [CrossRef]

7. Aradi S. Survey of deep reinforcement learning for motion planning of autonomous vehicles. IEEE Trans Intell Transp Syst. 2022;23(2):740–59. doi:10.1109/TITS.2020.3024655. [Google Scholar] [CrossRef]

8. Mollah MB, Zhao J, Niyato D, Guan YL, Yuen C, Sun S, et al. Blockchain for the Internet of vehicles towards intelligent transportation systems: a survey. IEEE Internet Things J. 2021;8(6):4157–85. doi:10.1109/JIOT.2020.3028368. [Google Scholar] [CrossRef]

9. Noor-A-Rahim M, Liu Z, Lee H, Khyam MO, He J, Pesch D, et al. 6G for vehicle-to-everything (V2X) communications: enabling technologies, challenges, and opportunities. Proc IEEE. 2022;110(6):712–34. doi:10.1109/JPROC.2022.3173031. [Google Scholar] [CrossRef]

10. Wang X, Ning Z, Guo S, Wang L. Imitation learning enabled task scheduling for online vehicular edge computing. IEEE Trans Mob Comput. 2022;21(2):598–611. doi:10.1109/TMC.2020.3012509. [Google Scholar] [CrossRef]

11. Mustafa E, Shuja J, Rehman F, Namoun A, Bilal M, Bilal K. Deep reinforcement learning and SQP-driven task offloading decisions in vehicular edge computing networks. Comput Netw. 2025;262:111180. doi:10.1016/j.comnet.2025.111180. [Google Scholar] [CrossRef]

12. Mustafa E, Shuja J, Rehman F, Namoun A, Bilal M, Iqbal A. Computation offloading in vehicular communications using PPO-based deep reinforcement learning. J Supercomput. 2025;81(4):547. doi:10.1007/s11227-025-07009-z. [Google Scholar] [CrossRef]

13. Yang X, Luo H, Sun Y, Guizani M. A novel hybrid-ARPPO algorithm for dynamic computation offloading in edge computing. IEEE Internet Things J. 2022;9(23):24065–78. doi:10.1109/JIOT.2022.3188928. [Google Scholar] [CrossRef]

14. Maleki H, Başaran M, Durak-Ata L. Handover-enabled dynamic computation offloading for vehicular edge computing networks. IEEE Trans Veh Technol. 2023;72(7):9394–405. doi:10.1109/TVT.2023.3247889. [Google Scholar] [CrossRef]

15. Zhao L, Li T, Zhang E, Lin Y, Wan S, Hawbani A, et al. Adaptive swarm intelligent offloading based on digital twin-assisted prediction in VEC. IEEE Trans Mob Comput. 2024;23(8):8158–74. doi:10.1109/TMC.2023.3344645. [Google Scholar] [CrossRef]

16. Shen R, Gao M, Li W, Li Y. Dynamic task offloading in distributed VEC networks: an exploration and exploitation assisted contract-theoretic approach. IEEE Trans Veh Technol. 2024;73(4):5717–29. doi:10.1109/TVT.2023.3332956. [Google Scholar] [CrossRef]

17. Raza S, Wang S, Ahmed M, Anwar MR, Mirza MA, Khan WU. Task offloading and resource allocation for IoV using 5G NR-V2X communication. IEEE Internet Things J. 2022;9(13):10397–410. doi:10.1109/JIOT.2021.3121796. [Google Scholar] [CrossRef]

18. Lv W, Yang P, Zheng T, Yi B, Ding Y, Wang Q, et al. Energy consumption and QoS-aware co-offloading for vehicular edge computing. IEEE Internet Things J. 2023;10(6):5214–25. doi:10.1109/JIOT.2022.3221966. [Google Scholar] [CrossRef]

19. Zhan W, Luo C, Wang J, Wang C, Min G, Duan H, et al. Deep-reinforcement-learning-based offloading scheduling for vehicular edge computing. IEEE Internet Things J. 2020;7(6):5449–65. doi:10.1109/JIOT.2020.2978830. [Google Scholar] [CrossRef]

20. Shen Q, Hu BJ, Xia E. Dependency-aware task offloading and service caching in vehicular edge computing. IEEE Trans Veh Technol. 2022;71(12):13182–97. doi:10.1109/TVT.2022.3196544. [Google Scholar] [CrossRef]

21. Du J, Sun Y, Zhang N, Xiong Z, Sun A, Ding Z. Cost-effective task offloading in NOMA-enabled vehicular mobile edge computing. IEEE Syst J. 2023;17(1):928–39. doi:10.1109/JSYST.2022.3167901. [Google Scholar] [CrossRef]

22. Zhao M, Yu JJ, Li WT, Liu D, Yao S, Feng W, et al. Energy-aware task offloading and resource allocation for time-sensitive services in mobile edge computing systems. IEEE Trans Veh Technol. 2021;70(10):10925–40. doi:10.1109/TVT.2021.3108508. [Google Scholar] [CrossRef]

23. He Q, Cui G, Zhang X, Chen F, Deng S, Jin H, et al. A game-theoretical approach for user allocation in edge computing environment. IEEE Trans Parallel Distrib Syst. 2020;31(3):515–29. doi:10.1109/TPDS.2019.2938944. [Google Scholar] [CrossRef]

24. Hu M, Xie Z, Wu D, Zhou Y, Chen X, Xiao L. Heterogeneous edge offloading with incomplete information: a minority game approach. IEEE Trans Parallel Distrib Syst. 2020;31(9):2139–54. doi:10.1109/TPDS.2020.2988161. [Google Scholar] [CrossRef]

25. Zhan Y, Guo S, Li P, Zhang J. A deep reinforcement learning based offloading game in edge computing. IEEE Trans Comput. 2020;69(6):883–93. doi:10.1109/TC.2020.2969148. [Google Scholar] [CrossRef]

26. Gong Y, Yao H, Wu D, Yuan W, Dong T, Yu FR. Computation offloading for rechargeable users in space-air-ground networks. IEEE Trans Veh Technol. 2023;72(3):3805–18. doi:10.1109/TVT.2022.3217079. [Google Scholar] [CrossRef]

27. Luo Y, Wang Y, Lei Y, Wang C, Zhang D, Ding W. Decentralized user allocation and dynamic service for multi-UAV-enabled MEC system. IEEE Trans Veh Technol. 2024;73(1):1306–21. doi:10.1109/TVT.2023.3308589. [Google Scholar] [CrossRef]

28. Salim A, Khedr AM, Osamy W. IoVSSA: efficient mobility-aware clustering algorithm in Internet of vehicles using sparrow search algorithm. IEEE Sens J. 2023;23(4):4239–55. doi:10.1109/JSEN.2022.3233903. [Google Scholar] [CrossRef]

29. Zhong R, Liu X, Liu Y, Chen Y. Multi-agent reinforcement learning in NOMA-aided UAV networks for cellular offloading. IEEE Trans Wirel Commun. 2022;21(3):1498–512. doi:10.1109/TWC.2021.3104633. [Google Scholar] [CrossRef]

30. Liu L, Zhao M, Yu M, Ahmad Jan M, Lan D, Taherkordi A. Mobility-aware multi-hop task offloading for autonomous driving in vehicular edge computing and networks. IEEE Trans Intell Transp Syst. 2023;24(2):2169–82. doi:10.1109/TITS.2022.3142566. [Google Scholar] [CrossRef]

31. Chen Y, Li K, Wu Y, Huang J, Zhao L. Energy efficient task offloading and resource allocation in air-ground integrated MEC systems: a distributed online approach. IEEE Trans Mob Comput. 2024;23(8):8129–42. doi:10.1109/TMC.2023.3346431. [Google Scholar] [CrossRef]