Machine Learning and Explainable AI-Guided Design and Optimization of High-Entropy Alloys as Binder Phases for WC-Based Cemented Carbides

1  Introduction

Tungsten carbide-based (WC-based) cemented carbides, renowned for their exceptional hardness, toughness, and wear resistance, are widely used in cutting tools, mining equipment, and high-wear components. The carbide precipitation strengthening mechanisms of cobalt (Co)-based binders at elevated temperatures have been extensively investigated. However, Co, the conventional binder phase, has increasingly become a bottleneck in the development of WC-based cemented carbides due to its scarcity, high cost, and the significant environmental impact of its extraction [1,2].

High-entropy alloys (HEAs), a novel class of multi-principal-element alloys, have garnered significant attention due to their outstanding mechanical properties, high-temperature resistance, and corrosion resistance. Through complex multi-element combinations, HEAs can form stable single-phase solid solutions or intermetallic compounds, exhibiting distinctive features such as the “high-entropy effect” and “sluggish diffusion effect”, which differentiate them from conventional alloys [3,4]. Cutting-edge research has demonstrated that composition design strategies based on configurational entropy can significantly enhance phase stability in HEAs. For instance, Wan et al. [5] highlighted the transformative potential of machine learning (ML) in accelerating the discovery of high-entropy compounds, including the efficient screening of multi-component systems through advanced data-driven approaches. Recent studies have explored the potential of HEAs as binder phases in cemented carbides. For example, Ghasemi et al. [6] investigated the application of chromium (Cr)-rich and iron (Fe)-rich HEAs binder phases in WC-based cemented carbides, demonstrating significantly enhanced wear resistance and thermal stability compared to traditional Co-based alloys. Further research has indicated that optimizing HEA compositions can effectively improve the overall mechanical properties of WC-based cemented carbides [7].

Despite the promising potential of HEAs in cemented carbides, the complexity of their composition design makes traditional experimental approaches costly and time-consuming when searching for optimal formulations. In recent years, the rapid advancement of ML techniques in materials science has provided an efficient solution for materials design. In particular, the emergence of adaptive ML frameworks has made it possible to extract underlying physical correlations from high-dimensional and heterogeneous datasets. ML can extract latent patterns from large-scale materials databases, establish composition-property prediction models, and offer insights into optimizing material properties [8]. For example, Schmidt et al. [9] comprehensively reviewed the application of ML in solid-state materials science, demonstrating its effectiveness in accelerating materials discovery, optimizing functional properties, and predicting structure-property relationships. Their work highlighted how data-driven approaches can overcome traditional trial-and-error methods, particularly in designing advanced materials such as perovskites, HEAs, and energy storage systems. These studies suggest that data-driven approaches can significantly enhance the efficiency of materials design while providing a scientific basis for optimizing complex material systems.

This study integrates HEAs design principles with ML techniques to explore the feasibility of replacing Co with HEAs as the binder phase in WC-based cemented carbides. A composition-property prediction model is developed to systematically analyze the effects of HEAs composition on cemented carbide mechanical properties. Furthermore, explainable artificial intelligence (XAI) techniques, including SHapley Additive exPlanations (SHAP) and Local Interpretable Model-agnostic Explanations (LIME), are employed to elucidate the influence of key alloying elements [10]. As ML models grow increasingly complex, understanding their internal logic and decision-making processes has become crucial. The interpretability of ML models ensures that predictions and insights can be effectively explained in a manner comprehensible to human researchers.

The key contributions of this study include developing an ML-driven composition-property prediction model for HEAs in cemented carbides and providing theoretical support for the rapid screening of high-performance formulations. Additionally, by employing feature selection methods and XAI techniques, this study reveals the mechanisms through which HEA elements influence the mechanical properties of cemented carbides, thereby enhancing the interpretability of model predictions. Moreover, the experimentally validated optimal HEAs formulation demonstrates superior mechanical properties, underscoring its potential for practical application in cemented carbides. Finally, due to the long experimental cycle and low efficiency of the traditional trial-and-error method for HEAs, our research team was unable to obtain alloy compositions with ideal mechanical properties (such as Vickers Hardness, HV) through 120 experimental groups. To address this issue, we introduced ML methods to optimize the composition design and property prediction of HEAs. This method significantly shortened the experimental cycle and successfully guided the rapid screening and development of HEAs with excellent hardness.

This research not only introduces new perspectives on the application of HEAs in cemented carbides but also contributes to the intelligent and efficient design of advanced materials. By combining ML with HEAs design principles, this study aims to drive the innovation of high-performance tool materials, meeting the growing industrial demands for enhanced tool properties.

2  Methods

To accurately model and optimize the “composition-property” relationship, this study employed a systematic data-driven approach. A high-quality composition-property database was first established, ensuring comprehensive and reliable data for analysis. Appropriate ML algorithms were then carefully selected to achieve an optimal balance between prediction accuracy and model interpretability. Furthermore, to validate the reliability of the model’s predictions, a series of experiments were conducted to assess the mechanical performance of the predicted optimal alloy compositions. This integrated approach enhances both the predictive power and practical applicability of the proposed model.

2.1 Construction and Evaluation of the Prediction Model

The methodology for model construction and evaluation in this study is illustrated in Fig. 1.

Figure 1: AI simulation process

2.1.1 Establishment of the Database and Data Screening

This study systematically integrated a dataset comprising 672 sets of mechanical property data for HEAs. Among them, 120 sets were original experimental data obtained by our research group over the past two years, based on classical compositional design principles for high-entropy binder phases in cemented carbides, prioritizing transition metal systems with solid solution strengthening potential (e.g., Co-nickel (Ni)-Fe-Cr-aluminum (Al)). Fig. 2 presents the correlation between five alloying elements (Co, Fe, Ni, Cr, Al) and the hardness of HEAs based on our team’s 120 original experimental data points. However, such simple correlation analysis cannot precisely reveal the individual contribution of each element to hardness—a limitation that will be addressed by our proposed interpretable ML model. Furthermore, Fig. 3 compares the average hardness values of HEAs with those of conventional Ni-based and Co-based alloys from our experimental dataset. The results demonstrate that the HEAs exhibit superior hardness performance compared to their traditional counterparts. The remaining 552 sets were curated from literature published between 2004 and 2022, selected based on the completeness of composition–property correspondence in HEAs studies. The resulting dataset encompasses 15 key compositional and performance-related features across 14 alloy systems, with a particular emphasis on composition design and hardness-related mechanical properties.

Figure 2: The correlation between the composition (a) and hardness (b) of the Co-Ni-Fe-Cr-Al quinary system

Figure 3: Comparison chart of the hardness of co-based alloys, Ni-based alloys, and HEAs

During the data preprocessing phase, we applied rigorous quality control procedures. First, samples lacking major constituent elements (defined as elements with atomic fractions ≥5%) or with incomplete mechanical property records were removed, reducing the dataset from 672 to 532 entries. Next, outlier detection was performed using the Grubbs’ test, followed by thermodynamic consistency screening based on mixing enthalpy (ΔHmix ∈ [–15, 5] kJ/mol) and atomic size difference (δ ≤ 6.5%). This yielded a refined dataset of 410 high-quality samples. The resulting composition-property database provides a reliable foundation for subsequent ML modeling efforts.

Subsequent screening and analysis following database construction revealed that common binder phases in high-entropy cemented carbides predominantly consist of Co, Ni, and Fe. This finding aligns with conclusions from previous studies on compositional design strategies in HEAs [11,12].

By combining literature review with systematic data analysis, this study not only validates existing research but also establishes a representative and optimized database. This work provides a scientific foundation for data-driven composition design and performance prediction of high-entropy binder phases in cemented carbides.

2.1.2 Construction of the Prediction Model

The HEAs dataset used in this study exhibits two key characteristics: a relatively small sample size and a high-dimensional feature space. These characteristics pose challenges for constructing an accurate prediction model, particularly when dealing with complex feature interactions. Therefore, supervised regression algorithms well-suited for small-sample, high-dimensional data were selected for model construction.

According to existing literature, Extreme Gradient Boosting (XGBoost), Random Forest (RF), and K-Nearest Neighbors (KNN) are among the most commonly used regression algorithms for such datasets. These methods have demonstrated strong adaptability and high predictive accuracy in scenarios involving multiple features and limited data availability [13–15]. To demonstrate the innovation of the experiment, we have also applied the Multilayer Perceptron (MLP) and Kolmogorov-Arnold Network (KAN) algorithms for the ML–based selection and optimization of HEAs.

To assess the suitability of different algorithms for this dataset, the coefficient of determination (R2) was chosen as the primary evaluation metric. This metric quantifies the proportion of variance in the target variable explained by the model. An R2 value closer to 1 indicates a better model fit, signifying that the algorithm effectively captures the relationship between input features and the target variable.

XGBoost

XGBoost is an efficient gradient-boosting algorithm that employs Classification and Regression Trees (CART) as base learners. It has been widely applied in regression and classification tasks involving large-scale datasets due to its high computational efficiency and strong generalization ability.

XGBoost utilizes an additive modeling approach, in which trees are sequentially added to optimize the objective function. At each iteration, the algorithm computes the negative gradient (pseudo-residual) of the current loss function and treats it as the new target value. By iteratively fitting new trees and refining model parameters, XGBoost minimizes the loss function and ultimately produces optimal predictive results [16,17].

Random Forest

RF is an ensemble learning algorithm that improves prediction accuracy by constructing multiple decision trees using the Bagging (Bootstrap Aggregating) method. Unlike traditional decision trees, RF introduces both random sampling and random feature selection during the construction of each tree. These mechanisms help reduce overfitting and enhance the model’s generalization capability.

During the prediction phase, RF aggregates the outputs of individual decision trees—using majority voting for classification tasks and averaging for regression tasks—to generate the final prediction [18,19].

One of the key advantages of RF is its ability to efficiently handle high-dimensional datasets, while also demonstrating strong robustness to noise and missing values. In the context of HEAs analysis, RF can manage numerous compositional and mechanical features while evaluating the importance of each feature. This capability provides valuable insights for further optimizing alloy design.

K-Nearest Neighbors

KNN algorithm is a simple yet effective supervised learning method applicable to both classification and regression tasks. The core principle of KNN involves computing the distance between a new data point and existing points in the training dataset, typically using Euclidean distance. The algorithm then selects the k nearest neighbors and determines the output based on majority voting for classification tasks or weighted averaging for regression tasks. KNN offers advantages such as ease of implementation and the absence of a training phase. However, as the dimensionality of the dataset increases, its computational complexity rises significantly, a phenomenon known as the “curse of dimensionality”, which can degrade performance in high-dimensional spaces. Despite these challenges, KNN remains valuable in HEAs prediction tasks, as it enables localized feature learning and helps uncover nonlinear relationships between alloy composition and mechanical properties [20].

Multilayer Perceptron

As a typical representative of the Feedforward Neural Network, the MLP achieves parameter optimization through the following mechanism: First, the input data undergoes nonlinear transformations in the hidden layers and is propagated forward to the output layer. Subsequently, based on the prediction error, the Backpropagation algorithm is used to calculate the gradient layer by layer, and the error signal is transmitted backward from the output layer to the input layer to update the connection weights and bias terms. This iterative process of “forward calculation-backward propagation” continuously optimizes the network parameters, causing the loss function (e.g., mean squared error) to gradually converge. Finally, a high-dimensional nonlinear mapping relationship is established between the input features (e.g., alloy composition) and the output targets (e.g., mechanical properties). Fig. 4a shows a schematic diagram of the network architecture of the MLP. Compared with traditional ML methods, the advantage of the MLP lies in the distributed representation ability of its hidden layers, which can effectively capture the complex structure-performance relationships in material systems. With the help of advanced analysis techniques, the MLP can further improve the accuracy and computational efficiency of material property prediction [21].

Figure 4: MLP (a)/KAN (b) structure and hyperparameter setting

Kolmogorov-Arnold Network

KAN, as an emerging neural network architecture, has its theoretical foundation rooted in the Kolmogorov-Arnold representation theorem (KART). This theorem holds an important position in the theory of function approximation. It rigorously proves that any multivariate continuous function can be decomposed into a superposition of a finite number of univariate functions and addition operations. KAN has no linear weights—each weight parameter is parameterized into a spline curve by a univariate function [22].

Unlike traditional neural networks, KAN uses B-spline basis functions to parametrically model the Kolmogorov-Arnold representation. As shown in Fig. 4b, the KAN constructs a spline space formed by the linear combination of local functions and transforms the model parameters into learnable basis-function coefficients. This parametric strategy not only ensures the function approximation ability but also endows the model with stronger interpretability. Its strengths in interpretability and computational efficiency enable effective mining of complex composition-property relationships, providing precise composition optimization and performance prediction guidance for multi-principal element alloy design.

In this study, we adopted two different network architectures for analysis: the MLP employed a six-layer linear structure (including one input layer, four hidden layers, and one output layer), while the KAN adopted a more concise three-layer KAN linear structure. Both models used the ReLU activation function and optimized the hyperparameter selection through the grid search method. The detailed training processes and parameter settings are respectively shown in Fig. 4a,b.

2.2 XAI Interpretability Analysis

Although ML methods have shown strong performance in predicting the mechanical properties of HEAs, their inherent “black-box” nature significantly limits the interpretability of the models. While feature importance evaluation methods can provide the relative contributions of each feature to the model’s predictions, these methods only reveal the importance ranking of features without quantifying their specific roles in individual predictions [10]. This becomes especially problematic when dealing with a single prediction sample, where it is difficult to clarify the exact contribution of each feature to the final predicted value, thus restricting the transparency of the model and understanding of its decision-making process.

Moreover, ML models can automatically capture complex nonlinear and high-order interactions between features. These interactions make the model’s behavior more intricate, increasing the difficulty of interpreting the model’s predictions [23]. To address these challenges, this study employs two XAI techniques: SHAP and LIME. SHAP, based on game theory, provides both global and local interpretability by calculating the marginal contribution of each feature to the model output, helping to reveal the underlying decision-making mechanisms of the model. LIME, in contrast, approximates the behavior of a complex model locally by fitting a simple, interpretable model in the vicinity of a prediction instance, offering an interpretable basis for the decision-making process of a single prediction [24,25]. The combination of these methods enhances the interpretability of the model, allows for a clearer understanding of the specific impact of HEAs composition on mechanical properties, and ultimately improves the transparency and reliability of the prediction results.

2.2.1 Global Shapley Additive Explanations

The SHAP method, derived from cooperative game theory, views the ML model as a “black box” and each input feature as a “player.” As illustrated in Fig. 5, the SHAP explanation process mirrors the structure of a game where players collaborate to achieve the maximum benefit. SHAP aims to quantify the contribution of each feature to the model’s predictions. By calculating the Shapley value for each feature, it is possible to assess the marginal contribution of that feature under different feature combinations, providing a comprehensive understanding of the model’s decision-making process [10,26].

Figure 5: SHAP explanation process

Shapley values not only help to evaluate the importance of features but also reveal their specific impact on the final prediction. A large absolute Shapley value indicates that the feature has a significant contribution to the prediction, whereas a value close to zero suggests minimal impact [27]. Compared to other feature importance evaluation methods, SHAP offers more accurate and stable explanations by considering feature interactions, particularly in complex, nonlinear models [28].

One of the main advantages of SHAP is its model-agnostic property, meaning it can be applied to various ML models, including tree-based models (e.g., XGBoost and RF) and neural networks. This versatility makes SHAP a valuable tool not only for providing interpretability in HEAs predictions but also for optimizing ML models and feature selection. Through SHAP analysis, researchers can better understand the specific contributions of each feature to model outputs, ultimately improving model performance, enabling data preprocessing, and informing feature engineering.

2.2.2 Local Interpretable Model-Agnostic Explanations

LIME is a local interpretability method that explains the predictions of a “black-box” model by approximating it within a localized region [24]. The core principle of LIME is to generate perturbed samples around the data point of interest and fit a simple, interpretable model (e.g., a linear model) to these perturbed samples [25]. This allows LIME to explain the behavior of complex models in a local context, making the results more intuitive.

Specifically, starting from the data point to be explained (shown as the red dot in Fig. 6), LIME generates multiple perturbed samples (blue dots) and assigns weights to them based on the distance to the original sample. It then fits a simple interpretable model using these weighted perturbed samples, with the decision boundary shown by the black line representing the result of the local fitting. This method is highly flexible and can be applied to any ML model, including linear regression, decision trees, and neural networks, without relying on the model’s internal structure or parameters [25].

Figure 6: LIME explanation process

In the context of HEAs property prediction, LIME not only helps identify the key factors driving the model’s predictions but also assists in diagnosing performance bottlenecks. By analyzing the local interpretations for different samples, researchers can identify areas or features where the model performs poorly and implement targeted improvements [24]. Additionally, LIME can visualize the interpretability results, providing an intuitive analysis tool that enhances model transparency and helps clarify the model’s decision-making process.

2.3 Experimental Procedure

To verify the reliability of the performance prediction model, eight predicted data points were randomly selected for experimental validation.

WC-based cemented carbides are an ultra-hard material fabricated using the powder metallurgy method, a process that consists of three primary stages: powder preparation, compaction, and sintering, as illustrated in Fig. 7. The raw material powders were weighed and mixed according to the selected compositions. A planetary ball mill was used for mixing, with anhydrous ethanol as the grinding medium.

Figure 7: Flow chart of HEAs experiment

After ball milling, the powders were retrieved and separated from the grinding balls using a sieve. Anhydrous ethanol was used to rinse the grinding jar and balls to ensure cleanliness. The powder mixture was then left to settle, allowing for the separation of the powder and ethanol. Once settled, the upper ethanol layer was removed via siphoning, leaving behind the precipitated powder. The remaining powder was dried in an oven at 80°C for 3 h. After drying, the agglomerated powder was finely ground using a mortar and pestle and then sieved to obtain a fine powder.

A 20 g sample of the prepared powder was subjected to spark plasma sintering (SPS) at a sintering temperature of 1200°C and a pressure of 30 MPa. Upon completion of the sintering process, cylindrical specimens were obtained, surface-ground, and polished before hardness measurements.

The mechanical properties of the HEAs were evaluated using the Vickers hardness (HV30) testing method.

3  Results and Discussion

3.1 Algorithm Selection

During the development of the ML model, the pre-processed dataset was randomly split into a training set and a test set using an 8:2 ratio. The training set was used for model training and hyperparameter optimization (it involves the step size for controlling the update of model parameters; to prevent overfitting, adjust the regularization weight, etc.), while the test set was employed to assess the model’s generalization performance, ensuring its applicability to unseen data.

Among the evaluated models, the optimized XGBoost algorithm achieved a coefficient of determination (R2) of 0.88 on the test set, indicating high prediction accuracy and stability in forecasting mechanical properties (HV). In contrast, the R2 values of the test sets for both the RF and KNN models were 0.83 (as shown in Fig. 8). Additionally, we investigated more advanced algorithms to perform regression tasks. As shown in Fig. 9, these are the fitting results of MLP and KAN, and the R2 values of the test set were 0.77 and 0.75, respectively. These results highlight the superior fitting ability and generalization performance of XGBoost, making it the most effective model for this task.

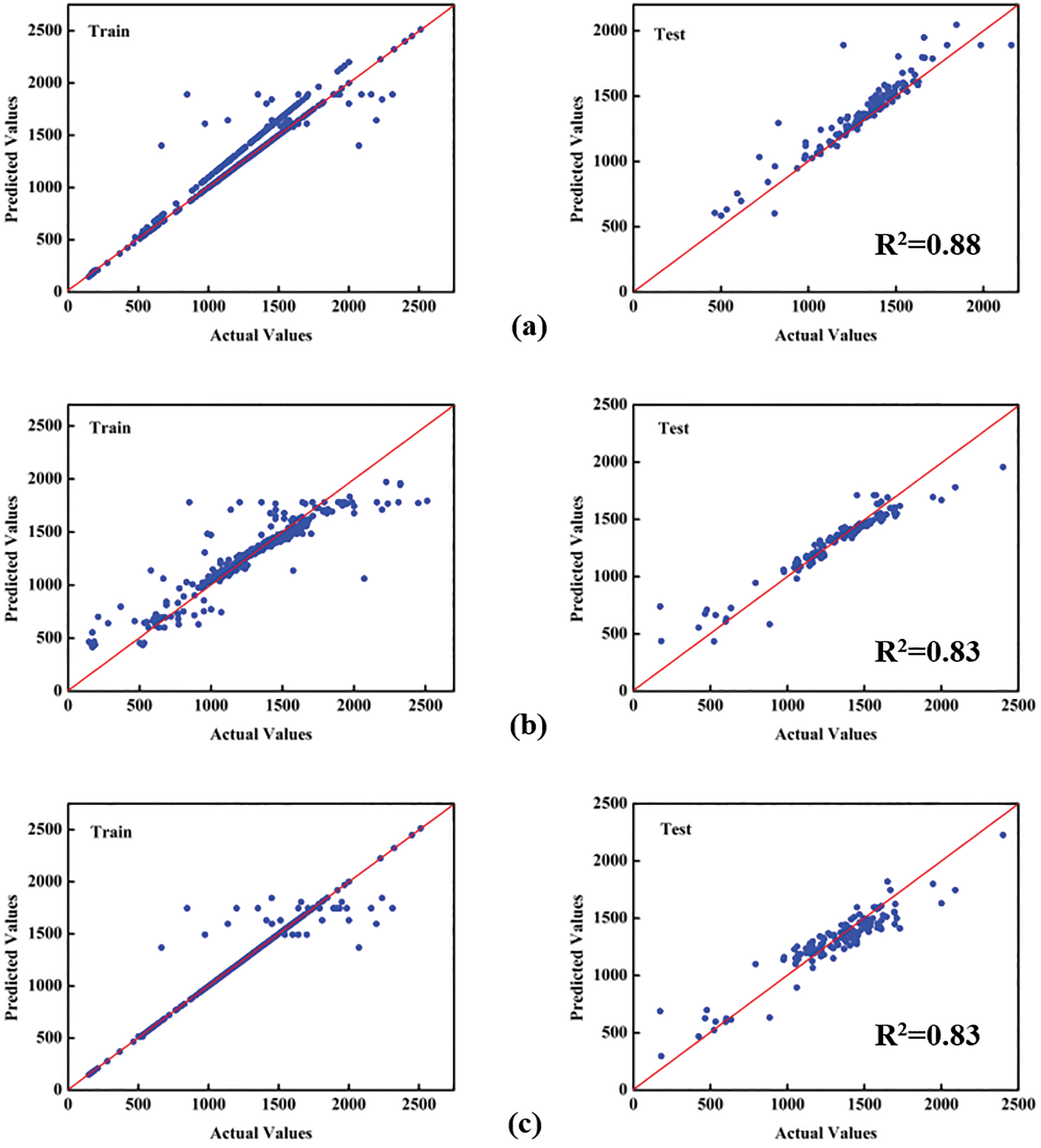
Figure 8: Comparison and selection of three model algorithms. (a) XGBoost; (b) Random Forest; (c) KNN

Figure 9: The fitting results of the MLP and KAN algorithm. (a) MLP; (b) KAN

As shown in Fig. 8a, the blue dots and round dots represent the data point distributions of the training and test sets, respectively, while the red solid line denotes the ideal case where the predicted values perfectly match the true values. From the figure, it is evident that the training set data points are densely clustered around the red solid line, indicating that the model achieves a strong fit to the training data. Although the test set data points exhibit slightly greater dispersion, the majority remain close to the red solid line, further confirming the model’s robustness and predictive capability.

Compared with RF, KNN, MLP, and KAN models, XGBoost demonstrates significant advantages in modeling the nonlinear characteristics of HEAs, owing to its implicit interaction learning mechanism based on the gradient-boosted tree framework. In this study, no explicit interaction terms were predefined; the input features consisted solely of elemental compositions selected through feature screening. The superior performance of XGBoost stems from its gradient-based optimization mechanism, which effectively captures both feature importance and complex inter-element interactions [29]. XGBoost continuously splits the nodes of the decision tree. Based on the distribution of the data and the importance of features, it automatically discovers and learns the potential relationships between features from the input data without the need for humans to define these interaction terms in advance. It can automatically identify which features have potential interaction relationships that affect the target variable. To a certain extent, this reduces the workload of manual feature engineering, and it can also discover some new and unexpected feature interactions, thus improving the performance of the model.

To further validate the model’s applicability, we employed cross-validation to assess its stability. The cross-validation results were consistent with the R2 value obtained from the test set, reinforcing the reliability of the XGBoost model in handling small-sample, high-dimensional datasets. The following are the calculation formulas and comparisons of the performance indicators of R2, mean absolute error (MAE), and root mean square error (RMSE) for the five algorithms.

R2=1−Σ(yi−y^i)2∑(yi−y¯)2(1)

MAE=1n∑i=1n|yi−y^i|(2)

MSE=1n∑i=1n(yi−y^i)2(3)

yi:True valuey^i:Predicted valuen: The number of samples

As shown in Table 1, the XGBoost model exhibits the best error consistency index, and its MAE/RMSE ratio (0.45) is significantly lower than that of RF (0.57), KNN (0.57), MLP (0.66), and KAN (0.61). This result indicates that the distribution of prediction errors of XGBoost is more concentrated, and it has better numerical stability. Further, by combining the comparative analysis of Figs. 8 and 9, it can be seen that the prediction results of the XGBoost model for the hardness values of HEAs have the highest degree of agreement with the experimental data (R2 = 0.88). Based on the above comprehensive performance evaluation, this study determines that XGBoost is the optimal algorithm for predicting the properties of HEAs.

XGBoost demonstrates a strong capability in handling complex nonlinear relationships and accurately capturing the intricate interactions among multiple principal elements in high-entropy binder phases, as well as variations in carbide content. Although the primary focus of the dataset in this study is on WC-based cemented carbide systems, the model was trained on data encompassing 14 distinct alloy systems. This enables the quantification of the differential effects of carbide content and high-entropy principal elements on hardness. As a result, the model can be effectively extrapolated to novel compositions featuring similar principal element combinations. Moreover, it accurately identifies the formation patterns across various carbide systems and elucidates their influence on mechanical performance, thereby enabling efficient screening and optimization of HEA materials across different systems.

The single model training cycle of our research team mainly consists of three key stages: (1) Data preparation stage: Through two years of data accumulation, we have carried out strict cleaning, annotation, and feature engineering on the original data to ensure that the dataset is of high quality and has good applicability. (2) Model selection and training stage, which takes about a week: In this stage, first, according to the specific task requirements, the most suitable model structure is screened out from a variety of candidate model architectures. Subsequently, through meticulous hyperparameter tuning, the model parameters are continuously adjusted through multiple rounds of training until the optimal algorithm performance is achieved. (3) The final verification and evaluation stage also take about a week. In this stage, an independent test set is used to comprehensively evaluate the trained model, and the possible overfitting or underfitting problems of the model are diagnosed by continuously monitoring various performance indicators. In addition, we have also designed systematic comparative experiments to verify the reliability and generalization ability of the ML algorithm through empirical research, ensuring that the research results have practical application value.

3.2 Results of Shapley Additive Explanations

During the prediction process of the XGBoost model, understanding the relationship between features and prediction outcomes is crucial for interpreting the model’s decision-making process. By analyzing SHAP values (as shown in Fig. 10), it is evident that the contents of WC, Fe, Co, and Ni are the key factors influencing the mechanical properties (HV) of HEAs. Specifically, WC exhibits the highest absolute SHAP value, indicating its dominant role in enhancing mechanical properties. This finding aligns with previous studies highlighting its extensive application in the strengthening design of cemented carbides and HEAs [6,7].

Figure 10: SHAP values of each feature for HV of HEAs

Furthermore, the contents of Fe, Co, and Ni also have a significant impact on HV, underscoring their critical role in mechanical strengthening through solid-solution hardening and lattice stabilization. SHAP analysis not only quantifies feature importance but also reveals the specific contribution directions of each feature to the prediction results. While existing research has suggested that the synergistic effect of Fe, Co, and Ni enhances the overall performance of alloys, a precise quantitative assessment of their respective contributions remains lacking. This study addresses this gap by leveraging SHAP values, providing a crucial foundation for further optimizing the compositional design of HEAs.

The model predictions demonstrate strong consistency with both SHAP for global interpretation and LIME for local analysis, thereby providing dual interpretability support that combines global reliability with local explainability for understanding the decision-making mechanisms of complex models in HEAs performance prediction and similar applications. The interpretation results of LIME will also be discussed in Section 3.4.

3.3 High-Throughput Prediction

The results of the SHAP analysis indicate that the hard phase WC and the primary binder phase elements—Co, Fe, and Ni—exert the most significant influence on the model’s predictive outcomes. In contrast, the effects of the secondary binder phase elements—Al, Cr, manganese (Mn), and molybdenum (Mo)—are comparatively less pronounced. Based on this insight, we applied the XGBoost model to conduct high-throughput predictions of the impact of binder phase composition on hardness (HV) in HEAs.

Specifically, the prediction process was carried out in two stages. First, based on the established database, we performed high-throughput calculations within the compositional constraints of 70% WC, with the primary binder phase elements (Co, Fe, Ni) varying within the ranges of 0%–30%, 0%–30%, and 0%–20%, respectively, to assess their influence on HV. Next, after determining the optimal content ranges of these primary elements, we adjusted the composition ranges of the secondary elements (Al, Cr, Mn, Mo) to 0%–20%, 0%–30%, 0%–20%, and 0%–20%, respectively, to further evaluate their contribution to HV. The XGBoost model was used to facilitate these high-throughput calculations. By adopting this stepwise prediction strategy, we aimed to efficiently identify alloy compositions with promising mechanical properties.

Based on the defined compositional ranges of the primary elements, we utilized the XGBoost model for high-throughput calculations, generating 86,927 data points. The relationships between the key elements (Co, Fe, and Ni) and mechanical properties were visualized through a 3D color surface mapping, as shown in Fig. 11. Analysis of Fig. 11 reveals that within the compositional ranges of Co (0–11 wt%), Fe (10–27.5 wt%), and Ni (0–4 wt%), the hardness (HV) of the HEAs exhibits a significant increase, indicating that alloys within this compositional region possess superior mechanical properties. This phenomenon can be attributed to the synergistic interactions among these elements: the combined effects of Co, Fe, and Ni may facilitate the formation of short-range ordered structures, stabilizing the face-centered cubic (FCC) phase structure. Additionally, the multi-element solid-solution strengthening mechanism enhances the hardness and strength of the alloy [30]. Furthermore, lattice distortion and the high-entropy effect likely contribute to the overall improvement of the alloy’s mechanical performance [31,32]. These findings align with recent studies that have explored the influence of elemental interactions on the microstructure and mechanical properties of HEAs [33]. The optimal compositional ranges for Co, Fe, and Ni obtained in this study provide valuable guidance for further optimizing the microstructure and mechanical performance of high-entropy cemented carbides.

Figure 11: Relationship between the principal components, Co-Fe-Ni and mechanical properties

Following the determination of the optimal Co, Fe, and Ni content ranges, we extended our high-throughput predictions by incorporating the secondary elements (Al, Cr, Mn, and Mo) and generating a total of 97,966 additional data points. The composition data of these four elements were systematically permuted and analyzed in pairs, and 3D color surface maps illustrating the relationships between HV and different compositional combinations (Al-Cr, Al-Mn, Al-Mo, Cr-Mn, Cr-Mo, Mn-Mo) were constructed, as shown in Fig. 12. The results indicate that in Fig. 12a,d,e, the combinations of Al-Cr, Cr-Mn, and Cr-Mo significantly enhance mechanical properties, with clear peak regions in the HV distribution. This suggests that Al, Cr, and Mn exhibit strong synergistic strengthening effects at specific ratios. Conversely, the combinations of Al-Mn, Al-Mo, and Mn-Mo in Fig. 12b,c,f exhibits relatively minor improvements in HV, with a more uniform data distribution. This may be attributed to the weaker effects of these elements on solid-solution strengthening, precipitate formation, and grain boundary interactions.

Figure 12: Relationship between Al, Cr, Mn, Mo, and mechanical properties

These findings are consistent with recent research conclusions regarding the influence of element interactions on the mechanical properties of HEAs, further validating the reliability of the XGBoost model in predicting alloy properties.

Building on the above compositional modeling and analysis, this study further explored the potential mechanisms by which Co, Fe, and Ni, along with the secondary combinations of Al-Cr, Cr-Mn, and Cr-Mo, enhance mechanical performance. The high-entropy effect of Co, Ni, and Fe contributes to improved phase stability and resistance to deformation [34]. The addition of Al influences phase evolution, stabilizing the FCC phase and potentially promoting precipitation strengthening under specific conditions [35]. Cr, known for its excellent oxidation resistance, plays a crucial role in stabilizing the solid-solution structure and refining the microstructure of HEAs [36]. Mo promotes the precipitation of hard phases (e.g., Mo2C), thereby enhancing wear resistance and hardness [37]. The synergistic interactions among these elements are likely the primary drivers of the exceptional mechanical properties observed in this five-element system.

To further validate the reliability and robustness of our findings, we systematically evaluated the predictive performance of different compositional regions using the XGBoost model. By computing R2 and RMSE, we found that the Co-Fe-Ni composition exhibited high fitting accuracy, with the correlation between model-predicted and experimentally measured values exceeding R2 > 0.9. This indicates strong generalization ability and high predictive accuracy within this compositional space. Additionally, the Al-Cr, Cr-Mn, and Cr-Mo combinations demonstrated high consistency in high-throughput predictions, further supporting their contributions to the mechanical properties of HEAs.

In conclusion, for the binder phase of high-entropy cemented carbides, a five-element system consisting of Co, Fe, and Ni, combined with Al-Cr, Cr-Mn, and Cr-Mo at optimal ratios, can significantly enhance mechanical properties. This research not only provides theoretical insights for optimizing the compositional design of HEAs but also highlights the potential of ML in materials science, facilitating the advancement of data-driven materials design methodologies. Meanwhile, combining the former conclusions with Fig. 3, we can also see that the HEA system designed based on the combination of ML algorithms and high-throughput calculations exhibits excellent mechanical properties, and its hardness value is indeed higher than that of traditional Co-Ni-based alloys.

3.4 Analysis of LIME Local Explanation Results

In this study, we employed LIME to further investigate the specific contributions of binder phase composition to the mechanical properties of HEAs at a localized level. The results of the LIME analysis are presented in Fig. 13. As shown in the figure, elements such as Co and Ni exhibit a significant positive contribution to the hardness of HEAs. This finding underscores their crucial roles in solid-solution strengthening and high-temperature stability, which help achieve an optimal balance between hardness and toughness.

Figure 13: LIME diagram of HEAs. (a)–(h) are all LIME analysis results between HV and components

A closer examination of Fig. 13e–h reveals a critical threshold in the influence of Fe content on mechanical properties. When Fe content is extremely low (Fe ≤ 0.0), its overall effect on mechanical properties remains positive, suggesting that a small amount of Fe enhances alloy performance. This improvement can be attributed to Fe’s ability to regulate the alloy’s phase structure, optimizing the balance between plasticity and hardness [38]. However, excessive Fe content may induce phase separation or reduce the alloy’s high-temperature stability. Therefore, precise control of Fe concentration is essential to achieve optimal mechanical properties.

Beyond the binder phase, the influence of the hard phase WC exhibits a distinct non-linear trend. When WC content is relatively low (≤65%), its contribution to mechanical properties is predominantly negative. This suggests that, at insufficient concentrations, WC may not form a continuous reinforcing phase, resulting in a negligible strengthening effect. However, when WC content exceeds 75%, a significant increase in hardness is observed, indicating a strong positive effect. This phenomenon suggests that in high-entropy cemented carbides, a continuous WC reinforcing phase effectively enhances grain-boundary strengthening and dispersion strengthening, aligning with findings from previous studies. Nonetheless, an excessively high WC content may lead to the formation of brittle phases, compromising the alloy’s fracture toughness. Therefore, optimizing WC content remains a critical aspect of high-entropy cemented carbide design, and we will explore this issue in future studies.

In conclusion, the local interpretability results obtained via LIME align well with the global feature importance analysis provided by SHAP, further confirming the critical roles of Co, Ni, and Fe in regulating the mechanical properties of HEAs. These insights not only deepen our understanding of the relationship between alloy microstructure and mechanical performance but also provide a scientific foundation for optimizing alloy composition. In future research, integrating microstructural characterization with molecular dynamics simulations may further elucidate the synergistic mechanisms among different elements, offering new strategies for the rational design of high-performance HEAs.

3.5 Experimental Verification

Through the integrated analysis from the dual perspectives of global SHAP and local LIME, this study systematically reveals the key regulatory role of the Co-Fe-Ni-Cr-Al metallic binder phase system on the hardness of HEAs. To verify the prediction reliability of the ML model, based on the methodological framework described in Section 2.1, we designed and prepared 8 sets of composition gradient samples for experimental verification: (1) The WC content (65%–90%) covers the typical compositional range of WC in cemented carbides; (2) The content of the binder phase is strictly controlled within the optimized range of 10%–35% (Table 2). This range not only avoids the insufficient effect of the binder phase effects at a low content but also prevents the deterioration of mechanical properties caused by a high content. As shown in Fig. 14, the experimentally measured values show good consistency with the model prediction results (with a small average error). This not only confirms the effectiveness of the model but also verifies, from an experimental perspective, the key role of the composition design of the binder phase in property regulation.

Figure 14: Comparison between hardness prediction and experimental results

The comparison results show that the deviation between the measured HV values and the predicted values is small, and the overall error is controlled within a reasonable range, verifying the high precision and generalization ability of the XGBoost prediction model. Especially in the samples with a high WC content (≥75%), the maximum deviation between the experimental value and the predicted value does not exceed 5%, indicating that the role of WC in strengthening HEAs has been experimentally supported. In addition, the experimental results of the binder phase Al, Fe, Co, and Ni under different ratios are also consistent with the predicted trends, further demonstrating the effectiveness of the model in revealing the composition-property relationship of HEAs.

These experimental verification results not only indicate that the feature-analysis method based on SHAP and LIME can effectively identify the key components affecting the properties of HEAs, but also demonstrate the feasibility and practicality of ML in material design. In the future, further integration of microstructural characterization (such as X-ray Diffraction, Scanning Electron Microscopy, Electron Backscatter Diffraction) and first-principles calculations will help to more deeply reveal the specific contributions of different elements to the alloy strengthening mechanism, providing more solid theoretical and experimental support for the intelligent design of high-performance HEAs.

At the same time, to increase the feasibility of the experimental work of this study, we also added numerical experiments. We imposed noise on the input data and compared the mechanical properties of five algorithm models. Meanwhile, a sensitivity analysis was carried out to identify the input parameters that have the greatest impact.

As shown in Fig. 15, the Robustness analysis results of five ML models (XGBoost, RF, KNN, MLP, KAN) are presented for the task of HEAs material optimization and selection under different levels of measurement noise (from 0% to 50%). Judging from the trends, as the noise level increases, the performance of all models fluctuates to varying degrees. However, XGBoost shows the strongest robustness, and its performance fluctuation is significantly lower than that of other models. Especially when the noise level is high (such as 30%–50%), the performance advantage of XGBoost is more prominent, indicating that it can better handle the noise interference in the data and is suitable for the HEAs material datasets with possible measurement errors in practical applications.

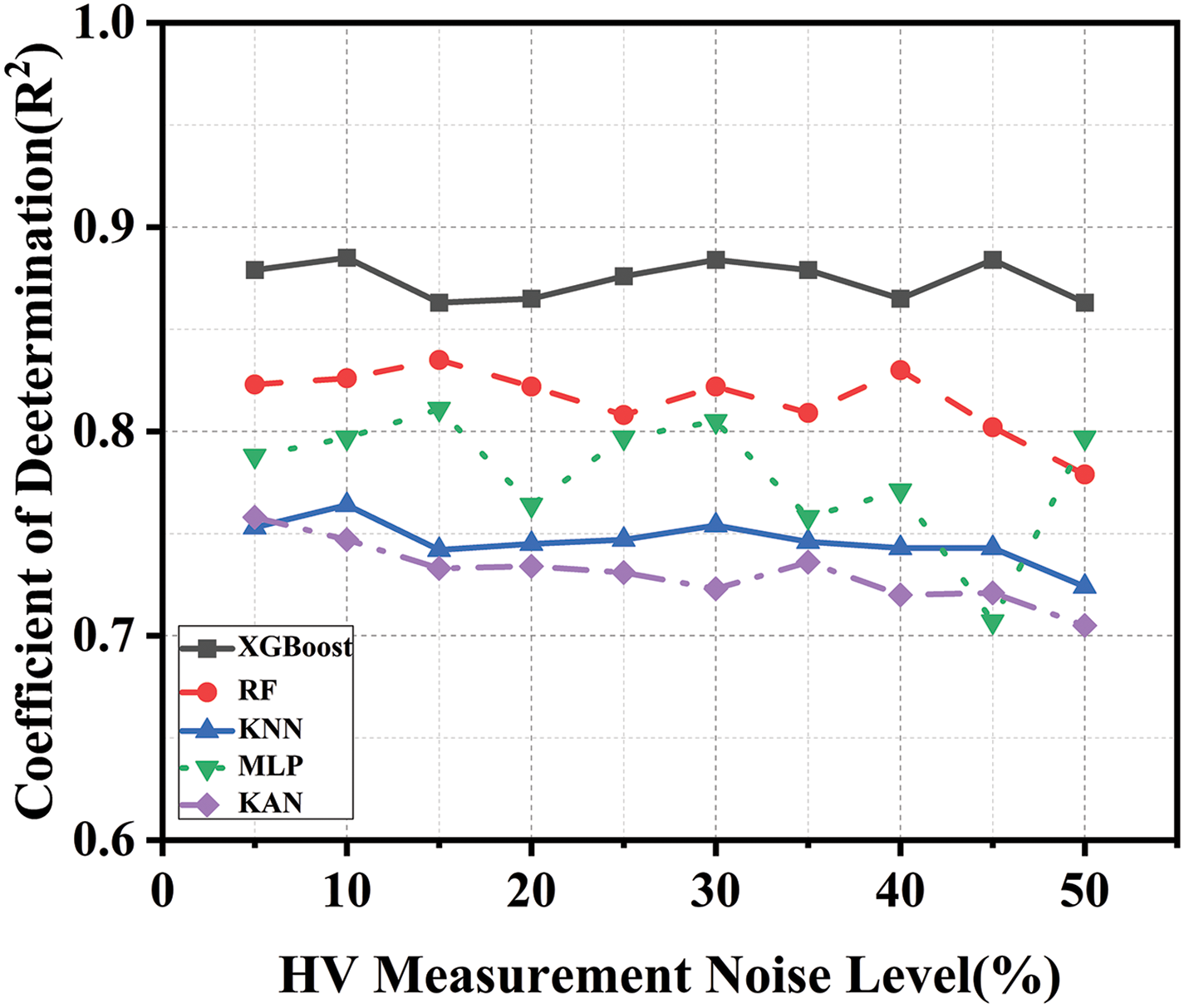
Figure 15: Robustness analysis

At the same time, to quantitatively evaluate the relative importance of each input variable to the model output and identify the influence of the interaction between input variables (the secondary elements) on the output, we conducted a systematic study on the data and performed a sensitivity analysis using the Sobol method. As shown in Fig. 16a,b, the influence degrees of single input variables on the mechanical properties of HEAs show obvious differences: the first-order indices (S) of the main elements Co, Fe, and Ni in the bonding phase are significantly higher than those of other elements (0.25–0.45). The influences of Co and Ni are relatively significant, followed by Fe, indicating that the independent effects of these main elements contribute the most to the output variables. Among the secondary elements in the bonding phase, Cr shows a significant influence, while the first-order indices of Al, Mn, and Mo are close to 0, indicating that their respective influences can be ignored. The ST values of Co/Fe/Ni are close to the S values, further verifying their dominant position; although Cr has a certain ST value (~0.01), it is mainly reflected through the interaction (see the second-order analysis). The above results are highly consistent with the SHAP interpretation results in Section 3.2, verifying the reliability of the analysis method.

Figure 16: Sensitivity analysis of a single input variable. (a) Co/Fe/Ni/Cr (b) Al/Mn/Mo

Regarding the interactions among secondary elements, Fig. 17 shows the analysis results of the second-order Sobol indices. It should be noted that the negative values appearing in the analysis may be due to the estimation fluctuations of the Monte Carlo simulation under a small-sample dataset, especially when the true value is close to zero (which is consistent with the characteristic of a relatively small sample size in this study). Nevertheless, the analysis results still show that the interaction intensities among the secondary elements (e.g., Al, Cr, Mn, Mo) in the binder phase are significantly lower than the independent effects of the main elements (e.g., Co, Fe, Ni). The Sobol index of Mn-Mo is close to zero, indicating that the non-linear effect is not significant. The results of the sensitivity analysis in this study show that the second-order interaction intensities among the secondary elements (Al/Cr/Mn/Mo) in the binder phase are significantly lower than the error range of the Monte Carlo simulation (|S2| < 0.014), and their weak effects may be masked by numerical calculation noise. This phenomenon is consistent with the inherent fluctuation characteristics of Sobol index estimation under small-sample conditions [39]. In addition, the absolute value of the negative value reflects the degree of estimation fluctuation—the larger the negative value, the more significant the fluctuation and the larger the estimation error.

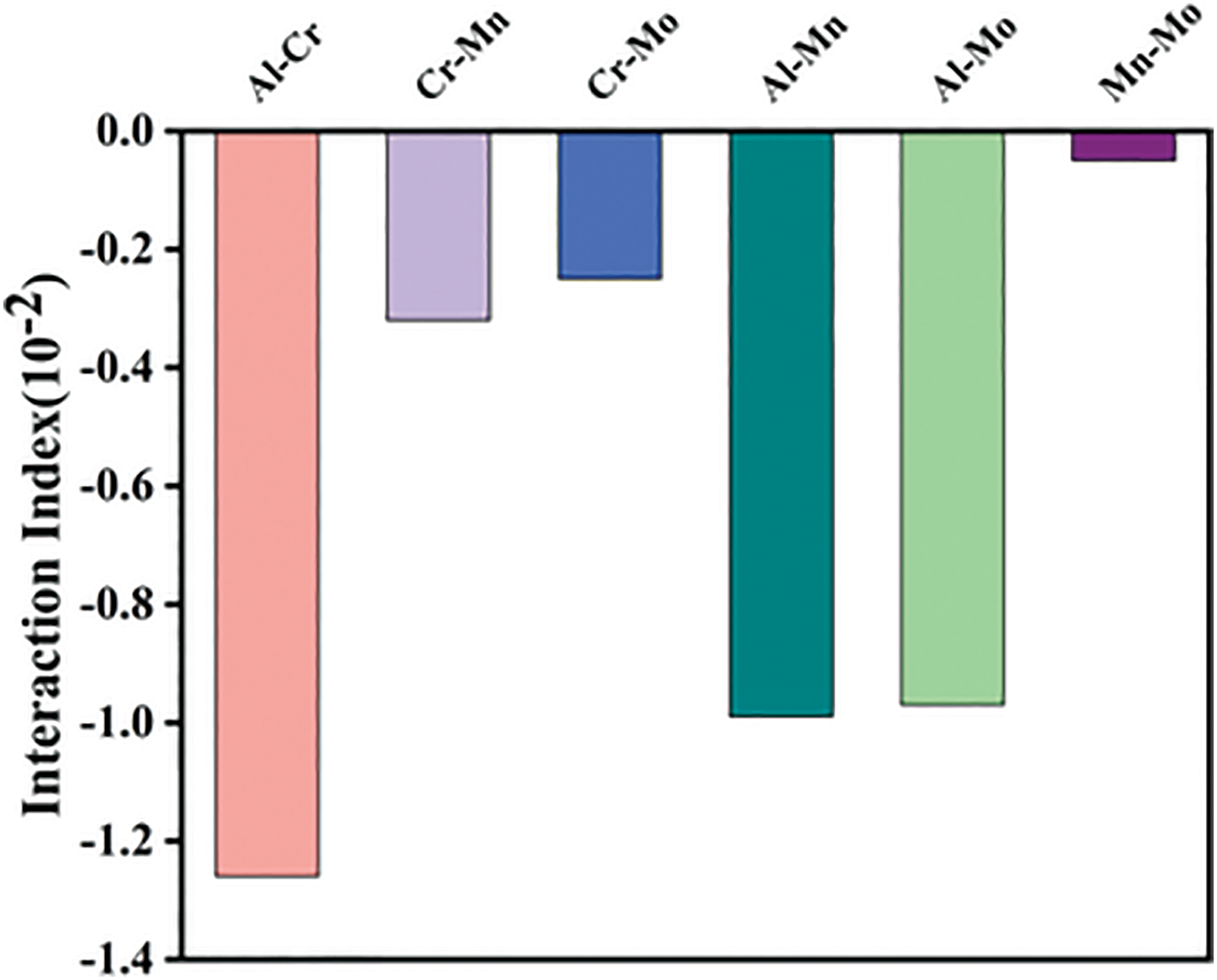
Figure 17: Sensitivity analysis of second-order interaction effects

Therefore, this numerical experiment further validates the credibility of our final choice of XGBoost as the core model for HEAs material optimization in this study, taking into account both the prediction accuracy and the anti-noise ability.

3.6 Finiteness and Instability

The HEAs dataset constructed in this study exhibits significant compositional diversity, encompassing 14 key elements. It fully covers the typical alloying systems used in high-entropy binder phase design, including solid-solution-strengthening transition metals (Fe/Co/Ni-based systems), carbide-forming elements (e.g., W, Mo, Ti), and grain boundary modifiers. In terms of performance space, the dataset spans a wide range of HV values, encompassing both traditional cemented carbides and novel HEAs. Synergistic distribution analysis of composition and performance reveals that the existing dataset effectively captures the relationship between the content of high-entropy constituents in the binder phase and the resulting alloy hardness. This provides the XGBoost model with a broad and representative feature space, facilitating the learning of complex correlations between compositional combinations and mechanical performance. However, the coverage of the compositional space in the dataset is inherently constrained by the scope of the collected data. Due to limitations in experimental resources and costs, it is not feasible to include all possible compositional permutations, and thus, the dataset retains certain limitations.

Consequently, the finiteness of the data, noise, and the unevenness of the data distribution will all give rise to uncertainties. For instance, the finiteness of HEAs data may not be able to comprehensively reflect the complex relationships of material properties, leading to significant uncertainties in the model’s predictions in unknown regions. Moreover, the complexity and assumptions inherent in the XGBoost model itself introduce uncertainties. Although it is capable of handling complex nonlinear relationships, inappropriate selection of the model structure may result in overfitting or underfitting, which will affect the accuracy and reliability of predictions.

3.7 Future Research Directions

3.7.1 Applications of Artificial Intelligence in Solving Partial Differential Equations

In recent years, with the significant improvement of computer hardware performance, the continuous innovation of ML algorithms, and the mature application of automatic differentiation algorithms in artificial intelligence frameworks such as PyTorch and TensorFlow, artificial intelligence has made significant progress in the field of solving partial differential equations [40]. This research currently mainly uses traditional ML algorithms. However, we are actively exploring cutting-edge algorithm technologies and also plan to introduce the method of solving partial differential equations with the help of artificial intelligence to the research fields of HEAs and other materials. Specifically, we plan to establish a learning model for partial differential equations, learn the internal laws of partial differential equations through training data, and then solve key problems in materials science. The following are the key advancement directions of this research:

Physics-Informed Neural Networks (PINNs)

Physics-Informed Neural Networks are an innovative deep-learning framework. By directly integrating the mathematical expressions of partial differential equations (PDEs) into the neural network training process, it enables efficient modeling of physical systems [41]. This method shows unique advantages in handling sparse, noisy, unstructured, and multi-fidelity data. In the research of HEAs, we plan to incorporate the basic principles, such as the laws of thermodynamics and the diffusion equation, which are incorporated into the neural network as loss functions. For example, by adding constraint terms to ensure that the alloy composition conforms to the stoichiometric relationship or making the model prediction results consistent with physical laws, a physically interpretable neural network model can be constructed.

Deep Energy Method (DEM)

DEM proposed by Samaniego et al. [42] has its core idea in utilizing the variational energy structure of the Boundary Value Problem (BVP). It directly takes the energy function of the system as the loss function of the Deep Neural Network (DNN) for optimization. This method, through the principle of physics-driven energy minimization, effectively ensures the mechanical consistency of the solution process, and thus it is named DEM.

Based on this theoretical framework, our research team plans to extend the core methodology of DEM to the field of material design and performance optimization of HEAs. Specifically, by constructing an energy-driven ML model, with the alloy composition as the input variable and the minimization of the strain energy density functional as the optimization objective, the loss function can be expressed as:

L(θ)=∫Ωψ(ε(uθ);c)dΩ(4)

ψ: the strain energy density function uθ: the displacement field predicted by the neural networkc: the parameter of the alloy composition

The optimal composition c* = argmincL(θ) is obtained as the output. The implementation of this method is expected to achieve the directional optimization of the mechanical properties of high entropy alloys and provide a new computational paradigm for material design.

Physics-Informed Neural Operator (PINO)

The Physics-Informed Neural Operator is a new algorithm framework that integrates physical modeling and deep learning [43]. This technology not only inherits the physical constraint idea of PINNs but also has the generalization ability of neural operators. It can perform functional mapping in the function space, thus efficiently predicting the evolution of physical fields under different initial/boundary conditions. We plan to integrate the thermodynamic and kinetic principles of HEAs into the PINO model through methods such as loss functions, regularization terms, or network structure design, to improve the accuracy and reliability of the model in predicting material properties.

3.7.2 Expansion Directions of ML-XAI

This research currently mainly focuses on the mechanical performance indicators of HEAs, such as hardness, fracture toughness, and flexural strength. To further expand the application scope of ML in the design and optimization of HEA materials, future research will be extended to multiple key performance indicators, including physical properties (e.g., thermal conductivity and electrical conductivity), corrosion resistance, wear resistance, and low-cost preparation processes.

3.7.3 Universality of the ML-XAI Framework

The ML-XAI framework developed by our team exhibits excellent universality characteristics. This framework can efficiently process massive material data (including information such as composition, structure, and preparation processes) and discover the potential correlation laws between material characteristics and properties. Even when faced with high-dimensional and complex-structured material data, ML-XAI can still automatically extract the most predictive key features. Based on this advantage, we plan to expand the application of this framework to other material systems, including but not limited to: predicting the optical/electrical properties of optoelectronic materials, predicting the mechanical/physical/chemical properties of polymer materials, and optimizing the key properties of other metallic materials [44]. This expansion will provide strong technical support for the Materials Genome Initiative and accelerate the research and development process of new materials.

4  Conclusions

(1)   This study established a characteristic database for cemented carbides with HEAs as the binder phase and applied the XGBoost model to predict HV, achieving an R2 of 0.88, which indicates strong predictive performance.

(2)   SHAP analysis clarified the decision-making mechanism of the model, identifying Al, Fe, Co, and Ni as key binder phase elements influencing mechanical properties.

(3)   High-throughput calculations determined an optimized binder phase composition. Results suggest that a five-element system—combining Co, Fe, and Ni with Al-Cr, Cr-Mn, and Cr-Mo—significantly enhances mechanical properties, providing data-driven guidance for alloy design.

(4)   LIME analysis and experimental validation of eight cemented carbide compositions confirmed alignment with SHAP results. The high correlation between model predictions and experimental values demonstrates the reliability of the XGBoost model.

(5)   By developing a composition-property prediction model with an interpretable framework, this study enhances model transparency and provides a theoretical foundation for replacing Co with HEAs in cemented carbides, advancing ML-driven materials design.

Acknowledgement: The authors acknowledge the Computers, Materials & Continua for their support of the paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing—Original Draft, Writing—Review & Editing: Jianping Li and Wan Xiong (First Author); Methodology: Tenghang Zhang; Supervision: Hao Cheng and Miaojin He; Validation: Kun Shen; Data Curation: Yu Zhang; Investigation: Junxin Song; Conceptualization, Funding Acquisition, Resources, Supervision, Validation, Writing—Original Draft, Writing—Review & Editing: Ying Deng and Qiaowang Chen (Corresponding Author). All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li K, Yang X, Shen S, Gu Y, Chen M, Ma J. Research and prospect of novel WC-HEA cemented carbide. Int J Adv Manuf Technol. 2024;130(5):2085–117. doi:10.1007/s00170-023-12770-7. [Google Scholar] [CrossRef]

2. Nie H, Zhang T. Development of manufacturing technology on WC-Co hardmetals. Tungsten. 2019;1(3):198–212. doi:10.1007/s42864-019-00025-6. [Google Scholar] [CrossRef]

3. Yeh JW, Chen SK, Lin SJ, Gan JY, Chin TS, Shun TT. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv Eng Mater. 2004;6(5):299–303. doi:10.1002/adem.200300567. [Google Scholar] [CrossRef]

4. Miracle DB, Senkov ON. A critical review of high-entropy alloys and related concepts. Acta Mater. 2017;122:448–511. doi:10.1016/j.actamat.2016.08.081. [Google Scholar] [CrossRef]

5. Wan X, Li Z, Yu W, Wang A, Ke X, Guo H. Machine learning paves the way for high entropy compounds exploration: challenges, progress, and outlook. Adv Mater. 2023;1:2305192. doi:10.1002/adma.202305192. [Google Scholar] [PubMed] [CrossRef]

6. Ghasemi A, Eivani AR, Abbasi SM, Jafarian HR, Ghosh M, Anijdan SHM. Al-Co-Cr-Fe-Ni-Ti high entropy alloys: a review of microstructural and mechanical properties at elevated temperatures. J Alloys Compd. 2025;1010(28):178216. doi:10.1016/j.jallcom.2024.178216. [Google Scholar] [CrossRef]

7. Ansh P, Modalavalasa K, Rao PKA. The design of high-entropy alloys with high hardness: a metaheuristic approach. Sci Rep. 2024;14(1):7692. doi:10.1038/s41598-024-57094-y. [Google Scholar] [PubMed] [CrossRef]

8. Ward L, Agrawal A, Choudhary A, Wolverton C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput Mater. 2016;2(1):16028. doi:10.1038/npjcompumats.2016.28. [Google Scholar] [CrossRef]

9. Schmidt J, Marques MR, Botti S, Marques MA. Recent advances and applications of machine learning in solid-state materials science. npj Comput Mater. 2019;5(1):83. doi:10.1038/s41524-019-0221-0. [Google Scholar] [CrossRef]

10. Lundberg SM, Lee SI. A unified approach to interpreting model predictions. Adv Neural Inf Process Syst. 2017;30:4765–74. [Google Scholar]

11. Liu H, Wang B, Chen P, Li D, Hao J, Yang H, et al. Hierarchical heterogeneous microstructure for enhanced wear resistance of CoCrFeMnNi high-entropy alloy coatings via in-situ rolling assisted laser cladding. J Manuf Process. 2025;141(8):105–20. doi:10.1016/j.jmapro.2025.02.066. [Google Scholar] [CrossRef]

12. Balaji V, Arivazhagan A, Anthony Xavior M. Phase structure, microstructure, and mechanical properties of FeCoCrNi-based eutectic high-entropy alloys reinforced with MWCNTs and Gr. J Sci Adv Mater Devices. 2025;10(2):100868. doi:10.1016/j.jsamd.2025.100868. [Google Scholar] [CrossRef]

13. Wang X, Zhang B, Xu Z, Li M, Skare M. A multi-dimensional decision framework based on the XGBoost algorithm and the constrained parametric approach. Sci Rep. 2025;15(1):4315. doi:10.1038/s41598-025-87207-0. [Google Scholar] [PubMed] [CrossRef]

14. Zhang W, Li P, Wang L, Fu X, Wan F, Wang Y, et al. Prediction of the yield strength of as-cast alloys using the random forest algorithm. Mater Today Commun. 2024;38(8):108520. doi:10.1016/j.mtcomm.2024.108520. [Google Scholar] [CrossRef]

15. Manzali Y, Barry KA, Flouchi R, Balouki Y, Elfar M. A feature weighted K-nearest neighbor algorithm based on association rules. J Ambient Intell Humaniz Comput. 2024;15(7):2995–3008. doi:10.1007/s12652-024-04793-z. [Google Scholar] [CrossRef]

16. Chen T, Guestrin C. XGBoost: a scalable tree boosting system. In: Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining; 2016 Aug 13–17; New York, NY, USA. [Google Scholar]

17. Choudhury A, Mondal A, Sarkar S. Searches for the BSM scenarios at the LHC using decision tree-based machine learning algorithms: a comparative study and review of random forest, AdaBoost, XGBoost, and LightGBM frameworks. Eur Phys J Spec Top. 2024;233(15–16):1–39. doi:10.1140/epjs/s11734-024-01308-x. [Google Scholar] [CrossRef]

18. Breiman L. Random forests. Mach Learn. 2001;45(1):5–32. [Google Scholar]

19. Elsayed N, Elaleem AS, Marie M. Improving prediction accuracy using random forest algorithm. Int J Adv Comput Sci Appl. 2024;15(4):436–41. doi:10.14569/ijacsa.2024.0150445. [Google Scholar] [CrossRef]

20. Cover T, Hart P. Nearest neighbor pattern classification. IEEE Trans Inf Theory. 1967;13(1):21–7. doi:10.1109/tit.1967.1053964. [Google Scholar] [CrossRef]

21. Myśliwiec P, Kubit A, Szawara P. Optimization of 2024-T3 aluminum alloy friction stir welding using random forest, XGBoost, and MLP machine learning techniques. Materials. 2024;17(7):1452. doi:10.3390/ma17071452. [Google Scholar] [PubMed] [CrossRef]

22. Liu Z, Wang Y, Vaidya S, Ruehle F, Halverson J, Soljačić M, et al. KAN: Kolmogorov-Arnold networks. arXiv:2404.19756. 2024. [Google Scholar]

23. Mersha M, Lam K, Wood J, AlShami A, Kalita J. Explainable artificial intelligence: a survey of needs, techniques, applications, and future direction. Neurocomputing. 2024;599(5):128111. doi:10.1016/j.neucom.2024.128111. [Google Scholar] [CrossRef]

24. Ribeiro MT, Singh S, Guestrin C. Explaining the predictions of any classifier. In: Proceedings of the the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2016 Aug 13–16; San Francisco, CA, USA. [Google Scholar]

25. Ribeiro MT, Singh S, Guestrin C. LIME: local interpretable model-agnostic explanations. [cited 2025 May 20]. Available from: https://homes.cs.washington.edu/~marcotcr/blog/lime/. [Google Scholar]

26. Shapley LS. A value for n-person games. Contrib Theory Games. 1953;2:307–17. [Google Scholar]

27. Vriens M, Vidden C, Bosch N. The benefits of Shapley value in key-driver analysis. Appl Mark Anal. 2021;6(3):269–78. [Google Scholar]

28. Molnar C. Interpretable machine learning: a guide for making black box models explainable. Victoria, BC, Canada: Leanpub Publishing; 2020. [Google Scholar]

29. Friedman JH. Greedy function approximation: a gradient boosting machine. Ann Stat. 2001;29(5):1189–232. doi:10.1214/aos/1013203451. [Google Scholar] [CrossRef]

30. Li HN, Zhang H, Chen D, Jiang Z. Comparative study of the microstructure and mechanical properties of WC/high-speed steel composite materials prepared with Co, Ni, and Fe binders. JOM. 2024;76(5):2120–31. doi:10.1007/s11837-024-06429-1. [Google Scholar] [CrossRef]

31. Qiu Z, Liu X, Yang T, Wang J, Wang Y, Ma W, et al. Synergistic enhancement of electromagnetic wave absorption and corrosion resistance properties of high entropy alloy through lattice distortion engineering. Adv Funct Mater. 2024;34(33):2400220. doi:10.1002/adfm.202400220. [Google Scholar] [CrossRef]

32. Abe T, Han K, Goto Y, Ohnuma I, Koyama T. Stabilization of equiatomic solutions due to the high-entropy effect. Mater Trans. 2023;64(4):877–84. doi:10.2320/matertrans.mt-m2022167. [Google Scholar] [CrossRef]

33. Alkan M, Alkan ED, Ari G. AlCoCrFeNi-based high-entropy superalloy coating applied onto the surface of Al-alloys. In: Proceedings of the TMS, 2025 154th Annual Meeting & Exhibition; 2025 Mar 23–27; Cham, Switzerland. [Google Scholar]

34. de la Obra AG, Sayagués MJ, Chicardi E, Gotor FJ. Development of Ti(C, N)-based cermets with (Co, Fe, Ni)-based high entropy alloys as binder phase. J Alloys Compd. 2020;814:152218. doi:10.1016/j.jallcom.2019.152218. [Google Scholar] [CrossRef]

35. Ma QY, Zhang W, Xiang CQ, Ren YL, Qiu KQ. Effect of Al addition on phase constituents and corrosion behaviors of AlxCrFeMo0.5Ni2 high-entropy alloys. J Mater Res Technol. 2025;35:1519–30. doi:10.1016/j.jmrt.2025.01.145. [Google Scholar] [CrossRef]

36. Wang Y, Li D, Wang S, Zhang M, Gong P, Hu Z. Effect of Cr content on the high temperature oxidation behavior of FeCoNiMnCrx porous high-entropy alloys. J Mater Res Technol. 2024;33:3324–33. doi:10.1016/j.jmrt.2024.10.025. [Google Scholar] [CrossRef]

37. Xu Z, Guo C, Deng Y, Wang X, Li A, Ma T. Effect of the synergistic effect of Cr and Mo on the solidification microstructure and mechanical properties of NiAl-based high-entropy alloys. J Alloys Compd. 2025;1010:177814. doi:10.1016/j.jallcom.2024.177814. [Google Scholar] [CrossRef]

38. Feng M, Lin T, Lian G, Chen C, Huang X. The influence of WC content on the microstructure and properties of laser cladding CoCrFeMnNiSi1.6 high-entropy alloy coatings. Ceram Int. 2024;50(24C):55286–306. doi:10.1016/j.ceramint.2024.10.384. [Google Scholar] [CrossRef]

39. Saltelli A, Annoni P, Azzini I, Campolongo F, Ratto M, Tarantola S. Variance-based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput Phys Commun. 2010;181(2):259–70. doi:10.1016/j.cpc.2009.09.018. [Google Scholar] [CrossRef]

40. Wang Y, Bai J, Lin Z, Wang Q, Anitescu C, Sun J, et al. Artificial intelligence for partial differential equations in computational mechanics: a review. arXiv:2410.19843. 2024. [Google Scholar]

41. Liu Y, Liu W, Yan X, Guo S, Zhang CA. Adaptive transfer learning for PINN. J Comput Phys. 2023;490:112305. [Google Scholar]

42. Samaniego E, Anitescu C, Goswami S, Nguyen-Thanh VM, Guo H, Hamdia K. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: concepts, implementation and applications. Comput Methods Appl Mech Eng. 2020;362(2):112790. doi:10.1016/j.cma.2019.112790. [Google Scholar] [CrossRef]

43. Eshaghi SM, Anitescu C, Thombre M, Wang Y, Zhuang X, Rabczuk T. Variational physics-informed neural operator (VINO) for solving partial differential equations. Comput Methods Appl Mech Eng. 2025;437(1):117785. doi:10.1016/j.cma.2025.117785. [Google Scholar] [CrossRef]

44. Kyungtae L, Balachandran PV. Explainable artificial intelligence approach for yield strength prediction in as-cast multi-principal element alloys. Materialia. 2022;26(5):101602. doi:10.1016/j.mtla.2022.101628. [Google Scholar] [CrossRef]