Optimized Metaheuristic Strategies for Addressing the Multi-Picker Robot Routing Problem in 3D Warehouse Operations

1  Introduction

In today’s rapidly evolving logistics landscape, efficient warehouse management is pivotal to maintaining a responsive and cost-effective supply chain. Warehouses are integral components of supply chains, performing critical tasks such as receiving, storage, picking, packing, and shipping of goods [1]. Among these, order picking is notably the most labor-intensive and costly process, contributing to approximately 60% of total operational costs [2]. As such, optimizing the order picking process, particularly in terms of minimizing picking time and travel distance, is essential for enhancing warehouse performance and customer satisfaction.

To meet the increasing demands of e-commerce and same-day delivery services, the integration of autonomous mobile robots has become a transformative trend in warehouse operations [3,4]. These robots enable faster, more accurate, and scalable order fulfillment. However, coordinating multiple robots in a shared environment, while ensuring minimal travel distance and balanced workloads, poses a complex optimization challenge-formally known as the Multi-Picker Robot Routing Problem. The MPRRP, which requires determining optimal routes for multiple robots under constraints such as energy, task allocation, and time, is an nondeterministic polynomial time-hard (NP-Hard) problem [5].

Despite extensive research into picker routing, most existing studies focus on 2D warehouse layouts and either single-picker scenarios or basic multi-robot coordination [6–8]. These models often oversimplify real warehouse environments, where racks, shelves, and pathways span multiple levels. In practice, many modern warehouses adopt vertical storage systems, effectively forming a three-dimensional (3D) layout to maximize space utilization. This introduces new challenges in robot coordination, vertical movement (e.g., elevators, lifts), and dynamic routing planning.

Moreover, while several works have applied metaheuristic algorithms such as Genetic Algorithms (GA) and Particle Swarm Optimization (PSO) to warehouse routing, these approaches often lack tailored strategies for 3D navigation or realistic energy modeling. The coupling of routing scheduling with energy-aware decision-making in multi-robot systems within a 3D warehouse environment remains an underexplored research direction.

This paper aims to bridge these gaps by making the following key contributions:

•   We present a novel 3D mathematical model for the MPRRP that captures the spatial complexity of multi-level warehouse environments, including aisle structure, shelf height, and robot movement across vertical and horizontal planes.

•   We propose two optimized metaheuristic algorithms, GA-MPRRP and PSO-MPRRP, which integrate problem-specific evolution operators and encoding schemes to effectively solve the MPRRP in 3D.

•   We demonstrate, through extensive simulation, that our methods outperform conventional techniques in terms of travel distance, energy efficiency, and computational scalability, especially under large-scale warehouse settings.

The remainder of this paper is organized as follows: Section 2 reviews related work in robotic routing and metaheuristic optimization. Section 3 details the problem formulation and constraints. Section 4 describes the proposed metaheuristic strategies, while Section 5 presents experimental results and analysis. Finally, Section 6 concludes the paper and highlights future research directions.

2  Related Works

In this section, we present the literature on warehousing problems related to our work as multi-picker robot routing problem (MPRRP).

The picker-routing problem in warehouses with 2D layouts is a well-known NP-Hard problem [1], making it particularly challenging to solve. Various methods have been proposed to tackle this problem, including exact algorithms [9], heuristics and metaheuristics [7,8,10], genetic algorithms, and stochastic models. These approaches are typically applied individually or in combination to improve computational efficiency. A comprehensive review by [6] highlights that most existing studies focus on conventional 2D warehouse layouts and often consider simplified settings, such as single-picker routing. Notably, exact methods remain rare due to their computational cost, especially for large-scale problems. For instance, study [9] introduces two exact algorithms that significantly improve a mixed-integer programming formulation and generalize existing dynamic programming approaches; however, these methods suffer from scalability issues. Other studies such as [7] and [8] emphasize heuristic-based strategies to address order picking with predefined routing policies or height-level constraints in high-bay systems. While these works demonstrate effective results in specific 2D settings, they are generally limited to single-picker scenarios and do not extend to full three-dimensional (3D) warehouse modeling.

In contrast, research on picker-routing in 3D environments remains limited. One relevant study [11] investigates a three-dimensional vehicle routing problem for fuel delivery and proposes a 3D Ant Colony Optimization algorithm. However, this work is outside the warehouse domain and focuses on vehicle routing rather than intra-warehouse picking by robots.

Recent developments in robot routing planning have addressed 2D multi-objective routing problems using evolutionary algorithms. For example, study [12] employs an improved NSGA-II algorithm, while study [13] introduces a self-learning mechanism based on an enhanced artificial bee colony algorithm. These studies contribute valuable algorithmic insights but do not consider warehouse-specific constraints or 3D environments with multiple pickers.

Despite the growing importance of automation in warehouse operations, research explicitly targeting the multi-picker robot routing problem in three-dimensional warehouse layouts remains scarce. To bridge this gap, our study proposes a novel problem formulation that jointly considers multi-robot coordination and spatial complexity in 3D warehouse environments. Furthermore, we introduce optimized metaheuristic strategies to enhance solution quality and scalability. This contribution is twofold: (i) a new mathematical model for multi-robot routing in 3D warehouses, and (ii) an effective algorithmic framework tailored to this complex logistics problem.

3  Preliminaries and Problem Formulation

3.1 Preliminaries

The MPRRP addresses the challenge of minimizing the total energy consumption of multiple picker robots tasked with retrieving required products from a structured parallel 3D warehouse layout, as shown in Fig. 1a. The warehouse consists of parallel shelves arranged systematically, with each shelf divided into multiple vertical layers. Each layer is further segmented into smaller storage cells, each containing a different quantity of a single product. A product type can be stored in multiple cells. A counter is set up in the warehouse to collect all picked products. Picker robots are tasked with retrieving items from specific cells based on predefined order lists, navigating in 3D space along the x, y, and z axes. Movements along the x-axis allow traversal across shelves, the y-axis facilitates navigation between parallel aisles, and the z-axis provides vertical access to different shelf layers. The warehouse cross-sections are shown in Fig. 1b–d.

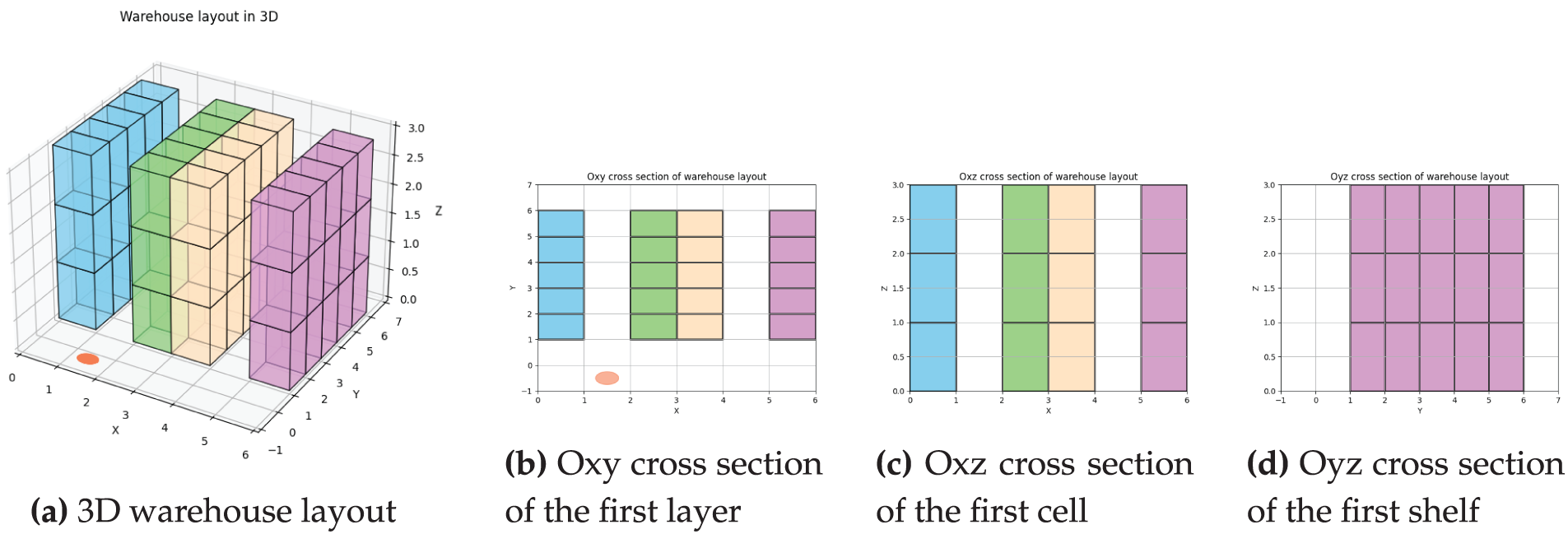
Figure 1: Warehouse layout with 4 shelves, 3 layers in a shelf and 5 cells in a layer

Given S parallel shelves, with S/2 aisles between the shelves to facilitate movement within the warehouse, each shelf is divided into L vertical layers, with C cells in each layer, creating a grid of storage spaces. The total number of cells B in the warehouse is given by B=S×L×C. Multiple types of products P are arranged in cells, with each type of product potentially occupying multiple cells. Each cell Bi contains a different quantity qi of a specific product pi, which has weight wi, where i∈[1,B]. The cell Bi is positioned at shelf index k, layer index h, and cell index g, which is stated in Eq. (1). Hence, i, as shown in Eq. (2), can be determined using k, h, and g.

k=⌊i−1L×K⌋h=⌊i−k×L×K−1K⌋g=i−k×L×K−h×K−1(1)

i=g×L×K+h×K+k+1(2)

Furthermore, Bi represents the point with coordinates (x,y,z) in the three-dimensional Cartesian coordinate system, which can be calculated from k, h, and g as shown in Eq. (3).

x=k+⌊k+12⌋y=g+1z=h(3)

Let the counter be an additional cell, B0, in the warehouse, located at the point with coordinates (1,−1,0). The minimum distance between two cells, Bi at (xi,yi,zi) and Bj at (xj,yj,zj), for all i,j∈[0,B] in the warehouse, is calculated as shown in Eq. (4).

Di,j=Dx(xi,xj)+Dy(yi,yj)+Dz(zi,zj)(4)

where:

Dx(xi,xj)=|xi−xj|(5)

Dy(yi,yj)={0,xi=xj|yi−yj|,|xi−xj|=2min(|yi+yj|,(2(k+1)−yi−yj)),otherwise(6)

Dz(zi,zj)={|zi−zj|,xi=xj and yi=yj|zi+zj|,otherwise(7)

Consider R picker robots, each beginning at the counter to collect the required products. Every robot has a maximum capacity Cr and follows a specific energy consumption model. All robots must start and end their journey at the counter, either after collecting all the required products or reaching their capacity limit. A robot’s tour, denoted as T, refers to the sequence of cells visited by the robot between two consecutive times when robot r returns to the counter, expressed as T={B0,Bi,…,B0|∃i∈[1,B]}. The robot r completes a total of Vr tours. A route Rr for robot r is formed by all its tours, i.e., Rr={Tvr|v∈[1,Vr]}. The overall routing for all robots is the collection of all individual robot routes, i.e., R={Rr|r∈[1,R]}.

The energy consumption of each robot includes the energy used for moving on the floor and the energy for going up and down. The moving energy consumption EMr for picker robot r to travel on the floor from Bi to Bj is determined by Eq. (8).

EMr(i,j)=(Dx(xi,xj)+Dy(yi,yj))WMr(8)

where WMr is the moving energy consumption per distance (Wh/m). The energy required for lifting and lowering, ELr, for picker robot r to travel from Bi to Bj is calculated in Eq. (9).

ELr(i,j)=Dz(zi,zj)WLr(9)

where WLr is the energy consumption for lifting and lowering per unit distance (Wh/m). The total energy consumption Ei,jr of picker robot r to travel from cell Bi to cell Bj and retrieve the required products from cell Bj is calculated in Eq. (10).

Ei,jr=EMr(i,j)+ELr(i,j)(10)

The energy consumption E0r of picker robot r while waiting at the counter for the next tour is calculated in Eq. (11).

E0r=(a0r−1)W0r(11)

where a0r is number of times that robot r returns to the counter in solution.

The total energy E consumed by all picker robots in the routing, while ensuring that all required products are picked up and brought to the counter, with the weight of all products in picker robot r being less than its maximum capacity CMr, is calculated in Eq. (12).

E=∑r=1R∑i=0B∑j=0BEi,jrai,jr+∑r=1RE0r(12)

where ai,jr has value 1 if the picker robot r visits cell Bj from cell Bi and 0 in other cases.

3.2 Problem Formulation

The problem can be stated as follows: A 3D warehouse layout consists of parallel shelves with multiple layers and cells, where each cell contains a specific type of product with varying quantities and weights, as illustrated in Fig. 1a. Products may be distributed across multiple cells. A list of required products must be collected by a team of picker robots. Each robot starts at the counter, retrieves the assigned products, and returns either after collecting all required items or when its maximum capacity is reached. The robot’s route is determined by the sequence of cells it visits. During operation, robots move along the floor, lift products between layers, and wait at the counter–each action consuming different amounts of energy. The goal is to determine the optimal routing for all robots that ensures the collection of all required products, satisfies the product demand constraints in Eq. (14), the robot operation conditions in Eqs. (15) and (18), and the capacity constraints in Eqs. (16), (17), and (19), while minimizing the total energy consumption as defined in Equation (specify equation number here if applicable).

The mathematical model of the problem is as follows.

Input:

•   ℬ={Bi|i=0..B}: Set of cells.

•   P: Number of product types in warehouse.

•   𝒫={pi,qi,wi|i=1..B}: Set of products in cells.

•   𝒰={pu,qu,wu|u=1..U}: Set of required products.

•   ℛ={r|r=1..R}: Set of picker robots.

•   𝒲={WMr,WLr,W0r|r=1..R}: Set of energy consumptions for moving, up and down per meter, and energy consumptions for waiting of the picker robots per time.

•   𝒞={Cr|r=1..R}: Set of capacities of the picker robots.

Output: R={Rr|∀r∈[1,R]}

Objective function:

min(E)=min(∑r=1R∑i=0B∑j=0BEi,jrai,jr+∑r=1RE0r)(13)

Constraints:

P≤B(14)

T={B0,Bi,...,B0|∀i∈[1,B]}(15)

∑u=1Uwuqu=∑r=1R∑i=1Bwiqirxir,∃xir∈{0,1},∀r∈[1,R],∀i∈[1,B](16)

where xr has value 1 if the picker robot r takes products from cell Bi and 0 in other cases; wi is the weight of the product in cell Bi; qir is the quantity of products in cell Bi collected by robot r.

∑r=1R∑i=1BwiqirxirxiTxT,r<Cr,∀r∈[1,R],∀T(17)

where xr has value 1 if the picker robot r takes products i and 0 in other cases; xiT has value 1 if the cell Bi is visited in tour T and 0 in other cases; xT,r has value 1 if the tour T is visited by robot r.

∑r=1Rqir≤qi,∀i∈[1,B](18)

pi=∅,qi=0,∀i=0(19)

4  Proposed Algorithms

Metaheuristic algorithms are powerful and flexible tools for solving diverse optimization problems [14–17]. They iteratively guide the search process by combining exploration and exploitation strategies [18]. A key challenge lies in designing problem-specific operators. In this section, we detail two tailored algorithms developed to effectively solve the MPRRP.

4.1 Solution Presentation

An individual (particle) is represented by a one-dimensional array, called a cell array, of length A, which corresponds to the number of cells storing the required product type. The array is expressed as [I1,I2,…,IA], where each element Ii corresponds to a cell index Bi, with i∈[1,A], and each Ii has a unique value. The individual is a permutation of theA indices of the cells storing the required products. As shown in Fig. 2a, the individual encoding is based on 6 cells containing the product types, selected from a warehouse of 20 cells. Cells that do not store the required products are excluded to reduce the array’s length, minimizing redundancy and improving the quality of the individual.

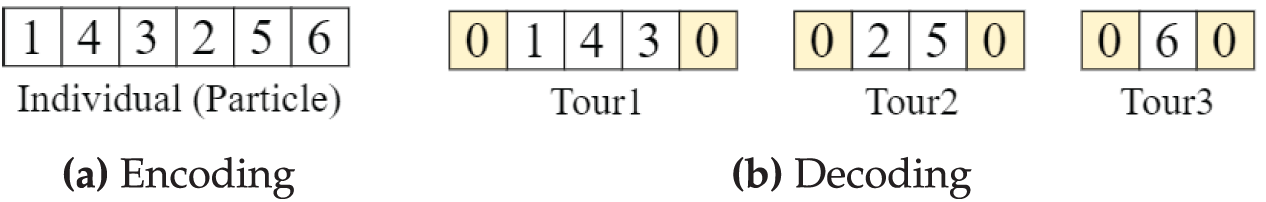
Figure 2: Demonstration of solution encoding and decoding

The greedy algorithm is used to decode an individual into multiple routes for each robot, considering the robot’s maximum capacity and the product weights in the tour. After completing a tour, the robot returns to the counter and begins a new tour. The sequence of elements in the cell array determines the order of cell visits in the robot’s tour. As shown in Fig. 2b, the individual is decoded into three tours: Tour1, Tour2, and Tour3. The ring policy is applied to distribute the tours among the robots (e.g., with 2 robots and 3 tours: Tour1→Robot1, Tour2→Robot2, Tour3→Robot1).

4.2 Evolution Algorithms

4.2.1 The PSO-MPRRP Algorithm

PSO-MPRRP, described in Algorithm 1, utilizes the XOR method to enhance exploration and exploitation. First, Xor1 is obtained by applying a bitwise XOR between the particle’s current position and its personal best (Pbest), capturing individual learning. Similarly, Xor2 is computed using the XOR operation between the current position and the global best (Gbest), incorporating swarm-wide knowledge. The Velocity is then generated using a one-point crossover between Xor1 and Xor2, serving as a mask. Finally, the new position is determined using an order crossover operator applied to three parents (the current position, Pbest, and Gbest), with the velocity as a mask guiding the recombination process. This hybrid approach, as shown in Fig. 3, enhances ability of PSO-MPRRP to maintain diversity while accelerating convergence, making it highly effective for solving the MPRRP problem.

Figure 3: Demonstration of PSO-MPRRP

The XOR method

The XOR method between two permutation positions applies an element-wise comparison operation. For each corresponding pair of elements at the same position index in two permutations, the operation sets the resulting value to 1 if the elements differ and to 0 if they are identical. This creates a binary mask indicating positions where the two permutations differ, as illustrated in Fig. 3a,b. For example in Fig. 3a, comparing positions [3, 4, 1, 2, 5, 6] and [2, 1, 4, 5, 3, 6] would yield [1, 1, 1, 1, 1, 0], indicating that elements at positions 1 to 5 are different. This binary representation enables the algorithm to identify which positions should be influenced by personal best (Pbest) or global best (Gbest) solutions during the position update process.

The update of velocity

To update Velocity, a one-point crossover is applied to combine the binary array representations of Xor1 and Xor2, as illustrated in Fig. 3c. In this method, a crossover point, denoted as point, is randomly selected within the length of the arrays. The arrays are then split at this point, creating two segments: one before and one after the crossover point. The offspring are generated by swapping the segments between the two parents at the crossover point.

The update of new position

The order crossover operator is applied to three parents: the current position, Pbest, and Gbest, guided by a velocity mask to generate a new position, as shown in Fig. 3d. The velocity mask indicates which parent’s element to select at each index, considering all three parents. For each index, the mask instructs the algorithm to choose one of the three parents’ elements at that position. Initially, elements from Pbest are taken in order, ensuring the sequence from Pbest is preserved. Next, elements from Gbest are selected, maintaining their order while avoiding duplicates of the already chosen elements from Pbest. Finally, for any remaining positions, elements from the current position are selected in order, ensuring the offspring maintains the structure of the current solution. This approach allows the exploration of promising solutions from all three parents, balancing the contributions from the current solution, Pbest, and Gbest, while preserving their relative order to generate a new, potentially improved position.

4.2.2 The GA-MPRRP Algorithm

The GA-MPRRP employs the crossover operator, mutation operator, and selection policy on the population in each generation, as described in Algorithm 2. The Multi-Point Order Crossover (MOX) operator ensures order preservation by selecting multiple crossover points and maintaining unique elements in the offspring. Additionally, swap mutation enhances exploration and prevents premature convergence. Selection is performed using the roulette wheel method, balancing the exploitation of high-quality solutions with the preservation of genetic diversity. This combination of MOX crossover, swap mutation, and roulette wheel selection enables an efficient search within complex solution spaces. These techniques are particularly effective for solving MPRRP problems, where maintaining solution integrity is crucial for convergence to optimal solutions.

The crossover operator

The MOX is used in GA-MPRRP to generate two offspring from two parents. After selecting two random points, p1 and p2, the offspring inherit the gene segment between these points, with the remaining genes taken in the order they appear in the parents. As shown in Fig. 4a, each parent is divided into three parts by two random crossover points. This operator ensures a valid permutation without duplicated cells. The OX operator introduces variability by creating new cell combinations while preserving order information, potentially maintaining high-quality tours. However, if the crossover points split advantageous tours, it may increase population diversity.

Figure 4: Illustration of the evolution operators GA-MPRRP

The mutation operator

The mutation operator swaps two random cells in the individual, as shown in Fig. 4b, where the second and fifth elements are swapped. This preserves the permutation structure, ensures a valid individual, and increases population diversity. While excessive use can disrupt high-quality solutions, when balanced, it helps prevent premature convergence and improves the algorithm’s ability to find optimal or near-optimal solutions.

The selection operator

In GA-MPRRP, roulette selection updates the population by selecting individuals based on fitness-proportional probabilities. A cumulative probability distribution is used, mapping random values to select individuals. This method favors fitter solutions while maintaining population diversity for effective optimization.

4.2.3 Complexity Analysis

The complexity of the proposed PSO-MPRRP and GA-MPRRP algorithms is analyzed with size be the population/swarm size and max_iter the number of iterations, defined as the number of fitness function evaluations. The fitness function computes the total energy consumption (Eq. (12)) for a solution. For each algorithm:

•   Initialization: Evaluating size individuals requires size fitness evaluations.

•   Iteration: Each of max_iter iterations, PSO-MPRRP evaluates size new positions, costing size fitness evaluations while GA-MPRRP evaluates size offsprings and costing size fitness evaluations.

Total fitness evaluations: O(size+max_iter×size)=O(max_iter×size). Thus, both algorithms have complexity O(max_iter×size).

5  Numerical Results

5.1 Problem Instances

The experimental data, presented in Table 1, includes parameters representing various warehouse and robot operation factors. These factors are essential for evaluating and optimizing the performance of metaheuristic algorithms in solving the multi-picker robot routing challenge. By varying these parameters, the paper examines the efficiency and effectiveness of the proposed strategies under different operational conditions.

5.2 Experimental Settings

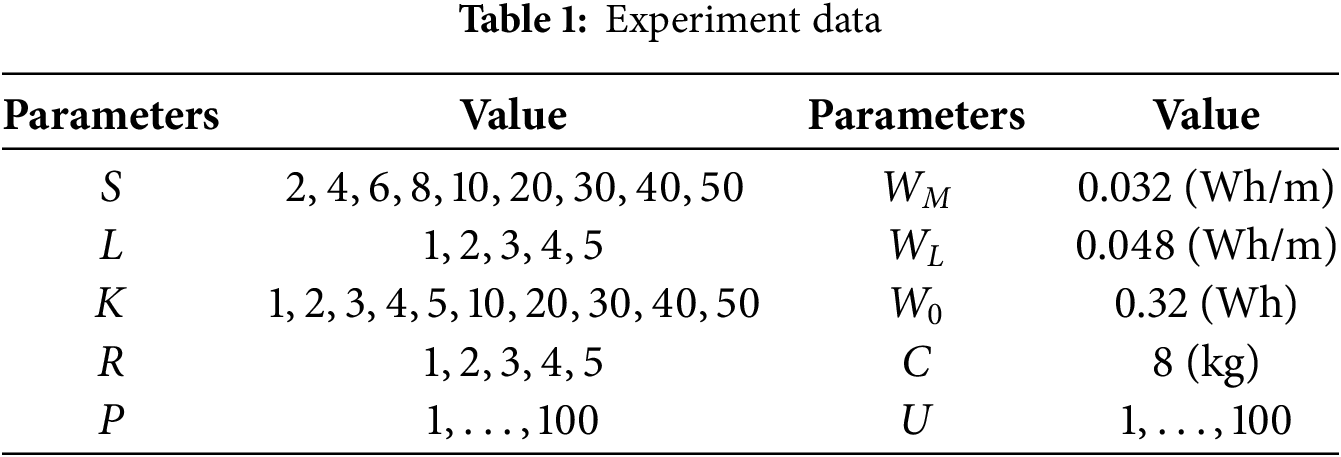
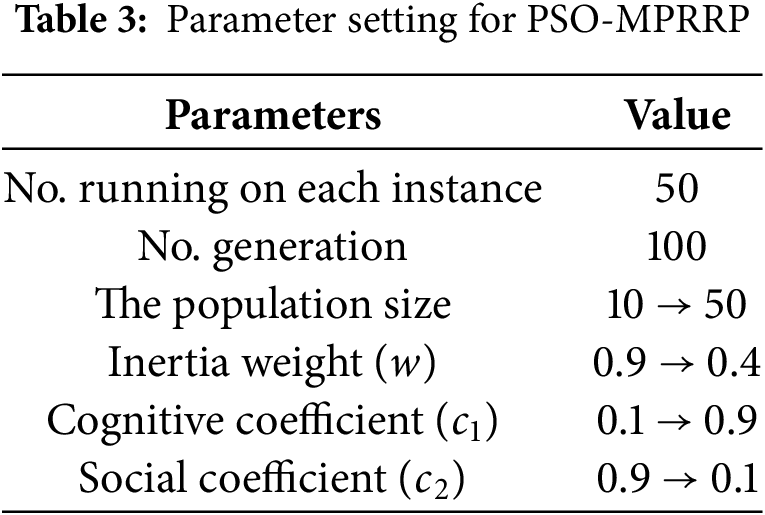
The experiments were performed on a computer featuring an Intel processor with a 1 GHz clock speed and 16 GB of RAM, providing adequate computational resources for testing. The implementation was done in Python, with the environment set up to efficiently support multiple runs, ensuring consistent and reliable results. All parameters of GA-MPRRP and PSO-MPRRP are set in detail in Tables 2 and 3, respectively.

5.3 Experiments Results

Visualization of the tours is presented in Fig. 5. The fitness improved 29% from generation 0 to 54 (23,344 to 16,608) in the data file 10_5_10, transforming chaotic overlapping tours into coordinated systematic ones. The optimization successfully minimized redundant overlap and demonstrated effective multi-robot coordination convergence.

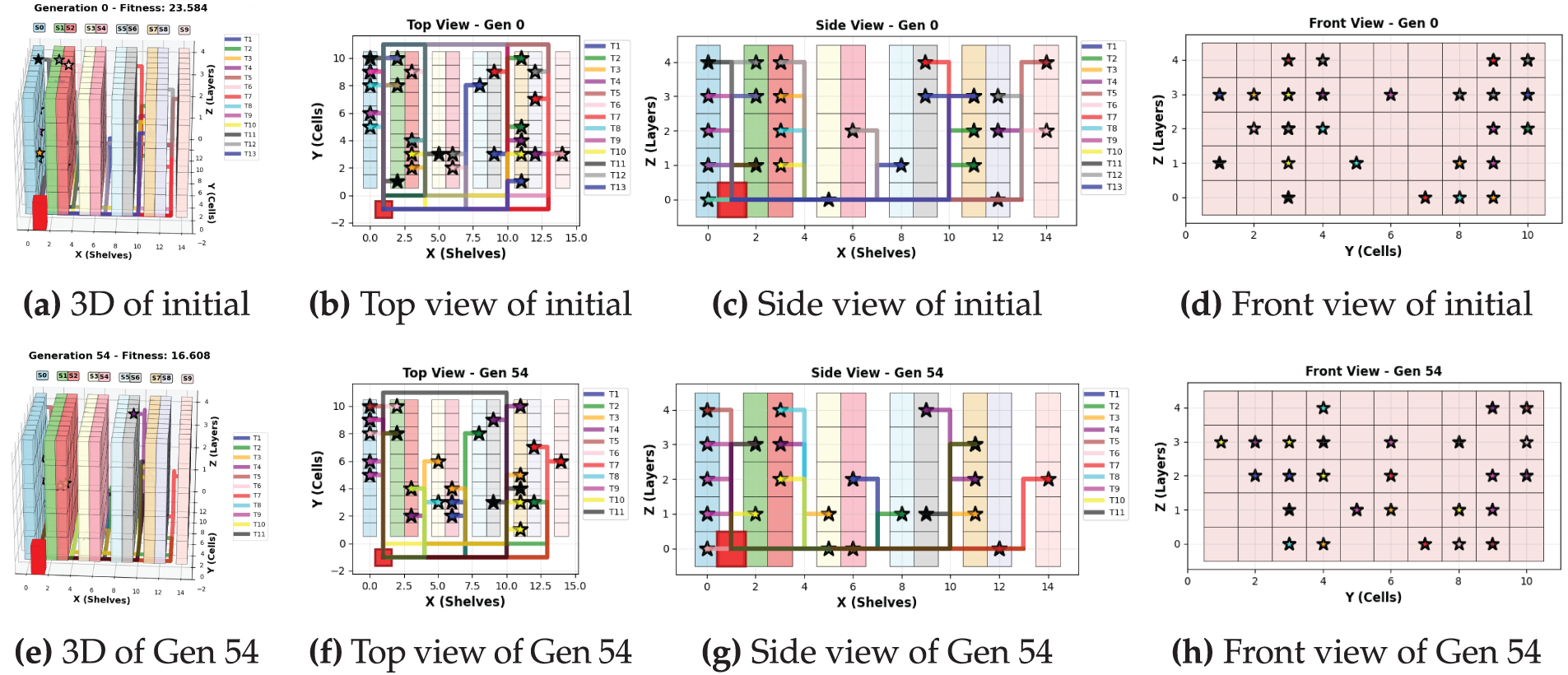
Figure 5: Visualization tours of 2 robots in the data file 10_5_10 with ring policy distribution: tours (T1, T3, T5, T7, T9, T11) assigned to Robot1, tours (T2, T4, T6, T8, T10) assigned to Robot2

Test the optimal parameters for the proposed algorithms: GA-MPRRP and PSO-MPRRP

Fig. 6a shows that the 0.6–0.4 combination (yellow line) achieves the lowest energy consumption, particularly after 20 generations, consistently outperforming other combinations. This indicates that prioritizing the particle’s own experience (c1 = 0.7) over the swarm’s experience (c2 = 0.3) leads to more effective optimization. Thus, c1 = 0.7 and c2 = 0.3 is the optimal setting for minimizing energy consumption. Fig. 6b demonstrates that a mutation rate of 0.6 with a crossover rate of 1 yields optimal performance in the GA-MPRRP. Fig. 6c shows that a swarm size of 20 (blue dotted line) results in the lowest energy consumption after about 30 s and maintains it throughout the simulation. Swarm sizes of 30, 40, and 50 improve energy consumption but do not match the efficiency of size 20. A swarm size of 10 performs well initially but plateaus at a higher energy level. Therefore, a swarm size of 20 is the most effective for minimizing energy consumption in this PSO implementation. Fig. 6d shows that a population size of 20 (blue dotted line) achieves the lowest energy consumption after 20 s and maintains it throughout the simulation. A population size of 10 improves quickly but plateaus at a higher energy level, while larger sizes (30, 40, and 50) lead to higher energy consumption and slower convergence. Thus, a population size of 20 is the most effective for minimizing energy consumption in this GA implementation.

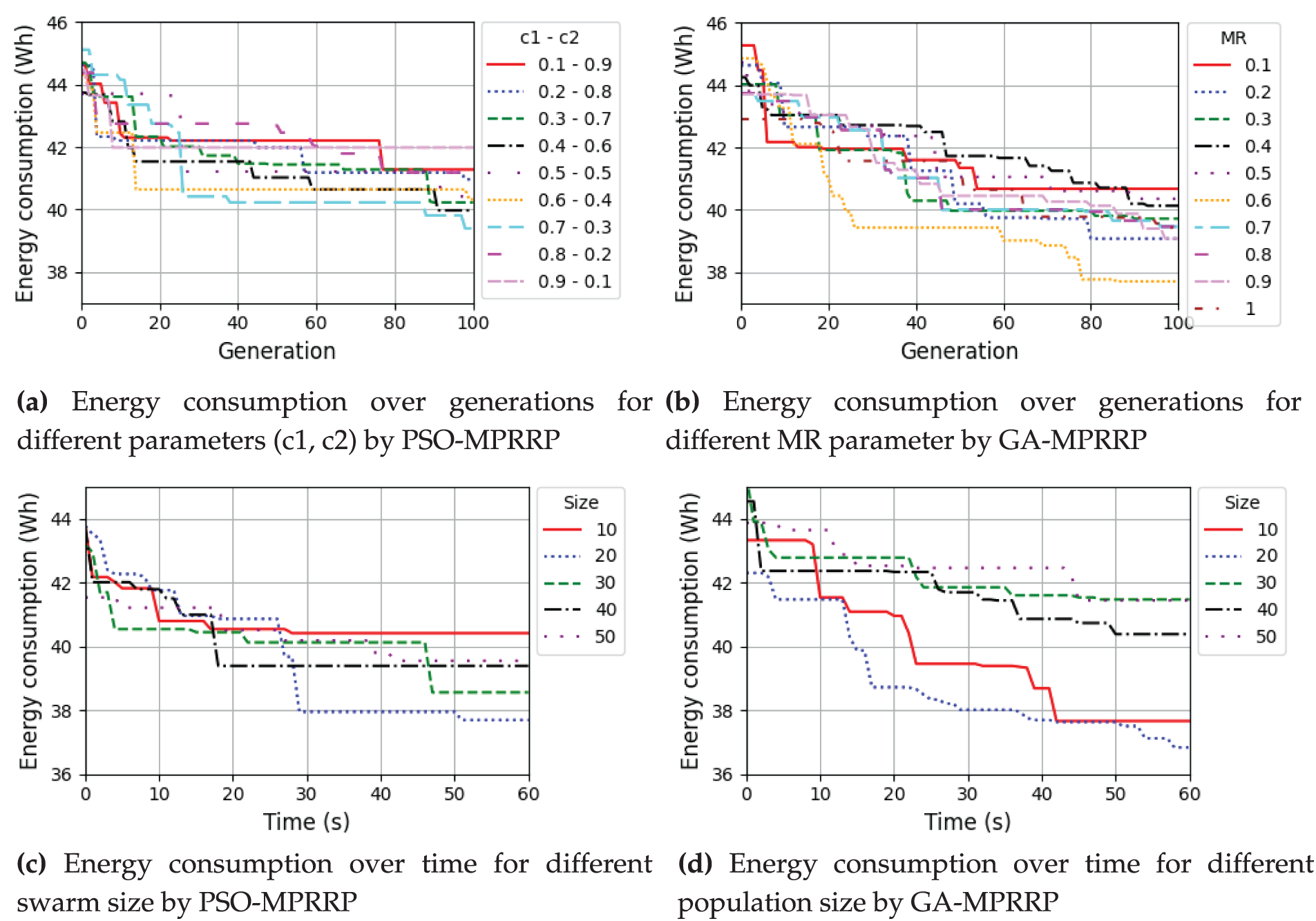
Figure 6: Energy consumption over generations and time for different parameters in the data file 10_3_10 with 3 picker robots, calculated by PSO-MPRRP and GA-MPRRP algorithm

Evaluate the performance of the two proposed algorithms under varying parameter settings

Fig. 7a compares the convergence of GA-MPRRP and PSO-MPRRP in terms of energy consumption over time. While PSO-MPRRP initially converges faster and achieves lower energy consumption, GA-MPRRP surpasses it after about 30 s, ultimately reaching a lower final energy consumption. This indicates that GA-MPRRP offers better long-term optimization, despite PSO-MPRRP’s quicker early convergence. Fig. 7b compares GA-MPRRP and PSO-MPRRP in terms of energy consumption and result consistency across varying robot counts. GA-MPRRP consistently achieves lower energy consumption and exhibits smaller error bars, indicating more stable performance. While PSO-MPRRP shows a trend of reduced energy consumption with more robots, its higher standard deviation indicates greater variability. Thus, GA-MPRRP outperforms PSO-MPRRP in both energy efficiency and robustness.

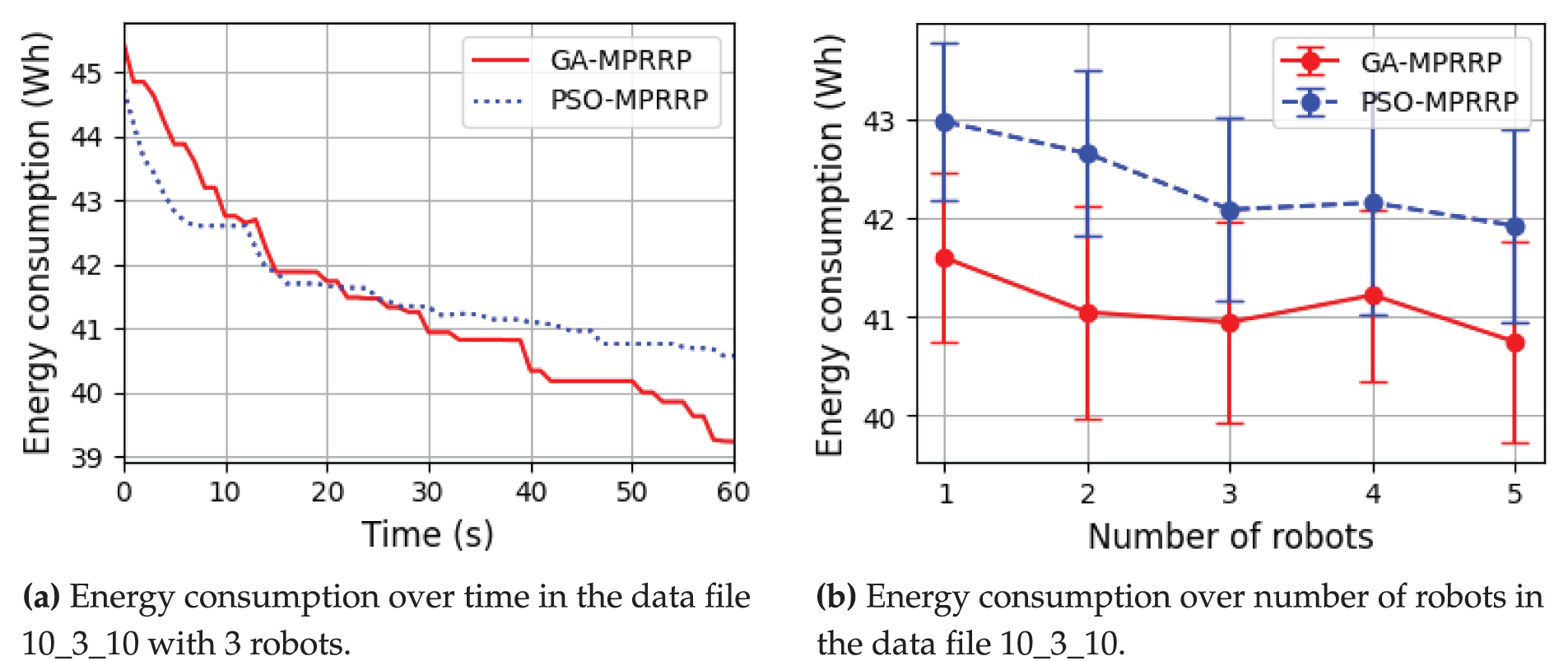
Figure 7: Energy consumption calculated by PSO-MPRRP and GA-MPRRP algorithm

6  Conclusion

This paper addresses MPRRP in warehouse operations, a crucial challenge for optimizing modern logistics and supply chains. We proposed a mathematical model and developed two metaheuristic algorithms, GA-MPRRP and PSO-MPRRP, to solve the problem efficiently. These approaches optimize robot routes, reduce operational costs, and minimize execution time. Experimental results validate the effectiveness of the proposed methods, with GA-MPRRP demonstrating superior solution quality through exploration, and PSO-MPRRP achieving faster convergence and computational efficiency. Despite these promising results, several limitations remain. The computational scalability of the algorithms in very large or real-time warehouse environments poses challenges. Moreover, the current evaluation relies on synthetic data, and the energy model used is simplified compared to real-world robotic dynamics. These factors may impact the direct applicability of the approach in highly dynamic or complex warehouse systems. Future work will explore hybridization with other metaheuristics, integration with learning-based methods for adaptive decision-making, and validation using real-world warehouse datasets. These directions aim to enhance the adaptability, robustness, and practical deployment of the proposed algorithms. In summary, GA-MPRRP and PSO-MPRRP represent a significant step forward in solving the MPRRP, offering scalable and intelligent solutions for enhancing the efficiency of automated warehouse operations.

Acknowledgement: This research was sponsored by Hanoi University of Industry, Hanoi, Vietnam.

Funding Statement: This research is funded by Hanoi University of Industry, Hanoi, Vietnam, under contract number 25−2024−RD/HD−DHCN.

Author Contributions: Thi My Binh Nguyen: methodology, supervision, software, writing—original draft, editing, and funding acquisition. Thi Ngoc Huyen Do: methodology, resource, writing—original draft, and editing. Thi Hoa Hue Nguyen: methodology, software, writing—original draft, funding acquisition. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data will be made available on request.

Ethics Approval: The study does not include human or animal subjects and is approved by the committee.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Boysen N, De Koster R, Weidinger F. Warehousing in the e-commerce era: a survey. Eur J Oper Res. 2019;277(2):396–411. doi:10.1016/j.ejor.2018.08.023. [Google Scholar] [CrossRef]

2. Casella G, Volpi A, Montanari R, Tebaldi L, Bottani E. Trends in order picking: a 2007–2022 review of the literature. Prod Manuf Res. 2023;11(1):2191115. [Google Scholar]

3. Yu S, Puchinger J, Sun S. Van-based robot hybrid pickup and delivery routing problem. Eur J Oper Res. 2022;298(3):894–914. doi:10.1016/j.ejor.2021.06.009. [Google Scholar] [CrossRef]

4. Zhang S, Zhuge D, Tan Z, Zhen L. Order picking optimization in a robotic mobile fulfillment system. Expert Syst Appl. 2022;209:118338. doi:10.1016/j.eswa.2022.118338. [Google Scholar] [CrossRef]

5. Shah B, Khanzode V. A comprehensive review of warehouse operational issues. Int J Logist Syst Manage. 2017;26(3):346–78. doi:10.1504/ijlsm.2017.081962. [Google Scholar] [CrossRef]

6. Masae M, Glock CH, Grosse EH. Order picker routing in warehouses: a systematic literature review. Int J Prod Econ. 2020;224:107564. doi:10.1016/j.ijpe.2019.107564. [Google Scholar] [CrossRef]

7. Silva A, Coelho LC, Darvish M, Renaud J. Integrating storage location and order picking problems in warehouse planning. Transp Res Part E Logist Transp Rev. 2020;140:102003. doi:10.1016/j.tre.2020.102003. [Google Scholar] [CrossRef]

8. Cano JA, Cortés P, Muñuzuri J, Correa-Espinal A. Solving the picker routing problem in multi-block high-level storage systems using metaheuristics. Flex Serv Manuf J. 2023;35(2):376–415. doi:10.1007/s10696-022-09445-y. [Google Scholar] [CrossRef]

9. Pansart L, Catusse N, Cambazard H. Exact algorithms for the order picking problem. Comput Oper Res. 2018;100:117–27. [Google Scholar]

10. Haouassi M, Kergosien Y, Mendoza JE, Rousseau LM. The picker routing problem in mixed-shelves, multi-block warehouses. Int J Product Res. 2025;63(4):1304–25. doi:10.1080/00207543.2024.2374845. [Google Scholar] [CrossRef]

11. Guo N, Qian B, Na J, Hu R, Mao JL. A three-dimensional ant colony optimization algorithm for multi-compartment vehicle routing problem considering carbon emissions. Appl Soft Comput. 2022;127:109326. doi:10.1016/j.asoc.2022.109326. [Google Scholar] [CrossRef]

12. Duan P, Yu Z, Gao K, Meng L, Han Y, Ye F. Solving the multi-objective path planning problem for mobile robot using an improved NSGA-II algorithm. Swarm Evol Comput. 2024;87:101576. doi:10.1016/j.swevo.2024.101576. [Google Scholar] [CrossRef]

13. Ye F, Duan P, Meng L, Sang H, Gao K. An enhanced artificial bee colony algorithm with self-learning optimization mechanism for multi-objective path planning problem. Eng Appl Artif Intell. 2025;149:110444. doi:10.1016/j.engappai.2025.110444. [Google Scholar] [CrossRef]

14. Binh NTM, Ngoc NH, Binh HTT, Van NK, Yu S. A family system based evolutionary algorithm for obstacle-evasion minimal exposure path problem in Internet of Things. Expert Syst Appl. 2022;200:116943. doi:10.1016/j.eswa.2022.116943. [Google Scholar] [CrossRef]

15. Binh NTM, Hoang Long D, Ngoc N, Thanh Binh HT, Phuong NK. Investigate evolutionary strategies for black-box attacks to deepfake forensic systems. In: Proceedings of the 11th International Symposium on Information and Communication Technology. Hanoi, Vietnam; 2022. p. 126–33. [Google Scholar]

16. Binh NTM, Thien NV, Luong HVD, Ngoc DT. An efficient approach to the k-strong barrier coverage problem under the probabilistic sensing model in wireless multimedia sensor networks. In: Ad hoc networks. Cham: Springer Nature Switzerland; 2024. p. 167–80. [Google Scholar]

17. Huong TT, Van Cuong L, Hai NM, Le NP, Vinh LT, BinhHTT. A bi-level optimized charging algorithm for energy depletion avoidance in wireless rechargeable sensor networks. Appl Intell. 2022;52(6):6812–34. doi:10.1007/s10489-021-02775-8. [Google Scholar] [CrossRef]

18. Hussain K, Mohd Salleh MN, Cheng S, Shi Y. Metaheuristic research: a comprehensive survey. Artif Intell Rev. 2019;52:2191–233. doi:10.1007/s10462-017-9605-z. [Google Scholar] [CrossRef]