Active Protection Scheme of DNN Intellectual Property Rights Based on Feature Layer Selection and Hyperchaotic Mapping

1  Introduction

Deep neural networks (DNNs) have achieved remarkable success across a wide range of tasks and have been extensively adopted in commercial applications over the past decade [1]. The development of high-performance DNN models typically demands access to large-scale datasets, substantial computational resources, and highly skilled personnel, rendering such models valuable intellectual property assets [2]. However, these models are increasingly vulnerable to unauthorized exploitation, including model stealing and reverse engineering, which pose significant threats to intellectual property rights. Consequently, protecting the intellectual property of DNNs has emerged as a critical research focus, and various techniques have been proposed to safeguard models against infringement.

Current intellectual property protection technologies for deep neural networks (DNNs) can be categorized into passive verification and active defense approaches [3], both of which exhibit inherent limitations. Passive verification methods primarily rely on embedding watermarks into models for subsequent ownership authentication [4,5]. Extensive research has been devoted to developing various watermarking techniques [6,7]. However, these approaches suffer from two major limitations: (1) Their reactive nature only allows post-infringement forensics, offering no means to proactively prevent unauthorized usage; and (2) the watermark embedding process typically requires full model retraining, leading to considerable computational and time overhead [8,9]. Active protection technologies, although capable of enabling access control through encryption, present their own challenges. Most existing solutions require retraining the entire network for parameter encryption, which entails significant encryption costs for already-trained DNN models. Furthermore, certain parameter encryption schemes demand complete encryption of all model parameters, similarly demanding considerable encryption overhead. These constraints pose substantial challenges for practical implementation in large-scale commercial models.

The fundamental dilemma of existing methodologies lies in their inability to balance security and efficiency. Passive approaches appear computationally efficient due to their encryption-free nature, yet critically lack proactive defense capabilities. Conversely, active methods enable real-time protection at the expense of practicality, as global parameter encryption and mandatory retraining impose prohibitive operational constraints. More critically, both paradigms fail to address the synergistic optimization between encryption granularity and algorithmic efficiency-excessive encryption squanders computational resources whereas simplistic encryption becomes vulnerable to reverse-engineering attacks. This paper proposes a dynamic fine-grained encryption framework that achieves dual optimization of security and efficiency through feature layer selection and 4D hyper-chaotic mapping. The main contributions of this paper include the following:

–   A novel active protection scheme for DNNs is proposed, which safeguards DNN models through a critical weight selection strategy and a dual encryption mechanism. This approach eliminates the need to retrain the DNN model or encrypt all model parameters.

–   A DNN critical weight selection strategy is designed to protect DNN IP by encrypting only a small subset of parameters that have the most significant impact on model performance.

–   A novel dual encryption strategy for critical weights is developed, leveraging a 4D Lorenz hyperchaotic map and an amplitude recovery mask to encrypt the positional information and values of critical weights, respectively. This ensures the protection of key model parameters.

2  Related Work

Passive verification. Uchida et al. [10] proposed for the first time a generalized framework for embedding watermarks in deep network models by embedding watermarks into model parameters via a parameter regularizer without compromising the performance of the model. Chen et al. [11] embedded unique fingerprints in the model parameters, and the model owner can verify the ownership of the model by identifying the embedded fingerprints. Wang et al. [12] inserted a separate neural network in DNN using selective weights for watermarking and changed the neural network to be used only in the training phase and watermark verification phase. However, references [10–12] all of these schemes embed watermarking directly in the internal weights of the model, which is easy to be detected and attacked. Adi et al. [13] proposed a black-box watermarking-based IP protection method for DNNs, which can be applied to most classification tasks and can be well combined with various learning algorithms. Le Merrer et al. [14] proposed a method to construct a watermarking algorithm using antagonistic samples using the zero-bit watermarking algorithm with trigger sets. This method only alters the sample labels without altering the original data and requires very few queries to extract the watermark. Li et al. [15] utilized frequency domain image watermarking to generate triggers to construct DNN watermarks, and this black box watermarking scheme can be effective in resisting fraudulent claims attacks due to the high stealthiness of frequency domain watermarking. References' [13–15] methods have broader application prospects, but the black-box watermarking method modifies the training dataset of the model, which inevitably affects the accuracy of the model, and may not be suitable for application in some domains with higher accuracy requirements. Existing studies on DNN IP protection primarily rely on passive verification mechanisms. These approaches often require substantial resources during the initial deployment phase and can only verify model ownership retrospectively, after an infringement has occurred. Moreover, they offer no effective defense against adversarial behaviors such as unauthorized usage or model tampering. As such, passive verification schemes are increasingly insufficient for modern IP protection demands. In response, active DNN IP protection aims to proactively prevent and detect misuse, attracting growing attention and emerging as a key research direction.

Active DNN Intellectual Property Protection: Several proactive DNN protection schemes have emerged in recent research. Pyone et al. [16] proposed an input preprocessing framework where authorized users must apply identical image transformations to utilize the DNN model effectively. Ren et al. [17] introduced a model-locking mechanism that generates correct inference results exclusively for users possessing specific authentication markers. Luo et al. [18] implemented hierarchical authorization through Laplacian mechanism-based output perturbations with varying intensity levels. Tian et al. [19] developed a selective encryption algorithm for IP protection while enabling tiered service functionalities. However, these methods universally require model retraining, incurring substantial encryption overhead. Hardware-assisted solutions have also been explored: Pan et al. [20] leveraged Physical Unclonable Functions (PUFs) to generate device-bound secret keys for weight permutation and diffusion-based encryption. Fan et al. [21] devised a passport-based protection strategy demonstrating strong resilience against model modification and ambiguity attacks. Chakraborty et al. [22] proposed a trusted device-embedded framework where DNNs serve as key-dependent functions, restricting model accessibility to authorized hardware owners. Although these hardware-based approaches achieve active protection, they still demand model retraining and often involve labor-intensive key embedding processes. Parameter encryption schemes present alternative solutions. Zhou et al. [23] created an access-controlled framework preventing unauthorized users from obtaining functional DNN models. Inspired by Zhu et al. [24] and Li et al.’s [25] chaotic image encryption, Lin et al. [26] developed a chaos mapping-based weight obfuscation method that scrambles convolutional/full-connected layer kernels into chaotically disordered states through positional ambiguity. While eliminating retraining requirements, these parameter-level approaches necessitate full-model encryption, resulting in prohibitive computational costs that hinder commercial deployment. Some more novel approaches have been proposed [27–29], but again the network needs to be retrained. All of the above works perform active authorization control on DNN models, so that only legitimate users can use the services provided by the model properly with a specific secret key, and illegitimate users cannot obtain the correct functionality of the model.

Most existing active DNN IP protection methods require either model retraining or specialized hardware support, leading to significant overhead in terms of time and computational resources. In contrast, the method proposed in this paper achieves IP protection by encrypting only a small subset of critical weights from selected feature layers. This design significantly reduces both computational and time costs, while maintaining high efficiency in both encryption and decryption processes. Unlike the chaotic weighting approach proposed by Lin et al. [26], which is limited to encrypting square-shaped parameter regions, our method supports encryption over arbitrarily shaped parameter subsets. Furthermore, by applying a dual-stage parameter selection strategy, our approach minimizes the number of parameters to be encrypted, thereby enhancing overall efficiency.

3  The Proposed Algorithm

3.1 Problem Statement

The overall concept of the proposed scheme is illustrated in Fig. 1. The DNN model, developed by the model owner at substantial computational and time costs, must be protected to prevent unauthorized exploitation. As depicted in the figure, both authorized users and potential attackers can access the encrypted model via a public cloud API. However, only authorized users possess the trusted decryption key provided by the model owner. Upon decryption, authorized users can fully restore the model and utilize its services as intended. In contrast, attackers, lacking the correct key, are restricted to an encrypted version of the model with significantly degraded inference accuracy. The goal of our scheme is to prevent unauthorized entities from benefiting from high-performance models, while ensuring that legitimate users experience no degradation in model accuracy or functionality after decryption.

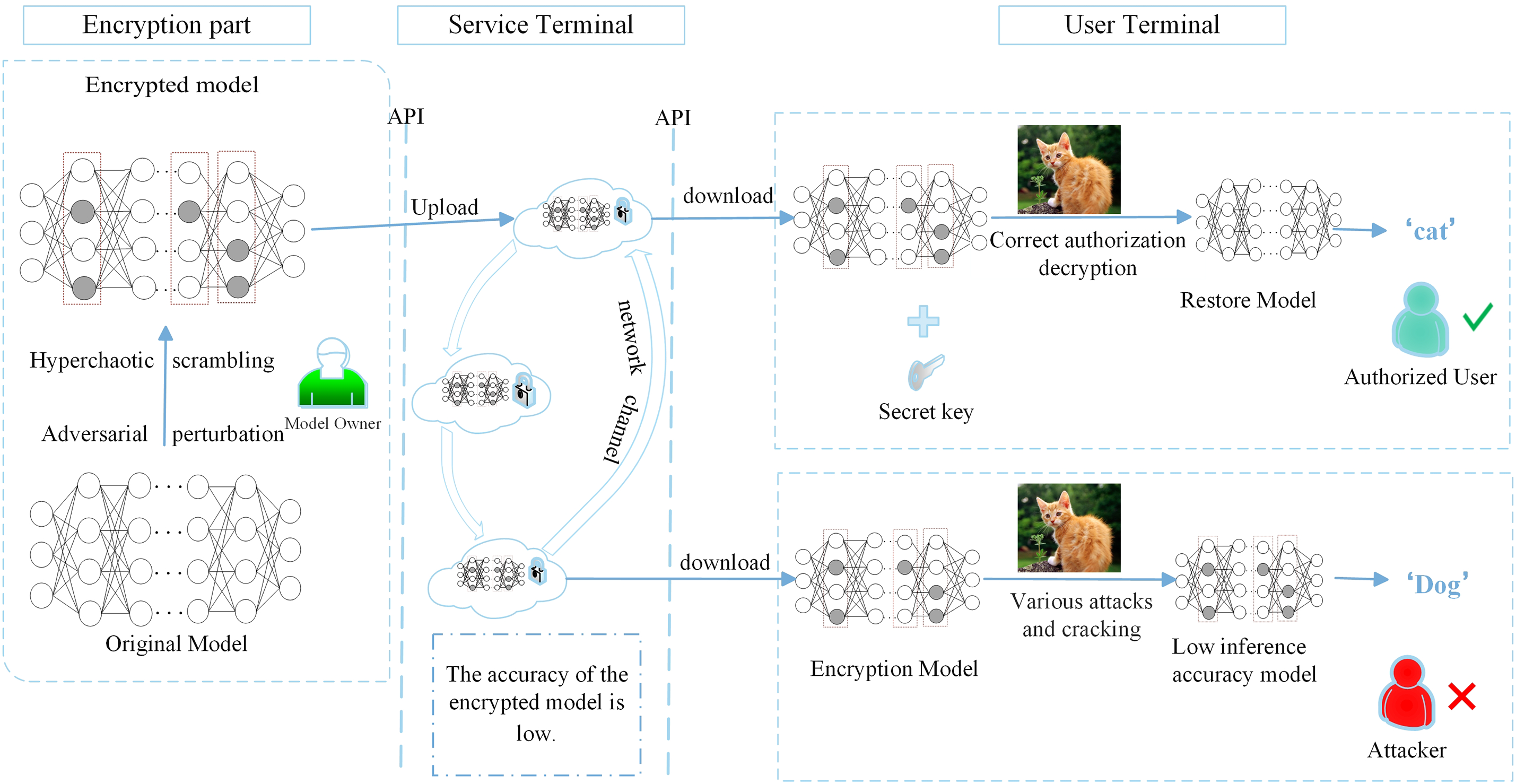
Figure 1: Overall flowchart of DNN IP protection

3.2 Model Encryption

During DNN model training, each convolutional layer of the network works together to optimize the model performance after a certain number of iterations. However, the role played by each convolutional layer is different, i.e., each convolutional layer has a different degree of influence on the model performance. Therefore, before selecting the weights for encryption, the model owner first sorts all the feature layers according to their importance according to the feature layer importance discrimination algorithm (Algorithm 1), sets a parameter p, which represents the proportion of the number of feature layers selected for encryption to the total number of feature layers, and then processes the selected encrypted layers to get the weights that have the greatest effect on the model, and then the weight positions are scrambled using a 4D Lorentz hyperchaotic system, and an Amplitude recovery maskis added to the weights for further encryption.

3.2.1 Structured Obfuscation

According to Algorithm 1, firstly sort all feature layers by importance, and add different degrees of disturbance to the weight of each feature layer. After each disturbance, calculate the change in model accuracy, obtain the accuracy drop value drop, and compare it with the drop threshold th. If it is greater than the threshold th, the feature layer will be marked as the layer to be encrypted, and the drop value drop will be retained. The initial threshold is set to 0.1. After all feature layers are selected, sort the feature layers by the drop value to obtain the feature layers to be encrypted. Here, the disturbance range and threshold th can be reasonably adjusted according to the task calculation amount and calculation time. In order to obtain a more accurate ranking of the importance of the convolutional layer, this paper selects a larger disturbance range and a smaller th value.

In this algorithm, the outer loop runs n times while the inner loop runs 10 times, resulting in a time complexity of O(n×10). The algorithm only retains the feature layer that has the most significant impact on model performance during each iteration, ultimately producing just a sorted list of feature layer importance. Therefore, its space complexity is O(1).

After selecting the target layer for encryption, a weight importance evaluation algorithm is applied to identify the most critical weights. Specifically, the parameter dimensions of a convolutional layer are C*N*K*K, where C, N, and K denote the number of input channels, output channels, and kernel size, respectively (typically 3*3 or 5*5). Due to structural differences across layers, the functional significance of individual kernels and their associated weights varies. Drawing inspiration from model pruning techniques, where less significant weights are removed to improve efficiency, we assess weight importance using the L1-norm. Since convolutional weights are multi-dimensional, they are first flattened into a one-dimensional array for ranking. The L1-norm values are then used to partially sort the weights. Based on a predefined encryption ratio, a selection function identifies the most impactful weights and their corresponding indices. The result is a list of selected weights and their positions, which defines the final encryption target.

After calculating the weight information to be encrypted, use the 4D Lorenz Hyperchaotic Map to scramble the weight position. The Eq. (1) is as follows:

{w1′=α1(w2−w1)+w2w3w2′=γ1w1−w2−w1w3+w4w3′=w1w2−β1w3w4′=ρ1w4−w1w3(1)

where, w1,w2,w3,w4 are state variables that changes over time. wi′ denotes the derivative of time t. The parameters α1,β1,γ1,ρ1 are the system parameters of the control system behaviour, which affect the dynamic characteristics of the system. When the parameter values are α1=10,β1=8/3,γ1=28 and 1.52≤ρ1≤0.06, the system exhibits hyperchaotic behavior. In this paper, ρ1=1.0 is taken. α1 regulates the coupling strength between w1 and w2. γ1 controls the strength of the response of w2 to w1, β1 determines the decay rate of w3, ρ1 controls the growth rate of w4. We use the Runge-Kutta-Fehlberg method (RKF45) to integrate the differential equations of the 4D Lorenz system and calculate four chaotic sequences X, Y, Z, and W with the same dimension as the encrypted parameters. The RKF45 method controls the error in the solution process by adaptively adjusting the step size. It is an explicit Runge-Kutta method with two different orders, usually fourth and fifth. At each time step, RKF45 calculates two estimates of the fifth and fourth order, and uses the difference between them to estimate the error to determine whether the step size needs to be adjusted to achieve the set accuracy. The following is the Runge-Kutta table in the general form of the RKF45 algorithm (Eq. (2)):

{k1=f(ti,yi)k2=f(ti+h4,yi+k14)k3=f(ti+3h8,yi+3hk132+9hk232)k4=f(ti+12h13,yi+1932hk12197−7200hk22197+7296hk32197)k5=f(ti+h,yi+439hk1216−8hk2+3680hk3513−845hk44104)k6=f(ti+h2,yi−8hk127+2hk2−3544hk32565+1859hk44104−11hk540)(2)

where, ti is the current time step, yi is the estimated value of the current step, f(ti,yi) represents the ordinary differential equation, which can usually be defined as dy/dt=f(t,y), k1,k2,k3,k4,k5,k6 are intermediate values, and h is the set step size. The step size set in this paper is h=0.01. Then, the linear combination of derivative terms can be obtained to calculate the Runge-Kutta approximation of the fourth-order yi+14 and the fifth-order yi+14 (Eq. (3)):

{yi+1(5)=yi+h(16k1135+6656k312825+28561k456430−9k550+2k655)yi+1(4)=yi+h(25k1216+1408k32565+2197k44104−k55)(3)

The error estimate can be obtained by taking the difference between the two approximations (Eq. (4)):

Ei=yi+1(5)−yi+1(4)(4)

Adjust the step size according to the error estimate to meet the predetermined error tolerance. If the error exceeds the tolerance, reduce the step size; if the error is within the tolerance, increase the step size appropriately. Next, sort the subscripts of the X, Y, Z, and W sequence elements in ascending (or descending) order according to their size, and obtain four new subscript sequences, as shown in the Eq. (5):

{Sh{Ix,Iy,Iz,Iw}=ξ(x),ξ(y),ξ(z),ξ(w)x,y,z,w=Φ(m1,m2,m3,m4)(5)

where, Sh is a dictionary used to store new sequences, Φ is a hyperchaotic map, m1,m2,m3,m4 are the sizes of the encrypted areas, and the ξ function is used to rearrange the X, Y, Z, and W sequences. Use the sequences Ix,Iy,Iz,Iw in the dictionary Sh to confuse the parameter dimensions that need to be encrypted. Then use Sh to rearrange the parameters that need to be encrypted and generate a decryption key. The final position of the original parameter is determined by the four chaotic sequences, achieving highly nonlinear obfuscation of the encryption layer. The obfuscation equation (Eq. (6)) can be expressed as:

(i′j′k′p′)=(lx(i)ly(j)lz(k)lw(p))(6)

where, i′,j′,k′,p′ are the positions after parameter confusion, and i,j,k,p are the positions before parameter confusion. Original parameter at position i,j,k,p migrates to i′,j′,k′,p′ creating interleaved scattering across all dimensions simultaneously, this architecture ensures that even partial parameter leakage reveals no structural patterns.

In this design, even if an attacker obtains a model with scrambled parameter positions, they cannot achieve high inference accuracy without the correct decryption key. The obfuscated model remains resistant to brute-force attacks, effectively preventing the recovery of its original performance. This mechanism thus provides strong protection for DNN intellectual property, making it difficult for unauthorized users to exploit the model. Furthermore, since the chaotic sequence used for scrambling is deterministically generated from fixed initial conditions, it does not need to be transmitted along with the model. Only the initial parameters are required to regenerate the same sequence during decryption, significantly reducing communication overhead.

3.2.2 Amplitude Recovery Mask Weights

In order to further improve the security of the encryption parameters, we add a small perturbation to the selected encryption weight value to further increase the difficulty for attackers to crack. Specifically, the loss function is recorded as Loss, the weight of the convolution layer l is recorded as Wl=[Wl1,Wl2,Wl3,…], where Wli,i∈(1,2,3,…) is the convolution kernel parameter, the model input is recorded as x, and the output result is recorded as y^, The gradient obtained during back propagation is Eq. (7):

∇WlLoss(x,y^)=[∂Loss(x,y^)∂Wl1,∂Loss(x,y^)∂Wl2,…](7)

And calculate the parameter with the largest absolute value of the partial derivative (Eq. (8)):

|∂Loss(x,y^)∂Wlt|=max[|∂Loss(x,y^)∂Wl1|,|∂Loss(x,y^)∂Wl2|,…](8)

After determining the encrypted weight Wlt, the Amplitude recovery maskper of the weight can be defined as Eq. (9):

per=μ×sign[∂Loss(x,y^)∂wlt]×[max(Wl)−min(Wl)](9)

where, μ is a hyperparameter with a very small value, which is used to control the perturbation per within a very small range. max(Wl) and min(Wl) are the maximum and minimum values of the weight of the encryption layer, respectively. The encryption weight Wlt is updated to (Wlt+per), and the unselected weight value will not be updated. The Crop() function is used to control the newly generated weight within a reasonable range so that it will not be detected by the attacker due to unreasonable weights. The public display is as follows (Eq. (10)):

Crop(Wlt+per)={Wlt+per,Wlt∈[Hl1,Hl2]Anew(Wlt+per),Wlt<Hl1Anew(Wlt+per),Wlt>Hl2Hl1=min(Wl)+ε×[max(Wl)−min(Wl)],Hl2=max(Wl)−ε×[max(Wl)−min(Wl)](10)

where, ε is a hyperparameter, Hl1 and Hl2 are two thresholds that control the range of weights after perturbation. Their function is to make the encrypted weights within a reasonable range after updating, and not too large or too small. The function Anew(Wlt+per), will perform two steps. In order to ensure that the original weights can be correctly decrypted, before updating the weights, the perturbation value per must be updated to per′, and then the weights are updated to Wlt. If the value of (Wlt+per) happens to be in the interval [Hl1,Hl2], the weights are not processed and are directly updated to the encrypted model. Otherwise, the parameters are updated according to the Anew(Wlt+per) function. The definition of the Anew(Wlt+per) function is as follows Eq. (11):

Anew(Wlt+per):{per′=Hl1−Wlt,Wlt<Hl1Wlt′=Hl1,Wlt<Hl1per′=Hl2−Wlt,Wlt>Hl2Wlt′=Hl2,Wlt>Hl2(11)

where, per′ and Wlt′ are the updated perturbation values and weights. per′=Hl1−Wlt,Wlt<Hl1 Recalibrate perturbation to reach lower threshold, Wlt′=Hl1,Wlt<Hl1Crop() weight to minimum allowable value. per′=Hl2−Wlt,Wlt>Hl2 Adjust perturbation to hit upper threshold, Wlt′=Hl2,Wlt>Hl2Crop() weight to maximum allowable value.

3.2.3 Key Generation

The composite key in our framework comprises three security elements:

K={a,b,c,d}⏟Chaotic seeds∪{(plt,vlt)}⏟l∈L∪{Sl,Wl,Hl}⏟Layer metadata(12)

where, {a,b,c,d}: Initial parameters of the 4D hyperchaotic map Φ, protected by AES-256 with 1014 possible combinations (NIST SP 800-22 validated), {(plt,vlt)}: Position-perturbation pairs where plt=Ix(i)‖Iy(j)‖Iz(k)‖Iw(p) denotes the 4D permuted index, and vlt=per′ is the amplitude-adjusted perturbation from Eq. (11), {Sl,Wl,Hl}: Spatial dimensions of encrypted layer l for decryption alignment Key Usage Example: For a convolutional layer with S×W×H×C=3×3×64×128, the key entry corresponding to position (2,1,5,33) would be: K(2,1,5,33)=(Ix(2)‖Iy(1)‖Iz(5)‖Iw(33), 0.127), where 0.127 is the calibrated perturbation bounded by [Hl1,Hl2]. Authorized users decrypt through:

Woriginal=ARMDecode(Wencrypted−vlt)∘Φ−1(a,b,c,d)(13)

While key transmission relies on established protocols (e.g., TLS 1.3 + RSA-4096), we mitigate interception risks through:

•   Dynamic key rotation: Regenerate {a,b,c,d} hourly via PUF (Physically Unclonable Functions)

•   Key fragmentation: Distribute K across multiple secure enclaves (SGX/TEE)

The encryption process of the encryption algorithm proposed in this article is shown in Algorithm 2.

The overall time complexity of the algorithm is O(nlogn)+O(n)+O(m)=O(nlogn+m), dominated by the sorting operation with O(nlogn), while chaotic sequence generation and region computation (each O(n)) as well as weight amplitude recovery (O(m)) contribute to the remaining costs. The space required for generating chaotic sequences is O(n). The GetArea(L) operation returns a region whose size correlates with the input layer L’s dimensions, assuming the returned region occupies O(n) space. In the weight scrambling operation, no new arrays are created—it merely swaps the positions of weight elements, resulting in O(1) space complexity. The amplitude recovery mask also demonstrates O(1) space complexity. Consequently, the total space complexity is O(n).

3.3 Model Decryption

Since the chaotic scrambling method selected is reversible, the decryption process is essentially the inverse process of encryption. As long as the transmitted key is correct, the original model can be quickly restored. First, subtract the added Amplitude recovery maskvalue to restore the encrypted weight value, and then generate the required chaotic sequence based on the initial value of the chaotic sequence, and perform chaotic scrambling in reverse order to restore the original position of the model and obtain the original DNN model. The decryption equation is as follows (Eq. (14)):

(ijkp)=(lx−(i′)ly−(j′)lz−(k′)lw−(p′))(14)

where, i′,j′,k′,p′ are the positions after parameter confusion, and i,j,k,p are the positions before parameter confusion. And lx−,ly−,lz−,lw− are the inverse sequences of the encrypted chaotic sequence.

4  Experimental Results and Analysis

4.1 Experimental Setup

Our method is evaluated on an NVIDIA GeForce RTX 4060 Laptop GPU with CUDA12.2 and CUDNN11.6. The CUDA Toolkit and cuDNN libraries compatible with PyTorch1.13+cu116 are installed, and PyTorch is configured to support GPU acceleration. In addition, Vscode is installed as a code editor for Python3.9.13. In this paper, four datasets, namely CIFAR-10 [30], CIFAR-100 [30], Fashion-MNIST [31], and ImageNet [32], are selected as experimental datasets. First, seven classification networks, namely EfficientNet [33], MobileNetV2 [34], MobileNetV3 [34], ResNet-18 [35], ResNet-50 [35], Shuffle-Net [36], and VGG-16 [37], are selected for evaluation on the above four datasets.

4.2 Feature Layer Importance Judgment

This paper introduces a feature layer importance evaluation algorithm to prioritize layers with significant influence on model performance, thereby narrowing the encryption scope. In our initial analysis, we assessed all feature layers including convolutional, pooling, and fully connected layers and observed that convolutional layers have the most critical impact on overall model accuracy. Subsequent experiments focused on evaluating the relative importance of each convolutional layer, with the results presented in Fig. 2. We trained ResNet-18 and VGG-16 on the CIFAR-10 dataset, achieving over 90% classification accuracy. Each convolutional layer was indexed as i. Where i∈(1,2,3,…,n), denotes the total number of convolutional layers. In total, 19 and 13 convolutional layers were evaluated for ResNet-18 and VGG-16, respectively.

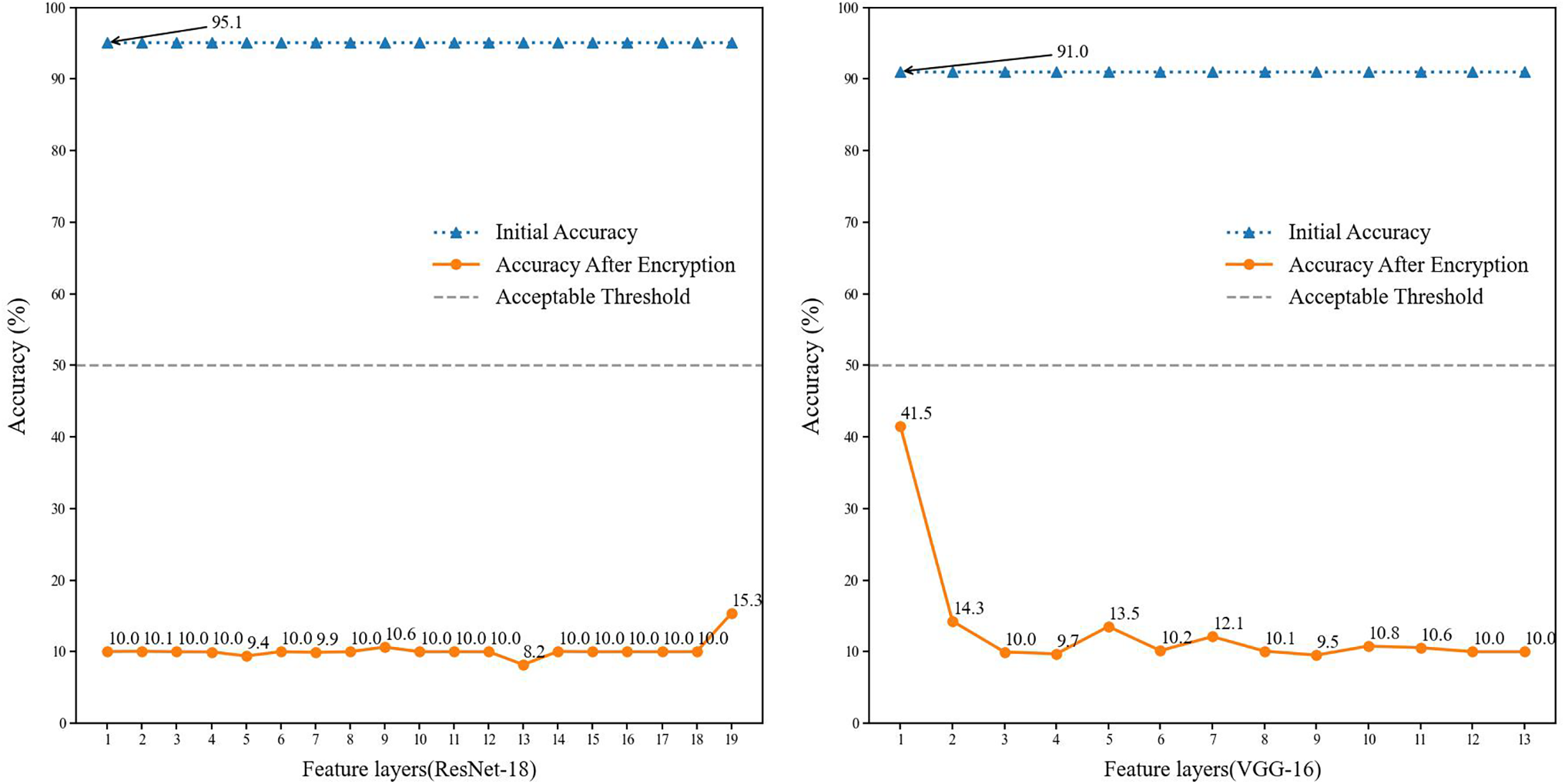
Figure 2: Analysis of the importance of feature layers

After selecting the layers to be encrypted, the number of encrypted weights is further reduced by arranging the L1 norm of each layer. The encryption ratio of each layer is set to 0.5% per layer. Different numbers of layers are selected for encryption according to the importance of the feature layer, and the performance changes of the model are observed. As shown in Fig. 3, in ResNet-18, only 0.5% of the parameters (184) of a convolutional layer need to be encrypted to reduce the model performance to 61.57%. Encrypting about 550 parameters of three layers can reduce the model accuracy to 19.59%, accounting for 0.016% and 0.049% of the total parameters, respectively. For the VGG-16 network, only 84 parameters of one layer need to be encrypted to reduce the model accuracy to 65.34%, and about 6600 parameters of three layers need to be encrypted to reduce the model accuracy to 43.95%, accounting for 0.0006% and 0.049% of the total parameters, respectively.

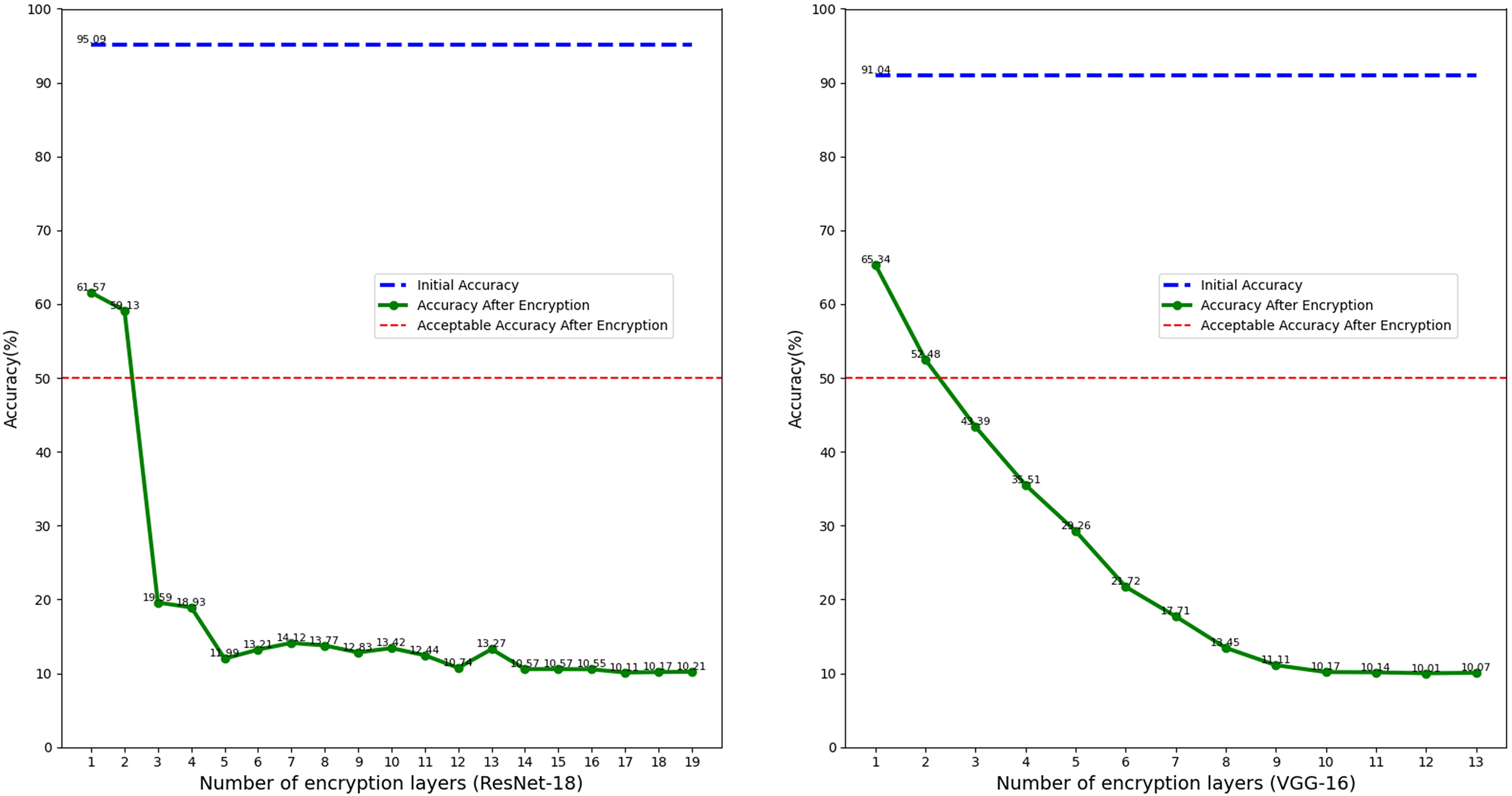
Figure 3: Selection of encryption feature layers initial accuracy represents the original accuracy of the model, accuracy after encryption represents the accuracy of the model after encryption, and acceptable accuracy after encryption represents the acceptable degree of accuracy reduction after encryption

4.3 Encryption Effects

Based on the above methodology, the encryption layer ratio δ=i/n is set to 0.8, and the encryption ratio within each selected layer is set to 0.01. All subsequent experiments adopt these fixed parameters. Table 1 summarizes the encryption results across four datasets, where seven classification networks are evaluated per dataset. For each model, we report the original accuracy, the accuracy after encryption, and the accuracy after decryption. Notably, for datasets with 10 categories such as CIFAR-10 and Fashion-MNIST, the encrypted model accuracy drops to approximately 10.00%, close to random guessing. For CIFAR-100 and ImageNet-200 (a subset with 200 classes), encryption accuracy falls to around 1.00% and 0.50%, respectively—also near the expected random baseline. These results demonstrate that the proposed method is highly stable across various datasets and architectures, exhibiting strong robustness.

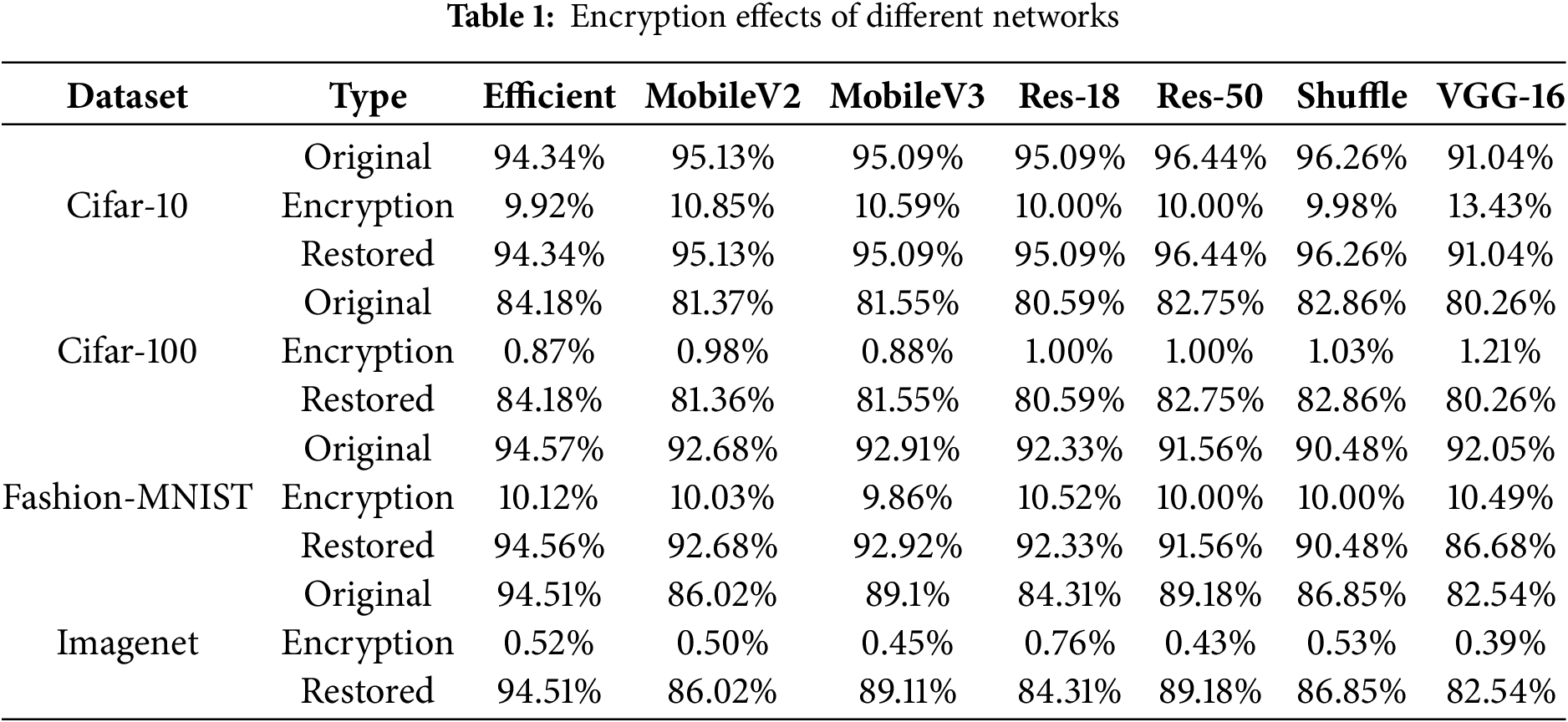
Furthermore, due to the reversibility of the proposed encryption scheme, model performance after decryption is nearly identical to the original. As shown in Table 1, the fluctuation in accuracy is typically within 0.01%, with only a few exceptional cases (highlighted in bold) showing minimal deviation. This indicates that the scheme introduces negligible performance loss, making it suitable for most DNNs unless extreme precision is required. Additionally, Table 2 reports the storage overhead of encrypted model files. The file sizes before and after encryption remain nearly unchanged, confirming the method’s lightweight design.

4.4 Model Decryption Time

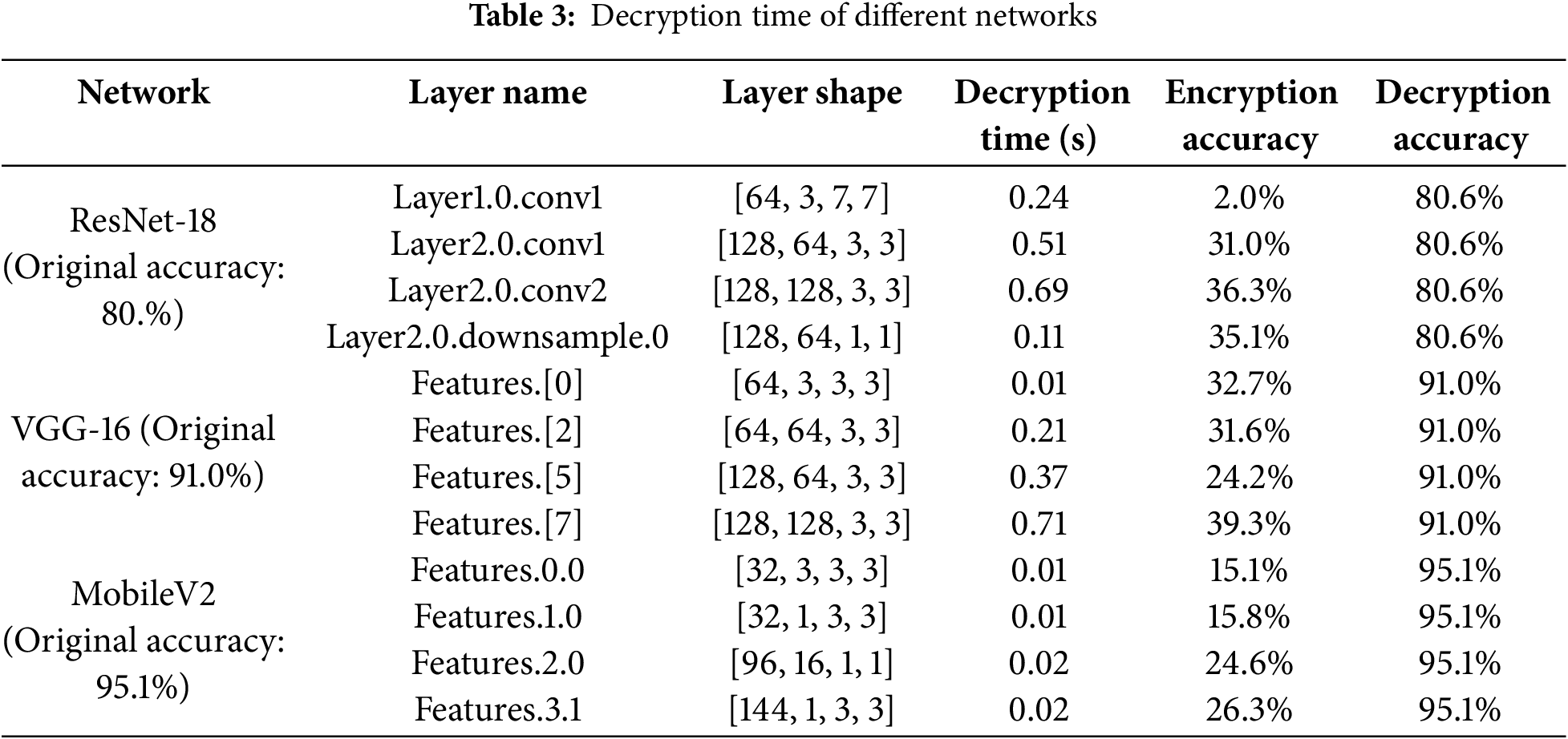
For a user-oriented network model, service response time is a criterion for measuring user experience. Therefore, the encryption algorithm should have a high decryption efficiency while protecting the intellectual property rights of the model owner to ensure a good user experience. Table 3 shows the decryption time of some encrypted feature layers of three networks, ResNet-18, VGG-16, and MobileNetV2, respectively, under the CIFAR-100 and CIFAR-10 datasets, as well as the accuracy changes of the encrypted model at this layer. The encryption ratio of the CIFAR-100 dataset used by ResNet-18 is set to 3%. It can be seen that the decryption model takes very little time, all within 1 second, but it is worth noting that the decryption time is affected by many factors such as the hardware conditions of the test device and the operating status of the device, and is also affected by the number of encrypted weights of the model. In different scenarios, the decryption time will vary. The accuracy of the model after encryption remains at a low level. After decryption, the model accuracy is basically not lost, which can well meet the various service needs of users.

4.5 Parameter Distribution Analysis Attacks

The attacker can infer which weights are encrypted based on the weight distribution of the model or the variance of the model weights. For this reason, this paper adds an adversarial perturbation to the encrypted weights so that the weight distribution and variance of the encrypted model remain basically unchanged. As shown in Fig. 4, this is an encrypted convolutional layer from ResNet-18 and VGG-16. The two figures on the left are the weight distributions of ResNet-18 and VGG-16 before encryption, and the two figures on the right are the weight distributions of ResNet-18 and VGG-16 after encryption. The two vertical lines represent the mean and variance of the model, respectively. It can be seen that the mean and variance changes before and after encryption are both in the range of 10−6. These experimental results show that the encrypted weights are invisible to attackers, and it is difficult for attackers to determine the location of the encrypted layer and the encrypted weights by analyzing the abnormality of the weights, that is, it is difficult to detect anomalies for these encrypted layers by analyzing weight changes.

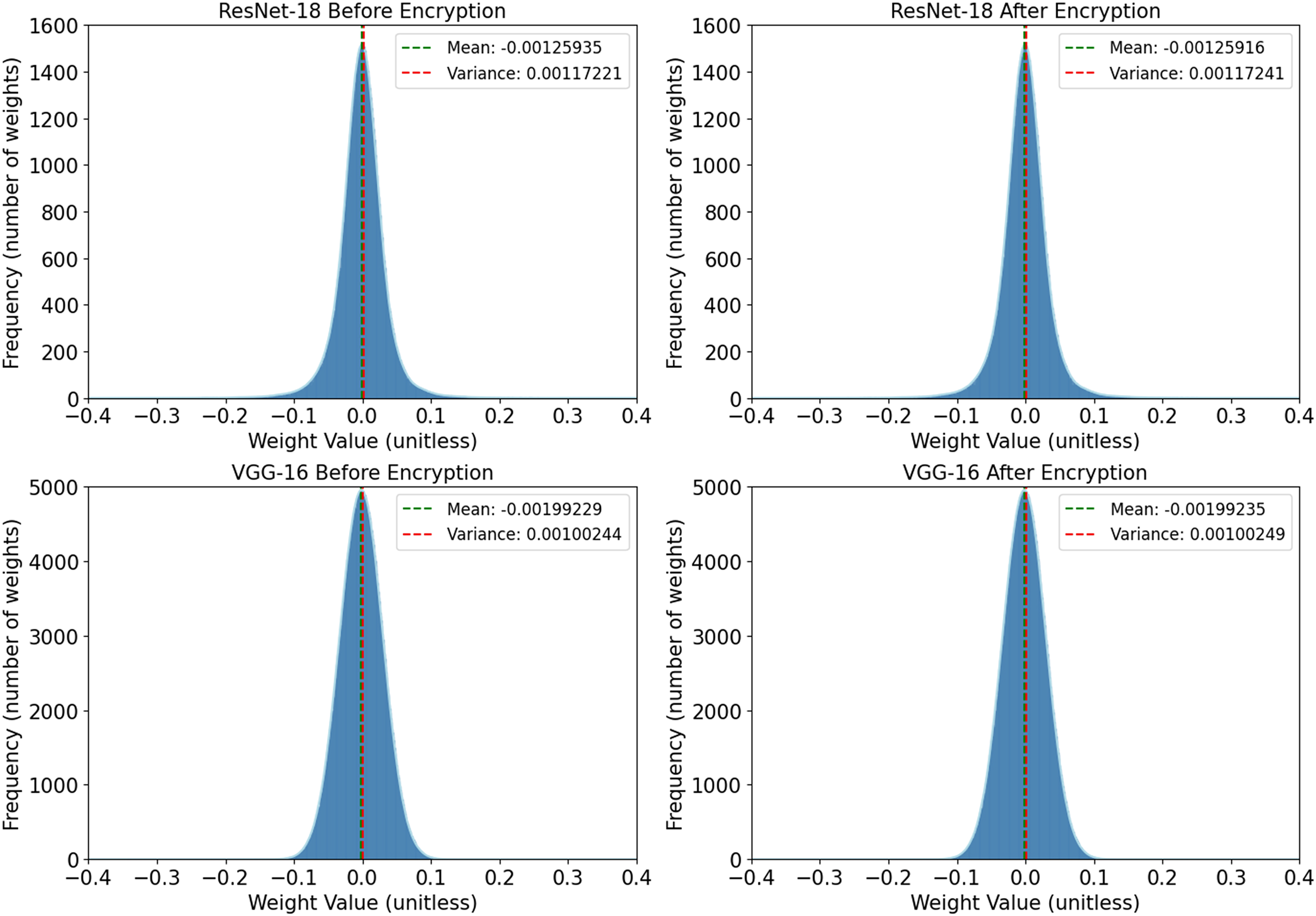
Figure 4: Weight distribution histogram mean represents the mean of the model weights, and variance represents the variance of the model weights

4.6 Model Fine-Tuning Attack

4.6.1 Fine-Tuning with Limited Data

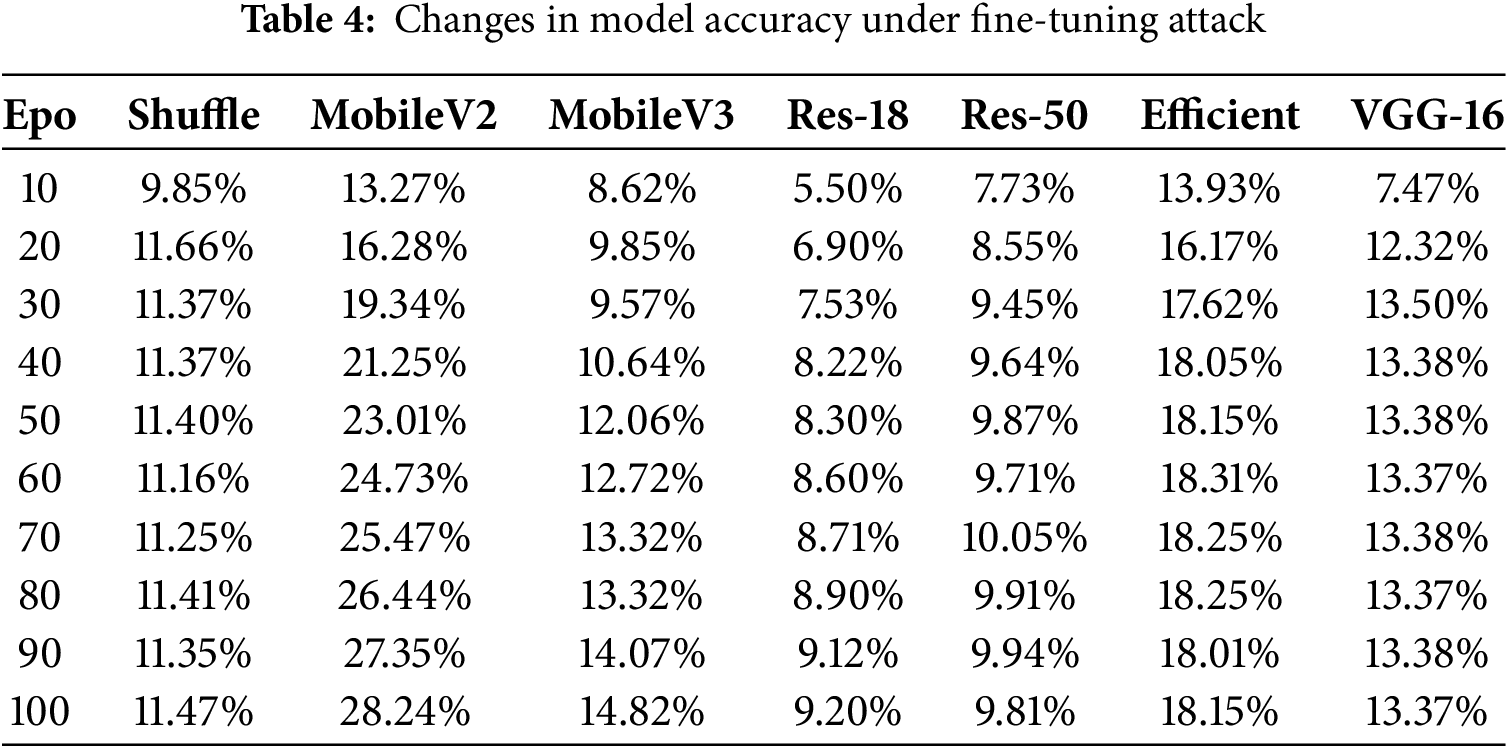
Since the encryption model can be obtained from the IoT system by all devices, an attacker can fine-tune the encryption model to invalidate the encryption and thus obtain the services of the original model. In the experiment, ShuffleNet, MobileNetV2, and MobileNetV3 use the CIFAR-10 dataset, while EfficientNet, ResNet-18, ResNet-50, and VGG-16 use the CIFAR-100 dataset for testing. 10% of the data in the test sets of the two datasets are selected for model fine-tuning attacks, and the remaining 90% of the data in the test sets are used as validation sets. The learning rate lr is set to 0.00001 to evaluate the change in the inference accuracy of the model when it is fine-tuned. The results are shown in Table 4. From the results, even after 100 epochs of reasoning, the reasoning accuracy of the fine-tuned encrypted model remains at a low level. Among the three models fine-tuned on CIFAR-10, only MobileNetV2 has a reasoning accuracy of 28.24%, while the accuracy of ShuffleNet and MobileNetV3 is only 11.47% and 14.82%, respectively. It is very close to the random selection accuracy of CIFAR-10 of 10%. The highest accuracy of the four networks on CIFAR-100 is only 18.31%, and the four models of ShuffleNet, EfficientNet, ResNet-50, and VGG-16 have already achieved the best fine-tuning accuracy before reaching 100 epochs, which means that even if the number of epochs continues to increase, the accuracy of the model will not be improved, which further illustrates the robustness of the encrypted model to fine-tuning attacks. Since the training cost of the entire original model is high and the attacker cannot have the private dataset of the model owner, fine-tuning the encrypted model with a small dataset cannot obtain the original accuracy of the model. Fine-tuning the model with a large dataset is equivalent to retraining the model, the fine-tuning attack loses its meaning.

4.6.2 Increase the Fine-tuning Ratio

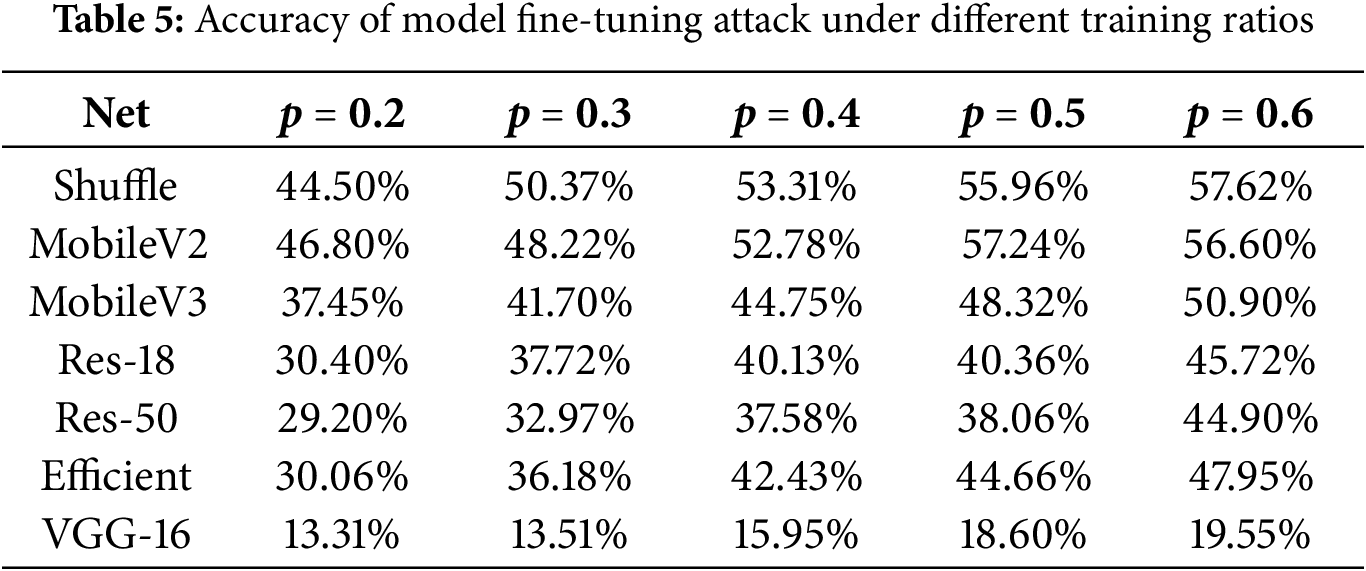
To further verify the model’s resistance to fine-tuning attacks, we assume that the attacker has a large number of annotated images for fine-tuning the model. Use a larger learning rate, set the learning rate lr to 0.001, and set a dataset ratio p, p∈(0.2,0.3,0.4,0.5,0.6). Use the same dataset for 100 epochs of attacks. As shown in Table 5, the model inference accuracy of the 7 networks after 100 epochs of attacks on the training datasets with different proportions. It can be seen that when p = 0.2, the inference accuracy of several networks is still below 50%, and even when p = 0.6, the model inference accuracy of the four networks tested using CIFAR-100 after 100 epochs of attacks is still below 50%, and the model accuracy of the model after 100 epochs of attacks on ShuffleNet is only 57.62%, which is still a big gap compared to the original accuracy of the model of 96.26%, which fully demonstrates the robustness of the proposed algorithm in resisting model fine-tuning attacks.

4.7 Model Pruning Attack

The attacker may prune the encrypted area of the model by pruning the model to obtain the original accuracy of the model. In this experiment, CIFAR-10 was used to perform pruning attacks on three networks, EfficientNet, MobileNetV2, and ResNet-18, while MobileNetV2, ResNet-50, and VGG-16 used the CIFAR-100 dataset. The pruning rate of the model was set from 0.0 to 0.7, where 0.0 represents the accuracy of the encrypted model and 0.7 represents a pruning rate of 70%. The results are shown in Table 6. Regardless of the pruning rate, the reasoning accuracy of the encrypted model remains at an extremely low level, close to the random selection accuracy. When the pruning rate is 0.5, several networks achieve the best pruning effect. If the pruning rate is further increased, the model reasoning accuracy is even lower. After pruning, the model reasoning accuracy is even lower than that after encryption. This shows that the model pruning attack not only does not prune the important weights of the encrypted model, but also prunes some less important weights that are not encrypted, resulting in a further reduction in the reasoning accuracy of the model. This shows that the algorithm we proposed does not continuously encrypt a series of adjacent weights, but selectively encrypts model weights, which can effectively resist model pruning attacks.

4.8 Ablation Experiments

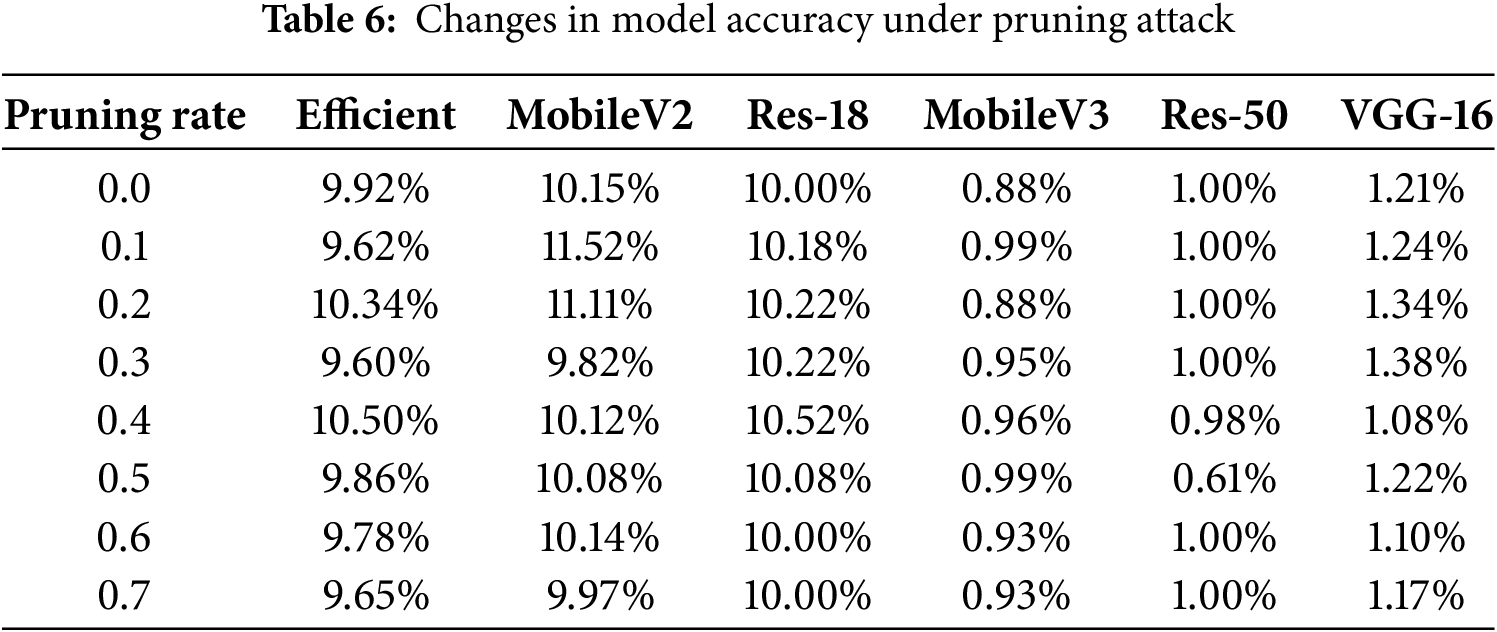
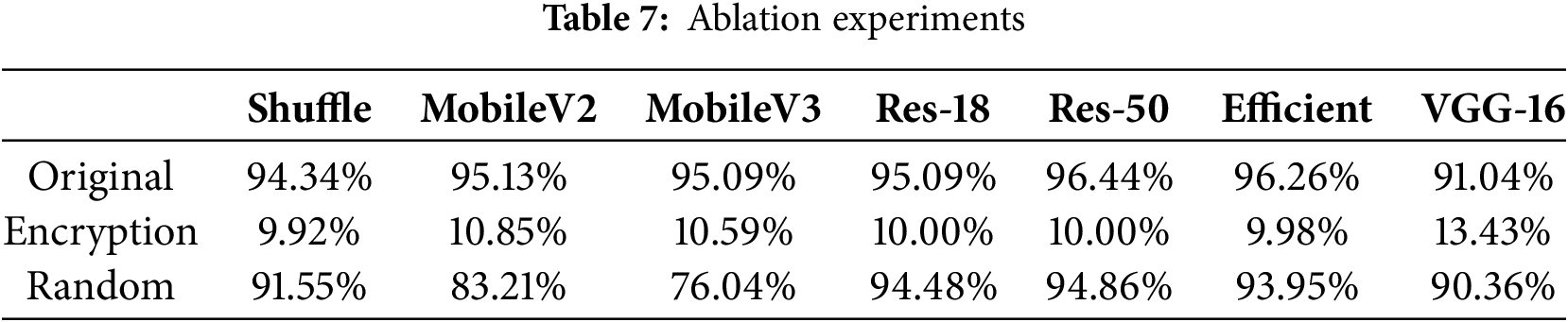
We performed ablation experiments and the results are shown in Table 7. The first row is the accuracy of the original model, the second row represents the accuracy of the encryption model, and the third row is the result of our random selection of the same number of weight encryption models.

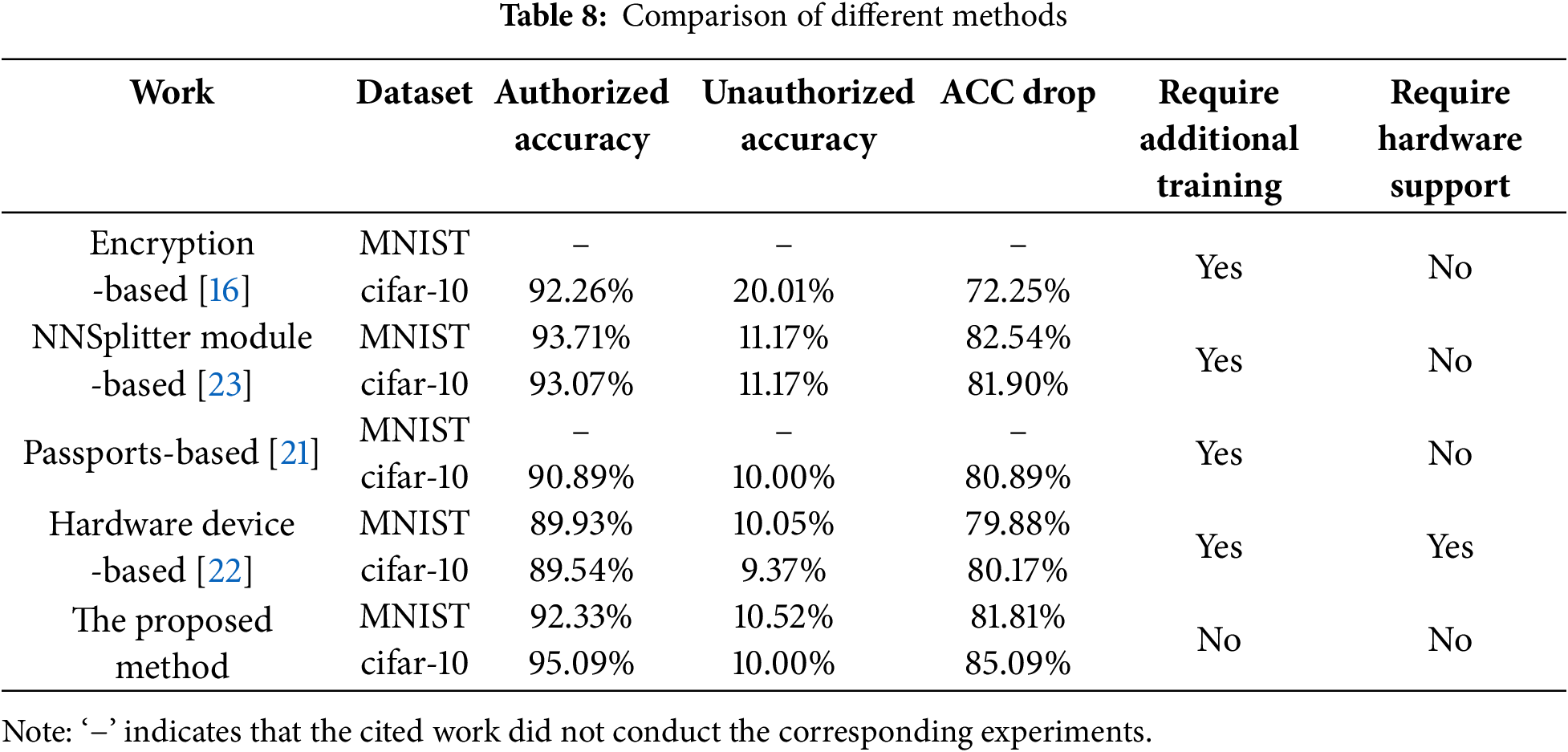
4.9 Comparison with SOTA Methods

We compare the proposed method with existing active DNN IP protection schemes. As shown in Table 8, we give the encryption effects of these schemes on Fashion-MNIST and cifar-10. The scheme proposed by Pyone et al. [16] requires image preprocessing when training and using the model, which undoubtedly consumes a lot of time, and retraining also consumes a lot of computing resources. The scheme proposed by Zhou et al. [23] also requires the full parameters of the cryptographic model, which cannot meet the needs of commercial applications. For work [21], attackers may find out the information of the model encryption weights through reverse engineering of the model. The scheme of work [22] not only requires retraining the model, but also requires the support of hardware equipment, which will also consume a lot of costs in commercial applications. Compared with previous work, the scheme proposed in this paper not only does not require retraining the model, but also does not require hardware equipment support, and decryption only takes a very short time, which can well meet the needs of commercial applications.

5  Conclusion

This paper presents a Model Active Protection Framework that secures DNN models at the source by encrypting only a small subset of critical weights. These encrypted weights remain statistically indistinguishable from normal values, making their locations hard to detect. The framework ensures efficient decryption with minimal computational overhead, enabling practical deployment. Experimental results show that, after encryption, model accuracy drops to near-random levels across seven classification networks and four benchmark datasets, effectively preventing unauthorized exploitation. Moreover, the scheme demonstrates strong resistance to common attacks such as model fine-tuning and pruning, underscoring its robustness. In summary, the proposed method offers a lightweight, resilient, and practical solution for protecting the integrity and confidentiality of DNN models in real-world scenarios.

Acknowledgement: Thank all the members who have contributed to this work with us.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant No. 62172280, in part by the Key Scientific Research Projects of Colleges and Universities in Henan Province, China under Grant No. 23A520006, and in part by Henan Provincial Science and Technology Research Project under Grant No. 222102210199.

Author Contributions: The authors confirm the following contributions to this article: Research concept and design: Xintao Duan and Yinhang Wu; Experimental, analytical, and interpretive results: Yinhang Wu and Zhao Wang; Drafted by Xintao Duan. Chuan Qin reviewed the results and approved the final version of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data openly available in a public repository.

Ethics Approval: Not the study included human or animal subjects.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Malhotra R, Singh P. Recent advances in deep learning models: a systematic literature review. Multimed Tools Appl. 2023;82(29):44977–5060. doi:10.1007/s11042-023-15295-z. [Google Scholar] [CrossRef]

2. Peng S, Chen Y, Xu J, Chen Z, Wang C, Jia X. Intellectual property protection of DNN models. World Wide Web. 2023;26(4):1877–911. doi:10.1007/s11280-022-01113-3. [Google Scholar] [CrossRef]

3. Li Z, Hu C, Zhang Y, Guo S. How to prove your model belongs to you: a blind-watermark based framework to protect intellectual property of DNN. In: Proceedings of the 35th Annual Computer Security Applications Conference; 2019 Dec 9–13; San Juan, Puerto Rico. p. 126–37. [Google Scholar]

4. Furukawa R, Sakazawa S. Generation management of white-box DNN model watermarking. In: 2023 IEEE 12th Global Conference on Consumer Electronics (GCCE); 2023 Oct 10–13; Nara, Japan. p. 792–3. [Google Scholar]

5. Chen H, Zhang W, Liu K, Chen K, Fang H, Yu N. Speech pattern based black-box model watermarking for automatic speech recognition. In: ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2022 May 22–27; Singapore. p. 3059–63. [Google Scholar]

6. Li Y, Wang H, Barni M. A survey of deep neural network watermarking techniques. Neurocomputing. 2021;461:171–93. doi:10.1016/j.neucom.2021.07.051. [Google Scholar] [CrossRef]

7. Ogundokun RO, Abikoye CO, Kumar Sahu A, Akinrotimi AO, Babatunde AN, Sadiku PO, et al. Enhancing security and ownership protection of neural networks using watermarking techniques: a systematic literature review using PRISMA. In: Multimedia watermarking. 1st ed. Singapore: Springer; 2024. p. 1–28. doi:10.1007/978-981-99-9803-6_1. [Google Scholar] [CrossRef]

8. Zhang J, Chen D, Liao J, Zhang W, Feng H, Hua G et al. Deep model intellectual property protection via deep watermarking. IEEE Trans Pattern Anal Mach Intell. 2021;44(8):4005–20. doi:10.1109/tpami.2021.3064850. [Google Scholar] [PubMed] [CrossRef]

9. Ye Z, Zhang X, Feng G. Deep neural networks watermark via universal deep hiding and metric learning. Neural Comput Appl. 2024;36(13):7421–38. doi:10.1007/s00521-024-09469-5. [Google Scholar] [CrossRef]

10. Uchida Y, Nagai Y, Sakazawa S, Satoh S. Embedding watermarks into deep neural networks. In: Proceedings of the 2017 ACM on International Conference on Multimedia Retrieval; 2017 Jun 6–9; Bucharest, Romania. p. 269–77. [Google Scholar]

11. Chen H, Rohani BD, Koushanfar F. Deepmarks: a digital fingerprinting framework for deep neural networks. arXiv:1804.03648. 2018. [Google Scholar]

12. Wang J, Wu H, Zhang X, Yao Y. Watermarking in deep neural networks via error back-propagation. Electron Imaging. 2020;32(4):1–9. doi:10.2352/issn.2470-1173.2020.4.mwsf-022. [Google Scholar] [CrossRef]

13. Adi Y, Baum C, Cisse M, Pinkas B, Keshet J. Turning your weakness into a strength: watermarking deep neural networks by backdooring. In: 27th USENIX Security Symposium (USENIX Security 18); 2018 Aug 15–17; Baltimore, MD, USA. p. 1615–31. [Google Scholar]

14. Le Merrer E, Perez P, Trédan G. Adversarial frontier stitching for remote neural network watermarking. Neural Comput Appl. 2020;32(13):9233–44. doi:10.1007/s00521-019-04434-z. [Google Scholar] [CrossRef]

15. Li M, Zhong Q, Zhang LY, Du Y, Zhang J, Xiang Y. Protecting the intellectual property of deep neural networks with watermarking: the frequency domain approach. In: 2020 IEEE 19th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom); 2020 Dec 29–2021 Jan 1; Guangzhou, China. p. 402–9. [Google Scholar]

16. Pyone A, Maung M, Kiya H. Training DNN model with secret key for model protection. In: 2020 IEEE 9th Global Conference on Consumer Electronics (GCCE); 2020 Oct 13–16; Kobe, Japan. p. 818–21. [Google Scholar]

17. Ren G, Wu J, Li G, Li S, Guizani M. Protecting intellectual property with reliable availability of learning models in AI-based cybersecurity services. IEEE Trans Dependable Secure Comput. 2022;21(2):600–17. doi:10.1109/tdsc.2022.3222972. [Google Scholar] [CrossRef]

18. Luo Y, Feng G, Zhang X. Hierarchical authorization of convolutional neural networks for multi-user. IEEE Signal Process Lett. 2021;28:1560–4. doi:10.1109/lsp.2021.3100307. [Google Scholar] [CrossRef]

19. Tian J, Zhou J, Duan J. Hierarchical services of convolutional neural networks via probabilistic selective encryption. IEEE Trans Serv Comput. 2021;16(1):343–55. doi:10.1109/tsc.2021.3136601. [Google Scholar] [CrossRef]

20. Pan Q, Dong M, Ota K, Wu J. Device-bind key-storageless hardware AI model IP protection: a PUF and permute-diffusion encryption-enabled approach. arXiv:2212.11133. 2022. [Google Scholar]

21. Fan L, Ng KW, Chan CS, Yang Q. DeepIPR: deep neural network ownership verification with passports. IEEE Trans Pattern Anal Mach Intell. 2022;44(10):6122–39. doi:10.1109/tpami.2021.3088846. [Google Scholar] [PubMed] [CrossRef]

22. Chakraborty A, Mondai A, Srivastava A. Hardware-assisted intellectual property protection of deep learning models. In: 2020 57th ACM/IEEE Design Automation Conference (DAC); 2020 Jul 20–24; San Francisco, CA, USA. p. 1–6. [Google Scholar]

23. Zhou T, Luo Y, Ren S, Xu X. NNSplitter: an active defense solution for DNN model via automated weight obfuscation. In: ICML’23: International Conference on Machine Learning; 2023 Jul 23–29; Honolulu, HI, USA. p. 42614–24. [Google Scholar]

24. Zhu H, Zhang X, Yu H, Zhao C, Zhu Z. An image encryption algorithm based on compound homogeneous hyper-chaotic system. Nonlinear Dyn. 2017;89(1):61–79. doi:10.1007/s11071-017-3436-y. [Google Scholar] [CrossRef]

25. Li Z, Peng C, Li L, Zhu X. A novel plaintext-related image encryption scheme using hyper-chaotic system. Nonlinear Dyn. 2018;94(2):1319–33. doi:10.1007/s11071-018-4426-4. [Google Scholar] [CrossRef]

26. Lin N, Chen X, Lu H, Li X. Chaotic weights: a novel approach to protect intellectual property of deep neural networks. IEEE Trans Comput-Aided Des Integr Circuits Syst. 2020;40(7):1327–39. doi:10.1109/tcad.2020.3018403. [Google Scholar] [CrossRef]

27. Mohseni A, Moaiyeri MH, Amirany A, Rezayati MH. Protecting the intellectual property of binary deep neural networks with efficient spintronic-based hardware obfuscation. IEEE Trans Circuits Syst I: Regul Pap. 2024;71(7):3146–56. doi:10.1109/tcsi.2024.3397925. [Google Scholar] [CrossRef]

28. Xue M, Wu Y, Zhang LY, Gu D, Zhang Y, Liu W. SSAT: active authorization control and user’s fingerprint tracking framework for DNN IP protection. ACM Trans Multimed Comput Commun Appl. 2024;20(10):1–24. doi:10.1145/3679202. [Google Scholar] [CrossRef]

29. Li P, Huang J, Wu H, Zhang Z, SecureNet Qi C. Proactive intellectual property protection and model security defense for DNNs based on backdoor learning. Neural Netw. 2024;174(3):106199. doi:10.1016/j.neunet.2024.106199. [Google Scholar] [PubMed] [CrossRef]

30. Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images. Technical Report. Toronto, ON, Canada: University of Toronto; 2009. [cited 2025 Mar 30]. Available from: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf. [Google Scholar]

31. Xiao H, Rasul K, Vollgraf R. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. arXiv:1708.07747. 2017. [Google Scholar]

32. Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L. ImageNet: a large-scale hierarchical image database. In: 2009 IEEE Conference on Computer Vision and Pattern Recognition; 2009 Jun 20–25; Miami, FL, USA. p. 248–55. [Google Scholar]

33. Tan M, Le Q. EfficientNet: rethinking model scaling for convolutional neural networks. In: International Conference on Machine Learning; 2019 Jun 9–15; Long Beach, CA, USA. p. 6105–14. [Google Scholar]

34. Sandler M, Howard A, Zhu M, Zhmoginov A, Chen LC. MobileNetV2: inverted residuals and linear bottlenecks. In: Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2018 Jun 18–23; Salt Lake City, UT, USA. [cited 2025 Mar 30]. Available from: https://arxiv.org/abs/1801.04381. [Google Scholar]

35. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition; 2016 Jun 27–30; Las Vegas, NV, USA. p. 770–8. [Google Scholar]

36. Zhang X, Zhou X, Lin M, Sun J. ShuffleNet: an extremely efficient convolutional neural network for mobile devices. In: Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. p. 6848–56. [Google Scholar]

37. Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556. 2014. [Google Scholar]