SA-WGAN Based Data Enhancement Method for Industrial Internet Intrusion Detection

1  Introduction

With the rapid advancement of digitalization and Internet technology, the Industrial Internet is significantly transforming our production methods and lifestyles. By interconnecting sensors, equipment, and production systems, the Industrial Internet facilitates real-time data collection, analysis, and application, thereby optimizing production processes, enhancing efficiency, and reducing costs. This technology not only fosters a fundamental shift in production models but also generates unprecedented business opportunities for enterprises. Consequently, the Industrial Internet has gradually become an essential engine for driving productivity and industrial development. However, unlike traditional industrial control systems that typically operate within isolated internal networks with minimal consideration for external threats [1], the extensive interconnection of new industrial equipment and the ongoing advancement of smart technologies have led to increasingly complex and diverse cybersecurity challenges for industrial Internet systems. These challenges encompass computer viruses, malware, distributed denial-of-service (DDoS) attacks, and more [2]. As external threats continue to evolve, traditional protection mechanisms are facing heightened demands, and the security of the industrial Internet is under significant strain. Therefore, industrial Internet intrusion detection technology has emerged to monitor, identify, and respond to potential security threats within the system. This technology aims to prevent malicious activities such as unauthorized access, data tampering, and device destruction, while providing continuous security protection for industrial control systems through innovations in system architecture [3,4] and optimizations in algorithm performance [5,6]. However, in practice, industrial Internet systems generate a substantial amount of normal traffic data, which constitutes the majority of the dataset. In contrast, abnormal traffic data—representing potential intrusions or attacks—remains relatively scarce. This imbalance in data poses significant challenges for intrusion detection systems. As a result, the model often focuses excessively on normal traffic data while neglecting abnormal traffic data during training. This not only restricts the model’s generalization capabilities but also risks creating a bias toward the majority class of samples, potentially hindering its ability to effectively identify security threats.

In order to address the issue of data imbalance in industrial Internet intrusion detection, this paper proposes a data enhancement method for intrusion detection that is based on the WGAN and a self-attention mechanism. The primary contributions of this paper are as follows:

(1)   A traditional GAN (Generative Adversarial Network) consists of a generator and a discriminator: the generator expands the dataset by creating new samples, while the discriminator evaluates the authenticity of these generated samples. In this study, we enhance the GAN framework using WGAN, which improves the stability of the training process and increases the diversity of the generated samples. This enhancement brings the generated data samples closer to real data and effectively addresses the issue of data imbalance.

(2)   To improve the quality of generated samples, the study integrates the self-attention mechanism into the generator of the WGAN. When generating new anomalous traffic data, the generator employs the self-attention mechanism to concentrate on key features within the data. This approach ensures that the generated anomalous traffic samples are not only quantitatively enhanced but also qualitatively closer to real anomalous traffic.

(3)   This paper demonstrates that this combination not only balances the category distribution within the dataset but also significantly improves the quality of the generated samples, allowing them to more closely align with actual attack patterns. The enhanced data samples effectively boost the accuracy and generalization capabilities of the intrusion detection model in detecting anomalous traffic, thereby providing a stronger safeguard for the security of industrial Internet systems.

2  Related Work

Early research in the field of intrusion detection did not adequately address the imbalance in data distribution among different classes of training samples. Consequently, many classification models tend to perform well only on the majority class of test samples. In contrast, the leakage rates for the minority class of test samples are significantly higher than average, with some individual instances of minority class attack traffic exhibiting leakage rates as high as 100%. In real network environments, these hard-to-detect intrusion flows are often more aggressive, thereby increasing network security risks. Given the widespread and challenging nature of the unbalanced dataset classification problem, researchers have investigated this issue in depth. Currently, methods for addressing the unbalanced data classification problem can be categorized into three main groups: data-level methods, algorithm-level methods, and Generative Adversarial Network (GAN)-based methods.

2.1 Data Enhancement Methods Based on the Data Level

The principle of data-level methods is to achieve a quantitative balance between the two types of data by adjusting the imbalanced ratio of minority and majority class samples in the dataset. There are two primary techniques for this: oversampling and undersampling.

Oversampling addresses class imbalance in datasets by increasing the number of samples in the minority class. Common techniques include SMOTE (Synthetic Minority Over-sampling Technique) and its variants. Among traditional oversampling methods, the SMOTE algorithm, proposed by Nitesh [7], is the most widely recognized. This algorithm expands minority class samples through random interpolation. While it is simple and effective for expanding minority class data, it is susceptible to generating noisy samples, particularly when the data dimensionality is high, which can adversely affect the model’s classification performance. Liang et al. [8] proposed the LR-SMOTE (Logistic Regression-Synthetic Minority Oversampling Technique) algorithm, which enhances the oversampling process by adjusting the distance between the generated data and the original samples. Experimental results indicate that LR-SMOTE outperforms the traditional SMOTE algorithm in terms of G-means value, F-measure value, and AUC. Gu et al. [9] introduced the CBSMOTE (CenterBorderline_SMOTE) algorithm, which improves data quality by extracting features from attack data. This algorithm effectively addresses the data imbalance problem and enhances classification performance and model generalization ability. Douzas et al. [10] proposed the KMeans-SMOTE algorithm, which combines K-means clustering with SMOTE. This method clusters a small number of samples and then synthesizes targeted oversampling points within different clusters. However, this approach incurs additional storage and computational overheads, which may lead to model overfitting.

Under-sampling methods address the challenges associated with oversampling techniques by either eliminating redundant samples from the majority class or retaining representative samples to create a balanced dataset. Existing under-sampling methods can be categorized into proximity-based methods and clustering-based methods. Proximity-based methods remove noise and redundant samples based on the labels of the nearest neighbors. For instance, Nwe and Lynn [11] employed the k-Nearest Neighbors (KNN) algorithm to eliminate majority class samples that are found among the nearest neighbors of minority class samples, thereby reducing class overlap. Vuttipittayamongkol and Elyan [12] proposed four nearest-neighbor-based methods and applied them to 24 public datasets from UCI and KEEL, with NB-REC and NB-TOMEK yielding particularly favorable results. Yan et al. [13] introduced the concept of spherical nearest neighbors to identify the nearest neighbor points of majority class samples and subsequently proposed two strategies (SDUS1 and SDUS2) for selecting representative majority class samples based on diversity indexes. Cluster-based methods select representative sample points through clustering algorithms. Ibrar et al. [14] utilized a cluster-center-based under-sampling method to reduce information loss by selecting the centroid of the majority class as a retained sample. Tsai et al. [15] proposed an under-sampling method based on cluster analysis and instance selection, known as CBIs (Cluster-based Instance Selection), which groups most classes of samples through cluster analysis and screens representative samples in each group to remove redundant data, achieve data balance, and improve classification performance. Although under-sampling methods possess the characteristics of independent classification algorithms and reliable sample data, current under-sampling methods typically rely on a single nearest neighbor or clustering information, making it challenging to accurately identify noisy samples and potentially leading to the loss of key information.

2.2 Data Enhancement Methods Based on Algorithm Level

Algorithmic-level methods focus on a limited number of class samples by adjusting the classification model. These methods primarily include cost-sensitive learning and ensemble learning. Cost-sensitive learning rebalances the classes by modifying the loss values, while ensemble learning addresses the issue of imbalanced data by combining multiple learners. Louk and Tama [16] employed the Focal Loss method to enhance learning effectiveness on imbalanced data by dynamically adjusting sample weights, decreasing the weight of easily categorized samples, and increasing the weight of hard-to-classify samples. This approach improves learning outcomes for unbalanced data. Mulyanto et al. [17] utilized Focal Loss as a loss function in conjunction with Deep Neural Networks (DNN) and Convolutional Neural Networks (CNN), assigning higher weights to hard-to-classify samples during training. Their experiments demonstrated that the combination of Focal Loss and CNN yielded the best results. Gupta et al. [18] addressed the imbalance problem by increasing the misclassification cost of attack class samples through cost-sensitive deep modeling and ensemble methods. Bedi et al. [19] tackled the category imbalance issue using a Siamese neural network, which classifies training samples by calculating the similarity between training samples and input samples, achieving a higher recall rate for a limited number of attack class samples. Subsequently, Bedi et al. [20] improved this method and proposed the I-SiamIDS method, which consists of a two-layer ensemble model. The first layer identifies attacks, while the second layer further classifies these attacks into specific categories. Li et al. [21] trained multiple CNN models by combining subsets of majority class samples with minority class samples to create several sub-datasets, deriving final results through a voting strategy. Du et al. [22] proposed a cost-sensitive online ensemble learning algorithm that integrates multiple equalization methods, including initial classifier construction, dynamic misclassification costs, sample sampling, and base classifier weight computation, thereby enhancing classification performance under unbalanced data streams. Mhawi et al. [23] introduced a novel integrated learning algorithm for network intrusion detection systems (IDSs) that combines feature selection with a CFS-FPA hybrid approach, utilizing AdaBoosting and Bagging to augment four classifiers: Support Vector Machine (SVM), Random Forest, Naive Bayes, and K-Nearest Neighbors (KNN). Although these approaches have made significant strides in improving the recognition rates of minority class samples, they also face challenges such as high computational complexity and the risk of overfitting.

2.3 Data Enhancement Methods Based on Generative Adversarial Network

In recent years, breakthroughs in deep learning technology have led to significant advancements in GAN based methods, which have proven effective in addressing data imbalance issues. These methods have rapidly infiltrated various multidisciplinary applications. For instance, interdisciplinary technologies are being explored in medical image synthesis (e.g., ophthalmic image generation), innovations in materials science (e.g., nanostructure-driven neuromorphic computing), and building automation design (e.g., intelligent layout generation). In the realm of medical diagnosis, GANs enhance the efficiency of diagnosis and treatment through image fusion and anomaly detection. In the field of financial technology, they improve the accuracy of market predictions by utilizing time-series data augmentation. Additionally, in the area of intrusion detection, GAN-based data generation methods have emerged as a key solution to the data imbalance problem.

Shahriar et al. [24] proposed a GAN-based IIDS that effectively addresses the challenges of data imbalance and missing data in Cyber-Physical Systems (CPS) by generating synthetic samples. Experiments demonstrate that this model outperforms traditional IDS in terms of attack detection and model stability. Ding et al. [25] introduced a Generative Adversarial Network-based Data Enhanced Intrusion Detection Method (TMG-IDS), which significantly improves detection effectiveness through a multiple generator structure and optimized classifiers. Lee and Park [26] utilized a generative adversarial network model to create new virtual data that closely resembles existing data, thereby addressing the data imbalance problem in intrusion detection. They also proposed a model categorized as a random forest to evaluate detection performance, with experimental results confirming the model’s effectiveness. Fu et al. [27] developed a method for generating intrusion detection data using generative adversarial networks. Initially, the overall data is digitized and normalized to maintain data integrity. The ACGAN model is then employed to learn the hidden features of the data and generate new samples. Finally, the similarity and validity of the generated data are assessed from multiple perspectives. Experimental results indicate that the data produced by this method shares similar characteristics with the original data and can effectively enhance the original dataset. Li et al. [28] applied generative adversarial networks for data augmentation to address the data imbalance issue. They combined convolutional neural networks with bidirectional long short-term memory networks (BiLSTM) for network intrusion detection, utilizing the CIC-IDS 2017 dataset to compare their model against machine learning methods such as random forests and decision trees. The experimental results reveal that their model significantly outperforms traditional models, demonstrating that the GAN-CNN-BiLSTM architecture enhances the efficiency of intrusion detection.

Compared to data-level and algorithm-level techniques, GANs can generate synthetic samples that closely resemble real data, particularly for datasets with complex features or structures. This capability enhances dataset expansion. However, the performance of GANs is significantly influenced by the model architecture; an inappropriate model structure can lead to training failures or low-quality generated samples. Therefore, selecting an appropriate model architecture is a critical consideration in GAN applications.

3  Overview of Generative Adversarial Networks

In 2014, Ian Goodfellow and his colleagues first proposed the GAN model, a neural network architecture designed for generative modeling [29]. Generative Adversarial Networks represent a significant innovation in the field of deep learning in recent years, and their unique structure and design principles demonstrate considerable potential across various applications. GANs consist of two neural networks: the Generator and the Discriminator. These networks engage in a competitive yet collaborative process to continuously optimize their performance in a scenario known as adversarial training, where the success of one network is contingent upon the failure of the other.

The goal of the Generator is to produce realistic data samples from random noise. Typically, it is a neural network that takes random vectors as input and transforms them into data samples that resemble the training data through a series of neural network layers. The Discriminator is another neural network designed to differentiate between the fake data generated by the Generator and the real data. During training, both the Generator and the Discriminator update their respective parameters using a backpropagation algorithm and gradient descent. The loss function for the Discriminator is generally based on its accuracy in distinguishing between real and generated data, while the loss function for the Generator is determined by how often the Discriminator misclassifies the generated data as real. By alternately updating the parameters of both the Generator and the Discriminator, the Generative Adversarial Network (GAN) can gradually enhance the quality of the generated data, making it increasingly similar to real data. The objective function of the GAN is presented in Eq. (1):

minGmaxDV(D,G)=Ex∼data[log⁡(D(x))]+Ez∼pz(z)[log⁡(1−D(G(z)))](1)

where D(x) denotes the probability that the discriminator classifies the data x as real, and G(z) represents the data generated by the generator based on the noise z. Additionally, let Ex∼data and Ez∼pz(z)denote the expectations of the true data and the noise data, respectively. This objective function embodies a zero-sum game, in which the generator aims to minimize the function while the discriminator seeks to maximize it.

The structure of the GAN model is illustrated in Fig. 1, which primarily consists of two components: the discriminator and the generator. The training process can be divided into the following steps:

(1)  Initialize Generators and Discriminators: Generators and discriminators are neural network models that require proper initialization. During this phase, the architectures of both the generators and discriminators are designed and constructed. Following this, initial values are assigned to the parameters of each network using either random initialization or specific weight initialization methods. These parameters include the weights and biases of the neural networks, which determine how the networks process inputs and generate outputs.

(2)  Training the Discriminator: At the outset of the training process, the discriminator is presented with a batch of real samples alongside a batch of fake samples generated by the generator. It classifies these samples and computes the loss function. Subsequently, the backpropagation algorithm is employed to update the weights of the discriminator, thereby enhancing its classification accuracy for both real and fake samples.

(3)  Training the Generator: The generator produces a batch of synthetic samples and presents them to the discriminator. The discriminator then evaluates these synthetic samples and computes the loss function. The backpropagation algorithm is employed to update the generator’s weights, thereby enhancing the likelihood that the samples it generates will be misclassified as real by the discriminator.

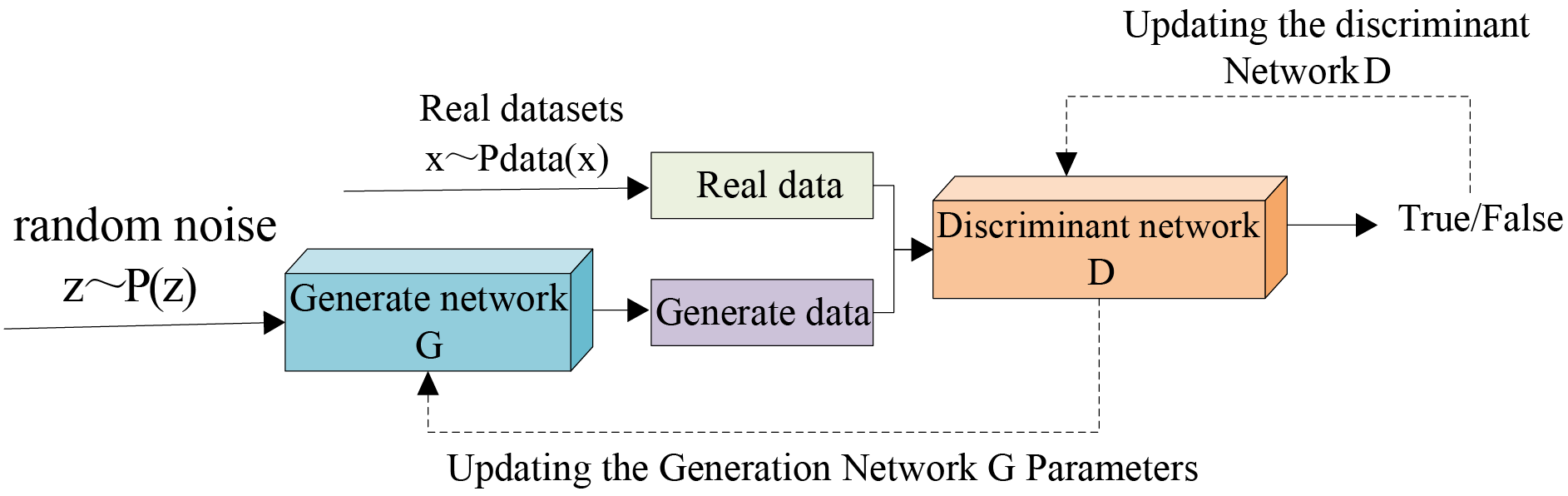
Figure 1: Structure of the basic model for generating adversarial networks

Repeat steps (2) and (3): alternately train the generator and the discriminator until either a predetermined number of training rounds is completed or the loss function converges.

4  Data Augmentation Model for Intrusion Detection Based on SA-WGAN

This study addresses the issue of data imbalance in industrial Internet intrusion detection by proposing a GAN enhancement method that incorporates a self-attention mechanism. Traditional methods often exhibit low detection rates when confronted with limited types of anomalous traffic. In this paper, we improve the generator structure and introduce the self-attention mechanism, enabling the model to concentrate on the key features of traffic data. This enhancement not only improves the quality of the generated samples but also optimizes computational efficiency. Experimental results demonstrate that the anomalous traffic data generated by this method significantly outperforms traditional generation methods in terms of fidelity and diversity. By augmenting the dataset, the intrusion detection model can be trained more effectively, thereby enhancing its ability to recognize potential security threats and ultimately improving the overall security of the industrial Internet.

4.1 Model Design

The data enhancement model based on the Generative Adversarial Network (SA-WGAN) can generate samples that closely resemble the real data distribution through the collaboration of two primary components: the generator and the discriminator. The generator produces high-quality samples utilizing an inverse convolutional layer and a self-attention mechanism, while the discriminator assesses the authenticity of the generated data. The model structure is shown in Fig. 2.

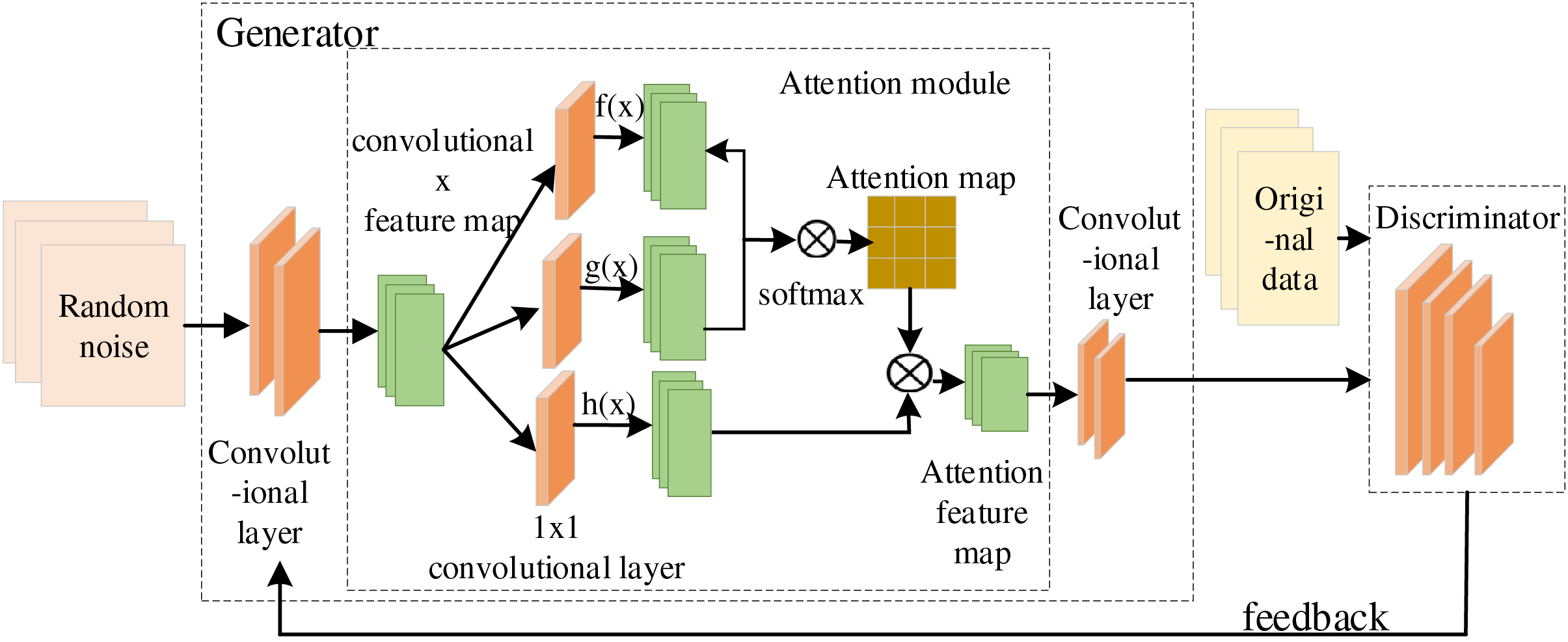
Figure 2: Structure of the SA-WGAN-based intrusion detection data enhancement model

(1) Generator

In the generator, a series of inverse convolution (also known as transposed convolution) layers are employed to progressively upsample the latent vectors of the inputs, resulting in samples with intricate structures and details. Furthermore, a self-attention mechanism is integrated into the model, enabling it to capture long-range dependencies and improve the quality of the generated samples by assessing the correlations between various locations in the input sequence. Ultimately, the generator produces samples that closely mimic the real data distribution, thereby facilitating data generation and enhancement.

(2) Attention module

In the attention mechanism module of the model, first, the input sequences are subjected to three different linear transformations (i.e., multiplied by the weight matrix) to obtain f(x), g(x), and h(x) with different output channel sizes. The purpose of these transformations is to map the input data to a new representation space for subsequent similarity computation and weighting operations, as shown in Eqs. (2)–(4). Where Wf, Wg, and Wh denote the weight matrices trained by different methods. Next, f(x) is transposed and multiplied by g(x) using Eq. (5) to obtain a similarity score matrix. Each element of this matrix represents the similarity between a query and a key. Then, a softmax function is applied to the similarity score matrix to transform it into an attention weight matrix. The softmax function converts the raw scores into a probability distribution with positive numbers and a sum of 1, which represents the importance of each key for the current query.

f(x)=Wfx(2)

g(x)=Wgx(3)

h(x)=Whx(4)

sij=f(xi)Tg(xi)(5)

Finally, a weighted sum is performed using the attention weight matrix pairs. Specifically, each h(x) vector is multiplied by its corresponding attention weight, and then all the weighted value vectors are summed to obtain the self-attentive output for the current query location. This process allows the model to dynamically aggregate information based on the similarity of different locations in the input sequence. The attention weights are calculated according to Eq. (6), where βj,i indicates the degree of influence of the model on the ith location when synthesizing the Jth region. Then, the attention feature map is obtained according to Eq. (7). Finally, the feature map with attention mechanism is combined with the feature vector x to obtain the feature mapping Y with attention mechanism by Eq. (8), where γ is the scale parameter.

βj,i=exp(sij)∑i=1Nexp(sij)(6)

oj=∑i=1Nβj,ih(xi)(7)

yi=γoj+xj(8)

(3) Discriminator

In the discriminator, features are progressively extracted from the input data through a series of one-dimensional convolutional layers, while the Leaky ReLU activation function enhances the model’s nonlinearity. As the network deepens, the number of channels is gradually increased to capture more complex features. The final output of the discriminator is a probability value that indicates the likelihood that the input sample is real, typically ranging between 0 and 1. If the output is close to 0, the discriminator considers the input sample to be a fake generated by the generator; conversely, if the output is close to 1, the discriminator considers the input to be real. An output near 0.5 indicates that the discriminator is uncertain about the authenticity of the input, suggesting that it lies in a fuzzy region between real and generated samples. During training, the discriminator’s objective is to maximize the probability of correctly classifying real and generated samples, thereby encouraging the generator to produce more realistic outputs while minimizing the probability of incorrect classifications to enhance the discriminator’s accuracy.

(4) Loss function

The Jensen-Shannon (JS) divergence [30], which is commonly employed as a loss function in traditional generative adversarial networks, quantifies the difference between the distribution of generated samples and that of real data. This measurement guides the generator in producing more realistic samples. However, the asymmetry inherent in the JS divergence between the two distributions can create an imbalance in the training process of both the generator and the discriminator. Such an imbalance may result in issues including training instability, mode collapse, and the vanishing or exploding gradient problem.

To address the issues in the original GAN, Arjovsky et al. [31] proposed utilizing the Wasserstein distance, also referred to as the Earth-Mover (EM) distance, to measure the distance between two distributions, rather than employing the Jensen-Shannon (JS) divergence. The Wasserstein distance is defined by the following Eq. (9):

W(Pr,Pg)=infγ∼∏(pr,pg)E(x,y)∼γ[||x−y||](9)

where Pr and Pg represent two probability distributions, and X and Y are the random variables in these distributions, respectively. inf denotes the lower bound, i.e., the smallest expected distance among all possible transmission modes. E(x,y)∼γ[||x−y||], on the other hand, denotes the expected value of the distance between random variables X and Y. The distance between X and Y is usually calculated based on some kind of distance metric (e.g., Euclidean distance). This expected value is usually computed based on some distance metric such as the Euclidean distance. Specifically, the Wasserstein distance attempts to find an optimal transmission method that minimizes the expected value of the distance between random variables during transmission from distribution Pr to distribution Pg. This transmission method can be understood as a kind of “bulldozing” process, in which the probability mass (which can be imagined as a mound of earth) is “bulldozed” from the Pr distribution to the Pg distribution, and the Wasserstein distance is the minimum cost of this bulldozing process. Since the inf in Eq. (9) cannot be solved directly, Arjovsky transforms it as shown in Eq. (10):

W(Pr,PG)=1Ksup||f||L≤KEx∼pr[f(x)]−Ex∼pg[f(x)](10)

The restriction on Eq. (10) is that the Lipchitz constant ||f||L of the function f does not exceed K, and the upper bound of Ex∼pr[f(x)]−Ex∼pg[f(x)] is taken for all possible satisfactions of the condition for f under this condition, and then Eq. (10) is transformed approximately as shown in Eq. (11):

W(Pr,PG)≈1Ksup||fω||L≤KEx∼pr[fω(x)]−Ex∼pg[fω(x)](11)

For the constraint ||fω||L≤K in Eq. (11), WGAN uses weight clipping to restrict all parameters fω of the discriminator ωi to not exceed [−c, c] to satisfy the Lipschitz continuity condition. This is done to ensure that the gradient of the discriminator is not too large or too small, thus making the training process more stable. Therefore, the objective function of WGAN is shown in Eq. (12):

V=Ex∼pr[D(x)]−Ex∼pg[D(x)](12)

Maximize Eq. (13) as much as possible under the restriction of not exceeding [−c, c], at which point V approximates the Wasserstein distance between Pr(x) and Pg(x). The loss functions of the generator and discriminator in WGAN are shown in Eqs. (13) and (14) as follows:

LD=−Ex∼pg[D(x)](13)

LG=Ex∼pg[D(x)]−Ex∼pr[D(x)](14)

Compared to the Jensen-Shannon (JS) divergence used in traditional GANs, the Wasserstein distance provides a more accurate measure of the difference between two probability distributions and offers greater stability in addressing issues such as gradient vanishing and mode collapse. By incorporating the Wasserstein distance as a loss function, WGAN is able to better guide the generator in producing realistic samples while enhancing training stability and convergence speed, thereby making the generative adversarial network more efficient and reliable. However, weight tailoring may lead to a waste of network parameters, as the tailoring operation restricts the parameters to their range, which may prevent the model from reaching its optimal solution. In addition, weight tailoring may cause the model to perform poorly in some cases because it is a coarser way to control the complexity of the model. In this paper, we choose to add a gradient penalty term to the loss function of WGAN, which acts directly on the gradient to ensure that the magnitude and direction of the gradient meet the requirements by penalizing the gradient of the discriminator. This method can control the gradient size more accurately and avoid the problem of disappearing or exploding gradients that may be caused by weight cropping. The loss function of the discriminator is shown in Eq. (15):

LD=Ex~∼pg[D(x~)]−Ex∼pr[D(x)]+λx^∼PpenaltyE[(||∇x^D(x^)||2−1)2](15)

where x~ is obtained by sampling from the generated pseudo-data distribution Pg, x is obtained by sampling from the real data distribution Pr, x^ denotes the data mixed by a certain proportion of x~ and x, x^∼Ppenalty denotes sampling uniformly on a straight line between any data obeying Prand Pg, ∇x^D(x^) denotes the derivative of D(x^) over x^ to compute the gradient, and λx^∼PpenaltyE(||∇x^D(x^)||2−1)2 that is the gradient penalization term, which denotes that the loss function will be the L2 paradigm of gradient of the input data constrained to be around 1.

Compared to traditional methods, such as weight clipping, the gradient penalty does not impose restrictions on the model’s parameters. Instead, it directly regulates the model’s complexity during the optimization process. This approach results in a more natural and smooth training experience while also enhancing training efficiency. Furthermore, by applying a penalty term to the gradient of the discriminator, the gradient penalty compels the discriminator to satisfy the Lipschitz constraint, which improves both the stability and performance of the model. This constraint ensures that the gradient of the discriminator in the input space remains bounded, thereby preventing issues such as exploding or vanishing gradients and making the training process more reliable.

4.2 Model Training Process

In this paper, data enhancement techniques are employed to improve the performance of intrusion detection models. The methodology is implemented through several steps. First, the raw data undergoes preprocessing, which includes low variance filtering, normalization, and unique heat coding. Next, random noise z is input into a generator to produce minority class samples, which are then combined with actual majority class samples to create a balanced dataset. In the data enhancement module, the generator enhances the training data by generating synthetic data G(z), while the discriminator evaluates and classifies both the real and generated data, outputting the classification results. Ultimately, after training the discriminator, the generator becomes capable of producing more realistic minority class samples, thereby improving the model’s classification performance for intrusion detection tasks. The final model is trained using the balanced dataset and outputs classification results, effectively enhancing the recognition capability of the intrusion detection module. The entire model training process is illustrated in Fig. 3.

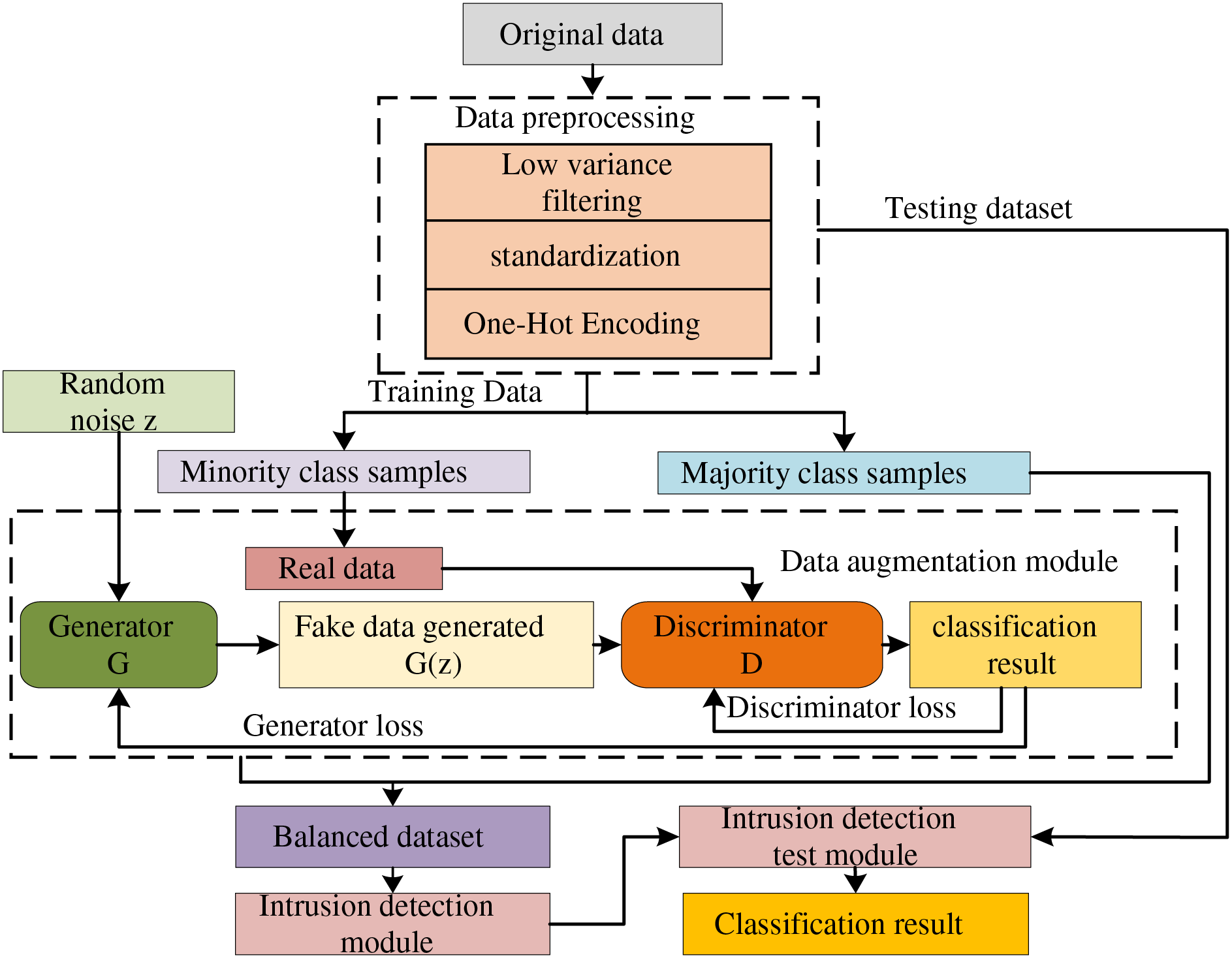
Figure 3: Model training process

5  Experiment and Analysis

5.1 Experimental Environment

The experimental environment described in this paper is based on a 64-bit Windows 10 system equipped with a 3.00 GHz Intel(R) Core (TM) i7-9700 CPU. The programming language utilized is Python 3.7.13, and the integrated development environment (IDE) employed is PyCharm. The experiments were conducted using the PyTorch 1.13.1 deep learning framework. All experiments were carried out under consistent hardware and software conditions, as well as identical algorithmic parameters.

5.2 Model Structural Parameters

The generator model comprises five layers, primarily including the transposed convolutional layer and the self-attention mechanism. The first through fourth layers progressively upsample the input data using the transposed convolutional layer to produce feature maps of varying sizes, while the final layer generates output samples of size 17. The self-attention mechanism is incorporated in the third layer to enable the generator to concentrate on the key features within the data, thereby enhancing the quality and fidelity of the generated samples, as illustrated in Table 1.

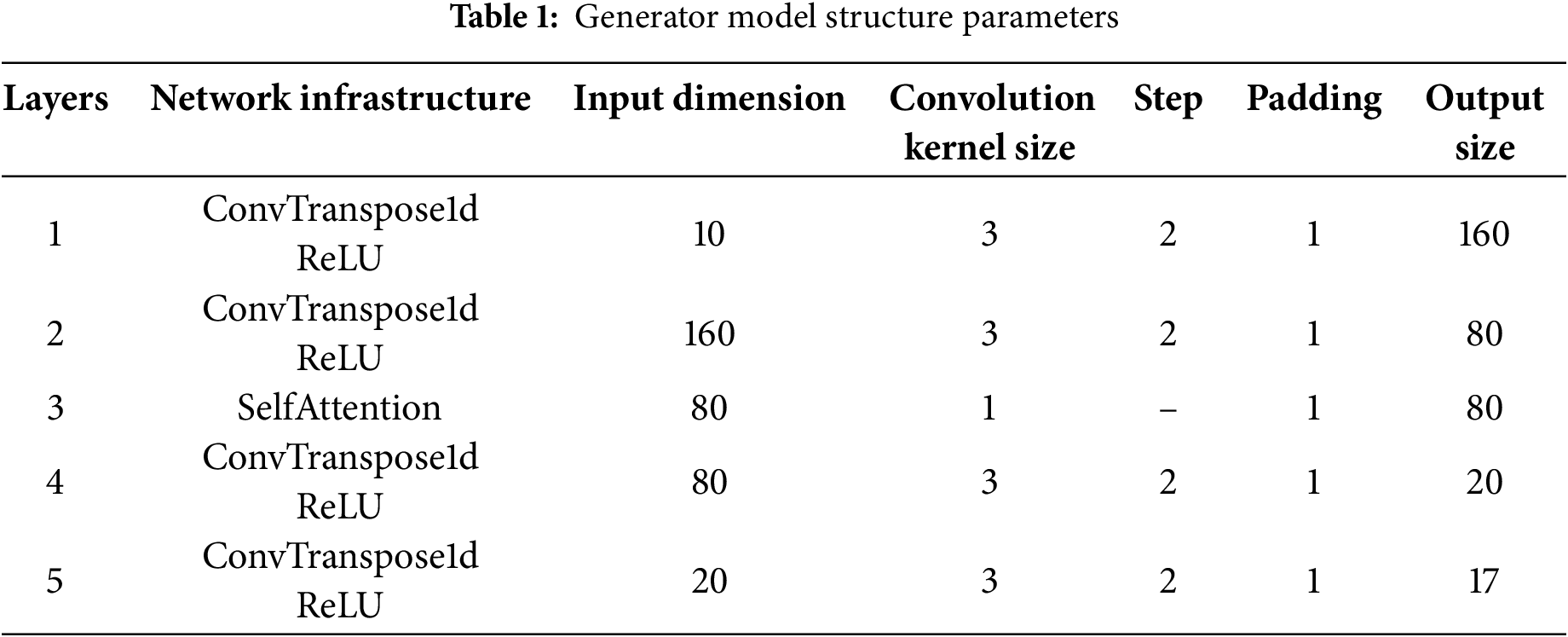
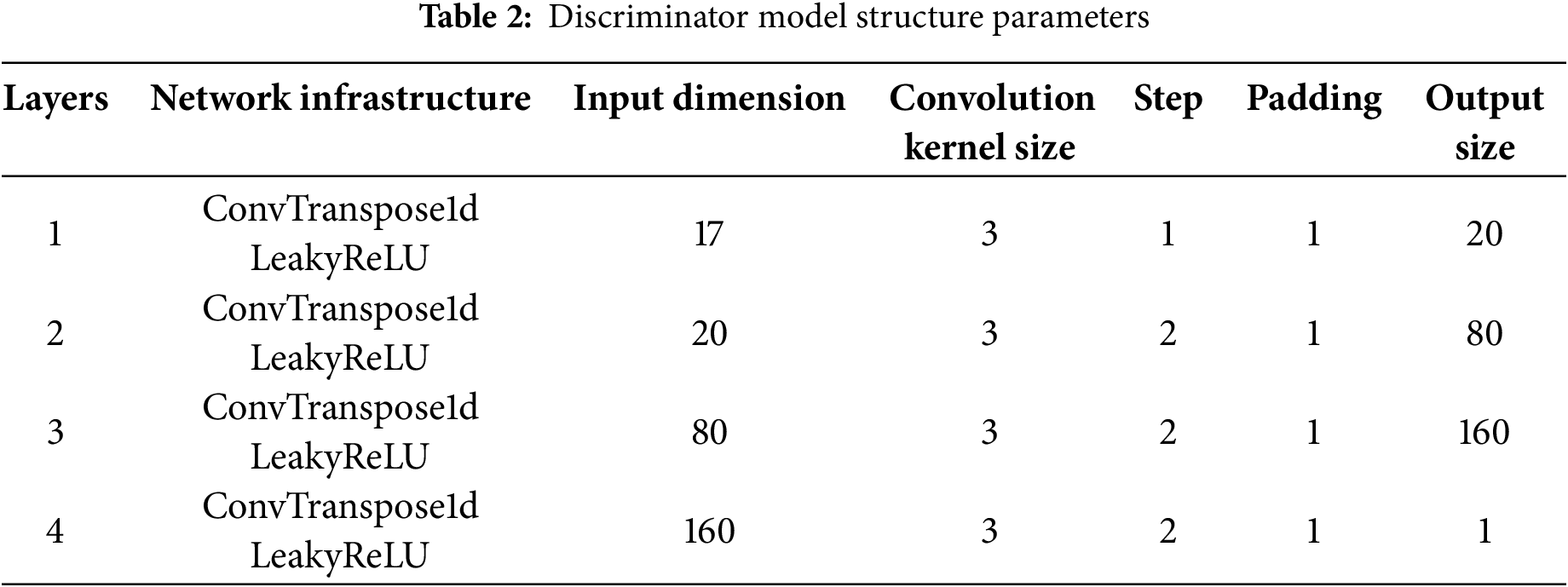
The discriminator model comprises four transposed convolutional layers, which are activated using the Leaky ReLU function. Each layer progressively extracts features from the samples produced by the generator and ultimately outputs a scalar value that indicates the probability of the sample being real. This structure aims to enhance the generator’s performance by evaluating the generated samples, thereby facilitating the generation process in relation to the training data. This is shown in Table 2.

5.3 Dataset

5.3.1 Dataset Description

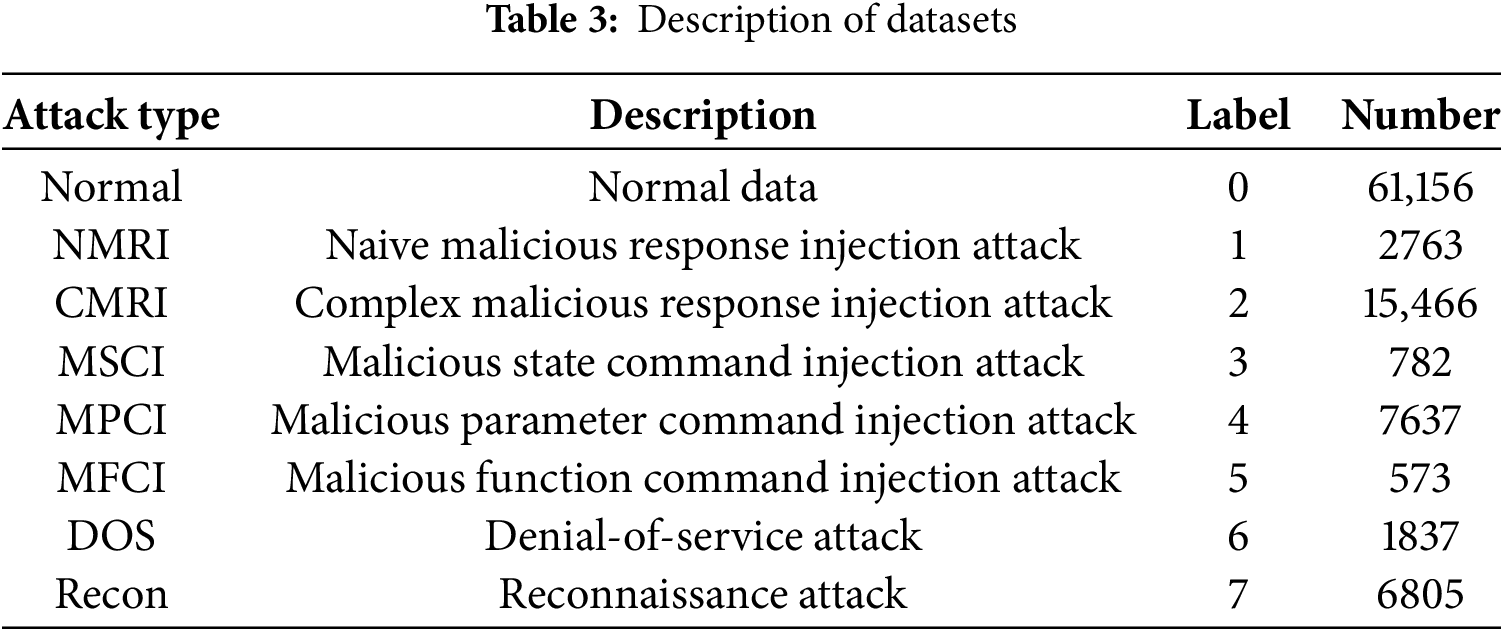
In 2014, Mississippi State University released a standardized dataset for intrusion detection in industrial control systems that is derived from network layer data from natural gas pipeline control systems [32]. The dataset contains network layer data from natural gas pipeline control systems covering a wide range of attack types and normal data. The specific attack types are shown in Table 3.

5.3.2 Data Preprocessing

It plays a crucial role in the experimentation and testing of industrial Internet intrusion detection models, significantly influencing their performance and detection accuracy. The data preprocessing described in this paper is primarily divided into three steps: low-variance filtering, normalization, and one-hot encoding.

(1) Low variance filter

The dataset discussed in this chapter is complex and variable, comprising numerous features. However, not all features are well-differentiated; some exhibit very low variance, indicating that they do not contribute significant information. These features are deemed unimportant and are subsequently removed. For example, if a feature accounts for 95% of the instance values across all input samples, it can be considered not particularly useful. A feature in which 100% of its values are identical provides no meaningful information. In this paper, we eliminate the nine feature columns with the lowest variance, resulting in a dataset with seventeen valid features.

(2) Normalization

The Gas Pipeline dataset comprises high-dimensional features characterized by significant intervals between their maximum and minimum values. In this paper, the feature values are mapped to a specific range of [0, 1] using min-max normalization. The normalization formula is presented in Eq. (16):

xp′=xq−min(xp)max(xp)−min(xp)(16)

(3) Unique thermal coding

Classifiers cannot directly process the unordered discrete features of natural gas pipeline datasets. In this paper, we employ solo thermal coding to create a mapping table for discrete feature data, transforming it into an ordered and continuous format. The dataset includes eight classification results: Normal (0), NMRI (1), CMRI (2), MSCI (3), MPCI (4), MFCI (5), DOS (6), and Recon (7). These classifications can be encoded as follows: (1, 0, 0, 0, 0, 0, 0, 0), (0, 1, 0, 0, 0, 0, 0, 0), (0, 0, 1, 0, 0, 0, 0, 0), (0, 0, 0, 1, 0, 0, 0, 0), (0, 0, 0, 0, 1, 0, 0, 0), (0, 0, 0, 0, 0, 1, 0, 0), (0, 0, 0, 0, 0, 0, 1, 0), and (0, 0, 0, 0, 0, 0, 0, 1). This is illustrated in Eq. (17):

One−hot encodi={(1,0,0,0,0,0,0,0),if the result is Normal(0).(0,1,0,0,0,0,0,0),if the result is NMRI(1).(0,0,1,0,0,0,0,0),if the result is CMRI(2).(0,0,0,1,0,0,0,0),if the result is MSCI(3).(0,0,0,0,1,0,0,0),if the result is MPCI(4).(0,0,0,0,0,1,0,0),if the result is MFCI(5).(0,0,0,0,0,0,1,0),if the result is DOS(6).(0,0,0,0,0,0,0,1),if the result is Recon(7).(17)

5.4 Analysis of Experimental Results

5.4.1 Data Set Description and Data Enhancement

This paper utilizes the natural gas pipeline dataset provided by Mississippi State University in 2014, which is characterized by data imbalance. Specifically, the dataset comprises 63.035% Normal type data, 15.941% CMRI type data, and 7.871% MPCI type data. In contrast, the MSCI type data constitutes only 0.806%, while the MFCI type data represents a mere 0.590%. Consequently, the experiments in this section concentrate on augmenting the two minority classes, MSCI and MFCI. The number of samples per class in the gas pipeline dataset without augmentation is shown in Fig. 4.

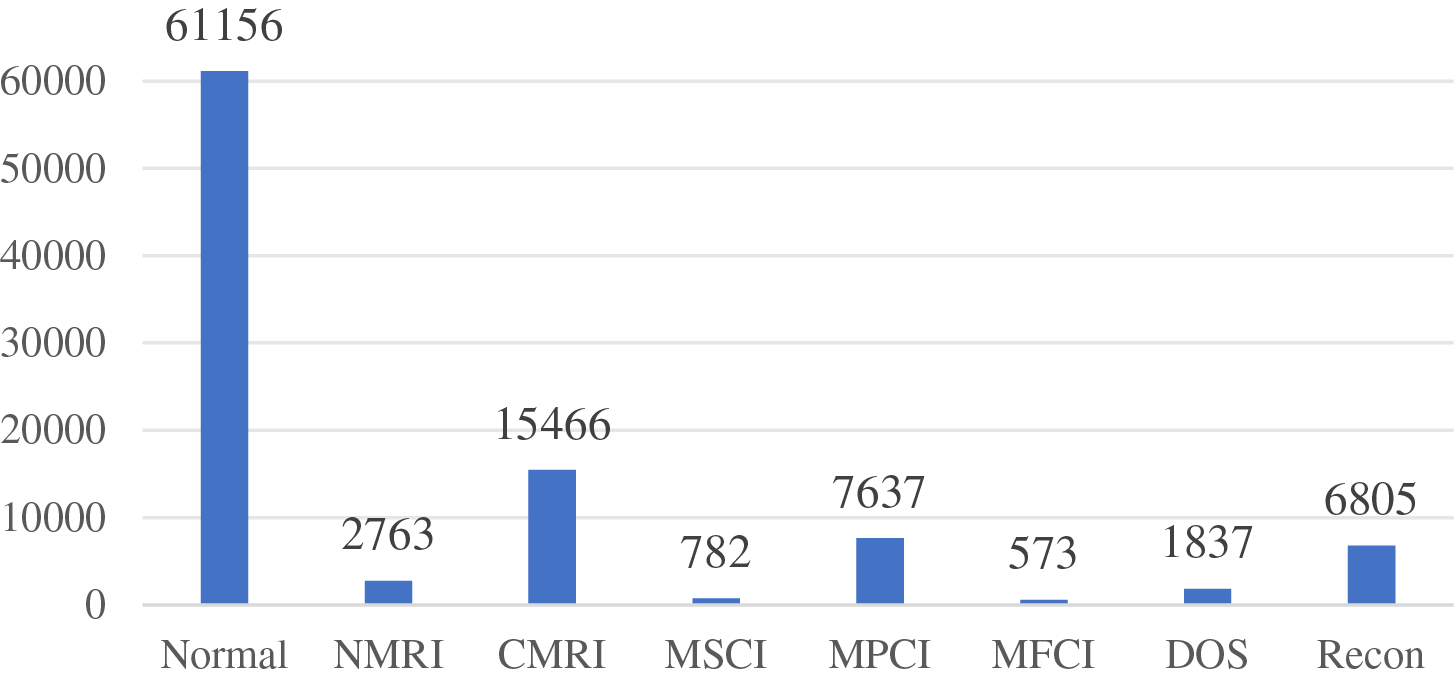
Figure 4: The number of samples of each category in the gas pipeline dataset before data augmentation

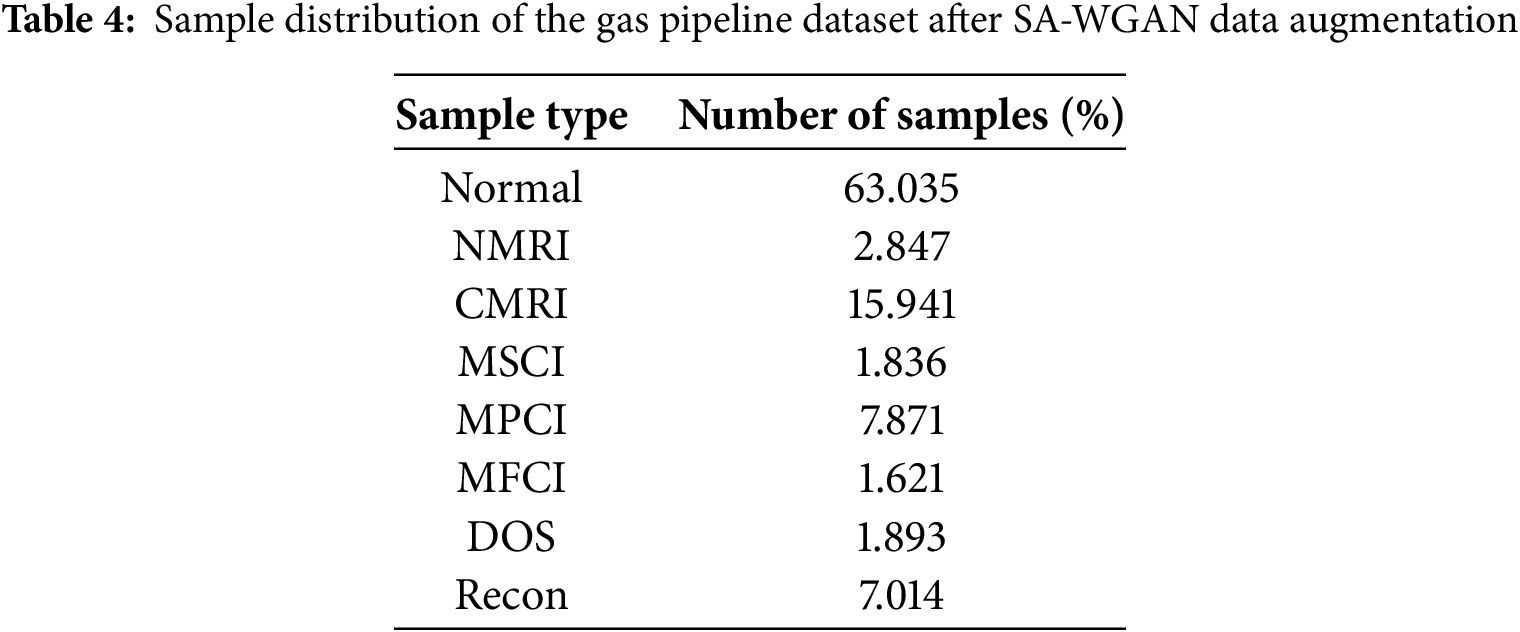
To balance the data categories in the natural gas pipeline industry dataset, this paper generates new samples for the two minority classes, MSCI and MFCI, which are underrepresented in the training set, using the SA-WGAN-based data augmentation method. After augmentation, the number of samples for the minority classes, MSCI and MFCI, was increased to match the other attack classes. Specifically, 1000 new samples were generated for each minority class using a generative adversarial network, and these new samples were merged with the original training set to create a new, data-enhanced dataset. This process effectively balanced the data categories within the dataset. The distribution and proportion of each category in the SA-WGAN-enhanced gas pipeline dataset are presented in Table 4.

In order to further evaluate the quality of samples generated by the SA-WGAN, we visualize and compare the original dataset with the SA-WGAN-augmented dataset using the t-distributed Stochastic Neighbor Embedding (t-SNE) technique. t-SNE is a nonlinear dimensionality reduction method that minimizes the Kullback-Leibler divergence between the data distributions in high-dimensional and low-dimensional spaces. This technique effectively maps high-dimensional data to a low-dimensional space while preserving both the local and global structures of the data.

Through t-SNE dimensionality reduction, we mapped the original dataset to a two-dimensional space and visualized the comparison with the dataset generated by SA-WGAN. Fig. 5 illustrates the t-SNE visualization results categorized by data source. Overall, the original data and the two types of data generated by SA-WGAN exhibit an overlapping distribution trend in the two-dimensional space, indicating that the generated samples share a high degree of similarity with the original data in the feature space. In the central region of the 2D space, the generated data form two dense, red, forked clusters, which enhance the two attack types, MSCI and MFCI, that have very few samples in the original dataset. These clusters are centrally generated in the core region of the target category within the high-dimensional feature space, resulting in the t-SNE mapping into distinct clusters after dimensionality reduction.

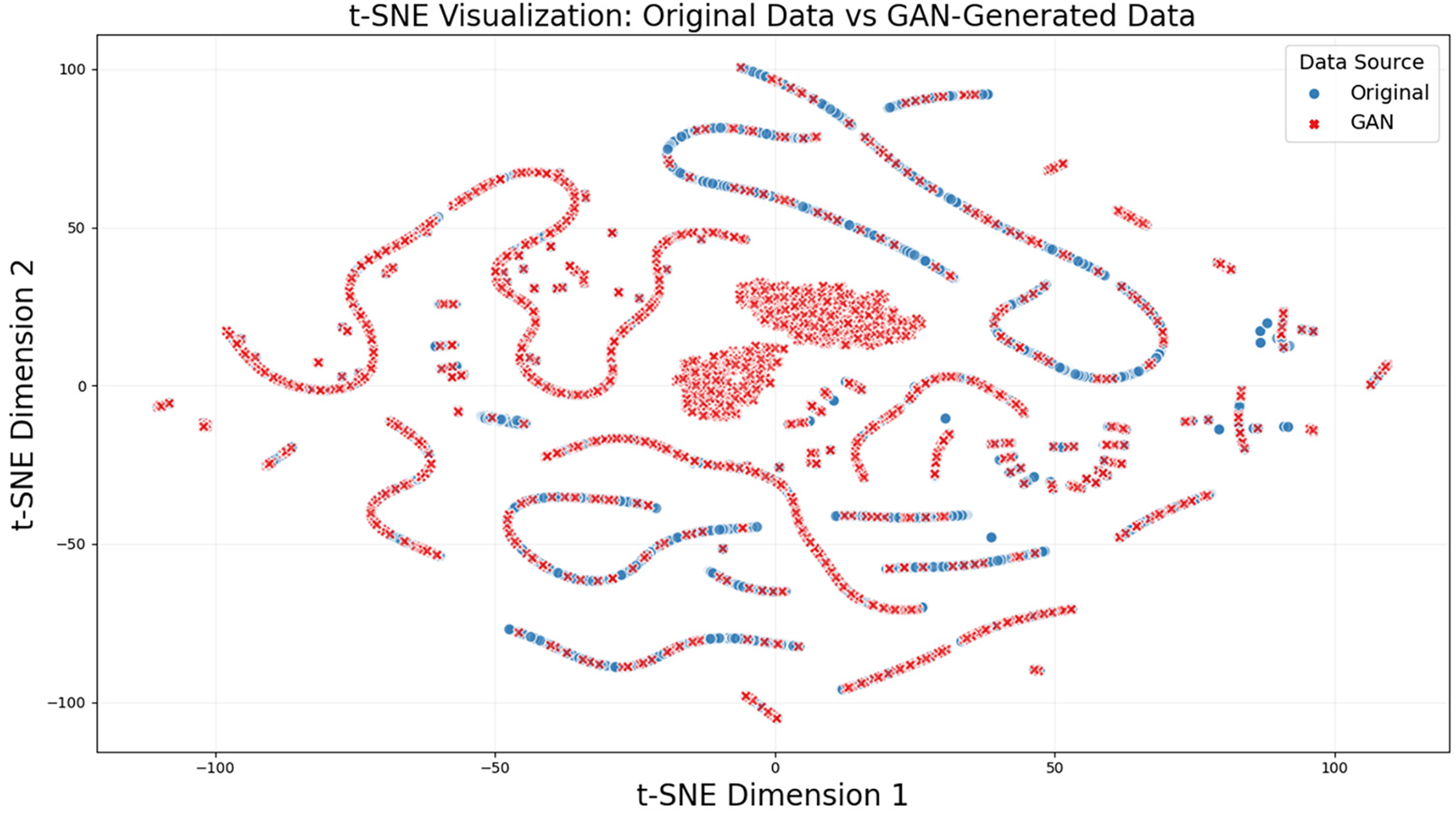
Figure 5: Visualization of the original data and the data distribution after data enhancement

5.4.2 Performance Comparison of Data Enhancement Methods

To assess the effectiveness of data enhancement methods based on GANs and attention mechanisms in the gas pipeline dataset, models were trained using the following datasets: the original gas pipeline training set, the dataset enhanced with GAN, the dataset enhanced with WGAN, and the dataset enhanced with SA-WGAN. The models were validated using the test set, with classification models constructed using both CNN and SRU (Simple Recurrent Unit), using 100 epochs for training. The results are presented in Table 5.

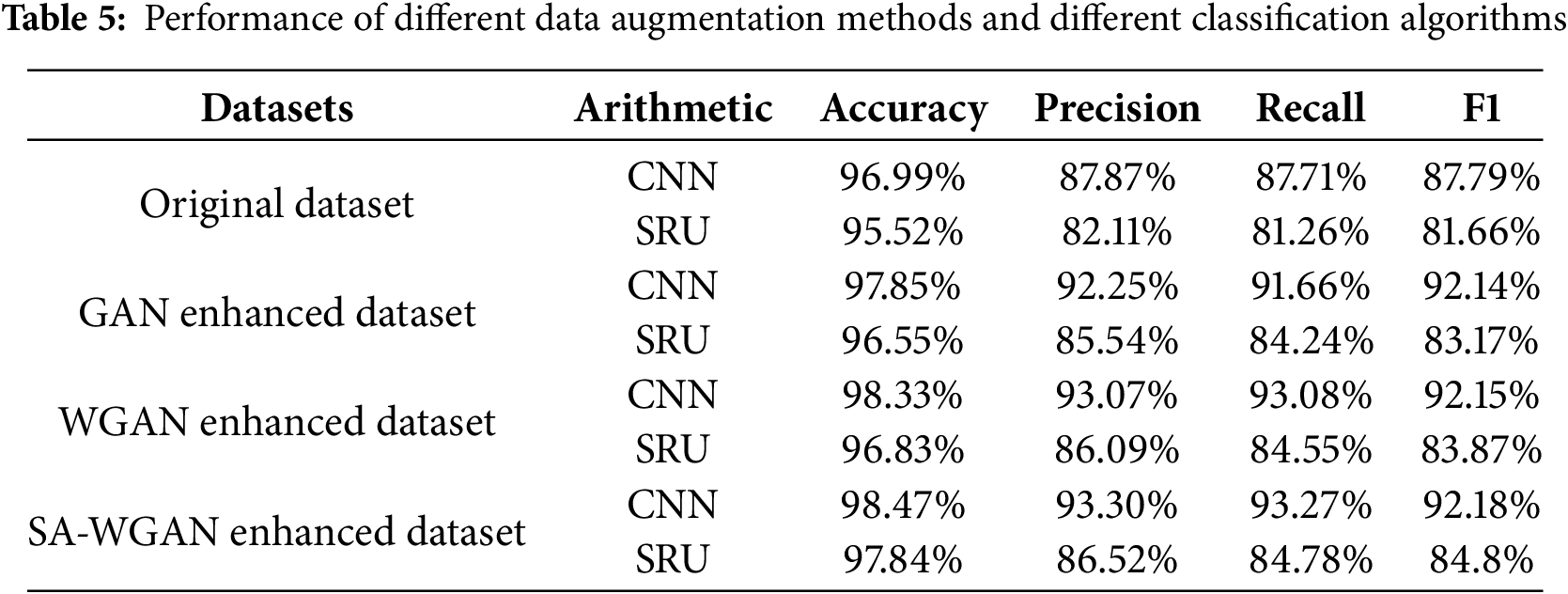
From Table 5, it can be observed that the detection results obtained from the dataset enhanced using the SA-WGAN algorithm are superior. On the original dataset, CNN achieved an accuracy of 96.99%, and SRU attained 95.52%. The CNN model outperforms the SRU in terms of accuracy, precision, recall, and F1 score. In the GAN-enhanced dataset, the CNN and SRU achieved accuracies of 97.85% and 96.55%, respectively, indicating an improvement over the original dataset, particularly in precision and recall, with a significant enhancement in CNN performance. On the WGAN-enhanced dataset, the accuracy of the CNN further increased to 98.33%, while the SRU reached 96.83%. However, the improvements in precision and recall were more modest compared to those observed in the GAN-enhanced dataset. Finally, on the dataset augmented with the SA-WGAN, the CNN’s accuracy reached 98.47%, accompanied by increases in precision, recall, and F1 score, highlighting the benefits of data augmentation and feature processing. Overall, the augmented datasets based on GAN and their variants significantly enhance model performance, particularly in the application of CNN models.

5.4.3 Performance Comparison of Data Enhancement Methods

To further assess the impact of the SA-WGAN-based intrusion detection data enhancement algorithm on detection performance, particularly concerning minority samples (MSCI and MFCI), experimental comparisons were conducted using a balanced training set. Fig. 6 represents the classification of the dataset after SA-WGAN data enhancement using a CNN classification model, and Fig. 7 represents the classification of the dataset after data enhancement using the SRU classification model.

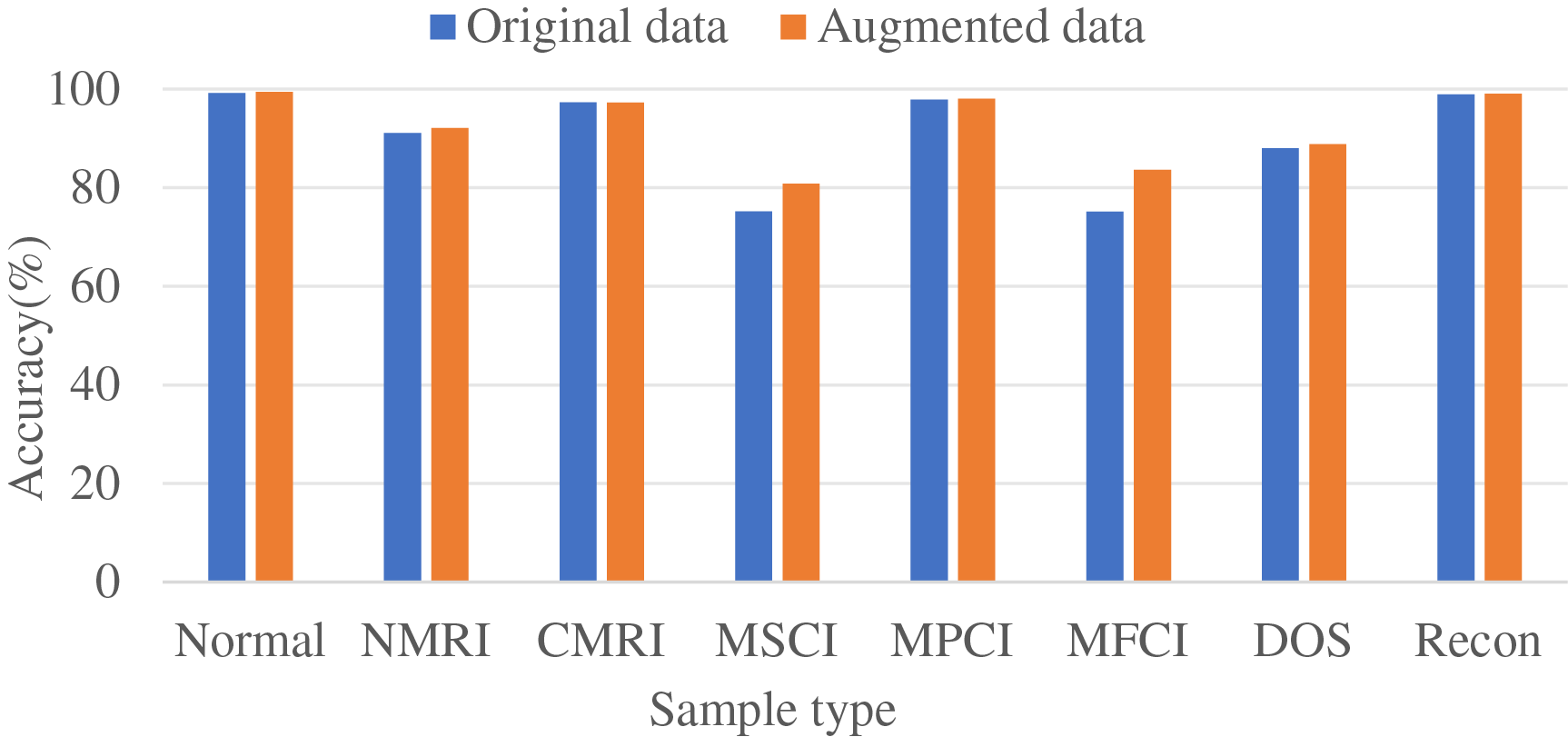
Figure 6: Comparison of recognition accuracy of attack samples based on the CNN model

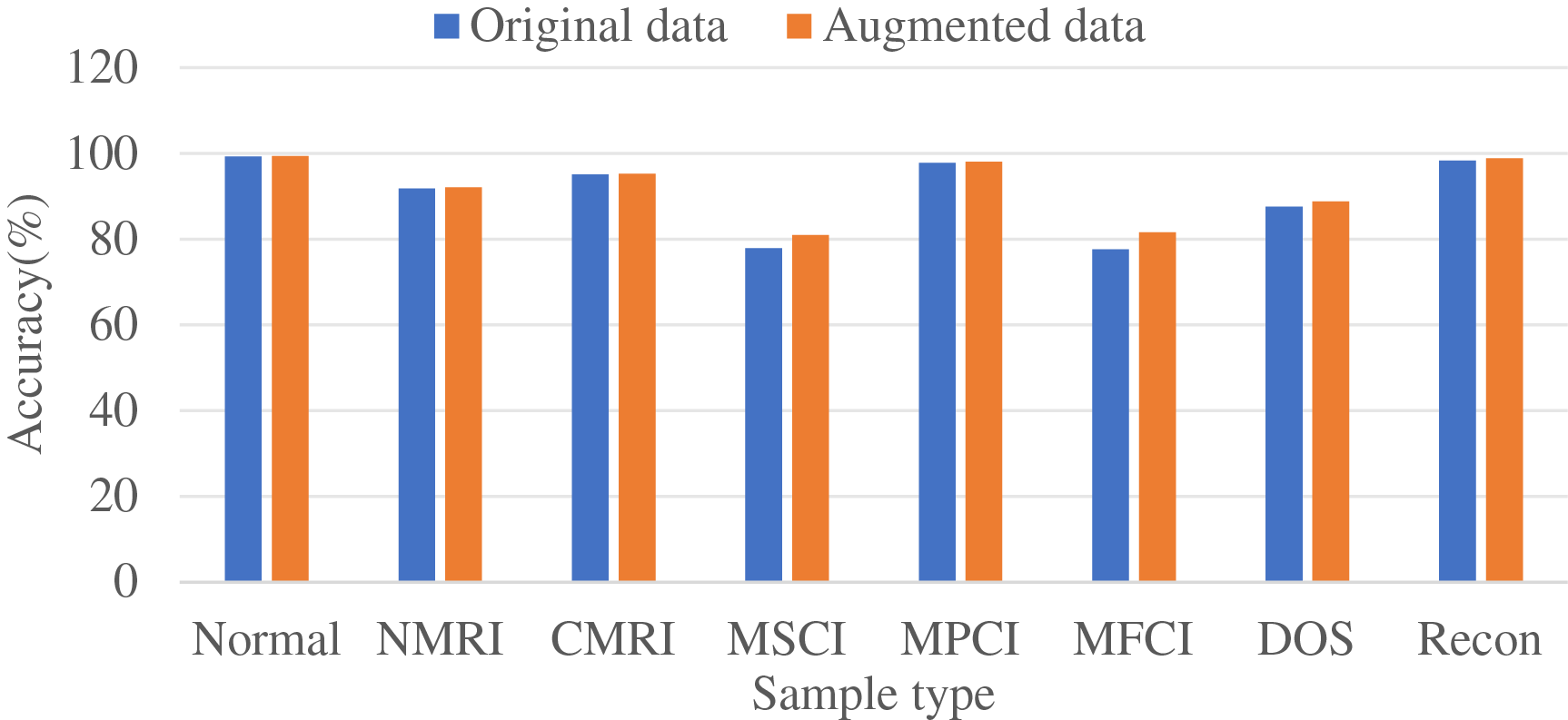
Figure 7: Comparison of recognition accuracy of attack samples based on the SRU model

The classification accuracy of most sample types is significantly enhanced with the introduction of the SA-WGAN in both CNN and SRUintrusion detection models. In both CNN and SRU frameworks, the detection accuracy for the Normal class remains stable, while the recognition performance for anomalous traffic categories, such as NMRI, CMRI, MSCI, MPCI, MFCI, DOS, and Recon, is optimized. Notably, the most significant improvements are observed in the MSCI and MFCI categories. This demonstrates that SA-WGAN effectively addresses the data distribution imbalance issue by emphasizing the key features of traffic through the self-attention mechanism. The generator enhances the diversity and authenticity of samples from underrepresented classes while simultaneously aiding the detection model in better capturing complex attack patterns and improving its generalization capabilities. Experimental results confirm that the integration of self-attention and generative adversarial networks not only bolsters the model’s robustness against various types of attacks in the industrial Internet but also underscores the method’s universal optimization value across different network architectures (CNN/SRU). This provides crucial technological support for enhancing the reliability of security protection systems.

6  Summarize

In this paper, we propose a data enhancement algorithm based on a SA-WGAN for industrial Internet intrusion detection, aimed at addressing the issue of class imbalance in network traffic data. By integrating the self-attention mechanism with the Wasserstein generative adversarial network, we achieve accurate feature extraction and high-quality data generation of attack samples from a limited number of classes. Experimental results demonstrate that our method significantly enhances the performance of anomalous traffic detection and validates the utility of the generated data in improving the detection model’s ability to identify attacks. However, this study has certain limitations. The current experiments are validated using specific industrial datasets due to the scarcity of publicly available datasets in the Industrial Internet domain, and the adaptability to multi-protocol hybrid scenarios requires further investigation. Future research could focus on achieving real-time, traffic-driven adaptive adjustments of data distribution through online learning mechanisms. Additionally, exploring cross-protocol knowledge transfer and developing lightweight generative architectures, while further integrating adversarial defense techniques, could enhance the bidirectional robustness of both the generated data and the detection model. This approach aims to advance the evolution of the industrial Internet security protection system towards a stage characterized by adaptability and high generalization.

Acknowledgement: I would like to express my heartfelt gratitude to all those who contributed to this paper. Their dedication and insights were crucial in shaping the outcomes of this work.

Funding Statement: This research is partially supported by the National Natural Science Foundation of China (62473341), Key Technologies R&D Program of Henan Province (242102211071, 252102211086, 252102210166).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yuan Feng, Yajie Si; draft manuscript preparation: Jianwei Zhang, Zengyu Cai; data collection: Hongying Zhao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials utilized in this review originate from publicly available databases and previously published studies, with proper citations included throughout the text. References to these sources can be found in the bibliography.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Iaiani M, Tugnoli A. Analysis of cybersecurity-related incidents in the process industry. Reliab Eng Syst Saf. 2021;209:107485. doi:10.1016/j.ress.2021.107485. [Google Scholar] [CrossRef]

2. Awotunde JB, Chakraborty C, Adeniyi AE. Intrusion detection in industrial internet of things network-based on deep learning model with rule-based feature selection. Wirel Commun Mob Comput. 2021;2021(1):7154587. doi:10.1155/2021/7154587. [Google Scholar] [CrossRef]

3. Soliman S, Oudah W, Aljuhani A. Deep learning-based intrusion detection approach for securing industrial Internet of Things. Alex Eng J. 2023;81:371–83. doi:10.1016/j.aej.2023.09.023. [Google Scholar] [CrossRef]

4. Gopi R, Sheeba R, Anguraj K, Chelladurai T, Alshahrani HM, Nemri N. Intelligent intrusion detection system for industrial internet of things environment. Comput Syst Sci Eng. 2023;44(2):1567–82. doi:10.32604/csse.2023.025216. [Google Scholar] [CrossRef]

5. Tharewal S, Ashfaque MW, Banu SS, Uma P, Hassen SM, Shabaz M. Intrusion detection system for industrial Internet of Things based on deep reinforcement learning. Wirel Commun Mob Comput. 2022;2022(1):9023719. doi:10.1155/2022/9023719. [Google Scholar] [CrossRef]

6. Gaber T, Awotunde JB, Folorunso SO, Ajagbe SA, Eldesouky E. Industrial internet of things intrusion detection method using machine learning and optimization techniques. Wirel Commun Mob Comput. 2023;2023(1):3939895. doi:10.1155/2023/3939895. [Google Scholar] [CrossRef]

7. Nitesh VC. SMOTE: synthetic minority over-sampling technique. J Artif Intell Res. 2022;16(1):321. doi:10.1613/jair.953. [Google Scholar] [CrossRef]

8. Liang XW, Jiang AP, Li T, Xue YY, Wang GT. LR-SMOTE—improved unbalanced data set oversampling based on K-means and SVM. 2002. Knowl-Based Syst. 2020;196(8):105845. doi:10.1016/j.knosys.2020.105845. [Google Scholar] [CrossRef]

9. Gu H, Lai Y, Wang Y, Liu J, Sun M, Mao B. DEIDS: a novel intrusion detection system for industrial control systems. Neural Comput Appl. 2022;34(12):9793–11. doi:10.1007/s00521-022-06965-4. [Google Scholar] [CrossRef]

10. Douzas G, Bacao F, Last F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf Sci. 2018;465(1):1–20. doi:10.1016/j.ins.2018.06.056. [Google Scholar] [CrossRef]

11. Nwe MM, Lynn KT. KNN-based overlapping samples filter approach for classification of imbalanced data. In: Lee R, editor. Software engineering research, management and applications. Cham, The Netherlands: Springer; 2020. doi:10.1007/978-3-030-24344-9_4. [Google Scholar] [CrossRef]

12. Vuttipittayamongkol P, Elyan E. Neighbourhood-based undersampling approach for handling imbalanced and overlapped data. Inf Sci. 2020;509(2):47–70. doi:10.1016/j.ins.2019.08.062. [Google Scholar] [CrossRef]

13. Yan Y, Zhu Y, Liu R, Zhang Y. Spatial distribution-based imbalanced undersampling. IEEE Trans Knowl Data Eng. 2022;35(6):6376–91. doi:10.1109/TKDE.2022.3161537. [Google Scholar] [CrossRef]

14. Ibrar M, Hassan MA, Shaukat K, Alam TM, Khurshid SK, Hameed AH. A machine learning-based model for stability prediction of decentralized power grid linked with renewable energy resources. Wirel Commun Mob Comput. 2022;2022(1):2697303. doi:10.1155/2022/2697303. [Google Scholar] [CrossRef]

15. Tsai CF, Lin WC, Hu YH, Yao GT. Under-sampling class imbalanced datasets by combining clustering analysis and instance selection. Inf Sci. 2019;477(1):47–54. doi:10.1016/j.ins.2018.10.029. [Google Scholar] [CrossRef]

16. Louk MHL, Tama BA. Dual-IDS: a bagging-based gradient boosting decision tree model for network anomaly intrusion detection system. Expert Syst Appl. 2023;213(1):119030. doi:10.1016/j.eswa.2022.119030. [Google Scholar] [CrossRef]

17. Mulyanto M, Faisal M, Prakosa SW, Leu JS. Effectiveness of focal loss for minority classification in network intrusion detection systems. Symmetry. 2020;13(1):4. doi:10.3390/sym13010004. [Google Scholar] [CrossRef]

18. Gupta N, Jindal V, Bedi P. CSE-IDS: using cost-sensitive deep learning and ensemble algorithms to handle class imbalance in network-based intrusion detection systems. Comput Secur. 2022;112(1):102499. doi:10.1016/j.cose.2021.102499. [Google Scholar] [CrossRef]

19. Bedi P, Gupta N, Jindal V. Siam-IDS: handling class imbalance problem in intrusion detection systems using siamese neural network. Procedia Comput Sci. 2020;171(6):780–9. doi:10.1016/j.procs.2020.04.085. [Google Scholar] [CrossRef]

20. Bedi P, Gupta N, Jindal V. I-SiamIDS: an improved Siam-IDS for handling class imbalance in network-based intrusion detection systems. Appl Intell. 2021;51(2):1133–51. doi:10.1007/s10489-020-01886-y. [Google Scholar] [CrossRef]

21. Li X, Kong K, Shen H, Wei Z, Liao X. Intrusion detection method based on imbalanced learning classification. J Exp Theor Artif Intell. 2024;36(5):657–77. doi:10.1080/0952813X.2022.2104384. [Google Scholar] [CrossRef]

22. Du H, Zhang Y, Gang K, Zhang L, Chen YC. Online ensemble learning algorithm for imbalanced data stream. Appl Soft Comput. 2021;107(1):107378. doi:10.1016/j.asoc.2021.107378. [Google Scholar] [CrossRef]

23. Mhawi DN, Aldallal A, Hassan S. Advanced feature-selection-based hybrid ensemble learning algorithms for network intrusion detection systems. Symmetry. 2022;14(7):1461. doi:10.3390/sym14071461. [Google Scholar] [CrossRef]

24. Shahriar MH, Haque NI, Rahman MA, Alonso M. G-IDS: generative adversarial networks assisted intrusion detection system. In: Proceedings of the 2020 IEEE 44th Annual Computers, Software, and Applications Conference (COMPSAC); 2020 Jul 13–17; Madrid, Spain. doi:10.1109/COMPSAC48688.2020.0-218. [Google Scholar] [CrossRef]

25. Ding H, Sun Y, Huang N, Shen Z, Cui X. TMG-GAN: generative adversarial networks-based imbalanced learning for network intrusion detection. IEEE Trans Inf Forensics Secur. 2023;19(27):1156–67. doi:10.1109/TIFS.2023.3331240. [Google Scholar] [CrossRef]

26. Lee J, Park K. GAN-based imbalanced data intrusion detection system. Pers Ubiquit Comput. 2021;25(1):121–8. doi:10.1007/s00779-019-01332-y. [Google Scholar] [CrossRef]

27. Fu W, Qian L, Zhu X. GAN-based intrusion detection data enhancement. In: Proceedings of the 33rd Chinese Control and Decision Conference (CCDC); 2021 May 22–24; Kunming, China. doi:10.1109/CCDC52312.2021.9602568. [Google Scholar] [CrossRef]

28. Li S, Li Q, Li M. A method for network intrusion detection based on GAN-CNN-BiLSTM. Int J Adv Comput Sci Appl. 2023;14(5):507–15. doi:10.14569/IJACSA.2023.0140554. [Google Scholar] [CrossRef]

29. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S. Generative adversarial nets. Advances in neural information processing systems. arXiv:1406.2661. 2014. [Google Scholar]

30. Menéndez ML, Pardo JA, Pardo L, Pardo MDC. The Jensen-Shannon divergence. J Frankl Inst. 1997;334(2):307–18. doi:10.1016/S0016-0032(96)00063-4. [Google Scholar] [CrossRef]

31. Arjovsky M, Chintala S, Bottou L. Wasserstein generative adversarial networks. In: Proceedings of the International Conference on Machine Learning; 2017 Aug 6–11; Sydney, Australia. doi:10.48550/arXiv.1701.07875. [Google Scholar] [CrossRef]

32. Morris T, Gao W. Industrial control system traffic data sets for intrusion detection research. In: Butts J, Shenoi S, editors. Critical infrastructure protection VIII. Berlin/Heidelberg, Germany: Springer; 2014. Vol. 441. doi:10.1007/978-3-662-45355-1_5. [Google Scholar] [CrossRef]