An Optimization of Weak Key Attacks Based on the BGF Decoding Algorithm

1  Introduction

With the rise of quantum computers, current public key encryption (PKE) schemes face unprecedented threats [1]. Traditional public key encryption methods, such as RSA and ECC, rely on the difficulty of integer factorization and discrete logarithm problems. However, quantum computers, by using the Shor algorithm [2], can solve these problems efficiently in polynomial time, thus invalidating traditional encryption methods. To address this challenge, the National Institute of Standards and Technology (NIST) is advancing a standardization project for Post-Quantum Cryptography (PQC), which aims to evaluate and finalize encryption schemes that can withstand quantum attacks [3]. In this context, a scheme called BIKE (Bit Flipping Key Encapsulation) has attracted a lot of attention and has entered the final stage of the NIST PQC standardization competition.

BIKE is a representative QC-MDPC (Quasi Cyclic Medium Density Parity Check) code-based scheme, which is relatively competitive both in terms of code length and efficiency and communication bandwidth, and its security relies on the difficult problem of proposed cyclic codes [4]. However, the DFR problem exists even though BIKE employs a state-of-the-art Black-Gray-Flip (BGF) decoder [5] to reduce the Decoding Failure Rate (DFR) and to improve the decoding efficiency. The security of BIKE’s IND-CCA relies on the average Decoding Failure Rate (DFR). The current analysis only gives an estimate of the DFR and does not give a proven upper bound [6]. Therefore, the BIKE instantiation using the BGF decoder does not formally declare IND-CCA security. Currently, attacks such as GJS [7], weak keys [8], and side channels [9] still exist against the decoding failure probability of BIKE schemes. For example, the amplification principle of Guo et al. [10] as well as Nilsson et al. [11] introduce a GJS reaction attack based on the QC-MDPC code structure, which utilizes the existence of a DFR in the decoding so that the attacker can fully recover the key. Drucker et al. [12] argued that the existence of a weak key affects the DFR and that quantitative proofs of the IND-CCA security of BIKE are needed. Wang et al. [8] proved that the existence of weak keys and quantization of the effect on the DFR of the decoder pose threats to the IND-CCA security of BIKE.

Although BIKE shows great potentiality in the field of post-quantum cryptography, its challenges in terms of DFR and other security aspects suggest that further research and improvements are necessary. To ensure that the final chosen post-quantum cryptography standard provides sufficient security and efficiency, this paper addresses the BIKE algorithm, analyzes the performance of its BGF decoder to reveal the factors that affect the DFR, and proposes a weak-key attack optimization scheme to evaluate the security of the BIKE scheme by the DFR test of the decoder.

2  Preliminaries

2.1 BIKE

BIKE (Bit Flipping Key Encapsulation) is a post-quantum cryptography-based key encapsulation mechanism that uses quasi-cyclic moderate-density parity-check (QC-MDPC) codes and the Niederreiter cryptosystem framework [13]. It features small key sizes, efficient algorithms, and low complexity [14]. Compared to the traditional McEliece cryptosystem, BIKE has smaller communication bandwidth requirements, making it suitable for bandwidth-constrained network environments. Its design is simple with minimal resource usage, making it suitable for both software implementations (such as servers and PCs) and hardware implementations (such as IoT devices and embedded systems) [15]. It is an efficient, flexible, and quantum-resistant cryptographic solution with broad application prospects in the field of post-quantum cryptography [16]. The algorithm of BIKE KEM is divided into three main steps: key generation, key encapsulation, and key decapsulation. The key encapsulation mechanism (KEM) is described as Algorithm 1.

To have λ bits of IND-CCA security, the parameters are r,ω,t, and decoder chosen in the setup such that:

1. QCCFr,w offers λ bits of security

2. QCSDr,t offers λ bits of security

3. |ℳ|=2ℓ≥2λ

4. DFR (decoder) ≤2−λ

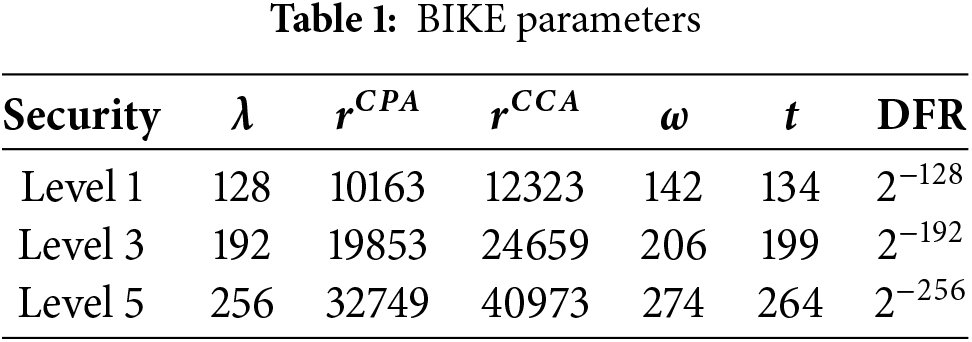
The NIST proposal identifies several security categories related to the strength of key search attacks on grouped ciphers (in the case of AES). The target security levels for BIKE are 1, 3, and 5, which correspond to the security levels of AES-128, AES-192, and AES-256, respectively. The BIKE parameters corresponding to different security levels are shown in Table 1:

2.2 BGF Decoding Algorithm

The BGF decoding algorithm (Black-Gray-Flip) is an improved version of Gallager’s bit-flip decoding method [17], addressing the issue of high decoding failure rates in MDPC codes. It employs two predefined thresholds to divide bits into two groups: the black set and the gray set. In the first step, bits with the highest number of unsatisfied parity checks are categorized as black bits and are flipped. Bits with fewer unsatisfied checks are considered gray bits and remain unchanged. In the subsequent step, if the number of unsatisfied checks on a bit exceeds a second threshold, black bits that breach this threshold are flipped back to their original state, and gray bits are flipped. After each operation, the algorithm updates the checksum and the count of unsatisfied checks, continuously adjusting to correct any incorrectly flipped bits. As a result, the BGF decoder focuses on fewer positions and has a higher concentration of errors compared to the traditional bit-flip decoder, improving flip accuracy and significantly reducing the likelihood of decoding failure. The specific steps are shown in Algorithms 2 and 3.

The reasonableness of the threshold selection can greatly affect the efficiency of the decoding. The threshold of the BGF decoder is defined as an affine function of the weight of the checker [18], but when the weight of the checker is between the average values, the threshold formula is also close to the affine function. Therefore, the lower limit of the threshold is given as:

threshold(|s′|)=max((d+1)/2,⌊a|s′|+b⌋)(1)

The BIKE 128-bit security parameter is used for the test as (d,t)=(71,134), the value required to achieve the target DFR for a given number of different iterations. The threshold parameter a=0.0069722, b=13.530. The code length of the BGF decoder, and the DFR relationship are shown in Fig. 1.

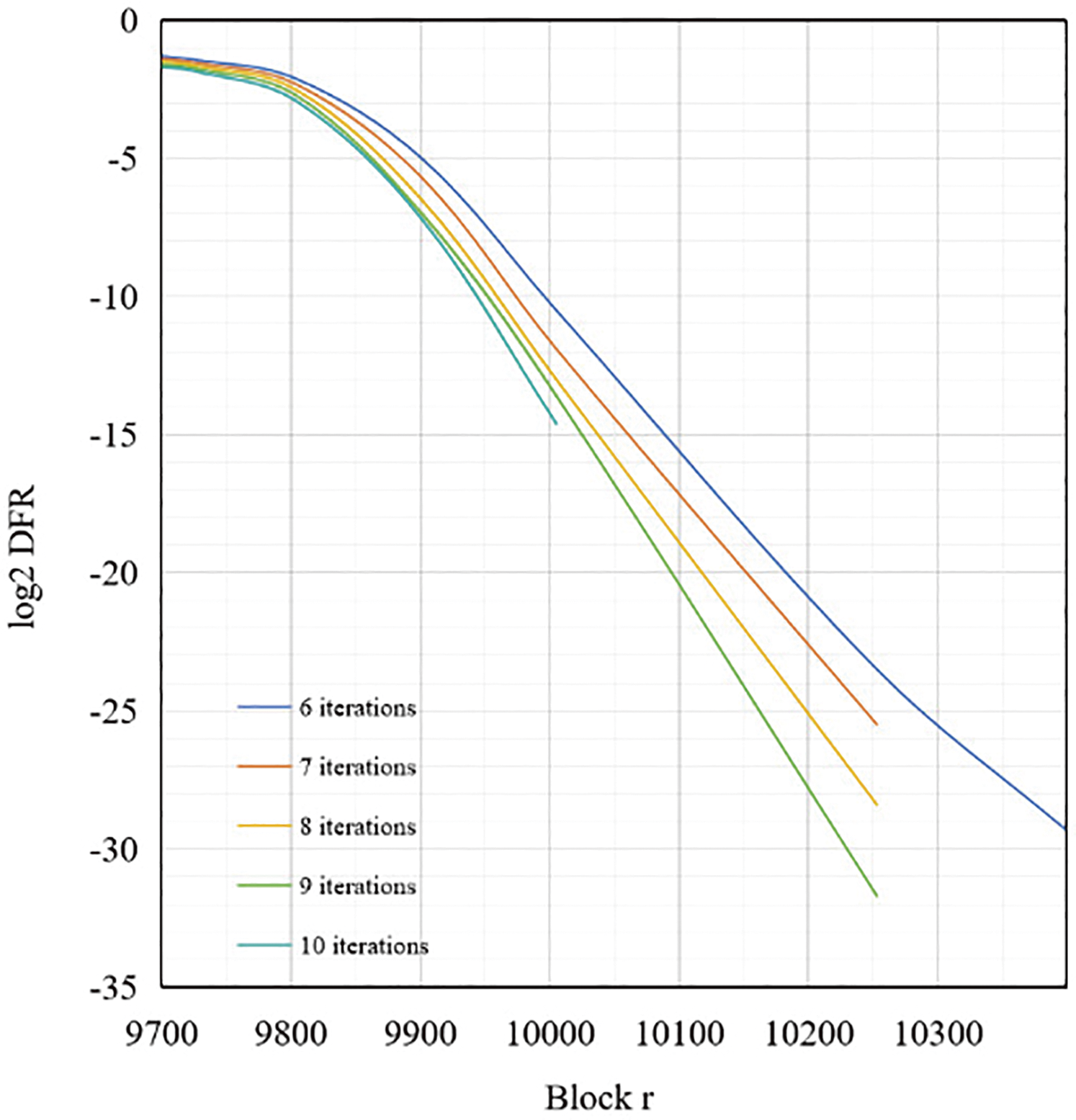
Figure 1: The relationship graph between Block length r and DFR

To accurately estimate the decoding failure probability DFR of this decoding algorithm, the extrapolation method Markovian model [19] is used, which is based on the fact that the DFR curve is a concave function, and the block value of the large parameter can be deduced by testing the DFR under the smaller code length parameter, given some of the parameters, i.e., r↦log⁡DFRD(r). For the decoder, security level λ, if DFRD(r)≥2−λ,r1<r2<r3, the following inequality can be obtained by defining the concavity of the Formula (2).

log⁡DFR𝒟(r3)≤log⁡DFR𝒟(r1)+log⁡DFR𝒟(r2)−log⁡DFR𝒟(r1)r2−r1⋅r3−r1(2)

To accurately assess p3, introduce the Bernoulli experimental function in statistics, assuming that p1 and p2 is the failure probability of two independent Bernoulli tests, in the total number of Bernoulli tests Ni in the sample to test failure situation Fi,i=1,2 and p3=p1−Ap21+A, the derivation of the formula is:

1K∫−∞tp3−∫−∞0es(F2+11+A)et(F1+1A+F2+11+A)(1−etA)N1−F1(1−es+t1+A)N2−F2dtds<α2(3)

1K∫ℓp3+∞∫−∞0es(F2+11+A)et(F1+1A+F2+11+A)(1−etA)N1−F1(1−es+t1+A)N2−F2dtds<α2(4)

K=A(1+A)B(F1+1,N1−F1+1)B(F2+1,N2−F2+1).(5)

Therefore, two methods, analog extrapolation and formula method, are used to test the decoding DFR lower bounds respectively. To ensure the security of IND-CCA and find the minimum block size, it is necessary to ensure that the selected parameter DFR is less than 2−λ. Where the parameters are chosen as (r1,r2,r3)=(9803,9901,12323), (d,t)=(71,134), and the confidence interval α is 0.01. The average DFR test results for the BGF decoding algorithm under the conditions of τ=3, IND-CCA security parameters λ=128,iterations=7, are shown in Table 2.

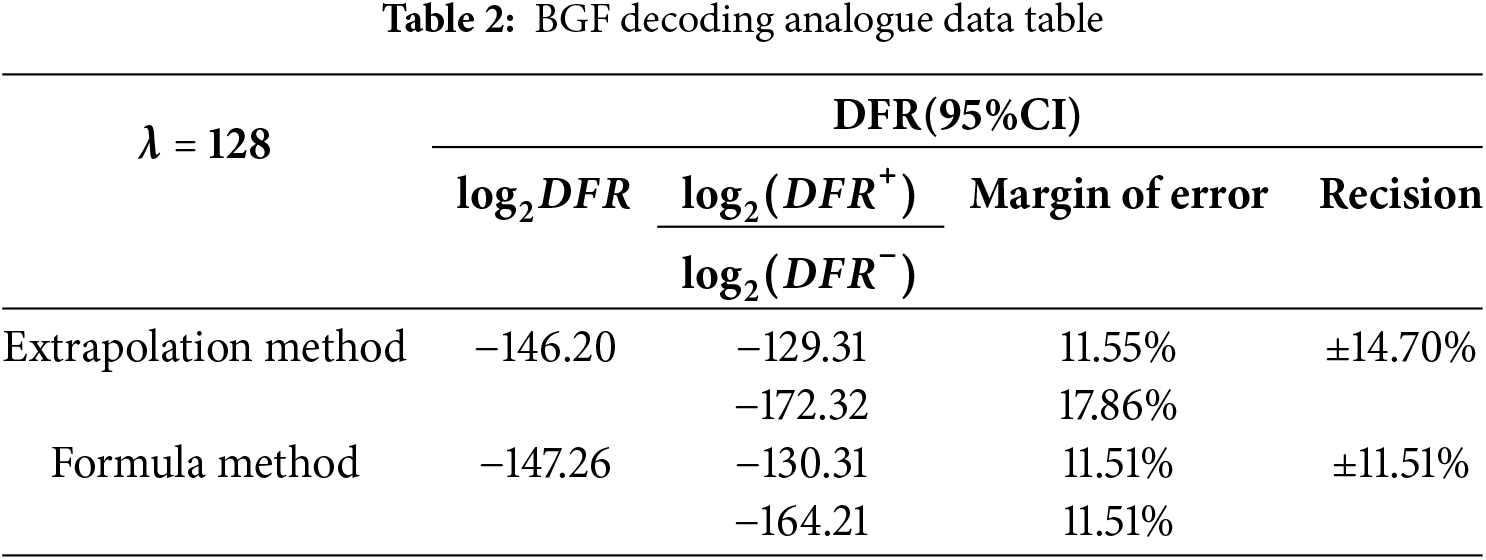
To more accurately evaluate the accuracy of these methods and their potential limitations when applied to practical BIKE parameters, this section provides a detailed analysis of their precision and margin of error. As specifically demonstrated in Table 2.

From Table 2, it can be seen that the BGF decoding algorithm can achieve a corresponding rCCA, which achieves better decoding efficiency than other variants of decoding algorithms [20] by exhibiting a lower DFR in constant time. However, the drawbacks are equally obvious, its efficient and accurate decoding sacrifices universality, and its error correction capability is limited in the face of longer code lengths or highly weighted code words, especially at high security levels.

3  DFR Analysis

Decoders for bit-flipping of QC-MDPC codes used by BIKE always have a non-negligible DFR. Although the BGF decoders currently used have a very small DFR, it does not formally declare the security of IND-CCA. This section analyzes the reasons for the existence of DFR and analyzes the special structures that may hinder the decoding to reveal the reasons that affect the decoding.

3.1 Distance Spectrum Analysis

In the GJS reaction attack, Guo [7] found that there is a strong correlation between the DFR and the distance spectrum of the key, and a large amount of information about the distance spectrum of the key can be collected from the decoding failure, and then the key can be recovered from the distance spectrum by the key recovery algorithm. Therefore, the distance spectrum of this attack is the key to whether the key can be recovered or not.

For h∈F2[x]/(xr−1), The number of occurrences of a distance can be called multiplicity, and the set of multiplicities is the distance spectrum, which can be expressed as [21]:

Spectrum(h)={(δ,μ(δ,h))∣δ∈{0,1,…,⌊r/2⌋}}(6)

Assuming that the multiplicities of the distance spectra are independent, then for 0≤m≤d,1≤δ≤⌊r/2⌋ and h∈F2[x]/(xr−1) then the multiplicity probability distribution formula is:

πm=Pr[μ(δ,h)=m]=𝒩m(rd)(7)

p≥m=Pr[maxδ∈{1,…,⌊r/2⌋}⁡μ(δ,h)≥m]=1−(1−πm)⌊r/2⌋(8)

p=m=Pr[maxδ∈{1,…,⌊r/2⌋}⁡μ(δ,h)=m]=p≥m−p≥m+1(9)

𝒩m=rd−m(d−1d−m−1)(r−d−1d−m−1)(10)

For a subsequent assessment of the effect of multiplicity on the DFR, the distribution of the parameters at three different security levels is plotted as Fig. 2. It can be observed that the probability of a specific multiplicity in the spectrum of a cyclic block is generally low (non-zero), with only a small percentage higher.

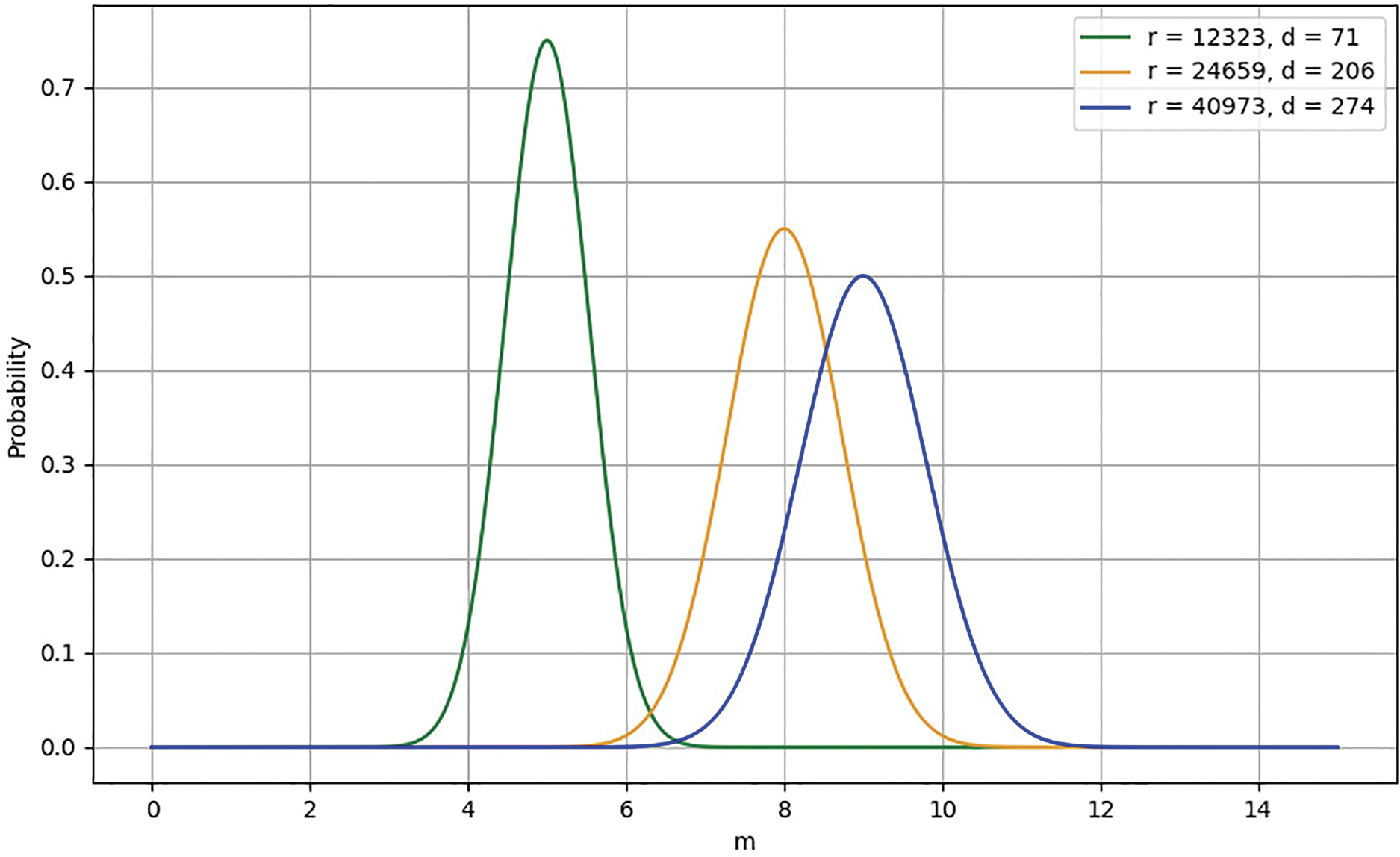
Figure 2: Probability analysis of multiplicity m

Therefore, this explains the strong correlation between the DFR and the distance between non-zero bits in the private key vector (the first row of the cyclic private key matrix) in the GJS attack. That is, if there is a distance between two non-zero bits in the same error pattern, then the probability of decoding failure is much smaller compared to the absence of such a distance.

Such a result is obvious, the result in the cyclic condition of the QC code, using the error pattern between the two 1’s of the distance and the private key vector of the same distance. Its checksum value decreases due to multiplicative cancellation when identical distances are encountered. The cancellation frequency is inversely proportional to the resultant checksum weight, with higher cancellation counts yielding lower weight values. Therefore, the probability of decoding error when the weight is 0 is greater than the probability of error when the weight is non-zero, and the corresponding DFR will be larger.

3.2 Checksum Analysis

In coding theory, the checker is an important factor affecting decoding. For bit-flip decoding, the number of iterations completes the decoding within 3–5 iterations on average, and further iterations have almost no effect on the decoding probability [22]. Therefore, the first correct flip greatly affects whether the decoding can be successful or not. In the first round of decoding, the number of errors ℓ in each checksum equation determines the number of correctly changed counters. For example, if the number of errors in a checksum equation is even, then all counters will be correctly changed; if it is odd, it means that there is at least one incorrect bit, in which case all counters will be incremented, but only one bit is incorrect. Thus, all but one counter will change correctly and the rest will increase incorrectly.

To more accurately analyze the effect of the number of errors in each checksum equation on the decoding, it is assumed that the number of errors involved in the equations obey the following distribution for any i∈{0,…,r−1},a∈{0,1},ℓ∈{0,…,min(ω,t)}, assuming that the number of errors involved in the equations H is chosen uniformly at random from ℋd,ω,r×n, and e uniformly at random from ℰn,t [23]:

Pr[ρi=ℓ∣si]=gsi(ℓ)𝒩gsi(11)

ga(ℓ)=(wℓ)(n−wt−ℓ)(nt)1a+2Z(ℓ)(12)

𝒩g1=∑ℓ is odd⁡(wℓ)(n−wt−ℓ)(nt), 𝒩g0=1−𝒩g1.(13)

where si∈{0,1},ℓ is the number of errors. When si=0, the number of errors involved in the equation is even, the distribution ρi is an odd multiple of the number of errors ℓ, and when si=0, the distribution is an even multiple of the number of errors.

Testing the parameters for selecting 128-bit security, it can be observed from the Table 3 that the probability decreases with an increase of ℓ and the average probability is generally lower for even multiples of the number of errors than for odd multiples. This is because when the number of errors is even, the number of counters correctly changed is w−ℓ, and the number of errors changed is ℓ. On the contrary, when the number of errors is odd, the number of counters correctly changed is ℓ, and the number of errors changed is w−ℓ. Thus, having an even number of counters helps in decoding, while having an odd number of counters ℓ has a negative effect on decoding.

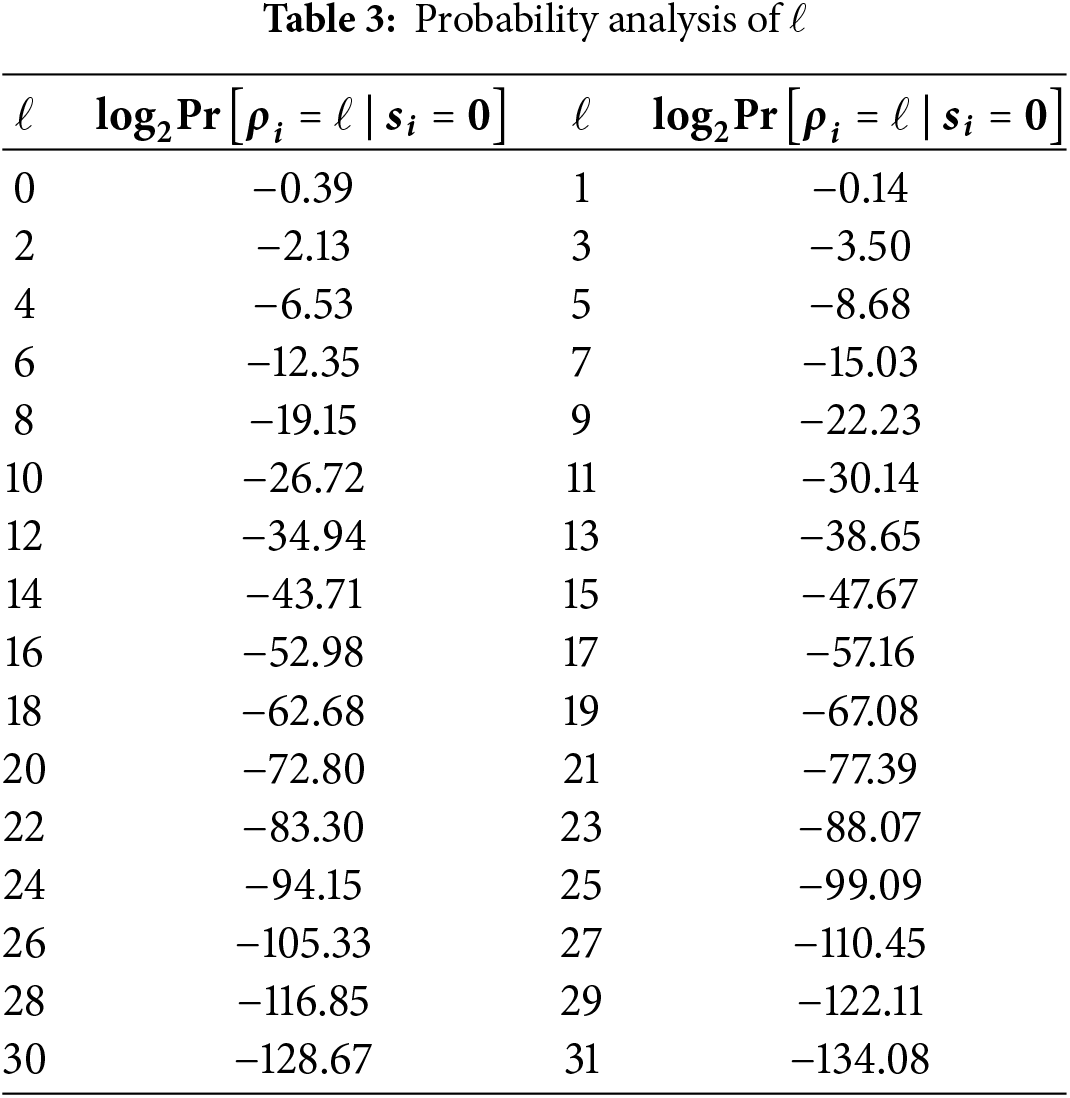
4  Optimization of Weak-Key Attack

4.1 Introduction

This scheme is based on the BGF decoding algorithm of the BIKE scheme. Building upon previous weak key attacks that only considered the multiplicity of the distance spectrum or the influence of error pattern near-codewords individually, it constructs a weak key that results from the combined effect of both the multiplicity of the key distance spectrum and the error pattern near-codewords.

4.2 Our Construction

The overall steps of the scheme are as follows:

1. (Constructing the key) Select the parameters (r,d,t) and multiplicity m, get the key h∈F2[x]/(xr−1),|h|=d,μ(δ,h)=m, where δ∈{0,1,…,⌊r/2⌋}.

2. (Sampling error patterns) Select specific parameters ℓ and collect the patterns of the near-codewords that satisfy the conditions ℓ=|hiT∗e| according to the key constructed h in the first step (ℓ denotes the number of keys and error vectors at the same position in the first check equation that are both 1).

3. (Measure the probability of decoding failure) Generate the ciphertext according to the BIKE encryption encapsulation, send the ciphertext to the target oracle predicate machine decoder decrypt the ciphertext, test the DFR under the small parameter block, and then use the model of the extrapolation method to test under the target parameter conditions.

4. (Analysis of search density) First calculate the search density of step 1, defined as the probability η(m), then calculate the search density of step 2, defined as probability η(ℓ), and finally calculate the density of the analysis as a whole, that is, the overall probability ηD=η(ℓ)⋅η(m).

5. (Analysis of security) Calculate the product of the two based on the results of Step 3 and Step 4, and perform a comparative analysis to determine whether the results are below the minimum requirements for NIST standardization, and thus whether there is a negative impact on decoding.

4.3 Scheme Analysis

Based on the analysis in Section 3, the multiplicity of the distance spectrum and the overlapping characteristics of the error vectors both impact decoding. The higher the multiplicity, the more complex the key structure, and the higher the decoding failure probability. Conversely, the higher the overlap of the error vectors, the poorer the error correction capability of the decoder [24].

The core advantage of this scheme lies in combining the key multiplicity with the overlapping characteristics of the near-codeword error vectors. These two factors work together on the decoder, significantly increasing the decoding failure probability without adding extra density. Theoretically, this combination can more effectively increase the DFR, thus enhancing the effectiveness of the attack.

4.4 Experimental Methodology

The scheme is based on BIKE’s BGF decoding algorithm and simulates the DFR of QC-MDPC codes under IND-CCA security conditions in the λ=128 case. Where the parameters of the BIKE scheme are (r,w,t)=(12323,142,134),w=2d. The parameter selection for the BGF implementation of the decoding algorithm is the same as in Section 2.

To ensure the accuracy of evaluating the DFR, for the multiplicity 5≤m≤20, the test values of r are r1=9717 and r2=9811, while for the multiplicity m>20, the block parameters of r are r1=10,099 and r2=10,271, the simulated decoding samples for each point are 106 times, the DFR with its iteration number of 7 is measured by distributing it under the condition of α=0.05, and the confidence interval value is 95%. Then, the test values of the DFR with the small parameters of r1 and r2 are extrapolated to r=12,323.

To test out the effect of key multiplicity and error pattern near-codewords on BIKE (i.e., BGF decoder), increase the weight of the constructed weak key multiplicity m from 5 to 30, and increase the constructed error pattern parameter ℓ from 5 to 25. The simulation results of the DFR tests are as follows [25].

According to the analysis in Table 4, it can be observed that, without considering the error model parameters ℓ, the DFR increases as the multiplicity of secret keys m increases, indicating that the failure probability of the decoding increases. At the same time, when the key has greater multiplicity, the DFR increases with the number of error parameters ℓ, showing that the error rate and the multiplicity of the secret key become more significant, and the probability of decoding failure increases.

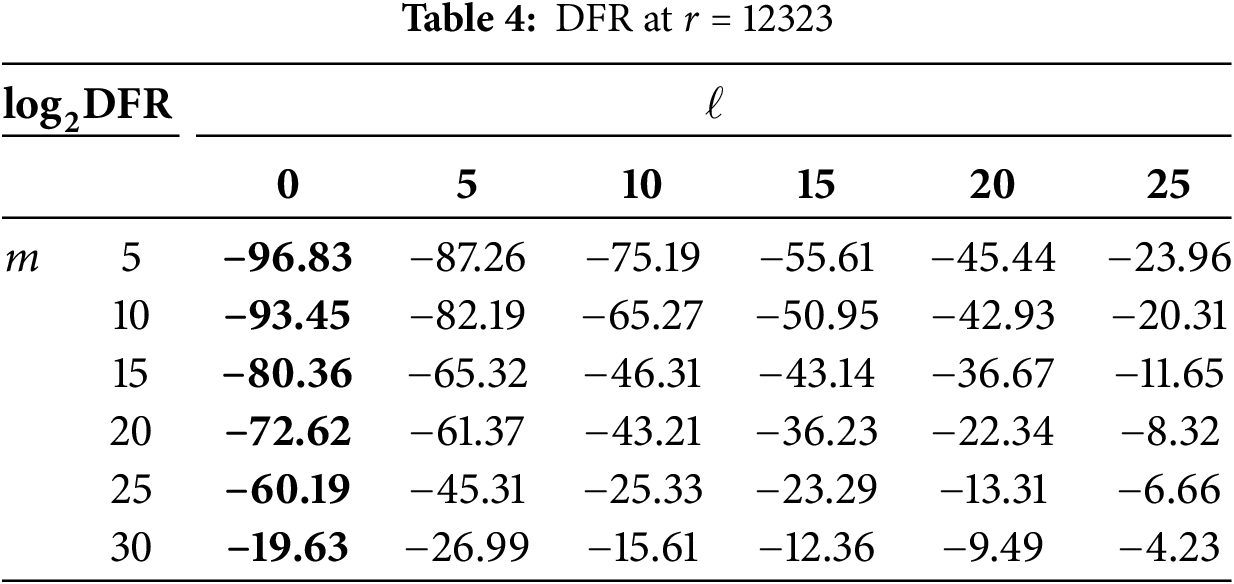
When considering multiple key multiplicities and error parameters, the increase in DFR is significant, and the impact of each factor is more prominent. This indicates that the key multiplicity and the near-codeword error vectors have a strong correlation with DFR, which has a major synergistic effect. By comparing the original data with ℓ=0, it can be seen that each row of DFR increases, explaining how the two factors interact to affect the decoding.

While DFR testing provides foundational insights, solely relying on this metric without assessing the attack method’s efficacy through holistic cryptanalysis is inadequate. For rigorous security evaluation, we must examine the cryptographic systematically, as developed in subsequent analysis.

4.5 Scheme Security Analysis

In order to gain insight into the impact of weak keys on the IND-CCA security of the BIKE mechanism, introduce the concept of P𝒟=η𝒟⋅DFR𝒟,ℋ. For weak keys, a set of weak keys is considered weak if there exists a set of weak keys such that the average DFR of the keys in it is higher than the average DFR of the overall set of keys and the density of the keys 𝒲 is sufficiently high that it significantly affects the average DFR of the overall set of keys for the security parameter λ, i.e.,

|𝒲||ℋ|DFR𝒟,ℋ>2−λ(14)

Therefore, the following inequality must be satisfied, otherwise the IND-CCA security of BIKE is considered to be potentially problematic as it is affected by weak keys.

P𝒟=|𝒲||ℋ|DFR𝒟,ℋ=η𝒟⋅DFR𝒟,ℋ<2−λ(15)

Under the IND-CCA language security condition, the attack collects the key of μ(δ,h)=m,0≤m<d. The multiplicity m of the distance spectrum of (r,d), and the upper bound of the weak key set of the decoder 𝒲 can be expressed as:

|𝒲(m)|≤2⌊r2⌋rd−m(d−1d−m−1)(r−d−1d−m−1)(16)

In particularly, when m=d−1 then the upper bound for the weak key set is |𝒲(m)|=2r⌊r/2⌋, however, for when m<d−1, then the upper bound is detailed in the distance spectral analysis 2.2. Thus, the overall upper η(m) bound on the density is:

η(m)=|𝒲(m)||ℋ(m)|≤2⋅r⌊r2⌋(d−1d−m−1)(r−d−1d−m−1)(d−m)(rd)(17)

For the near-codewords in 𝒩, assume that there exist weights ω such that ∀u∈𝒩, then ∀v∈𝒜t,ℓ(𝒩),|v−u|=w+t−2ℓ, giving an upper bound on the density η(𝒩) as [26]:

η(ℓ)=𝒟𝒩,t(ℓ)≤|𝒩|(dℓ)(r−dt−ℓ)(rt)(18)

The search complexity of this scheme is the product of the densities of the two, η𝒟=η(m)⋅η(ℓ). Therefore, the search density is upper bounded:

η𝒟=η(m)⋅η(ℓ)≤|𝒩|2⋅r⌊r2⌋(d−1d−m−1)(r−d−1d−m−1)(dℓ)(r−dt−ℓ)(d−m)(rd)(rt)(19)

To facilitate the analysis, the overall complexity of the scheme can be calculated according to the above formula, and the data are shown in Table 5.

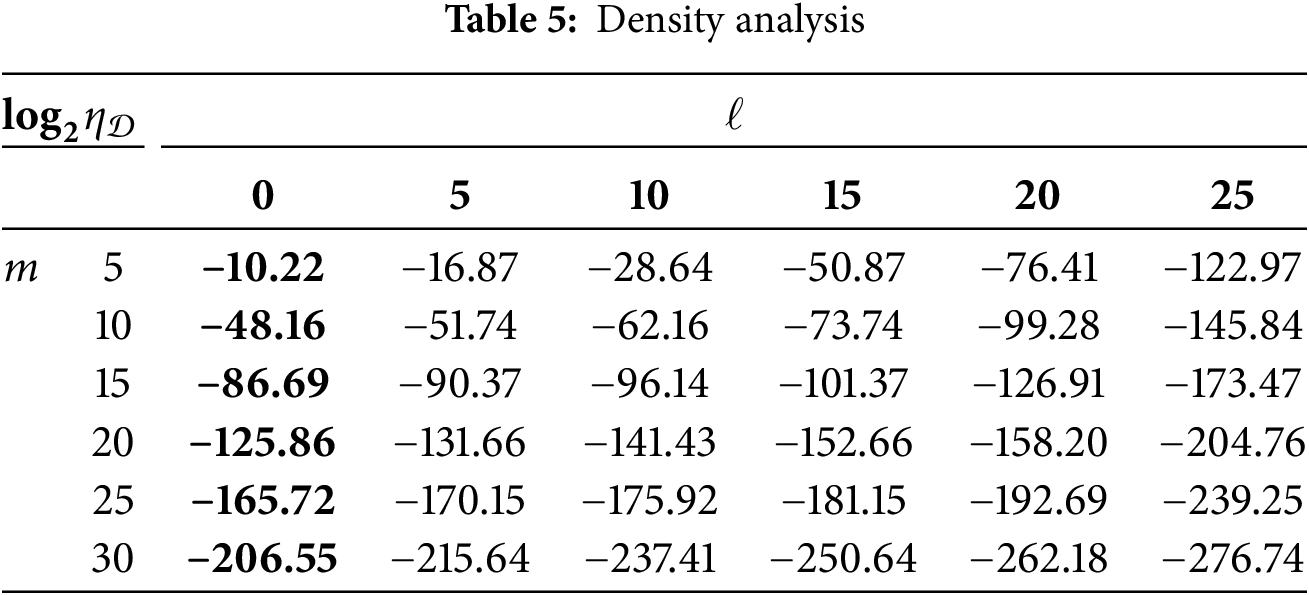
Without considering the error pattern parameter ℓ, the density gradually decreases as the multiplicity m increases. This is because the structure of high-multiplicity keys is more complex, making it more difficult to find keys with the same multiplicity. Similarly, without considering the multiplicity m, the density gradually decreases as the parameter ℓ increases. This indicates that the higher the overlap between the error vector and the key, the more difficult it is to find such an error vector.

When both the key multiplicity m and the error pattern parameter ℓ are considered simultaneously, the density is smaller than when only a single factor is considered. This is because meeting the conditions for both factors is more stringent. For example, when m=30 and ℓ=25, there are fewer keys that meet the requirements, and their density in the Table 5 is necessarily the smallest. However, the higher the search complexity, the more difficult it is for an attacker to find keys and error patterns that meet specific conditions.

To comprehensively analyze the variation of the upper bound of density under the influence of dual factors, a visualization of the density ηD as a function of m and ℓ was plotted based on formula 20. From the Fig. 3, it can be observed that high-density regions (such as the yellow areas) correspond to lower search complexity, indicating that attackers can more easily find weak keys or error patterns. Conversely, low-density regions (such as the deep purple areas) correspond to higher search complexity, meaning that attackers find it difficult to locate keys and error patterns that meet the specified conditions. Therefore, searching for keys and error vectors that satisfy both conditions simultaneously is extremely challenging, with a very low numerical density, as seen in the low-density deep purple regions, where the magnitude can be as low as 2−276.74. Compared to the total number of weak keys, this is negligible. However, more attention should be paid to the yellow regions at the front, where the density is extremely high. The average DFR in these regions may not meet security standards, and this part is highly likely to enhance the effectiveness of attacks. For an in-depth analysis to evaluate the IND-CCA security of the BIKE scheme in the presence of weak keys, after evaluating the overall density of the weak keys, it is also necessary to compute the value of P𝒟 (the product of the density and the DFR), which must satisfy the following inequality [27].

P𝒟=η𝒟⋅DFR𝒟,ℋ>2−λ(20)

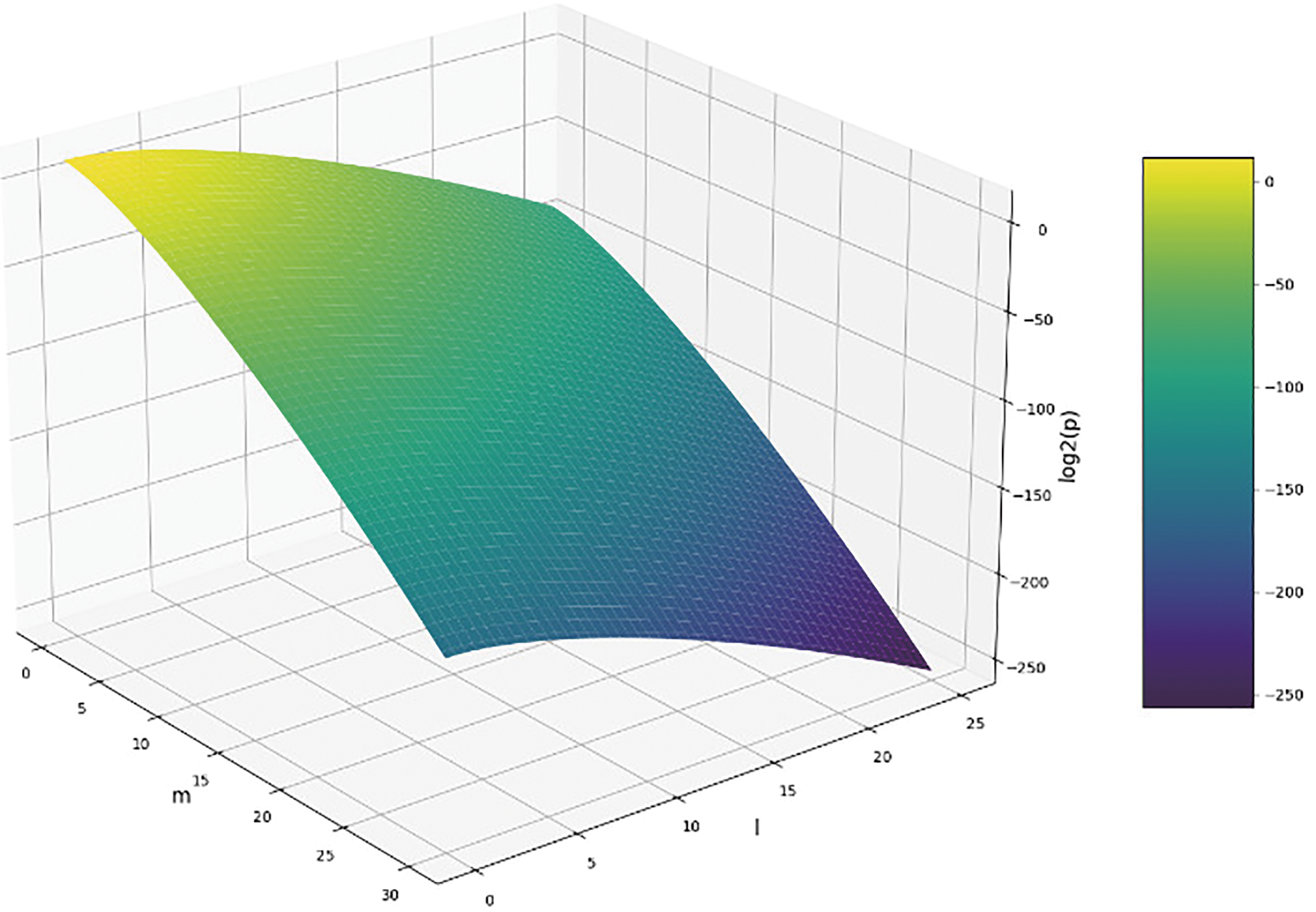
Figure 3: Bivariate density analysis plot

To explore the specific negative impact of the key on the security of the scheme, it is necessary to quantify the test results. Table 6 shows the quantized values of P𝒟 the product of η𝒟 and the DFR in Tables 4 and 5, which calculates the overall security of the scheme with the changes of the parameters variables and the values denoted by log2P𝒟.

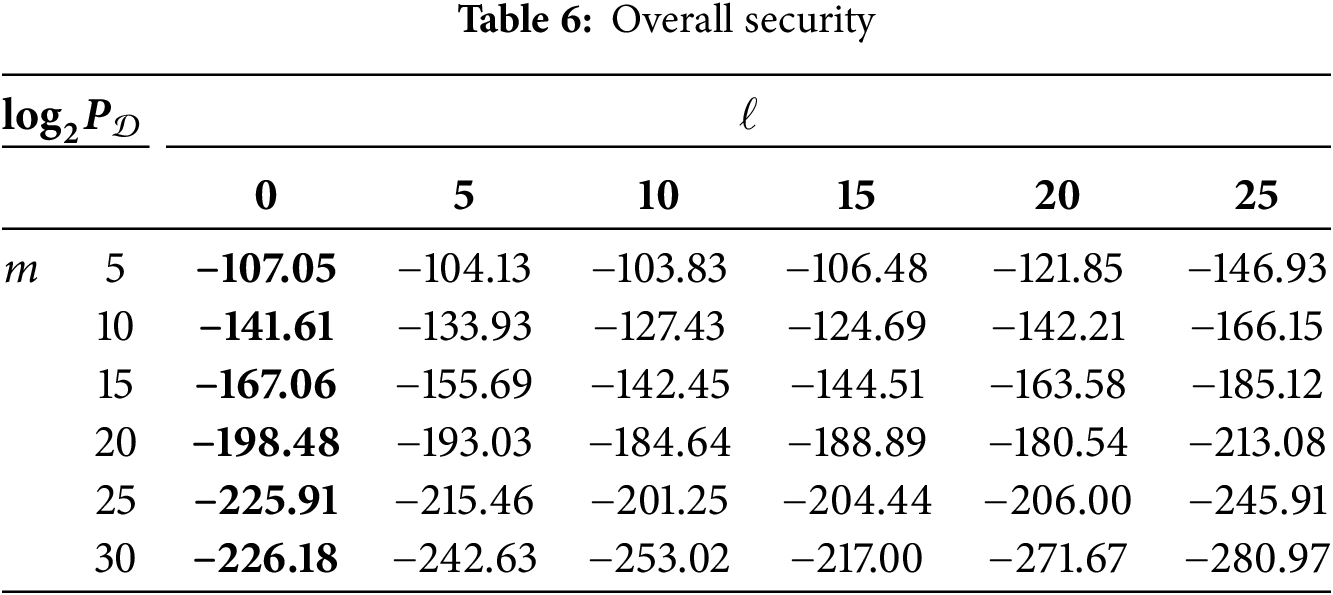
In Table 6, the value of P𝒟 reflects the effectiveness of the attacker’s. The lower the P𝒟 value, the worse the attacker’s effectiveness. For example, m=30 and ℓ=25,P𝒟=2−280.97, which means that the attacker can hardly find a key and error pattern that meet the conditions in this case. However, the higher the P𝒟 value, the better the attack effectiveness. For instance, when m=5 and ℓ=10, the P𝒟 value can reach up to 2−103.83, which is higher than 2−107.05, when m=5 and ℓ=0, improving the attack effectiveness by three percentage points.

To more intuitively demonstrate the improvement in attack effectiveness, Fig. 4 illustrates the enhancement within the region 5≤m≤25, 0<ℓ≤10 (hereinafter referred to as the effective region). In the effective region, for each m value, the three bar graphs from bottom to top represent ℓ values of 0, 5, and 10, respectively. By comparing the original data marked on the white background, it can be observed that the attack effectiveness is improved by an average of 5 to 6 percentage points, especially when m=15 and ℓ=15, where the maximum improvement can reach 14.7 percentage points.

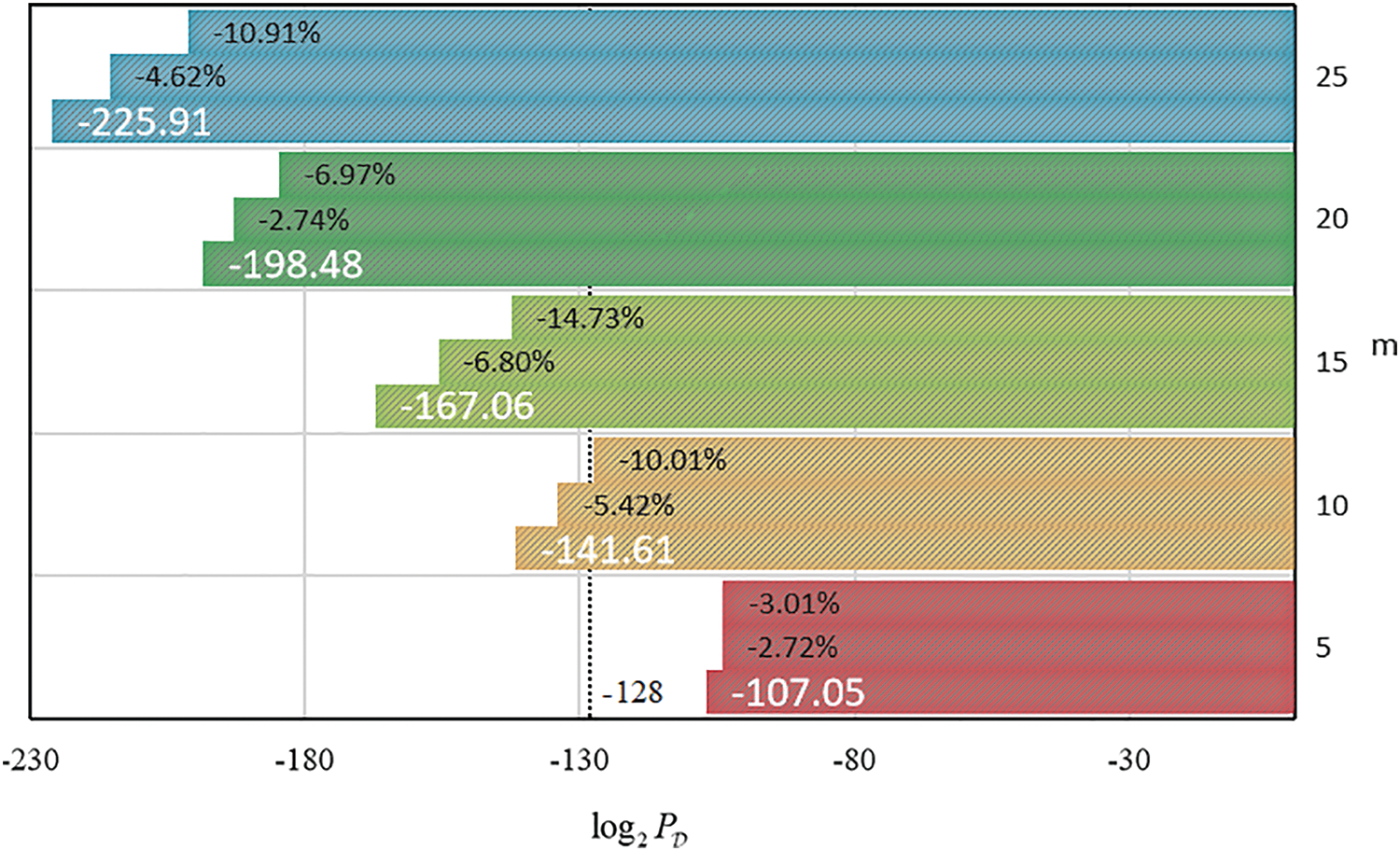
Figure 4: Effectiveness of scheme upgrading

Additionally, when m=10, by selecting an appropriate ℓ parameter (ℓ=10), the P𝒟 value can be increased to 2−127.43, which fails to meet the minimum NIST security standard of 128-bit. This indicates that attackers can effectively enhance their attack effectiveness by the ℓ parameter within the effective region. The bar graphs in Fig. 4 show the improvement in attack effectiveness under different combinations of m and ℓ, providing a more comprehensive understanding of the impact of key multiplicity and error vector parameters on the security of the BIKE scheme. This optimized attack scheme significantly enhances the effectiveness of the attack. By selecting appropriate parameters m and ℓ, the attack scheme achieves notable improvements within the effective region, with an average enhancement of 5 to 6 percentage points and a maximum improvement of up to 14.7 percentage points. The optimized scheme brings keys that originally met security standards close to or slightly below the NIST security threshold (for example, when m=10 and ℓ=10,P𝒟=2−127.43). The best attack effectiveness can reach 2−103.83, significantly increasing the efficiency of the attack and posing a potential threat to the existing BIKE algorithm.

4.6 Comparative Analysis

Wang et al. [8] re-evaluated the DFR of the QC-MDPC code-based scheme by introducing a new concept called the “gathering property”. The aggregation property is defined as follows: For(y0,y1)∈R2,R=F2[X]/(Xr−1), if there exists a consecutive sequence of m positions in y0 containing at least ωH(y0)−ϵ instances of the element 1, then it is said to satisfy the gathering property. Research has shown a strong correlation between the gathering property and the DFR of QC-MDPC codes. Experimental results indicate that when both the key and the error satisfy the gathering property, the DFR is significantly higher than the average level. Based on the gathering property, the following important theoretical results regarding the DFR of the QC-MDPC scheme were derived.

DFRavg≥2−116.61(21)

Reference [26] proposed a weak-key model construction method based on the multiplicity analysis of a single-variable distance spectrum (detailed analysis is provided in Section 3.1). The weak-key model structure is defined as h=(h0,h1), where each hi is generated via a mapping function ϕδ. The specific expression is:

hi=ϕδ(xl[(1+x+x2+…+xf−1)+hi′]), i∈{0,1}(22)

In this model, δ∈{1,2,3,…,[r/2]} represents the distance between non-zero bits in the weak key, while the parameter l∈{0,1,2,…,r−1} determines the starting position of the non-zero pattern. The mapping function ϕδ operates by replacing the variable x with xδ, ensuring that the distance between any two consecutive non-zero bits in the polynomial 1+x+x2+…+xf−1 remains constant at δ. The study further analyzed the impact of this weak-key model on the security of the BIKE scheme. For the BIKE scheme with parameters (r,ω,t)=(12323,142,134) and λ=128, the authors experimentally evaluated the performance of weak keys under IND-CCA. The relevant data is presented in Table 7.

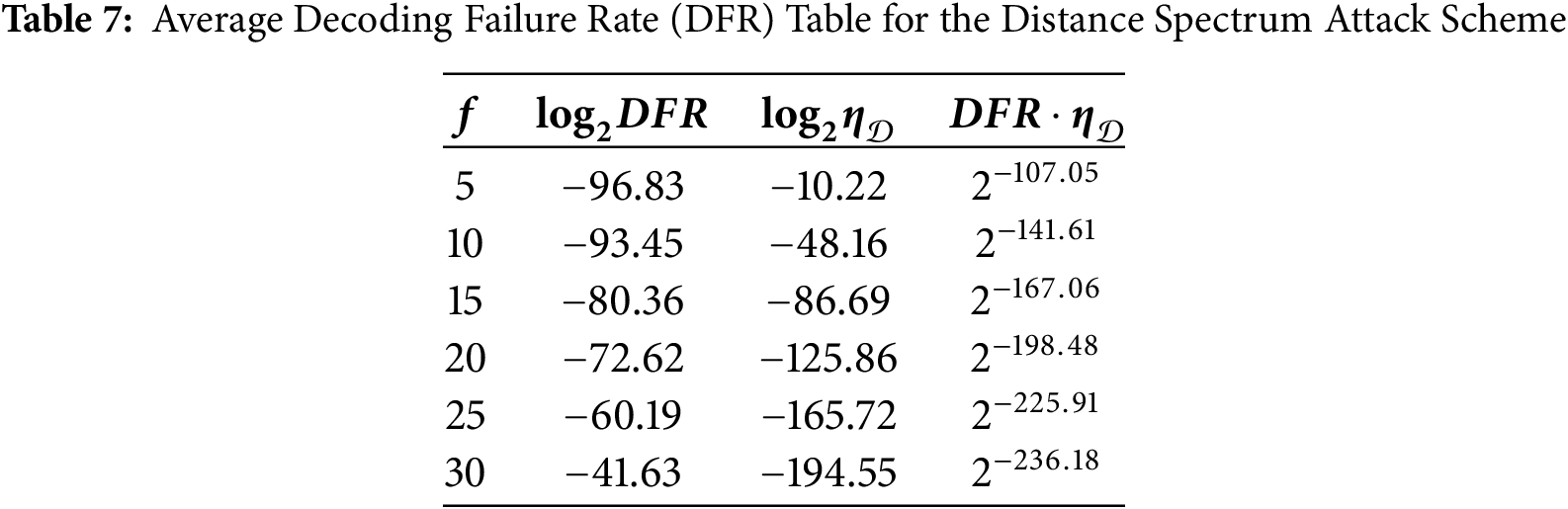
Compared to the aggregation degree scheme proposed by Wang et al. and the distance spectrum scheme in Reference [8], our proposed scheme demonstrates superior attack performance. In Wang et al.’s scheme, the lower bound of the average DFR is DFRavg≥2−116.61, while in Reference [23], the lower bound is 2−107.05. By optimizing the attack strategy, our scheme successfully increases the average DFR to DFRavg≥2−103.83. This improvement means attackers can trigger decoding failures with higher probability, thereby more easily extracting key-related information. A comparative analysis of the schemes is presented in Table 8.

The key innovation of our scheme lies in its ability to increase the decoding failure probability without introducing additional search density. This characteristic allows attackers to significantly enhance the success rate of key recovery while maintaining low computational resource consumption. Specifically, by refining the attack model and algorithms, our scheme enables attackers to more efficiently leverage decoding failure information for key recovery under the same computational complexity.

4.7 Weak-Key Detection

The general methods for dealing with weak keys primarily include three dimensions: static analysis, dynamic testing, and algorithm-specific detection. In terms of static analysis, the evaluation mainly relies on the following technical approaches: key space size analysis, repetition and predictable pattern recognition, known weak key dictionary comparison, and information entropy calculation. Dynamic testing employs practical attack validation techniques, including brute-force attempts, differential analysis, and linear analysis, to empirically assess the key’s resistance to attacks.

For algorithm-specific detection, the sample autocorrelation function test stands out due to its exceptional capability in detecting key periodicity. The principle of this method involves calculating the autocorrelation coefficient between the initial sequence and its left-shifted sequence by k positions, thereby quantifying the degree of internal correlation within the sequence. In practical implementation, by analyzing the distribution of autocorrelation coefficients at different lag orders, a significant peak at a specific lag order indicates the presence of correlation at that period. This method not only effectively identifies internal sequence variation characteristics but also accurately detects periodic properties of the sequence, making it particularly suitable for weak key periodicity detection based on distance spectrum analysis.

In summary, by integrating the technical approaches of static analysis, dynamic testing, and algorithm-specific detection, a comprehensive weak key detection system can be constructed. Among these, the autocorrelation function test, as a critical method in algorithm-specific detection, provides effective technical support for the periodic analysis of weak keys.

5  Conclusion

This study delves into the BGF decoding algorithm of the BIKE scheme and addressing its potential weak key issue, proposes an innovative optimized attack strategy. Through experiments, the specific impact of weak keys on the BGF decoder’s DFR is assessed. The analysis indicates that these weak keys pose a potential threat to the IND-CCA security of the BIKE scheme. Therefore, before claiming the IND-CCA security of the BIKE scheme, the security issues caused by weak keys must be addressed. In the future, this research will be extended to algorithms with higher security levels to further validate its universality and effectiveness. This study not only provides new insights into the security of the BIKE scheme but also offers a reference for the future security evaluation of post-quantum cryptography.

Acknowledgement: Not applicable.

Funding Statement: This research was funded by Beijing Institute of Electronic Science and Technology Postgraduate Excellence Demonstration Course Project (20230002Z0452).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Bing Liu; methodology, Bing Liu; software, Ting Nie; validation, Yansong Liu; formal analysis, Yansong Liu; investigation, Weibo Hu; resources, Ting Nie; data curation, Yansong Liu; writing—original draft preparation, Ting Nie; writing—review and editing, Bing Liu; visualization, Ting Nie; supervision, Bing Liu; project administration, Ting Nie; funding acquisition, Bing Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Bing Liu, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Li S, Chen Y, Chen L, Liao J, Kuang C, Li K, et al. Post-quantum security: opportunities and challenges. Sensors. 2023;23(21):8744. doi:10.3390/s23218744. [Google Scholar] [PubMed] [CrossRef]

2. Shor PW. Algorithms for quantum computation: discrete logarithms and factoring. In: Proceedings 35th Annual Symposium on Foundations of Computer Science. Santa Fe, NM, USA: IEEE; 1994. p. 124–34. [Google Scholar]

3. Alagic G, Alagic G, Apon D, Cooper D, Dang Q, Dang T, et al. Status report on the third round of the NIST post-quantum cryptography standardization process. Gaithersburg, MD, USA: National Institute of Standards and Technology; 2022. [Google Scholar]

4. Sendrier N. Code-based cryptography: state of the art and perspectives. IEEE Secur Priv. 2017;15(4):44–50. [Google Scholar]

5. Drucker N, Gueron S, Kostic D. QC-MDPC decoders with several shades of gray. In: International Conference on Post-Quantum Cryptography. Cham: Springer International Publishing; 2020. p. 35–50. [Google Scholar]

6. Aragon N, Barreto P, Bettaieb S, Bidoux L, Blazy O, Deneuville JC, et al. BIKE: bit flipping key encapsulation; 2022 [cited 2025 Apr 15]. Available from: https://bikesuite.org/files/v4.2/BIKE_Spec.2021.09.29.1.pdf. [Google Scholar]

7. Guo Q, Johansson T, Stankovski P. A key recovery attack on MDPC with CCA security using decoding errors. In: Advances in Cryptology–ASIACRYPT 2016: 22nd International Conference on the Theory and Application of Cryptology and Information Security; 2016 Dec 4–8; Hanoi, Vietnam. Berlin/Heidelberg, Germany: Springer; 2016. p. 789–815. [Google Scholar]

8. Wang T, Wang A, Wang X. Exploring decryption failures of BIKE: new class of weak keys and key recovery attacks. In: Annual International Cryptology Conference. Cham: Springer Nature Switzerland; 2023. p. 70–100. [Google Scholar]

9. Eaton E, Lequesne M, Parent A, Sendrier N. QC-MDPC: a timing attack and a CCA2 KEM. In: International Conference on Post-Quantum Cryptography. Cham: Springer International Publishing; 2018. p. 47–76. [Google Scholar]

10. Guo Q, Johansson T, Wagner PS. A key recovery reaction attack on QC-MDPC. IEEE Trans Inf Theory. 2018;65(3):1845–61. doi:10.1109/tit.2018.2877458. [Google Scholar] [CrossRef]

11. Nilsson A, Johansson T, Wagner PS. Error amplification in code-based cryptography. Cryptology ePrint Archive; 2018. doi:10.13154/tches.v2019.i1.238-258. [Google Scholar] [CrossRef]

12. Drucker N, Gueron S, Kostic D. On constant-time QC-MDPC decoding with negligible failure rate. Cryptology ePrint Archive; 2019 [cited 2025 Apr 15]. Available from: https://eprint.iacr.org/2017/604. [Google Scholar]

13. Niederreiter H. Knapsack-type cryptosystems and algebraic coding theory. Prob Control Inform Theory. 1986;15(2):157–66. [Google Scholar]

14. Fujisaki E, Okamoto T. Secure integration of asymmetric and symmetric encryption schemes. In: Annual International Cryptology Conference. Berlin/Heidelberg, Germany: Springer Berlin Heidelberg; 1999. p. 537–54. [Google Scholar]

15. Dent AW. A designer’s guide to KEMs. In: IMA International Conference on Cryptography and Coding. Berlin/ Heidelberg, Germany: Springer Berlin Heidelberg; 2003. p. 133–51. [Google Scholar]

16. Hofheinz D, Hövelmanns K, Kiltz E. A modular analysis of the Fujisaki-Okamoto transformation. In: Theory of Cryptography Conference. Cham: Springer International Publishing; 2017. p. 341–71. [Google Scholar]

17. Gallager R. Low-density parity-check codes. IRE Trans Inf Theory. 1962;8(1):21–8. doi:10.1109/tit.1962.1057683. [Google Scholar] [CrossRef]

18. Vasseur V. QC-MDPC codes DFR and the IND-CCA security of bike; 2022 [cited 2025 Apr 15]. Available from: https://ia.cr/2021/1458. [Google Scholar]

19. Sendrier N, Vasseur V. On the decoding failure rate of QC-MDPC bit-flipping decoders. In: Ding J, Steinwandt R, editors. Post-quantum cryptography. Cham: Springer; 2019. Vol. 11505. p. 404–16. [Google Scholar]

20. Sendrier N, Vasseur V. About low DFR for QC-MDPC decoding. In: International Conference on Post-Quantum Cryptography. Cham: Springer International Publishing; 2020. p. 20–34. [Google Scholar]

21. Vasseur V. Post-quantum cryptography: a study of the decoding of QC-MDPC codes. France: Université de Paris; 2021. [Google Scholar]

22. Chou T, Maezawa Y, Miyaji A. A closer look at the Guo-Johansson–Stankovski attack against QC-MDPC codes. In: International Conference on Information Security and Cryptology. Cham: Springer International Publishing; 2018. p. 341–53. [Google Scholar]

23. Sendrier N, Vasseur V. On the existence of weak keys for QC-MDPC decoding; 2020 [cited 2025 Apr 15]. Available from: https://ia.cr/2020/1232. [Google Scholar]

24. Nosouhi MR, Shah SW, Pan L, Zolotavkin Y, Nanda A, Gauravaram P, et al. Weak-key analysis for bike post-quantum key encapsulation mechanism. IEEE Trans Inf Forensics Secur. 2023;18(3):2160–74. doi:10.1109/tifs.2023.3264153. [Google Scholar] [CrossRef]

25. Sendrier N. Secure sampling of constant-weight words–application to bike. Cryptology ePrint Archive; 2021 [cited 2025 Apr 15]. Available from: https://ia.cr/2021/1631. [Google Scholar]

26. Arpin S, Billingsley TR, Hast DR, Lau JB, Perlner R, Robinson A. A study of error floor behavior in QC-MDPC codes. In: International Conference on Post-Quantum Cryptography. Cham: Springer International Publishing; 2022. p. 89–103. [Google Scholar]

27. Bardet M, Dragoi V, Luque JG, Otmani A. Weak keys for the quasi-cyclic MDPC public key encryption scheme. In: Progress in Cryptology–AFRICACRYPT 2016: 8th International Conference on Cryptology in Africa; 2016 Apr 13–15; Fes, Morocco: Springer International Publishing; 2016. p. 346–67. [Google Scholar]