Detection of False Data Injection Attacks: A Protected Federated Deep Learning Based on Encryption Mechanism

1  Introduction

As a crucial pillar of national infrastructure, ensuring power system security is paramount. With growing integration between the power system and the Internet [1], the smart grid [2] is regarded as the new generation in power systems, merging advanced network communication, intelligent control and automation technologies to strengthen monitoring, analysis and fault response capabilities for equipment and data [3]. Nevertheless, the deep coupling of information technology with physical power systems renders smart grids vulnerable to cyberattacks. Various types of adversarial attacks, such as label flipping, feature poisoning, vague generative adversarial network-based data poisoning attack (VagueGAN) [4], and even some unknown web attacks [5] keep emerging one after another, posing a huge threat to the normal and efficient operation of the smart grid. FDIA is a prominent representative among these threats, which is first proposed by Liu et al. in 2009 [6]. Specifically, attackers first monitor and analyze system data to comprehend normal operational patterns, then insert seemingly authentic false data to circumvent detection mechanisms, resulting in compromised data integrity, diminished system reliability, and even significant economic repercussions, exemplified by the severe 2015 Ukraine power grid attack [7].

In response to the occurrence of FDIA and its severe impacts, establishing effective detection and defense mechanisms is essential. Considerable research efforts have been dedicated to False Data Injection Attacks (FDIA). Numerous centralized FDIA detection methods, such as research [8–11], are capable of efficiently identifying anomalous data and significantly improving detection accuracy by integrating all power data into a central node for centralized analysis and training. However, these methods are highly dependent on central nodes, which increases the risk of single-point failures and makes the system particularly vulnerable to attacks targeting the central node. Meanwhile, as the system scales up, centralized methods will encounter scalability issues. For example, the computational and storage resources of centralized servers may reach their limits swiftly, which put tremendous pressure on centralized nodes. Extensive decentralized studies [12,13] effectively circumvent the aforementioned challenges by introducing distributed or decentralized ideas, but the lack of consideration of data leakage during transmission and sharing among multiple nodes or clients may threaten the security of the entire system. Furthermore, there are also some works [14,15] that capture information through temporal graphs or spatial graphs, which in turn aid in decision-making. Although they have achieved satisfactory results, constructing the graph only from a single perspective leads to one-sided information, thus limiting the further improvement of the detection accuracy.

It can be seen that most of the existing countermeasures cannot simultaneously guarantee the detection effectiveness, non-dependence on individual nodes as well as security during data transmission. Therefore, in this paper, we innovatively propose a FDIA detection scheme that combines federated learning, CKKS encryption system and STGNN detection model. By combining all advantages of each module, we can achieve a de-centralised, highly secure and accurate FDIA detection technology, addressing the shortcomings of existing research. Specifically, the Federated Averaging algorithm is first employed to alleviate the pressure on data storage as well as model training, thus reducing the reliance on centralized nodes. Subsequently, data security and model security are further guaranteed through leveraging the locally stored data for local model training and employing the CKKS homomorphic encryption mechanism to transmit model parameters. Finally, an enhanced spatial-temporal graph neural network (STGNN) proposed in [16] is used to capture the spatial-temporal correlations and extract more comprehensive features in training data, which significantly improves the detection accuracy of FDIA. In a word, the main contributions of this paper are as follows:

•   We propose a FDIA detection method based on the Federated Averaging algorithm, which enhances data privacy, eases central server load and lessens the dependence on the central node by locally performing training.

•   We innovatively apply the CKKS homomorphic encryption system to encrypt the weight parameters for upload, preventing hackers from inferring model information and safeguarding model security.

•   We employ an enhanced STGNN model, which is capable of extracting more comprehensive and accurate features by capturing the dependencies between temporal and spatial aspects, thereby enhancing the detection accuracy of FDIA.

The rest of this paper is structured as follows: Section 2 outlines the problem background and reviews related studies; Section 3 provides an overview of several algorithms involved in this paper; Section 4 details the proposed algorithm; Section 5 presents the experimental results along with clear analysis; Section 6 concludes this paper.

2  Background

In this section, we introduce the principles of FDIA and review the existing FDIA detection methods, offering a clear introduction of FDIA.

2.1 False Data Injection Attack

False Data Injection Attack (FDIA) is a type of network attack targeting networked control systems and power systems. In this attack, the attacker injects erroneous information into the system by tampering with sensor or communication data, which causes the system to make incorrect judgments or decisions and leads to system malfunctions or failures [17]. Based on the complex structure of the smart grid, the nonlinear measurement equation for state estimation can be established as Eq. (1):

z=h(x)+e,(1)

where z, h(x), x, e represent the vector of measurements, the nonlinear measurement function, the vector of state variables and the measurement error vector, respectively. After being subjected to a FDIA, the measurement is denoted by zf, as represented by Eq. (2):

zf=z+a,(2)

where a=[a1,a2,...,am]T is the attack vector of dimension m. Assuming x^ represents the normal state, the estimated state after FDIA can be expressed as xf in Eq. (3):

xf=x^+c,(3)

where c=[c1,c2,...,cn]T represents the estimation error vector of dimension n caused by the FDIA. Let the pre-attack and post-attack residuals be denoted as r and rf, respectively. They can be computed by Eq. (4):

r=z−h(x^),rf=zf−h(xf).(4)

By transforming Eqs. (2) and (3), rf can be derived as Eq. (5):

rf=zf−h(xf)=(z+a)−h(x^+c)=(z−h(x^))+(a−h(x^+c)+h(x^)).(5)

At this point, the attack vector a can be represented by Eq. (6):

a=rf−r+h(x^)−h(xf).(6)

Given the stealthy nature of FDIA, the residuals of the power grid remain unchanged before and after the attack, i.e., rf=r. Hence, a will be denoted as Eq. (7):

a=h(x^)−h(xf).(7)

Eq. (7) can be regarded as the constraint condition for the attack vector. Once this condition is fulfilled, FDIA can successfully bypass bad data detection [18].

2.2 FDIA Detection

Since FDIA is extremely harmful, it is imperative to establish an effective FDIA detection and defense mechanism. So far, numerous related researches have been conducted. Kosut et al. [8] propose an easy-to-compute heuristic algorithm which can trace undetectable destructive attacks in all scenarios. In addition, they also introduce the Bayesian formula for bad data problems and the optimized L∞ detector which is superior to the L2 norm-based detector, to better detect FDIA. Luo et al. [9] propose an unknown input observer (UIO)-based method for FDIA detection and isolation. Combining the internal physical dynamics as well as the residual properties of the UIO, an algorithm with adaptive threshold settings is proposed for fast detection of FDIA. In [10], Li et al. propose a security and resilience enhancement scheme (SECDM), designing a centralized FDIA detector that utilizes a decentralized homomorphic computation paradigm and a hierarchical knowledge-sharing algorithm for attack detection and mitigation in smart grids. Zhang et al. [11] integrate an autoencoder into a Generative Adversarial Network (GAN) to detect FDIA by capturing inconsistencies between anomalous data and normal measurements. Huang et al. and Huang et al. [12,13] abandon the traditional centralized detection framework and propose a distributed detection method based on edge computation. Although replacing the centralized framework with a distributed computing framework alleviates the computational pressure, the risk of data leakage during data transmission between the central server and edge users is not considered. Boyaci et al. [14] propose a GNN-based, scalable real-time FDIA detector by leveraging power grid physics and measurement spatial correlations. However, this approach only considers spatial correlations without taking the time series into account. Wu et al. [15] propose a robust FDIA model adaptable to topological changes and a distributed unsupervised detection method combining dynamic time warping and clustering techniques to effectively identify FDIA. Nevertheless, the method only considers the temporal correlation and ignores the spatial correlation of power data.

3  Preliminary

This section provides an overview of the current research status and principles of FedAvg, STGNN, and CKKS, which will serve as a research foundation for ProdFed in the following sections.

3.1 Federated Averaging Algorithm

As a classic and widely used distributed optimization algorithm in Federated Learning (FL), the Federated Averaging (FedAvg) algorithm is suitable for scenarios where data privacy is sensitive, communication costs are limited and data distribution is heterogeneous. This technology has been widely applied in fields with large amounts of data and high requirements for data security, such as healthcare [19,20], finance [21] and communications [22,23]. The FedAvg algorithm achieves data privacy preservation through local training and parameter aggregation, and has demonstrated some achievements [24,25] in FDIA detection field. Meanwhile, on the basis of optimizing the model using decentralized data, FedAvg reduces the number of communication rounds required for training by increasing client computation, thereby improving computational efficiency.

Specifically, its basic framework is shown in Fig. 1. Based on Stochastic Gradient Descent (SGD) [26], the FedAvg algorithm selects clients for local model training according to the actual situation. After multiple local iterations, the updates (such as weights or gradients) are uploaded to the central server for aggregation, thereby updating the global model. It allows participants to perform joint modeling without sharing the original data, thus ensuring data privacy. Meanwhile, multiple iterations are carried out locally, which reduces the communication cost. Since different grid nodes may have similar devices (the same features) but different operational data and fault conditions (different samples), the FedAvg algorithm enables all nodes to collaborate in training a more effective detector.

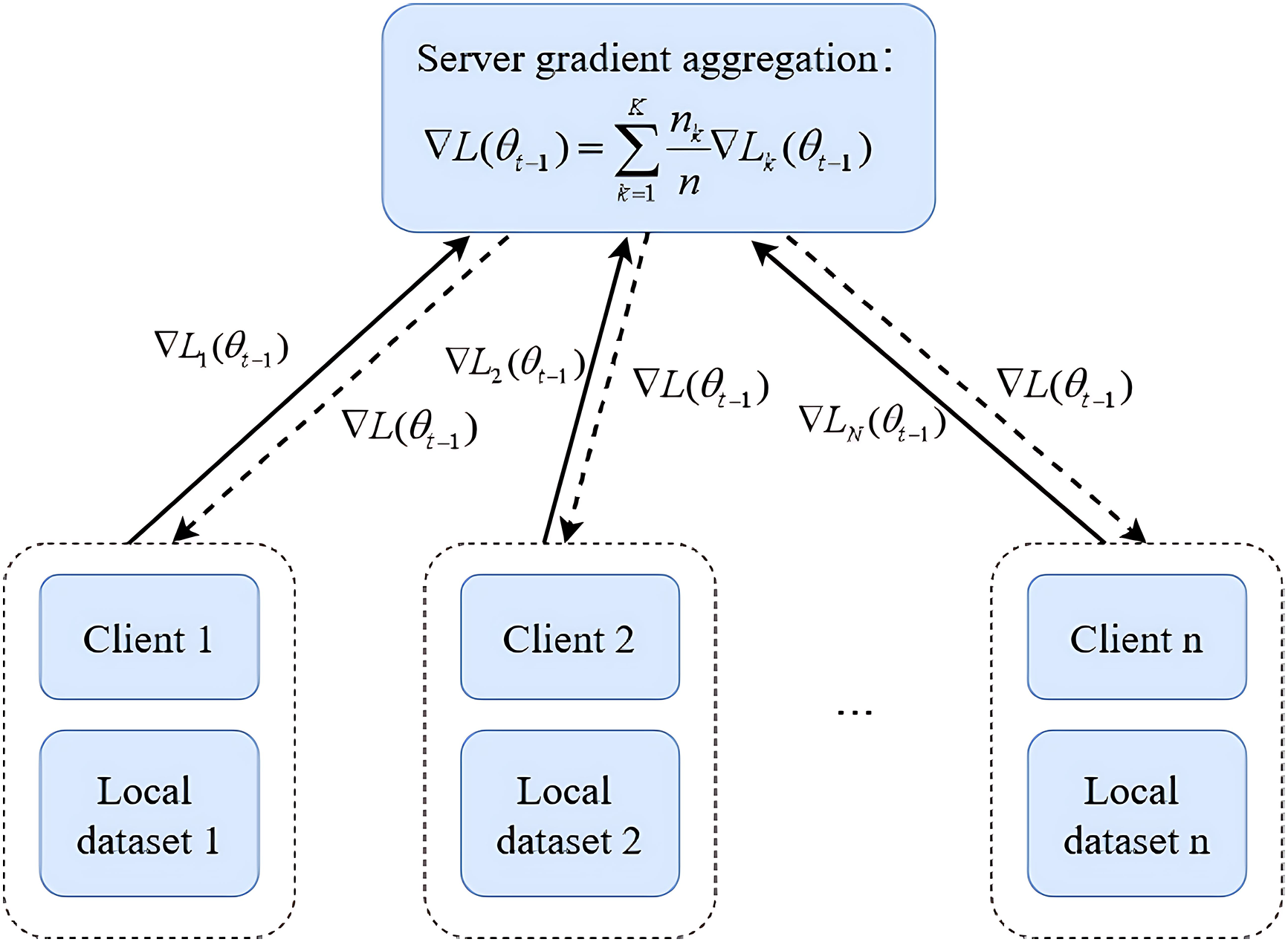
Figure 1: Federated averaging algorithm

3.2 Enhanced Spatial-Temporal Graph Neural Network

Aiming to simultaneously capture spatial and temporal dependencies in multivariate time series (MTS) [27] data, this paper adopts the spatial-temporal graphical neural network (STGNN), which has a promising application prospect in the fields of traffic prediction [28,29,30], medicine [31,32] and smart grid [33,34]. Moreover, it also holds promising prospects in the domain of attack identification [35,36] and abnormal data detection [37]. However, due to the low information density of time series data, STGNN can only extract information from short time intervals, struggling to capture long-term temporal sequences. To address this issue, the Enhanced Spatial-Temporal Graph Neural Network proposed in [16] is cited, which includes the Pre-training Stage and Forecasting Stage. Fig. 2 shows the flowchart.

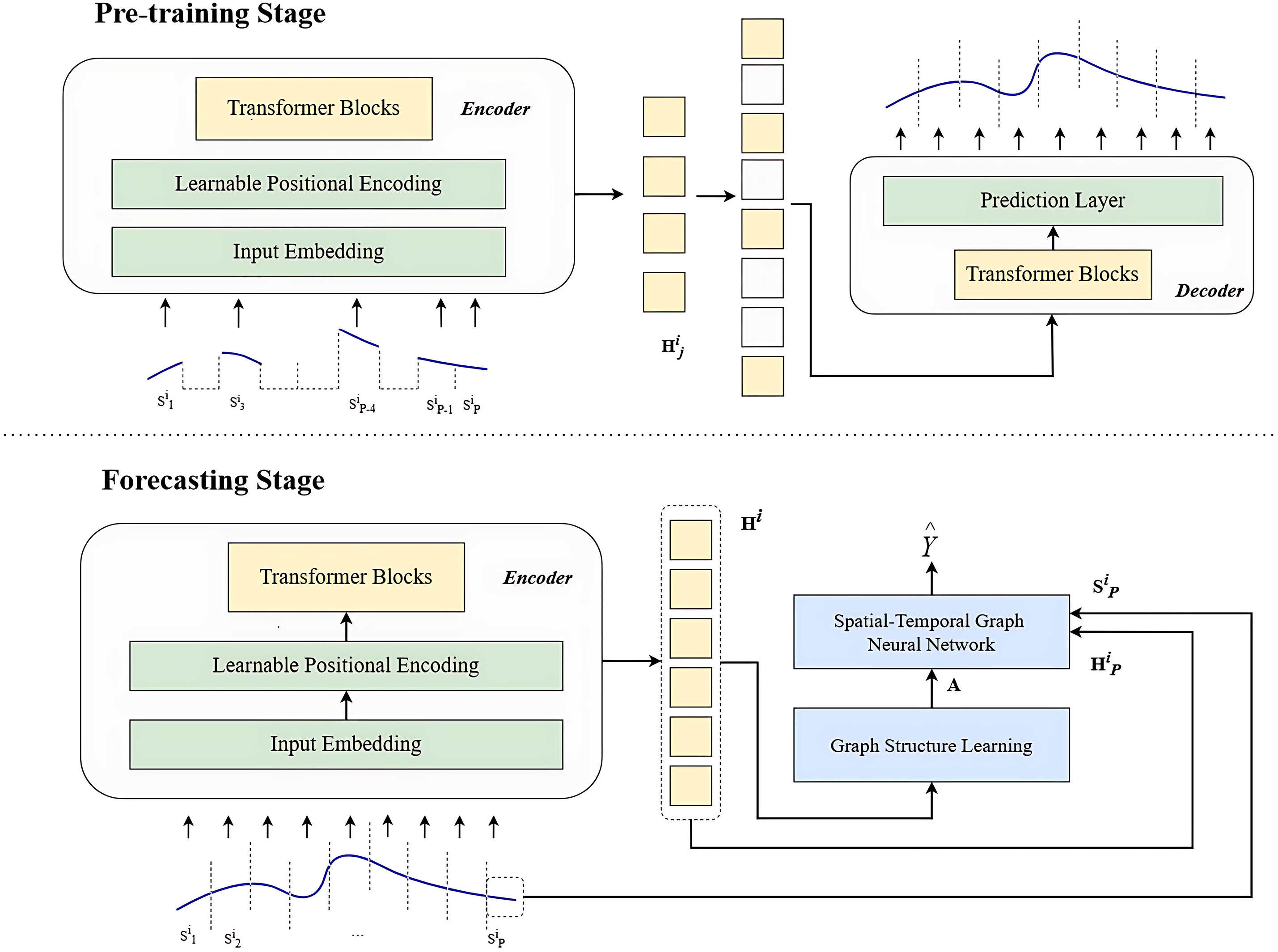
Figure 2: Enhanced spatial-temporal graph neural network

The Pre-training Stage includes four stages: Masking, Encoding, Decoding and Reconstruction.

•   Masking: In order to adapt to downstream model STGNNs and achieve efficient training, the input sequence is divided into non-overlapping segments which are selected for masking to create a challenging self-supervised task.

•   Encoding: The encoder only operates on unmasked fragments to generate latent representations which serve as preparations for subsequent tasks.

•   Decoding: The decoder operates on the full set of patches (including the mask tokens) to reconstruct the latent representations back to numerical information.

•   Reconstruction: The mean absolute error is calculated in parallel for all time series to evaluate the quality of reconstruction.

The Forecasting Stage includes two stages: Discrete Sparse Graph Learning and Downstream Spatial-Temporal Graph Neural Network.

•   Discrete Sparse Graph Learning: The pre-trained TSFormer is utilized for discrete sparse graph structure learning to address the challenges faced by STGNNs in graph structure learning, providing preparation for downstream tasks.

•   Downstream Spatial-Temporal Graph Neural Network: An enhanced STGNN framework combining TSFormer and Graph WaveNet is proposed to improve the performance and completion efficiency of downstream tasks.

3.3 CKKS Homomorphic Encryption

The Cheon-Kim-Kim-Song (CKKS) homomorphic encryption scheme, proposed by Cheon et al. in [38], is a widely adopted homomorphic encryption scheme based on the Brakerski Gentry Vaikuntenathan (BGV) or Brakerski Fan Vercauteren (BFV) schemes. It is distinguished primarily by its capability to process floating-point numbers through the introduction of approximate calculation, allowing for a certain degree of error. Compared with other traditional fully homomorphic encryption schemes, CKKS simplifies the details when processing floating-point numbers and has higher computational efficiency. Efficient encryption and decryption make it highly promising in the fields of machine learning [39–41] and privacy protection [42–45]. In this article, we utilize CKKS Homomorphic Encryption Algorithm to protect the model weight parameters during the information transmission process between the central server and the client, thus achieving the goal of protecting federated learning. The CKKS encryption parameters (e.g., polynomial degree, coefficient size) used in this article adhere to the security level settings recommended by the Homomorphic Encryption Standardization Group (HESG), with the specific configuration set to a 128-bit security level.

4  Methodology

The core idea of the ProFed scheme is to combine the Federated Averaging algorithm with CKKS homomorphic encryption to collaboratively train a FDlA detection model: Enhanced Spatial-Temporal Graph Neural Network for each client with locally stored data. Fig. 3 shows the flowchart of the ProFed-STGNN. The upper part illustrates the general workflow of federated learning, while the lower part outlines the corresponding steps taken for training local model (the pre-training enhanced STGNN). Specifically, the above process consists of Model Initialization, Local Model Training and Iteration, Encrypting Weights, Aggregating Model Weights and Updating Local Models.

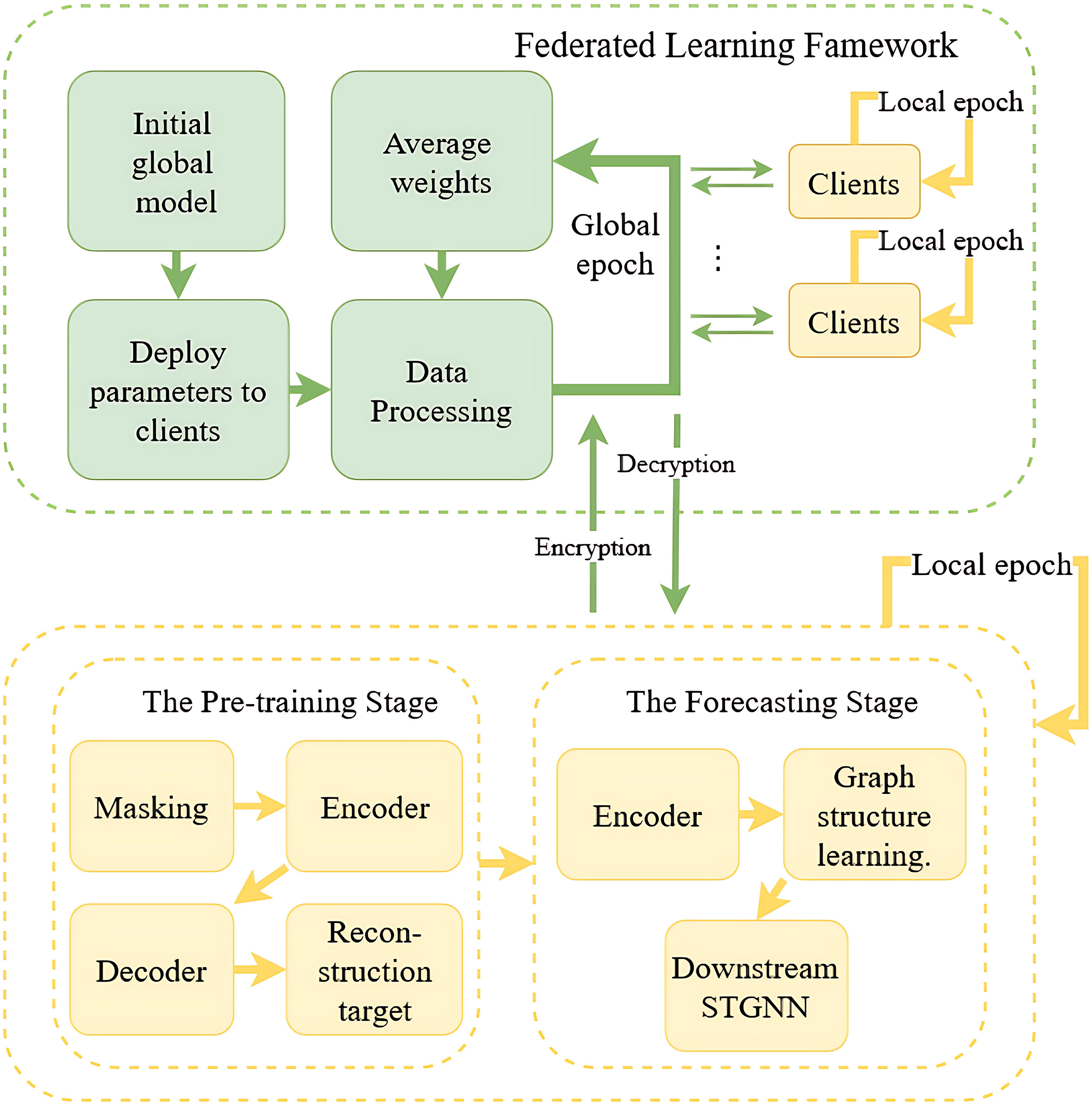
Figure 3: Flow chart of the ProFed-STGNN

4.1 Model Initialization

In ProFed, the central server first initializes the global model and sends the model parameters θ0 to each client. Meanwhile, according to the CKKS homomorphic encryption scheme, the key generator will generate the public key (PK) for encryption and the private key (SK) for decryption. The CKKS encryption scheme is constructed based on the Ring-LWE (Learning With Errors) problem, which has strong security assurance. In the ProFed scheme, the key generation depends on the security parameter λ, which represents the length of the bit-length sequence of the moduli used for encryption. Then, the generated key is leveraged to accomplish the encryption operation via polynomials defined over the ring Zq[x]/(xn+1), where n is the upper limit of polynomial degree, which is usually a power of 2. Zq[x] represents the polynomial ring of coefficients in Zq and q is the modulus, which is usually a large prime or a power of a prime.

4.2 Local Model Training and Iteration

4.2.1 Local Model Training

After initialization, each client uses local data to train a pre-trained enhanced FDIA detector based on enhanced spatial-temporal graph neural networks, which is described as the lower part of Fig. 3. Through extracting effective temporal information from long time series by unsupervised learning strategies (such as masked autoencoders), ProFed utilizes the pre-trained model to further enhance the model’s robustness against False Data Injection Attack (FDIA). In addition, ProFed introduces a graph structure learner which applies graph structure regularization and leverages TSFormer to reflect the dependencies between nodes to handle missing dependency graphs. This ensures the successful construction of the graph structure and provides useful information for the subsequent spatio-temporal graph neural network. As a result, the performance of STGNN is improved, empowering the module to identify abnormal data and detect potential attack behaviors with greater accuracy. In ProFed, by combining STGNN with pre-trained models, we can learn the temporal patterns from long-term historical time series effectively, generating segment-level representations rich in contextual information. These representations promote the performance of downstream models in FDIA detection, especially when dealing with complex power system data.

4.2.2 Iteration

ProFed employs federated learning (FL) to orchestrate interactions between a central server and clients. In each iteration, clients compute model updates (such as gradient or weight updates) based on their local power system datasets and the current global model parameters, enabling decentralized training without direct data sharing. To reduce computational costs and the number of communication rounds, ProFed utilizes the Federated Averaging (FedAvg) algorithm which is described in Section 3.1 during the iteration process.

In the t-th round of iteration, i-th client first receives the global model parameters θt. Then, multiple iterations are locally executed to update the model, aiming to minimize the loss function L(θit;Di) using the local dataset Di,

θit←θit−η▽L(θit;Di),(8)

where η is the learning rate; ▽L(θit;Di) is the gradient of the loss function with respect to the model parameters. For a client with ni local samples, the number of local updates per round is denoted as:

ui=EniB,(9)

where E represents the number of training epochs each client performs on its local dataset per round; B represents the local batch size used for client updates. ProFed utilizes the Federated Averaging algorithm, which enables clients to perform multiple iterations locally. By minimizing the transmission of intermediate results to the server, client-server communication is significantly reduced, effectively easing network transmission pressure and cutting communication costs. Meanwhile, the parallel local computing mode in ProFed allows the model to converge faster, significantly improving the overall training efficiency.

4.3 Encrypting Weights

In the ProFed framework, although the original data is not required in the data-sharing process, participants still need to upload model weights to build a federated model. These model weights are actually mappings of the original data, which can be reverse-engineered to obtain the original data, thus causing data leakage. To solve this problem, it is necessary to encrypt the model weight parameters using CKKS in ProFed to reduce the risk of data leakage during transmission between the central server and the clients. The encryption process first maps floating point numbers to polynomials and then encrypts them. Assuming that there are d parameters to be transmitted, the encryption complexity is O(d∗nlogn), where n represents the polynomial degree. The specific operations are as follows:

Epk(m)=(c1,c2),(10)

where m represents the real-valued model parameters (or updates); c1 and c2 are the two parts of the ciphertext and are constructed using a polynomial ring; pk is the public key.

As mentioned above, the ciphertext E(θit)=CKKS.Encrypt(pk,θit) is obtained by encrypting the local model parameters, thus reducing the risk of data information leakage during the subsequent transmission and aggregation processes. Meanwhile, this step enhances the confidentiality of the model weights or gradients uploaded by the clients, which may contain sensitive information.

4.4 Aggregating Model Weights

After each client sends the encrypted model parameters to the central server, rather than utilizing all clients, the central server randomly selects N clients from the received encrypted models and performs the aggregate operations. The server-side aggregation process mainly involves addition and multiplication operations. The addition has a complexity of O(d) and can be performed in batch, while the multiplication operation involves relinearization and modulus switching, which usually has a complexity of O(d∗n∗logn). Assuming that the number of aggregations T, the overall complexity of the encryption process is O(T∗d∗nlogn). Since the central server can access the public key, decryption is not required during the aggregation process. The weighted average of each obtained encrypted parameter is calculated for aggregation with the process shown in Eq. (11):

E(θt+1)=niNE(θit),(11)

where t represents the training round; i represents the client number; ni is the number of local samples for clients i; N is the number of selected clients.

4.5 Updating Local Models

In ProFed, the aggregated and updated parameters sent from the central server to each client are still in an encrypted form. So, the decryption of the ciphertext is carried out locally. Based on the Learning With Errors (LWE) problem, ProFed typically uses a private key (SK) to decrypt ciphertext. The decryption process mainly consists of ciphertext decoding and modular reduction, where ciphertext decoding is dominated by polynomial multiplication with complexity O(d*n log n). After decoding, the coefficients of the plaintext polynomial are reduced modulo, and the complexity of this reduction is O(d∗n). Assuming that the number of aggregations T, the overall complexity of the decryption process is O(T∗d∗nlogn). Therefore, the computational complexity of the Federated Averaging algorithm combined with CKKS encryption is O(T∗d∗nlogn). Given a ciphertext (c1,c2), the decryption process can be represented as Eq. (12):

Dsk(Epk(m))=m+error.(12)

Finally, each client will decrypt the ciphertext sent by the central server to obtain the updated model parameters θt+1=CKKS.Decrypt(sk,E(θt+1)), which are utilized to update their local models.

It’s worth noting that we assume that all clients have similar computational power to train the same local models. Additionally, this paper is based on theoretical analysis and does not consider practical issues such as data loss during communication.

5  Experenment

In this section, we first detail the data generation process and outline the specific settings for the experiment environment and hyperparameters. Then, we describe the evaluation metrics and the comparative algorithms. Finally, we present the experiment results and illustrate the superiority of the proposed method through charts.

5.1 Data Generation

1) Normal data: To simulate the normal operation of the actual power grid, we first generate normal data based on the IEEE 14-bus system and IEEE 118-bus system. These data are designed as a dataset with a mean equal to the base load with a 5% variance.

2) Compromised data: By injecting attacks into the IEEE 14-bus system and IEEE 118-bus system, a series of damaged data based on normal data is generated. Specifically, we set two levels of FDIA samples, weak attack and strong attack, based on the “strength” of the attack. Weak attack refers to the ratio of the average deviation of injected power to the standard value being less than 10%, the ratio of the average deviation of voltage amplitude to the standard value being less than 5%, and the average deviation of voltage angle being less than 2∘. Strong attack implies that the mean deviations of the above variables are respectively greater than 30%, 10%, and 5%, respectively. 10% nodes and 10% edges are randomly selected as attack nodes and edges.

3) Training and testing dataset settings: The training set contains 10,000 normal data samples and 10,000 damaged data samples, while the testing set contains 1000 normal data samples and 1000 compromised data samples. The ratio of weak attacks to strong attacks on damaged data is 1:1 in both the training and test sets.

5.2 Experiment Setting

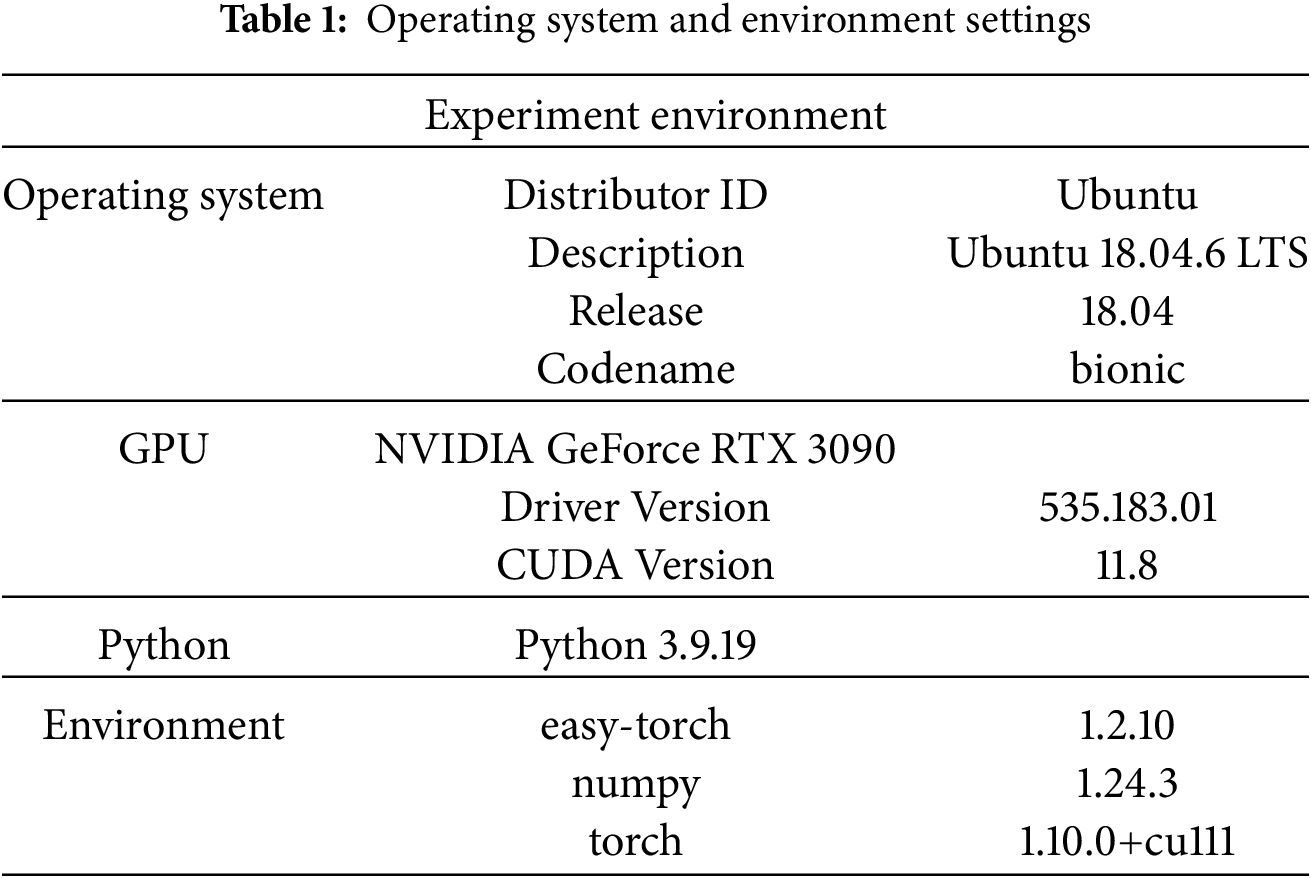
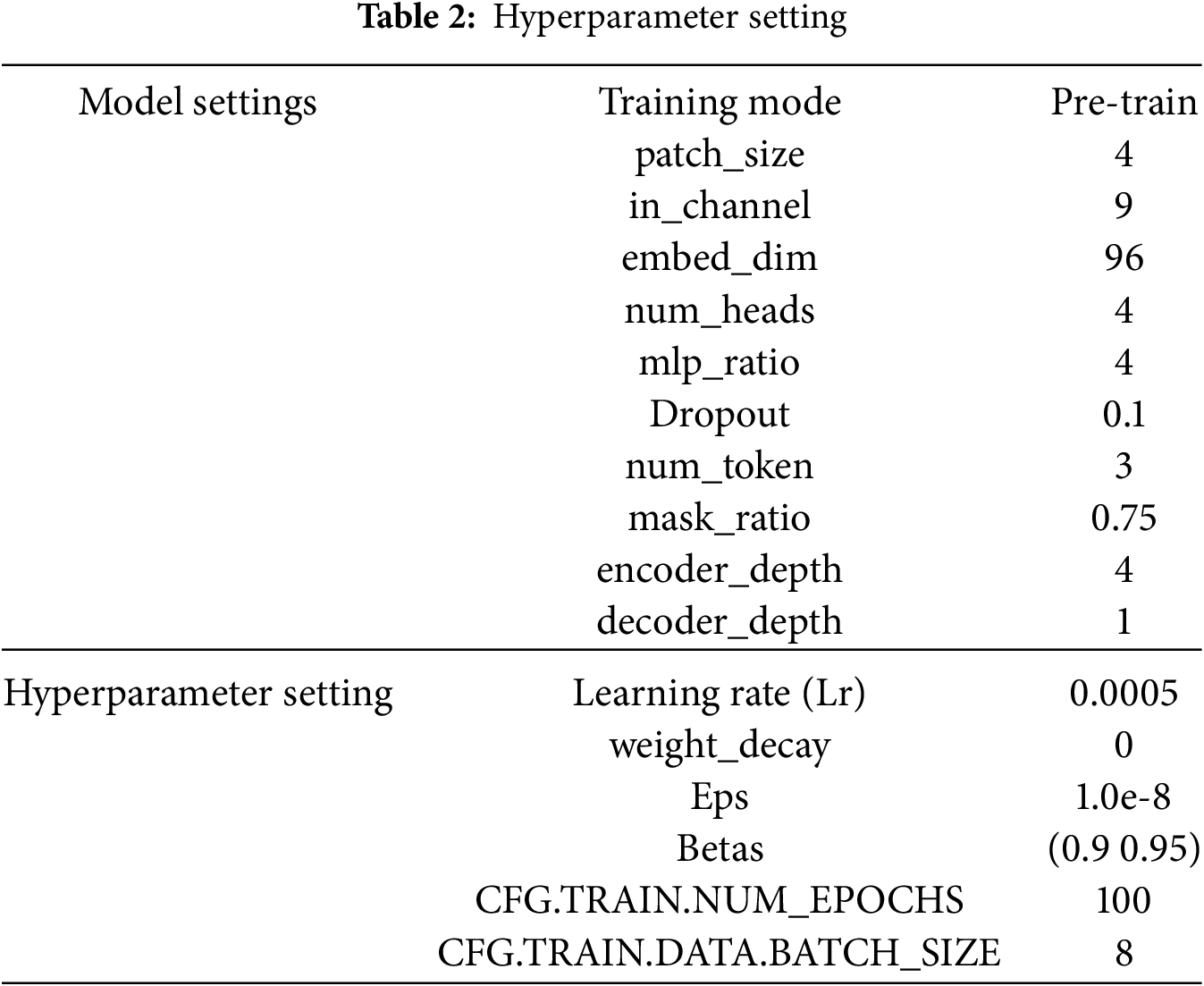
The specific environment settings and hyperparameter settings used in this article are shown in Tables 1 and 2, respectively.

5.3 Performance Evaluation Metrics

We choose precision, recall, F1-score [46] and Mean Absolute Error (MAE) [47] for evaluating the performance of the proposed method and exploring appropriate hyperparameter settings. Supposing that the meanings represented by TP, TN, FN, and FP are shown in Table 3, the aforementioned metrics are described as follows:

1. Precision (P): It indicates the proportion of actual positives among all samples predicted as positive.

Precision=TPTP+FP(13)

2. Recall (R): It represents the proportion of correctly predicted positives among all actual positives.

Recall=TPTP+FN(14)

3. F1-score (F): The F1-score is the harmonic mean of precision and recall, used to evaluate the model’s performance comprehensively, especially in cases of class imbalance.

F1−score=2×Precision×RecallPrecision+Recall(15)

4. Mean Absolute Error (MAE): MAE represents the average absolute error between predicted and observed values. It can be obtained by taking the mean of the MAEs from each communication round. The smaller the MAE value, the more ideal the actual operation of the model is. During the process of model performance evaluation, the MAE value can be influenced by the setting of hyperparameters. If the hyperparameters are improperly set, the actual values detected may exhibit a shift, resulting in an increased MAE value. Conversely, we can assess hyperparameter settings and the model performance by observing the fluctuations in MAE and calculating the average MAE value.

5.4 Experimental Result

1. IEEE 14-bus system: Tables 4 and 5, respectively, show the results from Convolutional Neural Networks (CNN) [48], Long Short-Term Memory (LSTM) [49] and the method proposed in this paper for the IEEE 14-bus system under weak attack and strong attack. We choose bus2 and bus3 as sampling points and communication rounds (CR), which represent the number of communication interactions between multiple clients and servers to train a shared model in federated learning, as independent variables to observe the changes in the evaluation metrics. It can be seen that with the increase of communication rounds (CR), the performance of each detection model gradually improves and eventually stabilizes. All evaluation metrics reach their maximum when CR = 6. Therefore, the distributed learning can widely utilize data from various sources to train models efficiently.

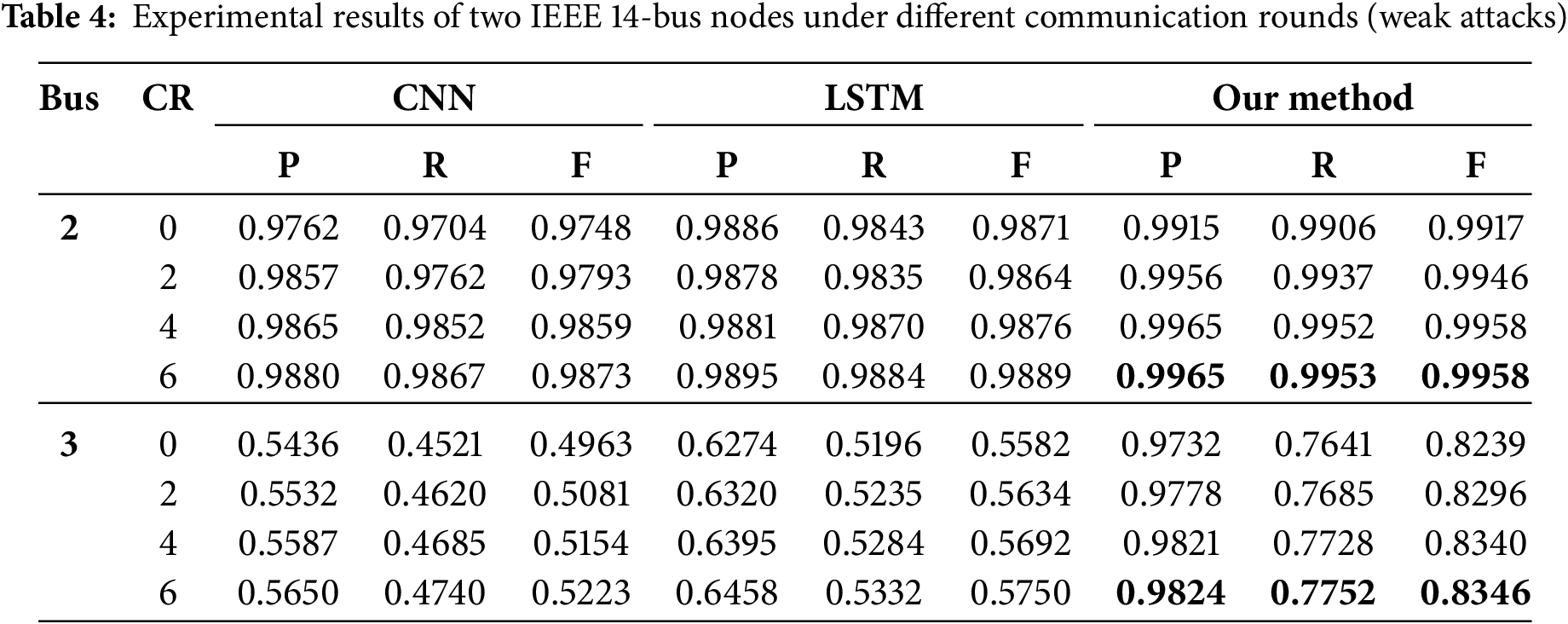
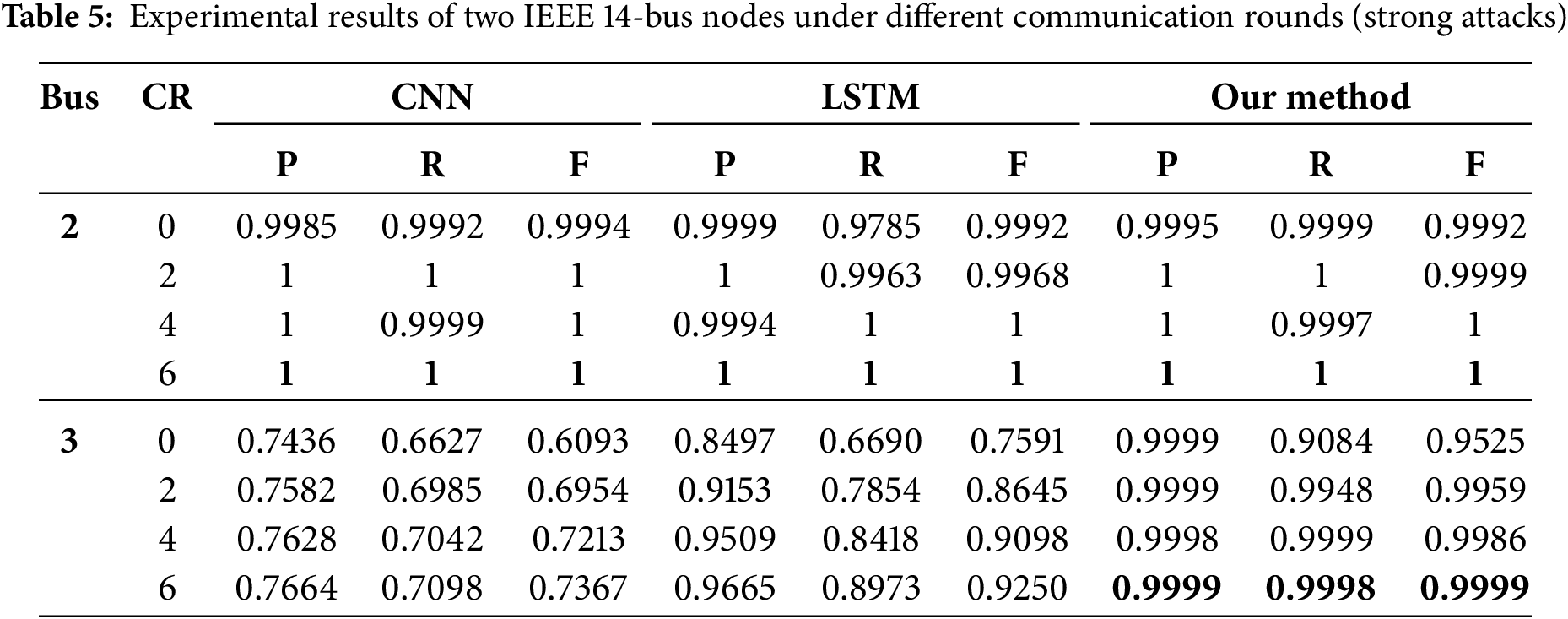
Under weak attacks, taking bus3 and CR = 6 as sampling points, the algorithm proposed in this paper respectively improves precision, recall, and F1 score by 0.4174, 0.3012, and 0.3123 compared to CNN, and 0.3366, 0.2420, and 0.2596 compared to LSTM. Under strong attacks, the algorithm proposed in this paper respectively improves precision, recall, and F1-score by 0.2336, 0.2902, and 0.2633 compared to CNN, and 0.0335, 0.1027, and 0.0750 compared to LSTM. It can be seen that the proposed method is superior to traditional deep learning models CNN and LSTM under both types of attacks. Finally, since the difference between normal data and compromised data is more pronounced under strong attacks, the detection performance is superior to that under weak attacks.

Fig. 4 illustrates the loss curve of the IEEE 14-bus system in the training process. It can be seen that the difference between training loss and validation loss is minimal, and with the increase in the number of communication rounds (CR), both training loss and validation loss decrease and finally stabilize at a lower value, which shows that the performance of the proposed model increases steadily and finally converges reasonably. In addition, the curve shows a reasonable fluctuation trend, indicating that the hyperparameters of the model have been well-adjusted without under-fitting or over-fitting.

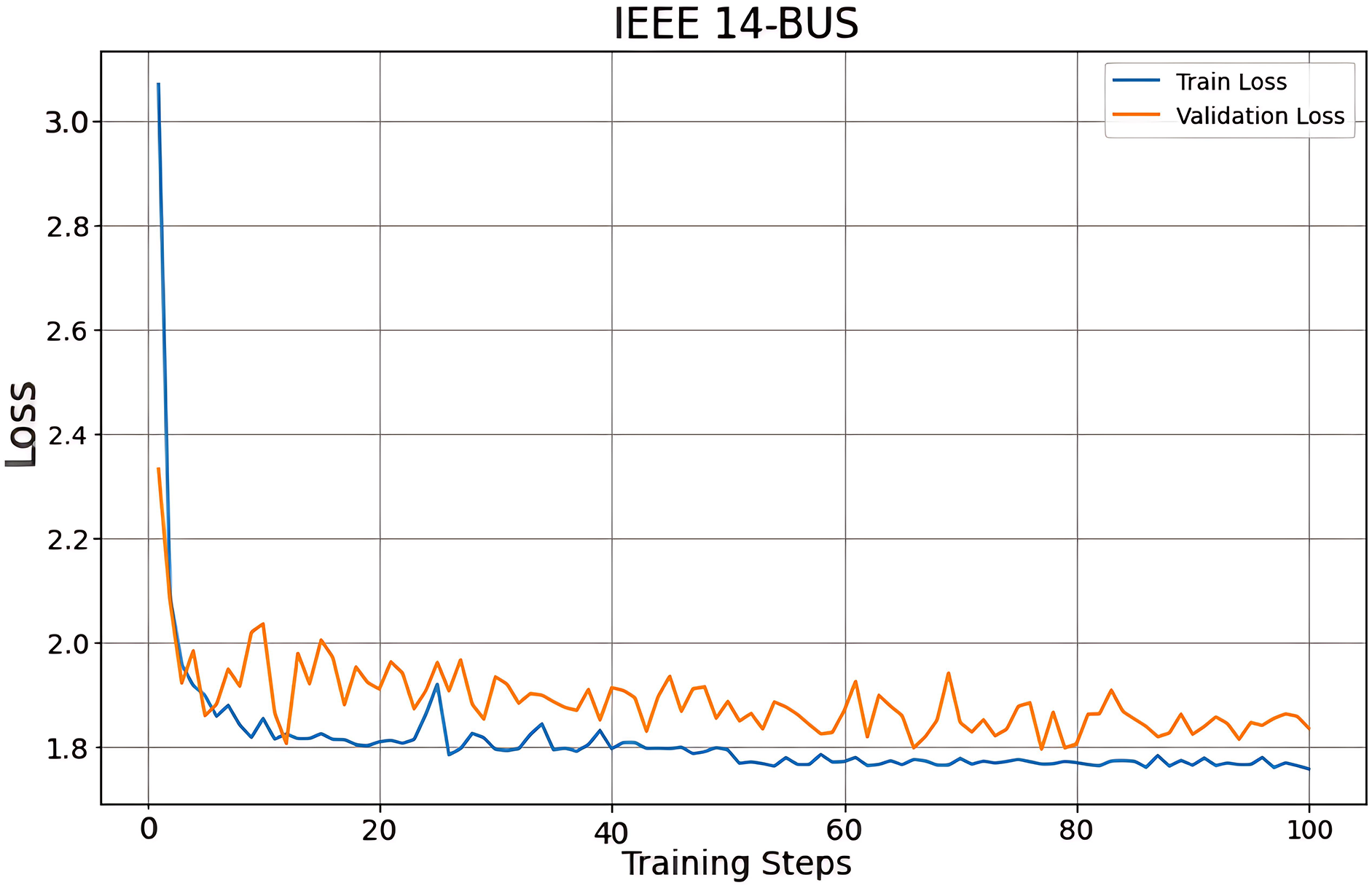
Figure 4: The loss curve during the training process of the IEEE 14-bus system

2. IEEE 118-bus system: Tables 6 and 7, respectively, show the evaluation metrics of CNN, LSTM, and the method proposed for the IEEE 118-bus system under weak and strong attacks. We select nodes 55 and 87 as sampling points to evaluate the performance changes of models with the increase of communication rounds (CR), and the results are similar to those obtained from the IEEE 14-bus system. Fig. 5 shows the loss curve during the training process of the IEEE 118-bus system, and its trend characteristics are basically the same as those of the IEEE 14-bus system, which indicates that the proposed method can be applied to both large and small systems.

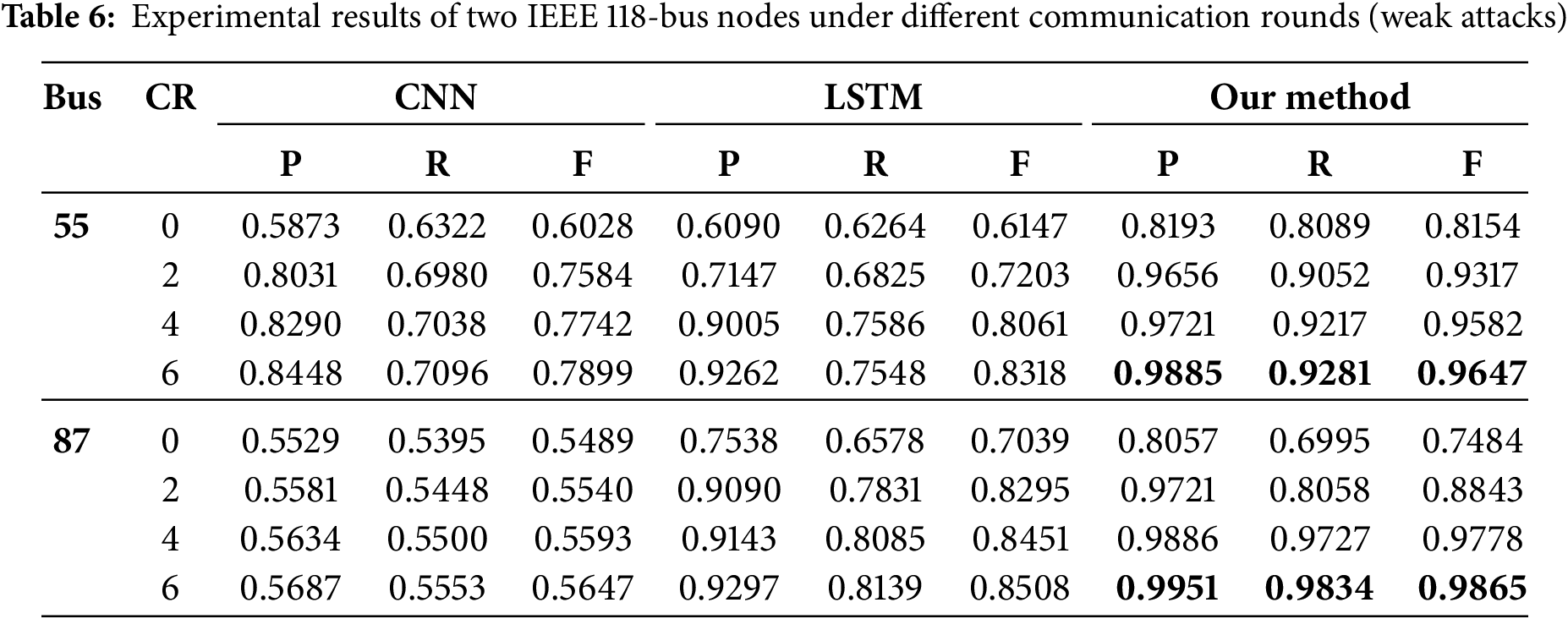
Figure 5: The loss curve during the training process of the IEEE 118-bus system

3. To reliably evaluate the performance of our proposed model and obtain suitable hyperparameter settings, we utilize 10-fold cross-validation to analyze and assess the model, calculating the MAE values and the average MAE. Fig. 6 shows that both the overall MAE and the average MAE are at a low level, which indicates that the model proposed in this paper has a small prediction error. In addition, by observing the fluctuations in the MAE data, it can be found that the MAE obtains the minimum in the 6th round of communication, which supports us in adjusting hyperparameters and optimizing the model.

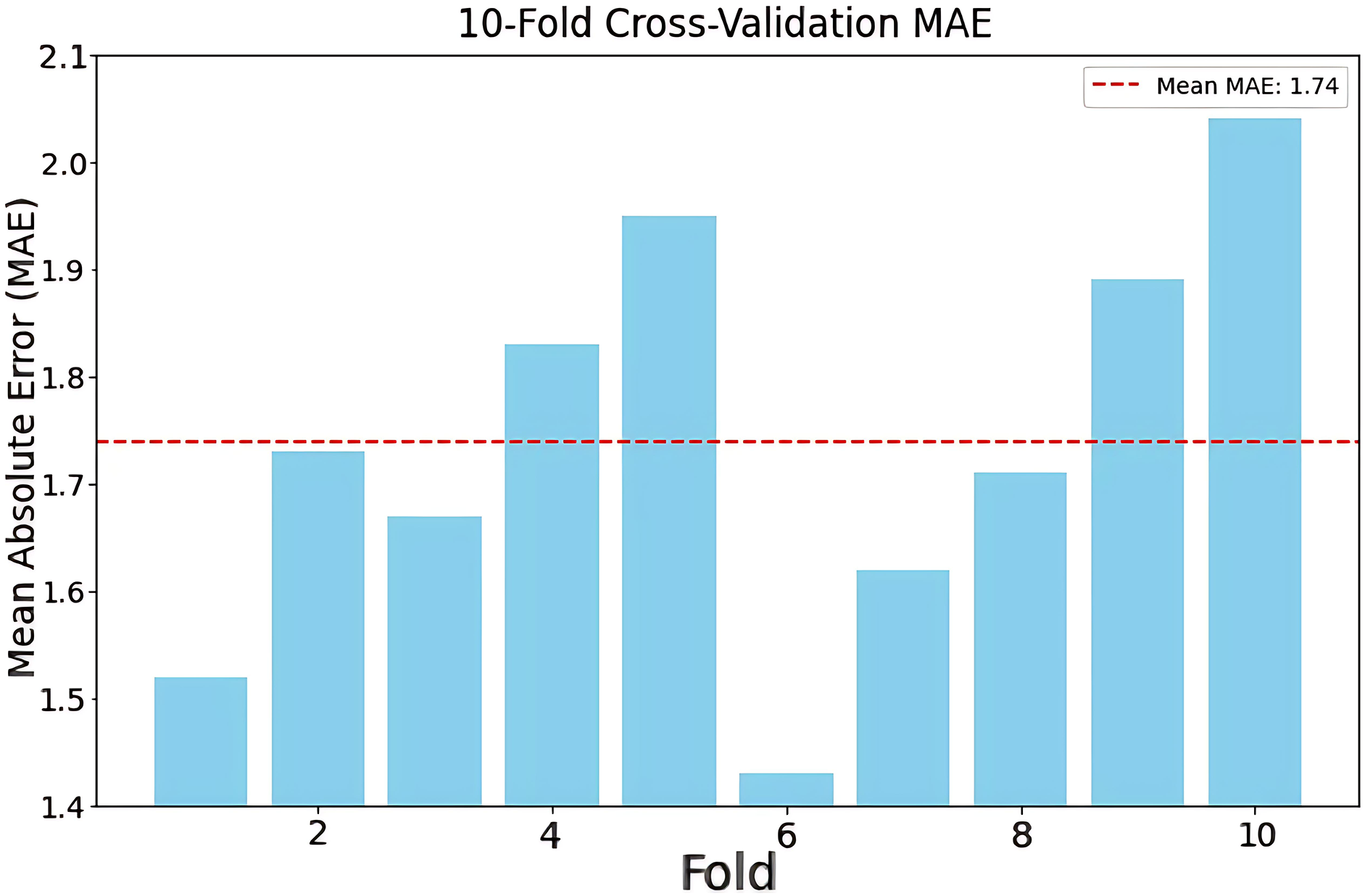
Figure 6: IEEE 14-bus system validation set 10-fold cross-validation loss plot

5.5 Discussion on Federated Aggregation Algorithm

In order to investigate the performance and technical characteristics of federated learning algorithms in different scenarios, we compare and analyze the Federated Average Algorithm (FedAvg) with other representative federated learning algorithms (e.g., Krum, FedProx), as these algorithms may exhibit distinct advantages under different scenarios [50]. The specific analysis process is as follows: 1) FedAvg balances simplicity and efficiency by averaging client updates after local training, making it suitable for large-scale deployments with reduced communication overhead. 2) Krum, in contrast, enhances robustness by selecting the update closest to the majority but at a higher computational cost due to pairwise distance calculations. 3) FedProx further addresses heterogeneous data distributions by mitigating local training bias via regularization, though it suffers from slower convergence in balanced datasets. It can be seen that different methods have their own advantages and disadvantages. Future work will explore tailored aggregation strategies to optimize trade-offs between robustness, efficiency, and adaptability.

5.6 Discussion on the Impact of CKKS Homomorphic Encryption

The introduction of CKKS will increase the training time to some extent for several reasons: 1.) Encryption and encoding operations are complex, which will increase the computational overhead and time. 2.) Homomorphic encryption operations (i.e., computations performed on encrypted data) are much slower than normal unencrypted arithmetic operations. 3.) Encrypted data is much larger than plaintext data (typically 10 to 100 times larger). Besides, unlike traditional fully homomorphic encryption, CKKS is an approximate homomorphic encryption, which may introduce some errors when encrypting and computing data. However, most studies (e.g., real-world reports from IBM, Microsoft) indicate that in real-world experiments, the effect of errors on model accuracy is small [51]. In the article, the impact is almost negligible.

6  Conclusion

Aiming at false data injection attacks faced by smart grids, this paper proposes a FDIA detection method based on the Federated Averaging algorithm. We first train an enhanced spatial-temporal graph neural network through pre-training and send the model parameter weights to the central server. Subsequently, we update the resultant model by aggregating the detection models from all the nodes and return it to each node. Additionally, we introduce the Cheon-Kim-Kim-Song (CKKS) homomorphic encryption scheme to protect the transmitted information, ensuring data security and minimizing the risk of data leakage. Numerous experiments have proven that the FDIA detection method proposed in this paper is effective and superior to traditional deep learning algorithms. It not only reduces the computational pressure on the central server but also has significant advantages in data privacy protection. Moreover, by utilizing pre-training enhanced spatial-temporal graph neural networks to mine sequences from both spatial and temporal perspectives, it captures more comprehensive contextual relationships, making data detection more accurate. Although the method proposed in this article demonstrates excellent performance in detecting FDIA, the efficiency issue of generating graph structures is also crucial as the complexity of smart grid structures increases. Meanwhile, during the decryption and aggregation process, there may be some potential vulnerabilities which may lead to key leakage. In the future, we will explore technologies such as non-disclosure key management, application of secure hardware and access control strategies to construct corresponding protection systems, thus further enhancing the security of the model. Furthermore, the emergence of sophisticated adversarial attacks, such as label flipping, underscores the urgent need for enhanced detection robustness in the face of evolving attack vectors. In the future, we will develop new detection methods to adapt to the increasingly complex modern power grid structures.

Acknowledgement: The authors would like to thank the Sichuan Science and Technology Program (2024YFHZ0015) and the Key Laboratory of Data Protection and Intelligent Management, Ministry of Education, Sichuan University (SCUSACXYD202401) for providing computational support and access to resources required for this research.

Funding Statement:: This work was supported in part by the Sichuan Science and Technology Program (2024YFHZ0015), the Key Laboratory of Data Protection and Intelligent Management, Ministry of Education, Sichuan University (SCUSACXYD202401).

Author Contributions: Conceptualization, Chenxin Lin; Methodology, Chenxin Lin; Software, Ximing Fan; Validation, Chenxin Lin, Zhan Wang and Yaochang Xu; Formal Analysis, Chenxin Lin and Yaochang Xu; Resources, Ximing Fan; Data Curation, Chenxin Lin; Writing—Original Draft Preparation, Chenxin Lin and Zhan Wang; Writing—Review and Editing, Chenxin Lin and Zhan Wang; Visualization, Yijia Xu; Supervision, Qun Zhou and Yijia Xu; Project Administration, Qun Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Gungor VC, Sahin D, Kocak T, Ergut S, Buccella C, Cecati C, et al. Smart grid technologies: communication technologies and standards. IEEE Trans Ind Inf. 2011;7(4):529–39. doi:10.1109/tii.2011.2166794. [Google Scholar] [CrossRef]

2. Ekanayake JB, Jenkins N, Liyanage KM, Wu J, Yokoyama A, et al. Smart grid: technology and applications. John Wiley & Sons; 2012. doi:10.1002/9781119968696. [Google Scholar] [CrossRef]

3. Yu X, Xue Y. Smart grids: a cyber–physical systems perspective. Proc IEEE. 2016;104(5):1058–70. doi:10.1109/JPROC.2015.2503119. [Google Scholar] [CrossRef]

4. Nowroozi E, Haider I, Taheri R, Conti M. Federated learning under attack: exposing vulnerabilities through data poisoning attacks in computer networks. IEEE Trans Netw Serv Manag. 2025;22(1):822–31. doi:10.1109/TNSM.2025.3525554. [Google Scholar] [CrossRef]

5. Xu Y, Zhang Q, Deng H, Liu Z, Yang C, Fang Y. Unknown web attack threat detection based on large language model. Appl Soft Comput. 2025;173(1):112905. doi:10.1016/j.asoc.2025.112905. [Google Scholar] [CrossRef]

6. Liu Y, Ning P, Reiter MK. False data injection attacks against state estimation in electric power grids. In: The 16th ACM Conference on Computer and Communications Security (CCS ’09); New York, NY, USA: ACM; 2009. p. 21–32. doi:10.1145/1653662.1653666. [Google Scholar] [CrossRef]

7. Defense Use Case. Analysis of the cyber attack on the Ukrainian power grid. Electricity Information Sharing and Analysis Center (E-ISAC). 2016;388(1-29):3. [cited 2025 Apr 15]. Available from: https://media.kasperskycontenthub.com/wp-content/uploads/sites/43/2016/05/20081514/E-ISAC_SANS_Ukraine_DUC_5.pdf. [Google Scholar]

8. Kosut O, Jia L, Thomas RJ, Tong L. Limiting false data attacks on power system state estimation. In: 2010 44th Annual Conference on Information Sciences and Systems (CISS). Princeton, NJ, USA: IEEE; 2010. p. 1–6. doi:10.1109/CISS.2010.5464816. [Google Scholar] [CrossRef]

9. Luo X, Wang X, Pan X, Guan X. Detection and isolation of false data injection attack for smart grids via unknown input observers. IET Generation Trans & Dist. 2019;13(8):1277–86. doi:10.1049/iet-gtd.2018.5139. [Google Scholar] [CrossRef]

10. Li B, Lu R, Xiao G, Li T, Choo KR. Detection of false data injection attacks on smart grids: A resilience–enhanced scheme. IEEE Trans Power Syst. 2022;37(4):2679–92. doi:10.1109/tpwrs.2021.3127353. [Google Scholar] [CrossRef]

11. Zhang Y, Wang J, Chen B. Detecting false data injection attacks in smart grids: a semi-supervised deep learning approach. IEEE Trans Smart Grid. 2021;12(1):623–34. doi:10.1109/TSG.2020.3010510. [Google Scholar] [CrossRef]

12. Huang C, Hong M, Fu S, Deng S. Distributed state estimation of active distribution networks considering false data injection attacks. Electric Power Engi Technol. 2022;41(3):22–32. doi:10.12158/j.2096-3203.2022.03.003. [Google Scholar] [CrossRef]

13. Huang D, He L, Sun J, Hu A. Distributed detection method for a false data attack in a power grid based on edge computing. Power Syst Prot Control. 2021;49(13):1–9. doi:10.19783/j.cnki.pspc.201130. [Google Scholar] [CrossRef]

14. Boyaci O, Umunnakwe A, Sahu A, Narimani MR, Ismail M, Davis KR, et al. Graph neural networks based detection of stealth false data injection attacks in smart grids. IEEE System J. 2021;16(2):2946–57. doi:10.1109/JSYST.2021.3109082. [Google Scholar] [CrossRef]

15. Wu Z, Zhang H, Jiang L, Li X. Distributed unsupervised detection for robust power system false data attacks via flexible dynamic time warping strategy. IEEE Transactions on Industrial Informatics. 2024;21(1):277–86. doi:10.1109/TII.2024.3452202. [Google Scholar] [CrossRef]

16. Shao Z, Zhang Z, Wang F, Xu Y. Pre-training enhanced spatial-temporal graph neural network for multivariate time series forecasting. In: Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining; Washington, DC, USA: ACM; 2022. p. 1567–77. doi:10.1145/3534678.3539396. [Google Scholar] [CrossRef]

17. Li Y, Wei X, Li Y, Dong Z, Shahidehpour M. Detection of false data injection attacks in smart grid: a secure federated deep learning approach. IEEE Trans Smart Grid. 2022;13(6):4862–72. doi:10.1109/TSG.2022.3204796. [Google Scholar] [CrossRef]

18. Deng R, Xiao G, Lu R, Liang H, Vasilakos AV. False data injection on state estimation in power systems—Attacks, impacts, and defense: a survey. IEEE Trans Industr Inform. 2016;13(2):411–23. doi:10.1109/TII.2016.2614396. [Google Scholar] [CrossRef]

19. Almodóvar A, Parras J, Zazo S. Propensity Weighted federated learning for treatment effect estimation in distributed imbalanced environments. Comput Biol Med. 2024;178(2):108779. doi:10.1016/j.compbiomed.2024.108779. [Google Scholar] [PubMed] [CrossRef]

20. Xia Y, Yang D, Li W, Myronenko A, Xu D, Obinata H, et al. Auto-FedAvg: learnable federated averaging for multi-institutional medical image segmentation. arXiv preprint. 2021. doi:10.48550/arXiv.2104.10195. [Google Scholar] [CrossRef]

21. Kong L, Zheng G, Brintrup A. A federated machine learning approach for order-level risk prediction in supply chain financing. Int J Prod Econ. 2024;268(1):109095. doi:10.1016/j.ijpe.2023.109095. [Google Scholar] [CrossRef]

22. Li Y, He Z, Gu X, Xu H, Ren S. AFedAvg: communication-efficient federated learning aggregation with adaptive communication frequency and gradient sparse. J Exp Theor Artif Intell. 2024;36(1):47–69. doi:10.1080/0952813x.2022.2079730. [Google Scholar] [CrossRef]

23. Li Z, Bilal M, Xu X, Jiang J, Cui Y. Federated learning-based cross-enterprise recommendation with graph neural networks. IEEE Trans Ind Inf. 2023;19(1):673–82. doi:10.1109/tii.2022.3203395. [Google Scholar] [CrossRef]

24. Lin WT, Chen G, Zhou X. Privacy-preserving federated learning for detecting false data injection attacks on power system. Electr Power Syst Res. 2024;229(22):110150. doi:10.1016/j.epsr.2024.110150. [Google Scholar] [CrossRef]

25. Tran HY, Hu J, Yin X, Pota HR. An efficient privacy-enhancing cross-silo federated learning and applications for false data injection attack detection in smart grids. IEEE Trans Inf Forensics Secur. 2023;18:2538–52. doi:10.1109/tifs.2023.3267892. [Google Scholar] [CrossRef]

26. Bottou L. Stochastic gradient descent tricks. In: Neural networks: tricks of the trade. 2nd ed. Berlin/Heidelberg: Springer Berlin Heidelberg; 2012. p. 421–36. doi:10.1007/978-3-642-35289-8_25. [Google Scholar] [CrossRef]

27. Huang C, Petukhina A. Multivariate time series analysis. In: Applied time series analysis and forecasting with python. Cham: Springer International Publishing; 2022. p. 215–56. doi:10.1007/978-3-031-13584-2_7. [Google Scholar] [CrossRef]

28. Ma J, Zhao J, Hou Y. Spatial-temporal transformer networks for traffic flow forecasting using a pre-trained language model. Sensors. 2024;24(17):5502. doi:10.3390/s24175502. [Google Scholar] [PubMed] [CrossRef]

29. Qi X, Hu W, Li B, Han K. STGNN-FAM: a traffic flow prediction model for spatiotemporal graph networks based on fusion of attention mechanisms. J Adv Transp. 2023;2023(1):8880530. doi:10.1155/2023/8880530. [Google Scholar] [CrossRef]

30. Pan YA, Li F, Li A, Niu Z, Liu Z. Urban intersection traffic flow prediction: a physics-guided stepwise framework utilizing spatio-temporal graph neural network algorithms. Multimodal Transp. 2025;4(2):100207. doi:10.1016/j.multra.2025.100207. [Google Scholar] [CrossRef]

31. Hu J, Zhou Y, Li H, Liang P. An interval forecast model for infectious diseases using fuzzy information granulation and spatial-temporal graph neural network. J Intell Fuzzy Syst. 2024;47(1–2):83–97. doi:10.3233/jifs-236766. [Google Scholar] [CrossRef]

32. Gharehbaghi A, Lindén M, Babic A. An artificial intelligent-based model for detecting systolic pathological patterns of phonocardiogram based on time-growing neural network. Appl Soft Comput. 2019;83:105615. doi:10.1016/j.asoc.2019.105615. [Google Scholar] [CrossRef]

33. Lv Y, Wang L, Long D, Hu Q, Hu Z. Multi-area short-term load forecasting based on spatiotemporal graph neural network. Eng Appl Artif Intell. 2024;138(5):109398. doi:10.1016/j.engappai.2024.109398. [Google Scholar] [CrossRef]

34. Zhuang W, Fan J, Xia M, Zhu K. A multi-scale spatial-temporal graph neural network-based method of multienergy load forecasting in integrated energy system. IEEE Trans Smart Grid. 2024;15(3):2652–66. doi:10.1109/TSG.2023.3315750. [Google Scholar] [CrossRef]

35. Wang X, Tang L, Xie H. Stealth FDIA localization in power systems using spatio-temporal graph neural networks. In: 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2); Hangzhou, China: IEEE; 2023. p. 4977–82. doi:10.1109/EI259745.2023.10513234. [Google Scholar] [CrossRef]

36. Wang J, Chen L, Wang KL, Liu JQ. Application layer DDoS detection method based on spatio-temporal graph neural network. Netinfo Secur. 2024;24(4):509–19. doi:10.3969/j.issn.1671-1122.2024.04.002. [Google Scholar] [CrossRef]

37. Qiu J, Zhang X, Wang T, Hou H, Wang S, Yang T. A GNN-based false data detection scheme for smart grids. Algorithms. 2025;18(3):166. doi:10.3390/a18030166. [Google Scholar] [CrossRef]

38. Cheon JH, Kim A, Kim M, Song Y. Homomorphic encryption for arithmetic of approximate numbers. In: Advances in Cryptology-ASIACRYPT 2017: 23rd International Conference on the Theory and Applications of Cryptology and Information Security. Hong Kong, China: Springer International Publishing; 2017. p. 409–37. doi:10.1007/978-3-319-70694-8_15. [Google Scholar] [CrossRef]

39. Wu W, Wang Y, Zhang Y, Wang L, Zhou L. Parallel secure inference for multiple models based on CKKS. In: Asia-Pacific Web (APWeb) and Web-Age Information Management (WAIM) Joint International Conference on Web and Big Data. Singapore: Springer Nature Singapore; 2024. p. 199–213. doi:10.1007/978-981-97-7241-4_13. [Google Scholar] [CrossRef]

40. Choi J, Choi J, Lee Y, Hong JS. Privacy-preserving rule induction using CKKS. IEEE Access. 2024;12(1):171540–58. doi:10.1109/access.2024.3498040. [Google Scholar] [CrossRef]

41. Li H, Mo W, Shen C, Pang L. EvalComp: bootstrapping based on homomorphic comparison function for CKKS. IEEE Trans Inform Forensic Secur. 2025;20(11):1349–61. doi:10.1109/tifs.2024.3516553. [Google Scholar] [CrossRef]

42. Su Y, Wang XA, Du W, Ge Y, Zhao K, Lv M. A secure data fitting scheme based on CKKS homomorphic encryption for medical IoT. J High Speed Netw. 2023;29(1):41–56. doi:10.3233/jhs-222016. [Google Scholar] [CrossRef]

43. Lee JW, Kang H, Lee Y, Choi W, Eom J, Deryabin M, et al. Privacy-preserving machine learning with fully homomorphic encryption for deep neural network. IEEE Access. 2022;10:30039–54. doi:10.1109/access.2022.3159694. [Google Scholar] [CrossRef]

44. Zhang Q, Wen Y, Huang Y, Li FP. Secure speech retrieval method using deep hashing and CKKS fully homomorphic encryption. Multimed Tools Appl. 2024;83(26):67469–500. doi:10.1007/s11042-024-18113-2. [Google Scholar] [CrossRef]

45. Yang T, Feng X, Cai S, Niu Y, Pen H. A privacy-preserving federated reinforcement learning method for multiple virtual power plants scheduling[J]. IEEE Trans Circuits Syst I Regul Pap. 2025;72(4):1939–50. doi:10.1109/TCSI.2024.3479427. [Google Scholar] [CrossRef]

46. Fathony RZA. Performance-aligned learning algorithms with statistical guarantees. Chicago: University of Illinois; 2019. [cited 2025 Apr 15]. Available from: https://www.proquest.com/docview/2342583943?sourcetype=Dissertations%20&%20Theses. [Google Scholar]

47. Hodson TO. Root-mean-square error (RMSE) or mean absolute error (MAEwhen to use them or not. Geosci Model Dev. 2022;15(14):5481–7. doi:10.5194/gmd-15-5481-2022. [Google Scholar] [CrossRef]

48. Alzubaidi L, Zhang J, Humaidi AJ, Al-Dujaili A, Duan Y, Al-Shamma O, et al. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J Big Data. 2021;8(1):53. doi:10.1186/s40537-021-00444-8. [Google Scholar] [PubMed] [CrossRef]

49. Yu Y, Si X, Hu C, Zhang J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019;31(7):1235–70. doi:10.1162/neco_a_01199. [Google Scholar] [PubMed] [CrossRef]

50. Taheri R, Arabikhan F, Gegov A, Akbari N. Robust aggregation function in federated learning. In: International Conference on Information and Knowledge Systems. Cham: Springer Nature Switzerland; 2024. p. 168–75. doi:10.1007/978-3-031-51664-1-12. [Google Scholar] [CrossRef]

51. Pan Y, Chao Z, He W, Yang J, Li H, Wang L. FedSHE: privacy preserving and efficient federated learning with adaptive segmented CKKS homomorphic encryption. Cybersecurity. 2024;7(1):40. doi:10.1186/s42400-024-00232-w. [Google Scholar] [CrossRef]