A Generative Neuro-Cognitive Architecture Using Quantum Algorithms for the Autonomous Behavior of a Smart Agent in a Simulation Environment

1  Introduction

Autonomous robot navigation in dynamic and unpredictable environments presents significant challenges in robotics research [1]. Traditional navigation approaches often struggle to adapt to complex environments with uncertainties inherent in real-world scenarios [1], and even recent surveys conclude that robust obstacle avoidance and path planning remain open problems [2]. However, the successful development of robust autonomous navigation systems has profound implications for various applications, including robotics, autonomous vehicles, and smart infrastructure. By enabling robots to navigate autonomously in complex environments, we can enhance efficiency, safety, and productivity in a wide range of industries and domains [1,2].

The primary purpose of this study is to propose a novel framework for autonomous robot behaviors driven by a generative neuro-cognitive architecture enhanced with quantum computing models. It is considered that quantum algorithms [3,4], which can process huge masses of information in a very short time, will play a vital role in the development of systems consisting of deep neural networks as a part of machine learning. By integrating quantum algorithms such as Grover’s iteration, Deutsch-Jozsa, and Bernstein-Vazirani algorithms along with a transformer-based reinforcement learning (RL) model inside the generative neuro-cognitive architecture, we aim to facilitate efficient decision-making and navigation in dynamic and complex environments. The neuro-cognitive architecture draws inspiration from principles observed in the human brain, enabling the robot to perceive its surroundings, interpret sensory information, and make cognitive decisions based on learned experiences. This study seeks to address the limitations of traditional navigation approaches and pave the way for more robust and adaptive autonomous navigation systems. Thus, the framework harnesses the computational power of quantum algorithms to optimize autonomous behaviors and learns from interactions with its environment, continuously refining its navigation strategies and adapting to changing conditions through high-dimensional state spaces more effectively. Through a brain-inspired modeling approach including transformer reinforcement learning (TRL), the proposed framework allows the robot to explore its environment as a conditional sequence modeling problem with multiple objectives, discover optimal paths, and minimize navigation errors while maximizing long-term rewards. Extensive simulations and real-world experiments conducted in diverse environments demonstrate the effectiveness of the proposed generative neuro-cognitive architecture by leveraging the quantum computing-powered TRL model for optimizing autonomous robot navigation tasks. The results highlight the superior performance of the neuro-cognitive framework enhanced with quantum computing models and reinforcement learning compared to traditional approaches. The proposed framework holds promising implications for advancing the capabilities of autonomous robots in navigation tasks, with potential applications spanning robotics, autonomous vehicles, and smart infrastructure.

Recent studies also strongly advocate the existence of possible relationships between quantum systems and cognitive functions [5–7]. Generally, neurocognitive architectures as integrated systems model the cognitive functions of the human brain [8], trying to replicate decision-making and memory; for instance, Juvina et al. [9] simulate emotional responses to decision-making in a cognitive architecture. In most studies, these architectures aim to explain how the human brain perceives its environment, processes behaviors, makes decisions/plans, and organizes information so that it can artificially realize high-level human mental concepts (emotion, attention, self-awareness, consciousness, etc.) [9,10]. Complex decision-making, interpretation, and adaptive planning processes that involve recursive task processing and meta-cognitive reasoning mechanisms are still great challenges for autonomous systems. Beyond the traditional artificial intelligence approaches that could not entirely deal with these cognitive functions, significant improvements have been made in cognitive architectures. Li et al. presented a quantum reinforcement learning (QRL) model incorporating the reinforcement learning (RL) method and the quantum theory [11]. An architecture with a value-updating algorithm based on the state superposition principle and quantum parallelism was developed [11]. The Q-values associated with state and action in conventional RL are recognized as the eigenstate (eigen-action) in QRL. In their study, the set of actions concerning the state was expressed as a quantum superposition state, and the eigenstate (eigen-action) was acquired by randomly measuring the simulated quantum state. According to rewards, their model obtained the likelihood of the eigen-action that is estimated in parallel by the probability amplitude [12,13]. Also, they analyzed some related qualities of QRL, including convergence, optimality, and balancing between exploration and exploitation, which indicate that this methodology makes a decent tradeoff between exploration and exploitation, utilizing the likelihood of sufficiency and may accelerate training through quantum parallelism [13–15]. They conducted various simulations and presented the consequences, indicating the effectiveness and superiority of the QRL algorithm for some comprehensive problems. Instead of conventional methods, a uniting architecture governed by principles of quantum mechanics is developed for more generalized cognitive models involving reasoning, decision-making, and planning with the capacity to represent more information [16]. Their architecture can constitute and expect various cognitive biases expressed in Lieder & Griffiths without heavy dependence on heuristics or presumptions of the computational assets of the mind [17]. A group of value-grounded quantum reinforcement learning models employing Grover’s iteration method is studied to update the policy, which is represented by a superposition of qubits related to each possible action [18]. An agent embodying Hierarchical Deep Q-Network (HDQfD) is developed on the Minecraft game platform for the MineRL competition so that the agent with HDQfD can easily remove low-quality expert data from the buffer [19]. According to this network, as a structured task-dependent replay buffer utilizing the hierarchical structure of expert trajectories, the adaptive prioritizing method, constructing sub-goals, and interpreting the sequence of meta-actions from the experimental data achieves success on imperfect environment model representations [19]. Heimann et al. studied quantum computing-based deep reinforcement learning methodology for learning navigation tasks using wheeled mobile robots in several simulated environments with increasing model complexity [20]. As one of the quantum machine learning (QML) studies, this methodology was realized by a hybrid quantum-classical setup involving a parameterized quantum circuit for autonomous robotic behaviors [20]. Yan et al. [21] presented a multi-agent quantum deep reinforcement learning framework replacing conventional function approximators with quantum circuits for distributed microgrid control. Similarly, for multi-agent settings, Yun et al. [22] introduced quantum meta-reinforcement learning techniques demonstrating improved adaptation capabilities. In contrast, our approach hybridizes a classical transformer-based network with quantum algorithms at the cognitive architecture level, offering a different integration paradigm where quantum enhancements assist meta-cognitive control rather than direct function approximation. These studies can be good examples of the emerging integration of quantum computation into agent learning pipelines. To show our contribution within this evolving quantum cognitive systems research landscape, our work differs by embedding quantum algorithms at the cognitive architecture level to accelerate meta-cognitive planning and decision optimization while maintaining a classical deep learning core for sequential decision modeling. This hybrid design approach allows us to integrate the power of deep neural networks with the search efficiency of quantum computation in Fig. 1.

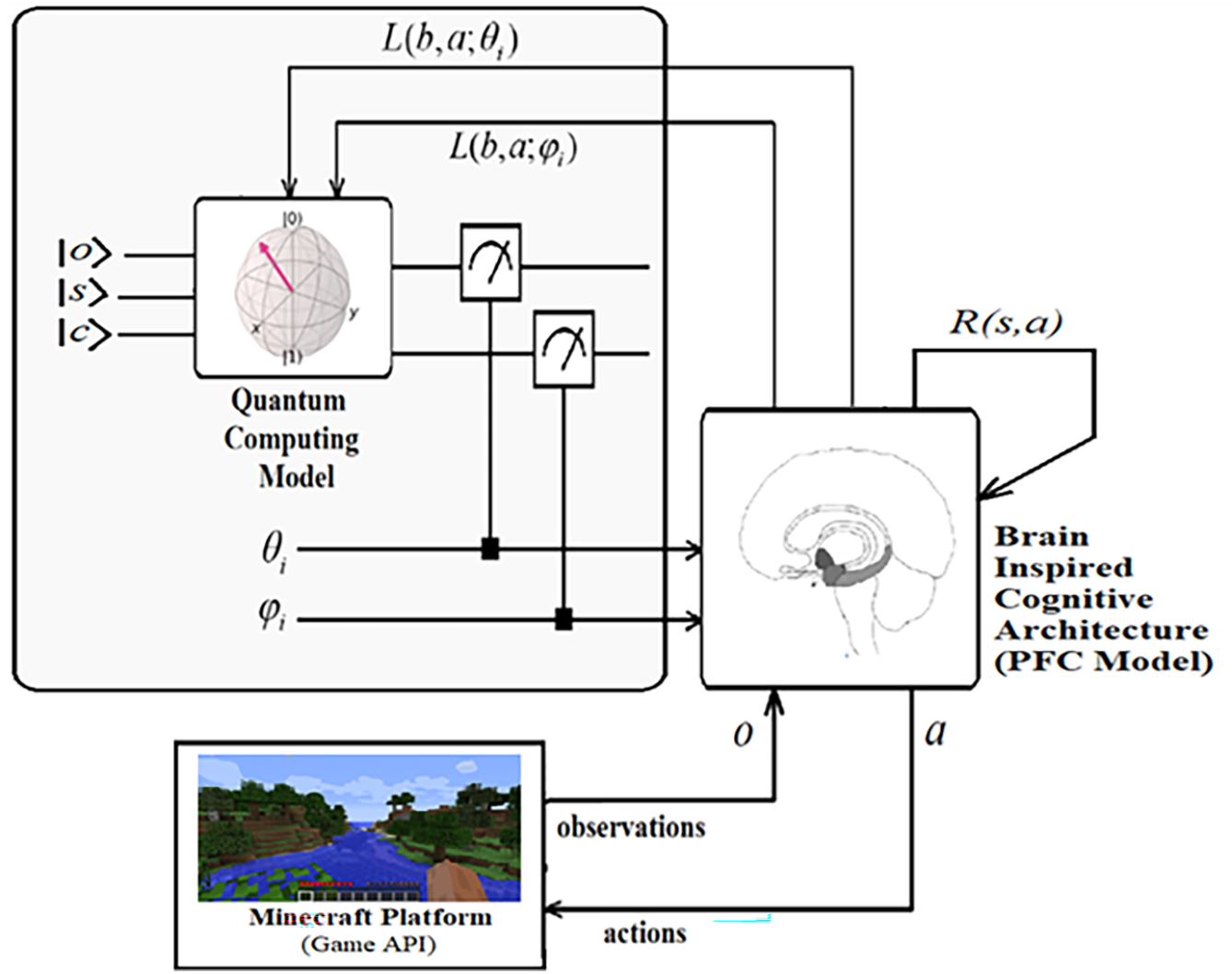
Figure 1: Quantum computing based brain inspired cognitive architecture

To shed light on these works, this study can be hypothesized based on two major research questions. One of them is related to whether the brain-inspired meta-cognitive architecture can simulate situation awareness by the contribution of the quantum computation model. Situation awareness, a crucial cognitive aspect, involves the agent’s ability to perceive its environment, make sense (e.g., risk analysis) of spatial-temporal relationships, and adapt its behavior accordingly. By integrating situation awareness into our model, we aim to develop algorithms and mechanisms that enable the agent to effectively navigate dynamic and uncertain environments. The approximation of situation-awareness deals with spatial-temporal reasoning skills trained by reinforcement learning in the computational model of lateral PFC during the interaction of the agent with its environment. In that case, if all these skills related to situation awareness guided by quantum algorithms are effective in the solution of the mentioned problems, it is expected that estimated costs of achieving multi-objective tasks such as navigate, search/collect, combat/escape, chop/build, and craft in the explorer scenario and the survivor scenario are decreased while accuracies (rewards) of them are increasing during the experiments. Another question arises from the point where the proposed brain-inspired architecture can ensure meta-cognition with the help of the quantum computation model. The meta-cognition hosted by the computational model of medial PFC, using an inverse reinforcement learning approach, involves regulating spatial-temporal reasoning skills and hierarchically learning sub-tasks while the agent is interacting with its environment. So, this feature allows the agent to enhance its problem-solving abilities. According to this, if the meta-cognition mechanism supported by quantum algorithms is generating admissible rewards to all cognitive functions related to situation awareness for optimizing complex decision-making, interpretation, and adaptive planning processes, convergence errors in reinforcement learning processes are decreased while success rates of multi-objective tasks such as navigate, search/collect, combat/escape, chop/build, and craft in the explorer scenario and the survivor scenario are increasing during the experiments. Quantum computing operations play a pivotal role in the meta-cognition aspect by enabling hierarchical learning of sub-tasks and providing explainability in the situation-awareness property. Quantum algorithms are employed to optimize the decision-making mechanism, allowing for an interpretable and transparent understanding of how the agent learns and accomplishes higher-level goals in dynamic environments with uncertainties.

The architecture initializes the agent by fetching a dataset from the Minecraft environment. During each iteration, the agent collects observations, processes them through the LPFC model to estimate belief states and actions, and further evaluates them via the MPFC model to perform meta-cognitive assessment. Using quantum optimization, the parameters of both cognitive layers are updated to improve decision-making and meta-level evaluations. This loop continuously refines the agent’s cognitive and meta-cognitive abilities through quantum-enhanced learning. The procedure is shown in Algorithm 1 below.

Our architecture is computationally inspired by the human prefrontal cortex (PFC), rather than intended as a biologically detailed model. While we take high-level inspiration from cognitive neuroscience (e.g., incorporating an executive meta-cognitive control analogous to PFC functions), we implement these functions with artificial neural networks and quantum algorithms instead of simulating neural circuitry. Unlike biologically realistic cortical models [8], our framework prioritizes functional integration with quantum computing modules over neural-level fidelity. This clarification positions our work in the realm of cognitive computing (drawing ideas from biology to improve AI agents) rather than as a literal neural simulation.

As great challenges, problem definition covers the issues that autonomous systems mostly suffer from complex decision-making, interpretation, and adaptive planning processes that involve recursive task processing and meta-cognitive reasoning mechanisms. Under conditions including unknown dynamic environments with spatial-temporal task/model uncertainties, they may not accurately process tasks with multi-objectives, such as explorer and survivor scenarios, by conventional computing approaches due to a lack of parallelization.

Thus, for the solution to the mentioned problems, we present a novel comprehensive quantum cognition framework (Fig. 1) that covers a brain-inspired computational model (prefrontal cortex) incorporating spatial-temporal reasoning tasks with multiple objectives and test it in the Minecraft game environment. The proposed framework consists of machine learning models and quantum computing procedures for smart agents exhibiting complex and chaotic processes of autonomous behaviors and cognitive activities.

•   Novel Quantum-Enhanced Cognitive Architecture: We propose a first-of-its-kind integration of quantum algorithms into a brain-inspired neuro-cognitive architecture (modeling prefrontal cortex functions) for autonomous agents. This theoretical framework introduces quantum computing to enhance meta-cognition and situation awareness in decision-making.

•   Transformer-Based Reinforcement Learning with Meta-Cognition: We develop a transformer reinforcement learning (TRL) module within the architecture, coupled with a meta-cognitive hierarchy that organizes sub-tasks. This contribution bridges deep learning (transformers) with cognitive modeling, enabling the agent to perform complex sequences of tasks with improved learning efficiency.

•   Comprehensive Validation in a Complex Simulation: We implement the integrated architecture in a rich, simulated Minecraft environment featuring multi-objective “explorer” and “survivor” scenarios. The experimental results demonstrate improved performance (faster learning convergence and higher success rates) compared to a classical approach, validating the potential benefits of the quantum enhancements. We also discuss implications for scaling to real-world tasks based on these findings.

The major contribution of this system is to emerge computational models of the situation-awareness and meta-cognition via quantum algorithms so that the smart agent can perform autonomous behaviors using a Minecraft game map involving the explorer and the survivor scenarios. These spatial-temporal reasoning tasks with multi-objectives are mainly modeled by the reinforcement learning approach in the lateral component of the computational prefrontal cortex model and their functions are regulated by the medial segment of the computational prefrontal cortex model with the inverse reinforcement learning algorithm, which is responsible for a reward generation operation. When quantum superposition states in the quantum circuit composed of classical registers and qubits are measured randomly, quantum states associated with various cognitive activities are collapsed to the eigenstate related to Q-values so that some sequence of actions as an actual response of the framework is generated. Inspired by the quantum parallelism and the state superposition property, the quantum computing-oriented working memory, where all cognitive tasks in the proposed prefrontal cortex model are processed, is a kind of associative memory stored in the network weights. In addition, weights of the network related to working memory enabling recalling, and prediction abilities, are updated by these deep learning approaches with the support of conventional quantum algorithms such as Grover’s iteration, Deutsch-Jozsa, and Bernstein-Vazirani algorithm.

All experiments in this study are performed in a simulated environment (the Minecraft game world), and while the results are promising, further work can be smoothly extended to apply the proposed architecture with physical robotic systems in real-world settings. Extensive simulations in a Minecraft-based environment demonstrate that the quantum-enhanced agent learns faster and achieves higher success rates in complex navigation and survival tasks in several scenarios when compared to a purely classical agent. The performance advantage is task-specific, and in certain subtasks such as fine-grained combat or sequential crafting, the classical agent performs comparably. We explicitly highlight this contextual variation in the results and present a detailed discussion rather than claiming uniform superiority.

2  Background

In this section, some background materials related to cognitive modeling, artificial intelligence, and quantum computing-based machine learning are required to be emphasized. There is a necessity to express crucial issues dealing with three major bases, such as machine learning, quantum computing, and quantum algorithms that solve some specific search and optimization problems via quantum computing approaches for this research.

2.1 Machine Learning Models

Currently, in conventional deep learning algorithms, the training data containing input data and target (class) information can be trained with high performance and tested with new data input. These deep learning algorithms may provide very efficient performances concerning the data set size, data set quality, the methods used in feature extraction, the hyperparameter set used in deep learning models, the activation functions, and the optimization algorithms. A deep neural network with a huge number of layers enables the agent to recognize objects at different levels of abstraction. Since a large amount of information workload is needed for the achievement of artificial mental functions and realizing cognitive tasks, various kinds of deep learning models may be evaluated, for instance, recurrent deep neural networks (long-short term memory (LSTM)), transformers, and deep reinforcement learning algorithms as deep Q-network (DQN). Particularly, as indicated by conditions, they may be consolidated in a hybrid artificial intelligence paradigm. The LSTM which is a recurrent neural network (RNN), like memory enactments in the human cerebrum may be artificially built by convolutional layers. It can equip short-term memory settings for a long-term period in the episodic memory image [23,24]. A generic segment of the LSTM is made out of a memory cell that contains input, output, and forget gates. The backpropagation through time calculation can be used to train the neural model [25,26]. Reinforcement learning (RL) has emerged as a powerful paradigm for training agents to make sequential decisions in various tasks, including natural language processing, robotics, and gaming. As a deep reinforcement learning model, the Q-learning algorithm with a deep neural network incorporated by a deep Q-network (DQN), may be re-composed by an LSTM model encapsulated with convolutional layers [27–29]. Inspired by the medial PFC of the human neocortex, DQN-based models that realize planning tasks can be related to meta-cognitive processes. The integration of reinforcement learning with transformer models has led to significant advancements in language understanding, generation, and translation tasks.

In the context of transformer reinforcement learning (Fig. 2), agents interact with an environment, take actions, and receive feedback in the form of rewards. The transformer architecture, originally proposed for sequence-to-sequence tasks like machine translation, has shown remarkable success in capturing long-range dependencies and contextual information in sequential data [30]. One common approach to combining reinforcement learning with transformers is through the use of policy gradients, where the parameters of the transformer model are updated based on the gradients of expected cumulative rewards. This allows the model to learn to make decisions that maximize long-term rewards, such as generating coherent and contextually appropriate text in language generation tasks [30]. Another approach is to use the transformer model as a function approximator in the Q-learning framework, where the model learns to estimate the expected future rewards of taking different actions in a given state [31]. This enables the agent to learn optimal policies by iteratively updating its Q-values based on the observed rewards and transitions between states [31]. The loss function of the model to enhancement in the training session is estimated as follows:

L(θi)=Es,a⌊(r+γmaxdQ(s′,a′|θi−1)−Q(s,a|θi))2⌋(1)

where θi is a learning parameter set. The experience memory replay (D) is a set of tuples comprised of (s, a, r, s′). A reinforcement reward and Q-value with the state (s) and action (a) pairs are expressed as r and Q(s, a), respectively. The experience memory replay is updated by the SGD algorithm, while it is attempting to minimize the loss function. Recent research has explored various applications of transformer reinforcement learning, including dialogue systems, recommendation systems, and autonomous agents. By leveraging the expressive power of transformer models and the learning capabilities of reinforcement learning algorithms, these approaches have demonstrated promising results in complex, real-world scenarios. Moreover, these techniques with deep learning exhibit more adaptable capacity estimate features to realize the achievement of human-level execution on robust social interaction including comprehensive planning tasks rather than the classic reinforcement learning approach [32]. Overall, transformer reinforcement learning represents a promising direction for advancing the capabilities of AI systems in a wide range of tasks, and continued research in this area is expected to drive further progress in the field.

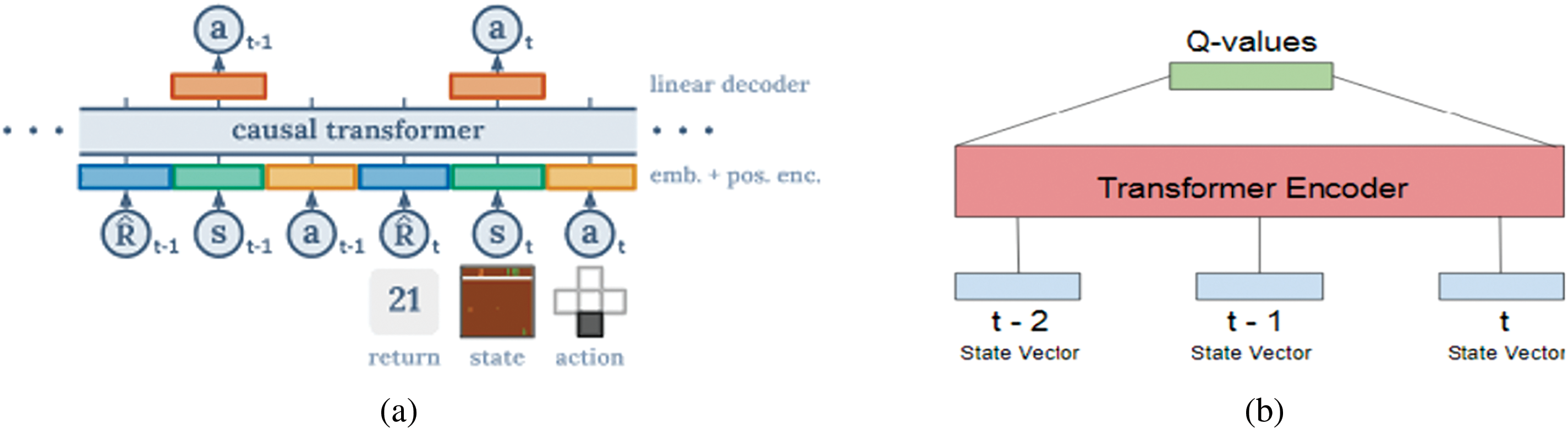
Figure 2: (a) Decision Transformer. Reprinted with permission from Ref. [30]. Copyright 2021, the authors of Ref. [30]. (b) Transformer Q Learning (TRL). Reprinted with permission from Ref. [31]. Copyright 2019, the authors of Ref. [31]

2.2 Quantum Computing

Instead of binary digit (bit) systems involving 0 and 1, employed by known information systems, quantum computers that use mathematical modeling (quantum computation) based on the nature of quantum mechanics, use qubit (single quantum bit) defined by the unit bi-dimensional vector as terminology with bra-ket notation |ψ⟩ where |0⟩ and |1⟩ are quantum states defined in complex vector space (Hilbert space) C2 [33].

|ψ⟩=α|0⟩+β|1⟩(2)

So single qubit |ψ⟩ which is a superposition state can be represented as a linear combination form that is computationally represented by basis (column) vectors such as |0⟩ = [1 0]T and |1⟩ = [0 1]T, respectively [33]. As complex coefficients, α and β which are defined in complex space should satisfy the rule |α|2 + |β|2 = 1. A possible qubit that satisfies this rule can be initialized as |ψ0⟩ = [1/√2 i/√2]T. In Fig. 3, it can be interpreted concerning the Bloch sphere represented by 2D vectors as:

|ψ⟩=cos⁡θ2|0⟩+eiφsin⁡θ2|1⟩(3)

where two variables θ and ϕ that define quantum state |ψ⟩ for a qubit in the Bloch sphere are angle values defined in R2 [33].

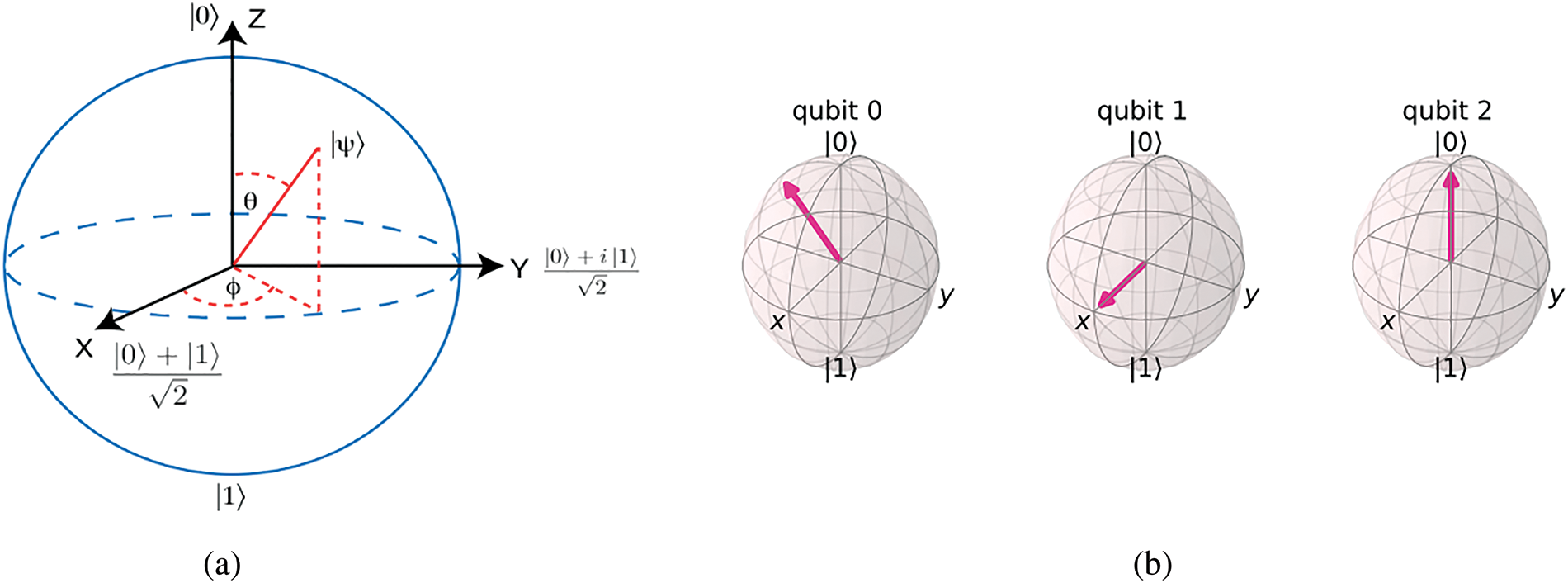
Figure 3: (a) The Bloch sphere for representation of quantum states of a qubit. Reprinted with permission from Ref. [34]. Copyright 2021, the authors of Ref. [34]. (b) Different qubit states are manipulated by quantum operators in the quantum circuit

When a qubit in superposition state |ψ⟩ is measured, the quantum state |ψ⟩ of the qubit in the quantum circuit is collapsed into one of its basic states |0⟩ or |1⟩ for measuring probability [33,34]. The probability of measuring quantum state |ψ⟩ concerning state |x⟩ can be expressed as P(|x⟩) = |〉x|〈ψ⟩|2 [34]. This property explains how to infer concrete knowledge from the quantum state. There are some implications of this rule involving normalization, global phase, and observer effect. According to quantum computation theory, there is a useful fundamental transformation which is the 2N × 2N dimensional unitary operator defined by unitary matrices U acting on the computational basis of N qubits [33]. As an essential principle of quantum parallelism required by a powerful quantum algorithm, this unitary transformation U obeying U†U = I produces a superposition state which is the result of all basis vectors of this state [33,34]. Where U† is the transpose conjugate of U and I is the unitary matrix with a convenient dimension. To define multi-qubit systems, larger vector spaces are needed within the framework of quantum computing [34].

As a kind of quantum algorithm, the Deutsch-Josza algorithm is based on a Deutsch-Josza problem. Although it can be solved by classical methods, a quantum algorithm solution providing better performance than the best classical algorithm might be advantageous to utilize a quantum computer as a computational method for a specific problem [35]. According to this, the problem given by an oracle function as a Boolean function f(x1, x2, x3, …, xn) → 0 or 1 for all xi are Boolean, evaluates whether this function is balanced or constant. A function accepting n-digit binary values as input is a constant function only if it returns an output as either a 0 or a 1 for any input values (all input combinations). In case a function returns 1 for half of the input domain and 0 for the other half, it is a balanced function. First of all, the n-qubit register is initialized to |0⟩, and the one-qubit register is initialized to |1⟩. Then a Hadamard gate is applied to all allocated qubits. After that, the quantum oracle |x⟩|y⟩ is implemented to |x⟩|y ⊕ f(x)⟩;

|ψi⟩=12n+1∑x=02n−1|x⟩(|f(x)⟩−|1⊕f(x)⟩)(4)

|ψi+1⟩=12n∑x=02n−1(−1)f(x)[∑y=02n−1(−1)x⋅y|y⟩](5)

At this point, the second single qubit register may be ignored. Finally, a Hadamard gate is applied again to each qubit in the first register and the first register is measured. According to this, the probability of measuring evaluates to 1 if f(x) is constant and 0 if f(x) is balanced. Bernstein-Vazirani algorithm can be considered as an extension formulation of the Deutsch-Josza algorithm. The difference of the Bernstein-Vazirani algorithm is that the oracle function given an input x is ensured to return the bitwise product of the input with some string s rather than the function is regarded as balanced or constant according to the Deutsch-Josza problem [36]. So, this algorithm struggles to obtain s for the oracle function which is described as f(x) = s.x(mod2) for any input x. In the first stage, the output qubit register is set to |-⟩ as the rest of the n-qubit register is initialized to |0⟩.

|000…0⟩→H⊗n12n∑x∈{0,1}n|x⟩→fs12n∑x∈{0,1}n(−1)s.x|x⟩(6)

Then a Hadamard gate is applied to all allocated qubits except the output qubit register. After that, the oracle function is evaluated and the Hadamard gate is subsequently performed. Eventually, the output qubit register |-⟩ is measured so that the algorithm proceeds to provide the hidden bit string by evaluating the quantum oracle function fs with the quantum superposition derived from the Hadamard transformation of |00…0⟩.

Grover’s algorithm is a promising candidate to solve unstructured search problems successfully [27]. This algorithm has a great run-time advantage in that it can quadratically speed up these problems with complex databases involving big data. As a complexity analysis, Grover’s algorithm can find an item to be searched in O(√N), while traditional methods can achieve in O(N) for N items [37]. Grover’s algorithm, which needs to create and solve a special oracle function f(x) uses an amplitude amplification trick or subroutine. f(x) = 0 occurs if x is not a solution; otherwise, in the case of f(x) = 1, ω = x is a valid solution. According to this, a possible oracle function can be described as:

Uf(ω)|x⟩=(−1)f(x)|x⟩(7)

The amplitude amplification procedure begins with the uniform superposition |s⟩, which is easily derived by |s⟩ = H(⨂n) |0n⟩. So, the oracle reflection U(f(ω)) can be applied to the state |s⟩. As an additional transformation, another reflection Us = 2|s⟩⟨s| –1 maps the state to Us Uf |s⟩ and completes the transformation. Grover’s algorithm can be utilized as an efficient iterative procedure that increases the probability of measuring any quantum state. In addition, it is possible to consolidate with other algorithms. The conditional phase-shift operation known as the phase gate is employed to execute Grover’s iteration (or Grover’s algorithm) via quantum bell states for reinforcing an optimal decision [37]. There are so many complex problems challenging to obtain a solution computationally by traditional search algorithms. However, Grover’s algorithm may relatively efficient way to verify a solution. For instance, it can be easily checked whether all the rules are satisfied to verify the solution for a Sudoku puzzle by quadratic run-time improvement.

3  Materials and Methods

In this study, the brain-inspired cognitive framework building on quantum algorithms investigates how the complex and chaotic processes of behavioral and cognitive activities can be modeled to exhibit autonomous behavior incorporating spatial-temporal reasoning skills for a smart agent as an autonomous life form with a virtual character in the simulation environment. In this quantum algorithms-oriented brain-inspired architecture involving a computational model of the prefrontal cortex, all activities between cognitive functions are evaluated by quantum entangled states so that an agent with a virtual character or a mobile robot might exhibit experience imitation of situation-awareness as well as meta-cognition during performing experiments with exploring and/or surviving scenarios in its dynamic environment with uncertainties. This requires coping with a huge amount of data processing power and capacity while behavioral response probabilities are evaluated.

We incorporate quantum operations in two main ways: (1) as training augmentations for evaluating state categories and binary patterns using Deutsch–Jozsa and Bernstein–Vazirani algorithms, and (2) in the agent’s decision-making loop via Grover’s algorithm to amplify the probability of selecting high-reward actions. During training, Deutsch–Jozsa is applied to determine whether certain environmental states match predefined patterns (e.g., “resource-rich” vs. “empty”) using a constant or balanced oracle. Bernstein–Vazirani is used to extract hidden bit strings representing optimal state-action sequences. These quantum circuits were implemented using Qiskit and executed on a classical simulator due to hardware constraints. Circuit design included Hadamard transformations, phase flips, and measurement steps tailored to each algorithm. Grover’s algorithm was implemented with custom oracle encoding reward-based action evaluation, followed by standard diffusion operations (inversion about the mean). Complexity-wise, Grover’s enables finding optimal actions in O(√N) steps, whereas classical search requires O(N). While simulated classically, these routines mimic the behavior of near-future quantum hardware.

Representation of these states involves larger vector spaces to express cognitive activities associated with quantum states with multi-qubit systems in the computational model of the prefrontal cortex as a quantum computing-based metacognitive architecture. According to this, for the state representing a specific activity of a cognitive function, quantum states with a multi-qubit system satisfying the rule ∑x=0,0,01,1,1 |Cx|2 = 1:

|Φ⟩=|ψ1⟩⊗|ψ2⟩⊗|ψ3⟩⊗.....|ψn⟩=∑x=000…0111…1Cx|x⟩(8)

where Cx is a complex coefficient and “⊗” stands for a tensor product. The probability of occurrence corresponding to state |x⟩ is |Cx|2 when quantum state |Φ⟩ is measured. As a result, the action sequence, which is an actual response of the framework, is produced when quantum superposition states in the quantum circuit composed of classical registers and qubits are measured randomly.

3.1 Computational Prefrontal Cortex Model

In this study, the proposed framework incorporates quantum algorithms with neuro-cognitive modeling involving large-scale bio-inspired structures so that next-generation artificial intelligence systems that allow simulating autonomous behaviors ensuring situation awareness and metacognition can be developed [38]. This work significantly extends our previous research presented in Daglarli (2020) [38], which focused on modeling prefrontal cortex–inspired meta-cognitive control for humanoid robots using classical reinforcement learning techniques. While Ref. [38] established a classical cognitive architecture framework, it did not incorporate quantum algorithms or address complex, multi-objective environments. In contrast, the current paper introduces a novel hybrid architecture that integrates quantum algorithms (Deutsch–Jozsa, Bernstein–Vazirani, and Grover’s search) with transformer-based deep reinforcement learning, enhancing both meta-cognition and situation awareness modules. Additionally, unlike [38], this work evaluates the proposed architecture in the rich and dynamic Minecraft simulation platform, tackling complex exploration and survival tasks with multiple objectives and environmental uncertainties. Furthermore, situation awareness is incorporated as an explicit module for the first time, alongside quantum-enhanced meta-cognition.

•   Meta-Cognition: The meta-cognition module acts as a high-level controller that monitors the agent’s progress on sub-tasks and can trigger re-planning or goal adjustments as needed. For example, if the agent is stuck on a sub-task or making insufficient progress, this module detects the issue and initiates a strategy change or sub-task switch. In this way, our meta-cognitive layer provides a form of self-monitoring of task performance (including implicit error detection when a sub-task fails) and dynamic re-planning capability.

•   Situation Awareness: This component builds an internal model of the world from the agent’s perceptions, aggregating spatial information over time. In practice, the situation awareness module maintains a state representation (for instance, constructing a map of the environment and tracking moving entities such as enemies or targets). We now explain that situation awareness is evaluated by the agent’s ability to anticipate environmental changes; for example, the agent uses its internal map and predictions of enemy movements to inform its decisions. This ties the previously abstract concept of “situation awareness” to a concrete predictive mechanism in our architecture.

•   Spatial-Temporal Reasoning: This term refers to the agent’s processing of spatial observations over time to discern patterns and predict trajectories. We clarify that in our implementation, spatial-temporal reasoning is realized through the transformer RL network, which ingests sequences of observations and extracts spatial-temporal features. Thus, the agent can reason about how the state of the environment evolves over an episode, leveraging the transformer’s sequence-processing capability.

The agent’s reinforcement learning policy is implemented using a transformer-based neural network (essentially adopting a Decision Transformer approach [32]) as a hybrid model that the transformer serves as the deep learning core of the agent’s “brain,” while the quantum algorithms act as auxiliary modules that guide or optimize certain decision-making processes. This transformer processes sequences of state (and action) inputs to capture temporal dependencies and outputs the agent’s action decisions at each step.

From the viewpoint of computational intelligence and cognitive neuroscience, this framework which is critical for many abilities such as meta-cognition, and situation awareness targets to realize a computational representation of the prefrontal cortex (PFC) composed of lateral and medial sub-structures with quantum computation-based machine learning algorithms and artificial intelligence approaches. Besides, the prefrontal cortex has very dense connections with other system modules so that cognitive skills like decision-making and planning abilities can be modulated. Specifically, the LPFC processes environmental observations ot and derives cognitive states st, applying quantum-enhanced reinforcement learning through transformer neural networks for robust spatial-temporal reasoning. The MPFC applies quantum-enhanced inverse reinforcement learning techniques to synthesize reward signals dynamically that direct meta-cognitive processes. Quantum computations enable fast convergence by effectively exploring high-dimensional cognitive state spaces. There is a continuous quantum computational output communication between LPFC and MPFC modules for providing integrated meta-cognitive monitoring and real-time adaptability in uncertain and dynamic environments.

3.1.1 Lateral Prefrontal Cortex (LPFC)

The computational lateral PFC (LPFC) model realizes spatial-temporal reasoning skills involving deep reinforcement learning-centered hybrid machine learning infrastructure by using quantum computing-based parameter estimation so that the mobile robot and/or the agent with a virtual character providing to evaluate situation awareness can efficiently perform rational tasks such as social interaction, survival tests during the execution of several possible scenarios (Algorithm 2).

The perception information (observations) ot is received as framework input. The st is the state derived from ot in the lateral PFC model, respectively.

|st⟩=∑xθx|ot⟩(9)

Each sub-task i in the computational lateral PFC model can be depicted as transitions (ot, st, st+1, at, Rt) which are stored in replay memory Di. Sub-policies where ϕi = fθ(Di) for each environment (task) Di are produced by the adaptation loop (internal cycle) behaving traditional RL policy learning as a sub-routine of the meta-reinforcement learning approach. The reward Rt is produced by the medial PFC model. The TRL model is employed by a computational model of lateral PFC involving a deep reinforcement learning algorithm with partially observable dynamics. The generated reward Rt broadcasting from mPFC and the observation data ot are concatenated and sent into the TRL model. The computed output of the network corresponds to approximate Q-values.

The neocortex-inspired computational model is utilized to obtain the state transition T and the observation O models. The state transition model is expressed as T(s, at, s′) = P(s′| s, a), and the observation model is defined as O(s′, at, ot) = P(o| s′, a). The belief propagation is calculated by the following equation:

bt(s′)=τ(bt−1,at,ot)=ηO(s′,at,ot)∑s∈ST(s,at,s′)bt−1(s)(10)

The reward function ρ(b, a) depending on the belief states is computed using the reward function based on the world states.

ρ(b,a)=∑s∈SR(s,at)bt(s)(11)

The Q-values of the system are learned according to the Bellman equation:

Qt(b,a;θi)=ρ(b,a)+γ∑b′τ(bt−1,at,ot)V(b′)(12)

Vt(b)=maxaQt(b,a)(13)

Maximizing the Q-values regarding actions provides to find the optimal value Vt(b). Gained points in the game and measured accuracy in tasks of the experiment are utilized as a source of reward inference mechanism to exhibit the situation-awareness property. It is expected that they increase during the implementation scenario of the experiments thanks to the helping of decision-making and planning activities of cognitive functions resulting from the computational LPFC model.

3.1.2 Medial Prefrontal Cortex (MPFC)

During interaction scenarios in experiments, the lateral PFC functions including the states of the spatial-temporal reasoning skills are supervised or regulated by the medial PFC (mPFC) module which is one of the most critical regions for the meta-cognition aspect. The computational model of the medial PFC module is responsible for many cognitive functions such as monitoring and reorganizing complex decision-making (e.g., planning or problem-solving), meta-reasoning, associative working memory, adaptive learning, behavior execution, multi-modal integration of action-reward and/or stimulus-reward association, and expectation (prediction) processes (Algorithm 3).

Furthermore, the computational mPFC module which works as a reward interpretation mechanism receives experience data identified with long-term or episodic memory, resulting from the hippocampus. This methodology behaves as an inverse reinforcement learning technique that performs reward estimation processing.

|ct⟩=∑yφy|st⟩(14)

To do this, first of all, the model constitutes the inference of the internal sub-states (c) extracted from b(st) and hippocampal information (othc, athc).

Racc(st,at)=P(c|b,ahct)(15)

Rofc(st,at)=P(c|b,ohct)(16)

The ACC module related to a sequence of past actions evaluates the action-reward correlation function Racc(st, at) as a part of the multi-objective reward generation process. Besides, the OFC module performs the reward generation processes associated with the stimulus-reward correlation function Rofc(st, at) shaping via a sequence of past observations (stimuli). The vmPFC module which is sensitive to internal sub-states manages the fusion of these correlation functions (the stimulus-reward and the action-reward) to generate an actual reward using another TRL model for an individual task composed of different sub-tasks.

P(c″|c′)=σ(ϕP(c′|b)+γ)|Φc⟩(17)

A probabilistic model network represents the cognitive map so that reasoning tasks that lead to consecutive or cyclic rational (cause-effect) relations (c′ →ϕi c′′), where φi defines the weight matrix of the network through extracted internal sub-states (c) can be realized. This provides information on why the action has to occur concerning the given state and reward as an explanatory feature of an inverse reinforcement learning model which allows exploring the relational connections between the input and output of the developed agent.

Rdmpfc(st,at)=Rvmpfc(st,at)+γ∑cP(c″|c′)P(c|b)(18)

As the external cycle of meta-reinforcement learning, the master strategy (policy) supervising all sub-policies (tasks) Di resulted in the adaptation loop (internal cycle) being generated. Thus, for an individual task, the computed output of the TRL model corresponding to approximate rewards generated in the vmPFC module is hierarchically learned by the dmPFC module undertaking the failure detection events (or conflict monitoring tasks) and working as a meta inverse reinforcement learning procedure.

3.2 Learning with Quantum Optimization

The quantum parallelism which is provided by axioms of quantum computing allows this meta-cognitive architecture simulating autonomous behaviors to realize distributed neuro-cognitive activities that involve the stochastic recursive mathematical models and dynamic nonlinear programming methodologies for an agent with virtual character as a situation-aware autonomous system. In addition, using the quantum search algorithms provides a great opportunity that incorporates the quantum circuit and the classical computational architecture which contains the prefrontal cortex (PFC) model with meta-cognitive functions for a situation-aware entity having autonomous behaviors. The following loss function L(b, a; θi) is minimized to optimize reinforcement learning processes of the computational model of lateral PFC.

L(b,a;θi)=Eb,a[(Qtarg⁡et(b,a;θi)−Qt(b,a;θi))2](19)

where α is a parameter related to training speed. The network weights θi computed by the quantum algorithm allow estimating the optimal Q-values via decreasing the difference between approximate Qt(b, a; θi) and actual (target) Q-values Qtarget(b, a; θi) which are computed by Bellman equation. Inverse reinforcement learning processes in the computational model of medial PFC are optimized by minimizing another loss function L(b, a; φi).

L(b,a;ϕi)=Eb,a[(Rtarg⁡et(b,a;ϕi)−Rt(b,a;ϕi))2](20)

where φi defines the weight matrix of the network to be calculated by the quantum algorithm for network loss function (fitness) so that its performance is guaranteed to be increased or maintained. Thus, the quantum computing-based training algorithm can easily obtain optimal reward R. This computed reward released from mPFC is utilized for the reinforcement learning progress of spatial-temporal reasoning skills which are hosted by modules of the lateral PFC.

For evaluation of loss functions, initialization of quantum state representation associated with network weights θi and φi representing meta-cognitive activities such as cause-effect based rational planning in the working memory of the prefrontal cortex model inspired meta-cognitive architecture are manipulated by quantum gates in the quantum circuit. Grover’s algorithm offering a quadratic speedup over classical algorithms can be utilized to estimate state parameters within an unsorted database of N-items in approximately √N steps as a quantum walking procedure optimizing initial circuit parametrization with the maximum probability of measuring these quantum states. According to this, a Grover diffusion operator Uψ is being applied to the state |ψ⟩.

Us=2|s⟩⟨s|−I(21)

U(θi)=L(b,a;θi)Us(22)

The procedure of Grover’s iteration requires a transformation operator. The oracle function selected as the loss function L(b, a; θi) is multiplied by the diffusion operator Us to create Grover’s iteration transformation U(θi). In the same way, another transformation U(φi) can be written using the diffusion operator Uc and the loss function L(b, a; φi) which is an oracle function.

Uc=2|c⟩⟨c|−I(23)

U(φj)=L(b,a;φj)Uc(24)

Computed gradients are utilized for performing gradient descent rule estimating network weights θi and φi. A classical non-linear optimizer with these gradients is employed to minimize the expected value by varying quantum state parameters that can dramatically affect performance so that network weights can be obtained.

θi+1=θi+α∇θU(θi)|s⟩(25)

φj+1=φj+α∇φU(φj)|c⟩(26)

According to the gradient descent principle, in this quantum optimization loop, these equations operating over its optimization surface are iterated for optimizing the training process until convergence so that learning processes and complex decision-making tasks involving meta-cognitive planning are performed faster and more robustly. A stochastic gradient descent (SGD) nonlinear optimizer with 1000 epochs is utilized to minimize expected values and obtain updated network weights. The training speed (learning rate) is set to 0.001. As a kind of quantum algorithm, the Deutsch-Josza algorithm which is based on a Deutsch-Josza problem is incorporated as a subroutine within a quantum optimization procedure. The Deutsch-Jozsa algorithm is used for detecting convergence of optimality during training of the procedure. Bernstein-Vazirani algorithm can be considered as an extension formulation of the Deutsch-Josza algorithm. The difference of the Bernstein-Vazirani algorithm is that the oracle function given an input x is ensured to return the bitwise product of the input with some string s rather than the function being regarded as balanced or constant according to the Deutsch-Josza problem.

Compared to classical argmax operations over Q-values, the quantum approach enables more scalable parallel evaluation. For small action spaces, simulated quantum search performs equivalently to classical maximum selection. However, in larger spaces or when the agent faces many near-optimal actions, the quantum routines (especially Grover’s algorithm) allow faster convergence to high-reward actions, even in simulation. This lays the groundwork for potential real-time gains on future quantum hardware.

4  Implementation and Results

In the implementation phase, experimental setup and initial conditions should be clearly defined. Implementation setups constitute the game implementation domain. The basic mechanics of the game are introduced in this implementation domain. Before passing to the setup, it is required to describe the general setting. Qiskit which is a cloud-based quantum computing library developed by IBM Q experience is utilized for quantum computing operations [34]. It allows not only performing simulation jobs but also implementing algorithms on real quantum hardware via a cloud-based gateway. Besides, as a machine learning framework, the TensorFlow library was employed to process neural networks and deep learning applications.

4.1 Experimental Setup

We utilize the MineRL simulator environment [39] and dataset [40] to design our scenarios, as they provide a rich set of tasks and human demonstrations that inform our experiment design. As a simulation environment considered for this research, Minecraft is an open-world first-person game based on the gathering of resources (e.g., wood from trees or walls from stones) and the creation of structures and items in which players can take many actions such as moving, exploring and build within a Minecraft map consisting of the 3D voxel space [39]. It provides an easily modifiable endless dynamic environment with a simplified physics engine. As an open-world game, this game which can be played in a single-player mode or a multi-player mode has no single certain objective. Instead of this, every player can develop his/her own story with different sub-goals which form a multitude of complex hierarchies. Minecraft with reduced environment continuity consisting of discrete cubic blocks allows simplifying state representation for world modeling [40]. Recent studies have tackled open-world multi-task learning with purely classical approaches [41,42]. For example, Cai et al. [41] use goal-aware representation learning for multiple tasks, and Yuan et al. [42] propose skill reinforcement learning for long-horizon tasks. These works, however, do not incorporate cognitive architectures or quantum computing, which is the focus of our study. Thus, Minecraft can be considered a comprehensive simulation domain to test the development of many artificial intelligence and machine learning applications including reinforcement and imitation learning-based methods. Project Malmo presents an API for reinforcement learning models to control agents having virtual characters within a Minecraft map in Fig. 4 [41]. With the development of this project, the research interest in terms of creating the artificial life simulation has increased to develop situation-aware autonomous agents ensuring cognitive perception, multi-task learning, and meta-cognition.

Figure 4: Snapshots from experiments using the Minecraft game

Minecraft allows the agent to perform many actions such as moving/turning in any direction, collecting/dropping an item, chopping something, and selecting/using a tool. Behaviors consisting of various sequences of actions constitute different hierarchically organized complex tasks [42]. They are formed by the aggregation of dependencies that are required to satisfy different needs and priorities for many objectives in Minecraft’s environment (map or world). Thus, Minecraft’s inherent difficulty is shaped by the size and complexity of these hierarchies [43]. One possible task example can be navigation which includes moving forward/backward or left/right, turning right/left actions so that the virtual character model can reach target locations or avoid obstacles/threads as behaviors. To build a structure (e.g., shelter), several useful actions such as collecting/dropping an item or chopping/destroying something may entail together with the help of another instance task as equipment or tool crafting, involving actions like selecting, modifying, and using items [43]. Besides collecting items and crafting tools in various tasks, more complex or abstract hierarchies arise through different features of gameplay, determining the agent’s life path in the experimental scenario. For instance, since players or artificial agents need to experience situation-dependent interactive scenarios such as combating enemies, building a shelter, and crafting a tool from several resources (items) necessary to survive, enabling exploration to gather many resources, these gameplay scenarios exhibit flexible hierarchies might require long period (or open-ended life span) [42,44]. The emergence of large language model-driven Minecraft agents [43] and hierarchical multi-agent navigation systems [44] demonstrates alternative approaches to autonomy in the same environment. In contrast, our approach provides a neuro-cognitive angle with quantum enhancements, offering improved learning performance as evidenced by our experiments.

The data collection and the feature extraction are very critical tasks. These processes entail long periods of gameplay with so many agents/humans multiple times. The content of the dataset involves a huge stack of memory replay employing observation, reward, and action. On the other hand, in nature, the reward information is implicit and cannot be provided directly as an observable feature. As the experimental environment, a 90,000 × 90,000 blocks Minecraft map is employed so that the autonomous agent equipped with the brain-inspired quantum metacognitive architecture can perform tasks related to explorer and survival-like implementation scenarios. This naturalistic Minecraft map includes mountains/hills, lavas, trenches, caves, valleys, rivers, lakes, sea, trees, plant cover, rocks, and soil as well as villagers, enemies (zombies, spiders, skeletons, etc.), and animals (cow, horse, chicken, pig, sheep, etc.). Buildings (houses, shelters, and depots) with walls, windows, doors, and furniture can be constructed with materials collected from this created environment.

4.2 Implementation Scenario

For this study, two main interaction scenarios are proposed for the autonomous behaviors of a smart agent in the Minecraft game setup within the dynamic environment. The agent simulating autonomous behaviors can easily establish an interaction with the environment and the non-player characters on the different sides of the map to learn a policy to optimally approximate the human-level performance in Fig. 5. According to the performed scenario, these tasks may be connected and the story within the scenario can be branched into different pathways while a virtual character with the agent is coming up to the optimal state. In some conditions, this virtual character can compete or collaborate with other players and/or non-player characters. For instance, a job update that involves tracking a new quest (a next objective) may have occurred when the virtual character delivers an item to a non-player character in the story as a role-playing scenario.

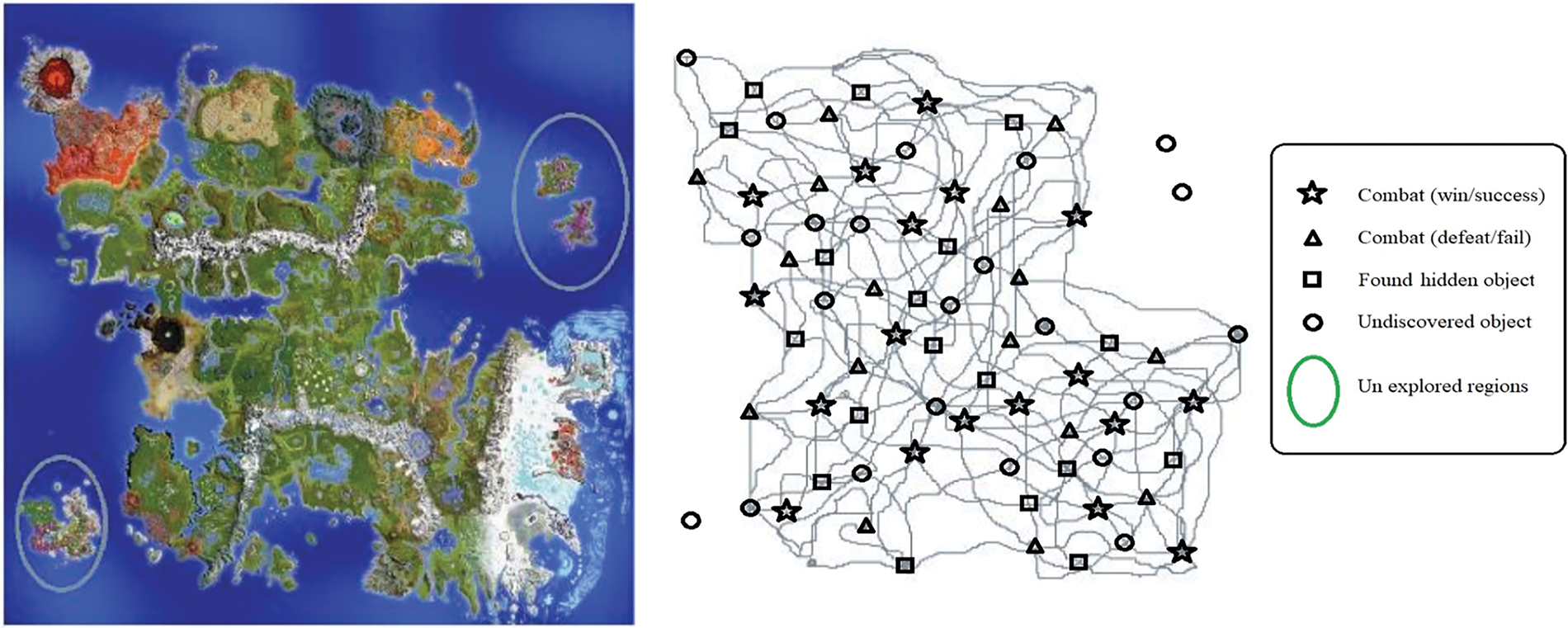
Figure 5: Trajectories of the autonomous agent and occurred event

The first implementation experiment is an explorer scenario including navigation-based behaviors and search-based tasks. In navigation-based behaviors, the agent performs particular movement patterns such as “move to a direction”, and “avoid obstacles” for accessing targets and discovering unknown territories depicted on the map. In addition, the other sub-tasks like “random wander”, “follow the clues (waypoints)”, and “detect and collect items” are employed to find hidden objects scattered around the proposed map in terms of search-based behaviors. These sub-tasks continue until the experiment is completed within a certain duration or the agent achieves reaching all targets and finding all hidden objects.

The second implementation experiment employs a survivor scenario. This scenario requires tasks that involve fighting (or escaping) and building a shelter for security needs. In addition, tasks such as crafting tools from collected resource items are considered in this scenario. During the experiment, the agent encounters many enemies and tries to eliminate them while it is exploring its territory and discovering hidden items for crafting tools. Then, the experiment is finalized if the agent successfully defeats all enemies or a certain duration is passed from the beginning of the experiment.

4.3 Experimental Results

In the experiments, proposed scenarios were performed using implementation platforms so that the system performance is evaluated and efficiency related to the mentioned research questions can be validated. To evaluate the outcomes of the system, it is required to capture the data stream by stacking image frames for data collection during implementation scenarios in experiments. In the first stage, after capturing the snapshot image from the video stream in the game, some pre-processing operations such as dimension reduction, gray-scale image conversion, and optimizing sampling rate are executed.

Before experiments, all system parameters related to learning models of brain-inspired meta-cognitive architecture as well as quantum states in quantum optimization algorithms are initialized. The convolution filter (weight tensor) size is selected as a stack of 4-time frames with the dimension of 84 × 110 × 2 indicating the image pattern of width, height, and depth, respectively. Initially, the alpha coefficient which is a learning rate parameter is 0.00025. The exploration probability which is constrained to its minimum by 0.01, is 1.0 at the start and its decay rate is 0.00001. The reward discounting rate (gamma) is 0.9. At the end of the experiments, the hypothesis based on both research questions is validated via the contribution of the quantum computing modeling approach.

In this paper, the MineRL dataset is utilized as one of the largest imitation learning datasets with over 60 million frames of recorded human player data, including various sub-datasets, and utilizing to perform experiments on the agent model that can adapt to a wide range of environments. As a meta-database that highlights many of the hardest problems such as exploring (navigating, collecting items, etc.) and surviving (tool crafting, combat, etc.), it covers a bunch of tasks where rewards are sparse and hard to define. In the explorer scenario, the smart agent is deployed on a diverse game map containing a variety of objects and creatures.

The agent employs its quantum computing-based neurocognitive architecture to explore the map, locate hidden objects, and record the number of successfully discovered objects. The performance of the agent is measured based on its discovery rate and the number of missed objects during the exploration. During the experiment, the smart agent successfully discovered a significant number of objects, demonstrating its proficiency in exploration and object detection. In the experiment of the survivor scenario, the smart agent faced a bunch of threats, including menacing monsters and creatures that posed potential dangers. The results of the survivor scenario experiment indicate that the smart agent successfully eliminated a majority of threats, exhibiting its capacity to adapt and make precise decisions with remarkable efficiency. Overall, the framework’s performance demonstrates a transformative impact on the agent’s abilities within both scenarios. The agent’s quantum parallelism enables efficient exploration, leading to the discovery of a substantial number of hidden objects in the explorer scenario. Moreover, its exceptional threat-elimination skills in the survivor scenario demonstrate the agent’s adaptive decision-making capabilities.

The efficiencies of the meta-cognition and the situation-awareness aspects were examined by reward trends as gaining scores in the game implementation platform for the experiment scenarios including explorer (Fig. 6a), and survivor (Fig. 6b), and mixed-scenario including both them (Fig. 6c), using Minecraft. Once outcomes are inspected, it is easily seen that rewards associated with autonomous behaviors incorporating meta-cognition and situation awareness are slightly better in experiment 3 than results related to meta-cognition in experiment 2 and results corresponding to situation awareness in experiment 1, as the rewards derived from the configuration without utilizing the quantum computing model in experiment 4 are remaining behind of experiments for all scenarios. Ripples in reward trends of the reinforcement learning process related to the situation-awareness involving skills such as spatial-temporal reasoning processes diminished as achieved scores in Minecraft map are rising in experiments, thanks to the meta-cognition procedure applying interpreted or re-generated rewards to all cognitive skills for organizing all sub-tasks that involve complex decision making, meta-cognitive planning, and reasoning activities.

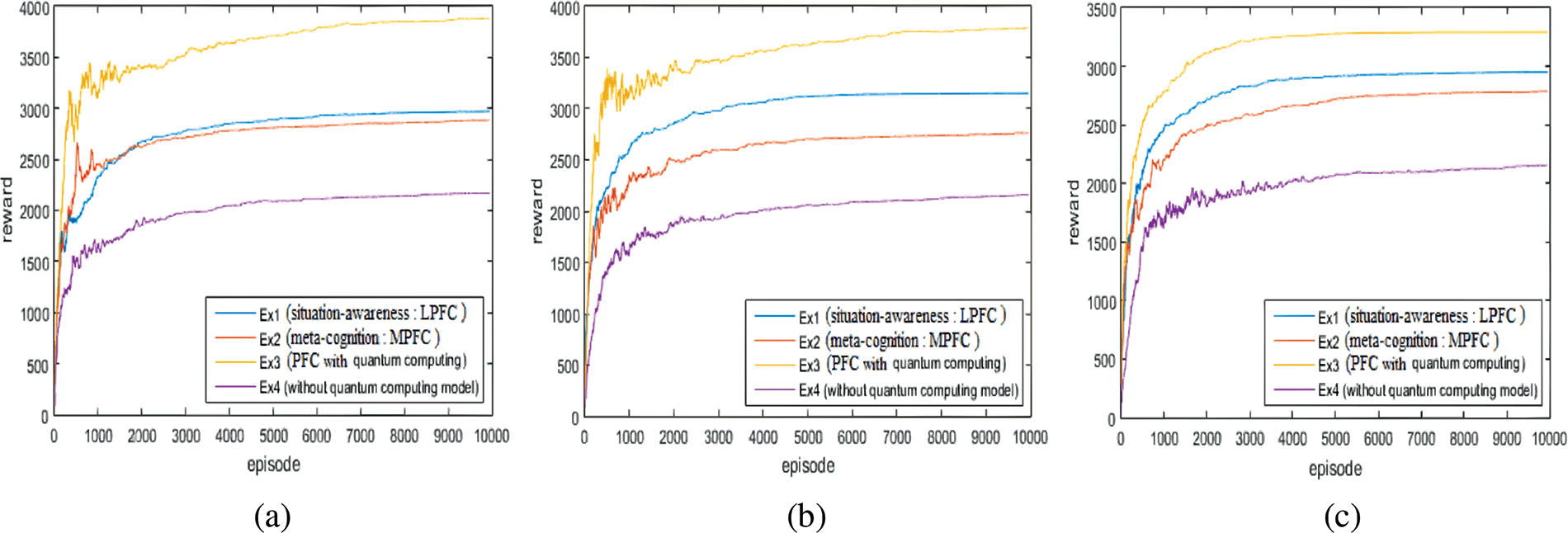
Figure 6: The rewards: (a) the explorer scenario (b) the survivor scenario, and (c) the mixed scenario with the Minecraft game

In addition, costs per training step (episode) indicating learning performances are observed during experiments (Fig. 7). Presented outcomes verify that costs computed by the loss function in the reinforcement learning process related to cognitive functions for decision-making and planning of autonomous task processing are reduced successfully via approximation of autonomy representation with the meta-cognition model and the situation-awareness property integrating quantum optimization algorithm for optimizing learning performances of the cognitive skills in experiment 3. Performances in experiment 4 that the quantum computing model is not employed are the worst for all scenarios. Although results in the experiment scenarios of the explorer (Fig. 7a) and the survivor (Fig. 7b) are close to each other, deviations related to the case without the quantum computing model are larger in the results of the mixed-scenario (Fig. 7c). Besides, the result of experiments except the fourth one is by far better in the explorer scenario with Minecraft (Fig. 7a). By the quantum optimization algorithm, it is shown that the decision-making activities are more robust and the training process is faster.

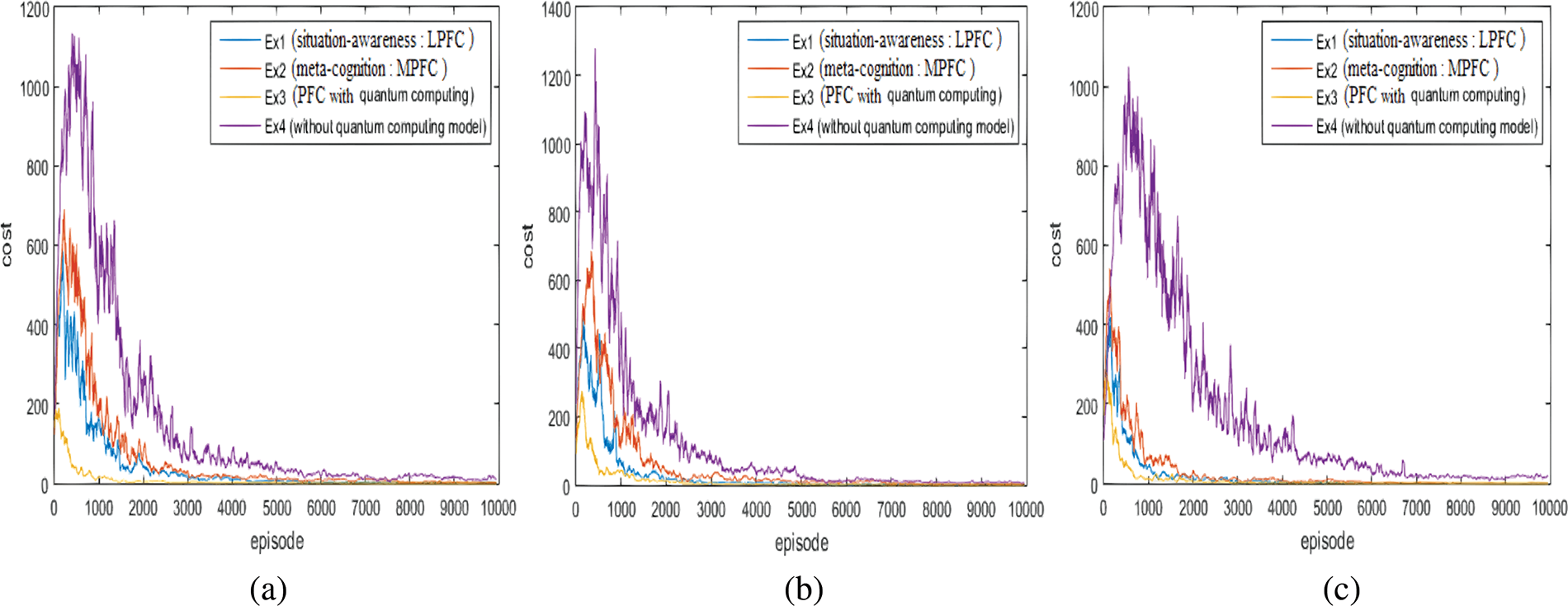
Figure 7: The costs: (a) the explorer scenario (b) the survivor scenario, and (c) the mixed scenario with the Minecraft game

Another significant efficiency indicator of this research is the steps per episode during experiments (Fig. 8). It can be investigated concerning different values of the learning rate parameter. Besides the first configuration (Fig. 8a) with the alpha coefficient (learning rate parameter) as 0.00025, the exploration probability set to 1.0, the decay rate chosen as 0.00001, and the reward discounting rate (gamma) which is 0.9, in the second configuration (Fig. 8b), the alpha coefficient (learning rate parameter), the exploration probability, the decay rate and the reward discounting rate (gamma) are 0.00275, 0.85, 0.00024, and 0.75, respectively. In the last configuration (Fig. 8c), the alpha coefficient (learning rate parameter), the exploration probability, the decay rate, and the reward discounting rate (gamma) are 0.06455, 0.75, 0.00187, and 0.6, respectively. To better interpret performance differences, learning curves were smoothed using a moving average technique with a window size of 10 episodes, highlighting overall trends and reducing high-frequency noise. The figure presents results for three different hyperparameter configurations. For all these configurations, the agent is trained and tested not on the Minecraft game platform, using a mixed scenario involving tasks of the explorer and the survivor scenarios. According to this, the third configuration has the most successful results concerning the first and second configurations. Even though there are some similarities between the results of the first and second configurations, the results of the second one are slightly better than the first configuration, whose results have more fluctuations as the least stable solution.

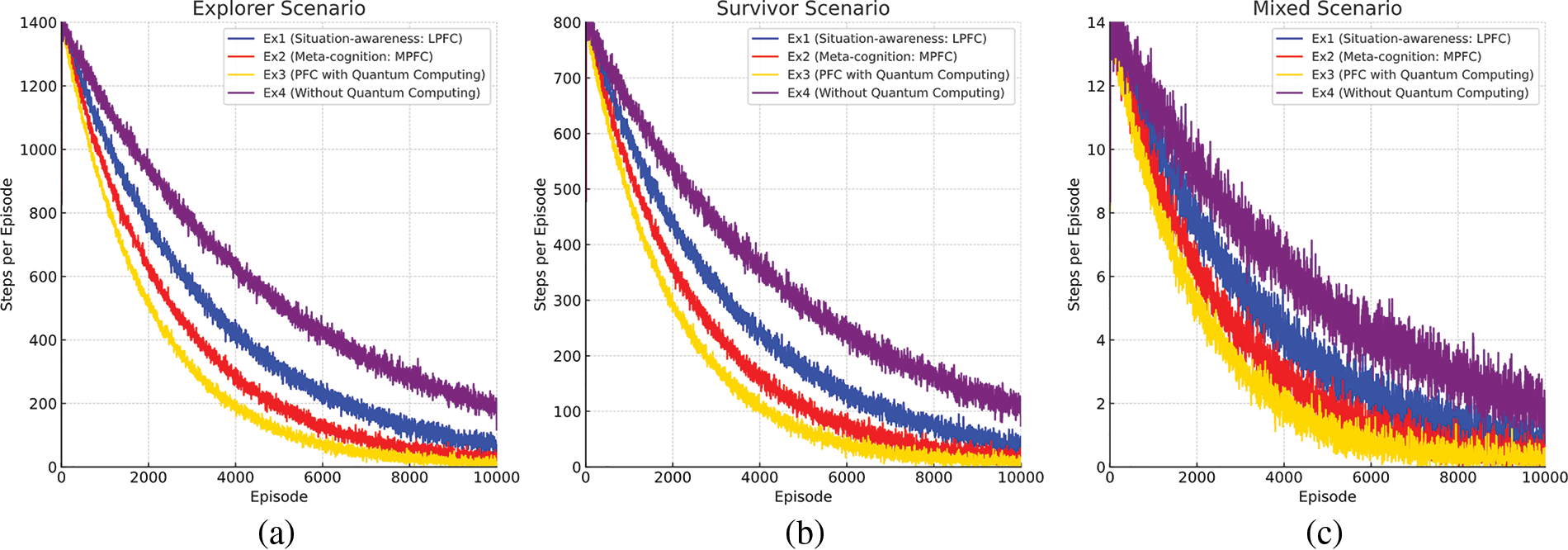
Figure 8: The steps per episode: (a) the explorer scenario (b) the survivor scenario, and (c) the mixed scenario with the Minecraft game

Various models are employed for comparison purposes so that supremacy between them has been demonstrated. Likewise, these comparisons are performed on the Minecraft game platform via experiments of explorer and survivor scenarios involving many interaction tasks involving chop, collect, build, combat, escape, search, and navigation. To evaluate research questions related to hypotheses ensuring situation awareness and meta-cognition, quantum computing-based training algorithms including iterative methods like Deutsch-Jozsa, Bernstein-Vazirani, and Grover’s algorithms are tested for a brain-inspired cognitive architecture involving deep reinforcement learning-oriented models. The values in the following tables correspond to the accuracy indicating the performance of the learning algorithms for the training and testing phases.

According to learning performances, results of these models that put forward the efficiency of the agent model are presented during experiments that the explorer scenario with several tasks such as finding and collecting items as well as crafting tools are taken into consideration on the Minecraft game platform in Table 1. For iterative or search models (Table 1), results of the Bernstein-Vazirani algorithm are better than the Deutsch-Jozsa algorithm by 9.21 and 6.44 scores for training and testing results, respectively in finding items task. Besides, outcomes that belong to the crafting tools task are worse in the Bernstein-Vazirani algorithm compared to results of the Deutsch-Jozsa algorithm by 3.43 and 3.37 percent for training and testing results, respectively. On the other hand, the best accuracies for quantum iterative or search algorithms are observed in Grover’s iteration in all tasks.

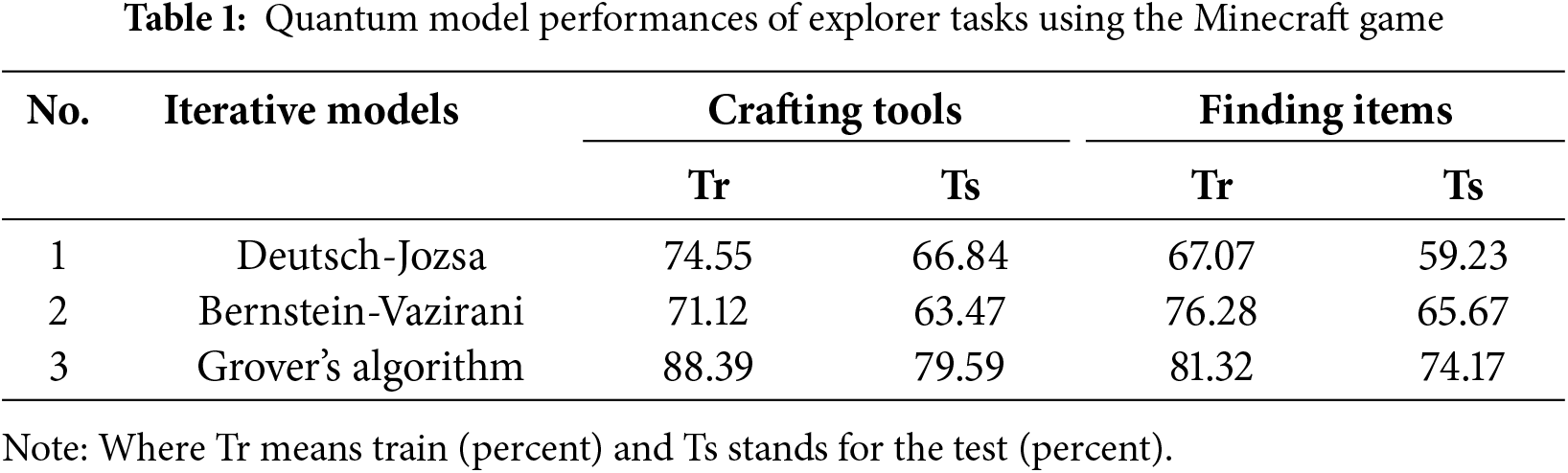
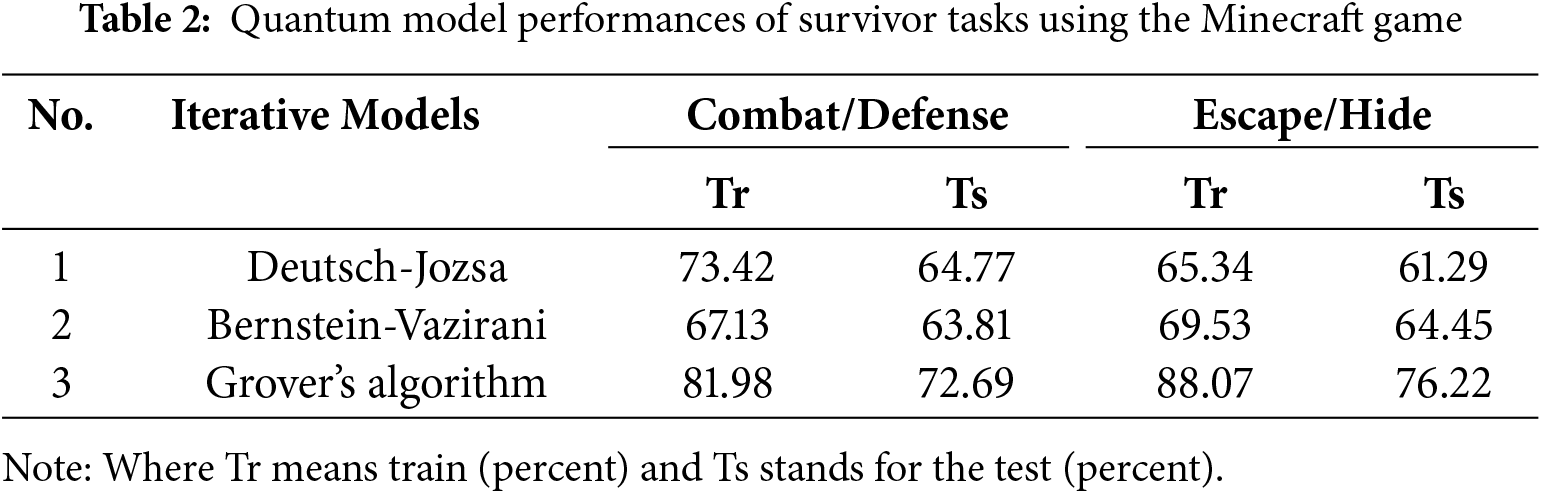
Table 2 shows the performance of the agent model on the Minecraft game platform, the results of these models are presented via experiments with the survivor scenario involving combat (or defense/block against the attacker) and escape (or hiding from the enemy) tasks. When results in iterative or search models are elaborately investigated, unlike the escape/hide task, model accuracies related to the Bernstein-Vazirani algorithm are slightly worse than Deutsch-Jozsa’s algorithm results in the combat/defense task. In the case of both tasks for iterative or search models, Grover’s iteration achieved the best results with an average accuracy % of 81.98–88.07 for training sessions and %72.69–76.22 for testing sessions, respectively.

The quantum-enhanced neuro-cognitive agent generally achieves higher success and learns faster than the classical counterpart, especially in tasks that involve exploratory/survivor behavior, hierarchical planning, or multi-goal decision making. In particular, sub-tasks requiring fine-grained motor control (such as real-time combat) or deterministic crafting sequences showed marginal or no improvement over the classical baseline. This indicates that quantum enhancement is successful in decision-making scenarios that benefit from efficient search or pattern evaluation, whereas in low-variability, deterministic tasks, classical methods. In the Survivor scenario, however, the efficiency gains were relatively modest. The quantum agent adapted slightly faster, but both agents ultimately converged. The results highlight that quantum modules provide an important benefit in situations involving a lot of searching or exploration, while their effectiveness declines in the case of tasks relying on reactive or rule-based behavior. This suggests that the quantum module primarily aids in strategic decision-making and early convergence, rather than low-level action optimization.

5  Conclusion

Thanks to emerging quantum information technologies, a revolution might take place in the field of artificial intelligence and machine learning technologies in the near future. Therefore, this study can lead to a progressive impact on smart agents and autonomous systems as synthetic life forms. While this study demonstrates the effectiveness of a quantum-enhanced cognitive architecture within a simulation environment (Minecraft), extending this approach to real-world robotics presents additional challenges and opportunities. The cognitive structure itself—including the meta-cognition, situation awareness, and transformer-based policy network—is designed in an environment-agnostic manner and could be adapted to operate on real robots. The agent’s decision cycle, involving perception, planning, action selection, and meta-cognitive monitoring, mirrors the modular control architectures used in modern robotics. Similarly, the quantum computational components (such as Grover’s algorithm for action optimization) could, in principle, be integrated via cloud-based quantum services to assist real robots in planning-intensive tasks. For instance, a mobile robot navigating an unfamiliar building could offload complex action search tasks to a quantum server while relying on classical control for real-time actuation. Thus, while hardware and deployment considerations are nontrivial, the conceptual architecture is translatable to physical systems.

The Minecraft simulation environment abstracts away important real-world factors such as sensor noise, actuation delays, continuous-time dynamics, and hardware resource constraints. Our agent benefits from full observability, idealized physics, and perfect perception, which simplifies the learning and decision-making process compared to a physical robot operating in an unpredictable, partially observable world. Moreover, our current use of classical simulation for quantum algorithms (via Qiskit) does not realize the true computational speedups that would occur on physical quantum processors; instead, we assume that future quantum hardware could provide these advantages. Thus, performance metrics reported here (learning speed, task success rates) may not directly extrapolate to real-world deployments. To bridge this gap, future work will include testing the cognitive architecture in high-fidelity physics simulators, applying domain randomization techniques to improve transferability, and eventually incorporating hardware-in-the-loop trials with real sensor data. Furthermore, integration with hybrid quantum-classical architectures (where quantum acceleration is selectively applied to planning modules) will be necessary to ensure real-time feasibility. We explicitly recognize that full real-world validation requires overcoming these challenges, and we have outlined a simulation-to-reality roadmap to progressively adapt the architecture for deployment beyond simulation.

These results underscore that our architecture’s benefits are context-specific. The conclusion one can draw is that quantum computing can enhance certain cognitive functions (like search and pattern detection) within an AI agent, leading to measurable performance gains, but it does not magically solve all challenges—areas like fine-grained control or domain-specific strategy still rely on robust learning and perhaps additional innovations. Besides, results highlight that combining quantum computing with cognitive architectures can improve agent performance in specific task categories, particularly those involving high-level planning, multi-objective navigation, or strategic decision-making. However, the performance gains are not uniform across all tasks. In certain cases—such as fine-grained combat or routine crafting—the classical architecture performs comparably. Thus, our architecture’s advantages are best interpreted as contextual enhancements rather than a one-size-fits-all improvement.

In structured Minecraft-based simulations, the quantum-enhanced agent achieved approximately 2× faster convergence to 80% task success in exploration scenarios and about 15% higher cumulative rewards compared to a classical agent baseline. These findings support the hypothesis that integrating quantum algorithms within cognitive control frameworks can improve learning speed and task performance, particularly in tasks requiring complex exploration and search. However, the performance gains were context-specific, with more modest improvements observed in stochastic combat-heavy tasks. In terms of learning performance, outcomes related to the computational framework of the brain-inspired cognitive model with quantum computing procedures that exhibit the qualification of the agent model during trials were introduced. Several models including quantum computing-based training algorithms composed of iterative methods or quantum search algorithms like Deutsch-Jozsa, Bernstein-Vazirani, and Grover’s algorithm were utilized to compare for demonstrate supremacy between them. When these results are investigated, Grover’s algorithm comes forward concerning Deutsch-Jozsa and Bernstein-Vazirani for iterative search models.

Building on this foundation, future work will pursue several paths: (1) extending the architecture to multi-agent systems, where quantum-enhanced meta-cognition could optimize collaboration and competition among agents; (2) adapting the system to real-world robotic platforms, starting with high-fidelity physics simulators and moving to physical robots; and (3) exploring advanced quantum machine learning methods, such as parameterized quantum circuits and hybrid quantum-classical policy models. By systematically addressing these next steps, we aim to translate the demonstrated simulation benefits into robust, scalable, real-world intelligent agents.

Acknowledgement: I would like to express my special thanks to Cognitive Systems Laboratory (CSL) as well as Artificial Intelligence and Data Science Research Center (ITUAI), Istanbul Technical University for their encouragement and opportunity throughout this research. In addition, I would like to express my special thanks all anonymous reviewers and the editor for their constructive comments.

Funding Statement: The author received no specific funding for this study.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The author declares no conflicts of interest to report regarding the present study.

References

1. Sun J, Zhao J, Hu X, Gao H, Yu J. Autonomous navigation system of indoor mobile robots using 2D lidar. Mathematics. 2023;11(6):1455. doi:10.3390/math11061455. [Google Scholar] [CrossRef]

2. Oroko JA, Nyakoe GN. Obstacle avoidance and path planning schemes for autonomous navigation of a mobile robot: a review. In: Proceedings of the 2012 Sustainable Research & Innovation (SRI) Conference; 2012 May 3–4; Juja, Kenya. [Google Scholar]

3. Vasques X. Machine learning theory and applications: hands-on use cases with python on classical and quantum machines. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 2024. 521 p. [Google Scholar]

4. Kou H, Zhang Y, Lee HP. Dynamic optimization based on quantum computation—a comprehensive review. Comput Struct. 2024;292:107255. doi:10.1016/j.compstruc.2023.107255. [Google Scholar] [CrossRef]

5. Pothos EM, Busemeyer JR, Shiffrin RM, Yearsley JM. The rational status of quantum cognition. J Exp Psychol Gen. 2017;146(7):968–87. doi:10.1037/xge0000312. [Google Scholar] [PubMed] [CrossRef]

6. Busemeyer JR, Fakhari P, Kvam P. Neural implementation of operations used in quantum cognition. Prog Biophys Mol Biol. 2017;130(3):53–60. doi:10.1016/j.pbiomolbio.2017.04.007. [Google Scholar] [PubMed] [CrossRef]

7. Yearsley JM. Advanced tools and concepts for quantum cognition: a tutorial. J Math Psychol. 2017;78(5):24–39. doi:10.1016/j.jmp.2016.07.005. [Google Scholar] [CrossRef]

8. Makoeva D, Nagoeva O, Anchokov M, Gurtueva I. Implementation of embodied cognition in multi-agent neurocognitive architecture. In: Proceedings of the Biologically Inspired Cognitive Architectures 2023; 2023 Oct 13–15; Ningbo, China. doi:10.1007/978-3-031-50381-8_58. [Google Scholar] [CrossRef]

9. Juvina I, Larue O, Hough A. Modeling valuation and core affect in a cognitive architecture: the impact of valence and arousal on memory and decision-making. Cogn Syst Res. 2018;48(1):4–24. doi:10.1016/j.cogsys.2017.06.002. [Google Scholar] [CrossRef]

10. Dağlarlı E, Dağlarlı SF, Günel GÖ., Köse H. Improving human-robot interaction based on joint attention. Appl Intell. 2017;47(1):62–82. doi:10.1007/s10489-016-0876-x. [Google Scholar] [CrossRef]

11. Li JA, Dong D, Wei Z, Liu Y, Pan Y, Nori F, et al. Quantum reinforcement learning during human decision-making. Nat Hum Behav. 2020;4(3):294–307. doi:10.1038/s41562-019-0804-2. [Google Scholar] [PubMed] [CrossRef]

12. Dong D, Chen C, Li H, Tarn TJ. Quantum reinforcement learning. IEEE Trans Syst Man Cybern Part B Cybern. 2008;38(5):1207–20. doi:10.1109/TSMCB.2008.925743. [Google Scholar] [PubMed] [CrossRef]

13. Dong D, Chen C, Chen Z. Quantum reinforcement learning. In: Advances in natural computation. Berlin/Heidelberg: Springer; 2005. p. 686–9. doi: 10.1007/11539117_97. [Google Scholar] [CrossRef]

14. Dong D, Chen C, Chu J, Tarn TJ. Robust quantum-inspired reinforcement learning for robot navigation. IEEE/ASME Trans Mechatron. 2012;17(1):86–97. doi:10.1109/TMECH.2010.2090896. [Google Scholar] [CrossRef]

15. Chen CL, Dong DY. Superposition-inspired reinforcement learning and quantum reinforcement learning. In: Weber C, Elshaw M, Mayer NM, editors. Reinforcement learning: theory and applications. Norderstedt, Germany: IntechOpen; 2008. [Google Scholar]

16. Moreira C, Wichert A. Quantum-like Bayesian networks for modeling decision making. Front Psychol. 2016;7:11. doi:10.3389/fpsyg.2016.00011. [Google Scholar] [PubMed] [CrossRef]

17. Moreira C, Fell L, Dehdashti S, Bruza P, Wichert A. Towards a quantum-like cognitive architecture for decision-making. arXiv:1905.05176. 2019. [Google Scholar]

18. Ganger M, Hu W. Quantum multiple Q-learning. Int J Intell Sci. 2019;9(1):1–22. doi:10.4236/ijis.2019.91001. [Google Scholar] [CrossRef]

19. Skrynnik A, Staroverov A, Aitygulov E, Aksenov K, Davydov V, Panov AI. Hierarchical deep Q-network from imperfect demonstrations in minecraft. Cogn Syst Res. 2021;65(7676):74–8. doi:10.1016/j.cogsys.2020.08.012. [Google Scholar] [CrossRef]

20. Hohenfeld H, Heimann D, Wiebe F, Kirchner F. Quantum deep reinforcement learning for robot navigation tasks. IEEE Access. 2024;12(7849):87217–36. doi:10.1109/access.2024.3417808. [Google Scholar] [CrossRef]

21. Yan R, Wang Y, Xu Y, Dai J. A multiagent quantum deep reinforcement learning method for distributed frequency control of islanded microgrids. IEEE Trans Control Netw Syst. 2022;9(4):1622–32. doi:10.1109/TCNS.2022.3140702. [Google Scholar] [CrossRef]

22. Yun WJ, Park J, Kim J. Quantum multi-agent meta reinforcement learning. Proc AAAI Conf Artif Intell. 2023;37(9):11087–95. doi:10.1609/aaai.v37i9.26313. [Google Scholar] [CrossRef]

23. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–44. doi:10.1038/nature14539. [Google Scholar] [PubMed] [CrossRef]

24. Goodfellow I, Bengio Y, Courville A. Deep learning. Cambridge, MA, USA: MIT Press; 2016. 800 p. [Google Scholar]

25. Zhang A, Lipton ZC, Li M, Smola AJ. Dive into deep learning. Cambridge, UK: Cambridge University Press; 2023. 574 p. [Google Scholar]

26. Sainath TN, Vinyals O, Senior A, Sak H. Convolutional, long short-term memory, fully connected deep neural networks. In: Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2015 Apr 19–24; South Brisbane, QLD, Australia. doi:10.1109/ICASSP.2015.7178838. [Google Scholar] [CrossRef]

27. Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-level control through deep reinforcement learning. Nature. 2015;518(7540):529–33. doi:10.1038/nature14236. [Google Scholar] [PubMed] [CrossRef]

28. Mnih V, Kavukcuoglu K, Silver D, Graves A, Antonoglou I, Wierstra D, et al. Playing atari with deep reinforcement learning. arXiv:1312.5602. 2013. [Google Scholar]

29. Hausknecht M, Stone P. Deep recurrent Q-learning for partially observable MDPs. arXiv:1507.06527. 2015. [Google Scholar]

30. Chen L, Lu K, Rajeswaran A, Lee K, Grover A, Laskin M, et al. Decision transformer: reinforcement learning via sequence modeling. arXiv:2106.01345v2. 2021. [Google Scholar]

31. Upadhyay U, Shah N, Ravikanti S, Medhe M. Transformer based reinforcement learning for games. arXiv:1912.03918. 2019. [Google Scholar]

32. Wu YH, Wang X, Hamaya M. Elastic decision transformer. Adv Neural Inf Process Syst 2023. 2024;36:18532–50. [Google Scholar]

33. Khang A. Applications and principles of quantum computing. Hershey, PA, USA: IGI Global; 2024. 491 p. [Google Scholar]

34. Bertels K, Sarkar A, Krol A, Budhrani R, Samadi J, Geoffroy E, et al. Quantum accelerator stack: a research roadmap. arXiv:2102.02035. 2021. [Google Scholar]

35. Oliveira AN, de Oliveira EVB, Santos AC, Villas-Bôas CJ. Quantum algorithms in IBMQ experience: deutsch-jozsa algorithm. arXiv:2109.07910. 2021. [Google Scholar]

36. Naseri M, Kondra TV, Goswami S, Fellous-Asiani M, Streltsov A. Entanglement and coherence in the Bernstein-vazirani algorithm. Phys Rev A. 2022;106(6):062429. doi:10.1103/physreva.106.062429. [Google Scholar] [CrossRef]

37. Gilliam A, Pistoia M, Gonciulea C. Optimizing quantum search using a generalized version of Grover’s algorithm. arXiv:2005.06468. 2020. [Google Scholar]

38. Daglarli E. Computational modeling of prefrontal cortex for meta-cognition of a humanoid robot. IEEE Access. 2020;8:98491–507. doi:10.1109/access.2020.2998396. [Google Scholar] [CrossRef]

39. Guss WH, Codel C, Hofmann K, Houghton B, Kuno N, Milani S, et al. Neurips 2019 competition: the MineRL competition on sample efficient reinforcement learning using human priors. arXiv:1904.10079. 2019. [Google Scholar]

40. Guss WH, Houghton B, Topin N, Wang P, Codel C, Veloso M, et al. MineRL: a large-scale dataset of minecraft demonstrations. arXiv:1907.13440. 2019. [Google Scholar]

41. Cai S, Wang Z, Ma X, Liu A, Liang Y. Open-world multi-task control through goal-aware representation learning and adaptive horizon prediction. In: Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2023 Jun 17–24; Vancouver, BC, Canada. doi:10.1109/CVPR52729.2023.01320. [Google Scholar] [CrossRef]

42. Yuan H, Zhang C, Wang H, Xie F, Cai P, Dong H, et al. Skill reinforcement learning and planning for open-world long-horizon tasks. arXiv:2303.16563. 2023. [Google Scholar]

43. Madge C, Poesio M. Large language models as minecraft agents. arXiv:2402.08392. 2024. [Google Scholar]

44. Zhao Z, Chen K, Guo D, Chai W, Ye T, Zhang Y, et al. Hierarchical auto-organizing system for open-ended multi-agent navigation. arXiv:2403.08282. 2024. [Google Scholar]