Application of Various Optimisation Methods in the Multi-Optimisation for Tribological Properties of Al–B₄C Composites

1  Introduction

The tribological properties of composite materials play a crucial role in the development of advanced engineering solutions, particularly in applications where wear resistance and friction reduction are essential. Aluminium alloys, such as AA2024, are widely used in industry due to their favourable mechanical properties and low density; however, their wear resistance is often limited [1]. To improve these characteristics, research has focused on developing composites with reinforcement particles, such as boron carbide (B4C), which significantly contribute to the enhancement of mechanical and tribological properties [2–4].

The addition of solid particles, such as B4C, enables modification of matrix properties, reducing wear and friction, which is critical for applications in the automotive parts industry, aviation, and other highly demanding environments including bulletproof vests and the containment of nuclear waste [5,6]. However, to achieve optimal performance of the composite, it is necessary to control the parameters of the production process precisely. Namely, parameters such as the percentage of reinforcement, grinding time, and applied normal load can significantly affect the final properties of the material.

Beder [7] investigated the effect of varying B4C particle content (0, 10, 20, and 40 wt.%) on the microstructure, mechanical properties, and wear in dry sliding conditions of Al2024 alloy-based composites. The composites were prepared using mechanical milling and hot-pressing methods. The results showed that increasing the B4C content leads to a higher presence of the θ (CuAl2) phase in the microstructure and an increase in the hardness of the samples. The highest volume loss during wear was recorded in the unreinforced samples, while those with the highest B4C content exhibited significantly reduced wear [7]. Gaylan et al. [8] produced Al–B4C metal matrix composites (MMCs) and studied their neutron shielding properties. The composite powders were prepared through high-energy planetary ball milling, and their microstructure was analysed using XRD (X-ray Diffraction) and SEM (Scanning Electron Microscopy)/EDX (Energy Dispersive X-ray Spectroscopy) techniques. The study concluded that the Al–B4C composites consisted of dominant aluminium and boron carbide phases, with a uniform distribution of B4C particles within the aluminium matrix. As the B4C content increased, the relative density of the composites decreased, while microhardness initially increased but later decreased at higher B4C contents. Corrosion resistance decreased with increasing B4C content, as reflected in an increase in both corrosion current and rate. In terms of neutron shielding, both experimental and simulation results demonstrated that an increase in B4C content improved the efficiency of shielding against thermal and fast neutrons [8].

In another study, Bayrak et al. investigated Al–B4C composites produced via vacuum hot pressing with up to 15 wt.% B4C particles. The microstructures, corrosion behaviour, and physical and tribological properties of the samples were examined. The results showed that an increase in the B4C content enhanced the wear resistance of aluminium and reduced its corrosion rate. However, the electrical conductivity of the aluminium decreased with higher B4C content and increased porosity, indicating a trade-off between mechanical and electrical properties [9].

To achieve the most reliable and accurate results in optimising production, processing, or testing parameters of composites, the Taguchi experimental method is applied. This method enables efficient determination of optimal process parameter values when optimising a single response. Taguchi method is simple to use and interpret, effective in reducing the number of experiments through orthogonal arrays and good at identifying factors that have the most significant impact on results. The disadvantages of the Taguchi method include its limitation in optimising multiple output parameters simultaneously and potential inaccuracy if there is substantial non-linearity in the system [10,11]. Murthy et al. applied the Taguchi technique to optimise process parameters for the fabrication of Al2024–B4C composites. The investigation onto the influence of B4C particle content (1, 3, and 5 wt.%), and aging duration (1, 3, and 5 h) as well as mesh size (100, 200, and 300) on ductility (%) and yield strength (N/mm2) was conducted. The most influential factor on the ductility of the formed composites is wt.% of B4C, followed by mesh size and ageing duration. For the yield strength of the formed composites, the most influential factor was the ageing duration, followed by mesh size and wt.% of B4C. It was concluded that the experimental results are in close agreement with the regression model equations for both ductility and yield strength, validating the experimental approach. The study demonstrated that the observed parameters significantly influence the mechanical properties of the Al2024–B4C composite, with optimal process parameters identified through statistical analysis, confirming the effectiveness of the chosen methods [12].

In addition to the previously discussed studies, another successful application of the Taguchi method was presented in Sunil et al. [13] investigation of Al2024–Gr–B4C hybrid composites produced by powder metallurgy technique with a fixed amount of graphite (3%) and different amounts of B4C (0%, 6% and 12 wt.%). The investigation focused on the effect of cutting speed, feed rate, depth of cut, and reinforcement wt.% on material removal rate (MRR) during a turning operation. MRR was calculated based on different combinations of cutting speeds (315, 400, and 500 rpm), feed rates (0.05, 0.10, and 0.15 mm/rev) and depth of cut (0.1, 0.2, and 0.3 mm), which were optimised using the Taguchi method with an L27 orthogonal array for experimental design. The machining process was most significantly influenced by cutting speed (29.45%), followed closely by the depth of cut (29.36%), feed rate (21.82%) and finally, the percentage of B4C (9.52%) [13]. However, in situations where it is necessary to optimise multiple output parameters with different quality characteristics, the application of multi-criteria optimisation through Grey Relational Analysis (GRA) proves to be a more suitable approach. The successful application of multi-criteria optimisation is found in the research of Gonfa et al. [14], who investigated aluminium composites reinforced with SiC and molybdenum disulfide (MoS2) particles. They concluded that adding SiC improved hardness, strength, and wear resistance, while MoS2 further enhanced wear resistance, but only up to a concentration of 2 wt.%. For optimisation of processing parameters, the Taguchi method was employed for single-response analysis, and the hybrid Taguchi-GRA method was used for multi-objective optimisation. These methods helped in predicting optimal processing conditions, including speed and mixing time, as well as the percentages of SiC and MoS2. The mentioned optimisation methods enabled the prediction of optimal processing conditions, resulting in a significant improvement in the mechanical and tribological properties of the composites.

Further confirmation of the effectiveness of Taguchi-GRA was found in the work of Ghosh et al. [15], who studied the tribological behaviour of the aluminium composite material Al–7.5% SiCp. Using the Taguchi-GRA method, the effects of parameters such as load, sliding speed and time on the friction and wear of the composites were investigated. The study showed that sliding time was the most significant parameter, while load and sliding speed also had a notable impact. SEM analysis confirmed that the abrasive wear mechanism dominated, further validating the conclusions on the successful application of optimisation methods to improve the tribological properties of composites. The advantages of the Taguchi-GRA method include efficiency in multi-criteria optimisation, simplicity of application, and increased process robustness. Limitations of Taguchi-GRA include the lack of a theoretical base for the factor weights, sensitivity to data normalisation, inability to model non-linear relationships, and the fact that it does not account for the mutual interactions of factors in the GRA phase [16]. Response Surface Methodology (RSM) is another optimisation method that enables the modelling of non-linear relationships between input and output parameters. This method is suitable for local optimisation and prediction of system behaviour, and analysis of the interaction effects of factors. Still, this method requires a larger number of experiments compared to the Taguchi method [17–19]. Abdelhady et al. [20] modelled the influence of normal load and sliding distance on the specific wear rate and CoF of AA6061-B4C composite using the RSM. The goal was to determine the combination of parameters that give minimal wear and friction. The optimal conditions were as follows: a volume fraction of 10%, an applied load of 20 N, and a sliding distance of 500 m. Another method suitable for multi-criteria decision making (MCDM), which is intuitive and easy to apply when the criteria are quantified, and that enables the ranking of alternatives in relation to the ideal and worst solutions, is the TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) and AHP (Analytical Hierarchy Process) methods. Some disadvantages of this method are that it requires a subjective determination of criteria weights (unless combined with Fuzzy or AHP-Analytic Hierarchy Process) and does not account for the statistical variability of the data [21,22]. Abbas et al. applied the integrated TOPSIS-Fuzzy approach to the multi-criteria optimisations of the Ti–6Al–4V alloy processing, demonstrating the effectiveness of this method in balancing multiple output parameters. Evolutionary algorithms, such as NSGA-II, offer the ability to explore large search spaces and identify Pareto-optimal fronts, as demonstrated in the optimisation of tribological behaviour in Al–SiC composites [23]. However, these methods often require high computational effort and may not always yield transparent decision criteria. NSGA-II has been effectively utilised for the multi-objective optimisation of machining parameters, focusing on balancing MRR and surface roughness (SR) in processes such as wire electrical discharge machining (WEDM) of Al6351-based composites. For instance, studies have demonstrated that NSGA-II can achieve a balance between productivity and precision in machining Al6351–SiC–Gr composites [23]. Sur and Erkan focused on optimising the surface quality of CFRP composite plates drilled with different types of drills, using processing parameters such as Taguchi, ANOVA, TOPSIS, and AHP methods. By using TOPSIS, and AHP, optimal results were achieved in the drilling optimisation of CFRP plates [24]. Additionally, Bodukuri and Kesha, in their research [25], focused on optimising the processing of aluminium composites reinforced with ceramics (SiC and B4C) using electrical discharge machining (EDM). The goal of the research was to study the impact of EDM parameters, specifically current pulse (I), pulse off time (P-Off), pulse on time (P-On), and tool lift (TL), on performance characteristics such as MRR, SR, tool wear rate (TWR) and crack density on the surface (SCD). Using the TOPSIS method for multi-objective optimisation, optimal parameters were determined to achieve maximum material removal rate and minimum tool wear. Mohankumar et al. [26] applied hybrid optimisation techniques, Entropy Weight Method (EWM), Taguchi approach, TOPSIS, and GRA for multi-criteria optimisation. The optimisation techniques are applied to evaluate the influence of Pulse ON time, Current, Voltage, and Pulse OFF time on SR, MRR, and Edge Wear Rate (EWR). Analysis of Variance (ANOVA) revealed significant impacts of parameters on SR, MRR, and EWR. Optimised parameters, based on TOPSIS and GRA, achieved a favourable balance: high MRR, minimal EWR, and acceptable SR, according to EWM-weighted priorities. After the confirmation experiments, the improvement in the closeness coefficient was 15%, and in the Grey Relational Grade (GRG), the improvement was 16%, thereby optimising SR, MRR, and EWR performance. More recently, Artificial Neural Networks (ANNs) have shown strong potential in predicting and optimising complex, non-linear relationships in composite materials, including wear, hardness, and strength. ANN is effective in modelling nonlinear and complex relationships, achieving high prediction accuracy. However, it requires a large amount of training data and it is more difficult to interpret—the “black box” approach [27,28]. A combination of ANOVA, regression, and ANN methods was performed by Kantheti et al. [29] for optimisation of critical parameters of Die-Sinking Electrical Discharge Machined (DS-EDM) AA7075–GR–B4C: Pulse on time (TON), pulse off time (TOFF), gap voltage (VS) and peak current (IP) that affect the MRR, Surface Roughness Rate (SRR) and Tool Wear Rate (TWR). The use of ANN, ANOVA, and regression analysis demonstrated a high correlation between the predicted and experimental values of MRR, SRR, and TWR, further validating the effectiveness of the optimised approach in achieving superior machining performance.

In contrast to previous studies, which typically rely on a single optimisation technique, this paper presents a novel hybrid approach that combines statistical, decision-making, and machine-learning methods. By integrating GRA with Taguchi design, AHP-TOPSIS for multi-criteria decision support, and ANN for predictive modelling, the research enables both multi-response optimisation and cross-validation of results. This approach enhances the reliability of parameter selection while significantly reducing the need for extensive experimental tests. The added predictive capability of ANN also provides insights into nonlinear relationships among input parameters and tribological properties.

This research focuses on the optimisation of the tribological behaviour—specifically wear loss (WL) and coefficient of friction (CoF) of AA2024–B4C composites under varying reinforcement content, milling time, and applied load. The proposed approach sets this research apart in terms of methodological depth, practical applicability, and experimental efficiency.

2  Experimental Procedure

2.1 Selection and Fabrication of Materials

In this study, AA2024 alloy powder with an average particle size of 25 µm was used as the composite matrix. The reinforcement was achieved by adding B4C powder (99.5% purity, average particle size of 5 µm) in amounts of 0, 10, and 15 wt.%. The selection of specific B4C ratios and milling times has been thoroughly discussed in a previous study. The mixtures underwent mechanical milling in a planetary ball mill at a speed of 400 rpm for 0, 15, and 25 h, using tungsten carbide balls (5 mm diameter) and containers (125 mL capacity), with a ball-to-powder weight ratio of 10:1 [30].

After milling, the powders were pre-compacted in a steel die under a pressure of 600 MPa to improve compaction and sinterability. The compacted samples were sintered in a vacuum at 560°C for 3 h, followed by additional uniaxial pressing under the same pressure using the hot-pressing method. The final cylindrical samples, with a diameter of 30 mm, were prepared for wear testing. More details on the process of obtaining these composite materials can be found in the literature [31].

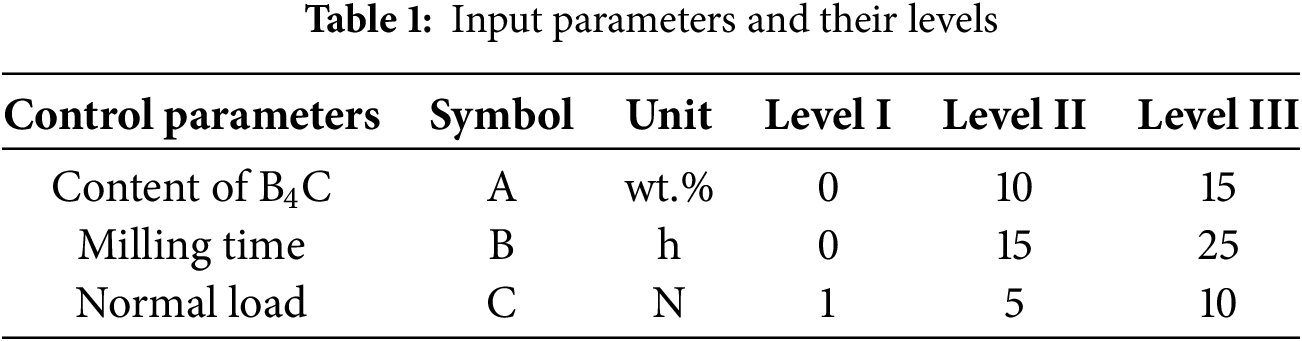
The control parameters selected for this research, namely B4C content (0, 10, and 15 wt.%), milling time (0, 15, and 25 h), and normal load (1, 5, and 10 N), were based on values frequently employed in the literature on AA2024–B4C composites processed by mechanical milling and powder metallurgy. B4C contents in the range of 10–15 wt.% have been widely investigated due to their demonstrated ability to significantly enhance mechanical properties such as hardness and microstructural uniformity without inducing excessive porosity or agglomeration [32]. Milling durations of up to 25 h were selected based on evidence showing that extended milling promotes a finer particle size distribution, better reinforcement dispersion, and improved mechanical performance due to increased work hardening and fragmentation [30]. Similarly, normal load values of 1 to 10 N are consistent with those used in standard tribological assessments to simulate varying wear conditions, with 10 N representing a commonly accepted upper range for evaluating the load-bearing performance of aluminium matrix composites [33].

2.2 Tribological Testing

Wear tests were conducted on samples produced by the hot-pressing method from AA2024–B4C composite powders, which were prepared with varying B4C contents and subjected to different milling durations. A Ducom brand universal wear testing device was used, and the ball-on-disc wear test method was applied according to ASTM G99-23 standard [34]. The tests were performed under loads of 1, 5, and 10 N, with a sliding speed of 0.1 m/s. Each sample was tested for a total sliding distance of 300 m. The WL was calculated by measuring the difference in the sample weights before and after testing. During the tests, the friction force values were obtained by analysing the average values supported by software tools [31].

2.3 Methodology of Applying Optimisation Methods

The tribological characterisation of new materials is essential for their successful industrial application while optimising the production parameters of composites play a crucial role in achieving the desired tribological properties. To accomplish this, the present study employs a hybrid optimisation strategy that combines three methods: Taguchi-GRA, AHP–TOPSIS, and ANN.

The Taguchi method is a robust statistical approach with a design of experiments that efficiently determines the influence of various parameters with a reduced number of experiments. When integrated with GRA, it becomes suitable for multi-response optimisation, allowing the conversion of multiple outputs, such as WL and CoF, into a single output known as the GRG, which helps identify optimal combinations of parameters for both output parameters simultaneously.

The AHP is a structured decision-making tool that uses pairwise comparisons to assign weights to evaluation criteria. These weights are then used in the TOPSIS method, which ranks each alternative based on its distance from the ideal and worst-case solutions. The combined AHP–TOPSIS approach enhances decision-making by providing a quantitative ranking of alternatives based on the importance of the criteria. By combining AHP and TOPSIS methods, an integrated approach is developed, which improves the decision-making process, especially in complex situations where a large number of criteria and alternatives are present. This combination enables the quantitative analysis and ranking of alternatives based on clearly defined priorities, which make transparent and well-argued decisions. The application of the AHP-TOPSIS method in combination with other applied methods enables a more precise selection of the most favourable solution, and at the same time verifies the obtained results.

ANNs are advanced machine learning models inspired by the human brain’s functioning. They are particularly effective in modelling complex, nonlinear relationships between input and output variables. In this study, an ANN is employed to predict the tribological properties (WL and CoF) based on the processing parameters (B4C content, milling time, and normal load), providing a reliable predictive model that complements the optimisation results.

This integrated optimisation approach enables multi-objective analysis, cross-verification of results, and predictive modelling—offering both accuracy and practical applicability. Compared to traditional single-method approaches, this methodology improves reliability of the parameter selection, reduces experimental costs, and enhances generalizability of the results.

The tribological characterisation of new materials is essential for their successful industrial application while optimising the production parameters of composites plays a crucial role in achieving the desired tribological properties. This study aims to produce composites based on AA2024 aluminium alloy, reinforced with 0, 10, and 15 wt.% B4C, using different milling times (0, 15, and 25 h) through high-energy ball milling and hot extrusion, to analyse their tribological efficiency and optimise the production parameters.

The methodology for applying optimisation methods involves creating a matrix using the Taguchi method, followed by ANOVA and S/N analysis for individual outputs, such as WL and CoF, which are essential for further multi-optimisation using Taguchi Grey Relational Analysis. Subsequently, the TOPSIS and AHP methods, along with ANN, will be applied for the multi-optimisation of tribological characteristics to determine the best solution for composite production intended for tribological applications.

The integration of Taguchi-GRA, AHP-TOPSIS, and ANN provides a comprehensive optimisation approach. Taguchi-GRA enables initial parameter screening and GRG-based optimisation. AHP-TOPSIS serves to validate these results through ranking based on weighted criteria. ANN offers a data-driven prediction model that generalizes the relationships and confirms the reliability of the selected parameters.

The aim of using optimisation methods is to significantly reduce production costs, minimise experimental expenses and drastically shorten the time required for conducting experiments. By utilising these methods, it is possible to efficiently identify optimal production parameters, not only optimising material quality but also enhancing the cost-effectiveness and productivity of the manufacturing process while reducing resources needed for testing and development.

2.4 Design of Experiments

In this study, three control parameters were chosen for the experimental design, as shown in Table 1. These parameters include the content of B4C (0, 10, and 15 wt.%), milling time (0, 15, and 25 h) and normal load (1, 5, and 10 N), each at three different levels. The chosen B4C content levels (0–15 wt.%) represent the practical reinforcement range for balancing mechanical strength and machinability. Milling time affects particle distribution and matrix refinement, while applied load directly influences wear behaviour. Based on these selected factors and their levels, a Taguchi L27 matrix was developed to investigate the tribological behaviour of aluminium composites. A total of 27 experiments were conducted, as presented in Table 2, to evaluate the effects of these parameters on the material’s tribological performance. The chosen B4C content levels (0–15 wt.%) represent the practical reinforcement range for balancing mechanical strength and machinability. Milling time affects particle distribution and matrix refinement, while applied load directly influences wear behaviour.

The experimental results were converted into a signal-to-noise (S/N) ratio, where the signal represents the mean value and the noise represents the standard deviation. Taguchi uses this ratio to assess quality characteristics through three loss functions: “smaller is better”, “larger is better” and “nominal is best”. In this study, the focus is on minimization, so the S/N ratio for achieving minimal WL and CoF was determined using the “smaller is better” criterion, calculated with the following equation [1,35,36]:

S/N=−10log⁡1n(∑y2)(1)

where y is experimental results and n is the number of experiments. The obtained results of WL and CoF were converted into the S/N ratio.

3  Results and Discussion

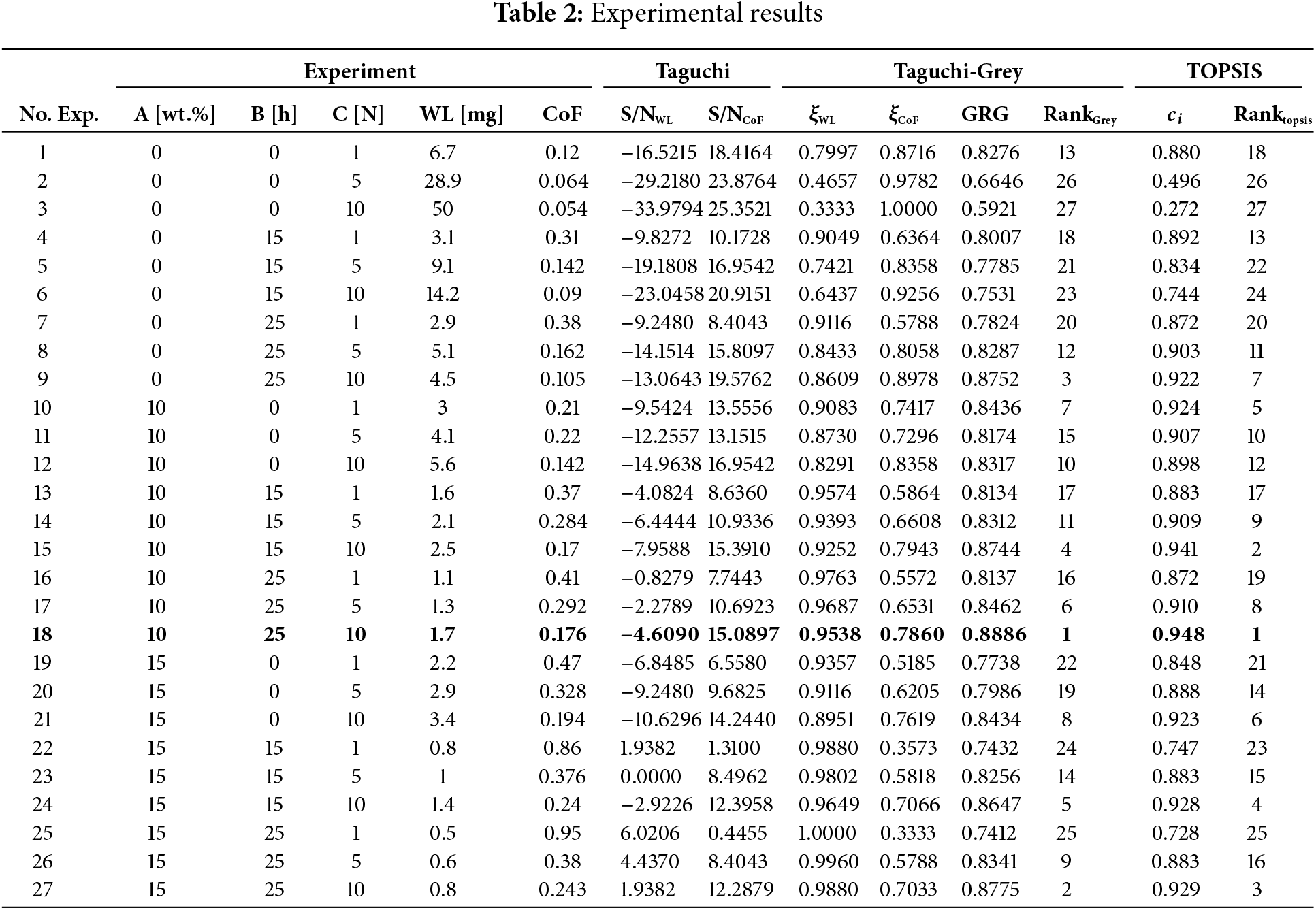
The tribological test results obtained from the 27 experimental combinations designed using the Taguchi L27 orthogonal array are summarized in Table 2. These values of WL and CoF were utilised in subsequent optimisation analyses using Taguchi-GRA, AHP-TOPSIS, and ANN models.

3.1 Analysis of S/N Ratios and Taguchi–Grey Relational Analysis

The interpretation of the S/N ratio results is independent of the selected quality characteristic. The ideal parameter setting is achieved by considering a higher S/N ratio, which indicates better quality characteristics, i.e., a smaller variance of the output characteristic around the desired value [37].

The results obtained from the S/N ratio analysis, shown in Table 3, clearly indicate that parameter A (B4C content) has the most significant influence on both observed outputs, WL and CoF. For WL, the second most important parameter is B (milling time), while the third is C (normal load). On the other hand, for CoF, the second-ranked parameter is C (normal load), while parameter B (milling time) is ranked third. The optimal combination of parameters for achieving the minimum values of WL and CoF can also be derived from Table 3. For the minimum WL, the optimal combination is A3B3C1, while for the minimum CoF, it is A1B1C3. Specifically, the minimum WL is achieved with 15 wt.% B4C, 25 h of milling, and a load of 1 N, while the minimum CoF is achieved with 0 wt.% B4C, 0 h of milling, and a load of 10 N.

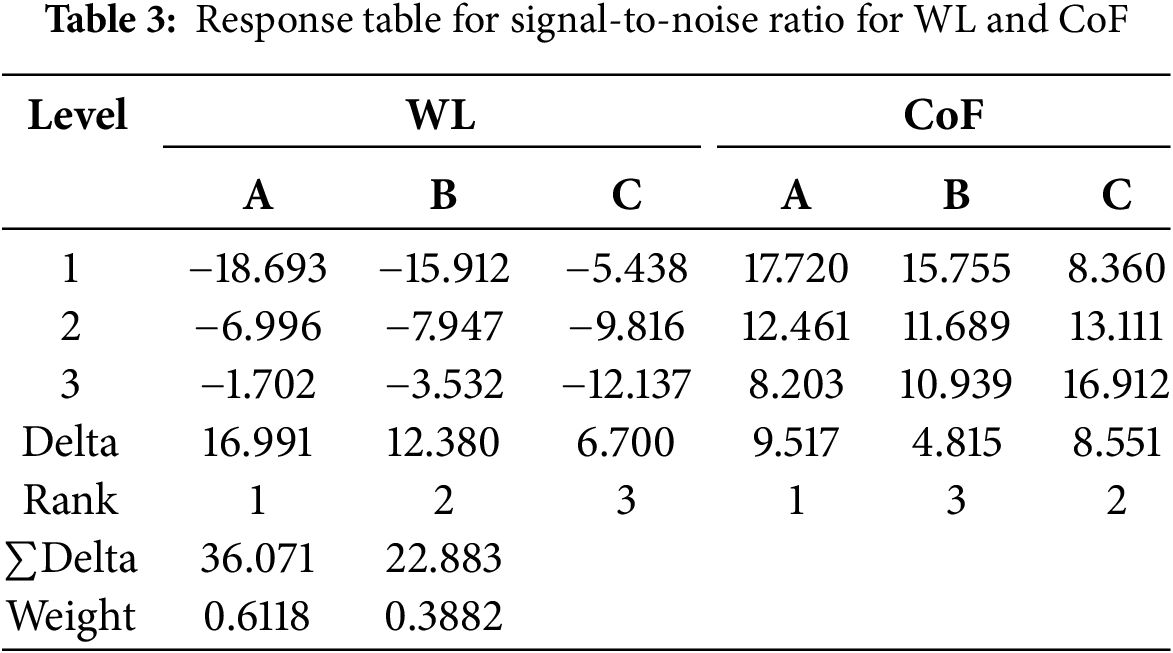
A more detailed ANOVA analysis could precisely determine the individual percentage influence of each parameter; however, since the objective of this research is multi-criteria optimisation, this type of analysis will not be presented. The S/N ratio analysis is crucial because it enables the definition of weight coefficients, as shown in Table 3, which will be of great importance for further analysis.

Although the Taguchi method was initially intended for single-response optimisation, multi-objective optimisation is made possible by integrating it with the GRA. Taguchi-GRA analysis was employed in this study to optimise the tribological properties of the composites, serving as a powerful tool for multi-criteria optimisation. This method enables the simultaneous analysis of multiple output parameters, integrating the benefits of the Taguchi method, known for its efficient process optimisation, with grey relational analysis, which facilitates the ranking and comparison of different variants based on multiple factors. Taguchi-GRA enables the identification of optimal process parameters, such as reinforcement content, milling time, and applied load, to achieve a minimal WL and an optimal CoF.

In this study, the responses (WL and CoF) were normalised and combined into a single Grey Relational Grade (GRG) using weighted Grey Relational Coefficient (GRC). This enables the optimisation of multiple performance criteria, transforming the problem into a single quality characteristic for analysis.

The optimisation process in GRA analysis involves the following steps: normalisation of the experimental results, calculation of deviations from normalised values, determination of GRC, and calculation of GRG. The experimental data are normalised within a range of 0 to 1, depending on the nature of the output parameters. There are three approaches to normalisation: “smaller is better”, “larger is better”, and “nominal is best”. In this study, the “smaller is better” method was applied for both output parameters, as the goal was to minimise the observed values.

To calculate the GRC-ξi, it is necessary first to calculate the absolute values of the difference using the normalised values for quality characteristics “smaller is better”. After obtaining the absolute value of the difference, the GRC is calculated by the corresponding equation [38]:

ξi(k)=Δmin+ζΔmaxΔ0i(k)+ζΔmax,(2)

where:

Δmin and Δmax—the minimal and maximal absolute values of the difference;

ζ—coefficient of difference, 0≤ζ≤1 (usually φ=0.5 [38]).

GRG-γi can be calculated using equations [37,39]:

γi=∑k=1nwkξi(k) or γi=1n∑k=1nξi(k),(3)

where: n represents the number of performance characteristics, wk denotes the weighting coefficients, and sometimes it is presumed that both outputs have the same impact on output and wk=0.5, but it is possible to calculate weighting coefficients and thus the impact of each output on the process characteristic, based on S/N using the equation:

wk=∑j=1pDeltai,j∑i=1m∑j=1pDeltai,j.(4)

By this approach, multi-output problems are effectively converted into single-output. The estimated GRG determines the overall performance characteristic for a multi-response process. A higher GRG value signifies a closer approximation to the optimum. The optimal parameter values can be identified using the Taguchi method, which focuses on maximizing the GRG.

Accurately determining the weighting coefficients for multiple responses (WL and CoF) is essential for obtaining reliable results in GRA analysis. The S/N ratio analysis provided the weighting coefficients for WL and CoF, which were found to be 0.6118 and 0.3882, respectively (Table 3). Using these coefficients and Eqs. (3) and (4), the final equation for the GRG was:

γ=0.6118⋅ξWL+0.3882⋅ξCoF(5)

where:

ξWL—GRC for WL;

ξCoF—GRC for CoF.

The trade-off between WL and CoF was addressed by assigning weights to each based on their signal-to-noise ratio deltas. WL was assigned a weight of 0.6118 and CoF 0.3882, reflecting its higher impact on tribological performance. These weights helped balance the optimisation objectives, ensuring that neither output dominated the decision-making process.

For a clear interpretation of the results, the grey relational analysis results are presented in the form of GRG, and its ranks are shown in Table 2. For further optimisation, ANOVA analysis was applied.

To determine the optimal parameter levels, an ANOVA analysis was conducted at a 95% confidence level. The results of this analysis are shown in Table 4, while the S/N ratio results are presented in Table 5 and illustrated in Fig. 1.

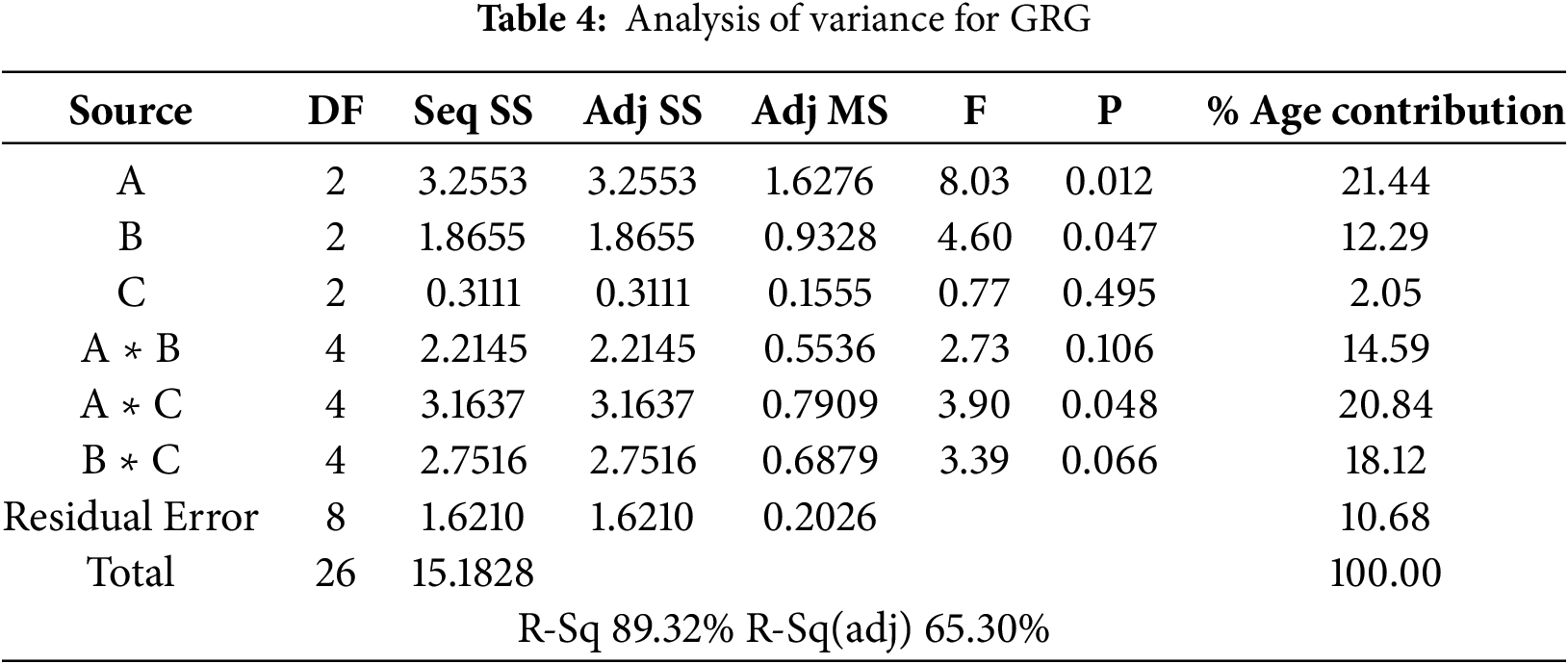
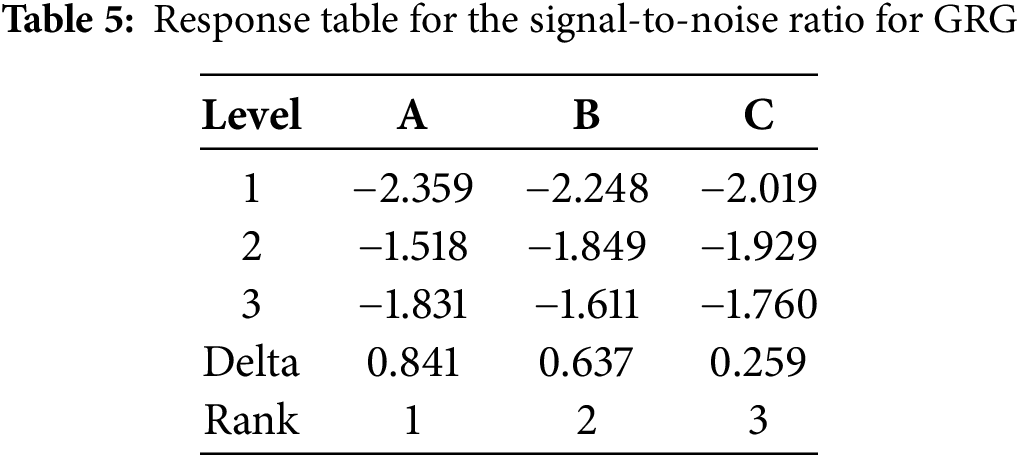
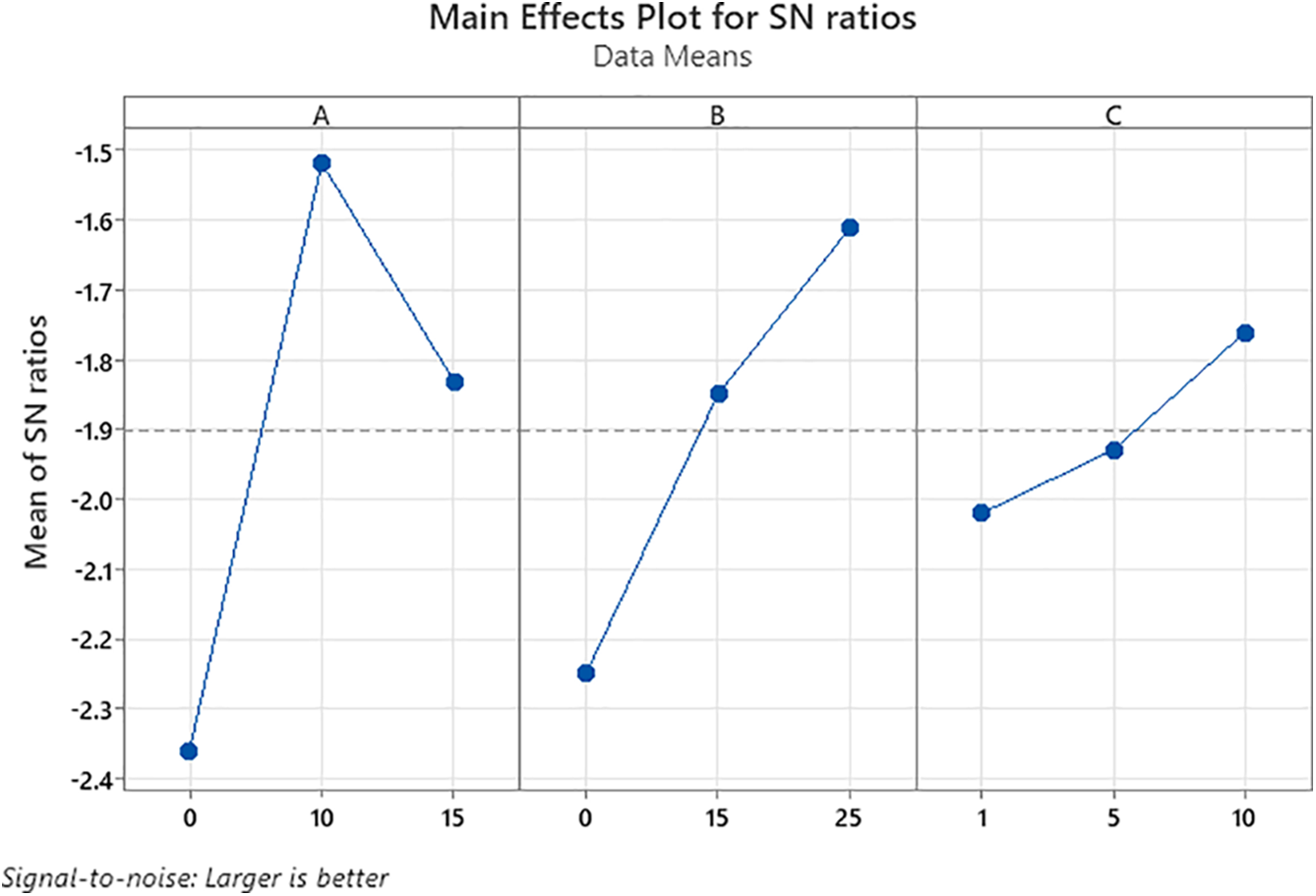
Figure 1: Response plot for GRG

Based on the analysis of the multi-criteria output parameter (GRG), it was determined that the B4C content has the most significant influence, at 21.44%, followed by milling time at 12.29%. In contrast normal load has the most negligible influence, at 2.05%. When examining the interactions between parameters, all interactions show a significant impact: A ∗ B with 14.59%, A ∗ C with 20.84%, and B ∗ C with 18.12%. The S/N ratio analysis for GRG is shown in Table 4. The p-values are less than 0.05 for the parameters B4C content and milling time (95% confidence level). Based on the results from Table 5 and Fig. 1, the optimal combination of parameters that accounts for both output parameters was identified. The combination A2B3C3 precisely represents the following values: 10 wt.% B4C content, 25 h of milling time, and a normal load of 10 N.

The need for applying ANOVA analysis arises from the goal of identifying which process parameter has the most dominant impact on the tribological characteristics of AA2024–B4C composites. Given the complexity of the interactions between factors, it is necessary to use a combined approach that includes the Taguchi method and GRA analysis. This approach enables the simultaneous consideration of multiple output parameters and the identification of the optimal combination of process parameters that results in the best tribological performance of the composite.

Based on the obtained results, it was determined that the most favourable combination of parameters is A2B3C3, meaning that the optimal conditions for the production of AA2024–B4C composites are achieved by selecting a B4C reinforcement content of 10 wt.%, using a milling time of 25 h and testing the tribological characteristics under a normal load of 10 N. This combination of parameters allows for the minimization of WL and CoF, significantly improving the composite’s performance under operating conditions.

Additionally, it was found that this combination of parameters fully matches the results of the GRA analysis, where it was ranked as the most optimal (rank 1 in Table 2—experiment 18), further confirming its validity and significance in the context of multi-criteria optimisation of the tribological characteristics of the composite material.

3.2 TOPSIS Analysis

In the field of MCDM, several different methods have been developed to find optimal solutions based on given criteria. Two of the most commonly used MCDM methods are the TOPSIS methods [40,41].

The AHP is a multi-criteria decision-making method used to address complex problems with numerous alternatives and criteria. Thomas Saaty developed it in the 1980s. The principle of the method is based on the hierarchical decomposition of a complex problem into smaller and clearer components. It is applied in almost all branches of industry, as well as in combination with other optimisation methods. It is most often used in combination with the TOPSIS method to properly define the weights of the given criteria [42–44].

The TOPSIS method is a multi-criteria decision-making approach designed to rank and select the most optimal solution by considering multiple criteria, developed by Hwang and Yoon. It is applied in various industries, including project management, financial analysis, marketing, and engineering. In the TOPSIS method, alternatives are ranked based on their distance from the positive ideal solution and the negative ideal solution. The distance is calculated using Euclidean distance, where the most optimal alternative is the one closest to the positive ideal solution and farthest from the negative ideal solution [43].

In scientific research, the combination of the TOPSIS method with the AHP method is common, aiming to achieve the most precise results. This approach is particularly beneficial in industries where decisions need to be made based on multiple factors, such as machining, material science, logistics, and engineering design. In summary, AHP determines the importance of the criteria, while TOPSIS uses this information to objectively rank alternatives, providing a comprehensive and reliable analysis for making optimal decisions.

The first step in implementing the TOPSIS method is to form a decision matrix based on the selected alternatives and criteria. After forming the decision matrix, the next step is to calculate the normalised decision matrix based on Eq. (6) [43]:

rij=xij∑i=1mxij2(6)

Defining the weights of the criteria and creating the weighted normalised decision matrix is the third step in the TOPSIS method. The weights of the criteria are determined using the AHP method, while the weighted normalised decision matrix is obtained by applying Eq. (7) [43]:

vij=wj⋅rij(7)

By following several basic steps of the AHP method, the definition of criterion weights was approached [40,42,43].

The formation of the comparison matrix (Eq. (8) [45]) represents the first step in the AHP method and is conducted using Saaty’s scale (Table 6).

A=[aij]=[1a12⋯a1n1a121⋯a2n⋯⋯⋯⋯1a1n1a2n⋯1](8)

Next is the calculation of the normalised weight (wj) using Eqs. (9) and (10) [45]:

wj=GMi∑i=1nGMi(9)

GMi=(∏i=1naij)1n(10)

Determining the maximum eigenvalue (λmax) of the comparison matrix, as well as the consistency index, is done using the following equations [45]:

CI=(λmax−n)(n−1)(11)

λmax=∑i=1ncvin,i=1,2,…,n and cvi=(A⋅wj)wj(12)

The random consistency index (RI) (Table 7) is calculated based on the data presented in Table 2.

The final step in the AHP method is calculating the consistency ratio (CR) using Eq. (13) [43]:

CR=CIRI(13)

If the CR value is 0.1 or lower, the determined weights of the criteria are accepted as valid. If the CR value is greater than 0.1, the criteria comparison is revisited and the remaining steps are repeated.

For the application of the TOPSIS method, the Taguchi L27 matrix (Table 2) was utilised, which was specifically designed for experimental and tribological testing purposes. The weights of the selected criteria were defined using the AHP method, based on Saaty’s scale (Table 6). A value of 2 was chosen from Saaty’s scale, resulting in the criteria weights of 62% for WL and 38% for the CoF. These weights correspond to those obtained using the Taguchi Grey method, thereby verifying of the results achieved by the Taguchi Grey method.

After forming the L27 matrix with the input parameters and criteria, the calculation of the decision matrix, the normalised decision matrix, and the definition of the Positive Ideal Solution (PIS) and Negative Ideal Solution (NIS) was carried out. PIS and NIC for WL were 0.005 and 0.501, respectively, while for CoF, PIS and NIC were 0.011 and 0.196, respectively.

After defining the PIS and NIS, the distance of each alternative from the positive ideal solution and the negative ideal solution was calculated using the Euclidean distance method. Subsequently, the relative closeness to the ideal solution was determined. Based on the ci values, the alternatives were ranked in descending order. Rank 1 is assigned to the alternative whose ci value is closest to 1. The obtained values are presented in Table 2.

Based on Table 2, it can be concluded that the most optimal combination of parameters is alternative 18 (experiment 18), with the following parameters: B4C content of 10 wt.%, milling time of 25 h and a load of 10 N, which results in a WL of 1.7 mg and CoF of 0.176. This combination achieved the best trade-off between minimizing WL and CoF, as it was verified by Taguchi-GRA and AHP-TOPSIS

The optimal reinforcement content of 10% B4C was also determined by Abdelhady et al., who used the response surface methodology (RSM) to optimise parameters such as load and sliding distance to achieve optimal performance in terms of wear resistance and CoF [20].

On the other hand, the most unfavourable alternative is alternative 3 (experiment 3), ranked 27, with the following parameters: a B4C concentration of 0%, a milling time of 0 h, and a load of 10 N, where WL is 50 mg, and CoF is 0.054.

From the above, it can be concluded that the presence of the B4C reinforcement significantly affects the tribological characteristics of the tested composite. Increasing the B4C reinforcement concentration resulted in a reduction in the wear of the observed materials.

These findings have significant practical implications, particularly in industrial applications where high wear resistance and stable tribological characteristics are crucial for the longevity and efficiency of components. By properly selecting processing parameters, an optimal balance between wear and friction can be achieved, thereby enhancing the material’s overall performance in real working conditions. The consistency of the results obtained through the Taguchi Grey and TOPSIS methods further confirms that the optimal parameter values have been reliably determined and can serve as guidelines for further research and industrial applications.

AHP-TOPSIS does not yield a functional mathematical optimum but instead ranks discrete alternatives based on their proximity to the ideal solution. In this study, AHP-TOPSIS validated the GRG-based Taguchi-GRA results by independently identifying the same optimal parameter combination.

Due to the fundamental differences in decision-making logic, some divergence in ranking is expected between the Taguchi-GRA and TOPSIS methods. However, both methods identified a consistent optimal condition, confirming the reliability of the selected parameters.

3.3 ANN Analysis

ANNs represent another advanced method used in this research. ANNs are particularly effective in modelling complex relationships between input and output parameters. In this study, ANNs were used for the simultaneous analysis of two output parameters: WL and CoF. This approach enables the prediction of the composite’s tribological performance based on variable input parameters, such as B4C content, milling time, and applied load, providing additional reliability in the optimisation process. The ANNs with different architectures were trained, and the network with 3-10-2 architecture had the highest overall regression coefficient, which was 0.99918 (Fig. 2). In the input layer, there were three input parameters: B4C weight percentage, milling time, and normal load to evaluate their effects on two output parameters (output layer): WL and CoF. The network type is feed-forward backpropagation with Levenberg-Marquardt training function, Mean Squared Error performance function, and hyperbolic tangent sigmoid transfer function. The performance graph of the trained network is shown in Fig. 3, while the comparative view of experimental results and ANN prediction for WL and CoF is presented in Fig. 4.

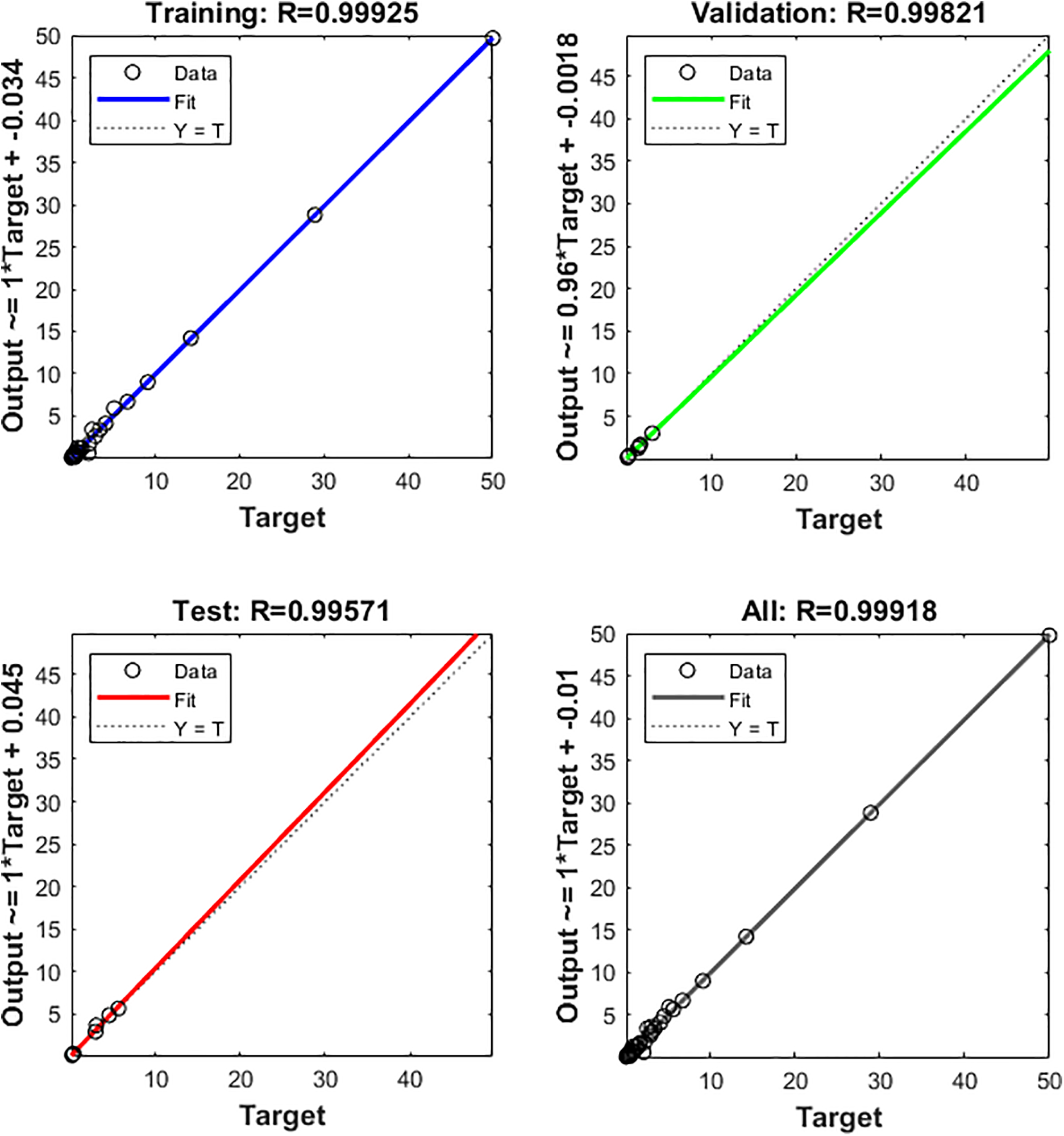
Figure 2: Regression coefficient for 3-10-2 ANN

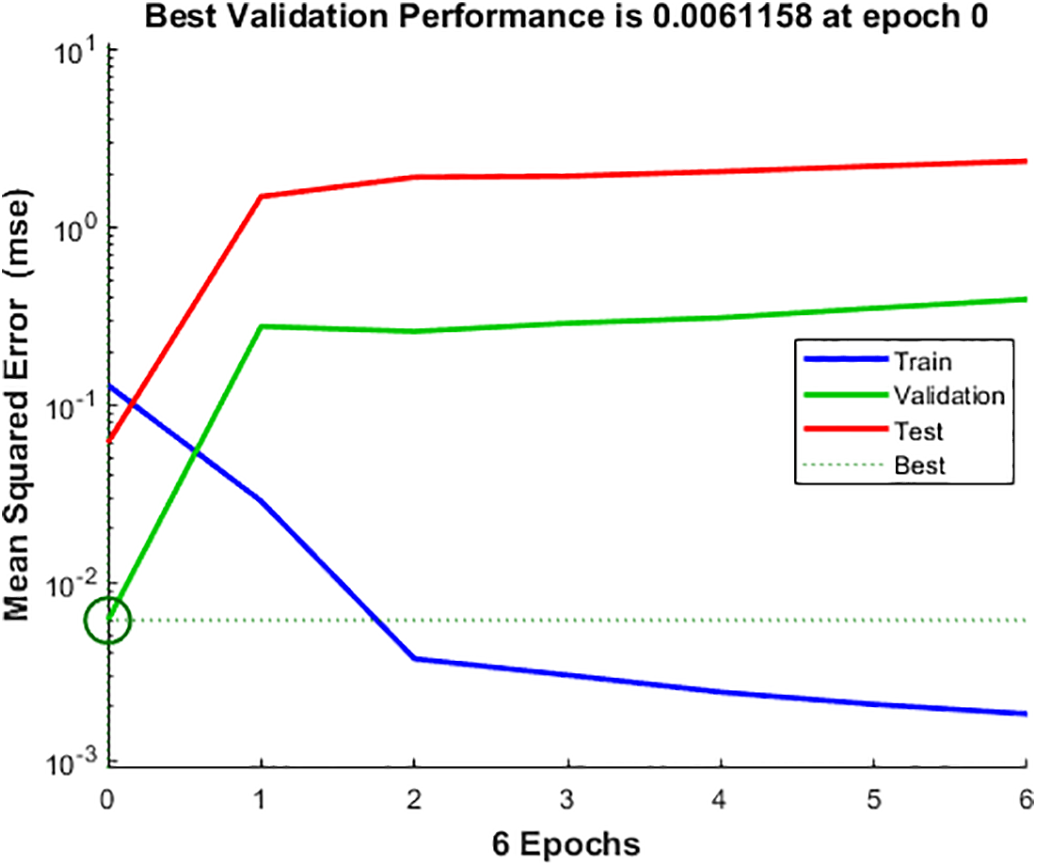
Figure 3: Network performance graph

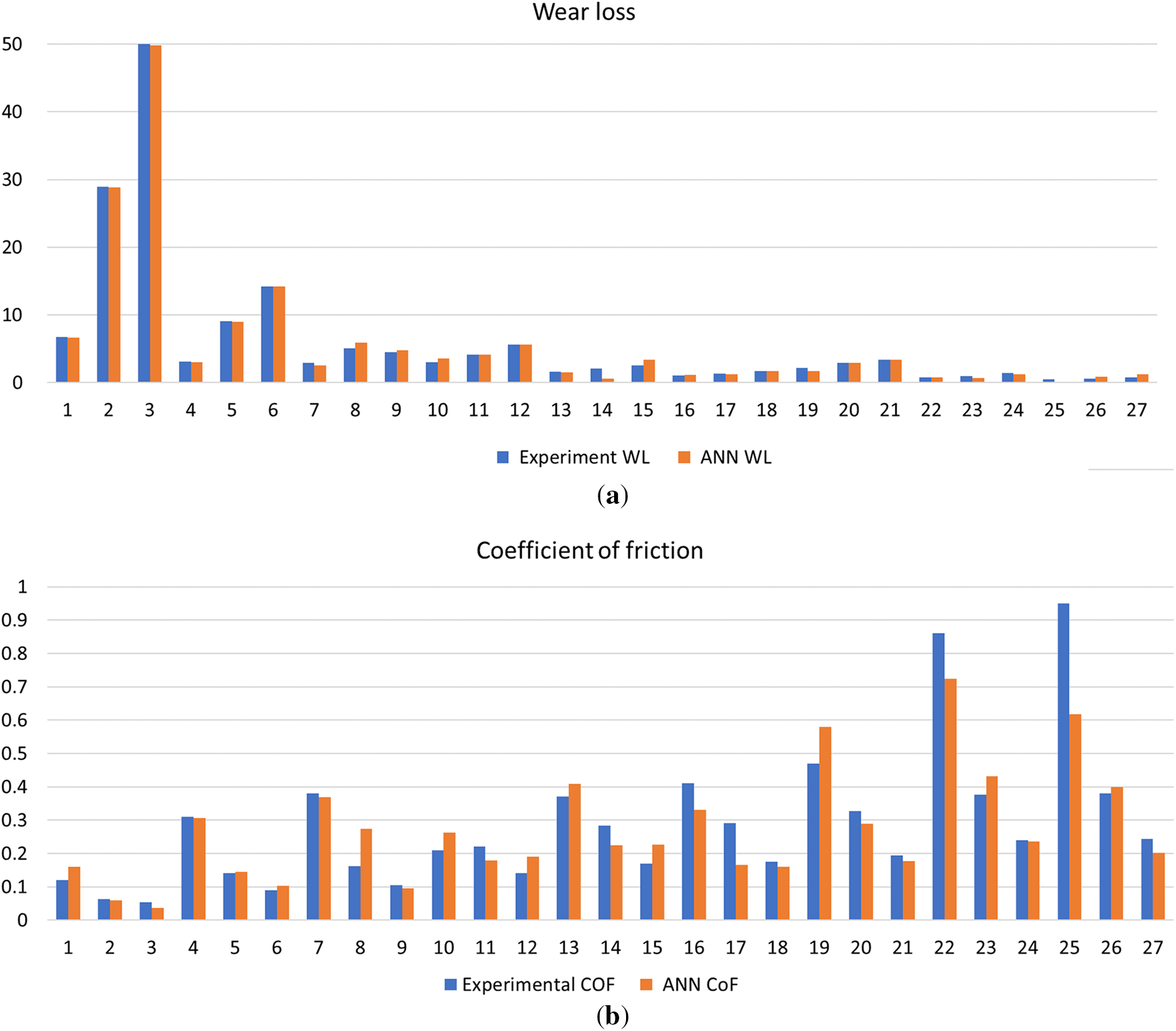
Figure 4: Comparative presentation of the results of the experiment and ANN prediction for (a) WL and (b) CoF

During the training of the neural network, signs of overfitting were observed, as evidenced by the performance plot (Fig. 3). In particular, the error curve shows an increase in validation and test errors after a certain number of epochs despite a continued decrease in training errors. This behaviour suggests that the model begins to overfit the training data and loses some of its generalisation ability. The likely causes of this behaviour include the relatively small dataset and the complexity of the network architecture.

However, based on the regression analysis presented in Fig. 2, where the regression coefficients (R) exceed 0.95 for the training, validation and testing phases, it can be concluded that the overfitting effect is not severe. Furthermore, statistical validation metrics such as Mean Squared Error (MSE), Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Coefficient of Determination (R2), were calculated using Eqs. (14)–(17) [47,48], to confirm that the model still performs reliably. The results of the validation are presented in Table 8. The MSE for WL was 0.19457, and for CoF it was 0.00741 indicating that the ANN has a more reliable prediction for CoF (the lower the value of MSE is the more reliable the prediction model).

MSE=1n∑i=1n(yi−yi^)2,(14)

MAE=1n∑i=1n|yi−yi^|,(15)

RMSE=MSE=1n∑i=1n(yi−yi^)2,(16)

R2=1−∑1n(yi−yi^)2∑1n(yi−y¯i)2,(17)

where: yi and yi^ are experimental and predicted values, respectively, y¯i is the mean value of the actual experimental values, and n is the number of experiments.

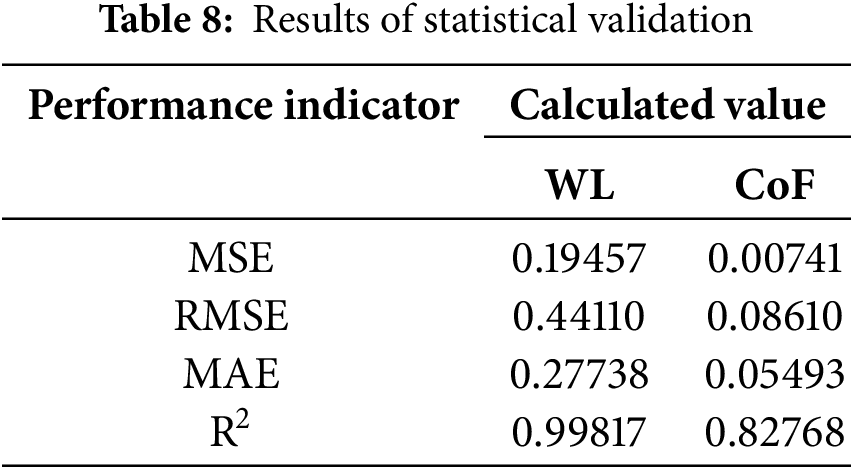
Based on the displayed performance indicators, it can be concluded that the model predicts WL very precisely, which confirms the high R2 (0.99817). On the other hand, the CoF prediction yields a lower R2 value of 0.82768, indicating acceptable predictive accuracy for this output. This difference may be due to the more direct and stable relationship between WL and the selected input parameters, higher non-linearity in the behaviour of CoF, the influence of factors not included in the model, or the difference in data ranges for individual outputs.

Despite this, the ANN model still achieved acceptable performance for CoF prediction, indicating that the selected parameters play a substantial, though not exclusive, role in frictional behaviour. Including additional descriptors such as surface roughness, real contact area, or in situ temperature could further improve model precision in future studies. Low values of MSE, RMSE, and MAE for both outputs confirm that the model performs well in minimizing prediction errors.

The comparison between experimental results and ANN predictions for WL shows a strong correlation. For the CoF, due to its more complex nature and values between 0 and 1, the deviations between experimental results and ANN predictions are more pronounced.

Although these methods show a good correlation with the experimental results, they have some limitations. The GRA and AHP–TOPSIS methods, while effective for multi-criteria decision-making, rely on the choice of normalisation techniques and subjective or semi-subjective weighting of output criteria. These factors can influence the final ranking and may vary if different normalisation or weighting are used. Moreover, GRA assumes independence between criteria, which may not always be true in tribological systems. ANNs offer high predictive accuracy, particularly for non-linear relationships, but they are also sensitive to overfitting, especially when trained on relatively small datasets. Their prediction ability might be limited if applied to significantly different material systems or operating conditions.

In summary, while previous investigations often apply only one optimisation method or focus on individual features, this investigation presents a comprehensive optimisation approach. It utilizes the L27 design of experiments, the Taguchi-GRA method for multi-criteria evaluation, AHP-TOPSIS for ranking and confirmation of results, and ANN for behaviour prediction. This approach not only improves the accuracy and reliability of the optimisation, but also significantly reduces the need for additional experiments, thus saving time and resources.

4  Conclusions

This research has successfully optimised the tribological characteristics of AA2024–B4C composites by employing a combination of advanced optimisation techniques, including Taguchi-GRA, TOPSIS, and ANN. Through systematic variation of key parameters, such as B4C content, milling time, and applied load, the study revealed their significant influence on crucial performance metrics including WL and the CoF.

The Taguchi–GRA method identified the optimal parameter combination (10 wt.% B4C, 25 h milling time, and 10 N load), which provided the most favourable trade-off between minimizing wear and reducing friction. This result was independently verified using the AHP–TOPSIS multi-criteria decision-making approach, further validating the robustness of the optimisation. Moreover, the application of ANN models ensured accurate prediction of tribological performance, with high coefficients of determination confirming the generalizability of the findings.

This hybrid optimisation framework not only improved the wear resistance and overall tribological behaviour of the composites but also demonstrated the potential for reducing experimental effort and production costs. The enhanced predictive capability offered by ANN supports more efficient design and performance adjustments of metal matrix composites.

This research not only demonstrates the effectiveness of multi-criteria optimisation in improving the efficiency, wear resistance, and overall quality of the composites but also highlights the potential for reducing production costs and accelerating experimental processes. The integration of ANN further enhanced the predictive accuracy of the output parameters, enabling more precise optimisation of the material’s performance. The findings have great practical significance, particularly for industrial applications that require high wear resistance and stable tribological properties. However, it is worth noting that real-world validation under industrial operating conditions was beyond the scope of this study. Future work will focus on large-scale testing and benchmarking of the optimised composites in actual automotive and aerospace tribological systems to fully confirm their practical applicability.

The optimised AA2024-B4C composites show strong potential for use in high-performance, wear-critical applications, particularly in the automotive and aerospace industries. The findings lay a solid foundation for future research aimed at developing composites tailored to specific engineering requirements with improved durability, efficiency, and reliability.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: Conceptualization, Slavica Miladinović, Sandra Gajević and Blaža Stojanović; methodology, Onur Güler and Serdar Özkaya; software, Slavica Miladinović, Sandra Gajević and Jelena Jovanović; validation, Slavica Miladinović, Sandra Gajević and Jelena Jovanović; formal analysis, Onur Güler and Serdar Özkaya; investigation, Slavica Miladinović, Sandra Gajević and Jelena Jovanović; resources, Onur Güler and Serdar Özkaya; data curation, Onur Güler and Serdar Özkaya; writing—original draft preparation, Slavica Miladinović and Sandra Gajević; writing—review and editing, Onur Güler, Serdar Özkaya and Blaža Stojanović; supervision, Blaža Stojanović. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data is contained in the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Satish Kumar T, Shalini S, Suganya Priyadharshini G, Raghu R. Parametric optimization of dry sliding wear behavior of A356 alloy-zircon composites. Tribol Ind. 2022;44(4):719–30. doi:10.24874/ti.1348.08.22.11. [Google Scholar] [CrossRef]

2. Akgümüş Gök D, Bayraktar C, Hoşkun M. A review on processing, mechanical and wear properties of Al matrix composites reinforced with Al2O3, SiC, B4C and MgO by powder metallurgy method. J Mater Res Technol. 2024;31(3):1132–50. doi:10.1016/j.jmrt.2024.06.110. [Google Scholar] [CrossRef]

3. Şenel MC, Kanca Y, Gürbüz M. Reciprocating sliding wear properties of sintered Al-B4C composites. Int J Miner Metall Mater. 2022;29(6):1261–9. doi:10.1007/s12613-020-2243-5. [Google Scholar] [CrossRef]

4. Baradeswaran A, Elaya Perumal A. Influence of B4C on the tribological and mechanical properties of Al7075-B4C composites. Compos Part B Eng. 2013;54(1):146–52. doi:10.1016/j.compositesb.2013.05.012. [Google Scholar] [CrossRef]

5. Prabha S, Raghavendra S, Koti V, Patil S. Fabrication and investigation of characteristics of Al2014-B4C composites using liquid metallurgy technique. J Inst Eng Ind Ser D. 2025;8(1):1–13. doi:10.1007/s40033-025-00884-z. [Google Scholar] [CrossRef]

6. Ubaid F, Matli PR, Shakoor RA, Parande G, Manakari V, Mohamed AMA, et al. Using B4C nanoparticles to enhance thermal and mechanical response of aluminum. Materials. 2017;10(6):621. doi:10.3390/ma10060621. [Google Scholar] [PubMed] [CrossRef]

7. Beder M. The effect of high B4C ratio on the improvement of mechanical properties and wear resistance of Al2024/B4C composites fabricated by mechanical milling-assisted hot pressing. Ceram Int. 2025;51(7):9528–47. doi:10.1016/j.ceramint.2025.01.287. [Google Scholar] [CrossRef]

8. Gaylan Y, Avar B, Panigrahi M, Aygün B, Karabulut A. Effect of the B4C content on microstructure, microhardness, corrosion, and neutron shielding properties of Al-B4C composites. Ceram Int. 2023;49(3):5479–88. doi:10.1016/j.ceramint.2022.10.071. [Google Scholar] [CrossRef]

9. Bayrak Y, Kisasoz A, Sezer R. Production and characterization of B4C content-dependent aluminum matrix composites fabricated via hot pressing. J Mater Eng Perform. 2025;34(2):1607–18. doi:10.1007/s11665-023-09093-9. [Google Scholar] [CrossRef]

10. Salih A, Zulkifli R, Azhari C, Shanmugam V, Al Shdaifat M. Optimization impact properties for biocomposites using taguchi method. J Mod Polym Chem Mater. 2022;1(1):3. doi:10.53964/jmpcm.2022003. [Google Scholar] [CrossRef]

11. Girish BM, Siddesh HS, Satish BM. Taguchi grey relational analysis for parametric optimization of severe plastic deformation process. SN Appl Sci. 2019;1(8):937. doi:10.1007/s42452-019-0982-6. [Google Scholar] [CrossRef]

12. Bharath L, Sreenivasa Reddy M, Girisha HN, Balakumar G. Optimization of ductility and yield strength on Al2024/B4C composite material using Taguchi Technique. IOP Conf Ser Mater Sci Eng. 2021;1055(1):012117. doi:10.1088/1757-899x/1055/1/012117. [Google Scholar] [CrossRef]

13. Sunil K, Kumar R, Ratnam C, Subrahmanyam B, Rao A. Fabrication and optimization of machining parameters on Al 2024-Gr-B4C hybrid MMCS during machining process. Int J Appl Eng Res. 2018;13(12):10551–8. [Google Scholar]

14. Gonfa BK, Sinha D, Vates UK, Badruddin IA, Hussien M, Kamangar S, et al. Investigation of mechanical and tribological behaviors of aluminum based hybrid metal matrix composite and multi-objective optimization. Materials. 2022;15(16):5607. doi:10.3390/ma15165607. [Google Scholar] [PubMed] [CrossRef]

15. Ghosh S, Sahoo P, Sutradhar G. Tribological performance optimization of Al-7.5% SiCp composites using the taguchi method and grey relational analysis. J Compos. 2013;2013(1–2):274527. doi:10.1155/2013/274527. [Google Scholar] [CrossRef]

16. Barragán-Trinidad M, Guadarrama-Pérez O, Guillén-Garcés RA, Bustos-Terrones V, Trevino-Quintanilla LG, Moeller-Chávez G. The grey-taguchi method, a statistical tool to optimize the photo-Fenton process: a review. Water. 2023;15(15):2685. doi:10.3390/w15152685. [Google Scholar] [CrossRef]

17. Kandala AVUK, Solomon DG, Arulraj JJ. Advantages of taguchi method compared to response surface methodology for achieving the best surface finish in wire electrical discharge machining (WEDM). JMechE. 2022;19(1):185–99. doi:10.24191/jmeche.v19i1.19696. [Google Scholar] [CrossRef]

18. Kumar R, Reji M. Response surface methodology (RSMan overview to analyze multivariate data. Indian J Microbiol Res. 2023;9(4):241–8. doi:10.18231/j.ijmr.2022.042. [Google Scholar] [CrossRef]

19. Kumar TS, Raghu R, Priyadharshini GS, Čep R, Kalita K. A study on microstructural, mechanical properties, and optimization of wear behaviour of friction stir processed AZ31/TiC composites using response surface methodology. Sci Rep. 2024;14(1):18729. doi:10.1038/s41598-024-69348-w. [Google Scholar] [PubMed] [CrossRef]

20. Abdelhady SS, Nabhan A, Zoalfakar SH, Elbadawi RE. Modeling of wear performance and surface roughness of AA6061-T6/B4C composite under dry sliding conditions by RSM. Proc Inst Mech Eng Part E J Process Mech Eng. 2024;235:09544089241276692. doi:10.1177/09544089241276692. [Google Scholar] [CrossRef]

21. Takele YF, Woldeyohannes AD. Optimal material selection for high temperature tribological application: an integrated multi criteria decision study. Discov Mater. 2025;5(1):33. doi:10.1007/s43939-025-00209-7. [Google Scholar] [CrossRef]

22. Madanchian M, Taherdoost H. A comprehensive guide to the TOPSIS method for multi-criteria decision making. Sustain Social Dev. 2023;1(1):2220. doi:10.54517/ssd.v1i1.2220. [Google Scholar] [CrossRef]

23. Dhoria SH, Subbaiah KV, Rao VDP. Multi-objective parametric optimization on WEDM of hybrid Al6351/SiC/gr composites using NSGA-II. J Inst Eng Ind Ser D. 2025;106(1):277–90. doi:10.1007/s40033-023-00632-1. [Google Scholar] [CrossRef]

24. Sur G, Erkan Ö. Surface quality optimization of CFRP plates drilled with standard and step drill bits using TAGUCHI, TOPSIS and AHP method. Eng Comput. 2021;38(5):2163–87. doi:10.1108/ec-04-2020-0202. [Google Scholar] [CrossRef]

25. Bodukuri AK, Kesha E. Multi-attribute optimization of EDM process parameters for machining of SiC and B4C particle reinforced Al6061 metal matrix composite adopting topsis method. Int J Adv Technol Eng Explor. 2021;8(79):735–52. doi:10.19101/ijatee.2021.874132. [Google Scholar] [CrossRef]

26. Mohankumar V, Kumarasamy SP, Palanisamy S, Kuriakose Mani A, Durairaj TK, Sillanpää M, et al. Process parameters optimization of EDM for hybrid aluminum MMC using hybrid optimization technique. Heliyon. 2024;10(15):e35555. doi:10.1016/j.heliyon.2024.e35555. [Google Scholar] [PubMed] [CrossRef]

27. Liang Y, Wei X, Peng Y, Wang X, Niu X. A review on recent applications of machine learning in mechanical properties of composites. Polym Compos. 2025;46(3):1939–60. doi:10.1002/pc.29082. [Google Scholar] [CrossRef]

28. Mijwil MM. Artificial neural networks advantages and disadvantages. Mesopotamian J Big Data. 2021;2021:29–31. doi:10.58496/mjbd/2021/006. [Google Scholar] [CrossRef]

29. Kantheti PR, Meena KL, Chekuri RBR. Maximizing machining efficiency and quality in AA7075/Gr/B4C HMMCs through advanced DS-EDM parameter optimization strategies. Eng Res Express. 2024;6(4):045504. doi:10.1088/2631-8695/ad7dcd. [Google Scholar] [CrossRef]

30. Ozkaya S, Canakci A. Effect of the B4C content and the milling time on the synthesis, consolidation and mechanical properties of AlCuMg-B4C nanocomposites synthesized by mechanical milling. Powder Technol. 2016;297:8–16. doi:10.1016/j.powtec.2016.04.004. [Google Scholar] [CrossRef]

31. Gajević S, Miladinović S, Güler O, Özkaya S, Stojanović B. Optimization of dry sliding wear in hot-pressed Al/B4C metal matrix composites using taguchi method and ANN. Materials. 2024;17(16):4056. doi:10.3390/ma17164056. [Google Scholar] [PubMed] [CrossRef]

32. Varol T, Canakci A. Effect of particle size and ratio of B4C reinforcement on properties and morphology of nanocrystalline Al2024-B4C composite powders. Powder Technol. 2013;246(4):462–72. doi:10.1016/j.powtec.2013.05.048. [Google Scholar] [CrossRef]

33. Çanakçı A, Karabacak AH, Çelebi M, Özkaya S, Arpacı KA. A study on the optimization of nano-B4C content for the best wear and corrosion properties of the Al-based hybrid nanocomposites. Arab J Sci Eng. 2024;49(11):14625–41. doi:10.1007/s13369-024-08736-w. [Google Scholar] [CrossRef]

34. G02 Committee. Test method for wear testing with a pin-on-disk apparatus. West Conshohocken, PA, USA: ASTM International; 2017. p. 1–6. doi:10.1520/G0099-23. [Google Scholar] [CrossRef]

35. Veličković S, Stojanović B, Babić M, Vencl A, Bobić I, Vadászné Bognár G, et al. Parametric optimization of the aluminium nanocomposites wear rate. J Braz Soc Mech Sci Eng. 2018;41(1):19. doi:10.1007/s40430-018-1531-8. [Google Scholar] [CrossRef]

36. Gajević S, Marković A, Milojević S, Ašonja A, Ivanović L, Stojanović B. Multi-objective optimization of tribological characteristics for aluminum composite using taguchi grey and TOPSIS approaches. Lubricants. 2024;12(5):171. doi:10.3390/lubricants12050171. [Google Scholar] [CrossRef]

37. Miladinović S, Gajević S, Savić S, Miletić I, Stojanović B, Vencl A. Tribological behaviour of hypereutectic Al-Si composites: a multi-response optimisation approach with ANN and taguchi grey method. Lubricants. 2024;12(2):61. doi:10.3390/lubricants12020061. [Google Scholar] [CrossRef]

38. Achuthamenon Sylajakumari P, Ramakrishnasamy R, Palaniappan G. Taguchi grey relational analysis for multi-response optimization of wear in co-continuous composite. Materials. 2018;11(9):1743. doi:10.3390/ma11091743. [Google Scholar] [PubMed] [CrossRef]

39. Rama Rao S, Padmanabhan G. Optimization of machining parameters in ECM of Al/B4C composites. J Manuf Sci Prod. 2013;13(3):145–53. doi:10.1515/jmsp-2012-0039. [Google Scholar] [CrossRef]

40. Emovon I, Oghenenyerovwho OS. Application of MCDM method in material selection for optimal design: a review. Results Mater. 2020;7(9):100115. doi:10.1016/j.rinma.2020.100115. [Google Scholar] [CrossRef]

41. Abishini AH, Karthikeyan KMB. Application of MCDM and Taguchi super ranking concept for materials selection problem. Mater Today Proc. 2023;72(3):2480–7. doi:10.1016/j.matpr.2022.09.526. [Google Scholar] [CrossRef]

42. Saaty T. The analytic hierarchy process (AHP). J Oper Res Soc. 1980;41:1073–6. [Google Scholar]

43. Iswari VD, Arini FY, Muslim MA. Decision support system for the selection of outstanding students using the AHP-TOPSIS combination method. Lontar Komputer J Ilmiah Teknologi Informasi. 2019;40. doi:10.24843/lkjiti.2019.v10.i01.p05. [Google Scholar] [CrossRef]

44. Chaurasiya PK, Rathod NJ, Jain PK, Pandey V, Shashikant, Lala K. Material selection for optimal design using multi-criteria decision making. In: Proceedings of the 2023 3rd International Conference on Advancement in Electronics & Communication Engineering (AECE); 2023 Nov 23–24; Ghaziabad, India. Piscataway, NJ, USA: IEEE; 2023. p. 206–10. doi:10.1109/AECE59614.2023.10428303. [Google Scholar] [CrossRef]

45. Shankar AN, Jagota V, Jamadon NH, Raffik R, Suneetha VL, Samori IA, et al. An AHP-TOPSIS approach for optimizing the mechanical performance of natural fiber-based green composites. Adv Mater Sci Eng. 2022;2022(3):1263237. doi:10.1155/2022/1263237. [Google Scholar] [CrossRef]

46. Sharma V, Meena ML, Kumar M, Patnaik A. Optimization of waste fly ash powder filled glass fiber reinforced epoxy composite by hybrid AHP-TOPSIS approach. Mater Today Proc. 2021;44:4789–94. doi:10.1016/j.matpr.2020.11.394. [Google Scholar] [CrossRef]

47. Osa-uwagboe N, Udu AG, Ghalati MK, Silberschmidt VV, Aremu A, Dong H, et al. A machine learning-enabled prediction of damage properties for fiber-reinforced polymer composites under out-of-plane loading. Eng Struct. 2024;308:117970. doi:10.1016/j.engstruct.2024.117970. [Google Scholar] [CrossRef]

48. Jierula A, Wang S, Oh TM, Wang P. Study on accuracy metrics for evaluating the predictions of damage locations in deep piles using artificial neural networks with acoustic emission data. Appl Sci. 2021;11(5):2314. doi:10.3390/app11052314. [Google Scholar] [CrossRef]