Hyper-Chaos and CNN-Based Image Encryption Scheme for Wireless Communication Transmission

1  Introduction

Wireless communication has evolved from 1G to 5G and is advancing at a rapid pace. 5G communication is a novel mobile communication technology, which has many features, including high data rates, low delay, and massive connectivity. It enables supporting applications of the Internet of Everything (IoE), such as the Internet of Things (IoT), virtual reality, and high-definition live streaming [1]. Moreover, countries around the world are actively advancing research and development of sixth-generation mobile communication technology (6G) to meet future communication requirements [2].

However, an increasing number of edge devices will connect to the network, leading to a rise in uncertainty. Therefore, communication security has consistently been a challenging issue in IoE technology. If the transmitted images are not rigorously secured, the performance of such wireless communication services is no longer reliable. Therefore, it is necessary to safeguard sensitive information during wireless communication transmission. Image encryption is the popular method for safeguarding the personal information of transmitted images [3,4].

Chaos theory, distinguished by its nonlinear dynamics, inherent unpredictability, and extreme sensitivity to initial conditions, has attracted significant interest in recent years [5]. The elaborate intricacies and inherent randomness of chaotic systems, combined with their acute dependency on initial states, endow them with pseudo-random properties that are highly desirable for image encryption applications [6]. Consequently, chaos-based image encryption algorithms are a leading trend in the field of image encryption [7,8].

However, conventional chaos-based image encryption algorithms often face critical challenges in key space security and dynamical degradation. Traditional one-dimensional chaotic systems, while computationally efficient, often exhibit oversimplified key spaces due to their limited control parameters and narrow chaotic ranges. This structural simplicity renders them vulnerable to exhaustive key searches and attacks. On the other hand, two-dimensional chaotic systems (e.g., Henon map, and coupled logistic maps) demonstrate improved chaotic behaviors through expanded parameter spaces, but significantly increased computational complexity [9,10]. Furthermore, the lack of adaptive mechanisms in traditional chaotic encryption often fails to resist different attacks.

To achieve a harmonious blend between the complexities of high-dimensional and the efficiencies of low-dimensional chaotic systems, this paper proposes an image encryption scheme based on the Iterative Hyper-Chaos system and CNN system. This scheme can offer an expanded key space coupled with more sophisticated dynamic behaviors. The encrypted images not only demonstrate superior distribution characteristics but also ensure robust protection against potential communication interference and threats. The main contributions are shown as follows.

(1)   A two-dimensional chaotic sequence is proposed by extending the one-dimensional chaotic sequence. The generated two-dimensional chaotic sequence can provide richer and more complex dynamic characteristics and randomness. Therefore, it can enhance the key space complexity and randomness, ensuring resistance against cryptanalysis.

(2)   An innovative CNN architecture is proposed for generating the key stream. The CNN architecture exhibits excellent nonlinearity and can further optimize the encryption process, and thus can ensure diversity, unpredictability, and non-replicable of the key stream.

(3)   Combining iterative hyper-chaos and CNN technologies, the proposed encryption method exhibits superior distribution characteristics, which underscores the robustness and efficacy.

The paper is organized as follows. Section 2 reviews the related works about our method. Section 3 provides a detailed introduction to the proposed encryption scheme, including an iterative hyper-chaotic system and CNN architecture. Moreover, the performance is verified through five key metrics in Section 4. Finally, the conclusion is shown in Section 5.

2  Related Works

2.1 Chaos Theory

Chaos is a highly irregular and highly sensitive dynamic phenomenon that occurs in deterministic nonlinear systems [11]. Chaotic systems typically exhibit the following basic characteristics, including sensitivity to initial values, non-periodicity, dense periodic orbits, topological mixing, attractors, orbital fractal structures, positive Lyapunov exponent, and so on.

Chaos mapping is an important support for chaotic systems, as its extreme sensitivity to initial values leads to highly complex and unpredictable behavior in deterministic systems. This makes it applied in spread spectrum communication, cryptography, image encryption, and other optimization algorithms [12–14]. Due to these characteristics, they can enhance the security of systems by generating complex, pseudo-random sequences. However, although low dimensional systems such as Logistic chaotic systems [15] and Tent chaotic systems [16] have simple structures and are easy to calculate, they also have problems such as limited pseudo randomness, limited complexity, limited key space, and uneven distribution, and weak resistance to attacks, which limit their performance and security in practical applications.

At the same time, high-dimensional chaotic sequences have larger parameter spaces and more complex dynamic behaviors. However, they also bring problems such as high computational complexity and slow iteration. This restricts the application of high-dimensional chaotic systems, especially in applications that require real-time and efficiency, where speed bottlenecks often affect their practical application effectiveness. Therefore, improving computational efficiency while ensuring sufficient security has always been a key direction in chaotic research.

2.2 Chaos for Image Encryption

The behavior complexity and sensitivity of chaotic systems determine their widespread application in image encryption. They are broadly categorized into low-dimensional and high-dimensional chaotic systems [17,18].

Low-dimensional chaotic systems are characterized by their straightforward structure and computational efficiency. Early iterations of image encryption algorithms predominantly leveraged such low-dimensional systems [19,20]. For instance, Zhou et al. [21] employed a combination of multiple low-dimensional chaotic maps for encryption. Feng et al. [22] more recently developed a novel 1D zero exclusion chaotic system that innovatively pays attention to the standard eight-pixel values, leading to enhanced encryption results. However, the simplicity of low-dimensional chaotic systems also means they have a more limited parameter space and reduced complexity in their dynamic behavior. This makes them more vulnerable to cracking under sophisticated attacks.

In contrast, high-dimensional chaotic systems offer a more intricate structure, which translates to a larger parameter space and more elaborate dynamic behavior [23–25]. Yan et al. [26] proposed two scrambling algorithms and one diffusion method by using a five-dimensional hyperchaotic system with memristors. Huang et al. [27] studied the shape dimension of 3D chaotic systems and applied it to the encryption scheme of color images. Despite these advances, the complex architecture of high-dimensional chaotic systems can lead to increased computational complexity and slower iterations. This, in turn, can affect the speed at which key streams are generated and pose challenges to the practical implementation of these algorithms.

In recent times, a plethora of innovative image encryption algorithms have emerged, a testament to the interdisciplinary synthesis of chaos theory with diverse fields [28–30]. Zhang et al. [31] addressed the issue of poor encryption performance of Galois domain multiplication operations for pixels with a value of ‘0’, and integrated DNA computing into Galois domain diffusion, achieving good improvement results. Guo et al. [32] presented a dual-channel encryption algorithm by using dual-channel ciphertexts. Huang et al. [33] presented an encryption method that utilizes the RAS algorithm and wavelet transform. Experimental outcomes have showcased the robust computational capabilities of these algorithms. However, in computer simulations, the efficiency of encoding and decoding processes is often relatively slow, and encryption systems demand stringent equipment and environmental conditions.

2.3 Deep Learning for Image Encryption

Deep learning has extraordinary generalization performance and nonlinearity, and thus it has been used in some encryption methods [34,35]. Man et al. [36] designed a dual-channel encryption method. The method introduces a convolutional neural network (CNN) for generating chaotic pointers. Ding et al. [37] introduced the generative adversarial network (GAN) to construct a private key. These networks are used for generating a random sequence as a key stream for the scrambling and diffusion process.

Maniyath et al. [38] proposed a deep-learning framework for improving image encryption schemes. These image encryption schemes use deep neural networks to produce an unpredictable key stream. The key stream sequence is unpredictable and suitable for image encryption systems. Sang et al. [39] presented a deep-auto-encoder-based encryption method for generating a highly random ciphertext image, which is critical for an encryption scheme. These described schemes use the deep neural network to generate secret keys and yield measurable outcomes, which motivates the exploration of more efficient integration between deep learning and chaotic systems.

3  Proposed Image Encryption Scheme

The image encryption method comprises two phases: the key stream generation phase and the diffusion and scrambling phase. It operates as a symmetric cryptographic system, where decryption mirrors the encryption process. The structure of the image encryption method is depicted in Fig. 1. The key streams are generated by a deep learning network. Then, the encrypted images are generated by diffusion and scrambling with an iterative-chaotic system. This can ensure that the signal can resist noise and attacks well during wireless transmission, ensuring communication security.

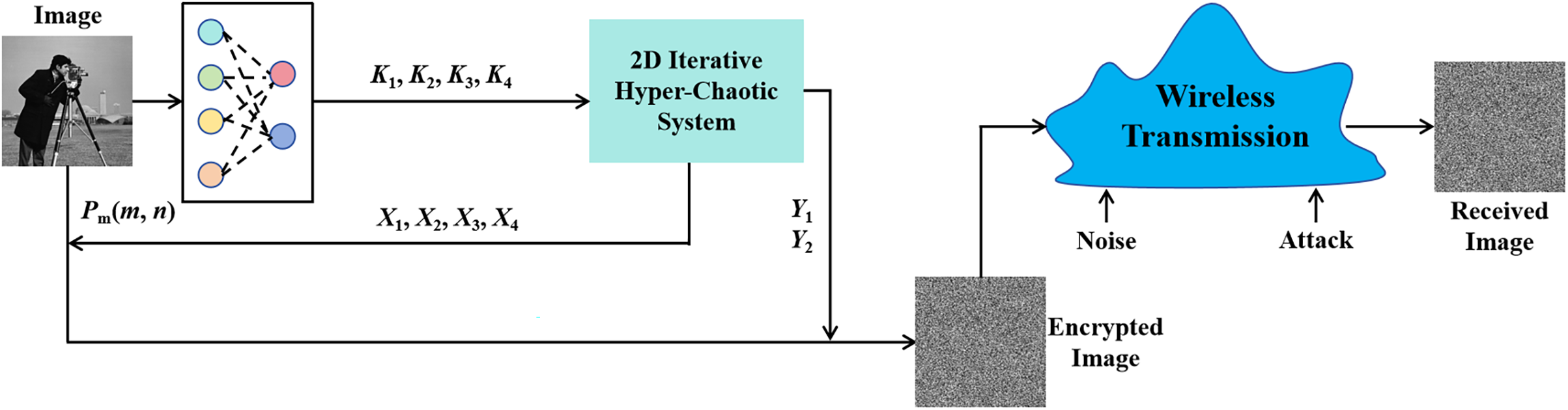
Figure 1: Schematic diagram of image encryption scheme

3.1 2D Iterative Hyper-Chaotic System

The traditional one-dimensional chaotic system is elegantly articulated through its mathematical representation, as illustrated in Eq. (1).

xn+1=sin⁡(παxn)(1)

xn denotes the iterative sequences, α is an essential component.

In response to the security issue of relatively small key space in 1D chaotic sequences, an innovative 2D iterative hyper-chaotic system is presented for image encryption. The mathematical formulation is elegantly depicted in Eq. (2).

{xn+1=cos⁡(πα⋅xnynβ)yn+1=sin⁡(πα⋅ynxnβ)(2)

xn and yn are the inputs, xn+1 and yn+1 are the outputs. The iterative sequences xn and yn have a value range of (−1, 1). α and β are essential components of the two-dimensional iterative hyper-chaotic system. α ranges over R+, while β is constrained to N+.

Distinct from 1D systems, 2D hyper-chaotic system unveils a spectrum of more intricate and sophisticated dynamic attributes and patterns. Coupled with an expanded parameter space within chaotic states, it aligns more effectively with the stringent requirements of image encryption.

Chaotic sequence attractors are pivotal in delineating and understanding the inherent dynamics of chaotic systems. The existence and characteristics of these attractors are critical for gauging the stability of chaotic sequences. A stable attractor ensures that the system’s trajectory consistently gravitates towards it, regardless of the chaotic sequence’s complexity within the phase space. Systems endowed with stable attractors tend to exhibit a diminished rate of exploration, as their states revolve around the attractor’s locus. In contrast, systems devoid of stable attractors are marked by an amplified rate of traversal, as they continuously evolve and venture into novel territories within the phase space. For cryptographic systems that require the generation of unpredictable random keys, those that showcase enhanced traversal are particularly advantageous.

Fig. 2 illustrates the behavior of the two-dimensional iterative hyper-chaotic attractors under a variety of control parameters, given the initial values x0 = 0.69344818165 and y0 = 0.98443984189. These results compellingly demonstrate the pronounced ergodicity of the two-dimensional iterative hyper-chaotic system, showcasing its attractors uniformly distributed across the phase space. This uniform dispersion indicates that the sequence possesses the desirable quality of randomness, an attribute that is highly beneficial for cryptographic applications.

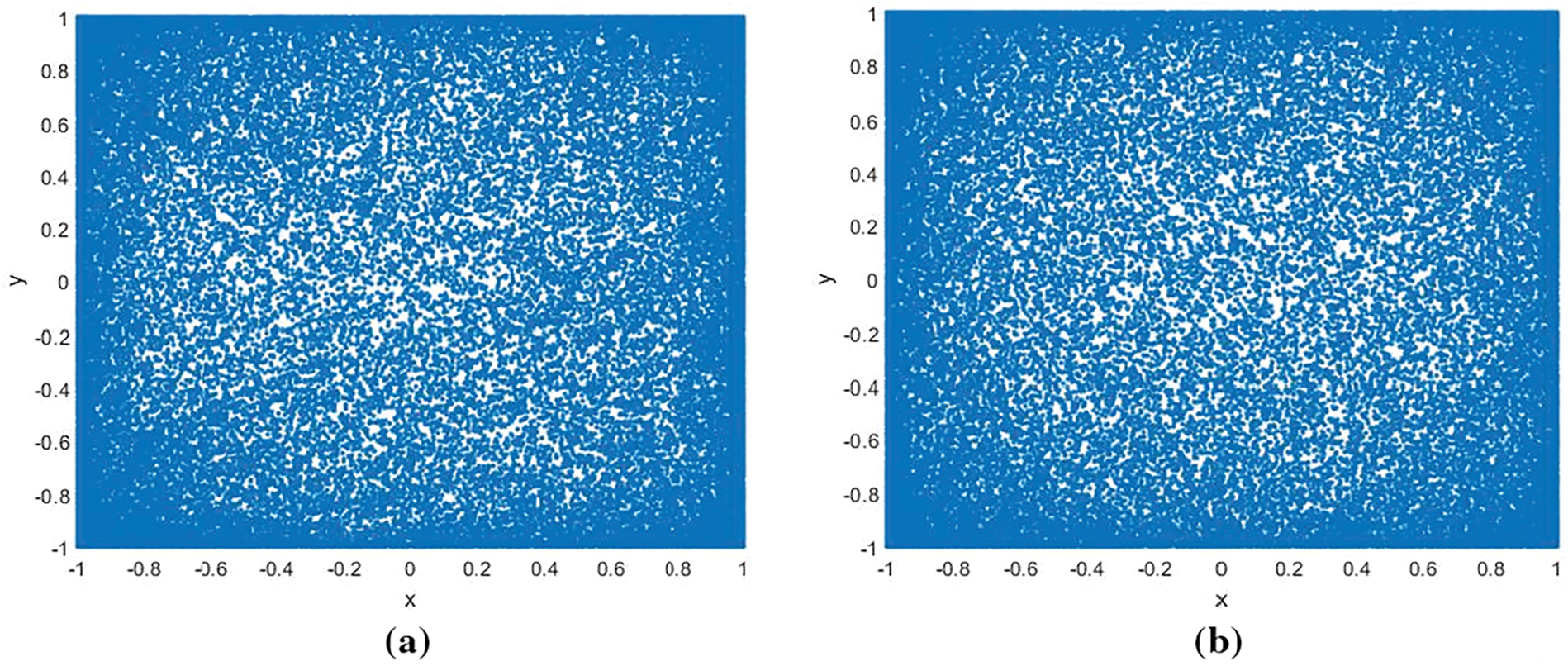
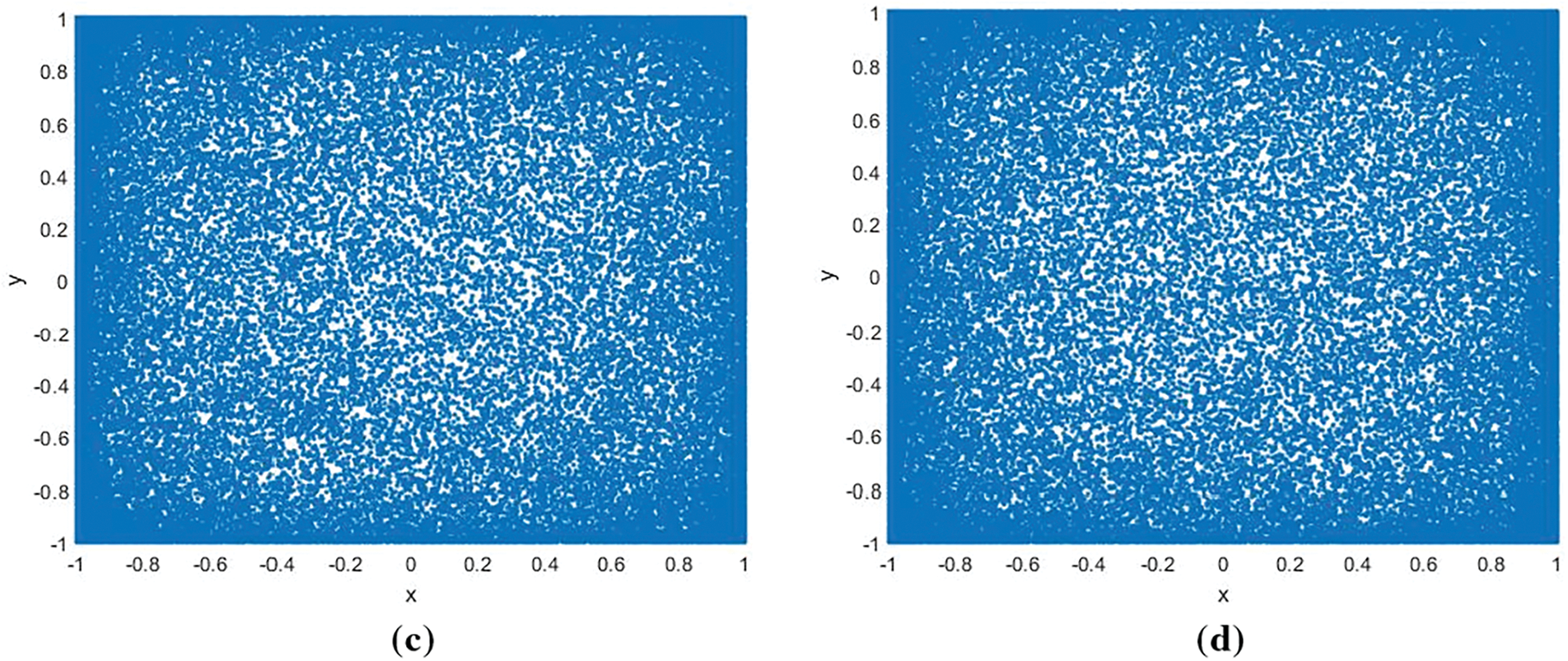
Figure 2: Two-dimensional iterative hyper-chaotic attractor with different parameters: (a) The attractor with the parameters α = 3.2, β = 2; (b) The attractor with the parameters α = 3.2, β = 8; (c) The attractor with the parameters α = 5, β = 2; (d) The attractor with the parameters α = 5, β = 8

The average Lyapunov exponent is a crucial quantitative metric for the dynamic characteristics of chaotic systems. It offers the rate at which small disturbances in the system amplify over time. Consequently, the average Lyapunov exponent holds a significant reference value in the analysis of chaotic systems. A positive Lyapunov exponent value denotes chaotic behavior, with its numerical magnitude indicating the level of chaos within the system. A larger Lyapunov exponent generally signifies heightened sensitivity to initial conditions. Table 1 presents the average Lyapunov exponent of the two-dimensional iterative hyper-chaotic system across various control parameters.

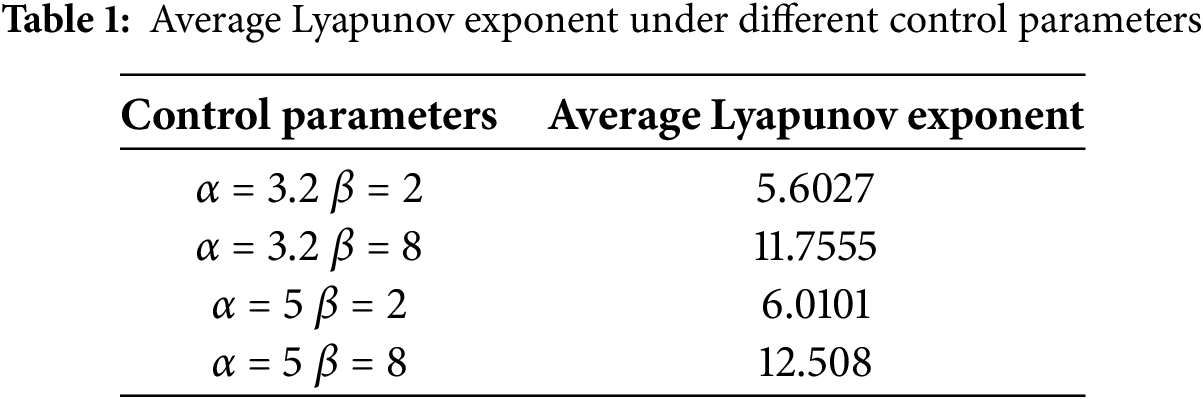
As shown in Table 1, the system evinces hyperchaotic traits, with its average Lyapunov exponent notably exceeding those observed in other chaotic systems. This distinction underscores the system’s superiority, suggesting a more pronounced sensitivity to initial conditions and a richer dynamic complexity that sets it apart in the realm of chaotic systems.

3.2 CNN Architecture for Key Generation

The proposed framework leverages a generative adversarial network (GAN) to dynamically synthesize cryptographic keys by fusing chaos theory with deep feature learning. Specifically, the generator (G) employs cascaded convolutional blocks to transform raw image features into chaotic system parameters, which are iteratively refined through adversarial training with the discriminator (D). The optimized parameters then drive a chaotic map to produce provably unpredictable keystreams. These keystreams are subsequently integrated via pixel-level XOR (Exclusive OR) operations to achieve nonlinear substitution.

The architecture of the network is displayed in Fig. 3. The generator consists of three downsample layers, six residual blocks, two transposed convolutional layers, and an ordinary convolutional layer. The discriminator consists of five convolutional layers. In addition, to enhance the generalization performance, instance normalization is applied for all convolutional layers.

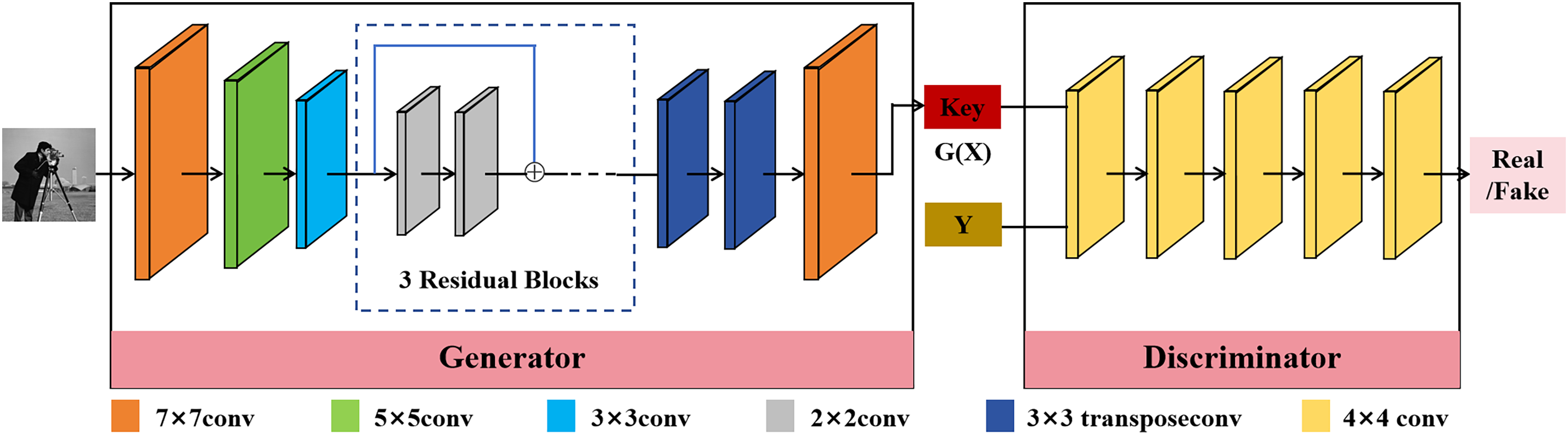
Figure 3: The CNN architecture for key generation

The proposed network first uses the generator to produce the keys from the original images. Then the discriminator whether the keys are real or fake. If the discrimination accuracy is nearly 50%, the generated keys have superior uncertainty and unpredictability.

Moreover, the loss function L includes the generator loss function LG and the discriminator loss function LD, as illustrated in Eq. (3).

L=LG+LD(3)

The loss function LG and LD are detailed in Eqs. (4) and (5), respectively.

LG=minG(Ex∼pdata(x)log⁡(1−D(G(x))))(4)

LD=maxD(Ey∼pdata(y)log⁡(D(y))+Ex∼pdata(x)log⁡(1−D(G(x))))(5)

G and D are a generator and a discriminator, respectively, x is the original image, and y is the data in the generation domain. The loss function LG and LD can achieve adversary during the training process. When the generator and the discriminator achieve an equilibrium state, the training results are optimal.

3.3 The Image Encryption Processing

(1)   The key stream generation phase

 The deep learning network can generate the key streams derived from the original image. As shown in Fig. 3, the paper employs the powerful nonlinearity of the CNN architecture to derive chaotic system keys. Throughout the convolution process, the network utilizes convolution kernels of 7 × 7, 5 × 5, and 3 × 3 for better feature extraction. Moreover, we use 3× residual blocks, to enhance uncertainty, non-replicability, and unpredictability of the key streams. The generated key streams are denoted as K1, K2, K3, K4.

(2)   The diffusion and scrambling phase

 Unlike conventional diffusion starting from a fixed position, the iterative hyper-chaos encryption method permits the diffusion process to originate from any arbitrary point within the image. This approach significantly amplifies the intricacy involved in decrypting the ciphertext images. The algorithm is described in the subsequent steps.

Step 1: Randomly select the initial diffusion position Pm(m, n).

Step 2: Process keys K1, K2, K3, and K4 to achieve the initial value by Eq. (6).

{α=mod(K1,1)×100+fix(K1);β=mod(round(K2×1010),35)+2;x0=mod(K3,1);y0=mod(K4,1).(6)

Then, input the initial parameter α, β, and the initial value x0, y0 into function [X, Y] = Chaos(α, β, x0, y0, N), where N is the number of iterations.

Step 3: Process X, and Y using equation Eq. (7) to obtain the four matrices required for rotational diffusion.

{X1=mod(X,256);X2=mod(Y,256);X3=mod(X+Y,256);X4=mod(X−Y,256).(7)

Select a matrix consisting of m elements from point X1 to form (1, m)′ and perform XOR operations upwards from point Pm to complete the first step of diffusion; Select matrices of appropriate size in X2, X3, and X4 to complete three diffusion operations to the left, down, and right, respectively.

In addition, for scrambling, Splice X, Y in function [X, Y] = Chaos (α, β, x0, y0, N), reorganize it into a matrix of 256 × 256, and sum each column in the matrix to obtain Y1, Y2 for scrambling. The scrambling process is shown in Eq. (8).

{P(i,j)=P(Y1(1,i),Y2(1,j));i∈[1,256],j∈[1,256].(8)

4  Performance Analysis

To evaluate the encryption performance and security performance, we will analyze six different evaluation terms. All methods were conducted on a computer equipped with an Intel i7-12700kf CPU and NVIDIA RTX 2080, and MATLAB 2016a version. The sizes of the experimental images are 256 × 256 and 512 × 512.

4.1 Visualization Analysis

The visualization analysis of encryption methods can evaluate the encryption results through a graphical interface, helping users intuitively understand the effects of the methods.

As shown in Figs. 4–6, visualization results show that our ciphertext image appears complete visual randomness with no discernible patterns or structural features. It is demonstrably completely impossible to achieve any meaningful information from ciphertext. Moreover, the ciphertext exhibits near-perfect visual congruence with its corresponding plaintext, which sufficiently demonstrates the effectiveness of encryption and the accuracy of decryption.

Figure 4: The visualization analysis of the image “Cameraman”: (a) Plaintext image; (b) Ciphertext image; (c) Decrypted image

Figure 5: The visualization analysis of the image “Goldhill”: (a) Plaintext image; (b) Ciphertext image; (c) Decrypted image

Figure 6: The visualization analysis of the image “Peppers”: (a) Plaintext image; (b) Ciphertext image; (c) Decrypted image

4.2 Histogram Analysis

Histogram analysis offers a straightforward representation of the pixel distribution. If the statistical properties are not effectively concealed within the ciphertext, it may allow malicious actors to statistically reconstruct the distribution of information in the plaintext through cryptanalysis. Therefore, the histogram distribution of ciphertext will affect the risk of ciphertext leakage.

Figs. 7–9 provide a comparative visualization of the image histograms, highlighting the transition from the plaintext distribution to the ciphertext distribution. The image histogram of the ciphertext is quite uniform, indicating that the statistical characteristics of the plaintext have been perfectly concealed and eliminated. The comparative results of the histogram underscore the ability to obscure the original statistical features, thereby enhancing information security.

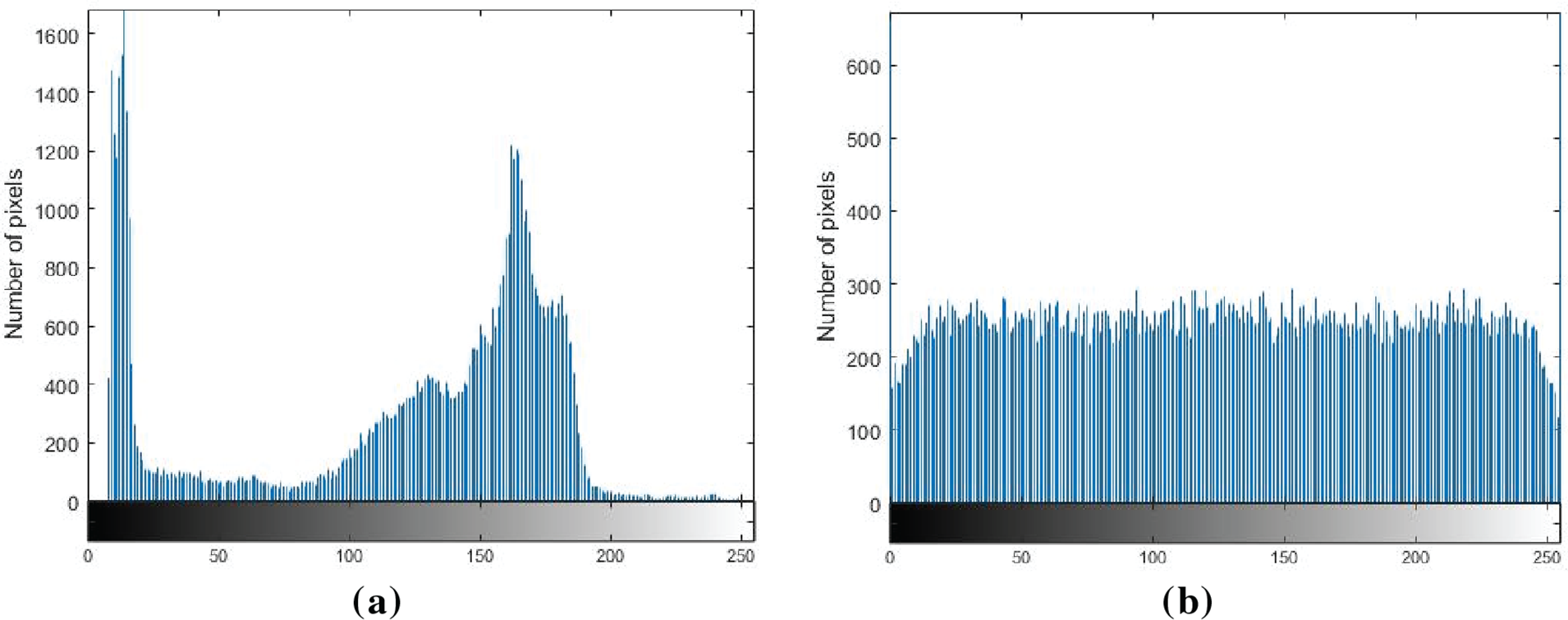
Figure 7: The histogram analysis of the image “Cameraman”: (a) Plaintext image; (b) Ciphertext image

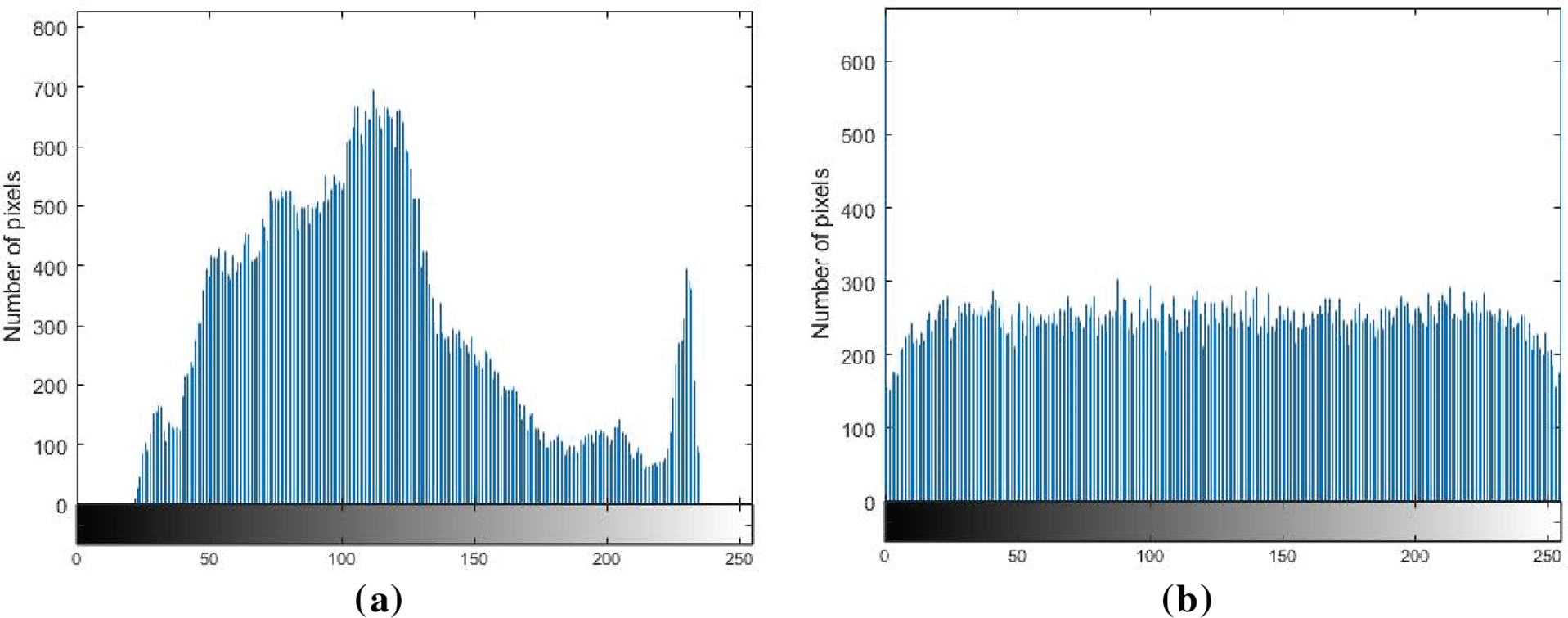
Figure 8: The histogram analysis of the image “Goldhill”: (a) Plaintext image; (b) Ciphertext image

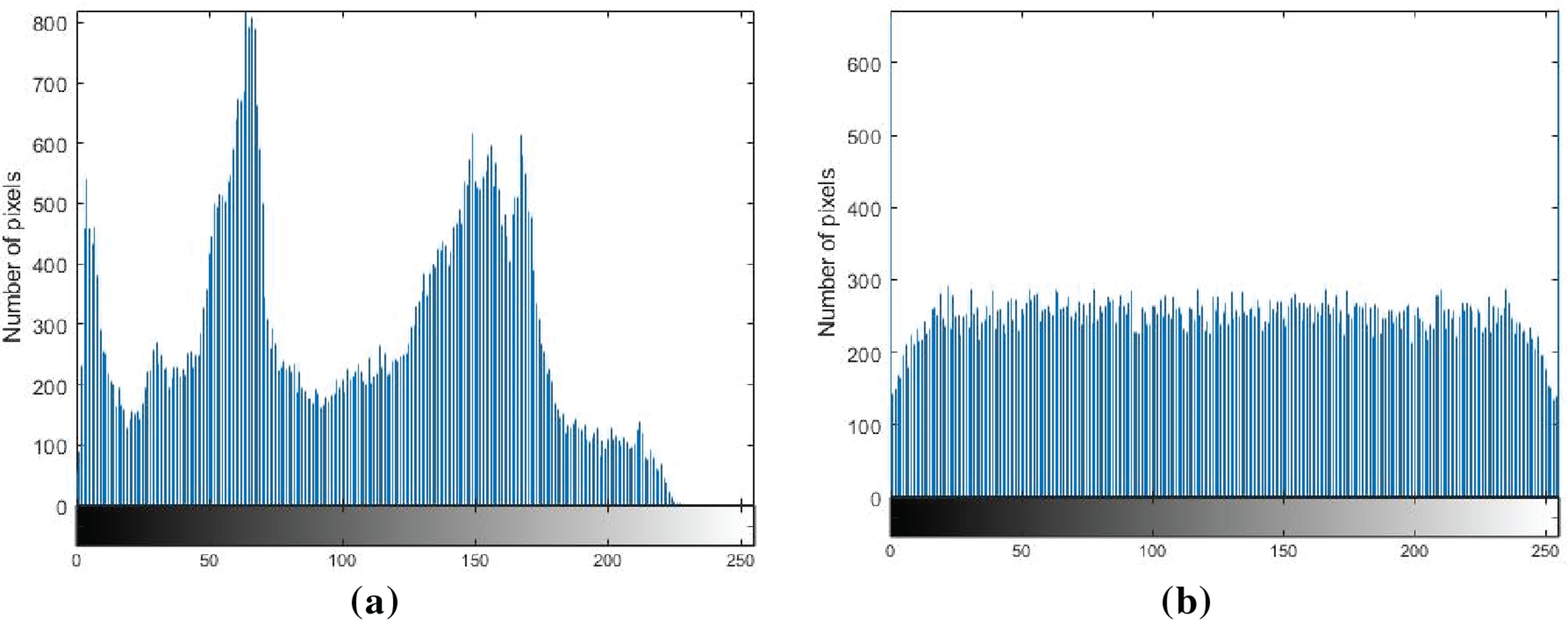
Figure 9: The histogram analysis of the image “Peppers”: (a) Plaintext image; (b) Ciphertext image

4.3 Information Entropy Analysis

The information entropy can measure the amount and complexity of information. Higher entropy values indicate greater image complexity and enhanced information content.

The information entropy of the proposed image encryption scheme is shown in Table 2. The experimental results show that the ciphertext information entropy is close to 8. Compared to the plaintext image, there is a significant improvement in information entropy, which proves that our scheme has an excellent encryption effect.

4.4 Correlation Analysis

Correlation analysis is instrumental in discerning the structural composition and information distribution. Attackers may exploit this by analyzing the correlation to infer patterns, which underscores the necessity for encryption to disrupt such relationships. A strong correlation is typically evidenced by a clustered scatter plot, whereas a weak or disrupted correlation results in a more dispersed pattern. Figs. 10–12 present a comparative correlation analysis conducted on different images.

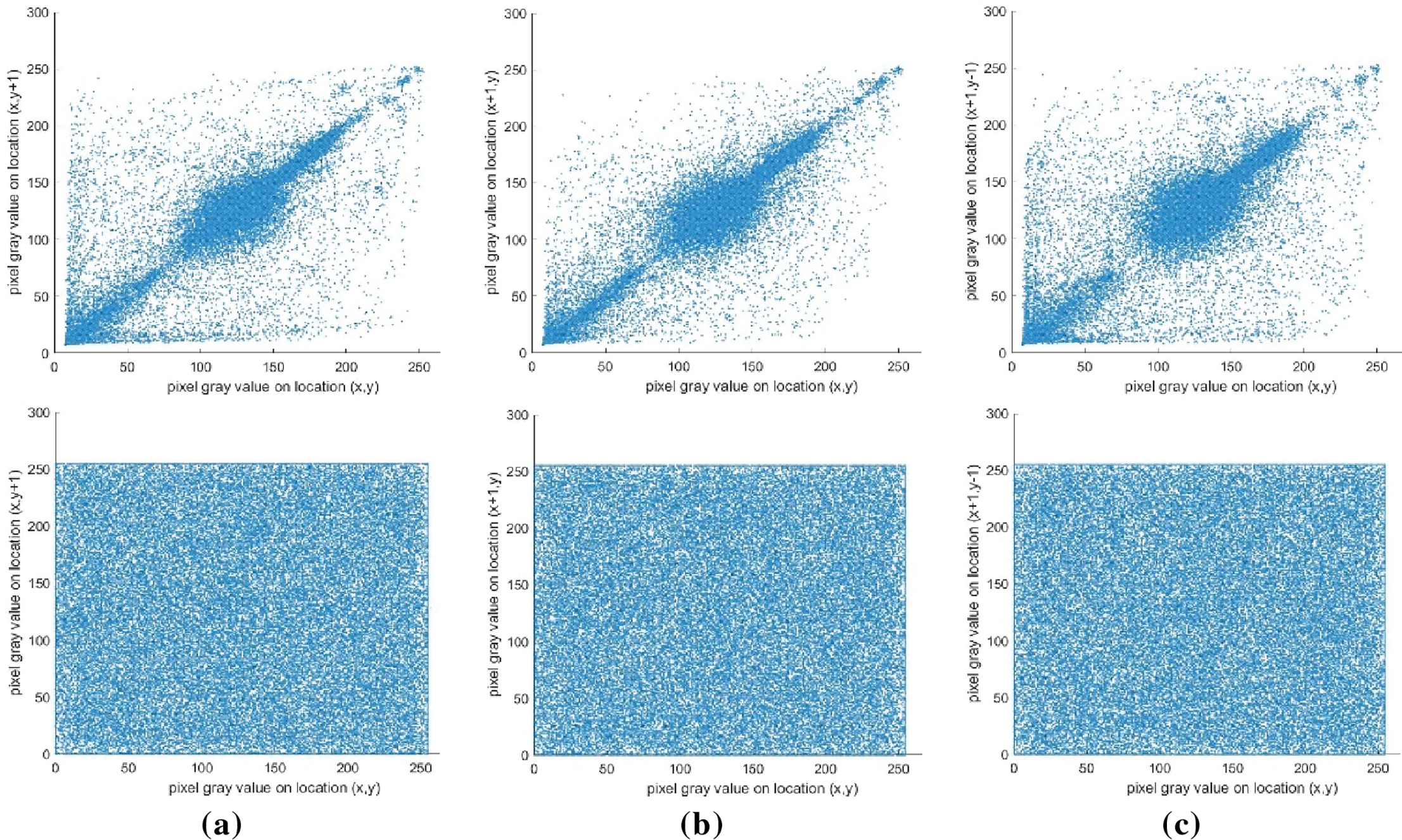
Figure 10: The correlation analysis of the image “Cameraman”: The first row denotes the plaintext; The second row denotes the ciphertext. (a) horizontal direction; (b) vertical direction; (c) diagonal direction

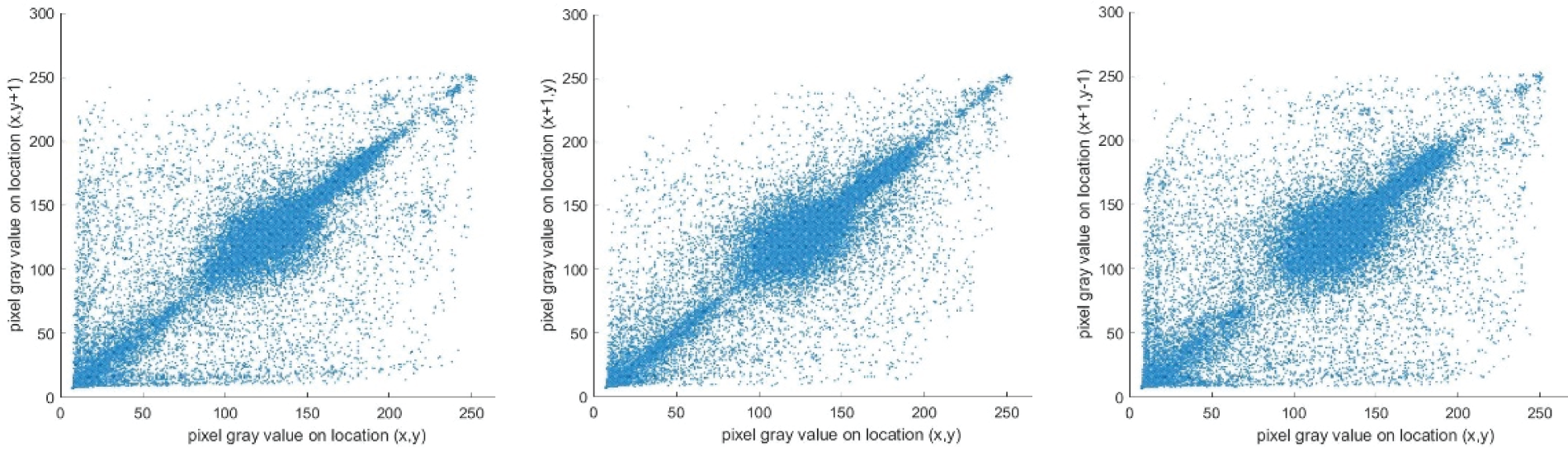
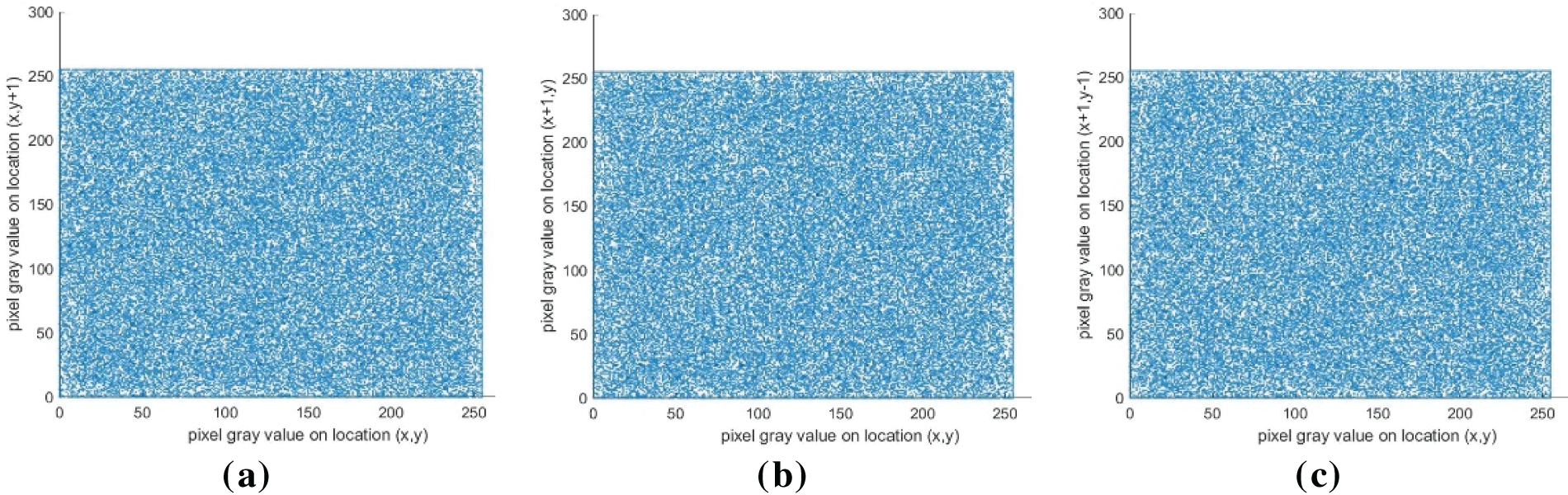
Figure 11: The correlation analysis of the image “Goldhill”: The first row denotes the plaintext; The second row denotes the ciphertext. (a) horizontal direction; (b) vertical direction; (c) diagonal direction

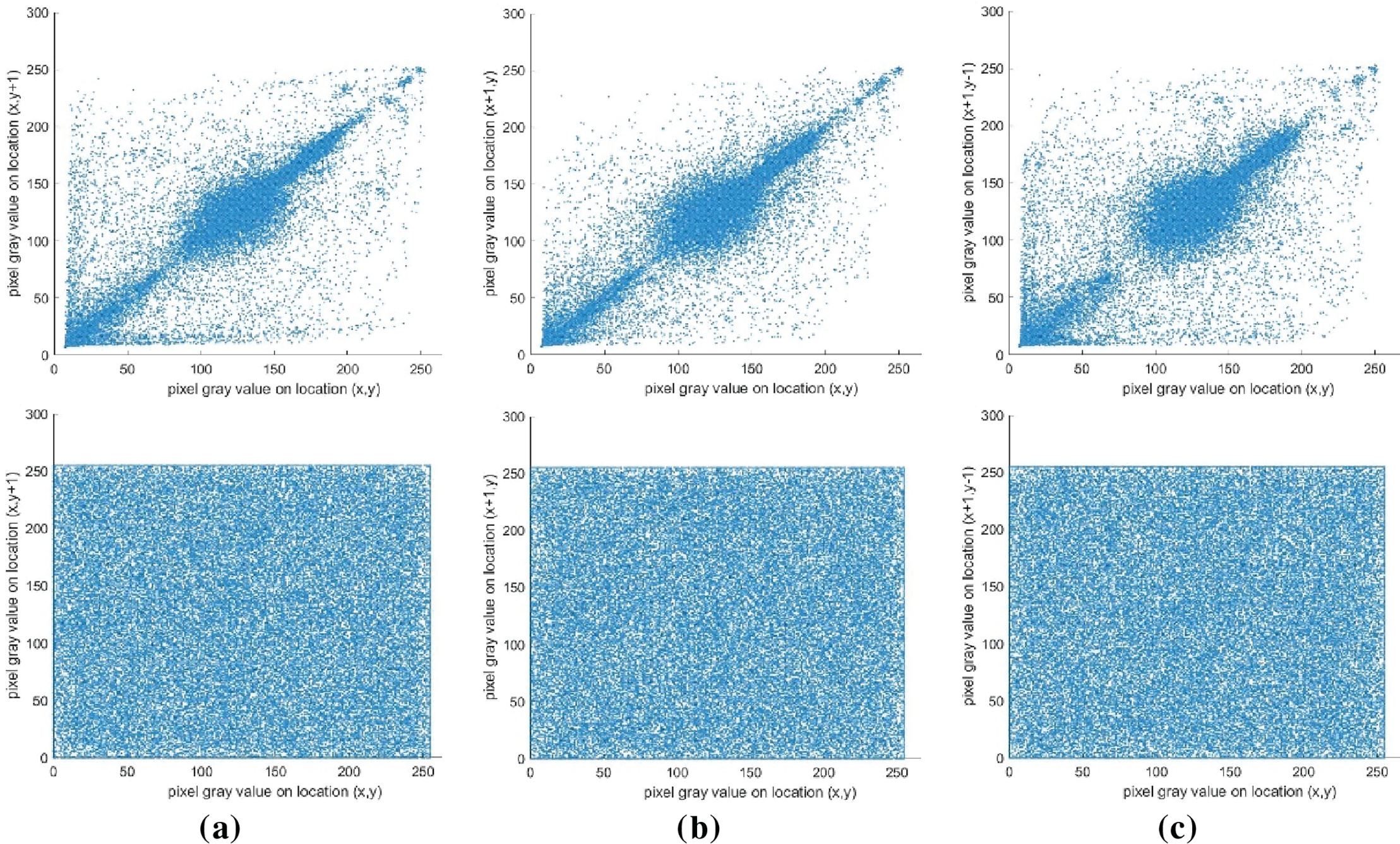
Figure 12: The correlation analysis of the image “Peppers”: The first row denotes the plaintext; The second row denotes the ciphertext. (a) horizontal direction; (b) vertical direction; (c) diagonal direction

The plaintext exhibits clustered scatter plots in all directions, indicating that the plaintext exhibits strong correlations. In contrast, the ciphertext exhibits a highly dispersed pattern in all directions. The results reveal that the proposed image encryption scheme can effectively eradicate any discernible correlation, thereby enhancing data security.

4.5 Differential Attack Analysis

A differential attack is a selective plaintext attack. The attack involves subtle modifications to the plaintext to compare the ciphertext before and after encryption. By analyzing these differences, attackers may attempt to obtain encryption keys. We encrypt the images before and after modification using the same key and introduce NPCR and UACI to analyze the differences between the two encrypted images. These two metrics are shown as follows.

NPCR=∑q,rT(q,r)W×H(9)

UACI=1W×H∑q,r|V1(q,r)−V2(q,r)|255(10)

T(q,r)={1,V1(q,r)≠V2(q,r)0,V1(q,r)=V2(q,r)(11)

W and H denote the width and height of the encrypted images. V1 and V2 denote the two encrypted images.

NPCR is used to measure the sensitivity of encryption algorithms to small changes in plaintext or key. A high NPCR value (close to the ideal value of 99.61%) denotes that the algorithm has strong diffusion and can effectively resist differential attacks. UACI reflects the degree of modification of the original pixels. A higher UACI value (close to the ideal value of 33.46%) denotes that the pixel changes significantly after encryption, which can effectively resist differential attacks. However, excessively high values may lead to excessive distortion of image information. Therefore, combining NPCR and UACE can effectively evaluate its ability to resist differential attacks.

To evaluate the resistance to the differential attacks, we compare our proposed method with the existing methods, including Refs. [17,20,24,35,40]. NPCR and UACI of various methods are shown in Table 3. Our method exhibits optimal resistance performance with an NCPR of 99.642% and a UACI of 33.465%. The method obtains high consistency in pixel variation and effectively scatters the intensity of modifications, which is challenging for detection and reverse encryption.

4.6 Resistance Analysis

During information transmission, if an attacker is unable to decrypt the ciphertext, they may resort to interference techniques to prevent the receiver from successfully decrypting the message, thereby achieving their objective. Two common methods for such attacks are cropping attacks and noise attacks. Fig. 13 illustrates the decryption effectiveness of our scheme under different levels of cropping attacks, while Fig. 14 shows the decryption effectiveness under various noise attacks. The results illustrate that our method exhibits powerful resistance to different attacks.

Figure 13: The decryption results under different pruning attacks: (a) Four corner cropping attack; (b) Edge cropping attack; (c) Central cropping attack; (d) The decryption results with four corner cropping; (e) The decryption results with edge cropping decryption; (f) The decryption results with central cropping decryption

Figure 14: The decryption results under different noise attacks: (a) The decryption results with 20% Salt and pepper attack; (b) The decryption results with 20% Gaussian attack; (c) The decryption results with 20% Spot attack

4.7 Ablation Experiments

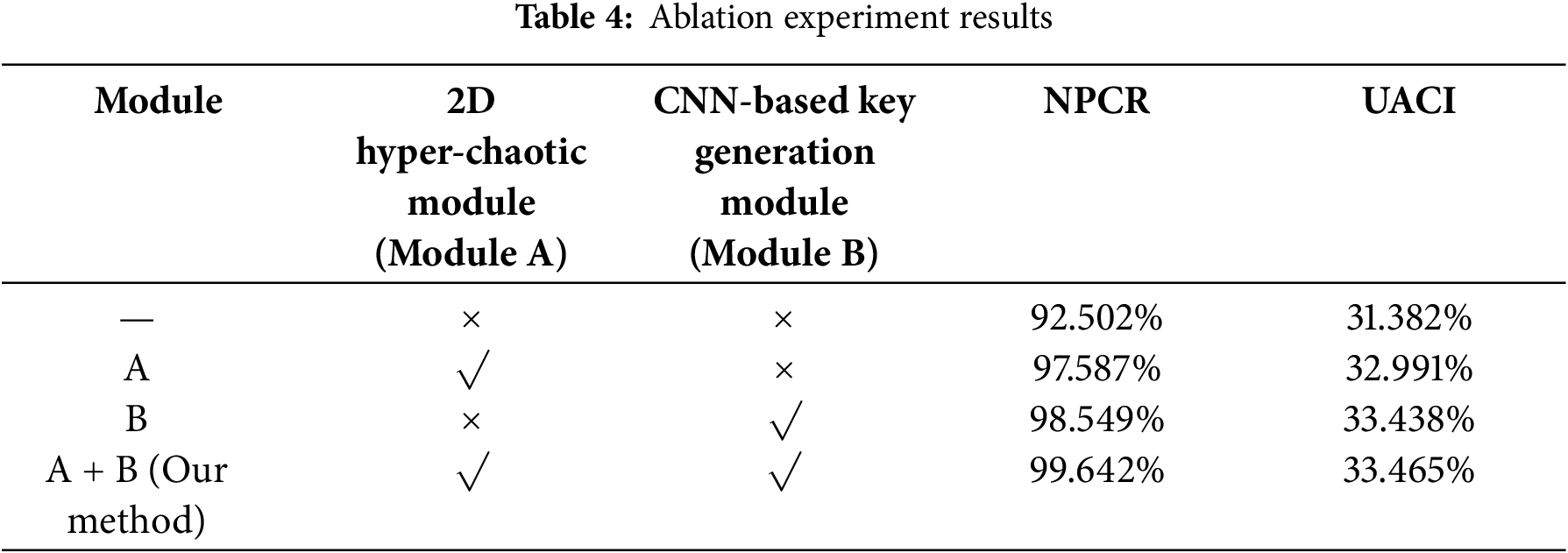
The ablation experiments were executed and composed of 2 stages, and each stage is shown as follows.

1.    Only 2D Iterative Hyper-Chaotic module (Module A) is carried out.

2.    Only CNN-based key generation module (Module B) is carried out.

3.    The combination of 2D Iterative Hyper-Chaotic module and CNN-based key generation module is carried out.

Specifically, take a picture of Cameraman, Goldhill, and Peppers as three examples. As shown in Table 4, ablation experiments have demonstrated the effectiveness of each proposed module.

5  Conclusions

To address the escalating challenges in safeguarding image security and overcoming the limitations of low-dimensional chaotic systems, which are vulnerable to attacks, and the complexities associated with high-dimensional system structures, this paper introduces a novel 2D iterative hyper-chaotic system. The system’s dynamic behavior and parameter space have been rigorously validated through attractors and average Lyapunov exponents, demonstrating superior chaotic properties compared to its lower dimensional counterparts.

Building upon the extraordinary generalization performance and powerful nonlinearity of CNN architecture, we construct a deep learning network for generating key streams, which enhances an unpredictability dimension for the encryption process. The security and efficacy of this scheme are substantiated through a comprehensive analysis, including different evaluation metric analyses. These evaluations confirm the high-security standards and practical utility of the combination of the two-dimensional iterative hyper-chaotic system and the deep learning network, highlighting its potential for broad application in wireless communication.

Acknowledgement: We would like to take this opportunity to express our heartfelt gratitude to all those who contributed to the completion of this article.

Funding Statement: This work was supported in part by the National Key Research and Development Program of China (No. 2021YFB3101500) and the Fundamental Research Funds for the Central Universities (No. 2023RC69).

Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Gang Liu, Guosheng Xu; data collection: Guoai Xu; validation: Chenyu Wang; writing—original draft: Gang Liu; writing—review & editing: Guosheng Xu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials used to support the findings of this study are available from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Chakaravarthi S, Saravanan S, Jagadeesh M, Nandhini S. IoT-based trusted wireless communication framework by machine learning approach. Meas Sens. 2024;34(6):101271. doi:10.1016/j.measen.2024.101271. [Google Scholar] [CrossRef]

2. Chen X, Tan J, Kang L, Tang F, Zhao M, Kato N. Frequency selective surface toward 6G communication systems: a contemporary survey. IEEE Commun Surv Tutor. 2024;26(3):1635–75. doi:10.1109/COMST.2024.3369250. [Google Scholar] [CrossRef]

3. Li L. A novel chaotic map application in image encryption algorithm. Expert Syst Appl. 2024;252(4):124316. doi:10.1016/j.eswa.2024.124316. [Google Scholar] [CrossRef]

4. Yang Y, Xiong X, Liu Z, Jin S, Wang J. High-performance encryption algorithms for dynamic images transmission. Electronics. 2024;13(1):131. doi:10.3390/electronics13010131. [Google Scholar] [CrossRef]

5. Zhang B, Liu L. Chaos-based image encryption: review, application, and challenges. Mathematics. 2023;11(11):2585. doi:10.3390/math11112585. [Google Scholar] [CrossRef]

6. Cao C, Sun K, Liu W. A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Process. 2018;143(1):122–33. doi:10.1016/j.sigpro.2017.08.020. [Google Scholar] [CrossRef]

7. Sanam N, ul Haq T, Tariq K. NTK-3D chaotic map and a non-associative LA-field sequences for image encryption. Comput Electr Eng. 2024;116(8):109196. doi:10.1016/j.compeleceng.2024.109196. [Google Scholar] [CrossRef]

8. Cai C, Cao Y, Jahanshahi H, Mou J, Sun B. 2D and 3D compatible chaotic image encryption system based on checkers rules and shift register. J Frankl Inst. 2024;361(9):106874. doi:10.1016/j.jfranklin.2024.106874. [Google Scholar] [CrossRef]

9. Hu Y, Wu H, Zhou L. Color image encryption base on a 2D hyperchaotic enhanced Henon map and cross diffusion. Alex Eng J. 2023;73(2):385–402. doi:10.1016/j.aej.2023.04.060. [Google Scholar] [CrossRef]

10. Hu Y, Wu H, Zhou L. A novel hyperchaotic 2D-SFCF with simple structure and its application in image encryption. Entropy. 2022;24(9):1266. doi:10.3390/e24091266. [Google Scholar] [PubMed] [CrossRef]

11. Jánosi D, Tél T. Overview of the advances in understanding chaos in low-dimensional dynamical systems subjected to parameter drift Parallel dynamical evolutions and climate change in simple systems. Phys Rep. 2024;1092(9):1–64. doi:10.1016/j.physrep.2024.09.003. [Google Scholar] [CrossRef]

12. Xu X, Zhang T, Mu Z, Ma Y, Liu M. Application of wavelet neural network with chaos theory for enhanced forecasting of pressure drop signals in vapor-liquid-solid fluidized bed evaporator. Chin J Chem Eng. 2025;78(4):67–81. doi:10.1016/j.cjche.2024.10.010. [Google Scholar] [CrossRef]

13. Smith-Escudero S, Dautartas A, Goliath JR, Lambert SP. Chaos theory and its applications in forensic anthropology. Forensic Sci Int Synergy. 2025;10(6):100587. doi:10.1016/j.fsisyn.2025.100587. [Google Scholar] [CrossRef]

14. Oueslati R, Manita G, Chhabra A, Korbaa O. Chaos game optimization: a comprehensive study of its variants, applications, and future directions. Comput Sci Rev. 2024;53(2):100647. doi:10.1016/j.cosrev.2024.100647. [Google Scholar] [CrossRef]

15. Alawida M. Enhancing logistic chaotic map for improved cryptographic security in random number generation. J Inf Secur Appl. 2024;80(1):103685. doi:10.1016/j.jisa.2023.103685. [Google Scholar] [CrossRef]

16. Zhang K, Liu Y, Wang X, Mei F, Kang H, Sun G. IBMRFO: improved binary Manta ray foraging optimization with chaotic tent map and adaptive somersault factor for feature selection. Expert Syst Appl. 2024;251(3):123977. doi:10.1016/j.eswa.2024.123977. [Google Scholar] [CrossRef]

17. Xiong G, Cai Z, Zhao S. A bit-plane encryption algorithm for RGB image based on modulo negabinary code and chaotic system. Digit Signal Process. 2023;141:104153. doi:10.1016/j.dsp.2023.104153. [Google Scholar] [CrossRef]

18. Vijayakumar M, Ahilan A. An optimized chaotic S-box for real-time image encryption scheme based on 4-dimensional memristive hyperchaotic map. Ain Shams Eng J. 2024;15(4):102620. doi:10.1016/j.asej.2023.102620. [Google Scholar] [CrossRef]

19. Liu L, Wang J. A cluster of 1D quadratic chaotic map and its applications in image encryption. Math Comput Simul. 2023;204(12):89–114. doi:10.1016/j.matcom.2022.07.030. [Google Scholar] [CrossRef]

20. Zhu S, Deng X, Zhang W, Zhu C. Image encryption scheme based on newly designed chaotic map and parallel DNA coding. Mathematics. 2023;11(1):231. doi:10.3390/math11010231. [Google Scholar] [CrossRef]

21. Zhou W, Wang X, Wang M, Li D. A new combination chaotic system and its application in a new Bit-level image encryption scheme. Opt Lasers Eng. 2022;149(6):106782. doi:10.1016/j.optlaseng.2021.106782. [Google Scholar] [CrossRef]

22. Feng X, Han G, Yan F, Shen D, Pang Z, Li Q. Local bit-level image encryption algorithm based on one dimensional zero excluded chaotic map. Phys Scr. 2024;99(6):065214. doi:10.1088/1402-4896/ad418d. [Google Scholar] [CrossRef]

23. Wang X, Ren Q, Jiang D. An adjustable visual image cryptosystem based on 6D hyperchaotic system and compressive sensing. Nonlinear Dyn. 2021;104(4):4543–67. doi:10.1007/s11071-021-06488-y. [Google Scholar] [CrossRef]

24. Dong Z, Zhang Z, Zhou H, Chen X. Color image compression and encryption algorithm based on 2D compressed sensing and hyperchaotic system. Comput Mater Contin. 2024;78(2):1977–93. doi:10.32604/cmc.2024.047233. [Google Scholar] [CrossRef]

25. Long G, Verma V, Jiang D, Yang Y, Ahmad M. A LE-controlled 4D non-degenerate hyperchaotic system and STP-CS model based efficient image encryption algorithm. Phys Scr. 2025;100(2):025228. doi:10.1088/1402-4896/ad9d8b. [Google Scholar] [CrossRef]

26. Yan S, Jiang D, Cui Y, Zhang H, Li L, Jiang J. A fractional-order hyperchaotic system that is period in integer-order case and its application in a novel high-quality color image encryption algorithm. Chaos Solitons Fractals. 2024;182:114793. doi:10.1016/j.chaos.2024.114793. [Google Scholar] [CrossRef]

27. Huang Y, Huang H, Huang Y, Wang Y, Yu F, Yu B, et al. Asymptotic shape synchronization in three-dimensional chaotic systems and its application in color image encryption. Chaos Solitons Fractals. 2024;184(6):114945. doi:10.1016/j.chaos.2024.114945. [Google Scholar] [CrossRef]

28. Ma Y. Research and application of big data encryption technology based on quantum lightweight image encryption. Results Phys. 2023;54(1/2):107057. doi:10.1016/j.rinp.2023.107057. [Google Scholar] [CrossRef]

29. Hong Y, Fang S, Su J, Xu W, Wei Y, Wu J, et al. A novel approach for image encryption with chaos-RNA. Comput Mater Contin. 2023;77(1):139–60. doi:10.32604/cmc.2023.043424. [Google Scholar] [CrossRef]

30. Erkan U, Toktas A, Memis S, Toktas F, Lai Q, Wen H, et al. OSMRD-IE: octal-based shuffling and multilayer rotational diffusing image encryption using 2-D hybrid Michalewicz-Ackley map. IEEE Internet Things J. 2024;11(21):35113–23. doi:10.1109/JIOT.2024.3432494. [Google Scholar] [CrossRef]

31. Zhang X, Liu G, Zou C. An image encryption method based on improved Lorenz chaotic system and Galois field. Appl Math Model. 2024;131(4):535–58. doi:10.1016/j.apm.2024.04.023. [Google Scholar] [CrossRef]

32. Guo Z, Chen SH, Zhou L, Gong LH. Optical image encryption and authentication scheme with computational ghost imaging. Appl Math Model. 2024;131(6):49–66. doi:10.1016/j.apm.2024.04.012. [Google Scholar] [CrossRef]

33. Huang H, Han Z. Computational ghost imaging encryption using RSA algorithm and discrete wavelet transform. Results Phys. 2024;56(1):107282. doi:10.1016/j.rinp.2023.107282. [Google Scholar] [CrossRef]

34. Singh OP, Singh KN, Singh AK, Agrawal AK. Deep learning-based image encryption techniques: fundamentals, current trends, challenges and future directions. Neurocomputing. 2025;612(3):128714. doi:10.1016/j.neucom.2024.128714. [Google Scholar] [CrossRef]

35. Feng L, Du J, Fu C. Digital image encryption algorithm based on double chaotic map and LSTM. Comput Mater Contin. 2023;77(2):1645–62. doi:10.32604/cmc.2023.042630. [Google Scholar] [CrossRef]

36. Man Z, Li J, Di X, Sheng Y, Liu Z. Double image encryption algorithm based on neural network and chaos. Chaos Solitons Fractals. 2021;152(24):111318. doi:10.1016/j.chaos.2021.111318. [Google Scholar] [CrossRef]

37. Ding Y, Tan F, Qin Z, Cao M, Choo KR, Qin Z. DeepKeyGen: a deep learning-based stream cipher generator for medical image encryption and decryption. IEEE Trans Neural Netw Learn Syst. 2022;33(9):4915–29. doi:10.1109/TNNLS.2021.3062754. [Google Scholar] [PubMed] [CrossRef]

38. Maniyath SR, Thanikaiselvan V. An efficient image encryption using deep neural network and chaotic map. Microprocess Microsyst. 2020;77(12):103134. doi:10.1016/j.micpro.2020.103134. [Google Scholar] [CrossRef]

39. Sang Y, Sang J, Alam MS. Image encryption based on logistic chaotic systems and deep autoencoder. Pattern Recognit Lett. 2022;153(5):59–66. doi:10.1016/j.patrec.2021.11.025. [Google Scholar] [CrossRef]

40. Yao W, Gao K, Zhang Z, Cui L, Zhang J. An image encryption algorithm based on a 3D chaotic Hopfield neural network and random row-column permutation. Front Phys. 2023;11:1162887. doi:10.3389/fphy.2023.1162887. [Google Scholar] [CrossRef]